Bài tập về số hữu tỉ minh họa chi tiết Toán lớp 7

Bài tập về số hữu tỉ minh họa chi tiết Toán lớp 7 1. Lý thuyết cần nhớ
Số hữu tỉ là số có thể viết dưới dạng a/b với a,b thuộc Z và b # 0 và được kí hiệu là Q.
Ví dụ: Các số 3; -1/2 ; 2/3 ;... là các số hữu tỉ.
Biểu diễn số hữu tỉ trên trục số: Mỗi số hữu tỉ được biểu diễn bởi một điểm
trên trục số và không phụ thuộc vào cách chọn phân số xác định của nó.
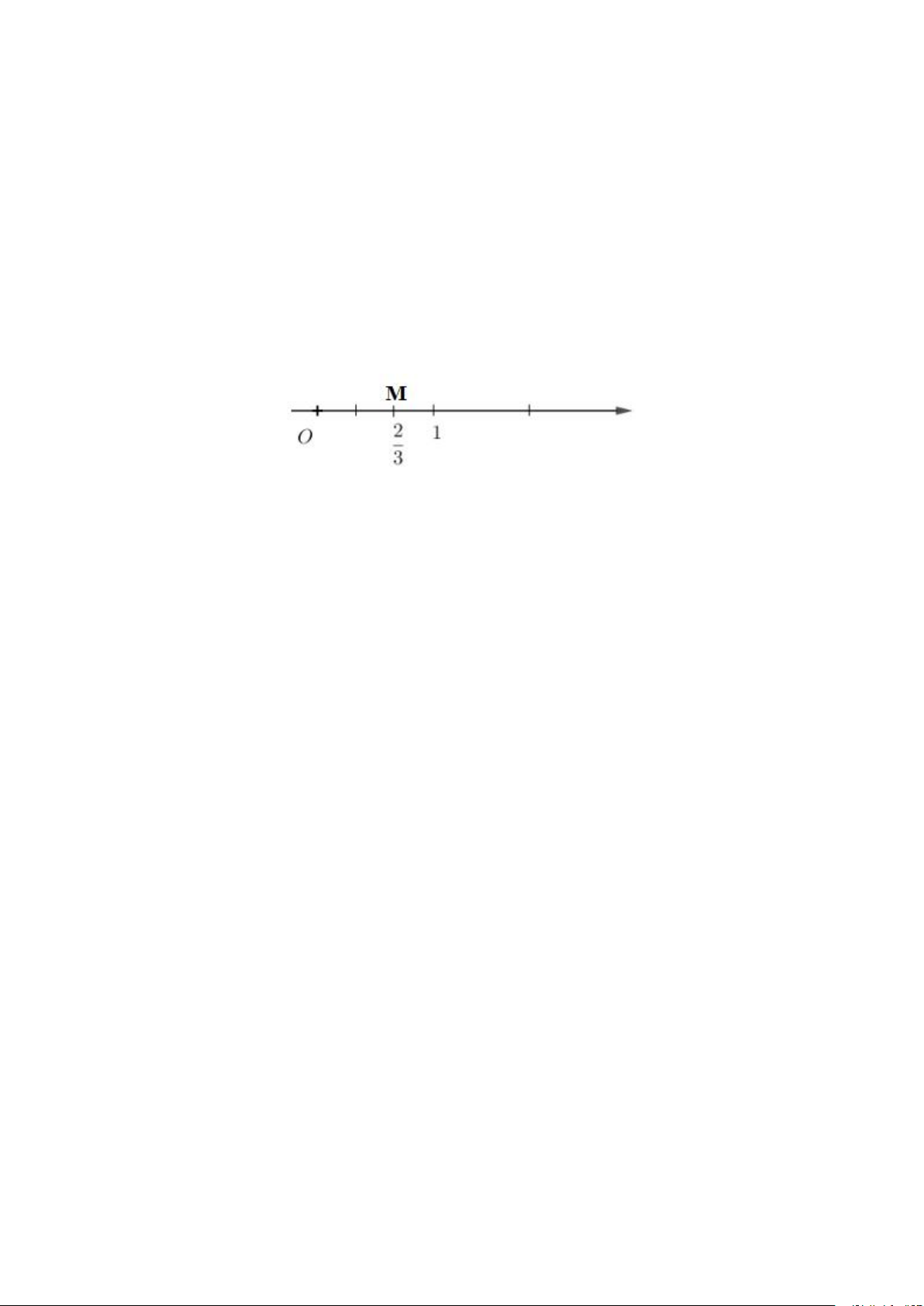
Ví dụ: Số hữu tỉ 2/3 được biểu diễn bởi điểm M trên trục số sau:
So sánh số hữu tỉ: Để so sánh hai số hữu tỉ x, y ta làm như sau:
- Viết x, y dưới dạng phân số cùng mẫu dương x = a/m y = b/m với m > 0
- So sánh các tủe là số nguyên aa và bb Nếu a > b thì x > y Nếu a = b thì x = y Nếu a < b thì x < y
Ví dụ: So sánh hai số x = 2/ -5 và y = -3/13
Ta có: x = 2/-5 = 2.(-13) / (-5) . (-13) = -26/65
y = -3/13 = -3.5 / 13.5 = 1-15/65
Mà -26 < -15 nên -26/65 < /65 hay x < y
Chú ý: - Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương
- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm
- Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm. Cộng, trừ số hữu tỉ:
- Ta có thể cộng, trừ số hữu tỉ x, y bằng cách viết chúng dưới dạng hai phân
số có cùng một mẫu dương rồi áp dụng quy tắc cộng, trừ phân số.
- Phép cộng số hữu tỉ có các tính chất của phép cộng phân số:
+ Tính chất giao hoán: x + y = y + x
+ Tính chất kết hợp: ( x + y) + z = x + ( y + z)
+ Cộng với số 0: x + 0 = x
+ Mỗi số hữu tỉ đều có một số đối, đối của x là - x + Quy tắc chuyển vế
- Khi chuyển vế một số hạng từ vế này sang vế kia của một đẳng thức thì ta
phải đổi dấu số hạng đó
NHân, chia hai số hữu tỉ:
- Ta có thể nhân, chia hai số hữu tỉ bằng viết chúng dưới dạng phân số rồi áp
dụng quy tắc nhân, chia phân số
- Phép nhân số hữu tỉ có các tính chất của phép nhân phân số:
+ Tính chất giao hoán: x . y = y.x
+ Tính chất kết hợp: (x.y) .z = x .(y.z)
+ Nhân số với số 1: x.1 = x
+ Tính chất phân phối của phép nhân đói với phép cộng.
+ Mỗi số hữu tỉ khác 0 đều có một số nghịch đảo: nghịch đảo của x là 1/x
- Các phép toán cộng, trừ, nhân chia cho các số hữu tỉ luôn cho ta kết quả là một số hữu tỉ
2. Bài tập về số hữu tỉ
Dạng 1: Thực hiện phép tính Phương pháp làm bài:
- Viết hai số hữu tỉ dưới dạng phân số
- Áp dụng quy tắc cộng trừ, nhân chia phân số để tính
- Rút gọn kết quả (nếu có thể)
Lưu ý: chỉ được áp dụng tính chất a. b + a.c = a. (b + c) a.c + b.c = (a + b) :c
- Không được áp dụng: a : b + a:c = a: (b +c)
Câu 1: Thực hiện phép tính:
a. -2/3 + -1/12 = (-8/12) + (-1/12) = (-9/12) = -3/4
b. 11/30 - 1/5 = 11/30 - 6/30 = 5/30 = 1/6
c. -5/2 : 3/4 = (-5/2) . (4/3) = -20/6 = -10/3
Dạng 2: Biểu diẽn số hữu tỉ trên trục số
Phương pháp: - Nếu a/b là số hữu tỉ dương ta chia khoảng độ dài 1 đơn vị và
làm b phần bằng nhau rồi lấy về phía chiều dương trục Õ a phần ta được vị trí của số a/b
Ví dụ: Biểu diễn số 5/4 ta chia các khoảng độ dài 1 đơn vị thành 4 phần bằng
nhau lấy 5 phần ta được phân số biểu diễn số 5/4
- Nếu a/b là số hữu tỉ âm thì ta có thể chia khoảng có độ dài bằng 1 đơn vị
làm b phần bằng nhau rồi lấy về phía chiều âm trục Õ a phần ta được vị trí của số a/b
Dạng 3: So sánh số hữu tỉ Phương pháp:
- Đưa về các phân số có cùng mẫu số dương rồi so sánh tử số
- So sánh với số 0, so sánh với số 1, so sánh với số -1....
- Dựa vào phần bù của 1
- So sánh với phân số trung gian (là phân số có tử số của phân số này mẫu số của phân số kia)
Bài 1: So sánh các số hữu tỉ sau: a. x = 17/20 ; y = 0,75
Ta có: y = 0.75 = 75/100 = 15/20 < 17/20 = x
b. x = 2000/2001 ; y = 2001/2002 Ta có: x = 2000/2001 1 - x = 1 - 2000/2001 = 1/2001 y = 2001/2002 1 -y = 1 - 2001/2002 = 1/2002
Dạng 4: Tìm điều kiện để một số hữu tỉ là số dương, âm là số 0 ( không âm, không dương)
Phương pháp: Dựa vào tính chất, a/b là số hữu tỉ dương nếu a và b cùng dấu
là số hữu tỉ âm nếu a và b trái dấu bằng 0 nếu a = 0
Dạng 5: Tìm các số hữu tỉ nằm trong một khoảng
Tìm a sao cho: 1/9 < 12/a < 3/2
Ta có: 12/108 < 12/a < 12/8 a = {9, 10, .... 107}
Phương pháp: đưa về các số hữu tỉ có cùng tử số hoặc mẫu số:
Dạng 6: Tìm x đề biểu thức nguyên Phương pháp:
- Nếu tử số không chứa x ta dùng dấu hiệu chia hết
- Nếu tử số chứa x dùng dấu hieuẹ chia hết hoặc dùng phương pháp tách tử số theo mẫu số
- Với các bài toán tìm đồng thời x, y ta nhóm x hoặc y rồi rút x hoặc y đưa về dạng phân thức.
Dạng 7: Các bài toán tìm x Phương pháp: - Quy đồng khử mẫu số
- Chuyển các số hạng chứa x về một vế các số hạng tự do về một vế (chuyển
vế đổi dấu( tồi tìm x
- Chú ý một tích bằng 0 khi một trong các thừa số bằng không
+ Chú ý: Các bài toán nâng cao: dạng luỹ thừa dạng giá trị tuyệt đối , dạng
tổng các bình phương bằng 0 các bài toán tìm x có quy luật.
>> Tham khảo: Số hữu tỉ là gì? Số vô tỉ là gì? Bài tập về số hữu tỉ và số vô tỉ 3. Bài tập tự luyện
Câu 1: Tìm giá trị của x trong dãy tính sau:
a. ( x + 2) + ( x + 12) + (x + 42) + (x +47) = 655
b. x + (x +1) +(x +2) + (x +3) + ... + (x +2009) = 2009 . 2010
Câu 2: Tính M = 1.2 + 2.3 + 3.4 + ... + 2009. 2010
Câu 3: Cho A = 3 + 32 + 33 + 34 + ... + 3100. Tìm số tự nhiên n biết rằng 2A + 3 = 3n
Câu 4: Cho M = 3 + 32 + 33 + 34 + ... + 3100
a. M có chia hết cho 4. cho 12 không? Vì sao\
b. Tìm số tự nhiên n biết rằng 2M + 3 = 3n
Câu 5: Trong các phân số phân số nào có biểu diễn số hữu tỉ 2/5 ; 6/-15 ; -3/7 ; 4/-12
Câu 6: So sánh các số hữu tỉ sau: a. x = 2/-5 và y = -3/13 b. x = -196/225 và y = 13/-15 c. x = 34/-4 và y = -8,6 d. x = 3/7 và y = 11/15
Câu 7: Trong các câu sau, câu nào đúng, câu nào sai?
a. Số hữu tỉ dương lớn hơn số hữu tỉ âm
b. Số hữu tỉ dương lớn hơn số tự nhiên
c. Số 0 là số hữu tỉ âm
d. Số nguyên dương là số hữu tỉ
Câu 8: Cho số hữu tỉ x = a -3/ 2 với giá trị nào của a thì" a. x là số nguyên dương b. x là số âm
c. x không là số dương và cũng không là số âm
Câu 9: Cho số hữu tỉ y = 2a-1 / -3 với giá trị nào của a thì: a. y là số nguyên dương b. y là số âm
c. y không là số dương và cũng không là số âm
Câu 10: Trọng lượng của một vật thể trên mặt trăng bằng khoảng 1/6 trọng
lượng của nó trên trái đất. Biết trọng lượng của một vật trên Trái Đất được
tính theo công thức: P = 10m với P là trọng lượng của vật tính theo đơn vị
niu- tơn; m là khối lườn của vật tính theo đơn vị ki lô gam. Nếu trên Trái đất
nhà du lịch vũ trụ có khối lượng là 75,5 kg thì trọng lượng của người đó trên
Mặt Trăng sẽ là bao nhiêu
Document Outline

• Bài tập về số hữu tỉ minh họa chi tiết Toán lớp 7
  • 1. Lý thuyết cần nhớ
  • 2. Bài tập về số hữu tỉ
  • 3. Bài tập tự luyện