BÀI T P CHƯƠNG III VÀ CHƯƠNG IV
1. M t phân xư ng có ba máy ho t ng c l p v i nhau. Xác su t trong th i gian t các máy b h ng l n lư t là 0,2; 0,1; 0,3.
a) Tìm quy lu t phân ph i xác su t c a smáy b h ng trong th i gian t.
b) Tìm kỳ v"ng và phương sai c a X. 2. Cho hàm f(x):
λx2(1−x), x∈[0,1] x= 0, x∉[0,1]
a) Xác nh h$ng s λ f(x) là hàm m t xác su t c a m t i lư ng ng%u nhiên X nào ó.
b) V i giá tr λ trên, hãy tìm kỳ v"ng M(x) và phương sai D(x). 3. Cho
i lư ng ng%u nhiên X có hàm phân bxác su t như sau: X 0 1 4 6 p 1/6 2/6 1/6 2/6
a) Tính kỳ v"ng và phương sai c a X. b) Tính P (1 ≤ X ≤ 3). 4. Cho
i lư ng ng%u nhiên X có hàm phân bxác su t như sau: F(x) = a + b.arctgx a) Tìm a, b.
b) Tìm xác su t P (0 ≤ X ≤ 1). c) Tìm hàm m t ca X. 5. Cho
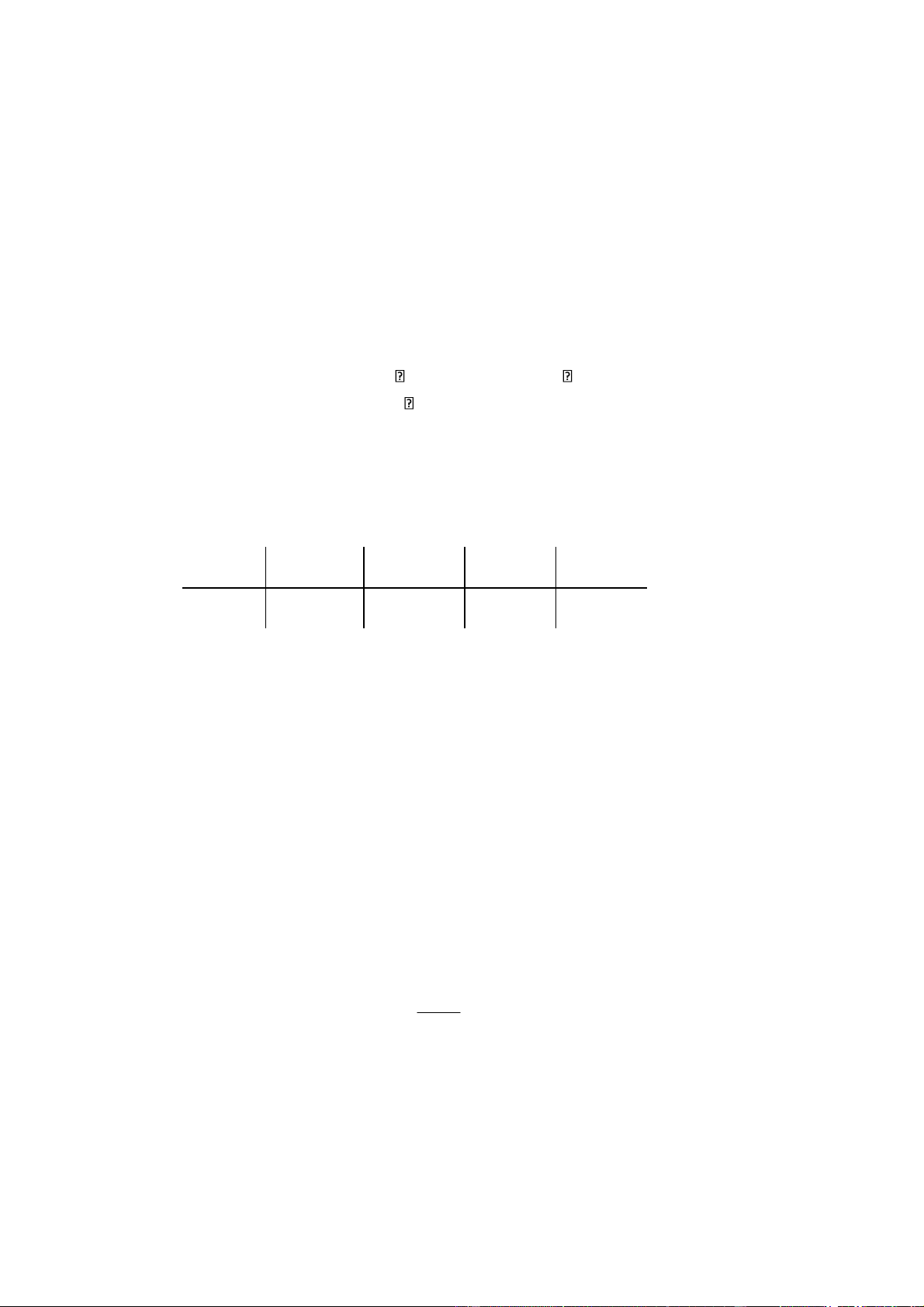
i lư ng ng%u nhiên X có hàm m t : a f ( )x =
2 (−∞< x <+∞) 1+ x a) Tìm a
b) Tìm xác su t p (0 < X < 1) c) Tìm F(x)
6. M t x th có n viên n b.n vào m/c tiêu cho 0n khi trúng m/c tiêu hay h0t n m i thôi. Xác su
t trúng m/c tiêu c a m2i viên n như nhau và b$ng p. Hãy l p b4ng phân ph i xác su t c a s n (X) mà x th ó b.n.
7. Cho hai i lư ng ng%u nhiên X và Y có b4ng phân bxác su t như sau: X 1 2 3 Y -2 -1 0 pi 0,1 0,3 0,6 pi 0,6 0,3 0,1
a) Tìm kỳ v"ng và phương sai c a chúng.
b) L p b4ng phân ph i xác su t c a X + Y và X.Y
8. M t x th b.n 100 viên n vào m/c tiêu. Xác su t trúng m/c tiêu c a m2i viên n là 0,8. Tìm xác su t : a) X th
ó b.n trúng không ít hơn 75 l n và không nhi5u hơn 90 l n.
b) Không ít hơn 75 l n b.n trúng. 9. M t x th b.n 5 viên
n vào m t m/c tiêu, xác su t trúng m/c tiêu c a m2i viên là 0,6.
a) Tìm quy lu t phân ph i xác su t c a s viên n trúng m/c tiêu (X).
b) Tìm kỳ v"ng M(X) và phương sai D(X).
10. 6 i lư ng ng%u nhiên X có hàm phân ph i xác su t: 0, x ≤ 0 2
F( )x = x ,0 ≤ x ≤1 1, x >1 Tìm các xác su t sau: a) p(0,25 ≤ X ≤ 0,75) b) p(X > 1)
11. Cho hai i lư ng ng%u nhiên X và Y có b4ng phân ph i xác su t như sau: X 1 2 3 Y -1 1 pi 0,3 0,4 0,3 pi 0,4 0,6
Hãy l p b4ng phân ph i xác su t c a X2vàX + Y.
12. Cho hai i lư ng ng%u nhiên X1vàX2cóquy lu t phân ph i xác su t như sau: X1 0 1 2 3 pi 0,2 0,4 0,3 0,1 Và X2 ∈B (2;0;3)
a) Tìm quy lu t phân ph i xác su tca Y = X1 + X2 b) Tìm M(Y), D(Y)
13. M t c u th ném bóng r2 400 l n. Xác su t ném trúng r2 c a m2i l b$ng
0,8. Tìm xác su t c u th ó ném trúng 300 l n. n 5u b$ng nhau và
14. Ngư i ta ti9n m t lo t chi ti0t có dài quy nh a = 20 cm. Gi4 s< dài chi ti0t tuân theo quy lu
t phân ph i chuNn v i µ= 20cm;σ= 0,2cm. Tính xác su t dài c a chi ti0t s4n xu t ra l9ch kh i
quy nh không quá ε= 0,3cm (dung sai).
15. M t nA công nhân Bng máy xe s i gCm 800 ng s i, xác su t Bt s i c a m2i ng trong vòng m
t gilà0,005. Tìm xác su t trong vòng m t gicó4 ng s i b Bt. 16. Tìm xác su t
cho i lư ng X có phân ph i chuNn v i tham s µ=1;σ2 = 4 n$m trong kho4ng (-5,4).
17. Véctơ ng%u nhiên (X,Y) có m t : A f (x y, ) = 2 2 2
π (16 + x )(25 + y ) a)Xác nh A. b)
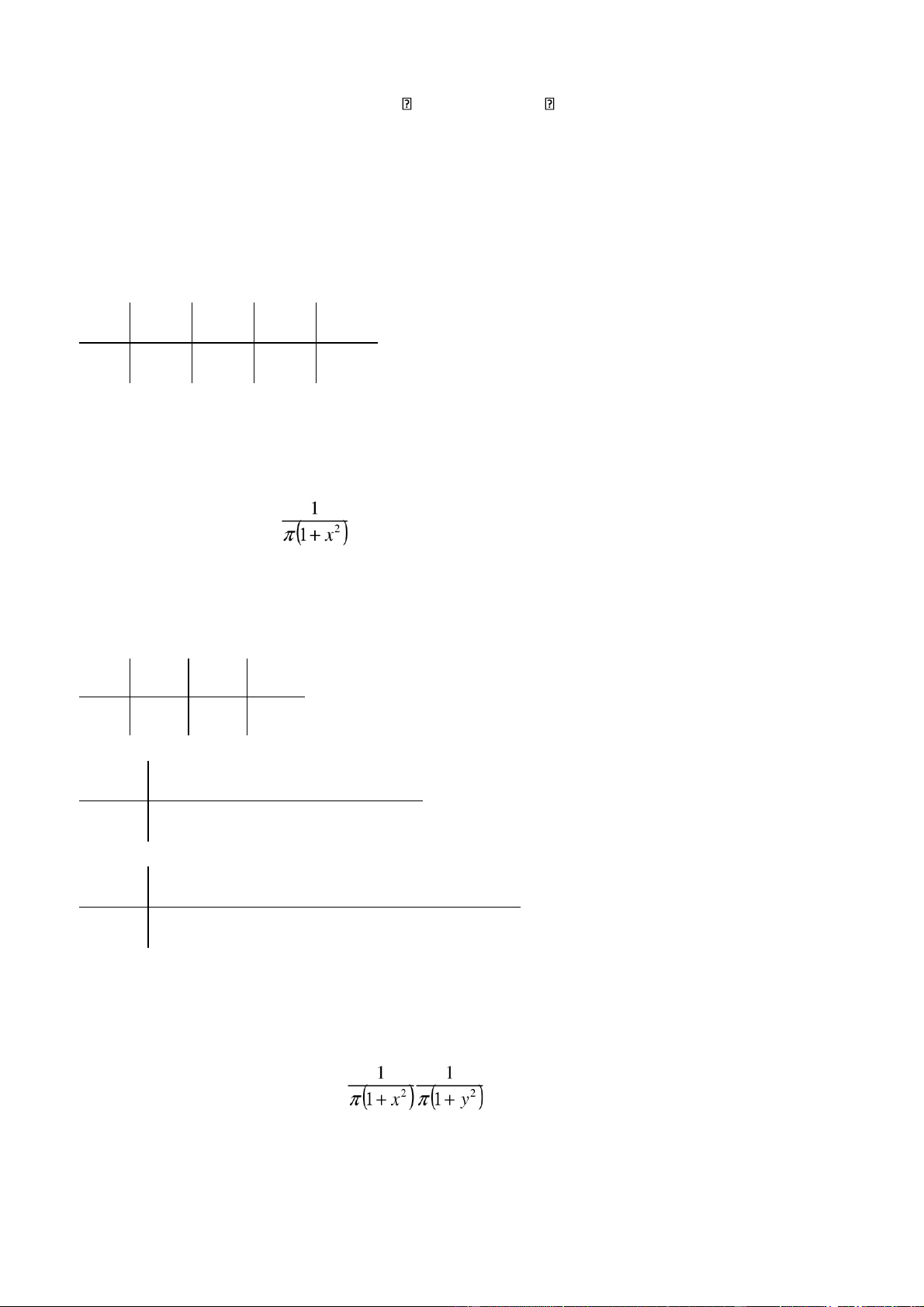
Tìm hàm phân ph i F(X,Y). 18. Véctơ ng%u nhiên (X,Y) có m t : a
f (x, y) = 2 2 2 2
1+ x + y + x .y a) Xác nh h$ng s a. b) ChBng minh X c l p v i Y.
19. Véctơ ng%u nhiên (X,Y) có m t :
a x( 2 + y2), x2 + y2 ≤ r2
f (x, y) = 2 2 2 0, x + y > r Tìm h9 s a.
HƯ NG D N VÀ ÁP SBÀI T P CHƯƠNG III, IV 1. a) X 0 1 2 3 pi 0,504 0,398 0,092 0,006 b) M(X) = 0,6 ; D(X) = 0,46
2. a) λ=12 b) M(X) = 3/5; D(X) = 1/25 3. a) M(X) = 3; p(X) = 5/3 b) p(1≤ X ≤ 3) = 1/3 4. a) a = 1/2, b=1/π c)
5. a) a=1/π b) p(0 < x <1) = 1/4 c) F(x) = 1/2 + 1/π.arctgx 8. a) 0,8882 b) 0,8943 11. X2 0 1 4 pi 0,3 0,4 0,3 X+Y -1 0 1 2 3 pi 0,12 0,16 0,30 0,24 0,18 12. a) Y 0 1 2 3 4 5 pi 0,098 0,280 0,333 0,211 0,069 0,009 b) M(Y) = 1,9; D(Y) = 1,23 13. 0,0023 14. 0,8644 15. 0,1954 16. 0,0372
17. A = 20, F(x,y) = (1/π.arctgx/4+1/2)( 1/πarctgy/4+1/2) 18. a) a = 1/π2 b) f (x y, ) = . V y c l p. 2 = 19. a 2 4 π r