







Preview text:
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
CĐ14: PHẦN HÌNH HỌC
Dạng toán: Tính số đo góc, chứng minh góc bằng nhau, so sánh góc
Dạng toán: Tính độ dài đoạn thẳng, chứng minh đoạn thẳng bằng nhau
Dạng toán: Chứng minh tam giác bằng nhau
Dạng toán: Chứng minh ba điểm thẳng hàng
Dạng toán: Bất đẳng thức tam giác
Dạng toán: Chứng minh song song, vuông góc
Dạng toán: Hình khối trong thực tiễn
Dạng toán: Bài toán chứng minh tổng hợp
Dạng toán: Tính số đo góc, chứng minh góc bằng nhau, so sánh góc A. Trắc nghiệm
Câu 1. (HSG 7 huyện Thanh Ba 2021 - 2022)
Cho a // b và = 1 A 2 1
B (hình vẽ bên ). Số đo 1 B bằng a 1 A b 1 B A. 30° . B. 60°. C. 90° . D. 45°. Lời giải Chọn B a 1 A b 2 1 B
Vì a//b nên = 1 A 2
B (đồng vị) và = 1 A 2 1 B Mà + 1 B 2 B =180°hay + 1 B 1 A =180° mà = 1 A 2 1 B (gt)
Trang 1/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 ⇒ + = ° ⇒ = ° ⇒ 1 B 2 1 B 180 3 1 B 180 1 B = 60°
Câu 2. (HSG 7 huyện Tam Nông, 2022 - 2023)
Cho hình vẽ AB//DE . Số đo BCD bằng D B E 135° A 120° C A. 75°. B. 85° . C. 45°. D. 65°. Lời giải Chọn A D B E 135° A 120° 1 2 C
Kẻ đường thẳng qua C và song song với AB .
Mà AB//DE nên đường thẳng đó cũng song song với DE . Do đó +
C1 ABC =180° và + C2 C E
D =180° (hai góc trong cùng phía) ⇒ = ° = ° ⇒ C1 60 , C2 45 BCD 180 = ° − 60° − 45° = 75°
Câu 3. (HSG 7 huyện Thanh Ba 2021 - 2022; huyện Tân An 2017 - 2018; huyện Lâm Thao 2016 - 2017) Cho
xOy = 50°, điểm A nằm trên Oy . Qua A vẽ tia Am . Để Am song song với Ox thì số đo của OAm là: A. 50° . B. 130° .
C. 50° và 130°. D. 80° . Lời giải Chọn C y y A A m m 50° 50° x x O O TH1 TH2
TH1: Vì Am // Ox nên +
AOx OAm =180° (hai góc trong cùng phía) Thay AOx = 50° , ta có : ° + 50 OAm =180°
Trang 2/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 ⇒
OAm =180° − 50° =130°
TH2: Vì Am // Ox nên =
AOx OAm (hai góc so le trong) mà AOx = 50° ⇒ OAm = 50°
Câu 4. (HSG 7 huyện Thảo Lâm, 2022 - 2023)
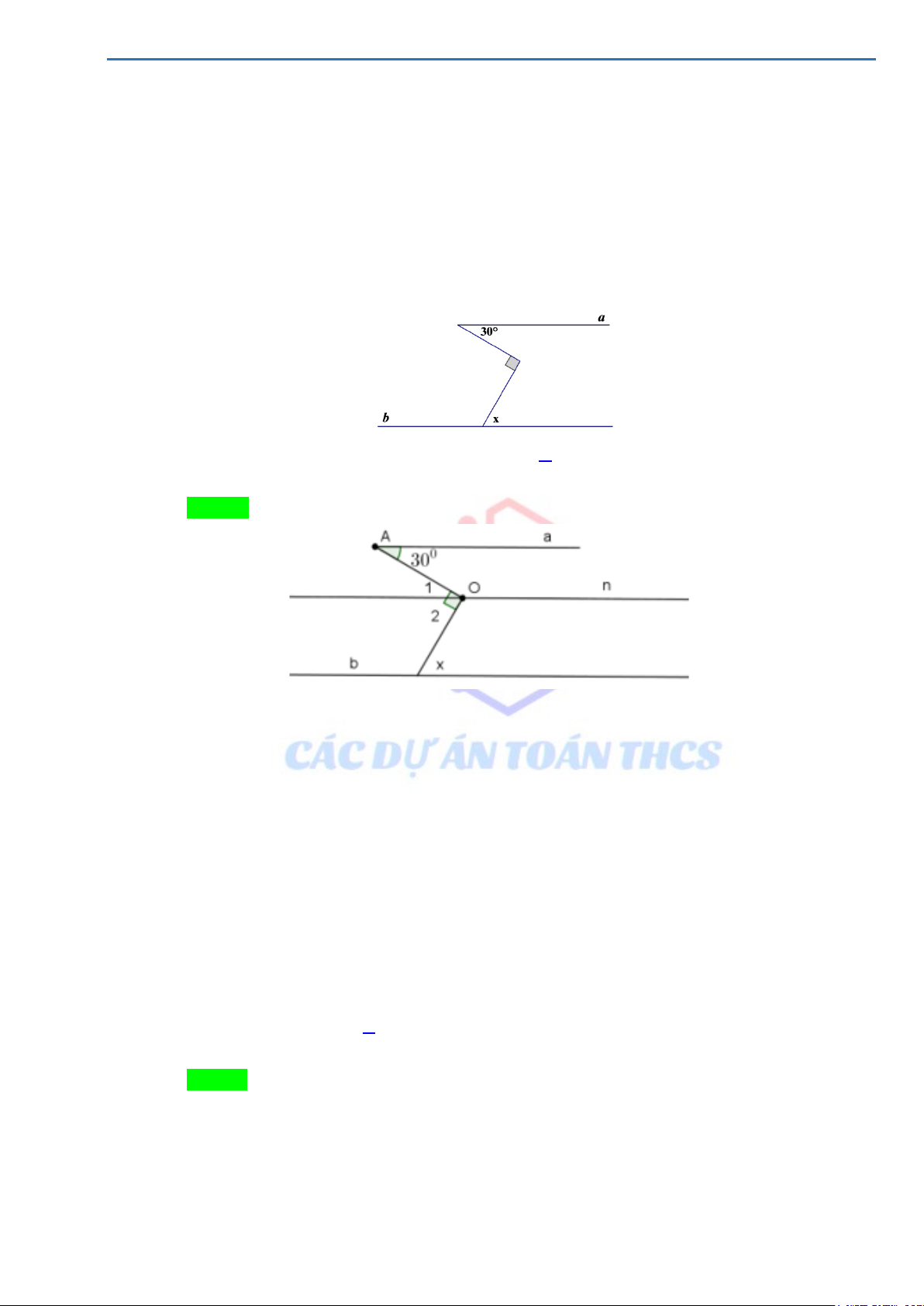
Cho a // b như hình vẽ bên. Số đo góc x bằng: A. 150 .° B. 90 .° C. 60 .° D. 30 .° Lời giải Chọn C
Kẻ n//a//b
Vì n // a ⇒ = 1 O
A ( 2 góc so le trong) ⇒ 1 O = 30° ⇒ = 2 O
O − 30° = 90° − 30° = 60° Vì ⇒ = n // b x 2 O (2 góc so le trong) ⇒ = x 2 O = 60°
Câu 5. (HSG 7 huyện Thanh Ba 2021 – 2022) Cho A
∆ BC có A = 40 ;° −
B C = 20° trên tia đối của AC lấy điểm E sao cho AE = A . B Số đo CBE là: A. 80° . B. 100° . C. 90° . D. 120° . Lời giải Chọn B
Trang 3/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 B 40° E A C
Xét tam giác ABC có + +
A B C =180° (định lí tồng ba góc trong tam giác ) và = ° −
A 40 ; B C = 20° Suy ra ° + ° +
B C =140° nên 140 20 = = ° B 80 ;C = 60 2 Xét A
∆ EB cân tại A (do AE = AB (gt) nên =
AEB ABE (tính chất của tam giác cân) (1) Lại có:
BAC là góc ngoài tam giác AEB = + BAC AEB ABE (2)
Từ (1) và (2) suy ra BAC ABE = = 20° 2 Do đó = +
CBE CBA ABE = 80° + 20° =100°
Câu 6. (HSG 7 huyện Thảo Lâm, 2022 - 2023) Cho A
∆ BC vuông tại A . Trên cạnh BC lấy điểm 2 điểm D và E sao cho BD = B ; A
CE = CA. Khi đó DAE có số đo là. A. 20°. B. 30° . C. 45°. D. 60°. Lời giải Chọn C Xét A
∆ CE cân tại C ⇒ = CAE CEA B
∆ AD cân tại B⇒ = BAD BDA ⇒ + = +
BAD CAE AED ADE ⇒ ° + = ° −
90 DAE 180 DAE ⇒
2DAE =180° − 90° = 90° 90 DAE ° ⇒ = = 45° 2 Vậy DAE = 45°
Trang 4/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
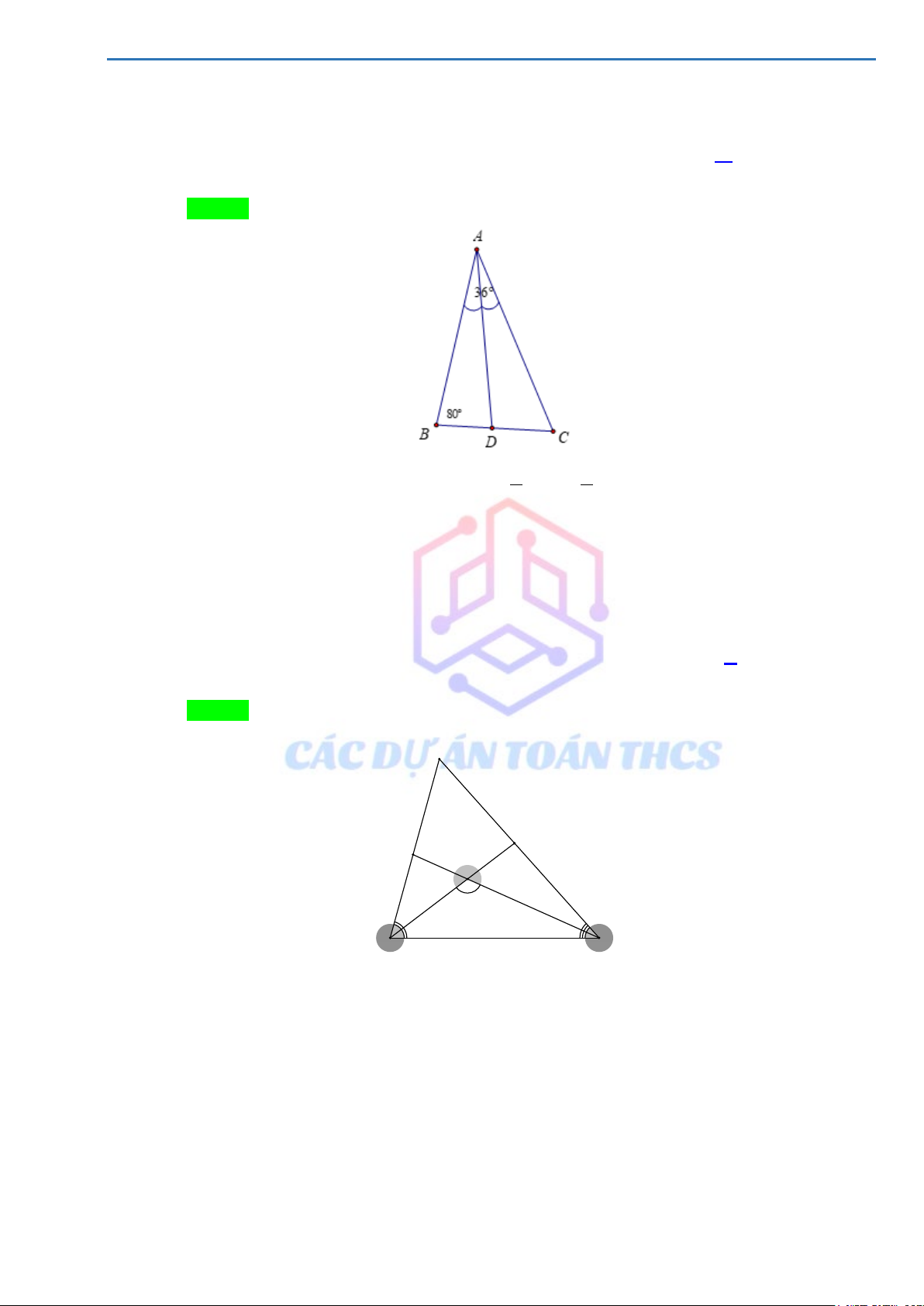
Câu 7. (HSG 7 huyện Sơn Động, 2022 - 2023)
Cho tam giác ABC có = °
B 80 , A = 36° . Tia phân giác
BAC cắt BC tại D . Số đo ADC là A. 90° . B. 88° . C. 82° . D. 98° . Lời giải Chọn D
Vì AD là phân giác của BAC nên 1 = 1 BAD BAC = ⋅36° =18° . 2 2 Vì
ADC là góc ngoài của A
∆ BD nên = + ADC
B BAD = 80° +18° = 98°.
Câu 8. (HSG 7 huyện Tam Nông, 2022 - 2023)
Cho tam giác ABC . Hai tia phân giác của B và C cắt nhau tại I . Nếu
BIC =120° thì số đo BAC bằng. A. 120° . B. 100° . C. 90° . D. 60°. Lời giải Chọn D A E I 120° B C
Trong tam giác BIC có +
IBC ICB =180° −120° = 60° ⇒ +
2IBC 2ICB = 2.60° Mà =
ABC 2IBC và = ACB 2ICB ⇒ + = ° ⇒ = ° − + ABC ACB 120
BAC 180 (ABC ACB) = 60°
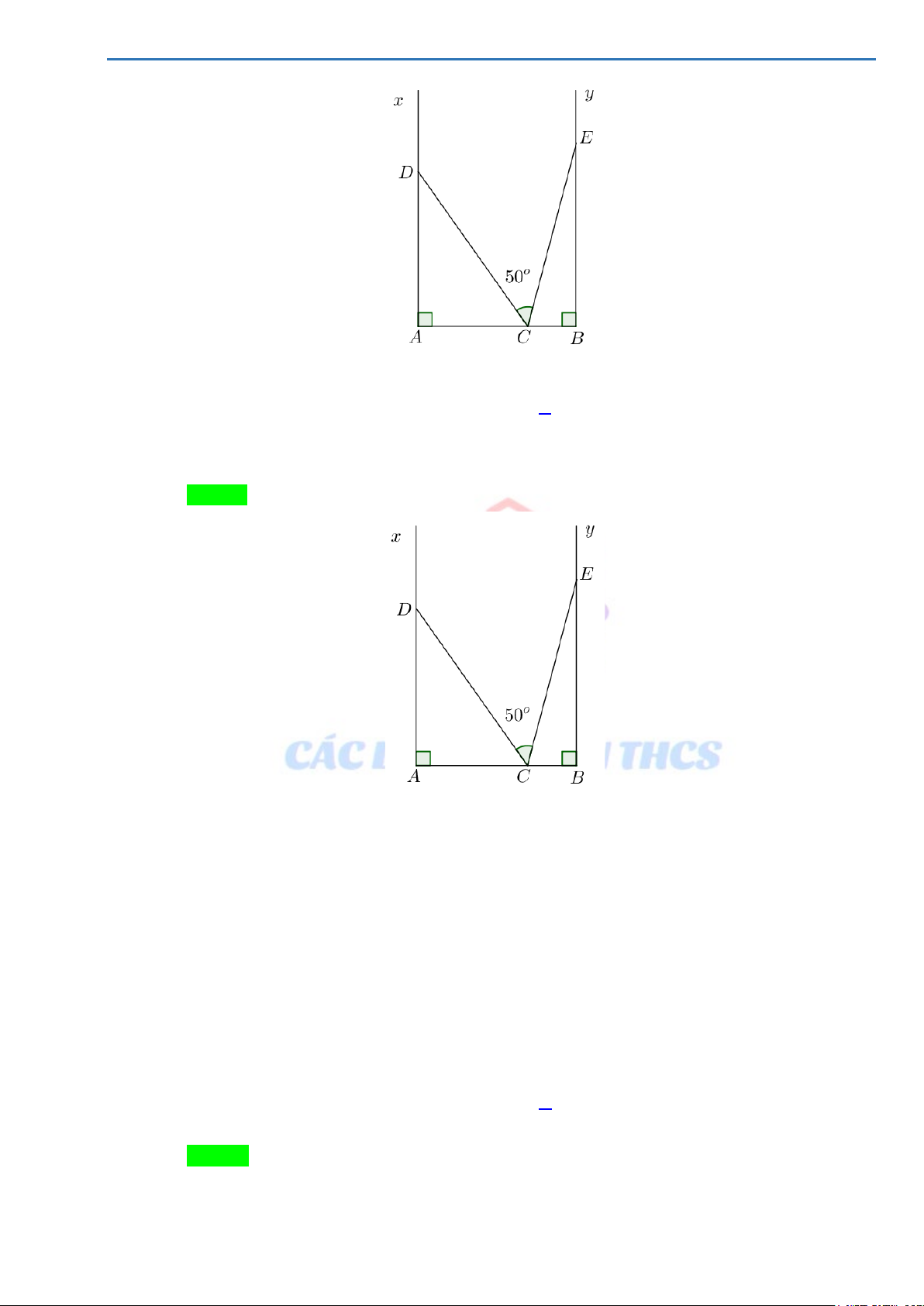
Câu 9. (HSG 7 Tam Nông, Phú Thọ 2021-2022)
Cho hình vẽ. Biết hai tia Ax, By vuông góc với AB . Trên hai tia Ax, By và đoạn AB lần
lượt lấy các điểm D, E,C sao cho DCE = 50° .
Trang 5/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 Khi đó A. + ADC CEB = 90° . B. + ADC CEB = 50° . C. + ADC CEB =100°. D. + ADC CEB = 80° . Lời giải Chọn B Xét A
∆ CD vuông tại A có +
ADC ACD = 90° (hai góc nhọn phụ nhau) Xét B
∆ CE vuông tại B có +
CEB BCE = 90° (hai góc nhọn phụ nhau) ⇒ + + +
ADC ACD BEC BCE =180° ⇒ + (ADC CEB)+ + (ACD BCE)=180° (1) Ta có + +
ACD DCE BCE =180° ⇒ + °+ ACD 50 BCE =180° ⇒ + ACD BCE =130° (2) Từ (1) và (2)⇒ +
(ADC CEB)+ °= °⇒ + 130 180 ADC CEB = 50°
Câu 10. (HSG 7 huyện Tam Nông, Phú Thọ 2021 - 2022)
Cho tam giác ABC cân tại A , A = 20°. Vẽ tam giác đều DBC ( D nằm trong tam giác ABC ). Tia phân giác
ABD cắt AC tại M . Số đo góc BDM là A. 140° . B. 150° . C. 160° . D. 170° . Lời giải Chọn C
Trang 6/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 A
∆ BC cân tại A , A = 20° suy ra 180 BAC 180 20 ABC BCA ° − ° − ° = = = = 80° 2 2 Mà DB ∆
C đều suy ra =
DBC BCD = 60° ⇒ =
ABD DCA = 80° − 60° = 20°
Có BM là tia phân giác của ABD suy ra 20 ABM MBD ° = = = 10° 2 +) Xét A ∆ BD và A ∆ CD có
BD = DC (cạnh DB ∆ C đều) Cạnh DA chung
AB = AC (vì tam giác ABC cân tại A ) Suy ra A ∆ BD = A
∆ CD (c.c.c) ⇒ = BDA CDA , =
BAD CAD (hai góc tương ứng) +) = BAD CAD mà BAC = 20° 20 BAD CAD ° ⇒ = = = 10° 2 +) có + +
BDA CDA BDC = 360° ⇒ + + ° = ° ⇒ + BDA CDA 60 360 BDA CDA = 300° mà =
BDA CDA suy ra = BDA CDA =150° (1) +) Xét A ∆ MB và B ∆ AD có = BAM ABD ( = 20° ) Cạnh AB chung = ABM BAD ( =10°) Suy ra A ∆ MB = B
∆ AD (g.c.g) ⇒ AM = DB ; MB = AD (hai cạnh tương ứng) +) Xét D ∆ MB và MD ∆ A có MB = AD = DBM MAD ( =10°) DB = AM Suy ra D ∆ MB = MD ∆ A (g.c.g) ⇒ =
ADM BMD (hai góc tương ứng) (2) +) Xét D
∆ MB có + +
BDM MBD BMD =180° ⇒ + + ° +
BDA ADM 10 BMD =180° (3) Từ (1), (2), (3) suy ra ⇒ ° + + ° + = ° ⇒ 150 ADM 10 ADM 180 ADM =10° ⇒ = +
BDM BDA ADM =150° +10° =160°
Trang 7/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
Câu 11. (HSG 7 huyện Hoài Nhơn 2018 – 2019)
Cho tam giác ABC cân tại A , A = 20°. Trên cạnh AB lấy điểm D sao cho AD = BC. Số đo của góc BDC là: A. 50° . B. 70°. C. 30° . D. 80° . Lời giải Chọn C
Vẽ tam giác đều EBC . Ta có: BC = CE = EB
Mà AD = BC (gt) Nên AD = BE . Chứng minh ∆ = ∆ ⇒ = AEB
AEC( .c .cc)
DAB DAC , do đó 20 EAB ° = = 10° 2 A
∆ BC cân tại A, mà A = 20 ( ° gt) ⇒
ABC = (180° − 20°) : 2 = 80° E ∆ BC đều nên
EBC = 60° , tia BE nằm giữa hai tia B , A BC ⇒
ABE = 80° − 60° = 20° Xét A ∆ BE và B
∆ AD có AB cạnh chung; =
ABE BAD = 20 ;° BE = AD Vậy A ∆ BE = B
∆ AD( .cg.g) ⇒ = BAE ABD =10° Mà = +
BDC BAD ABD (góc ngoài của A ∆ BD ) Nên
BDC = 20° +10° = 30° .
Câu 12. (HSG 7 huyện Tân An 2017 - 2018)
Cho tam giác ABC cân tại A , A = 20°. Trên cạnh AB lấy điểm D sao cho BD = BC . Số
đo của góc BDC là: A. 50° B. 70° C. 30° D. 80° Lời giải Chọn A
Trang 8/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 +) Xét A ∆ BC có: + +
BAC ABC ACB =180° (tổng ba góc trong một tam giác) ° + + 20 ABC ACB =180° ⇒ + ABC ACB =160° mà = ABC ACB ( A
∆ BC cân tại A ) ⇒ = ABC ACB = 80°
+) Ta có: AD = BC (gt) ⇒ B
∆ DC cân tại B . +) Xét B ∆ DC có: + +
DBC BDC BCD =180° (tổng ba góc trong một tam giác) ° + + 80 BDC BCD =180° + BDC BCD =100° mà = BDC BCD ( B
∆ DC cân tại B ) ⇒ = BDC BCD = 50°
Câu 13. (HSG 7 Tam Nông, Phú Thọ 2021-2022)
Cho tam giác ABC có = +
A 2B 2C . Các phân giác trong hai góc B và C cắt nhau tại I . Số đo góc BIC là A. 150° . B. 155° . C. 160° . D. 120° . Lời giải Chọn A Xét A
∆ BC có + +
A B C =180° (ĐL tổng ba góc của một tam giác)
Trang 9/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 ⇒ = °− + A 180 (B C) Ta có ° − + (B C)= + (B C)⇒ + 180 2 B C = 60°
Các phân giác trong hai góc B và C cắt nhau tại I nên ta có B = ; C IBC ICB = (t/c đường 2 2 phân giác của một góc) B C 60 IBC ICB + ° ⇒ + = = = 30° 2 2 Xét IB
∆ C có + +
IBC ICB BIC =180° (ĐL tổng ba góc của một tam giác) ⇒ °+ = ° ⇒
30 BIC 180 BIC =150°
Câu 14. (HSG 7 trường THCS Phan Đình Phùng 2017 - 2018)
Cho tam giác ABC vuông tại B, AB = 6, A = 30° . Phân giác góc C cắt AB tại D . Khi đó
độ dài đoạn thẳng BD và AD lần lượt là: A. 2;4 B. 3;3 C. 4;2 D. 1;5 Lời giải Chọn A
* Chứng minh nhận xét: Nếu một tam giác vuông có một góc nhọn bằng 30° thì cạnh góc
vuông đối diện với nó bằng nửa cạnh huyền. C M 1 2 B A Xét AB
C, ta có: B = 90° , A = 30°
Trên cạnh AC lấy điểm M sao cho CM = C B Ta có: BC ∆ M cân tại C . Mà +
C A = 90° (tính chất tam giác vuông) Suy ra: = ° − C 90
A = 90° − 30° = 60° Suy ra: BC ∆ M đều
Suy ra: BC = CM = BM và 1 B = 60° Ta có: + = 1 B B2 ABC = 90° ⇒ = ° − B2 90 1
B = 90° − 60° = 30° Trong B AM , ta có: = B2 A = 30° Suy ra: B
AM cân tại M (vì có 2 góc kề cạnh AB bằng nhau) Hay AM = B M
Trang 10/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
Suy ra: BC = CM = AM mà CM + MA = C A 1 ⇒ BC = AC . 2
Vậy: Nếu một tam giác vuông có một góc nhọn bằng 30° thì cạnh góc vuông đối diện với
nó bằng nửa cạnh huyền.
Áp dụng vào bài tập C M 1 2 30° B D A Ta có: = BCD DCA BCD 60° = =
= 30° ( Vì CD là tia phân giác của BCD ) 2 2 Xét DA C có: = A DCA= 30° ⇒ DA ∆
C cân tại D ⇒ DC = DA
Xét BDC vuông tại B, có BCD = 30° 1 ⇒ BD = DC 2 DC 3DC ⇒ BD + DA = + DC = = AB 2 2 ⇒ 3DC = 2AB 2AB 2.6 ⇒ DC = = = 4 3 3 ⇒ DC = DA = 4 1 1 ⇒ BD = DC = .4 = 2 2 2 B. Tự luận
Câu 1. (HSG 7 huyện Nghi Xuân 2022 - 2023)
Cho tam giác ABC có
BAC = 60° . Tia phân giác của góc B cắt AC ở D . Tia phân giác của
góc C cắt AB ở E ; BD và CE cắt nhau tại M . Tính EMD ? Lời giải B 1 2 E M 1 2 D C A Xét A
∆ BC có: + + = ° ⇒ + A ABC ACB 180 ABC ACB =120°
Trang 11/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 ⇒ + 2 B 1
C =120°: 2 = 60° Xét B
∆ MC có + + = ° ⇒ 2 B 1 C BMD 180
BMD =180° − 60° =120° ⇒ =
EMD BMD =120° (hai góc đối đỉnh) Vậy EDM =120°
Câu 2. (HSG 7 huyện Hoằng Hóa 2017 - 2018)
Cho tam giác đều ABC . M là một điểm nằm trong tam giác sao cho MA: MB : MC = 3: 4 :5.
Tính số đo góc AMB . Lời giải A N 1 3 2 M B C
Do MA: MB : MC = 3: 4 :5 Đặt MA MB MC = = = a 3 4 5
⇒ MA = 3a, MB = 4a, MC = 5a
Trên nửa mặt phẳng bờ AC dựng tam giác đều AMN .
⇒ AM = AN = MN = 3a và AMN = 60° Xét A ∆ BN và A ∆ CM có: AB = AC (gt)
AN = AM (= 3a) = = °− 1 A 3 A ( 60 2 A ) ⇒ A ∆ BN = A
∆ CM (c – g – c)
⇒ BN = CN = 5a Xét B ∆ MN có: 2 BN = ( a)2 2 5 = 25a 2 2
BM + MN = ( a)2 + ( a)2 2 4 3 = 25a 2 2 2
⇒ BN = BM + MN ⇒ B
∆ MN vuông tại M (định lý Pytago đảo) ⇒ NMB = 90° ⇒ = +
AMB AMN NMB = 90° + 60° =150°
Câu 3. (HSG 7 huyện Như Xuân, 2018 - 2019)
Trang 12/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
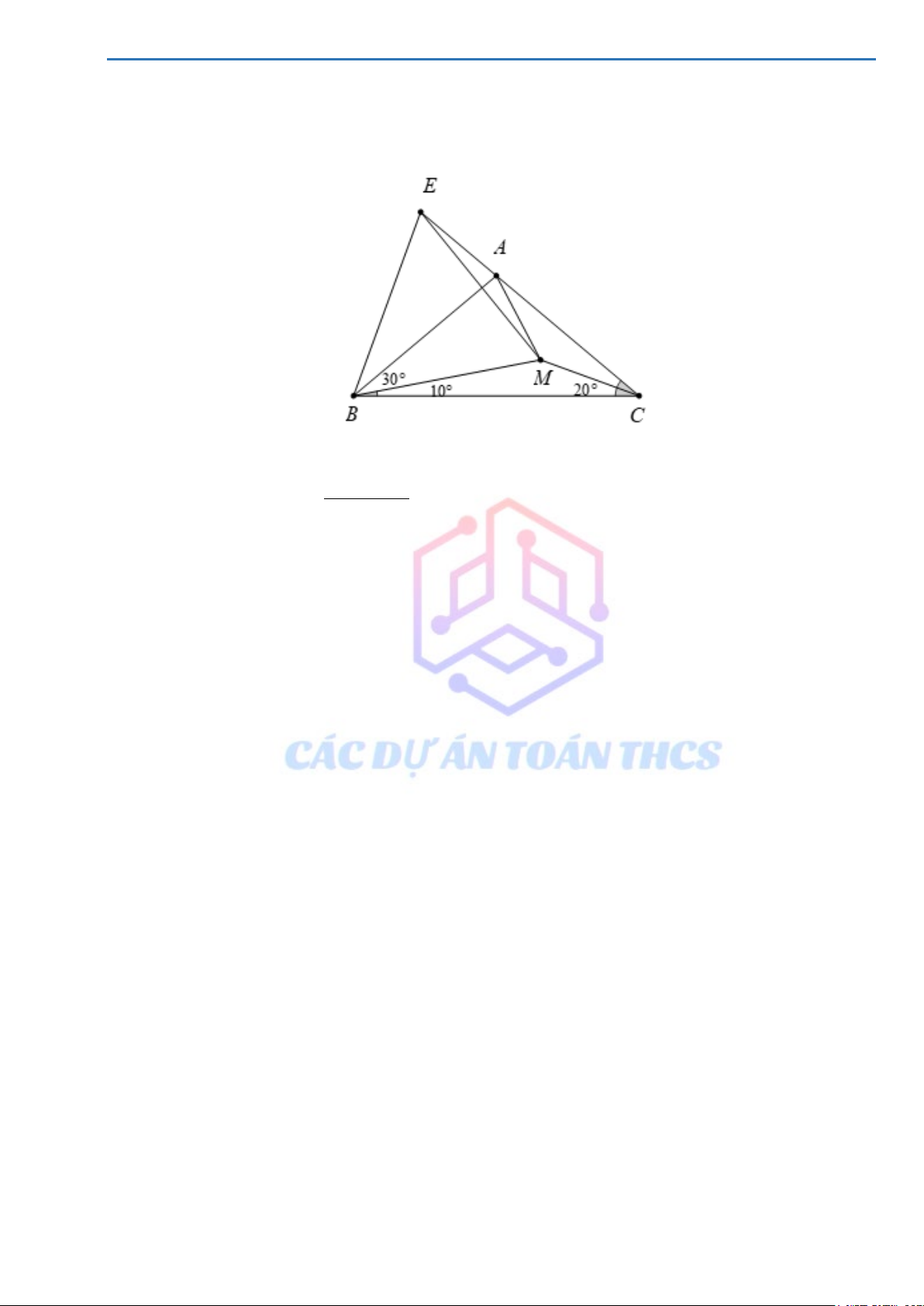
Cho tam giác ABC có =
BAC BCA = 80° . Ở miền trong của tam giác vẽ hai tia Ax và Cy cắt
BC, BA lần lượt tại D và E. Cho biết CAD = 60 ,°
ECA = 50° . Tính số đo ADE . Lời giải B F D E O A C
Kẻ tia CF sao cho
ACF = 60°(F ∈ AB),Tia CF cắt AD tại O ⇒ A ∆ OC; F
∆ OD đều⇒ OA = OC = AC;OF = OD = FD . A
∆ EC có: = °
EAC 80 , ACE = 50° ⇒ CEA = 50° ⇒ A
∆ EC cân tại A Có
EAO = 20° ⇒ = AEO AOE = 80° ⇒ EOF = 40° Suy ra = ° − ° − ° = ° = AFC 180 80 60 40 EOF ⇒ E
∆ OF cân tại E ⇒ EO = EF ⇒ F ∆ DE = ODE ∆ ( . c . c c) ⇒ = 1 = 1 ODE FDE FDA = 60° = 30° 2 2 Vậy ADE = 30° .
Câu 4. (HSG 7 huyện Diễn Châu 2022 - 2023; huyện Phù Ninh 2018 - 2019; huyện Nam Sách
2017 – 2018; trường Tân Lạc; huyện Ngọc Lặc 2015 - 2016)
Cho tam giác ABC có B = 45°, C =120° . Trên tia đối của tia CB lấy điểm D sao cho CD = 2 . CB Tính ADB ? Lời giải A 2 1 E 1 2 3 1 1 2 2 2 2 1 B C F D
Trên CA lấy điểm E sao cho AE = BE ⇒ E
∆ BA cân tại E
Trang 13/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 ⇒ = 1 B 1 A =15° ⇒ 2 B = 30° . Ta có = + 1 E 1 A 2
B = 30° (tính chất góc ngoài của tam giác) Do đó C
∆ BE cân tại C ⇒ CB = CE .
Gọi F là trung điểm CD ⇒ CB = CE = CF = FD .
Tam giác CEF cân tại C có = ° − C2 180 1
C = 60° nên CEF là tam giác đều.
⇒ CE = CF = FD = EF ⇒ E
∆ DF cân tại F . Suy ra = 2 F 1 D 3 E = = 30° 2
Xét tam giác CDE ta có: = + CED 2 E 3
E = 60° + 30° = 90° ( ) 1 Ta có: = 1 D 1 B ⇒ E
∆ BD cân tại E ⇒ EB = ED ⇒ EA = ED (= EB) (2) Từ ( ) 1 và (2) suy ra E
∆ DA vuông cân tại E ⇒ 2 D = 45° Vậy = + ADB 1 D 2
D = 30° + 45° = 75°.
Câu 5. (HSG 7 huyện Đông Hưng; huyện Vũ Thư 2022 - 2023)
Cho tam giác ABC có = °
BAC 15 , ABC = 45° , trên tia đối của tia CB lấy điểm D sao cho
CD = 2CB . Tính số đo ADC . Lời giải A 15° F E 45° 60° 30° B D C
Kẻ DE ⊥ CA . Xét A ∆ BC , có
ACB =180° − 45° −15° =120° ⇒ ACD = 60° hay ECD = 60° . Xét C
∆ ED có = °
CED 90 , ECD = 60° ⇒
EDC = 30° nên C
∆ ED là nửa tam giác đều.
Trên tia đối của tia EC lấy điểm F sao cho EC = EF . DC ∆
F có đường cao DE đồng thời là trung tuyến và có
ECD = 60° nên là tam giác đều. 1
⇒ CE = CD ⇒ CE = CB ⇒ E
∆ BC cân tại C 2 ⇒ = = ° = CBE CEB 30 EDC ⇒ E
∆ BD cân tại E . ⇒ EBA =15° ⇒ B
∆ EA cân tại E ⇒ EA = EB = ED ⇒ A
∆ ED vuông cân ⇒ ADE = 45° . Vậy = + ADB ADE EDB = 75°.
Câu 6. (HSG 7 huyện Kinh Môn 2022 - 2023; trường Ngô Gia Tự 2017 - 2018; trường Nguyễn
Du, huyện Nga Sơn 2016 - 2017)
Trang 14/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
Cho tam giác ABC có AB = AC , A =100°. Điểm M nằm trong tam giác ABC sao cho MBC =10°,
MCB = 20°. Tính số đo góc AMB . Lời giải
+) Ta có tam giác ABC cân tại A và A =100° 180 100 ABC ACB ° − ° ⇒ = = = 40°. 2
Trên tia CA lấy điểm E sao cho CE = CB ⇒ B
∆ CE cân tại C ⇒ = BEC EBC = 70° . +) Xét MC ∆ B và MC ∆ E có: MC chung = MCB MCE (= 20°)
CB = CE (cách lấy điểm E ) Suy ra MC ∆ B = MC ∆ E (c – g – c) ⇒ =
MBC MEC =10° ⇒ =
MBE MEB = 70° −10° = 60° ⇒ ME ∆
B đều ⇒ BM = BE . +) Ta có = −
MBA CBA CBM = 40° −10° = 30° Mặt khác = −
ABE MBE MBA = 60° − 30° = 30° Suy ra = ABE ABM (= 30°) +) Xét MA ∆ B và E ∆ AB có: AB chung = MBA EBA (= 30°) BM = BE (cmt) Suy ra M ∆ AB = E
∆ AB (c – g – c) ⇒ = AMB AEB = 70° .
Câu 7. (HSG 7 huyện Thạch Thành 2017- 2018)
Cho tam giác ABC vuông tại A . Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và
ACE . Gọi I là giao điểm của BE và CD . Chứng minh rằng
EIC = 60° và IA là tia phân giác của DIE . Lời giải
Trang 15/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 B D 1 I 2 1 A C 3 2 2 2 1 2 E =
DAC A + 90° = 60° + 90° =150° Ta có: 1 ⇒ = DAC BAE = BAE 2
A + 90° = 60° + 90° =150° Xét DA ∆ C và B ∆ AE có DA = BA (gt) = DAC BAE (cmt) AC = AE (gt) ⇒ D ∆ AC = B ∆ AE ( . c g.c)
⇒ BE = CD (hai cạnh tương ứng) Ta có : + + + 3 A 1 A BAC 2 A = 360° ⇔ 3
A + 60° + 90° + 60° = 360° ⇔ = ° = 3 A 150 DAC Xét DA ∆ E và B ∆ AE có DA = BA (gt) = 3 A DAC (cmt) AE chung ⇒ D ∆ AE = B ∆ AE ( . c g.c) ⇒ DE = BE Vậy B
∆ DE cân tại E Ta có: D ∆ AC = B ∆ AE (cmt) ⇒ = E C 1 1 (hai góc tương ứng) Lại có: + + I E ICE =180° IC ∆ E) 1 2 (tổng 3 góc trong ⇔ + − I
AEC E + C + C =180° 1 ( 1 ) ( 1 2) ⇔ + ° − +
I 60 E C + 60° =180° 1 1 1
Trang 16/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
⇔ I +120° =180° = (E C 1 1 ) 1 ⇔ I = 60° 1 Vì D ∆ AE = B
∆ AE (cmt) ⇒ = E E 1 2 (hai góc tương ứng)
⇒ EA là tia phân giác của DEI ( ) 1 D ∆ AC = B ∆ AE Vì ⇒ ∆ = ∆ ⇒ = DAC DAE D D 1 2 (hai góc tương ứng) D ∆ AE = B ∆ AE
⇒ DA là tia phân giác của EDC (2) Từ ( )
1 và (2) ⇒ A là giao điểm của 2 tia phân giác trong D ∆ IE
⇒ IAlà đường phân giác thứ 3 trong D ∆ IE
Vậy IAlà tia phân giác của DIE .
Câu 8. (HSG 7 Huyện 2017 - 2018)
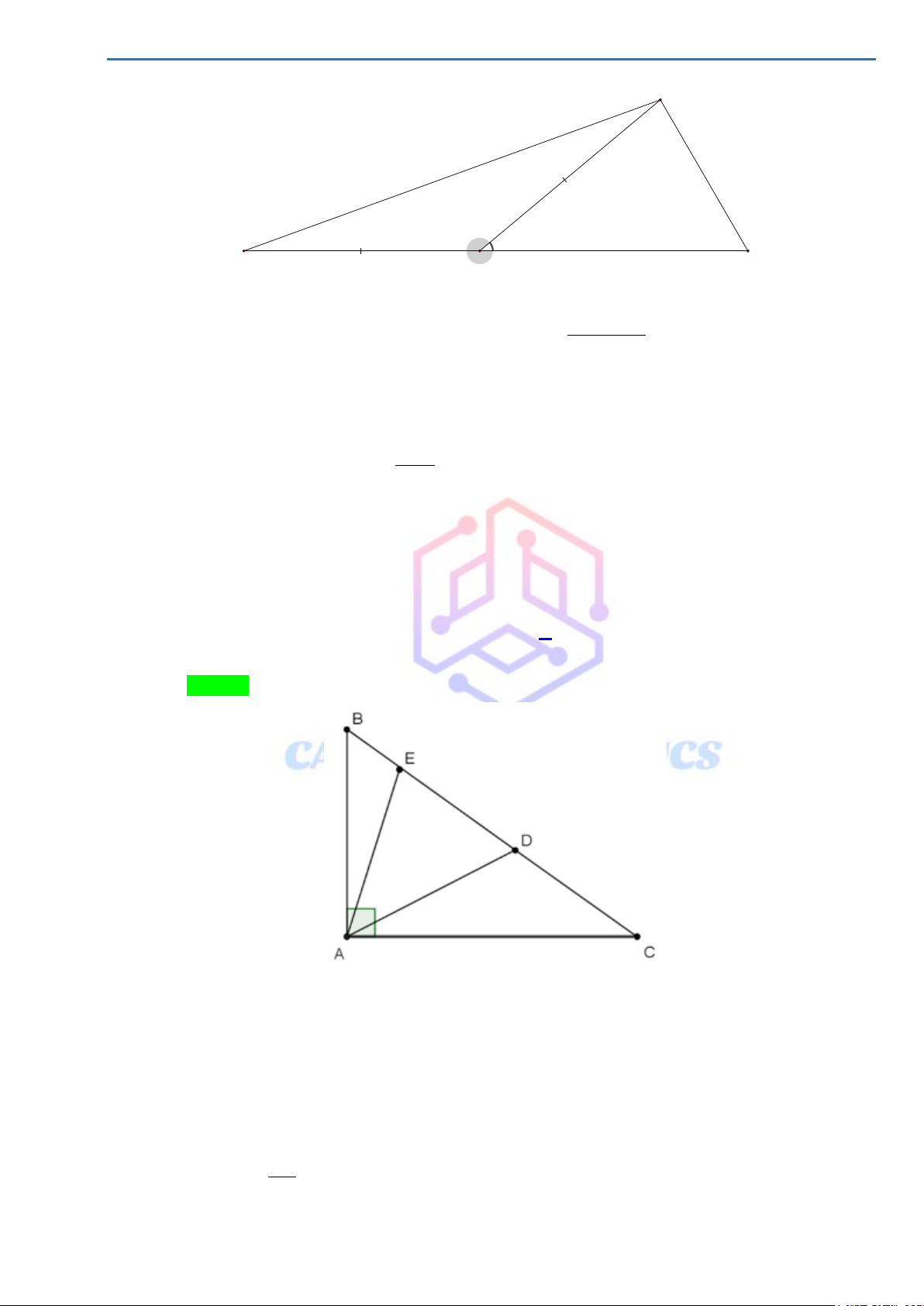
Cho tam giác ABC , M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao cho ME = .
MA Gọi I là một điểm trên AC , K là một điểm trên EB sao cho AI = EK . Từ E kẻ
EH ⊥ BC (H ∈ BC). Biết HBE = 50°; MEB = 25° . Tính HEM và BME . Lời giải A I M C B H K E Xét A ∆ MC và E ∆ MB có: AM = EM (gt) =
AMC EMB (đối đỉnh) BM = MC (gt) Nên A ∆ MC = E ∆ MB ( . c g.c) ⇒ AC = EB Vì ∆ = ∆ ⇒ = AMC EMB
MAC MEB , 2 góc ở vị trí so le trong được tạo bởi đường thẳng
AC, EB cắt đường thẳng AE ) ⇒ AC//BE Xét A ∆ MI và E
∆ MK có: AM = EM (gt) = MAI MEK ( A ∆ MC = E ∆ MB) AI = EK (gt)
Trang 17/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 ⇒ A ∆ MI = E ∆ MK ( . c g.c) ⇒ = AMI EMK Mà +
AMI IME =180° (Kề bù) ⇒ +
EMK IME =180° ⇒ ba điểm I, M , K thẳng hàng.
Trong tam giác vuông BHE (H =90°) có HBE = 50° ⇒ HEB = 40° ⇒ = −
HEM HEB MEB = 40° − 25° =15°
BME là góc ngoài tại đỉnh M của HE ∆ M nên = +
BME HEM MHE =15° + 90° =105°
(định lý góc ngoài của tam giác)
Câu 9. (HSG 7 trường THCS Hiệp Thạnh 2016 - 2017)
Cho tam giác ABC có 0
A =120 . Các đường phân giác AD và BE, tính số đo của góc BED Lời giải
Gọi Ax là tia đối của tia AB ta có: = 0 BAD DAC = 60 Xét A
∆ BD có AE là tia phân giác góc ngoài của đỉnh A ; BE là phân giác của góc B chúng
cắt nhau tại E nên DE là phân giác góc ngoài của D, Xét B
∆ ED có ADC ABC BAD 0 BED 1 D 2 B − = − = = = 30 2 2
Câu 10. (HSG 7 huyện Đức Thọ , 2022 - 2023) Tam giác ABC có x 0 = − 0
A 40 ; B C = 30 . Trên tia đối của tia AC lấy điểm E sao cho
AE = AB. Tính số đo góc CBE . Lời giải Ta có: + +
A B C =180° (tổng ba góc của tam giác) ⇒ + = ° −
B C 180 A=180° − 40° =140°
Trang 18/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7
Mà = °⇒ = ° B -C 30 B 85 ,C =55° Có: +
BAE BAC =180° (2 góc kề bù) ⇒ = °
BAE 180 - BAC =180°-40° =140° Xét ΔBAE có: AE = AB⇒ B ∆ AE cân tại E 180 - BAE 180 -140 ABE AEB ° ° ° ⇒ = = = = 20° 2 2 Vậy = +
CBE ABC ABE =85° + 20° =105°.
Câu 11. (HSG 7 huyện Quỳnh Phụ năm 2021 - 2022) Cho A
∆ BC có độ dài ba cạnh là BC = a, AC = ,
b AB = c thỏa mãn: 2 2 2
a + b > 5c .
Chứng minh rằng: C < 60° Lời giải Trong A ∆ BC : Giả sử 2 2
c ≥ a > 0 ⇒ c ≥ a Mà 2 2 2 2 2 2 2 2
a + b > 5c ⇒ a + b > 5a ⇒ b > 4a ⇒ b > 2a ( )1 Vì 2 2 2 2 2 2
c ≥ a ⇒ c + b ≥ a + b mà 2 2 2
a + b > 5c 2 2 2 2 2
⇒ c + b > 5c ⇒ b ≥ 4c ⇒ b > 2c (2) Từ ( )
1 và (2) ⇒ 2b > 2a + 2c ⇒ b > a + c (vô lý vì a,b,c là độ dài 3 cạnh của 1 tam giác). Vậy c < a
Lập luận tương tự có c < b
Suy ra c là cạnh ngắn nhất ⇒ C nhỏ nhất < C A ⇒ ⇒ < + +
3C A B C =180° ⇒ < ° ⇒ 3C 180 C < 60° < C B
Vậy C < 60°
Câu 12. (HSG 7 huyện Quốc Oai 2016 - 2017) Cho A
∆ BC, tia phân giác của A cắt BC tại D . Biết ADB = 85°. a) Tính − B C
b) Tính các góc của A ∆ BC nếu = 4.B 5.C Lời giải A 85o C B D
Trang 19/31
DỰ ÁN TÁCH ĐỀ HSG TOÁN 7 a) Xét A ∆ DC có
ADB là góc ngoài tại D Suy ra = + ADB C DAC = 85° ( ) 1 Xét A ∆ DB có
ADC là góc ngoài tại D Suy ra = +
ADC B BAD =180° −85° = 95° Mà =
DAC BAD (vì AD là tia phân giác của A ), suy ra + B DAC = 95° (2) Từ ( ) 1 và (2) suy ra −
B C = 95° −85° =10° b) Ta có =
4.B 5.C , suy ra B C = 5 4
Áp dụng tính chất dãy tỉ số bằng nhau ta có: − B C B C = = = 10° (Vì − B C =10° ) 5 4 5 − 4
Suy ra: B = 5.10° = 50°; C = 4.10° = 40° Xét A
∆ BC có + +
A B C =180° (Định lí tổng ba góc trong tam giác) Suy ra = ° − −
A 180 B C =180° − 50° − 40° = 90°.
Câu 13. (HSG 7 huyện 2022 - 2023)
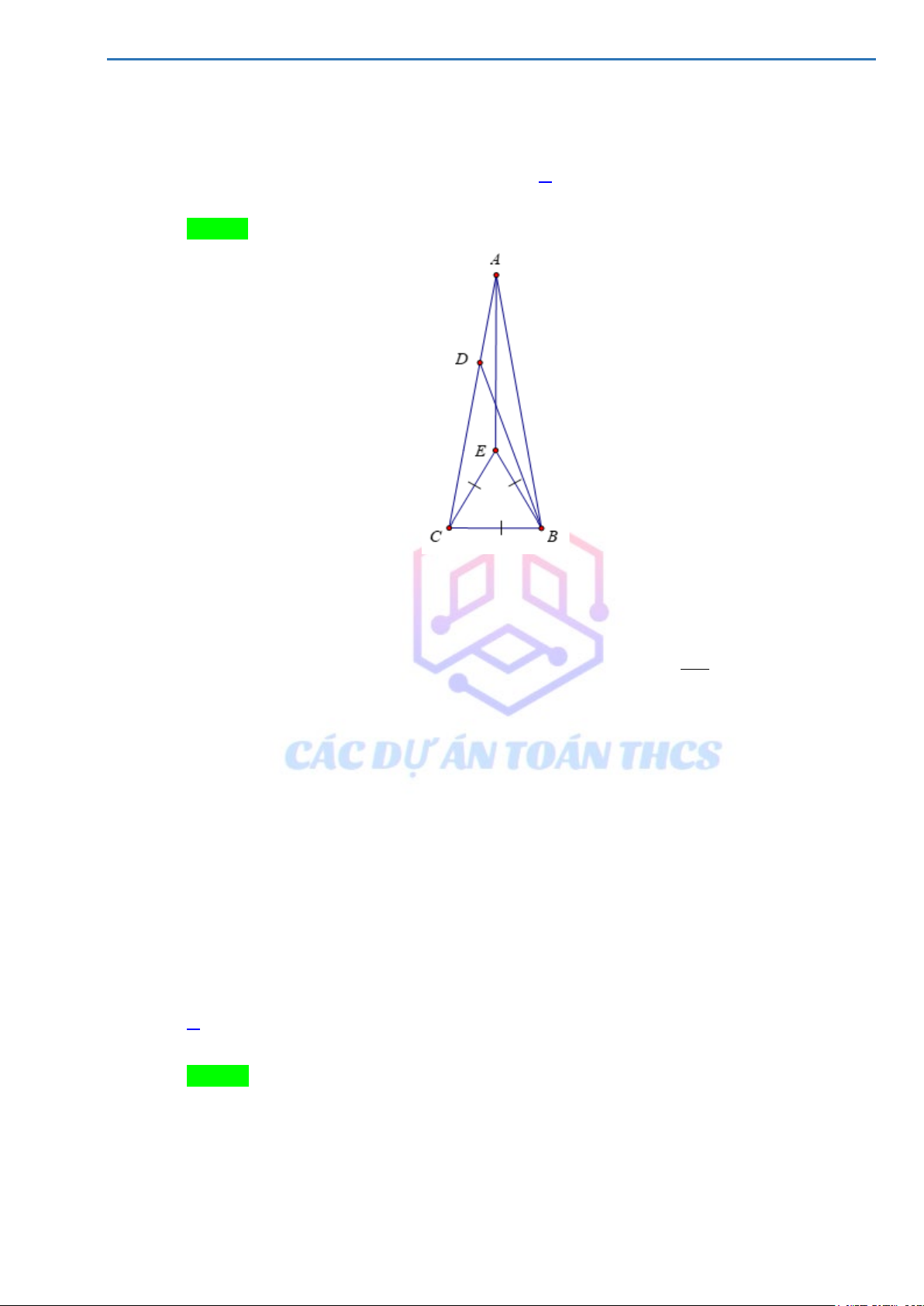
Cho tam giác nhọn ABC . Vẽ về phía ngoài tam giác ABC các tam giác đều ABD và ACE .
Gọi M là giao điểm của DC và BE . a) Chứng minh A ∆ BE = A ∆ DC b) Tính số đo BMC Lời giải E A D M C B Xét A ∆ BE và A ∆ DC có:
AD = AB ( A ∆ BD đều)
AC = AE ( A ∆ CE đều) = 0 = +
BAE DAC ( 60 BAC) ⇒ A ∆ BE = A ∆ DC (c.g.c) = +
BMC MCE CEM = + + MCA ACE CEM = + + AEM ACE CEM = + 0 0 0 AEC ACE = 60 + 60 =120
Trang 20/31




