




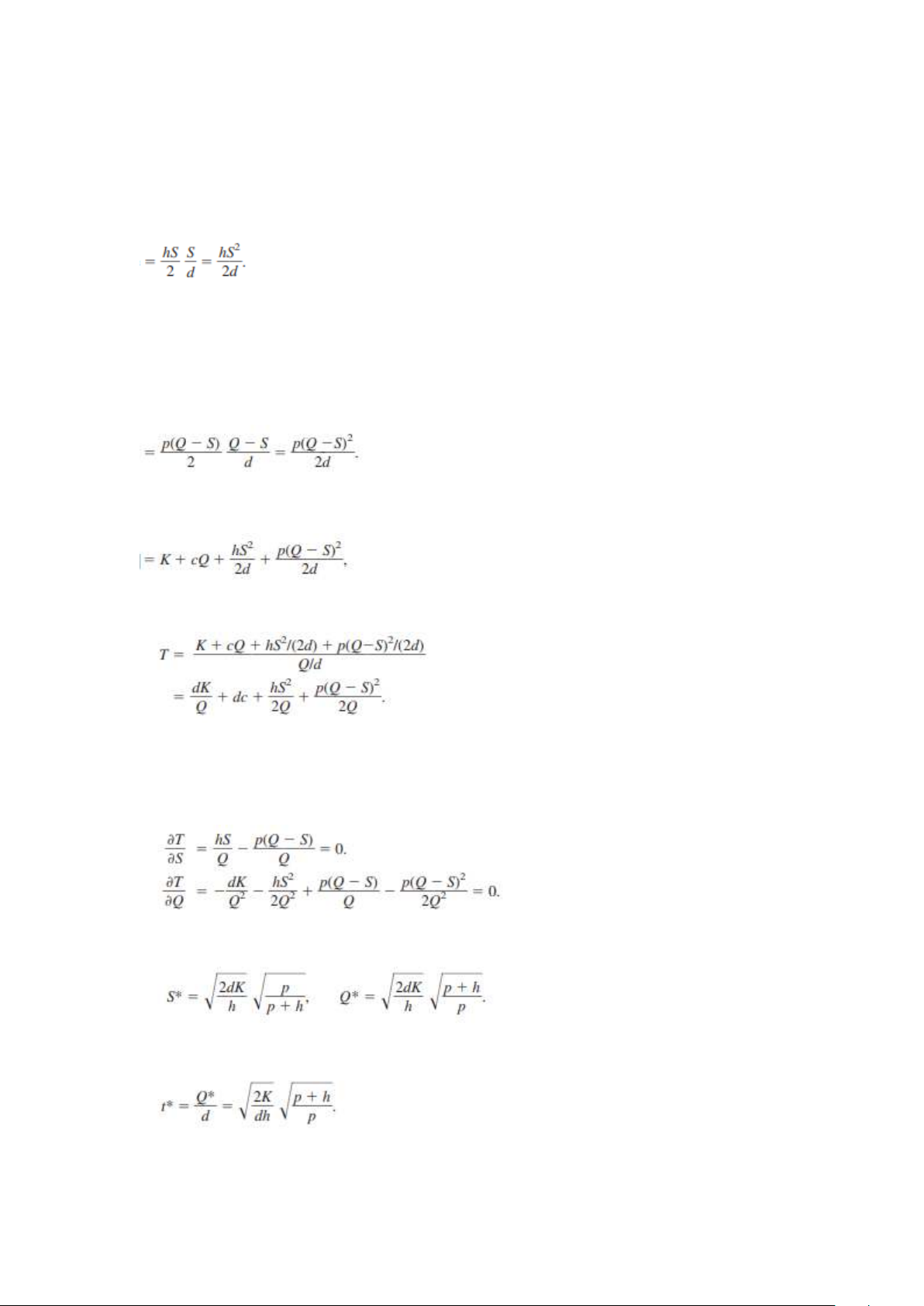







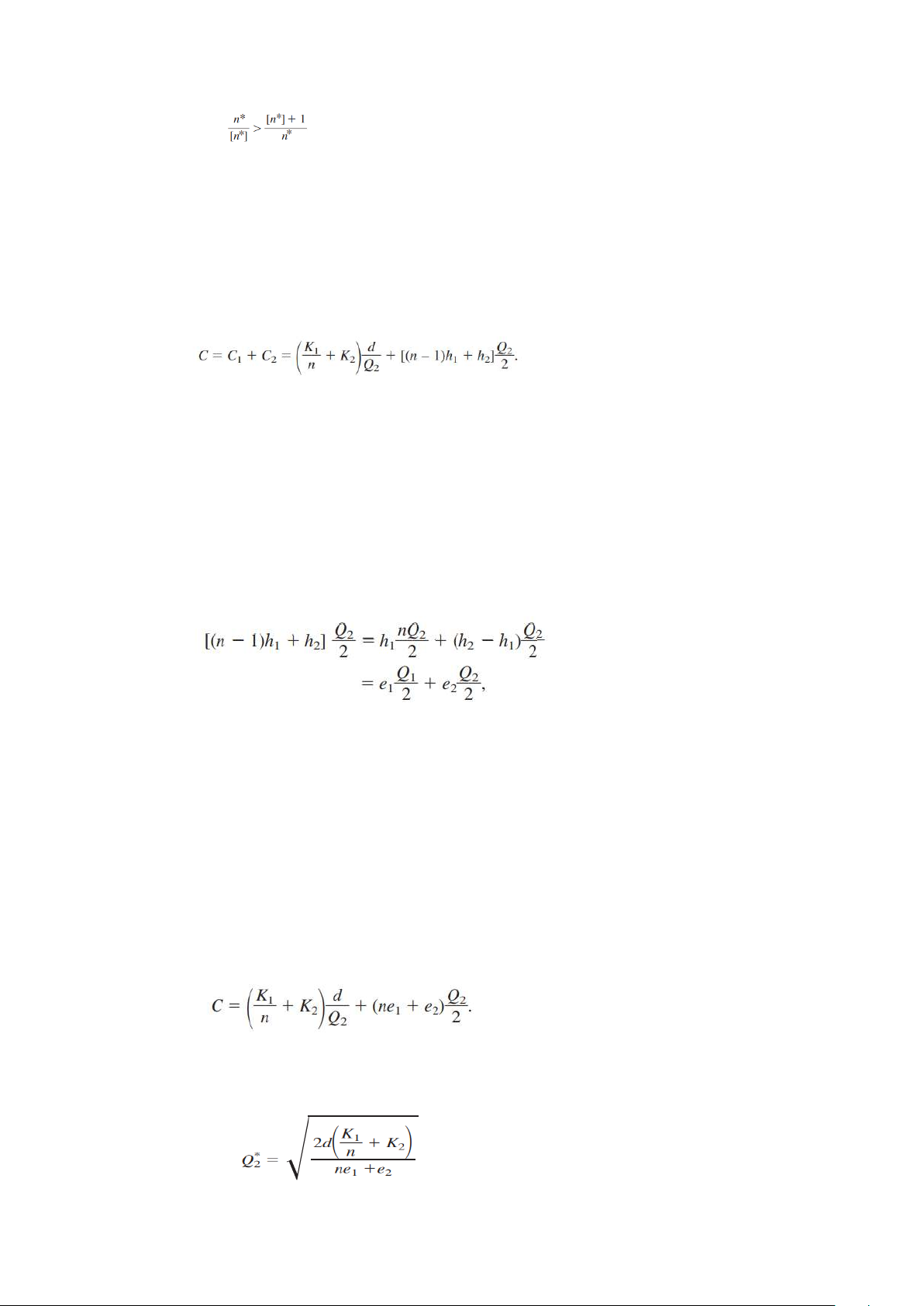









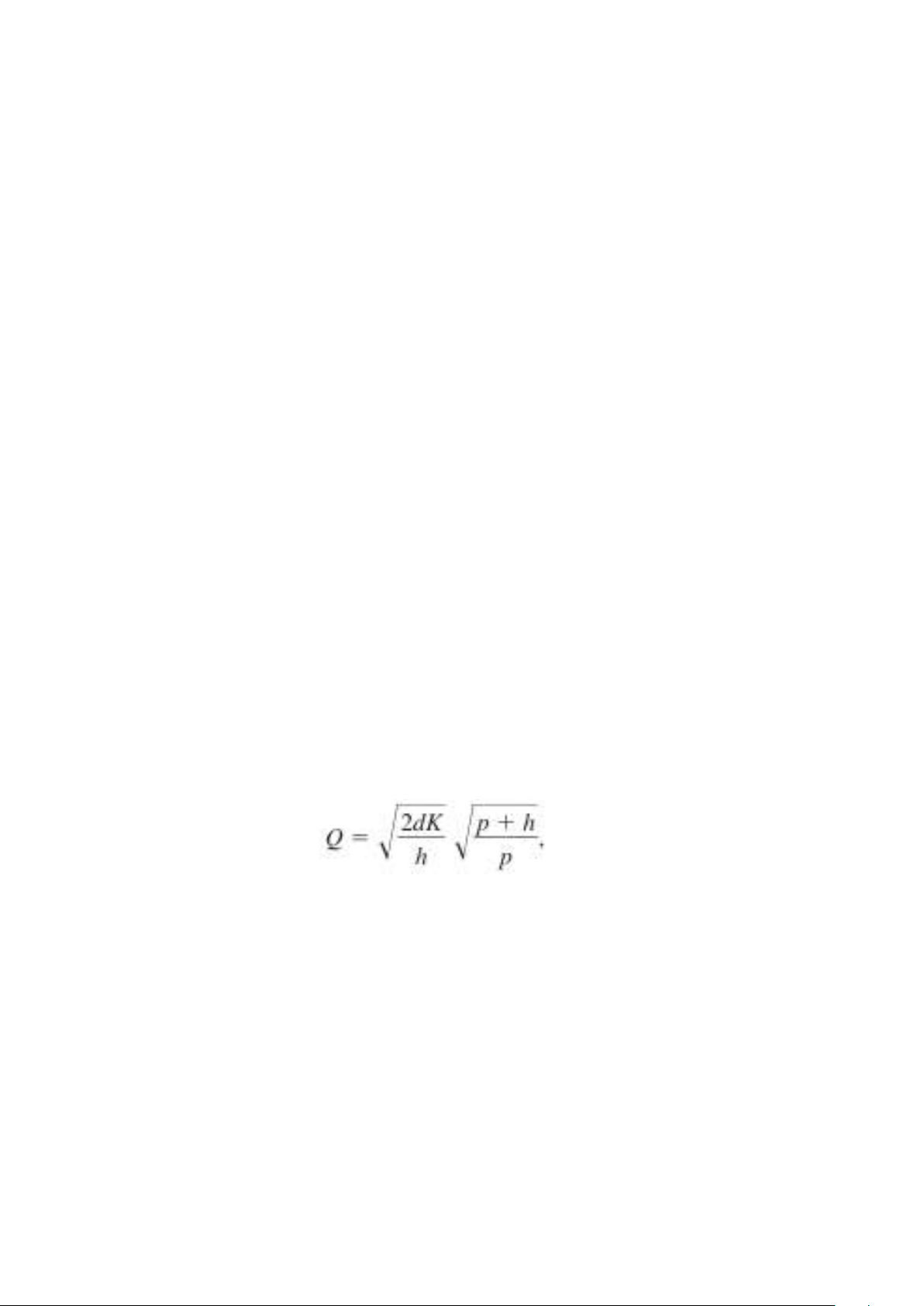






















Preview text:
TRƯỜNG ĐẠI HỌC KỸ THUẬT - CÔNG NGHỆ CẦN THƠ
KHOA QUẢN LÝ CÔNG NGHIỆP
HỌC PHẦN: KỸ THUẬT RA QUYẾT ĐỊNH
BẢN DỊCH TÓM TẮT CHƯƠNG 18 LÝ THUYẾT TỒN KHO
Giảng viên hướng dẫn: Phạm Thị Bích Trâm
Sinh viên thực hiện nhóm 6
Lê Thị Thanh Thảo: 2101326
Nguyễn Hữu Điền: 2101562 Liên Ngọc Trân: 210153
Nguyễn Phước Thịnh: 2100341 Trần Thái Bình: 2100392 Huỳnh Quốc Bảo: 2100705
Võ Minh Thùy Dương: 2100580 Cần Thơ, 2024 MỤC LỤC
CHƯƠNG 18: LÝ THUYẾT TỒN KHO 2
........................................................... 18.1 VÍ DỤ 2
...................................................................................................
18.2 THÀNH PHẦN CỦA MÔ HÌNH HÀNG TỒN KHO 3 .........................
18.3 CÁC MÔ HÌNH ĐÁNH GIÁ LIÊN TỤC XÁC ĐỊNH 4 .......................
18.4 MỘT MÔ HÌNH ĐÁNH GIÁ ĐỊNH KỲ XÁC ĐỊNH 10 ......................
18.5 MÔ HÌNH TỒN KHO ĐA CẤP XÁC ĐỊNH CHO QUẢN LÝ CHUỖI CUNG ỨNG 12
.................................................................................
18.6 MÔ HÌNH ĐÁNH GIÁ LIÊN TỤC NGẪU NHIÊN 28 .........................
18.7 MÔ HÌNH MỘT KỲ NGẪU NHIÊN ĐỐI VỚI CÁC SẢN PHẨM DỄ HỎNG 31
.................................................................................................. 18.8. QUẢN LÝ DOANH THU 43
................................................................ 18.9 KẾT LUẬN 51
....................................................................................... 1
CHƯƠNG 18: LÝ THUYẾT TỒN KHO
Quản lý hàng tồn kho khoa học bao gồm các bước sau:
1. Xây dựng mô hình toán học mô tả hoạt động của hệ thống kiểm kê.
2. Tìm kiếm một chính sách tồn kho tối ưu đối với mô hình này.
3. Sử dụng hệ thống xử lý thông tin trên máy tính để duy trì hồ sơ về mức tồn kho hiện tại.
4. Sử dụng bản ghi mức tồn kho hiện tại này, áp dụng chính sách tồn kho tối ưu
để báo hiệu thời điểm và số lượng cần bổ sung hàng tồn kho.
Các mô hình kiểm kê toán học được sử dụng với phương pháp này có
thể được chia thành hai loại lớn – mô hình xác định và mô hình ngẫu nhiên –
tùy theo khả năng dự đoán nhu cầu liên quan. 18.1 VÍ DỤ
Hai ví dụ trong các bối cảnh khá khác nhau (nhà sản xuất và nhà bán
buôn) trong đó cần phải phát triển chính sách tồn kho.
VÍ DỤ 1 Sản xuất loa cho TV
Một công ty sản xuất tivi sản xuất loa của riêng mình, loa này được sử
dụng để sản xuất tivi. Các tivi được lắp ráp trên dây chuyền sản xuất liên tục
với tốc độ 8.000 chiếc/tháng, mỗi bộ cần một loa. Loa được sản xuất theo lô vì
không đảm bảo phải thiết lập dây chuyền sản xuất liên tục và có thể sản xuất số
lượng tương đối lớn trong thời gian ngắn. Vì vậy, loa được đưa vào kho cho
đến khi cần lắp ráp thành tivi trên dây chuyền sản xuất. Công ty quan tâm đến
việc xác định khi nào nên sản xuất một lô loa và sản xuất bao nhiêu loa trong
mỗi lô. Một số chi phí phải được xem xét:
1. Mỗi lần sản xuất một lô, chi phí thiết lập sẽ phát sinh là 12.000 USD.
2. Chi phí sản xuất đơn vị của một chiếc loa (không bao gồm chi phí lắp đặt) là
10 USD, không phụ thuộc vào kích cỡ lô sản xuất.
3. Chi phí ước tính để giữ một chiếc loa trong kho là 0,30 USD mỗi tháng.
4. Tình trạng thiếu loa đôi khi vẫn xảy ra và ước tính rằng mỗi loa không có
sẵn khi được yêu cầu sẽ có giá 1,10 USD mỗi tháng.
Chính sách khoảng không quảng cáo cho ví dụ này ở trong phần. 18.3.
VÍ DỤ 2 Phân phối bán buôn xe đạp 2
Một nhà phân phối bán xe đạp gặp khó khăn với tình trạng thiếu mẫu xe
hiện đang xem xét lại chính sách tồn kho cho mẫu xe này. Nhà phân phối theo
đuổi mẫu xe đạp này từ nhà sản xuất hàng tháng và sau đó cung cấp nó cho các
cửa hàng xe đạp khác nhau ở miền Tây Hoa Kỳ để đáp ứng các đơn đặt hàng.
Tổng nhu cầu từ các cửa hàng xe đạp trong một tháng bất kỳ là bao nhiêu là
điều khá không chắc chắn. Vì vậy, câu hỏi đặt ra là: Nên đặt hàng bao nhiêu
chiếc xe đạp từ nhà sản xuất trong một tháng bất kỳ, với mức tồn kho tính đến tháng đó?
Nhà phân phối đã phân tích chi phí của mình và xác định rằng những
điều sau đây là quan trọng:
1 Chi phí đặt hàng ước tính là 2.000 USD và chi phí thực tế của mỗi chiếc xe
đạp là 350 USD cho người bán buôn này.
2. Chi phí lưu giữ là 10 USD cho mỗi chiếc xe đạp còn lại vào cuối tháng.
3. Chi phí thiếu hụt là 150 USD/chiếc xe đạp/tháng thiếu hụt.
Hai ví dụ trên cho biết về cách một công ty bổ sung hàng tồn kho. Một
khả năng là tự sản xuất. Hai là đặt hàng các sản phẩm từ một nhà cung cấp. Hai
ví dụ đều chỉ ra rằng tồn tại sự đánh đổi giữa các chi phí liên quan.
18.2 THÀNH PHẦN CỦA MÔ HÌNH HÀNG TỒN KHO
Một số chi phí quyết định khả năng sinh lời là (1) chi phí đặt hàng, (2) chi
phí lưu kho, (3) chi phí thiếu hụt. Các yếu tố liên quan khác bao gồm (4) doanh
thu, (5) chi phí thu hồi, (6) tỷ lệ chiết khấu. Sáu yếu tố này được mô tả lần lượt dưới đây.
Chi phí đặt hàng số lượng ȥ có thể được biểu thị bằng hàm c(ȥ). Dạng đơn
giản nhất của hàm này là dạng tỷ lệ thuận với số lượng đặt hàng, tức là c ȥ,
trong đó c đại diện cho đơn giá thanh toán. Một giả định phổ biến khác là c(ȥ)
bao gồm hai phần: một số hạng tỷ lệ thuận với số lượng đặt hàng và một số
hạng là hằng số K cho ȥ dương và bằng 0 cho ȥ = 0. Trong trường hợp này,
c(ȥ) = Chi phí đặt hàng ȥ {0 if ȥ=0 𝑘+𝑐 ȥ if ȥ>0
K = chi phí thiết lập và c = đơn giá
Hằng số K bao gồm chi phí hành chính của việc đặt hàng hoặc khi sản
xuất, các chi phí liên quan đến việc thiết lập để bắt đầu quá trình sản xuất.
Trong Ví dụ 1, loa được sản xuất và chi phí thiết lập cho quá trình sản
xuất là 12.000 USD. Hơn nữa, mỗi loa có giá 10 USD, do đó chi phí sản xuất
khi đặt hàng sản xuất một loạt loa được tính bằng 3
c(ȥ) = 12,000 + 10 ȥ, ȥ > 0
Trong ví dụ 2, nhà phân phối đặt hàng xe đạp từ nhà sản xuất và chi phí
đặt hàng được tính bằng
c(ȥ) = 2,000 + 350 ȥ, ȥ > 0.
Chi phí lưu giữ (đôi khi được gọi là chi phí lưu kho) bao gồm chi phí vốn gắn liền, không gian,...
Chi phí thiếu hụt phát sinh khi lượng hàng cần vượt lượng hàng sẵn
có.Trong một trường hợp, được gọi là tồn đọng, nhu cầu vượt mức không bị
mất đi mà thay vào đó được giữ lại cho đến khi có thể đáp ứng được khi đợt
giao hàng tiếp theo bổ sung thêm hàng tồn kho. Trường hợp thứ hai, được gọi
là không tồn đọng, nếu xảy ra tình trạng dư thừa nhu cầu so với lượng hàng
sẵn có, công ty không thể đợi đợt giao hàng tiếp theo để đáp ứng nhu cầu dư thừa.
Khi sử dụng các kỹ thuật định lượng để tìm kiếm chính sách tồn kho tối
ưu. Sử dụng tiêu chí giảm thiểu tổng chi phí (dự kiến) hoặc (chi phí chiết khấu
nếu khoảng thời gian dài). Tiêu chí hữu ích khác là giữ cho chính sách tồn kho
đơn giản, tức là giữ quy tắc cho biết thời điểm đặt hàng và số lượng đặt hàng.
18.3 CÁC MÔ HÌNH ĐÁNH GIÁ LIÊN TỤC XÁC ĐỊNH
Mô hình kinh tế đặt hàng (EOQ) là một mô hình đơn giản. Mô hình này
giả định rằng sản phẩm được rút từ kho với tỷ lệ không đổi được ký hiệu là "d",
và tồn kho được bổ sung thông qua đặt hàng lô hàng có kích thước cố định "Q"
đơn vị. Đối với mô hình EOQ cơ bản, chỉ có các chi phí sau cần được xem xét:
K = chi phí thiết lập cho việc đặt hàng một lô hàng,
c = chi phí đơn vị cho việc sản xuất hoặc mua mỗi đơn vị,
h = chi phí giữ hàng mỗi đơn vị mỗi đơn vị thời gian giữ trong kho.
Mục tiêu là xác định khi nào và bằng cách nào để bổ sung hàng tồn kho
sao cho giảm thiểu tổng các chi phí này mỗi đơn vị thời gian.
Giả định (Mô hình EOQ Cơ bản)
1. Một tỷ lệ nhu cầu biết trước và không đổi là d đơn vị mỗi đơn vị thời gian.
2. Số lượng đặt hàng (Q) để bổ sung hàng tồn kho đến một lần duy nhất khi
cần, nghĩa là khi mức tồn kho giảm về 0.
3. Không cho phép thiếu hụt dự định
Về giả định thứ 2, để đáp ứng giả định thứ 2, điểm đặt lại đơn hàng này cần được đặt tại. 4
Điểm đặt lại = (tốc độ nhu cầu) x (thời gian dẫn).
Độ dài chu kỳ được xem là thời gian giữa các lần sản xuất là Q/d.
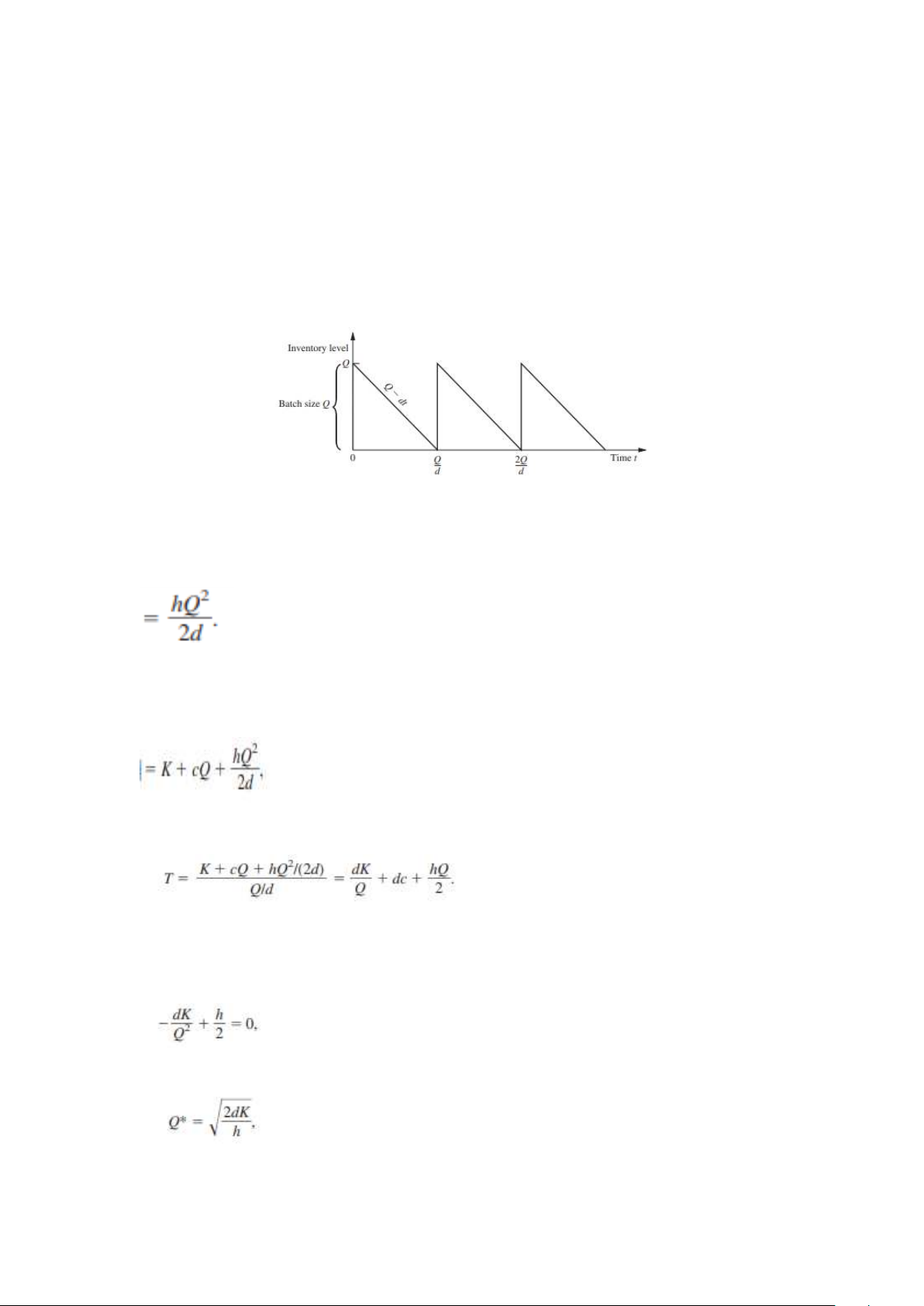
Chi phí sản xuất hoặc đặt hàng mỗi chu kỳ = K + cQ ■ HÌNH 18.1
Biểu đồ của mức tồn kho theo thời gian cho mô hình EOQ cơ bản.
Mức trung bình của tồn kho trong một chu kỳ là (Q + 0)/2 =Q/2 đơn vị, và chi
phí tương ứng là hQ/2 mỗi đơn vị thời gian. Vì độ dài chu kỳ là Q/d,
Chi phí giữ hàng mỗi chu kỳ Do đó,
Tổng chi phí mỗi chu kỳ
vì vậy, tổng chi phí mỗi đơn vị thời gian là
Giá trị của Q, gọi là Q*, mà làm giảm thiểu T được tìm bằng cách đặt đạo
hàm đầu tiên bằng không (và lưu ý rằng đạo hàm bậc hai là dương), điều này dẫn đến vì thế
Dây là công thức EOQ được biết đến rộng rãi. 5
(Nó cũng đôi khi được gọi là công thức căn bậc hai.) Thời gian chu kỳ tương ứng, gọi là t*, là
Quan sát thấy rằng Q* và t* thay đổi theo cách hợp lý và sáng tỏ khi có
thay đổi trong K, h, hoặc d. Khi chi phí thiết lập K tăng, cả Q* và t* đều tăng
(ít lần thiết lập hơn). Khi chi phí giữ hàng h tăng, cả Q* và t* giảm (mức tồn
kho nhỏ hơn). Khi tốc độ nhu cầu d tăng, Q* tăng (lô hàng lớn hơn) nhưng t*
giảm (thiết lập thường xuyên hơn).
Mô hình EOQ với Thiếu Hụt Dự Định khi tình trạng thiếu hụt hàng tồn
kho xuất hiện nhu cầu không thể được đáp ứng vì hàng tồn kho đã cạn kiệt. -
Thiếu hụt không dự định có thể xảy ra nếu tốc độ nhu cầu và giao hàng không đúng lịch trình.
Mô hình EOQ với Thiếu Hụt Dự Định giải quyết bằng cách thay đổi giả
định thứ ba của mô hình EOQ cơ bản. Giả định mới là:
Thiếu hụt dự định được cho phép. Khi xảy ra thiếu hụt, khách hàng bị -
ảnh hưởng sẽ chờ đợi sản phẩm trở lại có sẵn. Đơn hàng chờ của họ được đáp
ứng ngay lập tức khi số lượng đặt hàng đến để bổ sung hàng tồn kho. Đặt:
p là chi phí thiếu hụt mỗi đơn vị hàng trong mỗi đơn vị thời gian thiếu hụt, -
S là mức tồn kho ngay sau khi một lô hàng gồm Q đơn vị được thêm vào kho, -
Q S là thiếu hụt trong tồn kho ngay trước khi một lô hàng gồm Q đơn vị - - được thêm vào.
Tổng chi phí mỗi đơn vị thời gian bây giờ được tính từ các thành phần sau:
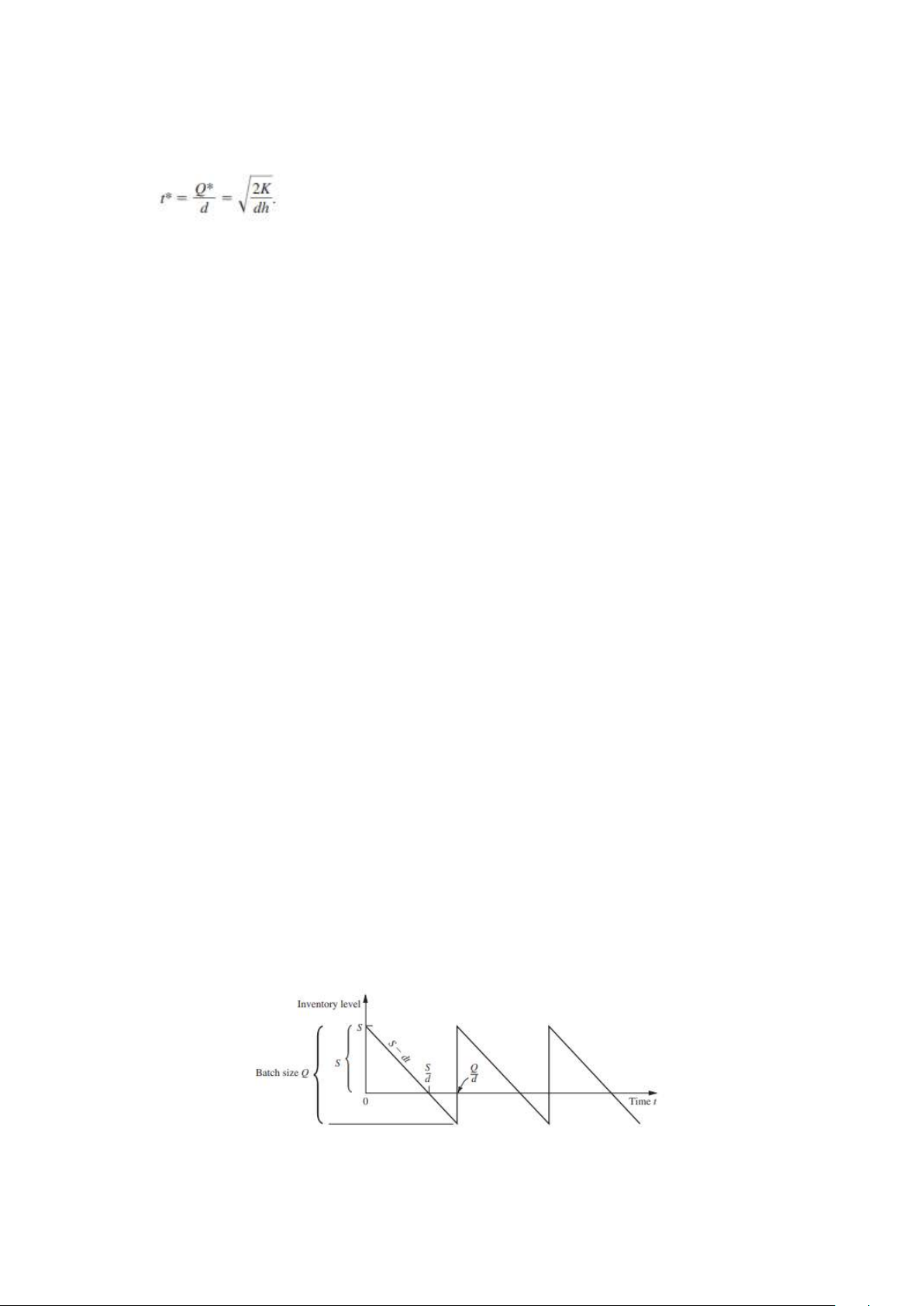
Chi phí sản xuất hoặc đặt hàng mỗi chu kỳ = K + cQ ■ HÌNH 18.2
Biểu đồ của mức tồn kho theo thời gian cho mô hình EOQ với thiếu hụt dự định. 6
Trong mỗi chu kỳ, mức tồn kho là dương trong một khoảng thời gian
S/d. Mức tồn kho trung bình trong khoảng thời gian này là (S 0)/2 S/2 đơn vị,
và chi phí tương ứng là hS/2 mỗi đơn vị thời gian. Do đó,
Chi phí giữ hàng mỗi chu kỳ
Thiếu hụt xảy ra trong một khoảng thời gian (Q S)/d. Lượng thiếu hụt -
trung bình trong khoảng thời gian này là (0 + Q S)/2 = (Q S)/2 đơn vị, và chi - -
phí tương ứng là p(Q S)/2 mỗi đơn vị thời gian. Do đó, -
Chi phí thiếu hụt mỗi chu kỳ
Tổng chi phí mỗi chu kỳ
và tổng chi phí mỗi đơn vị thời gian là
Trong mô hình này, có hai biến quyết định (S và Q), vì vậy các giá trị tối
ưu (S* và Q*) được tìm bằng cách đặt đạo hàm riêng của T/S và T/Q bằng không. Do đó,
Giải các phương trình này đồng thời dẫn đến
Độ dài chu kỳ tối ưu t* được cho bởi Thiếu hụt tối đa là 7
Ngoài ra, từ Hình 18.2, tỷ lệ thời gian không có thiếu hụt được cho bởi tính độc lập của K.
Khi p tiến đến vô cùng với h không đổi, Q* S* tiến dần về 0 trong khi -
cả Q* và t* tiến dần đến các giá trị của chúng cho mô hình EOQ cơ bản.
Ngược lại, khi h tiến đến vô cùng với p không đổi, S* sẽ bằng 0.
Mô hình EOQ với Chiết khấu Số lượng
Giả định mô hình EOQ với chiết khấu số lượng
Chi phí mỗi đơn vị của một mặt hàng phụ thuộc vào số lượng trong lô. -
Một động lực được cung cấp để đặt một đơn đặt hàng lớn bằng cách thay đổi
chi phí mỗi đơn vị cho một số lượng nhỏ bằng một chi phí mỗi đơn vị nhỏ hơn
cho mỗi mặt hàng trong một lô lớn hơn, và có thể là chi phí mỗi đơn vị nhỏ hơn
cho các lô lớn hơn. các giả định còn lại giống như cho mô hình EOQ cơ bản.
Ví dụ về loa TV được giới thiệu trong Phần 18.1.
Giả sử bây giờ chi phí mỗi loa là c1 = 11 đô la nếu số lượng dưới 10,000
loa được sản xuất, c2 = 10 đô la nếu sản xuất nằm giữa 10,000 và 80,000 loa,
và c3 = 9.50 đô la nếu sản xuất vượt quá 80,000 loa. Chính sách tối ưu là gì?
Giải pháp cho vấn đề cụ thể này sẽ tiết lộ phương pháp chung.
Từ các kết quả cho mô hình EOQ cơ bản, tổng chi phí mỗi đơn vị thời gian Tj
nếu chi phí mỗi đơn vị là cj được cho bởi
Biểu thức này giả định rằng h không phụ thuộc vào chi phí mỗi đơn vị
của các mặt hàng, nhưng một sự điều chỉnh nhỏ phổ biến là làm cho h tỉ lệ với
chi phí mỗi đơn vị để phản ánh việc chi phí vốn liên quan đến tồn kho biến đổi
theo cách này. Đối với K = 12,000, h = 0.30, và d = 8,000, giá trị này là
Giá trị Q làm giảm thiểu này là một giá trị khả thi cho hàm chi phí T2.
Đối với bất kỳ Q cố định nào, T2 < T1, vì vậy T1 có thể được loại bỏ khỏi xem
xét tiếp theo. Tuy nhiên, T3 không thể được loại bỏ ngay lập tức. Giá trị tối
thiểu khả thi của nó (điều này xảy ra khi Q = 80,000) phải được so sánh với T2 8
được đánh giá tại 25,298 (tức là 87,589 đô la). Vì T3 đánh giá tại 80,000 bằng
89,200 đô la, nên tốt hơn là sản xuất với số lượng là 25,298, vì vậy số lượng
này là giá trị tối ưu cho tập hợp các chiết khấu số lượng này.
Nếu chiết khấu số lượng dẫn đến chi phí mỗi đơn vị là 9 đô la (thay vì
9.50 đô la) khi sản xuất vượt quá 80,000, thì T3 được đánh giá tại 80,000 sẽ
bằng 85,200 đô la, và số lượng sản xuất tối ưu sẽ trở thành 80,000.
Dưới đây là tóm tắt về quy trình tổng quan:
1. Đối với mỗi chi phí mỗi đơn vị cj có sẵn, sử dụng công thức EOQ cho mô
hình EOQ để tính toán số lượng đặt hàng tối ưu Q*j của nó.
2. Đối với mỗi cj mà Q*j nằm trong phạm vi số lượng đặt hàng khả thi cho cj,
tính toán tổng chi phí mỗi đơn vị thời gian tương ứng Tj.
3. Đối với mỗi cj mà Q*j không nằm trong phạm vi số lượng đặt hàng khả thi
này, xác định số lượng đặt hàng Qj tại đầu mút của phạm vi khả thi này gần
nhất với Q*j. Tính toán tổng chi phí mỗi đơn vị thời gian Tj cho Qj và cj.
4. So sánh các giá trị Tj thu được cho tất cả các cj và chọn Tj tối thiểu. Sau đó,
chọn số lượng đặt hàng Qj thu được trong bước 2 hoặc 3 mà cho ra Tj tối thiểu này.
Nhận xét về các mô hình EOQ:
1. Nếu chi phí mỗi đơn vị của mặt hàng không thay đổi qua thời gian và không
phụ thuộc vào kích thước lô, thì chi phí này sẽ không ảnh hưởng đến kích
thước lô tối ưu trong các mô hình EOQ.
2. Các mô hình EOQ giả định rằng kích thước lô Q là cố định qua các chu kỳ.
Kích thước lô tối ưu Q* thực sự giảm tổng chi phí mỗi đơn vị thời gian cho
mọi chu kỳ, cho thấy rằng kích thước lô cố định này là tối ưu dù không có giả
định về kích thước lô cố định.
3. Trong các mô hình EOQ, mức tồn kho tối ưu không bao giờ vượt quá không.
4. Các mô hình EOQ đặt ra các giả định khá cứng nhắc, thường không thể hoàn
toàn đáp ứng trong thực tế.
Việc quản lý tồn kho của các sản phẩm yêu cầu phụ thuộc có thể phức
tạp hơn nhiều. Để hỗ trợ trong công việc này, kỹ thuật phổ biến là kế hoạch yêu
cầu vật liệu (MRP). MRP là một hệ thống dựa trên máy tính giúp lập kế hoạch,
lên lịch và kiểm soát việc sản xuất tất cả các thành phần của một sản phẩm cuối cùng.
Vai trò của Quản lý tồn kho Just-In-Time (JIT) 9
Giả sử chi phí thiết lập có thể giảm đáng kể từ 12.000 đô la ở ví dụ phần
18.1 xuống còn K = 1200 đô la. Điều này sẽ giảm kích thước lô sản xuất tối ưu
từ 25.298 loa xuống còn Q* = 2.530 loa, vì vậy một chuỗi sản xuất mới khởi
động hơn 3 lần mỗi tháng. Làm giảm chi phí thiết lập hàng năm và chi phí giữ
hàng hàng năm từ hơn 45.000 đô la xuống chỉ khoảng hơn 4.500 đô la mỗi cái.
Hệ thống JIT tập trung vào việc giảm mức tồn kho xuống mức tối thiểu
và cung cấp hàng hóa đúng lúc khi cần thiết.
Mặc dù JIT bị hiểu sai là không tương thích với mô hình EOQ. JIT tập
trung vào giảm chi phí thiết lập để số lượng đặt hàng tối ưu sẽ nhỏ. Nó cũng
giảm thời gian dẫn giao hàng, giảm sự không chắc chắn về số lượng cần thiết
khi giao hàng. Cải thiện bảo dưỡng định kỳ và quy trình sản xuất để đảm bảo
chất lượng cũng là điểm nhấn của JIT.
18.4 MỘT MÔ HÌNH ĐÁNH GIÁ ĐỊNH KỲ XÁC ĐỊNH
Mô hình đánh giá định kỳ được xem xét để lập kế hoạch sản xuất hoặc
đặt hàng cho các kỳ tiếp theo để bổ sung hàng tồn kho. Các nhu cầu trong các
kỳ tương ứng được biết trước và không giống nhau, được ký hiệu bằng nhu cầu cho kì i
Các chi phí được bao gồm trong mô hình này
K: chi phí thiết lập để sản xuất hoặc mua bất kỳ đơn vị nào để bổ sung -
hàng tồn kho vào đầu mỗi kỳ,
c: chi phí mỗi đơn vị để sản xuất hoặc mua từng đơn vị, -
h: chi phí giữ hàng cho mỗi đơn vị còn lại trong kho vào cuối mỗi kỳ - Một Ví dụ
Một nhà sản xuất máy bay nhận được đơn đặt hàng từ một tập đoàn lớn
cho 10 chiếc máy bay phản lực chuyên chở riêng tư. Đơn hàng yêu cầu các
máy bay được giao trong 4 giai đoạn khác nhau trong một khoảng thời gian.
Thiết lập cơ sở sản xuất đòi hỏi một chi phí thiết lập là 2 triệu đô la, và việc giữ
máy bay trong kho có chi phí là 200,000 đô la mỗi chiếc mỗi giai đoạn. Để
giảm chi phí lớn, nhà sản xuất muốn xác định lịch trình sản xuất ít tốn kém
nhất để đáp ứng đơn hàng này bằng cách sản xuất một số lượng nhỏ máy bay
ngay bây giờ và sau đó lặp lại việc thiết lập trong các giai đoạn sau để sản xuất thêm.
Do đó, sử dụng các ký hiệu của mô hình, các nhu cầu cho chiếc máy bay
cụ thể này trong bốn giai đoạn sắp tới (mùa) là
r1= 3, r2 = 2, r3 = 3, r4 = 2. 10
Sử dụng đơn vị triệu đô la, các chi phí liên quan là: K = 2, h = 0.2. Hình 18.4
Các mức tồn kho phát sinh từ một lịch sản xuất mẫu cho ví dụ về máy bay.
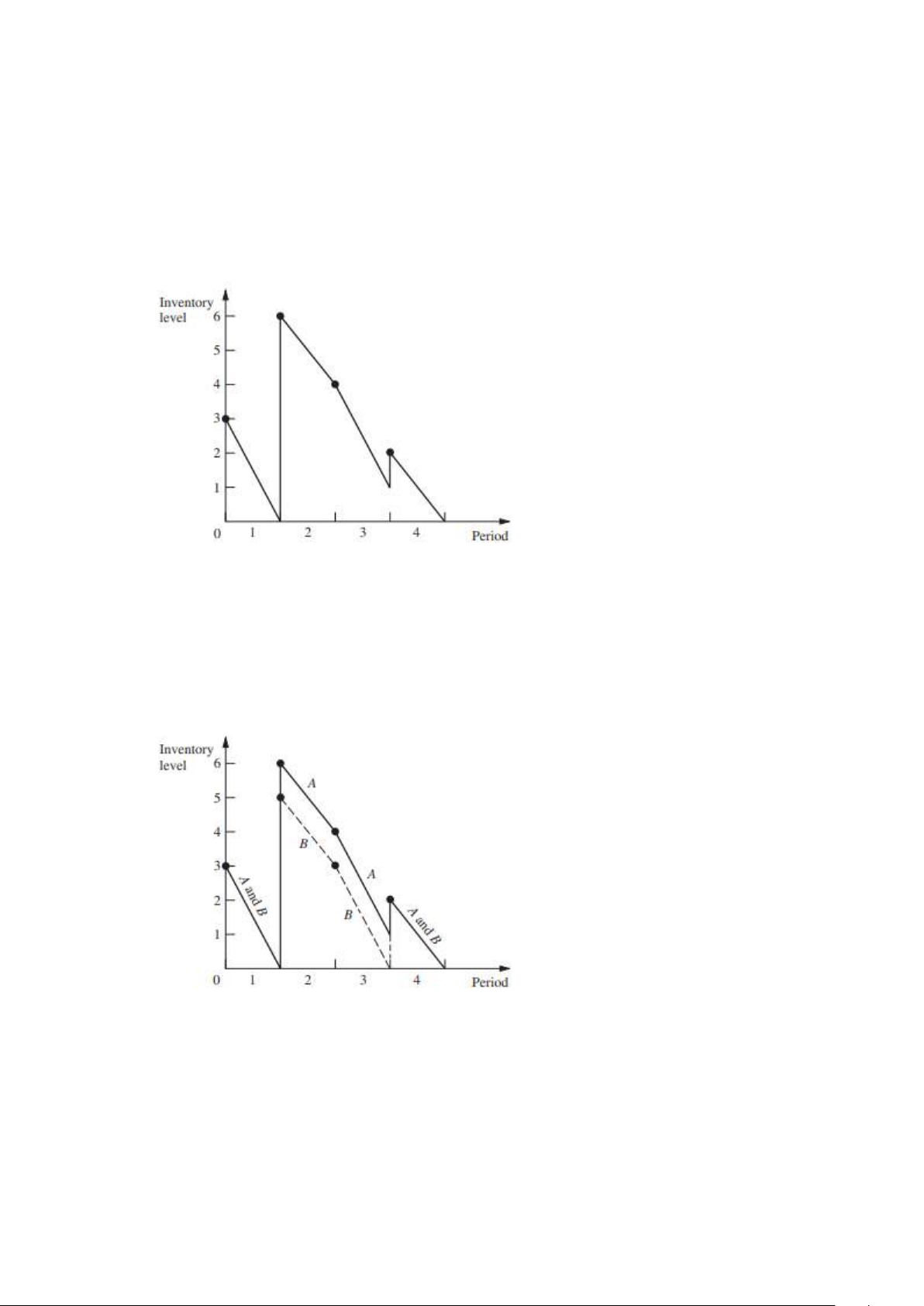
Ở đây, chúng ta sẽ tìm hiểu một thuật toán hiệu quả để tìm ra một chính
sách tồn kho tối ưu (hoặc tương đương, một lịch sản xuất tối ưu) cho mô hình
trên dựa trên thông tin cơ bản sau về bản chất của một chính sách tối ưu. ■ HÌNH 18.5
So sánh hai chính sách tồn kho (lịch sản xuất) cho ví dụ về máy bay.
Bằng cách sử dụng phương pháp lập trình động để giải quyết từng giai
đoạn theo chiều ngược, các giá trị Ci này có thể được tìm bằng cách trước tiên
tìm Cn, sau đó tìm Cn 1, và tiếp tục như vậy. Do đó, sau khi tìm thấy Cn, Cn 1, - - 11
. . . , Ci1, thì Ci có thể được tìm từ mối quan hệ đệ quy
trong đó j có thể được xem như là một chỉ số chỉ định (cuối của) giai đoạn khi
tồn kho đạt mức không lần đầu tiên sau khi sản xuất vào đầu giai đoạn i. Trong
khoảng thời gian từ giai đoạn i đến giai đoạn j, thuật ngữ với hệ số h đại diện
cho tổng chi phí giữ hàng trên khoảng thời gian này. Khi j = n, thuật ngữ Cn+1
= 0. Giá trị j cực tiểu cho thấy rằng nếu mức tồn kho thực sự giảm về không
khi bắt đầu giai đoạn i, thì sản xuất trong giai đoạn i nên đáp ứng tất cả nhu cầu
từ giai đoạn i qua giai đoạn j này.
Thuật toán để giải quyết mô hình bao gồm đơn giản là giải cho Cn, Cn-
1, . . . , C1 theo lần lượt. Đối với i = 1, giá trị j cực tiểu sau đó chỉ ra rằng sản
xuất trong giai đoạn 1 nên đáp ứng nhu cầu qua giai đoạn j, vì vậy sản xuất thứ
hai sẽ ở giai đoạn j + 1. Đối với i = j + 1, giá trị j cực tiểu mới xác định khoảng
thời gian được bao phủ bởi sản xuất thứ hai, và tiếp tục như vậy cho đến cuối.
Chúng tôi sẽ minh họa phương pháp này bằng ví dụ.
Việc áp dụng thuật toán này nhanh hơn nhiều so với phương pháp lập trình
động đầy đủ. Giống như trong lập trình động, Cn, Cn 1, . . . , C2 phải được tìm -
ra trước khi C1 được thu được. Tuy nhiên, số lượng tính toán nhỏ hơn nhiều, và
số lượng các lựa chọn về lượng sản xuất có giảm đi đáng kể.
18.5 MÔ HÌNH TỒN KHO ĐA CẤP XÁC ĐỊNH CHO QUẢN LÝ CHUỖI CUNG ỨNG
Để hỗ trợ quản lý chuỗi cung ứng, các mô hình tồn kho đa cấp bậc ngày
nay thường bao gồm các cấp bậc từ phần đầu của chuỗi cung ứng đến các cấp
bậc phân phối sản phẩm hoàn thiện. Cấp bậc đầu tiên có thể là tồn kho nguyên
liệu hoặc thành phần cuối cùng được sử dụng để sản xuất sản phẩm. Cấp bậc
thứ hai có thể là tồn kho các bộ phận con được sản xuất từ nguyên liệu hoặc
thành phần để chuẩn bị cho việc lắp ráp sau này vào sản phẩm cuối cùng. Một
mục tiêu phổ biến cho mô hình tồn kho đa cấp bậc là điều phối tồn kho ở mỗi
cấp độ sao cho chi phí tổng cộng liên quan đến hệ thống tồn kho tổng thể được tối thiểu hóa.
Một Mô hình cho Hệ thống Hai Cấp Bậc Liên tiếp
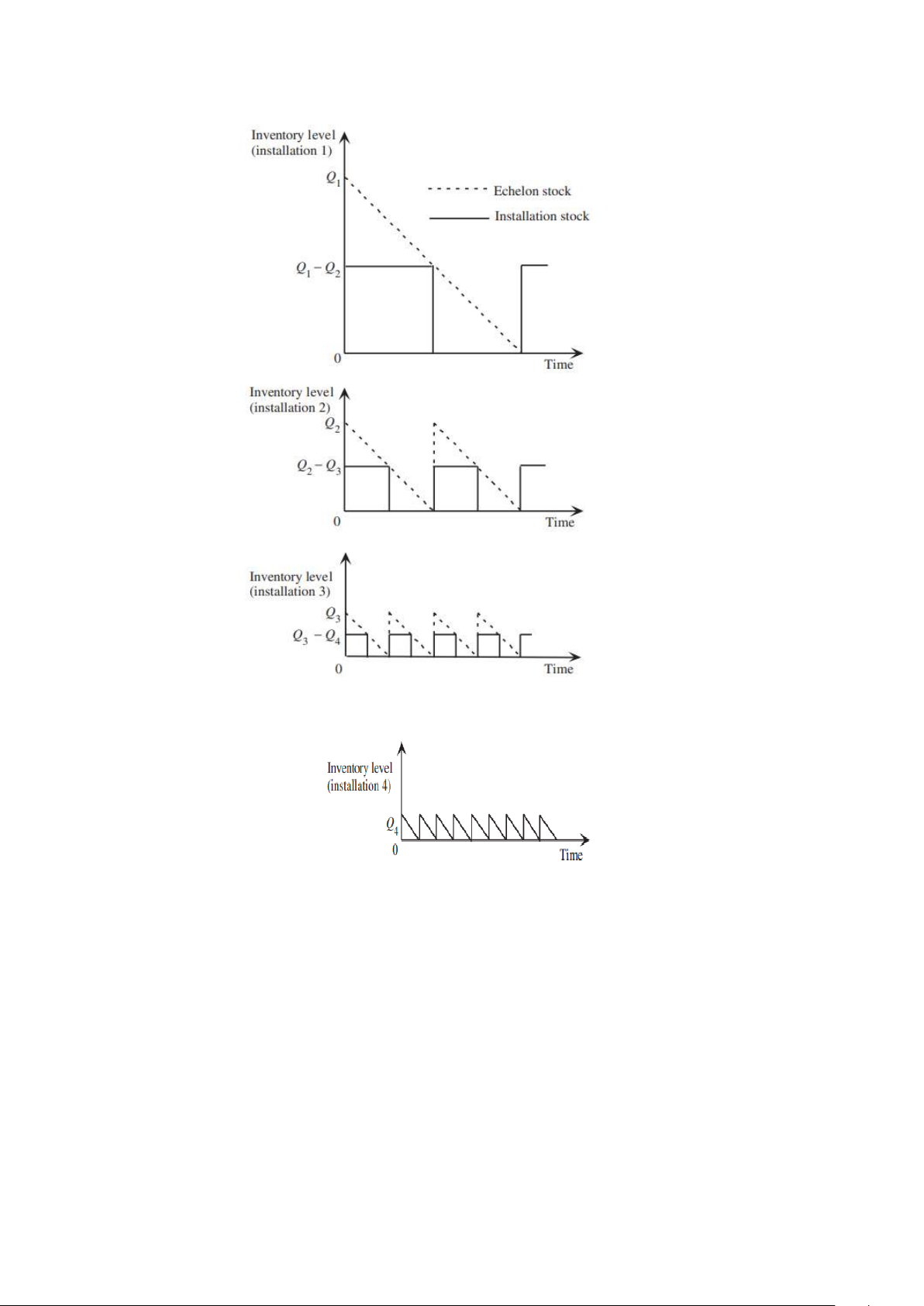
Một mô hình đơn giản cho hệ thống tồn kho đa cấp bậc là hệ thống có hai
cấp đặt và chỉ một cài đặt tại mỗi cấp. Hình 18.7 mô tả một hệ thống như vậy,
trong đó tồn kho tại cài đặt 1 được sử dụng để định kỳ nạp lại tồn kho tại cài
đặt 2. Ví dụ, cài đặt 1 có thể là một nhà máy sản xuất một sản phẩm cụ thể với 12
các chu trình sản xuất đôi khi, và cài đặt 2 có thể là trung tâm phân phối cho
sản phẩm đó. Hoặc, cài đặt 2 có thể là nhà máy sản xuất sản phẩm, trong khi
cài đặt 1 là một cơ sở khác nơi các thành phần cần thiết để sản xuất sản phẩm
đó được sản xuất hoặc nhận từ các nhà cung cấp.
Hình 18.7. Một hệ thống kiểm kê hai cấp nối tiếp Kiểm kê lúc Kiểm kê lúc lắp đặt 1 lắp đặt 2
Các đơn vị của mục 1 và mục 2 được xác định sao cho chính xác một đơn
vị của mục 1 cần thiết để có được một đơn vị của mục 2
Mô hình đặt ra các giả định sau đây.
Giả định cho Mô hình Hai Cấp Bậc Liên Tiếp
1. Các giả định của mô hình EOQ cơ bản đúng tại cài đặt 2.
2. Các chi phí liên quan tại lần lắp đặt 2 là chi phí thiết lập K2 mỗi khi đặt
hàng và chi phí giữ hàng h2 mỗi đơn vị mỗi đơn vị thời gian.
3. Cài đặt 1 sử dụng kho hàng của mình để cung cấp một lô Q2 đơn vị cho
cài đặt 2 ngay lập tức mỗi khi nhận được một đơn đặt hàng.
4. Một lượng đặt hàng của Q1 đơn vị được đặt vào thời gian để tái tồn
kho tại cài đặt 1 trước khi thiếu hụt xảy ra.
5. Tương tự như cài đặt 2, các chi phí liên quan tại cài đặt 1 là chi phí
thiết lập là K1 mỗi lần đặt hàng và chi phí giữ hàng là h1 mỗi đơn vị mỗi đơn vị thời gian.
6. Các đơn vị tăng giá trị khi chúng được nhận và xử lý tại cài đặt 2, vì vậy h1 < h2.
7. Mục tiêu là tối thiểu hóa tổng chi phí biến đổi mỗi đơn vị thời gian tại
hai cài đặt. (Điều này sẽ được ký hiệu là C.)
Từ "ngay lập tức" trong giả định 3 ngụ ý rằng không có thời gian chờ
giữa khi cài đặt 2 đặt hàng cho Q2 đơn vị và cài đặt 1 xử lý đơn hàng đó. 13
Mặc dù thời gian chờ bằng không và thời gian chờ cố định là tương
đương với mục đích mô hình hóa, cụ thể giả định thời gian chờ bằng không vì
nó giúp đơn giản hóa việc khái niệm cách mức tồn kho tại hai cài đặt thay đổi
đồng thời theo thời gian.
Mô hình của mức tồn kho theo thời gian cho cài đặt 1 phức tạp hơn một
chút so với cài đặt 2. Mỗi khi cài đặt 2 cần thêm Q2 đơn vị để cập nhật tồn kho
của mình, Q2 đơn vị cần được rút khỏi tồn kho của cài đặt 1. Điều này đòi hỏi
việc cài đặt 1 phải bổ sung hàng tồn kho của mình định kỳ, với số lượng đơn
đặt hàng Q1 đơn vị được đặt theo định kỳ.
Nếu việc nạp lại hàng hóa muộn hơn so với thời điểm này, cài đặt 1 sẽ
không thể cung cấp đúng thời hạn cho cài đặt 2, vì vậy điều này không chấp
nhận được. Nếu việc nạp lại hàng hóa sớm hơn, cài đặt 1 sẽ phải chịu chi phí
bổ sung để giữ hàng tồn kho này cho đến khi cần cung cấp cho cài đặt 2, vì vậy
việc trì hoãn nạp lại hàng hóa là tốt hơn.
Một chính sách tối ưu nên có Q1 đơn vị Q2 nQ2 trong đó n là một số
nguyên dương cố định. Hơn nữa, cài đặt 1 nên nạp lại hàng tồn kho của mình
với một lô Q1 đơn vị chỉ khi mức tồn kho của nó là không và đến lúc cung cấp
cài đặt 2 với một lô Q2 đơn vị.
Cụ thể, mỗi lần cài đặt 1 nhận một lô Q1 đơn vị, nó đồng thời cung cấp
cài đặt 2 với một lô các đơn vị Q2, vì vậy số lượng hàng tồn kho trên tay (gọi là
hàng tồn kho cài đặt) tại cài đặt 1 trở thành (Q1 Q2) đơn vị. Sau khi sau đó -
cung cấp cài đặt 2 với thêm hai lô đơn vị Q2
Việc mục tiêu là để giảm thiểu tổng chi phí biến đổi mỗi đơn vị thời gian
tại hai cài đặt, cách tiếp cận dễ nhất (và thường được sử dụng) sẽ là giải quyết
riêng lẻ cho các giá trị của Q2 và Q1 nQ2 mà giảm thiểu chi phí biến đổi tổng
cộng mỗi đơn vị tại cài đặt 2 và cài đặt 1, tương ứng.
Hãy bắt đầu bằng cách tối ưu hóa cài đặt 2 một cách độc lập. Vì các giả
định cho cài đặt 2 khớp chính xác với mô hình EOQ cơ bản, kết quả được trình
bày trong Mục 18.3 cho mô hình này có thể được sử dụng trực tiếp. Tổng chi
phí biến đổi mỗi đơn vị thời gian tại cài đặt này là.
Công thức này cho chi phí biến đổi tổng khác với công thức cho chi phí
tổng trong mô hình EOQ cơ bản bằng cách loại bỏ chi phí cố định D, trong đó c
là chi phí đơn vị của việc mua sản phẩm. Công thức EOQ cho biết lượng đặt
hàng tối ưu cho cài đặt này một mình là. 14
Vậy giá trị kết quả của C2 với Q2 = Q*2 là.
Bây giờ xem xét cài đặt 1 với một lượng đặt hàng là Q1 = nQ2. Hình 18.8
cho thấy rằng mức trung bình của mức tồn kho của cài đặt là (n + 1)Q2/2. Do
đó, vì cài đặt 1 cần phải nạp lại tồn kho của mình với Q1 đơn vị mỗi Q1/d =
nQ2/d đơn vị thời gian, tổng chi phí biến đổi mỗi đơn vị thời gian tại cài đặt 1 là.
Để tìm số lượng đặt hàng Q1 và Q2 mà làm giảm thiểu C1, cho Q2 bằng
Q*2, chúng ta cần giải quyết
để tìm giá trị của n làm giảm thiểu C1. Bỏ qua yêu cầu n phải là số
nguyên, điều này được thực hiện bằng cách lấy đạo hàm của C1 theo n, đặt đạo
hàm bằng không (lưu ý rằng đạo hàm bậc hai là dương đối với n dương), và
giải phương trình cho n, từ đó đạt được.
Nếu n* là một số nguyên, thì Q1= n*Q*2 là lượng đặt hàng tối ưu cho
việc lắp đặt 1, cho trước Q2 = Q*2. Nếu n* không phải là số nguyên, thì n* cần
được làm tròn lên hoặc xuống thành một số nguyên. Quy tắc để làm điều này là như sau. Quy trình làm tròn cho n*
Nếu n* < 1, chọn n = 1.
Nếu n* 1, hãy để [n*] là số nguyên lớn nhất <= n*, vậy [n*] <= n* < [n*]
+ 1, và sau đó làm tròn như sau. Nếu , chọn [n*]. 15 Nếu , chọn n = [n*] + 1.
Công thức cho n* cho biết rằng giá trị của nó phụ thuộc vào cả K1/K2 và
h2/h1. Nếu cả hai lượng này đều lớn hơn 1 đáng kể, thì n* cũng sẽ lớn hơn 1 đáng kể.
Tối Ưu Hóa Hai Cài Đặt Đồng Thời. Bằng cách thêm các chi phí tại các
cài đặt cá nhân được thu được ở trên, tổng chi phí biến đổi mỗi đơn vị thời gian tại hai cài đặt là
Chi phí lưu kho bên phải có một cách diễn giải thú vị về chi phí lưu kho
cho hàng tồn tại hai cài đặt. Đặc biệt, hãy để.
e1 = h1 = chi phí giữ hàng tầng lớp mỗi đơn vị mỗi đơn vị thời gian cho cài đặt 1,
e2 = h2 h1= chi phí giữ hàng tầng lớp mỗi đơn vị mỗi đơn vị thời gian - cho cài đặt 2.
Sau đó chi phí giữ hàng có thể được biểu diễn như
khi Q1/2 và Q2/2 là mức độ tồn kho trung bình của hàng tồn kho tại các
cài đặt 1 và 2, tương ứng. (Xem Hình 18.8.) Lý do mà e2 h2 h1 thay vì e2 = -
h2 là vì e1Q1/2 = h1Q1/2 đã bao gồm chi phí giữ hàng cho các đơn vị của mặt
hàng 1 ở hạ nguồn tại cài đặt 2, vì vậy e2 = h2 h1 chỉ cần phản ánh giá trị -
được thêm vào bằng cách chuyển đổi các đơn vị của mặt hàng 1 thành đơn vị
của mặt hàng 2 tại cài đặt 2. (Khái niệm này về việc sử dụng chi phí giữ hàng
tầng lớp dựa trên giá trị được thêm vào tại mỗi cài đặt sẽ đóng một vai trò quan
trọng hơn trong mô hình tiếp theo của chúng ta, nơi có nhiều hơn hai tầng lớp).
Sử dụng các chi phí giữ hàng này, chúng ta hiện có
Chuyển đổi theo Q2, đặt đạo hàm bằng không (đồng thời xác minh rằng
đạo hàm hai là dương cho Q2 dương), và giải phương trình cho Q2. 16
như lượng đặt hàng tối ưu (cho trước n) tại cài đặt 2. Lưu ý rằng điều này
giống hệt với công thức EOQ cho mô hình EOQ cơ bản trong đó tổng chi phí
thiết lập là K1/n K2 và tổng chi phí giữ hàng đơn vị là ne1+ e2.
Chèn biểu thức này cho Q* 2 vào C và thực hiện một số đơn giản hóa đại số.
Để giải quyết cho giá trị tối ưu của lượng đặt hàng tại cài đặt 1, Q1 nQ*2,
chúng ta cần tìm giá trị của n mà làm giảm thiểu C. Phương pháp thông thường
để làm điều này sẽ là việc lấy đạo hàm của C theo n, đặt đạo hàm này bằng
không, và giải phương trình để tìm n. Tuy nhiên, vì biểu thức của C liên quan
đến việc lấy căn bậc hai, việc làm này trực tiếp không phải là phương pháp tiện
lợi. Một phương pháp tiện lợi hơn là loại bỏ dấu căn bằng cách bình phương C
và làm giảm thiểu C2 thay vì, vì giá trị của n mà làm giảm thiểu C2 cũng là giá
trị làm giảm thiểu C. Do đó, chúng ta lấy đạo hàm của C2 theo n, đặt đạo hàm
này bằng không đến không, và giải phương trình này cho n. Vì đạo hàm bậc hai
là dương với n dương, điều này cho ra giá trị tối thiểu của n là
Điều này giống hệt với biểu thức cho n* được thu được trong phần tiếp theo trừ việc
h1 và h2 đã được thay thế bằng e1 và e2 ở đây. Khi n* không phải là một số nguyên,
quy trình làm tròn n* thành một số nguyên cũng giống như mô tả trong phần tiếp theo.
Nhận được n theo cách này cho phép tính Q*2 với biểu thức trên và sau đó đặt Q*1 = nQ*2.
Một ví dụ. Để minh họa các kết quả này, giả sử rằng các tham số của mô hình là.
K1 = $1,000, K2 = $100, h1 = $2, h2 = $3, d = 600.
Bảng 18.1 cung cấp các giá trị của Q*2, n*, n (giá trị được làm tròn của
n*), Q*1 và C* (tổng chi phí biến đổi kỹ thuật mỗi đơn vị thời gian) khi giải
quyết theo hai cách mô tả trong phần này. Do đó, cột thứ hai cung cấp kết quả
khi sử dụng phương pháp không chính xác của việc tối ưu hóa hai cài đặt một
cách riêng lẻ, trong khi cột thứ ba sử dụng phương pháp hợp lệ của việc tối ưu
hóa hai cài đặt đồng thời. 17
Một Mô hình cho Hệ thống Đa Cấp Liên tiếp.
Mở rộng phân tích trước đó cho các hệ thống tuần tự với hơn hai tầng.
Hình 18.9 mô tả loại hệ thống này, trong đó cài đặt 1 có hàng tồn kho
được cung cấp định kỳ, sau đó hàng tồn kho tại cài đặt 1 được sử dụng để cung
cấp hàng tồn kho tại cài đặt 2 định kỳ, sau đó cài đặt 2 làm tương tự cho cài đặt
3, và cứ thế đến cài đặt cuối cùng (cài đặt N).
Các mặt hàng được xử lý thành sản phẩm gần giống nhau tại các cài đặt khác
nhau được đề cập dưới dạng mặt hàng 1 ở cài đặt 1, mặt hàng 2 ở cài đặt 2, và tiếp tục như vậy.
Giả định cho mô hình đa cấp nối tiếp
1. Các giả thuyết của mô hình EOQ cơ bản (xem Mục 18.3) đúng tại cài
đặt N. Do đó, có một nhu cầu cố định biết của d đơn vị mỗi đơn vị thời gian,
một lượng đặt hàng của QN đơn vị được đặt vào thời gian để tái tồn kho khi
mức tồn kho giảm xuống không, và không cho phép thiếu hụt được lên kế hoạch.
2. Một lượng đặt hàng của Q1 đơn vị được đặt vào thời gian để tái tồn
kho tại cài đặt 1 trước khi xảy ra thiếu hụt.
3. Mỗi cài đặt ngoại trừ cài đặt N sử dụng tồn kho của mình để định kỳ tái
tồn kho của cài đặt tiếp theo. Do đó, cài đặt i (i = 1, 2, . . . , N 1) cung cấp một
lô hàng của Qi+1 đơn vị cho cài đặt (i 1) ngay lập tức mỗi khi một đơn đặt
hàng được nhận từ cài đặt (i + 1).
4. Các chi phí liên quan tại mỗi cài đặt i (i 1, 2, . . . , N) là một chi phí
thiết lập của Ki mỗi lần đặt hàng và một chi phí giữ hàng của hi mỗi đơn vị mỗi đơn vị thời gian. 18
5. Các đơn vị tăng giá trị mỗi khi chúng được nhận và xử lý tại cài đặt
tiếp theo, vì vậy h1 < h2 < hN.
6. Mục tiêu là tối thiểu hóa tổng chi phí biến đổi mỗi đơn vị thời gian tại
các cài đặt N. (Điều này sẽ được ký hiệu là C.)
Từ "ngay lập tức" trong giả định 3 ngụ ý rằng không có thời gian dẫn
giữa khi một cài đặt đặt hàng và cài đặt trước đó điền đơn hàng đó, mặc dù một
thời gian dẫn dương cố định không gây ra bất kỳ rắc rối nào. Với thời gian dẫn
bằng không, Hình 18.10 mở rộng Hình 18.8 để cho thấy cách mức tồn kho sẽ
biến đổi đồng thời tại các cài đặt khi có bốn cài đặt thay vì chỉ hai. Trong
trường hợp này, Qi = 2Qi+1 cho i = 1, 2, 3, vì vậy mỗi trong ba cài đặt đầu tiên
cần phải làm mới mức tồn kho của mình một lần cho mỗi hai lần nó làm mới
mức tồn kho của cài đặt tiếp theo. Do đó, khi một chu kỳ hoàn chỉnh của việc
làm mới tại tất cả bốn cài đặt bắt đầu vào thời điểm 0, Hình 18.10 cho thấy một
đơn đặt hàng gồm Q1 đơn vị đến cài đặt 1 khi mức tồn kho đã là không. Một
nửa trong số đơn đặt hàng này sau đó được sử dụng ngay lập tức để làm mới
mức tồn kho tại cài đặt 2. Cài đặt 2 sau đó làm điều tương tự cho cài đặt 3, và
cài đặt 3 làm điều tương tự cho cài đặt 4. Do đó, vào thời điểm 0, một số đơn vị
vừa đến cài đặt 1 được chuyển xuống dòng sản phẩm cuối cùng càng nhanh
càng tốt. Cài đặt cuối cùng sau đó ngay lập tức bắt đầu sử dụng mức tồn kho đã
được làm mới của sản phẩm cuối cùng để đáp ứng nhu cầu của d đơn vị mỗi
đơn vị thời gian cho sản phẩm đó. 19 ■ HÌNH 18.10
Mức tồn kho đồng bộ tại bốn cài đặt (N = 4) khi Qi 2Qi1 (i = 1, 2, 3), nơi
các đường thẳng liền nhau cho thấy mức tồn kho của cài đặt và các đường nét
đứt tương tự cho tồn kho hàng
Hãy nhớ rằng số lượng hàng tồn kho tại cài đặt 1 bao gồm số lượng hàng
tồn kho thực tế ở đó (tồn kho cài đặt) cộng với số lượng hàng tồn kho đã ở dưới
hệ thống tồn kho (và có thể đã được tích hợp vào sản phẩm hoàn thiện hơn) tại
các tầng lớp tiếp theo. Do đó, như các đường nét đứt trong Hình 18.10 cho 20
thấy, số lượng hàng tồn kho tại cài đặt 1 bắt đầu từ Q1 đơn vị vào thời điểm 0
và sau đó giảm với tốc độ d đơn vị mỗi đơn vị thời gian cho đến khi đến lúc đặt
hàng một lô hàng Q1 đơn vị khác, sau đó mẫu hình răng cưa tiếp tục. Số lượng
hàng tồn kho tại các cài đặt 2 và 3 tuân theo cùng một mẫu hình răng cưa,
nhưng với chu kỳ ngắn hơn. Số lượng hàng tồn kho tương đương với hàng tồn
kho cài đặt tại cài đặt 4, vì vậy số lượng hàng tồn kho lại tuân theo mẫu hình răng
Chúng ta cần sử dụng chi phí giữ hàng tầng hạng.
e1 = h1, e2 = h2 h1, e3 = h3 h2, . . . , eN = hN hN 1, - - - -
Nơi ei được hiểu là chi phí lưu trữ mỗi đơn vị mỗi đơn vị thời gian trên
giá trị được thêm vào bằng cách chuyển đổi mục (i 1) từ cài đặt (i 1) thành - - mục i tại cài đặt i.
Một chính sách tối ưu nên có Qi = niQi + 1 (i = 1, 2, . . . , N – 1), trong đó
ni là một số nguyên dương, cho mỗi chu kỳ nạp hàng. (Giá trị của ni có thể
khác nhau cho các chu kỳ nạp hàng khác nhau.) Hơn nữa, cài đặt i (i 1, 2, . . . ,
N – 1) nên nạp lại tồn kho của mình bằng một lô hàng gồm Qi đơn vị chỉ khi
mà mức tồn kho của nó là không và đến lúc cung cấp cho cài đặt (i + 1) một lô
hàng gồm Qi + 1 đơn vị.
Việc tìm ra một giải pháp tối ưu cho mô hình này khi N > 2 lại khá khó
khăn. Do đó, thường thực hiện hai sự xấp xỉ đơn giản để đưa ra một giải pháp.
Đơn giản hóa Xấp xỉ 1: Giả sử rằng lượng đặt hàng tại một cài đặt phải
giống nhau trên mỗi chu kỳ cung cấp. Do đó, Qi = niQi + 1 (i = 1,2, . . . , N –
1), trong đó ni là một số nguyên dương cố định.
Đơn giản hóa Xấp xỉ 2: ni = 2mi (i = 1, 2, . . . , N – 1), trong đó mi là một
số nguyên không âm, vì vậy các giá trị duy nhất được xem xét cho ni là 1, 2, 4, 8, . . . .
Tính chất Xấp xỉ 98 Phần trăm của Roundy: Vấn đề đã được sửa đổi được
đảm bảo cung cấp ít nhất 98 phần trăm xấp xỉ của vấn đề gốc theo cách sau. Số
tiền mà chi phí của một giải pháp tối ưu cho vấn đề đã được sửa đổi vượt quá
chi phí của một giải pháp tối ưu cho vấn đề gốc không bao giờ nhiều hơn 2
phần trăm (và thường sẽ ít hơn nhiều). Cụ thể, nếu
C* = chi phí biến đổi tổng cộng mỗi đơn vị thời gian của một giải pháp
tối ưu cho vấn đề ban đầu,
C = chi phí biến đổi tổng cộng mỗi đơn vị thời gian của một giải pháp tối
ưu cho vấn đề đã sửa đổi,sau đó C – C* <= 0.02 C*. 21
Điều này thường được gọi là xấp xỉ 98 phần trăm của Roundy vì công
thức và chứng minh của tính chất cơ bản này (cũng áp dụng cho một số loại hệ
thống tồn kho đa tầng tổng quát hơn) đã được phát triển bởi Giáo sư Robin
Roundy của Đại học Brigham Young.
Một hàm ý của hai sự xấp xỉ đơn giản là số lượng đặt hàng cho vấn đề đã
được sửa đổi phải thỏa mãn các bất đẳng thức yếu,
Q1 >= Q2 >= . . . >= QN.
Quy trình giải quyết vấn đề đã được sửa đổi có hai giai đoạn, trong đó các
bất đẳng thức này đóng một vai trò quan trọng trong giai đoạn 1. Cụ thể, xem
xét biến thể sau của cả vấn đề gốc và vấn đề đã sửa đổi.
Một Sự Nới Lỏng Của Vấn Đề: Tiếp tục giả định rằng lượng đặt hàng tại
một cài đặt phải giống nhau trên mỗi chu kỳ cung cấp. Tuy nhiên, thay thế xấp
xỉ đơn giản 2 bằng yêu cầu ít hạn chế hơn là Q1 >= Q2 >= . . . >= QN. Do đó,
hạn chế duy nhất đối với ni trong xấp xỉ đơn giản 1 là mỗi ni >= 1 (i = 1, 2, . . .
, N 1), mà không yêu cầu thậm chí ni phải là một số nguyên. Khi ni không -
phải là một số nguyên, sự không đồng bộ kết quả giữa các cài đặt được bỏ qua.
Mặc dù việc thư giãn này không phải là một biểu diễn thực tế của vấn đề
thực sự vì nó bỏ qua nhu cầu phối hợp việc cung cấp tại các cài đặt (và do đó
làm giảm chi phí giữ hàng thực sự), nhưng nó cung cấp một xấp xỉ rất dễ giải quyết.
Giai đoạn 1 của quy trình giải quyết vấn đề đã sửa đổi bao gồm việc giải
quyết bài toán thư giãn. Giai đoạn 2 sau đó sửa đổi giải pháp này bằng cách áp
đặt xấp xỉ đơn giản hóa 2.
Các bất đẳng thức yếu, Qi >= Qi + 1 (i = 1, 2, . . . , N 1), cho phép khả -
năng rằng Qi = Qi + 1. (Điều này tương ứng với việc có mi 0 trong ước lượng
đơn giản hóa 2.) Như được gợi ý bởi Hình 18.10, nếu Qi = Qi + 1, mỗi khi cài
đặt (i + 1) cần phải nạp lại tồn kho của mình với Qi + 1 đơn vị, cài đặt i cũng
cần phải đồng thời đặt hàng cùng số lượng đơn vị và sau đó (sau bất kỳ xử lý
cần thiết nào) chuyển toàn bộ lô hàng ngay lập tức đến cài đặt (i + 1). Do đó,
mặc dù đây là các cài đặt riêng biệt trong thực tế, cho mục đích mô hình hóa,
chúng ta có thể xem xét chúng như một cài đặt kết hợp duy nhất đang đặt một
đơn hàng cho Qi = Qi + 1 đơn vị với chi phí thiết lập là Ki + Ki + 1 và chi phí
giữ hàng theo tầng của ei + ei + 1. Việc hợp nhất các cài đặt (cho mục đích mô
hình hóa) này được tích hợp vào giai đoạn 1 của quy trình giải pháp.
Chúng tôi mô tả và đề cập đến hai giai đoạn của quy trình giải pháp theo lần lượt dưới đây. 22
Giai đoạn 1 của quy trình giải pháp.
Theo giả định 6 của mô hình cho biết mục tiêu là tối thiểu hóa C, tổng chi
phí biến đổi trên một đơn vị thời gian cho tất cả các quá trình lắp đặt. Bằng
cách sử dụng chi phí nắm giữ cấp bậc, tổng chi phí biến đổi trên một đơn vị
thời gian tại cài đặt i là
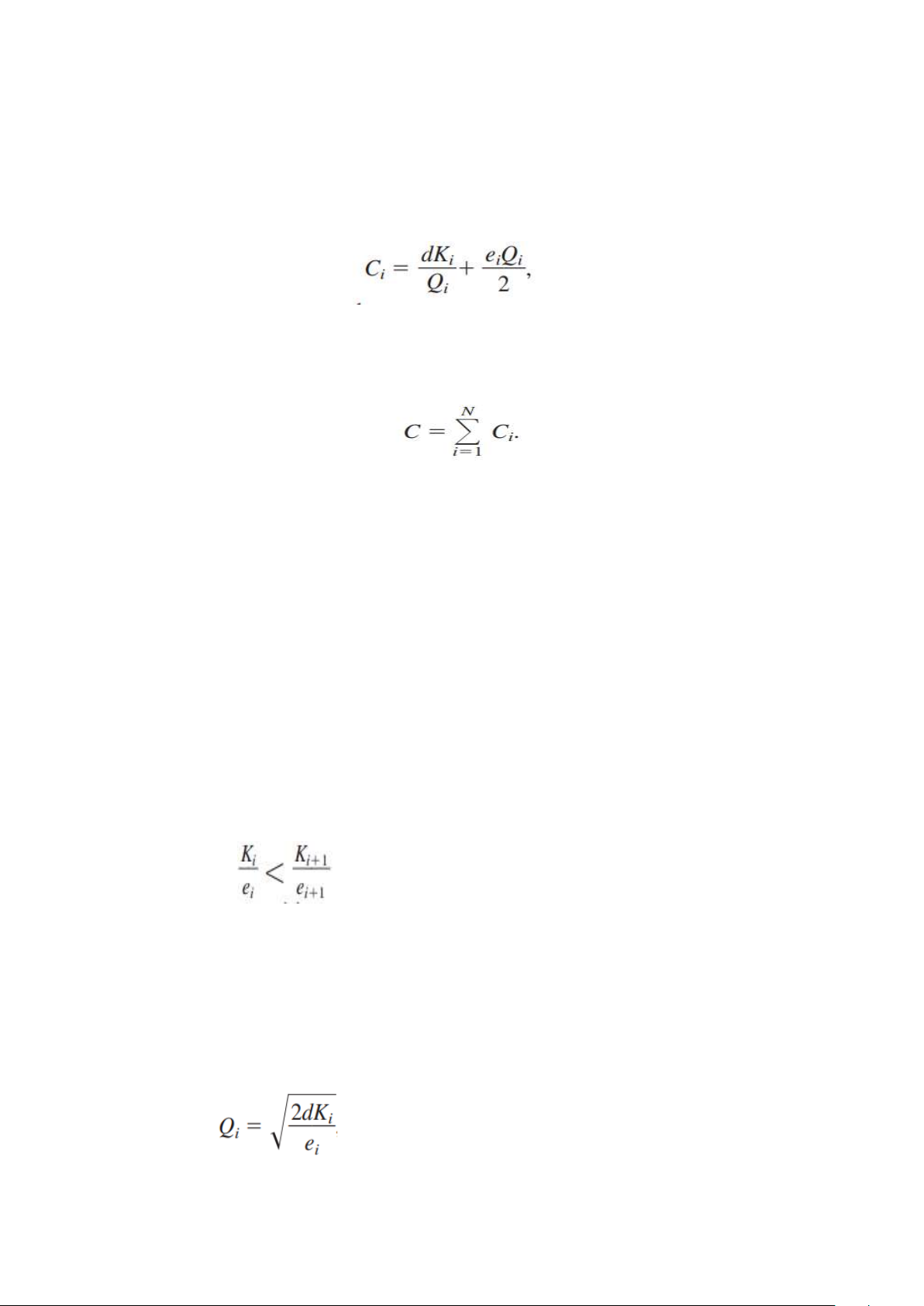
với i = 1, 2, . . . , N, Vì vậy:
(Biểu thức này đối với Ci giả định rằng lượng hàng tồn kho cấp bậc được
bổ sung ngay khi mức của nó về 0)
Lưu ý: Ci chỉ là tổng chi phí biến đổi trên một đơn vị thời gian cho một
lần lắp đặt thỏa mãn yêu cầu cơ bản mô hình EOQ
Công thức EOQ đơn giản được sử dụng để có được số lượng đặt hàng tại mỗi cài đặt.
Khi áp dụng công thức EOQ cho các cài đặt tương ứng, một tình huống
đặc biệt xuất hiện khi Ki/ei < Ki+1/ei+1, vì điều này sẽ dẫn đến Qi* < Q*i + 1,
điều này bị cấm bởi sự thoải mái của vấn đề. Để đáp ứng thì Qi >= Qi + 1, tốt
nhất có thể là đặt Qi = Qi + 1.
Phác thảo giai đoạn 1 (Giải quyết sự thư giãn) 1 Nếu
với i = 1, 2, . . . , N 1, xem cài đặt i và i + 1 như một -
cài đặt hợp nhất với chi phí thiết lập là Ki + Ki + 1 và chi phí giữ hàng theo cấp
độ là 𝑒𝑖+𝑒𝑖+1 trên mỗi đơn vị trên mỗi đơn vị thời gian. Sau khi hợp nhất, lặp
lại bước này cho bất kỳ cặp cài đặt liên tiếp khác (có thể bao gồm một cài đặt).
Sau đó, đánh số lại các lượt cài đặt cho phù hợp với N đặt lại làm tổng số lượt cài đặt mới. 2 Đặt
với i = 1, 2, . . ., N. 23 3 Đặt
, với i = 1, 2, . . ., N,
Giai đoạn 2 của quy trình giải pháp: được sử dụng để điều phối số
lượng đặt hàng. Thực hiện bằng cách làm tròn các lượng đặt hàng thu được
trong giai đoạn 1.Sau khi xác định tạm thời các giá trị của ni = 2mi sao cho Qi =
niQi + 1, bước cuối cùng là tinh chỉnh giá trị của QN để có được một giải pháp
tổng thể tối ưu cho vấn đề đã được sửa đổi.
Quy trình cuối cùng này liên quan đến việc biểu diễn mỗi Q i dưới dạng
của QN. Cụ thể, với mỗi ni sao cho Qi = niQi + 1, gọi pi là sản phẩm. p
với i = 1, 2, . . . , N 1,
i = nini + 1 . . . nN 1, - - Vì vậy Q
với i = 1, 2, . . . , N 1, i = piQN, -
Trong đó pN = 1, do đó, chi phí biến đổi tổng cộng mỗi đơn vị thời gian
tại tất cả các cài đặt là
Biểu thức này cũng có thể được hiểu là tổng chi phí biến đổi trên một đơn
vị thời gian cho một cơ sở tồn kho duy nhất đáp ứng được các yêu cầu cơ bản
mô hình EOQ đơn giản với chi phí thiết lập và chi phí lưu kho đơn vị là
Chi phí thiết lập =
, Chi phí giữ hàng đơn vị =
Do đó, giá trị QN làm cực tiểu C được tính theo công thức EOQ là 24
Bởi vì biểu thức này yêu cầu biết giá trị ni, giai đoạn 2 bắt đầu bằng cách
sử dụng giá trị của QN được tính toán trong giai đoạn 1 như một xấp xỉ của
Q*N, và sau đó sử dụng QN này để xác định ni (tạm thời), trước khi sử dụng
công thức này để tính toán Q*N.
Phác thảo giai đoạn 2 (Giải quyết vấn đề đã sửa đổi)
1. Đặt Q*N thành giá trị của QN thu được trong giai đoạn 1
2. Đối với i = N 1, N 2, . . . ,1 lần lượt, thực hiện như sau. Sử dụng giá - -
trị của Qi thu được trong giai đoạn 1, xác định giá trị số nguyên không âm của m sao cho Nếu , đặt ni = 2m và Nếu
, đặt ni = 2m + 1 và
3. Sử dụng các giá trị của ni được thu được trong bước 2 và các công thức
trên cho pi và Q*N để tính toán Q*N. Sau đó sử dụng Q*N này để lặp lại bước 2.
Nếu không có ni nào thay đổi, sử dụng (Q*1, Q*2, . . . , Q*N) làm giải pháp cho
vấn đề đã được điều chỉnh và tính toán chi phí tương ứng C. Nếu có bất kỳ ni
nào thay đổi, lặp lại bước 2 (bắt đầu với Q*N hiện tại) và sau đó bước 3 một lần
nữa. Sử dụng giải pháp thu được và tính toán C.
=> Quy trình cung cấp một giải pháp rất tốt cho vấn đề sửa đổi, đảm bảo
rằng giải pháp này sẽ cung cấp một xấp xỉ tốt của một giải pháp tối ưu cho vấn đề ban đầu.
Sẽ rất tốt nếu có thể kiểm tra xem 𝐶 đang ở gần đến đâu trên bất kỳ vấn
đề cụ thể nào mặc dù C* không biết. Hơn nữa, 𝐶 thường rất gần với C*. Do đó,
kiểm tra xem 𝐶 đang gần 𝐶 đến đâu đưa ra một ước lượng thận trọng về việc C
phải gần C* như thế nào, như tóm tắt dưới đây. Chi phí liên quan: vì vậy trong đó
𝐶 = chi phí của một giải pháp tối ưu cho vấn đề được nới lỏng,
C* = chi phí của một giải pháp tối ưu (không biết) cho vấn đề gốc,
𝐶 = chi phí của giải pháp được đạt được cho vấn đề đã được sửa đổi. 25
Ví dụ: C = 1.0047C cho ví dụ, được biết rằng 𝐶 nằm trong khoảng 0.47% của C*.
Một ví dụ. Xem xét một hệ thống tuần tự với bốn cài đặt có chi phí thiết
lập và chi phí giữ hàng đơn vị được hiển thị trong Bảng 18.2.
Bảng 18.2 Dữ liệu cho ví dụ về hệ thống tồn kho bốn tầng
Bước đầu là chuyển đổi chi phí tồn kho đơn vị h
i tại mỗi lần lắp đặt
thành chi phí tồn kho cấp đơn vị tương ứng ei phản ánh giá trị gia tăng ở mỗi lần cài đặt.
Áp dụng bước 1 của giai đoạn 1 của quy trình giải pháp để so sánh mỗi
Ki/ei với Ki+1/ei+1.
Các tỷ lệ này giảm từ trái sang phải ngoại trừ
Vì vậy, xemcài đặt 3 và 4 như một cài đặt kết hợp duy nhất cho mục đích
mô hình hóa. Sau khi kết hợp chi phí thiết lập và chi phí giữ hàng, ta hiện có dữ
liệu điều chỉnh trong Bảng 18.3.
Bảng 18.3 Dữ liệu đã điều chỉnh cho ví dụ bốn bậc sau khi hợp nhất cài đặt
3 và 4 cho mục đích mô hình hóa 26
Sử dụng dữ liệu đã điều chỉnh, Bảng 18.4 cho thấy kết quả của việc áp
dụng phần còn lại của quy trình giải pháp cho ví dụ này.
Bảng 18.4 Kết quả từ việc áp dụng quy trình giải pháp
cho ví dụ bốn tầng.
Cột thứ hai và thứ ba trình bày các phép tính thẳng từ các bước 2 và 3 của
giai đoạn 1. Đối với bước 1 của giai đoạn 2, Q3 = 400 trong cột thứ hai được
chuyển sang Q3* = 400 trong cột thứ tư. Đối với bước 2, chúng ta thấy rằng Vì Bởi vì
Đặt n2 = 21 = 2 và Q*2 n2Q*3 = 800. Tương tự, chúng tôi đặt n1 = 21 = 2 và
Q*1 = n1Q*2= 1600 vì và
Sau khi tính toán các Ci tương ứng, cột thứ tư và thứ năm của bảng tóm
tắt kết quả này từ việc áp dụng chỉ các bước 1 và 2 của giai đoạn 2.
Các cột cuối cùng của bảng sau đó tóm tắt kết quả từ việc hoàn thành quy
trình giải bằng cách áp dụng bước 3 của giai đoạn 2. Vì p1 = n1n4 và p2 = n2 =
2, công thức cho Q*N cho ra Q*3 = 425 là giá trị của Q3 là một phần của giải
pháp tối ưu tổng thể cho vấn đề đã được sửa đổi. Lặp lại bước 2 với Q*3 mới
này lại cho ra n2 = 2 và n1 = 2, vì vậy Q*2 = n2Q*3 = 850 và Q*1 = n1Q*2 =
1,700. Vì n2 và n1 không thay đổi so với lần thứ nhất qua bước 2, chúng ta thực
sự có giải pháp mong muốn cho vấn đề đã được sửa đổi, vì vậy các Ci được tính toán tương ứng. 27
18.6 MÔ HÌNH ĐÁNH GIÁ LIÊN TỤC NGẪU NHIÊN
Mô hình tồn kho ngẫu nhiên, được thiết kế để phân tích hệ thống tồn kho
khi có sự không chắc chắn đáng kể về nhu cầu trong tương lai.
Mức tồn kho được theo dõi liên tục để có thể đặt hàng mới ngay khi
mức tồn kho giảm xuống điểm đặt hàng lại.
Hệ thống kiểm kê được xem xét liên tục cho một sản phẩm cụ thể thông
thường sẽ dựa trên hai con số quan trọng:
R = điểm đặt hàng lại.
Q = số lượng đặt hàng.
Chính sách tồn kho: Bất cứ khi nào mức tồn kho của sản phẩm giảm
xuống R đơn vị, đặt hàng thêm Q đơn vị để bổ sung hàng tồn kho.
Chính sách như vậy thường được gọi là chính sách điểm đặt hàng lại,
chính sách số lượng đặt hàng hoặc gọi tắt là chính sách (R, Q)
Mô hình này có liên quan chặt chẽ với mô hình EOQ với tình trạng thiếu hụt theo kế hoạch.
Cần bổ sung thêm một số lượng hàng tồn kho an toàn khi thiết lập
điểm đặt hàng lại để tạo ra một số bước đệm cho việc có nhu cầu trên
mức trung bình trong thời gian đầu. Mặt khác, sự đánh đổi giữa các
yếu tố chi phí khác nhau thì giống nhau, do đó số lượng đặt hàng từ
hai mô hình phải giống nhau.
Xác định số lượng đặt hàng Q Trong đó:
d: nhu cầu trung bình trên một đơn vị thời gian K: chi phí thiết lập
h: chi phí lưu kho cho một đơn vị thời gian p: chi phí thiếu hụt
Q có kết quả gần đúng của số lượng đặt hàng tối ưu. Không có công
thức nào cho giá trị chính xác của số lượng đặt hàng tối ưu.
Xác định điểm đặt hàng lại R 28
Dựa trên mong muốn của ban quản lý mức độ phục vụ khách hàng. Mức
độ dịch vụ có thể được xác định theo một số cách khác nhau trong bối cảnh này, như đã nêu dưới.
Các biện pháp thay thế để đo lường mức độ dịch vụ
1. Xác suất tình trạng hết hàng sẽ không xảy ra giữa thời điểm đặt hàng và số
lượng đặt hàng được nhận.
2. Số lượng hàng tồn kho trung bình mỗi năm.
3. Tỷ lệ phần trăm trung bình của nhu cầu hàng năm có thể được đáp ứng ngay lập tức
4. Độ trễ trung bình trong việc lấp đầy các đơn hàng dự trữ khi xảy ra tình trạng hết hàng.
5. Độ trễ trung bình tổng thể trong việc thực hiện các đơn đặt hàng (ở đó độ trễ
khi không hết hàng là 0).
=> Biện pháp 1 có lẽ là biện pháp thuận tiện nhất vì vậy ta tập trung
vào trường hợp này. Ta sẽ biểu thị mức độ dịch vụ mong muốn theo thước đo này bằng L:
L = xác suất mong muốn của ban quản lý rằng tình trạng hết hàng sẽ
không xảy ra trong khoảng thời gian từ khi đặt số lượng đến khi nhận được số lượng đặt hàng.
D = nhu cầu trong thời gian thực hiện đơn hàng.
Khi phân phối đồng đều
Phân bố xác suất của D là phân bố đều trong khoảng từ a đến b, đặt - R = a + L(b-a) Mà:
Giá trị trung bình của phân phối này là
Lượng tồn kho an toàn (mức tồn kho dự kiến ngay trước khi số lượng đặt hàng được
nhận được) được tính bằng công thức sau 29
Khi phân phối không đồng đều 1. Chọn L 2. Tìm R sao cho
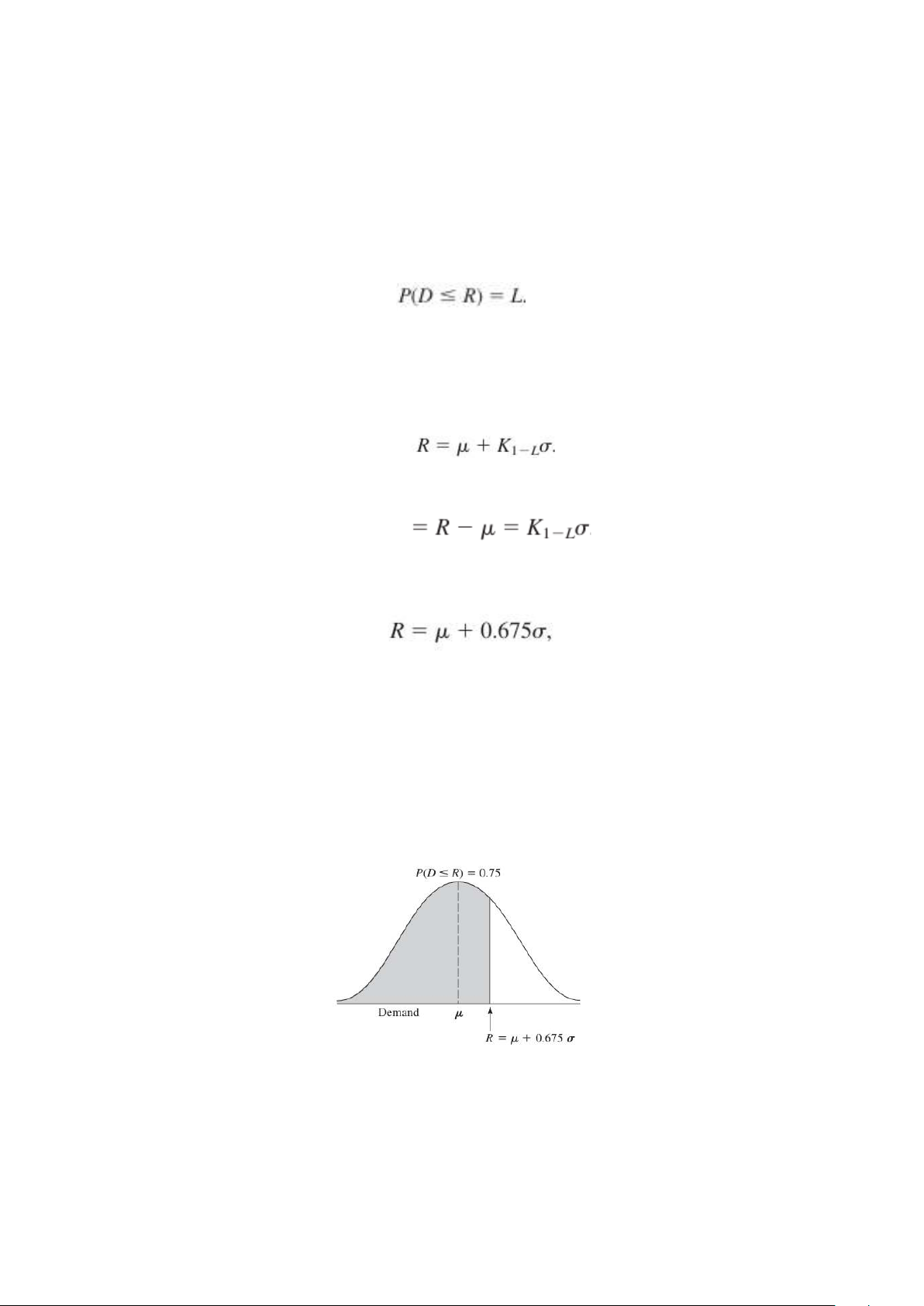
Ví dụ: giả sử D có phân phối chuẩn với giá trị trung bình 𝜇 và phương sai
𝜎2 , như thể hiện trong hình 18.13. Cho giá trị của L, bảng phân phối chuẩn đã
cho ở Phụ lục 5 để xác định giá trị của R. Cụ thể, tìm giá trị của K1 L trong -
bảng rồi thay vào công thức sau để tìm R
Lượng tồn kho an toàn thu được là
Ví dụ: nếu L = 0.75; K1 L = 0.675, vì vậy -
Vậy lượng dự trữ an toàn = 0.675𝜎 HÌNH 18.13
Tính toán điểm đặt hàng lại R cho ngẫu nhiên mô hình đánh giá liên tục khi L =
0.75 và phân phối xác suất của nhu cầu trong thời gian đầu là phân phối chuẩn
với trung bình 𝜇 và độ lệch chuẩn 𝜎 BÀI TOÁN
Cho chi phí thiết lập để sản xuất loa là K = 12000 USD, chi phí lưu kho
đơn vị là h = 0.30 USD/loa/tháng và chi phí thiếu hụt đơn vị là p = 30
$1.10/loa/tháng. Ban đầu, có một mức nhu cầu cố định là 8000 loa/tháng để lắp
ráp thành những chiếc tivi đang được sản xuất trên dây chuyền sản xuất với
mức giá cố định này. Tuy nhiên, doanh số bán TV khá biến động nên lượng tồn
kho của các bộ thành phẩm cũng dao động rất lớn. Để giảm chi phí lưu giữ
hàng tồn kho cho các bộ thành phẩm, ban quản lý đã quyết định điều chỉnh tốc
độ sản xuất cho các bộ đó hàng ngày để phù hợp hơn với sản lượng đầu ra với
các đơn đặt hàng đến.
Thời gian chuẩn bị là 1 tháng kể từ khi đặt hàng sản xuất loa cho đến khi
loa sẵn sàng để lắp ráp vào tivi. Nhu cầu về loa trong thời gian này là biến ngẫu
nhiên D có phân phối chuẩn với giá trị trung bình là 8000 và độ lệch chuẩn là
2000. Để giảm thiểu rủi ro làm gián đoạn dây chuyền sản xuất TV, ban quản lý
đã quyết định rằng lượng dự trữ an toàn cho loa phải đủ lớn để tránh tình trạng
hết hàng trong thời gian sản xuất này trong 95% thời gian Giải
Số lượng đặt hàng cho mỗi đợt sản xuất loa phải là:
Ban quản lý đã chọn mức dịch vụ L = 0.95 nên bảng ở Phụ lục 5 cho K1 L -
= 1.645. Do đó, điểm đặt hàng lại là R = μ + K 1 L𝜎 = 8000 + 1.645*2000 = - 11290.
Lượng tồn kho an toàn thu được là = R μ = 11290 – 8000 = 3290. -
18.7 MÔ HÌNH MỘT KỲ NGẪU NHIÊN ĐỐI VỚI CÁC SẢN PHẨM DỄ HỎNG
Một loại là một sản phẩm ổn định, sẽ vẫn có thể bán được vô thời hạn
nên không có thời hạn xử lý hàng tồn kho. Loại khác, ngược lại, là một sản
phẩm dễ hỏng, có thể được vận chuyển trong kho chỉ trong một khoảng thời
gian rất hạn chế trước khi nó không thể bán được nữa. Đây là loại sản phẩm mà
mô hình một giai đoạn (và các biến thể của nó) được trình bày trong phần này
được thiết kế. Đặc biệt, khoảng thời gian duy nhất trong mô hình là khoảng
thời gian rất hạn chế trước khi sản phẩm không thể bán được nữa.
Ví dụ: Một tờ báo của một ngày cụ thể chỉ có thể được kiểm kê trong
một ngày trước khi nó trở nên lỗi thời và cần được thay thế bằng tờ báo của
ngày hôm sau. Khi nhu cầu cho tờ báo là một biến ngẫu nhiên chủ sở hữu của
sạp báo cần chọn số lượng đặt hàng hàng ngày cung cấp phù hợp sự đánh đổi
giữa chi phí tiềm năng của việc đặt hàng quá mức và chi phí tiềm năng của việc 31
đặt hàng thiếu. Mô hình của phần này cho phép giải quyết số lượng đặt hàng
hàng ngày sẽ tối đa hóa lợi nhuận dự kiến.
Một số loại sản phẩm dễ hỏng
1. Tạp chí định kỳ, chẳng hạn như báo và tạp chí.
2. Hoa được bán bởi một người bán hoa.
3. Việc chế biến thực phẩm tươi sống được chế biến trong nhà hàng.
4. Sản phẩm, bao gồm cả trái cây và rau quả tươi, được bán trong cửa hàng tạp hóa. 5. Cây thông Noel.
6. Quần áo theo mùa, chẳng hạn như áo khoác mùa đông, trong đó bất kỳ hàng
hóa nào còn lại vào cuối mùa phải được bán với giá chiết khấu cao để giải
phóng không gian cho mùa tiếp theo.
7. Thiệp chúc mừng theo mùa.
8. Hàng hóa thời trang sẽ sớm lỗi mốt.
9. Xe mới vào cuối năm mô hình.
10. Bất kỳ sản phẩm nào sẽ sớm lỗi thời.
11. Phụ tùng thay thế quan trọng phải được sản xuất trong lần sản xuất cuối
cùng của một số mô hình của một sản phẩm (ví dụ: máy bay) để sử dụng khi
cần thiết trong toàn bộ trường dài cuộc sống của mô hình đó.
12. Đặt chỗ do hãng hàng không cung cấp cho một chuyến bay cụ thể, vì chỗ
ngồi còn trống trên chuyến bay có thể được xem là hàng tồn kho của một sản
phẩm dễ hỏng (chúng không thể được bán sau khi chuyến bay đã diễn ra). Một ví dụ
Nhà phân phối cảm thấy rằng ưu đãi này cung cấp một cơ hội lý tưởng
để thực hiện một đợt bán hàng cuối cùng cho khách hàng của mình (cửa hàng
xe đạp) cho mùa Giáng sinh sắp tới với mức giá giảm chỉ 450 đô la mỗi chiếc
xe đạp, do đó kiếm được lợi nhuận 250 đô la cho mỗi chiếc xe đạp. Do đó, bất
kỳ chiếc xe đạp nào không được bán trong đợt giảm giá này sẽ trở nên gần như
vô giá trị. Tuy nhiên, nhà phân phối tin rằng cô sẽ có thể xử lý bất kỳ chiếc xe
đạp nào còn lại sau Giáng sinh bằng cách bán chúng với giá danh nghĩa là 100
đô la mỗi chiếc (giá trị cứu hộ), do đó thu hồi một nửa chi phí mua hàng của
cô. Xem xét khoản lỗ này nếu cô ấy đặt hàng nhiều hơn cô ấy có thể bán, cũng
như lợi nhuận bị mất nếu cô ấy đặt hàng ít hơn có thể bán, nhà phân phối cần
quyết định số lượng đặt hàng nào để gửi cho nhà sản xuất. Kết hợp chi phí vốn
gắn liền với hàng tồn kho và các chi phí lưu trữ khác, chi phí hàng tồn kho này
được ước tính là $ 10 cho mỗi chiếc xe đạp còn lại trong kho sau Giáng sinh.
Do đó, xem xét giá trị cứu hộ là 100 đô la, chi phí giữ đơn vị là 90 đô la cho
mỗi chiếc xe đạp còn lại trong kho vào cuối. 32
Lợi nhuận = $ 450 x số được bán bởi nhà phân phối $ 200 x số được -
mua bởi nhà phân phối + $ 90 x số chưa bán và do đó được xử lý cho giá trị cứu hộ.
S = Số lượng nhà phân phối đã mua
= mức tồn kho (hàng tồn kho) sau khi nhận được giao dịch mua này (vì
không có hàng tồn kho ban đầu
D = nhu cầu của các cửa hàng xe đạp (một biến ngẫu nhiên), min{D, S} số đã bán, max{0, S D} số chưa bán. Sau đó
Lợi nhuận = 450 min{D, S} – 200S+ 90 max{0, S D}.
Thuật ngữ đầu tiên cũng có thể được viết là: 450 phút{D, SD= 450D 450 - max{0, D S}.
Thuật ngữ 450 max{0, D S} đại diện cho mất doanh thu do nhu cầu không - được đáp ứng.
Lợi nhuận liên quan = 450 max{0,max S} 200S + 90 max{0, S D} - - - -
Tổng chi phí = 450 max{0, D S}+ 200S 90 max{0, S D}. - - -
Các giả định của mô hình
1. Mỗi ứng dụng liên quan đến một sản phẩm dễ hỏng duy nhất.
2. Mỗi ứng dụng liên quan đến một khoảng thời gian duy nhất vì sản phẩm
không thể được bán sau này.
3. Tuy nhiên, sẽ có thể xử lý bất kỳ đơn vị sản phẩm nào còn lại tại
kết thúc giai đoạn, thậm chí có thể nhận được giá trị cứu hộ cho các đơn vị.
4. Có thể có một số hàng tồn kho ban đầu trong khoảng thời gian này, như được biểu thị bằng
I = hàng tồn kho ban đầu.
5. Quyết định duy nhất được đưa ra là số lượng đơn vị đặt hàng (thông qua mua
hoặc sản xuất) để chúng có thể được đưa vào hàng tồn kho vào đầu kỳ. Vậy
Q = số lượng đặt hàng,
S = mức tồn kho (hàng tồn kho) sau khi nhận được lệnh này = I + Q.
Với I, sẽ thuận tiện khi sử dụng S làm biến quyết định của mô hình, sau đó
Tự động xác định Q = S I. -
6. Nhu cầu rút đơn vị khỏi hàng tồn kho để bán (hoặc cho bất kỳ mục đích nào
khác) trong kỳ là biến ngẫu nhiên D.
7. Sau khi xóa doanh thu nếu nhu cầu được thỏa mãn (vì điều này độc lập với
quyết định S), mục tiêu trở thành giảm thiểu tổng chi phí dự kiến, trong đó
Các thành phần chi phí là 33
K = chi phí thiết lập để mua hoặc sản xuất toàn bộ lô đơn vị,
c = chi phí đơn vị để mua hoặc sản xuất từng đơn vị,
h = chi phí lưu giữ trên mỗi đơn vị còn lại vào cuối kỳ (bao gồm chi phí lưu trữ
trừ đi giá trị trục vớt),
p = chi phí thiếu hụt trên mỗi đơn vị nhu cầu không được thỏa mãn (bao gồm
doanh thu và chi phí bị mất thiện chí của khách hàng).
Phân tích mô hình không có hàng tồn kho ban đầu (I = 0 và không có chi phí thiết lập (K = 0)
Trước khi phân tích mô hình một cách tổng quát đầy đủ, sẽ hướng dẫn
bắt đầu bằng cách xem xét trường hợp đơn giản hơn trong đó I = 0 (không có
hàng tồn kho ban đầu) và K= 0 (không có chi phí thiết lập).
Quyết định về giá trị của S, số lượng hàng tồn kho cần mua, phụ thuộc
rất nhiều vào phân bố xác suất của cầu D. Nhiều hơn nhu cầu dự kiến có thể là
mong muốn, nhưng có lẽ ít hơn nhu cầu tối đa có thể. Một sự đánh đổi là cần
thiết giữa (1) rủi ro thiếu hụt và do đó phát sinh chi phí thiếu hụt và (2) rủi ro
có dư thừa và do đó phát sinh chi phí lãng phí cho việc đặt hàng và giữ các đơn
vị dư thừa. Điều này được thực hiện bằng cách giảm thiểu giá trị dự kiến (theo
nghĩa thống kê) của tổng các chi phí này.
Số tiền bán được đưa ra bởi
Do đó, chi phí phát sinh nếu nhu cầu là D và S được dự trữ được đưa ra bởi
Bởi vì nhu cầu là một biến ngẫu nhiên [với phân phối xác suất PD (d)], chi phí
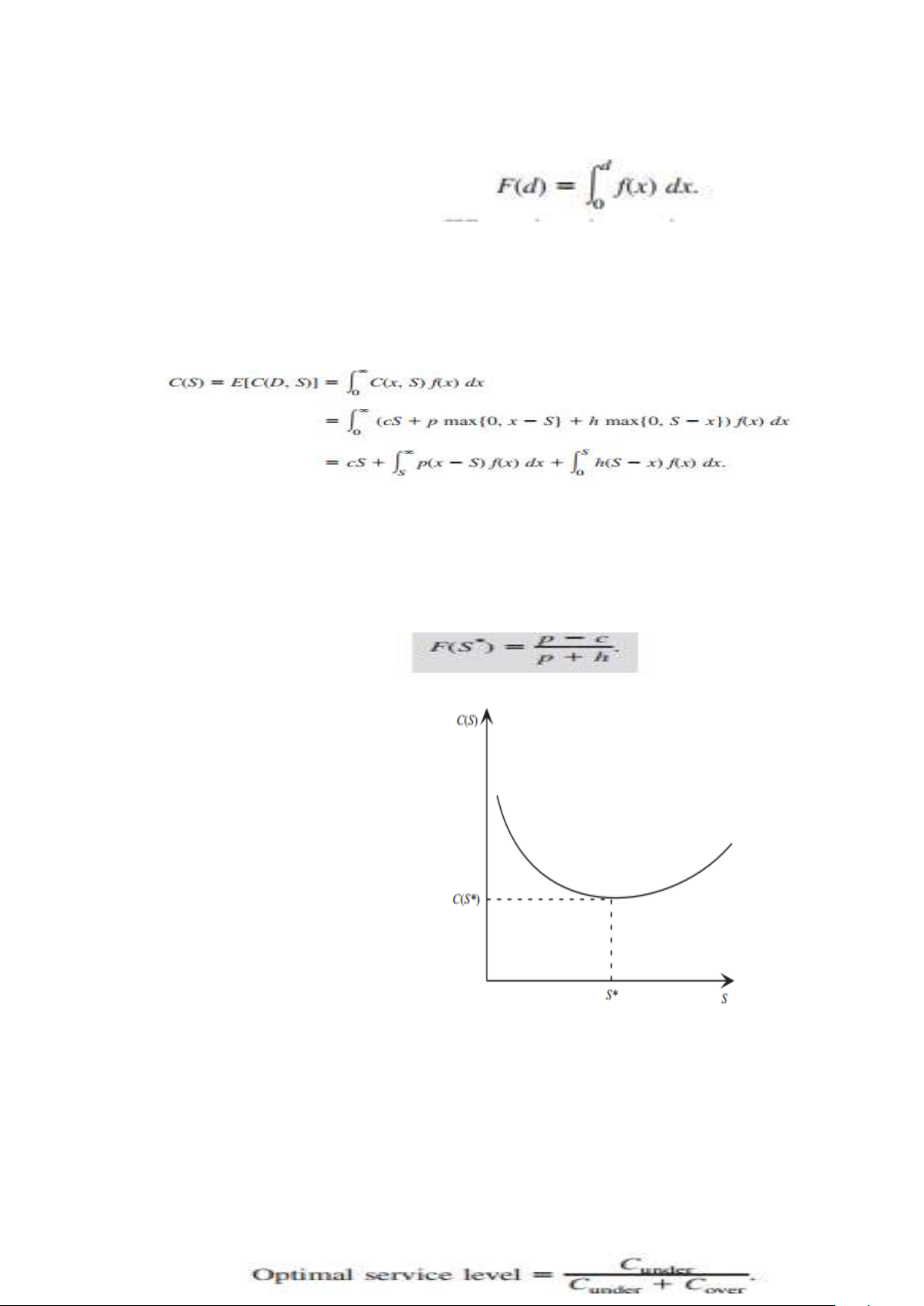
này cũng là một biến ngẫu nhiên. Chi phí dự kiến sau đó được đưa ra bởi C(S), trong đó
Hàm C(S) phụ thuộc vào phân bố xác suất của D, biến ngẫu nhiên rời rạc
này thường được xấp xỉ bởi một biến ngẫu nhiên liên tục. Hơn nữa, khi nhu cầu
dao động trên một số lượng lớn các giá trị có thể, xấp xỉ này thường sẽ mang
lại giá trị gần như chính xác của lượng hàng tồn kho tối ưu cho kho 34
Đối với biến ngẫu nhiên liên tục D này, hãy để
f(x) = hàm mật độ xác suất của D
F(d) = hàm phân phối tích lũy (CDF) của D,
Vì khi chọn mức tồn kho S,
CDF F (d) trở thành xác suất thiếu hụt sẽ không xảy ra trước khi giai đoạn kết
thúc. Như trong phần trước, xác suất này được gọi là mức dịch vụ được cung
cấp bởi số lượng đặt hàng. Chi phí dự kiến tương ứng C(S) được biểu thị bằng
Sau đó, cần phải tìm giá trị của S, giả sử S *, giảm thiểu C (S). Tìm một
công thức cho S * đòi hỏi một đạo hàm tương đối kéo dài và phức tạp, vì vậy
chúng sẽ chỉ đưa ra câu trả lời ở đây.
Cụ thể, bổ sung 1 thấy rằng mức tồn kho tối ưu S* là giá trị thỏa mãn ■ HÌNH 18.14
Đồ thị của C(S), dự kiến
Chi phí cho mô hình Stochastic Singleperiod cho dễ hỏng
Sản phẩm như một chức năng của S (mức tồn kho khi
số lượng đặt hàng Q = S I là - nhận được vào đầu
giai đoạn), cho rằng các
hàng tồn kho ban đầu là I = 0 và
chi phí thiết lập là K = 0.
Do đó, F (S *) là mức dịch vụ tối ưu và mức tồn kho tương ứng S * có thể
thu được bằng cách giải phương trình này bằng đại số hoặc bằng cách vẽ CDF
và sau đó xác định S * bằng đồ họa. Để giải thích phía bên phải của phương
trình này, tử số có thể được xem là
p c = chi phí đơn vị của việc đặt hàng thiếu = giảm lợi nhuận do không đặt - 35
hàng một đơn vị có thể có đã được bán trong kỳ. Tương tự
c + h = chi phí đơn vị đặt hàng quá mức = giảm lợi nhuận do đặt hàng một đơn
vị không thể bán được trong thời gian này.
Do đó, biểu thị chi phí đơn vị của việc đặt hàng thiếu và đặt hàng quá mức
bằng Cdưới và C trên, tương ứng, phương trình này chỉ định rằng
Khi nhu cầu có phân phối đồng đều hoặc theo cấp số nhân, tự động
thủ tục có sẵn trong Hướng dẫn IOR của bạn để tính S *. Một mẫu Excel tương
tự cũng được bao gồm trong các tệp Excel của chương này trên trang web của cuốn sách.
Nếu D được giả định là một biến ngẫu nhiên rời rạc có CDF
Một kết quả tương tự thu được. Trong đó, mức tồn kho tối ưu S* là số nguyên nhỏ nhất sao cho
Phần Ví dụ đã giải quyết trên trang web của cuốn sách cung cấp một ví dụ
khác liên quan đến việc đặt chỗ quá mức của hãng hàng không trong đó D là
một biến ngẫu nhiên rời rạc. Ví dụ dưới đây coi D là một biến ngẫu nhiên liên tục. Áp dụng vào ví dụ
Quay trở lại ví dụ về xe đạp được mô tả ở đầu phần này, chúng ta giả
định rằng nhu cầu có phân phối theo cấp số nhân với giá trị trung bình là
10.000, do đó hàm mật độ xác suất của nó là và CDF là
Từ dữ liệu được đưa ra, 36
C = 200, p = 450, h = 90.
Do đó, S* (mức tồn kho tối ưu cần đạt được ngay từ đầu để bắt đầu đáp
ứng nhu cầu) là giá trị thỏa mãn
Bằng cách sử dụng logarit tự nhiên (ký hiệu là ln), phương trình này có thể được giải như sau:
Do đó, nhà phân phối nên dự trữ 11.856 xe đạp trong mùa Giáng sinh. S*
có thể thu được từ mối quan hệ
Phân tích mô hình với hàng tồn kho ban đầu (I> 0) nhưng không có
chi phí thiết lập (K = 0)
Bây giờ hãy xem xét trường hợp I > 0, vì vậy đã có Iđơn vị trong kho đi
vào khoảng thời gian nhưng trước khi nhận được số lượng đặt hàng, Q = S – I.
(Ví dụ: trường hợp này sẽ phát sinh cho ví dụ xe đạp nếu nhà phân phối bắt đầu
với 500 xe đạp trước khi đặt hàng, vì vậy I = 500.) Chúng Itiếp tục giả định
rằng K = 0 (không có chi phí thiết lập). Cho
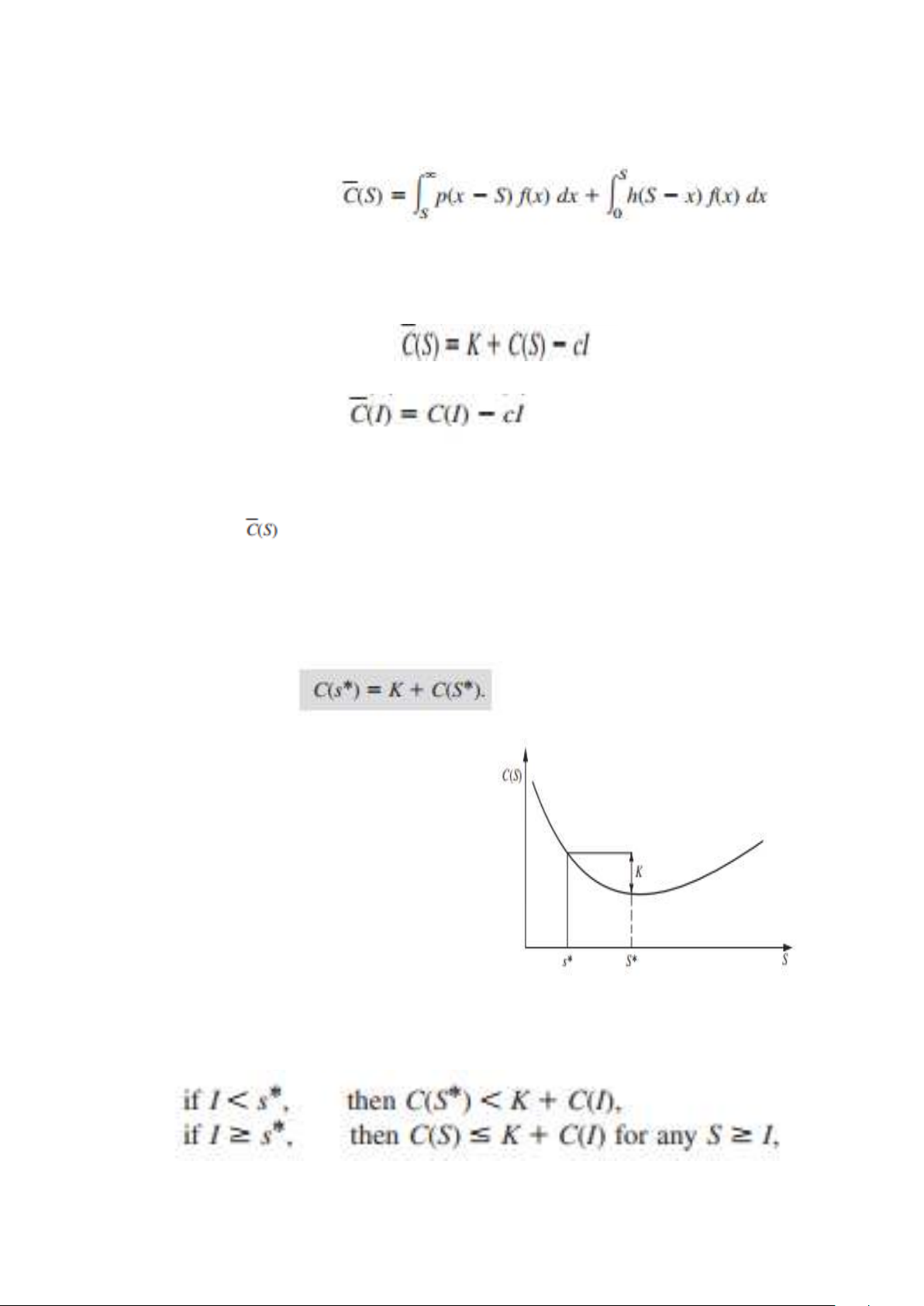
= chi phí dự kiến cho mô hình cho bất kỳ giá trị nào của I và K (bao gồm
cả giả định hiện tại rằng K = 0), cho rằng S là mức tồn kho thu được khi nhận
được số lượng đặt hàng vào đầu kỳ, vì vậy mục tiêu là chọn S ≥ I để Giảm thiểu .
S ≥ I Nó sẽ là hướng dẫn để so sánh
với hàm chi phí được sử dụng trong
tiểu mục trước (và được vẽ trong Hình 18.14),
C(S) = chi phí dự kiến cho mô hình, cho S, khi I = 0 và K = 0. Với K = 0, 37 Do đó,
giống với C (S) ngoại trừ số hạng đầu tiên, trong đó C (S) có cS thay vì c (S I). Do đó -
Vì I là một hằng số, điều này có nghĩa là
đạt được giá trị tối thiểu
của nó ở cùng giá trị S* như đối với C (S), như thể hiện trong Hình 18.14. Tuy
nhiên, vì S phải bị ràng buộc với S≥ I, nếu I > S*, Hình 18.14 chỉ ra rằng
sẽ được thu nhỏ hơn S ≥ I bằng cách đặt
S = I (tức là không đặt hàng). Điều này mang lại chính sách hàng tồn kho sau đây.
Chính sách hàng tồn kho tối ưu với I > 0 và K = 0
Nếu I< S*, hãy đặt hàng S* I để đưa mức tồn kho lên S*. -
Nếu I≥ S*, đừng gọi món,
trong đó S* một lần nữa thỏa mãn
Như vậy, trong ví dụ về xe đạp, nếu có 500 xe đạp trong tay, chính sách
tối ưu là để nâng mức tồn kho lên 11.856 xe đạp (nghĩa là đặt thêm 11.356 xe
đạp). Mặt khác, nếu đã có sẵn 12.000 xe đạp, chính sách tối ưu sẽ là không đặt hàng.
Phân tích mô hình với chi phí thiết lập (K > 0)
Bây giờ hãy xem xét phiên bản còn lại của mô hình trong đó K > 0, do
đó, chi phí thiết lập của K là phát sinh khi mua hoặc sản xuất toàn bộ lô đơn vị
được đặt hàng. (Ví dụ về xe đạp, nếu chi phí hành chính là 8.000 đô la sẽ phát
sinh để đặt hàng đặc biệt cho xe đạp cho mùa Giáng sinh, thì K 8.000.) Bây giờ
chúng Isẽ cho phép bất kỳ giá trị nào của hàng tồn kho ban đầu, vì vậy I≥ 0.
Với K >0, chi phí dự kiến C(S), với giá trị của biến quyết định S, là
Nếu một đơn hàng được đặt 38 Nếu không đặt hàng
Do đó, so với hàm chi phí dự kiến C (S) được vẽ trong Hình 18.14 ((giả định rằng I = 0 và K = 0)
Nếu một đơn hàng được đặt Nếu không đặt hàng
Bởi vì I là một hằng số, thuật ngữ cI trong cả hai biểu thức có thể được bỏ qua cho các mục đích Giảm thiểu
trên S ≥ I. Do đó, biểu đồ của C(S) trong Hình 18.14 có thể
được sử dụng để xác định xem có nên đặt hàng hay không và nếu có, nên chọn giá trị nào của s
Đây là những gì được thực hiện trong Hình 18.15, trong đó s * là giá trị của S sao cho ■ HÌNH 18.15 Đồ thị của C(S),
chi phí dự kiến (cho S) cho
Một kỳ Stochastic Stochastic
mô hình khi I = 0 và K = 0,
đang được sử dụng ở đây để
xác định các điểm quan trọng, s * và S *, tối ưu
Chính sách hàng tồn kho cho
Phiên bản của mô hình trong đó I≥0 và K > 0. Vậy 39
Nói cách khác, nếu hàng tồn kho ban đầu I nhỏ hơn s *, thì chi phí thiết
lập K là đáng giá vì đưa mức tồn kho lên S* (bằng cách đặt hàng S I) sẽ -
giảm chi phí còn lại dự kiến nhiều hơn K khi so sánh với không đặt hàng.
Tuy nhiên, nếu I> s *, thì không thể thu lại chi phí thiết lập K bằng cách đặt
hàng bất kỳ số tiền nào. (Nếu Is *, phát sinh chi phí thiết lập K để đặt hàng S *
s * sẽ giảm chi phí còn lại dự kiến bằng cùng số tiền này, vì vậy không có lý -
do gì để bận tâm đặt hàng.) Điều này dẫn đến chính sách hàng tồn kho sau đây.
Chính sách hàng tồn kho tối ưu với I ≥ 0 và K > 0
Nếu I< s*, hãy đặt hàng S* I để đưa mức tồn kho lên S*. -
Nếu I* ≥ s *, không đặt hàng. (Xem các công thức đóng hộp bóng mờ cho S *
và s * được đưa ra trước đó.)
Khi nhu cầu có phân phối đồng đều hoặc theo cấp số nhân, tự động
thủ tục có sẵn trong Hướng dẫn IOR của bạn để tính s * và S *. Áp dụng vào
ví dụ Giả sử rằng chi phí hành chính để đặt hàng đặc biệt cho xe đạp cho mùa
Giáng sinh sắp tới được ước tính là 8.000 đô la. Do đó, các tham số của mô hình bây giờ là
K = 8.000, c = 200, p = 450, h = 90. -
Như đã chỉ ra trước đó, nhu cầu về xe đạp được giả định là có phân phối theo
cấp số nhân với mức trung bình là 10.000.
Chúng Iđã tìm thấy trước đó cho ví dụ này rằng S* = 11.856.
Để tìm s*, chúng ta cần giải phương trình, C(s*) = K+ C(S*),
cho s*. Cắm hai lần vào biểu thức cho C (S) được đưa ra trong phần đầu của
phần này, với S s * ở phía bên trái của phương trình và S S * 11.856 ở phía bên
phải, phương trình trở thành
Sau khi tính toán dài để tính toán số ở phía bên tay phải và để giảm phía
bên trái đến một biểu thức đơn giản hơn về s *, phương trình này cuối cùng dẫn
đến giải pháp số, s* = 10.674. Do đó, chính sách tối ưu yêu cầu đưa mức tồn
kho lên S * = 11.856 xe đạp nếu số lượng trong tay nhỏ hơn s * = 10.674. Nếu
không, không có đơn đặt hàng nào được đặt.
Một giải pháp gần đúng cho chính sách tối ưu 40
Khi nhu cầu có phân phối theo cấp số nhân
Như được mô tả trong Phần 17.4, đối với phân bố hàm mũ có giá trị trung bình
là 1/α, hàm mật độ xác suất f(x) và CDF F(x) là Chúng ta có
Vì thế là giải pháp chính xác cho S*.
Để bắt đầu phát triển một xấp xỉ cho s *, chúng ta bắt đầu với phương trình chính xác, C(s*) = K +C(S*). Từ
Phương trình này trở thành
Hoặc ( bằng cách sử dụng kết quả trên cho S*).
Mặc dù phương trình cuối cùng này không có nghiệm dạng đóng cho S* nhưng
nó có thể được giải bằng số. Một giải pháp phân tích gần đúng cũng có thể thu
được như sau. Bằng cách cho phép 41 Và lưu ý rằng
Phương trình cuối cùng mang lại Làm giảm đến Nếu bằng 0
có thể mở rộng thành chuỗi Taylor quanh 0. Nếu bỏ qua
các số hạng ngoài số hạng bậc 2 thì kết quả sẽ trở thành Để có thể
Do đó, giá trị gần đúng mong muốn s* là
Sử dụng phép tính gần đúng này trong ví dụ về xe đạp và cho ra kết quả Để có thể
Khá gần với giá trị chính xác s*=10,674. 42
18.8. QUẢN LÝ DOANH THU
Điểm khởi đầu cho việc quản lý doanh thu là đạo luật bãi bỏ quy định
hàng không 1978, nới lỏng việc kiểm soát giá vé hàng không. Các hãng hàng
không giá rẻ và thuê chuyến sau đó tham gia thị trường để tận dụng lợi thế.
Hệ thống quản lý doanh thu phức tạp vào tháng 1 năm 2008. Hệ thống này bao gồm
(1) mô hình phản ứng của thị trường mô tả nhu cầu như một chức năng
của giá và các biến động lực khác, (2) phân tích chính sách giá của đối thủ cạnh
tranh, (3) mô hình đo lường lợi ích doanh thu của các chính sách giá khác
nhau,và (4) mô hình tối ưu hóa giá cả. Các khách sạn riêng lẻ hiện có người
quản lý doanh thu triển khai hệ thống với sự hỗ trợ của nhóm quản lý doanh
thu doanh nghiệp. Việc triển khai ban đầu hệ thống này đã đạt được doanh thu
tăng thêm là 145 triệu USD. Con số này dự kiến sẽ tăng lên khoảng 400 triệu
USD doanh thu bổ sung mỗi năm.
Nguồn: Koushik, D., J. A. Higbie và C. Eister: “Bán lẻ Tối ưu hóa giá tại
Tập đoàn khách sạn InterContinental, Giao diện, 42(1): 45–57, Tháng 1–Tháng 2. 2012
Giới thiệu hai mô hình cơ bản cho các loại cơ bản của quản lý doanh thu.
• Mô hình cho Giá vé Giảm giá được Kiểm soát Về Công suất
Một công ty có một lượng hàng tồn kho của một sản phẩm dễ hư hỏng cụ
thể (như là ghế trên một chuyến bay) để bán cho hai nhóm khách hàng (như là
du khách du lịch và khách kinh doanh trên chuyến bay). Nhóm khách hàng của
hạng 2 đến trước để mua từng đơn vị của sản phẩm với giá giảm giá được thiết
kế để đảm bảo toàn bộ lượng tồn kho có thể được bán trước khi sản phẩm
hỏng. Sau khi giá giảm giá không còn khả dụng, nhóm khách hàng của hạng 1
bắt đầu xuất hiện để mua từng đơn vị của sản phẩm với giá đầy đủ. Phân phối
xác suất của nhu cầu từ nhóm khách hàng hạng 1 được giả định là đã biết
trước. Quyết định cần được đưa ra là bao nhiêu tổng số hàng tồn kho nên được
dành riêng cho nhóm khách hàng hạng 1, để giá giảm giá sẽ được chấm dứt
sớm nếu tồn kho còn lại giảm xuống mức này trước khi đến hạn thông báo giảm giá.
Các tham số (và biến ngẫu nhiên) cho mô hình là:
L = Kích thước tồn kho của sản phẩm dễ tổn thương có sẵn để bán,
p1 = Giá trên mỗi đơn vị được thanh toán bởi khách hàng nhóm 1,
P2 = Giá trên mỗi đơn vị được thanh toán bởi khách hàng nhóm 2, với điều kiện p2 ≤ p1, 43
D = Nhu cầu từ khách hàng nhóm 1 (một biến ngẫu nhiên),
F(x) = Hàm phân phối tích lũy cho D, với F(x) = P(D ≤ x). Biến quyết định là:
X = Mức tồn kho phải được dành riêng cho khách hàng nhóm 1.
Chìa khóa để giải cho giá trị tối ưu của x, ký hiệu là x*, là đặt câu hỏi sau
và sau đó trả lời nó bằng cách thực hiện phân tích cận biên.
Câu hỏi: Giả sử có x đơn vị còn lại trong tồn kho trước thời hạn để yêu
cầu giá giảm giá p2, và một khách hàng thuộc nhóm 2 đến muốn mua một đơn
vị ở giá đó. Liệu yêu cầu này nên được chấp nhận hay từ chối?
Để giải quyết câu hỏi này, chúng ta cần so sánh doanh thu tăng thêm
(hoặc kỳ vọng thống kê của doanh thu tăng thêm) cho hai lựa chọn.
Nếu chấp nhận yêu cầu, doanh thu tăng thêm là p2. -
Nếu từ chối yêu cầu, doanh thu tăng thêm là: - 0, nếu D ≤ x 1 - p1, nếu D ≥ x Vì vậy
E (doanh thu tăng thêm) = p1 P(D ≥ x).
Do đó, yêu cầu để thực hiện bán cho khách hàng nhóm 2 nên được chấp nhận nếu p2 > p1 P(D ≥ x)
và nếu không thì từ chối. Lưu ý rằng P(D ≥ x) giảm khi x tăng. Do đó,
nếu bất phương trình này đúng đối với một giá trị cụ thể của x, giá trị này có
thể được tăng lên đến điểm quyết định x* trong đó
p2 ≤ p1 P(D ≥ x*) và p2 > p1 P(D ≥ x* + 1).
Sau đó, theo dõi rằng mức tồn kho tối ưu để dành cho khách hàng nhóm 1 là x*.
Tương đương, số đơn vị tối đa nên bán cho khách hàng nhóm 2 trước khi
dừng giá giảm giá p2 là L x*. -
Đến nay, chúng ta đã giả sử rằng khách hàng mua từng đơn vị sản phẩm
(như là các ghế trên chuyến bay của hãng hàng không), vì vậy phân phối xác
suất của D sẽ là phân phối rời rạc. Tuy nhiên, khi L lớn (như là số ghế trên một 44
chuyến bay của hãng hàng không lớn), việc sử dụng một phân phối liên tục có
thể thuận tiện tính toán hơn. p2 = p1 P(D > x*).
Vì P ( D > x*) = 1 P(D ≤ x*) = 1 F(x*), phương trình này cũng có thể - - được viết lại thành F (x*) = 1 𝑝2 - -𝑝1
(Khi sử dụng phân phối liên tục như một xấp xỉ nhưng x* giải phương
trình này không phải là số nguyên, x* nên được làm tròn xuống thành số
nguyên để thỏa mãn các biểu thức xác định giá trị tối ưu của x* được đề cập ở
cuối đoạn văn trước.) Phương trình sau rõ ràng cho thấy rằng tỷ lệ giữa p2 và
p1 đóng vai trò quan trọng trong việc xác định xác suất mà toàn bộ nhu cầu của
khách hàng nhóm 1 sẽ được đáp ứng.
Một ví dụ áp dụng mô hình này cho giá vé chiết khấu được kiểm soát năng lực
BLUE SKIES AIRLINES đã quyết định áp dụng mô hình này cho một
trong các chuyến bay của mình. Chuyến bay này có thể chấp nhận 200 chỗ đặt
chỗ trong cabin chính. (Con số này bao gồm khoản trợ cấp cho việc đặt vé quá
nhiều vì luôn có một số trường hợp lỡ chuyến). Chuyến bay thu hút một lượng
lớn khách số lượng lớn khách du lịch kinh doanh, những người thường đặt
phòng trong vòng một vài ngày của chuyến bay nhưng sẵn sàng trả giá vé
tương đối cao là 1.000 USD cho sự linh hoạt này. Tuy nhiên, phần lớn hành
khách cần phải là khách du lịch để có thể lấp đầy máy bay. Vì vậy, để thu hút
đủ lượng khách du lịch này, mức giảm giá rất thấp giá vé 200 USD được cung
cấp cho hành khách đặt chỗ trước ít nhất 14 ngày và đáp ứng một số hạn chế
khác (bao gồm cả việc không hoàn lại tiền).
Theo thuật ngữ của mô hình trên, khách hàng nhóm 1 là khách đi công
tác và khách hàng nhóm 2 là khách du lịch giải trí nên các tham số của mô hình là
L = 200, p1 = $1,000, p2 = $200.
Sử dụng dữ liệu về số lượng đặt chỗ được yêu cầu bởi nhóm khách hàng
nhóm 1 cho mỗi chuyến bay trong quá khứ, được ước lượng rằng phân phối
xác suất của số lượng đặt chỗ được yêu cầu bởi nhóm khách hàng này cho mỗi
chuyến bay trong tương lai được xấp xỉ bằng một phân phối chuẩn với giá trị trung bình µ = 60 và độ lệch chuẩn σ = 20. Do
đó, đây là phân phối cho biến ngẫu nhiên D trong mô hình, trong đó F(x) biểu
thị hàm phân phối tích luỹ cho D. Để giải cho x*, số lượng tối ưu của các khe 45
đặt chỗ để dành cho khách hàng nhóm 1, chúng ta sử dụng phương trình được cung cấp bởi mô hình.
Sử dụng bảng phân phối chuẩn do Phụ lục 5 cung cấp sẽ mang lại kết quả
Vì x* thực sự cần là một số nguyên, nó sau đó được làm tròn xuống (như
được xác định bởi mô hình) thành số nguyên 76. Bằng cách dành 76 chỗ cho
khách hàng sẵn lòng trả giá vé 1.000 đô la cho đặt chỗ trong vài ngày trước
chuyến bay, điều này ngụ ý rằng L x* = 124 là số lượng tối đa các đặt chỗ nên -
được bán với giá giảm giá 200 đô la trước khi dừng giá này, ngay cả khi điều
này xảy ra trước thời hạn 14 ngày trước chuyến bay.
• Mô hình đặt trước quá nhiều
Câu hỏi cơ bản mà mô hình đặt chỗ quá số lượng này đối mặt là làm thế
nào để đặt chỗ quá số lượng một cách sao cho lợi nhuận kỳ vọng của công ty là
lớn nhất. Mô hình đưa ra những giả định sau đây.
1. Khách hàng độc lập đặt chỗ cho một đơn vị tồn kho và sau đó có cùng
một xác suất cố định để thực sự đến đúng giờ để có được đơn vị.
2. Có một doanh thu ròng cố định được thu được cho mỗi đặt chỗ được chấp nhận.
3. Có một chi phí thiếu hụt cố định phát sinh mỗi khi một khách hàng có
đặt chỗ đến đúng giờ để có được một đơn vị tồn kho sau khi tồn kho đã được làm cạn kiệt.
Dựa trên những giả định này, mô hình có các tham số sau đây.
p = Xác suất rằng một khách hàng đặt chỗ cho một đơn vị tồn kho sẽ thực
sự đến đúng giờ để có được đơn vị.
r = Doanh thu ròng được thu được cho mỗi đặt chỗ được chấp nhận.
s = Chi phí thiếu hụt cho mỗi đơn vị nhu cầu không được đáp ứng.
L = Kích thước của tồn kho có sẵn.
Biến quyết định cho mô hình là
n = Số lượng khách hàng có thể được đặt chỗ cho một đơn vị tồn kho, nên
n L = Lượng đặt chỗ quá số lượng được phép. -
Cho giá trị của n, không chắc chắn là bao nhiêu trong số n khách hàng có
đặt chỗ cho một đơn vị tồn kho sẽ thực sự đến đúng giờ để có được đơn vị này. 46
Nói cách khác, nhu cầu rút lại các đơn vị từ tồn kho là bao nhiêu? Ký hiệu biến ngẫu nhiên này bằng
D (n) = Nhu cầu rút lại các đơn vị từ tồn kho.
Theo giả định 1, D(n) có phân phối nhị thức với tham số p, vì vậy.
Trong đó D(n) có giá trị trung bình là np và phương sai là np(1 p). -
Một biến ngẫu nhiên liên quan chặt chẽ và quan trọng trong phân tích của
chúng ta là nhu cầu không đáp ứng sẽ xảy ra khi n khách hàng được đặt chỗ.
Chúng ta ký hiệu biến ngẫu nhiên này bằng U (n), nên.
Chúng ta sẽ sử dụng phân tích cận biên (phân tích tác động của việc tăng
giá trị của biến quyết định n lên 1) để xác định giá trị tối ưu của n mà làm tăng
lợi nhuận kỳ vọng cực đại, do đó chúng ta sẽ cần biết tác động của việc tăng
giá trị của n lên 1 đối với E(U(n)).
Bắt đầu với n đặt chỗ, tác động của việc thêm một đặt chỗ là thêm 1 vào
nhu cầu không đáp ứng chỉ nếu cả hai sự kiện sau xảy ra. Một sự kiện cần thiết
là n đặt chỗ ban đầu dẫn đến việc làm cạn toàn bộ tồn kho, tức là D(n) ≥ L, và
sự kiện yêu cầu khác là khách hàng được thêm đặt chỗ thực sự sẽ đến đúng giờ
để cố gắng có được một đơn vị tồn kho. Nếu không, không có tác động nào đối
với nhu cầu không đáp ứng. Do đó, Giá trị của
▲E(U(n)) phụ thuộc vào giá trị của n vì P{D(n) ≥ L}, xác suất làm cạn
tồn kho, phụ thuộc vào n, số lượng đặt chỗ. Đối với n < L, ▲E(U(n)) = 0, trong khi
▲E(U(n)) tăng khi n tăng thêm vì xác suất làm cạn tồn kho tăng khi số lượng đặt chỗ tăng. 47
Biến ngẫu nhiên cuối cùng mà chúng ta quan tâm là lợi nhuận của công ty
sẽ xảy ra khi n khách hàng được đặt chỗ. Chúng ta ký hiệu biến ngẫu nhiên này bằng P(n), nên.
Như vừa được lưu ý ở trên, ▲E(U(n)) = 0 đối với n < L, trong khi
E(U(n)) tăng khi n tăng thêm. Do đó, E(P(n)) > 0 cho các giá trị của n tương
đối nhỏ và sau đó (giả sử r < s p) sẽ chuyển sang E(P(n)) 0 cho các giá trị của n
đủ lớn. Sau đó, ta có thể kết luận rằng n*, giá trị của n làm cho E(P(n)) đạt cực
đại, là giá trị thỏa mãn.
▲E(P(n* 1)) >0 và ▲E( P(n*)) ≤ 0, -
hoặc tương đương r > s p P{D( n* 1) ≥ L } và r ≤ s p P{D(n*) ≥ L ). -
Vì D (n) có phân phối nhị thức, việc giải cho n* theo cách này là rất trực
tiếp (mặc dù tính toán rất phiền toái).
Khi L lớn, việc sử dụng phân phối nhị thức để thực hiện các tính toán này
trở nên đặc biệt phiền toái. Do đó, trong thực tế, việc sử dụng xấp xỉ phân phối
chuẩn của phân phối nhị thức cho ứng dụng này là phổ biến (cũng như nhiều
ứng dụng khác). Cụ thể, phân phối chuẩn với trung bình là n p và phương sai là
n p (1 p) thường được sử dụng như là một xấp xỉ liên tục của phân phối nhị -
thức với các tham số n và p, vì phân phối này có cùng trung bình và phương
sai. Với phương pháp này, chúng ta giả sử ngay bây giờ rằng D(n) có phân phối
chuẩn này và xử lý n như một biến quyết định liên tục. Giá trị tối ưu của n sau
đó được xấp xỉ bằng phương trình.
Bằng cách sử dụng bảng cho phân phối chuẩn được đưa ra trong phụ lục
5, việc tính toán n* là rất trực tiếp, như sẽ được minh họa trong ví dụ sau. Nếu
n* không phải là một số nguyên, nó sẽ được làm tròn lên thành một số nguyên
để đáp ứng các biểu thức xác định giá trị nguyên tố ưu cho n* được mô tả ở
cuối đoạn văn trước đó. 48
Một ví dụ áp dụng mô hình đặt trước vượt mức này
TRANSCONTINENTAL AIRLINES có một chuyến bay hàng ngày (trừ
cuối tuần) từ San Francisco đến Chicago chủ yếu dành cho những người đi
công tác. Có 150 ghế trong một phòng máy bay. Giá vé trung bình mỗi ghế là
300 đô la. Đây là một loại vé không hoàn lại, vì vậy những người không xuất
hiện sẽ mất toàn bộ giá vé.
Chính sách của công ty là chấp nhận 10% đặt chỗ nhiều hơn so với số
lượng ghế có sẵn trên gần như tất cả các chuyến bay của mình, vì khoảng 10%
khách hàng của họ đặt chỗ cuối cùng lại không xuất hiện. Tuy nhiên, nếu trải
nghiệm với một chuyến bay cụ thể khác nhiều so với điều này, thì có thể thực
hiện ngoại lệ và nhóm OR được triệu hồi để phân tích xem chính sách đặt chỗ
quá số lượng nên là gì cho chuyến bay đó. Điều này vừa xảy ra liên quan đến
chuyến bay hàng ngày từ San Francisco đến Chicago. Ngay cả khi đã đạt đến
đủ 165 đặt chỗ (điều này xảy ra đối với hầu hết các chuyến bay), thường có
một số lượng đáng kể ghế trống. Trong quá trình thu thập dữ liệu, nhóm OR đã
phát hiện ra nguyên nhân. Chỉ có 80% khách hàng đặt chỗ cho chuyến bay này
thực sự đến để bay. 20% còn lại mất giá vé (hoặc, trong hầu hết các trường hợp,
để công ty của họ mất) vì kế hoạch của họ đã thay đổi.
Khi một khách hàng bị từ chối lên chuyến bay này, Transcontinental
Airlines sắp xếp để đưa khách hàng lên chuyến bay tiếp theo đến Chicago của
hãng hàng không khác. Chi phí trung bình của công ty để thực hiện điều này là
200 đô la. Ngoài ra, công ty tặng khách hàng một phiếu giá trị 400 đô la
(nhưng chỉ tốn cho công ty 300 đô la) để sử dụng cho một chuyến bay tương
lai. Công ty cũng cảm thấy rằng nên tính thêm 500 đô la cho chi phí không vật
chất của việc mất goodwill từ phía khách hàng bị từ chối lên chuyến bay. Do
đó, tổng chi phí khi bị từ chối lên chuyến bay được ước tính là 1.000 đô la.
p = 8, r = $300, s = $1,000, L = 150
Bởi vì L rất lớn, nhóm quyết định sử dụng xấp xỉ phân phối chuẩn của
phân phối nhị thức. Do đó, xấp xỉ này của n*, số lượng đặt chỗ tối ưu để chấp
nhận, được tìm bằng cách giải phương trình.
Trong đó D(n*) có phân phối chuẩn với trung bình µ = n p = 0.8n và
phương sai σ2= np (1 - p) = 0.16n, vì vậy σ= 0.4√n. Sử dụng bảng phân phối
chuẩn được đưa ra trong Phụ lục 5, vì σ= 0.375 và K2 = 0.32. 49 Làm giảm đến
Giải quyết để √n trong phương trình bậc hai này mang lại. Sau đó đưa ra. n* = (13.6)2 = 184.96
Vì x* thực sự cần phải là một số nguyên, nó sau đó được làm tròn lên
thành số nguyên là 185. 12 Kết luận là số lượng đặt chỗ cần chấp nhận cho
chuyến bay này nên được tăng từ 165 lên 185.
Kết quả là nhu cầu D(185) sẽ có ý nghĩa 0.8(185) = 148 và độ lệch chuẩn
của 0.4 √185 = 5.44. . Vì vậy, Transcontinental Airlines giờ đây có thể đạt
được gần như hoặc lấp đầy 150 chỗ ngồi của máy bay mà không gặp phải tình
trạng từ chối lên chuyến bay quá thường xuyên, bất cứ khi nào số lượng yêu
cầu đặt chỗ đạt tới 185. Do đó, mới chính sách tăng số lượng đặt chỗ được chấp
nhận từ 165 lên 185 sẽ làm tăng đáng kể lợi nhuận của công ty từ chuyến bay này. Mẫu khác
Có nhiều mô hình được sử dụng cho các loại quản lý doanh thu khác
nhau. Các mô hình này thường tích hợp một số ý tưởng được giới thiệu trong
hai mô hình được trình bày trong phần này. Dưới đây là danh sách một số xem
xét thực tế có thể cần phải được xem xét:
Cung cấp các cấp độ dịch vụ khác nhau (ví dụ: phòng hạng nhất, khu -
vực kinh doanh và khu vực kinh tế trên cùng một chuyến bay của hãng hàng không).
Tính phí khác nhau cho cùng một dịch vụ (ví dụ: giảm giá cho người -
cao tuổi, trẻ em, sinh viên, nhân viên, v.v.).
Tính phí khác nhau cho cùng một dịch vụ dựa trên việc bao nhiêu phần -
(nếu có) có thể hoàn lại khi hủy đặt trước.
Định giá động dựa trên thời điểm đặt chỗ và mức độ cần thiết của nhu cầu so với sức chứa.
Biến động mức đặt chỗ dựa trên thời gian còn lại và dự kiến hủy bỏ đến -
khi dịch vụ được cung cấp. 50
Có chi phí thiếu hụt phi tuyến tính cho việc đặt chỗ quá nhiều (ví dụ: -
một số khách hàng đầu tiên có thể tự nguyện chấp nhận bồi thường khiêm tốn
để từ chối dịch vụ nhưng sau đó nó trở nên đắt đỏ hơn).
Khách hàng mua gói dịch vụ kết hợp dưới nhiều điều kiện khác nhau (ví -
dụ: khách hàng hàng không sắp xếp một loạt các chuyến bay kết nối hoặc
khách sạn khách hàng ở lại nhiều đêm).
Khách hàng mua nhiều đơn vị (ví dụ: cặp đôi hoặc gia đình hoặc các - nhóm du lịch cùng nhau). 18.9 KẾT LUẬN
Chúng tôi chỉ giới thiệu các loại mô hình tồn kho cơ bản ở đây với mục
đích làm sáng tỏ bản chất chung của các mô hình hàng tồn kho.
Ví dụ, các mô hình Economic Order Quantity (EOQ) thường được sử
dụng rộng rãi và đôi khi được điều chỉnh để áp dụng cho các loại nhu cầu ngẫu
nhiên, như mô hình xem xét liên tục ngẫu nhiên. Mô hình một chu kỳ ngẫu
nhiên thì rất thuận tiện khi áp dụng cho các sản phẩm dễ hư hỏng..
Tuy nhiên, nhiều tình huống tồn kho vẫn mang theo những vấn đề phức
tạp mà các mô hình trong chương này không thể xem xét đầy đủ.
Phát triển mô hình hữu ích cho quản lý chuỗi cung ứng và mô hình quản
lý doanh thu phức tạp hơn là những hướng nghiên cứu đặc biệt quan trọng.
Nhiều nghiên cứu đang tiến hành để phát triển các mô hình quản lý doanh thu
phức tạp hơn, xem xét nhiều khía cạnh phức tạp hơn mà phát sinh trong thực
tế. Sự tiếp tục phát triển diễn ra trong việc tự động hóa xử lý dữ liệu tồn kho,
cùng với sự tăng trưởng trong quản lý tồn kho khoa học và hiệu quả. 51
TÀI LIỆU THAM KHẢO
1. Axsäter, S.: Inventory Control, 2nd ed., Springer, New York, 2006.
2. Bertsimas, D., and A. Thiele: “A Robust Optimization Approach to
Inventory Theory,” Operations Research, 54(1): 150–168, January– February 2006.
3. Bookbinder, J. H. (ed.): Handbook of Global Logistics: Transportation in
International Supply Chains, Springer, New York, 2013.
4. Choi, T. M. (ed.): Handbook of EOQ Inventory Problems: Stochastic and -
Deterministic Models and Applications, Springer, New York, 2013.
5. Choi, T. M. (ed.): Handbook of Newsvendor Problems: Models, Extensions -
and Applications, Springer, New York, 2012.
6. Goetschalckx, M.: Supply Chain Engineering, Springer, New York, 2011.
7. Harrison, T. P., H. L. Lee, and J. J. Neale (eds.): The Practice of Supply
Chain Management: Where Theory and Application Converge, Kluwer
Academic Publishers (now Springer), Boston, 2003.
8. Khouja, M.: “The Single Period (News Vendor) Problem: Literature Review - -
and Suggestions for Future Research,” Omega, 27: 537–553, 1999.
9. Muckstadt, J., and R. Roundy: “Analysis of Multi Stage Production -
Systems,” pp. 59–131 in Graves, S., A. Rinnooy Kan, and P. Zipken
(eds.): Handbook in Operations Research and Management Science,
Vol. 4, Logistics of Production and Inventory, North Holland,Amsterdam, - 1993.
10. Nahmias, S.: Perishable Inventory Systems, Springer, New York, 2011.
11. Simchi Levi, D., S. D. Wu, and Z. J. Shen (eds.): Handbook of Quantitative - -
Supply Chain Analysis, Kluwer Academic Publishers (now Springer), Boston, 2004.
12. Talluri, G., and K. van Ryzin: Theory and Practice of Yield Management,
Kluwer Academic Publishers (now Springer), Boston, 2004. (A 2nd
edition currently is in preparation.)
13. Tang, C. S., C. P. Teo, and K. K. Wei (eds.): Supply Chain Analysis: A -
Handbook on the Interaction of Information, System and Optimization, Springer, New York, 2008.
14. Tiwari, V., and S. Gavirneni: “ASP, The Art and Science of Practice:
Recoupling Inventory Control Research and Practice: Guidelines for Achieving
Synergy,” Interfaces, 37(2): 176–186, 52 March–April 2007.
15. Zipken, P. H.: Foundations of Inventory Management, McGraw Hill, - Boston, 2000. 53