Báo cáo bài tập lớn đề tài: Dự đoán ung thư vú môn Nhập môn Trí tuệ nhân tạo | Học viện Công Nghệ Bưu Chính Viễn Thông

lOMoAR cPSD| 58737056
H Ọ C VI Ệ N CÔNG NGH Ệ BƯU CHÍNH VI Ễ N THÔNG
KHOA AN TOÀN THÔNG TIN BÁO CÁO BÀI T Ậ
P L Ớ N H Ọ
C PH Ầ N: NH Ậ P MÔN TRÍ TU Ệ NHÂN T Ạ O Đ
Ề TÀI: D Ự ĐOÁN UNG THƯ VÚ Gi ả
ng viên hư ớ ng d ẫ n: Đào Th ị Thúy Qu ỳ nh
Nhóm môn h ọ c: 2
Nhóm BTL: 14
Sinh viên th ự
c hi ệ n: Lương Hà Anh Quân – B21DCAT 15 3 Trương H ả i Quân – B21DCAT1 58
Lê Quý Toàn – B21DC CN 117 Lê Anh Tu ấ n – B21DCAT2 05
~ Hà N ộ i, tháng 5 /202 4 ~ lOMoAR cPSD| 58737056 Mục lục I.
TỔNG QUAN GIẢI PHÁP ......................................................................... 2 1.
Giới thiệu ................................................................................................. 2 2.
Mục tiêu ................................................................................................... 2
II. CƠ SỞ LÝ THUYẾT ................................................................................ 2 1.
Maximum Likelihood Estimation .......................................................... 2 2.
Naive Bayes Classifier ............................................................................. 4 3.
Gaussian Naive Bayes ............................................................................. 5
III. DỮ LIỆU ................................................................................................... 6 1.
Giới thiệu về bộ dữ liệu ........................................................................... 6 2.
Giải thích các thông số ............................................................................ 7 3.
Biểu đồ trực quan hóa dữ liệu ................................................................ 8
3.1 Biểu đồ histogram ............................................................................... 8
3.2 Biểu đồ Heatmap ................................................................................10
IV. CÁC THƯ VIỆN SỬ DỤNG ...................................................................11 1.
Thư viện numpy .................................................................................... 12 2.
Thư viện Pandas .................................................................................... 12 3.
Thư viện Matplotlib .............................................................................. 12 4.
Thư viện Seaborn .................................................................................. 13 V. GIẢI THÍCH CODE
...................................................................................13 lOMoAR cPSD| 58737056 1
I. TỔNG QUAN GIẢI PHÁP 1. Giới thiệu
Trên toàn thế giới, ung thư vú là loại ung thư phổ biến nhất ở phụ nữ và có tỷ lệ tử
vong cao thứ hai. Chẩn đoán ung thư vú được thực hiện khi tìm thấy một khối u bất
thường (tự kiểm tra hoặc chụp X-quang) hoặc một đốm nhỏ của khối u. canxi được
nhìn thấy (trên X-quang). Sau khi tìm thấy một khối u đáng ngờ, bác sĩ sẽ tiến hành
chẩn đoán để xác định xem nó có phải là ung thư hay không và nếu có thì liệu nó
có lan sang các bộ phận khác của cơ thể hay không.
Bài toán trên liên quan đến việc dự đoán ung thư vú dựa trên các đặc trưng của khối
u, được biểu diễn qua bộ dữ liệu bao gồm các thông số khác nhau. Bộ dữ liệu này
chứa các thông tin đo lường về các khối u và cho biết việc bị ung thư vú hay không. 2. Mục tiêu
Mục tiêu của bài toán là xây dựng một mô hình phân loại để dự đoán mắc bệnh ung
thư vú dựa trên các đặc trưng đã cho. Cụ thể, bài toán sử dụng phương pháp Naive
Bayes với giả định các đặc trưng tuân theo phân phối Gaussian (Normal Distribution).
II.CƠ SỞ LÝ THUYẾT
1. Maximum Likelihood Estimation
Giả sử có các điểm dữ liệu x1, x2, …, xN. Giả sử thêm rằng ta đã biết các điểm dữ
liệu này tuân theo một phân phối nào đó được mô tả bởi bộ tham số 𝜃.
Maximum Likelihood Estimation là việc đi tìm bộ tham số 𝜃 sao cho xác suất sau
đây đạt giá trị lớn nhất:
Biểu thức (1) có ý nghĩa như thế nào và vì sao việc này có lý?
Giả sử rằng ta đã biết mô hình rồi, và mô hình này được mô tả bởi bộ tham số 𝜃.
Thế thì, 𝑝(𝑥1|𝜃) chính là xác suất xảy ra sự kiện 𝑥1 biết rằng mô hình là (được mô
tả bởi) 𝜃 (đây là một conditional probability). Và 𝑝(𝑥1,…,𝑥𝑁|𝜃) chính là xác suất
để toàn bộ các sự kiện 𝑥1,𝑥2,…,𝑥𝑁 xảy ra đồng thời (nó là một joint probability), 2
xác suất đồng thời này còn được gọi là likelihood. Ở đây, likelihood chính là hàm mục tiêu. lOMoAR cPSD| 58737056
Xác suất đồng thời này cần phải càng cao càng tốt. Việc này cũng giống như việc
đã biết kết quả, và ta cần đi tìm nguyên nhân sao cho xác suất xảy ra kết quả này
càng cao càng tốt. Maximum Likelihood chính là việc đi tìm bộ tham số 𝜃 sao cho Likelihood là lớn nhất.
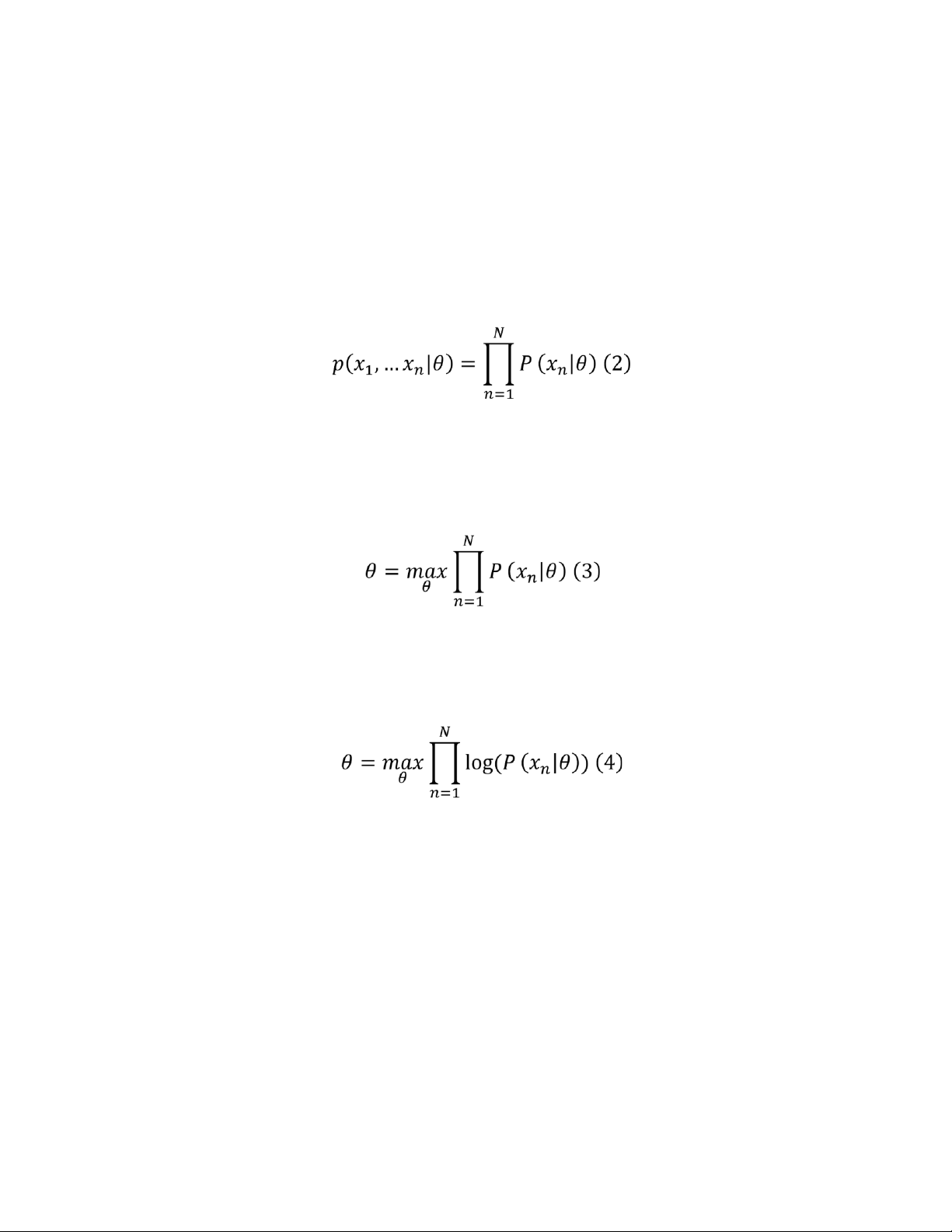
Việc giải trực tiếp bài toán (1) thường là phức tạp vì việc đi tìm mô hình xác suất
đồng thời cho toàn bộ dữ liệu là ít khi khả thi. Một cách tiếp cận phổ biến là giả sử
đơn giản rằng các điểm dữ liệu 𝑥𝑛 là độc lập với nhau, nếu biết tham số mô hình 𝜃
(độc lập có điều kiện). Nói cách khác, ta xấp xỉ likelihood trong (1) bởi:
Hai sự kiện 𝑥,𝑦 là độc lập nếu xác suất đồng thời của chúng bằng tích xác suất của
từng sự kiện: 𝑝(𝑥,𝑦)=𝑝(𝑥)𝑝(𝑦). Và khi là xác suất có điều kiện:
𝑝(𝑥,𝑦|𝑧)=𝑝(𝑥|𝑧)𝑝(𝑦|𝑧)). Lúc đó, bài toán (1) có thể được giải quyết bằng cách giải bài toán tối ưu sau:
Việc tối ưu hoá một tích thường phức tạp hơn việc tối ưu một tổng, vì vậy việc tối
đa hàm mục tiêu thường được chuyển về việc tối đa log của hàm mục tiêu. Bài
toán Maximum Likelihood được đưa về bài toán Maximum Log-likelihood: 3
2. Naive Bayes Classifier
Xét bài toán classification với 𝐶 classes 1,2,…,𝐶. Giả sử có một điểm dữ liệu 𝑥∈𝑅𝑑.
Hãy tính xác suất để điểm dữ liệu này rơi vào class 𝑐. Nói cách khác, hãy tính: p(y=c|x) (1)
hoặc viết gọn thành 𝑝(𝑐|𝑥).
Tức tính xác suất để đầu ra là class c𝑐 biết rằng đầu vào là vector 𝑥. lOMoAR cPSD| 58737056
Biểu thức này, nếu tính được, sẽ giúp chúng ta xác định được xác suất để điểm dữ
liệu rơi vào mỗi class. Từ đó có thể giúp xác định class của điểm dữ liệu đó bằng
cách chọn ra class có xác suất cao nhất:
Biểu thức (2) thường khó được tính trực tiếp. Thay vào đó, quy tắc Bayes thường được sử dụng:
Từ (3) sang (4) là vì quy tắc Bayes. Từ (4) sang (5) là vì mẫu số 𝑝(𝑥) không phụ thuộc vào 𝑐.
Tiếp tục xét biểu thức (5), 𝑝(𝑐) có thể được hiểu là xác suất để một điểm rơi vào
class 𝑐. Giá trị này có thể được tính bằng MLE, tức tỉ lệ số điểm dữ liệu trong tập
training rơi vào class này chia cho tổng số lượng dữ liệu trong tập training.
Thành phần còn lại 𝑝(𝑥|𝑐), tức phân phối của các điểm dữ liệu trong class 𝑐, thường
rất khó tính toán vì 𝑥 là một biến ngẫu nhiên nhiều chiều, cần rất rất nhiều dữ liệu
training để có thể xây dựng được phân phối đó. Để giúp cho việc tính toán được 4
đơn giản, người ta thường giả sử một cách đơn giản nhất rằng các thành phần của
biến ngẫu nhiên 𝑥 là độc lập với nhau, nếu biết 𝑐. Tức là:
Naive Bayes Classifier nhờ vào tính đơn giản , có tốc độ training và test rất nhanh.
Việc này giúp nó mang lại hiệu quả cao trong các bài toán large-scale.
Ở bước training, các phân phối 𝑝(𝑐) và p(𝑥𝑖|c),i=1,…,d sẽ được xác định dựa vào
training data. Việc xác định các giá trị này có thể dựa vào Maximum Likelihood Estimation
Ở bước test, với một điểm dữ liệu mới x𝑥, class của nó sẽ được xác đinh bởi: lOMoAR cPSD| 58737056
Việc này không ảnh hưởng tới kết quả vì log là một hàm đồng biến trên tập các số dương.
Cả việc training và test của Naive Bayes Classifier là cực kỳ nhanh khi so với các
phương pháp classification phức tạp khác. Việc giả sử các thành phần trong dữ
liệu là độc lập với nhau, nếu biết class, khiến cho việc tính toán mỗi phân phối
𝑝(𝑥𝑖|𝑐) trở nên cực kỳ nhanh.
Mỗi giá trị p(𝑐), 𝑐 = 1,2,…,𝐶 có thể được xác định như là tần suất xuất hiện của
class 𝑐 trong training data.
Việc tính toán 𝑝(𝑥𝑖|𝑐) phụ thuộc vào loại dữ liệu. Trong bài toán này ta sẽ sử dụng Gaussian Naive Bayes
3. Gaussian Naive Bayes 5
Mô hình này được sử dụng chủ yếu trong loại dữ liệu mà các thành phần là các biến liên tục.
Với mỗi chiều dữ liệu 𝑖 và một class 𝑐, 𝑥𝑖 tuân theo một phân phối chuẩn có kỳ vọng μci và phương sai Trong đó, bộ tham số
được xác định bằng Maximum Likelihood:
Đây là cách tính của thư viện sklearn. III. DỮ LIỆU
1. Giới thiệu về bộ dữ liệu
Tập dữ liệu về ung thư vú này được lấy từ Bệnh viện Đại học Wisconsin, Madison
từ Tiến sĩ William H. Wolberg. lOMoAR cPSD| 58737056
Bộ dữ liệu ung thư vú có thể được sử dụng cho nhiều mục đích khác nhau, bao gồm:
Phát triển các mô hình học máy để dự đoán ung thư vú.
Đánh giá hiệu quả của các phương pháp chẩn đoán ung thư vú khác nhau.
Nghiên cứu các yếu tố nguy cơ ung thư vú.
Các thông số này được sử dụng để huấn luyện mô hình học máy, giúp dự đoán
khả năng sẽ mắc ung thư vú hay không. Bằng cách phân tích các đặc trưng hình
thái học như bán kính, kết cấu, chu vi, diện tích và độ mịn, mô hình có thể nhận
biết các mẫu liên quan đến ung thư vú. Việc hiểu rõ ý nghĩa của từng thông số
không chỉ giúp cải thiện mô hình mà còn hỗ trợ các nhà nghiên cứu và bác sĩ
trong việc đưa ra các quyết định chẩn đoán và điều trị chính xác hơn. 6
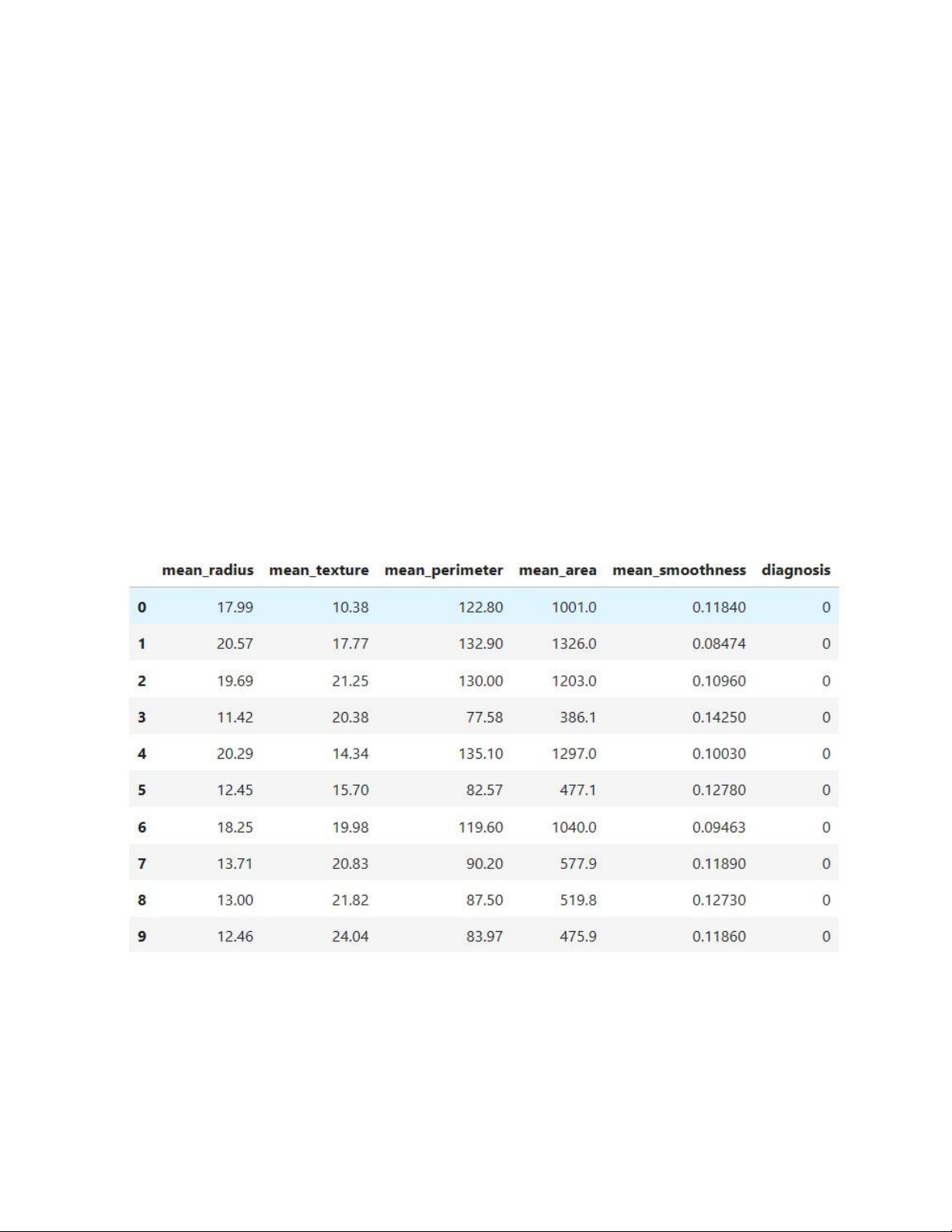
2. Giải thích các thông số
• mean_radius: Đường kính trung bình của khối u.
• mean_texture: Kết cấu trung bình của khối u.
• mean_perimeter: Chu vi trung bình của khối u.
• mean_area: Diện tích trung bình của khối u.
• mean_smoothness: Độ mịn trung bình của rìa khối u. lOMoAR cPSD| 58737056
• diagnosis: Chẩn đoán ung thư vú (0 = không mắc ung thư vú, 1 = mắc ung thư vú).
Ý nghĩa của các thuộc tính
• mean_radius: Đường kính trung bình của khối u là một chỉ báo về kích thước
của khối u. Khối u có đường kính trung bình lớn hơn có nhiều khả năng là ung thư hơn. 7
• mean_texture: Kết cấu trung bình thể hiện mức độ biến đổi của màu sắc trên
bề mặt khối u. Khối u có kết cấu mịn trung bình cao hơn có nhiều khả năng
là ít bị ung thư vú hơn.
• mean_perimeter: Chu vi trung bình của khối u là một chỉ báo về kích thước
của đường viền khối u. Khối u có chu vi trung bình lớn hơn có nhiều khả năng là ung thư hơn.
• mean_area: Diện tích trung bình của khối u là một chỉ báo về kích thước
tổng thể của khối u. Khối u có diện tích trung bình lớn hơn có nhiều khả năng là ung thư hơn.
• mean_smoothness: Độ mịn trung bình của rìa khối u là một chỉ báo về độ
đồng đều của rìa khối u. Khối u có độ mịn trung bình cao hơn có nhiều khả năng là lành tính hơn.
• diagnosis: Chẩn đoán ung thư vú là mục tiêu dự đoán của mô hình học máy.
Giá trị 0 cho biết không bị mắc ung thư vú, trong khi giá trị 1 cho biết kết quả bị ung thư vú. lOMoAR cPSD| 58737056
3. Biểu đồ trực quan hóa dữ liệu
3.1 Biểu đồ histogram 8
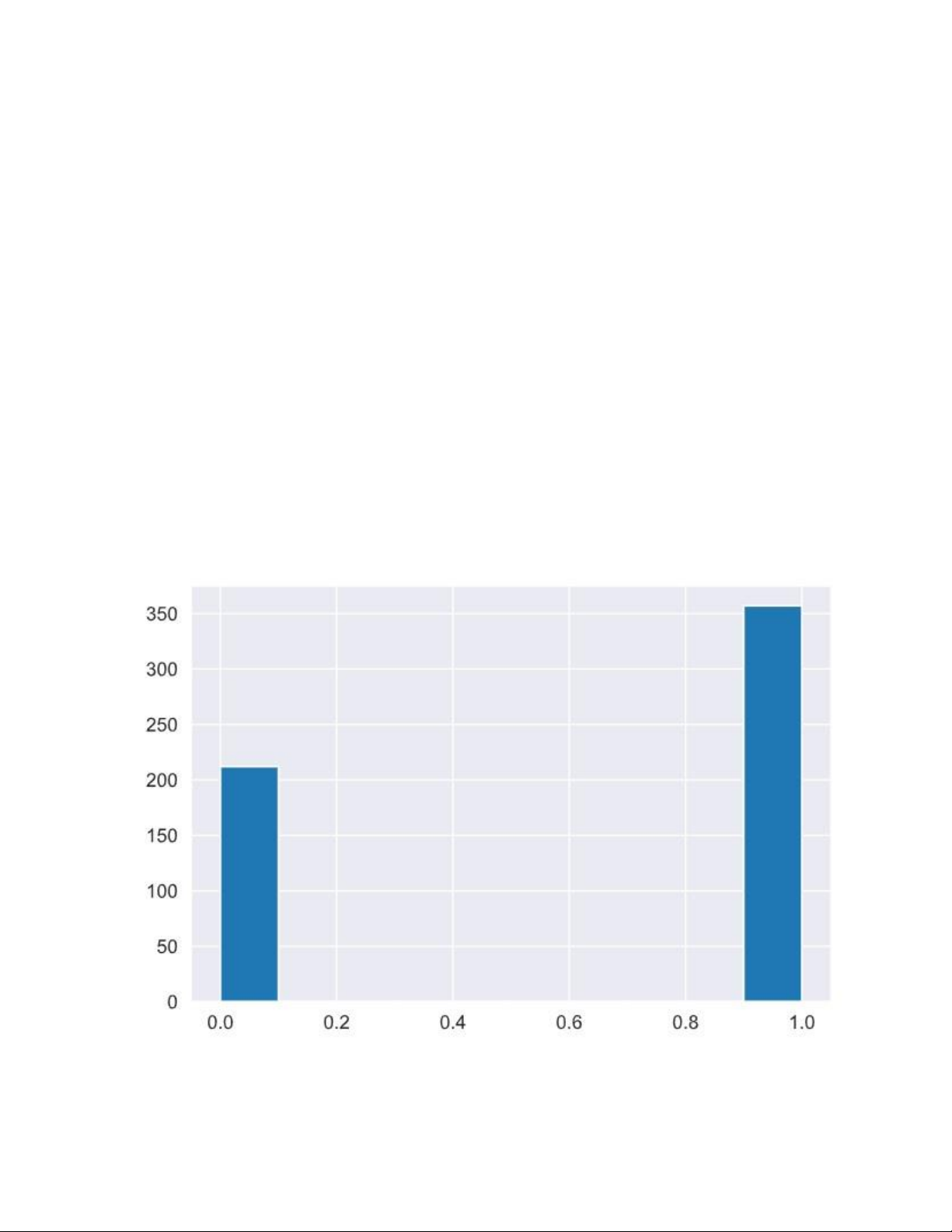
Biểu đồ này hiển thị phân bố của biến “diagnosis” trong tập dữ liệu ung thư vú.
Dưới đây là các chi tiết cụ thể: lOMoAR cPSD| 58737056 Mục Đích
- Phân loại khối u: Biến “diagnosis” phân loại khối u thành hai loại: không bị mắc
ung thư vú (“0”) và bị mắc ung thư vú (“1”).
- Phân bố mẫu: Biểu đồ cho thấy số lượng mẫu của mỗi loại khối u trong tập dữ liệu. Diễn Giải
- Trục x: Đại diện cho các giá trị của biến “diagnosis” (0 và 1).
- Trục y: Đại diện cho số lượng mẫu ứng với mỗi giá trị chẩn đoán. Ý Nghĩa 9
- Tỷ lệ mẫu: Biểu đồ này cho thấy sự cân bằng hoặc mất cân bằng giữa hai loại chẩn đoán.
- Quan trọng cho mô hình hóa: Hiểu rõ phân bố này giúp điều chỉnh phương pháp
xử lý dữ liệu, như sử dụng kỹ thuật cân bằng lại mẫu để cải thiện hiệu suất mô
hình học máy. Kết Luận
Biểu đồ histogram của biến “diagnosis” là công cụ hữu ích để đánh giá nhanh sự
phân bố của các loại chẩn đoán trong dữ liệu, giúp chuẩn bị tốt hơn cho các bước
phân tích và mô hình hóa tiếp theo. lOMoAR cPSD| 58737056
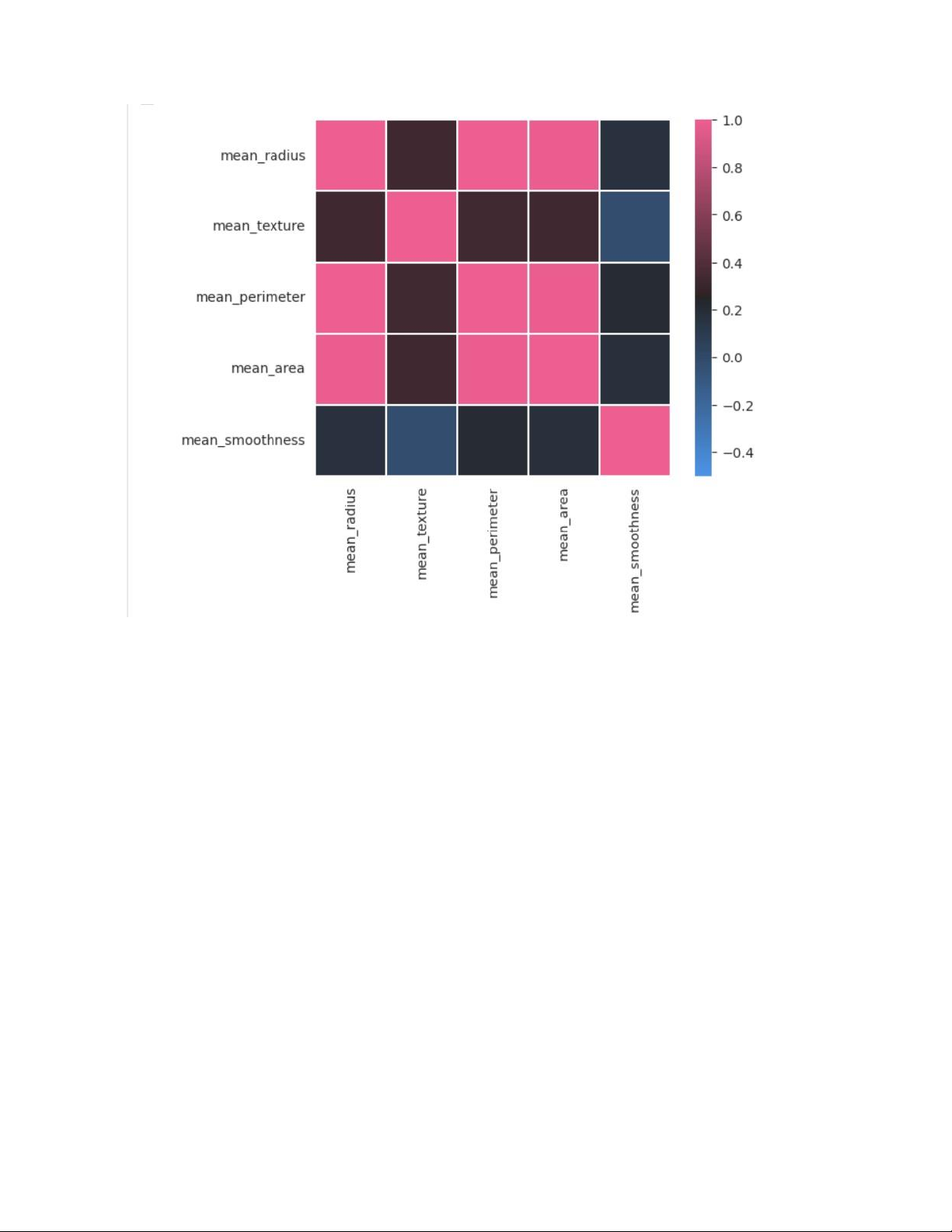
3.2 Biểu đồ Heatmap 10
Trong bài toán này, việc chọn các đặc trưng như mean_radius, mean_texture, và
mean_smoothness thay vì sử dụng tất cả các thông số có thể được giải thích chi tiết như sau:
• Khả năng phân biệt rõ ràng: Các đặc trưng này có khả năng phân biệt giữa
các lớp tốt. Điều này có thể được xác định thông qua phân tích thống kê và
trực quan hóa dữ liệu. Chẳng hạn, nếu một đặc trưng có sự khác biệt đáng kể
giữa các lớp, nó sẽ giúp mô hình Naive Bayes dễ dàng phân loại chính xác hơn.
• Tương quan thấp: Khi các đặc trưng ít tương quan với nhau, chúng cung cấp
thông tin độc lập và bổ sung cho mô hình. Tương quan thấp giữa các đặc
trưng giúp tránh tình trạng dư thừa thông tin, cải thiện hiệu suất của mô hình.
Đoạn mã sử dụng corr để tính toán ma trận tương quan, và dựa vào đó có thể
thấy rằng mean_radius, mean_texture, và mean_smoothness có tương quan
thấp, do đó chúng được chọn. lOMoAR cPSD| 58737056
• Đơn giản hóa mô hình: Sử dụng ít đặc trưng hơn giúp mô hình đơn giản hơn,
dễ hiểu hơn và giảm nguy cơ overfitting. Điều này đặc biệt quan trọng khi
làm việc với các thuật toán như Naive Bayes, vốn dựa trên giả định độc lập giữa các đặc trưng.
Trong bài toán lần này nhóm 7 không chọn mean_perimeter và mean_area thay
cho mean_radius do kết quả của việc thử nghiệm model ở cả 2 cách tiếp cận mang
lại kết quả thấp hơn.
IV.CÁC THƯ VIỆN SỬ DỤNG
Các thư viện được sử dụng:
• NumPy (np): Thư viện cung cấp các công cụ cho việc làm việc với mảng
và ma trận trong Python, làm cho việc tính toán số học trên dữ liệu nhanh chóng và dễ dàng hơn.
• Pandas (pd): Pandas là một thư viện mạnh mẽ cho phân tích dữ liệu trong
Python. Nó cung cấp các cấu trúc dữ liệu và công cụ xử lý dữ liệu để làm
cho việc làm việc với dữ liệu dạng bảng trở nên dễ dàng. 11
• Matplotlib (plt): Matplotlib là một thư viện trực quan hóa dữ liệu cơ bản
trong Python, cung cấp các công cụ để tạo ra các biểu đồ, đồ thị, hình ảnh,
và các loại hình vẽ khác để trình bày dữ liệu.
• Seaborn (sns): Seaborn là một thư viện trực quan hóa dữ liệu dựa trên
Matplotlib. Nó cung cấp giao diện cấp cao để tạo ra các biểu đồ thống kê
hấp dẫn và dễ đọc hơn so với Matplotlib. Đồng thời, Seaborn cũng cung
cấp một số chức năng hỗ trợ cho việc phân tích dữ liệu và trực quan hóa 1. Thư viện numpy
Trong đoạn mã được cung cấp, thư viện NumPy được sử dụng trong hàm tính toán
xác suất theo phân phối Gaussian (`calculate_likelihood_gaussian`), nơi nó được
sử dụng để tính toán các phép toán toán học như căn bậc hai và mũ. lOMoAR cPSD| 58737056 2. Thư viện Pandas
Trong đoạn mã được cung cấp, thư viện Pandas được sử dụng để đọc dữ liệu từ tệp
CSV và hiển thị một số hàng đầu tiên của DataFrame.
3. Thư viện Matplotlib 12
Đoạn mã này tạo ra một subplot với 1 hàng và 3 cột, chia sẻ trục y giữa các biểu
đồ. Sau đó, nó sử dụng thư viện Seaborn để vẽ histogram cho ba biến
`mean_radius`, `mean_smoothness`, và `mean_texture` từ dữ liệu `data` trên ba cột khác nhau của subplot. 4. Thư viện Seaborn
Đoạn mã này tính toán ma trận tương quan giữa các biến trong dữ liệu, sau đó sử
dụng Seaborn để vẽ heatmap của ma trận tương quan này. Heatmap được sử dụng
để trực quan hóa mối quan hệ tương quan giữa các biến, với các mức tương quan
được màu sắc hóa để dễ hiểu hóa. lOMoAR cPSD| 58737056 V.GIẢI THÍCH CODE
Calculate P(Y=y) for all possible y 13
Tìm xác suất p(yi) với mọi yi thuộc trong y. Các tham số truyền vào: •
df: DataFrame chứa dữ liệu •
Y: Tên cột chứa các lớp (cột target)
Hàm trả về một mảng gồm các xác suất của p(yi) với mọi yi thuộc trong y •
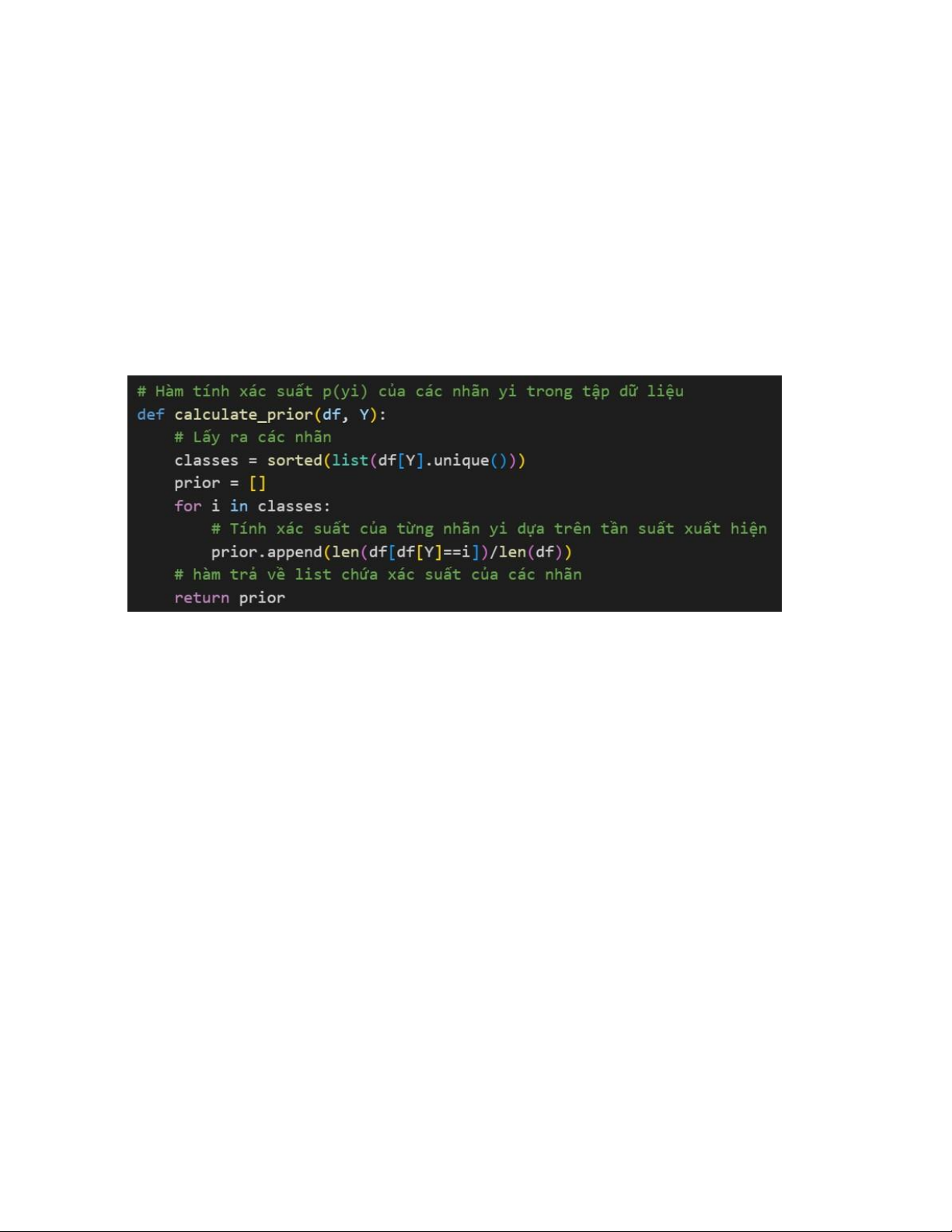
classes = sorted(list(df[Y].unique())) o Nhằm lấy ra các giá trị duy nhất
trong cột Y (hiểu là cột target - cột chứa các lớp để mô hình dự đoán phân lớp)
o Kết quả trả về của dòng này là một mảng gồm các giá trị duy nhất của
cột Y đã được sắp xếp •
prior = [] for i in classess: prior.append(len(df[df[Y]==i])/len(df))
o Tính xác suất cho từng lớp trong tập dữ liệu dựa trên tần suất xuất hiện của lớp đó
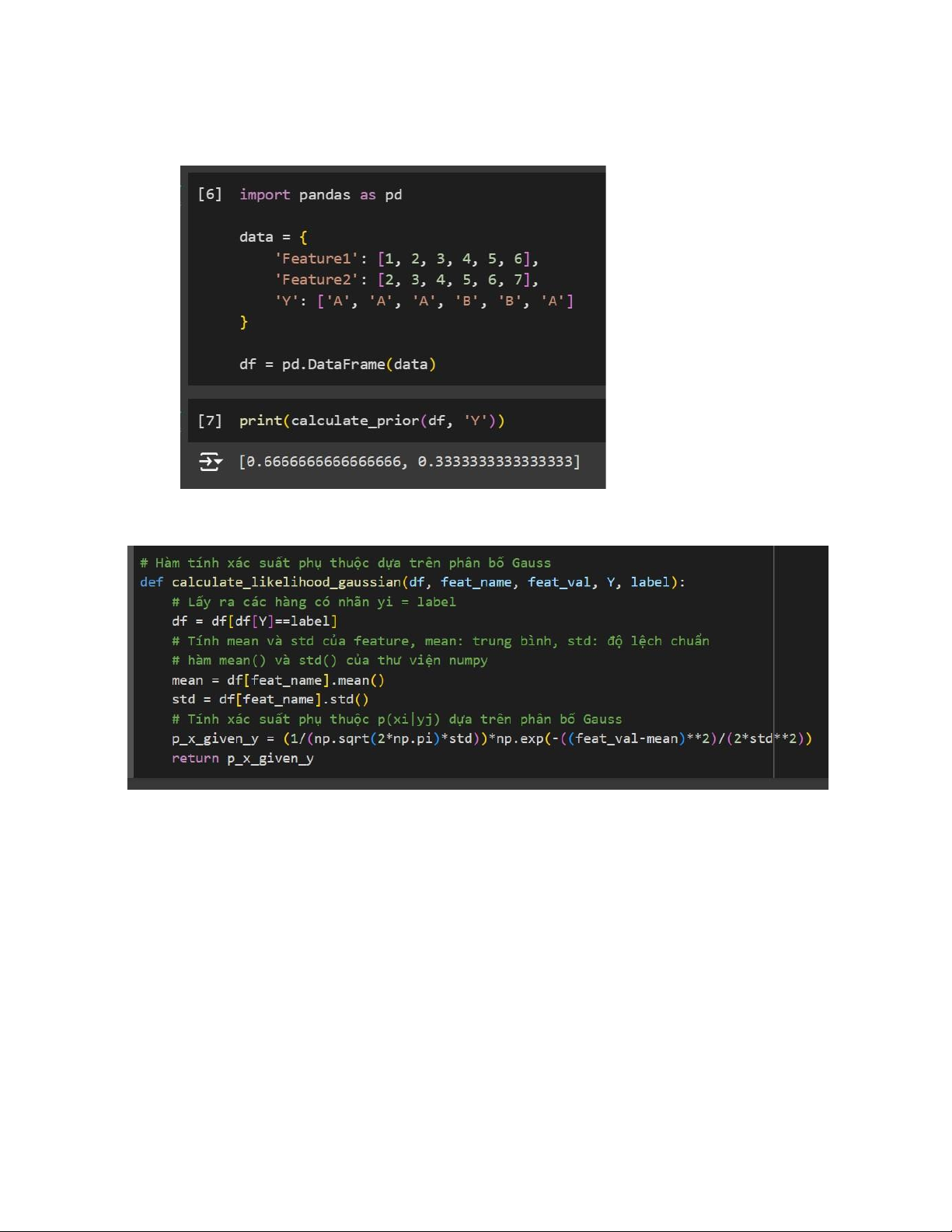
Ví dụ: Cho data như sau, ta sẽ nhận được kết quả (xác suất của lớp A và B tương ứng) lOMoAR cPSD| 58737056 14
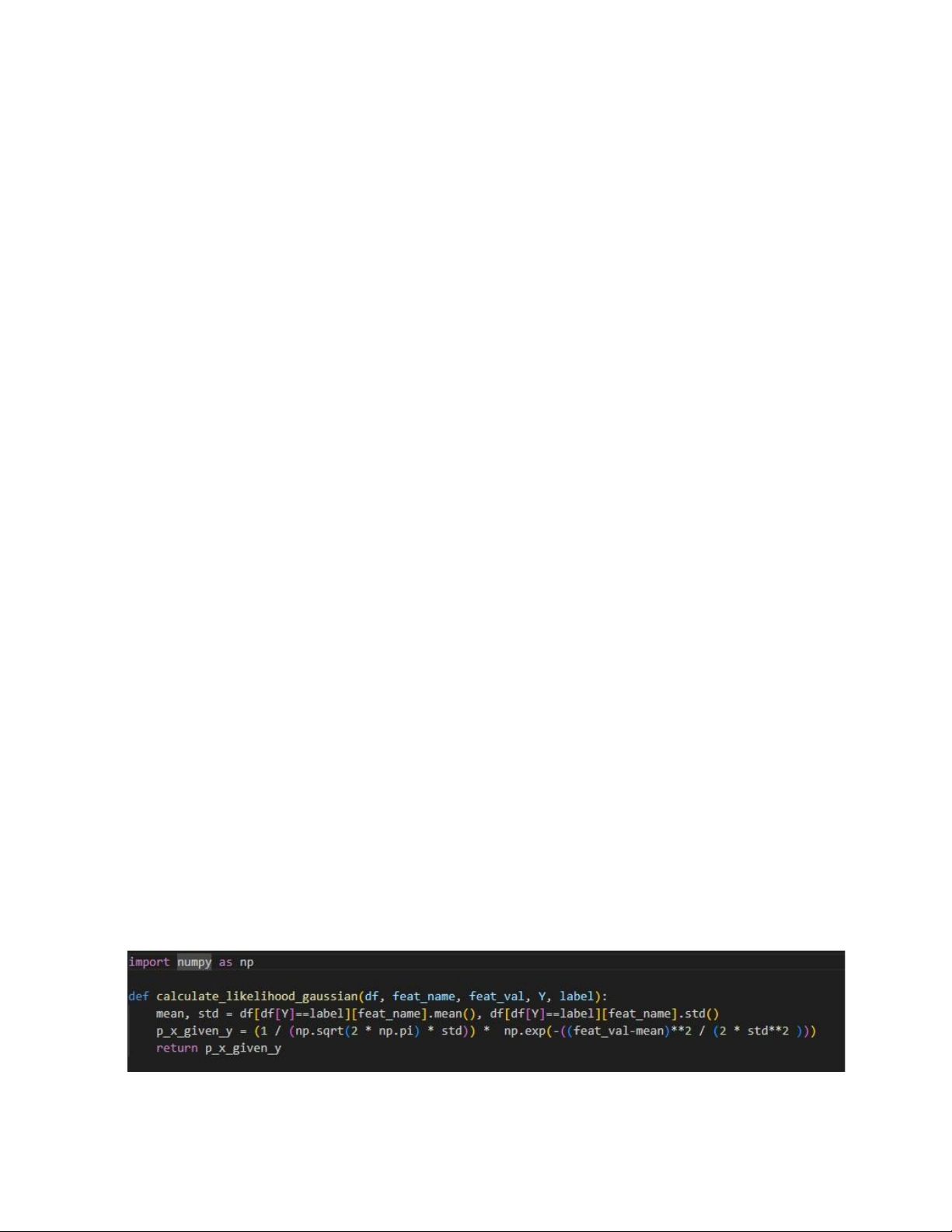
Calculate P(X=x|Y=y) using Gaussian dist.
Hàm này dùng để tính xác suất có điều kiện p(xi|yj) - xác suất có điều kiện của một
giá trị đặc trưng cho trước thuộc về một lớp cụ thể. Ở đây xác suất này được tính
dựa trên cách tiếp cận là Gaussian Naive Bayes, do dữ liệu là liên tục và tuân theo phân bố chuẩn. • Các tham số truyền vào: •
df: DataFrame chứa dữ liệu. •
feat_name: Tên cột đặc trưng cần tính xác suất. 15 •
feat_val: Giá trị của đặc trưng cần tính xác suất. •
Y: Tên cột chứa nhãn lớp. lOMoAR cPSD| 58737056 •
label: Nhãn lớp cụ thể cần tính xác suất có điều kiện.
Hàm trả về: xác suất có điều kiện p(xi | yj) được tính dựa trên công thức
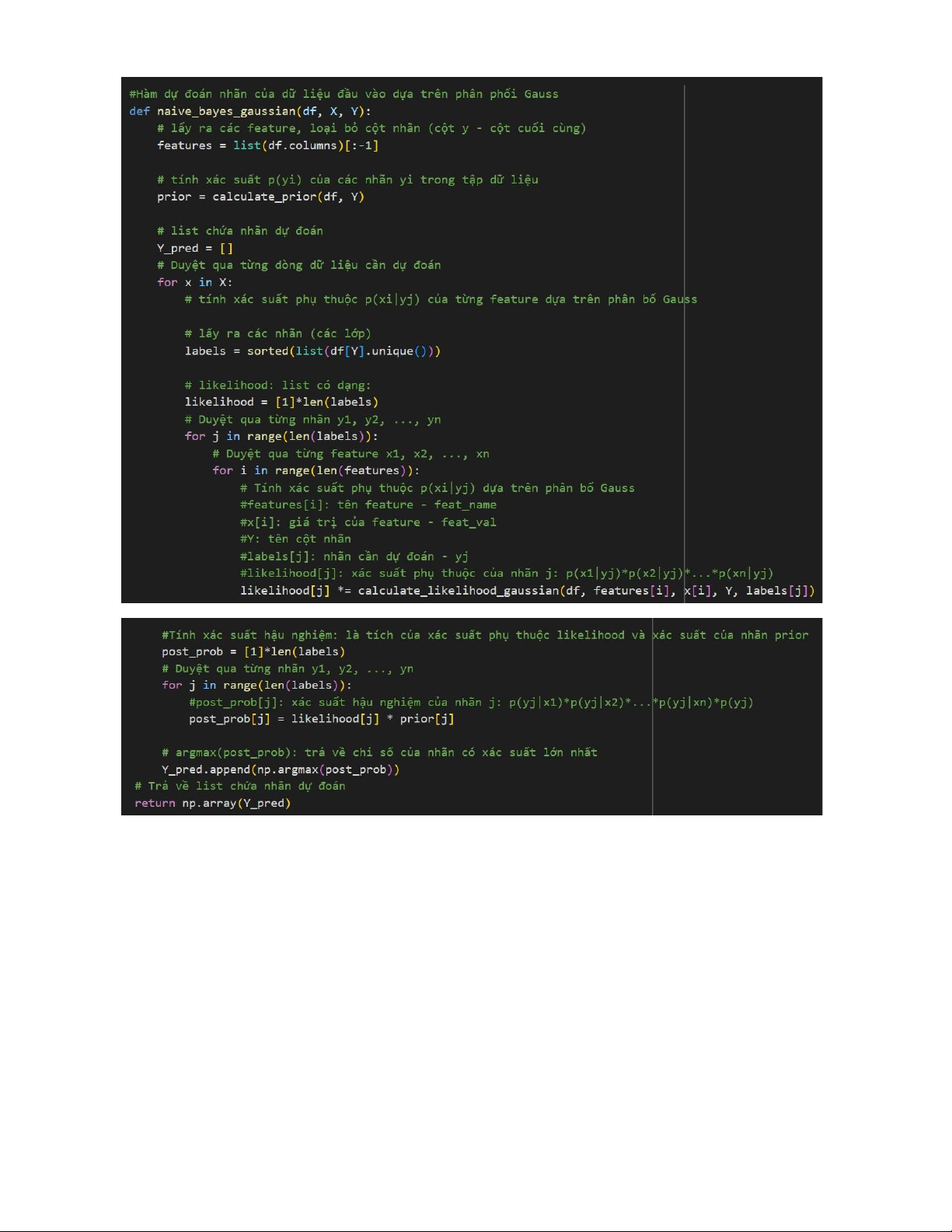
Calculate P(X=x1|Y=y)P(X=x2|Y=y)...P(X=xn|Y=y) * P(Y=y) for all y and find the maximum
Hàm chính của phân loại bayes đơn giản, trong trường hợp này sử dụng cách tiếp
cận phân bố chuẩn gauss do đặc điểm của dữ liệu của bài toán.
• Các tham số truyền vào:
o df: DataFrame chứa dữ liệu huấn luyện. o X: Tập các mẫu
dữ liệu cần dự đoán.
o Y: Tên cột chứa nhãn lớp cần dự đoán trong DataFrame df
• Hàm trả về list gồm các nhãn (các lớp) dự đoán tương ứng với từng dòng trong tập dữ liệu X. 16 lOMoAR cPSD| 58737056
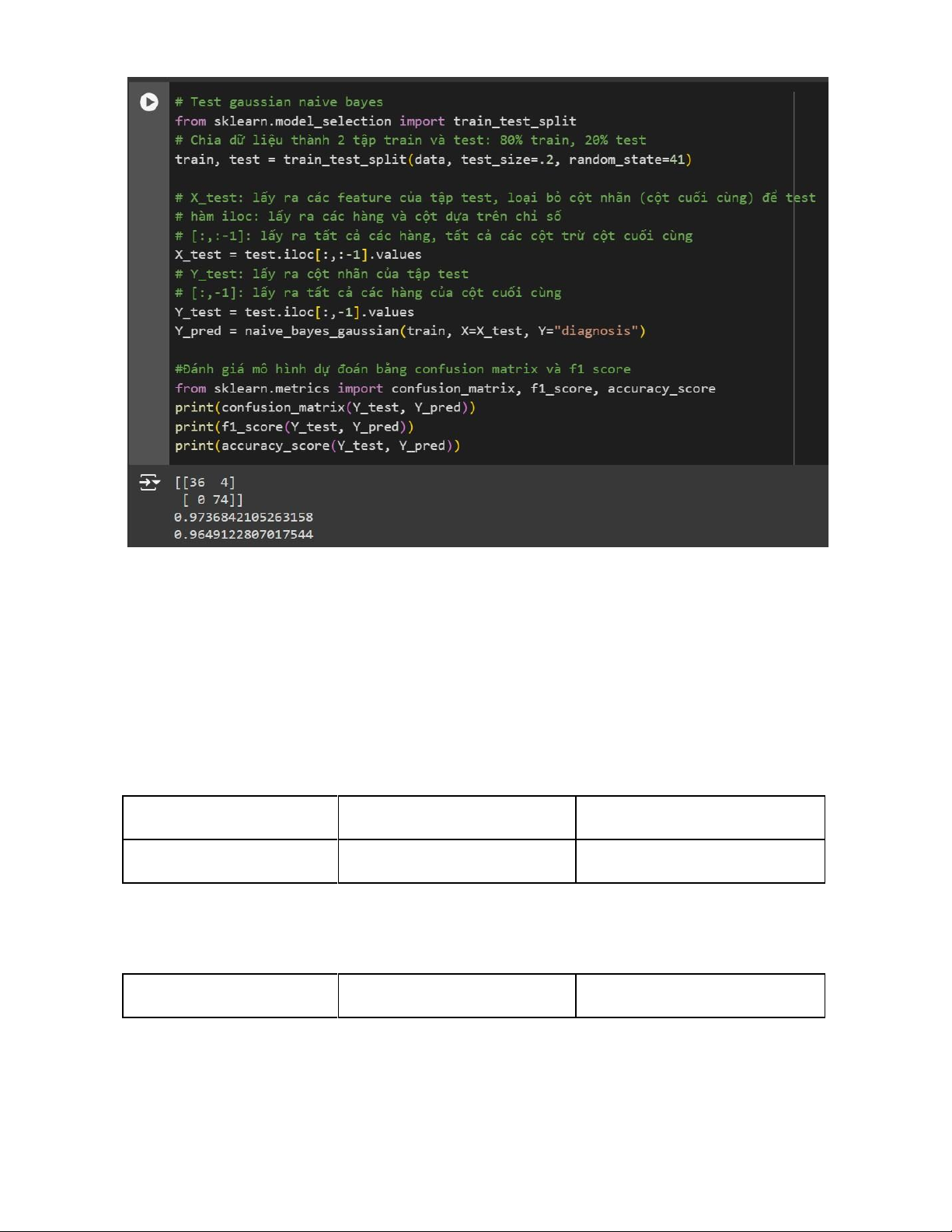
Chạy thử mô hình sử dụng hướng tiếp cận gauss 17 lOMoAR cPSD| 58737056
Nhóm thực hiện chạy mô hình trên bộ dữ liệu ở phần trên. Nhóm sẽ chia dữ liệu
thành 2 phần là train và test theo tỉ lệ 80:20.
Sau khi chạy mô hình và nhận được kết quả dự đoán là Y_pred, nhóm tiến hành đánh giá mô hình
• confusion_matrix (Ma trận nhầm lẫn): Cho biết số lượng dự đoán đúng và sai cho từng lớp Predicted Positive Predicted Negative Actual Positive True Positive False Positive 18 Actual Negative False Negative True Negative
• Kết quả ta nhận được là: o True Positives (TP) = 36: Số lượng mẫu thực tế
là dương tính (positive) và được dự đoán là dương tính. o False Negatives
(FN) = 4: Số lượng mẫu thực tế là dương tính nhưng được dự đoán là âm
tính (negative). o False Positives (FP) = 0: Số lượng mẫu thực tế là âm tính lOMoAR cPSD| 58737056
nhưng được dự đoán là dương tính. o True Negatives (TN) = 74: Số lượng
mẫu thực tế là âm tính và được dự đoán là âm tính. o
o accuracy_score (Độ chính xác của mô hình)
• Chỉ số Accuracy được tính dựa trên công thức
Kết quả của mô hình là 96,49% một kết quả có thể ứng dụng được trên thực tế.
• f1_score: Là điểm số đánh giá độ hiệu quả của mô hình. F1 score thường
được sử dụng trong các bài toán phân loại với dữ liệu không cân bằng. Trong
dữ liệu bài toán nhóm sử dụng: Có 357 mẫu dữ liệu cho ra kết quả là 1 (Có
mắc bệnh) và 212 mẫu dữ liệu cho kết quả là 0 (Không mắc bệnh). Có thể
thấy dữ liệu của bài toán này không thực sự cân bằng nên nhóm sử dụng
thêm thông số f1_score để đánh giá.
• Chỉ số f1_score được tính dựa trên công thức 19
• Precision (Độ chính xác):Tỷ lệ giữa số lượng dự đoán đúng trên tổng số dự đoán là đúng.
• Recall (Độ phủ): Tỷ lệ giữa số lượng dự đoán đúng trên tổng số lượng mẫu thuộc về lớp đó. lOMoAR cPSD| 58737056
• F1 score được tính dựa trên 2 chỉ số trên, nhằm nếu như mô hình có chỉ số
False Positive và False Negative cao thì F1 score sẽ phản ánh điều này rõ
ràng hơn so với Accuracy_Score. Điều này càng cần được chú ý trong những
bài toán nghiêm trọng như dự đoán về y tế.
• Mô hình cho ra chỉ số f1_score là 0,9737 là một chỉ số rất tốt.
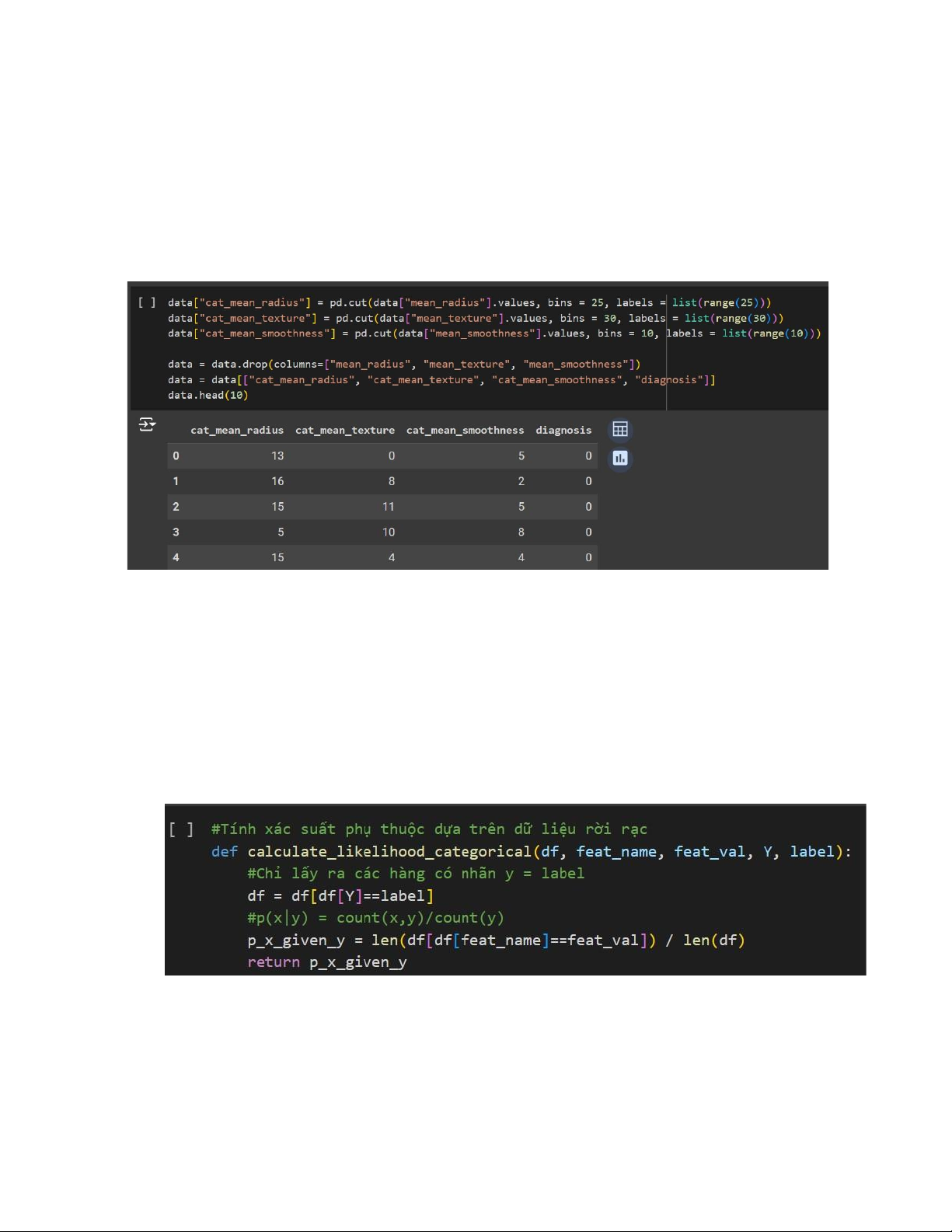
Chuyển từ dữ liệu liên tục sang dữ liệu rời rạc
Sử dụng hàm cut của thư viện pandas để rời rạc hóa dữ liệu. Dựa vào miền giá trị
của các features, nhóm chia dữ liệu thành các đoạn như trong code. 20
• Tính xác suất phụ thuộc p(xi | yj) o
Mục đích, các tham số đầu vào và giá trị trả về của hàm này vẫn giống với hàm calculate_likehood_gaussian.
o Tại đây chỉ khác ở cách tính xác suất p(xi | yi) do dữ liệu đã được rời
rạc hóa. Ta có thể tính xác suất dựa trên tần suất xuất hiện của xi với nhãn yj.