
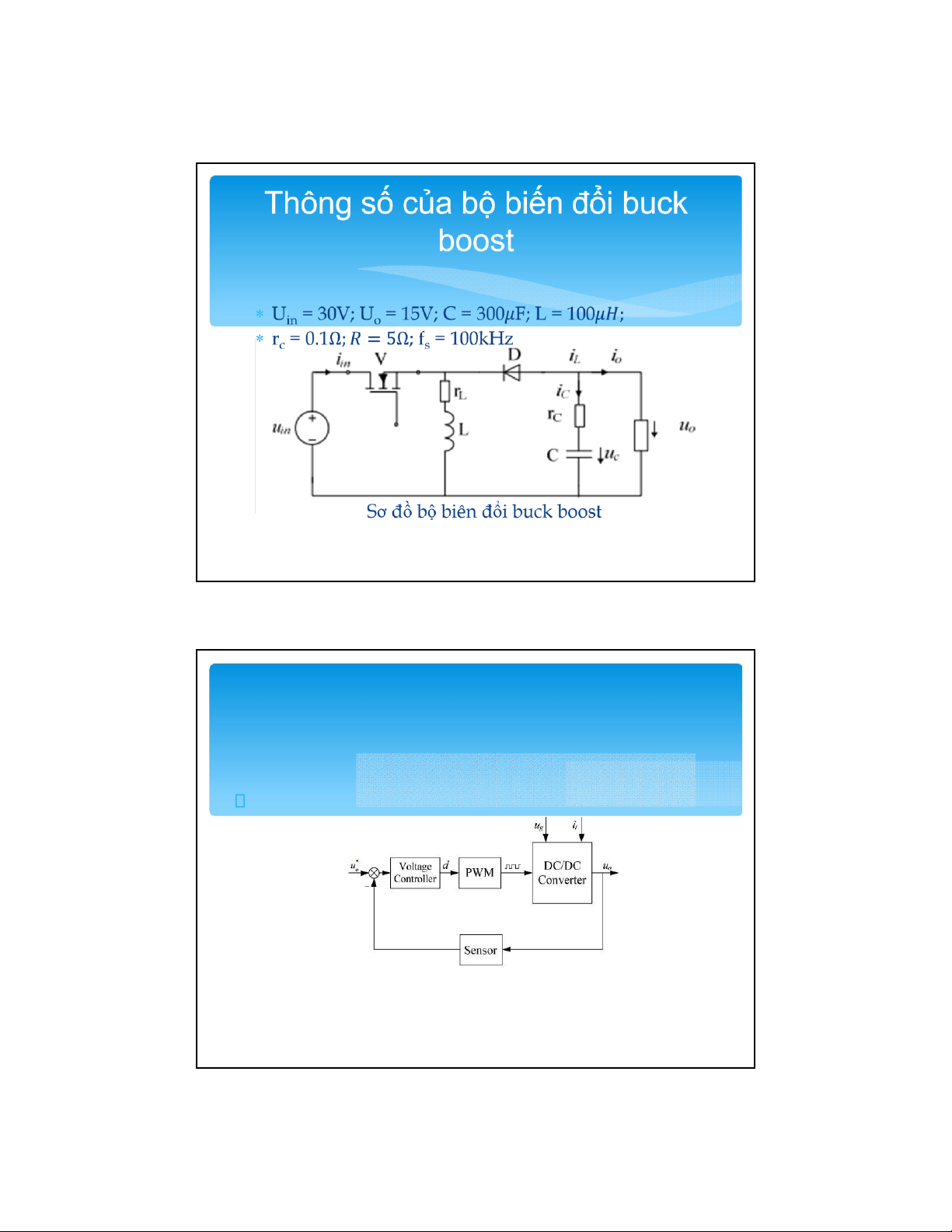







Preview text:
lOMoAR cPSD| 58511332 Đề
tài : T hiết kế cấu trúc điều
khiển bộ biến đổi buck boost
Giáo viên h ướ ng d ẫ n : Vũ Hoàng Ph ươ ng Sinh viên th ự c hi ệ n : Tr ầ n H ả i Hoàn : 20121734 Đ ặ ng Thành Chung: 20121320 Yêu cầu của đề tài
Thiết kế cấu trúc điều khiển theo chế độ diện áp
Mô phỏng cấu trúc điều khiển
Phân tích kết quả mô phỏng khi nguồn hoắc tải thay đổi lOMoAR cPSD| 58511332
Điều khiển theo điện áp
C ấ u trúc đi ề u khi ể n theo đi ệ n áp
➔Cần phải đưa ra cấu trúc và tổng hợp tham số cho bộ điều
chỉnh điện áp (Voltage controller). lOMoAR cPSD| 58511332 Phương án thiết kế
I. Mô hình hóa bộ biến đổi buck boost II. Thiết kế bộ bù III. Mô phỏng trên matlab
IV. Phân tích kết quả mô phỏng
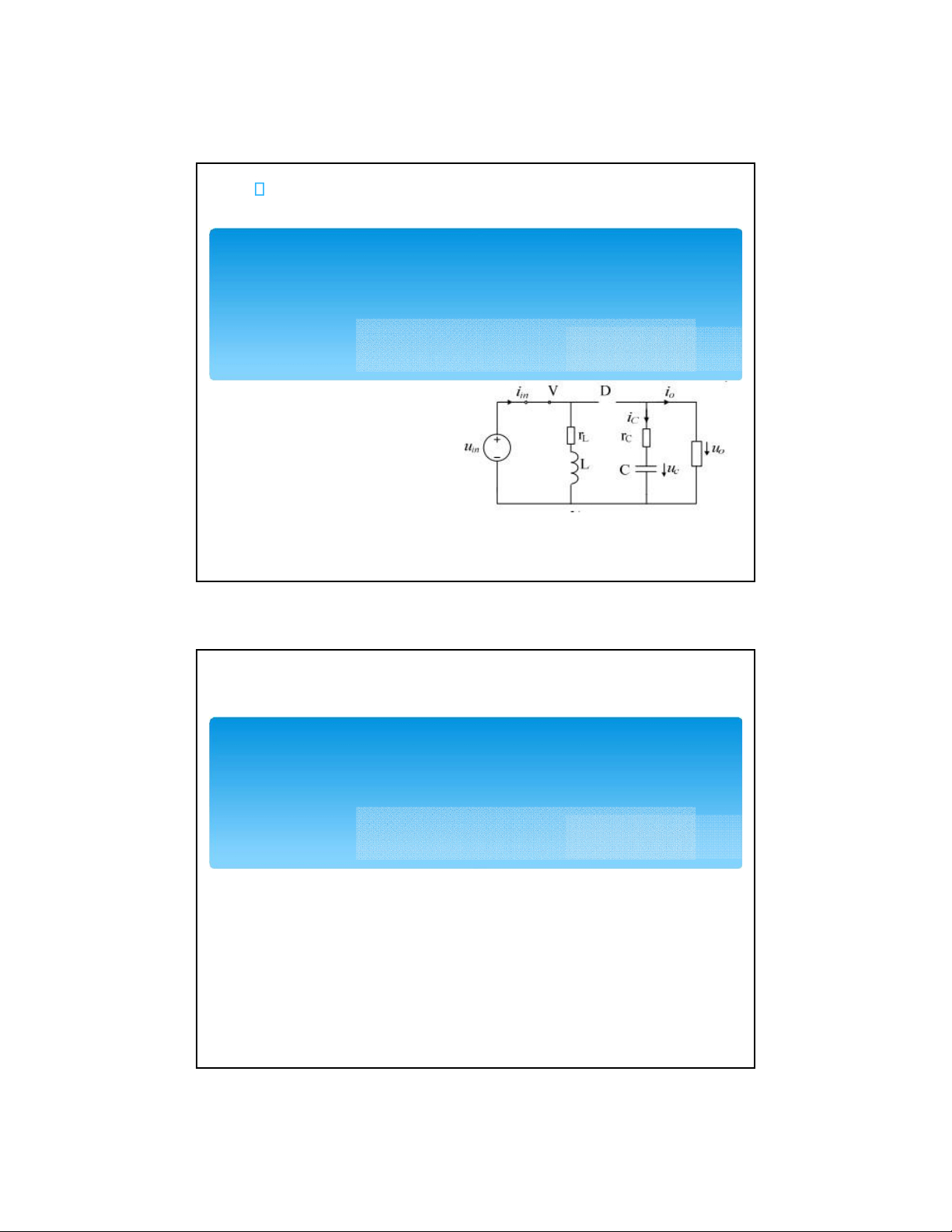
I. Mô hình hóa bộ biến đổi buck boost
Mô hình hóa theo phương pháp trung bình không gian trạng thái:
xác định phương trình mạch điện ở 2 trạng thái
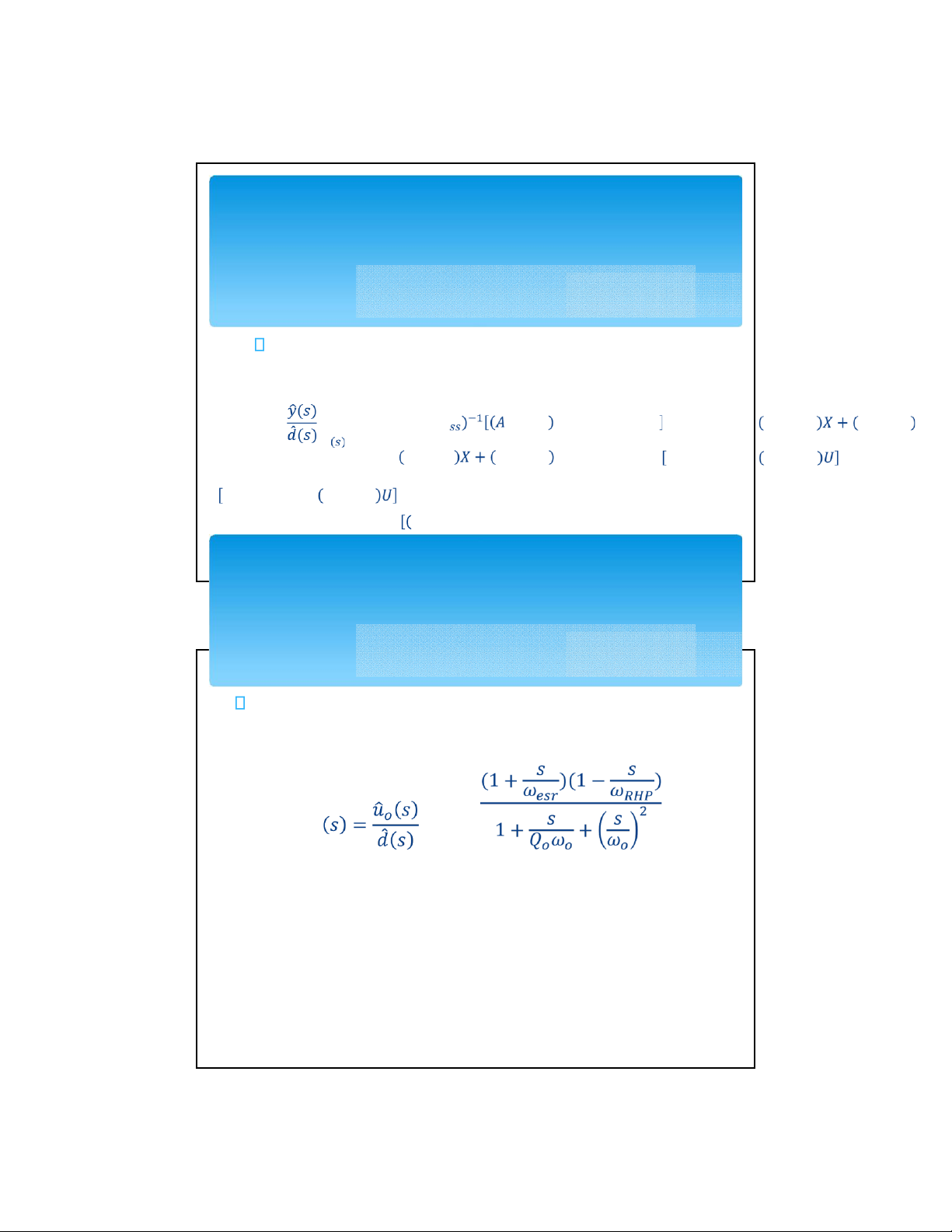
đóng mở của van và viết dưới dạng = + = + Với = và = lOMoAR cPSD| 58511332
Từ đó có thể tính được hàm truyền giữa đầu ra và
hệ số điều chế của bộ biến đổi buck boost
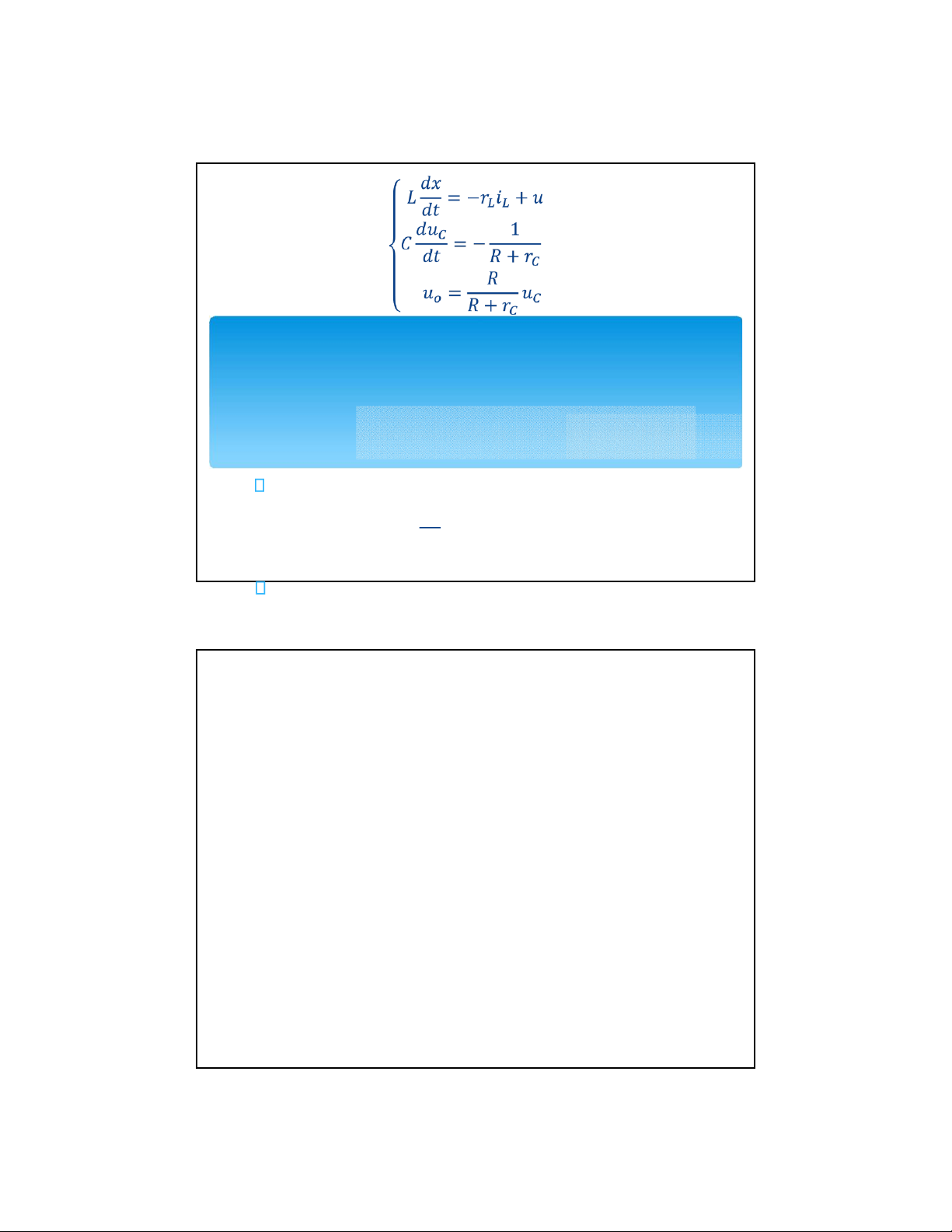
I. Mô hình hóa bộ biến đổi buck boost * Trang thái 1: V=ON D=OFF
I. Mô hình hóa bộ biến đổi buck boost
➔Dựa vào luật kirhoff xác định được hệ phương trình mạch điện như sau: lOMoAR cPSD| 58511332
I. Mô hình hóa bộ biến đổi buck boost
Viết lại hệ phương trình dạng = + = +
Từ đó ta xác định được các ma trận , , , lOMoAR cPSD| 58511332
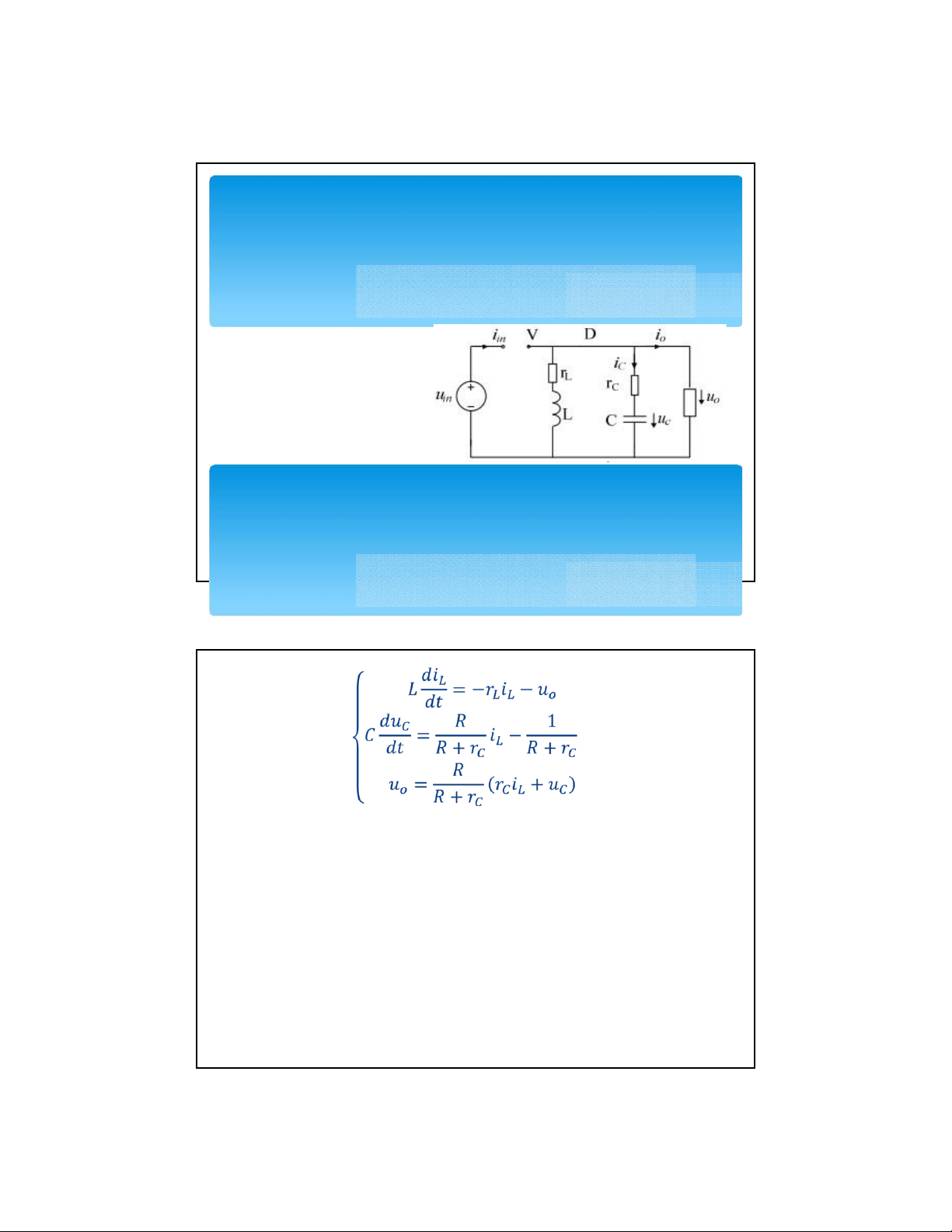
I. Mô hình hóa bộ biến đổi buck boost * Trang thái 1: V=OFF D=ON
I. Mô hình hóa bộ biến đổi buck boost
➔ Dựa vào luật kirhoff xác định được hệ phương
trình mạch điện như sau: lOMoAR cPSD| 58511332
I. Mô hình hóa bộ biến đổi buck boost
Viết lại hệ phương trình dưới dạng = + = +
Từ đó xác định được các ma trận , , ,
I. Mô hình hóa bộ biến đổi buck boost
Cuối cùng xác định được các ma trận A, B, C, D theo công thức như sau = + (1 − ) = [ + 1 − ] = [ + 1 − ] = [ + 1 − ] lOMoAR cPSD| 58511332
I. Mô hình hóa bộ biến đổi buck boost
Từ đó tính được hàm truyền đạt giữa đầu ra và hệ
số điều chế ( = 0) như sau: = ( − − − + − −
I. Mô hình hóa bộ biến đổi buck boost
Viết lại hàm truyền điện áp đầu ra và hệ số điều chế dưới dạng như sau: = lOMoAR cPSD| 58511332 lOMoAR cPSD| 58511332
I. Mô hình hóa bộ biến đổi buck boost
Độ dự trữ biên độ (GM) đặc trưng cho mức độ tiếp
cận giới hạn ổn định về phương diện biên độ.
Độ dự trữ pha (PM) đặc trưng cho mức độ tiếp cận
giới hạn ổn định về phương diện góc pha.
➔Hệ kín sẽ ổn định nếu PM và GM đều dương Hàm truyền
có tần số cắt là 7.22kHz độ dự trữ pha là
20.3 , độ dự trữ biên độ la 6.94
➔Hàm truyền có GM>0 và PM>0 nên hệ ổn định
➔Nhưng độ dự trữ pha và biên độ khá nhỏ nên cần thêm
bộ bù để tăng hệ số dự trữ pha giúp hệ thống ổn định
nhanh hơn, tín hiệu ra bám sát giá trị đặt. lOMoAR cPSD| 58511332 hay =
Do có thành phần tích phân giúp triệt tiêu sai lệch tĩnh điều chỉnh II. Thiết kế bộ bù
B ướ c 1: m ộ t đi ể m c ự c đ ặ t t ả i g ố c m ặ t ph ẳ ng ph ứ c ( m ạ ch
➔Các bước thực hiện:
vòng có chứa thành phần tích phân) Bước 2: chọn = = = 400 Bước 3: chọn = = 5305.2 Bước 4: chọn = = 1326.3 Bước 5: à
đều nhỏ hơn nên chọn các điểm cực như trên Bước 6: <= 10 Bước 7: <= 2.12kHz Bước 8: > 2 = 1.225 Chọn = 1.5 lOMoAR cPSD| 58511332 II. Thiết kế bộ bù
Từ các bước trên ta xác định được hàm
Sử dụng lệnh “[mag,phase]=bode( ,2*pi*1500)”
“[mag,phase]=bode( ,2*pi*1500)”
Từ đó xác định được biên độ của
Biên độ của bộ bù đước xác định như sau: 1 = = 46.5 lOMoAR cPSD| 58511332
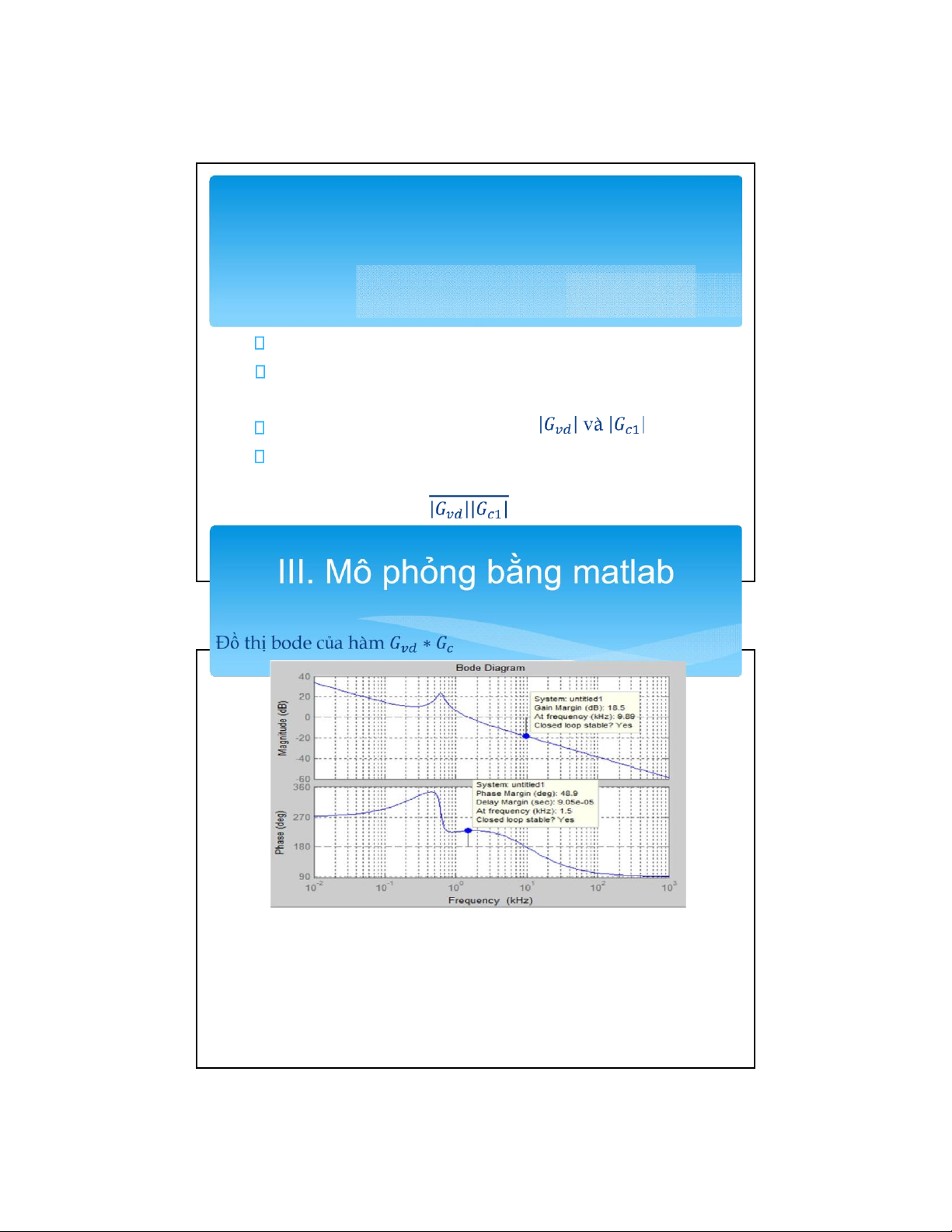
III. Mô phỏng bằng matlab Hàm truyền ∗
có tần số cắt là 1.5kHz và hệ số
dự trữ pha là 48.9 , hệ số dự trữ biên độ la 18.5
➔Độ dự trữ pha và biên độ đã khá lớn, lớn hơn so với lúc chưa có bộ bù GM: 18.5 so với 6.94 PM: 48.9 so với 20.3
III. Mô phỏng bằng matlab Code m-file trong matlab:
uin=30;u0=15;L=100e-6;C=300e-6;rc=0.1;fx=100e3;R=5;
D=u0/(u0+uin);iL=u0/((1-D)*R);
w_esr=1/(rc*C);w_RHP=R*((1-D)^2)/(L*D);
w0=(1-D)/sqrt(L*C);Q=R*(1-D)*sqrt(C/L); Gvdo=uin/((1-D)^2); fc=1500;
num1=Gvdo*[-1/(w_esr*w_RHP) (1/(w_esr)-1/(w_RHP)) 1]; den1=[1/(w0*w0) 1/(Q*w0) 1]; Gvd=tf(num1,den1);
wz1=2*pi*400;wz2=2*pi*400;wp1=w_esr;wp2=w_RHP;
num2=[1/(wz1*wz2) (1/wz1+1/wz2) 1];
den2=[1/(wp1*wp2) (1/wp1+1/wp2) 1];
Gc1=tf(num2,den2)*tf(1,[1 0]);
[mag1,phase1]=bode(Gvd,2*pi*fc);
[mag2,phase2]=bode(Gc1,2*pi*fc); kc=1/(mag1*mag2);Gc=kc*Gc1; lOMoAR cPSD| 58511332
III. Mô phỏng bằng matlab
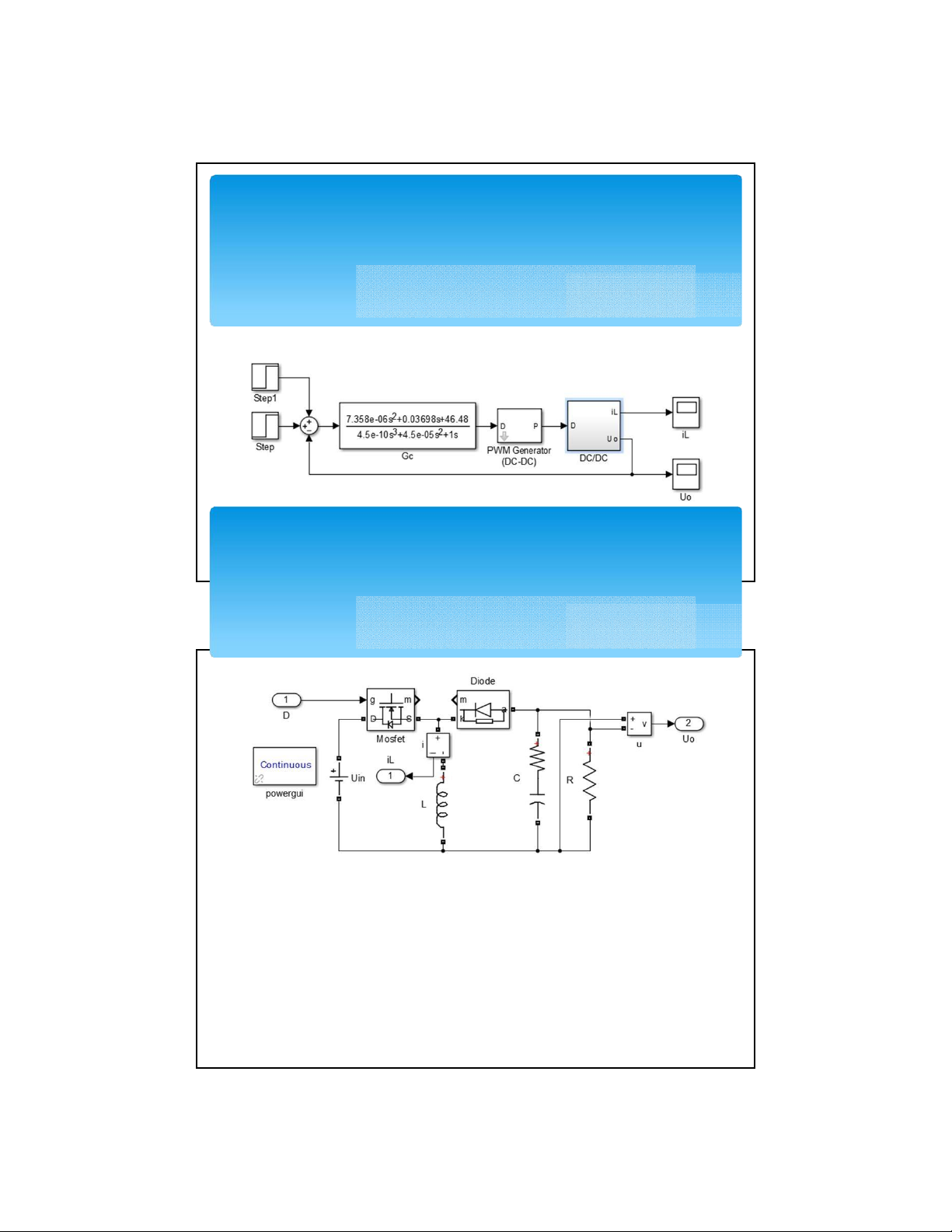
S ơ đ ồ mô ph ỏ ng simulink
III. Mô phỏng bằng matlab Kh ố i DC/DC lOMoAR cPSD| 58511332
III. Mô phỏng bằng matlab Đ ồ th ị dòng iL lOMoAR cPSD| 58511332
IV. Phân tích kết quả mô phỏng
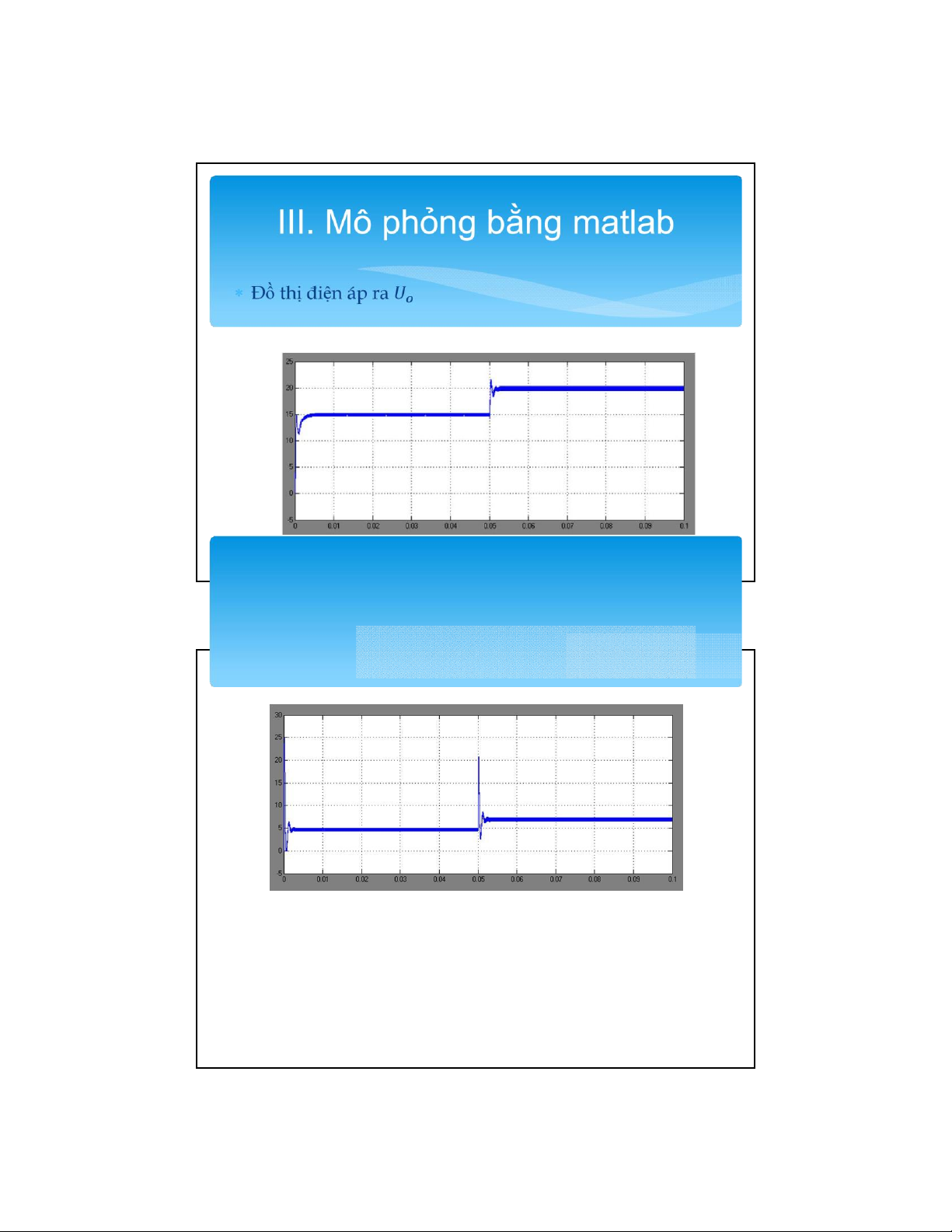
Qua đồ thị có thể thấy giá trị điện áp bám sát giá trị đặt,
có độ đập mạch từ 14.68 – 15.18V, độ đập mạch điện áp
nhỏ hơn 10% điện áp ra (15V).
Giá trị iL cũng ổn định nhưng độ quá điều chỉnh lúc ban
đầu khá lớn cần phải hiệu chinh thêm
➔bộ điều chỉnh khá ổn, khi thay đổi tải hoặc thay đổi đầu ra
thì điện áp ra vẫn bám giá trị đặt, nhưng cần có biện pháp
giảm độ quá điều chỉnh dòng iL chẳng hạn như làm trễ tín
hiệu vào, hoặc thêm bộ hạn chế dòng điện hoặc cũng có
thể chuyển sang phương pháp điều khiển theo dòng điện



