Báo cáo thí nghiệm 1: Bộ tạo sóng môn Xử lý tín hiệu số trên FPGA | Trường Đại học Bách khoa - Đại học Quốc gia Thành phố Hồ Chí Minh

ĐẠI HỌC QUỐC GIA TP HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
KHOA ĐIỆN – ĐIỆN TỬ
🙞···☼···🙜
Thí Nghiệm 1: BỘ TẠO SÓNG
MÔN: Xử Lý Tín Hiệu Số trên FPGA
Giảng viên hướng dẫn: Nguyễn Tấn Hùng
Lớp: L01 – Nhóm: 12 Danh sánh nhóm
Sinh viên thực hiện Mã số sinh viên Võ Bùi Thu Hằng 2210919 Lê Trường Thọ 2213319 Nguyễn Minh Toàn 2213534
Thành phố Hồ Chí Minh, tháng 9, năm 2024 GIỚI THIỆU
Ngày nay, với sự phát triển nhanh chóng của công nghệ điện tử và kỹ thuật số, hầu
hết các phòng thí nghiệm trong các trường cao đẳng và đại học đều được trang bị các
thiết bị hiện đại, trong đó máy tạo sóng là một trong những công cụ không thể thiếu.
Những thiết bị này có khả năng tạo ra nhiều dạng sóng cơ bản như sóng sine, sóng
vuông, sóng tam giác, sóng răng cưa, …, nhằm phục vụ cho việc kiểm tra, đo lường và
mô phỏng các hiện tượng của mạch điện. Không chỉ dừng lại ở đó, các máy này còn
cho phép người dùng điều chỉnh linh hoạt các thông số quan trọng như biên bộ, tần số
và chu kỳ xung (duty cycle). Chính sự đa dạng và khả năng tùy chỉnh cao như vậy khiến
người học như chúng em đặc ra câu hỏi: bằng cách nào một thiết bị có thể tạo ra nhiều
loại tín hiệu khác nhau như vậy? Và liệu chúng ta có thể tự mình thiết kế một hệ thống
tương tự như vậy hay không?
Xuất phát từ những thắc mắc trên, bài thí nghiệm 1 được xây dựng nhằm giúp sinh
viên tìm hiểu nguyên lý và phương pháp tạo dạng sóng. Mục tiêu chính là thiết kế và
triển khai một bộ tạo sóng trên FPGA. Máy tạo sóng cần đáp ứng khả năng tạo ra nhiều
tín hiệu khác nhau, bao gồm sóng sine, sóng vuông, sóng tam giác, sóng răng cưa và
sóng ECG. Bên cạnh đó, người thực hiện phải có thể tùy chỉnh các tham số của sóng
như biên độ, tần số và duty cycle (nếu có thể). Đặc biệt, hệ thống còn được yêu cầu tích
hợp thêm khả năng thêm nhiễu vào tín hiệu.
Qua bài thí nghiệm này, sinh viên có thể nắm và hiểu được cách thức tạo ra các dạng
sóng cơ bản bằng phần cứng số. Qua đó, giúp sinh viên có thể rèn luyện tư duy thiết kế,
khả năng xử lý, phân tích lỗi xà xây dựng mô hình phần cứng thực tế trên FPGA. BỘ TẠO SÓNG
1. Định nghĩa các dạng sóng:
Dạng sóng (waveform) là những biểu diễn đồ họa thể hiện sự thay đổi của một tín
hiệu theo thời gian. Các dạng sóng được yêu cầu thực hiện trong bài thí nhiệm 1 này
gồm có: sóng sin, sóng vuông, sóng tam giác, sóng răng cưa và sóng ECG.
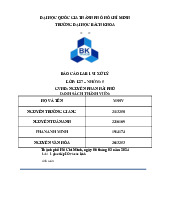
Sóng sine: là một dạng sóng tuần hoàn có biên độ thay đổi theo hàm sin hoặc cos, nó
có dạng trơn, mượt và đối xứng. Sóng sin thường xuất hiện trong các tín hiệu tự nhiên
như sao động điện, âm thanh, và gần gũi nhất là dòng điện 220V AC mà chúng ta vẫn dùng mỗi ngày.
Hình 1. Sóng sine (Sine Wave)
Sóng vuông: là một dạng sóng tuần hoàn chỉ gồm hai mức: cao và thấp. Sóng vuông
có biên đổi chuyển đổi gần như tức thời, tạo ra các cạnh lên và xuống rất dốc. Nó được
tạo thành từ rất nhiều thành phần hài bậc lẻ (thành phần tần số bậc lẻ).
Hình 2. Sóng vuông (Square Wave)
Sóng tam giác: là một dạng sóng tuyến tính lên và xuống, nó có biên độ tăng đều từ
mức thấp đến mức cao rồi giảm đều tương tự như vậy, tạo thành hình tam giác. Sóng
tam giác được tạo ra từ nhiều thành phần hài bậc lẻ như sóng vuông, nhưng có biên độ giảm nhanh.
Hình 3. Sóng tam giác (Triangle Wave)
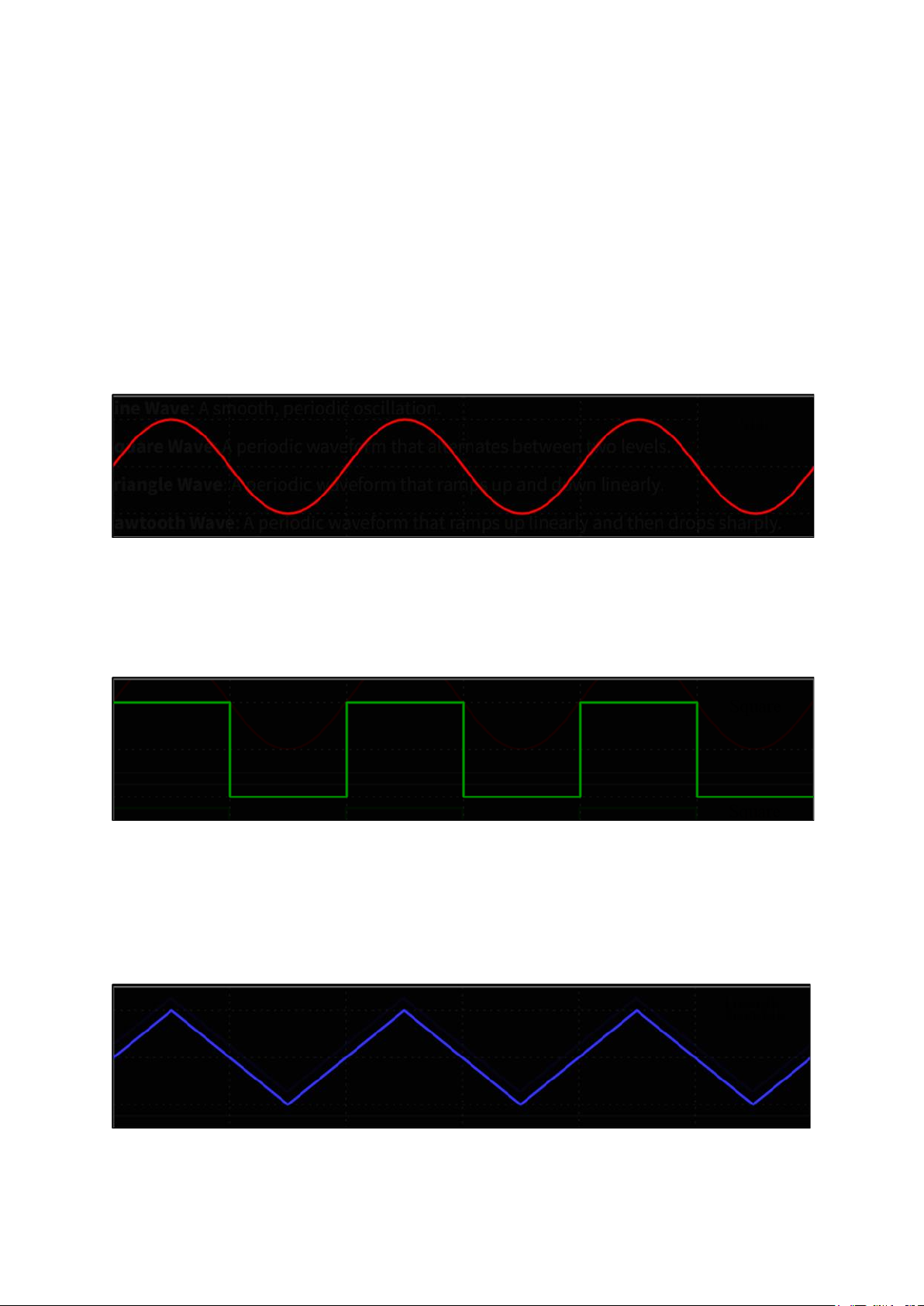
Sóng răng cưa: là một dạng sóng tăng tuyến tính rồi giảm đột ngột, nó có đặc điểm
là một cạnh lên chậm (tuyến tính) và một cạnh xuống rất nhanh. Sóng răng cưa được
tạo thành từ cả các thành phần hài bậc chẵn và lẻ.
Hình 4. Sóng răng cưa (Sawtooth Wave)
Sóng ECG: là một dạng tín hiệu sinh học ghi lại hoạt động của tim. Một chu kỳ của
sóng ECG gồm các pha đặc trưng: sóng P (khử phân cực tâm nhĩ), phức bộ QRS (khử
phân cực tâm thất), và sóng T (tái phân cực tâm thất). Sóng ECG là một dạng sóng
không đối xứng và có nhiều đỉnh đặc trưng.
Hình 5. Sóng ECG (Electrocardiogram Wave)
2. Thiết kế bộ tạo sóng:
Bộ tạo sóng của nhóm em được thiết kế theo các tiêu chí được cho ở bảng bên dưới: Loại sóng Tần số Sóng vuông 24.41 kHz Sóng tam giác 24.41 kHz Sóng răng cưa 48.83 kHz Sóng sine 97.66 kHz Sóng ECG 97.66 kHz Chức năng Chọn sóng 5 loại Thay đổi tần số f÷2, f, f×2 Thay đổi biên độ 5 mức Thêm nhiễu
Nhiễu răng cưa 390.625 kHz
Ngôn ngữ phần cứng Verilog HDL Tần số clock 50 MHz
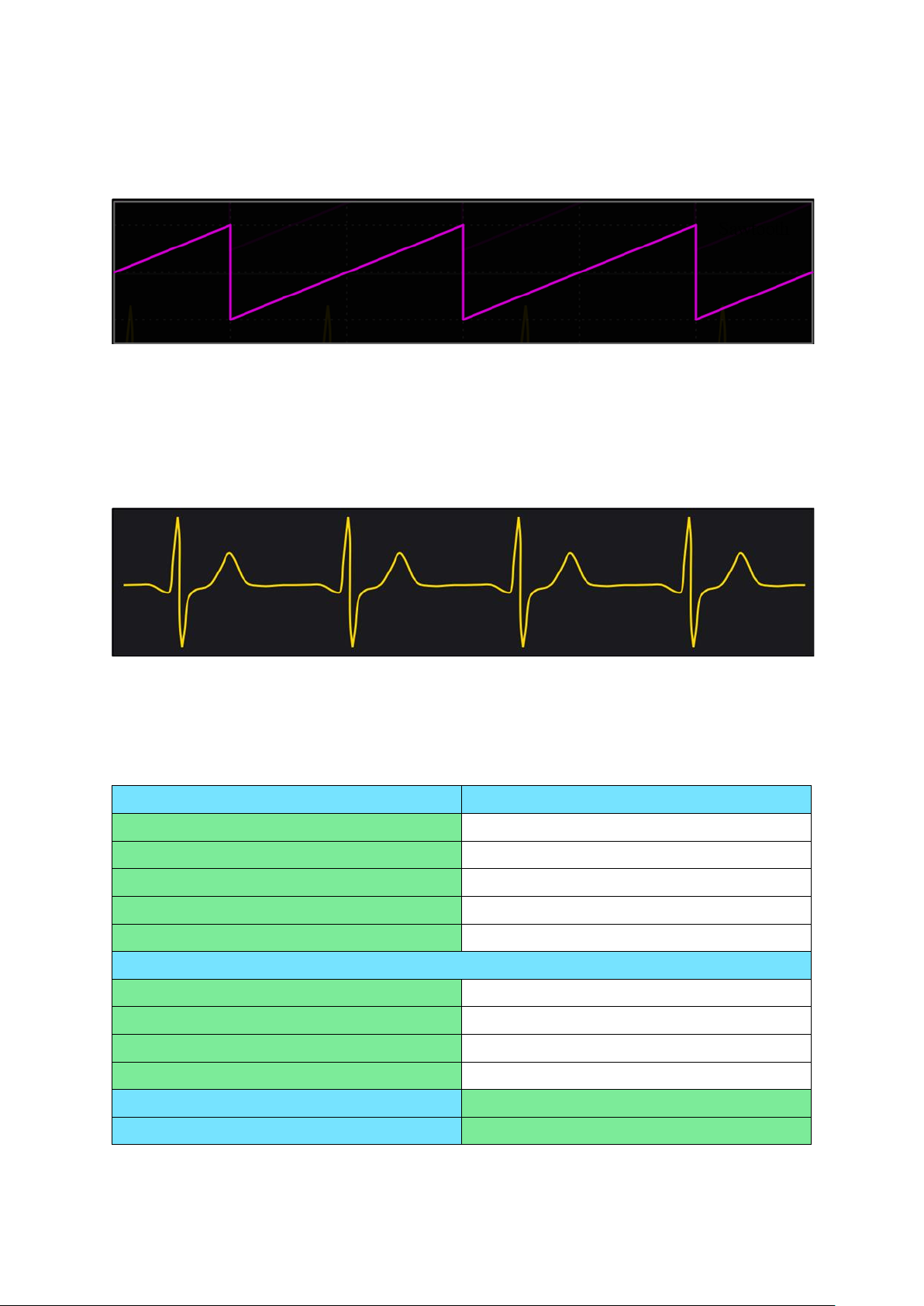
Hình 6. Sơ đồ khối của bộ tạo sóng
3. Triển khai các dạng sóng:
3.1. Sóng vuông, sóng tam giác và sóng răng cưa:
Để tạo ra sóng vuông, sóng tam giác và sóng răng cưa, nhóm em dùng phương pháp
đếm Counter. Counter là một bộ đếm nhị phân, giá trị của nó sẽ tăng theo từng cạnh lên
của xung clock, nó được dùng để xác định thời điểm thay đổi trạng thái của tín hiệu. 3.1.1. Sóng vuông:
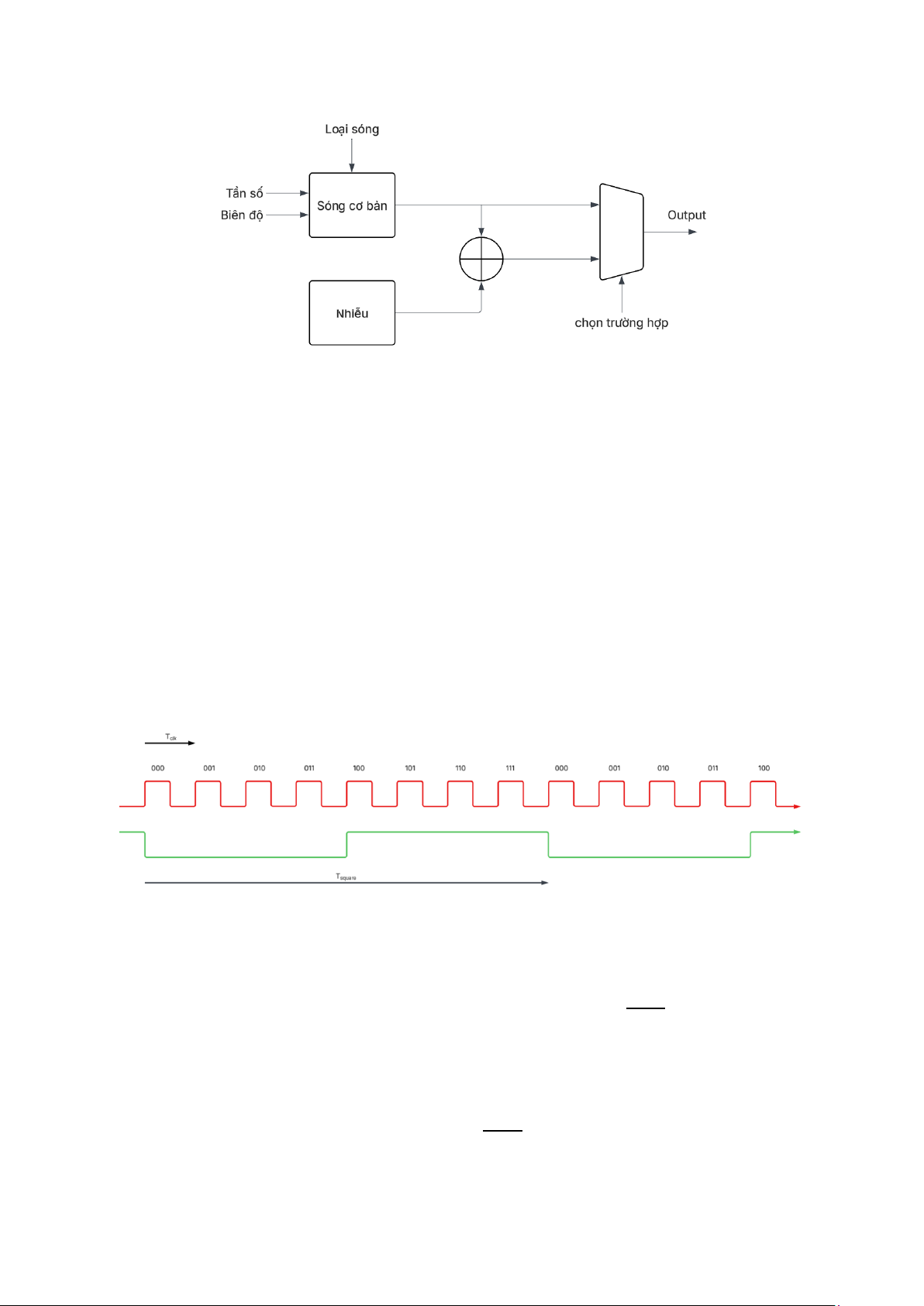
Để minh họa cách tạo ra sóng vuông, giả sử dùng 2 bit để tạo ra sóng vuông và dùng
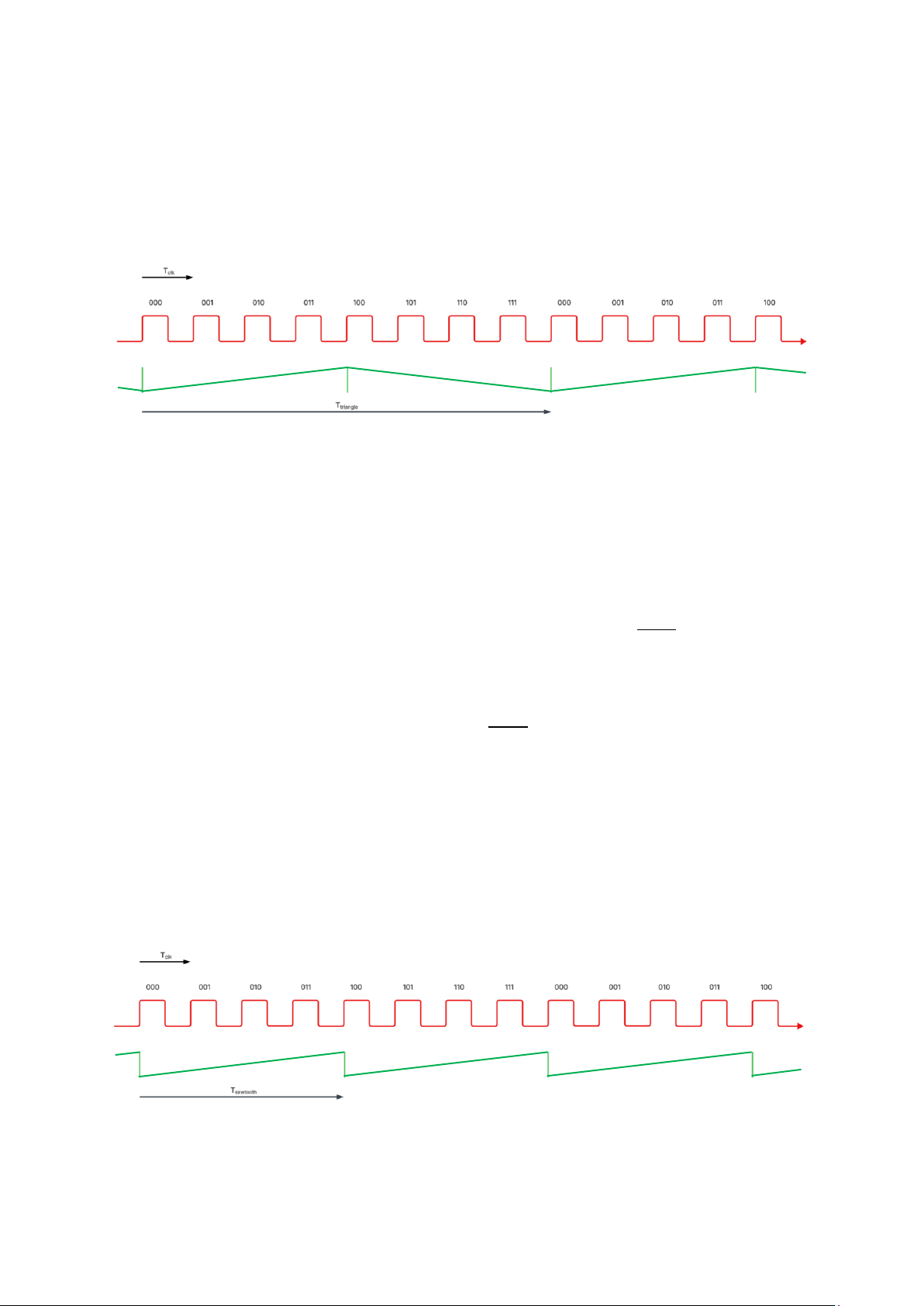
bit thứ 3 (counter[2]) của counter làm thời điểm thay đổi trạng thái của sóng vuông.
Nếu counter[2] = 0 thì sóng vuông có mức 0, ngược lại, counter[2] = 1 thì sóng vuông
có mức 1 (nguồn tham khảo [1]).
Hình 7. Minh họa cách dùng Counter để tạo sóng vuông
Từ hình minh họa, có thể rút ra mối quan hệ sau: 𝑓 𝑇 𝑐𝑙𝑘
𝑠𝑞𝑢𝑎𝑟𝑒 = 8 ∙ 𝑇𝑐𝑙𝑘 = 22+1 ∙ 𝑇𝑐𝑙𝑘 ⟺ 𝑓𝑠𝑞𝑢𝑎𝑟𝑒 = 22+1
Từ mối quan hệ trên, ta tổng quát hóa mối quan hệ giữa tần số của sóng vuông với tần số clock: 𝑓 𝑓 𝑐𝑙𝑘
𝑠𝑞𝑢𝑎𝑟𝑒 = 2𝑛+1
Với n là số bit dùng để tạo sóng vuông (sóng vuông được tạo từ n bit).
3.1.2. Sóng tam giác:
Để minh họa cách tạo sóng tam giác, giả sử dùng 2 bit để tạo sóng tam giác và dùng
bit thứ 3 của counter làm thời thời điểm thay đổi trạng thái của sóng tam giác. Nếu
counter[2] = 0 thì sóng tam giác tăng dần biên độ, ngược lại, counter[2] = 1 thì sóng
tam giác giảm dần biên độ (nguồn tham khảo [1]).
Hình 8. Minh họa cách dùng Counter để tạo sóng tam giác
Thực tế, chỉ mỗi khi có cạnh lên clock thì biên độ sóng tam giác mới tăng hoặc giảm đi
một bậc, thế nên đường cong của sóng tam giác sẽ rất gồ ghề. Vì vậy, còn sử dụng nhiều
bit để mô tả và clock tốc độ cao để nhìn dạng sóng được đẹp và mượt hơn.
Từ hình minh họa, giống sóng vuông, có được mối quan hệ sau: 𝑓 𝑇 𝑐𝑙𝑘
𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 = 8 ∙ 𝑇𝑐𝑙𝑘 = 22+1 ∙ 𝑇𝑐𝑙𝑘 ⟺ 𝑓𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 = 22+1
Tương tự như vậy, tổng quát mối quan hệ giữa tần số của sóng tam giác với tần số clock: 𝑓 𝑓 𝑐𝑙𝑘
𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 = 2𝑛+1
Với n là số bit dùng để tạo sóng tam giác (sóng tam giác được tạo từ n bit).
3.1.3. Sóng răng cưa:
Để minh họa cách tạo sóng răng cưa, tiếp tục giả sử dùng 2 bit để tạo sóng răng cưa.
Counter đếm tăng dần thì biên độ sóng răng cưa cũng tăng dần, do chỉ sử dụng 2 bit để
mô tả, khi bit thứ 3 của counter được đếm, biên độ của sóng răng về 0 do bị tràn bit (nguồn tham khảo [1]).
Hình 9. Minh họa cách dùng Counter để tạo sóng răng cưa
Tương tự như sóng tam giác, thực tế, chỉ mỗi khi có cạnh lên của clock thì biên độ của
sóng răng cưa mới tăng. Vì vậy còn dùng nhiều bit để mô tả và clock tốc độ cao để sóng
răng cưa được đẹp và mượt hơn.
Từ hình minh họa, có thể rút ra mối quan hệ sau: 𝑓 𝑇 𝑐𝑙𝑘
𝑠𝑎𝑤𝑡𝑜𝑜𝑡ℎ = 4 ∙ 𝑇𝑐𝑙𝑘 = 22 ∙ 𝑇𝑐𝑙𝑘 ⟺ 𝑓𝑠𝑎𝑤𝑡𝑜ọ𝑡ℎ = 22
Từ mối quan hệ trên, ta tổng quát hóa mối quan hệ giữa tần số sóng răng cưa với tần số clock: 𝑓 𝑓 𝑐𝑙𝑘
𝑠𝑎𝑤𝑡𝑜𝑜𝑡ℎ = 2𝑛
Với n là số bit dùng để tạo sóng răng cưa (sóng răng cưa được tạo từ n bit).
3.1.4. Tần số sóng vuông, sóng tam giác và sóng răng cưa:
Sử dụng 10 bit (n=10) và tần số clock 50 MHz để tạo sóng vuông, sóng tam giác và
sóng răng cưa, áp dụng các mối quan vừa tìm được ở trên, ta có tần số của các sóng là: Loại sóng Tần số Sóng vuông 24.41 kHz Sóng tam giác 24.41 kHz Sóng răng cưa 48.83 kHz
3.2. Sóng sine và sóng ECG:
Để tạo sóng sine và sóng ECG, nhóm em sử dùng phần mềm Matlab. Đây là một
công cụ mạnh, nó cho phép tạo và xuất các giá trị sóng sine, sóng ECG ra file text. 3.2.1. Sóng sine:
Để có được file text các giá trị của dạng sóng sine 10 bit bằng cách sử dụng matlab, ta làm theo các cách sau:
Một hàm sine, như đã biết, có giá trị như sau: −1 ≤ sin(𝑥) ≤ 1
Để hàm sine không có giá trị âm và chỉ thuộc khoảng từ 0 đến 1, ta cộng thêm 1 vào
hàm sine và chia tất cả cho 2: sin(𝑥) + 1 0 ≤ ≤ 1 2
Sau các bước trên, sóng sine đã có giá trị trong khoảng [0; 1]. Trong khi đó, một sóng
sine 10 bit có giá trị bé nhất là 0 và lớn nhất là 210 − 1 = 1023. Vì vậy, ta nhân biểu
thức trên với 1023 để có được sóng sine được biểu diễn theo 10 bit. sin(𝑥) + 1 0 ≤ × 1023 ≤ 1023 2
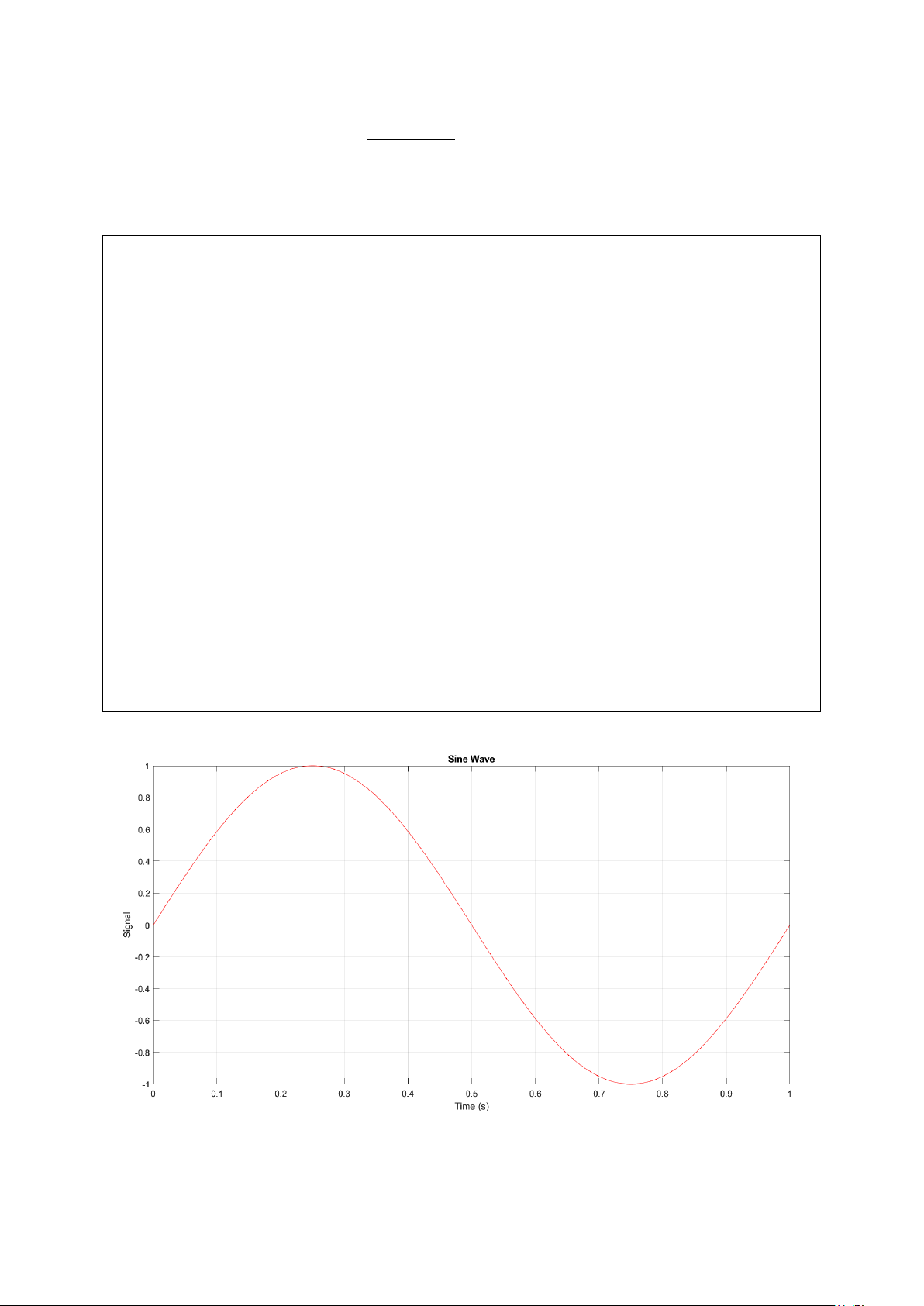
Viết chương trình trên Matlab, tạo một sóng sine có 512 mẫu, từ đó xuất ra file text lưu
các giá trị của sóng sine dùng 10 bit: % số mẫu: N = 512; % tạo sóng sine: t = 0:1/N:1; y = sin(2*pi*t); h = figure('color', [1 1 1]); plot(t, y, 'r'); grid on; title('Sine Wave'); ylabel('Signal'); xlabel('Time (s)');
% chuẩn hóa sóng sine về [0:1]: y_norm = (y + 1)/2;
% chuyển sóng sine sang sóng sine 10 bit:
y_10bit = round(y_norm * 1023); % xuất file text:
fid = fopen('sin_table.txt','w'); n = length(y_10bit); for k = 1:n index = k - 1;
fprintf(fid, "mem[%d] <= 10'h%X;\n", index, y_10bit(k)); end fclose(fid);
Hình 10. Sóng sine được tạo bởi Matlab 3.2.2. Sóng ECG:
Đối với sóng ECG, sử dụng Matlab, viết chương trình các biểu thức mô phỏng các
pha đặc trưng PQRST của sóng ECG. Sau đó chuẩn hóa nó về khoảng [0; 1] và nhân
với 1023 để chuyển nó về dạng 10 bit.
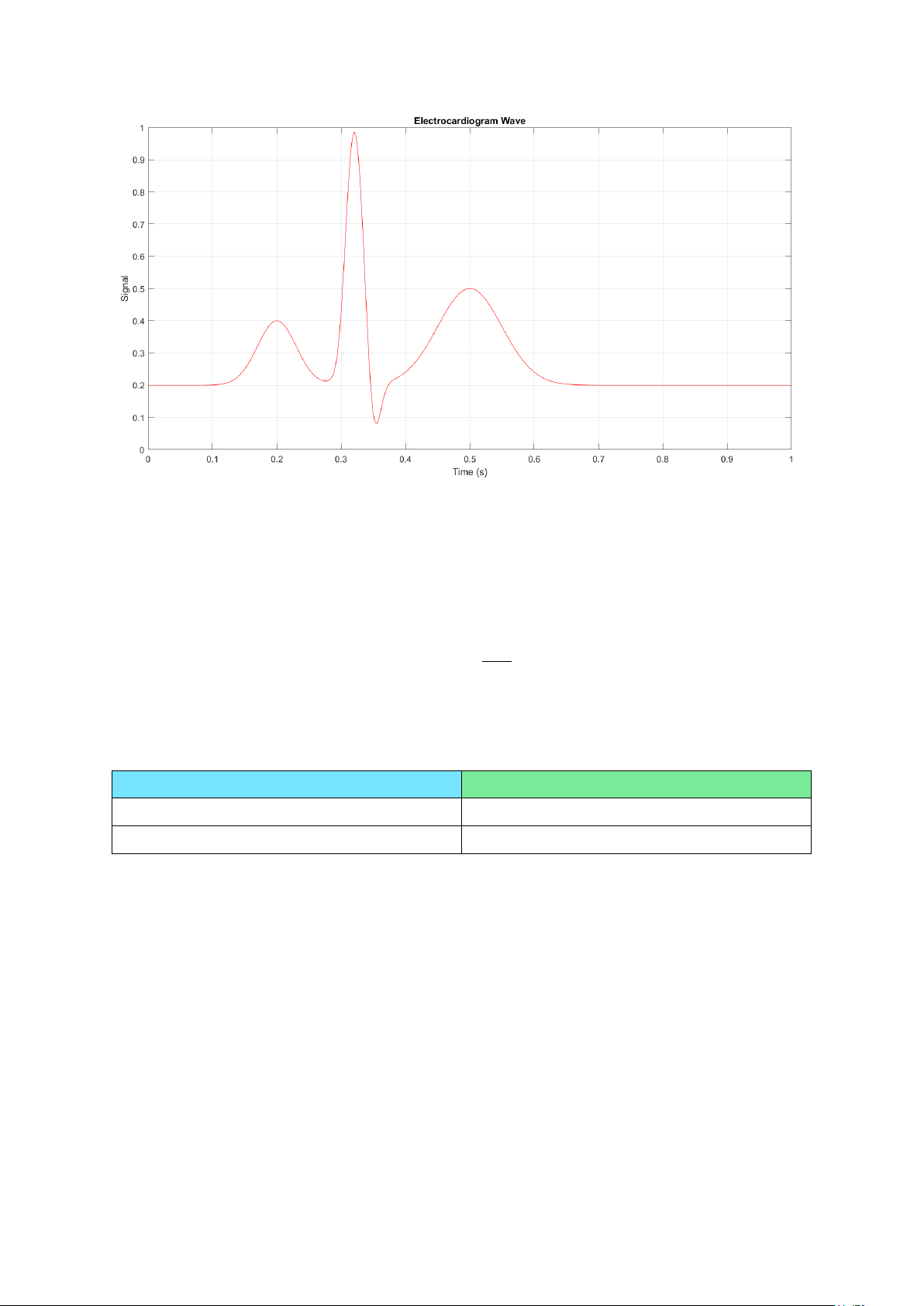
Viết chương trình Matlab, tạo sóng ECG có 512 mẫu, từ đó xuất ra file text lưu các giá
trị cúa sóng ECG dùng 10 bit: % số mẫu: N = 512; % tạo sóng ECG: t = 0:1/N:1;
P = 0.2*exp(-((t-0.2).^2)/(2*0.03^2));
Q = -0.1*exp(-((t-0.3).^2)/(2*0.01^2));
R = 0.8*exp(-((t-0.32).^2)/(2*0.015^2));
S = -0.2*exp(-((t-0.35).^2)/(2*0.01^2));
T = 0.3*exp(-((t-0.5).^2)/(2*0.05^2));
ecg_beat = P + Q + R + S + T + 0.2; % +0.2 là để sóng thuộc [0:1] figure('color', [1 1 1]);
plot(t, ecg_beat,'r'); grid on;
title('Electrocardiogram Wave'); ylabel('Signal'); xlabel('Time (s)');
% chuẩn hóa sóng ECG [0:1]:
ecg_norm = (ecg_beat - min(ecg_beat)) / (max(ecg_beat) - min(ecg_beat));
% chuyển sóng ECG sang 10-bit:
ecg_10bit = round(ecg_norm * 1023); % xuất file text:
fid = fopen('ecg_table.txt','w'); n = length(ecg_10bit); for k = 1:n index = k - 1;
fprintf(fid, "mem[%d] <= 10'h%X;\n", index, ecg_10bit(k)); end fclose(fid);
Hình 11. Sóng ECG được tạo bởi Matlab
3.2.3. Tần số sóng sine và sóng ECG:
Số mẫu được lấy cho sóng sine và sóng ECG là 512 mẫu, tần số clock được dùng là
50 MHz, vậy tần số của hai sóng này được cho bởi công thức: 𝑓 𝑓 𝑐𝑙𝑘 𝑤𝑎𝑣𝑒 = 𝑁
Với N là số mẫu được lấy của sóng.
Từ đây, ta tính được tần số của sóng sine và sóng ECG là: Loại sóng Tần số Sóng sine 97.66 kHz Sóng tam giác 97.66 kHz
4. Triển khai các chức năng của bộ tạo sóng:
4.1. Tần số:
Để thay đổi tần số của sóng, ta chỉ cần thay đổi tốc độ tăng của counter. Ví dụ, nếu
muốn tần số tăng gấp đôi, ta chỉ cần tăng counter từ tăng 1 mỗi khi có cạnh lên, thành
tăng 2 mỗi khi có cạnh lên.
Bây giờ, câu hỏi đặt ra ở đây là: “làm thế nào để giảm tần số đi một nữa?”. Ta không
thể để counter tăng 0,5 mỗi khi có cạnh lên được vì ngôn ngữ Verilog chỉ hỗ trợ số nguyên.
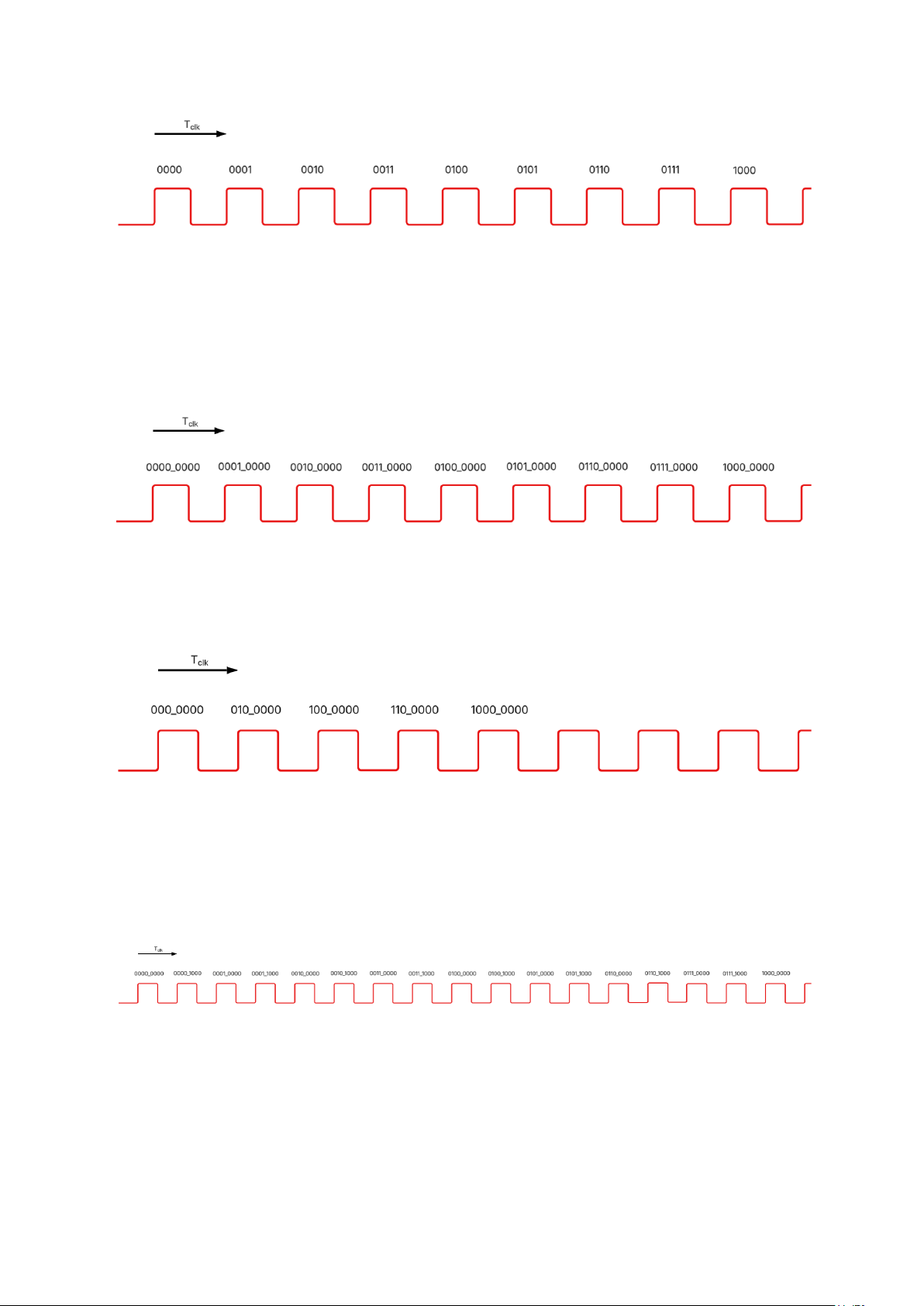
Để giải quyết vấn đề này, giả sử, ban đầu counter có 4 bit (counter[3:0]) và tăng 1 khi
có cạnh lên của clock, khi này ta tính thời gian để counter đạt giá trị là 1000.
Hình 12. Minh họa Counter tăng 1 mỗi cạnh lên của clock
Từ hình có thể thấy, thời gian để counter đạt giá trị 1000 là 8𝑇 (tính cả clock 0). 𝑐𝑙𝑘
Giờ ta hãy tăng counter thêm 4 bit, 4 bit này có mục đích duy nhất là để đếm mỗi khi
có clock cạnh lên, 4 bit ban đầu vẫn là 4 bit chính ta quan tâm. Để counter vẫn đạt được
giá trị 1000 sau 8𝑇 , thì mỗi khi có cạnh lên counter còn tăng 16 (tức 0001_0000). 𝑐𝑙𝑘
Hình 13. Minh họa Counter tăng 16 mỗi cạnh lên của clock
Nếu bây giờ counter tăng 32 (tức 0010_0000) mỗi cạnh lên của clock, tính thời gian để
counter đạt giá trị 1000.
Hình 14. Minh họa Counter tăng 32 mỗi cạnh lên của clock
Từ hình minh họa, có thể thấy, chỉ cần 4𝑇 thì counter đã đạt giá trị 1000. 𝑐𝑙𝑘
Nếu bây giờ counter tăng 8 (tức 0000_1000) mỗi cạnh lên của clock, tính thời gian để
counter đạt giá trị 1000.
Hình 15. Minh họa Counter tăng 8 mỗi cạnh lên của clock
Từ hình minh họa, có thể thấy, cần mất tận 16𝑇 thì counter mới đat được giá trị 1000. 𝑐𝑙𝑘
Kết luận lại, để có thể tăng tần số sóng lên gấp đôi hoặc giảm tần số sóng đi một nửa,
ta cần phải thêm còn 4 bit đếm vào counter. Dưới đây là bảng tóm tắt việc tăng counter
trên mỗi clock ảnh hưởng đến tần số của sóng: Tăng 8/clock Tăng 16/clock Tăng 32/clock 𝑓 ÷ 2 𝑓 𝑓 × 2
4.2. Biên độ:
Để thay đổi biên độ của sóng, ta chỉ cần nhân sóng với một hệ số bé hơn 1. Lấy một
ví dụ đơn giản, gọi A là biên độ của một hàm sine, chọn một hệ số bất kỳ, ví dụ là 2,
vậy ta có thể có các giá trị biên độ của hàm sine là: 0 1 𝐴 2 𝐴 × = 0 𝐴 × = 𝐴 × = 𝐴 2 2 2 2
Tổng quát hơn nếu ta chọn hệ số càng lớn, thì ta càng có thể phân chia biên độ của một
dạng sóng ra càng nhiều. Lấy một ví dụ nữa, nếu ta chọn hệ số là 16, thì ta có thể phân
chia biên độ của một sóng ra 16 phần (xem như không tính phần 0). A/16 A/8 3A/16 A/4 5A/16 3A/8 7A/16 A/2 9A/16 5A/8 11A/16 3A/4 13A/16 7A/8 15A/16 A
Nhóm em thiết kế cho phép chỉnh biên độ theo bảng bên dưới: Mức biên độ Mức 1 Mức 2 Mức 3 Mức 4 Mức 5 4A/16 8A/16 12A/16 15A/16 A 4.3. Nhiễu:
Nhiễu của nhóm em là một sóng răng cưa dùng 7 bit, có tần số 390.625 kHz. Nhiễu
này được tạo ra trực tiếp từ phần cứng (code Verilog) giống như các dạng sóng vuông,
sóng tam giác và sóng răng cưa bên trên.
Tuy nhiên, nhiễu được tạo ra bằng phương pháp đếm counter chỉ có giá trị từ 0 đến
27 − 1 = 127. Điều này làm cho khi thêm nhiễu vào tín hiệu thì nó chỉ có thể làm biên
độ tín hiệu tăng. Muốn cho nhiễu vừa có thể làm giảm và tăng biên độ của sóng thì
nhóm em cần chuyển nhiễu về dạng số bù 2.
Đầu tiên cần thêm 1 bit vào thanh ghi chứ nhiễu để làm bit dấu, sau đó lấy toàn bộ thanh
ghi này trừ đi cho 26 = 64. Đến đây, nhóm em đã có nhiễu sóng răng cưa có giá trị từ -64 đến 63.
Bảng các thông số nhiễu được tóm tắt ở bảng bên dưới: Nhiễu Loại Tần số Giá trị Sóng răng cưa 390.625 kHz −64 đến 63
5. Mô phỏng bộ tạo sóng:
5.1. Kết quả mô phỏng bộ tạo sóng:
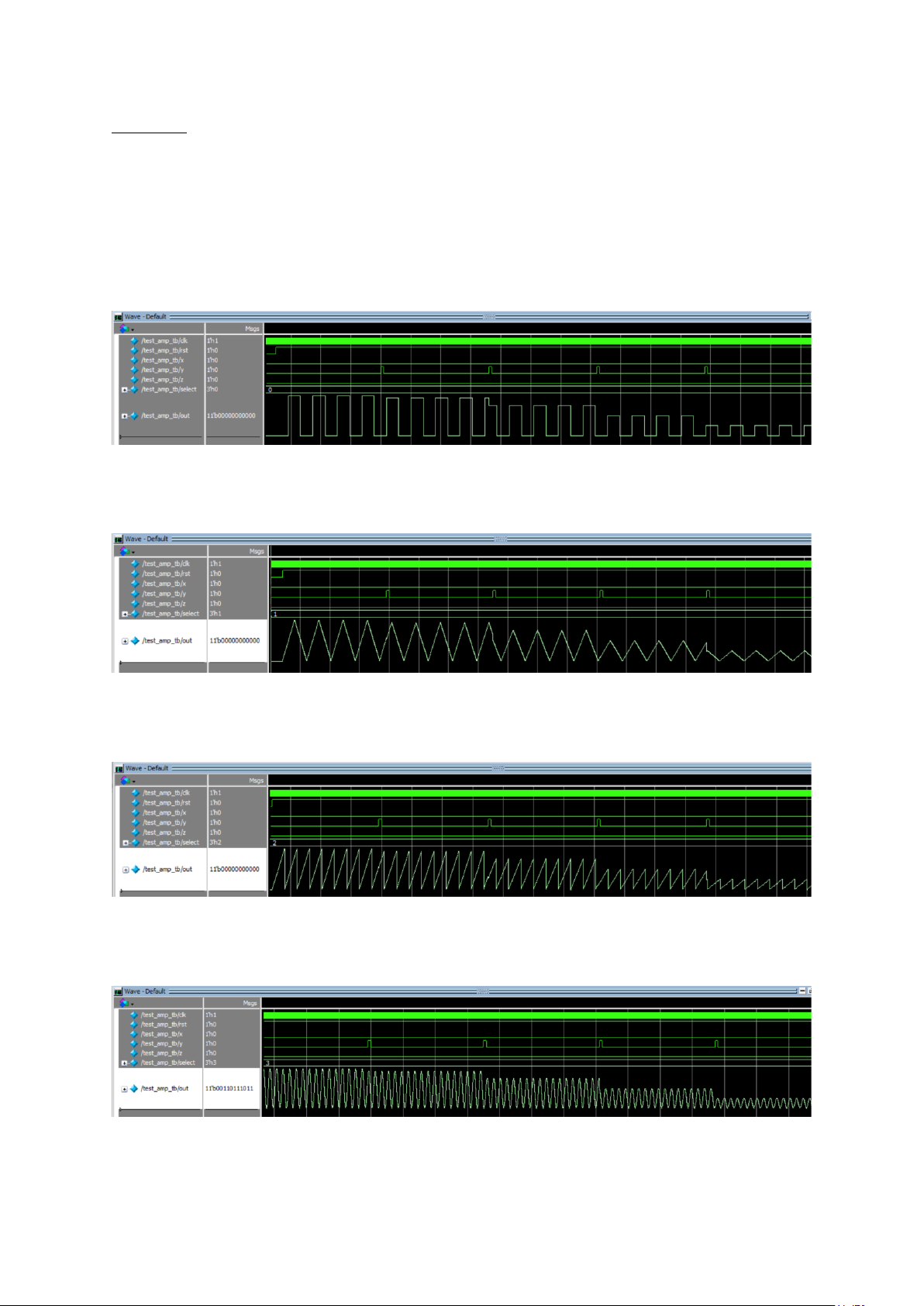
5.1.1. Các dạng sóng:
Các dạng sóng được tạo bởi bộ tạo sóng: - Sóng vuông:
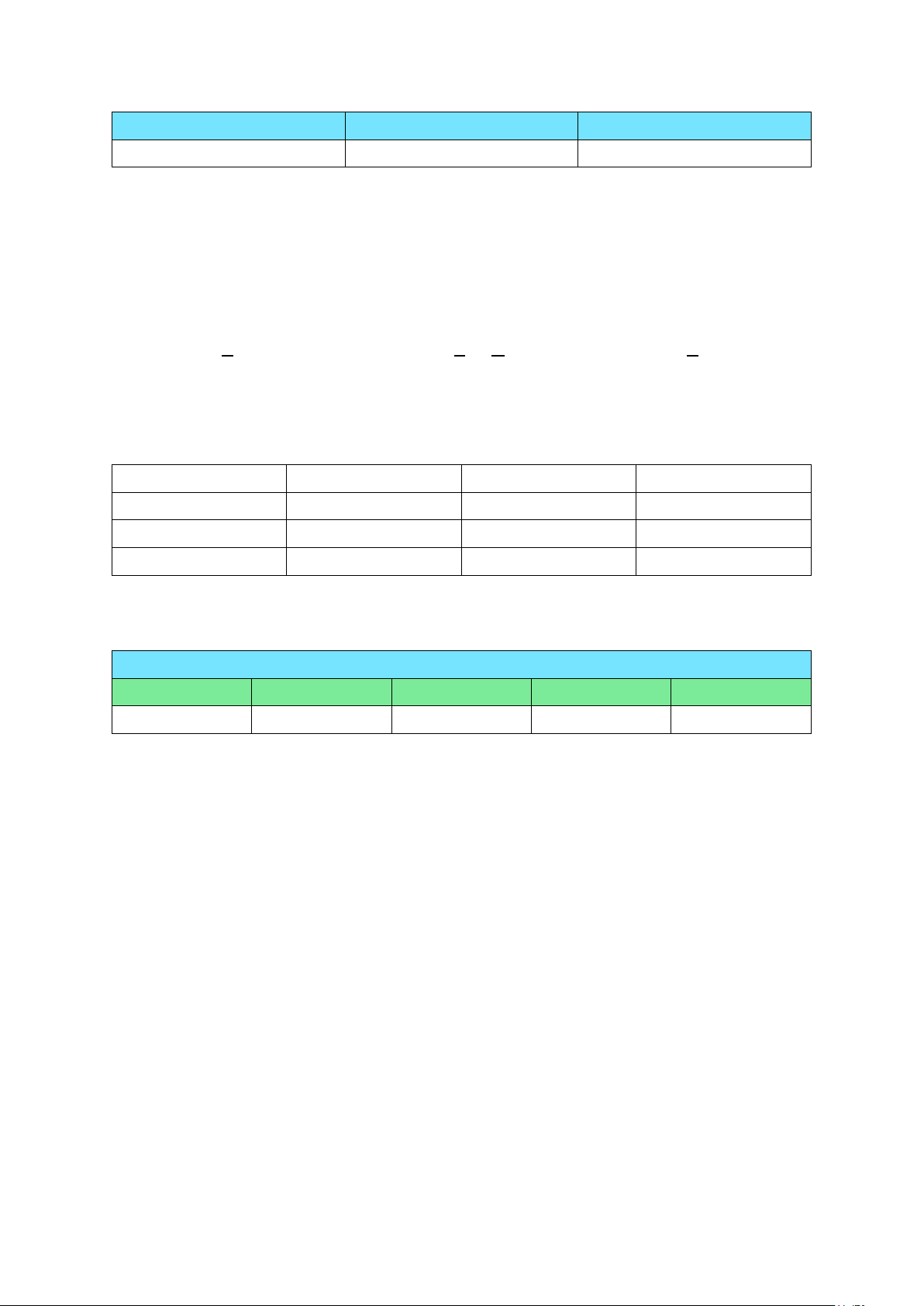
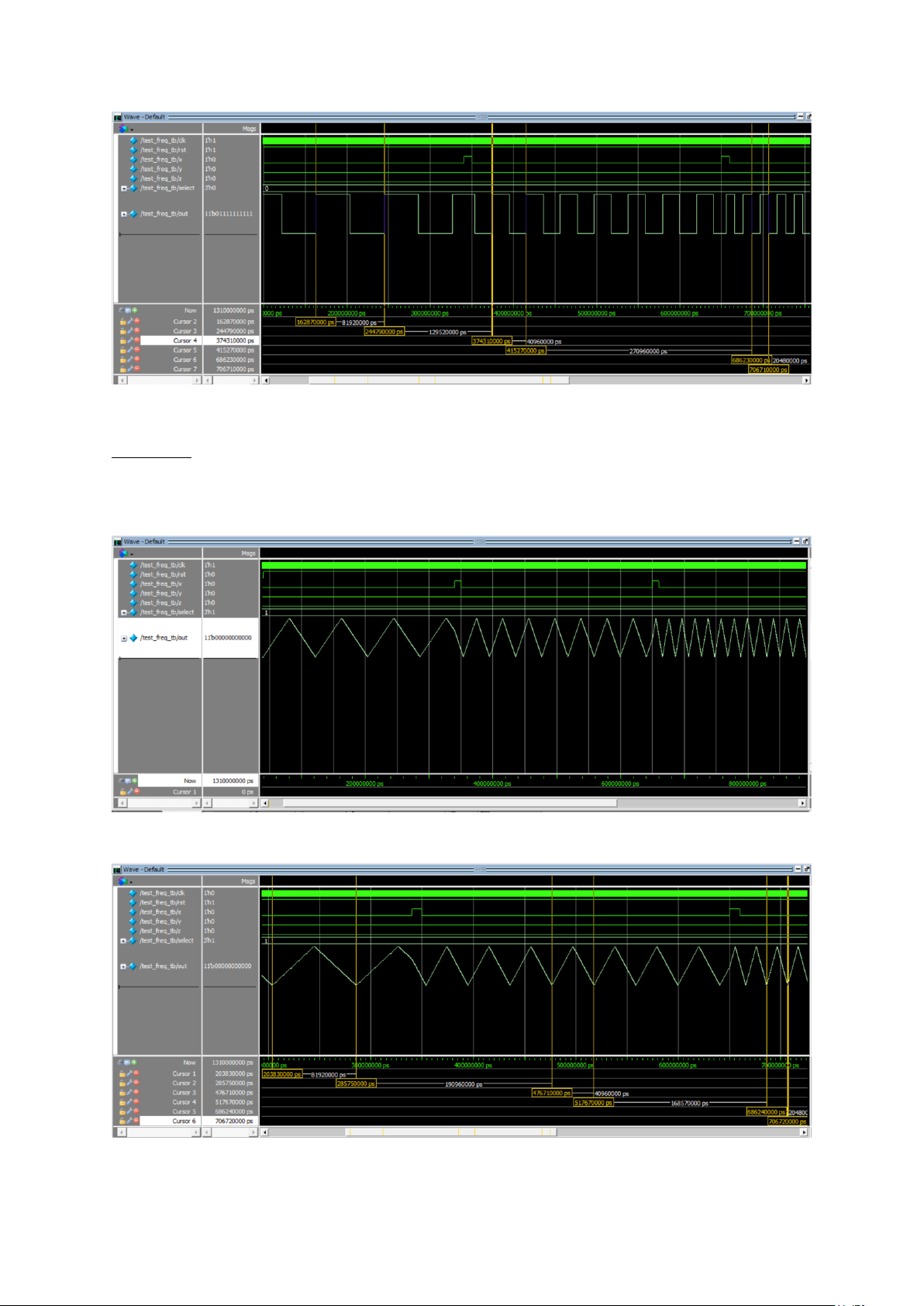
Hình 16. Sóng vuông tạo bởi bộ tạo sóng
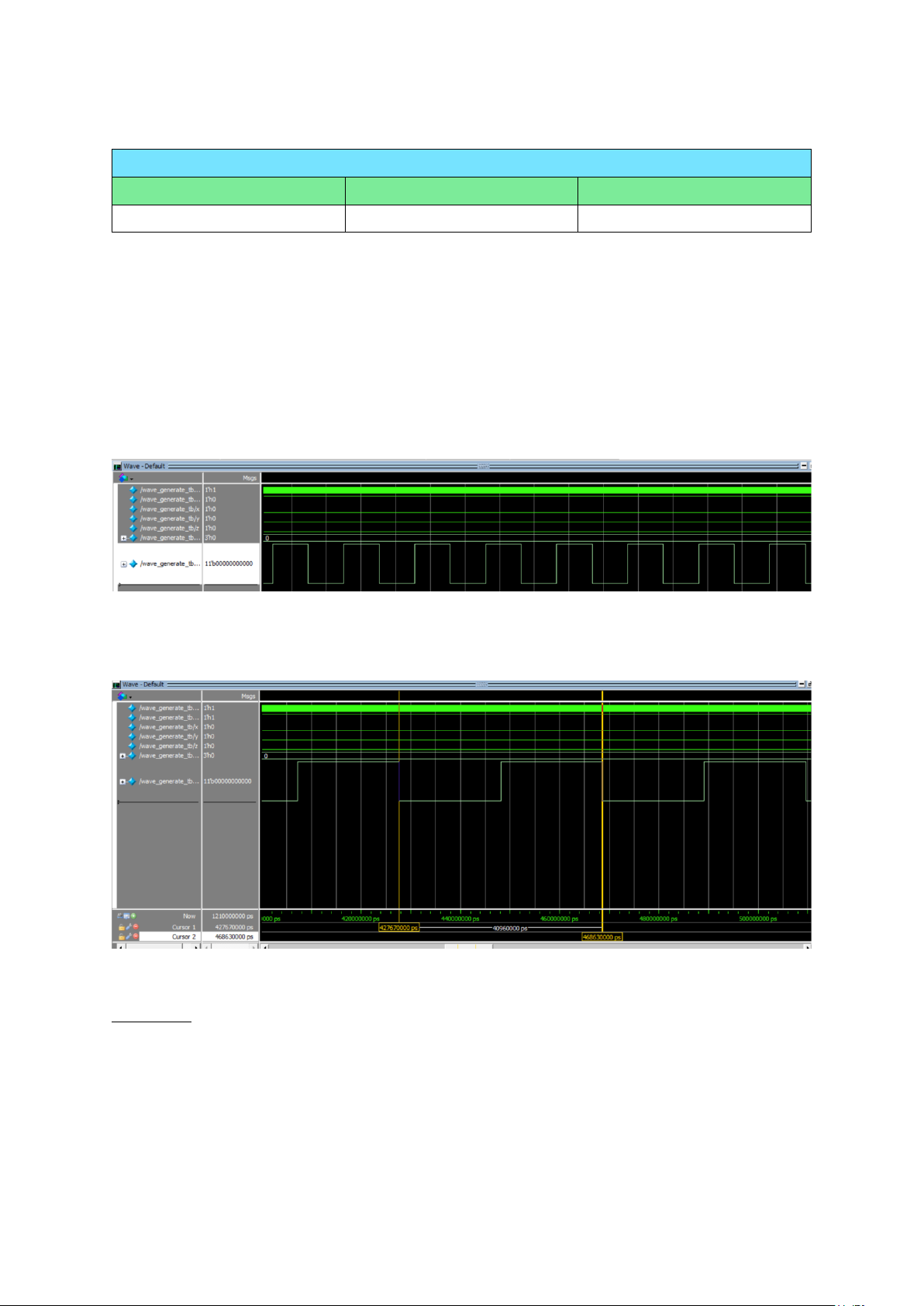
Hình 17. Kiểm tra tần số sóng vuông
Nhận xét: sóng vuông được tạo từ bộ tạo sóng rất đẹp và đúng với định nghĩa, tần số
đúng theo tính toán là 24.41 kHz - Sóng tam giác:
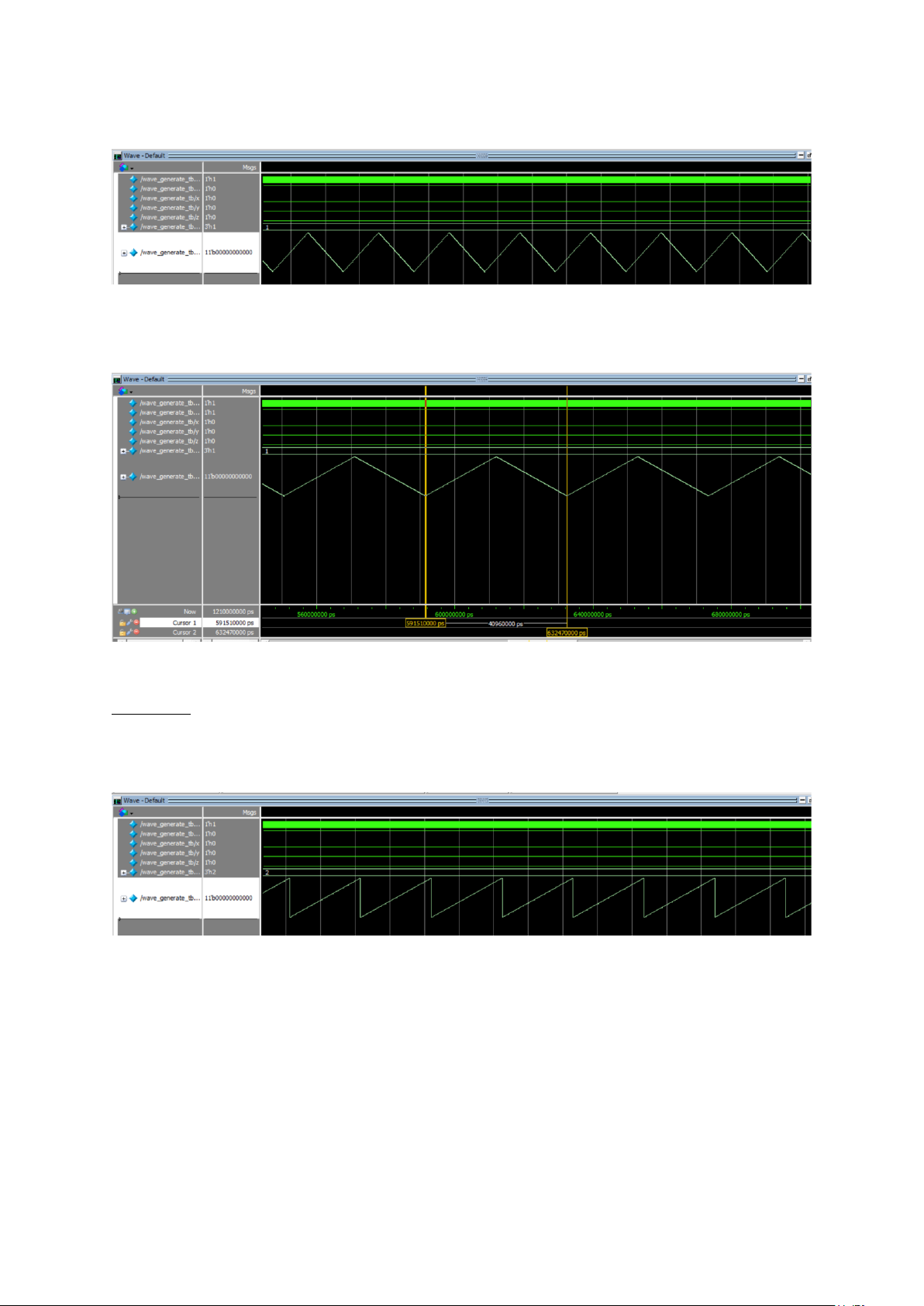
Hình 18. Sóng tam giác tạo bởi bộ tạo sóng
Hình 19. Kiểm tra tần số sóng tam giác
Nhận xét: sóng tam giác được tạo từ bộ tạo sóng rất đẹp và đúng với định nghĩa, tần số
sóng đúng theo tính toán là 24.41 kHz. - Sóng răng cưa:
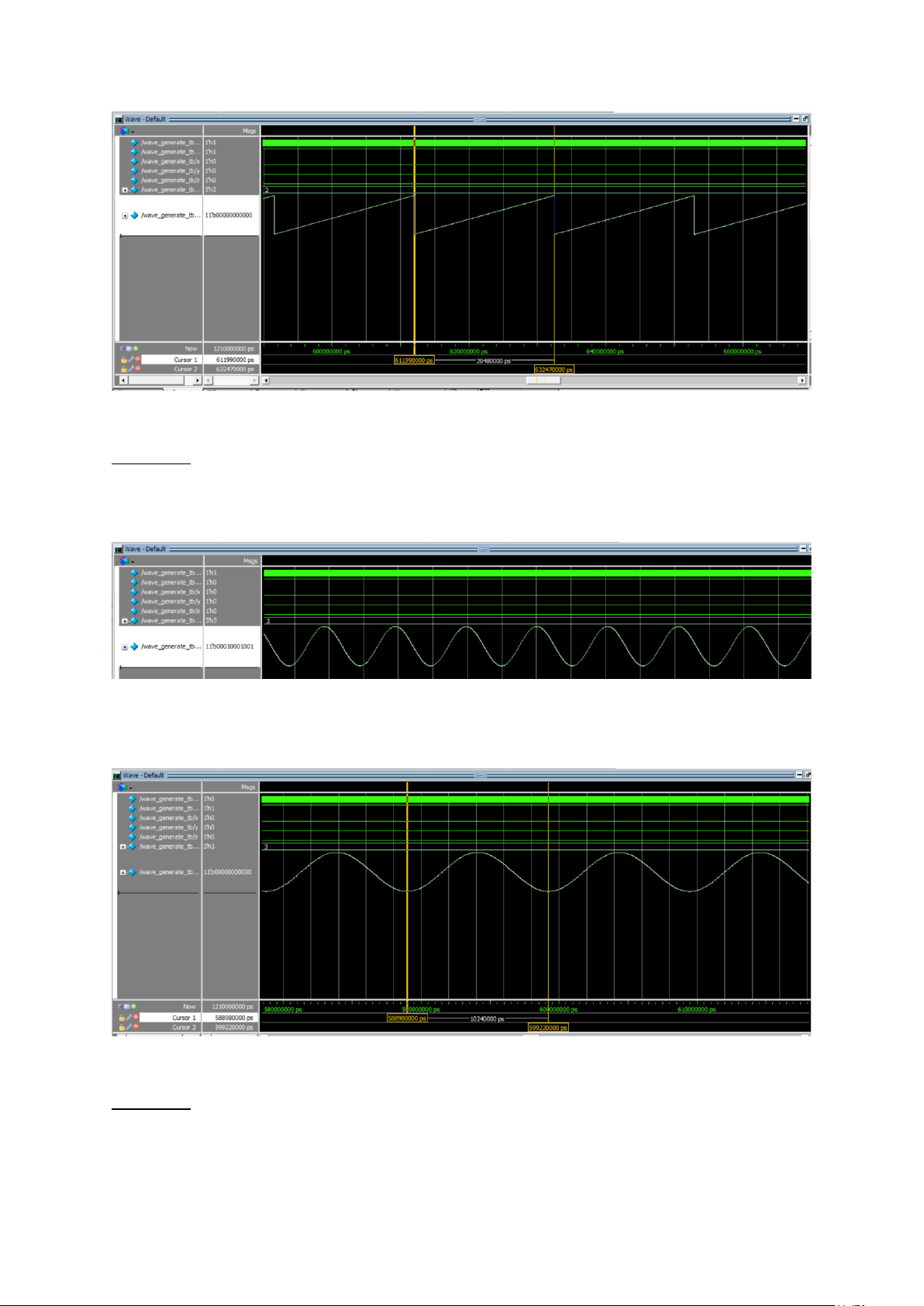
Hình 20. Sóng răng cưa tạo bởi bộ tạo sóng
Hình 21. Kiểm tra tần số sóng răng cưa
Nhận xét: sóng răng cưa được tạo từ bộ tạo sóng rất đẹp và đúng với định nghĩa, tần số
sóng đúng với tính toán là 48.83 kHz. - Sóng sine:
Hình 22. Sóng sine tạo bởi bộ tạo sóng
Hình 23. Kiểm tra tần số sóng sine
Nhận xét: sóng sine được tạo từ bộ tạo sóng rất đẹp, mượt và đúng với định nghĩa, tần
số sóng đúng với tính toán là 97.66 kHz. - Sóng ECG:
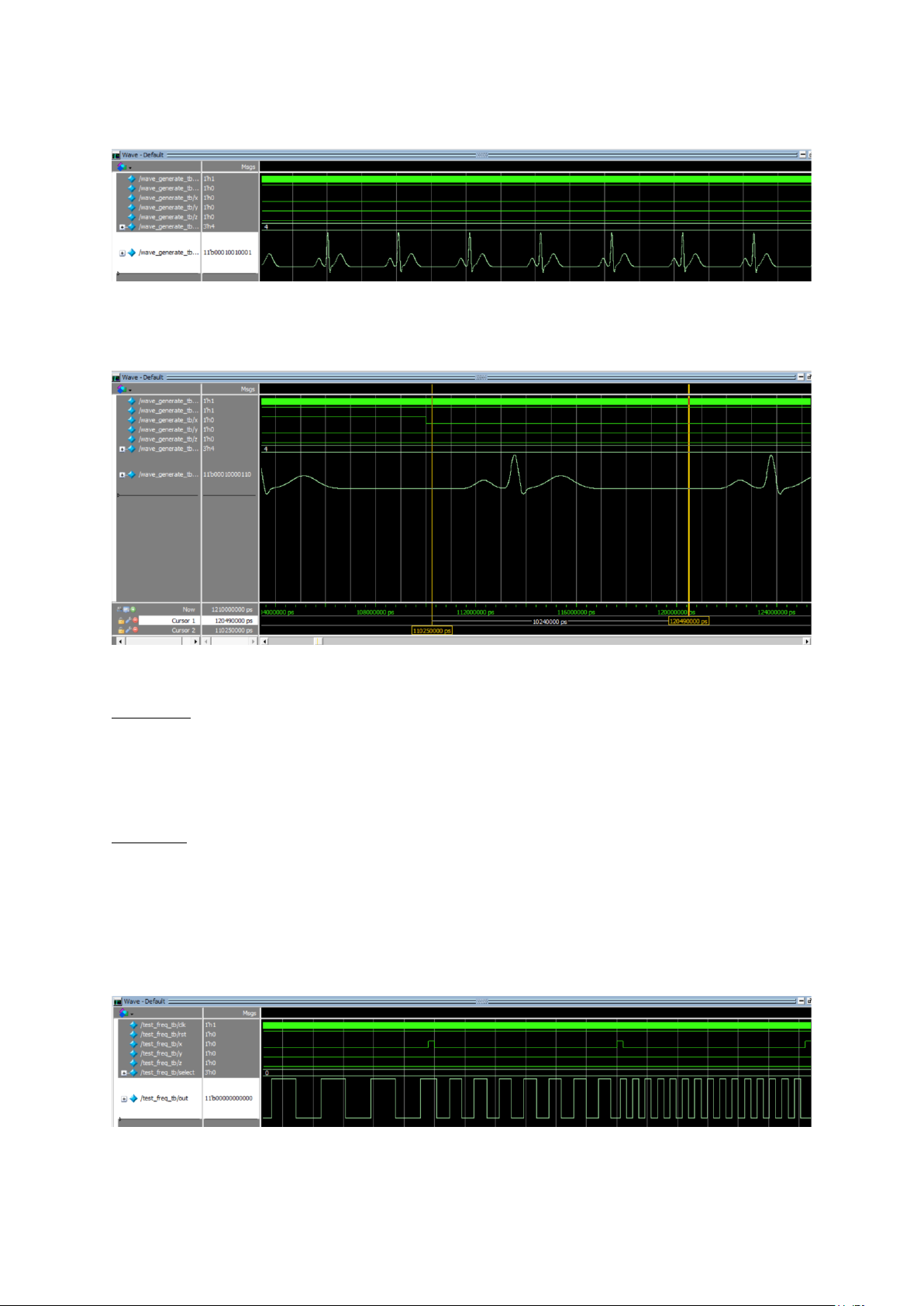
Hình 24. Sóng ECG tạo bởi bộ tạo sóng
Hình 25. Kiểm tra tần số sóng ECG
Nhận xét: sóng ECG được tạo từ bộ tạo sóng mặc dù nhìn đẹp nhưng khi phóng to thì
xuất hiện khá rõ các hình bậc thang, sóng có hình dạng khá giống với định nghĩa, tần
số sóng đúng tới tính toán là 97.66 kHz. Kết luận:
Bộ tạo sóng đã tạo được đúng các dạng sóng với tần số chuẩn đúng với yêu cầu ban
đầu đặt ra. Hình dạng của các sóng đẹp và đúng với định nghĩa.
5.1.2. Thay đổi tần số các dạng sóng: - Sóng vuông:
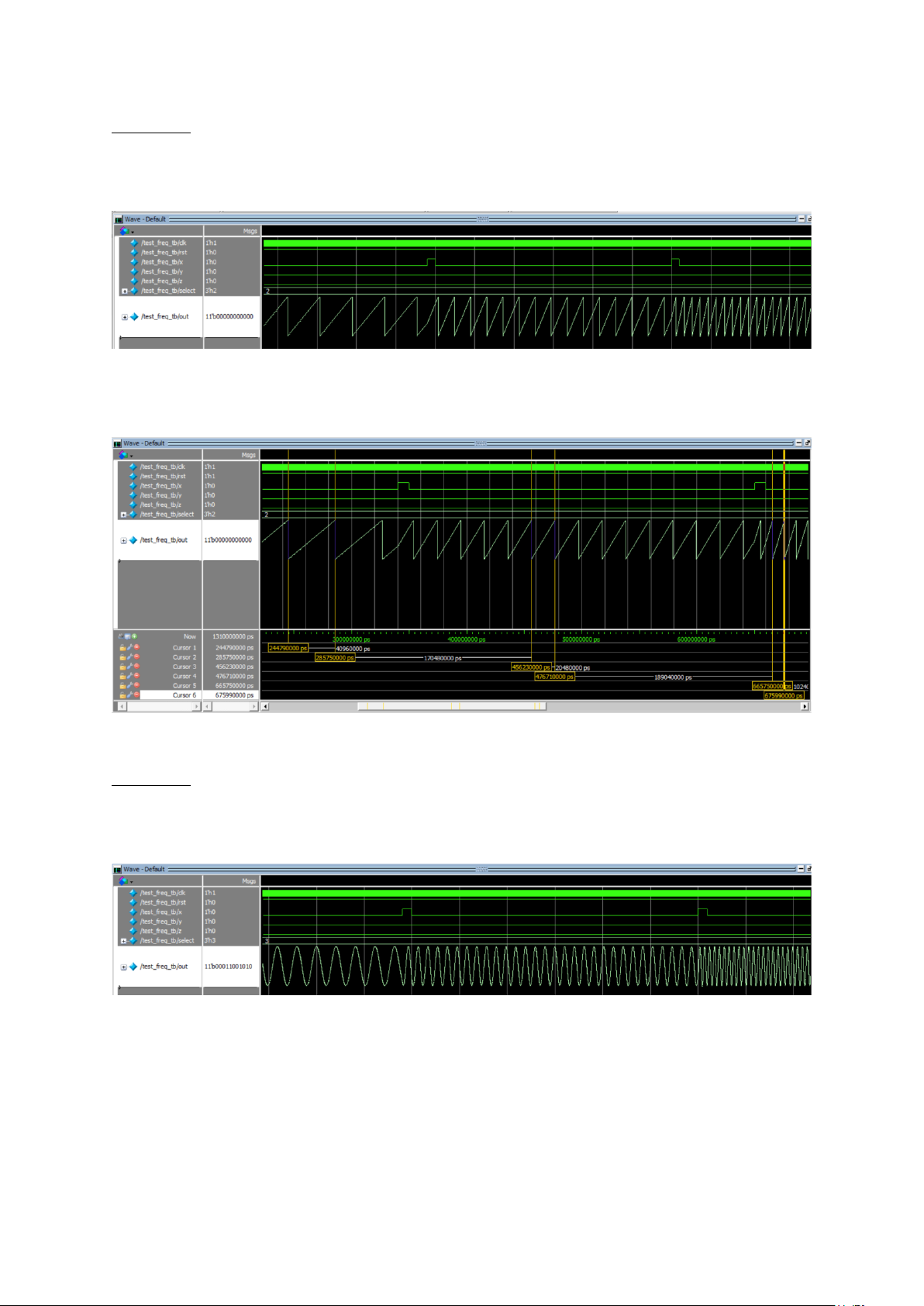
Hình 26. Sóng vuông qua 3 mức tần số
Hình 27. Kiểm tra 3 mức tần số của sóng vuông
Nhận xét: các tần số của sóng vuông đều đúng với 3 mức tần số là 12.21 kHz, 24.41 kHz và 48.83 kHz. - Sóng tam giác:
Hình 28. Sóng tam giác qua 3 mức tần số
Hình 29. Kiểm tra 3 mức tần số của sóng tam giác
Nhận xét: các tần số của sóng tam giác đều đúng với 3 mức tần số là 12.21 kHz, 24.41 kHz và 48.83 kHz. - Sóng răng cưa:
Hình 30. Sóng răng cưa qua 3 mức tần số
Hình 31. Kiểm tra 3 mức tần số của sóng răng cưa
Nhận xét: các tần số của sóng răng cưa đều đúng với 3 mức tần số là 24.41 kHz, 48.83 kHz và 97.66 kHz. - Sóng sine:
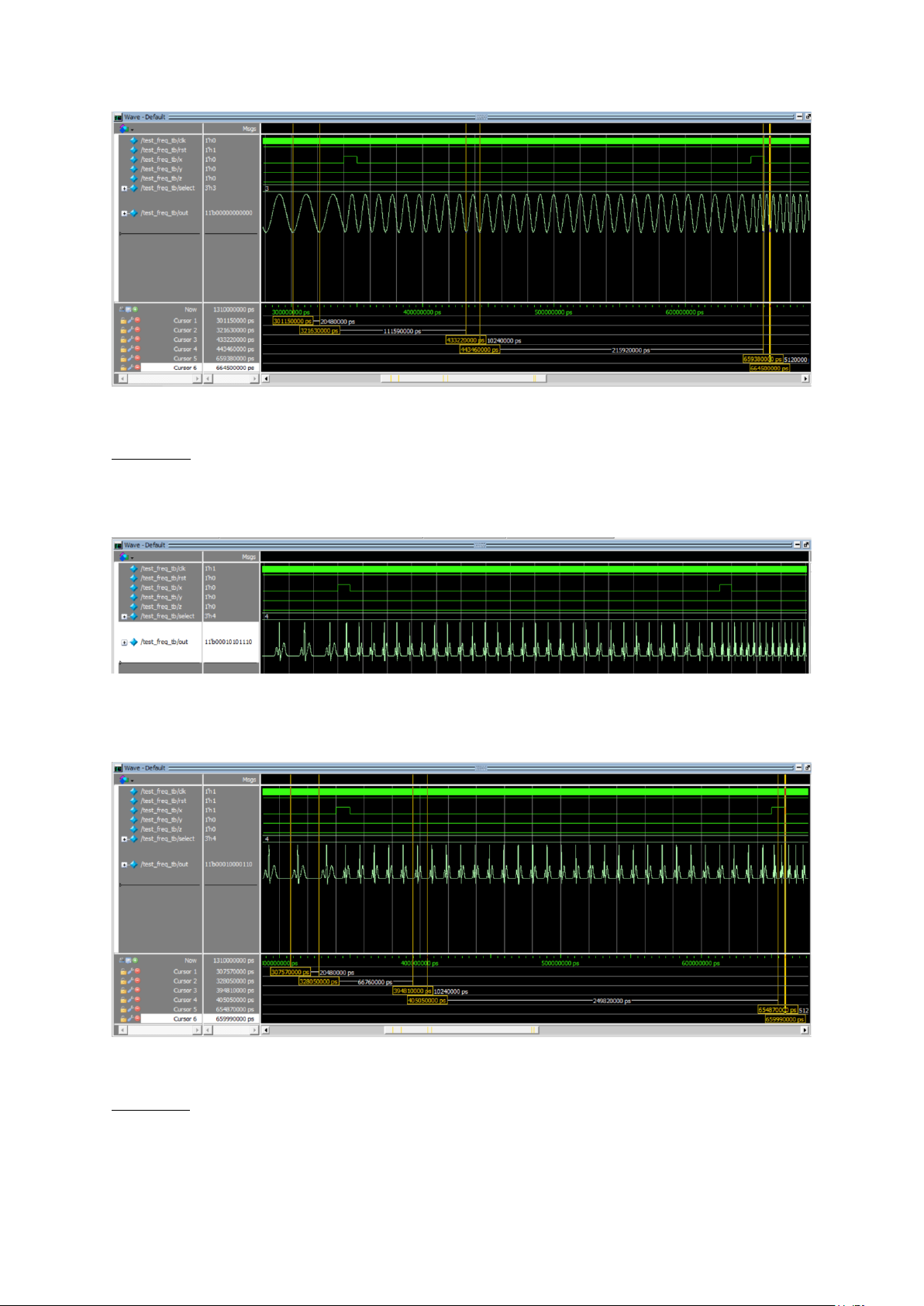
Hình 32. Sóng sine qua 3 mức tần số
Hình 33. Kiểm tra 3 mức tần số của sóng sine
Nhận xét: các tần số của sóng sine đều đúng với 3 mức tần số là 48.83 kHz, 97.66 kHz và 195.31 kHz. - Sóng ECG:
Hình 34. Sóng ECG qua 3 mức tần số
Hình 35. Kiểm tra 3 mức tần số của sóng ECG
Nhận xét: các tần số của sóng ECG đều đúng với 3 mức tần số là 48.83 kHz, 97.66 kHz và 195.31 kHz.
Kết luận: chức năng thay đổi tần số của bộ tạo sóng đã hoạt động đúng với yêu cầu đạt ra.
5.1.3. Thay đổi biên độ các dạng sóng:
Chính tần số về mức giảm phân nửa tần số chuẩn để dễ dàng quan sát các sóng có tần số chuẩn cao. - Sóng vuông:
Hình 36. Sóng vuông qua 5 mức biên độ - Sóng tam giác:
Hình 37. Sóng tam giác qua 5 mức biên độ - Sóng răng cưa:
Hình 38. Sóng răng cưa qua 5 mức biên độ - Sóng sine:
Hình 39. Sóng sine qua 5 mức biên độ