Báo cáo thí nghiệm cơ học chất - mô tả, trình tự và kết quả | Môn Cơ học chất lưu - Trường Đại học Bách khoa Hà Nội

lOMoARcPSD| 45315597
Bài 1: XÁC ĐỊNH CHẾ ĐỘ CHẢY CỦA CHẤT LỎNG TRONG ỐNG TIẾT DIỆN TRÒN
Mục đích: Bằng thí nghiệm minh họa các chế độ chảy của chất lỏng và tính toán số Reynolds (Re). Cơ sở lý thuyết
Tổn thất năng lượng của dòng có liên quan mật thiết với trạng thái của chất lưu. Năm
1883, nhà vật lý học người Anh Osborne Reynolds đã thực hiện nhiều thí nghiệm
làm với các loại đường ống và các loại chất lưu khác nhau đã phát hiện ra sự tồn tại hai chế độ chảy:
- Chế độ chảy trong đó các phân tố chất lưu chuyển động thành từng lớp riêng rẽ, không
xáo trộn lẫn nhau gọi là chế độ chảy tầng.
- Chế độ chảy trong đó các phân tố chất lưu chuyển động hỗn loạn, xáo trộn vào nhau
gọi là chế độ chảy rối.
Trạng thái dòng chảy được xác định qua một tổ hợp không thứ nguyên – gọi là số Reynolds (số Re): trong đó:
v – vận tốc trung bình dòng chảy, m/s; d – đường kính ống trụ tròn, m; –
độ nhớt động học chất lỏng, m2/s.
Số Reynolds tới hạn Reth được dùng làm tiêu chuẩn phân định trạng thái chảy
của chất lỏng. Khi dòng chảy có Re < Reth thì trạng thái của nó là chảy tầng và khi
dòng chảy có Re >> Reth thì trạng thái của nó là chảy rối. Đối với dòng chảy đầy
trong ống tròn thẳng: Reth = 2300.
MÔ TẢ THIẾT BỊ THÍ NGHIỆM
Thiết bị thí nghiệm được biểu diễn trên hình vẽ 1. Nước được cấp qua van cấp vào bình
điều tiết A và sẽ chảy qua ống thí nghiệm Reynolds 3 (ống thủy tinh trong suốt để
dễ dàng quan sát trạng thái chảy) sang bình điều tiết B. Ở các bình điều tiết A và B
mực nước được duy trì ổn định. Nước màu được đổ vào bình chứa lOMoARcPSD| 45315597
1. Khóa 2 được dùng để điều chỉnh lưu lượng nước màu chảy từ bình chứa 1 qua
ống 3. Dùng van 4 điều chỉnh vận tốc dòng chảy qua ống 3 để có các trạng thái chảy
khác nhau trong ống thí nghiệm Reynolds 3 và trên lưu lượng kế 5 sẽ hiện thị giá trị
lưu lượng tương ứng với từng trạng thái chảy.
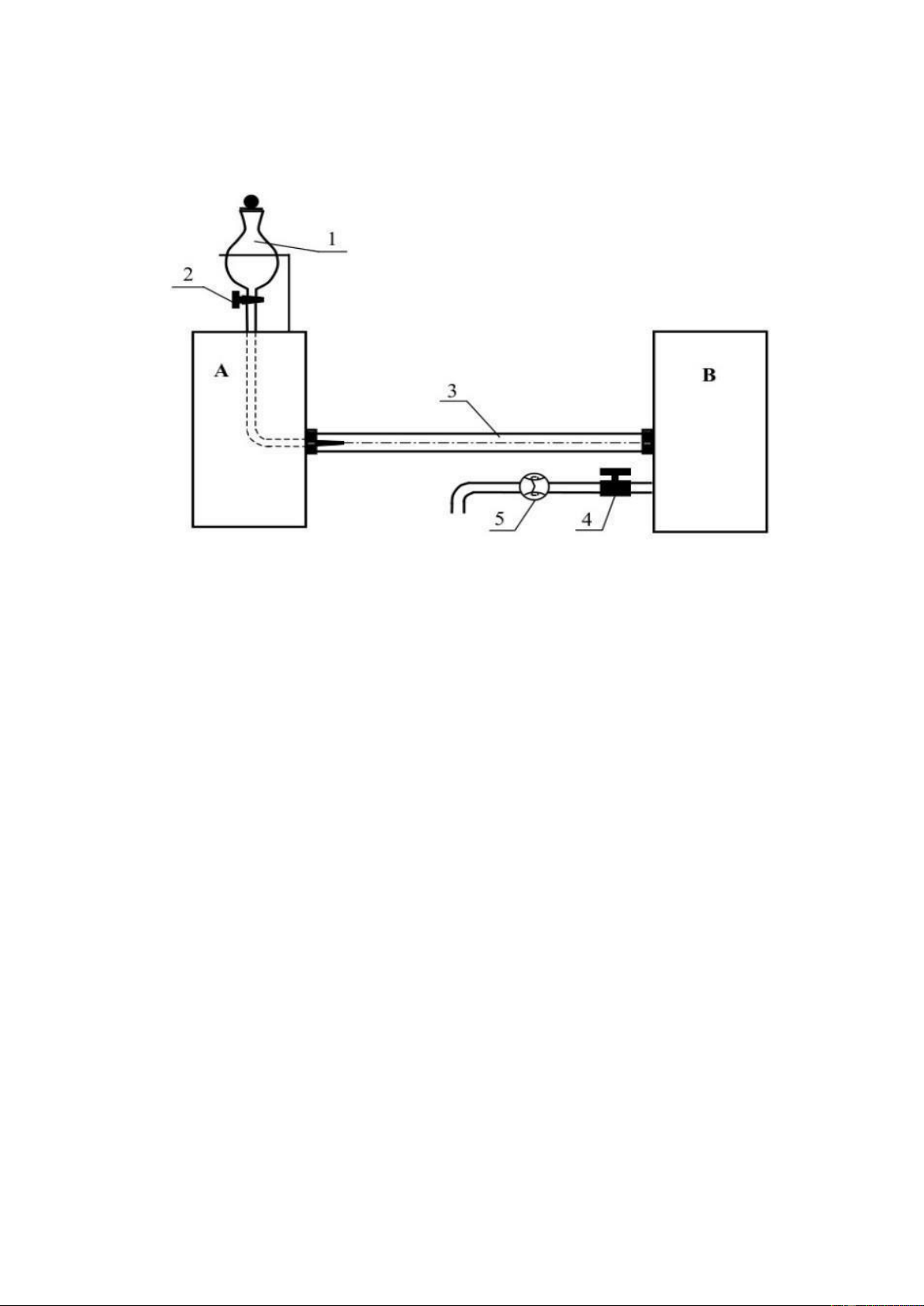
Hình 1. Sơ đồ thí nghiệm Reynolds
A, B. Các bình chứa nước; 1. Bình nước màu; 2. Khóa bình nước màu; 3. Ống
thí nghiệm Reynolds; 4. Van điều chỉnh lưu lượng; 5. Lưu lượng kế.
TRÌNH TỰ THÍ NGHIỆM
1. Nghiên cứu cơ sở lý thuyết về các trạng thái chảy của dòng chất lỏng có áp chảy
ồn định trong ống trụ tròn.
2. Làm quen với thiết bị thí nghiệm và thiết bị đo.
3. Mở van cấp để cấp nước cho các bình điều tiết A và B và đợi đến khi các bình
được cung cấp đủ nước để có thể tiến hành thí nghiệm. Trong thời gian chờ đợi thì
pha nước màu và đổ vào bình chứa nước màu 1.
4. Dùng nhiệt kế đo nhiệt độ của nước để xác định hệ số nhớt động học tương ứng.
5. Mở khóa 2 và điều chỉnh lưu lượng nước màu đủ quan sát (nếu dòng nước màu to,
dòng nước màu sẽ bị lắng xuống, khó thực hiện thí nghiệm).
6. Mở van 4 để điều chỉnh vận tốc dòng chảy qua ống 3 từ bé đến lớn sao cho dòng
chảy ở trạng thái chảy tầng, chảy quá độ và chảy rối; rồi điều chỉnh vận tốc dòng
chảy qua ống 3 từ vận tốc lớn về bé, tức là điều chỉnh trạng thái dòng chảy về quá lOMoARcPSD| 45315597
độ và về chảy tầng (hình vẽ 2). Ghi lại giá trị lưu lượng trên lưu lượng kế 5 tương
ứng với từng trạng thái chảy mà ta quan sát được.
7. Tiến hành thí nghiệm với ba đến năm chu kỳ tăng và giảm vận tốc qua ống 3
Hình 2. Hình ảnh dòng nước màu trong các trạng thái chảy
XỬ LÍ KẾT QUẢ THÍ NGHIỆM
Kết quả thí nghiệm trình bày vào trong bảng 1.
1. Trạng thái dòng chảy (khi quan sát), các số liệu lưu lượng Qi và nhiệt độ của nước t
được ghi lại vào các cột [2], [3] và [5] tương ứng trong bảng 1.
2. Ứng với mỗi giá trị lưu lượng Qi đo được ở cột [3] trong bảng 1 ta tính được vận
tốc trung bình vi của dòng chảy theo công thức:
Trong đó d – đường kính tiết diện mặt cắt ống 3.
3. Độ nhớt động học của nước ν được tính từ giá trị nhiệt độ của nước (mà ta đo được
ở cột [5] trong bảng 1) theo bảng 2 hoặc theo công thức Poise:
Trong đó t - nhiệt độ của nước, 0C. Giá trị tính được cần điền vào cột [6] bảng 1.
4. Tính trị số Re ứng với từng vận tốc vi rồi ghi lại vào cột [7] bảng 1.
5. Từ các giá trị Re thu được ta ghi trạng thái dòng chảy tương ứng với nó vào cột [8].
Bảng 1- Kết quả thí nghiệm Reynolds STT Trạng Q(m3/s) T(oC) 𝜈 Re thái thời Trạng thái chảy tốc độ(m/s) chảy (kết gian (quan quả tính sát) ) lOMoARcPSD| 45315597 1
tầng 150 1.35135E05 0.010759167 13 1.20302E06 357.737508 tầng 2
tầng 157 1.27389E05 0.010142399 13 1.20302E06 337.230262 tầng 3
178 1.1236E05 0.008945824 13 1.20302E06 297.444669 tầng tầng 4
tầng 140 1.42857E05 0.011373976 13 1.20302E06 378.179651 tầng 5
tầng 145 1.37931E05 0.01098177 13 1.20302E06 365.138974 tầng 6 rối
32 0.0000625 0.049761146 13 1.20302E06 1654.53597 tầng 7 rối
23 8.69565E05 0.069232899 13 1.20302E06 2301.96309 rối 8 rối 20 0.0001
0.079617834 13 1.20302E06 2647.25756 rối 9 rối 25
0.00008 0.063694268 13 1.20302E06 2117.80605 tầng
Bảng 2- Độ nhớt động học của nƣớc t (oC) 10o 20o 30o 40o 50o 60o 80o 100o 0o n.107 (m2/s)
17,92 13,06 10,06 8,05 6,59 5,56 4,8 3,7 2,95
Nhận xét, đánh giá kết quả thí nghiệm:
So sánh trạng thái dòng chảy theo kết quả tính toán được (ở cột [8]) với trạng
thái chảy mà ta quan sát khi làm thí nghiệm (ở cột [2]) rồi đưa ra nhận xét, đánh giá.
Nếu không có sự phù hợp thì chỉ rõ các nguyên nhân có thể có.
Trong quá trình đo lường trạng thái chảy nhóm thí nghiệm đã
quan sát thấy sự khác biệt giữa trạng thái chảy thực tế và trạng thái chảy
tính toán tại các lần đo đo 6 và 9, khi so sánh với lý thuyết chung về số lOMoARcPSD| 45315597
Reynolds (Re) < 2300 (phản ánh trạng thái chảy tầng) và Re > 2300 (phản
ánh trạng thái chảy rối của dòng). Sự không phù hợp này có thể được
giải thích bởi các yếu tố sai số, bao gồm sai số từ quá trình thực nghiệm,
sai số từ dụng cụ đo, và sai số chủ quan do quan sát không chính xác của
người thực hiện thí nghiệm đối với dòng chảy. lOMoARcPSD| 45315597
Bài 2 – XÁC ĐỊNH CÁC THÀNH PHẦN TRONG PHƢƠNG TRÌNH BERNOULLI
Mục đích: Vẽ đường năng và đường đo áp sau khi xác định các thành phần trong
phương trình Bernoulli bằng thí nghiệm. CƠ SỞ LÝ THUYẾT
Phương trình Bernoulli là phương trình năng lượng viết cho một đơn vị trong
lượng chất lỏng. Phương trình Bernoulli đối với toàn dòng chất lỏng thực, không
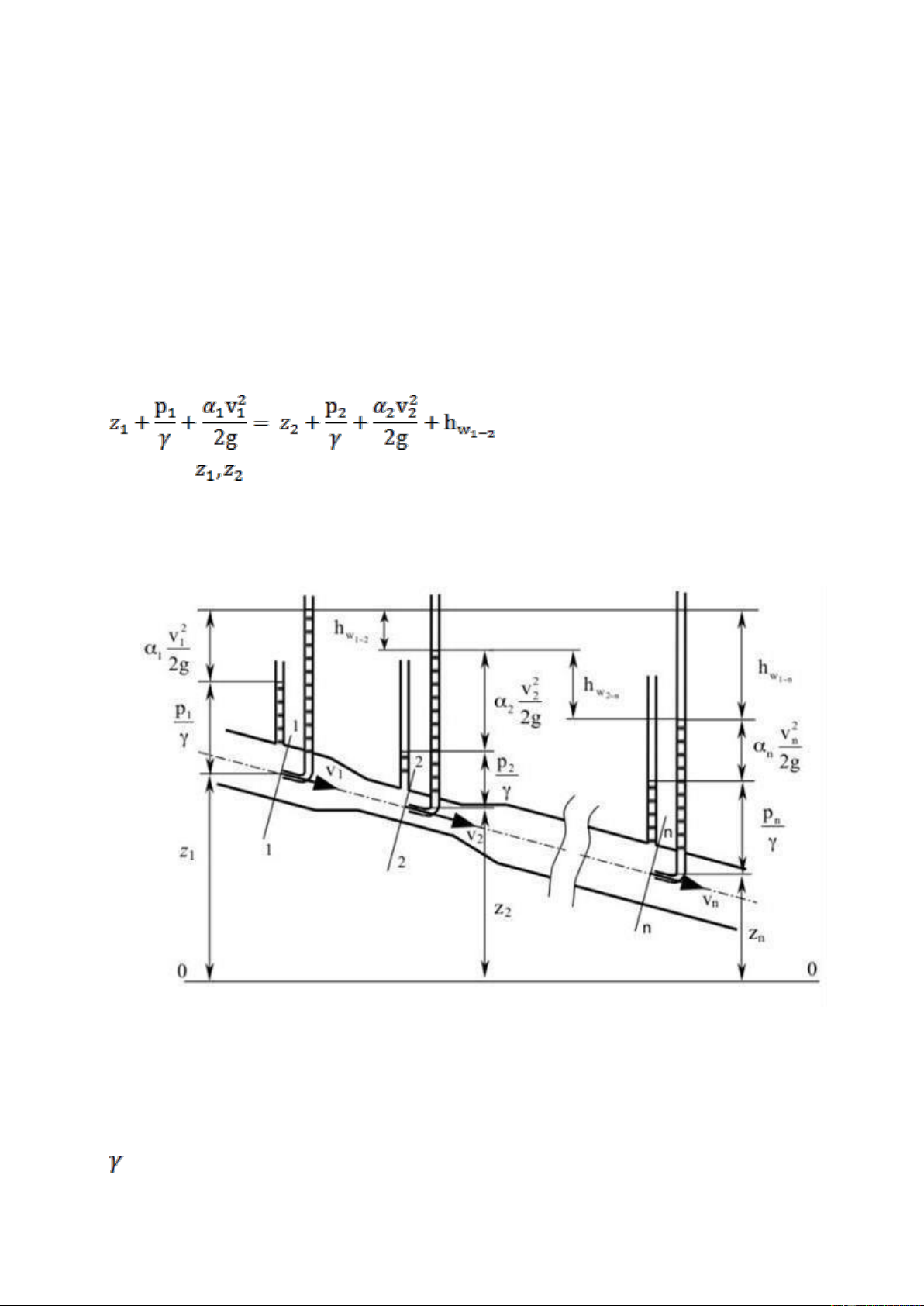
nén được, chuyển động ổn định từ mặt cắt 1 – 1 đến mặt cắt 2 - 2 (hình vẽ 3) có dạng:
trong đó: – năng lượng vị trí của dòng chảy ở tâm mặt cắt ướt 1-1 và 2-2 so với mặt
chuẩn 0-0 bất kỳ được gọi là vị năng đơn vị hay độ cao hình học;
Hình 3. Sơ đồ dòng chảy qua đoạn ống có kích thước khác nhau trong đó: –
trọng lượng riêng của chất lỏng; –
áp suất tại tâm mặt cắt 1-1 và 2-2; lOMoARcPSD| 45315597
– áp năng của một đơn vị trọng lượng chất lỏng do áp suất gây ra tại mặt cắt
1-1 và 2-2, gọi là áp năng đơn vị hay độ cao đo áp;
- thế năng đơn bị hay cột áp thủy tĩnh tại mặt cắt 1-1 và 2-2; 1
- hệ số hiệu chỉnh động năng hay hệ số Coriolis tại mặt cắt 1-1 và 2-2 , 2
v1, v2 – vận tốc trung bình tại mặt cắt 1-1 và 2-2;
– động năng đơn vị hay độ cao vận tốc tại mặt cắt 1-1 và ,
2-2; – tổn thất năng lượng đơn vị trong đoạn chảy từ mặt cắt 1-1 đến 2-2.
MÔ TẢ THIẾT BỊ THÍ NGHIỆM
Thiết bị thí nghiệm được biểu diễn trên hình vẽ 4. Nước được cấp qua van cấp vào
bình điều tiết A và sẽ chảy qua ống thí nghiệm Bernoulli 1 sang bình điều tiết B. lOMoARcPSD| 45315597
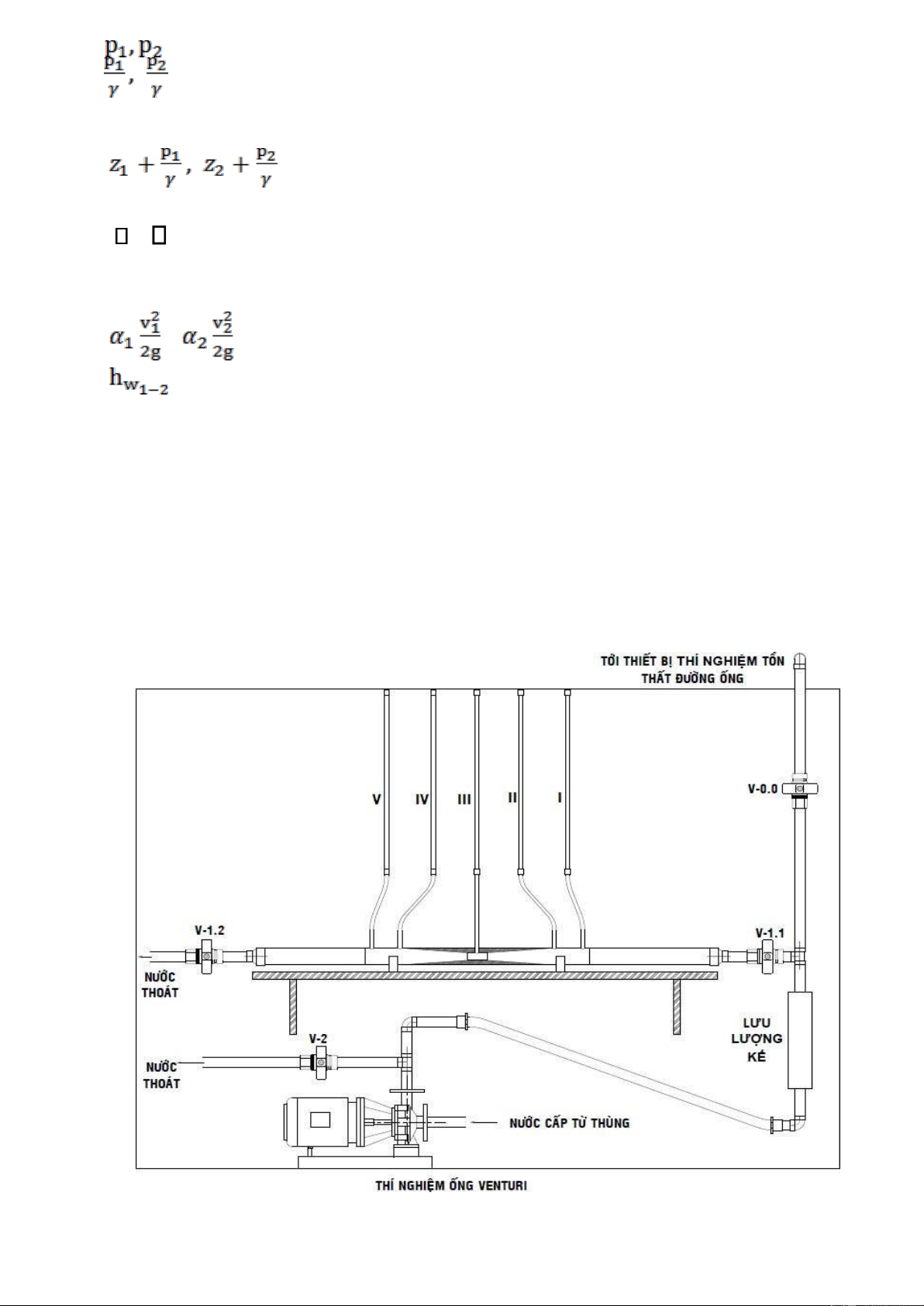
Hình 4. Sơ đồ ống thí nghiệm Bernoulli
A, B. Các bình chứa nước; 1. Ống thí nghiệm Bemoulli; 2. Van điều chỉnh lưu lượng;
3. Lưu lượng kế; I, II, III, IV và V. Các ống đo áp điều tiết B. Ở các bình điều tiết A
và B mực nước được duy trì ổn định. Trên ống thí nghiệm Bernoulli 1 có gắn các
ống đo áp I, II, III, IV và V tương ứng với 5 mặt cắt đã chọn. Đường kính của ống
d1 = 2.6 cm ; d2 = 1.3 cm. Dùng van 2 chiều điều chỉnh vận tốc dòng chảy qua ống
thí nghiệm Bernoulli 1, trên lưu lượng kế 3 sẽ hiển thị giá trị lưu lượng tương ứng
với từng vận tốc của dòng chảy.
TRÌNH TỰ THÍ NGHIỆM 1.
Nghiên cứu cơ sở lý thuyết về phương trình Bernoulli đối với toàn dòng chất
lỏng thực, không nén được, chuyển động ổn định. 2.
Làm quen với thiết bị thí nghiệm và thiết bị đo. 3.
Mở van V-1.1 và V-2.1 100%, van V-1.2 đóng. 4. Bật máy bơm nước. 5.
Điều chỉnh van V-2.1 để điều chỉnh lưu lượng nước đi qua ống venturi. Khi các
ống I, II, III, IV, V hết bọt khí và mực nước trong khoảng hiển thị, mở van V1.2 100%. 6.
Điều chỉnh V-2.1 đạt lưu lượng ................ và ghi số liệu trên các cột I, II, III,
IV, V (ghi số liệu 3 lần sau mỗi 1 phút). 7.
Tắt máy bơm. Đóng van V-1.1. lOMoARcPSD| 45315597
XỬ LÝ KẾT QUẢ THÍ NGHIỆM 1.
Ghi các giá trị lưu lượng Qi hiển thị trên lưu lượn kế vào cột [2] của bảng 3. 2.
Ứng với mỗi giá trị lưu lượng Qi đo được nói trên ta tính được vận tốc trung
bình vi của dòng chảy tại các mặt cắt tương ứng theo công thức: trong đó d -
đường kính tiết diện mặt cắt của ống d1 = 26mm và d2 = 13mm. Ghi các giá trị
tính được vào cột [3] của bảng 3. 3.
Từ các giá trị vi vừa tìm được ta tính các thành phần của phương trình
Bernoulli (ở đây, ta lấy = 1). Ghi các giá trị vào các cột [4], [7], [11],
[15] và [19] tương ứng của bảng 3. 4.
Theo cao độ của các ống đo áp I, II, III, IV và V ta xác định được trị số
tại các mặt cắt tương ứng (xem hình vẽ 4) (Nếu chọn mặt chuẩn đi qua
trục của ống thì ta có zi = 0). Ghi các giá trị vừa tìm được vào các cột [5], [8],
[12], [16] và [20] tương ứng của bảng 3. 5.
Các giá trị tổn thất cột áp ở các cột [9], [13], [17] và [21] trong bảng 3 được tính
từ phương trình Bernoulli (Ví dụ cần tính
ở cột [9] ta sẽ lấy tổng
giá trị cột [7] và cột [8] trừ đi tổng giá trị cột [4] và cột [5]) 6.
Từ số liệu ở bảng 3 và sơ đồ ống thí nghiệm Bernoulli (trên hình vẽ 4) vẽ đường năng và đường đo áp.
Bảng 3. Kết quả thí nghiệm các thành phần trong phương trình Bernoulli lOMoAR cPSD| 45315597 lOMoAR cPSD| 45315597 11
Downloaded by H?u mai (maihauhaumai@gmail.com) TT Q(m3/s) v v v lOMoARcPSD| 45315597 1 2 3 (m/s) (m/s) (m/s) (m) [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] 1 0.00025 0.450 0.0103 0.341 0.450 0.0103 0.336 0.005 1.800 0.165 2 0.00025 0.450 0.0103 0.347 0.450 0.0103 0.341 0.005 1.800 0.165 3 0.00025 0.450 0.0103 0.336 0.450 0.0103 0.331 0.005 1.800 0.165 4 0.00031 0.550 0.0154 0.459 0.550 0.0154 0.454 0.010 2.200 0.247 5 0.00031 0.550 0.0154 0.454 0.550 0.0154 0.449 0.010 2.200 0.247 TT 𝑣2 v z 5 5+𝑝5 𝛼 (m/s) a 𝛾 (m) 5𝑣52 4 4 z3+𝑝4 v4 2𝑔 z 2𝑔 4+𝑝4 𝛾 (m/s) 𝛾 [1] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] 1 0.224 0.043 0.450 0.010 0.245 0.134 0.450 0.010 0.265 0.020 2 0.234 0.048 0.450 0.010 0.255 0.134 0.450 0.010 0.275 0.020 3 0.214 0.038 0.450 0.010 0.245 0.124 0.450 0.010 0.270 0.025 4 0.306 0.084 0.550 0.015 0.331 0.206 0.550 0.015 0.362 0.031 5 0.306 0.089 0.550 0.015 0.326 0.211 0.550 0.015 0.357 0.031 Ghi chú: lOMoARcPSD| 45315597
Để kết quả thí nghiệm có độ chính xác cao cần điều chỉnh van 2 sao cho dòng chảy qua
ống Bernoulli là dòng chảy rối.
NHẬN XÉT, ĐÁNH GIÁ KẾT QUẢ THÍ NGHIỆM
So sánh giữa các đường năng và đường đo áp được vẽ dựa trên kết quả thực
nghiệm và lý thuyết cho thấy sự không đồng nhất do tồn tại độ sai số cụ thể.
Nguyên nhân của hiện tượng này có thể được giải thích bởi nhiều yếu tố: do các bộ
phận của thiết bị bị rò nước, có thể vẫn còn bọt khí trong ống, và mực nước không ổn
định khi đo. Điều này dẫn đến việc chỉ số liệu có tính tương đối, không đồng nhất khi so
sánh với giả định lý thuyết. lOMoARcPSD| 45315597
Bài 3- XÁC ĐỊNH TỔN THẤT THỦY LỰC DỌC ĐƯỜNG
Mục đích: Bằng thí nghiệm tính hệ số cản dọc đường. CƠ SỞ LÝ THUYẾT
Phương trình Bernoulli đối với toàn dòng chất lỏng thực, không nén được,
chuyển động ổn định từ mặt cắt 1-1 đến mặt cắt 2-2 có dạng: trong đó: là tổn
thất thủy lực khi dòng chảy chuyển động từ mặt cắt 1-1 đến mặt cắt 2-2 (hình vẽ 3). Giá trị
bao gồm tổn thất thủy lực dọc đường h , tổn thất thủy lực cục bộ h d c:
Tổn thất thủy lực dọc đường hd cho dòng chảy đều trong ống tròn, theo Darcy,
có thể được xác định theo công thức sau:
trong đó: – chiều dài đoạn dòng chảy, m; d – đường kính ống, m; v – vận tốc trung
bình của dòng chảy, m/s; g – gia tốc trọng trường, m/s2; – hệ số sức cản dọc đường (hệ số ma sát).
Hệ số ma sát phụ thuộc vào trạng thái dòng chảy của chất lỏng (tức là Re) và
đặc trưng hình học của ống dẫn, cụ thể là độ nhám tương đối của thành ống nhám của ống (với -
độ nhô của mặt nhám và d – đường kính trong của
ống). Một cách tổng quát, ta có: Mối quan hệ
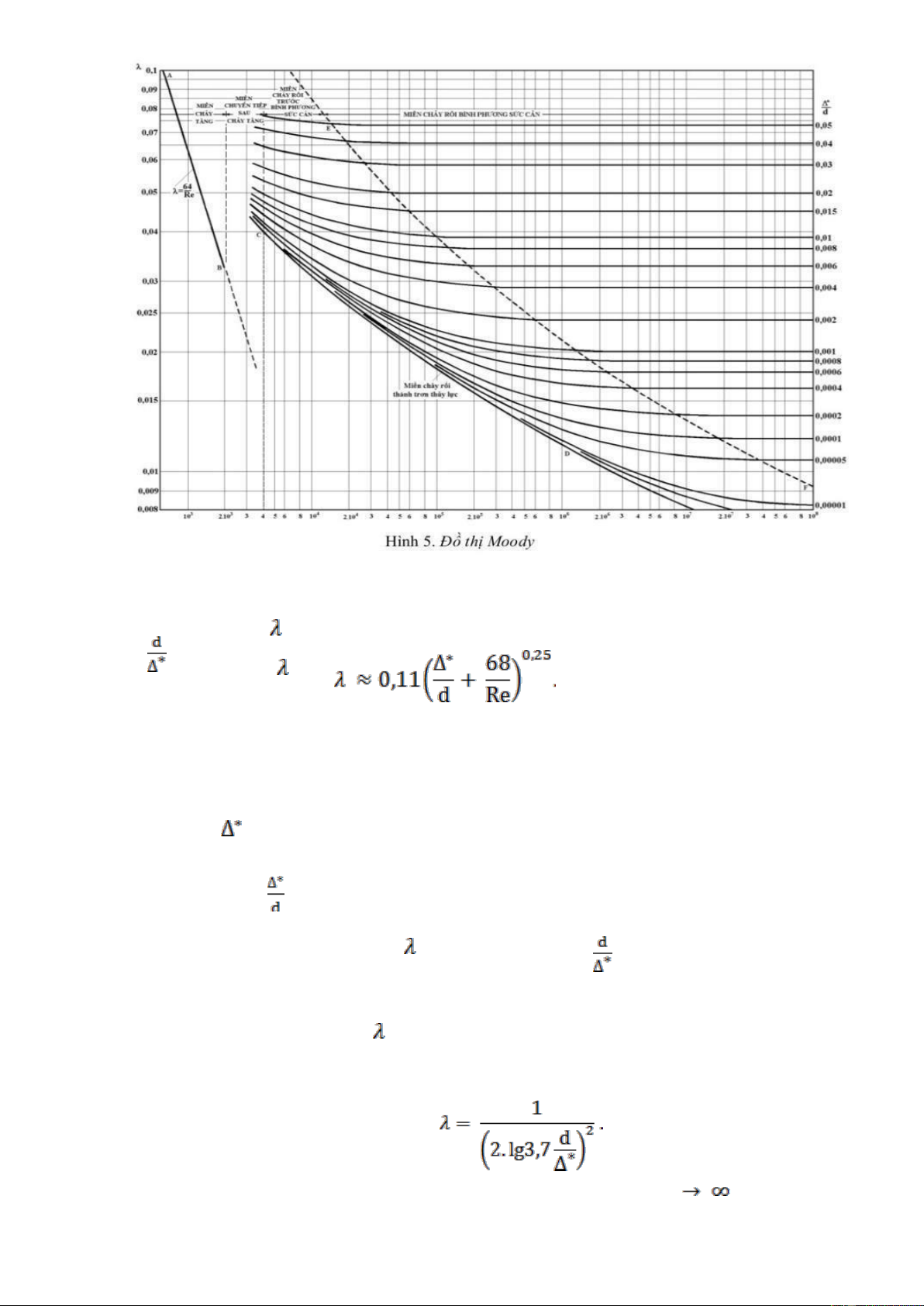
được Moody biểu diễn dưới dạng đồ thị ( - đồ thị
Moody, hình vẽ 5) và đồ thị này chỉ đúng cho ống thép tròn. lOMoARcPSD| 45315597
Phân tích đồ thị Moody, ta có thể chia nó thành 5 khi vực sau:
Khu vực 1 – khu vực chảy tầng (Re ). Hệ số ma sát chỉ
phụ thuộc vào Re mà không phụ thuộc vào (đoạn thẳng
AB trên hình vẽ 5). Khi đó:
Khu vực 2 – khu vực quá độ từ chảy tầng sang chảy rối (2300 < Re <104)
Trong khi vực này hệ số ma sát có quy luật biến thiên phức tạp (giữa điểm B
và điểm C). Các phương trình nghiên cứu của các tác giả đã đưa ra các công thức
thực nghiệm khác nhau để xác định. Frenken đã đưa ra công thức thực nghiệm sau:
Hoặc có thể sử dụng công thức Bladius cho dải Re < 105.
Khu vực 3 – Khu vực chảy rối ống trơn thủy lực.
Hệ số ma sát chỉ phụ thuộc vào Re mà không phụ thuộc vào (Quy luật biến
thiên tương ứng với đoạn thẳng CD trên hình vẽ 5). Một số công thức thực nghiệm: 5
-Công thức Bladius khi Re 10 :
-Công thức Cônacốp khi 4000 < Re < 3.106:
Khu vực 4 – khu vực chảy rối trước bình phương sức cản, hoặc không hoàn
toàn thành nhám (20 < Re < 500 ). lOMoARcPSD| 45315597
Khu vực giữa đoạn thẳng CD và đoạn thẳng EF trên hình vẽ 5. Trong khu vực này hệ số ma sát
phụ thuộc vào Re và phụ thuộc vào , có thể sử
dụng công thực Altsul để tính :
Trị số của các loại ống khác nhau được cho ở phụ lục 3.
Khu vực 5 – khu vực chảy rối thành nhám hoàn toàn, hay khu vực bình phương
sức cản (Re > 500 ). Khu vực nằm bên phải đoạn thẳng EF.
Trong khu vực này hệ số ma sát
chỉ phụ thuộc vào mà không phụ thuộc vào Re.
Một số công thực để xác định trong miền này: - Công thức Prandtl – Nicuradse:
- Công thức Shifrinson (nhận được từ công thức Altsul khi Re : lOMoARcPSD| 45315597 lOMoARcPSD| 45315597
MÔ TẢ THIẾT BỊ THÍ NGHIÊM
Thiết bị thí nghiệm được biểu diễn trên hình vẽ 6. Nước được cấp qua van cấp
vào bình điều tiết A và sẽ chảy qua ống thí nghiệm tổn thất thủy lực dòng đường 1
(đường kính d = 1,5 cm) sang bình điều tiết B. Ở các bình điều tiết A và B mực nước
được duy trì ổn định. Trên ống thí nghiệm này có gắn các ống đo áp I và II tương
ứng với hai mặt cắt 1-1 và 2-2 đã chọn. Khoảng cách giữa hai ống đo áp này là =
60 cm. Dùng van 2 điều chỉnh vận tốc dòng chảy qua ống thí nghiệm tổn thất thủy
lực dọc đường 1, trên lưu lượng kế 3 sẽ hiển thị giá trị lưu lượng tương ứng với từng
vận tốc của dòng chảy.
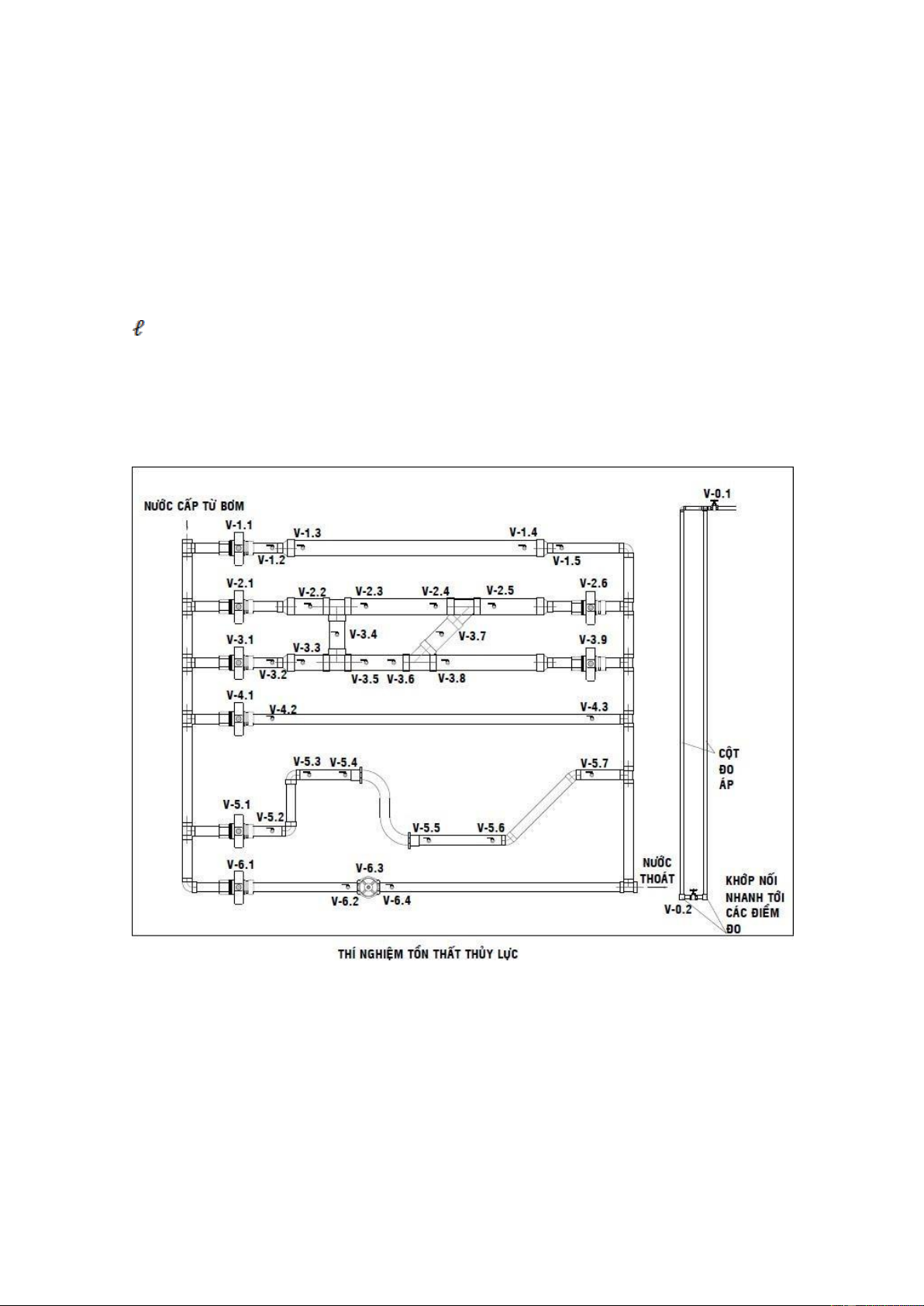
Hình 6. Ống thí nghiệm tổn thất thủy lực dọc đường lOMoARcPSD| 45315597
TRÌNH TỰ THÍ NGHIỆM
1. Nghiên cứu cơ sở lý thuyết về tổn thất thủy lực dọc đường đối với dòng chảy đều trong ống.
2. Làm quen với thiết bị thí nghiệm và thiết bị đo.
3. Kiểm tra đảm bảo tất cả các van đều ở trạng thái đóng 100%.
4. Mở van V-2 100% và van V-0.0 100% ở phía sau thiết bị. Van thoát V-
0.1 và van thông V-0.2 mở 100%. Mở các van V-1.1, V-4.1, V-5.1 V- 6.1.
- Đo trở lực đường dài: a/ Mở van V-4.1 và điều chỉnh lưu lượng bằng
van V-2. Khóa van V-0.1 và V-0.2 khi đảm bảo cột nước trong 2 ống
đo áp bằng nhau. Cắm 2 đầu đo vào vị trí 2 van V-4.2 và V-4.3. b/ Ghi
lại giá trị chênh lệch giữa 2 cột đo áp.
c/ Khóa van V-4.2 và V-4.3. Rút các đầu nối ra khỏi van. Mở van V-2 100%,
đóng van V-4.1 lại và kết thúc thí nghiệm.
- Đo trở lực qua van: Tương tự như đo trở lực đường dài. lOMoARcPSD| 45315597
XỬ LÝ KẾT QUẢ THÍ NGHIỆM
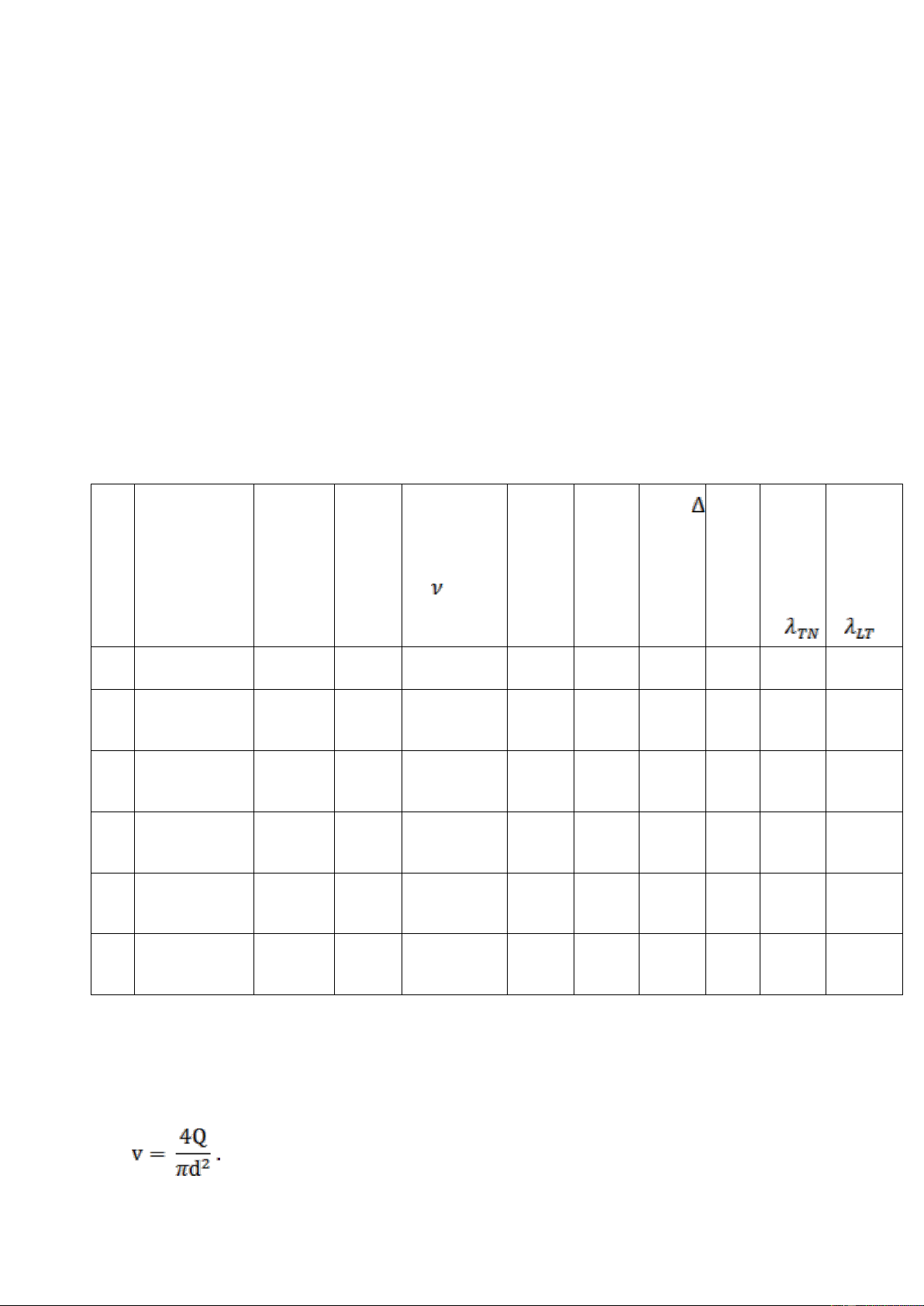
Bảng 4- Kết quả thí nghiệm tổn thất thủy lực dọc đƣờng Trạng thái v chảy quan Q h Tt (m/s) h Re h1 2 sát (m3/s) (mm) (mm) (m m) (m2/s) [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]
Chảy rối 0.00011 0.622 1.156.10^-6 8070 810 220 590 0.748 0.0327 1
Chảy rối 0.00011 0.622 1.156.10^-6 8070 810 220 590 0.748 0.0327 2
Chảy rối 0.00014 0.792 1.156.10^-6 10276 810 220 590 0.544 0.0300 3
Chảy rối 0.00014 0.792 1.156.10^-6 10276 650 370 280 0.258 0.0300 4 / / / / / / / / / / 5
1. Trạng thái dòng chảy và các số liệu lưu lượng Qi hiển thị trên lưu lượng kế 3
được ghi lại vào các cột [2] và [3] tương ứng trong bảng 4.
2. Ứng với mỗi giá trị lưu lượng Qi đo được nói trên ta tính được vận tốc trung