TRƯỜNG ĐẠI HỌC PHENIKAA KHOA ĐIỆN – ĐIỆN TỬ
BÀI THÍ NGHIỆM HỆ
THỐNG ĐIỀU KHIỂN SỐ Mã học phần: EEE703209 Nhóm ngành/ngành: 7520216
Họ và tên SV: Nguyễn Hoàng Hiệp
Mã lớp: EEE703029-1-1-23(NO1) Mã số SV: 20010703 GVHD: TS. Phạm Văn Thiêm
Lưu ý: Sau mỗi buổi thực hành, GVHD cần ký xác nhận vào kết quả thực hành; Sinh viên nộp
quyển thực hành này sau khi hoàn thành bài thí nghiệm Hà Nội 2023 lOMoARcPSD|47880655 Mục lục
1 Đánh giá kết quả thí nghiệm 5
1.1 Rubric-R1: Báo cáo thực
hành .................................................................5 1.2 Rubric-R2: Trình bày
và đóng quyển báo cáo .........................................5 1.3 Đánh giá điểm thực
hành ..........................................................................6
2 Mô hình hoá các hệ thống điều khiển 7 2.1 Đối tượng thí
nghiệm ................................................................................7
2.2 Kết quả thực hành và nhận
xét .................................................................8
3 Xác định mô hình gián đoạn của ĐCMC 9 3.1 Đối tượng thí
nghiệm ................................................................................9
3.2 Báo cáo thí nghiệm và nhận xét kết
quả ................................................10
4 Tổng hợp vòng điều chỉnh dòng phần fíng 11 4.1 Đối tượng thí
nghiệm ..............................................................................11
4.2 Báo caó thí nghiệm và nhận
xét .............................................................12
5 Tổng hợp vòng điều chỉnh dòng phần fíng 13 5.1 Đối tượng thí
nghiệm ..............................................................................13
5.2 Báo cáo thí nghiệm và nhận xét kết
quả ................................................14 2 Chương 1
Đánh giá kết quả thí nghiệm Nội dung 5 5 6 1.1
Rubric-R1: Báo cáo thực hành Tiêu chí đánh giá Điểm
Không làm đạt 50% số lượng bài thực hành được giao Điểm (0 − 3.9) Nộp đủ 50% và đúng Điểm (4 − 5.4) Hoàn thành 70% và đúng
Điểm (5.5 − 6.9)
Hoàn thành 90% và đúng Điểm (7.0 − 8.4) Hoàn thành 100% và đúng Điểm (8.5 − 10)
Bảng 1.1: Rubric điểm thí nghiệm
Lưu ý: Bài thực thành được coi là "hoàn thành" nếu thỏa mãn 02 tiêu chí:
1) Trình bày các bước giải quyết yêu cầu đề bài
2) Trình bày rõ ràng chi tiết các bước phần mô phỏng và thực nghiệm 1.2
Rubric-R2: Trình bày và đóng quyển báo cáo Tiêu chí đánh giá Điểm
Quyển trình bày ko cẩn thận,và không đóng thành quyển Điểm (0 − 3.9)
Quyển trình bày ko cẩn thận, không rõ ràng Điểm (4 − 5.4)
Đóng quyển, trình bày không rõ ràng
Điểm (5.5 − 8.4)
Trình bày sạch sẽ, rõ ràng và có đóng quyển Điểm (8.5 − 10)
Bảng 1.2: Rubric điểm trình bày báo cáo
Lưu ý: Bài thực hành được gọi là đóng quyển nếu quyển báo cáo được gián mép và đóng bìa cẩn thận;
Bài thực thành được coi la trình bày cẩn thận nếu được viết rõ ràng dễ đọc và sử dụng một mầu mực duy nhất. 1.3
Đánh giá điểm thực hành
Thành phần đánh giá Trọng số điểm Tiêu chí
Phần 1.1 − 1.3 5% Rubric-R1 Phần 1.4 5% Rubric-R1 Phần 1.5 10% Rubric-R1 Phần 1.6 20% Rubric-R1 Phần 1.7 20% Rubric-R1 Phần 2.2 15% Rubric-R1 lOMoARcPSD|47880655 Phần 2.3 15% Rubric-R1
Trình bày và đóng quyển 10% Rubric-R2
Bảng 1.3: Đánh giá điểm thực hành Chương 2
Mô hình hoá các hệ thống điều khiển 2.1
Đối tượng thí nghiệm
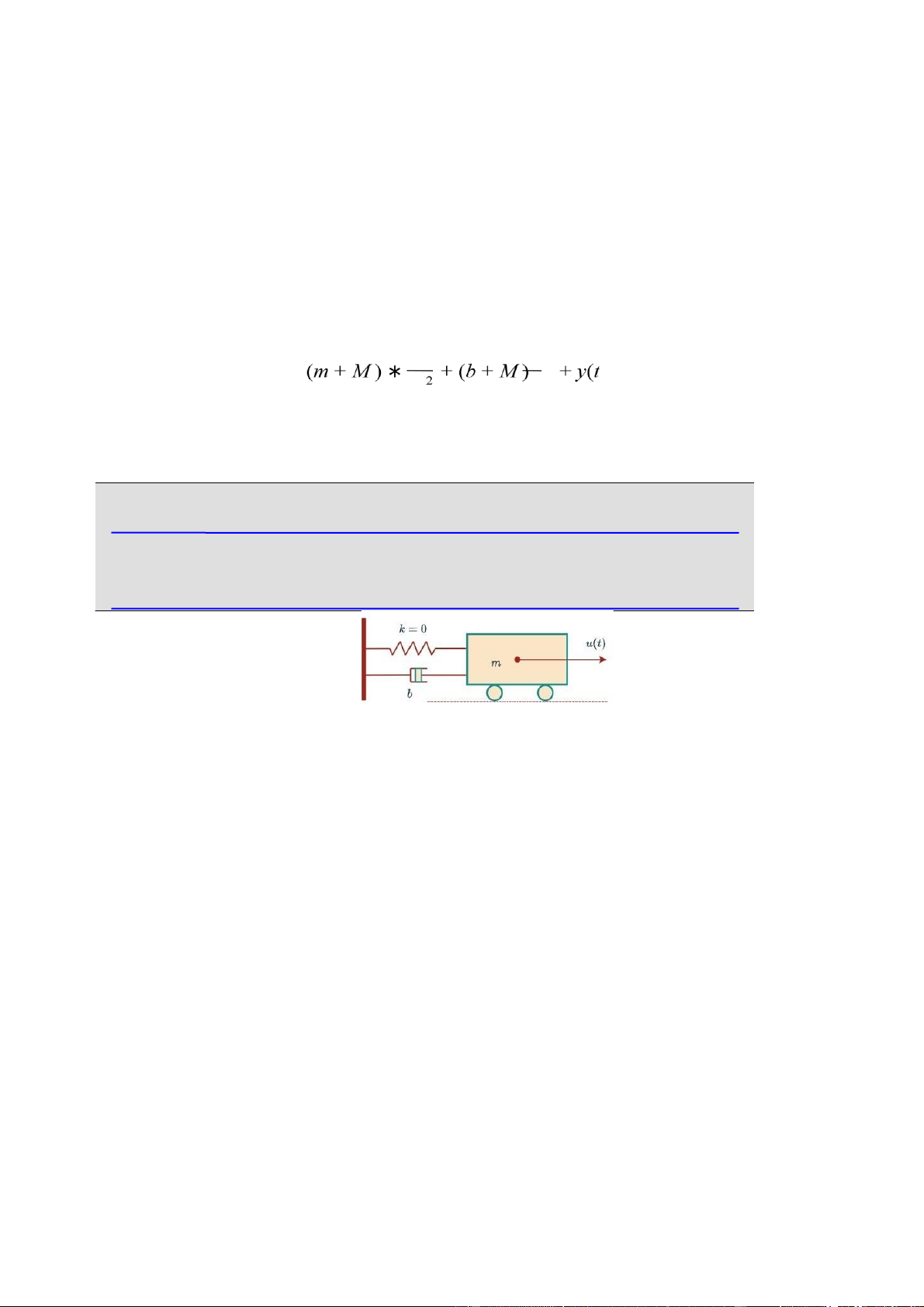
Cho phương trình vi phân mô tả hệ thống d2y dy ) = ku(t) dt dt
−4 tham số của hệ thống m = 500kg; b = 15N,
k = 5 và M = MSSV (4 : 8) ∗ 10 . Nội dung YÊU Cầu 7 8 1. Sử dụng phương
pháp đã học để xác định hàm truyền đạt, và
phương trình trạng thái.
2. Vẽ các đáp ứng của
hệ thống với các lệnh initial, impulse, step
và lsim với u(t) = 5
sin(2πt) và u(t) = 5
sin(0.5πt) + 2 cos(2πt).
3. Sử dụng lệnh c2d của MATLAB để tìm hàm truyền đạt trên miền ảnh z theo các
phương pháp ZOH, FOH và Tustin với chu kỳ trích mẫu được chọn là Ts = 0, 1s và 0, 01s.
4. Mô phỏng khảo sát, so sánh kết quả mô phỏng ở câu 2 với mô hình gián đoạn thu
được ở câu 3 (Sử dụng cả m-file và simulink để khảo sát) 2.2
Kết quả thực hành và nhận xét
2.2.1: Bài làm Matlab %% Ý a: m = 500 %kg b = 15 %N k = 5 M = 703*10^-4
% Ham truyen dat va mo hinh khong gian
num = {[k+M]} den = {[m+M b+M 1]} H = tf(num,den) systf = ss(H)
- Ta xác định các hệ số của u(t) và gán nó là biến “num”, các hệ số của y(t) và gán là
“den”. Khi đó ta xác định được hàm truyền đạt và mô hình không gian trạng thái. %% Ý b: t = 0:1:500 %da u vao u1 lOMoARcPSD|47880655 u1 = 5 * sin(0.5*pi*t); %dau vao u2
u2 = 5*sin(0.5*pi*t) + 2*cos(0.4*pi*t);
cond = input ('nhap gia tri: ') %nhap gia tri cua choosing
if cond == 1 %xet dieu kien cua if %Tinh dap ung cua he thong x0 = [-5 5]
[y ,t ,x] = initial(sys,x0,t) elseif cond == 2 %Ham dap ung xung Dirac sys = ss(systf) [y ,t ,x] = impulse(sys,t) elseif cond == 3 %xung buoc nhay, ham qua do [y,t,x]= step(sys,t) elseif cond == 4 %dap ung tin hieu bat ki
[u,t] = gensig('sin',1,10,0.1)
[y,t,x] = lsim(sys,5*u1,t) else cond == 5 [y,t,x] = lsim(sys,u2,10) end % bieu do figure(1); subplot(211); plot(t,y,'b'); legend('y');
xlabel('Time(s)'); ylabel('Output'); subplot(212);
plot(t,x(:,1),'r',t,x(:,2),'b'); legend('x1','x2');
xlabel('Time(s)'); ylabel('Output');
- Ý này sử dụng hàm “c2d” để tìm hàm truyền đạt trên miền ảnh Z bằng các phương
pháp “tustin”, “zoh” và “foh” với Ts=0.1s và 0.01s Chương 3
Xác định mô hình gián đoạn của ĐCMC 3.1
Đối tượng thí nghiệm
Cho sơ đồ cấu trúc của ĐCMC được minh họa như hình dưới đây với các thông số cho như bảng sau Điện trở phần ứng
RA − M = 250mΩ Điện cảm phần ứng
LA − M = 4mH Từ Nội dung thông định 9 mức 10 Ψ − M = 0.04 Moment quán tính
J − M = 0.012kgm2 Hằng số động cơ
ke = 236.8 + M ∗ 102, kM = 38.2 + M ∗ 10−3
Hằng số thời gian phần ứng TA = La/Ra Mã số SV
M = MSSV (4 : 8) ∗ 10−4. YÊU Cầu:
1. Sử dụng phương pháp đã học để xác định hàm truyền kín trên miền ảnh z. Chu kỳ
trích mẫu được chọn là Ts = 0, 1ms và 0, 01ms
2. Sử dụng lệnh c2d của MATLAB để tìm hàm truyền đạt trên miền ảnh z theo các
phương pháp ZOH, FOH và Tustin. lOMoARcPSD|47880655
3. Mô phỏng khảo sát, so sánh, nhận xét kết quả với 3 mô hình gián đoạn thu được
ở câu 2 sử dụng lệnh initial, impluse, step và lsim với u(t) = 5 sin(0.5πt) và u(t) =
5 sin(0.5πt) + 2 cos(0.4πt) (Sử dụng cả m-file và simulink để khảo sát).
4. Xây dựng mô hình trạng thái của ĐCMC trên miền thời gian liên tục. Sử dụng
phương pháp đã học để gián đoạn hóa mô hình với giả thiết chu kỳ trích mẫu Ts =
0, 01s và Ts = 0, 1s. Mô phỏng khảo sát đáp ứng bước nhảy của 2 mô hình thu
được (Sử dụng cả m-file và simulink để khảo sát). 3.2
Báo cáo thí nghiệm và nhận xét kết quả 3.2.1 Bài làm matlab %% Ý a: % thông số M=702*10^-4 ke = 236,8 + M*10^2 km = 38,2 +M*10^-3 Ra= 250*10^-3 +M La = M + 4*10^-3 phi = 0.04 +M J = 0.012 + M Ta = La/Ra G1 = 1/Ra G2 = tf(1,[1 Ta]) G3 = km*phi G4 = tf(1,[2*pi*J 0]) G5 = ke*phi G12 = series (G1,G2) G34 = series(G3,G4) G1234 = series (G12, G34) G = feedback(G1234,G5,-1)
- Ở ý a, ta sử dụng các hàm series để kết nối các khối lại với nhau, sau đó sử dụng
“feedback” để tìm hàm phản hồi ngược về %% ý B: Ts = 0.1 zoh = c2d(G,Ts,'zoh') foh = c2d(G,Ts,'foh') tustin = c2d(G,Ts,'tustin') Ts1 = 0.01 zoh1 =c2d(G,Ts1,'zoh') foh1 = c2d(G,Ts1,'foh') tustin1 =
c2d(G,Ts1,'tustin') - Ý này sử
dùng hàm “c2d” để tìm hàm truyền
đạt trên miền ảnh Z bằng các phương
pháp “tustin”, “zoh” và “foh” với Ts = 0.1 và 0.01 %% Ý c: t = 0:1:100 sys=ss(G)
cond = input('Nhap gia tri: ') x0 = [-5, 5] if cond == 1 [y,t,x] = initial(sys,x0,t) elseif cond ==2 [y,t,x] = impulse(sys,t) elseif cond == 3 [y,t,x ] == step(sys,t) elseif cond == 4 u = 5*sin(0.5*pi*t)
[u,t] = gensig('sin',1,10,0.1)
[y,t,x ] = lsim(sys,5*u,t) else cond == 5
u = 5*sin(0.5*pi*t) + 2*cos(0.4*pi*t)
[u,t] = gensig('sin',1,10,0.1)
[y,t,x ] = lsim(sys,u,t) end figure(1);
subplot(211); plot(t,y,'b'); legend('y');
xlabel('Time(s)'); ylabel('Output'); subplot(212);
plot(t,x(:,1),'r',t,x(:,2),'b'); legend('x1','x2');
xlabel('Time(s)'); ylabel('Output');
- Tiếp đến ta sử dụng các hàm “initial”, “step”,”impulse” và “lsim” để xác định các
đáp ứng của hệ thống. Sau đó vẽ đồ thị bằng “plot” để mô phỏng kết quả đã tính toán ở trên. Chương 4
Tổng hợp vòng điều chỉnh dòng phần ứng 4.1
Đối tượng thí nghiệm
Giả thiết bỏ qua sức từ động cảm ứng eA, thực hiện thiết kế vòng điều chỉnh lOMoARcPSD|47880655
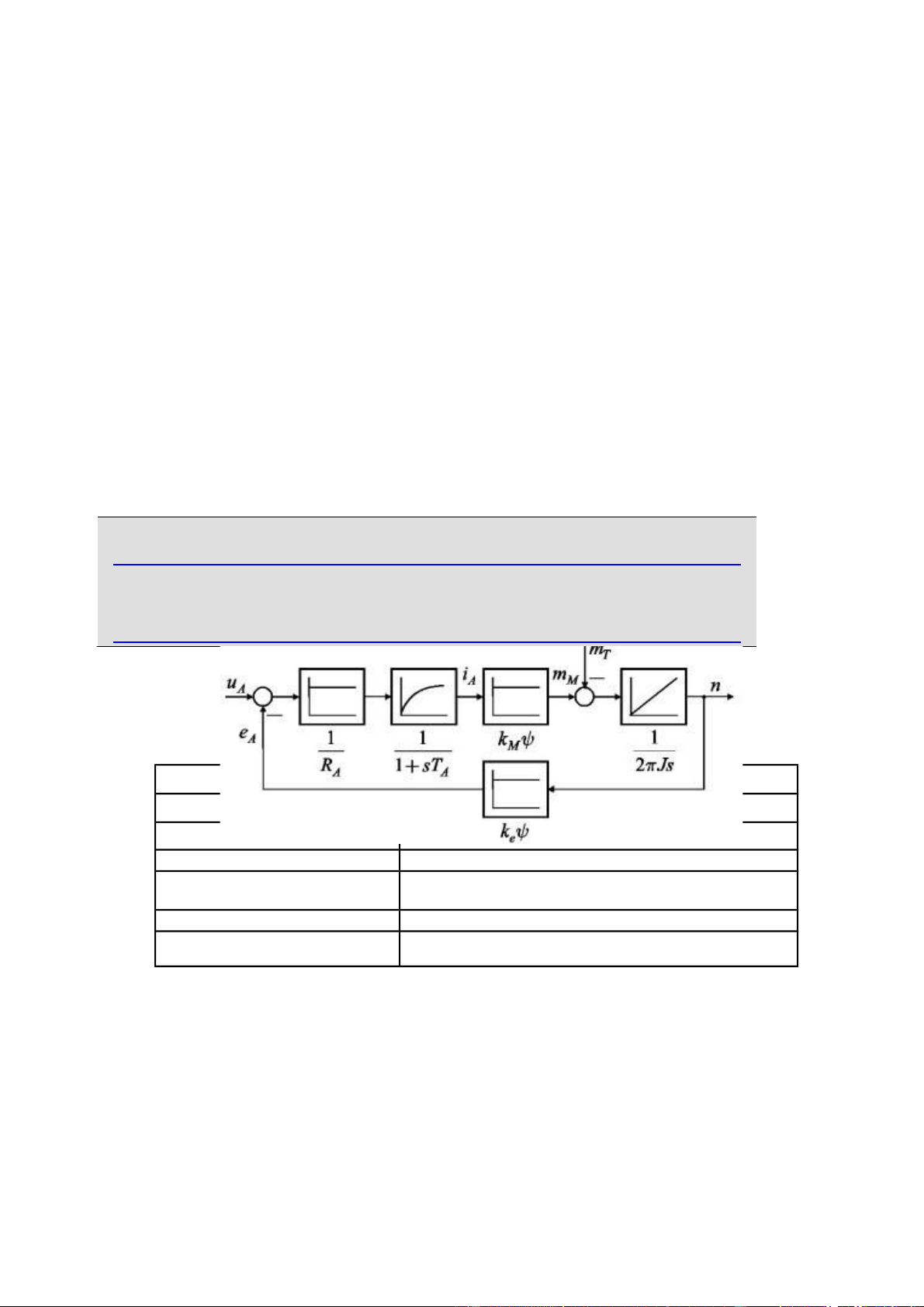
(viết tắt: ĐC) dòng cho ĐCMC với cấu trúc được mô tả như hình 4.1
Hình 4.1: Sơ đồ điều khiển DCMC theo cấu trúc casecade
Vòng ĐC dòng phần ứng iA với độ chính xác cao và quán tính nhỏ, tạo khả năng
áp đặt nhanh dòng phần ứng iA (và do đó áp đặt không trễ mômen quay mM ) là điều kiện Nội dung tiên quyết, 11 bảo 12 đảm
chất lượng ĐK cho ĐCMC. Vì vậy, các phương pháp thiết kế bộ ĐK kiểu bù
(Compensation Controller, còn gọi là: phương pháp cân bằng mô hình) hoặc kiểu
Dead-Beat (DeadBeat Controller) hay được sử dụng. Trong đó vòng ĐC, thiết bị
chỉnh lưu được mô tả tương đương một khâu quán tính bậc nhất đứng liền sau khâu
ĐC dòng trong hình 4.1 , với giả thiết có hằng số thời gian Tt = 100µs. Mô hình
đối tượng ĐK dòng đã được xây dựng ở bài tập thực hành số 1. YÊU Cầu:
1. Sử dụng phương pháp đã học để xác định hàm truyền trên miền ảnh z thích hợp
để thiết kế vòng điều khiển dòng phần ứng. Chu kỳ trích mẫu được chọn là Ts
= 0, 1ms và 0, 01ms
2. Sử dụng lệnh c2d của MATLAB để tìm hàm truyền đạt trên miền ảnh z theo
các phương pháp ZOH, FOH và Tustin.
3. Hãy thiết kế bộ ĐC dòng theo phương pháp Dead-Beat với L(z−1) là một đa
thức bậc 1 hoặc 2. Mô phỏng khảo sát đặc điểm của vòng ĐC đã thiết kế.
4. Hãy thiết kế bộ ĐC dòng theo phương pháp cân bằng mô hình sao cho tốc độ
đáp ứng của giá trị thực là 2 và 3 chu kỳ Ts. Mô phỏng khảo sát đặc điểm của vòng ĐC đã thiết kế.
5. Phân tích so sánh các kết quả mô phỏng đã thu được ở câu 3 và 4. 4.2
Báo caó thí nghiệm và nhận xét 4.2.1 Bài làm matlab %% ý 1 M = 703*10^-4 Ra = M + 250*10^-3 %Ohm La = M + 4*10^-3 %H phi= M + 0.04 J = M + 0.012 %kg*m^2 ke = 236.8 + M km = 38.2 + M Ta = La/Ra H = ke*phi Tt = 100*10^-6 %s % feedback 1. G1 = tf(1,[Tt 1]) G2 = 1/Ra G3 = tf( 1, [Ta 1]) Gf1 = series ( G3, G2) Gf2 = series (Gf1, G1) Ga = feedback ( Gf2, -1) num=Ga.Numerator{1} den=Ga.Denominator{1} disp(Ga)
- Ý đầu tiên, sử dụng hàm “Series” để kết nối 2 đối tượng với nhau là và . Sau đó lại
dùng hàm “Series” để kết nối với 2 khối trên. Cuối cùng dùng hàm “feedback” là hàm phản hồi về.
- Dùng hàm “Numerator” và “Denominator” để tìm các giá trị hệ số của tử và mẫu từ
hàm “feedback” bên trên. %% ý 2 % voi Ts= 0.0001
zoh = c2d(Ga,0.1*10^-3, 'zoh') foh =
c2d(Ga,0.1*10^-3,'foh') tustin = c2d (Ga,0.1*10^-3,'tustin')
%voi Ts = 0.01*10^-3 zoh1 = c2d(Ga, 0.01*10^-3, 'zoh') foh1 =
c2d(Ga,0.01*10^-3, 'foh') tustin1 = c2d(Ga,0.01*10^-3, 'tustin')
- Ý này sử dụng hàm “c2d” để tìm hàm truyền đạt trên miền ảnh Z bằng các phương
pháp “tustin”, “zoh” và “foh”. %% cân b ngằ Ts = 0.0001 G_cur = c2d( Gf2,Ts,'zoh') %Current control lOMoARcPSD|47880655
G_m = tf ([0.7 0.2 0.1], [1 0 0 0], Ts)
G_conCur = G_m/((1-G_m)*G_cur) num1 = G_conCur.Numerator{1}; den1 = G_conCur.Denominator{1} %% Dead_beat Ts = 0.0001 Gz = c2d( Gf2,Ts,'zoh') num2 = G_cur.Numerator{1}; den2 = G_cur.Denominator{1}; Gzf = filt(num2, den2,Ts) numf= Gzf.Numerator{1} denf=Gzf.Denominator{1} % lay a,b b1= numf(2) b2= numf(3) a1 = denf(2) a2 = denf(3) %tim q q0 = 1/sum(numf) q1 = q0*a1 q2 = q0*a2 p1 = q0*b1 p2 = q0*b2 % bo dieu khien
Gc = filt([q0 q1 q2], [1 -p1 -p2], Ts) numC= Gc.Numerator{1} denC=Gc.Denominator{1}
- Tiếp tới là thiết kế bộ điều khiển theo phương pháp cân bằng và Dead-Beat. Hai
phương pháp này khác nhau ở chỗ, Dead-Beat thì chúng ta phải tự tay tìm các hệ số
q1,q2,.. và p1,p2 . Còn phương pháp cân bằng thì chúng ta được chọn hệ số của
q1,q2,q3,.. và p1,p2,p3,… nhưng tổng giá trị của p phải bằng 1 và giá trị của q0 + q1 phải bằng giá trị q2.
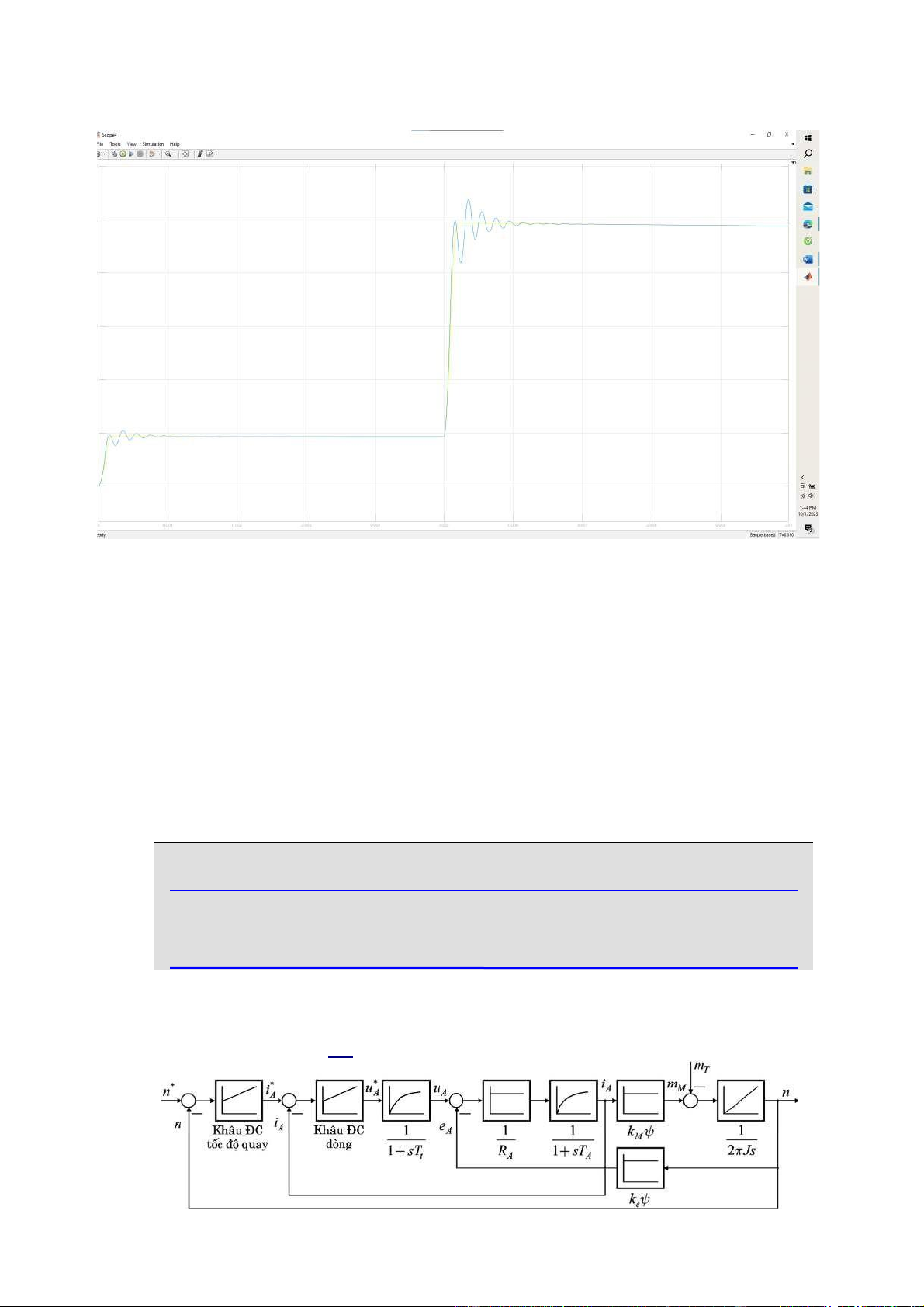
4.2.2 Kết quả mô phỏng so sánh 2 phương pháp Dead-beat và cân bằng Nhận xét:
Hình ảnh trên cho thấy đường màu xanh là của phương pháp cân bằng sẽ không ổn định
bằng đường màu vàng của phương pháp Dead-beat.
Như vậy, theo phương pháp Dead-Beat hệ thống sẽ ổn định hơn phương pháp cân bằng. Chương 5
Tổng hợp vòng điều chỉnh dòng phần ứng Nội dung 13 14 5.1
Đối tượng thí nghiệm
Thực hiện thiết kế vòng điều chỉnh (viết tắt: ĐC) tốc độ cho ĐCMC với cấu trúc
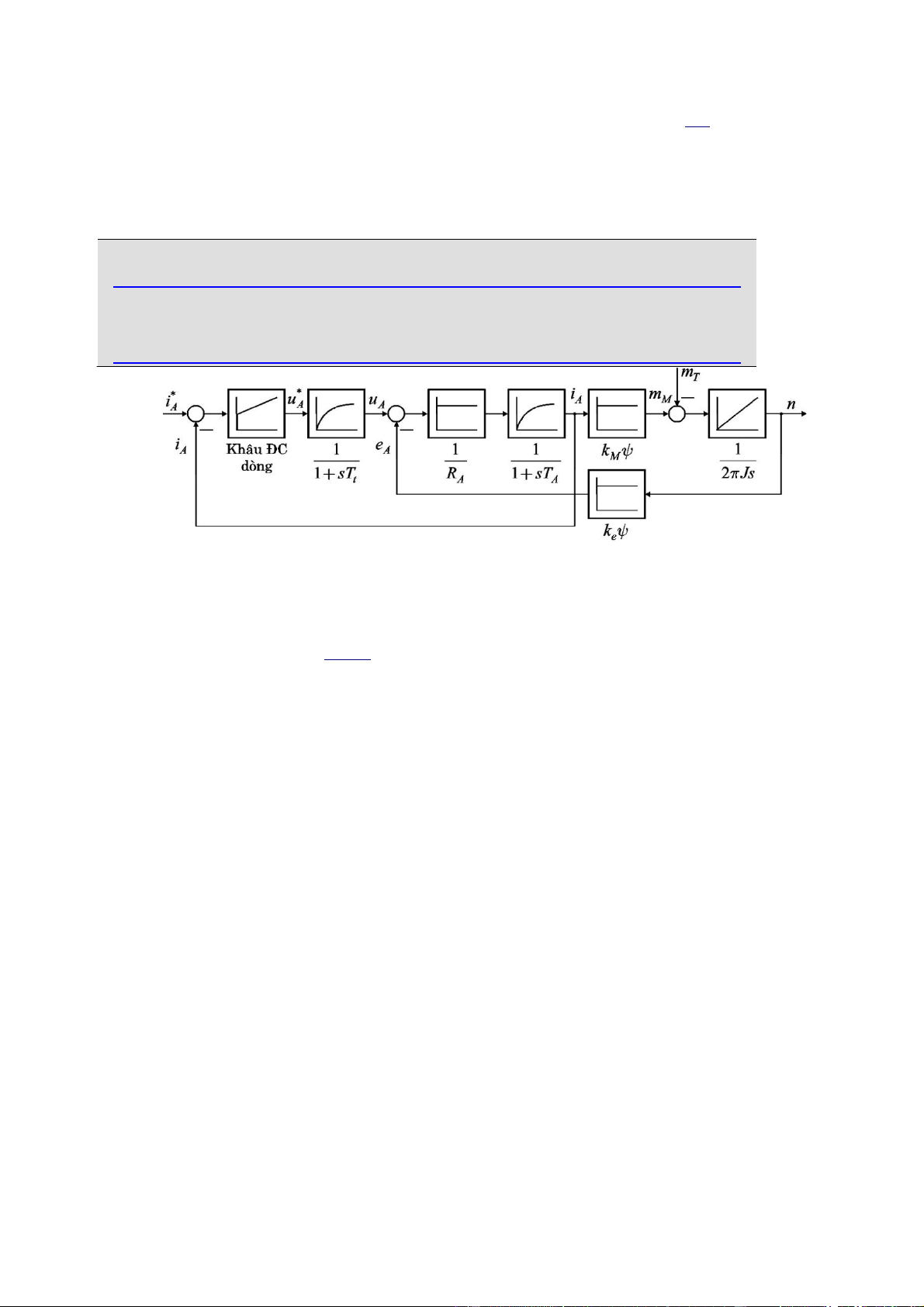
được mô tả như hình 5.1 lOMoARcPSD|47880655
Hình 5.1: Sơ đồ điều khiển tốc độ DCMC theo cấu trúc casecade YÊU Cầu:
1. Trên cơ sở vòng ĐC dòng phần ứng đã thiết kế ở bài thực hành số 2, hãy vận
dụng kiến thức để xác định hàm truyền đạt trên miền ảnh z của đối tượng,
phục vụ thiết kế khâu ĐC tốc độ quay.
2. Sử dụng lệnh c2d của MATLAB để tìm hàm truyền đạt trên miền ảnh z theo
các phương pháp ZOH, FOH và Tustin.
3. Tổng hợp (thiết kế) bộ điều chỉnh PI cho tốc độ động cơ.
4. Mô phỏng khảo sát vòng ĐC tốc độ quay cho 2 trường hợp: a) Giá trị đặt của
tốc độ quay thay đổi dưới dạng bước nhảy; b) Phụ tải thay đổi đột biến dưới dạng bước nhảy. 5.2
Báo cáo thí nghiệm và nhận xét kết quả 5.2.1 Bài làm matlab %% ý a M = 703*10^-4 Ra = M + 250*10^-3 %Ohm La = M + 4*10^-3 %H phi= M + 0.04 J = M + 0.012 %kg*m^2 ke = 236.8 + M km = 38.2 + M Ta = La/Ra H = ke*phi Tt = 100*10^-6 %s % feedback 1. G1 = tf(1,[Tt 1]) G2 = 1/Ra G3 = tf( 1, [Ta 1]) G4 = km*phi G5 = tf(1,[2*pi*J 0]) Gf1 = series ( G3, G2) Gf2 = series (Gf1, G1) G45 = series(G4,G5) Gt = series(Gf2,G45) Ga = feedback ( Gt, - 1) num=Ga.Numerator{1} den=Ga.Denominator{1} disp(Ga)
Ý đầu tiên, sử dụng hàm “Series” để kết nối 2 đối tượng với nhau là và . Sau đó lại
dùng hàm “Series” để kết nối với 2 khối trên. Cuối cùng dùng hàm “feedback” là hàm phản hồi về.
Dùng hàm “Numerator” và “Denominator” để tìm các giá trị hệ số của tử và mẫu từ
hàm “feedback” bên trên. %% ý b % voi Ts= 0.01 zoh = c2d(Ga,0.01, 'zoh') foh = c2d(Ga,0.01,'foh') tustin = c2d (Ga,0.01,'tustin') %voi Ts = 0.01*10^-3 zoh1 = c2d(Ga, 0.1, 'zoh') foh1 = c2d(Ga,0.1, 'foh')
tustin1 = c2d(Ga,0.1,'tustin')
Ý này sử dụng hàm “c2d” để tìm hàm truyền đạt trên miền ảnh Z bằng các phương pháp
“tustin”, “zoh” và “foh”. %% ý c Gt1 = tf(1,[2*Tt 1]) G_obj= series (G45,Gt1) Tc = 0.01 Gcs=series(tf(1,[Tc 0]),1/G_obj) num3=Gcs.Numerator{1} den3=Gcs.Denominator{1} a1 =
num3(1) a2=num3(2) b2=den3(2) P = a2/b2 D = a1/b2