





Preview text:
ĐÁP ÁN
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
ĐỀ THI ĐÁNH GIÁ NĂNG LỰC SƯ PHẠM
THÁNG ………………… Mã đề 001 MÔN THI: TOÁN
(Thời gian làm bài 90 phút, không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN ( 7 điểm)
Câu 1. Hàm số y 5
4sin 2x cos 2x có tất cả bao nhiêu giá trị nguyên? A. 3 B. 4 C. 5 D. 6 Lời giải Chọn C Ta có y
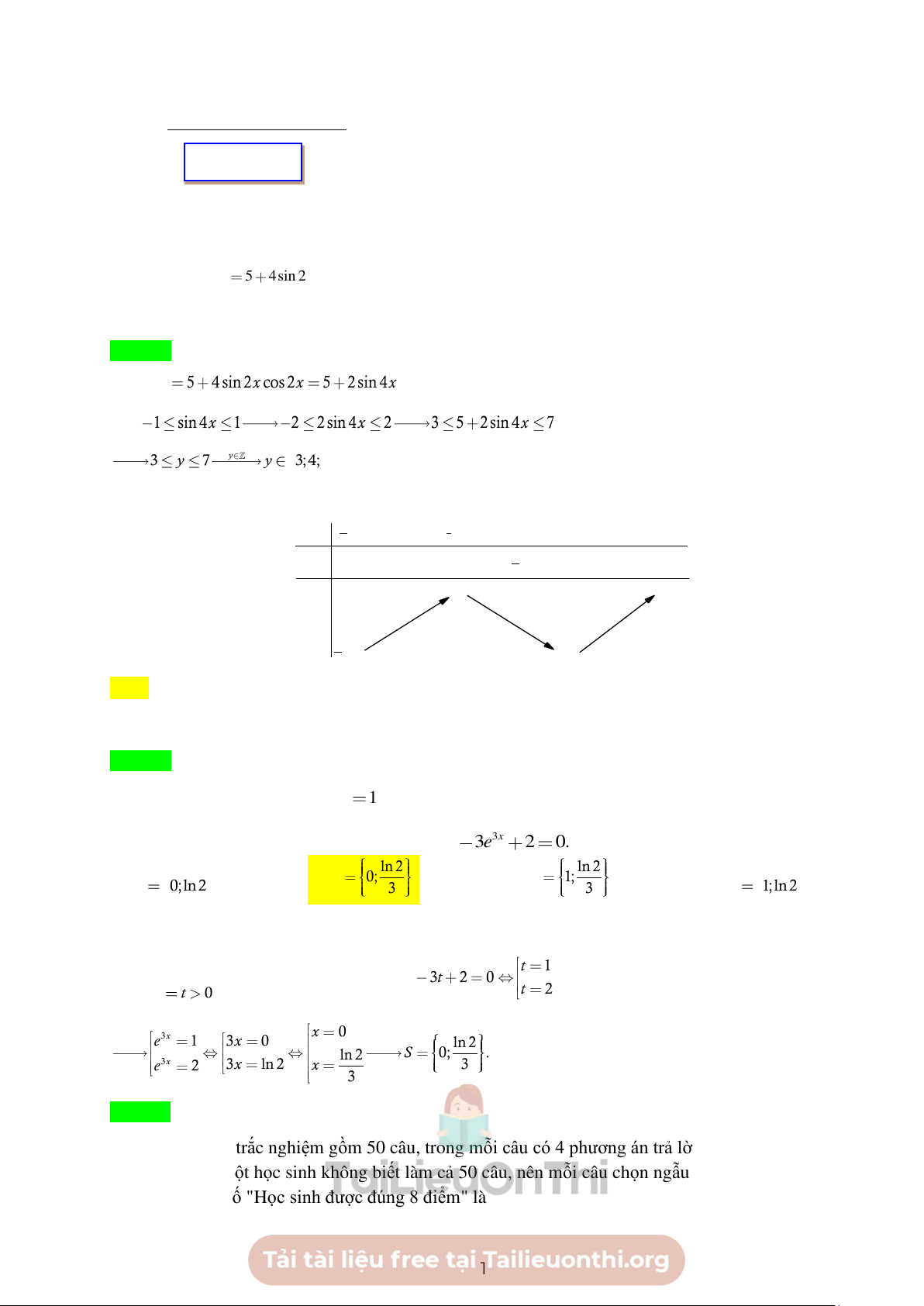
5 4 sin 2x cos 2x 5 2 sin 4x . Mà 1 sin 4x 1 2 2sin 4x 2 3 5 2sin 4x 7 3 7 y y y
3;4;5;6;7 nên y có 5 giá trị nguyên.
Câu 2. Cho hàm số y = f ( x) có bảng biến thiên như hình bên. Giá trị cực tiểu của hàm số bằng x ∞ 1 3 + ∞ y' + 0 0 + + ∞ 5 y ∞ 1 A. 1 . B. 3 . C. 5 . D. 1 − . Lời giải. Chọn A
Nhìn bảng biến thiên ta thấy y 1 . ct
Câu 3. Tìm tập S nghiệm của phương trình 6x 3 3 x e e 2 0. ln 2 ln 2 S 0; S 1; S 0;ln 2 S 1;ln 2 A. . B. 3 . C. 3 . D. . Lời giải. t 1 2 t 3t 2 0 Đặ 3x t 2 t e t
0 . Phương trình trở thành . 3x x 0 e 1 3x 0 ln 2 ln 2 S 0; . 3x e 2 3x ln 2 x 3 3 Chọn B
Câu 4. Một đề thi trắc nghiệm gồm 50 câu, trong mỗi câu có 4 phương án trả lời và có duy nhất một
phương án đúng. Một học sinh không biết làm cả 50 câu, nên mỗi câu chọn ngẫu nhiên một phương án.
Xác suất của biến cố "Học sinh được đúng 8 điểm" là 1
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
---------------------------------------------------------------------------------------------------------------------------------------------------- 40 10 40 40 10 40 10 C .3 1 1 3 1 3 A. 50 . B. 40 C . . C. . . D. 40 C . . . 40 4 50 4 4 4 50 4 4 Lời giải Chọn D
Gọi P là xác suất của biến cố "Học sinh được đúng 8 điểm" 40 10 1 3
Áp dụng công thức Bernoulli ta có: 40 P=C . . 50 4 4 3 5 4 3 4 Câu 5. Biết
f ( x) dx = và
f (t ) dt = . Tính f (u) du . 3 5 0 0 3 8 14 17 16 A. . B. . C. − . D. − . 15 15 15 15 Lời giải Chọn D 4 3 4 Ta có f
(u)du = f
(u)du + f (u)du . 0 0 3 3 3 5 4 4 3 Mà
f (u) du = f ( x) dx = và
f (u) du = f (t) dt = . 3 5 0 0 0 0 4 4 3 5 3 5 16 Nên
= + f (u)du f (u)du = − = − . 5 3 5 3 15 3 3
Câu 6. Trong không gian Oxyz, cho mặt phẳng (P) : x + 2y −3z − 4 = 0 và điểm A(1; 2 − ;− ) 3 . Phương
trình đường thẳng đi qua A và vuông góc với mặt phẳng (P) là x −1 y + 2 z + 3 x +1 y − 2 z − 3 A. = = . B. = = . 1 2 3 − 1 2 3 − x −1 y − 2 z + 3 x −1 y + 2 z + 3 C. = = = = 1 2 − 3 − . D. 1 2 − 3 − . Lời giải Chọn A
Dễ thấy vectơ chỉ phương của đường thẳng d đi qua A và vuông góc với (P) là một vectơ pháp tuyến của mặt phẳng (P).
Nên vectơ chỉ phương của đường thẳng d là: u (1;2; 3
− ). Và đường thẳng đi qua A(1;-2;-3) nên phương − + + trình đườ x 1 y 2 z 3 ng thẳng d là: = = 1 2 3 −
Câu 7. Người ta đo độ dài thân của 80 con cá rô được nuôi ở một khu vực. Kết quả được biểu diễn ở
biểu đồ tần số tương đối ghép nhóm sau (đơn vị: cm). 2
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
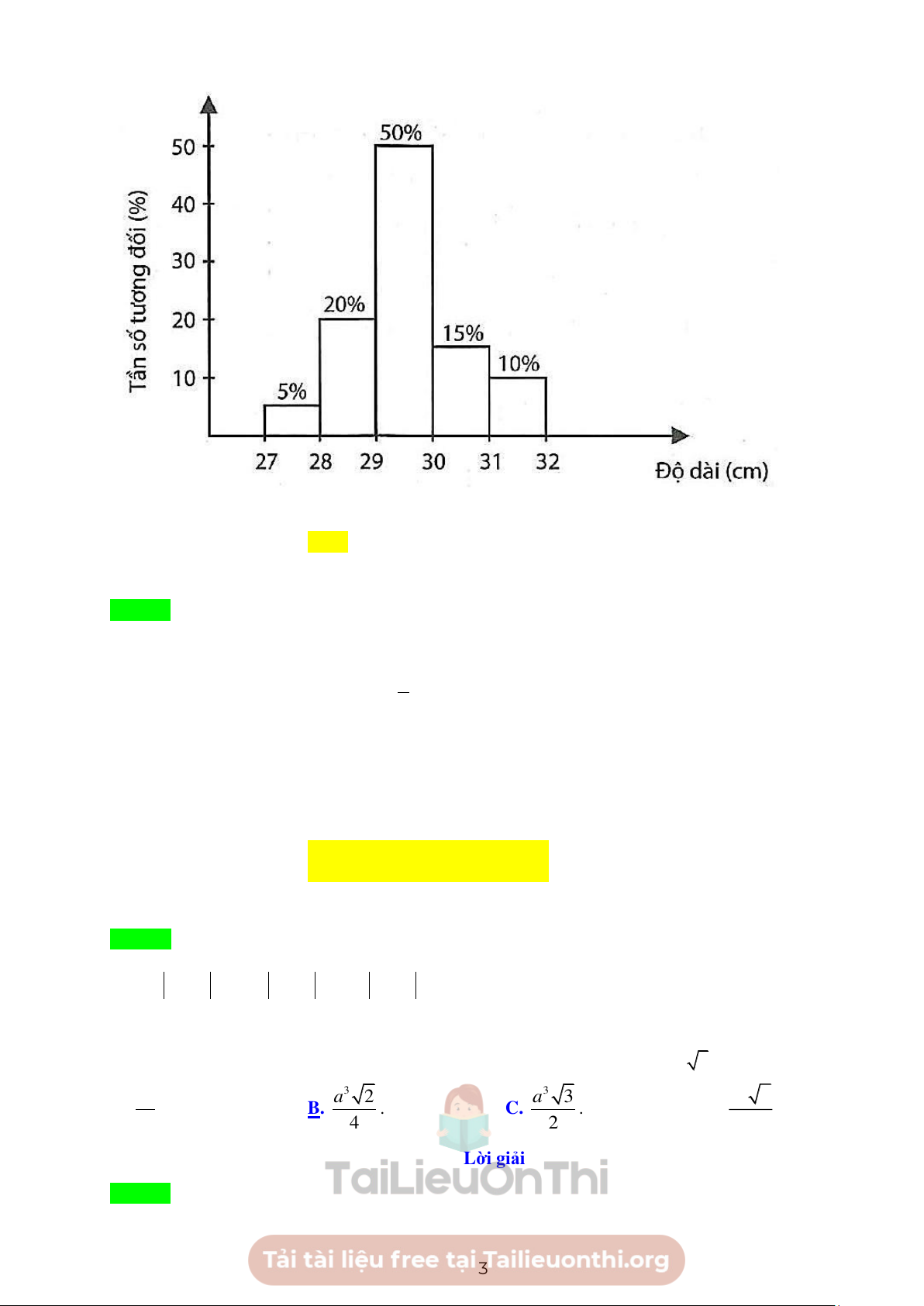
Số con cá có độ dài thân nhỏ hơn 29 cm là: A. 5. B. 20 C. 25 D. 16 Lời giải Chọn B
Dựa vào biểu đồ thì số con cá có độ dài thân nhỏ hơn 29 cm là 25% của 80 con 1
Nên số lượng cá thỏa mãn yêu cầu là: .80 = 20 4
Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y = 2 và các đường thẳng y = 2; x = 1 − ;x = 2 có giá trị bằng 2 2
A. (2x − 2)dx .
B. (2x − 2)dx 1 1 − 2 1 2
C. (2 − 2x )dx .
D. (2 − 2x ) + (2x dx − 2)dx . 1 − 1 − 1 Lời giải Chọn D 2 1 2 1 = 2x − 2 = 2x − 2 + 2x − 2 = (2−2x) 2 + (2x S dx dx dx dx − 2) . dx . 1 − 1 − 1 1 − 1
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , tam giác SAB đều nằm trong mặt
phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp. Biết rằng AB = a 3; AC = . a 3 a 3 a 2 3 a 3 3 a 2 A. . B. . C. . D. . 2 4 2 2 Lời giải Chọn B 3
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
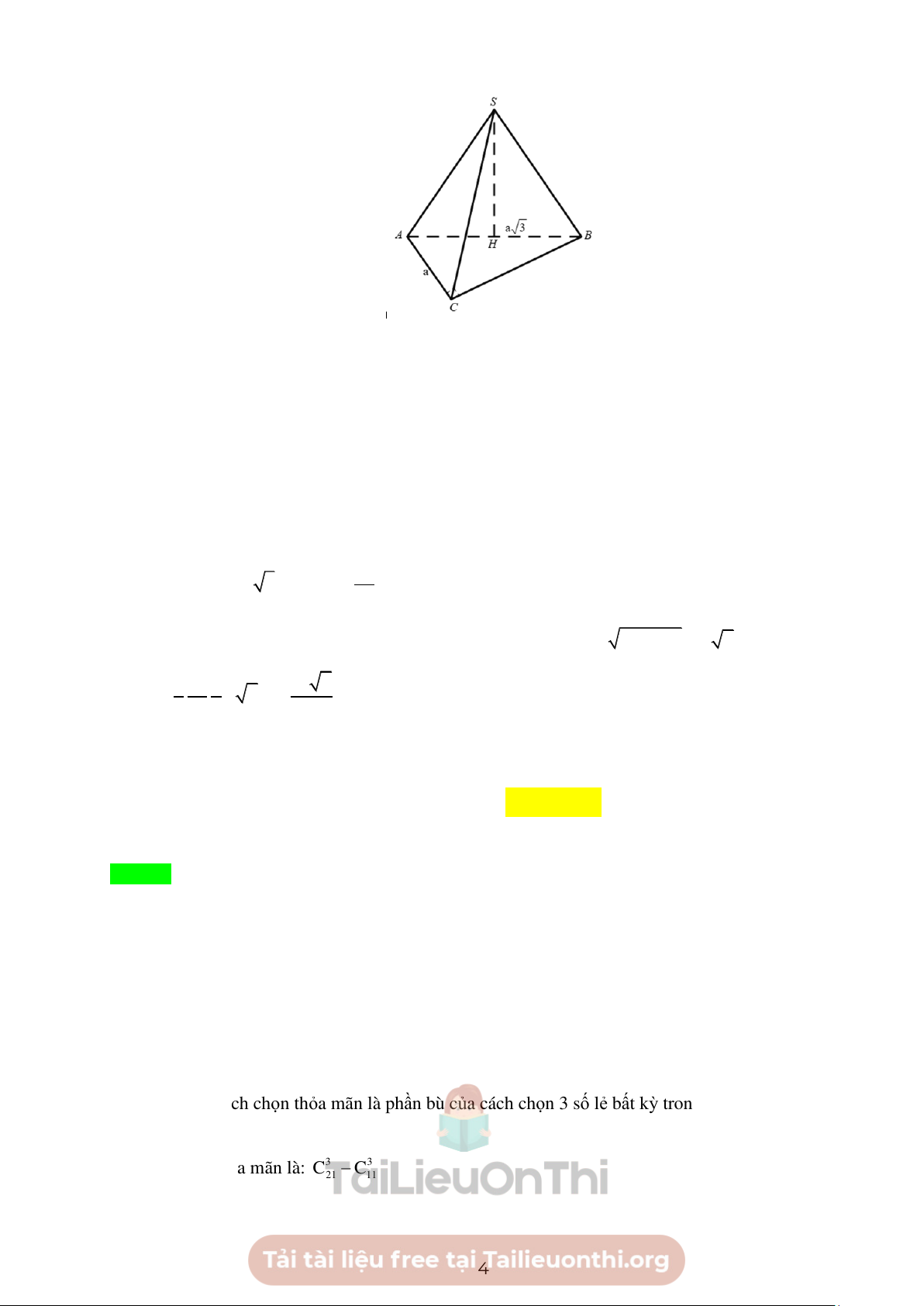
Trong mặt phẳng (SAB) .Gọi H là trung điểm của AB . S
AB đều SH ⊥ A . B Ta có: SH ⊥ AB (
SAB) ( ABC ) = AB SH ⊥ ( ABC ). ( SAB) ⊥ ( ABC ) 3a S
AB đều AB = a 3 SH = . 2 ABC
là tam giác vuông cân tại C 2 2 2 2 2
AB = AC + BC BC = 3a − a = a 2. 3 1 3a 1 a 2 V = a 2.a = . S.ABC 3 2 2 4
Câu 10. Có 21 thẻ được viết các số tự nhiên liên tiếp từ 1 đến 21 (mỗi thẻ viết đúng một số). Có bao
nhiêu cách chọn ra 3 thẻ thoả mãn tích của 3 số trên 3 thẻ được chọn là số chẵn? A. 3 C . B. 3 A . C. 3 3 C − C . D. 3 3 C − C . 21 21 21 11 21 10 Lời giải Chọn C
Gọi A = 1;2;.....;2
1 là tập hợp các số được đánh số trên thẻ.
Chọn ngẫu nhiên 3 thẻ bất kỳ ta có: 3 C (lựa chọn) 21
Trong tập A có 11 số tự nhiên lẻ. Ta chọn 3 số lẻ bất kỳ có: 3 C (lựa chọn) 11
Khi đó, để tích 3 thẻ được chọn là một số chẵn thì trong 3 thẻ được chọn ít nhất có một thẻ là số chẵn.
Vậy số lượng cách chọn thỏa mãn là phần bù của cách chọn 3 số lẻ bất kỳ trong việc chọn ngẫu nhiên 3 thẻ
Số cách chọn thỏa mãn là: 3 3 C − C 21 11 4
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
---------------------------------------------------------------------------------------------------------------------------------------------------- ax + b
Câu 11. Cho hàm số y =
có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi cx + d trong các số , b ,
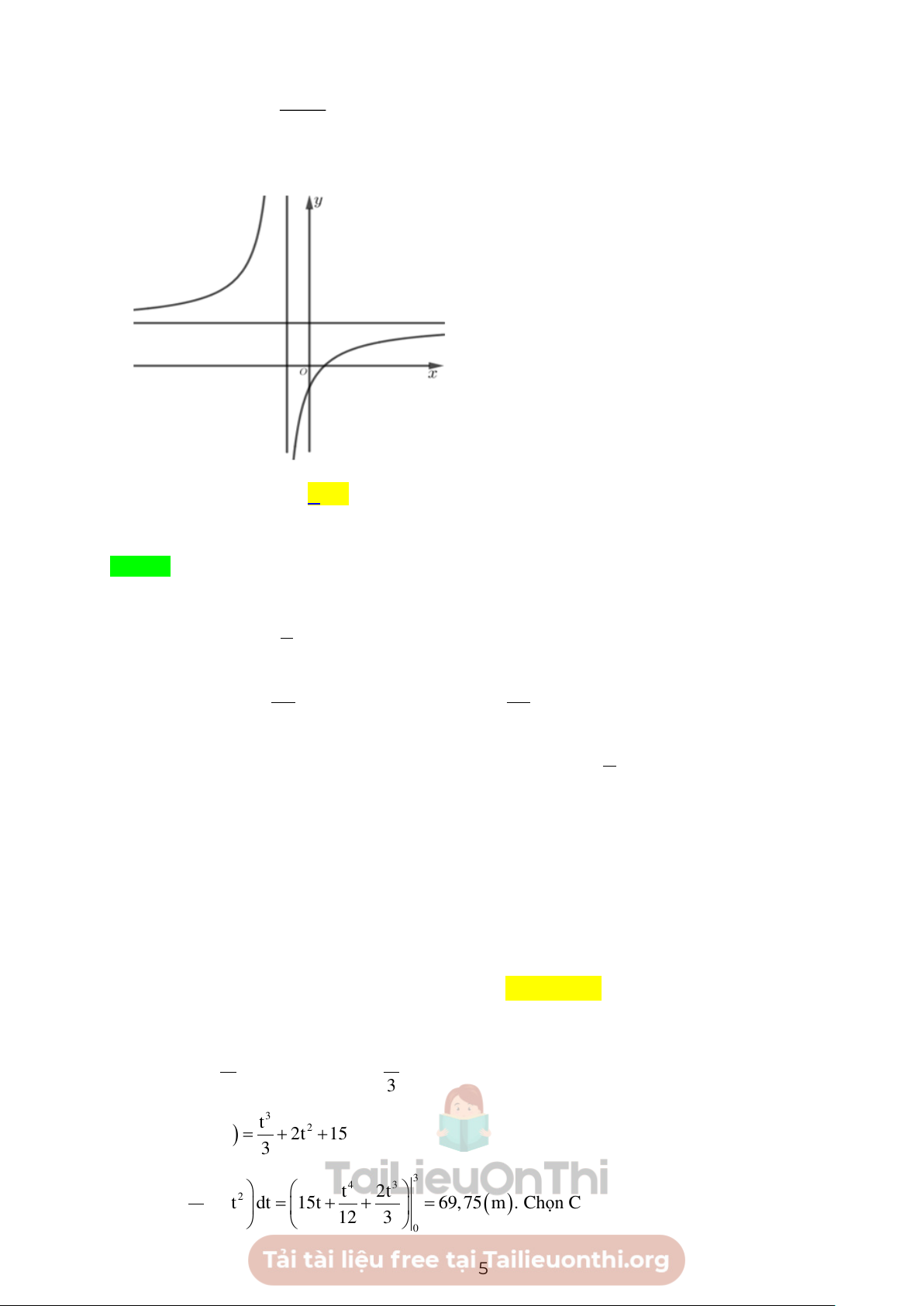
c d có tất cả bao nhiêu số dương? A. 1. B. 2 . C. 0 . D. 3 . Lời giải Chọn B
Nhìn vào đồ thị ta thấy: • a Tiệm cận ngang y =
nằm trên trục hoành nên c 0 (vì a 0 ) c − − • d d
Tiệm cận đứng x =
nằm bên trái trục tung nên
0. Suy ra d 0 (vì c 0 ) c c • b
Giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên 0. d
Suy ra b 0 (vì d 0 )
Vậy 𝑐 > 0, 𝑑 > 0.
Câu 12. Một chất điểm đang chuyển động với vận tốc v = 15 m / s thì tăng vận tốc với gia tốc 0 ( ) 2 = + ( 2 a t t
4t m / s ). Quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc là A. 67, 25 m . B. 68, 25 m. C. 69, 75 m. D. 70, 25 m . Đáp án (t + 4t) 3 t dt = + 2t + C v(t) 3 t 2 2 2 = + 2t + C . 3 3
v (0) = 15 v (t) 3 t 2 = + 2t +15 3 3 3 3 4 3 t t 2t 2 s = 15 + + 2t dt = 15t + + = 69,75(m). Chọn C 3 12 3 0 0 5
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
Câu 13. Trong không gian Oxyz, hình chiếu vuông góc của điểm M(1;2; 4
− ) trên trục Ox là điểm có toạ độ A. (0;2;0) . B. (1;0;0) . C. (0;0; 4 − ) . D. (1; 2; 4 − ). Lời giải Chọn B
Khi chiếu vuông góc điểm M lên trục Ox thì tung độ và cao độ đều = 0
Câu 14. Một cấp số cộng gồm bốn số hạng, biết tổng của chúng bằng 20 và tổng các bình phương của
chúng bằng 120. Tìm các số hạng của cấp số cộng đó. A. 8 − ,−6,−4,−2. B. 1,3,5,7. C. 2, 4,6,8. D. 7 − ,−5,−3,−1. Lời giải Chọn C
Không mất tính tổng quát, giả sử bốn số hạng của cấp số cộng đó là a −3 ; x a − ; x a + ;
x a + 3x với công
sai là d = 2x ( x 0). Khi đó, ta có:
(a −3x)+(a − x)+(a + x)+ (a + 3x) = 20 4a = 20 a = 5 ( do x 0 2 2 ( ) a − 3x
)2 +(a − x)2 +(a + x)2 +(a +3x)2 =120 4a + 20x =120 x =1
Vậy bốn số hạng của cấp số cộng cần tìm là 2, 4,6,8 .
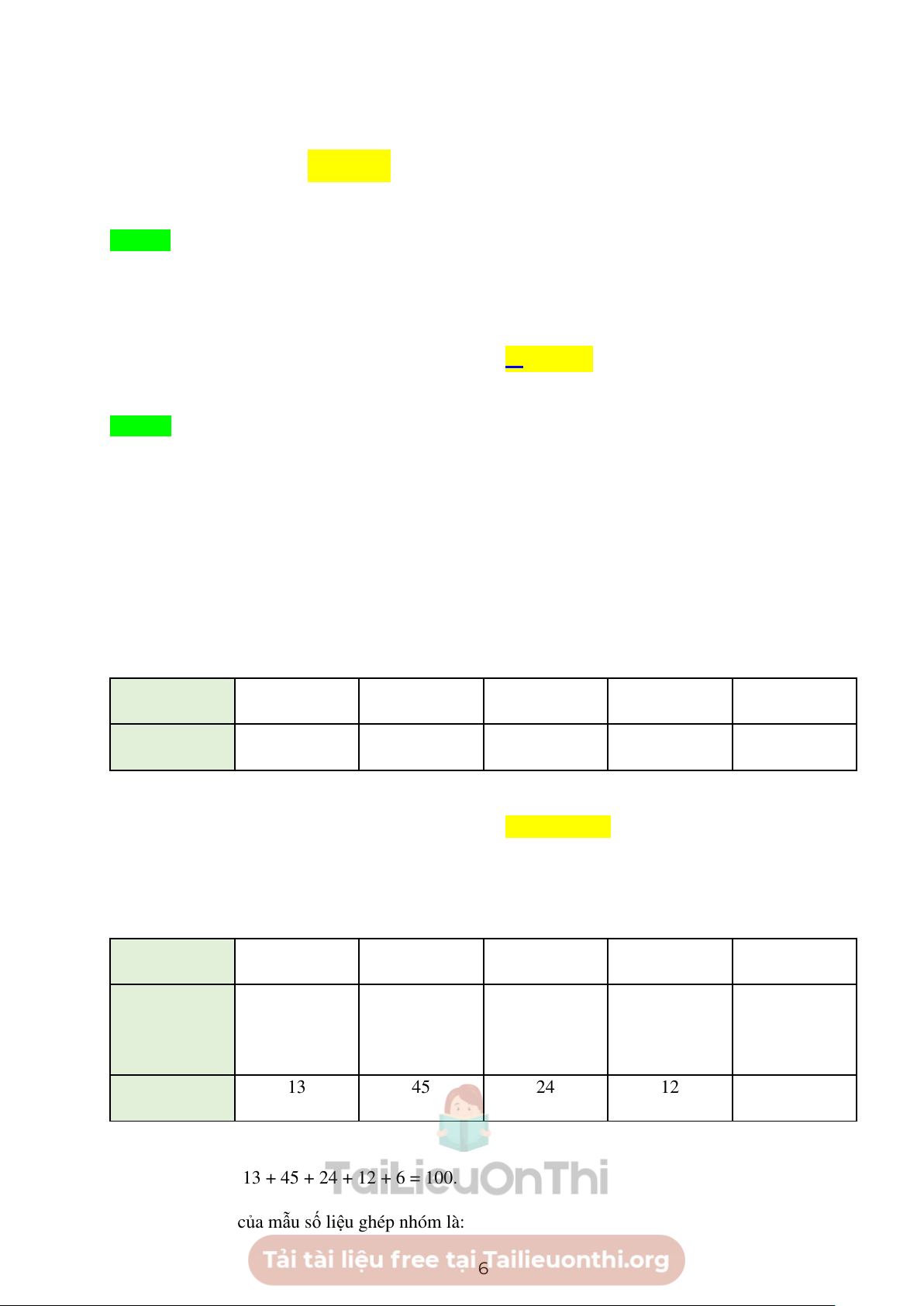
Câu 15. Bảng dưới đây thống kê cự li ném tạ của một vận động viên. Cự li (m) [19; 19,5) [19,5; 20) [20; 20,5) [20,5; 21) [21; 21,5) Tần số 13 45 24 12 6
Số trung bình của mẫu số liệu ghép nhóm xấp xỉ là A. 20.02 m . B. 20.15 m . C. 20.015 m . D. 20.05 m . Lời giải Ta có bảng sau: Cự li (m) [19; 19,5) [19,5; 20) [20; 20,5) [20,5; 21) [21; 21,5) Giá trị 19,25 19,75 20,25 20,75 21,25 đại diện Tần số 13 45 24 12 6
Cỡ mẫu là n = 13 + 45 + 24 + 12 + 6 = 100.
Số trung bình của mẫu số liệu ghép nhóm là: 6
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
13.19, 25 + 45.19, 75 + 24.20, 25 +12.20, 75 + 6.21, 25 x = = 20,015 100
Câu 16. Áo khoác HNUE trước khi xuất khẩu sang Anh phải qua 2 lần kiểm tra, nếu cả hai lần đều đạt thì
chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 98% sản phẩm làm ra qua được lần kiểm tra
thứ nhất, và 95% sản phẩm qua được lần kiểm tra đầu sẽ tiếp tục qua được lần kiểm tra thứ hai. Tìm xác
suất để 1 chiếc áo khoác đủ tiêu chuẩn xuất khẩu? 95 931 95 98 A. . B. . C. . D. . 98 1000 100 100 Lời giải Chọn B
Gọi A là biến cố ” qua được lần kiểm tra đầu tiên” P( ) A = 0,98
Gọi B là biên cố “qua được lần kiểm tra thứ 2” P(B | ) A = 0,95
chiếc áo khoác đủ tiêu chuẩn xuất khẩu phải thỏa mãn 2 điều kiện trên hay ta đi tính P( A B) P A B ta có P (B A) ( ) = = = = P ( A) P ( A
B) P (B A) P ( A) 931 | | . 0,95.0,98 1000
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI ( 3 điểm) 1
Câu 1. Một vật chuyển động theo quy luật 3 2 s = −
t + 9t với t (giây) là khoảng thời gian tính từ lúc 2
bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Xác định tính
đúng sai của các khẳng định sau: Khẳng định Đúng Sai
(a) Vật chuyển động được 400 m trong 10 giây đầu tiên. 3 (b) 2
v(t) = s (
t) = − t +18t 2 (c) v (
t) = 0 t = 6 (d) v (10) = 30 Lời giải
Quãng đường vật chuyển động được trong 10 giây đầu : s(10) = 400. Vận tốc tại thời điểm t là 3 2
v(t) = s (
t) = − t +18t với t 0;1 0 . 2 Ta có : v ( t) = 3
− t +18 = 0 t = 6 .
Suy ra: v (0) = 0;v(10) = 30;v(6) = 54 . Vậy vận tốc lớn nhất của vật đạt được bằng 54 (m/s) . 7
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
Câu 2. Trong không gian Oxyz, cho hai mặt phẳng (P) : 2x − y + z +1 = 0 , (Q): 4x − 2y + 2z +3 = 0 . Khẳng định Đúng Sai (a) n (2; 1 − ; )
1 là một vectơ pháp tuyến của (P) . (b) (P) / / (Q) . 3 (c) Điểm I 0; ;0 không thuộc (Q). 2 1
(d) Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng . 6 Đáp án
a) Đ; b) Đ; c) S; d) S.
PHẦN III. TRẢ LỜI NGẮN Câu 1.
Công ty HSA & TSA Việt Nam muốn làm đường ống dẫn từ một điểm A trên bờ đến một điểm
B trên một hòn đảo. Hòn đảo cách bờ biển 6km. Giá thành để xây đường ống trên bờ là
50.000USD mỗi km, và 130.000USD mỗi km để xây dưới nước. B’ là điểm trên bờ sao cho
BB’ vuông góc với bờ biển. Khoảng cách từ A đến B’ là 9km. Vị trí C trên đoạn AB’ sao cho
khi nối ống theo hướng ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng: Lời giải Trả lời: 6.5
Ta đặt: B'C = x(km),(0 x 9) Ta có: 2 2 2 BC =
B ' B + B 'C =
36 + x , AC = 9 − x
Gọi F(x) là hàm chi phí xây dựng đường ống nước từ ACB Ta có: F ( x) 2
=130.000. 36 + x + 50.000(9 − x)(USD)
Câu toán trở thành tìm x sao cho F(x) đạt GTNN. F ( x) 130.000 ' = x − 50.000. 2 36 + x F '( x) 130.000 2 = 0
x − 50.000 = 0 13x = 5 36 + x 2 36 + x 25 5 2 x = x = = 2,5 4 2
Vì F(x) là hàm liên tục trên đoạn 0;9 nên ta có: F ( ) = F ( ) 5 0 1.230.000, 9 = 1.406.000, F =1.170.000 2
Vậy chi phí nhỏ nhất khi C cách A khoảng bằng 9km-2,5km=6,5km.
Câu 2. Một phần thiết kế của một công trình đang xây dựng có dạng như hình bên, trong đó ABCD là hình vuông cạnh 6 m, = = =
AM, BN, DP cùng vuông góc với (ABCD), AM 4 m , BN 3 m, DP 2 m .
Góc giữa hai mặt phẳng (ABCD) và (MNP) (làm tròn kết quả đến hàng đơn vị của độ) là n với n là số 8
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
nguyên. Giá trị của n là bao nhiêu? Trả lời: 20. Lời giải
Chọn hệ trục Oxy như hình vẽ với đơn vị của mỗi trục là mét, A(0;0;0), B(6;0;0) ,
D(0;6;0), M(0;0;4), N(6;0;3), P(0;6;2). Phương trình mặt phẳng (MNP) là x + 2y + 6z − 24 = 0 , vectơ
pháp tuyến của (MNP) là n = (1;2;6) .
(ABCD) có vectơ pháp tuyến k = (0;0 ) ;1 . = (( ) ( )) 1.0 + 2.0 + 6.1 6 41 cosn cos ABCD , MNP = = . 2 2 2 2 2 2 + + + + 41 1 2 6 . 0 0 1 Suy ra n = 20 .
Câu 3. Theo thống kê xác suất để hai ngày liên tiếp có mưa ở một thành phố vào mùa hè là 0,5; còn
không mưa là 0,3. Biết các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng. Tính xác
suất để ngày thứ hai có mưa, biết ngày đầu không mưa.
Trả lời: ……0,25…… Lời giải Gọi ,
A B lần lượt là biến cố để trời mua vào ngày thứ nhất và trời mưa vào ngày thứ hai, theo bài ra, ta có:
P( AB) = 0, 5; P( AB) = 0, 3 .
Do các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng nên:
1− P( AB) + P( AB)
P( AB) = P( AB) = = 0,1. 2 Suy ra: P( )
A = P( AB) + P( AB) = 0, 4 .
Xác suất để ngày thứ hai có mưa, biết ngày đầu không mưa là: P( AB) 0,1 P(B | ) A = = = 0, 25 . P( ) A 0, 4 9
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
Câu 4. Có bao nhiêu số tự nhiên có bảy chữ số đôi một khác nhau, trong đó đứng liền giữa hai chữ số 1 và 3 là chữ số 2. Trả lời: 7440. Lời giải:
Vì chữ số 2 đứng liền giữa hai chữ số 1 và 3 nên số cần lập có bộ ba số 123 hoặc 321,
TH1: Số cần lập có bộ ba số 123.
Nếu bộ ba số 123 đứng đầu thì số có dạng 123abcd . Có 4
A = 840 cách chọn bốn số , a , b , c d nên có 4 A = 840 số, 7 7
Nếu bộ ba số 123 không đứng đầu thì số có 4 vị trí đặt bộ ba số 123,
Có 6 cách chọn số đứng đầu và có 3
A = 120 cách chọn ba số , b , c d , 6 Theo quy tắc nhân có 3
6 4 A = 2880 số. 6
Theo quy tắc cộng có 840 + 2880 = 3720 số.
TH2: Số cần lập có bộ ba số 321.
Do vai trò của bộ ba số 123 và 321 như nhau nên có 2(840 + 2880) = 7440 . PHẦN IV. TỰ LUẬN
Câu 5. Một cửa sổ gồm phần dưới là một hình chữ nhật và phần vòm có hình bán nguyệt được mô tả ở
hình. Biết chu vi của cửa sổ là 5 m. Tìm x và y để diện tích của cửa sổ lớn nhất thì Lời giải x 10 − (2 + )x
Chu vi của cửa sổ là: x + 2 y + = 5 . Do đó, y = . 2 4 2 2 x (4 )x 20x
Diện tích của cửa sổ là: S xy − + + = + = . 8 8 10 5
Diện tích của cửa sổ lớn nhất khi x = 1,4( m), y = 0,7( m) . 4 + 4 + 10
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
Câu 6. Cho hình lăng trụ AB . C A B C
có đáy ABC là tam giác đều cạnh bằng 1 , BB tạo với đáy một
góc 60 , hình chiếu của A lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC . Tính khoảng
cách từ C đến mặt phẳng (ABB) . Lời giải A' B' C' J 60 I A B H C 3 3 Ta có A A
H = 60 A H = AH.tan A A H = 3 = . 2 2
Kẻ HI ⊥ AB tại I và HJ ⊥ A I tại J .
Ta có: d(C,( ABB)) = 2d(H,(AA B )) = 2HJ . 1 1 1 1 1 3 = + = + HJ = . 2 2 2 2 2 HJ HA HI 3 2 13 3 2 4
Vậy d(C (ABB)) 3 13 , = . 13
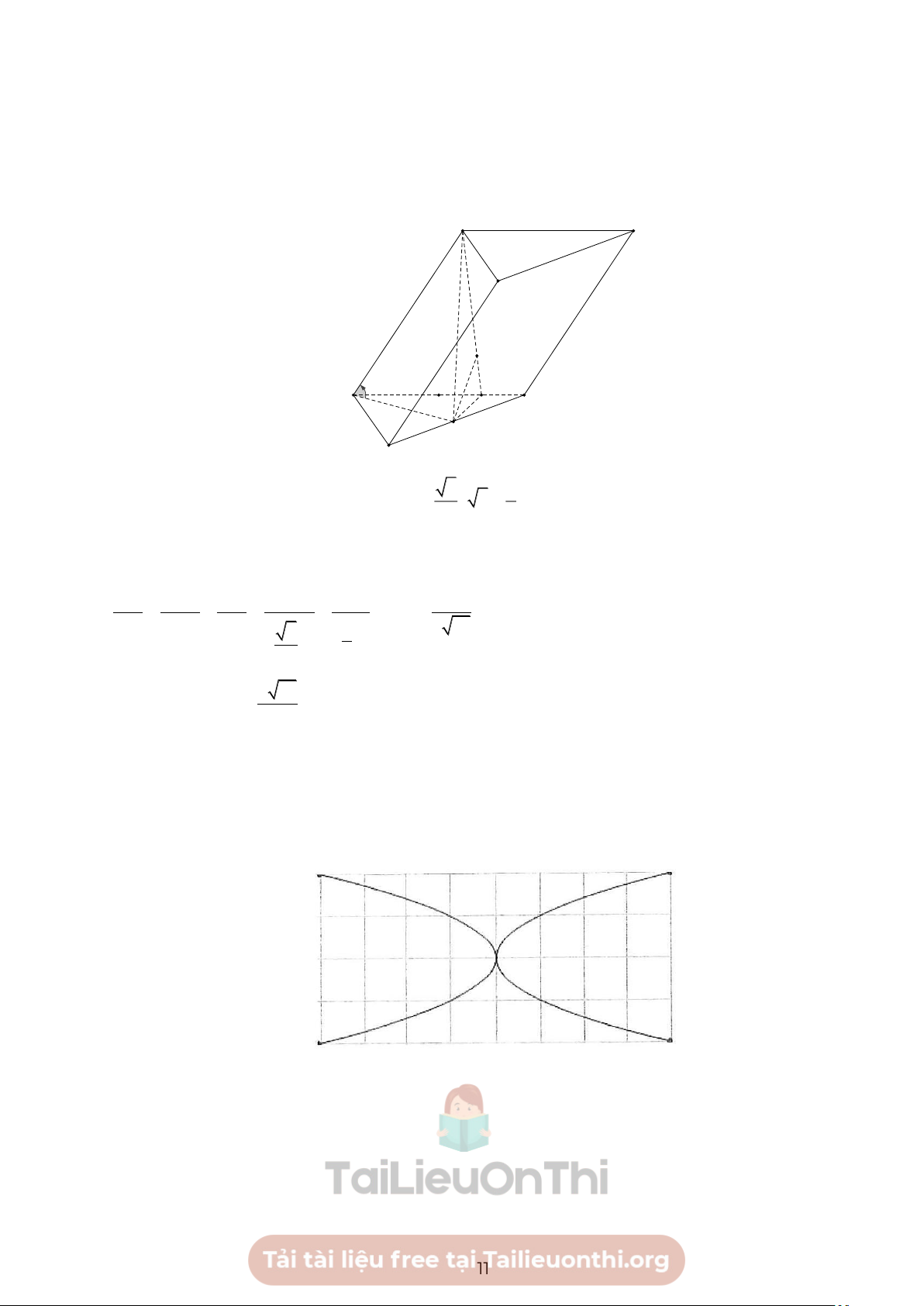
Câu 7. Một nhà thiết kế cần làm một cái logo có dạng hình chữ nhật kích thước 40 cm80 cm . Trong
logo đó có hai đường parabol chung đỉnh, cùng trục đối xứng chứa đường trung bình của hình chữ nhật và
hai parabol đi qua đỉnh của hình chữ nhật (hình bên). Nhà thiết kế có kế hoạch làm màu nền là màu xanh
phần phía trên của cả hai đường parabol và phần phía dưới của cả hai đường parabol, phần còn lại là màu
khác. Diện tích phần màu xanh là bao nhiêu 2
dm (làm tròn kết quả đến hàng phần mười)? 11
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
---------------------------------------------------------------------------------------------------------------------------------------------------- Đáp số: 10,7.
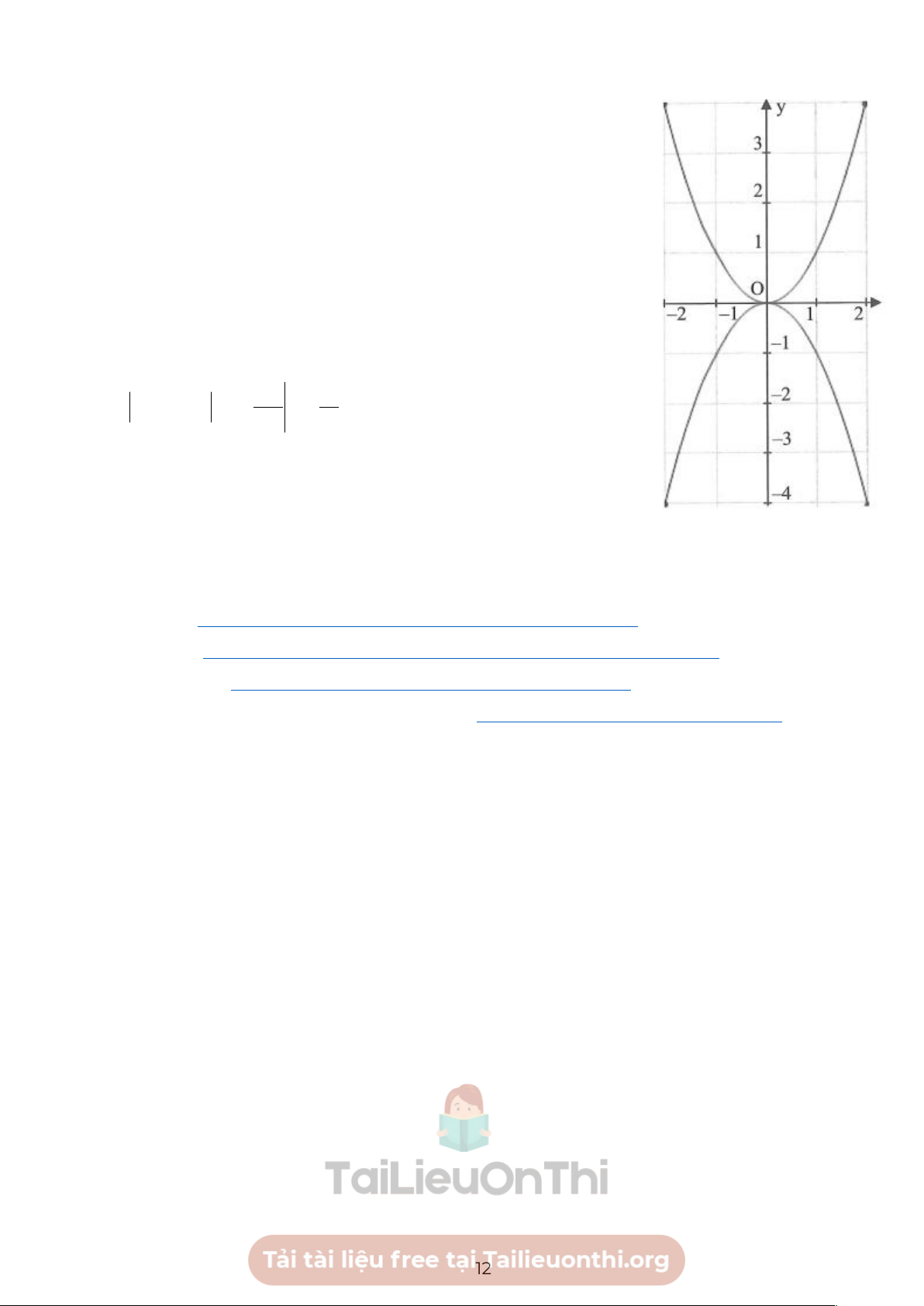
Chọn hệ trục toạ độ Oxy như hình bên với đơn vị của hai trục là dm.
Đường parabol phía trên có phương trình 2
y = ax và đi qua các điểm ( 2
− ;4),(2;4) . Suy ra a =1. Đường parabol phía dưới có phương trình 2 y = a x
và đi qua các điểm ( 2 − ; 4 − ),(2; 4 − ). Suy ra a = 1 − . Diện tích của hình chữ nhật là = ( 2 4.8
32 dm ) . Diện tích phần màu xanh bằng diện
tích hình phẳng giới hạn bởi hai đường parabol 2 y = x , 2 y = −x và các đường thẳng x = 2 − ,x = 2 . Ta có 2 2 S = x − (−x ) 3 2x 32 2 2 dx = = 10,7( 2 dm ). 3 3 2 − 2 −
-------------------------------------------------- Hết --------------------------------------------------
• Nhóm ôn thi ĐGNL ĐGTD TN
THPT: https://www.facebook.com/groups/dodaihoc.tlot
• Nhóm Góc ôn thi Đánh giá tư duy – Đánh giá năng lực – TN THPT
• Fanpage: https://www.facebook.com/tailieuonthipage
• Nhóm Zalo (update khi có nhóm mới): https://tailieuonthi.org/nhom-zalo 12
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
---------------------------------------------------------------------------------------------------------------------------------------------------- TAILIEUONTHI.ORG
ĐỀ THI ĐÁNH GIÁ NĂNG LỰC SƯ PHẠM MÔN THI: TOÁN Mã đề 002
(Thời gian làm bài 90 phút, không kể thời gian giao đề)
A. TÔ TRÊN PHIẾU TRẢ LỜI TRẮC NGHIỆM
Phần I (4 điểm). Thí sinh trả lời từ câu 1 đến câu 16. Đối với mỗi câu, thí sinh chỉ chọn một phương án. Câu 1:
Tổng nghiệm của cos x =1 trên 0; 201 8 bằng : A. 1010 B. ( 1009 2 2 − ) 1 C. 1019090 D. ( 1010 2 − ) 1 Lời giải Chọn C Ta có: +
x = k2 x 0; 2 ; 4 ;...; 2018 1009. (2 2018)
x = 2 + 4 +...+ 2018 = = 1019090 2
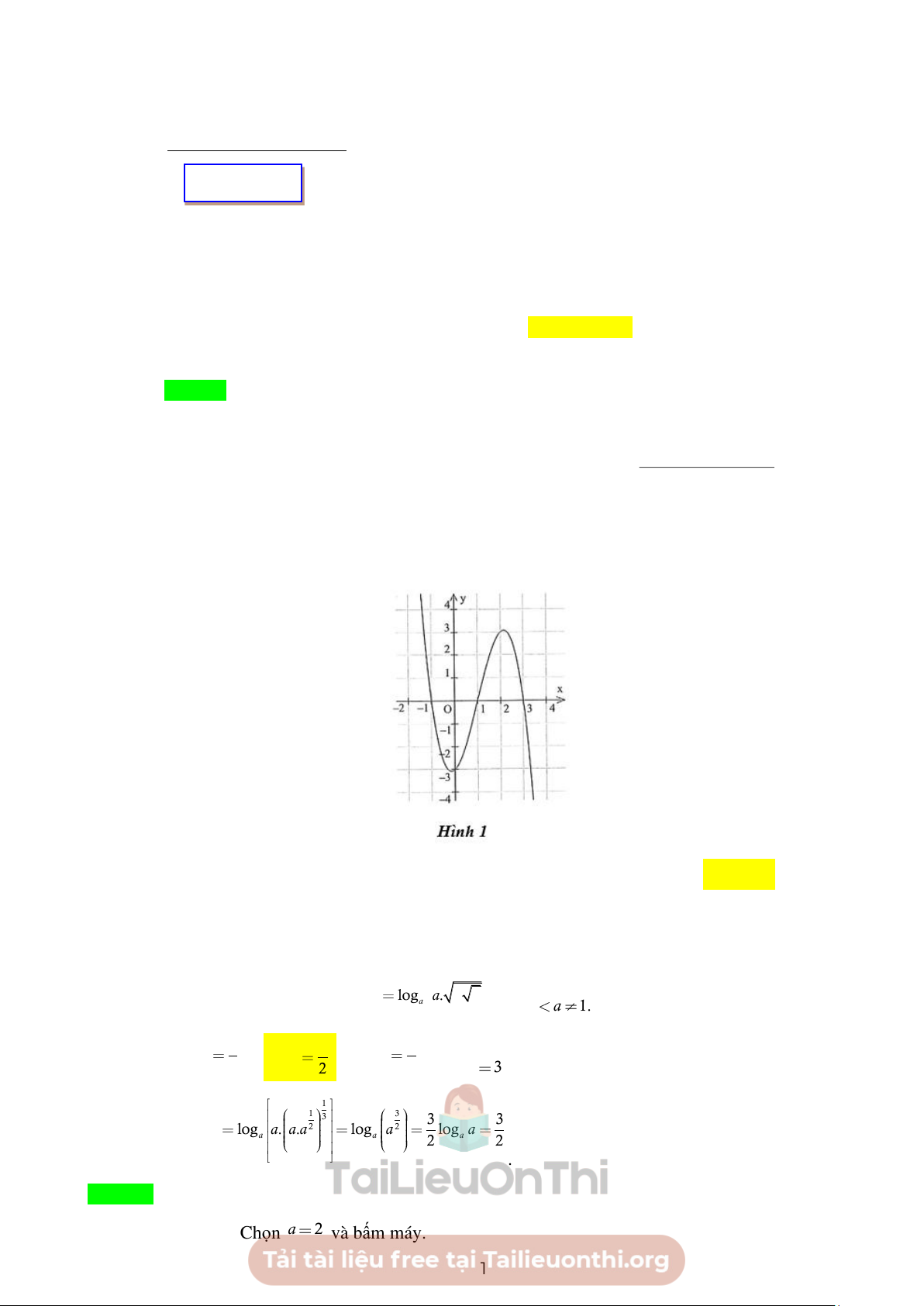
Câu 2. Cho hàm số y = f ( x) có đồ thị đạo hàm y = f ( x) như Hình 1. Hàm số y = f (x) nghịch biến trên khoảng A. ( 2 − ;0) . B. (1; 2) . C. (1; ) 3 . D. (4;5) . Lời giải
Từ đồ thị hàm số y = f ( x) ta thấy f ( x) 0 x
(4;5) nên hàm số nghịch biến trên (4;5) . 3 P log . a a a a Câu 3.
Tính giá trị của biểu thức với 0 a 1. 1 2 P 3 P P A. 3 . B. 2 . C. 3 . D. P 3 . 1 1 3 3 3 3 2 2 P log . a . a a log a log a a a 2 a 2 Lời giải. Ta có . Chọn B.
Cách trắc nghiệm: Chọn a 2 và bấm máy. 1
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
Câu 4. Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên
hai con xúc xắc bằng 6. Biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm. 2 1 1 5 A. . B. . C. . D. . 6 2 6 6 Lời giải Chọn C.
Gọi A là biến cố “con xúc xắc thứ nhất xuất hiện mặt 4 chấm”
Gọi B là biến cố “ Tổng số chấm xuất hiện trên 2 con xúc xắc bằng 6”.
Khi con xúc xắc thứ nhất đã xuất hiện mặt 4 chấm thì thì lần thứ hai xuất hiện 2 chấm thì tổng hai lần xuất
hiện là 6 chấm thì P (B A) 1 | = 6 5 dx Câu 5. Giả sử = ln c
. Giá trị của c là 2x − 1 1 A. 9. B. 3. C. 81. D. 8. Lời giải Chọn B 5 dx 1 5 1 Ta có
= ln 2x −1 = ln 3 − ln1 = ln 3 . 1 2x −1 2 2 1
Do đó c = 9 thỏa mãn yêu cầu bài toán.
Câu 6. Trong không gian Oxyz , cho ba điểm A(1;2;− ) 1 , B(3;0; ) 1 và C (2;2; 2
− ). Đường thẳng đi qua A
và vuông góc với mặt phẳng ( ABC ) có phương trình là: x −1 y − 2 z +1 x +1 y + 2 z −1 A. = = . B. = = . 1 2 − 3 1 2 1 x −1 y − 2 z −1 x −1 y − 2 z +1 C. = = . D. = = . 1 2 1 − 1 2 1 Lời giải Chọn A. Ta có AB = (2; 2
− ;2) , AC = (1;0;− ) 1 .
Mặt phẳng ( ABC ) có một véctơ pháp tuyến là n = A , B AC = (2;4;2) .
Đường thẳng vuông góc với mặt phẳng ( ABC) có một véctơ chỉ phương là u = (1;2 ) ;1 . − − + Đườ x y z
ng thẳng đi qua A và vuông góc với mặt phẳng ( ABC ) có phương trình là 1 2 1 = = . 1 2 1 2
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
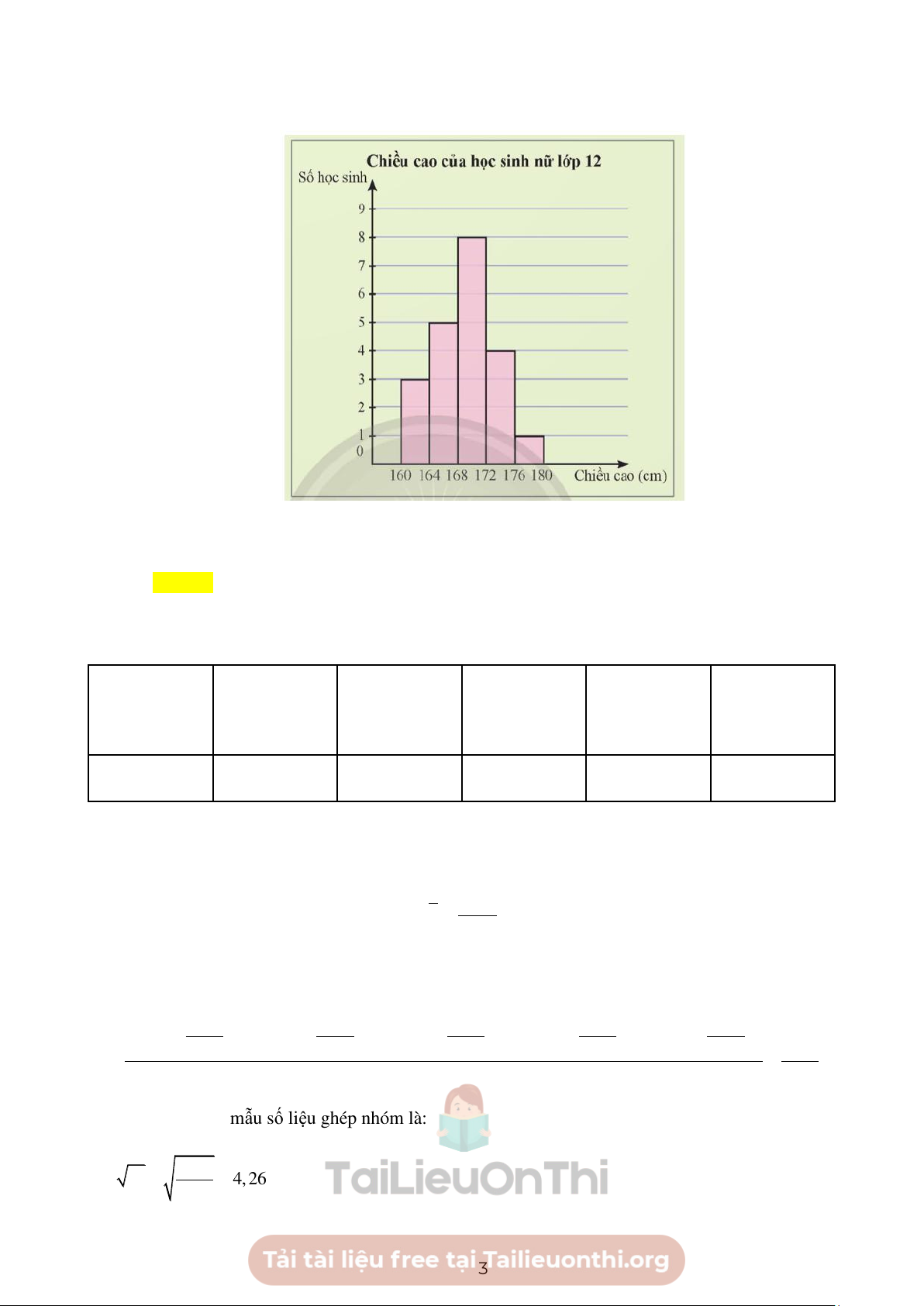
Câu 7. Trong buổi kiểm tra sức khỏe đầu năm của một lớp 12
Xét mẫu số liệu mới gồm các giá trị đại diện của các nhóm, tần số của mỗi giá trị đại diện bằng tần số của
nhóm tương ứng. Hãy tính độ lệch chuẩn của mẫu số liệu mới. A. 4,26. B. 4,25. C. 4. D. 4,2 Lời giải
Ta có bảng thống kê mẫu số liệu mới: Giá trị 162 166 170 174 178 đại diện Số học sinh 3 5 8 4 1 Cỡ mẫu n = 21. 3550
Số trung bình của mẫu số liệu ghép nhóm là: x = 21
Phương sai của mẫu số liệu ghép nhóm là: 2 2 2 2 2 3550 3550 3550 3550 3550 3 162 − + 5 166 − +8 170 − + 4 174 − +1 178 − 21 21 21 21 21 8000 2 s = = 18,14 21 441
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: 8000 2 s = s = 4,26 441 3
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
---------------------------------------------------------------------------------------------------------------------------------------------------- 1
Câu 8. Diện tích của hình phẳng giới hạn bởi đồ thị hàm số y =
ln x, trục hoành và đường thẳng x = e x bằng 1 1 A. . B. . C. 2 . D. 1. 4 2 Lời giải Chọn B 1 Ta có
ln x = 0 x = 1 x e e Do đó diệ 1 1
n tích hình phẳng cần tìm là: S = ln x dx = ln . x d(lnx) = . x 2 1 1 Câu 9.
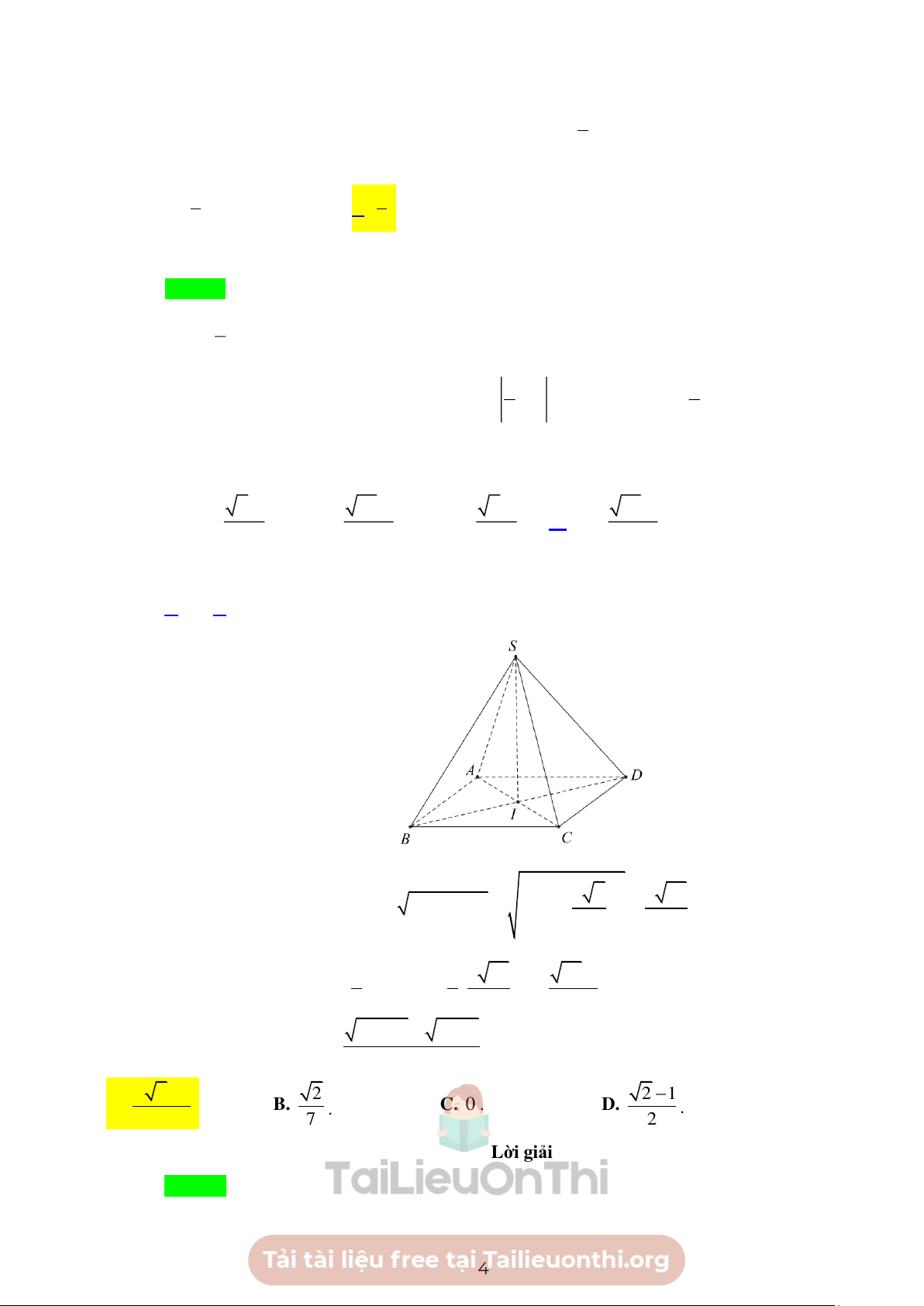
Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V
của khối chóp đã cho. 3 2a 3 14a 3 2a 3 14a A. V = B. V = C. V = D. V = 2 2 6 6 Lời giải Chọn D 2 a 2 a 14
Chiều cao của khối chóp: SI = 2 SA − 2 AI = 2 4a − = 2 2 3 1 1 a 14 14a
Thể tích khối chóp: V = SI.S = 2 . a = 3 ABCD 3 2 6 2 2 2x +1 − x +1
Câu 10. Giá trị của giới hạn lim x→− 2x + là: 2 − 2 +1 2 2 −1 A. . B. . C. 0 . D. . 2 7 2 Lời giải Chọn A 4
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
---------------------------------------------------------------------------------------------------------------------------------------------------- 1 1 x 2 + − x 1+ 2 2 x x Ta có lim x→− 2 x(2 + ) x 1 1 − 2 + + 1+ 2 2 x x = lim x→− 2 2 + x − + = 2 1 2 ax + b
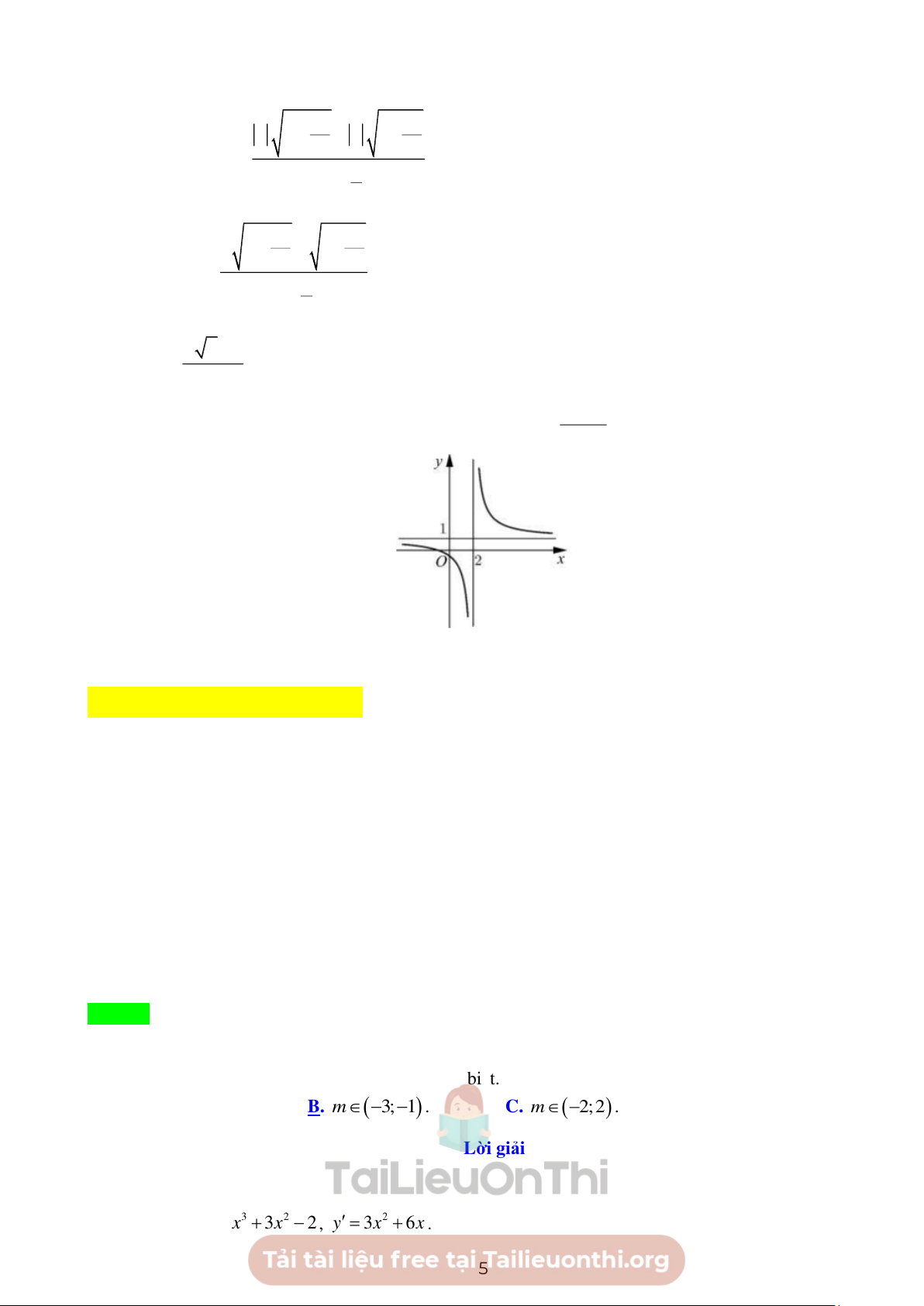
Câu 11. Đường cong của hình vẽ bên là đồ thị của hàm số y = với , a , b ,
c d là các số thực. cx + d
Mệnh đề nào sau đây là đúng?
A. y ' 0với x (− ; 2)(2;+). B. − + y ' 0 với x ( ;2) (2; ).
C. y ' 0 với x (− ; ) 1 (1;+) .
D. y ' 0 với x (− ; ) 1 (1;+) . Lời giải
Từ đồ thị thấy y = f ( )
x nghịch biến trên (− ; 2)và(2;+)
=> y ' 0với x (− ; 2)(2;+). Chọn A
Câu 12. Tìm tất cả các giá trị của tham số m để phương trình 3 2
x + 3x − 2 = 2m + 4 có ba nghiệm phân biệt. A. m 3 − ;− 1 . B. m( 3 − ;− ) 1 . C. m( 2 − ;2) . D. m 2 − ;2 . Lời giải Chọn B Xét hàm số 3 2
y = x + 3x − 2 , 2
y = 3x + 6x . 5
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
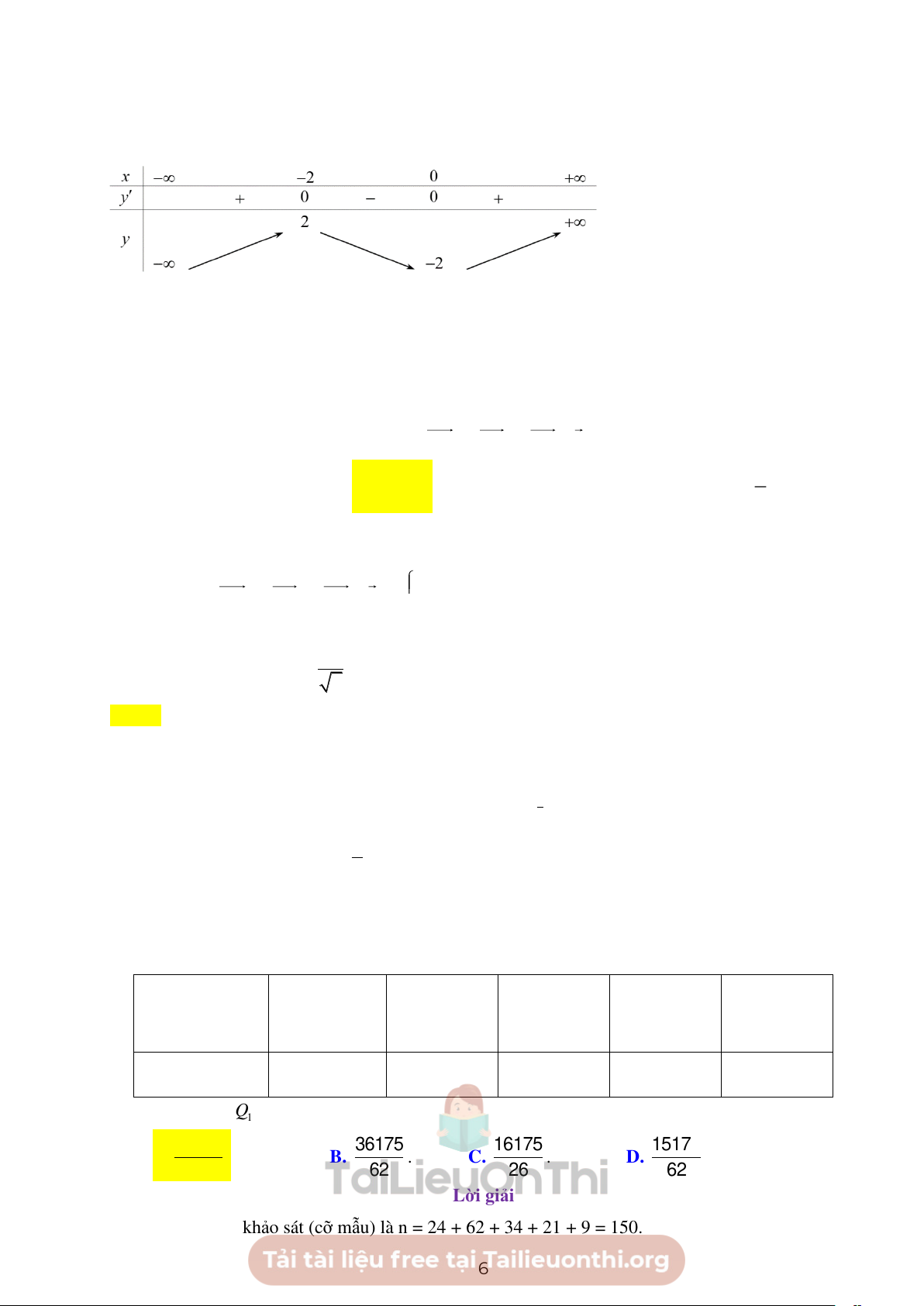
---------------------------------------------------------------------------------------------------------------------------------------------------- Lập bảng biến thiên
Số nghiệm của phương trình 3 2
x + 3x − 2 = 2m + 4( )
* bằng số giao điểm của đồ thị hàm số 3 2
y = x + 3x − 2 và đường thẳng y = 2m + 4 .
Dựa vào bảng biến thiên suy ra PT (*) có 3 nghiệm phân biệt khi 2
− 2m + 4 2 3 − m 1 − .
Câu 13. Cho A(0; )
3 , B(4;2) . Điểm D thỏa OD + 2DA− 2DB = 0 , tọa độ D là: 5 A. ( 3 − ;3) . B. (8; 2 − ) . C. ( 8 − ;2) . D. 2; . 2 Lời giải Chọn B
x − 0 + 2 − x − − x = x = D (0 D ) 2(4 D ) 0 8
Ta có: OD + 2DA − 2DB = 0 D
y − 0 + 2 − y − − y = y = − D (3 D ) 2(2 D ) 0 2 D 6 2
Câu 14. Trong khai triển x + , hệ số của 3
x ,( x 0) là: x A. 60 . B. 80 . C. 160 . D. 240 . Lời giải Chọn A. 1 −
Số hạng tổng quát trong khai triển trên là 6−k k 2 T = k k C .x 2 .x k 1 + 6 1
Yêu cầu bài toán xảy ra khi 6 − k −
k = 3 k = 2 . 2 Khi đó hệ số của 3 x là: 2 2 C .2 = 60 . 6
Câu 15. Kết quả điều tra tổng khối lượng bưởi thu hoạch trong năm 2025 của một số hộ gia đình ở Phú
Diễn được ghi lại ở bảng sau: Tổng số bưởi [200; 250) [250; 300) [300; 350) [350; 400) [400; 450) (kilogam) Số hộ gia đình 24 62 34 21 9
Hãy tìm tứ phân vị Q 1 16175 36175 16175 15175 A. . B. . C. . D. 62 62 26 62 Lời giải
Số hộ gia đình được khảo sát (cỡ mẫu) là n = 24 + 62 + 34 + 21 + 9 = 150. 6
Chia sẻ miễn phí tại website: Tailieuonthi.org
Group: Góc ôn thi đánh giá tư duy – đánh giá năng lực – TN THPT
----------------------------------------------------------------------------------------------------------------------------------------------------
Gọi x ; x ;...; x
là tổng khối lượng bưởi thu hoạch trong năm 2025 của 150 hộ gia đình được xếp theo thứ 1 2 150 tự không giảm. Ta có:
x ;...; x 200; 250 1 24 )
x ;...; x 300;350 25 86 ) x ;...; x 300;350 87 120 ) x ;...; x 350;400 121 141 ) x ;...; x 400;450 142 150 )
Do đó, đối với dãy số liệu x ; x ;...; x thì 1 2 150
Tứ phân vị thứ nhất Q là x 250;300 . Do đó, tứ phân thứ nhất của mẫu số liệu ghép nhóm là: 38 ) 1 150 − 24 16175 4 Q = 250 + 300 − 250 = 1 ( ) 62 62
Câu 16. Trong mặt phẳng tọa độ Oxy cho đường tròn (C ) có tâm I (1; − )
1 bán kính R = 5 . Biết rằng
đường thẳng (d) :3x − 4y +8 = 0 cắt đường tròn (C ) tại hai điểm phân biệt ,
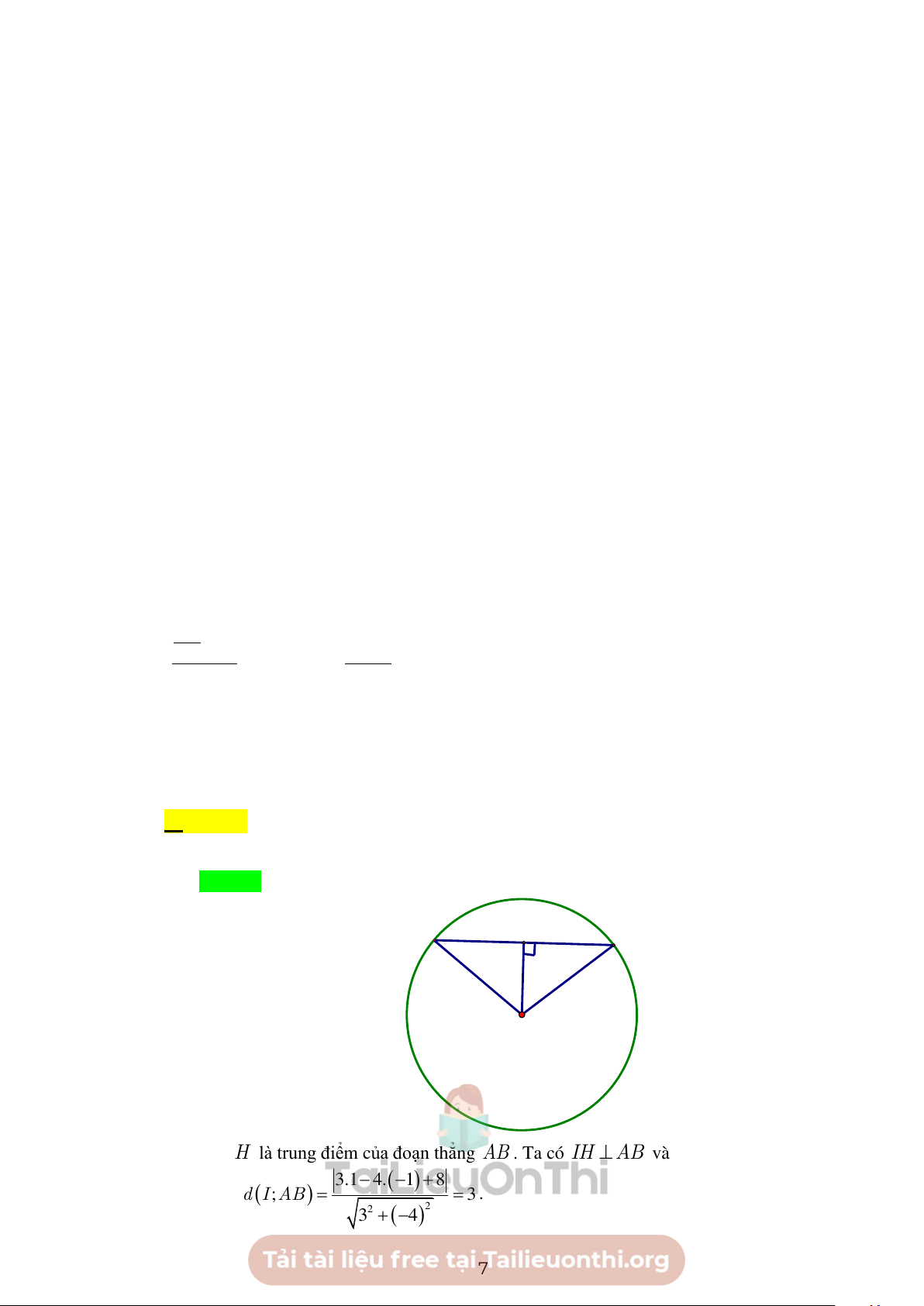
A B . Tính độ dài đoạn thẳng AB . A. AB = 8 . B. AB = 4 . C. AB = 3. . D. AB = 6 . Lời giải Chọn A A H B I
Gọi H là trung điểm của đoạn thẳng AB . Ta có IH ⊥ AB và − − +
IH = d (I AB) 3.1 4.( ) 1 8 ; = = 3 . 3 + ( 4 − )2 2 7
