Bộ đề cơ bản ôn thi THPT Quốc gia môn Toán

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 tài liệu bộ đề cơ bản ôn thi THPT Quốc gia môn Toán có đáp án và lời giải chi tiết.

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

124 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 01_______________
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
32i
có tọa độ là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
3; 2 .
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
7
logyx
là
A.
1
.y
x
B.
1
.
ln7
y
x
C.
D.
1
.
ln7
y
x

Câu 3: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
..
e
y e x
B.
1
.
e
yx
C.
1
.
1
e
x
y
e
D.
..
e
y e x
Câu 4: Tập nghiệm của bất phương trình
24
x
là
A.
;2
B.
0;2
C.
;2
D.
0;2
Câu 5: Cho cấp số nhân
n
u
với
1
5u
và
2
2u
. Công bội của cấp số nhân đó bằng
A.
1
. B.
28
. C.
5
2
. D.
2
5
.
Câu 6: Trong không gian
,Oxyz
cho mặt phẳng
:3 2 0P x z
. Vectơ no dưới đây l một vectơ
php tuyn của
P
?
A.
4
1;0; 1 . n
B.
1
3; 1;2 .n
C.
3
3; 1;0 .n
D.
2
3;0; 1 .n
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị như hình bên dưới :
Tọa độ giao điểm của đồ thị hàm số đã cho với trục tung là
A.
0; 2 .
B.
2;0 .
C.
2;0 .
D.
0;2 .
Câu 8: Cho hàm số
fx
và
gx
liên tục trên đoạn
0;1
và
11
00
d 1, d 3f x x g x x

. Tích phân
1
0
2 3 df x g x x


bằng
A.
9
. B.
5
. C.
10
. D.
11
.
Câu 9: Hàm số no có đồ thị l đường cong trong hình vẽ bên dưới?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
A.
42
41y x x
. B.
1
2
x
y
x
. C.
32
41y x x
. D.
2
21yx
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 1 9S x y z
. Tìm tọa độ tâm
I
và tính bán kính
R
của
.S
A.
1;2;1I
và
3.R
B.
1; 2; 1I 
và
3.R
C.
1;2;1I
và
9.R
D.
1; 2; 1I 
và
9.R
Câu 11: Trong không gian
,Oxyz
góc giữa hai mặt phẳng
Oxy
và
Oxz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
45 .
Câu 12: Cho số phức
2,zi
phần ảo của số phức
2
z
là
A.
4.
B.
4.i
C.
3.
D.
1.
Câu 13: Cho khối lập phương có cạnh bằng
3.
Thể tích khối lập phương đã cho bằng
A.
9.
B.
27.
C.
18.
D.
3.
Câu 14: Cho khối chóp
.S ABC
có đy l tam gic vuông tại
, 2, 4,A AB AC SA
vuông góc với đy v
3SA
(tham khảo hình bên).
C
B
A
S
Thể tích khối chóp đã cho bằng
A.
9.
B.
8.
C.
4.
D.
3.
Câu 15: Cho đường thẳng
và mặt cầu
;.S O R
Gọi
d
là khoảng cách từ
O
đn
và
.dR
Số giao
điểm của
và
;S O R
là
A.
1.
B.
2.
C.
0.
D. Vô số.
Câu 16: Phần ảo của số phức
là
A.
3.
B.
7.
C.
7.
D.
3.
Câu 17: Cho khối nón có đường cao
,h
độ di đường sinh
l
v bn kính đy
.r
Diện tích xung quanh
xq
S
của khối nón được tính theo công thức no dưới đây?
A.
xq
S rl
. B.
1
2
xq
S rl
. C.
2
xq
S rl
. D.
xq
S rh
.
Câu 18: Trong không gian
,Oxyz
đường thẳng
1 2 3
:
3 4 5
x y z
d


đi qua điểm no sau đây?
A.
1; 2;3
. B.
1;2; 3
. C.
3; 4; 5
. D.
3;4;5
.
Câu 19: Cho hàm số
42
y ax bx c
có đồ thị l đường cong như hình bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
x
y
-1
-1
-2
O
1
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là
A.
0; 1 .
B.
1;0 .
C.
1; 2 .
D.
Câu 20: Tiệm cận ngang của đồ thị hàm số
41
2
x
y
x
l đường thẳng có phương trình l
A.
4.y
B.
4.x
C.
2.x
D.
2.y
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
;2 .
B.
0;2 .
C.
0;1 .
D.
;1 .
Câu 22: Cho tập
M
có 10 phần tử. Số tập con gồm 3 phần tử của tập hợp
M
là
A.
3!.
B.
10!.
C.
3
10
.A
D.
3
10
.C
Câu 23: Cho
dsin .x x f x C
Khẳng định no dưới đây đúng?
A.
cos .
f x x
B.
cos .
f x x
C.
sin .
f x x
D.
sin .
f x x
Câu 24: Nu
4
2
3 d 12f x x x


thì
4
2
df x x
bằng
A.
6
. B.
0
. C.
2
. D.
10
3
.
Câu 25: Cho hàm số
sin 1f x x x
. Khẳng định no dưới đây đúng?
A.
2
d cos
2
x
f x x x x C
. B.
2
d cos
2
x
f x x x x C
.
C.
d cos 1f x x x C
. D.
2
d cos
2
x
f x x x C
.
Câu 26: Cho hàm số
()y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng bin trên các khoảng no dưới đây?
A.
0; 2
. B.
0; 
. C.
0; 4
. D.
1;1
.
Câu 27: Cho hàm số
y f x
có bảng bin thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Đồ thị hàm số
y f x
có điểm cực tiểu là
A.
0;2
. B.
3; 4
. C.
3
CT
x
. D.
.
Câu 28: Cho
a
,
b
là các số thực dương tùy ý. Khẳng định no sau đây đúng?
A.
ln ln lnab a b
. B.
ln ln lna b a b
.
C.
ln ln .lnab a b
. D.
ln ln .lna b a b
.
Câu 29: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
21y x x
và trục hoành. Thể tích của vật
thể tròn xoay khi quay
H
quanh trục hoành bằng
A.
9
8
. B.
81
80
. C.
81
80
. D.
9
8
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau:
Góc giữa đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 31: Cho hàm số
y f x
có bảng bin thiên như sau:
Tập hợp tất cả các giá trị của
m
để phương trình
f x m
có ba nghiệm thực phân biệt
A.
4;2 .
B.
4;2 .
C.
4;2 .
D.
4;2 .
Câu 32: Cho hàm số
fx
có đạo hàm
2
3
1 2 , .
f x x x x x
Khoảng nghịch bin của hàm
số là
A.
2;0
. B.
; 2 ; 0;1
. C.
; 2 ; 0; 
. D.
2;0 ; 1; 
.
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ
15
số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số lẻ bằng
A.
1
7
. B.
8
15
. C.
4
15
. D.
1
14
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 34: Tích các nghiệm của phương trình
1
5
log 6 36 1
xx

bằng
A.
6
log 5.
B.
5
log 6.
C.
5.
D.
0.
Câu 35: Cho số phức
z
thỏa mãn
12z i z
. Trong mặt phẳng phức, quỹ tích điểm biểu diễn
các số phức
z
A. l đường thẳng
3 1 0xy
. B. l đường thẳng
3 1 0xy
.
C. l đường thẳng
3 1 0xy
. D. l đường thẳng
3 1 0xy
.
Câu 36: Trong không gian
Oxyz
, vit phương trình đường thẳng
đi qua
1;1;0M
và vuông góc
với mặt phẳng
: 4 2 0Q x y z
?
A.
1
4
1
xt
yt
z


. B.
1
14
xt
yt
zt



. C.
2
54
1


xt
yt
zt
. D.
1
14
xt
yt
zt

.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxy
có
tọa độ là
A.
1; 2;3
. B.
1;2; 3
. C.
1; 2; 3
. D.
1;2;0
.
Câu 38: Cho lăng trụ tam gic đều
.ABC A B C
có tất cả các cạnh bằng
a
. Thể tích khối trụ có hai đy
là hai hình tròn ngoại tip hai đy của lăng trụ đã cho bằng
A.
3
a
. B.
3
12
a
. C.
3
3
a
. D.
3
4
3
a
.
Câu 39: Cắt khối nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đy một góc bằng
0
60
ta được thit diện là một tam giác vuông cân cạnh huyền
2a
. Thể tích khối nón
N
bằng
A.
3
53
24
a
. B.
3
53
72
a
. C.
3
53
8
a
. D.
3
3
72
a
.
Câu 40: Trong không gian
,Oxyz
phương trình mặt phẳng
()P
song song v cch đều hai đường
thẳng
1
:d
2
1 1 1
x y z

và
2
:d
12
2 1 1
x y z


là
A.
2 2 1 0 xz
. B.
2 2 1 0 yz
. C.
2 2 1 0 xy
. D.
2 2 1 0 yz
.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
32i
có tọa độ là
A.
2;3 .
B.
2;3 .
C.
3;2 .
D.
3; 2 .
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
7
logyx
là
A.
1
.y
x
B.
1
.
ln7
y
x
C.
D.
1
.
ln7
y
x

Câu 3: Trên khoảng
0; ,
đạo hàm của hàm số
e
yx
là
A.
1
..
e
y e x
B.
1
.
e
yx
C.
1
.
1
e
x
y
e
D.
..
e
y e x
Câu 4: Tập nghiệm của bất phương trình
24
x
là
A.
;2
B.
0;2
C.
;2
D.
0;2
Lời giải:
Ta có
2 4 2
x
x
Tập nghiệm của bất phương trình l
;2
.
Câu 5: Cho cấp số nhân
n
u
với
1
5u
và
2
2u
. Công bội của cấp số nhân đó bằng
A.
1
. B.
28
. C.
5
2
. D.
2
5
.
Lời giải:
Công bội của cấp số nhân đó bằng
2
1
2
5
u
q
u

.
Câu 6: Trong không gian
,Oxyz
cho mặt phẳng
:3 2 0P x z
. Vectơ no dưới đây l một vectơ
php tuyn của
P
?
A.
4
1;0; 1 . n
B.
1
3; 1;2 .n
C.
3
3; 1;0 .n
D.
2
3;0; 1 .n
Lời giải:
Vectơ php tuyn của mặt phẳng
:3 2 0P x z
l
2
3;0; 1n 
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị như hình bên dưới :
Tọa độ giao điểm của đồ thị hàm số đã cho với trục tung là
A.
0; 2 .
B.
2;0 .
C.
2;0 .
D.
0;2 .
Câu 8: Cho hàm số
fx
và
gx
liên tục trên đoạn
0;1
và
11
00
d 1, d 3f x x g x x

. Tích phân
1
0
2 3 df x g x x


bằng
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
A.
9
. B.
5
. C.
10
. D.
11
.
Lời giải:
Ta có
1 1 1
0 0 0
2 3 d 2 d 3 d 2.1 3.3 11f x g x x f x x g x x


.
Câu 9: Hàm số no có đồ thị l đường cong trong hình vẽ bên dưới?
A.
42
41y x x
. B.
1
2
x
y
x
. C.
32
41y x x
. D.
2
21yx
.
Lời giải:
Từ đồ thị ta thấy hàm số có 3 điểm cực trị, suy ra hình vẽ l đồ thị hàm số
42
41y x x
.
Câu 10: Trong không gian
,Oxyz
cho mặt cầu
2 2 2
: 1 2 1 9S x y z
. Tìm tọa độ tâm
I
và tính bán kính
R
của
.S
A.
1;2;1I
và
3.R
B.
1; 2; 1I 
và
3.R
C.
1;2;1I
và
9.R
D.
1; 2; 1I 
và
9.R
Câu 11: Trong không gian
,Oxyz
góc giữa hai mặt phẳng
Oxy
và
Oxz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
45 .
Câu 12: Cho số phức
2,zi
phần ảo của số phức
2
z
là
A.
4.
B.
4.i
C.
3.
D.
1.
Lời giải:
Ta có:
2
2
2 3 4 .z i i
Câu 13: Cho khối lập phương có cạnh bằng
3.
Thể tích khối lập phương đã cho bằng
A.
9.
B.
27.
C.
18.
D.
3.
Câu 14: Cho khối chóp
.S ABC
có đy là tam giác vuông tại
, 2, 4,A AB AC SA
vuông góc với đy v
3SA
(tham khảo hình bên).
C
B
A
S
Thể tích khối chóp đã cho bằng
A.
9.
B.
8.
C.
4.
D.
3.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Lời giải:
Ta có:
.
1 1 1
. . . 4.
3 3 2
S ABC ABC
V SA S SA AB AC
Câu 15: Cho đường thẳng
và mặt cầu
;.S O R
Gọi
d
là khoảng cách từ
O
đn
và
.dR
Số giao
điểm của
và
;S O R
là
A.
1.
B.
2.
C.
0.
D. Vô số.
Câu 16: Phần ảo của số phức
là
A.
3.
B.
7.
C.
7.
D.
3.
Câu 17: Cho khối nón có đường cao
,h
độ di đường sinh
l
v bn kính đy
.r
Diện tích xung quanh
xq
S
của khối nón được tính theo công thức no dưới đây?
A.
xq
S rl
. B.
1
2
xq
S rl
. C.
2
xq
S rl
. D.
xq
S rh
.
Câu 18: Trong không gian
,Oxyz
đường thẳng
1 2 3
:
3 4 5
x y z
d


đi qua điểm no sau đây?
A.
1; 2;3
. B.
1;2; 3
. C.
3; 4; 5
. D.
3;4;5
.
Câu 19: Cho hàm số
42
y ax bx c
có đồ thị l đường cong như hình bên dưới:
x
y
-1
-1
-2
O
1
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là
A.
0; 1 .
B.
1;0 .
C.
1; 2 .
D.
Câu 20: Tiệm cận ngang của đồ thị hàm số
41
2
x
y
x
l đường thẳng có phương trình l
A.
4.y
B.
4.x
C.
2.x
D.
2.y
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
;2 .
B.
0;2 .
C.
0;1 .
D.
;1 .
Lời giải:
Ta có:
2
0
log 1 0;2 .
2
x
xx
x

Câu 22: Cho tập
M
có 10 phần tử. Số tập con gồm 3 phần tử của tập hợp
M
là
A.
3!.
B.
10!.
C.
3
10
.A
D.
3
10
.C
Câu 23: Cho
dsin .x x f x C
Khẳng định no dưới đây đúng?
A.
cos .
f x x
B.
cos .
f x x
C.
sin .
f x x
D.
sin .
f x x
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Câu 24: Nu
4
2
3 d 12f x x x


thì
4
2
df x x
bằng
A.
6
. B.
0
. C.
2
. D.
10
3
.
Lời giải:
Ta có
4
2
3 d 12f x x x


4 4 4
2
2 2 2
4
1
3 d d 12 3 d 12
2
2
f x x x x f x x x
44
22
3 d 6 12 d 2f x x f x x

.
Câu 25: Cho hàm số
sin 1f x x x
. Khẳng định no dưới đây đúng?
A.
2
d cos
2
x
f x x x x C
. B.
2
d cos
2
x
f x x x x C
.
C.
d cos 1f x x x C
. D.
2
d cos
2
x
f x x x C
.
Câu 26: Cho hàm số
()y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng bin trên các khoảng no dưới đây?
A.
0; 2
. B.
0; 
. C.
0; 4
. D.
1;1
.
Câu 27: Cho hàm số
y f x
có bảng bin thiên như sau:
Đồ thị hàm số
y f x
có điểm cực tiểu là
A.
0;2
. B.
3; 4
. C.
3
CT
x
. D.
.
Lời giải:
Dựa vào bảng bin thiên, ta có đồ thị hàm số
y f x
có điểm cực tiểu là
3; 4
.
Câu 28: Cho
a
,
b
là các số thực dương tùy ý. Khẳng định no sau đây đúng?
A.
ln ln lnab a b
. B.
ln ln lna b a b
.
C.
ln ln .lnab a b
. D.
ln ln .lna b a b
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Theo quy tắc logarit ta có:
ln ln lnab a b
.
Câu 29: Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
21y x x
và trục hoành. Thể tích của vật
thể tròn xoay khi quay
H
quanh trục hoành bằng
A.
9
8
. B.
81
80
. C.
81
80
. D.
9
8
.
Lời giải:
+ Phương trình honh độ giao điểm:
2
1
2 1 0
1
2
x
xx
x

.
+ Thể tích cần tìm là
d
1
2
2
1
2
81
21
80
V x x x
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau:
Góc giữa đường thẳng
AB
và mặt phẳng
ABC
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Lời giải:
Do
AA A B C
nên
;.AB A B C A B A
Do tam giác
AA B
vuông cân nên
45 .A B A


Câu 31: Cho hàm số
y f x
có bảng bin thiên như sau:
Tập hợp tất cả các giá trị của
m
để phương trình
f x m
có ba nghiệm thực phân biệt
A.
4;2 .
B.
4;2 .
C.
4;2 .
D.
4;2 .
Lời giải:
Số nghiệm của phương trình
f x m
là số giao điểm của đồ thị hàm số
y f x
v đường
thẳng
ym
. Dựa vào bảng bin thiên ta thấy
4;2m
.
Câu 32: Cho hàm số
fx
có đạo hàm
2
3
1 2 , .
f x x x x x
Khoảng nghịch bin của hàm
số là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
A.
2;0
. B.
; 2 ; 0;1
. C.
; 2 ; 0; 
. D.
2;0 ; 1; 
.
Lời giải:
Ta có:
2
00
1
x
f x x
x

.
Bảng xét dấu:
Vậy hàm số nghịch bin trên khoảng
2;0
.
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ
15
số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số lẻ bằng
A.
1
7
. B.
8
15
. C.
4
15
. D.
1
14
.
Lời giải:
Không gian mẫu
2
15
105C
.
Để tổng hai số là một số lẻ ta chọn 1 số lẻ và 1 số chẵn nên ta có
8.7 56
.
Xác suất cần tìm là
56 8
105 15
.
Câu 34: Tích các nghiệm của phương trình
1
5
log 6 36 1
xx

bằng
A.
6
log 5.
B.
5
log 6.
C.
5.
D.
0.
Lời giải:
Điều kiện xc định:
1
6 36 0
xx

Khi đó, phương trình
11
5
log 6 36 1 6 36 5
x x x x
(thoả điều kiện)
6
36 6.6 5 0
6 1 0
6 5 log 5
xx
x
x
x
x
Vậy tích các nghiệm của phương trình đã cho bằng 0.
Câu 35: Cho số phức
z
thỏa mãn
12z i z
. Trong mặt phẳng phức, quỹ tích điểm biểu diễn
các số phức
z
A. l đường thẳng
3 1 0xy
. B. l đường thẳng
3 1 0xy
.
C. l đường thẳng
3 1 0xy
. D. l đường thẳng
3 1 0xy
.
Lời giải:
Gọi
,z x yi x y
.
Ta có
12z i z
2 2 2
2
1 1 2x y x y
3 1 0xy
.
Vậy quỹ tích điểm biểu diễn các số phức
z
l đường thẳng
3 1 0xy
.
Câu 36: Trong không gian
Oxyz
, vit phương trình đường thẳng
đi qua
1;1;0M
và vuông góc
với mặt phẳng
: 4 2 0Q x y z
?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
A.
1
4
1
xt
yt
z


. B.
1
14
xt
yt
zt



. C.
2
54
1


xt
yt
zt
. D.
1
14
xt
yt
zt

.
Lời giải:
Do đường thẳng
vuông góc với mặt phẳng
: 4 2 0Q x y z
nên đường thẳng
nhận
1; 4; 1u
làm một vectơ chỉ phương.
Kiểm tra phương n C thỏa mãn.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxy
có
tọa độ là
A.
1; 2;3
. B.
1;2; 3
. C.
1; 2; 3
. D.
1;2;0
.
Câu 38: Cho lăng trụ tam gic đều
.ABC A B C
có tất cả các cạnh bằng
a
. Thể tích khối trụ có hai đy
là hai hình tròn ngoại tip hai đy của lăng trụ đã cho bằng
A.
3
a
. B.
3
12
a
. C.
3
3
a
. D.
3
4
3
a
.
Lời giải:
Bn kính đường tròn ngoại tip đy của lăng trụ là
3
3
a
R
.
Thể tích khối trụ là
2
3
3
.
33
aa
Va





.
Câu 39: Cắt khối nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đy một góc bằng
0
60
ta được thit diện là một tam giác vuông cân cạnh huyền
2a
. Thể tích khối nón
N
bằng
A.
3
53
24
a
. B.
3
53
72
a
. C.
3
53
8
a
. D.
3
3
72
a
.
Lời giải:
Giả sử khối nón
N
có đỉnh là
S
, tâm đy l
O
và thit diện là giác vuông cân
SAB
.
Gọi
I
l trung điểm của
AB
, khi đó
0
60SIO
,
1
,2
2
SI AB a SB SA a
.
Ta có
2
0 2 2 2
3 3 5
.sin60 , 2
2 4 2
a a a
SO SI OB SB SO a
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Vậy
2
3
2
1 1 5 3 5 3
. . . . .
3 3 2 2 24
a a a
V OB SO





.
Câu 40: Trong không gian
,Oxyz
phương trình mặt phẳng
()P
song song v cch đều hai đường
thẳng
1
:d
2
1 1 1
x y z

và
2
:d
12
2 1 1
x y z


là
A.
2 2 1 0 xz
. B.
2 2 1 0 yz
. C.
2 2 1 0 xy
. D.
2 2 1 0 yz
.
Lời giải:
Đường thẳng
1
d
đi qua điểm
(2;0;0)M
v có véc tơ chỉ phương
1
( 1;1;1)u 
.
Đường thẳng
2
d
đi qua điểm
(0;1;2)N
v có véc tơ chỉ phương
2
(2; 1; 1)u
.
Gọi
I
l trung điểm của đoạn thẳng
MN
, suy ra
1
(1; ;1)
2
I
.
Vì mặt phẳng
()P
song song với hai đường thẳng
1
d
và
2
d
nên mặt phẳng
()P
đi qua
I
nhận
véc tơ
12
[ , ] ( 2;0; 1)n u u
lm véc tơ php tuyn. Do đó phương trình mặt phẳng là
11
( ):0.( 1) 1.( ) 1.( 1) 0 0 2 2 1 0.
22
P x y z y z y z
Vậy, phương trình mặt phẳng
()P
:
2 2 1 0.yz
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 02_______________
Câu 1: Cho số phức
23zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z
là điểm có
tọa độ là
A.
2;3
. B.
3; 2
. C.
3;2
. D.
2; 3
.
Câu 2: Đạo hàm của hàm số
10
x
y
là
A.
10
ln10
x
y
. B.
10 .ln10
x
y
. C.
10
x
y
. D.
10
10 log
x
ye
.
Câu 3: Tập xác định
D
của hàm số
1
3
2yx
là
A.
;2D 
. B.
;D  
. C.
;2D 
. D.
2;D 
.
Câu 4: Bất phương trình
3 81 0
x

có tất cả bao nhiêu nghiệm nguyên dương?
A.
3
. B.
4
. C. vô số. D.
5
.
Câu 5: Cho cấp số nhân
()
n
u
với
1
1u
và
4
8u
. Công bội của cấp số nhân đã cho bằng
A.
2.
B.
7.
C.
8.
D.
4.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:. P x y z4 3 2 0
Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng
P
?
A.
;;n
2
1 4 3
. B.
;; n
3
1 4 3
. C.
4
1; 4;3n
. D.
;;n
1
1 4 3
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Cho hàm số
fx
có đạo hàm trên ,
12 f
và
3 2.f
Tính
3
1
d
I f x x
.
A.
4.I
B.
0.I
C.
3.I
D.
4.I
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới?
A.
42
23y x x
. B.
3
33y x x
. C.
42
23y x x
. D.
42
23y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
:S
2 2 2
2 6 4 2 0. x y z x y z
Xác định tọa độ
tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 3;2 , 16IR
. B.
1; 3;2 , 4IR
. C.
1;3; 2 , 16IR
.D.
1;3; 2 , 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oyz
và
Oxz
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
Câu 12: Các điểm
, , , M N P Q
trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
1 2 3 4
, , ,z z z z
. Khi đó
1 2 3 4
3w z z z z
bằng
Q
P
N
M
-1
3
1
-2
2
x
y
O
1
-1
2
-2
-3
A.
64wi
. B.
64wi
. C.
43wi
. D.
34wi
.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
1
2
V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Câu 14: Cho khối hộp chữ nhật
.ABCD A B C D
có
2, 3, 4
AB AD AA
(tham khảo hình vẽ).
D
C
B
A
D'
C'
B'
A'
Thể tích khối hộp đã cho bằng
A.
24
. B.
20
. C.
9
. D.
8
.
Câu 15: Một khối cầu có bán kính bằng
2
, một mặt phẳng
cắt khối cầu đó theo một hình tròn có
diện tích là
2
. Khoảng cách từ tâm khối cầu đến mặt phẳng
bằng
A.
2
. B.
1
. C.
2
2
. D.
2
4
.
Câu 16: Môđun của số phức
34zi
bằng
A.
5
. B.
3
. C.
7
. D.
7
.
Câu 17: Tính chiều cao
h
của hình trụ biết chiều cao
h
bằng bán kính đáy và thể tích khối trụ đó là
8
.
A.
3
32h
. B.
3
4h
. C.
22h
. D.
2h
.
Câu 18: Trong không gian
Oxyz
, điểm nào dưới đây không thuộc đường thẳng
12
:
2 1 1
x y z
d


?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
A.
1; 2;0Q
. B.
1;2;0M
. C.
1; 3;1N 
. D.
3; 1; 1P 
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2x
. C.
0x
. D.
1x
.
Câu 20: Đường tiệm cận đứng của đồ thị hàm số
32
1
x
y
x
có phương trình là
A.
2x 
. B.
1x 
. C.
3x
. D.
1x
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
(0;1]
. B.
( ;2]
. C.
0;2
. D.
(0;2].
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là
A.
12
P
. B. 36. C.
3
12
C
. D.
3
12
A
.
Câu 23: Cho hàm số
y f x
thỏa mãn
2 7cosf x x

,
03f
. Mệnh đề nào dưới đây đúng?
A.
2 7sin 3f x x x
. B.
2 7sin 3f x x
.
C.
2 sin 9f x x x
. D.
2 7sin 3f x x x
.
Câu 24: Nếu
4
0
d5f x x
và
4
2
d1f x x 
thì
2
0
df x x
bằng
A.
6
. B.
4
. C.
4
. D.
6
.
Câu 25: Họ tất cả các nguyên hàm của hàm số
24
x
f x x
là
A.
2
2 ln2 2
x
xC
. B.
2
2
2
ln2
x
xC
. C.
2 ln2
x
C
. D.
2
ln2
x
C
.
Câu 26: Cho hàm số
fx
có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng
;1
.
B. Hàm số đã cho nghịch biến trên khoảng
0;1
.
C. Hàm số đã cho đồng biến trên khoảng
1; 
.
D. Hàm số đã cho nghịch biến trên khoảng
3; 2
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 27: Cho hàm số
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A.
3y 
. B.
1y
. C.
4y 
. D.
4y
.
Câu 28: Biết
5
2
logyx
. Khi đó
A.
5logyx
. B.
2
5logyx
. C.
2
5 logyx
. D.
2
1
log
5
yx
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
là
A.
9
2
V
. B.
81
10
V
. C.
81
10
V
. D.
9
2
V
.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với
mặt phẳng đáy và
32
2
a
SA
(minh họa như hình bên dưới).
Góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 31: Cho hàm số
23
2
x
y
x
có đồ thị
(C)
và đường thẳng
:d y x m
. Với tất cả giá trị nào của
m
thì
d
cắt
(C)
tại hai điểm phân biệt?
A.
2m
. B.
2m
. C.
6m
. D.
2
6
m
m
.
Câu 32: Cho hàm số
y f x
liên tục trên , có đạo hàm
23
2 2 5 ,
f x x x x x
.
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
;2
. B.
5;
. C.
2;5
. D.
2; 
.
Câu 33: Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10,
lấy ngẫu nhiên
5
quả cầu.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho 3 bằng
A.
11
12
. B.
5
12
. C.
7
12
. D.
1
12
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 34: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Tính
12
xx
.
A.
12
4xx
. B.
12
1
8
xx
. C.
12
1
2
xx
. D.
12
3xx 
.
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
,z x yi x y
thỏa mãn
23z i z i
là đường thẳng có phương trình là
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
qua
3;5;6M
và vuông góc với mặt phẳng
:2 3 4 2 0P x y z
thì đường thẳng
d
có phương trình là
A.
3 5 6
2 3 4
xyz

. B.
3 5 6
234
x y z

.
C.
3 5 6
2 3 4
x y z


. D.
1 2 10
2 3 4

x y z
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxz
có
tọa độ là
A.
1;2;3
. B.
1;2; 3
. C.
1;0; 3
. D.
1; 2;3
.
Câu 38: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng
2
, thiết
diện thu được là hình vuông có diện tích bằng
25
. Thể tích khối trụ bằng
A.
10 2
3
. B.
205
4
. C.
205
12
. D.
10 2
9
.
Câu 39: Cho hình nón có chiều cao bằng
25
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng
93
. Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng
A.
32 5
3
. B.
32
. C.
18 5
3
. D.
32 5
.
Câu 40: Trong không gian
,Oxyz
phương trình đường thẳng đi qua
1;2;4A
song song với
P
:
2 4 0x y z
và cắt đường thẳng
:d
2 2 2
3 1 5
x y z

có phương trình là
A.
1
2
42
xt
y
zt


. B.
12
2
42
xt
y
zt


. C.
12
2
44
xt
y
zt

. D.
1
2
42
xt
y
zt



.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức
23zi
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
z
là điểm có
tọa độ là
A.
2;3
. B.
3; 2
. C.
3;2
. D.
2; 3
.
Lời giải:
Câu 2: Đạo hàm của hàm số
10
x
y
là
A.
10
ln10
x
y
. B.
10 .ln10
x
y
. C.
10
x
y
. D.
10
10 log
x
ye
.
Lời giải:
10 10 .ln10
xx
yy
.
Câu 3: Tập xác định
D
của hàm số
1
3
2yx
là
A.
;2D 
. B.
;D  
. C.
;2D 
. D.
2;D 
.
Lời giải:
Tập xác định:
2 0 2xx
Vậy tập xác định của hàm số là
;2D 
.
Câu 4: Bất phương trình
3 81 0
x

có tất cả bao nhiêu nghiệm nguyên dương?
A.
3
. B.
4
. C. vô số. D.
5
.
Lời giải:
Ta có:
*
3 81 0 3 81 4 1;2;3;4 .
x
xx
xx

Câu 5: Cho cấp số nhân
()
n
u
với
1
1u
và
4
8u
. Công bội của cấp số nhân đã cho bằng
A.
2.
B.
7.
C.
8.
D.
4.
Lời giải:
Ta có:
33
41
. 8 2.u u q q q
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:. P x y z4 3 2 0
Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng
P
?
A.
;;n
2
1 4 3
. B.
;; n
3
1 4 3
. C.
4
1; 4;3n
. D.
;;n
1
1 4 3
.
Lời giải:
Mặt phẳng
: P x y z4 3 2 0
có một vectơ pháp tuyến là
;;n
2
1 4 3
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Cho hàm số
fx
có đạo hàm trên ,
12 f
và
3 2.f
Tính
3
1
d
I f x x
.
A.
4.I
B.
0.I
C.
3.I
D.
4.I
Lời giải:
Ta có
3
1
dI f x x
3
3 1 2 2 4
1
f x f f
.
Vậy
4I
.
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới?
A.
42
23y x x
. B.
3
33y x x
. C.
42
23y x x
. D.
42
23y x x
.
Lời giải:
Nhìn hình vẽ ta thấy là đồ thị hàm bậc 4 trùng phương
42
0f x ax bx c a
có hệ số
a
dương. Do vậy chọn đáp án D.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
:S
2 2 2
2 6 4 2 0. x y z x y z
Xác định tọa độ
tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1; 3;2 , 16IR
. B.
1; 3;2 , 4IR
. C.
1;3; 2 , 16IR
.D.
1;3; 2 , 4IR
.
Lời giải:
Ta có mặt cầu
S
:
2 2 2
2 6 4 2 0. x y z x y z
có tâm
1; 3;2I
và bán kính
2
22
1 3 2 2 4R
.
Vậy mặt cầu
S
có tâm
1; 3;2I
và bán kính
4R
.
Câu 11: Trong không gian
Oxyz
, góc giữa hai mặt phẳng
Oyz
và
Oxz
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
Câu 12: Các điểm
, , , M N P Q
trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
1 2 3 4
, , ,z z z z
. Khi đó
1 2 3 4
3w z z z z
bằng
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Q
P
N
M
-1
3
1
-2
2
x
y
O
1
-1
2
-2
-3
A.
64wi
. B.
64wi
. C.
43wi
. D.
34wi
.
Lời giải:
Ta có
1 2 3 4
3 2 ; 2 ; 3 ; 2 2z i z i z i z i
.
Suy ra
1 2 3 4
3 3 3 2 2 3 2 2 6 4w z z z z i i i i i
.
Câu 13: Thể tích của khối lăng trụ có diện tích đáy
B
và chiều cao
h
là
A.
1
2
V Bh
. B.
1
3
V Bh
. C.
1
6
V Bh
. D.
V Bh
.
Câu 14: Cho khối hộp chữ nhật
.ABCD A B C D
có
2, 3, 4
AB AD AA
(tham khảo hình vẽ).
D
C
B
A
D'
C'
B'
A'
Thể tích khối hộp đã cho bằng
A.
24
. B.
20
. C.
9
. D.
8
.
Lời giải:
Thể tích khối hộp chữ nhật đã cho bằng:
2.3.4 24V 
.
Câu 15: Một khối cầu có bán kính bằng
2
, một mặt phẳng
cắt khối cầu đó theo một hình tròn có
diện tích là
2
. Khoảng cách từ tâm khối cầu đến mặt phẳng
bằng
A.
2
. B.
1
. C.
2
2
. D.
2
4
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Gọi
,OH
lần lượt là tâm khối cầu và tâm hình tròn.
,Rr
lần lượt là bán kính mặt cầu và bán
kính hình tròn.
Diện tích hình tròn
2
2
2
S
s r r

.
Gọi
h
là khoảng cách từ tâm khối cầu đến mặt phẳng
suy ra
22
2.h R r
Câu 16: Môđun của số phức
34zi
bằng
A.
5
. B.
3
. C.
7
. D.
7
.
Lời giải:
Ta có:
32
3 4 5z
.
Câu 17: Tính chiều cao
h
của hình trụ biết chiều cao
h
bằng bán kính đáy và thể tích khối trụ đó là
8
.
A.
3
32h
. B.
3
4h
. C.
22h
. D.
2h
.
Lời giải:
Gọi
R
là bán kính của hình trụ khi đó
Rh
.
Ta có thể tích khối trụ là
23
V R h h


3
8
82
V
hh

.
Vậy chiều cao của khối trụ là
2h
.
Câu 18: Trong không gian
Oxyz
, điểm nào dưới đây không thuộc đường thẳng
12
:
2 1 1
x y z
d


?
A.
1; 2;0Q
. B.
1;2;0M
. C.
1; 3;1N 
. D.
3; 1; 1P 
.
Lời giải:
Điểm
12
;;
2 1 1
a b c
I a b c d

đúng.
Kiểm tra các điểm
; ; ;Q M N P
trong các phương án A, B, C, D ta thay điểm
1;2;0M
vào
phương trình
d
ta có:
1 1 2 2 0
2 1 1

(vô lý) . Vậy điểm
M
không thuộc đường thẳng
d
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2x
. C.
0x
. D.
1x
.
Lời giải:
Vì
y
đổi dấu từ âm sang dương duy nhất tại
2x
nên hàm số đã cho đạt cực tiểu tại
2x
Câu 20: Đường tiệm cận đứng của đồ thị hàm số
32
1
x
y
x
có phương trình là
A.
2x 
. B.
1x 
. C.
3x
. D.
1x
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Ta có:
( 1) ( 1)
32
lim lim
1
xx
x
y
x


.
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng
1x 
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1x
là
A.
(0;1]
. B.
( ;2]
. C.
0;2
. D.
(0;2].
Lời giải:
Điều kiện:
0.x
Bất phương trình đã cho tương đương
0
02
2
x
x
x
Vậy tập nghiệm của bất phương trình là
(0;2].S
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là
A.
12
P
. B. 36. C.
3
12
C
. D.
3
12
A
.
Lời giải:
Cách chọn 3 học sinh trong 12 học sinh không xếp thứ tự là tổ hợp chập 3 của 12:
3
12
C
Câu 23: Cho hàm số
y f x
thỏa mãn
2 7cosf x x

,
03f
. Mệnh đề nào dưới đây đúng?
A.
2 7sin 3f x x x
. B.
2 7sin 3f x x
.
C.
2 sin 9f x x x
. D.
2 7sin 3f x x x
.
Lời giải:
Ta có:
2 7cos 2 7sinf x x dx x x C
.
Mặt khác:
0 3 3fC
2 7sin 3f x x x
.
Câu 24: Nếu
4
0
d5f x x
và
4
2
d1f x x 
thì
2
0
df x x
bằng
A.
6
. B.
4
. C.
4
. D.
6
.
Lời giải:
Ta có
4 2 4 2 4 4
0 0 2 0 0 2
d d d d d d 5 1 6f x x f x x f x x f x x f x x f x x
.
Câu 25: Họ tất cả các nguyên hàm của hàm số
24
x
f x x
là
A.
2
2 ln2 2
x
xC
. B.
2
2
2
ln2
x
xC
. C.
2 ln2
x
C
. D.
2
ln2
x
C
.
Lời giải:
Ta có
2
2
d 2 4 d 2
ln2
x
x
f x x x x x C

.
Câu 26: Cho hàm số
fx
có bảng biến biên dưới đây:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng
;1
.
B. Hàm số đã cho nghịch biến trên khoảng
0;1
.
C. Hàm số đã cho đồng biến trên khoảng
1; 
.
D. Hàm số đã cho nghịch biến trên khoảng
3; 2
.
Lời giải:
Câu A: Sai vì hàm số không liên tục từ
;1
.
Câu B: Đúng vì hàm số nghịch biến trên khoảng
2;1
và khoảng
2;1
chứa khoảng
0;1
Câu C: Đúng quá rõ ràng.
Câu D: Đúng vì hàm số nghịch biến trên khoảng
;2
và khoảng
;2
chứa khoảng
3; 2
Câu 27: Cho hàm số
fx
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là
A.
3y 
. B.
1y
. C.
4y 
. D.
4y
.
Lời giải:
Từ bảng biến thiên của hàm số
y f x
, suy ra giá trị cực tiểu của hàm số là
4y 
(đạt tại
3)x 
.
Câu 28: Biết
5
2
logyx
. Khi đó
A.
5logyx
. B.
2
5logyx
. C.
2
5 logyx
. D.
2
1
log
5
yx
.
Lời giải:
Ta có
5
22
log 5logy x x
.
Câu 29: Gọi
H
là hình phẳng giới hạn bởi đồ thị hàm số
2
54y x x
và trục
Ox
. Thể tích của
khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
là
A.
9
2
V
. B.
81
10
V
. C.
81
10
V
. D.
9
2
V
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Phương trình hoành độ giao điểm của đồ thị hàm số
2
54y x x
và trục
Ox
ta có:
2
1
5 4 0
4
x
xx
x
Thể tích của khối tròn xoay sinh ra khi quay hình
H
quanh trục
Ox
44
2
22
11
81
54
10
V f x dx x x dx


.
Câu 30: Cho hình chóp
.S ABCD
có đáy là hình thoi tâm
O
,
ABD
đều cạnh
2a
,
SA
vuông góc với
mặt phẳng đáy và
32
2
a
SA
(minh họa như hình bên dưới).
Góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải:
Do
SA ABCD
nên hình chiếu vuông góc của
SO
lên mặt phẳng
ABC D
là
AO
. Khi đó
góc giữa đường thẳng
SO
và mặt phẳng
ABC D
là
SOA
.
ABD
đều cạnh
2a
nên
36
22
a
AO AB
.
SOA
vuông tại
A
có
32
2
a
SA
,
6
2
a
AO
nên
3 2 6
tan : 3
22
SA a a
SOA
AO
60SOA
.
Vậy góc giữa đường thẳng
SO
và mặt phẳng
ABC D
bằng
60
.
Câu 31: Cho hàm số
23
2
x
y
x
có đồ thị
(C)
và đường thẳng
:d y x m
. Với tất cả giá trị nào của
m
thì
d
cắt
(C)
tại hai điểm phân biệt?
A.
2m
. B.
2m
. C.
6m
. D.
2
6
m
m
.
Lời giải:
Phương trình hoành độ giao điểm là
2
23
( 2) 2 3 ( 2)( ) 2 3 0 (1)
2
x
x m x x x x m x mx m
x
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Để
d
cắt
(C)
tại hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt khác
2
2
0
2
.
6
( 2) 2 2 3 0
m
m
mm


Câu 32: Cho hàm số
y f x
liên tục trên , có đạo hàm
23
2 2 5 ,
f x x x x x
.
Hàm số
y f x
nghịch biến trên khoảng nào sau đây?
A.
;2
. B.
5;
. C.
2;5
. D.
2; 
.
Lời giải:
Xét phương trình
0fx
23
2
2 2 5 0 2.
5
x
x x x x
x
Bảng xét dấu:
Suy ra hàm số
()y f x
nghịch biến trên khoảng
2;5
.
Câu 33: Một hộp chứa
10
quả cầu được đánh số theo thứ tự từ
1
đến
10,
lấy ngẫu nhiên
5
quả cầu.
Xác suất để tích các số ghi trên
5
quả cầu đó chia hết cho 3 bằng
A.
11
12
. B.
5
12
. C.
7
12
. D.
1
12
.
Lời giải:
Số phần tử của không gian mẫu
5
10
nC
.
Gọi
A
là biến cố: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó chia hết cho 3”
Biến cố
A
: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó không chia hết cho 3”
Tính
nA
:
Để tích các số trên 5 quả cầu được chọn không chia hết cho 3 thì trong 5 quả cầu đó không có
các quả cầu mang số 3, 6, 9. Vậy
5
7
n A C
.
5
7
5
10
1
12
nA
C
PA
nC
.
11
1
12
P A P A
.
Câu 34: Biết phương trình
2
22
log 2log 2 1 0xx
có hai nghiệm
12
,xx
. Tính
12
xx
.
A.
12
4xx
. B.
12
1
8
xx
. C.
12
1
2
xx
. D.
12
3xx 
.
Lời giải:
ĐKXĐ:
0x
.
Ta có
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
22
2 2 2 2
2
2
log 2log 2 1 0 log 2log 3 0
1
log 1
2
log 3
8


x x x x
x
x
x
x
Vậy
12
4xx
.
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức
,z x yi x y
thỏa mãn
23z i z i
là đường thẳng có phương trình là
A.
1yx
. B.
1yx
. C.
1yx
. D.
1yx
.
Lời giải:
2 3 2 1 3z i z i x y i x y i
2 2 2
2 2 2 2 2
2 1 3 4 4 2 1 6 9x y x y x x y y x y y
4 4 4 1y x y x
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
qua
3;5;6M
và vuông góc với mặt phẳng
:2 3 4 2 0P x y z
thì đường thẳng
d
có phương trình là
A.
3 5 6
2 3 4
xyz

. B.
3 5 6
234
x y z

.
C.
3 5 6
2 3 4
x y z


. D.
1 2 10
2 3 4

x y z
.
Lời giải:
Ta có
:2 3 4 2 0P x y z
có vectơ pháp tuyến
2; 3;4n 
.
dP
d
nhận vectơ pháp tuyến của
P
làm vectơ chỉ phương.
Do đó đường thẳng
d
qua
3;5;6M
và có vectơ chỉ phương
2; 3;4u 
.
Kiểm tra phương án D thỏa mãn.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua mặt phẳng
Oxz
có
tọa độ là
A.
1;2;3
. B.
1;2; 3
. C.
1;0; 3
. D.
1; 2;3
.
Câu 38: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng
2
, thiết
diện thu được là hình vuông có diện tích bằng
25
. Thể tích khối trụ bằng
A.
10 2
3
. B.
205
4
. C.
205
12
. D.
10 2
9
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Từ đề bài ta có diện tích hình vuông
''ABB A
bằng
25
suy ra
'5AB BB
. Kẻ
OH AB
,
H
là trung điểm của
AB
thì
', ' ' , ' ' 2 d OO ABB A d O ABB A OH
.
Ta có
2
2 2 2
41
22



AB
OA OH AH OH
.
Suy ra khối trụ có
41
' 5;
2
h BB r OA
, vậy
2
205
4
V r h

.
Câu 39: Cho hình nón có chiều cao bằng
25
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng
93
. Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng
A.
32 5
3
. B.
32
. C.
18 5
3
. D.
32 5
.
Lời giải:
Ta có
2
3
93
4

SGF
S SG
2
36SG
6 l SG
* Bán kính đường tròn đáy là
2
2 2 2
6 2 5 4 r l h
* Thể tích khối nón là
22
1 1 32 5
. . .4 .2 5
3 3 3
V r h
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Câu 40: Trong không gian
,Oxyz
phương trình đường thẳng đi qua
1;2;4A
song song với
P
:
2 4 0x y z
và cắt đường thẳng
:d
2 2 2
3 1 5
x y z

có phương trình là
A.
1
2
42
xt
y
zt


. B.
12
2
42
xt
y
zt


. C.
12
2
44
xt
y
zt

. D.
1
2
42
xt
y
zt



.
Lời giải:
Ta có:
2;1;1
P
n
là một vec tơ pháp tuyến của mặt phẳng
P
.
Phương trình tham số của đường thẳng
d
là:
23
2,
25
xt
y t t
zt


.
Gọi
là đường thẳng cần tìm. Gọi
M
là giao điểm của
và
d
2 3 ;2 ;2 5M t t t
1 3 ; ; 2 5AM t t t
Do
// P
nên
. 0 2 1 3 2 5 0 12 0 0
P
AM n t t t t t
1;0; 2AM
.
Phương trình đường thẳng
đi qua
1;2;4A
và nhận
1;0; 2AM 
là một vec tơ chỉ
phương là:
1
2,
42
xt
yt
zt



.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 03_______________
Câu 1: Trong mặt phẳng tọa độ
Oxy
, số phức
23zi
được biểu diễn bởi điểm nào sau đây?
A.
3;2Q
. B.
2;3N
. C.
3;2P
. D.
2; 3M
.
Câu 2: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln 2
x
yx
.
Câu 3: Tập xác định của hàm số
1
2
log 2yx
là
A. . B.
2; 
. C.
2;
. D.
0;
.
Câu 4: Tập nghiệm của bất phương trình
1
2
2
x



là
A.
;1
. B.
0;
. C.
1; 
. D.
;1
.
Câu 5: Cho cấp số nhân
n
u
với
1
3u
và công bội
2q 
. Số hạng thứ
7
của cấp số nhân đó là
A.
384
. B.
192
. C.
192
. D.
384
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
( ) :P
1
2 1 3
y
xz
. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
( )?P
A.
2
(2;1;3).n
B.
4
( 3;6; 2).n
C.
1
(3;6;2).n
D.
3
( 3;6;2).n 
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Nếu
35
03
d 3, d 7

f x x f x x
thì
5
0
f x dx
bằng
A.
7
. B.
4
. C.
10
. D.
4
.
Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong ở hình vẽ bên dưới ?
A.
32
43 y x x
. B.
3 2
34y x x
. C.
3 2
4y x x
. D.
3
34 y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 1 2 1 4S x y z
. Tọa độ tâm
I
và
bán kính
R
của mặt cầu là
A.
1; 2;1 ; 4IR
. B.
1;2; 1 ; 2IR
.
C.
1; 2;1 ; 2IR
. D.
1;2; 1 ; 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Oy
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Biết
1; 2M
và
2;3N
lần lượt là hai điểm biểu diễn cho hai số phức
1
z
và
2
z
trên mặt
phẳng tọa độ
Oxy
. Khi đó, số phức
12
.zz
là
A.
15 i
. B
8.i
C.
26 i
. D.
3 i
.
Câu 13: Cho hình hộp có đáy là hình vuông cạnh bằng
a
và chiều cao
3a
. Thể tích của khối hộp đã
cho bằng
A.
3
a
. B.
3
1
3
a
. C.
3
3a
. D.
3
9a
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
ABCD
và
3SA a
(tham khảo hình vẽ).
Thể tích khối chóp
.S ABCD
bằng
A.
3
3a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Câu 15: Cho khối cầu có bán kính
2R
. Thể tích của khối cầu đã cho bằng
A.
32
3
. B.
16
3
. C.
16
. D.
32
.
Câu 16: Phần ảo của số phức
18 12zi
là
A.
12
. B.
12
. C.
12i
. D.
18
.
Câu 17: Thể tích của khối nón có chiều cao
h
, bán kính đáy
r
bằng
A.
2
1
3
rh
. B.
1
3
rh
. C.
2
1
3
rh
. D.
2
rh
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 3 1
x y z
d

. Điểm nào dưới đây thuộc
đường thẳng
d
?
A.
2;3;1 .Q
B.
1; 2; 1 .M 
C.
1;2;3 .P
D.
1;2; 1 .N
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.

. C.
11
. D.
1
.
Câu 20: Đường tiệm cận ngang của đồ thị hàm số
31
2
x
y
x
là
A.
1
3
y
. B.
3y
. C.
3y
. D.
2y
.
Câu 21: Tập nghiệm của bất phương trình
0,5 1
x
là
A.
;2
. B.
0;
. C.
;0
. D.
2;
.
Câu 22: Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp
1;2;3;4;5 ?X
A.
2
5
A
. B.
2
5
C
. C.
2
5
. D.
5
2
.
Câu 23: Nếu
d
6
0
18f x x
thì
d
2
0
3f x x
bằng
A.
6
. B.
12
. C.
36
. D.
54
.
Câu 24: Cho
6
2
d5f x x
. Khi đó
6
2
6 3 df x x


bằng
A.
9
. B.
9
. C.
1
. D.
21
.
Câu 25: Xác định
2
sin 2 d .
xx
A.
sin4
8
x
C
. B.
sin4
28
xx
C
. C.
3
cos 2
3
x
C
. D.
sin4
28
xx
C
.
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2; .
B.
1; .
C.
;3 .
D.
;. 
Câu 27: Cho hàm số
y f x
có đạo hàm liên tục trên
và có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Giá trị cực tiểu của hàm số bằng
A.
1
. B.
2
. C.
0
. D.
1
.
Câu 28: Với
,ab
là các số dương tùy ý,
25
3
log ab
bằng
A.
33
2log 5logab
. B.
3
10log ab
. C.
3
7log ab
. D.
33
10 log logab
.
Câu 29: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
y x x
và trục
hoành quanh trục hoành là
A.
3
V
. B.
30
V
. C.
15
V
. D.
5
V
.
Câu 30: Cho hình chóp
.S ABCD
có
ABCD
là hình thang vuông tại
A
và
D
, cạnh bên
SD
vuông góc
với đáy,
, 2 , 3AB AD a CD a SA a
.
Góc giữa
SB
và
SAD
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Câu 31: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
4 4 2 0x x m
có
4
nghiệm phân biệt?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
xm
nghịch biến trên khoảng
0;4
?
A.
6
. B.
7
. C.
5
. D.
11
.
Câu 33: Một hộp chứa 12 tấm thẻ được đánh số bằng các số tự nhiên liên tiếp từ 1 đến 12. Chọn ngẫu
nhiên ra ba tấm thẻ. Xác suất để tích số ghi trên ba tấm thẻ là một số chẵn bằng
A.
11
12
. B.
1
3
. C.
10
11
. D.
1
2
.
Câu 34: Tính tổng các nghiệm của phương trình
11
2 2 5
xx

A.
0
. B.
2
. C.
1
2
. D.
2
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 35: Trong mặt phẳng
Oxy
, tập hợp các điểm biểu diễn số phức
z
thoã điều kiện
3 2 1 2z i i
A. Đường thẳng vuông góc với trục
Ox
. B. Đường tròn tâm
3; 2I
, bán kính
5R
.
C.
Đường tròn tâm
3; 2I
, bán kính
5R
. D. Đường thẳng vuông góc với trục
Oy
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
đi qua điểm
1;2;3A
và vuông góc với mặt phẳng
:4 3 7 1 0x y z
có phương trình tham số là
A.
14
23
37
xt
yt
zt
. B.
54
53
47


xt
yt
zt
C.
13
24
37
xt
yt
zt



D.
18
26
3 14
xt
yt
zt
Câu 37: Trong mặt phẳng
Oxyz
, mặt cầu
S
có tâm thuộc trục
Ox
và đi qua hai điểm
1;2;1 , 1;0;3AB
có bán kính bằng
A.
3
. B.
23
. C.
3
. D.
9
.
Câu 38: Cho khối nón
N
có chiều cao bằng
3a
. Cắt hình nón đó bởi một mặt phẳng song song với
mặt đáy, cách mặt đáy một khoảng bằng
a
thu được thiết diện có diện tích bằng
2
64
.
9
a
Khi
đó, thể tích của khối nón
N
bằng
A.
3
16 a
. B.
3
48a
. C.
3
16a
. D.
3
48 a
.
Câu 39: Cho hình trụ có chiều cao bằng
8cm
. Một mặt phẳng
song song với trục của hình trụ
cách trục một khoảng bằng
5cm
và mp
cắt hình trụ theo thiết diện có diện tích bằng
2
32cm
. Khi đó diện tích toàn phần của hình trụ đã cho bằng
A.
2
24 cm
. B.
2
16 cm
. C.
2
66 cm
. D.
2
11 cm
.
Câu 40: Trong không gian
,Oxyz
cho điểm
(1;0;1)M
và đường thẳng
1 2 3
:.
1 2 3
x y z
d

Đường
thẳng đi qua
,M
vuông góc với
d
và cắt
Oz
có phương trình là
A.
13
0
1
xt
y
zt


. B.
13
0
1
xt
y
zt


. C.
13
1
xt
yt
zt


. D.
13
0
1
xt
y
zt


.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng tọa độ
Oxy
, số phức
23zi
được biểu diễn bởi điểm nào sau đây?
A.
3;2Q
. B.
2;3N
. C.
3;2P
. D.
2; 3M
.
Lời giải:
Trong mặt phẳng tọa độ
Oxy
, số phức
23zi
được biểu diễn bởi điểm
2; 3M
.
Câu 2: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln 2
x
yx
.
Lời giải:
Hàm số
2
x
y
có đạo hàm là
' 2 .ln2
x
y
.
Câu 3: Tập xác định của hàm số
1
2
log 2yx
là
A. . B.
2; 
. C.
2;
. D.
0;
.
Lời giải:
Điều kiện xác định:
2 0 2 2;x x x 
.
Câu 4: Tập nghiệm của bất phương trình
1
2
2
x



là
A.
;1
. B.
0;
. C.
1; 
. D.
;1
.
Lời giải:
1
1
2 2 2 1 1
2
x
x
xx



Câu 5: Cho cấp số nhân
n
u
với
1
3u
và công bội
2q 
. Số hạng thứ
7
của cấp số nhân đó là
A.
384
. B.
192
. C.
192
. D.
384
.
Lời giải:
Số hạng thứ
7
của cấp số nhân đó là
6
6
71
. 3. 2 192u u q
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
( ) :P
1
2 1 3
y
xz
. Vectơ nào dưới đây là một vectơ
pháp tuyến của mặt phẳng
( )?P
A.
2
(2;1;3).n
B.
4
( 3;6; 2).n
C.
1
(3;6;2).n
D.
3
( 3;6;2).n 
Lời giải:
Ta có:
1 3 6 2 6 0
2 1 3
y
xz
x y z
. Do đó vectơ pháp tuyến là
1
(3;6;2).n
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hình bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
x
y
O
-2
2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
A.
0; 2
. B.
2;0
. C.
2;0
. D.
0;2
.
Câu 8: Nếu
35
03
d 3, d 7

f x x f x x
thì
5
0
f x dx
bằng
A.
7
. B.
4
. C.
10
. D.
4
.
Lời giải:
Ta có:
5 3 5
0 0 3
3 7 10f x dx f x dx f x dx
.
Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong ở hình vẽ bên dưới ?
A.
32
43 y x x
. B.
3 2
34y x x
. C.
3 2
4y x x
. D.
3
34 y x x
.
Lời giải:
Nhánh cuối đồ thị đi xuống suy ra hệ số ứng với bậc cao nhất là số âm, nên loại đáp án
B
và
D
Nhận thấy điểm
1;0
thuộc đồ thị, ta thay
1x
và
0y
vào các đáp án còn lại, chọn
được đáp án
A
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 1 2 1 4S x y z
. Tọa độ tâm
I
và
bán kính
R
của mặt cầu là
A.
1; 2;1 ; 4IR
. B.
1;2; 1 ; 2IR
.
C.
1; 2;1 ; 2IR
. D.
1;2; 1 ; 4IR
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Oy
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Biết
1; 2M
và
2;3N
lần lượt là hai điểm biểu diễn cho hai số phức
1
z
và
2
z
trên mặt
phẳng tọa độ
Oxy
. Khi đó, số phức
12
.zz
là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
15 i
. B.
8 i
. C.
26 i
. D.
3 i
.
Lời giải:
Ta có :
12
1 2 ; 2 3z i z i
. Từ đó suy ra :
12
. 1 2 . 2 3 8z z i i i
.
Câu 13: Cho hình hộp có đáy là hình vuông cạnh bằng
a
và chiều cao
3a
. Thể tích của khối hộp đã
cho bằng
A.
3
a
. B.
3
1
3
a
. C.
3
3a
. D.
3
9a
.
Lời giải:
Thể tích của khối hộp:
23
. .3 3V B h a a a
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
ABCD
và
3SA a
(tham khảo hình vẽ).
Thể tích khối chóp
.S ABCD
bằng
A.
3
3a
. B.
3
3a
. C.
3
a
. D.
3
3
3
a
.
Lời giải:
Ta có
3
2
.
1 1 3
. . 3 .
3 3 3
S ABCD ABCD
a
V SA S a a
.
Câu 15: Cho khối cầu có bán kính
2R
. Thể tích của khối cầu đã cho bằng
A.
32
3
. B.
16
3
. C.
16
. D.
32
.
Lời giải:
Thể tích của khối cầu là
33
4 4 32
. . .2
3 3 3
VR
.
Câu 16: Phần ảo của số phức
18 12zi
là
A.
12
. B.
12
. C.
12i
. D.
18
.
Lời giải:
Phần ảo của số phức
18 12zi
là
12
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Câu 17: Thể tích của khối nón có chiều cao
h
, bán kính đáy
r
bằng
A.
2
1
3
rh
. B.
1
3
rh
. C.
2
1
3
rh
. D.
2
rh
.
Lời giải:
Thể tích của khối nón đã cho là
2
1
3
V r h
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
2 3 1
x y z
d

. Điểm nào dưới đây thuộc
đường thẳng
d
?
A.
2;3;1 .Q
B.
1; 2; 1 .M 
C.
1;2;3 .P
D.
1;2; 1 .N
Lời giải:
Đường thẳng
d
đi qua
0 0 0
;;M x y z
có một véc tơ chỉ phương là
;;u a b c
thì
d
có phương
trình chính tắc là
0 0 0
:
x x y y z z
d
a b c

.
Vậy
1 2 1
:
2 3 1
x y z
d

đi qua điểm
1; 2; 1M 
hay
1; 2; 1M 
thuộc đường thẳng
d
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.

. C.
11
. D.
1
.
Lời giải:
Từ bảng biến thiên của hàm số
y f x
,ta thấy giá trị cực đại của hàm số là
11
.
Câu 20: Đường tiệm cận ngang của đồ thị hàm số
31
2
x
y
x
là
A.
1
3
y
. B.
3y
. C.
3y
. D.
2y
.
Lời giải:
Ta có:
31
lim 3
2
x
x
x
;
31
lim 3
2
x
x
x
nên TCN
3y
.
Câu 21: Tập nghiệm của bất phương trình
0,5 1
x
là
A.
;2
. B.
0;
. C.
;0
. D.
2;
.
Lời giải:
Ta có:
0
0,5 1 0,5 0,5 0
xx
x
.
Câu 22: Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp
1;2;3;4;5 ?X
A.
2
5
A
. B.
2
5
C
. C.
2
5
. D.
5
2
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Lời giải:
Mỗi số tự nhiên có hai chữ số khác nhau có các chữ số lấy từ tập
X
là một chỉnh hợp chập 2
của 5 phần tử, do đó ta được
2
5
A
số.
Câu 23: Nếu
d
6
0
18f x x
thì
d
2
0
3f x x
bằng
A.
6
. B.
12
. C.
36
. D.
54
.
Lời giải:
Xét tích phân
2
0
3dI f x x
Đặt
3tx
. Khi đó
d
d 3d d
3
t
t x x
.
Với
0 0; 2 6x t x t
.
Khi đó
66
00
d 1 1
. d .18 6
3 3 3
t
I f t f t t

.
Câu 24: Cho
6
2
d5f x x
. Khi đó
6
2
6 3 df x x


bằng
A.
9
. B.
9
. C.
1
. D.
21
.
Lời giải:
Ta có:
6 6 6
2 2 2
6 3 d 6 d 3 df x x x f x x


6
2
6
6 3 d 6. 6 2 3.5 9
2
x f x x
.
Câu 25: Xác định
2
sin 2 d .
xx
A.
sin4
8
x
C
. B.
sin4
28
xx
C
. C.
3
cos 2
3
x
C
. D.
sin4
28
xx
C
.
Lời giải:
Ta có
2
1 cos4
sin 2 d d
2
x
x x x

11
d cos4 d 4
28
x x x

sin4
.
28
xx
C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2; .
B.
1; .
C.
;3 .
D.
;. 
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Từ Bảng biến thiên suy ra hàm số đã cho đồng biến trên
(2; )
.
Câu 27: Cho hàm số
y f x
có đạo hàm liên tục trên
và có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số bằng
A.
1
. B.
2
. C.
0
. D.
1
.
Lời giải:
Từ BBT, ta có giá trị cực tiểu của hàm số là:
CT
1y 
.
Câu 28: Với
,ab
là các số dương tùy ý,
25
3
log ab
bằng
A.
33
2log 5logab
. B.
3
10log ab
. C.
3
7log ab
. D.
33
10 log logab
.
Lời giải:
Ta có:
2 5 2 5
3 3 3 3 3
log log log 2log 5loga b a b a b
.
Câu 29: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
y x x
và trục
hoành quanh trục hoành là
A.
3
V
. B.
30
V
. C.
15
V
. D.
5
V
.
Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số
2
y x x
và trục hoành là
2
0
0
1
x
xx
x
.
Vậy
1
2
2
0
d
30
V x x x
.
Câu 30: Cho hình chóp
.S ABCD
có
ABCD
là hình thang vuông tại
A
và
D
, cạnh bên
SD
vuông góc
với đáy,
, 2 , 3AB AD a CD a SA a
.
Góc giữa
SB
và
SAD
bằng
A.
30
. B.
60
. C.
45
. D.
90
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Ta có:
AB AD
AB SAD
AB SD

,,SB SAD SB SA BSA
.
Tam giác
SAB
vuông tại
1
tan 30
3
AB
A BSA BSA
SA
.
Câu 31: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
42
4 4 2 0x x m
có
4
nghiệm phân biệt?
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải:
Ta có :
42
4 4 2 0x x m
42
4 4 2x x m
1
.
Số nghiệm của phương trình
1
là số giao điểm của đồ thị hàm số
42
44y x x
và đường
thẳng
2ym
.
Xét hàm số
42
44y x x
;
3
48y x x

,
0
0
2
x
y
x


.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có: Phương trình
1
có 4 nghiệm phân biệt khi
8 2 4m
24m
.
Vì
m
nguyên nên
3m
.
Câu 32: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
xm
nghịch biến trên khoảng
0;4
?
A.
6
. B.
7
. C.
5
. D.
11
.
Lời giải:
Tập xác định
\
4
m
D



.
Ta có
2
2
36
4
m
y
xm
.
Hàm số đã cho nghịch biến trên khoảng
0;4
khi và chỉ khi
2
36 0
0;4
4
m
m

66
0
4
4
4
m
m
m
66
06
0
16
m
m
m
m

.
Vì
m
nguyên nên
0;1;2;3;4;5m
.
Vậy có
6
giá trị của
m
thỏa mãn yêu cầu bài toán.
x


y
y
2
0
0
8
4
0
2
0
8


Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Câu 33: Một hộp chứa 12 tấm thẻ được đánh số bằng các số tự nhiên liên tiếp từ 1 đến 12. Chọn ngẫu
nhiên ra ba tấm thẻ. Xác suất để tích số ghi trên ba tấm thẻ là một số chẵn bằng
A.
11
12
. B.
1
3
. C.
10
11
. D.
1
2
.
Lời giải:
Chọn 3 trong 12 tấm thẻ có
3
12
220C
cách
220n
.
Gọi biến cố A: “tích số ghi trên ba tấm thẻ là một số lẻ”
Khi đó
3
6
20n A C
.
Nên
20 1
220 11
nA
PA
n
.
Suy ra xác suất để tích số ghi trên ba tấm thẻ là một số chẵn là
1 10
11
11 11
PA
.
Câu 34: Tính tổng các nghiệm của phương trình
11
2 2 5
xx

A.
0
. B.
2
. C.
1
2
. D.
2
.
Lời giải:
Ta có:
11
1
2 2 5 2.2 2. 5
2
x x x
x

.
Đặt
20
x
tt
, phương trình trở thành:
2
2
22
1
2
2 5 2 5 2 0
1
1
1
2
2
2
x
x
t
x
t t t
x
t
t

.
Vậy tổng tất cả các nghiệm của phương trình là 0.
Câu 35: Trong mặt phẳng
Oxy
, tập hợp các điểm biểu diễn số phức
z
thoã điều kiện
3 2 1 2z i i
A. Đường thẳng vuông góc với trục
Ox
. B. Đường tròn tâm
3; 2I
, bán kính
5R
.
C.
Đường tròn tâm
3; 2I
, bán kính
5R
. D. Đường thẳng vuông góc với trục
Oy
.
Lời giải:
Gọi số phức
,z x yi xy
.
Khi đó
22
3 2 1 2 3 2 1 2 3 2 5z i i x y i i x y
Vậy tập hợp các điểm biểu diễn số phức
z
thoã điều kiện đề bài là đường tròn tâm
3; 2I
,
bán kính
5R
.
Câu 36: Trong không gian
Oxyz
, đường thẳng
d
đi qua điểm
1;2;3A
và vuông góc với mặt phẳng
:4 3 7 1 0x y z
có phương trình tham số là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
A.
14
23
37
xt
yt
zt
. B.
54
53
47


xt
yt
zt
C.
13
24
37
xt
yt
zt



D.
18
26
3 14
xt
yt
zt
Lời giải:
Mặt phẳng
có VTPT
4;3; 7n
.
Đường thẳng
d
vuông góc với mp
nên
d
nhận
4;3; 7n
làm 1 VTCP.
Đường thẳng
d
đi qua điểm
1;2;3A
và có vtcp
4;3; 7 .n
Kiểm tra phương án B thỏa mãn.
Câu 37: Trong mặt phẳng
Oxyz
, mặt cầu
S
có tâm thuộc trục
Ox
và đi qua hai điểm
1;2;1 , 1;0;3AB
có bán kính bằng
A.
3
. B.
23
. C.
3
. D.
9
.
Lời giải:
Giả sử tâm
;0;0I a Ox
.
Ta có
22
22
1 4 1 1 0 9AI BI a a
1 1;0;0aI
2 2 2
1 1 0 2 0 1 3R AI
.
Câu 38: Cho khối nón
N
có chiều cao bằng
3a
. Cắt hình nón đó bởi một mặt phẳng song song với
mặt đáy, cách mặt đáy một khoảng bằng
a
thu được thiết diện có diện tích bằng
2
64
.
9
a
Khi
đó, thể tích của khối nón
N
bằng
A.
3
16 a
. B.
3
48a
. C.
3
16a
. D.
3
48 a
.
Lời giải:
Ta có:
3SO h a
;
2
22
64 8
93
TD
S r HK a HK a
.
Do thiết diện song song và cách mặt đáy một đoạn bằng
a
nên
2.HO a SH SO OH a
Xét
SOA SHK
, ta có:
.
4
OA SO SO HK
OA a
HK SH SH
.
Vậy
2 2 3
11
. . .16 .3 16
33
N
V R h a a a
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Câu 39: Cho hình trụ có chiều cao bằng
8cm
. Một mặt phẳng
song song với trục của hình trụ
cách trục một khoảng bằng
5cm
và mp
cắt hình trụ theo thiết diện có diện tích bằng
2
32cm
. Khi đó diện tích toàn phần của hình trụ đã cho bằng
A.
2
24 cm
. B.
2
16 cm
. C.
2
66 cm
. D.
2
11 cm
.
Lời giải:
D
O
B
O'
C
A
M
Theo giả thiết, mp
cắt hình trụ theo thiết diện là hình chữ nhật và giả sử là
ABCD
.
Ta có:
2
8
4
. 32
AD OO cm
AB cm
AD AB cm


.
Gọi
M
là trung điểm
AB
Suy ra
2
2 2 2
2 5 2 3MB cm OB OM MB cm
Khi đó hình trụ có bán kính đáy
3r cm
và độ dài đường sinh
8l cm
.
Diện tích toàn phần của hình trụ là
2
2 2 .3. 8 3 66
tp
S r l r cm
.
Câu 40: Trong không gian
,Oxyz
cho điểm
(1;0;1)M
và đường thẳng
1 2 3
:.
1 2 3
x y z
d

Đường
thẳng đi qua
,M
vuông góc với
d
và cắt
Oz
có phương trình là
A.
13
0
1
xt
y
zt


. B.
13
0
1
xt
y
zt


. C.
13
1
xt
yt
zt


. D.
13
0
1
xt
y
zt


.
Lời giải:
Gọi
là đường thẳng cần tìm và
.N Oz
Ta có
(0;0; ).Nc
Vì
qua
,MN
và
M Oz
nên
( 1;0; 1)MN c
là VTCP của
.
d
có 1 VTCP
(1;2;3)u
và
d
nên
41
0 1 3( 1) 0 ( 1;0; ).
33
MN u c c MN
Chọn
( 3;0;1)v
là 1 VTCP của
, phương trình tham số của đường thẳng
là
13
0
1
xt
y
zt


.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 04_______________
Câu 1: Số phức nào sau đây có biểu diễn hình học là điểm
3;5M
?
A.
35zi
. B.
35zi
. C.
35zi
. D.
35zi
.
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
lnyx
là
A.
1
.
10
y
x
B.
1
.
y
x
C.
1
.
y
ex
D.
.
e
y
x
Câu 3: Tập xác định
D
của hàm số
23
yx
là
A.
0;D
. B.
D
. C.
0;D
. D.
\0D
.
Câu 4: Tập nghim của bt phương trnh
ln 1x
là
A.
;e 
. B.
0;e
. C.
;e
. D.
;e
.
Câu 5: Cho cp số nhân
n
u
có
1
2u
và có công bội bằng
3
. Giá trị
2
u
bằng
A.
5
. B.
9
. C.
8
. D.
6
.
Câu 6: Trong không gian
Oxyz
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
Oxy
?
A.
1;1;1m
. B.
1;0;0i
. C.
0;1;0j
. D.
0;0;1k
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hnh bên dưới:
x
y
O
-2
2
Số giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 8: Cho
6
2
d4
f x x
và
6
2
d5
g x x
, khi đó
6
2
3d


f x g x x
bằng
A.
19
. B.
17
. C.
11
. D.
7
.
Câu 9: Đường cong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
1y x x
. B.
. C.
. D.
3
21y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, mặt cầu có tâm
2; 1;3I
, bán kính
3R
có phương trnh là
A.
2 2 2
2 1 3 3x y z
. B.
2 2 2
2 1 3 3x y z
.
C.
2 2 2
2 1 3 3x y z
. D.
2 2 2
3 1 3 3x y z
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Ox
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 6x yi i x i
, với
i
là đơn vị ảo.
A.
1, 3xy
. B.
1, 1xy
. C.
1, 1xy
. D.
1, 3xy
.
Câu 13: Cho khối chóp có din tích đáy
6B
và chiều cao
8h
. Thể tích của khối chóp đã cho bằng
A.
16
. B.
48
. C.
8
. D.
14
.
Câu 14: Thể tích khối lăng trụ tam giác đều có tt cả các cạnh đều bằng
a
bằng
B
C
A
B
C
A
A.
3
3
12
a
. B.
3
a
. C.
3
2a
. D.
3
3
4
a
.
Câu 15: Cho mặt cầu
S
, bán kính
R
và mặt phẳng
. Biết khoảng cách từ tâm của mặt cầu
S
tới
mặt phẳng
bằng
R
. Khẳng định nào sau đây đúng?
A. Mặt phẳng
a
cắt mặt cầu
S
.
B. Thiết din của mặt phẳng
với mặt cầu
S
là một đường tròn.
C. Mặt phẳng
a
tiếp xúc với mặt cầu
S
.
D. Mặt phẳng
a
với mặt cầu
S
không có điểm chung.
Câu 16: Cho số phức
12zi
. Số phức liên hợp của
z
là
A.
12i
. B.
12i
. C.
2 i
. D.
12i
.
Câu 17: Cho hnh nón có độ dài đường sinh bằng
3a
và bán kính đáy bằng
a
. Din tích xung quanh
của hnh nón đã cho bằng
A.
2
12 a
. B.
2
3 a
. C.
2
6 a
. D.
2
a
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
32
:1
23
xt
d y t
zt



. Điểm nào dưới đây thuộc
d
?
A.
3;1;2M
. B.
2;1;3Q
. C.
3; 1; 2P
. D.
2;1;3N
.
Câu 19: Cho hàm số
fx
có bảng xét du
fx
như sau:
Hoành độ điểm cực tiểu của hàm số đã cho bằng
A.
1
. B.
0
. C.
1
. D.
1
và
1
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 20: Bảng biến thiên sau đây là của hàm số nào ?
A.
1
.
2
x
y
x
B.
1
.
1
x
y
x
C.
21
.
2
x
y
x
D.
3
.
2
x
y
x


Câu 21: Tập nghim của bt phương trnh
1
24
x
là
A.
;3 .
B.
;5 .
C.
1;3 .
D.
1; .
Câu 22: Từ 10 điểm phân bit trong không gian có thể tạo thành bao nhiêu vectơ khác vectơ
0
?
A.
10
2
. B.
10
P
. C.
2
10
A
. D.
2
10
C
.
Câu 23: Cho hàm số
y f x
xác định và liên tục trên
đồng thời thoả mãn:
( ) 3 5sinf x x

,
(0) 14f
. Khẳng định nào sau đây đúng?
A.
( ) 3 5f


. B.
( ) 3 5sin 9f x x x
.
C.
( ) 3 5cos 9f x x x
. D.
3
9
22
f





.
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x


bằng
A. 12. B. 18. C.
27
. D. 10.
Câu 25: Họ tt cả các nguyên hàm của hàm số
cos 6f x x x
là
A.
2
sin 3x x C
. B.
sin xC
. C.
2
sin 3x x C
. D.
2
sin 6x x C
.
Câu 26: Cho hàm số
y f x
có đồ thị như hnh bên dưới:
Mnh đề nào sau đây đúng?
A. Hàm số
fx
nghịch biến trên
2;5
. B. Hàm số
fx
nghịch biến trên
0;5
.
C. Hàm số
fx
đồng biến trên
;0
. D. Hàm số
fx
đồng biến trên
5;
.
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Hàm số đã cho đạt cực tiểu tại
A.
1x
. B.
3.y
C.
3x
. D.
1y 
.
Câu 28: Cho khối trụ
T
,
là mặt phẳng đi qua trục và cắt khối trụ
T
theo thiết din là hình
vuông cạnh 2a. Thể tích khối trụ
T
bằng
A.
3
3
a
B.
3
2.a
C.
3
2
3
a
. D.
3
.a
Câu 29: Cho
a
là số thực dương khác
1
. Giá trị của
3
log
a
a
bằng
A.
0.
B.
1
.
3
C.
3.
D.
3.
Câu 30: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và
trục hoành quay quanh trục
Ox
là
A.
4
3
V
. B.
16
15
V
. C.
16
15
V
. D.
4
3
V
.
Câu 31: Cho hnh chóp
.S ABC
có đáy
ABC
là tam giác vuông cạnh huyền
BC a
. Hnh chiếu
vuông góc của
S
lên
ABC
trng với trung điểm của
BC
.
H
A
C
B
S
Biết
SB a
. Tính số đo của góc giữa
SA
và
ABC
.
A.
75
. B.
30
. C.
60
. D.
45
.
Câu 32: Cho hàm số bậc ba
y f x
có đồ thị như hnh vẽ bên dưới:
Số giá trị nguyên của tham số
m
để đường thẳng
ym
cắt đồ thị hàm số đã cho tại ba điểm
phân bit là
A. Vô số. B.
3
. C. 0. D.
5
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 33: Có bao nhiêu giá trị nguyên của tham số thực m để hàm số
32
4 9 5y x mx m x
nghịch biến trên khoảng
; 
?
A. 5. B. 7. C. 4. D. 6.
Câu 34: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong
hộp. Xác sut để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng bằng
A.
11
18
. B.
5
18
. C.
75
408
. D.
95
408
.
Câu 35: Phương trnh
9 4.3 3 0
xx
có tổng các nghim là
A.
1
. B.
4
. C.
1
. D.
4
.
Câu 36: Gọi
12
;zz
là hai nghim phức của phương trnh
2
2 2 0zz
. Tập hợp các điểm bểu diễn
của số phức
w
thỏa mãn
12
w z w z
là đường thẳng có phương trnh
A.
0xy
. B.
0x
. C.
0xy
. D.
0y
.
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
và đường thẳng
3 1 7
:
2 1 2
x y z
d

. Đường
thẳng
đi qua
A
và song song với
d
có phương trnh là
A.
13
2
37
xt
yt
zt



. B.
3
12
73
xt
yt
zt


. C.
32
3
12



xt
yt
zt
. D.
2
12
23
xt
yt
zt


.
Câu 38: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua trục
Oz
có tọa độ là
A.
1;2; 3
. B.
1;2; 3
. C.
1; 2;0
. D.
1; 2;3
.
Câu 39: Cắt hình nón bởi một mặt phẳng đi qua đỉnh và tạo với mặt phẳng đáy một góc
60
được
thiết din là một tam giác vuông cân có cạnh huyền bằng
4.
Tính thể tích của khối nón ban
đầu.
A.
10 3
.
3
V
B.
53
.
3
V
C.
3
.
3
V
D.
53
.
3
V
Câu 40: Trong không gian
Oxyz
, viết phương trnh đường thẳng
d
đi qua điểm
1;2; 1M
, song
song với mặt phẳng
:3P x y z
và vuông góc với đường thẳng
3
: 3 3
2
xt
yt
zt


.
A.
15
23
12
xt
yt
zt


. B.
1
23
12
xt
yt
zt


. C.
1
2
1
xt
yt
zt


. D.
5
32
2



xt
yt
zt
.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Số phức nào sau đây có biểu diễn hình học là điểm
3;5M
?
A.
35zi
. B.
35zi
. C.
35zi
. D.
35zi
.
Lời giải:
3;5M
là điểm biểu diễn hình học của số phức
35zi
.
Câu 2: Trên khoảng
0; ,
đạo hàm của hàm số
lnyx
là
A.
1
.
10
y
x
B.
1
.
y
x
C.
1
.
y
ex
D.
.
e
y
x
Câu 3: Tập xác định
D
của hàm số
23
yx
là
A.
0;D
. B.
D
. C.
0;D
. D.
\0D
.
Lời giải:
Do hàm số
23
yx
là hàm số lũy thừa với số mũ không nguyên nên để hàm số xác định thì
0x
.
Vậy hàm số
23
yx
có tập xác định là
0;D
.
Câu 4: Tập nghim của bt phương trnh
ln 1x
là
A.
;e 
. B.
0;e
. C.
;e
. D.
;e
.
Lời giải:
Ta có
1
0
ln 1 0
x
x x e
xe
.
Từ đây ta suy ra tập nghim của bt phương trnh đã cho là
0;e
.
Câu 5: Cho cp số nhân
n
u
có
1
2u
và có công bội bằng
3
. Giá trị
2
u
bằng
A.
5
. B.
9
. C.
8
. D.
6
.
Lời giải:
Ta có:
21
. 2. 3 6u u q
.
Câu 6: Trong không gian
Oxyz
, vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
Oxy
?
A.
1;1;1m
. B.
1;0;0i
. C.
0;1;0j
. D.
0;0;1k
.
Lời giải:
Vì
Oz
vuông góc với mặt phẳng
Oxy
, nên vectơ pháp tuyến của mặt phẳng
Oxy
là
0;0;1k
.
Câu 7: Cho hàm số
ax b
y
cx d
có đồ thị là đường cong trong hnh bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
x
y
O
-2
2
Số giao điểm của đồ thị hàm số đã cho và trục hoành là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 8: Cho
6
2
d4
f x x
và
6
2
d5
g x x
, khi đó
6
2
3d


f x g x x
bằng
A.
19
. B.
17
. C.
11
. D.
7
.
Lời giải:
Ta có
6 6 6
2 2 2
3 3 3.4 5 7f x g x dx f x dx g x dx


.
Câu 9: Đường cong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
1y x x
. B.
. C.
. D.
3
21y x x
.
Lời giải:
Dựa vào hình vẽ ta có tin cận đứng
1x
và tim cận ngang
1y
.
Câu 10: Trong không gian
Oxyz
, mặt cầu có tâm
2; 1;3I
, bán kính
3R
có phương trnh là
A.
2 2 2
2 1 3 3x y z
. B.
2 2 2
2 1 3 3x y z
.
C.
2 2 2
2 1 3 3x y z
. D.
2 2 2
3 1 3 3x y z
.
Lời giải:
Mặt cầu có tâm
2; 1;3I
, bán kính
3R
có phương trnh là
2 2 2
2 1 3 3x y z
.
Câu 11: Trong không gian
Oxyz
, góc giữa mặt phẳng
Oyz
và trục
Ox
bằng
A.
30 .
B.
90 .
C.
60 .
D.
0.
Câu 12: Tìm hai số thực
x
và
y
thỏa mãn
2 3 1 3 6x yi i x i
, với
i
là đơn vị ảo.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
A.
1, 3xy
. B.
1, 1xy
. C.
1, 1xy
. D.
1, 3xy
.
Lời giải:
Ta có
2 1 1
2 3 1 3 6 2 1 3 3 6
3 3 6 3
x x x
x yi i x i x y i x i
yy



.
Câu 13: Cho khối chóp có din tích đáy
6B
và chiều cao
8h
. Thể tích của khối chóp đã cho bằng
A.
16
. B.
48
. C.
8
. D.
14
.
Lời giải:
Thể tích của khối chóp
11
. .6.8 16
33
V B h
.
Vậy thể tích của khối chóp đã cho bằng
16
.
Câu 14: Thể tích khối lăng trụ tam giác đều có tt cả các cạnh đều bằng
a
bằng
B
C
A
B
C
A
A.
3
3
12
a
. B.
3
a
. C.
3
2a
. D.
3
3
4
a
.
Lời giải:
B
C
A
B
C
A
Thể tích khối lăng trụ là
23
33
..
44
aa
V B h a
.
Câu 15: Cho mặt cầu
S
, bán kính
R
và mặt phẳng
. Biết khoảng cách từ tâm của mặt cầu
S
tới
mặt phẳng
bằng
R
. Khẳng định nào sau đây đúng?
A. Mặt phẳng
a
cắt mặt cầu
S
.
B. Thiết din của mặt phẳng
với mặt cầu
S
là một đường tròn.
C. Mặt phẳng
a
tiếp xúc với mặt cầu
S
.
D. Mặt phẳng
a
với mặt cầu
S
không có điểm chung.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Khoảng cách từ tâm mặt cầu đến mặt phẳng bằng đúng bán kính nên mặt phẳng tiếp xúc mặt
cầu.
Câu 16: Cho số phức
12zi
. Số phức liên hợp của
z
là
A.
12i
. B.
12i
. C.
2 i
. D.
12i
.
Lời giải:
Theo định nghĩa số phức liên hợp ta có
12i
là số phức liên hợp của
12zi
.
Câu 17: Cho hnh nón có độ dài đường sinh bằng
3a
và bán kính đáy bằng
a
. Din tích xung quanh
của hnh nón đã cho bằng
A.
2
12 a
. B.
2
3 a
. C.
2
6 a
. D.
2
a
.
Lời giải:
Hnh nón có độ dài đường sinh
3la
, bán kính đáy
ra
có din tích xung quanh là
2
. .3 3
xq
S rl a a a
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
32
:1
23
xt
d y t
zt



. Điểm nào dưới đây thuộc
d
?
A.
3;1;2M
. B.
2;1;3Q
. C.
3; 1; 2P
. D.
2;1;3N
.
Câu 19: Cho hàm số
fx
có bảng xét du
fx
như sau:
Hoành độ điểm cực tiểu của hàm số đã cho bằng
A.
1
. B.
0
. C.
1
. D.
1
và
1
.
Lời giải:
Do
fx
xác định và đổi du từ âm sang dương khi đi qua 1, nên hoành độ điểm cực tiểu
của hàm số bằng 1.
Câu 20: Bảng biến thiên sau đây là của hàm số nào ?
A.
1
.
2
x
y
x
B.
1
.
1
x
y
x
C.
21
.
2
x
y
x
D.
3
.
2
x
y
x


Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Lời giải:
Từ BBT suy ra:
Tim cận đứng của ĐTHS là:
2x
. Loại B.
Tim cận ngang của ĐTHS là:
1y
. Loại C.
Du của đạo hàm:
'
0y
. Loại D.
Câu 21: Tập nghim của bt phương trnh
1
24
x
là
A.
;3 .
B.
;5 .
C.
1;3 .
D.
1; .
Lời giải:
Ta có:
1
2 4 1 2 3.
x
xx
Câu 22: Từ 10 điểm phân bit trong không gian có thể tạo thành bao nhiêu vectơ khác vectơ
0
?
A.
10
2
. B.
10
P
. C.
2
10
A
. D.
2
10
C
.
Lời giải:
Chọn 2 điểm từ 10 điểm phân bit đã cho rồi xếp vào 2 vị trí điểm đầu - điểm cuối của véc tơ
Số véc tơ tạo thành là
2
10
A
.
Câu 23: Cho hàm số
y f x
xác định và liên tục trên
đồng thời thoả mãn:
( ) 3 5sinf x x

,
(0) 14f
. Khẳng định nào sau đây đúng?
A.
( ) 3 5f


. B.
( ) 3 5sin 9f x x x
.
C.
( ) 3 5cos 9f x x x
. D.
3
9
22
f





.
Lời giải:
Ta có
( )d 3 5s n 3cd 5oi sf x x x Cf x x x x

.
Mà
93.0 5co(0) 14s0f C C
.
Suy ra
3 5cos 9.f x x x
Do đó
93. 5co
3
22
9
2
s
2
f




.
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x


bằng
A. 12. B. 18. C.
27
. D. 10.
Lời giải:
Ta có:
4 4 4
4
2 2 3
0
0 0 0
2 ( ) 3 d 2 ( )d 3 d 2.37 74 64 10


f x x x f x x x x x
.
Câu 25: Họ tt cả các nguyên hàm của hàm số
cos 6f x x x
là
A.
2
sin 3x x C
. B.
sin xC
. C.
2
sin 3x x C
. D.
2
sin 6x x C
.
Lời giải:
Ta có
d cos 6 df x x x x x

2
sin 3x x C
. Vậy chọn A.
Câu 26: Cho hàm số
y f x
có đồ thị như hnh bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Mnh đề nào sau đây đúng?
A. Hàm số
fx
nghịch biến trên
2;5
. B. Hàm số
fx
nghịch biến trên
0;5
.
C. Hàm số
fx
đồng biến trên
;0
. D. Hàm số
fx
đồng biến trên
5;
.
Lời giải:
Dựa vào đồ thị hàm số
y f x
, hàm số
fx
đồng biến trên
5;
.
Câu 27: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
1x
. B.
3.y
C.
3x
. D.
1y 
.
Lời giải:
Từ bảng biến thiên ta thy hàm số đã cho đạt cực tiểu tại
3x
.
Câu 28: Cho khối trụ
T
,
là mặt phẳng đi qua trục và cắt khối trụ
T
theo thiết din là hình
vuông cạnh 2a. Thể tích khối trụ
T
bằng
A.
3
3
a
B.
3
2.a
C.
3
2
3
a
. D.
3
.a
Lời giải:
Thiết din của khối trụ
T
được cắt bởi mặt phẳng
là hình vuông cạnh bằng
2a
nên ta
có
2l h a
, bán kính đường tròn đáy bằng
1
.2
2
r a a
. Vậy
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
2 2 3
. .2 2 .V B h r h a a a
Câu 29: Cho
a
là số thực dương khác
1
. Giá trị của
3
log
a
a
bằng
A.
0.
B.
1
.
3
C.
3.
D.
3.
Lời giải:
Ta có
1
3
3
11
log log log .
33
a a a
a a a
Câu 30: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và
trục hoành quay quanh trục
Ox
là
A.
4
3
V
. B.
16
15
V
. C.
16
15
V
. D.
4
3
V
.
Lời giải:
Hoành độ giao điểm của đồ thị hàm số
2
43y x x
và trục hoành là nghim phương trnh
2
1
4 3 0
3
x
xx
x
.
Do đó, thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số
2
43y x x
và trục hoành quay quanh trục
Ox
là
3
2
2
1
4 3 dV x x x
3
4 3 2
1
8 22 24 9 dx x x x x
3
53
42
1
22 16
2 12 9
5 3 15
xx
x x x



.
Câu 31: Cho hnh chóp
.S ABC
có đáy
ABC
là tam giác vuông cạnh huyền
BC a
. Hnh chiếu
vuông góc của
S
lên
ABC
trng với trung điểm của
BC
.
H
A
C
B
S
Biết
SB a
. Tính số đo của góc giữa
SA
và
ABC
.
A.
75
. B.
30
. C.
60
. D.
45
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
H
A
C
B
S
Gọi
H
là trung điểm của
BC
.
Theo giả thiết ta có
SH ABC
và góc giữa
SA
và
ABC
là góc
SAH
.
Ta có
2
2 2 2
3
42
aa
SH SB BH a
và
1
22
a
AH BC
.
Ta có
3
2
tan 3 60
2
a
SH
SAH SAH
a
AH
.
Vậy góc giữa
SA
và
ABC
bằng
60
.
Câu 32: Cho hàm số bậc ba
y f x
có đồ thị như hnh vẽ bên dưới:
Số giá trị nguyên của tham số
m
để đường thẳng
ym
cắt đồ thị hàm số đã cho tại ba điểm
phân bit là
A. Vô số. B.
3
. C. 0. D.
5
.
Lời giải:
Từ đồ thị ta thy để đường thẳng
ym
cắt đồ thị hàm số đã cho tại ba điểm phân bit khi
15m
. Vì
m
nguyên nên
2;3;4m
.
Vậy có 3 giá trị nguyên của
m
thoả mãn yêu cầu bài toán
Câu 33: Có bao nhiêu giá trị nguyên của tham số thực m để hàm số
32
4 9 5y x mx m x
nghịch biến trên khoảng
; 
?
A. 5. B. 7. C. 4. D. 6.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Ta có
2
' 3 2 4 9y x mx m
.
Hàm số nghịch biến trên
; 
' 0,yx
2
' 12 27 0 9 3m m m
(*)
Từ (*) suy ra
9; 8; 7; 6; 5; 4; 3m
là các giá trị nguyên của m thỏa mãn yêu cầu
của bài toán.
Câu 34: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong
hộp. Xác sut để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng bằng
A.
11
18
. B.
5
18
. C.
75
408
. D.
95
408
.
Lời giải:
Số phần tử của không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi.
Suy ra
5
18
C
.
Gọi
A
là biến cố 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng. Ta có các
trường hợp thuận lợi cho biến cố
A
là:
TH 1: Chọn 1 viên bi đỏ, 1 viên bi vàng và 3 viên bi xanh. Có
..
1 1 3
6 7 5
CCC
cách chọn.
TH 2: Chọn 2 viên bi đỏ, 2 viên bi vàng và 1 viên bi xanh. Có
..
2 2 1
6 7 5
CCC
cách chọn.
Do đó số phần tử của biến cố
A
là
. . . .
1 1 3 2 2 1
6 7 5 6 7 5
A C C C C C C
.
Vậy xác sut cần tính là
. . . .
1 1 3 2 2 1
6 7 5 6 7 5
5
18
A
C C C C C C 95
PA
C 408
.
Câu 35: Phương trnh
9 4.3 3 0
xx
có tổng các nghim là
A.
1
. B.
4
. C.
1
. D.
4
.
Lời giải:
Ta có:
2
3 1 0
9 4.3 3 0 3 4.3 3 0
1
33
x
x x x x
x
x
x

.
Vậy tổng các nghim của phương trnh là
1
.
Câu 36: Gọi
12
;zz
là hai nghim phức của phương trnh
2
2 2 0zz
. Tập hợp các điểm bểu diễn
của số phức
w
thỏa mãn
12
w z w z
là đường thẳng có phương trnh
A.
0xy
. B.
0x
. C.
0xy
. D.
0y
.
Lời giải:
Phương trnh
2
1
2 2 0
1
zi
zz
zi


.
Gọi
;,w x yi x y
12
2 2 2 2
1 1 1 1
1 1 1 1 0.
w z w z x y i x y i
x y x y y
Do đó tập hợp các điểm bểu diễn của số phức
w
là đường thẳng có phương trnh
0.y
Câu 37: Trong không gian
Oxyz
, cho điểm
1;2;3A
và đường thẳng
3 1 7
:
2 1 2
x y z
d

. Đường
thẳng
đi qua
A
và song song với
d
có phương trnh là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
A.
13
2
37
xt
yt
zt



. B.
3
12
73
xt
yt
zt


. C.
32
3
12



xt
yt
zt
. D.
2
12
23
xt
yt
zt


.
Lời giải:
Vectơ chỉ phương của đường thẳng
d
là
2;1; 2
d
u 
.
Do
//d
nên
có vectơ chỉ phương là
2;1; 2
d
uu
và
đi qua
A
.
Kiểm tra phương án C thỏa mãn.
Câu 38: Trong không gian
Oxyz
, cho điểm
1;2;3A
. Điểm đối xứng với
A
qua trục
Oz
có tọa độ là
A.
1;2; 3
. B.
1;2; 3
. C.
1; 2;0
. D.
1; 2;3
.
Câu 39: Cắt hình nón bởi một mặt phẳng đi qua đỉnh và tạo với mặt phẳng đáy một góc
0
60
được
thiết din là một tam giác vuông cân có cạnh huyền bằng
4.
Tính thể tích của khối nón ban
đầu.
A.
10 3
.
3
V
B.
53
.
3
V
C.
3
.
3
V
D.
53
.
3
V
Lời giải:
Giả sử hnh nón đỉnh
S
tâm
O
, thiết din qua đỉnh ở giả thiết là tam giác vuông cân
SAB
.
Gọi
K
là trung điểm của
AB
, suy ra góc giữa
SAB
và mặt đáy là
60SKO 
.
Ta có
1
42
2
AB SK AB
và
22SA SB
.
Tam giác
SKO
vuông tại
: .tan 3O SO SK SKO
.
Tam giác
SAO
vuông tại
22
:5O AO SA SO
.
Thể tích khối nón
2
1 5 3
..
33
V AO SO


.
Câu 40: Trong không gian
Oxyz
, viết phương trnh đường thẳng
d
đi qua điểm
1;2; 1M
, song
song với mặt phẳng
:3P x y z
và vuông góc với đường thẳng
3
: 3 3
2
xt
yt
zt


.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
A.
15
23
12
xt
yt
zt


. B.
1
23
12
xt
yt
zt


. C.
1
2
1
xt
yt
zt


. D.
5
32
2



xt
yt
zt
.
Lời giải:
VTPT của mặt phẳng
: 1;1; 1
P
Pn 
.
VTCP của đường thẳng
: 1;3;2u

.
VTCP của đường thẳng
:;
dP
d u n u


5; 3;2
.
Vậy phương trnh tham số của đường thẳng
15
: 2 3
12
xt
d y t
zt


.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 05_______________
Câu 1: Điểm
M
trong hình vẽ là điểm biểu diễn số phức nào dưới đây?
A.
2.zi
B.
2.zi
C.
2.zi
D.
2.zi
Câu 2: Đạo hàm của hàm số
2023
x
y
là
A.
1
.2023
x
yx
. B.
2023
ln2023
x
y
. C.
2023 .ln2023
x
y
. D.
2023
x
y
.
Câu 3: Hàm số
ln 2 1yx
có đạo hàm là
A.
2
ln 2 1
y
xx
. B.
1
21
y
x
. C.
2
21
y
x
. D.
1
2 1 ln2
y
x
.
Câu 4: Tập nghiệm của bất phương trình
39
x
là
A.
2;
. B.
0;2
. C.
0;
. D.
2;
.
Câu 5: Cho cấp số cộng
n
u
có
1
3u
và
2
1u 
. Công sai của cấp số cộng đó bằng
A.
1
. B.
4
. C.
4
. D.
2
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng nào dưới đây nhận
3;1; 7n 
là một vectơ pháp
tuyến?
A.
3 7 0xz
. B.
3 7 1 0x y z
. C.
3 7 0xy
. D.
3 7 3 0x y z
.
Câu 7: Cho hàm số
fx
có bảng biến thiên như sau:
Số nghiệm của phương trình
25fx
là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 8: Cho
5
2
d 10
f x x
. Khi đó,
5
2
2 3 d


f x x
bằng
A.
32
. B.
36
. C.
42
. D.
46
.
Câu 9: Hàm số nào có đồ thị là hình vẽ sau đây?
A.
32
34y x x
. B.
42
34y x x
. C.
32
34y x x
. D.
21
35
x
y
x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 2 1 3 9. S x y z
Tọa độ tâm của mặt cầu
S
là
A.
2;1;3 .
B.
2; 1;3 .
C.
2;1; 3 .
D.
2; 1; 3 .
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oxy
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho hai số phức
1
12zi
,
2
26zi
. Tích
12
.zz
bằng
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Câu 13: Cho hình lập phương có cạnh bằng
3
. Tổng diện tích các mặt của hình lập phương đã cho
bằng
A.
54
. B.
12
. C.
36
. D.
24
.
Câu 14: Cho khối tứ diện
ABCD
có
,,AB AC AD
đôi một vuông góc và
2 , 3 AB AC a AD a
. Thể
tích của khối tứ diện đó là
A.
3
4Va
. B.
3
2Va
. C.
3
Va
. D.
3
3Va
.
Câu 15: Diện tích
S
của mặt cầu có bán kính
r
được tính theo công thức nào dưới đây?
A.
2
4Sr
. B.
2
Sr
. C.
2
4
3
Sr
. D.
2
1
3
Sr
.
Câu 16: Trong các số phức sau, số phức nào dưới đây là số thuần ảo?
A.
1 i
. B.
3i
. C.
2
. D.
5
.
Câu 17: Thể tích của khối nón có đường kính đường tròn đáy là
4,
đường cao bằng
6
là
A.
8.
V
B.
C.
24 .
V
D.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
21
3
3
1
:
zyx
đi qua điểm nào dưới đây?
A.
3; 1;0N
. B.
3; 1;2P
. C.
1;3;0M
. D.
1; 3;0Q
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Giá trị cực đại của hàm số đã cho là
A.
1
. B.
1
. C.
0
. D.
2
.
Câu 20: Cho hàm số
y f x
có
lim 1
x
fx

và
lim 1
x
fx


. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1y
và đường thẳng
1y 
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1x
và đường thẳng
1x 
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 21: Tập nghiệm của bất phương trình
2
log 1 3x 
là
A.
;8S 
. B.
;7S 
. C.
1; 8S 
. D.
1; 7S 
.
Câu 22: Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng?
A.
300
. B.
15
. C.
35
. D.
20
.
Câu 23: Cho
d 
x x F x C
. Khẳng định nào dưới đây đúng?
A.
1
Fx
. B.
F x x
. C.
2
2

x
F x C
. D.
F x x
.
Câu 24: Nếu
2
1
d3
f x x
và
2
3
d1
f x x
thì
3
1
d
f x x
bằng
A. 4. B.
2
. C.
2
. D.
4
.
Câu 25: Cho hàm số
cosf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d sin .f x x x x C
B.
2
d sin .f x x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d sin .
2
x
f x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;2
. B.
3; 
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị như hình bên dưới:
Giá trị cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aalog 3 log 2
bằng
A.
loga
. B.
2
log
3
. C.
2
log 6a
. D.
3
log .
2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
2y x x
và
0y
quanh trục
Ox
là
A.
16
15
V 
B.
16
9
V 
C.
16
9
V 
D.
16
15
V 
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
SA a
(tham
khảo hình vẽ).
C
B
A
S
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
f x m
có ba
nghiệm thực phân biệt. Tổng tất cả các phần tử của
S
bằng
A.
3
. B.
5
. C.
3
. D.
4
.
Câu 32: Cho hàm số
()y f x
liên tục trên và có đạo hàm
2
2 1 3 , .
f x x x x x
Hàm
số đồng biến trên khoảng nào dưới đây?
A.
; 1 .
B.
;0 .
C.
3; .
D.
1;3 .
Câu 33: Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được
3
quả cầu màu xanh là
A.
4
.
455
B.
24
.
455
C.
4
.
165
D.
33
.
91
Câu 34: Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ
bằng
16
. Thể tích của khối trụ đã cho bằng
A.
24
. B.
32
. C.
16
. D.
8
.
Câu 35: Cho phương trình
2
24
log 8log 1 0.xx
Giải phương trình trên bằng cách đặt
2
log ,tx
ta
thu được phương trình nào dưới đây?
A.
2
8 1 0.tt
B.
2
4 1 0.tt
C.
2
16 1 0.tt
D.
2
6 1 0.tt
Câu 36: Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
1
12zi
,
2
25zi
,
3
24zi
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình
hành là
A.
17i
. B.
5 i
. C.
15i
. D.
35i
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 37: Trong không gian
Oxyz
, đường thẳng đi qua điểm
3;2;1M
và vuông góc với mặt phẳng
:2 5 4 0P x y
có phương trình là
A.
32
25
1


xt
yt
z
. B.
32
25
1


xt
yt
z
. C.
32
25


xt
yt
zt
. D.
32
2 5 .
1


xt
yt
z
Câu 38: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oxz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 39: Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2,a
cạnh bên bằng
3a
. Khoảng cách từ
A
đến
SCD
bằng
A.
14
3
a
. B.
14
4
a
. C.
14a
. D.
14
2
a
.
Câu 40: Cho hình nón
N
có chiều cao
3.h
Một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo một thiết diện là tam giác vuông có diện tích bằng
8.
Tính thể tích của khối nón giới
hạn bởi hình nón
.N
A.
16 .
B.
21 .
C.
12 .
D.
7.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Điểm
M
trong hình vẽ là điểm biểu diễn số phức nào dưới đây?
A.
2.zi
B.
2.zi
C.
2.zi
D.
2.zi
Lời giải:
Điểm
M
trong hình vẽ là điểm biểu diễn số phức:
2zi
.
Câu 2: Đạo hàm của hàm số
2023
x
y
là
A.
1
.2023
x
yx
. B.
2023
ln2023
x
y
. C.
2023 .ln2023
x
y
. D.
2023
x
y
.
Câu 3: Hàm số
ln 2 1yx
có đạo hàm là
A.
2
ln 2 1
y
xx
. B.
1
21
y
x
. C.
2
21
y
x
. D.
1
2 1 ln2
y
x
.
Lời giải:
Hàm số
ln 2 1yx
có đạo hàm là
2
21
y
x
.
Câu 4: Tập nghiệm của bất phương trình
39
x
là
A.
2;
. B.
0;2
. C.
0;
. D.
2;
.
Lời giải:
Ta có
2
3 9 3 3 2 2;
xx
xx
.
Vậy tập nghiệm của bất phương trình là
2;
.
Câu 5: Cho cấp số cộng
n
u
có
1
3u
và
2
1u 
. Công sai của cấp số cộng đó bằng
A.
1
. B.
4
. C.
4
. D.
2
.
Lời giải:
Ta có
2211
1 3 4ddu u u u
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng nào dưới đây nhận
3;1; 7n 
là một vectơ pháp
tuyến?
A.
3 7 0xz
. B.
3 7 1 0x y z
. C.
3 7 0xy
. D.
3 7 3 0x y z
.
Lời giải:
Phương trình mặt phẳng
3 7 3 0x y z
có một vectơ pháp tuyến là
3;1; 7n 
.
Câu 7: Cho hàm số
fx
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm của phương trình
25fx
là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải:
Ta có:
5
25
2
f x f x
.
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
5
2
y
. Từ đồ thị ta thấy có ba giao điểm.
Vậy phương trình đã cho có ba nghiệm.
Câu 8: Cho
5
2
d 10
f x x
. Khi đó
5
2
2 3 d


f x x
bằng
A.
32
. B.
36
. C.
42
. D.
46
.
Lời giải:
Ta có
5 5 5
2 2 2
2 3 d 2d 3 d 36.


f x x x f x x
Câu 9: Hàm số nào có đồ thị là hình vẽ sau đây?
A.
32
34y x x
. B.
42
34y x x
. C.
32
34y x x
. D.
21
35
x
y
x
.
Lời giải:
Dựa vào hình dạng đồ thị, ta thấy đây là đồ thị của hàm số bậc 3, với hệ số
0 lim
x
ay


. Nên loại B và D.
Khi
04xy
.
Câu 10: Trong không gian
,Oxyz
mặt cầu
2 2 2
: 2 1 3 9. S x y z
Tọa độ tâm của mặt cầu
S
là
A.
2;1;3 .
B.
2; 1;3 .
C.
2;1; 3 .
D.
2; 1; 3 .
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Lời giải:
Phương trình
2 2 2
2; 1;3
2 1 3 9
3
I
x y z
R

Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oxy
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho hai số phức
1
12zi
,
2
26zi
. Tích
12
.zz
bằng
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Lời giải:
Ta có
12
. 1 2 2 6 14 2z z i i i
.
Câu 13: Cho hình lập phương có cạnh bằng
3
. Tổng diện tích các mặt của hình lập phương đã cho
bằng
A.
54
. B.
12
. C.
36
. D.
24
.
Lời giải:
Tổng diện tích các mặt của hình lập phương là:
2
6.3 54S 
.
Câu 14: Cho khối tứ diện
ABCD
có
,,AB AC AD
đôi một vuông góc và
2 , 3 AB AC a AD a
. Thể
tích của khối tứ diện đó là
A.
3
4Va
. B.
3
2Va
. C.
3
Va
. D.
3
3Va
.
Lời giải:
Do khối tứ diện
ABCD
có
,,AB AC AD
đôi một vuông góc nên
3
1
. . 2
6

ABCD
V AB AC AD a
.
Câu 15: Diện tích
S
của mặt cầu có bán kính
r
được tính theo công thức nào dưới đây?
A.
2
4Sr
. B.
2
Sr
. C.
2
4
3
Sr
. D.
2
1
3
Sr
.
Câu 16: Trong các số phức sau, số phức nào dưới đây là số thuần ảo?
A.
1 i
. B.
3i
. C.
2
. D.
5
.
Lời giải:
Số phức
3i
là số phức thuần ảo.
Câu 17: Thể tích của khối nón có đường kính đường tròn đáy là
4,
đường cao bằng
6
là
A.
8.
V
B.
C.
24 .
V
D.
Lời giải:
22
11
.6.2 8
33
V hR
.
Câu 18: Trong không gian
Oxyz
, cho đường thẳng
21
3
3
1
:
zyx
đi qua điểm nào dưới đây?
A.
3; 1;0N
. B.
3; 1;2P
. C.
1;3;0M
. D.
1; 3;0Q
.
Lời giải:
Ta có:
2
0
1
33
3
11
Suy ra điểm
0;3;1M
thuộc đường thẳng
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Giá trị cực đại của hàm số đã cho là
A.
1
. B.
1
. C.
0
. D.
2
.
Lời giải:
Qua đồ thị hàm số
y f x
ta thấy giá trị cực đại của hàm số bằng
1
.
Câu 20: Cho hàm số
y f x
có
lim 1
x
fx

và
lim 1
x
fx


. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1y
và đường thẳng
1y 
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng
1x
và đường thẳng
1x 
.
Lời giải:
Vì
lim 1
x
fx

và
lim 1
x
fx


nên đồ thị hàm số đã cho có hai tiệm cận ngang là đường
thẳng
1y
và đường thẳng
1y 
.
Câu 21: Tập nghiệm của bất phương trình
2
log x 1 3
là
A.
;8S 
. B.
;7S 
. C.
1; 8S 
. D.
1; 7S 
.
Lời giải:
Ta có:
2
log 1 3x 
3
0 1 2x
17x
Vậy tập nghiệm của bất phương trình
2
13log x 
là
1; 7 .S
Câu 22: Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng?
A.
300
. B.
15
. C.
35
. D.
20
.
Lời giải:
Lớp có
20 15 35
học sinh.
Suy ra số cách chọn một học sinh của lớp 10A để làm lớp trưởng là
1
35
35C
.
Câu 23: Cho
d 
x x F x C
. Khẳng định nào dưới đây đúng?
A.
1
Fx
. B.
F x x
. C.
2
2

x
F x C
. D.
F x x
.
Lời giải:
Ta có
d



F x x x x
.
Câu 24: Nếu
2
1
dx 3fx
và
2
3
dx 1fx
thì
3
1
dxfx
bằng
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
A. 4. B.
2
. C.
2
. D.
4
.
Lời giải:
Ta có
23
32
dx 1 dx 1f x f x

khi đó
3 2 3
1 1 2
dx dx dx 3 1 2f x f x f x
.
Câu 25: Cho hàm số
cosf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d sin .f x x x x C
B.
2
d sin .f x x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d sin .
2
x
f x x x C
Lời giải:
2
d cos d n .
2
si
x
f x x x x x x C

Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;2
. B.
3; 
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Giá trị cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aalog 3 log 2
bằng
A.
loga
. B.
2
log
3
. C.
2
log 6a
. D.
3
log .
2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
2y x x
và
0y
quanh trục
Ox
là
A.
16
15
V 
B.
16
9
V 
C.
16
9
V 
D.
16
15
V 
Lời giải:
Phương trình hoành độ giao điểm của đường
2
2y x x
và đường
0y
là
2
0
20
2
x
xx
x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Thể tích là
22
53
2
2 4 3 2 4
00
2
16
2 d 4 4 d 4. .
0
5 3 15




xx
V x x x x x x x x
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
SA a
(tham
khảo hình vẽ).
C
B
A
S
Góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Lời giải:
Ta có:
SA ABC
nên góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
SBA
.
Do tam giác
SAB
vuông cân tại
45A SBA
.
Vậy góc giữa đường thẳng
SB
và mặt phẳng
ABC
bằng
45
.
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
f x m
có ba
nghiệm thực phân biệt. Tổng tất cả các phần tử của
S
bằng
A.
3
. B.
5
. C.
3
. D.
4
.
Lời giải:
Số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
:d y m
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Dựa vào hình vẽ, ta có:
Phương trình
f x m
có ba nghiệm thực phân biệt khi đường thẳng
:d y m
cắt đồ thị
hàm số
y f x
tại ba điểm phân biệt, tức là
31m
. Mà
m
nên
2; 1;0m
.
Câu 32: Cho hàm số
()y f x
liên tục trên và có đạo hàm
2
'( ) 2 ( 1)(3 ), . f x x x x x
Hàm số
đồng biến trên khoảng nào dưới đây?
A.
; 1 .
B.
;0 .
C.
3; .
D.
1;3 .
Lời giải:
Ta có:
0
'( ) 0 1
3
x
f x x
x
Bảng xét dấu:
Căn cứ bảng xét dấu ta thấy hàm số đồng biến trên
( 1;3)
.
Câu 33: Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được
3
quả cầu màu xanh là
A.
4
.
455
B.
24
.
455
C.
4
.
165
D.
33
.
91
Lời giải:
Số phần tử của không gian mẫu
3
15
nC
455
.
Gọi
A
là biến cố "
3
quả cầu lấy được đều là màu xanh". Suy ra
3
4
n A C
4
.
Vậy xác suất cần tìm là
4
455
PA
.
Câu 34: Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ
bằng
16
. Thể tích của khối trụ đã cho bằng
A.
24
. B.
32
. C.
16
. D.
8
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Ta có thiết diện qua trục là hình vuông nên
2hR
Diện tích xung quanh bằng
16
nên
2 16 (*)Rh

Thay
2hR
vào
(*)
ta được
2
2 8 2RR
24hR
Thể tích khối trụ bằng :
2
.4.4 16V R h
.
Câu 35: Cho phương trình
2
24
log 8log 1 0.xx
Giải phương trình trên bằng cách đặt
2
log ,tx
ta
thu được phương trình nào dưới đây?
A.
2
8 1 0.tt
B.
2
4 1 0.tt
C.
2
16 1 0.tt
D.
2
6 1 0.tt
Lời giải:
Ta có:
22
2 4 2 2
log 8log 1 0 log 4log 1 0.x x x x
Đặt
2
log ,tx
phương trình trở thành
2
3 1 0.tt
Câu 36: Cho
A
,
B
,
C
tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức
1
12zi
,
2
25zi
,
3
24zi
. Số phức
z
biểu diễn bởi điểm
D
sao cho tứ giác
ABCD
là hình bình
hành là
A.
17i
. B.
5 i
. C.
15i
. D.
35i
.
Lời giải:
Ta có
1;2A
,
2;5B
,
2;4C
.
Gọi
;D x y
.Ta có
3;3AB 
,
2 ;4DC x y
.
Để
ABCD
là hình bình hành thì
AB DC
2 3 5
4 3 1
xx
yy




.
Vậy
5zi
.
Câu 37: Trong không gian
Oxyz
, đường thẳng đi qua điểm
3;2;1M
và vuông góc với mặt phẳng
:2 5 4 0P x y
có phương trình là
A.
32
25
1


xt
yt
z
. B.
32
25
1


xt
yt
z
. C.
32
25


xt
yt
zt
. D.
32
2 5 .
1


xt
yt
z
Lời giải:
Gọi
d
là đường thẳng đi qua điểm
M
và vuông góc với mặt phẳng
P
Ta có
2; 5;0
d
P
d P u n
32
: : 2 5
2; 5;0
1
3;2;1
d
xt
d d y t
Q a M
z
u
u




Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Câu 38: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oxz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 39: Cho hình chóp đều
.S ABCD
có cạnh đáy bằng
2,a
cạnh bên bằng
3a
. Khoảng cách từ
A
đến
SCD
bằng
A.
14
3
a
. B.
14
4
a
. C.
14a
. D.
14
2
a
.
Lời giải:
2a
2a
3a
O
D
S
A
B
C
Gọi
.O AC BD
Do
.S ABCD
chóp đều nên đáy
ABCD
là hình vuông và
SO ABCD
.
Ta có:
,
2
,

d A SCD
AC
d O SCD OC
, 2. , 2 d A SCD d O SCD h
.
Xét
ACD
vuông tại
D
có:
22
AC AD CD
2 2 2CD a
2 OC OD a
.
Xét
SOC
vuông tại O có:
22
SO SC OC
2
2
32aa
7 a
.
Do tứ diện
SOCD
có ba cạnh
,OS
,OC
OD
đôi một vuông góc
2 2 2 2
1 1 1 1
h OS OC OD
222
2
1 1 1 8
7
7 2 2
a
aaa
14
4

a
h
.
Vậy khoảng cách từ
A
đến
SCD
bằng
14
2
a
.
Câu 40: Cho hình nón
N
có chiều cao
3.h
Một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo một thiết diện là tam giác vuông có diện tích bằng
8.
Tính thể tích của khối nón giới
hạn bởi hình nón
.N
A.
16 .
B.
21 .
C.
12 .
D.
7.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
S
A
B
O
h
r
l
Gọi thiết diện là tam giác
,.SAB SA SB l
Theo giả thiết:
2
8 8 4.
2
SAB
l
Sl
Bán kính của
N
là
22
7.r l h
Vậy thể tích khối nón là
2
1
7.
3
V h r


________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 06_______________
Câu 1: Trên mặt phẳng tọa độ, cho
4; 3M
là điểm biểu diễn của số phức
z
. Phần ảo của
z
bằng
A.
4
. B.
3i
. C.
4
. D.
3
.
Câu 2: Tập xác định của hàm số
3
2
yx
là
A.
0;
. B.
2;
. C. . D.
\0
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2
logyx
là
A.
1
ln2
y
x
. B.
ln2
y
x
. C.
1
y
x
. D.
1
2
y
x
.
Câu 4: Tập các nghiệm của bất phương trình
26
x
là
A.
2
log 6;
. B.
;3
. C.
3; 
. D.
2
;log 6
.
Câu 5: Cho cấp số cộng
n
u
có số hạng đầu
1
2u
và số hạng thứ tư
4
17u
. Công sai của cấp số
cộng đã cho bằng
A.
15
2
. B.
5
. C.
3
. D.
15
.
Câu 6: Trong không gian
,Oxyz
mặt phẳng
( ): 1
2 2 1
x y z
P
, có một vectơ pháp tuyến là
A.
3
(2;2; 1)n 
. B.
4
(1;1; 2)n 
. C.
1
(2; 2; 1)n
. D.
2
( 2; 2;1)n
.
Câu 7: Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
60fx
là
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 8: Cho
1
2
0
2 3 d 1
x x f x x
. Tính
1
0
df x x
.
A.
1
3
. B.
5
3
. C.
1
9
. D.
5
9
.
Câu 9: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào?
A.
3
32y x x
. B.
3
32y x x
. C.
42
2y x x
. D.
3
32y x x
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 2 0S x y z y z
. Bán kính mặt cầu
S
bằng
A.
1
. B.
7
. C.
22
. D.
7
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 11: Trong không gian
,Oxyz
góc giữa trục
Ox
và
Oz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
z
thỏa mãn
12i z i
. Môđun của số phức
z
bằng
A.
10
2
. B.
3
. C.
2
. D.
10
.
Câu 13: Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a
. Thể tích của khối lăng trụ đã cho là
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
3
a
V
. D.
3
Va
.
Câu 14: Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA ABC
,
SA a
(tham khảo hình
vẽ).
S
A
B
C
Thể tích của khối chóp đã cho bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
12
a
.
Câu 15: Nếu tăng bán kính của một khối cầu gấp
3
lần thì thể tích khối cầu đó thay đổi như thế nào?
A. Thể tích tăng gấp
6
lần. B. Thể tích tăng gấp
9
lần.
C. Thể tích tăng gấp
3
lần. D. Thể tích tăng gấp
27
lần.
Câu 16: Cho số phức bất kì
,z a bi a b
. Khẳng định nào sau đây đúng?
A.
22
z a b
. B.
22
z a b
. C.
33
z a b
. D.
22
z a b
.
Câu 17: Cho tam giác
ABC
vuông tại
A
,
AB a
và
3AC a
. Tính độ dài đường sinh
l
của hình
nón có được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
2la
. B.
2la
. C.
3la
. D.
la
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
12
:
2 1 3
x y z
d


đi qua điểm nào dưới đây?
A.
2; 1;3A
. B.
1;2;0C
. C.
1; 2;0D
. D.
0;2; 1B
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm giá trị cực đại
CÐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
A.
3
CÐ
y
và
0
CT
y
. B.
3
CÐ
y
và
2
CT
y 
.
C.
2
CÐ
y 
và
2
CT
y
. D.
2
CÐ
y
và
0
CT
y
.
Câu 20: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số
2
2
x
y
x
?
A.
2x
. B.
2x 
. C.
1y
. D.
1y 
.
Câu 21: Tập nghiệm của bất phương trình
3
log 2 1 2x 
là
A.
1
;5
2
S


. B.
1
;5
2
S



. C.
;5S 
. D.
5;S
.
Câu 22: Có
3
cây bút đỏ,
4
cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút
từ hộp bút đó?
A.
7
. B.
4
. C.
12
. D.
3
.
Câu 23: Cho
dsin .x x G x C
Đạo hàm hàm số
2y G x x
là
A.
2sin 1.yx

B.
2sin 1.yx

C.
2sin .yx
D.
2
2cos .
2
x
y x C
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x


bằng
A. 12. B. 18. C.
27
. D. 10.
Câu 25: Cho hàm số
sinf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d cos .
2
x
f x x x C
B.
2
d cos .
2
x
f x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d cos .
2
x
f x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;2
. B.
2;
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Điểm cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aa
33
log 5 log 2
bằng
A.
3
log 3 .a
B.
3
2
log .
5
C.
2
3
log 10a
. D.
3
5
log .
2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
y x x
và
0y
quanh trục
Ox
là
A.
16
15
V 
B.
16
15
V
C.
1
30
V
D.
30
V
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
2AB SA
(tham khảo hình vẽ).
C
B
A
S
Góc giữa hai mặt phẳng
SBC
và
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
x
y
2
-2
-1
O
1
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có ba nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 32: Cho hàm số
y f x
có
1 3 , .f x x x x x
Hàm số
y f x
đồng biến trên khoảng
nào dưới đây?
A.
;0 .
B.
0;1 .
C.
1;2 .
D.
2; .
Câu 33: Chọn ngẫu nhiên 2 số tự nhiên khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn
được hai số có tổng là một số chẵn bằng
A.
1
2
. B.
13
25
. C.
12
25
. D.
313
625
.
Câu 34: Số nghiệm của phương trình
22
22
3 10.3 9 0
x x x x
là
A.
4.
B.
1.
C.
0.
D.
2.
Câu 35: Cho số phức
z
thỏa mãn
1 4.zi
Biết tập hợp các điểm biểu diễn số phức
w 3 4 1 2i z i
là đường tròn
.C
Tìm tâm
I
và bán kính
R
của đường tròn
.C
A.
2; 5 , 20.IR
B.
2; 5 , 4.IR
C.
2;5 , 4.IR
D.
2;5 , 20.IR
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 36: Trong không gian
Oxyz
, viết phương trình tham số của đường thẳng đi qua hai điểm
1;2; 3 , 2; 3;1AB
.
A.
1
25
32
xt
yt
zt


. B.
2
35
14
xt
yt
zt


. C.
3
85
54
xt
yt
zt


. D.
1
25
34
xt
yt
zt



.
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oyz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;7 .
Câu 38: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng
a
. Gọi
M
là trung điểm của
AA
.
Khoảng cách từ
M
đến mặt phẳng
AB C
bằng
A.
2
4
a
. B.
21
7
a
. C.
2
2
a
. D.
21
14
a
.
Câu 39: Cho hình nón
N
có chiều cao
2.ha
Một mặt phẳng
P
đi qua đỉnh của hình nón và cắt
hình hình nón theo một thiết diện là tam giác đều có diện tích bằng
2
16 3
.
9
a
Góc giữa
P
và
mặt đáy của
N
bằng
A.
90 .
B.
45 .
C.
60 .
D.
30 .
Câu 40: Trong không gian
,Oxyz
cho điểm
0; 2; 0M
và đường thẳng
43
:2
1
xt
d y t
zt


. Đường thẳng đi
qua
M
, cắt và vuông góc với
d
có phương trình là
A.
2
.
1 1 2

x y z
B.
1
.
1 1 2


x y z
C.
11
.
1 1 2


x y z
D.
1
.
1 1 2

x y z
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, cho
4; 3M
là điểm biểu diễn của số phức
z
. Phần ảo của
z
bằng
A.
4
. B.
3i
. C.
4
. D.
3
.
Lời giải:
Ta có:
43zi
nên phần ảo của
z
bằng
3
.
Câu 2: Tập xác định của hàm số
3
2
yx
là
A.
0;
. B.
2;
. C. . D.
\0
.
Lời giải:
Tập xác định của hàm số
3
2
yx
là
0;
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2
logyx
là
A.
1
ln2
y
x
. B.
ln2
y
x
. C.
1
y
x
. D.
1
2
y
x
.
Lời giải:
Áp dụng công thức
1
log
ln
a
x
xa
. Ta có
1
ln2
y
x
Câu 4: Tập các nghiệm của bất phương trình
26
x
là
A.
2
log 6;
. B.
;3
. C.
3; 
. D.
2
;log 6
.
Lời giải:
26
x
2
log 6x
2
log 6;x 
.
Câu 5: Cho cấp số cộng
n
u
có số hạng đầu
1
2u
và số hạng thứ tư
4
17u
. Công sai của cấp số
cộng đã cho bằng
A.
15
2
. B.
5
. C.
3
. D.
15
.
Lời giải:
Ta có
41
41
17 2
35
33
uu
u u d d
.
Câu 6: Trong không gian
,Oxyz
mặt phẳng
( ): 1
2 2 1
x y z
P
, có một vectơ pháp tuyến là
A.
3
(2;2; 1)n 
. B.
4
(1;1; 2)n 
. C.
1
(2; 2; 1)n
. D.
2
( 2; 2;1)n
.
Lời giải:
Ta có
1 2 2 2 2 0
2 2 1
x y z
x y z x y z
Vậy một vectơ pháp tuyến của mặt phẳng
()P
là
4
(1;1; 2)n 
.
Câu 7: Cho hàm số
y f x
có bảng biến thiên như sau:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm của phương trình
60fx
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải:
Ta có
6 0 6f x f x
.
Đường thẳng
6y
cắt đồ thị
y f x
tại 2 điểm phân biệt.
Câu 8: Cho
1
2
0
2 3 d 1
x x f x x
. Tính
1
0
df x x
.
A.
1
3
. B.
5
3
. C.
1
9
. D.
5
9
.
Lời giải:
Ta có
1
1 1 1
3
22
0 0 0
0
2
2 3 d 1 3 d 1 3 d 1
33
x
x x f x x x f x x f x x



1
0
5
d
9
f x x

.
Câu 9: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào?
A.
3
32y x x
. B.
3
32y x x
. C.
42
2y x x
. D.
3
32y x x
.
Lời giải:
Nhánh cuối của đồ thị đi xuống nên
0a
, đồ thị có hai điểm cực trị nên
.0ac
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 2 0S x y z y z
. Bán kính mặt cầu
S
bằng
A.
1
. B.
7
. C.
22
. D.
7
.
Lời giải:
Ta có
2 2 2
0
1
: 2 4 2 0
2
2
a
b
S x y z y z
c
d


.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Khi đó, bán kính mặt cầu
S
là
2
22
0 1 2 2 7R
.
Câu 11: Trong không gian
,Oxyz
góc giữa trục
Ox
và
Oz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
z
thỏa mãn
12i z i
. Môđun của số phức
z
bằng
A.
10
2
. B.
3
. C.
2
. D.
10
.
Lời giải:
Ta có
2 1 3 1 3
12
1 2 2 2 2
i
i z i z z i z i
i
.
Vậy
22
1 3 10
2 2 2
z
.
Câu 13: Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
BA BC a
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
6
a
V
. B.
3
2
a
V
. C.
3
3
a
V
. D.
3
Va
.
Lời giải:
Ta có:
3
. ' ' '
11
. ' . . ' . . . .
2 2 3
ABC A B C ABC
a
V S BB BA BC BB a a a
Câu 14: Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA ABC
,
SA a
(tham khảo hình
vẽ).
S
A
B
C
Thể tích của khối chóp đã cho bằng
A.
3
3
4
a
. B.
3
3
6
a
. C.
3
3a
. D.
3
3
12
a
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
S
A
B
C
Vì
SA ABC
nên ta có
SA
là đường cao của hình chóp hay
h SA a
.
Do đáy của hình chóp là tam giác đều cạnh
a
nên ta có:
2
3
4
a
S
.
Khi đó thể tích của khối chóp đã cho là:
1
.
3
V S h
23
1 3 3
..
3 4 12
aa
a
(đvtt).
Câu 15: Nếu tăng bán kính của một khối cầu gấp
3
lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp
6
lần. B. Thể tích tăng gấp
9
lần.
C. Thể tích tăng gấp
3
lần. D. Thể tích tăng gấp
27
lần.
Lời giải:
Gọi
R
là bán kính của khối cầu lúc đầu và
R
là bán kính khối cầu lúc sau.
3RR

.
Khi đó:
3
33
4 4 4
3 .27. 27
3 3 3
V R R R V

.
Vậy thể tích lúc sau tăng gấp
27
lần.
Câu 16: Cho số phức bất kì
,z a bi a b
. Khẳng định nào sau đây đúng?
A.
22
z a b
. B.
22
z a b
. C.
33
z a b
. D.
22
z a b
.
Câu 17: Cho tam giác
ABC
vuông tại
A
,
AB a
và
3AC a
. Tính độ dài đường sinh
l
của hình
nón có được khi quay tam giác
ABC
xung quanh trục
AB
.
A.
2la
. B.
2la
. C.
3la
. D.
la
.
Lời giải:
Quay tam giác
ABC
xung quanh trục
AB
suy ra
h AB a
và
3r AC a
.
Đường sinh
l
của hình nón bằng
22
2l r h a
.
Câu 18: Trong không gian
Oxyz
, đường thẳng
12
:
2 1 3
x y z
d


đi qua điểm nào dưới đây?
A.
2; 1;3A
. B.
1;2;0C
. C.
1; 2;0D
. D.
0;2; 1B
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Lần lượt thay tọa độ các điểm vào phương trình đường thẳng
d
.
Kiểm tra
2; 1;3 :A
2 1 1 2 3 3
1
2 1 3 2
(sai)
Ad
.
Kiểm tra
1;2;0 :C
1 1 2 2 0
00
2 1 3
Cd
.
Câu 19: Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm giá trị cực đại
CÐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
3
CÐ
y
và
0
CT
y
. B.
3
CÐ
y
và
2
CT
y 
.
C.
2
CÐ
y 
và
2
CT
y
. D.
2
CÐ
y
và
0
CT
y
.
Câu 20: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số
2
2
x
y
x
?
A.
2x
. B.
2x 
. C.
1y
. D.
1y 
.
Lời giải:
Ta có:
2
lim 1 1
2
x
x
y
x




là tiệm cận ngang của đồ thị hàm số.
Câu 21: Tập nghiệm
S
của bất phương trình
3
log 2 1 2x 
là
A.
1
;5
2
S


. B.
1
;5
2
S



. C.
;5S 
. D.
5;S
.
Lời giải:
Ta có
3
2
1
2 1 0
1
log 2 1 2 ; 5
2
2 1 3
2
5
x
x
xx
x
x






.
Câu 22: Có
3
cây bút đỏ,
4
cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút
từ hộp bút đó?
A.
7
. B.
4
. C.
12
. D.
3
.
Lời giải:
Chọn
1
cây bút từ
7
cây bút nên có
7
cách chọn.
Câu 23: Cho
sin d .
x x G x C
Đạo hàm hàm số
2y G x x
là
A.
2sin 1.yx

B.
2sin 1.yx

C.
2sin .yx
D.
2
2cos .
2
x
y x C
Lời giải:
Ta có
2 2sin 1.y G x x x
Câu 24: Nếu
d
4
0
( ) 37f x x
thì
d
4
2
0
2 ( ) 3f x x x


bằng
A. 12. B. 18. C.
27
. D. 10.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Lời giải:
Ta có:
4 4 4
4
2 2 3
0
0 0 0
2 ( ) 3 d 2 ( )d 3 d 2.37 74 64 10


f x x x f x x x x x
.
Câu 25: Cho hàm số
sinf x x x
. Khẳng định nào dưới đây đúng?
A.
2
d cos .
2
x
f x x x C
B.
2
d cos .
2
x
f x x x C
C.
2
d sin .
2
x
f x x x C
D.
2
d cos .
2
x
f x x x C
Lời giải:
2
d sin d cos .
2

x
f x x x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;2
. B.
2;
. C.
;1
. D.
2;3
.
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Điểm cực tiểu của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
aa
33
log 5 log 2
bằng
A.
3
log 3 .a
B.
3
2
log .
5
C.
2
3
log 10a
. D.
3
5
log .
2
Lời giải:
Ta có
aa
3 3 3 3
55
log 5 log 2 log log .
22
a
a
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
y x x
và
0y
quanh trục
Ox
là
A.
16
15
V 
B.
16
15
V
C.
1
30
V
D.
30
V
Lời giải:
Phương trình hoành độ giao điểm của đường
2
y x x
và đường
0y
là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
2
0
0
1
x
xx
x
.
Thể tích là
11
5 4 3
2
2 4 3 2
00
1
d 2 d .
0
5 2 3 30




x x x
V x x x x x x x
Câu 30: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
,a
SA
vuông góc với đáy và
2AB SA
(tham khảo hình vẽ).
C
B
A
S
Góc giữa hai mặt phẳng
SBC
và
ABC
bằng
A.
60 .
B.
30
C.
90
D.
45
Lời giải:
M
C
B
A
S
Dựng
,AM BC M
là trung điểm
.BC
Ta có:
.
SA BC
BC SAM
AM BC

Suy ra, góc giữa hai mặt phẳng
SBC
và
ABC
bằng
SMA
.
Xét tam giác
SAM
vuông tại
1
: tan 30 .
3
SA
A SMA SMA
AM

Vậy góc giữa hai mặt phẳng
SBC
và
ABC
bằng
30 .
Câu 31: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
x
y
2
-2
-1
O
1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có ba nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải:
Số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
:d y m
.
x
y
m
2
-2
-1
O
1
Dựa vào hình vẽ, ta có:
Phương trình
f x m
có ba nghiệm thực phân biệt khi đường thẳng
:d y m
cắt đồ thị
hàm số
y f x
tại ba điểm phân biệt, tức là
22 m
. Mà
m
nên
1;0;1m
.
Câu 32: Cho hàm số
y f x
có
1 3 , .f x x x x x
Hàm số
y f x
đồng biến trên khoảng
nào dưới đây?
A.
;0 .
B.
0;1 .
C.
1;2 .
D.
2; .
Lời giải:
Ta có:
0
0 1.
3
x
f x x
x
Bảng xét dấu:
x

0
1
3

fx
0
0
0
Câu 33: Chọn ngẫu nhiên 2 số tự nhiên khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn
được hai số có tổng là một số chẵn bằng
A.
1
2
. B.
13
25
. C.
12
25
. D.
313
625
.
Lời giải:
2
25
300nC
.
Trong 25 số nguyên dương đầu tiên có 13 số lẻ và 12 số chẵn
Gọi
A
là biến cố chọn được hai số có tổng là 1 số chẵn.
Chọn 2 số lẻ trong 13 số lẻ hoặc chọn 2 số chẵn trong 12 số chẵn
22
13 12
144n A C C
.
Vậy
144 12
.
300 25
nA
pA
n
Câu 34: Số nghiệm của phương trình
22
22
3 10.3 9 0
x x x x
là
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
A.
4.
B.
1.
C.
0.
D.
2.
Lời giải:
Điều kiện:
.x
Phương trình
22
2
3 10.3 9 0 *
x x x x
Đặt
2
30
xx
t

, phương trình
*
trở thành:
(tháa m·n)
(tháa m·n)
2
1
10 9 0 .
9
t
tt
t
+) Với
1,t
ta có:
2
2
0
3 1 0 .
1
xx
x
xx
x

+) Với
9,t
ta có:
2
22
1
3 9 2 2 0 .
2
xx
x
x x x x
x

Kết luận: Vậy tập nghiệm của phương trình là
2; 1;0;1 .S
Câu 35: Cho số phức
z
thỏa mãn
1 4.zi
Biết tập hợp các điểm biểu diễn số phức
w 3 4 1 2i z i
là đường tròn
.C
Tìm tâm
I
và bán kính
R
của đường tròn
.C
A.
2; 5 , 20.IR
B.
2; 5 , 4.IR
C.
2;5 , 4.IR
D.
2;5 , 20.IR
Lời giải:
Đặt
w , . x yi x y
Từ giả thiết:
w 3 4 1 2i z i
w+1 2
34
i
z
i

w+1 2
11
34
i
z i i
i
w+2 5
1
34
i
zi
i
w+2 5 1 3 4 w+2 5 20 i z i i i
22
2 5 20xy
22
2 5 400.xy
Vậy tập hợp điểm biểu diễn số phức
w
là đường tròn tâm
2; 5 ,I 
bán kính
20.R
Câu 36: Trong không gian
Oxyz
, viết phương trình tham số của đường thẳng đi qua hai điểm
1;2; 3 , 2; 3;1AB
.
A.
1
25
32
xt
yt
zt


. B.
2
35
14
xt
yt
zt


. C.
3
85
54
xt
yt
zt


. D.
1
25
34
xt
yt
zt



.
Lời giải:
Gọi
là đường thẳng đi qua
,AB
thì
nhận
1; 5;4AB 
làm VTCP.
Do đó loại đáp án A và. B.
Phương trình chính tắc của
là:
1 2 3
1 5 4
x y z

.
Ta thấy
3; 8;5M
nên
có phương trình tham số là:
3
85
54
xt
yt
zt


.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên mặt
phẳng
Oyz
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;7 .
Câu 38: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng
a
. Gọi
M
là trung điểm của
AA
.
Khoảng cách từ
M
đến mặt phẳng
AB C
bằng
A.
2
4
a
. B.
21
7
a
. C.
2
2
a
. D.
21
14
a
.
Lời giải:
Trong
ABB A

, gọi
E
là giao điểm của
BM
và
AB
. Khi đó hai tam giác
EAM
và
EB B
đồng dạng. Do đó
,
11
,,
, 2 2
d M AB C
EM MA
d M AB C d B AB C
d B AB C EB BB


.
Từ
B
kẻ
BN AC
thì
N
là trung điểm của
AC
và
3
2
a
BN
,
BB a
.
Kẻ
BI B N
thì
22
21
,
7
BB BN a
d B AB C BI
BB BN
.
Vậy
1 21
,,
2 14
a
d M AB C d B AB C

.
Câu 39: Cho hình nón
N
có chiều cao
2.ha
Một mặt phẳng
P
đi qua đỉnh của hình nón và cắt
hình hình nón theo một thiết diện là tam giác đều có diện tích bằng
2
16 3
.
9
a
Góc giữa
P
và
mặt đáy của
N
bằng
A.
90 .
B.
45 .
C.
60 .
D.
30 .
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
l
r
h
H
O
B
A
S
Gọi thiết diện là tam giác
,.SAB SA SB l
Theo giả thiết:
2 2 2
16 3 3 16 3 8
.
9 4 9 3
SAB
a l a a
Sl
Gọi
H
là trung điểm
®¸y nãn;AB SAB SHO
và
3 4 3
.
23
la
SH 
Xét tam giác
SOH
vuông tại
o
3
: sin 60 .
2
SO
O SHO SHO
SH
Câu 40: Trong không gian
,Oxyz
cho điểm
0; 2; 0M
và đường thẳng
43
:2
1
xt
d y t
zt


. Đường thẳng đi
qua
M
, cắt và vuông góc với
d
có phương trình là
A.
2
.
1 1 2

x y z
B.
1
.
1 1 2


x y z
C.
11
.
1 1 2


x y z
D.
1
.
1 1 2

x y z
Lời giải:
Ta có :
4;2; 1
:
3;1;1
d
qua N
d
vtcpu

Gọi
H
là hình chiếu vuông góc của
M
lên
d
MH d
Hd
.0
d
MH u
Hd
43
2
1
3 2 0
xt
yt
zt
x y z


1;1; 2H
.
Đường thẳng
đi qua
M
và vuông góc với
d
có véctơ chỉ phương là
1; 1; 2MH
.
Suy ra, phương trình
2
:
1 1 2
x y z
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 07_______________
Câu 1: Trên mặt phẳng toạ độ
Oxy
, biết
1;2M
là điểm biểu diễn số phức
z
, phần thực của
z
bằng
A.
1
. B.
2
. C.
1
. D.
2
.
Câu 2: Tập xác định của hàm số
logyx
là
A.
1; 
. B.
0;
. C.
0;
. D.
1; 
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2023
logyx
là
A.
1
ln2023
y
x
. B.
ln2023
y
x
. C.
1
y
x
. D.
1
2023
y
x
.
Câu 4: Tập nghiệm của bất phương trình
52
x
là
A.
5
(log 2; ).
B.
( ; ). 
C.
2
;.
5




D.
2
(log 5; )
Câu 5: Cho cấp số nhân
n
u
có
2
2u
và
3
4u 
. Công bội của cấp số nhân đã cho bằng
A.
2
. B.
6
. C.
6
. D.
2
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:3 2 2 0P x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của
P
?
A.
2
2; 1;2n 
. B.
4
3;2;1n
. C.
3
3;2;2n
. D.
1
3;2; 1n 
.
Câu 7: Cho hàm số
y f x
có đồ thị là đường cong như hình vẽ bên dưới:
Số nghiệm của phương trình
2fx
bằng
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 8: Biết
2
1
d6f x x
,
5
2
d1f x x
, tính
5
1
dI f x x
.
A.
5I
. B.
5I 
. C.
7I
. D.
4I
.
Câu 9: Bảng biến thiên sau đây là của hàm số nào?
A.
3
2
x
fx
x
. B.
3
.
2
x
fx
x
C.
3
2
x
fx
x
. D.
23
.
2
x
fx
x
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 8 2 1 0S x y z x y
. Tìm tọa độ tâm và bán
kính của mặt cầu
S
.
A.
4;1;0I
và
4R
. B.
4; 1;0I
và
2R
.
C.
4;1;0I
và
2R
. D.
4; 1;0I
và
4R
.
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oyz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
25zi
. Tìm số phức
w iz z
.
A.
73wi
. B.
33wi
. C.
37wi
. D.
77wi
.
Câu 13: Cho khối lăng trụ đứng có chiều cao bằng
5m
, đáy là hình vuông có cạnh bằng
4m
. Thể tích
khối lăng trụ đã cho bằng
A.
3
80m
. B.
3
20m
. C.
3
40m
. D.
3
60m
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA ABCD
,
2SA a
. Tính
thể tích khối chóp
A.
3
4
3
a
V
. B.
3
4
3
a
V
. C.
3
4Va
. D.
3
4Va
.
Câu 15: Cho mặt cầu
S
có tâm
O
, bán kính
2r
. Một điểm
M
trong không gian thỏa mãn
2OM
. Mệnh đề nào sau đây đúng?
A.
M
là điểm nằm trong mặt cầu
S
. B.
M
là tâm của mặt cầu
S
.
C.
M
là điểm nằm trên mặt cầu
S
. D.
M
là điểm nằm ngoài mặt cầu
S
.
Câu 16: Khẳng định nào sau đây sai?
A. Số
2021i
là số thuần ảo.
B. Số
0
là số phức có mô đun nhỏ nhất.
C. Với số phức
z
bất kì,
z
và
z
là hai số đối nhau.
D. Số phức
z
và số phức
z
có môđun bằng nhau.
Câu 17: Cho hình trụ có bán kính đáy
3r
và chiều cao
4h
. Diện tích xung quanh của hình trụ đã
cho bằng
A.
12
. B.
24
. C.
36
. D.
42
.
Câu 18: Trong không gian
Oxyz
, điểm nào sau đây thuộc đường thẳng
12
:1
xt
yt
zt


?
A.
1; 1; 1M
. B.
2;1; 1N
. C.
1; 1;0P
. D.
2; 1;1Q
.
Câu 19: Cho hàm số
fx
có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
2
. B.
5
. C.
3
. D.
1
.
Câu 20: Cho hàm số
y f x
thỏa mãn
lim 0.

x
fx
Khẳng định nào sau đây đúng?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
A. Đồ thị hàm số có đường tiệm cận ngang
2y
.
B. Đồ thị hàm số có đường tiệm cận đứng
2x
.
C. Đồ thị hàm số có đường tiệm cận ngang
0y
.
D. Đồ thị hàm số có đường tiệm cận đứng
2x
.
Câu 21: Tập nghiệm của bất phương trình
2
log 1 1x 
là
A.
3; 
. B.
;3
. C.
1;3
. D.
1;3
.
Câu 22: Có
8
quả ổi và
6
quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả đó?
A.
48
. B.
24
. C.
14
. D.
18
.
Câu 23: Cho
3
d 
x x F x C
. Khẳng định nào dưới đây đúng?
A.
21
F
. B.
8.2
F
C.
24
F
. D.
2 16
F
Câu 24: Nếu
1
0
2 d 2f x x x


thì
1
0
df x x
bằng
A. 1. B. 2. C. 0. D. 4.
Câu 25: Cho hàm số
sin cosf x x x
. Khẳng định nào dưới đây đúng?
A.
d sin cos .
f x x x x C
B.
d sin cos .
f x x x x C
C.
d sin cos .
f x x x x C
D.
d sin cos .
f x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
A.
0 1 .ff
B.
1 2 .ff
C.
4 5 .ff
D.
4 5 .ff
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Điểm cực đại của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
3
2
log a
bằng
A.
2
log 3 .a
B.
2
3 log .a
C.
2
log .a
D.
2
3log .a
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
4y x x
và
0y
quanh trục
Ox
là
A.
501
15
V
B.
501
15
V
C.
512
15
V
D.
512
15
V
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
Câu 30: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
1;0
B.
1;0 .
C.
0;1 .
D.
0; 1 .
Câu 31: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông cân tại
B
và
2AB a
.(minh họa như hình vẽ).
A
C
B
S
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
60
. B.
45
. C.
30
. D.
90
.
Câu 32: Cho hàm số
42
y f x ax bx c
có đồ thị là đường cong trong hình bên dưới:
x
y
-5
-1
O
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Câu 33: Cho hàm số
y f x
có đạo hàm
22
' 1 ,y f x x x x
. Hàm số
y f x
đồng
biến trên khoảng nào dưới đây?
A.
2;
. B.
0;2
. C.
1;1
. D.
;1
.
Câu 34: Một hộp chứa
11
quả cầu gồm
5
quả màu xanh và
6
quả cầu màu đỏ. Chọn ngẫu nhiên đồng
thời
2
quả cầu từ hộp đó. Xác suất để
2
quả cầu chọn ra cùng màu bằng
A.
5
.
22
B.
6
.
11
C.
5
.
11
D.
8
.
11
Câu 35: Tính tổng
T
tất cả các nghiệm thực của phương trình
4.9 13.6 9.4 0.
x x x
A.
13
4
T
. B.
3T
. C.
1
4
T
. D.
2T
.
Câu 36: Trong không gian
Oxyz
, cho 3 điểm
2;1; 1A
,
1;0;4B
,
0; 2; 1C 
. Phương trình mặt
phẳng đi qua
A
và vuông góc với
BC
là
A.
2 5 5 0x y z
. B.
2 5 5 0x y z
. C.
2 5 0xy
. D.
2 5 5 0x y z
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên trục
Oy
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 38: Cho hình nón đỉnh
S
, đáy là đường tròn tâm
O
bán kính
5R
, góc ở đỉnh bằng
60
. Một
mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm
A
và
B
sao cho
6AB
.
Tính khoảng cách từ
O
đến
SAB
.
A.
20 273
90
. B.
20 270
91
. C.
20 271
91
. D.
20 273
91
.
Câu 39: Trong không gian
,Oxyz
cho mặt phẳng
: 4 2 1 0P x y z
và điểm
(4;2;1)M
. Khi đó
điểm đối xứng với
M
qua mặt phẳng
P
có tọa độ là
A.
( 4;0; 3)
. B.
( 4; 4; 1)
. C.
(4;2;1)
. D.
( 2;0;5)
.
Câu 40: Cho hình trụ
T
có chiều cao bằng
8a
. Một mặt phẳng
song song với trục và cách trục
của hình trụ này một khoảng bằng
3a
, đồng thời
cắt
T
theo thiết diện là một hình
vuông. Diện tích xung quanh của hình trụ đã cho bằng
A.
2
80 a
. B.
2
40 a
. C.
2
30 a
. D.
2
60 a
.
________________________HẾT________________________
LỜI GIẢI CHI TIẾT
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
Câu 1: Trên mặt phẳng toạ độ
Oxy
, biết
1;2M
là điểm biểu diễn số phức
z
, phần thực của
z
bằng
A.
1
. B.
2
. C.
1
. D.
2
.
Lời giải:
Vì
1;2M
là điểm biểu diễn số phức
z
nên ta có
12zi
.
Suy ra phần thực của
z
bằng
1
.
Câu 2: Tập xác định của hàm số
logyx
là
A.
1; 
. B.
0;
. C.
0;
. D.
1; 
.
Lời giải:
Hàm số
logyx
xác định
0x
.
Vậy tập xác định của hàm số là:
0;D 
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
2023
logyx
là
A.
1
ln2023
y
x
. B.
ln2023
y
x
. C.
1
y
x
. D.
1
2023
y
x
.
Lời giải:
Áp dụng công thức
1
log
ln
a
x
xa
. Ta có
1
.
ln2023
y
x
Câu 4: Tập nghiệm của bất phương trình
52
x
là
A.
5
(log 2; ).
B.
( ; ). 
C.
2
;.
5




D.
2
(log 5; )
Lời giải:
5
5 2 log 2
x
x
.
Câu 5: Cho cấp số nhân
n
u
có
2
2u
và
3
4u 
. Công bội của cấp số nhân đã cho bằng
A.
2
. B.
6
. C.
6
. D.
2
.
Lời giải:
Công bội của cấp số nhân là
3
2
4
2
2
u
q
u
.
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
:3 2 2 0P x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của
P
?
A.
2
2; 1;2n 
. B.
4
3;2;1n
. C.
3
3;2;2n
. D.
1
3;2; 1n 
.
Lời giải:
Véc-tơ pháp tuyến của
P
là
1
3;2; 1n 
.
Câu 7: Cho hàm số
y f x
có đồ thị là đường cong như hình vẽ bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm của phương trình
2fx
bằng
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải:
Ta có số nghiệm của phương trình
2fx
là số giao điểm của đồ thị hàm số
()y f x
và
đường thẳng
2y 
.
Căn cứ vào đồ thị hàm số ta có số giao điểm bằng 2
Vậy phương trình đã cho có 2 nghiệm.
Câu 8: Biết
2
1
d6f x x
,
5
2
d1f x x
, tính
5
1
dI f x x
.
A.
5I
. B.
5I 
. C.
7I
. D.
4I
.
Lời giải:
Ta có:
5 2 5
1 1 2
d d d 6 1 7I f x x f x x f x x
.
Câu 9: Bảng biến thiên sau đây là của hàm số nào?
A.
3
2
x
fx
x
. B.
3
.
2
x
fx
x
C.
3
2
x
fx
x
. D.
23
.
2
x
fx
x
Lời giải:
Ta có
lim 1
x
fx

suy ra đồ thị hàm số có một tiệm cận ngang là
1y
.
2
lim
x
fx

2x
mà một tiệm cận đứng của đồ thị hàm số.
Dựa vào bảng biến thiên, nhận thấy hàm số đồng biến trên từng khoảng xác định.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 8 2 1 0S x y z x y
. Tìm tọa độ tâm và bán
kính của mặt cầu
S
.
A.
4;1;0I
và
4R
. B.
4; 1;0I
và
2R
.
C.
4;1;0I
và
2R
. D.
4; 1;0I
và
4R
.
Lời giải:
Từ phương trình của mặt cầu suy ra tâm
4; 1;0I
và bán kính
2
22
4 1 0 1 4.R
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Câu 11: Trong không gian
,Oxyz
cho điểm
1;0;0 .A
Góc giữa đường thẳng
OA
và mặt phẳng
Oyz
bằng
A.
90 .
B.
60 .
C.
30 .
D.
0.
Câu 12: Cho số phức
25zi
. Tìm số phức
w iz z
.
A.
73wi
. B.
33wi
. C.
37wi
. D.
77wi
.
Lời giải:
2 5 2 5 5 2 2 5 3 3w iz z i i i i i i
.
Câu 13: Cho khối lăng trụ đứng có chiều cao bằng
5m
, đáy là hình vuông có cạnh bằng
4m
. Thể tích
khối lăng trụ đã cho bằng
A.
3
80m
. B.
3
20m
. C.
3
40m
. D.
3
60m
.
Lời giải:
Ta có diện tích đáy khối lăng trụ đứng là
22
4 16Sm
.
Vậy thể tích khối lăng trụ đã cho
3
16.5 80V Sh m
.
Câu 14: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA ABCD
,
2SA a
. Tính
thể tích khối chóp
A.
3
4
3
a
V
. B.
3
4
3
a
V
. C.
3
4Va
. D.
3
4Va
.
Lời giải:
D
C
B
A
S
Diện tích hình vuông
ABCD
là:
2
2
22
ABCD
S a a
Thể tích khối chóp
.S ABCD
là:
3
2
.
1 1 4
. .2 .2
3 3 3
S ABCD ABCD
a
V SAS a a
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Câu 15: Cho mặt cầu
S
có tâm
O
, bán kính
2r
. Một điểm
M
trong không gian thỏa mãn
2OM
. Mệnh đề nào sau đây đúng?
A.
M
là điểm nằm trong mặt cầu
S
. B.
M
là tâm của mặt cầu
S
.
C.
M
là điểm nằm trên mặt cầu
S
. D.
M
là điểm nằm ngoài mặt cầu
S
.
Lời giải:
Vì
2OM r
M
là điểm nằm trên mặt cầu
S
.
Câu 16: Khẳng định nào sau đây sai?
A. Số
2021i
là số thuần ảo.
B. Số
0
là số phức có mô đun nhỏ nhất.
C. Với số phức
z
bất kì,
z
và
z
là hai số đối nhau.
D. Số phức
z
và số phức
z
có môđun bằng nhau.
Lời giải:
Ta có:
z
và
z
được gọi là 2 số phức liên hợp do đó C sai.
Câu 17: Cho hình trụ có bán kính đáy
3r
và chiều cao
4h
. Diện tích xung quanh của hình trụ đã
cho bằng
A.
12
. B.
24
. C.
36
. D.
42
.
Lời giải:
Diện tích xung quanh của hình trụ đã cho là
2 24
xq
S rh


.
Câu 18: Trong không gian
Oxyz
, điểm nào sau đây thuộc đường thẳng
12
:1
xt
yt
zt


?
A.
1; 1; 1M
. B.
2;1; 1N
. C.
1; 1;0P
. D.
2; 1;1Q
.
Lời giải:
Đường thẳng
12
:1
xt
yt
zt


đi qua điểm
1; 1;0P
vì
1 1 2
1 1 0
0
t
tt
t


.
Câu 19: Cho hàm số
fx
có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
2
. B.
5
. C.
3
. D.
1
.
Lời giải:
Từ bảng xét dấu của đạo hàm thì hàm số đã cho có 2 cực trị.
Câu 20: Cho hàm số
y f x
thỏa mãn
lim 0.

x
fx
Khẳng định nào sau đây đúng?
A. Đồ thị hàm số có đường tiệm cận ngang
2y
.
B. Đồ thị hàm số có đường tiệm cận đứng
2x
.
C. Đồ thị hàm số có đường tiệm cận ngang
0y
.
D. Đồ thị hàm số có đường tiệm cận đứng
2x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Câu 21: Tập nghiệm của bất phương trình
2
log 1 1x 
là
A.
3; 
. B.
;3
. C.
1;3
. D.
1;3
.
Lời giải:
2
log 1 1 0 1 2 1 3.x x x
Câu 22: Có
8
quả ổi và
6
quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả đó?
A.
48
. B.
24
. C.
14
. D.
18
.
Lời giải:
Theo quy tắc cộng có
8 6 14
cách chọn ra một quả trong các quả đã cho.
Câu 23: Cho
3
d 
x x F x C
. Khẳng định nào dưới đây đúng?
A.
21
F
. B.
8.2
F
C.
24
F
. D.
2 16
F
Lời giải:
Ta có
33
d 8.2



F x x x x F
Câu 24: Nếu
1
0
2 d 2f x x x


thì
1
0
df x x
bằng
A. 1. B. 2. C. 0. D. 4.
Lời giải:
Ta có:
1 1 1 1
2
0
0 0 0 0
1
2 d 2 d 2 d 2 d 2f x x x f x x x x f x x x


11
00
d 1 0 2 d 1.f x x f x x

Câu 25: Cho hàm số
sin cosf x x x
. Khẳng định nào dưới đây đúng?
A.
d sin cos .
f x x x x C
B.
d sin cos .
f x x x x C
C.
d sin cos .
f x x x x C
D.
d sin cos .
f x x x x C
Lời giải:
d sin cos d cos sin .

f x x x x x x x C
Câu 26: Cho hàm số
()y f x
có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
A.
0 1 .ff
B.
1 2 .ff
C.
4 5 .ff
D.
4 5 .ff
Câu 27: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Điểm cực đại của hàm số đã cho là
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 28: Với
a
là số thực dương tùy ý,
3
2
log a
bằng
A.
2
log 3 .a
B.
2
3 log .a
C.
2
log .a
D.
2
3log .a
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường
2
4y x x
và
0y
quanh trục
Ox
là
A.
501
15
V
B.
501
15
V
C.
512
15
V
D.
512
15
V
Lời giải:
Phương trình hoành độ giao điểm của đường
2
4y x x
và đường
0y
là
2
0
40
4
x
xx
x
.
Thể tích là
44
53
2
2 4 3 2 4
00
4
16 512
4 d 8 16 d 2 .
0
5 3 15




xx
V x x x x x x x x
Câu 30: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
1;0
B.
1;0 .
C.
0;1 .
D.
0; 1 .
Lời giải:
Ta có:
1
2
2
1 1;1
2 2 0 .
1 1; 1
z i A
zz
z i B
I
là trung điểm
1;0 .AB I
Câu 31: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt phẳng
ABC
,
2SA a
, tam giác
ABC
vuông cân tại
B
và
2AB a
.(minh họa như hình vẽ).
A
C
B
S
Góc giữa đường thẳng
SC
và mặt phẳng
ABC
bằng
A.
60
. B.
45
. C.
30
. D.
90
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
Lời giải:
A
C
B
S
Ta có:
SC A BC C
SA ABC

,( ) ( , )SC ABC SC AC SCA
.
Mà:
2 2 2 2
2 2 2AC AB BC a a a SA
.
Vì
SAC
vuông cân tại
A
nên ta có
45SCA 
.
Câu 32: Cho hàm số
42
y f x ax bx c
có đồ thị là đường cong trong hình bên dưới:
x
y
-5
-1
O
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
f x m
có bốn nghiệm thực
phân biệt?
A.
4
. B.
5
. C.
3
. D.
2
.
Lời giải:
Số nghiệm của phương trình
f x m
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
:d y m
.
x
y
m
-5
-1
O
Dựa vào hình vẽ, ta có:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
Phương trình
f x m
có bốn nghiệm thực phân biệt khi đường thẳng
:d y m
cắt đồ thị
hàm số
y f x
tại bốn điểm phân biệt, tức là
51 m
.
Mà
m
nên
4; 3; 2 m
.
Câu 33: Cho hàm số
y f x
có đạo hàm
22
' 1 ,y f x x x x
. Hàm số
y f x
đồng
biến trên khoảng nào dưới đây?
A.
2;
. B.
0;2
. C.
1;1
. D.
;1
.
Lời giải:
Ta có:
0
'0
1
x
fx
x


' '( )y f x y f x
Hàm số
y f x
đồng biến khi và chỉ khi
'( ) 0 ' 0f x f x
1 1 1 1. xx
Câu 34: Một hộp chứa
11
quả cầu gồm
5
quả màu xanh và
6
quả cầu màu đỏ. Chọn ngẫu nhiên đồng
thời
2
quả cầu từ hộp đó. Xác suất để
2
quả cầu chọn ra cùng màu bằng
A.
5
.
22
B.
6
.
11
C.
5
.
11
D.
8
.
11
Lời giải:
Số cách lấy ra 2 quả cầu trong 11 quả là
2
11
C
, Suy ra
2
11
nC
Gọi A là biến cố lấy được 2 quả cùng màu. Suy ra
22
56
n A C C
Xác suất của biến cố A là
22
56
2
11
5
.
11

CC
PA
C
Câu 35: Tính tổng
T
tất cả các nghiệm thực của phương trình
4.9 13.6 9.4 0.
x x x
A.
13
4
T
. B.
3T
. C.
1
4
T
. D.
2T
.
Lời giải:
Phương trình
96
4. 13. 9 0
44
xx
2
33
4. 13. 9 0
22
xx
.
Đặt
3
,0
2
x
tt




.
Phương trình trở thành:
2
1
4 13 9 0
9
4
t
tt
t
( thỏa mãn).
+)
3
1 1 0
2
x
tx



.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
+)
9 3 9
2
4 2 4
x
tx



.
Câu 36: Trong không gian
Oxyz
, cho 3 điểm
2;1; 1A
,
1;0;4B
,
0; 2; 1C 
. Phương trình mặt
phẳng đi qua
A
và vuông góc với
BC
là
A.
2 5 5 0x y z
. B.
2 5 5 0x y z
. C.
2 5 0xy
. D.
2 5 5 0x y z
.
Lời giải:
Ta có
1; 2; 5BC 
.
Vậy phương trình mặt phẳng đi qua
A
và vuông góc với
BC
là:
1 2 2 1 5 1 0 2 5 5 0x y z x y z
.
Câu 37: Trong không gian
Oxyz
, cho điểm
3;5;7A
. Hình chiếu vuông góc của điểm
A
lên trục
Oy
có tọa độ là
A.
3;5;7 .
B.
3;5;0 .
C.
3;0;7 .
D.
0;5;0 .
Câu 38: Cho hình nón đỉnh
S
, đáy là đường tròn tâm
O
bán kính
5R
, góc ở đỉnh bằng
60
. Một
mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm
A
và
B
sao cho
6AB
.
Tính khoảng cách từ
O
đến
SAB
.
A.
20 273
90
. B.
20 270
91
. C.
20 271
91
. D.
20 273
91
.
Lời giải:
Gọi
I
là trung điểm
AB OI AB
.
Mà
AB SO
(vì
SO
vuông góc với đáy)
AB SIO SAB SIO
Trong
SIO
vẽ
SAB SIOOK SI
OK SAB
,OK d O SAB
.
Góc ở đỉnh bằng
60
30 ASO
, mà
5 5 3OA R SO
IAO
vuông tại
I
có:
5, 3 4
2
AB
OA AI OI
SOI
vuông tại
O
, đường cao
OK
có:
2 2 2
1 1 1 20 273
91
OK
OK SO OI
.
Vậy
20 273
91
,d O SAB
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Câu 39: Trong không gian
,Oxyz
cho mặt phẳng
: 4 2 1 0P x y z
và điểm
(4;2;1)M
. Khi đó
điểm đối xứng với
M
qua mặt phẳng
P
có tọa độ là
A.
( 4;0; 3)
. B.
( 4; 4; 1)
. C.
(4;2;1)
. D.
( 2;0;5)
.
Lời giải:
Phương trình đường thẳng
d
qua
M
vuông góc với
P
là
44
2
12
xt
yt
zt



Gọi
H d P
0;1; 1H
.
M
đối xứng với
M
qua
P
nên
H
là trung điểm
MM
4;0; 3M
.
Câu 40: Cho hình trụ
T
có chiều cao bằng
8a
. Một mặt phẳng
song song với trục và cách trục
của hình trụ này một khoảng bằng
3a
, đồng thời
cắt
T
theo thiết diện là một hình
vuông. Diện tích xung quanh của hình trụ đã cho bằng
A.
2
80 a
. B.
2
40 a
. C.
2
30 a
. D.
2
60 a
.
Lời giải:
Gọi trục của hình trụ là
OO
8OO a

.
Mặt phẳng
cắt hình trụ theo thiết diện là hình vuông
ABCD
8AB AD a
Theo giả thiết
;3d OO ABCD a
.
Kẻ
OH AB
OH ABCD
; ; 3d OO ABCD d O ABCD OH a

.
Xét tam giác
OAH
vuông tại
H
ta có:
2 2 2
OA OH AH
5OA a
.
Diện tích xung quanh của hình trụ bằng:
2
xq
S rh
2 .5 .8aa
2
80 a
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 1
_______________ĐỀ SỐ 08_______________
Câu 1: Trong mặt phẳng
,Oxy
điểm
3; 2M
là điểm biểu diễn của số phức nào dưới đây ?
A.
23zi
. B.
32zi
. C.
3 2 .zi
D.
23zi
.
Câu 2: Hệ số góc của tiếp tuyến với đồ thị hàm số
ln 1yx
tại điểm có hoành độ
2x
là
A. 1. B.
ln 2
. C.
1
3
. D.
1
3ln2
.
Câu 3: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln 2
x
yx
.
Câu 4: Tập nghiệm của bất phương trình
21
3 27
x
là
A.
1
;
2




. B.
3;
. C.
2;
. D.
1
;
3




.
Câu 5: Cho cấp số cộng
()
n
u
có
1
2027u
và công sai
3d 
. Số hạng
3
u
A.
3
3
2027( 3)u 
. B.
3
2021u
. C.
3
2020u
. D.
3
2054u
.
Câu 6: Trong không gian
Oxyz
, mặt phẳng
:3 4 3 0x y z
có một vectơ pháp tuyến là
A.
3;4; 1m
. B.
3;4;1n
. C.
6;8;2a
. D.
3;4; 1 b
.
Câu 7: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình
3fx
là
A.
1
. B.
2
. C. 0. D. 3.
Câu 8: Cho
d
2
1
( ) 2f x x
và
d
2
1
( ) 1g x x

. Giá trị của
d
2
1
2 ( ) 3 ( )f x g x x


bằng
A. 1. B. 5. C. 7. D.
7
.
Câu 9: Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
31y x x
. B.
3
31y x x
. C.
42
21y x x
. D.
3
31y x x
.
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 2) ( 1) ( 1) 9 S x y z
. Tọa độ tâm
I
và bán
kính
R
của
S
là
A.
( 2;1; 1), 3. IR
B.
( 2;1; 1), 9. IR
C.
(2; 1;1), 3.IR
D.
(2; 1;1), 9.IR
Câu 11: Trong không gian
Oxyz
, cho hai điểm
1;1;2A
và
3; 5;0B
. Tọa độ trung điểm của đoạn
thẳng
AB
là
A.
2; 4;2
B.
4; 6;2
C.
1; 2;1
D.
2; 3; 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 2
Câu 12: Cho hai số phức
1
37zi
và
2
23zi
. Tìm số phức
12
z z z
.
A.
1 10zi
. B.
54zi
. C.
3 10zi
. D.
33zi
.
Câu 13: Cho khối lăng trụ đứng có diện tích đáy bằng
2
2a
và cạnh bên bằng
3a
. Thể tích khối lăng
trụ đã cho bằng
A.
3
2a
B.
3
3a
C.
3
18a
D.
3
6a
Câu 14: Cho hình chóp
.S ABC
có đường cao
,SA
tam giác
ABC
vuông tại
A
có
2AB
,
4AC
. Gọi
H
là trung điểm của
BC
(tham khảo hình vẽ).
H
C
B
A
S
Biết diện tích tam giác
SAH
bằng 2, thể tích của khối chóp
.S ABC
bằng
A.
16 5
5
. B.
16 5
15
. C.
45
9
. D.
45
3
.
Câu 15: Cắt một mặt cầu
S
bởi một mặt phẳng qua tâm được thiết diện là hình tròn đường kính
bằng
4.cm
Tính thể tích của khối cầu đã cho.
A.
3
256
.
2
cm
B.
3
16 .
cm
C.
3
32
.
3
cm
D.
3
64 .
cm
Câu 16: Môđun của số phức
1zi
bằng
A.
1
. B.
0
. C.
2
. D.
2
.
Câu 17: Cho hình trụ có bán kính đáy bằng
5
và chiều cao bằng
7
. Diện tích xung quanh của hình trụ
đã cho bằng
A.
175
.
3
B.
175 .
C.
70 .
D.
35 .
Câu 18: Trong không gian
,Oxyz
điểm nào dưới đây thuộc đường thẳng
12
:3
45
xt
d y t
zt


?
A.
3; 2 ; 1P 
. B.
2 ;1; 5N
. C.
1; 3; 4M
. D.
4;1; 3Q
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng
;ab
?
A.
4
. B.
2
. C.
7
. D.
3
.
Câu 20: Tiệm cận đứng của đồ thị hàm số
35
2
x
y
x
là
A.
2x
. B.
2y
. C.
3x
. D.
3y
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 3
Câu 21: Bất phương trình
22
log (3 2) log (6 5 )xx
có tập nghiệm là
( ; )ab
. Tổng
ab
bằng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Câu 22: Có
10
cái bút khác nhau và
8
quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A.
80
. B.
70
. C.
90
. D.
60
.
Câu 23: Cho hàm số
2
x
f x x e
. Tìm một nguyên hàm
Fx
của hàm số
fx
thỏa mãn
0 2023F
.
A.
2
2022
x
F x x e
. B.
2
2022
x
F x x e
.
C.
2
2021
x
F x x e
. D.
2023
x
F x e
.
Câu 24: Cho
2
2
d1f x x
,
4
2
d4f t t

. Tính
4
2
dI f y y
.
A.
5I
. B.
3I
. C.
3I 
. D.
5I 
.
Câu 25: Họ nguyên hàm của hàm số
3
2f x x
x

là
A.
2
3
2.C
x

B.
2
2
3
.xC
x

C.
2
ln .x x C
D.
2
3ln .x x C
Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây?
A.
2;
. B.
;1
. C.
0;
. D.
0;2
.
Câu 27: Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại
0x
. B. Hàm số đạt cực tiểu tại
4x 
.
C. Hàm số đạt cực đại tại
2x 
. D. Hàm số đạt cực đại tại
1x
.
Câu 28: Với
a
và
b
là hai số thực dương tùy ý;
34
2
log ab
bằng
A.
22
11
log log .
34
ab
B.
22
3log 4log .ab
C.
24
2 log log .ab
D.
22
4log 3log .ab
Câu 29: Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
,
0y
. Quay
H
quanh trục hoành
tạo thành khối tròn xoay có thể tích được tính bởi công thức nào dưới đây?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 4
A.
2
2
0
2 d .
x x x
B.
2
2
2
0
2 d .
x x x
C.
2
2
2
0
2 d .
x x x
D.
2
2
0
2 d .
x x x
Câu 30: Cho hình lập phương
.
ABCD A B C D
. Góc giữa đường thẳng
AB
và mặt phẳng
ABC D
bằng
A.
60 .
B.
90 .
C.
30 .
D.
45 .
Câu 31: Cho hàm số bậc ba
32
34y x x
có đồ thị như hình vẽ bên dưới:
x
y
-1
2
4
O
Tìm tất cả các giá trị thực của
m
sao cho phương trình
32
3 4 0x x m
có 3 nghiệm thực
phân biệt.
A.
24m
. B.
04m
. C.
4
0
m
m
. D.
04m
.
Câu 32: Hàm số
y f x
liên tục trên và có đạo hàm
2
1 1 , .
f x x x x x
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
1;2 .
B.
1;0 .
C.
0;1 .
D.
2; 1 .
Câu 33: Một hộp chứa
15
quả cầu gồm
6
quả màu đỏ được đánh số từ
1
đến
6
và
9
quả màu xanh
được đánh số từ
1
đến
9
. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả
khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
A.
9
.
35
B.
18
.
35
C.
4
.
35
D.
1
.
7
Câu 34: Tích tất cả các nghiệm của phương trình
2
log 2log 3 0 xx
bằng
A.
1
.
10
B.
100.
C.
10.
D.
1
.
100
Câu 35: Trong mặt phẳng
,Oxy
tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn
| 3 | 2zi
là
A. đường tròn
22
3 1 4xy
. B. đường tròn
22
3 1 4xy
.
C. đường tròn
22
3 1 2xy
. D. đường thẳng
3 2 0.xy
Câu 36: Trong không gian
,Oxyz
phương trình đường thẳng đi qua hai điểm
;;A 1 1 2
và
là
A.
xt
yt
zt


12
1.
22
B.
xt
yt
zt
12
1.
22
C.
xt
yt
zt



32
.
42
D.
xt
yt
zt


52
1.
62
Câu 37: Trong không gian
,Oxyz
cho
23a i j k
. Tọa độ của vectơ
a
là
A.
1;2; 3
. B.
2; 3; 1
. C.
2; 1; 3
. D.
3;2; 1
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 5
Câu 38: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,2AB a AD a
SA ABCD
và
SA a
(tham khảo hình vẽ)
Khoảng cách từ
A
đến mặt phẳng
SBD
bằng
A.
3
2
a
. B.
21
7
a
. C.
10
5
a
. D.
2
5
a
.
Câu 39: Trong không gian
,Oxyz
gọi
H
hình chiếu vuông góc của
2;0;1M
lên đường thẳng
12
:
1 2 1
x y z
. Tìm tọa độ điểm
H
.
A.
2;2;3H
. B.
0; 2;1H
. C.
1;0;2H
. D.
1; 4;0H 
.
Câu 40: Một hình trụ có bán kính bằng
2a
. Hai điểm
,AB
lần lượt thuộc hai đường tròn đáy sao cho
4A B a
. Biết khoảng cách giữa
AB
và trục bằng
a
. Tính thể tích khối trụ đã cho.
A.
3
2
Va
. B.
3
82
3
a
V
. C.
3
42
Va
. D.
3
8
Va
.
________________________HẾT________________________
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 6
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng
,Oxy
điểm
3; 2M
là điểm biểu diễn của số phức nào dưới đây ?
A.
23zi
. B.
32zi
. C.
3 2 .zi
D.
23zi
.
Lời giải:
Số phức thoả mãn yêu cầu đề bài là:
32zi
.
Câu 2: Hệ số góc của tiếp tuyến với đồ thị hàm số
ln 1yx
tại điểm có hoành độ
2x
là
A. 1. B.
ln 2
. C.
1
3
. D.
1
3ln2
.
Lời giải:
Ta có
1
'
1
y
x
. Hệ số góc của tiếp tuyến với đồ thị hàm số
ln 1yx
tại điểm có hoành độ
2x
là:
1
'2
3
y
.
Câu 3: Đạo hàm của hàm số
2
x
y
là
A.
1
.2
x
yx
. B.
2 .ln 2
x
y
. C.
2
x
y
. D.
1
.2 .ln 2
x
yx
.
Lời giải:
Hàm số
2
x
y
có đạo hàm là
' 2 .ln2
x
y
.
Câu 4: Tập nghiệm của bất phương trình
21
3 27
x
là
A.
1
;
2




. B.
3;
. C.
2;
. D.
1
;
3




.
Lời giải:
2 1 2 1 3
3 27 3 3 2 1 3 2
xx
xx

.
Vậy bất phương trình có tập nghiệm
2;S
.
Câu 5: Cho cấp số cộng
()
n
u
có
1
2027u
và công sai
3d 
. Số hạng
3
u
A.
3
3
2027( 3)u 
. B.
3
2021u
. C.
3
2020u
. D.
3
2054u
.
Lời giải:
31
2 2027 2.( 3) 2021u u d
Câu 6: Trong không gian
Oxyz
, mặt phẳng
:3 4 3 0x y z
có một vectơ pháp tuyến là
A.
3;4; 1m
. B.
3;4;1n
. C.
6;8;2a
. D.
3;4; 1 b
.
Lời giải:
Mặt phẳng
:3 4 3 0x y z
có một vectơ pháp tuyến là
3; 4; 1u
nên vectơ
6;8;2a
cũng là một vectơ pháp tuyến của mặt phẳng
.
Câu 7: Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ bên dưới:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 7
Số nghiệm thực của phương trình
3fx
là
A.
1
. B.
2
. C. 0. D. 3.
Lời giải:
Số nghiệm của phương trình
3fx
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
3y
.
Ta có đường thẳng
3y
song song với trục hoành và cắt trục tung tại điểm có tọa độ
0;3
.
Từ đồ thị ta thấy đường thẳng
3y
cắt đồ thị hàm số
y f x
tại hai điểm phân biệt. Do đó
phương trình
3fx
có 2 nghiệm thực phân biệt.
Câu 8: Cho
d
2
1
( ) 2f x x
và
d
2
1
( ) 1g x x

. Giá trị của
d
2
1
2 ( ) 3 ( )f x g x x


bằng
A. 1. B. 5. C. 7. D.
7
.
Lời giải:
Áp dụng tính chất của tích phân ta có
2 2 2
1 1 1
2 ( ) 3 ( ) 2 ( ) 3 ( ) 4 3 1f x g x dx f x dx g x dx


.
Câu 9: Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây?
A.
32
31y x x
. B.
3
31y x x
. C.
42
21y x x
. D.
3
31y x x
.
Lời giải:
Quan sát hình dạng đồ thị ta loại đáp án hàm số
42
21y x x
do trên hình hàm số có hai
cực trị mà đáp án này hàm số có 3 cực trị.
Do nhánh bên phải của đồ thị đi lên nên loại đáp án
3
31y x x
.
Mặt khác quan sát đồ thị có hai điểm cực trị là
1x 
.
Xét đáp án A có
2
0
3 6 0
2
x
y x x
x
nên loại đáp án này.
Vậy hình trên là đồ thị hàm số
3
31y x x
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 8
Câu 10: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ):( 2) ( 1) ( 1) 9 S x y z
. Tọa độ tâm
I
và bán
kính
R
của
S
là
A.
( 2;1; 1), 3. IR
B.
( 2;1; 1), 9. IR
C.
(2; 1;1), 3.IR
D.
(2; 1;1), 9.IR
Câu 11: Trong không gian
Oxyz
, cho hai điểm
1;1;2A
và
3; 5;0B
. Tọa độ trung điểm của đoạn
thẳng
AB
là
A.
2; 4;2
B.
4; 6;2
C.
1; 2;1
D.
2; 3; 1
Câu 12: Cho hai số phức
1
37zi
và
2
23zi
. Tìm số phức
12
z z z
.
A.
1 10zi
. B.
54zi
. C.
3 10zi
. D.
33zi
.
Lời giải:
Ta có:
12
z z z
3 7 2 3 5 4i i i
.
Câu 13: Cho khối lăng trụ đứng có diện tích đáy bằng
2
2a
và cạnh bên bằng
3a
. Thể tích khối lăng
trụ đã cho bằng
A.
3
2a
B.
3
3a
C.
3
18a
D.
3
6a
Lời giải:
23
. 2 .3 6 V B h a a a
Câu 14: Cho hình chóp
.S ABC
có đường cao
,SA
tam giác
ABC
vuông tại
A
có
2AB
,
4AC
. Gọi
H
là trung điểm của
BC
(tham khảo hình vẽ).
H
C
B
A
S
Biết diện tích tam giác
SAH
bằng 2, thể tích của khối chóp
.S ABC
bằng
A.
16 5
5
. B.
16 5
15
. C.
45
9
. D.
45
3
.
Lời giải:
H
A
C
B
S
Xét tam giác
ABC
vuông tại
A
:
2 2 2 2
2 4 2 5BC AB AC
.
Suy ra
11
.2 5 5
22
AH BC
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 9
Xét tam giác
SAH
vuông tại
A
:
1 1 4 5
. 2 . 5
2 2 5
SAH
S SA AH SA SA
.
Diện tích tam giác
ABC
:
11
. .2.4 4
22
ABC
S AB AC
.
Thể tích khối chóp
.S ABC
:
.
1 1 4 5 16 5
. . .4
3 3 5 15
S ABC ABC
V SA S
.
Câu 15: Cắt một mặt cầu
S
bởi một mặt phẳng qua tâm được thiết diện là hình tròn đường kính
bằng
4.cm
Tính thể tích của khối cầu đã cho.
A.
3
256
.
2
cm
B.
3
16 .
cm
C.
3
32
.
3
cm
D.
3
64 .
cm
Lời giải:
Bán kính
R
của hình tròn thu được bằng bán kính của mặt cầu.
Đường kính hình tròn là:
2 4 2 . R R cm
Thể tích khối cầu là:
3 3 3
4 4 32
.2 .
3 3 3

V R cm
Câu 16: Môđun của số phức
1zi
bằng
A.
1
. B.
0
. C.
2
. D.
2
.
Lời giải:
Ta có
2
2
1 1 2z
.
Câu 17: Cho hình trụ có bán kính đáy bằng
5
và chiều cao bằng
7
. Diện tích xung quanh của hình trụ
đã cho bằng
A.
175
.
3
B.
175 .
C.
70 .
D.
35 .
Lời giải:
Ta có
5; 7 r l h
. Suy ra
2 5 702 . .7
xq
S rl
Câu 18: Trong không gian
,Oxyz
điểm nào dưới đây thuộc đường thẳng
12
:3
45
xt
d y t
zt


?
A.
3; 2 ; 1P 
. B.
2 ;1; 5N
. C.
1; 3; 4M
. D.
4;1; 3Q
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng
;ab
?
A.
4
. B.
2
. C.
7
. D.
3
.
Lời giải:
Từ đồ thị hàm số suy ra hàm số có 3 điểm cực tiểu trên khoảng
;ab
.
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 10
Câu 20: Tiệm cận đứng của đồ thị hàm số
35
2
x
y
x
là
A.
2x
. B.
2y
. C.
3x
. D.
3y
.
Lời giải:
Ta có
22
35
lim lim
2



xx
x
y
x
;
22
35
lim lim
2



xx
x
y
x
.
Vậy tiệm cận đứng của đồ thị hàm số là
2x
.
Câu 21: Bất phương trình
22
log (3 2) log (6 5 )xx
có tập nghiệm là
( ; )ab
. Tổng
ab
bằng
A.
8
3
. B.
28
15
. C.
26
5
. D.
11
5
.
Lời giải:
22
8 8 1
log (3 2) log (6 5 ) 3 2 6 5 0
66
55
xx
x x x x
xx







Suy ra bất phương trình có tập nghiệm là:
6
1; .
5



Vậy tổng
6 11
1
55
ab
.
Câu 22: Có
10
cái bút khác nhau và
8
quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A.
80
. B.
70
. C.
90
. D.
60
.
Lời giải:
Có
10
cách chọn bút và
8
cách chọn sách.
Số cách chọn một cái bút và một quyển sách là
10.8 80
.
Câu 23: Cho hàm số
2
x
f x x e
. Tìm một nguyên hàm
Fx
của hàm số
fx
thỏa mãn
0 2023F
.
A.
2
2022
x
F x x e
. B.
2
2022
x
F x x e
.
C.
2
2021
x
F x x e
. D.
2023
x
F x e
.
Lời giải:
Ta có
2
2

xx
f x dx x e dx x e C
.
Có
Fx
là một nguyên hàm của
fx
và
0 2023F
.
Suy ra
2
0 2023
x
F x x e C
F
1 2023 2022 CC
.
Vậy
2
2022
x
F x x e
.
Câu 24: Cho
2
2
d1f x x
,
4
2
d4f t t

. Tính
4
2
dI f y y
.
A.
5I
. B.
3I
. C.
3I 
. D.
5I 
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 11
Do tích phân không phụ thuộc vào biến số nên
44
22
d d 4f t t f x x


.
Ta có
4 4 4 2
2 2 2 2
d d d d 4 1 5I f y y f x x f x x f x x

.
Câu 25: Họ nguyên hàm của hàm số
3
2f x x
x

là
A.
2
3
2.C
x

B.
2
2
3
.xC
x

C.
2
ln .x x C
D.
2
3ln .x x C
Lời giải:
2
3
2 3ln .f x dx x dx x x C
x




Câu 26: Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây?
A.
2;
. B.
;1
. C.
0;
. D.
0;2
.
Câu 27: Cho hàm số
y f x
xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại
0x
. B. Hàm số đạt cực tiểu tại
4x 
.
C. Hàm số đạt cực đại tại
2x 
. D. Hàm số đạt cực đại tại
1x
.
Lời giải:
Dựa vào bảng biến thiên của hàm số
y f x
ta thấy hàm số đạt cực đại tại
2x 
.
Câu 28: Với
a
và
b
là hai số thực dương tùy ý;
34
2
log ab
bằng
A.
22
11
log log .
34
ab
B.
22
3log 4log .ab
C.
24
2 log log .ab
D.
22
4log 3log .ab
Lời giải:
Ta có:
3 4 3 4
2 2 2 2 2
log log log 3log 4loga b a b a b
nên B đúng.
Câu 29: Cho hình phẳng
H
giới hạn bởi các đường
2
2y x x
,
0y
. Quay
H
quanh trục hoành
tạo thành khối tròn xoay có thể tích được tính bởi công thức nào dưới đây?
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 12
A.
2
2
0
2 d .
x x x
B.
2
2
2
0
2 d .
x x x
C.
2
2
2
0
2 d .
x x x
D.
2
2
0
2 d .
x x x
Lời giải:
Theo công thức ta chọn
2
2
2
0
2d
V x x x
.
Câu 30: Cho hình lập phương
.
ABCD A B C D
. Góc giữa đường thẳng
AB
và mặt phẳng
ABC D
bằng
A.
60 .
B.
90 .
C.
30 .
D.
45 .
Lời giải:
A'
D'
B'
C'
B
C
A
D
Góc giữa
AB
và mặt phẳng
ABC D
là góc
0
45
B AB
.
Câu 31: Cho hàm số bậc ba
32
34y x x
có đồ thị như hình vẽ bên dưới:
x
y
-1
2
4
O
Tìm tất cả các giá trị thực của
m
sao cho phương trình
32
3 4 0x x m
có 3 nghiệm thực
phân biệt.
A.
24m
. B.
04m
. C.
4
0
m
m
. D.
04m
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 13
x
y
-1
2
4
O
Ta có
3 2 3 2
3 4 0 3 4x x m x x m
. Số nghiệm của phương trình trên là số giao điểm
của đồ thị hàm số
32
34y x x
và đường thẳng
ym
.
Dựa vào đồ thị ta thấy đồ thị hàm số
32
34y x x
và đường thẳng
ym
cắt nhau tại 3
điểm phân biệt khi và chỉ khi
04m
.
Câu 32: Hàm số
y f x
liên tục trên và có đạo hàm
2
1 1 , .
f x x x x x
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
1;2 .
B.
1;0 .
C.
0;1 .
D.
2; 1 .
Lời giải:
Xét hàm số
y f x
có
2
2
1 1 1 1f x x x x x x x
.
2
0
0 1 1 0 1
1
x
f x x x x x
x

.
Suy ra bảng xét dấu của hàm
fx
:
Từ bảng xét dấu của hàm
fx
suy ra hàm số
y f x
nghịch biến trên khoảng
1;0
Câu 33: Một hộp chứa
15
quả cầu gồm
6
quả màu đỏ được đánh số từ
1
đến
6
và
9
quả màu xanh
được đánh số từ
1
đến
9
. Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả
khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng
A.
9
.
35
B.
18
.
35
C.
4
.
35
D.
1
.
7
Lời giải:
Số cách lấy ngẫu nhiên
2
quả cầu từ hộp là:
2
15
105C
cách
Để tổng hai số ghi trên hai quả cầu là số chẵn ta có
2
TH sau:
TH 1: Hai quả cầu khác màu cùng đánh số lẻ:
11
35
. 15CC
cách
TH 2: Hai quả cầu khác màu nhau cùng đánh số chẵn:
11
34
. 12CC
cách
Vậy xác suất cần tính là:
12 15 9
.
105 35
P

Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 14
Câu 34: Tích tất cả các nghiệm của phương trình
2
log 2log 3 0 xx
bằng
A.
1
.
10
B.
100.
C.
10.
D.
1
.
100
Lời giải:
Ta có:
2
3
3
0
10
log 1
10
log 2log 3 0
log 3
10
10


x
x
x
x
xx
x
x
x
Vậy
12
1
..
100
xx
Câu 35: Trong mặt phẳng
,Oxy
tập hợp các điểm
M
biểu diễn số phức
z
thỏa mãn
| 3 | 2zi
là
A. đường tròn
22
3 1 4xy
. B. đường tròn
22
3 1 4xy
.
C. đường tròn
22
3 1 2xy
. D. đường thẳng
3 2 0.xy
Lời giải:
Đặt
,z x yi x y
. Ta có
2 2 2 2
3 2 3 1 2 3 1 4.z i x y x y
Câu 36: Trong không gian
,Oxyz
phương trình đường thẳng đi qua hai điểm
;;A 1 1 2
và
là
A.
xt
yt
zt


12
1.
22
B.
xt
yt
zt
12
1.
22
C.
xt
yt
zt



32
.
42
D.
xt
yt
zt


52
1.
62
Lời giải:
Kiểm tra sự kiện:
Ad
và vectơ chỉ phương
;;AB 2 1 2
ta thấy phương án D thỏa mãn.
Câu 37: Trong không gian
,Oxyz
cho
23a i j k
. Tọa độ của vectơ
a
là
A.
1;2; 3
. B.
2; 3; 1
. C.
2; 1; 3
. D.
3;2; 1
.
Câu 38: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
,2AB a AD a
SA ABCD
và
SA a
(tham khảo hình vẽ)
Khoảng cách từ
A
đến mặt phẳng
SBD
bằng
A.
3
2
a
. B.
21
7
a
. C.
10
5
a
. D.
2
5
a
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 15
Gọi
K
là hình chiếu vuông góc của
A
trên
BD
.
Khi đó:
AK BD
BD SAK
BD SA

.
mà
BD SBD
suy ra
SBD SAK
mà
SBD SAK SK
nên kẻ
AH SK
thì
AH SBD
.
Vậy
,d A SBD AH
Xét tứ diện vuông
AS BD
suy ra
22222222
2
51
2
111111
aaaaASABADAH
.
Suy ra
5
10a
AH
. Vậy
5
10
))(,(
a
SBDAd
.
Câu 39: Trong không gian
,Oxyz
gọi
H
hình chiếu vuông góc của
2;0;1M
lên đường thẳng
12
:
1 2 1
x y z
. Tìm tọa độ điểm
H
.
A.
2;2;3H
. B.
0; 2;1H
. C.
1;0;2H
. D.
1; 4;0H 
.
Lời giải:
Ta có
1
:2
2
xt
yt
zt



t
mà
1;2 ; 2 1;2 ; 1H H t t t MH t t t
.
Đường thẳng
có một VTCP là
1;2;1u
.
Khi đó
. 0 1 4 1 0 0 1;0;2MH MH u t t t t H
.
Câu 40: Một hình trụ có bán kính bằng
2a
. Hai điểm
,AB
lần lượt thuộc hai đường tròn đáy sao cho
4A B a
. Biết khoảng cách giữa
AB
và trục bằng
a
. Tính thể tích khối trụ đã cho.
A.
3
2
Va
. B.
3
82
3
a
V
. C.
3
42
Va
. D.
3
8
Va
.
Lời giải:
Bộ đề cơ bản Ôn thi THPT Quốc gia
Trang 16
a
Dựng các đường sinh
AC
và
BD
.
Ta có
//OO ACBD
, , ,d OO AB d OO ACBD d O ACBD

.
Gọi
H
là trung điểm của
BC
OH ACBD
,.d O ACBD OH a
Tam giác
OHC
vuông tại
H
suy ra
3HC a
nên
23BC a
Tam giác
ABC
vuông tại
C
2AC OO a
.
Vậy khối trụ đã cho có thể tích
2 2 3
.4 .2 8V r h a a a
.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023
| 1/124
| | Tải xuống

Có thể bạn quan tâm:

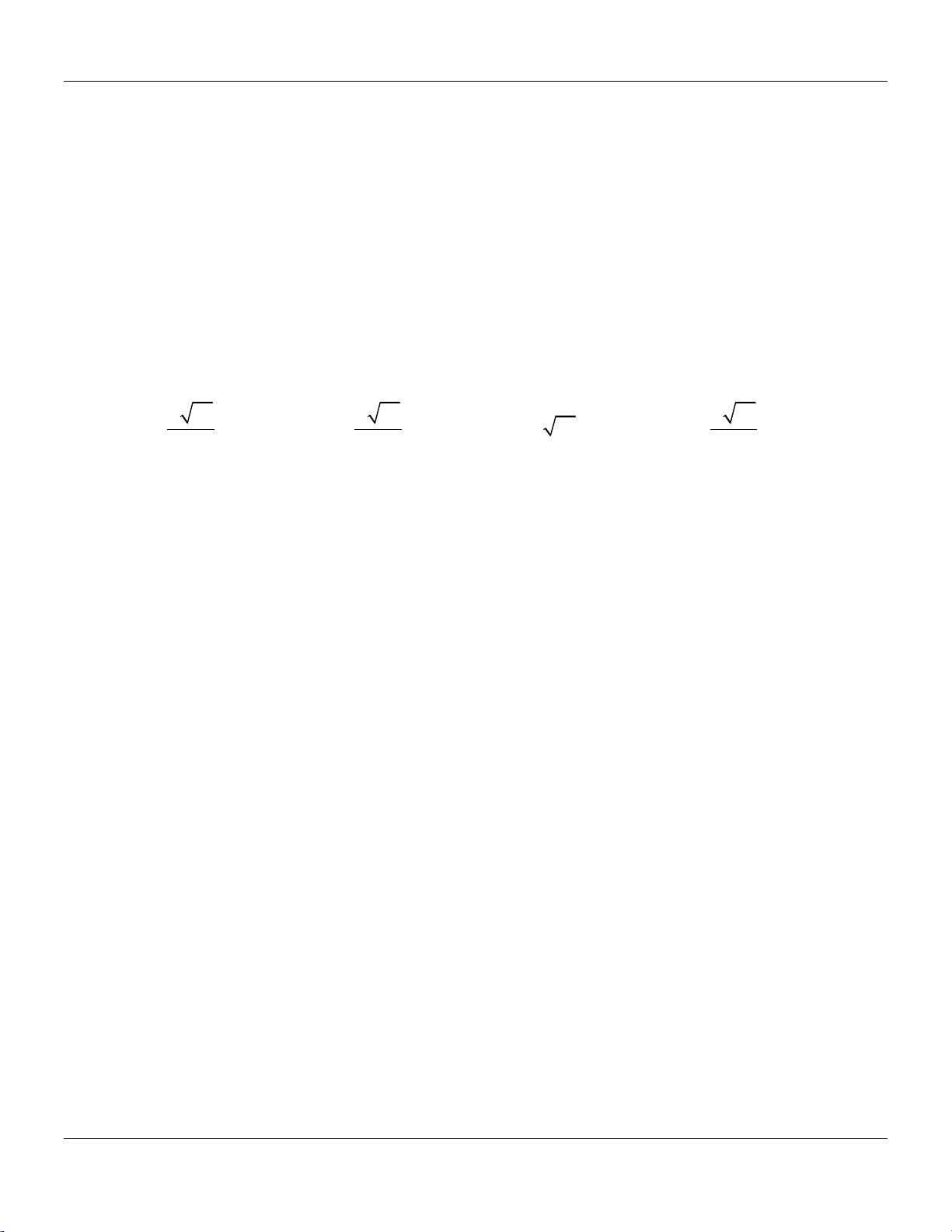
Preview text:

Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 01_______________
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 3  2i có tọa độ là A. 2;3. B. 2;3. C. 3; 2. D. 3; 2.
Câu 2: Trên khoảng 0;  , đạo hàm của hàm số y  log x là 7 1 1 ln 7 1
A. y  . B. y  . C. y  . D. y   . x xln7 x x ln7
Câu 3: Trên khoảng 0;  , đạo hàm của hàm số e y x là e1 x A. e 1 y e.x    . B. e 1 y x    . C. y  . D.   . e y e x . e  1
Câu 4: Tập nghiệm của bất phương trình 2x  4 là A.  ;  2 B. 0; 2 C.  ;  2 D. 0; 2
Câu 5: Cho cấp số nhân u u  5 u  2 n  với 1 và 2
. Công bội của cấp số nhân đó bằng 5 2 A. 1. B. 28 . C. . D. . 2 5
Câu 6: Trong không gian Oxyz, cho mặt phẳng  P : 3x z  2  0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của  P ? A. n  1  ;0; 1  . B. n  3; 1  ;2 . C. n  3; 1  ;0 . D. n  3;0; 1  . 2   3   1   4   ax b
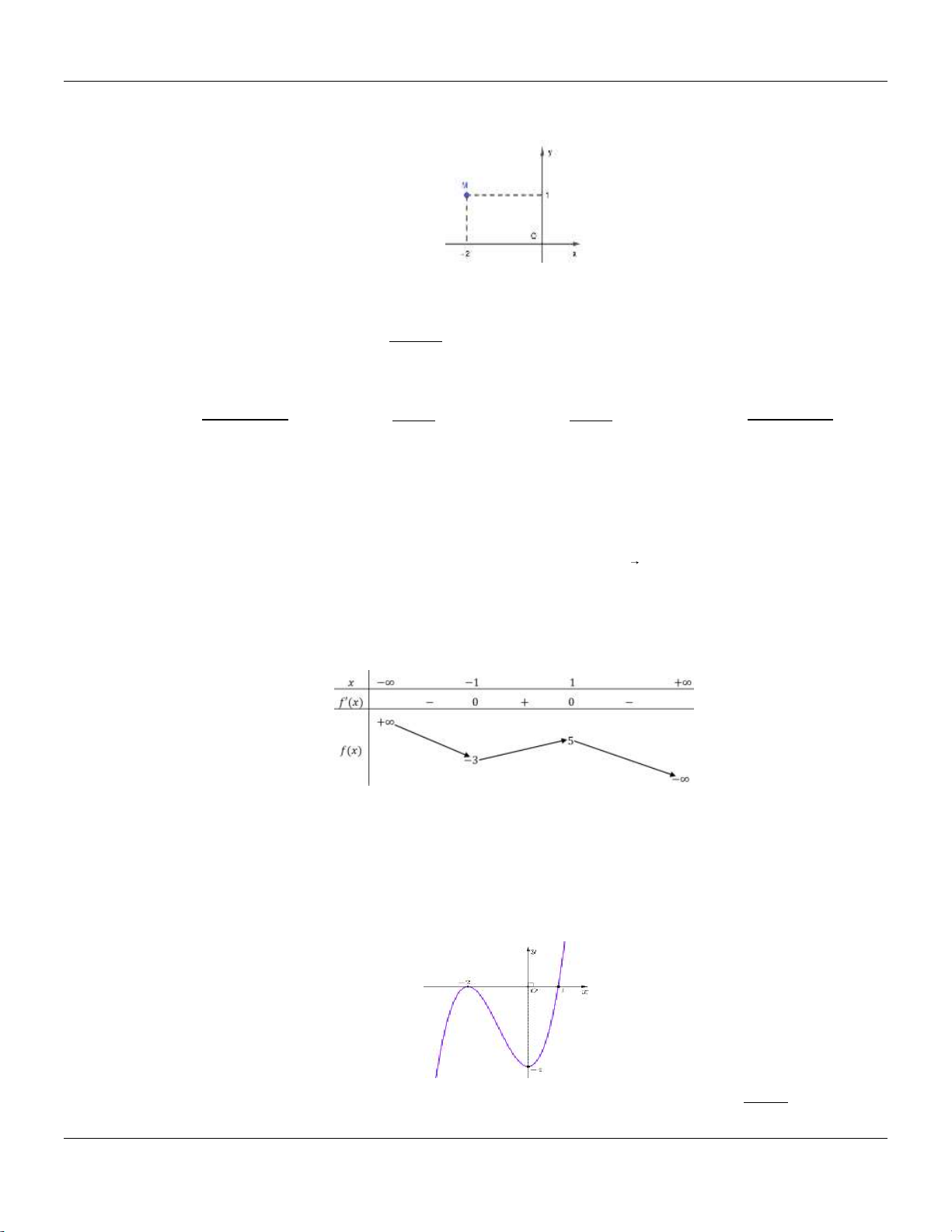
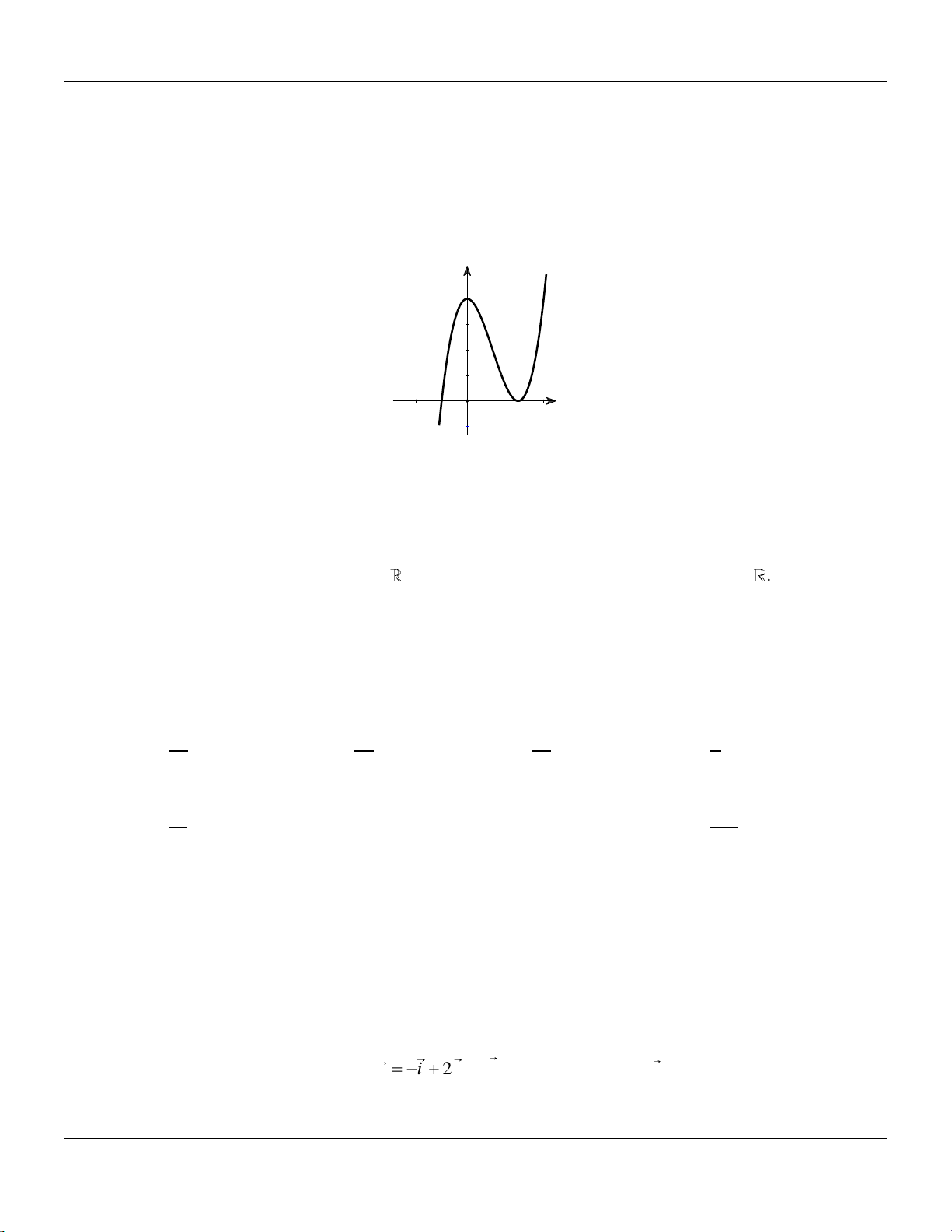
Câu 7: Cho hàm số y
có đồ thị như hình bên dưới : cx d
Tọa độ giao điểm của đồ thị hàm số đã cho với trục tung là A. 0; 2  . B. 2;0.
C. 2;0. D. 0; 2. 1 1
Câu 8: Cho hàm số f x và g x liên tục trên đoạn 0;  1 và f
 xdx 1, g
 xdx  3. Tích phân 0 0 1 2 f
 x3gxdx  bằng 0 A. 9 . B. 5 . C. 10 . D. 11.
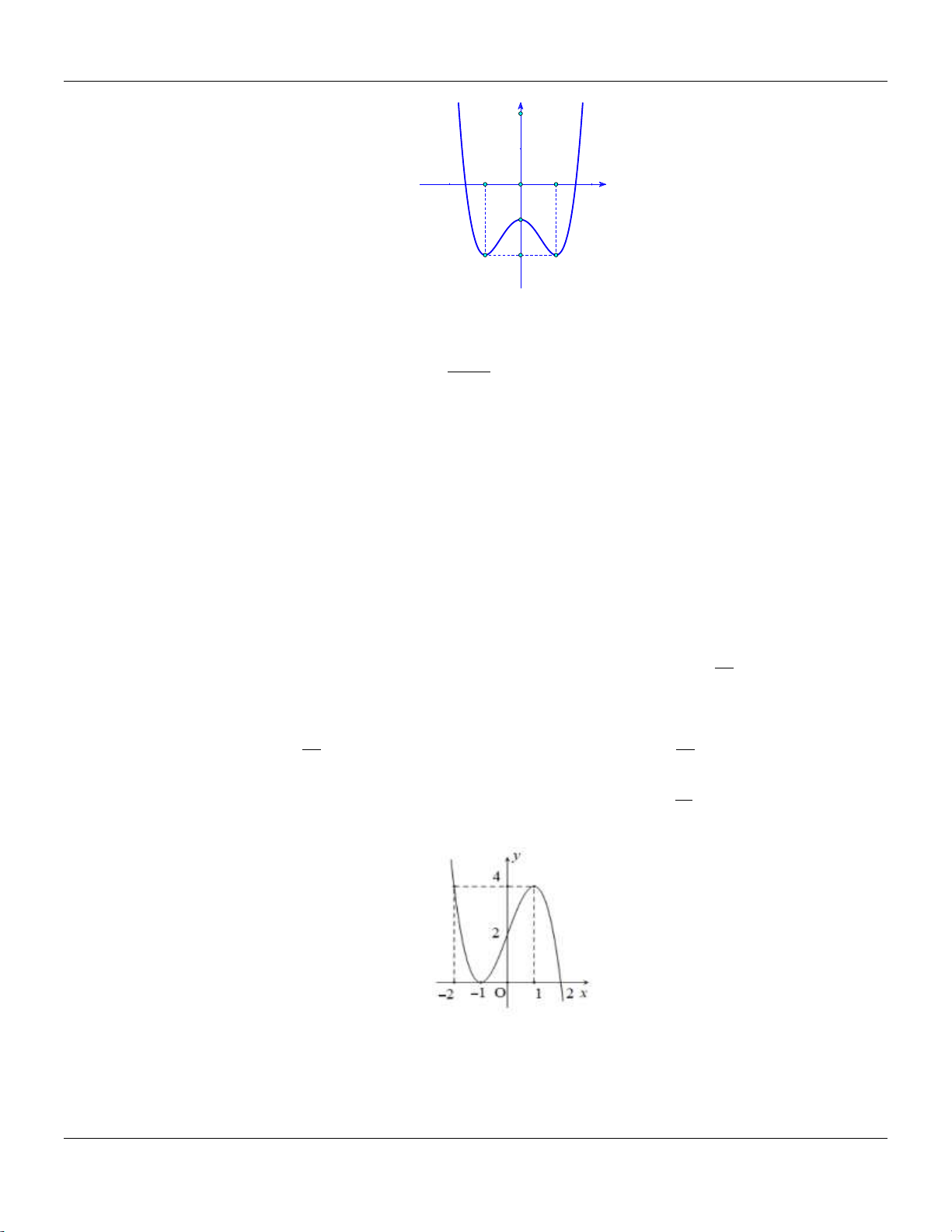
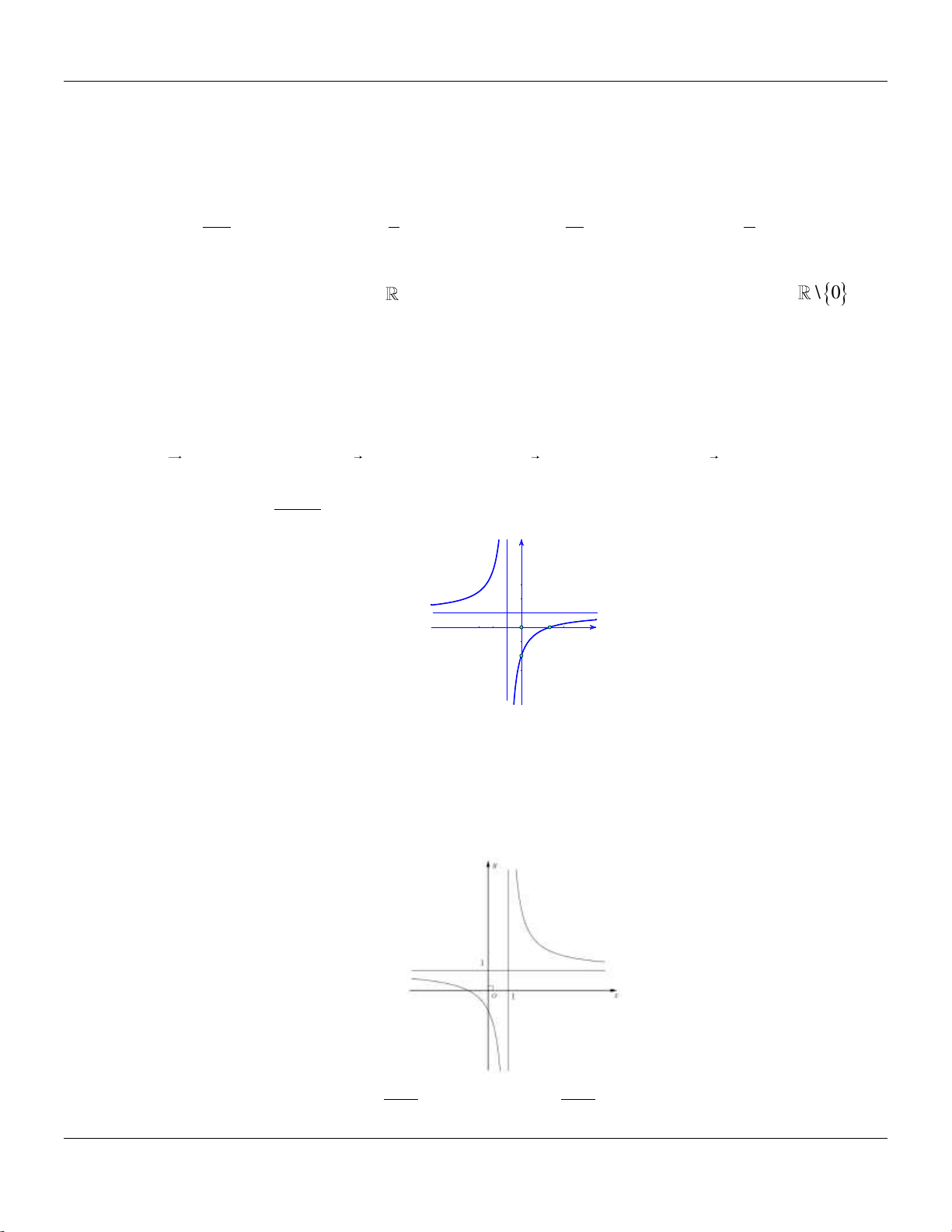
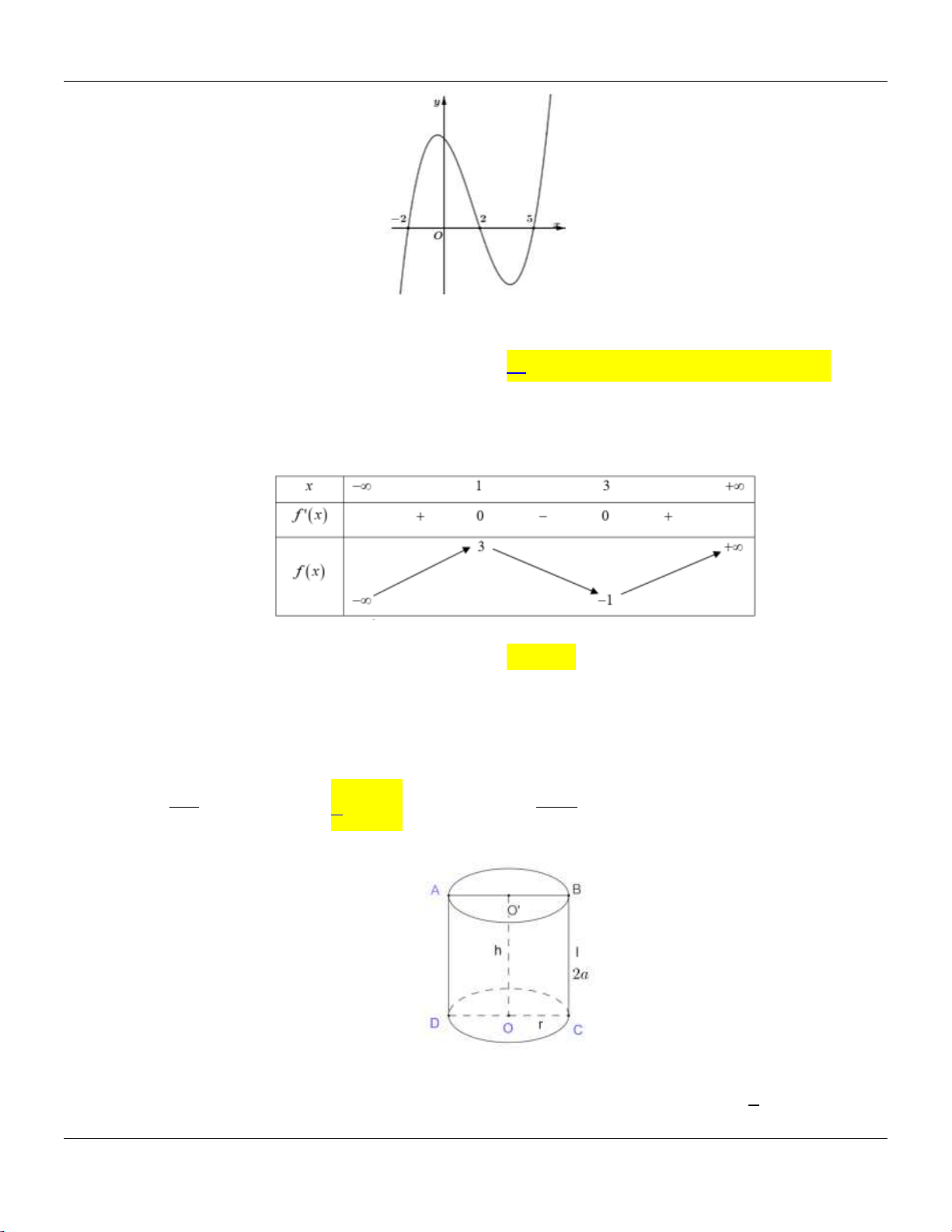
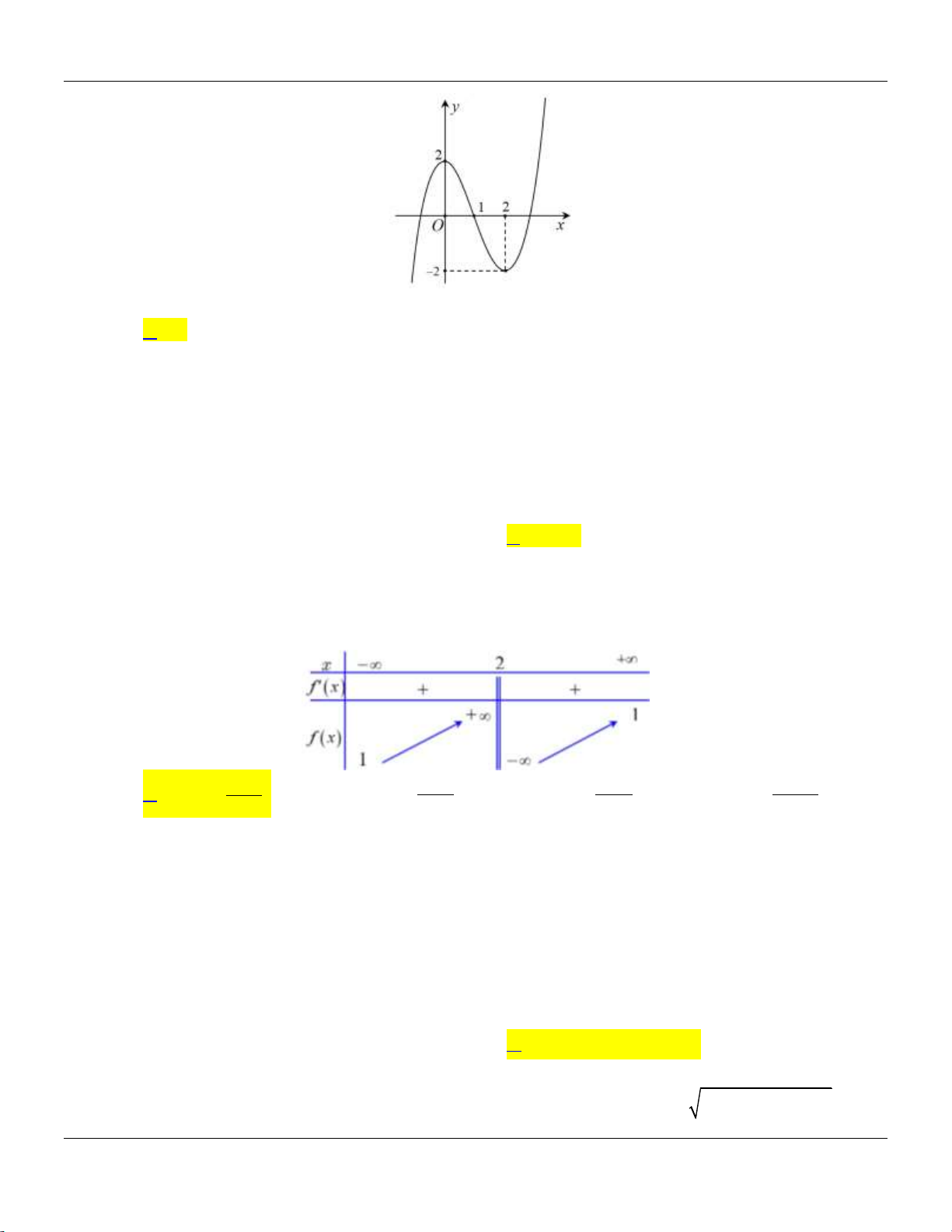
Câu 9: Hàm số nào có đồ thị là đường cong trong hình vẽ bên dưới? Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia x 1 A. 4 2
y x  4x 1. B. y
y x x  . D. 2 y  2x 1 . x  . C. 3 2 4 1 2 2 2 2
Câu 10: Trong không gian Oxyz, cho mặt cầu S  :  x   1
  y  2  z   1
 9 . Tìm tọa độ tâm I
và tính bán kính R của S . A. I  1  ;2 
;1 và R  3. B. I 1; 2  ;  1 và R  3. C. I  1  ;2 
;1 và R  9. D. I 1; 2  ;  1 và R  9.
Câu 11: Trong không gian Oxyz, góc giữa hai mặt phẳng Oxy và Oxz bằng A. 90 .  B. 60 .  C. 30 .  D. 45 . 
Câu 12: Cho số phức z  2  i, phần ảo của số phức 2 z là A. 4. B. 4 . i C. 3. D. 1.
Câu 13: Cho khối lập phương có cạnh bằng 3. Thể tích khối lập phương đã cho bằng A. 9. B. 27. C. 18. D. 3.
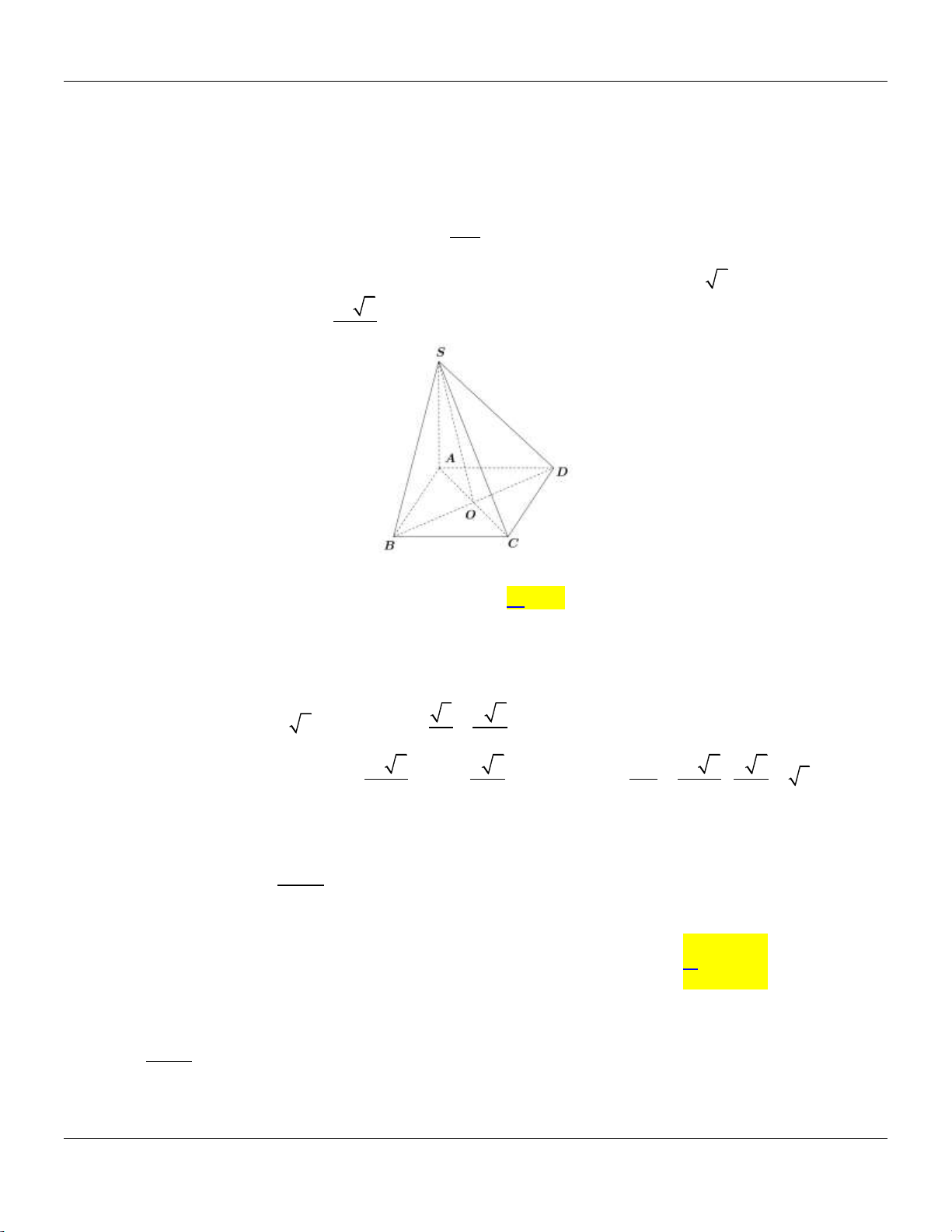
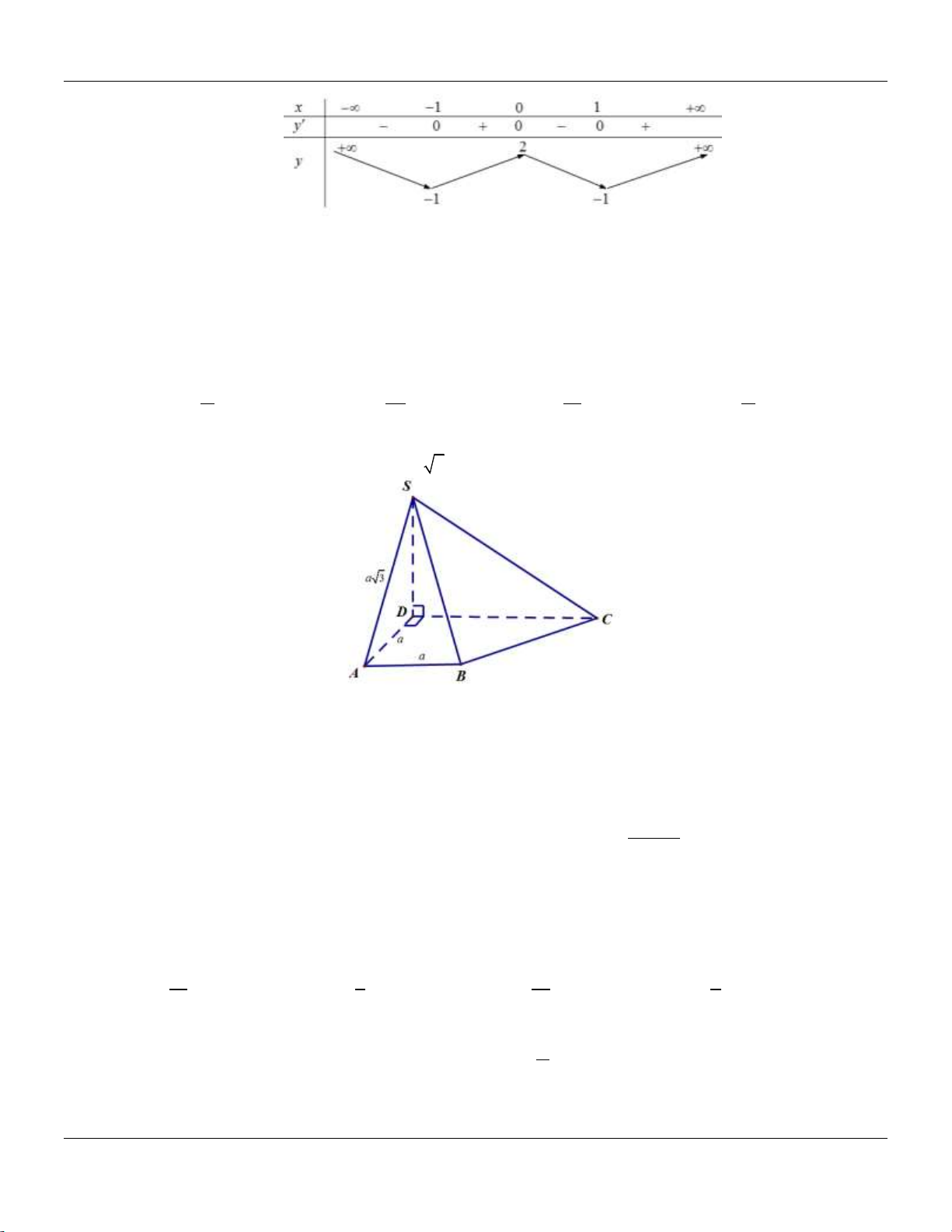
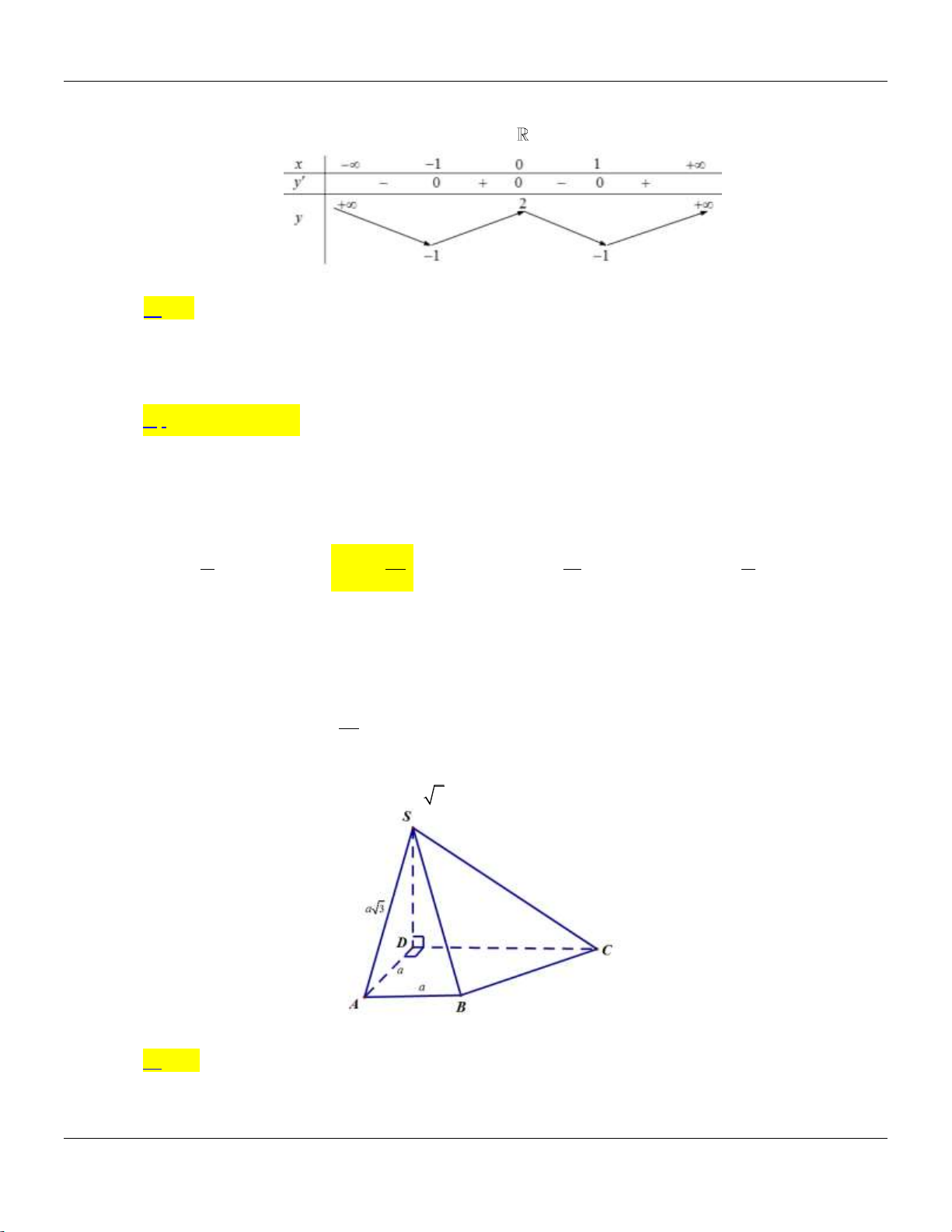
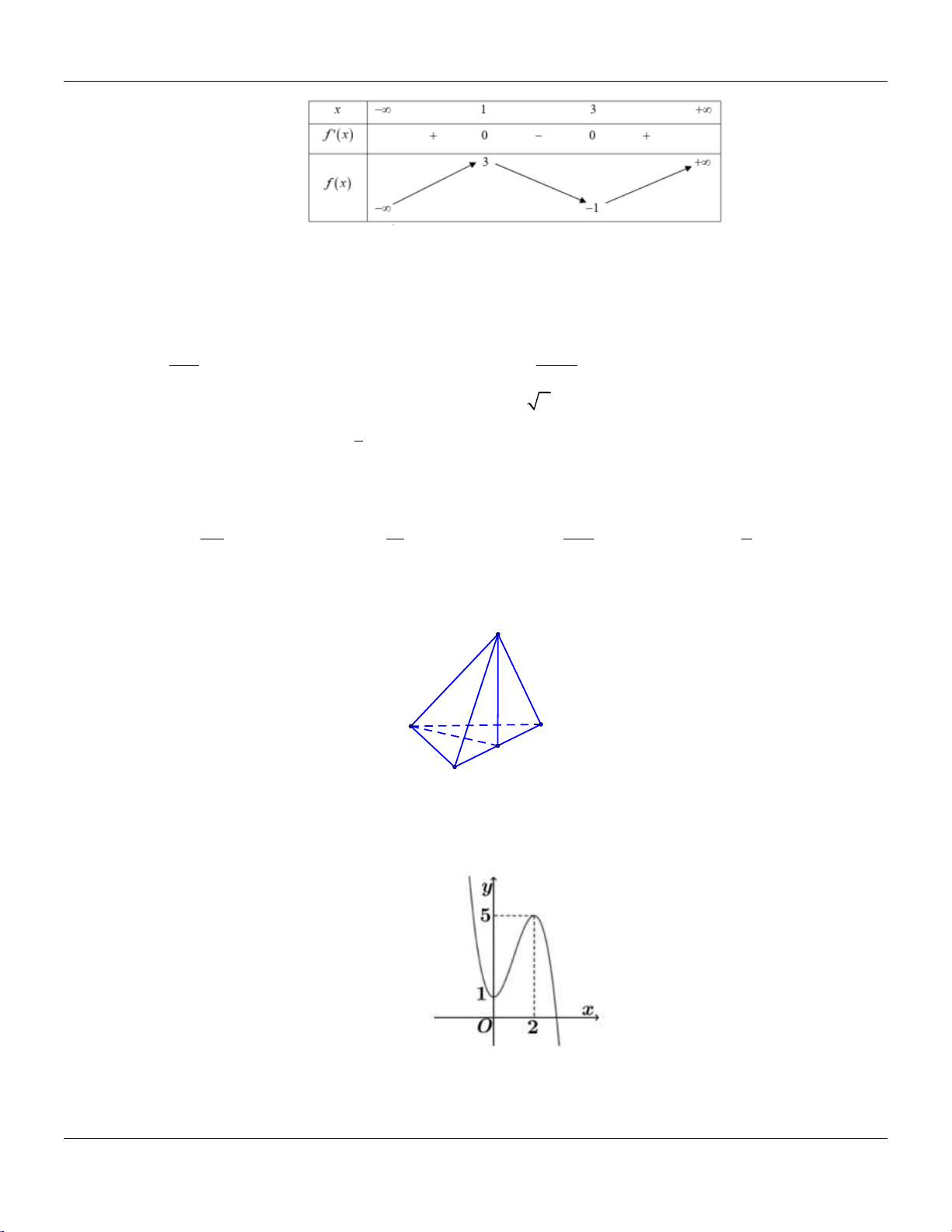
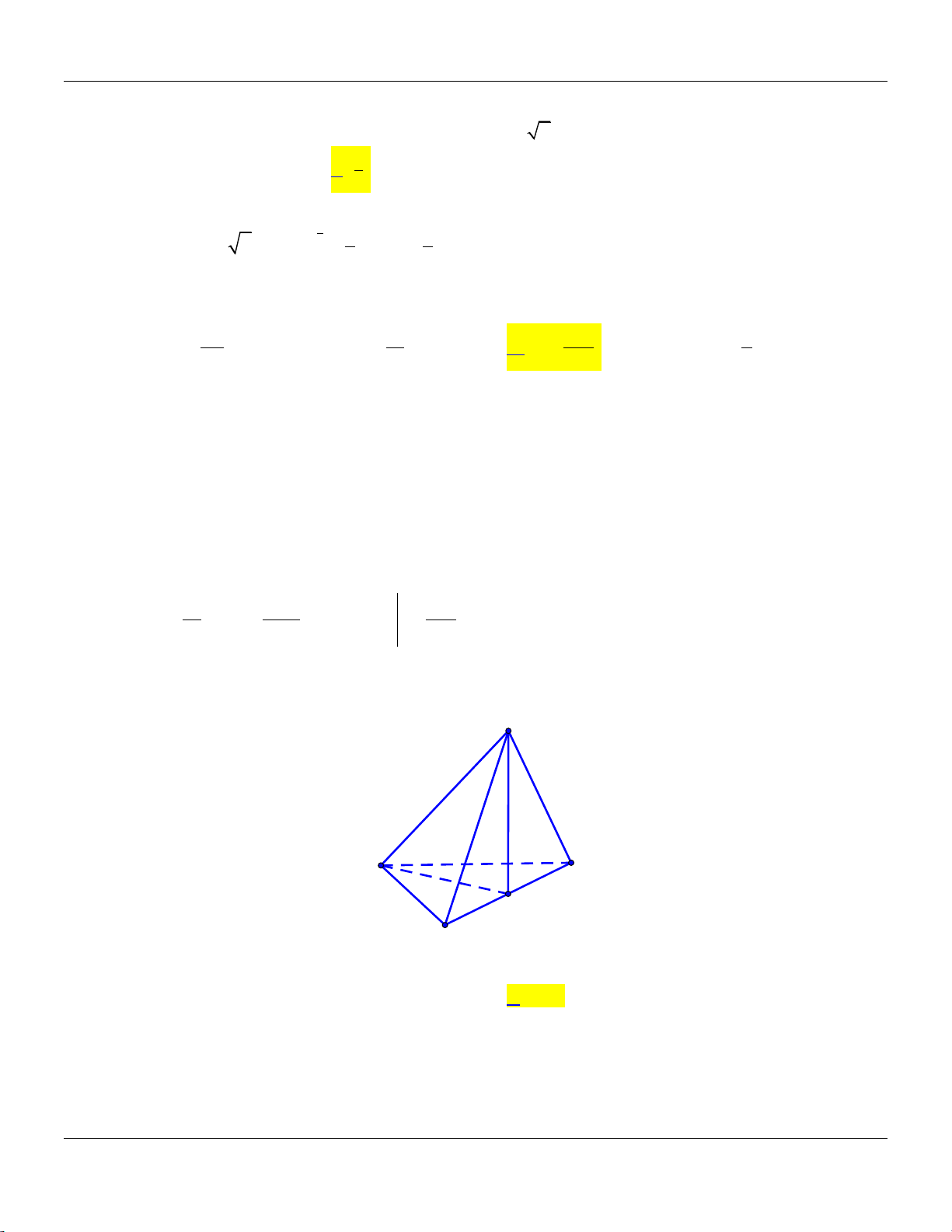
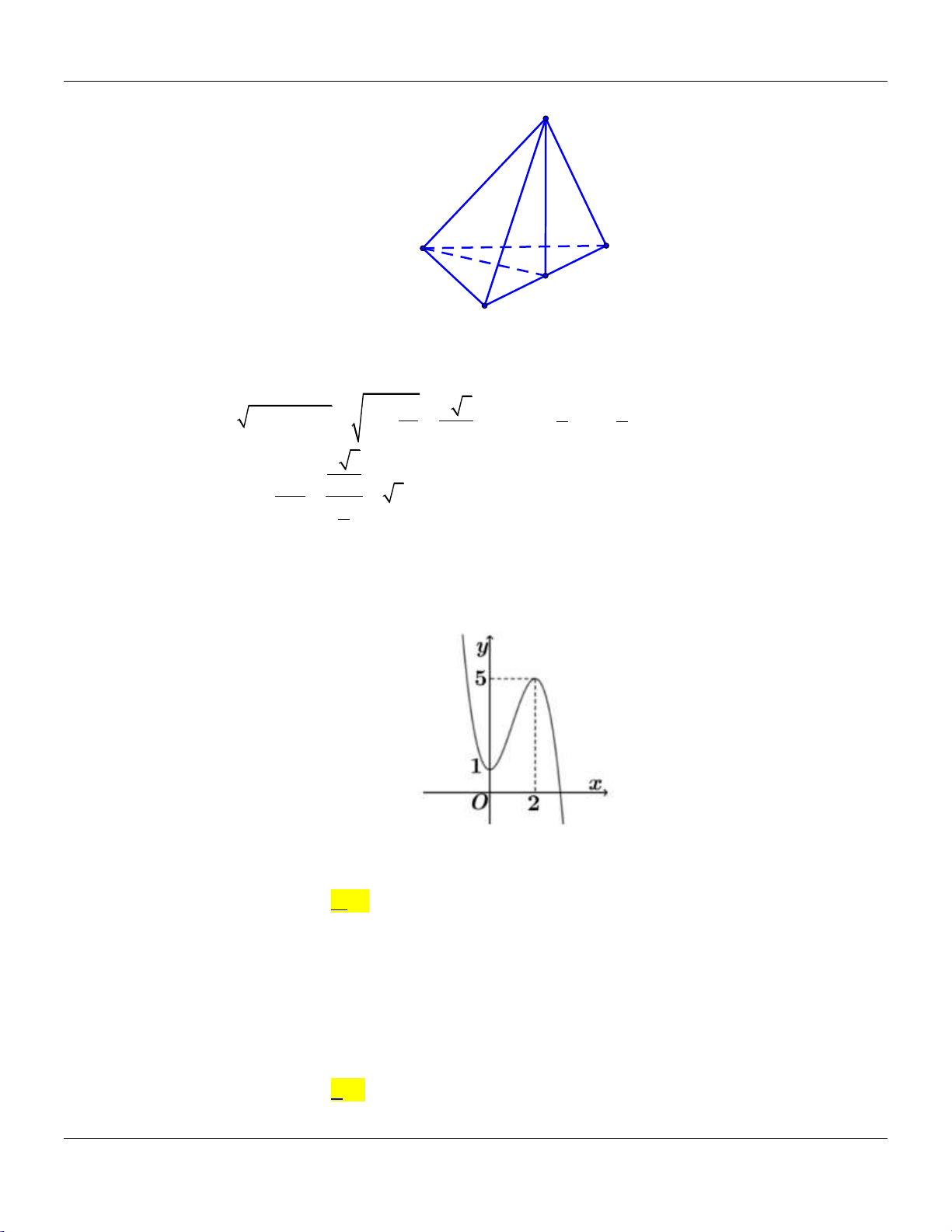
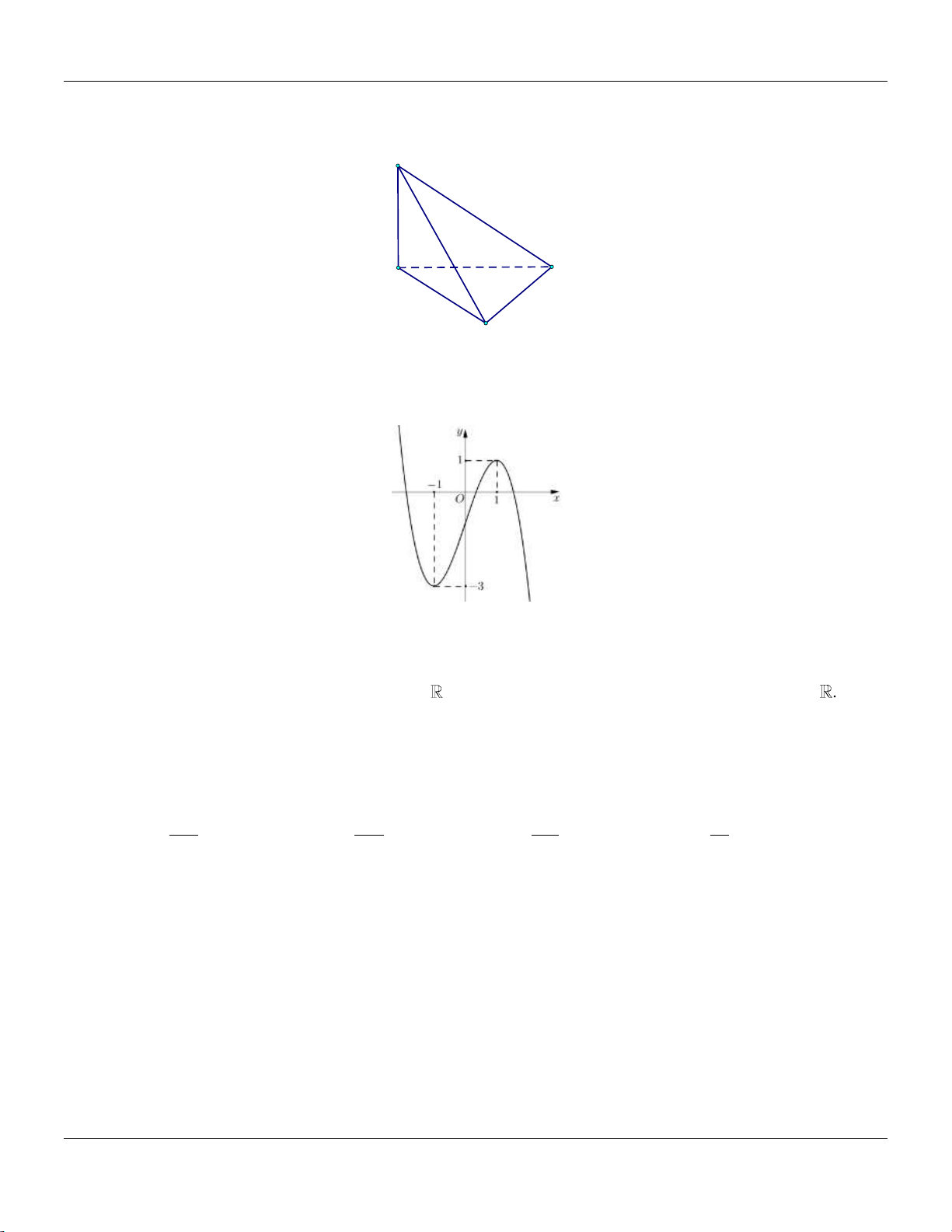
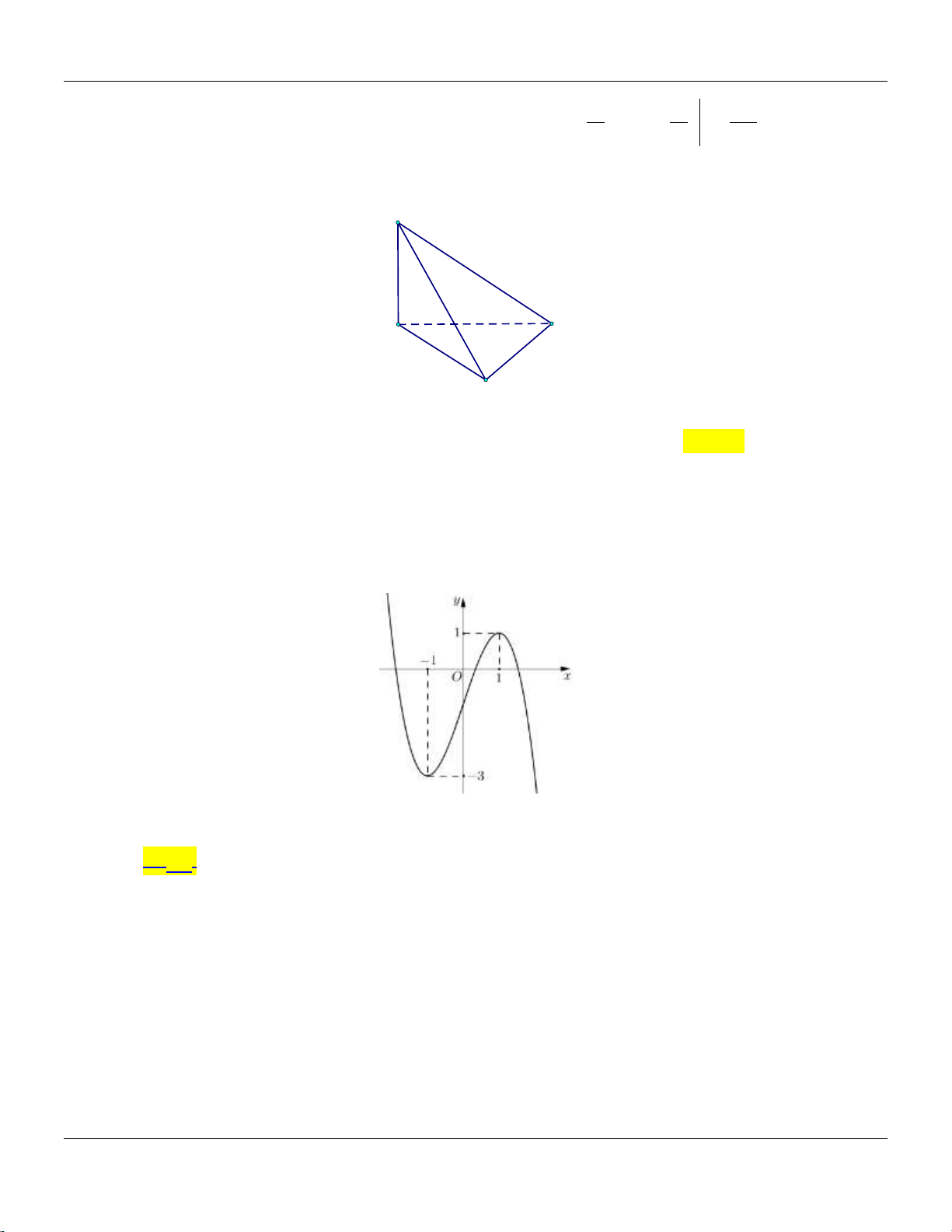
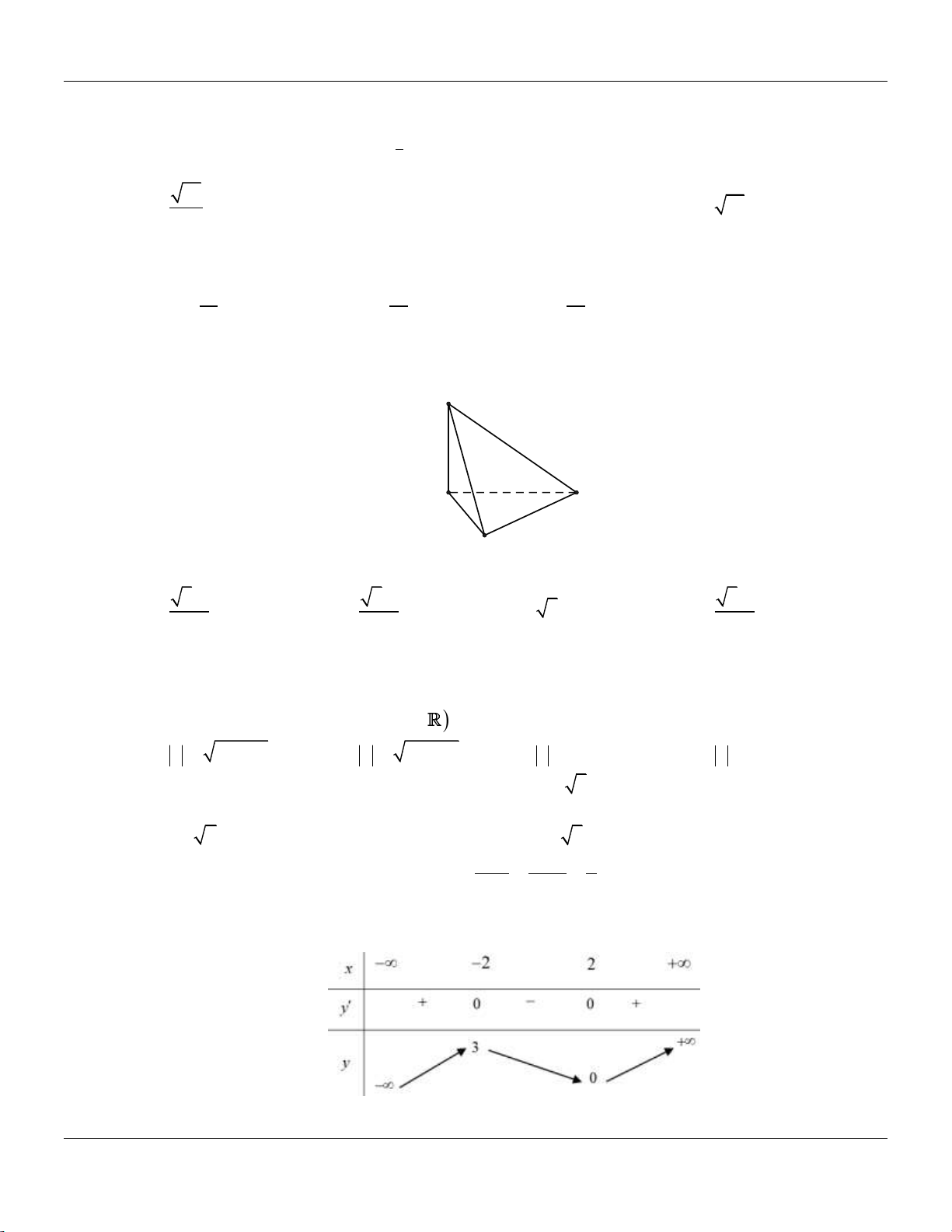
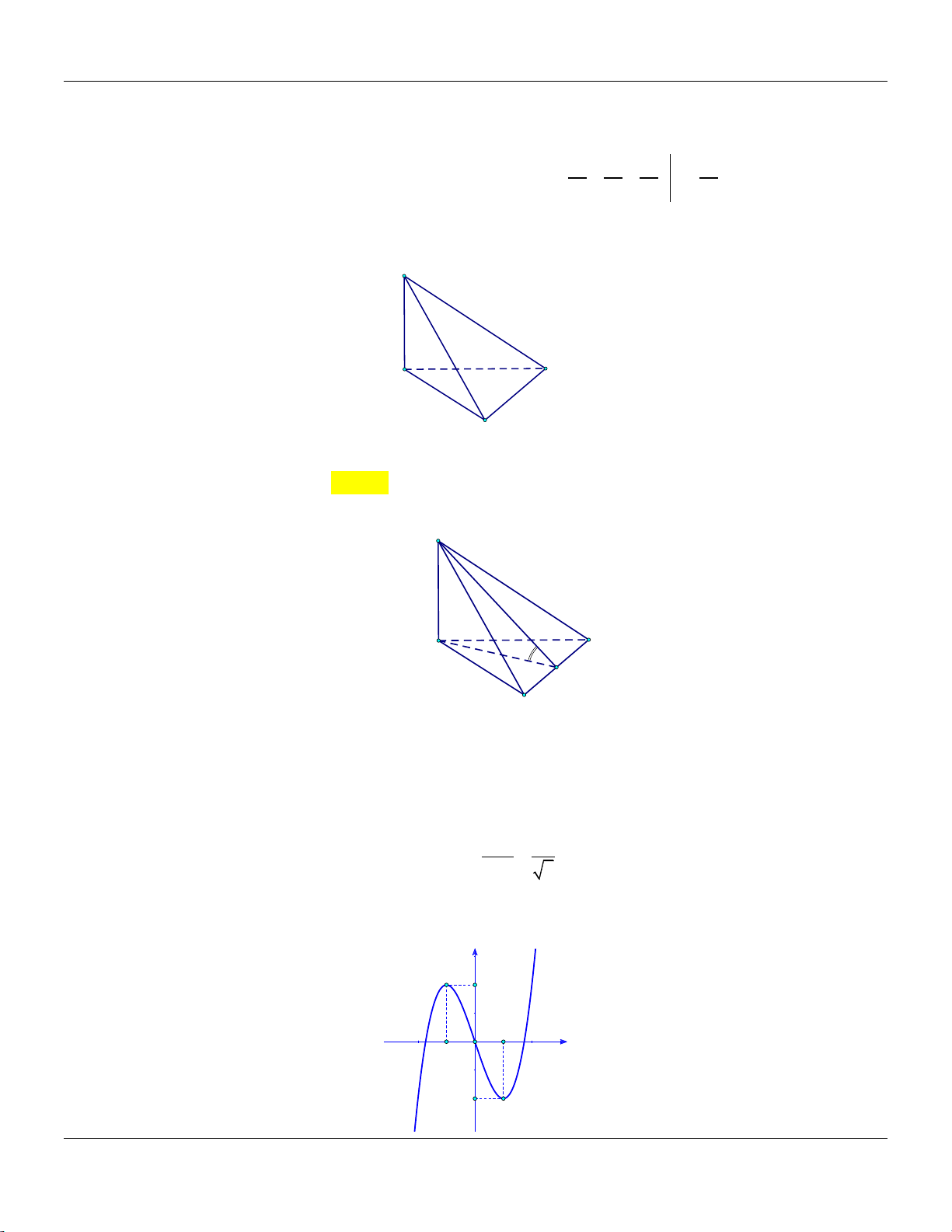
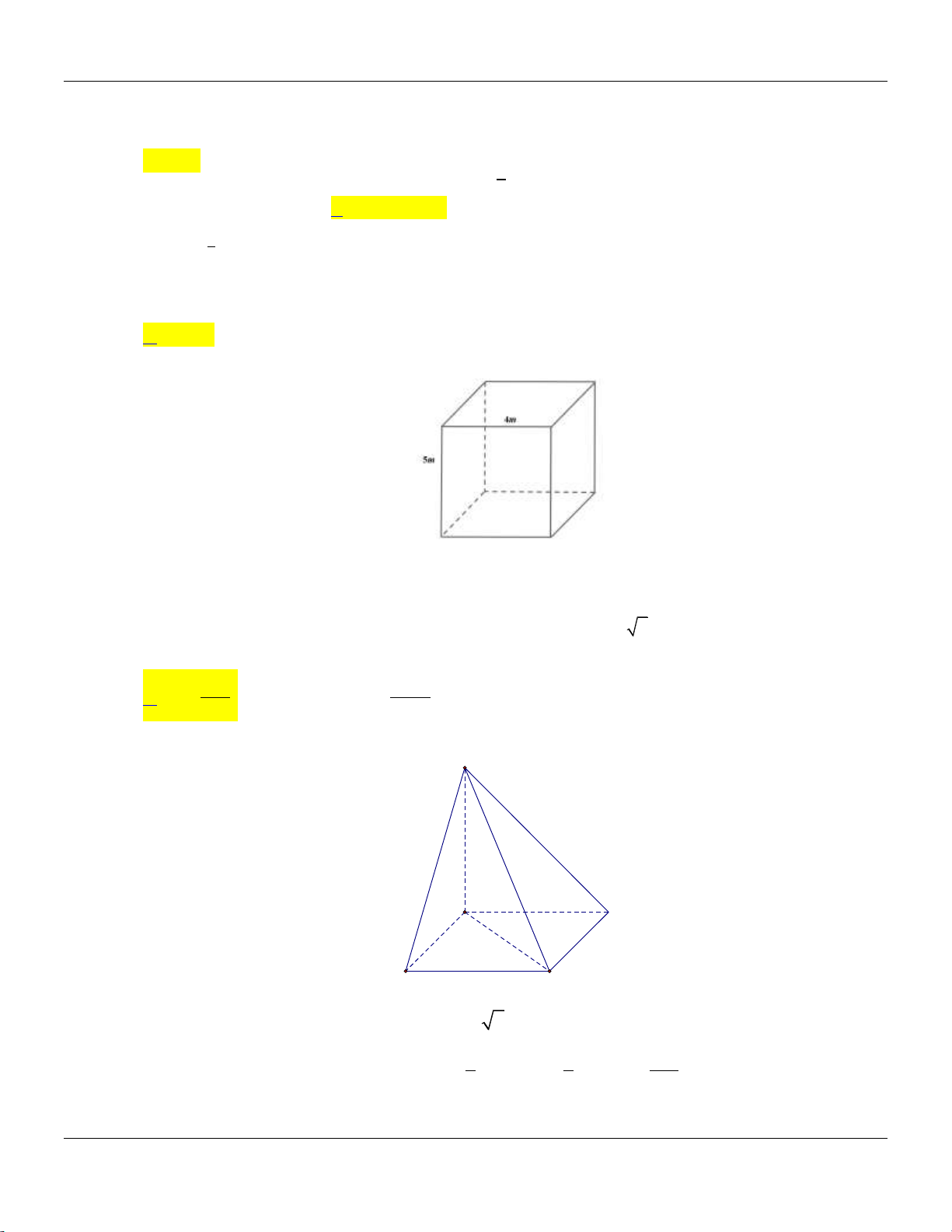
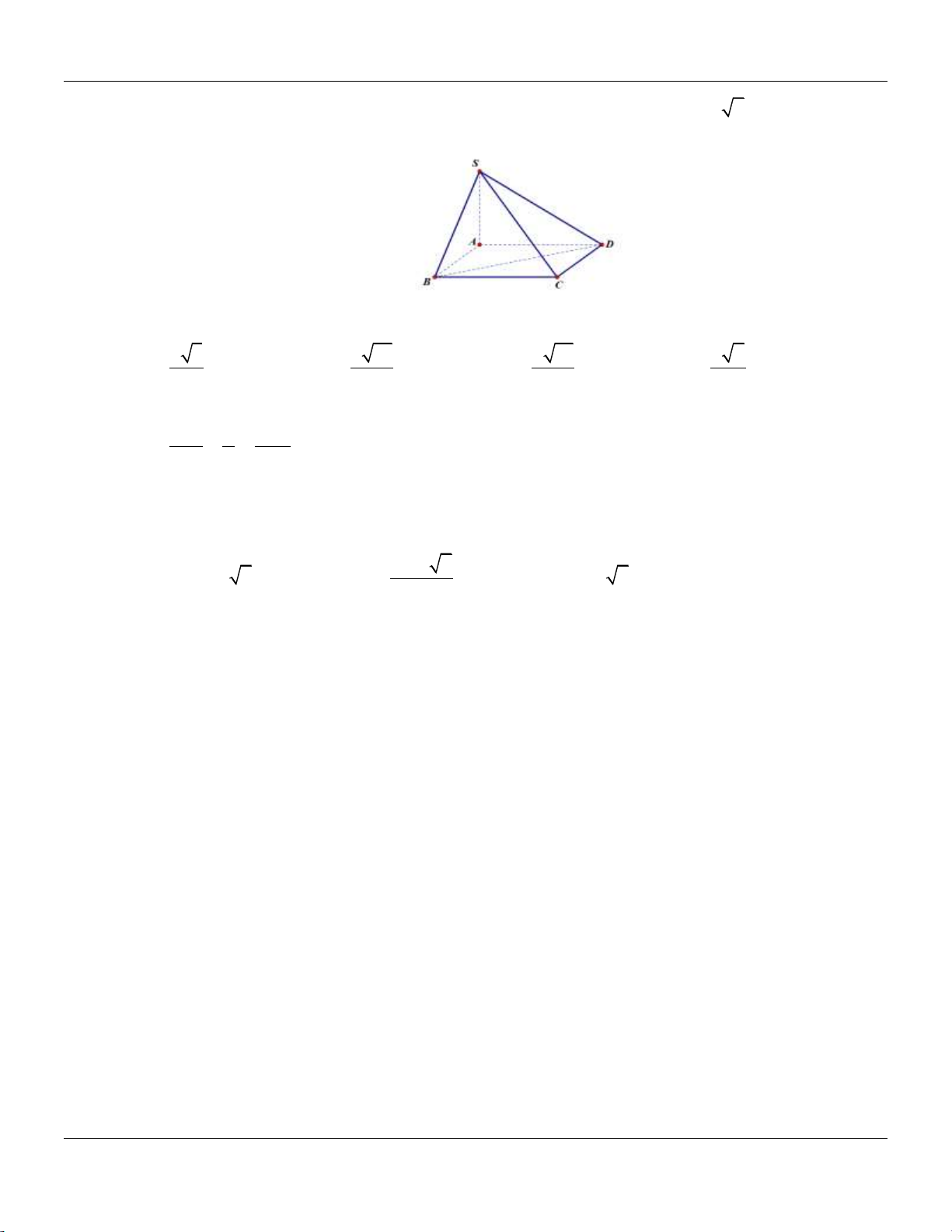
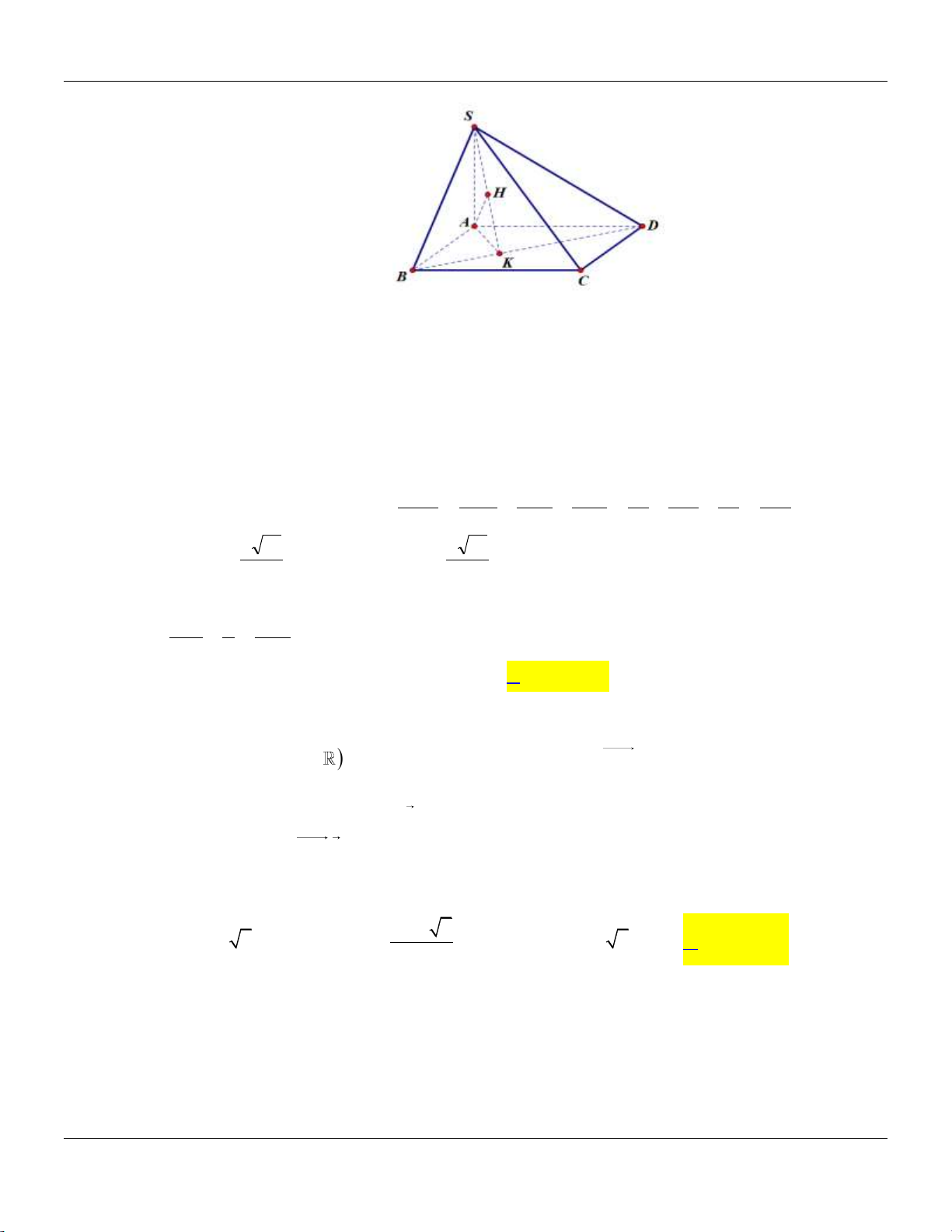
Câu 14: Cho khối chóp .
S ABC có đáy là tam giác vuông tại A, AB  2, AC  4,SA vuông góc với đáy và
SA  3 (tham khảo hình bên). S A C B
Thể tích khối chóp đã cho bằng A. 9. B. 8. C. 4. D. 3.
Câu 15: Cho đường thẳng  và mặt cầu SO; R. Gọi d là khoảng cách từ O đến  và d  . R Số giao
điểm của  và SO; R là A. 1. B. 2. C. 0. D. Vô số.
Câu 16: Phần ảo của số phức z  3  7i là A. 3. B. 7. C. 7. D. 3.
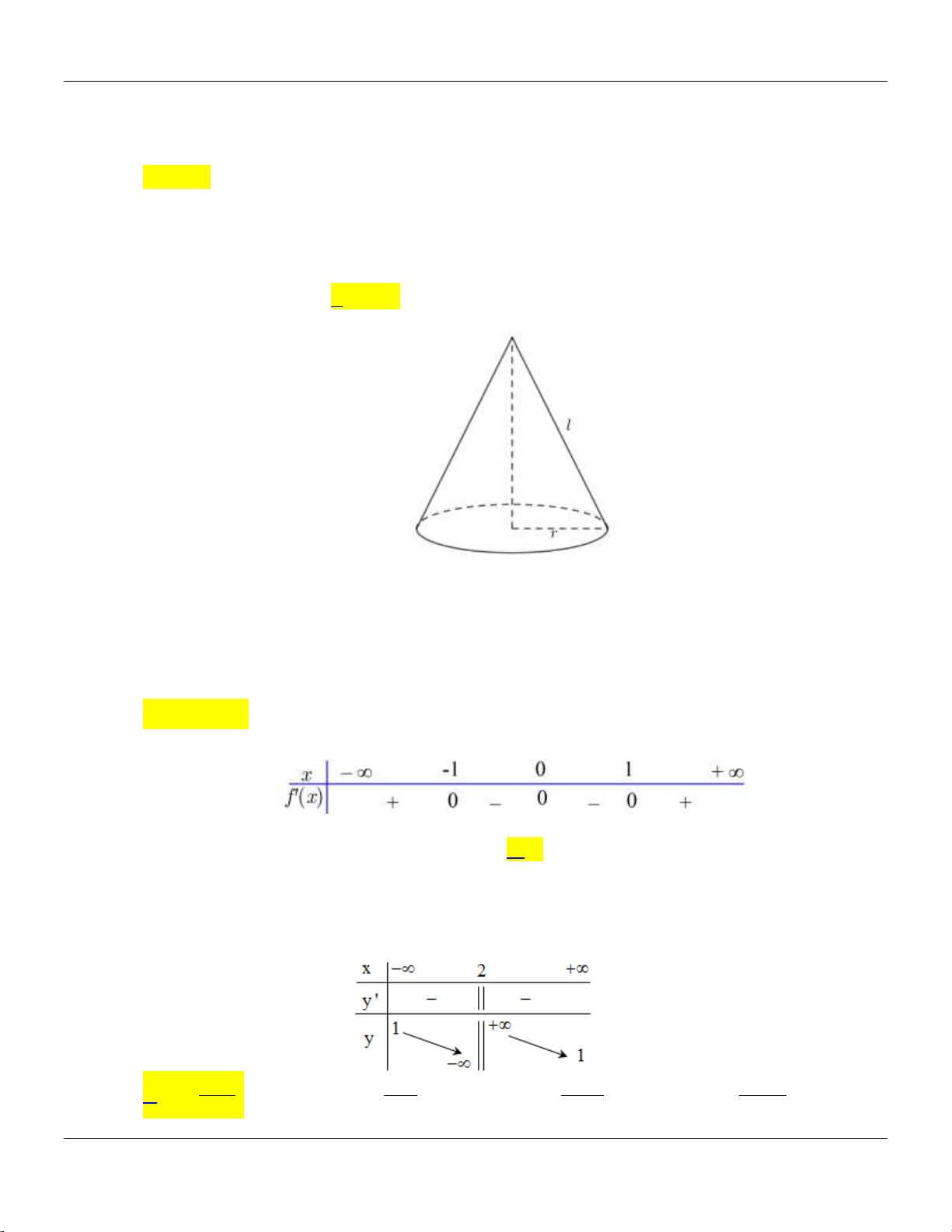
Câu 17: Cho khối nón có đường cao h, độ dài đường sinh l và bán kính đáy r. Diện tích xung quanh
Sxq của khối nón được tính theo công thức nào dưới đây?
A. S   rl   S   rl S   rh xq . B. 1 S rl . C. 2 . D. . xq xq xq 2 x 1 y  2 z  3
Câu 18: Trong không gian Oxyz, đường thẳng d :  
đi qua điểm nào sau đây? 3 4  5 
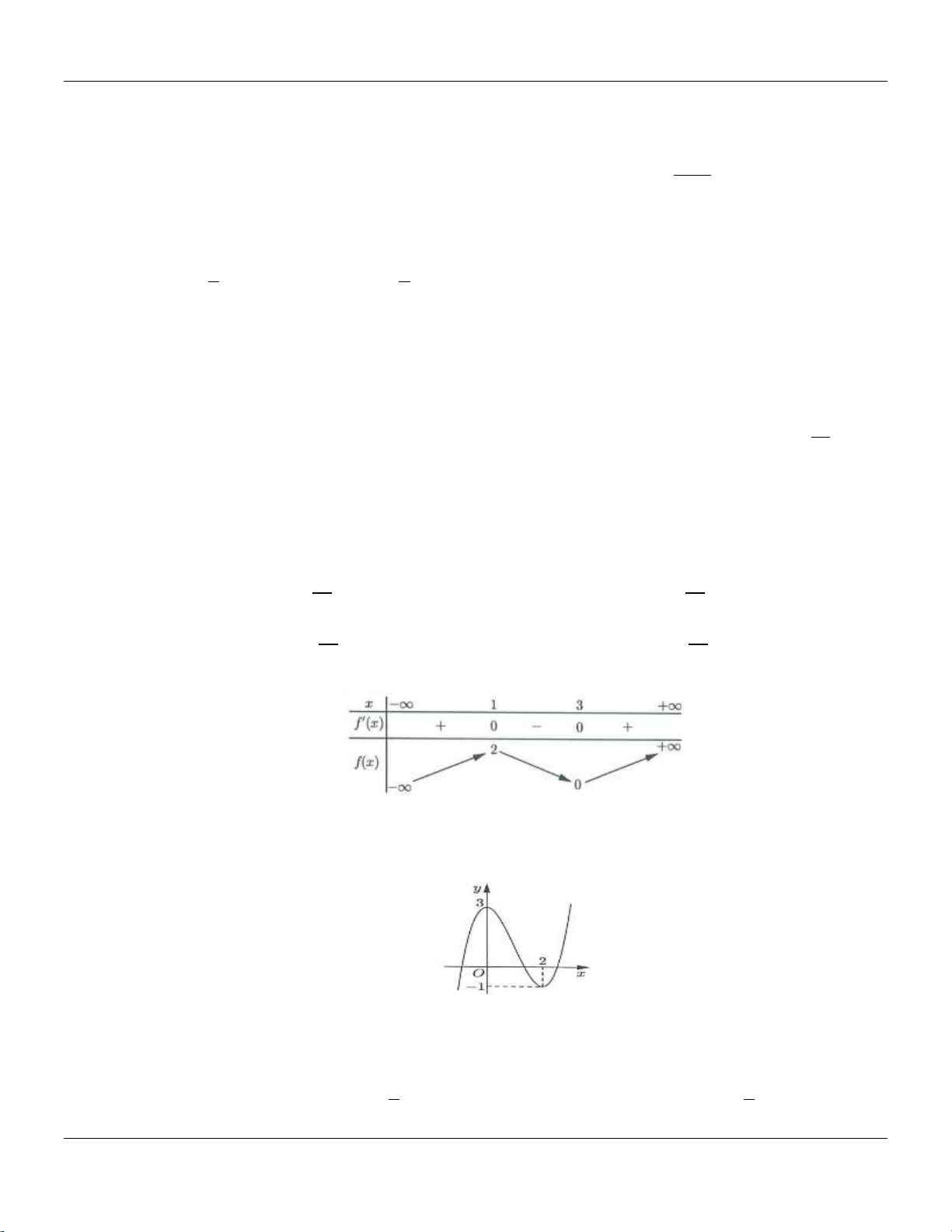
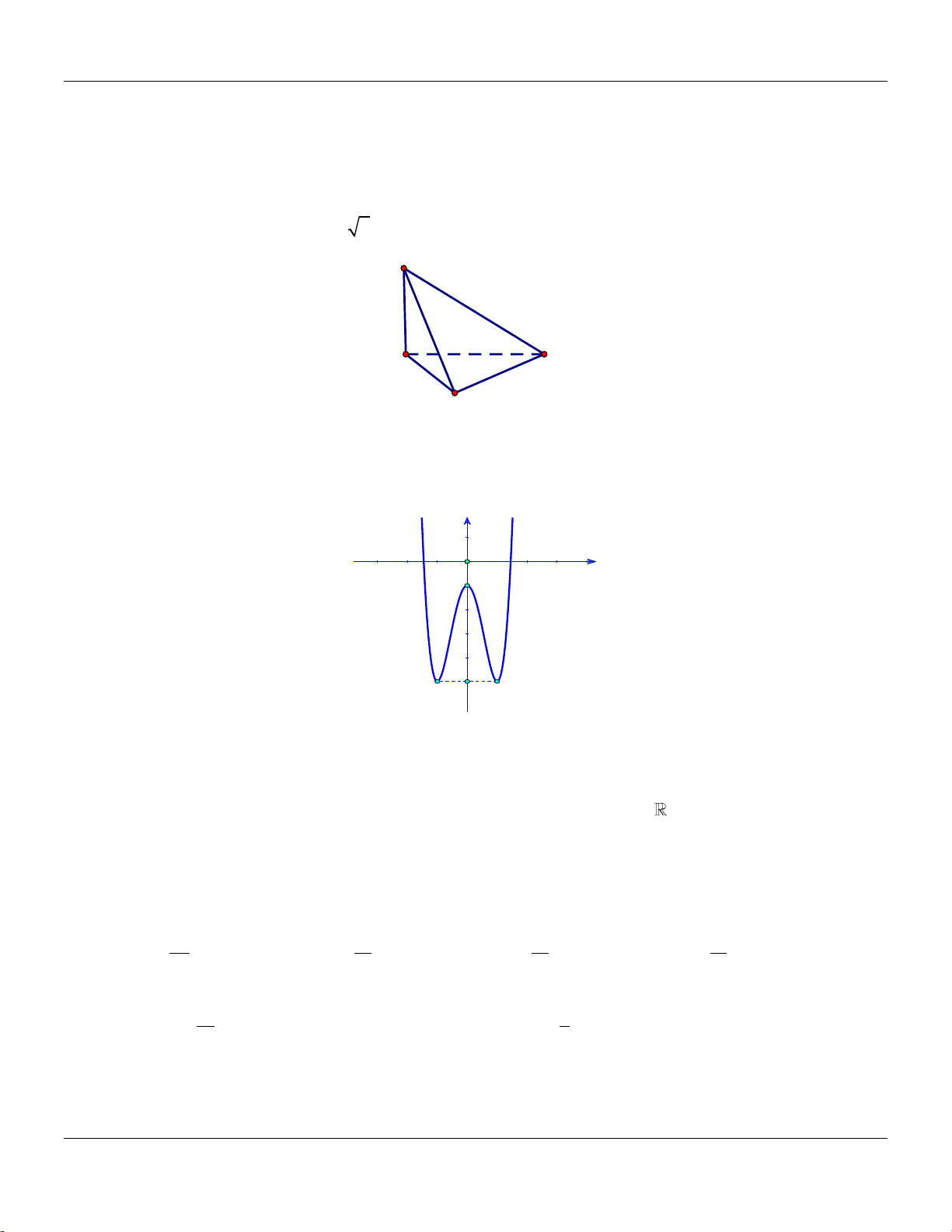
A. 1; 2;3 . B.  1  ;2; 3   . C. 3; 4  ; 5   . D. 3; 4;5 . Câu 19: Cho hàm số 4 2
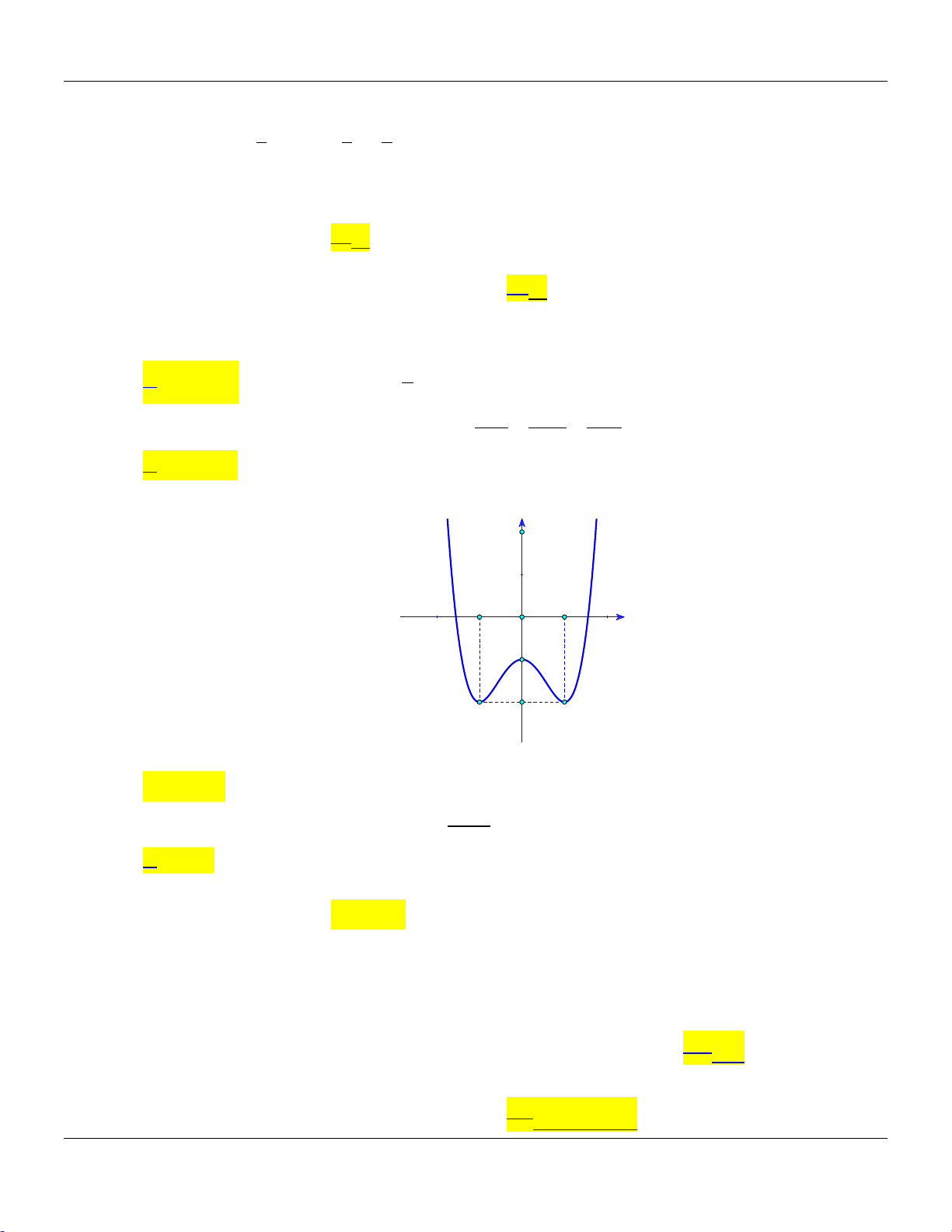
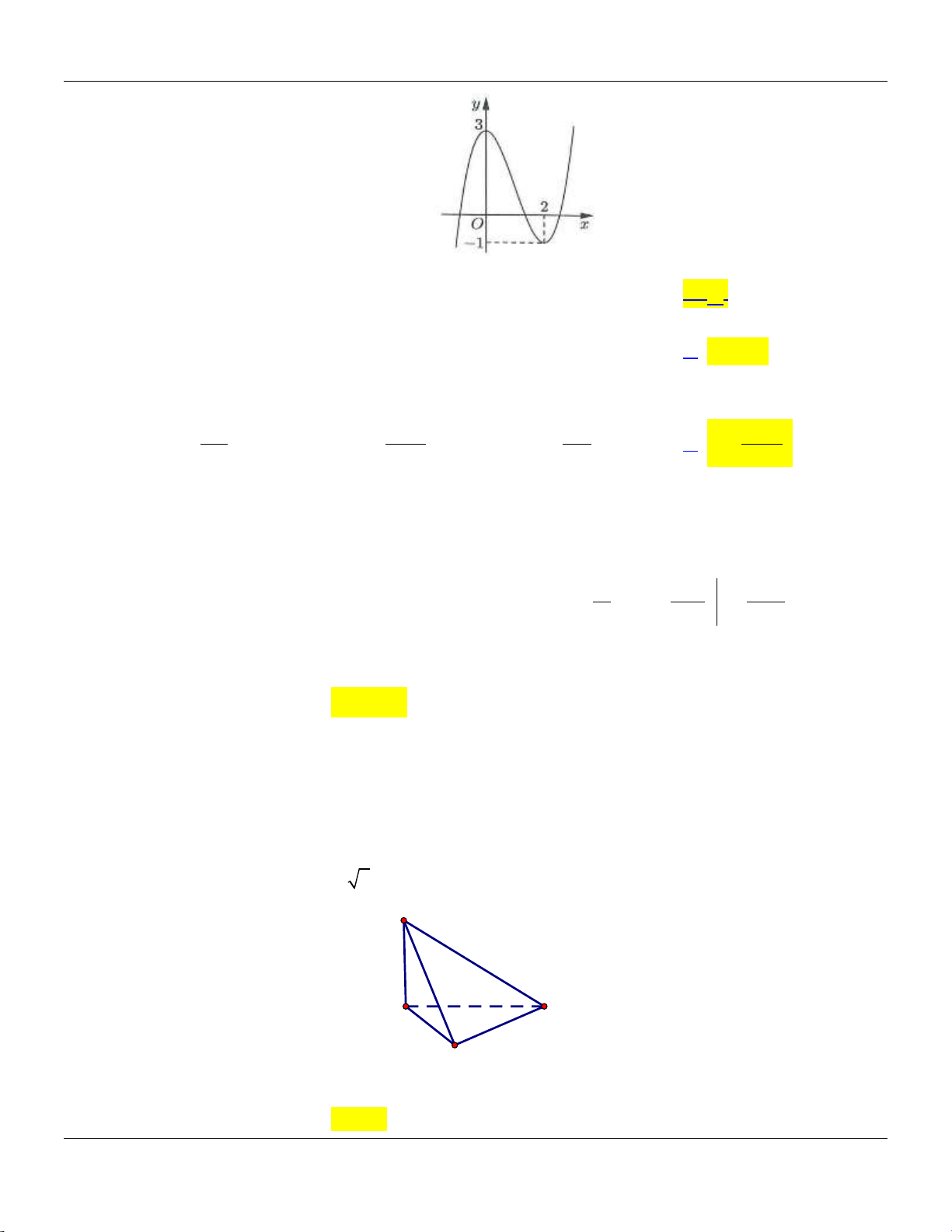
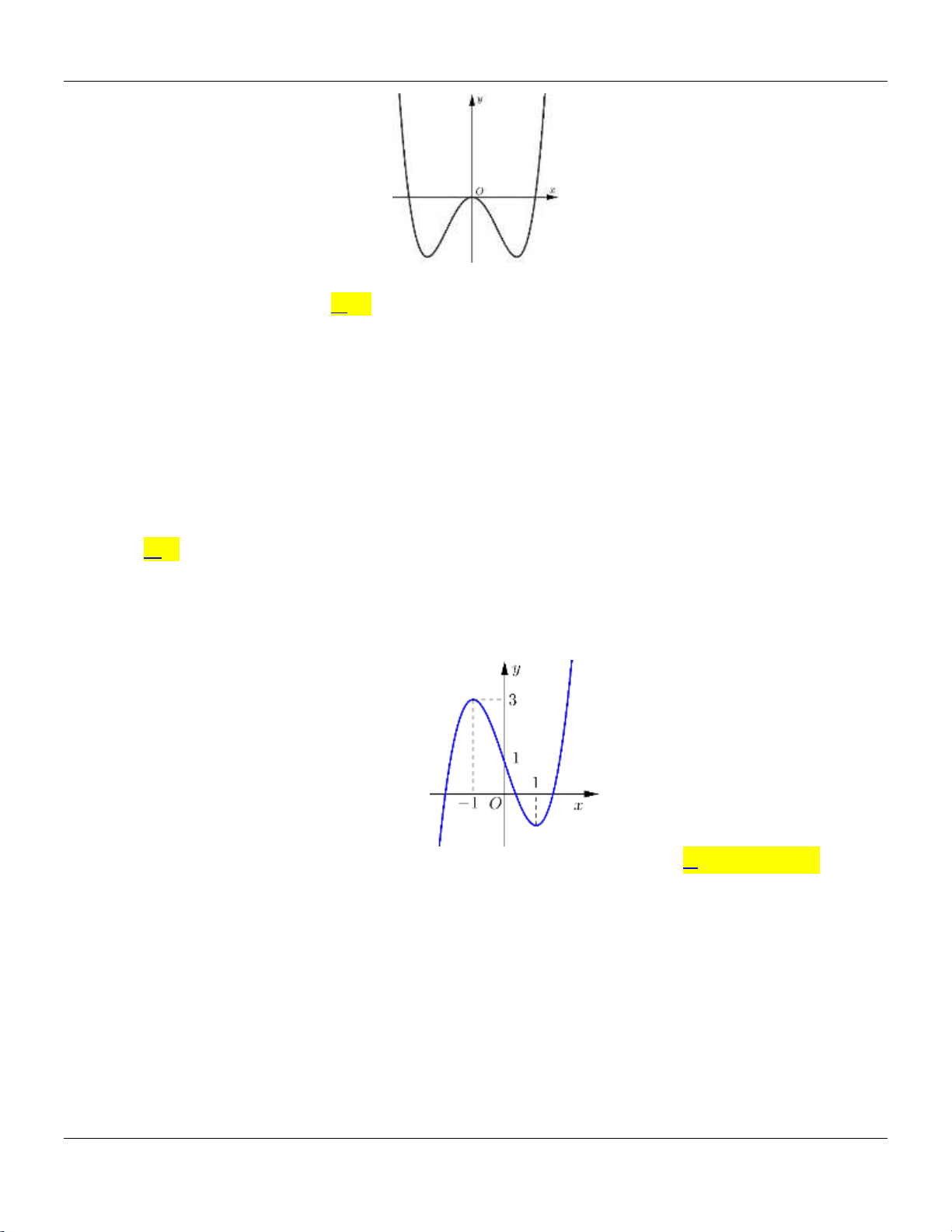
y ax bx c có đồ thị là đường cong như hình bên dưới: Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia y -1 1 x O -1 -2
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là A. 0;   1 . B. 1;0. C. 1; 2. D. 1; 2. 4x  1
Câu 20: Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình là x  2
A. y  4.
B. x  4.
C. x  2. D. y  2.
Câu 21: Tập nghiệm của bất phương trình log x  1 là 2 A.  ;  2. B. 0; 2. C. 0;  1 . D.  ;   1 .
Câu 22: Cho tập M có 10 phần tử. Số tập con gồm 3 phần tử của tập hợp M là A. 3!. B. 10!. C. 3 A . D. 3 C . 10 10 Câu 23: Cho sin d x x f
xC. Khẳng định nào dưới đây đúng?
A. f  x  cos . x
B. f  x   cos . x
C. f  x  sin . x
D. f  x   sin . x 4 4
Câu 24: Nếu 3 f
 x xdx 12 
thì f x dx  bằng 2 2 10 A. 6 . B. 0 . C. 2 . D. . 3
Câu 25: Cho hàm số f x  s inx x 1. Khẳng định nào dưới đây đúng? x x A. f  x 2 dx  cosx
x C . B. f  x 2
dx  cosx
x C . 2 2 x C. f
 xdx  cosx 1C . D. f  x 2
dx  cosx   C . 2
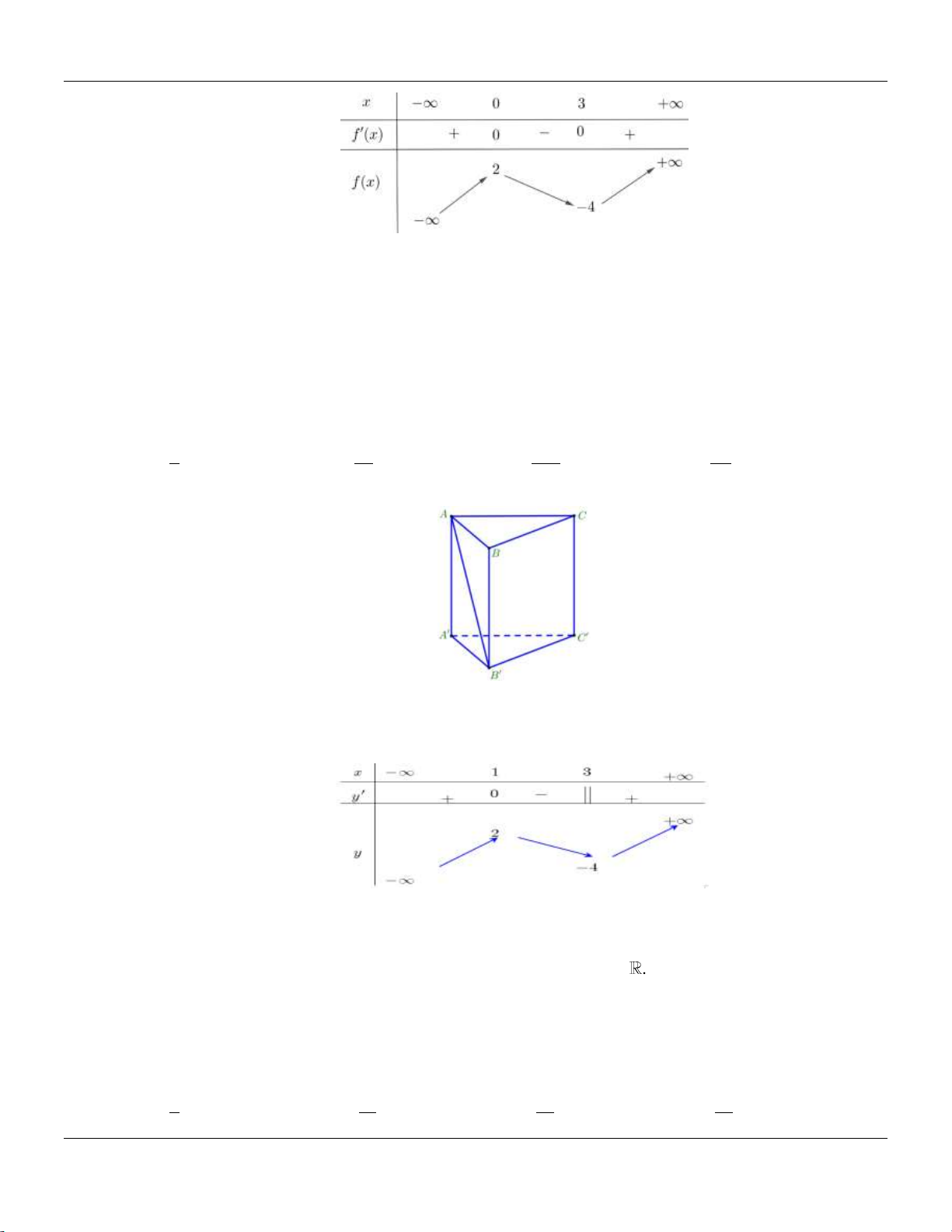
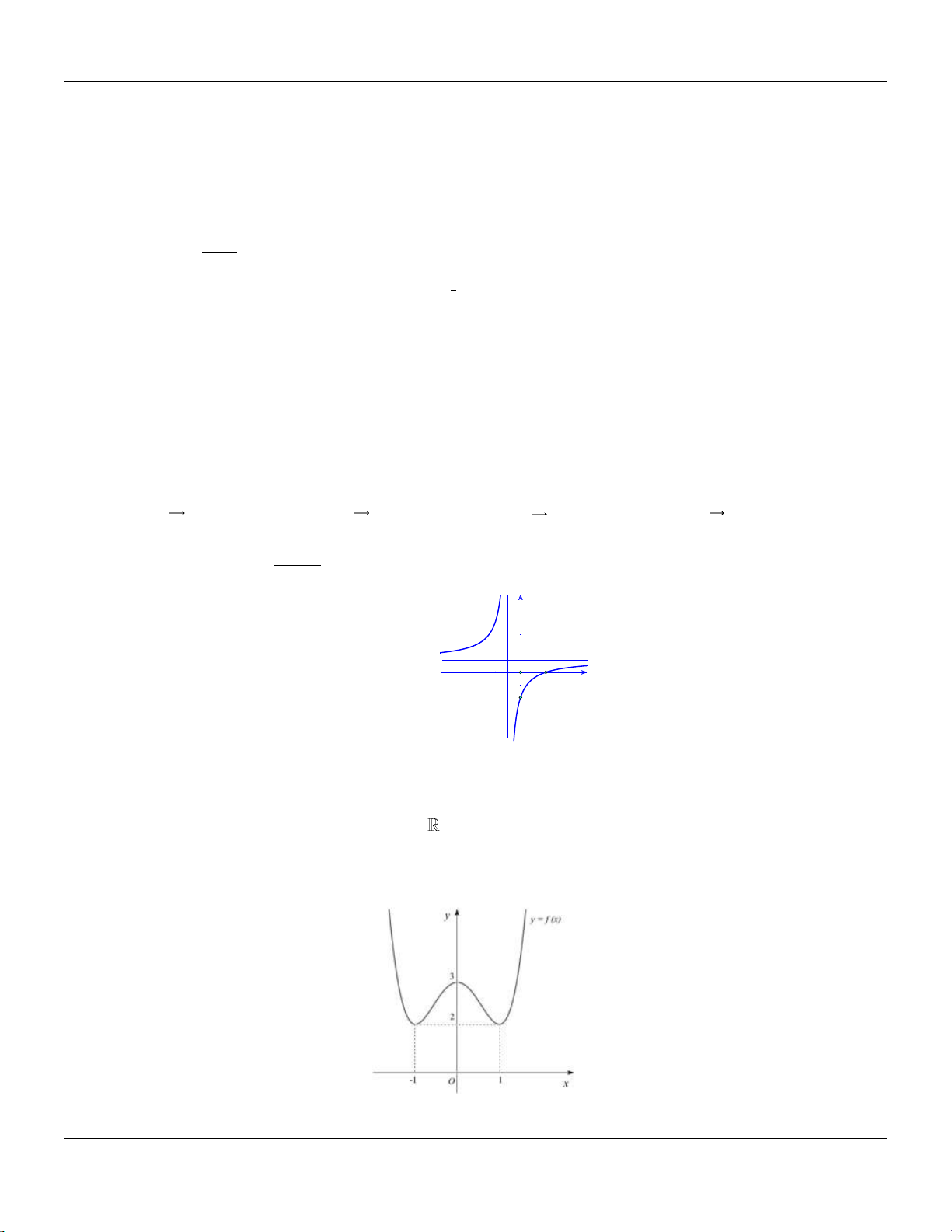
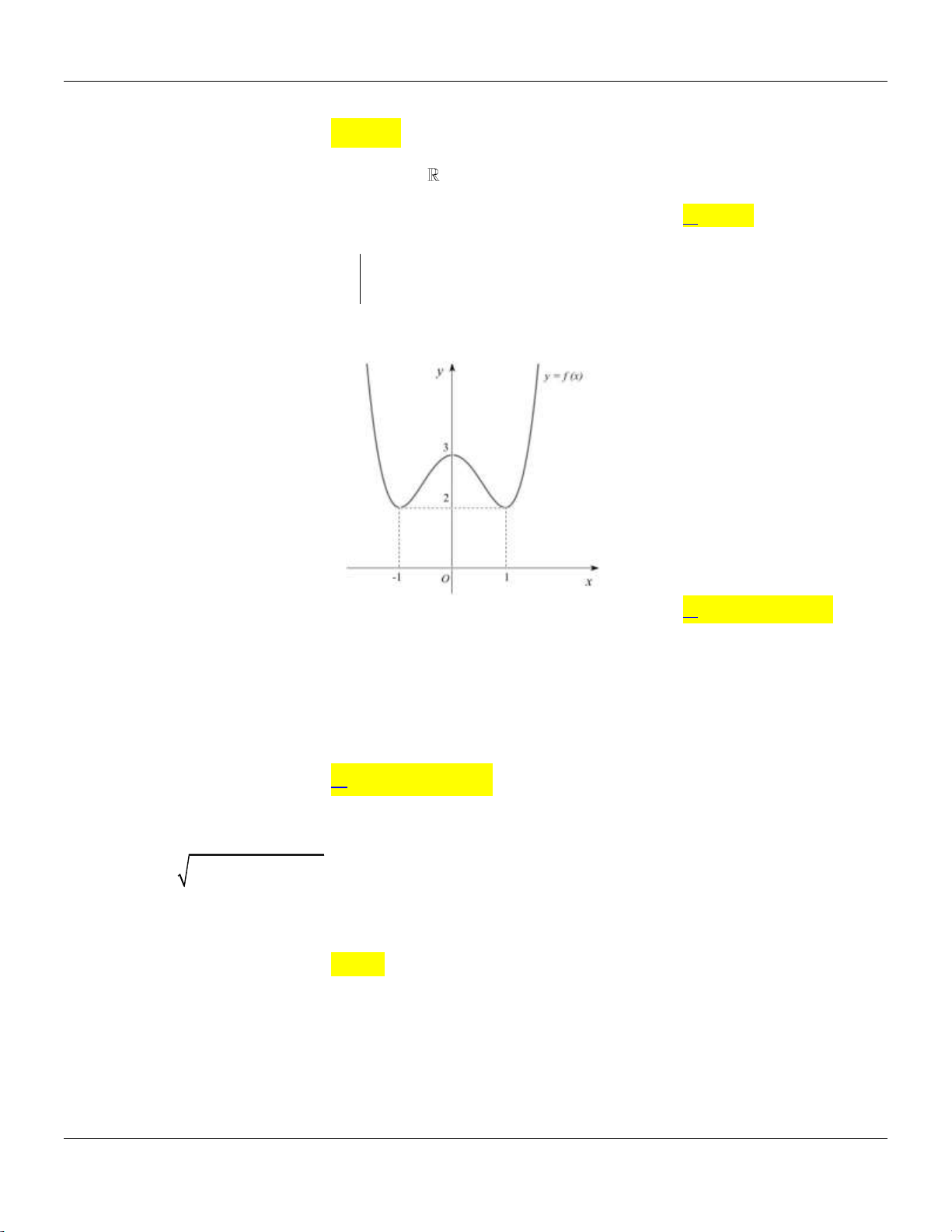
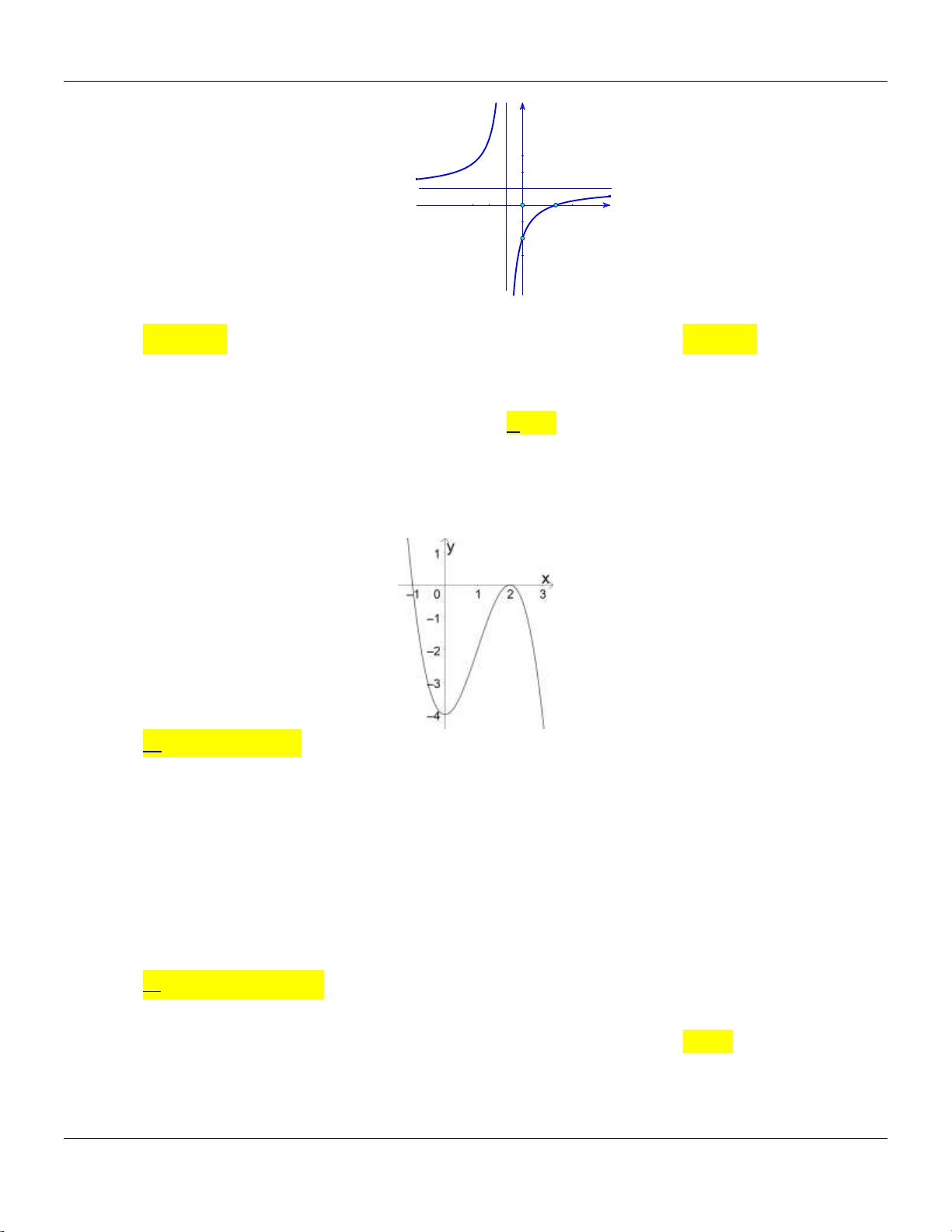
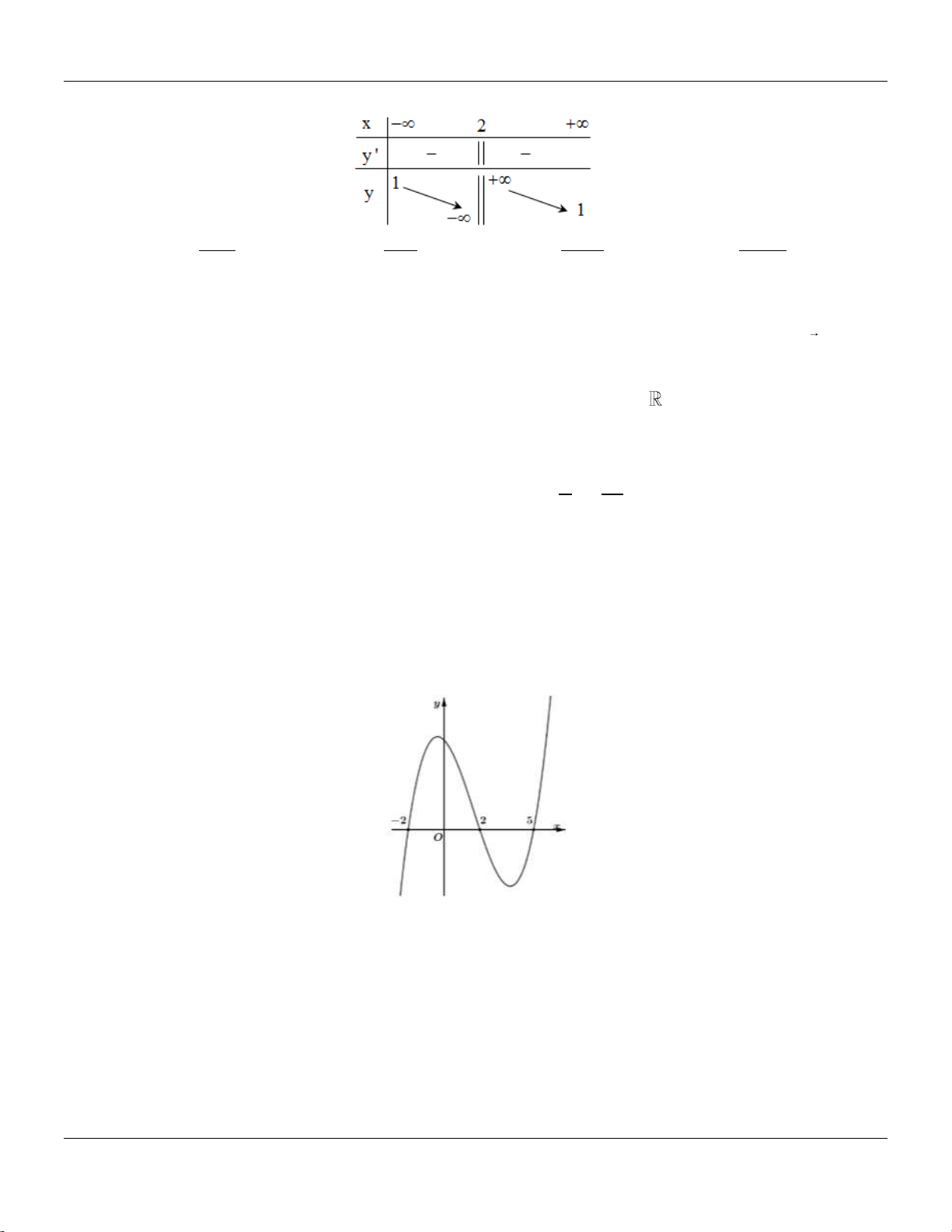
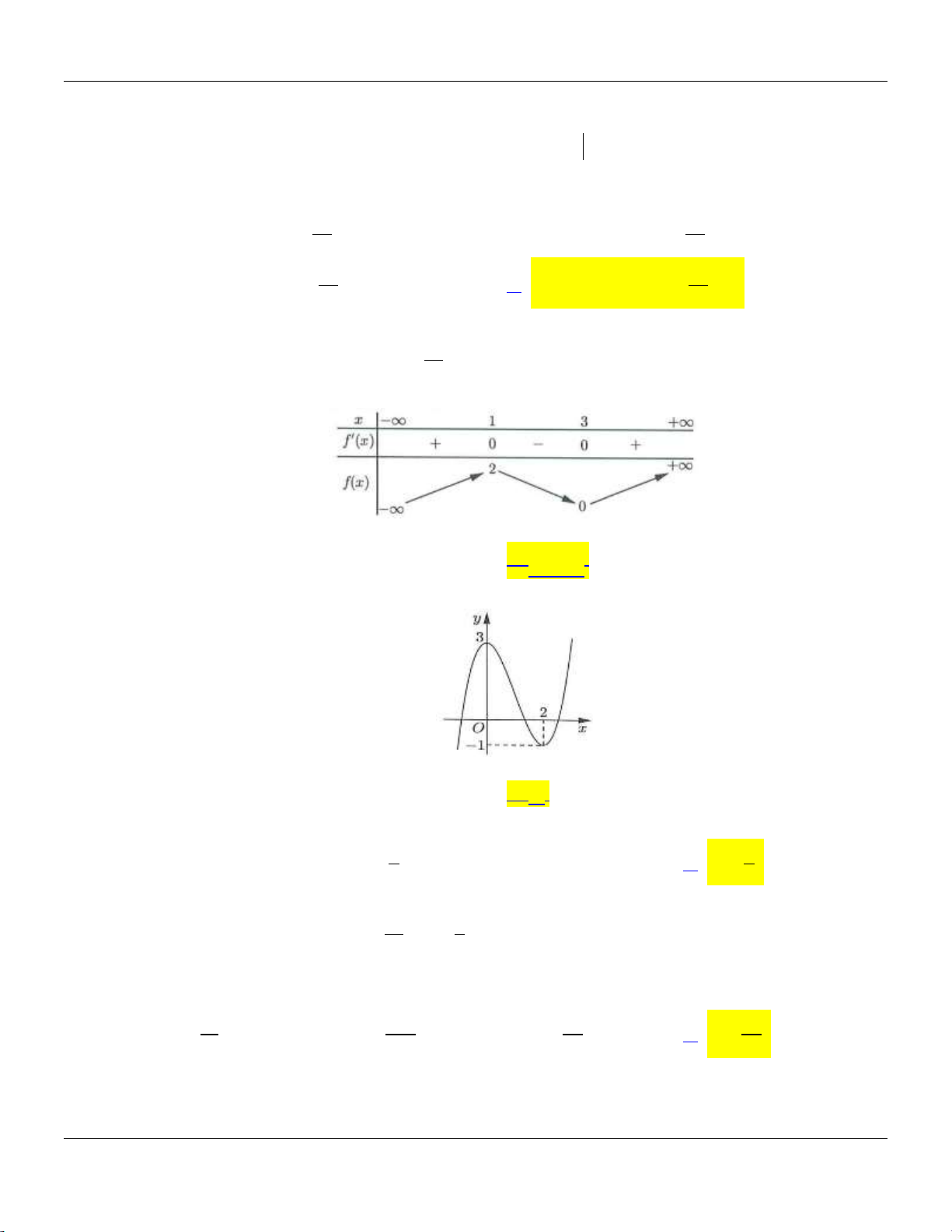
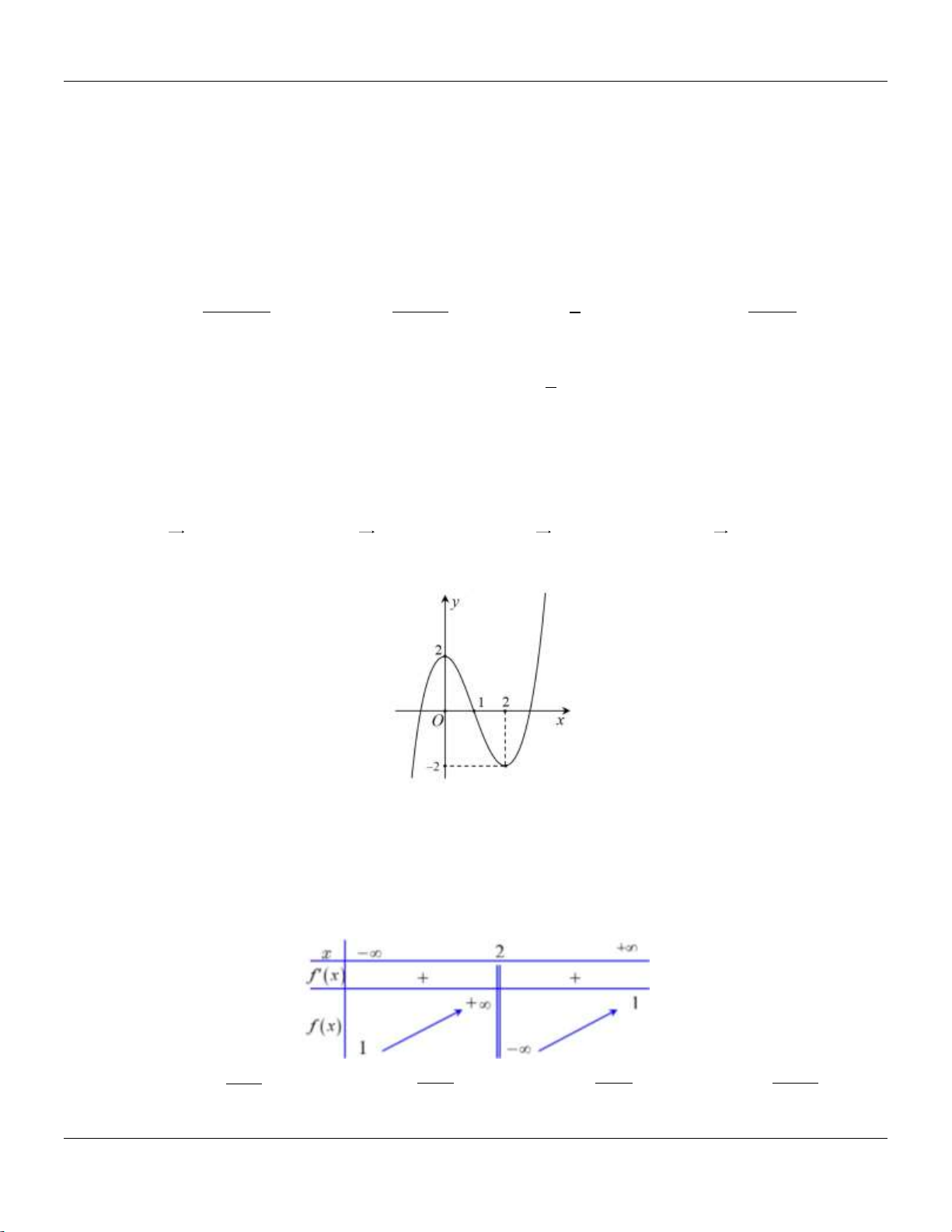
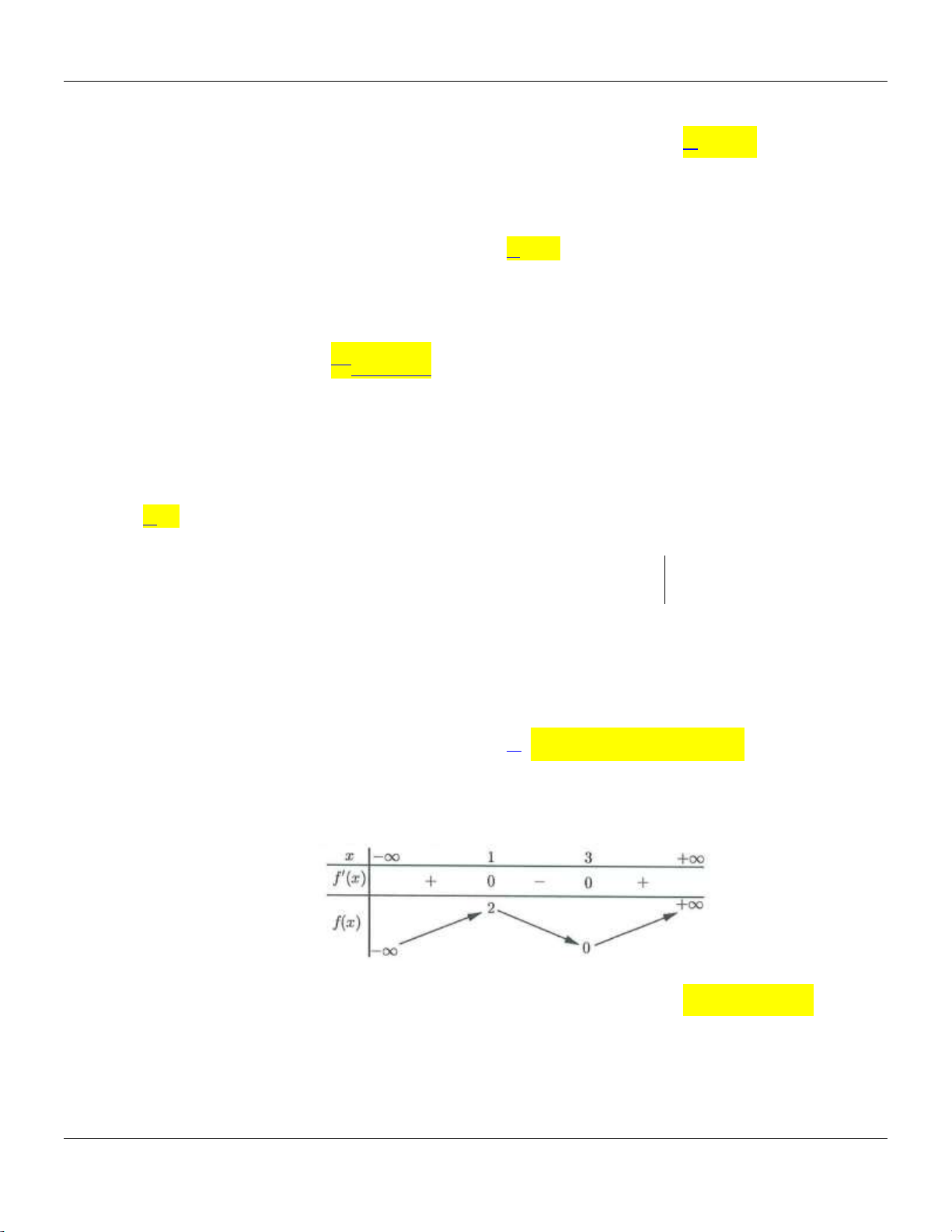
Câu 26: Cho hàm số y f (x) có đồ thị như hình vẽ bên.
Hàm số đã cho đồng biến trên các khoảng nào dưới đây? A. 0; 2 .
B. 0;   . C. 0; 4 . D. 1;  1 .
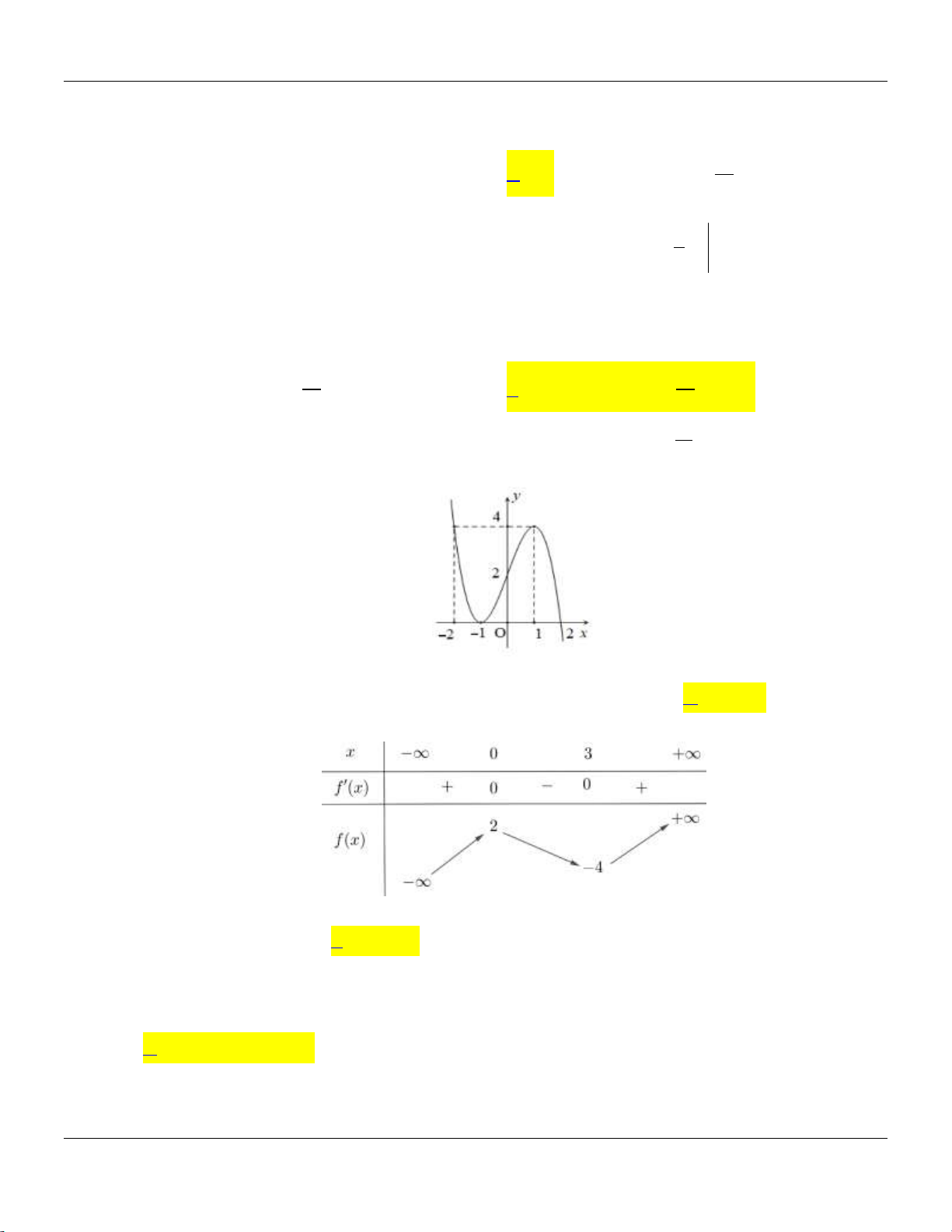
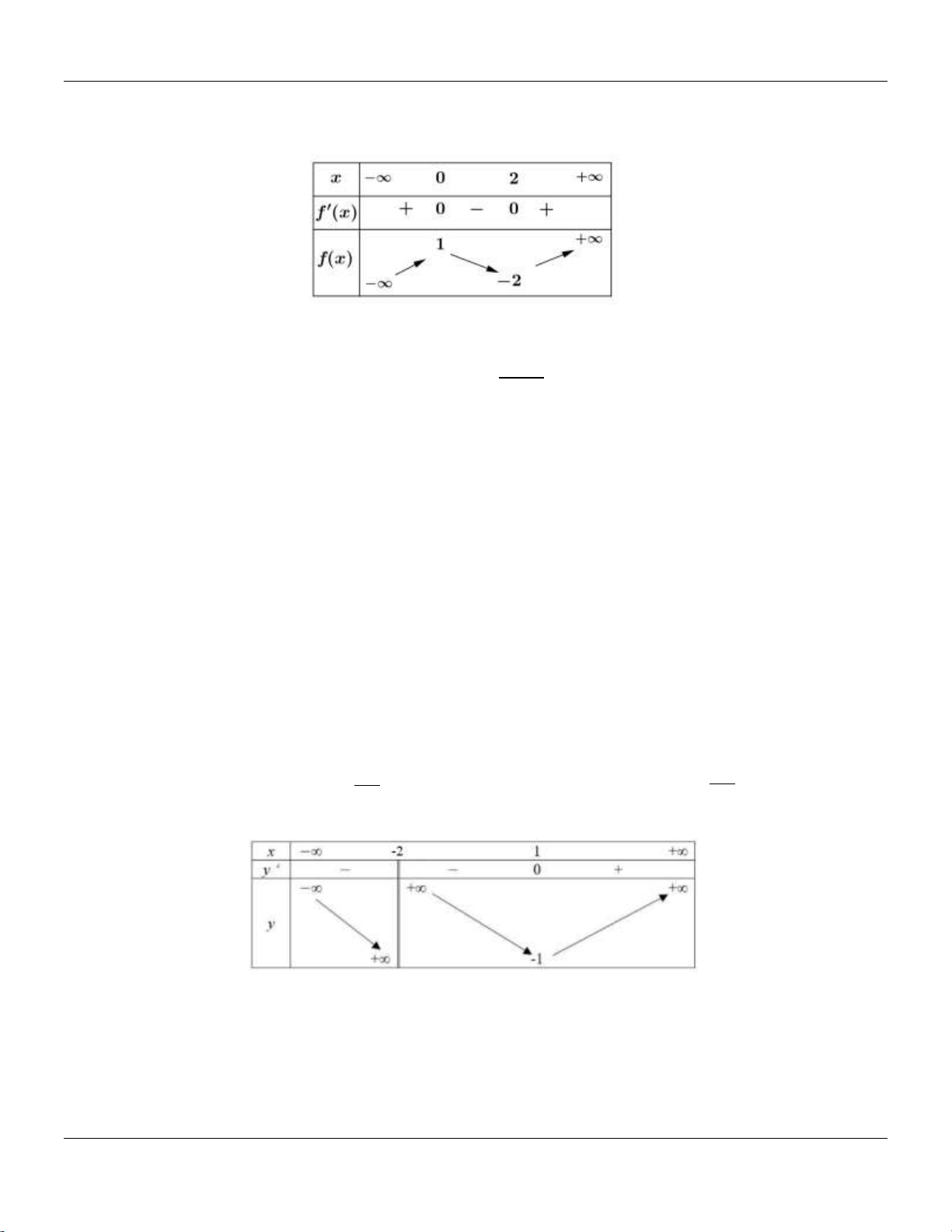
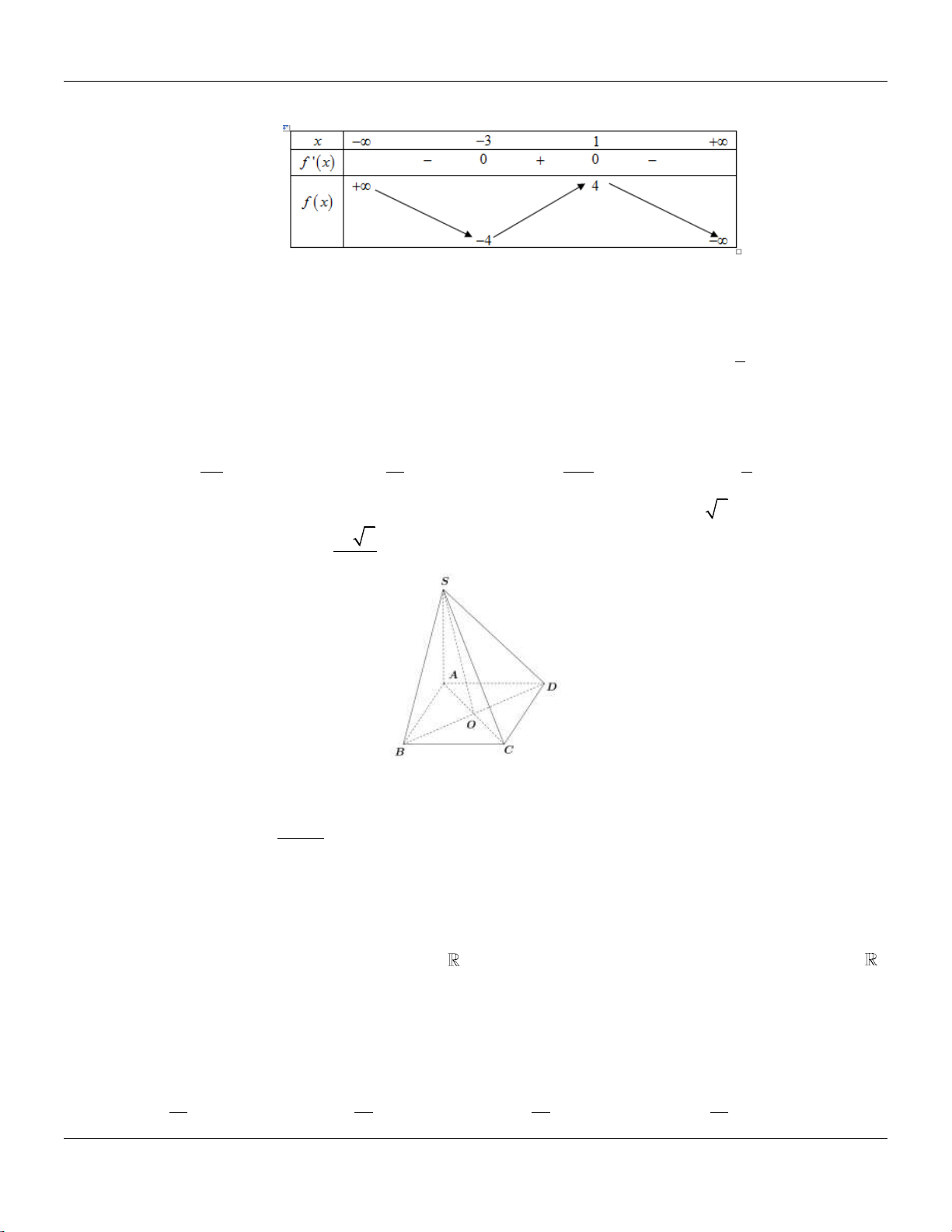
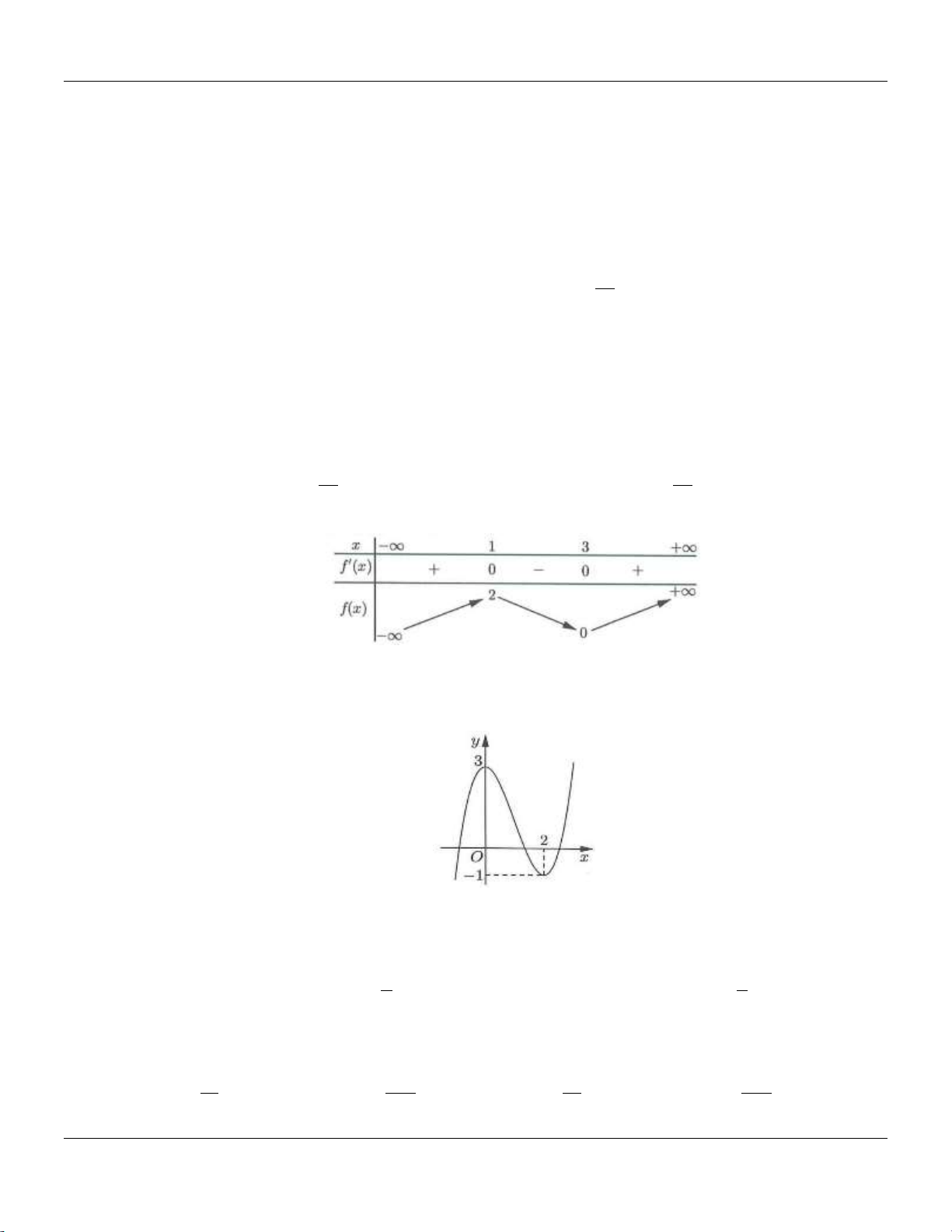
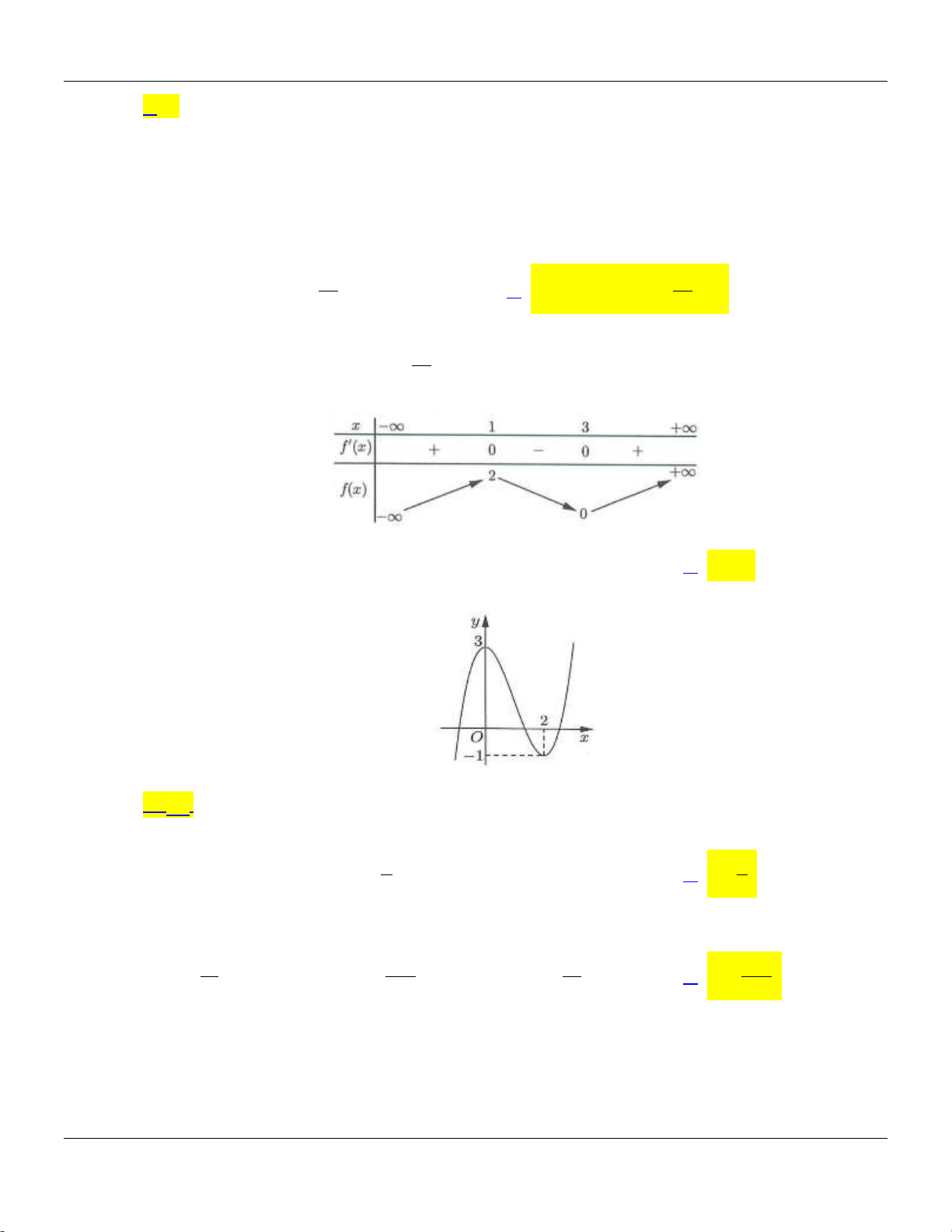
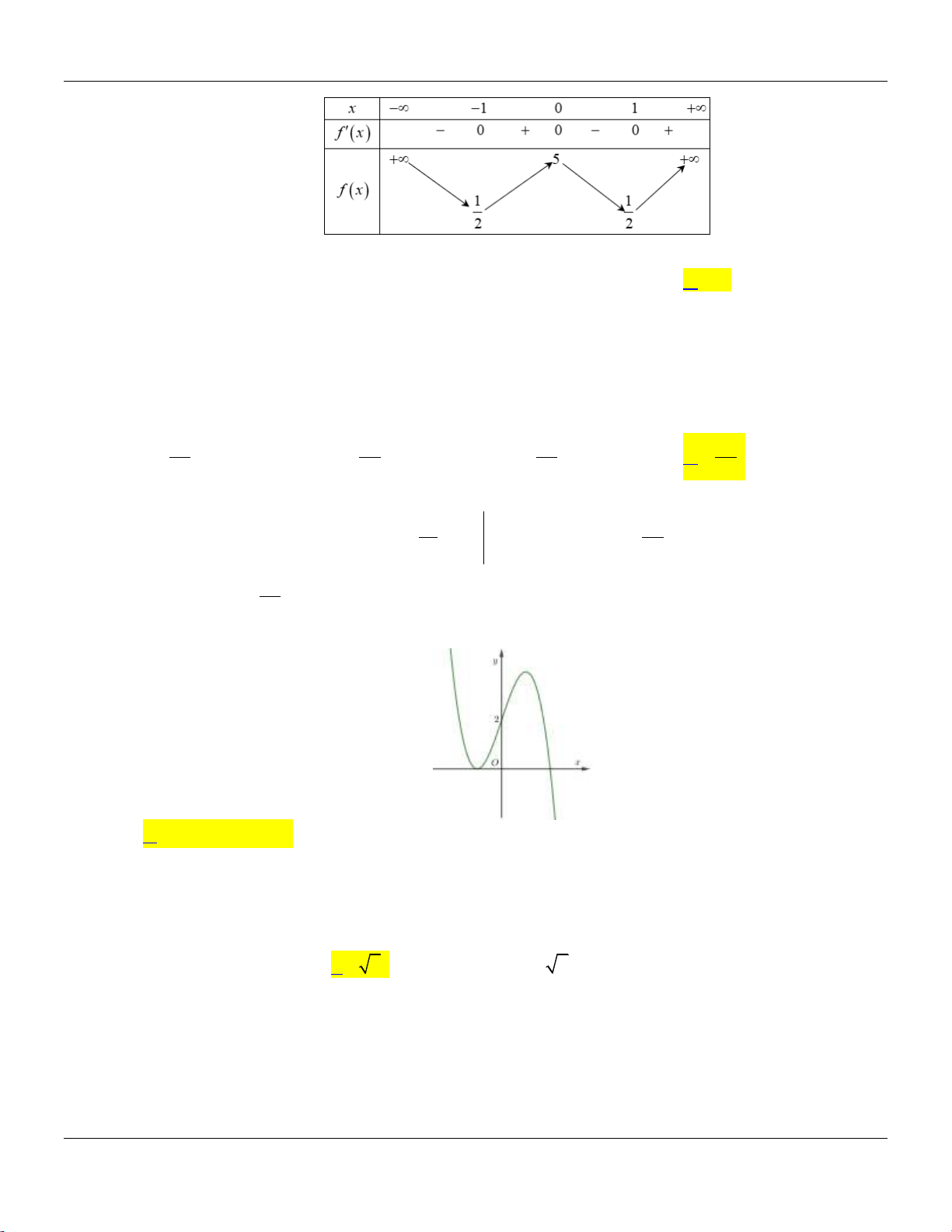
Câu 27: Cho hàm số y f x có bảng biến thiên như sau: Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Đồ thị hàm số y f x có điểm cực tiểu là A. 0; 2 .
B. 3;  4 . C. x  3. D. y  4. CT CT
Câu 28: Cho a , b là các số thực dương tùy ý. Khẳng định nào sau đây đúng?
A. ln ab  ln a  ln b .
B. ln a b  ln a  ln b .
C. ln ab  ln . a ln b .
D. ln a b  ln . a ln b .
Câu 29: Cho hình phẳng H giới hạn bởi đồ thị hàm số 2
y  2x x  1 và trục hoành. Thể tích của vật
thể tròn xoay khi quay H quanh trục hoành bằng 9 81 81 9 A. . B. . C. . D. . 8 80 80 8
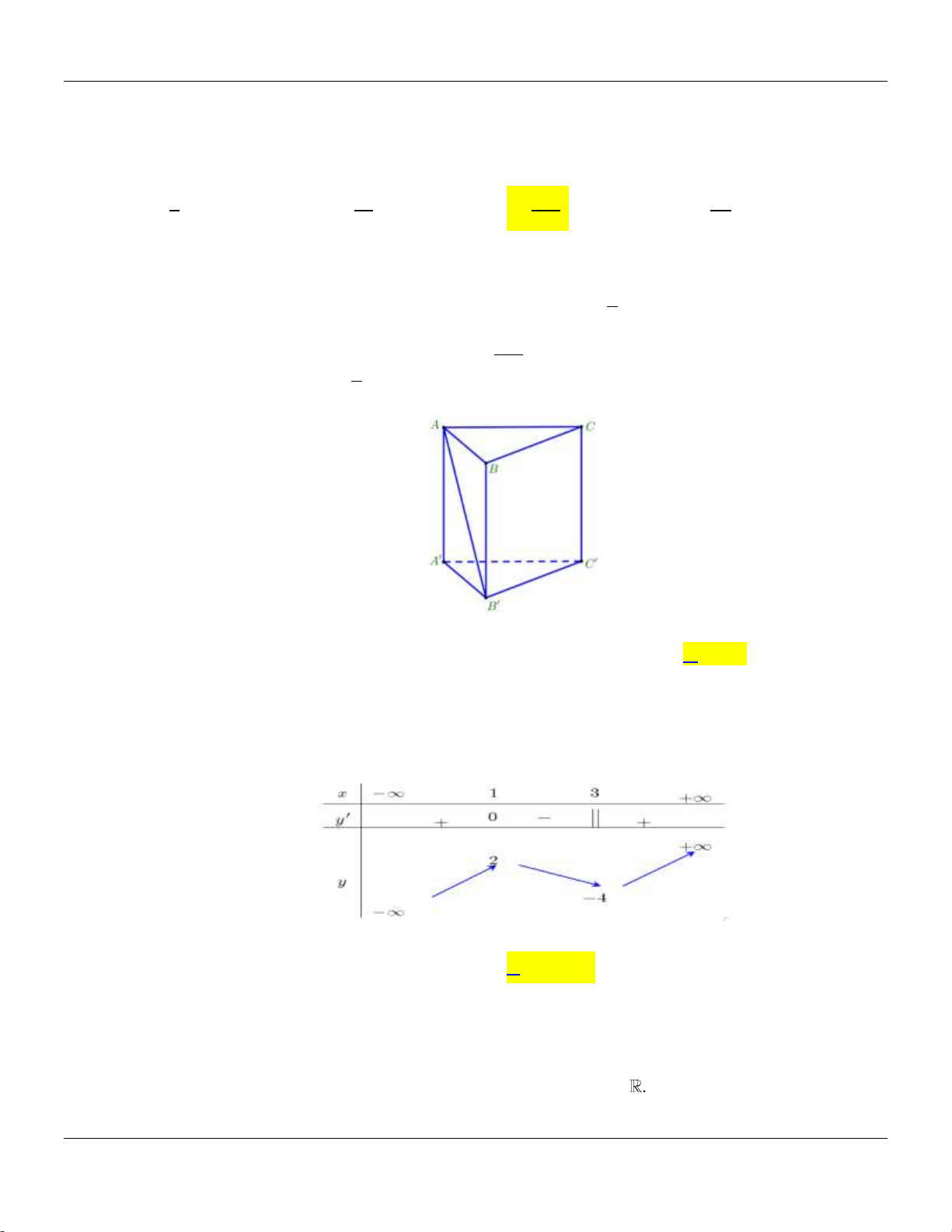
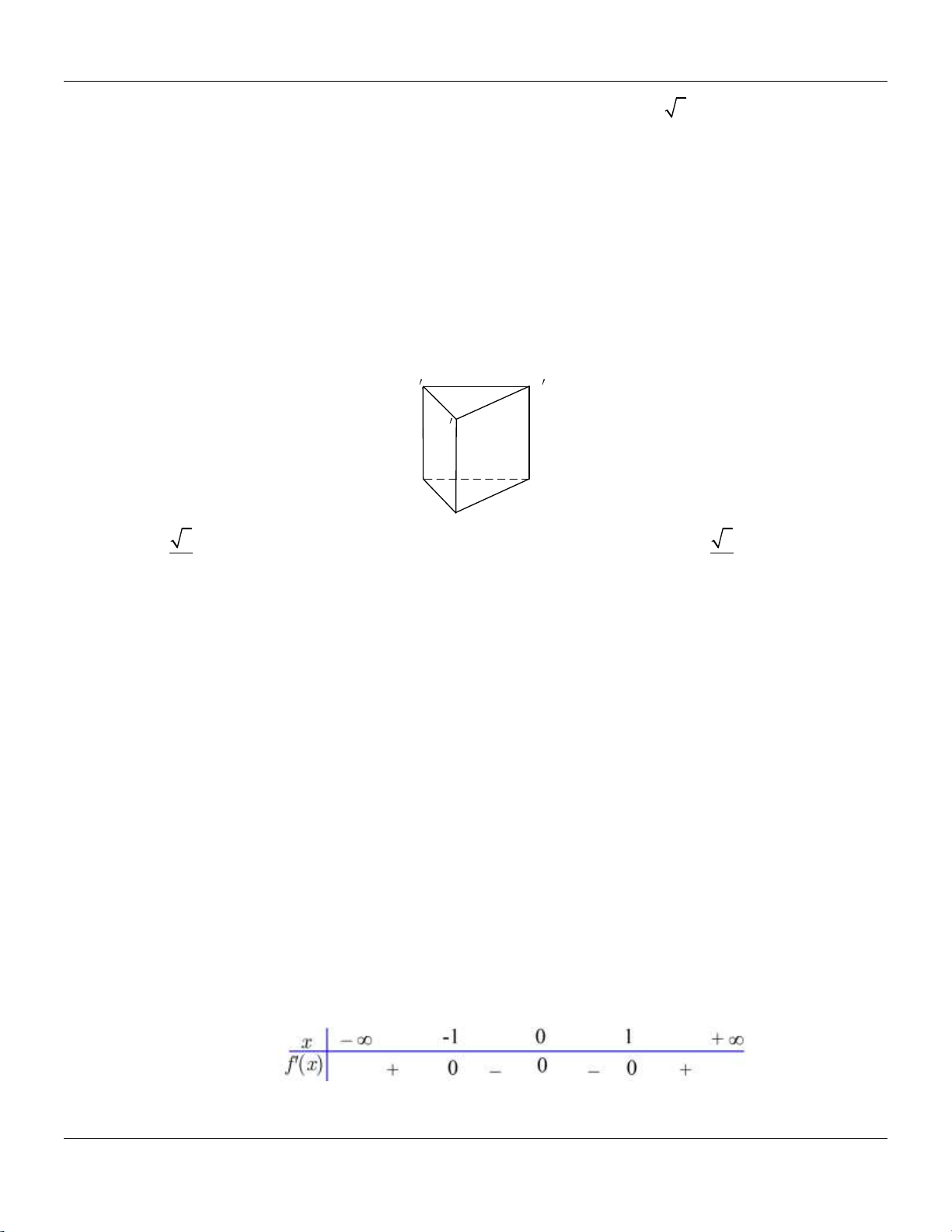
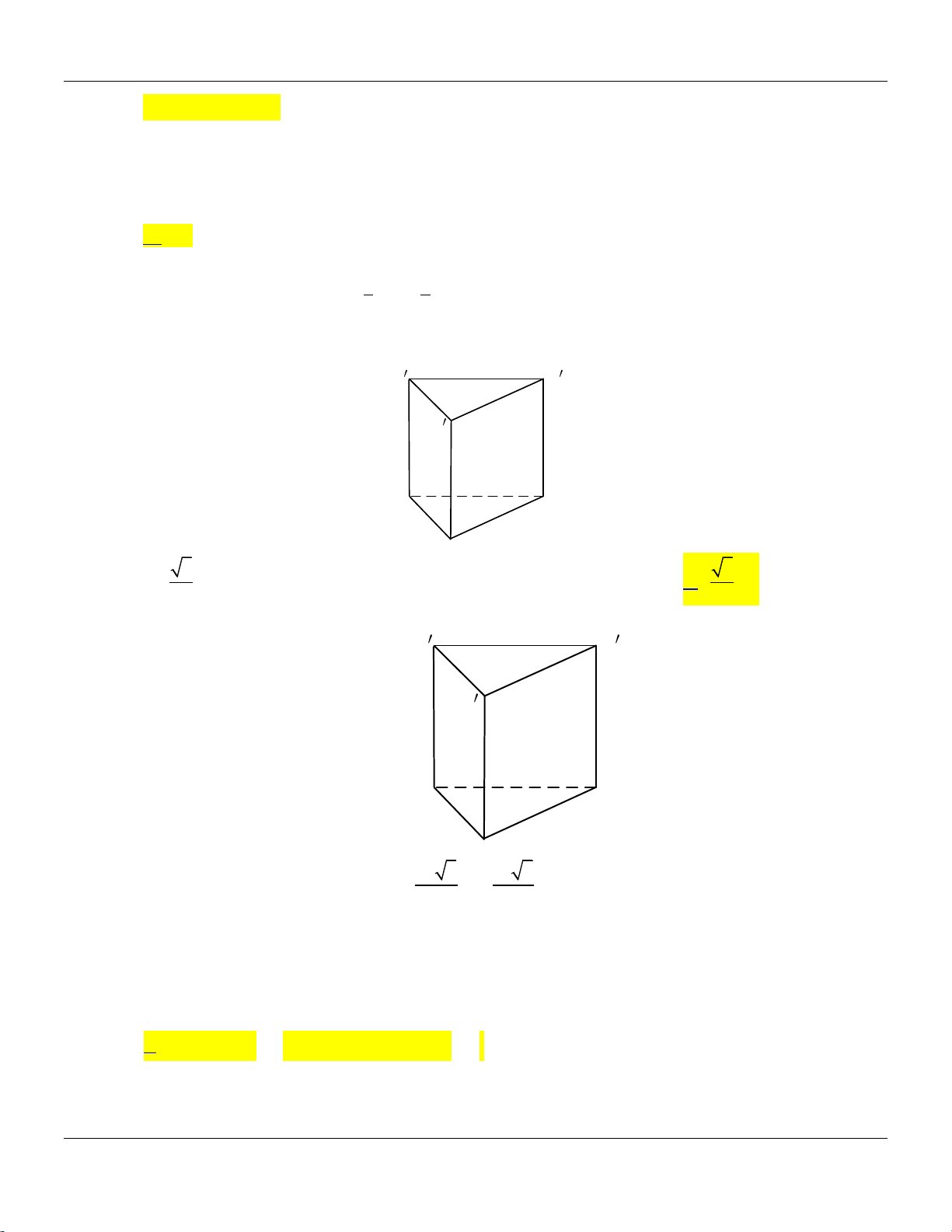
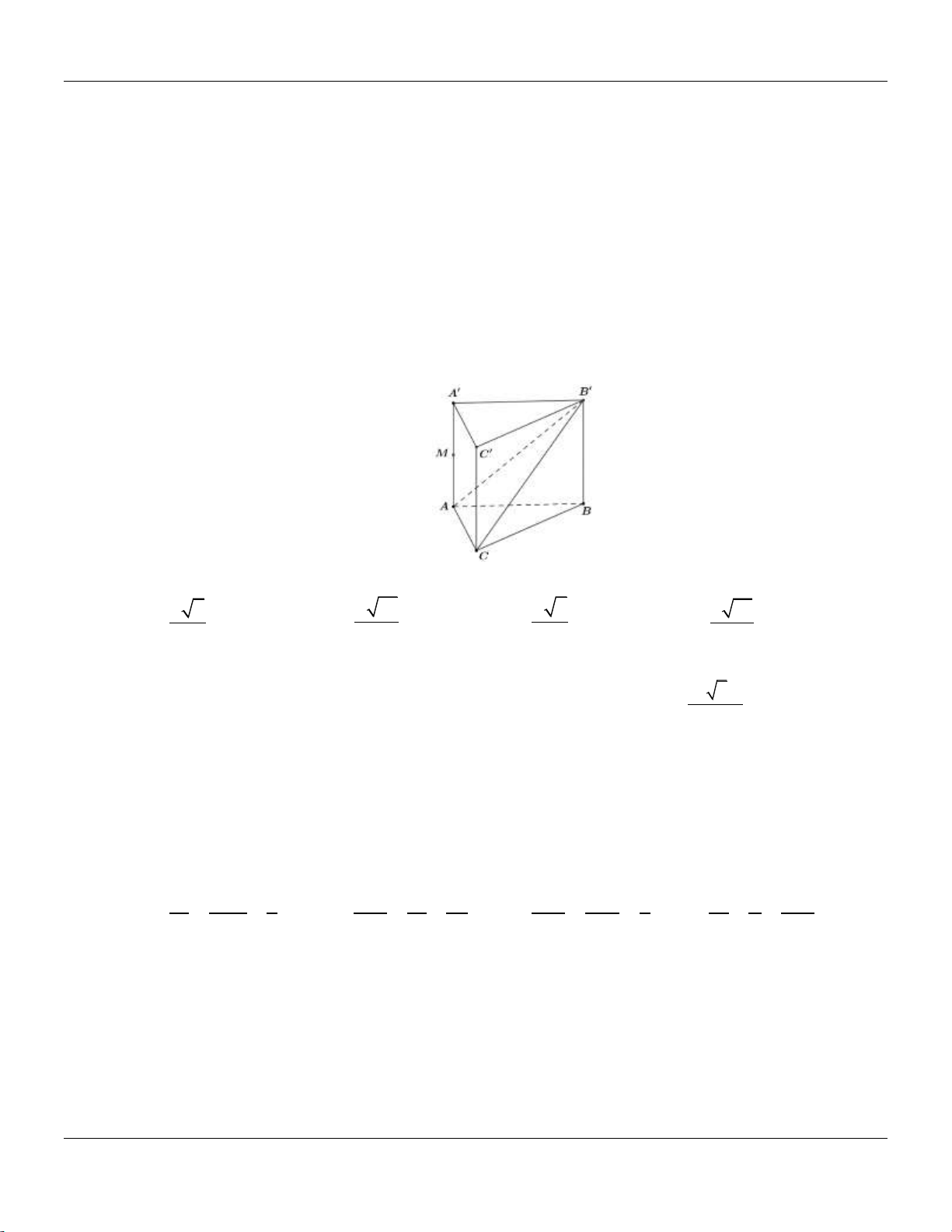
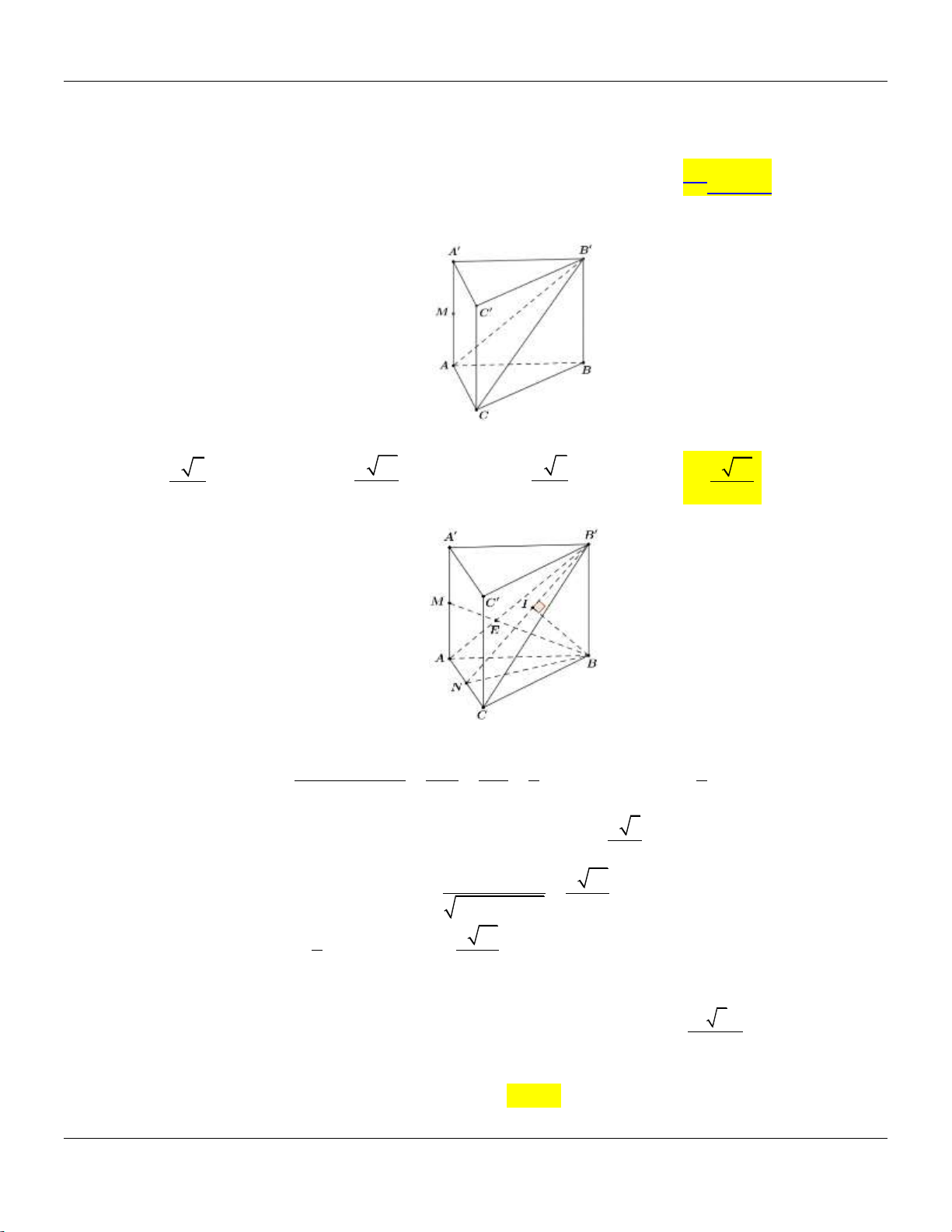
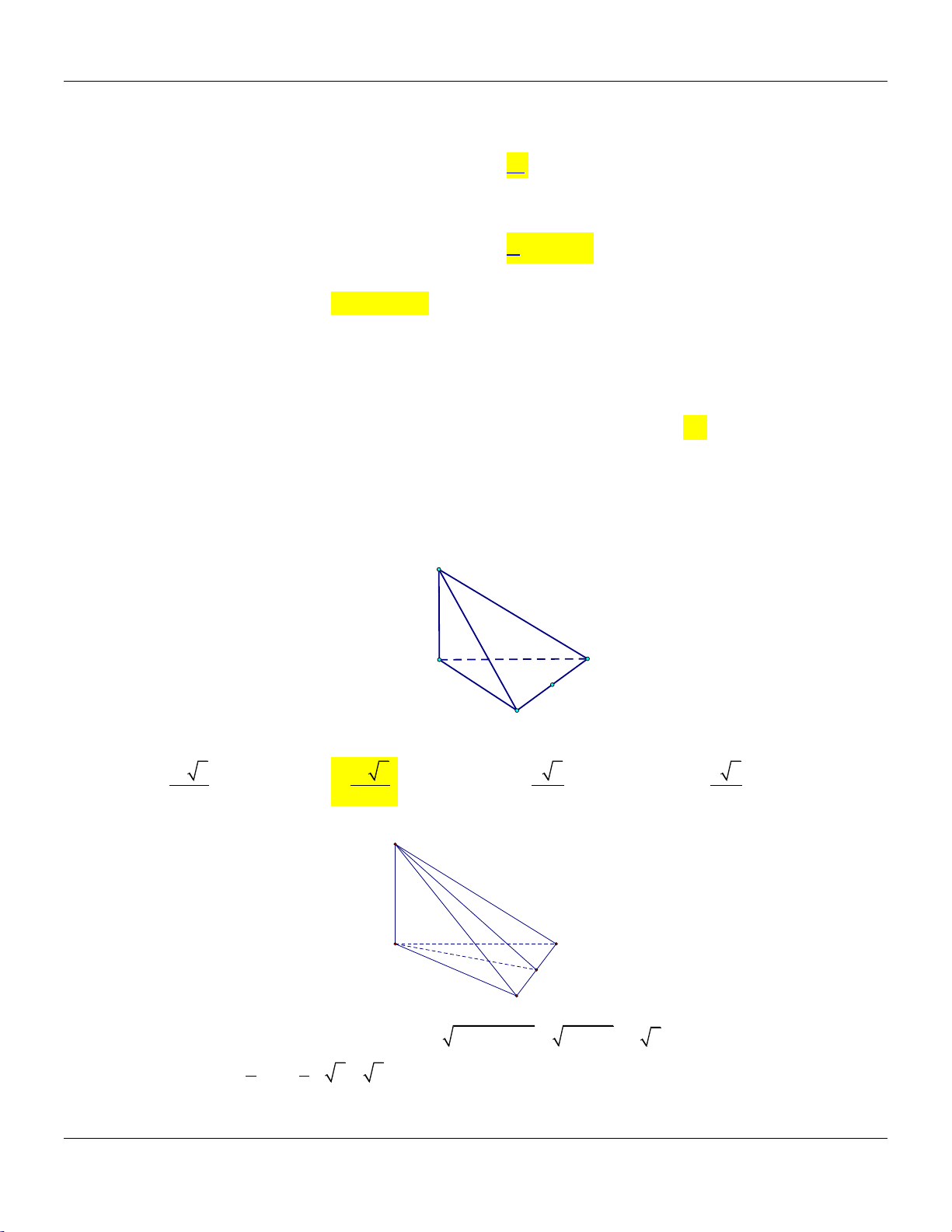
Câu 30: Cho hình lăng trụ đứng ABC.AB C
  có tất cả các cạnh bằng nhau:
Góc giữa đường thẳng AB và mặt phẳng  AB C  bằng A. 30 . B. 90 . C. 60 . D. 45 .
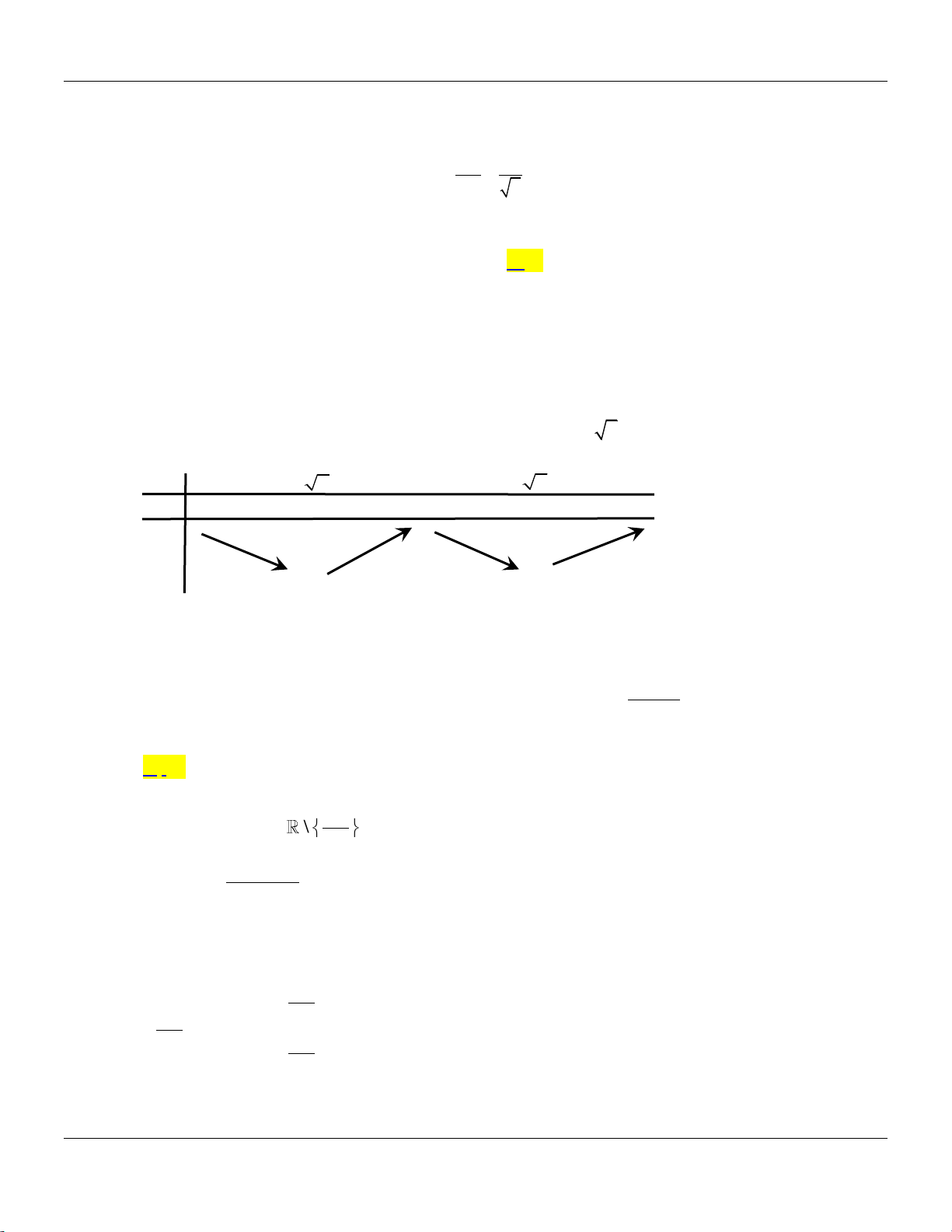
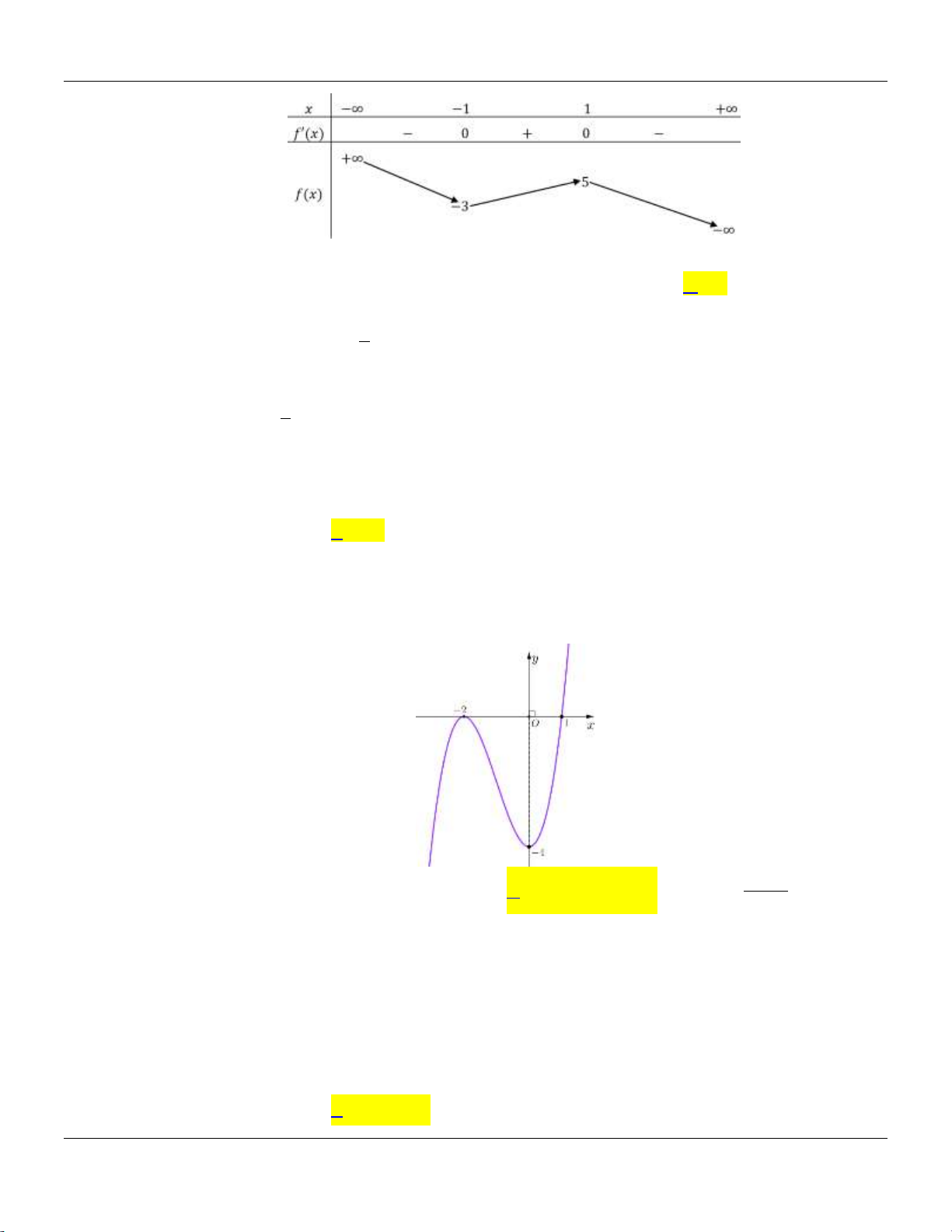
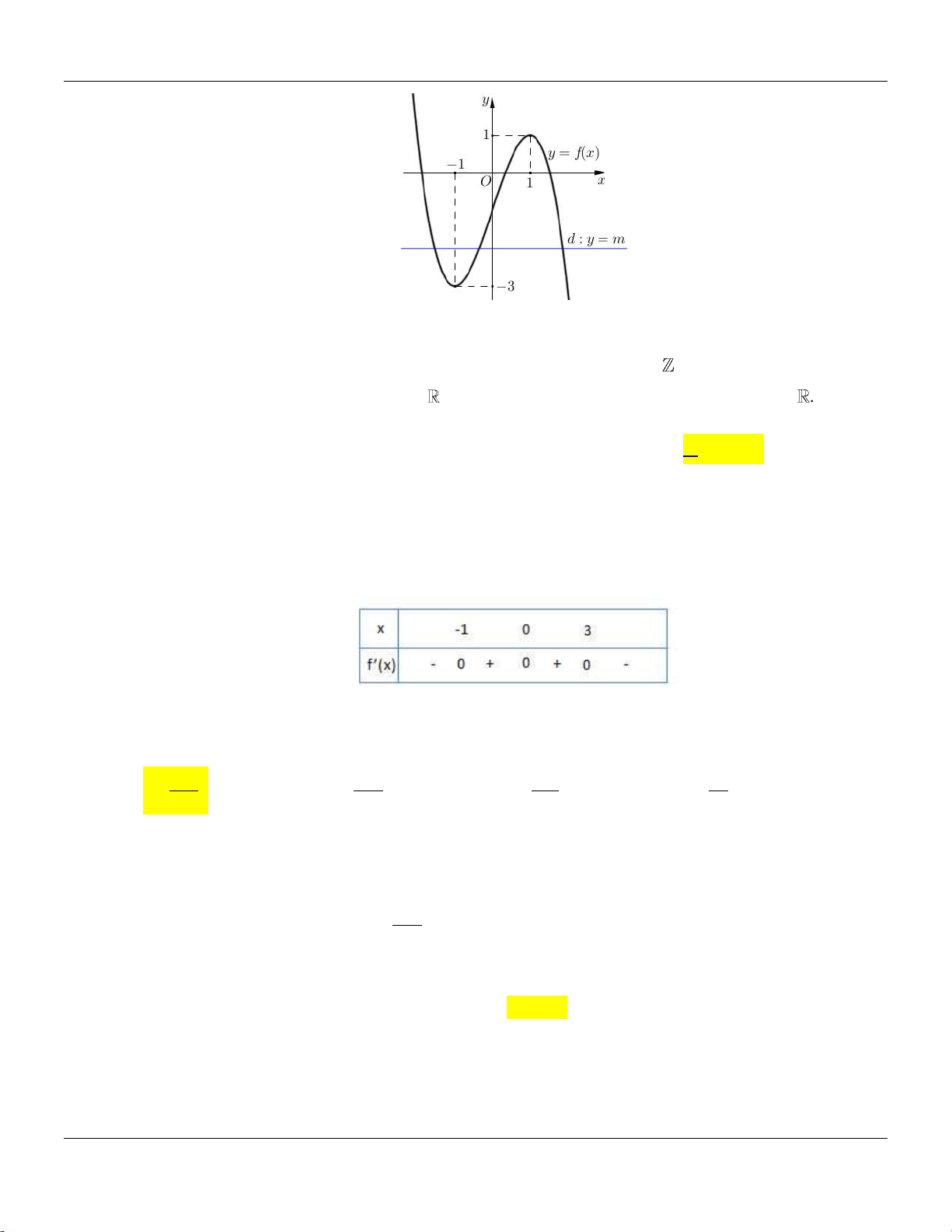
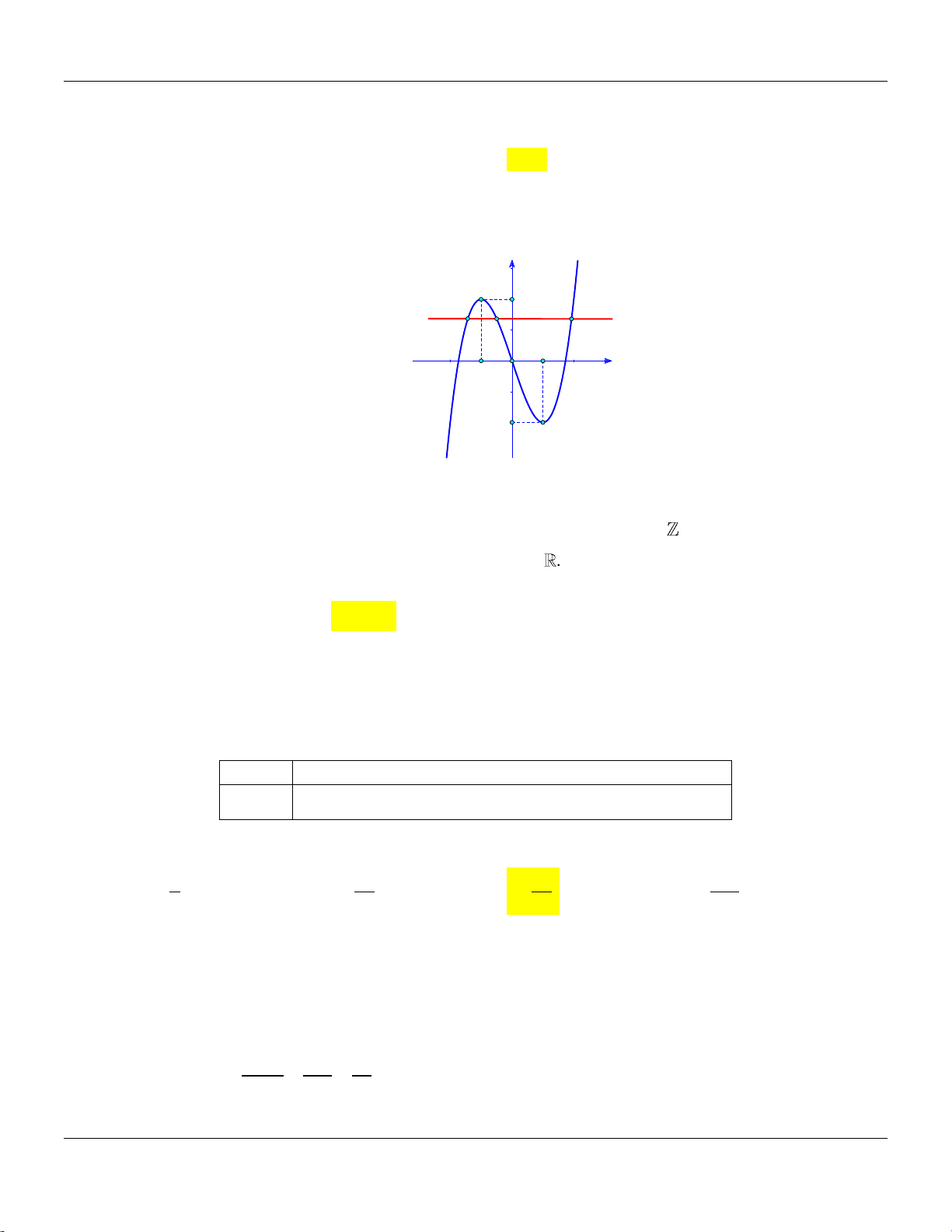
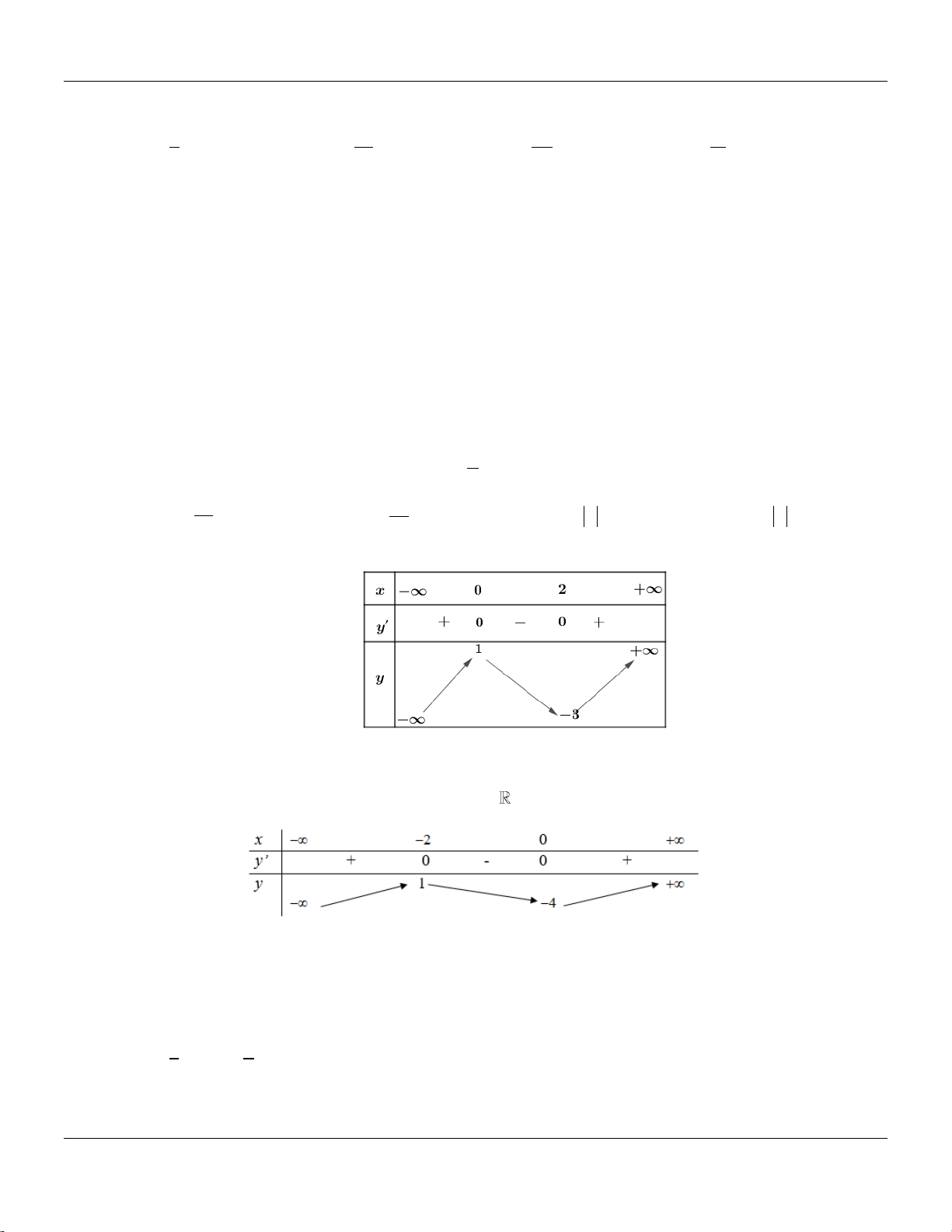
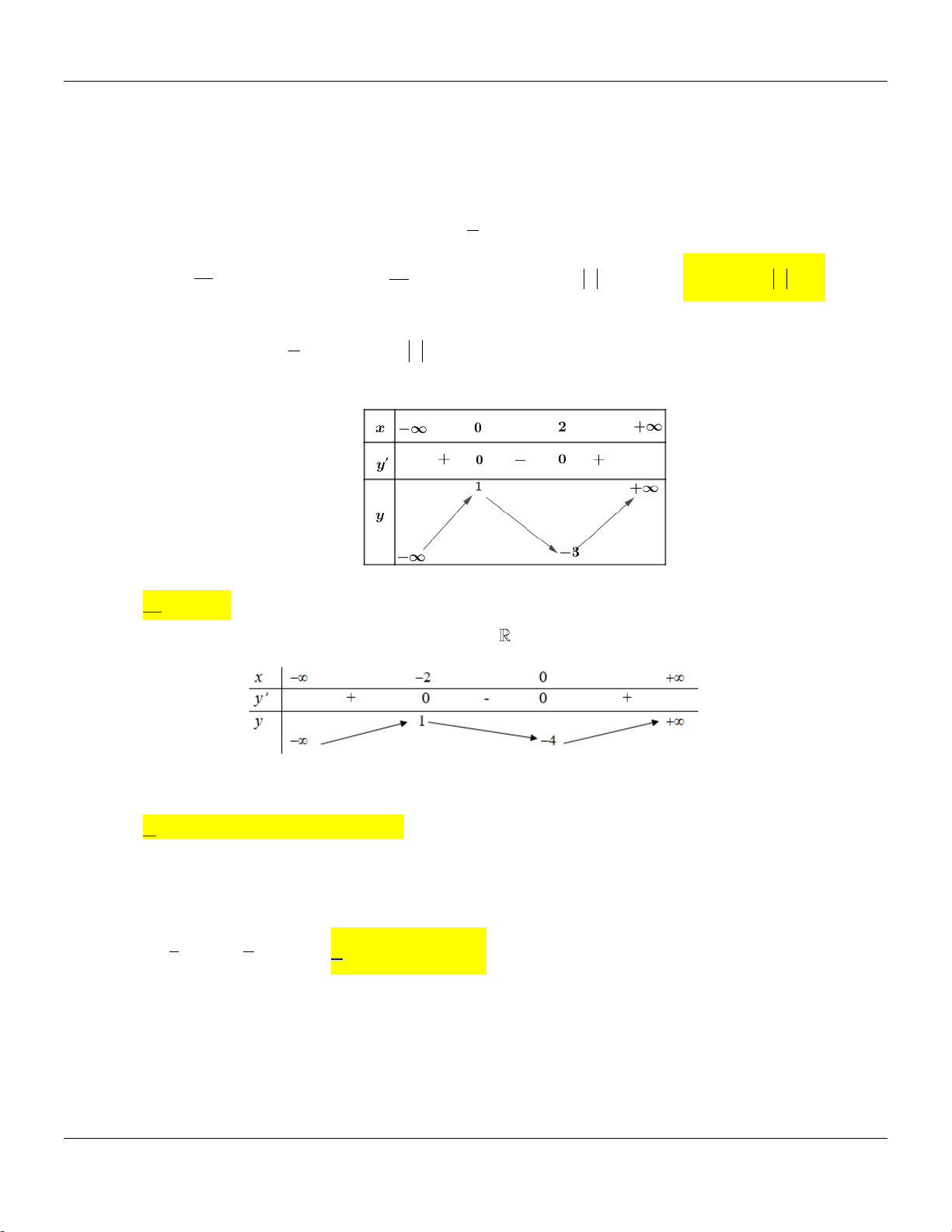
Câu 31: Cho hàm số y f x có bảng biến thiên như sau:
Tập hợp tất cả các giá trị của m để phương trình f x  m có ba nghiệm thực phân biệt
A. 4; 2. B. 4; 2.
C. 4; 2. D. 4; 2. 3 2
Câu 32: Cho hàm số f x có đạo hàm f  x  x x   1
x  2,x . Khoảng nghịch biến của hàm số là A. 2;0 . B.  ;  2  ;0;  1 . C.  ;  2
 ;0;. D.  2  ;0;1; .
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số lẻ bằng 1 8 4 1 A. . B. . C. . D. . 7 15 15 14 Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 34: Tích các nghiệm của phương trình log  x 1
6   36x  1 bằng 5  A. log 5. B. log 6. C. 5. D. 0. 6 5
Câu 35: Cho số phức z thỏa mãn z 1 i z  2 . Trong mặt phẳng phức, quỹ tích điểm biểu diễn các số phức z
A. là đường thẳng 3x y 1  0 .
B. là đường thẳng 3x y 1  0 .
C. là đường thẳng 3x y 1  0 .
D. là đường thẳng 3x y 1  0 .
Câu 36: Trong không gian Oxyz , viết phương trình đường thẳng  đi qua M  1  ;1;0 và vuông góc
với mặt phẳng Q : x  4y z  2  0 ?  x 1 tx 1 tx  2   tx  1   t     A. y  4   t .
B. y  1 4t .
C. y  5  4t .
D. y  1 4t .     z  1   z t   z  1  t z t
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua mặt phẳng Oxy có tọa độ là A. 1; 2;3 . B. 1; 2; 3  . C.  1  ; 2  ; 3   . D. 1; 2;0 .
Câu 38: Cho lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng a . Thể tích khối trụ có hai đáy
là hai hình tròn ngoại tiếp hai đáy của lăng trụ đã cho bằng 3  a 3  a 3 4 a A. 3  a . B. . C. . D. . 12 3 3
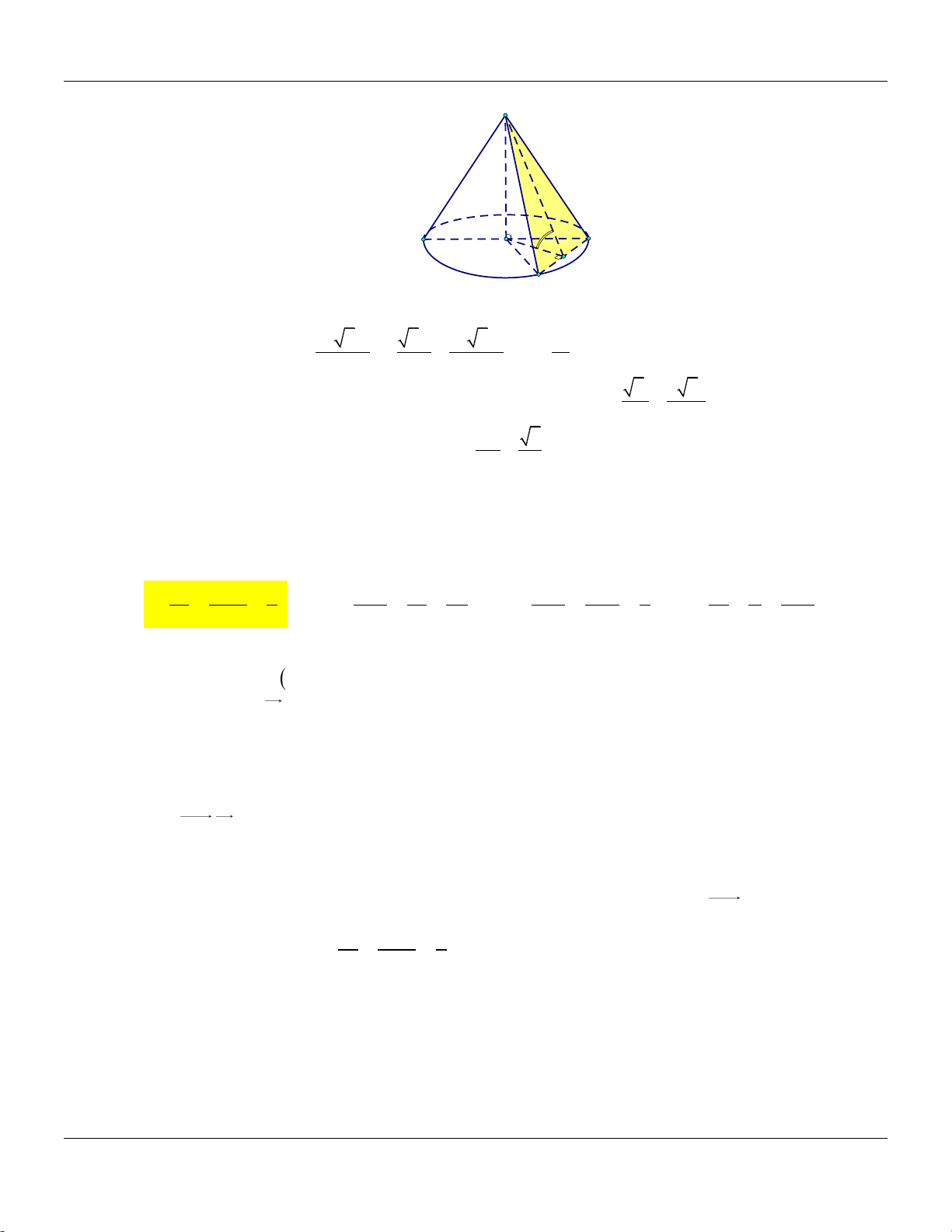
Câu 39: Cắt khối nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
60 ta được thiết diện là một tam giác vuông cân cạnh huyền 2a . Thể tích khối nón  N  bằng 3 5 3 a 3 5 3 a 3 5 3 a 3 3 a A. . B. . C. . D. . 24 72 8 72
Câu 40: Trong không gian Oxyz, phương trình mặt phẳng (P) song song và cách đều hai đường x  2 y z x y 1 z  2 thẳng d :   và d :   là 1 2 1  1 1 2 1  1 
A. 2x  2z 1  0 .
B. 2 y  2z 1  0 .
C. 2x  2 y 1  0 .
D. 2 y  2z 1  0 .
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 3  2i có tọa độ là A. 2;3. B. 2;3. C. 3; 2. D. 3; 2.
Câu 2: Trên khoảng 0;  , đạo hàm của hàm số y  log x là 7 1 1 ln 7 1
A. y  . B. y  . C. y  . D. y   . x xln7 x x ln7
Câu 3: Trên khoảng 0;  , đạo hàm của hàm số e y x là e1 x A. e 1 y e.x    . B. e 1 y x    . C. y  . D.   . e y e x . e  1
Câu 4: Tập nghiệm của bất phương trình 2x  4 là A.  ;  2 B. 0; 2 C.  ;  2 D. 0; 2 Lời giải:
Ta có 2x  4  x  2  Tập nghiệm của bất phương trình là  ;  2 .
Câu 5: Cho cấp số nhân u u  5 u  2 n  với 1 và 2
. Công bội của cấp số nhân đó bằng 5 2 A. 1. B. 28 . C. . D. . 2 5 Lời giải: u 2
Công bội của cấp số nhân đó bằng 2 q   . u 5 1
Câu 6: Trong không gian Oxyz, cho mặt phẳng  P : 3x z  2  0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của  P ? A. n  1  ;0; 1  . B. n  3; 1  ;2 . C. n  3; 1  ;0 . D. n  3;0; 1  . 2   3   1   4   Lời giải:
Vectơ pháp tuyến của mặt phẳng  P : 3x z  2  0 là n  3;0; 1  . 2   ax b
Câu 7: Cho hàm số y
có đồ thị như hình bên dưới : cx d
Tọa độ giao điểm của đồ thị hàm số đã cho với trục tung là A. 0; 2  . B. 2;0.
C. 2;0. D. 0; 2. 1 1
Câu 8: Cho hàm số f x và g x liên tục trên đoạn 0;  1 và f
 xdx 1, g
 xdx  3. Tích phân 0 0 1 2 f
 x3gxdx  bằng 0 Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia A. 9 . B. 5 . C. 10 . D. 11. Lời giải: 1 1 1 Ta có 2 f
 x3gxdx  2 f
 xdx3 g
 xdx  2.13.311. 0 0 0
Câu 9: Hàm số nào có đồ thị là đường cong trong hình vẽ bên dưới? x 1 A. 4 2
y x  4x 1. B. y
y x x  . D. 2 y  2x 1 . x  . C. 3 2 4 1 2 Lời giải:
Từ đồ thị ta thấy hàm số có 3 điểm cực trị, suy ra hình vẽ là đồ thị hàm số 4 2
y x  4x 1. 2 2 2
Câu 10: Trong không gian Oxyz, cho mặt cầu S  :  x   1
  y  2  z   1
 9 . Tìm tọa độ tâm I
và tính bán kính R của S . A. I  1  ;2 
;1 và R  3. B. I 1; 2  ;  1 và R  3. C. I  1  ;2 
;1 và R  9. D. I 1; 2  ;  1 và R  9.
Câu 11: Trong không gian Oxyz, góc giữa hai mặt phẳng Oxy và Oxz bằng A. 90 .  B. 60 .  C. 30 .  D. 45 . 
Câu 12: Cho số phức z  2  i, phần ảo của số phức 2 z là A. 4. B. 4 . i C. 3. D. 1. Lời giải:
Ta có: z    i2 2 2  3  4i.
Câu 13: Cho khối lập phương có cạnh bằng 3. Thể tích khối lập phương đã cho bằng A. 9. B. 27. C. 18. D. 3.
Câu 14: Cho khối chóp .
S ABC có đáy là tam giác vuông tại A, AB  2, AC  4,SA vuông góc với đáy và
SA  3 (tham khảo hình bên). S A C B
Thể tích khối chóp đã cho bằng A. 9. B. 8. C. 4. D. 3. Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia Lời giải: 1 1 1 Ta có: VS . A SS . A A . B AC  4. S.ABC 3 ABC 3 2
Câu 15: Cho đường thẳng  và mặt cầu SO; R. Gọi d là khoảng cách từ O đến  và d  . R Số giao
điểm của  và SO; R là A. 1. B. 2. C. 0. D. Vô số.
Câu 16: Phần ảo của số phức z  3  7i là A. 3. B. 7. C. 7. D. 3.
Câu 17: Cho khối nón có đường cao h, độ dài đường sinh l và bán kính đáy r. Diện tích xung quanh
Sxq của khối nón được tính theo công thức nào dưới đây?
A. S   rl   S   rl S   rh xq . B. 1 S rl . C. 2 . D. . xq xq xq 2 x 1 y  2 z  3
Câu 18: Trong không gian Oxyz, đường thẳng d :  
đi qua điểm nào sau đây? 3 4  5 
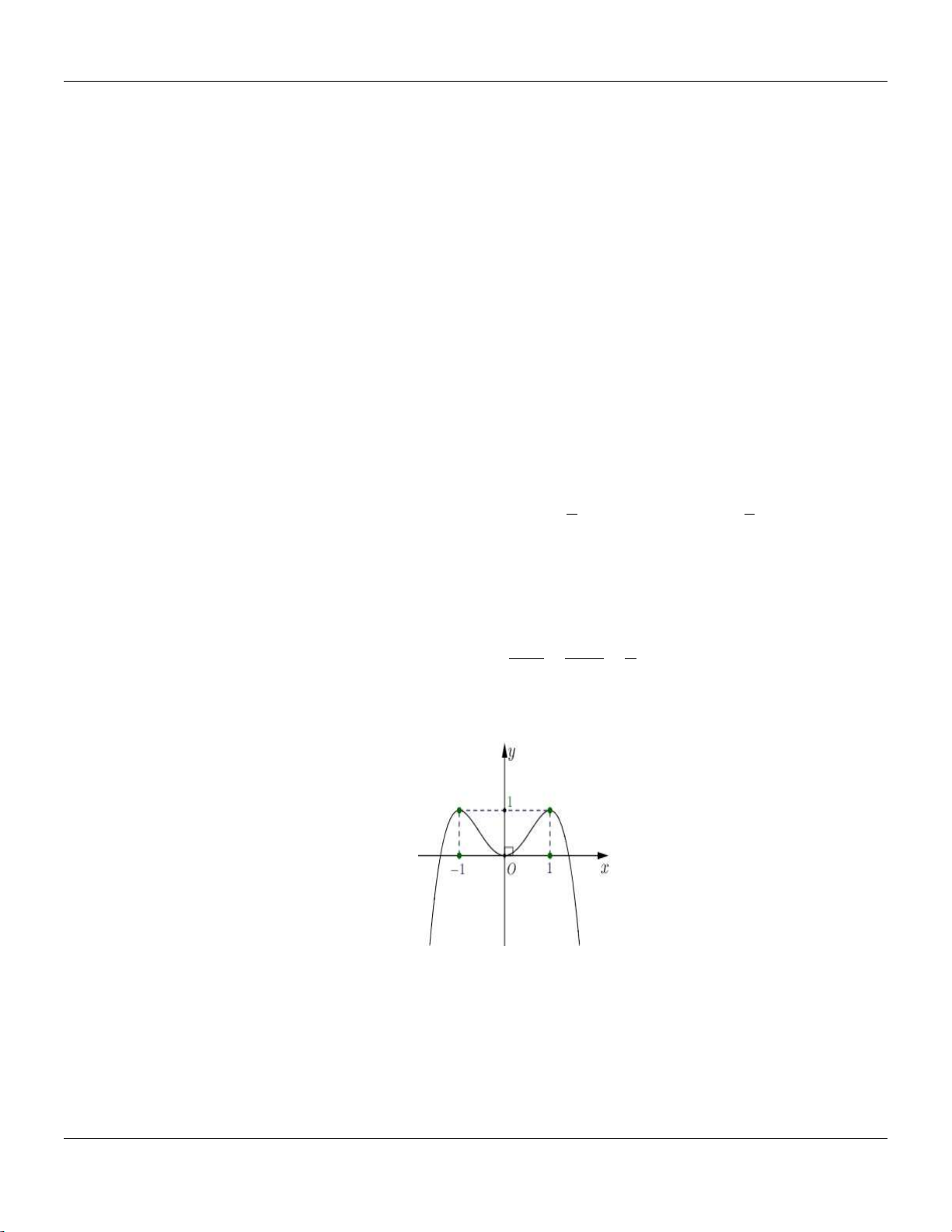
A. 1; 2;3 . B.  1  ;2; 3   . C. 3; 4  ; 5   . D. 3; 4;5 . Câu 19: Cho hàm số 4 2
y ax bx c có đồ thị là đường cong như hình bên dưới: y -1 1 x O -1 -2
Điểm cực đại của đồ thị hàm số đã cho có tọa độ là A. 0;   1 . B. 1;0. C. 1; 2. D. 1; 2. 4x  1
Câu 20: Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình là x  2
A. y  4.
B. x  4.
C. x  2. D. y  2.
Câu 21: Tập nghiệm của bất phương trình log x  1 là 2 A.  ;  2. B. 0; 2. C. 0;  1 . D.  ;   1 . Lời giải: x  0
Ta có: log x  1    x 0;2 . 2   x   2
Câu 22: Cho tập M có 10 phần tử. Số tập con gồm 3 phần tử của tập hợp M là A. 3!. B. 10!. C. 3 A . D. 3 C . 10 10 Câu 23: Cho sin d x x f
xC. Khẳng định nào dưới đây đúng?
A. f  x  cos . x
B. f  x   cos . x
C. f  x  sin . x
D. f  x   sin . x Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia 4 4
Câu 24: Nếu 3 f
 x xdx 12 
thì f xdx  bằng 2 2 10 A. 6 . B. 0 . C. 2 . D. . 3 Lời giải: 4 4 4 4 1 4 Ta có 3 f
 x xdx 12   3 f
 xdx d
x x  12  3 f   x 2 dx x 12 2 2 2 2 2 2 4 4  3 f
 xdx6 12  f
 xdx  2. 2 2
Câu 25: Cho hàm số f x  s inx x 1. Khẳng định nào dưới đây đúng? x x A. f  x 2 dx  cosx
x C . B. f  x 2
dx  cosx
x C . 2 2 x C. f
 xdx  cosx 1C . D. f  x 2
dx  cosx   C . 2
Câu 26: Cho hàm số y f (x) có đồ thị như hình vẽ bên.
Hàm số đã cho đồng biến trên các khoảng nào dưới đây? A. 0; 2 .
B. 0;   . C. 0; 4 . D. 1;  1 .
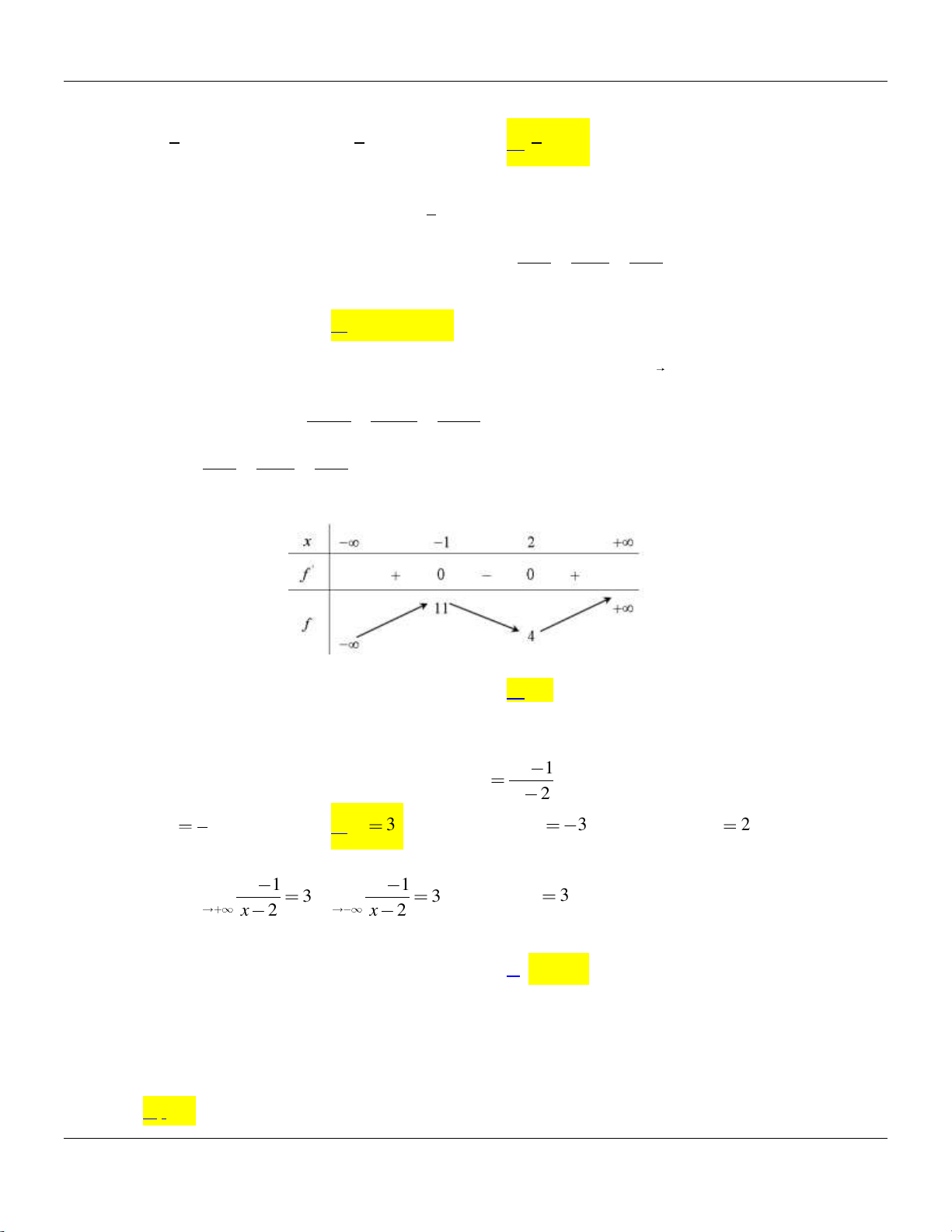
Câu 27: Cho hàm số y f x có bảng biến thiên như sau:
Đồ thị hàm số y f x có điểm cực tiểu là A. 0; 2 .
B. 3;  4 . C. x  3. D. y  4. CT CT Lời giải:
Dựa vào bảng biến thiên, ta có đồ thị hàm số y f x có điểm cực tiểu là 3;  4 .
Câu 28: Cho a , b là các số thực dương tùy ý. Khẳng định nào sau đây đúng?
A. ln ab  ln a  ln b .
B. ln a b  ln a  ln b .
C. ln ab  ln . a ln b .
D. ln a b  ln . a ln b . Lời giải: Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia
Theo quy tắc logarit ta có: ln ab  ln a  ln b .
Câu 29: Cho hình phẳng H giới hạn bởi đồ thị hàm số 2
y  2x x  1 và trục hoành. Thể tích của vật
thể tròn xoay khi quay H quanh trục hoành bằng 9 81 81 9 A. . B. . C. . D. . 8 80 80 8 Lời giải: x  1
+ Phương trình hoành độ giao điểm: 2 
2x x  1  0  1  . x    2 1 2 81
+ Thể tích cần tìm là V    2
2x x  1 dx   .  80 1 2
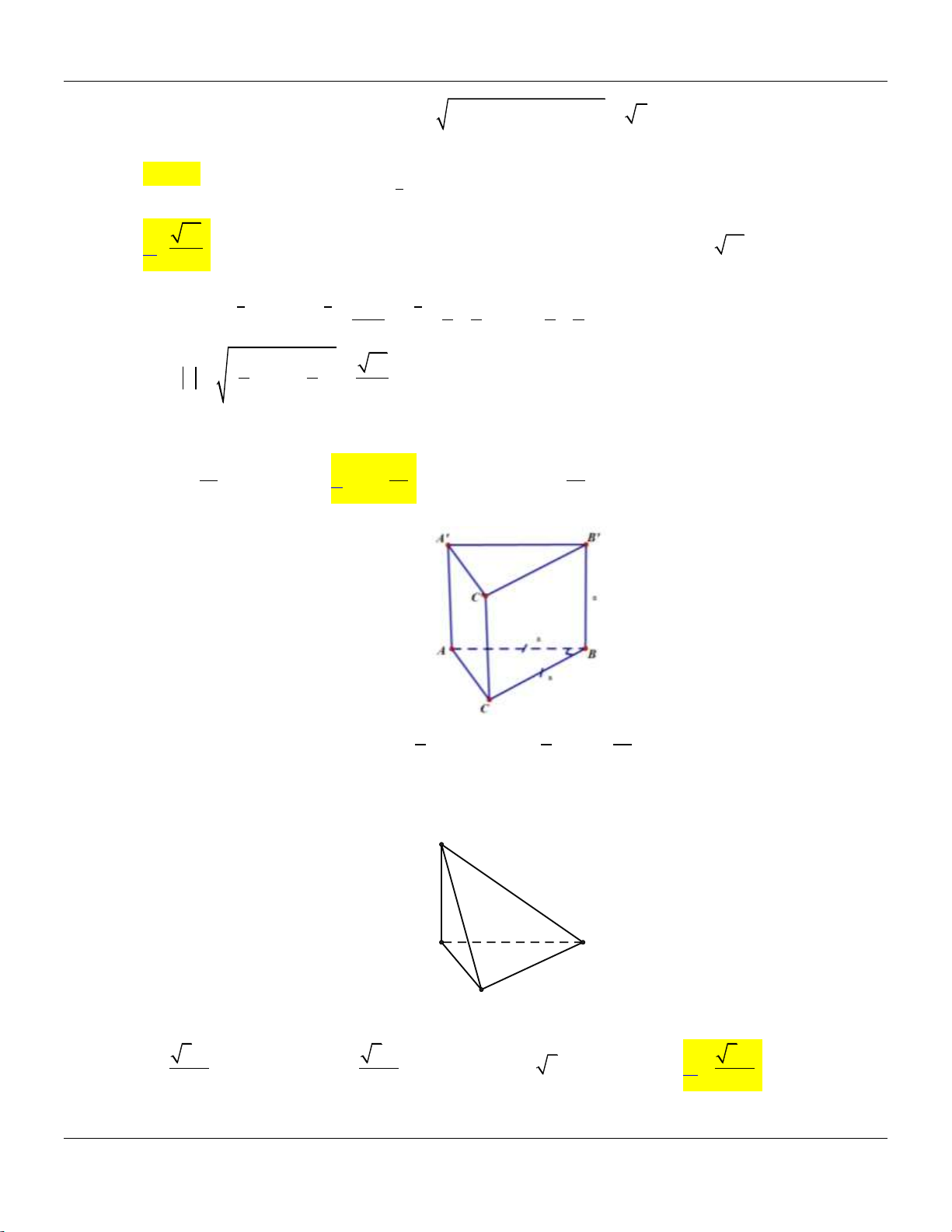
Câu 30: Cho hình lăng trụ đứng ABC.AB C
  có tất cả các cạnh bằng nhau:
Góc giữa đường thẳng AB và mặt phẳng  AB C  bằng A. 30 . B. 90 . C. 60 . D. 45 . Lời giải:
Do AA   A BC
  nên AB ;A BC    A B   . A Do tam giác AA B
 vuông cân nên A BA   45 .
Câu 31: Cho hàm số y f x có bảng biến thiên như sau:
Tập hợp tất cả các giá trị của m để phương trình f x  m có ba nghiệm thực phân biệt
A. 4; 2.
B. 4; 2.
C. 4; 2. D. 4; 2. Lời giải:
Số nghiệm của phương trình f x  m là số giao điểm của đồ thị hàm số y f x và đường
thẳng y m . Dựa vào bảng biến thiên ta thấy m  4  ;2 . 3 2
Câu 32: Cho hàm số f x có đạo hàm f  x  x x  
1  x  2,x  . Khoảng nghịch biến của hàm số là Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia A. 2;0 . B.  ;  2  ;0;  1 . C.  ;  2
 ;0;. D.  2  ;0;1; . Lời giải: x  2  
Ta có: f  x  0  x  0  . x 1  Bảng xét dấu:
Vậy hàm số nghịch biến trên khoảng 2;0 .
Câu 33: Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được
hai số có tổng là một số lẻ bằng 1 8 4 1 A. . B. . C. . D. . 7 15 15 14 Lời giải: Không gian mẫu 2 C  105 . 15
Để tổng hai số là một số lẻ ta chọn 1 số lẻ và 1 số chẵn nên ta có 8.7  56 . 56 8 Xác suất cần tìm là  . 105 15
Câu 34: Tích các nghiệm của phương trình log  x 1
6   36x  1 bằng 5  A. log 5. B. log 6. C. 5. D. 0. 6 5 Lời giải:
Điều kiện xác định: x 1 6   36x  0
Khi đó, phương trình log  x 1 6  36x x 1 1 6    
 36x  5 (thoả điều kiện) 5  3
 6x  6.6x  5  0
6x 1  x  0
 6x 5 x log 5  6
Vậy tích các nghiệm của phương trình đã cho bằng 0.
Câu 35: Cho số phức z thỏa mãn z 1 i z  2 . Trong mặt phẳng phức, quỹ tích điểm biểu diễn các số phức z
A. là đường thẳng 3x y 1  0 .
B. là đường thẳng 3x y 1  0 .
C. là đường thẳng 3x y 1  0 .
D. là đường thẳng 3x y 1  0 . Lời giải:
Gọi z x yi x, y   . 2 2 2
Ta có z 1 i z  2   x     y     x   2 1 1 2
y  3x y 1  0 .
Vậy quỹ tích điểm biểu diễn các số phức z là đường thẳng 3x y 1  0 .
Câu 36: Trong không gian Oxyz , viết phương trình đường thẳng  đi qua M  1  ;1;0 và vuông góc
với mặt phẳng Q : x  4y z  2  0 ? Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc giax 1 tx 1 tx  2   tx  1   t     A. y  4   t .
B. y  1 4t .
C. y  5  4t .
D. y  1 4t .     z  1   z t   z  1  t z tLời giải:
Do đường thẳng  vuông góc với mặt phẳng Q : x  4y z  2  0 nên đường thẳng  nhận u  1; 4  ; 1
  làm một vectơ chỉ phương.
Kiểm tra phương án C thỏa mãn.
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua mặt phẳng Oxy có tọa độ là A. 1; 2;3 . B. 1; 2; 3  . C.  1  ; 2  ; 3   . D. 1; 2;0 .
Câu 38: Cho lăng trụ tam giác đều ABC.AB C
  có tất cả các cạnh bằng a . Thể tích khối trụ có hai đáy
là hai hình tròn ngoại tiếp hai đáy của lăng trụ đã cho bằng 3  a 3  a 3 4 a A. 3  a . B. . C. . D. . 12 3 3 Lời giải: a 3
Bán kính đường tròn ngoại tiếp đáy của lăng trụ là R  . 3 2 3  a 3   a
Thể tích khối trụ là V  . a       . 3 3  
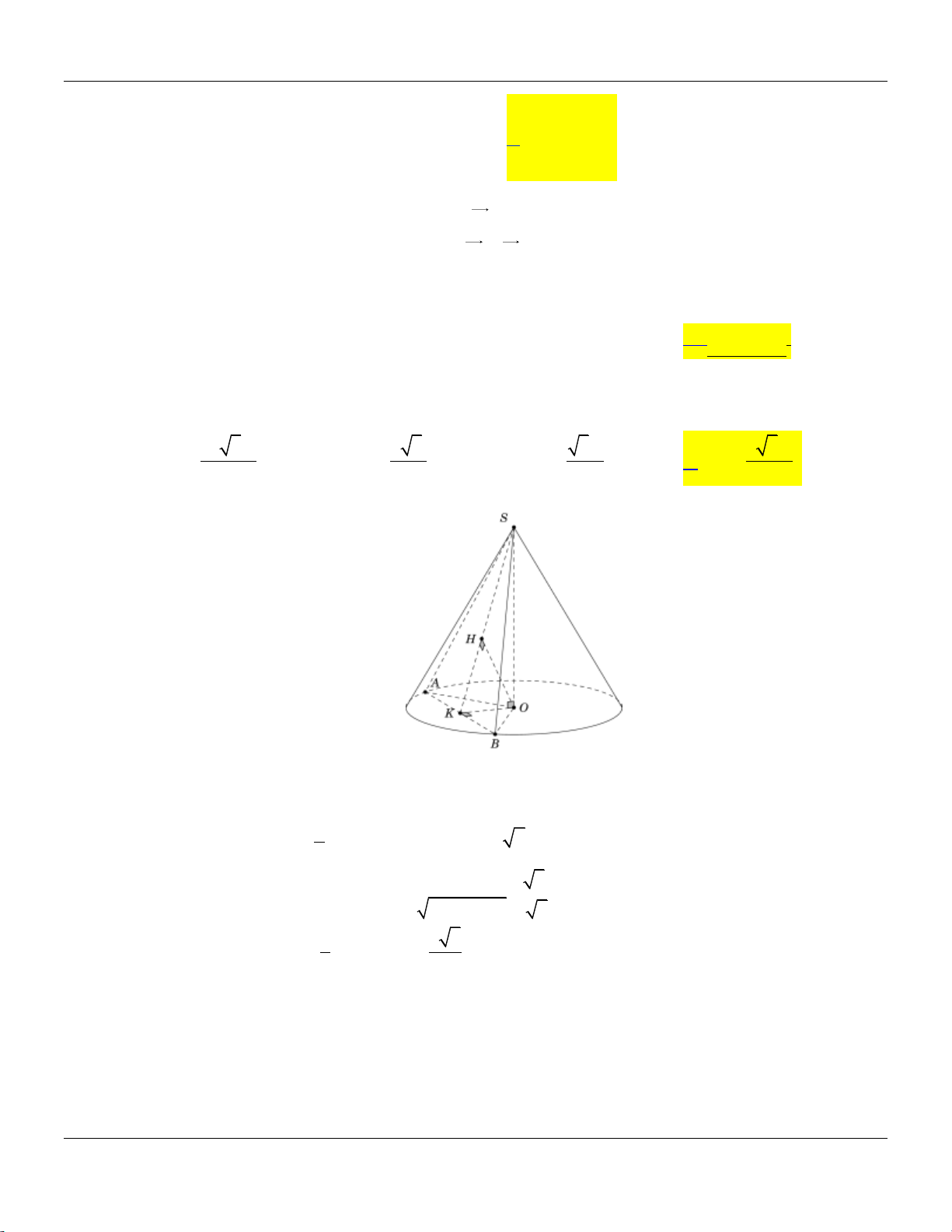
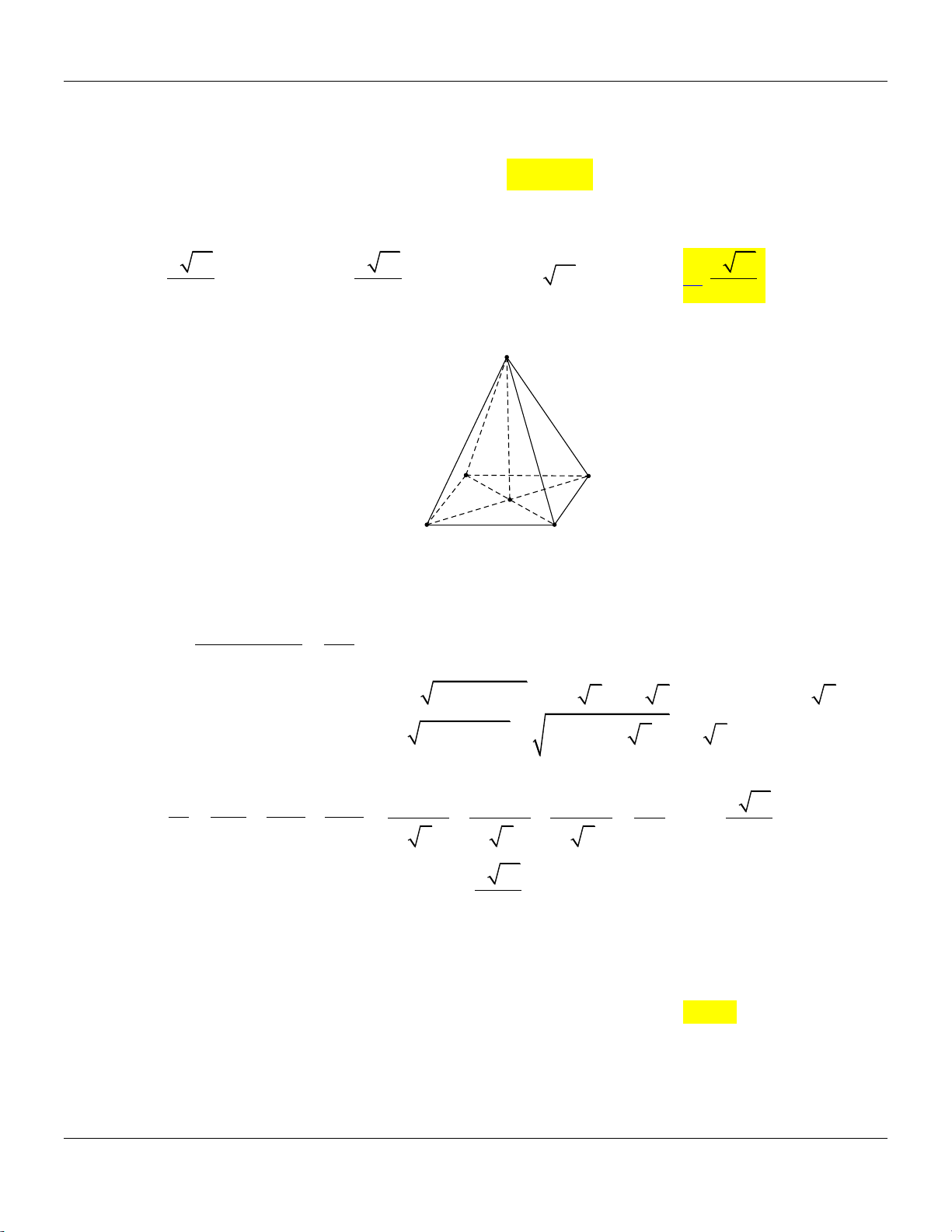
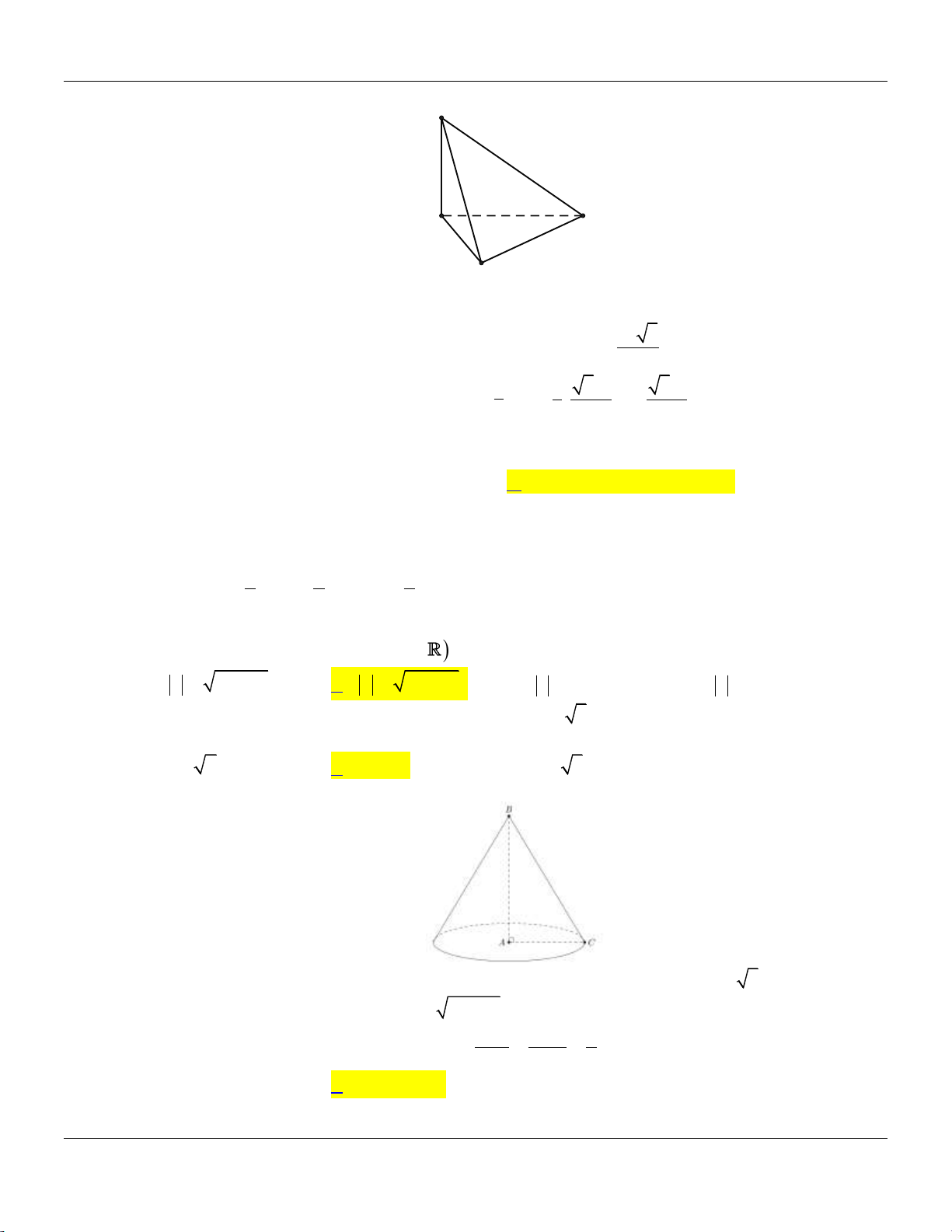
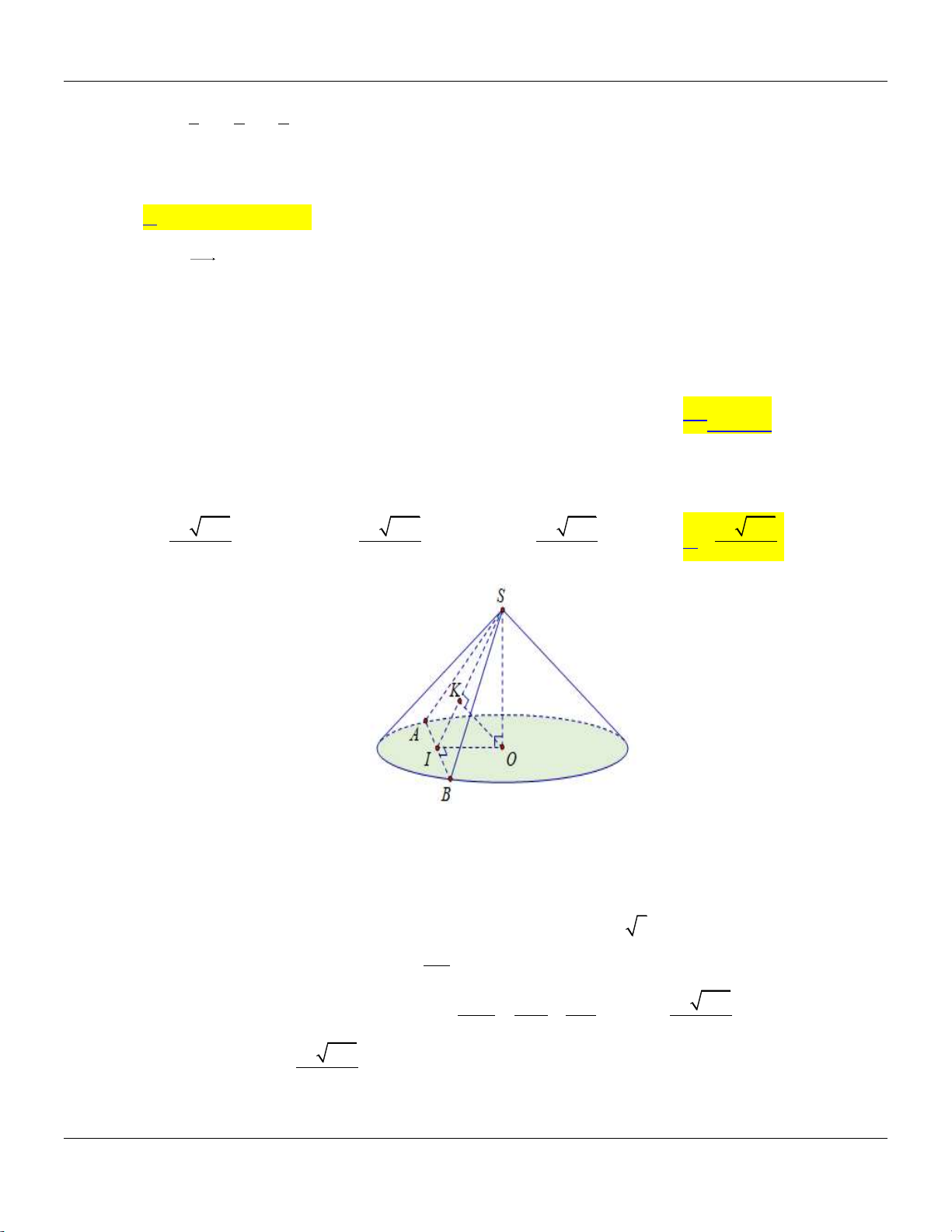
Câu 39: Cắt khối nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
60 ta được thiết diện là một tam giác vuông cân cạnh huyền 2a . Thể tích khối nón  N  bằng 3 5 3 a 3 5 3 a 3 5 3 a 3 3 a A. . B. . C. . D. . 24 72 8 72 Lời giải:
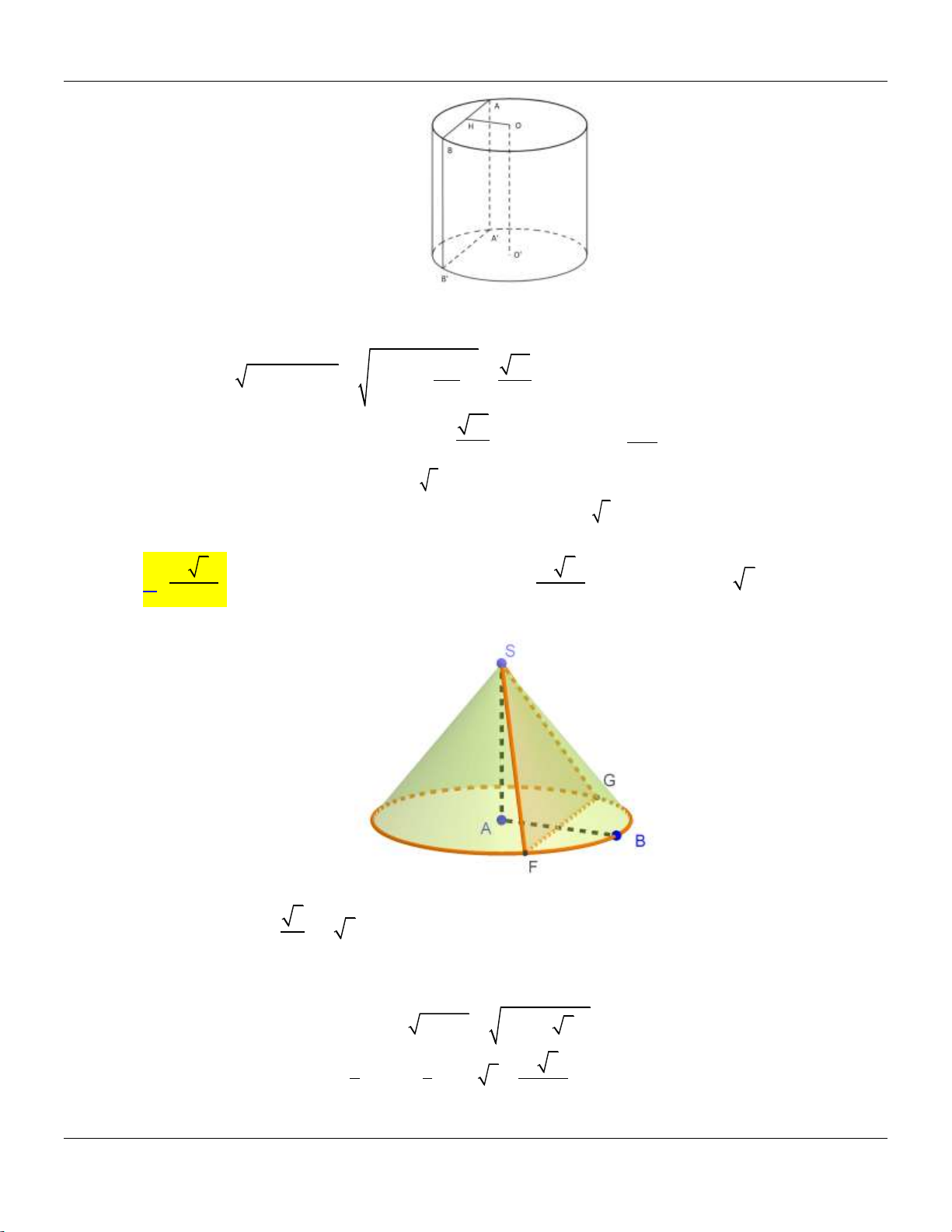
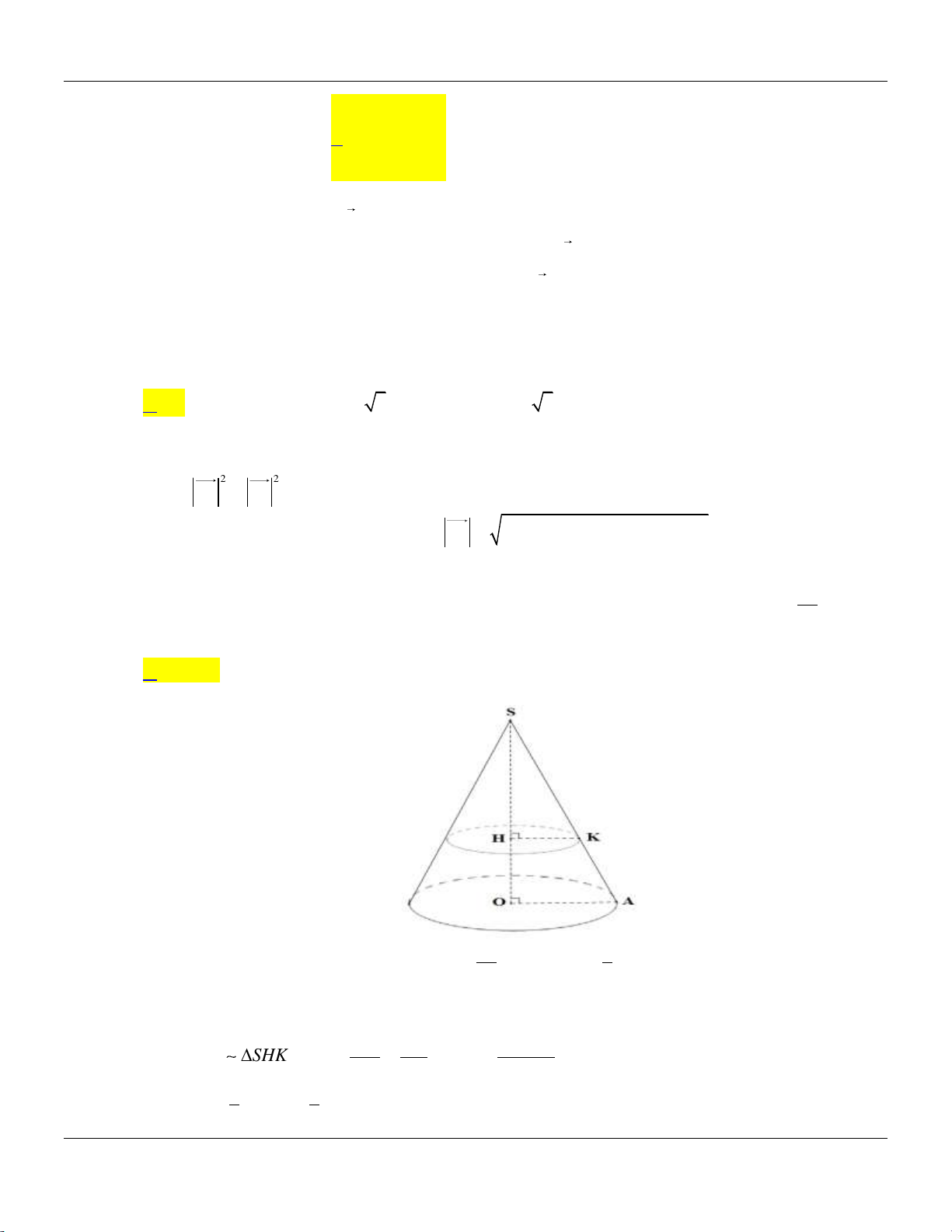
Giả sử khối nón  N  có đỉnh là S , tâm đáy là O và thiết diện là giác vuông cân SAB . 1
Gọi I là trung điểm của AB , khi đó 0
SIO  60 , SI
AB a, SB SA a 2 . 2 2 a 3 3a a 5 Ta có 0 2 2 2
SO SI.sin 60  ,OB
SB SO  2a   . 2 4 2 Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 3 1 1
a 5  a 3 5 3a Vậy 2
V  . .OB .SO   .  .    . 3 3 2 2 24  
Câu 40: Trong không gian Oxyz, phương trình mặt phẳng (P) song song và cách đều hai đường x  2 y z x y 1 z  2 thẳng d :   và d :   là 1 2 1  1 1 2 1  1 
A. 2x  2z 1  0 .
B. 2 y  2z 1  0 .
C. 2x  2 y 1  0 .
D. 2 y  2z 1  0 . Lời giải:
Đường thẳng d đi qua điểm M (2;0;0) và có véc tơ chỉ phương u  ( 1  ;1;1) . 1 1
Đường thẳng d đi qua điểm N (0;1; 2) và có véc tơ chỉ phương u  (2; 1  ; 1  ) . 2 2 1
Gọi I là trung điểm của đoạn thẳng MN , suy ra I (1; ;1) . 2
Vì mặt phẳng (P) song song với hai đường thẳng d và d nên mặt phẳng (P) đi qua I nhận 1 2
véc tơ n  [u    1, u 2 ]
( 2; 0; 1) làm véc tơ pháp tuyến. Do đó phương trình mặt phẳng là 1 1
(P) : 0.(x 1) 1.( y  ) 1.(z 1)  0  y z
 0  2y  2z 1  0. 2 2
Vậy, phương trình mặt phẳng (P) : 2 y  2z 1  0.
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 02_______________
Câu 1: Cho số phức z  2  3i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z là điểm có tọa độ là A. 2;3 .
B. 3;  2 . C. 3; 2 . D. 2;  3 .
Câu 2: Đạo hàm của hàm số 10x y  là 10x A. y  . B. 10x y  .ln10 . C. 10x y  . D.   10x y log e . ln10 10
Câu 3: Tập xác định D của hàm số y    x13 2 là
A. D   ;  2. B. D   ;  .
C. D   ;  2 .
D. D  2;  .
Câu 4: Bất phương trình 3x  81  0 có tất cả bao nhiêu nghiệm nguyên dương? A. 3 . B. 4 . C. vô số. D. 5 .
Câu 5: Cho cấp số nhân (u ) với u  1 và u  8 . Công bội của cấp số nhân đã cho bằng n 1 4 A. 2. B. 7. C. 8. D. 4.
Câu 6: Trong không gian Oxyz , cho mặt phẳng  P : x  4 y  3z  2  0. Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng  P ? A. n  1 4 3 n  1 4 3 n   n  1 4 3 2  ; ;  . B. 3  ; ; . C. 1; 4;3 . D. 1  ; ;  . 4   ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d y O 2 x -2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0; 2 . 3
Câu 8: Cho hàm số f x có đạo hàm trên , f   1  2
 và f 3  2. Tính I f   xdx. 1  A. I  4. B. I  0. C. I  3. D. I  4.
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới? A. 4 2
y  x  2x  3 . B. 3
y x  3x  3 . C. 4 2
y  x  2x  3 . D. 4 2
y x  2x  3 . Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 10: Trong không gian Oxyz , cho mặt cầu S  : 2 2 2
x y z  2x  6 y  4z  2  0. Xác định tọa độ
tâm I và bán kính R của mặt cầu S  . A. I 1; 3
 ;2, R 16 . B. I 1; 3
 ;2, R  4 . C. I  1  ;3; 2
 , R 16 .D. I  1  ;3; 2
 , R  4 .
Câu 11: Trong không gian Oxyz , góc giữa hai mặt phẳng Oyz và Oxz bằng A. 30 .  B. 90 .  C. 60 .  D. 45 . 
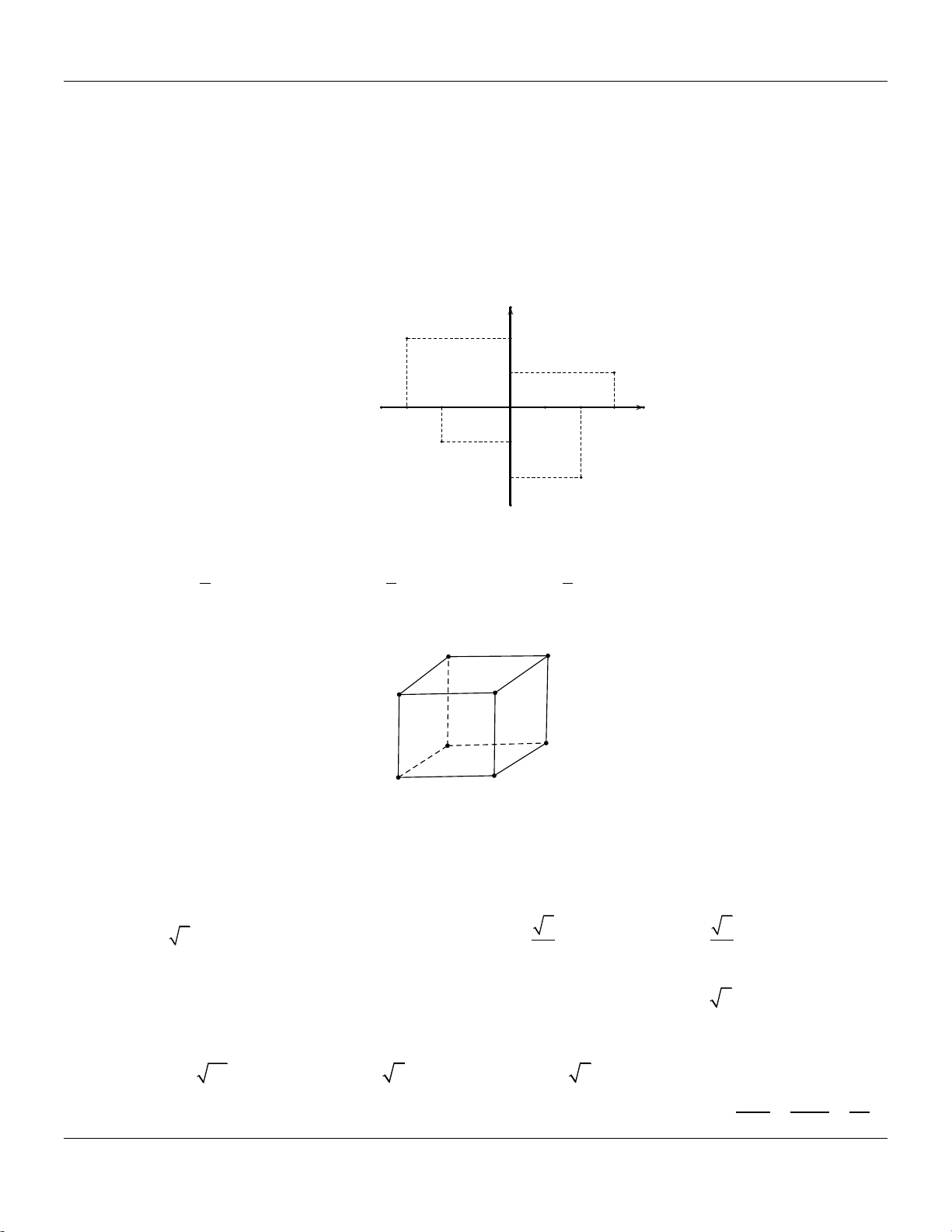
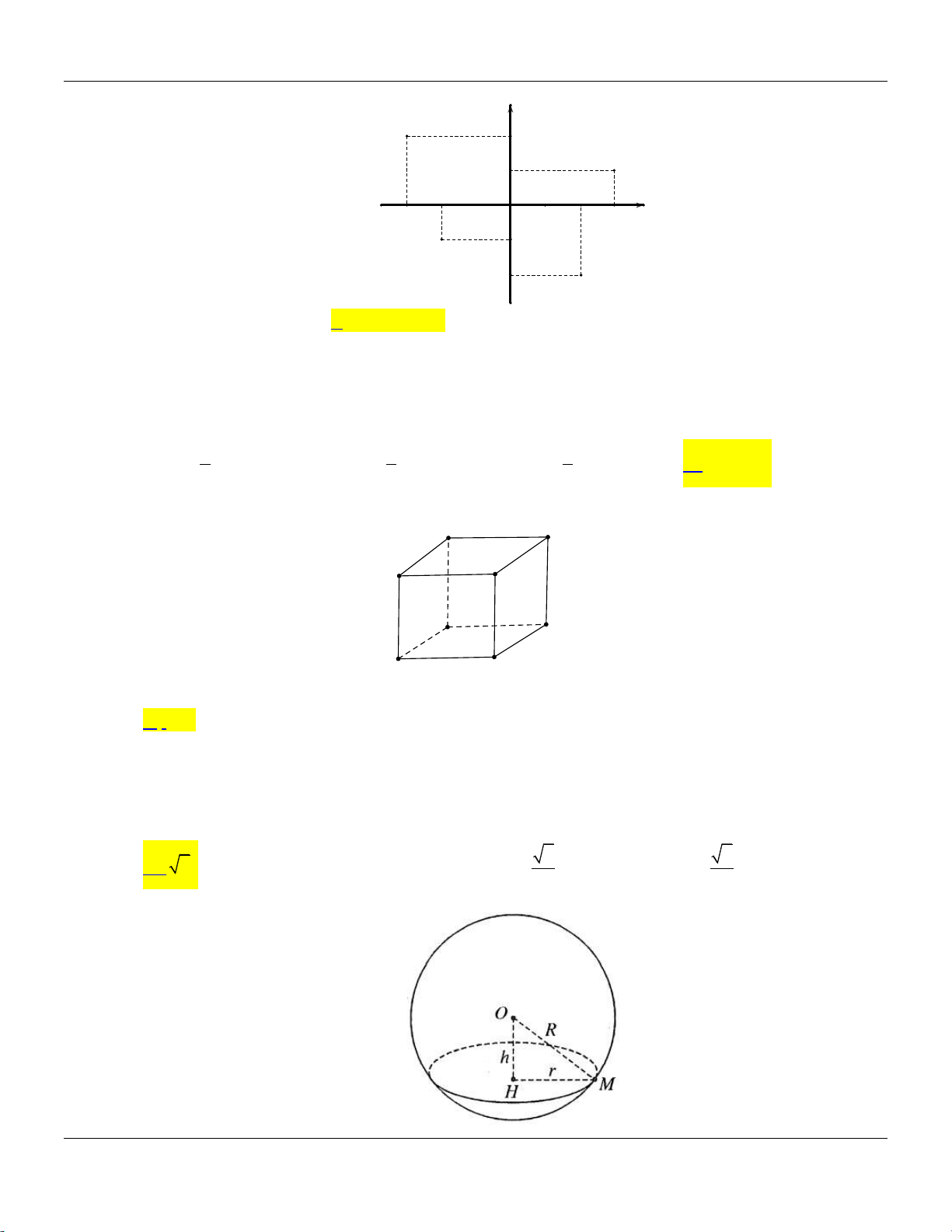
Câu 12: Các điểm M , N , P, Q trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
z , z , z , z . Khi đó w  3z z z z bằng 1 2 3 4 1 2 3 4 y M 2 1 P -3 -1 O 1 2 3 x -2 -1 N Q -2
A. w  6  4i .
B. w  6  4i .
C. w  4  3i .
D. w  3  4i .
Câu 13: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 1 1 1 A. V Bh . B. V Bh . C. V Bh .
D. V Bh . 2 3 6
Câu 14: Cho khối hộp chữ nhật ABC . D AB CD
  có AB  2, AD  3, 
AA  4 (tham khảo hình vẽ). A' D' C' B' A D B C
Thể tích khối hộp đã cho bằng A. 24 . B. 20 . C. 9 . D. 8 .
Câu 15: Một khối cầu có bán kính bằng 2 , một mặt phẳng   cắt khối cầu đó theo một hình tròn có
diện tích là 2 . Khoảng cách từ tâm khối cầu đến mặt phẳng   bằng 2 2 A. 2 . B. 1 . C. . D. . 2 4
Câu 16: Môđun của số phức z  3  4i bằng A. 5 . B. 3 . C. 7 . D. 7 .
Câu 17: Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích khối trụ đó là 8 . A. 3 h  32 . B. 3 h  4 . C. h  2 2 . D. h  2 . x 1 y  2 z
Câu 18: Trong không gian Oxyz , điểm nào dưới đây không thuộc đường thẳng d :   2 1 1  ? Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia A. Q 1; 2  ;0 . B. M  1  ;2;0 . C. N  1  ; 3  ;  1 . D. P 3; 1  ;  1 .
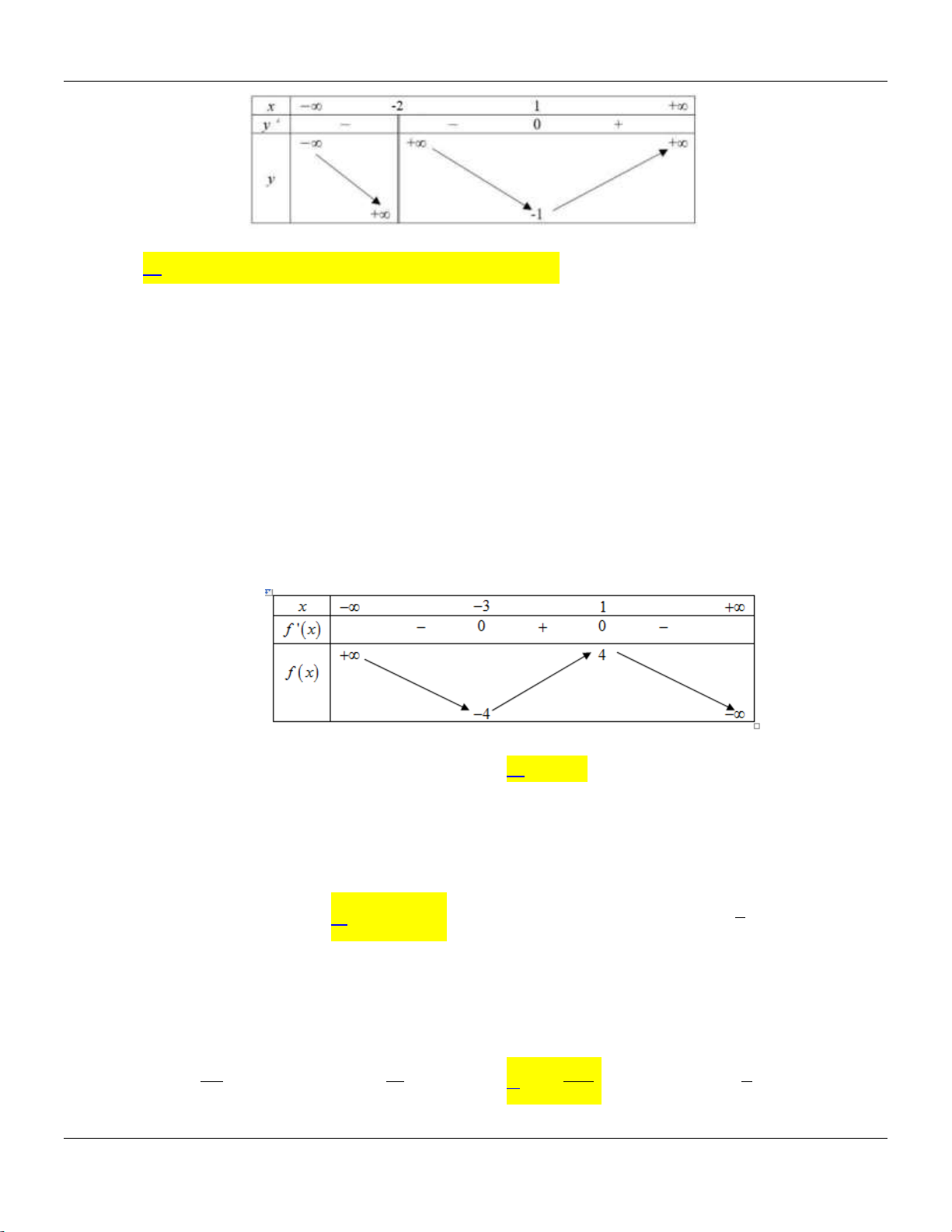
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  2 . B. x  2 . C. x  0 .
D. x  1 . 3x  2
Câu 20: Đường tiệm cận đứng của đồ thị hàm số y  có phương trình là x 1 A. x  2 . B. x  1 . C. x  3 . D. x  1 .
Câu 21: Tập nghiệm của bất phương trình log x  1 là 2 A. (0;1] . B. (; 2] . C. 0; 2. D. (0; 2].
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là A. P . B. 36. C. 3 C . D. 3 A . 12 12 12
Câu 23: Cho hàm số y f x thỏa mãn f  x  2  7 cos x , f 0  3 . Mệnh đề nào dưới đây đúng?
A. f x  2x  7 sin x  3.
B. f x  2  7 sin x  3 .
C. f x  2x  sin x  9 .
D. f x  2x  7 sin x  3. 4 4 2 Câu 24: Nếu f
 xdx  5 và f xdx  1  
thì f xdx  bằng 0 2 0 A. 6 . B. 4 . C. 4  . D. 6  . x
Câu 25: Họ tất cả các nguyên hàm của hàm số f x  2  4x là x 2x 2 A. x 2
2 ln 2  2x C . B. 2  x 2x C .
C. 2 ln 2  C . D. C . ln 2 ln 2
Câu 26: Cho hàm số f x có bảng biến biên dưới đây:
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng  ;    1 .
B. Hàm số đã cho nghịch biến trên khoảng 0;  1 .
C. Hàm số đã cho đồng biến trên khoảng 1;  .
D. Hàm số đã cho nghịch biến trên khoảng 3; 2 . Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 27: Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là A. y  3 . B. y  1. C. y  4 . D. y  4 . Câu 28: Biết 5
y  log x . Khi đó 2 1
A. y  5log x .
B. y  5log x .
C. y  5  log x .
D. y  log x . 2 2 2 5
Câu 29: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  5x  4 và trục Ox . Thể tích của
khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox là 9 81 81 9 A. V  . B. V  . C. V  . D. V  . 2 10 10 2
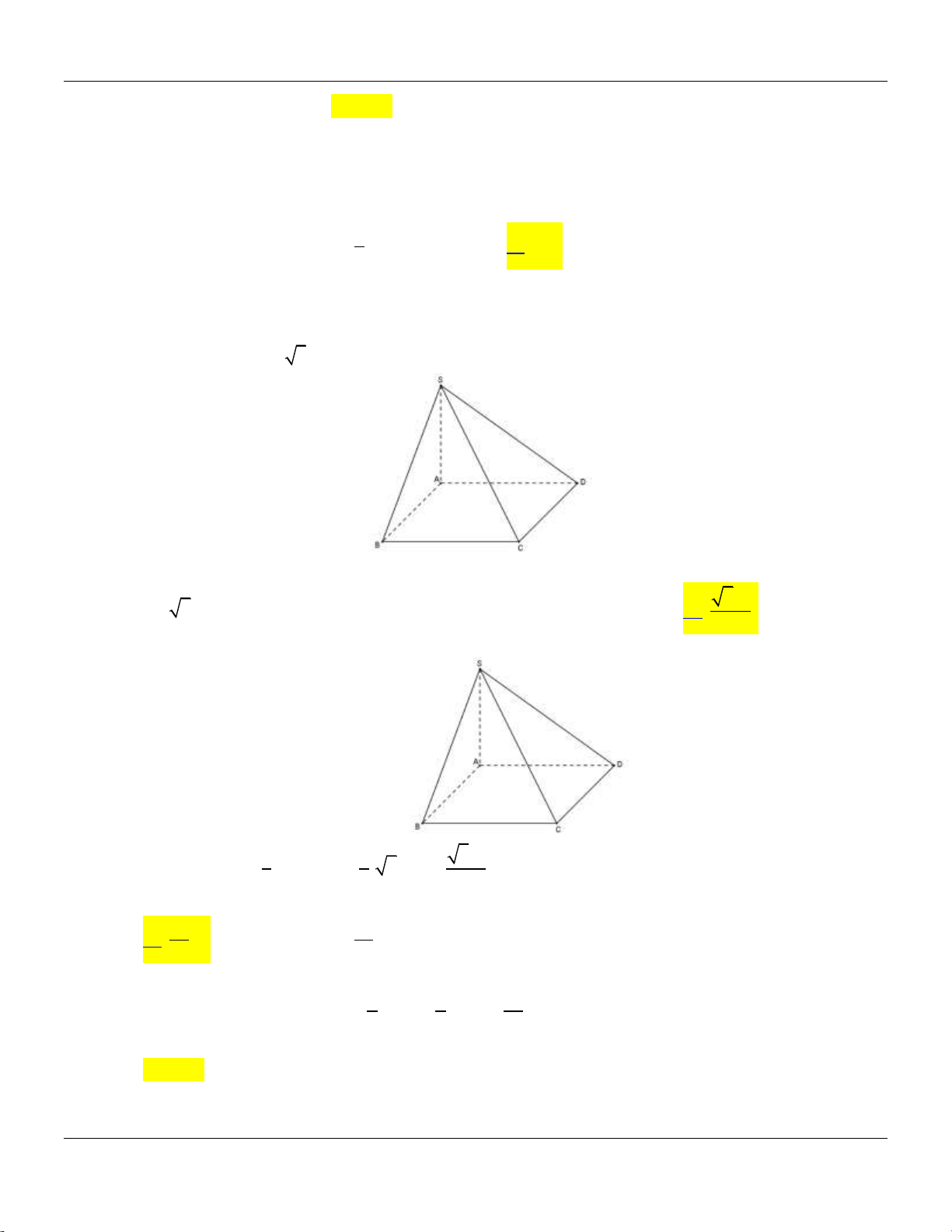
Câu 30: Cho hình chóp S.ABCD có đáy là hình thoi tâm O , ABD đều cạnh a 2 , SA vuông góc với 3a 2
mặt phẳng đáy và SA
(minh họa như hình bên dưới). 2
Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 . 2x  3
Câu 31: Cho hàm số y
có đồ thị (C) và đường thẳng d : y x m . Với tất cả giá trị nào của x  2
m thì d cắt (C) tại hai điểm phân biệt? m  2
A. m  2 .
B. m  2 . C. m  6 . D.  . m  6 2 3
Câu 32: Cho hàm số y f x liên tục trên
, có đạo hàm f  x  2  x  x  2  x  5,x  .
Hàm số y f x nghịch biến trên khoảng nào sau đây? A.  ;  2. B. 5;  . C. 2;5 .
D. 2;  .
Câu 33: Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10, lấy ngẫu nhiên 5 quả cầu.
Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng 11 5 7 1 A. . B. . C. . D. . 12 12 12 12 Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 34: Biết phương trình 2 log x  2 log
2x 1  0 có hai nghiệm x , x . Tính x x . 2 2   1 2 1 2 1 1 A. x x  4 . B. x x  . C. x x  .
D. x x  3 . 1 2 1 2 8 1 2 2 1 2
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z x yi  , x y   thỏa mãn
z  2  i z  3i là đường thẳng có phương trình là
A. y x 1.
B. y  x 1.
C. y x 1.
D. y  x 1 .
Câu 36: Trong không gian Oxyz , đường thẳng d qua M  3
 ;5;6 và vuông góc với mặt phẳng
P:2x 3y  4z  2  0 thì đường thẳng d có phương trình là x  3 y  5 z  6 x  3 y  5 z  6 A.     . 2 3  . B. 4 2 3 4 x  3 y  5 z  6 x 1 y  2 z 10 C.     . 2 3  4  . D. 2 3  4
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua mặt phẳng Oxz có tọa độ là A. 1; 2;3 . B. 1; 2; 3  . C.  1  ;0; 3   . D. 1; 2;3 .
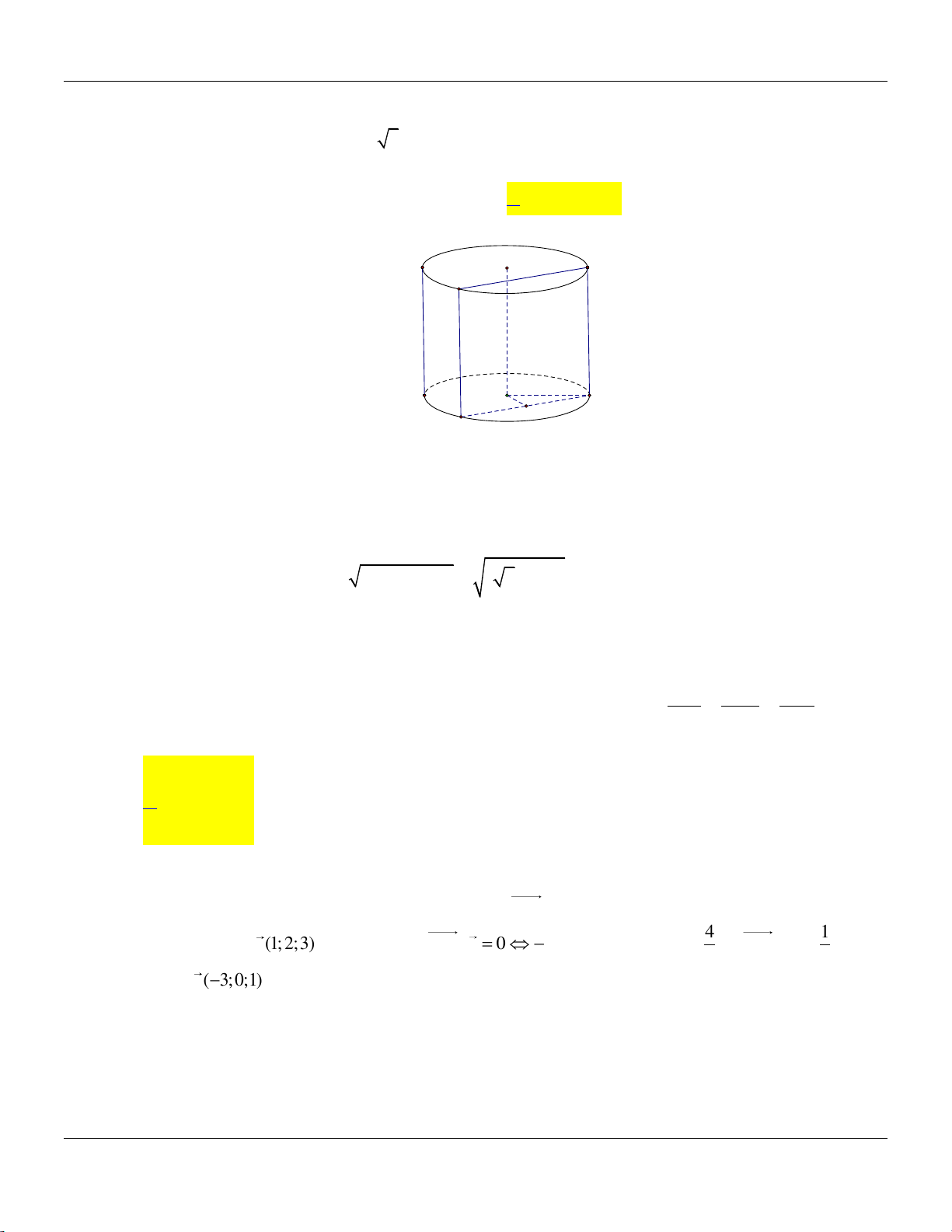
Câu 38: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 2 , thiết
diện thu được là hình vuông có diện tích bằng 25 . Thể tích khối trụ bằng 10 2 205 205 10 2 A.  . B.  . C.  . D.  . 3 4 12 9
Câu 39: Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng 32 5 18 5 A. . B. 32 . C. . D. 32 5 . 3 3
Câu 40: Trong không gian Oxyz, phương trình đường thẳng đi qua A1; 2; 4 song song với  P : x  2 y  2 z  2
2x y z  4  0 và cắt đường thẳng d :   có phương trình là 3 1 5 x 1 tx 1 2tx  1   2tx 1 t     A. y  2 . B.  y  2 . C.  y  2 . D.  y  2  .     z  4  2tz  4  2tz  4  4tz  4  2t
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Cho số phức z  2  3i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức z là điểm có tọa độ là A. 2;3 .
B. 3;  2 . C. 3; 2 . D. 2;  3 . Lời giải:
Câu 2: Đạo hàm của hàm số 10x y  là 10x A. y  . B. 10x y  .ln10 . C. 10x y  . D.   10x y log e . ln10 10 Lời giải: 10x   10 .x y y ln10 .
Câu 3: Tập xác định D của hàm số y    x13 2 là
A. D   ;  2. B. D   ;  .
C. D   ;  2 .
D. D  2;  . Lời giải:
Tập xác định: 2  x  0  x  2
Vậy tập xác định của hàm số là D   ;  2 .
Câu 4: Bất phương trình 3x  81  0 có tất cả bao nhiêu nghiệm nguyên dương? A. 3 . B. 4 . C. vô số. D. 5 . Lời giải: * Ta có: 3x 81 0 3x 81 x 4 x        x1;2;3;  4 .
Câu 5: Cho cấp số nhân (u ) với u  1 và u  8 . Công bội của cấp số nhân đã cho bằng n 1 4 A. 2. B. 7. C. 8. D. 4. Lời giải: Ta có: 3 3
u u .q q  8  q  2. 4 1
Câu 6: Trong không gian Oxyz , cho mặt phẳng  P : x  4 y  3z  2  0. Vectơ nào sau đây là vectơ
pháp tuyến của mặt phẳng  P ? A. n  1 4 3 n  1 4 3 n   n  1 4 3 2  ; ;  . B. 3  ; ; . C. 1; 4;3 . D. 1  ; ;  . 4   Lời giải:
Mặt phẳng  P : x  4 y  3z  2  0 có một vectơ pháp tuyến là n  1 4 3 2  ; ;  . ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d y O 2 x -2 Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0; 2 . 3
Câu 8: Cho hàm số f x có đạo hàm trên , f   1  2
 và f 3  2. Tính I f   xdx. 1  A. I  4. B. I  0. C. I  3. D. I  4. Lời giải: 3 3 Ta có I f
 xdx f x  f 3 f  1  2 2    4 1  . 1  Vậy I  4 .
Câu 9: Đồ thị hàm số nào dưới đây có dạng đường cong như hình bên dưới? A. 4 2
y  x  2x  3 . B. 3
y x  3x  3 . C. 4 2
y  x  2x  3 . D. 4 2
y x  2x  3 . Lời giải:
Nhìn hình vẽ ta thấy là đồ thị hàm bậc 4 trùng phương f x  4 2
ax bx c a  0 có hệ số a
dương. Do vậy chọn đáp án D.
Câu 10: Trong không gian Oxyz , cho mặt cầu S  : 2 2 2
x y z  2x  6 y  4z  2  0. Xác định tọa độ
tâm I và bán kính R của mặt cầu S  . A. I 1; 3
 ;2, R 16 . B. I 1; 3
 ;2, R  4 . C. I  1  ;3; 2
 , R 16 .D. I  1  ;3; 2
 , R  4 . Lời giải:
Ta có mặt cầu S  : 2 2 2
x y z  2x  6 y  4z  2  0. có tâm I 1; 3  ;2 và bán kính R    2 2 2 1 3  2  2  4 .
Vậy mặt cầu S  có tâm I 1; 3
 ;2 và bán kính R  4 .
Câu 11: Trong không gian Oxyz , góc giữa hai mặt phẳng Oyz và Oxz bằng A. 30 .  B. 90 .  C. 60 .  D. 45 . 
Câu 12: Các điểm M , N , P, Q trong hình vẽ bên là điểm bểu diễn lần lượt của các số phức
z , z , z , z . Khi đó w  3z z z z bằng 1 2 3 4 1 2 3 4 Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia y M 2 1 P -3 -1 O 1 2 3 x -2 -1 N Q -2
A. w  6  4i .
B. w  6  4i .
C. w  4  3i .
D. w  3  4i . Lời giải:
Ta có z  3  2i; z  2
  i; z  3 ;i z  2  2i . 1 2 3 4
Suy ra w  3z z z z  3 3   2i  2
  i  3 i  2  2i  6   4i . 1 2 3 4        
Câu 13: Thể tích của khối lăng trụ có diện tích đáy B và chiều cao h là 1 1 1 A. V Bh . B. V Bh . C. V Bh .
D. V Bh . 2 3 6
Câu 14: Cho khối hộp chữ nhật ABC . D AB CD
  có AB  2, AD  3, 
AA  4 (tham khảo hình vẽ). A' D' C' B' A D B C
Thể tích khối hộp đã cho bằng A. 24 . B. 20 . C. 9 . D. 8 . Lời giải:
Thể tích khối hộp chữ nhật đã cho bằng: V  2.3.4  24 .
Câu 15: Một khối cầu có bán kính bằng 2 , một mặt phẳng   cắt khối cầu đó theo một hình tròn có
diện tích là 2 . Khoảng cách từ tâm khối cầu đến mặt phẳng   bằng 2 2 A. 2 . B. 1 . C. . D. . 2 4 Lời giải: Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia
Gọi O, H lần lượt là tâm khối cầu và tâm hình tròn. R ,r lần lượt là bán kính mặt cầu và bán kính hình tròn. S  Diện tích hình tròn 2 2
s   r r    2   .
Gọi h là khoảng cách từ tâm khối cầu đến mặt phẳng   suy ra 2 2
h R r  2.
Câu 16: Môđun của số phức z  3  4i bằng A. 5 . B. 3 . C. 7 . D. 7 . Lời giải: Ta có: 3 2 z  3  4  5 .
Câu 17: Tính chiều cao h của hình trụ biết chiều cao h bằng bán kính đáy và thể tích khối trụ đó là 8 . A. 3 h  32 . B. 3 h  4 . C. h  2 2 . D. h  2 . Lời giải:
Gọi R là bán kính của hình trụ khi đó R h . V 8
Ta có thể tích khối trụ là 2 3
V   R h   h 3  h    8  h  2   .
Vậy chiều cao của khối trụ là h  2 . x 1 y  2 z
Câu 18: Trong không gian Oxyz , điểm nào dưới đây không thuộc đường thẳng d :   2 1 1  ? A. Q 1; 2  ;0 . B. M  1  ;2;0 . C. N  1  ; 3  ;  1 . D. P 3; 1  ;  1 . Lời giải: a b c
Điểm I a b c 1 2 ; ; d    2 1 1  đúng. Kiểm tra các điểm ;
Q M ; N; P trong các phương án A, B, C, D ta thay điểm M  1  ;2;0 vào 1  1 2  2 0
phương trình d ta có:   2 1 1
 (vô lý) . Vậy điểm M không thuộc đường thẳng d .
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  2 . B. x  2 . C. x  0 .
D. x  1 . Lời giải:
Vì y đổi dấu từ âm sang dương duy nhất tại x  2 nên hàm số đã cho đạt cực tiểu tại x  2 3x  2
Câu 20: Đường tiệm cận đứng của đồ thị hàm số y  có phương trình là x 1 A. x  2 . B. x  1 . C. x  3 . D. x  1 . Lời giải: Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia 3x  2 Ta có: lim y  lim   .   x (  1  ) x (  1  ) x  1
Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng x  1 .
Câu 21: Tập nghiệm của bất phương trình log x  1 là 2 A. (0;1] . B. (; 2] . C. 0; 2. D. (0; 2]. Lời giải:
Điều kiện: x  0. x  0
Bất phương trình đã cho tương đương   0  x  2 x  2
Vậy tập nghiệm của bất phương trình là S  (0; 2].
Câu 22: Số cách phân công 3 học sinh trong 12 học sinh đi lao động là A. P . B. 36. C. 3 C . D. 3 A . 12 12 12 Lời giải:
Cách chọn 3 học sinh trong 12 học sinh không xếp thứ tự là tổ hợp chập 3 của 12: 3 C 12
Câu 23: Cho hàm số y f x thỏa mãn f  x  2  7 cos x , f 0  3 . Mệnh đề nào dưới đây đúng?
A. f x  2x  7 sin x  3.
B. f x  2  7 sin x  3 .
C. f x  2x  sin x  9 .
D. f x  2x  7 sin x  3. Lời giải:
Ta có: f x  2  7cos xdx  2x  7sin x C .
Mặt khác: f 0  3  C  3  f x  2x  7 sin x  3 . 4 4 2 Câu 24: Nếu f
 xdx  5 và f xdx  1  
thì f xdx  bằng 0 2 0 A. 6 . B. 4 . C. 4  . D. 6  . Lời giải: 4 2 4 2 4 4 Ta có f
 xdx f
 xdxf
 xdx f
 xdx f
 xdx f  xdx 5     1  6 . 0 0 2 0 0 2 x
Câu 25: Họ tất cả các nguyên hàm của hàm số f x  2  4x là x 2x 2 A. x 2
2 ln 2  2x C . B. 2  x 2x C .
C. 2 ln 2  C . D. C . ln 2 ln 2 Lời giải: 2x x Ta có f
 xdx  2 4x 2 dx   2x C . ln 2
Câu 26: Cho hàm số f x có bảng biến biên dưới đây: Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia
Mệnh đề nào sau đây sai ?
A. Hàm số đã cho nghịch biến trên khoảng  ;    1 .
B. Hàm số đã cho nghịch biến trên khoảng 0;  1 .
C. Hàm số đã cho đồng biến trên khoảng 1;  .
D. Hàm số đã cho nghịch biến trên khoảng 3; 2 . Lời giải:
Câu A: Sai vì hàm số không liên tục từ  ;    1 .
Câu B: Đúng vì hàm số nghịch biến trên khoảng 2;  1 và khoảng 2;  1 chứa khoảng
0; 1 Câu C: Đúng quá rõ ràng.
Câu D: Đúng vì hàm số nghịch biến trên khoảng  ;
 2và khoảng  ;  2chứa khoảng 3;2
Câu 27: Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số là A. y  3 . B. y  1. C. y  4 . D. y  4 . Lời giải:
Từ bảng biến thiên của hàm số y f x , suy ra giá trị cực tiểu của hàm số là y  4 (đạt tại x  3) . Câu 28: Biết 5
y  log x . Khi đó 2 1
A. y  5log x .
B. y  5log x .
C. y  5  log x .
D. y  log x . 2 2 2 5 Lời giải: Ta có 5
y  log x  5 log x . 2 2
Câu 29: Gọi  H  là hình phẳng giới hạn bởi đồ thị hàm số 2
y x  5x  4 và trục Ox . Thể tích của
khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox là 9 81 81 9 A. V  . B. V  . C. V  . D. V  . 2 10 10 2 Lời giải: Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc gia
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y x  5x  4 và trục Ox ta có: x 1 2
x  5x  4  0   x  4
Thể tích của khối tròn xoay sinh ra khi quay hình  H  quanh trục Ox 4 4  V  
f xdx    x  5x  42 81 2 2 dx    . 10 1 1
Câu 30: Cho hình chóp S.ABCD có đáy là hình thoi tâm O , ABD đều cạnh a 2 , SA vuông góc với 3a 2
mặt phẳng đáy và SA
(minh họa như hình bên dưới). 2
Góc giữa đường thẳng SO và mặt phẳng  ABCD bằng A. 45 . B. 30 . C. 60 . D. 90 . Lời giải:
Do SA   ABCD nên hình chiếu vuông góc của SO lên mặt phẳng  ABCD là AO . Khi đó
góc giữa đường thẳng SO và mặt phẳng  ABCD là SOA .  3 a 6
ABD đều cạnh a 2 nên AO AB  . 2 2  3a 2 a 6 SA 3a 2 a 6
SOA vuông tại A có SA  , AO  nên tan SOA   :  3 2 2 AO 2 2  SOA  60.
Vậy góc giữa đường thẳng SO và mặt phẳng  ABCD bằng 60 . 2x  3
Câu 31: Cho hàm số y
có đồ thị (C) và đường thẳng d : y x m . Với tất cả giá trị nào của x  2
m thì d cắt (C) tại hai điểm phân biệt? m  2
A. m  2 .
B. m  2 . C. m  6 . D.  . m  6 Lời giải:
Phương trình hoành độ giao điểm là 2x  3 2
x m (x  2
 )  2x  3  (x  2)(x  )
m x mx  2m  3  0 (1) x  2 Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia
Để d cắt (C) tại hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân   0 m  2 biệt khác 2     .  2 ( 2
 )  2m  2m  3  0 m  6 2 3
Câu 32: Cho hàm số y f x liên tục trên
, có đạo hàm f  x  2  x  x  2  x  5,x  .
Hàm số y f x nghịch biến trên khoảng nào sau đây? A.  ;  2. B. 5;  . C. 2;5 .
D. 2;  . Lời giải: x  2 2 3 
Xét phương trình f  x  0  2  x  x  2  x  5  0  x  2  .  x  5  Bảng xét dấu:
Suy ra hàm số y f (x) nghịch biến trên khoảng 2;5 .
Câu 33: Một hộp chứa 10 quả cầu được đánh số theo thứ tự từ 1 đến 10, lấy ngẫu nhiên 5 quả cầu.
Xác suất để tích các số ghi trên 5 quả cầu đó chia hết cho 3 bằng 11 5 7 1 A. . B. . C. . D. . 12 12 12 12 Lời giải:
Số phần tử của không gian mẫu n  5  C . 10
Gọi A là biến cố: “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó chia hết cho 3”
 Biến cố A : “Lấy được 5 quả cầu có tích các số trên 5 quả cầu đó không chia hết cho 3”
Tính n A :
Để tích các số trên 5 quả cầu được chọn không chia hết cho 3 thì trong 5 quả cầu đó không có
các quả cầu mang số 3, 6, 9. Vậy n A 5  C . 7
P AnA 5 C 1 7    . n  5 C 12 10
PA   PA 11 1  . 12
Câu 34: Biết phương trình 2 log x  2 log
2x 1  0 có hai nghiệm x , x . Tính x x . 2 2   1 2 1 2 1 1 A. x x  4 . B. x x  . C. x x  .
D. x x  3 . 1 2 1 2 8 1 2 2 1 2 Lời giải:
ĐKXĐ: x  0 . Ta có Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia 2
log x  2 log 2x 2
1  0  log x  2log x  3  0 2 2 2 2  1 log x  1  x  2     2 log x  3   2 x  8
Vậy x x  4 . 1 2
Câu 35: Trên mặt phẳng tọa độ, tập hợp các điểm biểu diễn số phức z x yi  , x y   thỏa mãn
z  2  i z  3i là đường thẳng có phương trình là
A. y x 1.
B. y  x 1.
C. y x 1.
D. y  x 1 . Lời giải:
z  2  i z  3i   x  2   y  
1 i x   y  3i
 x  2   y  2  x   y  2 2 2 2 2 2 2 1 3
x  4x  4  y  2y 1 x y  6y  9
4 y  4x  4  y x 1.
Câu 36: Trong không gian Oxyz , đường thẳng d qua M  3
 ;5;6 và vuông góc với mặt phẳng
P:2x 3y  4z  2  0 thì đường thẳng d có phương trình là x  3 y  5 z  6 x  3 y  5 z  6 A.     . 2 3  . B. 4 2 3 4 x  3 y  5 z  6 x 1 y  2 z 10 C.     . 2 3  4  . D. 2 3  4 Lời giải:
Ta có  P : 2x  3y  4z  2  0 có vectơ pháp tuyến n  2; 3  ;4.
d   P  d nhận vectơ pháp tuyến của  P làm vectơ chỉ phương.
Do đó đường thẳng d qua M  3
 ;5;6 và có vectơ chỉ phương u  2; 3  ;4.
Kiểm tra phương án D thỏa mãn.
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua mặt phẳng Oxz có tọa độ là A. 1; 2;3 . B. 1; 2; 3  . C.  1  ;0; 3   . D. 1; 2;3 .
Câu 38: Cắt hình trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 2 , thiết
diện thu được là hình vuông có diện tích bằng 25 . Thể tích khối trụ bằng 10 2 205 205 10 2 A.  . B.  . C.  . D.  . 3 4 12 9 Lời giải: Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc gia
Từ đề bài ta có diện tích hình vuông ABB ' A ' bằng 25 suy ra AB BB '  5 . Kẻ OH AB , H
là trung điểm của AB thì d OO ', ABB ' A'  d O, ABB ' A'  OH  2 . 2  AB  41 Ta có 2 2 2
OA OH AH OH     .  2  2 41 205
Suy ra khối trụ có h BB '  5; r OA  , vậy 2
V   r h   . 2 4
Câu 39: Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng 32 5 18 5 A. . B. 32 . C. . D. 32 5 . 3 3 Lời giải: 3 Ta có 2 SSG  9 3 SGF 4 2  SG  36
l SG  6
* Bán kính đường tròn đáy là r l h    2 2 2 2 6 2 5  4 1 1 32 5 * Thể tích khối nón là 2 2 V  .  r .h  .4  .2 5  . 3 3 3 Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 40: Trong không gian Oxyz, phương trình đường thẳng đi qua A1; 2; 4 song song với  P : x  2 y  2 z  2
2x y z  4  0 và cắt đường thẳng d :   có phương trình là 3 1 5 x 1 tx 1 2tx  1   2tx 1 t     A. y  2 . B.  y  2 . C.  y  2 . D.  y  2  .     z  4  2tz  4  2tz  4  4tz  4  2tLời giải: Ta có: n
là một vec tơ pháp tuyến của mặt phẳng  P . P 2;1  ;1
x  2  3t
Phương trình tham số của đường thẳng d là:  y  2  t , t  . z  25t
Gọi  là đường thẳng cần tìm. Gọi M là giao điểm của  và d M 2  3t; 2  t; 2  5t
AM  1 3t;t; 2   5t
Do  //  P nên AM .n  0  21 3t   t   2
  5t  0  12t  0  t  0 PAM  1;0; 2   .
Phương trình đường thẳng  đi qua A1; 2; 4 và nhận AM  1;0; 2
  là một vec tơ chỉ x 1 t
phương là:  y  2 , t  . z  4 2t
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 16
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 03_______________
Câu 1: Trong mặt phẳng tọa độ Oxy , số phức z  2  3i được biểu diễn bởi điểm nào sau đây?
A. Q 3; 2 .
B. N 2;3 .
C. P 3; 2 . D. M 2; 3   .
Câu 2: Đạo hàm của hàm số 2x y  là A. 1 .2x y x    . B. 2 . x y  ln 2 . C. 2x y  . D. x 1 y .2 x    .ln 2 .
Câu 3: Tập xác định của hàm số y  log x  2 là 1   2 A. .
B. 2;  . C. 2;  . D. 0;  . x  1 
Câu 4: Tập nghiệm của bất phương trình  2   là  2  A. ;   1 .
B. 0;  .
C. 1;  . D.  ;    1 .
Câu 5: Cho cấp số nhân u với u  3 và công bội q  2 . Số hạng thứ 7 của cấp số nhân đó là n  1 A. 384 . B. 192 . C. 192 . D. 384 . x y z
Câu 6: Trong không gian Oxyz , cho mặt phẳng (P) :
   1. Vectơ nào dưới đây là một vectơ 2 1 3
pháp tuyến của mặt phẳng (P)?
A. n  (2;1; 3). B. n  ( 3;  6; 2  ).
C. n  (3;6; 2). D. n  ( 3;  6;2). 2 4 1 3 ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d y O 2 x -2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0; 2 . 3 5 5
Câu 8: Nếu  f xdx  3,  f xdx  7 thì f xdx  bằng 0 3 0 A. 7 . B. 4 . C. 10 . D. 4  .
Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong ở hình vẽ bên dưới ? A. 3 2
y  x  3x  4 . B. 3 2
y x  3x  4 . C. 3 2
y  x x  4 . D. 3
y x  3x  4 . Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 2 2
Câu 10: Trong không gian Oxyz , cho mặt cầu S  :  x  
1   y  2   z   1
 4 . Tọa độ tâm I và
bán kính R của mặt cầu là A. I   1  ; 2   ;1 ; R  4 .
B. I  1; 2;   1 ; R  2 . C. I   1  ; 2   ;1 ; R  2 .
D. I  1; 2;  1 ; R  4 .
Câu 11: Trong không gian Oxyz , góc giữa mặt phẳng Oyz và trục Oy bằng A. 30 .  B. 90 .  C. 60 .  D. 0 . 
Câu 12: Biết M 1; 2
  và N 2;3 lần lượt là hai điểm biểu diễn cho hai số phức z z 1 và 2 trên mặt
phẳng tọa độ Oxy . Khi đó, số phức z .z 1 2 là A. 1 5i . B 8  . i C. 2  6i . D. 3  i .
Câu 13: Cho hình hộp có đáy là hình vuông cạnh bằng a và chiều cao 3a . Thể tích của khối hộp đã cho bằng 1 A. 3 a . B. 3 a . C. 3 3a . D. 3 9a . 3
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
ABCD và SA  3a (tham khảo hình vẽ).
Thể tích khối chóp S.ABCD bằng 3 3a A. 3 3a . B. 3 3a . C. 3 a . D. . 3
Câu 15: Cho khối cầu có bán kính R  2 . Thể tích của khối cầu đã cho bằng 32 16 A.  . B.  . C. 16 . D. 32 . 3 3
Câu 16: Phần ảo của số phức z  18 12i là A. 12 . B. 12 . C. 12i . D. 18 .
Câu 17: Thể tích của khối nón có chiều cao h , bán kính đáy r bằng 1 1 1 A. 2  rh . B. rh . C. 2  r h . D. 2  r h . 3 3 3 x 1 y  2 z 1
Câu 18: Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc 2 3 1 đường thẳng d ? A. Q 2;3  ;1 . B. M 1; 2  ;  1 .
C. P 1; 2;3.
D. N 1; 2;   1 .
Câu 19: Cho hàm số y f x có bảng biến thiên như sau: Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Giá trị cực đại của hàm số đã cho bằng A. 2 . B.  . C. 11. D. 1. 3x 1
Câu 20: Đường tiệm cận ngang của đồ thị hàm số y là x 2 1 A. y . B. y 3 . C. y 3 . D. y 2 . 3 x
Câu 21: Tập nghiệm của bất phương trình 0,5  1 là A.  ;  2 .
B. 0;  . C.  ;  0 . D. 2;  .
Câu 22: Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp X  1; 2;3; 4;  5 ? A. 2 A . B. 2 C . C. 2 5 . D. 5 2 . 5 5 6 2 Câu 23: Nếu f
 xdx 18 thì f 3xdx  bằng 0 0 A. 6 . B. 12 . C. 36 . D. 54 . 6 6 Câu 24: Cho f
 xdx  5. Khi đó 63f  xdx  bằng 2 2 A. 9 . B. 9  . C. 1. D. 21 . Câu 25: Xác định 2 sin 2 d .  x x sin 4x x sin 4x 3 cos 2x x sin 4x A. C . B.   C . C.   C . D.   C . 8 2 8 3 2 8
Câu 26: Cho hàm số y
f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 2; . B. 1; . C.  ;  3. D.  ;  .
Câu 27: Cho hàm số y f x có đạo hàm liên tục trên và có bảng biến thiên như sau: Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Giá trị cực tiểu của hàm số bằng A. 1  . B. 2 . C. 0 . D. 1.
Câu 28: Với a,b là các số dương tùy ý, log  2 5 a b bằng 3 
A. 2 log a  5log b . B. 10 log ab . C. 7 log ab .
D. 10log a  log b . 3 3  3   3   3 3
Câu 29: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y x x và trục
hoành quanh trục hoành là     A. V  . B. V  . C. V  . D. V  . 3 30 15 5
Câu 30: Cho hình chóp .
S ABCD có ABCD là hình thang vuông tại A và D , cạnh bên SD vuông góc
với đáy, AB AD a,CD  2a,SA a 3 .
Góc giữa SB và SAD bằng A. 30 . B. 60 . C. 45 . D. 90 .
Câu 31: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x  4x  4  2m  0 có 4 nghiệm phân biệt? A. 4 . B. 2 . C. 1. D. 3 . mx  9
Câu 32: Có bao nhiêu giá trị nguyên của tham số m để hàm số y  4x  nghịch biến trên khoảng m 0;4 ? A. 6 . B. 7 . C. 5 . D. 11.
Câu 33: Một hộp chứa 12 tấm thẻ được đánh số bằng các số tự nhiên liên tiếp từ 1 đến 12. Chọn ngẫu
nhiên ra ba tấm thẻ. Xác suất để tích số ghi trên ba tấm thẻ là một số chẵn bằng 11 1 10 1 A. . B. . C. . D. . 12 3 11 2
Câu 34: Tính tổng các nghiệm của phương trình x 1  1 2
 2 x  5 1 A. 0 . B. 2 . C. . D. 2  . 2 Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 35: Trong mặt phẳng Oxy , tập hợp các điểm biểu diễn số phức z thoã điều kiện
z  3  2i  1  2i
A. Đường thẳng vuông góc với trục Ox .
B. Đường tròn tâm I 3; 2
  , bán kính R  5 .
C. Đường tròn tâm I 3; 2
 , bán kính R  5 . D. Đường thẳng vuông góc với trục Oy .
Câu 36: Trong không gian Oxyz , đường thẳng d đi qua điểm A1; 2;3 và vuông góc với mặt phẳng
 :4x 3y 7z 1 0 có phương trình tham số là
x  1 4t
x  5  4tx 1 3tx  1   8t     A. y  2   3t .
B. y  5  3t
C. y  2  4t D. y  2   6t     z  3   7tz  4   7  t z  3  7tz  3  14t
Câu 37: Trong mặt phẳng Oxyz , mặt cầu S  có tâm thuộc trục Ox và đi qua hai điểm
A1;2;1, B  1
 ;0;3 có bán kính bằng A. 3 . B. 2 3 . C. 3 . D. 9 .
Câu 38: Cho khối nón  N  có chiều cao bằng 3a . Cắt hình nón đó bởi một mặt phẳng song song với 64
mặt đáy, cách mặt đáy một khoảng bằng a thu được thiết diện có diện tích bằng 2  a .Khi 9
đó, thể tích của khối nón  N  bằng A. 3 16 a . B. 3 48a . C. 3 16a . D. 3 48 a .
Câu 39: Cho hình trụ có chiều cao bằng 8cm . Một mặt phẳng   song song với trục của hình trụ
cách trục một khoảng bằng 5cm và mp   cắt hình trụ theo thiết diện có diện tích bằng 2
32cm . Khi đó diện tích toàn phần của hình trụ đã cho bằng A.   2 24 cm  . B.   2 16 cm  . C.   2 66 cm  . D.   2 11 cm  . x 1 y  2 z  3
Câu 40: Trong không gian Oxyz, cho điểm M (1; 0;1) và đường thẳng d :   . Đường 1 2 3
thẳng đi qua M , vuông góc với d và cắt Oz có phương trình là x 1 3tx 1 3tx 1 3tx 1 3t     A. y  0 . B. y  0 .
C. y t . D. y  0 .     z  1 tz  1 tz  1 tz  1 t
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng tọa độ Oxy , số phức z  2  3i được biểu diễn bởi điểm nào sau đây?
A. Q 3; 2 .
B. N 2;3 .
C. P 3; 2 . D. M 2; 3   . Lời giải:
Trong mặt phẳng tọa độ Oxy , số phức z  2  3i được biểu diễn bởi điểm M 2; 3
  .
Câu 2: Đạo hàm của hàm số 2x y  là A. 1 .2x y x    . B. 2 . x y  ln 2 . C. 2x y  . D. x 1 y .2 x    .ln 2 . Lời giải: Hàm số 2x y  có đạo hàm là ' 2 . x y  ln 2 .
Câu 3: Tập xác định của hàm số y  log x  2 là 1   2 A. .
B. 2;  . C. 2;  . D. 0;  . Lời giải:
Điều kiện xác định: x  2  0  x  2
  x 2;. x  1 
Câu 4: Tập nghiệm của bất phương trình  2   là  2  A. ;   1 .
B. 0;  .
C. 1;  . D.  ;    1 . Lời giải: x  1  x 1
 2  2  2  x 1  x  1     2 
Câu 5: Cho cấp số nhân u với u  3 và công bội q  2 . Số hạng thứ 7 của cấp số nhân đó là n  1 A. 384 . B. 192 . C. 192 . D. 384 . Lời giải:
Số hạng thứ 7 của cấp số nhân đó là u u .q  3. 2  6 6  192 . 7 1 x y z
Câu 6: Trong không gian Oxyz , cho mặt phẳng (P) :
   1. Vectơ nào dưới đây là một vectơ 2 1 3
pháp tuyến của mặt phẳng (P)?
A. n  (2;1; 3). B. n  ( 3;  6; 2  ).
C. n  (3;6; 2). D. n  ( 3;  6;2). 2 4 1 3 Lời giải: x y z Ta có: 
  1  3x  6y  2z  6  0 . Do đó vectơ pháp tuyến là n (3;6;2). 2 1 3 1 ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia y O 2 x -2
Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là A. 0; 2 . B. 2;0 . C. 2;0 . D. 0; 2 . 3 5 5
Câu 8: Nếu  f xdx  3,  f xdx  7 thì f xdx  bằng 0 3 0 A. 7 . B. 4 . C. 10 . D. 4  . Lời giải: 5 3 5 Ta có: f
 xdx f
 xdx f
 xdx  37 10 . 0 0 3
Câu 9: Hàm số nào dưới đây có đồ thị dạng như đường cong ở hình vẽ bên dưới ? A. 3 2
y  x  3x  4 . B. 3 2
y x  3x  4 . C. 3 2
y  x x  4 . D. 3
y x  3x  4 . Lời giải:
Nhánh cuối đồ thị đi xuống suy ra hệ số ứng với bậc cao nhất là số âm, nên loại đáp án B và D
Nhận thấy điểm 1;0 thuộc đồ thị, ta thay x  1 và y  0 vào các đáp án còn lại, chọn được đáp án A . 2 2 2
Câu 10: Trong không gian Oxyz , cho mặt cầu S  :  x  
1   y  2   z   1
 4 . Tọa độ tâm I và
bán kính R của mặt cầu là A. I   1  ; 2   ;1 ; R  4 .
B. I  1; 2;   1 ; R  2 . C. I   1  ; 2   ;1 ; R  2 .
D. I  1; 2;  1 ; R  4 .
Câu 11: Trong không gian Oxyz , góc giữa mặt phẳng Oyz và trục Oy bằng A. 30 .  B. 90 .  C. 60 .  D. 0 . 
Câu 12: Biết M 1; 2
  và N 2;3 lần lượt là hai điểm biểu diễn cho hai số phức z z 1 và 2 trên mặt
phẳng tọa độ Oxy . Khi đó, số phức z .z 1 2 là Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia A. 1 5i . B. 8  i . C. 2  6i . D. 3  i . Lời giải:
Ta có : z  1 2 ; i z  2  3i
z .z  1 2i . 2  3i  8 i 1 2 . Từ đó suy ra : 1 2     .
Câu 13: Cho hình hộp có đáy là hình vuông cạnh bằng a và chiều cao 3a . Thể tích của khối hộp đã cho bằng 1 A. 3 a . B. 3 a . C. 3 3a . D. 3 9a . 3 Lời giải:
Thể tích của khối hộp: 2 3 V  .
B h a .3a  3a .
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
ABCD và SA  3a (tham khảo hình vẽ).
Thể tích khối chóp S.ABCD bằng 3 3a A. 3 3a . B. 3 3a . C. 3 a . D. . 3 Lời giải: 3 1 1 3a Ta có 2 VS . A S  . 3 . a a  . S .ABCD 3 ABCD 3 3
Câu 15: Cho khối cầu có bán kính R  2 . Thể tích của khối cầu đã cho bằng 32 16 A.  . B.  . C. 16 . D. 32 . 3 3 Lời giải: 4 4 32
Thể tích của khối cầu là 3 3 V  .R  ..2   . 3 3 3
Câu 16: Phần ảo của số phức z  18 12i là A. 12 . B. 12 . C. 12i . D. 18 . Lời giải:
Phần ảo của số phức z  18 12i là 12 . Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 17: Thể tích của khối nón có chiều cao h , bán kính đáy r bằng 1 1 1 A. 2  rh . B. rh . C. 2  r h . D. 2  r h . 3 3 3 Lời giải: 1
Thể tích của khối nón đã cho là 2 V   r h . 3 x 1 y  2 z 1
Câu 18: Trong không gian Oxyz , cho đường thẳng d :  
. Điểm nào dưới đây thuộc 2 3 1 đường thẳng d ? A. Q 2;3  ;1 . B. M 1; 2  ;  1 .
C. P 1; 2;3.
D. N 1; 2;   1 . Lời giải:
Đường thẳng d đi qua M x ; y ; z có một véc tơ chỉ phương là u   ; a ;
b c thì d có phương 0 0 0  x x y y z z trình chính tắc là 0 0 0 d :   . a b c x 1 y  2 z 1 Vậy d :  
đi qua điểm M 1; 2  ;  1 hay M 1; 2  ; 
1 thuộc đường thẳng d . 2 3 1
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 2 . B.  . C. 11. D. 1. Lời giải:
Từ bảng biến thiên của hàm số y f x ,ta thấy giá trị cực đại của hàm số là 11. 3x 1
Câu 20: Đường tiệm cận ngang của đồ thị hàm số y là x 2 1 A. y . B. y 3 . C. y 3 . D. y 2 . 3 Lời giải: 3x 1 3x 1 Ta có: lim 3 ; lim 3 nên TCN y 3 . x x 2 x x 2 x
Câu 21: Tập nghiệm của bất phương trình 0,5  1 là A.  ;  2 .
B. 0;  . C.  ;  0 . D. 2;  . Lời giải: x x Ta có: 
       0 0, 5 1 0, 5 0, 5  x  0 .
Câu 22: Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp X  1; 2;3; 4;  5 ? A. 2 A . B. 2 C . C. 2 5 . D. 5 2 . 5 5 Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia Lời giải:
Mỗi số tự nhiên có hai chữ số khác nhau có các chữ số lấy từ tập X là một chỉnh hợp chập 2
của 5 phần tử, do đó ta được 2 A số. 5 6 2 Câu 23: Nếu f
 xdx 18 thì f 3xdx  bằng 0 0 A. 6 . B. 12 . C. 36 . D. 54 . Lời giải: 2 Xét tích phân I f  3xdx 0 dt
Đặt t  3x . Khi đó dt  3dx   dx . 3
Với x  0  t  0; x  2  t  6 . 6 6 dt 1 1 Khi đó I f
 t  . f
 tdt  .18  6. 3 3 3 0 0 6 6 Câu 24: Cho f
 xdx  5. Khi đó 63f  xdx  bằng 2 2 A. 9 . B. 9  . C. 1. D. 21 . Lời giải: 6 6 6 6 6 Ta có: 6  3 f 
xdx  6 dx 3 f  
 xdx  6x 3 f
 xdx  6.6 23.5  9 . 2 2 2 2 2 Câu 25: Xác định 2 sin 2 d .  x x sin 4x x sin 4x 3 cos 2x x sin 4x A. C . B.   C . C.   C . D.   C . 8 2 8 3 2 8 Lời giải: 1  cos 4x 1 1 x sin 4x Ta có 2 sin 2 d x x  dx    dx  cos 4 d x   4x    C. 2 2 8 2 8
Câu 26: Cho hàm số y
f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 2; . B. 1; . C.  ;  3. D.  ;  . Lời giải: Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia
Từ Bảng biến thiên suy ra hàm số đã cho đồng biến trên (2; ) .
Câu 27: Cho hàm số y f x có đạo hàm liên tục trên và có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số bằng A. 1  . B. 2 . C. 0 . D. 1. Lời giải:
Từ BBT, ta có giá trị cực tiểu của hàm số là: y  1. CT
Câu 28: Với a,b là các số dương tùy ý, log  2 5 a b bằng 3 
A. 2 log a  5log b . B. 10 log ab . C. 7 log ab .
D. 10log a  log b . 3 3  3   3   3 3 Lời giải: Ta có: log  2 5 a b  2 5
 log a  log b  2log a  5log b . 3 3 3 3 3
Câu 29: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số 2
y x x và trục
hoành quanh trục hoành là     A. V  . B. V  . C. V  . D. V  . 3 30 15 5 Lời giải:
Phương trình hoành độ giao điểm của đồ thị hàm số 2
y x x và trục hoành là x  0 2
x x  0   . x 1 1 2  Vậy V    2
x x dx   . 30 0
Câu 30: Cho hình chóp .
S ABCD có ABCD là hình thang vuông tại A và D , cạnh bên SD vuông góc
với đáy, AB AD a,CD  2a,SA a 3 .
Góc giữa SB và SAD bằng A. 30 . B. 60 . C. 45 . D. 90 . Lời giải: Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc gia AB AD Ta có:
  AB  SAD  SB,SAD  SB,SA  BSA . AB SD AB 1
Tam giác SAB vuông tại A  tan BSA    BSA  30 . SA 3
Câu 31: Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình 4 2
x  4x  4  2m  0 có 4 nghiệm phân biệt? A. 4 . B. 2 . C. 1. D. 3 . Lời giải: Ta có : 4 2
x  4x  4  2m  0 4 2
x  4x  4  2m   1 .
Số nghiệm của phương trình  
1 là số giao điểm của đồ thị hàm số 4 2
y x  4x  4 và đường
thẳng y  2m . x  0 Xét hàm số 4 2
y x  4x  4 ; 3
y  4x  8x , y  0   . x   2 Bảng biến thiên: x   2 0 2  y   0  0  0     4 y   8 8
Dựa vào bảng biến thiên ta có: Phương trình  
1 có 4 nghiệm phân biệt khi
8  2m  4  2  m  4 .
Vì m nguyên nên m  3 . mx  9
Câu 32: Có bao nhiêu giá trị nguyên của tham số m để hàm số y  4x  nghịch biến trên khoảng m 0;4 ? A. 6 . B. 7 . C. 5 . D. 11. Lời giải: m
Tập xác định D  \   .  4  2 m  36 Ta có y   . 4x m2
Hàm số đã cho nghịch biến trên khoảng 0; 4 khi và chỉ khi 6  m  6  2     m  36  0   6 m 6  m     0    m   m  0  0  m  6 .  4  0;4     4 m       m 16 4   4
Vì m nguyên nên m 0;1; 2;3; 4;  5 .
Vậy có 6 giá trị của m thỏa mãn yêu cầu bài toán. Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 33: Một hộp chứa 12 tấm thẻ được đánh số bằng các số tự nhiên liên tiếp từ 1 đến 12. Chọn ngẫu
nhiên ra ba tấm thẻ. Xác suất để tích số ghi trên ba tấm thẻ là một số chẵn bằng 11 1 10 1 A. . B. . C. . D. . 12 3 11 2 Lời giải:
Chọn 3 trong 12 tấm thẻ có 3
C  220 cách  n   220 . 12
Gọi biến cố A: “tích số ghi trên ba tấm thẻ là một số lẻ”
Khi đó n A 3  C  20 . 6 n A 20 1 Nên P A      . n  220 11
Suy ra xác suất để tích số ghi trên ba tấm thẻ là một số chẵn là  P A 1 10 1 1  . 11 11
Câu 34: Tính tổng các nghiệm của phương trình x 1  1 2
 2 x  5 1 A. 0 . B. 2 . C. . D. 2  . 2 Lời giải: x x x 1 Ta có: 1 1 2  2  5  2.2  2.  5 . 2x x
Đặt t  2 t  0 , phương trình trở thành: t  2  2x  2 2  x  1 2   2t
 5  2t  5t  2  0  1    . x 1 tt  2  x  1   2  2
Vậy tổng tất cả các nghiệm của phương trình là 0.
Câu 35: Trong mặt phẳng Oxy , tập hợp các điểm biểu diễn số phức z thoã điều kiện
z  3  2i  1  2i
A. Đường thẳng vuông góc với trục Ox .
B. Đường tròn tâm I 3; 2
  , bán kính R  5 .
C. Đường tròn tâm I 3; 2
 , bán kính R  5 . D. Đường thẳng vuông góc với trục Oy . Lời giải:
Gọi số phức z x yi, xy  . 2 2
Khi đó z  3  2i  1 2i x  3   y  2i  1 2i   x  3   y  2  5
Vậy tập hợp các điểm biểu diễn số phức z thoã điều kiện đề bài là đường tròn tâm I 3; 2 , bán kính R  5 .
Câu 36: Trong không gian Oxyz , đường thẳng d đi qua điểm A1; 2;3 và vuông góc với mặt phẳng
 :4x 3y 7z 1 0 có phương trình tham số là Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia
x  1 4t
x  5  4tx 1 3tx  1   8t     A. y  2   3t .
B. y  5  3t
C. y  2  4t D. y  2   6t     z  3   7tz  4   7  t z  3  7tz  3  14tLời giải:
Mặt phẳng   có VTPT n 4;3; 7   .
Đường thẳng d vuông góc với mp   nên d nhận n  4;3; 7 làm 1 VTCP.
Đường thẳng d đi qua điểm A1; 2;3 và có vtcp n  4;3; 7  .
Kiểm tra phương án B thỏa mãn.
Câu 37: Trong mặt phẳng Oxyz , mặt cầu S  có tâm thuộc trục Ox và đi qua hai điểm
A1;2;1, B  1
 ;0;3 có bán kính bằng A. 3 . B. 2 3 . C. 3 . D. 9 . Lời giải:
Giả sử tâm I a;0;0 Ox . 2 2
Ta có AI BI  a  2    a  2 1 4 1 1  0  9  a  1   I  1
 ;0;0  R AI    2    2    2 1 1 0 2 0 1  3.
Câu 38: Cho khối nón  N  có chiều cao bằng 3a . Cắt hình nón đó bởi một mặt phẳng song song với 64
mặt đáy, cách mặt đáy một khoảng bằng a thu được thiết diện có diện tích bằng 2  a .Khi 9
đó, thể tích của khối nón  N  bằng A. 3 16 a . B. 3 48a . C. 3 16a . D. 3 48 a . Lời giải: 64 8
Ta có: SO h  3a ; S
  r   HK
a HK a . TD  2 2 2 9 3 Do thiết diện song song và cách mặt đáy một đoạn bằng a nên
HO a SH SO OH  2 . a OA SO S . O HK Xét SOA SHK , ta có:   OA   4a . HK SH SH 1 1 Vậy 2 2 3        V R h a a a . N  . . .16 .3 16 3 3 Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 39: Cho hình trụ có chiều cao bằng 8cm . Một mặt phẳng   song song với trục của hình trụ
cách trục một khoảng bằng 5cm và mp   cắt hình trụ theo thiết diện có diện tích bằng 2
32cm . Khi đó diện tích toàn phần của hình trụ đã cho bằng A.   2 24 cm  . B.   2 16 cm  . C.   2 66 cm  . D.   2 11 cm  . Lời giải: O' D C O B M A
Theo giả thiết, mp   cắt hình trụ theo thiết diện là hình chữ nhật và giả sử là ABCD .
AD OO  8cm Ta có: 
AB  4cm . 2 A . D AB  32cm
Gọi M là trung điểm AB
Suy ra MB cm OB OM MB   2 2 2 2 2 5  2  3cm
Khi đó hình trụ có bán kính đáy r  3cm và độ dài đường sinh l  8cm .
Diện tích toàn phần của hình trụ là
S   r l r          2 2 2 .3. 8 3 66 cm . tpx 1 y  2 z  3
Câu 40: Trong không gian Oxyz, cho điểm M (1; 0;1) và đường thẳng d :   . Đường 1 2 3
thẳng đi qua M , vuông góc với d và cắt Oz có phương trình là x 1 3tx 1 3tx 1 3tx 1 3t     A. y  0 . B. y  0 .
C. y t . D. y  0 .     z  1 tz  1 tz  1 tz  1 tLời giải:
Gọi  là đường thẳng cần tìm và N    Oz.
Ta có N (0;0; c). Vì  qua M , N và M Oz nên MN (1;0; c 1) là VTCP của  . 4 1
d có 1 VTCP u(1; 2;3) và   d nên MN u  0  1
  3(c 1)  0  c   MN( 1  ;0; ). 3 3 Chọn v( 3
 ;0;1) là 1 VTCP của  , phương trình tham số của đường thẳng  là x 1 3t  y  0 . z 1t
________________________HẾT________________________ Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc gia
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 16
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 04_______________
Câu 1: Số phức nào sau đây có biểu diễn hình học là điểm M 3;5 ?
A. z  3  5i .
B. z  3  5i .
C. z  3  5i .
D. z  3  5i .
Câu 2: Trên khoảng 0;  , đạo hàm của hàm số y  ln x là 1 1 1 A. y  . B. y  . C. y  . D.   e y . 10x x ex x Câu 3: Tập xác định  D của hàm số 2 3 y x là
A. D  0;   . B. D  .
C. D 0;  . D. D  \   0 .
Câu 4: Tập nghiệm của bất phương trình ln x  1 là A.  ; e  . B. 0;e . C.  ;  e. D.  ;  e .
Câu 5: Cho cấp số nhân u
có u  2 và có công bội bằng 3
 . Giá trị u bằng n  1 2 A. 5  . B. 9 . C. 8  . D. 6  .
Câu 6: Trong không gian Oxyz , vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng Oxy ?
A. m  1;1  ;1 .
B. i  1;0;0 .
C. j  0;1;0 .
D. k  0;0  ;1 . ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d y O 2 x -2
Số giao điểm của đồ thị hàm số đã cho và trục hoành là A. 0 . B. 1. C. 2 . D. 3 . 6 6 6
Câu 8: Cho  f xdx  4 và  g xdx  5 , khi đó 3
 f x gxd  x bằng 2 2 2 A. 19 . B. 17 . C.11. D. 7 .
Câu 9: Đường cong hình vẽ là đồ thị hàm số nào dưới đây? x 1 x 1 A. 3 2
y x x 1 . B. y y
y  x x  . x  . C. 1 x  . D. 3 2 1 1 Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 10: Trong không gian Oxyz , mặt cầu có tâm I 2; 1
 ;3 , bán kính R  3 có phương trình là 2 2 2 2 2 2
A. x  2   y  
1   z  3  3 .
B. x  2   y  
1   z  3  3 . 2 2 2 2 2 2
C. x  2   y  
1   z  3  3 .
D. x  3   y  
1   z  3  3 .
Câu 11: Trong không gian Oxyz , góc giữa mặt phẳng Oyz và trục Ox bằng A. 30 .  B. 90 .  C. 60 .  D. 0 . 
Câu 12: Tìm hai số thực x và y thỏa mãn 2x  3yi  1  3i  x  6i , với i là đơn vị ảo.
A. x  1, y  3 .
B. x  1, y  1 .
C. x  1, y  1.
D. x  1, y  3.
Câu 13: Cho khối chóp có diện tích đáy B  6 và chiều cao h  8 . Thể tích của khối chóp đã cho bằng A. 16 . B. 48 . C. 8 . D. 14 .
Câu 14: Thể tích khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a bằng A C B A C B 3 3 A. 3 a . B. 3 a . C. 3 2a . D. 3 a . 12 4
Câu 15: Cho mặt cầu S , bán kính R và mặt phẳng   . Biết khoảng cách từ tâm của mặt cầu S tới
mặt phẳng   bằng R . Khẳng định nào sau đây đúng?
A. Mặt phẳng a cắt mặt cầu S .
B. Thiết diện của mặt phẳng   với mặt cầu S là một đường tròn.
C. Mặt phẳng a tiếp xúc với mặt cầu S .
D. Mặt phẳng a với mặt cầu S không có điểm chung.
Câu 16: Cho số phức z  1 2i . Số phức liên hợp của z là A. 1 2i . B. 1 2i . C. 2  i . D. 1 2i .
Câu 17: Cho hình nón có độ dài đường sinh bằng 3a và bán kính đáy bằng a . Diện tích xung quanh
của hình nón đã cho bằng A. 2 12 a . B. 2 3 a . C. 2 6 a . D. 2  a .
x  3  2t
Câu 18: Trong không gian Oxyz , cho đường thẳng d :  y  1 t . Điểm nào dưới đây thuộc d ? z  23t
A. M 3;1; 2 .
B. Q 2;1;3 . C. P  3  ; 1  ; 2  . D. N  2  ;1;3 .
Câu 19: Cho hàm số f x có bảng xét dấu f  x như sau:
Hoành độ điểm cực tiểu của hàm số đã cho bằng A. 1  . B. 0 . C. 1. D. 1 và 1  . Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 20: Bảng biến thiên sau đây là của hàm số nào ? x 1 x 1 2x 1 x  3 A. y  . B. y  . C. y  . D. y  . x  2 x 1 x  2 x  2
Câu 21: Tập nghiệm của bất phương trình x 1 2   4 là A.  ;  3. B.  ;  5. C. 1;3. D. 1; .
Câu 22: Từ 10 điểm phân biệt trong không gian có thể tạo thành bao nhiêu vectơ khác vectơ 0 ? A. 10 2 . B. P . C. 2 A . D. 2 C . 10 10 10
Câu 23: Cho hàm số y f x
xác định và liên tục trên đồng thời thoả mãn: f (
x)  3 5sin x , f (0) 14 . Khẳng định nào sau đây đúng?
A. f ( )  3  5 .
B. f (x)  3x  5sin x  9 .    3
C. f (x)  3x  5cos x  9 . D. f   9   .  2  2 4 4
Câu 24: Nếu f (x)dx  37  thì 2
2 f(x)  3x dx   bằng 0 0 A. 12. B. 18. C. 27 . D. 10.
Câu 25: Họ tất cả các nguyên hàm của hàm số f x  cos x  6x là A. 2
sin x  3x C . B.  sin x C . C. 2
sin x  3x C . D. 2
sin x  6x C .
Câu 26: Cho hàm số y f x có đồ thị như hình bên dưới:
Mệnh đề nào sau đây đúng?
A. Hàm số f x nghịch biến trên 2;5 .
B. Hàm số f x nghịch biến trên 0;5 .
C. Hàm số f x đồng biến trên  ;  0.
D. Hàm số f x đồng biến trên 5;  .
Câu 27: Cho hàm số y f x có bảng biến thiên như sau: Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Hàm số đã cho đạt cực tiểu tại
A. x  1 .
B. y  3.
C. x  3 .
D. y  1.
Câu 28: Cho khối trụ T  ,   là mặt phẳng đi qua trục và cắt khối trụ T  theo thiết diện là hình
vuông cạnh 2a. Thể tích khối trụ T  bằng 3  a 3 2 a A. B. 3 2 a . C. . D. 3  a . 3 3
Câu 29: Cho a là số thực dương khác 1. Giá trị của 3 log a bằng a 1 A. 0. B. . C. 3. D. 3. 3
Câu 30: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  3 và
trục hoành quay quanh trục Ox là 4 16 16 4 A. V  . B. V  . C. V  . D. V  . 3 15 15 3
Câu 31: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC a . Hình chiếu
vuông góc của S lên  ABC  trùng với trung điểm của BC . S A C H B
Biết SB a . Tính số đo của góc giữa SA và  ABC  . A. 75 . B. 30 . C. 60 . D. 45 .
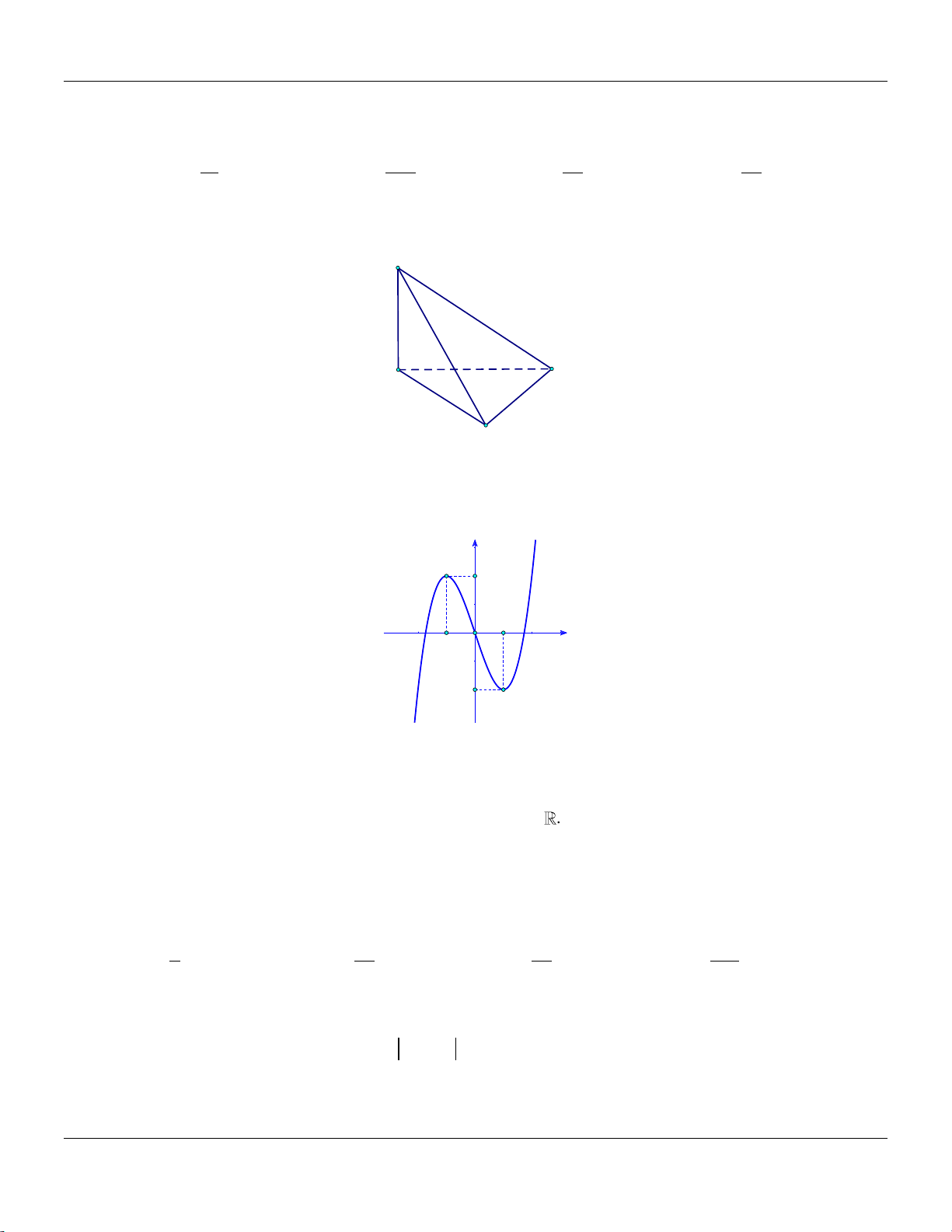
Câu 32: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên dưới:
Số giá trị nguyên của tham số m để đường thẳng y m cắt đồ thị hàm số đã cho tại ba điểm phân biệt là A. Vô số. B. 3 . C. 0. D. 5 . Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 33: Có bao nhiêu giá trị nguyên của tham số thực m để hàm số 3 2
y  x mx  4m  9 x  5
nghịch biến trên khoảng  ;   ? A. 5. B. 7. C. 4. D. 6.
Câu 34: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong
hộp. Xác suất để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng bằng 11 5 75 95 A. . B. . C. . D. . 18 18 408 408
Câu 35: Phương trình 9x 4.3x
 3  0 có tổng các nghiệm là A. 1  . B. 4 . C. 1. D. 4  .
Câu 36: Gọi z ; z là hai nghiệm phức của phương trình 2
z  2z  2  0 . Tập hợp các điểm bểu diễn 1 2
của số phức w thỏa mãn w z w z là đường thẳng có phương trình 1 2
A. x y  0 . B. x  0 .
C. x y  0 . D. y  0 . x  3 y 1 z  7
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 và đường thẳng d :   . Đường 2 1 2 
thẳng  đi qua A và song song với d có phương trình là x 1 3t
x  3  tx  3 2t
x  2  t    
A. y  2  t .
B. y  1 2t .
C. y  3  t .
D.y  1 2t .     z  3  7tz  7   3tz  1 2  t z  2   3t
Câu 38: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua trục Oz có tọa độ là A.  1  ;2; 3   . B. 1; 2; 3  . C.  1  ; 2  ;0. D.  1  ; 2  ;3 .
Câu 39: Cắt hình nón bởi một mặt phẳng đi qua đỉnh và tạo với mặt phẳng đáy một góc 60 được
thiết diện là một tam giác vuông cân có cạnh huyền bằng 4. Tính thể tích của khối nón ban đầu. 10 3  5 3 3  5 3  A. V  . B. V  . C. V  . D. V  . 3 3 3 3
Câu 40: Trong không gian Oxyz , viết phương trình đường thẳng d đi qua điểm M 1; 2;  1 , song x  3  t
song với mặt phẳng  P : x y z  3 và vuông góc với đường thẳng  :  y  3  3t . z  2t  x 1 5tx 1 tx 1 tx  5  t    
A. y  2  3t .
B. y  2  3t .
C. y  2  t .
D. y  3  2t .     z  1   2tz  1   2tz  1   tz  2   t
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Số phức nào sau đây có biểu diễn hình học là điểm M 3;5 ?
A. z  3  5i .
B. z  3  5i .
C. z  3  5i .
D. z  3  5i . Lời giải:
M 3;5 là điểm biểu diễn hình học của số phức z  3  5i .
Câu 2: Trên khoảng 0;  , đạo hàm của hàm số y  ln x là 1 1 1 A. y  . B. y  . C. y  . D.   e y . 10x x ex x Câu 3: Tập xác định  D của hàm số 2 3 y x là
A. D  0;   . B. D  .
C. D 0;  . D. D  \   0 . Lời giải: Do hàm số 2 3 y x
là hàm số lũy thừa với số mũ không nguyên nên để hàm số xác định thì x  0 . Vậy hàm số 2 3 y x
có tập xác định là D  0;   .
Câu 4: Tập nghiệm của bất phương trình ln x  1 là A.  ; e  . B. 0;e . C.  ;  e. D.  ;  e . Lời giải: x  0
Ta có ln x  1  
 0  x e . 1 x e
Từ đây ta suy ra tập nghiệm của bất phương trình đã cho là 0;e .
Câu 5: Cho cấp số nhân u
có u  2 và có công bội bằng 3
 . Giá trị u bằng n  1 2 A. 5  . B. 9 . C. 8  . D. 6  . Lời giải:
Ta có: u u .q  2. 3   6  . 2 1  
Câu 6: Trong không gian Oxyz , vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng Oxy ?
A. m  1;1  ;1 .
B. i  1;0;0 .
C. j  0;1;0 .
D. k  0;0  ;1 . Lời giải:
Vì Oz vuông góc với mặt phẳng Oxy , nên vectơ pháp tuyến của mặt phẳng Oxy là k  0;0  ;1 . ax b
Câu 7: Cho hàm số y
có đồ thị là đường cong trong hình bên dưới: cx d Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia y O 2 x -2
Số giao điểm của đồ thị hàm số đã cho và trục hoành là A. 0 . B. 1. C. 2 . D. 3 . 6 6 6
Câu 8: Cho  f xdx  4 và  g xdx  5 , khi đó 3
 f x gxd  x bằng 2 2 2 A. 19 . B. 17 . C.11. D. 7 . Lời giải: 6 6 6 Ta có 3 f
 x gxdx  3 f
 xdxg
 xdx  3.45  7 . 2 2 2
Câu 9: Đường cong hình vẽ là đồ thị hàm số nào dưới đây? x 1 x 1 A. 3 2
y x x 1 . B. y y
y  x x  . x  . C. 1 x  . D. 3 2 1 1 Lời giải:
Dựa vào hình vẽ ta có tiện cận đứng x  1 và tiệm cận ngang y  1.
Câu 10: Trong không gian Oxyz , mặt cầu có tâm I 2; 1
 ;3 , bán kính R  3 có phương trình là 2 2 2 2 2 2
A. x  2   y  
1   z  3  3 .
B. x  2   y  
1   z  3  3 . 2 2 2 2 2 2
C. x  2   y  
1   z  3  3 .
D. x  3   y  
1   z  3  3 . Lời giải:
Mặt cầu có tâm I 2; 1
 ;3 , bán kính R  3 có phương trình là
x  2  y  2 z  2 2 1 3  3 .
Câu 11: Trong không gian Oxyz , góc giữa mặt phẳng Oyz và trục Ox bằng A. 30 .  B. 90 .  C. 60 .  D. 0 . 
Câu 12: Tìm hai số thực x và y thỏa mãn 2x  3yi  1  3i  x  6i , với i là đơn vị ảo. Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia
A. x  1, y  3 .
B. x  1, y  1 .
C. x  1, y  1.
D. x  1, y  3. Lời giải: x   xx  
Ta có  x yi    i  x i x    y   2 1 1 2 3 1 3 6 2 1 3
3 i x  6i     .  3  y  3  6  y  3 
Câu 13: Cho khối chóp có diện tích đáy B  6 và chiều cao h  8 . Thể tích của khối chóp đã cho bằng A. 16 . B. 48 . C. 8 . D. 14 . Lời giải: 1 1
Thể tích của khối chóp V  .
B h  .6.8  16 . 3 3
Vậy thể tích của khối chóp đã cho bằng 16 .
Câu 14: Thể tích khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a bằng A C B A C B 3 3 A. 3 a . B. 3 a . C. 3 2a . D. 3 a . 12 4 Lời giải: A C B A C B 2 3 a 3 a 3
Thể tích khối lăng trụ là V  . B h  .a  . 4 4
Câu 15: Cho mặt cầu S , bán kính R và mặt phẳng   . Biết khoảng cách từ tâm của mặt cầu S tới
mặt phẳng   bằng R . Khẳng định nào sau đây đúng?
A. Mặt phẳng a cắt mặt cầu S .
B. Thiết diện của mặt phẳng   với mặt cầu S là một đường tròn.
C. Mặt phẳng a tiếp xúc với mặt cầu S .
D. Mặt phẳng a với mặt cầu S không có điểm chung. Lời giải: Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia
Khoảng cách từ tâm mặt cầu đến mặt phẳng bằng đúng bán kính nên mặt phẳng tiếp xúc mặt cầu.
Câu 16: Cho số phức z  1 2i . Số phức liên hợp của z là A. 1 2i . B. 1 2i . C. 2  i . D. 1 2i . Lời giải:
Theo định nghĩa số phức liên hợp ta có1 2i là số phức liên hợp của z  1 2i .
Câu 17: Cho hình nón có độ dài đường sinh bằng 3a và bán kính đáy bằng a . Diện tích xung quanh
của hình nón đã cho bằng A. 2 12 a . B. 2 3 a . C. 2 6 a . D. 2  a . Lời giải:
Hình nón có độ dài đường sinh l  3a , bán kính đáy r a có diện tích xung quanh là 2 S   rl  . .3
a a  3 a . xq
x  3  2t
Câu 18: Trong không gian Oxyz , cho đường thẳng d :  y  1 t . Điểm nào dưới đây thuộc d ? z  23t
A. M 3;1; 2 .
B. Q 2;1;3 . C. P  3  ; 1  ; 2  . D. N  2  ;1;3 .
Câu 19: Cho hàm số f x có bảng xét dấu f  x như sau:
Hoành độ điểm cực tiểu của hàm số đã cho bằng A. 1  . B. 0 . C. 1. D. 1 và 1  . Lời giải:
Do f  x xác định và đổi dấu từ âm sang dương khi đi qua 1, nên hoành độ điểm cực tiểu của hàm số bằng 1.
Câu 20: Bảng biến thiên sau đây là của hàm số nào ? x 1 x 1 2x 1 x  3 A. y  . B. y  . C. y  . D. y  . x  2 x 1 x  2 x  2 Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia Lời giải:
Từ BBT suy ra:
Tiệm cận đứng của ĐTHS là: x  2 . Loại B.
Tiệm cận ngang của ĐTHS là: y  1. Loại C. Dấu của đạo hàm: '
y  0 . Loại D.
Câu 21: Tập nghiệm của bất phương trình x 1 2   4 là A.  ;  3. B.  ;  5. C. 1;3. D. 1; . Lời giải:  Ta có: x 1 2
 4  x 1  2  x  3.
Câu 22: Từ 10 điểm phân biệt trong không gian có thể tạo thành bao nhiêu vectơ khác vectơ 0 ? A. 10 2 . B. P . C. 2 A . D. 2 C . 10 10 10 Lời giải:
Chọn 2 điểm từ 10 điểm phân biệt đã cho rồi xếp vào 2 vị trí điểm đầu - điểm cuối của véc tơ
 Số véc tơ tạo thành là 2 A . 10
Câu 23: Cho hàm số y f x
xác định và liên tục trên đồng thời thoả mãn: f (
x)  3 5sin x , f (0) 14 . Khẳng định nào sau đây đúng?
A. f ( )  3  5 .
B. f (x)  3x  5sin x  9 .    3
C. f (x)  3x  5cos x  9 . D. f   9   .  2  2 Lời giải:
Ta có f x  f (  x)dx  
35s ni xdx  3x5cosxC .
Mà f (0)  3.0  5cos 0  C  14  C  9 .
Suy ra f x  3x  5cos x  9.        3 Do đó f  3.  5cos 9  9       .  2  2  2  2 4 4
Câu 24: Nếu f (x)dx  37  thì 2
2 f(x)  3x dx   bằng 0 0 A. 12. B. 18. C. 27 . D. 10. Lời giải: 4 4 4 4 Ta có: 2 2 3
2 f (x) 3x  dx  2 f (x)dx 3 x dx  2.37  x  74  64 10     . 0 0 0 0
Câu 25: Họ tất cả các nguyên hàm của hàm số f x  cos x  6x là A. 2
sin x  3x C . B.  sin x C . C. 2
sin x  3x C . D. 2
sin x  6x C . Lời giải: Ta có f
 xdx  cos x6xdx 2
 sin x  3x C . Vậy chọn A.
Câu 26: Cho hàm số y f x có đồ thị như hình bên dưới: Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia
Mệnh đề nào sau đây đúng?
A. Hàm số f x nghịch biến trên 2;5 .
B. Hàm số f x nghịch biến trên 0;5 .
C. Hàm số f x đồng biến trên  ;  0.
D. Hàm số f x đồng biến trên 5;  . Lời giải:
Dựa vào đồ thị hàm số y f x , hàm số f x đồng biến trên 5;  .
Câu 27: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A. x  1 .
B. y  3.
C. x  3 .
D. y  1. Lời giải:
Từ bảng biến thiên ta thấy hàm số đã cho đạt cực tiểu tại x  3 .
Câu 28: Cho khối trụ T  ,   là mặt phẳng đi qua trục và cắt khối trụ T  theo thiết diện là hình
vuông cạnh 2a. Thể tích khối trụ T  bằng 3  a 3 2 a A. B. 3 2 a . C. . D. 3  a . 3 3 Lời giải:
Thiết diện của khối trụ T  được cắt bởi mặt phẳng   là hình vuông cạnh bằng 2a nên ta 1 có
l h  2a , bán kính đường tròn đáy bằng r  .2a a . Vậy 2 Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 2 3 V  .
B h   r h   a .2a  2 a .
Câu 29: Cho a là số thực dương khác 1. Giá trị của 3 log a bằng a 1 A. 0. B. . C. 3. D. 3. 3 Lời giải: 1 1 1 Ta có 3 3 log
a  log a  log a  . a a 3 a 3
Câu 30: Thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  3 và
trục hoành quay quanh trục Ox là 4 16 16 4 A. V  . B. V  . C. V  . D. V  . 3 15 15 3 Lời giải:
Hoành độ giao điểm của đồ thị hàm số 2
y x  4x  3 và trục hoành là nghiệm phương trình x 1 2
x  4x  3  0   . x  3
Do đó, thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số 2
y x  4x  3
và trục hoành quay quanh trục Ox là 3 3 2 V    2
x  4x  3 dx    4 3 2
x  8x  22x  24x  9dx 1 1 3 5 3  x 22x  16 4 2     2x
12x  9x   .  5 3  15 1
Câu 31: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC a . Hình chiếu
vuông góc của S lên  ABC  trùng với trung điểm của BC . S A C H B
Biết SB a . Tính số đo của góc giữa SA và  ABC  . A. 75 . B. 30 . C. 60 . D. 45 . Lời giải: Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia S A C H B
Gọi H là trung điểm của BC .
Theo giả thiết ta có SH   ABC  và góc giữa SA và  ABC  là góc SAH . 2 a a 3 1 a Ta có 2 2 2 SH
SB BH a   và AH BC  . 4 2 2 2 a 3 SH Ta có 2 tan SAH  
 3  SAH  60 . AH a 2
Vậy góc giữa SA và  ABC  bằng 60 .
Câu 32: Cho hàm số bậc ba y f x có đồ thị như hình vẽ bên dưới:
Số giá trị nguyên của tham số m để đường thẳng y m cắt đồ thị hàm số đã cho tại ba điểm phân biệt là A. Vô số. B. 3 . C. 0. D. 5 . Lời giải:
Từ đồ thị ta thấy để đường thẳng y m cắt đồ thị hàm số đã cho tại ba điểm phân biệt khi
1  m  5 . Vì m nguyên nên m 2;3;  4 .
Vậy có 3 giá trị nguyên của m thoả mãn yêu cầu bài toán
Câu 33: Có bao nhiêu giá trị nguyên của tham số thực m để hàm số 3 2
y  x mx  4m  9 x  5
nghịch biến trên khoảng  ;   ? A. 5. B. 7. C. 4. D. 6. Lời giải: Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia Ta có 2 y '  3
x  2mx  4m  9.
Hàm số nghịch biến trên  ;
   y'  0, x   2
  '  m 12m  27  0  9   m  3  (*)
Từ (*) suy ra m  9  ; 8  ; 7  ;6;5;4; 
3 là các giá trị nguyên của m thỏa mãn yêu cầu của bài toán.
Câu 34: Một hộp có 5 viên bi xanh, 6 viên bi đỏ và 7 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong
hộp. Xác suất để 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng bằng 11 5 75 95 A. . B. . C. . D. . 18 18 408 408 Lời giải:
Số phần tử của không gian mẫu là số cách chọn ngẫu nhiên 5 viên bi từ hộp chứa 18 viên bi. Suy ra 5   C . 18
Gọi A là biến cố 5 viên bi được chọn có đủ ba màu và số bi đỏ bằng số bi vàng. Ta có các
trường hợp thuận lợi cho biến cố A là:
TH 1: Chọn 1 viên bi đỏ, 1 viên bi vàng và 3 viên bi xanh. Có 1 C . 1 C . 3 C cách chọn. 6 7 5
TH 2: Chọn 2 viên bi đỏ, 2 viên bi vàng và 1 viên bi xanh. Có 2 C . 2 C . 1 C cách chọn. 6 7 5
Do đó số phần tử của biến cố A là 1
A C . 1 C . 3 2
C C . 2 C . 1 C . 6 7 5 6 7 5 1 1 3 2 2 1 A C C C C C C 95
Vậy xác suất cần tính là PA . . . . 6 7 5 6 7 5    5  . C 408 18
Câu 35: Phương trình 9x 4.3x
 3  0 có tổng các nghiệm là A. 1  . B. 4 . C. 1. D. 4  . Lời giải: 3x  1 x  0 Ta có: x x 2
9  4.3  3  0  3 x  4.3x  3  0     . 3x  3 x  1
Vậy tổng các nghiệm của phương trình là 1.
Câu 36: Gọi z ; z là hai nghiệm phức của phương trình 2
z  2z  2  0 . Tập hợp các điểm bểu diễn 1 2
của số phức w thỏa mãn w z w z là đường thẳng có phương trình 1 2
A. x y  0 . B. x  0 .
C. x y  0 . D. y  0 . Lời giải: z 1 i Phương trình 2
z  2z  2  0   . z 1 i
Gọi w x yi ; x, y
w z w z x 1  y 1 i x 1  y 1 i 1 2          x  2 1   y  2 1  x  2 1   y  2 1  y  0.
Do đó tập hợp các điểm bểu diễn của số phức w là đường thẳng có phương trình y  0. x  3 y 1 z  7
Câu 37: Trong không gian Oxyz , cho điểm A1; 2;3 và đường thẳng d :   . Đường 2 1 2 
thẳng  đi qua A và song song với d có phương trình là Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc giax 1 3t
x  3  tx  3 2t
x  2  t    
A. y  2  t .
B. y  1 2t .
C. y  3  t .
D.y  1 2t .     z  3  7tz  7   3tz  1 2  t z  2   3tLời giải:
Vectơ chỉ phương của đường thẳng d là u  2;1;  2 . d
Do  / /d nên  có vectơ chỉ phương là u u   
2;1; 2 và  đi qua A . d
Kiểm tra phương án C thỏa mãn.
Câu 38: Trong không gian Oxyz , cho điểm A1; 2;3 . Điểm đối xứng với A qua trục Oz có tọa độ là A.  1  ;2; 3   . B. 1; 2; 3  . C.  1  ; 2  ;0. D.  1  ; 2  ;3 .
Câu 39: Cắt hình nón bởi một mặt phẳng đi qua đỉnh và tạo với mặt phẳng đáy một góc 0 60 được
thiết diện là một tam giác vuông cân có cạnh huyền bằng 4. Tính thể tích của khối nón ban đầu. 10 3  5 3 3  5 3  A. V  . B. V  . C. V  . D. V  . 3 3 3 3 Lời giải:
Giả sử hình nón đỉnh S  tâm O , thiết diện qua đỉnh ở giả thiết là tam giác vuông cân SAB .
Gọi K là trung điểm của AB , suy ra góc giữa SAB và mặt đáy là SKO  60 . 1
Ta có AB  4  SK
AB  2 và SA SB  2 2 . 2
Tam giác SKO vuông tại O : SO SK.tan SKO  3 .
Tam giác SAO vuông tại 2 2 O : AO
SA SO  5 . 1 5 3 Thể tích khối nón 2
V   .AO .SO   . 3 3
Câu 40: Trong không gian Oxyz , viết phương trình đường thẳng d đi qua điểm M 1; 2;  1 , song x  3  t
song với mặt phẳng  P : x y z  3 và vuông góc với đường thẳng  :  y  3  3t . z  2t  Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc giax 1 5tx 1 tx 1 tx  5  t    
A. y  2  3t .
B. y  2  3t .
C. y  2  t .
D. y  3  2t .     z  1   2tz  1   2tz  1   tz  2   t Lời giải:
VTPT của mặt phẳng  P : n   P 1;1;  1 .
VTCP của đường thẳng  : u  1;3; 2 .
VTCP của đường thẳng d  : u      d
nP;u   5; 3;2 . x 1 5t
Vậy phương trình tham số của đường thẳng d  :  y  2  3t . z  1   2t
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 16
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 05_______________
Câu 1: Điểm M trong hình vẽ là điểm biểu diễn số phức nào dưới đây?
A. z  2  . i
B. z  2  i.
C. z  2  i.
D. z  2  i.
Câu 2: Đạo hàm của hàm số 2023x y  là 2023x A. 1 .2023x y x    . B. y  . C. 2023x y  .ln 2023 . D. 2023x y  . ln 2023
Câu 3: Hàm số y  ln 2x   1 có đạo hàm là 2 1 2 1 A. y  . B. y  . C. y  . D. y  .
x ln 2x   1 2x 1 2x 1 2x  1ln2
Câu 4: Tập nghiệm của bất phương trình 3x  9 là
A. 2;  . B. 0;2 .
C. 0;  . D.  2;    .
Câu 5: Cho cấp số cộng u có u  3 và u  1. Công sai của cấp số cộng đó bằng n  1 2 A. 1. B. 4  . C. 4 . D. 2 .
Câu 6: Trong không gian Oxyz , mặt phẳng nào dưới đây nhận n  3;1; 7
  là một vectơ pháp tuyến?
A. 3x z  7  0 .
B. 3x y  7z 1  0 . C. 3x y  7  0 .
D. 3x y  7z  3  0 .
Câu 7: Cho hàm số f x có bảng biến thiên như sau:
Số nghiệm của phương trình 2 f x  5 là A. 0 . B. 2 . C. 1. D. 3 . 5 5
Câu 8: Cho  f xdx 10 . Khi đó, 2  3  f x d  x bằng 2 2 A. 32 . B. 36 . C. 42 . D. 46 .
Câu 9: Hàm số nào có đồ thị là hình vẽ sau đây? 2x 1 A. 3 2
y x  3x  4 . B. 4 2
y x  3x  4 . C. 3 2
y x  3x  4 . D. y  . 3x  5 Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 2 2
Câu 10: Trong không gian Oxyz, mặt cầu S  : x  2   y  
1   z  3  9. Tọa độ tâm của mặt cầu S là
A. 2;1;3. B. 2; 1  ;3. C.  2  ;1; 3  . D.  2  ; 1  ; 3  .
Câu 11: Trong không gian Oxyz, cho điểm A1;0;0. Góc giữa đường thẳng OA và mặt phẳng Oxy bằng A. 90 .  B. 60 .  C. 30 .  D. 0 . 
Câu 12: Cho hai số phức z  1 2i , z  2  6i . Tích z .z bằng 1 2 1 2
A. 10  2i .
B. 2 12i .
C. 14 10i . D. 14  2i .
Câu 13: Cho hình lập phương có cạnh bằng 3 . Tổng diện tích các mặt của hình lập phương đã cho bằng A. 54 . B. 12 . C. 36 . D. 24 .
Câu 14: Cho khối tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB AC  2a, AD  3a . Thể
tích của khối tứ diện đó là A. 3
V  4a . B. 3
V  2a . C. 3
V a . D. 3
V  3a .
Câu 15: Diện tích S của mặt cầu có bán kính r được tính theo công thức nào dưới đây? 4 1 A. 2
S  4 r . B. 2
S   r . C. 2 S   r . D. 2 S   r . 3 3
Câu 16: Trong các số phức sau, số phức nào dưới đây là số thuần ảo?
A. 1 i .
B. 3i . C. 2 . D. 5  .
Câu 17: Thể tích của khối nón có đường kính đường tròn đáy là 4, đường cao bằng 6 là
A. V  8 .
B. V  32 .
C. V  24 .
D. V  96 . x  1 y  3 z
Câu 18: Trong không gian Oxyz , cho đường thẳng  : 
 đi qua điểm nào dưới đây? 3 1 2 A. N 3; 1  ;0 . B. P3; 1  ;2 . C. M  1  ;3;0 . D. Q1; 3  ;0 .
Câu 19: Cho hàm số y f x có đồ thị như hình vẽ bên dưới:
Giá trị cực đại của hàm số đã cho là A. 1. B. 1  . C. 0 . D. 2 .
Câu 20: Cho hàm số y f x có lim f x  1 và lim f x  1
 . Khẳng định nào sau đây đúng? x x
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng y  1 và đường thẳng y  1.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng x  1 và đường thẳng x  1 . Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 21: Tập nghiệm của bất phương trình log x  1  3 là 2  
A. S   ;  8.
B. S   ;  7 . C. S   1  ; 8 . D. S   1  ; 7 .
Câu 22: Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng? A. 300 . B. 15 . C. 35 . D. 20 . Câu 23: Cho d   
x x F x C . Khẳng định nào dưới đây đúng? x
A. F x  1.
B. F x  x .
C. F x 2   C .
D. F x  x . 2 2 2 3
Câu 24: Nếu  f xdx  3 và  f xdx 1 thì  d  f x x bằng 1 3 1 A. 4. B. 2  . C. 2 . D. 4  .
Câu 25: Cho hàm số f x  cos x x . Khẳng định nào dưới đây đúng? A. f  x 2 dx  sin 
x x C. B. f  x 2
dx  sin x x C. x x C. f  x 2 dx  s  in x   C. D. f  x 2 dx  sin x   C. 2 2
Câu 26: Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; 2 .
B. 3;  . C.   ;1  . D. 2;3 .
Câu 27: Cho hàm số bậc ba y f x có đồ thị như hình bên dưới:
Giá trị cực tiểu của hàm số đã cho là A. 1  . B. 3 . C. 2 . D. 0 .
Câu 28: Với a là số thực dương tùy ý, log  a 3   log2a bằng 2 3
A. log a . B. log . C.  2 log 6a  . D. log . 3 2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y x  2x và
y  0 quanh trục Ox là 16 16 16 16 A. V   B. V   C. V   D. V   15 9 9 15 Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 30: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy và SA a (tham khảo hình vẽ). S C A B
Góc giữa đường thẳng SB và mặt phẳng  ABC  bằng A. 60 .  B. 30 C. 90 D. 45
Câu 31: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình f x  m có ba
nghiệm thực phân biệt. Tổng tất cả các phần tử của S bằng A. 3  . B. 5 . C. 3 . D. 4 .
Câu 32: Cho hàm số y f (x) liên tục trên
và có đạo hàm f  x 2
 2x x  
1 3  x,x  . Hàm
số đồng biến trên khoảng nào dưới đây? A.  ;    1 . B.  ;  0. C. 3; . D. 1;3.
Câu 33: Từ một hộp chứa 11 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được 3 quả cầu màu xanh là 4 24 4 33 A. . B. . C. . D. . 455 455 165 91
Câu 34: Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ
bằng 16 . Thể tích của khối trụ đã cho bằng A. 24 . B. 32 . C. 16 . D. 8 .
Câu 35: Cho phương trình 2
log x  8 log x  1  0. Giải phương trình trên bằng cách đặt t  log x, ta 2 4 2
thu được phương trình nào dưới đây? A. 2
t  8t  1  0. B. 2
t  4t  1  0. C. 2
t  16t  1  0. D. 2
t  6t  1  0.
Câu 36: Cho A , B , C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z  1 2i , 1 z  2
  5i , z  2  4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình 2 3 hành là
A. 1 7i .
B. 5  i .
C. 1 5i . D. 3  5i . Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 37: Trong không gian Oxyz , đường thẳng đi qua điểm M 3;2;1 và vuông góc với mặt phẳng
P:2x 5y  4  0 có phương trình là
x  3  2t
x  3  2t
x  3  2tx  3 2t    
A. y  2  5t .
B. y  2  5t .
C. y  2  5t .
D. y  2  5t .     z  1  z  1  z   t z  1 
Câu 38: Trong không gian Oxyz , cho điểm A3;5;7 . Hình chiếu vuông góc của điểm A lên mặt
phẳng Oxz có tọa độ là A. 3;5;7. B. 3;5;0.
C. 3;0;7. D. 0;5;0.
Câu 39: Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a . Khoảng cách từ A
đến  SCD bằng a 14 a 14 a 14 A. . B. . C. a 14 . D. . 3 4 2
Câu 40: Cho hình nón N có chiều cao h  3. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo một thiết diện là tam giác vuông có diện tích bằng 8. Tính thể tích của khối nón giới
hạn bởi hình nón N. A. 16 . B. 21 . C. 12 . D. 7 .
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Điểm M trong hình vẽ là điểm biểu diễn số phức nào dưới đây?
A. z  2  . i
B. z  2  i.
C. z  2  i.
D. z  2  i. Lời giải:
Điểm M trong hình vẽ là điểm biểu diễn số phức: z  2   i .
Câu 2: Đạo hàm của hàm số 2023x y  là 2023x A. 1 .2023x y x    . B. y  . C. 2023x y  .ln 2023 . D. 2023x y  . ln 2023
Câu 3: Hàm số y  ln 2x   1 có đạo hàm là 2 1 2 1 A. y  . B. y  . C. y  . D. y  .
x ln 2x   1 2x 1 2x 1 2x  1ln2 Lời giải: 2
Hàm số y  ln 2x  
1 có đạo hàm là y  . 2x 1
Câu 4: Tập nghiệm của bất phương trình 3x  9 là
A. 2;  . B. 0;2 .
C. 0;  . D.  2;    . Lời giải: Ta có x x 2
3  9  3  3  x  2  x  2;  .
Vậy tập nghiệm của bất phương trình là 2;  .
Câu 5: Cho cấp số cộng u có u  3 và u  1. Công sai của cấp số cộng đó bằng n  1 2 A. 1. B. 4  . C. 4 . D. 2 . Lời giải:
Ta có u u d d u u  1   3  4 . 2 1 2 1
Câu 6: Trong không gian Oxyz , mặt phẳng nào dưới đây nhận n  3;1; 7
  là một vectơ pháp tuyến?
A. 3x z  7  0 .
B. 3x y  7z 1  0 . C. 3x y  7  0 .
D. 3x y  7z  3  0 . Lời giải:
Phương trình mặt phẳng 3x y  7z  3  0 có một vectơ pháp tuyến là n  3;1; 7  .
Câu 7: Cho hàm số f x có bảng biến thiên như sau: Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia
Số nghiệm của phương trình 2 f x  5 là A. 0 . B. 2 . C. 1. D. 3 . Lời giải:
Ta có: f x   f x 5 2 5  . 2
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y f x và đường thẳng 5 y
. Từ đồ thị ta thấy có ba giao điểm. 2
Vậy phương trình đã cho có ba nghiệm. 5 5
Câu 8: Cho  f xdx 10. Khi đó 2  3  f x d    x bằng 2 2 A. 32 . B. 36 . C. 42 . D. 46 . Lời giải: 5 5 5 Ta có 2  3  f x d
x  2dx  3  
f xdx  36. 2 2 2
Câu 9: Hàm số nào có đồ thị là hình vẽ sau đây? 2x 1 A. 3 2
y x  3x  4 . B. 4 2
y x  3x  4 . C. 3 2
y x  3x  4 . D. y  . 3x  5 Lời giải:
Dựa vào hình dạng đồ thị, ta thấy đây là đồ thị của hàm số bậc 3, với hệ số
a  0 lim y   . Nên loại B và D. x 
Khi x  0  y  4 . 2 2 2
Câu 10: Trong không gian Oxyz, mặt cầu S  : x  2   y  
1   z  3  9. Tọa độ tâm của mặt cầu S là
A. 2;1;3. B. 2; 1  ;3. C.  2  ;1; 3  . D.  2  ; 1  ; 3  . Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia Lời giải:   2 2 2 I 2; 1;3
Phương trình  x  2   y   1   z  3    9   R  3
Câu 11: Trong không gian Oxyz, cho điểm A1;0;0. Góc giữa đường thẳng OA và mặt phẳng Oxy bằng A. 90 .  B. 60 .  C. 30 .  D. 0 . 
Câu 12: Cho hai số phức z  1 2i , z  2  6i . Tích z .z bằng 1 2 1 2
A. 10  2i .
B. 2 12i .
C. 14 10i . D. 14  2i . Lời giải:
Ta có z .z  1 2i 2  6i  14  2i . 1 2   
Câu 13: Cho hình lập phương có cạnh bằng 3 . Tổng diện tích các mặt của hình lập phương đã cho bằng A. 54 . B. 12 . C. 36 . D. 24 . Lời giải:
Tổng diện tích các mặt của hình lập phương là: 2 S  6.3  54 .
Câu 14: Cho khối tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB AC  2a, AD  3a . Thể
tích của khối tứ diện đó là A. 3
V  4a . B. 3
V  2a . C. 3
V a . D. 3
V  3a . Lời giải: 1
Do khối tứ diện ABCD có AB, AC, AD đôi một vuông góc nên 3 VA .
B AC.AD  2a . ABCD 6
Câu 15: Diện tích S của mặt cầu có bán kính r được tính theo công thức nào dưới đây? 4 1 A. 2
S  4 r . B. 2
S   r . C. 2 S   r . D. 2 S   r . 3 3
Câu 16: Trong các số phức sau, số phức nào dưới đây là số thuần ảo?
A. 1 i .
B. 3i . C. 2 . D. 5  . Lời giải:
Số phức 3i là số phức thuần ảo.
Câu 17: Thể tích của khối nón có đường kính đường tròn đáy là 4, đường cao bằng 6 là
A. V  8 .
B. V  32 .
C. V  24 .
D. V  96 . Lời giải: 1 1 2 2
V   hR   .6.2  8 . 3 3 x  1 y  3 z
Câu 18: Trong không gian Oxyz , cho đường thẳng  : 
 đi qua điểm nào dưới đây? 3 1 2 A. N 3; 1  ;0 . B. P3; 1  ;2 . C. M  1  ;3;0 . D. Q1; 3  ;0 . Lời giải: 11 3  3 0 Ta có: 
 Suy ra điểm M  0 ; 3 ; 1
 thuộc đường thẳng  3 1 2
Câu 19: Cho hàm số y f x có đồ thị như hình vẽ bên dưới: Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia
Giá trị cực đại của hàm số đã cho là A. 1. B. 1  . C. 0 . D. 2 . Lời giải:
Qua đồ thị hàm số y f x ta thấy giá trị cực đại của hàm số bằng 1.
Câu 20: Cho hàm số y f x có lim f x  1 và lim f x  1
 . Khẳng định nào sau đây đúng? x x
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng y  1 và đường thẳng y  1.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là đường thẳng x  1 và đường thẳng x  1 . Lời giải:
Vì lim f x  1 và lim f x  1
 nên đồ thị hàm số đã cho có hai tiệm cận ngang là đường x x
thẳng y  1 và đường thẳng y  1.
Câu 21: Tập nghiệm của bất phương trình log x 1  3 là 2  
A. S   ;  8.
B. S   ;  7 . C. S   1  ; 8 . D. S   1  ; 7 . Lời giải:
Ta có: log x  1  3 3
 0  x 1 2  1 x  7 2  
Vậy tập nghiệm của bất phương trình log
x 1  3 là S   1  ; 7. 2  
Câu 22: Lớp 10A có 20 học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ra một học sinh của
lớp 10A để làm lớp trưởng? A. 300 . B. 15 . C. 35 . D. 20 . Lời giải:
Lớp có 20 15  35 học sinh.
Suy ra số cách chọn một học sinh của lớp 10A để làm lớp trưởng là 1 C  35 . 35 Câu 23: Cho d   
x x F x C . Khẳng định nào dưới đây đúng? x
A. F x  1.
B. F x  x .
C. F x 2   C .
D. F x  x . 2 Lời giải:  
Ta có F x    d
x x   x . 2 2 3 Câu 24: Nếu f
 xdx  3 và f
 xdx 1 thì f x  dx bằng 1 3 1 Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia A. 4. B. 2  . C. 2 . D. 4  . Lời giải: 2 3 3 2 3
Ta có f xdx  1 f xdx  1    khi đó f
 xdx  f
 xdx  f
 xdx  31 2 . 3 2 1 1 2
Câu 25: Cho hàm số f x  cos x x . Khẳng định nào dưới đây đúng? A. f  x 2 dx  sin 
x x C. B. f  x 2
dx  sin x x C. x x C. f  x 2 dx  s  in x   C. D. f  x 2 dx  sin x   C. 2 2 Lời giải:
   x   xx 2 x f x d cos dx  n si x   C. 2
Câu 26: Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 0; 2 .
B. 3;  . C.   ;1  . D. 2;3 .
Câu 27: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới:
Giá trị cực tiểu của hàm số đã cho là A. 1  . B. 3 . C. 2 . D. 0 .
Câu 28: Với a là số thực dương tùy ý, log  a 3   log2a bằng 2 3
A. log a . B. log . C.  2 log 6a  . D. log . 3 2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y x  2x và
y  0 quanh trục Ox là 16 16 16 16 A. V   B. V   C. V   D. V   15 9 9 15 Lời giải:
Phương trình hoành độ giao điểm của đường 2
y x  2x và đường y  0 là x  0 2
x  2x  0   . x  2 Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 2 5 3 2  x x  2 16
Thể tích là V   2
x  2x dx   4 3 2
x  4x  4x  4 dx    x  4.   . 5 3 0 15   0 0
Câu 30: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy và SA a (tham khảo hình vẽ). S C A B
Góc giữa đường thẳng SB và mặt phẳng  ABC  bằng A. 60 .  B. 30 C. 90 D. 45 Lời giải:
Ta có: SA   ABC nên góc giữa đường thẳng SB và mặt phẳng  ABC  bằng SBA .
Do tam giác SAB vuông cân tại A SBA  45 .
Vậy góc giữa đường thẳng SB và mặt phẳng  ABC  bằng 45 .
Câu 31: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình f x  m có ba
nghiệm thực phân biệt. Tổng tất cả các phần tử của S bằng A. 3  . B. 5 . C. 3 . D. 4 . Lời giải:
Số nghiệm của phương trình f x  m bằng số giao điểm của đồ thị hàm số y f x và
đường thẳng d : y m . Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc gia
Dựa vào hình vẽ, ta có:
Phương trình f x  m có ba nghiệm thực phân biệt khi đường thẳng d : y m cắt đồ thị
hàm số y f x tại ba điểm phân biệt, tức là 3
  m  1. Mà m  nên m 2  ; 1  ;  0 .
Câu 32: Cho hàm số y f (x) liên tục trên và có đạo hàm 2
f '(x)  2x (x 1)(3  x), x  . Hàm số
đồng biến trên khoảng nào dưới đây? A.  ;    1 . B.  ;  0. C. 3; . D. 1;3. Lời giải: x  0 
Ta có: f '(x)  0  x  1   x  3  Bảng xét dấu:
Căn cứ bảng xét dấu ta thấy hàm số đồng biến trên (1;3) .
Câu 33: Từ một hộp chứa 11 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Xác suất để lấy được 3 quả cầu màu xanh là 4 24 4 33 A. . B. . C. . D. . 455 455 165 91 Lời giải:
Số phần tử của không gian mẫu n  3  C  455 . 15
Gọi A là biến cố " 3 quả cầu lấy được đều là màu xanh". Suy ra n A 3  C  4 . 4
Vậy xác suất cần tìm là P A 4  . 455
Câu 34: Một khối trụ có thiết diện qua trục là một hình vuông. Biết diện tích xung quanh của khối trụ
bằng 16 . Thể tích của khối trụ đã cho bằng A. 24 . B. 32 . C. 16 . D. 8 . Lời giải: Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia
Ta có thiết diện qua trục là hình vuông nên h  2R
Diện tích xung quanh bằng 16 nên 2 Rh  16 (*)
Thay h  2R vào (*) ta được 2
2R  8  R  2  h  2R  4
Thể tích khối trụ bằng : 2
V   R h   .4.4  16 .
Câu 35: Cho phương trình 2
log x  8 log x  1  0. Giải phương trình trên bằng cách đặt t  log x, ta 2 4 2
thu được phương trình nào dưới đây? A. 2
t  8t  1  0. B. 2
t  4t  1  0. C. 2
t  16t  1  0. D. 2
t  6t  1  0. Lời giải: Ta có: 2 2
log x  8 log x  1  0  log x  4 log x  1  0. 2 4 2 2
Đặt t  log x, phương trình trở thành 2
t  3t  1  0. 2
Câu 36: Cho A , B , C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z  1 2i , 1 z  2
  5i , z  2  4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình 2 3 hành là
A. 1 7i .
B. 5  i .
C. 1 5i . D. 3  5i . Lời giải:
Ta có A1; 2 , B 2;5 , C 2; 4 . Gọi D  ;
x y  .Ta có AB   3
 ;3 , DC  2  ; x 4  y  . 2  x  3  x  5
Để ABCD là hình bình hành thì AB DC     . 4  y  3 y 1
Vậy z  5  i .
Câu 37: Trong không gian Oxyz , đường thẳng đi qua điểm M 3;2;1 và vuông góc với mặt phẳng
P:2x 5y  4  0 có phương trình là
x  3  2t
x  3  2t
x  3  2tx  3 2t    
A. y  2  5t .
B. y  2  5t .
C. y  2  5t .
D. y  2  5t .     z  1  z  1  z   t z  1  Lời giải:
Gọi d là đường thẳng đi qua điểm M và vuông góc với mặt phẳng  P
Ta có d   P  u n  2; 5  ;0 d P    x   t Qa u M  3;2  3 2   d  ;1 : 
 d  y   t u     d   : 2 5 2; 5; 0 z 1  Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 38: Trong không gian Oxyz , cho điểm A3;5;7 . Hình chiếu vuông góc của điểm A lên mặt
phẳng Oxz có tọa độ là A. 3;5;7. B. 3;5;0.
C. 3;0;7. D. 0;5;0.
Câu 39: Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a . Khoảng cách từ A
đến  SCD bằng a 14 a 14 a 14 A. . B. . C. a 14 . D. . 3 4 2 Lời giải: S 3a A D 2a O B 2a C
Gọi O AC  . BD
Do S.ABCD chóp đều nên đáy ABCD là hình vuông và SO   ABCD . d  , A SCD AC Ta có:  d  ,
A SCD  2.d O,SCD  2h .
d O SCD   2 , OC
Xét ACD vuông tại D có: 2 2 AC
AD CD CD 2  2a 2  OC OD a 2 .
Xét SOC vuông tại O có: 2 2 SO
SC OC   a  a 2 2 3 2  a 7 .
Do tứ diện SOCD có ba cạnh OS, OC, OD đôi một vuông góc 1 1 1 1     1 1 1 8     14   a h . 2 2 2 2 h OS OC OD  2  2  2 2 7 7 2 2 a a a a 4 a 14
Vậy khoảng cách từ A đến  SCD bằng . 2
Câu 40: Cho hình nón N có chiều cao h  3. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình
nón theo một thiết diện là tam giác vuông có diện tích bằng 8. Tính thể tích của khối nón giới
hạn bởi hình nón N. A. 16 . B. 21 . C. 12 . D. 7 . Lời giải: Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc gia S l h A O r B
Gọi thiết diện là tam giác SAB,SA SB  .l 2 l Theo giả thiết: S  8   8  l  4. SAB 2
Bán kính của N là 2 2
r l h  7. 1
Vậy thể tích khối nón là 2
V hr  7 . 3
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 06_______________
Câu 1: Trên mặt phẳng tọa độ, cho M 4; 3
  là điểm biểu diễn của số phức z . Phần ảo của z bằng A. 4 .
B. 3i . C. 4  . D. 3  . 3
Câu 2: Tập xác định của hàm số 2
y x là
A. 0;  .
B. 2;  . C. . D. \   0 .
Câu 3: Trên khoảng 0;  , đạo hàm của hàm số y  log x là 2 1 ln 2 1 1 A. y  . B. y  . C. y  . D. y  . x ln 2 x x 2x
Câu 4: Tập các nghiệm của bất phương trình 2x  6 là
A. log 6;  . B.  ;3   .
C. 3;  . D.  ;  log 6 . 2  2 
Câu 5: Cho cấp số cộng u có số hạng đầu u  2 và số hạng thứ tư u  17 . Công sai của cấp số n  1 4 cộng đã cho bằng 15 A. . B. 5 . C. 3 . D. 15 . 2 x y z
Câu 6: Trong không gian Oxyz, mặt phẳng (P) :  
1, có một vectơ pháp tuyến là 2 2 1 
A. n  (2; 2; 1  ) .
B. n  (1;1; 2)  .
C. n  (2; 2  ; 1  ) .
D. n  ( 2  ; 2  ;1) . 3 4 1 2
Câu 7: Cho hàm số y f x có bảng biến thiên như sau:
Số nghiệm của phương trình f x  6  0 là A. 3 . B. 1. C. 4 . D. 2 . 1 1 Câu 8: Cho  2
x  2x  3 f xdx 1. Tính f xdx  . 0 0 1  5  1  5  A. . B. . C. . D. . 3 3 9 9
Câu 9: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào? A. 3
y  x  3x  2 . B. 3
y  x  3x  2 . C. 4 2
y x x  2 . D. 3
y x  3x  2 .
Câu 10: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  2 y  4z  2  0 . Bán kính mặt cầu S  bằng A. 1. B. 7 . C. 2 2 . D. 7 . Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 11: Trong không gian Oxyz, góc giữa trục Ox và Oz bằng A. 90 .  B. 60 .  C. 30 .  D. 0 . 
Câu 12: Cho số phức z thỏa mãn 1 iz  2  i . Môđun của số phức z bằng 10 A. . B. 3 . C. 2 . D. 10 . 2
Câu 13: Cho khối lăng trụ đứng AB . C A BC
  có BB  a , đáy ABC là tam giác vuông cân tại B và
BA BC a . Thể tích của khối lăng trụ đã cho là 3 a 3 a 3 a A. V  . B. V  . C. V  . D. 3 V a . 6 2 3
Câu 14: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a , SA   ABC  , SA a (tham khảo hình vẽ). S A C B
Thể tích của khối chóp đã cho bằng 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 4 6 12
Câu 15: Nếu tăng bán kính của một khối cầu gấp 3 lần thì thể tích khối cầu đó thay đổi như thế nào?
A. Thể tích tăng gấp 6 lần.
B. Thể tích tăng gấp 9 lần.
C. Thể tích tăng gấp 3 lần.
D. Thể tích tăng gấp 27 lần.
Câu 16: Cho số phức bất kì z a bia,b   . Khẳng định nào sau đây đúng? A. 2 2 z
a b . B. 2 2 z
a b . C. 3 3
z a b . D. 2 2
z a b .
Câu 17: Cho tam giác ABC vuông tại A , AB a và AC a 3 . Tính độ dài đường sinh l của hình
nón có được khi quay tam giác ABC xung quanh trục AB .
A. l  2a .
B. l  2a .
C. l  3a .
D. l a . x 1 y  2 z
Câu 18: Trong không gian Oxyz , đường thẳng d : 
 đi qua điểm nào dưới đây? 2 1  3 A. A2; 1  ;3 . B. C  1  ;2;0 . C. D 1; 2  ;0 .
D. B 0; 2;   1 .
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Tìm giá trị cực đại y và giá trị cực tiểu y của hàm số đã cho. CÐ CT Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia A. y
 3 và y  0 . B. y
 3 và y  2. CÐ CT CÐ CT C. y
 2 và y  2 . D. y
 2 và y  0 . CÐ CT CÐ CT x  2
Câu 20: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y x ? 2
A. x  2 .
B. x  2 .
C. y  1. D. y  1.
Câu 21: Tập nghiệm của bất phương trình log 2x 1  2 là 3   1   1  A. S  ;5   . B. S  ;5   .
C. S   ;5   .
D. S  5;  . 2   2 
Câu 22: Có 3 cây bút đỏ, 4 cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút từ hộp bút đó? A. 7 . B. 4 . C. 12 . D. 3 . Câu 23: Cho sin d x x G
xC. Đạo hàm hàm số y  2Gx x là 2 x
A. y  2 sin x  1.
B. y  2 sin x  1.
C. y  2 sin . x D. y  2  cos x   C. 2 4 4
Câu 24: Nếu f (x)dx  37  thì 2
2 f(x)  3x dx   bằng 0 0 A. 12. B. 18. C. 27 . D. 10.
Câu 25: Cho hàm số f x  sin x x . Khẳng định nào dưới đây đúng? x x
A. f x 2 dx  cos x   C.
B. f x 2
dx   cos x   C. 2 2 x x C. f  x 2 dx  s  in x   C.
D. f x 2
dx   cos x   C. 2 2
Câu 26: Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 0; 2 .
B. 2;  . C.   ;1  . D. 2;3 .
Câu 27: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới:
Điểm cực tiểu của hàm số đã cho là A. 1  . B. 3 . C. 2 . D. 0 .
Câu 28: Với a là số thực dương tùy ý, log  a 5   log 2a bằng 3 3  2 5 A. log 3 . a B. log . C. log  2 3 10a  . D. log . 3 3 5 3 2 Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y x x và
y  0 quanh trục Ox là 16 16 1  A. V   B. V   C. V   D. V   15 15 30 30
Câu 30: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy và AB  2SA (tham khảo hình vẽ). S C A B
Góc giữa hai mặt phẳng SBC và  ABC  bằng A. 60 .  B. 30 C. 90 D. 45
Câu 31: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới: y 2 1 x -1 O -2
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có ba nghiệm thực phân biệt? A. 4 . B. 5 . C. 3 . D. 2 .
Câu 32: Cho hàm số y f x có f x  xx  1x  3 , x
  . Hàm số y f x đồng biến trên khoảng nào dưới đây?
A. ;0. B. 0;1. C. 1; 2.
D. 2; .
Câu 33: Chọn ngẫu nhiên 2 số tự nhiên khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn
được hai số có tổng là một số chẵn bằng 1 13 12 313 A. . B. . C. . D. . 2 25 25 625 2 2
Câu 34: Số nghiệm của phương trình 2x 2 3
x  10.3x x  9  0 là A. 4. B. 1. C. 0. D. 2.
Câu 35: Cho số phức z thỏa mãn z 1 i  4. Biết tập hợp các điểm biểu diễn số phức
w  3  4iz 1 2i là đường tròn C . Tìm tâm I và bán kính R của đường tròn C . A. I  2
 ; 5, R  20. B. I  2
 ; 5, R  4. C. I  2
 ;5, R  4. D. I  2  ;5, R  20. Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 36: Trong không gian Oxyz , viết phương trình tham số của đường thẳng đi qua hai điểm
A1; 2; 3, B 2; 3;  1 . x  1 tx  2  tx  3  tx  1 t    
A. y  2  5t . B. y  3   5t . C. y  8   5t .
D. y  2  5t .     z  3   2tz  1  4tz  5  4tz  3  4t
Câu 37: Trong không gian Oxyz , cho điểm A3;5;7 . Hình chiếu vuông góc của điểm A lên mặt
phẳng Oyz có tọa độ là A. 3;5;7. B. 3;5;0.
C. 3;0;7. D. 0;5;7.
Câu 38: Cho hình lăng trụ đứng ABC.AB C
  có tất cả các cạnh bằng a . Gọi M là trung điểm của AA .
Khoảng cách từ M đến mặt phẳng  AB C   bằng a 2 a 21 a 2 a 21 A. . B. . C. . D. . 4 7 2 14
Câu 39: Cho hình nón N có chiều cao h  2 .
a Một mặt phẳng P đi qua đỉnh của hình nón và cắt 2 16 3a
hình hình nón theo một thiết diện là tam giác đều có diện tích bằng
. Góc giữa P và 9
mặt đáy của N bằng A. 90 .  B. 45 .  C. 60 .  D. 30 . 
x  4  3t
Câu 40: Trong không gian Oxyz, cho điểm M 0; 2; 0 và đường thẳng d : y  2  t . Đường thẳng đi
z  1t
qua M , cắt và vuông góc với d có phương trình là x y  2 z x 1 y z x 1 y 1 z x y z 1 A.   . B.   . C.   . D.   . 1  1 2 1 1  2  1 1 2 1  1 2
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Trên mặt phẳng tọa độ, cho M 4; 3
  là điểm biểu diễn của số phức z . Phần ảo của z bằng A. 4 .
B. 3i . C. 4  . D. 3  . Lời giải:
Ta có: z  4  3i nên phần ảo của z bằng 3  . 3
Câu 2: Tập xác định của hàm số 2
y x là
A. 0;  .
B. 2;  . C. . D. \   0 . Lời giải: 3
Tập xác định của hàm số 2
y x là 0;  .
Câu 3: Trên khoảng 0;  , đạo hàm của hàm số y  log x là 2 1 ln 2 1 1 A. y  . B. y  . C. y  . D. y  . x ln 2 x x 2x Lời giải:  1 Áp dụng công thức  x  . Ta có y  a  1 log x ln a x ln 2
Câu 4: Tập các nghiệm của bất phương trình 2x  6 là
A. log 6;  . B.  ;3   .
C. 3;  . D.  ;  log 6 . 2  2  Lời giải:
2x  6  x  log 6  x  log 6;  . 2  2
Câu 5: Cho cấp số cộng u có số hạng đầu u  2 và số hạng thứ tư u  17 . Công sai của cấp số n  1 4 cộng đã cho bằng 15 A. . B. 5 . C. 3 . D. 15 . 2 Lời giải: u u 17  2 Ta có 4 1
u u  3d d    5. 4 1 3 3 x y z
Câu 6: Trong không gian Oxyz, mặt phẳng (P) :  
1, có một vectơ pháp tuyến là 2 2 1 
A. n  (2; 2; 1  ) .
B. n  (1;1; 2)  .
C. n  (2; 2  ; 1  ) .
D. n  ( 2  ; 2  ;1) . 3 4 1 2 Lời giải: x y z Ta có  
1  x y  2z  2
  x y  2z  2  0 2 2 1 
Vậy một vectơ pháp tuyến của mặt phẳng (P) là n  (1;1; 2)  . 4
Câu 7: Cho hàm số y f x có bảng biến thiên như sau: Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia
Số nghiệm của phương trình f x  6  0 là A. 3 . B. 1. C. 4 . D. 2 . Lời giải:
Ta có f x  6  0  f x  6 .
Đường thẳng y  6 cắt đồ thị y f x tại 2 điểm phân biệt. 1 1 Câu 8: Cho  2
x  2x  3 f xdx 1. Tính f xdx  . 0 0 1  5  1  5  A. . B. . C. . D. . 3 3 9 9 Lời giải: 1 1 3 1 1  x  2 Ta có  2
x  2x  3 f x 2 dx  1   x  3 f  
 xdx 1 3 f
 xdx 1  3  3 0 0 0 0 1   f x 5 dx   . 9 0
Câu 9: Đường cong trong hình vẽ bên là đồ thị của một hàm số nào? A. 3
y  x  3x  2 . B. 3
y  x  3x  2 . C. 4 2
y x x  2 . D. 3
y x  3x  2 . Lời giải:
Nhánh cuối của đồ thị đi xuống nên a  0 , đồ thị có hai điểm cực trị nên . a c  0 .
Câu 10: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  2 y  4z  2  0 . Bán kính mặt cầu S  bằng A. 1. B. 7 . C. 2 2 . D. 7 . Lời giải: a  0 b   1 Ta có S  2 2 2
: x y z  2 y  4z  2  0   . c  2   d  2  Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia 2
Khi đó, bán kính mặt cầu S  là 2 2 R  0 1   2    2    7 .
Câu 11: Trong không gian Oxyz, góc giữa trục Ox và Oz bằng A. 90 .  B. 60 .  C. 30 .  D. 0 . 
Câu 12: Cho số phức z thỏa mãn 1 iz  2  i . Môđun của số phức z bằng 10 A. . B. 3 . C. 2 . D. 10 . 2 Lời giải: i Ta có   i 2 1 3 1 3 1
z  2  i z
z   i z   i 1 . i 2 2 2 2 2 2  1   3  10 Vậy z         .  2   2  2
Câu 13: Cho khối lăng trụ đứng AB . C A BC
  có BB  a , đáy ABC là tam giác vuông cân tại B và
BA BC a . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a 3 a A. V  . B. V  . C. V  . D. 3 V a . 6 2 3 Lời giải: 3 1 1 a Ta có: VS .BB '  B . A BC.BB '  . . a . a a  .
ABC.A'B'C ' ABC 2 2 3
Câu 14: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a , SA   ABC  , SA a (tham khảo hình vẽ). S A C B
Thể tích của khối chóp đã cho bằng 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 4 6 12 Lời giải: Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia S A C B
Vì SA   ABC  nên ta có SA là đường cao của hình chóp hay h SA a . 2 a 3
Do đáy của hình chóp là tam giác đều cạnh a nên ta có: S  . 4 1 2 3 1 3a 3a
Khi đó thể tích của khối chóp đã cho là: V S.h  . .a  (đvtt). 3 3 4 12
Câu 15: Nếu tăng bán kính của một khối cầu gấp 3 lần thì thể tích thay đổi như thế nào?
A. Thể tích tăng gấp 6 lần.
B. Thể tích tăng gấp 9 lần.
C. Thể tích tăng gấp 3 lần.
D. Thể tích tăng gấp 27 lần. Lời giải:
Gọi R là bán kính của khối cầu lúc đầu và R là bán kính khối cầu lúc sau.
R  3R . 4 4 4
Khi đó: V    R   3R3 3 3
 .27.R  27V . 3 3 3
Vậy thể tích lúc sau tăng gấp 27 lần.
Câu 16: Cho số phức bất kì z a bia,b   . Khẳng định nào sau đây đúng? A. 2 2 z
a b . B. 2 2 z
a b . C. 3 3
z a b . D. 2 2
z a b .
Câu 17: Cho tam giác ABC vuông tại A , AB a và AC a 3 . Tính độ dài đường sinh l của hình
nón có được khi quay tam giác ABC xung quanh trục AB .
A. l  2a .
B. l  2a .
C. l  3a .
D. l a . Lời giải:
Quay tam giác ABC xung quanh trục AB suy ra h AB a và r AC a 3 .
Đường sinh l của hình nón bằng 2 2 l
r h  2a . x 1 y  2 z
Câu 18: Trong không gian Oxyz , đường thẳng d : 
 đi qua điểm nào dưới đây? 2 1  3 A. A2; 1  ;3 . B. C  1  ;2;0 . C. D 1; 2  ;0 .
D. B 0; 2;   1 . Lời giải: Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia
Lần lượt thay tọa độ các điểm vào phương trình đường thẳng d . 2 1 1   2 3 3 Kiểm tra A2; 1  ;3 : 
  1 (sai)  Ad . 2 1  3 2 1  1 2  2 0 Kiểm tra C  1  ;2;0 : 
  0  0  C d . 2 1  3
Câu 19: Cho hàm số y f x có bảng biến thiên như sau:
Tìm giá trị cực đại y và giá trị cực tiểu y của hàm số đã cho. CÐ CT A. y
 3 và y  0 . B. y
 3 và y  2. CÐ CT CÐ CT C. y
 2 và y  2 . D. y
 2 và y  0 . CÐ CT CÐ CT x  2
Câu 20: Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y x ? 2
A. x  2 .
B. x  2 .
C. y  1. D. y  1. Lời giải: x  2  Ta có: lim 1 y 1  
là tiệm cận ngang của đồ thị hàm số.
x  x  2 
Câu 21: Tập nghiệm S của bất phương trình log 2x 1  2 là 3   1   1  A. S  ;5   . B. S  ;5   .
C. S   ;5   .
D. S  5;  . 2   2  Lời giải:  1 2x 1  0 x   1 
Ta có log 2x 1  2     2  x  ; 5   . 3   2 2x 1 3   2   x  5
Câu 22: Có 3 cây bút đỏ, 4 cây bút xanh trong một hộp bút. Hỏi có bao nhiêu cách lấy ra một cây bút từ hộp bút đó? A. 7 . B. 4 . C. 12 . D. 3 . Lời giải:
Chọn 1 cây bút từ 7 cây bút nên có 7 cách chọn. Câu 23: Cho sin d 
x x GxC. Đạo hàm hàm số y  2Gx x là 2 x
A. y  2 sin x  1.
B. y  2 sin x  1.
C. y  2 sin . x D. y  2  cos x   C. 2 Lời giải:
Ta có y  2Gx  x  2sin x  1. 4 4
Câu 24: Nếu f (x)dx  37  thì 2
2 f(x)  3x dx   bằng 0 0 A. 12. B. 18. C. 27 . D. 10. Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia Lời giải: 4 4 4 4 Ta có: 2 2 3
2 f (x) 3x  dx  2 f (x)dx 3 x dx  2.37  x  74  64 10     . 0 0 0 0
Câu 25: Cho hàm số f x  sin x x . Khẳng định nào dưới đây đúng? x x
A. f x 2 dx  cos x   C.
B. f x 2
dx   cos x   C. 2 2 x x C. f  x 2 dx  s  in x   C.
D. f x 2
dx   cos x   C. 2 2 Lời giải:
   x   xx 2 x f x d sin
dx   cos x   C. 2
Câu 26: Cho hàm số y f (x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 0; 2 .
B. 2;  . C.   ;1  . D. 2;3 .
Câu 27: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới:
Điểm cực tiểu của hàm số đã cho là A. 1  . B. 3 . C. 2 . D. 0 .
Câu 28: Với a là số thực dương tùy ý, log  a 5   log 2a bằng 3 3  2 5 A. log 3 . a B. log . C. log  2 3 10a  . D. log . 3 3 5 3 2 Lời giải: 5a 5 Ta có log  a 5   log  a 2  log  log . 3 3  3 3 2a 2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y x x và
y  0 quanh trục Ox là 16 16 1  A. V   B. V   C. V   D. V   15 15 30 30 Lời giải:
Phương trình hoành độ giao điểm của đường 2
y x x và đường y  0 là Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc giax  0 2
x x  0   . x  1 1 1 5 4 3 2  x x x  1 
Thể tích là V   2
x x dx   4 3 2
x  2x x dx       . 5 2 3 0 30   0 0
Câu 30: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy và AB  2SA (tham khảo hình vẽ). S C A B
Góc giữa hai mặt phẳng SBC và  ABC  bằng A. 60 .  B. 30 C. 90 D. 45 Lời giải: S C A M B
Dựng AM BC, M là trung điểm BC. SA BC Ta có:  
BC  SAM. AM   BC
Suy ra, góc giữa hai mặt phẳng SBC và  ABC  bằng SMA . SA 1
Xét tam giác SAM vuông tại A : tanSMA    SMA  30 .  AM 3
Vậy góc giữa hai mặt phẳng SBC  và  ABC  bằng 30 . 
Câu 31: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới: y 2 1 x -1 O -2 Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có ba nghiệm thực phân biệt? A. 4 . B. 5 . C. 3 . D. 2 . Lời giải:
Số nghiệm của phương trình f x  m bằng số giao điểm của đồ thị hàm số y f x và
đường thẳng d : y m . y 2 m 1 x -1 O -2
Dựa vào hình vẽ, ta có:
Phương trình f x  m có ba nghiệm thực phân biệt khi đường thẳng d : y m cắt đồ thị
hàm số y f x tại ba điểm phân biệt, tức là 2  m  2 . Mà m  nên m  1  ;0;  1 .
Câu 32: Cho hàm số y f x có f x  xx  1x  3 , x
  . Hàm số y f x đồng biến trên khoảng nào dưới đây?
A. ;0. B. 0;1. C. 1; 2.
D. 2; . Lời giải: x  0 
Ta có: f x  0  x  1.  x  3  Bảng xét dấu: x  0 1 3  f x  0  0  0 
Câu 33: Chọn ngẫu nhiên 2 số tự nhiên khác nhau từ 25 số nguyên dương đầu tiên. Xác suất để chọn
được hai số có tổng là một số chẵn bằng 1 13 12 313 A. . B. . C. . D. . 2 25 25 625
Lời giải: n  2  C  300 . 25
Trong 25 số nguyên dương đầu tiên có 13 số lẻ và 12 số chẵn
Gọi A là biến cố chọn được hai số có tổng là 1 số chẵn.
Chọn 2 số lẻ trong 13 số lẻ hoặc chọn 2 số chẵn trong 12 số chẵn  n A 2 2
C C 144. 13 12 n A 144 12 Vậy p A      n  . 300 25 2 2
Câu 34: Số nghiệm của phương trình 2x 2 3
x  10.3x x  9  0 là Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia A. 4. B. 1. C. 0. D. 2. Lời giải:
Điều kiện: x  . 2 2 2
Phương trình  3x x  10.3x x  9  0 *   2 t 1 (tháa m·n) Đặt 3x x t  
 0 , phương trình * trở thành: 2t 10t  9  0   . t   9 (tháa m·n)   2  x 0
+) Với t  1, ta có: x x 2 3
 1  x x  0   . x  1     2  x 1
+) Với t  9, ta có: x x 2 2 3
 9  x x  2  x x  2  0   . x  2  
Kết luận: Vậy tập nghiệm của phương trình là S   2  ; 1;0;  1 .
Câu 35: Cho số phức z thỏa mãn z 1 i  4. Biết tập hợp các điểm biểu diễn số phức
w  3  4iz 1 2i là đường tròn C . Tìm tâm I và bán kính R của đường tròn C . A. I  2
 ; 5, R  20. B. I  2
 ; 5, R  4. C. I  2
 ;5, R  4. D. I  2  ;5, R  20. Lời giải:
Đặt w  x yi x, y  .  i w+1 2i
Từ giả thiết: w  3  4iz 1 w+1 2 2i z
z 1 i  1 i 3  4i 3  4i w+2  5   i z 1 i
 w+2  5i z 1 i 3 4i  w+2  5i  20 3  4i   2 2
x  2   y  2 2 5
 20  x  2   y  5  400.
Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I  2
 ; 5, bán kính R  20.
Câu 36: Trong không gian Oxyz , viết phương trình tham số của đường thẳng đi qua hai điểm
A1; 2; 3, B 2; 3;  1 . x  1 tx  2  tx  3  tx  1 t    
A. y  2  5t . B. y  3   5t . C. y  8   5t .
D. y  2  5t .     z  3   2tz  1  4tz  5  4tz  3  4tLời giải:
Gọi  là đường thẳng đi qua ,
A B thì  nhận AB  1; 5;4 làm VTCP.
Do đó loại đáp án A và. B. x 1 y  2 z  3
Phương trình chính tắc của  là:   1 5  . 4 x  3  t
Ta thấy M 3; 8;5   nên  có phương trình tham số là:  y  8   5t . z  5 4t  Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 37: Trong không gian Oxyz , cho điểm A3;5;7 . Hình chiếu vuông góc của điểm A lên mặt
phẳng Oyz có tọa độ là A. 3;5;7. B. 3;5;0.
C. 3;0;7. D. 0;5;7.
Câu 38: Cho hình lăng trụ đứng ABC.AB C
  có tất cả các cạnh bằng a . Gọi M là trung điểm của AA .
Khoảng cách từ M đến mặt phẳng  AB C   bằng a 2 a 21 a 2 a 21 A. . B. . C. . D. . 4 7 2 14 Lời giải: Trong  ABB A
  , gọi E là giao điểm của BM và AB. Khi đó hai tam giác EAM và EB B
d M , AB C   EM MA 1 1 đồng dạng. Do đó         d
d M , AB C
d B, AB C B,  AB C       EB BB . 2 2 a 3
Từ B kẻ BN AC thì N là trung điểm của AC và BN  , BB  a . 2 BB  BN a 21 Kẻ BI B N
 thì d B, AB C    BI   . 2 2   7 BB BN 1 a 21
Vậy d M , AB C
   d B, AB C    . 2 14
Câu 39: Cho hình nón N có chiều cao h  2 .
a Một mặt phẳng P đi qua đỉnh của hình nón và cắt 2 16 3a
hình hình nón theo một thiết diện là tam giác đều có diện tích bằng
. Góc giữa P và 9
mặt đáy của N bằng A. 90 .  B. 45 .  C. 60 .  D. 30 .  Lời giải: Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc gia S l h A O r H B
Gọi thiết diện là tam giác SAB,SA SB  .l 2 2 2 16 3a 3l 16 3a 8a Theo giả thiết: S     l  . SAB 9 4 9 3 3l 4 3a
Gọi H là trung điểm AB   SAB;®¸ynãn  SHO và SH   . 2 3 SO 3
Xét tam giác SOH vuông tại O : sinSHO    SHO  o 60 . SH 2
x  4  3t
Câu 40: Trong không gian Oxyz, cho điểm M 0; 2; 0 và đường thẳng d : y  2  t . Đường thẳng đi
z  1t
qua M , cắt và vuông góc với d có phương trình là x y  2 z x 1 y z x 1 y 1 z x y z 1 A.   . B.   . C.   . D.   . 1  1 2 1 1  2  1 1 2 1  1 2 Lời giải: qua N 4;2;   1 Ta có : d : vtcp u   3;1;  1 dMH d Gọi H là hình chiếu vuông góc của M lên d   H d
x  4  3t   MH.u  0
y  2  t d    
H 1;1; 2 . H d z  1 t  3
 x y  2 z  0
Đường thẳng  đi qua M và vuông góc với d có véctơ chỉ phương là MH  1; 1;  2 . x y  2 z Suy ra, phương trình  :   1  . 1 2
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 16
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 07_______________
Câu 1: Trên mặt phẳng toạ độ Oxy , biết M  1
 ;2 là điểm biểu diễn số phức z , phần thực của z bằng A. 1  . B. 2 . C. 1. D. 2  .
Câu 2: Tập xác định của hàm số y  log x là A. 1  ;  .
B. 0;  . C. 0;   . D. 1;  .
Câu 3: Trên khoảng 0;  , đạo hàm của hàm số y  log x là 2023 1 ln 2023 1 1 A. y  . B. y  . C. y  . D. y  . x ln 2023 x x 2023x
Câu 4: Tập nghiệm của bất phương trình 5x  2 là  2 
A. (log 2; ). B. ( ;  ). C. ;  . D. (log 5; ) 5    2 5 
Câu 5: Cho cấp số nhân u có u  2 và u  4 . Công bội của cấp số nhân đã cho bằng n  2 3 A. 2  . B. 6  . C. 6 . D. 2 .
Câu 6: Trong không gian Oxyz , cho mặt phẳng  P : 3x  2y z  2  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của  P ? A. n  2; 1  ;2 .
B. n  3; 2;1 .
C. n  3; 2; 2 .
D. n  3; 2; 1  . 1   3   4   2  
Câu 7: Cho hàm số y f x có đồ thị là đường cong như hình vẽ bên dưới:
Số nghiệm của phương trình f x  2  bằng A. 2 . B. 3 . C. 1. D. 0 . 2 5 5 Câu 8: Biết f
 xdx  6, f
 xdx 1, tính I f  xdx. 1 2 1 A. I  5 .
B. I  5 .
C. I  7 .
D. I  4 .
Câu 9: Bảng biến thiên sau đây là của hàm số nào? x x x x
A. f x 3  .
B. f x 3  .
C. f x 3  .
D. f x 2 3  . x  2 2  x x  2 x  2 Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 10: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  8x  2 y 1  0 . Tìm tọa độ tâm và bán
kính của mặt cầu S  . A. I  4
 ;1;0 và R  4 .
B. I 4; 1;0 và R  2 .
C. I  4
 ;1;0 và R  2 .
D. I 4; 1;0 và R  4 .
Câu 11: Trong không gian Oxyz, cho điểm A1;0;0. Góc giữa đường thẳng OA và mặt phẳng Oyz bằng A. 90 .  B. 60 .  C. 30 .  D. 0 . 
Câu 12: Cho số phức z  2  5i . Tìm số phức w iz z .
A. w  7  3i .
B. w  3  3i .
C. w  3  7i .
D. w  7  7i .
Câu 13: Cho khối lăng trụ đứng có chiều cao bằng 5m , đáy là hình vuông có cạnh bằng 4m . Thể tích
khối lăng trụ đã cho bằng A. 3 80m . B. 3 20m . C. 3 40m . D. 3 60m .
Câu 14: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a 2 , SA   ABCD , SA  2a . Tính thể tích khối chóp . S ABCD. 3 4a 3 4 a A. V  . B. V  . C. 3 V  4a . D. 3 V  4 a . 3 3
Câu 15: Cho mặt cầu S  có tâm O , bán kính r  2 . Một điểm M trong không gian thỏa mãn
OM  2 . Mệnh đề nào sau đây đúng?
A. M là điểm nằm trong mặt cầu S  .
B. M là tâm của mặt cầu S  .
C. M là điểm nằm trên mặt cầu S  .
D. M là điểm nằm ngoài mặt cầu S  .
Câu 16: Khẳng định nào sau đây sai?
A. Số 2021i là số thuần ảo.
B. Số 0 là số phức có mô đun nhỏ nhất.
C. Với số phức z bất kì, z và z là hai số đối nhau.
D. Số phức z và số phức z có môđun bằng nhau.
Câu 17: Cho hình trụ có bán kính đáy r  3 và chiều cao h  4 . Diện tích xung quanh của hình trụ đã cho bằng A. 12 . B. 24 . C. 36 . D. 42 . x 1 2t
Câu 18: Trong không gian Oxyz , điểm nào sau đây thuộc đường thẳng  :  y  1   t ? z t  
A. M 1; 1;   1 .
B. N  2  ;1;  1 .
C. P 1; 1;0 .
D. Q 2;   1;1 .
Câu 19: Cho hàm số f x có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 2 . B. 5 . C. 3 . D. 1.
Câu 20: Cho hàm số y f x thỏa mãn lim f x  0. Khẳng định nào sau đây đúng? x Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia
A. Đồ thị hàm số có đường tiệm cận ngang y  2 .
B. Đồ thị hàm số có đường tiệm cận đứng x  2 .
C. Đồ thị hàm số có đường tiệm cận ngang y  0 .
D. Đồ thị hàm số có đường tiệm cận đứng x  2 .
Câu 21: Tập nghiệm của bất phương trình log x 1  1 là 2  
A. 3;  . B.  ;3   . C. 1;  3 . D. 1;3 .
Câu 22: Có 8 quả ổi và 6 quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả đó? A. 48 . B. 24 . C. 14 . D. 18 . Câu 23: Cho 3d   
x x F x C . Khẳng định nào dưới đây đúng?
A. F2  1 .
B. F2  8.
C. F2  4 .
D. F2  16 1 1
Câu 24: Nếu  f
 x2xdx 2 
thì f xdx  bằng 0 0 A. 1. B. 2. C. 0. D. 4.
Câu 25: Cho hàm số f x  sin x  cos x . Khẳng định nào dưới đây đúng?
A. f xdx  sin x  cos x C.
B. f xdx  sin x  cos x C.
C. f xdx  sin x  cos x C.
D. f xdx  sin x  cos x C.
Câu 26: Cho hàm số y f (x) có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
A. f 0  f   1 . B. f  
1  f 2.
C. f 4  f 5.
D. f 4  f 5.
Câu 27: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới:
Điểm cực đại của hàm số đã cho là A. 1  . B. 3 . C. 2 . D. 0 .
Câu 28: Với a là số thực dương tùy ý, 3 log a bằng 2 A. log 3 . a B. 3  log . a C. log . a D. 3log . a 2 2 2 2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y x  4x và
y  0 quanh trục Ox là 501 501 512 512 A. V   B. V   C. V   D. V   15 15 15 15 Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 30: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng AB là 1 2 A. 1;0
B. 1;0. C. 0;1. D. 0; 1  .
Câu 31: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  , SA  2a , tam giác ABC
vuông cân tại B và AB  2a .(minh họa như hình vẽ). S A C B
Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng A. 60 . B. 45 . C. 30 . D. 90 .
Câu 32: Cho hàm số y f x 4 2 
ax bx c có đồ thị là đường cong trong hình bên dưới: y x O -1 -5
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm thực phân biệt? A. 4 . B. 5 . C. 3 . D. 2 .
Câu 33: Cho hàm số y f x có đạo hàm y f x 2  x  2 ' x   1 , x
  . Hàm số y f x đồng
biến trên khoảng nào dưới đây?
A. 2;  . B. 0; 2 . C. 1;  1 . D.  ;    1 .
Câu 34: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và 6 quả cầu màu đỏ. Chọn ngẫu nhiên đồng
thời 2 quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng 5 6 5 8 A. . B. . C. . D. . 22 11 11 11
Câu 35: Tính tổng T tất cả các nghiệm thực của phương trình 4.9x 13.6x 9.4x    0. 13 1 A. T  .
B. T  3 . C. T  . D. T  2 . 4 4
Câu 36: Trong không gian Oxyz , cho 3 điểm A2;1;   1 , B  1
 ;0;4 , C 0; 2;  1 . Phương trình mặt
phẳng đi qua A và vuông góc với BC là
A. x  2 y  5z  5  0 . B. 2x y  5z  5  0 . C. x  2 y  5  0 .
D. x  2 y  5z  5  0 . Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 37: Trong không gian Oxyz , cho điểm A3;5;7 . Hình chiếu vuông góc của điểm A lên trục Oy có tọa độ là A. 3;5;7. B. 3;5;0.
C. 3;0;7. D. 0;5;0.
Câu 38: Cho hình nón đỉnh S , đáy là đường tròn tâm O bán kính R  5 , góc ở đỉnh bằng 60 . Một
mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho AB  6 .
Tính khoảng cách từ O đến SAB . 20 273 20 270 20 271 20 273 A. . B. . C. . D. . 90 91 91 91
Câu 39: Trong không gian Oxyz, cho mặt phẳng  P : 4x y  2z 1  0 và điểm M (4; 2;1) . Khi đó
điểm đối xứng với M qua mặt phẳng  P có tọa độ là A. ( 4  ;0; 3  ) . B. ( 4  ; 4  ; 1  ) . C. (4; 2;1) . D. (2; 0;5) .
Câu 40: Cho hình trụ T  có chiều cao bằng 8a . Một mặt phẳng   song song với trục và cách trục
của hình trụ này một khoảng bằng 3a , đồng thời   cắt T  theo thiết diện là một hình
vuông. Diện tích xung quanh của hình trụ đã cho bằng A. 2 80 a . B. 2 40 a . C. 2 30 a . D. 2 60 a .
________________________HẾT________________________
LỜI GIẢI CHI TIẾT Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 1: Trên mặt phẳng toạ độ Oxy , biết M  1
 ;2 là điểm biểu diễn số phức z , phần thực của z bằng A. 1  . B. 2 . C. 1. D. 2  . Lời giải: Vì M  1
 ;2 là điểm biểu diễn số phức z nên ta có z  1 2i .
Suy ra phần thực của z bằng 1  .
Câu 2: Tập xác định của hàm số y  log x là A. 1  ;  .
B. 0;  . C. 0;   . D. 1;  . Lời giải:
Hàm số y  log x xác định  x  0 .
Vậy tập xác định của hàm số là: D  0; .
Câu 3: Trên khoảng 0;  , đạo hàm của hàm số y  log x là 2023 1 ln 2023 1 1 A. y  . B. y  . C. y  . D. y  . x ln 2023 x x 2023x Lời giải:  1 Áp dụng công thức  x  . Ta có y  . a  1 log x ln a x ln 2023
Câu 4: Tập nghiệm của bất phương trình 5x  2 là  2 
A. (log 2; ). B. ( ;  ). C. ;  . D. (log 5; ) 5    2 5  Lời giải:
5x  2  x  log 2 . 5
Câu 5: Cho cấp số nhân u có u  2 và u  4 . Công bội của cấp số nhân đã cho bằng n  2 3 A. 2  . B. 6  . C. 6 . D. 2 . Lời giải: u 4 
Công bội của cấp số nhân là 3 q    2  . u 2 2
Câu 6: Trong không gian Oxyz , cho mặt phẳng  P : 3x  2y z  2  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của  P ? A. n  2; 1  ;2 .
B. n  3; 2;1 .
C. n  3; 2; 2 .
D. n  3; 2; 1  . 1   3   4   2   Lời giải:
Véc-tơ pháp tuyến của  P là n  3; 2; 1  . 1  
Câu 7: Cho hàm số y f x có đồ thị là đường cong như hình vẽ bên dưới: Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia
Số nghiệm của phương trình f x  2  bằng A. 2 . B. 3 . C. 1. D. 0 . Lời giải:
Ta có số nghiệm của phương trình f x  2
 là số giao điểm của đồ thị hàm số y f (x) và
đường thẳng y  2 .
Căn cứ vào đồ thị hàm số ta có số giao điểm bằng 2
Vậy phương trình đã cho có 2 nghiệm. 2 5 5 Câu 8: Biết f
 xdx  6, f
 xdx 1, tính I f  xdx. 1 2 1 A. I  5 .
B. I  5 .
C. I  7 .
D. I  4 . Lời giải: 5 2 5 Ta có: I f
 xdx f
 xdx f
 xdx 61 7. 1 1 2
Câu 9: Bảng biến thiên sau đây là của hàm số nào? x x x x
A. f x 3  .
B. f x 3  .
C. f x 3  .
D. f x 2 3  . x  2 2  x x  2 x  2 Lời giải:
Ta có lim f x  1 suy ra đồ thị hàm số có một tiệm cận ngang là y  1. x
lim f x    x  2 mà một tiệm cận đứng của đồ thị hàm số.  x2
Dựa vào bảng biến thiên, nhận thấy hàm số đồng biến trên từng khoảng xác định.
Câu 10: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  8x  2 y 1  0 . Tìm tọa độ tâm và bán
kính của mặt cầu S  . A. I  4
 ;1;0 và R  4 .
B. I 4; 1;0 và R  2 .
C. I  4
 ;1;0 và R  2 .
D. I 4; 1;0 và R  4 . Lời giải:
Từ phương trình của mặt cầu suy ra tâm I 4; 1;0 và bán kính R    2 2 2 4 1  0 1  4. Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 11: Trong không gian Oxyz, cho điểm A1;0;0. Góc giữa đường thẳng OA và mặt phẳng Oyz bằng A. 90 .  B. 60 .  C. 30 .  D. 0 . 
Câu 12: Cho số phức z  2  5i . Tìm số phức w iz z .
A. w  7  3i .
B. w  3  3i .
C. w  3  7i .
D. w  7  7i . Lời giải:
w iz z i 2  5i  2  5i  5
  2i  2  5i  3   3i .
Câu 13: Cho khối lăng trụ đứng có chiều cao bằng 5m , đáy là hình vuông có cạnh bằng 4m . Thể tích
khối lăng trụ đã cho bằng A. 3 80m . B. 3 20m . C. 3 40m . D. 3 60m . Lời giải:
Ta có diện tích đáy khối lăng trụ đứng là 2 S    2 4 16 m  .
Vậy thể tích khối lăng trụ đã cho V Sh    3 16.5 80 m  .
Câu 14: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a 2 , SA   ABCD , SA  2a . Tính thể tích khối chóp . S ABCD. 3 4a 3 4 a A. V  . B. V  . C. 3 V  4a . D. 3 V  4 a . 3 3 Lời giải: S A D B C
Diện tích hình vuông ABCD là: S  a 2 2 2  2a ABCD 3 1 1 4a
Thể tích khối chóp S.ABCD là: 2 VS . A S  .2a .2a S. ABCD 3 ABCD 3 3 Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 15: Cho mặt cầu S  có tâm O , bán kính r  2 . Một điểm M trong không gian thỏa mãn
OM  2 . Mệnh đề nào sau đây đúng?
A. M là điểm nằm trong mặt cầu S  .
B. M là tâm của mặt cầu S  .
C. M là điểm nằm trên mặt cầu S  .
D. M là điểm nằm ngoài mặt cầu S  . Lời giải:
Vì OM  2  r M là điểm nằm trên mặt cầu S  .
Câu 16: Khẳng định nào sau đây sai?
A. Số 2021i là số thuần ảo.
B. Số 0 là số phức có mô đun nhỏ nhất.
C. Với số phức z bất kì, z và z là hai số đối nhau.
D. Số phức z và số phức z có môđun bằng nhau. Lời giải:
Ta có: z và z được gọi là 2 số phức liên hợp do đó C sai.
Câu 17: Cho hình trụ có bán kính đáy r  3 và chiều cao h  4 . Diện tích xung quanh của hình trụ đã cho bằng A. 12 . B. 24 . C. 36 . D. 42 . Lời giải:
Diện tích xung quanh của hình trụ đã cho là S  2 rh  24 . xqx 1 2t
Câu 18: Trong không gian Oxyz , điểm nào sau đây thuộc đường thẳng  :  y  1   t ? z t  
A. M 1; 1;   1 .
B. N  2  ;1;  1 .
C. P 1; 1;0 .
D. Q 2;   1;1 . Lời giải: x 1 2t 1  1 2t  
Đường thẳng  :  y  1
  t đi qua điểm P1;1;0 vì  1   1
  t t  0 .   z t   0  t  
Câu 19: Cho hàm số f x có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 2 . B. 5 . C. 3 . D. 1. Lời giải:
Từ bảng xét dấu của đạo hàm thì hàm số đã cho có 2 cực trị.
Câu 20: Cho hàm số y f x thỏa mãn lim f x  0. Khẳng định nào sau đây đúng? x
A. Đồ thị hàm số có đường tiệm cận ngang y  2 .
B. Đồ thị hàm số có đường tiệm cận đứng x  2 .
C. Đồ thị hàm số có đường tiệm cận ngang y  0 .
D. Đồ thị hàm số có đường tiệm cận đứng x  2 . Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 21: Tập nghiệm của bất phương trình log x 1  1 là 2  
A. 3;  . B.  ;3   . C. 1;  3 . D. 1;3 . Lời giải: log
x 1  1  0  x 1  2  1  x  3. 2  
Câu 22: Có 8 quả ổi và 6 quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả đó? A. 48 . B. 24 . C. 14 . D. 18 . Lời giải:
Theo quy tắc cộng có 8  6  14 cách chọn ra một quả trong các quả đã cho. Câu 23: Cho 3d   
x x F x C . Khẳng định nào dưới đây đúng?
A. F2  1 .
B. F2  8.
C. F2  4 .
D. F2  16 Lời giải:  
Ta có F x    3  x x  3 d  x   F 2  8. 1 1
Câu 24: Nếu  f
 x2xdx 2 
thì f xdx  bằng 0 0 A. 1. B. 2. C. 0. D. 4. Lời giải: 1 1 1 1 1 Ta có:  f
 x2xdx 2 f
 xdx 2 d x x  2  f   x 2 dx x  2 0 0 0 0 0 1 1  f
 xdx102 f
 xdx1. 0 0
Câu 25: Cho hàm số f x  sin x  cos x . Khẳng định nào dưới đây đúng?
A. f xdx  sin x  cos x C.
B. f xdx  sin x  cos x C.
C. f xdx  sin x  cos x C.
D. f xdx  sin x  cos x C. Lời giải:
f xdx  sin xcos xdx  cos xsin xC.
Câu 26: Cho hàm số y f (x) có bảng biến thiên như sau:
Khẳng định nào dưới đây đúng?
A. f 0  f   1 . B. f  
1  f 2.
C. f 4  f 5.
D. f 4  f 5.
Câu 27: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên dưới: Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia
Điểm cực đại của hàm số đã cho là A. 1  . B. 3 . C. 2 . D. 0 .
Câu 28: Với a là số thực dương tùy ý, 3 log a bằng 2 A. log 3 . a B. 3  log . a C. log . a D. 3log . a 2 2 2 2
Câu 29: Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường 2
y x  4x và
y  0 quanh trục Ox là 501 501 512 512 A. V   B. V   C. V   D. V   15 15 15 15 Lời giải:
Phương trình hoành độ giao điểm của đường 2
y x  4x và đường y  0 là x  0 2
x  4x  0   . x  4 4 4 5 3 2  x 16x  4 512
Thể tích là V   2
x  4x dx   4 3 2
x  8x 16x  4 dx    2x    . 5 3 0 15   0 0
Câu 30: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng AB là 1 2 A. 1;0
B. 1;0. C. 0;1. D. 0; 1  . Lời giải: z  1
  i A 1  ;1 2 1  
Ta có: z  2z  2  0   . z  1
  i B 1  ; 1   2  
I là trung điểm AB I  1  ;0.
Câu 31: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng  ABC  , SA  2a , tam giác ABC
vuông cân tại B và AB  2a .(minh họa như hình vẽ). S A C B
Góc giữa đường thẳng SC và mặt phẳng  ABC  bằng A. 60 . B. 45 . C. 30 . D. 90 . Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc gia Lời giải: S A C BSC  
ABC  C Ta có: 
 SC,(ABC)  (SC, AC)  SCA. SA    ABC Mà: 2 2 2 2 AC
AB BC  2a  2a  2a SA .
Vì SAC vuông cân tại A nên ta có SCA  45 .
Câu 32: Cho hàm số y f x 4 2 
ax bx c có đồ thị là đường cong trong hình bên dưới: y x O -1 -5
Có bao nhiêu giá trị nguyên của tham số m để phương trình f x  m có bốn nghiệm thực phân biệt? A. 4 . B. 5 . C. 3 . D. 2 . Lời giải:
Số nghiệm của phương trình f x  m bằng số giao điểm của đồ thị hàm số y f x và
đường thẳng d : y m . y x O -1 m -5
Dựa vào hình vẽ, ta có: Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia
Phương trình f x  m có bốn nghiệm thực phân biệt khi đường thẳng d : y m cắt đồ thị
hàm số y f x tại bốn điểm phân biệt, tức là 5  m  1.
Mà m  nên m  4  ; 3  ;  2 .
Câu 33: Cho hàm số y f x có đạo hàm y f x 2  x  2 ' x   1 , x
  . Hàm số y f x đồng
biến trên khoảng nào dưới đây?
A. 2;  . B. 0; 2 . C. 1;  1 . D.  ;    1 . Lời giải: x
Ta có: f x 0 '  0   x  1 
y f x  y '   f '(x)
Hàm số y f x đồng biến khi và chỉ khi
f '(x)  0  f 'x  0  1 x 1  1  x  1.
Câu 34: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và 6 quả cầu màu đỏ. Chọn ngẫu nhiên đồng
thời 2 quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng 5 6 5 8 A. . B. . C. . D. . 22 11 11 11 Lời giải:
Số cách lấy ra 2 quả cầu trong 11 quả là 2
C , Suy ra n  2  C 11 11
Gọi A là biến cố lấy được 2 quả cùng màu. Suy ra n A 2 2  C C 5 6 C C 5
Xác suất của biến cố A là P A 2 2 5 6   . 2 C 11 11
Câu 35: Tính tổng T tất cả các nghiệm thực của phương trình 4.9x 13.6x 9.4x    0. 13 1 A. T  .
B. T  3 . C. T  . D. T  2 . 4 4 Lời giải: x x  2x x 9   6   3   3  Phương trình  4.  13.  9      0  4.  13.  9      0 .  4   4   2   2  x  3  Đặt t  , t    0 .  2  t  1 Phương trình trở thành: 2 
4t  13t  9  0  9  ( thỏa mãn). t   4 x  3  +) t  1   1  x    0 .  2  Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia x 9  3  9 +) t     x    2 . 4  2  4
Câu 36: Trong không gian Oxyz , cho 3 điểm A2;1;   1 , B  1
 ;0;4 , C 0; 2;  1 . Phương trình mặt
phẳng đi qua A và vuông góc với BC là
A. x  2 y  5z  5  0 . B. 2x y  5z  5  0 . C. x  2 y  5  0 .
D. x  2 y  5z  5  0 . Lời giải:
Ta có BC 1;  2;  5 .
Vậy phương trình mặt phẳng đi qua A và vuông góc với BC là:
1 x  2  2 y   1  5 z  
1  0  x  2 y  5z  5  0 .
Câu 37: Trong không gian Oxyz , cho điểm A3;5;7 . Hình chiếu vuông góc của điểm A lên trục Oy có tọa độ là A. 3;5;7. B. 3;5;0.
C. 3;0;7. D. 0;5;0.
Câu 38: Cho hình nón đỉnh S , đáy là đường tròn tâm O bán kính R  5 , góc ở đỉnh bằng 60 . Một
mặt phẳng qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho AB  6 .
Tính khoảng cách từ O đến SAB . 20 273 20 270 20 271 20 273 A. . B. . C. . D. . 90 91 91 91 Lời giải:
Gọi I là trung điểm ABOI AB .
Mà AB SO (vì SO vuông góc với đáy)
AB  SIO  SAB  SIO
Trong SIO vẽ OK SI  SAB  SIO  OK  SAB  OK d O,SAB .
Góc ở đỉnh bằng 60  ASO  30 , mà OA R  5  SO  5 3  AB
IAO vuông tại I có: OA  5, AI   3  OI  4 2  1 1 1 20 273
SOI vuông tại O , đường cao OK có:    OK  . 2 2 2 OK SO OI 91
Vậy d O,SAB 20 273  . 91 Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 39: Trong không gian Oxyz, cho mặt phẳng  P : 4x y  2z 1  0 và điểm M (4; 2;1) . Khi đó
điểm đối xứng với M qua mặt phẳng  P có tọa độ là A. ( 4  ;0; 3  ) . B. ( 4  ; 4  ; 1  ) . C. (4; 2;1) . D. (2; 0;5) . Lời giải:
x  4  4t
Phương trình đường thẳng d qua M vuông góc với  P là  y  2  t z 1 2t
Gọi H d   P  H 0;1;   1 .
M  đối xứng với M qua  P nên H là trung điểm MM   M  4  ;0; 3   .
Câu 40: Cho hình trụ T  có chiều cao bằng 8a . Một mặt phẳng   song song với trục và cách trục
của hình trụ này một khoảng bằng 3a , đồng thời   cắt T  theo thiết diện là một hình
vuông. Diện tích xung quanh của hình trụ đã cho bằng A. 2 80 a . B. 2 40 a . C. 2 30 a . D. 2 60 a . Lời giải:
Gọi trục của hình trụ là OO  OO  8a .
Mặt phẳng   cắt hình trụ theo thiết diện là hình vuông ABCD AB AD  8a
Theo giả thiết d OO ; ABCD  3a .
Kẻ OH AB OH   ABCD  d OO ; ABCD  d O ; ABCD  OH  3a .
Xét tam giác OAH vuông tại H ta có: 2 2 2
OA OH AH OA  5a .
Diện tích xung quanh của hình trụ bằng: S
 2 rh  2.5 .8 a a 2  80 a . xq
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc gia Trang 16
Bộ đề cơ bản Ôn thi THPT Quốc gia
_______________ĐỀ SỐ 08_______________
Câu 1: Trong mặt phẳng Oxy, điểm M 3; 2
  là điểm biểu diễn của số phức nào dưới đây ?
A. z  2  3i .
B. z  3  2i .
C. z  3  2 . i
D. z  2  3i .
Câu 2: Hệ số góc của tiếp tuyến với đồ thị hàm số y  ln  x  
1 tại điểm có hoành độ x  2 là 1 1 A. 1. B. ln 2 . C. . D. . 3 3ln 2
Câu 3: Đạo hàm của hàm số 2x y  là A. 1 .2x y x    . B. 2 . x y  ln 2 . C. 2x y  . D. x 1 y .2 x    .ln 2 . Câu 4:
Tập nghiệm của bất phương trình 2x 1 3  27 là  1   1  A. ;    . B. 3;   . C. 2;   . D. ;     .  2   3 
Câu 5: Cho cấp số cộng (u ) có u  2027 và công sai d  3 . Số hạng u n 1 3 A. 3 u  2027( 3)  .
B. u  2021.
C. u  2020 .
D. u  2054 . 3 3 3 3
Câu 6: Trong không gian Oxyz , mặt phẳng   : 3x  4y z  3  0 có một vectơ pháp tuyến là
A. m  3; 4;   1 .
B. n  3; 4  ;1 . C. a   6  ;8;2 . D. b   3  ;4;  1 .
Câu 7: Cho hàm số bậc bốn y f x có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình f x  3 là A. 1. B. 2 . C. 0. D. 3. 2 2 2
Câu 8: Cho f (x d ) x  2  và ( g x d ) x  1  
. Giá trị của 2 f (x)  3 ( g x) dx    bằng 1  1  1  A. 1. B. 5. C. 7. D. 7 .
Câu 9: Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây? A. 3 2
y x  3x 1. B. 3
y  x  3x 1. C. 4 2
y x  2x 1. D. 3
y x  3x 1.
Câu 10: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : ( x  2)  ( y 1)  ( z 1
 )  9 . Tọa độ tâm I và bán
kính R của S  là A. I ( 2
 ;1;1), R  3. B. I ( 2  ;1; 1
 ), R  9. C. I(2;1;1), R  3.
D. I (2; 1;1), R  9.
Câu 11: Trong không gian Oxyz , cho hai điểm A 1
 ;1;2 và B3; 5
 ;0 . Tọa độ trung điểm của đoạn thẳng AB là A. 2; 4; 2 B. 4; 6; 2 C. 1; 2;  1 D. 2; 3  ;  1 Trang 1
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 12: Cho hai số phức       1 z
3 7i và z2 2 3i . Tìm số phức z 1 z z2 .
A. z  110i .
B. z  5  4i .
C. z  3 10i .
D. z  3  3i .
Câu 13: Cho khối lăng trụ đứng có diện tích đáy bằng 2
2a và cạnh bên bằng 3a . Thể tích khối lăng trụ đã cho bằng A. 3 2a B. 3 3a C. 3 18a D. 3 6a
Câu 14: Cho hình chóp .
S ABC có đường cao SA, tam giác ABC vuông tại A có AB  2 , AC  4 . Gọi
H là trung điểm của BC (tham khảo hình vẽ). S C A H B
Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp . S ABC bằng 16 5 16 5 4 5 4 5 A. . B. . C. . D. . 5 15 9 3
Câu 15: Cắt một mặt cầu S  bởi một mặt phẳng qua tâm được thiết diện là hình tròn đường kính bằng 4 .
cm Tính thể tích của khối cầu đã cho. 256 32 A.  3 cm . B.   3 16 cm . C.  3 cm . D.   3 64 cm . 2 3
Câu 16: Môđun của số phức z  1  i bằng A. 1. B. 0 . C. 2 . D. 2 .
Câu 17: Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình trụ đã cho bằng 175 A. . B. 175 .  C. 70 .  D. 35 .  3 x 1 2t
Câu 18: Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng d  :  y  3   t ? z  45t
A. P 3 ;  2 ;   1 .
B. N 2 ;1; 5 .
C. M 1;  3 ; 4 .
D. Q 4 ;1; 3 .
Câu 19: Cho hàm số y f x có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng a;b ? A. 4 . B. 2 . C. 7 . D. 3 . 3x  5
Câu 20: Tiệm cận đứng của đồ thị hàm số y  là x  2 A. x  2 . B. y  2 . C. x  3 . D. y  3 . Trang 2
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 21: Bất phương trình log (3x  2)  log (6  5x) có tập nghiệm là (a;b) . Tổng a b bằng 2 2 8 28 26 11 A. . B. . C. . D. . 3 15 5 5
Câu 22: Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn? A. 80 . B. 70 . C. 90 . D. 60 . Câu 23: Cho hàm số    2  x f x
x e . Tìm một nguyên hàm F x của hàm số f x thỏa mãn F 0  2023 . A.   2   x F x x e  2022 . B.   2   x F x x e  2022 . C.   2   x F x x e  2021 . D.    x F x e  2023 . 2 4 4 Câu 24: Cho f
 xdx 1, f tdt  4   . Tính I f  ydy . 2  2  2 A. I  5 . B. I  3 . C. I  3 . D. I  5 .
Câu 25: Họ nguyên hàm của hàm số f x 3  2x  là x 3 3 A. 2   C. B. 2 x   C. C. 2
x  ln x C. D. 2
x  3ln x C. 2 x 2 x
Câu 26: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây? A. 2;  . B.   ;1  . C. 0;  . D. 0; 2 .
Câu 27: Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại x  0 .
B. Hàm số đạt cực tiểu tại x  4 .
C. Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực đại tại x  1 .
Câu 28: Với a và b là hai số thực dương tùy ý; log  3 4 a b bằng 2  1 1 A. log a  log . b
B. 3log a  4 log .
b C. 2log a  log b . D. 4 log a  3log . b 2 4  2 2 3 4 2 2 2 2
Câu 29: Cho hình phẳng  H  giới hạn bởi các đường 2
y  2x x , y  0 . Quay  H  quanh trục hoành
tạo thành khối tròn xoay có thể tích được tính bởi công thức nào dưới đây? Trang 3
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 2 2 2 2 2 A.  2 2   x x d .x B.   2 2 
x x  d .x C.  2 2 
x x  d .x D.   2 2   x x d .x 0 0 0 0
Câu 30: Cho hình lập phương ABC . D
A BCD . Góc giữa đường thẳng AB và mặt phẳng  ABCD bằng A. 60 .  B. 90 .  C. 30 .  D. 45 . 
Câu 31: Cho hàm số bậc ba 3 2
y x  3x  4 có đồ thị như hình vẽ bên dưới: y 4 -1 2 O x
Tìm tất cả các giá trị thực của m sao cho phương trình 3 2
x  3x  4  m  0 có 3 nghiệm thực phân biệt. m  4
A. 2  m  4 .
B. 0  m  4 . C.  .
D. 0  m  4 . m  0
Câu 32: Hàm số y f x liên tục trên và có đạo hàm f  x  x x   2 1 x  
1 ,x  . Hàm số
y f x nghịch biến trên khoảng nào dưới đây? A. 1; 2. B. 1;0. C. 0;  1 . D. 2;   1 .
Câu 33: Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh
được đánh số từ 1 đến 9 . Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả
khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng 9 18 4 1 A. . B. . C. . D. . 35 35 35 7
Câu 34: Tích tất cả các nghiệm của phương trình 2
log x  2 log x  3  0 bằng 1 1 A. . B. 100. C. 10. D. . 10 100
Câu 35: Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn | z  3  i | 2 là 2 2 2 2
A. đường tròn  x  3   y   1  4 .
B. đường tròn  x  3   y   1  4 . 2 2
C. đường tròn  x  3   y   1  2 .
D. đường thẳng 3x y  2  0.
Câu 36: Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A ; 1 ; 1 2 và B ; 3 ; 0 4 là
x  1  2t
x  1  2t
x  3  2t
x  5  2t    
A. y  1  t .
B. y  1  t .
C. y t  .
D. y  1  t .    
z  2  2t
z  2  2tz  4  2tz  6  2t
Câu 37: Trong không gian Oxyz, cho a  i  2 j  3k . Tọa độ của vectơ a là A.  1  ;2; 3   . B. 2; 3  ;   1 . C. 2; 1  ; 3   . D.  3  ;2;  1 . Trang 4
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD a 2 SA   ABCD và
SA a (tham khảo hình vẽ)
Khoảng cách từ A đến mặt phẳng  SBD bằng a 3 a 21 a 10 a 2 A. . B. . C. . D. . 2 7 5 5
Câu 39: Trong không gian Oxyz, gọi H hình chiếu vuông góc của M 2;0  ;1 lên đường thẳng x 1 y z  2  :  
. Tìm tọa độ điểm H . 1 2 1
A. H 2; 2;3 .
B. H 0; 2   ;1 .
C. H 1;0;2 .
D. H  1  ; 4  ;0 .
Câu 40: Một hình trụ có bán kính bằng 2a . Hai điểm ,
A B lần lượt thuộc hai đường tròn đáy sao cho
AB  4a . Biết khoảng cách giữa AB và trục bằng a . Tính thể tích khối trụ đã cho. 3 8 2 A. 3 V   a 2 . B. a V . C. 3 V  4 a 2 . D. 3 V  8 a . 3
________________________HẾT________________________ Trang 5
Bộ đề cơ bản Ôn thi THPT Quốc gia
LỜI GIẢI CHI TIẾT
Câu 1: Trong mặt phẳng Oxy, điểm M 3; 2
  là điểm biểu diễn của số phức nào dưới đây ?
A. z  2  3i .
B. z  3  2i .
C. z  3  2 . i
D. z  2  3i . Lời giải:
Số phức thoả mãn yêu cầu đề bài là: z  3  2i .
Câu 2: Hệ số góc của tiếp tuyến với đồ thị hàm số y  ln  x  
1 tại điểm có hoành độ x  2 là 1 1 A. 1. B. ln 2 . C. . D. . 3 3ln 2 Lời giải: 1 Ta có y ' 
. Hệ số góc của tiếp tuyến với đồ thị hàm số y  ln  x  
1 tại điểm có hoành độ x 1
x  2 là: y   1 ' 2  . 3
Câu 3: Đạo hàm của hàm số 2x y  là A. 1 .2x y x    . B. 2 . x y  ln 2 . C. 2x y  . D. x 1 y .2 x    .ln 2 . Lời giải: Hàm số 2x y  có đạo hàm là ' 2 . x y  ln 2 . Câu 4:
Tập nghiệm của bất phương trình 2x 1 3  27 là  1   1  A. ;    . B. 3;   . C. 2;   . D. ;     .  2   3  Lời giải: 2 x 1  2 x 1  3 3  27  3
 3  2x 1  3  x  2 .
Vậy bất phương trình có tập nghiệm S  2;   .
Câu 5: Cho cấp số cộng (u ) có u  2027 và công sai d  3 . Số hạng u n 1 3 A. 3 u  2027( 3)  .
B. u  2021.
C. u  2020 .
D. u  2054 . 3 3 3 3 Lời giải:
u u  2d  2027  2.( 3)   2021 3 1
Câu 6: Trong không gian Oxyz , mặt phẳng   : 3x  4y z  3  0 có một vectơ pháp tuyến là
A. m  3; 4;   1 .
B. n  3; 4  ;1 . C. a   6  ;8;2 . D. b   3  ;4;  1 . Lời giải:
Mặt phẳng   : 3x  4y z  3  0 có một vectơ pháp tuyến là u  3; 4  ;  1 nên vectơ a   6
 ;8;2 cũng là một vectơ pháp tuyến của mặt phẳng   .
Câu 7: Cho hàm số bậc bốn y f x có đồ thị như hình vẽ bên dưới: Trang 6
Bộ đề cơ bản Ôn thi THPT Quốc gia
Số nghiệm thực của phương trình f x  3 là A. 1. B. 2 . C. 0. D. 3. Lời giải:
Số nghiệm của phương trình f x  3 bằng số giao điểm của đồ thị hàm số y f x và
đường thẳng y  3 .
Ta có đường thẳng y  3 song song với trục hoành và cắt trục tung tại điểm có tọa độ 0;3 .
Từ đồ thị ta thấy đường thẳng y  3 cắt đồ thị hàm số y f x tại hai điểm phân biệt. Do đó
phương trình f x  3 có 2 nghiệm thực phân biệt. 2 2 2
Câu 8: Cho f (x d ) x  2  và ( g x d ) x  1  
. Giá trị của 2 f (x)  3 ( g x) dx    bằng 1  1  1  A. 1. B. 5. C. 7. D. 7 . Lời giải: 2 2 2
Áp dụng tính chất của tích phân ta có 2 f (x)  3 (
g x) dx  2 f (x)dx  3 (
g x)dx  4  3  1      . 1  1  1 
Câu 9: Đường cong trong hình vẽ là đồ thị hàm số nào dưới đây? A. 3 2
y x  3x 1. B. 3
y  x  3x 1. C. 4 2
y x  2x 1. D. 3
y x  3x 1. Lời giải:
Quan sát hình dạng đồ thị ta loại đáp án hàm số 4 2
y x  2x 1 do trên hình hàm số có hai
cực trị mà đáp án này hàm số có 3 cực trị.
Do nhánh bên phải của đồ thị đi lên nên loại đáp án 3
y  x  3x 1.
Mặt khác quan sát đồ thị có hai điểm cực trị là x  1 . x  0 Xét đáp án A có 2
y  3x  6x  0   nên loại đáp án này. x  2
Vậy hình trên là đồ thị hàm số 3
y x  3x 1. Trang 7
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 10: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : ( x  2)  ( y 1)  ( z 1
 )  9 . Tọa độ tâm I và bán
kính R của S  là A. I ( 2
 ;1;1), R  3. B. I ( 2  ;1; 1
 ), R  9. C. I(2;1;1), R  3.
D. I (2; 1;1), R  9.
Câu 11: Trong không gian Oxyz , cho hai điểm A 1
 ;1;2 và B3; 5
 ;0 . Tọa độ trung điểm của đoạn thẳng AB là A. 2; 4; 2 B. 4; 6; 2 C. 1; 2;  1 D. 2; 3  ;  1
Câu 12: Cho hai số phức       1 z
3 7i và z2 2 3i . Tìm số phức z 1 z z2 .
A. z  110i .
B. z  5  4i .
C. z  3 10i .
D. z  3  3i . Lời giải: Ta có: z         1 z
z2 3 7i 2 3i 5 4i .
Câu 13: Cho khối lăng trụ đứng có diện tích đáy bằng 2
2a và cạnh bên bằng 3a . Thể tích khối lăng trụ đã cho bằng A. 3 2a B. 3 3a C. 3 18a D. 3 6a Lời giải: 2 3 V  .
B h  2a .3a  6a
Câu 14: Cho hình chóp .
S ABC có đường cao SA, tam giác ABC vuông tại A có AB  2 , AC  4 . Gọi
H là trung điểm của BC (tham khảo hình vẽ). S C A H B
Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp . S ABC bằng 16 5 16 5 4 5 4 5 A. . B. . C. . D. . 5 15 9 3 Lời giải: S A C H B
Xét tam giác ABC vuông tại A : 2 2 2 2
BC AB AC  2  4  2 5 . 1 1
Suy ra AH BC  .2 5  5 . 2 2 Trang 8
Bộ đề cơ bản Ôn thi THPT Quốc gia 1 1 4 5
Xét tam giác SAH vuông tại A : S  . SA AH  2  . SA 5  SA  . SAH 2 2 5 1 1
Diện tích tam giác ABC : SA . B AC  .2.4  4 . ABC 2 2 1 1 4 5 16 5 Thể tích khối chóp . S ABC : VS . A S  . .4  . S.ABC 3 ABC 3 5 15
Câu 15: Cắt một mặt cầu S  bởi một mặt phẳng qua tâm được thiết diện là hình tròn đường kính bằng 4 .
cm Tính thể tích của khối cầu đã cho. 256 32 A.  3 cm . B.   3 16 cm . C.  3 cm . D.   3 64 cm . 2 3 Lời giải:
Bán kính R của hình tròn thu được bằng bán kính của mặt cầu.
Đường kính hình tròn là: 2R  4  R  2 c . m 4 4 32 Thể tích khối cầu là: 3 3 V   R  .2   3 cm . 3 3 3
Câu 16: Môđun của số phức z  1  i bằng A. 1. B. 0 . C. 2 . D. 2 . Lời giải:
Ta có z   2 2 1 1  2 .
Câu 17: Cho hình trụ có bán kính đáy bằng 5 và chiều cao bằng 7 . Diện tích xung quanh của hình trụ đã cho bằng 175 A. . B. 175 .  C. 70 .  D. 35 .  3 Lời giải:
Ta có r  5;l h  7 . Suy ra S  2rl  2 5 . .7  70 xqx 1 2t
Câu 18: Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng d  :  y  3   t ? z  45t
A. P 3 ;  2 ;   1 .
B. N 2 ;1; 5 .
C. M 1;  3 ; 4 .
D. Q 4 ;1; 3 .
Câu 19: Cho hàm số y f x có đồ thị như hình vẽ bên dưới:
Hàm số có bao nhiêu điểm cực tiểu trên khoảng a;b ? A. 4 . B. 2 . C. 7 . D. 3 . Lời giải:
Từ đồ thị hàm số suy ra hàm số có 3 điểm cực tiểu trên khoảng a;b . Trang 9
Bộ đề cơ bản Ôn thi THPT Quốc gia 3x  5
Câu 20: Tiệm cận đứng của đồ thị hàm số y  là x  2 A. x  2 . B. y  2 . C. x  3 . D. y  3 . Lời giải: 3x  5 3x  5 Ta có lim y  lim
  ; lim y  lim   .     x2 x2 x  2 x2 x2 x  2
Vậy tiệm cận đứng của đồ thị hàm số là x  2 .
Câu 21: Bất phương trình log (3x  2)  log (6  5x) có tập nghiệm là (a;b) . Tổng a b bằng 2 2 8 28 26 11 A. . B. . C. . D. . 3 15 5 5 Lời giải: 8  x  8 x 1  
log (3x  2)  log (6  5x)  3x  2  6  5x  0     2 2 6 6 x x     5  5  6 
Suy ra bất phương trình có tập nghiệm là: 1; .    5  6 11
Vậy tổng a b  1  . 5 5
Câu 22: Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
một cái bút và một quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn? A. 80 . B. 70 . C. 90 . D. 60 . Lời giải:
Có 10 cách chọn bút và 8 cách chọn sách.
Số cách chọn một cái bút và một quyển sách là 10.8  80 . Câu 23: Cho hàm số    2  x f x
x e . Tìm một nguyên hàm F x của hàm số f x thỏa mãn F 0  2023 . A.   2   x F x x e  2022 . B.   2   x F x x e  2022 . C.   2   x F x x e  2021 . D.    x F x e  2023 . Lời giải: Ta có       2 2      x x f x dx x e dx x e C .
Có F x là một nguyên hàm của f x và F 0  2023 .    2   x F x x e C Suy ra 
 1 C  2023  C  2022 .
F 0  2023 Vậy   2   x F x x e  2022 . 2 4 4 Câu 24: Cho f
 xdx 1, f tdt  4   . Tính I f  ydy . 2  2  2 A. I  5 . B. I  3 . C. I  3 . D. I  5 . Lời giải: Trang 10
Bộ đề cơ bản Ôn thi THPT Quốc gia 4 4
Do tích phân không phụ thuộc vào biến số nên
f t dt
f xdx  4    . 2  2  4 4 4 2 Ta có I
f y dy f xdx
f xdx
f xdx  4  1  5      . 2 2 2  2 
Câu 25: Họ nguyên hàm của hàm số f x 3  2x  là x 3 3 A. 2   C. B. 2 x   C. C. 2
x  ln x C. D. 2
x  3ln x C. 2 x 2 x Lời giải:   f  x 3 2 dx  2x
dx x  3ln x C.   x
Câu 26: Cho hàm số y f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây? A. 2;  . B.   ;1  . C. 0;  . D. 0; 2 .
Câu 27: Cho hàm số y f x xác định, liên tục trên và có bảng biến thiên như sau:
Khẳng định nào sau đây đúng?
A. Hàm số đạt cực đại tại x  0 .
B. Hàm số đạt cực tiểu tại x  4 .
C. Hàm số đạt cực đại tại x  2 .
D. Hàm số đạt cực đại tại x  1 . Lời giải:
Dựa vào bảng biến thiên của hàm số y f x ta thấy hàm số đạt cực đại tại x  2 .
Câu 28: Với a và b là hai số thực dương tùy ý; log  3 4 a b bằng 2  1 1 A. log a  log . b
B. 3log a  4 log .
b C. 2log a  log b . D. 4 log a  3log . b 2 4  2 2 3 4 2 2 2 2 Lời giải: Ta có: log  3 4 a b  3 4
 log a  log b  3log a  4log b nên B đúng. 2 2 2 2 2
Câu 29: Cho hình phẳng  H  giới hạn bởi các đường 2
y  2x x , y  0 . Quay  H  quanh trục hoành
tạo thành khối tròn xoay có thể tích được tính bởi công thức nào dưới đây? Trang 11
Bộ đề cơ bản Ôn thi THPT Quốc gia 2 2 2 2 2 2 A.  2 2   x x d .x B.   2 2 
x x  d .x C.  2 2 
x x  d .x D.   2 2   x x d .x 0 0 0 0 Lời giải: 2 2
Theo công thức ta chọn V    2 2x   x  dx . 0
Câu 30: Cho hình lập phương ABC . D
A BCD . Góc giữa đường thẳng AB và mặt phẳng  ABCD bằng A. 60 .  B. 90 .  C. 30 .  D. 45 .  Lời giải: D' A' B' C' A D B C
Góc giữa AB và mặt phẳng  ABCD là góc 0 BAB  45 .
Câu 31: Cho hàm số bậc ba 3 2
y x  3x  4 có đồ thị như hình vẽ bên dưới: y 4 -1 2 O x
Tìm tất cả các giá trị thực của m sao cho phương trình 3 2
x  3x  4  m  0 có 3 nghiệm thực phân biệt. m  4
A. 2  m  4 .
B. 0  m  4 . C.  .
D. 0  m  4 . m  0 Lời giải: Trang 12
Bộ đề cơ bản Ôn thi THPT Quốc gia y 4 -1 2 O x Ta có 3 2 3 2
x  3x  4  m  0  x  3x  4  m . Số nghiệm của phương trình trên là số giao điểm của đồ thị hàm số 3 2
y x  3x  4 và đường thẳng y m .
Dựa vào đồ thị ta thấy đồ thị hàm số 3 2
y x  3x  4 và đường thẳng y m cắt nhau tại 3
điểm phân biệt khi và chỉ khi 0  m  4 .
Câu 32: Hàm số y f x liên tục trên và có đạo hàm f  x  x x   2 1 x  
1 ,x  . Hàm số
y f x nghịch biến trên khoảng nào dưới đây? A. 1; 2. B. 1;0. C. 0;  1 . D. 2;   1 . Lời giải: 2
Xét hàm số y f x có f   x  x x   2 1 x  
1  x x   1  x   1 .  x  0 
f   x  0  x x  2 1  x   1  0  x  1  . x  1  
Suy ra bảng xét dấu của hàm f   x :
Từ bảng xét dấu của hàm f  x suy ra hàm số y f x nghịch biến trên khoảng 1;0
Câu 33: Một hộp chứa 15 quả cầu gồm 6 quả màu đỏ được đánh số từ 1 đến 6 và 9 quả màu xanh
được đánh số từ 1 đến 9 . Lấy ngẫu nhiên hai quả từ hộp đó, xác suất để lấy được hai quả
khác màu đồng thời tổng hai số ghi trên chúng là số chẵn bằng 9 18 4 1 A. . B. . C. . D. . 35 35 35 7 Lời giải:
Số cách lấy ngẫu nhiên 2 quả cầu từ hộp là: 2 C  105 cách 15
Để tổng hai số ghi trên hai quả cầu là số chẵn ta có 2 TH sau:
TH 1: Hai quả cầu khác màu cùng đánh số lẻ: 1 1
C .C  15 cách 3 5
TH 2: Hai quả cầu khác màu nhau cùng đánh số chẵn: 1 1
C .C  12 cách 3 4 12  15 9
Vậy xác suất cần tính là: P   . 105 35 Trang 13
Bộ đề cơ bản Ôn thi THPT Quốc gia
Câu 34: Tích tất cả các nghiệm của phương trình 2
log x  2 log x  3  0 bằng 1 1 A. . B. 100. C. 10. D. . 10 100 Lời giải: x  0 log x 1  x 10 Ta có: 2
log x  2 log x  3  0 
 x 10   3 log x  3   x 10 3 x 10 1 Vậy x .x  . 1 2 100
Câu 35: Trong mặt phẳng Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn | z  3  i | 2 là 2 2 2 2
A. đường tròn  x  3   y   1  4 .
B. đường tròn  x  3   y   1  4 . 2 2
C. đường tròn  x  3   y   1  2 .
D. đường thẳng 3x y  2  0. Lời giải: 2 2 2 2
Đặt z x yi x, y   . Ta có z  3  i  2   x  3   y   1
 2  x 3   y   1  4.
Câu 36: Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A ; 1 ; 1 2 và B ; 3 ; 0 4 là
x  1  2t
x  1  2t
x  3  2t
x  5  2t    
A. y  1  t .
B. y  1  t .
C. y t  .
D. y  1  t .    
z  2  2t
z  2  2tz  4  2tz  6  2tLời giải:
Kiểm tra sự kiện: A d và vectơ chỉ phương AB   ; 2  ;
1 2 ta thấy phương án D thỏa mãn.
Câu 37: Trong không gian Oxyz, cho a  i  2 j  3k . Tọa độ của vectơ a là A.  1  ;2; 3   . B. 2; 3  ;   1 . C. 2; 1  ; 3   . D.  3  ;2;  1 .
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD a 2 SA   ABCD và
SA a (tham khảo hình vẽ)
Khoảng cách từ A đến mặt phẳng  SBD bằng a 3 a 21 a 10 a 2 A. . B. . C. . D. . 2 7 5 5 Lời giải: Trang 14
Bộ đề cơ bản Ôn thi THPT Quốc gia
Gọi K là hình chiếu vuông góc của A trên BD . AK BD Khi đó:
  BD  SAK  . BD SA
mà BD  SBD suy ra SBD  SAK
mà SBD  SAK   SK nên kẻ AH SK thì AH  SBD . Vậy d  ,
A SBD  AH 1 1 1 1 1 1 1 5
Xét tứ diện vuông ASBD suy ra        . 2 2 2 2 2 2 2 2 AH AD AB AS a 2a a 2a a 10 a 10 Suy ra AH  . Vậy d ( , A (SB )) D  . 5 5
Câu 39: Trong không gian Oxyz, gọi H hình chiếu vuông góc của M 2;0  ;1 lên đường thẳng x 1 y z  2  :  
. Tìm tọa độ điểm H . 1 2 1
A. H 2; 2;3 .
B. H 0; 2   ;1 .
C. H 1;0;2 .
D. H  1  ; 4  ;0 . Lời giải: x 1 t
Ta có  :  y  2t t   mà H    H t 1; 2t;t  2  MH  t 1; 2t;t   1 . z  2t
Đường thẳng  có một VTCP là u  1;2  ;1 .
Khi đó MH    MH.u  0  t  
1  4t  t  
1  0  t  0  H 1;0; 2 .
Câu 40: Một hình trụ có bán kính bằng 2a . Hai điểm ,
A B lần lượt thuộc hai đường tròn đáy sao cho
AB  4a . Biết khoảng cách giữa AB và trục bằng a . Tính thể tích khối trụ đã cho. 3 8 2 A. 3 V   a 2 . B. a V . C. 3 V  4 a 2 . D. 3 V  8 a . 3 Lời giải: Trang 15
Bộ đề cơ bản Ôn thi THPT Quốc gia a
Dựng các đường sinh AC và BD .
Ta có OO //  ACBD  d OO , AB  d OO , ACBD  d O, ACBD .
Gọi H là trung điểm của BC OH   ACBD  d O, ACBD  OH  . a
Tam giác OHC vuông tại H suy ra HC a 3 nên BC  2a 3
Tam giác ABC vuông tại C AC OO  2a .
Vậy khối trụ đã cho có thể tích 2 2 3
V   r h   .4a .2a  8 a .
________________________HẾT________________________
Huế, 10h30’ Ngày 01 tháng 4 năm 2023 Trang 16