BT lập trình môn Toán rời rạc| Môn Toán rời rạc| Trường Đại học Bách Khoa Hà Nội

Bài tập lập trình 2: Tô màu đồ thị
Bạn đã biết trong bài giảng:
Định lý 1. Cho G là đồ thị với mọi đỉnh đều có bậc ≤ k. Nếu G không chính quy, vậy thì χ(G) ≤ k.
Chứng minh của mệnh đề này cho chúng ta cách xây dựng thứ tự các đỉnh để thuật toán tham
lam tô màu đỉnh dùng không quá k màu (cho đồ thị không chính quy). Bài tập này yêu cầu bạn
cài đặt thuật toán này.
Nhiệm vụ: Nhập đồ thị từ bàn phím dưới dạng danh sách cạnh. Đưa ra màn hình một cách tô màu đồ thị dùng
• Không nhiều hơn k màu nếu G không chính quy.
• Không nhiều hơn k + 1 màu nếu G chính quy.
Dữ liệu vào: Từ file dothi.txt trong đó
• Dòng đầu tiên ghi hai số nguyên n và m là số đỉnh và số cạnh của đồ thị;
• Ở m dòng tiếp theo, mỗi dòng ghi hai số nguyên tương ứng với một cạnh của đồ thị.
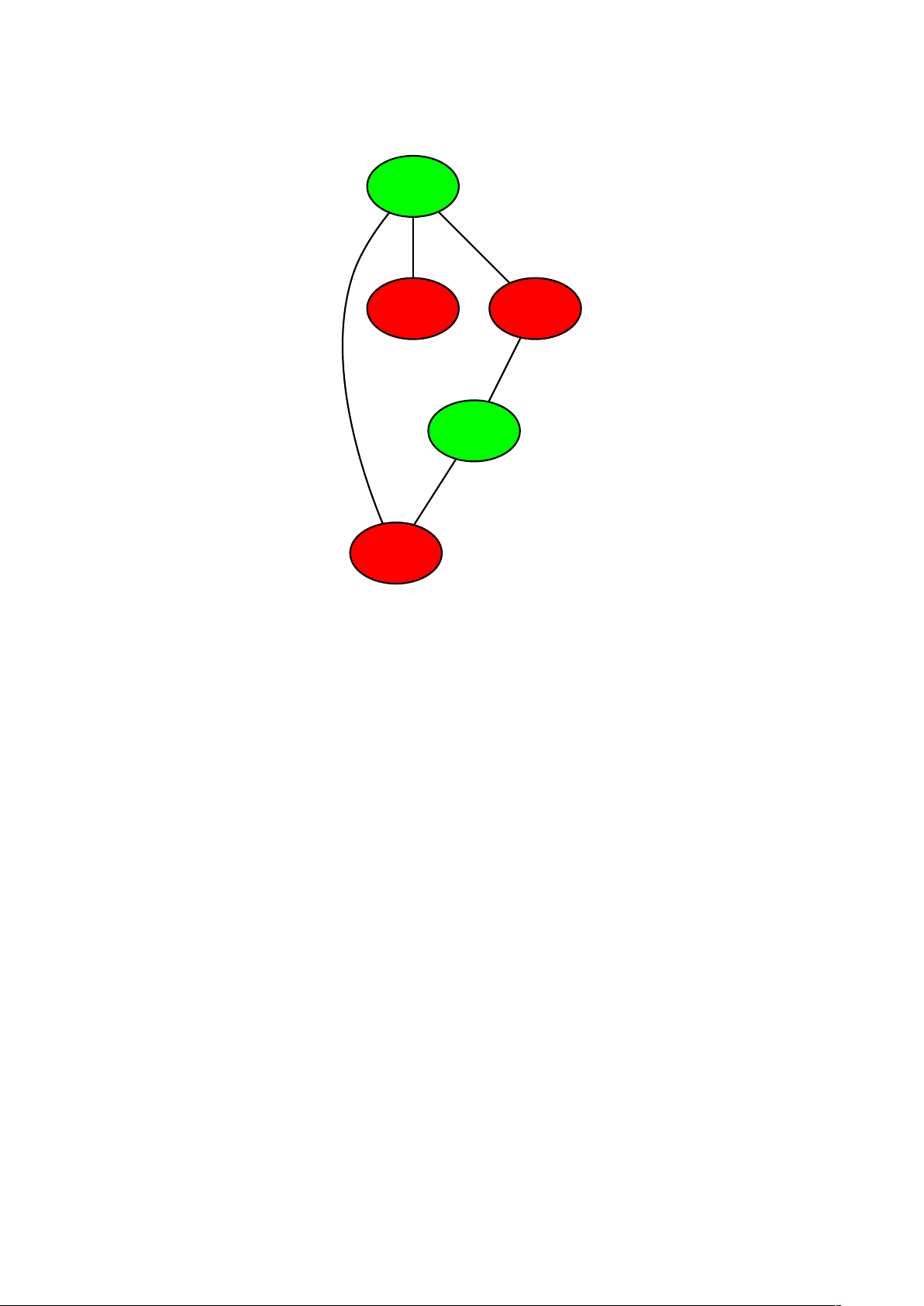
Dữ liệu ra: file dothitomau.dot biểu diễn đồ thị ở dạng ngôn ngữ DOT với các đỉnh đã được tô màu. Ví dụ: Dữ liệu vào Dữ liệu ra 4 5 graph dothi 1 2 { 2 3
5 [fillcolor=red, style=filled]; 3 4
4 [fillcolor=red, style=filled]; 4 1
1 [fillcolor=green, style=filled]; 1 5
3 [fillcolor=green, style=filled];
2 [fillcolor=red, style=filled]; 1 -- 2; 2 -- 3; 3 -- 4; 4 -- 1; 1 -- 5; }
Với dữ liệu ra dothitomau.dot, ta biên dịch với chương trình graphviz:
dot -Tpdf dothitomau.dot -o graph.pdf
thì được file graph.pdf với nội dung như Hình 1.
Tài liệu về ngôn ngữ DOT:. Tài liệu Drawing graphs with dot có thể download tại link dưới đây:
https://www.graphviz.org/pdf/dotguide.pdf 1 2 1 5 2 3 4
Hình 1. Đồ thị được tô màu của ví dụ trước
Bài tập 3: Tìm kiếm trên đồ thị lớn
A. Xét tập dữ liệu sgb-words ở địa chỉ:
http://www-cs-faculty.stanford.edu/~knuth/sgb-words.txt
Tập dữ liệu này chứa phần lớn các từ tiếng Anh độ dài 5. Từ dữ liệu này, ta xây dựng đồ thị
G = (V, E) với tập đỉnh V = “ mọi từ trong sgb-words ”, và giữa hai từ u và v trong G có cạnh
nối nếu u, v khác nhau ở đúng một vị trí.
Dễ thấy, trong đồ thị G, dãy từ
words, wolds, golds, goads, grads, grade, grape, graph
là một đường đi với đỉnh bắt đầu là từ words và đỉnh kết thúc là từ graph.
(a) Hãy viết chương trình đếm số thành phần liên thông của đồ thị G.
(b) Hãy viết chương trình nhập vào từ bắt đầu u và từ kết thúc v; hiện ra màn hình một
đường đi ngắn nhất từ u tới v.
B. Vẫn từ tập dữ liệu sgb-words, ta xây dựng đồ thị có hướng D với tập đỉnh là “ mọi từ trong
sgb-words”, và một từ u có cung nối với một từ v khác nếu bốn chữ cuối của u xuất hiện
trong v (tính cả số lần xuất hiện).
Đồ thị có hướng D có 94, 084 cung và 5757 đỉnh. Đường đi có hướng ngắn nhất từ words tới graph là
words → dross → soars → orcas → chars → sharp → graph
và ta có thể quay lại từ words trong năm bước,
graph → harps → prats → astro → trows → words
(a) Hãy viết chương trình đếm số thành phần liên thông mạnh của đồ thị D.
(b) Hãy viết chương trình nhập vào một từ u và hiện ra màn hình các từ cùng thành phần
liên thông mạnh với từ u.
(c) Hãy viết chương trình nhập vào từ bắt đầu u và từ kết thúc v; hiện ra màn hình một
đường đi ngắn nhất từ u tới v. 1
Bài tập lập trình 1: Nén cây
Mỗi cây gán nhãn với n đỉnh có thể biểu diễn duy nhất bởi Prufer code của nó. Do kích thước
ngắn của Prufer code, ta xem nó như một biểu diễn nén của cây. Bạn hãy viết chương trình nhập
vào một cây gán nhãn và in ra màn hình Prufer code của nó.
Cụ thể, bạn phải cài đặt chương trình làm việc sau.
• Input (nhập từ bàn phím): Cây gán nhãn {0, ..., n − 1} với số đỉnh n < 100000. Cây này
được biểu diễn bởi danh sách cạnh.
• Output (ra màn hình): Mã Prufer code của cây này.
Ví dụ: Với dữ liệu vào: 9 1 6 0 2 7 5 0 3 2 4 2 6 8 4 2 9 6 1 6 5 9 2 9 7 9 8 3 0
Dòng đầu tiên thể hiện số cạnh của cây; mỗi dòng tiếp theo thể hiện một cạnh của cây.
Với dữ liệu này, chương trình nên output ra mã Prufer: 6 0 2 6 2 9 9 2
Test chương trình: Để test chương trình của mình, bạn có thể sử dụng mã nguồn sinh cây gán
nhãn ngẫu nhiên từ mã Prufer (trong thư mục PruferCodes); và sử dụng cây này như Input của
chương trình để tìm lại mã Prufer. Chú ý:
• Bạn chỉ submit file source code lên hệ thống
• Hệ thống sẽ tự kiểm tra việc sao chép bài. Mọi bài sao chép (dù chỉ 1 phần) sẽ bị điểm 0 và bị cảnh cáo. 1
Bài tập lập trình 4: Lập lịch di chuyển cho Robot 1. Mô tả bài toán
Có hai con robot A và B di chuyển trên một đồ thị có trọng số G. Do cả hai robot đều được điều
khiển bởi sóng radio nên chúng không thể ở gần nhau trong khoảng cách r. Ban đầu hai robot
đứng ở đỉnh a và đỉnh b trên G. Robot tại a muốn di chuyển đến đỉnh c dọc theo một đường đi
trong G, và robot tại b muốn di chuyển đến đỉnh d. Việc di chuyển này có thể mô ta dưới dạng
việc lập lịch di chuyển: tại mỗi thời điểm, lịch di chuyển xác định chỉ một robot di chuyển qua
một cạnh, từ một đỉnh tới một hàng xóm; cuối cùng, robot từ đỉnh a nên ở đỉnh c, và robot từ b nên ở đỉnh d.
Một lịch di chuyển gọi là không gây nhiễu nếu không có thời điểm nào mà hai robot lại đứng ở
hai đỉnh có khoảng cách1 ≤ r, với tham số r cho trước.
Bạn hãy viết chương trình nhập vào một đồ thị có trọng số G, hai đỉnh bắt đầu a và b, hai đỉnh
kết thúc c và d, và tham số r > 0. Thông báo ra màn hình một lịch di chuyển nếu có; nếu không
có thông báo ’Không thể!’. Input:
• Dòng đầu tiên là số đỉnh n < 100 và số cạnh m của đồ thị G.
• m dòng tiếp theo mỗi dòng gồm 3 số x y w thể hiện: Đồ thị G có cạnh {x, y} với trọng số w.
• dòng tiếp theo chứa bốn số a b c d là đỉnh bắt đầu và kết thúc của hai robot.
• dòng cuối cùng là số r > 0.
Output: Bao gồm nhiều dòng, mỗi dòng là hai số u v thể hiện các đỉnh mà hai robot đứng tại
mỗi thời điểm trong lịch di chuyển.
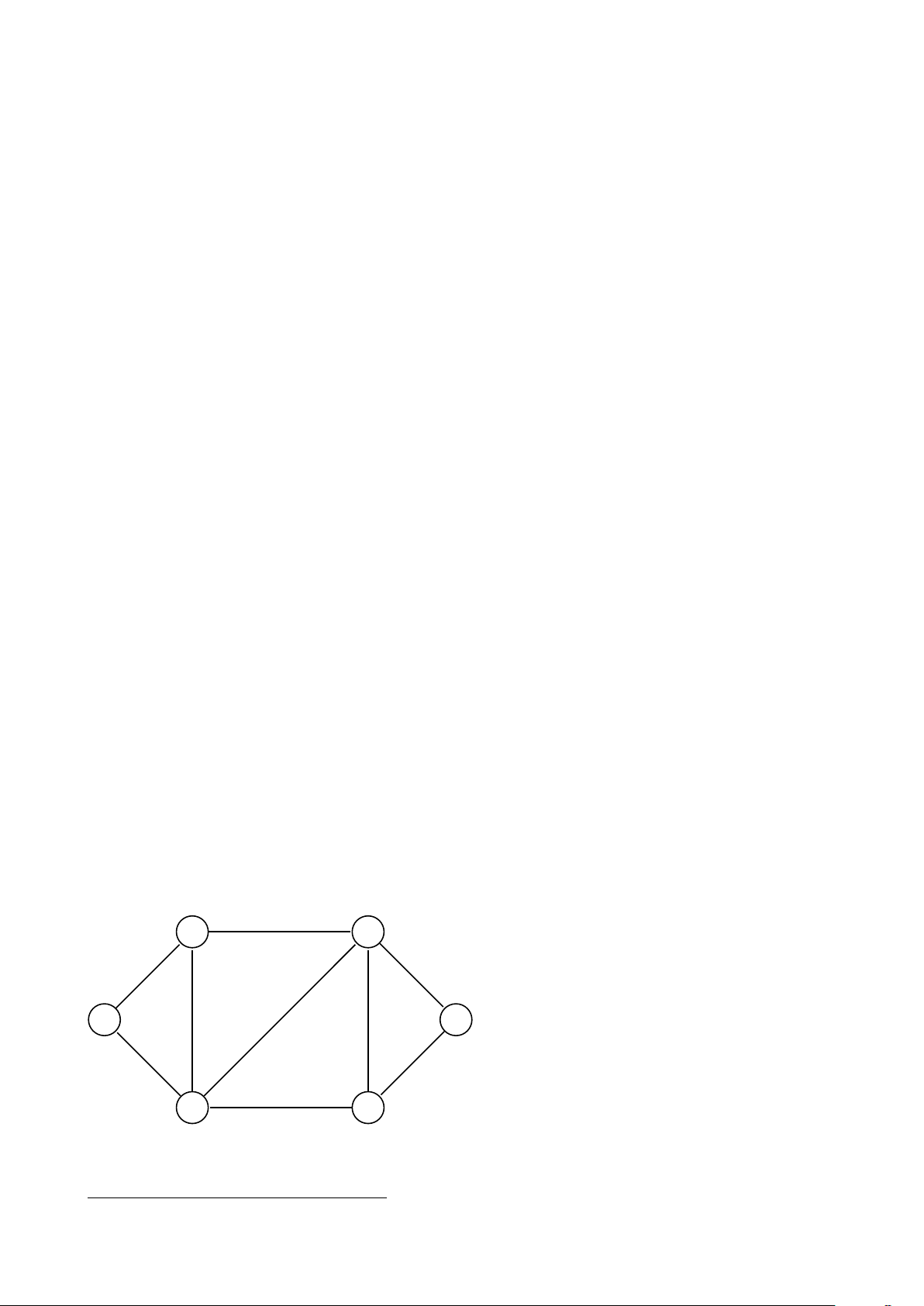
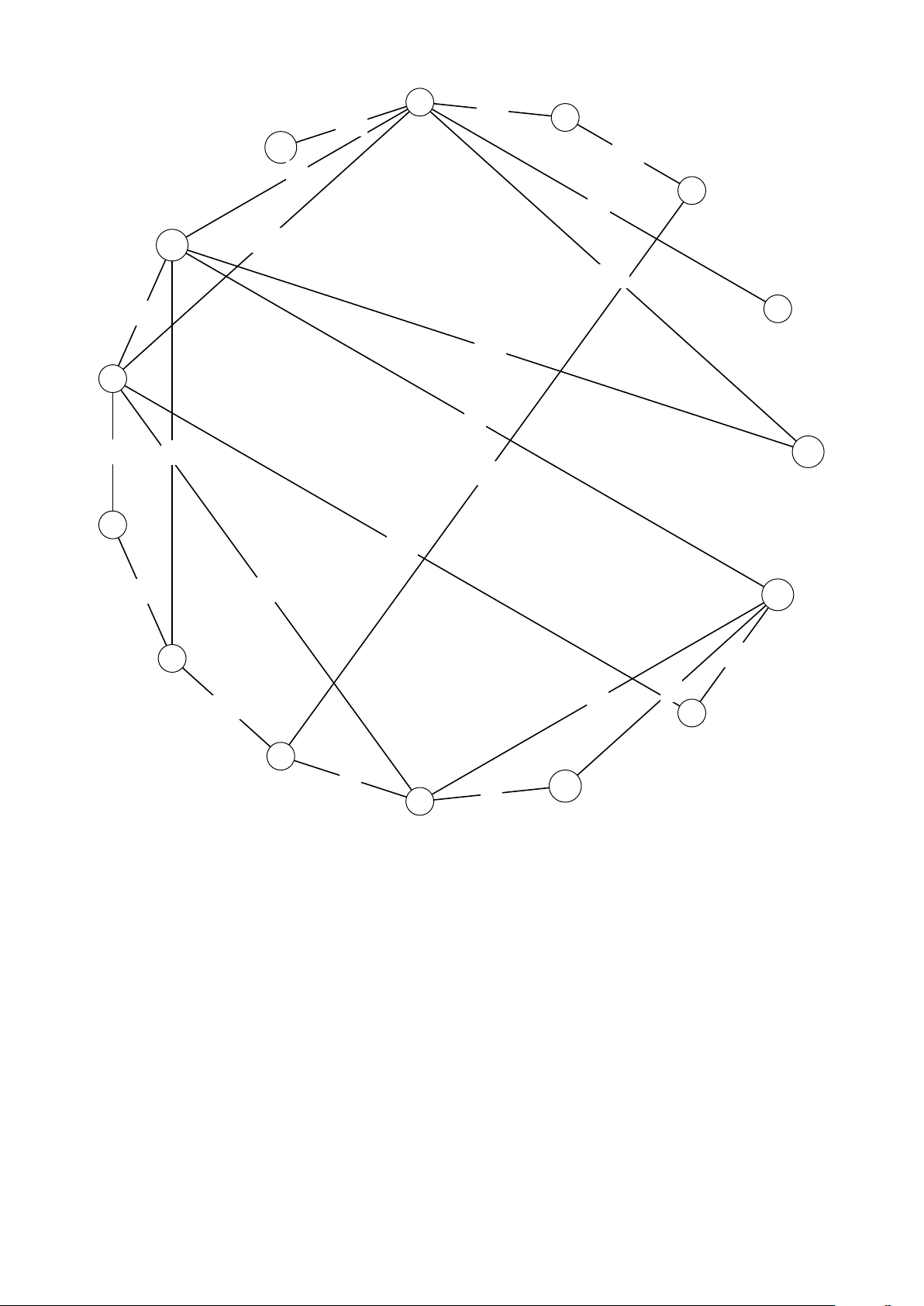
Ví dụ: Xét đồ thị dưới đây với các đỉnh bắt đầu a = 0, b = 2; các đỉnh kết thúc c = 2, d = 3; và
r = 4. Ta có một lịch di chuyển được chỉ ra ở dưới đây. Khoảng cách cặp đỉnh được chỉ ra ở cột
cuối để chứng minh rằng đây là một lịch di chuyển không gây nhiễu. 1 1 2 6 2
Lịch di chuyển khoảng cách 0 2 7 7 0 7 9 5 0 3 5 1 3 8 2 3 7 1 5 4 3 4
Nếu ta thay r trong ví dụ trên bằng 5, thì không có lịch di chuyển không nhiễu nào cả.
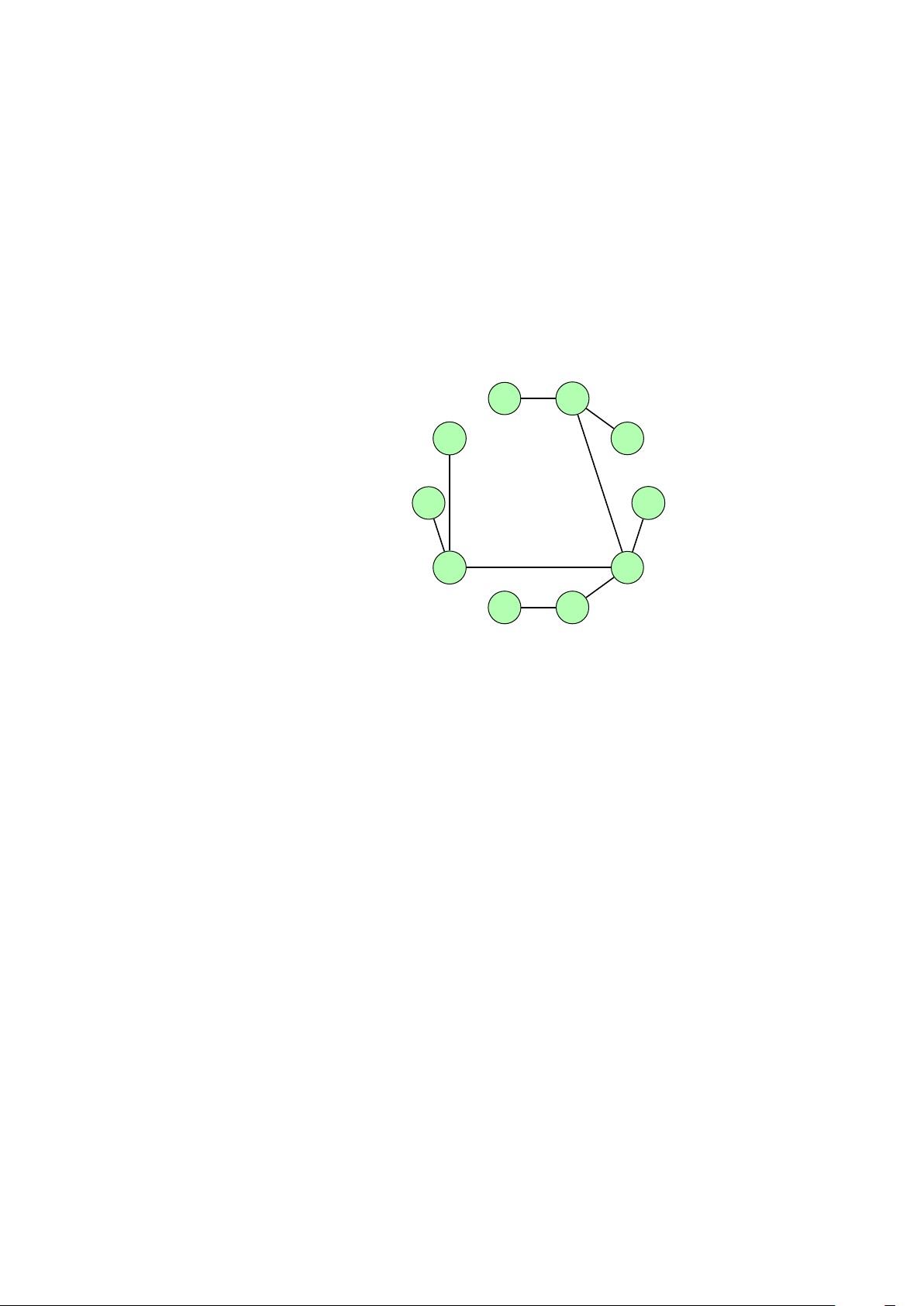
1khoảng cách là độ dài đường đi ngắn nhất 1 2 2. Một số dữ liệu Test Dữ liệu Test 1 10 12 // n m 0 4 10 0 9 11 1 4 9 2 6 5
Lịch di chuyển khoảng cách 2 8 1 1 3 20 3 4 11 1 4 9 3 6 5 1 0 19 4 5 2 4 0 10 5 7 9 3 0 21 7 8 3 3 4 11 7 9 10 8 9 4 1 3 // a b 3 4 // c d 7 // r 3 11 4 5 9 6 1 2 10 5 0 5 9 11 7 10 9 3 4 2 1 8
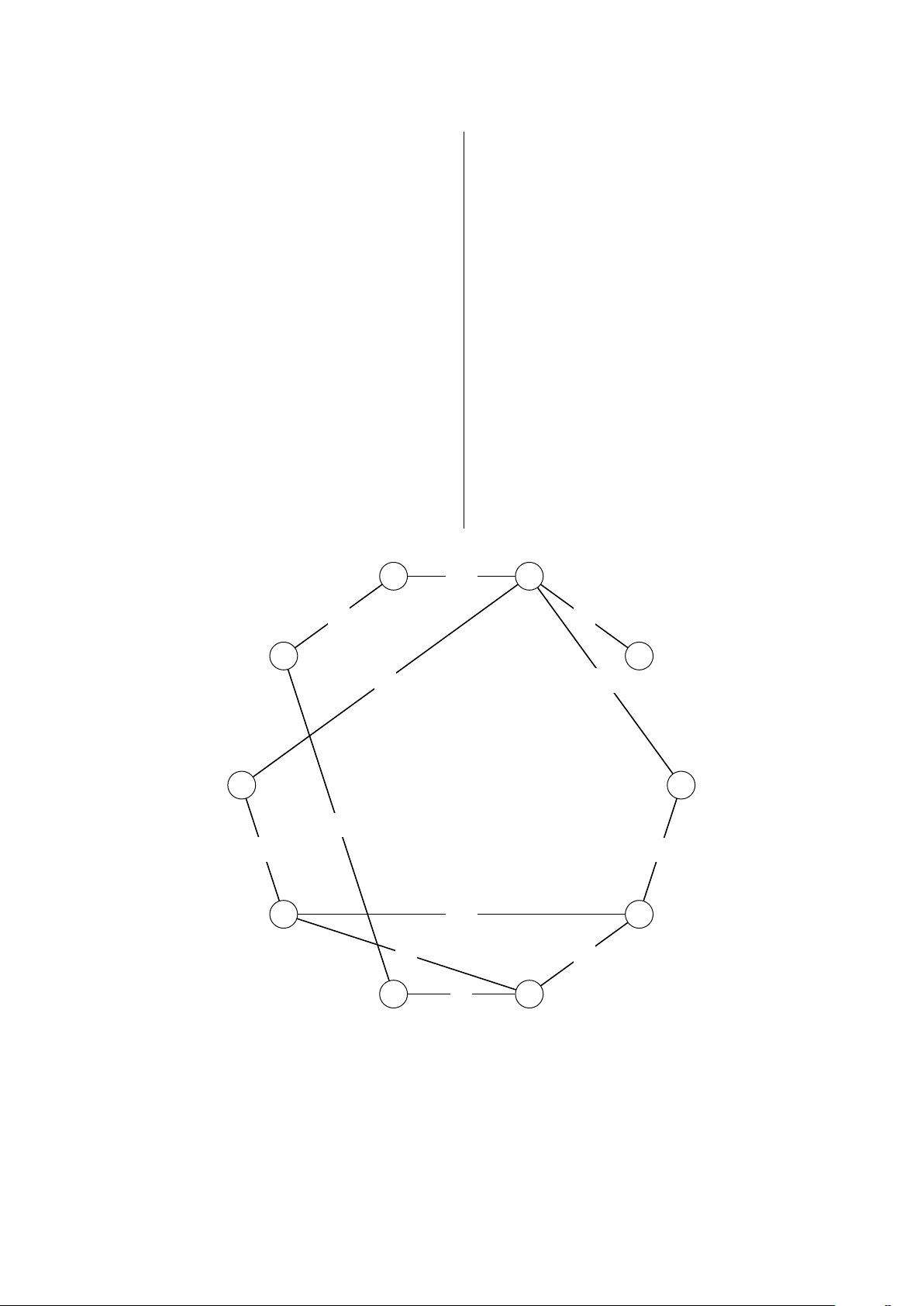
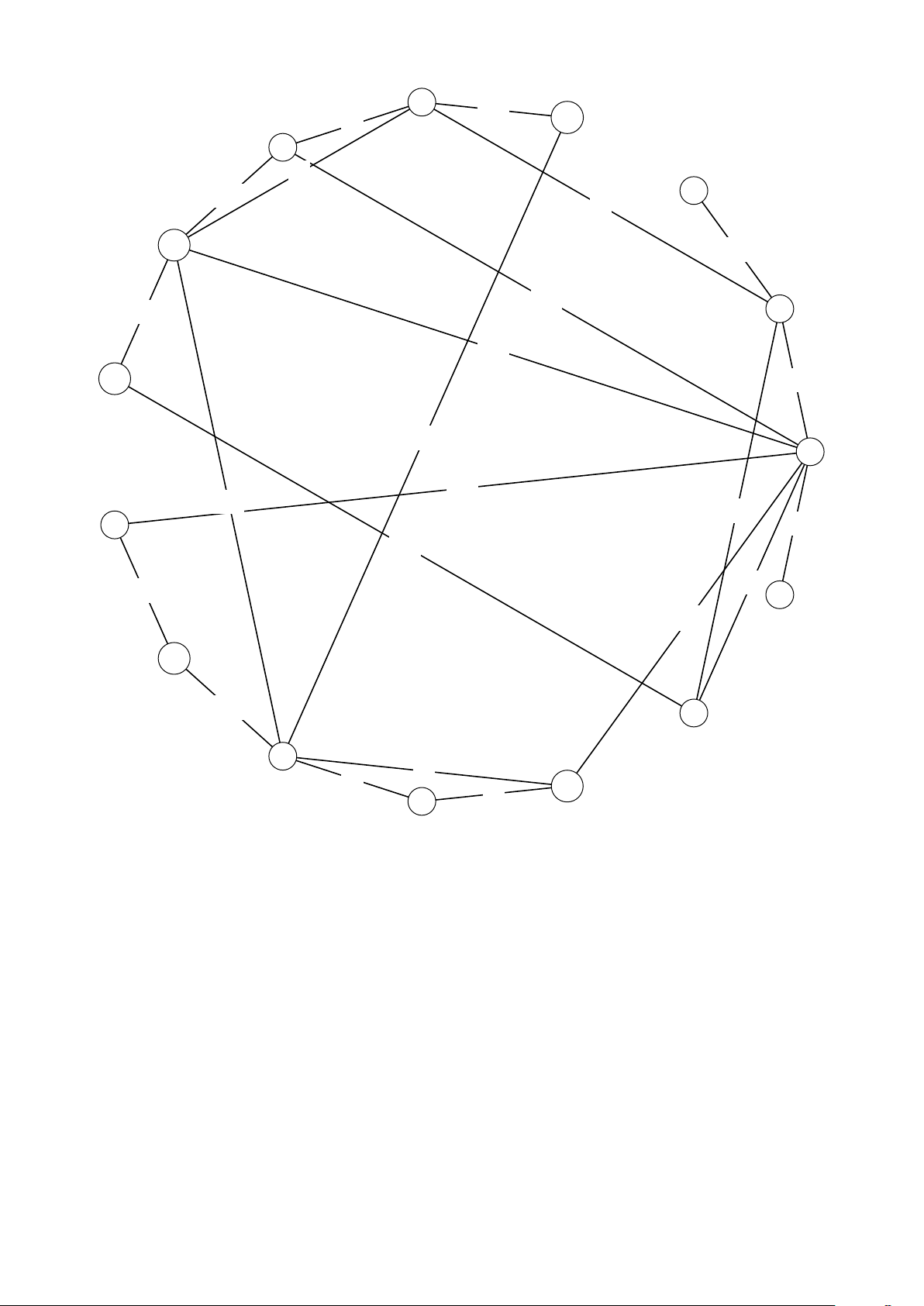
Hình 1. Đồ thị của dữ liệu Test 1 3 Dữ liệu Test 2 15 22 // n m 0 8 11 0 11 7 1 4 15 1 7 13 2 3 2 2 4 12 2 8 10 2 10 13
Lịch di chuyển khoảng cách 2 12 6 1 3 29 2 13 13 7 3 21 5 8 5 6 3 19 5 9 14 6 2 17 6 7 2 6 4 29 6 8 7 8 4 22 6 11 5 2 4 12 6 14 3 3 4 14 7 9 11 8 12 7 9 12 9 10 12 15 11 12 7 11 14 8 1 3 // a b 3 4 // c d 7 // r 4 Dữ liệu Test 3 15 23 // n m 0 2 3 0 9 6 0 10 11 1 9 5 2 4 15 2 5 14 2 7 1 2 9 5 2 11 6
Lịch di chuyển khoảng cách 2 12 14 1 3 23 3 6 7 1 12 19 3 11 7 9 12 14 3 12 10 9 4 10 3 13 14 2 4 15 3 14 14 12 4 8 4 8 2 3 4 18 4 12 11 5 13 15 6 11 2 8 9 8 8 12 6 8 14 11 10 12 3 1 3 // a b 3 4 // c d 7 // r 5 2 12 4 13 13 15 6 1 2 12 10 13 3 7 15 8 7 5 9 10 13 5 11 14 7 11 9 7 5 8 11 0 7 2 14 6 3
Hình 2. Đồ thị của dữ liệu Test 2 6 8 11 14 2 4 6 1 11 8 12 5 15 9 3 14 10 5 14 2 14 10 6 5 1 11 3 15 7 6 13 14 0 3 7 7 11 6 2
Hình 3. Đồ thị của Test 3 Toán Rời Rạc Thực hành 9
Có n chàng trai và n cô gái. Mỗi chàng trai m xếp hạng các cô gái dưới dạng một dãy
w1, w2, . . . , wn.
Ta nói rằng chàng trai m thích cô wi hơn cô wj nếu cô wi đứng trước cô wj trong dãy này.
Ta gọi dãy này là danh sách ưu tiên của m. Tương tự, mỗi cô gái cũng có một danh sách ưu tiên của mình.
Cần tìm cách ghép cặp mỗi chàng trai với một cô gái để tổ thức đám cưới sao cho không
tồn tại hai người khác giới thích nhau hơn vợ/chồng của họ. Những cuộc hôn nhân như
vậy gọi là ”bền vững”.
• Dữ liệu vào gồm:
– Dòng đầu tiên là số n.
– n dòng tiếp theo, mỗi dòng gồm n số nguyên là danh sách ưu tiên của mỗi chàng trai.
– n dòng tiếp theo, mỗi dòng gồm một dãy n số nguyên là danh sách ưu tiên của mỗi cô gái.
• Dữ liệu ra gồm: n cặp i, j thể hiện sẽ tổ chức đám cưới cho chàng trai i và cô gái j
đảm bảo họ có cuộc hôn nhân bền vững.
Ví dụ: Xét bảng dữ liệu vào và ra như sau: Dữ liệu vào Dữ liệu ra 5 3 2 5 1 4 5 1 1 2 5 3 4 2 2 4 3 2 1 5 4 3 1 3 4 2 5 3 4 1 2 4 5 3 1 5 3 5 2 1 4 5 2 1 4 3 4 3 5 1 2 1 2 3 4 5 2 3 4 1 5 1
• Dòng đầu tiên ở cột Dữ liệu vào chỉ ra rằng có 5 chàng trai và 5 cô gái.
• 5 dòng tiếp theo lần lượt là danh sách ưu tiên của chàng trai 1, 2,. . ., 5 đối với các
cô gái. Ví dụ, bảng trên chỉ ra rằng: chàng 1 thích
– cô 3 hơn cô 2,
– cô 2 hơn cô 5,
– cô 5 hơn cô 1,
– cô 1 hơn cô 4.
• 5 dòng tiếp theo lần lượt là danh sách ưu tiên của cô 1, cô 2,…, cô 5 đối với các chàng
trai. Ví dụ, bảng trên chỉ ra rằng: cô 1 thích
– chàng 3 hơn chàng 5,
– chàng 5 hơn chàng 2,
– chàng 2 hơn chàng 1,
– chàng 1 hơn chàng 4.
• Còn cột Dữ liệu ra chỉ ra rằng ta có thể ghép chàng 5 với cô 1, chàng 2 với cô 2,
chàng 4 với cô 3, chàng 3 với cô 4, và chàng 1 với cô 5 để các cuộc hôn nhân đều bền vững. 2
Algorithm 1: Thuật toán Gale-Shapley
Khởi tạo mọi chàng trai m ∈ M và mọi cô gái w ∈ W là độc thân;
while có một chàng trai m độc thân và vẫn chưa đính hôn với cô gái nào do
Chọn chàng trai m này;
Xét w là cô gái m thích nhất trong danh sách những cô mà m chưa đề nghị cưới;
if w là độc thân then (m, w) đính hôn; else
/* w hiện tại đang đính hôn với m′ */
if w thích m′ hơn m then
m lại trở thành độc thân; else
/* w thích m hơn m′ */
(m, w) đính hôn với nhau;
m′ trở thành độc thân;
return tập S gồm các cặp đính hôn; 3