

















Preview text:
Bài tập 11 Câu hỏi 1
Nén dữ liệu thường sử dụng trong lưu trữ và truyền dữ liệu. Giả sử bạn muốn dùng nén dữ liệu
kết hợp với mã hóa. Lựa chọn nào dưới đây có có ý nghĩa nhất:
1. Nén sau đó mã hóa.
2. Mã hóa sau đó nén.
3. Thứ tự không quan trọng – không trường hợp nào nén được dữ liệu.
4. Thứ tự không quan trọng – cả hai đều tốt. Câu hỏi 2
Giả sử bạn biết mã hóa của thông điệp “attack at dawn” dùng one time pad encryption là 6c73d5240a948c86981bc294814d
(bản rõ ở dạng mã ASCII 8-bit và bản mã được viết ở dạng hexa). Bản mã của thông điệp "attack
at dusk"với cùng khóa OTP là gì ? Câu hỏi 3
Xét G : {0, 1}s → {0, 1}n là một PRG an toàn. Những PRG nào dưới đây cũng an toàn (có thể có nhiều đáp án đúng):
G0(k) = G(0)
G0(k) = G(k ⊕ 1s)
G0(k) = G(k)
0 (ở đây ký hiệu phép ghép)
G0(k) = reverse(G(k)) với reverse(x ) là ảnh gương của xâu x , có nghĩa rằng bit đầu của x
là bit cuối của reverse(x), bit thứ hai của x là bit thứ hai tính từ cuối của reverse(x),. . . . Câu hỏi 4
Xét G : K → {0, 1}n là một PRG an toàn. Ta định nghĩa G0(k ) = ) ^ ) 1, k2 G(k1 G(k2
với V là phép toán AND bit. Xét statistic test A trên {0, 1}n định nghĩa dưới đây:
A(x) outputs LSB(x), là bit phải nhất của x. Lợi thế Adv [
PRG A, G0] bằng bao nhiêu ? Bạn có thể giả sử rằng LSB(G(k)) bằng 0 với đúng một
nửa số seed k trong K.
1https://class.coursera.org/crypto-012/ 1 Câu hỏi 5
Xét (E, D) là một hệ mã (one-time) semantically secure với không gian khóa K = {0, 1}`. Một
ngân hàng mong muốn tách khóa giải mã k thuộc K = {0, 1}` thành hai khóa p1 và p2 sao cho
để giải mã bắt buộc cần cả hai khóa. Khóa p1 có thể đưa cho một nhân viên và p2 cho một nhân
viên khác, và cả hai người phải cùng tham gia thì quá trình giải mã mới có thể tiến hành.
Ngân hàng sinh ngẫu nhiên khóa k =
1 thuộc {0, 1}` và đặt k0 ← k ⊕ k k. 1
1. Chú ý rằng k1 ⊕ k01
Ngân hàng có thể đưa k1 cho một nhân viên và k0 cho nhân viên khác. Cả hai phải có mặt thì 1
quá trình giải mã mới tiến hành được bởi vì bản thân mỗi khóa không chứa thông tin về khóa bí
mật k (chú ý rằng mỗi phần là một one-time pad encryption của k).
Bây giờ, giả sử ngân hàng muốn tách k thành ba phần p1, p2, p3 sao cho chỉ cần hai trong số ba
khóa là có thể giải mã được. Việc này đảm bảo rằng dù một nhân viên bị ốm thì việc giải mã vẫn
có thể tiến hành. Để làm điều này, ngân hàng sinh ngẫu nhiên hai cặp (k ) ) 1, k0 và (k như trên 1 2, k02 sao cho k = = 1 ⊕ k0 k
k. Ngân hàng nên gán các phần thế nào để chỉ cần hai phần vẫn có 1 2 ⊕ k02
thể giải mã được khóa k, nhưng chỉ có một phần thì không thể ? 1. p = ( ) = ( ) = ( ) 1 k1, k2 , p2 k1, k2 , p3 k02 2. p = ( ) = ( ) = ( ) 1 k1, k2 , p2 k2, k0 , p k0 2 3 2 3. p = ( ) = ( ) = ( ) 1 k1, k2 , p2 k0 , p k0 1 3 2 4. p = ( ) = ( ) = ( ) 1 k1, k2 , p2 k0 , k , p k0 1 2 3 2 5. p = ( ) = ( ) = ( ) 1 k1, k2 , p2 k0 , k0 , p k0 1 2 3 2 Câu hỏi 6
Xét M = C = K = {0, 1, 2, . . . , 255} và xét hệ mã sau đây định nghĩa trên (K, M, C):
E(k, m) = m + k (mod 256) ;
D(k, c) = c − k (mod 256) .
Hệ mã này có phải là bí mật tuyệt đối không? Câu hỏi 7
Xét (E, D) là một hệ mã (one-time) semantically secure với không gian bản rõ và bản mã đều là
{0, 1}n. Sơ đồ mã hóa nào dưới đây là (one-time) semantically secure?
1. E0(k, m) = E(k, m) k
2. E0(k, m) = E(k, m) LSB(m)
3. E0( (k, k0), m) = E(k, m)
E (k0, m)
4. E0(k, m) = tính c ← E(k, m) và output c c
(tức là output c hai lần)
5. E0(k, m) = E(0n, m)
6. E0(k, m) = 0 E(k, m) (tức là thêm 0 vào đầu bản mã) 2 Câu hỏi 8
Ngành công nghiệp phim muốn bảo vệ nội dung số của các đĩa DVD. Chúng ta phát triển một
phương pháp để bảo vệ các đĩa Blu-ray gọi là AACS.
Giả sử tổng số đầu đọc DVD trên thế giới nhiều nhất là n (ví dụ n = 232). Ta xem n đầu đọc như
các nút lá của một cây nhị phân có độ cao log n. Mỗi nút trong cây nhị phân này chứa một khóa 2
AES k . Các khóa này được giữ bí mật khỏi người dùng và không đổi. Lúc sản xuất, mỗi đầu đọc i
DVD được gán một số seri i ∈ [0, n − 1]. Xét tập các nút S dọc theo đường đi từ gốc tới nút lá i i
trên cây nhị phân. Nhà sản xuất các đầu đọc DVD nhúng trong mỗi đầu đọc có số i một số khóa
gắn với nút trong tập S . Một đĩa DVD phim i
m được mã hóa bởi
E(kroot, k) E (k, m)
với k là khóa AES ngẫu nhiên, gọi là khóa nội dụng, và kroot là khóa gắn với gốc của cây. Bởi vì
mọi đầu đọc DVD đều có khóa kroot nên chúng có thể giải mã phim m. Ta gọi E(kroot, k) là header
và E(k, m) là body. Dưới đây, mỗi DVD header chứa nhiều bản mã của khóa nội dung k, mỗi bản
mã là mã hóa của khóa k dùng khóa k trong cây. i
Giả sử các khóa được nhúng trong đầu đọc DVD có số r bị lộ do hackers tấn công và bị đưa lên
Internet. Mục đích của bài tập này là chỉ ra cách để khi nhà sản xuất phim phân phối một đĩa
phim DVD mới, họ có thể mã hóa nội dung của DVD dùng nhiều header hơn một chút (chứa
khoảng log n khóa) sao cho mọi đầu đọc DVD, ngoại trừ đầu đọc có số r, có thể giải mã phim. 2
Thực ra, các hãng sản xuất phim sẽ loại bỏ đầu đọc có số r mà không ảnh hưởng đến các đầu đọc khác.
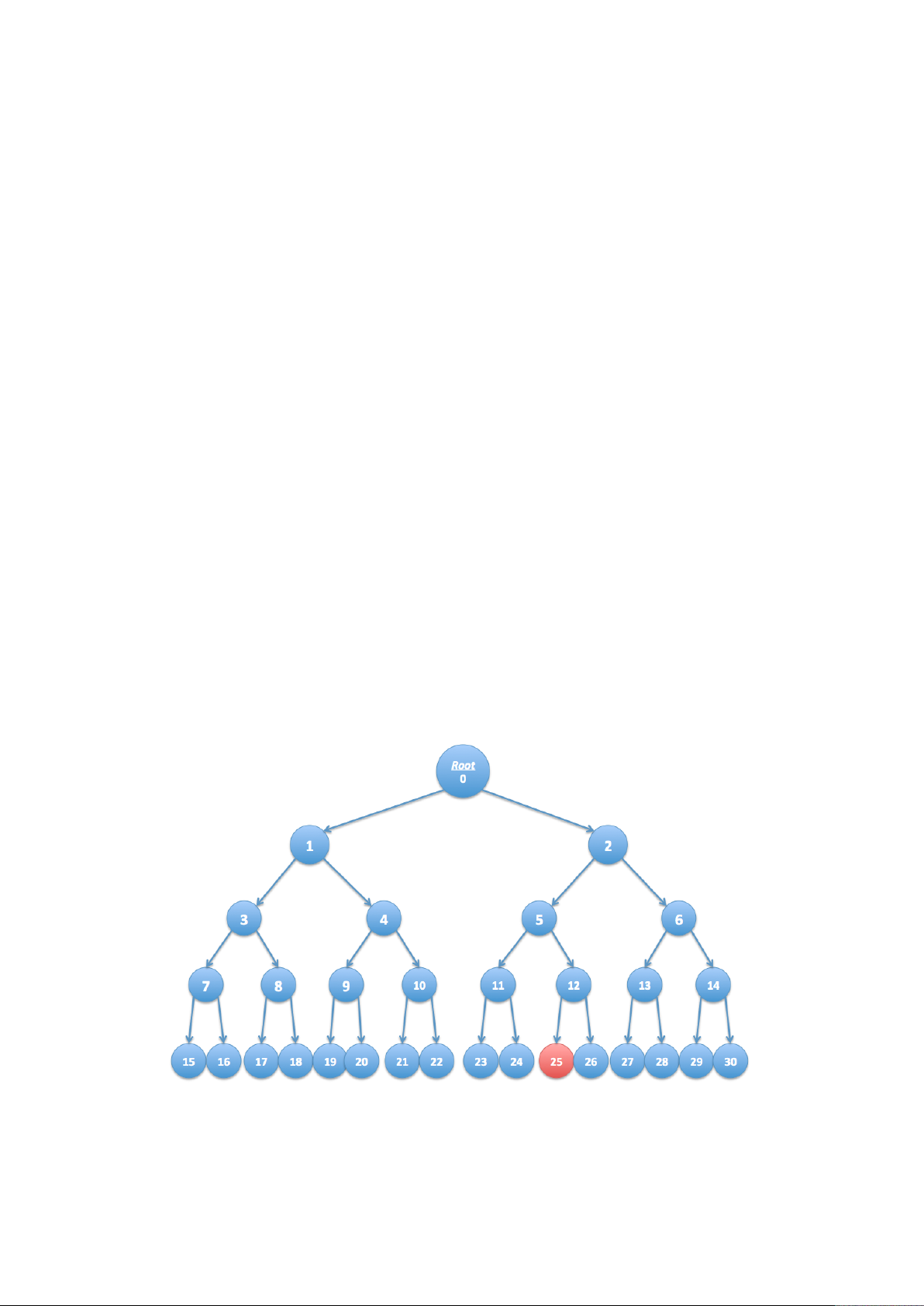
Như chỉ ra dưới đây, xét cây với n = 16 lá. Giả sử nút lá có nhãn 25 tương ứng với đầu đọc DVD
có khóa bị lộ. Hãy đánh dấu các khóa dưới đây mà khóa k cần mã hóa sao cho mọi đầu đọc khác
với đầu đọc 25 có thể giải mã DVD. Gợi ý: Chỉ bốn khóa cần mã. 6 1 15 25 11 8 26 16 3 Câu hỏi 9
Tiếp câu hỏi trước, nếu có n đầu đọc DVD, số khóa cần thiết dùng để mã hóa khóa nội dung k
nếu có đúng một đầu đọc DVD cần thu hồi? log n 2 n − 1 n/2 p 2 n Câu hỏi 10
Tiếp câu hỏi 8, giả sử các nút lá gán nhãn 16, 18, and 25 tương ứng với các khóa đầu đọc DVD bị
lộ. Đánh dấu tập nhỏ nhất các khóa cần dùng để mã hóa khóa nội dung k sao cho mọi đầu đọc
khác các đầu đọc 16, 18, 25 có thể giải mã DVD. Gợi ý: Chỉ cần sáu khóa. 14 15 26 23 4 17 21 0 6 11 4 Homework 21 Câu hỏi 1
Xét năm sự kiện sau. Hãy liệt kê các sự kiện này theo thứ tự từ sự kiện có xác suất xuất hiện
nhiều nhất đến ít nhất?
1. Chọn một khóa ngẫu nhiên AES 128-bit đúng ngay lần đầu tiên.
2. Thắng sổ xô với 1 triệu người chơi (xác suất là 1/106).
3. Xác suất thắng sổ xố với 1 triệu người chơi những 5 lần liên tiếp (xác suất là (1/106)5).
4. Xác suất thắng sổ xố với 1 triệu người chơi những 6 lần liên tiếp.
5. Xác suất thắng sổ xố với 1 triệu người chơi những 7 lần liên tiếp. Câu hỏi 2
Giả sử rằng bằng cách sử dụng phần cứng rẻ tiền, bạn có thể xây dựng một máy tính khoảng
$200 mà có thể tính toán vét cạn khoảng 1 tỷ khóa AES mỗi giây. Giả sử một tổ chức muốn tấn
công tìm kiếm vén cạn để tìm một khóa AES 128-bit và sẵn sàng chi 4 nghìn tỷ đô la ($4 ∗ 1012)
để mua các máy này (đây là ngân sách hàng năm của Hoa Kỳ). Với các máy tính này, tổ chức này
mất bao lâu thì có thể tìm được một khóa AES 128-bit bằng cách vét cạn? Bỏ qua các chi phí bổ
sung như điện và bảo trì.
1. Nhiều hơn một triệu năm nhưng ít hơn một tỷ (109) năm.
2. Nhiều hơn một tháng nhưng chưa đầy một năm.
3. Nhiều hơn 100 năm nhưng chưa đầy một triệu năm.
4. Nhiều hơn một ngày nhưng ít hơn một tuần.
5. Nhiều hơn một tỷ (109) năm. Câu hỏi 3
Xét PRF an toàn F : {0, 1}n × {0, 1}n → {0, 1}n (cụ thể, một PRF với không gian khóa, không gian
đầu vào, không gian đầu ra đều là {0, 1}n và giả sử n = 128. PRF nào dưới đây là an toàn (có thể
có nhiều hơn một câu trả lời đúng):
1. F 0(k, x) = k L x
2. F 0(k, x) = reverse(F(k, x)) với reverse( y) là ảnh gương của xâu y, tức là bit đầu của y là bit
cuối của của reverse( y), bit thứ hai của y là bit thứ hai tính từ cuối của reverse( y), và v.v.
3. F 0(k, x) = F(k, x) L F(k, x ⊕ 1n).
4. F 0(k, x) = F(k, x)
0 (ở đây ký hiệu phép ghép) 5. F 0((k )
1, k2 , x ) = F (k1, x )
F (k2, x) (ở đây ký hiệu phép ghép)
1https://class.coursera.org/crypto-012/ 1
6. F 0(k, x) = F(k, x)[0, . . . , n − 2] (i.e., F0(k, x) đạt được bằng cách bỏ đi bit cuối của F(k, x)) Câu hỏi 4
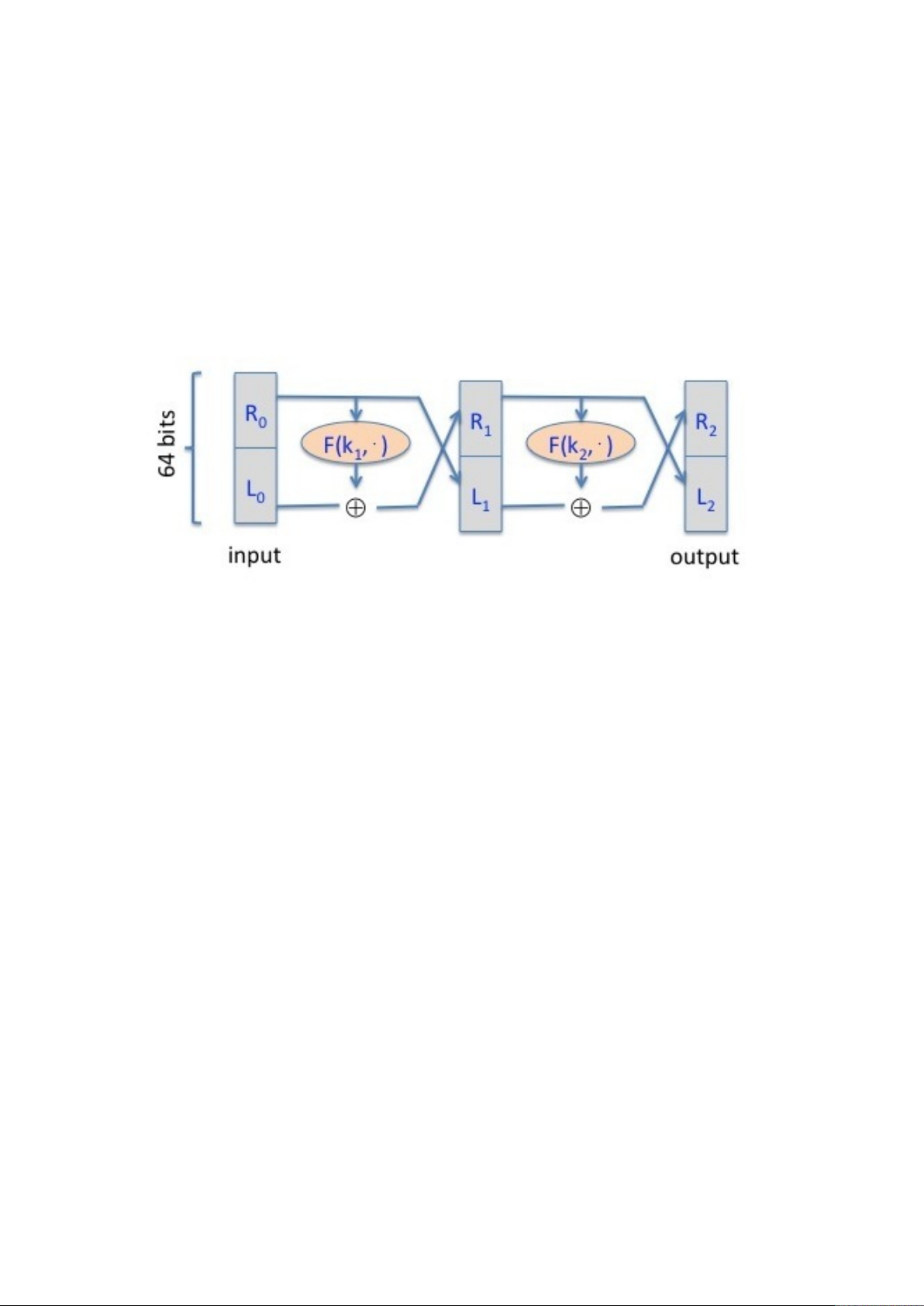
Nhắc lại rằng định lý Luby-Rackoff thảo luận trong Lecture 3.2 khẳng định rằng việc áp dụng
mạng Feistel ba vòng cho một PRF an toàn cho ta một hệ mã khối an toàn. Ta cùng xem chuyện
gì xảy ra nếu ta chỉ sử dụng mạng Feistel hai vòng. Xét F : K × {0, 1}32 → {0, 1}32 là một PRF an
toàn. Nhắc lại rằng mạng Feistel 2-vòng được định nghĩa bởi PRP F2 : K2 × {0, 1}64 → {0, 1}64. Ở
đây R0 là 32 bits phải của 64-bit đầu vào và L0 là 32 bit trái.
Một trong các dòng dưới đây là output của PRP F2 này dùng một khóa ngẫu nhiên, trong khi ba
output khác là output của một hoán vị ngẫu nhiên thật f : {0, 1}64 → {0, 1}64. Mọi dãy 64-bit
outputs đều được mã hóa như các xâu hex độ dài 16. Bạn có thể chỉ ra output của PRP này
không? Chú ý rằng, vì bạn có thể phân biệt được ouput của F2 với ngẫu nhiên, nên F2 không phải
là mã khối an toàn. Đây chính là cái mà chúng tôi muốn chỉ ra.
Gợi ý: Đầu tiên ta nên tìm cách nhận biết được mẫu có phải là xor của F ( (
2 ·, 064) và F2 ·, 132032).
Sau đó cố gắng nhận biết mẫu này trong output.
1. Với input 064 thì output là "5f67abaf 5210722b". Với input 132032 thì output là "bbe033c0 0bc9330e".
2. Với input 064 thì output là "2d1cfa42 c0b1d266". Với input 132032 thì output là "eea6e3dd b2146dd0".
3. Với input 064 thì output là "e86d2de2 e1387ae9". Với input 132032 thì output là "1792d21d b645c008".
4. Với input 064 thì output là "4af53267 1351e2e1". Với input 132032 thì output là "87a40cfa 8dd39154". Câu hỏi 5
Nonce-based CBC. Nhắc lại rằng trong lecture 4.4 chúng ta đã nói rằng nếu người ta muôn dùng
mã hóa CBC với nonce không ngẫu nhiên duy nhất thì nonce đầu tiên phải được mã hóa với một
khóa PRP độc lập và kết quả sau đó được dùng như CBC IV. Ta cùng xem chuyện gì xảy ra nếu ta
mã hóa nonce với cùng khóa PRP như khóa dùng cho mã hóa CBC. 2
Xét F : K × {0, 1}` → {0, 1}` là một PRP an toàn, ví dụ, ` = 128. Xét n là một nonce và giả sử
người ta mã hóa thông điệp m bằng cách: đầu tiên tính I V = F(k, n) và sau đó dùng IV này trong
mã hóa CBC dùng F (k, ·). Để ý rằng cùng khóa k được dùng cho tính IV và cho mã hóa CBC. Ta
chứng minh rằng kết quả là hệ thống không phải là một nonce-based CPA an toàn.
Kẻ tấn công bắt đầu bằng cách hỏi mã hóa của hai khối m = (0`, 0`) với nonce n = 0`. Anh
ta nhận lại được hai khối bản mã (c )
0, c1 . Quan sát rằng, theo định nghĩa của CBC ta biết rằng c = ) = L 1
F (k, c0 . Tiếp theo, kẻ tấn công hỏi mã hóa của một khối thông điệp m1 c0 c1 với nonce
n = c0. Anh ta nhận lại được một khối bản mã c0 . 0
Quan hệ nào dưới đây là đúng với c0, c1, c00? Để ý rằng quan hệ này giúp kẻ tấn công thắng trong
nonce-based CPA game với lợi thế 1. 1. c = 1 0` 2. c = L 1 c0 c00 3. c = 1 c00 4. c = L 0 c1 c00 Câu hỏi 6
Xét thông điệp m gồm ` khối AES (ví dụ ` = 100). Alice mã hóa m dùng CBC mode và truyền
bản mã kết quả tới Bob. Do mạng lỗi, khối bản mã số `/2 bị mất trong khi truyền. Mọi bản mã
khác được truyền và nhận đúng. Khi Bob giải mã bản mã nhận được, bao nhiêu khối bản rõ sẽ bị mất? Câu hỏi 7
Xét thông điệp m bao gồm ` khối AES (ví dụ ` = 100). Alice mã hóa m dùng randomized counter
mode và truyền bản mã kết quả tới Bob. Do mạng lỗi, bản mã số `/2 bị mất trong khi truyền.
Mọi khối bản mã khác được truyền và nhận đúng. Khi Bob giải mã bản mã nhận được, bao nhiêu khối bản rõ bị mất? Câu hỏi 8
Nhắc lại rằng hệ mã không giấu đầy đủ thông tin về độ dài của thông điệp truyền. Lộ thông tin
về độ dài của web requests được dùng để nghe trộm thông tin trên traffic HTTPS tới một số trang
web, như thông tin chuẩn bị thuế, Google searches, và trang sức khỏe. Giả sử rằng kẻ tấn công
nhận được một gói tin mà anh ta biết rằng phần nội dung gói tin được mã hóa dùng AES trong
CBC mode với IV ngẫu nhiên. Nội dung gói tin được mã hóa là 128 bytes. Thông điệp nào dưới
đây có thể đoán là giải mã của nội dung gói tin:
1. ’The most direct computation would be for the enemy to try all 2^r possible keys, one by one.’
2. ’If qualified opinions incline to believe in the exponential conjecture, then
I think we cannot afford not to make use of it.’ 3
3. ’We see immediately that one needs little information to begin to break down the process.’
4. ’In this letter I make some remarks on a general principle relevant to enciphering in general and my machine.’ Câu hỏi 9
Xét R := {0, 1}4 và xét PRF F : R5 × R → R được định nghĩa như sau: t = k[0] for i = 1 to 4 do
F (k, x) :=
if (x[i − 1] == 1) t = t ⊕ k[i] output t
Có nghĩa rằng, khóa là k = (k[0], k[1], k[2], k[3], k[4]) trong R5 và giá trị của hàm tại, ví dụ,
0101 được định nghĩa bởi F (k, 0101) = k[0] ⊕ k[2] ⊕ k[4].
Với một khóa ngẫu nhiên k mà bạn không biết, bạn nhận ra rằng
F (k, 0110) = 0011 and F(k, 0101) = 1010 and F(k, 1110) = 0110.
Giá trị của F (k, 1101) là gì? Để ý rằng vì bạn có thể dự đoán hàm tại một điểm mới, hàm này
không phải là PRF an toàn. 4 Bài tập 31 Câu hỏi 1
Giả sử một hệ MAC (S, V ) được dùng để bảo vệ các file trong hệ thống bằng cách thêm một MAC
tag vào mỗi file. Thuật toán ký MAC S được áp dụng trên nội dung của file và không có gì khác.
Kiểu tấn công giả mạo nào dưới đây mà hệ thống này không thể chống được?
1. Hoán đổi hai file trong hệ thống file.
2. Thay thế tag và nội dung của một file bằng tag và nội dung của file đặt trên máy tính khác
cũng được bảo vệ bởi cùng hệ MAC, nhưng với khóa khác.
3. Thay thế nội dung của một file với việc ghép hai file trên hệ thống.
4. Xóa byte cuối của nội dung file. Câu hỏi 2
Xét một hệ MAC an toàn (S, V ) trên (K, M, T ) với M = {0, 1}n và T = {0, 1}128 (cụ thể, không
gian khóa là K, không gian thông điệp là {0, 1}n, và không gian tag là {0, 1}128). MAC nào dưới
đây là MAC an toàn: (ở đây, ta dùng ký hiệu là ghép xâu).
1. S0(k, m) = S(k, m[0, . . . , n − 2] 0) và
V 0(k, m, t) = V (k, m[0, . . . , n − 2] 0, t)
2. S0(k, m) = S(k, m)[0, . . . , 126] và
V 0(k, m, t) = V (k, m, t0) hoặc V (k, m, t1)
(i.e., V 0(k, m, t) outputs “1” nếu hoặc t0 hoặc t1 là tag hợp lệ cho m).
3. S0(k, m) = S(k, mm) và
V 0(k, m, t) = V (k, mm, t).
¨V (k, m, t) if m 6= 0n
4. S0(k, m) = S(k, m)
và V 0(k, m, t) = “1” otherwise
5. S0(k, m) = S(k, m) và
V 0(k, m, t) = V (k, m, t) or V (k, m ⊕ 1n, t)
(cụ thể, V 0(k, m, t) outputs “1” nếu t là một tag hợp lệ cho hoặc m hoặc m ⊕ 1n). 6. S0((k ) 1, k2 , m) =
S(k1, m), S(k2, m) và V 0 (k ) ) = ) )
1, k2 , m, (t1, t2
V (k1, m, t1 and V (k2, m, t2
(cụ thể, V 0 (k ) )
1, k2 , m, (t1, t2
outputs “1” nếu cả t1 và t2 đều là tag hợp lệ). Câu hỏi 3
Nhắc lại rằng ECBC-MAC dùng một IV cố định (trong bài giảng chúng ta đơn giản đặt IV bằng
0). Giả sử nếu ta chọn IV ngẫu nhiên cho mỗi thông điệp bằng cách ký và kèm IV trong tag. Nói
cách khác, S(k, m) := r, ECBC ( (
r k, m) ở đó ECBCr k, m) tham chiếu đến hàm ECBC dùng r như
IV. Thuật toán kiểm tra V nhận k, thông điệp m, và tag (r, t) outputs “1” nếu t = ECBC ( r k, m) và
outputs “0” trong trường hợp ngược lại.
1https://class.coursera.org/crypto-012/ 1
Hệ MAC xây dựng theo cách này là không an toàn. Kẻ tấn công có thể truy vấn cho thông điệp
kích thước 1-block m và nhận được tag (r, t). Anh ta, sau đó, sinh ra thông điệp giả mạo như sau:
(ta giả sử rằng hệ mã khối sử dụng là hệ trên khối n-bit)
1. Tag (r, t ⊕ r) là một tag hợp lệ cho thông điệp kích thước 1-block 0n.
2. Tag (m ⊕ t, t) là một tag hợp lệ cho thông điệp kích thước 1-block 0n.
3. Tag (r ⊕ 1n, t) là tag hợp lệ cho thông điệp kích thước 1-block m ⊕ 1n.
4. Tag (m ⊕ t, r) là tag hợp lệ cho thông điệp kích thước 1-block 0n. Câu hỏi 4
Giả sử Alice đang phát quảng bá (broadcasting) các gói tin cho 6 người B1, . . . , B6. Những người
nhận nên đảm bảo rằng các gói tin anh ta nhận được gửi bởi Alice.
Alice quyết định sử dụng MAC. Giả sử Alice và B1, . . . , B6 cùng chia sẻ một khóa bí mật k. Alice
tính tag cho mọi gói tin cô ấy gửi sử dụng khóa k. Mỗi người dùng B kiểm tra tag khi nhận gói i
tin và loại bỏ gói tin nếu tag không hợp lệ. Alice để ý rằng sơ đồ này không an toàn bởi vì người
dùng B1 có thể dùng khóa k để gửi tag hợp lệ cho người dùng B1, . . . , B6 và anh ta có thể lừa mọi
người nghĩ rằng các gói tin này được gửi từ Alice.
Vì vậy, Alice đặt một tập gồm 4 khóa bí mật S = {k1, . . . , k4}. Cô ấy đưa cho mỗi người dùng Bi
một tập con Si ⊆ S khóa. Khi Alice truyền một gói tin cô ấy thêm 4 tags vào gói tin bằng cách
tính tag tương ứng với 4 khóa cô ấy có. Khi người dùng B nhận một gói tin, anh ấy chấp nhận nó i
là đúng nếu và chỉ nếu mọi tag tương ứng với các khóa trong S của anh ấy là đúng. Ví dụ, nếu i
người dùng B1 được đưa {k1, k2} anh ấy sẽ chấp nhận một gói tin đến chỉ nếu cả tag đầu tiên và
tag thứ hai đều hợp lệ. Để ý rằng B1 không thể kiểm tra tính hợp lệ của tag thứ 3 hoặc thứ 4 vì
anh ta không có k3 hoặc k4.
Alice nên gán khóa cho 6 người dùng thế nào để không có người dùng nào có thể mạo danh Alice
để gửi tin cho người dùng khác? 1. S = = = = = = 1
{k1, k2}, S2 {k1}, S3
{k1, k4}, S4
{k2, k3}, S5
{k2, k4}, S6 {k3, k4} 2. S = = = = = = 1
{k1, k2}, S2
{k1, k3}, S3
{k1, k4}, S4
{k2, k3, k4}, S5
{k2, k3}, S6 {k3, k4} 3. S = = = = = = 1
{k1, k2}, S2
{k1, k3}, S3
{k1, k4}, S4
{k2, k3}, S5
{k2, k4}, S6 {k3, k4} 4. S = = = = = = 1
{k1, k2}, S2
{k1, k3}, S3
{k1, k4}, S4
{k2, k3}, S5
{k2, k4}, S6 {k4} Câu hỏi 5
Xét CBC MAC với hàm mã hóa dựa trên AES. Giả sử rằng ta tính tag cho một thông điệp dài m
bao gồm n khối AES. Xét m0 là thông điệp dài n-block sinh từ m bằng cách đảo bit cuối của m
(cụ thể, nếu bit cuối của m là b thì bit cuối của m0 là b ⊕ 1). Cần bao nhiêu lần gọi AES để có thể
tính tag cho m0 từ tag của m và khóa MAC? (trong câu hỏi này, ta có thể bỏ qua việc padding mà
đơn giản giả sử rằng độ dài thông điệp là chia hết cho kích thước khối của AES) 1. 4 3. 2 2. 5 4. n 2 Câu hỏi 6
Xét H : M → T là một hàm băm kháng xung đột. Hàm băm nào dưới đây cũng là kháng xung
đột: (như thường lệ, ta dùng ký hiệu cho phép toán ghép xâu).
1. H0(m) = H(mm)
2. H0(m) = H(m) ⊕ H(m)
3. H0(m) = H(|m|) (cụ thể, hash độ dài của m)
4. H0(m) = H(m) L H(m ⊕ 1|m|) (với m ⊕ 1|m| là phần bù của m)
5. H0(m) = H(m) H (m)
6. H0(m) = H(0)
7. H0(m) = H(m) H (0) Câu hỏi 7
Giả sử rằng H1 và H2 là các hàm băm kháng xung đột ánh xạ các input trong tập M vào {0, 1}256.
Mục đích của chúng ta là chỉ ra rằng hàm H ( (
2 H1 m)) cũng là kháng xung đột. Chúng ta chứng
minh bằng phản chứng như sau: giả sử H ( (
2 H1 ·)) không kháng xung đột, có nghĩa rằng, ta có
x 6= y thỏa mãn H ( ( ( (
2 H1 x )) = H2 H1 y )). Ta xây dựng một xung đột hoặc cho H1 hoặc cho H2.
Điều này chỉ ra rằng nếu H ( (
1 và H2 là kháng xung đột thì H2 H1 ·)) cũng kháng xung đột. Khẳng
định nào dưới đây là đúng:
1. Hoặc x, H ( (
1 y ) là xung đột cho H2 hoặc H2 x ), y là xung đột cho H1.
2. Hoặc x, y là xung đột cho H ( (
2 hoặc H1 x ), H1 y ) là xung đột cho H1.
3. Hoặc x, y là xung đột cho H ( (
1 hoặc H1 x ), H1 y ) là xung đột cho H2. 4. Hoặc H ( (
2 x ), H2 y ) là xung đột cho H1 hoặc x , y là xung đột cho H2. Câu hỏi 8
Trong câu hỏi dưới đây, bạn được hỏi tìm xung đột cho hai hàm nén: f (
1 x , y ) = AES( y, x ) M y and f (
2 x , y ) = AES( x , x ) M y
với AES(x, y) là mã hóa AES-128 của y dưới khóa x.
Mục đích của bạn là tìm hai cặp phân biệt (x ) ) ) ) ( ) =
1, y1 , ( x2, y2 , ( x3, y3 , ( x4, y4
thỏa mãn f1 x1, y1 f ( ) ( ) = ( ) 1 x2, y2
and f2 x3, y3
f2 x4, y4 . Nói cách khác, hai cặp đầu tiên là xung đột cho f1 và hai
cặp sau là xung đột cho f2. Câu hỏi 9
Xét H : M → T là một hàm băm ngẫu nhiên với |M| |T | (cụ thể kích thước của M lớn hơn kích
thước của T ). Trong bài giảng ta đã chỉ ra rằng việc tìm xung đột cho H có thể thực hiện trong 3
O |T |1/2 lần lấy mẫu ngẫu nhiên của H. Bao nhiêu mẫu ngẫu nhiên cần lấy cho đến khi ta đạt
được ba xung đột, cụ thể, là ba xâu x, y, z trong M sao cho H(x) = H( y) = H(z)?
1. O |T |1/3 3. O |T |
2. O |T |1/2
4. O |T |2/3 4 Bài tập 41 Câu hỏi 1
Một kẻ tấn công bắt được bản mã sau (hex encoded):
20814804c1767293b99f1d9cab3bc3e7 ac1e37bfb15599e5f40eef805488281d
Anh ta biết rằng bản rõ là thông điệp “Pay Bob 100$” (ở dạng ASCII, bỏ quả nháy kép). Anh ta
cũng biết rằng hệ mã được dùng là CBC với IV ngẫu nhiên cùng với hệ mã khối AES. Hãy chỉ ra
rằng kẻ tấn công có thể thay đổi bản mã để khi giải mã trở thành “Pay Bob 500$”. Bản mã (ở
dạng hexa) là gì ? Điều này chỉ ra rằng CBC không đảm bảo tính toàn vẹn. Câu hỏi 2
Xét (E, D) là một hệ mã với không gian khóa K, không gian thông điệp {0, 1}n và không gian bản
mã {0, 1}s. Giả sử (E, D) là hệ mã có xác thực. Hệ mã nào sau đây cũng có xác thực: (như thông
thường, ta sử dụng k để ký hiệu phép ghép xâu) 1. E0 (k ) = 1, k2 , m
E(k2, E(k1, m)) và ¨ D(k D0 (k ) =
1, D(k2, c))
nếu D(k2, c) 6= ⊥ 1, k2 , c ⊥ ngược lại
2. E0(k, m) = c ← E(k, m), output (c, c) và
¨ D(k, c ) nếu c = c D0(k, (c ) ) = 1 1 2 1, c2 ⊥ ngược lại
3. E0(k, m) = E(k, m), 0 và
D0(k, (c, b) ) = D(k, c)
4. E0(k, m) = E(k, m), E(k, m) và D0(k, (c ) ) = ) 1, c2 D(k, c1 Câu hỏi 3
Giả sử chúng ta cần xây dựng một ứng dụng để mã hóa nhiều thông điệp với cùng một khóa. Hệ
mã nào chúng ta nên sử dụng? (ta tạm thời bỏ quả vấn đề sinh và quản lý khóa)
1. sử dụng cài đặt chuẩn của một trong các hệ mã xác thực GCM, CCM, EAX or OCB. 2. tự cài đặt OCB
3. tự cài Encrypt-and-MAC
4. dùng cài đặt chuẩn của randomized counter mode.
1https://class.coursera.org/crypto-012/ 1 Câu hỏi 4
Xét (E, D) là hệ mã đối xứng với không gian thông điệp M (xem M chỉ bao gồm các thông điệp
ngắn, ví dụ 32 bytes). Ta định nghĩa hệ MAC (S, V ) cho các thông điệp trong M như sau:
¨1 nếu D(k, t) = m
S(k, m) := E(k, m) ;
V (k, m, t) := 0 ngược lại
Hệ mã (E, D) cần tính chất nào dưới đây để thỏa mãn hệ MAC trên an toàn?
1. an toàn ngữ nghĩa (semantic security) dưới chosen plaintext attack (CPA) 2. hệ mã xác thực
3. bí mật tuyệt đối
4. an toàn ngữ nghĩa Câu hỏi 5
Trong lecture 8.1 chúng ta đã thảo luận cách dẫn xuất các khóa phiên từ khóa bí mật. Vấn đề nảy
sinh khi khóa bí mật không phải ngẫu nhiên đều. Trong câu hỏi này chúng ta chứng minh rằng
dùng một PRF với một khóa ngẫu nhiên không đều có thể tạo ra giá trị ngẫu nhiên không đều.
Điều này chỉ ra rằng khóa phiên không thể dẫn xuất trực tiếp dùng khóa bí mật không đều làm
khóa trong PRF. Vì vậy người ta phải sử dụng hàm dẫn xuất khóa như HKDF.
Giả sử k là một khóa bí mật không đều được lấy mẫu từ không gian khóa {0, 1}256. Đặc biệt, k
được lấy mẫu từ tập mọi khóa ở đó cả 128 bit cao nhất đều bằng 0. Nói cách khác, k được chọn
ngẫu nhiên đều từ một tập con không gian khóa. Chính xác hơn,
¨1/2128 if MSB (c) = 0128
for all c ∈ {0, 1}256 : Pr[k = c] = 128 0 ngược lại
Xét F (k, x) là một PRF an toàn với không gian đầu vào {0, 1}256. Hàm nào dưới đây là PRF an
toàn khi k ngẫu nhiên đều trong {0, 1}256 nhưng không an toàn khi khóa được lấy mẫu từ phân
phối không đều như ở trên?
¨ F(k, x) nếu MSB (k) = 0128
1. F 0(k, x) = 128 0256 ngược lại
2. F 0(k, x) = F(k, x)
¨ F(k, x) nếu MSB (k) 6= 1128
3. F 0(k, x) = 128 0256 ngược lại
¨ F(k, x) nếu MSB (k) 6= 0128
4. F 0(k, x) = 128 1256 ngược lại Câu hỏi 6
Kịch bản nào dưới đây có thể chấp nhận để sử dụng hệ mã có xác thực đơn định(DAE) như SIV? 2
1. để mã hóa nhiều bản ghi trong một cơ sở dữ liệu với cùng một khóa khi cùng một bản ghi có
thể lặp lại nhiều lần.
2. khi các thông điệp có cấu trúc đủ đảm bảo rằng mọi thông điệp được mã hóa là duy nhất.
3. khi một thông điệp cố định được mã lặp lại dùng cùng một khóa.
4. để mã hóa riêng nhiều gói tin trong một hội thoại (voice conversation) với cùng một khóa. Câu hỏi 7
Xét E(k, x) là một hệ mã khối an toàn. Xét hệ mã tweakable block cipher sau đây: E0 (k ) =
1, k2 , t , x
E(k1, x) M E(k2, t).
Đây có là tweakable block cipher an toàn?
1. có, ta đã giả sử rằng E là mã khối an toàn.
2. không vì với t 6= t0 ta có E0((k ) ) ) )
1, k2 , t , 0) M E0((k1, k2 , t 0, 1) = E0((k1, k2 , t 0, 1) M E0((k1, k2 , t 0, 0)
3. không vì với x 6= x0 ta có E0((k ) ) ) )
1, k2 , 0, x ) M E0((k1, k2 , 0, x ) = E0((k1, k2 , 0, x 0) M E0((k1, k2 , 0, x 0)
4. không vì với x 6= x0 ta có E0((k ) ) ) )
1, k2 , 0, x ) M E0((k1, k2 , 1, x ) = E0((k1, k2 , 0, x 0) M E0((k1, k2 , 1, x 0)
5. không vì với x 6= x0 và t 6= t0 ta có E0((k ) ) ) )
1, k2 , t , x ) M E0((k1, k2 , t 0, x ) = E0((k1, k2 , t , x 0) M E0((k1, k2 , t 0, x ) Câu hỏi 8
Trong lecture 8.5 chúng ta đã thảo luận về mã hóa bảo toàn định dạng (format preserving
encryption): một PRP trên miền {0, . . . , s − 1} với một số giá trị xác định trước của s. Nhắc lại
rằng cách xây dựng mà ta trình bày thực hiện trên hai bước, ở đó bước thứ hai hoạt động lặp lại
PRP cho đến khi output thuộc vào tập {0, . . . , s − 1}.
Giả sử ta cố gắng xây dựng một hệ mã bảo toàn định dạng cho credit card từ AES chỉ dùng bước
thứ hai. Có nghĩa rằng, ta bắt đầu với một PRP trên miền {0, 1}128 từ đó ta muốn xây dựng một
PRP trên miền1016. Nếu ta chỉ dùng bước (2), ta cần lặp (trung bình) AES bao nhiêu lần cho mỗi
lần tính PRP với trên 1016? 1. 2128
3. 2128/1016 ≈ 3.4 × 1022 2. 1016/2128 4. 4 3 Câu hỏi 9
Xét (E, D) là một tweakable block cipher an toàn. Ta định nghĩa MAC (S, V ) sau:
¨1 nếu E(k, m,0) = tag
S(k, m) := E(k, m, 0) ;
V (k, m, tag) := 0 ngược lại
Nói cách khác, thông điệp m được dùng như tweak và bản rõ đưa vào E luôn được đặt bằng 0.
Đây có phải là MAC an toàn? 1. có
2. phụ thuộc vào tweakable block cipher. 3. không Câu hỏi 9
Trong Lecture 7.6 chúng ta đã thảo luận về padding oracle attacks. Kiểu tấn công chọn bản mã
(chosen-ciphertext attacks) này có thể phá các cài đặt sai của sơ đồ MAC-then-encrypt. Xét hệ
thống cài đặt MAC-then-encrypt với mã hóa dùng CBC với random IV và AES như hệ mã khối.
Giả sử hệ thống bị tấn công bởi padding oracle attack. Một kẻ tấn công lấy được bản mã 64-byte c
(16 bytes đầu tiên của c là IV và 48 bytes còn lại là nội dung được mã). Kẻ tấn công cần chọn
bao nhiêu queries (trong trường hợp tồi nhất) để có thể giải mã toàn bộ 48 byte nội dung này?
Nhắc lại rằng padding oracle attacks chỉ giải mã một byte nội dung mỗi lần. 1. 12288 3. 12240 2. 256 4. 65536 4 Homework 51 Question 1
Consider the toy key exchange protocol using an online trusted 3rd party (TTP) discussed in
Lecture 9.1. Suppose Alice, Bob, and Carol are three users of this system (among many others)
and each have a secret key with the TTP denoted ka, kb, kc respectively. They wish to generate
a group session key kABC that will be known to Alice, Bob, and Carol but unknown to an
eavesdropper. How would you modify the protocol in the lecture to accomodate a group key
exchange of this type? (note that all these protocols are insecure against active attacks)
1. Alice contacts the TTP. TTP generates a random kABC and sends to Alice
E(ka, kABC), ticket1 ← kABC, ticket2 ← kABC
Alice sends ticket1 to Bob and ticket2 to Carol.
2. Alice contacts the TTP. TTP generates random kABC and sends to Alice
E(ka, kABC),
ticket1 ← E(kb, kABC),
ticket2 ← E(kc, kABC).
Alice sends ticket1 to Bob and ticket2 to Carol.
3. Alice contacts the TTP. TTP generates a random kABC and sends to Alice
E(ka, kABC),
ticket1 ← E(kb, kABC),
ticket2 ← E(kc, kABC)
Alice sends kABC to Bob and kABC to Carol.
4. Alice contacts the TTP. TTP generates a random kAB and a random kAC. It sends to Alice
E(ka, kAB),
ticket1 ← E(kb, kAB),
ticket2 ← E(kc, kAC).
Alice sends ticket1 to Bob and ticket2 to Carol. Question 2
Let G be a finite cyclic group (e.g. G = Z∗p) with generator g. Suppose the Diffie-Hellman
function DHg(gx, gy) = gxy is difficult to compute in G. Which of the following functions is
also difficult to compute: As usual, identify the f below for which the contra-positive holds: if
f (·, ·) is easy to compute then so is DHg(·, ·). If you can show that then it will follow that if
DHg is hard to compute in G then so must be f . 1.
f (gx, gy) = gxy+1 2.
f (gx, gy) = gx(y+1) 3.
f (gx, gy) = (g2)x+y √ 4.
f (gx, gy) = ( g)x+y
1https://class.coursera.org/crypto-012/ 1 Question 3
Suppose we modify the Diffie-Hellman protocol so that Alice operates as usual, namely chooses
a random a in {1, . . . , p − 1} and sends to Bob A ← ga. Bob, however, chooses a random b in
{1,..., p − 1} and sends to Alice B ← g1/b. What shared secret can they generate and how would they do it?
1. secret = gab. Alice computes the secret as Ba and Bob computes Ab.
2. secret = ga/b. Alice computes the secret as Ba and Bob computes A1/b.
3. secret = ga/b. Alice computes the secret as B1/b and Bob computes Aa.
4. secret = gab. Alice computes the secret as B1/a and Bob computes Ab. Question 4
Consider the toy key exchange protocol using public key encryption described in Lecture 9.4.
Suppose that when sending his reply c ← E(pk, x) to Alice, Bob appends a MAC t := S(x, c) to
the ciphertext so that what is sent to Alice is the pair (c,t). Alice verifies the tag t and rejects
the message from Bob if the tag does not verify. Will this additional step prevent the man in the
middle attack described in the lecture?
1. it depends on what MAC system is used.
2. it depends on what public key encryption system is used. 3. yes 4. no Question 5
The numbers 7 and 23 are relatively prime and therefore there must exist integers a and b such
that 7a + 23b = 1. Find such a pair of integers (a, b) with the smallest possible a > 0. Given
this pair, can you determine the inverse of 7 in Z23? Question 6
Solve the equation 3x + 2 = 7 in Z19. Question 7
How many elements are there in Z∗ ? 35 2 Question 8
How much is 210001 mod 11? (please do not use a calculator for this) Question 9
While we are at it, how much is 2245 mod 35?
Hint: use Euler’s theorem (you should not need a calculator) Question 10
What is the order of 2 in Z∗ ? 35 Question 11
Which of the following numbers is a generator of Z∗ ? 13 1. 7,
⟨7⟩ = {1,7,10,5,9,11,12,6,3,8,4,2} 2. 5,
⟨5⟩ = {1,5,12,8} 3. 9,
⟨9⟩ = {1,9,3} 4. 2,
⟨2⟩ = {1,2,4,8,3,6,12,11,9,5,10,7} 5. 3,
⟨3⟩ = {1,3,9} Question 12
Solve the equation x2 + 4x + 1 = 0 in Z23. Use the method described in lecture 9.3 using the quadratic formula. Question 13
What is the 11th root of 2 in Z19? (i.e. what is 21/11 in Z19)
Hint: observe that 11−1 = 5 in Z18. Question 14
What is the discete log of 5 base 2 in Z13? (i.e. what is Dlog2(5))
Recall that the powers of 2 in Z13 are
⟨2⟩ = {1,2,4,8,3,6,12,11,9,5,10,7} 3 Question 15
If p is a prime, how many generators are there in Z∗p? 1. (p − 1)/2 2. p − 1 3. φ(p) 4. φ(p − 1) 4




