
















Preview text:
CÁC DẠNG BÀI TẬP BÀI PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Dạng 1: Xác định các yếu tố cơ bản của đường thẳng trong không gian. Vị trí tương đối trong không gian
Phương pháp: Trong không gian Oxyz , vectơ u = ( ; a ;
b c) 0 là vectơ chỉ phương của đường thẳng
thì vecto m = k.u cũng là vectơ chỉ phương của đường thẳng .
x = x + at 0
Phương trình tham số : y = y + bt t
có vectơ chỉ phương u = (a;b;c) (hệ số trước t). 0 ( )
z = z + ct 0 − − − Phương trình chính tắc x x y y z z 0 0 0 : = =
có vectơ chỉ phương u = (a;b;c) (hệ số ở mẫu). a b c Nhận xét:
■ Với phương trình tham số lấy đúng thứ tự hệ số trước tham số t .
■ Với phương trình chính tắc lấy hệ số dưới mẫu.
■ Nếu giả thiết chưa đúng cấu trúc, ta phải sắp xếp lại rồi mới lấy hệ số.
A. BÀI TẬP TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Trong không gian với hệ tọa độ Oxyz , vectơ nào là một vectơ chỉ phương của đường thẳng có x − y − phương trình 1 3 3 = = z ? 3 2 1 A. 3 2 a = 3; ;1 .
B. a = (9;2;3) . C. a = (3;2; ) 1 .
D. a = 3; ; −1 . 2 3 Lời giải x − y − − − Ta có: 1 3 3 = =
z x 1 y z 3 = = 3 2 1 3 2 1 − 3
Một vectơ chỉ phương của đường thẳng có phương trình là 2 a = 3; ; −1 . 3
Câu 2: Trong không gian Oxyz , cho đường thẳng D vuông góc với mặt phẳng ( ) có phương trình
x + 2z + 3 = 0 . Một vectơ chỉ phương của D là
A. a = (1;0;2) .
B. a = (2;−1;0) .
C. a = (1;2;3) .
D. a = (2;0;− ) 1 . Lời giải
Đường thẳng D vuông góc với mặt phẳng ( ) : x + 2z + 3 = 0 có một vectơ chỉ phương là a = (1;0;2) .
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho OA = 2i + 3 j − 5k; OB = 2
− j − 4k . Một vectơ chỉ
phương của đường thẳng AB là Trang 1 A. a = ( 2 − ;−5;− ) 1 .
B. a = (2;5;− ) 1 .
C. a = (2;5;−9) .
D. a = (2;1;−9) . Lời giải
Một vectơ chỉ phương của đường thẳng AB là a = (2;5;− ) 1 . x − 3 y − 4 z +1
Câu 4: Trong không gian Oxyz , cho đường thẳng d : = =
. Vectơ nào dưới đây là một 2 5 − 3
vectơ chỉ phương của d ?
A. a = (3;4;− ) 1 .
B. a = (2;−5;3) . C. a = ( 3 − ;− 4; ) 1 .
D. a = (2;−5;−3). Lời giải x − 3 y − 4 z +1
Một vectơ chỉ phương của đường thẳng d : = = là a = (2;−5;3) . 2 5 − 3 x = 2 − t
Câu 5: Trong không gian Oxyz , đường thẳng d : y = 1+ 2t có một vectơ chỉ phương là z = 3+t A. a = ( 1 − ;2; ) 1 .
B. a = (2;1;3) .
C. a = (1;2;3) .
D. a = (2;0;− ) 1 . Lời giải x = 2 − t
Đường thẳng d : y = 1+ 2t có một vectơ chỉ phương là a = ( 1 − ;2; ) 1 . z = 3+t
Câu 6: Trong không gian Oxyz, tọa độ nào sau đây là tọa độ của một véctơ chỉ phương của đường x = 2 + 4t
thẳng : y =1− 6t ,(t )? z = 9t A. 1 1 3 a = ; ; .
B. a = (2;1;0) . C. a = (4;− 1 1 3 6;0) . D. a = ; − ; . 3 2 4 3 2 4 Lời giải x = 2 + 4t
Một vectơ chỉ phương của đường thẳng 1 1 3
: y = 1− 6t là a = ; − ; . 3 2 4 z = 9t x + 1 y − 2 z − 1
Câu 7: Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d : = = ? 1 − 3 3
A. Q(1;− 2;− ) 1 . B. N ( 1 − ;3;2). C. A(1;2 ) ;1 . D. P( 1 − ;2 ) ;1 . Lời giải x + 1 y − 2 z − 1
Điểm thuộc đường thẳng d : = = là P( 1 − ;2 ) ;1 . 1 − 3 3 x −1 y − 2 z +1
Câu 8: Trong không gian Oxyz, cho đường thẳng d : = =
. Điểm nào sau đây thuộc d ? 2 3 1 − A. Q( 1 − ;− 2 ) ;1 . B. N ( 1 − ;3;2). C. A(2;3;− ) 1 . D. P (1;2;− ) 1 . Trang 2 Lời giải x −1 y − 2 z +1
Điểm thuộc đường thẳng d : = = là P (1;2;− ) 1 . 2 3 1 − x =1− t
Câu 9: Trong không gian Oxyz , điểm nào dưới đây thuộc đường thẳng d : y = 5 + t ? z = 2+3t A. Q( 1 − ;1;3) .
B. N (1;−1;3) . C. A( 2 − ;5;− 2). D. P(1;5;2) . Lời giải x =1− t
Điểm thuộc đường thẳng d : y = 5 + t là P(1;5;2) . z = 2+3t x =1+ 2t
Câu 10: Trong không gian Oxyz , đường thẳng d : y = 3 − t không đi qua điểm nào dưới đây? z =1−t A. Q(3;2;0) . B. N (5;1;− ) 1 . C. A(1;3; ) 1 . D. P(0;1;2) . Lời giải x =1+ 2t
Điểm không thuộc đường thẳng d : y = 3 − t là P(0;1;2) . z =1−t − + − Câu 11: x y z
Trong không gian Oxyz , cho đường thẳng 1 2 4 : = =
. Trong các điểm sau đây, 3 5 − 1
điểm nào không thuộc đường thẳng ?
A. M (4;− 7;− 2) .
B. N (7;−12;6) .
C. P(10;−17;7) .
D. Q(13;− 22;8) . Lời giải
Thế tọa độ M (4;− 7;− 2) vào phương trình đường thẳng ta được 4 −1 7 − + 2 2 − − 4 = = 1 = 1 = 6 − (vô lý). 3 5 − 1
Suy ra M không thuộc đường thẳng .
Thế tọa độ N (7;−12;6) vào phương trình đường thẳng ta được 7 −1 12 − + 2 6 − 4 = = 2 = 2 = 2 (đúng). 3 5 − 1
Suy ra N thuộc đường thẳng .
Thế tọa độ P(10;−17;7) vào phương trình đường thẳng ta được 10 −1 1 − 7 + 2 7 − 4 = = 3 = 3 = 3 (đúng). 3 5 − 1 Trang 3
Suy ra P thuộc đường thẳng .
Thế tọa độ Q(13;− 22;8) vào phương trình đường thẳng ta được 13 −1 2 − 2 + 2 8 − 4 = = 4 = 4 = 4 (đúng). 3 5 − 1
Suy ra Q thuộc đường thẳng . x = 2 + 3t
Câu 12: Trong không gian Oxyz , cho đường thẳng : y = 1
− + t (t ) . Véc tơ nào sau đây là một z = 5 − 2t
véc tơ chỉ phương của đường thẳng ?
A. u = (2;−1;5) . B. (2;−1;− 2) .
C. u = (3;1;5) .
D. u = (3;1;− 2) . Lời giải
Một vectơ chỉ phương của đường thẳng là u = (3;1;− 2) . − + − Câu 13: x y z
Trong không gian Oxyz , cho đường thẳng 1 2 4 : = =
. Véc tơ nào sau đây là một 3 5 − 1
véc tơ chỉ phương của đường thẳng ?
A. u = (1;− 2;4).
B. u = (3;− 5; ) 1 . C. u = ( 1 − ;2;− 4).
D. u = (3;− 5;4). Lời giải
Một véc tơ chỉ phương của đường thẳng là u = (3;− 5; ) 1 .
Câu 14: Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng x −1 y + 1 z x − 3 y − 3 z + 2 : = = , : = = 1 2 2 2 3 1 − 2 − 1
A. song song với .
B. chéo với . 1 2 1 2
C. cắt .
D. trùng với . 1 2 1 2 Lời giải Vì 2 2
nên vectơ chỉ phương u = 2;2;3 của đường thẳng không cùng phương với 1 ( ) − 1 1 2 −
vectơ chỉ phương u = 1 − ; 2
− ;1 của suy ra chéo với hoặc cắt . 2 ( ) 2 1 2 1 2 Lấy M (1; 1
− ;0) , N 3;3; 2
− . Ta có MN = (2;4; 2 − ). 1 ( ) 2
Khi đó u ,u .MN = 0
u ,u , MN đồng phẳng. 1 2 suy ra 1 2 Vậy cắt . 1 2 x = 1+ t x = 1+ 2t '
Câu 15: Trong không gian Oxyz , cho hai đường thẳng d : y = 2 + t và d ': y = 1
− + 2t ' . Mệnh đề nào z = 3 − t z = 2 − 2t ' sau đây đúng?
A. Hai đường thẳng d và d chéo nhau. Trang 4
B. Hai đường thẳng d và d song song với nhau.
C. Hai đường thẳng d và d cắt nhau.
D. Hai đường thẳng d và d trùng nhau. Lời giải
Đường thẳng d có vectơ chỉ phương u = 1;1; 1 − 1 ( )
Đường thẳng d có vectơ chỉ phương u = 2;2; 2 − . 2 ( )
Ta có u = 2.u nên đường thẳng d và d ' song song hoặc trùng nhau. 2 1
Chọn điểm M (1;2;3) thuộc đường thẳng d , thay tọa độ điểm M vào phương trình đường 1 =1+ 2t
thẳng d ' , ta có d : 2 = 1
− + 2t vô nghiệm, vậy M không thuộc đường thẳng d nên 2 đường 3 = 2− 2t thẳng song song nhau. − + Câu 16: x y z
Trong không gian với hệ toạ độ Oxyz , cho hai đường thẳng thẳng 1 2 d : = = và 2 1 − 1 x = 1 − + 2t
d : y = 1+ t
. Khẳng định nào sau đây là khẳng định đúng? z = 3
A. d và d chéo nhau.
B. d song song với d .
C. d trùng với d .
D. d cắt d tại điểm A(0;1; 2 − ). Lời giải
Làm bằng phương pháp tự luận:
Đường thẳng d đi qua điểm M (0;1;− 2) và có vectơ chỉ phương u = (2;−1; ) 1 .
Đường thẳng d đi qua điểm N ( 1
− ;1;3) và có vectơ chỉ phương v = (2;1;0).
u,v = ( 1 − ;2;4) , MN = ( 1
− ;0;5) u,v.MN = 21 0
d và d chéo nhau.
Làm bằng phương pháp trắc nghiệm: Ta có: u = (2;−1; )
1 và v = (2;1;0) không cùng phương Đáp án B, C loại. Điểm A(0;1; 2
− ) không thuộc đường thẳng d Đáp án D loại. x = 4 + 4t − + − Câu 17: x 8 y 2 z 3
Trong không gian Oxyz , cho đường thẳng : = =
và : y = 3 − t . Giá trị 1 2 4 m −1 2 z = 2 + 2t
của m để và vuông góc là 1 2 A. m = 1 . B. m = −1. C. m = 3 . D. m = −3 . Lời giải Trang 5
Đường thẳng qua M 8; 2
− ;3 và có véctơ chỉ phương u = 2;4;m −1 . 1 ( ) 1 ( ) 1
Đường thẳng qua M 4;3;2 và có véctơ chỉ phương u = 4; 1 − ;2 . 2 ( ) 2 ( ) 2
Ta có: và vuông góc kh u .u = 0 8 − 4 + 2m − 2 = 0 m = 1 − 1 2 1 2 − − − Câu 18: x 1 y 7 z 3
Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng d : = = và 1 2 1 4 x y − 3 z + 4 d : = =
cắt nhau tại điểm M có toạ độ bằng 2 3 2 − 1
A. M (0;3;− 4) .
B. M (1;7;3) . C. M ( 3 − ;5;− 5) .
D. M (3;− 5;5) . Lời giải
Chuyển hai đường thẳng đã cho về dạng phương trình tham số, sau đó: 3 t ' = 1+ 2t t ' = 1 − Xét hệ phương trình: 3
− 2t ' = 7 + t t = 2 − 4
− + t ' = 3 + 4t
Suy ra hai đường thẳng cắt nhau tại điểm M ( 3 − ;5;− 5) .
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. − − − Câu 1: x y z
Trong không gian Oxyz , cho đường thẳng 1 3 2 d : = =
. Xét tính đúng sai của các 1 1 − 2 khẳng định sau:
a) Điểm M (1;3;2) nằm trên đường thẳng d .
b) Một vectơ chỉ phương của d là u = (1;3;2) x = 1+ t
c) Đường thẳng d song song với đường thẳng : y = 3 − t . z = 2 + 2t x = 3 − t
d) Đường thẳng d và đường thẳng d : y = t là hai đường chéo nhau. z = 1 − − 3t Lời giải
a) Đúng: Tọa độ điểm M (1;3;2) thỏa mãn phương trình d
b) Vectơ chỉ phương của d là là u(1; 1 − ;2) x = 1+ t
c) Sai: Đường thẳng d song song với đường thẳng : y = 3 − t . z = 2 + 2t x = 1+ t x −1 y − 3 z − 2 d : = =
y = 3 − t 1 1 − 2 z = 2 + 2t Trang 6 1
+ t = 1+ t Xét hệ phương trình 3
− t = 3 − t
hệ có vô số nghiệm nên d
2 + 2t = 2 + 2t x = 3 − t
d) Đúng: Đường thẳng d và đường thẳng d : y = t là hai đường chéo nhau. z = 1 − − 3t
Đường thẳng d đi qua điểm M (1;3;2) có vectơ chỉ phương là u = (1; 1
− ;2) và đường thẳng d đi qua N (0;0;− )
1 có vectơ chỉ phương là u = ( 3 − ;1;− ) 1 .
Ta có u,u.MN = 21 0
nên d và d chéo nhau. x = 1+ 2t
Câu 2: Trong không gian Oxyz, cho đường thẳng : y = 3 + t (t ). Xét tính đúng sai của các z = 4 − 5t khẳng định sau:
a) Một vectơ chỉ phương của đường thẳng là: u = (1;3;4).
b) Điểm A(5;5;− 6) thuộc đường thẳng . x = 2 + 3t
c) Đường thẳng d : y = 4t
(t ) vuông góc với đường thẳng . z = 3+ 2t
d) Đường thẳng cắt mặt phẳng (Oxz) tại điểm M ( 5 − ;0;19). Lời giải
a) Sai: Đường thẳng có một vectơ chỉ phương là u = (2;1; 5 − ) . 5 = 1+ 2t b) Đúng: Ta có: 5 = 3 + t t = 2. 6 − = 4 − 5t c) Đúng: Ta có: u =
− và u = (3;4;2 và dễ thấy: u .u = 0 . d ) (2;1; 5) d
d) Đúng: Ta có: y = 0 3 + t = 0 t = 3 − nên điểm M ( 5
− ;0;19) là giao điểm của đường
thẳng và mặt phẳng (Oxz) .
Câu 3: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng , lần lượt có phương 1 2 − − + − + trình là: x 1 y 2 z 1 x 4 y 1 z : = = và : = = . Xets 1 1 1 − 2 2 3 1 1 −
a) Đường thẳng có một vectơ chỉ phương là: u = 1; 1
− ;2 và đi qua điểm A( 1 − ; 2 − ; ) 1 . 1 ( ) 1 b) Điểm M (10;1; 2
− ) thuộc đường thẳng . Xét tính đúng sai của các khẳng định sau: 2
c) Đường thẳng vuông góc với đường thẳng . 1 2
d) Đường thẳng và đường thẳng là hai đường thẳng chéo nhau. 1 2 Lời giải Trang 7
a) Sai: Đường thẳng có một vectơ chỉ phương là: u = 1; 1
− ;2 và đi qua điểm A(1;2;− ) 1 1 ( ) 1 − + − b) Đúng: Ta có 10 4 1 1 2 = = là mệnh đề đúng. 3 1 1 − c) Đúng: Ta có: u = − và u = (3;4; 2
− và dễ thấy: u .u = 0 . d ) (2;1; 5) d
d) Đúng: Đường thẳng có một vectơ chỉ phương là: u = 1; 1 − ;2 và đi qua điểm 1 ( ) 1 A(1;2;− )
1 . Đường thẳng có một vectơ chỉ phương là: u = 3;1; 1 − và đi qua điểm 2 ( ) 2 M (10;1; 2 − ). Ta có: MA = (9; 1 − ;− )
1 và u ,u .MA = 2 − 0 1 2 .
Câu 4: Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng , lần lượt có phương 1 2 − + + + − trình là: x y 3 z 3 x 4 y 2 z 4 : = = và : = =
. Xét tính đúng sai của các khẳng 1 1 1 − 2 2 2 1 1 − định sau:
a) Đường thẳng có một vectơ chỉ phương là: u = 1; 1
− ;2 và đi qua điểm A( 1 − ;4; 5 − ). 1 ( ) 1
b) Đường thẳng không cắt trục toạ độ Oz . 2
c) Đường thẳng song song với đường thẳng . 1 2
d) Đường thẳng và đường thẳng là hai đường thẳng chéo nhau. 1 2 Lời giải
a) Đúng: Đường thẳng có một vectơ chỉ phương là: u = (1; 1 − ;2) và đi qua điểm 1 A( 1 − ;4; 5 − )
b) Sai: Đường thẳng cắt trục toạ độ Oz tại M (0;0;2) . 2
c) Sai: Ta có: u = 1; 1 − ;2 và u = 2;1; 1
− nên u ,u không cùng phương. 2 ( ) 1 ( ) d
d) Sai: Đường thẳng có một vectơ chỉ phương là: u = 1; 1
− ;2 và đi qua điểm A( 1 − ;4; 5 − ). 1 ( ) 1
Đường thẳng có một vectơ chỉ phương là: u = 2;1; 1
− và đi qua điểm M ( 4 − ; 2 − ;4) . 2 ( ) 2 Ta có: MA = ( 3 − ; 6
− ;9) và u ,u .MA = 0 1 2 .
PHẦN III. Câu trắc nghiệm trả lời ngắn
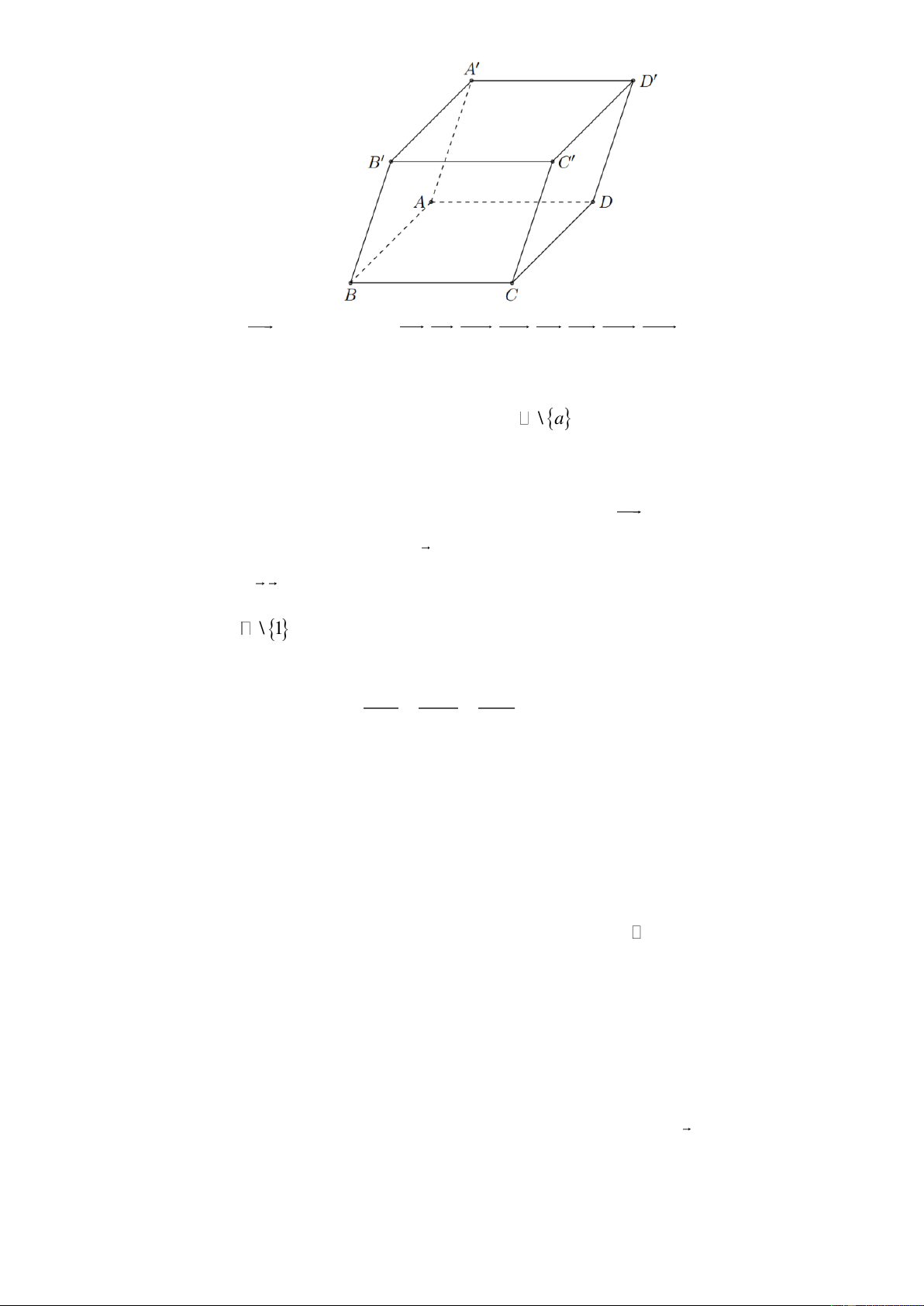
Câu 1: Cho hình hộp AB . CD A B C D
. Có bao nhiêu vectơ chỉ phương của đường thẳng AB có điểm
đầu và điểm cuối là đỉnh của hình hộp. Lời giải Trang 8
Đường thẳng AB nhận các vectơ AB, B , A A B , B A ,C , D DC,C D , D C là các vectơ chỉ phương.
Vậy có 8 vectơ thỏa mãn. Câu 2:
Trong không gian với hệ tọa độ Oxyz . Khi m \
a thì đường thẳng d đi qua hai điểm A(1;2;0); B( ; m 1
− ;3) cắt mặt phẳng (P) : x + y + z − 6 = 0 . Giá trị của a bằng bao nhiêu ? Lời giải
Đường thẳng d đi qua điểm A(1;2;0) và có vecto chỉ phương AB(m −1; 3 − ;3)
Mặt phẳng ( P) có vecto pháp tuyến n(1;1; ) 1
d cắt ( P) .
n u = m −1− 3 + 3 = 2 0 m 1 Vậy với m \
1 thì d cắt ( P) nên a = 1.
Câu 3: Trong không gian Oxyz , cho các điểm M ( 1 − ;3; ) 1 , N ( 2 − ;1; 2
− ) , P(1;2;3) , Q(2; 1 − ;2) , x − y − z − S (1;2; 3
− ) . Đường thẳng 1 2 3 d : = =
đi qua bao nhiêu điểm trong số các điểm đã 2 1 − 2 cho? Lời giải Ta có: M ( 1 − ;3; )
1 , P(1;2;3) (d ) ; N ( 2 − ;1; 2 − ),Q(2; 1 − ;2),S (1;2; 3 − )(d )
Vậy đường thẳng (d ) đi qua hai điểm. x = 1+ 2t
Câu 4: Trong không gian Oxyz , cho đường thẳng d : y = 2 − t ,t và các điểm M ( 1 − ;3; ) 1 , z = 3+ 2t N ( 2 − ;1; 2
− ) , P(1;2;3) , Q(2; 1
− ;2) , S (1;2; 3
− ) . Có mấy điểm không thuộc đường thẳng (d ) cho trước? Lời giải Ta có: M ( 1 − ;3; )
1 , P(1;2;3) (d ) ; N ( 2 − ;1; 2 − ),Q(2; 1 − ;2),S (1;2; 3 − )(d ) Câu 5:
Trong không gian Oxyz , cho hai điểm A( 1 − ;2;4) và B(5;2; 2 − ). Biết u = ( ; a ; b ) 1 là vectơ chỉ
phương của đường thẳng là đường đối xứng với AB qua mặt phẳng (Oyz) . Tính a + b Lời giải Trang 9
Do A(1;2;4) và B( 5 − ;2; 2
− ) là hai điểm đối xứng với ,
A B qua mặt phẳng (Oyz) vậy nên
đường thẳng đi qua A và B nên nhận AB = ( 6 − ;0; 6
− ) là vectơ chỉ phương.
Khi đó nhận u = (1;0; )
1 là vecto chỉ phương a = 1;b = 0 a + b = 1. x −1 y + 4 z − 5 Câu 6:
Trong không gian với hệ trục tọa độ Oxyz , cho hai đường thẳng : = = và 2 3 1 x + 3 y + 2 z − 3 : = =
đối xứng với nhau qua mặt phẳng ( P) . Biết ( P) có vectơ pháp tuyến 2 3 1 là n = ( ; a ;
b 3) . Tính a + b . Lời giải
Đường thẳng qua A(1; 4
− ;5) và nhận u = (2;3; ) 1 là vecto chỉ phương. Đường thẳng qua B( 3 − ; 2
− ;3) và nhận u = (2;3; )
1 là vecto chỉ phương ∥ .
Gọi A là điểm trên
sao cho AA ⊥ . Do A A( 3 − + 2t; 2
− + 3t;3 + t) AA = ( 4
− + 2t;2 + 3t; 2 − + t). 2
Do AA ⊥ AA .u = 0 8
− + 4t + 6 + 9t − 2 + t = 0 t = 7 17 − 8 − 23 24 − 20 12 − 4 A ; ; AA = ; ; = − . (6; 5 − ;3) 7 7 7 7 7 7 7
Khi đó (P) nhận n = (6; 5
− ;3) là vectơ pháp tuyến a = 6;b = 5
− a + b = 1.
B. BÀI TẬP TỰ LUẬN
Bài tập 1: Trong không gian Oxyz, xác định một vectơ chỉ phương của đường thẳng dưới đây: x = 2 − t x −1 y − 2 z +1 − − − a) x 1 y 2 z
d : y = 1+ 2t b) d : = = c) 1 d : = = 2 1 2 2 2 1 z = 3 + t Lời giải a) Đường thẳng r
d có một vectơ chỉ phương là u = ( 1 − ; 2; ) 1 . b) Đường thẳng r
d có một vectơ chỉ phương là v = (2;1; 2). − − − − − − c) Ta viết lại x 1 y 1 2 z x 1 y 1 z 2 r d : = = d : = = u = 2; 2; 1 − . 1 ( ) 2 2 1 2 2 1 −
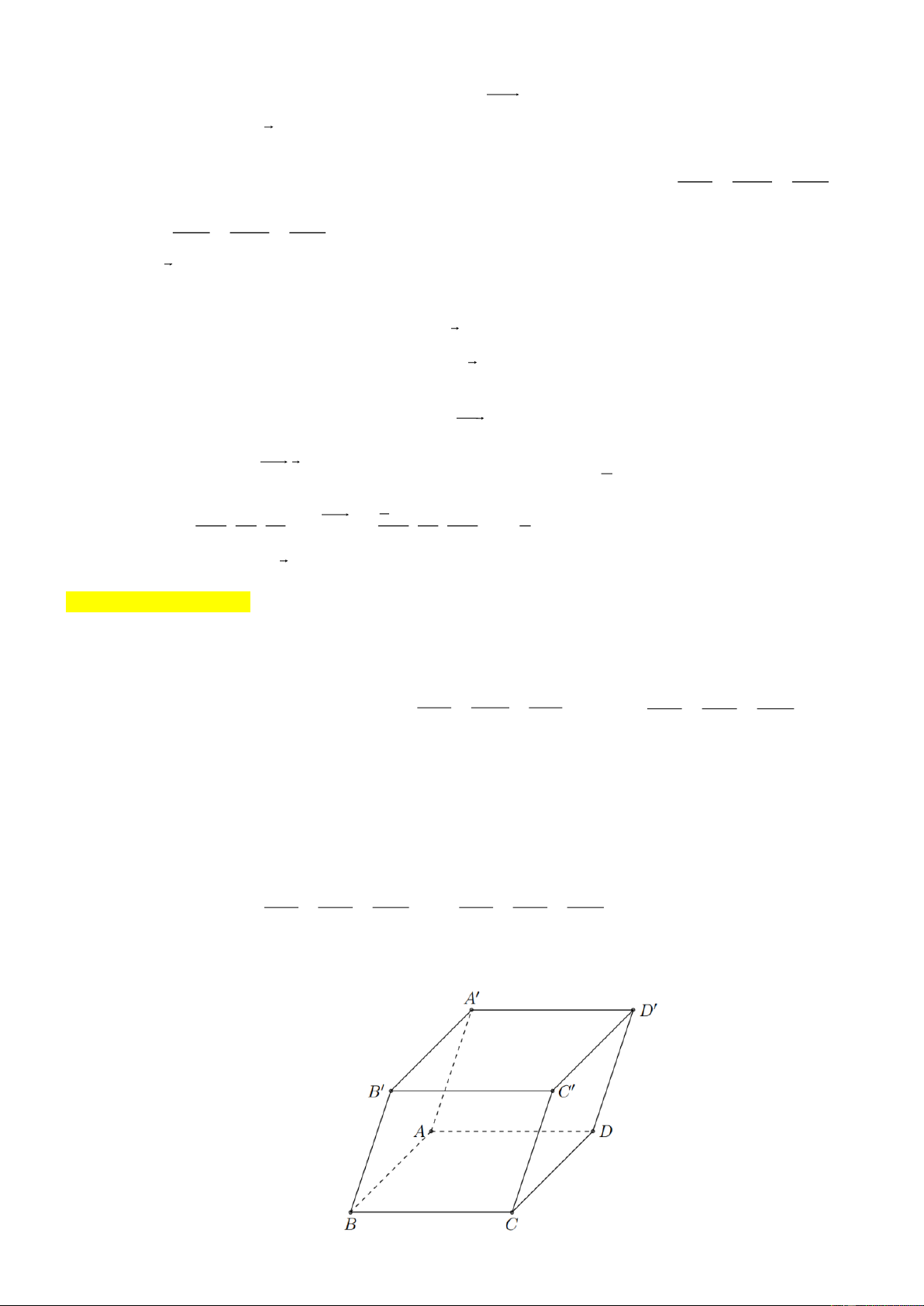
Bài tập 2: Cho hình hộp ABC . D AB C D
. Trong các vectơ có điểm đầu và điểm cuối là các đỉnh của
hình hộp, những véc tơ nào là véc tơ chỉ phương của đường thẳng AC ? Trang 10 Lời giải
Vì AC song song với AC nên các vectơ chỉ phương của đường thẳng AC thỏa bài toán là
các vectơ sau đây: AC ,CA, A C ,C A . x = 2 + 3t
Bài tập 3: Trong không gian Oxyz , cho đường thẳng : y = 1
− + t (t ). Trong các điểm sau đây, z = 5− 2t
điểm nào thuộc đường thẳng ?
A. M (11;2;4) .
B. N (5;0;3) .
C. P (10;3;− 3) . D. Q(8;−3; ) 1 . Lời giải 11 = 2 + 3t t = 3
Thế tọa độ M (11;2;4) vào phương trình đường thẳng ta được 2 = 1 − + t t = 3 4 = 5 − 2t 1 t = 2
Vì hệ phương trình trên vô nghiệm nên M không thuộc đường thẳng . 5 = 2 + 3t t =1
Thế tọa độ N (5;0;3) vào phương trình đường thẳng ta được 0 = 1 − + t t =1 3 = 5 − 2t t = 1
Vì hệ phương trình trên có nghiệm nên N thuộc đường thẳng . 8 t = 10 = 2 + 3t 3
Thế tọa độ P (10;3;− 3) vào phương trình đường thẳng ta được 3 = 1 − + t t = 4 3 − = 5 − 2t t = 4
Vì hệ phương trình trên vô nghiệm nên P không thuộc đường thẳng . 8 = 2 + 3t t = 2
Thế tọa độ Q(8;−3; )
1 vào phương trình đường thẳng ta được 3 − = 1 − + t t = 2 − 1 = 5 − 2t t = 2
Vì hệ phương trình trên vô nghiệm nên Q không thuộc đường thẳng .
Bài tập 4: Trong không gian Oxyz , xét vị trí tương đối của các cặp đường thẳng sau: x = 1+ t x = 2 + 2t
a) d : y = 2t (t R ) và d : y = 3 + 4t(t R) z = 3 − t z = 5 − 2t x = 1+ 2t − + + b) x y z d : y = 1
− + 3t (t R) và 1 2 1 d : = = 3 2 2 z = 5 + t Trang 11 − − − + c) x y 1 z x y z d : = = và 1 2 2 d : = = 1 1 − 2 5 1 2 − Lời giải
a) Ta có các vectơ chỉ phương của d và d lần lượt là a = (1;2;− ) 1 và a = (2;4; 2 − ) .
Vì a = 2a nên a và a cùng phương d và d song song với nhau hoặc trùng nhau.
Xét điểm M (1;0;3) d nên ta có M d nên d ∥ d .
b) Ta có d và d lần lượt nhận a = (2;3; )
1 và a = (3;2;2) là các vectơ chỉ phương.
Vì a và a không cùng phương nên d và d cắt nhau hoặc chéo nhau.
Đường thẳng d qua M (1; 2 − ;− )
1 ; có VTCP a = (3;2;2) nên có phương trình là: x = 1+ 3t d : y = 2
− + 2t(t R) z = 1 − + 2t 3 t = − 5 1
+ 2t = 1+ 3t Xét hệ phương trình : 2 1 − + 3t = 2
− + 2t t = − Hệ vô nghiệm 5 5 + t = 1 − + 2t 5 + t = 1 − + 2t
Vậy hai đường thẳng d và d chéo nhau.
c) Ta có: d đi qua M (0;1;0) và có vectơ chỉ phương a = (1; 1 − ;2) ;
Đường thẳng d đi qua M (1;2; 2
− ) và có vectơ chỉ phương a = (5;1; 2 − ) .
Nên phương trình tham số của d và d lần lượt là: x = t x = 1+ 5t
d : y = 1− t và d : y = 2 + t z = 2t z = 2 − − 2t 2 t = 1+ 5t t − 5t = 1 t = − Xét hệ phương trình 3 1
− t = 2 + t t − − t = 1
hệ có nghiệm duy nhất 1 2t = 2 − − 2t 2t + 2t = 2 − t = − 3
Vậy hai đường thẳng d và d cắt nhau.
Dạng 2: Viết phương trình đường thẳng
Phương pháp: Ta thường gặp các dạng toán sau:
Dạng 1: Đường thẳng đi qua một điểm và có một vectơ chỉ phương:
Trong không gian Oxyz , phương trình đường thẳng đi qua M và có vectơ chỉ phương a = (a;b;c) Trang 12
x = x + at 0 − − −
Khi đó phương trình đường thẳng x x y y z z
y = y + bt hoặc 0 0 0 = =
nếu a;b; c 0 . 0 a b c
z = z + ct 0
Chú ý: Phương trình tìm được không nằm trong các phương án, ta có thể thay tọa độ điểm mà đường
thẳng đi qua để kiểm tra.
Dạng 2: Phương trình đường thẳng đi qua hai điểm:
Trong không gian Oxyz , viết phương trình đường thẳng qua hai điểm A và B .
■ Chọn A hoặc B là điểm mà đi qua.
■ Nhận AB làm VTCP → u = AB .
Lưu ý: Phương trình tìm được không nằm trong các phương án, ta có thể thay tọa độ điểm mà đường
thẳng đi qua để kiểm tra.
Dạng 3: Đường thẳng là giao tuyến của hai mặt phẳng
Trong không gian Oxyz , viết phương trình đường thẳng
Giao tuyến của hai mặt phẳng ( ) : Ax + By + Cz + D = 0 và ( ) : A x + B y
+ C z + D = 0 ■ Cho 1 trong 3 ẩn ; x ;
y z = 0 để tìm 2 ẩn còn lại
By + Cz + D = 0 y = ? ■ x = 0 ⎯⎯ → M (0;?;?) B y
+ C z + D = 0 z = ?
u = n ;n ■ Vecto chỉ phương .
Lưu ý: Phương trình tìm được không nằm trong các phương án, ta có thể thay tọa độ điểm mà đường
thẳng đi qua để kiểm tra
A. BÀI TẬP TRẮC NGHIỆM
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho điểm A(1;2;0) . Viết phương trình đường thẳng đi qua A , vuông góc và cắt trục Ox . Trang 13 x = 1 x = 1− t x = 1+ t x = 1
A. y = t
B. y = 2 + t
C. y = 2 + t
D. y = t z = t z = 0 z = 0 z = 0 Lời giải Nhận thấy (
A 1;2;0) (Oxy) .
Đường thẳng đi qua A , vuông góc và cắt trục Ox đi qua A và hình chiếu vuông góc
của A trên Ox . x = 1 x = 1
Phương trình : y = 2 + t , hay : y = t . z = 0 z = 0
Câu 2: Cho điểm A( 1
− ;1;0) .Viết phương trình đường thẳng đi qua A , cắt trục Ox , sao cho góc tạo
bởi với hai trục Ox,Oy bằng nhau. x = 1 − + 2t x = 1 − + t x = 1 − + t x = t
A. y =1− t
B. y = 1− 2t
C. y = 1− t
D. y = 1− t z = 0 z = 0 z = 0 z = 0 Lời giải Nhận thấy A( 1 − ;1;0)(Oxy) . x = 1 − + t
Nhận thấy đường thẳng : y = 1− t đi qua ,
A O thỏa mãn yêu cầu bài toán. z = 0 + − Câu 3: x y z Cho điểm (
A 1;2;3) và đường thẳng 1 3 d : = =
. Viết phương trình đường thẳng đi 2 1 2 −
qua A , vuông góc với đường thẳng d và cắt trục Oz . − − − − − − A. x 1 y 2 z 3 = = x y z B. 1 2 3 = = 1 2 − 2 1 2 2 − − − − − − C. x 1 y 2 z 3 = = x y z D. 1 2 3 = = 1 2 4 1 − 2 2 Lời giải
Đường thẳng cắt trục Oz tại B(0;0;b) BA = (1;2;3 − b) là vectơ chỉ phương của đường thẳng .
Vì ⊥ d B .
A u = 0 2 + 2 − 2(3 − b) = 0 b = 1 BA = (1;2;2 . d ) − − −
Vậy phương trình là x 1 y 2 z 3 = = . 1 2 2
Câu 4: Trong không gian Oxyz , cho điểm A(1;0;3) .Viết phương trình đường thẳng đi qua A , cắt hai trục O ,
x Oz tại M , N sao cho AM = 2AN . Trang 14 x = 1 − − 2t x = 1 − + 2t x = 1+ t x = 1+ 2t A. y = 0 B. y = 0 C. y = 0 D. y = 0 z = 3t z = 3t z = 3 + 3t z = 3t Lời giải Ta có: M ( ;
m 0;0), N (0;0;n) (m n) ; AM = (m −1;0; 3 − ), AN = ( 1 − ;0;n − 3) . m = 1 − m −1 = 2 −
Theo đề bài: AM = AN 3 M (− ) 3 2 1;0;0 , N 0;0; . 3 − = 2n − 6 n = 2 2 x = 1 − + 2t
Vậy phương trình : y = 0 . z = 3t − + − + Câu 5: x 1 y 1 z x y 1 z 1 Cho điểm A(1; 2 − ; )
1 và 2 đường thẳng d : = = , d : = = . Phương 1 1 − 2 3 − 2 1 − 2 1
trình đường thẳng d đi qua A cắt hai đường thẳng d ,d là 3 1 2 − + − − + − A. x 1 y 2 1 z = = x y z B. 2 6 6 = = 1 − 4 5 − 1 − 4 5 − − + − − + − C. x 1 y 2 z 1 = = x y z D. 2 6 6 = = 1 − 4 5 1 − 4 5 Lời giải
Gọi giao điểm của đường thẳng d với hai đường thẳng d ,d lần lượt là M , N . 3 1 2
Ta có: M (1− t;−1+ 2t;− 3t), N(− ; u 1 + 2 ; u −1 + u) AM = ( t − ,2t +1, 3 − t − ) 1 , AN = ( u
− −1,2u + 3,u − 2) . 1 − = (− − ) t = t k u 1 t − + ku + k = 0 2 Có ,
A M , N thẳng hàng nên 2t +1 = k (2u + 3) 2t − 2ku − 3k = 1 − k =1 3
− t −1 = k (u − 2) 3
− t − ku + 2k = 1 1 ku = − 2 1 5 − 1 AM = − ,2, = ( 1 − ;4; 5 − ). 2 2 2
Phương trình đường thẳng d đi qua A có vectơ chỉ phương u = 1 − ;4; 5 − là: 3 ( ) 3 x − 1 y + 2 z − 1 = = . 1 − 4 5 −
Nhận thấy điểm M (2; 6
− ;6)d do đó phướng trình d được viết lại thành: 3 3 x − 2 y + 6 z − 6 = = . 1 − 4 5 − Trang 15 x = 1− t − + − Câu 6: x 2 y 2 z 3
Cho hai đường thẳng d : = =
;d : y = 1+ 2t và điểm A(1;2;3) . Đường 1 2 2 1 − 1 z = 1 − + t
thẳng đi qua A , vuông góc với d và cắt d có phương trình là 1 2 − − − − − − A. x 1 y 2 z 3 = = . x y z B. 1 2 3 = = . 1 3 1 1 − 3 − 1 − − − − − − −
C. x 1 2 y z 3 = = . x y z D. 1 2 3 = = . 1 3 − 5 − 1 3 5 Lời giải
Gọi giao điểm của đường thẳng với đường thẳng d là M (1− t;1+ 2t; 1 − + t) . 2 Ta có: AM = ( t
− ;2t −1;t − 4).
vuông góc d AM.u = 0 2
− t − 2t +1+ t − 4 = 0 t = 1 − M 2; 1 − ; 2 − . 1 1 ( )
đi qua A(1;2;3) và có vectơ chỉ phương AM = (1; 3 − ; 5 − ) . − − − − − −
Phương trình chính tắc : x 1 y 2 z 3 = = hay 1 x y 2 z 3 = = . 1 3 − 5 − 1 3 5
Câu 7: Trong không gian Oxyz , cho tam giác nhọn ABC có E (2;2; ) 1 , 8 4 8 F − ; ; , O(0;0;0) lần 3 3 3
lượt là chân đường cao hạ từ các đỉnh ,
A B,C xuống các cạnh BC,C ,
A AB . Viết phương trình − đường thẳng đi qua x y z
A cắt trục Ox tại điểm có hoành độ nguyên và tạo với 1 d : = = 2 2 1 − một góc 51 , cos = . 9 + + − − A. x 3 y z = = x 4 y 1 z 1 B. = = 7 1 1 − 7 1 1 − − − − C. x 3 y z = = x 3 y z D. = = 7 1 1 7 1 1 Lời giải o O
EH = OBH = 90 − BAC Ta có
OEH = FEH . o
FEH = FCH = 90 − BAC o
FOH = FAH = 90 − ACB Tương tự ta có FOH = EOH . o
EOH = EBH = 90 − ACB
Suy ra trực tâm H của tam giác ABC cũng chính là tâm đường tròn nội tiếp tam giác ABC .
Do đó: EF.HO + O .
E HF + OF.HE = 0 5HO + 3HF + 4HE = 0 H (0;1; ) 1 . Trang 16 x = 2k Do ,
A H , E thẳng hàng nên HA = k HE y = k +1 A(2k;k +1; ) 1 . z =1
Do OH ⊥ OA nên O .
A OH = 0 1.(k + ) 1 +1 = 0 k = 2 − A( 4 − ;−1; ) 1 .
Gọi M = Ox , M ( ;
m 0;0) và AM = (m + 4;1;− ) 1 ; u = (2;2;− ) 1 . d AM u + + d m m cos( ; d ) . 2 11 51 2 11 = = = 2 2 AM . u + + 9 m 8m 18.3 3 m + 8m + 18 d m = 3 ( 2
51 m + 8m +18) = 9( 2 4m + 44m + 12 ) 2
1 15m + 12m −171 = 0 19 m = − 5
M (3;0;0), AM = (7;1;− ) 1 . − −
Vậy phương trình : x 3 y z = = 7 1 1
Câu 8: Đường thẳng đi qua điểm M (3;1; )
1 , nằm trong mặt phẳng ( ) : x + y − z − 3 = 0 , cắt x = 3 x = 1
d : y = 1+ 3t và tạo với đường thẳng d : y = 4 + 3t một góc nhỏ nhất, thì phương trình của 1 z = 1 − 2t z = 3 − − 2t là: x = 1 x = 8 + 5t x = 1+ 2t x = 1+ 5t
A. y = t − . B. y = 3 − − 4t .
C. y =1− t .
D. y =1− 4t . z = 2t z = 2 + t z = 3 − 2t z = 3 + 2t Lời giải
Ta thấy: M ( ) . Đường thẳng d có vectơ chỉ phương là u = (0;3;− 2) .
Mặt phẳng ( ) có vectơ pháp tuyến là n = (1;1;− ) 1 . Vì . u n = 0.1+ 3.1+ ( 2 − ).(− )
1 = 5 0 nên d cắt ( ) .
Dễ thấy M d ,d ∥ d . 1 1 Lấy N (3;4;− )
1 d . Gọi K , H lần lượt là hình chiếu vuông góc của N trên mặt phẳng ( ) 1 và đường thẳng . Ta có: ( NH NK
d, ) = (d , = NMH và sin NMH = . 1 ) MN MN
Do vậy (d,) nhỏ nhất khi K H hay là đường thẳng MK . Trang 17 x = 3 + t
Đường thẳng NK có phương trình: y = 4 + t . z = 1 − − t
Tọa độ K ứng với t là nghiệm của phương trình: ( + t) + ( + t) − (− − t) 5 3 4 1
− 3 = 0 t = − . 3 Suy ra 4 7 2 K ; ; . 3 3 3
Đường thẳng có vectơ chỉ phương là 5 4 1 1 MK = − ; ; − = − (5;− 4; ) 1 3 3 3 3 x = 3 + 5t x = 8 + 5t
Đường thẳng có phương trình: y =1− 4t hay y = 3 − − 4t . z = 1 + t z = 2 + t
Câu 9: Trong không gian Oxyz , cho đường thẳng là giao tuyến của hai mặt phẳng (P) : z −1 = 0 và
(Q): x + y + z −3 = 0. Gọi d là đường thẳng nằm trong mặt phẳng (P), cắt đường thẳng x − 1 y − 2 z − 3 = =
và vuông góc với đường thẳng . Phương trình của đường thẳng d là 1 1 − 1 − x = 3 + t x = 3 − t x = 3 + t x = 3 + t
A. y = t .
B. y = t .
C. y = t .
D. y = t − . z = 1 + t z = 1 z = 1 z = 1 + t Lời giải Đặt n = (0;0; ) 1 và n =
lần lượt là vectơ pháp tuyến của (P) và (Q) . Q (1;1; )1 P
Do = (P) (Q) nên có một véctơ chỉ phương u = n ,n = − . ( 1;1;0 P Q )
Đường thẳng d nằm trong (P) và d ⊥ nên d có một véctơ chỉ phương là u = n P , u d = ( 1 − ; 1 − ;0) . − − − Gọi x 1 y 2 z 3 d : = =
và A = d d A = d (P) 1 1 − 1 − z −1 = 0 z = 1
Xét hệ phương trình x −1 y − 2 z − 3 y = 0 A(3;0; ) 1 . = = 1 1 − 1 − x = 3 x = 3 + t
Do đó phương trình đường thẳng d : y = t . z =1 Trang 18 + − − Câu 10: x y z
Trong không gian với hệ tọa độ Oxyz cho đường thẳng (d ) 1 1 2 : = = và mặt phẳng 2 1 3
(P): x − y − z −1= 0. Viết pt đường thẳng () đi qua điểm A(1;1 ; − 2) , biết () // ( P) và () cắt d . − − + − − + A. x 1 y 1 z 2 = = . x y z B. 1 1 2 = = . 1 1 − 1 − 2 1 3 − − + − − + C. x 1 y 1 z 2 = = . x y z D. 1 1 2 = = . 8 3 5 2 1 1 Lời giải
Gọi M = (d ) () M ( 1 − + 2t;1 + t; 2 + 3t ) .
Khi đó AM = (2t − 2; t ; 3
t + 4) là một vectơ chỉ phương của () . Hai mặt phẳng () // ( P) AM ⊥ n = - − . P (1; 1; ) ( n với 1 P) ( ) AM. = − (
n ) = 0 2t − 2 − t − 3t − 4 = 0 t 3 AM = ( 8 − ; − 3; − 5) . P − − +
Vậy () x 1 y 1 z 2 : = = . 8 3 5
Câu 11: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x + 2y + z − 4 = 0 và đường thẳng x + 1 y z + 2 d : = =
. Viết phương trình đường thẳng nằm trong mặt phẳng (P) , đồng thời 2 1 3
cắt và vuông góc với đường thẳng d . − − − − − − A. x 1 y 1 z 1 = = . x y z B. 1 1 1 = = . 5 1 − 3 − 5 1 3 − − + − + + − C. x 1 y 1 z 1 = = . x y z D. 1 3 1 = = . 5 1 − 2 5 1 − 3 Lời giải
Vectơ pháp tuyến của mặt phẳng (P) là: n = (1;2; ) ( ) 1 . P
Vectơ chỉ phương của đường thẳng d là u = (2;1;3 . d ) x = 1 − + 2t
Phương trình tham số của đường thẳng d : y = t . z = 2 − + 3t Xét phương trình: 1
− + 2t + 2t − 2 + 3t − 4 = 0 7t − 7 = 0 t = 1.
Suy ra giao điểm của đường thẳng d và mặt phẳng (P) là A(1;1; ) 1 . Ta có: A .
Vectơ chỉ phương của đường thẳng là: u = n ,u = − − P (5; 1; 3 d ) ( ) . − − −
Phương trình chính tắc của đường thẳng x 1 y 1 z 1 : = = . 5 1 − 3 − Trang 19
Câu 12: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : x + 2y + 2z + 5 = 0 và đường thẳng x − 1 y − 1 z d : =
= . Đường thẳng nằm trên mặt phẳng (P) , đồng thời vuông góc và cắt 2 2 1
đường thẳng d có phương trình là + + + + + + A. x 1 y 1 z 1 = = . x y z B. 1 1 1 = = . 2 3 2 2 3 − 2 − − − − + − C. x 1 y 1 z 1 = = . x y z D. 1 1 1 = = . 2 − 3 2 − 2 3 − 2 Lời giải
Vectơ pháp tuyến của (P) là n = (3;2;− )
1 , vectơ chỉ phương của d là u = (2; 2; ) 1 .
u, n = (2; − 3; 2)
là vectơ chỉ phương của .
Mặt khác, do cắt d nên đi qua giao điểm M của d và mặt phẳng (P) .
Tọa độ giao điểm M của d và (P) là nghiệm hệ phương trình sau: x = 1+ 2t t = 1 − y = 1+ 2t x = 1 − M ( 1 − ; −1; − ) 1 . z = t y = 1 −
x + 2y + 2z + 5 = 0 z = 1 − + + +
Vậy phương trình đường thẳng là x 1 y 1 z 1 = = . 2 3 − 2 − − − Câu 13: x y z
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 1 2 3 d : = = và mặt phẳng 2 1 − 1
(P): 2x + y + z +1= 0. Viết phương trình đường thẳng qua giao điểm của đường thẳng d với
(P), nằm trên mặt phẳng (P) và vuông góc với đường thẳng d. x = 2 − − t x = 1 − + t x = 3 − − t x = 2 − + t A. y = 2 − . B. y = 0 . C. y = 4 . D. y = 2 − . z = 3 + 2t z = 1 − 2t z = 1 + 2t z = 4 − 2t Lời giải
Gọi là đường thẳng cần tìm
Gọi H = d (P) , suy ra H(1+ 2t;2 − t;3 + t) thay tọa độ H và (P)
2(1+ 2t ) + (2 − t ) + (3 + t ) +1 = 0 t = −2 suy ra H ( 3 − ;4; ) 1
Vì đường thằng nằm trong (P) nên nhận n = (2;1; )
1 làm vectơ pháp tuyến của đường thẳng d .
Vì đường thằng vuông góc với d nên nhận u = (2; 1 − ; )
1 làm vectơ pháp tuyết của đường d thẳng . Trang 20




