lOMoAR cPSD| 36066900 lOMoAR cPSD| 36066900
Các dạng toán và phương pháp giải toán ở Tiểu học.
I. Tìm hai số khi biết tổng và hiệu của chúng.
Cách giải bài toán: “Tìm hai số khi biết tổng và hiệu của hai số đó.” Phương pháp chung:
- Xác định tổng của hai số đó.
- Xác định hiệu của hai số đó.
- Vẽ sơ đồ (có thể không cần vẽ).
- Tìm mỗi số phải tìm. Số nhỏ Số lớn
= (tổng – hiệu)/2
= (tổng – hiệu)/2 ➢ Lưu ý:
✓ Thông thường các bài toán dành cho học sinh khá giỏi, người ta
thường cho tổng hoặc hiệu dưới hình thức khác nên khi giải nhất thiết
phải xác định được tổng và hiệu của hai số phải tìm.
✓ Khi tìm được hai số cần tìm phải thử lại xem có phù hợp với đề bài chưa.
✓ Thông thường bài toán có 2 cách giải: + Cách 1: Tìm số nhỏ trước
+ Cách 2: Tìm số lớn trước
Hướng dẫn và giải bài tập
Bài 1: Cả hai lớp 4A và 4B trồng được 600 cây. Lớp 4A trồng được ít hơn
lớp 4B là 50 cây. Hỏi mỗi lớp trồng được bao nhiêu cây?
Cách 1: Giải bằng phương pháp đại số (phương pháp lập hệ phương trình) Giải
Gọi a là số cây lớp 4A trồng được.
Gọi b là số cây lớp 4B trồng được.
Điều kiện: a>0, b>0, a
Cả hai lớp 4A và 4B trồng được 600 cây, nghĩa là: a + b = 600 (1)
Lớp 4A trồng được ít hơn lớp 4B là 50 cây, nghĩa là: lOMoAR cPSD| 36066900 b – a = 50 (2)
Từ (1) và (2), ta có hệ phương trình:
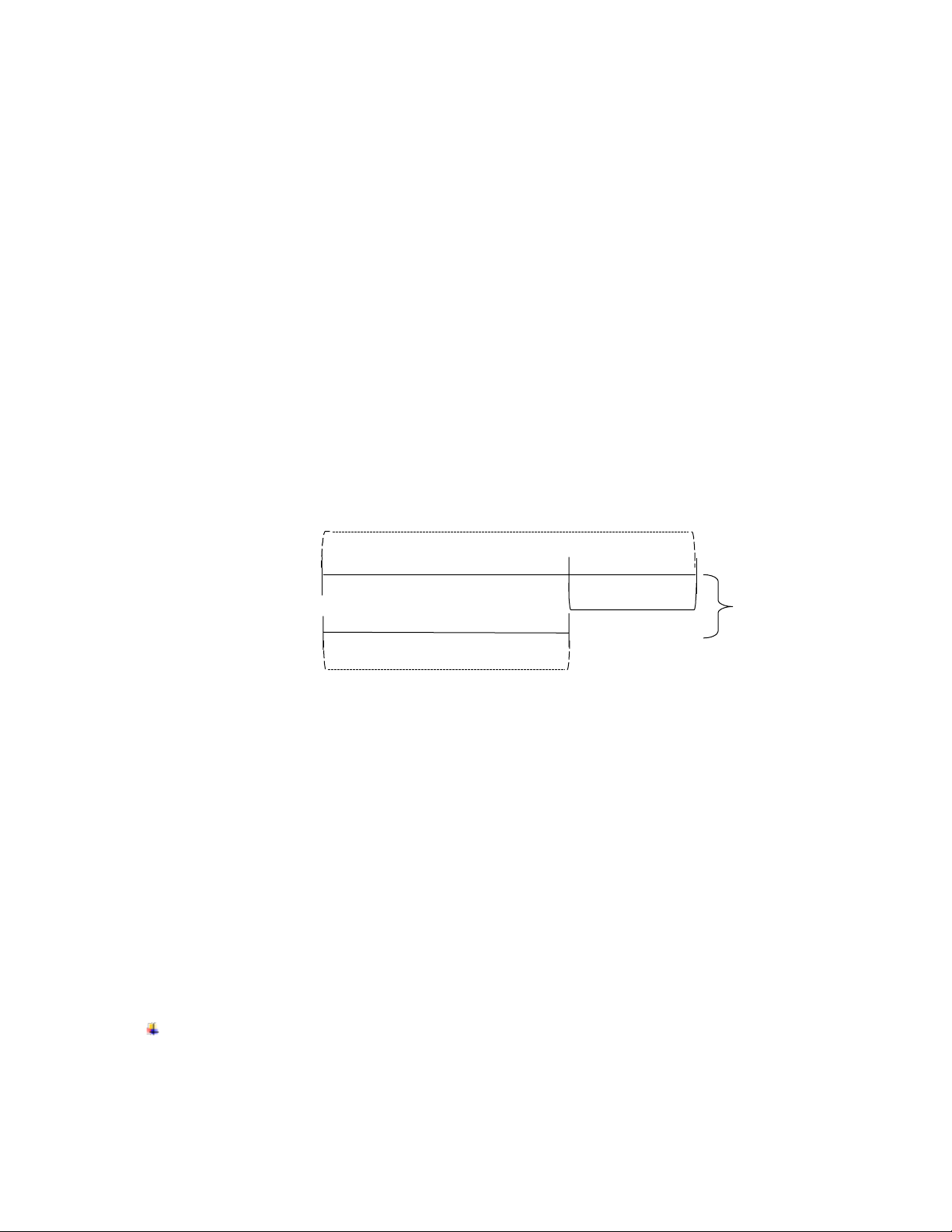
Cách 2: Giải bằng phương pháp tiểu học: Tóm tắt: ? Số cây lớp 4B: ; 600 cây Số cây lớp 4A: 50 cây ? Giải
Hai lần số cây của lớp 4A là:
600 – 50 = 550 (cây)
Số cây lớp 4A là: 550 : 2 = 275 (cây)
Số cây lớp 4B là:
600 – 275 = 325 (cây) Đáp số:
Số cây lớp 4A: 275(cây)
Số cây lớp 4B: 325 (cây)
Bài 2: Tuổi bố và tuổi con cộng lại được 58 tuổi. Bố hơn con 38 tuổi. Hỏi
bố bao nhiêu tuổi, con bao nhiêu tuổi?
Cách 1: Giải bằng phương pháp đại số (phương pháp lập hệ phương trình) lOMoAR cPSD| 36066900 Giải
Gọi a là tuổi của bố, b là tuổi của con
Điều kiện: a và là số nguyên dương
Tuổi của bố và con cộng lại được 58 tuổi, nghĩa là: a + b = 58 (1)
Bố hơn con 38 tuổi, nghĩa là: a – b = 38 (2)
Từ (1) và (2), ta có hệ phương trình:
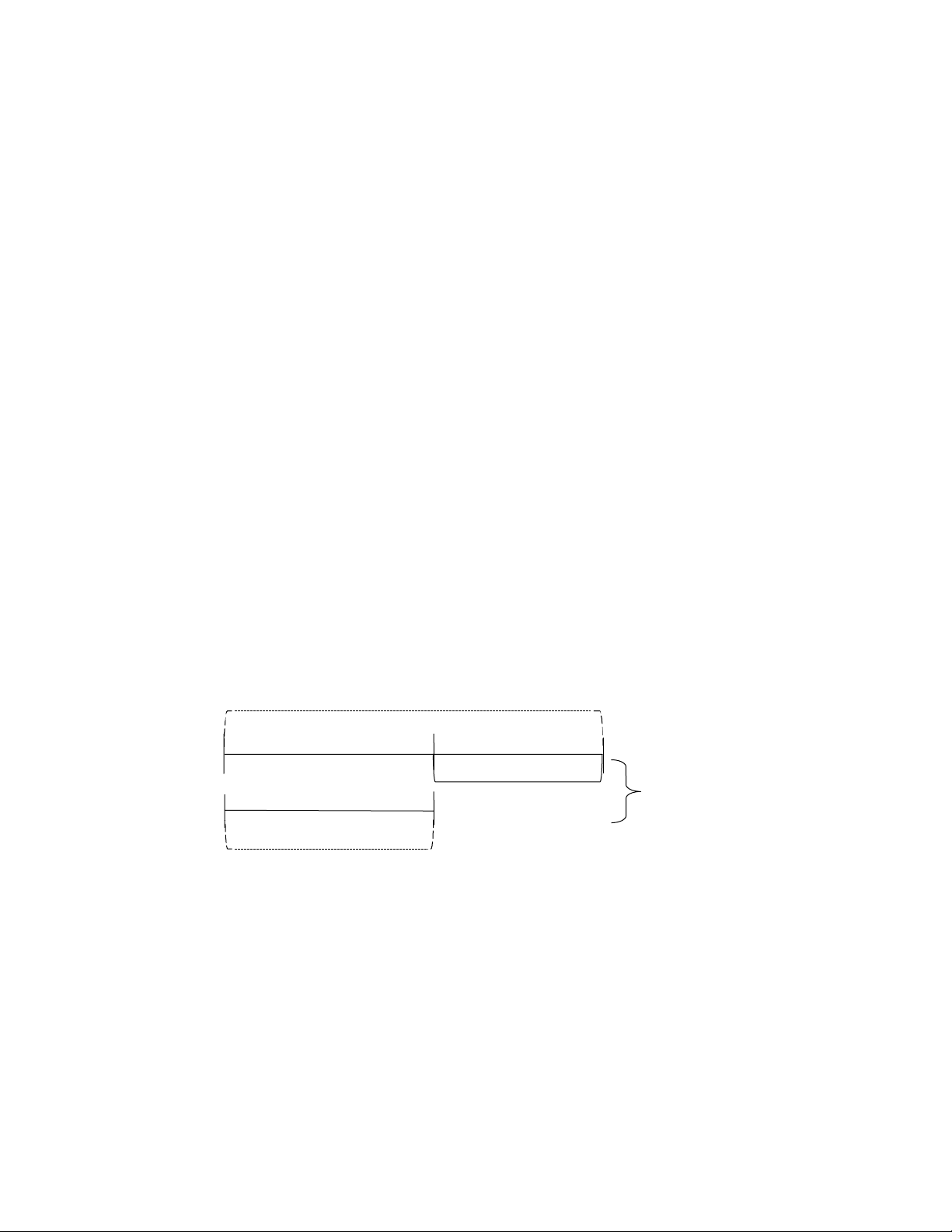
Cách 2: Giải bằng phương pháp tiểu học Tóm tắt ? Tuổi bố: Tuổi 58 tuổi con: 38 tuổi ? Giải
Hai lần tuổi bố là: 58 + 38 = 96 (tuổi) Tuổi bố là: 96 : 2 = 48 (tuổi) Tuổi con là:
58 – 48 = 10 (tuổi) lOMoAR cPSD| 36066900 Đáp số:
Tuổi bố: 48 tuổi
Tuổi con: 10 tuổi
II. Tìm hai số khi biết tổng (hiệu) và tỉ số của chúng.
❖ Cách giải chung bài toán về tìm hai số khi biết tổng và tỉ
Phương pháp chung:
Bước 1: Vẽ sơ đồ theo dữ kiện bài ra.
Bước 2: Tìm tổng số phần bằng nhau.
Bước 3: Tìm số bé và số lớn (Có thể tìm số lớn trước hoặc tìm sau và ngược lại)
✓ Số bé = (Tổng : số phần bằng nhau) x số phần của số bé (Tổng – số lớn)
✓ Số lớn = (Tổng : số phần bằng nhau) x số phần của số lớn (Tổng – số bé)
Bước 4: Kết luận đáp số
(Học sinh có thể tiến hành thêm bước thử lại để kiểm tra kết quả) ❖
Trường hợp đặc biệt các bài toán về tìm hai số khi biết tổng và tỉ số
Đề bài nhiều bài toán lại không cho dữ kiện đầy đủ về tổng và tỉ số mà chỉ cho dữ kiện như sau:
✓ Thiếu (ẩn) tổng (cho biết tỉ số, không cho biết tổng)
✓ Thiếu (ẩn) tỉ (Cho biết tổng số, không cho biết tỉ số)
✓ Cho dữ kiện thêm, bớt số, tạo tổng (tỉ) mới tìm số ban đầu.
Với những bài toán cho dữ kiện như vậy, cần tiến hành thêm một bước chuyển
về bài toán cơ bản.
Bài 1: Một hình chữ nhật có cho vi bằng 100m. Chiều dài bằng chiều
rộng. Tìm chiều dài và chiều rộng của hình chữ nhật.
Cách 1: Giải bằng phương pháp đại số (phương pháp đại số) Giải
Gọi a là chiều rộng hình chữ nhật, b là chiều dài hình chữ nhật
Điều kiện: a và b là số dương, b > a.
Một hình chữ nhật có chu vi bằng 100m, nghĩa là: lOMoAR cPSD| 36066900 (a + b) x 2 = 100 (1)
Chiều dài bằng chiều rộng, nghĩa là: b = a (2)
Từ (1) và (2) ta có hệ phương trình:
Cách 2: Giải bằng phương pháp tiểu học Tóm tắt Chiều dài: Chiều 50 m rộng: Giải
Nửa chu vi hình chữ nhật là: 100 : 2 = 50 (mét)
Tổng số phần bằng nhau là: 3 + 2 = 5 (phần)
Chiều dài hình chữ nhật là: 50 : 5 x 3 = 30 (mét)
Chiều rộng hình chữ nhật là: 50 : 5 x 2 = 20 (mét) Đáp số:
Chiều dài: 30 mét
Chiều rộng: 20 mét lOMoAR cPSD| 36066900
III. Phương pháp giả thuyết tạm
IV. Phương pháp khử
V. Tìm hai số biết hai hiệu số