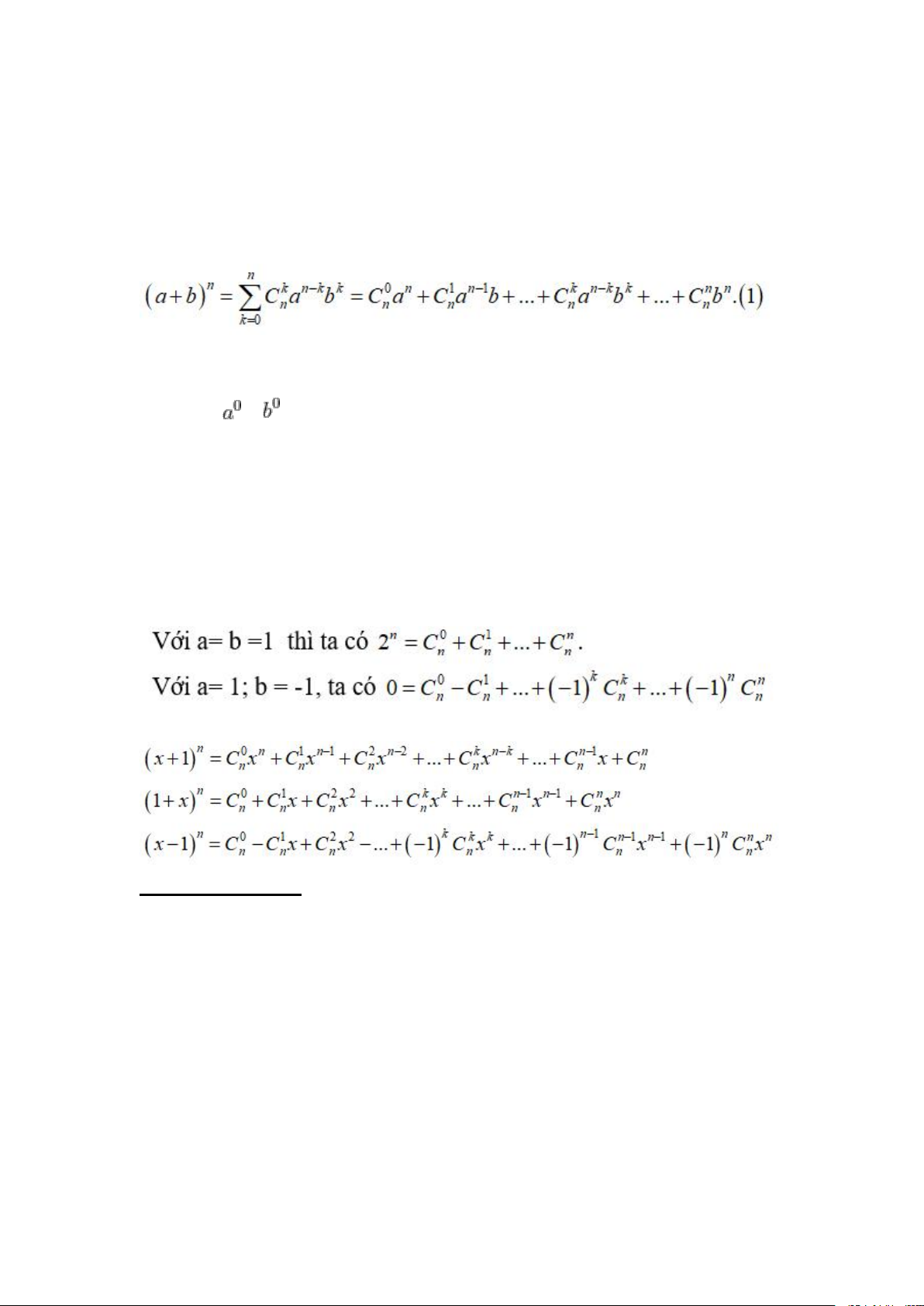




Preview text:
Cách khai triển nhị thức Newton: tìm hệ số, số hạng trong khai triển
1. Công thức nhị thức Niu-tơn
Với a, b là các số thực và n là sô nguyên dương, ta có:
Công thức trên được gọi là công thức nhị thức Newton (viết tắt là Nhị thức Newton). Quy ước: = = 1 Chú ý :
Trong biểu thức ở vế phải của công thức (1)
+ Số các hạng tử là n + 1.
+ Các hạng tử có số mũ của a giảm dần từ n đến 0, số mũ của b tăng dần từ
0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n.
+ Các hệ số của mỗi hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau. Hệ quả :
Các dạng khai triển cơ bản nhị thức Newton * Tam giác Pascal.
Tam giác Pascal được thiết lập theo quy luật sau :
- Đỉnh được ghi số 1. Tiếp theo là hàng thứ nhất ghi hai số 1.
- ¬Nếu biết hàng thứ n ( n≥1) thì hàng thứ n+1tiếp theo được thiết lập bằng
cách cộng hai số liên tiếp của hàng thứ n rồi viết kết quả xuống hàng dưới ở
vị trí giữa hai số này. Sau đó viết số 1 ở đầu và cuối hàng.
2. Công thức tìm hệ số, số hạng trong triển khai nhị thức Niu - tơn 2.1. Tổng hợp lý thuyết
Xét khai triển: (với a,b là các hệ số; x,y là biến)
- Số hàng thứ k + 1 của khai triển:
- Hệ số của số hạng thứ k + 1 của khai triển:
2.2. Các công thức tìm hệ số trong nhị thức Niu - tơn * Với khai triển
(p, q là các hằng số), ta có: Số hạng chứa
ứng với giá trị k thỏa mãn np – pk + qk = m. Từ đó tìm
Vậy hệ số của số hạng chứa xm là: với giá trị k đã tìm được ở trên. * Với khai triển P(x) = (p,q là các hằng số)
Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của * Chú ý:
- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa , hệ số phải tìm bằng 0.
- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa .
2.3 Công thức tìm số hạng trong nhị thức Niu - tơn * Với khai triển (p, q là các hằng số) Ta có: Số hạng chứa
ứng với giá trị k thỏa mãn: np – pk + qk = m Từ đó tìm Vậy số hạng chứa
là: với giá trị k đã tìm được ở trên. * Với khai triển P(x) = (p, q là các hằng số) Ta có:
Từ số hạng tổng quát của hai khai triển trên ta tính được số hạng chứa .
3. Bài tập vận dụng liên quan
Bài tập 1: Viết khai triển theo công thức nhị thức Newton: a. b. c. d.
Bài tập 2: Viết khai triển theo công thức nhị thức Newton: a. b. Hướng dẫn giải a. Khai triển Newton của b. Khai triển Newton của
Bài tập 3: Tìm hệ số của trong khai triển biểu thức Hướng dẫn giải Ta có: Số hạng chứa
trong khai triển ứng với k = 7. Khi đó hệ số của số hạng chứa
Bài tập 3: Tìm hệ số không chứa x trong khai triển sau: biết rằng Hướng dẫn giải Ta có: Do đó biểu thức khai triển là =
Số hạng không chứa x ứng với k: 36 - 4k = 0 <=> k=9
Số hạng không chưa x là: = -112640
Bài tập 4: Xét khai triển:
a. Viết số hạng thứ k + 1 trong khai triển.
b. Số hạng nào trong khai triển không chứa x.
c. Xác định hệ số của trong khai triển. Hướng dẫn giải
Số hạng không chứa x trong khai triển ứng với k là: 20 - 2k = 0 <=> k = 10
Số hạng không chứa x trong khai triển là: Số hạng chứa
trong khai triển ứng với k là: 20 - 2k = 4 <=> k = 8 Vậy số hạng chứa
trong khai triển có hệ số là:
Bài tập 5: Một nhóm tình nguyện viên gồm 4 học sinh lớp 10A, 5 học sinh lớp
10B và 6 học sinh lớp 10C. Để tham gia một công việc tình nguyện, nhóm có bao nhiêu cách cử ra: a) 1 thành viên của nhóm?
b) 3 thành viên của nhóm đang học ở ba lớp khác nhau?
c) 2 thành viên của nhóm đang học ở hai lớp khác nhau? Lời giải:
a) Số thành viên của nhóm là 4 + 5 + 6 = 15 (thành viên)
Số cách để nhóm cử ra một thành viên của nhóm tham gia một công việc tình
nguyện là tổ hợp chập 1 của 15. Do đó ta có số cách cử một thành viên trong nhóm là: = 15 (cách)
Vậy số cách cử một thành viên trong nhóm là 15 cách.
b) Số cách để nhóm cử ra ba thành viên của nhóm đang học ở ba lớp khác
nhau tham gia một công việc tình nguyện là: = 120 (cách).
Vậy có 120 cách để nhóm cử ra ba thành viên của nhóm đang học ở ba lớp
khác nhau tham gia một công việc tình nguyện.
c) Số cách cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau có thể có 3 phương án khác nhau:
- Phương án 1: 1 thành viên lớp 10A và 1 thành viên lớp 10B, có 20 (cách).
- Phương án 2: 1 thành viên lớp 10B và 1 thành viên lớp 10C, có 30(cách). fdfgfg bgfgf
- Phương án 3: 1 thành viên lớp 10A và 1 thành viên lớp 10C, có 24(cách).
Theo quy tắc cộng, có tất cả 20 + 30 + 24 = 74 cách cử ra 2 thành viên của
nhóm đang học ở hai lớp khác nhau tham gia một công việc tình nguyện.
Bài tập 6: Một khóa số có 3 vòng số (mỗi vòng gồm 10 số, từ 0 đến 9) như
Hình 1. Người dùng cần đặt mật mã cho khóa là một dãy số có ba chữ số. Để
mở khóa, cần xoay các vòng số đề dãy phía trước khóa trùng với mật mã đã
chọn. Có bao nhiêu cách chọn mật mã cho khóa?
Đáp án: Có tất cả 1000 cách chọn mật mã cho khóa
Bài số 7: Thực đơn tại một quán cơm văn phòng có 6 món mặn, 5 món rau và
3 món canh. Tại đây, một nhóm khách muốn chọn bữa trưa gồm cơm, 2 món
mặn, 2 món rau và 1 món canh. Nhóm khách có bao nhiêu cách chọn?
Đáp án: Nhóm khách có tất cả 450 cách chọn một bữa trưa
Bài tập 8: Một nhóm gồm 4 chàng trai và 6 cô gái. Họ muốn chọn ra 3 người
để tham gia một nhóm làm việc. Có bao nhiêu cách chọn nhóm?
Đáp án: Có 120 cách chọn một nhóm làm việc gồm 3 người từ tổng số 10 người này
Bài tập 9: Có 8 cuốn sách văn học và 6 cuốn sách khoa học. Một người đọc
muốn chọn 4 cuốn sách từ tổng số sách trên. Có bao nhiêu cách chọn?
Bài tập 10: Một hội thảo có 5 bài thuyết trình. Một người tham dự muốn chọn
3 bài để tham gia nghe. Có bao nhiêu cách chọn?
Đáp án: có 1001 cách chọn 4 cuốn sách từ tổng số 14 cuốn sách trên.
Bài tập 11: Một hội chợ có 10 quán bán đồ ăn, 8 quán bán đồ uống và 5 quán
bán đồ chơi. Một người tham dự muốn ghé thăm 4 quán từ các loại hội chợ
trên. Có bao nhiêu cách chọn?
Đáp án: có 1771 cách chọn 4 quán từ tổng số 23 quán trên.
Bài tập 12: Một bộ bài từ 1 đến 10 (tức là có 10 lá bài) được xếp ngẫu nhiên.
Tính xác suất để lá bài đầu tiên có giá trị là 3, lá bài thứ hai có giá trị lớn hơn
5 và lá bài thứ ba có giá trị là số chẵn.
Đáp án: xác suất để lá bài đầu tiên có giá trị là 3, lá bài thứ hai có giá trị lớn
hơn 5 và lá bài thứ ba có giá trị là số chẵn là 0.0055%.
Bài tập 13: Một hội thi vẽ có 5 thí sinh nam và 7 thí sinh nữ. Ban giám khảo
muốn chọn ra 3 người đoạt giải, trong đó có ít nhất 1 thí sinh nam. Có bao nhiêu cách chọn?
Đáp án: có 185 cách chọn 3 người đoạt giải, trong đó ít nhất có 1 thí sinh nam.
Document Outline
- Cách khai triển nhị thức Newton: tìm hệ số, số hạn
- 1. Công thức nhị thức Niu-tơn
- 2. Công thức tìm hệ số, số hạng trong triển khai n
- 2.1. Tổng hợp lý thuyết
- 2.2. Các công thức tìm hệ số trong nhị thức Niu -
- 2.3 Công thức tìm số hạng trong nhị thức Niu - tơn
- 3. Bài tập vận dụng liên quan




