Cách tính khoảng cách giữa hai đường thẳng | Chuyên đề Toán 12

Cách tính khoảng cách giữa hai đường thẳng trong oxyz
A. Công thức tính khoảng cách giữa hai đường thẳng
Cho hai đường thẳng d và  bất kì. Khi đó để tính khoảng cách giữa hai đường
thẳng ta có thể thực hiện theo hai cách như sau:
Cách 1. Tính khoảng cách từ 1 điểm bất kì thuộc đường thẳng này đến đường thẳng còn lại.
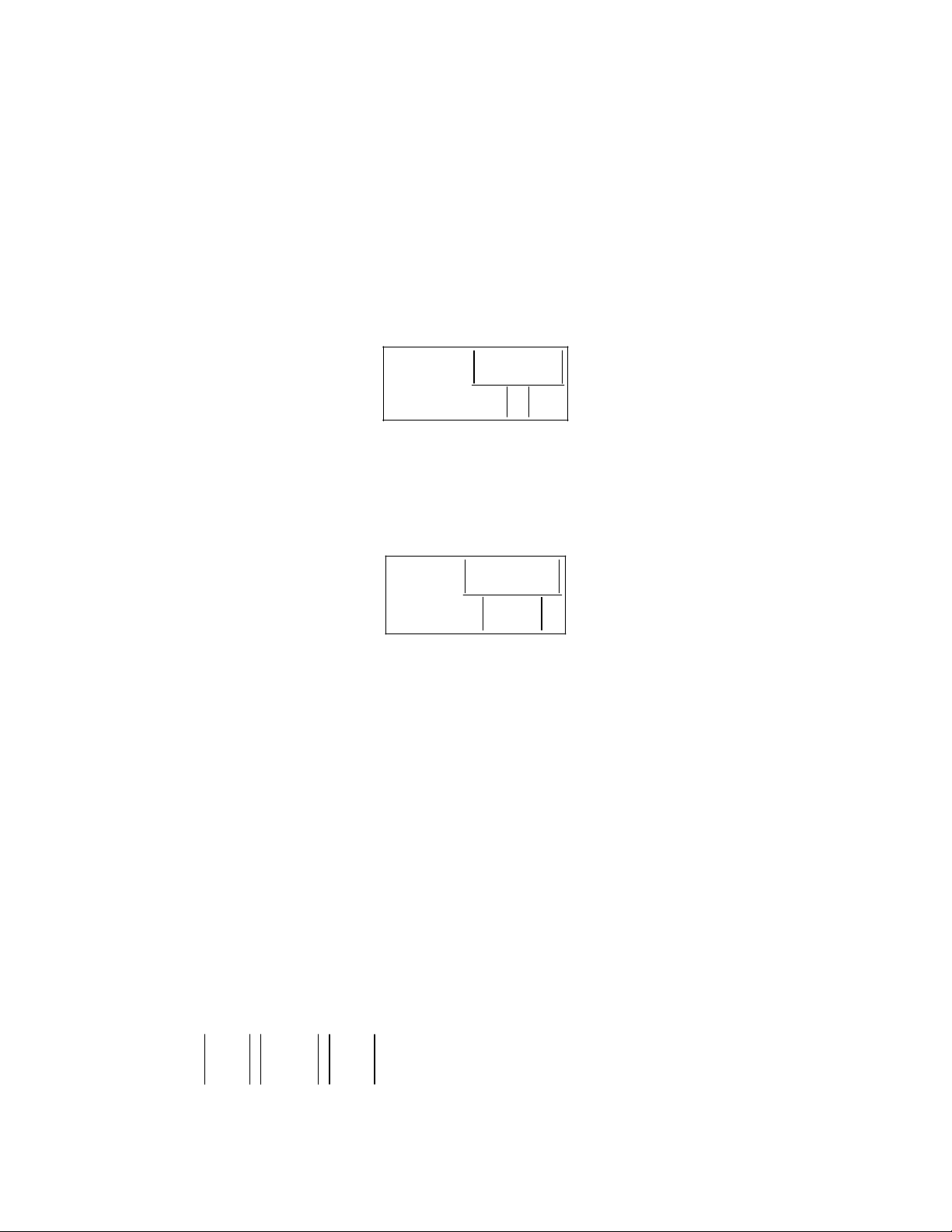
Khoảng cách từ điểm M  d đến đường thẳng  
 đi qua điểm M và có vectơ chỉ phương a 0    a   , M M d M ,  0      a
Cách 2. Áp dụng công thức tính khoảng cách của hai đường thẳng chéo nhau
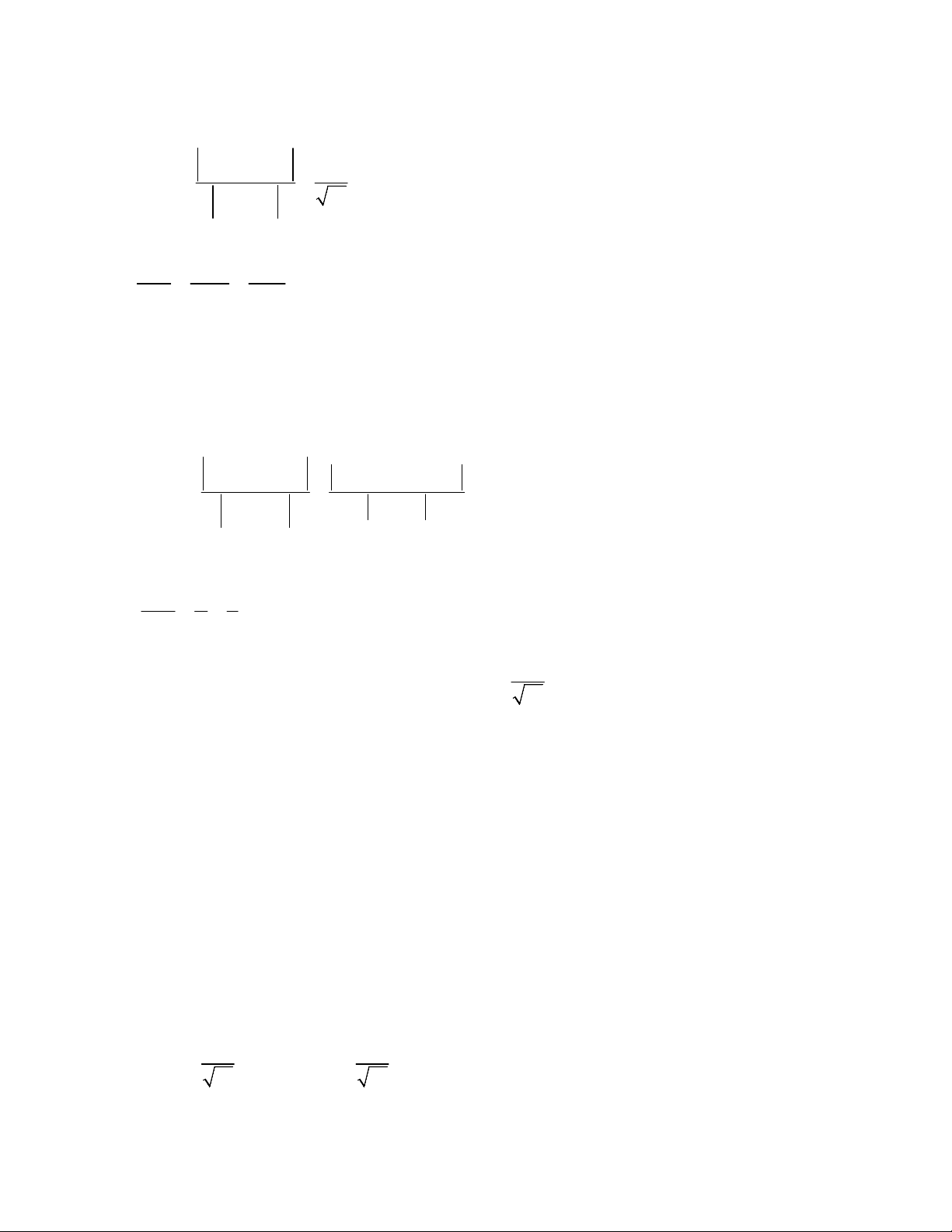
Khoảng cách giữa hai đường thẳng chéo nhau: 
d đi qua điểm M và có vectơ chỉ phương a1 
 đi qua điểm N và có vectơ chỉ phương a2
  
a ,a .MN d d,  1 2 =      a ,a  1 2  
C. Bài tập tính khoảng cách giữa hai đường thẳng x  1 t
Ví dụ. Trong không gian 
Oxyz ,cho hai đường thẳng d : y  t ;t   và z  t  x  2t '
d ': y  1
  t ';t '  . Khoảng cách giữa hai đường thẳng d và d ' bằng bao z   t ' nhiêu? Hướng dẫn giải 
Đường thẳng d đi qua điểm A1;0;0 và có vectơ chỉ phương u    d  1;1; 1
Đường thẳng d ' đi qua điểm B0; 1
 ;0 và có vectơ chỉ phương   u  AB    d 2;1;1 ; 1; 1;0 '      
 1 1 1 1 1 1  u u        d ; d ; ; 2; 1; 3 '      1 1 1 2 2 1 
Khoảng cách giữa hai đường thẳng d và d ' là:
   u u  AB d ; d .
d d;d ' '   1     u u  d ; 14 d '  
Ví dụ. Trong không gian với hệ tọa độ Oxyz , tính khoảng cách giữa đường thẳng
x 1 y  2 z  4 d :   và trục Ox . 2 4  3 Hướng dẫn giải 
Đường thẳng d có vectơ chỉ phương u  
và đi qua điểm M 1; 2  ;4 d 2; 4;3 
Trục Ox có vectơ chỉ phương u 
và đi qua điểm N 1;0;0 Ox 1;0;0
Khoảng cách giữa đường thẳng d và trục Ox là:
   u u  MN d ; Ox . 
d d;Ox   0;3;4.0;2; 4      u u  d ;   2 0;3;4 Ox  
Ví dụ. Trong không gian Oxyz , cho hai đường thẳng x  1 t x 1 : y z d ,d :   
y  2  t ; t 
. Gọi S là tập hợp tất cả các số d ,d 1 2   m sao cho 2 1 3 1 2 z   m
chéo nhau và khoảng cách giữa chúng bằng 5 . Tính tổng tất cả các phần tử 19 của S . Hướng dẫn giải  
Vectơ chỉ phương của d ,d là u  2;1;3 ,u  1;1;0 1   2   1 2   
Khi đó: n  u ,u   3;3;1 . 1 2    
Gọi P là mặt phẳng chứa d song song với d . 1 2 
Tức là, P qua A1;0;0 và nhận n làm vectơ pháp tuyến.
Ta có phương trình P :3x 3y  z 3  0
Xét điểm B1;2;md . Do d ,d chéo nhau nên BP  m  6. 2 1 2 Lại có: d  5 5 d ;d   d ; B P  1 2     19 19 3 6  m 3 5 m  1    19 19  m  11
Vậy tổng các phần tử của S là 1  11 1  2.