Cách tính xác suất có điều kiện | Chuyên đề Toán 12

Cách tính xác suất có điều kiện
Trong thực tế, ta thường phải cập nhật xác suất của một biến cố khi biết thêm
một thông tin nào đó. Nếu có thông tin biến cố B xảy ra, cần cập nhật xác suất
của biến cố A , tức là tính xác suất có điều kiện của A khi biết biến cố B đã xảy ra.
A. Định nghĩa xác suất có điều kiện
Cho hai biến cố A và B . Xác suất của biến cố A với điều kiện biến cố B đã xảy
ra được gọi là xác suất của A với điều kiện B , kí hiệu P A | B.
Công thức tính xác suất có điều kiện
Nếu PB  0 thì  P AB P A | B    PB Chú ý:
Nếu PB  0 thì P AB  P B.P A | B 
Nếu A và B là hai biến cố bất kì thì P AB  P A.P B | A  P B .P A | B 
Công thức trên được gọi là công thức nhân xác suất. Cho n AB
A và B là hai biến cố với PB  0. Khi đó, ta có: P A | B    , trong đó nB
n AB là số các trường hợp thuận lợi của biến cố AB ; nB là số các trường hợp
thuận lợi của biến cố B .
Công thức xác suất
Nếu A và B là hai biến cố bất kì, với PB  0 thì: PA | B 1 P A| B
Cho A và B là hai biến cố với 0  P A 1; 0  P B1 .
Khi đó, A và B là hai biến cố độc lập khi và chỉ khi: P A  P A | B  P A | B  và
PB  P B | A  P B | A 
Tính chất trên giải thích vì sao hai biến cố độc lập nếu việc xảy ra hay không xảy
ra của biến này không làm ảnh hưởng đến xác suất của biến cố kia.
Chú ý 1: Cho hai biến cố độc lập A và B với 0  P A 1; 0  P B1 .
P A  P A | B  P A | B 
PB  P B | A  P B | A  Chú ý 2:
P A  P A  1
P A | B  P A | B 1
P AB  P AB   P A
P AB  P AB  P B  Chú ý 3:
Xác suất của một biến cố có thể phụ thuộc vào nhiều yếu tố, điều kiện khác nhau
nào đó mà có thể được nói ra hoặc không nói ra (điều kiện hiểu ngầm).
Để chỉ ra một cách cụ thể hơn về việc xác suất của một sự kiện A nào đó phụ
thuộc vào một điều kiện B nào đó ra sao, ta sử dụng xác suất có điều kiện.
Những bài toán xảy ra xác suất có điều kiện, thường đi kèm với việc sử dụng
quy tắc nhân xác suất, khi gặp bài toán này ta cần lưu ý đến sự độc lập của biến
cố để vận dụng công thức đúng.
B. Bài tập minh họa tính xác suất có điều kiện Yêu cầu cần đạt Nhận biêt:
Nhận biết được khái niệm về xác suất có điều kiện Thông hiểu:
Giải thích được ý nghĩa của xác suất có điều kiện trong những tình huống thực tiễn quen thuộc.
Bài 1. Gieo một con xúc xắc. Gọi A là biến cố xuất hiện mặt 2 chấm và B là biến
cố xuất hiện mặt có số chấm là số chẵn. Tính: P A | B . Hướng dẫn giải
P A B P AB n AB 1 |    Ta có: PB n B 3 .
Bài 2. Trong một hộp có 4 viên bi màu trắng và 9 viên bi màu đen, các viên bi có
cùng kích thước và khối lượng. Lấy lần lượt mỗi lần một viên bi trong hộp,
không hoàn lại. Tính xác xuất để viên bi lấy ở lần thứ hai là màu đen, biết rằng
viên bi lấy ở lần thứ nhất cũng là màu đen. Hướng dẫn giải
Gọi B là biến cố viên bi lấy ở lần thứ nhất là màu đen.
A là biến cố viên bi lấy ở lần thứ hai là màu đen.
Ta cần tính P A | B .
Cách 1: Bằng định nghĩa
Do lần thứ nhất lấy được viên bi màu đen nên trong hộp còn 12 viên bi, trong đó
có 4 viên bi màu trắng và 8 viên bi màu đen. Vậy P A B 8 2 |   . 12 3
Cách 2: Bằng công thức
Số cách chọn 1 viên bi ở mỗi lần thứ nhất và thứ hai lần lượt là 13 và 12 cách
chọn nên n 13.12
Có 9 cách chọn 1 viên bi màu đen ở lần thứ nhất và 12 cách chọn 1 viên bi ở lần
thứ hai nên nB 
 P B  nB 9.12 9 9.12    . n 13.12 13
AB là biến cố cả hai lần đều chọn được viên bi màu đen
 n AB 
 P AB  n AB 9.8 6 9.8    . n 13.12 13 6  P AB P A | B   13 2    PB 9 3 Vậy 13 .
C. Bài tập tính xác suất có điều kiện có đáp án
Bài tập 1. Theo một số liệu thống kê của dự án Plan, tại một xã của một tỉnh miền
núi phía Bắc chỉ có 2 dân tộc Mông và Dao sinh sống, có số trẻ em dưới 5 tuổi là
300 em, kết quả điều tra năm 2023 được cho như bảng dưới đây : Kêt quả điều tra
Người Mông Người Dao Suy dinh dưỡng 27 24 Không suy dinh 153 96 dưỡng
Chọn ngẫu nhiên một trẻ em dưới 5 tuổi của xã.
a) Tính xác suất chọn được một trẻ em dưới 5 tuổi của xã là người Mông và bị suy dinh dưỡng.
b) Tính xác suất trẻ em người Mông bị suy dinh dưỡng.
c) Tính xác suất trẻ em người Dao bị suy dinh dưỡng.
Bài tập 2. Một bình đựng 50 viên bi kích thước, chất liệu như nhau, trong đó có
30 viên bi trắng và 20 viên bi xanh. Lấy ngẫu nhiên ra một viên bi không hoàn
lại, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên
bi trắng ở lần thứ nhất và một viên bi xanh ở lần thứ hai.
Bài tập 3. Một công ty bảo hiểm nhận thấy có 52% số người mua bảo hiểm ô tô
là nam và có 39% số người mua bảo hiểm ô tô là nam trên 40 tuổi. Biết một
người mua bảo hiểm ô tô là nam, tính xác suất người đó trên 40 tuổi.
Bài tập 4. Kết quả khảo sát những bệnh nhân là học sinh bị tai nạn xe máy điện
về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:
Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 60% .
Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là 90% .
Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu là 15% .
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách đối với học sinh
khi di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu
khi gặp tai nạn bao nhiêu lần?
Đáp án bài tập tự rèn luyện Bài tập 1
Gọi A là biến cố chọn được một trẻ em dưới 5 tuổi của xã bị suy dinh dưỡng.
B là biến cố chọn được một trẻ em dưới 5 tuổi của xã là dân tộc Mông.
(a) Ta có n  300
AB là biến cố : Trẻ em dưới 5 tuổi được chọn là người Mông và bị suy dinh dưỡng.
 n AB 
 P AB  n AB 27 27    . n 0,09 300
(b) Số lượng trẻ em dưới 5 tuổi của xã là dân tộc Mông là nB  27 153 180
Xác suất chọn được một trẻ em dưới 5 tuổi của xã là dân tộc Mông là PB 180 3    0,6 . 300 5
Xác suất trẻ em dưới 5 tuổi bị suy dinh dưỡng của xã là dân tộc Mông:
P A B P AB 0,09 |    . PB 0,15 0,6
(c) Xác suất chọn một trẻ em dưới 5 tuổi của xã là dân tộc Dao là
PB 1 P B  0,4
AB là biến cố : Trẻ em được chọn bị suy dinh dưỡng và là người Dao
 nAB   P AB 24 24   0,08 . 300
Xác suất trẻ em dưới 5 tuổi bị suy dinh dưỡng của xã là dân tộc Dao :
PA B PAB 0,08 |    . PB 0,2 0,4 Bài tập 2
Gọi A là biến cố: “Lấy được một viên bi trắng ở lần thứ nhất”
Gọi B là biến cố: “Lấy được một viên bi xanh ở lần thứ hai”.
Ta cần tính: P AB.
Vì có 30 viên bi trắng trong tổng số 50 viên bi nên P A 30 3   50 5
Nếu A đã xảy ra, tức là một viên bi trắng đã được lấy ra ở lần thứ nhất, còn lại
trong bình 49 viên bi, trong đó bi xanh là 20 viên bi. Do đó PB A 20 |  49
Theo công thức nhân xác suất: P AB  P A P B A 3 20 12 . |  .  . 5 49 49
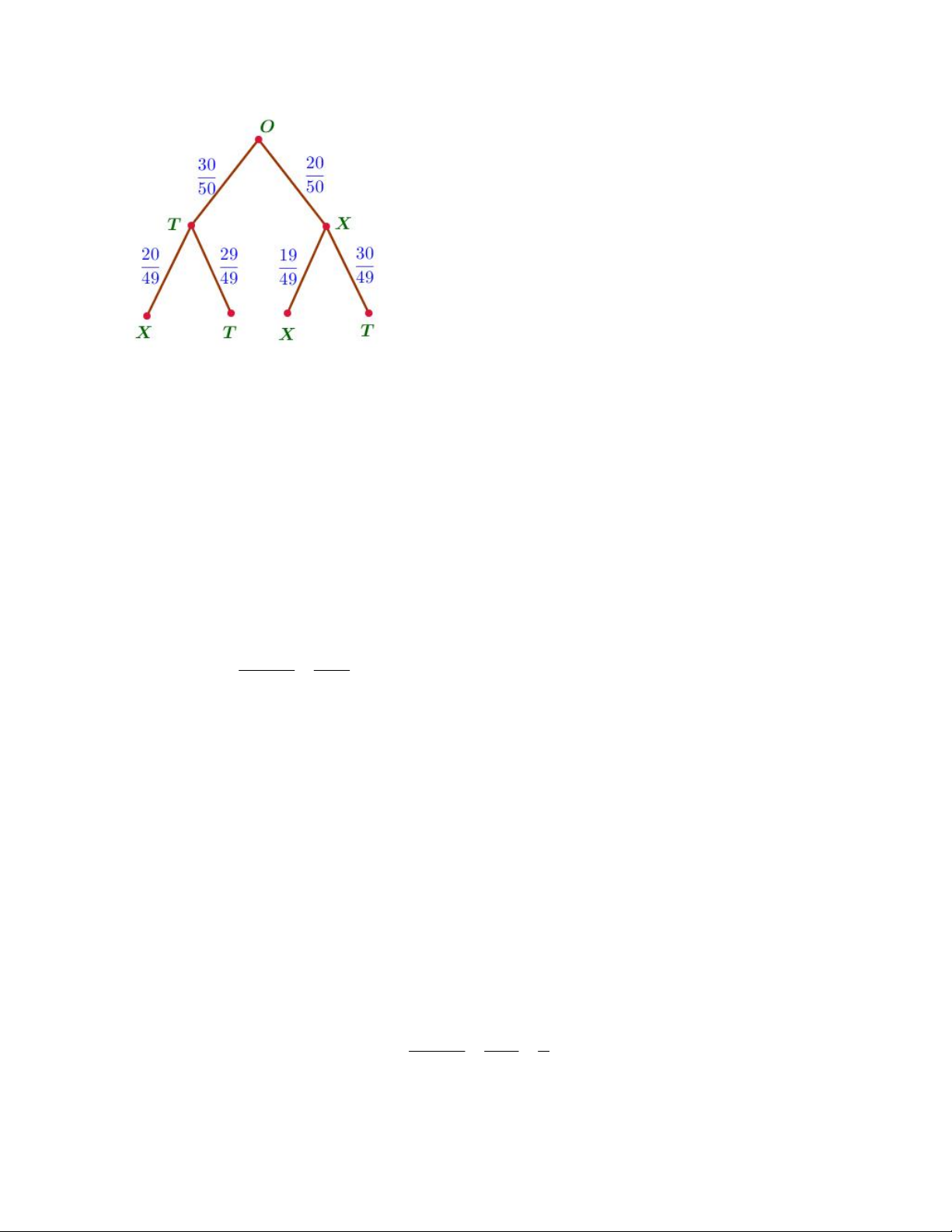
Mô tả bằng sơ đồ cây Bài tập 3
Gọi A là biến cố “Người mua bảo hiểm ô tô là nam”
B là biến cố “Người mua bảo hiểm ô tô trên 40 tuổi”.
Ta cần tính PB | A .
Do có 52% người mua bảo hiểm ô tô là nam nên P A  0,52 .
Do có 39% số người mua bảo hiểm ô tô là nam trên 40 tuổi nên P AB  0,39 .
Vậy PB A P AB 0,39 |    . P A 0,75 0,52 Bài tập 4
Gọi A là biến cố “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn ”.
B : “ Bệnh nhân đội mũ bảo hiểm đúng cách ”.
AB : “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn và đội mũ bảo hiểm đúng cách ”.
Theo đề ra ta có P AB 15%  0,15 ; PB  90%  0,9 ; P A  60%  0,6
Xác suất để HS bị chấn thương vùng đầu khi gặp tai nạn, biết HS đó đã đội mũ
bảo hiểm đúng cách là: P A B P AB 0,15 1 |    PB 0,9 6
Vậy việc đội mũ bảo hiểm đúng cách đối với học sinh khi di chuyển bằng xe máy
điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn số lần là 0,6  3,6lần. 1 6