

Preview text:
Tailieumontoan.com
Điện thoại (Zalo) 039.373.2038
CẨM NANG CHINH PHỤC
HÌNH HỌC VÀO LỚP 10
(Liệu hệ tài liệu word môn toán SĐT (zalo) : 039.373.2038)
Tài liệu sưu tầm, ngày 15 tháng 8 năm 2023
Website: tailieumontoan.com Môc lôc Trang CHƯƠNG 1
HỆ THỨC LƯỢNG TRONG TÁC VUÔNG CHƯƠNG 2 ĐƯỜNG TRÒN CHƯƠNG 3
CÁC ĐỊNH LÝ, BÀI TOÁN HÌNH HỌC CHƯƠNG 4
PHÂN TÍCH VÀ GIẢI 23 ĐỀ CHUYÊN TOÁN
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 521
Website: tailieumontoan.com
CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Dưới đây là các hệ thức về mối liên hệ của các cạnh, các góc, đường chiếu và đường cao trong một tam giác vuông. Cho A
∆ BC vuông tại A. Giả sử AH là đường cao của tam giác. Khi đó ta có các hệ thức sau: 2
1) BH.BC = BA và 2
CH .CB = CA 2 2) . HB HC = HA
3) AH.BC = B . A CA 1 1 1 4) = + 2 2 2 HA BA CA CA = BA = CA = BA 5) sin B , cos B , tan B , cot B = (tương tự với góc C ) CB BC BA CA = = 1 = = 1 ˆ = = 6) sin B cos C, sin C cos B, tanB cotC, tan C cot B cot B cot C
Trên đây tôi đã nhắc lại một số hệ thức cơ bản nhất về mối liên hệ gữa các cạnh, các góc, đường
chiếu và đường cao trong một tam giác vuông. Dưới đây là hệ thống bài tập giúp bạn đọc ghi nhớ và
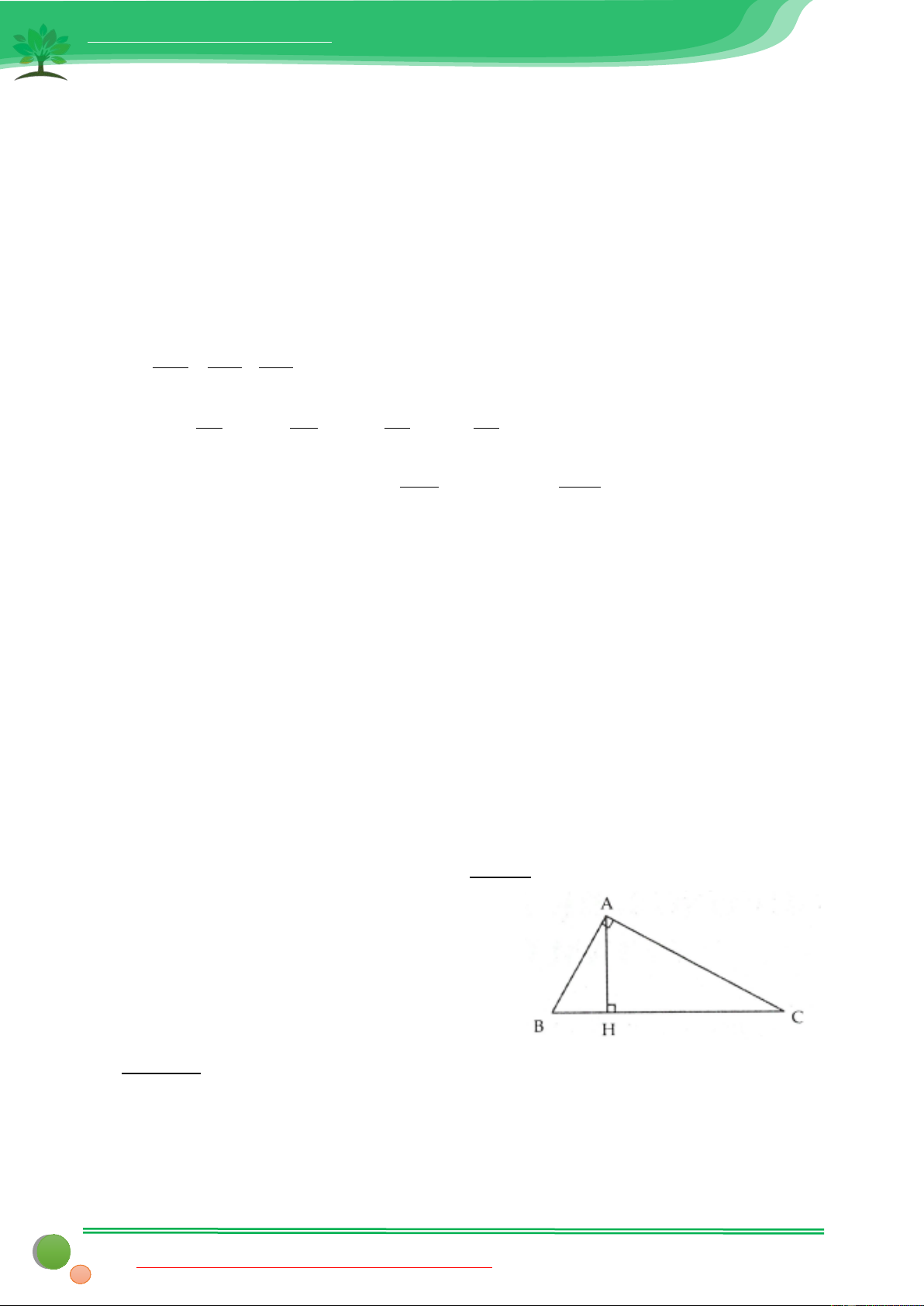
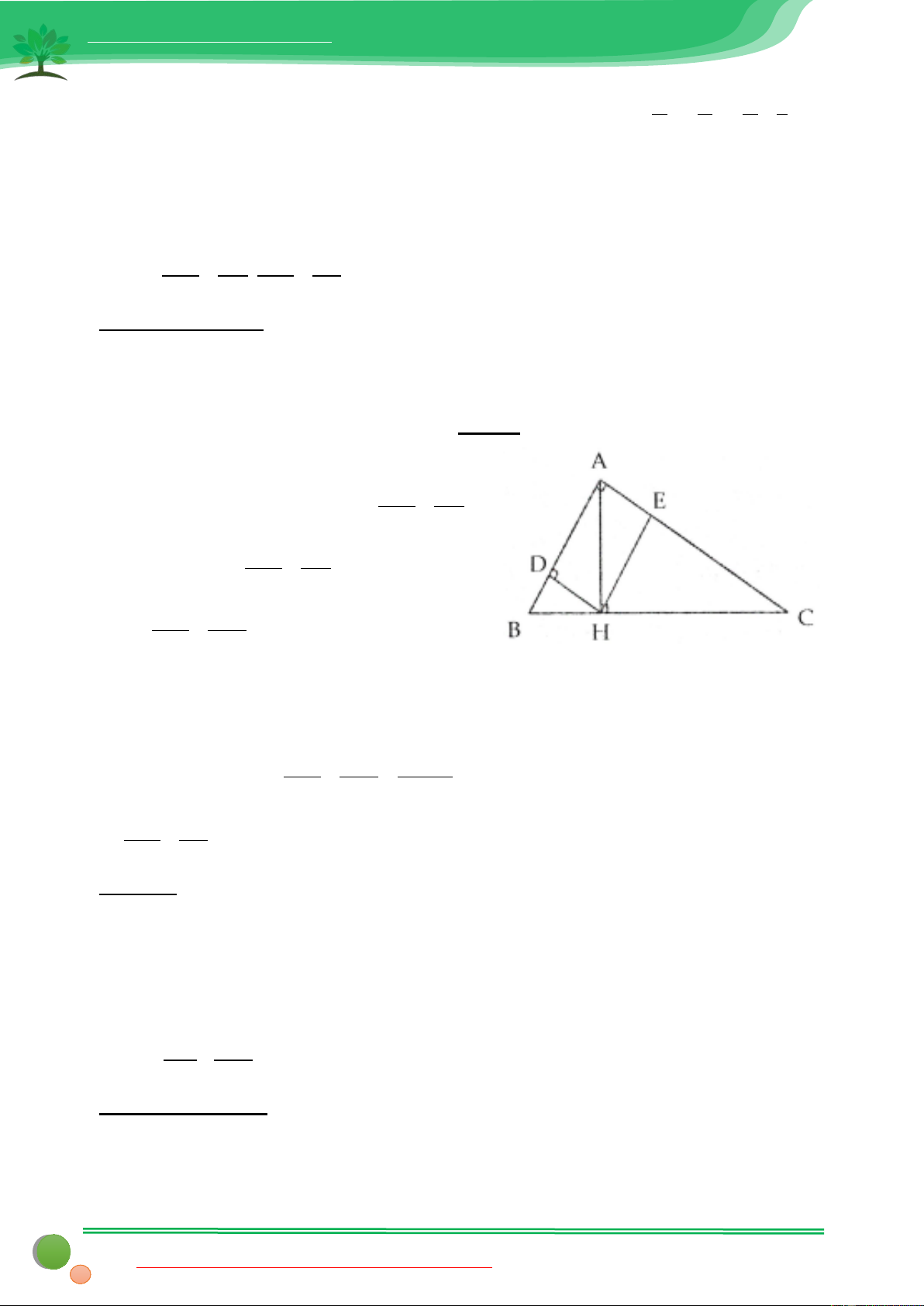
sử dụng thành thạo các công thức này trong các bài toán. Bài 1: Cho A
∆ BC vuông tại A đường cao AH . Biết BH = 9,CH =16.Giải tam giác ABC .
Định hướng lời giải: Ở đây bài toán yêu cầu giải tam giác ABC tức là chúng ta cần tìm độ dài 3
cạnh của tam giác. Điều này hoàn toàn dễ dàng ta chỉ cần sử dụng các hệ thức ở trên thì bài toán sẽ
được giải quyết. Dễ thấy BC = BH + CH = 25 . Để tính các cạnh AB,AC ta sẽ sử dụng hệ thức 1) ở trên ta được 2
BA = BH .BC = 225 ⇒ BA = 15 và 2
CA = CH.CB = 400 ⇒ CA = 20 . Từ đó ta đã tìm
được độ dài các cạnh của A
∆ BC . Ngoài ra ta hoàn toàn có thể tính được độ dài đường cao, diện tích và chu vi A ∆ BC Lời giải
Ta có BC = BH + CH = 25 Trong tam giác A
∆ BC vuông tại A đường cao AH Ta có: 2
AB = BC.HB = 225 ⇒ AB = 15 2
CA = BC.CH = 400 ⇒ CA = 20
Nhận xét: Như vậy đối với A
∆ BC vuông tại A và có đường cao AH. Ta chỉ cần biết được độ dài 2
trong số các cạnh AB, BC,C , A ,
HA HB, HC ta hoàn toàn có thể xác định được tất cả các yếu tố còn lại của A
∆ BC . Từ đó ta sẽ có các bài toán sau: Cho A
∆ BC vuông tại A đường cao AH
1) Biết AC = 12, BC = 15. Tính độ dài các đoạn AB, BH ,CH , AH.
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 1
Website: tailieumontoan.com
2) Biết AC = 10, HC = 8 . Tính độ dài các đoạn AB, BC, BH , AH.
3) Biết AB = 15, AH = 12 . Tính độ dài các đoạn AC, BC,CH , BH .
4) Biết BC = 25, AH = 12 . Tính độ dài các đoạn AC, AB,CH , BH . Bài 2: Cho A
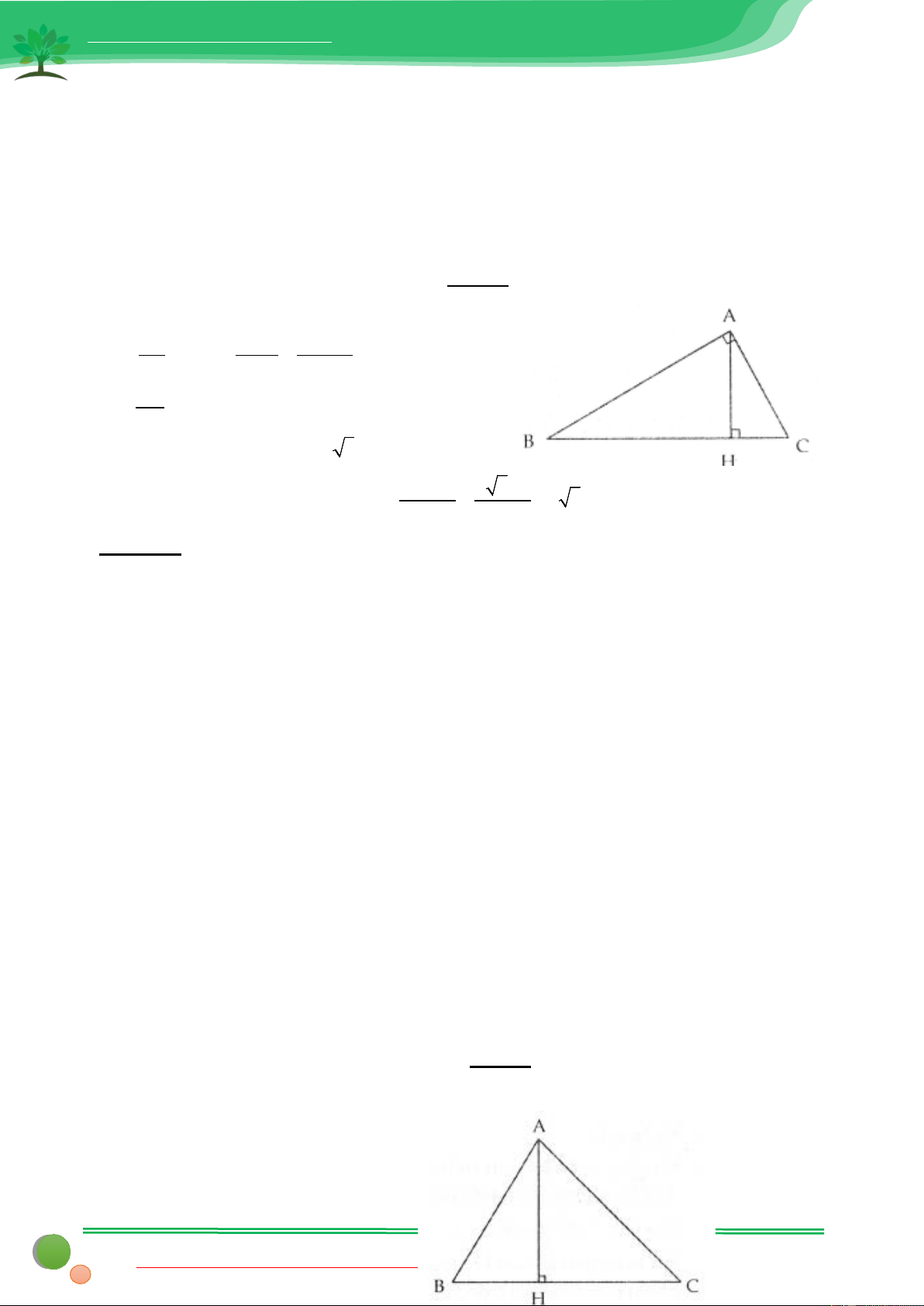
∆ BC vuông tại A đường cao AH. Biết =
AC 12, C = 60° . Giải tam giác ABC và tính độ dài đường cao AH Lời giải
Áp dụng hệ thức 5) ta sẽ có: CA AC 12 cos C = ⇒ BC = = = CB 24 cos C cos 60° AB sin C = BC ⇒ = AB
BC.sin C = 12.sin 60° = 6 3 A . B AC 6 3.12
Lại có AH.BC = 2S = A . B AC ⇒ AH = = = 3 3 ABC ∆ BC 24
Nhận xét: Ở bài toán 1 ta thấy nếu biết được 2 yếu tố về cạnh và đường cao trong A ∆ BC vuông thì ta
hoàn toàn xác định được các yếu tố còn lại trong tam giác. Đến bài toán 2 này ta thấy rằng nếu trong
tam giác ABC vuông mà ta biết được 1 yếu tố về cạnh và một yếu tố về góc thì các yếu tố còn lại cũng
hoàn toàn được xác định. Từ đó sẽ dẫn đến các bài toán sau: Cho A
∆ BC vuông tại A có đường cao AH 1) Biết = BC 10, C = 30 .
° Tính độ dài các đoạn AB, AC, BH,CH, AH 2) Biết = AH
5, C = 60° . Tính độ dài các đoạn AB, BC,C , A BH , CH 3) Biết = CH
8, C = 45° . Tính độ dài các đoạn AB, BC,C , A BH , AH
4) Biết AB : AC = 3 : 4 và BC = 15 . Tính độ dài các đoạn BH ,CH
Ở 2 bài toán trên ta đều xét tam giác ABC vuông. Bây giờ ta chuyển sang xét các tam giác không vuông. Bài 3: Cho A
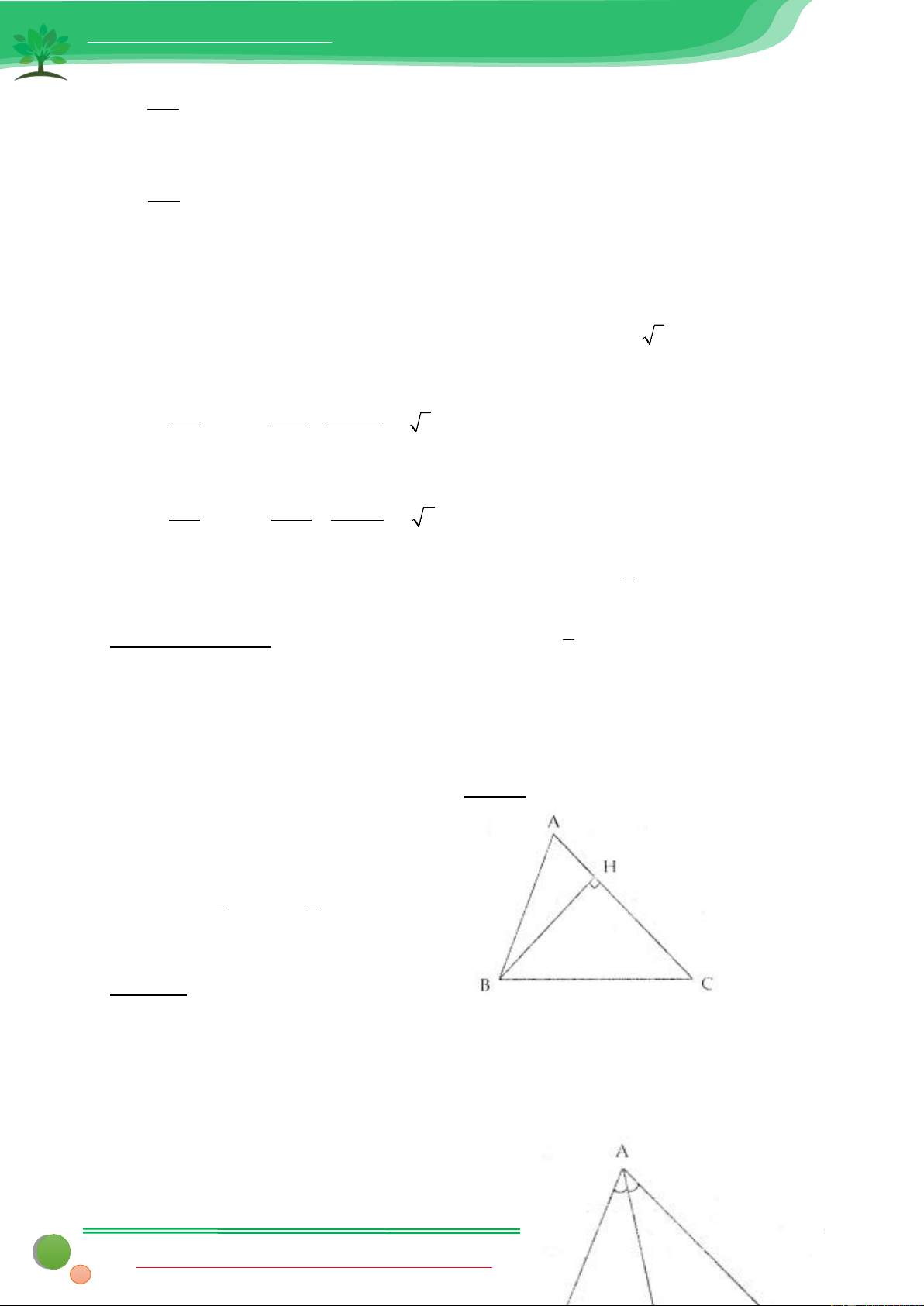
∆ BC có 3 góc nhọn, đường cao AH a) Chứng minh = + BC
AH .(cot B cot C) b) Biết = = ° AH 6, B
60 , C = 45° . Giải tam giác ABC Lời giải
a. Ta thấy trên hình có 2 tam giác ABH và ACH đều vuông tại H từ đó ta có thể áp dụng hệ thức lượng trong các tam giác này + Trong A
∆ BH vuông tại H có:
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 2
Website: tailieumontoan.com BH = ⇒ = cot B BH AH .cot B (1) AH + Trong A
∆ CH vuông tại H có: CH = ⇒ = cot C CH AH .cot C (2) AH + Từ (1) và (2), suy ra: = + = + BC BH HC
AH .(cot B cot C) b. Theo phần a) ta có: = + BC
AH .(cot B cot C) = 6(cot 60° + cot 45°) = 2( 3 + 3) + Trong A
∆ BH vuông tại H có: AH AH 6 sin B = ⇒ AB = = = AB 4 3 sin B sin 30° + Trong A
∆ CH vuông tại H có: AH AH 6 sin C = ⇒ AC = = = AC 6 2 sin C sin 45° 1 Bài 4: Cho A
∆ BC có A nhọn. Chứng minh diện tích tam giác ABC là = S A . B AC.sin A 2 1
Định hướng lời giải: Ta đã biết diện tích tam giác thì bằn g cạnh đáy x chiều cao như vậy ở bài 2
toán này ta sẽ phải hạ chiều cao từ 1 đỉnh của tam giác. Quan sát điều cần chứng minh ta thấy sin A
nên ta sẽ phải dựng đường cao hạ từ đỉnh B hoặc C của A
∆ BC . Từ đó áp dụng hệ thức lượng trong
tam giác vuông ta dễ dàng có điều phải chứng minh. Lời giải
Hạ BH ⊥ AC(H ∈ AC) Trong ∆ ABH có = BH AB sin A Do đó 1 1 = = S BH .AC A . B AC.sin A ABC ∆ 2 2 ⇒ đpcm
Nhận xét:
- Rõ ràng ta hoàn toàn có thể mở rộng bài toán này cho hình bình hành ABCD vì thực chất hình bình
hành ABCD bằng 2 lần diện tích tam giác ABD do đó = S A . B A . D sin . A ABCD
- Bài toán trên là một bài toán khá cơ bản tuy nhiên nó có ứng dụng rất nhiều trong các bài toán khác nhau.
Dưới đây là một số bài toán như vậy:
1) (Tính độ dài đường phân giác trong tam giác)
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 3
Website: tailieumontoan.com Xét A
∆ BC nhọn có đường phân giác AD(D ∈ BC) Ta có S = S + S ABC ∆ ABD ∆ AC ∆ D
Theo bài toán trên ta suy ra: 1 1 A 1 A A . B AC.sin A = A . B A . D sin + AC.A . D sin 2 2 2 2 2 A 2 os c .A . B AC A . B AC.sin A 2 ⇒ AD = = A AB + AC ( AB + AC).sin 2 A A ( Ta có công thức sin A = 2 sin os c
. Công thức này chứng minh cũng không quá khó khăn, ta sẽ xét 2 2 A
∆ BC cân tại A và kẻ các đường các đường cao AH, BK sau đó sử dụng hệ thức lượng giác các tam
giác vuông. Việc chứng minh cụ thể xin được dành cho bạn đọc). 2) Cho A
∆ BC có A < 90° . Trên cạnh AB, AC lần lượt lấy các điểm B ',C '. Chứng minh rằng S AB AC ABC ∆ = . S AB '.AC ' AB ∆ 'C'
Áp dụng bài toán trên ta có: 1 A . B AC.sin A S A . B AC ABC ∆ 2 = = S 1 AB '.AC ' AB ∆ 'C'
AB '.AC '.sin A 2 ⇒ đpcm
Các bài tập dưới đây xin mời các bạn đọc tự chứng minh: 1. Cho A
∆ BC nhọn. Kẻ đường thẳng d song song với BC và cắt các cạnh AB, AC lần lượt tại D, E . Tìm
vị trí của d để diện tích B
∆ DE đạt giá trị lớn nhất.
2. Cho tứ giác ABCD có 2 đường chéo cắt nhau tại O. Biết
AOD < 90° . Chứng minh: 1 = S( AOD ABCD) AC.BD.sin 2 3. Cho A
∆ BC vuông tại A. Từ trung điểm E của cạnh AC kẻ EF ⊥ BC a. Chứng minh = AF BE.c osC b. Biết = BC
10, C = 60° . Tính diện tích tứ giác ABFE
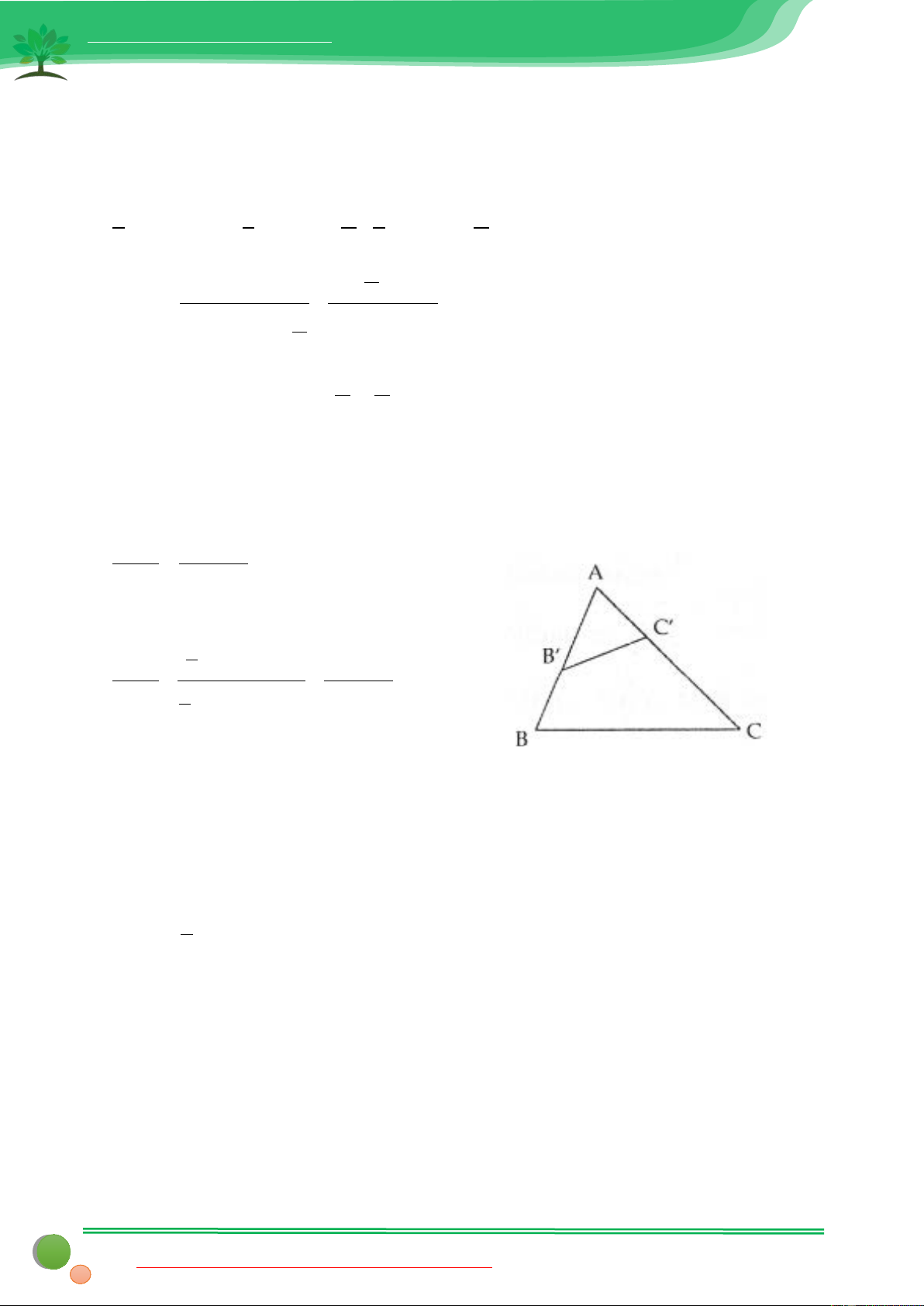
c. AF và BE cắt cạnh tại O. Tính sin AOB Bài 5: Cho A
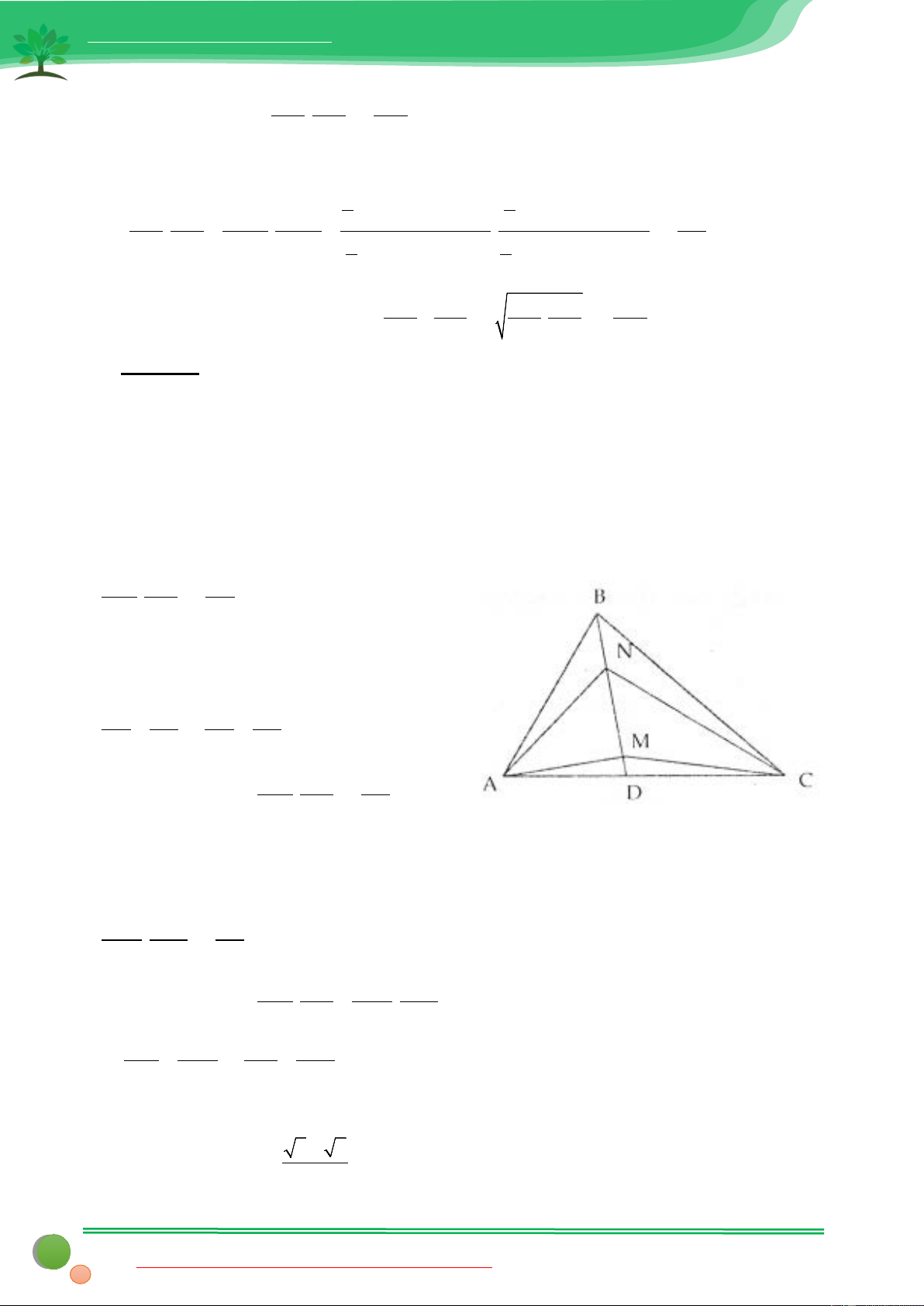
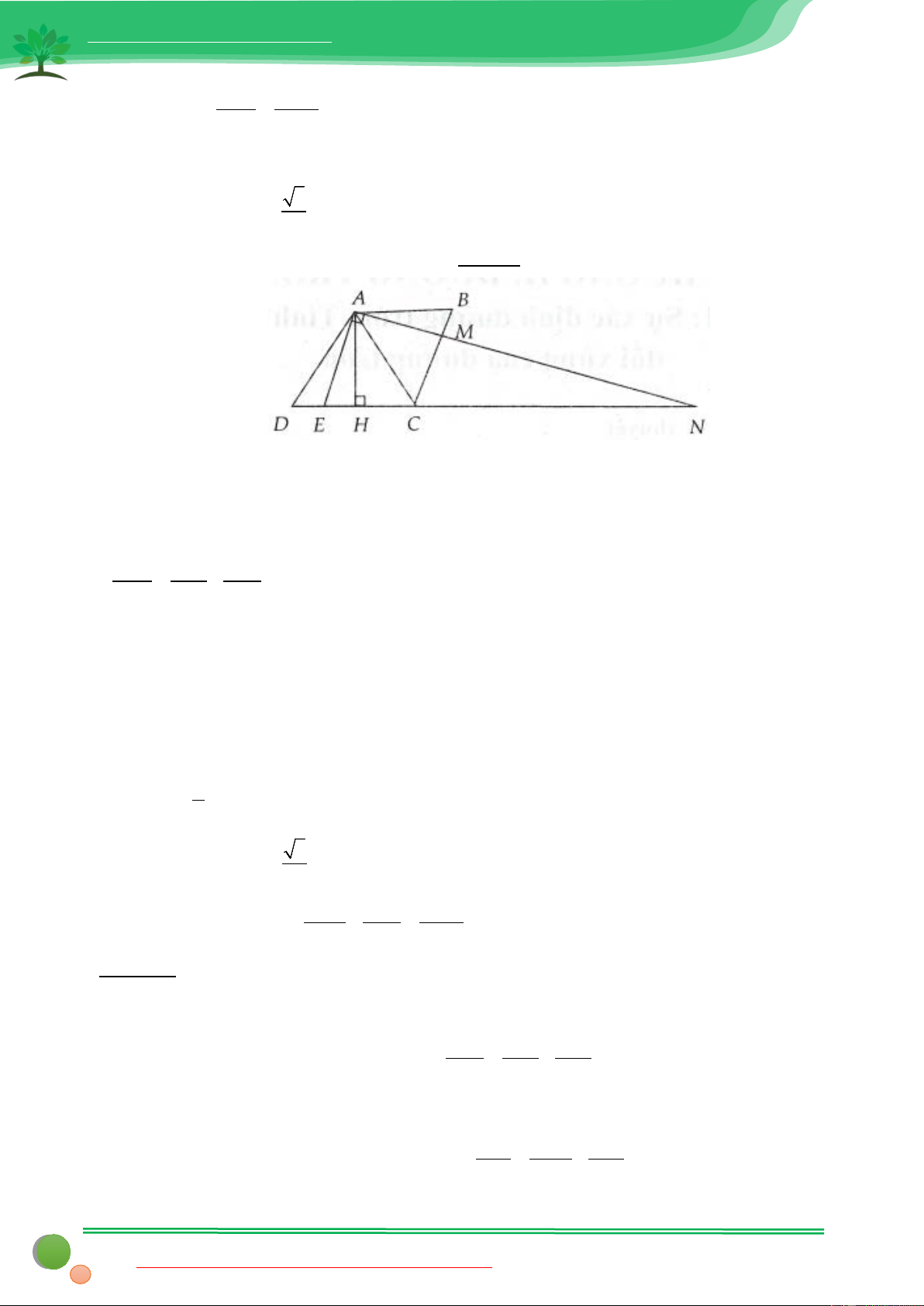
∆ BC . Trên cạnh BC lấy hai điểm M , N sao cho = BAM CAN Chứng minh rằng:
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 4
Website: tailieumontoan.com 2 2 BM CM AM BM BN AB . a . = . b . = CN BN AN CN CM AC BM CM AM . c + ≥ 2 CN BN AN
(Đề thi chuyên Toán THPT Hùng Vương năm 2000)
Định hướng lời giải: Quan sát vào hình vẽ và các tỉ số cần chứng minh ở trên ta sẽ nghĩ ngay đến tỉ lệ
diện tích các tam giác có chung đường cao. BM S CM S Ta có ngay ABM ∆ = và AC ∆ M =
. Giả thiết lại cho = BAM
CAN nên ta sẽ nghĩ đến công thức CN S BN S AC ∆ N ABN ∆
diện tích dựa vào góc đã chứng minh ở bài 4. Áp dụng công thức đó ta sẽ có: 1 1 AB . AM .sin BAM AC . AM .sin CAM S AB . AM S ABM ∆ 2 = = và AC ∆ M 2 = S 1 AC . AN S 1 ABN ∆ AC ∆ N AC . AN .sin CAN AB . AN .sin BAN 2 2 S AC . A M Do = ⇒ = AC ∆ M BAM CAN BAN CAM ⇒ =
từ đó kết hợp lại ta sẽ giải quyết được phần a) S AB . A N ABN ∆ BM CM AM
và b). Phần c) yêu cầu chứng minh bất đẳng thức + ≥ 2
mà theo phần a) ta đã biết tích CN BN AN 2 BM CM AM . =
một cách tự nhiên ta sẽ nghĩ đến việc áp dụng bất đẳng thức Cosi cho 2 tỉ số BM CN BN AN CN 2 CM BM CM BM CM AM AM và . Ta có + ≥ 2 . = 2 = 2 . BN CN BN CN BN AN AN
Từ đó ta có điều cần chứng minh. Lời giải
a. Dễ thấy các tam giác A ∆ BM , A ∆ CN, A ∆ BN, A
∆ CM có cùng chiều cao hạ từ đỉnh A do đó ta có: BM CM S S . ABM ∆ = . AC ∆ M CN BN S S AC ∆ N ABN ∆
Áp dụng công thức tính diện tích tam giác 1 = S
XY.XZ.sin X ta có X ∆ YZ 2 BM CM S S ABM ∆ AC ∆ M . = . CN BN S S AC ∆ N ABN ∆ 1 1 AB .AM .sin BAM AC .AM .sin CAM 2 2 = . (*) 1 1 AC .AN .sin CAN AB .AN .sin BAN 2 2
Lại có = ⇒ − = − ⇒ = BAM CAN BAC BAM BAC CAN BAN CAM
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 5
Website: tailieumontoan.com 2 Do đó từ BM CM AM (*) suy ra . = CN BN AN
b. Tương tự phần a) ta có: 1 1 2 AB.AM .sin BAM AB.AN.sin BAN BM BN S S AB ABM ∆ ABN ∆ 2 2 . = . = . = CN CM S S 1 AC AC ∆ N AC ∆ M 1 AC.AN.sin CAN AC.AM .sin CAM 2 2 BM CM BM CM AM
c. Áp dụng bất đẳng thức Cosi, ta có: + ≥ 2 . = 2 CN BN CN BN AN
Nhận xét: Hai đường thẳng AM, AN ở bài toán trên được gọi là hai đường đẳng giác trong A ∆ BC .
Hệ thức ở phần b) là một hệ thức khá quan trọng đó là một trong những tính chất của đường đẳng
giác trong tam giác. Từ hệ thức này ta có thể giải quyết bài toán khá khó sau đây: Cho A
∆ BC có BD là phân giác trong của
ABC . Trên đoạn BD lấy 2 điểm M, N sao cho = CAM
BAN . Chứng minh = ACM BCN + Trong A ∆ BD có = DAM
BAN nên theo phần b) bài toán trên ta sẽ có: 2 BN BM AB . = ( ) 1 DM DN AD
Do BD là phân giác của
ABC nên theo tính chất
đường phân giác trong tam giác ta có: AD AB AB BC = ⇒ = (2) CD BC AD CD 2 BN BM BC Từ (1) và (2), suy ra: . = (3) DM DN CD
Mặt khác trên đoạn BD ta lấy điểm M ' sao cho = BCN DCM ' + Trong B ∆ CD có = BCN
DCM ' nên theo phần b) bài toán trên ta sẽ có: 2 BN BM ' BC . = (4) DM ' DN CD BN BM BN BM ' Từ (3) và (4), suy ra: . = . DM DN DM ' DN BM BM ' BM BM ' ⇒ = ⇒ =
⇒ BM = BM ' ⇒ M ≡ M ' DM DM ' BD BD Do đó = BCN ACM (đpcm) 6 + 2
Bài 6: Chứng minh sin 75° = 4
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 6
Website: tailieumontoan.com
( Đề thi chuyên Toán – Tin, Hà Tây năm 2000-2001)
Định hướng lời giải: Để tính đượcsin 75° việc đầu tiên chắc chắn ta phải dựng một tam giác vuông
có 2 góc nhọn là 75° và15° . Ta giả sử có tam giác ABC vuông tại A và có = ° B 75 , C = 15 . ° Tiếp theo
ta sẽ khai thác một số tính chất của tam giác vuông mà tính chất đầu tiên ta nghĩ tới sẽ là đường trung 1
tuyến từ đỉnh của góc vuông có độ dài bằng
độ dài cạnh huyền. Như vậy, nếu gọi I là trung điểm của 2 BC
BC thì ta sẽ có IA = IB = IC =
= a và ta để ý rằng tam giác IAB cân mà có B = 75° nên AIB = 30° . 2
Từ đây ta sẽ nghĩ ngay đến việc hạ đường cao AH thì ta sẽ hoàn toàn tính được độ dài AH , HI theo a.
Từ đó dễ dàng tính được độ dài của AC theo a nên ta sẽ thu được điều phải chứng minh. Lời giải Giả sử A
∆ BC có vuông tại A và có = ° B 75 , C = 15 , ° BC = 2a
Gọi I là trung điểm của BC Do A
∆ BC vuông tại A nên ta có IA = IB = IC = a ⇒ IA
∆ B cân tại I có = ° ⇒ B 75 AIB = 30°
Kẻ AH ⊥ BC ( H ∈ BC ) a Trong A
∆ HI vuông tại H có AH = AI.sin 30° = 2 3 = .co 3 s a IH AI 0° = 2 a + a (2 3 3 )
Do đóCH = CI + IH = a + = 2 2 a 2 + 3 a 2 2 2 ( )2 2 2 Ta có: 2
AC = AH + HC = + = a (2+ 3) 4 4
⇒ AC = a 2 + 3 Trong A
∆ BC vuông tại A có sin
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 7
Website: tailieumontoan.com ° = AC a 2 + 3 2 + 3 6 + 2 sin 75 sin B = = = = ⇒ đpcm BC 2a 2 4
Nhận xét: Cũng với cách làm tương tự ta hoàn toàn có thể tính được giá trị lượng giác của các góc khác
như 18 ,°36 ,°54 ,°72°. Mời bạn đọc thử sức với các bài toán đó. A a Bài 7: Cho A
∆ BC có độ dài các cạnh BC, AC, AB lần lượt là a,b,c . Chứng minh rằng sin ≤ 2 b + . c
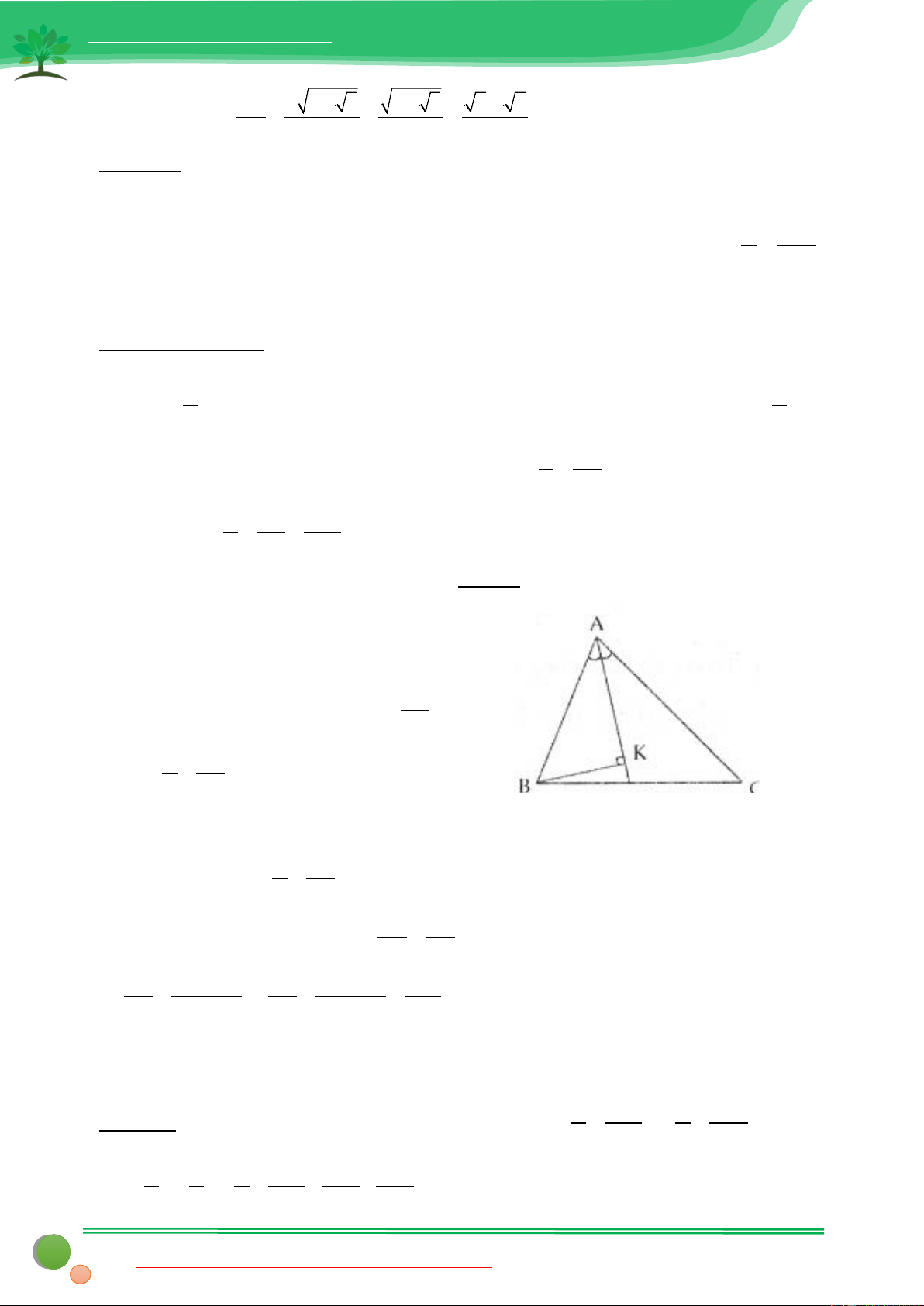
(Đề thi chuyên tỉnh Trà Vinh năm học 2013-2014) A a
Định hướng lời giải: Đề bài yêu cầu chứng minh sin ≤
như vậy chắc chắn ta sẽ nghĩ đến việc 2 b + c A A tạo ra góc
bằng cách dựng tia phân giác AD của góc A. Tiếp theo để làm xuất hiện sin thì ý tưởng 2 2 A BK
tự nhiên là hạ BK ⊥ AD ta sẽ có A
∆ BK vuông tại K vàsin =
. Mặt khác, ta lại dễ dàng thấy rằng 2 AB A BD a
BK ≤ BD ⇒ sin ≤ = 2 AB b + c Lời giải
Kẻ đường phân giác AD của
A( D ∈ BC )
Hạ BK ⊥ AD ( K ∈ AD) BK Trong A
∆ BK vuông tại K có sin KAB = BA A BK Hay sin = ( ) 1 2 BA Trong B
∆ DK vuông tại K cạnh huyền BD có BK ≤ BD(2) A BD Từ (1) và (2) suy ra sin ≤ (3) 2 BA DB AB
Do AD là phân giác của A nên ta có: = DC AC BD AB BD BC a ⇒ = ⇒ = = (4) BC AB + AC BA AB + AC b + c A a Từ (3) và(4), ta có: sin ≤ ⇒ đpcm 2 b + c B b C c
Nhận xét: Tương tự với các góc
B, C của A
∆ BC ta cũng có sin ≤ ;sin ≤ . Từ đó ta sẽ 2 c + a 2 a + b A B C a b c có sin .sin .sin ≤ + +
. Áp dụng bất đẳng thức quen thuộc sau 2 2 2 b + c c + a a + b
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 8
Website: tailieumontoan.com ( A B C 1
a + b)(b + c)(c + a) ≥ 8abc ta sẽ được một bất đẳng thức khá đẹp mắt sin .sin .sin ≤ 2 2 2 8
Ngoài việc tính toán các đại lượng hình học, các hệ thức lượng trong tam giác vuông còn có ứng dụng
trong việc chứng minh các đẳng thức hình học. Ta sẽ xem xét một bài toán sau: Bài 8: Cho A
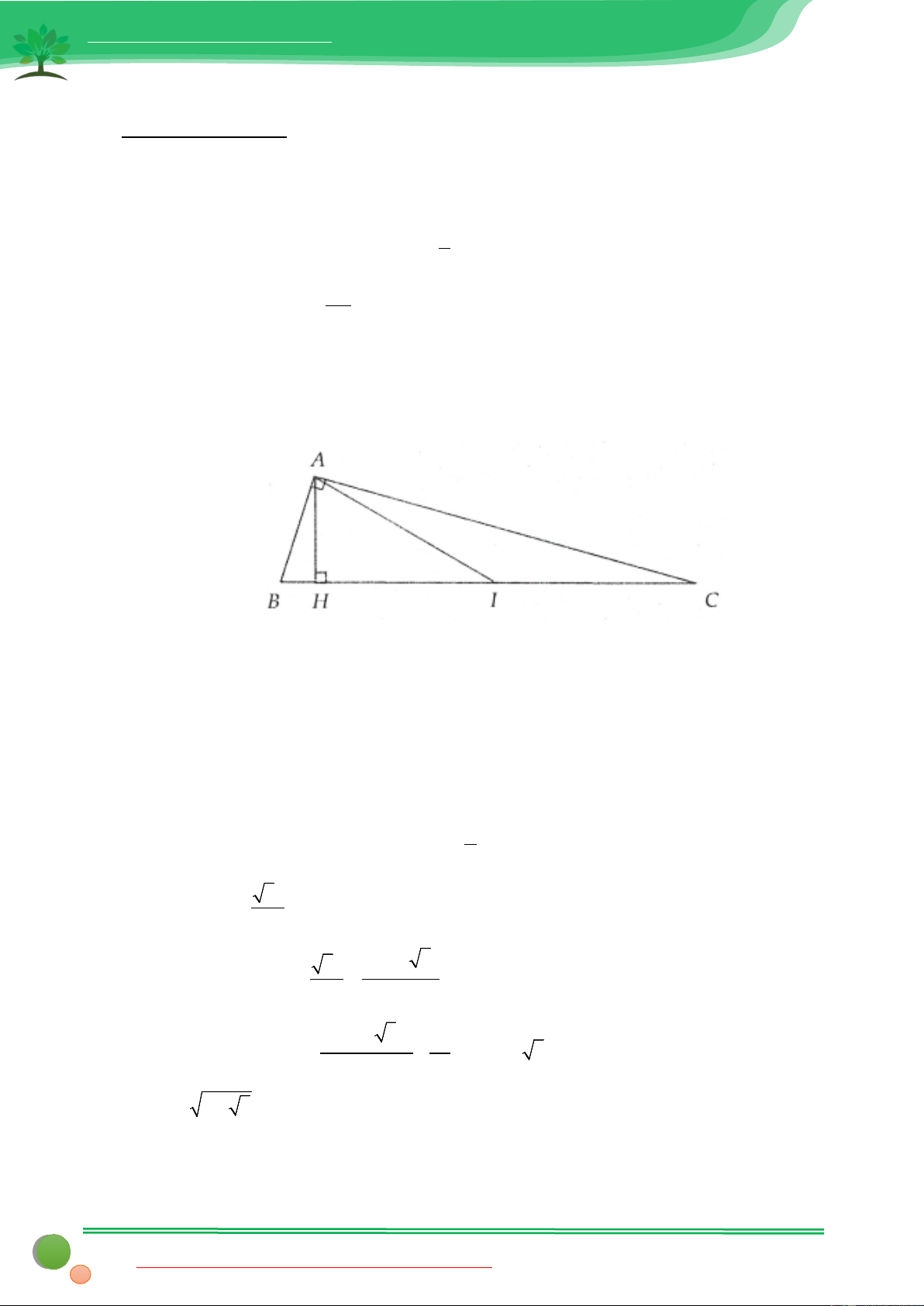
∆ BC vuông tại A. Đường cao AH, HD, HE lần lượt là các đường cao của A ∆ HB và A ∆ HC . 2 3 AB HB AB DB Chứng minh = ; = 2 3 AC HC AC EC
Định hướng lời giải: Từ các tam giác vuông A ∆ BC, H ∆ AB và HA ∆
C ta dễ dàng thiết lập được mối liên
hệ giữa các đoạn AB, AC, BH ,CH , HD, HE, DB, EC với nhau bởi các hệ thức lượng trong tam giác
vuông nên sẽ không khó khăn gì để thu được điểu phải chứng minh. Lời giải a. Trong A
∆ BC vuông tại A đường cao AH có: 2 AB HB 2 2
AB = BH .BC; AC = CH .CB ⇒ = 2 AC HC 2 AB HB b. Theo phần a) có = 2 AC HC 4 2 AB HB ⇒ = 1 2 4 ( ) AC HC Trong HA ∆
B vuông tại H có đường cao HD có 2 HB = B . D BA(2) Trong HA ∆
C vuông tại H có đường cao HE có 2
HC = EC.AC (3) 4 2 AB HB B . D BA Từ (1), (2) và (3) suy ra: = = 2 4 AC HC CE .CA 3 AB DB ⇒ = ⇒ đpcm 3 AC EC
Nhận xét: Đây cũng là một bài tập đơn giản giúp chúng ta có thể nhớ và vận dụng linh hoạt các hệ thức
lượng trong tam giác vuông vào các bài tập tính toán cũng như chứng minh đẳng thức.
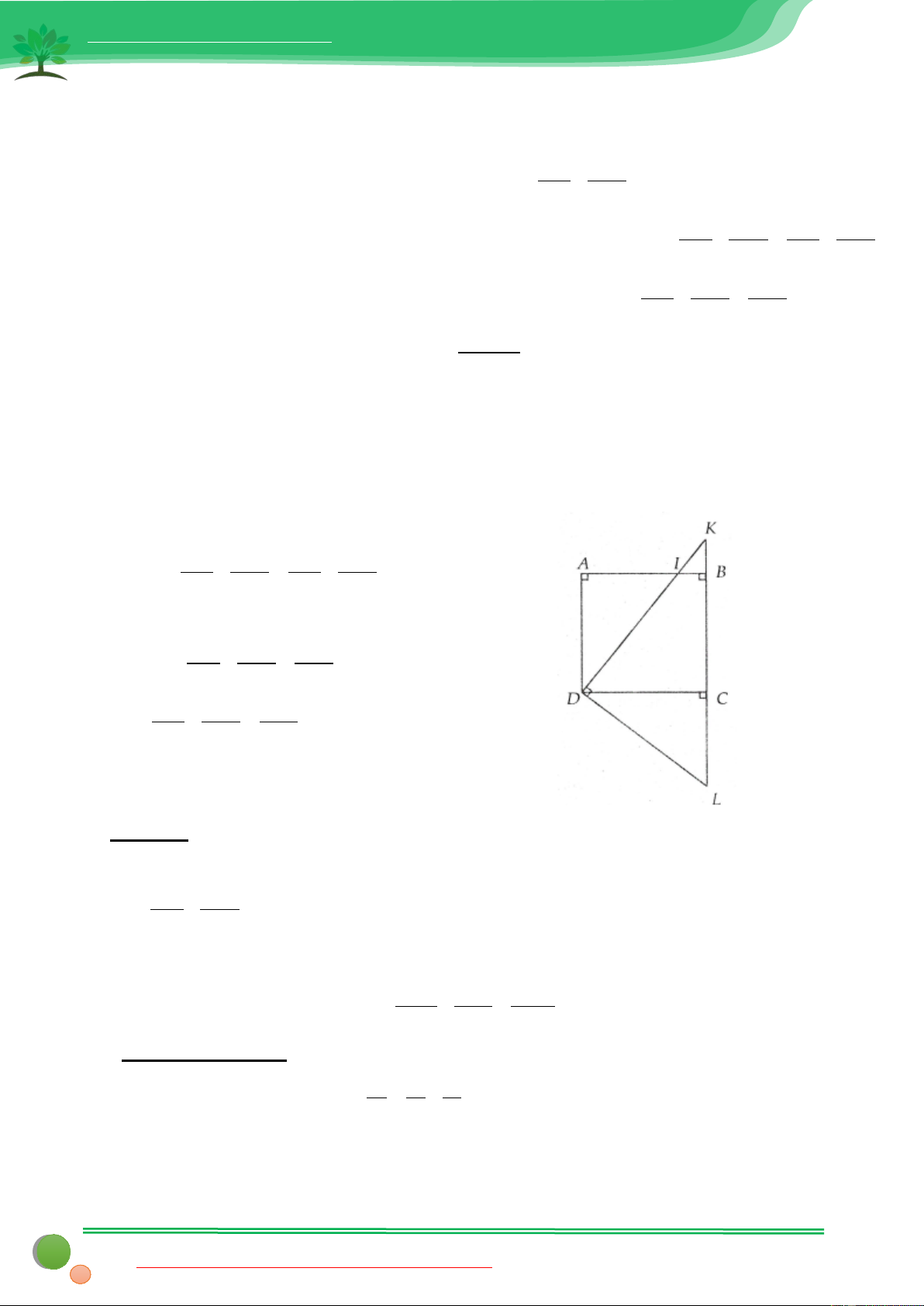
Bài 9: Cho hình vuông ABCD. Gọi I là điểm nằm giữa A, B. Tia DI cắt CB ở K. Đường thẳng qua D
vuông góc với DI và cắt BC tại L . Chứng minh: a. D
∆ IL là tam giác cân 1 1 b. Tổng +
không thay đổi khi I thay đổi trên AB. 2 2 DI DK
Định hướng lời giải: Phần a) bài toán yêu cầu chứng minh D
∆ IL là tam giác cân. Nhìn từ hình vẽ ta thấy D
∆ IL cân tại D như vậy ta cần chứng minh = DIL
DLI hoặc DI = DL . Quan sát thể hình ta thấy
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 9
Website: tailieumontoan.com
rằng việc chứng minh 2 cạnh DI = DL là dễ dàng hơn vì trong 2 A ∆ DI và C
∆ DL đều có góc vuông có 1
cặp cạnh bằng nhau mà ta dễ dàng nhận ra = ADI
CDL vì cùng phụ với CDI ⇒ A ∆ DI = C ∆ DL ⇒ 1 1
DI = DL ta có đpcm. Phần b yêu cầu chứng minh tổng +
không đổi khi I thay đổi trên AB. 2 2 DI DK 1 1 1 1
Rõ ràng phần a) của bài toán là một gợi ý cho phần b) khi ta có DI = DL ⇒ + = + 2 2 2 2 DI DK DL DK 1 1 1
mà theo hệ thức lượng trong DL ∆
K vuông tại D có đường cao DC nên + = không đổi. 2 2 2 DL DK DC Lời giải a. Ta có: + = =
° = = + ⇒ = ADI IDC ADC 90 IDL IDC CDL ADI CDL ( ) 1 Lại có = = DAI 90
DCL và AD = DC (2)
Từ (1) và (2), suy ra: A ∆ DI = C
∆ DL (g.c.g) ⇒ DI = DL ⇒ DI ∆ L cân tại D
b. Theo phần a) ta có DI = DL Do đó 1 1 1 1 + = + 2 2 2 2 DI DK DL DK
Trong tam giác DKL vuông tại D, đường cao 1 1 1 DC có + = không đổi 2 2 2 DL DK DC 1 1 1 ⇒ + = không đổi khi I thay 2 2 2 DI DK DC đổi trên AB
Nhận xét: Bài toán này sẽ khó hơn rất nhiều nếu bỏ đi phần a) của bài 7 ta sẽ có bài toán sau: Cho
hình vuông ABCD. Điểm I thay đổi trên cạnh AB. Đường thẳng DI cắt tia BC tại K. Chứng minh rằng 1 1 tổng +
không thay đổi khi I thay đổi trên cạnh AB. 2 2 DI DK
Bài 10: Cho hình thoi ABCD có
A = 120° . Kẻ tia Ax sao cho
BAx = 15° . Tia Bx cắt cạnh BC tại M và cắt đườ 1 1 4
ng thẳng CD tại N. Chứng minh rằng: + = 2 2 2 AM AN 3AB
Định hướng lời giải: Đẳng thức cần chứng minh gợi cho ta đến đẳng thức về mối liên hệ về cạnh và đườ 1 1 1
ng cao trong tam giác vuông = +
. Từ đó ta thấy nó cũng mang một chút hơi hướng như 2 2 2 h b c
bài 8. Ta sẽ tạo một tam giác vuông có độ dài 2 cạnh góc vuông là AM và AN. Quan sát thể hình ta sẽ
dựng AE ⊥ AN ( E ∈ DC ) và dựng AH ⊥ DC ( H ∈ DC ) . Như vậy ta sẽ chỉ cần chứng minh được
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 10
Website: tailieumontoan.com 1 4 AE = AM và =
. Việc chứng minh AE = AM hoàn toàn tương tự như phần a) của bài 8. 2 2 AH 3AB
Theo giả thiết có
A = 120° nên dễ thấy A ∆ DC đều 3
⇒ AH = sin 60 . ° AD =
AB từ đó ta sẽ có đpcm. 2 Lời giải
Qua A kẻ đường thẳng vuông góc với Ax và cắt đoạn DC tại E
Hạ AH ⊥ CD ( H ∈CD)
Trong tam giác EAN vuông tại A, đường cao AH có: 1 1 1 = + (1) 2 2 2 AH AE AN
Mặt khác, ta có: = − − DAE DAB EAN
NAB = 120° − 90° −15° = 15° ⇒ = DAE MAB Mà = = AD AB,B D ⇒ A ∆ DE = A
∆ BM (g.c.g) ⇒ AE = AM( 2 )
Do ABCD là hình thoi có A = 120° ⇒ 1 = DAC A = 60° ⇒ A
∆ DC là tam giác đều 2 3
⇒ AH = AD.cos60° = AB (3) 2 1 1 4
Từ (1), (2) và (3), suy ra: + = ⇒ đpcm 2 2 2 AM AN 3AB
Nhận xét: Dưới đây là một số bài toán có ý tưởng tương tự như 2 bài toán trên:
Bài toán 1: Cho hình thang vuông ABCD có = A
D = 90° và AD = BC ( AB < DC ) . Gọi E là giao điểm 1 1 1
của hai đường thẳng DA và CB. Chứng minh: = + 2 2 2 AD BC EC
Bài toán 2: Cho hình chữ nhật ABCD với AD = t.AB (t > 0) . Lấy điểm M trên cạnh BC. Đường thẳng 1 1 1
AM cắt đường thẳng CD tại P. Chứng minh rằng: = + 2 2 2 AB AM AP
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 11
Website: tailieumontoan.com
CHƯƠNG II : ĐƯỜNG TRÒN
BÀI 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn I. Tóm tắt lý thuyết
1) Cho đường tròn (O) bán kính R kí hiệu là (O;R)
Xét vị trí điểm M trên mặt phẳng so với vị trí của (O;R):
_ Điểm M thuộc (O;R) khi và chỉ khi OM = R
_ Điểm M nằm bên trong (O;R) khi và chỉ khi OM < R
_ Điểm M nằm bên ngoài (O;R) khi và chỉ khi OM > R
2) Đường tròn là hình có tâm đối xứng.Tâm của đường tròn chính là tâm đối xứng của đường tròn đó
3) Đường tròn là hình có trục đối xứng. Đường kính bất kì của đường tròn đều là trục đối xứng của đường tròn đó II .Bài tập
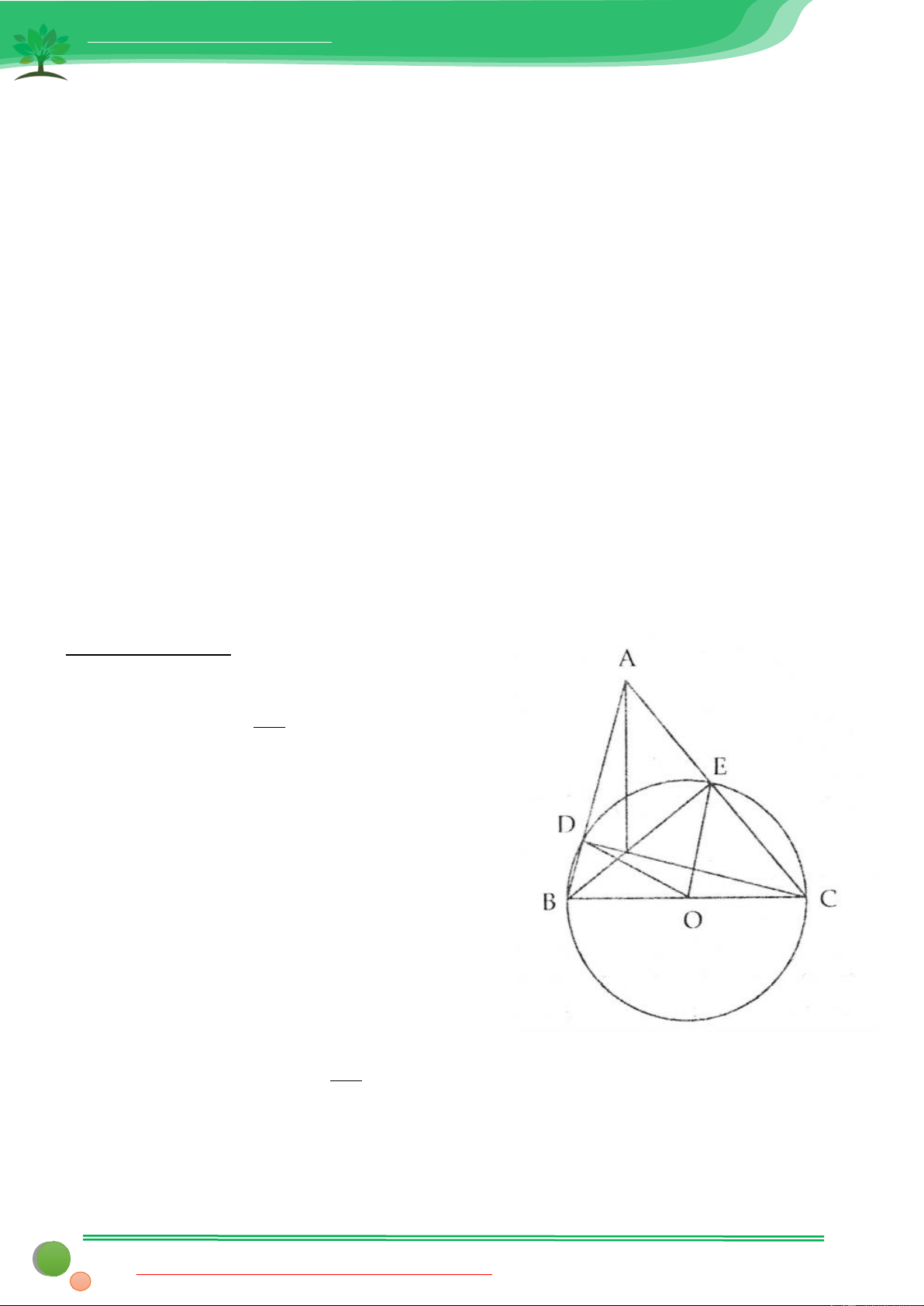
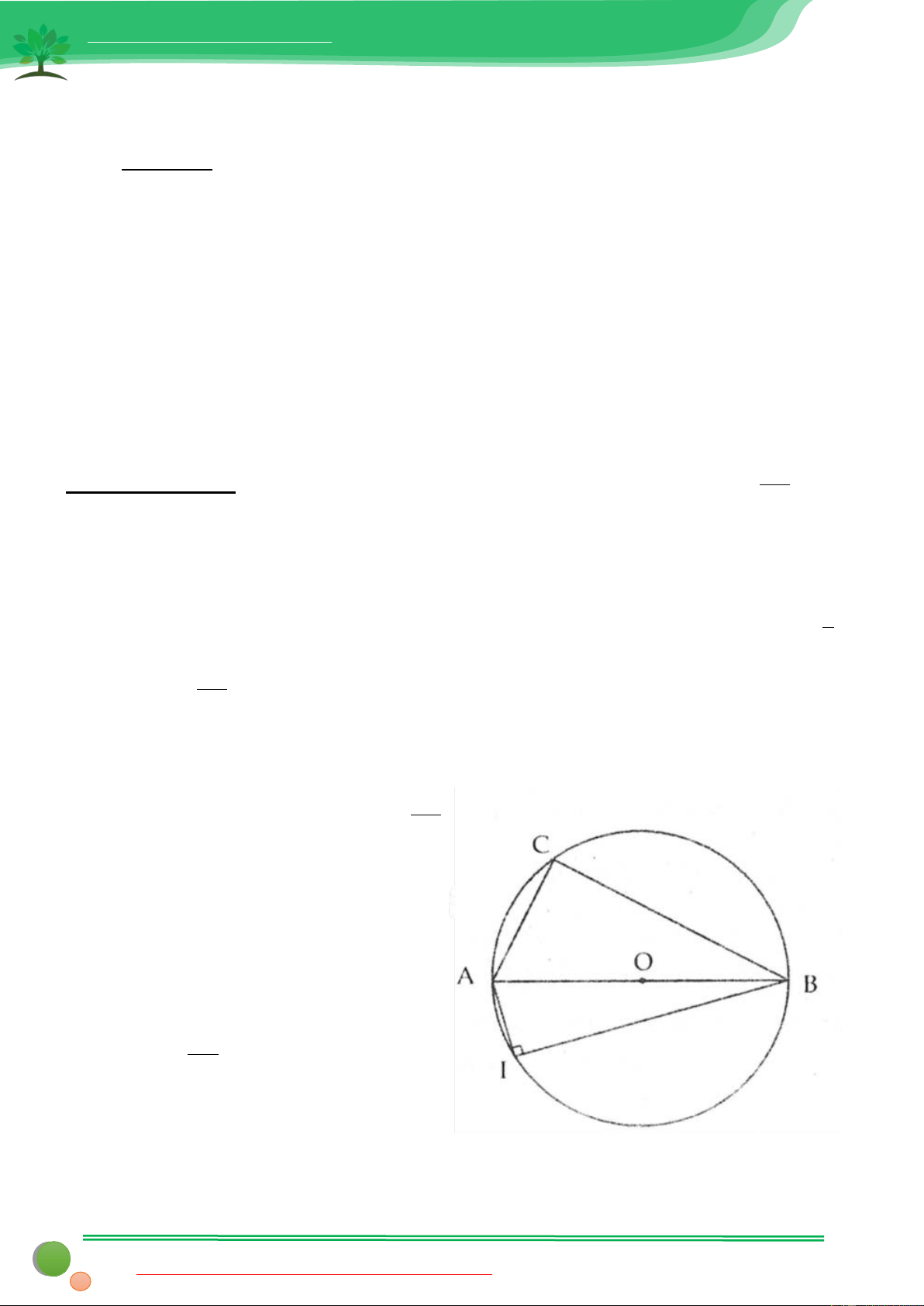
Bài 1: Cho tam giác nhọn ABC .Vẽ đường tròn (O) có đường kính BC và cắt cạnh AB, AC theo thứ tự ở D, E
a. Chứng minh CD ⊥ AB,BE ⊥ AC
b. Gọi K là giao điểm của BE và CD. Chứng minh rằng AK ⊥ BC
Định hướng lời giải :
Ta dễ dàng nhận thấy OB = OC = OD = OE BC
từ đó suy ra OD = OE = 2
Mà OD, OE lần lượt là các đường trung
tuyến trong ∆BDC và ∆BEC nên ta có 2
tam giác này vuông tại D, E hay suy ra
CD ⊥ AB và BE ⊥ AC
Như vậy ta có BE, CD là các đường cao của ∆ABC
⇒ K = BE ∩CD là trực tâm của ∆ABC nên ta sẽ có AK ⊥ BC Lời giải:
a. Do D, E thuộc đường tròn (O) đường kính BC BC
⇒OD = OE = OB = OC = 2
⇒ các tam giác BDC và BEC là các tam giác vuông tại D và E
⇒ BE ⊥ AC và CD ⊥ AB
b. Ta thấy trong tam giác ABC có các đường cao BE và CD
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 1
Website: tailieumontoan.com
Lại có K là giao điểm của BE và CD
⇒ K là trực tâm của ∆ABC ⇒ AK ⊥ BC
Nhận xét : Từ bài toán này ta rút ra nhận xét đó là với mỗi điểm M bất kì thuộc đường tròn đường
kính BC thì ta sẽ có BMC = 90° . Nhận xét này là khá quan trọng và sẽ được dùng trong rất nhiều
các bài toán trong suốt chương trình hình học 9
Bài 2: Cho 3 dây AB, BC, CA của một đường tròn (O;R) trong đó AB là đường kính
a. Chứng minh ACB = 90°
b. Tìm tập hợp điểm I nhìn đoạn thẳng AB đã cho dưới một góc vuông
c. Dựng ∆ABC vuông có cạnh huyền AB cố định đã cho bằng 5cm, cạnh góc vuông AC = 3cm
d. Dựng trực tâm của ∆ABC có cạnh AB = 5cm,BC = 4,5cm,CA = 4cm Định hướ AB
ng lời giải : Tương tự như phần a) bài 1 dễ thấy OA = OB = OC = R do đó OC = 2
Mà OC là trung tuyến trong ∆ABC nên ∆ABC vuông tại C hay ACB = 90°
Phần b) yêu cầu tìm tập hợp điểm I nhìn đoạn thẳng AB dưới 1 góc vuông tức là AIB = 90° . Như vậy tam 1
giác ∆AIB vuông tại I nên điều đầu tiên ta nghĩ đến đó là đường trung tuyến từ I có độ dài bằng cạnh 2 AB , do đó AB OI =
= R nên I ∈(O;R) từ đó suy ra tập hợp điểm I chính là đường tròn (O;R). Phần c) và 2
d) ta chỉ cần dựa vào kết quả của phần b) và bài 1 sẽ được giải quyết Lời giải: AB
a. Dễ thấy OA = OB = OC = R ⇒ OC = 2
Mà OC là đường trung tuyến của ∆ABC ⇒ ∆
ABC vuông tại C ⇒ ACB = 90° b. Phần thuận Ta có AIB = °
90 ⇒ ∆AIB vuông tại I
Mà IO là đường trung tuyến của ∆AIB AB ⇒OI =
= R ⇒ I ∈(O;R) 2
* Phần đảo : Với I ∈ (O;R)
Theo phần a) dễ thấy AIB = 90°
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 2
Website: tailieumontoan.com
Vậy nên ta có tập hợp các điểm I nhìn đoạn thẳng AB một góc vuông là đường tròn (O) sao cho AB là đường kính
c. Dựng đường tròn đường kính AB = 5cm
Dựng dây AC = 3cm (ta luôn dựng được vì 3cm < 5cm )
Từ đó ta sẽ dựng được tam giác ABC vuông tại C có AB = 5cm,CA = 3cm
d. Đầu tiên ta dễ dàng dựng được ∆ABC (dựng bằng compa)
Tiếp theo ta sẽ dựng đường tròn (O,2cm) với O là trung điểm của AC. Khi đó AC là đường kính của
đường tròn này. Gọi D, E là các giao điểm của đường tròn (O) với các cạnh AB, BC. Khi đó nếu gọi
H là giao điểm của AD và CE thì H chính là trực tâm của ∆ABC (theo bài 1)
Nhận xét : Bài toán này chính là hệ quả trực tiếp của phần nhận xét ở bài 1. Với kiến thức ở phần lí
thuyết trong bài này ta vẫn chưa được sử dụng ngay nhận xét đó nhưng nó có thể giúp cho ta phát
triển và giải quyết vấn đề của bài toán rất nhanh
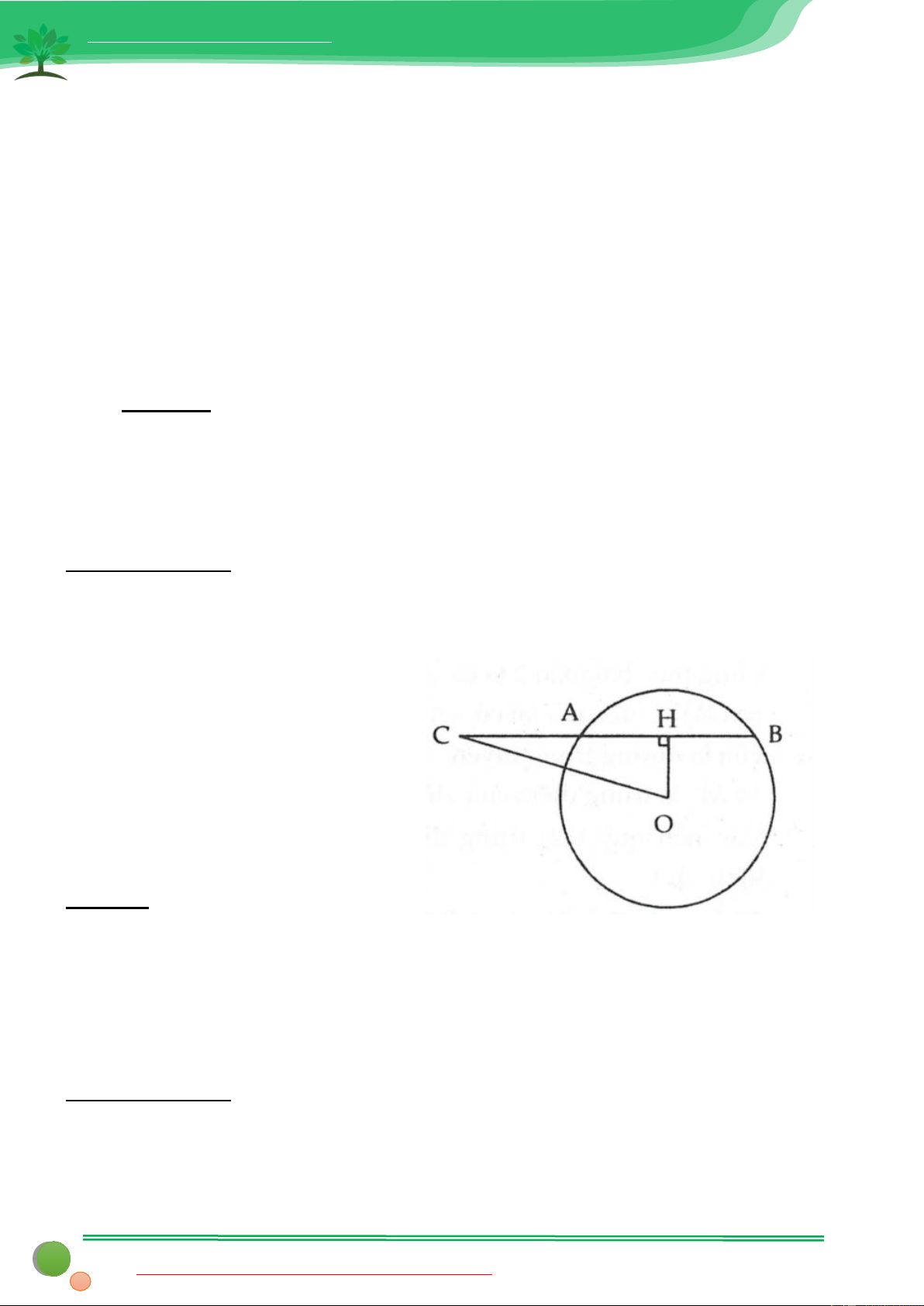
Bài 3: Cho AB là dây cung của đường tròn (O;R) (AB không là đường kính). C là điểm trên tia đối của tia
AB. Chứng minh điểm C nằm ngoài đường tròn (O;R)
Định hướng lời giải :
Để chứng minh được C nằm ngoài đường tròn (O;R) ta cần chứng minh OC > R hay OC >OA . Điều này
giúp ta nghĩ đến việc dựng đường phụ OH ⊥ AB để vận dụng quan hệ đường xiên và hình chiếu Lời giải:
Hạ OH ⊥ AB (H ∈ AB )
Do C nằm trên tia đối của tia AB nên
dễ thấy HC > HA
Theo quan hệ đường xiên và hình
chiếu ta suy ra OC > OA hay OC > R
⇒ C nằm ngoài đường tròn (O;R) ⇒ đpcm Nhận xét :
_ Ta có bài tập tương tự sau : Cho AB là dây cung của đường tròn (O;R) (AB không là đường kính). C là
điểm nằm trên đoạn thẳng AB. Chứng minh điểm C nằm trong đường tròn (O;R)
_ Hai bài tập này giúp ta chứng minh được định lí không tồn tại đường tròn nào đi qua 3 điểm thẳng hàng
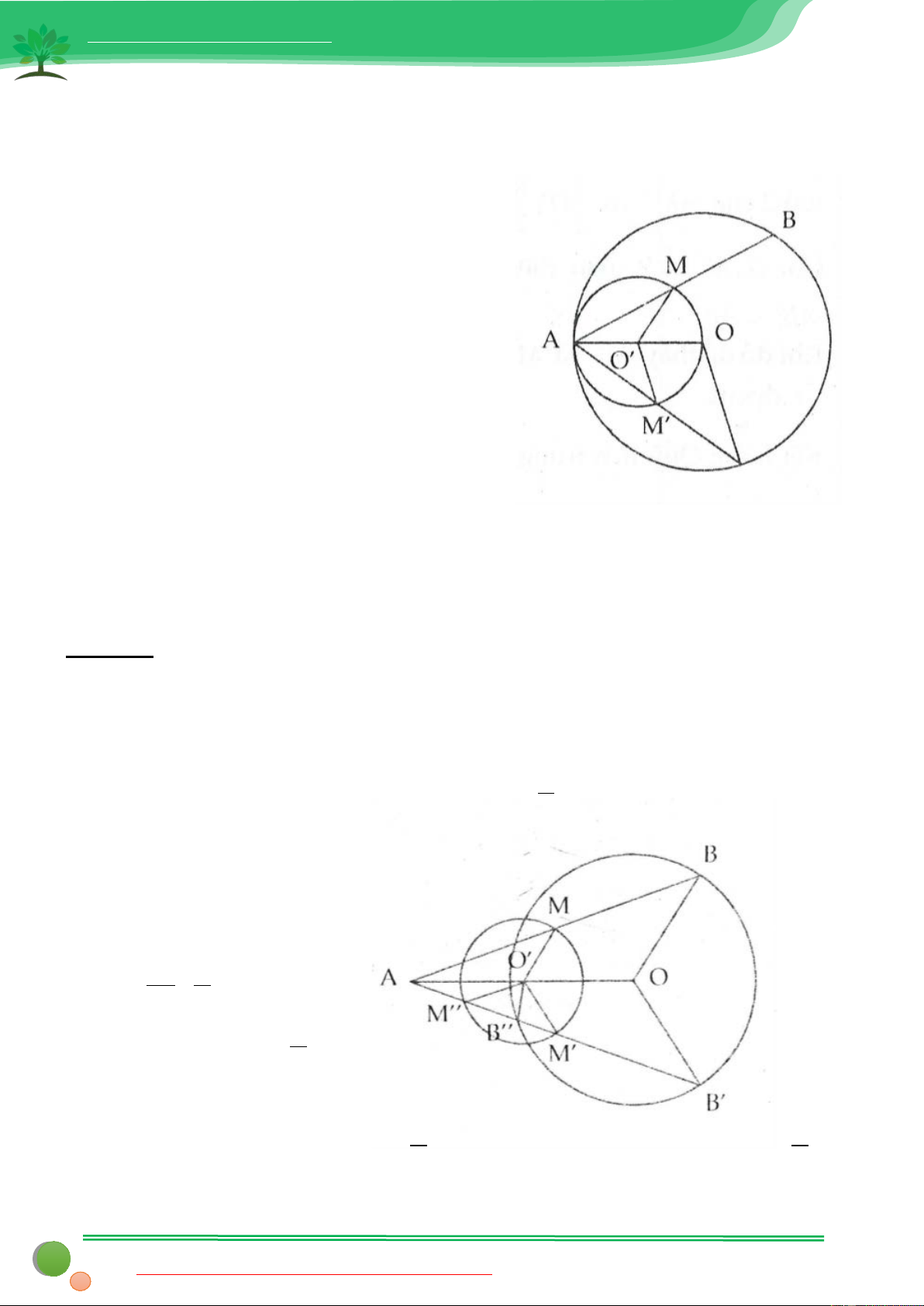
Bài 4: Cho đường tròn (O) và điểm A cố định trên đường tròn, điểm B chuyển động trên đường tròn. Tìm
quỹ tích trung điểm M của dây AB
Định hướng lời giải :
Đối với những bài toán tìm quỹ tích với những hình vẽ đơn giản không quá phức tạp ta thường vẽ một 1 vài
điểm trên để hình dung dễ hơn quỹ tích của chúng. Ở bài toán này ta sẽ lấy thêm 2 hoặc 3 điểm B trên đường
tròn để xác định quỹ tích trung điểm của chúng. Ta để ý rằng OA =OB tức là tam giác OAB cân tại O, do
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 3
Website: tailieumontoan.com đó OM vừa là đườ
ng trung tuyến vừa là đường cao trong tam giác OAB ⇒ AMO = 90° . Theo phần b) bài
toán 2 ta có quỹ tích của điểm M là đường tròn đường kính OA từ đó ta có được đpcm Lời giải: * Phần thuận
Ta có OA = OB nên tam giác AOB cân tại O
Do đó trung tuyến OM đồng thời là đườ
ng cao của ∆AOB ⇒ AMO = ° 90
Theo bài toán 2 điểm M thuộc đường
tròn (O′) có đường kính là AO cố định * Phần đảo
Gọi M ′ là điểm bất kì trên đường tròn đường kính AO
Gọi B′ là giao điểm thứ 2 của đường thẳng AM ′ với (O)
Cũng theo bài toán 2 ta có AM O ′ = 90°
⇒ OM ′ ⊥ AB′ mà lại có ∆AOB′ cân tại O do đó OM ′ vừa là đường cao vừa là đường trung tuyến
⇒ M ′ là trung điểm của AB′
Vậy nên quỹ tích trung điểm M của đoạn AB là đường tròn đường kính AO
Nhận xét :Tiếp theo ta sẽ thử khảo sát bài toán này với trường hợp điểm A nằm trong hoặc nằm ngoài
đường tròn (O;R). Do 2 trường hợp tương tự nhau, nên ta sẽ trình bày 1 trường hợp điểm A nằm ngoài đường tròn (O;R)
Với trường hợp này ta cũng vẽ một số vị trí của điểm B để dự đoán quỹ tích của điểm M chuyển động trên đườ R
ng tròn có tâm O′ là trung điểm của OA và có bán kính là 2 * Phần thuận
Gọi O′ là trung điểm của OA Khi đó ta có O M ′ là đường
trung bình của ∆AOB OB R ⇒O M ′ = = 2 2 ⇒ R
M thuộc đường tròn O ;′ 2 * Phần đảo R R
Gọi M ′ là điểm bất kì thuộc đường tròn O ;′
và M ′′ là giao điểm thứ 2 của AM ′ với O ;′ 2 2 Gọi B ,
′ B′′ là 2 giao điểm của đường thẳng AM ′ với (O;R) sao cho AB′′ < AB′
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 4
Website: tailieumontoan.com
Khi đó dễ thấy M ′ và M ′′ lần lượt là trung điểm của AB′ và AB′′ ⇒ đpcm R
Kết luận : Quỹ tích trung điểm M của AB là đường tròn tâm O ;′
với O′ là trung điểm của OA 2
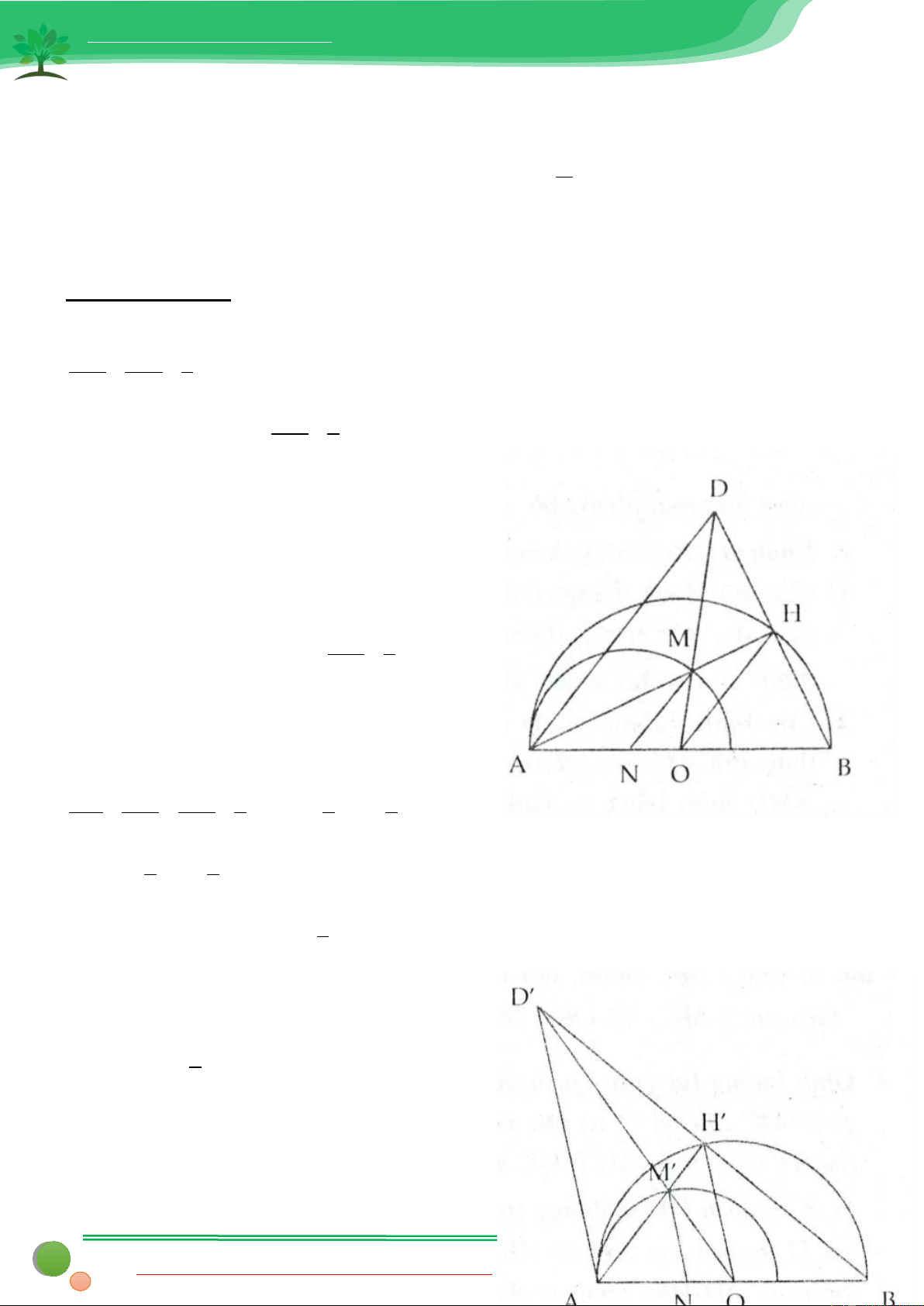
Bài 5: Cho nửa đường tròn (O) đường kính AB cố định. H là một điểm bất kì trên cung AB. Trên tia BH lấy
một điểm D sao cho H là trung điểm của BD. Đoạn thẳng DO cắt AH tại M. Tìm quỹ tích của điểm M
Định hướng lời giải :
Hoàn toàn dễ dàng nhận ra điểm M chính là trọng tâm của ∆ABD nên ta sẽ thu ngay được tỉ lệ AM DM 2 =
= . Điều này giúp ta nghĩ đến việc kẻ đường thẳng song song từ M với đường thẳng OH cắt AH DO 3 AM 2
AO tại N để lợi dụng tỉ số
= để suy ra điểm N cố định và đoạn NM có độ dài không đổi. Từ đó suy AH 3
ra được quỹ tích của M là một đường tròn tâm N cố định Lời giải: * Phần thuận :
Trong ∆ABD có đường trung tuyến AH và DO cắt nhau tại M ⇒ AM
M là trọng tâm của ∆ABD ⇒ = 2 AH 3
Từ M kẻ đường thẳng song song với OH
và cắt đoạn thẳng AB tại N
Theo định lí Tales, ta có : AN MN AM 2 2 2 = =
= ⇒ AN = AO = R ⇒ N cố định AO OH AH 3 3 3 2 2 và NM = OH = R 3 3 ⇒ 2
M thuộc nửa đường tròn N ; R
cùng thuộc nửa mặt phẳng bờ AB so với nửa đường tròn (O) 3 * Phần đảo :
Gọi M ′ là một điểm bất kì thuộc nửa đườ 2 ng tròn N ; R cùng thuộc nửa 3
mặt phẳng bờ AB so với nửa đường tròn (O)
Gọi H ′ là giao điểm của AM ′ với nửa đường tròn (O;R)
Trên tia BH ′ lấy điểm D ′ sao cho H D ′ ′ = H B ′
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 5
Website: tailieumontoan.com
Ta cần chứng minh OD ′ đi qua điểm M ′ 2 R NM ′ 2 AN NM ′ 2 Thật vậy ta có : 3 = = ⇒ = = OH ′ R 3 AO OH ′ 3
Theo định lí Tales đảo ⇒ MN ′ / /OH ′ AM ′ Do đó 2 = ⇒ M ′ ∆ABD AH ′ là trọng tâm của ′ 3 ⇒ trung tuyến D O
′ đi qua M ′ ⇒ đpcm 2
Vậy nên quỹ tích của điểm M là nửa đường tròn N ; R
nằm trên cùng nửa mặt phẳng bờ AB so với nửa 3 đường tròn (O;R)
Nhận xét : Dưới đây là một số bài toán tương tự :
1. Cho một đoạn thẳng cố định AB có độ dài bằng 2a. Gọi I là trung điểm của AB, K là trung điểm của đoạ
n IB. Trên tia Kx kẻ tùy ý, lấy một điểm M sao cho KMB = MAB . Tìm quỹ tích của điểm M
2. Cho hình vuông ABCD cạnh bằng a. Một đoạn thẳng MN có độ dài thay đổi, M chạy trên AB, N
chạy trên AD sao cho chu vi tam giác AMN luôn bằng 2a. Gọi H là chân đường vuông góc hạ từ C
xuống MN. Chứng minh rằng H luôn luôn nằm trên một đường tròn cố định
3. Cho nửa đường tròn (O) đường kính AB, M là một điểm chuyển động trên đường tròn (O). C là một
điểm trên tia AM sao cho AC = BM . Chứng minh rằng đường thẳng d vuông góc với AM tại C
luôn đi qua một điểm cố định
Bài 6:Cho ∆ABC nhọn, nội tiếp trong đường tròn (O). Gọi H là trực tâm của ∆ABC . Vẽ
OK ⊥ BC (K ∈ BC ) . Chứng minh AH = 2OK
Định hướng lời giải :
Quan sát hình vẽ ta dễ dàng nhận ra OK ⊥ BC vì tam giác BOC cân tại O và OK là đường trung tuyến nên
đồng thời là đường cao. Từ đó ta thấy AH / /OK mà đề bài yêu cầu chứng minh AH = 2OK nên ta sẽ dự
đoán OK là đường trung bình của tam giác nào đó chứa cạnh AH, gọi D là giao của AO và HK. Ta cần
chứng minh O, K lần lượt là trung điểm của của AD, HK. Từ đó ta nhận thấy D nằm trên đường tròn (O) Lời giải:
Gọi D là giao của AO và HK
Gọi D ′ là giao của AO với (O)
Ta sẽ chứng minh D ≡ D ′
Khi đó AD ′ là đường kính của (O)
Theo các bài toán ở trên ta dễ dàng ′
chứng minh được ACD = ABD ′ = 90°
Do đó AC ⊥ CD ′;AB ⊥ BD ′
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 6
Website: tailieumontoan.com
⇒ BH / /CD ;′CH / /BD ′
⇒ BHCD ′ là hình bình hành
⇒ HD ′ đi qua trung điểm của BC hay HD ′ đi qua K
⇒ D ′ = HK ∩ AO ⇒ D ≡ D ′
⇒O,K lần lượt là trung điểm của AD, HD ⇒ 1
OK là đường trung bình của ∆AHD ⇒ OK = AH ⇒ đpcm 2 Nhận xét :
_ Kết quả của bài toán vẫn đúng trong trường hợp ∆ABC tù
_ Đây là bài toán không quá khó nhưng nó có ứng dụng trong rất nhiều bài toán hay và khó. Dưới đây là một số bài toán như vậy :
1. (Đường thẳng Ơle) Cho ∆ABC nhọn nội tiếp trong đường tròn (O), H là trực tâm, G là trọng tâm
của ∆ABC . Chứng minh O, G, H thẳng hàng
2. Cho đường tròn (O;R) và điểm P cố định ở ngoài đường tròn, vẽ tiếp tuyến PA và cát tuyến bất kì
PBC (A,B,C thuộc (O)). Tìm quỹ tích trực tâm H của tam giác ABC
3. Cho ∆ABC nội tiếp đường tròn (O). Gọi D, E, F tương ứng là trung điểm của BC, CA, AB. Kẻ các
đường thẳng DD ,′EE ,′FF ′ sao cho DD ′ / /OA,EE′ / /OB,FF ′ / /OC . Chứng minh rằng các đường thẳng DD ,
′ EE ,′FF ′ đồng quy
4. (Đề thi THPT chuyên Hùng Vương 2013-2014) Cho điểm A cố định trên đường tròn (O;R). Gọi AB,
AC là 2 dây cung của (O;R) thay đổi sao cho AB.AC = 3R . Xác định vị trí của B, C trên (O) để
diện tích tam giác ABC lớn nhất
Bài 7: Cho 3 điểm A, B, C bất kì và đường tròn (O) bán kính l. Chứng minh rằng luôn tồn tại điểm M thuộc đường tròn (O ) ;1 thỏa mãn :
MA + MB + MC ≥ 3
Định hướng lời giải :
Bài toán yêu cầu chứng minh tồn tại điểm M thuộc đường tròn (O )
;1 thỏa mãn MA + MB + MC ≥ 3 thì
việc đầu tiên ta nghĩ đến là xét 1 điểm M thuộc đường tròn. Ta thấy việc xét 1 điểm M vẫn chưa thu được
điều gì nên cần phải xét thêm những điểm M khác thuộc đường tròn (O )
;1 . Bây giờ nếu xét thêm các điểm khác thuộc (O )
;1 thì ý tưởng sẽ là tìm các điểm có một mối liên hệ gì đó với M và điểm đầu tiên ta nghĩ đến
đó chính là điểm M ′ đối xứng với M qua O hay MM ′ chính là đường kính đường tròn (O ) ;1 ⇒ MM ′ = 2.
Đến đây ta sẽ áp dụng bất đẳng thức tam giác thì thu được MA + M A′ ≥ MM ′ = 2
Tương tự MB + M B′ ≥ 2,MC + M C ′ ≥ 2
Cộng theo vế các bất đẳng thức ta được :
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 7





