Câu hỏi và bài tập Chương 1 môn Toán thống kê | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

Thống kê Toán học
CÂU HỎI VÀ BÀI TẬP CHƯƠNG I
Bài 1. Sắp xếp lại và vẽ đồ thị biểu diễn dãy số liệu sau: 39 41 40 42 41 40 42 44 40 43 43 41 43 39 42 40 41 42 39 41 38 43 39 42 39 41 37 43 39 41 40 42 40 41 42 40 43 38 39 41 41 42 43 40
Bài 2. Cho dãy số liệu sau: 47 45 41 34 20 26 38 53 45 38 31 20 43 44 27 22 29 45 55 42 29 32 27 37 61 30 35 33 27 43 50
a) Tính trung vị, trung bình mẫu và phương sai mẫu;
b) Chia dãy số liệu trên thành nhóm có độ dài 5 và vẽ đa giác tần số.
Bài 3. Năng suất của một loại cây trên 36 thửa đất là: 19,2 17,7 20,0 21,1 21,5 18,5 20,6 19,3 19,0 18,2 17,1 19,2 19,1 15,2 19,5 17,3 16,3 19,6 17,5 19,1 19,7 16,0 16,7 16,4 20,8 19,3 16,0 17,4 15,3 17,2 17,6 11,5 11,4 46,1 17,8 20,0
Tính trung vị, trung bình mẫu, phương sai mẫu, và tứ phân vị. Bài 4.
Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng A và B được cho ở bảng sau: Cân nặng (g) [150;155) [155;160) [160;165) [165;170) [170;175) Số cam ở lô hàng A 2 6 12 4 1 Số cam ở lô hàng B 1 3 7 10 4
a) Hãy ước lượng cân nặng trung bình của mỗi quả cam ở lô hàng A và lô hàng B .
b) Nếu so sánh theo số trung bình thì cam ở lô hàng nào nặng hơn?
Bài 5. Cân nặng của 28 học sinh nam lớp 11 được cho như sau:
55,4 62,6 54,2 56,8 58,8 59,4 60,7 58 59,5 63,6 61,8 52,3 63,4 57,9
49,7 45,1 56,2 63,2 46,1 49,6 59,1 55,3 55,8 45,5 46,8 54 49,2 52,6 P. N. Hoa Page 1 Thống kê Toán học
a) Hãy chia mẫu dữ liệu trên thành 5 nhóm, lập bảng tần số ghép nhóm và xác
định giá trị đại diện cho mỗi nhóm.
b) Hãy ước lượng cân nặng trung bình của học sinh lớp 11.
Bài 6. Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà
ở mức giả nào. Kết quả khảo sát được ghi lại ở bảng sau: Mức giá [10;14) [14;18) [18;22) [22;26) [26;30) (triệu đồng/ 2 m ) Số khách hàng 54 78 120 45 12
a) Tìm trung bình, trung vị và mốt của mẫu số liệu ghép nhóm trên.
b) Công ty nên xây nhà ở mức giá nào để nhiều người có nhu cầu mua nhất? Bài 7.
Kết quả khảo sát cân nặng của 1 thùng táo ở một lô hàng cho trong bảng sau:
Cân nặng (g) [150;155) 155;160 160;165 165;170 170;175 Số quả táo 4 7 12 6 2
Hãy tìm trung vị và tứ phân vị của mẫu số liệu ghép nhóm trên. Bài 8.
Trong tuần lễ bảo vệ môi trường, các học sinh khối 12 tiến hành thu
nhặt vỏ lon nước ngọt để tái chế. Nhà trường thống kê kết quả thu nhặt vỏ lon
nước ngọt của học sinh khối 12 ở bảng sau: Số vỏ lon 11;1  5 16;20 21;2  5 26;3  0 31;3  5 Số học sinh 58 87 54 44 23
Hãy tìm trung vị và tứ phân vị của mẫu số liệu ghép nhóm trên. Bài 9.
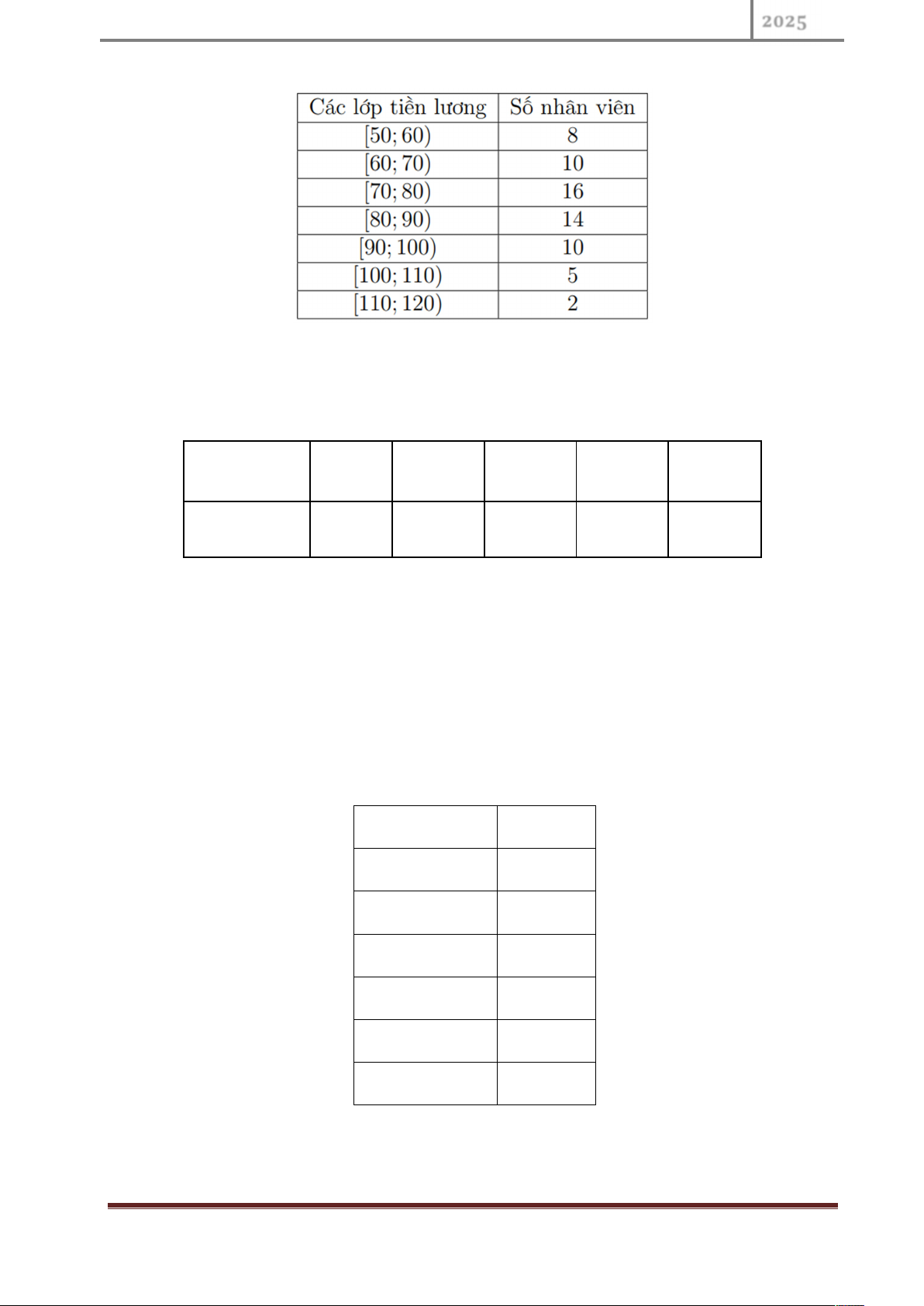
Tiền lương nhận được trong 1 giờ làm việc của nhân viên công ty A
được thống kê theo mẫu số liệu ghép nhóm sau (đơn vị: ngàn đồng): P. N. Hoa Page 2 Thống kê Toán học
Hãy xác định các tứ phân vị của mẫu số liệu trên.
Bài 10. Mức lương hàng tháng ở 1 công ty được Công đoàn thu thập theo bảng
sau( đơn vị triệu đồng): Mức lương
6;10 10;15 15;20 20;25 25;30 Nhân viên 17 38 27 21 7
a) Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
b) Chủ tịch Công đoàn muốn đề nghị hỗ trợ cho nhóm 25% số nhân viên có mức
lương thấp nhất và ước lượng rằng số nhân viên này không ít hơn 10. Nhận định
của chủ tịch có hợp lí hay không? Bài 11.
Bảng dưới biểu diễn mẫu số liệu ghép nhóm về chiều cao (đơn vị:
centimét) của 36 học sinh nam lớp 12 ở một trường trung học phổ thông. Tìm
khoảng biến thiên, các tứ phân vị và phương sai của mẫu số liệu ghép nhóm đó. Nhóm Tần số [160;163) 6 [163;166) 11 [166;169) 9 [169;172) 7 [172;175) 3 n  36 Bài 12.
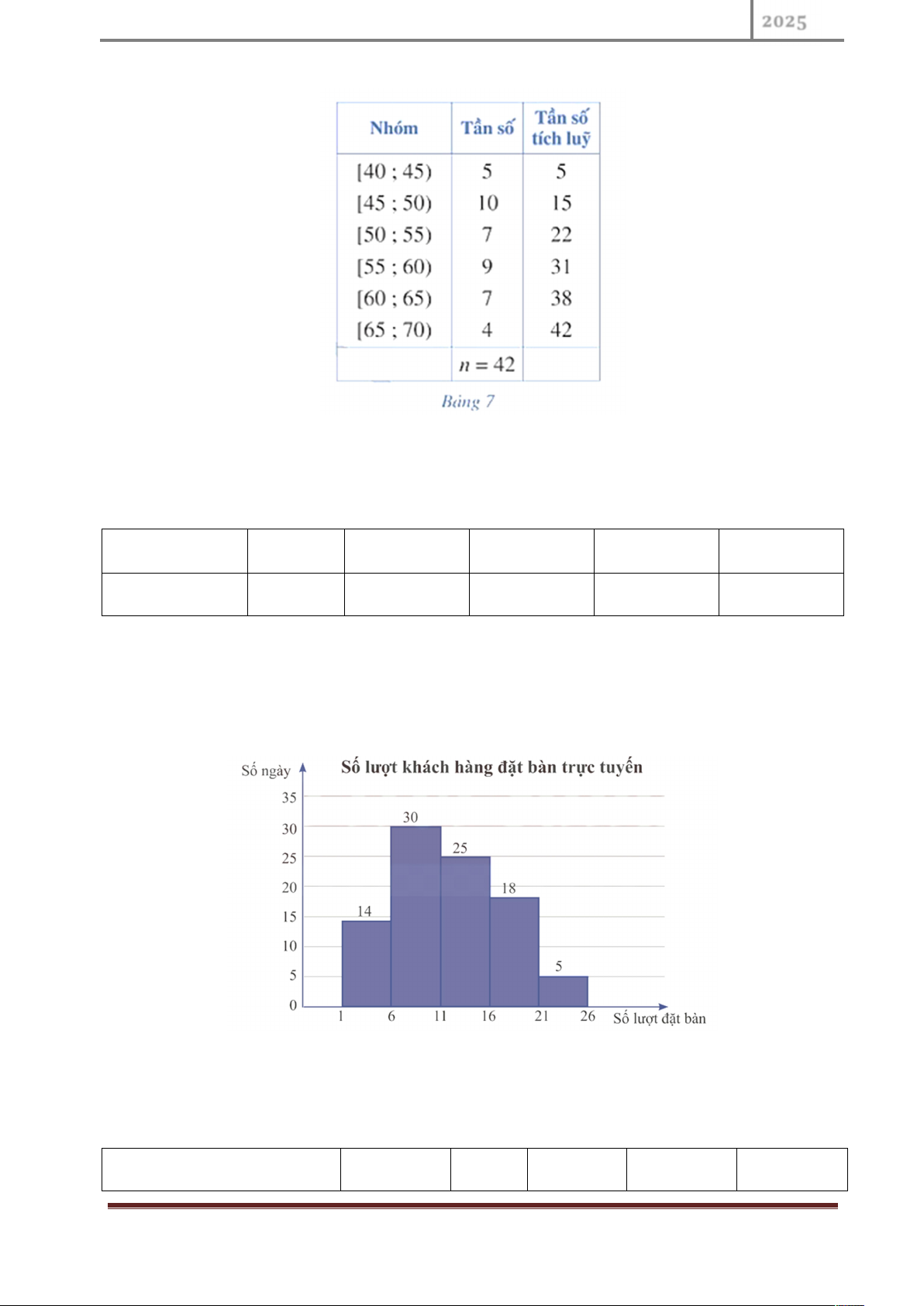
Bảng dưới biểu diễn mẫu số liệu ghép nhóm vể chiều cao của 42
mẫu cây ở một vườn thực vật (đơn vị: centimét). Tính khoảng tứ phân vị của
mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng phẩn mười nếu cần). P. N. Hoa Page 3 Thống kê Toán học Bài 13.
Bảng sau thống kê cân nặng của 50 quả xoài Thanh Ca được lựa
chọn ngẫu nhiên sau khi thu hoạch ở một nông trường. Hãy tìm khoảng tứ phân
vị của mẫu số liệu ghép nhóm đó
Cân nặng (g) [250;290) [290;330) [330;370) [370; 410) [410;450) Số quả xoài 3 13 18 11 5 Bài 14.
Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình
thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất
biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày
có từ 6 đến dưới 11 lượt đặt bàn;...
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên. Bài 15.
Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận
động viên được ghi lại ở bảng sau:
Thời gian luyện tập (giờ) [0; 2) [2;4) [4;6) [6;8) [8;10) P. N. Hoa Page 4 Thống kê Toán học Số vận động viên 3 8 12 12 4
Hãy tìm trung vị, các tứ phân vị, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm trên. Bài 16.
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại
của người đó trong một tuần ở bảng sau:
Thời gian (đơn vị: [0;60) [60;120) [120;180) [180; 240) [240;300) [300;360) giây) Số cuộc gọi 8 10 7 5 2 1
Hãy tìm trung vị, các tứ phân vị, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm trên. Bài 17.
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau: Điểm số [5, 5;10, 5) [10,5;15,5) [15,5; 20, 5) [20,5; 25,5) Số trận 3 9 2 6
Hãy tìm trung vị, các tứ phân vị, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm trên. Bài 18.
Thời gian sử dụng điện thoại trong một ngày của 30 sinh viên được
ghi lại ở bảng sau (đơn vị: phút). Thời gian (phút) [0;60) [60;120) [120;180) [180; 240) [240;300) Số sinh viên 2 7 7 10 4
Hãy tìm trung vị, các tứ phân vị, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm trên. Bài 19.
Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của
60 thí sinh được cho mẫu số liệu ghép nhóm như sau: Điểm [0;9,5) [9,5;19,5) [19,5;29,5) [29,5;39,5) [39,5;49,5) Số thí sinh 1 2 4 6 15 Điểm [49,5;59,5) [59,5;69,5) [69,5;79,5) [79,5;89,5) [89,5;99,5) Số thí sinh 12 10 6 3 1 P. N. Hoa Page 5 Thống kê Toán học
Tính trung vị, các tứ phân vị, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm trên. Bài 20.
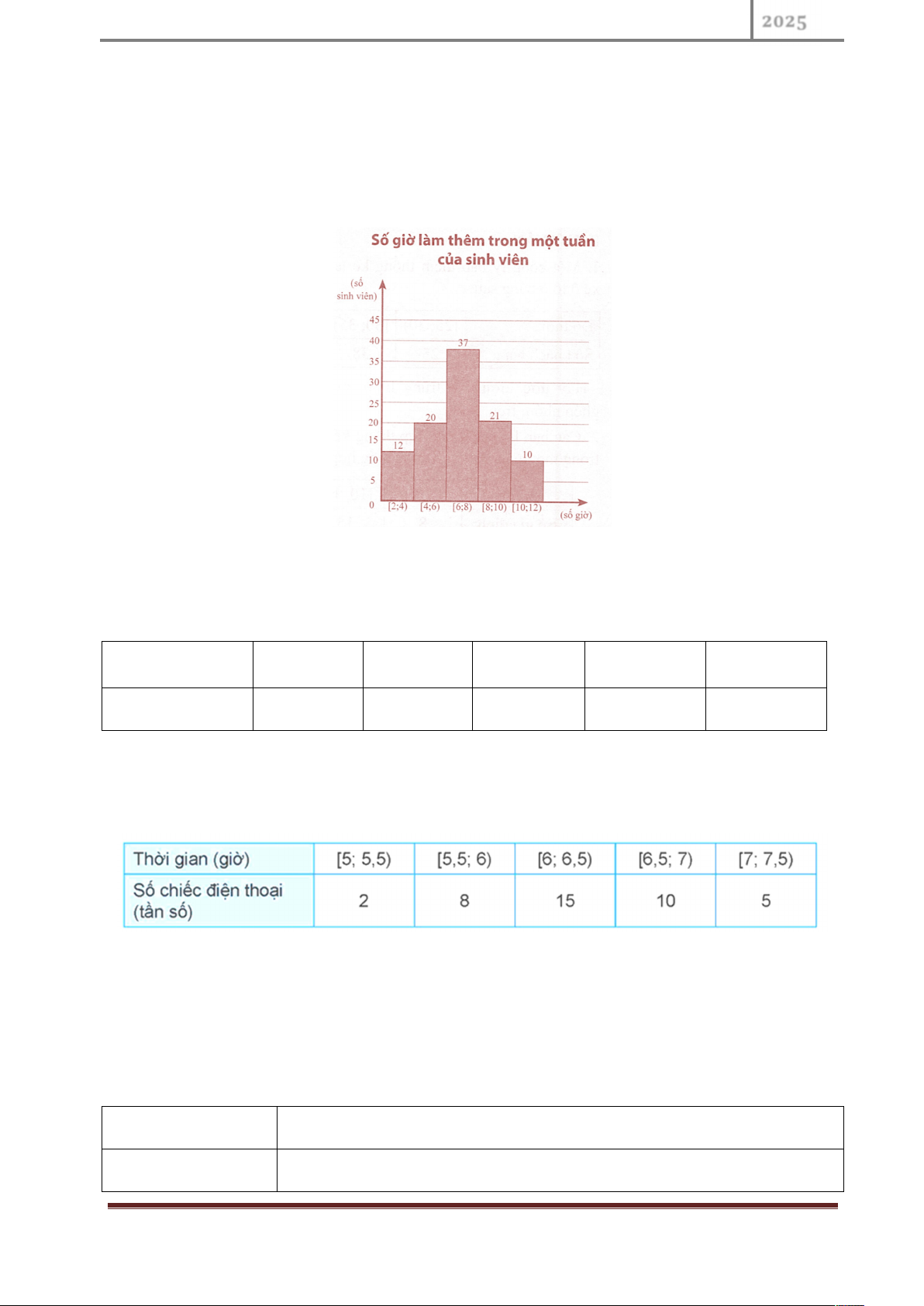
Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh
viên được cho ở biểu đồ bên.
Tìm khoảng tứ phân vị của số liệu đó.
Bài 21. Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm (kết quả được
làm tròn đến hàng phần trăm) Chiều cao (cm) 160;164 164;168 168;172 172;176 176;180 Số học sinh 3 5 8 4 1
Bài 22. Để đánh giá chất lượng một loại pin điện thoại mới, người ta ghi lại
thời gian nghe nhạc liên tục của điện thoại được sạc đầy pin cho đến khi hết pin cho kết quả như sau:
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả được làm tròn đến hàng phần trăm) Bài 23.
Để ước lượng mức xăng tiêu hao trung bình cho một lọai xe ô tô
chạy từ A đến B, phòng kỹ thuật của công ty vận tải đã quan sát mức xăng tiêu
hao (X lít) trong 30 chuyến xe. Kết quả cho như sau: Mức xăng(X lít)
(9,6-9,8] (9,8-10] (10-10,2] (10,2-10,4] (10,4-10,6] Số chuyến 3 5 10 8 4 P. N. Hoa Page 6 Thống kê Toán học
Giả thiết mức xăng tiêu hao X tuân theo luật chuẩn. a)
Hãy ước lượng mức xăng tiêu hao trung bình. b)
Với độ tin cậy 95% xăng tiêu hao trung bình nằm trong khoảng nào? Bài 24.
Điều tra 365 điểm trồng lúa của một huyện. Kết qủa cho như sau: Năng suất 25 30 33 34 35 36 37 39 40 (X :tạ/ha) Số hộ 6 13 38 74 106 85 30 10 3
Giả thiết X tuân theo luật chuẩn. a)
Hãy chỉ ra ước lượng năng suất lúa trung bình/ha. b)
Với độ tin cậy 95% năng suất lúa trung bình/ha nằm trong khoảng nào? Bài 25.
Một nhân viên chọn ngẫu nhiên một mẫu kích thước = 12 hóa
đơn trong số các hóa đơn bán hàng của công ty và thu được các giá trị sau (đơn
vị: ngàn đồng): 875, 1231, 453, 522, 2130, 1550, 309, 760, 498, 999, 1320, 1021. Hãy
tìm một ước lượng của giá trị trung bình và phương sai của các giá trị các hóa đơn bán hàng. Bài 26.
Tuổi thọ của một loại bóng đèn được biết theo quy luật chuẩn với độ lệch chuẩn 100 giờ.
a) Chọn ngẫu nhiên 100 bóng để thử nghiệm, thấy mỗi bóng tuổi thọ trung bình
là 1000 giờ. Hãy ước lượng tuổi thọ trung bình của bóng đèn xí nghiệp sản xuất với độ tin cậy 95%.
b) Với độ chính xác là 15 giờ. Hãy xác định độ tin cậy.
c) Với độ chính xác là 25 giờ và độ tin cậy là 95% thì cần thử nghiệm bao nhiêu bóng? Bài 27.
Trọng lượng các bao gạo tại một cửa hàng lương thực là một đại
lượng ngẫu nhiên có phân phối chuẩn. Cân kiểm tra 20 bao, thấy ̅ = 48 , và phương sai mẫu = (0,5) . a)
Với độ tin cậy 95% hãy ước lượng trọng lượng trung bình của một bao bột mì thuộc cửa hàng. b)
Với độ chính xác 0,26 kg, xác định độ tin cậy. c)
Với độ chính xác 160 g, độ tin cậy là 95% . Tính cỡ mẫu n. Bài 28.
Để ước lượng số cá trong hồ, người ta đánh bắt 2000 con, đánh dấu P. N. Hoa Page 7 Thống kê Toán học
rồi thả xuống. Vài ngày sau, ta lại đánh bắt 400 con thì thấy có 80 con cá được
đánh dấu. Với độ tin cậy 95%, hãy ước lượng số cá có trong hồ. Bài 29.
Một nhân viên nghiên cứu thị trường phỏng vấn ngẫu nhiên 18
người xem họ có (C) hay không (K) tiêu dùng một loại sản phẩm và thu được
dãy câu trả lời như sau: CKKCCCKCKCCCKCKCCK. Hãy ước lượng tỉ lệ khách
hàng dùng loại sản phẩm đó với độ tin cậy 99%. Bài 30.
Một xí nghiệp đưa ra thị trường một sản phẩm mới. Để xem đánh
giá của người tiêu dùng đối với loại sản phẩm mới này như thế nào, người ta
phát cho mỗi người mua hàng đó một phiếu thăm dò và yêu cầu gửi lại cho xí
nghiệp chậm nhất là sau ba tháng. Vì điều kiện thời gian nên xí nghiệp không
thể hỏi ý kiến của tất cả các khách hàng trong cả nước, cho nên họ chỉ gửi phiếu
thăm dò cho khách hàng ở Hà Nội. Kết quả sau ba tháng xí nghiệp nhận được
300 phiếu thăm dò trong đó có 90 phiếu tỏ ra là thích loại sản phẩm này (cả về chức năng và giá cả)
a) Hãy ước lượng tỷ lệ thực khách hàng thích loại sản phẩm này.
b) Với độ tin cậy 95 phần trăm tỷ lệ đó cao nhất là bao nhiêu ?
c) Muốn nhận được ước lượng khoảng cho tỷ lệ thực với độ chính xác 0,03
thì cần thăm dò thêm bao nhiêu phiếu nữa ?
d) Với mẫu n = 300, ước lượng khoảng có độ chính xác là 0,0436 thì độ tin cậy
của kết luận về ước lượng là khoảng bao nhiêu? Bài 31.
Để nghiên cứu tuổi thọ của một loại bóng đèn, người ta thắp thử 100
bóng thì thu được số liệu sau: Tuổi thọ (X giờ) Số bóng Tuổi thọ (X giờ) Số bóng 1010-1030 2 1110-1130 20 1030-1050 3 1130-1150 12 1050-1070 8 1150-1170 10 1070-1090 13 1170-1190 6 1090-1110 25 1190-1210 1
Sau khi cải tiến kĩ thuật, người ta lại thắp 100 bóng thì thu được bảng số liệu sau: Tuổi thọ (Y giờ) Số bóng Tuổi thọ (X giờ) Số bóng P. N. Hoa Page 8 Thống kê Toán học 1150 10 1180 30 1160 15 1190 15 1170 20 1200 10
a) Hãy chỉ ra ước lượng điểm và ước lượng khoảng ( = 0,05)cho tuổi thọ
trung bình và bình phương độ lệch của tuổi thọ bóng đèn trước và sau khi cải tiến.
b) Với độ tin cậy 95% có thể nói việc cải tiến kỹ thuật đã làm tăng tuổi thọ
trung bình của bóng đèn lên ít nhất bao nhiêu giờ.
c) Nếu ước lượng khoảng cho EX có độ chính xác là 6,05 thì độ tin cậy tương ứng là bao nhiêu.
d) Nếu muốn ước lượng khoảng cho EX với độ tin cậy 95%, độ chính xác là
5 thì cần quan sát thêm bao nhiêu bóng đèn nữa.
Giả sử X và Y đều tuân theo luật chuẩn.
-------------------------*&*------------------------- P. N. Hoa Page 9