Chương 2 – cấu trúc bộ lọc môn Xử lý tín hiệu số | Học viện kỹ thuật quân sự

THIẾT KẾ BỘ LỌC SỐ
Chương 2 – Cấu trúc bộ lọc Hồ Phước Tiến
Trường Đại học Bách Khoa – Đại học Đà Nẵng Giới thiệu chung
• Bộ lọc: dùng để xử lý tín hiệu • Thiết kế bộ lọc:
– Loại bộ lọc (FIR hay IIR)
– Cấu trúc bộ lọc (cách thức thực hiện bộ lọc)
• FIR là trường hợp riêng của IIR
• Tuy nhiên, bộ lọc FIR được xem xét riêng lẻ 2 Các khối cơ bản
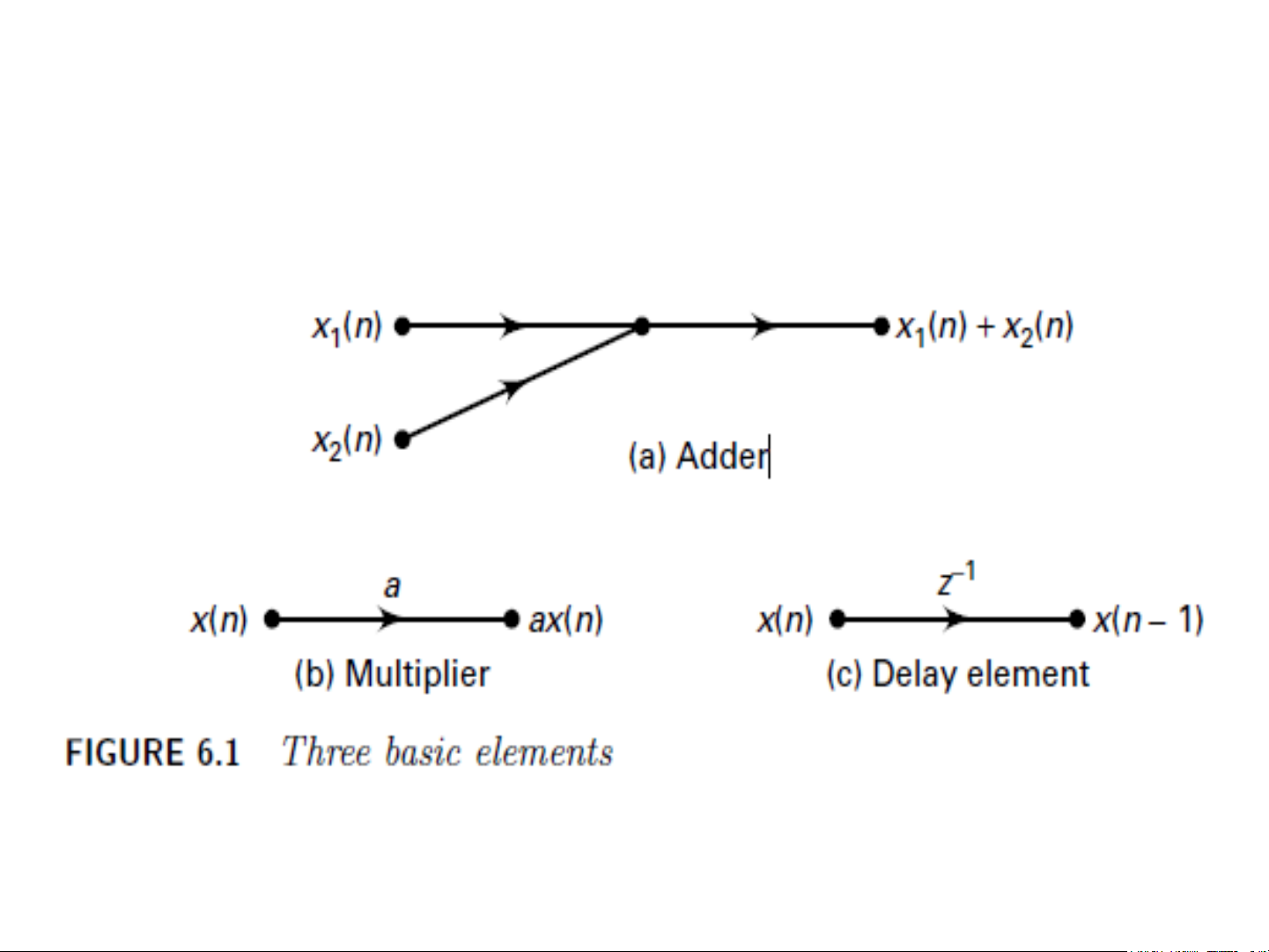
• Xem xét hệ thống tuyến tính bất biến LTI • Ba khối cơ bản – Bộ cộng – Bộ nhân – Bộ trễ
• Từ ba khối cơ bản, có thể thực hiện được các cấu trúc
khác nhau đối với bộ lọc FIR và IIR 3 Các khối cơ bản 4 Nội dung chính
• Cấu trúc bộ lọc IIR – Dạng trực tiếp – Dạng nối tiếp – Dạng song song
• Cấu trúc bộ lọc FIR – Dạng trực tiếp – Dạng nối tiếp – Dạng pha tuyến tính
– Dạng lấy mẫu tần số
• Cấu trúc lattice (FIR & IIR) 5
Cấu trúc bộ lọc IIR
• Hàm hệ thống của bộ lọc IIR (bậc N) 𝐵(𝑧) 𝑀 𝑛=0 𝑏 𝑏 𝐻 𝑧 = =
𝑛𝑧−𝑛 = 0 + 𝑏1𝑧−1 + ⋯ + 𝑏𝑀𝑧−𝑀 𝐴(𝑧) 𝑁 𝑎 𝑛=0 𝑛𝑧−𝑛
1 + 𝑎1𝑧−1 + ⋯ + 𝑎𝑁𝑧−𝑁
• Phương trình sai phân bộ lọc IIR 𝑀 𝑁
𝑦 𝑛 = 𝑏𝑚𝑥(𝑛 − 𝑚) − 𝑎𝑚𝑦 𝑛 − 𝑚 𝑚=0 𝑚=1 6
Cấu trúc bộ lọc IIR
• Dạng trực tiếp (direct form)
• Dạng nối tiếp (cascade form): gồm các khối bậc 2 (biquad) nối tiếp nhau
– Mỗi khối biquad có dạng trực tiếp
• Dạng song song (parallel form): gồm tổng các khối bậc 2 (biquad) 7
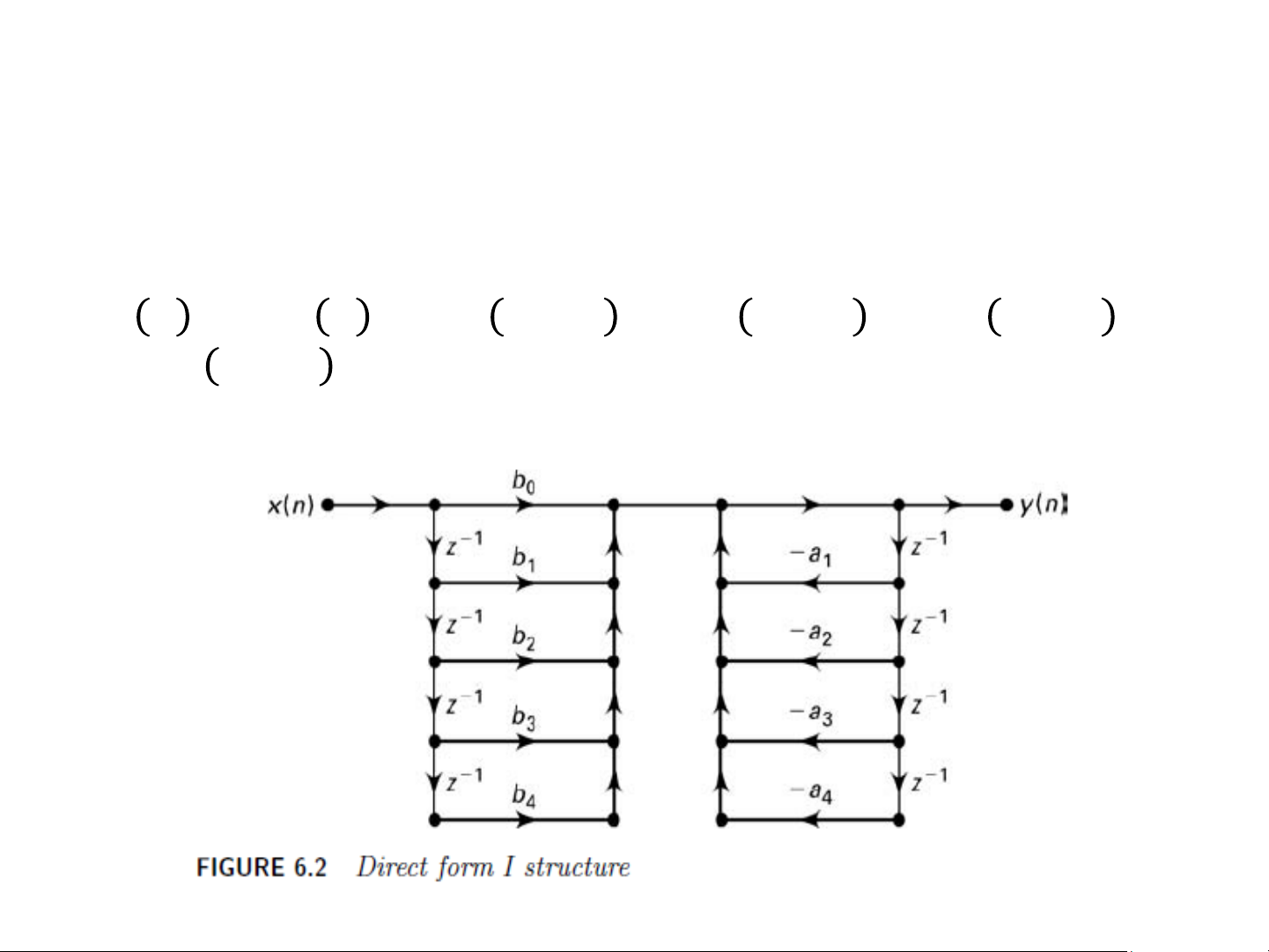
IIR – Dạng trực tiếp (direct) • Bộ lọc bậc 4
𝑦 𝑛 = 𝑏0𝑥 𝑛 + 𝑏1𝑥 𝑛 − 1 + 𝑏2𝑥 𝑛 − 2 + 𝑏3𝑥 𝑛 − 3 +
𝑏4𝑥 𝑛 − 4 − 𝑎1𝑦(𝑛 − 1) − 𝑎2𝑦(𝑛 − 2) − 𝑎3𝑦(𝑛 − 3) − 𝑎4𝑦(𝑛 − 4) 8
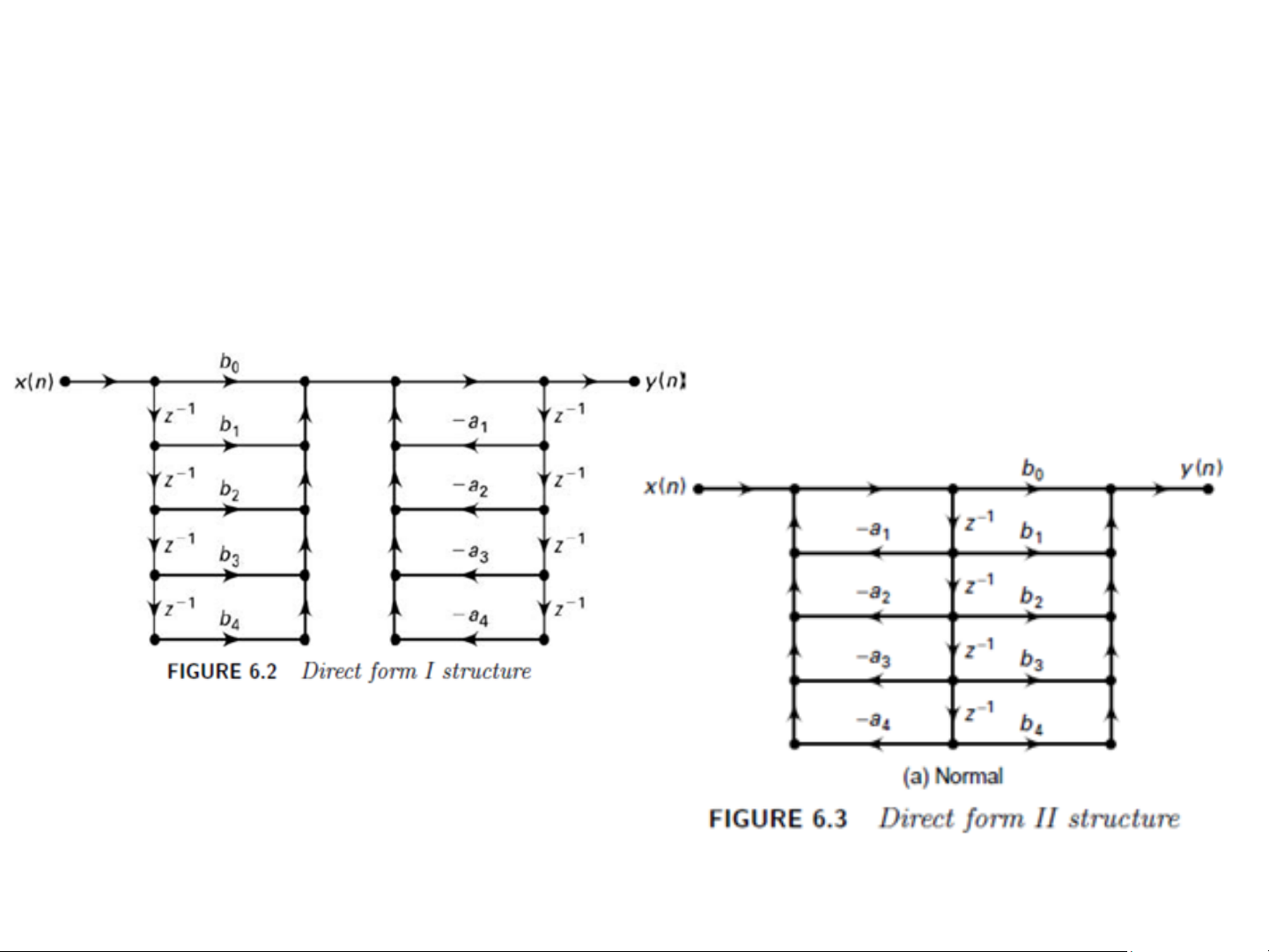
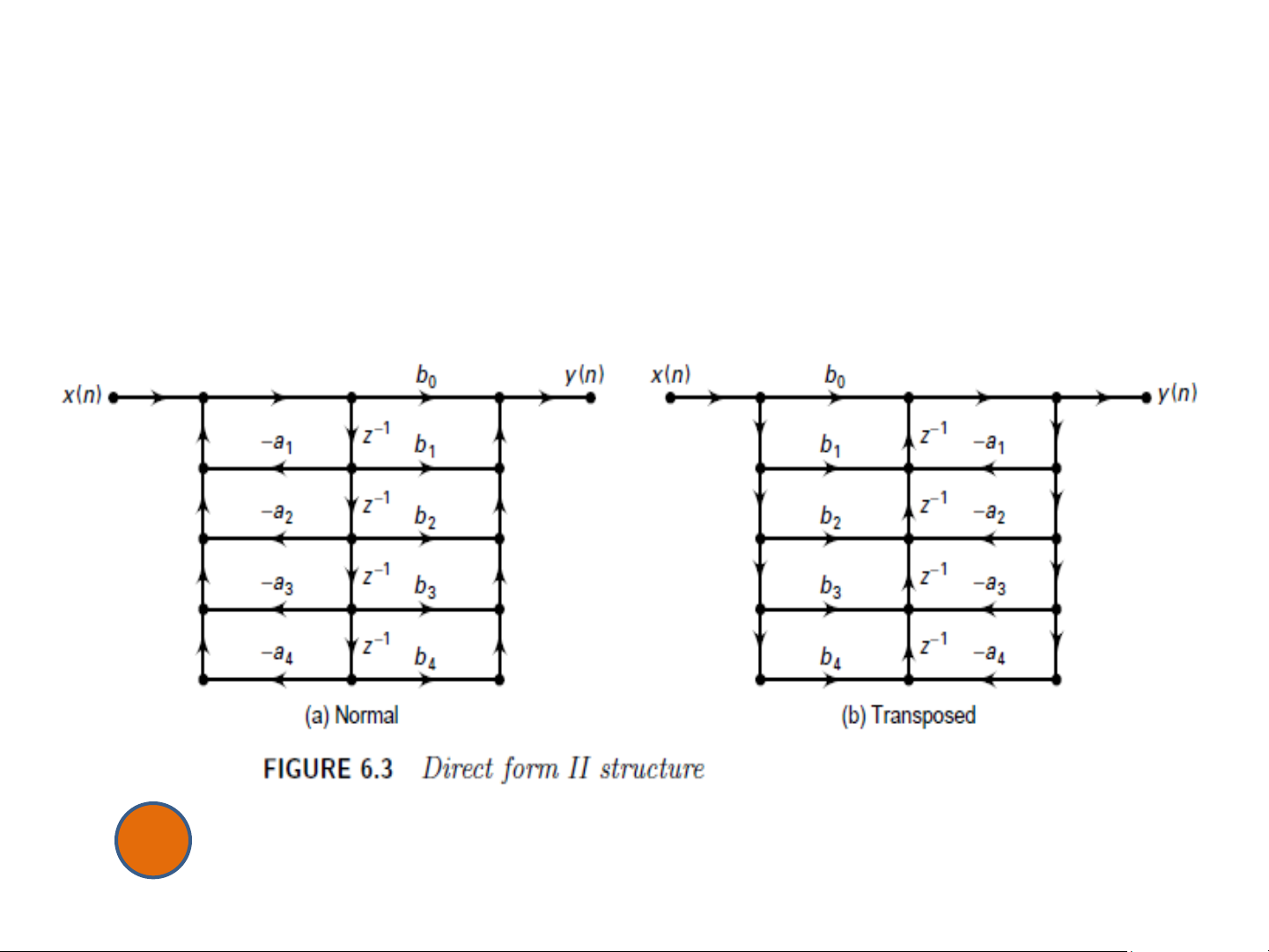
IIR – Dạng trực tiếp
• Hoán vị hai khối trong cấu trúc trực tiếp loại I để được
cấu trúc trực tiếp loại II (canonical) 9
IIR – Dạng trực tiếp
• Cấu trúc chuyển vị (transposed structure): để tạo ra một cấu trúc tương đương
– Đảo ngược tất cả các hướng
– Tất cả các nút rẽ nhánh được thay bằng bộ cộng, và
tất cả các bộ cộng được thay bằng nút rẽ nhánh
– Hoán vị đầu ra và đầu vào 10
IIR – Dạng trực tiếp
• Cấu trúc chuyển vị (transposed structure) ? Bài tập P6.3 11
IIR – Dạng trực tiếp
• Matlab: cấu trúc trực tiếp được thể hiện bằng hai vector:
b chứa các hệ số 𝑏𝑘 và a chứa các hệ số 𝑎𝑘
• Lệnh filter : lọc tín hiệu dùng dạng trực tiếp
• Hàm Hd = dfilt.df2t(b,a) chuyển cấu trúc trực tiếp thành
cấu trúc trực tiếp loại II chuyển vị 12
IIR – Dạng nối tiếp (cascade)
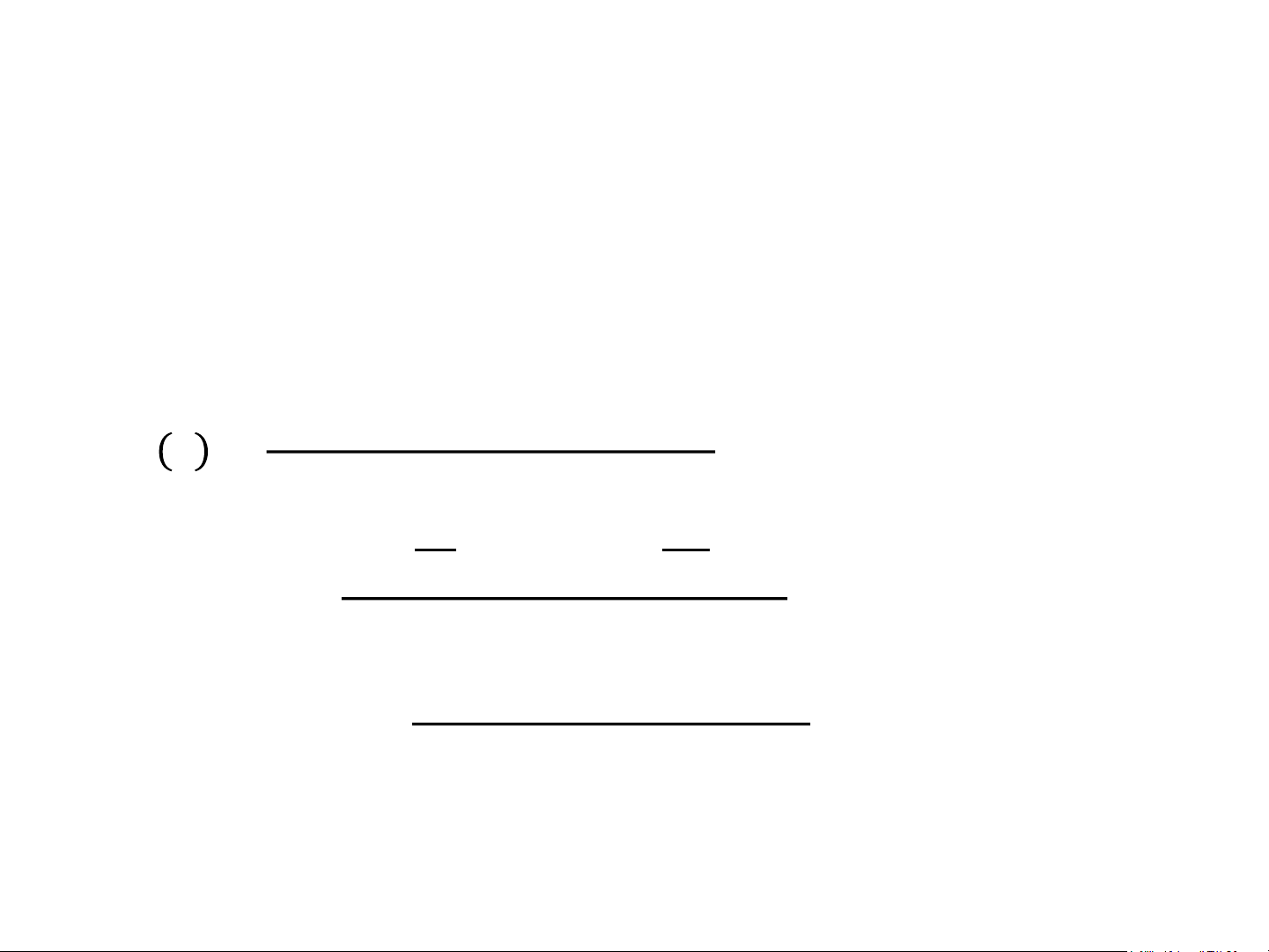
• H(z) được viết thành tích các khối bậc 2 có hệ số thực (giả sử N chẵn). 𝑏
𝐻 𝑧 = 0 + 𝑏1𝑧−1 + ⋯ + 𝑏𝑁𝑧−𝑁
1 + 𝑎1𝑧−1 + ⋯ + 𝑎𝑁𝑧−𝑁 𝑏 𝑏 1 + 1 𝑁
𝑏 𝑧−1 + ⋯ + 𝑏 𝑧−𝑁 = 𝑏 0 0 0
1 + 𝑎1𝑧−1 + ⋯ + 𝑎𝑁𝑧−𝑁 𝐾 1 + 𝐵 = 𝑏
𝑘,1𝑧−1 + 𝐵𝑘,2𝑧−2 0
1 + 𝐴𝑘,1𝑧−1 + 𝐴𝑘,2𝑧−2 𝑘=1 13
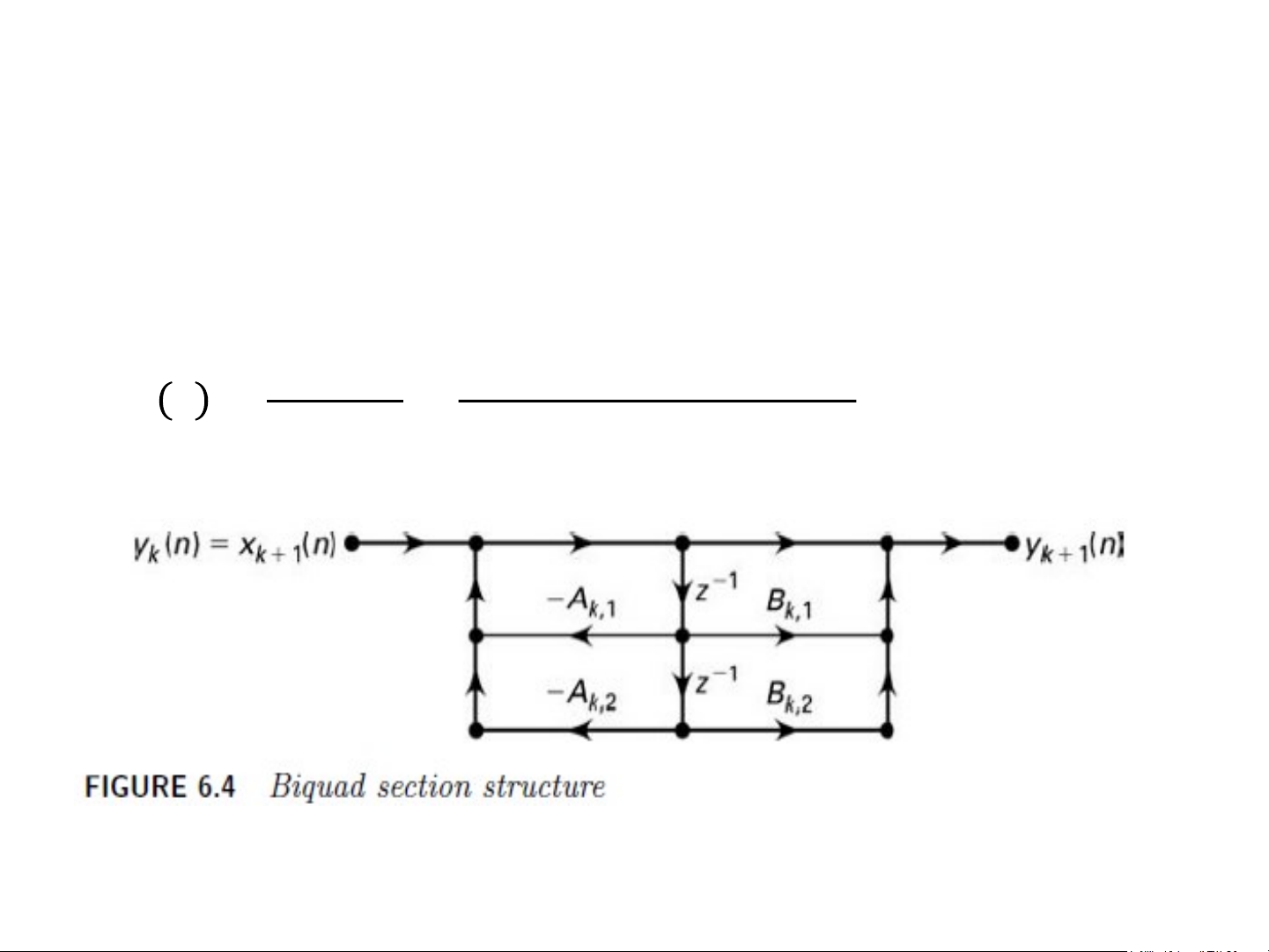
IIR – Dạng nối tiếp (cascade)
• Biquad thứ k (dạng trực tiếp loại II) 𝑌 1 + 𝐵 𝐻 𝑘+1(𝑧)
𝑘,1𝑧−1 + 𝐵𝑘,2𝑧−2 𝑘 𝑧 = = , 𝑘 = 1, . . , 𝐾 𝑌 𝑘(𝑧)
1 + 𝐴𝑘,1𝑧−1 + 𝐴𝑘,2𝑧−2 14
IIR – Dạng nối tiếp (cascade)
• Bộ lọc nối tiếp bậc 4 15
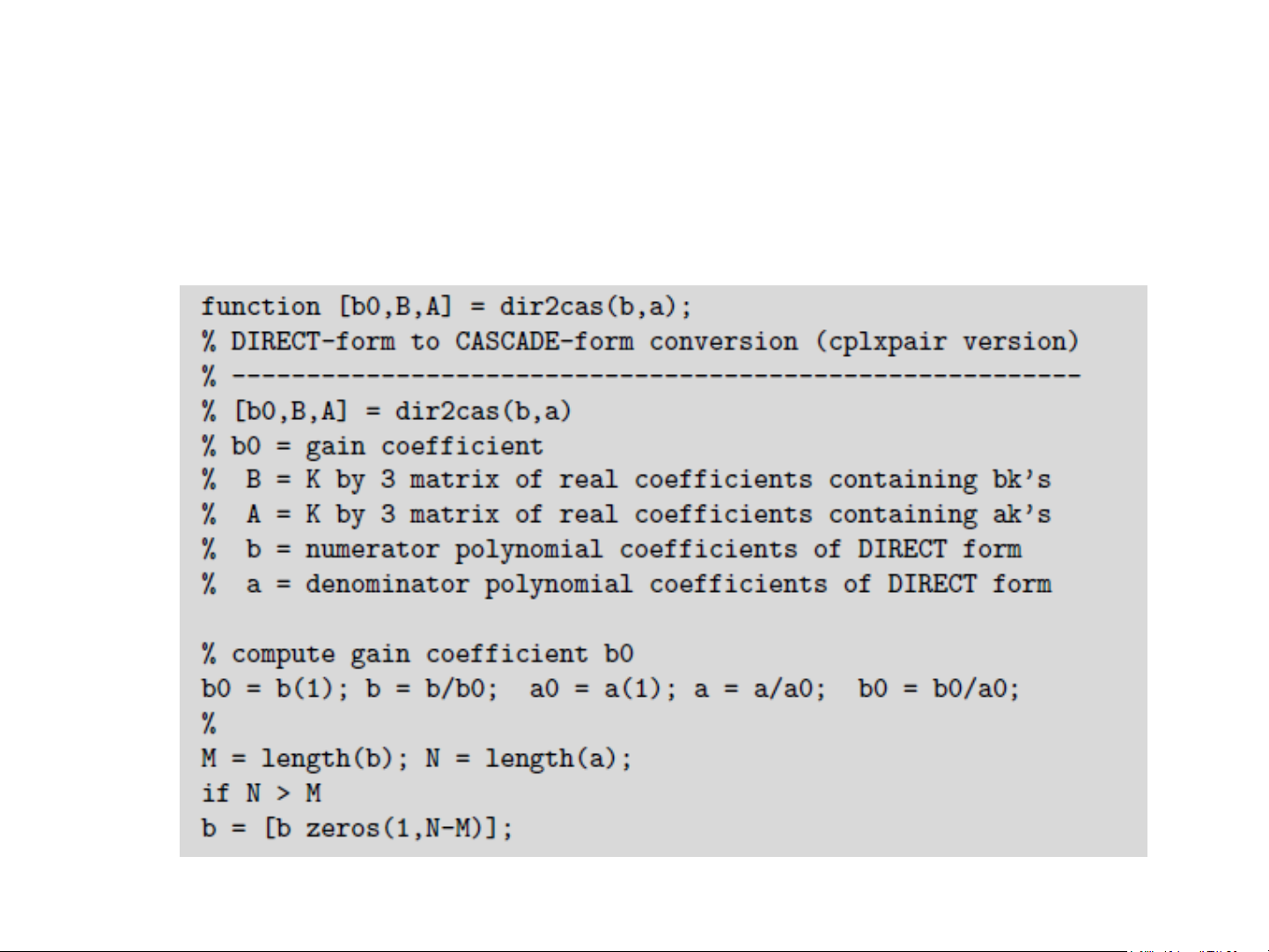
IIR – Dạng nối tiếp (cascade) Matlab
• Lệnh [b0,B,A] = dir2cas(b,a)
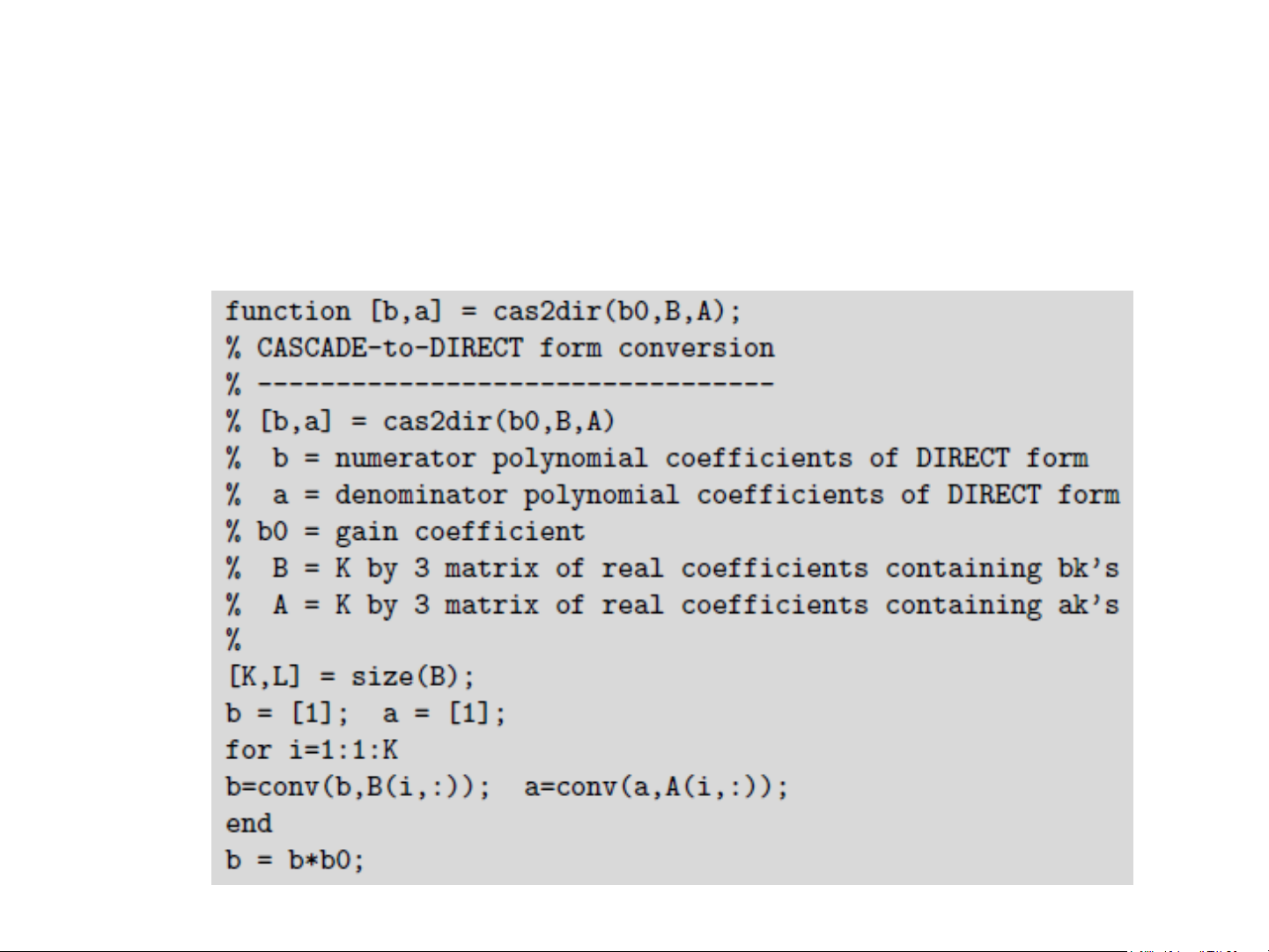
• Lệnh [b,a] = cas2dir(b0,B,A)
• Lệnh y = casfiltr(b0,B,A,x) thực hiện lọc tín hiệu với cấu
trúc bộ lọc dạng nối tiếp 16
IIR – Dạng nối tiếp (cascade) Matlab 17
IIR – Dạng nối tiếp (cascade) Matlab 18
IIR – Dạng nối tiếp (cascade) Matlab 19
IIR – Dạng nối tiếp (cascade) • Ví dụ: 20