Chapter 5_Linear transformation | Bài giảng đại số tuyến tính

Algebra Linear transformation PhD. Nguyen Tuan Long
Faculty of Economic Mathematics Functions Definition
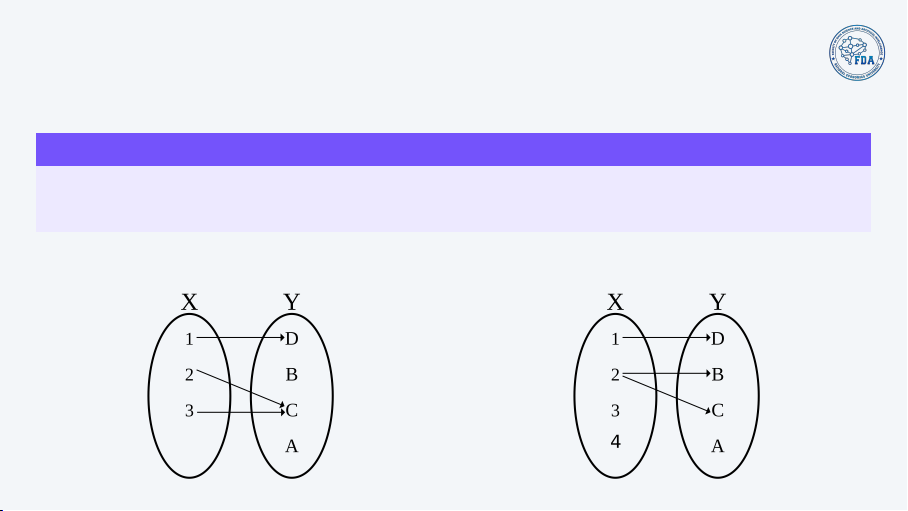
A function f : X → Y assigns to each element x of X (called domain) exactly one
element y of Y (called codomain). A function is sometime called map or mapping. function NOT function 2/20 Functions Examples
• A univariate function: f : R → R with f(x) = x2
• A bivariate function: f : R2 → R with f(x1, x2) = 2x1 + 3x2
• A multivariate function: f : Rn → R with f(x1, . . . , xn) = a1x1 + · · · + anxn
• A polynomial function: f : R2 → R with f(x1, x2) = 2x2 + 3x2 − x 1 2
1x2 + 4x1 + 5x2 Definition
• One-to-one (or injective) function: f : X → Y: if x, x′ ∈ X, x ̸= x′ then f(x) ̸= f(x′)
• Onto function (or surjective) function: f : X → Y: for every y ∈ Y there exists
x ∈ X such that f(x) = y
• Bijective function f : X → Y is the function that is both injective and surjective.3/20 Transformation Definition
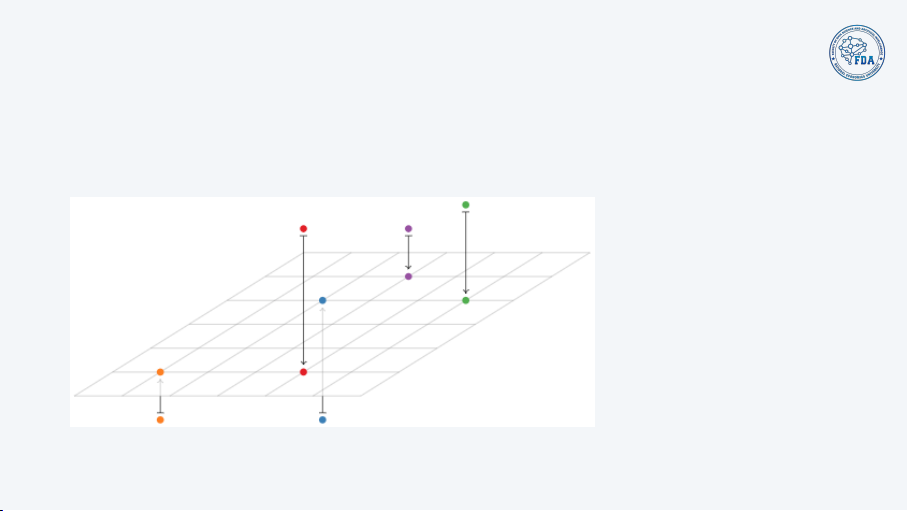
A transformation is a function T from Rn to Rm.
• Rn is called the domain of T
• Rm is called the codomain of T
• For x ∈ Rn, the vector T(x) is called the image of x under T
• The set of images {T(x) | x ∈ Rn} is called the range of T 4/20 Matrix Transformation Definition
Let A = [aij] ∈ Rm×n be a matrix. The matrix transformation associated to A is the
transformation T from Rn to Rm, defined by T(x) = Ax.
The range of T is the column space of A.        
a11x1 + · · · + a1nxn a11 a12 a1n  .   .   .   .  Ax =  ..  = x . . .
1  .  + x2  .  + · · · + xn  . 
am1x1 + · · · + amnxn am1 am2 amn
meaning the outputs of T(x) = Ax are exactly the linear combinations of the columns of A. 5/20
Projection onto the xy-plane       1 0 0 x x
0 1 0 y = y 0 0 0 z 0 6/20 Reflection [ ] [ ] [ ] −1 0 x −x = 0 1 y y 7/20 Dilation [ ] [ ] [ ] 1.5 0 x x = 1.5 0 1.5 y y 8/20 Rotation [ ] [ ] [ ] 0 −1 x −y = 1 0 y x 9/20 Question
Let T(x) = Ax is a matrix transformation from R2 to R3 where     1 1 [ ] 7 3 A = 0 1 and let u = , b = 5 4 1 1 7 • Find T(u).
• Find a vector v ∈ R2 such that T(v) = b. Is there more than one?
• Does there exist a vector w ∈ R3 such that there is more than one v ∈ R2 with T(v) = w?
• Find a vector w ∈ R3 which is not in range of T. 10/20
One-to-one transformation Definition
A transformation T from Rn to Rm is one-to-one if one of the following holds:
• for every b ∈ Rm, there is at most one vector x ∈ Rn such that T(x) = b
• for every x, y ∈ Rn with x ̸= y, then T(x) ̸= T(y).
• for every x, y ∈ Rn, if T(x) ̸= T(y) then x ̸= y. Examples
• The matrix transformation associated with the identify matrix is one-to-one. 11/20
One-to-one transformation Properties
Let T : Rn → Rm be a matrix transformation associated with a matrix A. The following statements are equivalent: • T is one-to-one
• for every b ∈ Rm, the equation T(x) = b has at most one solution
• for every b ∈ Rm, the equation Ax = b has a unique solution or is inconsistent
• Ax = 0 has only the trivial solution
• The columns of A are linearly independent
• The range of T has dimension n . 12/20
One-to-one transformation Examples
Check which of the following matrix transformations are one-to-one?     1 0 1 0 1 [ ] [ ] 1 1 0 1 −1 2 A = 0 1 ,
B = 0 1 0 , C = , D = 0 1 1 −2 2 −4 1 0 0 0 0 13/20 Onto transformation Definition
A transformation T from Rn to Rm is onto if one of the following holds:
• for every b ∈ Rm, there is at least one vector x ∈ Rn such that T(x) = b
• the range of T is equal to the codomain of T Examples
• The matrix transformation associated with identify matrix is onto. 14/20 Onto transformation Properties
Let T : Rn → Rm be a matrix transformation associated with a matrix A. The following statements are equivalent: • T is onto
• for every b ∈ Rm, the equation T(x) = b has at least one solution
• for every b ∈ Rm, the equation Ax = b is consistent
• The columns of A spans Rm
• The range of T has dimension m . 15/20 Onto transformation Examples
Check which of the following matrix transformations are onto? [ ]   1 0 [ ] 1 1 0 1 −1 2 A = , B = 0 1 , C = 0 1 1 −2 2 −4 1 0 16/20 Linear transformation Definition
A transformation T from Rn to Rm is linear if
T(x + y) = T(x) + T(y)
T(rx) = rT(x)
for all vectors x, y and all scalars r.
Every matrix transformation is a linear transformation and vice versa. 17/20
Non-linear transformation
Verify that following transformations are not linear? [ ] [ ] [ ] [ ] [ ] [ ] x |x| x xy x 2x + 1 T1 = , T = , T = , y y 2 y y 3 = y x − 2y 18/20
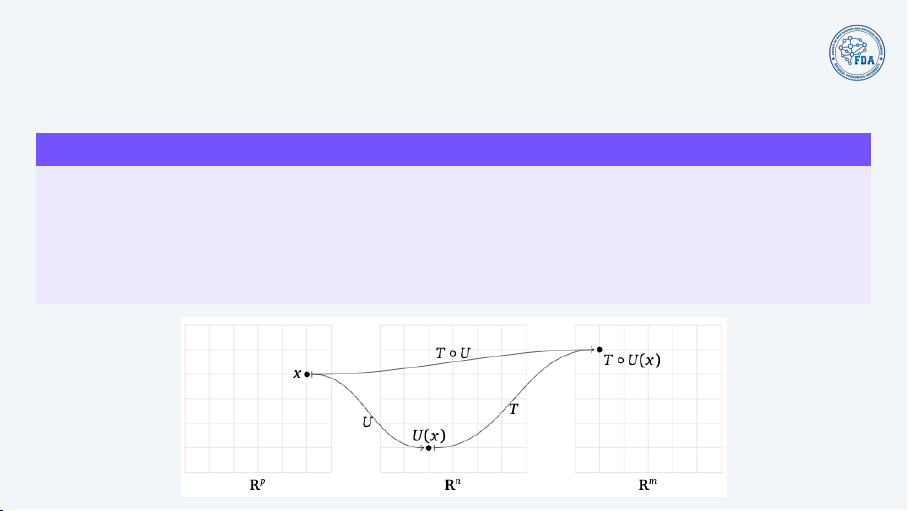
Composition of linear transformations Definition
Let T : Rn → Rm and U : Rp → Rn be linear transformations. Their composition is the
transformation T ◦ U : Rp → Rm defined by
(T ◦ U)(x) = T(U(x)). 19/20
Composition of linear transformations Examples
Let T : R3 → R2 and U : R2 → R3 be linear transformations: [ ]   1 0 1 1 0 T(x) = x,
and U(x) = 0 1 x. 0 1 1 1 0
The composition is a transformation T ◦ U : R2 → R2, for which the associated matrix is [ ] [ ]   1 0 1 1 1 1 0 = 0 1 1 1 0 1 1 1 0 20/20