











Preview text:
2021/8/16
GIỚI THIỆU HỌC PHẦN
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 1
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 2
GIỚI THIỆU HỌC PHẦN
GIỚI THIỆU HỌC PHẦN
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 3
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 4
GIỚI THIỆU VỀ PHÂN LOẠI MẬT MÃ Mã dòng Mật mã đối xứng ã Mã khối m ật Hàm băm m không khóa Hàm băm n Hàm băm có có oá khóa t Mật mã khóa công khai ật hu Chữ kí số T Sinh số ngẫu nhiên
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 5 16 August 2021 | Page 6
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 1 2021/8/16 BÀI 01 - MỤC TIÊU
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 7
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 8
TỔNG QUAN VỀ MẬT MÃ HỌC Tránh bị truy nhập Tránh bị sử dụng Khả Tránh bị tiết lộ dụng Bí Tránh bị gián đoạn mật Toàn vẹn Tránh bị sửa đổi
Tránh bị phá hoại trái phép
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin 16 August 2021 | Page 9
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 10
Các mối đe dọa an toàn thông tin trong
hệ thống thông tin liên lạc
Các loại chung của mối đe
Phân tích hệ quả của việc thực dọa
hiện các mối đe dọa
Vi phạm quy tắc kiểm soát truy
cập đến các tài nguyên
Mối đe dọa bên trong
Vi phạm tính bí mật
Mối đe dọa bên ngoài
Vi phạm tính toàn vẹn
Vi phạm tính sẵn sàng phục vụ
Mối đe dọa kết hợp của hệ thống
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 11
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 12 2 2021/8/16 • Mã hóa
• Hàm băm, mã xác thực thông điệp (MAC) Dịch vụ Kỹ thuật • Chữ kí số
Đảm bảo tính bí mật Mã hóa
Đảm bảo tính toàn vẹn
Chữ ký số, hàm băm, MAC Xác thực Chữ ký số, MAC Chống chối bỏ Chữ ký số
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 13
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 14 Biến đổi A/D Mã nguồn Mã bảo mật Mã kênh Nguồn tin Kênh truyền (Tạp âm, đa đường, giao thoa, nhiễu, nghe trộm ...) Nhận tin Biến đổi D/A Giải mã nguồn Giải mã bảo mật Giải mã kênh
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 15
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 16
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 17
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 18 3 2021/8/16
P là tập hữu hạn các bản rõ có thể
C là tập hữu hạn các bản mã có thể
K là tập hữu hạn các khoá có thể
𝐸𝑘: P → C - là quy tắc mã hóa với khóa 𝑘 ∈ K. Tập {𝐸𝑘: 𝑘 ∈ K} ký hiệu là E,
còn tập {𝐸𝑘(𝑥): 𝑥 ∈ P} ký hiệu là 𝐸𝑘(P).
𝐷𝑘: 𝐸𝑘(P) → P - là quy tắc giải mã với khóa 𝑘 ∈ K. Tập {𝐷𝑘: 𝑘 ∈ K} ký hiệu là D.
Với mỗi 𝑘 ∈ K sẽ được mô tả dưới dạng 𝑘 = (𝑘𝑒, 𝑘𝑑), trong đó: 𝑘𝑒 - là
khóa dùng cho mã hóa, 𝑘𝑑 - là khóa dùng cho giải mã. Khi đó 𝐸𝑘 được
hiểu là hàm 𝐸𝑘 , 𝐷 𝑒
𝑘 được hiểu là hàm 𝐷𝑘𝑑
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 19
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 20
Định nghĩa hệ mật: Một hệ mật là bộ 5 (P, C, K, E, D) thoả mãn các điều kiện sau: Mã hóa
1) ∀𝑥 ∈ P, 𝑘 ∈ K ta có: 𝐷𝑘 𝐸𝑘 𝑥 = 𝑥; 2) Bản rõ Bản mã
C = ራ 𝐸𝑘(P) 𝑘∈K Giải mã Ghi chú: • Mã hóa: 𝑦 = 𝐸
Quá trình chung của hệ mật 𝑘 𝑥 𝑒
• Giải mã: 𝑥 = 𝐷𝑘 𝑦 𝑑
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 21
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 22
Mã hóa đối xứng: biết được khóa mã hóa dễ dàng suy ra được khóa giải
mã (thông thường 𝑘e= 𝑘d) 𝑐 = 𝐸 (m) 𝑘𝑒 m ciphertext E D 𝐷 (c) = m 𝑘 plaintext 𝑑 𝑘 eavesdropping 𝑒 𝑘𝑑 adversary encryption key decryption key
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 23
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 24 4 2021/8/16
Mã hóa bất đối xứng: Mỗi bên có một khoá công khai và một khoá bí mật • . Mã khối:
- Bên gửi dùng khoá công khai của bên nhận để mã hoá.
- Bên nhận dùng khoá bí mật của mình để giải mã. 𝑐 = 𝐸 (m) 𝑘𝑒 m ciphertext E D 𝐷 (c) = m 𝑘 plaintext 𝑑 𝑘 attacker 𝑒 𝑘𝑑 (public) encryption key (private) decryption key
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 25
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 26 Mã dòng: Bộ kí tự: chữ cái latin Nguồn khóa ki Nguồn khóa MÃ HÓA ngẫu nhiên ngẫu nhiên Khóa ngẫu nhiên: PWKAX Thông điệp: HELLO k
c m k i i i i ci H E L L O Bản mã Rõ (7) (4) (11) (11) (14) P W K A X Khóa Nguồn tin
m c k (15) (22) (10) (0) (23) m i i i i W A V ? ? Hệ mật Vernam Bản rõ Mã (22) (0) (21) (?) (?) (One-Time Pad)
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 27
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 28 Bộ kí tự: chữ cái latin K K GIẢI MÃ Khóa ngẫu nhiên: PWKAX Mở rộng khóa Mở rộng khóa Bản mã: WAVLL zi z W A V L L
c m z i Mã i i i c (22) (0) (21) (11) (11) i Bản mã E D P W K A X Khóa (15) (22) (10) (0) (23) Nguồn tin H E L L O m c z i i i Rõ mi (7) (4) (11) (11) (14) Bản rõ
m , z , c 0, 1 i i i
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 29
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 30 5 2021/8/16 K K
• Khối «mở rộng khóa»
• Là bộ sinh số giả ngẫu nhiên (PRNG) Mở rộng khóa Mở rộng khóa z • Là quan trọng nhất i
• Quyết định độ an toàn của mã dòng z c e m i i z i i c •Phân loại i Bản mã E D
• z chỉ phụ thuộc K: «mã dòng đồng bộ» i • z phụ thuộc c , c
, ..., c : «mã dòng tự đồng i i-n i-n+1 i-1 Nguồn tin m d c bộ» i z i m i i
m , c , z A Bản rõ i i i
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 31
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 32
16 August 2021 | Page 33
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 34
• Sơ đồ khối của một hệ truyền tin mật sử dụng hệ mật KBM?
• Các phương pháp chính của hệ mật KBM?
• Yếu điểm của mã đơn biểu vs mã đa biểu? • Hệ mật tích?
• Thám mã một số hệ mã cổ điển dựa trên phương pháp thống kê?
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 35
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 36 6 2021/8/16
Sơ đồ khối của một hệ truyền tin mật
• Các hệ mật thay thế đơn biểu Oscar
• Khi khóa đã được chọn thì mỗi kí tự của bản rõ được ánh xạ Bản rõ Bản mã Bản mã Bản rõ
đến một kí tự duy nhất của bản mã. Bộ mã hóa Kênh mở Bộ giải mã
• Như vậy độ dài của khóa ở đây là 26 và số khóa có thể có là 26!. (không an toàn) Alice Bob Kênh an toàn Nguồn khóa
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 37
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 38
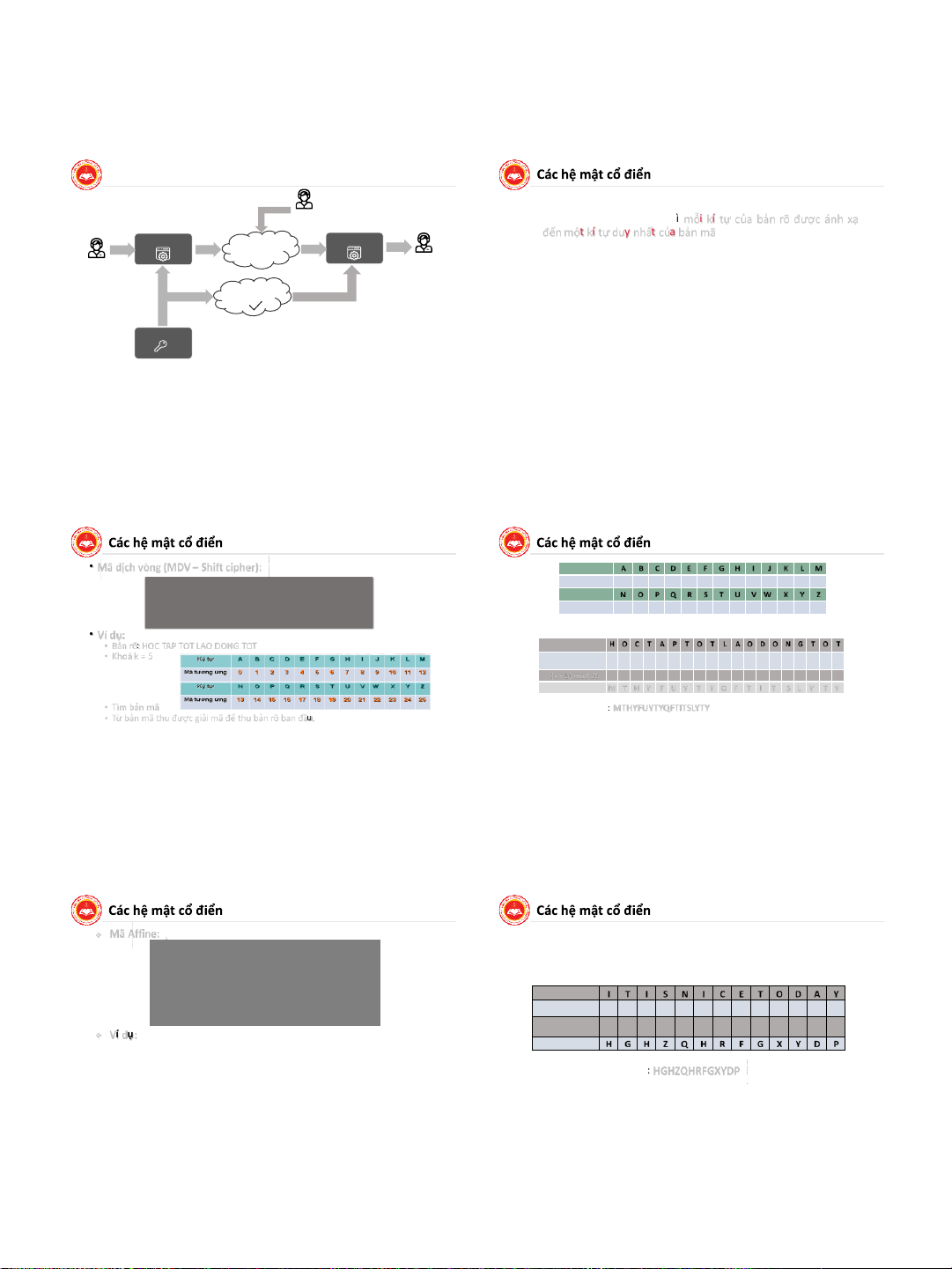
• Mã dịch vòng (MDV – Shift cipher): Ký tự A B C D E F G H I J K L M Giả sử P = C = K = Z Mã tương ứng 0 1 2 3 4 5 6 7 8 9 10 11 12
26 với 0 ≤ k ≤ 25, ta định nghĩa: Ký tự N O P Q R S T U V W X Y Z y = ek(x) = x + k mod 26 Mã tương ứng 13 14 15 16 17 18 19 20 21 22 23 24 25 x = dk(y) = y - k mod 26 • Ví dụ:
• Bản rõ: HOC TAP TOT LAO DONG TOT Bản rõ H O C T A P T O T L A O D O N G T O T • Khoá k = 5 Mã tương ứng (x)
19 0 15 19 14 19 11 0 14 3 14 13 6 19 14 19 (x + 5) mod 26
12 19 7 24 5 20 24 19 24 16 5 19 8 19 18 11 24 19 24 Bản mã
M T H Y F U Y T Y Q F T I T S L Y T Y • Tìm bản mã
Bản mã thu được: MTHYFUYTYQFTITSLYTY
• Từ bản mã thu được giải mã để thu bản rõ ban đầu. Giải mã: SV tự làm!
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 39
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 40 Mã Affine: Giải:
Cho P = C = Z26, K = Z26 x Z26. Giả sử:
Tìm bản mã của bản rõ: It is nice today
K = {(a,b) Z26 x Z26; UCLN (a, 26) = 1} ■ Ta có hàm mã: e
Với k = (a, b) K ta định nghĩa: k(x) = 7x + 3 mod 26 Ký tự I T I S N I C E T O D A Y y = ek(x) = ax + b mod 26 Mã (x) 8 9 8 18 13 8 2 4 19 14 3 0 24
x = dk(y) = a-1(y – b) mod 26 7x + 3 mod 26 7 6 7 25 16 7 17 5 6 23 24 3 15 Ví dụ: Bản mã H G H Z Q H R F G X Y D P
Cho k = (7, 3). Bản rõ: It is nice today ■ Tìm bản mã.
Bản mã thu được là: HGHZQHRFGXYDP ■
Giải mã bản mã thu được
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 41
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 42 7 2021/8/16 Giải:
• Nhận xét về các hệ mật thay thế đơn biểu: •
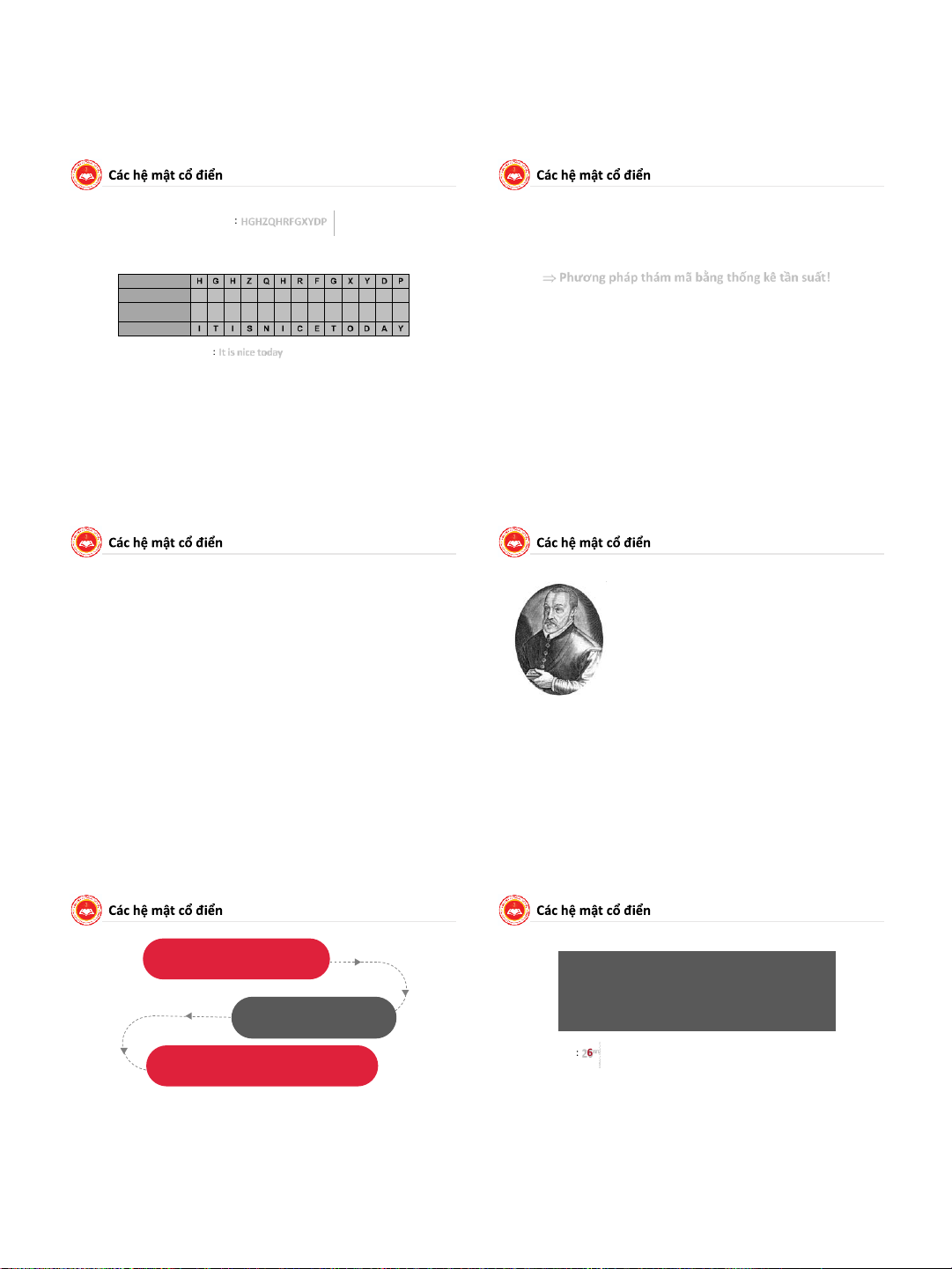
Tìm bản rõ của bản mã: HGHZQHRFGXYDP
Mỗi ký tự của bản rõ được ánh xạ đến một ký tự duy nhất của bản mã. ■ Ta có hàm mã:
• Các đặc trưng về ngôn ngữ, tần suất xuất hiện của các chữ
dk(y) = 7-1.(y - 3) mod 26 = 15.(y – 3) mod 26
trong bản rõ và chữ tương ứng trong bản mã là như nhau Bản mã H G H Z Q H R F G X Y D P
Phương pháp thám mã bằng thống kê tần suất! Mã (y) 7 6 7 25 16 7 17 5 6 23 24 3 15 15(y – 3) mod 26 8 19 8 18 13 8 2 4 19 14 3 0 24 Bản rõ I T I S N I C E T O D A Y
Bản mã thu được là: It is nice today
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 43
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 44
• Các hệ mật thay thế đa biểu
Hệ mật thay thế đa biểu:
• Yếu điểm của các mã pháp đơn biểu • Hệ Vigenere:
• Một hướng khác làm tăng độ an toàn cho mã trên bảng chữ là
• Blaise de Vigènere (1523 – 1596)
sử dụng nhiều bảng chữ để mã. • Ý tưởng:
• Mỗi chữ sẽ được mã bằng bất kì chữ nào trong bản mã tùy
• Sử dụng một loạt mã Caesar khác nhau dựa
thuộc vào ngữ cảnh khi mã hóa. Làm như vậy để trải bằng tần
trên các kí tự của một từ khóa
suất các chữ xuất hiện trong bản mã. Do đó làm mất bớt cấu
• Dễ hiểu và dễ thực hiện
trúc của bản rõ được thể hiện trên bản mã và làm cho mã thám đa bảng khó hơn.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 45
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 46
• Mô tả hệ mã Vigenere:
Biến đổi bảng chữ cái A, B, …, Z thành các
Cho m là số nguyên dương. Ta định nghĩa P = C = K = (Z kí tự 0, 1, …25 26)m. Với khoá
k = (k1, k2, …, km) ta xác định:
ek(x1, x2…,xm) = (x1 + k1, x2 + k2,… xm + km) Và d
Khóa (từ khóa) là một chuỗi các kí tự
k(y1, y2,…, ym) = (y1 - k1, y2 - k2,… ym - km) có độ dài m
(Các phép toán đều thực hiện trên Z26.) • Nhận xét: • Số khoá: 26m
Thông điệp được chia thành các khối độ dài m. Mỗi
lần mã hóa sẽ thực hiện biến đổi đồng thời m kí tự
Tấn công tìm khoá vét cạn là không khả thi
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 47
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 48 8 2021/8/16
• Ví dụ minh hoạ: • Giải: • m = 6, k = cipher
• Ta có từ khoá CIPHER, tương ứng với dãy số: k = (2, 8, 15, 7, 4, 17)
• Bản rõ: Information security
• Chuyển các ký tự rõ thành mã trên Z26 rồi cộng với từ khoá
• Hãy mã hoá bản rõ trên Bản rõ I N F O R M A T I O N S E C U R I T Y
• Giải mã bản mã vừa thu được Mã 8 13 5 14 17 12 0 19 8 14 13 18 4 2 20 17 8 19 24 Khoá 2 8 15 7 4 17 2 8 15 7 4 17 2 8 15 7 4 17 2 Bản mã 10 21 20 21 21 3 2 1 23 21 17 9 6 10 9 24 12 10 0
• Chuyển các ký tự số thành chữ cái tương ứng. Ta có bản mã: KVUVVDCBXVRJGKJYMKA
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 49
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 50 Bản rõ I N F O R M A T I O N S E C U R I T Y
Bản mã K V U V V D C B X V R J G K J Y M K A • Nhận xét?
• Như vậy có chữ mã khác nhau cho cùng một chữ của bản rõ.
• Ví dụ: Chữ I được mã bởi các chữ: K, X, M; chữ N được mã bởi các chữ V, R; ...
Tần suất của các chữ bị là phẳng, nghĩa là tần suất xuất hiện các chữ trên bản
mã tương đối đều nhau.
• Tuy nhiên chưa mất hoàn toàn, do độ dài của khoá có hạn, nên có thể
tạo nên chu kỳ vòng lặp, hoặc việc lặp do ngẫu nhiên
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 51
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 52 Hệ mật Hill: • Cho ma trận:
Lester S.Hill đưa ra năm 1929 a a 11 12
Ý tưởng: lấy m tổ hợp tuyến tính của m kí tự trong một phần tử bản A
rõ để tạo ra một phần tử m kí tự trong một phần tử của bản mã. a a 21 22 Mô tả:
• Định thức detA = a .a – a .a 11 22 12 21
Cho m là số nguyên dương cố định. Cho P = C = (Z26)m. k = {các
ma trận khả nghịch cấp m x m trên Z
• Ma trận là khả nghịch det A ≠ 0 26}:
Với k K, ta xác định:
• Vì các phép toán tính theo modulo 26 nên phải có điều kiện: UCLN(detA, 26) = 1. ek(x) = xk • Ma trận nghịch đảo: d a a 22 12 k(y) = yk-1 1 A 1 det A .
(Các phép toán đều thực hiện trên Z 26.) a a 21 11
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 53
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 54 9 2021/8/16
• Ví dụ minh hoạ: • •
Các hệ mật thay thế không tuần hoàn Bản rõ: “july” •
• Phép thế lý tưởng là dùng nhiều bảng chữ cái để không nhận diện Ma trận khoá: 11 8
được phân bố tần suất k • 3 7
Điều gì xảy ra nếu văn bản được mã bằng số bảng chữ cái không hạn chế?
• Tìm bản mã của bản rõ trên
• Vigenere đề xuất hệ mật khoá tự sinh (hệ mật khoá chạy)
• Từ bản mã thu được tìm bản rõ ban đầu.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 55
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 56
• Hệ mật khoá chạy: • Ý tưởng: • Mã hoá bản rõ
Từ khoá được nối tiếp bằng chính bản rõ, sau đó sử dụng mã Vigenere để mã
• Khi biết từ khoá, giải được một số chữ của bản rõ rồi dùng chúng giải nốt phần còn lại Khoá D E C E P T W E I V A E
R E D I S C O V E R E D S A V
• Sự cải tiến này gây mất khái niệm chu kỳ. • Bản rõ
W E A R E D I S C O V E R E D S A V E Y O U R S E L F Ví dụ: • Key = deceptive Bản mã
Z I C V T W Q N G K Z E I I G A S X S T S L V V W L A
• Bản rõ: we are discovered save yourself
• Hãy mã hoá bản rõ trên.
• Giải mã bản mã thu được
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 57
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 58 • Hệ mật OTP O V E R E D S A V
• Do Gillbert Vernam đưa ra 1971 • Mô tả: Khoá D E C E P T I V E
Bản mã Z I C V T W Q N G K Z E I I G A S X S T S L V V W L A
P = C = K = (Z2)n, n 1 là số nguyên, K (Z2)n, Bản rõ W E E A R E E D D I I S C
O V E R E D S A V E Y O U R S E L F
với x = (x1, …, xn) và K = (K1, …, Kn), ta có hàm mã hoá: e K(x) = (x1 K1, …, xn Kn)
Phép mã đồng nhất với phép giải. Nếu y = (y1, …, yn) ta có: d K(y) = (y1 K1, …, yn Kn)
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 59
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 60 10 2021/8/16
• Hệ mật hoán vị (MHV): • MHV: • Ý tưởng:
Cho m là số nguyên dương xác định. Cho P = C = (Z
• Các chữ trong bản rõ không được thay thế bằng các chữ khác mà chỉ 26)m
thay đổi vị trí giữa các chữ trong bản rõ.
k là tất cả hoán vị có thể có của {1, 2, …,m}: • Nhận xét? •
Với khoá , ta xác định:
Bản mã có cùng tần suất xuất hiện các chữ như trong bản gốc • Dễ thám mã
e(x1, …,xm) = (x(1), …, x(m)) d -1 -1
(y (1), …, y (m)) = (x1, …,xm)
(Trong đó -1 là hoán vị ngược của )
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 61
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 62 • • Ví dụ 1: Mã hóa: •
• B1: Nhóm bản rõ thành các nhóm 6 kí tự
m =6; khóa là phép hoán vị sau: 1 2 3 4 5 6 3 5 1 6 4 2 • •
B2: Mỗi nhóm 6 kí tự sẽ được sắp xếp lại theo theo phép HV (3, 5, 1,
Khi đó phép HV ngược -1: 6, 4, 2), ta có: 1 2 3 4 5 6 3 6 1 5 2 4 • Khi đó ta có bản mã:
• Bản rõ: asecondclasscarriageonthetrain
EOANCSLSDSACRICARAOTGHNERIENAT
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 63
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 64 • Giải mã: • Hệ mật tích:
• B1: Nhóm bản mã thành các nhóm 6 kí tự
• Ý tưởng: kết hợp các hệ mật bằng cách tạo tích của chúng.
• Xét các hệ mật có C = P (các hệ mật loại này được gọi là tự đồng cấu)
Giả sử S1 = (P, P, K1, E1, D1) và S2 = (P, P, K2, E2, D2) là hai hệ mật tự đồng cấu có × •
cùng không gian bản mã , rõ. Khi đó tích S S
B2: Mỗi nhóm 6 kí tự sẽ được sắp xếp lại theo theo phép HV -1 (3, 6, 1 và S2 (KH: S1 2) được xác định là hệ mật (P, P, K × K 1, 5, 2, 4), ta có: 1 2, E, D) Với khoá k = (k 1, k2) trong đó k1 K1, k2 K2 ta xác định: 𝑒 𝑘 𝑥 = 𝑒 𝑒 (𝑥) 1,𝑘2 𝑘2 𝑘1
• Khi đó ta có bản rõ tương ứng: Và quy tắc giải mã:
asecondclasscarriageonthetrain 𝑑 𝑘 𝑥 = 𝑑 𝑒 (𝑥) 1,𝑘2 𝑘2 𝑘1
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 65
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 66 11 2021/8/16
• Thám mã một số hệ mật cổ điển:
• Phương pháp thám mã bằng thống kê tần suất:
• Nhận xét về các hệ mật thay thế đơn biểu:
• Ngôn ngữ có tính dư thừa
• Mỗi ký tự của bản rõ được ánh xạ đến một ký tự duy nhất của
• Ví dụ: tiếng Anh, chữ E được sử dụng nhiều nhất; sau đó đến các chữ bản mã.
T, R, N, I, O, A, S. Một số chữ rất ít dùng như: Z, J, K, Q, X
• Các đặc trưng về ngôn ngữ, tần suất xuất hiện của các chữ trong
• Các bộ chữ thường xuất hiện: th, nt, lrd, shll, …
bản rõ và chữ tương ứng trong bản mã là như nhau
• Bằng phương pháp thống kê, ta có thể xây dựng các bảng các tần
Phương pháp thám mã bằng thống kê tần suất!
suất các chữ đơn, cặp hay bộ ba các chữ
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 67
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 68
• Ví dụ: Giả sử ta có bản mã
• Thám mã Affine bằng phương pháp thống kê tần suất.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 69
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 70
• Bước 1: xác định tần suất
• Bước 2: Tách nhóm Kí tự Tần suất Kí tự Tần suất xuất hiện xuất hiện
• Từ bảng tần suất, giả sử G 22 I 5
• G (6) là mã hóa của E (4) N 21 K 4
• N (13) là mã hóa của T (19) R 21 L 4
• Thiết lập hệ phương trình B 16 Q 4 O 16 E 3 4a + b = 6 W 13 P 3 19a + b = 13 Z 11 F 2 A 9 T 2
• Giải hệ được a = 23, b = - 8 = 18. Ta có hàm mã: D 9 M 1 ek(x) = 23x + 18 mod 26 H 7 U 1
• Hàm giải mã tương ứng: J 6 V 1
dk(y) = 17(y – 18) = (17y + 6) mod 26
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 71
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 72 12 2021/8/16
• Bước 3: Tìm bản rõ
• Quay lại bước 2
• Từ hàm giải mã, ta có bản rõ tương ứng:
• Giả sử G là mã hóa của T • N là mã hóa của E • Ta lại có hệ: 19a + b = 6 4a + b = 13
• Giải hệ được a = 3, b = 1. Ta có hàm mã:
• Nhận xét gì về bản rõ? ek(x) = 3x + 1 mod 26
• Hàm giải mã tương ứng:
dk(y) = 9(y – 1) = 9y + 17 mod 26
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 73
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 74
• Bước 3: Bản rõ tương ứng
• Ví dụ minh hoạ:
• Giả sử ta dùng hệ mật Hill với bản rõ: “Friday”, bản mã tương ứng “ZIQVSO”
“The art of war teaches us to rely not • Hãy tìm ma trận khoá.
on the likelihood of the enemy’s not • Giải:
coming but on our own readiness to
• Ta có FR (5; 17), ID (8;3), AY (0; 24)
receive him not on the chance of his
ZI (25; 8) QV( 16; 21); SO (18; 14)
not attacking but rather on the fact that • PT: 25 8 5 17
e have made our position unassailable” .K 16 21 8 3 1
5 17 25 8 9 1 25 8 7 15 K . .
8 3 16 21 2 15 16 21 4 19
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 75
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 76
Bài 02. Các hệ mật KBM
• Thám mã hệ mã Vigerner: đọc thêm tài liệu [4, 1.2 chapter 1] Mục tiêu:
Thực hiện làm thành thạo các bài tập minh họa phần lí thuyết về các
hệ mật cổ điển học trong Bài 01
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 77
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 78 13 2021/8/16 • Bài 1. • Bài 3.
• Bản rõ P được mã bằng mã Affine với k = (7, 11), đầu ra tiếp tục được
• Ta có phương thức mã hoán vị như sau : Giả sử m, n là các số nguyên
mã bằng hệ mã Vigenere với từ khóa là CIPHER thu bản mã
dương. Ta viết bản rõ theo từng hàng thành một ma trận nxm. Sau đó
BNNIECQDZSSGHG. Hãy tìm P ban đầu
tạo ra bản mã bằng cách lấy các cột của ma trận này. Cho n = 3, m = 5 • Bài 2.
em hãy mô tả cách giải mã bản mã ’’WAT ORW REI DBN SUD ’’ thu được
bằng phương pháp đã nêu ở trên
• Giải mã bản mã QQCD thu được khi mã bản rõ bằng hệ mã Hill. Cho 5 8 • Bài 4. khóa k = 12 7
• Hãy giải mã bản mã “ZFFPXNZXXQ” thu được từ mã Affine. Biết rằng “P”
là mã hóa của “y”, “Z” là mã hóa của “s”.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 79
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 80
Bài 03. Các hệ mật hiện đại
Nguyên lí thiết kế mã khối?
Thuật toán mã khối DES
Các bước thực hiện thuật toán DES
Vấn đề liên quan tới DES? Biến thể của DES?
Nắm vững cơ sở toán học của hệ mã AES, cấu trúc SPN, thuật toán AES
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 81
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 82 Mã khối Mã khối
• Nguyên lí thiết kế mã khối:
• Chuẩn mã dữ liệu DES
• Theo Shannon có 2 nguyên tắc cơ sở để độ bảo mật cao đó là việc tạo ra • Giới thiệu về DES
tính xáo trộn (confussion) và tính khuếch tán (diffusion) • Thuật toán DES
• Tính xáo trộn: sự phụ thuộc vào bản mã đối với bản rõ phải thực sự phức • Double DES và Triple DES
tạp để gây rắc rối, cảm giác xáo trộn đối với kẻ thám mã có ý định phân tích
tìm quy luật để phá mã. Quan hệ của mã – tin là phi tuyến
• Khuếch tán: làm khuếch tán những mẩu văn bản mang đặc tính thống kê
(gây ra do dư thừa ngôn ngữ) lẫn vào toàn bộ văn bản. Nhờ đó gây khó
khăn cho kẻ phá hoại trong việc dò mã trên cơ sở thống kê các mẫu lặp lại
cao. Sự thay đổi 1 bit trong 1 khối bản rõ phải dẫn tới sự thay đổi hoàn
toàn trong khối mã tạo ra
• Một cách đơn giản, xáo trộn được thực hiện bằng phép thế, khuếch tán
được thực hiện bằng phép đổi chỗ hay hoán vị
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 83
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 84 14 2021/8/16 Mã khối Mã khối
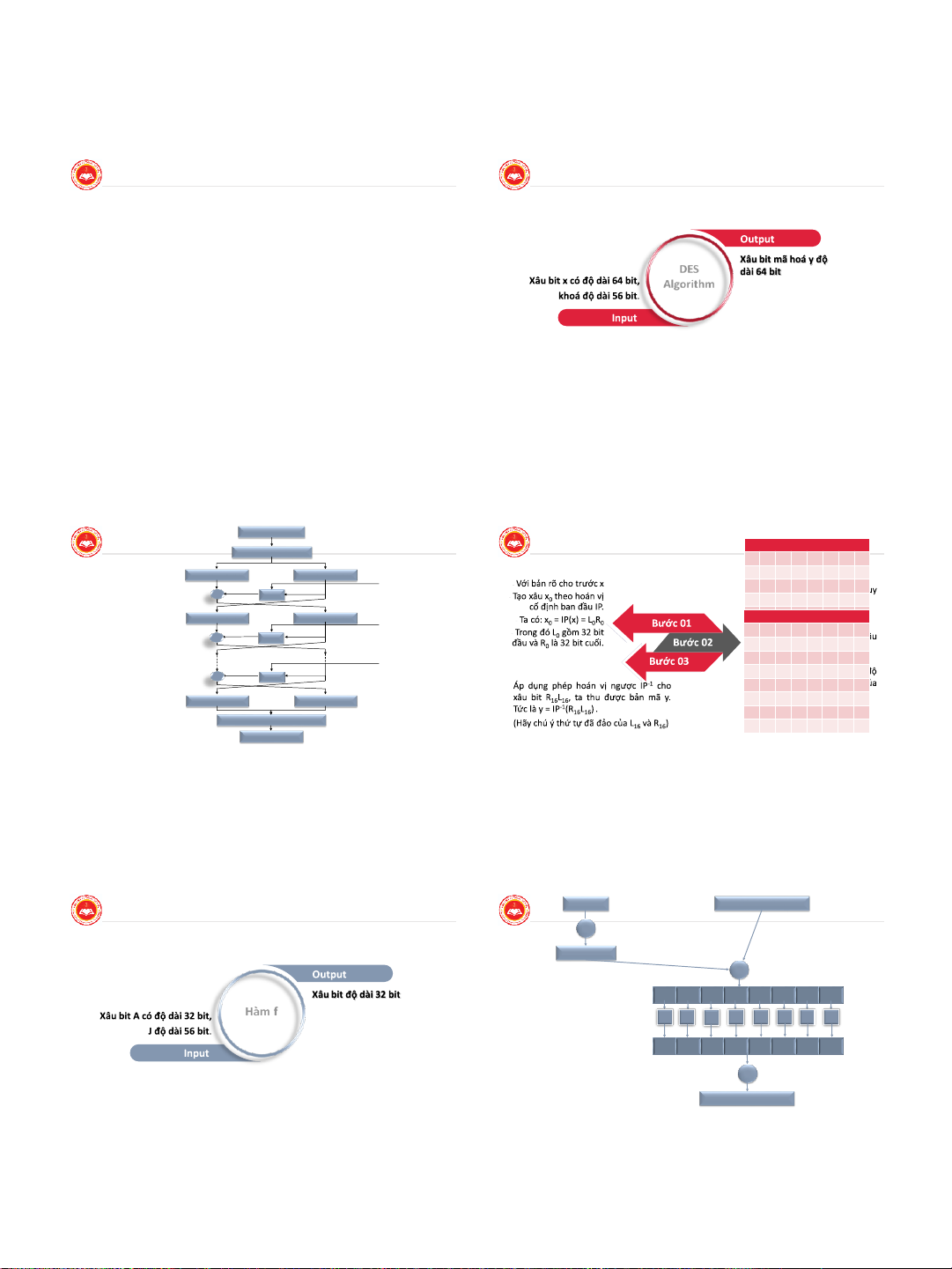
• Giới thiệu về DES
• Năm 1972, Viện tiêu chuẩn và công nghệ quốc gia Hoa kỳ (National
Institute of Standards and Technology-NIST) đặt ra yêu cầu xây dựng một
thuật toán mã hoá bảo mật thông tin với yêu cầu là dễ thực hiện, sử
dụng được rộng rãi trong nhiều lĩnh vực và mức độ bảo mật cao.
• Năm 1974, IBM giới thiệu thuật toán Lucifer, thuật toán này đáp ứng hầu DES
hết các yêu cầu của NIST. Algorithm
• Sau một số sửa đổi, năm 1976, Lucifer được NIST công nhận là chuẩn
quốc gia Hoa kỳ và được đổi tên thành Data Encryption Standard (DES).
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 85
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 86 Input x 64 bits Mã khối IP Initial Pemutation 58 50 42 34 26 18 10 2
Mô tả thuật toán: Left 32 bits Right 32 bits 60 52 44 36 28 20 12 4 K1 62 54 46 38 30 22 14 6 + f 64 56 48 40 32 24 16 8 57 49 41 33 25 17 9 1 Left 32 bits Right 32 bits IP-1 K2 59 51 43 35 27 19 11 3 40 8 48 16 56 24 64 32 + f 61 53 45 37 29 21 13 5 39 7 47 15 55 23 63 31 63 55 47 39 31 23 15 7 38 6 46 14 54 22 62 30 K16 37 5 45 13 53 21 61 29 + f 36 4 44 12 52 20 60 28 Left 32 bits Right 32 bits 35 3 43 11 51 19 59 27 34 2 42 10 50 18 58 26
Inverse Initial Permutation 33 1 41 9 49 17 57 25
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin Output y 64 bits
16 August 2021 | Page 87
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 88 Mã khối A J 32 bit 48 bit E E(A) 48 bit 48 bit + B1 B2 B3 B4 B5 B6 B7 B8 Hàm f S1 S S 2 S3 S4 5 S6 S7 S8 C1 C2 C3 C4 C5 C6 C7 C8 32 bit P 32 bit f(A,J)
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 89
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 90 15 2021/8/16 Mã khối Mã khối • Dùng 8 bảng S BẢNG CHỌN E BIT
1S2,…,S8 ( được gọi là các hộp S ). Với mỗi Si là một
Lặp lại 2 bit cuối của
bảng 416 cố định có các hàng là các số nguyên từ 0 đến 15. Với 32 1 2 3 4 5 hàng trên
xâu bit có độ dài 6 (kí hiệu Bi = b1 b2 b3 b4 b5 b6), ta tính Sj(Bj) như 4 5 6 7 8 9 sau: 8 9 10 11 12 13
• Hai bit b1b6 xác định biểu diễn nhị phân hàng r của Sj (0 r 3) 12 13 14 15 16 17
• Bốn bit (b2 b3 b4 b5) xác định biểu diễn nhị phân của cột c của Sj (0 c 15). • 16 17 18 19 20 21
Khi đó Sj(Bj) sẽ xác định phần tử Sj(r, c) ; phần tử này viết dưới dạng nhị
phân là một xâu bit có độ dài 4 20 21 22 23 24 25
• Bằng cách tương tự tính các C
Lặp lại 2 bit cuối của j = Sj(Bj) , (1 j 8). 24 25 26 27 28 29 hàng trên 28 29 30 31 32 1
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 91
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 92 Mã khối S3 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8 Các hộp thế: 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7 S1 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 S 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8 4 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14 S2 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10 S5 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 93
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 94 S6 Mã khối 12 1 10 15 9 2 6 8 0 13 3 4 14 7 15 11 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8
3 tính chất của S – box được NSA công bố 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13
Các bít vào luôn phụ thuộc không tuyến tính vào các bít ra S7 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1
Sửa đổi ở một bit vào làm thay đổi ít nhất là hai bit ra. 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6
Khi một bit vào được giữ cố định và 5 bit con lại cho thay đổi thì S-boxes thể 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12
hiện một tính chất được gọi là ‘phân bố đồng nhất ‘ (uniform distribution): S
so sánh số lượng bit số 0 và 1 ở các đầu ra luôn ở mức cân bằng. Tính chất 8 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7
này khiến cho việc áp dụng phân tích theo lý thuyết thông kê để tìm cách phá 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8 S-boxes là vô ích. 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 95
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 96 16 2021/8/16 Mã khối Mã khối
Xâu bit C = C1 C2 … C8 có độ dài 32 được hoán vị theo phép hoán vị cố
• Các bước tính bảng khóa DES:
định P. Xâu kết quả là P(C) được xác định là f(A, J).
• Với một khoá k 64 bit cho trước, ta loại bỏ các bit kiểm tra tính chẵn lẻ và
hoán vị các bit còn lại của k theo phép hoán vị cố định PC-1. Ta viết: PC- P 1(k) = C 16 7 20 21 0D0
• Với i thay đổi từ 1 đến 16: 29 12 28 17 Ci = LSi(Ci-1) 1 15 23 26 Di = LSi(Di-1) 5 18 31 10
• Dịch trái 1 bit tương ứng với các vòng 1, 2, 9, 16 2 8 24 14
• Dịch trái 2 bit tương ứng với các vòng 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 32 27 3 9 19 13 30 6 22 11 4 25
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 97
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 98 Mã khối Mã khối K Tính bảng khóa DES
Các hoán vị PC – 1 và PC – 2: PC – 1 PC – 1 PC – 1 C 57 49 41 33 25 17 9 14 17 11 24 1 5 0 D0 1 58 50 42 34 26 18 3 28 15 6 21 10 LS1 LS1 10 2 59 51 43 35 27 23 19 12 4 26 8 19 11 3 60 52 44 36 16 7 27 20 13 2 C PC – 2 K 1 D1 1 63 55 47 39 31 23 15 41 52 31 37 47 55 ⁞ 7 62 54 46 38 30 22 30 40 51 45 33 48 LS16 LS16 14 6 61 53 45 37 29 44 49 39 56 34 53 21 13 5 28 20 12 4 46 42 50 36 29 32 C16 D16 PC – 2 K16
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 99
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 100 Mã khối Mã khối
• Tính chất của DES
• Tính chất của DES
• Tác dụng đồng loạt: Khi ta thay đổi 1 bit trong khoá sẽ gây ra tác động đồng loạt làm • …
thay đổi nhiều bit trên bản mã. Đây là tính chất mong muốn của khoá trong thuật
• Khóa nửa yếu: Có 6 cặp khóa nửa yếu
toán mã hoá. Nếu thay đổi 1 bít đầu vào hoặc khoá sẽ kéo theo thay đổi một nửa số • Là cặp (k (𝐸
𝑥 ) = 𝑥 với mọi x
bít đầu ra. Do đó không thể đoán khoá được. Co thể nói rằng DES thể hiện tác động
1, k2) sao cho 𝐸𝑘1 𝑘2 đồng loạt mạnh
• DES không là nhóm dưới phép hợp hàm
• Tính chất bù: Ký hiệu ҧ𝑥 là bù của x theo từng bít, ta có Khóa yếu Cặp khóa bán yếu
𝐸𝑘 𝑥 = 𝑦 ⟺ 𝐸ത𝑘 ҧ𝑥 = ത𝑦 1)
01FE 01FE 01FE 01FE FE01 FE01 FE01 FE01 • 1) 0101 0101 0101 0101
Khóa yếu: DES có 4 khóa yếu 2)
1FE0 0EF1 0EF1 0EF1 E01F E01F F10E F10E
• k được gọi là khóa yếu nếu 𝐸𝑘(𝐸𝑘 𝑥 ) = 𝑥; x 2) FEFE FEFE FEFE FEFE 3)
01E0 01E0 01F1 01F1 E001 E001 F101 F101
• Khóa nửa yếu: Có 6 cặp khóa nửa yếu 3) 1F1F 1F1F 0E0E 0E0E 4) •
1FFE 1FFE 0EFE OEFE FE1F FE1F FE0E FE0E Là cặp (k (𝐸 𝑥 ) = 𝑥 1, k2) sao cho 𝐸𝑘 với mọi x 1 𝑘2 • 5)
DES không là nhóm dưới phép hợp hàm 4) E0E0 E0E0 F1F1 F1F1
011F 011F 010E 010E 1F01 1E01 0E01 0E01 6)
E0FE E0FE F1FE F1FE FEE0 FEE0 FEF1 FEF1
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 101
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 102 17 2021/8/16 Mã khối DES bội ba
Các biến thể của DES M C DES DES M C K1() DES-1K2() K1() Bản rõ DES bội hai DES Bản mã K1() DESK1() Bản rõ Bản mã Mã hóa: K1 K2 K1 Với TDES việc tìm C = DES K
Mã hóa TDES với 2 khóa C DES DES 1 DES M khóa vét cạn yêu K2[DESK1(M)] 1 K2 1 K K2 1 K cầu khoảng: 2112 Giải mã: phép tính TDES, bởi M = DES -1 -1 C M vậy thực tế khó có K1 [DESK2 (C)] C M DES-1 DES K1() K2() DES-1K1() thể thám mã thành
Có 256 sự lựa chọn cho khóa K1 DES-1 Bản mã Bản rõ K2() DES-1K1() công.
và 256 sự lựa chọn cho khóa K Bản mã Bản rõ 2. K1 K2 K1
Bởi vậy có 2112 sự lựa chọn cho K1 K2 cặp khóa (K
Giải mã TDES với 2 khóa M DES 1 1
K 1 DES K 2 DES K 1 C 1, K2)
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 103
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
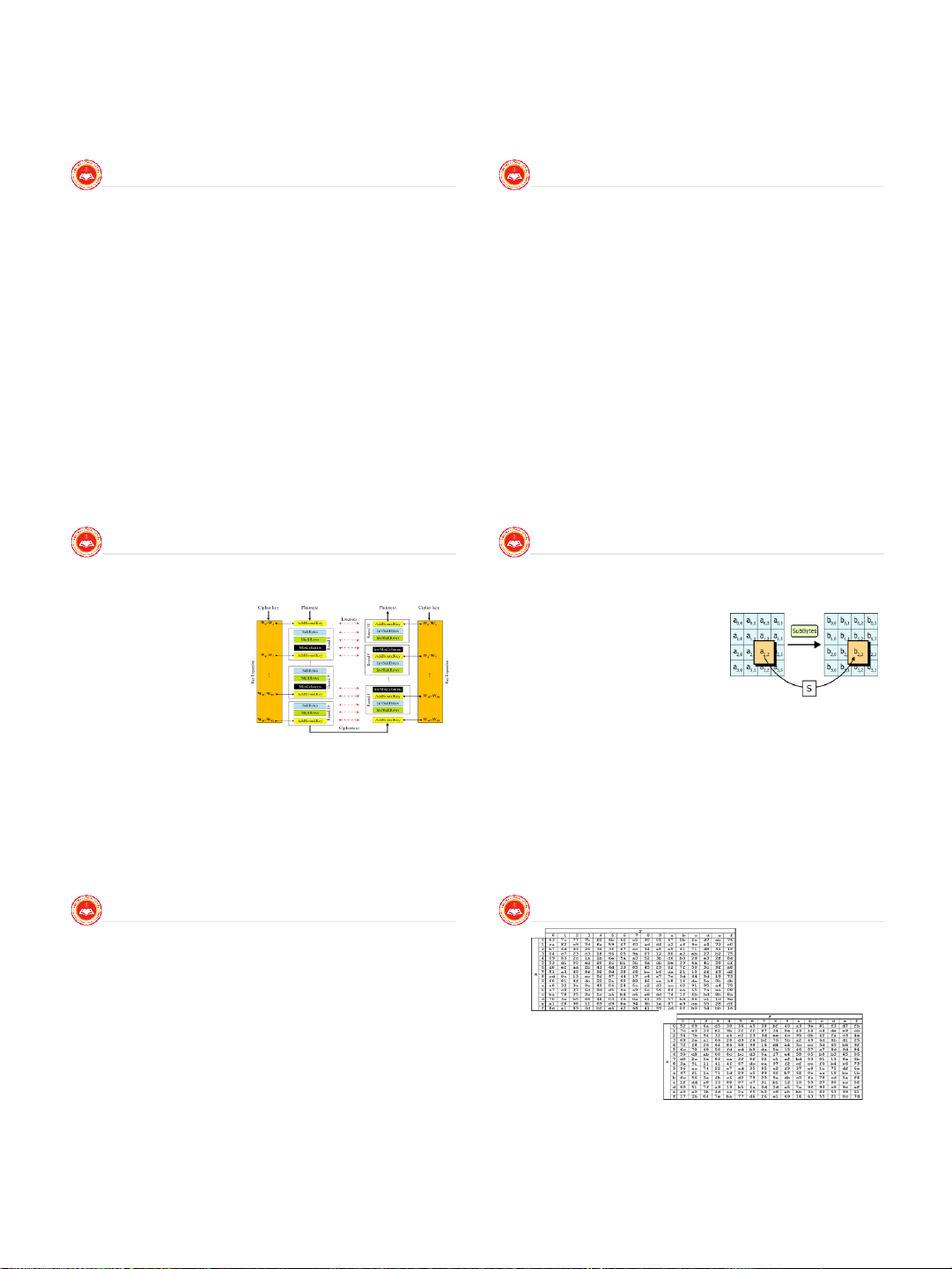
16 August 2021 | Page 104 Mã khối Mã khối Thuật toán AES:
Yêu cầu của AES
Là mã khối đối xứng khoá riêng. Nguồn gốc:
Kích thước khối dữ liệu 128 bit và độ dài khoá là tùy biến: 128, 192 ■
Rõ ràng cần phải thay thế DES, vì có những tấn công về mặt lý hoặc 256 bit.
thuyết có thể bẻ được nó.
Chuẩn mã mới phải mạnh và nhanh hơn Triple DES. Mã mới có cơ sở lí
thuyết mạnh để thời gian sống của chuẩn khoảng 20-30 năm (cộng ■
Do đó Viện chuẩn quốc gia Hoa kỳ US NIST ra lời kêu gọi tìm kiếm
chuẩn mã mới vào năm 1997. Sau đó có 15 đề cử được chấp nhận thêm thời gian lưu trữ).
vào tháng 6 năm 1998. Và được rút gọn còn 5 ứng cử viên vào
Khi đưa ra thành chuẩn yêu cầu cung cấp chi tiết thiết kế và đặc tả đầy
đủ. Đảm bảo rằng chuẩn mã mới cài đặt hiệu quả trên cả C và Java.
tháng 6 năm 1999. Đến tháng 10 năm 2000, mã Rijndael được chọn
làm chuẩn mã nâng cao và được xuất bản là chuẩn FIPS PUB 197 vào 11/2001.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 105
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 106 Mã khối Mã khối
Cơ sở toán học của thuật toán AES: trong AES các phép toán
Phép nhân: được thực hiện trên GF(28) bằng cách nhân hai đa thức rút
cộng và nhân được thực hiện trên các byte trong trường hữu hạn
gọn theo mođulo của một đa thức bất khả quy m(x). Trong AES đa thức bất GF(28) khả quy này là: Phép cộng: ■ A = (a m(x) = x8 + x4 + x3 + x +1.
1 a2 a3 a4 a5 a6 a7 a8); B = (b1 b2 b3 b4 b5 b6 b7 b8) ■
C = A + B = (c1 c2 c3 c4 c5 c6 c7 c8)
Ví dụ: A = C3H, B = 85H tương ứng với ■
Trong đó: Ci = ai+bi mod 2, 1 ≤ i ≤ 8.
a(x) = x7 + x6 + x +1 và b(x) = x7 + x2 + 1. Khi đó: C= A.B ■
Ví dụ: tổng của A = 73H; B = 4EH là: ●
Dạng cơ số Hexa: 73H + 4EH = 3DH
c(x) = a(x).b(x) mod (x8 + x4 + x3 + x +1) ●
Dạng nhị phân: 01110011 + 01001110 = 00111101
c(x) = x7 + x5 + x3 +x2 + x hay C = AEH = 10101110 ● Dạng đa thức:
(x6 + x5 + x4 + x + 1) + (x6 + x3 + x2 + x) = (x5 + x4 + x3 + x2 + 1)
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 107
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 108 18 2021/8/16 Mã khối Mã khối Phép xtime()
Chuẩn mã nâng cao AES – Rijndael: có các đặc trưng sau: Tính (57)●(13)
Có 128/192/256 bit khoá và 128 bit khối dữ liệu.
Ta có (13) = (01) (02) (10) Lặp hơi khác với Fiestel
(57)●(02) = xtime(57) = (10101110) = (ae) ■
Chia dữ liệu thành 4 nhóm – 4 byte
(57)●(04) = xtime(ae) = (01011100) (00011011) = (01000111) = (47) ■
Thao tác trên cả khối mỗi vòng
(57)●(08) = xtime(47) = (10001110) = (8e) ■ Thiết kế để:
(57)●(10) = xtime(8e) = (00011100) (00011011) = (07) ●
Chống lại các tấn công đã biết
Từ đó (57) ●(13) = 57●{(01) (02) (10)} ●
Tốc độ nhanh và nén mã trên nhiều CPU
= (57) (57) ● (02) (57) ● (10) = (57) (ae) (07) ●
Đơn giản trong thiết kế
= (01010111) (10101110) (00000111) = (11111110) = (fe)
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 109
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 110 Mã khối Mã khối
Có 10/12/14 vòng lặp tương ứng với kích thước khóa (128, 192 và 256 bit), SubBytes:
trong đó mỗi vòng bao gồm
Là quá trình thay thế (phi tuyến) trong
Phép thế byte (dùng một S box cho từng byte)
đó mỗi byte sẽ được thay thế bằng
Dịch hàng (hoán vị byte giữa
một byte khác theo bảng tra nhóm/cột)
Sử dụng một bảng 16 x 16 byte chứa
Trộn cột (sử dụng nhân ma trận
hoán vị của tất cả 256 giá trị 8 bit của các cột)
Mỗi byte trạng thái được thay bởi byte
Cộng khoá vòng (XOR trạng thái
trên hàng xác định bởi 4 bit trái và cột
dữ liệu với khoá vòng).
xác định bởi 4 bit phải.
Ví dụ: Chẳng hạn {8d} được thay bởi
hàng 8, cột d, mà giá trị sẽ là {5d}.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 111
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 112 Mã khối Mã khối
Hộp thế S-Box được xây dựng dựa trên phép biến đổi phi tuyến: y= A x-1 + c (1)
trên trường hữu hạn GF(28). Hộp thế S-box 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 1 1 1 1 0 0 0 1 0 A c 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 1 Hộp thế ngược InvS-box 0 0 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 0
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 113
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
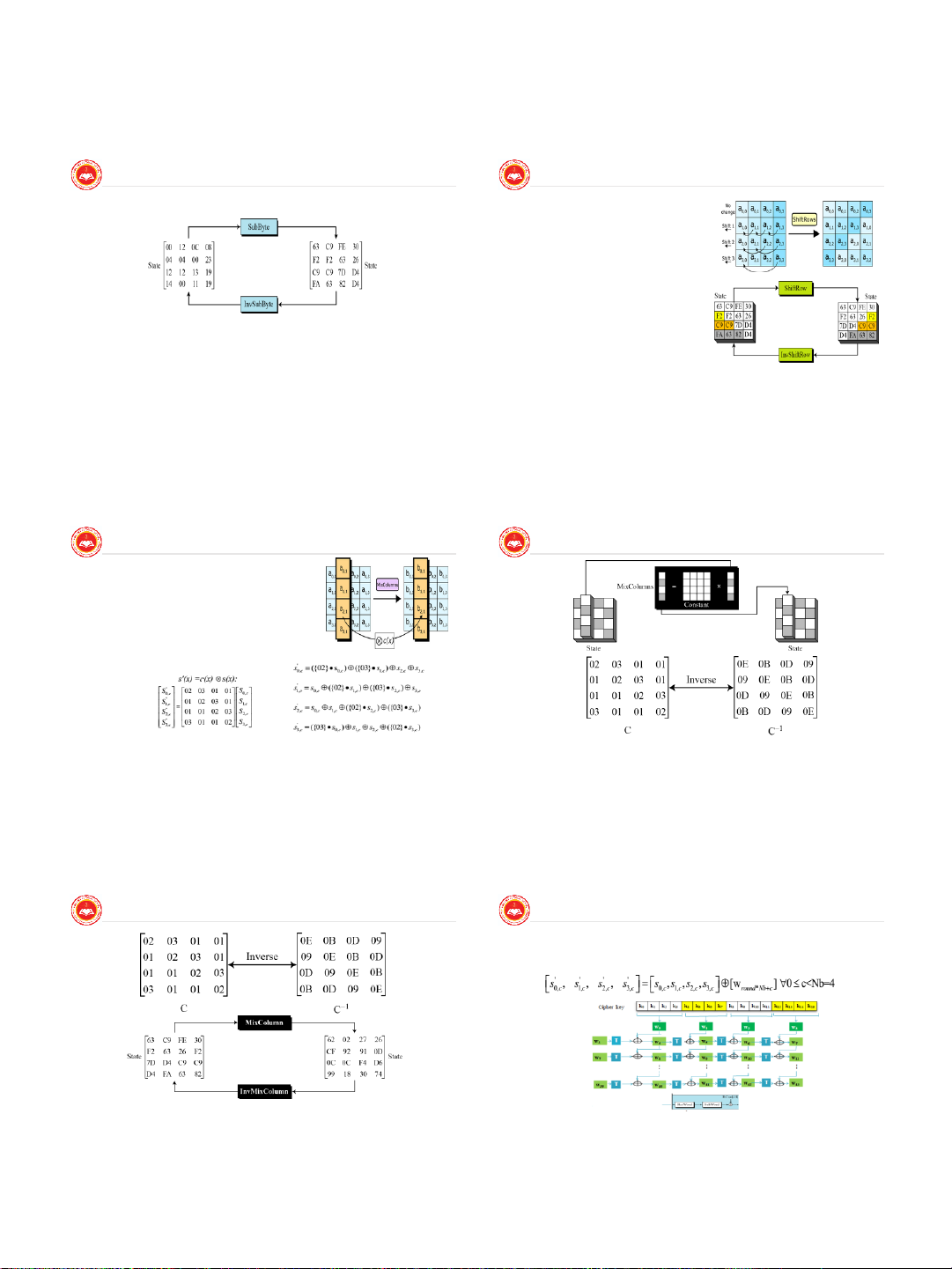
16 August 2021 | Page 114 19 2021/8/16 Mã khối Mã khối ShiftRows
Đổi chỗ, các hàng trong khối được dịch vòng Hàng 1 không đổi
Hàng 2 dịch vòng quanh 1 byte sang trái
Hàng 3 dịch vòng quanh 2 byte sang trái
Hàng 4 dịch vòng quanh 3 byte sang trái
Việc Giải mã thực hiện dịch ngược lại sang phải
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 115
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 116 Mã khối Mã khối MixColums
Hàm này làm việc trên mỗi cột của trạng thái.
Với mỗi trạng thái, hàm MixColumns (State) thực hiện lặp lại 4 lần.
Nó coi mỗi cột của mảng trạng thái như một đa
thức gồm 4 hạng tử và được nhân theo modulo
x4+1 với một đa thức cố định c(x):
c(x) = {03}x3 + {01}x2+{01}x +{02}
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 117
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 118 Mã khối Mã khối AddRoundKey:
Một khóa vòng (Round Key) sẽ được cộng vào mảng trạng thái bằng
một thao tác XOR theo từng bit.
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 119
Bộ môn Khoa Học An Toàn Thông Tin – Khoa An Toàn Thông Tin
16 August 2021 | Page 120 20


