Chương 17 : Ứng dụng sinh các hoán vị | Cấu trúc dữ liệu và giải thuật

Chöông 17 – ÖÙng duïng sinh caùc hoaùn vò
Chöông 17 – ÖÙNG DUÏNG SINH CAÙC HOAÙN VÒ
ÖÙng duïng naøy minh hoïa söï söû duïng caû hai loaïi danh saùch: danh saùch toång
quaùt vaø DSLK trong maûng lieân tuïc. ÖÙng duïng naøy seõ sinh ra n! caùch hoaùn vò cuûa
n ñoái töôïng moät caùch hieäu quaû nhaát. Chuùng ta goïi caùc hoaùn vò cuûa n ñoái töôïng
khaùc nhau laø taát caû caùc phöông aùn thieát laäp chuùng theo moïi thöù töï coù theå coù.
Chuùng ta coù theå choïn baát kyø ñoái töôïng naøo trong n ñoái töôïng ñaët taïi vò trí ñaàu
tieân, sau ñoù coù theå choïn baát kyø trong n-1 ñoái töôïng coøn laïi ñaët taïi vò trí thöù hai,
vaø cöù theá tieáp tuïc. Caùc choïn löïa naøy ñoäc laäp nhau neân toång soá caùch choïn löïa laø:
n x (n-1) x (n-2) x ... x 2 x 1 = n!
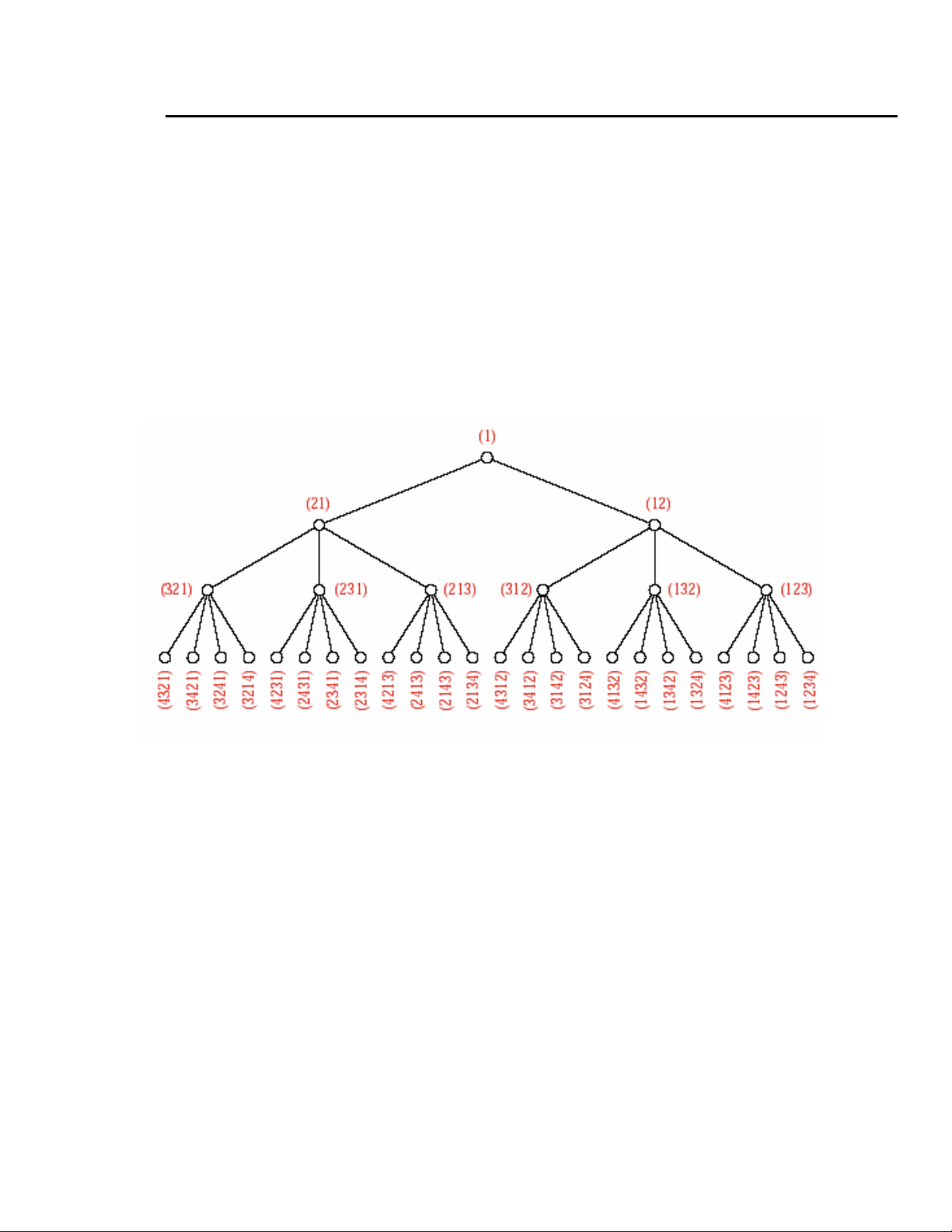
Hình 17.1- Sinh caùc hoaùn vò cho {1, 2, 3, 4} 17.1. YÙ töôûng
Chuùng ta xaùc ñònh caùc hoaùn vò qua caùc nuùt treân caây. Ñaàu tieân chæ coù 1 ôû goác
caây. Chuùng ta coù hai hoaùn vò cuûa {1, 2} baèng caùch ghi 2 beân traùi, sau ñoù beân phaûi
cuûa 1. Töông töï, saùu hoaùn vò cuûa {1, 2, 3} coù ñöôïc töø (2, 1) vaø (1, 2) baèng caùch
theâm 3 vaøo caû ba vò trí coù theå (traùi, giöõa, phaûi). Nhö vaäy caùc hoaùn vò cuûa {1, 2, ..., k} coù ñöôïc nhö sau:
Ñoái vôùi moãi hoaùn vò cuûa {1, 2, ..., k-1} chuùng ta ñöa caùc phaàn töû vaøo moät list.
Sau ñoù cheøn k vaøo moïi vò trí coù theå trong list ñoù ñeå coù ñöôïc k hoaùn vò khaùc nhau cuûa {1, 2, ..., k}.
Giaûi thuaät naøy minh hoïa vieäc söû duïng ñeä quy ñeå hoaøn thaønh caùc coâng vieäc ñaõ
taïm hoaõn. Chuùng ta seõ vieát moät haøm, ñaàu tieân laø theâm 1 vaøo moät danh saùch roãng,
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät 395
Chöông 17 – ÖÙng duïng sinh caùc hoaùn vò
sau ñoù goïi ñeä quy ñeå theâm laàn löôït caùc soá khaùc töø 2 ñeán n vaøo danh saùch. Laàn goïi
ñeä quy ñaàu tieân seõ theâm 2 vaøo danh saùch chæ chöùa coù 1, giaû söû theâm 2 beân traùi
cuûa 1, vaø trì hoaõn caùc khaû naêng theâm khaùc (nhö laø theâm 2 beân phaûi cuûa 1), ñeå
goïi ñeä quy tieáp. Cuoái cuøng, laàn goïi ñeä quy thöù n seõ theâm n vaøo danh saùch. Baèng
caùch naøy, baét ñaàu töø moät caáu truùc caây, chuùng ta phaùt trieån moät giaûi thuaät trong ñoù
caây naøy trôû thaønh moät caây ñeä quy. 17.2. Tinh cheá
Chuùng ta seõ phaùt trieån giaûi thuaät treân cuï theå hôn. Haøm theâm caùc soá töø 1 ñeán n
ñeå sinh n! hoaùn vò seõ ñöôïc goïi nhö sau: permute(1, n)
Giaû söû ñaõ coù k-1 soá ñaõ ñöôïc theâm vaøo danh saùch, haøm sau seõ theâm caùc soá coøn
laïi töø k ñeán n vaøo danh saùch:
void permute(int k,int n) /*
pre: Töø 1 ñeán k - 1 ñaõ coù trong danh saùch caùc hoaùn vò;
post: Cheøn caùc soá nguyeân töø k ñeán n vaøo danh saùch caùc hoaùn vò. */ {
for // vôùi moãi vò trí trong k vò trí coù theå trong danh saùch. {
// Cheøn k vaøo vò trí naøy.
if (k == n) process_permutation;
else permute(k + 1, n);
// Laáy k ra khoûi vò trí vöøa cheøn. } }
Khi coù ñöôïc moät hoaùn vò ñaày ñuû cuûa {1, 2, ..., n}, chuùng ta coù theå in keát
quaû, hoaëc gôûi keát quaû nhö laø thoâng soá vaøo cho moät baøi toaùn naøo khaùc, ñoù laø nhieäm
vuï cuûa haøm process_permutation. 17.3. Thuû tuïc chung
Ñeå chuyeån giaûi thuaät thaønh chöông trình C++, chuùng ta coù caùc teân bieán nhö
sau: danh saùch caùc soá nguyeân permutation chöùa hoaùn vò cuûa caùc soá; new_entry,
thay cho k, laø soá nguyeân seõ ñöôïc theâm vaøo; vaø degree, thay cho n, laø soá caùc
phaàn töû caàn hoaùn vò.
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät 396
Chöông 17 – ÖÙng duïng sinh caùc hoaùn vò
void permute(int new_entry, int degree, List &permutation) /*
pre: permutation chöùa 1 hoaùn vò vôùi caùc phaàn töû töø 1 ñeán new_entry - 1.
post: Moïi hoaùn vò cuûa degree phaàn töû ñöôïc taïo neân töø hoaùn vò ñaõ coù vaø seõ ñöôïc xöû lyù trong haøm process_permutation.
uses: haøm permute moät caùch ñeä quy, haøm process_permutation, vaø caùc haøm cuûa List. */ {
for (int current = 0; current < permutation.size() + 1; current++) {
permutation.insert(current, new_entry); if (new_entry == degree)
process_permutation(permutation); else
permute(new_entry + 1, degree, permutation);
permutation.remove(current, new_entry); } }
Haøm treân ñaây coù theå söû duïng vôùi baát kyø hieän thöïc naøo cuûa danh saùch maø
chuùng ta ñaõ laøm quen (DSLK söû duïng con troû, danh saùch lieân tuïc, DSLK trong
maûng lieân tuïc). Vieäc xaây döïng öùng duïng ñaày ñuû ñeå sinh caùc hoaùn vò xem nhö baøi
taäp. Tuy nhieân chuùng ta seõ thaáy raèng öu ñieåm cuûa DSLK trong maûng lieân tuïc raát
thích hôïp ñoái vôùi baøi toaùn naøy trong phaàn tieáp theo döôùi ñaây.o3
17.4. Toái öu hoùa caáu truùc döõ lieäu ñeå taêng toác ñoä cho chöông trình sinh caùc hoaùn vò
n! taêng raát nhanh khi n taêng. Do ñoù soá hoaùn vò coù ñöôïc seõ raát lôùn. ÖÙng duïng
treân laø moät trong caùc öùng duïng maø söï toái öu hoùa ñeå taêng toác ñoä chöông trình raát
ñaùng ñeå traû giaù, ngay caû khi aûnh höôûng ñeán tính deã ñoïc cuûa chöông trình. Chuùng
ta seõ duøng DSLK trong maûng lieân tuïc coù keøm moät chuùt caûi tieán cho baøi toaùn treân.
Chuùng ta haõy xem xeùt moät vaøi caùch toå chöùc döõ lieäu theo höôùng laøm taêng toác ñoä
chöông trình caøng nhanh caøng toát. Chuùng ta söû duïng moät danh saùch ñeå chöùa caùc
soá caàn hoaùn vò. Moãi laàn goïi ñeä quy ñeàu phaûi caäp nhaät caùc phaàn töû trong danh
saùch. Do chuùng ta phaûi thöôøng xuyeân theâm vaø loaïi phaàn töû cuûa danh saùch, DSLK
toû ra thích hôïp hôn danh saùch lieân tuïc. Maët khaùc, do toång soá phaàn töû trong danh
saùch khoâng bao giôø vöôït quaù n, chuùng ta neân söû duïng DSLK trong maûng lieân tuïc
thay vì DSLK trong boä nhôù ñoäng.
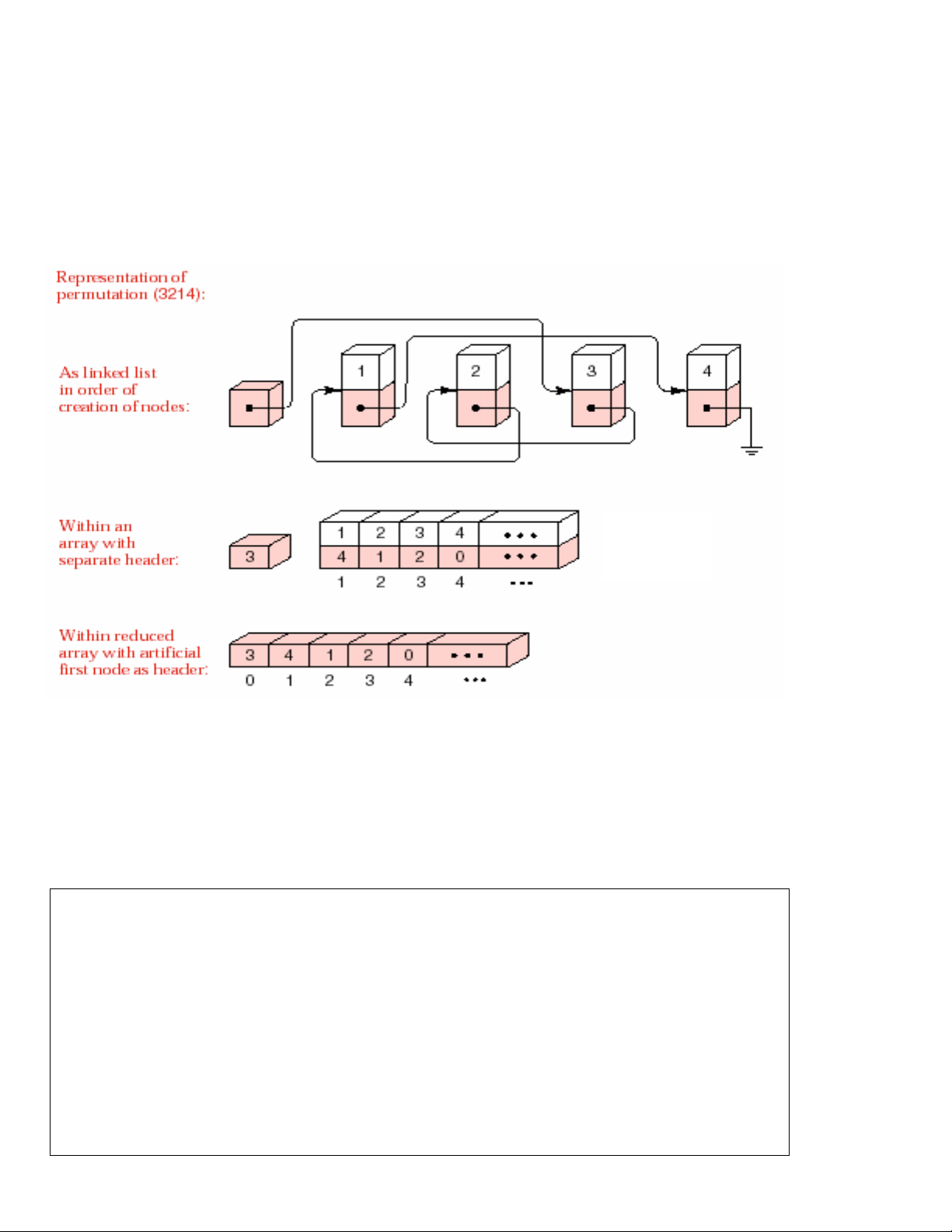
Hình 17.2 minh hoïa caùch toå chöùc caáu truùc döõ lieäu. Hình treân cuøng laø DSLK
cho hoaùn vò (3, 2, 1, 4). Hình beân döôùi bieåu dieãn hoaùn vò naøy trong DSLK trong
maûng lieân tuïc. Ñaëc bieät trong hình naøy, chuùng ta nhaän thaáy, trò cuûa phaàn töû ñöôïc
theâm vaøo cuõng chính baèng chæ soá cuûa phaàn töû trong array, neân vieäc löu caùc trò naøy
khoâng caàn thieát nöõa. (Chuùng ta chuù yù raèng, trong giaûi thuaät ñeä quy, caùc soá ñöôïc
theâm vaøo danh saùch theo thöù töï taêng daàn, neân moãi phaàn töû seõ chieám vò trí trong
maûng ñuùng baèng trò cuûa noù; caùc hoaùn vò khaùc nhau cuûa caùc phaàn töû naøy ñöôïc phaân
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät 397
Chöông 17 – ÖÙng duïng sinh caùc hoaùn vò
bieät bôûi thöù töï cuûa chuùng trong danh saùch, ñoù chính laø söï khaùc nhau veà caùch noái
caùc tham chieáu). Cuoái cuøng chæ coøn caùc tham chieáu laø caàn löu trong maûng (hình
döôùi cuøng trong hình 17.2). Node 0 duøng ñeå chöùa ñaàu vaøo cuûa DSLK trong maûng
lieân tuïc. Trong chöông trình döôùi ñaây chuùng ta vieát laïi caùc coâng vieäc theâm vaø loaïi
phaàn töû trong danh saùch thay vì goïi caùc phöông thöùc cuûa danh saùch ñeå taêng hieäu quaû toái ña. (entry) (next)
Hình 17.2 – Caáu truùc döõ lieäu chöùa hoaùn vò 17.5. Chöông trình
Chuùng ta coù haøm permute ñaõ ñöôïc caûi tieán:
void permute(int new_entry, int degree, int *permutation) /*
pre: permutation chöùa 1 hoaùn vò vôùi caùc phaàn töû töø 1 ñeán new_entry - 1.
post: Moïi hoaùn vò cuûa degree phaàn töû ñöôïc taïo neân töø hoaùn vò ñaõ coù vaø seõ ñöôïc xöû lyù trong haøm process_permutation.
uses: haøm permute moät caùch ñeä quy, haøm process_permutation. */ { int current = 0; do {
permutation[new_entry] = permutation[current];
permutation[current] = new_entry;
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät 398
Chöông 17 – ÖÙng duïng sinh caùc hoaùn vò if (new_entry == degree)
process_permutation(permutation); else
permute(new_entry + 1, degree, permutation);
permutation[current] = permutation[new_entry];
current = permutation[current]; } while (current != 0); }
Chöông trình chính thöïc hieän caùc khai baùo vaø khôûi taïo: main() /*
pre: Ngöôøi söû duïng nhaäp vaøo degree laø soá phaàn töû caàn hoaùn vò.
post: Moïi hoaùn vò cuûa degree phaàn töû ñöôïc in ra. */ { int degree;
int permutation[max_degree + 1];
cout << "Number of elements to permute? "; cin >> degree;
if (degree < 1 || degree > max_degree)
cout << "Number must be between 1 and " << max_degree << endl; else { permutation[0] = 0;
permute(1, degree, permutation); } }
Danh saùch permutation laøm thoâng soá cho haøm process_permutation chöùa
caùch noái keát caùc phaàn töû trong moät hoaùn vò, chuùng ta coù theå in caùc soá nguyeân cuûa
moät caùch hoaùn vò nhö sau:
void process_permutation(int *permutation) /*
pre: permutation trong caáu truùc lieân keát bôûi caùc chæ soá.
post: permutation ñöôïc in ra. */ { int current = 0;
while (permutation[current] != 0) {
cout << permutation[current] << " ";
current = permutation[current]; } cout << endl; }
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät 399
Chöông 17 – ÖÙng duïng sinh caùc hoaùn vò
Giaùo trình Caáu truùc döõ lieäu vaø Giaûi thuaät 400