Chương 3: Xử lý số liệu thực nghiệm bằng toán thống kê | Lí thuyết Xác suất thống kê | Trường Đại học khoa học Tự nhiên

CHƯƠNG 3
XỬ LÝ SỐ LIỆU THỰC NGHIỆM BẰNG TOÁN HỌC THỐNG KÊ 3.1 CÁC SỐ CÓ Ý NGHĨA
Số các số có ý nghĩa là số cực tiểu các chữ số cần thiết để biểu diễn một giá trị đã
cho trong khoa học mà không làm mất độ chính xác của phép đo đó. Biểu diễn các số
của phép đo tuân theo quy tắc sau:
1. Số “0” có thể là một phần của phép đo, nhưng nó cũng có thể chỉ là một số chỉ hệ
thập phân, hay nói cách khác là số các con số có nghĩa của phép đo không phụ
thuộc vào vị trí của điểm chỉ hệ thập phân. Thí dụ 92,067mm có thể biểu diễn
92067 µm hoặc 9,2067 cm hoặc 0,92067 dm hoặc 0,092067 m. Tất cả các số hạng
trên đều có 5 số có ý nghĩa. Trong hai trường hợp sau cùng, số “0” không có ý
nghĩa, được dùng để chỉ hệ thập phân, các trường hợp còn lại, số “0” đều có ý nghĩa.
Khi số “0” đứng ở cuối cùng, nó cũng có ý nghĩa, thí dụ 727,0 ; 100,0 … Thí
dụ 3.1 Tìm số các số có ý nghĩa trong các số sau:
0,216 (có 3 số có ý nghĩa) 90,7
(có 3 số có ý nghĩa) 800,0 (có 4 số có ý nghĩa) 0,0670 (có 3 số có ý nghĩa)
2. Con số chìa khóa của một phép đo quyết định số các con số có ý nghĩa. Trong một
bài toán có nhiều phép tính, số hạng nào có giá trị tuyệt đối thấp nhất là con số chìa khoá.
3. Trong một bài toán có nhiều phép tính, các số lẻ được giữ cho tới phép tính cuối
cùng trước khi làm tròn.
4. Quy tắc làm tròn: nếu chữ số cuối cùng cần làm tròn > 5 thì số trước đó +1, nếu số
cần làm tròn < 5 thì bỏ số đó và số trước đó không thay đổi. 3.2 CÁC LOẠI SAI SỐ
3.2.1 Sai số tuyệt đối
Sai số tuyệt đối là hiệu số giữa giá trị trung bình và giá trị thực. e = x-µ
trong đó x là trung bình số học của các giá trị thực nghiệm, µ là giá trị thực
Sai số tuyệt đối không cho ta thấy được độ đúng của phép phân tích, muốn biết ta phải xét sai số tương đối.
3.2.2 Sai số tương đối
Sai số tương đối là tỷ số giữa sai số tuyệt đối và giá trị thực µ.
S= ε =x-μ =G-Đ; (3.1) x μ Đ
Thông thường sai số tương đối biểu diễn bằng S% = ε .100 = G -Đ.100. Sai số tương μ Đ
đối cho ta biết độ đúng của phép xác định.
Thí dụ nhìn vào hai phép xác định sau ta chỉ có thể nhận ra độ đúng của từng phép xác
định khi dùng sai số tương đối.
Bảng 3.1: Sai số tương đối Thí nghiệm Giá trị đo Giá trị thực e S % 1 45,8 45,2 0,6 1,3% 2 216 215,4 0,6 0,3%
3.2.3 Sai số hệ thống
Là sai số do các nguyên nhân cố định gây ra, thường lặp đi lặp lại trong các thí nghiệm.
Các giá trị thường lệch về một phía luôn mang dấu ”+” hoặc dấu “-“. Sai số hệ thống
thường do phương pháp sai, dụng cụ đo không đúng.v.v.
3.2.4 Sai số ngẫu nhiên
Là sai số do các nguyên nhân không cố định, khách quan gây ra, nó phản ánh sự sai lệch
giữa từng giá trị riêng lẻ và giá trị trung bình, ngoài ra nó còn phản ánh độ lặp lại của phương pháp
3.3 CÁC ĐẠI LƯỢNG TRUNG BÌNH
3.3.1 Trung bình số học là trung bình
cộng của các giá trị riêng lẻ.
Zả sử có n thí nghiệm thu được n giá trị thí nghiệm x1 , x2 ...xn
x= x1 + + +x2 ... xn =åxi (3.2) n n
3.3.2 Trung bình bình phương
Là căn bậc hai của tổng các giá trị bình phương chia cho n x 2 2 2 2 1 + x ... 2 ++ x x å x n i bp = = n n (3.3)
3.4 CÁC ĐẠI LƯỢNG ĐẶC TRƯNG CHO ĐỘ PHÂN TÁN
3.4.1 Độ lệch trung bình d
Độ lệch là sự chênh lệch giữa giá trị riêng lẻ và giá trị trung bình còn Độ lệch trung bình
là trung bình cộng giữa giá trị riêng lẻ và giá trị trung bình có lấy giá trị tuyệt đối å xi -x d = n (3.4)
3.4.2 Phương sai
Phương sai là đại lượng đặc trưng cho sai lệch của các số liệu thực nghiệm so
với giá trị trung bình. Phương sai là một trong những đặc tính thống kê quan trọng nhất
của sai số ngẫu nhiên. Theo định luật phân bố chuẩn thì khi phương sai giảm, sự phân
bố tốt hơn, cận sẽ giảm, phép phân tích càng chính xác.
Phương sai là trung bình cộng các bình phương của hiệu số giữa các giá trị riêng
lẻ và giá trị trung bình:
å(x -x)2 S2 = i khi n < 20 (3.5) n-1 å(x -x)2 s2 = i khi n > 20 (3.6) n
S2 và s2 đều gọi là phương sai, n-1 là số bậc tự do
3.4.3 Độ lệch chuẩn
Độ lệch chuẩn cũng như phương sai đều đặc trưng cho sự dao động của các số
liệu hay là độ phân tán của các kết quả so với giá trị trung bình.
Độ lệch chuẩn là căn bậc hai của tổng bình phương độ lệch của các số liệu khỏi
giá trị trung bình chia cho số bậc tự do. (
å x i - x) 2 2 S = S = n - 1 (x x) 2 1 å 2 - (3.7) s s= = n (3.8)
3.4.4 Độ lệch chuẩn trung bình S x
Độ lệch chuẩn trung bình là độ lệch chuẩn chia cho căn bậc hai của n lần thí nghiệm
Sx= S = å(xi -x)2 (3.9) n n n( -1)
3.4.5 Độ lệch chuẩn tương đối và hệ số biến động
(Relative standard deviation, RSD and coefficient of variation, CV) Độ lệch
chuẩn tương đối được xác định bằng cách chia độ lệch chuẩn cho giá trị trung bình của
các số liệu thực nghiệm. Nó thường được biểu diễn bằng phần ngàn hay phần trăm. RSD = S .1000 phần ngàn x
Độ lệch chuẩn tương đối nhân với 100% còn được gọi là hệ số biến động CV = S .100 phần trăm x
Thí dụ 3.2 Phân tích Pb trong máu cho biết hàm lượng tính theo ppm như sau:
x : 0,752; 0,756; 0,752; 0,751; 0,760 ppm
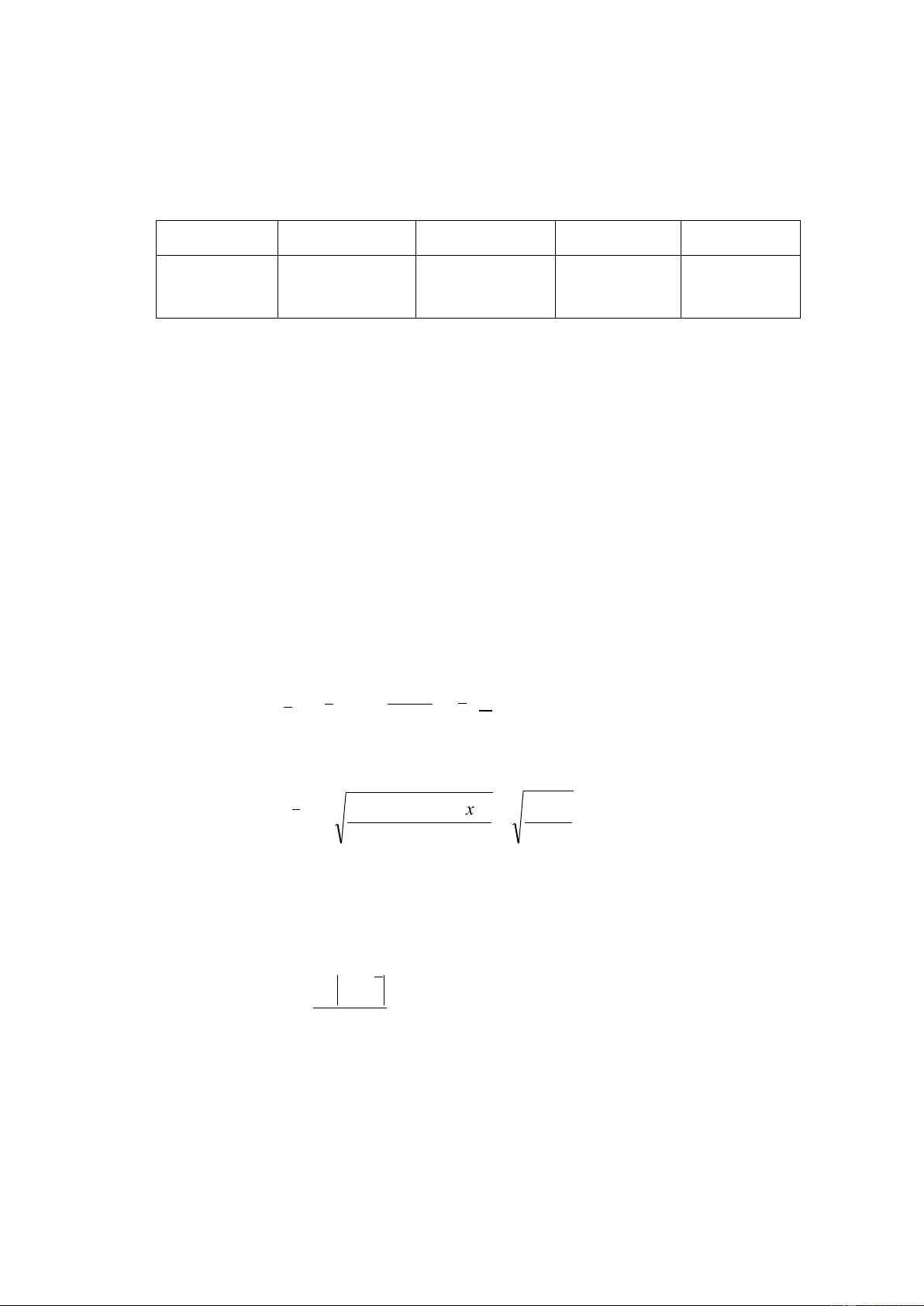
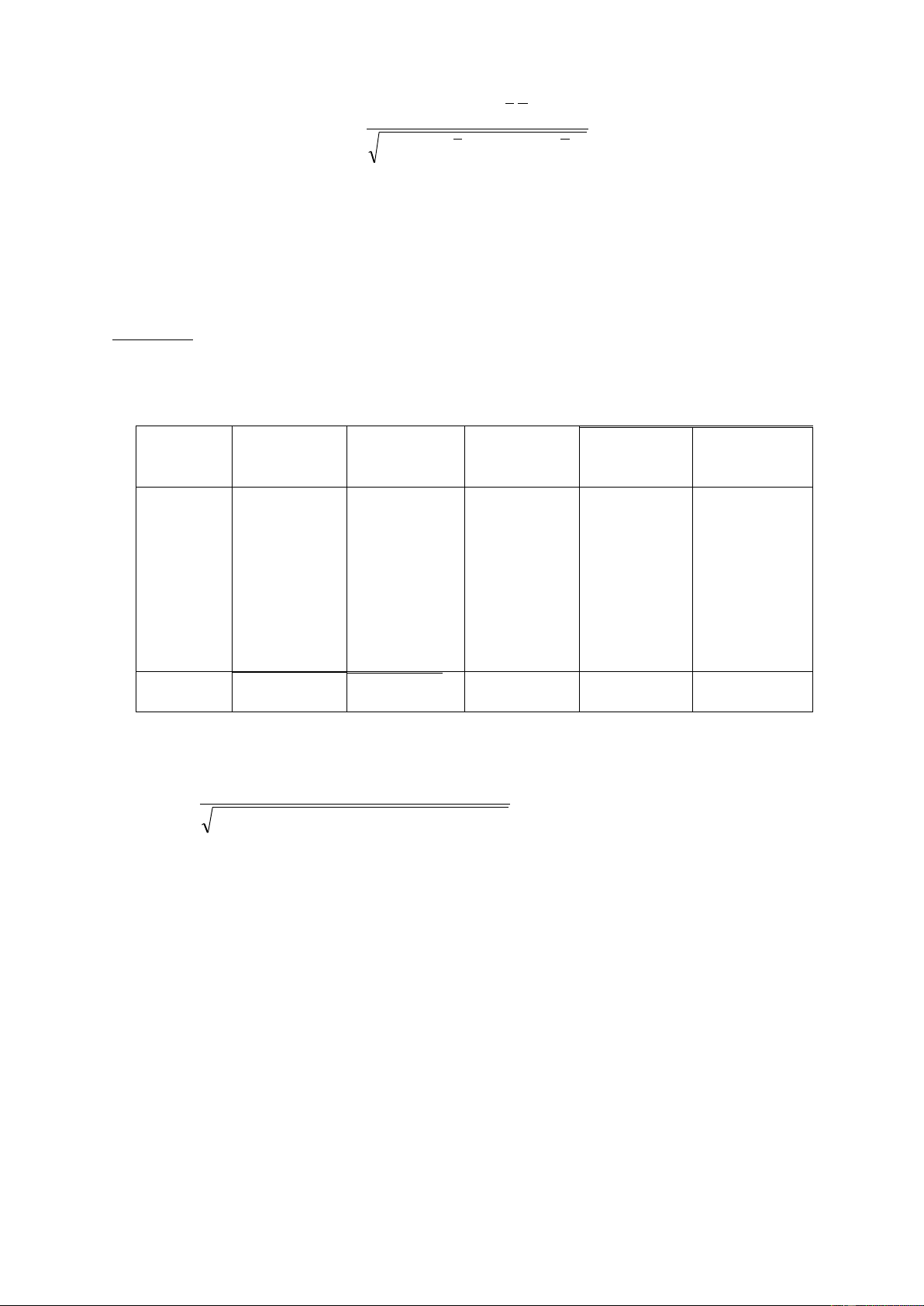
(0,752-0,754)2 + +... (0,760-0,754)2 S = =0,0038 5 1- RSD =
.1000 = 5,0 phần ngàn; CV = .100 = 0,5 %
Độ lệch chuẩn tương đối chỉ rõ mức độ sai số của dữ kiện thực nghiệm rõ hơn độ lệch chuẩn tuyệt đối. 3.5 CÁC LOẠI PHÂN BỐ
3.5.1 Phân bố chuẩn hay phân bố Gauxơ (Gauss)
Khi sai số của phép phân tích là sai số ngẫu nhiên thì các kết quả gần với giá trị thực,
nó phân bố xung quanh giá trị thực. Số thí nghiệm càng nhiều, x càng tiến tới giá trị thực µ.
Theo lý thuyết toán học hàm số phân bố chuẩn y phụ thuộc biến số x có dạng: -0,5æç x-µö÷2 y= 1 .e è 2s ø (3.10) s p2
Hàm số đạt giá trị cực đại khi x= µ ; khi đó 1 y = sp 2
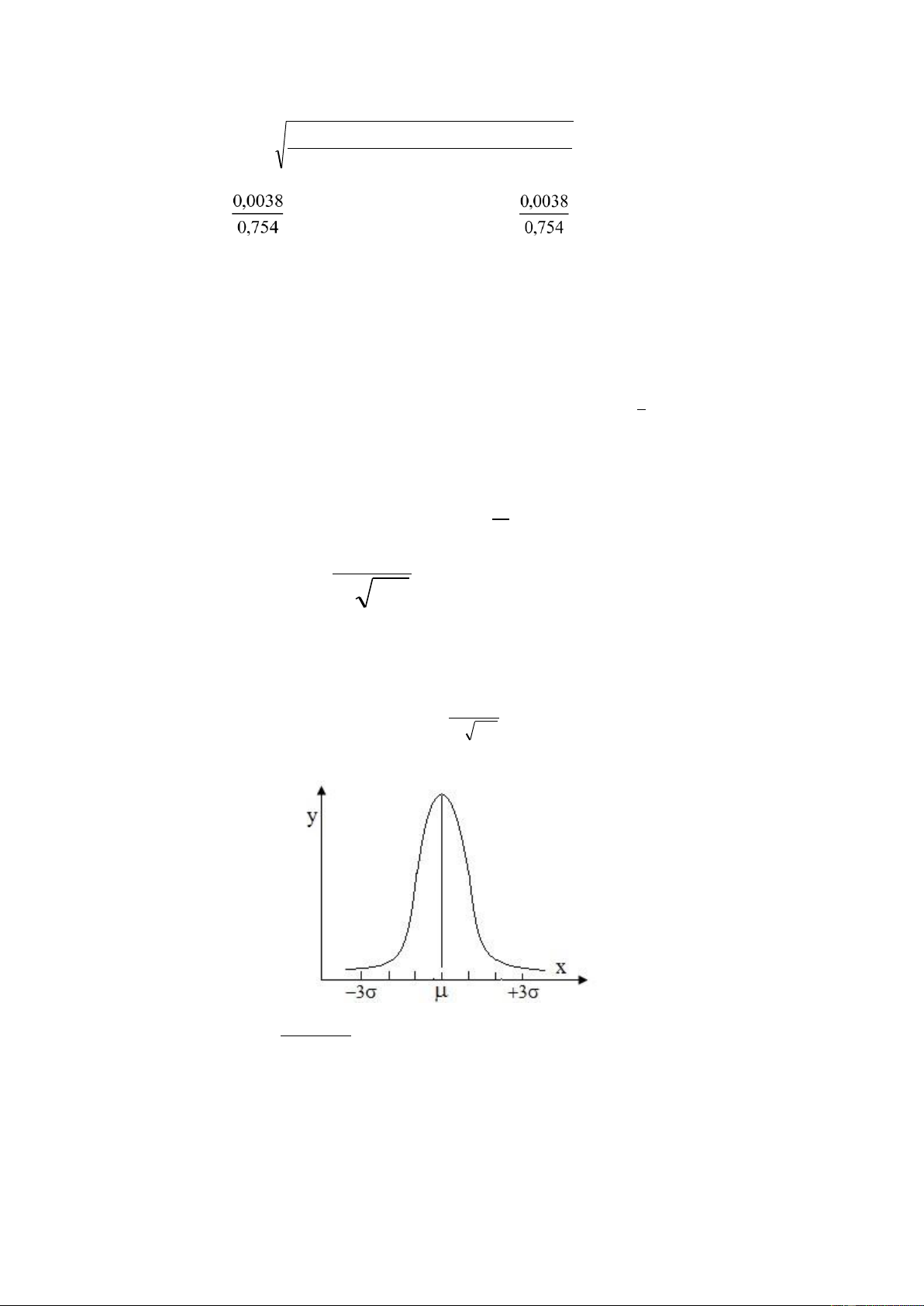
Đường phân bố có dạng: y
Hình 3.1: Phân bố chuẩn (GAUSS)
Như chúng ta đã đề cập ở trên, s là đại lượng đặc trưng cho sự phân tán. là sự sai lệch
gữa các giá trị riêng lẻ và giá trị trung bình (trong trường hợp này là giá trị thực). Khi s
càng nhỏ, y càng lớn. Sự xuất hiện giá trị thực nghiệm tương ứng diện tích của parabol
xác lập bởi đường cong và trục hoành từ -¥ đến +¥ bằng 1. Khi chọn khoảng ± s có
nghĩa độ tin cậy của giá trị thực nghiệm đạt 68,3%, còn ± 2s là 95,46%, còn ± 3s là
99,9%. Thông thường để có độ tin cậy cao, người ta áp dụng quy tắc ± 3s.
3.5.2 Phân bố thực nghiệm
Giả sử nghiên cứu xác suất xuất hiện của mặt đồng xu bằng cách tung nó nhiều lần, giả
sử tung 1000 lần, chia làm 9 đợt, chúng ta thấy sự xuất hiện một nửa số lần mặt phải và
một nửa số lần mặt trái chiếm giá trị cao nhất, tiếp theo số lần xuất hiện từng mặt càng
cao càng giảm dần khi tiến về hai phía của giá trị này.
Bảng 3.2: Xác suất xuất hiện mặt phải (trái) của đồng xu STT Mặt phải/ trái Xác xuất xuất hiện 1 1 (1/9) 0.01 0.05 2 2 (2/8) 0.32 0.65 3 3 (3/7) 0.84 0.62 4 4 (4/6) 0.38 0.04 5 5 (5/5) 0.01 6 6 (6/4) 7 7 (7/3) 8 8 (8/2) 9 9 (9/1)
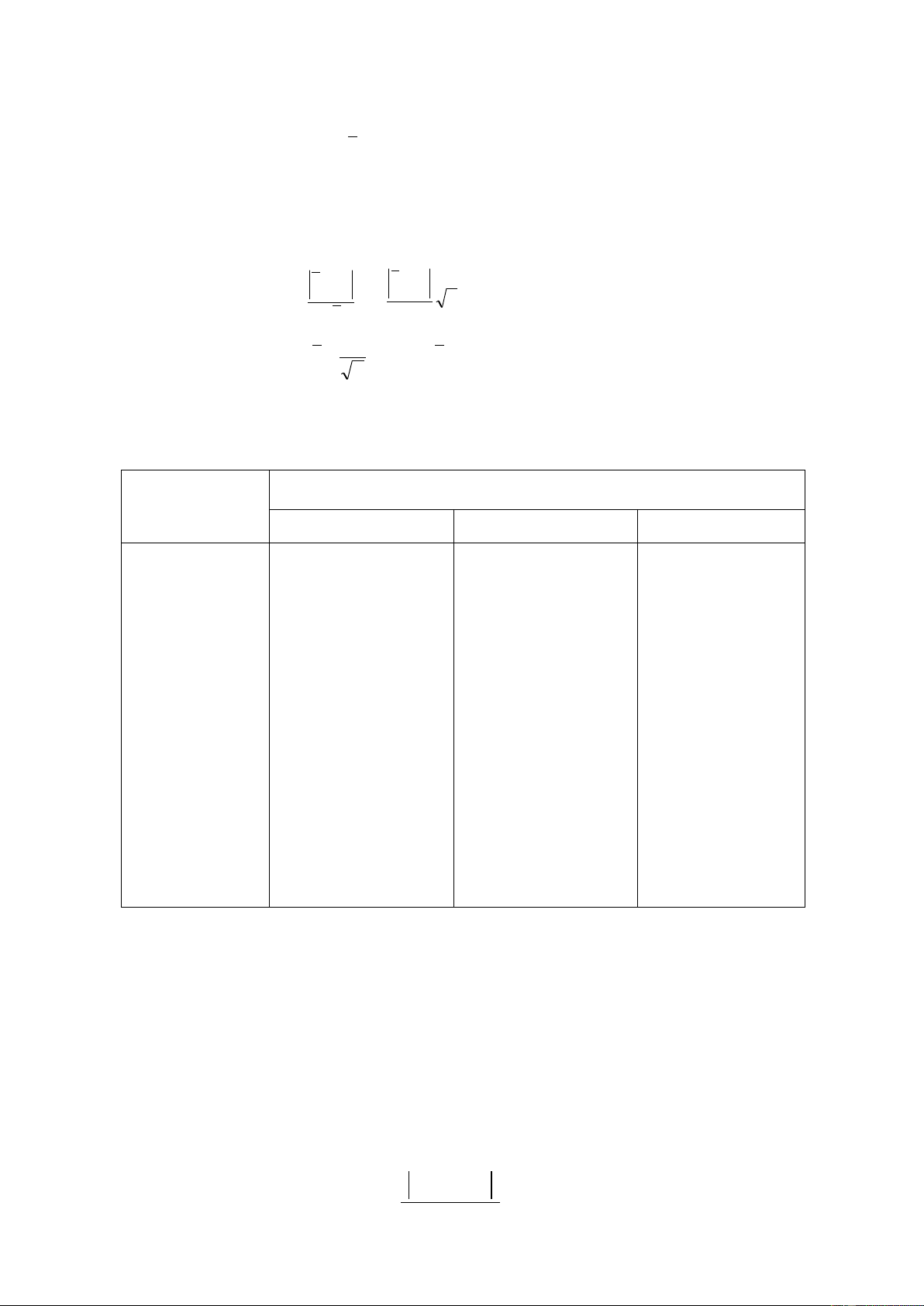
Biểu diễn kết quả trên bằng đồ thị ta thấy dạng đường parabol xuất hiện (hình 3.2). B ### 0.8 0.6 0.4 0.2 0.0 1 2 3 4 5 6 7 8 9 Thi nghiem
Hình 3.2: Phân bố thực nghiệm
Như vậy, nếu nối các giá trị thực nghiệm lại ta cũng thấy xuất hiện đường cong dạng
parabol có cực đại tại xuất hiện mặt phải và mặt trái đều là 50%. 3.6 BIÊN GIỚI TIN CẬY
Biên giới tin cậy là khoảng giá trị trong đó chứa giá trị thực µ. Nếu sai số ngẫu nhiên s
tuân theo phân bố chuẩn thì có thể xác định được biên giới tin cậy µ = x ± 0,67
với xác suất 50% n s µ = x ± 1,96 với xác suất 95% n s µ = x ± 2,58 với xác suất 99% n
Tuy nhiên số thí nghiệm thường nhỏ, phải dùng chuẩn Student để xác định biên giới tin
cậy. Chuẩn Student được tính theo công thức: x -µ x-µ t = =
n ; từ đây rút ra: Sx S tS μ= ±x hay:μ= ±x ε n
trong đó e là biên giới tin cậy
Bảng 3.3: Giá trị t với xác suất P và số bậc tự do K K=n-1 Xác xuất P 90% 95% 99% 1 6,31 12,7 63,7 2 2,92 4,3 9,92 3 2,35 3,18 5,84 4 2,13 2,78 4,60 5 2,01 2,57 4,03 6 1,94 2,45 3,71 7 1,89 2,36 3,5 8 1,86 2,31 3,36 9 1,83 2,26 3,25 10 1,81 2,23 3,17 15 1,75 2,13 2,95 20 1,73 2,06 2,79
3.7 SỬ DỤNG CÁC CÔNG CỤ CHUẨN ĐỂ XỬ LÝ CÁC SỐ LIỆU
3.7.1 Chuẩn Đisơn (loại bỏ các số liệu sai thô):
Trong thực tế, các số liệu thực nghiệm thu được không phải lúc nào cũng tuân theo ý
muốn. Những sai số ngẫu nhiên không theo một quy luật nào, nhưng điều trở ngại mhất
là các số liệu quá sai lệch so với các số liệu còn lại. Các số liệu đó ta gọi là các số liệu
sai thô. Nếu để các số liệu này trong dãy số liệu thu được mà dem xử lý thì kết quả
không phản ánh đúng giá trị thực của phép đo. Để loại trừ các số liệu sai thô, Dison đưa
ra công thức sau để tìm giá trị Q thực nghiệm, viết tắt là QTN: xn -xn+1
QTN = xmax -xmin (3.11)
xn là giá trị cần kiểm tra. Sau khi có giá trị QTN, đem so với giá trị Q lý thuyết (QLT) đã
được tính theo bảng sau:
Bảng 3.4: Giá trị Q với các xác suất P n Xác suát P 90% 95% 99% 3 0,98 0,94 0,99 4 0,68 0,77 0,89 5 0,56 0,64 0,76 6 0,48 0,56 0,70 7 0,43 0,51 0,64 8 0,40 0,48 0,58
Nếu QTN> QLT, ta nói giá trị đo thu được (xn) quá sai lệch hay sai thô, phải loại bỏ,
ngược lại nếu QTN < QLT, ta nói số liệu thu được chấp nhận được.
Thí dụ 3.3: Phân tích hàm lượng Pb trong mẫu, có dãy số liệu
Bảng 3.5: Phân tích Pb TN Các giá trị x xmax= 3,21; xmin= 2,11 1 2,11 2 2,19 Q= = 0,85 3 2.25 Theo bảng n=6; P=95% Q=0,56 4 2,32
Như vậy Qtn>Qlt phải loại giá trị 3,21. Còn 5 5 2,38
số liệu đều sử dụng được. 6 3,21
3.7.2 Chuẩn Fisơ
Một kết quả phân tích có thể mang
một ý nghĩa lớn, thí dụ chỉ tiêu phân tích cho một một hợp đồng kinh tế lớn, một vụ
trọng án hay một kỳ thi thể thao lớn ... Như vậy kết quả phân tích cần phải được xem
xét kỹ, kết quả phải đúng và chính xác. Thông thường, người ta có thể dùng hai phương
pháp để so sánh, đôi khi có thể dùng hai hay nhiều phòng thí nghiệm để so sánh.
Chuẩn Fisơ dựa trên việc so sánh phương sai của hai tập số liệu hay hai phương
pháp trên một chỉ tiêu thí nghiệm. Hai phương sai trùng nhau là rất hiếm, trong trường
hợp lệch nhau, thì mức độ nào có thể cho phép? Tiêu chuẩn Fisơ đưa ra các giá trị nhất
định tương ứng với số bậc tự do tương ứng với độ tin cậy P=0,95. Biểu thức Fisơ: = F SS1222 (3.12) trong đó S 2 2
1 , S2 là phương sai của phương pháp 1 và phương pháp 2.
Bảng 3.6: Giá trị F lý thuyết với P=0,95 và các bậc tự do của 2 phương pháp k1 k2 2 3 4 5 6 8 10 12 2 19
19,16 19,25 19,3 19,33 19,37 19,39 19,41 3
9,55 9,28 9,12 9,01 8,94 8,84 8,78 8,74 4
6,94 6,59 6,39 6,26 6,16 6,04 5,96 5,91 5
5,79 5,41 5,19 5,05 4,95 4,82 4,74 4,68 6
5,14 4,76 4,53 4,39 4,28 4,15 4,06 4,00 7
4,74 4,35 4,12 3,97 3,87 3,73 3,63 3,57 8
4,46 4,07 3,84 3,69 3,57 3,44 3,34 3,28 9
4,26 3,86 3,63 3,48 3,37 3,23 3,13 3,07 10 4,10
3,71 3,48 3,33 3,22 3,07 2,97 2,91 11
3,98 3,59 3,36 3,20 3,09 2,95 2,86 2,79 12
2,88 3,49 3,26 3,11 3,00 2,85 2,76 2,69 15
3,98 3,29 3,06 2,90 2,79 2,64 2,55 2,48 20
3,49 3,10 2,87 2,71 2,60 2,45 2,35 2,28
Nếu Ftn < Flt thì 2 phương pháp đồng nhất
Nếu Ftn > Flt thì 2 phương pháp không đồng nhất
3.7.3 Dùng chuẩn Student để kiểm đánh giá phương pháp
Một trong các ứng dụng của chuẩn Student là đánh giá sai số hệ thống. Khi sử dụng
công cụ này, dựa vào độ lệch giữa giá trị trung bình và giá trị thực hoặc so sánh các giá
trị trung bình của các phương pháp ta biết được phương pháp có mắc sai số hệ thống
không hoặc có đồng nhất không. Có ba kiểu đánh giá theo chuẩn student:
a) So sánh dãy số thí nghiệm có giá trị trung bình và độ lệch chuẩn của nó với giá trị
thực, tìm ra được giá trị “t” thực nghiệm. Tra bảng để có giá trị “t” lí thuyết từ đó rút ra
kết luận về sai số của các phương pháp. Chuẩn student có công thức: x -µ x-µ
t = = n (3.13) Sx S
Nếu ttn>tlt có nghĩa là x và µ khác nhau nhiều nên mắc sai số hệ thống
Nếu ttnx và µ không khác nhau nhiều nên không mắc sai số hệ thống.
Thí dụ 3.4 Khi phân tích sunfua trong các mẫu than theo phương pháp mới có các kết
quả: 3,29; 3,22; 3,30 và 3,23 %. Tuy nhiên một phương pháp tiêu chuẩn khác đã tìm
được hàm lượng sunfua là 3,19%. Đánh giá phương pháp mới có mắc sai số hệ thống không. Giải: x = 3,26 ( 3 29 , - 3 19 , ) 2 + ( , 3 22 - 3 19 , ) 2 + ( 3 30 , - 3 19 , ) 2 +( 3 23 , 3 19 , ) 2 - S = 3 = 0,04
Áp dụng công thức 11.13 ta có 3,26 - 3,19 tTN = 4 = 3,41 0,04
Theo bảng t khi sử dụng độ tin cậy 95% và số bậc tự do 3 có tLT = 3,18. Như vậy
tTN lớn hơn tLT, hai phương pháp không đồng nhất, phương pháp đo mới mắc sai số hệ thống.
b) Hai phương pháp đo trên một mẫu phân tích cho hai dãy kết quả, hoặc một phương
pháp đo cho hai mẫu phân tích cũng cho hai dãy kết quả. Giá trị “tTN” được xác định theo công thức: tTN= x1 -x2 nn1 2 (3.14) Stc n n1 + 2
trong đó Stc là độ lệch chuẩn tổng cộng được tính theo công thức: ) ) Stc = å(x ( (
i -x1 2 +å(x j -x2 2 = S n12 1 -1)+S n22 2 -1) (3.15) n n1 + 2 -2 n n1 + 2 -2
Từ tTN và tLT cũng là cơ sở để đánh giá sự đồng nhất của hai phương pháp
Thí dụ 3.5 Thí nghiệm của Lord Rayleigh xác định tỷ trọng khí nitơ trong không khí và
khí nitơ điều chế theo phương pháp hoá học, cho hai dãy số liệu sau: Dãy1 từ không khí
Dãy 2 từ phản ứng hoá học 2,31017 2,30143 2,30986 2,29890 2,31010 2,29816 2,31001 2,30182 2,31024 2,29869 2,31010 2,29940 2,31028 2,29849 2,29889
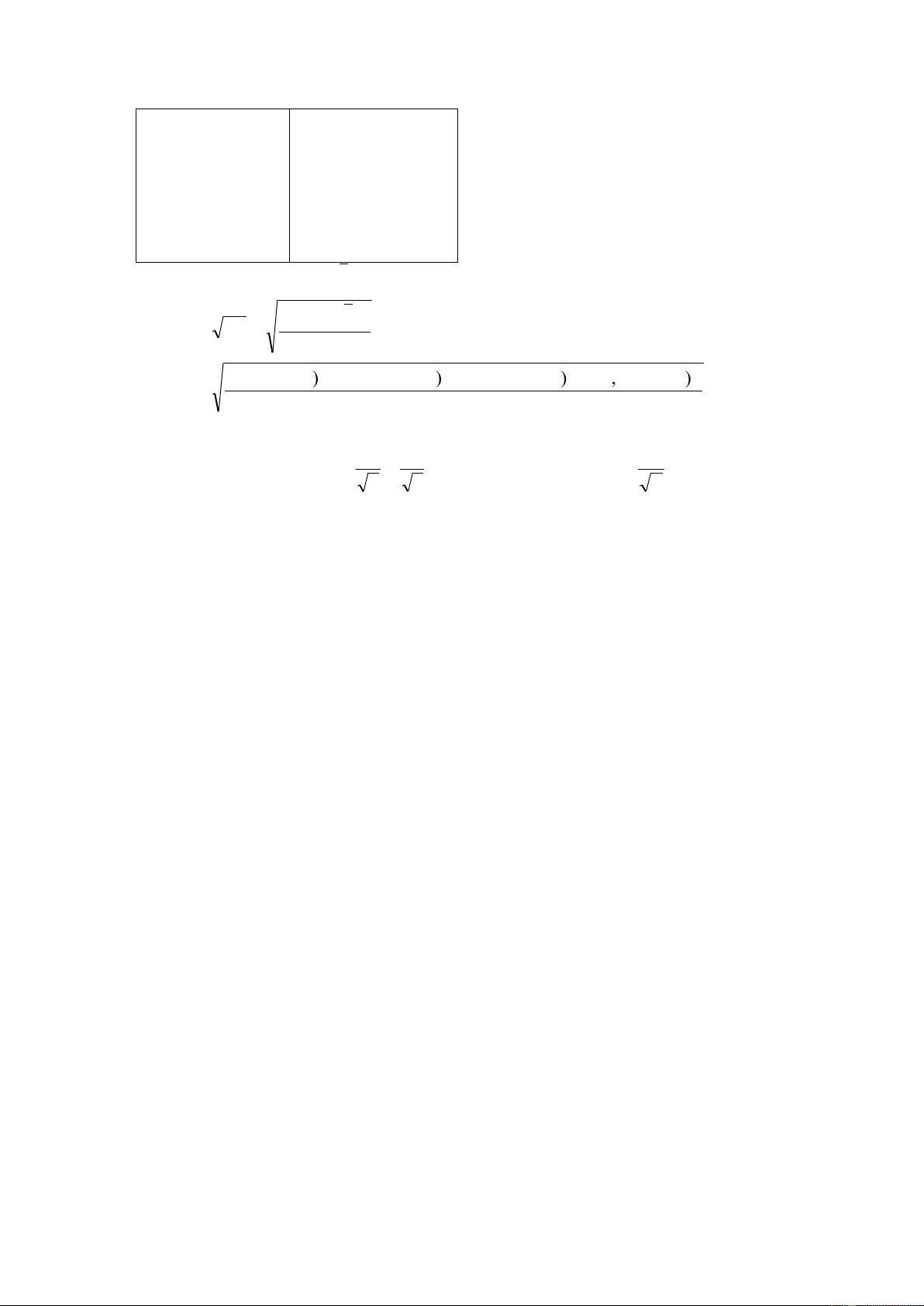
x1 = 2,31011 x2 = 2,29947 S1 = 0,00014 S2 = 0,00138
Stc = (0,00014) (2 7 -1) (+ 0,00138) (2 8 -1) = 0,00102 7 +8- 2
ttc = 2.31011- 2,29947 7 8x =20,2 0,00102 7 + 8
Với bậc tự do 7 + 8 - 2 =13 và độ tin cậy 95%, tLT có giá trị nằm trong khoảng 2,23 đến
2,13 như vậy tTN lớn hơn tLT điều đó chứng tỏ rằng hai khí nitơ không đồng nhất và sau
đó tác giả phát hiện ra khí nitơ điều chế từ không khí còn chứa tạp chất argon.
c) Dùng hai phương pháp khác nhau để đo nhiều mẫu nhưng mỗi mẫu đo một lần với 1
phương pháp. Dùng tTN được tính theo công thức: = S d d tTN n (3.16)
trong đó d là độ lệch trung bình của tất cả các phép đo đối với hai phương pháp, n
là số cặp thực nghiệm, Sd được xác định theo biểu thức:
Sd = å(d di - )2 (3.17) n-1
Thí dụ 3.6 Hai phương pháp A và B xác định các mẫu colesterol cho các kết quả sau:
Bảng 3.7: Phân tích colesterol trong máu Mẫu Phương pháp A Phương pháp B Độ lệch di 1 1,46 1,42 0,04 2 2,22 2,38 -0,16 3 2,84 2,67 0,17 4 1,97 1,80 0,17 5 1,13 1,09 0,04 6 2,35 2,25 0,10 di = + 0,06 Giải: ( 2 2 2 2 0 04 , - 0 06 , ) +( - 0 16 , - 0 06 , ) + ( 20 17 , - , 0 06 ) +( 010 , - 0 06 , ) S d = = 0,12 6 - 1 0 06 , t 6 =1 20 , TN 0 12 , =
Tra bảng khi áp dụng độ tin cậy 95%, bậc tự do bằng 5 có tLT = 2,57.
Như vậy kết luận hai phương pháp A và B đòng nhất về mặt kỹ thuật.
3.7.4 Hệ số tương quan r để so sánh hai phương pháp
Có 2 dãy số liệu : x1 x2 x3 x4 x5 ... và y1 y2 y3 y4 y5 ...
Dãy x có đại lượng trung bình x, dãy y có đại lượng y . Hệ số tương quan r được định nghĩa:
r =å (xi -nSx y).(xS yi - y) (3.18)
Để thuận tiện cho tính toán ta dùng phương trình sau: r = åx yi i -nx y. (3.19) (åx 2 2
i -nx2).(åyi -ny2) với -1 £ r £ +1
• Khi 0,9 < r < 0,95 chỉ ra hai dãy số có sự đồng nhất vừa phải
• Khi 0,95 < r < 0,99 chỉ ra hai dãy số có sự đồng nhất tốt
• Khi r > 0,99 có thể xem hệ số tương quan rất tốt
Thí dụ 3.7: Khi phân tích ure trong máu bằng hai phương pháp quang thu được 2 dãy số
liệu, dãy A của phương pháp A và dãy B của phương pháp tiêu chuẩn, có các số liệu sau:
Bảng 3.8: Phân tích ure trong máu Mẫu PP A PP B Di Di- D (D D - i )2 (chuẩn) 1 10,2 10,5 -0,3 -0,6 0,36 2 12,7 11,9 8,7 0,8 0,5 0,25 3 8,6 16,9 -0,1 -0,4 0,16 4 17,5 10,9 0,6 0,3 0,09 5 11,2 11,1 0,3 0,0 0,00 6 11,5 0,4 0,1 0,01 x = 12,0 y = 11,7 S= 0,17 S = 0,87 S(xi)2 = 903,2; S(yi)2 = 855,2 ; S(xi yi) = 878,5
Áp dụng phương trình 3.19 có r = 878,5- (6).(12,0).(11,7) = 0,99
[903,2 - (6).(12,0)2].[855,2 - (6).11,7) ]2
Kết luận hai phương pháp A và B đồng nhất hay phương pháp A tương đương phương pháp tiêu chuẩn
3.7.5 Phương pháp bình phương tối thiểu để biểu diễn phương trình đường chuẩn
Khi lập dãy số liệu biểu diễn sự phụ thuộc tuyến tính giữa tín hiệu đo vào nồng độ
chất, ta có phương trình: yi = axi + b
Để tìm được các hệ số a,b cho đúng có nghĩa là làm thế nào để tìm được đường
thẳng đúng nhất phù hợp với tất cả các điểm trên đường chuẩn (mỗi điểm đều có sai
số)? Phương trình đó có dạng: yt = axi + b
Nói một cách khác, một đường thẳng phù hợp là đường biểu diễn sự liên hệ giữa
giá trị y và các giá trị riêng lẻ x (xi) sao cho tổng các độ lệch nhỏ nhất. Vì một số độ lệch
này có giá trị dương hoặc âm nên được tối thiểu hoá theo tổng bình phương số dư.
Do đó có thể dùng thuật ngữ phương pháp bình phương tối thiểu.
S = S (yi -yt)2 = S yi - (axi + b)]2
Theo phương pháp bình phương tối thiểu, các hệ số a, b trong phương trình được tính theo công thức:
å(x x yi - )( i -y) ; b= y ax- a= å 2
(x xi - )
Phương trình tương đương sau dễ áp dụng hơn ( x y ) a= n 2
åx yi i - å åi i 2 (åxi ) åxi - n
Thí dụ 3.8 Vitamin B2 được xác định bằng phương pháp đo quang cho dãy số liệu sau:
Bảng 3.9: Số liệu phân tích vitamin B12 xi (µg/ml) yi xi2 xiyi 0,000 0,0 0,0000 0,00 0,100 5,8 0,0100 0,58 0,200 12,2 0,0400 2,44 0,400 22.3 0,1600 8,92 0,800 43,3 0,6400 34,64 Sx 2 i = 1,500 Syi = 83,6 Sxi = 0,850 Sxiyi = 46,5 x = 0,300 y =16,72 (Sxi)2 = 2,250 46,58 -1,500-83,6 Giải: a== 5
53,75; b = 16,72 - (53,75 . 0,300) = 0,60 0,850- 2 250 , Phương trình tìm 5 được: y = 53,8 x + 0,6
Trường hợp mẫu phân tích có y = 15,4 ; nồng độ B2 là 15,4 = 53,8 x + 0,6 x = 0,275 µg/ml
3.7.6 Đánh giá và biểu diễn kết quả thực nghiệm theo phương pháp thống kê Từ
các số liệu trong thí dụ 11.1 trên đây sau khi loại giá trị thô có có
Bảng 3.10: Số liệu phân tích Pb TN Các giá trị x 1 2,11 2 2,19 3 2.25 4 2,32 5 2,38 x = 2 25 , (
å x i - x) 2 2 S = S = n - 1 (2 11 , - 2 , ) 25 2 +(2 19 , - 2 , ) 25 2 +(2 32 , - 2 , ) 25 2 +(2 38 , - , 2 ) 25 2 S = 4
S = 0,1 vậy: S = 0,1 = 0,047. Từ biểu thức e= tS (3.20) n 5 n
Tra bảng t khi n=5, P=95%, có tlt = 2,78, vậy e = 2,78x0,047= 0,13
Kết quả thực nghiệm là: µ = 2,25 ± 0,13