







Preview text:
4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh I SÈ TUYN TNH
Ch÷ìng 4. nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 1 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
Nèi ti¸p kh¡i ni»m ¡nh x¤ trong ch÷ìng 1, ch÷ìng 4 nghi¶n cùu mët lo¤i
¡nh x¤ °c bi»t khi tªp nguçn v tªp ½ch l c¡c khæng gian v²c tì, ÷ñc gåi l ¡nh x¤ tuy¸n t½nh.
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 2 / 30
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh 4.1. nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 3 / 30
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 3 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 3 / 30
Mët ¡nh x¤ tuy¸n t½nh tø khæng gian v²c tì V v o ch½nh nâ ÷ñc gåi l
mët to¡n tû tuy¸n t½nh hay ph²p bi¸n êi t½nh t½nh tr¶n V . 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
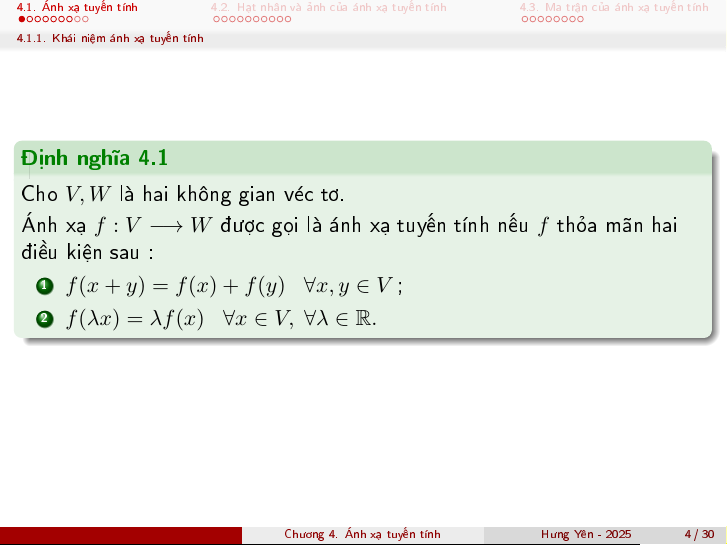
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh ành ngh¾a 4.1
Cho V, W l hai khæng gian v²c tì.
nh x¤ f : V −→ W ÷ñc gåi l ¡nh x¤ tuy¸n t½nh n¸u f thäa m¢n hai i·u ki»n sau : 1
f (x + y) = f (x) + f (y) ∀x, y ∈ V ; 2
f (λx) = λf (x) ∀x ∈ V, ∀λ ∈ R.
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 4 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh ành ngh¾a 4.1
Cho V, W l hai khæng gian v²c tì.
nh x¤ f : V −→ W ÷ñc gåi l ¡nh x¤ tuy¸n t½nh n¸u f thäa m¢n hai i·u ki»n sau : 1
f (x + y) = f (x) + f (y) ∀x, y ∈ V ; 2
f (λx) = λf (x) ∀x ∈ V, ∀λ ∈ R.
Mët ¡nh x¤ tuy¸n t½nh tø khæng gian v²c tì V v o ch½nh nâ ÷ñc gåi l
mët to¡n tû tuy¸n t½nh hay ph²p bi¸n êi t½nh t½nh tr¶n V .
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 4 / 30 Líi gi£i : L§y b§t ký x = (x 2 2
1, x2) ∈ R , y = (y1, y2) ∈ R , λ ∈ R Khi â : x + y = (x 2 2
1 + y1, x2 + y2) ∈ R , λx = (λx1, λx2) ∈ R , ta câ :
f (x) = f (x1, x2) = (x1 + x2, x1 − x2, 2x1 + x2)
f (y) = f (y1, y2) = (y1 + y2, y1 − y2, 2y1 + y2) 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh V½ dö 4.1 Cho ¡nh x¤ f : 2 3 R → R
x = (x1, x2) 7→ w = f (x) = (x1 + x2, x1 − x2, 2x1 + x2)
Chùng minh f l mët ¡nh x¤ tuy¸n t½nh.
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 5 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh V½ dö 4.1 Cho ¡nh x¤ f : 2 3 R → R
x = (x1, x2) 7→ w = f (x) = (x1 + x2, x1 − x2, 2x1 + x2)
Chùng minh f l mët ¡nh x¤ tuy¸n t½nh. Líi gi£i : L§y b§t ký x = (x 2 2
1, x2) ∈ R , y = (y1, y2) ∈ R , λ ∈ R Khi â : x + y = (x 2 2
1 + y1, x2 + y2) ∈ R , λx = (λx1, λx2) ∈ R , ta câ :
f (x) = f (x1, x2) = (x1 + x2, x1 − x2, 2x1 + x2)
f (y) = f (y1, y2) = (y1 + y2, y1 − y2, 2y1 + y2)
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 5 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh V½ dö 4.1 Kiºm tra hai i·u ki»n : 1)f(x + y) =f(x1 + y1, x2 + y2) =
(x1 + y1) + (x2 + y2), (x1 + y1) − (x2 + y2), 2(x1 + y1) + (x2 + y2) =
(x1 + x2) + (y1 + y2), (x1 − x2) + (y1 − y2), (2x1 + x2) + (2y1 + y2)
=(x1 + x2, x1 − x2, 2x1 + x2) + (y1 + y2, y1 − y2, 2y1 + y2)
=f(x1, x2) + f(y1, y2) = f(x) + f(y). 2)f(λx)
= f (λx1, λx2) = (λx1 + λx2, λx1 − λx2, 2λx1 + λx2)
= λ(x1 + x2), λ(x1 − x2), λ(2x1 + x2)
= λ(x1 + x2, x1 − x2, 2x1 + x2) = λf (x)
Tø 1) v 2) ta câ f l ¡nh x¤ tuy¸n t½nh.
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 6 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
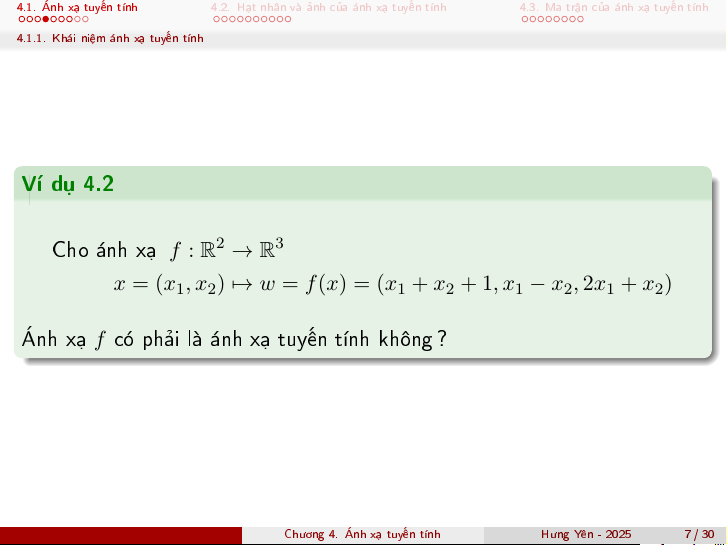
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh V½ dö 4.2 Cho ¡nh x¤ f : 2 3 R → R
x = (x1, x2) 7→ w = f (x) = (x1 + x2 + 1, x1 − x2, 2x1 + x2)
nh x¤ f câ ph£i l ¡nh x¤ tuy¸n t½nh khæng ?
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 7 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh V½ dö 4.2 Líi gi£i : L§y b§t ký x = (x 2 2
1, x2) ∈ R , y = (y1, y2) ∈ R Khi â : x + y = (x 2 1 + y1, x2 + y2) ∈ R
f (x) = (x1 + x2 + 1, x1 − x2, 2x1 + x2)
f (y) = (y1 + y2 + 1, y1 − y2, 2y1 + y2) f (x + y) = f (x1 + y1, x2 + y2)
= (x1 + y1) + (x2 + y2) + 1, (x1 + y1) − (x2 + y2), 2(x1 + y1) + (x2 + y2) =
(x1 + x2) + (y1 + y2) + 1, (x1 − x2) + (y1 − y2), (2x1 + x2) + (2y1 + y2)
=(x1 +x2 +1, x1 −x2, 2x1 +x2)+(y1 +y2 +1, y1 −y2, 2y1 +y2)+(−1, 0, 0)
=f(x1, x2) + f(y1, y2) + (−1, 0, 0) ̸= f(x) + f(y).
Vªy, ¡nh x¤ f khæng ph£i l ¡nh x¤ tuy¸n t½nh.
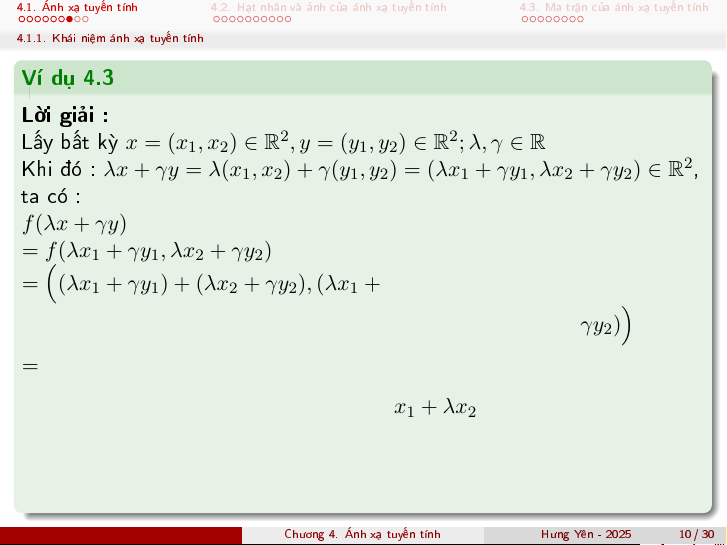
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 8 / 30 V½ dö 4.3
Chùng minh l¤i b i to¡n trong V½ dö 4.1 sû döng Nhªn x²t 4.1 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
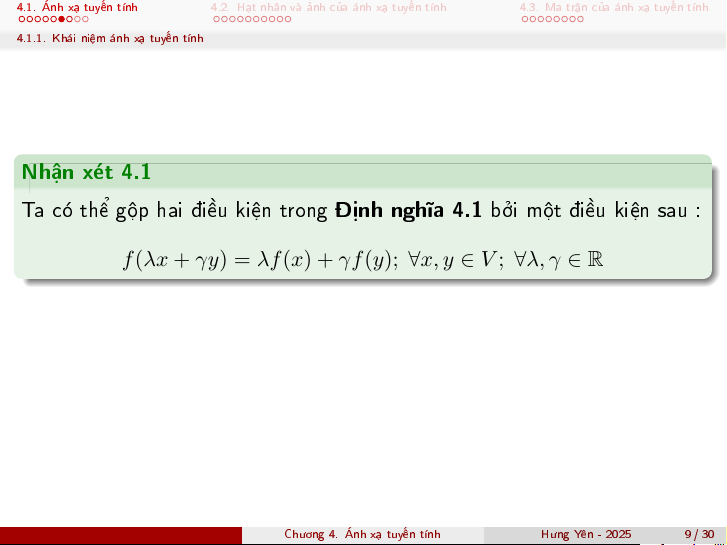
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh Nhªn x²t 4.1
Ta câ thº gëp hai i·u ki»n trong ành ngh¾a 4.1 bði mët i·u ki»n sau :
f (λx + γy) = λf (x) + γf (y); ∀x, y ∈ V ; ∀λ, γ ∈ R
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 9 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh Nhªn x²t 4.1
Ta câ thº gëp hai i·u ki»n trong ành ngh¾a 4.1 bði mët i·u ki»n sau :
f (λx + γy) = λf (x) + γf (y); ∀x, y ∈ V ; ∀λ, γ ∈ R V½ dö 4.3
Chùng minh l¤i b i to¡n trong V½ dö 4.1 sû döng Nhªn x²t 4.1
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 9 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.1. Kh¡i ni»m ¡nh x¤ tuy¸n t½nh V½ dö 4.3 Líi gi£i : L§y b§t ký x = (x 2 2
1, x2) ∈ R , y = (y1, y2) ∈ R ; λ, γ ∈ R Khi â : λx + γy = λ(x 2
1, x2) + γ(y1, y2) = (λx1 + γy1, λx2 + γy2) ∈ R , ta câ : f (λx + γy) = f (λx1 + γy1, λx2 + γy2)
= (λx1 + γy1) + (λx2 + γy2), (λx1 + γy1) − (λx2 + γy2), 2(λx1 + γy1) + (λx2 + γy2)
= (λx1 + λx2) + (γy1 + γy2), (λx1 − λx2) + (γy1 − γy2),
(2λx1 + λx2) + (2γy1 + γy2)
= (λx1 + λx2, λx1 − λx2, 2λx1 + λx2) + (γy1 + γy2, γy1 − γy2, 2γy1 + γy2)
= λ(x1 + x2, x1 − x2, 2x1 + x2) + γ(y1 + y2, y1 − y2, 2y1 + y2) = λf (x) + γf (y)
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 10 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.2. T½nh ch§t v c¡c ph²p to¡n
C¡c t½nh ch§t cõa ¡nh x¤ tuy¸n t½nh ành lþ 4.3
V v W l hai khæng gian v²c tì. N¸u f : V → W l mët ¡nh x¤ tuy¸n t½nh th¼ : 1 f (θV ) = θW 2 f (−x) = −f (x), ∀x ∈ V 3 f (x − y) = f (x) − f (y), ∀x, y ∈ V
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 11 / 30 M»nh · 4.2
N¸u f : V → W v g : W → T l hai ¡nh x¤ tuy¸n t½nh th¼ ¡nh x¤ t½ch
h = gof công l ¡nh x¤ tuy¸n t½nh. 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.2. T½nh ch§t v c¡c ph²p to¡n
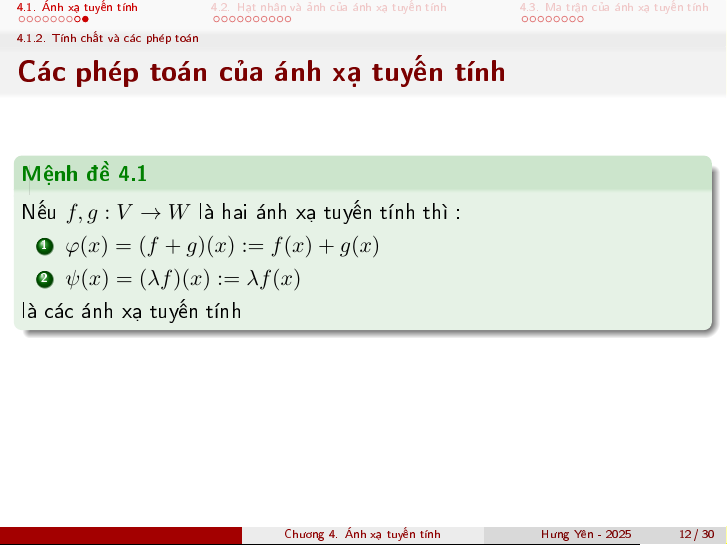
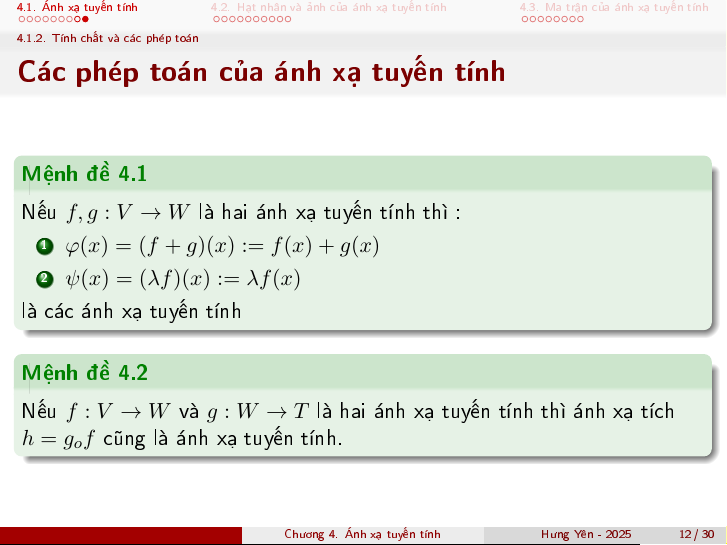
C¡c ph²p to¡n cõa ¡nh x¤ tuy¸n t½nh M»nh · 4.1
N¸u f, g : V → W l hai ¡nh x¤ tuy¸n t½nh th¼ : 1
φ(x) = (f + g)(x) := f (x) + g(x) 2 ψ(x) = (λf )(x) := λf (x) l c¡c ¡nh x¤ tuy¸n t½nh
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 12 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh
4.1.2. T½nh ch§t v c¡c ph²p to¡n
C¡c ph²p to¡n cõa ¡nh x¤ tuy¸n t½nh M»nh · 4.1
N¸u f, g : V → W l hai ¡nh x¤ tuy¸n t½nh th¼ : 1
φ(x) = (f + g)(x) := f (x) + g(x) 2 ψ(x) = (λf )(x) := λf (x) l c¡c ¡nh x¤ tuy¸n t½nh M»nh · 4.2
N¸u f : V → W v g : W → T l hai ¡nh x¤ tuy¸n t½nh th¼ ¡nh x¤ t½ch
h = gof công l ¡nh x¤ tuy¸n t½nh.
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 12 / 30 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh 4.2.1. Kh¡i ni»m ành ngh¾a 4.2
V v W l hai khæng gian v²c tì, f : V → W l mët ¡nh x¤ tuy¸n t½nh. Khi â :
Tªp t§t c£ c¡c ph¦n tû cõa V câ £nh l θW ∈ W gåi l h¤t nh¥n cõa f , kþ hi»u Ker(f ) :
Ker(f ) := {x ∈ V |f (x) = θW }
Tªp t§t c£ c¡c ph¦n tû cõa W l £nh cõa ½t nh§t mët ph¦n tû cõa V
gåi l £nh cõa f, kþ hi»u Im(f) :
Im(f ) := {w ∈ W |∃x ∈ V : f (x) = w} Nh÷ vªy Im(f) = f(V ).
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 13 / 30 Ta câ : Ker(f ) = {x = (x 2
1, x2) ∈ R |f (x) = θ 3 = (0, 0, 0)} R
L§y b§t ký x = (x1, x2) ∈ Ker(f), khi â : x ( 1 + x2 = 0 x1 = 0 f (x) = (0, 0, 0) ⇔ x1 − x2 = 0 ⇔ x 2 = 0 2x1 + x2 = 0
Vªy Ker(f) = {x = (0, 0)} = {θ 2} R 4.1. nh x¤ tuy¸n t½nh
4.2. H¤t nh¥n v £nh cõa ¡nh x¤ tuy¸n t½nh
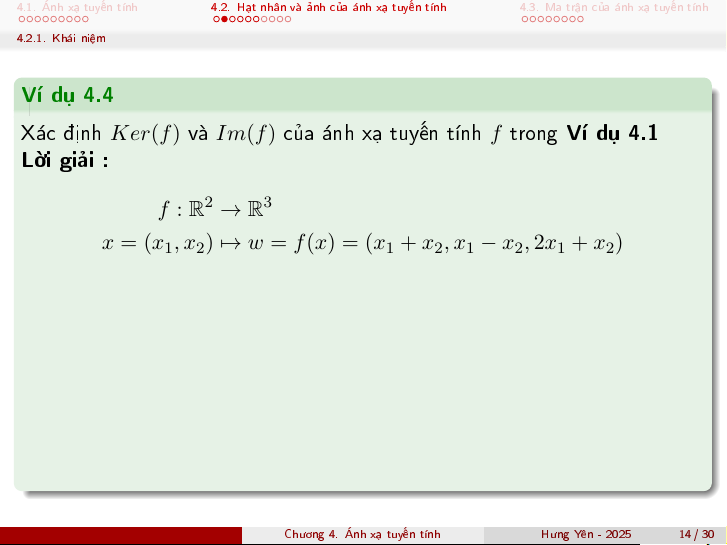
4.3. Ma trªn cõa ¡nh x¤ tuy¸n t½nh 4.2.1. Kh¡i ni»m V½ dö 4.4
X¡c ành Ker(f) v Im(f) cõa ¡nh x¤ tuy¸n t½nh f trong V½ dö 4.1 Líi gi£i : f : 2 3 R → R
x = (x1, x2) 7→ w = f (x) = (x1 + x2, x1 − x2, 2x1 + x2)
Ch÷ìng 4. nh x¤ tuy¸n t½nh H÷ng Y¶n - 2025 14 / 30