Chương 4: Khảo sát tính ổn định của hệ thống | Bài giảng Điều khiển tự động

Chương 4: Khảo sát tính ổn định của hệ thống
4.1_ Khái niệm tính ổn định
4.2_ Tiêu chuẩn ổn định đại số (Routh)
4.3_ Tiêu chuẩn ổn định tần số (Bode)
4.4_ Phương pháp quỹ đạo nghiệm số 1
4.1 Khái niệm tính ổn định 
Ổn định là yêu cầu cơ bản của hệ thống ĐKTĐ. 
Ổn định BIBO: (Bound Input- Bound Output, vào chặn ra chặn)
Hệ thống được gọi là ổn định BIBO nếu với tín hiệu vào hữu hạn
thì tín hiệu ra cũng hữu hạn. Tức là nếu |r(t)|< thì |y(t)|< .
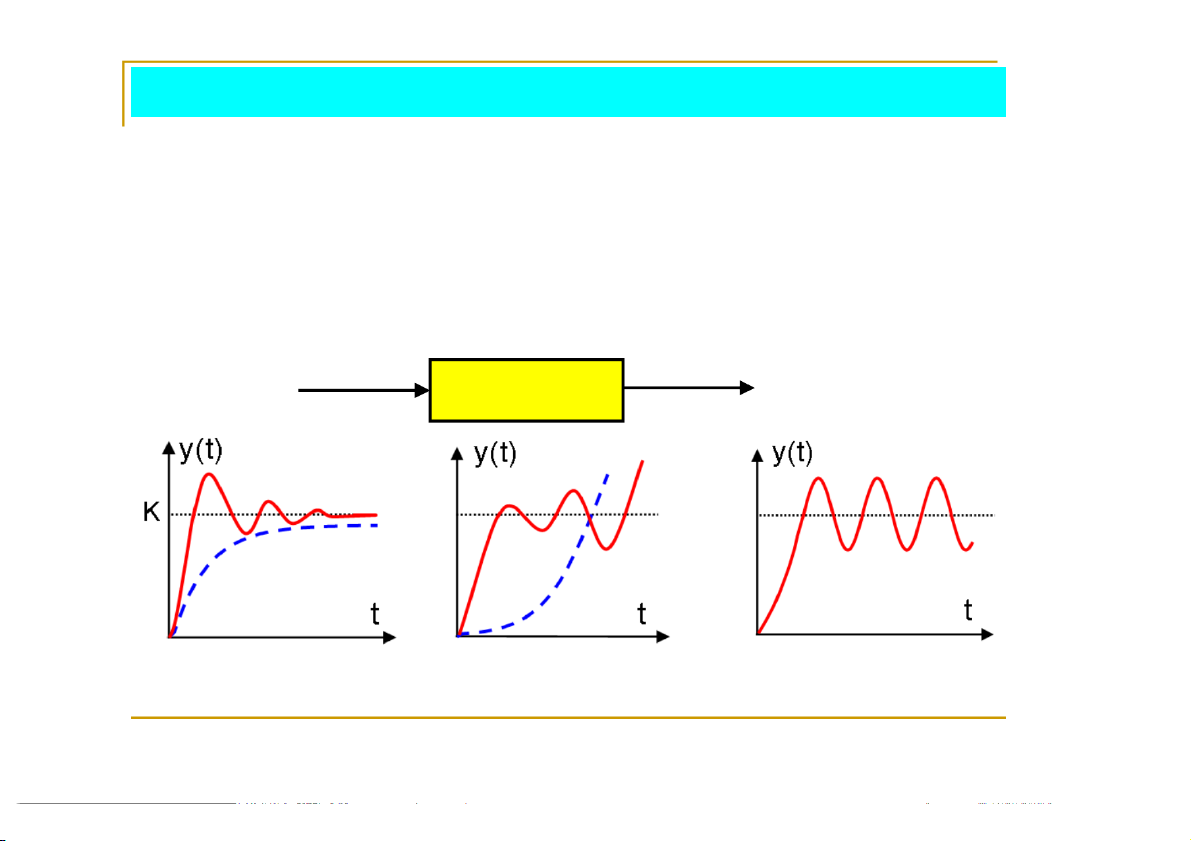
Ví dụ: hệ ổn định BIBO  với r(t) = 1(t) thì y() = const. r(t) y(t) Hệ thống Hệ ổn định không ổn định
giới hạn ổn định 2
4.1 Khái niệm tính ổn định
 Ổn định tiệm cận (Lyapunov): Hệ ổn định tiệm cận nếu
như khi có nhiễu tức thời đánh bật hệ ra khỏi trạng thái
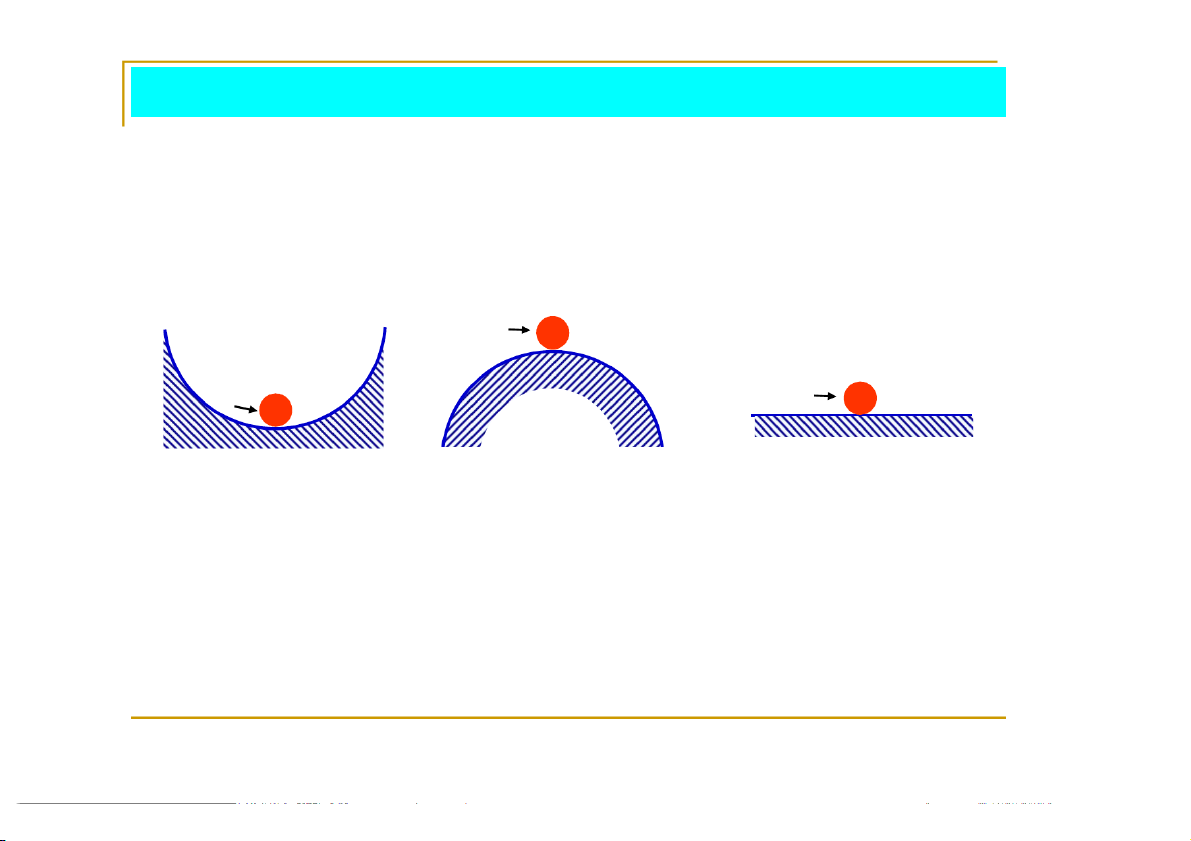
cân bằng thì sau đó hệ có khả năng tự quay về trạng thái cân bằng ban đầu. Hệ ổn định không ổn định
giới hạn ổn định
 Với hệ tuyến tính thì hai khái niệm ổn định nêu trên là
tương đương. Hệ tuyến tính đạt ổn định BIBO thì cũng
sẽ ổn định tiệm cận và ngược lại. 3
4.1 Khái niệm tính ổn định 
Xét hệ thống tuyến tính có PTVP: n n 1  m m 1 d y d y d r d  r a  a  ...  a y(t)  b  b  ...  b r(t) n n n 1  n 1  0 m m m 1  m 1  0 dt dt dt dt
Đáp ứng của hệ cũng là nghiệm PTVP: y(t) = y (t) + y 0 qđ (t)
y0(t)_ là nghiệm riêng của PTVP.
yqđ(t)_ Là nghiệm tổng quát của PTVP.
Ta thấy nếu r(t) hữu hạn thì y (t) cũng hữu hạn, nên: 0
Tính ổn định của hệ chỉ phụ thuộc thành phần quá độ yqđ(t). 4
4.1 Khái niệm tính ổn định n t Tổng quát: y (t)  C  esi qd i i1
Ci _là hằng số phụ thuộc thông số của hệ và điều kiện đầu. s n n 1 a s  a s    a 
i _là nghiệm của phương trình đặc tính: ... 0 n n 1  0
si cũng gọi là cực của hệ thống. s 
i có thể là số thực (=i) hay số phức (= j i i)
Từ nhận xét nêu trên ta có thể định nghĩa cách khác về ổn định:
Một hệ thống tuyến tính được gọi là ổn định nếu quá trình quá
độ tắt dần theo thời gian. Hệ thống không ổn định nếu QTQĐ tăng
dần. Hệ thống ở giới hạn ổn định nếu QTQĐ không đổi hoặc dao
động với biên độ không đổi . Hệ ổn định  5
4.1 Khái niệm tính ổn định
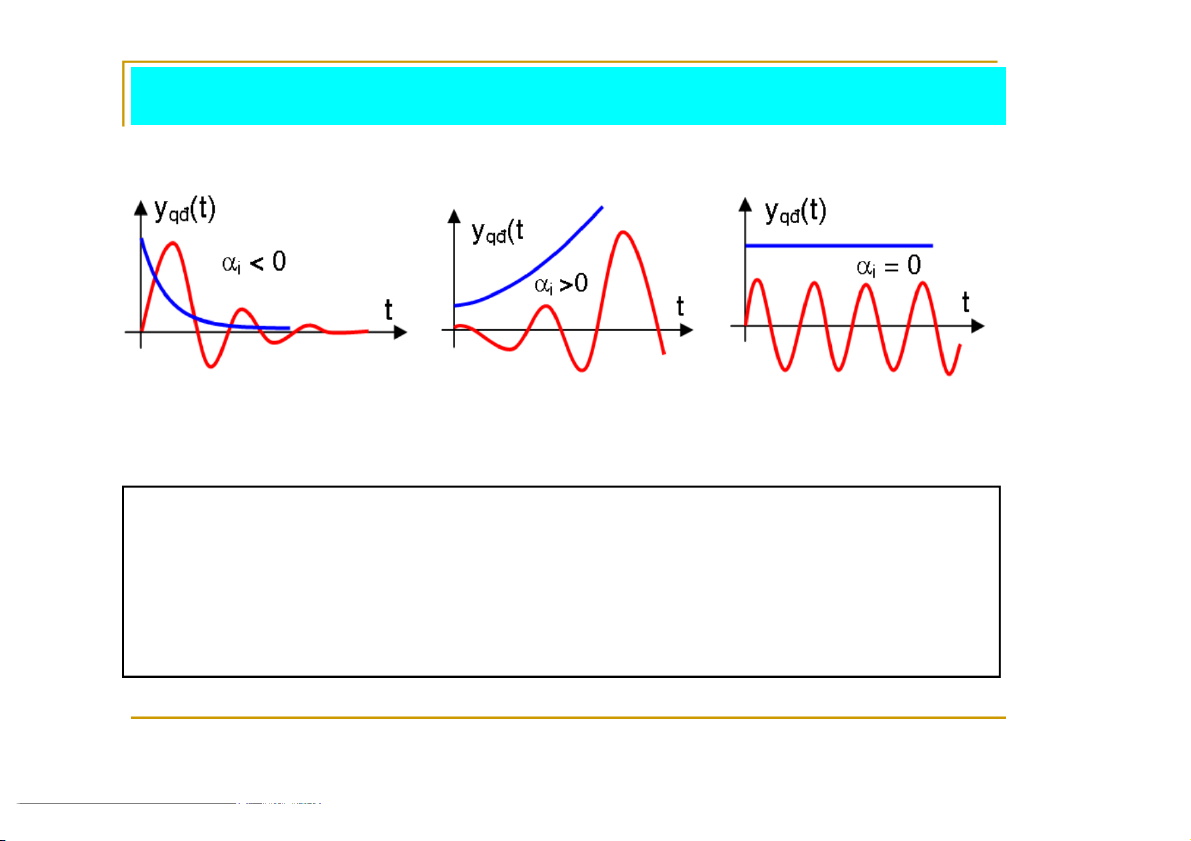
Xét các trường hợp cụ thể, ta có: Hệ ổn định Không ổn định
Giới hạn ổn định
Kết luận: Tính ổn định của hệ phụ thuộc các nghiệm si của PTĐT.
- Hệ ổn định  Mọi s có phần thực<0  Mọi s là nghiệm trái. i i
- Hệ không ổn định   s có ph.thực>0   s là nghiệm phải. i i
- Hệ ở giới hạn ổn định   s 
i có i = 0, các s còn lại có i i <0.
  si nằm trên trục ảo , các nghiệm còn lại là nghiệm trái. 6
4.1 Khái niệm tính ổn định 
Ví dụ, xét hệ có hàm truyền: 2s 5 G(s)  2 (s  8)(s  6s 13) 2
Phương trình đặc tính: (s  8)(s  6s 13)  0
PTĐT có 3 nghiệm: s = -8 và s = -3 2j 1 2,3 
Cả 3 nghiệm đều có phần thực âm nên hệ thống ổn định.
Để tránh phải giải PTĐT, ta có các phương pháp
xét ổn định một cách gián tiếp, tiện dụng hơn. Đó là:
- Tiêu chuẩn ổn định đại số Routh, Hurwitz.
- Tiêu chuẩn ổn định tần số Nyquist, Bode.
- Phương pháp quỹ đạo nghiệm. - … 7
4.2 Tiêu chuẩn ổn định đại số
- Tiêu chuẩn đại số tìm điều kiện ràng buộc giữa các hệ số
của phương trình đặc tính để hệ thống ổn định.
- Áp dụng được cho cả hệ hở và hệ kín.
4.2.1 Điều kiện cần
ĐK cần để hệ ổn định là Tất cả các hệ số của PTĐT đều >0. PTĐT: a n n-1 ns + a s n-1
+…+a0=0  ĐK cần: a0,a ,…,a 1 n >0 Ví dụ, xét hệ có PTĐT: 3 2 s  4s  5s  7  0
 Không ổn định vì hệ số a2<0 4 2 s  5s  6s  2  0
 Không ổn định vì hệ số a3=0 4 3 2
s  4s  5s  6s  2  0  Chưa kết luận được, mới thoả ĐK cần 8
4.2 Tiêu chuẩn ổn định đại số
4.2.2 Tiêu chuẩn Routh
Xét hệ có phương trình đặc tính: n n 1
a s  a s  ...  a  0 n n 1  0
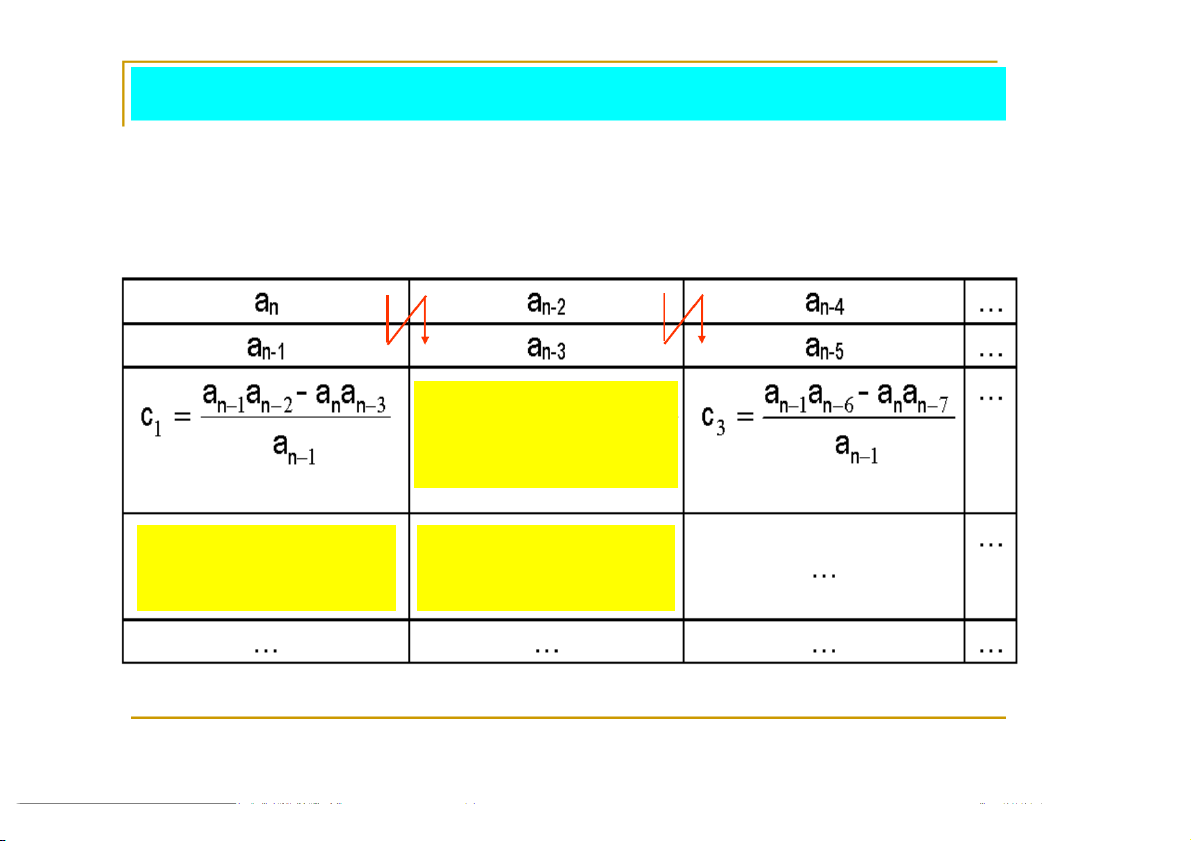
Lập bảng Routh gồm (n+1) hàng: 9
4.2 Tiêu chuẩn ổn định đại số
Phát biểu tiêu chuẩn Routh:
- Cần và đủ để hệ thống ổn định là các hệ số ở cột một
bảng Routh đều dương.
- Số lần đổi dấu ở cột một bằng số nghiệm của phương
trình đặc tính có phần thực dương (=số nghiệm phải).
Ví dụ 1. Xét ổn định hệ thống có PTĐT: 4 3 2
s  2s  7s  4s  3  0
Ví dụ 2. Xét ổn định hệ có PTĐT: 5 4 3 2
s  4s  5s  4s  7s  8  0
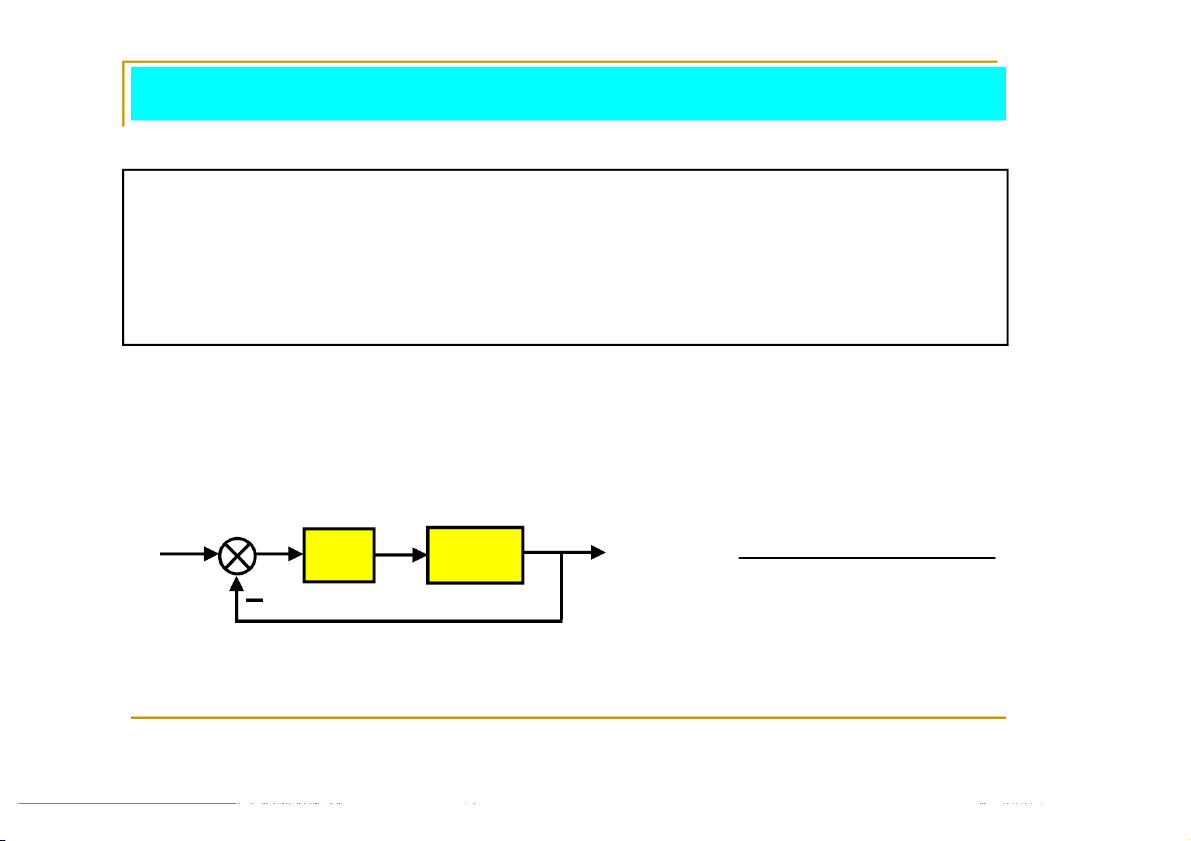
Ví dụ 3. Xét hệ thống có sơ đồ khối: r y 1 K G(s) G(s)  2 s(3s  2)(s  4s  1)
Hãy tìm khoảng giá trị của K để hệ thống ổn định. 10
4.2 Tiêu chuẩn ổn định đại số
Giải. Phương trình đặc tính của hệ: K 1  K.G(s)  0  1  0 2 s(3s  2)(s  4s 1) 3 2
 s(3s 14s 11s  2)  K  0 4 3 2
 3s 14s  11s  2s  K  0 Bảng Routh: 3 11 K
Điều kiện để hệ ổn định: 14 2 0 74 49K  0 74 / 7 K 0 K  0  74  49K 0 74    37 0 K 49 K 11
4.2 Tiêu chuẩn ổn định đại số
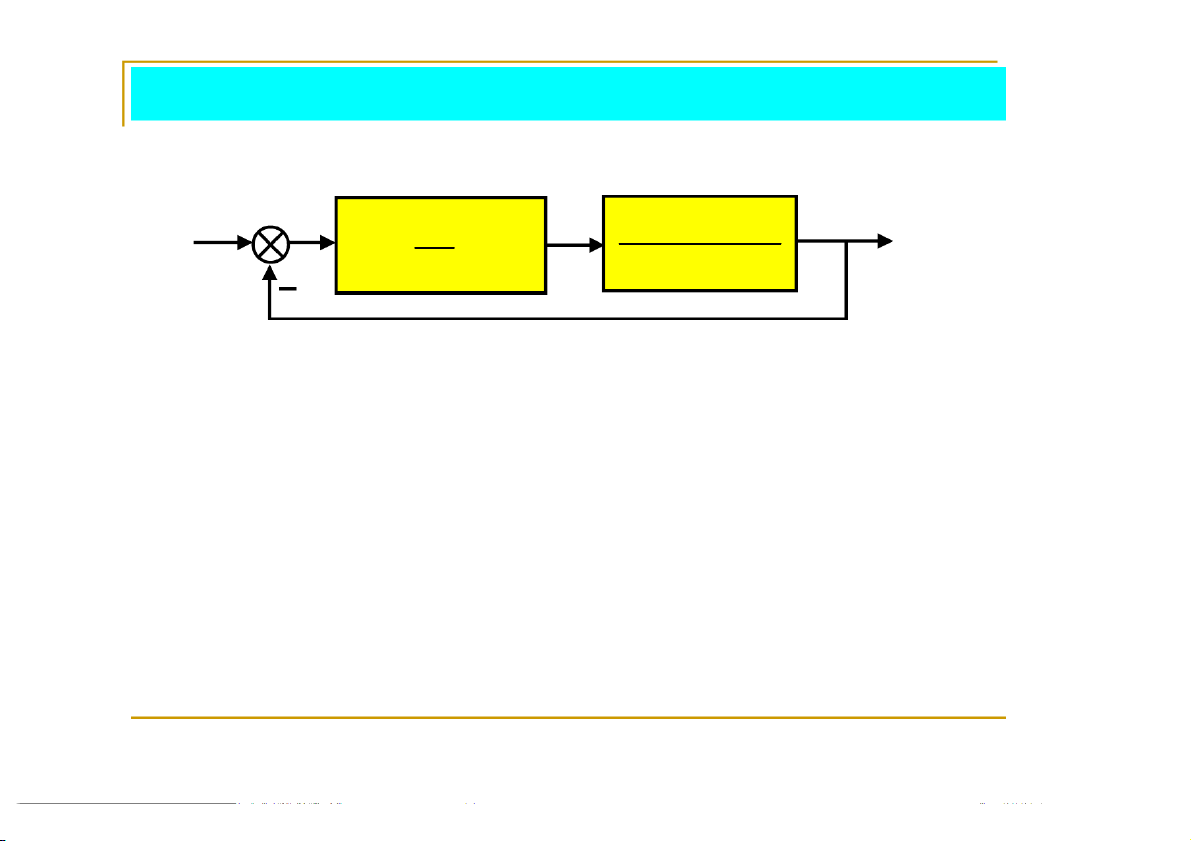
Ví dụ 4. Xét hệ thống có sơ đồ khối: r y K 16 I K + +K s P D 2 s s 12s  20
a) Cho KD=2; K = 38. Tìm khoảng giá trị của K để hệ thống P I luôn ổn định.
b) Cho KD=2. Tìm biểu thức quan hệ giữa KP và KI để hệ thống luôn ổn định.
Đáp số: (  44)(628) 16K  0 I a)  0  K 1727  I K  0  I 44(20 16K ) 16K  0 P I  0  K  44K  55 b) I P K  0  I 12
4.3 Tiêu chuẩn ổn định tần số
4.3.1 Độ dự trữ ổn định, tiêu chuẩn Bode
Mục đích: Đánh giá mức độ ổn định của hệ thống. 
Tần số cắt biên c là tần số tại đó A()=1, tức L()= 0 dB. 
Tần số cắt pha - là tần số tại đó ()= - =-180. 
Độ dự trữ biên độ GM (Gain Margin) đặc trưng cho mức độ
tiếp cận giới hạn ổn định về phương diện biên độ. GM  L( ) 
: đơn vị dB, dùng với biểu đồ Bode.
- Giá trị GM=0dB  giới hạn ổn định. - Do A()= y nên GM cũng thể hiện 0/r0
mức cho phép tăng hệ số
khuếch đại K mà hệ thống vẫn ổn định. 
Độ dự trữ pha PM (Phase Margin) đặc trưng cho mức độ tiếp
cận giới hạn ổn định về phương diện góc pha. PM =180+ ( ) c 13
4.3.1 Độ dự trữ ổn định, tiêu chuẩn Bode 
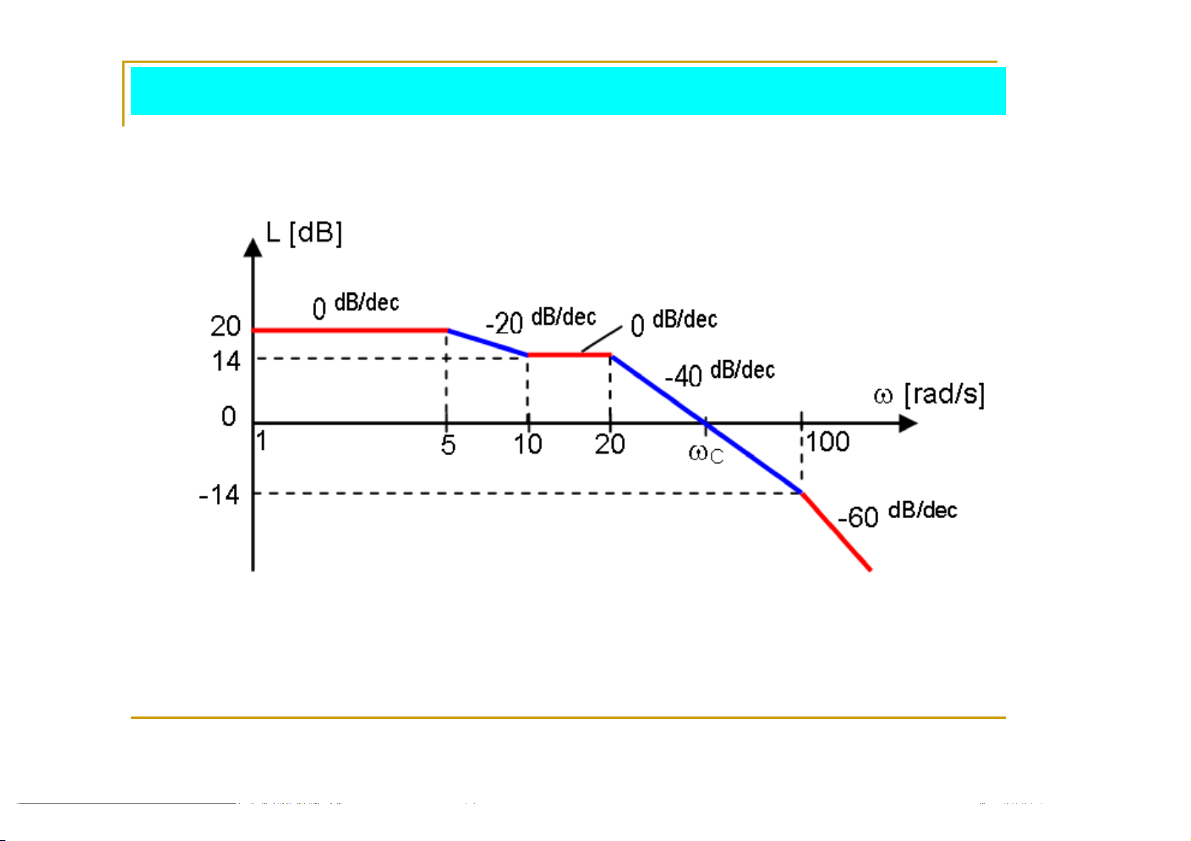
Xác định GM và PM từ biểu đồ Bode GM  L( )  26 -20 -80 -230 PM = 180+ ( ) c 14
4.3.4 Độ dự trữ ổn định, tiêu chuẩn Bode  Tiêu chuẩn Bode
Hệ kín ổn định nếu hệ hở có dự trữ biên và dự trữ pha đều >0.
Hệ kín ổn định  hệ hở có GM>0 [dB] và PM >0 []. 
Trường hợp đặc biệt Hệ kín ổn định  Hệ hở ổn định và
PM=180+(c) = >0 15
4.3.4 Độ dự trữ ổn định, tiêu chuẩn Bode
 Ví dụ 1. Xét tính ổn định của hệ kín có hàm truyền vòng hở : K(s 10) G(s)  ; K=500  1 2 1  (s  5)(s 100) s  s  1    400 20 
Giải. Viết lại hàm truyền hệ hở:  1  10 s   1 10  G(s)  1  1  1 2 1  s 1 s 1 s  s 1      5 100  400 20  1 1 1 1 10 s+1 1 1 1 1 2 10 s+1 s+1 s + s+1 5 100 400 20 P VPB1 PT1 PT PT 1 2    g=10 g=100  g=5 g=20 16
4.3.4 Độ dự trữ ổn định, tiêu chuẩn Bode
 Hệ số khuếch đại chung: K =10 Biên độ 20lgK = 20dB   
 Các tần số gãy:  = 5, 10, 20, 100 [rad/s]
 Gọi L5 , L10 ,…là giá trị L tại các tần số  = 5, 10, …[rad/s] L 20 20 lg(10 / 5) 14dB ; L  L  14dB 10     2  0 1  0 L 14 40 lg(100 / 20) 14dB 1      00 17
4.3.4 Độ dự trữ ổn định, tiêu chuẩn Bode
 Tính góc pha tại tần số cắt biên L  L  14 c  20 14 
 -40 [dB/dec]  lg( /20)   0,35 lg( /20) lg( c /20) 40 c c 0,35
Tần số cắt biên:   (20)(10 )  44,8  45 [rad/s] c  1    1   1   1  ( ) 20
  arctg   arctg  arctg   arctg  2  10   5   100   1 1    400 
( )  arctg 4,5  arctg 9  arctg 0,45  arctg 0  ,55 c        
 77,5  83, 7  24, 2 151, 2  18  1, 6
 Xét ổn định hệ kín
Độ dự trữ pha: PM= 180 +  (c) = -1,6 <0
nên hệ kín không ổn định 18
4.3.4 Độ dự trữ ổn định, tiêu chuẩn Bode
 Ví dụ 2: Xét tính ổn định của hệ kín có hàm truyền vòng hở : 6400(s  25)
G(s)  (s 4)(s 100) 2s 12s100
Giải. Viết lại hàm truyền hệ hở:  1  4 s 1    25  G(s)  1  1  1 2 12  s 1 s  1 s  s 1      4 100 100 100 
 Hệ số khuếch đại chung: K =4 20lgK = 12dB  
 Các tần số gãy:  = 4, 10, 25, 100 [rad/s]
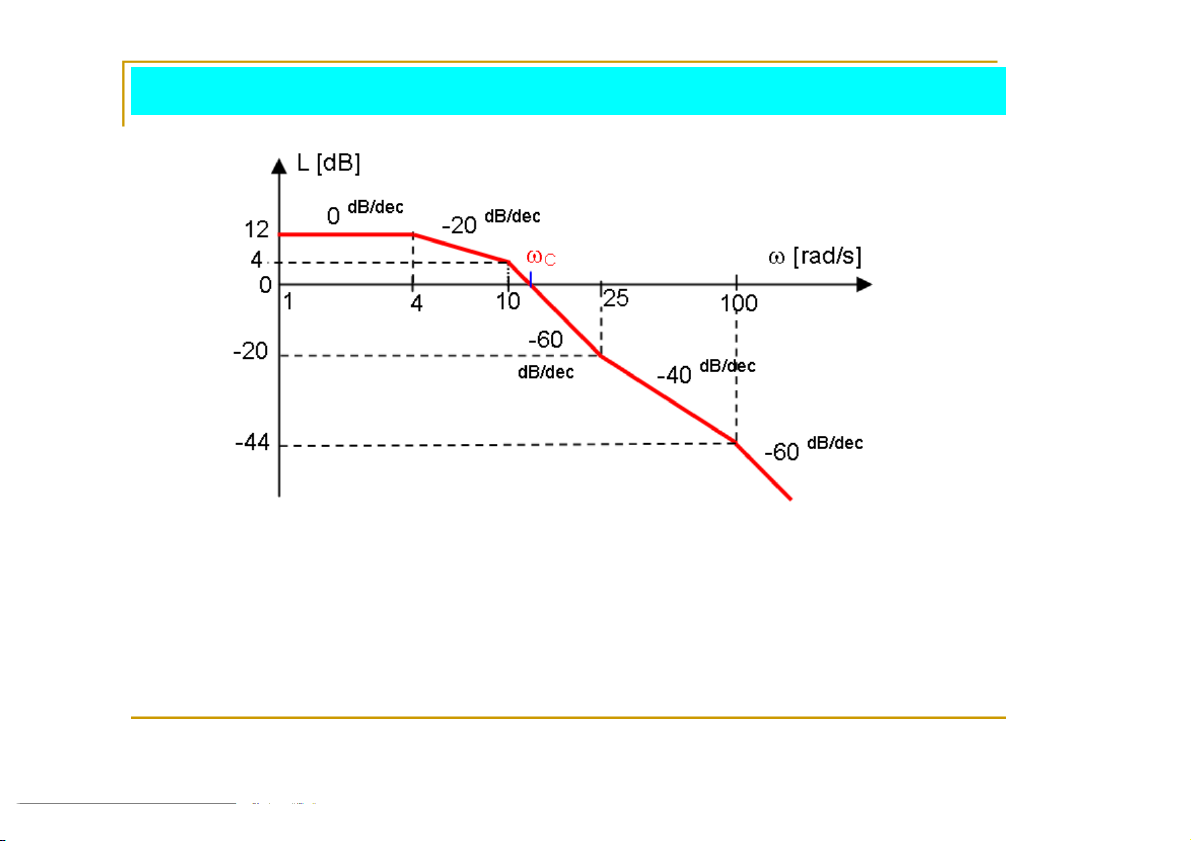
 Gọi L4 , L10 ,…là giá trị L tại các tần số  = 4, 10, …[rad/s] 19
4.3.4 Độ dự trữ ổn định, tiêu chuẩn Bode L
 L  20lg(10 / 4)  12  20 lg(2,5)  4dB 1  0 4 L  L
 60lg(25 /10)  4  60 lg(2,5)  20dB 2  5 1  0 L  L
 40lg(100 / 25)  20 40 lg 4  44dB 1  00 25 20