Chương 4 Kỹ thuật CMOS trong thiết kế mạch số độngSVs

PHÂN TÍCH VÀ THIẾT KẾ MẠCH TÍCH HỢP SỐ-TƯƠNG TỰ GS: Chu Mạnh Hoàng
Khoa Vật liệu điện tử và Linh kiện
Truòng Vật Liệu, Đại học Bách khoa Hà Nội
CHƯƠNG 4: KỸ THUẬT CMOS TRONG
THIẾT KẾ MẠCH SỐ ĐỘNG
4.1. Thiết kế mạch Adder
4.2. Thiết kế mạch Multiplexers
4.3. Thiết kế mạch Latch
4.4. Thiết kế mạch Memory 2
4.1. Thiết kế mạch Adder Cơ sở lý thuyết: Phép Cộng Logic:
- Phép cộng logic, hay còn gọi là phép OR logic, là một trong những phép toán cơ bản trong đại số Boole.
Phép toán này được sử dụng rộng rãi trong lĩnh vực điện tử số và lý thuyết mạch logic để xử lý và thiết kế các mạch số.
- Phép cộng logic giữa hai biến A và B được ký hiệu là A + B hoặc A V B. Kết quả của phép cộng logic chỉ
bằng 0 khi cả hai biến đều bằng 0, và bằng 1 trong các trường hợp còn lại, cụ thể. - Xét hai bit A và B: VD: Cộng 2 số 0111 
Nếu A = 0 và B = 0, kết quả sẽ là 0 và không có bit nhớ. nhị phân 
Nếu A = 0 và B = 1, kết quả sẽ là 1 và không có bit nhớ. 1110 
Nếu A = 1 và B = 0, kết quả sẽ là 1 và không có bit nhớ. 10101 
Nếu A = 1 và B = 1, kết quả sẽ là 0 và có một bit nhớ (carry) sang vị trí tiếp theo.
Phép cộng logic có thể được biểu diễn bằng công thức: trong đó: Sum = A  B
 là phép XOR (Exclusive OR) Carry = A  B  là phép AND 3
4.1. Thiết kế mạch Adder
Bảng Chân Lý của Phép Cộng Logic
- Bảng chân lý của phép cộng logic là một bảng thể hiện tất cả các khả năng đầu vào và kết quả đầu ra tương
ứng của một phép cộng logic giữa hai bit. Bảng chân lý của phép cộng logic như sau: A B Sum Carry 0 0 0 0 1 0 1 0 0 1 1 0 1 1 1 1 
A và B là các bit đầu vào. 
Sum là kết quả của phép cộng logic giữa A và B. 
Carry là bit nhớ được sinh ra khi cả A và B đều là 1.
Khi A và B đều bằng 1, kết quả là 0 và có một bit nhớ (Carry) được sinh ra. Đây là nền tảng cho
các phép toán nhị phân phức tạp hơn trong các hệ thống kỹ thuật số. 4
4.1. Thiết kế mạch Adder
Ứng Dụng của Phép Cộng Logic
- Phép cộng logic có nhiều ứng dụng quan trọng trong lĩnh vực khoa học máy tính và kỹ thuật số. Dưới đây là
một số ứng dụng tiêu biểu của phép cộng logic:
+ Mạch số học: Phép cộng logic là thành phần cơ bản trong các mạch số học như bộ cộng (adder). Bộ cộng
là một mạch logic thực hiện phép cộng hai số nhị phân. Có hai loại bộ cộng chính: o
Bộ cộng nửa (Half Adder): Thực hiện phép cộng của hai bit và cho ra kết quả tổng và bit nhớ. o
Bộ cộng toàn phần (Full Adder): Thực hiện phép cộng của ba bit (bao gồm cả bit nhớ từ phép
cộng trước đó) và cho ra kết quả tổng và bit nhớ mới.
+ Bộ xử lý trung tâm (CPU): Phép cộng logic được sử dụng trong các đơn vị xử lý số học và logic (ALU) của
CPU để thực hiện các phép toán cơ bản như cộng, trừ, nhân và chia. Đây là các hoạt động cơ bản cần thiết cho
việc xử lý dữ liệu trong máy tính.
+ Thiết kế mạch số: Phép cộng logic được sử dụng rộng rãi trong thiết kế các mạch số và vi mạch. Các mạch
logic số, bao gồm các mạch tổ hợp và mạch tuần tự, đều dựa vào các phép toán logic cơ bản như AND, OR, NOT và phép cộng logic. 5
4.1. Thiết kế mạch Adder
Ứng Dụng của Phép Cộng Logic
+ Xử lý tín hiệu số: Trong lĩnh vực xử lý tín hiệu số, phép cộng logic được sử dụng để thực hiện các phép toán
trên các tín hiệu số. Các bộ lọc số và các hệ thống xử lý tín hiệu thường sử dụng các phép toán logic để xử lý và phân tích tín hiệu.
+ Lập trình và thuật toán: Phép cộng logic cũng được sử dụng trong lập trình và các thuật toán máy tính. Các
ngôn ngữ lập trình cung cấp các phép toán logic để xử lý các biến nhị phân và thực hiện các phép toán trên các
bit. Điều này rất hữu ích trong các ứng dụng yêu cầu xử lý dữ liệu nhị phân hoặc tối ưu hóa hiệu suất. 6
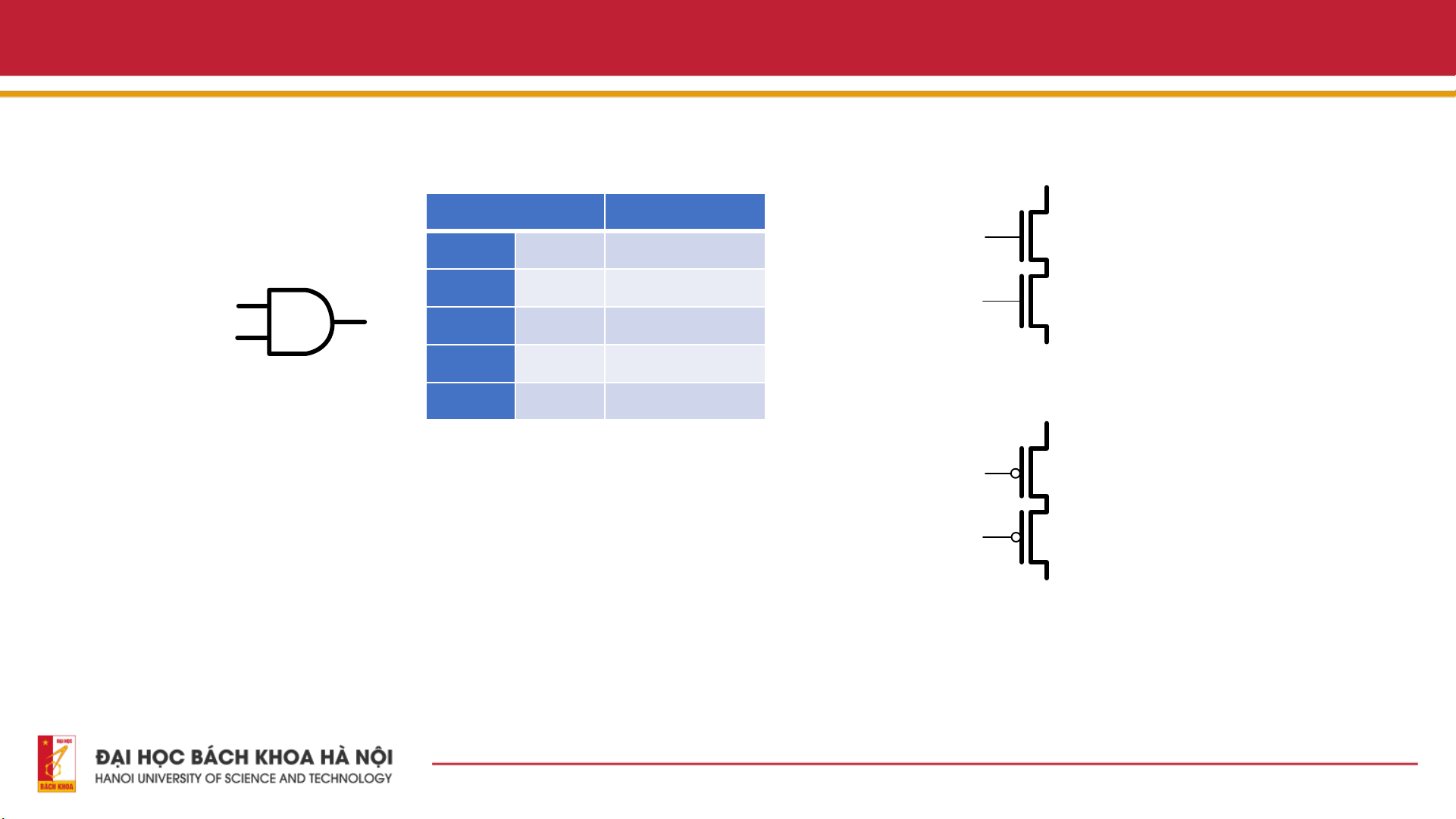
4.1. Thiết kế mạch Adder
Các cổng logic cơ bản Bảng chân lý 1. Cổng AND Input Output Y = AB A A B Y = AB nMOS1 - Ký hiệu 0 0 0 B A nMOS2 Out 1 0 0 B 0 1 0 Y = A·B 1 1 1 A pMOS1 B pMOS2 Y = A·B 7
4.1. Thiết kế mạch Adder
Các cổng logic cơ bản
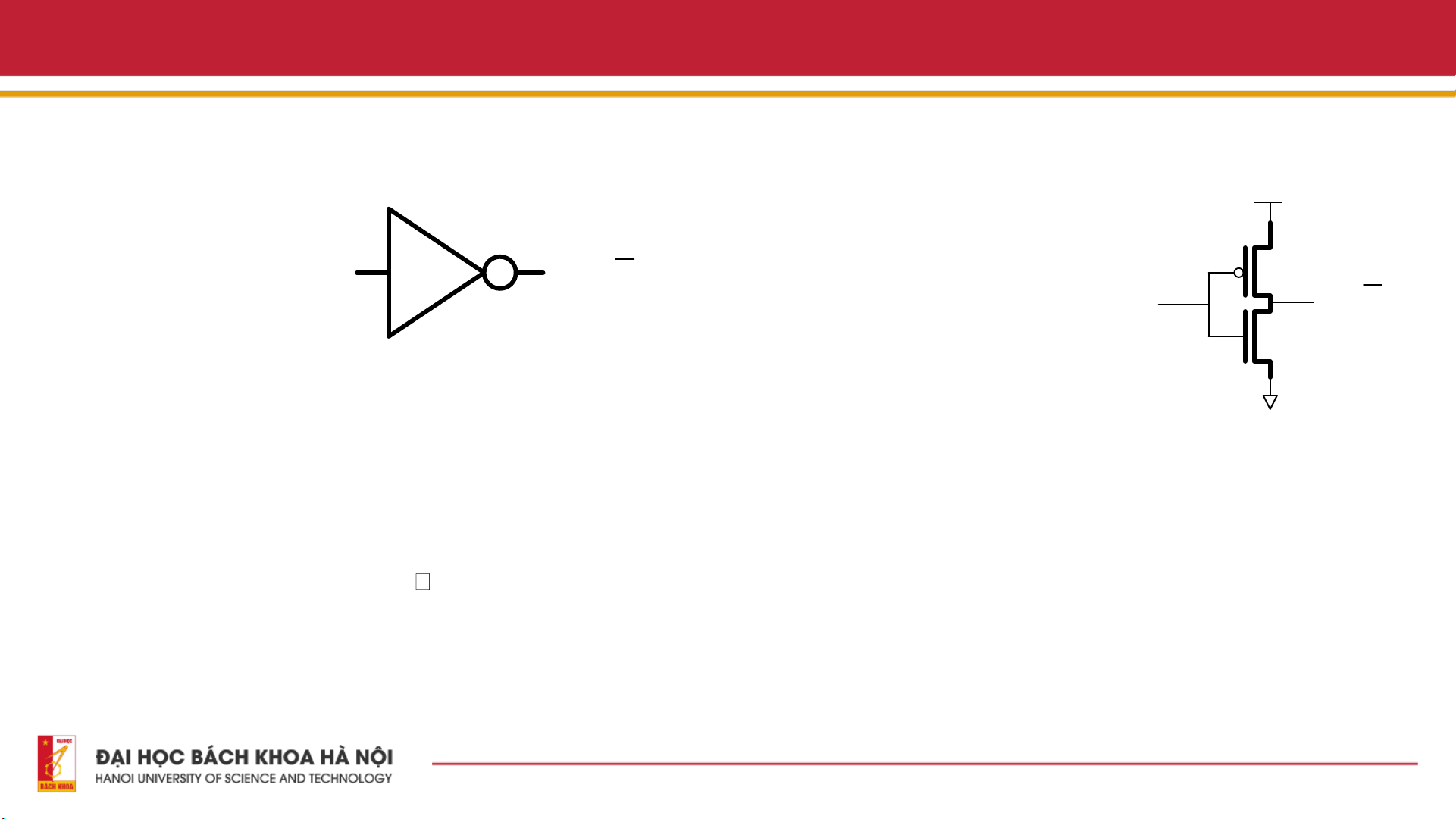
+ Kí hiệu và sơ đồ mạch cấu trúc 2. Cổng NOT
logic CMOS của cổng đảo sử VDD
dụng 1 transitor pMOS kéo lên - Ký hiệu V và 1 transitor nMOS kéo A DD Y = A xuống GND. pMOS A Y = A
+ Transitor nMOS tích cực mức cao; nMOS
+ Transitor pMOS tích cực mức thấp. GND
+ Khi ngõ vào A = 0: nMOS  OFF và pMOS  ON
 Ngõ ra Y kéo lên VDD, Y = 1
+Ngược lại, khi A = 1: nMOS  ON, pMOS  OFF.
 Ngõ ra Y kéo xuống GND, Y=0 8
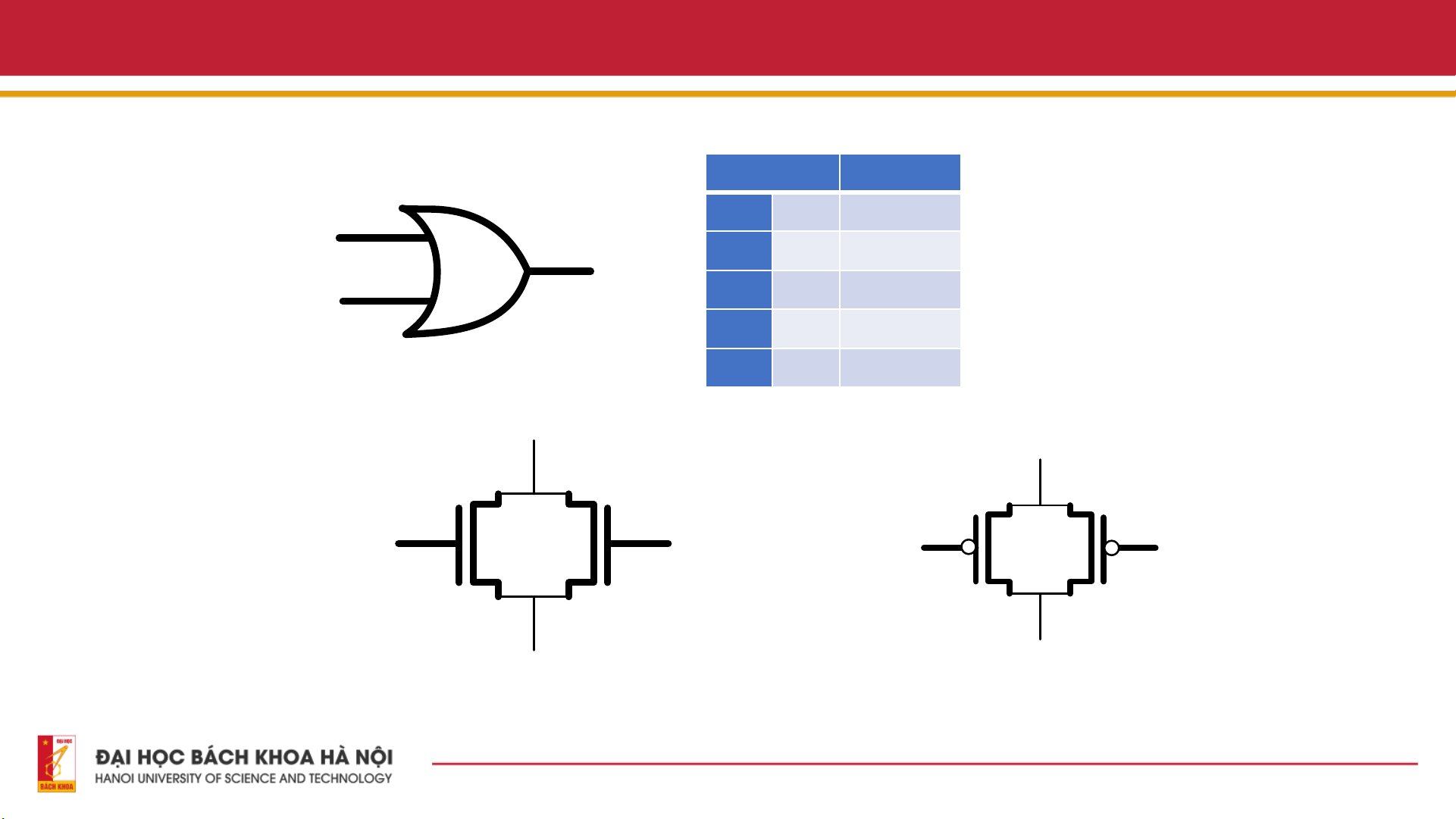
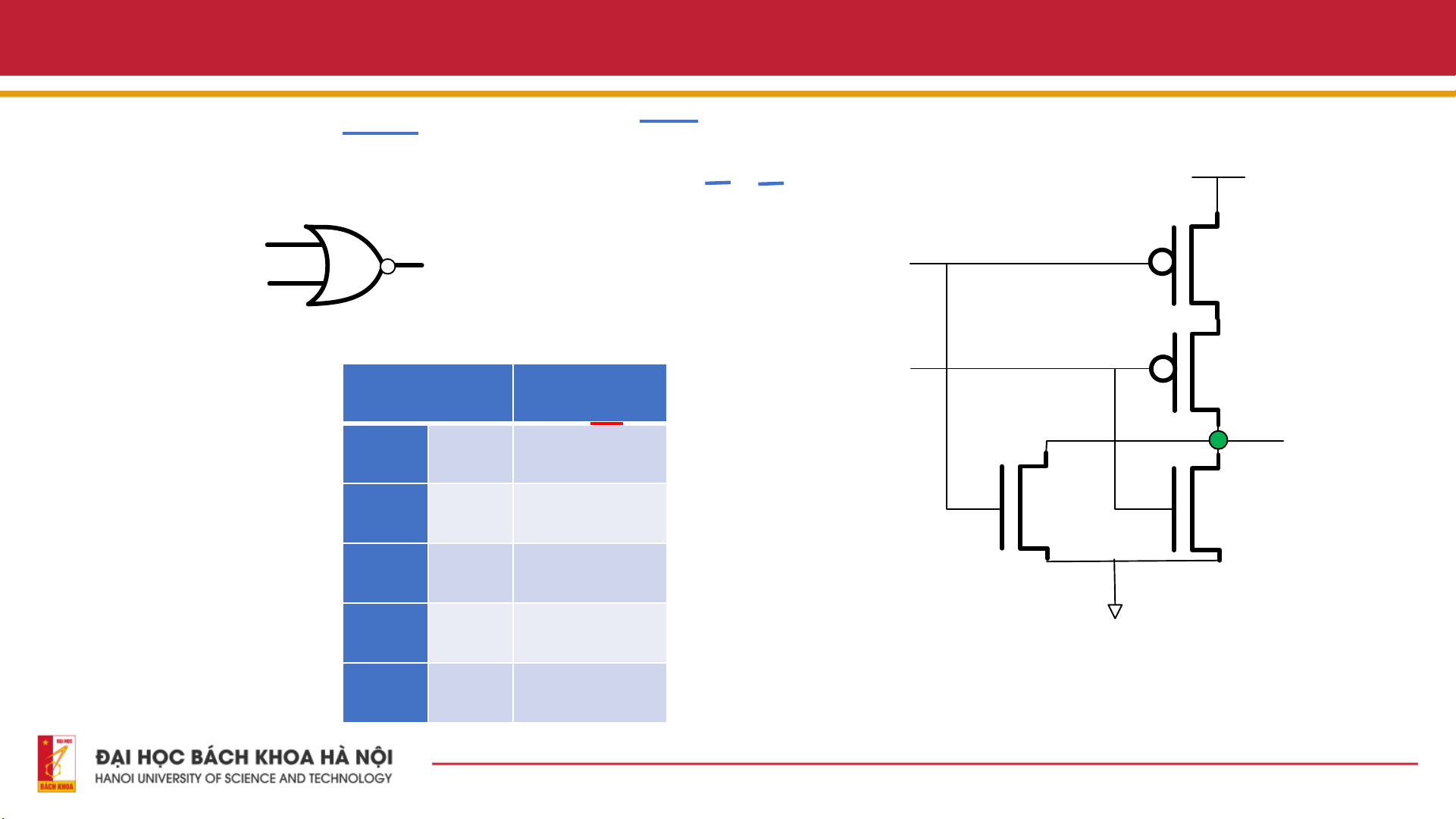
4.1. Thiết kế mạch Adder 3. Cổng OR Bảng chân lý Y = A + B Input Output A B Y = A+B - Ký hiệu A 0 0 0 Out 1 0 1 B 0 1 1 1 1 1 nMOS1 nMOS2 pMOS1 pMOS2 A B A B Y Y 9
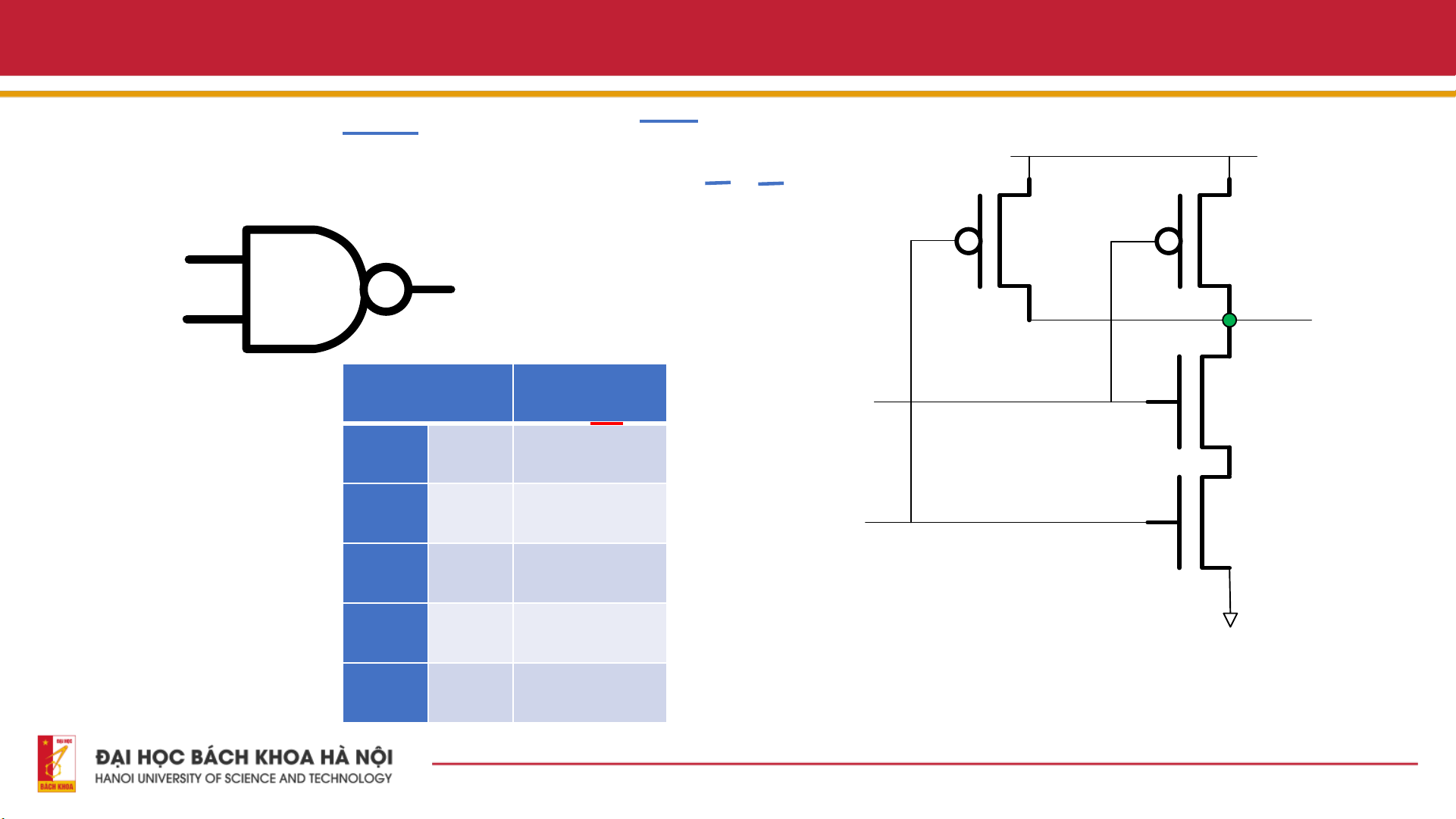
4.1. Thiết kế mạch Adder 4. Cổng NAND Y = A  B Pulldown Y = A  B - Ký hiệu Pullup Y = A + B A Out B Y Input Output A A B Y = AB 0 0 1 B 1 0 1 0 1 1 GND 1 1 0 10
4.1. Thiết kế mạch Adder
Bài tập: Vẽ cổng NAND 3 ngõ vào dung transistor MOS Đáp án: Y A B C GND 11
4.1. Thiết kế mạch Adder 5. Cổng NOR Y = A + B Pulldown Y = A + B - Ký hiệu Pullup Y = A  B A Out A B B Input Output A B Y = A+B Y 0 0 1 1 0 0 0 1 0 GND 1 1 0 12
4.1. Thiết kế mạch Adder Bài tập
vẽ sơ đồ nguyên lý cổng NOR 3 ngõ vào dùng transistor CMOS A Đáp án: B C Y GND 13
4.1. Thiết kế mạch Adder 14
4.1. Thiết kế mạch Adder
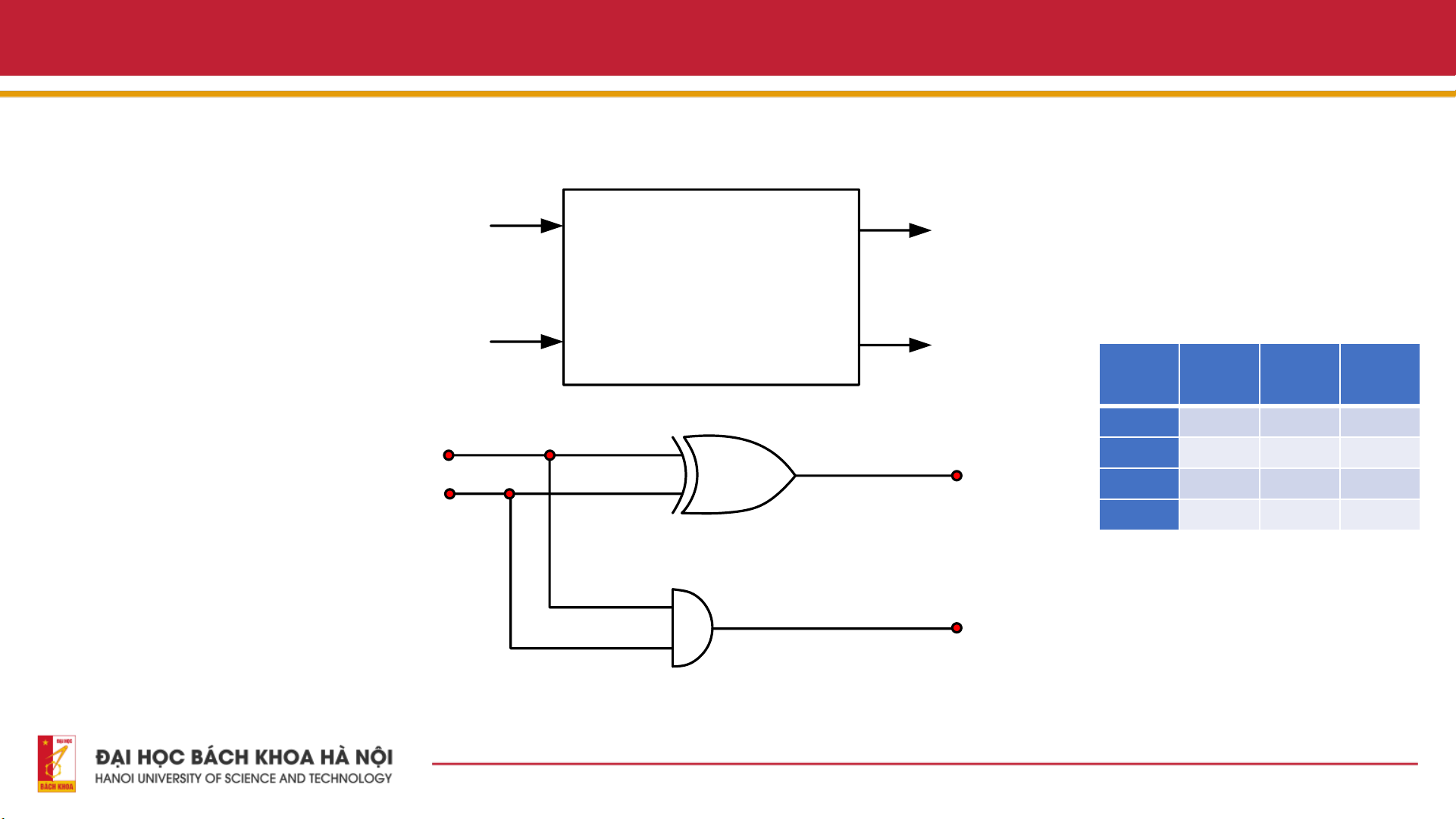
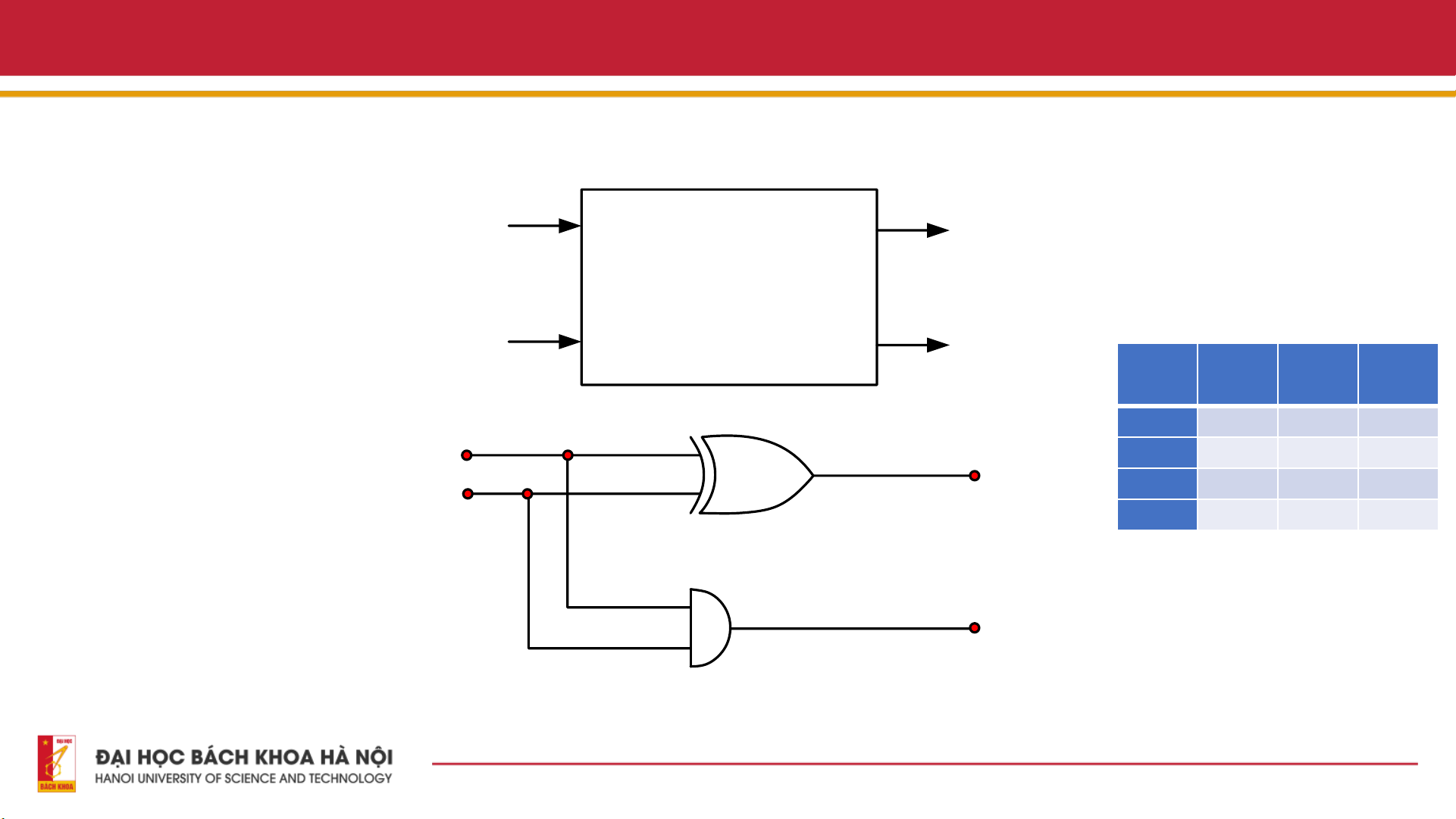
- Thiết kế mạch số là nền tảng
của điện tử hiện đại, và việc
triển khai các mạch số học cơ A Sum bản như Half Adder, Full Adder và cổng NAND đóng Input Mạch bán cộng output
vai trò nền tảng trong lĩnh vực
Bảng sự thật của bộ bán cộng này. B Carry out A B SUM CARR - Các mạch nền tảng cho Y
các phép tính số học trong 0 0 0 0 1
hệ thống số là mạch bán A 4 0 1 1 0 Sum 2 1 0 1 0
cộng và mạch toàn cộng. B Cổng XOR 1 1 0 1
Mạch toàn cộng mở rộng
chức năng này để tính đến 1 phép nhớ, cho phép cộng 3 Carry out
nhiều bit. Mạch bán cộng 2 Cổng AND
tính toán tổng và phép nhớ
của hai chữ số nhị phân.
Sơ đồ khối và sơ đồ mạch của bộ cộng nửa 15
4.1. Thiết kế mạch Adder
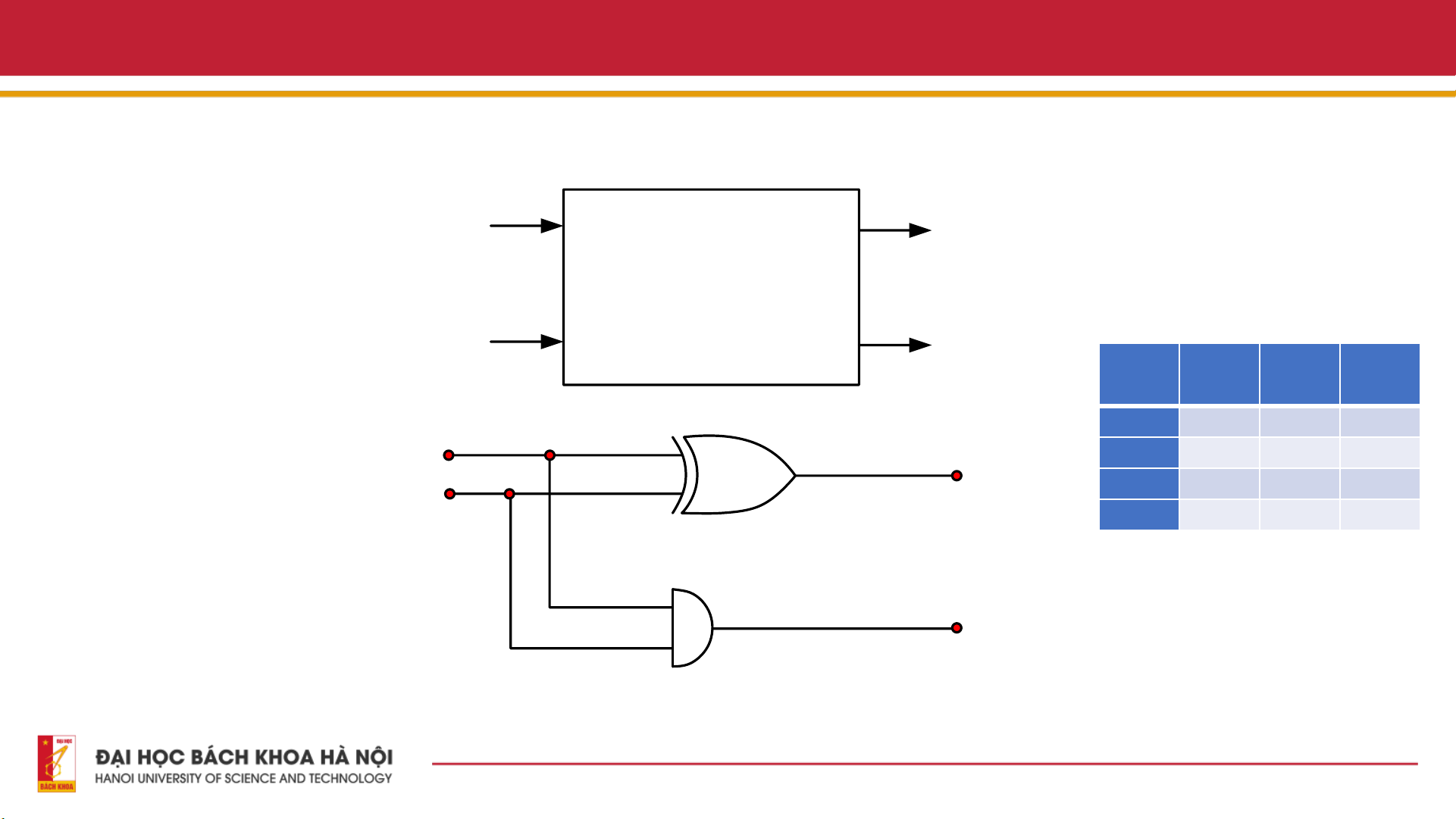
- Mạch bán cộng là một mạch
logic số thực hiện phép cộng nhị A Sum
phân của hai số nhị phân một bit.
Mạch có hai đầu vào, A và B, và Input Mạch bán cộng output
hai đầu ra, SUM và CARRY. Đầu
Bảng sự thật của bộ bán cộng
ra SUM là bit có trọng số thấp B Carry out A B SUM CARR
nhất (LSB) của kết quả, trong khi Y
đầu ra CARRY là bit có trọng số 0 0 0 0
cao nhất (MSB) của kết quả, cho 1 A 4 0 1 1 0
biết liệu có sự chuyển tiếp từ phép Sum 2 1 0 1 0 B
cộng hai đầu vào hay không. Cổng XOR 1 1 0 1
Mạch bán cộng có thể được thực
hiện bằng cách sử dụng các cổng 1 cơ bản như cổng 3 XOR và cổng Carry out 2 AND. Cổng AND
Sơ đồ khối và sơ đồ mạch của bộ cộng nửa 16
4.1. Thiết kế mạch Adder
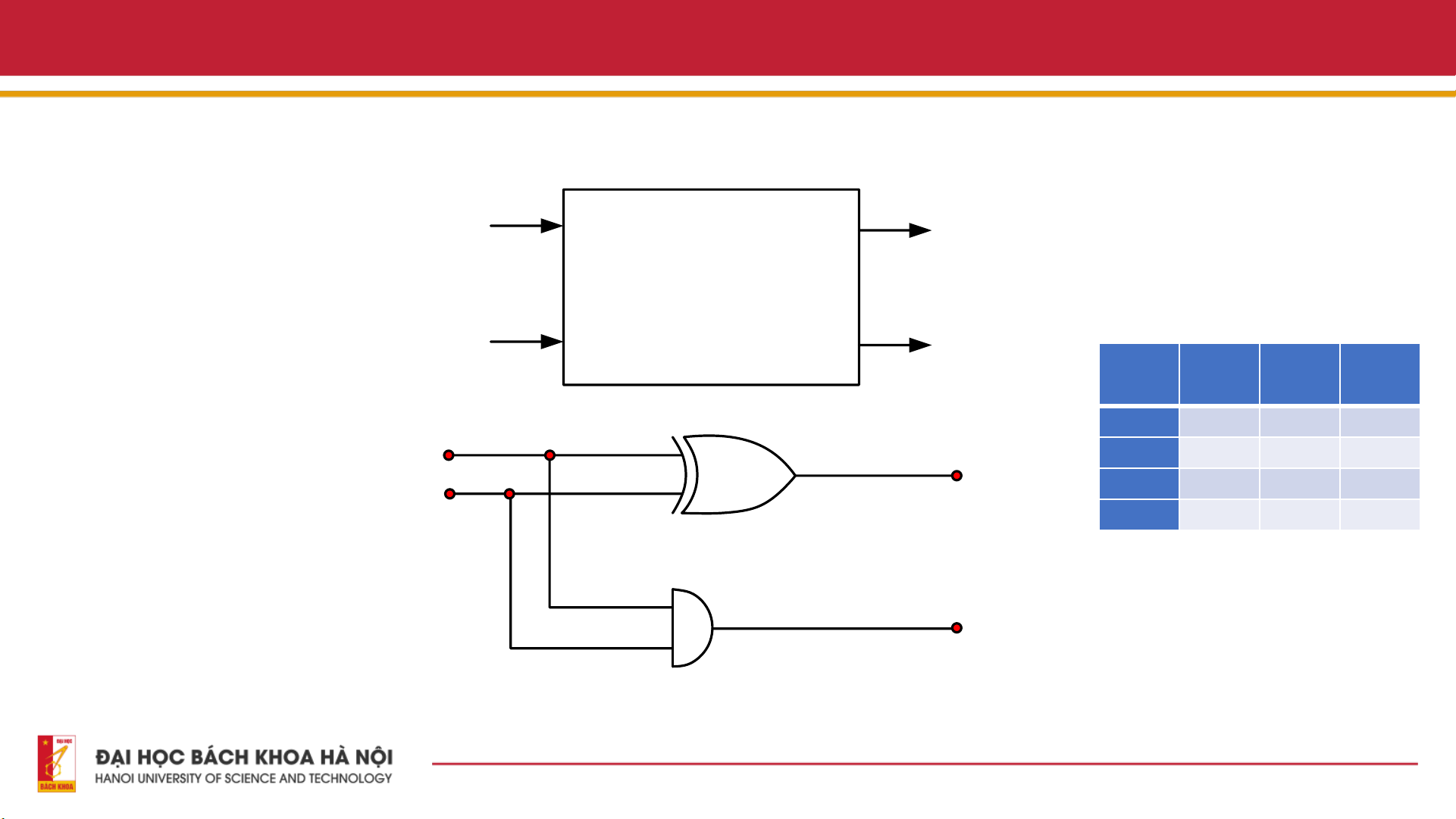
- Bộ bán cộng là một khối xây
dựng cơ bản cho các mạch
cộng phức tạp hơn như bộ A Sum
cộng đầy đủ và bộ cộng nhiều
bit. Nó thực hiện phép cộng Input Mạch bán cộng output
nhị phân của hai đầu vào một
Bảng sự thật của bộ bán cộng B Carry out
bit, A và B, và cung cấp hai A B SUM CARR đầu Y ra, SUM và CARRY. Đầu 0 0 0 0
ra SUM là bit có trọng số thấp 1 A 4 0 1 1 0
nhất (LSB) của kết quả, tức là Sum 2 1 0 1 0 B
phép XOR của hai đầu vào A Cổng XOR 1 1 0 1
và B. Cổng XOR thực hiện
phép cộng cho các chữ số nhị 1 3
phân, trong đó "1" chỉ được Carry out 2 tạo Cổng AND ra ở đầu ra SUM khi một
trong các đầu vào là "1".
Sơ đồ khối và sơ đồ mạch của bộ cộng nửa 17
4.1. Thiết kế mạch Adder
- Ngõ ra CARRY là bit có ý nghĩa
nhất (MSB) của kết quả, cho biết liệu
có sự chuyển tiếp từ phép cộng của
hai đầu vào hay không. Ngõ ra A Sum
CARRY là AND của hai đầu vào A Input Mạch bán cộng output
và B. Cổng AND chỉ tạo ra số "1"
Bảng sự thật của bộ bán cộng
trong ngõ ra CARRY khi cả hai đầu B Carry out A B SUM CARR
vào đều là "1". Mạch cộng bán phần Y
là mạch số học tổ hợp cộng hai số và 0 0 0 0
tạo ra một bit tổng (s) và một bit nhớ 1 A 4 0 1 1 0
(c) ở đầu ra. Phép cộng 2 bit được Sum 2 1 0 1 0 B
thực hiện bằng một mạch tổ hợp gọi Cổng XOR 1 1 0 1
là mạch cộng bán phần. Các biến đầu
vào là các bit tăng cường (augend 1
bit) và bit cộng, còn các biến đầu ra 3 Carry out 2
là các bit tổng và bit nhớ. A và B là Cổng AND hai bit đầu vào.
Sơ đồ khối và sơ đồ mạch của bộ cộng nửa 18
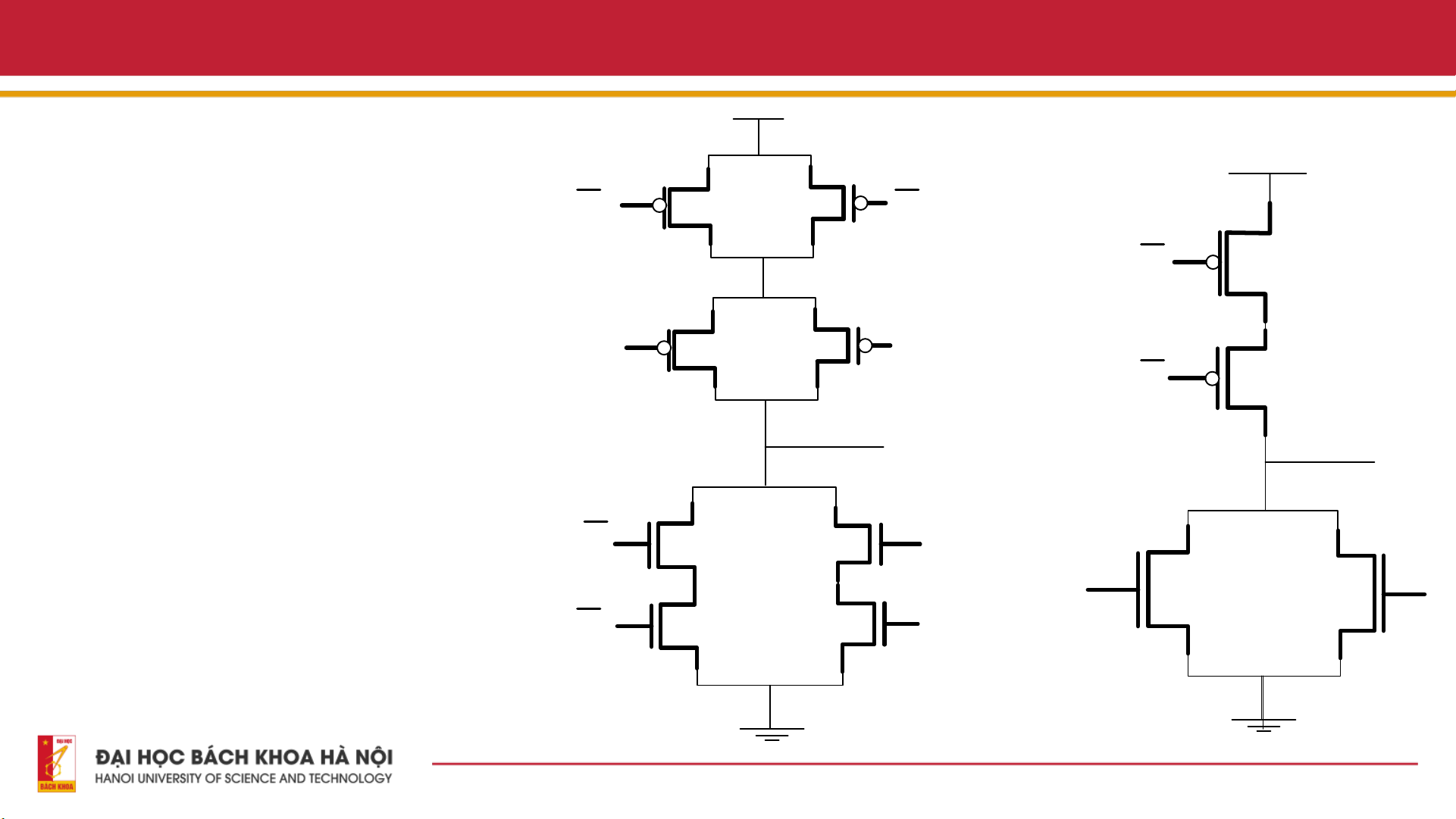
4.1. Thiết kế mạch Adder VDD VDD
- Mạch tích hợp số thường sử dụng công
nghệ CMOS tĩnh vì tính linh hoạt và mức A B
tiêu thụ điện năng thấp. Các transistor được cấu A
hình theo cách bổ sung để đạt
được chức năng logic trong việc triển
khai CMOS của các mạch này. A B B Sum u A A A B B B 19 THANK YOU ! 20