Chuyên đề đường tiệm cận của đồ thị hàm số từ cơ bản đến nâng cao

Tài liệu gồm 200 trang, được biên soạn bởi thầy giáo Huỳnh Văn Ánh, bao gồm lý thuyết, hệ thống bài tập trắc nghiệm và hệ thống bài tập tự luận chuyên đề đường tiệm cận của đồ thị hàm số từ cơ bản đến nâng cao.. Mời bạn đọc đón xem!

56 28 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

200 trang 1 tháng trước

Tác giả:

Profile Lê Phương
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 201
Sưu tầm và biên soạn
BÀI 3. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
I. Đường tiệm cận ngang
Cho hàm số
( )
y fx=
có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng
(, )a +∞
;
( ,)a−∞
;
(,)−∞ +∞
.Đường thẳng
0
yy=
được gọi là đường TCN (hay TCN) của
đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
0
lim ( )
x
fx y
→−∞
=
;
0
lim ( )
x
fx y
→+∞
=
Ví dụ. Tìm đường tiệm cận ngang của đồ thi hàm số
3
21
x
y
x
−
=
+
.
Lời giải
Tập xác định
1
\
2
D

= −


Ta có
và
31
lim
2 12
x
x
x
→−∞
−
=
+
Vậy đường tiệm cận ngang của đồ thị hàm số
3
21
x
y
x
−
=
+
là đường thẳng
1
2
y =
.
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT VÀ VẼ
ĐỒ THỊ CỦA HÀM SỐ
LÝ THUYẾT.
I
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 202
Sưu tầm và biên soạn
II. Đường tiệm cận đứng
Đường thẳng
0
xx=
được gọi là đường tiệm cận đứng
(TCĐ) của đồ thị hàm số
( )
y fx
=
nếu thỏa mãn ít nhất
một trong các điều kiện sau:
0
lim ( )
xx
fx
+
→
= +∞
;
0
lim ( )
xx
fx
+
→
= −∞
0
lim ( )
xx
fx
−
→
= +∞
;
0
lim ( )
xx
fx
−
→
= −∞
Lưu ý:
i) Hàm
ax b
y
cx d
+
=
+
với
0ac ≠
có tiệm cận đứng
d
x
c
= −
; tiệm cận ngang
a
y
c
=
.
ii) Hàm
(
)
( )
fx
y
gx
=
với
( ) ( )
,f x gx
là những hàm đa thức
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang
0y =
.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang
n
n
a
y
b
=
với
,
nn
ab
là hệ số của lũy thừa cao
nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
+)
0
xx=
là tiệm cận đứng
( ) ( )
( ) ( )
( )
( )
0
00
00
0; 0
0
lim
xx
gx f x
gx f x
fx
gx
→
= ≠
= =
⇔
= ±∞
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 203
Sưu tầm và biên soạn
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử
dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm:
Giới hạn
Thao tác trên máy tính
o
xx
+
→
CALC
10
10
o
x
−
+
o
xx
−
→
CALC
10
10
o
x
−
−
x → +∞
CALC
10
10
x → −∞
CALC
10
10−
Ví dụ 1: Tìm đường tiệm cận đứng của đồ thi hàm số
2
2
x
y
x
+
=
−
.
Lời giải
Tập xác định
{ }
\2D
=
Ta có
2
2
lim
2
x
x
x
+
→
+
= +∞
−
, suy ra đường tiệm cận đứng của đồ thị hàm số là
2x =
.
Ví dụ 2: Tìm đường tiệm cận đứng của đồ thi hàm số
34
21
x
y
x
+
=
−
.
Lời giải
Tập xác định
1
\
2
D

=


Ta có
1
2
34
lim
21
x
x
x
+

→


+
= +∞
−
, suy ra đường tiệm cận đứng của đồ thị hàm số là
1
2
x =
.
Lời bình: Đường tiệm cận đứng của đồ thị hàm số
ax b
y
cx d
+
=
+
là đường thẳng
d
x
c
= −
.
Ví dụ 3. Tìm đường tiệm cận đứng của đồ thi hàm số
2
2
1
2
xx
y
xx
−+
=
−−
.
Lời giải
Tập xác định
{ }
\ 2; 1
D = −
Ta có
2
2
2
1
lim
2
x
xx
xx
+
→
−+
= +∞
−−
,
2
2
1
1
lim
2
x
xx
xx
+
→−
−+
= −∞
−−
Vậy phương trình đường tiệm cận đứng của đồ thị hàm số là đường thẳng
2x =
và
1x = −
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 204
Sưu tầm và biên soạn
III. Đường tiệm cận xiên
Đường thẳng
y ax b= +
được gọi là một đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị
hàm số
(
)
y fx=
nếu
(
)
(
)
lim 0
x
f x ax b
→−∞
−+=


hoặc
(
)
( )
lim 0
x
f x ax b
→+∞
−+=


.
Đường thẳng
y ax b= +
là tiệm cận xiên của đồ thị hàm số
(
)
y fx=
được minh họa như sau
Để tìm tiệm cận xiên của đồ thị hàm số ta cần tính hệ số
,ab
trong phương trình của đường tiệm
cận xiên
y ax b= +
theo công thức như sau
+
( )
lim
x
fx
a
x
→+∞
=
,
( )
lim
x
b f x ax
→+∞
= −


hoặc
( )
lim
x
fx
a
x
→−∞
=
,
( )
lim
x
b f x ax
→−∞
= −


+ Khi
0a =
thì đồ thị của hàm số có tiệm cận ngang là đường thẳng
yb
=
.
Ví dụ. Tìm đường tiệm cận xiên của đồ thi hàm số
( )
2
31
2
xx
fx
x
−+
=
−
.
Lời giải
Tập xác định
{ }
\2D
=
.
Ta có
( )
( )
22
2
31 31
lim lim lim 1
22
xx x
fx
xx xx
a
x xx x x
→+∞ →+∞ →+∞
−+ −+
= = = =
−−
.
Ta có
( )
( )
2
2
22
31
lim lim
2
31 2
31 2
lim lim
22
xx
xx
xx
b f x ax x
x
x x xx
xx xx
xx
→+∞ →+∞
→+∞ →+∞

−+
= −= −



−


− +− −

− +− +
= =


−−


1
lim 1
2
x
x
x
→+∞
−+

= = −

−

Vậy đường tiệm cận xiên là
1yx= −
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 205
Sưu tầm và biên soạn
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC
Câu 1: Cho hàm số
23
()
2
x
y fx
x
−
= =
+
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()y fx=
.
Câu 2: Cho hàm số
2
23
()
2
xx
y fx
x
+−
= =
+
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số
()y fx=
.
Câu 3: Cho hàm số
2
23
()
2
xx
y fx
x
−+ +
= =
+
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số
()y fx=
.
Câu 4: Cho hàm số
2
6
()
2
xx
y fx
x
−−
= =
−
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ
thị hàm số
()
y fx=
.
Câu 5: Cho hàm số
2
6
()
1
xx
y fx
x
+−
= =
+
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 6: Cho hàm số
2
6
()
1
xx
y fx
x
− ++
= =
−
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA
HÀM SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
Câu 7: Cho hàm số
()y fx=
có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
()y fx=
.
Câu 8: Cho hàm số
()fx
có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số
1
()
y
fx
=
?
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 206
Sưu tầm và biên soạn
Câu 9: Cho hàm số
(
)
y fx
=
xác định, liên tục trên
{ }
\1
và có bảng biến thiên như sau:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho?
Câu 10: Cho hàm số
()
y fx=
xác định trên
{
}
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang?
Câu 11: Cho hàm số
()y fx=
xác định trên
{ }
\1
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tìm các giá trị nguyên của
[
)
0;5
m ∈
để đồ thị hàm số
( )
y fx
=
có 3 đường tiệm cận đứng
và ngang?
Câu 12: Cho hàm số
()fx
có đồ thị như hình vẽ bên.
Tìm phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số trên.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 207
Sưu tầm và biên soạn
Câu 13: Cho đồ thị hàm số
(
)
y fx
=
như hình bên. Đồ thị có bao nhiêu đường tiệm cận đứng và tiệm
cận ngang?
Câu 14: Cho hàm số
(
)
y fx
=
có đồ thị như hình vẽ.
Phương trình đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là?
Câu 15: Cho hàm số
(
)
y fx=
có đồ thị như hình vẽ.
Phương trình đường tiệm cận xiên của đồ thị hàm số là?
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 208
Sưu tầm và biên soạn
Câu 16: Tìm tiệm cận xiên của đồ thị hàm số
2
22
1
xx
y
x
−+
=
−
DẠNG 3: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ HÀM HỢP
Các dạng trong chủ đề: Cho hàm số
( )
y fx=
biết bảng biến thiên hoặc đồ thị. Tìm các đường
tiệm cận đứng và tiệm cận ngang của đồ thị
( )
y gx=
thuộc một trong các dạng sau
1)
(
)
()
y f ux=
,
2)
( )
()y g fx=
,
3)
( )
(u( ))y gf x=
,
4)
( )
, ()y gxfx=
,
5)
( )
, (u(x))y gxf=
.
Phương pháp giải: Gọi
( )
G
là đồ thị hàm số
( )
y gx=
.
1)Tìm tiệm cận ngang.
Xét hàm số dạng
( )
()
()
ux
gx
vx
=
.Một dấu hiệu thường dùng để nhận biết
( )
G
có tiệm cận ngang:
+ Hàm số
( )
y gx=
xác định trên
( )
;a +∞
hoặc trên
( )
;a−∞
.
+ Bậc của
(x)u
≤
Bậc của
(x)
v
.
+
0
lim ( )
x
gx y
→+∞
=
hoặc
0
lim ( )
x
gx y
→−∞
=
⇒
Đường thẳng
0
yy
=
là tiệm cận ngang của
( )
G
.
2)Tìm tiệm cận đứng.
Xét dạng hàm số
( )
()
()
ux
gx
vx
=
. Một dấu hiệu thường dùng để nhận biết đường thẳng
0
xx=
là
tiệm cận đứng của
( )
G
:
+
0
()0vx =
và
0
()0ux
≠
,
( )
gx
xác định trên
( )
0
;ax
hoặc
( )
0
;xb
.
+ Ít nhất một trong hai giới hạn
( ) ( )
00
lim , lim
xx xx
gx gx
+−
→→
là giới hạn vô cực.
⇒
Đường thẳng
0
xx=
là tiệm cận đứng của
( )
G
.
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số
( )
y fx=
.
Câu 17: Cho hàm số
( )
y fx=
có bảng biến thiên như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
21
y
fx
=
−
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 209
Sưu tầm và biên soạn
Câu 18: Cho hàm số
( )
y fx=
liên tục trên
\1
và có bảng biến thiên như sau
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
1
()
23
y gx
fx
= =
−
Câu 19: Cho hàm số
(
) (
)
32
,,,f x ax bx cx d a b c d R= + ++ ∈
có đồ thị như hình vẽ.
Đồ thị hàm số
(
)
(
)
(
)
( )
( )
22
2
43
2
++ +
=
−
x x xx
gx
fx fx
có bao nhiêu đường tiệm cận đứng?
Câu 20: Cho đồ thị hàm đa thức bậc bốn
()y fx=
như hình vẽ bên dưới.
Hỏi đồ thị của hàm số
( )
62 2
2
( 1)( 5 ). 2
()
() 2 () 2 10
x x xx x
gx
f x fx x
+− −
=

−−

có bao nhiêu đường tiệm cận đứng và
tiệm cận ngang.
Câu 21: Cho hàm số
( )
32
f x ax bx cx d= + ++
là hàm số đa thức với hệ số thực, có đồ thị
()C
như hình
vẽ bên.
Tìm số tiệm cận đứng của đồ thị hàm số
( )
( )
( ) ( ) ( )
2
2
32 1
1
xx x
gx
x f x fx
−+ −
=

+−

.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 210
Sưu tầm và biên soạn
Câu 22: Cho hàm số bậc ba
()y fx=
có đồ thị như hình vẽ bên.
Tìm số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
2
( 1)( 1)
()
() 2 ()
xx
y gx
f x fx
+−
= =
−
.
Câu 23: Cho hàm số
( )
32
y f x ax bx cx d= = + ++
,
( )
0a ≠
có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
(
)
( )
( )
(
)
(
)
(
)
2
2
2
23xx x
y gx
x x fx fx
+−
= =

−+

.
Câu 24: Cho hàm số bậc ba
()y fx=
có đồ thị như hình vẽ bên.
Tìm số đường tiệm cận đứng của đồ thị hàm số
2
()
() 1
x
y gx
fx
+
= =
+
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 211
Sưu tầm và biên soạn
Câu 25: Cho hàm số
(
)
y fx
=
liên tục trên
\1
và có bảng biến thiên như sau
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
2
22y gx f x x= = −−
.
Câu 26: Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình
dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
2
1
x
y gx f
x
−

= =

+

Câu 27: Cho hàm số
(
)
y fx=
là hàm đa thức liên tục trên
và có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
( )
(
)
1
fx
y gx
fx
= =
−
.
Câu 28: Cho hàm số
( )
y fx=
xác định, liên tục trên
và có bảng biến thiên như sau:
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 212
Sưu tầm và biên soạn
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
( )
( )
3
3
11
=
++ −
gx
fx x
.
DẠNG 3: MỘT SỐ BÀI TOÁN VỀ TIỆM CẬN CHỨA THAM SỐ
Câu 29: Tìm các giá trị thực của tham số
m
để đồ thị hàm số
7
1
mx
y
mx
+
=
−
có tiệm cận đứng đi qua điểm
( )
1; 2A −
.
Câu 30: Tìm các giá trị thực của tham số
m
để đồ thị hàm số
( )
2
2x
fx
x xm
−
=
++
có ba đường tiệm cận.
Câu 31: Tìm tham số m để đồ thì hàm số
( 1) 5
2
m xm
y
xm
+−
=
−
có tiệm cận ngang là đường thẳng
1
y =
.
Câu 32: Tìm các tham số
m
để đồ thị hàm số
2
1
4
x
y
x mx
−
=
++
có đúng hai đường tiệm cận?
Câu 33: Cho hàm số
2
1
mx m
y
x
+
=
−
. Với giá trị nào của
m
thì đường tiệm cận đứng, tiệm cận ngang của
đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là 8?
Câu 34: Biết đồ thị
(
)
C
của hàm số
ax b
y
cx d
+
=
+
đi qua điểm
(
)
1; 7
A −
và giao điểm hai tiệm cận của
( )
C
là điểm
( )
2;3I −
. Biết
c
là số nguyên dương và
a, c
là các số nguyên tố cùng nhau. Tìm các số
,,,abcd
.
Câu 35: Cho hàm số
2
34
xm
y
xx
−
=
+−
. Giá trị nào của
m
để đồ thị hàm số đã cho có đúng 1 tiệm cận đứng?
Câu 36: Cho hàm số
2xm
y
xm
+
=
−
. Tìm tất cả các giá trị của
m
để đồ thị hàm số có 2 đường tiệm cận cùng
với hai trục tọa độ tạo thành một hình vuông
Câu 37: Cho hàm số
2
1
24
x
y
x mx
−
=
−+
. Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số có
đúng ba đường tiệm cận.
Câu 38: Biết rằng đồ thị hàm số
1
2
ax
y
bx
có tiệm cận đứng là
2x
và tiệm cận ngang là
3y
. Tìm
,
ab
.
Câu 39: Tính tổng bình phương tất cả các giá trị của
m
để đồ thị hàm số
2
2 35 6y x x mx= − ++ −
có tiệm cận ngang.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 1
Sưu tầm và biên soạn
BÀI 3. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
I. Đường tiệm cận ngang
Cho hàm số
( )
y fx=
có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng
(, )a +∞
;
( ,)a−∞
;
(,)−∞ +∞
.Đường thẳng
0
yy=
được gọi là đường TCN (hay TCN) của
đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
0
lim ( )
x
fx y
→−∞
=
;
0
lim ( )
x
fx y
→+∞
=
Ví dụ. Tìm đường tiệm cận ngang của đồ thi hàm số
3
21
x
y
x
−
=
+
.
Lời giải
Tập xác định
1
\
2
D

= −


Ta có
và
31
lim
2 12
x
x
x
→−∞
−
=
+
Vậy đường tiệm cận ngang của đồ thị hàm số
3
21
x
y
x
−
=
+
là đường thẳng
1
2
y =
.
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT VÀ VẼ
ĐỒ THỊ CỦA HÀM SỐ
LÝ THUYẾT.
I
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 2
Sưu tầm và biên soạn
II. Đường tiệm cận đứng
Đường thẳng
0
xx=
được gọi là đường tiệm cận đứng
(TCĐ) của đồ thị hàm số
( )
y fx
=
nếu thỏa mãn ít nhất
một trong các điều kiện sau:
0
lim ( )
xx
fx
+
→
= +∞
;
0
lim ( )
xx
fx
+
→
= −∞
0
lim ( )
xx
fx
−
→
= +∞
;
0
lim ( )
xx
fx
−
→
= −∞
Lưu ý:
i) Hàm
ax b
y
cx d
+
=
+
với
0ac ≠
có tiệm cận đứng
d
x
c
= −
; tiệm cận ngang
a
y
c
=
.
ii) Hàm
(
)
( )
fx
y
gx
=
với
( ) ( )
,f x gx
là những hàm đa thức
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang
0y =
.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang
n
n
a
y
b
=
với
,
nn
ab
là hệ số của lũy thừa cao
nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
+)
0
xx=
là tiệm cận đứng
( ) ( )
( ) ( )
( )
( )
0
00
00
0; 0
0
lim
xx
gx f x
gx f x
fx
gx
→
= ≠
= =
⇔
= ±∞
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 3
Sưu tầm và biên soạn
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử
dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm:
Giới hạn
Thao tác trên máy tính
o
xx
+
→
CALC
10
10
o
x
−
+
o
xx
−
→
CALC
10
10
o
x
−
−
x → +∞
CALC
10
10
x → −∞
CALC
10
10−
Ví dụ 1: Tìm đường tiệm cận đứng của đồ thi hàm số
2
2
x
y
x
+
=
−
.
Lời giải
Tập xác định
{ }
\2D
=
Ta có
2
2
lim
2
x
x
x
+
→
+
= +∞
−
, suy ra đường tiệm cận đứng của đồ thị hàm số là
2x =
.
Ví dụ 2: Tìm đường tiệm cận đứng của đồ thi hàm số
34
21
x
y
x
+
=
−
.
Lời giải
Tập xác định
1
\
2
D

=


Ta có
1
2
34
lim
21
x
x
x
+

→


+
= +∞
−
, suy ra đường tiệm cận đứng của đồ thị hàm số là
1
2
x =
.
Lời bình: Đường tiệm cận đứng của đồ thị hàm số
ax b
y
cx d
+
=
+
là đường thẳng
d
x
c
= −
.
Ví dụ 3. Tìm đường tiệm cận đứng của đồ thi hàm số
2
2
1
2
xx
y
xx
−+
=
−−
.
Lời giải
Tập xác định
{ }
\ 2; 1D = −
Ta có
2
2
2
1
lim
2
x
xx
xx
+
→
−+
= +∞
−−
,
2
2
1
1
lim
2
x
xx
xx
+
→−
−+
= −∞
−−
Vậy phương trình đường tiệm cận đứng của đồ thị hàm số là đường thẳng
2x =
và
1x = −
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 4
Sưu tầm và biên soạn
III. Đường tiệm cận xiên
Đường thẳng
y ax b= +
được gọi là một đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị
hàm số
(
)
y fx=
nếu
( ) ( )
lim 0
x
f x ax b
→−∞
−+=


hoặc
( ) ( )
lim 0
x
f x ax b
→+∞
−+=


.
Đường thẳng
y ax b= +
là tiệm cận xiên của đồ thị hàm số
( )
y fx=
được minh họa như sau
Để tìm tiệm cận xiên của đồ thị hàm số ta cần tính hệ số
,ab
trong phương trình của đường tiệm
cận xiên
y ax b
= +
theo công thức như sau
+
( )
lim
x
fx
a
x
→+∞
=
,
( )
lim
x
b f x ax
→+∞
= −


hoặc
( )
lim
x
fx
a
x
→−∞
=
,
(
)
lim
x
b f x ax
→−∞
= −


+ Khi
0a =
thì đồ thị của hàm số có tiệm cận ngang là đường thẳng
yb
=
.
Ví dụ. Tìm đường tiệm cận xiên của đồ thi hàm số
( )
2
31
2
xx
fx
x
−+
=
−
.
Lời giải
Tập xác định
{ }
\2D =
.
Ta có
( )
( )
22
2
31 31
lim lim lim 1
22
xx x
fx
xx xx
a
x xx x x
→+∞ →+∞ →+∞
−+ −+
= = = =
−−
.
Ta có
( )
( )
2
2
22
31
lim lim
2
31 2
31 2
lim lim
22
xx
xx
xx
b f x ax x
x
x x xx
xx xx
xx
→+∞ →+∞
→+∞ →+∞

−+
= −= −



−


− +− −

− +− +
= =


−−


1
lim 1
2
x
x
x
→+∞
−+

= = −

−

Vậy đường tiệm cận xiên là
1yx= −
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 5
Sưu tầm và biên soạn
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC
Câu 1: Cho hàm số
23
()
2
x
y fx
x
−
= =
+
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị
hàm số
()y fx=
.
Lời giải
Vì
lim 2; lim 2
xx
yy
→−∞ →+∞
= =
nên đồ thị hàm số có 1 tiệm cận ngang là
2
y =
.
Vì
22
lim ; lim
xx
yy
+−
→− →−
= −∞ = +∞
nên đồ thị hàm số có 1 tiệm cận đứng
2
x
= −
.
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 2: Cho hàm số
2
23
()
2
xx
y fx
x
+−
= =
+
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số
()y fx
=
.
Lời giải
Ta có
( )
( )
( )
( )
2
2
23
lim lim 1
2
23 3
lim lim lim 0
22
xx
xx x
fx
xx
a
x xx
xx
b fx x x
xx
→−∞ →−∞
→−∞ →−∞ →−∞
+−
= = =
+

+− −
= −= −= =



++

Vậy đường thẳng
yx=
là tiệm cận xiên của đồ thị hàm số đã cho khi
x → −∞
.
Ta lại có
( )
( )
( )
( )
2
2
23
lim lim 1
2
23 3
lim lim lim 0
22
xx
xx x
fx
xx
a
x xx
xx
b fx x x
xx
→+∞ →+∞
→+∞ →+∞ →+∞
+−
= = =
+

+− −
= −= −= =



++

Vậy đường thẳng
yx=
là tiệm cận xiên của đồ thị hàm số đã cho khi
x → +∞
.
Ta có:
22
lim ; lim
xx
yy
+−
→− →−
= −∞ = +∞
nên đồ thị hàm số có 1 tiệm cận đứng
2x = −
.
Câu 3: Cho hàm số
2
23
()
2
xx
y fx
x
−+ +
= =
+
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số
()y fx=
.
Lời giải
Ta có
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 6
Sưu tầm và biên soạn
( )
( )
( )
( )
2
2
2
23
1
23
lim lim lim 1
2
2
1
3
4
23 43
lim lim lim lim 4
2
22
1
xx x
x x xx
fx
xx
xx
a
x xx
x
xx x
x
b fx x x
xx
x
→−∞ →−∞ →−∞
→−∞ →−∞ →−∞ →−∞
−+ +
−+ +
= = = = −
+
+
+

−+ + +
= += += = =



++

+
Vậy đường thẳng
4yx=−+
là tiệm cận xiên của đồ thị hàm số đã cho khi
x
→ −∞
.
Ta lại có
( )
( )
( )
( )
2
2
2
23
1
23
lim lim lim 1
2
2
1
3
4
23 43
lim lim lim lim 4
2
22
1
xx x
x x xx
fx
xx
xx
a
x xx
x
xx x
x
b fx x x
xx
x
→+∞ →+∞ →+∞
→+∞ →+∞ →+∞ →+∞
−+ +
−+ +
= = = = −
+
+
+

−+ + +
= += += = =



++

+
Vậy đường thẳng
4yx=−+
là tiệm cận xiên của đồ thị hàm số đã cho khi
x → +∞
.
Ta có:
22
lim ; lim
xx
yy
+−
→− →−
= −∞ = +∞
nên đồ thị hàm số có 1 tiệm cận đứng
2x = −
.
Câu 4: Cho hàm số
2
6
()
2
xx
y fx
x
−−
= =
−
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 5: Cho hàm số
2
6
()
1
xx
y fx
x
+−
= =
+
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Câu 6: Cho hàm số
2
6
()
1
xx
y fx
x
− ++
= =
−
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ
thị hàm số
()y fx=
.
Lời giải
Ta có
( )
( )
( )
( )
2
2
2
16
1
6
lim lim lim 1
1
1
1
6
66
lim lim lim lim 0
2
11
1
xx x
x x xx
fx
xx
xx
a
x xx
x
xx
x
b fx x x
xx
x
→−∞ →−∞ →−∞
→−∞ →−∞ →−∞ →−∞
−+ +
− ++
= = = = −
−
+

− ++
= += += = =



−−

+
Vậy đường thẳng
yx= −
là tiệm cận xiên của đồ thị hàm số đã cho khi
x → −∞
.
Ta lại có
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 7
Sưu tầm và biên soạn
( )
( )
( )
(
)
2
2
2
16
1
6
lim lim lim 1
1
1
1
6
66
lim lim lim lim 0
2
11
1
xx x
x x xx
fx
xx
xx
a
x xx
x
xx
x
b fx x x
xx
x
→+∞ →+∞ →+∞
→+∞ →+∞ →+∞ →+∞
−+ +
− ++
= = = = −
−
+

− ++
= += += = =



−−

+
Vậy đường thẳng
yx= −
là tiệm cận xiên của đồ thị hàm số đã cho khi
x → +∞
.
Ta có:
11
lim ; lim
xx
yy
+−
→→
= +∞ = −∞
nên đồ thị hàm số có 1 tiệm cận đứng
1x =
.
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA
HÀM SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
Câu 7: Cho hàm số
()y fx=
có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
()
y fx=
.
Lời giải
Vì
lim ; lim 3
xx
yy
→−∞ →+∞
= −∞ =
nên đồ thị hàm số có 1 tiệm cận ngang là
3y =
.
Vì
4
lim
xx
y
+
→
= +∞
nên đồ thị hàm số có 1 tiệm cận đứng
4
xx
=
.
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 8: Cho hàm số
()fx
có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số
1
()
y
fx
=
?
Lời giải
Vì
1
lim 0; lim
3
xx
yy
→−∞ →+∞
= =
nên đồ thị hàm số có 1 tiệm cận ngang
0
y =
và
1
3
y =
.
Từ bảng biến thiên, ta có
(x) 0f =
có hai nghiệm
2
xx=
và
( )
1
;xa x= ∈ −∞
.
Dễ thấy
lim
xa
y
+
→
= +∞
và
2
lim
xx
y
+
→
= +∞
nên đồ thị hàm số có 2 tiệm cận đứng là
2
xx=
và
xa=
Do đó đồ thị hàm số có tổng số 4 đường tiệm cận kể cả đứng và ngang.
Câu 9: Cho hàm số
( )
y fx=
xác định, liên tục trên
{ }
\1
và có bảng biến thiên như sau:
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Page 8
Sưu tầm và biên soạn
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho?
Lời giải
Tập xác định:
{ }
\1D =
.
Ta có
(
)
( )
lim 2; lim 2
xx
fx fx
→−∞ →+∞
= =
. Do đó
2
y =
là đường tiệm cận ngang của đồ thị hàm số.
Câu 10: Cho hàm số
()
y fx=
xác định trên
{
}
\0
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang?
Lời giải
Tập xác định:
{ }
\0D =
.
Ta có
(
)
lim
x
fx
→−∞
= +∞
;
(
)
lim
x
fx
→+∞
= −∞
do đó đồ thị hàm số không có tiệm cận ngang.
(
)
0
lim 0
x
fx x
+
→
= −∞ ⇒ =
là đường tiệm cận đứng duy nhất của đồ thị hàm số.
Câu 11: Cho hàm số
()y fx=
xác định trên
{ }
\1
, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như sau:
Tìm các giá trị nguyên của
[
)
0;5m ∈
để đồ thị hàm số
(
)
y fx=
có 3 đường tiệm cận đứng
và ngang?
Lời giải
Tập xác định
{ }
\1D =
. Ta có
( )
lim 2 2
x
fx y
→−∞
=⇒=
là đường tiệm cận ngang.
( )
1
lim 1
x
fx x
−
→
= −∞ ⇒ =
là tiệm cận đứng.
( )
lim
x
fx m y m
→+∞
=⇒=
là đường tiệm cận ngang.
| 1/200
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
ỨNG DỤNG ĐẠO HÀM NG ƯƠ
I ĐỂ KHẢO SÁT VÀ VẼ CH
ĐỒ THỊ CỦA HÀM SỐ
BÀI 3. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ I LÝ THUYẾT.
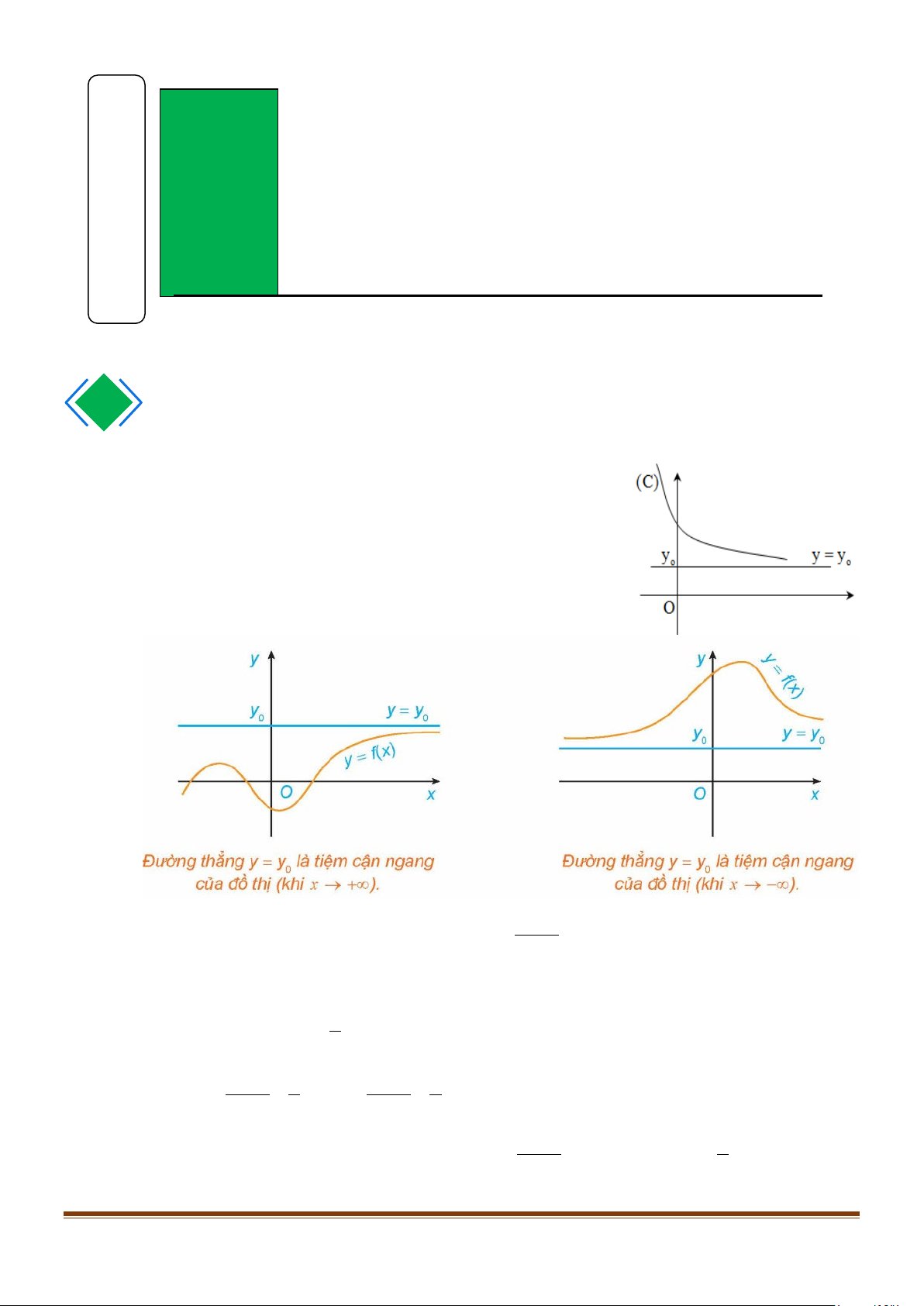
I. Đường tiệm cận ngang
Cho hàm số y = f (x) có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng (a,+∞) ; (−∞,a) ; (−∞,+∞)
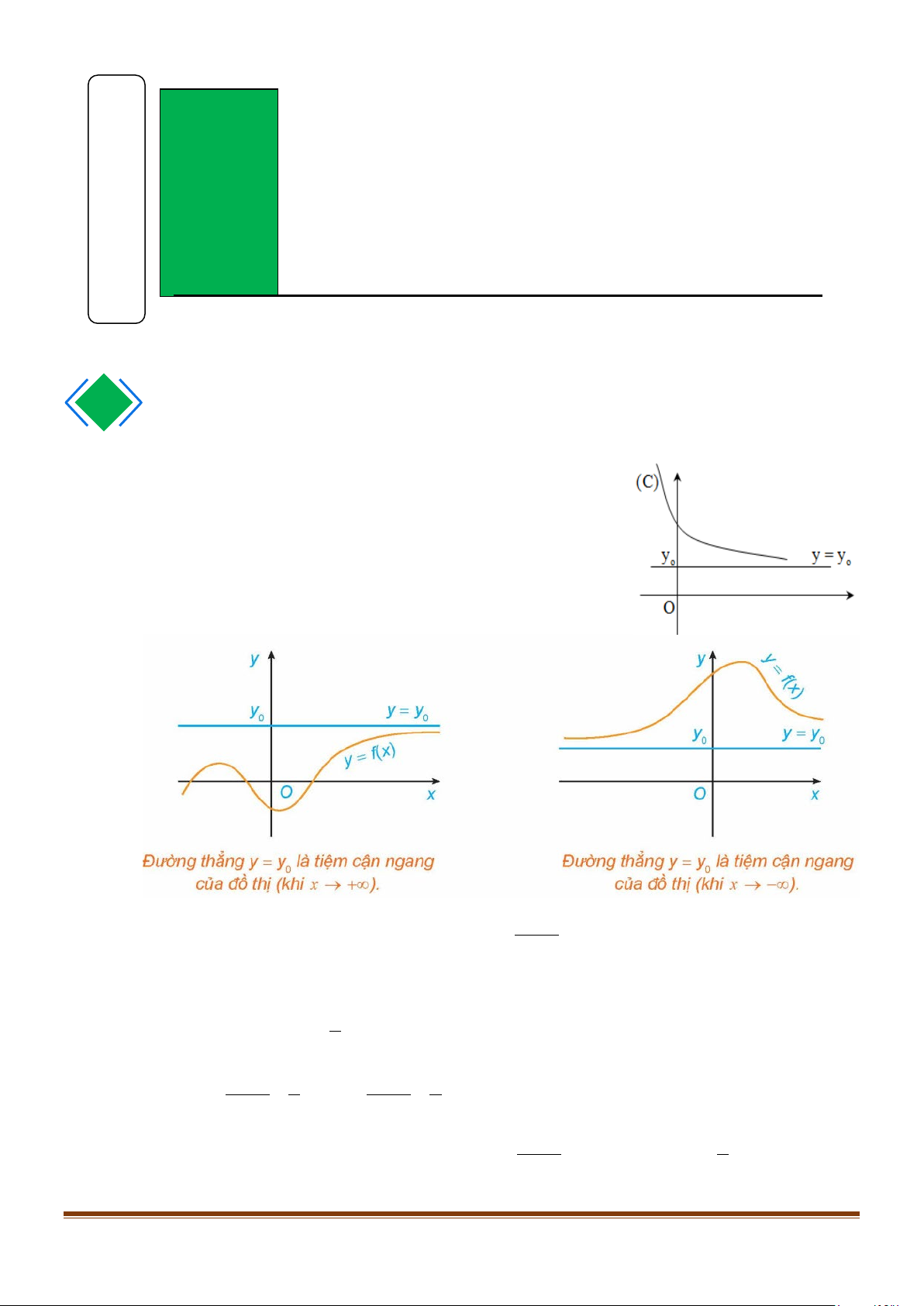
.Đường thẳng y = y được gọi là đường TCN (hay TCN) của 0
đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
lim f (x) = y ; lim f (x) = y 0 x→−∞ 0 x→+∞
Ví dụ. Tìm đường tiệm cận ngang của đồ thi hàm số x − 3 y = . 2x +1 Lời giải Tập xác định  1 D  \  = − 2   Ta có x − 3 1 lim − = và x 3 1 lim = x→+∞ 2x +1 2
x→−∞ 2x +1 2
Vậy đường tiệm cận ngang của đồ thị hàm số x − 3 y = là đường thẳng 1 y = . 2x +1 2 Page 201
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
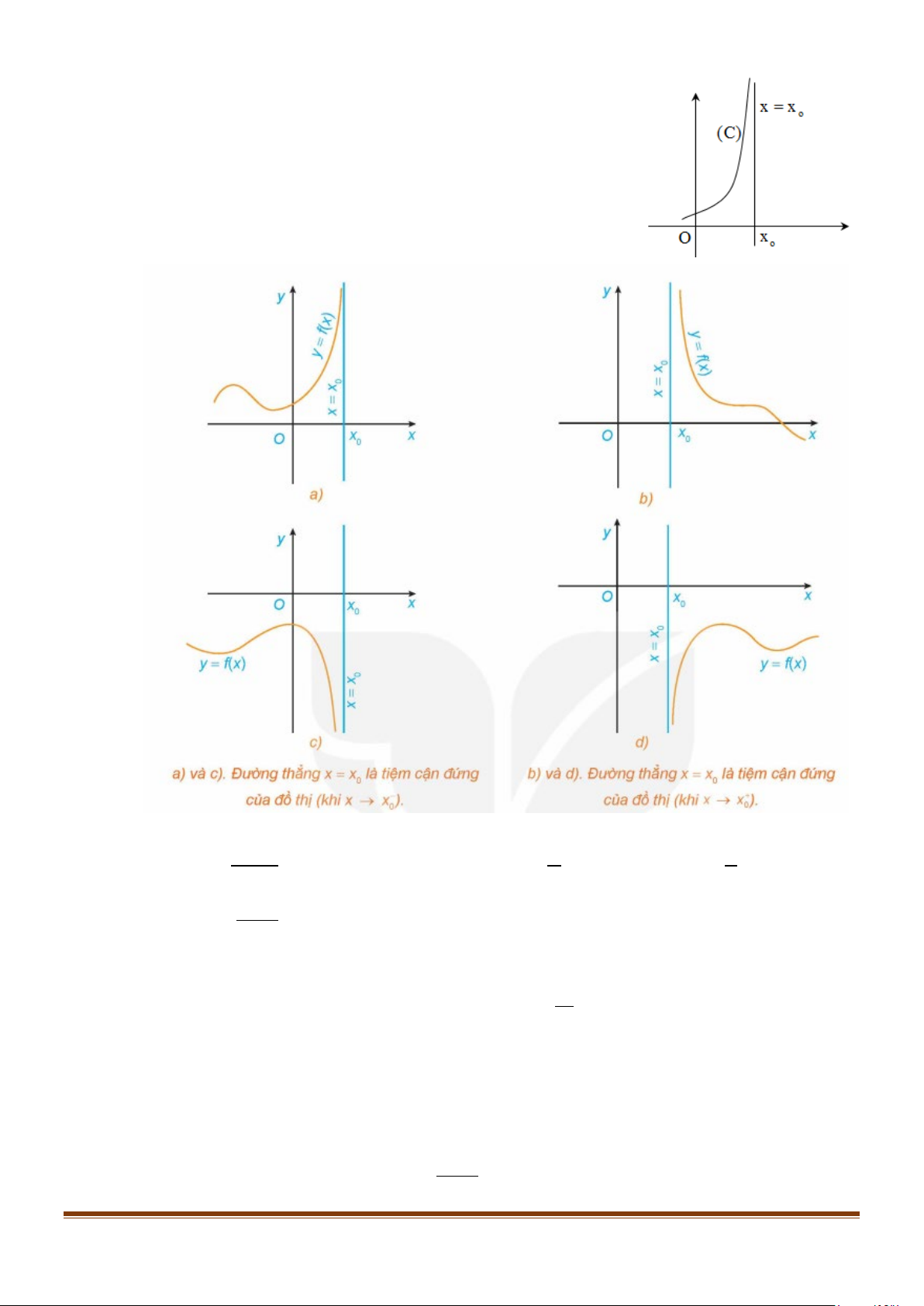
II. Đường tiệm cận đứng
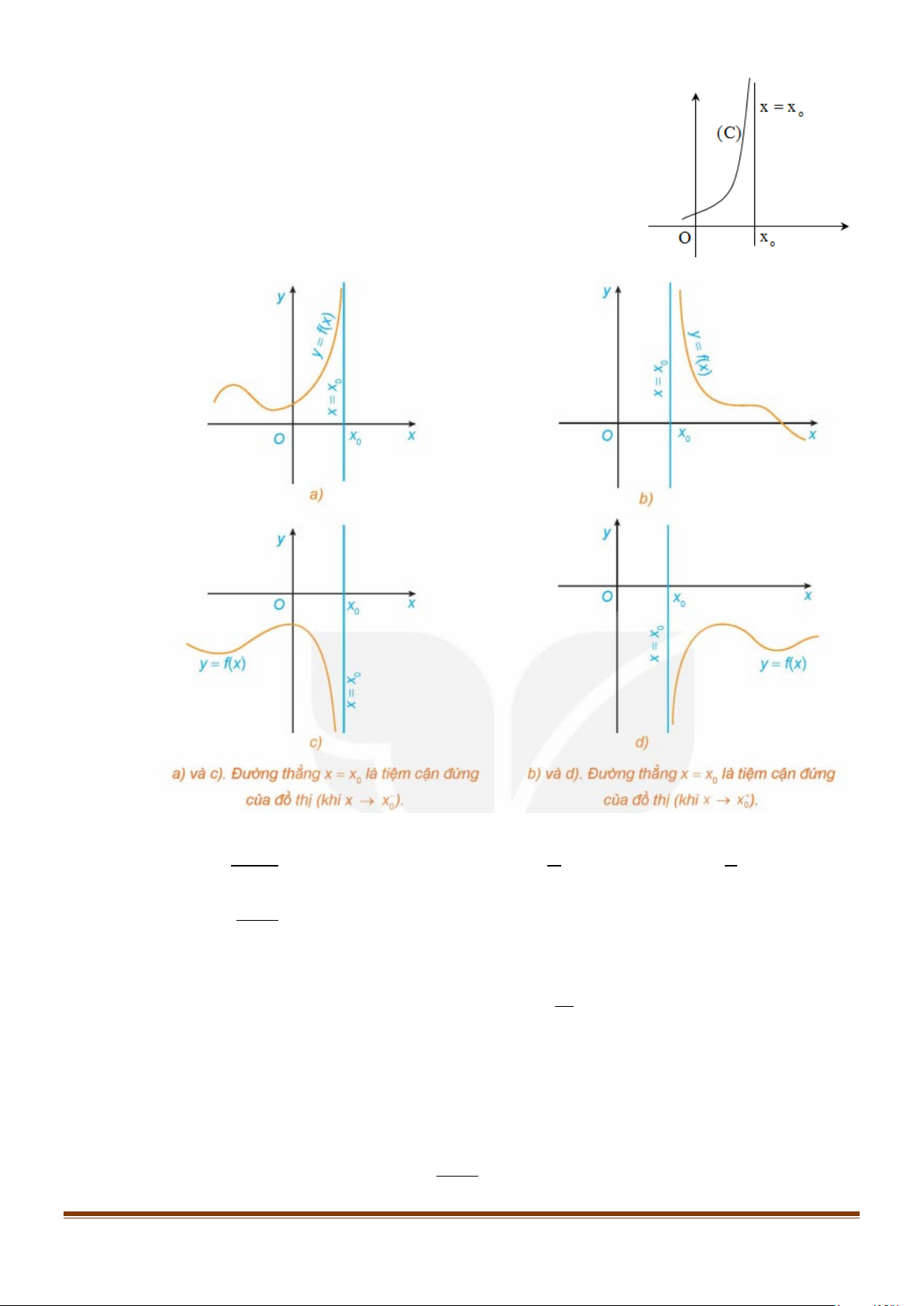
Đường thẳng x = x được gọi là đường tiệm cận đứng 0
(TCĐ) của đồ thị hàm số y = f (x) nếu thỏa mãn ít nhất
một trong các điều kiện sau:
lim f (x) = +∞ ; lim f (x) = −∞ x + → + 0 x x→ 0 x
lim f (x) = +∞ ; lim f (x) = −∞ x − → − 0 x x→ 0 xLưu ý: + i) Hàm ax b y =
với ac ≠ 0 có tiệm cận đứng d
x = − ; tiệm cận ngang a y = . cx + d c c f (x) ii) Hàm y =
với f (x), g (x) là những hàm đa thức g (x)
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang y = 0.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang an y =
với a b là hệ số của lũy thừa cao n , b n n
nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
g (x = 0; f x ≠ 0 0 ) ( 0)  
g ( x = f x = 0 0 ) ( 0)
+) x = x là tiệm cận đứng ⇔ . 0    f (x)  lim = ±∞  x→  0 x g   (x) Page 202
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm: Giới hạn
Thao tác trên máy tính x x+ → CALC 10 x − + o 10 o x x− → CALC 10 x − − o 10 o x → +∞ CALC 10 10 x → −∞ CALC 10 10 −
Ví dụ 1: Tìm đường tiệm cận đứng của đồ thi hàm số x + 2 y = . x − 2 Lời giải
Tập xác định D =  \{ } 2 Ta có x + 2 lim
= +∞ , suy ra đường tiệm cận đứng của đồ thị hàm số là x = 2 . x 2+ → x − 2
Ví dụ 2: Tìm đường tiệm cận đứng của đồ thi hàm số 3x + 4 y = . 2x −1 Lời giải Tập xác định 1 D  \  =  2   + Ta có 3x 4 lim
= +∞ , suy ra đường tiệm cận đứng của đồ thị hàm số là 1 x = . 1 +   − 2 → 2x 1 x  2   +
Lời bình: Đường tiệm cận đứng của đồ thị hàm số ax b y = là đường thẳng d x = − . cx + d c 2
Ví dụ 3. Tìm đường tiệm cận đứng của đồ thi hàm số x − x +1 y = . 2 x − x − 2 Lời giải
Tập xác định D =  \{2;− } 1 2 2 Ta có x − x +1 lim − + = +∞ , x x 1 lim = −∞ + 2
x→2 x − x − 2 + 2 x→ 1 − x − x − 2
Vậy phương trình đường tiệm cận đứng của đồ thị hàm số là đường thẳng x = 2 và x = 1 − . Page 203
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
III. Đường tiệm cận xiên
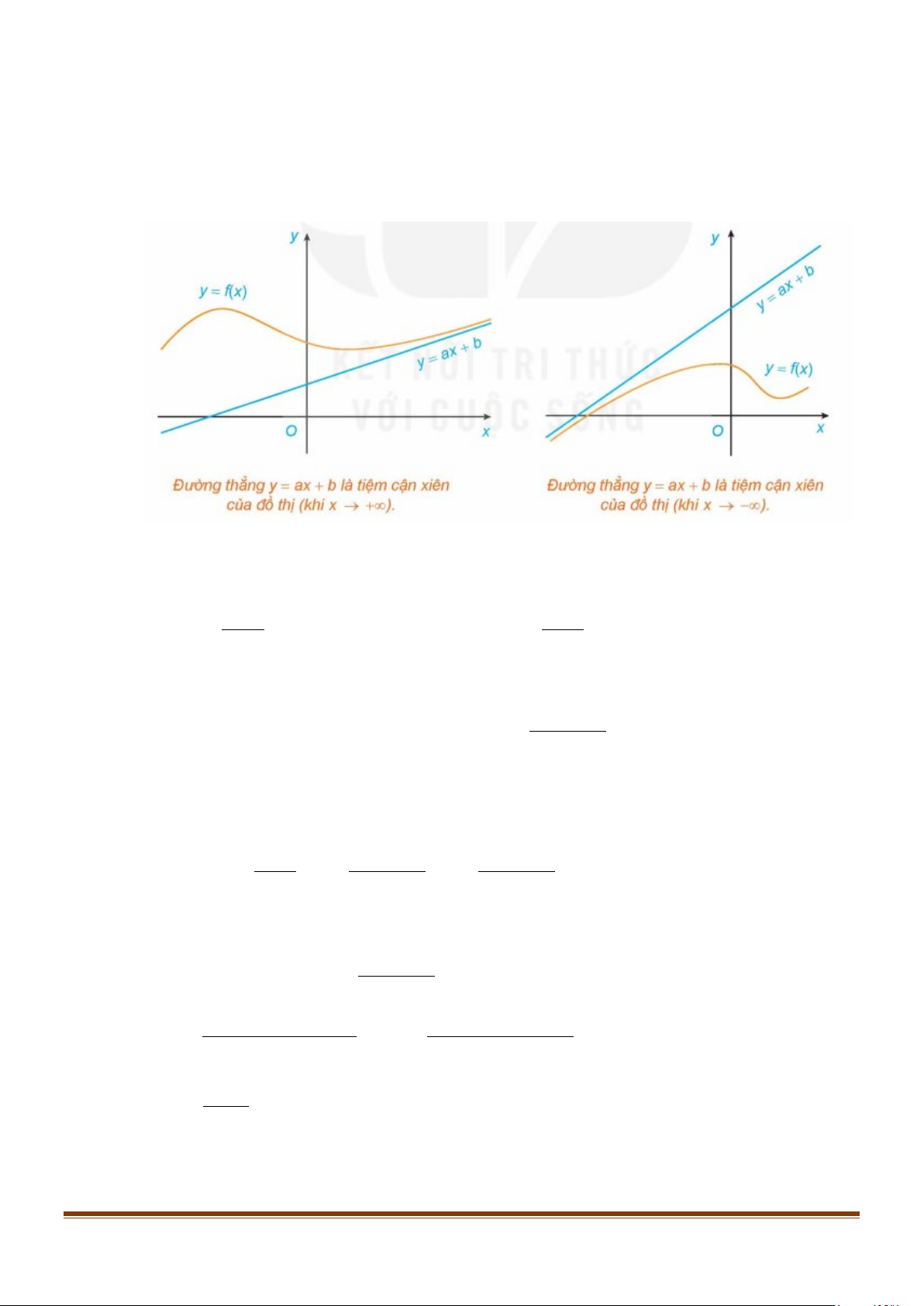
Đường thẳng y = ax + b được gọi là một đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị
hàm số y = f (x) nếu lim  f
 ( x) − (ax + b) = 0  hoặc lim  f
 ( x) − (ax + b) = 0  . x→−∞ x→+∞
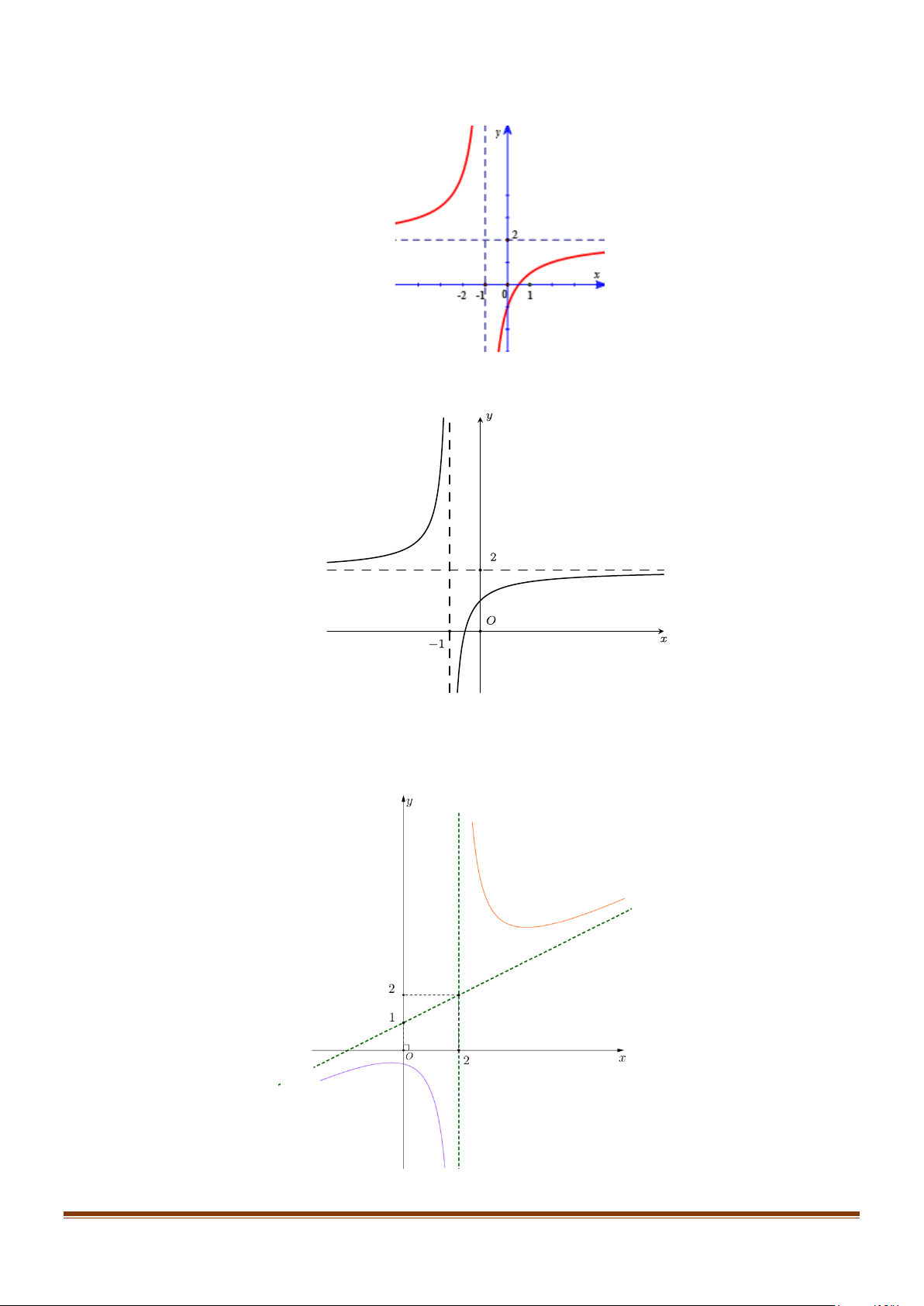
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y = f (x) được minh họa như sau
Để tìm tiệm cận xiên của đồ thị hàm số ta cần tính hệ số a,b trong phương trình của đường tiệm
cận xiên y = ax + b theo công thức như sau f (x) f (x) + a = lim
, b = lim  f (x) − ax   hoặc a = lim
, b = lim  f (x) − ax   x→+∞ x x→+∞ x→−∞ x x→−∞
+ Khi a = 0 thì đồ thị của hàm số có tiệm cận ngang là đường thẳng y = b. 2
Ví dụ. Tìm đường tiệm cận xiên của đồ thi hàm số f (x) x −3x +1 = . x − 2 Lời giải
Tập xác định D =  \{ } 2 . f (x) 2 2 Ta có x − 3x +1 x − 3x +1 a = lim = lim = = . x→+∞ x x
→+∞ x ( x − 2) lim 1 2 x→+∞ x − 2x Ta có 2  − +  b =  f  ( x) x 3x 1 lim − ax = lim   − xx→+∞ x→+∞  x − 2  2
x − 3x +1− x(x − 2) 2 2 
x − 3x +1− x + 2  = lim   = lim x   x→+∞  x − 2 x→+∞   x − 2   −x +1 lim  = = 1 −  
x→+∞  x − 2 
Vậy đường tiệm cận xiên là y = x −1. Page 204
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
II HỆ THỐNG BÀI TẬP TỰ LUẬN.
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC 2x −3
Câu 1: Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị x + 2
hàm số y = f (x) . 2 x + 2x − 3
Câu 2: Cho hàm số y = f (x) =
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số x + 2
y = f (x) . 2 −x + 2x + 3
Câu 3: Cho hàm số y = f (x) =
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số x + 2
y = f (x) . 2 − − Câu 4: x x 6
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ x − 2
thị hàm số y = f (x) . 2 + − Câu 5: x x 6
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ x +1
thị hàm số y = f (x) . 2 − + + Câu 6: x x 6
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ x −1
thị hàm số y = f (x) .
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA
HÀM SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
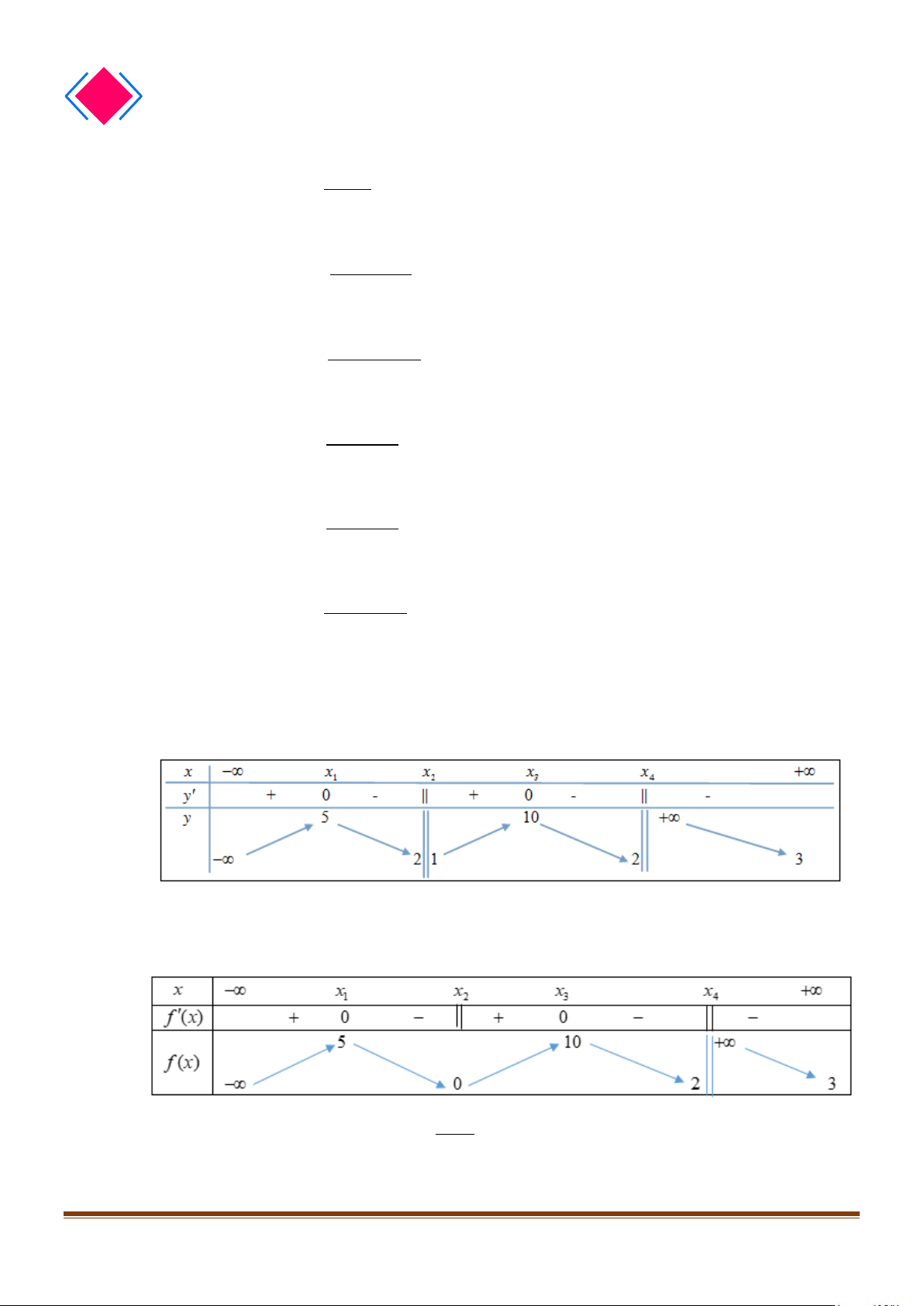
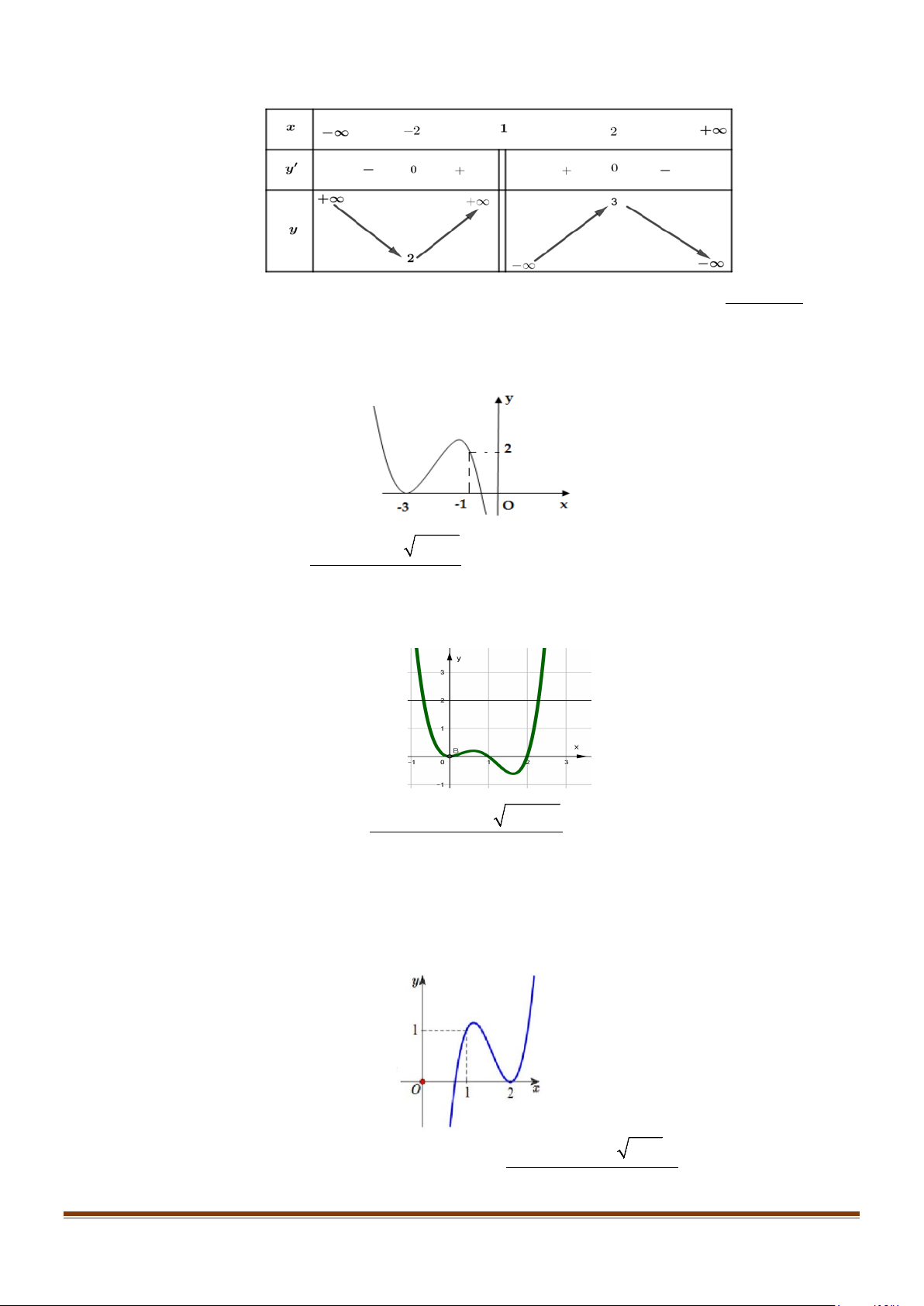
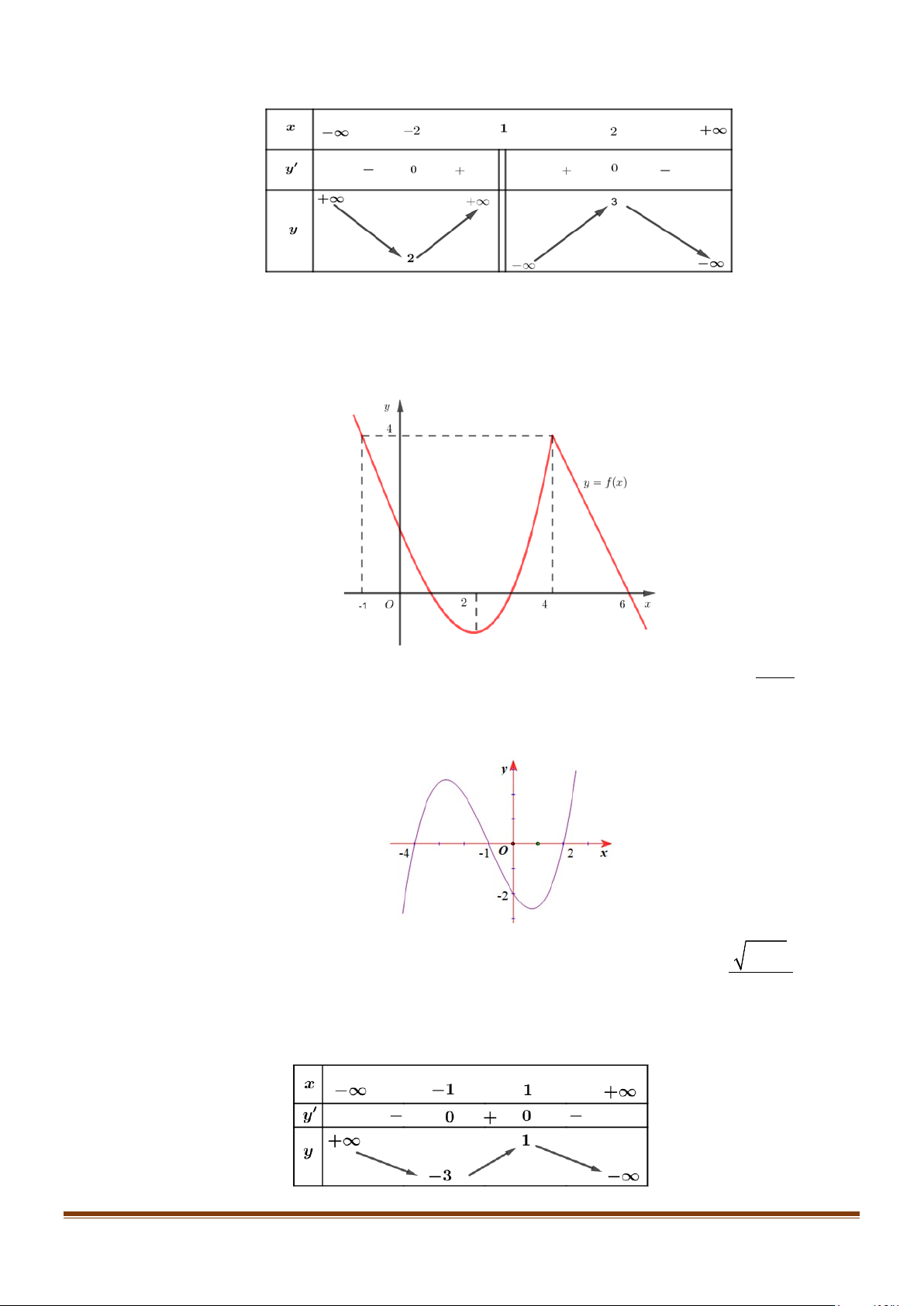
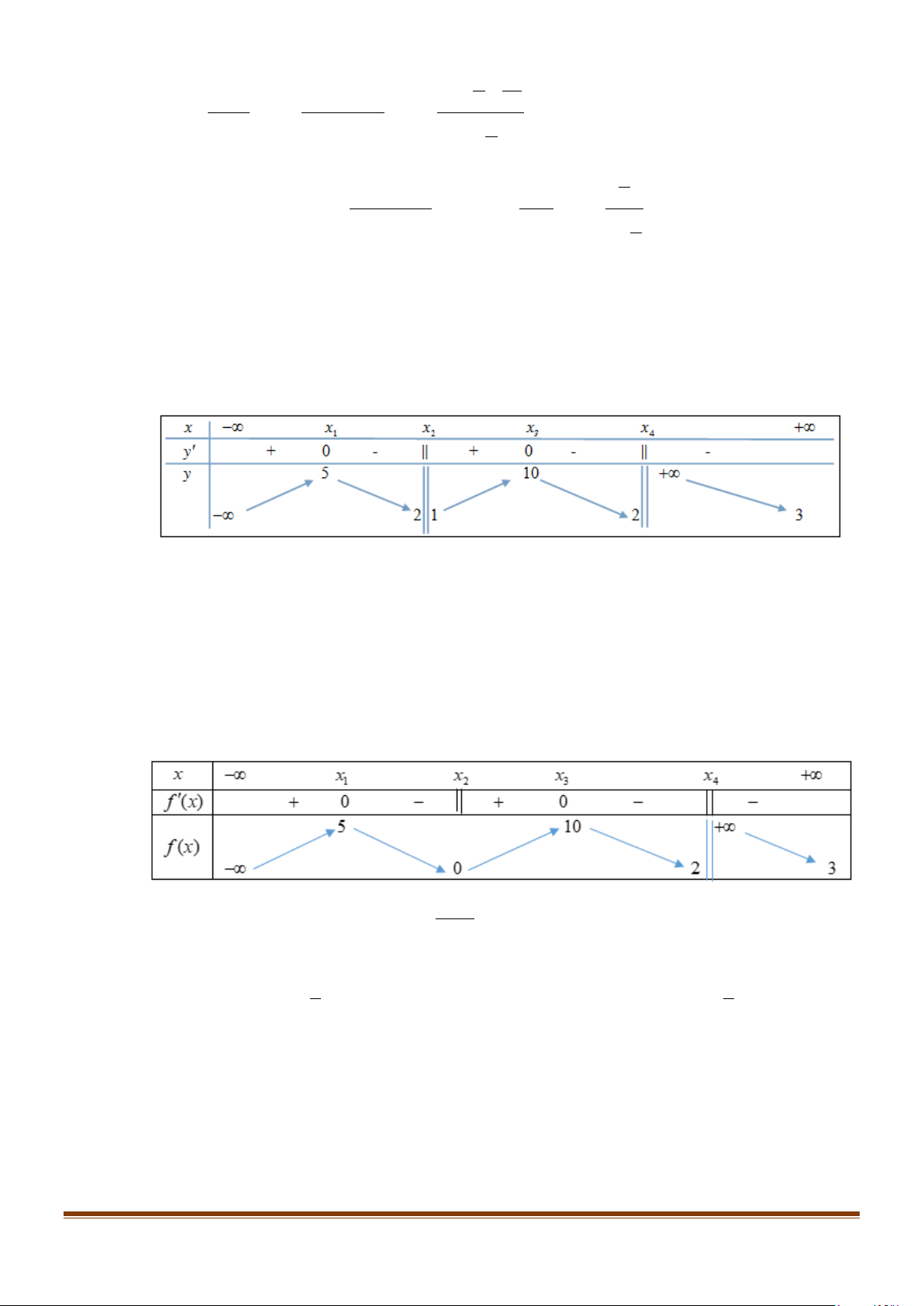
Câu 7: Cho hàm số y = f (x) có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f (x) .
Câu 8: Cho hàm số f (x) có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số 1 y = ? f (x) Page 205
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
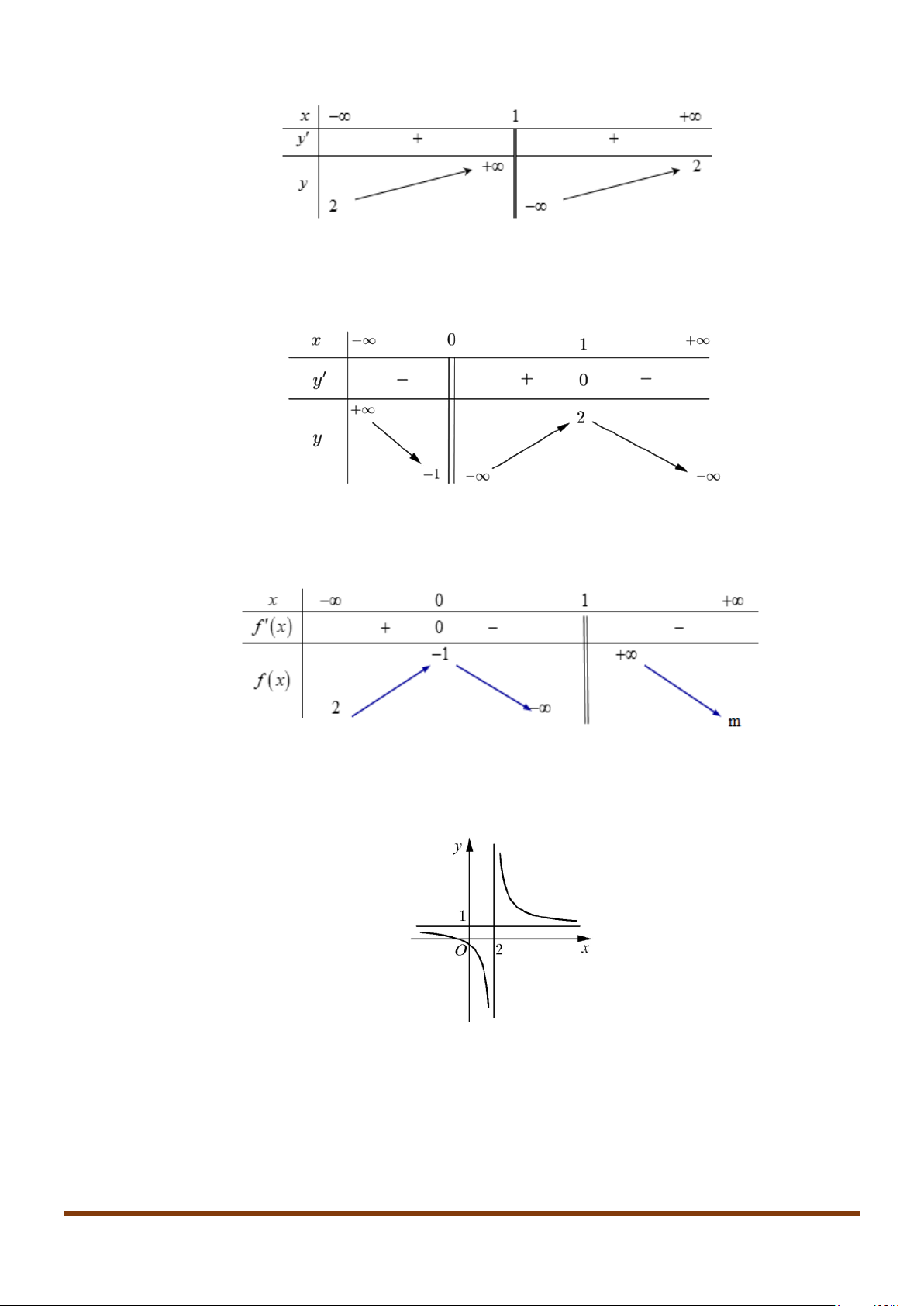
Câu 9: Cho hàm số y = f (x) xác định, liên tục trên  \{ }
1 và có bảng biến thiên như sau:
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho?
Câu 10: Cho hàm số y = f (x) xác định trên  \{ }
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang?
Câu 11: Cho hàm số y = f (x) xác định trên  \{ }
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm các giá trị nguyên của m∈[0;5) để đồ thị hàm số y = f ( x) có 3 đường tiệm cận đứng và ngang?
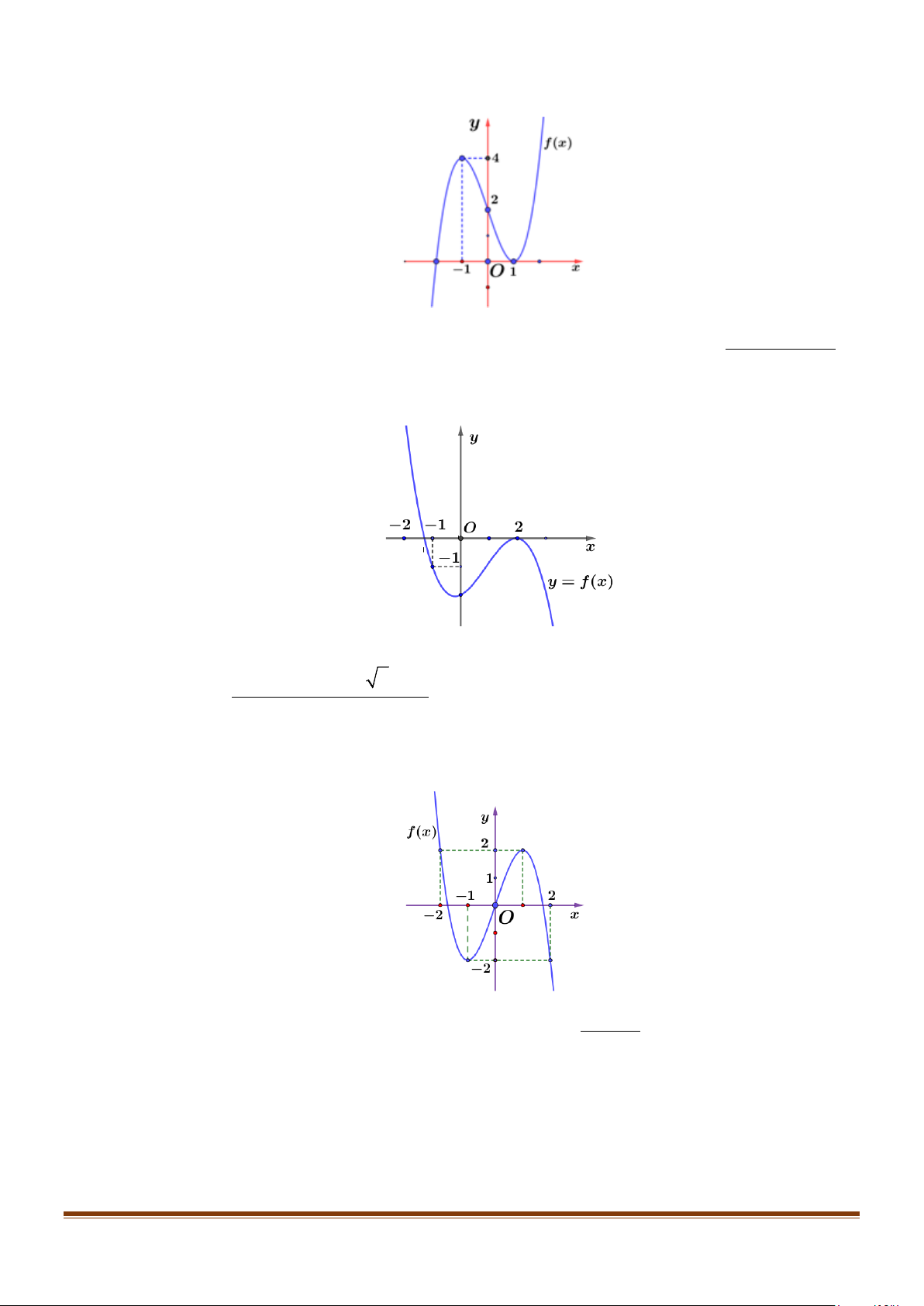
Câu 12: Cho hàm số f (x) có đồ thị như hình vẽ bên.
Tìm phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số trên. Page 206
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Câu 13: Cho đồ thị hàm số y = f (x) như hình bên. Đồ thị có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Câu 14: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Phương trình đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là?
Câu 15: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Phương trình đường tiệm cận xiên của đồ thị hàm số là? Page 207
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ 2 − + Câu 16: x 2x 2
Tìm tiệm cận xiên của đồ thị hàm số y = x −1
DẠNG 3: TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ HÀM HỢP
Các dạng trong chủ đề: Cho hàm số y = f (x) biết bảng biến thiên hoặc đồ thị. Tìm các đường
tiệm cận đứng và tiệm cận ngang của đồ thị y = g (x) thuộc một trong các dạng sau
1) y = f (u(x)) ,
2) y = g ( f (x)) ,
3) y = g ( f (u(x))) ,
4) y = g (x, f (x)),
5) y = g (x, f (u(x))) .
Phương pháp giải: Gọi (G) là đồ thị hàm số y = g (x) . 1)Tìm tiệm cận ngang.
Xét hàm số dạng g (x) u(x) =
.Một dấu hiệu thường dùng để nhận biết (G) có tiệm cận ngang: v(x)
+ Hàm số y = g (x) xác định trên ( ;
a +∞) hoặc trên ( ; −∞ a) .
+ Bậc của u(x) ≤ Bậc của v(x) .
+ lim g(x) = y hoặc lim g(x) = y ⇒ Đường thẳng y = y là tiệm cận ngang của(G) . 0 x→+∞ 0 x→−∞ 0
2)Tìm tiệm cận đứng.
Xét dạng hàm số g (x) u(x) =
. Một dấu hiệu thường dùng để nhận biết đường thẳng x = x v(x) 0 là
tiệm cận đứng của (G) :
+ v(x ) = 0 và u(x ) ≠ 0 , g (x) xác định trên ( ;
a x hoặc (x ;b . 0 ) 0 ) 0 0
+ Ít nhất một trong hai giới hạn lim g (x), lim g (x) là giới hạn vô cực. x + − → 0 x x→ 0 x
⇒ Đường thẳng x = x là tiệm cận đứng của (G) . 0
Trong chủ đề này, các dấu hiệu nhận biết ở trên dựa vào bảng biến thiên hoặc đồ thị của hàm số
y = f (x) .
Câu 17: Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây 1
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = . 2 f (x) −1 Page 208
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Câu 18: Cho hàm số y = f ( x) liên tục trên  \  
1 và có bảng biến thiên như sau 1
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g(x) = 2 f (x) −3
Câu 19: Cho hàm số f (x) 3 2
= ax + bx + cx + d (a, ,
b c,d ∈ R) có đồ thị như hình vẽ.
( 2x +4x+3) 2x + x
Đồ thị hàm số g (x) =
có bao nhiêu đường tiệm cận đứng?
( f (x))2 −2 f (x)
Câu 20: Cho đồ thị hàm đa thức bậc bốn y = f (x) như hình vẽ bên dưới. 6 2 2
Hỏi đồ thị của hàm số
(x +1)(x − 5x). x − 2 ( ) x g x =
có bao nhiêu đường tiệm cận đứng và 2
f (x) − 2 f (x)(2x −10)   tiệm cận ngang.
Câu 21: Cho hàm số ( ) 3 2
f x = ax + bx + cx + d là hàm số đa thức với hệ số thực, có đồ thị (C) như hình vẽ bên.
( 2x −3x+2) x−1
Tìm số tiệm cận đứng của đồ thị hàm số g (x) = ( . x + ) 2
1  f (x) − f (x)   Page 209
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Câu 22: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. 2 (x +1)(x −1)
Tìm số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = g(x) = . 2
f (x) − 2 f (x)
Câu 23: Cho hàm số = ( ) 3 2
y f x = ax + bx + cx + d , (a ≠ 0) có đồ thị như hình dưới đây
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số ( 2x +2x−3) = ( ) x y g x = ( .
x x)( f (x))2 2 f (x) − +  
Câu 24: Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. x + 2
Tìm số đường tiệm cận đứng của đồ thị hàm số y = g(x) = f (x)+1. Page 210
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Câu 25: Cho hàm số y = f ( x) liên tục trên  \  
1 và có bảng biến thiên như sau
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g (x) = f ( 2
x − 2x − 2) .
Câu 26: Cho hàm số y = f (x) liên tục trên  và có đồ thị như hình dưới đây  − x
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g ( x) 2 = f   x 1  + 
Câu 27: Cho hàm số y = f (x) là hàm đa thức liên tục trên  và có đồ thị như hình dưới đây f x
Tìm số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = g (x) ( ) = . f (x) −1
Câu 28: Cho hàm số y = f (x) xác định, liên tục trên  và có bảng biến thiên như sau: Page 211
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Tìm số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số g (x) 3 = . f ( 3 x + x + ) 1 −1
DẠNG 3: MỘT SỐ BÀI TOÁN VỀ TIỆM CẬN CHỨA THAM SỐ
Câu 29: Tìm các giá trị thực của tham số m để đồ thị hàm số mx + 7 y =
có tiệm cận đứng đi qua điểm mx −1 A(1; 2 − ) .
Câu 30: Tìm các giá trị thực của tham số m để đồ thị hàm số f (x) x − 2 =
có ba đường tiệm cận. 2 x + x + m
Câu 31: Tìm tham số m để đồ thì hàm số
(m +1)x − 5m y =
có tiệm cận ngang là đường thẳng y =1. 2x − m
Câu 32: Tìm các tham số m để đồ thị hàm số x −1 y =
có đúng hai đường tiệm cận? 2 x + mx + 4 Câu 33: Cho hàm số 2mx + m y =
. Với giá trị nào của m thì đường tiệm cận đứng, tiệm cận ngang của x −1
đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là 8?
Câu 34: Biết đồ thị (C) của hàm số ax + b y = đi qua điểm A( 1;
− 7) và giao điểm hai tiệm cận của (C) cx + d là điểm I ( 2;
− 3). Biết c là số nguyên dương và a,c là các số nguyên tố cùng nhau. Tìm các số
a,b,c, d . Câu 35: Cho hàm số x − m y =
. Giá trị nào của m để đồ thị hàm số đã cho có đúng 1 tiệm cận đứng? 2 x + 3x − 4 Câu 36: Cho hàm số 2x + m y =
. Tìm tất cả các giá trị của m để đồ thị hàm số có 2 đường tiệm cận cùng x − m
với hai trục tọa độ tạo thành một hình vuông Câu 37: Cho hàm số 1− x y =
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có 2 x − 2mx + 4
đúng ba đường tiệm cận.
Câu 38: Biết rằng đồ thị hàm số ax 1 y
có tiệm cận đứng là x  2 và tiệm cận ngang là y  3 . Tìm bx 2 a,b .
Câu 39: Tính tổng bình phương tất cả các giá trị của m để đồ thị hàm số 2
y = 2x −3x + 5 + mx − 6
có tiệm cận ngang. Page 212
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
ỨNG DỤNG ĐẠO HÀM NG ƯƠ
I ĐỂ KHẢO SÁT VÀ VẼ CH
ĐỒ THỊ CỦA HÀM SỐ
BÀI 3. ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ I LÝ THUYẾT.
I. Đường tiệm cận ngang
Cho hàm số y = f (x) có xác định trên một khoảng vô hạn
là khoảng có một trong các dạng (a,+∞) ; (−∞,a) ; (−∞,+∞)
.Đường thẳng y = y được gọi là đường TCN (hay TCN) của 0
đồ thị nếu thỏa mãn ít nhất một trong các điều kiện sau:
lim f (x) = y ; lim f (x) = y 0 x→−∞ 0 x→+∞
Ví dụ. Tìm đường tiệm cận ngang của đồ thi hàm số x − 3 y = . 2x +1 Lời giải Tập xác định  1 D  \  = − 2   Ta có x − 3 1 lim − = và x 3 1 lim = x→+∞ 2x +1 2
x→−∞ 2x +1 2
Vậy đường tiệm cận ngang của đồ thị hàm số x − 3 y = là đường thẳng 1 y = . 2x +1 2 Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
II. Đường tiệm cận đứng
Đường thẳng x = x được gọi là đường tiệm cận đứng 0
(TCĐ) của đồ thị hàm số y = f (x) nếu thỏa mãn ít nhất
một trong các điều kiện sau:
lim f (x) = +∞ ; lim f (x) = −∞ x + → + 0 x x→ 0 x
lim f (x) = +∞ ; lim f (x) = −∞ x − → − 0 x x→ 0 xLưu ý: + i) Hàm ax b y =
với ac ≠ 0 có tiệm cận đứng d
x = − ; tiệm cận ngang a y = . cx + d c c f (x) ii) Hàm y =
với f (x), g (x) là những hàm đa thức g (x)
+) Nếu bậc tử nhỏ hơn bậc mẫu thì có tiệm cận ngang y = 0.
+) Nếu bậc tử bằng bậc mẫu thì có tiệm cận ngang an y =
với a b là hệ số của lũy thừa cao n , b n n
nhất trên tử và dưới mẫu.
+) Nếu bậc tử lớn hơn bậc mẫu thì không có tiệm cận ngang.
g (x = 0; f x ≠ 0 0 ) ( 0)  
g ( x = f x = 0 0 ) ( 0)
+) x = x là tiệm cận đứng ⇔ . 0    f (x)  lim = ±∞  x→  0 x g   (x) Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
iii) Ứng dụng máy tính CASIO để tìm tiệm cận đứng hoặc tiệm cận ngang
Để tìm tiệm cận đứng hoặc tiệm cận ngang của một hàm số thông qua máy tính CASIO, ta sử dụng phím CALC trên máy.
Một số lưu ý về kết quả và cách bấm: Giới hạn
Thao tác trên máy tính x x+ → CALC 10 x − + o 10 o x x− → CALC 10 x − − o 10 o x → +∞ CALC 10 10 x → −∞ CALC 10 10 −
Ví dụ 1: Tìm đường tiệm cận đứng của đồ thi hàm số x + 2 y = . x − 2 Lời giải
Tập xác định D =  \{ } 2 Ta có x + 2 lim
= +∞ , suy ra đường tiệm cận đứng của đồ thị hàm số là x = 2 . x 2+ → x − 2
Ví dụ 2: Tìm đường tiệm cận đứng của đồ thi hàm số 3x + 4 y = . 2x −1 Lời giải Tập xác định 1 D  \  =  2   Ta có 3x + 4 lim
= +∞ , suy ra đường tiệm cận đứng của đồ thị hàm số là 1 x = . 1 +   − 2 → 2x 1 x  2   +
Lời bình: Đường tiệm cận đứng của đồ thị hàm số ax b y = là đường thẳng d x = − . cx + d c 2
Ví dụ 3. Tìm đường tiệm cận đứng của đồ thi hàm số x − x +1 y = . 2 x − x − 2 Lời giải
Tập xác định D =  \{2;− } 1 2 2 Ta có x − x +1 lim − + = +∞ , x x 1 lim = −∞ + 2
x→2 x − x − 2 + 2 x→ 1 − x − x − 2
Vậy phương trình đường tiệm cận đứng của đồ thị hàm số là đường thẳng x = 2 và x = 1 − . Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
III. Đường tiệm cận xiên
Đường thẳng y = ax + b được gọi là một đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị
hàm số y = f (x) nếu lim  f
 ( x) − (ax + b) = 0  hoặc lim  f
 ( x) − (ax + b) = 0  . x→−∞ x→+∞
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y = f (x) được minh họa như sau
Để tìm tiệm cận xiên của đồ thị hàm số ta cần tính hệ số a,b trong phương trình của đường tiệm
cận xiên y = ax + b theo công thức như sau f (x) f (x) + a = lim
, b = lim  f (x) − ax   hoặc a = lim
, b = lim  f (x) − ax   x→+∞ x x→+∞ x→−∞ x x→−∞
+ Khi a = 0 thì đồ thị của hàm số có tiệm cận ngang là đường thẳng y = b. 2
Ví dụ. Tìm đường tiệm cận xiên của đồ thi hàm số f (x) x −3x +1 = . x − 2 Lời giải
Tập xác định D =  \{ } 2 . f (x) 2 2 Ta có x − 3x +1 x − 3x +1 a = lim = lim = = . x→+∞ x x
→+∞ x ( x − 2) lim 1 2 x→+∞ x − 2x Ta có 2  − +  b =  f  ( x) x 3x 1 lim − ax = lim   − xx→+∞ x→+∞  x − 2  2
x − 3x +1− x(x − 2) 2 2 
x − 3x +1− x + 2  = lim   = lim x   x→+∞  x − 2 x→+∞   x − 2   −x +1 lim  = = 1 −  
x→+∞  x − 2 
Vậy đường tiệm cận xiên là y = x −1. Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
II HỆ THỐNG BÀI TẬP TỰ LUẬN.
DẠNG 1: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CHO BỞI CÔNG THỨC 2x −3
Câu 1: Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị x + 2
hàm số y = f (x) . Lời giải
Vì lim y = 2; lim y = 2 nên đồ thị hàm số có 1 tiệm cận ngang là y = 2 . x→−∞ x→+∞ Vì lim y = ;
−∞ lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = 2 − . x 2+ x 2− →− →−
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang. 2 x + 2x − 3
Câu 2: Cho hàm số y = f (x) =
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số x + 2
y = f (x) . Lời giải Ta có f (x) 2 x + 2x − 3 a = lim = lim = x→−∞ x x
→−∞ x ( x + ) 1 2 2  + −  bf  ( x) x 2x 3 3 lim x lim   x − = − = −  = = x→−∞
x→−∞  (x + ) lim 0 2 x→−∞ x + 2 
Vậy đường thẳng y = x là tiệm cận xiên của đồ thị hàm số đã cho khi x → −∞ . Ta lại có f (x) 2 x + 2x − 3 a = lim = lim = x→+∞ x x
→+∞ x ( x + ) 1 2 2  + −  bf  ( x) x 2x 3 3 lim x lim   x − = − = −  = = x→+∞
x→+∞  (x + ) lim 0 2 x→+∞ x + 2 
Vậy đường thẳng y = x là tiệm cận xiên của đồ thị hàm số đã cho khi x → +∞ . Ta có: lim y = ;
−∞ lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = 2 − . x 2+ x 2− →− →− 2 −x + 2x + 3
Câu 3: Cho hàm số y = f (x) =
. Tìm tiệm cận xiên và tiệm cận đứng của đồ thị hàm số x + 2
y = f (x) . Lời giải Ta có Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ 2 3 f (x) 2 1 − + + 2 −x + 2x + 3 = lim = lim x x a = = − x→−∞ x x →−∞ x(x + 2) lim 1 x→−∞ 2 1+ x 3 2 4 + =  ( ) −x + 2x + 3  4x + 3 lim +  = lim x b f x x  + x = = = x→−∞
x→−∞  (x + 2) lim lim 4 x→−∞ x + 2 x→−∞ 2  1+ x
Vậy đường thẳng y = −x + 4 là tiệm cận xiên của đồ thị hàm số đã cho khi x → −∞ . Ta lại có 2 3 f (x) 2 1 − + + 2 −x + 2x + 3 = lim = lim x x a = = − x→+∞ x x →+∞ x(x + 2) lim 1 x→+∞ 2 1+ x 3 2 4 + =  ( ) −x + 2x + 3  4x + 3 lim +  = lim x b f x x  + x = = = x→+∞
x→+∞  (x + 2) lim lim 4 x→+∞ x + 2 x→+∞ 2  1+ x
Vậy đường thẳng y = −x + 4 là tiệm cận xiên của đồ thị hàm số đã cho khi x → +∞ . Ta có: lim y = ;
−∞ lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = 2 − . x 2+ x 2− →− →− 2 − − Câu 4: x x 6
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ x − 2
thị hàm số y = f (x) . 2 + − Câu 5: x x 6
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ x +1
thị hàm số y = f (x) . 2 − + + Câu 6: x x 6
Cho hàm số y = f (x) =
. Tìm tổng số đường tiệm cận xiên và tiệm cận đứng của đồ x −1
thị hàm số y = f (x) . Lời giải Ta có 1 6 f (x) 2 1 − + + 2 −x + x + 6 = lim = lim x x a = = − x→−∞ x x →−∞ x(x − ) lim 1 1 x→−∞ 1 1+ x 6 2 =  ( ) −x + x + 6  6 lim +  = lim x b f x x  + x = = = x→−∞
x→−∞  (x − ) lim lim 0 1
x→−∞ x −1 x→−∞ 2  1+ x
Vậy đường thẳng y = −x là tiệm cận xiên của đồ thị hàm số đã cho khi x → −∞ . Ta lại có Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ 1 6 f (x) 2 1 − + + 2 −x + x + 6 = lim = lim x x a = = − x→+∞ x x →+∞ x(x − ) lim 1 1 x→+∞ 1 1+ x 6 2 =  ( ) −x + x + 6  6 lim +  = lim x b f x x  + x = = = x→+∞
x→+∞  (x − ) lim lim 0 1
x→+∞ x −1 x→+∞ 2  1+ x
Vậy đường thẳng y = −x là tiệm cận xiên của đồ thị hàm số đã cho khi x → +∞ . Ta có: lim y = ;
+∞ lim y = −∞ nên đồ thị hàm số có 1 tiệm cận đứng x =1. x 1+ x 1− → →
DẠNG 2: TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ BIẾT BBT CỦA HÀM SỐ, ĐỒ THỊ CỦA
HÀM SỐ ĐÓ HOẶC HÀM SỐ LIÊN QUAN
Câu 7: Cho hàm số y = f (x) có bảng biến thiên
Tìm tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = f (x) . Lời giải Vì lim y = ;
−∞ lim y = 3 nên đồ thị hàm số có 1 tiệm cận ngang là y = 3. x→−∞ x→+∞
Vì lim y = +∞ nên đồ thị hàm số có 1 tiệm cận đứng x = x . x + → 4 4 x
Do đó đồ thị hàm số có tổng số 2 tiệm cận kể cả đứng và ngang.
Câu 8: Cho hàm số f (x) có bảng biến thiên
Tìm số tiệm cận của đồ thị hàm số 1 y = ? f (x) Lời giải Vì 1
lim y = 0; lim y = nên đồ thị hàm số có 1 tiệm cận ngang y = 0 và 1 y = . x→−∞ x→+∞ 3 3
Từ bảng biến thiên, ta có f (x) = 0 có hai nghiệm x = x và x = a ∈( ; −∞ x . 1 ) 2
Dễ thấy lim y = +∞ và lim y = +∞ nên đồ thị hàm số có 2 tiệm cận đứng là x = x và x = a x a+ → x + → 2 2 x
Do đó đồ thị hàm số có tổng số 4 đường tiệm cận kể cả đứng và ngang.
Câu 9: Cho hàm số y = f (x) xác định, liên tục trên  \{ }
1 và có bảng biến thiên như sau: Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số đã cho? Lời giải
Tập xác định: D =  \{ } 1 .
Ta có lim f (x) = 2; lim f (x) = 2 . Do đó y = 2 là đường tiệm cận ngang của đồ thị hàm số. x→−∞ x→+∞
Câu 10: Cho hàm số y = f (x) xác định trên  \{ }
0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hỏi đồ thị hàm số trên có bao nhiêu đường tiệm cận đứng và ngang? Lời giải
Tập xác định: D =  \{ } 0 . Ta có
lim f (x) = +∞ ; lim f (x) = −∞ do đó đồ thị hàm số không có tiệm cận ngang. x→−∞ x→+∞
lim f (x) = −∞ ⇒ x = 0 là đường tiệm cận đứng duy nhất của đồ thị hàm số. x 0+ →
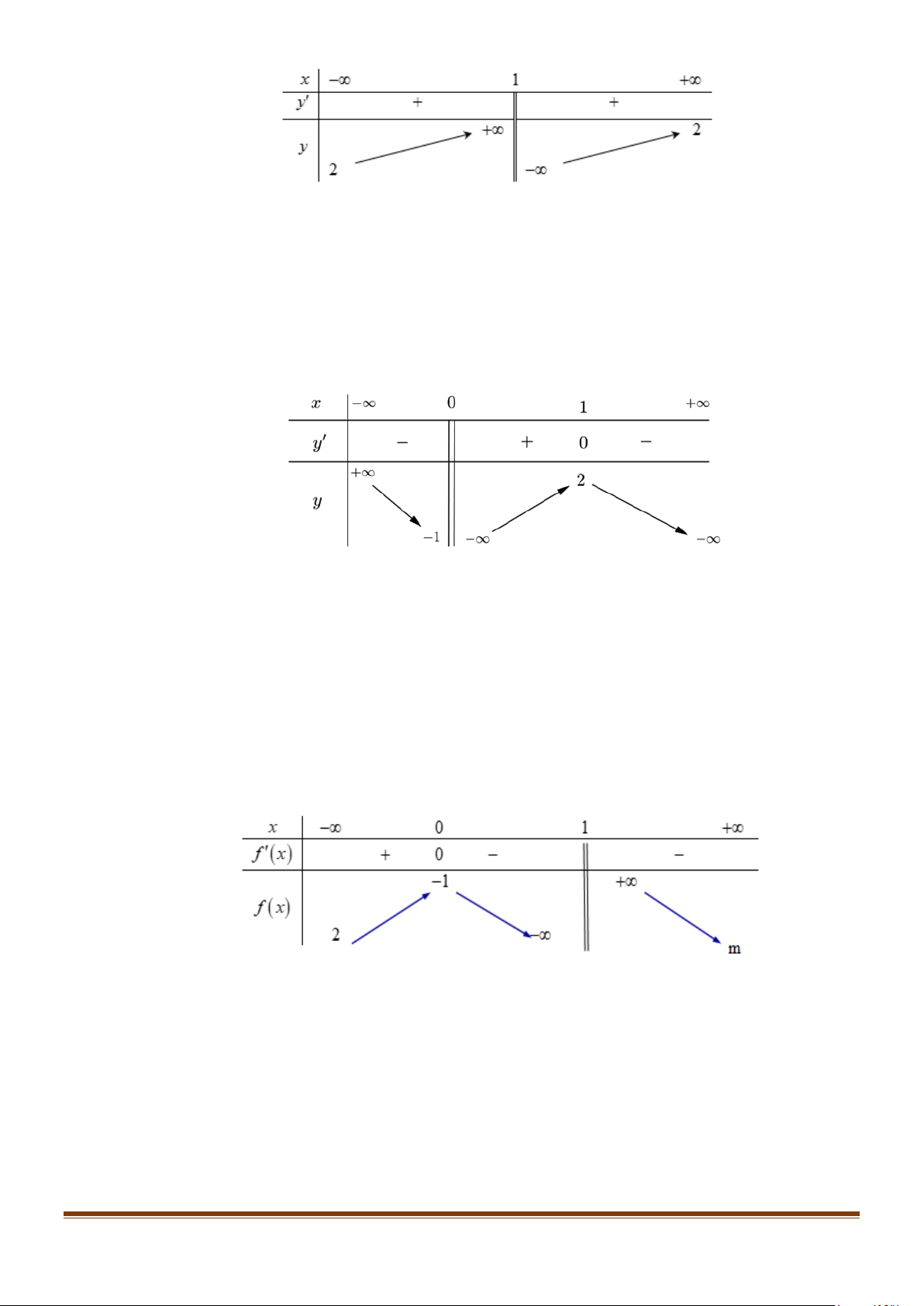
Câu 11: Cho hàm số y = f (x) xác định trên  \{ }
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm các giá trị nguyên của m∈[0;5) để đồ thị hàm số y = f ( x) có 3 đường tiệm cận đứng và ngang? Lời giải
Tập xác định D =  \{ } 1 . Ta có
lim f (x) = 2 ⇒ y = 2 là đường tiệm cận ngang. x→−∞
lim f (x) = −∞ ⇒ x =1 là tiệm cận đứng. x 1− →
lim f (x) = m ⇒ y = m là đường tiệm cận ngang. x→+∞ Page 8
Sưu tầm và biên soạn