Chuyên đề phương pháp tọa độ trong không gian oxyz tự luận và trắc nghiệm

Chuyên đề phương pháp tọa độ trong không gian oxyz tự luận và trắc nghiệm có lời giải và đáp án được soạn dưới dạng file PDF gồm 92 trang. Đề thi có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mời các bạn cùng đón xem ở dưới.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

92 trang 7 tháng trước

Tác giả:

Profile ha phan
Trang1


I. H T TRONG KHÔNG GIAN
1. H t
Trong không gian, xét ba trc
xOx
; ; vuông góc vi nhau tt. Gi ln
 các trc ; ; . H ba try gi là h trc t -
các vuông góc trong không gian hay h t .
m c gi là gc t.
Chú ý: và .
2. T ca mm
 (x : hoành độ, y : tung độ, z : cao độ)
Chú ý:
.
Cho



3. T 
nh 
Nhn xét:
II. BIU THC T C
nh lý:Trong không gian cho
y Oy
z Oz
,,i j k

xOx
y Oy
z Oz
Oxyz
Oxyz
O
2 2 2
1i j k
; ; . . .M x y z OM x i y j z k
0; 0; 0M Oxy z M Oyz x M Oxz y
0; 0; 0M Ox y z M Oy x z M Oz x y
; ; ; ;
A A A B B B
A x y z x y z
;;
B A B A B A
AB x x y y z z
2 2 2
B A B A B A
AB AB x x y y z z
;;
2 2 2
A B A B A B
x x y y z x
M



;;
3 3 3
A B C A B C A B C
x x x y y y z z z
G



;;
4 4 4
A B C D A B C D A B C D
x x x x y y y y z z z z
G



; ; . . .u x y z u x i y j z k
; ; ; ;M x y z OM x y z
Oxyz
1 2 3 1 2 3
; ; ; ; ; ;a a a a b b b b k R

Trang2
H qu: Trong không gian cho

m thì:
*
*T m M cn thng AB là
NG
1. Biu thc t cng
nh lý:Trong không gian ng c và c
nh bi:
2. ng dng
(vi )
T CU
nh lý: Trong không gian , mt cu tâm       
.
1 1 2 2 3 3
;;a b a b a b a b

1 2 3 1 2 3
; ; ; ;ka k a a a ka ka ka
Oxyz
1 2 3 1 2 3
; ; ; ; ; ;a a a a b b b b k R

0 0;0;0 ; 1;0;0 ; 0;1;0 ; 0;0;1 ;i j k
a
0b b a kb k R
11
1 2 3
2 2 1 2 3
1 2 3
33
, , , 0
a kb
a a a
a kb b b b
b b b
a kb
; ; ; ;
A A A B B B
A x y z x y z
;;
B A B A B A
AB OB OA x x y y z z
;;
2 2 2
A B A B A B
x x y y z z
M



Oxyz
1 2 3
;;a a a a
1 2 3
;;b b b b
1 1 2 2 3 3
. . . .a b a b a b a b

1 1 2 2 3 3
. . . 0a b a b a b a b

2 2 2
1 2 3
a a a a
2
2 2 2
1 2 3
a a a a
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
. . . .
cos ,
.
.
a b a b a b a b
ab
ab
a a a b b b





,0ab
Oxyz
S
;;I a b c
2 2 2
2
x a y b z c r
Trang3
Nhn xét: t cu 
.


Trong không gian  và 
 và  
Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

()

 và 
 :
 :
 :
 :
Chú ý:


– 
 

2 2 2
2 2 2 0x y z ax by cz d
2 2 2 2
d a b c r
2 2 2
r a b c d
;;M a b c

1 2 3
;;a a a a
1 2 3
;;b b b b
a
b
,ab


2 3 3 1
12
2 3 3 2 3 1 1 3 1 2 2 1
2 3 3 1 1 2
, ; ; ; ;
a a a a
aa
a b a b a b a b a b a b a b
b b b b b b





, ; ,a b a a b b

,,a b b a

, ; , ; , ;i j k j k i i k j
[ , ] . .sin ,a b a b a b
,ab
c
, . 0a b c



ABCD
,
ABCD
S AB AD


ABC
1
,
2
ABC
S AB AC


' ' ' '
, . '
ABCDA B C D
V AB AD AA


ABCD
1
,.
6
ABCD
V AB AC AD


Trang4


{Tìm tọa độ điểm, tọa độ vecto thỏa tính chất nào đó, tìm tọa độ trung điểm, trọng tâm, trực
tâm, đỉnh của hình bình hành, đỉnh của một hình đa diện,…}
PHN 1: CÁC VÍ D
Ví d1. Trong không gian vi h to   , , .
Tìm t  .
Li gii
Ta có:
Suy ra:
. Vy .
Ví d2. Trong không gian vi h to  m .
1/ Tìm t m  t giác là hình bình hành.
2/ Tìm t tâm I ca hình bình hành .
Li gii
1/ T giác là hình bình hành
m I là tâm hình bình hành
m ca AC .
Ví d3. Trong không gian vi h to  m . Tìm t
m Mthuc mt phng m A, B, C ?
Oxyz
(2; 5;3)a 
0;2; 1b 
1;7;2c
42d a b c
2; 5;3a 
4 0;8; 4b 
2 2;14;4c
42d a b c
2; 5;3 0;8; 4 2;14;4
2 0 2; 5 8 14;3 4 4
0; 27;3
0; 27;3d 

Oxyz
1;2;4 , 2; 1;0 , 2;3; 1A B C
D
ABCD
ABCD
ABCD
3
6 3;6;3
3
D C B A
D C B A
D C B A
x x x x
AD BC y y y y D
z z z z
ABCD
2
153
;;
2 2 2 2
2
AC
I
AC
I
AC
I
xx
x
yy
yI
zz
z



Oxyz
1; 1;5 , 3;4;4 , 4;6;1A B C
Oxy
Trang5
Li gii
Gi m cn tìm.
Vì u nên ta có:
.
Vy .
Ví d4. Trong không gian vi h to  m , gi là hình chiu vuông góc
ca trên trc . Tìm t m cn thng ?
Li gii
Vì là hình chiu vuông góc ca lên trc nên
Gi m Suy ra
Ví d5. Trong không gian vi h t cho , . Tìm các giá tr
ca  tam giác u?
Li gii
Gm cn thng AB
Ta có: , ,
u khi và ch khi
Vy: là các giá tr cn tìm.
VN DNG THP VÀ VN DNG CAO
Ví d6. Trong không gian vi h t , cho tam giác có
. Gi   ng phân giác trong góc ca tam
giác Tìm t m
Li gii
22
; ;0 , , ; 0M x y Oxy x y x y
M
,,A B C
22
22
AM BM
MA MB MC
AM CM
2 2 2 2 2 2
2 2 2 2 2 2
1 1 0 5 3 4 0 4
1 1 0 5 4 6 0 1
x y x y
x y x y
4 10 14 0 2 5 7 16
2 4 12 0 2 6 5
x y x y x
x y x y y
16; 5;0M
Oxyz
2;4;6K
'K
K
Oz
'OK
'K
2;4;6K
Oz
' 0;0;6 .K
1 1 1
;;I x y z
'.OK
0;0;3 .I
Oxyz
( 2;2; 1)A 
2;3;0 ,B
;3; 1Cx
x
ABC
51
2; ;
22
M




2AB
2
1
( 2)
2
CM x
22
1
3 1 6
( 2) ( 2) 1
3
2 2 2
x
CM AB x x
x


1
3
x
x


Oxyz
ABC
2;0; 3 , 4;1; 1 , 4; 4;1A B C
D
A
.ABC
.D
Trang6
Theo tính cht phân giác trong, ta có:
Mà:
T .
Ví d7. Cho hình hp
1/ Chng minh:
2/ Cho . Tính t nh còn li ca hình hp.
Li gii
1/ Ta có: ; và
Suy ra: 
2/ S dng công thc hai vecto b   c:
Ví d8. Trong không gian vi h t u có và
m nm trong mt phng  nh  .
1/ Tìm t m .
2/ Tìm t m bit là t diu.
Li gii
1/ Vì nên .
Ta có:
Tam giác u nên
.
1
DB AB AB
DB DC
DC AC AC
3; 6AB AC
2
21
1 2 2 4; ;
33
2
C D B D
C D B D
C D B D
x x x x
DC DB y y y y D
z z z z



. ' ' ' 'ABCD A B C D
' ' 2 ' 0AC CA C C
1;0;1 , 2;1;2 , ' 4;5; 5 , 1; 1;1A B C D
''AC AC CC
''C A CA
' ' 2 ' 2 ' 2 ' 0AC CA C C CC AC CA C C
2;0;2 , ' 4;6; 5 , ' 3;5; 6 , ' 3;4; 6C B A D
Oxyz
ABC
5;3; 1 , 2;3; 4AB
C
Oxy
3
C
D
ABCD
C Oxy
; ;0C x y
3;0; 3 , 5; 3;1 , 2 ; 3;4AB AC x y BC x y y
ABC
22
22
AB AC AB AC
AC BC
AC BC


22
2 2 2 2
5 3 1 18
11
42
5 3 1 2 3 16
xy
xx
yy
x y x y




A
B
C
D
Trang7
Vì  nh  .
2/ Gi .
 .
u nên t diu khi và ch khi
.
Vy: .
PHN 2: CÂU HI TRC NGHIM
Câu 1. [2H3-1.1-1] Trong không gian   thì

A. . B. . C. . D. .
Li gii
Chn A
.
Câu 2. [2H3-1.1-1]   , ,
 là:
A. . B. . C. . D. .
Li gii
Chn C
Có
C
1;2;0C
;;D x y z
5; 3; 1 ; 2; 3; 4 ; 1; 2;AD x y z BD x y z CD x y z
32AD BD CD AB
2 2 2 2 2 2
2 2 2 2 2
2
2 2 2
5 3 1 2 3 4
5 3 1 1 2
5 3 1 18
x y z x y z
x y z x y z
x y z
2 2 2
1
16 5
5 3 1 18
zx
yx
x y z

2
10
3
12
2
16 5 6
3
1
3 16 20 0
7
3
x
z x x
y x y y
z
xx
z


10 2 7
2;6; 1 ; ;
3 3 3
DD



Oxyz
,,i j k
;;M x y z
OM
xi y j kz
xi y j kz
x j yi kz
xi y j kz
OM xi y j kz
Oxyz
(2; 5;3)a 
0;2; 1b 
1;7;2c
42d a b c
(0;27;3)
1;2; 7
0; 27;3
0;27; 3
42d a b c
2; 5;3 4 0;2; 1 2 1;7;2
2; 5;3 0;8; 4 2;14;4
Trang8
.
Vy .
Câu 3. [2H3-1.1-2]        , cho tam giác 
và   
A. . B. . C. . D. .
Li gii
Chn D
T trng tâm .
Vy .
Câu 4. [2H3-1.1-2]        , cho hình bình hành có
(  là:
A. . B. . C. . D. .
Li gii
Chn B
Ta có .
.
Gi I là tâm hình bình hành m .
Câu 5. [2H3-1.1-2]   
A. . B. . C. . D. .
Li gii
Chn A
Vi hình chiu vuông góc ca lên trc là .
Câu 6. [2H3-1.1-2]    
   
A. . B. . C. . D. .
Li gii
2 0 2; 5 8 14;3 4 4
0; 27;3
0; 27;3d 

Oxyz
ABC
3; 2;5 , 2;1; 3AB
5;1;1C
G
ABC
2;0; 1G
2;1; 1G
2;0;1G
2;0;1G
;;
3 3 3
A B C A B C A B C
x x x y y y z z z
G



2;0;1G
2;0;1G
Oxyz
OABD
1;1;0 ,OA 
1;1;0OB
O
OABD
1;0;0
11
; ;0
22



1;0;1
1;1;0
1;1;0 1;1;0OA A
1;1;0 1;1;0OB B
.OABD
11
; ;0
22
OB I



2;5;0M
M
Oy
0;5;0M
0; 5;0M
2;5;0M
2;0;0M
;;M a b c
M
Oy
1
0; ;0Mb
Oxyz
2;4;6K
'K
K
Oz
'OK
1;0;0
0;0;3
0;2;0
1;2;3
Trang9
Chn B
Vì là hình chiu vuông góc ca lên trc nên .
Gi m Suy ra .
Câu 7. [2H3-1.1-2]   

A. . B. . C. . D. .
Li gii
Chn C
Vi hình chiu vuông góc ca lên mt phng là .
Câu 8. [2H3-1.1-2] Trong không gian  ,  
  là:
A. . B. . C. . D. .
Li gii
Chn B
, 
.
Câu 9. [2H3-1.1-2]           
  là:
A. . B. . C. . D. .
Li gii
Chn C
Ta có: .
 t giác là hình bình hành thì .
Câu 10. [2H3-1.1-2]        , cho
  
  là:
'K
2;4;6K
Oz
' 0;0;6K
1 1 1
;;I x y z
'.OK
0;0;3I
1;2; 3M
M
Oxy
0;2; 3M
1;0; 3M
1;2;0M
1;2;3M
;;M a b c
M
Oxy
1
; ;0M a b
Oxyz
(1;2; 3)B
(7;4; 2)C
E
2CE EB
E
8
3;3;
3



88
3; ;
33



1
1;2;
3



88
;3;
33



( ; ; )E x y z
8
3
23
8
3
x
CE EB y
z

Oxyz
2;0;0 , 0; 3;0 , 0;0;4M N P
MNPQ
Q
2; 3;4
3;4;2
2;3;4
2; 3; 4
2; 3;0 , ; ; 4
Q Q Q
MN QP x y z
MNPQ
22
33
0 4 4
QQ
QQ
QQ
xx
MN QP y y
zz





Oxyz
1;0;0 , 0;1;0 , 0;0;1 , 1;1;1A B C D
,MN
,AB CD
G
MN
Trang10
A. . B. . C. . D. .
Li gii
Chn B
Vì M m ca AB nên .
N m ca CD nên .
 .
Câu 11. [2H3-1.1-1]                

A. . B. . C. . D. .
Li gii
Chn A
Ta thy vi ;  ng vi .
Câu 12. [2H3-1.1-2]  , ,
. 
 

A. . B. . C. . D. .
Li gii
Chn C
, 
.
Câu 13. [2H3-1.1-2]          
A, B, C  là:
A. . B. . C. . D. .
Li gii
Chn B
Có .
111
;;
333



111
;;
222



222
;;
333



111
;;
444



11
; ;0
22
M



11
; ;1
22
N



111
;;
222
G



Oxyz
(1;2;2)a
1 2 2
;;
3 3 3



1 2 2
;;
3 3 3



1 2 2
;;
3 3 3



111
;;
333



1 2 2
; ; 1
3 3 3
uu




1 1 2 2
;;
3 3 3 3
ua





a
Oxyz
(1;2; 1)A
(2; 1;3)B
( 2;3;3)C
;;M a b c
ABCM
2 2 2
P a b c
42
43
44
45
( ; ; )M x y z
ABCM
1 2 2
2 3 1 ( 3;6; 1) P 44
1 3 3
x
AM BC y M
z
Oxyz
2; 3;4 , 1; ; 1 ;4;3A B y C x
5x + y
42
41
40
36
1; 3; 5 ; 2;7; 1AB y AC x
Trang11
 m A, B, C thng hàng thì  .
Vy .
Câu 14. [2H3-1.1-2]   
AB  
A. . B. . C. . D. .
Li gii
Chn A
Gi s m cn tìm.
n AB theo t s nên ta có: .
.
Vy .
Câu 15. [2H3-1.1-2]   
A. . B. . C. . D. .
Li gii
Chn D
Vi i xng ca qua mt phng là
Câu 16. [2H3-1.1-3]    

A. . B. . C. . D. .
Li gii
Chn A
AB
AC
1 3 5
2 7 1
y
x

9
; 32
5
xy
5x + y = 41
5x + y = 41
Oxyz
1;1;0 , 2;0; 3AB
1
2
k 
42
; ; 1
33
M



22
; ; 2
33
M



12
; ;1
33
M



22
; ; 2
33
M




;;M x y z
1
2
k 
1
2
MA MB
4
1
12
3
2
12
10
23
1
1
3
2
x
xx
y y y
z
zz






42
; ; 1
33
M



3;2; 1M
M
Oxy
3;2;0M
3; 2; 1M

3; 2;1M
3;2;1M
;;M a b c
M
Oxy
;;M a b c
3;2; 1M
;;M a b c
Oy
abc
0
4
6
2
Trang12
Vi i xng ca qua trc là
.
Câu 17. [2H3-1.1-3] Trong không gian  có

A. . B. . C. . D. .
Li gii
Chn B
Câu 18. [2H3-1.1-3] Trong không gian       
 
A. . B. . C. . D. .
Li gii
Chn C
.
m nên .
.
Câu 19. [2H3-1.1-4]  
M A, B, C 
A. . B. . C. . D. .
Li gii
Chn A
Gi m cn tìm.
Vì u , , nên ta có:
Vy .
Câu 20. [2H3-1.1-4]  , cho 
   là:
;;M a b c
M
Oy
;;M a b c

3;2;1 0M a b c
Oxyz
ABCD
(1;0;2), ( 2;1;3), (3;2;4), (6;9; 5)A B C D
ABCD
8;12;4G
2;3;1G
14
3;3;
4
G



18
9; ; 30
4
G




Oxyz
(1;2;1), (2; 1;2)AB
M
Ox
,AB
1 1 3
;;
222
M



1
;0;0
2
M



3
;0;0
2
M



13
0; ;
22
M



;0;0M Ox M a
M
,AB
22
2 2 2 2 2 2
1 2 1 2 2 1MA MB a a
3
23
2
aa
Oxyz
1; 1;5 , 3;4;4 , 4;6;1A B C
16; 5;0M
6; 5;0M
6;5;0M
12;5;0M
22
; ;0 , ; 0M x y x y x y
M
A
B
C
MA MB MC
2 2 2 2 2 2 2 2 2
1 1 0 5 3 4 0 4 4 6 0 1x y x y x y
2 2 27 6 8 41 8 12 53x y x y x y
4 10 14 0 2 5 7 16
2 4 12 0 2 6 5
x y x y x
x y x y y
16; 5;0M
Oxyz
2;1; 1 , 3;0;1 , 2; 1;3A B C
D
Oy
ABCD
D
Trang13
A. . B. . C. . D. .
Li gii
Chn C
m thuc trc có t  . Ta có , và
. D thy
,
,
nên hoc .

{ Tích vô hướng hai vt, góc giữa hai vt, độ dài vt, độ dài đường trung tuyến, phân giác,đường
cao, diện tích tam giác, chu vi tam giác…}
PHN 1: CÁC VÍ D
Ví d 1. Trong không gian cho tam giác ABC có .Tính
Li gii
Ta có:
Suy ra: .
Ví d 2. Trong không gian vi h to  , cho tam giác ABC bit , B i xng vi A qua
mt phng ( ), C i xng vi B qua gc t O. Tính din tích tam giác ABC ?
Li gii
 i xng vi A qua mt phng ( )
i xng vi B qua gc t O
.
Ví d 3. Trong không gian vi h to  , cho tam giác có , ,
. Gi m trên cnh sao cho  n thng .
Li gii
0; 7;0
0;8;0
0; 7;0
0;8;0
0; 8;0
0;7;0
D
Oy
0
(0; ;0)Dy
1; 1;2AB 
0; 2;4AC 
0
2; 1;1AD y
1 2 2 1 1 1
, ; ; 0; 4; 2
2 4 4 0 0 2
AB AC





0
11
5 , . 2 4
66
ABCD
V AB AC AD y


0
7y 
0
8y
m
2; 1;3 , 3;0; 2 , 5; 1; 6A B C
cosBAC
1;1; 5 ; 3;0; 9AB AC
. 16 8 30
cos cos ;
. 45
3 30
AB AC
BAC AB AC
AB AC
Oxyz
1;2;3A
Oxy
Oxy
(1;2; 3)B
C( 1; 2;3)
1
(0;0; 6); ( 2; 4;0) S ; 6 5
2
ABC
AB AC AB AC


Oxyz
ABC
2;0;0A
0;3;1B
3;6;4C
M
BC
2MC MB
AM
Trang14
m thuc cnh nên , suy ra t m là
.
V dài bng:
.
Ví d 4.Trong không gian vi h to  cho hai vecto tha mãn
1) Tính .
2) Tính góc gia hai vecto và .
Li gii
1) Ta có:
.
2) Ta có: và .
.
Ví d 5.Trong không gian vi h t cho , . Tìm các giá tr
ca  tam giác u?
Li gii
Gm cn thng .
Ta có: , , .
u khi và ch khi
.
Vy: là các giá tr cn tìm.
M
BC
2MC MB
M
( 2)
1
1 ( 2)
( 2)
4
1 ( 2)
( 2)
2
1 ( 2)
CB
M
CB
M
CB
M
xx
yy
zz
x
y
z







AM
22
22
22
1() 2 4 0 2(2 0) 9
M A M A M A
x zy zxy 
Oxyz
,ab

0
; 120 ; 2; 3a b a b
2ab

a
32x a b
. . .cos ; 3ab a b a b
2
22
2 4 . 4 52 2 2 13a b a a b b a b
2
. 2 2 . 6a x a a b a a b
2
3 2 6x a b
0
.1
cos ; ; 60
2
.
ax
a x a x
ax


Oxyz
( 2;2; 1)A 
2;3;0 ,B
;3; 1Cx
x
ABC
AB
51
2; ;
22
M




2AB
2
1
( 2)
2
CM x
22
1
3 1 6
( 2) ( 2) 1
3
2 2 2
x
CM AB x x
x


1
3
x
x


Trang15
Ví d 6.Trong không gian , cho hình hp ch nht nh A trùng vi gc ,
, . Gm ca cnh .Tính th tích
ca khi t din
.
Li gii
Ta có : .
Vy th tích ca khi t din là: .
PHN 2: CÂU HI TRC NGHIM
Câu 1. [2H3-1.2-1]  
A. . B. . C. . D. .
Li gii
Chn B
Câu 2. [2H3-1.2-1]  
A. . B. . C. . D. .
Li gii
Chn A
.
Câu 3. [2H3-1.2-1]   
A. . B. . C. . D. .
Li gii
Chn B
Vi .
Câu 4. [2H3-1.2-1]   
A.25. B.5. C. 4. D. 0.
Li gii
m
. ' ' ' 'ABCD A B C D
O
;0;0Ba
0; ;0 , ' 0;0;D a A b
,0ab
'CC
'BDA M
; ;0 , ' ; ; ; ;
2
b
C a a C a a b M a a



2
2
; ;0
, ; ; ; ' ;0;b
22
0; ;
2
3
, . '
2
BD a a
ab ab
BD BM a BA a
b
BM a
ab
BD BM BA











'BDA M
2
'
1
, . '
64
BDA M
ab
V BD BM BA



2;2;5 , 0;1;2ab

10
12
13
14
1;2;3 , 0;1;1AB
AB
6
8
10
12
2
2 2 2 2 2
0 1 1 2 1 3 6
B A B A B A
AB x x y y z z
1;2; 3M
M
Oxy
14
3
1
2
; ; , 3M a b c d M Oxy c
2;5;0M
M
Ox
Trang16
Chn B
Vi
Câu 5. [2H3-1.2-2]           
sai ?
A. . B. . C. . D. .
Li gii
Chn D
.
.
.
.
Câu 6. [2H3-1.2-2]  Tam giác là
A.Tam giác có ba góc nhn. B. nh .
C. nh . D. u.
Li gii
Chn A
 không vuông.
không cân.
Câu 7. [2H3-1.2-1]   và  và khác  
A. . B. . C. . D. .
Li gii
Chn D
Câu 8. [2H3-1.2-2]   .
?
A. . B.  . C. . D. .
Li gii
Chn C
2 2 2 2
; ; , 5 0 5M a b c d M Ox b c
Oxyz
1;1;0 , 1;10 , 1;1;1a b c
2a
3c
ab

cb

22
( 1) 1 0 2a
222
1 1 1 3c
. 1 .1 1.1 0.0 0a b a b
. 1.1 1.1 0.1 2bc

1;2;0 , 1;0; 1 , 0; 1;2 .A B C
ABC
A
A
(0; 2; 1); ( 1; 3;2)AB AC
.0AB AC 
ABC
AB AC
ABC
a
b
a
b
0
cos
.
ab
ab


.
.
ab
ab


.
.
ab
ab


.
.
ab
ab


Oxyz
1;1;0 , 1;10 , 1;1;1a b c
.1ac

a
c
2
cos ,
6
bc

0abc
Trang17

.
Câu 9. [2H3-1.2-2] Trong không gian  
 là
A. . B. . C. . D. .
Li gii
Chn C
Xét .
Ta có: ; .
 ;
Suyra : .
Câu 10. [2H3-1.2-2]            
   
là:
A. . B. . C. . D. .
Li gii
Chn D
Có
;
Mà
Vy .
Câu 11. [2H3-1.2-2]        , cho tam giác có ,
,   sao cho 

. 1.1 1.1 0.1 0 .ac a c
1;3;1 0.abc
1.1 1.1 0.1 2
cos ,
1 1. 1 1 1 6
bc



Oxyz
1;2;0 , 1;1;3 , 0; 2;5A B C
, , ,A B C D
D
1; 1;6D
1;2;3D
0;3;0D
0;0;2D
2;5;0D
1; 1;6D
2; 1;3AB
1; 4;5AC
1;1;0AD 
, 7;7;7AB AC


, . 0AB AC AD


Oxyz
ABCD
2; 1;6 , 3; 1; 4 ,AB
5; 1;0 ,C
1;2;1D
ABCD
9
7
6
5
8;0;4 ; 4;3;5 ; 5;0;10BC BD BA
, 12; 24;24BC BD


, . 180BC BD BA


1
. , . 30
6
ABCD
V BC BD BA



22
2
11
. , . 12 24 24 18
22
ABC
S BC BD


1
..
3
ABCD BCD
V AH S
3.
5
ABCD
BCD
V
AH
S
5AH
Oxyz
ABC
2;0;0A
0;3;1B
3;6;4C
M
BC
2MC MB
AM
Trang18
A. . B. . C. . D. .
Li gii
Chn C
m thuc cnh nên , suy ra t m là
.
Vy .
Câu 12. [2H3-1.2-2]            và
 là:
A. . B. . C. . D. .
Li gii
Chn A
Có
.
Vy .
Câu 13. [2H3-1.2-2]        , cho tam giác có
 là:
A. . B. . C. . D. .
Li gii
Chn C
33
27
29
30
M
BC
2MC MB
M
( 2)
1
1 ( 2)
( 2)
4
1 ( 2)
( 2)
2
1 ( 2)
CB
M
CB
M
CB
M
xx
yy
zz
x
y
z







AM
22
22
22
1() 2 4 0 2(2 0) 9
M A M A M A
x zy zxy 
Oxyz
2;2;1 , 1;0;2AB
1;2;3C
ABC
35
2
35
45
5
2
3; 2;1 ; 1;0;2AB AC
, 4; 5;2AB AC


22
2
1 1 3 5
. , 4 5 2
2 2 2
ABC
S AB AC


35
2
ABC
S
Oxyz
ABC
1;0;1 ,A
0;2;3 ,B
2;1;0C
C
26
26
2
26
3
26
1;2;2 , 1;1; 1AB AC
Trang19
 ng cao k t ca tam giác là : .
Câu 14. [2H3-1.2-2] Cho  
A. . B. . C. . D. .
Li gii
Chn A
Tính .
.
Câu 15. [2H3-1.2-2] Trong không gian   
 
A. . B. .
C. . D. .
Li gii
Chn A
 nên .
Câu 16. [2H3-1.2-2]         
 
 là
A. . B. . C. . D. .
Li gii
Chn C
Tính
, vi ,
C
ABC
,
26
,
3
AB AC
d C AB
AB



1; 2;0 , 3;3;2 , 1;2;2 , 3;3;1A B C D
ABCD
3
4
5
6
2;5;2 , 2;4;2 , 2;5;1AB AC AD
1
, . 3
6
V AB AC AD



Oxyz
ABCD
D
ABCD
,.
.
AB AC AD
h
AB AC




,.
1
3
.
AB AC AD
h
AB AC


,.
.
AB AC AD
h
AB AC


,.
1
3
.
AB AC AD
h
AB AC




1 1 1
. . , .
3 2 6
ABCD
V h AB AC AB AC AD

,.
.
AB AC AD
h
AB AC




Oxyz
1; 2;0 , 3;3;2 , 1;2;2 , 3;3;1A B C D
ABCD
D
ABC
9
2
9
7
9
72
9
14
2;5;2 , 2;4;2 , 2;5;1AB AC AD
1
, . 3
6
V AB AC AD



1
.
3
V B h
1
, 7 2
2
ABC
B S AB AC


,h d D ABC
Trang20
.
áp dng công thc c:
.
Câu 17. [2H3-1.2-3]  và  và  
A. . B. . C. . D. .
Li gii
Chn A
Ta có .
Câu 18. [2H3-1.2-3] Cho và   thì

A. . B. . C. . D. .
Li gii
Chn C
.
Câu 19. [2H3-1.2-3] Cho  và  ,
  thì 
A. . B. . C. . D. .
Li gii
Chn D
.
.
Câu 20. [2H3-1.2-3]        ,cho tam giác có
B là:
A. . B. . C. . D. .
Li gii
3 3.3 9
7 2 7 2
V
h
B
,.
18 9
14 2 7 2
.
AB AC AD
h
AB AC




a
b
0
60
2; 4ab

ab

27
23
25
2
2 2 2
2 .cos , 4 16 8 28 2 7a b a b a b a b a b
1;1;1u
0;1;mv
,uv

0
45
m
13
3
23
3
2
2
2
2
1
1.0 1.1 1. 1
cos 2 1 3 1 2 3
3 1 2 1
2
3. 1
m
m
m m m
mm
m


2; 5,ab

a
b
2
3
; 2 .u ka b v a b
u
v
k
6
45
45
6
6
45
45
6
2
. 2 4 50 2 1 cos 0
3
u v ka b a b k k a b
45
6 45 0
6
kk
Oxyz
ABC
1;2; 1A
, 2; 1;3B
,C 4;7;5
2 74
2 74
3
3 76
2
3 76
Trang21
Chn B
Gng phân trong ca góc B thu l:
.
Vy .
Câu 21. [2H3-1.2-3]        , cho tam giác ABC có ,
. AM là:
A. . B. . C. . D. .
Li gii
Chn C
Ta có: .
.
Câu 22. [2H3-1.2-4]        , cho hình chóp S.OAMN 
   và    
chóp S.OAMN là:
A. . B. . C. . D. .
Li gii
Chn A
Có
.

{các bài toán tìm tâm I, bán kính R, xác định xem một phương trình có phải là phương trình
mặt cầu hay không, tìm điều kiện (có chứa tham số m) để một phương trình là phương trình
mặt cầu, các bài toán về họ mặt cầu, bài toán quỹ tích….}
PHN 1: CÁC VÍ D
1 2 11 8 14 2 74
; ;1 ; ; 2
2 3 3 3 3 3
DA BA
D BD BD
BC
DC

2 74
3
BD
Oxyz
( 3;0;4)AB 
(5; 2;4)AC 
23
42
32
53
1 1 1 1
2 2 2 2
AM AB BM AB BC AB BA AC AB AC

2
22
1; 1;4 1 1 4 18 3 2AM AM
Oxyz
0;0;1 , 1;1;0 , ;0;0 ,S A M m
0; ;0Nn
0, 0mn
6mn
1
2
4
6
1;1;0 , ;0;0 , 0; ;0OA OM m ON n
11
,
22
11
,
22
11
.6 3
22
OAM
OAN
OAMN OAM OAN
S OA OM m
S OA ON n
S S S m n






.
11
. , . .1.3 1
33
S OAMN OAMN
V d S OAMN S
Trang22
Ví d1. nh t tâm I, bán kính R ca mt cu ?
Li gii
Mt cu có tâm , bán kính .
Ví d2. Cho mt cu . Chng minh rng:Mt cu tip xúc vi mt phng
. Tìm t tim .
Li gii
 có tâm , bán kính .
Ta có 
   .
 thì nên
.
Ví d3. Trong khoâng gian vi h t  , cho b m ,
. Tìm t ng tròn ngoi tip tam giác .
Li gii
Ta có:   
 .
 
Suy ra  .
             
 : 
  


 có tâm , bán kính .
 
2 2 2
: 2 4 6 5 0S x y z x y z
S
1;2;3I
3R
2 2 2
:( 1) ( 2) 9S x y z
:2 2 5 0P x y z
M
S
1; 0; 2I
3R
2 2 2
2 0 2 5
( ; ( )) 3
2 2 1
d I P R

M
I
P
;;M x y z
1; ; 2IM x y z
()
13
.
11 20 17
;;
2 2 1
9 9 9
2 2 5 0
P
x y z
IM t n
M
MP
x y z







Oxyz
3;3;0A
3;0;3 , 0;3;3 , 3;3;3B C D
ABC
0; 3;3 , 3;0;3AB AC
, 9; 9; 9 1;1;1AB AC n


ABC
: 6 0ABC x y z
;;I a b c
ABC
60
02
0
I ABC
abc
IA IB b c a b c
IB IC a b


2;2;2I
,Oxyz
P
2 2 4 0x y z
S
2 2 2
2 4 6 11 0x y z x y z
P
S
S
1;2;3I
5R
I
2 4 3 4
: , 3
3
P d I P R
Trang23
  
  
  
. Bán kính .
   .
Tìm    


 có tâm , bán kính .
   .
 .
 
.
  
 .
PHN 2: CÂU HI TRC NGHIM
Câu 1. [2H3-1.3-1]          
 và tính bán kính là:
A. và . B. và .
C. và . D. và .
Li gii
Chn A
Tâm và bán kính .
P
S
, Hr
H
I
P
H
12
3
22
0 (3;0;2)
3
2
2 2 4 0
xt
x
yt
yH
zt
z
x y z






22
4r R IH
2
:2 2 3 0P x y z m m
2 2 2
: 1 1 1 9S x y z
m
P
S
m
S
1; 1;1I
3R
I
P
1 1 1
:
2 2 1
x y z
P
2
31
,3
3
mm
S d I P R

2
2
3 10 0
5, 2
3 8 0 VN
mm
mm
mm
:2 2 10 0P x y z
A
1 1 1
2 2 1
2 2 10 0
x y z
x y z

3, 1, 2 3;1;2x y z A
Oxyz
2 2 2
: 1 2 1 16S x y z
I
R
1;2;1I
4R
1; 2; 1I 
4R
1;2;1I
16R
1; 2; 1I 
16R
1;2;1I
4R
Trang24
Câu 2. [2H3-1.3-1]             
có tâm I là:
A. và . B. và .
C. và . D. và .
Li gii
Chn D
Mt cu có tâm , bán kính .
Câu 3. [2H3-1.3-1]  không 
A. . B. .
C. . D. .
Li gii
Chn C
Vì .
Câu 4. [2H3-1.3-2]      

A. m chung vi (S). B. ct (S) theo mng tròn.
C. tip xúc vi (S). D. a (S).
Li gii
Chn C
Mt cu có tâm , bán kính .
Ta có: nên ct (S) theo mng tròn.
Tâm thuc mt phng .
Câu 5. [2H3-1.3-2]  
  là:
A. và . B. và .
C. và . D. và .
Li gii
Chn A
Do bốn đáp án là khác nhau về bán kính nên ta chỉ tính bán kính cho đơn giản.
Oxyz
08108
222
yxzyx
4; 5;4I
57R
4; 5;4I
7R
4;5;0I
7R
4; 5;0I
7R
4; 5;0I
7R
2 2 2
100 0x y z
2 2 2
3 3 3 48 36 297 0x y z y y
2 2 2
12 16 100 0x y z y y
2 2 2
1 2 2 9 0x y z
2
2
6 0 4 0
:4 2 3 1 0x y z
2 2 2
: 2 4 6 0S x y z x y z
S
1; 2; 3I 
14R
,0d I R

1; 2; 3I 
Oxyz
2 2 9 0x y z
2 2 2
6 4 2 86 0x y z x y z
1;2;3I
8r
1;2;3I
4r
1; 2;3I
2r
1;2; 3I
9r
Trang25
Mt cu có tâm , bán kính là .
Khong cách t tâm mt cn mt phng là :
.
Vng tròn giao tuyn là : .
Câu 6. [2H3-1.3-2]           
   .  
  
A. . B. . C. . D. .
Li gii
Chn A
Mt phng tip xúc vi mt cu tm t tha và
L t th t     và thì ch     a vì
và
Câu 7. [2H3-1.3-2] 
A. . B. .
C. . D. .
Li gii
Chn A
Câu 8. [2H3-1.3-2]   .  là
  .  
A. B. C.3. D.
Li gii
Chn A
Tâm .
Vì  nên ta có
3; 2;1O 
10R
22
2
2 3 2. 2 1 9
6
2 2 1
d

22
8r R d
Oxyz
2 2 2
: 2 4 6 5 0S x y z x y z
:2 2 1 0x y z
S
M
1;1;1
1;2;3
3;3; 3
2;1;0
S
M
M
.S
M
4
S
2.1 1 2.1 1 0
222
1 1 1 2.1 4.1 6.1 5 0.
2 2 2
20x y z x
2 2 2
2 1 0x y z x y
2
2 2 2
2 2 2 1x y x y z x
2
2
21x y xy z
2;4;1 , 2;0;3AB
1
: 1 2
2
xt
d y t
zt


S
,AB
d
S
3 3.
6.
2 3.
1 ;1 2 ; 2I d I t t t
3 ; 3 2 ; 3 ; 1 ;1 2 ; 5AI t t t BI t t t
S
,AB
Trang26
Vy bán kính mt cu :
Câu 9. [2H3-1.3-2]          
    
 là:
A. hoc . B. hoc .
C. . D. .
Li gii
Chn B
có tâm và bán kính .
tip xúc
Câu 10. [2H3-1.3-2]    S) : .
 và là:
A. . B. .
C. . D. và (S) không ct nhau.
Li gii
Chn C
T m là nghim h 
Câu 11. [2H3-1.3-2]  và A, B 
Oy 
2 2 2 2 2 2
22
3 3 2 3 1 1 2 5
4 0 0 3; 3; 3
IA IB IA IB t t t t t t
t t IA
S
22
2
3 3 3 3 3.R IA
P
()S
2 2 2 2
:2 2 4 5 0; ( ): 2 2 2 6 0P x y z m m S x y z x y z
m
P
()S
1m
5m 
1m 
5m
1m 
5m
2 2 2
( ): 2 2 2 6 0S x y z x y z
1; 1;1I
3R
P
()S
;d I P R
2
2
2 2 2
2.1 2.( 1) 1.1 4 5
3 4 4 9
2 2 1
mm
mm

2
2
2
4 4 9 1
4 5 0 .
5
4 4 9
m m m
mm
m
mm
2 2 3
:
2 3 2
x y z
d

2
22
29x y z
S
0;0;2 , 2;2; 3AB
2;3;2A
2;2; 3A 
2
22
22
23
0 2;2; 3 .
32
29
xt
yt
tA
zt
x y z

2;1; 1A
1;0;1B
Trang27
A. . B. .
C. . D. .
Li gii
Chn D
Gi trên Oy vì
ng kính bng .
Câu 12. [2H3-1.3-2]   
có bán kính là:
A.5. B.4. C.2. D. .
Li gii
Chn A
Gi là hình chiu ca tâm lên trc
Vy mt cu có bán kính : .
Câu 13. [2H3-1.3-2]   và
 
A.4. B.5. C. . D. .
Li gii
Chn B
Gi là hình chiu ca lên . .
Câu 14. [2H3-1.3-3]   
 là :
A. . B.14. C. . D.7.
Li gii
Chn C
22
6
42
26
0; ;0It
IA IB
2 0;2;0tI
6R IA
26
Oxyz
6;3; 4I
Ox
5
H
I
.Ox
6;0;0 .H Ox H
2
22
0 3 4 5R IH
Oxyz
3;3; 4I
Oy
5
5
2
I
I
Oy
0;3;0I
2
22
3 0 4 5R II
Oxyz
1;3;5I
:1
2-
xt
d y t
zt
7
14
00
0
0
0; 1;2 ; 1; 1; 1
,
1;4;3
; 14
1; 1; 1
M d M VTCP a
M I a
MI
d I d
a
a


Trang28
Câu 15. [2H3-1.3-2]  , cho  
 . Bán kính là:
A. . B. . C. . D. .
Li gii
Chn D
Câu 16. [2H3-1.3-3]       
có bán kính là:
A. . B. . C. . D. .
Li gii
Chn A
Gt cu ngoi tip t din có dng:
Vì thuc mt cu nên ta có h 
Câu 17. [2H3-1.3-3]     

A. . B. . C. . D. .
Li gii
Chn D
Oxyz
S
2;1; 1I
:2 2 3 0P x y z
S
2
9
2
3
4
3
2
2.2 2.1 1 3
; 2.
4 4 1
R d I P

Oxyz
ABCD
1;0;0 ,A
0;1;0 , 0;0;1 , 1;1;1B C D
3
2
2
3
3
4
S
ABCD
2 2 2
2 2 2 0x y z ax by cz d
2 2 2
0.a b c d
1;0;0 ,A
0;1;0 , 0;0;1 , 1;1;1B C D
S
222
2 2 2
2 2 2
222
1
2
1 0 0 2 .1 2 .0 2 .0 0
21
1
0 1 0 2 .0 2 .1 2 .0 0 2 1
.
2
21
0 0 1 2 .0 2 .1 2 .1 0
1
2 2 2 3
1 1 1 2 .1 2 .1 2 .1 0
2
0
a
a b c d
ad
a b c d b d
b
cd
a b c d
c
a b c d
a b c d
d

222
1 1 1 3
.
2 2 2 2
R
Oxyz
2 2 2
2 2 1 4 5 0x y z mx m y z m
13mm
5
1
2
m
3m
5
1
2
mm
Trang29
       t cu khi
Câu 18. [2H3-1.3-3]        
   là:
A. . B. . C. . D. .
Li gii
Chn C
T lun: Mt cu có tâm , bán kính
nên mt phng và mt cu m chung.
Gi ng thng qua và vuông góc vi ,
m ca và m có t . Vì khong cách t
n ln nht nên .
Trc nghim:Th m có t không thuc mt cu
nên loi.
Khong cách t m n là: .
Khong cách t m n là: .
Khong cách t m n là: .
Câu 19. [2H3-1.3-4]    
qua  
A. 3. B.2. C. . D. .
Li gii
Chn B
22
22
1
1 2 5 0 2 7 5 0 .
5
2
m
m m m m m
m
A
2 2 2
: 2 2 2 0S x y z x z
A
:2 2 6 0P x y z
A
1;0; 3
1 4 2
;;
3 3 3



7 4 1
;;
3 3 3




1 4 5
;;
3 3 3




1;0; 1I
2R
,3d I P R
P
S
d
I
P
12
:2
1
xt
d y t
zt


d
S
7 4 1 1 4 4
; ; , ; ;
3 3 3 3 3 3
A
P
7 4 1
;;
3 3 3
A




1 4 2
;;
3 3 3



S
1;0; 3
P
5
3
7 4 1
;;
3 3 3




P
13
3
1 4 5
;;
3 3 3




P
1
3
2;1;2A
22
2
: 1 1 9S x y z
P
A
S
3
2
1
2
Trang30
Mt cu có tâm , bán kính . D thm nm trong mt cu nên mt
phng c và vuông góc vi .
 .
ng tròn là : .
Câu 20. [2H3-1.3-4]            
.        
là:
A. . B. . C. . D. .
Li gii
Chn C
Gi là tâm mt cu ngoi tip t din , ta có:
là tâm mt cu ngoi tip t din
Vy .
Cách 2:   t cu có dng ,
Thay t vào 
S dng MTCT gii h n  .
S
0;1;1I
3R
A
P
A
IA
:2 6 0P x z
22
9 5 2r R IA
Oxyz
ABCD
1; 2; 1 , 5;10; 1 , 4;1; 1 ,A B C
8; 2;2D 
ABCD
2;3; 5
2; 4;3
2;4;5
1; 3;4
(a;b;c)I
ABCD
2 2 2
2
2 2 2
2
2 2 2
2
2 2 2 2
1 ; 2 ; 1 c 1 2 1 c
5 ;10 ; 1 c 5 10 1 c
4 ;1 ; 1 c 4 1 1 c
( 8 ; 2 ;2 c) ( 8 ) ( 2 ) (2 c)
IA a b IA a b
IB a b IB a b
IC a b IC a b
ID a b IA a b
; ;cI a b
ABCD
22
22
22
6 6 12
12 24 120 2
4 2;4;5
18 6 66 5
ab
IA IB
a b a
IA IC I
a c c
I
b
A ID




( 2;4;5)I
2 2 2
: 2 2 2 0S x y z ax by cz d
2 2 2
0a b c d
, , ,A B C D
S
, , ,a b c d
,,I a b c
Trang31

{Viết phương trình mặt cầu biết tâm và bán kính, biết tâm và đi qua điểm, biết đường kính, mặt
cầu đi qua 2 điểm và có tâm thuộc trục tọa độ, mặt cầu đi qua 3 điểm có tâm thuộc mặt phẳng
tọa độ, mặt cầu đi qua 3 điểm và có bán kính, mặt cầu ngoại tiếp tứ diện,. mặt cầu có tâm và
tiếp xúc với trục tọa độ, có tâm và tx với mặt phẳng tọa độ, có tâm và tiếp xúc với mặt cầu
khác,…}
PHN 1: CÁC VÍ D
   có tâm bán kính .

 .
   

  .
Ta có .
Suy ra tâm và bán kính .
 .
 Có tâm  .

  nên suy ra .
 .
 Có tâm  .

 .
 .
             
và .

 có tâm .
S
S
1;2;3I
5R
2 2 2
:( 1) ( 2) ( 3) 5S x y z
S
Ox
1;2;1 , 3;1; 2AB
I
;0;0I Ox I x
2 2 2
2 2 2 2 2
1 2 1 3 1 2IA IB x x
2x
2;0;0I
22
6R IB
2 2 2
( ):( 2) 6S x y z
6;3; 4I
Oy
S
Oy
,3R d I Oy
2 2 2
: 6 3 4 9S x y z
1;1;2I
: 2 2 1 0P x y z
222
1 2 4 1
8
,
3
1 2 2
R d I P


2 2 2
64
: 1 1 2
9
S x y z
2 1 1
:
3 2 2
x y z
d

: 2 2 2 0P x y z
: 2 2 4 0Q x y z
S
2 3 ;1 2 ;1 2I d I t t t
Trang32
  và nên
và .
 .
    sao cho

   .
Ta có nên 
.
      
.
 .
PHN 2: CÂU HI TRC NGHIM
Câu 1. [2H3-1.3-1]   tâm
và có bán kính là:
A. . B. .
C. . D. .
Li gii
Chn B
t cu tâm và có bán kính là:
.
Vy: Mt cu tâm , bán kính 
.
Câu 2. [2H3-1.3-1]   , bán kính

A. . B. .
S
P
Q
,,d I P d I Q R
2 3 6 3
4 11 11
2 3 6 3 2; ;
3 3 3 3 3
tt
t t t I




2
3
R
22
2
11 11 4
:2
3 3 9
S x y z
1;3;5I
23
:
1 1 1
x y z
,AB
12AB
2; 3; 0M
1;1;1u

1; 6; 5IM
, 1; 4; 5 ,IM u



2
22
2
22
,
1 4 5
, 14
1 1 1
IM u
dI
u


,AB
2
22
, 14 36 50
2
AB
R d I



2 2 2
1 3 5 50x y z
Oxyz
S
1; 2;2I
23R
2 2 2
1 2 2 12x y z
2 2 2
1 2 2 12x y z
2 2 2
1 2 2 6x y z
2 2 2
1 2 2 6x y z
S
a; ;I b c
R
2 2 2
2
x a y b z c R
3; 1;2I
4R
2 2 2
1 2 2 12x y z
Oxyz
3; 1;2I
4R
2 2 2
3 1 2 16x y z
2 2 2
3 1 2 4x y z
Trang33
C. . D. .
Li gii
Chn D
Mt cu tâm , bán kính 
.
Câu 3. [2H3-1.3-1]   và
 là:
A. . B. .
C. . D. .
Li gii
Chn C
Tâm  .
 : .
Câu 4. [2H3-1.3-2]   

A. . B. .
C. . D. .
Li gii
Chn A
Mt cu tâm ng kính bng 10 nên có bán kính 
.
Câu 5. [2H3-1.3-2]               
và 
A. . B. .
C. . D. .
Li gii
Chn C
Tâm m cng kính , bán kính mt cu là
2 2 2
3 1 2 4x y z
2 2 2
3 1 2 16x y z
3; 1;2I
4R
2 2 2
3 1 2 16x y z
Oxyz
1;1; 2I
2; 1;0M
2 2 2
1 1 2 9x y z
2 2 2
1 1 2 3x y z
2 2 2
1 1 2 9x y z
2 2 2
1 1 2 3x y z
1;1; 2I
3R IM
S
2 2 2
1 1 2 9x y z
Oxyz
1;2;0I
22
2
1 2 25x y z
22
2
1 2 100x y z
22
2
1 2 25x y z
22
2
1 2 100x y z
1;2;0I
5R
22
2
1 2 25x y z
Oxyz
AB
1;3; 4A
1; 1;0A
2 2 2
1 1 2 8x y z
2 2 2
1 1 2 4x y z
2 2 2
1 1 2 8x y z
2 2 2
1 1 2 4x y z
I
AB
1;1; 2I
22R IB
Trang34
t cu : .
Câu 6. [2H3-1.3-2]   . 
  .
A. . B. .
C. . D. .
Li gii
Chn D
Gi là hình chiu ca lên , ta có: .
là bán kính mt cu cn tìm.
PT mt cu cn tìm là: .
Câu 7. [2H3-1.3-2]   có tâm 
 
A. . B. .
C. . D. .
Li gii
Chn B
Mt cu có tâm và tip xúc vi mt phng nên có bán
kính 
Câu 8. [2H3-1.3-2]   
 
A. . B. .
C. . D. .
Li gii
Chn A
. Vây .
Câu 9. [2H3-1.3-2]  
 là:
S
2 2 2
1 1 2 8x y z
Oxyz
1; 2;3I
I
Oy
2 2 2
1 2 3 15x y z
2 2 2
1 2 3 30x y z
2 2 2
1 2 3 20x y z
2 2 2
1 2 3 10x y z
M
1; 2;3I
Oy
0; 2;0M
1;0; 3IM
10R IM
2 2 2
1 2 3 10x y z
Oxyz
S
1;2;1I
( ): 2 2 2 0P x y z
2 2 2
1 2 1 3x y z
2 2 2
1 2 1 9x y z
2 2 2
1 2 1 3x y z
2 2 2
1 2 1 9x y z
S
1;2;1I
( ): 2 2 2 0P x y z
1 2.2 2.1 2
3
1 4 4
R


2 2 2
1 2 1 9.x y z
Oxyz
2;1; 1I
Oyz
2 2 2
2 1 1 4x y z
2 2 2
2 1 1 1x y z
2 2 2
2 1 1 4x y z
2 2 2
2 1 1 2x y z
2
2
: 0 ; 2
1
Oyz x R d I Oyz
2 2 2
: 2 1 1 4S x y z
Oxyz
Ox
3;1;0 , 5;5;0AB
Trang35
A. . B. .
C. . D. .
Li gii
Chn C
Lt th t m vào  a vì
và
Câu 10. [2H3-1.3-2]   
  .
A. . B. .
C. . D. .
Li gii
Chn B
Ta có là mt cu có tâm thuc mt phng có tâm .
Suy ra có dng: .
Ta có .
.
Câu 11. [2H3-1.3-3]            có tâm
 : .
A. . B. .
C. . D. .
Li gii
Chn B
Gi có bán kính .
Ta có qua , có VTCP .
tip xúc vng thng .
2
22
9 10x y z
2
22
10 5 2x y z
2
22
10 50x y z
2
22
10 25x y z
,A
B
4
2
22
3 10 1 0 50
2
22
5 10 5 0 50.
Oxyz
S
Oxy
1;2; 4 , 1; 3;1 ,AB
2;2;3C
22
2
2 1 16 0x y z
2 2 2
4 2 21 0x y z x y
2 2 2
4 2 21 0x y z x y
2 2 2
4 2 6 21 0x y z x y z
S
Oxy S
( ; ;0)I a b
S
2 2 2
2 2 0x y z ax by c
1;2; 4
2
1; 3;1 1
21
2;2;3
AS
a
B S b
c
CS





2 2 2
: 4 2 21 0S x y z x y
Oxyz
S
4;2; 1I
d
2 1 1
2 1 2
x y z

2 2 2
4 2 1 16x y z
2 2 2
4 2 1 16x y z
2 2 2
8 4 2 5 0x y z x y z
2 2 2
8 4 2 5 0x y z x y z
S
R
d
(2; 1;1)A
(2;1;2)
d
u
S
d
;
;4
d
d
IA u
R d I d
u


Trang36
.
Câu 12. [2H3-1.3-2] Trong không gian  , cho  
 ?
A. . B. .
C. . D. .
Li gii
Chn D
Mt cng kính có tâm m . Bán kính .
Câu 13. [2H3-1.3-2]  
  ?
A. . B. .
C. . D. .
Li gii
Chn C
.
t cu cn tìm có dng: .
Cách 2: theo công th   t cu có tâm bán kính có dng
. Ta loi câu A và D.
Bán kính . Nên ta chn câu C.
Câu 14. [2H3-1.3-3]      Oxyz S) có tâm  
 P): .    P    S     
 S) là:
A. . B. .
C. . D. .
Li gii
Chn D
2 2 2
4 2 1 16x y z
Oxyz
2; 6;4A
OA
2 2 2
2 6 4 56x y z
2 2 2
2 6 4 56x y z
2 2 2
1 3 2 14x y z
2 2 2
1 3 2 14x y z
OA
1; 3;2I
OA
56
22
OA
R 
Oxyz
1;2; 1I
: 2 2 8 0P x y z
2 2 2
1 2 1 3x y z
2 2 2
1 2 1 3x y z
2 2 2
1 2 1 9x y z
2 2 2
1 2 1 9x y z
,
22
2
1 2.2 2. 1 8
3
1 2 2
IP
Rd
2 2 2
1 2 1 9x y z
;;I a b c
R
2 2 2
2
x a y b z c R
,
22
2
1 2.2 2. 1 8
3
1 2 2
IP
Rd
(2;1;1)I
2 2 2 0x y z
2 2 2
1 1 1 8x y z
2 2 2
2 1 1 10x y z
2 2 2
2 1 1 8x y z
2 2 2
2 1 1 10x y z
Trang37
Ta có .
Bán kính mt cu là .
Câu 15. [2H3-1.3-3]  
 .  và có
 .
A. . B. .
C. . D. .
Li gii
Chn D
t cu có dng: , ta có
Ly v tr v ca cho ; cho ; kt hc h
.
Vt cu là .
Trc nghim:
Thay t vào tt cu t

Thay t t cu lo
Câu 16. [2H3-1.3-3]   và
   
 
A. . B. .
C. . D. .
Li gii
Chn D
2 2 2
2.2 1 2.1 2
( ;( )) 3
2 1 2
d d I P

2 2 2
22
1 10 : 2 1 1 10R d S x y z
Oxyz
2;0;1 , 1;0;0 , 1;1;1A B C
: 2 0P x y z
,,A B C
P
2 2 2
2 1 0x y z x z
2 2 2
2 1 0x y z x y
2 2 2
2 2 1 0x y z x y
2 2 2
2 2 1 0x y z x z
()S
2 2 2
2 2 2 0x y z ax by cz d
2;0;1 4 2 5 1
1;0;0 2 1 2
1;1;1 2 2 2 3 3
2 4
A S a c d
B S a d
C S a b c d
I P a b c







1
2
2
3
2 2 4 1
2 2 2 0 1
21
a c a
b c b d
a b c c





2 2 2
2 2 1 0x y z x z
1;0;0B
2;0;1A
Oxyz
( ): 2 2 3 0P x y z
(1;3; 1)I
S
I
()P
2
:S
2 2 2
( 1) ( 3) ( 1) 5x y z
:S
2 2 2
( 1) ( 3) ( 1) 5x y z
:S
2 2 2
( 1) ( 3) ( 1) 3x y z
:S
2 2 2
( 1) ( 3) ( 1) 5x y z
Trang38
Bán kính cng tròn giao tuyn ca và là .
.
Bán kính mt cu là .
  t cu tâm và bán kính là
.
Câu 17. [2H3-1.3-3]   
, ,  là:
A. . B. .
C. . D. .
Li gii
Chn B
  .
 nên
  , , .
Nên
. .
 có tâm bán kính .
 : .
Câu 18. [2H3-1.3-4]   : và
: .  và 

A. . B. .
S
P
2
1
2
r

2323
,2
4 1 4
d d I P

S
22
5R r d
S
1;3; 1I
5R
:S
2 2 2
( 1) ( 3) ( 1) 5x y z
Oxyz
S
1;2; 4A
1; 3;1B
2;2;3C
Oxy
22
2
7 3 83
2 2 2
x y z
22
2
2 1 26x y z
22
2
7 3 81
2 2 2
x y z
22
2
7 3 83
2 2 2
x y z
;;I a b c
S
Oxy
; ;0I a b
S
1;2; 4A
1; 3;1B
2;2;3C
IA IB IC
2 2 2 2
2 2 2 2
1 2 16 1 3 1
1 2 16 2 2 9
a b a b
a b a b
2 4 2
10 10 1
aa
bb





S
2;1;0I
26R IA
S
22
2
2 1 26x y z
Oxyz
1
d
1
0
5
xt
y
zt

2
d
0
42
53
x
yt
zt


1
d
2
d
22
2
2 3 17x y z
22
2
2 3 25x y z
Trang39
C. . D. .
Li gii
Chn A
có vtcp .
có vtcp .
.
.
.
n vuông góc chung cng thng và
.
 .
Mt cng kính có tâm và bán kính 
.
Câu 19. [2H3-1.3-4]   và
 ,  , và có tâm 
 .
A. . B. .
C. . D. .
Li gii
Chn A
 ng thng .
Ta có: .
Vì mt cu m , nên: .
2 2 2
2 3 1 25x y z
2 2 2
2 3 1 25x y z
1
d
1
1;0;1u

2
d
2
0; 2;3u 
1
1; 0; 5A d A t t
2
0;4 2 ; 5 3B d B t t

1 ,4 2 ,10 3AB t t t t

AB
1
d
2
d
1
1
1 10 3 ' 0
.0
2 3 ' 9 3
2 4 2 ' 3 10 3 ' 0
3 13 ' 22 ' 1
.0
t t t
ABu
t t t
t t t
t t t
ABu



4;0; 2 , 0;6;2AB
AB
2;3;0I
17
2
AB
R 
22
2
2 3 17x y z
Oxyz
1
:
2 1 2
x y z
d

2;1;0A
2;3;2B
A
B
I
d
2 2 2
1 1 2 17x y z
2 2 2
1 1 2 17x y z
2 2 2
3 1 2 5x y z
2 2 2
3 1 2 5x y z
12
:
2
xt
d y t
zt


1 2 ; 1: 2
1 2 ; ; 2
3 2 ; 3; 2 2
AB t t t
I d I t t t
BI t t t
S
A
B
22
R IA IB IA IB
Trang40
.
t cu cn tìm là: .
Câu 20. [2H3-1.3-4]  
 :  ,
.
A. và .
B. và .
C. và .
D. và .
Li gii
Chn D
* Gi là tâm mt cu .
* Vì  nên .
  và nên:
.
 tâm bán kính .
 .
 tâm bán kính .
 .
2 2 2 2 2 2
1 2 1 2 3 2 3 2 2t t t t t t
20 20 0 1tt
1; 1;2 17I R IA
S
2 2 2
1 1 2 17x y z
Oxyz
S
d
2
0
x
y

: 2 8 0P x z
:2 5 0Q x z
22
2
144
2 11
5
x y z
22
2
16
2 11
5
x y z
22
2
121
2 11
5
x y z
22
2
126
2 11
5
x y z
22
2
134
2 11
5
x y z
22
2
164
2 11
5
x y z
22
2
144
2 11
5
x y z
22
2
16
23
5
x y z
;;I a b c
S
I
2
:
0
x
d
y

2;0;Iz
S
P
Q
,,d I P d I Q
2 2 8 4 5
55
zz

2 10 1zz
2 10 1
2 10 1
zz
zz
11
3
z
z


11z 
2;0; 11I 
12
,
5
R d I P
22
2
144
: 2 11
5
S x y z
3z 
2;0; 3I 
4
,
5
R d I P
22
2
16
: 2 11
5
S x y z
Trang41
T PHNG

A. 
B. .
Bài toán 1: Vi   t phng   m và có vtpt
Bài toán 2:Vit phng m M và có c 
c.
Bài toán 3: Vit phng m không thng hàng
Bài toán 4:  

Bài toán 5: Mt phngvà mt cu.
Bài toán 6: Mt phn góc.
Bài toán 7: Mt phn khong cách.
C. 
 -  ng dn gii chi tit u
S 
NB: 10 TH: 15 VDT: 15 VDC: 10
P
( ; ; )
o o o
M x y z
()
( ; ; )
P
n A B C
()P
, ab

()P
, , A B C
()P
Trang42
A LÝ THUYT CN NM
n, c 
  




 




  







 
 1 
 1   




ng quát ca mt phng:


   

 
ng hc bit:







O











:




 








.
0n

()P
n
( ).P
, ab

()P
( ).P
, ab

()P
,n a b


( ).P
0n

()P
. , ( 0)k n k
( ).P
( ) : 0.P Ax By Cz D
()P
( ) : 0P Ax By Cz D
()
( ; ; )
P
n A B C
( ).P
( ),P
()


( ; ; )
( ): ( ): .( ) .( )
tpt : ( ;
( ) 0
;)
.
o o o
oo
P
o
n A B
M x y z
P P A x x B y y C z
C
z
()P
()P
0D
( ): 0P Ax By Cz
()P
0A
( ) : 0P By Cz D
( ) P Ox
()P Ox
0B
( ) : 0P Ax Cz D
( ) P Oy
()P Oy
0C
( ): 0P Ax By D
( ) P Oz
()P Oz
0AB
( ): 0P Cz D
( ) ( )P Oxy
( ) ( )P Oxy
0AC
( ): 0P By D
( ) ( )P Oxz
( ) ( )P Oxz
0BC
( ): 0P Ax D
( ) ( )P Oyz
( ) ( )P Oyz
()P
()P
P
()P
n
uuur
Trang43



 







 ().
  

B .
Bài toán 1: Vi   t phng   m và có vtpt


Áp dng:
Ví d 1:  M d A
và B,



a) b)
c) d)
AB A, B cho

Mă
t phă
ng trung trư
c của đoạn AB là mp đi qua và vuông góc tại trung điểm I của AB.



a) b) c)
()P
( ;0;0), (0; ;0), (0;0; )A a B b C c
( ): 1
x y z
P
a b c
( ; ; )
M M M
M x y z
( ) : 0P Ax By Cz D
2 2 2
( ;( ))
M M M
Ax By Cz D
d M P
A B C


P
( ; ; )
o o o
M x y z
()
( ; ; )
P
n A B C
()


( ; ; )
( ):
( ): .( ) .( )
tpt : ( ;
( ) 0
;)
.
o o o
oo
P
o
n A B
M x y z
P
P A x x B y C z z
C
y
()mp P
Đ
2
()

( ):
:
P
Pd
M
mp P
VTP
i
T n u AB
qua


( 1;2;3), (2; 4;3), (4;5;6).M A B
(0;0;0), ( 2; 1;3), (4; 2;1).M A B
(2; 4;0), (5;1;7), ( 1; 1; 1).M A B
(3;0;0), (0; 5;0), (0;0; 7).M A B
()P
Đ
()

2 2 2

(
: ( ; ; )
):
A B A B A B
P B A B A B A
x x y y z z
i qua I
VTPT n AB x x y y z
mp
z
P



(2;0;1), (0; 2;3).AB
(1;3; 4), ( 1;2;2).AB
(2;1;1), (2; 1; 1).AB
Trang44
           



1. 
a) và b) và
c) và d) và
2. 2013 NC)   
A   
qua A  ?
 và
3.         
  ?

 M 





a) b)
c) d)
()mp P
( ; ; )
o o o
M x y z
( ) : 0Q Ax By Cz D
Đ
( ) ( )

( ):

)
o o o
PQ
M x y z
mp P
VTPT n n A B C
i qua

(3;3;3)M
( ): 2 3 6 0.Q x y z
(2;1;5)M
( ) ( )Q Oxy
(1; 2;1)M
( ): 2 3 0.Q x y
( 1;1;0)M
( ) : 2 10 0.Q x y z
,Oxyz
( 1;3; 2)A 
( ): 2 2 5 0.P x y z
( ).P
()Q
()P
2
,( )
3
d A P
( ): 2 2 3 0.Q x y z
()P
( ):2 3 6 14 0mp Q x y z
()P
5
( ) : 2 3 6 35 0.P x y z
()P
, ab

Đ
()

( ):

,
P
M
mp P
VTPT n a b
i qua


(1;2; 3), (2;1;2), (3;2; 1).M a b
(1; 2;3), (3; 1; 2), (0;3;4).M a b
( 1;3;4), (2;7;2), (3;2;4).M a b
( 4;0;5), (6; 1;3), (3;2;1).M a b
Trang45
  vuông góc và


a)
b)
   :
a) b)
c) d)
    
1
2014)         cho
 d
và  d 
 và
( 2010 
 ) 


  .
a) 


 
d  .
b)  sao cho M O 

. 
 M  :
()mp P
,M
()mp Q
( ) :mp P
2
( ) ( )

( ):

o o o
P
PQ
M x y z
mp P
vtpt n n
qu
u
a



(1;1;1),M
( ): 2 1 0,Q x y z
11
:
2 1 3
x y z
(3;2;1),M
Q x y z
13
: 2 , ( ).
33
xt
y t t
zt


()P
, AB
()mp Q
Đ
( ) ( )

( ):

PP
PQ
A hay B
mp P
VT
i
PT n AB n
qua



(0;1;0), (1;2; 2)
( ):2 3 13 0
AB
Q x y z
(3;1; 1), (2; 1;4)
( ):2 3 1 0
AB
Q x y z

(2; 1;3), ( 4;7; 9)
( ):3 4 8 5 0
AB
Q x y z
(3; 1; 2), ( 3;1;2)
( ):2 2 2 5 0
AB
Q x y z
,Oxyz
( ) : 2 2 1 0mp P x y z
23
( ) :
1 2 3
x y z
d

( ).mp P
()Q
( ).mp P
73
; 3;
22
M



( ) : 8 5 13 0.Q x y z
,Oxyz
1
( ) :
2 1 1
x y z
d

:2 2 2 0P x y z
()Q
( ) ( ).QP
Md
( ).mp P
( ): 2 2 0Q x y
(0;1;0).M
()P
Trang46


  

VTCP

a) b)
c) d)
(TNTHPT 2010  



O 
 O 

 và
 


a)
b)
c)
   và song
song
u
Đ
()

( ):

P
M
mp P
VTPT n AM
i qu
u
a


42
2; 3;1 , : 2 3
3
xt
M y t
zt


2
1;4; 3 , : 1 2
13
xt
M y t
zt


1 2 5
4; 2;3 , :
3 4 2
x y z
M
2 1 0
2;1;4 , :
2 2 5 0
x y z
M
x y z

,Oxyz
11
:
2 2 1
x y z
.
()P
.
,
( ; ) 1
MO u
dO
u


( ) : 2 2 0.P x y z
()P
12
, :
12
12
()

( ):

P
M hay M
mp P
vtp
qu
t n u u
a



1
3
: 1 2 , ( ),
3
xt
y t t
zt

2
1
: 2 , ( )
4
xt
y t t
zt



1
30
:,
2 1 0
x y z
xy
2
1
: 2 , ( )
3
xt
y t t
zt


1
2 4 0
:,
2 6 0
x y z
x y z
2
20
:
2 7 0
xz
yz
12
, .
()P
1
2
Trang47


a)
b)
c)
 qua M  :


a)
b)
( 2009 

) 




cho




  . 



 
 


  .

. .
( 2010 

) 






  . 



sao cho 

 và  .

. .
12
1
()

( ):

P
M
mp P
vtpt n u u
qua




1
12
: 3 , ,
23
xt
y t t
zt

2
2
: 1 ,
32
xt
y t t
zt


1
21
:,
3 2 2
x y z
2
11
:
1 2 4
x y z
1
2 4 0
:
2 2 4 0
x y z
x y z
2
1
: 2 ,
12
xt
y t t
zt


()mp P
( ), ( )mp

( ) ( ) ( )

( ):

P
mp P
vtpt n n n
qua M



(1; 3;2),M
( ) : 2 5 1 0,x y z
( ): 2 3 4 0.x y z
2; 1;1 ,M
:2 1 0,xz
:0y
,Oxyz
1
: 2 3 4 0P x y z
2
:3 2 1 0P x y z
P
1;1;1 ,A
1
P
2
P
:4 5 2 1 0P x y z
,Oxyz
: 3 0P x y z
: 1 0Q x y z
R
R
P
Q
,2d O R
: 2 2 0R x z
Trang48
             

 ?

  




a) b)
c) d)
 (THPT 2011 NC)  cho
  
 và
 M 
  và 
Cho:
Cho:

a)
b)
 

  
 
( ),P
()P
( ) : 1 0,x y z
( ):2 3 4 0x y z
()P
26
( ): 4 3 26 0.P x y z
()P
, , A B C
Đ
()
, (
( ):

)
ABC
mp P
VTPT n A
i qua A hay
B AC
B hay C


(2; 5;1), (3;4; 2), (0;0; 1).A B C
(1; 2;4), (3;2; 1), ( 2;1; 3).A B C
(3; 5;2), (1; 2;0), (0; 3;7).A B C
( 1;2;3), (2; 4;3), (4;5;6).A B C
,Oxyz
(0;0;3),A
( 1; 2;1),B 
( 1;0;2).C
( ).ABC
ABC
.A
( ) :2 2 6 0ABC x y z
35
5
AH 
P
,

PP
,AB
,A B P
1 1 1 1
2 2 2 2
...
...;...;...
...
o
o
o
A x B y C z D
x
z z A P
y
A x B y C z D

1 1 1 1
2 2 2 2
...
...;...;...
...
o
o
o
B y C z A x D
y
x x B P
z
B y C z A x D

Đ 
:

:
P
mp P
VTPT n AB
i qua M
AM


2;0;1 ,M
: 2 4 0,x y z
:2 4 0x y z
1;2; 3 ,M
:2 3 5 0,x y z
:3 2 5 1 0x y z
()P
P
, ,

Trang49
a)
b)
   
 
a)
b)
              
và  
 
Bài toán 5: Mt phngvà mt cu
  
a) 
b) 
Ví d -LN 2-2018) Trong không gian vi h ta
 , cho mt cu   m ,
. Gi là mt phm , sao cho thit din ca vi mt
cu có din tích nh nht. Khi vi i dng .
Tính .
A. . B. . C. . D. .
Li gii

: 2 4 0,yz
: 3 0,x y z
: 2 0x y z
: 4 2 5 0,x y z
: 4 5 0,yz
:2 19 0xy
P
, ,

:2 3 4 0,xy
:2 3 5 0,yz
:2 3 2 0x y z
: 2 4 0,yz
: 3 0,x y z
: 2 0x y z
()P
( ): 3 2 0xz
( ): 2 1 0,yz
1
0;0;
2
M



73
18
( ) : 5 1 0P x y z
( ):5 17 19 27 0.P x y z
P
S
:H
2 2 2
: 3 1 2 24S x y z
1;3;0H
2 2 2
: 6 2 4 5 0S x y z x y z
4;3;0H
Oxyz
2 2 2
: 1 2 3 16S x y z
1;0;2A
1;2;2B
P
A
B
P
S
P
: 3 0P ax by cz
T a b c
3
3
0
2
Trang50
 bán kính là .
Ta có ,   trên và 

 
 suy ra qua  .
Ta có suy ra   và .
 .
 .
Oxyz và 
 d và
Ox
(S) có tâm I(1; 1; 2), bán kính R = 2. d có VTCP .
(P) // d, Ox
(P) có VTPT
PT của (P) có dạng: .
(P) tiếp xúc với (S)
(P): hoặc (P): .
Oxyz
   P):       Q   
P(S).
(S) có tâm I(–1; 2; 0) và bán kính R = 3; (P) có VTPT .
PT (Q) đi qua M có dạng:
I
H
A
B
K
1;2;3I
4R
A
B
K
I
AB
H
I
2 2 2
S r R IH

IH
IH IK
P
,AB
IK
5IA IB
K
AB
0;1;2K
1;1;1KI
: 1 2 0P x y z
30x y z
3T 
33
2 2 1
x y z

2 2 2
2x 2 4z 2 0x y z y
(2;2;1)u
, (0;1; 2)n u i

2z 0yD
( ,( ))d I P R
22
14
2
12
D
3 2 5D 
3 2 5
3 2 5
D
D


2z 3 2 5 0y
2z 3 2 5 0y
2 2 2
2 4 4 0x y z x y
30xz
(3;1; 1)M
(1;0;1)
P
n
2 2 2
( 3) ( 1) ( 1) 0, 0A x B y C z A B C
Trang51
(Q) tiếp xúc với (S)
(*)
(**)
Từ (*), (**)
Với . Chọn B = 1, A = 2, C = –2
PT (Q):
Với . Chọn B = –7, A = 4, C = –4
PT (Q):
Câu hỏi tương tự:
a) Với , .
ĐS: hoặc .
         Oxyz   
. Px 
 .
(S) có tâm I(1; –2; –1), bán kính R = 3. (P) chứa Ox
(P): ay + bz = 0.
Mặt khác đường tròn thiết diện có bán kính bằng 3 cho nên (P) đi qua tâm I.
Suy ra: –2a – b = 0 b = –2a (a 0)
(P): y – 2z = 0.
         xyz    
   .    
Pd  .
(S) có tâm , bán kính R = 2.
PT mặt phẳng (P) có dạng: .
Chọn .
Ta có:
+ Với (1)
(P): + Với (2)
(P):
               ,
2 2 2
( ,( )) 4 3d I Q R A B C A B C
( ) ( ) . 0 0
QP
Q P n n A C C A

2 2 2 2
5 3 2 8 7 10 0B A A B B A AB
2 7A 4A B B
2AB
2 2 9 0x y z
7A 4B
4 7 4 9 0x y z
2 2 2
( ): 2 4 4 5 0S x y z x y z
( ): 2 6 5 0, (1;1;2)P x y z M
( ): 2 2 6 0Q x y z
( ) :11 10 2 5 0Q x y z
2 2 2
S x y z x y z
3r
2 2 2
x y z x y z
20
:
2 6 0
xy
d
xz
1r
( 1;1; 1)I 
2 2 2
0 ( 0)ax by cz d a b c
(2;0; 2), (3;1;0)M N d
22
()
()
( ,( ))
MP
NP
d I P R r

,2 ( ), 3 (1)
17 7 ,2 ( ), 3 (2)
a b c a b d a b
a b c a b d a b
40x y z
7 17 5 4 0x y z
Oxyz
1
1
:
2 1 1
x y z
Trang52
và  
  và .
(P): hoc (P):
          Oxyz,    S   
 
 .


S
 .
Do (
) // (
) nên (
) có phương trình 2x + 2y – z + D = 0 (D 17)
(S) có tâm I(1; –2; 3), bán kính R = 5. Đường tròn có chu vi 6
nên có bán kính r = 3.
Khoảng cách từ I tới (
) là h =
Do đó
Vậy (
) có phương trình .
Câu hỏi tương tự:
a) , , .
ĐS:
Bài toán 6: Mt phn góc.
 Oz  
?
 
      và   góc  
?
 
        Oxyz     ):
       góc 60
0
    
Oz.
(
) qua điểm và có VTCP . (P) có VTPT .
2
1
:
1 1 1
x y z

:S
2 2 2
x y z x y z
S
1
2
3 3 2 0yz
3 3 2 0yz
2 2 2
2 4 6 11 0x y z x y z
 x y z
6p
2 2 2 2
5 3 4Rr
2 2 2
7
2.1 2( 2) 3
4 5 12
17 (loaïi)
2 2 ( 1)
D
D
D
D

x y z
22
2 4 6 11 0
2
( ): y z x y zSx
( ):2 2 19 0x y z
8p
( ): 2 2 1 0x y z
()mp P
( ):2 11 3 0Q x y z
30
o
( ): 0Px
( ):3 4 0.P x y
()P
(3;0;1), (6; 2;1)AB
()P
()Oyz
2
cos
7
( ) :2 3 6 12 0mp P x y z
( ): 2 3 6 0.mp P x y z
1
1 1 2
x y z


2 2 1 0x y z
(1;0;0)A
(1; 1; 2)u
(2; 2; 1)n
Trang53
Giao điểm cho . (
) có VTPT
(
) và (P): tạo thành góc 60
0
nên:
hay
Kết luận: hay
Oxyz, (P) 
d     ,     
 góc
mà
Lấy . (P) qua A
PT (P) có dạng: .
(P) qua B nên:
.
Chọn .
+ Với
+ Với
.
xyz, cho  
 
  .
PT mặt phẳng (Q) có dạng: .
Ta có:
Phương trình mp(Q): hoặc (Q): .
(0;0; )Mm
( 1;0; )AM m
, ( ; 2;1)n AM u m m


2 2 1 0x y z
2
2
1 1 1
cos , 2 4 1 0
22
2 4 5
n n m m
mm


22m 
22m 
(0;0;2 2)M
(0;0;2 2)M
xy
xz
Q x y z
22
cos
9
(0;1;0), (1;3;2)A B d
Ax By Cz B
A B C B
(2 2 )A B C
P B C x By Cz B
2 2 2
2 2 2 2
22
cos
9
3 (2 2 )
B C B C
B C B C

22
 B BC C
5
1 1;
13
C B B
1BC
P x y z
5
, 1
13
BC
  P x y z
( 1;2; 3), (2; 1; 6)AB
( ) : 2 3 0P x y z
3
cos
6
2 2 2
0 ( 0)ax by cz d a b c
()
()
3
cos
6
AQ
BQ
2 2 2
2 3 0
2a 6 0
23
6
1 4 1
a b c d
b c d
a b c
abc

4 , 3 , 15
, 0,
a b c b d b
a b c d b
4 3 15 0x y z
30xy
Trang54
Câu hỏi tương tự:
a) , .
ĐS: (Q): hoặc (Q): .
 , cho  
 và  
d   .
ĐS: hoặc
xyz và
 
 .
Giả sử PT mặt phẳng (R): .
Ta có: (1);
(2)
Từ (1) và (2)
Với : chọn
PT mặt phẳng
Với : chọn
PT mặt phẳng
Câu hỏi tương tự:
a) Với .
ĐS: hoặc
          xyz, cho      
và  
  .
Đáp số: (P): hoặc (P): .
Câu hỏi tương tự:
(0;0;1), (1;1;0)AB
1
( ) ( ),cos
6
P Oxy

2 1 0x y z
2 1 0x y z
Oxyz
d
: 3 0P x y z
:2 4 0Q x y z
R
Oxy
0
60
: 2 2 2 0R x y z
: 2 2 2 0R x y z
( ) :5 2 5 1 0P x y z
( ) : 4 8 12 0Q x y z
()R
0
45
2 2 2
ax z 0 ( 0)by c d a b c
( ) ( ) 5 2 5 0R P a b c
0
2 2 2
4 8 2
cos(( ),( )) cos45
2
9
a b c
RQ
abc


22
7 6 0
7
ac
a ac c
ca

ac
1, 0, 1a b c
( ): 0R x z
7ca
1, 20, 7a b c
( ): 20 7 0R x y z
0
( ): 2 0,( ) ( ), (2; 3;1), 45P x y z Q Oyz M
( ): 1 0R x y
( ) :5 3 4 23 0R x y z
1
1 1 1
:
1 1 3
x y z
2
:
1 2 1
x y z
1
2
0
30
5 11 2 4 0x y z
2 2 0x y z
Trang55
a) Với , , .
ĐS: (P): hoặc (P):
b) , , .
ĐS: (P):
hoặc (P):
xyz, 
x, Oy  .
Gọi là VTPT của (P). Các VTCP của trục Ox, Oy là .
Ta có:
PT mặt phẳng (P): hoặc
          xyz, cho    và
 d và

PT mặt phẳng (P) có dạng: . Gọi .
Chọn hai điểm . Ta có:
(P):
TH1: Nếu a = 0 thì
.
TH2: Nếu a
0 thì . Đặt và
1
2
:
1 1 1
x y z
2
2 3 5
:
2 1 1
x y z
0
30
2 2 2 0x y z
2 4 0x y z
1
11
:
2 1 1
x y z
2
21
:
1 1 1
x y z
0
30
(18 114) 21 (15 2 114) (3 114) 0x y z
(18 114) 21 (15 2 114) (3 114) 0x y z
(1;2;3)M
00
45 , 30
( ; ; )n a b c
(1;0;0), (0;1;0)ij

2
sin( ,( ))
2
1
sin( ,( ))
2
Ox P
Oy P
2ab
cb
2( 1) ( 2) ( 3) 0x y z
2( 1) ( 2) ( 3) 0x y z
2 5 0x y z
1 1 3
:
2 1 1
x y z
d

2 2 2
ax z 0 ( 0)by c d a b c
(( ),( ))PQ
( 1; 1;3), (1;0;4)M N d
()
( ) 7 4
M P c a b
N P d a b



( 2 ) 7 4 0ax by a b z a b
22
3
cos .
6
5 4 2
ab
a ab b

2
33
cos .
2
6
2
b
b

0
30
2
1
3
cos .
6
5 4 2
b
a
bb
aa




b
x
a
2
( ) cosfx
Trang56
Xét hàm số .
Dựa vào BBT, ta thấy
Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn .
Vậy: (P): .
Câu hỏi tương tự:
a) Với (Q): , . ĐS: .
b) Với . ĐS: .
c) Với , . ĐS: .
xyz, cho  
 

ĐS: .
Câu hỏi tương tự:
a) . ĐS: .
          , cho    
   
PT mặt phẳng (P) có dạng: . Gọi .
Chọn hai điểm . Ta có:
(P):
.
TH1: Nếu b = 0 thì .
2
2
9 2 1
( ) .
6 5 4 2
xx
fx
xx


00
min ( ) 0 cos 0 90 30fx

1, 1, 4b c d
40yz
x y z
12
:
1 2 1
x y z
d


( ) : 2 5 3 0P x y z
12
( ) ( ), :
1 1 2
x y z
Q Oxy d

( ): 3 0P x y z
( ) : 2 2 0Q x y z
: 1 2
2
xt
d y t
zt


( ): 3 0P x y z
( 1; 1;3), (1;0;4)MN
: 2 5 0Q x y z
( ) : 4 0P y z
(1;2; 1), ( 1;1;2),( ) ( )M N Q Oxy
( ) :6 3 5 7 0P x y z
Oxyz
1
:2
2
xt
d y t
zt

P
d
Oy
2 2 2
ax z 0 ( 0)by c d a b c
(( ), )P Oy
(1; 2;0), (0; 1;2)M N d
( ) 2
( ) 2
M P c a b
N P d a b



20
2
ab
ax by z a b
22
2
sin
5 5 2
b
a b ab

0
0
Trang57
TH2: Nếu b
0 thì . Đặt và .
Xét hàm số . Dựa vào BBT, ta được
.
Vậy
lớn nhất khi . Chọn
(P): .
xyz, cho  và
 sao cho 
 
đi qua và có VTCP .Vì nên .
PT mặt phẳng (P) có dạng:
Ta có: .
Gọi
TH1: Với B = 0 thì
TH2: Với B
0. Đặt , ta được:
Xét hàm số . Dựa vào BBT ta có: khi
Khi đó .
So sánh TH1 và TH2

lớn nhất với khi .
Phương trình mặt phẳng (P): .
xyz, cho  và
             d    
2
2
sin
5 5 2
aa
bb




a
x
b
2
( ) sinfx
2
4
()
5 2 5
fx
xx

51
max ( )
65
f x x
0
0
1
5
a
b
1, 5, 2, 9a b c d
5 2 9 0xyz
1
12
:
1 2 1
x y z
d


2
21
:
2 1 2
x y z
d


1
d
2
d
1
d
(1; 2;0)M
(1;2; 1)u 
1
()dP
()MP
( 1) ( 2) 0A x B y Cz
2 2 2
( 0)A B C
( ) . 0 2d P u n C A B

2
(( ), )Pd
2
22
22
4 3 1 (4 3 )
sin .
3 2 4 5
3. 2 4 5
A B A B
A AB B
A AB B




22
sin
3
A
t
B
2
2
1 (4 3)
sin .
3 2 4 5
t
tt

2
2
(4 3)
()
2 4 5
t
ft
tt

25
max ( )
7
ft
7t 
7
A
B

53
sin ( 7)
9
f
53
sin
9
7
A
B

7 5 9 0 x y z
1 2 1
:
1 1 1
x y z
d

(2; 1;0)A
Trang58
xy
ĐS: .
xyz, cho  

y 
ĐS: hoặc .
Bài toán 7: Mt phn khong cách.
Oxyz
  .
PT mặt phẳng (P) qua O nên có dạng: (với ).
Vì (P)
(Q) nên:
(1)
(2)
Từ (1) và (2) ta được:
Từ (3): B = 0
C = –A. Chọn A = 1, C = –1
(P):
Từ (4): 8A + 5B = 0. Chọn A = 5, B = –8
C = 3
(P): .
xyz : và
, 
, d  
 ( )

Ta có:
.
 
 .
Với . Chọn
Phương trình (P): .
Câu hỏi tương tự:
( ): 2 1 0P x y z
2 2 0x y z
(1;1; 1)A
( ) : 0P y z
( ): 2 5 6 0P x y z
0x y z
2
Ax z 0By C
2 2 2
0A B C
1. 1. 1. 0A B C
C A B
( ,( )) 2d M P
2 2 2
2
2
A B C
A B C


2 2 2 2
( 2 ) 2( )A B C A B C
2
8A 5 0BB
0 (3)
8A 5 0 (4)
B
B

0xz
5x 8 3z 0y
13
1 1 4
x y z

ax 2 0by cz b
2 2 2
0abc
(1;1;4)u
2 2 2
40
()
5
4
( ;( ))
a b c
P
ab
d A P d
abc


P
4
2
ac
ac

4ac
4, 1 8a c b
4 8 16 0x y z
2ac
2, 1 2a c b
2x 2 4 0yz
Trang59
a) Với .
ĐS: hoặc .
xyz 
  d 
3.
(d) đi qua điểm và có VTCT . Gọi với là
VTPT của (P).
PT mặt phẳng (P): (1).
Do (P) chứa (d) nên: (2)
(3)
Từ (2) và (3), chọn
PT mặt phẳng (P): .
xyz, cho  .
 .
PT mặt phẳng (P) có dạng: .
Ta có:
.
+ Với (1)
PT mặt phẳng (P):
+ Với (2)
PT mặt phẳng (P): .
xyz, cho  , ,
, 

PT mặt phẳng (P) có dạng: .
1
: ; (0;3; 2), 3
1 1 4
x y z
Md
( ): 2 2 8 0P x y z
( ) :4 8 26 0P x y z
( ): 1 2
1
xt
d y t
z
( 1;2;3)A
(0; 1;1)M
(1;2;0)u
( ; ; )n a b c
2 2 2
0abc
( 0) ( 1) ( 1) 0 0a x b y c z ax by cz b c
. 0 2 0 2u n a b a b

22
2 2 2 2 2
3 2 5 2
,( ) 3 3 3 5 2 3 5
5
a b c b c
d A P b c b c
a b c b c
2
22
4 4 0 2 0 2b bc c b c c b
1b 
2, 2ac
2 2 1 0x y z
( 1;1;0), (0;0; 2), (1;1;1)M N I
3
2 2 2
0 ( 0)ax by cz d a b c
()
()
( ,( )) 3
MP
NP
d I P
,2 , (1)
5 7 ,2 , (2)
a b c a b d a b
a b c a b d a b
20x y z
7 5 2 0x y z
(1; 1;2)A
(1;3;0)B
( 3;4;1)C
(1;2;1)D
2 2 2
0 ( 0)ax by cz d a b c
Trang60
Ta có:
+ Với
(P): .
+ Với
(P): .
Câu hỏi tương tự:
a) Với .
ĐS: hoặc .
               , ,
   
   .
Vì O
(P) nên , với .
Do A
(P)
(1) và (2)
Từ (1) và (2)
hoặc .
Với thì
Với thì
Câu hỏi tương tự:
a) Với . ĐS: hoặc .
           , cho ba  , ,
và :  
 .
PT có dạng: , với
Do nên: (1); nên (2)
()
()
( ,( )) ( ,( ))
AP
BP
d C P d D P
2 2 2 2 2 2
20
30
3a 4 2
a b c d
a b d
b c d a b c d
a b c a b c
2 , 4 , 7
2 , , 4
b a c a d a
c a b a d a
2 , 4 , 7b a c a d a
2 4 7 0x y z
2 , , 4c a b a d a
2 4 0x y z
(1;2;1), ( 2;1;3), (2; 1;1), (0;3;1)A B C D
( ): 4 2 7 15 0P x y z
( ) : 2 3 5 0P x z
Oxyz
(1;2;3)A
(0; 1;2)B
(1;1;1)C
()P
A
O
B
()P
C
()P
( ) : 0P ax by cz
2 2 2
0abc
2 3 0a b c
( ,( )) ( ,( )) 2d B P d C P b c a b c
0b
0c
0b
3ac
( ):3 0P x z
0c
2ab
( ) :2 0P x y
(1;2;0), (0;4;0), (0;0;3)A B C
6 3 4 0x y z
6 3 4 0x y z
Oxyz
(1;1; 1)A
(1;1;2)B
( 1;2; 2)C 
2 2 1 0x y z
()
2IB IC
()
ax 0by cz d
2 2 2
0abc
(1;1; 1) ( )A

0a b c d
( ) ( )P
2 2 0a b c
2IB IC
( ,( )) 2 ( ;( ))d B d C

2 2 2 2 2 2
2 2 2
2
a b c d a b c d
a b c a b c
Trang61
Từ (1), (2), (3) ta có 2 trường hợp sau:
TH1: .
Chọn
:
TH2: .
Chọn
:
Vậy: : hoặc :
Trong không xyz 
trình , . 
 .
Ta có đi qua A(2;2;3), có , đi qua và có .
Do (P) cách đều nên (P) song song với
PT mặt phẳng (P) có dạng:
Do (P) cách đều suy ra
Phương trình mặt phẳng (P):
xyz 
trình , . (P) 
và ,   .
Ta có: đi qua và có VTCP
đi qua và có VTCP là
3 3 6 0
(3)
5 2 3 0
a b c d
a b c d
0
13
2 2 0 ; ;
22
3 3 6 0
a b c d
a b c b a c a d a
a b c d

2 1; 2; 3a b c d
()
2 2 3 0x y z
0
33
2 2 0 ; ;
22
5 2 3 0
a b c d
a b c b a c a d a
a b c d
2 3; 2; 3a b c d
()
2 3 2 3 0x y z
()
2 2 3 0x y z
()
2 3 2 3 0x y z
12
,dd
1
2 2 3
:
2 1 3
x y z
d

2
1 2 1
:
2 1 4
x y z
d

12
,dd
1
d
1
(2;1;3)
d
u
2
d
(1;2;1)B
2
(2; 1;4)
d
u 
12
,dd
12
,dd
12
, (7; 2; 4)
P d d
n u u
7 2 4 0x y z d
12
,dd
( ,( )) ( ,( ))d A P d B P
7.2 2.2 4.3 7.1 2.2 4.1
69 69
dd
3
21
2
d d d
14 4 8 3 0x y z
12
,dd
1
1
:2
1
xt
d y t
z


2
2 1 1
:
1 2 2
x y z
d

1
d
2
d
1
d
2
d
1
d
(1;2;1)A
1
(1; 1;0)u 
2
d
(2;1; 1)B
2
(1; 2;2)u 
Trang62
Gọi là VTPT của (P), vì (P) song song với và nên
Phương trìnht (P): .
;
+ Với + Với
Trong xyz, 
 ,  .
(S) có tâm , bán kính .
PT mặt phẳng (P) có dạng:
Ta có:
+ Với (1)
Phương trình của (P):
+ Với (2)
Phương trình của (P):
xyz . 

Ta có .Do đó xảy ra nên mặt phẳng (P) cần
tìm là mặt phẳng đi qua A và vuông góc với OA. Ta có
Vậy phương trình mặt phẳng (P): .
xyz
 

Gọi H là hình chiếu của A trên d
d(d, (P)) = d(H, (P)). Giả sử điểm I là hình chiếu của H
lên (P), ta có
HI lớn nhất khi . Vậy (P) cần tìm là mặt phẳng đi qua A và
nhận làm VTPT
(P): .
n
1
d
2
d
12
, ( 2; 2; 1)n u u
2 2 0x y z m
1
7
( ,( )) ( ;( ))
3
m
d d P d A P

2
5
( ,( )) ( ,( ))
3
m
d d P d B P

12
( ,( )) 2 ( ,( ))d d P d d P
7 2. 5mm
7 2(5 )
7 2(5 )
mm
mm
17
3;
3
mm
3m 
P x y z
17
3
m 
17
( ): 2 2 0
3
P x y z
(0; 1;2)A
(1;0;3)B
2 2 2
( 1) ( 2) ( 1) 2x y z
(1;2; 1)I
2R
2 2 2
0 ( 0)ax by cz d a b c
()
()
( ,( ))
AP
BP
d I P R
, , 2 3 (1)
3 8 , , 2 3 (2)
a b c a b d a b
a b c a b d a b
10xy
8 3 5 7 0x y z
(2; 1;1)A
( ,( ))d O P OA
max
( ,( ))d O P OA
()OA P
(2; 1;1)OA 
2 6 0x y z
11
2 1 3
x y z

AH HI
AI
AH
7 5 77 0x y z
Trang63
xyzd
 d) và
I(d và
d
Gọi (P) là mặt phẳng chứa
, thì hoặc . Gọi H là hình chiếu vuông góc
của I trên (P). Ta luôn có và .
Mặt khác
Trong (P), ; do đó . Lúc này (P) ở vị trí (P
0
)
IA tại A.
Vectơ pháp tuyến của (P
0
) là , cùng phương với .
Phương trình của mặt phẳng (P
0
) là: .
     , cho   và
      

PT mặt phẳng (P) có dạng: .
(P) có VTPT , d đi qua điểm và có VTCP .
Vì (P)
d nên
. Xét 2 trường hợp:
TH1: Nếu b = 0 thì (P): . Khi đó: .
TH2: Nếu b
0. Chọn ta được (P): .
Khi đó:
Vậy
. Khi đó: (P): .
Câu hỏi tương tự:
a) . ĐS:
2 ; 2 ; 2 2x t y t z t
( ) ( )Pd
( ) ( )Pd
IH IA
IH AH
( ,( )) ( ,( ))
()
d d P d I P IH
HP

IH IA
axIH = IA H Am 
6;0; 3n IA
2;0; 1v 
2( 4) 1.( 1) 2 9 0x z x z
Oxyz
12
:
2 1 2
x y z
d


(2;5;3)A
P
d
A
P
2 2 2
ax z 0 ( 0)by c d a b c
( ; ; )n a b c
(1;0;2)M
(2;1;2)u
()
.0
MP
nu

20
2 2 0
a c d
a b c
2 (2 )c a b
d a b

10xz
( ,( )) 0d A P
1b
2 2 (2 1) 2 2 0ax y a z a
22
99
( ,( )) 3 2
8 4 5
13
22
22
d A P
aa
a





max ( ,( )) 3 2d A P
11
20
24
aa
4 3 0x y z
112
: , (5;1;6)
2 1 5
x y z
dA

( ): 2 1 0P x y z
Trang64
b) . ĐS:
xyz và 
   

 ,
;
Nếu B = 0 thì d(K, (P)) = 0 (loại)
Nếu thì
Dấu “=” xảy ra khi B = –C. Chọn C = 1. Khi đó PT (P): .
12
: , (1;4;2)
1 1 2
x y z
dA


( ) :5 13 4 21 0P x y z
(0; 1;2)M
( 1;1;3)N
P
,MN
(0;0;2)K
P
( 1) ( 2) 0 2 0Ax B y C z Ax By Cz B C
2 2 2
( 0)A B C
( 1;1;3) ( ) 3 2 0 2N P A B C B C A B C
( ):(2 ) 2 0P B C x By Cz B C
( ,( ))
22
4 2 4
d K P
B C BC
B

0B
2 2 2
11
( ,( ))
2
4 2 4
2 1 2
B
d K P
B C BC
C
B





x y z
Trang65
C 
Phn I: 10 CÂU NHN BIT
Câu 1. Trong không gian t , mt phm nhn vi

A. B.
C. D. .
Câu 2. Trong không gian vi h t Oxyza mt phng là:
A. B. C. D.
Câu 3. Trong không gian vi h t Oxyz, mn ca mt phng là:
A. B. C. D.
Câu 4. Trong không gian vi h t Oxyzc mt phng :
A. B. C. D.
Câu 5. Trong không gian vi h t Oxyz, mt phng ct các trc t lt ti
vi 
A. B. C. D.
Câu 6. Trong không gian vi h t  Oxyz, cho hai mt phng và
. Kh
A. và ct nhau. B.
C. D.
Câu 7. Trong không gian vi h t Oxyz, mt pha trc :
A. B. C. D.
Câu 8. Trong không gian vi h t Oxyz, mt phi trc :
A. B. C. D.
Câu 9. Trong không gian vi h t Oxyz, mt phi mt phng ?
A. B. C. D.
Câu 10. Trong không gian vi h t  Oxyz, khong cách t gc t  n mt phng
bng:
A. B. C. D.
Phn II: 15 CÂU THÔNG HIU
Câu 11. Gi s là mn ca mt phng . Khnh nào sai?
Oxyz
0 0 0
;;M x y z
;;n a b c
2 2 2
0abc
0 0 0
0x x a y y b z z c
0 0 0
0x x a y y b z z c
0 0 0
0a x x b y y c z z
0 0 0
0a x x b y y c z z
Oxy
0x
0y
0z
0xy
3 4 0xz
1; 3; 4n
1;3;4n
1;0;3n 
1;0;3n
2 3 4 0x y z
1; 2;3M
1;1;1N
4;0;1E
0; 2;0F
,,Ox Oy Oz
;0;0 , 0, ;0 , 0;0;A a B b C c
0abc
1
x y z
a b c
10
x y z
a b c
1ax by cz
1bcx cay abz
: 2 3 4 0P x y z
: 2 4 6 4 0Q x y z
P
Q
PQ
//PQ
PQ
Ox
0yz
20xy
20x y z
20xz
Oy
20y 
2 3 1 0xz
2 3 4 0x y z
20xz
Oyz
20z
2 1 0z
20x
2 1 0x
O
: 2 2 1 0P x y z
1
1
9
1
3
1
3
n
P
Trang66
A. Giá ca vuông góc vi . B.    n ca
C. là m . D. không ph    n
ca .
Câu 12. Cho c nm trên mt phng . Kh
A. là mn ca .
B. là mn ca nu 
C. là mn ca khi và ch khi
D. là mn ca khi 
Câu 13. Trong không gian vi h to  Oxyz, có hai giá tr ca tham s  hai mt phng
và vuông góc vi
nhau. Tính tng các bình pa hai s 
A. B. C. D.
Câu 14. Trong không gian vi h t Oxyz, mt ph và vuông góc vi trc có

A. B. C. D.
Câu 15. Trong không gian vi h t Oxyz, mt ph và cha trc 
trình là:
A. B. C. D.
Câu 16. Trong không gian vi h t  Oxyz  m và hai mt phng
và . Mt phng  ng thi vuông góc vi
c và 
A. B.
C. D.
Câu 17. Trong không gian vi h t Oxyzm . Mt phng trung
trc cn thng 
A. B.
C. D.
Câu 18. Trong không gian vi h t Oxyzm . Mt phng
n
P
\0kn k
P
n
0
1
2017
n
P
12
,uu
P
12
,n u u


P
12
,n u u


P
12
,uu
12
,n u u


P
12
uu
12
,n u u


P
12
,uu
m
: 3 2 1 0P x y z
: 2 1 1 2 2 4 14 0Q m x m m y m z
19
4
13
4
29
4
17
4
1;2;3A
Oy
230x y z
40xz
20y 
3 10 0xz
1;2;3A
Oz
3z
230x y z
20xy
2 5 0xy
1;2;3M
: 2 3 0Q x y
: 3 4 0R y z
P
M
Q
R
6 3 3 0x y z
7 5 28 0x y z
6 3 9 0x y z
750x y z
1;2;3 , 1; 2; 3AB
AB
2 4 6 28 0x y z
2 4 6 28 0x y z
20x y z
230x y z
1;0;0 , 0;2;0 , 0;0;3A B C
Trang67

A. B. C. D.
Câu 19. Trong không gian vi h t Oxyzm vi . Gi lt
là hình chiu ca trên các mt phng t a mt
phng là:
A. B. C. D.
Câu 20. Trong không gian vi h t Oxyz, mt phng c t và song song vi
mt phng 
A. B. C. D.
Câu 21. Trong không gian vi h t  Oxyz, mt phng song song vi mt phng
và cách mt khong b
A. B.
C. D.
Câu 22. Trong không gian vi h t Oxyz, mt phng m và cách gc ta
 mt khong ln nhg trình là:
A. B. C. D.
Câu 23. Trong không gian vi h t  Oxyz, mt phng song song v  ng thng
và nhn?
A. B. C. D.
Câu 24. Trong không gian vi h t Oxyz, mt phng  và ct các trc t
lt ti sao cho là trng tâm tam giác a
là:
A. B. C. D.
Câu 25. Trong không gian vi h trc t Oxyzm t phng (P)
qua M, ct các trc t lt ti I, J, K mà M là trc tâm ca tam giác IJK là
A. B.
C. D.
ABC
6 3 2 6 0x y z
0
1 2 3
x y z
6 3 2 6 0x y z
1
1 2 3
x y z
;;M a b c
0abc
,,A B C
M
,,Oxy Oyz Ozx
ABC
1
x y z
a b c
0
x y z
a b c
2
x y z
a b c
3
x y z
a b c
P
O
: 2 3 4 0Q x y z
2 3 4 0x y z
230x y z
2 3 0x y z
2 4 6 0x y z
P
: 2 2 1 0Q x y z
Q
2 2 8 0x y z
2 2 10 0x y z
2 2 8 0
2 2 10 0
x y z
x y z
2 2 2 0x y z
P
1; 2;3M
2 3 6 0x y z
20x y z
2 3 12 0x y z
2 3 14 0x y z
P
1
21
:
2 3 4
x y z
2
2
: 3 2
1
xt
yt
zt


5;6; 7n
5; 6;7n 
5; 6;7n
5; 6; 7n
P
1;2;3M
,,Ox Oy Oz
,,A B C
M
ABC
P
2 3 14 0x y z
1
1 2 3
x y z
1
3 6 9
x y z
60x y z
4;5;6M
1
12 15 18
x y z
1
4 5 6
x y z
2 3 32 0x y z
4 5 6 77 0xyz
Trang68
Phn III: 15 CÂU VN DNG THP
Câu 26. Trong không gian vi h to  Oxyz, t phng (Pm , ct
các tia Ox, Oy, Oz ti A, B, C sao cho biu thc có giá tr nh nht là:
A. B. C. D.
Câu 27. Trong không gian vi h t  Oxyz, cho mt phng  m
. Mt phng i xng vi  m   
. Giá tr ca là:
A. B. C. D.
Câu 28. Trong không gian vi h t Oxyzm 
trình mt phng là . Giá tr ca bng
A. B. C. D.
Câu 29. Trong không gian vi h t Oxyz, cho hai mt cu và
ct nhau theo giao tuyn là mng tròn . Vit
t phng chng tròn :
A. B.
C. D.
Câu 30. Trong không gian vi h t Oxyzm và mt phng (P):
. Mt phng (Qm A, B và vuông góc vi mt phng (P) có

A. B. C. D.
Câu 31. Trong không gian vi h to  Oxyz   ng thng và   
, . Mt phng (P) cha (d ) và có

A. Không tn ti B. C. D.
Câu 32. Trong không gian vi h trc Oxyz, cho mt cu (S): .
t phng (P) cha trc Ox và ct mt cu (S) theo mng tròn có bán kính
là:
A. B. C. D.
Câu 33. 


 
 xyz, Gi là mt phng ch  ng thng
và . Khong cách t m n
bng:
(1;2;3)M
2 2 2
1 1 1
OA OB OC

60x y z
3
1 2 3
x y z
2 3 14 0x y z
1
1 2 3
x y z
:4 3 7 3 0P x y z
1; 1;2I
Q
P
I
40x by cz d
b c d
2
0
1
1
0;1;2 , 2; 2;1 , 2;1;0A B C
ABC
0ax y cz d
ad
4
2
4
2
2 2 2
1
: 1 2 3 16S x y z
2 2 2
2
: 1 2 3 25S x y z
C
P
C
2 3 9 0x y z
2 3 9 0x y z
4 8 12 9 0x y z
4 8 12 9 0x y z
2;4;1 , 1;1;3AB
x y z
3 9 0x y z
3 10 0xy
8 12 61 0yz
2 3 11 0yz
1
()d
2
()d
1
112
( );
2 3 1
x y z
d

2
4 1 3
( ):
6 9 3
x y z
d

1
2
()d
0x y z
2 3 1 0x y z
5 10 0x y z
2 2 2
x y z x y z
3r
20yz
0x
20yz
0yz
P
1
1
( ):
1 2 3
x y z
d


2
14
( ):
1 2 5
x y z
d


1;2;3M
P
Trang69
A. B. C. D.
Câu 34. Trong không gian vi h to  Oxyzng thng d: và mt cu (S):
. Lt phng (P) song song vi d và trc Ox,
ng thi tip xúc vi mt cu (S).
A. B. C. D.
Câu 35. Trong không gian vi h to  Oxyz, cho mt cu (S   
và mt phng (
x + 2y z + 17 = 0. Mt
phng (
) song song vi (
) và ct (S) theo giao tuyng tròn có chu vi bng có
 . Giá tr ca bng:
A. B.
C. D. hoc
Câu 36. Trong không gian vi h to  Oxyz, vit phng (P) qua O, vuông góc vi
mt phng (Q): m M(1; 2; 1) mt khong bng .
A. B. C. D.
Câu 37. Trong không gian vi h to  Oxyz, cho t din ABCD vi , , ,
. Vit phng (PA, B sao cho khong cách t C n (P) bng
khong cách t D n (P).
A. B. C. D.
Câu 38. Trong không gian vi h to  Oxyz  ng thng l 
, . Vit phu hai
ng thng .
A. B.
C. D.
Câu 39. Trong không gian vi h t Oxyzng thng m .
Vitrình mt phng (P) cha d sao cho khong cách t A n (P) là ln nht.
A. B. C. D.
Câu 40. Trong không gian vi h t  Oxyz  m  ng th  
trình: . Lt phi d và khong
4
6
8
6
2
6
6
32
2 2 1
x y z

2 2 2
2x 2 4z 1 0x y z y
2 2 0xy
2z 8 0y
2z 2 0
2z 8 0
y
y
2z 2 0
2z 8 0
y
y
2 2 2
2 4 6 11 0x y z x y z
6p
10ax by cz
T a b c
3T
3
7
T
3
7
T 
3
17
T
3
7
T 
0x y z
2
0
5 8 3 0
xy
x y z

0
2 5 3 0
yz
x y z

0
5 8 3 0
xz
x y z

2 5 7 0
2 5 3 0
xyz
x y z

(1; 1;2)A
(1;3;0)B
( 3;4;1)C
(1;2;1)D
2 4 7 0x y z
2 4 0x y z
2 4 7 0
2 4 0
x y z
x y z
2 4 7 0
2 4 0
x y z
x y z
12
,dd
1
2 2 3
:
2 1 3
x y z
d

2
1 2 1
:
2 1 4
x y z
d

12
,dd
7 2 4 3 0x y z
7 2 4 3 0x y z
14 4 8 13 0x y z
14 4 8 3 0x y z
12
:
2 1 2
x y z
d


(2;5;3)A
4 3 0x y z
5 3 0x y z
10xz
2 2 6 0x y z
10;2; –1A
11
2 1 3
x y z

Trang70
cách t d ti (P) là ln nht.
A. B. C. D.
Phn IV: 10 CÂU VN DNG CAO
Câu 41. Trong không gian vi h t Oxyz, cho mt cu (S): và mt
phng (P): t phng (Qm vuông góc vi
mt phng (P) và tip xúc vi mt cu (S) có dng . Giá tr ca
bng:
A. B. C. hoc D. hoc
Câu 42. Trong không gian vi h t  Oxyz, cho hai mt phng và
. Gi là mt ph  c t O, không cha trc ,
vuông góc vi mt phng (P) và to vi mt phng (Q) mt góc . Khong cách t
n bng:
A. B. C. D. hoc
Câu 43. Trong không gian vi h t Oxyz, cho mt phng (Q): ng thng
. Vit phng (P) chng thng d và to vi mt
phng (Q) mt góc nh nht.
A. B. C. D.
Câu 44. Trong không gian vi h t  Oxyz   ng thng và
t phng (P) cha sao cho góc gia mt phng (P) và
ng thng là ln nht là: . Giá tr ca bng
A. B. C. D.
Câu 45. Trong không gian to    m , và mt cu
. Mt phng  và ct
theo giao tuyng tròn có bán kính nh nht. Tính .
A. B. C. D.
Câu 46. Trong không gian to  m và mt phng . Gi
là mt phng song song vi (P) và ct hai tia tm B, C sao cho tam giác
ABC có din tích bng 6. Gi s  a là: . Giá tr ca
bng
A. B. C. D.
Câu 47. Trong không gian vi h to  Oxyz, mt phng (Pm , ct các tia Ox, Oy,
Oz ti A, B, C sao cho th tích t din OABC có giá tr nh nh   
7 5 77 0x y z
2 19 0x y z
2 3 19 0x y z
5 3 77 0x y z
2 2 2
2 4 4 0x y z x y
30xz
(3;1; 1)M
90ax by cz
abc
0
7
1
7
7
1
( ) :5 2 5 1 0P x y z
( ) : 4 8 12 0Q x y z
()R
Oy
0
45
1; 2;3M
R
32
5
31 2
15
2
2
32
5
2 5 0x y z
1 1 3
:
2 1 1
x y z
d

40yz
30x y z
2 6 0x y z
2 1 0xy
1
12
:
1 2 1
x y z
d


2
21
:
2 1 2
x y z
d


1
d
2
d
0ax y cz d
T a c d
3T
0T
13
4
T 
6T 
,Oxyz
3; 2;6A
0;1;0B
2 2 2
: 1 2 3 25S x y z
: 2 0P ax by cz
,AB
S
T a b c
2T
3T
4T
5T
,Oxyz
(2;2;4)A
( ) :P
40x y z
Q
,Ox
Oy
Q
40ax by cz
abc
3
6
12
3
(9;1;1)M
Trang71
. Giá tr ca bng
A. B. C. D.
Câu 48. Trong không gian vi h to  Oxyz, m , . Gi là
mt phng sao cho khong cách t m A n mt phng bng 15 và khong cách t m
B n mt phng bng 2. Mt phng 
A. B. C. D.
Câu 49. Trong không gian vi h to  Oxyz,  ng thng
, vi . Khi  i thì
luôn nm trong mt mt phng c nh . Tính ?
A. B. C. D.
Câu 50. Trong không gian vi h to  Oxyz,   m , , vi
tha mãn . Bit rng khi i thì qu tích tâm mt cu ngoi
tip t din thuc mt mt phng c nh. Tính khong cách t m
n mt phng .
A. B. C. D.
------------------------HT---------------------------

Phn I: 10 CÂU NHN BIT
Câu 1. Trong không gian t , mt phm nhn vi

A. B.
C. D. .
ng dn gii:
Ch
Câu 2. Trong không gian vi h t Oxyza mt phng là:
A. B. C. D.
ng dn gii: Ch
Câu 3. Trong không gian vi h t Oxyz, mn ca mt phng là:
A. B. C. D.
ng dn gii: Ch
0x By Cz D
B C D
9
27
45
19
1; 2; 3A
6;10; 3B 
P
P
P
P
8; 3;1M
18; 3;11M
52; 7;13M
40; 2; 15M
4 3 2 3 8 7
:
2 1 1 4 3
m
x m y m z m
d
m m m

31
1; ;
42
m



m
m
d
: 6 0P ax by cz
abc
10
9
7
8
;0;0Aa
0; ;0Bb
0;0;Cc
, , 0abc
2abc
,,abc
OABC
P
2016;0;0M
P
2015
3
2016
2016
3
2014
3
Oxyz
0 0 0
;;M x y z
;;n a b c
2 2 2
0abc
0 0 0
0x x a y y b z z c
0 0 0
0x x a y y b z z c
0 0 0
0a x x b y y c z z
0 0 0
0a x x b y y c z z
0 0 0
0a x x b y y c z z
Oxy
0x
0y
0z
0xy
3 4 0xz
1; 3; 4n
1;3;4n
1;0;3n 
1;0;3n
Trang72
Câu 4. Trong không gian vi h t Oxyzc mt phng :
A. B. C. D.
ng dn gii: Ch
Câu 5. Trong không gian vi h t Oxyz, mt phng ct các trc t lt ti
vi 
A. B. C. D.
ng dn gii: Ch
Câu 6. Trong không gian vi h t  Oxyz, cho hai mt phng và
. Kh
A. và ct nhau. B. C. D.
ng dn gii: Vì nên . Ch
Câu 7. Trong không gian vi h t Oxyz, mt pha trc :
A. B. C. D.
ng dn gii: Mt phng cha trc ng: . Ch
Câu 8. Trong không gian vi h t Oxyz, mt phi trc :
A. B. C. D.
ng dn gii: Mt phng song song vi trc    ng:
. Ch
Câu 9. Trong không gian vi h t Oxyz, mt phi mt phng ?
A. B. C. D.
ng dn gii: Mt phng song song vi mt phng    ng
. Ch
Câu 10. Trong không gian vi h t  Oxyz, khong cách t gc t  n mt phng
bng:
A. B. C. D.
ng dn gii: Ta có . Ch
Phn II: 15 CÂU THÔNG HIU
2 3 4 0x y z
1; 2;3M
1;1;1N
4;0;1E
0; 2;0F
,,Ox Oy Oz
;0;0 , 0, ;0 , 0;0;A a B b C c
0abc
1
x y z
a b c
10
x y z
a b c
1ax by cz
1bcx cay abz
: 2 3 4 0P x y z
: 2 4 6 4 0Q x y z
P
Q
PQ
//PQ
PQ
1 2 3 4
2 4 6 4



//PQ
Ox
0yz
20xy
20x y z
20xz
Ox
0by cz
Oy
20y 
2 3 1 0xz
2 3 4 0x y z
20xz
Oy
00ax cz d d
Oyz
20z
2 1 0z
20x
2 1 0x
Oyz
00
0x x x
O
: 2 2 1 0P x y z
1
1
9
1
3
1
3
2
22
0 2.0 2.0 1
1
,
3
1 2 2
d O P

Trang73
Câu 11. Gi s là mn ca mt phng . Khnh nào sai?
A. Giá ca vuông góc vi . B.    n ca
C. là m . D. không ph    n
ca .
ng dn gii:
Vì n ca nên n ca
. Ch
Câu 12. Cho c nm trên mt phng . Kh
A. là mn ca .
B. là mn ca nu 
C. là mn ca khi và ch khi
D. là mn ca khi 
ng dn gii: Ch
Câu 13. Trong không gian vi h to  Oxyz, có hai giá tr ca tham s  hai mt phng
và vuông góc vi
nhau. Tính ta hai s 
A. B. C. D.
ng dn gii:
Ta có
Suy ra . Ch B.
u:
u hoc do tính toán sai.
Câu 14. Trong không gian vi h t Oxyz, mt ph và vuông góc vi trc có

A. B. C. D.
n
P
n
P
\0kn k
P
n
0
1
2017
n
P
\0kn k
P
1
2017
n
P
12
,uu
P
12
,n u u


P
12
,n u u


P
12
,uu
12
,n u u


P
12
uu
12
,n u u


P
12
,uu
m
: 3 2 1 0P x y z
: 2 1 1 2 2 4 14 0Q m x m m y m z
19
4
13
4
29
4
17
4
2
1
1 2 1 3 1 2 2 2 4 0 2 3 0
3
2
m
P Q m m m m m m
m

2
2
3 13
1
24



1;2;3A
Oy
230x y z
40xz
20y 
3 10 0xz
Trang74
ng dn gii:
n ca mt phng là t phng là: .
Ch C.
u:
A. Nhm t m thành t n.
B. Nht phng vuông góc vi t phng song song
vi
D. Mt u thêm.
Câu 15. Trong không gian vi h t Oxyz, mt ph và cha trc 
trình là:
A. B. C. D.
ng dn gii:
  t phng cha trc là . Thay t    c
 . Chán C.
u:
A. Nhm mt phng cha vi mt phng vuông góc vi .
B. Nhn v
D. Mu khi ki
Câu 16. Trong không gian vi h t  Oxyz  m và hai mt phng
và . Mt phng  ng thi vuông góc vi
c và 
A. B.
C. D.
ng dn gii:
n ca và lt là .
    n ca là . Suy ra pt
. Chn C.
u:
A. Tính nhn thành .
B. Tính nhm c vtpt .
D. Mu thêm do nh B.
0;1;0j
20y 
Oy
Oy
1;2;3A
Oz
3z
230x y z
20xy
2 5 0xy
Oz
0ax by
1;2;3A
2ab
20xy
Oz
Oz
1;2;3M
: 2 3 0Q x y
: 3 4 0R y z
P
M
Q
R
6 3 3 0x y z
7 5 28 0x y z
6 3 9 0x y z
750x y z
Q
R
1; 2;0 , 0;1;3
QR
nn
P
, 6; 3;1
P Q R
n n n


:6 3 9 0P x y z
6;3;1
1; 2;3 , 1;3; 4
QR
nn
1;7;5
P
n 
Trang75
Câu 17. Trong không gian vi h t Oxyzm . Mt phng trung
trc cn thng 
A. B. C.
D.
ng dn gii:
m ca là n ca mt phng trung trc là
t phng trung trc là . Ch D.
u:
A, B. c i thay
 hoc .
C. Ht phng trung trc ca phi cha c và nên thay c t
u tha mãn.
Câu 18. Trong không gian vi h t Oxyzm . Mt phng

A. B. C. D.
ng dn gii:
n chc . Ch D.
u:
u khi hc sinh ch bit th t m.
Câu 19. Trong không gian vi h t Oxyzm vi . Gi lt
là hình chiu ca trên các mt phng t a mt
phng là:
A. B. C. D.
ng dn gii:
Cách 1: Thay t  C.
Cách 2: Mt phng ct các trc t tm
 .
u:
A. Nhm t hình chiu trên mt phng t vi t hình chiu trên các trc t.
1;2;3 , 1; 2; 3AB
AB
2 4 6 28 0x y z
2 4 6 28 0x y z
20x y z
230x y z
AB
0;0;0O
1;2;3OA
230x y z
2; 4; 6AB
A
B
AB
A
B
,AB
1;0;0 , 0;2;0 , 0;0;3A B C
ABC
6 3 2 6 0x y z
0
1 2 3
x y z
6 3 2 6 0x y z
1
1 2 3
x y z
1
1 2 3
x y z
;;M a b c
0abc
,,A B C
M
,,Oxy Oyz Ozx
ABC
1
x y z
a b c
0
x y z
a b c
2
x y z
a b c
3
x y z
a b c
; ;0 , 0; ; , ;0;A a b B b c C a c
ABC
,,Ox Oy Oz
2 ;0;0 , 0;2 ;0 , 0;0;2abc
11
2 2 2
x y z x y z
a b c a b c
Trang76
u thêm.
Câu 20. Trong không gian vi h t Oxyz, mt phng c t và song song vi
mt phng 
A. B. C. D.
ng dn gii:
Vì (PO nên loi A. Vì (P) song song vi (Q) nên chc D.
Câu 21. Trong không gian vi h t  Oxyz, mt phng song song vi mt phng
và cách mt khong b
A. B. C. D.
ng dn gii:
Vì a là .
Khong cách gia và bng .
a là hoc .
u:
A, B. Nhm công thc tính khong cách không có du tr tuyi trên t
thc.
D. Không bit công thc tính khong cách gia hai mt phng. Cng thêm 3 vào pt ca .
Câu 22. Trong không gian vi h t Oxyz, mt phng m và cách gc ta
 mt khong ln nh
A. B. C. D.
ng dn gii:
Khong cách  cn tìm nhn 
tuyn. Ch D.
u:
u gây nhiu nu dùng phép th. C u thu kin
 . Vic th bng công thc khong cách s mt nhiu thi gian.
Câu 23. Trong không gian vi h t  Oxyz, mt phng song song v  ng thng
P
O
: 2 3 4 0Q x y z
2 3 4 0x y z
230x y z
2 3 0x y z
2 4 6 0x y z
P
: 2 2 1 0Q x y z
Q
2 2 8 0x y z
2 2 10 0x y z
2 2 8 0
2 2 10 0
x y z
x y z
2 2 2 0x y z
//PQ
P
2 2 0 1x y z D D
P
Q
2
22
8
1
( ),( ) 3
10
1 2 2
D
D
d P Q
D

P
2 2 8 0x y z
2 2 10 0x y z
Q
P
1; 2;3M
2 3 6 0x y z
20x y z
2 3 12 0x y z
2 3 14 0x y z
;d O P OH OM
P
1; 2;3OM 
P
M
P
Trang77
và nhn?
A. B. C. D.
ng dn gii:
l        . Suy ra
Vì nên . Chn  c .
Ch D.
u:
A, B, C do tính sai công thc nên nhm du.
Câu 24. Trong không gian vi h t Oxyz, mt phng  và ct các trc t
lt ti sao cho là trng tâm tam giác a
là:
A. B. C. D.
ng dn gii:
Gi suy ra trng tâm là .
n chn ca là: . Ch C.
u:
A. Nhm trng tâm thành trc tâm ca tam giác .
B. Nhm A, B, C là hình chiu ca M trên các trc t.
D. Mu dng gn vi t l 1:1:1.
Câu 25. Trong không gian vi h trc t Oxyzm t phng (P)
qua M, ct các trc t lt ti I, J, K mà M là trc tâm ca tam giác IJK là
A. B. C. D.

M là trực tâm tam giác IJK suy ra hay có vectơ pháp tuyến là
1
21
:
2 3 4
x y z
2
2
: 3 2
1
xt
yt
zt


5;6; 7n
5; 6;7n 
5; 6;7n
5; 6; 7n
12
,
12
2; 3;4 , 1;2; 1uu
12
, 5;6;7uu



1
2
//
//
P
P
1
12
2
,0
P
P
P
nu
n k u u k
nu


1k 
5; 6; 7
P
n
P
1;2;3M
,,Ox Oy Oz
,,A B C
M
ABC
P
2 3 14 0x y z
1
1 2 3
x y z
1
3 6 9
x y z
60x y z
;0;0 , 0; ;0 , 0;0;A a B b C c
; ; 3, 6, 9
3 3 3
abc
M a b c



P
1
3 6 9
x y z
1;2;3M
ABC
4;5;6M
1
12 15 18
x y z
1
4 5 6
x y z
2 3 32 0x y z
4 5 6 77 0xyz
OM P
P
4;5;6OM
Trang78
Vậy phương trình mặt phẳng (P): . Chọn đáp án D.
u:
A. Nhm trc tâm và trng tâm. Suy ra .
B. Hiu là hình chiu ca trên các trc t.
C. Mu thêm.
Phn III: 15 CÂU VN DNG THP
Câu 26. Trong không gian vi h to  Oxyz, t phng (Pm , ct
các tia Ox, Oy, Oz ti A, B, C sao cho biu thc có giá tr nh nht là:
A. B. C. D.
ng dn gii:
Gi là hình chiu ca trên mt phng . Ta có .
 nh nht thì ln nht. Mt khác nên ln nht
bng khi . Hay  n là .
a là: . Ch
u:
A. Nhm ln khi s dng bng thc Cô si: và da
u kin xng thc suy ra nh nht bng khi
.
T n là .
u thêm.
Câu 27. Trong không gian vi h t  Oxyz, cho mt phng  m
. Mt phng i xng vi  m   
. Giá tr ca là:
A. B. C. D.
ng dn gii:
4 5 6 77 0xyz
12;0;0 , 0;15;0 , 0;0;18I J K
,,I J K
M
(1;2;3)M
2 2 2
1 1 1
OA OB OC

60x y z
3
1 2 3
x y z
2 3 14 0x y z
1
1 2 3
x y z
H
O
P
2 2 2 2
1 1 1 1
OA OB OC OH
2 2 2
1 1 1
OA OB OC

OH
OH OM
OH
OM
HM
OM P
P
1;2;3OM
P
2 3 14 0x y z
3
2 2 2 2 2 2
1 1 1 1
3
OA OB OC OA OB OC
2 2 2
1 1 1
OA OB OC

3
2 2 2
1
3
OA OB OC
OA OB OC
1;1;1n
:4 3 7 3 0P x y z
1; 1;2I
Q
P
I
40x by cz d
b c d
2
0
1
1
Trang79
Cách 1: Biu thc t ci xng tâm là: thay vào pt ca
c
hay pt
. Ch C.
Cách 2: Ta có  m .
i xng ca qua là . Vì nên .
u:
u.
Câu 28. Trong không gian vi h t Oxyzm 
trình mt phng là . Giá tr ca bng
A. B. C. D.
ng dn gii:
Cách 1: ,
suy ra .
 . Ch D.
Cách 2: Thay t   m    a suy ra
 . Ch D.
u:
A. Do tính nh       n là nên pt
.
B. Do gii h  bn các h s t do
sang bên phi du bng nên kt qu i du
C. Mu thêm.
1; 1;2I
2'
2'
4'
xx
yy
zz


P
4 2 ' 3 2 ' 7 4 ' 3 0x y z
4 ' 3 ' 7 ' 11 0x y z
:4 3 7 11 0 3 7 11 1Q x y z b c d
//QP
:4 3 7 0Q x y z d
0;1;0AP
A
I
' 2; 3;4A
'AQ
11d
0;1;2 , 2; 2;1 , 2;1;0A B C
ABC
0ax y cz d
ad
4
2
4
2
2; 3; 1 , 2;0; 2 2 1;0;1AB AC
()
1
, 3; 3;3 3 1;1; 1
2
ABC
n AB AC



: 1 0 2P x y z a d
,,A B C
P
2 1 1
2 2 1
2 1 1
c d a
a c d c
a d d





2ad
1;1;1
: 3 0P x y z
2 1 0
2 2 0
2 1 0
cd
a c d
ad
1; 1ad
Trang80
Câu 29. Trong không gian vi h t Oxyz, cho hai mt cu và
ct nhau theo giao tuyn là mng tròn . Vit
t phng chng tròn :
A. B. C. D.
ng dn gii:
Vì khong cách gia hai tâm nên và ct nhau theo
mng tròn. Mt phng chng tròn này là mt pha và .
L   tr    c . Ch  
D.
u:
i nên không loc ph
nào c.
V m giao ca mt phng vi làm mt thi gian.
Câu 30. Trong không gian vi h t Oxyzm và mt phng (P):
. Mt phng (Qm A, B và vuông góc vi mt phng (P) có

A. B. C. D.


(Q) có VTPT
. Ch D.
u:
A. Th t A và B thy tha mãn.
B. Th thy vuông góc vi .
C. Vi vàng chc .
Câu 31. Trong không gian vi h to  Oxyz   ng thng và   
, . Mt phng (P) cha (d ) và có

A. Không tn ti B. C. D.
ng dn gii:
Ta có    .
2 2 2
1
: 1 2 3 16S x y z
2 2 2
2
: 1 2 3 25S x y z
C
P
C
2 3 9 0x y z
2 3 9 0x y z
4 8 12 9 0x y z
4 8 12 9 0x y z
1 2 1 2
56 9 4 5I I R R
1
S
2
S
1
S
2
S
2
S
1
S
4 8 12 9 0x y z
12
II
P
12
II
2;4;1 , 1;1;3AB
x y z
3 9 0x y z
3 10 0xy
8 12 61 0yz
2 3 11 0yz
, (0; 8; 12) 0
P
n n AB



( ): 2 3 11 0Q y z
P
, (0; 8; 12) 0
P
n n AB



1
()d
2
()d
1
112
( );
2 3 1
x y z
d

2
4 1 3
( ):
6 9 3
x y z
d

1
2
()d
0x y z
2 3 1 0x y z
5 10 0x y z
1
d
1
1; 1;2M
1
2;3;1u

Trang81
   .
Vì và  và  .
n ca là  là:
. Chn (D).
u:
A. Do tính nên kt lun không tn ti .
B. Thay nhm t  ng t 
C. Vì nên chn luôn .
Câu 32. Trong không gian vi h trc Oxyz, cho mt cu (S): .
t phng (P) cha trc Ox và ct mt cu (S) theo mng tròn có bán kính
là:
A. B. C. D.
ng dn gii:
(S) có tâm I(1; –2; –1), bán kính R = 3. (P) chứa Ox
(P): ay + bz = 0.
Mặt khác đường tròn giao tuyến có bán kính bằng 3 cho nên (P) đi qua tâm I.
Suy ra: –2a – b = 0 b = –2a (a 0)
(P): y – 2z = 0. Chọn đáp án A.
u:
B. Nhm mt phng cha trc là:
C. Tính nhm h s ca và thành .
D. Mu thêm.
Câu 33. 



 xyz, Gi là mt phng ch  ng thng
và . Khong cách t m n
bng:
A. B. C. D.
ng dn gii:
qua và có , qua và có .
,
đồng phẳng.
(P) có VTPT và đi qua M
1
nên có phương trình .
2
d
2
4;1;3M
2
6;9;3u
1
u

2
u
1
u

12
3;2;1MM
12
//dd
P
1 1 2
, 1;1; 5
P
n u M M


P
5 10 0x y z
12
, 0;0;0 0uu



P
5;5;5
P
n 
21
3uu
1p
nu
2 2 2
x y z x y z
3r
20yz
0x
20yz
0yz
Ox
0x
y
z
2ab
P
1
1
( ):
1 2 3
x y z
d


2
14
( ):
1 2 5
x y z
d


1;2;3M
P
4
6
8
6
2
6
6
1
d
1
(0; 1;0)M
1
(1; 2; 3)u
2
d
2
(0;1;4)M
2
(1;2;5)u
12
; ( 4; 8;4) 0uu

12
(0;2;4)MM
1 2 1 2
; . 0u u M M

12
,dd
(1;2; 1)n 
2 2 0x y z
Trang82
Khong cách . Ch A.
u:
B. n thành c pt
u thêm.
Câu 34. Trong không gian vi h to  Oxyzng thng d: và mt cu (S):
. Lt phng (P) song song vi d và trc Ox,
ng thi tip xúc vi mt cu (S).
A. B. C. D.
ng dn gii:
(S) có tâm I(1; 1; 2), bán kính . d có VTCP .
(P) // d, Ox
(P) có VTPT
PT của (P) có dạng: .
(P) tiếp xúc với (S)
(P): hoặc (P): .
Vì điểm và nên mặt phẳng cần tìm là
u:
A: Th bng máy tính thy
C. Quên kim tra tính song song ca (P) và d.
D. Tính nhm c .
Câu 35. Trong không gian vi h to  Oxyz, cho mt cu (S   
và mt phng (
x + 2y z + 17 = 0. Mt
phng (
) song song vi (
) và ct (S) theo giao tuyng tròn có chu vi bng có
 . Giá tr ca bng:
A. B. C. D. hoc
ng dn gii:
Do (
) // (
) nên (
) có phương trình 2x + 2y – z + D = 0 (D 17)
4
;
6
d M P
(1; 2; 1)n
2 2 0x y z
32
2 2 1
x y z

2 2 2
2x 2 4z 1 0x y z y
2 2 0xy
2z 8 0y
2z 2 0
2z 8 0
y
y
2z 2 0
2z 8 0
y
y
5R
(2;2;1)u
, (0;1; 2)n u i

2z 0yD
( ,( ))d I P R
22
14
5
12
D
35D
2
8
D
D

2 2 0yz
2z 8 0y
3;2;0Md
3;2;0 : 2 2 0M P y z
: 2 8 0P y z
;5d I P
35D
2
8
D
D
2 2 2
2 4 6 11 0x y z x y z
6p
10ax by cz
T a b c
3T
3
7
T
3
7
T 
3
17
T
3
7
T 
Trang83
(S) có tâm I(1; –2; 3), bán kính R = 5. Đường tròn có chu vi 6
nên có bán kính r = 3.
Khoảng cách từ I tới (
) là h =
Do đó
Vậy (
) có phương trình . Suy ra . Chọn
C.
nhiu:
A.  ý  .
B.       nên t pt suy ra
.
D.  u kin song song ca và du kin .
Câu 36. Trong không gian vi h to  Oxyz, vit phng (P) qua O, vuông góc vi
mt phng (Q): m M(1; 2; 1) mt khong bng .
A. B. C. D.
ng dn gii:
PT mặt phẳng (P) qua O nên có dạng: (với ).
Vì (P)
(Q) nên:
(1)
(2)
Từ (1) và (2) ta được:
Từ (3): B = 0
C = –A. Chọn A = 1, C = –1
(P):
Từ (4): 8A + 5B = 0. Chọn A = 5, B = –8
C = 3
(P): . Chọn đáp án
C.
u:
u v mt hình thc, hoc làm tn thi gian khi s dng cách
th u ki bài.
Câu 37. Trong không gian vi h to  Oxyz, cho t din ABCD vi , , ,
. Vit phng (PA, B sao cho khong cách t C n (P) bng
khong cách t D n (P).
2 2 2 2
5 3 4Rr
2 2 2
7
2.1 2( 2) 3
4 5 12
17 (loaïi)
2 2 ( 1)
D
D
D
D

x y z
2 2 1
10
7 7 7
x y z
3
7
T 
1d
10ax by cz
10ax by cz
2 2 1
10
7 7 7
x y z
3
7
T
17D
0x y z
2
0
5 8 3 0
xy
x y z

0
2 5 3 0
yz
x y z

0
5 8 3 0
xz
x y z

2 5 7 0
2 5 3 0
xyz
x y z

Ax z 0By C
2 2 2
0A B C
1. 1. 1. 0A B C
C A B
( ,( )) 2d M P
2 2 2
2
2
A B C
A B C


2 2 2 2
( 2 ) 2( )A B C A B C
2
8A 5 0BB
0 (3)
8A 5 0 (4)
B
B

0xz
5x 8 3z 0y
(1; 1;2)A
(1;3;0)B
( 3;4;1)C
(1;2;1)D
Trang84
A. B. C. D.
ng dn gii:
Cách 1: PT mặt phẳng (P) có dạng: .
Ta có:
+ Với
(P): .
+ Với
(P): .
Cách 2: Ta có , m ca
là .
Mt phng  u nên:
TH1: cha và song song vi
TH2: m
u:
A: Ch xét c TH1.
B. u thêm.
Câu 38. Trong không gian vi h to  Oxyz  ng thng l 
, . Vit phu hai
ng thng .
A. B. C. D.
ng dn gii:
Cách 1: Ta có đi qua A(2;2;3), có , đi qua và có .
Do (P) cách đều nên (P) song song với
PT mặt phẳng (P) có dạng:
Do (P) cách đều suy ra
2 4 7 0x y z
2 4 0x y z
2 4 7 0
2 4 0
x y z
x y z
2 4 7 0
2 4 0
x y z
x y z
2 2 2
0 ( 0)ax by cz d a b c
()
()
( ,( )) ( ,( ))
AP
BP
d C P d D P
2 2 2 2 2 2
20
30
3a 4 2
a b c d
a b d
b c d a b c d
a b c a b c
2 , 4 , 7
2 , , 4
b a c a d a
c a b a d a
2 , 4 , 7b a c a d a
2 4 7 0x y z
2 , , 4c a b a d a
2 4 0x y z
0;4; 2 2 0;2; 1AB
4; 2;0 2 2; 1;0CD
CD
1;3;1I
P
,AB
,CD
P
AB
CD
: 2 4 7 0P x y z
P
,,A B I
: 2 4 0P x y z
12
,dd
1
2 2 3
:
2 1 3
x y z
d

2
1 2 1
:
2 1 4
x y z
d

12
,dd
7 2 4 3 0x y z
7 2 4 3 0x y z
14 4 8 13 0x y z
14 4 8 3 0x y z
1
d
1
(2;1;3)
d
u
2
d
(1;2;1)B
2
(2; 1;4)
d
u 
12
,dd
12
,dd
12
, (7; 2; 4)
P d d
n u u
7 2 4 0x y z d
12
,dd
( ,( )) ( ,( ))d A P d B P
Trang85
Phương trình mặt phẳng (P):
Cách 2: Ta có đi qua A(2;2;3), có , đi qua và có .
Do (P) cách đều nên (P) song song với
Mặt khác (P) đi qua trung điểm của đoạn là nên pt (P) là:
u:
u v hình thc hong.
Câu 39. Trong không gian vi h t Oxyzng thng m .
Vit t phng (P) cha d sao cho khong cách t A n (P) là ln nht.
A. B. C. D.
ng dn gii:
Ta có .
Suy ra ln nht bng khi hay
.
Suy ra .
Ta có  và có vtcp là .
. Suy ra
. Suy ra pt .
u:
B. Mt ph và vuông góc vi nên nu th tính khong cách thì
c kt qu bng .
C. Là mt phng cha A và d.
D. Mt phng qua và vuông góc vi .
Câu 40. Trong không gian vi h t Oxyz  m A(10; 2;   ng th
trình: . Lt phi d và khong
cách t d ti (P) là ln nht.
7.2 2.2 4.3 7.1 2.2 4.1
69 69
dd
3
21
2
d d d
14 4 8 3 0x y z
1
d
1
(2;1;3)
d
u
2
d
(1;2;1)B
2
(2; 1;4)
d
u 
12
,dd
12
,dd
12
, (7; 2; 4)
P d d
n u u
AB
3
;2;2
2
I



14 4 8 3 0x y z
12
:
2 1 2
x y z
d


(2;5;3)A
4 3 0x y z
5 3 0x y z
10xz
2 2 6 0x y z
;;d A P AH AK d A d
;d A P
;d A d
HK
AK P
;d A P
d
1;0;2M
2;1;2
d
u
1;5;1MA
;
11
, 9;0;9 1;0; 1
99
d
dA
n u MA


;
, 1;4; 1
Pd
dA
n u n


: 4 3 0P x y z
1;0;2M
AM
AM AK
M
d
11
2 1 3
x y z

P
d
A
H
K
Trang86
A. B. C. D.
ng dn gii:
Gọi H là hình chiếu của A trên d
d(d, (P)) = d(H, (P)). Giả sử điểm I là hình chiếu của H
lên (P), ta có
HI lớn nhất khi . Vậy (P) cần tìm là mặt phẳng đi qua A và
nhận làm VTPT
(P): .
u:
u làm mt nhiu th th u kin nu chn cách
th.
C. Nhm mt phng song song vi d thành mt phng vuông góc vi d
D. Nu tính khot qu ln nht, tuy nhiên mt phng 
 A.
Phn IV: 10 CÂU VN DNG CAO
Câu 41. Trong không gian vi h t Oxyz, cho mt cu (S): và mt
phng (P): t phng (Qm vuông góc vi
mt phng (P) và tip xúc vi mt cu (S) có dng . Giá tr ca
bng:
A. B. C. hoc D. hoc
ng dn gii:
(S) có tâm I(–1; 2; 0) và bán kính R = 3; (P) có VTPT .
PT (Q) đi qua M có dạng:
(Q) tiếp xúc với (S)
(*)
(**)
Từ (*), (**)
Với . Chọn B = 1, A = 2, C = –2
PT (Q):
Với . Chọn B = –7, A = 4, C = –4
PT (Q):
Ch C.
 nhiu:
A. Vì nên d n ca là .
u thêm.
Câu 42. Trong không gian vi h t  Oxyz, cho hai mt phng và
. Gi là mt ph  c t O, không cha trc ,
vuông góc vi mt phng (P) và to vi mt phng (Q) mt góc . Khong cách t
7 5 77 0x y z
2 19 0x y z
2 3 19 0x y z
5 3 77 0x y z
AH HI
AI
AH
7 5 77 0x y z
2 2 2
2 4 4 0x y z x y
30xz
(3;1; 1)M
90ax by cz
abc
0
7
1
7
7
1
(1;0;1)
P
n
2 2 2
( 3) ( 1) ( 1) 0, 0A x B y C z A B C
2 2 2
( ,( )) 4 3d I Q R A B C A B C
( ) ( ) . 0 0
QP
Q P n n A C C A

2 2 2 2
5 3 2 8 7 10 0B A A B B A AB
2 7A 4A B B
2AB
2 2 9 0x y z
7A 4B
4 7 4 9 0x y z
QP
Q
1;0; 1
( ) :5 2 5 1 0P x y z
( ) : 4 8 12 0Q x y z
()R
Oy
0
45
Trang87
n bng:
A. B. C. D. hoc
ng dn gii:
Giả sử PT mặt phẳng (R): .
Ta có: (1);
(2)
Từ (1) và (2)
Với : chọn
PT mặt phẳng (loại)
Với : chọn
PT mặt phẳng (thỏa mãn)
Suy ra . Chọn đáp án A.
u:
B. m .
C. Ch gic cho pt .
D. Không loc pt .
Câu 43. Trong không gian vi h t Oxyz, cho mt phng (Q): ng thng
. Vit phng (P) chng thng d và to vi mt
phng (Q) mt góc nh nht.
A. B. C. D.
ng dn gii:
Ghi nhớ: Góc gia và ln nht bng và nh nht bng góc gia và .
Gi , , , lt là hình chiu ca trên
và .
a và bng , góc gia và
bng .
Vì nên , suy ra
1; 2;3M
R
32
5
31 2
15
2
2
32
5
2 2 2
ax z 0 ( 0)by c d a b c
( ) ( ) 5 2 5 0R P a b c
0
2 2 2
4 8 2
cos(( ),( )) cos45
2
9
a b c
RQ
abc


22
7 6 0
7
ac
a ac c
ca

ac
1, 0, 1a b c
( ): 0R x z
7ca
1, 20, 7a b c
( ): 20 7 0R x y z
32
;
5
d M R
1;2;3M
ac
0xz
0xz
2 5 0x y z
1 1 3
:
2 1 1
x y z
d

40yz
30x y z
2 6 0x y z
2 1 0xy
P
Q
0
90
d
Q
PQ
,M d M Q
I d Q
,HK
M
Q
P
Q
MKH
d
Q
MIH
HK 
HI HK
Q
P
d
I
M
H
K
Trang88
 . Suy ra nh nht bng khi hay .
Suy ra n ca  a .
 và .
C th: Ta có    . Mt phng có
n .
Suy ra . .
Vy . Chán A.
u:
B. ng mt ln cng hp này góc là ln
nht ).
C. Nu th bng cách tính góc gia hai mt ph nht bng .
D. u cho vic th xem mt phng có chng thng hay không.
Câu 44. Trong không gian vi h t  Oxyz   ng thng và
t phng (P) cha sao cho góc gia mt phng (P) và
ng thng là ln nht là: . Giá tr ca bng
A. B. C. D.
ng dn gii:
T m bt k trên k ng thng song song vi .
Ly thuc không thuc . Gi l t là hình
chiu ca trên và . Gi lt là góc gia và
, và .
Ta có suy ra .
 ln nht bng khi hay .
Ta có đi qua và có VTCP .   .
n ca mt phng là .
tan tan
MH MH
MKH MIH
HK HI
MKH MIH
MKH
MIH
KI
MI 
MIH 
MIH
,
dQ
MIH
u n u n



,
Pd
n u u


d
1; 1;3M 
2;1;1
d
u
Q
1;2; 1
Q
n 
11
, 3;3;3 1;1;1
33
dQ
u u n


, 0; 3;3 3 0;1; 1
Pd
n u u


: 4 0P y z
0
90
0
0
d
1
12
:
1 2 1
x y z
d


2
21
:
2 1 2
x y z
d


1
d
2
d
0ax y cz d
T a c d
3T
0T
13
4
T 
6T 
I
1
d
'
2
d
2
d
M
2
'd
P
,HK
M
P
1
d
,

2
'd
P
2
'd
1
d
sin sin
MH MK
MI MI


HK
MK P
1
d
(1; 2;0)I
1
(1;2; 1)u 
2
d
2
2; 1;2u 
MIK
1 1 2
, 3; 4; 5n u u


P
d1
d2'
d2
H
I
M
K
Trang89
n ca là .
Phương trình mặt phẳng (P): .
u:
B. a và ln nht bng khi 
ca . Suy ra .
C. ng ca và c n
ca c pt
D. Sau khi vic pt thì vi vàng tính
Câu 45. Trong không gian to    m , và mt cu
. Mt phng  và ct
theo giao tuyng tròn có bán kính nh nht. Tính .
A. B. C. D.
ng dn gii:
 ng tròn giao tuyn có bán kính nh nht thì
khong cách ln nht. Mà
nên ln nht khi hay mt phng
cha và vuông góc vi .
Suy ra .
Ta có .
Suy ra .
    a . Suy ra . Ch  
B.
u:
u thêm.
C. Nhm n ca . Do ch tính theo quán tính mt ln tích
 ng thì công nh     n ca mt phng c    c
.
Câu 46. Trong không gian to  m và mt phng . Gi
là mt phng song song vi (P) và ct hai tia tm B, C sao cho tam giác
P
11
, 14;2; 10
P
n u n


7 5 9 0 x y z
2
d
P
0
90
2
dP
:2 2 4 0P x y z
0T
1
u

2
u
3; 4; 5
P
13
3 4 5 11 0
4
x y z T
14 2 10 18 0x y z
6T a c d
,Oxyz
3; 2;6A
0;1;0B
2 2 2
: 1 2 3 25S x y z
: 2 0P ax by cz
,AB
S
T a b c
2T
3T
4T
5T
IH
;IH IK d I AB
IH
HK
P
AB
IK
;P mp AB I Q
1
, 5;1; 2
3
Q
n AB AI



1
, 0;12;6 6 0;2;1
3
PQ
n n AB



:0 2 2 0P x y z
3T a b c
5;1; 2
Q
n 
P
5 2 2 0x y z
,Oxyz
(2;2;4)A
( ) :P
40x y z
Q
,Ox
Oy
P
I
A
B
H
K
Trang90
ABC có din tích bng 6. Gi s  a là: . Giá tr ca
bng
A. B. C. D.

Vì (Q) // (P) nên (Q): . Giả sử
.
. Chọn đáp án B.
:
  .
C, D 
Câu 47. Trong không gian vi h to  Oxyz, mt phng (Pm , ct các tia Ox, Oy,
Oz ti A, B, C sao cho th tích t din OABC có giá tr nh nh   
. Giá tr ca bng
A. B. C. D.
ng dn gii:
Giá s .
t phng (P) có dng: .
Ta có: (1); (2)
(1) 
Du "=" xy ra (P):
Suy ra
u:
B, C, D do cng sai .
Câu 48. Trong không gian vi h to  Oxyz, m , . Gi là
mt phng sao cho khong cách t m A n mt phng bng 15 và khong cách t m
B n mt phng bng 2. Mt phng 
A. B. C. D.
ng dn gii:
Q
40ax by cz
abc
3
6
12
3
0 ( 4)x y z d d
( ) Ox, ( )B Q C Q Oy
( ;0;0), (0; ;0) ( 0)B d C d d
1
,6
2
ABC
S AB AC



2d 
( ): 2 0Q x y z
2 2 2 4 0 6x y z a b c
20x y z
3abc
(9;1;1)M
0x By Cz D
B C D
9
27
45
19
( ;0;0) , (0; ;0) , (0;0; )A a Ox B b Oy C c Oz
( , , 0)abc
1
x y z
a b c
(9;1;1) ( )MP
9 1 1
1
abc
1
6
OABC
V abc
9abc bc ac ab
2
3
3 9( )abc
32
( ) 27.9( ) 243abc abc abc
27
9
3
9 1 1
1
3
a
bc ac ab
b
c
abc


1
27 3 3
x y z
9 9 27 0x y z
9B C D
B C D
1; 2; 3A
6;10; 3B 
P
P
P
P
8; 3;1M
18; 3;11M
52; 7;13M
40; 2; 15M
Trang91
Gi s c mt phng (P) tha mãn yêu cu bài toán. Gi H, K lt là hình
chiu ca A, B trên (P). Ta có :
Mà y dng thc (1) phi xy ra
i tm H tha mãn
Gi
Vt phng (P) là mt phH nhn làm vtpt, nên có
 m thuc .
ChD.
u:
u thêm.
Câu 49. Trong không gian vi h to  Oxyz,  ng thng
, vi . Khi  i thì
luôn nm trong mt mt phng c nh . Tính ?
A. B. C. D.
ng dn gii:
.
. Suy ra . Ch
D.
u:
u thêm.
Câu 50. Trong không gian vi h to  Oxyz,   m , , vi
tha mãn . Bit rng khi i thì qu tích tâm mt cu ngoi
tip t din thuc mt mt phng c nh. Tính khong cách t m
,( ) 15
,( ) 2
d A P AH
d B P BK


13 15 12 13 (1)AH BK AB
()H K P AB
15
2
AH BH
HK
( ; ; )H x y z
88
15
1 ( 6)
13
2
15 154 88 154
2 ( 10) ; ; 3 .
2 13 13 13
15
3
3 ( 3)
2
x
xx
y y y K H
z
zz









( 5;12;0)AB
( ) :5 12 176 0P x y
40; 2; 15M
P
4 3 2 3 8 7
:
2 1 1 4 3
m
x m y m z m
d
m m m

31
1; ;
42
m



m
m
d
: 6 0P ax by cz
abc
10
9
7
8
4 3 2 3 8 7
:
2 1 1 4 3
m
x m y m z m
d
m m m

4 3 2 1
2 9 3
2 3 1
45
8 7 4 3
x m m t
x y t
y m m t
y z t
z m m t

2 3 4 6 10 3z 6 0x y y z x y
1 10 3 8abc
;0;0Aa
0; ;0Bb
0;0;Cc
, , 0abc
2abc
,,abc
OABC
P
Trang92
n mt phng .
A. B. C. D.
ng dn gii:
D c t tâm mt cu ngoi tip t din
là
.
T gi thit  thuc mt
phng c nh . Suy ra .
Chn A.
u:
B,C. Vì nên nu HS không bit làm có th chn thiên v s và .
D. Do HS có th nhm pt là ly ngay t gi thia
 m .
----------------------------------------------------Ht----------------------------------------------------
2016;0;0M
P
2015
3
2016
2016
3
2014
3
OABC
;;
2 2 2
a b c
I



21
2 2 2
a b c
abc
I
: 1 0P x y z
2015
;
3
d M P
2016;0;0M
2016
2016
3
20x y z
I
I
H
z
O
x
y
C
A
B
K
| 1/92
| | Tải xuống

Có thể bạn quan tâm:

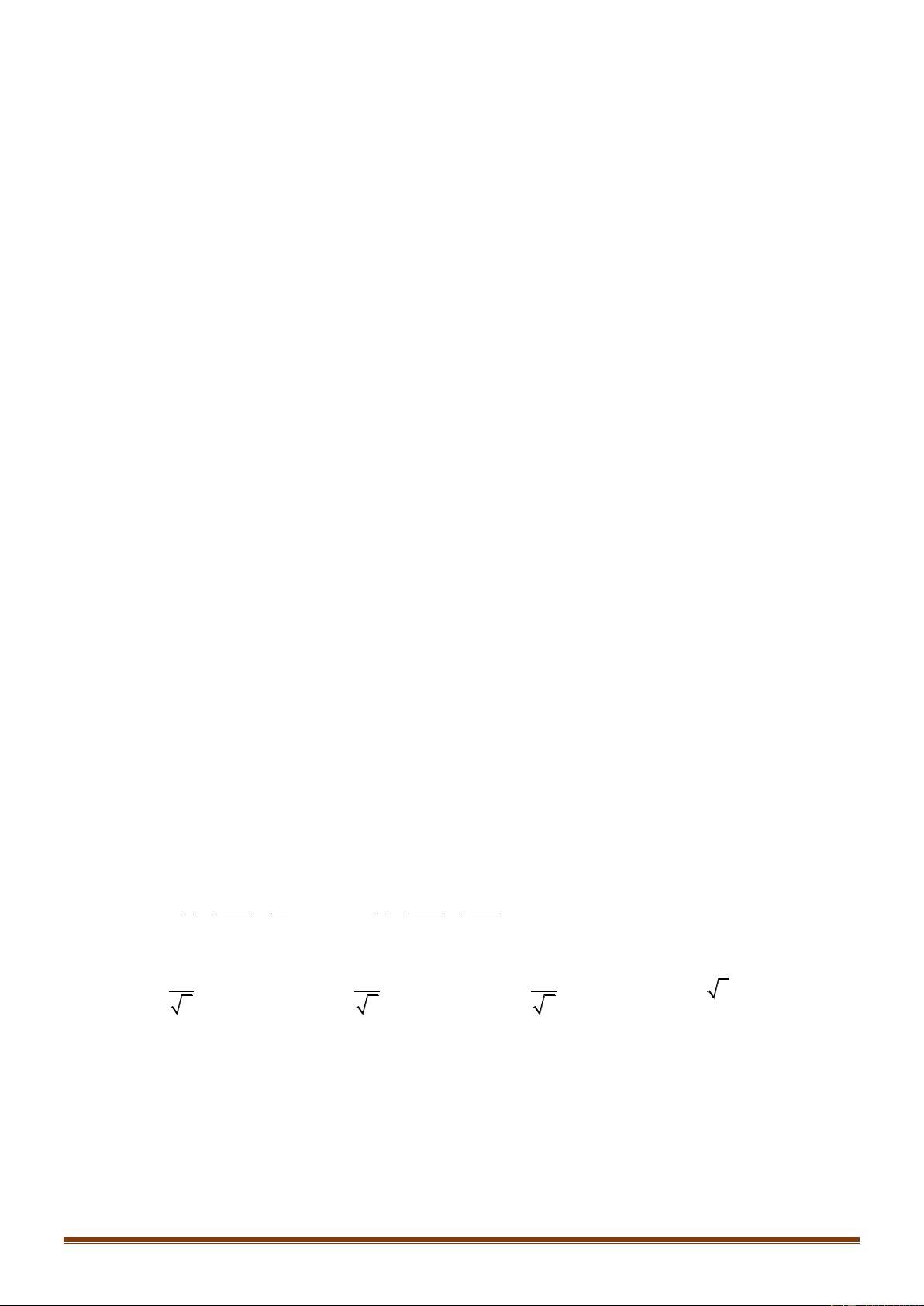
Preview text:

BÀI 1. HỆ TỌA ĐỘ TRONG KHÔNG GIAN
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN NẮM
I. HỆ TỌA ĐỘ TRONG KHÔNG GIAN 1. Hệ tọa độ   
Trong không gian, xét ba trục x Ox ; y Oy ; z O
z vuông góc với nhau từng đôi một. Gọi i , j, k lần
lượt là các vectơ đơn vị các trục x Ox ; y Oy ; z O
z . Hệ ba trục như vậy gọi là hệ trục tọa độ Đề-
các vuông góc Oxyz trong không gian hay hệ tọa độ Oxyz .
Điểm O được gọi là gốc tọa độ.          2 2 2
Chú ý: i j k  1 và . i j  .
i k k. j  0 .
2. Tọa độ của một điểm    
a) Định nghĩa: M  ;
x y; z   OM  .
x i y. j z.k (x : hoành độ, y : tung độ, z : cao độ)
Chú ý: M Oxy  z  0; M Oyz  x  0; M Oxz  y  0
M Ox y z  0;M Oy x z  0;M Oz x y  0 .
b) Tính chất: Cho Ax ; y ; z  x ; y ; z A A A B B B 
AB  x x ; y y ; z z B A B A B A  
AB AB  x xy yz z B A 2
B A2  B A2      x x y y z x
Toạ độ trung điểm M của đoạn thẳng AB: A B M ; A B ; A B    2 2 2 
 Toạ độ trọng tâm G của tam giác ABC:
x x x y y y z z z A B C G ; A B C ; A B C    3 3 3 
 Toạ độ trọng tâm G của tứ diện ABCD:
x x x x y y y y z z z z A B C D G ; A B C D ; A B C D    4 4 4  3. Tọa độ vectơ     
Định nghĩa: u   ;
x y; z   u  . x i  .
y j z.k 
Nhận xét: M   ;
x y; z   OM   ; x y; z
II. BIỂU THỨC TỌA ĐỘ CỦA PHÉP TOÁN VECTƠ  
Định lý:Trong không gian Oxyz cho a  a ;a ;a ;b b ;b ;b ;k R 1 2 3   1 2 3 Trang1  
a b  a b ;a b ;a b 1 1 2 2 3 3  
ka k a ;a ;a ka ;ka ;ka 1 2 3   1 2 3  
Hệ quả: Trong không gian Oxyz cho a  a ;a ;a ;b b ;b ;b ;k R 1 2 3   1 2 3 a b 1 1    
a b  a b 2 2 a b  3 3    
 0  0;0;0;i  1;0;0; j  0;1;0;k  0;0;  1 ;      
a cùng phương bb  0  a kbk R a kb 1 1  a a a 1 2 3
 a kb   
, b ,b ,b  0 2 2  1 2 3  b b b  1 2 3 a kb  3 3
Cho hai điểm Ax ; y ; z x ; y ; z A A A B B B  thì:   
* AB OB OA   x x ; y y ; z z B A B A B A
x x y y z z
*Tọa độ trung điểm M của đoạn thẳng AB là A B M ; A B ; A B    2 2 2 
III. TÍCH VÔ HƢỚNG
1. Biểu thức tọa độ của tích vô hƣớng  
Định lý:Trong không gian Oxyz , tích vô hướng của hai vectơ a  a ;a ;a
b  b ;b ;b 1 2 3  1 2 3  và được   xác định bởi: .
a b a .b a .b a .b 1 1 2 2 3 3 2. Ứng dụng  
a b a .b a .b a .b  0 1 1 2 2 3 3   2 2 2 a
a a a 1 2 3   2 2 2 2
a a a a 1 2 3           a b a b a b a b cosa,b . . . . 1 1 2 2 3 3     (với , a b  0 ) 2 2 2 2 2 2 a . b
a a a . b b b 1 2 3 1 2 3
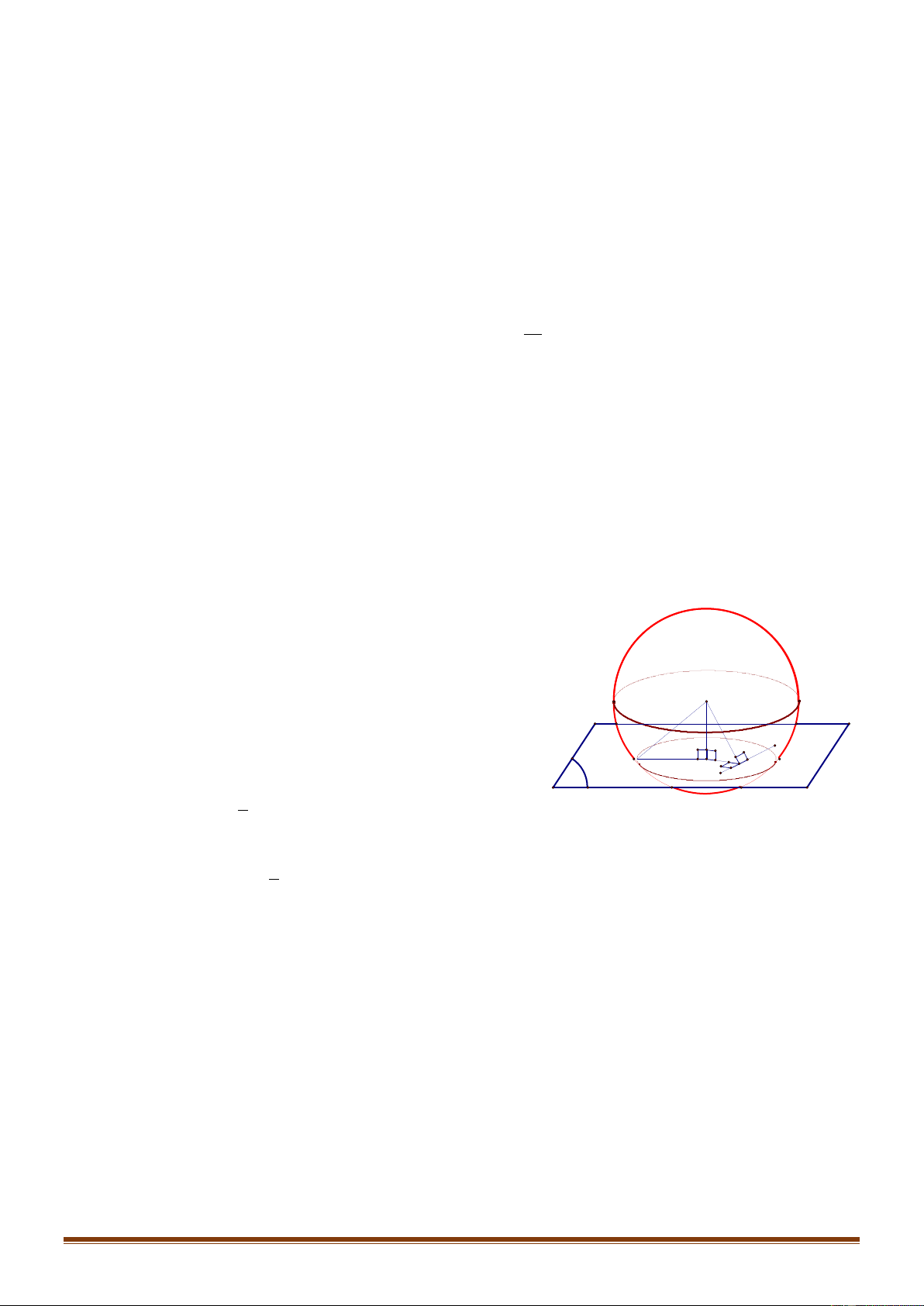
IV. PHƢƠNG TRÌNH MẶT CẦU
Định lý: Trong không gian Oxyz , mặt cầu S  tâm I  ; a ;
b c bán kính r có phương trình là:
  2   2   2 2 x a y b z cr . Trang2
Nhận xét: Phương trình mặt cầucòn có thểviết dưới dạng: 2 2 2
x y z  2ax  2by  2cz d  0 với 2 2 2 2
d a b c r 2 2 2
r a b c d .
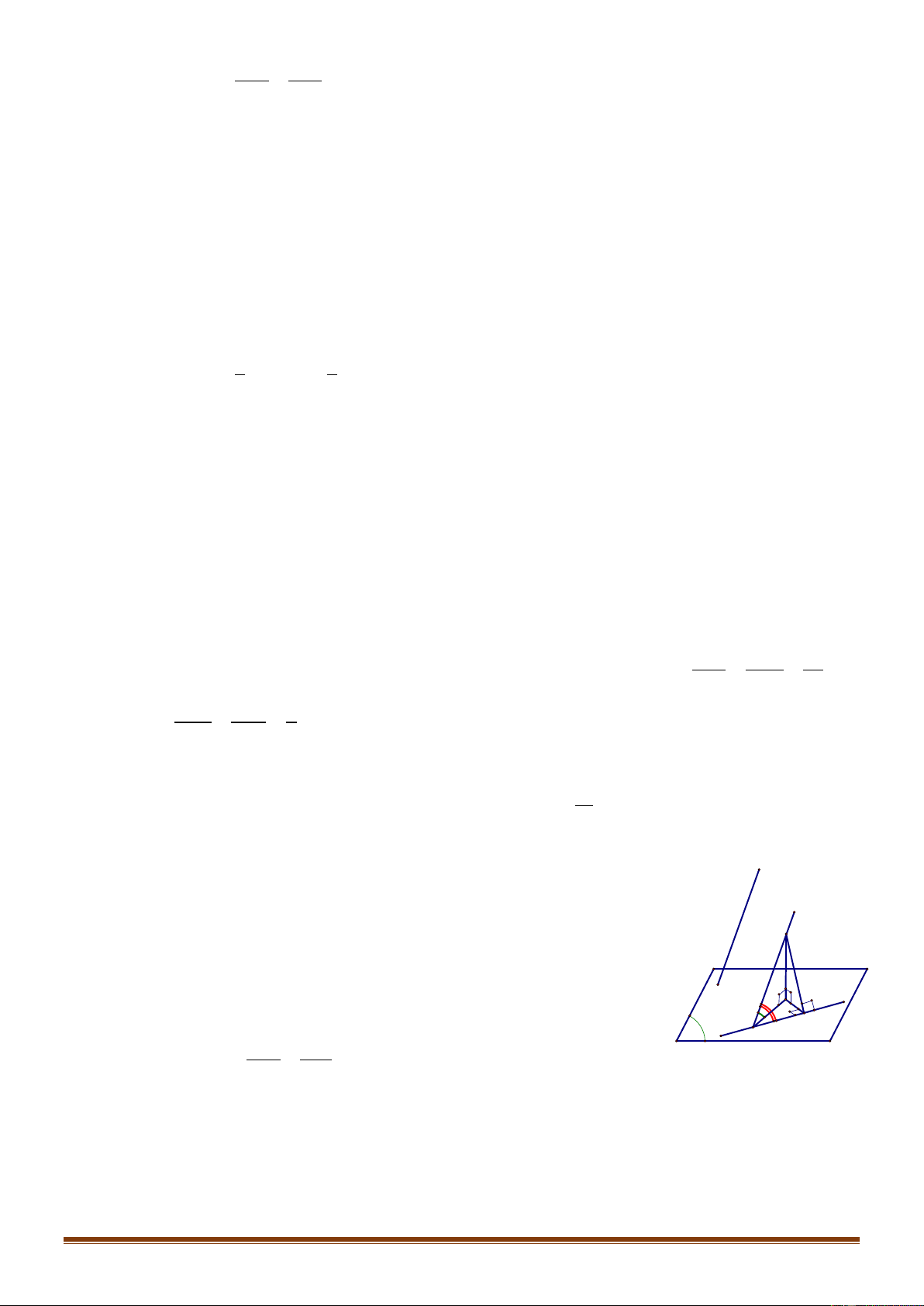
V. TÍCH CÓ HƢỚNG CỦA HAI VECTƠ 1. Định nghĩa  
Trong không gian M  ; a ;
b c cho hai vectơ a  a ;a ;a
b  b ;b ;b 1 2 3  1 2 3  và . Tích có hướng   
của hai vectơ a và b kí hiệu là a,b , được xác định bởi     a a a a a a  2 3 3 1 1 2
a,b   ; ;
  a b a b ;a b a b ;a b a b 2 3 3 2 3 1 1 3 1 2 2 1    b b b b b b  2 3 3 1 1 2 
Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số. 2. Tính chất         , a b  ; a  , a b  b           , a b    , b a               i
 , j  k;  j,k  ;i i
 ,k  j;              [ , a ]
b a . b .sin  ,
a b (Chƣơng trình nâng cao)
3. Ứng dụng của tích có hƣớng: (Chƣơng trình nâng cao)    
Điều kiện đồng phẳng của ba vectơ: a,b và c đồng phẳng   , a b.c  0   
Diện tích hình bình hành ABCD: S  AB,ADABCD     1
Diện tích tam giác ABC : S  AB,ACABC   2
  
Thể tích khối hộp ABCDA'B'C'D' : V
 AB, AD.AA'
ABCDA' B 'C ' D '  
   1
Thể tích tứ diện ABCD : V
 AB,AC.AD ABCD   6 Chú ý:
– Tích vô hƣớngcủa hai vectơ thường sử dụng để chứng minh hai đường thẳng vuông góc, tính
góc giữa hai đường thẳng.
– Tích có hƣớngcủa hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ
diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương. Trang3
B. PHÂN LOẠI VÀ PHƢƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Các bài toán liên quan tọa độ điểm, tọa độ của vectơ
{Tìm tọa độ điểm, tọa độ vecto thỏa tính chất nào đó, tìm tọa độ trung điểm, trọng tâm, trực
tâm, đỉnh của hình bình hành, đỉnh của một hình đa diện,…}
PHẦN 1: CÁC VÍ DỤ   
Ví dụ1. Trong không gian với hệ toạ độ Oxyz , cho ba vectơ: a  (2; 5
 ;3) , b  0;2; 
1 , c  1;7;2 .    
Tìm tọa độ vectơ d a  4b  2c . Lời giải  Ta có: a  2; 5  ;3  4b  0;8;4  2c  2;14;4    
Suy ra: d a  4b  2c  2; 5  ;3 0;8; 4   2;14;4  2 0  2; 5
 8 14;3 4  4   0; 2
 7;3. Vậy d  0;27;3 .
Ví dụ2. Trong không gian với hệ toạ độ Oxyz , cho ba điểm A1; 2; 4, B 2; 1  ;0,C  2  ;3;  1 .
1/ Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.
2/ Tìm tọa độ tâm I của hình bình hành ABCD . Lời giải
x x x x  3  D C B A   
1/ Tứ giác ABCD là hình bình hành  AD BC  y y y y  6  D D C B A  3;6;3
z z z z  3  D C B A
2/ Điểm I là tâm hình bình hành ABCD x x A C x   I 2       y y 1 5 3 I là trung điểm của AC A C  y   I  ; ;   . I 2   2 2 2   z z A C z   I  2
Ví dụ3. Trong không gian với hệ toạ độ Oxyz , cho ba điểm A1; 1
 ;5,B3;4;4,C4;6;  1 . Tìm tọa độ
điểm Mthuộc mặt phẳng Oxy và cách đều các điểm A, B, C ? Trang4 Lời giải
Gọi M x y Oxy  2 2 ; ;0 , ,
x y   ; x y  0 là điểm cần tìm. 2 2 AM BM Vì M cách đều ,
A B, C nên ta có: MA MB MC   2 2 AM CM   x   2 1   y  2
1  0  52   x  32   y  42  0  42  x  2 1   y  2
1  0  52   x  42   y  62  0  2 1
4x 10y 14  0
2x  5y  7 x 16       .
2x  4y 12  0
x  2y  6 y  5  Vậy M 16; 5  ;0 .
Ví dụ4. Trong không gian với hệ toạ độ Oxyz , cho điểm K 2;4;6 , gọi K ' là hình chiếu vuông góc
của K trên trục Oz . Tìm tọa độ trung điểm của đoạn thẳng OK '? Lời giải
Vì K ' là hình chiếu vuông góc của K 2;4;6 lên trục Oz nên K '0;0;6.
Gọi I x ; y ; z I 0;0;3. 1 1
1  là trung điểm OK '. Suy ra
Ví dụ5. Trong không gian với hệ tọa độ Oxyz cho (
A 2; 2; 1) , B 2  ;3;0, C  ; x 3;   1 . Tìm các giá trị
của x để tam giác ABC đều? Lời giải
Gọi M là trung điểm của đoạn thẳng AB  5 1  1 Ta có: M 2  ; ;   , AB  2 , 2
CM  (x  2)   2 2  2
Tam giác ABC đều khi và chỉ khi 3 1 6 x  1  2 2 CM AB  (x  2)    (x  2) 1  2 2 2 x  3  x  1 Vậy:
là các giá trị cần tìm.  x  3
VẬN DỤNG THẤP VÀ VẬN DỤNG CAO Ví dụ6. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A 2  ;0; 3  ,B 4  ;1;  1 ,C  4  ; 4  ; 
1 . Gọi D là chân đường phân giác trong góc A của tam giác .
ABC Tìm tọa độ điểm . D Lời giải Trang5 A B D C
Theo tính chất phân giác trong, ta có: DB AB  AB    DB   DC   1 DC AC AC
Mà: AB  3; AC  6 x x  2  x x C DB D     2 1  Từ   1  DC  2
DB  y y  2
y y D    C DB D 4; ;   .    z z   z zC DB D 3 3 2
Ví dụ7. Cho hình hộp ABC .
D A' B'C ' D'    
1/ Chứng minh: AC '  CA'  2C 'C  0 2/ Cho A1;0; 
1 , B2;1;2,C '4;5; 5  , D1; 1  ; 
1 . Tính tọa độ các đỉnh còn lại của hình hộp. Lời giải 
  
   
1/ Ta có: AC '  AC CC ' ; CA'  CC '  C ' A và C ' A'  CA   
    
Suy ra: AC '  CA'  2C 'C  2CC '  AC CA  2C 'C  0 (đpcm) 2/ Sử dụng công thức hai vecto bằng nhau ta được:
C 2;0;2, B'4;6; 5  , A'3;5; 6  , D'3;4; 6  
Ví dụ8. Trong không gian với hệ tọa độ Oxyz , cho tam giác đều ABC có A5;3;  1 , B 2;3; 4   và
điểm C nằm trong mặt phẳng Oxy có tung độ nhỏ hơn 3 .
1/ Tìm tọa độ điểm C .
2/ Tìm tọa độ điểm D biết ABCD là tứ diện đều. Lời giải
1/ Vì C Oxy nên C  ; x y;0 .    Ta có: AB   3  ;0; 3
 , AC  x  5; y  3; 
1 , BC   x  2 y; y  3;4 2 2 AB AC AB AC
Tam giác ABC đều nên    2 2 AC BC AC BC   x 5 
2  y 32 118
x 1 x 1       .   x  
2  y  2   x  2  y  2 
y  4 y  2 5 3 1 2 3 16 Trang6
Vì C có tung độ nhỏ hơn 3 nên C 1;2;0 . 2/ Gọi D ; x ; y z .   
Khi đó: AD   x  5; y  3; z  
1 ; BD   x  2; y  3; z  4;CD   x 1; y  2; z  .
Vì tam giác ABC đều nên tứ diện ABCD đều khi và chỉ khi AD BD CD AB  3 2 
x 52  y 32 z  2 1
 x  22   y  32  z  42 
  x 52   y 32  z  2 1  x  2 1   y  22 2  z  
x  52   y  32   z  2 1  18   10 x    z  1 x 3       z 1 x x 2       2
y 16  5x
 y 16 5x
 y  6  y   .   3     2 x  5       
2  y 32 z  2 1 18 3x 16x 20 0 z 1   7 z    3   Vậy: D   10 2 7 2;6; 1  D ;  ;    .  3 3 3 
PHẦN 2: CÂU HỎI TRẮC NGHIỆM    Câu 1.
[2H3-1.1-1] Trong không gian Oxyz , gọi i, j, k là các vectơ đơn vị, khi đó với M  ; x y; z  thì  OM bằng:            
A. xi y j k z .
B. xi y j k z .
C. x j yi k z .
D. xi y j k z . Lời giải Chọn A    
OM xi y j k z .   Câu 2.
[2H3-1.1-1] Trong không gian với hệ toạ độ Oxyz , cho ba vectơ: a  (2; 5
 ;3) ,b  0;2;  1 ,     
c  1;7;2 . Tọa độ vectơ d a  4b  2c là: A. (0; 27;3) . B. 1;2; 7   . C. 0; 2  7;3 . D. 0;27; 3   . Lời giải Chọn C    
Có d a  4b  2c  2; 5  ;3  40;2;  1  21;7;2  2; 5  ;3 0;8; 4   2;14;4 Trang7  2 0  2; 5
 8 14;3 4  4  0; 2  7;3. 
Vậy d  0;27;3 . Câu 3.
[2H3-1.1-2] Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC với A3; 2  ;5,B 2  ;1; 3
 và C 5;1; 
1 . Trọng tâm G của tam giác ABC có tọa độ là:
A. G 2;0;  1 .
B. G 2;1;  1 . C. G  2  ;0;  1 . D. G 2;0;  1 . Lời giải Chọn D
x x x y y y z z z  Tọa độ trọng tâm A B C G ; A B C ; A B C    G2;0;  1 .  3 3 3  Vậy G 2;0;  1 . Câu 4.
[2H3-1.1-2] Trong không gian với hệ toạ độ Oxyz , cho hình bình hành OABD có   OA   1
 ;1;0, OB  1;1;0 (O là gốc toạ độ) . Toạ độ tâm hình bình hành OABD là:  1 1  A. 1;0;0 . B. ; ;0   . C. 1;0;  1 . D. 1;1;0 .  2 2  Lời giải Chọn B  Ta có OA   1  ;1;0  A 1  ;1;0 . 
OB  1;1;0  B 1;1;0 .  1 1 
Gọi I là tâm hình bình hành OAB .
D Suy ra I là trung điểm OB I ; ;0  .  2 2  Câu 5.
[2H3-1.1-2]Cho điểm M  2
 ;5;0, hình chiếu vuông góc của điểm M trên trục Oy là điểm
A. M 0;5;0 . B. M 0; 5  ;0 .
C. M 2;5;0 . D. M  2  ;0;0 . Lời giải Chọn A Với M  ; a ;
b c  hình chiếu vuông góc của M lên trục Oy là M 0; ; b 0 1   . Câu 6.
[2H3-1.1-2] Trong không gian với hệ toạ độ Oxyz , cho điểm K 2;4;6 , gọi K ' là hình chiếu
vuông góc của K trên trục Oz , khi đó trung điểm OK ' có toạ độ là A. 1;0;0 . B. 0;0;3 . C. 0;2;0 . D. 1;2;3 . Lời giải Trang8 Chọn B
Vì K ' là hình chiếu vuông góc của K 2;4;6 lên trục Oz nên K '0;0;6 .
Gọi I x ; y ; z I 0;0;3 1 1
1  là trung điểm OK '. Suy ra . Câu 7.
[2H3-1.1-2] Cho điểm M 1;2; 3
  , hình chiếu vuông góc của điểm M trên mặt phẳng Oxy là điểm
A. M 0;2; 3   .
B. M 1;0; 3   .
C. M 1;2;0 .
D. M 1;2;3 . Lời giải Chọn C Với M  ; a ;
b c  hình chiếu vuông góc của M lên mặt phẳng Oxy là M ; a ; b 0 1   . Câu 8.
[2H3-1.1-2] Trong không gian Oxyz , cho 2 điểm B(1; 2; 3) , C(7; 4; 2)
 . Nếu E là điểm thỏa  
mãn đẳng thức CE  2EB thì tọa độ điểm E là:  8   8 8   1   8 8  A. 3;3;    . B. 3; ;    . C. 1;2;   . D. ;3;    .  3   3 3   3   3 3  Lời giải Chọn B  8 x   3    E( ;
x y; z) , từ CE  2EB   y  3 .  8 z    3 Câu 9. [2H3-1.1-2] Trong không gian với hệ toạ độ Oxyz , cho 3 điểm
M 2;0;0, N 0; 3
 ;0, P0;0;4 . Nếu MNPQ là hình bình hành thì toạ độ của điểm Q là: A.  2  ; 3  ;4 . B. 3;4;2 . C. 2;3;4 . D.  2  ; 3  ; 4  . Lời giải Chọn C   Ta có: MN   2  ; 3
 ;0,QP  x ;y ;z  4 Q Q Q .  2   xx  2 Q Q    
Để tứ giác MNPQ là hình bình hành thì MN QP   3
   y  y  3 Q Q .   0  z  4 z  4  QQ Câu 10. [2H3-1.1-2] Trong không gian với hệ toạ độ Oxyz , cho
A1;0;0, B0;1;0, C 0;0;  1 , D1;1; 
1 . Gọi M , N lần lượt là trung điểm của AB,CD . Toạ độ
điểm G là trung điểm MN là: Trang9 A.  1 1 1  . B.  1 1 1  . C.  2 2 2  . D.  1 1 1  . ; ;   ; ;   ; ;   ; ;    3 3 3   2 2 2   3 3 3   4 4 4  Lời giải Chọn B  1 1 
Vì M là trung điểm của AB nên M ; ;0   .  2 2   1 1 
N là trung điểm của CD nên N ; ;1   .  2 2   1 1 1  Do đó G ; ;   .  2 2 2 
Câu 11. [2H3-1.1-1] Trong không gian với hệ toạ độ Oxyz , vectơ đơn vị cùng hướng với vec tơ
a  (1;2;2) có tọa độ là:  1 2 2   1 2 2   1 2 2   1 1 1  A. ; ;   . B.  ; ;   . C. ;  ;   . D. ; ; .    3 3 3   3 3 3   3 3 3   3 3 3  Lời giải Chọn A   1 2 2    1   1 2 2   Ta thấy với u  ; ;  u 1   ; u a  ; ; 
 là vectơ đơn vị cùng hướng với a .  3 3 3  3  3 3 3 
Câu 12. [2H3-1.1-2]Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm (
A 1; 2; 1) , B(2; 1  ;3) ,
C(2;3;3) . Điểm M  ; a ;
b c là đỉnh thứ tư của hình bình hành ABCM , khi đó 2 2 2
P a b c có giá trị bằng A. 42 . B. 43. C. 44 . D. 45 . Lời giải Chọn C M ( ;
x y; z) , ABCM là hình bình hành thì x 1  2   2   
AM BC   y  2  3 1  M ( 3  ;6; 1  )  P  44 . z 1 33 
Câu 13. [2H3-1.1-2]Trong không gian với hệ toạ độ Oxyz , cho ba điểm A2; 3  ;4,B1; ; y   1 C  ;
x 4;3 . Để ba điểm A, B, C thẳng hàng thì tổng giá trị 5x + y là: A. 42 . B. 41 . C. 40 . D. 36 . Lời giải Chọn B   Có AB   1  ; y  3; 5
 ; AC  x  2;7;  1 . Trang10   1 y  3 5
Để ba điểm A, B, C thẳng hàng thì AB cùng phương AC    . x  2 7 1  9
x  ; y  32 5  5x + y = 41 Vậy 5x + y = 41 .
Câu 14. [2H3-1.1-2] Trong không gian với hệ toạ độ Oxyz , cho hai điểm A1;1;0, B2;0; 3   . Điểm 1
M chia đoạn AB theo tỉ số k   có tọa độ là: 2  4 2   2 2   1 2   2 2  A. M ; ; 1    . B. M ; ; 2    . C. M ; ;1   . D. M ; ; 2    .  3 3   3 3   3 3   3 3  Lời giải Chọn A Giả sử M  ;
x y; z  là điểm cần tìm. 1  
Vì M chia đoạn AB theo tỉ số k   1
nên ta có: MA   MB . 2 2  1 
1 x   2  x 4 x    2 3    1 
   y     y 2 1 0  y  . 2 3    1    z      zz 1 3   2   4 2  Vậy M ; ; 1    .  3 3 
Câu 15. [2H3-1.1-2]Cho điểm M 3;2; 
1 , điểm đối xứng của M qua mặt phẳng Oxy là điểm
A. M 3;2;0 . B. M 3; 2  ;  1 . C. M 3; 2  ;  1 .
D. M 3;2;  1 . Lời giải Chọn D Với M  ; a ;
b c  điểm đối xứng của M qua mặt phẳng Oxy là M  ; a ;
b c
Câu 16. [2H3-1.1-3] Cho điểm M 3;2;  1 , điểm M  ; a ;
b c đối xứng của M qua trục Oy , khi đó
a b c bằng A. 0 . B. 4 . C. 6 . D. 2 . Lời giải Chọn A Trang11 Với
 điểm đối xứng của qua trục là    M  ; a ; b cM Oy M  ; a ; b c  M 3  ;2; 
1  a b c  0 .
Câu 17. [2H3-1.1-3] Trong không gian Oxyz , cho tứ diện ABCD có ( A 1;0; 2), B( 2
 ;1;3),C(3;2;4), D(6;9; 5
 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD  14   18 
A. G 8;12;4 . B. G 2;3;  1 . C. G 3;3;   . D. G 9  ; ; 3  0   .  4   4  Lời giải Chọn B
Câu 18. [2H3-1.1-3] Trong không gian Oxyz , cho hai điểm (
A 1; 2;1), B(2; 1
 ;2) . Điểm M trên trục
Ox và cách đều hai điểm ,
A B có tọa độ là  1 1 3   1   3   1 3  A. M ; ;   . B. M ;0;0   . C. M ;0;0   . D. M 0; ;   .  2 2 2   2   2   2 2  Lời giải Chọn C
M Ox M  ; a 0;0 . 2 2
M cách đều hai điểm , A B nên 2 2
MA MB    a 2 2      a 2 2 1 2 1 2  2 1 . 3
 2a  3  a  . 2
Câu 19. [2H3-1.1-4] Trong không gian với hệ toạ độ Oxyz , cho ba điểm A1; 1
 ;5,B3;4;4,C4;6;  1
. Điểm M thuộc mặt phẳng (Oxy) và cách đều các điểm A, B, C có tọa độ là: A. M 16; 5  ;0 . B. M 6; 5  ;0 . C. M  6  ;5;0.
D. M 12;5;0 . Lời giải Chọn A
Gọi M x y   2 2 ; ;0 ,
x y   ; x y  0 là điểm cần tìm.
Vì M cách đều A , B , C nên ta có: MA MB MC
 x  2   y  2    2  x  2   y  2    2  x  2   y  2    2 1 1 0 5 3 4 0 4 4 6 0 1   2
x  2y  27  6
x 8y  41  8
x 12y  53
4x 10y 14  0
2x  5y  7 x 16       Vậy M 16; 5  ;0 .
2x  4y 12  0
x  2y  6 y  5 
Câu 20. [2H3-1.1-4] Trong không gian với hệ toạ độ Oxyz , cho A2;1;  1 , B 3;0;  1 ,C 2; 1  ;3 điểm
D thuộc Oy và thể tích của tứ diện ABCD bằng 5. Toạ độ của D là: Trang12 0; 7  ;0 0; 8  ;0 A. . B. . C. . D. . 0; 7  ;0 0;8;0   0;8;0 0;7;0 Lời giải Chọn C  
Điểm D thuộc trục Oy có tọa độ D(0; y ;0) . Ta có AB  1; 1
 ;2 , AC  0; 2  ;4 và 0 
AD  2; y 1;1 0  . Dễ thấy    1  2 2 1 1 1  
AB, AC   ; ;   0; 4  ; 2   ,   2  4 4 0 0 2   
1    1  5  V
 AB, AC.AD  2  4y , ABCD 0   6 6 nên y  7  hoặc y  8 . 0 0
Dạng 2: Tích vô hƣớng và các ứng dụng của tích vô hƣớng
{ Tích vô hướng hai vt, góc giữa hai vt, độ dài vt, độ dài đường trung tuyến, phân giác,đường
cao, diện tích tam giác, chu vi tam giác…}
PHẦN 1: CÁC VÍ DỤ
Ví dụ 1. Trong không gian m cho tam giác ABC có A2; 1  ;3, B3;0; 2  ,C5; 1  ; 6  .Tính  cos BAC Lời giải  
Ta có: AB  1;1; 5
 ; AC  3;0; 9       AB AC Suy ra:  BAC  AB AC . 16 8 30 cos cos ;    . A . B AC 3 30 45
Ví dụ 2. Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC biết A1;2;3 , B đối xứng với A qua
mặt phẳng ( Oxy ), C đối xứng với B qua gốc tọa độ O. Tính diện tích tam giác ABC ? Lời giải
Theo đề bài: B đối xứng với A qua mặt phẳng (Oxy ) B(1;2;3)
C đối xứng với B qua gốc tọa độ O C(1;2;3)   1    AB  (0;0; 6)  ; AC  ( 2  ; 4  ;0)  S   ; AB AC   6 5  . ABC   2
Ví dụ 3. Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC có A2;0;0 , B 0;3;  1 , C  3  ;6;4
. Gọi M là điểm trên cạnh BC sao cho MC  2MB . Tính độ dài đoạn thẳng AM . Lời giải Trang13  
Vì điểm M thuộc cạnh BC nên MC  2
MB , suy ra tọa độ điểm M là  x  ( 2)  x C B x   1   M 1 ( 2)    y  ( 2)  y C By   4 . M 1 ( 2)    z  ( 2)  z C Bz   2 M  1 ( 2) 
Vậy độ dài AM bằng:
x x 2  y y 2 2
 (z z )    22  4  02 2 1  (2  0)  29 M A M A M A .      
Ví dụ 4.Trong không gian với hệ toạ độ Oxyz cho hai vecto ,
a b thỏa mãn a b 0 ;
120 ; a  2; b  3  
1) Tính a  2b .    
2) Tính góc giữa hai vecto a và x  3a  2b . Lời giải       1) Ta có: .
a b a . b .cos ; a b  3         
 a b2 2 2 2  a  4 .
a b  4b  52  a  2b  2 13 .           
2) Ta có: a x a a b 2 . 2  a  2 .
a b  6 và x   a b2 3 2  6 .        a x .ax 1 cos ;
      ;ax 0  60 . a . x 2
Ví dụ 5.Trong không gian với hệ tọa độ Oxyz cho (
A 2; 2; 1) , B 2  ;3;0, C  ; x 3;   1 . Tìm các giá trị
của x để tam giác ABC đều? Lời giải
Gọi M là trung điểm của đoạn thẳng AB .  5 1  1 Ta có: M 2  ; ;   , AB  2 , 2
CM  (x  2)  .  2 2  2
Tam giác ABC đều khi và chỉ khi 3 1 6 x  1  2 2 CM AB  (x  2)  
 (x  2) 1  . 2 2 2 x  3  x  1 Vậy:
là các giá trị cần tìm.  x  3 Trang14
Ví dụ 6.Trong không gian m , cho hình hộp chữ nhật ABC .
D A' B'C ' D' có đỉnh A trùng với gốc O , B  ;
a 0;0 , D0; ;
a 0, A'0;0;b a,b  0 . Gọi M là trung điểm của cạnh CC ' .Tính thể tích
của khối tứ diện BDA' M . Lời giải b  Ta có : C  ; a ; a 0,C ' ; a ; a b  M ; a ; a  .  2   BD   ; a ; a 0     ab ab   2 
 BD, BM   ; ; a ; BA'  b       a;0;b BM  0; ; a  2 2      2  2
   3a b
 BD, BM .BA'     2 2
1    a b
Vậy thể tích của khối tứ diện BDA' M là: V
 BD, BM .BA'  . BDA'M   6 4
PHẦN 2: CÂU HỎI TRẮC NGHIỆM   Câu 1.
[2H3-1.2-1] Tích vô hướng của hai vectơ a   2
 ;2;5,b  0;1;2 trong không gian bằng: A.10 . B.12 . C.13 . D.14 . Lời giải Chọn B Câu 2.
[2H3-1.2-1]Trong không gian cho hai điểm A 1
 ;2;3, B0;1; 
1 , độ dài đoạn AB bằng A. 6 . B. 8 . C. 10 . D. 12 . Lời giải Chọn A 
AB   x xy yz z         B A 2
B A2  B A2   2  2  2 0 1 1 2 1 3 6 . Câu 3.
[2H3-1.2-1]Cho điểm M 1;2; 3
  , khoảng cách từ điểm M đến mặt phẳng Oxy bằng A. 14 . B. 3 . C.1 . D. 2 . Lời giải Chọn B Với M  ; a ;
b c  d M ,Oxy  c  3 . Câu 4.
[2H3-1.2-1]Cho điểm M  2
 ;5;0, khoảng cách từ điểm M đến trục Ox bằng A.25. B.5. C. 4. D. 0. Lời giải Trang15 Chọn B
Với M a b c  d M Ox 2 2 2 2 ; ; ,
b c  5  0  5 Câu 5. [2H3-1.2-2] Trong không gian với hệ toạ độ Oxyz , cho ba vectơ    a   1
 ;1;0,b  1;10,c  1;1; 
1 . Trong các mệnh đề sau, mệnh đề nào sai ?       A. a  2 . B. c  3 .
C. a b .
D. c b . Lời giải Chọn D  2 2 a  ( 1  ) 1  0  2 .  2 2 2
c  1 1 1  3 .     . a b   
1 .11.1 0.0  0  a b .   .
b c  1.11.1 0.1  2 . Câu 6.
[2H3-1.2-2] Cho 3 điểm A1;2;0, B1;0;  1 , C 0; 1
 ;2. Tam giác ABC là
A.Tam giác có ba góc nhọn.
B. Tam giác cân đỉnh A .
C. Tam giác vuông đỉnh A . D. Tam giác đều. Lời giải Chọn A     AB  (0; 2  ; 1  ); AC  ( 1  ; 3  ;2) . Ta thấy A .
B AC  0  ABC  không vuông.  
AB AC ABC  không cân.      Câu 7.
[2H3-1.2-1] Gọi  là góc giữa hai vectơ a và b , với a và b khác 0 , khi đó cos bằng:         a b . a b  . a b . a b A.   . B.   . C.   . D.   . a . b a . b a . b a . b Lời giải Chọn D    Câu 8.
[2H3-1.2-2] Trong không gian với hệ toạ độ Oxyz , cho ba vectơ a  1
 ;1;0,b1;10,c1;1;  1 .
Trong các mệnh đề sau, mệnh đề nào đúng ?           A. . a c  1.
B. a cùng phương c . C.b c 2 cos ,  .
D. a b c  0 . 6 Lời giải Chọn C Trang16   
 Nên đáp án A và B sai. . a c  1
 .11.1 0.1 0  a  . c    
a b c  1;3;  1  0.     b c 1.1 1.1 0.1 2 cos ,   . 11. 111 6 Câu 9.
[2H3-1.2-2] Trong không gian Oxyz cho ba điểm A1;2;0, B 1  ;1;3,C0; 2  ;5 . Để 4 điểm ,
A B,C, D đồng phẳng thì tọa độ điểm D là A. D1; 1  ;6 .
B. D 1;2;3 .
C. D 0;3;0 .
D. D 0;0;2 . Lời giải Chọn C Xét D 2  ;5;0 . D1; 1  ;6   
Ta có: AB  2;1;3 ; AC  1; 4;5 . AD  1;1;0   Do đó: A ,
B AC  7;7;7 ;  
   Suyra :  A ,
B AC.AD  0 .   Câu 10. [2H3-1.2-2]
Trong không gian với hệ toạ độ Oxyz , cho tứ diện ABCD biết A2; 1  ;6,B 3  ; 1  ; 4  , C5; 1  ;0, D1;2; 
1 . Độ dài đường cao AH của tứ diện ABCD là: A. 9 . B. 7 . C. 6 . D. 5 . Lời giải Chọn D   
Có BC  8;0;4; BD  4;3;5; BA  5;0;10  
  
BC,BD   1  2; 2
 4;24; BC,BD.BA 180     1
   V
 . BC, BD.BA  30 ABCD   6 1   1 S
 . BC, BD  .      ABC  122  242 2 24 18   2 2 1 V Mà V  3. .AH .S ABCD     AH 5 ABCD 3 BCD S BCD Vậy AH  5 .
Câu 11. [2H3-1.2-2] Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC có A2;0;0 , B 0;3;  1 , C  3
 ;6;4 . Gọi M là điểm trên cạnh BC sao cho MC  2MB . Độ dài đoạn AM bằng Trang17 A. . B. . C. . D. . 3 3 2 7 29 30 Lời giải Chọn C  
Vì điểm M thuộc cạnh BC nên MC  2
MB , suy ra tọa độ điểm M là  x  ( 2)  x C B x   1   M 1 ( 2)    y  ( 2)  y C By   4 . M 1 ( 2)    z  ( 2)  z C Bz   2 M  1 ( 2)  2 2 2 2 Vậy AM
x x   y y  2
 (z z )    2  4  0 2 1  (2  0)  29 M A M A M A .
Câu 12. [2H3-1.2-2] Trong không gian với hệ toạ độ Oxyz , cho ba điểm A 2  ;2;  1 , B 1;0;2 và C  1
 ;2;3 . Diện tích tam giác ABC là: 3 5 5 A. . B. 3 5 . C. 4 5 . D. . 2 2 Lời giải Chọn A   Có AB  3; 2  ;  1 ; AC  1;0;2   A , B AC   4  ; 5  ;2   1   1 S  . A , B AC       ABC   42  52 3 5 2 2 .   2 2 2 3 5 Vậy S   . ABC 2
Câu 13. [2H3-1.2-2] Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC có A1;0;  1 ,
B 0;2;3, C 2;1;0 . Độ dài đường cao của tam giác kẻ từ C là: 26 26 A. 26 . B. . C. . D. 26 . 2 3 Lời giải Chọn C  
AB   1;2;2, AC  1;1;  1 Trang18   AB AC  
Độ dài đường cao kẻ từ C của tam giác ABC là : d C AB , 26 ,    . AB 3
Câu 14. [2H3-1.2-2] Cho A1; 2
 ;0,B3;3;2,C 1
 ;2;2, D3;3; 
1 . Thể tích của tứ diện ABCD bằng A. 3 . B. 4 . C. 5 . D. 6 . Lời giải Chọn A   
Tính AB  2;5;2, AC   2
 ;4;2, AD  2;5;  1 .
1    V
AB, AC.AD  3 .   6
Câu 15. [2H3-1.2-2] Trong không gian Oxyz cho tứ diện ABCD . Độ dài đường cao vẽ từ D của tứ
diện ABCD cho bởi công thức nào sau đây:
   
  
AB, AC .AD    AB, AC. 1 AD   A. h    . B. h    . A . B AC    3 . AB AC
  
  
AB, AC.AD     AB, AC . 1 AD   C. h    . D. h    . A . B AC 3  . AB AC    Lời giải Chọn A
     1 1  
1   
AB, AC .AD   Vì V  . h  . AB AC  
AB, AC.AD nên h    . ABCD     3 2 6 A . B AC    Câu 16. [2H3-1.2-2] Trong không gian tọa độ Oxyz , cho bốn điểm A1; 2
 ;0,B3;3;2,C 1
 ;2;2, D3;3; 
1 . Độ dài đường cao của tứ diện ABCD hạ từ đỉnh D
xuống mặt phẳng  ABC là 9 9 9 9 A. . B. . C. . D. . 2 7 7 2 14 Lời giải Chọn C   
Tính AB 2;5;2, AC  2
 ;4;2, AD2;5;  1
1    V
AB, AC.AD  3   6 1   V  1 .
B h , với B S
  AB, AC  7 2 h d  , D ABC   ,   3 ABC 2 Trang19 3V 3.3 9  h    . B 7 2 7 2
  
AB, AC.AD   18 9 h      .  
áp dụng công thức ở câu trên ta được: A . B AC 14 2 7 2        
Câu 17. [2H3-1.2-3] Cho hai vectơ a và b tạo với nhau góc 0
60 và a  2; b  4 . Khi đó a b bằng A. 2 7 . B. 2 3 . C. 2 5 . D. 2 . Lời giải Chọn A   2  2  2      
Ta có a b a b  2 a b .cos a,b  4 16  8  28  a b  2 7 .    
Câu 18. [2H3-1.2-3] Cho u  1;1; 
1 và v  0;1;m . Để góc giữa hai vectơ u,v có số đo bằng 0 45 thì m bằng A.1 3 . B.  3 . C. 2  3 . D. 3 . Lời giải Chọn C m     m  cos    2 m   1 1.0 1.1 1. 1 2 1  3 m 1    m   3. m 1 2 3  m   1  2m   2 3 2 2 2 1 .     2      
Câu 19. [2H3-1.2-3] Cho a  2; b  5, góc giữa hai vectơ a và b bằng , u ka  ;
b v a  2 . b 3  
Để u vuông góc với v thì k bằng 6 6 45 A.  45 . B. . C. . D.  . 45 6 45 6 Lời giải Chọn D         
u v  ka b a b  k    k   2 . 2 4 50 2 1 a b cos  0 . 3 45
 6k  45  0  k   . 6
Câu 20. [2H3-1.2-3] Trong không gian với hệ toạ độ Oxyz ,cho tam giác ABC có A1;2;  1 , B 2; 1  ;3 ,C 4
 ;7;5 . Độ dài đường phân giác trong của góc B là: 2 74 3 76 A. 2 74 . B. . C. . D. 3 76 . 3 2 Lời giải Trang20 Chọn B
Gọi D là chân đường phân trong của góc B thuộc tam giác ABC, khi đó ta có tỷ lệ:  DA BA 1  2  11    8  14  2 74       D ; ;1  BD  ; ; 2   BD  .     DC BC 2  3 3   3 3  3 2 74 Vậy BD  . 3 
Câu 21. [2H3-1.2-3] Trong không gian với hệ toạ độ Oxyz , cho tam giác ABC có AB  ( 3  ;0;4) ,  AC  (5; 2
 ;4) . Độ dài trung tuyến AM là: A. 2 3 . B. 4 2 . C. 3 2 . D. 5 3 . Lời giải Chọn C   
 1   1   1  1 
Ta có: AM AB BM AB BC AB
BAAC ABAC . 2 2 2 2  
AM      AM    2 2 2 1; 1;4 1 1  4  18  3 2 .
Câu 22. [2H3-1.2-4] Trong không gian với hệ toạ độ Oxyz , cho hình chóp S.OAMN với S 0;0; 
1 , A1;1;0, M  ;
m 0;0, N 0; ;
n 0 , trong đó m  0, n  0 và m n  6 . Thể tích hình chóp S.OAMN là: A.1 . B. 2 . C. 4 . D. 6 . Lời giải Chọn A   
Có OA  1;1;0,OM   ;
m 0;0,ON  0; ; n 0 1   1 S  O , A OM   m OAM   2 2 1   1 S  O , A ON   n OAN   2 2 1 SSSm n   OAMN OAM OAN   1.6 3 2 2 1 1 V
 .d S, OAMN .S  .1.3  1 S .OAMN    . 3 OAMN 3
Dạng 3: Xác định phƣơng trình mặt cầu, tìm các thuộc tính của mặt cầu
{các bài toán tìm tâm I, bán kính R, xác định xem một phương trình có phải là phương trình
mặt cầu hay không, tìm điều kiện (có chứa tham số m) để một phương trình là phương trình
mặt cầu, các bài toán về họ mặt cầu, bài toán quỹ tích….}
PHẦN 1: CÁC VÍ DỤ Trang21
Ví dụ1. Xác định tọa độ tâm I, bán kính R của mặt cầu S  2 2 2
: x y z  2x  4 y  6z  5  0 ? Lời giải
Mặt cầu  S  có tâm I  1
 ;2;3 , bán kính R  3.
Ví dụ2. Cho mặt cầu S  2 2 2
:(x 1)  y  (z  2)  9 . Chứng minh rằng:Mặt cầu tiếp xúc với mặt phẳng
P:2x  2y z 5  0. Tìm tọa độ tiếp điểm M . Lời giải
Mặt cầu S  có tâm I 1; 0; 2 , bán kính R  3. 2  0  2  5
Ta có d(I; (P)) 
 3  R nên mặt phẳng tiếp xúc với mặt cầu. 2 2 2 2  2 1
Tiếp điểm M là hình chiếu của I trên mặt phẳng P .  Gọi M  ;
x y; z  thì IM   x 1; y; z  2 nên    x 1 y z  3
IM t.n      ( P) 11 20 17    2 2 1  M  ;  ;   . M   P   9 9 9 
2x  2y z  5  0 Ví dụ3. Trong khoâng gian với hệ tọa độ Oxyz , cho bốn điểm A3;3;0 ,
B3;0;3,C 0;3;3, D3;3;3 . Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC . Lời giải      Ta có: AB  0; 3  ;3, AC   3  ;0;3  A , B AC   9  ; 9  ; 9
   n  1;1;  1 là VTPT của  
ABC . Suy ra phương trình ABC: x y z 6  0 . Gọi I  ; a ;
b c là tâm đường tròn ngoại tiếp tam giác ABC
I  ABC
a b c  6  0  
Suy ra IA IBb   c  0
a b c  2 . Vậy I 2;2;2 .   IB IC a b  0  
Ví dụ4. Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng P có phương trình :
2x  2 y z  4  0 và mặt cầu  S  : 2 2 2
x y z  2x  4 y  6z 11  0 . Chứng minh rằng mặt
phẳng P cắt mặt cầu S  theo một đường tròn. Xác định toạ độ tâm và tính bán kính của đường tròn đó. Lời giải
Mặt cầu S  có tâm I 1;2;3 , bán kính R  5.   
Khoảng cách từ I đến Pd I P 2 4 3 4 : ,   3  R 3 Trang22
Suy ra mặt phẳng P cắt mặt cầu S  theo một đường tròn.
Gọi H , r lần lượt là tâm và bán kính đường tròn đó, suy ra H là hình chiếu vuông góc của I
lên mặt phẳng P nên tọa độ của H là nghiệm của hệ: x 1 2t  x  3
y  2  2t  
 y  0  H(3;0;2) . Bán kính 2 2
r R IH  4 . z  3  t  z  2 
2x  2y z  4  0 Ví dụ5. 2 2 2
Cho mặt phẳng  P 2
: 2x  2 y z m  3m  0 và mặt cầu S  :  x   1   y   1   z   1  9 .
Tìm m để mặt phẳng  P tiếp xúc với mặt cầu  S  . Với m vừa tìm được hãy xác định tọa độ tiếp điểm. Lời giải
Mặt cầu S  có tâm I 1; 1  ; 
1 , bán kính R  3.
Gọi  là đường thẳng đi qua I , vuông góc với P . x 1 y 1 z 1 Suy ra phương trình  :   . 2 2 1 2 m  3m 1
Mặt phẳng P tiếp xúc với mặt cầu S  d I,P  R   3 3 2
m  3m 10  0    m  5  ,m  2 . 2
m  3m  8  0 VN
Khi đó P : 2x  2y z 10  0 . Tọa độ tiếp điểm A là nghiệm của hệ:
x 1 y 1 z 1     2 2
1 , giải hệ này ta được x  3, y  1, z  2  A3;1;2 .
2x  2y z 10  0
PHẦN 2: CÂU HỎI TRẮC NGHIỆM Câu 1. [2H3-1.3-1] Trong không gian với hệ tọa độ Oxyz , mặt cầu
S x  2  y  2 z  2 : 1 2 1
16 có tọa độ tâm I và tính bán kính R là: A. I  1  ;2;  1 và R  4 .
B. I 1; 2;  1 và R  4 . C. I  1  ;2;  1 và R 16 .
D. I 1; 2;  1 và R 16 . Lời giải Chọn A Tâm I  1  ;2; 
1 và bán kính R  4 . Trang23 Câu 2.
[2H3-1.3-1] Trong không gian với hệ tọa độ Oxyz , mặt cầu có phương trình 2 2 2
x y z  8x 10y  8  0 có tâm I và bán kính R lần lượt là:
A. I 4; 5;4 và R  57 .
B. I 4; 5;4 và R  7 .
C. I 4;5;0 và R  7 .
D. I 4; 5;0 và R  7 . Lời giải Chọn D
Mặt cầu có tâm I 4; 5;0 , bán kính R  7 . Câu 3.
[2H3-1.3-1] Biểu thức nào sau đây không là phương trình mặt cầu. A. 2 2 2
x y z 100  0 . B. 2 2 2 3
x  3y  3z  48y  36y  297  0 . 2 2 2 C. 2 2 2
x y z 12 y 16 y 100  0 . D. x  
1   y  2   z  2  9  0 . Lời giải Chọn C Vì  2 2 6  0  4  0 . Câu 4. [2H3-1.3-2] Cho mặt phẳng
:4x 2y 3z 1 0 và mặt cầu S 2 2 2
: x y z  2x  4 y  6z  0 . Khi đó mệnh đề nào sau đây là mệnh đề sai:
A.   có điểm chung với (S).
B.   cắt (S) theo một đường tròn.
C.   tiếp xúc với (S).
D.   đi qua tâm của (S). Lời giải Chọn C
Mặt cầu  S  có tâm I 1; 2;3 , bán kính R  14 .
Ta có: d I,   0  R nên   cắt (S) theo một đường tròn.
Tâm I 1; 2;3 thuộc mặt phẳng   . Câu 5.
[2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , tọa độ tâm và bán kính của đường tròn
giao tuyến của mặt phẳng 2x  2y z  9  0 và mặt cầu 2 2 2
x y z  6x  4 y  2z  86  0 là: A. I  1
 ;2;3 và r  8 .
B. I 1;2;3 và r  4 . C. I 1; 2
 ;3 và r  2 . D. I 1;2; 3
  và r  9 . Lời giải Chọn A
Do bốn đáp án là khác nhau về bán kính nên ta chỉ tính bán kính cho đơn giản. Trang24
Mặt cầu có tâm O   3; 2; 
1 , bán kính là R 10 .
Khoảng cách từ tâm mặt cầu đến mặt phẳng là : 2 3  2. 2   1 9 d   6 . 2   2  2   2 2 1
Vậy bán kính đường tròn giao tuyến là : 2 2 r R d  8 . Câu 6. [2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , cho mặt cầu S 2 2 2
: x y z  2x  4 y  6z  5  0 và mặt phẳng   : 2x y  2z 1  0 . Mặt phẳng  
tiếp xúc với mặt cầu S  tại điểm M có tọa độ là: A. 1;1;  1 . B. 1;2;3 . C. 3;3; 3   . D.  2  ;1;0 . Lời giải Chọn A
Mặt phẳng   tiếp xúc với mặt cầu  S  tại điểm M  tọa độ M thỏa   và  S .
Lần lượt thế tọa độ M ở 4 phương án vào   và  S  thì chỉ có phương án A thỏa vì 2.11 2.11  0 và 2 2 2
1 1 1  2.1 4.1 6.1 5  0. Câu 7.
[2H3-1.3-2] Phương trình nào sau đây là phương trình mặt cầu ? A. 2 2 2
x y z  2x  0 . B. 2 2 2
x y z  2x y 1  0 .
C. x y   x y2 2 2 2 2 2
z  2x 1.
D. x y2 2
 2xy z 1 . Lời giải Chọn A x 1 tCâu 8.
[2H3-1.3-2] Cho các điểm A 2  ;4; 
1 , B 2;0;3 và đường thẳng d : y 1 2t . Gọi S  là z  2   t  mặt cầu đi qua ,
A B và có tâm thuộc đường thẳng d . Bán kính mặt cầu  S  bằng: A. 3 3. B. 6. C.3. D. 2 3. Lời giải Chọn A
Tâm I d I 1 t;1 2t; 2   t .  
AI  3 t; 3   2t; 3
  t; BI   1
  t;1 2t; 5   t
Vì S  đi qua , A B nên ta có Trang25
IA IB IA IB    t 2    t 2    t 2    t 2    t 2    t 2 2 2 3 3 2 3 1 1 2 5 
 4t  0  t  0  IA  3; 3  ; 3    2 2
Vậy bán kính mặt cầu  S  : 2
R IA  3  3  3  3 3. Câu 9.
[2H3-1.3-2] Cho mặt phẳng  P và mặt cầu (S ) có phương trình lần lượt là P 2 2 2 2
: 2x  2 y z m  4m  5  0; (S) : x y z  2x  2y  2z  6  0 . Giá trị của m để
P tiếp xúc (S) là:
A. m 1 hoặc m  5  . B. m  1  hoặc m  5 . C. m  1 . D. m  5 . Lời giải Chọn B  2 2 2
(S) : x y z  2x  2 y  2z  6  0 có tâm I 1; 1  ; 
1 và bán kính R  3.
P tiếp xúc (S )  d I;P  R 2 2.1 2.( 1
 ) 1.1 m  4m  5 2 
 3  m  4m  4  9 2 2 2 2  2 1 2
m  4m  4  9 m  1  2  
m  4m  5  0  .  2
m  4m  4  9  m  5 x  2 y  2 z  3
Câu 10. [2H3-1.3-2] Cho đường thẳng d :  
và mặt cầu (S) : x y   z  2 2 2 2  9 . 2 3 2
Tọa độ giao điểm của  và S  là:
A. A0;0;2, B 2  ;2; 3   .
B. A2;3;2 . C. A 2  ;2; 3   .
D.  và (S) không cắt nhau. Lời giải Chọn C
Tọa độ giao điểm là nghiệm hệ phương trình: x  2   2ty  23t  
t  0  A 2  ;2; 3  .
z  3  2t  x y   z  22 2 2  9
Câu 11. [2H3-1.3-2] Cho các điểm A2;1;  1 và B 1;0; 
1 . Mặt cầu đi qua hai điểm A, B và tâm thuộc
trục Oy có đường kính là: Trang26 A. . B. . 2 2 6 C. . D. . 4 2 2 6 Lời giải Chọn D
Gọi I 0;t;0 trên Oy vì IA IB t  2  I 0;2;0
R IA  6  đường kính bằng 2 6 .
Câu 12. [2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , mặt cầu tâm I 6;3; 4
  tiếp xúc với trục Ox có bán kính là: A.5. B.4. C.2. D. 5 . Lời giải Chọn A
Gọi H là hình chiếu của tâm I lên trục . Ox
H Ox H 6;0;0. 
Vậy mặt cầu có bán kính : R IH    2 2 2 0 3  4  5 .
Câu 13. [2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , bán kính của mặt cầu tâm I 3;3; 4   và
tiếp xúc với trục Oy bằng: 5 A.4. B.5. C. 5 . D. . 2 Lời giải Chọn B 
Gọi I  là hình chiếu của I lên Oy .  I0;3;0  R II   2 2 2 3  0  4  5 .
Câu 14. [2H3-1.3-3] Trong không gian với hệ toạ độ Oxyz , bán kính của mặt cầu tâm I 1;3;5 và tiếp x t
xúc với đường thẳng d : y  1   t là : z  2-tA. 7 . B.14. C. 14 . D.7. Lời giải Chọn C 
M d M 0; 1
 ;2 ;VTCP a  1; 1  ; 1  0 0        M I   1;4;3 M I, a   
d I;d  0 0     a   1; 1  ;  14 1 a Trang27
Câu 15. [2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , cho  S  là mặt cầu tâm I 2;1;  1 và tiếp
xúc với mặt phẳng P : 2x  2y z  3  0 . Bán kính S  là: 2 2 4 A. . B. . C. . D. 2 . 9 3 3 Lời giải Chọn D    
R d I P 2.2 2.1   1 3 ;   2. 4  4 1
Câu 16. [2H3-1.3-3] Trong không gian với hệ toạ độ Oxyz , mặt cầu ngoại tiếp tứ diện ABCD với
A1;0;0, B0;1;0, C 0;0;  1 , D1;1;  1 có bán kính là: 3 3 A. . B. 2 . C. 3 . D. . 2 4 Lời giải Chọn A
Gọi phương trình mặt cầu  S  ngoại tiếp tứ diện ABCD có dạng: 2 2 2
x y z  2ax  2by  2cz d  0  2 2 2
a b c d  0.
Vì A1;0;0, B0;1;0, C 0;0;  1 , D1;1; 
1 thuộc mặt cầu S  nên ta có hệ phương trình:  1 a   2 2 2         2 1 0 0 2 .1 a 2 .0 b 2 .0 c d 0  2
a d  1     2 2 2 1  0 1  0  2 .0 a  2 .1 b  2 .0 c d  0  2
b d  1  b        2 . 2 2 2 0  0 1  2 .0 a  2 .1 b  2 .1 c d  0 2
c d  1    1                   2 2 2 2a 2b 2c d 3 c 1 1 1 2 .1 a 2 .1 b 2 .1 c d 0 2  d  0 2 2 2  1   1   1  3 R     .        2   2   2  2
Câu 17. [2H3-1.3-3] Trong không gian với hệ toạ độ Oxyz , với giá trị nào của m thì phương trình 2 2 2
x y z  2mx  2m  
1 y  4z  5m  0 là phương trình mặt cầu ?
A. m 1 m  5 3 . B.1  m  . C. m  5 3 .
D. m  1 m  . 2 2 Lời giải Chọn D Trang28 Phương trình đã cho là phương trình mặt cầu khi m 1
m2 m 2 2 2 1 2 5m 0 2m 7m 5 0             5 . m   2
Câu 18. [2H3-1.3-3] Biết điểm A thuộc mặt cầu S  2 2 2
: x y z  2x  2z  2  0 sao cho khoảng
cách từ A đến mặt phẳng P :2x  2y z  6  0 lớn nhất . Khi đó tọa độ điểm A là:  1 4 2   7 4 1   1 4 5  A. 1;0; 3   . B. ;  ;   . C. ; ;    . D.  ; ;    .  3 3 3   3 3 3   3 3 3  Lời giải Chọn C
Tự luận: Mặt cầu có tâm I 1;0;  1 , bán kính R  2
d I,P  3  R nên mặt phẳng P và mặt cầu S  không có điểm chung. x 1 2t
Gọi d là đường thẳng qua I và vuông góc với  P , d : y   2t z  1   t   7 4 1   1 4 4 
giao điểm của d và S  là hai điểm có tọa độ ; ; ,  ; ;      . Vì khoảng cách từ  3 3 3   3 3 3   7 4 1 
A đến  P lớn nhất nên A ; ;   .  3 3 3    1 4 2 
Trắc nghiệm:Thử 4 phương án thấy điểm có tọa độ ;  ; 
 không thuộc mặt cầu S   3 3 3  nên loại. 5
Khoảng cách từ điểm 1;0; 3
  đến P là: . 3  7 4 1  13 Khoảng cách từ điểm ; ;  
 đến P là: .  3 3 3  3  1 4 5  1
Khoảng cách từ điểm  ; ;  
 đến P là: .  3 3 3  3 2 2
Câu 19. [2H3-1.3-4] Cho điểm A2;1;2 và mặt cầu S  2
: x   y   1   z   1
 9 mặt phẳng P đi
qua A và cắt  S  theo thiết diện là đường tròn có bán kính nhỏ nhất. Bán kính nhỏ nhất đó là: 3 1 A. 3. B.2. C. . D. . 2 2 Lời giải Chọn B Trang29
Mặt cầu  S  có tâm I 0;1; 
1 , bán kính R  3. Dễ thấy điểm A nằm trong mặt cầu nên mặt
phẳng  P cần tìm đi qua A và vuông góc với IA .
Do đó : P :2x z  6  0 .
Bán kính đường tròn là : 2 2 r
R IA  9  5  2 .
Câu 20. [2H3-1.3-4] Trong không gian với hệ toạ độ Oxyz , cho tứ diện ABCD với A1; 2  ;  1 , B 5  ;10;  1 ,C 4;1;  1 , D 8  ; 2
 ;2 . Tâm I của mặt cầu ngoại tiếp tứ diện ABCD là: A.  2  ;3; 5   . B. 2; 4  ;3 . C.  2  ;4;5 . D. 1; 3  ;4 . Lời giải Chọn C
Gọi I (a; b;c) là tâm mặt cầu ngoại tiếp tứ diện ABCD , ta có:  IA  1 ; a 2   ; b 1
  c  IA  1 a2   2   b2   1   c2 2  IB   5   ; a 10  ; b 1
  c  IB   5
  a2  10 b2   1   c2 2  IC  4  ; a 1 ; b 1
  c  IC  4  a2  1b2   1   c2 2  2 2 2 2 ID  ( 8   ; a 2   ;
b 2  c)  IA  ( 8   a)  ( 2
  b)  (2  c) I  ; a ;
b c là tâm mặt cầu ngoại tiếp tứ diện ABCD 2 2 IA IB 1
 2a  24b  1  20 a  2     2 2
 IA IC  6a  6b 12  b   4  I  2  ;4;5    2 2 IA ID 18a  6c  6  6 c  5    Vậy I (2; 4;5) .
Cách 2: Phương trình mặt cầu có dạng S  2 2 2
: x y z  2ax  2by  2cz d  0 , 2 2 2
a b c d  0 Thay tọa độ ,
A B,C, D vào  S  ta được 4 phương trình.
Sử dụng MTCT giải hệ phương trình 4 ẩn  a,b, c, d . Lúc đó I a, , b c . Trang30
Dạng 4: Viết phƣơng trình mặt cầu
{Viết phương trình mặt cầu biết tâm và bán kính, biết tâm và đi qua điểm, biết đường kính, mặt
cầu đi qua 2 điểm và có tâm thuộc trục tọa độ, mặt cầu đi qua 3 điểm có tâm thuộc mặt phẳng
tọa độ, mặt cầu đi qua 3 điểm và có bán kính, mặt cầu ngoại tiếp tứ diện,. mặt cầu có tâm và
tiếp xúc với trục tọa độ, có tâm và tx với mặt phẳng tọa độ, có tâm và tiếp xúc với mặt cầu khác,…}
PHẦN 1: CÁC VÍ DỤ
Ví dụ1. Lập phương trình mặt cầu S  biết mặt cầu S  có tâm I 1;2;3 bán kính R  5 . Lời giải
Phương trình mặt cầu S  2 2 2
: (x 1)  ( y  2)  (z  3)  5 .
Ví dụ2. Mặt cầu S  có tâm nằm trên Ox và đi qua A1;2;  1 , B 3;1; 2   Lời giải
Gọi I là tâm mặt cầu. Vì I Ox I  ; x 0;0 . 2 2 2 Ta có 2 2
IA IB   x   2 2    x   2 1 2 1 3 1   2    x  2.
Suy ra tâm I 2;0;0 và bán kính 2 2
R IB  6 .
Vậy phương trình mặt cầu 2 2 2
(S ) : (x  2)  y z  6 .
Ví dụ3. Có tâm I 6;3; 4
  và tiếp xúc với Oy . Lời giải
Vì mặt cầu S  tiếp xúc với Oy nên suy ra R d I,Oy  3 .
Vậy phương trình S   x  2   y  2  z  2 : 6 3 4  9 .
Ví dụ4. Có tâm I 1;1;2 và tiếp xúc với mp P : x  2y  2z 1  0 . Lời giải 1 2  4 1
Ta có, bán kính mặt cầu R d I P 8 ,   . 2 2 2   3 1 2 2
Vậy phương trình mặt cầu S   x  2   y  2   z  2 64 : 1 1 2  . 9 x  2 y 1 z 1
Ví dụ5. Có tâm nằm trên đường thẳng d :  
và tiếp xúc với hai mặt phẳng 3 2 2
P: x  2y 2z 2  0 và Q: x  2y 2z  4  0. Lời giải
Vì mặt cầu S  có tâm I d I 2  3t;1 2t;1 2t . Trang31
Mặt cầu S  tiếp xúc với hai mp P và Q nên d I,P  d I,Q  R 2  3t 6  3t 4  11 11     2 2  3t  6
  3t t   I 2  ; ;   và R  . 3 3 3  3 3  3 2 2    
Vậy phương trình mặt cầu S   x  2 11 11 4 : 2  y   z       .  3   3  9   Ví dụ6. x 2 y 3 z
Mặt cầu có tâm I 1;3;5 và cắt  :   tại hai điểm ,
A B sao cho AB  12 1 1 1 Lời giải
Đường thẳng  qua điểm M 2;  3; 0 và có véc tơ chỉ phương là u      1;1;  1 .   
Ta có IM  1; 6; 5 nên IM , u     1; 4; 5, do đó     2   2 2        d I    IM , u 1  4 5 ,     14 . u   2 2 2 1 1 1
Vì mặt cầu cắt  tại hai điểm ,
A B nên bán kính mặt cầu được xác định theo công thức : 2  AB  2 2
R d I,     14  36  50   .  2 
Vậy mặt cầu cần tìm có phương trình là:  x  2   y  2   z  2 1 3 5  50 .
PHẦN 2: CÂU HỎI TRẮC NGHIỆM Câu 1.
[2H3-1.3-1] Trong không gian với hệ tọa độ Oxyz , phương trình mặt cầu  S  tâm I 1; 2  ;2
và có bán kính R  2 3 là: 2 2 2 2 2 2 A. x  
1   y  2   z  2  12 . B. x  
1   y  2   z  2  12. 2 2 2 2 2 2 C. x  
1   y  2   z  2  6 . D. x  
1   y  2   z  2  6 . Lời giải Chọn B Phương trình mặ 2 2 2
t cầu  S  tâm I a; ;
b c và có bán kính R là:            2 x a y b z cR .
Vậy: Mặt cầu tâm I 3;1;2 , bán kính R  4 có phương trình là: 2 2 2 x  
1   y  2   z  2  12. Câu 2.
[2H3-1.3-1] Trong không gian với hệ tọa độ Oxyz , mặt cầu tâm I 3;1;2 , bán kính R  4 có phương trình là: 2 2 2 2 2 2
A. x  3   y  
1   z  2  16 . B. x   3   y  
1   z  2  4 . Trang32 2 2 2 2 2 2
C. x  3   y  
1   z  2  4 .
D. x  3   y  
1   z  2  16 . Lời giải Chọn D
Mặt cầu tâm I 3;1;2 , bán kính R  4 có phương trình là: 2 2 2
x 3  y  
1   z  2  16 . Câu 3.
[2H3-1.3-1] Trong không gian với hệ tọa độ Oxyz , phương trình mặt cầu có tâm I 1;1; 2 và
đi qua điểm M 2;1;0 là: 2 2 2 2 2 2 A. x   1   y  
1   z  2  9 .
B. x   1   y  
1   z  2  3 . 2 2 2 2 2 2 C. x   1   y  
1   z  2  9 .
D. x   1   y  
1   z  2  3 . Lời giải Chọn C Tâm I 1;1; 2
  , bán kính mặt cầu là R IM  3.
nên phương trình mặt cầu  2 2 2
S  :  x   1   y  
1   z  2  9 . Câu 4.
[2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , mặt cầu tâm I  1
 ;2;0 đường kính bằng 10 có phương trình là: 2 2 2 2
A. x     y   2 1 2  z  25 .
B.x     y   2 1 2  z 100 . 2 2 2 2
C.x     y   2 1 2  z  25 .
D.x     y   2 1 2  z 100 . Lời giải Chọn A
Mặt cầu tâm I  1
 ;2;0 đường kính bằng 10 nên có bán kính R  5 có phương trình: 2 2
x    y   2 1 2  z  25 . Câu 5.
[2H3-1.3-2] Trong không gian với hệ tọa độ Oxyz , mặt cầu có đường kính AB AB với
A1;3; 4 và A1;1;0 có phương trình là: 2 2 2 2 2 2 A. x   1   y  
1   z  2  8 . B. x   1   y  
1   z  2  4 . 2 2 2 2 2 2 C. x   1   y  
1   z  2  8 . D. x   1   y  
1   z  2  4 . Lời giải Chọn C
Tâm I là trung điểm của đường kính AB I 1;1; 2 , bán kính mặt cầu là R IB  2 2 Trang33 nên phương trình mặ 2 2 2
t cầu  S  :  x   1   y  
1   z  2  8 . Câu 6.
[2H3-1.3-2] Trong không gian với hệ tọa độ Oxyz , cho điểm I 1; 2;3 . Viết phương trình
mặt cầu tâm I và tiếp xúc với trục Oy . 2 2 2 2 2 2 A. x  
1   y  2   z  3  15 . B. x  
1   y  2   z  3  30 . 2 2 2 2 2 2 C. x  
1   y  2   z  3  20 . D.  x  
1   y  2   z  3  10 . Lời giải Chọn D
Gọi M là hình chiếu của I 1; 2;3 lên Oy , ta có: M 0; 2;0 .  IM   1
 ;0; 3  R IM  10 là bán kính mặt cầu cần tìm. 2 2 2
PT mặt cầu cần tìm là:  x  
1   y  2   z  3  10 . Câu 7.
[2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , mặt cầu  S  có tâm I  1  ;2;  1 và tiếp xúc
với mặt phẳng (P) : x  2y  2z  2  0 có phương trình: 2 2 2 2 2 2 A. x  
1   y  2   z   1  3 . B. x  
1   y  2   z   1  9 . 2 2 2 2 2 2 C. x  
1   y  2   z   1  3 . D. x  
1   y  2   z   1  9 . Lời giải Chọn B
Mặt cầu  S  có tâm I  1  ;2; 
1 và tiếp xúc với mặt phẳng (P) : x  2 y  2z  2  0 nên có bán 1   2.2  2.1 2 2 2 2 kính R
 3 có phương trình: x  
1   y  2   z   1  9. 1 4  4 Câu 8.
[2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , mặt cầu tâm I 2;1;  1 tiếp xúc với mặt
phẳng Oyz có phương trình là: 2 2 2 2 2 2
A.x  2   y   1   z   1  4 .
B.x  2   y   1   z   1  1 . 2 2 2 2 2 2
C. x  2   y   1   z   1  4 .
D.x  2   y   1   z   1  2 . Lời giải Chọn A  2 2 2
Oyzx   R d I Oyz 2 : 0 ; 
 2 . Vây S:x  2  y   1   z   1  4 . 2 1 Câu 9.
[2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz , phương trình mặt cầu có tâm thuộc trục
Ox và đi qua hai điểm A3;1;0, B 5;5;0 là: Trang34 A. . B. . x  2 2 2 9
y z 10 x  2 2 2 10
y z  5 2 C. x  2 2 2 10
y z  50 . D. x  2 2 2 10
y z  25 . Lời giải Chọn C
Lần lượt thế tọa độ điểm ,
A B vào 4 phương án. Chỉ có phương án A thỏa vì   2 2 2 3 10
1  0  50 và   2 2 2 5 10  5  0  50.
Câu 10. [2H3-1.3-2] Trong không gian với hệ toạ độ Oxyz ,viết phương trìnhmặt cầu  S  có tâm thuộc
mặt phẳng Oxy và đi qua ba điểm A1;2; 4  , B1; 3  ;  1 , C 2;2;3 . 2 2
A. x     y   2 2 1  z 16  0 . B. 2 2 2
x y z  4x  2 y  21  0 . C. 2 2 2
x y z  4x  2 y  21  0 . D. 2 2 2
x y z  4x  2 y  6z  21  0 . Lời giải Chọn B
Ta có  S  là mặt cầu có tâm thuộc mặt phẳng Oxy  S  có tâm I (a; ; b 0) .
Suy ra  S  có dạng: 2 2 2
x y z  2ax  2by c  0 . A1;2; 4  S  a  2    Ta có B1; 3  ; 
1  S   b  1 .   C  Sc  21 2; 2;3     S 2 2 2
: x y z  4x  2 y  21  0 .
Câu 11. [2H3-1.3-3] Trong không gian với hệ toạ độ Oxyz ,viết phương trìnhmặt cầu  S  có tâm x  2 y 1 z 1 I 4;2; 
1 và tiếp xúc với đường thẳng d :   . 2 1 2 2 2 2 2 2 2
A. x  4   y  2   z   1  16 .
B. x  4   y  2   z   1  16 . C. 2 2 2
x y z  8x  4 y  2z  5  0 . D. 2 2 2
x y z  8x  4 y  2z  5  0 . Lời giải Chọn B
Gọi  S  có bán kính R .  Ta có d qua (
A 2; 1;1) , có VTCP u  (2;1;2) d .      IA ud  
S  tiếp xúc với đường thẳng d R d I d  ; ;    4 . ud Trang35
 x  2  y  2 z  2 4 2 1  16 .
Câu 12. [2H3-1.3-2] Trong không gian với hệ tọa độ Oxyz , cho điểm A2; 6
 ;4 . Phương trình nào
sau đây là phương trình mặt cầu đường kính OA ? 2 2 2 2 2 2
A. x  2   y  6   z  4  56 .
B. x  2   y  6   z  4  56 . 2 2 2 2 2 2 C. x  
1   y  3   z  2 14 . D. x  
1   y  3   z  2  14 . Lời giải Chọn D OA 56
Mặt cầu đường kính OA có tâm I 1; 3
 ;2là trung điểm OA . Bán kính R   . 2 2
Câu 13. [2H3-1.3-2] Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình
của mặt cầu có tâm I 1;2; 
1 và tiếp xúc với mặt phẳng  P : x  2y  2z  8  0 ? 2 2 2 2 2 2 A. x  
1   y  2   z   1  3 . B. x  
1   y  2   z   1  3 . 2 2 2 2 2 2 C. x  
1   y  2   z   1  9 . D. x  
1   y  2   z   1  9 . Lời giải Chọn C 1 2.2  2.  1  8 R d   3 . I ,P 1   2  2   2  2 2 Phương trình mặ 2 2 2
t cầu cần tìm có dạng:  x  
1   y  2   z   1  9 .
Cách 2: theo công thức phương trình mặt cầu có tâm I  ; a ;
b c bán kính R có dạng
  2   2   2 2 x a y b z c
R . Ta loại câu A và D. 1 2.2  2.  1  8
Bán kính R d
 3 . Nên ta chọn câu C. I ,P 1   2  2   2  2 2
Câu 14. [2H3-1.3-3] Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I (2;1;1) và mặt
phẳng (P): 2x y  2z  2  0 . Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một
đường tròn có bán kính bằng 1. Phương trình của mặt cầu (S) là: 2 2 2 2 2 2 A. x   1   y   1   z   1  8 .
B. x  2   y   1   z   1  10 . 2 2 2 2 2 2
C. x  2   y   1   z   1  8 .
D. x  2   y   1   z   1  10 . Lời giải Chọn D Trang36 2.2 1 2.1 2
Ta có d d (I;(P))   3. 2 2 2 2 1  2 2 2 2 Bán kính mặt cầu là 2 2 R
d 1  10  S  :  x  2   y   1   z   1 10 .
Câu 15. [2H3-1.3-3] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A2;0; 
1 , B 1;0;0,C 1;1;  1
và mặt phẳng P : x y z  2  0 . Viết phương trình mặt cầu đi qua ba điểm , A B,C và có
tâm thuộc mặt phẳng P . A. 2 2 2
x y z x  2z 1  0 . B. 2 2 2
x y z x  2 y 1  0 . C. 2 2 2
x y z  2x  2 y 1  0 . D. 2 2 2
x y z  2x  2z 1  0 . Lời giải Chọn D
Phương mặt cầu (S ) có dạng: 2 2 2
x y z  2ax  2by  2cz d  0 , ta có A2;0;  1  S   4  a
 2c d  5    1  
B1;0;0S   2  ad  1  2    C  1;1;  1  S  2
a  2b  2c d  3   3   I   P
a b c  2  4
 Lấy vế trừ vế của  
1 cho 2 ; 2 cho 3 ; kết hợp (4) ta được hệ  2
a  2c  4  a 1  
2b 2c  2  b   0 d 1.  
a b c  2 c  1  
Vậy phương trình mặt cầu là 2 2 2
x y z  2x  2z 1  0 . Trắc nghiệm:
Thay tọa độ B1;0;0 vào từng phương trình mặt cầu ở từng đáp án loại được đáp án A và đáp án B.
Thay tọa độ A2;0; 
1 vào phương trình mặt cầu loại được đáp án C.
Câu 16. [2H3-1.3-3] Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng (P) : 2x y  2z  3  0 và
I (1;3; 1) . Gọi  S  là mặt cầu tâm I và cắt mặt phẳng (P) theo một đường tròn có chu vi
bằng 2 . Viết phương trình mặt cầu (S). A. S  : 2 2 2
(x 1)  ( y  3)  (z 1)  5 . B. S  : 2 2 2
(x 1)  ( y  3)  (z 1)  5 . C. S  : 2 2 2
(x 1)  ( y  3)  (z 1)  3 . D. S  : 2 2 2
(x 1)  ( y  3)  (z 1)  5 . Lời giải Chọn D Trang37 2
Bán kính của đường tròn giao tuyến của  S  và  P là r   1 . 2   
d d I P 2 3 2 3 ,   2 . 4 1 4
Bán kính mặt cầu  S  là 2 2
R r d  5 .
Phương trình mặt cầu S  tâm I 1;3;  1 và bán kính R  5 là S  : 2 2 2
(x 1)  ( y  3)  (z 1)  5 .
Câu 17. [2H3-1.3-3] Trong không gian với hệ tọa độ Oxyz , phương trình mặt cầu  S  qua ba điểm
A1;2; 4 , B1; 3; 
1 , C 2;2;3 và có tâm nằm trên mp Oxy là: 2 2  7   3  83 2 2 A. 2 x   y   z      .
B.  x     y   2 2 1  z  26 .  2   2  2 2 2  2 2 7   3  81  7   3  83 C. 2 x   y   z      . D. 2 x   y   z      .  2   2  2  2   2  2 Lời giải Chọn B * Gọi I  ; a ;
b c là tâm mặt cầu S  .
* Vì I thuộc mp Oxy nên I  ; a ; b 0
* Mặt khác S  qua ba điểm A1;2; 4 , B1; 3;  1 , C 2;2;3 .   a   2
1  b  22 16  a  2
1  b  32 1
Nên IA IB IC     a   2
1  b  22 16  a  22  b  22  9 2a  4  a  2  .     . 1  0b 10 b  1
* Vậy S  có tâm I  2
 ;1;0 bán kính R IA  26 . * P.trình mặt cầu  2 2
S  :  x     y   2 2 1  z  26 . x 1 t
Câu 18. [2H3-1.3-4] Trong không gian với hệ toạ độ Oxyz , cho hai đường thẳng d   1  : y 0 và z  5   t  x  0   d     dd2 1  2  : y
4 2t . Mặt cầu nhận đoạn vuông góc chung của và làm đường kính có
z  53t  phương trình là: 2 2 2 2
A. x     y   2 2 3  z  17 .
B. x     y   2 2 3  z  25 . Trang38 2 2 2 2 2 2
C. x  2   y  3   z   1  25 .
D. x  2   y  3   z   1  25 . Lời giải Chọn A   d u  1;0;1 1   1  có vtcp .   d u  0; 2;3 2   2  có vtcp . A 
d A 1 t;0; 5   t 1   . B
  d B 0;4  2t ;53t 2    .  AB   1
  t,4  2t ,1
 0  3t  t .
AB là đoạn vuông góc chung của hai đường thẳng dd2 1  và   A . B u  0  1
  t 10  3t ' t  0   2
t  3t '  9  t   3 1          .    2 AB u  
 4  2t '  310  3t ' t  0  3
t 13t '  2  2 t  '  1 . 0  1 Khi đó: A4;0; 2
 , B0;6;2 . AB
Mặt cầu đường kính AB có tâm I 2;3;0 và bán kính R   17 có phương trình: 2
x  2  y  2 2 2 3  z  17 . x 1 y z
Câu 19. [2H3-1.3-4] Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d :   và 2 1 2 
hai điểm A2;1;0 , B 2
 ;3;2.Viết phương trình mặt cầu đi qua A , B và có tâm I thuộc đường thẳng d . 2 2 2 2 2 2 A. x   1   y  
1   z  2 17 .
B. x   1   y  
1   z  2  17 . 2 2 2 2 2 2
C. x  3   y  
1   z  2  5.
D. x  3   y  
1   z  2  5 . Lời giải Chọn A x 1 2t
Phương trình tham số đường thẳng d : y t . z  2  t   AB    1
  2t;t 1: 2t
Ta có: I d I 1 2t;t; 2t    . BI  
3 2t;t 3;22t
Vì mặt cầu  S  đi qua hai điểm A , B nên: 2 2
R IA IB IA IB . Trang39
   t2 t  2  t2    t2  t  2    t2 1 2 1 2 3 2 3 2 2
 20t  20  0  t  1   I  1
 ;1;2  R IA  17 . Phương trình mặ 2 2 2
t cầu  S  cần tìm là:  x   1   y  
1   z  2 17 .
Câu 20. [2H3-1.3-4]Trong không gian với hệ tọa độ Oxyz , phương trình mặt cầu  S  có tâm nằm trên x  2 
đường thẳng d : 
và tiếp xúc với hai mặt phẳng  P : x  2z  8  0 , Q : 2x z  5  0 y  0 . 2 2 144 2 2 16
A. x  2 2
y  z   11  và  x  2 2
y  z   11  . 5 5 2 2 121 2 2 126
B. x  2 2
y  z 1  1  và  x  2 2
y  z   11  . 5 5 2 2 134 2 2 164
C. x  2 2
y  z   11  và  x  2 2
y  z   11  . 5 5 2 2 144 2 2 16
D.  x  2 2
y  z   11  và  x  2 2
y  z  3  . 5 5 Lời giải Chọn D * Gọi I  ; a ;
b c là tâm mặt cầu S  . x  2 
* Vì I thuộc đường thẳng d :  nên I  2  ;0; z . y  0
* Mặt khác S  tiếp xúc với P và Q nên: d I,P  d I,Q 2   2z 8 4   z  5   5 5  z    zz  11   2  z 10  1 2 10 1 z   .  
2z 10 1 zz  3  * Với z  11   tâm I  2  ;0;1 
1  bán kính R d I P 12 ,  . 5 2 2 144
ta được  S  : x  2 2
y  z   11  . 5 * Với z  3   tâm I  2
 ;0;3  bán kính R d I P 4 ,  . 5 2 2 16
ta được  S  : x  2 2
y  z 1  1  . 5 Trang40
PHƢƠNG TRÌNH MẶT PHẲNG NỘI DUNG A. LÝ THUYẾT
B. MỘT SỐ BÀI TOÁN VIẾT PHƢƠNG TRÌNH MẶT PHẲNG THƢỜNG GẶP.
Bài toán 1: Viết phƣơng trình mặt phẳng P đi qua điểm M (x ; y ; z ) và có vtpt o o o  n  ( ; A B;C) ( P )
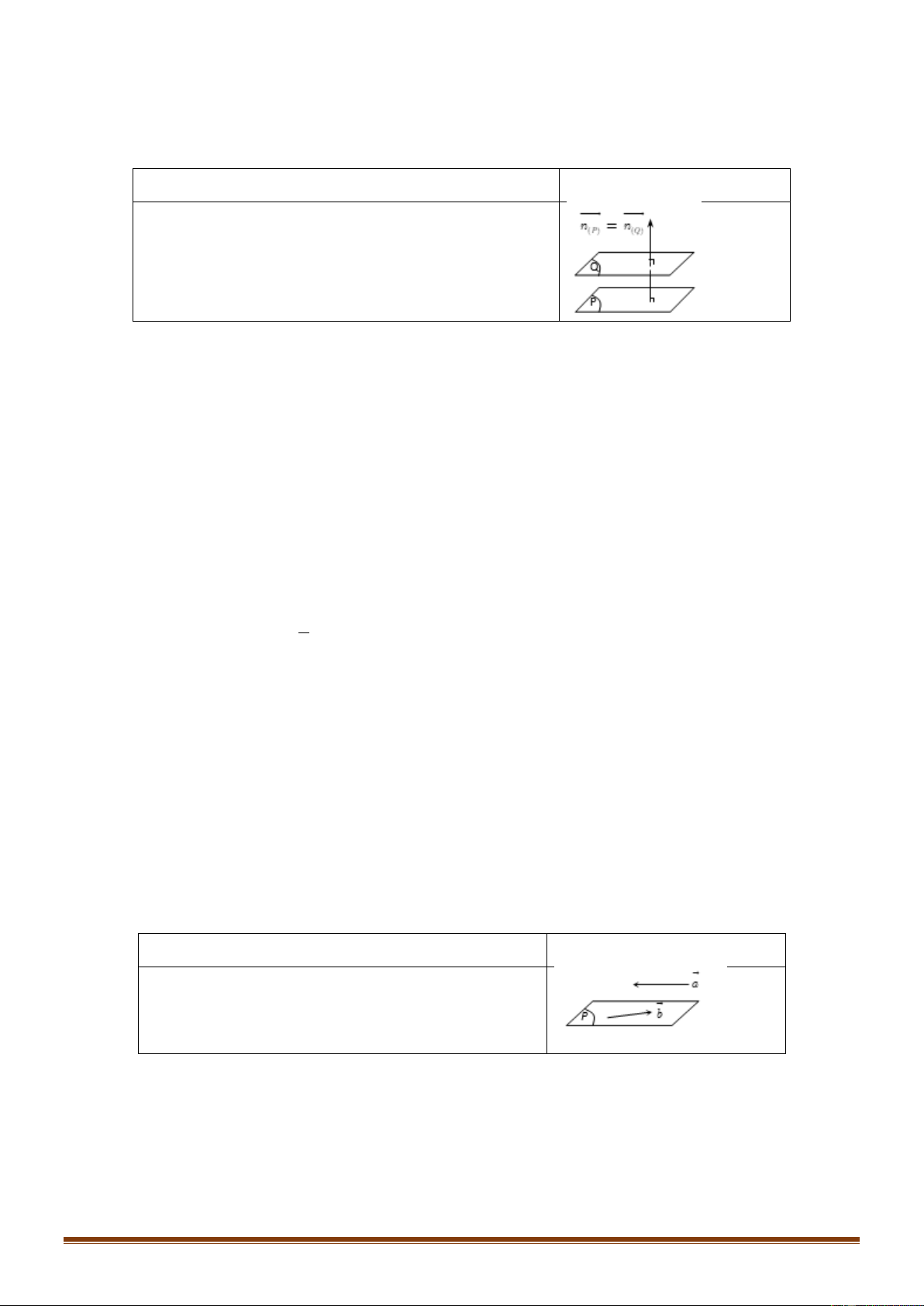
Bài toán 2:Viết phƣơng trình mặt phẳng (P) đi qua điểm M và có cặp véctơ chỉ phƣơng  
a, b cho trƣớc.
Bài toán 3: Viết phƣơng trình mặt phẳng (P) đi qua ba điểm ,
A B, C không thẳng hàng
Bài toán 4: Viết phƣơng trình mặt phẳng (P) đi qua giao tuyến của hai mặt phẳng và thỏa
mãn điều kiện cho trƣớc:
Bài toán 5: Mặt phẳngvà mặt cầu.
Bài toán 6: Mặt phẳngliên quan đến góc.
Bài toán 7: Mặt phẳngliên quan đến khoảng cách.
C. BÀI TẬP TRẮC NGHIỆM:
Đề - Đáp án – Hƣớng dẫn giải chi tiết – Phân tích phƣơng án nhiễu
Số lƣợng 50 câu, trong đó NB: 10 TH: 15 VDT: 15 VDC: 10 Trang41
A – LÝ THUYẾT CẦN NẮM
1) Véctơ pháp tuyến, cặp véctơ chỉ phƣơng   
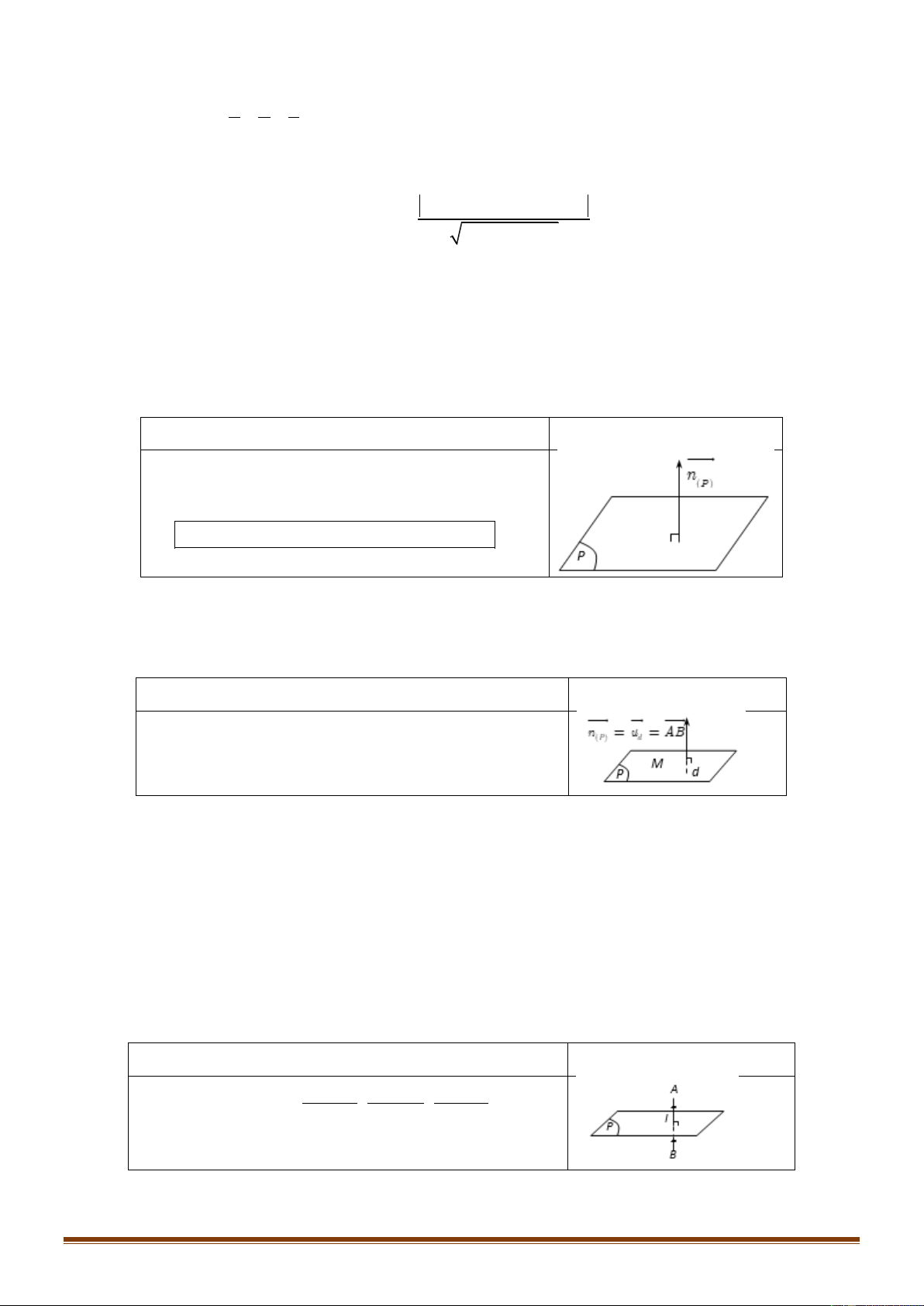
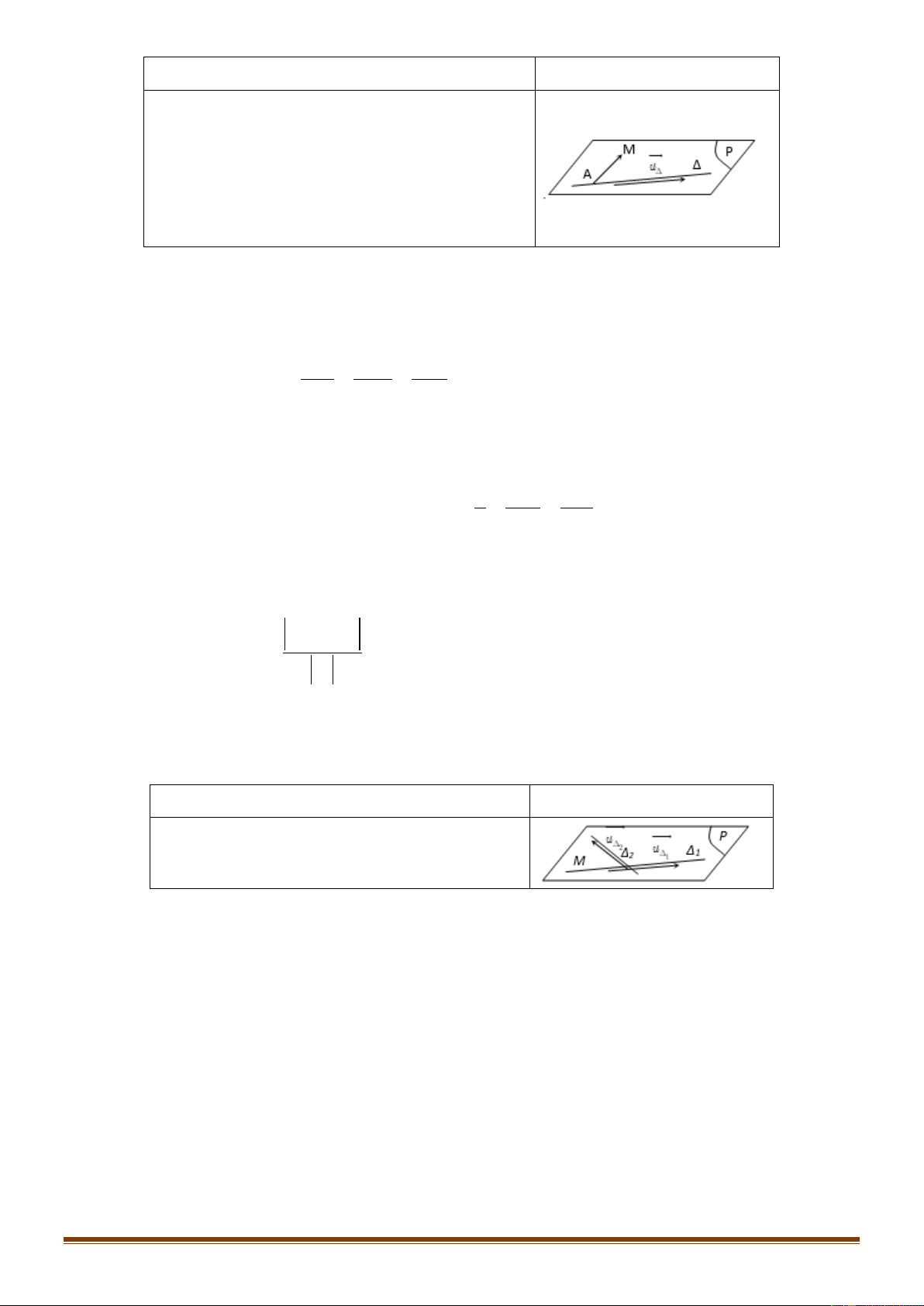
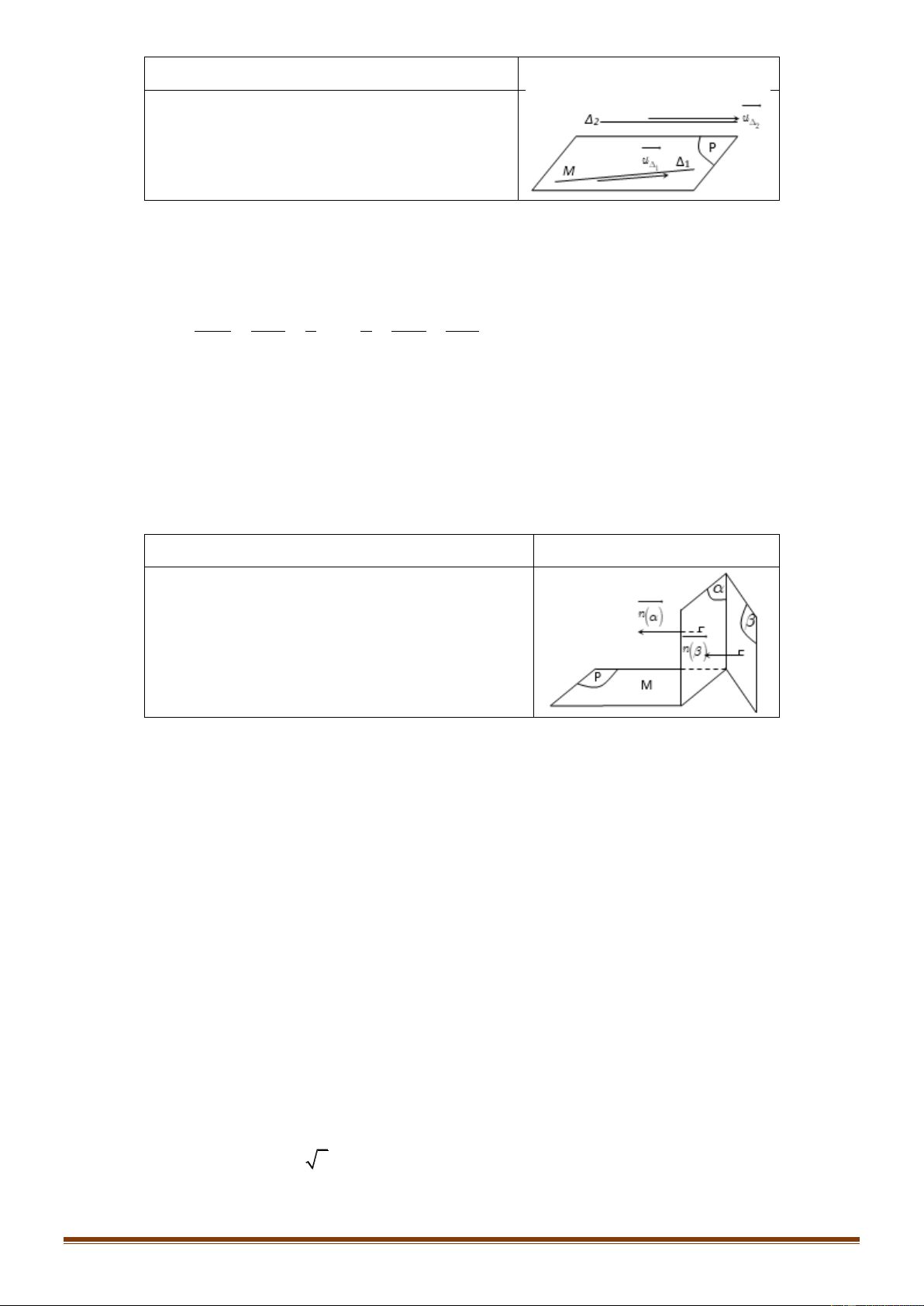
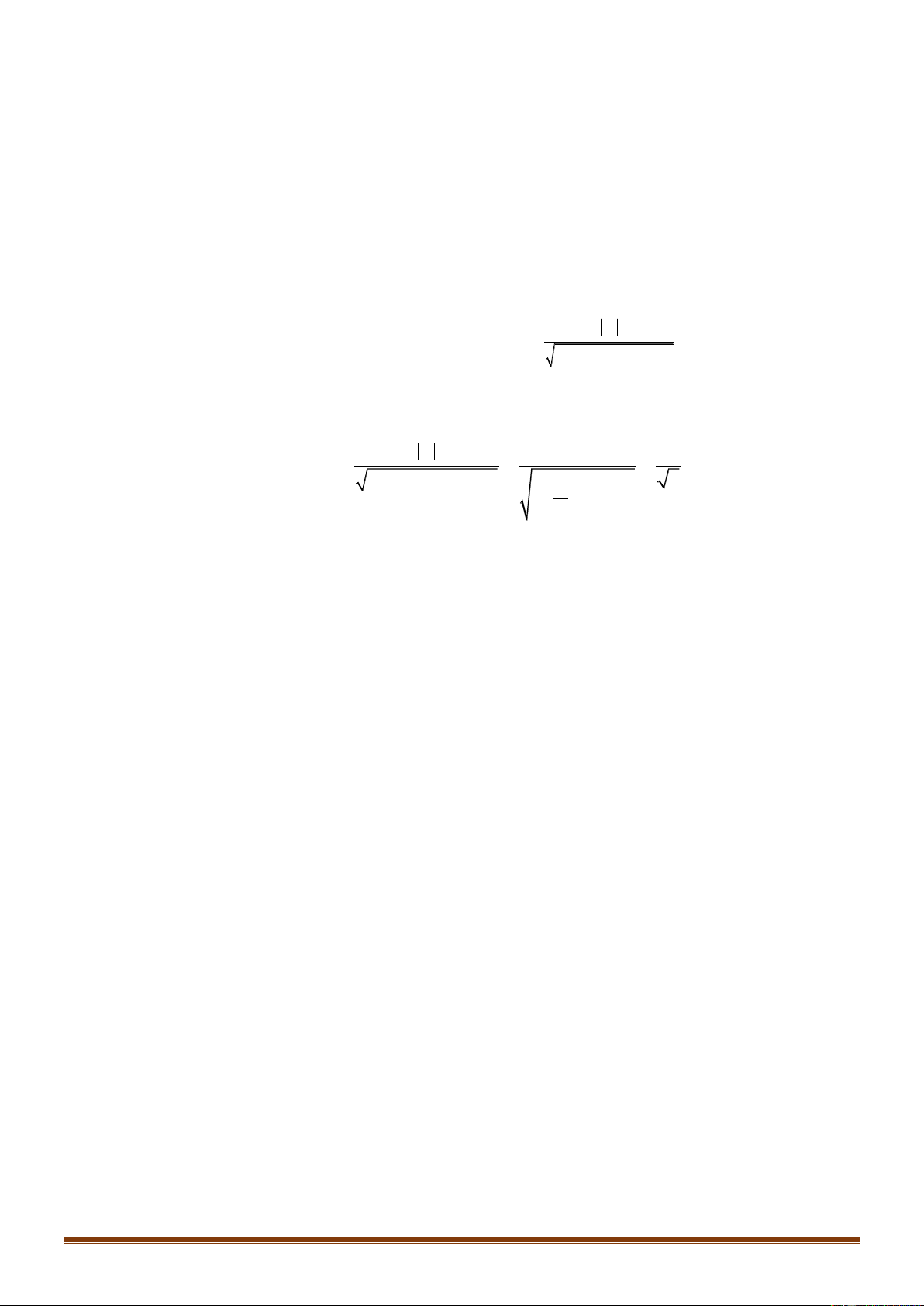
 Véctơ n  0 là véctơ pháp tuyến của mặt phẳng (P) nếu giá n vuông góc với (P).  
 Hai véctơ a, b không cùng phương là că ̣p véctơ chỉ uuur
phƣơng của mặt phẳng (P) nếu giá của chúng song song n(P )
hoă ̣c nằm trên mă ̣t phẳng (P).  
 Nếu a, b là một cặp véctơ chỉ phương của mặt phẳng (P) P   
thì n  a,b là 1 véctơ pháp tuyến của mặt phẳng (P).     
 Nếu n  0 là 1 véctơ pháp tuyến của mặt phẳng (P) thì k. ,
n (k  0) cũng là véctơ pháp
tuyến của mă ̣t phẳng (P).
2) Phƣơng trình tổng quát của mặt phẳng: (P) : Ax By Cz D  0. 
 Nếu mă ̣t phẳng (P) có phương trình (P) : Ax By Cz D  0 thì n  ( ;
A B;C) là một ( P )
véctơ pháp tuyến của mặt phẳng (P).
 Để viết phương trình mặt phẳng (P), ta cần xác định 1 điểm đi qua và 1 véctơ pháp tuyến. •
 qua M (x ; y ; z )  o o o (P) :    (P) : .
A (x x )  .
B ( y y )  C (
. z z )  0  •  v o o o tpt : n ( ; A ; B C)   ( P)
3) Các trƣờng hợp đặc biệt: Các hệ số
Phương trình mă ̣t phẳng (P) Tính chất mặt phẳng (P) D  0
(P) : Ax By Cz  0
(P) đi qua gốc to ̣a độ O A  0
(P) : By Cz D  0
(P)  Ox hoă ̣c (P)  Ox B  0
(P) : Ax Cz D  0
(P)  Oy hoă ̣c (P)  Oy C  0
(P) : Ax By D  0
(P)  Oz hoă ̣c (P)  Oz A B  0
(P) : Cz D  0
(P)  (Oxy) hoă ̣c (P)  (Oxy) A C  0
(P) : By D  0
(P)  (Oxz) hoă ̣c (P)  (Oxz) B C  0
(P) : Ax D  0
(P)  (Oyz) hoă ̣c (P)  (Oyz) Lƣu ý:
 Nếu trong phương trình của mă ̣t phẳng (P) không chứa ẩn nào thì (P) song song hoă ̣c
chứa tru ̣c tương ứng. Trang42
 Phương trình mă ̣t phẳng (P) cắt các tru ̣c to ̣a đô ̣ ta ̣i các điểm (
A a; 0; 0), B(0; ;
b 0), C(0; 0; c) x y z
là (P) :    1 (gọi là phương trình mặt theo đoạn chắn). a b c
 Khoảng cách từ điểm M (x ; y ; z ) đến mặt phẳng (P) : Ax By Cz D  0 được xác M M M
Ax By Cz D
định bởi công thức: d(M;(P)) M M M   2 2 2
A B C
B – MỘT SỐ BÀI TOÁN VIẾT PHƢƠNG TRÌNH MẶT PHẲNG THƢỜNG GẶP.
Bài toán 1: Viết phƣơng trình mặt phẳng P đi qua điểm M (x ; y ; z ) và có vtpt o o o  n  ( ; A B;C) ( P ) Phƣơng pháp Minh họa •
 qua M (x ; y ; z )  o o o (P) :   •  vtpt : n  ( ; A ; B C)  ( P)  (P) : .
A (x x )  .
B ( y y )  C (
. z z )  0  o o o Áp dụng:
Ví dụ 1: Viết phương trình mp(P) đi qua M và vuông góc với đường thẳng d đi qua 2 điểm A và B, Phƣơng pháp Minh họa •
i qua M 2 Đ  P
 mp(P) :     •
VTPT : n u AB  ( P) d với: a) M ( 1  ;2;3), ( A 2; 4
 ;3), B(4;5;6). b) M (0;0;0), ( A 2  ; 1  ;3), B(4; 2  ;1). c) M (2; 4  ;0), ( A 5;1; 7), B( 1  ; 1  ; 1  ). d) M (3;0;0), ( A 0; 5  ;0), B(0;0; 7  ).
Ví dụ 2: Viết phƣơng trình mặt phẳng trung trực của đoạn thẳng AB với tọa độ A, B cho trƣớc:
Mặt phẳng trung trực (P) của đoạn AB là mp đi qua và vuông góc tại trung điểm I của AB. Phƣơng pháp Minh họa       • Đi qua x x y y z z A B I ; A B ; A B    mp(P) :   2 2 2    •
VTPT : n AB  (x x ; y y ; z z )  ( P) B A B A B A Vận dụng a) (
A 2; 0;1), B(0; 2  ;3). b) ( A 1;3; 4),  B( 1  ;2;2). c) ( A 2;1;1), B(2; 1  ; 1  ). Trang43
Ví dụ 3: Viết phƣơng trình mp(P) đi qua M (x ; y ; z ) và song song với o o o
(Q) : Ax By Cz D  0 hƣơng pháp Minh họa •  Đ
i qua M (x , y , z )  o o o mp(P) :    •
VTPT : n n  ( ; A ; B C)  ( P) (Q) Vận dụng:
1. Viết ptmp (P) đi qua M và song song với mp(Q) trong các trường hợp sau:
a) M (3;3;3) và (Q) : 2x  3y z  6  0. b) M (2;1;5) và (Q)  (Oxy) c) M (1; 2
 ;1) và (Q) : 2x y  3  0. d) M (1;1;0) và (Q) : x  2y z 10  0.
2.(ĐH D – 2013 NC) Trong không gian với hệ trục Oxyz, cho điểm ( A 1  ;3; 2)  và mặt phẳng
(P) : x  2 y  2z  5  0. Tính khoảng cách từ A đến (P). Viết phương trình mặt phẳng (Q) đi
qua A và song song với (P) ?
Đáp số. d A P  2 , ( ) 
và (Q) : x  2 y  2z  3  0. 3
3.Viết phương trình mặt phẳng (P) song song với mp(Q) : 2x  3y  6z 14  0 và khoảng
cách từ gốc tọa độ đến mặt phẳng (P) bằng 5 ?
Đáp số. (P) : 2x  3y  6z  35  0.
Bài toán 2:Viết phƣơng trình mặt phẳng (P) đi qua điểm M và có cặp véctơ chỉ phƣơng  
a, b cho trƣớc Phƣơng pháp Minh họa •  Đ i qua Mmp(P) :     • VTPT : n  a,b  ( P)    Vận dụng: Ví dụ 1:     a) M (1; 2; 3
 ), a  (2;1;2), b  (3;2; 1  ). b) M(1; 2  ;3), a  (3; 1  ; 2  ), b  (0;3;4).     c) M ( 1
 ;3;4), a  (2;7;2), b  (3;2;4). d) M( 4  ;0;5), a  (6; 1
 ;3), b  (3;2;1). Trang44
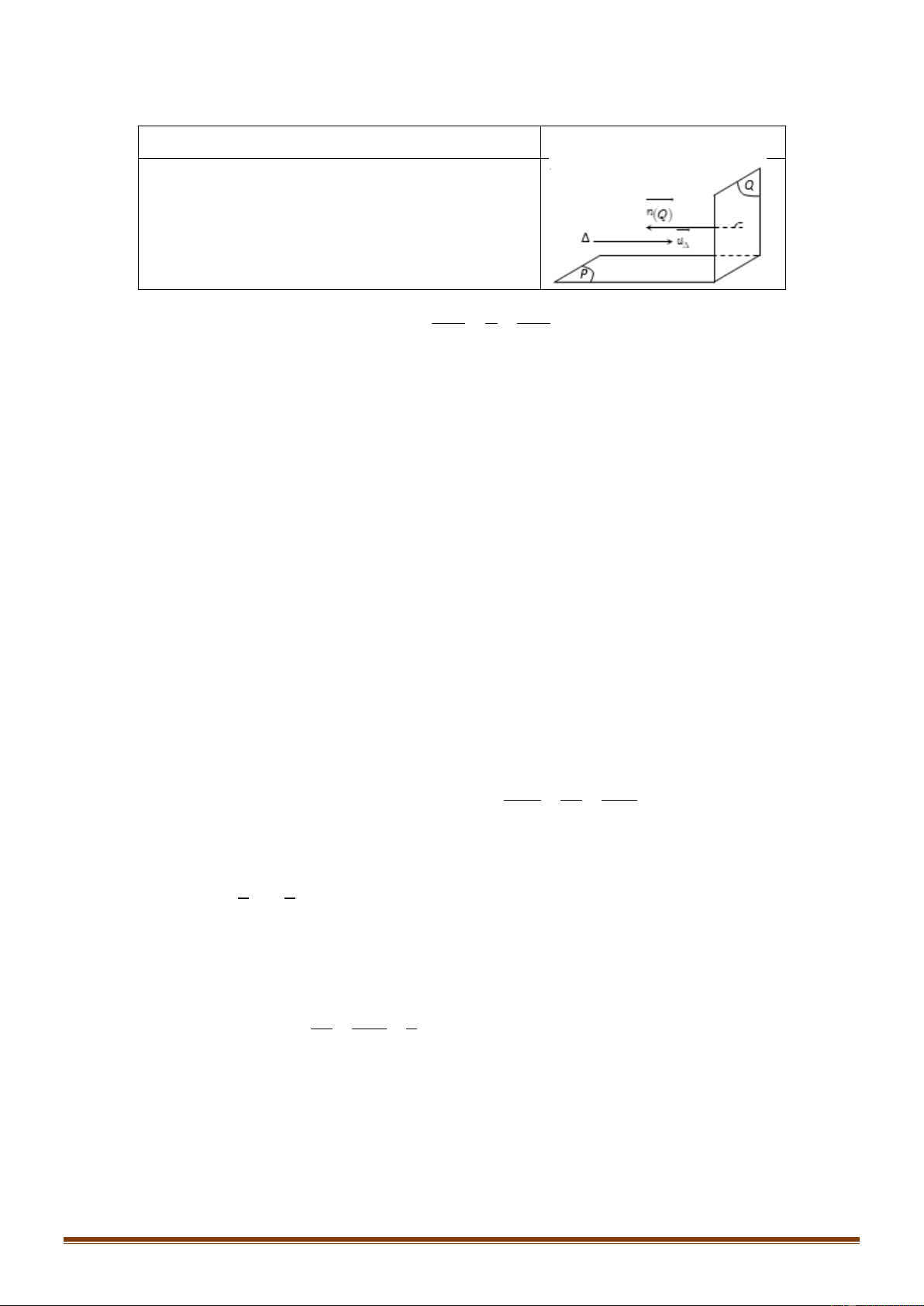
Ví dụ 2:Viết phương trình đi qua vuông góc và   mp(P) M , mp(Q) mp(P) : Phƣơng pháp Minh họa •
qua M x , y , z 2  o o o   P
 mp(P) :     • vtpt : n  n ,u   ( P) (Q)     x y z
a) M (1;1;1), (Q) : 2x y z 1  1 1 0,  :    2 1 3 x 13t
b) M (3; 2;1), (Q) : 2x  3y – z  0,  :  y  2  t , (t   ). z  33t
Ví dụ 3: Viết phương trình mặt phẳng (P) đi qua ,
A B và vuông góc với mp(Q) : •  Đ i qua ,
A (hay B)  PP
 mp(P) :     • VTPT : n  AB,n   ( P) (Q)     (0
A ;1;0), B(1; 2; 2  )  ( A 3;1; 1  ), ( B 2; 1  ;4) a)  b)  (
Q) : 2x y  3z 13  0 (
Q) : 2x y  3z 1 0  ( A 2; 1  ;3), B( 4  ;7; 9  )  ( A 3; 1  ; 2  ), B( 3  ;1;2) c)  d)  (
Q) :3x  4y 8z 5  0 (
Q) : 2x  2y  2z  5  0
Ví dụ 4: (ĐH A, A1 – 2014) Trong không gian với hệ trục tọa độ Oxyz, cho x y z
mp(P) : 2x y  2z 1  2 3
0 và đường thẳng (d ) :  
 Tìm tọa độ giao điểm của d 1 2  3
và mp(P). Viết phương trình mặt phẳng (Q) chứa d và vuông góc với mp(P).  7 3  Đáp số. M ; 3  ; 
 và (Q) : x  8y  5z 13  0.  2 2 
Ví dụ 5: (CĐ – 2010 – Chƣơng trình nâng cao ) Trong không gian với hệ trục tọa độ Oxyz, x y 1 z
cho đường thẳng (d) : 
 và mặt phẳng P: 2x y  2z  2  0 . 2 1 1
a) Viết phương trình mă ̣t phẳng (Q) chứa d và (Q)  (P). .
b) Tìm tọa độ điểm M d sao cho M cách đều O và mặt phẳng mp(P).
Đáp số. (Q) : x  2y  2  0 và M (0;1;0).
Ví dụ 6: Viết phương trình của mặt phẳng (P) đi qua điểm M và chứa đường thẳng  : Trang45 Phƣơng pháp Minh họa
Trên đƣờng thẳng Δ lấy điểm A và xác định 
VTCP u •  Đ i qua M
Khi đó mp(P) :     • VTPT : n  AM ,u   ( P)    
x  4  2tx  2  t   a) M 2; 3   ;1 ,
 : y  2 3t b) M 1;4; 3
 ,  : y  1   2t   z  3  tz  1 3t x y z
x y z   c) M    1 2 5 4; 2;3 ,  :   d) M   2 1 0 2;1; 4 ,  :  3 4 2
x  2y  2z  5  0
Ví dụ 7: (TNTHPT – 2010 – Chƣơng trình nâng cao) Trong không gian với hệ trục tọa độ x y 1 z 1
Oxyz, cho đường thẳng có phương trình  :    2 2  1
a) Tính khoảng cách từ O đến đường thẳng . 
b) Viết phương trình mặt phẳng (P) chứa điểm O và chứa đường thẳng .    MO,u     Đáp số. d ( ; O )  
 1 và (P) : x  2y  2z  0. u
Ví dụ 8: Viết phương trình của mặt phẳng (P) đi qua hai đường thẳng cắt nhau  ,  : 1 2 Phƣơng pháp Minh họa •
qua M  , (hay M  ) 1 2  mp(P) :     • vtpt : n  u ,u   ( P)      1 2 x  3t
x  1 t  
a)  :  y  1 2t , (t   ),  :  y  2t , (t  ) 1 2   z  3 t
z  4  t x  1 t
x y z  3  0  b)  :  ,  :  y  2
  t , (t   ) 1  2
2x y 1  0  z  3  t
x  2y z  4  0
x z  2  0 c)  :  ,  :  1
2x y z  6  0 2
y  2z  7  0
Ví dụ 9: Cho 2 đường thẳng chéo nhau  ,  . Hãy viết phương trình (P) chứa  và song 1 2 1 song  2 Trang46 Phƣơng pháp Minh họa •
qua M 1  mp(P) :     • vtpt : n  u ,u   ( P)      1 2 x  1 2tx  2t  
a)  :  y  3  t
, t   ,  :  y  1 t , t  2   1     z  2   3t
z  3  2tx  2 y 1 z x y 1 z 1 b)  :   ,  :   1 2 3 2  2 1 2 4 x 1 t
x  2y z  4  0  c)  : 
 : y  2 t , t  2   1
x  2y  2z  4  0 z 1 2t
Ví dụ 10: Viết phương trình mp(P) qua M và vuông góc với hai mp mp( ), ( ) : Phƣơng pháp Minh họa •  qua Mmp(P) :     • vtpt : n  n ,n   ( P) ( ) ( )    a) M (1; 3
 ;2), ( ) : x  2y  5z 1  0, ( ) : 2x  3y z  4  0. b) M 2; 1  ; 
1 ,   : 2x z 1  0,   : y  0
Ví dụ 11: (CĐ – 2009 – Chƣơng trình chuẩn) Trong không gian với hê ̣ tru ̣c to ̣a đô ̣ Oxyz, cho
đường các mă ̣t phẳng P : x  2y  3z  4  0
P :3x  2y z 1 0 2  1  và . Viết phương trình
mă ̣t phẳng P đi qua điểm A1;1; 
1 , vuông góc hai mă ̣t phẳng  PP2  1  và .
Đáp số. P : 4x 5y  2z 1 0 .
Ví dụ 12: (ĐH D – 2010 – Chƣơng trình chuẩn) Trong không gian với hê ̣ tru ̣c to ̣a đô ̣ Oxyz,
cho hai mă ̣t phẳng P : x y z  3  0 và Q : x y z 1  0 . Viết phương trình mă ̣t phẳng
R sao cho R vuông góc với P và Q đồng thời d  ,
O R  2 .
Đáp số. R : x z  2 2  0 . Trang47
Ví dụ 13: Viết phương trình mặt phẳng (P), biết rằng (P) vuông góc với hai
( ) : x y z 1  0, ( ) : 2x y  3z  4  0 và khoảng cách từ gốc tọa độ đến mặt phẳng (P) bằng 26 ?
Đáp số. (P) : 4x y  3z  26  0.
Bài toán 3: Viết phƣơng trình mặt phẳng (P) đi qua ba điểm ,
A B, C không thẳng hàng Phƣơng pháp Minh họa •  Đ i qua ,
A (hay B hay C)  mp(P) :     • VTPT : n  A , B AC   ( ABC )    Vận dụng: Ví dụ 1: a) ( A 2; 5  ;1), B(3;4; 2),  C(0; 0; 1  ). b) ( A 1; 2  ;4), B(3;2; 1  ), C( 2  ;1; 3  ). c) ( A 3; 5  ;2), B(1; 2  ;0), C(0; 3  ;7). d) (
A 1; 2;3), B(2; 4  ;3), C(4;5;6).
Ví dụ 2: (THPT – 2011 NC) Trong không gian với hệ trục Oxyz, cho (
A 0; 0;3), B(1; 2;1),
C(1; 0; 2). Viết phương trình mặt phẳng ( ABC). Tính độ dài đường cao của ABC  kẻ từ . A
Đáp số. (ABC) : 2x y  2z  6  3 5 0 và AH   5
Ví dụ 3:Viết phương trình mặt phẳng P đi qua điểm M và giao tuyến của hai mặt phẳng  ,   PP
 Chọn ,
A B thuộc giao tuyến hai mặt phẳng   và    ,
A B  P. Cụ thể:
A x B y   C z D    1 1  1 o 1  x ...
Cho: z z      AP o
...;...;...  
A x B y   C z D  y  ... 2 2  2 o 2 
B y C z   A x D    1 1  1 o 1  y ...
Cho: x x      BP o
...;...;...  
B y C z   A x D  z  ... 2 2  2 o 2  •  Đ i qua M
Khi đó mpP :  
  • VTPT :      n AB AM P ,    a) M 2;0 
;1 ,   : x  2y z  4  0,   : 2x y z  4  0 b) M 1; 2; 3
 ,  : 2x 3y z 5  0,  :3x  2y 5z 1 0
Bài toán 4: Viết phƣơng trình mặt phẳng (P) đi qua giao tuyến của hai mặt phẳng và thỏa
mãn điều kiện cho trƣớc:
Ví dụ 1: Viết phương trình mặt phẳng P qua giao tuyến của hai mặt phẳng  ,  , đồng
thời song song với mặt phẳng   cho trước Trang48
a)   : y  2z  4  0,   : x y z  3  0,   : x y z  2  0
b)   : x  4 y  2z  5  0,   : y  4z  5  0,   : 2x y 19  0
Ví dụ 2: Viết phương trình mặt phẳng P qua giao tuyến của hai mặt phẳng  ,  , đồng
thời vuông góc với mặt phẳng   cho trước
a)   : 2x  3y  4  0,   : 2y  3z  5  0,   : 2x y  3z  2  0
b)   : y  2z  4  0,   : x y z  3  0,   : x y z  2  0
Ví dụ 3: Viết phương trình mặt phẳng (P) qua giao tuyến của hai mặt phẳng   7 3
( ) : x  3z  2  0 và ( ) : y  2z 1  1
0, đồng thời cách điểm M 0;0;   một khoảng   2  18
Đáp số. (P) : x y  5z 1  0 hoặc (P) : 5x 17 y 19z  27  0.
Bài toán 5: Mặt phẳngvà mặt cầu
Ví dụ 1: Viết phương trình mặt phẳng P tiếp xúc với mặt cầu S  cho trước tại điểm H : 2 2 2
a) S  :  x  3   y  
1   z  2  24 tại H  1  ;3;0 b) S  2 2 2
: x y z  6x  2 y  4z  5  0 tại H 4;3;0
Ví dụ 2: (CHUYÊN LAM SƠN THANH HÓA-LẦN 2-2018) Trong không gian với hệ tọa độ 2 2 2
Oxyz , cho mặt cầu S  :  x  
1   y  2   z  3  16 và các điểm A1;0; 2 , B  1
 ;2;2 . Gọi P là mặt phẳng đi qua hai điểm A , B sao cho thiết diện của P với mặt
cầu  S  có diện tích nhỏ nhất. Khi viết phương trình  P dưới dạng  P : ax by cz  3  0 .
Tính T a b c . A. 3 . B. 3  . C. 0 . D. 2  . Lời giải Chọn B Trang49 I B H A K
Mặt cầu có tâm I 1;2;3 bán kính là R  4 .
Ta có A , B nằm trong mặt cầu. Gọi K là hình chiếu của I trên AB và H là hình chiếu của
I lên thiết diện.
Ta có diện tích thiết diện bằng 2      2 2 S r
R IH  . Do đó diện tích thiết diện nhỏ nhất khi
IH lớn nhất. Mà IH IK suy ra  P qua ,
A B và vuông góc với IK . 
Ta có IA IB  5 suy ra K là trung điểm của AB . Vậy K 0;1; 2 và KI  1;1;  1 .
Vậy P :  x  
1  y   z  2  0  x y z  3  0 . Vậy T  3  . x  3 y  3 z
Ví dụ 3: Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d:   và mặt 2 2 1 cầu (S): 2 2 2
x y z  2x  2 y  4z  2  0 . Lập phương trình mặt phẳng (P) song song với d và
trục Ox, đồng thời tiếp xúc với mặt cầu (S).  
(S) có tâm I(1; 1; 2), bán kính R = 2. d có VTCP u  (2; 2;1) .   
(P) // d, Ox (P) có VTPT n  u, i   (0;1; 2
 ) PT của (P) có dạng: y  2z  D  0 . 1 4  DD  
(P) tiếp xúc với (S) d (I , (P))  R   2  D  3  3 2 5 2 5   2 2 1  2 D  3 2 5
(P): y  2z 3 2 5  0 hoặc (P): y  2z 3 2 5  0 .
Ví dụ 4: Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): 2 2 2
x y z  2x  4 y  4  0
và mặt phẳng (P): x z 3  0 . Viết phương trình mặt phẳng (Q) đi qua điểm M (3;1; 1)
vuông góc với mặt phẳng (P) và tiếp xúc với mặt cầu (S).  
(S) có tâm I(–1; 2; 0) và bán kính R = 3; (P) có VTPT n  (1; 0;1) . P
PT (Q) đi qua M có dạng: 2 2 2 (
A x  3)  B( y 1)  C(z 1)  0, A B C  0 Trang50
(Q) tiếp xúc với (S) 2 2 2
d (I , (Q))  R  4
A B C  3 A B C (*)   ( ) Q  ( )
P n .n  0  A C  0  C  A (**) Q P Từ (*), (**)  2 2 2 2
B  5A  3 2A B  8B  7 A 10AB  0  A  2B  7A  4  B
Với A  2B . Chọn B = 1, A = 2, C = –2 PT (Q): 2x y  2z  9  0 Với 7A  4
B . Chọn B = –7, A = 4, C = –4 PT (Q): 4x  7y  4z  9  0
Câu hỏi tương tự: a) Với 2 2 2
(S) : x y z  2x  4 y  4z  5  0 , (P) : 2x y  6z  5  0, M (1;1; 2) .
ĐS: (Q) : 2x  2 y z  6  0 hoặc (Q) :11x 10y  2z  5  0 . Ví dụ 5: Trong không gian với hệ trục Oxyz, cho mặt cầu S 2 2 2
: x y z – 2x  4y  2z – 3  0 . Viết phương trình mặt phẳng (P) chứa trục Ox và cắt
mặt cầu (S) theo một đường tròn có bán kính r  3 .
(S) có tâm I(1; –2; –1), bán kính R = 3. (P) chứa Ox (P): ay + bz = 0.
Mặt khác đường tròn thiết diện có bán kính bằng 3 cho nên (P) đi qua tâm I.
Suy ra: –2a – b = 0 b = –2a (a 0) (P): y – 2z = 0.
Ví dụ 6: Trong không gian với hệ trục Oxyz, cho mặt cầu (S):
x y   2 2 2
x y z  2x  2 y  2z –1  2 0
0 và đường thẳng d : 
. Viết phương trình mặt
2x z  6  0
phẳng (P) chứa d và cắt mặt cầu (S) theo một đường tròn có bán kính r  1 .
(S) có tâm I(1;1;1) , bán kính R = 2.
PT mặt phẳng (P) có dạng: 2 2 2
ax by cz d  0 (a b c  0) . Chọn M (2; 0; 2), 
N (3;1; 0)  d . M (P)  a  , b 2c  (  a  ) b , d  3  a b (1)
Ta có: N  (P)     1  7a  7  , b 2c  (  a  ) b , d  3  a b (2) 2 2
d(I,(P))  R r
+ Với (1) (P): x y z  4  0 + Với (2) (P): 7x 17 y  5z  4  0 x y 1 z
Ví dụ 7: Trong không gian với hệ toạ độ Oxyz , cho hai đường thẳng  :   1 , 2 1 1 Trang51 x 1 y z  :   S: 2 2 2
x y z – 2x  2 y  4z – 3  0 2 và mặt cầu
. Viết phương trình tiếp 1 1 1
diện của mặt cầu S  , biết tiếp diện đó song song với hai đường thẳng  và  . 1 2
(P): y z 33 2  0 hoặc (P): y z 33 2  0
Ví dụ 8: Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình 2 2 2
x y z  2x  4 y  6z 11  0 và mặt phẳng () có phương trình 2x  2 y – z  17  0 .
Viết phương trình mặt phẳng () song song với () và cắt (S) theo giao tuyến là đường tròn có
chu vi bằng p  6 .
Do () // () nên () có phương trình 2x + 2y – z + D = 0 (D 17)
(S) có tâm I(1; –2; 3), bán kính R = 5. Đường tròn có chu vi 6 nên có bán kính r = 3.
Khoảng cách từ I tới () là h = 2 2 2 2
R r  5  3  4 2.1 2( 2  )  3 DD  7  Do đó  4  5   D 12   2 2 2    D 17 (loaïi) 2 2 ( 1)
Vậy () có phương trình 2x  2 y – z – 7  0 .
Câu hỏi tương tự: 2 2 2
a) (S) : x y z  2x  4y  6z 11  0 , () : 2x y  2z 19  0 , p  8 .
ĐS: ( ) : 2x y  2z 1  0
Bài toán 6: Mặt phẳngliên quan đến góc.
Ví dụ 1: Viết phương trình mp(P) chứa trục Oz và tạo với ( )
Q : 2x y  11z  3  0 một góc 30o   ?
Đáp số. (P) : x  0 hoặc (P) : 3x  4 y  0.
Ví dụ 2: Viết (P) đi qua (
A 3; 0;1), B(6; 2
 ;1) và (P) tạo với (Oyz) góc  thỏa mãn 2 cos  ? 7
Đáp số. mp(P) : 2x  3y  6z 12  0 hoặc mp(P) : 2x  3y  6z  0.
Ví dụ 3: Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng () chứa đường thẳng (): x 1 y z  
và tạo với mặt phẳng (P): 2x  2 y z 1  0 một góc 600. Tìm tọa độ giao 1 1  2 
điểm M của mặt phẳng () với trục Oz.   
() qua điểm (
A 1; 0; 0) và có VTCP u  (1; 1; 2) . (P) có VTPT n  (2; 2  ; 1  ) . Trang52    
Giao điểm M (0;0; m) cho AM  ( 1  ;0; )
m . () có VTPT n   AM ,u   ( ; m m  2;1)
() và (P): 2x  2 y z 1  0 tạo thành góc 600 nên:  
cos n, n  1 1 1 2  
  2m  4m 1 0  m  2 2 hay m  2 2 2 2   2 2m 4m 5
Kết luận: M (0;0; 2  2) hay M (0;0; 2  2)
Ví dụ 4: Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng (P) đi qua giao
tuyếnd của hai mặt phẳng ( ) : 2x – y –1  0 , ( ) : 2x – z  0 và tạo với mặt phẳng ( 2 2
Q) : x – 2 y  2z – 1  0 một góc  mà cos  9 Lấy (
A 0;1; 0), B(1;3; 2)  d . (P) qua A PT (P) có dạng: Ax By Cz – B  0 .
(P) qua B nên: A 3B  2C – B  0  A  (2B  2C)
 (P) : (2B  2C)x By Cz – B  0 2
B  2C  2B  2C 2 2 cos    2 2
13B  8BC – 5C  0 . 2 2 2    9 3 (2B 2C) B C 5
Chọn C  1  B  1; B . 13
+ Với B C 1 (P) : 4
x y z –1  0 5 + Với B
, C  1  (P) : 23
x  5y 13z – 5  0 . 13
Ví dụ 5: Trong không gian với hệ tọa độ Oxyz, cho hai điểm ( A 1  ;2; 3  ), B(2; 1  ; 6)  và mặt
phẳng (P) : x  2 y z  3  0 . Viết phương trình mặt phẳng (Q) chứa AB và tạo với mặt phẳng 3
(P) một góc  thoả mãn cos  . 6
PT mặt phẳng (Q) có dạng: 2 2 2
ax by cz d  0 (a b c  0) . A(Q)
a  2b  3c d  0   a  4  , b c  3  , b d  1  5b
Ta có: B  (Q)
 2a b  6c d  0      a   ,
b c  0, d b   3 
a  2b c 3 cos     6  2 2 2      6 a b c 1 4 1
Phương trình mp(Q): 4x y  3z 15  0 hoặc (Q): x y  3  0 . Trang53
Câu hỏi tương tự: 1 a) (
A 0; 0;1), B(1;1; 0) , (P)  (Oxy), cos  . 6
ĐS: (Q): 2x y z 1  0 hoặc (Q): x  2 y z 1  0 .
Ví dụ 6: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d là giao tuyến của hai mặt
phẳng P : x y z  3  0 và Q : 2x y z  4  0 . Viết phương trình mặt phẳng  R chứa
đường thẳng d và tạo với mặt phẳng Oxy một góc 0   60 .
ĐS: R : 2x y z  2  2  0 hoặc R : 2x y z  2  2  0
Ví dụ 7: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P) : 5x  2y  5z 1  0 và
(Q) : x  4 y  8z 12  0 . Lập phương trình mặt phẳng (R) đi qua điểm M trùng với gốc tọa độ
O, vuông góc với mặt phẳng (P) và tạo với mặt phẳng (Q) một góc 0   45 .
Giả sử PT mặt phẳng (R): 2 2 2 ax  by  z
c d  0 (a b c  0) .
Ta có: (R)  (P)  5a  2b  5c  0 (1);
a  4b  8c 2 0
cos((R), (Q))  cos 45   (2) 2 2 2   2 9 a b ca cTừ (1) và (2)  2 2
7a  6ac c  0   c  7a
Với a  c : chọn a 1,b  0,c  1 PT mặt phẳng (R) : x z  0
Với c  7a : chọn a 1,b  20,c  7  PT mặt phẳng (R) : x  20y  7z  0
Câu hỏi tương tự: a) Với 0
(P) : x y  2z  0, (Q)  (Oyz), M (2; 3  ;1),  45 .
ĐS: (R) : x y 1  0 hoặc (R) : 5x  3y  4z  23  0
Ví dụ 8: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng có phương trình: x 1 y 1 z 1  x y z :    :    1 và 2
. Viết phương trình mặt phẳng (P) chứa và tạo 1 1 3 1 2  1 1 với  một góc 0   30 . 2
Đáp số: (P): 5x 11y  2z  4  0 hoặc (P): 2x y z  2  0 .
Câu hỏi tương tự: Trang54 x y  2 z x  2 y  3 z  5 a) Với  :    :   0   30 1 , 2 , . 1 1 1 2 1 1 
ĐS: (P): x  2y  2z  2  0 hoặc (P): x  2y z  4  0 x 1 y z 1 x y  2 z 1 b)  :    :   0   30 1 , 2 , . 2 1 1 1 1  1
ĐS: (P): (18 114)x  21y  (15  2 114)z (3 114)  0
hoặc (P): (18  114)x  21y  (15  2 114)z  (3  114)  0
Ví dụ 9: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm
M (1; 2;3) và tạo với các trục Ox, Oy các góc tương ứng là 0 0 45 , 30 .    
Gọi n  (a; ;
b c) là VTPT của (P). Các VTCP của trục Ox, Oy là i  (1;0;0), j  (0;1;0) .  2 s
 in(Ox,(P))    2  a  2 b Ta có:    1   c b sin(Oy, (P))   2
PT mặt phẳng (P): 2(x 1)  ( y  2)  (z  3)  0 hoặc  2(x 1)  ( y  2)  (z  3)  0
Ví dụ 10: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2 y z  5  0 và x 1 y 1 z  3 đường thẳng d :  
. Viết phương trình mặt phẳng (P) chứa đường thẳng d và 2 1 1
tạo với mặt phẳng (Q) một góc nhỏ nhất.
PT mặt phẳng (P) có dạng: 2 2 2 ax  by  z
c d  0 (a b c  
0) . Gọi   ((P), (Q)) . M P c
  a b
Chọn hai điểm M ( 1  ; 1  ;3), N(1;0;4)  ( ) d . Ta có:    N (P)
d  7a  4b  3 a b
(P): ax by  (2a b)z  7a  4b  0  cos   . 2 2 6
5a  4ab  2b 3 b 3
TH1: Nếu a = 0 thì cos  .   0   30 . 2 6 2 2b b 1 3 a b
TH2: Nếu a 0 thì cos  .
. Đặt x và 2
f (x)  cos  2 6 bb a 5  4  2  aa  Trang55 2 9 x  2x 1
Xét hàm số f (x)  . . 2
6 5  4x  2x
Dựa vào BBT, ta thấy 0 0
min f (x)  0  cos  0    90  30
Do đó chỉ có trường hợp 1 thoả mãn, tức a = 0. Khi đó chọn b  1,c  1, d  4 .
Vậy: (P): y z  4  0 .
Câu hỏi tương tự: x 1 y  2 z
a) Với (Q): x  2 y  2z – 3  0 , d :  
. ĐS: (P) : x  2y  5z 3   0 . 1 2 1  x 1 y  2 z
b) Với (Q)  (Oxy), d : 
. ĐS: (P) : x y z  3  0 . 1  1 2 x t  
c) Với (Q) : 2x y z  2  0 , d :  y  1
  2t . ĐS: (P) : x y z  3  0 .  z  2  t
Ví dụ 11: Trong không gian với hệ tọa độ Oxyz, cho hai điểm M ( 1  ; 1
 ;3), N(1;0;4) và mặt
phẳng Q : x  2y z  5  0 . Viết phương trình mặt phẳng (P) đi qua M, N và tạo với (Q) một góc nhỏ nhất.
ĐS: (P) : y z  4  0 .
Câu hỏi tương tự: a) M (1; 2; 1  ), N( 1
 ;1;2),(Q)  (Oxy) . ĐS: (P) : 6x  3y  5z  7  0 . x  1 t
Ví dụ 12: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d : y  2   t . Viết  z  2t
phương trình mặt phẳng  P chứa đường thẳng d và tạo với trục Oy một góc lớn nhất.
PT mặt phẳng (P) có dạng: 2 2 2 ax  by  z
c d  0 (a b c  
0) . Gọi   ((P), Oy) . M P
c a b
Chọn hai điểm M (1; 2  ;0), N(0; 1  ;2)  ( ) 2 d . Ta có:    N (P)
d  a  2b   a b 2 b
(P): ax by
z a  2b  0  sin  . 2 2 2
5a  5b  2ab TH1: Nếu b = 0 thì 0   0 . Trang56 2 a
TH2: Nếu b 0 thì sin 
. Đặt x và 2
f (x)  sin  . 2  a a b 5   5  2  b b 4 5 1
Xét hàm số f (x) 
. Dựa vào BBT, ta được max f (x)   x   0   0 . 2 5x  2x  5 6 5 a 1
Vậy lớn nhất khi
. Chọn a 1,b  5,c  2
 , d  9 (P): x  5y  2z  9  0 . b 5 x 1 y  2 z
Ví dụ 13: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   1 và 1 2 1  x  2 y 1 z d :   d 2
. Viết phương trình mặt phẳng (P) chứa
sao cho góc giữa mặt phẳng 2 1 2 1
(P) và đường thẳng d là lớn nhất. 2  
d đi qua M (1; 2; 0) và có VTCP u  (1; 2; 1
 ) .Vì d  (P) nên M  (P) . 1 1
PT mặt phẳng (P) có dạng: (
A x 1)  B( y  2)  Cz  0 2 2 2
( A B C  0)  
Ta có: d  (P)  u.n  0  C A  2B . 2 4A 3B 1 (4 A 3B) Gọi
  ((P), d ) sin     . 2 2 2 2 2   3
2 A  4 AB  5 3. 2 4 5 B A AB B 2 2
TH1: Với B = 0 thì sin  3 A 2 1 (4t 3)
TH2: Với B 0. Đặt t , ta được: sin   . B 2 3 2t  4t  5 2 (4t  3) 25 A
Xét hàm số f (t) 
. Dựa vào BBT ta có: max f (t)  khi t  7    7 2 2t  4t  5 7 B 5 3
Khi đó sin  f ( 7)   . 9 5 3 A
So sánh TH1 và TH2  lớn nhất với sin  khi  7 . 9 B
Phương trình mặt phẳng (P): 7x y  5z 9   0 . x 1 y  2 z 1
Ví dụ 13: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và 1 1 1  điểm (
A 2; 1; 0) . Viết phương trình mặt phẳng (P) qua A, song song với d và tạo với mặt Trang57
phẳng (Oxy) một góc nhỏ nhất.
ĐS: (P) : x y  2z 1  0 .
Ví dụ 14: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): 2x y z  2  0 và điểm ( A 1;1; 1
 ) . Viết phương trình mặt phẳng (P) đi qua điểm A, vuông góc với mặt phẳng (Q) và
tạo với trục Oy một góc lớn nhất.
ĐS: (P) : y z  0 hoặc (P) : 2x  5y z  6  0 .
Bài toán 7: Mặt phẳngliên quan đến khoảng cách.
Ví dụ 1: Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng (P) qua O, vuông
góc với mặt phẳng (Q): x y z  0 và cách điểm M(1; 2; –1) một khoảng bằng 2 .
PT mặt phẳng (P) qua O nên có dạng: Ax  By Cz  0 (với 2 2 2
A B C  0 ).
Vì (P) (Q) nên: 1.A1.B 1.C  0 C  AB (1)    A 2B C d(M , ( ) P )  2   2  2 2 2 2
( A  2B C)  2( A B C ) (2) 2 2 2
A B CB
Từ (1) và (2) ta được: 2 8AB  5B  0 (3) 0  8  A  5B  0 (4)
Từ (3): B = 0 C = –A. Chọn A = 1, C = –1 (P): x z  0
Từ (4): 8A + 5B = 0. Chọn A = 5, B = –8 C = 3 (P): 5x 8y  3z  0 . x 1 y  3 z
Ví dụ 12: Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng  :   và 1 1 4
điểm M(0; –2; 0). Viết phương trình mặt phẳng (P) đi qua điểm M, song song với đường thẳng
, đồng thời khoảng cách d giữa đường thẳng  và mặt phẳng (P) bằng 4.
Phƣơng trình mp (P) đi qua M(0; –2; 0) có dạng: ax  by cz  2b  0 ( 2 2 2
a b c  0 )  
đi qua điểm A(1; 3; 0) và có một VTCP u  (1;1; 4)
a b  4c  0  P (P)  a  4c Ta có:    a  5b   . d( ;
A (P))  d  4  a  2  c 2 2 2
a b c
Với a  4c . Chọn a  4,c 1 b  8
 Phƣơng trình (P): 4x 8y z 16  0 . Với a  2
c . Chọn a  2,c  1 b  2  Phương trình (P): 2x  2y z  4  0 .
Câu hỏi tương tự: Trang58 x y z 1 a) Với  :  
; M (0;3; 2), d  3 . 1 1 4
ĐS: (P) : 2x  2y z  8  0 hoặc (P) : 4x  8y z  26  0 . x t
Ví dụ 13: Trong không gian với hệ toạ độ Oxyz, cho đường thẳng (d) : y  1
  2t và điểm z 1  (
A 1; 2;3) . Viết phương trình mặt phẳng (P) chứa đường thẳng (d) sao cho khoảng cách từ
điểm A đến mặt phẳng (P) bằng 3.   
(d) đi qua điểm M (0; 1;1) và có VTCT u  (1; 2;0) . Gọi n  (a; ; b c) với 2 2 2
a b c  0 là VTPT của (P).
PT mặt phẳng (P): a(x  0)  b( y 1)  c(z 1)  0  ax by cz b c  0 (1).  
Do (P) chứa (d) nên: .
u n  0  a  2b  0  a  2  b (2)
a b c b c d , A (P) 3 2 5 2 2 2  3   3 
 3  5b  2c  3 5b c 2 2 2 2 2
a b c 5b c
b bc c    b c2 2 2 4 4 0 2
 0  c  2b (3)
Từ (2) và (3), chọn b  1
  a  2,c  2  PT mặt phẳng (P): 2x y  2z 1  0 .
Ví dụ 4: Trong không gian với hệ toạ độ Oxyz, cho các điểm M ( 1  ;1;0), N(0;0; 2)  , I(1;1;1) .
Viết phương trình mặt phẳng (P) qua A và B, đồng thời khoảng cách từ I đến (P) bằng 3 .
PT mặt phẳng (P) có dạng: 2 2 2
ax by cz d  0 (a b c  0) . M (P)  a   ,
b 2c a  ,
b d a b (1)
Ta có: N  (P)   .   5  a  7 ,
b 2c a  ,
b d a b (2)
d(I,(P))  3
+ Với (1) PT mặt phẳng (P): x y z  2  0
+ Với (2) PT mặt phẳng (P): 7x  5 y z  2  0 .
Ví dụ 5: Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với (
A 1; 1; 2) , B(1;3; 0) , C( 3
 ;4;1) , D(1;2;1) . Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C
đến (P) bằng khoảng cách từ D đến (P).
PT mặt phẳng (P) có dạng: 2 2 2
ax by cz d  0 (a b c  0) . Trang59 A(P)
a b  2c d  0  
Ta có: B  (P)
 a  3b d  0  
d(C,(P))  d(D,(P)) 3
 a  4b c d
a  2b c d    2 2 2 2 2 2 
a b c
a b c       b 2 , a c 4 , a d 7a  c  2 , a b  , a d  4  a
+ Với b  2a, c  4a, d  7
a (P): x  2y  4z  7  0 .
+ Với c  2a, b a, d  4
a (P): x y  2z  4  0 .
Câu hỏi tương tự: a) Với ( A 1; 2;1), B( 2  ;1;3),C(2; 1
 ;1), D(0;3;1) .
ĐS: (P) : 4x  2 y  7z 15  0 hoặc (P) : 2x  3z  5  0 .
Ví dụ 6: Trong không gian với hệ trục tọa độ Oxyz , cho các điểm (
A 1; 2; 3) , B(0; 1; 2) ,
C(1;1;1) . Viết phương trình mặt phẳng (P) đi qua A và gốc tọa độ O sao cho khoảng cách từ
B đến (P) bằng khoảng cách từ C đến (P) .
Vì O (P) nên (P) : ax by cz  0 , với 2 2 2
a b c  0 .
Do A (P) a  2b  3c  0 (1) và d (B, (P))  d (C, (P))  b
  2c a b c (2)
Từ (1) và (2) b  0 hoặc c  0 .
Với b  0thì a  3
c (P) :3x z  0  Với c  0 thì a  2
b  (P) : 2x y  0
Câu hỏi tương tự: a) Với (
A 1; 2; 0), B(0; 4; 0), C(0; 0;3) . ĐS: 6
x  3y  4z  0 hoặc 6x  3y  4z  0 .
Ví dụ 7: Trong không gian với hệ trục tọa độ Oxyz , cho ba điểm ( A 1;1; 1  ) , B(1;1;2) , C(1; 2; 2
 ) và mặt phẳng (P): x  2y  2z 1  0 . Viết phương trình mặt phẳng ( ) đi qua A,
vuông góc với mặt phẳng (P), cắt đường thẳng BC tại I sao cho IB  2IC .
PT ( ) có dạng: ax  by cz d  0 , với 2 2 2
a b c  0 Do ( A 1;1; 1
 ) () nên: a b c d  0 (1); ()  (P) nên a 2b  2c  0 (2)
a b  2c d
a  2b  2c d
IB  2IC d (B, ( ))  2d (C;( ))   2 2 2 2 2 2 2
a b c
a b c Trang60 3
a 3b  6c d  0  (3)
a  5b  2c  3d  0
Từ (1), (2), (3) ta có 2 trường hợp sau:
a b c d  0  1  3 
TH1: a  2b  2c  0  b  ; a c   ; a d a . 2 2
3a 3b6c d  0 
Chọn a  2  b  1; c  2; d  3  ( ) : 2x y  2z  3  0
a b c d  0  3 3 
TH2: a  2b  2c  0  b  ; a c  ; a d a . 2 2
a 5b 2c 3d  0 
Chọn a  2  b  3; c  2; d  3  ( ) : 2x  3y  2z  3  0
Vậy: ( ) : 2x y  2z  3  0 hoặc ( ) : 2x  3y  2z  3  0
Ví dụ 8: Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng d , d lần lượt có phương 1 2 x  2 y  2 z  3 x 1 y  2 z 1 trình d :   d :   1 , 2
. Viết phương trình mặt phẳng cách đều 2 1 3 2 1  4
hai đường thẳng d , d . 1 2   
Ta có d đi qua A(2;2;3), có u
 (2;1;3) , d đi qua B(1;2;1) và có u  (2; 1  ;4) . 1 d1 2 d 2   
Do (P) cách đều d , d nên (P) song song với d , d n  u ,u  (7; 2  ; 4  ) P d1 d 2  1 2 1 2
PT mặt phẳng (P) có dạng: 7x  2y  4z d  0
Do (P) cách đều d , d suy ra d ( ,
A (P))  d (B, (P)) 1 2        7.2 2.2 4.3 d 7.1 2.2 4.1 d  3
d  2  d 1  d 69 69 2
Phương trình mặt phẳng (P): 14x  4y 8z  3  0
Ví dụ 9: Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng d , d lần lượt có phương 1 2 x 1 tx  2 y 1 z 1
trình d :  y  2  t d :   1 , 2
. Viết phương trình mặt phẳng (P) song song với  1 2  2 z  1 
d và d , sao cho khoảng cách từ d đến (P) gấp hai lần khoảng cách từ d đến (P). 1 2 1 2   Ta có: d đi qua (
A 1; 2;1) và có VTCP u  (1; 1  ;0) 1 1 
d đi qua B(2;1; 1) và có VTCP là u  (1; 2  ;2) 2 2 Trang61    
Gọi n là VTPT của (P), vì (P) song song với d và d nên n  u ,u  ( 2  ; 2  ; 1  ) 1 2  1 2
Phương trìnht (P): 2x  2y z m  0 . 7  m 5  m
d (d , (P))  d ( ; A (P)) 
d (d , (P))  d ( , B (P))  1 ; 2 3 3   m   m 17
d (d , (P))  2d (d , (P))  7  m  2. 5  7 2(5 ) m   m  3;  m   1 2  7  m  2  (5 ) m 3 17 + Với m  3
  (P) : 2x  2y z – 3  0 + Với m    17
(P) : 2x  2 y z   0 3 3
Ví dụ 10: Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng (P) đi qua hai điểm (
A 0; 1; 2) , B(1; 0;3) và tiếp xúc với mặt cầu (S): 2 2 2
(x 1)  ( y  2)  (z 1)  2 .
(S) có tâm I(1;2; 1
 ) , bán kính R  2 .
PT mặt phẳng (P) có dạng: 2 2 2
ax by cz d  0 (a b c  0) A(P)  a   ,
b c  a  ,
b d  2a  3b (1)
Ta có: B  (P)    3  a  8  ,
b c  a  ,
b d  2a  3b (2)
d(I,(P))  R
+ Với (1) Phương trình của (P): x y 1  0
+ Với (2) Phương trình của (P): 8x  3y  5z  7  0
Ví dụ 11: Trong không gian với hệ tọa độ Oxyz, cho điểm (
A 2; 1;1) . Viết phương trình mặt
phẳng (P) đi qua điểm A và cáchgốc tọa độ O một khoảng lớn nhất.
Ta có d(O,(P))  OA .Do đó d(O,(P))
OA xảy ra OA  (P) nên mặt phẳng (P) cần max 
tìm là mặt phẳng đi qua A và vuông góc với OA. Ta có OA  (2; 1  ;1)
Vậy phương trình mặt phẳng (P): 2x y z  6  0 .
Ví dụ 12: Trong không gian với hệ tọa độ Oxyz, cho điểm A(10; 2; –1) và đường thẳng d có x 1 y z 1 phương trình:  
. Lập phương trình mặt phẳng (P) đi qua A, song song với d và 2 1 3
khoảng cách từ d tới (P) là lớn nhất.
Gọi H là hình chiếu của A trên d d(d, (P)) = d(H, (P)). Giả sử điểm I là hình chiếu của H
lên (P), ta có AH HI HI lớn nhất khi A I . Vậy (P) cần tìm là mặt phẳng đi qua A và 
nhận AH làm VTPT (P): 7x y  5z  77  0 . Trang62
Ví dụ 13: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng (d) có phương trình tham số x  2
  t; y  2
t; z  2  2t . Gọi  là đường thẳng qua điểm A(4;0;–1) song song với (d) và
I(–2;0;2) là hình chiếu vuông góc của A trên (d). Viết phương trình của mặt phẳng chứa  và
có khoảng cách đến (d) là lớn nhất.
Gọi (P) là mặt phẳng chứa , thì (P) (d) hoặc (P)  (d) . Gọi H là hình chiếu vuông góc
của I trên (P). Ta luôn có IH IA và IH AH .
d(d,(P))  d(I,(P))  IH Mặt khác H (P)
Trong (P), IH IA ; do đó a
m xIH = IA  H  A . Lúc này (P) ở vị trí (P0) IA tại A.   
Vectơ pháp tuyến của (P
n IA  6;0; 3 v  2;0;   0) là , cùng phương với 1 .
Phương trình của mặt phẳng (P        0) là: 2( x 4) 1.(z 1) 2x z 9 0 . x 1 y z  2
Ví dụ 14: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   và 2 1 2 điểm (
A 2;5;3) . Viết phương trình mặt phẳng  P chứa d sao cho khoảng cách từ A đến
P là lớn nhất.
PT mặt phẳng (P) có dạng: 2 2 2 ax  by  z
c d  0 (a b c  0) .  
(P) có VTPT n  (a; ;
b c) , d đi qua điểm M (1; 0; 2) và có VTCP u  (2;1; 2) . M  (P)
a  2c d  0 2c  (  2a  ) b
Vì (P) d nên       
. Xét 2 trường hợp: n.u  0
2a b  2c  0
d a b
TH1: Nếu b = 0 thì (P): x z 1  0 . Khi đó: d ( ,
A (P))  0 .
TH2: Nếu b 0. Chọn b 1 ta được (P): 2ax  2 y  (2a 1)z  2a  2  0 . Khi đó: 9 9 d ( , A (P))    3 2 2 2 8a  4a  5  1  3 2 2a     2  2 Vậy max d( , A ( ) P )  1 1 3 2  2a
 0  a   . Khi đó: (P): x  4y z  3  0 . 2 4
Câu hỏi tương tự: x 1 y 1 z  2 a) d :   , (
A 5;1; 6) . ĐS: (P) : 2x y z 1  0 2 1 5 Trang63 x 1 y  2 z b) d :   , (
A 1; 4; 2) . ĐS: (P) : 5x 13y  4z  21  0 1 1 2
Ví dụ 15: Trong không gian toạ độ Oxyz, cho hai điểm M (0; 1  ;2) và N( 1  ;1;3) . Viết phương
trình mặt phẳng  P đi qua M , N sao cho khoảng cách từ điểm K(0;0;2) đến mặt phẳng  P là lớn nhất.
PT (P) có dạng: Ax B(y 1)  C(z  2)  0  Ax By Cz B  2C  0 , 2 2 2
( A B C  0) N ( 1
 ;1;3) (P)  A B  3C B  2C  0  A  2B CB
(P) : (2B C)x By Cz B  2C  0 ; d(K, (P))  2 2
4B  2C  4BC
Nếu B = 0 thì d(K, (P)) = 0 (loại) B 1 1
Nếu B  0 thì d (K , (P))    2 2 2
4B  2C  4BC 2  C  2  1  2  B
Dấu “=” xảy ra khi B = –C. Chọn C = 1. Khi đó PT (P): x y – z  3  0 . Trang64
C – BÀI TẬP TRẮC NGHIỆM
Phần I: 10 CÂU NHẬN BIẾT Câu 1.
Trong không gian tọa độ Oxyz , mặt phẳng đi qua điểm M x ; y ; z n  a; ; b c 0 0 0  nhận với 2 2 2
a b c  0 làm vectơ pháp tuyến có phương trình là: A. x
x a y
y b z z c  0 x
x a y
y b z z c  0 0   0   0   0   0   0   B.
C. a x x b y y c z z  0
a x x b y y c z z  0 0   0   0  0   0   0  D. . Câu 2.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt phẳng Oxy là: A. x  0 B. y  0 C. z  0
D. x y  0 Câu 3.
Trong không gian với hệ tọa độ Oxyz, một vectơ pháp tuyến của mặt phẳng x 3z  4  0 là:    
A. n  1; 3; 4
B. n  1;3; 4
C. n  1;0;3
D. n  1;0;3 Câu 4.
Trong không gian với hệ tọa độ Oxyz, điểm nào sau đây thuộc mặt phẳng x  2 y  3z  4  0 : A. M 1; 2  ;3 B. N 1;1  ;1 C. E 4;0  ;1 D. F 0; 2  ;0 Câu 5.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A ;
a 0;0, B 0, ;
b 0, C 0;0;c với abc  0 có phương trình là: x y z x y z A.    1 B.
  1  0 C. ax by cz  1
D. bcx cay abz  1 a b c a b c Câu 6.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng  P : x  2y  3z  4  0 và Q: 2
x  4y  6z  4  0 . Khẳng định nào đúng?
A. P và Q cắt nhau.
B. P  Q
C. P / / Q
D. P  QCâu 7.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào sau đây chứa trục Ox :
A. y z  0 B. 2
x y  0
C. 2x y z  0 D. 2
x z  0 Câu 8.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào sau đây song song với trục Oy :
A. y  2  0
B. 2x  3z 1  0
C. 2x y  3z  4  0 D. 2
x z  0 Câu 9.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào sau đây song song với mặt phẳng Oyz  ? A. 2z  0 B. 2  z 1 0 C. 2  x  0 D. 2  x 1 0
Câu 10. Trong không gian với hệ tọa độ Oxyz, khoảng cách từ gốc tọa độ O đến mặt phẳng
P: x 2y  2z 1 0 bằng: 1 1 1 A. 1 B. C. D.  9 3 3
Phần II: 15 CÂU THÔNG HIỂU
Câu 11. Giả sử n là một vectơ pháp tuyến của mặt phẳng  P . Khẳng định nào sai? Trang65  
A. Giá của n vuông góc với  P .
B. k n k   \  
0  là vectơ pháp tuyến của P   1 
C. n là một vectơ khác 0 . D.
n không phải là vectơ pháp tuyến 2017 của  P .  
Câu 12. Cho u , uP 1
2 là hai vectơ có giá song song hoặc nằm trên mặt phẳng
. Khẳng định nào đúng?   
A. n u
 ,u  là một vectơ pháp tuyến của P . 1 2       
B. n u
 ,u  là một vectơ pháp tuyến của P nếu u , u không cùng phương. 1 2   1 2     
C. n u
 ,u  là một vectơ pháp tuyến của P khi và chỉ khi u u 1 2   1 2     
D. n u
 ,u  là một vectơ pháp tuyến của P khi u , u 1 2 cùng phương. 1 2  
Câu 13. Trong không gian với hệ toạ độ Oxyz, có hai giá trị của tham số m để hai mặt phẳng
P: x 3y  2z 1 0 và Q:2m 
1 x m1 2my  2m  4 z 14  0 vuông góc với
nhau. Tính tổng các bình phương của hai số đó. 19 13 29 17 A. B. C. D. 4 4 4 4
Câu 14. Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua A1; 2;3 và vuông góc với trục Oy có phương trình là:
A. x  2 y  3z  0
B. x z  4  0
C. y  2  0
D. x  3z 10  0
Câu 15. Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua A1; 2;3 và chứa trục Oz có phương trình là: A. z  3
B. x  2 y  3z  0
C. 2x y  0
D. x  2 y  5  0
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho điểm M 1; 2;3 và hai mặt phẳng
Q: x 2y 3  0 và R: y 3z 4  0 . Mặt phẳng P đi qua M đồng thời vuông góc với
cả Q và  R có phương trình là: A. 6
x  3y z  3  0
B. x  7 y  5z  28  0
C. 6x  3y z  9  0
D. x  7 y  5z  0
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1; 2;3, B  1  ; 2  ; 3   . Mặt phẳng trung
trực của đoạn thẳng AB có phương trình là:
A. 2x  4 y  6z  28  0
B. 2x  4 y  6z  28  0
C. x  2 y z  0
D. x  2 y  3z  0
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A1;0;0, B 0; 2;0, C 0;0;3 . Mặt phẳng Trang66
ABC có phương trình là: x y z x y z
A. 6x  3y  2z  6  0 B.    0
C. 6x  3y  2z  6  0 D.    1 1 2 3 1 2 3
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho điểm M  ; a ;
b c với abc  0. Gọi ,
A B, C lần lượt
là hình chiếu của M trên các mặt phẳng tọa độ Oxy, Oyz, Ozx . Phương trình của mặt
phẳng  ABC  là: x y z x y z x y z x y z A.    1 B.    0 C.    2 D.    3 a b c a b c a b c a b c
Câu 20. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P đi qua gốc tọa độ O và song song với
mặt phẳng Q : x  2y  3z  4  0 có phương trình là:
A. x  2 y  3z  4  0
B. x  2 y  3z  0
C. x  2 y  3z  0
D. 2x  4 y  6z  0
Câu 21. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P song song với mặt phẳng
Q: x 2y  2z 1 0 và cách Q một khoảng bằng 3 có phương trình là:
A. x  2 y  2z  8  0
B. x  2 y  2z 10  0
x  2y  2z 8  0 C.
D. x  2 y  2z  2  0 
x  2y  2z 10  0
Câu 22. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P đi qua điểm M 1; 2
 ;3 và cách gốc tọa
độ một khoảng lớn nhất có phương trình là:
A. x  2 y  3z  6  0
B. x y z  2  0
C. x  2 y  3z 12  0 D. x  2 y  3z 14  0
Câu 23. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P song song với hai đường thẳng x  2  t x  2 y 1 z   :  
 : y  3 2t 1 và
nhận vectơ nào sau đây làm vectơ pháp tuyến? 2 3  4 2 z 1t      A. n   5  ;6; 7  
B. n  5; 6;7 C. n   5  ; 6  ;7 D. n  5; 6  ; 7  
Câu 24. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P đi qua M 1; 2;3 và cắt các trục tọa độ
Ox, Oy, Oz lần lượt tại ,
A B, C sao cho M là trọng tâm tam giác ABC . Phương trình của P là: x y z x y z
A. x  2 y  3z 14  0 B.    1 C.    1
D. x y z  6  0 1 2 3 3 6 9
Câu 25. Trong không gian với hệ trục tọa độ Oxyz, cho điểm M 4;5;6 . Phương trình mặt phẳng (P)
qua M, cắt các trục tọa độ lần lượt tại I, J, K mà M là trực tâm của tam giác IJK là x y z x y z A.    1 B.    1 12 15 18 4 5 6
C. x  2 y  3z  32  0
D. 4x  5 y  6z  77  0 Trang67
Phần III: 15 CÂU VẬN DỤNG THẤP
Câu 26. Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M (1; 2;3) , cắt 1 1 1
các tia Ox, Oy, Oz tại A, B, C sao cho biểu thức  
có giá trị nhỏ nhất là: 2 2 2 OA OB OC x y z x y z
A. x y z  6  0 B.    3
C. x  2 y  3z 14  0 D.    1 1 2 3 1 2 3
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng  P : 4x  3y  7z  3  0 và điểm I 1; 1
 ;2 . Mặt phẳng Q đối xứng với P qua điểm I có phương trình
4x by cz d  0 . Giá trị của b c d là: A. 2 B. 0 C. 1 D. 1
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A0;1; 2, B 2; 2  ;  1 , C  2  ;1;0 . Phương
trình mặt phẳng  ABC  là ax y cz d  0 . Giá trị của a d bằng A. 4  B. 2  C. 4 D. 2 2 2 2
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu S : x 1  y  2  z  3  16 1        và
S : x 1  y  2  z 3  25 C 2   2  2  2
cắt nhau theo giao tuyến là một đường tròn . Viết
phương trình mặt phẳng P chứa đường tròn C :
A. x  2 y  3z  9  0
B. x  2 y  3z  9  0
C. 4x  8 y 12z  9  0
D. 4x  8 y 12z  9  0
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2; 4;  1 , B  1
 ;1;3 và mặt phẳng (P):
x – 3y  2z – 5  0 . Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình là
A. x y  3z  9  0
B. 3x y 10  0
C. 8 y 12z  61  0
D. 2 y  3z 11  0
Câu 31. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng (d ) và (d ) có phương trình: 1 2 x 1 y 1 z  2 x  4 y 1 z  3 (d );   (d ) :   (d ) 1 , 2
. Mặt phẳng (P) chứa (d ) và có 2 3 1 6 9 3 1 2 phương trình là A. Không tồn tại
B. x y z  0
C. 2x  3y z 1  0 D. x y  5z 10  0
Câu 32. Trong không gian với hệ trục Oxyz, cho mặt cầu (S): 2 2 2
x y z – 2x  4 y  2z – 3  0 .
Phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S) theo một đường tròn có bán kính r  3 là:
A. y  2z  0 B. x  0
C. 2 y z  0
D. y z  0
Câu 33. Trong không gian với hê ̣ to ̣a
đô ̣ O xyz, Gọi P là mặt phẳng chứa hai đường thẳng x y 1 z x y 1 z  4 (d ) :   (d ) :   M 1; 2;3 P 1 và . Khoảng cách từ điểm đến 1 2  3  2 1 2 5 bằng: Trang68 4 8 2 A. B. C. D. 6 6 6 6 x  3 y  2 z
Câu 34. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d: 
 và mặt cầu (S): 2 2 1 2 2 2
x y z  2x  2 y  4z 1  0 . Lập phương trình mặt phẳng (P) song song với d và trục Ox,
đồng thời tiếp xúc với mặt cầu (S). y    y  2z  2  0
A. 2x y  2  0
B. y  2z  8  2z 2 0 0 C. D.   y  2z 8  0 y  2z 8  0
Câu 35. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình 2 2 2
x y z  2x  4 y  6z 11  0 và mặt phẳng () có phương trình 2x + 2y – z + 17 = 0. Mặt
phẳng () song song với () và cắt (S) theo giao tuyến là đường tròn có chu vi bằng p  6 có
phương trình ax by cz 1  0 . Giá trị của T a b c bằng: A. T  3 3 B. T  7 3 C. T   3 D. T  3 hoặc T   7 17 7
Câu 36. Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng (P) qua O, vuông góc với
mặt phẳng (Q): x y z  0 và cách điểm M(1; 2; –1) một khoảng bằng 2 . x y  0
y z  0 x z  0
2x  5y  7z  0 A. B. C. D.     5
x 8y  3z  0
2x  5y  3z  0 5
x 8y  3z  0
2x 5y  3z  0
Câu 37. Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với (
A 1; 1; 2) , B(1;3; 0) , C( 3  ;4;1) ,
D(1; 2;1) . Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng
khoảng cách từ D đến (P).
x y z  
x  2y  4z  7  0
A. x  2 y  4z  7  0
B. x y  2z  4  2 4 7 0 0 C. D.  
x y  2z  4  0
x y  2z  4  0
Câu 38. Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng d , d lần lượt có phương trình 1 2 x  2 y  2 z  3 x 1 y  2 z 1 d :   d :   1 , 2
. Viết phương trình mặt phẳng cách đều hai 2 1 3 2 1  4
đường thẳng d , d . 1 2
A. 7x  2 y  4z  3  0
B. 7x  2 y  4z  3  0
C. 14x  4 y  8z 13  0
D. 14x  4 y  8z  3  0 x 1 y z  2
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và điểm ( A 2;5;3) . 2 1 2
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. x  4 y z  3  0
B. x  5 y z  3  0
C. x z 1  0
D. 2x y  2z  6  0
Câu 40. Trong không gian với hệ tọa độ Oxyz, cho điểm A10;2; – 
1 và đường thẳng d có phương x 1 y z 1 trình:  
. Lập phương trình mặt phẳng (P) đi qua A, song song với d và khoảng 2 1 3 Trang69
cách từ d tới (P) là lớn nhất.
A. 7x y  5z  77  0 B. 2x y z 19  0 C. 2x y  3z 19  0 D. 5x y  3z  77  0
Phần IV: 10 CÂU VẬN DỤNG CAO
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): 2 2 2
x y z  2x  4 y  4  0 và mặt
phẳng (P): x z  3  0 . Phương trình mặt phẳng (Q) đi qua điểm M (3;1; 1) vuông góc với
mặt phẳng (P) và tiếp xúc với mặt cầu (S) có dạng ax by cz  9  0 . Giá trị của a b c bằng: A. 0 B. 7 C. 1 hoặc 7  D. 7 hoặc 1
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P) : 5x  2 y  5z 1  0 và
(Q) : x  4 y  8z 12  0 . Gọi (R) là mặt phẳng đi qua gốc tọa độ O, không chứa trục Oy ,
vuông góc với mặt phẳng (P) và tạo với mặt phẳng (Q) một góc 0 45 . Khoảng cách từ M 1; 2
 ;3 đến R bằng: 3 2 31 2 3 2 A. B. C. 2 D. 2 hoặc 5 15 5
Câu 43. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2 y z  5  0 và đường thẳng x 1 y 1 z  3 d :  
. Viết phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt 2 1 1
phẳng (Q) một góc nhỏ nhất.
A. y z  4  0
B. x y z  3  0
C. x  2 y z  6  0
D. x  2 y 1  0 x 1 y  2 z
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   1 và 1 2 1  x  2 y 1 z d :   d 2
. Phương trình mặt phẳng (P) chứa
sao cho góc giữa mặt phẳng (P) và 2 1 2 1
đường thẳng d là lớn nhất là: ax y cz d  0 . Giá trị của T a c d bằng 2 A. T  3 B. T  13 0 C. T   D. T  6  4
Câu 45. Trong không gian toạ độ Oxyz, cho hai điểm A3; 2
 ;6 , B0;1;0 và mặt cầu
S x  2  y  2 z  2 : 1 2 3
 25 . Mặt phẳng P : ax by cz  2  0 đi qua , A B và cắt
S theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T abc . A. T  2 B. T  3 C. T  4 D. T  5
Câu 46. Trong không gian toạ độ Oxyz, cho điểm (
A 2; 2; 4) và mặt phẳng (P) : x y z  4  0 . Gọi
Q là mặt phẳng song song với (P) và cắt hai tia Ox, Oy tại 2 điểm B, C sao cho tam giác
ABC có diện tích bằng 6. Giả sử phương trình của Q là: ax by cz  4  0 . Giá trị của
a b c bằng A. 3 B. 6  C. 12 D. 3 
Câu 47. Trong không gian với hệ toạ độ Oxyz, mặt phẳng (P) đi qua điểm M (9;1;1) , cắt các tia Ox, Oy,
Oz tại A, B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất có phương trình Trang70
x By Cz D  0 . Giá trị của B C D bằng A. 9  B. 27  C. 45 D. 19
Câu 48. Trong không gian với hệ toạ độ Oxyz, cho hai điểm A 1  ; 2  ; 3   , B 6  ;10; 3
  . Gọi P là
mặt phẳng sao cho khoảng cách từ điểm A đến mặt phẳng  P bằng 15 và khoảng cách từ điểm
B đến mặt phẳng  P bằng 2. Mặt phẳng  P đi qua điểm nào sau đây? A. M 8; 3  ;  1 B. M 18; 3  ;1  1 C. M 52; 7  ;13 D. M  4  0; 2  ; 1  5 Câu 49. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng  x m y m z m   3 1  d   m   1  ; ;  mdmm  4 3 2 3 8 7 : , với . Khi thay đổi thì 2m 1 m 1 4m  3  4 2 
luôn nằm trong một mặt phẳng cố định  P : ax by cz  6  0 . Tính a b c ? A. 10 B. 9 C. 7 D. 8
Câu 50. Trong không gian với hệ toạ độ Oxyz, cho các điểm A ;
a 0; 0 , B 0; ;
b 0 , C 0;0;c với
a, b, c  0 thỏa mãn a b c  2 . Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại
tiếp tứ diện OABC thuộc một mặt phẳng  P cố định. Tính khoảng cách từ điểm
M 2016;0;0 đến mặt phẳng  P . 2015 2016 2014 A. B. 2016 C. D. 3 3 3
------------------------HẾT--------------------------- ĐÁP ÁN
Phần I: 10 CÂU NHẬN BIẾT Câu 1.
Trong không gian tọa độ Oxyz , mặt phẳng đi qua điểm M x ; y ; z n  a; ; b c 0 0 0  nhận với 2 2 2
a b c  0 làm vectơ pháp tuyến có phương trình là: A. x
x a y
y b z z c  0 x
x a y
y b z z c  0 0   0   0   0   0   0   B.
C. a x x b y y c z z  0
a x x b y y c z z  0 0   0   0  0   0   0  D. . Hƣớng dẫn giải:
Chọn đáp án D: a x x b y y c z z  0 0   0   0  Câu 2.
Trong không gian với hệ tọa độ Oxyz, phương trình của mặt phẳng Oxy là: A. x  0 B. y  0 C. z  0
D. x y  0
Hƣớng dẫn giải: Chọn đáp án C Câu 3.
Trong không gian với hệ tọa độ Oxyz, một vectơ pháp tuyến của mặt phẳng x 3z  4  0 là:    
A. n  1; 3; 4
B. n  1;3; 4
C. n  1;0;3
D. n  1;0;3
Hƣớng dẫn giải: Chọn đáp án C Trang71 Câu 4.
Trong không gian với hệ tọa độ Oxyz, điểm nào sau đây thuộc mặt phẳng x  2 y  3z  4  0 : A. M 1; 2  ;3 B. N 1;1  ;1 C. E 4;0  ;1 D. F 0; 2  ;0
Hƣớng dẫn giải: Chọn đáp án D Câu 5.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A ;
a 0;0, B 0, ;
b 0, C 0;0;c với abc  0 có phương trình là: x y z x y z A.    1 B.
  1  0 C. ax by cz  1
D. bcx cay abz  1 a b c a b c
Hƣớng dẫn giải: Chọn đáp án A Câu 6.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng  P : x  2y  3z  4  0 và Q: 2
x  4y  6z  4  0 . Khẳng định nào đúng?
A. P và Q cắt nhau.
B. P  Q
C. P / / QD.
P  Q 1 2  3 4 
Hƣớng dẫn giải: Vì   
nên  P / / Q . Chọn đáp án C 2 4 6  4 Câu 7.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào sau đây chứa trục Ox :
A. y z  0 B. 2
x y  0
C. 2x y z  0 D. 2
x z  0
Hƣớng dẫn giải: Mặt phẳng chứa trục Ox có phương trình dạng: by cz  0 . Chọn đáp án A Câu 8.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào sau đây song song với trục Oy :
A. y  2  0
B. 2x  3z 1  0
C. 2x y  3z  4  0 D. 2
x z  0
Hƣớng dẫn giải: Mặt phẳng song song với trục Oy có phương trình dạng:
ax cz d  0 d  0 . Chọn đáp án B Câu 9.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng nào sau đây song song với mặt phẳng Oyz  ? A. 2z  0 B. 2  z 1 0 C. 2  x  0 D. 2  x 1 0
Hƣớng dẫn giải: Mặt phẳng song song với mặt phẳng Oyz có phương trình dạng x x x  0 0  0  . Chọn đáp án D
Câu 10. Trong không gian với hệ tọa độ Oxyz, khoảng cách từ gốc tọa độ O đến mặt phẳng
P: x 2y  2z 1 0 bằng: 1 1 1 A. 1 B. C. D.  9 3 3 0  2.0  2.0 1 Hƣớ 1
ng dẫn giải: Ta có d O,P   . Chọn đáp án C   2 2 2 3 1 2  2
Phần II: 15 CÂU THÔNG HIỂU Trang72 
Câu 11. Giả sử n là một vectơ pháp tuyến của mặt phẳng  P . Khẳng định nào sai?  
A. Giá của n vuông góc với  P .
B. k n k   \  
0  là vectơ pháp tuyến của P   1 
C. n là một vectơ khác 0 . D.
n không phải là vectơ pháp tuyến 2017 của  P . Hƣớng dẫn giải:  1 
Vì k n k   \  
0  là vectơ pháp tuyến của P nên 
n cũng là vectơ pháp tuyến của 2017
P . Chọn đáp án D  
Câu 12. Cho u , uP 1
2 là hai vectơ có giá song song hoặc nằm trên mặt phẳng
. Khẳng định nào đúng?   
A. n u
 ,u  là một vectơ pháp tuyến của P . 1 2       
B. n u
 ,u  là một vectơ pháp tuyến của P nếu u , u không cùng phương. 1 2   1 2     
C. n u
 ,u  là một vectơ pháp tuyến của P khi và chỉ khi u u 1 2   1 2     
D. n u
 ,u  là một vectơ pháp tuyến của P khi u , u 1 2 cùng phương. 1 2  
Hƣớng dẫn giải: Chọn đáp án B
Câu 13. Trong không gian với hệ toạ độ Oxyz, có hai giá trị của tham số m để hai mặt phẳng
P: x 3y  2z 1 0 và Q:2m 
1 x m1 2my  2m  4 z 14  0 vuông góc với
nhau. Tính tổng các bình phương của hai số đó. 19 13 29 17 A. B. C. D. 4 4 4 4 Hƣớng dẫn giải: m 1 
Ta có  P  Q  12m  
1  3m 1 2m  22m  4 2
 0  2m m  3  0  3 m    2 2  3  13 Suy ra 2 1      . Chọn đáp án B.  2  4 Phƣơng án nhiễu:
A, C, D là các phương án gây nhiễu hoặc do tính toán sai.
Câu 14. Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua A1; 2;3 và vuông góc với trục Oy có phương trình là:
A. x  2 y  3z  0
B. x z  4  0
C. y  2  0
D. x  3z 10  0 Trang73 Hƣớng dẫn giải:
Vectơ pháp tuyến của mặt phẳng là j  0;1;0 nên phương trình mặt phẳng là: y  2  0 . Chọn đáp án C. Phƣơng án nhiễu:
A. Nhầm tọa độ điểm thành tọa độ vectơ pháp tuyến.
B. Nhầm phương trình mặt phẳng vuông góc với Oy thành phương trình mặt phẳng song song với Oy
D. Một phương án gây nhiễu thêm.
Câu 15. Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua A1; 2;3 và chứa trục Oz có phương trình là: A. z  3
B. x  2 y  3z  0
C. 2x y  0
D. x  2 y  5  0 Hƣớng dẫn giải:
Phương trình mặt phẳng chứa trục Oz là ax by  0 . Thay tọa độ A1;2;3 vào pt được a  2
b . Suy ra phương trình 2x y  0 . Chọn đáp án C. Phƣơng án nhiễu:
A. Nhầm mặt phẳng chứa Oz với mặt phẳng vuông góc với Oz .
B. Nhầm vectơ pháp tuyến với điểm đi qua.
D. Một phương án gây nhiễu khi kiểm tra điểm đi qua.
Câu 16. Trong không gian với hệ tọa độ Oxyz, cho điểm M 1; 2;3 và hai mặt phẳng
Q: x 2y 3  0 và R: y 3z 4  0 . Mặt phẳng P đi qua M đồng thời vuông góc với
cả Q và  R có phương trình là: A. 6
x  3y z  3  0 B. x  7y  5z  28  0
C. 6x  3y z  9  0
D. x  7 y  5z  0 Hƣớng dẫn giải:  
Ta có vectơ pháp tuyến của Q và R lần lượt là n  1; 2
 ;0, n  0;1;3 Q R .   
Suy ra vectơ pháp tuyến của P là n  n ,n     P Q R  6; 3;  1 . Suy ra pt  
P:6x 3y z 9  0 . Chọn C. Phƣơng án nhiễu:
A. Tính nhầm vectơ pháp tuyến thành  6  ;3;  1 .   
B. Tính nhầm n  1; 2
 ;3, n  1;3; 4  n   1  ;7;5 PQ R  nên được vtpt .
D. Một phương án gây nhiễu thêm do nhầm như B. Trang74
Câu 17. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A1; 2;3, B  1  ; 2  ; 3   . Mặt phẳng trung
trực của đoạn thẳng AB có phương trình là:
A. 2x  4 y  6z  28  0 B. 2x  4 y  6z  28  0 C.
x  2 y z  0
D. x  2 y  3z  0 Hƣớng dẫn giải: 
Trung điểm của AB là O 0;0;0 , vectơ pháp tuyến của mặt phẳng trung trực là OA  1;2;3
nên phương trình mặt phẳng trung trực là x  2y  3z  0 . Chọn đáp án D. Phƣơng án nhiễu:  A,
B. Tính được AB  2; 4; 6 là vectơ pháp tuyến, nhưng lại thay
điểm đi qua là A hoặc B .
C. Học sinh nghĩ mặt phẳng trung trực của AB phải chứa cả A và B nên thay cả tọa độ , A B vào đều thỏa mãn.
Câu 18. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A1;0;0, B 0; 2;0, C 0;0;3 . Mặt phẳng
ABC có phương trình là: x y z x y z
A. 6x  3y  2z  6  0 B.    0
C. 6x  3y  2z  6  0 D.    1 1 2 3 1 2 3 Hƣớng dẫn giải: x y z
Dùng phương trình đoạn chắn ta được    1 . Chọn đáp án D. 1 2 3 Phƣơng án nhiễu:
A, B, C là các phương án gây nhiễu khi học sinh chỉ biết thử tọa độ điểm.
Câu 19. Trong không gian với hệ tọa độ Oxyz, cho điểm M  ; a ;
b c với abc  0. Gọi ,
A B, C lần lượt
là hình chiếu của M trên các mặt phẳng tọa độ Oxy, Oyz, Ozx . Phương trình của mặt
phẳng  ABC  là: x y z x y z x y z x y z A.    1 B.    0 C.    2 D.    3 a b c a b c a b c a b c Hƣớng dẫn giải:
Cách 1: Thay tọa độ A ; a ;
b 0, B 0; ; b c, C  ;
a 0;c vào các pt ta được đáp án C.
Cách 2: Mặt phẳng  ABC  cắt các trục tọa độ Ox, Oy, Oz tại các điểm  x y z x y z 2 ; a 0;0, 0;2 ;
b 0, 0;0;2c nên phương trình là    1     1 . 2a 2b 2c a b c Phƣơng án nhiễu:
A. Nhầm tọa độ hình chiếu trên mặt phẳng tọa độ với tọa độ hình chiếu trên các trục tọa độ. Trang75
B và D là các phương án gây nhiễu thêm.
Câu 20. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P đi qua gốc tọa độ O và song song với
mặt phẳng Q : x  2y  3z  4  0 có phương trình là:
A. x  2 y  3z  4  0
B. x  2 y  3z  0
C. x  2 y  3z  0
D. 2x  4 y  6z  0 Hƣớng dẫn giải:
Vì (P) đi qua O nên loại A. Vì (P) song song với (Q) nên chọn được D.
Câu 21. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P song song với mặt phẳng
Q: x 2y  2z 1 0 và cách Q một khoảng bằng 3 có phương trình là:
x y z  
A. x  2 y  2z  8  0
B. x  2 y  2z 10  2 2 8 0 0 C. D.
x  2y  2z 10  0
x  2 y  2z  2  0 Hƣớng dẫn giải:
Vì  P / / Q nên phương trình của  P là x  2y  2z D  0  D    1 . D 1 D  8
Khoảng cách giữa  P và Q bằng d (P),(Q)   3  .     2 2 2  D  10  1 2 2
Suy ra phương trình của P là x  2y  2z  8  0 hoặc x  2y  2z 10  0 . Phƣơng án nhiễu: A,
B. Nhầm công thức tính khoảng cách không có dấu trị tuyệt đối trên tử thức.
D. Không biết công thức tính khoảng cách giữa hai mặt phẳng. Cộng thêm 3 vào pt của Q .
Câu 22. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P đi qua điểm M 1; 2
 ;3 và cách gốc tọa
độ một khoảng lớn nhất có phương trình là:
A. x  2 y  3z  6  0
B. x y z  2  0
C. x  2 y  3z 12  0 D. x  2 y  3z 14  0 Hƣớng dẫn giải:  Khoảng cách d  ;
O P  OH OM do đó P cần tìm nhận OM  1; 2  ;3 làm vectơ pháp
tuyến. Chọn đáp án D. Phƣơng án nhiễu:
Các phương án A, B, C đều gây nhiễu nếu dùng phép thử. Cả 4 đáp án đều thỏa mãn điều kiện
P đi qua M . Việc thử bằng công thức khoảng cách sẽ mất nhiều thời gian.
Câu 23. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P song song với hai đường thẳng Trang76 x  2  t x  2 y 1 z   :  
 : y  3 2t 1 và
nhận vectơ nào sau đây làm vectơ pháp tuyến? 2 3  4 2 z 1t      A. n   5  ;6; 7  
B. n  5; 6;7 C. n   5  ; 6  ;7 D. n  5; 6  ; 7   Hƣớng dẫn giải:  
 ,  lần lượt có các vectơ chỉ phương là u  2;3;4 , u  1;2;1 1   2   . Suy ra 1 2   u  ,u   5  ;6;7 1 2         P   / / n u     1 Vì  nên P 1
   n k u ,u k  0 k  1  n  5; 6  ; 7  PP 1 2  . Chọn ta được .     P   / /   2 n uP 2 Chọn đáp án D. Phƣơng án nhiễu:
A, B, C do tính sai công thức nên nhầm dấu.
Câu 24. Trong không gian với hệ tọa độ Oxyz, mặt phẳng  P đi qua M 1; 2;3 và cắt các trục tọa độ
Ox, Oy, Oz lần lượt tại ,
A B, C sao cho M là trọng tâm tam giác ABC . Phương trình của P là: x y z x y z
A. x  2 y  3z 14  0 B.    1 C.    1
D. x y z  6  0 1 2 3 3 6 9 Hƣớng dẫn giải: a b c  Gọi A ;
a 0;0, B 0; ;
b 0, C 0;0;c suy ra trọng tâm là M ; ;
a  3,b  6,c  9   .  3 3 3  x y z
Phương trình đoạn chắn của P là:    1 . Chọn đáp án C. 3 6 9 Phƣơng án nhiễu:
A. Nhầm trọng tâm M 1; 2;3 thành trực tâm của tam giác ABC .
B. Nhầm A, B, C là hình chiếu của M trên các trục tọa độ.
D. Một phương án nhiễu dựa trên suy đoán trọng tâm thường gắn với tỉ lệ 1:1:1.
Câu 25. Trong không gian với hệ trục tọa độ Oxyz, cho điểm M 4;5;6 . Phương trình mặt phẳng (P)
qua M, cắt các trục tọa độ lần lượt tại I, J, K mà M là trực tâm của tam giác IJK là x y z x y z A.    1 B.    1
C. x  2 y  3z  32  0 D. 12 15 18 4 5 6
4x  5 y  6z  77  0 Hướng dẫn giải: 
M là trực tâm tam giác IJK suy ra OM   P hay P có vectơ pháp tuyến là OM  4;5;6 Trang77
Vậy phương trình mặt phẳng (P): 4x  5 y  6z  77  0 . Chọn đáp án D. Phƣơng án nhiễu:
A. Nhầm trực tâm và trọng tâm. Suy ra I 12;0;0, J 0;15;0, K 0;0;18 .
B. Hiểu I , J , K là hình chiếu của M trên các trục tọa độ.
C. Một phương án gây nhiễu thêm.
Phần III: 15 CÂU VẬN DỤNG THẤP
Câu 26. Trong không gian với hệ toạ độ Oxyz, phương trình mặt phẳng (P) đi qua điểm M (1; 2;3) , cắt 1 1 1
các tia Ox, Oy, Oz tại A, B, C sao cho biểu thức  
có giá trị nhỏ nhất là: 2 2 2 OA OB OC x y z x y z
A. x y z  6  0 B.    3
C. x  2 y  3z 14  0 D.    1 1 2 3 1 2 3 Hƣớng dẫn giải: 1 1 1 1
Gọi H là hình chiếu của O trên mặt phẳng  P . Ta có    . 2 2 2 2 OA OB OC OH 1 1 1 Để  
nhỏ nhất thì OH lớn nhất. Mặt khác OH OM nên OH lớn nhất 2 2 2 OA OB OC 
bằng OM khi H M . Hay OM   P , nghĩa là  P có vectơ pháp tuyến là OM  1; 2;3 .
Suy ra phương trình của P là: x  2y  3z 14  0 . Chọn đáp án (C). Phƣơng án nhiễu: 1 1 1 1
A. Nhầm lẫn khi sử dụng bất đẳng thức Cô si: 3    3 và dựa 2 2 2 2 2 2 OA OB OC OA OB OC 1 1 1 1
vào điều kiện xảy ra đẳng thức suy ra   nhỏ nhất bằng 3 3 khi 2 2 2 OA OB OC 2 2 2 OA OB OC
OA OB OC . 
Từ đó suy ra vectơ pháp tuyến là n  1;1  ;1 .
B và D là các phương án gây nhiễu thêm.
Câu 27. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng  P : 4x  3y  7z  3  0 và điểm I 1; 1
 ;2 . Mặt phẳng Q đối xứng với P qua điểm I có phương trình
4x by cz d  0 . Giá trị của b c d là: A. 2 B. 0 C. 1 D. 1 Hƣớng dẫn giải: Trang78
x  2  x ' 
Cách 1: Biểu thức tọa độ của phép đối xứng tâm I 1; 1
 ;2 là: y  2
  y ' thay vào pt của z  4 z'  P được
42  x '  3 2
  y ' 74  z ' 3  0  4x' 3y ' 7z '11  0 hay pt
Q:4x 3y 7z 11 0  bc d  3
  7 111. Chọn đáp án C.
Cách 2: Ta có Q / /  P nên phương trình Q : 4x  3y  7z d  0 . Điểm A0;1;0  P .
Điểm đối xứng của A qua I là A'2; 3
 ;4 . Vì A'Q nên d 11. Phƣơng án nhiễu:
A, B, D là các phương án gây nhiễu.
Câu 28. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A0;1; 2, B 2; 2  ;  1 , C  2  ;1;0 . Phương
trình mặt phẳng  ABC  là ax y cz d  0 . Giá trị của a d bằng A. 4  B. 2  C. 4 D. 2 Hƣớng dẫn giải:   Cách 1: AB  2; 3  ; 
1 , AC  2;0; 2  21;0;  1 , 
 1  suy ra nA , B AC  3  ; 3  ;3  3  1;1; 1  ( ABC )     .    2 
Do đó pt P : x y z 1  0  a d  2 . Chọn đáp án D.
Cách 2: Thay tọa độ các điểm ,
A B, C vào phương trình của  P suy ra  2c d  1  a 1  
2a c d  2  c   1    2
a d  1  d  1  
Do đó a d  2 . Chọn đáp án D. Phƣơng án nhiễu:
A. Do tính nhầm tích có hướng được vectơ pháp tuyến là  1  ;1;  1 nên pt
P:x y z 3  0 . 
2c d 1  0 
B. Do giải hệ phương trình 2a c d  2  0 bằng MTBT nhưng quên chuyển các hệ số tự do  2
a d 1  0 
sang bên phải dấu bằng nên kết quả đổi dấu a  1  ; d  1 
C. Một đáp án gây nhiễu thêm. Trang79 2 2 2
Câu 29. Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu S : x 1  y  2  z  3  16 1        và
S : x 1  y  2  z 3  25 C 2   2  2  2
cắt nhau theo giao tuyến là một đường tròn . Viết
phương trình mặt phẳng P chứa đường tròn C :
A. x  2 y  3z  9  0
B. x  2 y  3z  9  0 C. 4x  8 y 12z  9  0 D.
4x  8 y 12z  9  0 Hƣớng dẫn giải:
Vì khoảng cách giữa hai tâm I I  56  9  4  5  R RSS2  1  1 2 1 2 nên và cắt nhau theo
một đường tròn. Mặt phẳng chứa đường tròn này là mặt phẳng đẳng phương của  SS2  1  và .
Lấy phương trình  SS
4x  8 y 12z  9  0 1  2  trừ phương trình ta được . Chọn đáp án D. Phƣơng án nhiễu: 
A, B, C đều có vectơ pháp tuyến cùng phương với I I
1 2 nên không loại ngay được phương án nào cả.
Vấn đề tìm điểm giao của mặt phẳng  P với I I làm mất thời gian. 1 2
Câu 30. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A2; 4;  1 , B  1
 ;1;3 và mặt phẳng (P):
x – 3y  2z – 5  0 . Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình là
A. x y  3z  9  0
B. 3x y 10  0
C. 8 y 12z  61  0
D. 2 y  3z 11  0 Hướng dẫn giải:    
(Q) đi qua A, B và vuông góc với (P) (Q) có VTPT n  n , AB  (0; 8  ; 1  2)  0   P
 (Q) : 2y  3z 11  0 . Chọn đáp án D. Phƣơng án nhiễu:
A. Thử tọa độ A và B thấy thỏa mãn.
B. Thử thấy vuông góc với  P .    
C. Vội vàng chọn đáp án khi tính được n  n , AB  (0; 8  ; 1  2)  0  P.
Câu 31. Trong không gian với hệ toạ độ Oxyz, cho 2 đường thẳng (d ) và (d ) có phương trình: 1 2 x 1 y 1 z  2 x  4 y 1 z  3 (d );   (d ) :   (d ) 1 , 2
. Mặt phẳng (P) chứa (d ) và có 2 3 1 6 9 3 1 2 phương trình là A. Không tồn tại
B. x y z  0
C. 2x  3y z 1  0 D. x y  5z 10  0 Hƣớng dẫn giải: 
Ta có d đi qua M 1; 1  ;2 u  2;3;1 1   1   có vectơ chỉ phương . 1 Trang80  d đi qua M 4;1;3 u  6;9;3 2   2   có vectơ chỉ phương . 2     Vì u u u M M  3; 2;1 d / /d 1 2   1 và 2 cùng phương, 1 và không cùng phương nên . 1 2   
Vectơ pháp tuyến của P là n u  ,M M   1;1; 5  PP 1 1 2  . Suy ra phương trình là:  
x y  5z 10  0 . Chọn (D). Phƣơng án nhiễu:    A. Do tính u
 ,u   0;0;0  0 P 1 2  
nên kết luận không tồn tại .   
B. Thay nhầm tọa độ vectơ chỉ phương bằng tọa độ điểm đi qua: n  5;5;5 P     
C. Vì u  3u n u 2 1 nên chọn luôn . p 1
Câu 32. Trong không gian với hệ trục Oxyz, cho mặt cầu (S): 2 2 2
x y z – 2x  4 y  2z – 3  0 .
Phương trình mặt phẳng (P) chứa trục Ox và cắt mặt cầu (S) theo một đường tròn có bán kính r  3 là:
A. y  2z  0 B. x  0
C. 2 y z  0
D. y z  0
Hƣớng dẫn giải:
(S) có tâm I(1; –2; –1), bán kính R = 3. (P) chứa Ox (P): ay + bz = 0.
Mặt khác đường tròn giao tuyến có bán kính bằng 3 cho nên (P) đi qua tâm I.
Suy ra: –2a – b = 0 b = –2a (a 0) (P): y – 2z = 0. Chọn đáp án A. Phƣơng án nhiễu:
B. Nhầm mặt phẳng chứa trục Ox là: x  0
C. Tính nhầm hệ số của y và z thành a  2  b .
D. Một phương án gây nhiễu thêm.
Câu 33. Trong không gian với hê ̣ to ̣a đô ̣ O
xyz, Gọi  P là mặt phẳng chứa hai đường thẳng x y 1 z x y 1 z  4 (d ) :   (d ) :   M 1; 2;3 P 1 và . Khoảng cách từ điểm đến 1 2  3  2 1 2 5 bằng: 4 8 2 A. B. C. D. 6 6 6 6 Hƣớng dẫn giải:   d qua M (0; 1
 ;0) và có u  (1; 2  ; 3
 ) , d qua M (0;1;4) và có u  (1;2;5) . 1 1 1 2 2 2         u ;u  ( 4  ; 8
 ;4)  0 M M  (0;2;4)
u ;u .M M  0 d ,d 1 2  1 2  , 1 2   đồng phẳng. 1 2 1 2 
(P) có VTPT n  (1; 2; 1  ) và đi qua M    
1 nên có phương trình x 2 y z 2 0 . Trang81
Khoảng cách d M P 4 ;  . Chọn đáp án A. 6 Phƣơng án nhiễu:
B. Tính sai vectơ pháp tuyến thành n  (1; 2; 1) nên được pt x  2 y z  2  0
C, D là các phương án gây nhiễu thêm. x  3 y  2 z
Câu 34. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d: 
 và mặt cầu (S): 2 2 1 2 2 2
x y z  2x  2 y  4z 1  0 . Lập phương trình mặt phẳng (P) song song với d và trục Ox,
đồng thời tiếp xúc với mặt cầu (S). y    y  2z  2  0
A. 2x y  2  0
B. y  2z  8  2z 2 0 0 C. D.   y  2z 8  0 y  2z 8  0
Hƣớng dẫn giải:
(S) có tâm I(1; 1; 2), bán kính R  5 . d có VTCP u  (2; 2;1) .   
(P) // d, Ox (P) có VTPT n  u,i   (0;1; 2
 )  PT của (P) có dạng: y  2z  D  0 . 1 4  DD  
(P) tiếp xúc với (S) d (I , (P))  R   5  D 3  2 5   2 2 1  2 D  8
(P): y  2z  2  0 hoặc (P): y  2z  8  0 .
Vì điểm M 3;2;0d và M 3;2;0P : y  2z  2  0 nên mặt phẳng cần tìm là
P: y 2z 8  0 Phƣơng án nhiễu:
A: Thử bằng máy tính thấy d I; P  5
C. Quên kiểm tra tính song song của (P) và d. D
D. Tính nhầm D  3  2 5 được .  D  8
Câu 35. Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình 2 2 2
x y z  2x  4 y  6z 11  0 và mặt phẳng () có phương trình 2x + 2y – z + 17 = 0. Mặt
phẳng () song song với () và cắt (S) theo giao tuyến là đường tròn có chu vi bằng p  6 có
phương trình ax by cz 1  0 . Giá trị của T a b c bằng: A. T  3 3 B. T  3 C. T   3 D. T  hoặc 7 7 17 3 T   7 Hƣớng dẫn giải:
Do () // () nên () có phương trình 2x + 2y – z + D = 0 (D 17) Trang82
(S) có tâm I(1; –2; 3), bán kính R = 5. Đường tròn có chu vi 6 nên có bán kính r = 3.
Khoảng cách từ I tới () là h = 2 2 2 2
R r  5  3  4 2.1 2( 2  )  3 DD  7  Do đó  4  5   D 12   2 2 2    D 17 (loaïi) 2 2 ( 1) 2 2 1
Vậy () có phương trình 2x  2 y – z – 7  0   x y z 1  3
0 . Suy ra T   . Chọn 7 7 7 7 C. Phƣơng án nhiễu:
A. Không để ý d  1 trong phương trình ax by cz 1  0 .
B. Không để ý đến phương trình ax by cz 1  2 2 1 0 nên từ pt x y z 1  0 suy ra 7 7 7 3 T  . 7
D. Không để ý điều kiện song song của   và   dẫn đến không có điều kiện D 17 .
Câu 36. Trong không gian với hệ toạ độ Oxyz, viết phương trình mặt phẳng (P) qua O, vuông góc với
mặt phẳng (Q): x y z  0 và cách điểm M(1; 2; –1) một khoảng bằng 2 . x y  0
y z  0 x z  0
2x  5y  7z  0 A. B. C. D.     5
x 8y  3z  0
2x  5y  3z  0 5
x 8y  3z  0
2x 5y  3z  0 Hƣớng dẫn giải:
PT mặt phẳng (P) qua O nên có dạng: Ax  By Cz  0 (với 2 2 2
A B C  0 ).
Vì (P) (Q) nên: 1.A 1.B 1.C  0  C  AB (1)
A  2B C d(M , ( ) P )  2   2  2 2 2 2
( A  2B C)  2( A B C ) (2) 2 2 2
A B CB
Từ (1) và (2) ta được: 2 8AB  5B  0 (3) 0  8  A  5B  0 (4)
Từ (3): B = 0 C = –A. Chọn A = 1, C = –1 (P): x z  0
Từ (4): 8A + 5B = 0. Chọn A = 5, B = –8 C = 3 (P): 5x  8 y  3z  0 . Chọn đáp án C. Phƣơng án nhiễu:
A, B, D là các phương án gây nhiễu về mặt hình thức, hoặc làm tốn thời gian khi sử dụng cách
thử các điều kiện trong đề bài.
Câu 37. Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với (
A 1; 1; 2) , B(1;3; 0) , C( 3  ;4;1) ,
D(1; 2;1) . Viết phương trình mặt phẳng (P) đi qua A, B sao cho khoảng cách từ C đến (P) bằng
khoảng cách từ D đến (P). Trang83
x y z  
x  2y  4z  7  0
A. x  2 y  4z  7  0
B. x y  2z  4  2 4 7 0 0 C. D.  
x y  2z  4  0
x y  2z  4  0 Hƣớng dẫn giải:
Cách 1: PT mặt phẳng (P) có dạng: 2 2 2
ax by cz d  0 (a b c  0) . A(P)
a b  2c d  0  
Ta có: B  (P)
 a  3b d  0  
d(C,(P))  d(D,(P)) 3
 a  4b c d
a  2b c d    2 2 2 2 2 2 
a b c
a b c       b 2 , a c 4 , a d 7a  c  2 , a b  , a d  4  a
+ Với b  2a, c  4a, d  7
a (P): x  2y  4z  7  0 .
+ Với c  2a, b a, d  4
a (P): x y  2z  4  0 .  
Cách 2: Ta có AB  0; 4; 2    20;2;  1 , CD  4; 2  ;0  22; 1
 ;0 . Trung điểm của CD là I  1  ;3  ;1 .
Mặt phẳng  P đi qua ,
A B và cách đều C, D nên:
TH1:  P chứa AB và song song với CD   P : x  2y  4z  7  0
TH2:  P đi qua 3 điểm ,
A B, I   P : x y  2z  4  0 Phƣơng án nhiễu: A: Chỉ xét được TH1.
B. D là các phương án gây nhiễu thêm.
Câu 38. Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng d , d lần lượt có phương trình 1 2 x  2 y  2 z  3 x 1 y  2 z 1 d :   d :   1 , 2
. Viết phương trình mặt phẳng cách đều hai 2 1 3 2 1  4
đường thẳng d , d . 1 2
A. 7x  2 y  4z  3  0 B. 7x  2 y  4z  3  0 C. 14x  4 y  8z 13  0 D.
14x  4 y  8z  3  0 Hƣớng dẫn giải:  
Cách 1: Ta có d đi qua A(2;2;3), có u
 (2;1;3) , d đi qua B(1;2;1) và có u  (2; 1  ;4) . 1 d1 2 d 2   
Do (P) cách đều d , d nên (P) song song với d , d n  u ,u  (7; 2  ; 4  ) P d1 d 2  1 2 1 2
PT mặt phẳng (P) có dạng: 7x  2y  4z d  0
Do (P) cách đều d , d suy ra d ( ,
A (P))  d (B, (P)) 1 2 Trang84        7.2 2.2 4.3 d 7.1 2.2 4.1 d  3
d  2  d 1  d 69 69 2
Phương trình mặt phẳng (P): 14x  4y 8z  3  0  
Cách 2: Ta có d đi qua A(2;2;3), có u
 (2;1;3) , d đi qua B(1;2;1) và có u  (2; 1  ;4) . 1 d1 2 d 2   
Do (P) cách đều d , d nên (P) song song với d , d n  u ,u  (7; 2  ; 4  ) P d1 d 2  1 2 1 2  3 
Mặt khác (P) đi qua trung điểm của đoạn AB là I ; 2; 2   nên pt (P) là:  2 
14x  4 y  8z  3  0 Phƣơng án nhiễu:
A, B, C là các phương án nhiễu về hình thức hoặc do tính sai tích có hướng. x 1 y z  2
Câu 39. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d :   và điểm ( A 2;5;3) . 2 1 2
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. x  4 y z  3  0
B. x  5 y z  3  0
C. x z 1  0
D. 2x y  2z  6  0 Hƣớng dẫn giải: Ta có d  ;
A P  AH AK d  ; A d  . A Suy ra d  ;
A P lớn nhất bằng d  ;
A d  khi H K hay
AK   P . d H
Suy ra d; A   P . K P 
Ta có d đi qua M 1;0; 2 và có vtcp là u  2;1; 2 d  .   1   1 MA  1;5;  1 . Suy ra n
  u , MA   9;0;9  1;0;1 d ; A d         9 9    n u  ,n   1  ;4; 1 
P: x 4y z 3  0 P d d ;A   . Suy ra pt .     Phương án nhiễu:
B. Mặt phẳng này đi qua M 1;0; 2 và vuông góc với AM nên nếu thử tính khoảng cách thì
được kết quả bằng AM AK .
C. Là mặt phẳng chứa A và d.
D. Một phương án gây nhiễu thêm. Đây là mặt phẳng qua M và vuông góc với d .
Câu 40. Trong không gian với hệ tọa độ Oxyz, cho điểm A(10; 2; –1) và đường thẳng d có phương x 1 y z 1 trình:  
. Lập phương trình mặt phẳng (P) đi qua A, song song với d và khoảng 2 1 3
cách từ d tới (P) là lớn nhất. Trang85
A. 7x y  5z  77  0 B. 2x y z 19  0 C. 2x y  3z 19  0 D. 5x y  3z  77  0 Hƣớng dẫn giải:
Gọi H là hình chiếu của A trên d d(d, (P)) = d(H, (P)). Giả sử điểm I là hình chiếu của H
lên (P), ta có AH HI HI lớn nhất khi A I . Vậy (P) cần tìm là mặt phẳng đi qua A và 
nhận AH làm VTPT (P): 7x y  5z  77  0 . Phƣơng án nhiễu:
B, C, D là các phương án nhiễu làm mất nhiều thời gian để thử các điều kiện nếu chọn cách thử.
C. Nhầm mặt phẳng song song với d thành mặt phẳng vuông góc với d
D. Nếu tính khoảng cách thì đáp án D cho kết quả lớn nhất, tuy nhiên mặt phẳng ở đáp án D không đi qua
A.
Phần IV: 10 CÂU VẬN DỤNG CAO
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): 2 2 2
x y z  2x  4 y  4  0 và mặt
phẳng (P): x z  3  0 . Phương trình mặt phẳng (Q) đi qua điểm M (3;1; 1) vuông góc với
mặt phẳng (P) và tiếp xúc với mặt cầu (S) có dạng ax by cz  9  0 . Giá trị của a b c bằng: A. 0 B. 7 C. 1 hoặc 7  D. 7 hoặc 1
Hƣớng dẫn giải:
(S) có tâm I(–1; 2; 0) và bán kính R = 3; (P) có VTPT n  (1; 0;1) . P
PT (Q) đi qua M có dạng: 2 2 2 (
A x  3)  B( y 1)  C(z 1)  0, A B C  0
(Q) tiếp xúc với (S)  2 2 2
d (I , (Q))  R  4
A B C  3 A B C (*)   ( ) Q  ( )
P n .n  0  A C  0  C  A (**) Q P Từ (*), (**)  2 2 2 2
B  5A  3 2A B  8B  7 A 10AB  0  A  2B  7A  4  B
Với A  2B . Chọn B = 1, A = 2, C = –2 PT (Q): 2x y  2z  9  0 Với 7A  4
B . Chọn B = –7, A = 4, C = –4 PT (Q): 4x  7y  4z  9  0 Chọn đáp án C. Phƣơng án nhiễu:
A. Vì Q   P nên dự đoán vectơ pháp tuyến của Q là 1;0; 1  .
B và D là các phương án gây nhiễu thêm.
Câu 42. Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P) : 5x  2 y  5z 1  0 và
(Q) : x  4 y  8z 12  0 . Gọi (R) là mặt phẳng đi qua gốc tọa độ O, không chứa trục Oy ,
vuông góc với mặt phẳng (P) và tạo với mặt phẳng (Q) một góc 0 45 . Khoảng cách từ Trang86 M 1; 2
 ;3 đến R bằng: 3 2 31 2 3 2 A. B. C. 2 D. 2 hoặc 5 15 5 Hƣớng dẫn giải:
Giả sử PT mặt phẳng (R): 2 2 2 ax  by  z
c d  0 (a b c  0) .
Ta có: (R)  (P)  5a  2b  5c  0 (1);
a  4b  8c 2 0
cos((R), (Q))  cos 45   (2) 2 2 2   2 9 a b ca cTừ (1) và (2)  2 2
7a  6ac c  0   c  7a
Với a  c : chọn a 1,b  0,c  1 PT mặt phẳng (R) : x z  0 (loại)
Với c  7a : chọn a 1,b  20,c  7  PT mặt phẳng (R) : x  20y  7z  0 (thỏa mãn)
Suy ra d M R 3 2 ; 
. Chọn đáp án A. 5 Phƣơng án nhiễu:
B. Thay sai điểm M 1; 2;3 .
C. Chỉ giải được a  c cho pt x z  0 .
D. Không loại được pt x z  0 .
Câu 43. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (Q): x  2 y z  5  0 và đường thẳng x 1 y 1 z  3 d :  
. Viết phương trình mặt phẳng (P) chứa đường thẳng d và tạo với mặt 2 1 1
phẳng (Q) một góc nhỏ nhất.
A. y z  4  0
B. x y z  3  0
C. x  2 y z  6  0
D. x  2 y 1  0 Hƣớng dẫn giải:
Ghi nhớ: Góc giữa  P và Q lớn nhất bằng 0
90 và nhỏ nhất bằng góc giữa d và Q .
Gọi    P  Q , M d, M Q , I d  Q , H , K lần lượt là hình chiếu của M trên Q và  . Khi đó góc giữ 
a  P và Q bằng MKH , góc giữa d và P Q  bằng MIH . M d Vì HK   nên HI HK , suy ra  I H Trang87 K Q  MH MH  tan MKH    tan MIH HK HI Do đó  
MKH MIH . Suy ra 
MKH nhỏ nhất bằng 
MIH khi K I hay MI   .
Suy ra MIH    hay vectơ pháp tuyến của  MIH  là vectơ chỉ phương của  .       
Do đó ta có u nu
n  và n u  ,u  .  MIH , d Q   P d    
Cụ thể: Ta có d đi qua M  1  ; 1
 ;3 và có vectơ chỉ phương u  Qd 2;1;  1 . Mặt phẳng có 
vectơ pháp tuyến n   Q 1;2;  1 .  1   1    Suy ra u  u ,n      n u  ,u       P d  0; 3;  3 30;1;   1 d Q  3;3;3  1;1  ;1 . .   3 3  
Vậy  P : y z  4  0 . Chọn đáp án A. Phƣơng án nhiễu:
B. Tính tích có hướng một lần đã cho là vectơ pháp tuyến của (P) (Trường hợp này góc là lớn nhất 0 90 ).
C. Nếu thử bằng cách tính góc giữa hai mặt phẳng thì đáp án này cho góc nhỏ nhất bằng 0 0 .
D. Phương án nhiễu cho việc thử xem mặt phẳng có chứa đường thẳng d hay không. x 1 y  2 z
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   1 và 1 2 1  x  2 y 1 z d :   d 2
. Phương trình mặt phẳng (P) chứa
sao cho góc giữa mặt phẳng (P) và 2 1 2 1
đường thẳng d là lớn nhất là: ax y cz d  0 . Giá trị của T a c d bằng 2 A. T  3 B. T  13 0 C. T   D. T  6  4 Hƣớng dẫn giải:
Từ điểm I bất kỳ trên d kẻ đường thẳng '
d song song với d . 1 2 2 d2'
Lấy M thuộc d ' không thuộc  P . Gọi H , K lần lượt là hình M 2 d2
chiếu của M trên  P và d . Gọi  ,  lần lượt là góc giữa d ' và 1 2  H
P , d ' và d . 2 1 d1 P I K MH MK Ta có sin   
 sin suy ra    . MI MI
Do đó  lớn nhất bằng  khi H K hay MK  P .  
Ta có d đi qua I (1; 2; 0) và có VTCP u  (1; 2; 1
 ) . d có vectơ chỉ phương u  2; 1  ;2 2   . 1 1 2   
Do đó vectơ pháp tuyến của mặt phẳng MIK  là n u  ,u   3; 4  ; 5  1 1 2  .   Trang88   
Vectơ pháp tuyến của P là n u  ,n   1  4;2; 1  0 P 1 1   .  
Phương trình mặt phẳng (P): 7x y  5z 9   0 . Phƣơng án nhiễu:
B. Do nghĩ góc giữa d và  P lớn nhất bằng 0 90 khi d P 2
  . Do đó suy ra phương trình 2
của  P : 2x y  2z  4  0 . Suy ra T  0 .  
C. Sau khi tính tích có hướng của u u 3; 4  ; 5   1 và 2 được
thì nghĩ đó là vectơ pháp tuyến 13
của  P nên được pt 3x  4 y  5z 11  0  T   4
D. Sau khi viết được pt 14x  2 y 10z 18  0 thì vội vàng tính T a c d  6 
Câu 45. Trong không gian toạ độ Oxyz, cho hai điểm A3; 2
 ;6 , B0;1;0 và mặt cầu
S x  2  y  2 z  2 : 1 2 3
 25 . Mặt phẳng P : ax by cz  2  0 đi qua , A B và cắt
S theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T abc . A. T  2 B. T  3 C. T  4 D. T  5 Hƣớng dẫn giải:
Để đường tròn giao tuyến có bán kính nhỏ nhất thì
khoảng cách IH lớn nhất. Mà IH IK d I; AB
nên IH lớn nhất khi H K hay mặt phẳng  P I
chứa AB và vuông góc với IK . B
Suy ra  P  mp A ;
B I   Q . P H K A  1   Ta có n A , B AI   Q 5;1; 2 .   3    1  Suy ra n n , AB   PQ 0;12;6 60;2;  1 .   3 
Do đó phương trình của P : 0x  2y z  2  0 . Suy ra T a b c  3. Chọn đáp án B. Phƣơng án nhiễu:
A, D là các phương án gây nhiễu thêm. 
C. Nhầm n  5;1; 2 PQ
 là vectơ pháp tuyến của
. Do chỉ tính theo quán tính một lần tích
có hướng thì công nhận luôn là vectơ pháp tuyến của mặt phẳng cần tìm. Do đó được
5x y  2z  2  0 .
Câu 46. Trong không gian toạ độ Oxyz, cho điểm (
A 2; 2; 4) và mặt phẳng (P) : x y z  4  0 . Gọi
Q là mặt phẳng song song với (P) và cắt hai tia Ox, Oy tại 2 điểm B, C sao cho tam giác Trang89
ABC có diện tích bằng 6. Giả sử phương trình của Q là: ax by cz  4  0 . Giá trị của
a b c bằng A. 3 B. 6  C. 12 D. 3  Hƣớng dẫn giải:
Vì (Q) // (P) nên (Q): x y z d  0 (d  4) . Giả sử B  (Q)  Ox, C  (Q)  Oy  
B(d;0;0),C(0;d;0) (d  1 0) . S
 AB, AC  6 d  2  ABC 2
 (Q) : x y z  2  0  2
x  2y  2z  4  0  a b c  6 . Chọn đáp án B. Phƣơng án nhiễu:
A: Sau khi tìm được pt x y z  2  0 thì vội vàng tính a b c  3.
C, D là các phương án nhiễu thêm.
Câu 47. Trong không gian với hệ toạ độ Oxyz, mặt phẳng (P) đi qua điểm M (9;1;1) , cắt các tia Ox, Oy,
Oz tại A, B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất có phương trình
x By Cz D  0 . Giá trị của B C D bằng A. 9  B. 27  C. 45 D. 19 Hƣớng dẫn giải: Giá sử (
A a; 0; 0)  Ox, B(0; ;
b 0)  Oy, C(0; 0; c)  Oz (a, , b c  0) . x y z
Khi đó PT mặt phẳng (P) có dạng:    1 . a b c Ta có: M (9;1;1)  9 1 1 (P)     1 1 (1); Vabc OABC (2) a b c 6
(1)  abc  9bc ac ab ≥ 2 3 3 9(abc)  3 2
(abc)  27.9(abc)  abc  243 9
bc ac aba  27   x y z Dấu "=" xảy ra   9 1 1  b   3  (P):
   1  x  9y  9z  27  0    1   27 3 3 a b cc  3
Suy ra B C D  9  Phƣơng án nhiễu:
B, C, D do cộng sai B C D .
Câu 48. Trong không gian với hệ toạ độ Oxyz, cho hai điểm A 1  ; 2  ; 3   , B 6  ;10; 3
  . Gọi P là
mặt phẳng sao cho khoảng cách từ điểm A đến mặt phẳng  P bằng 15 và khoảng cách từ điểm
B đến mặt phẳng  P bằng 2. Mặt phẳng  P đi qua điểm nào sau đây? A. M 8; 3  ;  1 B. M 18; 3  ;1  1 C. M 52; 7  ;13 D. M  4  0; 2  ; 1  5 Hƣớng dẫn giải: Trang90
Giả sử ta xác định được mặt phẳng (P) thỏa mãn yêu cầu bài toán. Gọi H, K lần lượt là hình d   ,
A (P)  AH  15
chiếu của A, B trên (P). Ta có :  d
 B,(P)  BK  2
Mà 13  15 12  AH BK AB  13 (1) . Như vậy dấu đẳng thức ở (1) phải xảy ra
 15  AH BH
Điều đó tương đương với H K  (P)  AB tại điểm H thỏa mãn  2 H K  15  88  x 1  (x  6) x    2 13    15  154  8  8 154  Gọi H ( ;
x y; z)   y  2 
( y 10)   y   K H ; ; 3  .   2 13    13 13   15 z  3  z  3  (z  3)    2  
Vậy phương trình mặt phẳng (P) là mặt phẳng đi qua H nhận ( AB 5
 ;12;0) làm vtpt, nên có
phương trình (P) : 5x 12y 176  0 . Suy ra điểm M  4  0; 2  ; 1
 5 thuộc P . Chọn đáp án D. Phƣơng án nhiễu:
A, B, C là các phương án gây nhiễu thêm. Câu 49. Trong không gian với hệ toạ độ Oxyz, cho đường thẳng  x m y m z m   3 1  d   m   1  ; ;  mdmm  4 3 2 3 8 7 : , với . Khi thay đổi thì 2m 1 m 1 4m  3  4 2 
luôn nằm trong một mặt phẳng cố định  P : ax by cz  6  0 . Tính a b c ? A. 10 B. 9 C. 7 D. 8 Hƣớng dẫn giải:
x  4m  3 2m   1 tx m y m z m  
x  2y  9   3t d  
 y  2m  3 m   1 t   m  4 3 2 3 8 7 : . 2m 1 m 1 4m  3     
m    m    4 y z 5 t z 8 7 4 3 t
x  2y  34y z  6  x 10y 3z 6  0 . Suy ra a bc 1103 8 . Chọn đáp án D. Phƣơng án nhiễu:
A, B, C là các phương án gây nhiễu thêm.
Câu 50. Trong không gian với hệ toạ độ Oxyz, cho các điểm A ;
a 0; 0 , B 0; ;
b 0 , C 0;0;c với
a, b, c  0 thỏa mãn a b c  2 . Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại
tiếp tứ diện OABC thuộc một mặt phẳng  P cố định. Tính khoảng cách từ điểm Trang91
M 2016;0;0 đến mặt phẳng  P . 2015 2016 2014 A. B. 2016 C. D. 3 3 3 Hƣớng dẫn giải: z
Dễ dàng suy ra được tọa độ tâm mặt cầu ngoại tiếp tứ diện OABC C là  a b c I ; ;   .  K 2 2 2  I O B a b c
Từ giả thiết a b c  2 
   1 . Do đó I thuộc mặt y 2 2 2 A H
phẳng cố định  P : x y z 1  0 . Suy ra d M P 2015 ;  . 3 x Chọn A. Phƣơng án nhiễu: 2016
B,C. Vì M 2016;0;0 nên nếu HS không biết làm có thể chọn thiên về số 2016 và . 3
D. Do HS có thể nhầm pt là x y z  2  0 lấy ngay từ giả thiết, do không tìm được đúng tọa độ điểm I .
----------------------------------------------------Hết---------------------------------------------------- Trang92