

















Preview text:
ttt TOÁN TỪ TÂM TỌA ĐỘ trong MẶT PHẲNG TÁC GIẢ TOÁN TỪ TÂM Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG MỤC LỤC
Bài 1. TỌA ĐỘ VECTƠ TRONG MẶT PHẲNG A. Lý thuyết
1. Trục tọa độ .................................................................................................................................... 3
2. Hệ trục tọa độ ............................................................................................................................... 3
3. Biểu thức tọa độ của các phép toán vectơ ................................................................................ 4
4. Ứng dụng biểu thức tọa độ của các phép toán vecto ............................................................. 5
B. Các dạng bài tập
Dạng 1. Tọa độ trên trục ........................................................................................................... 6
Dạng 2. Tọa độ trên hệ trục ..................................................................................................... 9 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................. 14
B. Câu hỏi – Trả lời đúng/sai ....................................................................................................... 16
C. Câu hỏi – Trả lời ngắn.............................................................................................................. 19
Bài 2. PHƯƠNG TRÌNH ĐƯỜNG THẲNG A. Lý thuyết
1. Véc tơ chỉ phương và vectơ pháp tuyến của đường thẳng ................................................. 21
2. Liên hệ giữa VTCP và VTPT .................................................................................................... 22
3. Phương trình đường thẳng ...................................................................................................... 22
B. Các dạng bài tập
Dạng 1. Phương trình tham số của đường thẳng .............................................................. 24
Dạng 2. Phương trình tổng quát của đường thẳng ........................................................... 26
Dạng 3. Vị trí tương đối của đường thẳng ......................................................................... 28
Dạng 4. Khoảng cách từ một điểm đến đường thẳng ....................................................... 32 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................. 34
B. Câu hỏi – Trả lời đúng/sai ....................................................................................................... 36
C. Câu hỏi – Trả lời ngắn.............................................................................................................. 39
Bài 3. PHƯƠNG TRÌNH ĐƯỜNG TRÒN A. Lý thuyết
1. Phương trình đường tròn ......................................................................................................... 41
2. Phương trình tiếp tuyến của đường tròn ............................................................................... 41
3. Vị trí tương đối .......................................................................................................................... 42
B. Các dạng bài tập
Dạng 1. Nhận diện phương trình đường tròn – tìm tâm & bán kính ........................... 43
» TOÁN TỪ T ÂM – 0901.837.432 Trang 1 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
Dạng 2. Viết phương trình đường tròn .............................................................................. 46
Dạng 3. Vị trí tương đối giữa đường tròn & đường thẳng ............................................. 49
Dạng 4. Vị trí tương đối giữa đường tròn & đường tròn ................................................ 53
Dạng 5. Tiếp tuyến của đường tròn .................................................................................... 56 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................ 60
B. Câu hỏi – Trả lời đúng/sai ...................................................................................................... 63
C. Câu hỏi – Trả lời ngắn ............................................................................................................. 65
Bài 4. BA ĐƯỜNG CONIC A. Lý thuyết
1. Elip .............................................................................................................................................. 68
2. Hypebol ...................................................................................................................................... 68
3. Parabol ........................................................................................................................................ 69
B. Các dạng bài tập
Dạng 1. Phương trình Elip .................................................................................................... 70
Dạng 2. Phương trình Hypebol ........................................................................................... 73
Dạng 3. Phương trình Parabol ............................................................................................. 76 C. Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm ................................................................................................ 78
B. Câu hỏi – Trả lời đúng/sai ...................................................................................................... 82
C. Câu hỏi – Trả lời ngắn ............................................................................................................. 90
» TOÁN TỪ T ÂM – 0901.837.432 Trang 2 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Chương 09 Bài 1.
TỌA ĐỘ VECTƠ TRONG MẶT PHẲNG Lý thuyết 1. Trục tọa độ 1.1. Định nghĩa Định nghĩa
» Trục tọa độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm
gọi là điểm gốc và một vectơ đơn vị . » Điểm gọi là gốc tọa độ.
» Hướng của vecto đơn vị là hướng của trục. O
» Ta kí hiệu trục đó là
1.2. Tọa đ ộ của vectơ và của điểm trên trục Định nghĩa
» Cho vectơ nằm trên trục
khi đó số được gọi là tọa độ của vectơ trên trục khi và chỉ khi . » Cho điểm nằm trên trục khi đó số
được gọi là tọa độ của điểm trên trục khi và chỉ khi . Như vậy tọa điểm là tọa độ vectơ . 2. Hệ trục tọ a độ 2.1. Định nghĩa Định nghĩa
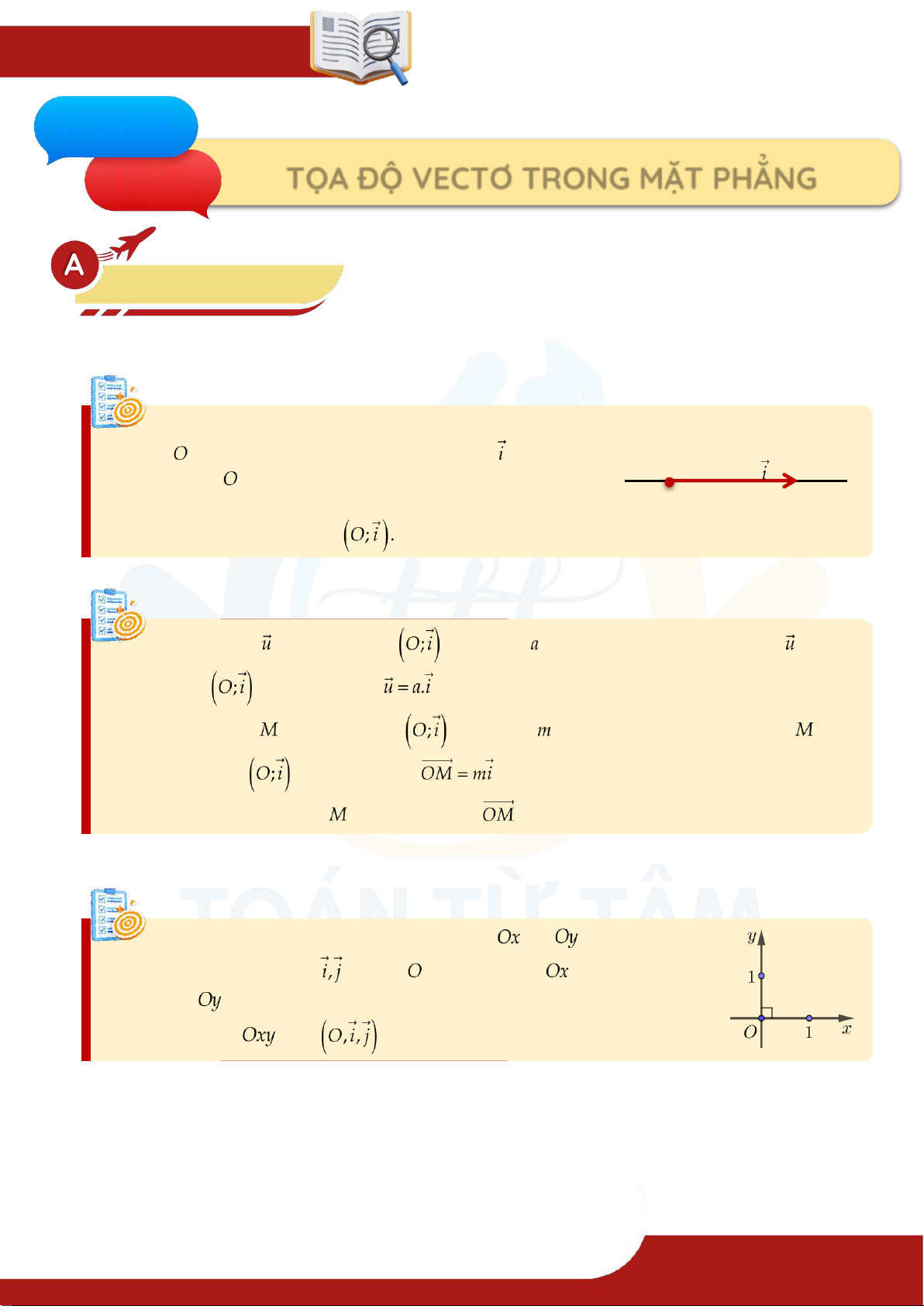
» Hệ trục tọa độ gồm hai trục vuông góc và với hai vectơ đơn vị lần lượt là . Điểm là gốc tọa độ, gọi là trục hoành và gọi là trục tung. Kí hiệu: hay .
2.2. Tọa đ ộ điểm, tọa độ vectơ
» TOÁN TỪ T ÂM – 0901.837.432 Trang 3 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Định nghĩa
» Trong hệ trục tọa độ , cặp số
được gọi là tọa độ của vectơ Kí hiệu: hay .
» Trong hệ trục tọa độ , tọa độ của vectơ
gọi là tọa độ của điểm . Kí hiệu: hay .
2.3. Tọa đ ộ trung điểm của đoạn thẳng. Tọa độ trọng tâm tam giác »
là trung điểm của đoạn . » là trọng tâm tam giác .
3. Biểu thức tọa độ của các phép toán vectơ Cho
và số thực . Khi đó ta có ⑴ ⑵ ⑶
⑷ cùng phương với tồn tại số sao cho . ⑸ Cho hai điểm thì .
» TOÁN TỪ T ÂM – 0901.837.432 Trang 4 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
4. Ứng dụng biểu thức tọa độ của các phép toán vecto
Trên mặt phẳng tọa độ , cho hai vectơ và hai điểm Ta có: ⑴ ⑵ cùng phương ⑶ ⑷ . ⑸ ( và đều khác )
» TOÁN TỪ T ÂM – 0901.837.432 Trang 5 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Các dạng bài tập
Dạng 1. Tọa độ trên trục Phương pháp
Tọa độ trên trục của điểm & vecto:
» Cho vectơ nằm trên trục
khi đó số được gọi là tọa độ của vectơ trên trục khi và chỉ khi . » Cho điểm nằm trên trục khi đó số
được gọi là tọa độ của điểm trên trục khi và chỉ khi . Như vậy tọa điểm là tọa độ vectơ . Ví dụ 1.1. Trên trục cho 2 điểm
có tọa độ lần lượt là và 5.
⑴ Tìm tọa độ của .
⑵ Tìm tọa độ trung điểm của đoạn thẳng .
⑶ Tìm tọa độ của điểm sao cho .
⑷ Tìm tọa độ điểm sao cho .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 6 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Ví dụ 1.2. Trên trục cho 2 điểm
có tọa độ lần lượt là và 1 .
⑴ Tìm tọa độ điểm sao cho .
⑵ Tìm tọa độ điểm sao cho .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 1.3. Trên trục tọa độ cho hai điểm
có tọa độ lần lượt là .
⑴ Tìm tọa độ điểm sao cho .
⑵ Tìm tọa độ trung điểm của .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 7 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Ví dụ 1.4. Trên trục tọa độ cho bốn điểm bất kỳ. Chứng minh
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 1.5. Trên trục , cho 3 điểm
có tọa độ lần lượt là . Tìm điểm sao cho .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 8 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
Dạng 2. Tọa độ trên hệ trục Phương pháp ⑴
là trung điểm của đoạn .
⑵ là trọng tâm tam giác . » Cho
và số thực . Khi đó ta có ⑴ ⑵ ⑶
⑷ cùng phương với tồn tại số sao cho . ⑸ ⑹ ( đều khác ) ⑺ Cho hai điểm thì . ⑻ . Ví dụ 2.1.
Trong mặt phẳng tọa độ , cho .
⑴ Tìm tọa độ trung điểm của đoạn thẳng .
⑵ Tìm tọa độ trọng tâm tam giác .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 9 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
........................................................................................................................................................ Ví dụ 2.2.
Trong mặt phẳng tọa độ , cho
⑴ Tìm tọa độ các vectơ .
⑵ Phân tích vectơ theo hai vectơ ; .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.3.
Trong mặt phẳng tọa độ , cho 3 điểm .
⑴ Chứng minh 3 điểm tạo thành tam giác.
⑵ Tìm tọa độ điểm sao cho là hình bình hành.
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 10 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
........................................................................................................................................................ Ví dụ 2.4. Cho
⑴ Tìm tọa độ của ⑵ Tìm sao cho:
⑶ Biểu diễn vectơ theo .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.5. Cho 4 điểm . Hãy biểu diễn theo các vectơ .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 11 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Ví dụ 2.6. Tìm để ⑴ 2 vectơ và cùng phương. ⑵ 3 điểm thẳng hàng.
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.7. Cho ba điểm
⑴ Chứng minh ba điểm không thẳng hàng .
⑵ Tìm toạ độ điểm , sao cho
là hình bình hành.
⑶ Tìm toạ độ trọng tâm của tam giác .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 12 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................ Ví dụ 2.8. Cho hai điểm
⑴ Tìm toạ độ điểm thoả mãn .
⑵ Tìm điểm đối xứng với qua . ⑶ Tìm điểm trên trục , sao cho thẳng hàng. ⑷ Tìm điểm trên sao cho
là hình thang có cạnh đáy .
Lời giải
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
........................................................................................................................................................
» TOÁN TỪ T ÂM – 0901.837.432 Trang 13 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Luyện tập
A. Câu hỏi – Trả lời trắc nghiệm
» Câu 1. Trong hệ trục toạ độ Oxy , toạ độ của vectơ a 8j 3i bằng
A. a 3;8 .
B. a 3; 8 .
C. a 8; 3 .
D. a 8; 3 .
» Câu 2. Trong mặt phẳng Oxy , cho hai điểm B 1
;3 và C3;
1 . Độ dài vectơ BC bằng A. 6 . B. 2 5 . C. 2 . D. 5 .
» Câu 3. Trong mặt phẳng với hệ trục tọa độ Oxy , cho điểm A1;3 và B0; 6 . Khẳng định nào sau đây đúng?
A. AB 5; 3 .
B. AB 1; 3 .
C. AB 3; 5 .
D. AB 1;3 .
» Câu 4. Cho A 1 ;
1 , B1;3 ,C 2
;0. Tìm x sao cho AB xBC 2 2 3 3 A. x B. x C. x D. x 3 3 2 2
» Câu 5. Cho các vectơ a 1; 2 , b 2; 6 . Khi đó góc giữa chúng là A. 45o . B. o 60 . C. o 30 . D. o 135 .
» Câu 6. Cho các vectơ a 1; 3 , b 2; 5 . Tính tích vô hướng của aa 2b A. 16. B. 26 . C. 36 . D. 16 .
» Câu 7. Trong mặt phẳng Oxy , cho a 2;
1 và b 3; 4 . Khẳng định nào sau đây là sai?
A. Tích vô hướng của hai vectơ đã cho là 10 .
B. Độ lớn của vectơ a là 5 .
C. Độ lớn của vectơ b là 5 .
D. Góc giữa hai vectơ là 90o .
» Câu 8. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u 3; 4 và v 8; 6 . Khẳng định nào sau đây đúng? 1
A. u v . B. M 0;
. và v cùng phương. 2
C. u vuông góc với v .
D. u v. 1
» Câu 9. Trong hệ tọa độ Oxy cho u i 5 .
j Tọa độ của vecto u là 2 1 1 A. u ; 5 . B. u ; 5 .
C. u 1;10.
D. u 1; 10. 2 2
» Câu 10. Trong mặt phẳng tọa độ Oxy , a (5; 2) , b 1
( 0; 6 2x) . Tìm x để a; b cùng phương? A. 1. B. 1 . C. 2. D. 2 .
» Câu 11. Trong hệ trục tọa độ Oxy , cho hai điểm M 1; 1 , N 4; 1
. Tính độ dài véctơ MN .
A. MN 13 .
B. MN 5 .
C. MN 29 . D. MN 3 .
» TOÁN TỪ T ÂM – 0901.837.432 Trang 14 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG
» Câu 12. Trong mặt phẳng tọa độ Oxy, cho ba điểm A3;
1 , B2;10 , C 4
; 2 Tính tích vô hướng A . B AC A. A . B AC 40 B. .
AB AC 40 C. A . B AC 26 D. . AB AC 26
» Câu 13. Trên trục O;i cho ba điểm A, B, C có tọa độ lần lượt là 5
; 2; 4. Khi đó tọa độ điểm M
thảo mãn 2MA 3MC 4MB 0 là: 10 10 5 5 A. B. C. D. 3 9 3 4
» Câu 14. Trên trục x'Ox cho tọa độ các điểm B, C lần lượt là m 2 và 2
m 3m 2. Tìm m để đoạn
thẳng BC có độ dài nhỏ nhất. A. m 2 B. m 1 C. m 1 D. m 2
» Câu 15. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 3; 2 và b 1; 7. Tìm tọa độ vectơ
c biết c.a 9 và c.b 20
A. c 1; 3
B. c 1; 3 C. c 1; 3
D. c 1; 3
» Câu 16. Cho OM 2;
1 , ON 3;
1 . Tính góc của OM,ON 2 2 A. o 135 . B. . C. 1 o 35 . D. . 2 2
» Câu 17. Cặp vectơ nào sau đây vuông góc?
A. a 2;
1 và b 3; 4 .
B. a 3; 4 và b 3; 4 .
C. a 2; 3 và b 6; 4 .
D. a 7; 3 và b 3; 7 .
» Câu 18. Cho tam giác ABC có A1; 2 , B 1 ; 1 , C 5; 1 .Tính cos A 2 1 1 2 A. . B. . C. . D. . 5 5 5 5
» Câu 19. Trong mặt phẳng O;i, j cho 2 vectơ : a 3i 6j và b 8i 4 .j Kết luận nào sau đây sai? A. . a b 0.
B. a b .
C. a . b 0 . D. . a b 0 .
» Câu 20. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a 2; 3 , b 4;
1 và c ka mb với
k, m . Biết rằng vectơ c vuông góc với vectơ a b. Khẳng định nào sau đây đúng?
A. 2k 2m
B. 3k 2m
C. 2k 3m 0
D. 3k 2m 0.
» Câu 21. Trong mặt phẳng Oxy cho A 1 ; 1 , B1; 3 , C 1; 1
. Khảng định nào sau đây đúng.
A. AB 4; 2 , BC 2; 4 .
B. AB BC .
C. Tam giác ABC vuông cân tại A .
D. Tam giác ABC vuông cân tại B .
» Câu 22. Trong mặt phẳng tọa độ Oxy, cho hai điểm A1; 2 và B 3 ;
1 . Tìm tọa độ điểm C thuộc
trục tung sao cho tam giác ABC vuông tại . A
A. C 0; 6 .
B. C 5;0 . C. C 3; 1 . D. C 0; 6 .
» Câu 23. Cho tam giác ABC có A 1
; 2,B0;3,C5;2. Tìm tọa độ chân đường cao hạ từ đỉnh
A của tam giác ABC .
» TOÁN TỪ T ÂM – 0901.837.432 Trang 15 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG A. 0;3 .
B. 0; 3 . C. 3; 0 . D. 3 ;0 .
» Câu 24. Cho điểm A 2 ;
3 và vectơ AM 3i 2j .Vectơ nào trong hình là vectơ AM ? A. V B. V C. V D. V 1 2 3 4
» Câu 25. Trong mặt phẳng Oxy , cho hai điểm B 1
;3 và C3;
1 . Tìm tọa độ điểm A sao cho tam
giác ABC vuông cân tại A .
A. A0;0 hoặc A2; 4 .
B. A0;0 hoặc A2; 4 .
C. A0;0 hoặc A 2 ; 4 .
D. A0;0 hoặc A 2 ; 4.
» Câu 26. Cho véc tơ a 1; 2 . Với giá trị nào của y thì véc tơ b 3; y tạo với véctơ a một góc 45 y 1 y 1 A. y 9 . B. . C. . D. y 1 . y 9 y 9
» Câu 27. Trong mặt phẳng toạ độ Oxy, cho ABC có A 3
;3,B1;4,C2; 5
. Tọa độ điểm M
thỏa mãn 2MA BC 4CM là: 1 5 1 5 1 5 5 1 A. M ; B. M ; C. M ; D. M ; 6 6 6 6 6 6 6 6
» Câu 28. Trong mặt phẳng với hệ tọa độ Oxy , cho hai vectơ u 1; 2 và v 4m ; 2m 2 . Tìm m
để vectơ u vuông góc với v . 1 1 A. m . B. m . C. m 1. D. m 1 . 2 2 2
» Câu 29. Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trọng tâm G ; 0 , biết 3 M 1; 1
là trung điểm của cạnh BC . Tọa độ đỉnh A là A. 2; 0 . B. 2 ; 0 . C. 0; 2 . D. 0; 2 .
» Câu 30. Trong hệ tọa độ Oxy, cho 3 điểm A 1 ; 1 , B0;
1 ,C 3; 0 . Xác định tọa độ giao điểm I
của AD và BG với D thuộc BC và 2BD 5DC , G là trọng tâm ABC 5 1 35 35 A. I ;1 B. I ;1 C. I ; 2 D. I ;1 9 9 9 9
B. Câu hỏi – Trả lời đúng/sai
» Câu 31. Trong mặt phẳng toạ độ, cho các điểm A0; 2; B1; 1 ;C 1 ; 2 . Các điểm A , B ,C lần 1
lượt chia các đoạn BC,CA, AB theo các tỉ số 1 ; ; 2 . Khi đó: 2
» TOÁN TỪ T ÂM – 0901.837.432 Trang 16 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Mệnh đề Đúng Sai 1 (a) A 0; 2 (b) B 2;6 1 4
(c) C ; 3 3 (d) Ba điểm A ,
B ,C thẳng hàng.
» Câu 32. Cho A0; 1 ; B2; 3 ;C 1; 7 . Khi đó: Mệnh đề Đúng Sai
(a) Nếu B là trung điểm của AM thì tọa độ điểm M 1; 2 .
(b) Nếu C là trọng tâm của tam giác ABG thì tọa độ điểm G1; 3 .
Nếu D là đỉnh thứ tư của hình bình hành ABCD thì tọa độ điểm (c) D 1 ; 3 .
Nếu E là điểm thuộc trục hoành sao cho AE vuông góc với BC thì
(d) tọa độ E4;0.
» Câu 33. Trong mặt phẳng toạ độ Oxy , cho A 2 ;5,B 4 ; 2
,C1;5. Khi đó: Mệnh đề Đúng Sai
(a) Ba điểm A, B,C không thẳng hàng. 5 8 (b) G
; là tọa độ trọng tâm của tam giác ABC . 3 3
(c) Tứ giác ABCD là hình bình hành khi đó tọa độ điểm D là D3;10 (d) ACB 45
» Câu 34. Trong mặt phẳng tọa độ Oxy , cho các vectơ a 2;3 ,b 1 ; 2,c 6 ; 4. Khi đó: Mệnh đề Đúng Sai (a) a 13
(b) b 3 (c) c 13 13 3
Vectơ d cùng phương với a và có độ dài bằng có tọa độ 1 ; 2 2 (d) 3 hay 1 ; . 2
» Câu 35. Trong mặt phẳng tọa độ Oxy , cho các vectơ a 2; 2 ,b 4;
1 và c 0; 1 . Khi đó: Mệnh đề Đúng Sai
(a) 2a b 3c 0; 2
(b) Vectơ e 1;
1 cùng phương, cùng hướng với vectơ a 1 (c) Vectơ f 1 ;
cùng phương, cùng hướng với vectơ b 4
» TOÁN TỪ T ÂM – 0901.837.432 Trang 17 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG 1 5
(d) a b c 2 2
» Câu 36. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có các đỉnh thỏa mãn
OA 2i j ,OB i j ,OC 4i j . Khi đó: Mệnh đề Đúng Sai
(a) A2; 1 , B1; 1 ,C 4; 1 3
(b) E là trung điểm AB nên E ; 0 2 2 1
(c) G là trọng tâm ABC nên G ; 3 3
(d) Điểm D sao cho ABCD là hình bình hành nên D2; 1
» Câu 37. Trong mặt phẳng tọa độ Oxy , cho các điểm A 4 ;
1 , B2; 4 ,C 2; 2 . Khi đó: Mệnh đề Đúng Sai
(a) Tọa độ điểm D sao cho C là trọng tâm tam giác ABD là D8;1 1
(b) BC 0; 6 ; AC 6; 3
Tọa độ điểm E thuộc trục hoành sao cho A, B, E thẳng hàng là (c) E 6 ;0
(d) Tọa độ F thỏa mãn AF BC 2AC 2CF là F 20;5
» Câu 38. Trong mặt phẳng tọa độ Oxy , cho ba điểm A 2 ;
1 ; B1;3; C 2; 3 . Khi đó: Mệnh đề Đúng Sai
(a) A, B,C là ba đỉnh một tam giác
(b) Điểm I 0; 2
là trung điểm của AB 5
(c) Điểm M thuộc Ox sao cho AM BM bé nhất có hoành độ bằng 4
(d) Điểm N thuộc Oy sao cho BN CN bé nhất có tung độ bằng 2
» Câu 39. Cho tam giác ABC có ba đỉnh A1; 2 , B 2
;6, C9;8. Khi đó: Mệnh đề Đúng Sai
(a) Tam giác ABC vuông tại A . 11
(b) Tâm đường tròn ngoại tiếp của tam giác ABC có tọa độ là ;1 2
(c) Tam giác ABC có diện tích bằng 25 (đơn vị diện tích). 1 3
(d) Điểm H thuộc BC sao cho AH ngắn nhất có tọa độ là ; 5 5
» Câu 40. Trên màn hình ra đa của một đài kiểm soát không lưu (được coi như mặt phẳng tọa độ
Oxy với đơn vị trên các trục tính theo ki-lô-mét, một máy bay trực thăng chuyển động
thẳng đều từ thành phố A có tọa độ 600; 200 đến thành phố B có tọa độ 200;500 và
thời gian bay quãng đường AB là 3 giờ. Biết tọa độ M x; y là tọa độ của máy bay trực
thăng tại thời điểm sau khi xuất phát 1 giờ. Khi đó:
» TOÁN TỪ T ÂM – 0901.837.432 Trang 18 .. Ch ương 09
TỌA ĐỘ TRONG MẶT PHẲNG Mệnh đề Đúng Sai
(a) AM x 600 ; y 200
(b) AM 3AB 1400 (c) M ; 300 3
(d) AB 400 ;300
C. Câu hỏi – Trả lời ngắn
» Câu 41. Với m 0 thì có bao nhiêu u 2m 1; 2
cùng phương với v 2 ; m 3.
Điền đáp số:
» Câu 42. Trong mặt phẳng tọa độ Oxy , cho các vectơ a (2; 1 ),b 1 ( ;1) và d 2
2m 2;1 m . Có
bao nhiêu giá trị dương của tham số m để d cùng phương với a .
Điền đáp số:
» Câu 43. Trong mặt phẳng tọa độ Oxy , cho hai điểm M 5; 3 , N 3
;5. Xác định giá trị hoành độ
của điểm P sao cho ba điểm M, N, P thẳng hàng. Biết điểm P nằm trên trục hoành.
Điền đáp số:
» Câu 44. Cho các điểm A1; 2 , B 2
;0;C0;5, tính tổng tung độ và hoahf độ điểm M biết rằng
AM 2BM 3CM 0 . Kết quả làm tròn đến hàng phần mười.
Điền đáp số:
» Câu 45. Trong mặt phẳng toạ độ Oxy , cho a ;
m 2 ,b 3
;n và c 2 ;
m 7 . Tính m n biết
rằng c a b , với ;
m n là các số tự nhiên.
Điền đáp số:
» Câu 46. Trong mặt phẳng toạ độ Oxy , cho A2; 2; B1; 3 ;C 3
;0 . Xác định hoành độ điểm E thoả mãn AE 2 AB3AC .
Điền đáp số:
» Câu 47. Trong mặt phẳng toạ độ Oxy , cho tam giác ABC có A 3 ; 4; B 1 ; 2 , C8; 1 . Có bao
nhiêu điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng ba lần
diện tích của tam giác ABM .
Điền đáp số:
» Câu 48. Trong mặt phẳng toạ độ Oxy , cho hai điểm A1;5 , B9;3 . Có bao nhiêu điểm M thuộc
trục hoành thỏa mãn AMB 90 .
Điền đáp số:
» Câu 49. Trong mặt phẳng toạ độ Oxy , cho hai vectơ a 3 ; m 4m
1 và b 2; 2 (với m là
tham số). Tìm giá trị của m để góc giữa hai vectơ a và b bằng 45 .
Điền đáp số:
» TOÁN TỪ T ÂM – 0901.837.432 Trang 19 ..




