Chuyên đề số tập hợp các số thực toán lớp 7 (có lời giải chi tiết )

Tổng hợp Chuyên đề số tập hợp các số  toán lớp 7 (có lời giải) được biến soạn gồm 37 trang . Các bạn tham khảo và ôn tập kiến thức cho kì thi sắp tới .Chúc các bạn đạt kết quả cao nhé!!!

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 7

Môn: Toán 7

Thông tin:

37 trang 8 tháng trước

Tác giả:

Profile Hiền Trần
Trang 1
a
CHUYÊN ĐỀ : TẬP HỢP CÁC SỐ THỰC
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Số thực, trục số thực.
-
Số hữu tỉ và số vô tỉ được gọi chung là số thực.
-
Tập hợp các số thực được kí hiệu là .
-
Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu
diễn một số thực. Vì vậy, người ta gọi trục số là trục số thực.
* Chú ý:
-
Mỗi số thực a đều có một số đối kí hiệu là a .
-
Tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
2. Thứ tự trong tập hợp các số thực.
-
Các số thực đều viết được dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể có thể so sánh
hai số thực tương tự như so sánh hai số hữu tỉ viết dưới dạng số thập phân.
-
Với a,b , ta có a
hoặc a hoặc a b .
-
Cho
a
,
b
,
c
. Nếu a
và b
thì a
( tính chất bắc cầu ).
-
Nếu 0
3. Giá trị tuyệt đối của một số thực
-
Khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a , kí hiệu a .
* Nhận xét:
-
Giá trị tuyệt đối của
0
là
0
.
-
Giá trị tuyệt đối của một số dương là chính nó.
-
Giá trị tuyệt đối của một số âm là số đối của nó.
* Các tính chất hay sử dụng của giá trị tuyệt đối
Với a thì
a ;
a
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. TẬP HỢP SỐ THỰC – SO SÁNH CÁC SỐ HỮU TỈ
I.
Phương pháp giải:
-
Sử dụng kí hiệu của tập hợp số
Bạn cần nhớ: quan hệ giữa các tập hợp số: và .
Tập hợp các số tự nhiên kí hiệu là ;
Tập hợp các số nguyên kí hiệu là ;
Tập hợp các số hữu tỉ kí hiệu là ;
Tập hợp các số vô tỉ kí hiệu là ;
Tập hợp các số thực kí hiệu là ;
b
b
b
c
c
a b
thì a
b .
a a
;
a
0
khi a
0 ;
a a khi a
0 ;
a khi a
0
Trang 2
b
a
b
17

0, 33
7
-
So sánh các số thực
+ Việc so sánh các số thực được làm tương tự như so sánh các số hữu tỉ viết dưới dạng số thập phân.
+ Đặc biệt, với a, b là hai số thực dương thì:
a
; a
II.
Bài toán.
* NHẬN BIẾT
Bài 1. Điền ký hiệu
, ,
vào ô trống để được khẳng định đúng.
a)
5
d)
. b)
2
3
. e) 
I
.
c)
3
.
5
. f) .
Lời giải
a)
5
d)
b)
2
I
3
e)
-
c)
3
5
f)
Bài 2. Điền các kí hiệu , , vào các ô trống:
a)
c) 1, 4142135...
Lời giải
; b) 0,52 41 ;
; d) .
a) ;
b) 0, 52 41
;
c)
1, 4142135...
; d) .
Bài 3. Điền kí hiệu thích hợp vào ô trống để được khẳng định đúng?
a) 3 ; b) .
Lời giải
a) 3 ; b) .
Bài 4. Tìm số đối của các số
0, 75;
Lời giải
Số đối của 0, 75 là
Số đối của
là
8
13
Số đối của là
Bài 5. So sánh các số thực:
a)
3, 7373737373......
với
3, 7474747474....
b)
0,1845
và
0,184147....
c)
6,8218218.....
và
6, 6218
d)
7,321321321 .....
và
b
a
2
b
2
25
25
17
0, 33
8
;
13
7
0, 75
8
13
7
7,325
Trang 3
3
8
2
8
10 8 8,306623.... 8,32
65 1 63 1
65
63
24
0,16
9
145
25
24
8100
90
2
Lời giải
a)
3, 7373737373......
<
3, 7474747474....
b)
0,1845
<
0,184147....
c)
6,8218218.....
>
6, 6218
d)
7,321321321 .....
>
Bài 6. So sánh số 1, 7(32) với số .
Lời giải
Ta có 3 1, 732050808...< 1, 7(32)
* THÔNG HIỂU
Bài 7. Tìm số lớn nhất trong các số sau:
Lời giải
Ta có 69 8,306623....
Vì Vậy số lớn nhất là 8, 32 .
Bài 8. Không dùng máy tính, cho biết trong hai khẳng định dưới đây, khẳng định nào đúng, khẳng định
nào sai?
a) b)
Lời giải
a) Đúng
Vì
b) Đúng
Vì
do đó
do đó
Bài 9. So sánh (không dùng máy tính):
Lời giải
Ta có 6
Bài 10. So sánh các số thực sau:
và 6 .
a) và 5 . b)
c) và 0, 4 . d) 4. và .
Lời giải
a) Vì
b) Ta có :
5
nên 5
90
9.10
90
7,325
( 8)
2
; 8, 32;
69; 100.
100
10
1
8
1
7
65 1 63 1
8
7
1
8
1
7
34,9
36
34,9
81.100
và
81. 100
.
24
81.100
81. 100
Trang 4
81. 100
0,
4
2
9
145
144
9
x
x
x
4
9
16
25
.
81
64
49
1
4
1
9
1
36
1, 69
1, 96
c) Ta có :
d) Ta có :
Vậy
Vậy
.
0, 4
0, 4
4.
4.3
12
và
12
Vậy
4.
145
.
Bài 11.
Tìm các số thực không âm
x
, biết:
a)
Lời giải
a)
0
. b)
0
1
. c)
2
. d)
3
.
Vậy
b)
x
0
x 0 .
1
.
x
1
2
(thỏa mãn)
Vậy
c)
x 1
(thỏa mãn)
x 1 .
2
x
2
2
Vậy
d)
x 4
x 4 .
3
x
3
2
(thỏa mãn)
Vậy
x 9
(thỏa mãn)
x 9 .
Bài 12. Thực hiện phép tính
a)
b)
.
c)
. d)
.
Lời giải
a)
81.100
0,16
0,16
x
x
x
x
x
1, 44
Trang 5
9
16
25
64
49
b)
2
3
4
5
14
.
9
8
7
8
.
4
81
Trang 6
1
4
1
9
1
36
1, 44
1, 69
1, 96
10
9
100
10
10
0, 09
0,3
2
0,5
0,5
35
0,5
35
x 1
x
2
c)
1
1
1
3
2
1
4
2
.
2 3 6 6 6 3
d)
1, 2
1, 3
1, 4
1, 5
.
* VẬN DỤNG
Bài 13. Sắp xếp các số thực sau theo thứ tự tăng dần :
a) 1, 4142135; 0,(3) ; ; 3 ;
b) 0,5;
Lời giải
a) Ta có :
0,(3)
1
3
0,(4) ; 3. ;0,3 ;

3
10
Mà
1
1.4142135 3
10
3
0,(3) 1.4142135 3
c) Ta có :

0,3
0,3
*
3.
Mà
3.
3.2
6
Mà 0,(4) 0,3 
0,(4) 0,3 3.
Bài 14.
Tìm
x
, biết:
a) 1 với
x
1
. b)
2 với
x
2
.
c)
Lời giải
19
với
x 19 . d)
3 .
a)
Vậy
b)
1
x
1
1
x 2 (thỏa mãn).
2
.
x
2
2
2
25.4
4
35
10
25.4
25.4
0,5
4
36
36
35
4
35
36
4
x 2
19 x
x
2
1
x
1
Trang 7
19
x
x
2
1
Vậy
c)
Vậy
d)

x
2
(thỏa mãn)
x 2 .
19
19
x
19
2
19
x
361
x
19
361
x
342
(thỏa mãn)
x 342.
3
x
2
1
3
2
x
2
8
x 
Vậy
x
8
.
Bài 15.
Tìm
x
, biết:
a)
x
2
2
0
. b)
5
x
2
1
. c)
1
x
2
3 . d)
x
1
2
1
0
.
7
Lời giải
a)
x
2
2
0
x
2
2
x
Vậy
x 2 .
b)
5
x
2
1
.
Vậy
x
2
4
x 2
x
2
.
c)
1
x
2
3
1 x 
TH1: 1 x 
x 1
8
2
3
3
3
Trang 8
0, 25
16
25
0, 09
36
4
25
9
64
0, 25
0, 09
36
4
25
9
64
196
4
.
1, 44
9
0,81
1, 21
9
225
9
144
TH2: 1 x 

Vậy
x 1
x
1
3
.
d)
x
1
2
1
0
7
x
1
2
1
7
Vì
x
1
2
0 , mà
1
0
7
Không có giá trị nào của x thỏa mãn đề bài
Vậy không có x thỏa mãn đề bài.
Bài 16. Thực hiện phép tính:
a)
4.
c)
2.
. b)
5
.
d)
3
.
2
3
.
3
0, 04
:
.
Lời giải
a)
4.
2.

4.5
2.
2
20
4
60
4
56
.
3 3 3 3 3
b)
5
3
5.4
0,5
3.
4
20
1
12
5 2 5
200
5
24
219
.
10 10 10 10
c)
1
.
1, 21
0,5.1,1
0,3
6
6, 25
.
4
3
.
3 2
1
8
3 3
8
6 8 16
d)
2
3
0, 04
:
.
3.
.
.
.
.
5

Bài 17. Thực hiện phép tính:
2 5
5
3
5 5
3 5 3
a)
5.
6.
. b)
5
5
36
.
25
c)
.
d)
5.
7
.
400
:
.
20


Lời giải
3
3
25
4
9
16
1
.
1, 21
4
25
4
9
16
16
25
81
49
4
0, 25
Trang 9
81
196
4
.
1, 44
9
0,81
9
225
2
x
3
a)
5.
6.
5.9 6.
7
2
45 21
24
b)
5
5
5.0,5 13 5.
6
5
2,5
13
6
4, 5
c)
2
.1, 2 0,9 1,1
3
0,8
2
2,8
5.
7
d)
20
.
400
:

5.
3
7
.20
:
3
15 20
12

1 7
:
3
12
8:
3
12
32
Câu 18. Hai bạn Hoa và Mai chuẩn bị đi dã ngoại cùng một nhóm bạn lớp 7A. Để chuẩn bị cho chuyến
đi dã ngoại hai bạn đã đi mua một số đồ. Hoa mua
1
3
gói dâu tây, biết một gói dâu tây có giá
400000
đồng. Một thùng nước ngọt giá
250000
đồng, Mai mua
1
2
thùng nước này. Hỏi trong hai người, ai mua
hết nhiều tiền hơn?
Lời giải
Ta có:
400000
390000
130000
260000
250000
125000
.
3 3 2 2
Từ đó suy ra
400000
250000
.
3 2
Vậy Hoa mua hết nhiều tiền hơn Mai .
* VẬN DỤNG CAO
Bài 19. a) Tìm giá trị lớn nhất của các biểu thức :
A
.
49
4
0, 25
36
25
1, 21
9
144
Trang 10
5
x
2
x
x
5
x
2
2
x
3
x
2
x
x
x
2 x
b) Tìm giá trị lớn nhất của các biểu thức : A .
Lời giải
a)
Xét
A
Ta có :
0
với mọi x không âm
3
3
với mọi
x
không âm
2
2
x
3
3
với mọi x không âm
A
2
3
với mọi x không âm
Dấu “
” xảy ra khi và chỉ khi
A có giá trị lớn nhất bằng
2
3
khi
0
hay
x 0
x 0
b)
Xét
A
Ta có:
0
với mọi x không âm
2
2
5
2
với mọi x không âm
với mọi x không âm
A
5
2
với mọi x không âm
Dấu “
” xảy ra khi x 0
Giá trị lớn nhất của A là
5
2
khi
x 0
Bài 20. a) Tìm giá trị nhỏ nhất của các biểu thức : D
3
.
b) Tìm giá trị nhỏ nhất của các biểu thức :
D
6
.
Lời giải
a)
Xét:
D
3
Ta có:
0
với mọi
x
không âm
2
2
3
3
2
2
x
3
x
x
5
x
2
x
Trang 11
3
x
x
x
3 x
0
a
D
3
2
Dấu “
”xảy ra khi
x 0
Vậy D có giá trị nhỏ nhất bằng
3
khi
2
x 0
b)
Xét D
6
Ta có :
0
với mọi x không âm
3
3
với mọi x không âm
6
6
3
với mọi x không âm
D 2
Dấu ‘
’ xảy ra khi
x 0
Vậy giá trị nhỏ nhất của D là 2 khi
x 0 .
Bài 21. Tìm x nguyên để
Lời giải
a)
Ta có:
x 5
x
2
có giá trị nguyên.
x 5
x 2 7
1
7
x 2 x 2 x 2
Để
x 5
x
2
nhận giá trị nguyên thì
7
x
2
nguyên
Do đó x 2 Ư 7
1;1;
7; 7
Ta có bảng :
x 2
1
1
7
7
x
3
1
9
5
Vậy
x
3;
1;
9;5
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC.
I. Phương pháp giải:
- Giá trị tuyệt đối của một số hữu tỉ x , kí hiệu là x
Được xác định như sau:
x
x khi x 0
- Với x , x
khi đó:
x khi x < 0
+) Nếu a thì x 0 ;
+) Nếu a
thì
x
hoặc x ;
a
0
a
Trang 12
b
0
k
.
x b a a
b a b
4 4
7 7
7
2
7
2
+) Nếu a
* Chú ý:
+ Ta có:
k
.
x
thì x
;
Dấu “=” xảy ra k.x 0 .
+ Ta có: k.x ;
Dấu “=” xảy ra k.x b 0 .
+ Ta có: a . Dấu “=” xảy ra khi a.b
II. Bài toán.
* NHẬN BIẾT
Bài 1. Tìm x biết:
a)
x
4
7
Lời giải
b)
x
3
11
c)
x
0, 749
d)
x 5
1
7
a) b)
Bài 2. Tính:
c) 0, 749 0, 749
d) 5
1
7
5
1
7
a)
a)
Bài 3. Tính:
0,17
Lời giải
0,17 0,17
b)
12, 5
16, 5
b)
12, 5
16, 5
4
4
a)
2, 5 7, 5
b)
1, 2 3 6, 4
c) 
Lời giải
a)
2, 5 7, 5 2, 5 7, 5 10
b)
1, 2 3 6, 4 1, 2.3 6, 4 3, 6 6, 4 10
c)
7
15
22
11
2 2 2
Bài 4.
Tìm
x
, biết:
a)
x
b)
x
Lời giải
a)
x
b)
Vì
x
với mọi x
0
0
k
.
x a a
k
.
x a a
k
.
x b a a
0
3 3
11 11
15
2
15
2
13
17
13
0
Trang 13
13
3
8
7
11
3
8
2
5
1, 6 3, 6
2, 2
2
5
2
25
4
9
Vậy x
hoặc
x Vậy không tìm được giá trị x thoả mãn
x
Bài 5.
Tìm
x
, biết:
Lời giải
a)
x
1, 2
a)
x
1, 2
b)
x
3
4
b)
x
3
4
x
1, 2
hoặc
* THÔNG HIỂU
x
1, 2
x
3
4
hoặc
x
3
4
Bài 6. Tìm số đối của các số
5, 5
;
; 
Lời giải
Ta có
5, 5
5, 5
;
3
;
8
7
11
Vậy số đối của
Số đối của
5, 5
là
3
8
là
5,5
Số đối của 
là
7
11
Bài 7. Tính giá trị các biểu thức sau:
a)
5,9
2
b)
c)
2

3
5
7
Lời giải
a)
5,9
2
5,9
2
3,9
b)
1, 6.3, 6
2, 2
5, 76
2, 2
3,56
c)
2
3
2
2
3
0
3
3
5
7
5 5 7 7 7
Bài 8. Tính:
a)
6
4
. b)
5
3
25 5 9 5
Lời giải
x
13
13; x
13
17
7
11
3
8
7
11
1, 6 3, 6
2, 2
8
5
Trang 14
4
9
8
5
1, 3
a)
6
4
=
6
4
2
=
6
20
2
12
25 5
25 5 25
25 25 25 25
b)
5
3
=
5
3
4
8
=
5
4
3
8
9
5
11 2
9 5
9 5 9 5
9 9
5 5
9 5

Bài 9. Cho
a 6 ; b 3 ; c 2
, hãy tính:
a)
a
b
c
b)
a
b
c
.
Lời giải
Ta có
a 6
6
;
b
3
3
;
c
2
2
. Do đó:
a)
a
b
c
6
3
2
11
11
b)
a
b
c
6
3
2
7
7
Bài 10. So sánh:
a)
7
11
và
7 11
b)
8
15
và
8 15
Lời giải
a)
Ta có:
7
11
18
18
7
11
7
11
18
Vậy
7
11
=
7 11
b)
Ta có:
8
15
7 7
8
15
8
15
23
Vậy
8
15
8 15
Bài 11
. Tìm
x
biết:
a) 1,8 x 0, 5
Lời giải
a) 1,8 x 0, 5
1,8
x
0,5
TH1:
1,8 x 0,5
x
x
b)
x
2
1
7
c)
3
x
2
4
TH 2:
1,8
x
0,5
x
x
Vậy
x
hoặc
x
b)
x
2
1
7
2
25
1,8 0,5
1,8 0,5
1, 3
2, 3
2, 3
Trang 15
5
7
2
2
2
3
2
2
3
3
x
2
1
7
TH 1:
x
2
1
7
x
x
TH 2:
x
2
1
7
x
x
Vậy x hoặc
x
c)
3
x
2
4
3
x
2
4
TH 1: 3x 2 4
3
x
x
TH 2: 3x 2 4
3
x
x
Vậy
x
hoặc
x
* VẬN DỤNG
Bài 12. Tìm x , biết:
a)
x
2 . b)
x
1
2
.
c)
x
3
3
1
.
Lời giải
a)
x
x
TH1:
x
x
0
TH2:
x
x 2
Vậy
x
0; 2
2
b)
x
1
2
x
1
TH1:
x
1
2
2
1
2
7
1
2
7
5
7
9
7
9
7
6
2
2
3
2
3
2
2
2
2
2
2
2
3
Trang 16
3
3
1
4
x
3
TH2:
x
1
2
x
1
Vậy
x
3
3; 1
3
c)
x
3
3
1
x
3
2
x 3 2
TH1:
x
3
2
x
5
TH2:
x
3
2
x
1
Vậy
x
5;1
Bài 13. Tìm x biết:
a)
1
x
2
1
4 3 2
Lời giải
a)
1
x
2
1
4 3 2
1
x
1
2
4 2 3
x
1
6
b)
2
x
Vì
x 0
với mọi
x
Không tìm được giá trị của x thoả mãn.
b)
2
x
2
x
2
x
Suy ra 2x
2
x
2
x
hoặc
2
x
hoặc
2
x
hoặc
2
x
3
1 2 5
1
4
1 2 5
1 5 2
1 3
1 3
1
3
3 1
3 1
4
2
Trang 17
4

x
2
hoặc
x
1
Vậy
x
2
hoặc
x
1
.
Bài 14.
Tìm các số không âm
x
, biết:
a)
x .
4x
3
0
.
b) x
1
1
3
.
2 4 2
Lời giải
a)
x .
4x
3
0
TH1:
x
0
x 0 (thỏa mãn)
TH2:
4
x
3
0
x
3
(thỏa mãn)
4
Vậy
x
0;
3
4

b)
x
1
1
3
x
1
3
1

x
1
7
x
1
7
2 4 2
TH1:
2 2 4 2 4 2 4
x
1
7
2 4
x
9
(thỏa mãn)
4
TH2:
x
1
7
2 4
x
5
4
( loại )
Vậy
x
9


Bài 15. Tìm x biết:
a) 5x 3 7 x
Lời giải
a) 5x 3 7 x
5
x
3
7
x
hoặc
5
x
3
x
7
b) 2x 1 1 x
Trang 18
10
5
3
5
3
0
2
3
TH 1 : 5x 3 7 x
5x
TH 2 : 5x 3 x 7
5x
6
x
4
x
Vậy
x
x
x
hoặc
x 1
.
b) 2x 1 1 x
2
x
1
1
x
hoặc
2
x
1
x
1
TH 1: 2x 1 1 x
2x
3
x
x
TH 2: 2x 1 x 1
2
x
x
Vậy x hoặc x
Bài 16.
Tìm
x
biết:
a)
2
x
1
2
x
1
b) 1 3x 1 3x
c)
x
1
1
x
d)
2x
1
1
2x
2 2 3 3
Lời giải
a)
2
x
1
2
x
1
2
x
1
2
x
1
Suy ra
2x
2x
x
b) 1 3x 1 3x
1
Suy ra
1
x
Vậy
x
Vậy
x
c)
x
1
1
x
d)
2x
1
1
2x
2 2
x
1
x
1
3 3
Suy ra
2x
2 2
Suy ra
x
x
Vậy
x
2x
x
Vậy
x
x 7 3
x 3 7
4
1
x 1 1
x
1 1
2
2
3
0
3
x
3
x
1
1 0
3x 0
1
1
3
1
2
1
3
1
2
1
0
3
1
0
2
1
3
1
2
1
6
1
2
1
6
Trang 19
2
x
0
1
1 2
x
2
3
3
t / m
4
3
4
* VẬN DỤNG CAO
Bài 17. Rút gọn:
a)
A
x
x
b
)
C
x
1
x
a)
A
Lời giải
x
x
TH1: nếu x thì x x . Khi đó
A x x 2x
TH2: nếu x thì x x . Khi đó
A x x 0
Vậy A khi x
A khi x
b)
C
x
1
x
TH1: nếu
x
thì
x
1
x
1. Khi đó C x 1 x 1
TH2: nếu x
thì
x
1 1
x . Khi đó C 1 x x 1 2x
Vậy C khi
x
C khi x
Bài 18. Tìm x biết:
a) 3x 1 x 2 khi
x b)
x
8
x
2
0
c)
x
2
1
0
Lời giải
d)
x
2
1
0
a) 3x 1 x 2 khi x
3
x
Suy ra
3x
3x
hoặc
3x
3x
4x 2x
Vậy
x x
x hoặc
x
b) Vì
x 8 0
và
x 2 0
với mọi
x
.
Nên
x 8 x 2 0
0
0
0
0
1
1
1
1
2
1 2
x
1 2 x
1 x 2
x 2
1
x 1 2
1
1
t / m
2
1
2
Trang 20
8 0
Khi
x
và
x
2 0
Trang 21
8 0
1
1 x 0
3
0
4
x
x
2
1
0
Suy ra x và x
và x
Vậy không tìm được giá trị x thoả mãn.
c)
x
2
1
0
Vậy
hoặc x
x ; x
d)
x
2
1
0
Vì
x
2
với mọi x nên x
2
với mọi x
Vậy không tìm được giá trị x thoả mãn
x
2
1 0
Bài 19. Rút gọn các biểu thức sau:
Lời giải
E 2 x 1 3 x
E 2 x 1 3 x
TH 1: Nếu
x
E
thì
x 1
x 1
và
x x
. Khi đó :
TH 2: Nếu
E
thì
x 1
x
1
và
x x
. Khi đó :
TH 3: Nếu
x
E
thì
x 1
x 1
và
x x
. Khi đó :
Vậy
E
E
E
khi
x
khi
khi
x
Bài 20. Tìm x, y, z
biết:
a)
x
y
1
0
;
b)
x
1
2
y
1
x
y
z
0
3
a)
Vì
Lời giải
x
và
y 1 0
với mọi
x
,
y
.
Nên
x
và
y
1
0
y
x
2
1
2 0
x
8
2
x 1
1
1
0
1 0
1
2 x 1 3 x
2x 2 3x
5x 2
1 x 0
2 x 1 3 x 2x 2 3x
x 2
0
2 x 1 3x 2x 2 3x 5x 2
5x 2
1
x 2
5x 2
0
3
4
3
4
x
3
4
0
1 0
Trang 22
3
4
3
4
1
0
3
1
0
3
1
2
1
3
1
2
1
3
1
14
5
10
và
y
x
và
y
Vậy
x
;
y
b)
Vì
x
0
;
y
1
3
0
;
x y z 0
với mọi
x
,
y
,
z
, Nên:
x
1
2
y
1
x
y
z
0
3
và
y
và
x
và
y
và x
x và y và
z
Vậy x ; y ;
z
Bài 21. Tìm x thoả mãn
2 x 1 3 x 12
Lời giải
2 x 1 3 x 12
TH 1: Nếu
x
thì
x 1
x 1
và
x x
. Khi đó :
2
x
1
3
x
12
2
x
2
3
x
12
5
x
2
12
5x
14
x
( thoả mãn )
TH 2: Nếu thì
x 1
x
1
và
x x
. Khi đó :
2
x
1
3
x
12
2
x
2
3
x
12
x
2
12
x
10
x
( không thoả mãn )
TH 3: Nếu
x
thì
x 1
x
1
và
x x
. Khi đó :
x
3
4
0
1 0
1
1
1
2
x
1
2
0
y z 0
x
1
2
0
y z 0
0
1 1 5
2 3 6
5
6
1 x 0
0
Trang 23
5
14
5
5
4
0
0
x
x
5
3
3
5
3
x
3
5x
x
( thoả mãn )
Vậy
x
; x
Bài 22. Tìm giá trị nhỏ nhất của biểu thức:
a)
A
1
2 x
1
2 2
b) B x
2
y 2 5
Lời giải
a)
A
1
2 x
1
2 2
Ta có
x
với mọi x
Do đó
A
1
2 x
1
1
với mọi x .
2 2 2
Dấu “=” xảy ra, tức
A
x
1
.
2
Vậy giá trị nhỏ nhất của
A
bằng
1
2
khi
x
b)
B x
2
y 2 5
Ta có
x
2
với mọi x ;
y
với mọi
y
Do đó
B x
2

y 2 5 5
với mọi
x; y
.
Dấu “=” xảy ra, tức
B
Vậy giá trị nhỏ nhất của
B
bằng khi
Bài 23. Tìm giá trị nhỏ nhất của biểu thức:
C 3x 5 3x 9
Lời giải
C 3x 5 3x 9
Do đó
C
3x 5 9 3x
Dấu “=” xảy ra, tức C khi
3x
TH 1:
2
x
2
x
5
x
1
2
2
3
x
12
3
x
12
12
10
5
1
0
2
1
khi x
2
1
2
0
x
1
2
0
1
2
0
2 0
5 khi
x
2
0
y 2 0
khi
x
y
0
2
x 0
y 2
3x 5 9 3x
4 C 4
5 9 3x 0
3
x
5
9 3
x
Trang 24
3
x
5
9 3
x
0
0
x
x
5
3
3
8
2 0
2 0
8
1 3 3
1
2 x
1
3
1
3
1
3
2
2
3
1
5
1, 75; 2; 0;5
3
;
6
;
22
;
7
5.
TH 2: Không tìm được x thoả mãn.
Vậy giá trị nhỏ nhất của
C
khi
5
3
x 3
.
Bài 24. Tìm giá trị lớn nhất của biểu thức:
a) A 8 6 x 2
b)
B
Lời giải
a)
A 8 6 x 2
Ta có
x
2 0
với mọi x . Do đó
A 8 6 x 2 8
với mọi x .
Dấu “=” xảy ra, tức
A khi
x
khi
x
khi
x
Vậy giá trị lớn nhất của
A
khi
x
2
.
b)
B
Ta có
x 1 0
với mọi x . Do đó
2 x
với mọi x .
Suy ra
B
1
3
với mọi x .
Dấu “=” xảy ra, tức
B
khi x
Vậy giá trị lớn nhất của
B
khi x
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. TẬP HỢP SỐ THỰC
* NHẬN BIẾT
Bài 1. Điền các kí hiệu , , vào các ô trống:
a) ; b) 1
d) ; e)
; c) ;
; f) .
Bài 2. Dùng máy tính để so sánh
* THÔNG HIỂU
Bài 3. Tìm x biết:
với
2,(23)
.
a) x
2
400 ; b) x
2
64 0 ; c) 5x
2
10
9 .
Bài 4. Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:
4
1
2 x
1
3
2
1
2 x
1
3
1 0 x 1 0 x 1
1
9
5
Trang 25
225
1
5
196
3
17
13
161
2 1
5 4
x
0, 4
0
Bài 5. Tính:
M
2
1
3, 5 : 4
1
3
1
7, 5
.
3 6 7
* VẬN DỤNG
Bài 6. Tìm x biết
x
2
4 x
2
3 0
.
Bài 7. So sánh hai số:
A
1 ; B
* VẬN DỤNG CAO
Bài 8.
Cho
A
x 1
. Tìm
x
để
A
nhận giá trị nguyên
x 1
Bài 9. Tìm GTNN của biểu thức
P
1

2
Bài 10. Tìm GTLN của biểu thức Q =
7 2
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA SỐ THỰC
* NHẬN BIẾT
Bài 1. Tính
x
, biết:
a)
x
. b)
x
c)
x
Bài 2. Tính x , biết:
a)
x
; b)
x
0
;
c)
x
* THÔNG HIỂU
Bài 3. Tính x , biết:
a)
x
; b)
x
Bài 4. Tìm x , biết:
a)
3, 6
b)
x
* VẬN DỤNG
Bài 5. Rút gọn các biểu thức sau:
a)
C 3 x 5 3x 5
Bài 6. Tìm x biết:
b)
D
x 1 x 3
1
6
x
x
1
15, 08
3
7
8, 7
0, 5 3, 9
0
3, 5 7, 5
Trang 26
10
1
2
x
2
5
10 9
3
1
5
a)
1 2x x 7
b)
x 1 2
.
x 3 3
0
c)
x
2
3x 0
d)
x
2
1
x
2
x
* VẬN DỤNG CAO
Bài 7. Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
A
b) B
Bài 8. Tìm giá trị nhỏ nhất của biểu thức:
a)
A
b)
B
Bài 9. Tìm giá trị lớn nhất của các biểu thức sau:
a)
C
1, 5
x 2,1
; b)
D
c)
A
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. TẬP HỢP SỐ THỰC
* NHẬN BIẾT
Bài 1. Điền các kí hiệu , , vào các ô trống:
a)
d)
Bài 2. Dùng máy tính để so sánh với 2,(23)
ĐS: Ta có
5
2, 2360667...
2,(23) . Vậy
* THÔNG HIỂU
Bài 3. Tìm x biết:
2,(23)
.
a)
x
2
400
b)
x
2
x
20; x
20
;
c) 5x
2
Không tìm được x thoả mãn .
Bài 4. Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:
x
6
13
x 2,8 7, 9
x
1, 5 5, 7
5, 7 2, 7 x
x
8 141
139 272
5
64 0
x
2
64 x
8; x
8
;
b) 1
;
c) 2
;
;
e)
9
; f)
.
Trang 27
225
1
5
196
225
1
5
1
5
196
1
6
x 1
x 1
1
ĐS:
Bài 5. Tính:
M
2
1
3, 5 : 4
1
3
1
7, 5
.
ĐS:
M
7 7
:
3 6 7
25 22 15
35
:
43 15 155
.
3 2 6 7 2 6 42 2 86
* VẬN DỤNG
Bài 6. Tìm x biết
x
2
4 x
2
3 0
.
ĐS:
x
2
x
2
4
0
hoặc
x
2
3
0
x
2
4
hoặc
x
2
3
Bài 7. So sánh hai số:
A
1 ; B
ĐS:
A
1
15
1
14
B
14
Do đó
A
* VẬN DỤNG CAO
Bài 8.
Cho
A
x 1
. Tìm
x
để
A
nhận giá trị nguyên
x 1
Đáp số:
A 1
Để
A
nhận giá trị nguyên thì
x
1
là ước của
2
.
Vậy
x
Bài 9. Tìm GTNN của biểu thức
P
Đ/S:
P
min
2
khi
x
Bài 10. Tìm GTLN của biểu thức Q =
7 2
x
2;
3;
3; 2
1, 75; 2; 0;5
3
;
6
;
22
;
7
5.
2; 1, 75;0; 5; ;
22
;5
3
.
7 6
4
x
2
3 0
1
6
1
5
1
6
B
2
x 1
0; 4;9
1
2
x
0
x
1
Trang 28
3
17
13
161
8, 7
x
0, 4
0
x 4; x
3, 2
3, 5 4, 5
x 0
5
3
1
max
Đ/S:
Q
7
khi
x
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA SỐ THỰC
* NHẬN BIẾT
Bài 1. Tính x , biết: a)
x
. b)
x
c)
x
ĐS:
a)
x
. b)
x
c) x
Bài 2. Tính x , biết: a)
x
; b) x
0 ;
c) x
ĐS:
a)
x
3
; x
3
; b)
x
0
;
c)
x
Không tìm được x
7 7
* THÔNG HIỂU
Bài 3. Tính x , biết:
a)
x
2
1
5 4
b)
x
Bài 4. Tìm x , biết:
a)
3, 6
b)
x
c)
x
Không tìm được x .
* VẬN DỤNG
Bài 5. Rút gọn các biểu thức sau:
a)
C 3 x 5 3x 5
Nếu
x
thì
C
10
.
Nếu
x
5
thì
C
b)
D x 1 x 3
Nếu
Nếu
x
thì
D
thì
D
Nếu
x
thì
D
1
15, 08
3
17
13
161
15, 08
3
7
8, 7
x
13
; x
20
3
20
0, 5 3, 9
0
x 3, 4; x
4, 4
3, 5 7, 5
x
11;
x
4
20 6x
2x 2
3 x 1
2
2x 2
Trang 29
x
2; 8
x
3; 0;1; 6
x 3; 0
x 1;
1
2
Bài 6. Tìm x biết:
a) 1 2x x 7
1 2x 7 x
với
x
7
1
2x
7
x
hoặc
1
2x
7
x
b)
x 1 2
.
x 3 3
0
x 1 2
0
hoặc
x 3 3
0
x 1 2
hoặc
x 3 3
c)
x
2
3x 0
x
2
3x
0
x
x
3
0
d)
x
2
1
x
2
x
x
2
1
x
2
x
hoặc
x
2
1
x
2
x
* VẬN DỤNG CAO
Bài 7. Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
A
A
min
b) B
B
min
Bài 8. Tìm giá trị nhỏ nhất của biểu thức:
a)
A
A
min
b)
B
x
6
13
6
13
x
0
x 2,8 7, 9
7, 9 x
2,8
10
1
2
x
10 x
1
2
x
1, 5 5, 7
Trang 30
17
8
;
13
7
3
B
min
Bài 9. Tìm giá trị lớn nhất của các biểu thức sau:
a)
C
1, 5
x 2,1
;
C
max
b)
D
D
max
c)
A
A
max
PHIẾU BÀI TẬP
( Nội dung là toàn bộ bài tập đã có trên )
Dạng 1. TẬP HỢP SỐ THỰC
* NHẬN BIẾT
Bài 1.
Điền ký hiệu
,
,
vào ô trống để được khẳng định đúng.
a)
5
d)
. b)
2
3
. e)

I
.
c)
3
.
5
. f) .
Bài 2. Điền các kí hiệu , , vào các ô trống:
a)
c)
1, 4142135...
;
b)
0, 52 41
;
; d) .
Bài 3. Điền kí hiệu thích hợp vào ô trống để được khẳng định đúng?
a) 3 ; b) .
Bài 4. Tìm số đối của các số
0, 75;
Bài 5. So sánh các số thực:
d)
3, 7373737373......
với
3, 7474747474....
e)
0,1845
và
0,184147....
f)
6,8218218.....
và
6, 6218
d)
7,321321321 .....
và
Bài 6. So sánh số 1, 7(32) với số .
* THÔNG HIỂU
5, 7
x
1, 5
1, 5
x
2,1
5, 7 2, 7 x
5, 7
x
2, 7
x
8 141
139 272
141
x
272
8
139
25
0, 33
7,325
Trang 31
65 1 63
1
24
0,16
9
145
x
4
9
16
25
.
81
64
49
1
4
1
9
1
36
1, 44
1, 69
1, 96
10
x
1
19
x
0, 25
16
25
1
.
1, 21
4
0, 09
36
4
25
9
64
Bài 7. Tìm số lớn nhất trong các số sau:
Bài 8. Không dùng máy tính, cho biết trong hai khẳng định dưới đây, khẳng định nào đúng, khẳng định
nào sai?
a) b)
Bài 9. So sánh (không dùng máy tính):
Bài 10. So sánh các số thực sau:
và
6
.
a)
và
5
.
b)
c) và
0, 4
. d)
4.
và .
Bài 11. Tìm các số thực không âm x, biết:
a)
0
. b)
1
.
c)
2
.
d)
3
.
Bài 12. Thực hiện phép tính
a)
b)
.
c)
. d) .
* VẬN DỤNG
Bài 13. Sắp xếp các số thực sau theo thứ tự tăng dần :
a)
1, 4142135; 0,(3) ;
; 3 ;
b) 0,5;
Bài 14. Tìm x, biết:
0,(4) ; 3.
;0,3 ;
a)
1
với
x
1
.
b)
2
với
x
2
.
c)
19
với
x
19
.
d)
3
.
Bài 15. Tìm x, biết:
a)
x
2
2 0 . b)
5
x
2
1
. c)
1
x
2
3
. d)
x
1
2
1
0
.
7
Bài 16. Thực hiện phép tính:
a)
4.
2.
. b)
5
3
.
c)
.
d)
3
.
2

3
0, 04
:
.

Bài 17. Thực hiện phép tính:
( 8)
2
; 8, 32; 69; 100.
1
8
1
7
34,9
81.100
và
81. 100
.
x
x
x
25.4
4
35
x
2
x
2
1
25
4
9
16
Trang 32
196
36
25
4
. 1, 44
9
9
225
9
144
2
x
3
5
x
2
2
x
3
x
7
2
a)
5.
6.
. b)
5
5
.
5.
7
c)
. d)
20
. 400
:
.

Câu 18. Hai bạn Hoa và Mai chuẩn bị đi dã ngoại cùng một nhóm bạn lớp 7A. Để chuẩn bị cho chuyến
đi dã ngoại hai bạn đã đi mua một số đồ. Hoa mua
1
3
gói dâu tây, biết một gói dâu tây có giá 400000
đồng. Một thùng nước ngọt giá 250000 đồng, Mai mua
1
2
thùng nước này. Hỏi trong hai người, ai mua
hết nhiều tiền hơn?
* VẬN DỤNG CAO
Bài 19.
a) Tìm giá trị lớn nhất của các biểu thức :
A
.
b)
Tìm giá trị lớn nhất của các biểu thức :
A
.
Bài 20. a) Tìm giá trị nhỏ nhất của các biểu thức :
D
3
.
b) Tìm giá trị nhỏ nhất của các biểu thức :
D
6
.
Bài 21. Tìm x nguyên để
x
5
x
2
có giá trị nguyên.
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC.
* NHẬN BIẾT
Bài 1. Tìm
x
biết:
a)
x
4
7
b)
x
3
11
c)
x
0, 749
d)
x 5
1
7
Bài 2. Tính:
b)
Bài 3. Tính:
0,17 0,17
b)
12, 5 16, 5
a)
2, 5 7, 5
b)
1, 2 3 6, 4
c)
Bài 4. Tìm x , biết:
a)
x
b)
x
Bài 5. Tìm x , biết:
1, 21
0,81
81
49
4
0, 25
15
2
13
17
Trang 33
3
8
2
5
2
25
4
9
2
3
1
4
a) x 1, 2
b)
x
1
3
2 4
* THÔNG HIỂU
Bài 6. Tìm số đối của các số
5, 5
; ;
Bài 7. Tính giá trị các biểu thức sau:
a)
5,9 2
b)
c)
2
3
5
7
Bài 8. Tính:
a)
6
4
.
b)
5
3
25 5 9 5
Bài 9. Cho
a 6 ; b 3 ; c 2
, hãy tính:
a)
a b
c
b)
a b c
.
Bài 10. So sánh:
a)
7 11
và
7 11
b)
8
15

và
8 15
Bài 11. Tìm x biết:
a)
1,8 x 0, 5
* VẬN DỤNG
Bài 12. Tìm x , biết:
b)
x
2
1
7
c)
3x 2 4
a)
x
2
.
b)
x
1
2
. c)
x 3 3 1
.
Bài 13. Tìm x biết:
a)
x
2
1
3 2
b)
2x
Bài 14. Tìm các số không âm x , biết:
a)
x .
4x 3
0
.
b)
x
1
3
.
4 2
Bài 15. Tìm x biết:
a)
5x 3 7 x
Bài 16. Tìm x biết:
a)
2x 1 2x 1
b)
2x 1 1 x
b)
1 3x 1 3x
c)
x
1
1
x
d)
2x
1
1
2x
7
11
1, 6 3, 6
2, 2
8
5
1 2 5
1
2
Trang 34
2 2 3 3
Trang 35
2
2
2
3
1
5
1, 75; 2; 0;5
3
;
6
;
22
;
7
5.
* VẬN DỤNG CAO
Bài 17. Rút gọn:
a) A 
x x
b
)
C
x 1 x
Bài 18. Tìm x biết:
a)
3x 1 x 2 khi
x b)
x 8 x 2 0
c)
x
2
1
0
d)
x
2
1
0
Bài 19. Rút gọn các biểu thức sau:
E 2 x 1 3 x
Bài 20. Tìm x, y, z
biết:
a)
x
y
1
0
;
b)
x
1
2
y
1
x
y
z
0
3
Bài 21. Tìm x thoả mãn
2 x 1 3 x 12
Bài 22. Tìm giá trị nhỏ nhất của biểu thức:
a)
A
1
2 x
1
2 2
b)
B x
2
y 2 5
Bài 23. Tìm giá trị nhỏ nhất của biểu thức:
C 3x 5 3x 9
Bài 24. Tìm giá trị lớn nhất của biểu thức:
a)
A 8 6 x 2
b)
B
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. TẬP HỢP SỐ THỰC
* NHẬN BIẾT
Bài 1. Điền các kí hiệu , , vào các ô trống:
a) ; b) 1
d) ; e)
; c) ;
; f) .
Bài 2. Dùng máy tính để so sánh
* THÔNG HIỂU
Bài 3. Tìm x biết:
với
2,(23)
.
a) x
2
400 ; b) x
2
64 0 ; c) 5x
2
10
9 .
Bài 4. Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:
3
4
1
2 x
1
3
9
5
Trang 36
225
1
5
196
3
17
13
161
2 1
5 4
x
0, 4
0
Bài 5. Tính:
M
2
1
3, 5 : 4
1
3
1
7, 5
.
3 6 7
* VẬN DỤNG
Bài 6. Tìm x biết
x
2
4 x
2
3 0
.
Bài 7. So sánh hai số:
A
1 ; B
* VẬN DỤNG CAO
Bài 8.
Cho
A
x 1
. Tìm
x
để
A
nhận giá trị nguyên
x 1
Bài 9. Tìm GTNN của biểu thức
P
1

2
Bài 10. Tìm GTLN của biểu thức Q =
7 2
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA SỐ THỰC
* NHẬN BIẾT
Bài 1. Tính
x
, biết:
a)
x
. b)
x
c)
x
Bài 2. Tính x , biết:
a)
x
; b)
x
0
;
c)
x
* THÔNG HIỂU
Bài 3. Tính x , biết:
a)
x
; b)
x
Bài 4. Tìm x , biết:
a)
3, 6
b)
x
c)
x
* VẬN DỤNG
Bài 5. Rút gọn các biểu thức sau:
a)
C 3 x 5 3x 5
b)
D
x 1 x 3
1
6
x
x
1
15, 08
3
7
8, 7
0, 5 3, 9
0
3, 5 7, 5
3, 5 4, 5
x 0
Trang 37
10
1
2
x
Bài 6. Tìm x biết:
a) 1 2x x 7
b)
x 1 2
.
x 3 3
0
c)
x
2
3x 0
d)
x
2
1
x
2
x
* VẬN DỤNG CAO
Bài 7. Tìm giá trị nhỏ nhất của các biểu thức sau:
a)
A
b) B
Bài 8. Tìm giá trị nhỏ nhất của biểu thức:
a)
A
b)
B
Bài 9. Tìm giá trị lớn nhất của các biểu thức sau:
a)
C
1, 5
x 2,1
; b)
D
c)
A
HẾT
x
6
13
x 2,8 7, 9
x
1, 5 5, 7
5, 7 2, 7 x
x
8 141
139 272
| 1/37
| | Tải xuống

Có thể bạn quan tâm:

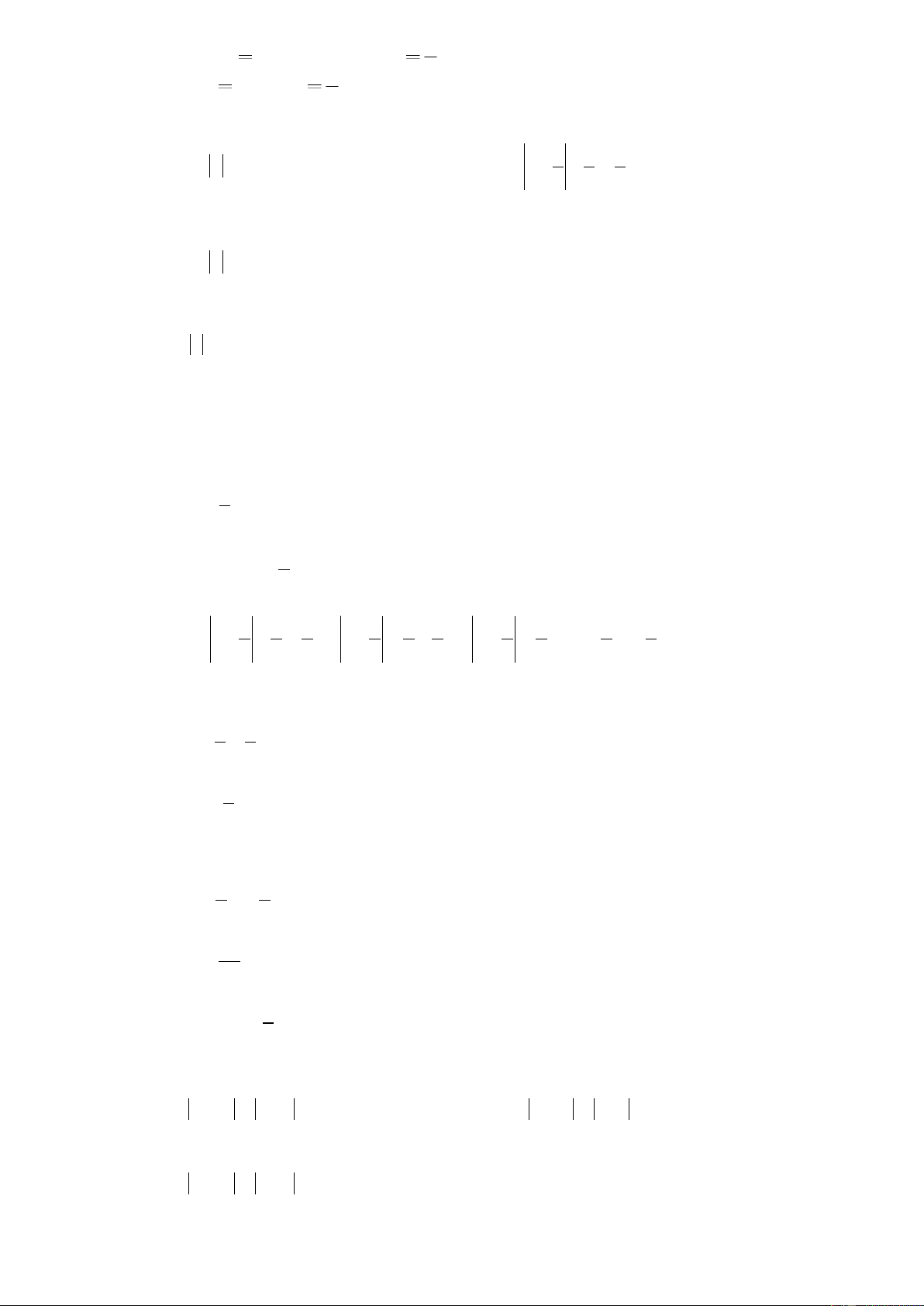
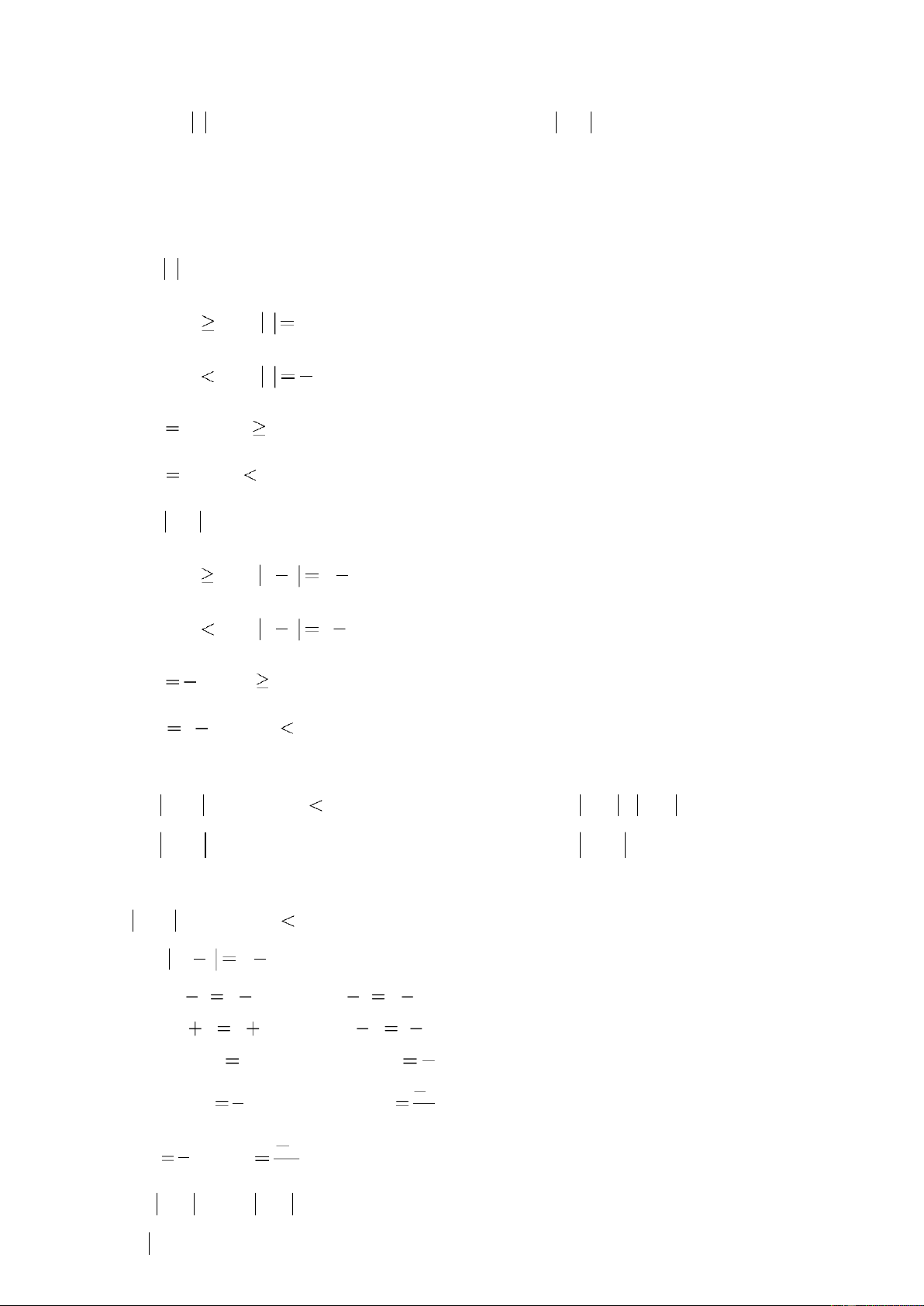
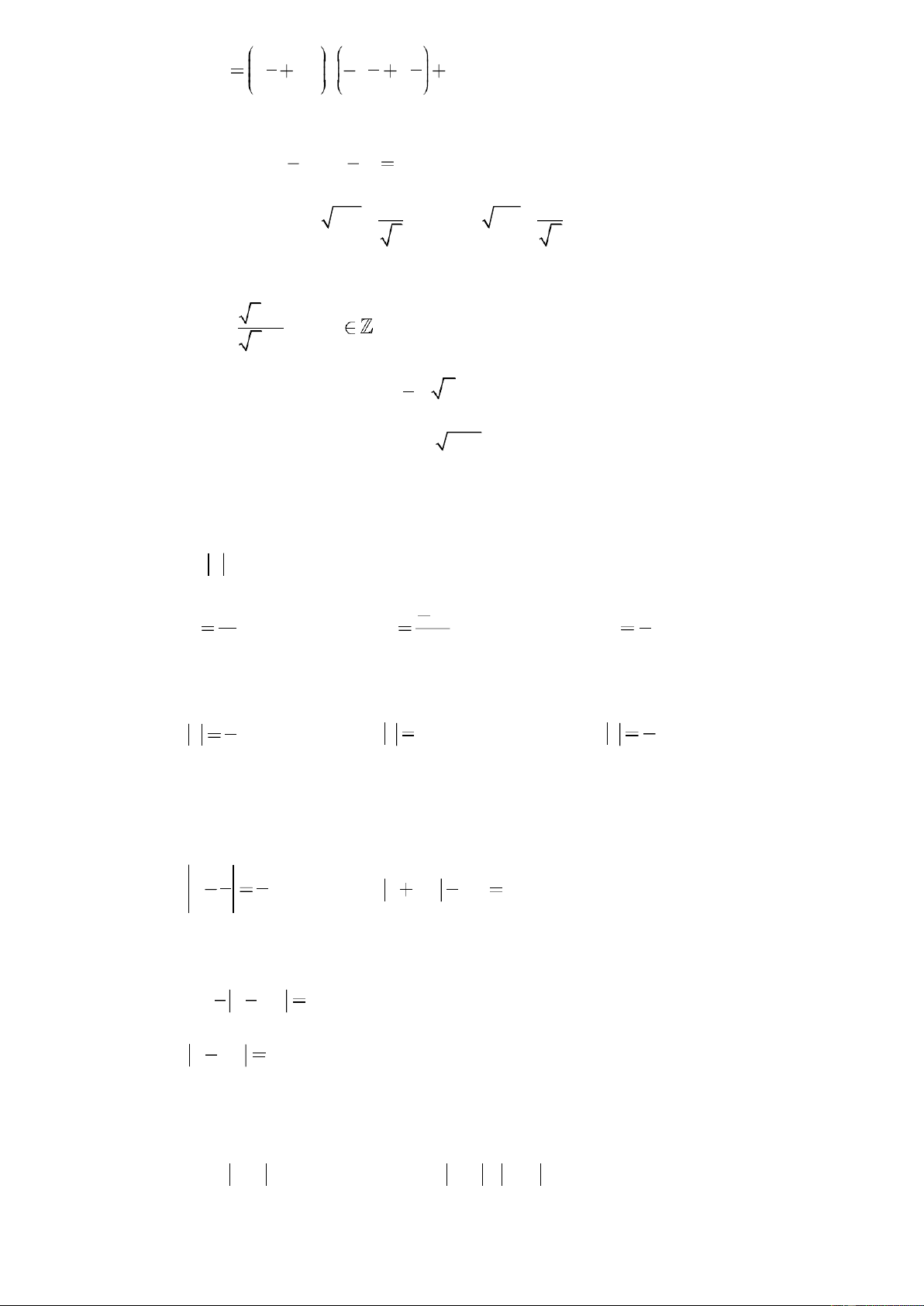
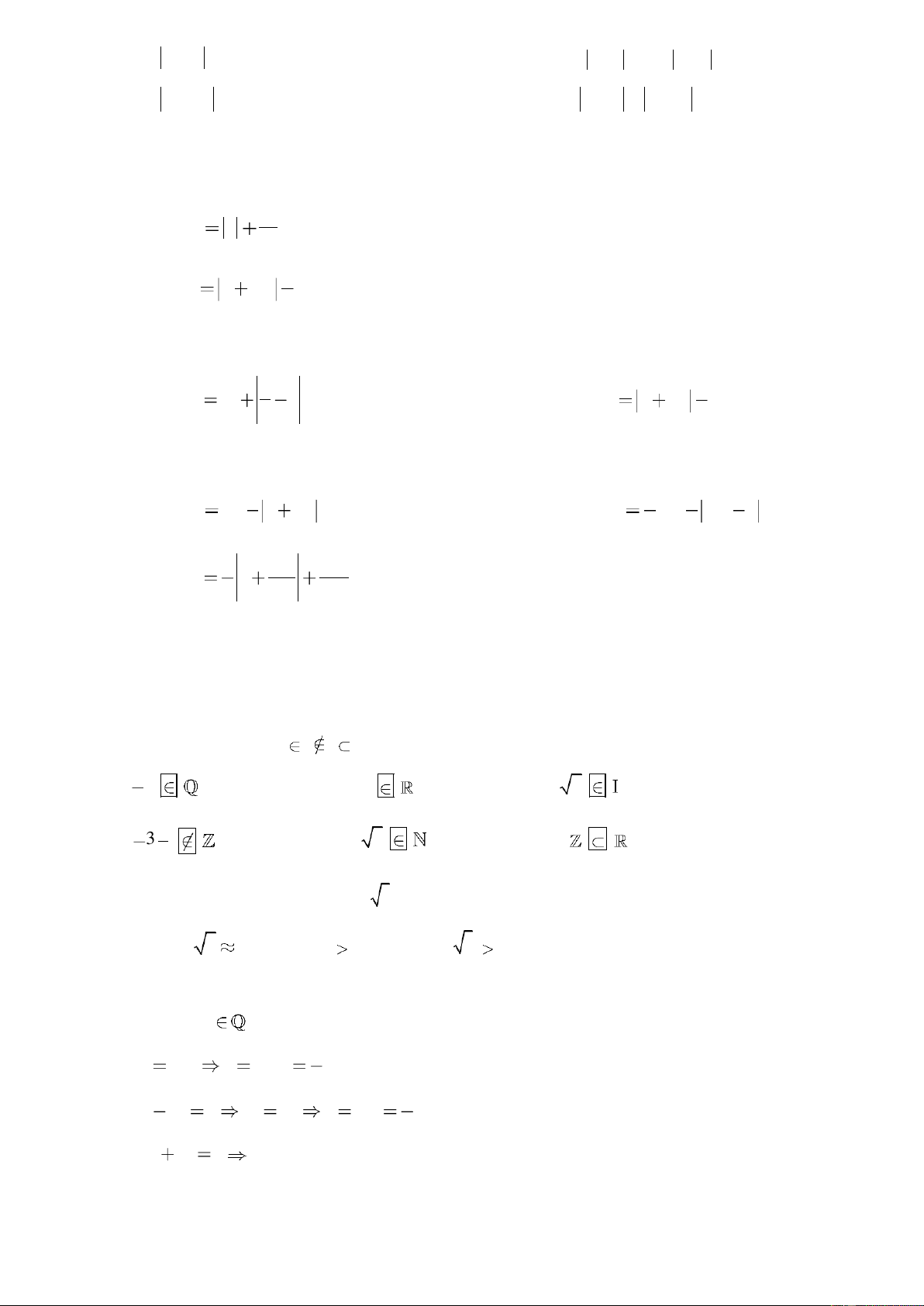
Preview text:

CHUYÊN ĐỀ : TẬP HỢP CÁC SỐ THỰC
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Số thực, trục số thực.
- Số hữu tỉ và số vô tỉ được gọi chung là số thực.
- Tập hợp các số thực được kí hiệu là .
- Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu
diễn một số thực. Vì vậy, người ta gọi trục số là trục số thực. * Chú ý:
- Mỗi số thực a đều có một số đối kí hiệu là a .
- Tập số thực cũng có các phép toán với các tính chất như trong tập số hữu tỉ.
2. Thứ tự trong tập hợp các số thực.
- Các số thực đều viết được dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể có thể so sánh
hai số thực tương tự như so sánh hai số hữu tỉ viết dưới dạng số thập phân. - Với a,b , ta có a
b hoặc a b hoặc a b .
- Cho a,b, c
. Nếu a b và b c thì a c ( tính chất bắc cầu ).
- Nếu 0 a b thì a b .
3. Giá trị tuyệt đối của một số thực
- Khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a , kí hiệu a . * Nhận xét:
- Giá trị tuyệt đối của 0 là 0 .
- Giá trị tuyệt đối của một số dương là chính nó.
- Giá trị tuyệt đối của một số âm là số đối của nó.
* Các tính chất hay sử dụng của giá trị tuyệt đối Với a thì a 0 ; a a ; a a ; a 0 khi a 0 ; a a khi a 0 ; a a khi a 0
PHẦN II. CÁC DẠNG BÀI.
Dạng 1. TẬP HỢP SỐ THỰC – SO SÁNH CÁC SỐ HỮU TỈ I. Phương pháp giải:
- Sử dụng kí hiệu của tập hợp số
Bạn cần nhớ: quan hệ giữa các tập hợp số: và .
Tập hợp các số tự nhiên kí hiệu là ;
Tập hợp các số nguyên kí hiệu là ;
Tập hợp các số hữu tỉ kí hiệu là ;
Tập hợp các số vô tỉ kí hiệu là ;
Tập hợp các số thực kí hiệu là ; Trang 1
- So sánh các số thực
+ Việc so sánh các số thực được làm tương tự như so sánh các số hữu tỉ viết dưới dạng số thập phân.
+ Đặc biệt, với a, b là hai số thực dương thì: a b a b ; a b a2 b2 II. Bài toán. * NHẬN BIẾT
Bài 1. Điền ký hiệu, ,  vào ô trống để được khẳng định đúng. 2 3 a) 5 . b) I . c) .   3 5 d) . e)  . f) 17 . 25 Lời giải 2 3 a) 5 b) I c)     3 5 d) e) - f)    25  17 
Bài 2. Điền các kí hiệu , , vào các ô trống: a) 0, 33 ; b) 0,52 41 ; c) 1, 4142135... ; d) . Lời giải a) 0, 33 ; b) 0, 52 41 ; c) 1, 4142135... ; d) .
Bài 3. Điền kí hiệu thích hợp vào ô trống để được khẳng định đúng? a) 3 ; b) . Lời giải a) 3 ; b) . 8
Bài 4. Tìm số đối của các số 0, 75; ; 7 13 Lời giải
Số đối của 0, 75 là 0, 75 8 Số 8 đối của là 13 13 Số đối của 7 là 7
Bài 5. So sánh các số thực:
a) 3, 7373737373...... với 3, 7474747474.... b) 0,1845 và 0,184147.... c) 6,8218218..... và 6, 6218
d) 7,321321321 ..... và 7,325 Trang 2 Lời giải
a) 3, 7373737373...... < 3, 7474747474.... b) 0,1845 < 0,184147....
c) 6,8218218..... > 6, 6218 d) 7,321321321 ..... > 7,325
Bài 6. So sánh số 1, 7(32) với số 3 . Lời giải
Ta có 3 1, 732050808...< 1, 7(32) * THÔNG HIỂU
Bài 7. Tìm số lớn nhất trong các số sau: ( 8)2 ; 8, 32; 69; 100. Lời giải 2 Ta có 8 8 69 8,306623.... 100 10
Vì 10 8 8,306623.... 8,32 Vậy số lớn nhất là 8, 32 .
Bài 8. Không dùng máy tính, cho biết trong hai khẳng định dưới đây, khẳng định nào đúng, khẳng định nào sai? 1 1 a) 65 1 63 1 b) 8 7 Lời giải a) Đúng Vì 65 63 do đó 65 1 63 1 b) Đúng 1 1 Vì 8 7 do đó 8 7
Bài 9. So sánh (không dùng máy tính): và 6 . 34,9 Lời giải Ta có 6 36 34,9
Bài 10. So sánh các số thực sau: a) 24 và 5 . b) 81.100 và 81. 100 . c) 0,16 và 0, 4 . d) 4. 9 và 145 . Lời giải a) Vì  25  5 nên 24 24  5 b) Ta có :    81.100 8100 902 90 81. 100  9.10  90 Trang 3 Vậy  81. 81.100 100 . c) Ta có :  0,16 0, 42  0, 4 Vậy  0, 4 0,16 d) Ta có : 4. 9  4.3  12 và  145  144 12 Vậy 4. 9  145 .
Bài 11. Tìm các số thực không âm x , biết: a) x  0 . b) x  1. c) x  2 . d) x  3 . Lời giải a) x  0
x  0 (thỏa mãn) Vậy x  0 . b) x  1.  x  12
x  1 (thỏa mãn) Vậy x 1 . c) x  2  x  22
x  4 (thỏa mãn) Vậy x  4 . d) x  3  x  32
 x  9 (thỏa mãn) Vậy x  9 .
Bài 12. Thực hiện phép tính a) 4  9  16   25 . b) 81  64 49 . 1 1 1 c)   . d)   1, 44 1, 69 1, 96 . 4 9 36 Lời giải a) Trang 4 4  9  16  
25 2  3  4  5  14 . 81   64  49 9  8  7  8 . b) Trang 5 1 1 1 3  2 1 4 2 1 1 1 c)         . 4 9 36 2 3 6 6 6 3 d)  1, 44  1, 69 
1, 96 1, 2 1, 3 1, 4  1, 5 . * VẬN DỤNG
Bài 13. Sắp xếp các số thực sau theo thứ tự tăng dần :
a) 1, 4142135; 0,(3) ; 10 ; 3 ; 25.4
b) 0,5;  0,(4) ; 3. 4 ;0,3 ; 35 Lời giải a) Ta có : 1 0,(3)  3 10   9  3 25.4  100  10 1 Mà
 1.4142135  3  10  10 3
0,(3)  1.4142135  3  10  25.4 c) Ta có :  0,5 0, 09  0, 32  0,3  0,5  0,3
* 3. 4  3.2  6  36 Mà 36   35  3. 4  35
Mà 0,(4)  0,3 0,5  35  36 
 0,(4)  0,3 0,5  35  3. 4
Bài 14. Tìm x , biết:
a) x 1  1 với x  1. b)
 2 với x  2 . x  2 c)
 19 với x  19 . d)  3 . 19  x x2 1 Lời giải a)  1 x 1  x 1  1
Vậy x  2 (thỏa mãn). b)  x  2 2 .  x  2  22 Trang 6
x  2 (thỏa mãn) Vậy x  2 . c)  19  x 19
 19  x  192
 19  x  361
 x  19  361
 x  342 (thỏa mãn) Vậy x  342. d) x2 1  3  x2 1  32  x2  8   x   8  Vậy x  8 .
Bài 15. Tìm x , biết: 1 a) x2  2  0 . b) 5  x2  1 .
c) 1 x2  3 .
d)  x 12   0 . 7 Lời giải a) x2  2  0  x2  2  x   2  Vậy x  2 . b) 5  x2  1 .  x2  4  x  2 Vậy x  2 . c) 1 x2  3
 1 x   3  TH1: 1 x  3   x  1 3 Trang 7
TH2: 1 x   3  
 x  1 3 
Vậy x 1 3 . 1
d)  x 12   0 7  1
x 12   7 1
Vì  x 12  0 , mà   0 7
Không có giá trị nào của x thỏa mãn đề bài
Vậy không có x thỏa mãn đề bài.
Bài 16. Thực hiện phép tính: 4 a) 4. 25  2. . b) 5 16  0, 25 16  3 . 9 25 1  . 1, 21  3   . d) . 9 c) 0, 09 36 4  3  0, 04  4 2 25 : . 64    Lời giải 4  2  4  60  4  56 a) 4. 25  2. 4.5  2. 20  . 9 3 3 3 3 3 4 16  1 12 b) 5 16  20  0, 25  3  5.4  0,5  3. 25 5 2 5  200 5 24 219    . 10 10 10 10 1 c) . 1, 21  
 0,5.1,1 0,3  6  6, 25 . 0, 09 36 4  3   3 2 1  8  3 3  8 6 8 16 .  4 9   25 64 d)  3 0, 04 :    .  3. .
   .  .  . 5   2  2 5 5  3  5 5  3 5 3
Bài 17. Thực hiện phép tính: 49 36 a) 5. 81  6. . b) 5 0, 25  196  5 . 4 25  7  c) 4   . d) 5.  . 400 : . . 1, 44  9 0,81 1, 21 9 20  9  225  144 Lời giải Trang 8 49 a) 5. 81  6. 4  7 5.9  6. 2  45  21  24 36 b) 5 0, 25  196  5 25  6 5.0,5 13  5. 5  2,5 13  6  4, 5 4 . 1, 44 c)  0,81  1, 21  9  2 .1, 2  0,9 1,1 3  0,8  2  2,8  7  5.    9 d)  9 225 . 400  144 20 :     3 7   3  5. 15  20 .20 : 12    3 1 7 : 12  3 8: 12  32
Câu 18. Hai bạn Hoa và Mai chuẩn bị đi dã ngoại cùng một nhóm bạn lớp 7A. Để chuẩn bị cho chuyến đi 1
dã ngoại hai bạn đã đi mua một số đồ. Hoa mua gói dâu tây, biết một gói dâu tây có giá 400000 3 đồng. 1
Một thùng nước ngọt giá 250000 đồng, Mai mua thùng nước này. Hỏi trong hai người, ai mua 2 hết nhiều tiền hơn? Lời giải 400000 390000 260000 250000 Ta có:   130000    125000 . 3 3 2 2 Từ 400000 250000 đó suy ra  . 3 2
Vậy Hoa mua hết nhiều tiền hơn Mai . * VẬN DỤNG CAO 2
Bài 19. a) Tìm giá trị lớn nhất của các biểu thức : A  . x  3 Trang 9 5
b) Tìm giá trị lớn nhất của các biểu thức : A  . x  2 Lời giải 2 a) Xét A   x  3 Ta có :
x  0 với mọi x không âm
x  3  3 với mọi x không âm  2 2
 với mọi x không âm x  3 3  2
A  với mọi x không âm 3
Dấu “  ” xảy ra khi và chỉ khi x  0 hay x  0 2
A có giá trị lớn nhất bằng khi x  0 3 5 b) Xét A   x  2 Ta có:
x  0 với mọi x không âm
x  2  2 với mọi x không âm 5  5
 với mọi x không âm x  2 2  5
A  với mọi x không âm 2
Dấu “  ” xảy ra khi x  0 5
Giá trị lớn nhất của A là khi x  0 2 3
Bài 20. a) Tìm giá trị nhỏ nhất của các biểu thức : D  . 2  x 6
b) Tìm giá trị nhỏ nhất của các biểu thức : D  . 3  x Lời giải 3 a) Xét: D  2  x Ta có:
x  0 với mọi x không âm
 2  x  2  3 3  2  x 2 Trang 10   3 D  2
Dấu “  ”xảy ra khi x  0 3
Vậy D có giá trị nhỏ nhất bằng khi x  0 2 6 b) Xét D  3  x Ta có :
x  0 với mọi x không âm
 3  x  3 với mọi x không âm  6 6 
với mọi x không âm 3  x 3  D  2
Dấu ‘  ’ xảy ra khi x  0
Vậy giá trị nhỏ nhất của D là 2 khi x  0 . x  5
Bài 21. Tìm x nguyên để có giá trị nguyên. x  2 Lời giải a) Ta có:
x  5  x  2  7 7  1 x  2 x  2 x  2 7 Để x  5
nhận giá trị nguyên thì nguyên x  2 x  2
Do đó x  2 Ư 7  1;1; 7; 7 Ta có bảng : x 2 1 1 7 7 x 3 1 9 5
Vậy x 3; 1; 9;5 
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC.
I. Phương pháp giải:
- Giá trị tuyệt đối của một số hữu tỉ x , kí hiệu là x Được x khi x 0
xác định như sau: x x khi x < 0 - Với x , x a khi đó: +) Nếu a 0 thì x 0 ; +) Nếu a 0 thì x a hoặc x a ; Trang 11
+) Nếu a 0 thì x * Chú ý: + Ta có: k.x 0 k.x a a ; k.x a a Dấu “=” xảy ra k.x 0 . + Ta có: k.x b 0 k.x b a a ; k.x b a a Dấu “=” xảy ra k.x b 0 . + Ta có: a b
a b . Dấu “=” xảy ra khi a.b 0 II. Bài toán. * NHẬN BIẾT
Bài 1. Tìm x biết: 4  1 a) x  3 b) x  c) x  0, 749 d) x  5 7 11 7 Lời giải 1 1 4 4 a) b) 3 3 c) 0, 749  0, 749 d) 5  5 7 7 11 11 7 7 Bài 2. Tính: a) 0,17 b) 12, 5 16, 5 Lời giải a) 0,17  0,17
b) 12, 5 16, 5  4  4 Bài 3. Tính:  7 a) 2, 5  7, 5 b) 1, 2 3  6, 4 c)  15 2  2 Lời giải
a) 2, 5  7, 5  2, 5  7, 5  10
b) 1, 2 3  6, 4  1, 2.3  6, 4  3, 6  6, 4  10  7 15 22 7 c)  15     11 2 2 2 2 2
Bài 4. Tìm x , biết: a) x 13 b) x 17 Lời giải a) x 13 b) Vì x 0 với mọi x Trang 12 x 13 hoặc x 13
Vậy không tìm được giá trị x thoả mãn Vậy x 13; x 13 x 17
Bài 5. Tìm x , biết: 3 b) x  a) x  1, 2 4 Lời giải 3 a) x  1, 2 b) x  4 3 3
x  1, 2 hoặc x  1, 2
x  hoặc x  4 4 * THÔNG HIỂU 3
Bài 6. Tìm số đối của các số 5, 5 ; ;  7 8  11 Lời giải 3 7 3 ;  7 Ta có 5, 5  5, 5 ;   8 8 11 11
Vậy số đối của 5, 5 là 5,5 3 3 Số đối của là  8 8 7
Số đối của  7 là  11 11
Bài 7. Tính giá trị các biểu thức sau: 2 a) 5,9  2 b) c)     3   2      1, 6 3, 6 2, 2 5 5 7   Lời giải
a) 5,9  2  5,9  2  3,9 b) 1, 6 3, 6
2, 2  1, 6.3, 6  2, 2  5, 76  2, 2  3,56 2  3  2 2 3 3 3 c)     
     0   5 5 7 7 7 5 2 7 5   Bài 8. Tính: 6 4 5 3 a)    2 . b)    4  8 25 5 25 9 5 9 5 Lời giải Trang 13 6 4 a)    6 4 2 6 20 2 12 2 =   =    25 5 25 25 5 25 25 25 25 25 5 3  5 4   3 8  9 5 b)     5 3 4 8 =        11  2   = 9 5 9 5 9 5    5 5 9 5     4 8 9 5 9 9    
Bài 9. Cho a  6 ; b  3 ; c   2 , hãy tính:
a b c .
a) a b  c b) Lời giải
Ta có a  6  6 ; b  3  3 ; c   2  2 . Do đó:
a) a b  c  6  3  2  11  11
b) a b c  6  3  2  7  7 Bài 10. So sánh:  a) 7 11 và 7  11
b) 8  15 và 8  15 Lời giải
a) Ta có: 7 11  18  18 7  11  7 11  18 Vậy 7 11 = 7  11
b) Ta có: 8  15  7  7
8  15  8 15  23
Vậy 8  15  8  15
Bài 11. Tìm x biết: 2  a) 1,8  x  0, 5 b) x  1 c) 3x  2  4 7 Lời giải a) 1,8  x  0, 5
 1,8  x  0,5 TH1: 1,8  x  0,5
TH 2: 1,8  x  0,5 x 1,8 0,5 x 1,8 0,5 x 1, 3 x 2, 3
Vậy x 1, 3 hoặc x 2, 3 2 b) x   1 7 Trang 14  2 x   1 7 2 2 TH 1: x   1 TH 2: x   1 7 7 2 2 x 1 x 1 7 7 5 9 x x 7 7 5 Vậy 9 x hoặc x 7 7 c) 3x  2  4  3x  2  4 TH 1: 3x  2  4
TH 2: 3x  2  4 3x 6 3x 2 2 x 2 x 3 Vậy 2 x 2 hoặc x 3 * VẬN DỤNG
Bài 12. Tìm x , biết: a) 2  x  2 .
b) x 1  3  2 . c) x  3  3 1. Lời giải a) 2  x  2 
 2  x   2 TH1: 2 x  2 x  0 TH2: 2  x   2 x  2 2
Vậy x 0; 2 2  b) x 1  3  2
x 1   3  2 TH1: x 1  3  2 Trang 15 x  3  3 TH2: x 1   3  2 x   3 1
Vậy x 3  3; 1 3  c) x  3  3 1  x  3  2  x  3  2 TH1: x  3  2 x  5 TH2: x  3  2 x 1 Vậy x 5;1 
Bài 13. Tìm x biết: 1 2 1 a)  x   b) 2x 1 2 5 4 3 2 Lời giải 1 2 1 a)  x   4 3 2 1  1 2 x   4 2 3  1  1 x  4 6 1 Vì
x  0 với mọi x 4
Không tìm được giá trị của x thoả mãn. b) 2x 1 2 5 2x 1 5 2 2x 1 3
Suy ra 2x 1 3 hoặc 2x 1 3 2x 3 1 hoặc 2x 3 1 2x 4 hoặc 2x 2 Trang 16 x 2 hoặc x 1
Vậy x 2 hoặc x 1 .
Bài 14. Tìm các số không âm x , biết: 1 1 3
a) x .4x  3  0 . b) x    . 2 4 2 Lời giải
a) x .4x  3  0 TH1: x  0 x  0 (thỏa mãn) TH2: 4x  3  0 3 x  (thỏa mãn) 4  3  Vậy x  0;      4     1 1 3 1 3 1 1 7 1 7
b) x     x
   x    x    2 4 2 2 2 4 2 4 2 4 TH1: 1 7 x   2 4 9 x  (thỏa mãn) 4 TH2: 1 7 x    2 4  5 x  ( loại ) 4 9 
Vậy x   4  
Bài 15. Tìm x biết:
a) 5x  3  7  x
b) 2x 1  1 x Lời giải
a) 5x  3  7  x
 5x  3  7  x hoặc 5x  3  x  7 Trang 17
TH 1 : 5x  3  7  x
TH 2 : 5x  3  x  7 5x x 7 3 5x x 3 7 6x 10 4x 4 5 x x 1 3 5 Vậy x hoặc x 1. 3
b) 2x 1  1 x
2x 1  1 x hoặc 2x 1  x 1
TH 1: 2x 1 1 x
TH 2: 2x 1  x 1 2x x 1 1 2x x 1 1 3x 2 x 0 2 x 3 2 Vậy x hoặc x 0 3
Bài 16. Tìm x biết:
a) 2x 1  2x  1
b) 1 3x 1  3x 1 1 1 1 c) x    x
d) 2x    2x 2 2 3 3 Lời giải
a) 2x 1  2x  1
b) 1 3x 1  3x
2x 1  2x 1 1 3x 3x 1 Suy ra 2x 1 0 Suy ra 1 3x 0 1 2x 1 x 3 1 1 x Vậy x 2 3 Vậy 1 x 2 1 1 1 1 c) x    x d) 2x    2x 2 2 3 3 1 1 x   x  Suy ra 2x 1 0 2 2 3 1 1 Suy ra x 0 2x 2 3 1 1 x x 2 6 Vậy 1 1 x Vậy x 2 6 Trang 18 * VẬN DỤNG CAO Bài 17. Rút gọn: C 
a) A  x x x 1  x b ) Lời giải
a) A  x x
TH1: nếu x 0 thì x
x . Khi đó A x x  2x
TH2: nếu x 0 thì x
x . Khi đó A  x x  0
Vậy A 2x khi x 0 A 0 khi x 0
b) C x 1  x
TH1: nếu x 1 thì x 1
x 1. Khi đó C x 1 x  1
TH2: nếu x 1 thì x 1
1 x . Khi đó C  1 x x  1 2x Vậy C 1 khi x 1 C 1 2x khi x 1
Bài 18. Tìm x biết:
a) 3x 1  x  2 khi x 2
b) x  8  x  2  0 c) x2 1  0 d) x2 1  0 Lời giải
a) 3x 1  x  2 khi x 2 3x 1 2 x
Suy ra 3x 1 2 x hoặc 3x 1 x 2 3x x 2 1 3x x 1 2 4x 3 2x 1 3 1 t / m x x t / m 4 2 3 Vậy 1 x hoặc x 4 2
b) Vì x  8  0 và x  2  0 với mọi x .
Nên x  8  x  2  0 Trang 19
Khi x 8 0 và x 2 0 Trang 20
Suy ra x 8 0 và x 2 0 x 8 và x 2 x
Vậy không tìm được giá trị x thoả mãn. c) x2 1  0 x2 1 0 x2 1 x 1 hoặ c x 1 Vậy x 1 ; x 1 d) x2 1  0 Vì x2
0 với mọi x nên x2 1 0 với mọi x
Vậy không tìm được giá trị x thoả mãn x2 1  0
Bài 19. Rút gọn các biểu thức sau: E  2 x 1  3 x Lời giải
E  2 x 1  3 x TH 1: Nếu x 1 thì x 1 x 1và x x . Khi đó : E 2 x 1 3 x 2x 2 3x 5x 2
TH 2: Nếu 1 x 0 thì x 1 x 1 và x x . Khi đó : E 2 x 1 3 x 2x 2 3x x 2
TH 3: Nếu x 0 thì x 1 x 1và x x . Khi đó : E 2 x 1 3x 2x 2 3x 5x 2 Vậy E 5x 2 khi x 1 E x 2 khi 1 x 0
E 5x 2 khi x 0
Bài 20. Tìm x, y, z  biết:  1 3  1 a) x   y 1  0 ; b) x
y   x y z  0 4 2 3 Lời giải 3 a) Vì x
0 và y 1  0 với mọi x, y  . 4 Nên x  3  y 1  0  4 3 x 0 và y 1 0 4 Trang 21 3 x 0 và y 1 0 4 3 x và y 1 4 3 Vậy x ; y 1 4  1 b) Vì x 
1  0 ; y   0 ; x y z  0 với mọi x, y, z  , Nên: 2 3 1 x   1
y   x y z  0 2 3 1 1 x 0 và y 0 và x y z 0 2 3 1 1 x 0 và y 0 và x y z 0 2 3 1 1 1 1 5 x và y và z 0 2 3 2 3 6 1 1 Vậy 5 x ; y ; z 2 3 6
Bài 21. Tìm x thoả mãn 2 x 1  3 x  12 Lời giải
2 x 1  3 x  12 TH 1: Nếu x 1 thì x 1 x 1và x x . Khi đó : 2 x 1 3 x 12 2x 2 3x 12 5x 2 12 5x 14 14 x ( thoả mãn ) 5
TH 2: Nếu 1 x 0 thì x 1 x 1 và x x . Khi đó : 2 x 1 3 x 12 2x 2 3x 12 x 2 12 x 10 x 10 ( không thoả mãn )
TH 3: Nếu x 0 thì x 1 x 1 và x x . Khi đó : Trang 22 2 x 1 3x 12 2x 2 3x 12 5x 2 12 5x 10 x 5 ( thoả mãn ) 14 Vậy x ; x 5 5
Bài 22. Tìm giá trị nhỏ nhất của biểu thức: 1 1
a) A   2 x  2 2
b) B x2  y  2  5 Lời giải 1 1
a) A   2 x  2 2 Ta có x 1 0 với mọi x 2 1 1 1
Do đó A   2 x   với mọi x . 2 2 2 1 1 1 Dấu 1
“=” xảy ra, tức A khi x x . 0 x 0 2 2 2 2 Vậy 1
giá trị nhỏ nhất của 1 A bằng khi x 2 2
b) B x2  y  2  5 Ta có x2
0 với mọi x ; y 2 0 với mọi y
Do đó B x2  y  2  5  5 với mọi x; y . x2 0 x 0
Dấu “=” xảy ra, tức B 5 khi khi y 2 0 y 2 x 0
Vậy giá trị nhỏ nhất của B bằng 5 khi y 2
Bài 23. Tìm giá trị nhỏ nhất của biểu thức: C  3x  5  3x  9 Lời giải
C  3x  5  3x  9  3x  5  9  3x 3x 5 9 3x Do đó C 4 C 4
Dấu “=” xảy ra, tức C 4 khi 3x 5 9 3x 0 5 3x 5 0 x 5 TH 1: 3 x 3 9 3x 0 3 x 3 Trang 23 5 3x 5 0 x TH 2: 3
Không tìm được x thoả mãn. 9 3x 0 x 3 5
Vậy giá trị nhỏ nhất của C khi 4 x 3 . 3
Bài 24. Tìm giá trị lớn nhất của biểu thức:
a) A  8  6 x  2 1 b) B   2 x 1  3 Lời giải
a) A  8  6 x  2 Ta có x 2
0 với mọi x . Do đó A  8  6 x  2  8 với mọi x .
Dấu “=” xảy ra, tức A 8 khi x 2 0 khi x 2 0 khi x 2 Vậy khi x 2 .
giá trị lớn nhất của 8 A 1 b) B   2 x 1  3 Ta có x 1
0 với mọi x . Do đó 2 x 1 3 3 với mọi x . 1 1 Suy ra B   với mọi x . 2 x 1  3 3 1
Dấu “=” xảy ra, tức B khi x 1 0 x 1 0 x 1 3
Vậy giá trị lớn nhất của khi x 1 B 1 3
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. TẬP HỢP SỐ THỰC * NHẬN BIẾT
Bài 1. Điền các kí hiệu , , vào các ô trống: a) 2 ; b) 1 ; c) 2 ; 1 d) 3 ; e) 9 ; f) . 5
Bài 2. Dùng máy tính để so sánh 5 với 2,(23) . * THÔNG HIỂU Bài 3. Tìm x biết: a) x2 400 ; b) x2 64 0 ; c) 5x2 10 9 .
Bài 4. Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn: 3 1, 75; 2; 0;5 ; 22 ; ; 5. 6 7 Trang 24 1 1 1
Bài 5. Tính: M 2 3, 5 : 4 3 7, 5 . 3 6 7 * VẬN DỤNG
Bài 6. Tìm x biết x2 4 x2 3 0 . 1 1
Bài 7. So sánh hai số: A  225  1 ; B  196  5  6 * VẬN DỤNG CAO x 1
Bài 8. Cho A  . Tìm x
để A nhận giá trị nguyên x 1 1
Bài 9. Tìm GTNN của biểu thức P   x 2
Bài 10. Tìm GTLN của biểu thức Q = 7  2 x 1
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA SỐ THỰC * NHẬN BIẾT
Bài 1. Tính x , biết: 3 13 a) x . b) x c) x 15, 08 17 161
Bài 2. Tính x , biết: 3 a) x ; b) x 0 ; c) x 8, 7 7 * THÔNG HIỂU
Bài 3. Tính x , biết: 2 1 a) x ; b) x 0, 5 3, 9 0 5 4
Bài 4. Tìm x , biết: a) 3, 6 x 0, 4 0 b) x 3, 5 7, 5 * VẬN DỤNG  
Bài 5. Rút gọn các biểu thức sau:
a) C  3 x  5  3x  5
b) D  x 1  x  3
Bài 6. Tìm x biết: Trang 25
a) 1 2x x  7
b)  x 1  2. x  3  3  0
c) x2  3x  0
d) x2 1  x2  x * VẬN DỤNG CAO
Bài 7. Tìm giá trị nhỏ nhất của các biểu thức sau: 6 a) A x 13 b) B x 2,8 7, 9
Bài 8. Tìm giá trị nhỏ nhất của biểu thức: 1 a) A 10 x b) B x 1, 5 5, 7 2
Bài 9. Tìm giá trị lớn nhất của các biểu thức sau: a) C 1, 5 x 2,1 ; b) D 5, 7 2, 7 x 8 141 c) A x 139 272
ĐÁP SỐ BÀI TẬP TỰ LUYỆN
Dạng 1. TẬP HỢP SỐ THỰC * NHẬN BIẾT
Bài 1. Điền các kí hiệu , , vào các ô trống: a) 2 ; b) 1 ; c) 2 ; 1 d) 3 ; e) 9 ; f) . 5
Bài 2. Dùng máy tính để so sánh 5 với 2,(23)
ĐS: Ta có 5 2, 2360667... 2,(23) . Vậy 5 2,(23) . * THÔNG HIỂU Bài 3. Tìm x biết: a) x2 400 x 20; x 20 ; b) x2 64 0 x2 64 x 8; x 8 c) 5x2 10 9
Không tìm được x thoả mãn .
Bài 4. Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn: Trang 26 3 1, 75; 2; 0;5 ; 22 ; ; 5. 6 7 22 3 ĐS: 2; 1, 75;0; 5; ; ;5 . 7 6 1 1 1
Bài 5. Tính: M 2 3, 5 : 4 3 7, 5 . 3 6 7 ĐS: 43 15 155 M 7 7 25 22 15 35 : : . 3 2 6 7 2 6 42 2 86 * VẬN DỤNG
Bài 6. Tìm x biết x2 4 x2 3 0 . ĐS: x2 4 x2 3 0
x2  4  0 hoặc x2  3  0  x2  4 hoặc x2  3 x 2; 3; 3; 2 1 1
Bài 7. So sánh hai số: A  225  1 ; B  196  5  6 1 1 1 ĐS: A  225  1  15  1  14   5 5 5  1 1 B   196  14  6  6 Do đó A B * VẬN DỤNG CAO x 1
Bài 8. Cho A  . Tìm x
để A nhận giá trị nguyên x 1 x 1 2
Đáp số: A   1 x 1  x 1
Để A nhận giá trị nguyên thì x 1 là ước của 2 . Vậy x 0; 4;9 1
Bài 9. Tìm GTNN của biểu thức P x 2 1 Đ/S: P  khi x 0 min 2
Bài 10. Tìm GTLN của biểu thức Q = 7  2 x 1 Trang 27 Đ/S: Q 7 khi x 1 max
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA SỐ THỰC * NHẬN BIẾT 3 13
Bài 1. Tính x , biết: a) x . b) x c) x 15, 08 17 161 ĐS: 3 13 a) x . b) x c) x 15, 08 17 161 3
Bài 2. Tính x , biết: a) x ; b) x 0 ; c) x 8, 7 7 ĐS: 3 3 a) x ; x ; b) x 0 ; c) x 8, 7 Không tìm được x 7 7 * THÔNG HIỂU
Bài 3. Tính x , biết: 2 1 a) x   13 3 x ; x 5 4 20 20 b) x 0, 5 3, 9 0 x 3, 4; x 4, 4
Bài 4. Tìm x , biết: a) 3, 6 x 0, 4 0 x 4; x 3, 2 b) x 3, 5 7, 5 x 11; x 4 c) x 3, 5 4, 5 x 0
Không tìm được x . * VẬN DỤNG
Bài 5. Rút gọn các biểu thức sau:
a) C  3 x  5  3x  5
Nếu x 5 thì C 10 .
Nếu x 5 thì C 20 6x
b) D x 1  x  3 Nếu x 3 thì D 2x 2
Nếu 3 x 1 thì D 2
Nếu x 1 thì D 2x 2 Trang 28
Bài 6. Tìm x biết:
a) 1 2x x  7
 1 2x  7  x với x  7
1 2x  7  x hoặc 1 2x  7  x x 2; 8
b)  x 1  2. x  3  3  0
  x 1  2  0 hoặc  x  3  3  0
x 1  2 hoặc x  3  3 x 3; 0;1; 6
c) x2  3x  0
x2  3x  0
x x  3  0 x 3; 0
d) x2 1  x2  x
x2 1  x2  x hoặc x2 1  x2  x 1 x 1; 2 * VẬN DỤNG CAO
Bài 7. Tìm giá trị nhỏ nhất của các biểu thức sau: 6 a) A x 13 6 A x 0 min 13 b) B x 2,8 7, 9 B 7, 9 x 2,8 min
Bài 8. Tìm giá trị nhỏ nhất của biểu thức: 1 a) A 10 x 2 1 A 10 x min 2 b) B x 1, 5 5, 7 Trang 29 B 5, 7 x 1, 5 min
Bài 9. Tìm giá trị lớn nhất của các biểu thức sau: a) C 1, 5 x 2,1 ; C 1, 5 x 2,1 max b) D 5, 7 2, 7 x D 5, 7 x 2, 7 max 8 141 c) A x 139 272 141 8 A x max 272 139 PHIẾU BÀI TẬP
( Nội dung là toàn bộ bài tập đã có trên )
Dạng 1. TẬP HỢP SỐ THỰC * NHẬN BIẾT
Bài 1. Điền ký hiệu, ,  vào ô trống để được khẳng định đúng. 2 3 a) 5 . b) I . c) .   3 5 d) . e)  . f) 17 . 25
Bài 2. Điền các kí hiệu , , vào các ô trống: a) 0, 33 ; b) 0, 52 41 ; c) 1, 4142135... ; d) .
Bài 3. Điền kí hiệu thích hợp vào ô trống để được khẳng định đúng? a) 3 ; b) . 8
Bài 4. Tìm số đối của các số 0, 75; ; 7 13
Bài 5. So sánh các số thực:
d) 3, 7373737373...... với 3, 7474747474.... e) 0,1845 và 0,184147.... f) 6,8218218..... và 6, 6218
d) 7,321321321 ..... và 7,325
Bài 6. So sánh số 1, 7(32) với số 3 . * THÔNG HIỂU Trang 30
Bài 7. Tìm số lớn nhất trong các số sau: ( 8)2 ; 8, 32; 69; 100.
Bài 8. Không dùng máy tính, cho biết trong hai khẳng định dưới đây, khẳng định nào đúng, khẳng định nào sai? 1 1 a) 65 1 63 1 b) 8 7
Bài 9. So sánh (không dùng máy tính): 34,9 và 6 .
Bài 10. So sánh các số thực sau: a) 24 và 5 . b) 81.100 và 81. 100 . c) 0,16 và 0, 4 . d) 4. 9 và . 145
Bài 11. Tìm các số thực không âm x, biết: a) x  0 . b) x  1. c) x  2 . d) x  3 .
Bài 12. Thực hiện phép tính a) 4  9  16   25 . b) 81  64 49 . 1 1 1 c)   .
d) 1, 44  1, 69  1, 96 . 4 9 36 * VẬN DỤNG
Bài 13. Sắp xếp các số thực sau theo thứ tự tăng dần :
a) 1, 4142135; 0,(3) ; 10 ; 3 ; 25.4
b) 0,5;  0,(4) ; 3. 4 ;0,3 ; 35
Bài 14. Tìm x, biết:
a) x 1  1 với x  1.
b) x  2  2 với x  2 .
c) 19  x  19 với x  19. d) x2 1  3 .
Bài 15. Tìm x, biết: 1 a) x2  2  0 . b) 5  x2  1 .
c) 1 x2  3 .
d)  x 12   0 . 7
Bài 16. Thực hiện phép tính: a) 4.  2. 25 4 . b) 5 16  0, 25 16  3 . 9 25 1  3  c) . 1, 21   . d) . 9  0, 09 36 4 2 3  0, 04  : . 4 25 64  
Bài 17. Thực hiện phép tính: Trang 31 a) 5. 81  6. 49 . b) 5  0, 25 196 36  5 . 4 25  7  4 5.   . 1, 44 9 9  0,81 1, 21  c) 9  . d)  225 . 400  144   20 : .
Câu 18. Hai bạn Hoa và Mai chuẩn bị đi dã ngoại cùng một nhóm bạn lớp 7A. Để chuẩn bị cho chuyến đi 1
dã ngoại hai bạn đã đi mua một số đồ. Hoa mua gói dâu tây, biết một gói dâu tây có giá 400000 3 đồng. 1
Một thùng nước ngọt giá 250000 đồng, Mai mua thùng nước này. Hỏi trong hai người, ai mua 2 hết nhiều tiền hơn? * VẬN DỤNG CAO 2
Bài 19. a) Tìm giá trị lớn nhất của các biểu thức : A  . x  3 5
b) Tìm giá trị lớn nhất của các biểu thức : A  . x  2 3
Bài 20. a) Tìm giá trị nhỏ nhất của các biểu thức : D   . 2  x 6
b) Tìm giá trị nhỏ nhất của các biểu thức : D   . 3  x x  5
Bài 21. Tìm x nguyên để có giá trị nguyên. x  2
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA MỘT SỐ THỰC. * NHẬN BIẾT
Bài 1. Tìm x biết: 4  1 a) x  3 b) x  c) x  0, 749 d) x  5 7 11 7 Bài 2. Tính: b) 0,17  0,17 b) 12, 5 16, 5 Bài 3. Tính:  7  a) 2, 5  7, 5 b) 1, 2 3  6, 4 15 2 2 c)  
Bài 4. Tìm x , biết: a) x 13 b) x 17
Bài 5. Tìm x , biết: Trang 32 1 3 a) x  1, 2 b) x   2 4 * THÔNG HIỂU 3
Bài 6. Tìm số đối của các số 5, 5 ; ;  7 8  11
Bài 7. Tính giá trị các biểu thức sau: 2 a) 5,9  2 b)
c)    2  3   1, 6 3, 6 2, 2      5 5 7   Bài 8. Tính: 6 4 5 3 a)    2 . b)    4  8 25 5 25 9 5 9 5
Bài 9. Cho a  6 ; b  3 ; c   2 , hãy tính:
a b c .
a) a b  c b) Bài 10. So sánh:  a) 7 11 và 7  11
b) 8  15 và 8  15
Bài 11. Tìm x biết: 2  a) 1,8  x  0, 5 b) x  1 c) 3x  2  4 7 * VẬN DỤNG
Bài 12. Tìm x , biết: a) 2  x  2 .
b) x 1  3  2 . c) x  3  3 1.
Bài 13. Tìm x biết: 1 2 1 a)  x   b) 2x 1 2 5 4 3 2
Bài 14. Tìm các số không âm x , biết: 1 1  3
a) x .4x  3  0 . b) x   . 2 4 2
Bài 15. Tìm x biết:
a) 5x  3  7  x
b) 2x 1  1 x
Bài 16. Tìm x biết:
a) 2x 1  2x  1
b) 1 3x 1  3x 1 1 1 1 c) x    x
d) 2x    2x Trang 33 2 2 3 3 Trang 34 * VẬN DỤNG CAO Bài 17. Rút gọn: C 
a) A  x x x 1  x b )
Bài 18. Tìm x biết:
a) 3x 1  x  2 khi x 2
b) x  8  x  2  0 c) x2 1  0 d) x2 1  0
Bài 19. Rút gọn các biểu thức sau: E  2 x 1  3 x
Bài 20. Tìm x, y, z  biết:  1 3  1 a) x   y 1  0 ; b) x
y   x y z  0 4 2 3
Bài 21. Tìm x thoả mãn 2 x 1  3 x  12
Bài 22. Tìm giá trị nhỏ nhất của biểu thức: 1 1
a) A   2 x  2 2
b) B x2  y  2  5
Bài 23. Tìm giá trị nhỏ nhất của biểu thức: C  3x  5  3x  9
Bài 24. Tìm giá trị lớn nhất của biểu thức:
a) A  8  6 x  2 1 b) B   2 x 1  3
Phần III. BÀI TẬP TỰ LUYỆN
Dạng 1. TẬP HỢP SỐ THỰC * NHẬN BIẾT
Bài 1. Điền các kí hiệu , , vào các ô trống: a) 2 ; b) 1 ; c) 2 ; 1 d) 3 ; e) 9 ; f) . 5
Bài 2. Dùng máy tính để so sánh 5 với 2,(23) . * THÔNG HIỂU Bài 3. Tìm x biết: a) x2 400 ; b) x2 64 0 ; c) 5x2 10 9 .
Bài 4. Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn: 3 1, 75; 2; 0;5 ; 22 ; ; 5. 6 7 Trang 35 1 1 1
Bài 5. Tính: M 2 3, 5 : 4 3 7, 5 . 3 6 7 * VẬN DỤNG
Bài 6. Tìm x biết x2 4 x2 3 0 . 1 1
Bài 7. So sánh hai số: A  225  1 ; B  196  5  6 * VẬN DỤNG CAO x 1
Bài 8. Cho A  . Tìm x
để A nhận giá trị nguyên x 1 1
Bài 9. Tìm GTNN của biểu thức P   x 2
Bài 10. Tìm GTLN của biểu thức Q = 7  2 x 1
Dạng 2. GIÁ TRỊ TUYỆT ĐỐI CỦA SỐ THỰC * NHẬN BIẾT
Bài 1. Tính x , biết: 3 13 a) x . b) x c) x 15, 08 17 161
Bài 2. Tính x , biết: 3 a) x ; b) x 0 ; c) x 8, 7 7 * THÔNG HIỂU
Bài 3. Tính x , biết: 2 1 a) x ; b) x 0, 5 3, 9 0 5 4
Bài 4. Tìm x , biết: a) 3, 6 x 0, 4 0 b) x 3, 5 7, 5 c) x 3, 5 4, 5 x 0 * VẬN DỤNG  
Bài 5. Rút gọn các biểu thức sau:
a) C  3 x  5  3x  5
b) D  x 1  x  3 Trang 36
Bài 6. Tìm x biết:
a) 1 2x x  7
b)  x 1  2. x  3  3  0
c) x2  3x  0
d) x2 1  x2  x * VẬN DỤNG CAO
Bài 7. Tìm giá trị nhỏ nhất của các biểu thức sau: 6 a) A x 13 b) B x 2,8 7, 9
Bài 8. Tìm giá trị nhỏ nhất của biểu thức: 1 a) A 10 x b) B x 1, 5 5, 7 2
Bài 9. Tìm giá trị lớn nhất của các biểu thức sau: a) C 1, 5 x 2,1 ; b) D 5, 7 2, 7 x 8 141 c) A x 139 272 HẾT Trang 37