






























Preview text:
CHƯƠNG 1: SỐ HỮU TỈ
Bài 1: TẬP HỢP SỐ HỮU TỈ
I. LÍ THUYẾT TRỌNG TÂM
1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số: a
a) Khái niệm: Số hữu tỉ là số viết được dưới dạng phân số
với a,b ;b 0 b
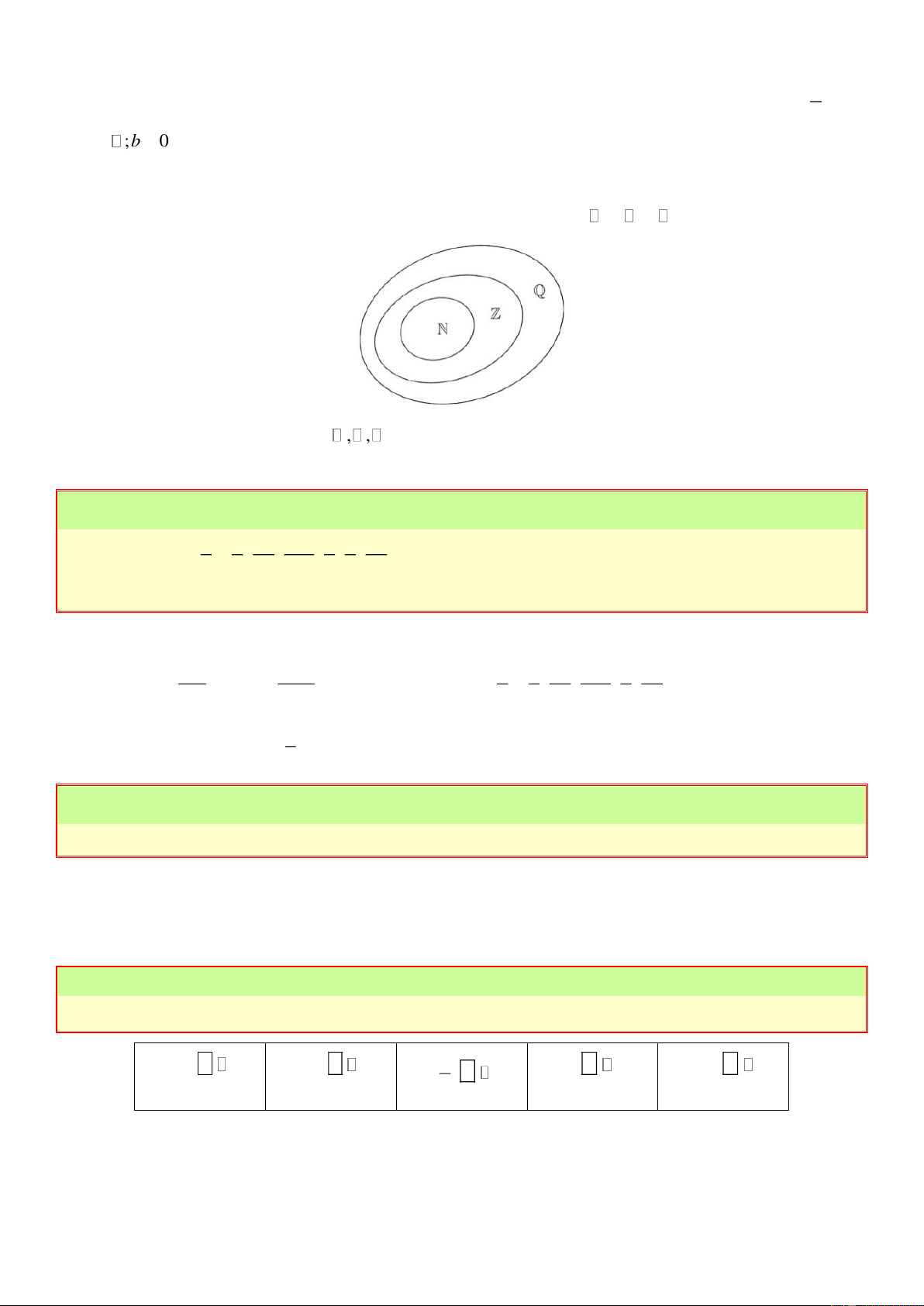
Tập hợp số hữu tỉ được kí hiệu là . a a
*) Chú ý: Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ là b b
*) Nhận xét: Các số thập phân đều viết được dưới dạng phân số thập phân nên chúng đều là các
số hữu tỉ. Số nguyên, hỗn số cũng là các số hữu tỉ
b) Biểu diễn số hữu tỉ trên trục số
+ Biểu diễn số hữu tỉ trên trục số: Tương tự như đối với số nguyên, ta có thể biểu diễn mọi số hữu tỉ trên trục số
+ Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a
+ Nhận xét: Trên trục số, hai điểm biểu diễn hai số hữu tỉ đối nhau a và a nằm về hai phía khác
nhau só với điểm O và có cùng khoảng cách đến O
2. Thứ tự trong tập hợp các số hữu tỉ
+ Ta có thể so sánh hai số hũu tỉ bất kì bằngg cách viết chúng dưới dạng phân số rồi só sánh hai phân số đó
+ Với hai số hữu tỉ x, y ta luôn có hoặc x y hoặc x y hoặc x y .
+ Cho ba số hữu tỉ a, , b c , ta có:
Nếu a b và b c thì a c (tính chất bắc cầu)
+ Trên trục số, nếu a b thì điểm a nằm trước điểm b *) Chú ý:
+ Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương;
+ Số hữu tỉ nhỏ hơn 0 được gọi là số hữu tỉ âm.
+ Số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
II. CÁC DẠNG BÀI TẬP
Dạng 1: Nhận biết các số hữu tỉ, quan hệ trên tập hợp số Phương pháp giải: Trang 1 a
+ Muốn xác định xem một số có là số hữu tỉ hay không, ta hãy biến đổi xem số đó có dạng với b
a,b ;b 0 hay không.
+ Mối quan hệ giữa các tập hợp số đã biết với tập hợp số hữu tỉ: .
+ Sử dụng các kí hiệu , , , ,
, , để biểu diễn mối quan hệ giữa số và tập hợp hoặc giữa các tập hợp với nhau. Bài 1: 5 2 2 1 3 0 3 9 Cho các số sau: ;3 ; ; ; ; ; ;3,5;0;6, 25 4 5 7 17 3 0 9
, hãy cho biết số nào là số hữu tỉ, số nào không phải là số hữu tỉ? Lời giải 35 625 5 2 2 1 3 0 9 Ta viết: 3,5 ;0, 625
. Vậy các số hữu tỉ là ;3 ; ; ; ; ;3,5;0;6, 25 100 1000 4 5 7 17 3 9 3
Số không phải số hữu tỉ là (vì có mẫu số là 0). 0 Bài 2: Số nguyên ... 2; 1
;0;1;2;... có là số hữu tỉ không? Vì sao? Lời giải
Vì các số nguyên đề có thể viết được dưới dạng phân số với mẫu số là 1 nên các số nguyên đều là số hữu tỉ. Bài 3: Điền kí hiệu ;
thích hợp vào ô trống: 6,5 6,5 4 2 0 -3,5 7 Lời giải Trang 2 6,5 6,5 4 2 0 -3,5 7 Bài 4: Điền kí hiệu ;
thích hợp vào ô trống: 5 5 5 1 0 5 8 Lời giải 5 5 5 1 0 5 8 Bài 5:
Điền các kí hiệu ¥ ,¤ ,¢ vào ô trống cho đúng (điền tất cả các khả năng có thể): a) 11..... b) 2 6..... 1 3 c) ..... d) ..... 5 4 Lời giải
a) Có thể điền ¥ , ¢ , ¤ b) Có thể điền ¢ , ¤ c) Có thể điền ¤ d) Có thể điền ¤ Bài 6:
Điền các kí hiệu thích hợp , , , , , , vào ô trống: 1 7 3 ; ; . 2 9 Hướng dẫn giải 1 3 ; 2 7 ; . 9 Trang 3 Bài 7:
Điền các kí hiệu thích hợp , , , , , , vào ô trống: 10 3 1 ; 1 ; ; ; 2 8 4 1 2 ; ; ; . 9 4 5 Lời giải 10 10 1 ; 1 ; do = 5 ; 2 2 3 4 1 2 ; ; , ; ; ; . 8 9 4 5 Chú ý:
+ Kí hiệu là “thuộc”.
+ Kí hiệu là “không thuộc”.
+ Kí hiệu là “tập hợp con”.
+ Kí hiệu là “chứa trong” hoặc “chứa”. + Kí hiệu
là “tập hợp các số tự nhiên”. Bài 8: Điền kí hiệu , ,
thích hợp và ô trống: 5 2 4 ; ; 8 ; ; 3 9 1 2 2 ; ; ; . 11 7 19 Lời giải 5 2 4 ; ; 8 ; ; 3 9 1 2 2 ; ; ; . 11 7 19 Bài 9:
Điền các kí hiệu ; ; thích hợp vào ô trống (điền tất cả các khả năng có thể): 2 6 ; 22 ; ; ; 23 5 3 ; ; 21 ;; 1 . 7 4 Lời giải Trang 4 2 6 ; ; 22 ; ; ; ; ; ; 23 5 3 ; ; ; 21 ; 1 ; . 7 4 Bài 10:
Khẳng định nào dưới đây sai?
A. Số 19 là một số tự nhiên. B. Số 5
là một số nguyên âm. 15 C. Số là một số hữu tỉ.
D. Số 0 là một số hữu tỉ dương. 19 Lời giải Chọn đáp án D
Vì số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương. Bài 11:
Viết Đ vào ô có khẳng định đúng và S vào ô có khẳng định sai:
1. Số nguyên là số hữu tỉ
2. Số nguyên âm không là số hữu tỉ âm 3. Tập hợp
gồm các số hữu tỉ âm và các số hữu tỉ dương 1 4. Số 1 là số hữu tỉ 2 1 5. Số không là số hữu tỉ 5 Lời giải 1. Đ 2. S 3. S 4. Đ 5. S Bài 12:
Các số hữu tỉ sau là âm hay dương? 5 4 3 a) b) c) 7 9 8 14 5 d) e) 9 8 Lời giải Số hữu tỉ dương là 3 8 5 4 14 5 Số hữu tỉ âm là ; ; ; 7 9 9 8 Trang 5 Bài 13:
Các số hữu tỉ sau là âm hay dương? 3 2 a) b) 5 9 0 c) 4 d) 3 Lời giải 3 a) là số hữu tỉ dương 5 2 b) là số hữu tỉ dương 9
c) 4 là số hữu tỉ âm 0 d)
0 không là số hữu tỉ âm cũng không là số hữu tỉ dương. 3 Bài 14: 11 7 5 1 1
Tìm số đối của các số sau: ; 4 ; ; 0; ; ; 2 6 7 3 2 Lời giải 11 7 5 1 1 11 7 5 1 1 Số đối của ; 4 ; ; 0; ; ; lần lượt là ; 4; ; 0; ; ; 2 6 7 3 2 2 6 7 3 2 Bài 15: 1 3
Tìm số đối của các số sau: 3 ; 5 ; ; 8 2 4 Lời giải 1 3 1 3 Số đối của 3 ; 5 ; ; 8 lần lượt là 3 ;5; ; 8 2 4 2 4 Bài 16:
Dãy số nào dưới đây cùng biểu diễn một số hữu tỉ 3 6 5 1 0 a) 0 ,3; ; b) 5; ; 10 20 1 2 2 7 1 4 9 6 3 c) ; ; d) ; ; 13 17 26 12 8 4 Lời giải Trang 6 3 6 a) Ta có: 0 ,3
. Dãy số này không biểu diễn một số hữu tỉ 10 20 5 1 0 b) Ta có: 5
. Dãy số này không biểu diễn một số hữu tỉ 1 2 2 7 1 4 c)
. Dãy số này không biểu diễn một số hữu tỉ 13 17 26 9 6 3 d) ; ;
. Dãy số này không biểu diễn một số hữu tỉ 12 8 4 Bài 17: 5
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ
, từ đó rút ra dạng tổng quát của 4 5
các phân số bằng phân số . 4 1 0 15 2 0 1 9 25 12 , , , , , 4 12 1 6 16 2 0 15 Lời giải 1 0 5 15 5 2 0 5 1 9 5 25 12 5
Rút gọn các phân số ta được: , , , , , 4 4 12 4 1 6 4 16 4 2 0 15 4 5 1 0 15 25
Vậy các phân số biểu diễn số hữu tỉ là , , 4 8 12 2 0 5 5k
Dạng tổng quát của các phân số bằng phân số là
k ,k 0 4 4k Bài 18: 14
a) Tìm 3 phân số bằng cạc phân số 21 4
b) Tìm 3 phân số bằng cạc phân số 12 Lời giải 14 2 4 16 a) Ta có: 21 3 6 24 4 1 2 8 b) Ta có: 1 2 3 6 2 4 Bài 19:
Viết dạng chung của các số hữu tỉ bằng: 123123 434343 a) b) 164164 868686 Trang 7 Lời giải 1 23123 1 23.1001 1 23 a) Ta có: 164164 164.1001 164 123123 123. m
Vậy dạng chung của số hữu tỉ là
với m , m 0 164164 164.m 434343 1.434343 1 a) Ta có: 868686 2.434343 2 434343 1.m
Vậy dạng chung của số hữu tỉ là
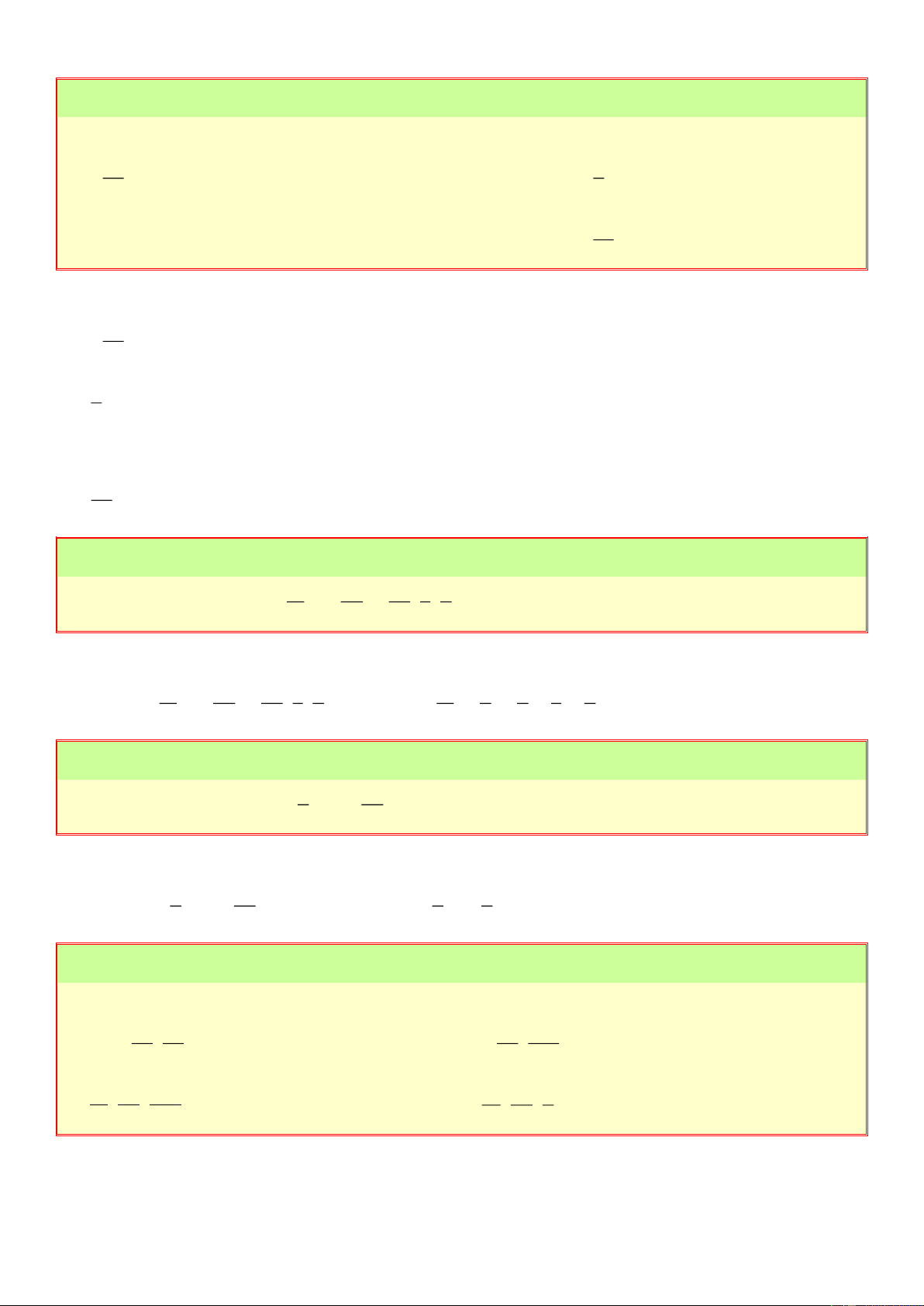
với m , m 0 868686 2.m 3 5 -2 -1 0 1 2 3 Bài 20: 2,3 3 5 12 0 2 3 Cho các số sau: ; 1 ; ; ; ; ;
; 1, 6;0,35 . Hãy cho biết số nào là số hữu tỉ, số nào 5 4 9 7 8 0 3
không phải là số hữu tỉ? Lời giải 3 5 12 0 3 Các số hữu tỉ là 1 ; ; ; ; ; 1, 6; 0,35 4 9 7 8 3 2, 3 2
Số không phải là số hữu tỉ là ; 5 0 Bài 21:
Các số hữu tỉ sau là âm hay dương? 1 3 2 ; ; ; 6 4 11 5 Lời giải 3 2 Số hữu tỉ dương là: ; 11 5 1
Số hữu tỉ âm là: ; 6 4 Bài 22: 3 4 2
Tìm số đối của các số: 5 ; 9 ; ; 5 ; ;0,56 . 7 1 1 3 Lời giải Trang 8 3 4 2 3 4 2 Số đối của 5 ; 9 ; ; 5
; ;0,56 lần lượt là: 5 ;9; ; 5 ; ; 0,56 7 1 1 3 7 11 3 Bài 23: 2
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ ? 5 8 9 10 6 9 ; ; ; ; 20 12 25 15 15 Lời giải 2 2 Ta có
. Rút gọn các phân số đã cho ta được: 5 5 8 4 9 3 10 2 6 2 9 3 ; ; ; ; 20 5 1 2 4 25 5 1 5 5 15 5 2 10 6
Vậy các phân số biểu diễn số hữu ti là: ; . 5 25 15 Bài 24:
Biểu diễn các số hữu tỉ sau trên cùng một trục số. 1 3 3 a) b) c) 4 4 4 14 7 d) e) 9 4 Lời giải 3 3 3 3 1 4 5 7 3 Ta có: ; ; 1 ; 1 . 4 4 4 4 9 9 4 4 -2 -1 0 1 2 -14 3 -1 -3 7 9 -4 4 -4 4 Bài 25: Hãy tìm năm phân số 2 bằng phân số . 7 Lời giải Năm phân số 2 4 6 8 10 12 bằng phân số là: ; ; ; ; 7 14 21 28 35 42 Bài 26: Trang 9
Tìm số nguyên x để các số sau là số hữu tỉ: x 3 7 a) b) c) 11 x 3x Lời giải a) Để x
là số hữu tỉ thì x . 11 b) Để 3
là số hữu tỉ thì x và x 0 . Suy ra x là số nguyên khác 0 . x c) Để 7 là số hữu tỉ thì và
. Suy ra x là số nguyên khác 3x 3x 0 0 . 3x Bài 27:
Tìm số nguyên x để các số sau là số hữu tỉ: 5 4 a) b) x 3 5x 10 Lời giải a) Để 5
là số hữu tỉ thì x 3 và x 3 0 x 3. x 3 5
Vậy khi x là số nguyên khác 3 thì là số hữu tỉ x 3 b) Để 4
là số hữu tỉ thì 5x 10 và 5x 10 0 x 2 . 5x 10 4
Vậy khi x là số nguyên khác 2 thì là số hữu tỉ. 5x 10 Bài 28:
Tìm tất cả các số nguyên x để các phân số sau có giá trị là số nguyên: 10x 9 x 10 a) A b) B 2x 3 x 5 Lời giải 10x 9 6 a) A 5 2x 3 2x 3 6 A
2x 3 Ư(6) 2x 3 2x 3 6
; 3 ; 2 ; 1; 1; 2; 3 ; 6
x 0; 1 ; 2; 3 , x Trang 10 x 10 5 b) B 1
. Làm tương tự câu a ta được x {4;6;0;10}. x 5 x 5 Bài 29:
Cho số x thỏa mãn 2
x 5 . Hỏi số x có là số hữu tỉ không? Lời giải
x không thể là số hữu tỉ.
Dạng 2: Biểu diễn số hữu tỉ
Bài toán 1: Biểu diễn số hữu tỉ trên trục số *) Phương pháp giải:
Để biểu diễn một số hữu tỉ trên trục số, ta thường làm như sau:
Bước 1. Ta viết số đó dưới dạng phân số có mẫu dương. Khi đó mẫu của phân số sẽ cho ta biết
đoạn thẳng đơn vị được chia thành bao nhiêu phần bằng nhau.
Bước 2. Lấy đoạn thẳng mới làm đơn vị.
Bước 3. Số hữu tỉ dương (âm) nằm bên phải (trái) điểm 0 và cách điểm 0 một khoảng bằng giá trị
tuyệt đối của số hữu tỉ đó. Bài 1: 3 Biểu diễn số hữu tỉ trên trục số. 4 Lời giải
Chia các đoạn thẳng đơn vị ra làm 4 phần bằng nhau. 1
Lấy đoạn thẳng mới làm đơn vị (bằng đơn vị cũ). 4
Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 3 đơn vị mới.
Điểm vừa lấy là điểm phải tìm. Bài 2: Trang 11 3 Biểu diễn số hữu tỉ trên trục số. 5 Lời giải 3 3 Ta có 5 5
Chia các đoạn thẳng đơn vị ra làm 5 phần bằng nhau. 1
Lấy đoạn thẳng mới làm đơn vị (bằng đơn vị cũ). 5
Lấy điểm nằm bên trái điểm 0, cách điểm 0 một đoạn bằng 3 đơn vị mới.
Điểm vừa lấy là điểm phải tìm. Bài 3:
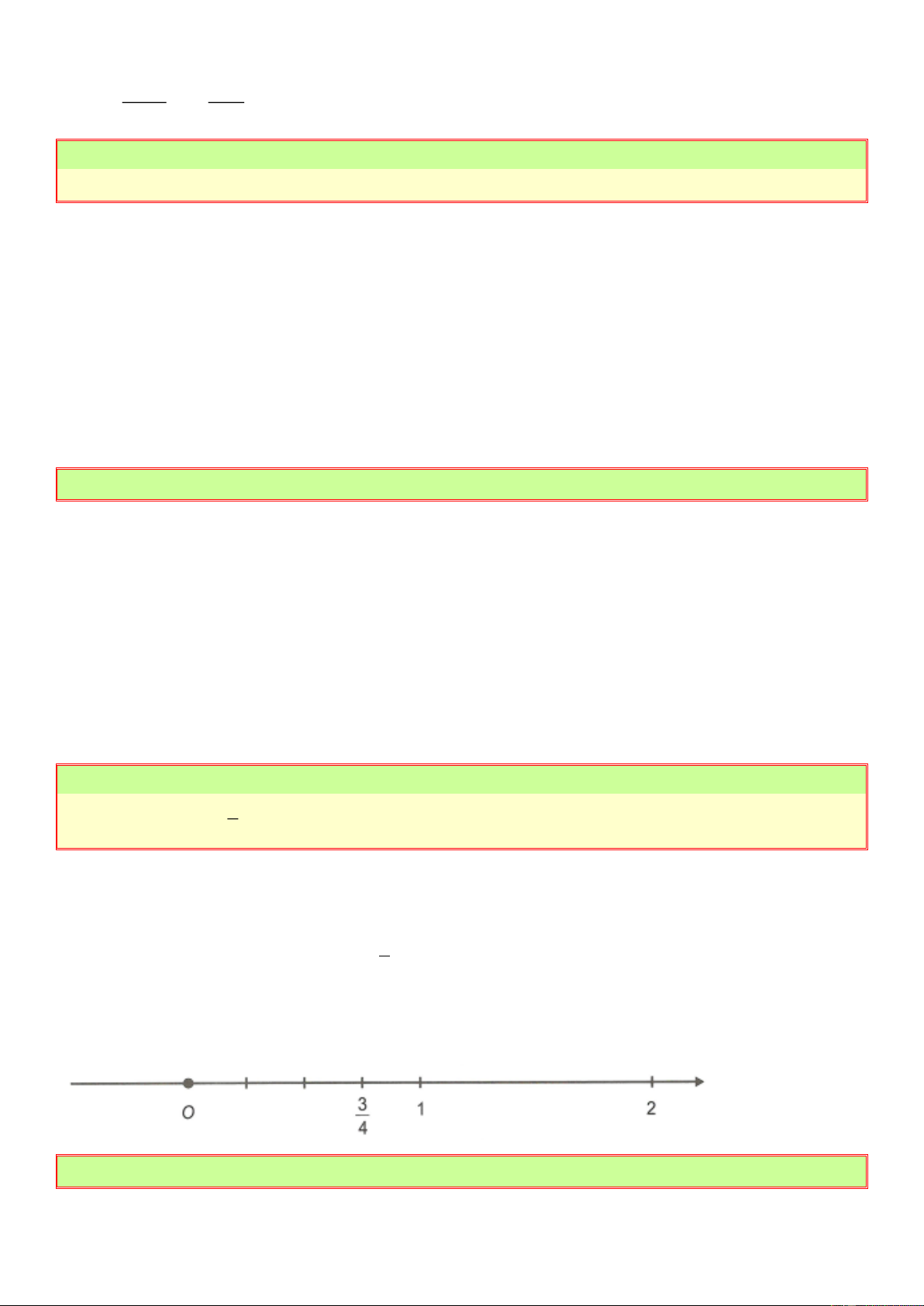
Điền số thích hợp vào chỗ trống: -1 -1 0 1 1 2 3 Lời giải -1 -1 0 1 1 2 -1 3 1 4 -1 3 2 3 Bài 4: 5 4 3
Biểu diễn số hữu tỉ ; ; trên trục số. 4 4 5 Lời giải 5
Biểu diễn số hữu tỉ 4 -5 4 -2 -1 0 1 2 3 Trang 12 4 Biểu diễn số hữu tỉ 1 4 -2 -1 0 1 2 3 4 3 Biểu diễn số hữu tỉ 5
Bài toán 2: Biểu diễn số hữu tỉ dưới dạng các phân số bằng nhau *) Phương pháp giải: a
Số hữu tỉ thường được biểu diễn dưới dạng phân số tối giản
với a,b ;b 0 . b Bài 1 6 4 4 20 Cho các phân số sau: ; ; ; 15 1 2 1 0 8 2
Những phân số nào biểu diễn số hữu tỉ ? 5 Hướng dẫn giải 2 2 6 2 4 1 4 2 20 5 Ta có
. Rút gọn các phân số đã cho ta được: ; ; ; 5 5 15 5 1 2 3 1 0 5 8 2 2 6 4
Vậy các phân số biểu diễn số hữu tỉ là: và . 5 15 10 Bài 2: 3 1 1
Biểu diễn các số hữu tỉ sau trên trục số: ; ; 2 3 4 Lời giải 3 1 1
Biểu diễn các số hữu tỉ ; ; trên trục số như sau: 2 3 4 Bài 3: Trang 13 9 1 4 4 12 2 Cho các phân số sau ; ; ;
. Những phân số nào biểu diễn số hữu tỉ ? 6 21 6 20 3 Lời giải 2 2 Ta có: . 3 3 9 3 1 4 2 4 2 12 3
Rút gọn các phân số đã cho ta được: ; ; ; 6 2 21 3 6 3 2 0 5 2 14 4
Vậy các phân số biểu diễn số hữu tỉ là: và . 3 21 6 Bài 4: 2 1 1 4 4 2 35 5 2 8 7 a) Cho các phân số ; ; ; ; ;
. Những phân số nào biểu diễn số hữu tỉ ? 27 19 5 4 4 5 7 36 9 7
b) Biểu diễn số hữu tỉ trên trục số. 9 Lời giải 2 1 7 2 8 7 35 3 5 7 a) Ta có: ; ; 27 9 36 9 4 5 45 9 7 2 1 2 8 35
Vậy các phân số biểu diễn số hữu tỉ là: ; và . 9 27 36 45 7
b) Biểu diễn các số hữu tỉ trên trục số như sau: 9 Bài 5: 3
Trong các phân số sau, phân số nào không bằng phân số ? 5 6 9 A. B. 11 15 6 3 C. D. 10 5 Lời giải
Các đáp án B, C, D sau khi rút gọn ta đều đượ 3 c phân số . 5 Bài 6: 1 2 5 5 Biểu diễn các số: ; 0, 25; ;
bởi các điểm trên cùng một trục số ta được bao nhiêu điểm 4 1 00 20 phân biệt?
A. Một điểm. B. Hai điểm. Trang 14 C. Ba điểm. D. Bốn điểm. Lời giải Đưa các số 1 1 25 1 5 1
hữu tỉ về dạng phân số tối giản, ta có: ; 0, 25 ; ; . 4 4 1 00 4 20 4 1
Vậy các số trên cùng biểu diễn bởi điểm trên trục số. 4 Bài 7: 14 24 26 2 8 72 12 Trong các phân số ; ; ; ;
có bao nhiêu phân số bằng phân số ? 18 26 2 8 30 78 13 A. 1. B. 2. C. 3. D. 4. Lời giải 14 7 24 12 26 13 2 8 1 4 72 12 ; ; ; ; . 18 9 26 13 2 8 14 30 15 78 13 12
Vậy có hai phân số biểu diễn phân số . 13
Dạng 3: So sánh hai số hữu tỉ
*) Phương pháp giải:
+ Viết các số hữu tỉ dưới dạng phân số có cùng mẫu dương: So sánh các tử số, phân số nào có tử
nhỏ hơn thì phân số đó nhỏ hơn.
+ So sánh các số trung gian ( 0,1,... );
+ So sánh với phần hơn hoặc phần bù;
+ So sánh thương hai số hữu tỉ (khác 0 ) với 1;
+ Áp dụng tính chất bắc cầu và các bất đẳng thức đã chứng minh trong bài Bài 1: 11 8
So sánh các số hữu tỉ sau: và . 6 9 Hướng dẫn giải 8 8 9 9 1 1 3 3 8 8 1 6 Ta có ; 6 18 9 9 18 33 16 1 1 8 Vì 3 3 1 6 nên hay 18 18 6 9 Trang 15 Bài 2: So sánh các số sau: 25 20 15 21 19 23 a) và ; b) và ; c) và . 20 25 21 49 49 47 Hướng dẫn giải 25 20 25 20 a) Ta có 0 và 0 nên . 20 25 20 25 15 5 21 3 5 3 15 21 b) Ta có ; . Vì nên 21 7 49 7 7 7 21 49 19 23 23 23 c) Ta có: và . Do đó 19 23 49 49 49 47 49 47 Bài 3:
So sánh các số hữu tỉ sau: 998 999 315 316 2020 2018 a) và ; b) và ; c) và . 555 556 380 381 2019 2019 Hướng dẫn giải
a) Ta thấy 998 555 999 556 443 nên ta so sánh hai phân số qua phần bù 998 443 999 443 Ta có 1 ; 1 555 555 556 556 443 443 999 998 999 998 Vì nên 1 1 hay 556 555 556 555 556 555 b) Ta thấy 380 3 15 381 3
16 65 nên ta so sánh hai phân số bằng cách cộng thêm 1. 3 15 65 3 16 65 Ta có 1 ; 1 380 380 381 381 65 65 3 15 3 16 3 15 3 16 Vì nên 1 1 hay . 380 381 380 381 380 381 2020 c) Ta có 2020 2019 nên 1 2019 2018 Lại có 2018 2019 nên 1 2019 Do đó 2020 2018 . 2019 2019 Chú ý:
Ngoài phương pháp so sánh bằng cách quy đồng mẫu số, ta có thể sử dụng các phương pháp Trang 16 khác như:
+ So sánh qua một phân số trung gian. + So sánh qua phần bù.
+ Đưa về so sánh hai phân số có cùng tử số. Bài 4:
So sánh các số hữu tỉ sau: 7 11 5 7 a) và ; b) và ; 8 12 8 10 24 19 9 27 c) và ; d) và . 35 30 21 63 Lời giải 7 21 11 22 a) Ta có ; 8 24 12 24 21 22 7 11 Vì 21 22 nên hay . 24 24 8 12 5 3 7 3 b) Ta có 1 ; 1 8 8 10 10 3 3 5 7 5 7 Vì nên 1 1 hay 8 10 8 10 8 10 24 11 19 11 c) Ta có 1 ; 1 35 35 30 30 11 11 11 11 24 19 Vì nên 1 1 hay 35 30 35 30 35 30 9 3 27 2 7 3 d) Ta có ; 21 7 6 3 63 7 9 27 Suy ra . 21 63 Bài 5:
So sánh các số hữu tỉ sau: 9 5 4 15 a) và ; b) và ; 70 42 27 63 13 9 9 20 c) và ; d) và . 15 11 17 21 Lời giải Trang 17 9 27 5 25 a) Ta có ; 70 210 42 210 27 25 9 5 Vì 27 25 nên hay 210 210 70 42 4 2 8 15 1 5 4 5 b) Ta có ; 27 189 6 3 63 189 28 45 4 15 Vì 2 8 4 5 nên hay 189 189 27 63 13 2 9 2 c) Ta có 1 ; 1 15 15 11 11 2 2 2 2 13 9 Vì nên 1 1 hay 15 11 15 11 15 11 9 2 0 20 9 20 d) Ta có 0; 0 nên . 17 2 1 21 17 21 Bài 6: 1 2 3 1 6 1 1 1 1 4 9
Sắp xếp các số hữu tỉ ; ; ; ; ; ;
theo thứ tự giảm dần. 19 19 19 19 19 19 19 Lời giải 1 6 1 4 1 2 1 1 9 3 1 Vì 1 6 1 4 1 2 1 1 9 3 1 nên 19 19 19 19 19 19 19 1 3 9 1 1 1 2 1 4 1 6
Sắp xếp các số theo thứ tự giảm dần: ; ; ; ; ; ; 19 19 19 19 19 19 19 Bài 7: 1 6 1 6 19
Sắp xếp các số hữu tỉ ; ; theo thứ tự tăng dần. 27 29 27 Lời giải 16 16 16 16 Có 27 29 nên . Suy ra 27 29 27 29 1 6 1 9 Lại có 1 6 1 9 nên 27 27 19 1 6 1 6 Vậy . 27 27 29 19 1 6 1 6
Sắp xếp các số theo thứ tự tăng dần: ; ; 27 27 29 Bài 8:
So sánh các số hữu tỉ sau. 3 5 2 3 a) và b) và 7 7 5 5 Trang 18 4 5 3 3 c) và d) và 9 9 8 8 Lời giải 3 5 a) và 7 7 3 5 Vì 3 5 nên 7 7 2 3 b) và 5 5 2 3 Vì 2 3 nên 5 5 4 5 c) và 9 9 4 4 5 5 Ta có: ; 9 9 9 9 4 5 4 5 Vì nên 9 9 9 9 3 3 d) và 8 8 3 3 3 3 Ta có: ; 8 8 8 8 Vậy 3 3 8 8 Bài 9:
So sánh các số hữu tỉ sau: 5 3 3 3 1 3 a) và b) và ; c) và . 4 4 5 4 21 27 Lời giải 5 3 a) Ta có 5 4 nên 4 4 3 3 3 3 b) Ta có nên 5 4 5 4 3 1 1 1 1 3 c) Ta có mà nên 27 9 21 9 21 27 Bài 10: Trang 19 1 2 3 1 6 1 1 1 1 4 1 9
Sắp xếp các số hữu tỉ sau theo thứ tự giảm dần: ; ; ; ; ; ; 17 17 17 17 17 17 17 Lời giải 1 3 1 1 1 2 1 4 1 6 1 9 Ta có : 17 17 17 17 17 17 17
Các số được sắp xếp theo thứ tự giảm dần là: 1 3 1 1 1 2 1 4 1 6 1 9 : : ; ; ; ; 17 17 17 17 17 17 17 Bài 11:
Sắp xếp các số hữu tỉ sau theo thứ tự tăng dần. 5 5 5 5 5 5 5 ; ; ; ; ; ; 9 7 2 4 8 3 11 Lời giải 5 5 5 5 5 5 5 5 5 5 5 5 5 5 Ta có : 11 9 8 7 4 3 2 11 9 8 7 4 3 2
Các số được sắp xếp theo thứ tự tăng dần là: 5 5 5 5 5 5 5 ; ; ; ; ; ; 2 3 4 7 8 9 11 Bài 12:
So sánh các số hữu tỉ sau một cách nhanh nhất: 1 46 1 21 13 2019 2020 a) và ; b) và ; c) và . 43 89 23 12 2019 2019 Lời giải 1 46 1 1 46 1 a) Ta có: 0 và 0 nên 43 89 43 89 21 13 21 13 b) Ta có: <1 và 1 nên < 23 12 23 12 2019 2020 2019 2020 c) Ta có: =1 và 1 nên 2019 2019 2019 2019 Bài 13:
So sánh các số hữu tỉ sau một cách nhanh nhất: 1 a) x 0 ,125 và y 8 5
b) b) x 0, 75 và y 4 Trang 20 1 7 1 71717 c) x và y 23 232323 Lời giải 1 a) x 0 ,125 và y 8 1 1 1 Ta có: x 0 ,125 ; y 8 8 8 Vậy x y 5
b) x 0, 75 và y 4 3 3 5
Ta có: x 0, 75 mà 4 4 4 Vậy x y 1 7 1 71717 c) x và y 23 232323 1 7 1 7.10101 1 71717 Ta có: x 23 23.10101 232323 Vậy x y Bài 14:
So sánh các số hữu tỉ sau một cách nhanh nhất: 3131 31 2021 2022 2019 2020 a) và b) và ; c) và 1313 13 2021 2021 2018 2019 Lời giải 3131 31.101 31 3131 31 a) Ta có: = = = 1313 13.101 13 1313 13 2021 2022 2021 2022 b) Ta có: =1 và 1 nên 2021 2021 2021 2021 2019 1 2020 1 1 1 2019 2020 c) Ta có: =1+ và 1 mà nên 2018 2018 2019 2019 2018 2019 2018 2019 Bài 15:
So sánh các số hữu tỉ sau một cách nhanh nhất: 7 a) 1 ,6 và 4 2018 2019 b) và 2019 2020 Trang 21 - 1234 - 4321 c) và 1244 4331 Lời giải 8 3 7 3 3 3 3 3 a) Ta có 1 ,6 1 và 1
. Ta lại có nên 1+ 1 5 5 4 4 5 4 5 4 3 3 1 > 1 5 4 8 7 5 4 7 Vậy 1 ,6> . 4 2018 1 2019 1 1 1 2018 2019 b) Ta có: =1 và 1 mà nên 2019 2019 2020 2020 2019 2020 2019 2020 -1234 10 -4321 10 c)Ta có: + 1 = ; + 1 = 1244 1244 4331 4331 10 10 -1234 4 321 Mà 1244 < 4331 +1 > +1 1244 4331 1244 4331 -1234 -4321 Vậy > 1244 4331 Bài 16:
So sánh các số hữu tỉ sau một cách nhanh nhất: 11 25 -31 313131 3246 45984 a) và b) và c) và 33 76 -32 323232 3247 45983 Lời giải 11 25 a) và 33 76 1 1 1 2 5 2 5 25 Ta có : 33 3 75 76 7 6 1 1 25 Vậy 33 7 6 -31 313131 b) và -32 323232 -31 31 31.10101 313131 Ta có: = = = -32 32 32.10101 323232 Trang 22 -31 313131 Vậy = . -32 323232 3246 45984 c) và 3247 45983 3246 -45984 3246 -45984 Ta có: > -1 > . Vậy > -3247 45983 -3247 45983 Bài 17: Quy đồ 1 5 3 1 7
ng rồi sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn: , , , , 3 12 4 4 12 Lời giải 1 4 3 9 1 3
Ta thực hiện quy đồng mẫu số với mẫu số chung là 12: , , 3 12 4 12 4 12 9 7 5 4 3 3 7 5 1 1 Do 12 12 12 12 12 4 12 12 3 4 Bài 18: 1 0 5 1 9 2 17
Sắp xếp các số hữu tỉ sau theo thứ tự từ lớn đến bé: , , 0, , , ,1. 8 12 19 1 0 15 Lời giải 17 5
Các số hữu tỉ dương: 5 17 ,
,1. Sắp xếp theo thứ tự từ lớn đến bé ta được: 1 ; 12 15 15 12 1 0 1 9 2 Các số hữu tỉ âm: , 1 ,
Sắp xếp theo thứ tự từ lớn đến bé ta được: 8 19 1 0 2 1 9 1 0 ; 1 0 19 8 17 5 2 1 9 1 0
Vậy sắp xếp theo thứ tự từ lớn đến bé ta được: 1 0 15 12 1 0 19 8 Bài 19: 4 7 Lớp 7B có
số học sinh thích học toán,
số học sinh thích học văn, 23 số học sinh thích học 5 10 25
anh. Môn học nào được nhiều bạn học sinh lớp 7B yêu thích nhất? Lời giải 4 40 7 35 23 46 Ta có: ; ; 5 50 10 50 25 50 35 40 46 7 4 23 Vì nên 50 50 50 10 5 25 Trang 23 23 Hay lớn nhất. 25
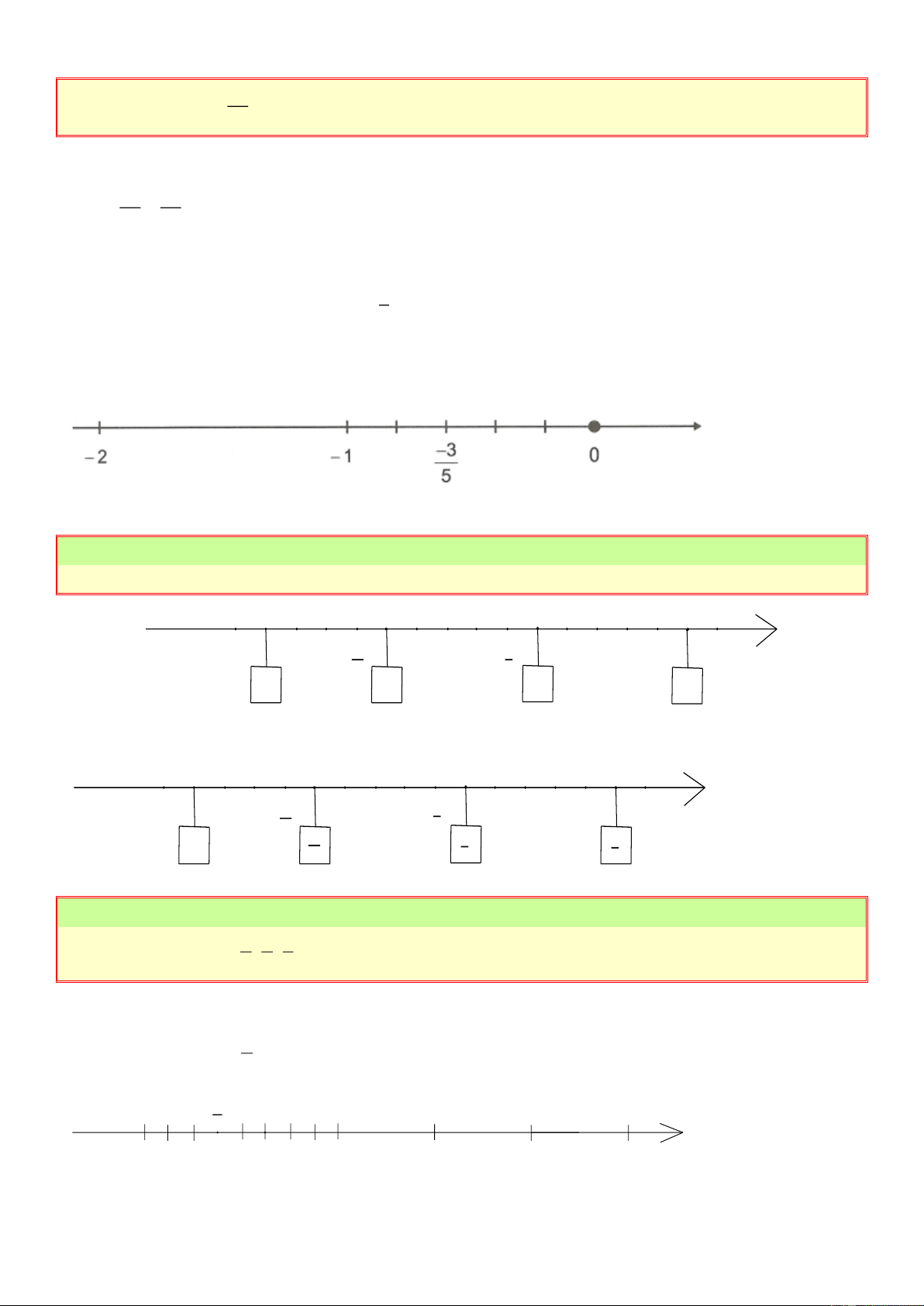
Vậy môn tiếng anh được nhiều bạn học sinh lớp 7B yêu thích nhất. Bài 20: Lưới nào sẫm nhất?
a) Đối với mỗi lưới ô vuông ở hình trên, hãy lập một phân số có tử là số ô sẫm, mẫu là tổng số ô sẫm và trắng.
b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô sẫm so
với tổng số ô là lớn nhất). Lời giải 2 5 4 8 11 a) . A ; . B ; C. ; . D ; E. 6 12 15 20 30 b) 2 20 5 25 4 16 Ta có: ; ; ; 6 60 12 60 15 60 8 24 11 22 ; 20 60 30 60 16 20 22 24 25 Mà 60 60 60 60 60 4 2 11 8 5 Nên . 15 6 30 20 12
Vậy lưới B sẫm nhất. Bài 21:
Nhiệt độ của Matxcơva các tháng trong năm 2020 được thống kê như sau: Trang 24 Lời giải Tháng 1 2 3 4 5 6 7 8 9 10 11 12 Nhiệt
độ(độ C) – 3,75 – 7,6 – 1,2 0 7,5 8,63 19,2 17,5 11,3 14,5 15 12,5
Hãy sắp xếp nhiệt độ của các tháng theo thứ tự từ lớn đến bé.
Lời giải: Nhiệt độ của Matxcơva các tháng trong năm 2020 được sắp xếp theo thứ tự từ lớn đến
bé là: 19, 2; 17,5; 15; 14,5; 12,5; 11,3; 8, 63; 7,5; 0; 1, 2; 3, 75; 7, 6. Bài 22: 1 1
Hãy viết bốn số hữu tỉ xen giữa và 2 3 Lời giải 1 1 5 1 1 0 Ta có: = và 2 30 3 30 1 1 1 4 1 3 1 2 1 1
Bốn số hữu tỉ xen giữa và là , , , 2 3 30 30 30 30 Bài 23:
Viết 3 số hữu tỉ có mẫu khác nhau lớn hơn -1 nhưng nhỏ hơn 4 ? 3 5 Lời giải -1 4 -5 12 -5 -3 1 10 12 Ta có : < Þ < Þ < < < < 3 5 15 15 15 15 15 15 15 -5 -1 1 2 12 Þ < < < < 15 5 15 3 15 -1 -1 1 2 4 Þ < < < < 3 5 15 3 5 -1 1 2
Vậy 3 phân số cần tìm: ; ; 5 15 3 Bài 24: Tìm phân số có:
a) Mẫu số bằng 5 , lớn hơn 5 và nhỏ hơn 2 . 7 7
b) Tử số bằng 8 , lớn hơn 5 và nhỏ hơn 5 . 9 7 Lời giải Trang 25 x a) Gọi
x là phân số cần tìm. Theo đề bài ta có: 5 5 x 2 2 5 7x 1 0 2 5 7x 1 0 7 5 7 35 35 35
Mặt khác 7x 7 nên 7x 2 1; 1 4 . Với 7x 2 1 x 3 , Với 7x 1 4 x 2 . 3 2
Vậy các phân số cần tìm là ; . 5 5 8 b) Gọi
x , x 0 là phân số cần tìm. Theo đề bài ta có: x 5 8 5 40 40 40 56 5x 72 9 x 7 72 5x 56
Mặt khác 5x 5 nên 5x 60;65;7 0 .
Với 5x 60 x 12
Với 5x 65 x 13
Với 5x 70 x 14. 8 8 8
Vậy các phân số cần tìm là ; ; . 12 13 14 Bài 25: x x 4 x 1
Tìm phân số x ¢ sao cho: 9 9 7 9 Lời giải x 4 x 1 7x 36 7 x 1 Ta có: 9 7 9 63 63 63 x x 36 7 36 7 1 x x 1 7 36 Mà 5
6 . Suy ra x 5. 7 5
Vậy phân số cần tìm là: 9 Bài 26: Cho * *
a ¢ , b ¥ , n ¥ . Trang 26 a a n
a) Nếu a b , hãy so sánh hai số và b b n a a n
b) Nếu a b , hãy so sánh hai số và b b n Lời giải a) Ta có: * a b an bn n ¥
an ab bn ab an b bn a Vì * *
b ¥ , n ¥ nên b 0; n b 0 a a n b b n b) Ta có: * a b an bn n ¥
an ab bn ab an b bn a Vì * *
b ¥ , n ¥ nên b 0; n b 0 a a n b b n Bài 27: x x 2018 Cho ,
x y , y 0 , hãy so sánh hai số hữu tỉ: và y y 2018 Lời giải x x x 2018 * Nếu 1 (theo kết quả bài 19) y y y 2018 x x x 2018 * Nếu 1 ( theo kết quả bài 19) y y y 2018 Bài 28: m n m m n n
a) Chứng tỏ rằng nếu x, y dương và thì x y x x y y
b) Áp dụng kết quả câu a.Viết ba số hữu tỉ khác tử số và mẫu số sao cho chúng lớn hơn 1 và 5 nhỏ hơn 1 . 6 Lời giải m n a)Ta có
và x 0, y 0 x y Trang 27
my nx my mx nx mx my mx nx mx
x(x y)
x(x y)
m x y
x m n
x x y
x x y m m n x x y m n Ta có
và x 0, y 0 x y
nx my nx ny my ny nx ny my ny
y x y
y x y
n x y
y m n
y x y
y x y n m n y x y
Vậy ta có điều cần chứng minh. 1 1 1 2 1 b) Ta có: 5 6 5 11 6 1 2 1 3 2 5 11 5 16 11 1 3 1 4 3 5 16 5 21 16 1 4 3 2 1 Vậy 5 21 16 11 6 Bài 29: x y x x y y
Chứng tỏ rằng nếu x, y, z , z 0 và thì z z z 2z z Lời giải x y
Theo kết quả bài 21, ta có:
(Với x, y, z , z 0 ) z z x x y x y y Suy ra: . z z z 2z z Bài 30: Trang 28 m p m p Cho hai số hữu tỉ và với ,
n q 0 . Chứng tỏ rằng: Nếu mq np thì n q n q Lời giải m mq p np mq np m p Ta có: ,
Mặt khác mq np và nq 0 do n 0,q 0 nên n nq q nq nq nq n q Bài 31:
Tìm x ¢ để: x 3 x a)
là số hữu tỉ dương. b) 5 là số hữu tỉ âm. x 7 x 10 Lời giải x 3 a)
là số hữu tỉ dương khi: x 7 x 3 0 x 3 0 hoặc x 7 0 x 7 0 x 3 0 x 3 * x 7 1 x 7 0 x 7 x 3 0 x 3 * x 3 2 x 7 0 x 7 Kết hợp
1 và 2 , ta được: x 3 hoặc x 7 Vậy khi x 3 x 3
hoặc x 7 thì là số hữu tỉ dương. x 7 x 5 a) là số hữu tỉ âm khi: x 10 x 5 0 x 5 0 hoặc x 10 0 x 10 0 x 5 0 x 5 *
5 x 10 1 x 10 0 x 10 x 5 0 x 5 * x 2 x 10 0 x 10 Kết hợp
1 và 2 , ta được: 5 x 10 Vậy khi x 5 5 x 10 thì là số hữu tỉ âm. x 10
BÀI TẬP TỰ LUYỆN DẠNG TOÁN Trang 29 Bài 1:
So sánh các số hữu tỉ sau. 1 1 1 1 a) và b) và 4 100 2 3 2 3 5 c) và d) 2 ,5 và 3 5 2 Lời giải 1 1 a) và 4 100 1 1 1 1 Vì 0; 0 nên 4 100 4 100 1 1 b) và 2 3 1 1 1 1 Vì 2 3 2 3 2 3 c) và 3 5 3 3 2 Ta có: 5 5 3 Vậy 2 3 3 5 5 d) 2 ,5 và 2 5 5 Ta có: 2 ,5 2 2 Vậy 5 2 ,5 2 Bài 2:
So sánh các số hữu tỉ sau: 2 7 4 4 a) và b) và ; 9 9 7 3 3 12 c) và . 5 20 Lời giải 2 7 a) Ta có 2 7 nên 9 9 Trang 30 4 4 4 4 b) Ta có nên 7 3 7 3 12 3.4 3 c) Ta có = 20 5.4 5 3 12 Vậy = 5 20 Bài 3:
Sắp xếp các số hữu tỉ sau theo thứ tự tăng dần. 6 2 1 2 8 1 7 2 5 3 ; ; ; ; ; ; 13 13 13 13 13 13 13 Lời giải 2 5 1 7 1 2 8 6 3 2 Ta có : 13 13 13 13 13 13 13
Các số được sắp xếp theo thứ tự tăng dần là: 2 5 1 7 1 2 8 6 3 2 ; ; ; ; ; ; 13 13 13 13 13 13 13 Bài 4:
So sánh các số hữu tỉ sau: 1 3 2 3 a) x và y b) x và y 2 4 5 7 3 c) x và 0 5 Lời giải 1 2 3 2 3 a) x
và y . Ta có: nên x y 2 4 4 4 4 2 2 1 4 3 1 5 1 4 1 5 b) x và y . Ta có 1 4 1 5 và 35 > 0 nên hay x y 5 5 35 7 35 35 35 c) x 0 Bài 5:
So sánh các số hữu tỉ sau: 2017 14 45 777 a) x và y b) x và y 2018 13 81 999 1 110 17 c) x 2 và y d) x và y 0, 75 5 50 20 Lời giải Trang 31 2017 14 a) x 1
y nên x y 2018 13 4 5 5 777 7 77 :111 7 b) x ; y
nên ta có x y 81 9 9 99 999 :111 9 1 1 1 1 10 c) x 2
y nên x y 5 5 50 3 15 17 d) y 0, 75 nên x y 4 20 20 Bài 6: So sánh các phân số sau: 1234 4319 22 51 -18 -23 a) và b) và c) và 1235 4320 -67 -152 91 114 Lời giải 1234 4319 a) và 1235 4320 1234 -1 4319 -1 - 1 = ; - 1 = 1235 1235 4320 4320 -1 -1 1234 4319 Có 1235 < 4320 < -1 < -1 1235 4320 1235 4320 1234 4319 Vậy < 1235 4320 22 51 b) và -67 -152 22 -22 -22 -1 -51 -51 51 22 51 = > = = > = . Vậy > -67 67 66 3 153 152 -152 -67 -152 -18 -23 c) và 91 114 -18 -18 -1 -23 -23 -18 -23 > = = > . Vậy > 91 90 5 115 114 91 114 Bài 7: 14 24 5 0 4 25 7 234 45
Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn: , , , , , , , 2 8 23 46 6 30 5 2 35 46 Lời giải Trang 32
+ Các số hữu tỉ dương: 14 4 25 7 4 4 5 25 14 7 7 , , , Vì 1 và
, nên sắp xếp theo thứ 8 6 30 5 6 6 6 30 8 4 5
tự từ bé đến lớn ta được: 4 25 7 14 1 6 30 5 8 24 5 0 234 45 45 5 0 25 24 234 Các số hữu tỉ âm: , , , 2 Vì 2 1 và 1 nên sắp 23 46 2 35 46 46 46 23 23 235
xếp theo thứ tự từ bé đến lớn ta được: 45 5 0 24 234 2 1 46 46 23 2 35 45 5 0 24 234 4 25 7 14 Vậy: 2 46 46 23 2 35 6 30 5 8 Bài 8:
So sánh các số hữu tỉ sau: 47 65 33 34 29 47 a) và b) và c) và 83 73 37 35 59 93 Lời giải 47 47 65 a)Ta có: 83 73 73 47 65 Vậy 83 73 33 34 34 3 3 3 4 3 4 b)Ta có: 37 37 35 37 37 35 33 34 Vậy 37 35 29 29 1 30 1 47 47 1 c) Ta có: ; 59 59 1 60 2 93 94 2 29 47 Vậy 59 93 Bài 9:
So sánh các số hữu tỉ sau: 456 465 173 1 6 a) và b) và 23 32 457 47 Lời giải Trang 33 456 456 456 9 465 a) Ta có 1 nên 23 23 23 9 32 173 173 1 7313 1 60 1 6 b)Ta có 1 nên 457 457 457 13 470 47 Bài 10:
Trong dịp hè, bạn An muốn mua một số vở để chuẩn bị cho năm học mới. Cửa hàng có 2 loại
vở: 6 quyển vở Hồng Hà có giá 65 nghìn đồng và 9 quyển vở Campus có giá 103 nghìn đồng.
Hỏi để tiết kiệm tiền bạn An nên mua loại vở nào? Lời giải
Giá tiền mỗi quyển vở Hồng Hà là: 65 (nghìn đồng). 6
Giá tiền mỗi quyển vở Campus là: 103 (nghìn đồng). 9
Quy đồng mẫu số hai phân số ta có: 65 195 103 206 ; 6 18 9 18 195 206 65 103 Vì nên . 18 18 6 9
Vậy để tiết kiệm tiền bạn An nên mua vở Hồng Hà. Bài 11: Tìm các phân số:
a) Có mẫu số là 30 , lớn hơn 2 và nhỏ hơn 1 . 5 6 b) Có tử số là 15
, lớn hơn 5 và nhỏ hơn 3 . 6 4 Lời giải 2 12 1 5 12 5 11 10 9 8 7 6 a) ; . Vậy x x ; ; ; ; ; 5 30 6 30 30 30 30 30 30 30 30 30 5 15 3 15 1 5 1 5 1 5 b) ; . Vậy x x 6 18 4 20 18 20 19
Dạng 4. Tìm điều kiện để một số hữu tỉ là số âm (dương) hay số nguyên *) Phương pháp giải:
- Số hữu tỉ âm là những số hữu tỉ nhỏ hơn 0.
- Số hữu tỉ dương là những số hữu tỉ lớn hơn 0.
- Số 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương a - Số hữu tỉ
là số hữu tỉ dương khi a, b cùng dấu. b Trang 34 a - Số hữu tỉ
là số hữu tỉ âm khi a, b khác dấu. b a - Số hữu tỉ
bằng 0 khi a 0 và b 0 . b
Chú ý: 0 không là số âm cũng không là số dương. a - Số hữu tỉ
là số nguyên khi a b hay b là ước của a. b Bài 1:
Tìm số nguyên x để các số sau là số hữu tỉ: x 5 5 a) b) c) 7 x 2x Lời giải a) Để x
là số hữu tỉ thì x . 7 b) Để 5
là số hữu tỉ thì x và x 0 . Suy ra x là số nguyên khác 0 . x c) Để 5
là số hữu tỉ thì 2x
và 2x 0 . Suy ra x là số nguyên khác 0 . 2x Bài 2:
Tìm số nguyên x để các số sau là số hữu tỉ: 1 2 a) b) x 1 2x 4 Lời giải a) Để 1
là số hữu tỉ thì x 1 và x 1 0 x , x 1. x 1 1
Vậy khi x là số nguyên khác 1thì là số hữu tỉ x 1 b) Để 2
là số hữu tỉ thì 2x 4 và 2x 4 0 x , x 2 . 2x 4 2
Vậy khi x là số nguyên khác 2 thì là số hữu tỉ. 2x 4 Bài 3: 101
Tìm số nguyên x để số hữu tỉ A là số nguyên. x 7 Lời giải Trang 35 Để 101 A ¢ thì
¢ x 7Ư 101 x 7
x 7{1;1; 1 01;101} Ta có bảng sau: x 7 1 1 101 101 x 8 6 108 94 101
Vậy khi x { 8; 6 ; 1
08;94} thì số hữu tỉ A là số nguyên. x 7 Bài 4: 20m 11
Cho số hữu tỉ x
. Với giá trị nào của m thì: 2019 a) x là số dương b) x là số âm. Lời giải 20m 11
a) Số hữu tỉ x là số dương khi: 2019 20m 11 1 1 x
0 20m 11 0 m 2 019 20 20m 11
b) Số hữu tỉ x là số âm khi: 2019 20m 11 1 1 x
0 20m 11 0 m 2 019 20 Bài 5: a 5
Cho số hữu tỉ: x
. Với giá trị nào của a thì: 2 a) x là số dương b) x là số âm
c) x không là số dương và cũng không là số âm. Lời giải a
a) x là số dương khi:
5 0 a 5 0 a 5 2 a 5
b) x là số âm khi:
0 a 5 0 a 5 2 a 5
c) x không là số dương và cũng không là số âm khi:
0 a 5 0 a 5 2 Bài 6: Trang 36 12 Cho x
(b ¢ ) . Với giá trị nào của b thì: b 5
a) x là số hữu tỉ b) x 1 Lời giải a) Để 12 x
(b ¢ ) là số hữu tỉ thì b 15 0 b 15 b 5 12 b) Ta có : x 1 1
12 (b 5) b 7 b 5 Bài 7: a 2
Cho số hữu tỉ x
(a ¢ ) . Với giá trị nào của a thì x là số nguyên? 5 Lời giải a 2 Số hữu tỉ x
(a ¢ ) là số nguyên khi: a 2 5
M a 2 5k(k ¢ ) a 5k 2 5 Bài 8: a 5
Cho số hữu tỉ: x
(a 0) . Với giá trị nguyên nào của a thì x là số nguyên? a Lời giải a 5 5 Ta có: x 1 (a 0) . a a 5
Suy ra x ¢ khi ¢ a U (5) a Vậy a 5 ; 1 ;1; 5 Bài 9: x 1
Tìm tất cả các số nguyên x để số hữu tỉ A
x 2có giá trị là số nguyên. x 2 Lời giải x 1 3 Ta có: A 1 x 2 x 2 x 2 3
Do x , để A là sô nguyên thì phải là số nguyên x 2 Hay (x 2) Ư(3) x 2 3 ; 1 ; 1 ; 3 Ta có bảng sau: Trang 37 x 2 3 1 1 3 x 1 1 3 5 x 1 Vậy khi x 1 ; 1 ; 3;
5 thì số hữu tỉ A
x 2có giá trị là số nguyên. x 2 Bài 10: 2x 1
Tìm tất cả các số nguyên x để số hữu tỉ B
x 5có giá trị là số nguyên. x 5 Lời giải 2x 1 11 Ta có: B 2 ( với x 5 ) x 5 x 5 11 Suy ra: B
Z x 5 Ư(11) x 5 x 5 1 1; 1 ; 1 ; 1 1 Ta có bảng sau: x 5 11 1 1 11 x 16 6 4 6 2x 1 Vậy khi x 1 6; 6 ; 4;
6 thì số hữu tỉ B
x 5có giá trị là số nguyên. x 5 Bài 11: x 3
Tìm số nguyên x để số hữu tỉ D là số nguyên 2x Lời giải
Ta có: D ¢ thì 2D ¢ . 2x 6 3 2D 1 . 2x x
Để D ¢ thì 2D ¢ và 2D là số chẵn. 3 3 Suy ra ¢ và là số lẻ (1) x x
x Ư 3 x{1;1; 3 ;3} (2)
Từ (1) và (2) ta có x { 1;1; 3
;3} thỏa mãn điều kiện đề bài x 3
Vậy khi x { 1;1; 3
;3}thì số hữu tỉ D là số nguyên. 2x Bài 12: Trang 38
Cho số x thỏa mãn 2
x 2 . Hỏi số x có là số hữu tỉ không? Lời giải Giả sử a
x là số hữu tỉ : x
;a,b 1; a ¢ ,b ¢ ,b 0 b 2 a Ta có: 2 2 2 x 2
2 a 2b 2 b Suy ra: 2 a 2 M a 2
M a 2mm¢ Khi đó: 2 2 2 2 2
4m 2b 2m b b 2 M b 2 M Mà a 2 M và b 2
M mâu thuẫn với giả sử a,b 1
Vậy x không thể là số hữu tỉ. Bài 13: 2a 1 o số hữu tỉ x
. Với giá trị nào của a thì: 2
a) x là số hữu tỉ dương?
b) x là số hữu tỉ âm?
c) x không là số hữu tỉ dương cũng không là số hữu tỉ âm? d) x là số nguyên? Lời giải a) Để a
x là số dương thì 2 1 0 2 1
Mà 2 0 nên 2a 1 0 a 2 1 Vậy a
thì x là số hữu tỉ dương. 2 b) Để 2a 1 x là số âm thì 0 2 1
Mà 2 0 nên 2a 1 0 a 2 1 Vậy a
thì x là số hữu tỉ âm. 2 c) Để 2a 1
x không là số dương cũng không là số âm thì 0 2 1
Mà 2 0 nên 2a 1 0 a 2 1 Vậy a
thì x không là số hữu tỉ dương, cũng không là số hữu tỉ âm. 2 Trang 39
d) Để x là số nguyên thì 2a 1 2 . Suy ra:
2a 1 2k, k 1
2a 2k 1 a k , k 2 1
Vậy a k , k
thì x là số nguyên. 2 Bài 14: a
Cho số hữu tỉ x
. Với giá trị nào của a thì 2 a 1
a) x là số hữu tỉ âm?
b) x không là số hữu tỉ âm, x cũng không là số hữu tỉ dương? Lời giải Ta có 2 a 0, a nên 2
a 1 1 0 hay 2 a 1 0 a . Do đó: a
a) x là số hữu tỉ nếu 0 , suy ra a 0 2 a 1 a
b) x không là số hữu tỉ âm, x cũng không là số hữu tỉ dương nếu
0 , suy ra a 0 . 2 a 1 Bài 15: 7
Cho số hữu tỉ x
. Xác định số nguyên a để x là số nguyên dương. a 1 Lời giải
Để x thì 7 a 1 hay a 1 ¦ 7 7 ; 1 ;1; 7 . Ta có bảng sau: a 1 7 1 1 7 a 8 2 0 6
Mà x là số nguyên dương nên 7 0 a 1
Mà 7 0 nên a 1 0 a 1 a 0; 6 7
Với a 0 ta có x 7 0 1 7
Với a 6 ta có x 1 6 1 Vậy a 0;
6 thì x là số nguyên dương. Bài 16: 3a 7
Cho số hữu tỉ x
. Với giá trị nào của a thì 5
a) x là số hữu tỉ dương? Trang 40
b) x là số hữu tỉ âm?
c) x không là số hữu tỉ dương và cũng không là số hữu tỉ âm? Lời giải a) Để a 7
x là số hữu tỉ dương thì 3 7 0 . Mà 5
0 nên 3a 7 0 suy ra a 5 3 b) Để 3a 7 7
x là số hữu tỉ âm thì 0 . Mà 5
0 nên 3a 7 0 suy ra a . 5 3 c) Để 3a 7
x không là số hữu tỉ dương cũng không là số hữu tỉ âm thì 0 . Mà 5 0 nên 5 7
3a 7 0 suy ra a . 3 Bài 17: 3n 1
Cho số hữu tỉ x
. Với giá trị nào của a thì 4
a) x là số hữu tỉ dương?
b) x là số hữu tỉ âm?
c) x không là số hữu tỉ dương cũng không là số hữu tỉ âm? Lời giải a) Để 3n 1 1
x là số hữu tỉ dương thì
0 3n 1 0 do 4 0 3n 1 n . 4 3 b) Để 3n 1 1
x là số hữu tỉ âm thì
0 3n 1 0 3n 1 n . 4 3
c) Để x không là số hữu tỉ dương cũng không là số hữu tỉ âm thì 3n 1 1
0 3n 1 0 3n 1 n 4 3 Bài 18: 7
Cho số hữu tỉ x
. Tìm số nguyên n để x nhận giá trị là số nguyên. n 1 Lời giải Để 7 x
thì n 1¦ 7 1 ; 7 n 1 Ta lập bảng: n 1 7 1 1 7 n 6 0 2 8 Vậy n 6 ;0;2;
8 thì x nhận giá trị nguyên.
BÀI TẬP TỰ LUYỆN DẠNG TOÁN Trang 41 Bài 1:
Tìm số nguyên a,b sao cho: 3 a 3 8 12 2 a) b) 8 10 5 19 b 5 Lời giải 3 a 3 1 5 4a 2 4 a) Ta có: . 8 10 5 40 40 40 1 5 4a 2 15 4 a 6 4
Mà a ¢ , suy ra: a 4 ; 5 8 12 2 2 12 8 24 24 24 b) Ta có: 19 b 5 5 b 19 60 2 b 57 57 57 2 b 60 3 0 b 2
Mà b ¢ , suy ra b 29 Bài 2:
Tìm x ¢ để: x 5 x 5 a) là số hữu tỉ dương b) là số hữu tỉ âm. x 10 x 7 Lời giải x 5 a)
là số hữu tỉ dương khi: x 10 x 5 0 x 5 0 hoặc x 10 0 x 10 0 x 5 0 x 5 * x 10 1 x 10 0 x 10 x 5 0 x 5 * x 52 x 10 0 x 10 Kết hợp
1 và 2 , ta được: x 5 hoặc x 10 Vậy khi x 5
x 5 hoặc x 10 thì là số hữu tỉ dương. x 10 x 5 b) là số hữu tỉ âm khi: x 7 Trang 42 x 5 0 x 5 0 hoặc x 7 0 x 7 0 x 5 0 x 5 * x 1 x 7 0 x 7 x 5 0 x 5 * 7 x 52 x 7 0 x 7 Kết hợp 1 và 2 , ta được: 7 x 5 Vậy khi x 5 7 x 5 thì là số hữu tỉ âm. x 7 Trang 43




