Chuyên đề tỉ số thể tích khối đa diện hình 12 có đáp án và lời giải chi tiết

CHUYÊN ĐỀ TỈ SỐ THỂ TÍCH
GIẢI NHANH CÁC CÂU HỎI TRẮC NGHIỆMTHI TỐT NGHIỆP THPT
A. CÁC CÔNG THỨC GIẢI NHANH TỈ SỐ THỂ TÍCH KHỐI ĐA DIỆN
1. Tỉ số thể tích khối chóp tam giác
Cho khối chóp tam giác S.ABC . Mặt phẳng  P cắt các đường thẳng S ,
A SB, SC lần lượt tại V
SA' SB ' SC '
A', B ',C ' . Khi đó ta có S.A'B'C'  . . . V SA SB SC S.ABC
Ví dụ 1.Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA  2a và SA vuông góc với đáy.
Gọi M , N lần lượt là hình chiếu vuông góc của A lên các đường thẳng SB và SC . Tính tỉ số thể tích V .ABCNM . VS.ABC Lời giải S N A C M B 2 SM SM .SB SA 4 Ta có    . 2 2 SB SB SB 5 SN 4 Tương tự  . SC 5 2 V SM SN  4  V 9 S . AMN  .    . A BCNM   V SB SC  5  V 25 S . ABC S .ABC
2. Tỉ số thể tích khối chóp có đáy là hình bình hành
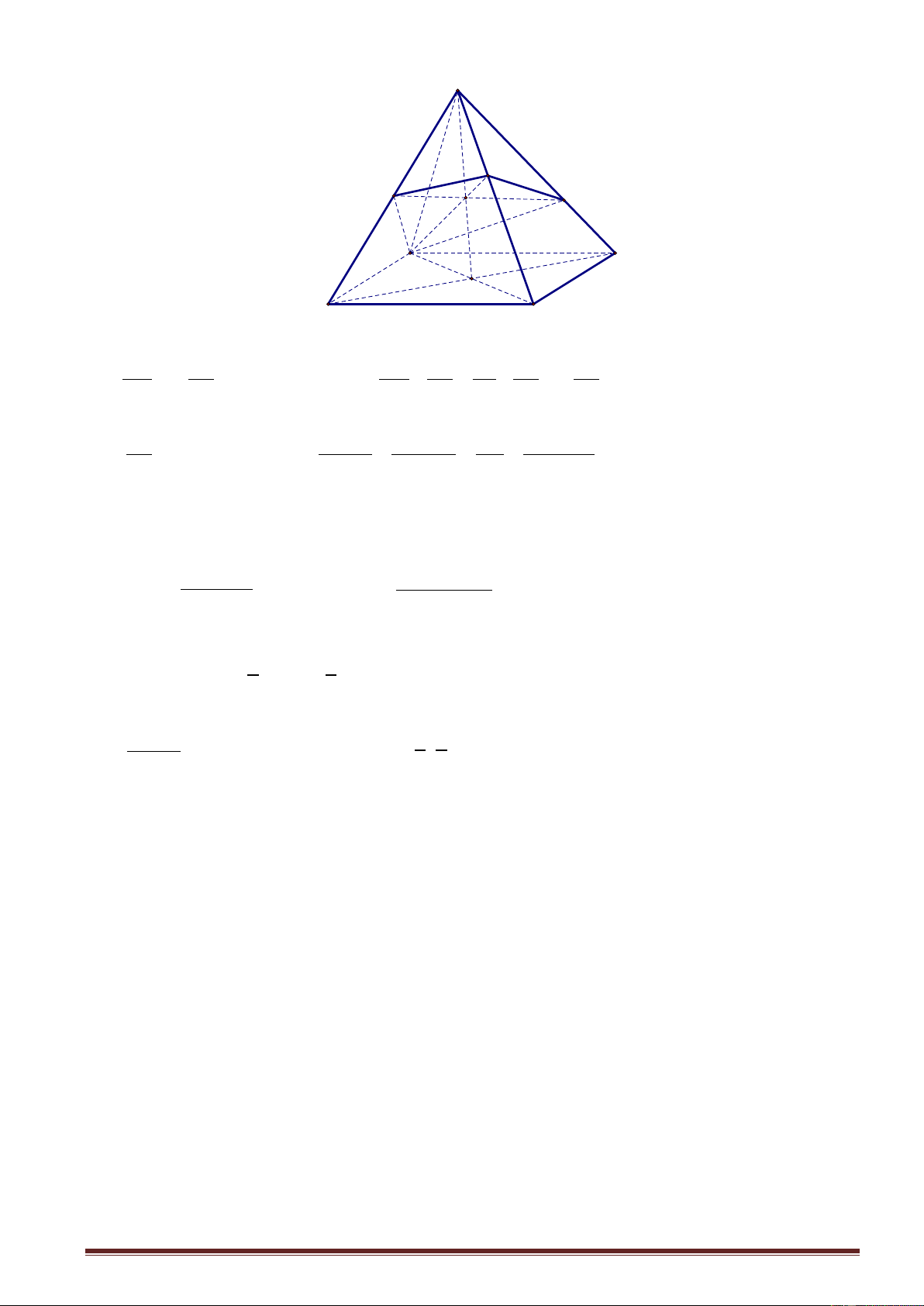
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Mặt phẳng  P cắtcác cạnh S ,
A SB, SC, SD, SO lần lượt tại A ', B ',C ', D ' và O' .Ta có SA SC SB SD SO a)     2. . SA ' SC ' SB ' SD ' SO ' Trang1 SA SB SC SD V
x  y  z  t b) Đặt x  , y  , z  , t 
. Ta có S.A'B'C'D'  . SA ' SB ' SC ' SD ' V 4xyzt S.ABCD
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SB , điểm V
P thuộc cạnh SD sao cho SP  2PD. Mặt phẳng  AMP cắt SC tại N . Tính tỷ số S.AMNP . VS.ABCD Lời giải S N M P I A D O B C SA SC SB SD SC 3 SC 5 Ta có     1  2    SA SN SM SP SN 2 SN 2 5 3 1 2   V 7 Vậy S.AMNP 2 2   V 5 3 30 S . ABCD 4.1.2. . 2 2
Ví dụ 3. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng  P chứa cạnh AB và
đi qua điểm M trên SC chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau. Tính tỷ số SM k  . SC Lời giải Trang2 S N M A D B C
AB  P
Gọi N   P  SC ta có 
nên MN //CD . AB//CD SM SC SD 1 Ta có k     SC SM SN k 1 1 11    Khi đó V 1 1 1 1 1 5 5 1 SABMN k k     1 0    k  . V 1 2 2 k k k 2 2 SABCD 4. 2 k
Ví dụ 4. Cho hình chóp S.ABCD có thể tích bằng V , đáy ABCD là hình vuông; SA   ABCD và
SC hợp với đáy một góc bằng 30 . Mặt phẳng  P đi qua A và vuông góc với SC , cắt các cạnh
SB, SC, SD lần lượt tại E, F , K . Tính thể tích khối chóp S.AEFK . Lời giải S F K E D A O B C 2 SB SB 2 SD SD SB SD Ta có  . Tương tự  nên  . 2 SE SA 2 SK SA SE SK Trang3 2 SC SC SC SB SD SB SD 5 Mà   4 ( do S  CA vuông tại  0 , A SCA  30 )nên 1    5    2 SF SA SF SE SK SE SK 2 V 10 1 V V S.AEFK S.ABCD   V   . S . V 5 5 10 AEFK 10 10 S. ABCD 4.1.4. . 2 2
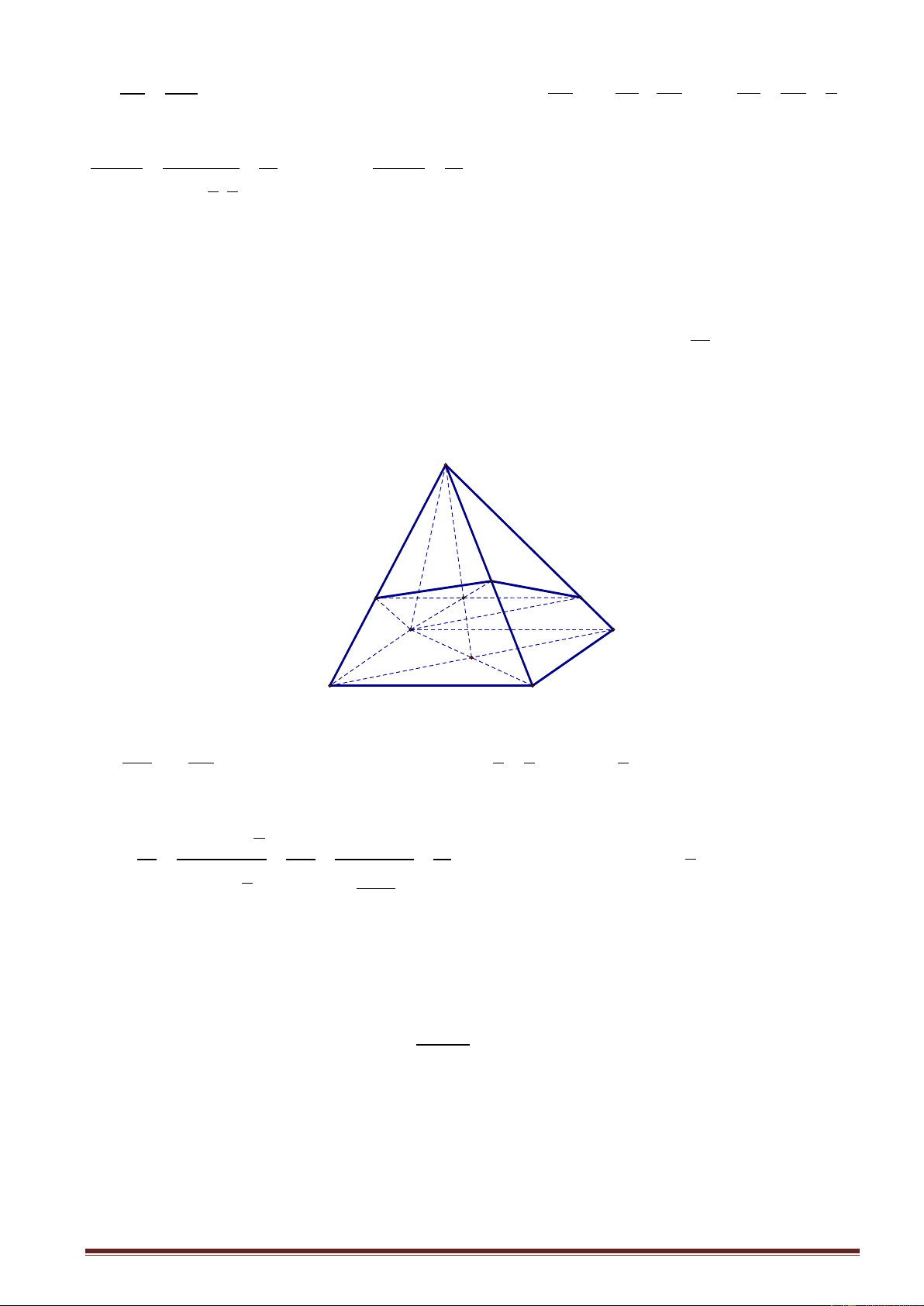
Ví dụ 5. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành; điểm Inằm trên SC sao cho
IS  2IC . Mặt phẳng  P chứa cạnh AI cắt cạnh SB, SD lần lượt tại M , N . Gọi V ',V lần lượt là V '
thể tích khối chóp S.AMIN và S.ABCD . Tính giá trị nhỏ nhất của tỉ số thể tích . V Lời giải S I M N D A O B C SB SD 3 5 5 Đặt  x,
 y  x, y  1 . Ta có  x  y  1   x  y  . SM SN 2 2 2 3 x  y 1 V ' 5 5 8 5 Ta có 2    
. Dấu bằng xảy ra khi x  y  . 2 V 3 6xy  x  y  15 4 4 . x .1. y 6 2    2 
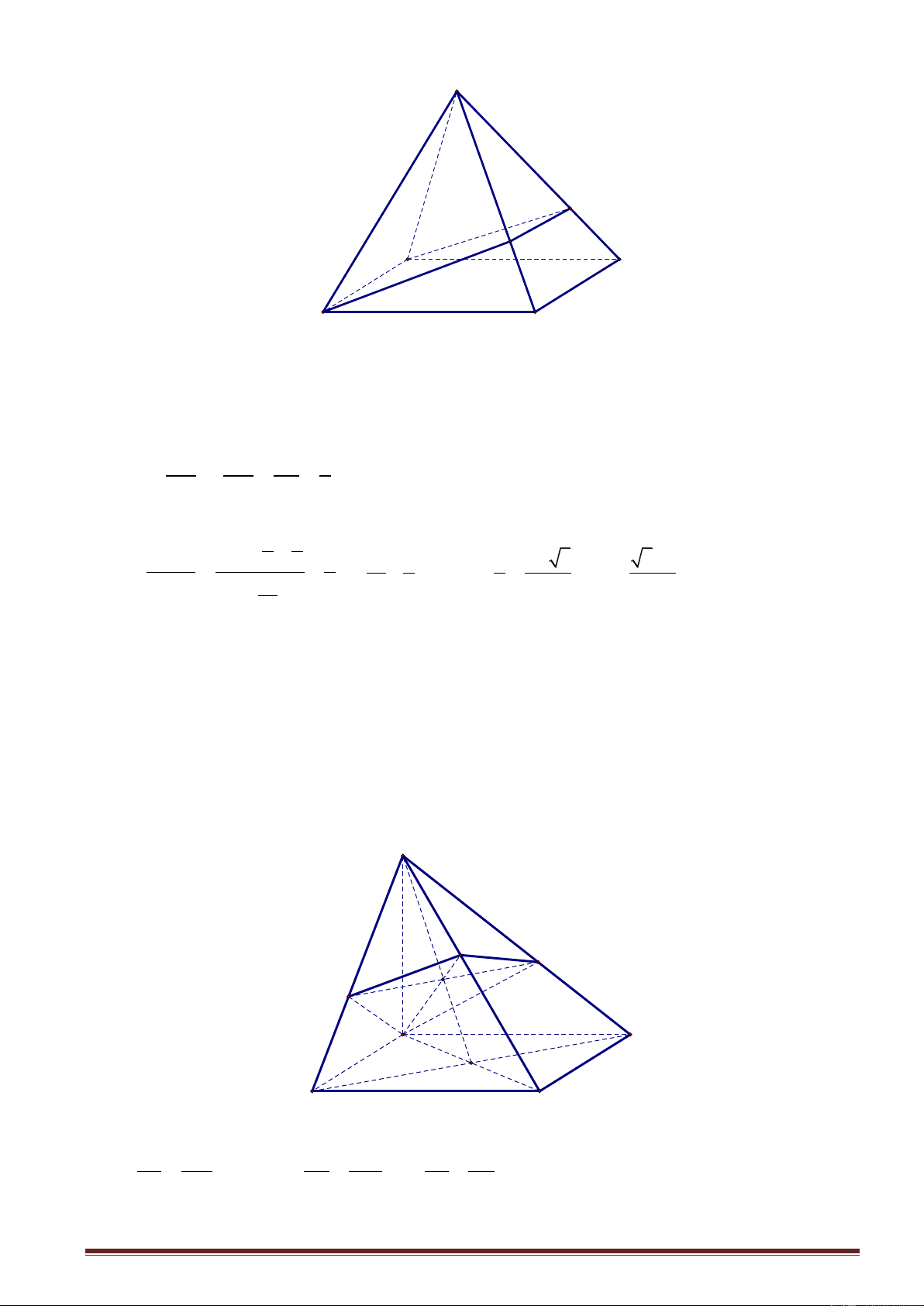
Ví dụ 6.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Mặt phẳng   thay đổi
luôn đi qua B , trung điểm I của SO và cắt các cạnh ,
SA SC và SD lần lượt tại M , N và . P Tính V
giá trị lớn nhất và giá trị nhỏ nhất của tỷ số S.BMPN . VS.ABCD Lời giải Trang4 S P M N I B C O A D SA SC SA SC SB SD SO Đặt  x,
 y  x, y  1 .Ta có     2.  4 SM SN SM SN SB SP SI SD V 8 2 2 Nên
 3; x  y  4 . Từ đó S.BMPN    SP V 4. . x . y 3.1 3xy 3x 4  x S .ABCD  
Từ x  y  4  x  4  y  3 vì y  1. 2 2 4  2x
Xét f  x 
  f 'x     0  x  2
x   x , 1 x 3 3 4
3x4  x 2    2 1 Ta có f  
1  f 3  ; f 2  . 9 6 V 1 2
Vậy S.BMPN đạt GTNN, GTLN lần lượt là , . V 6 9 S .ABCD Trang5
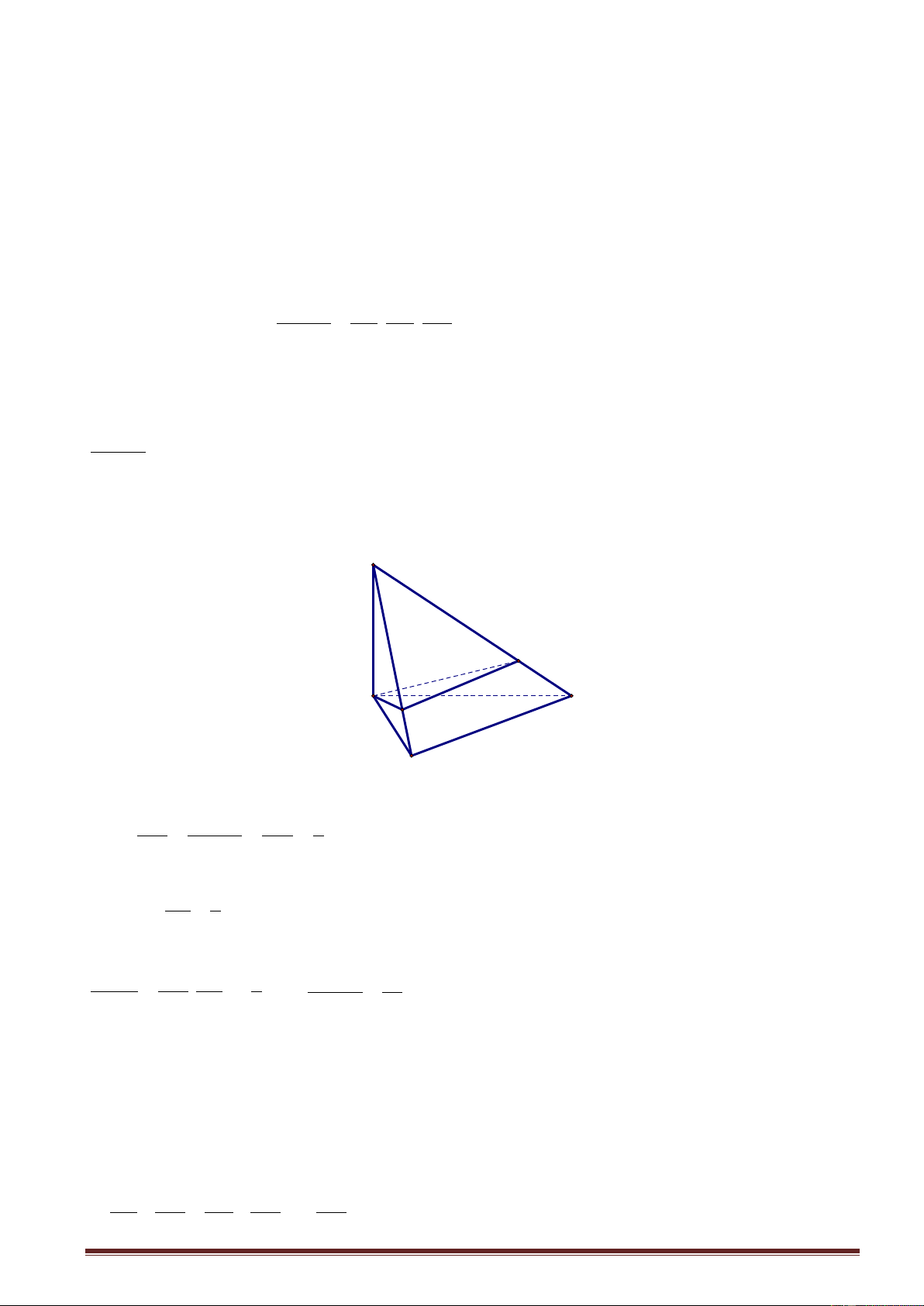
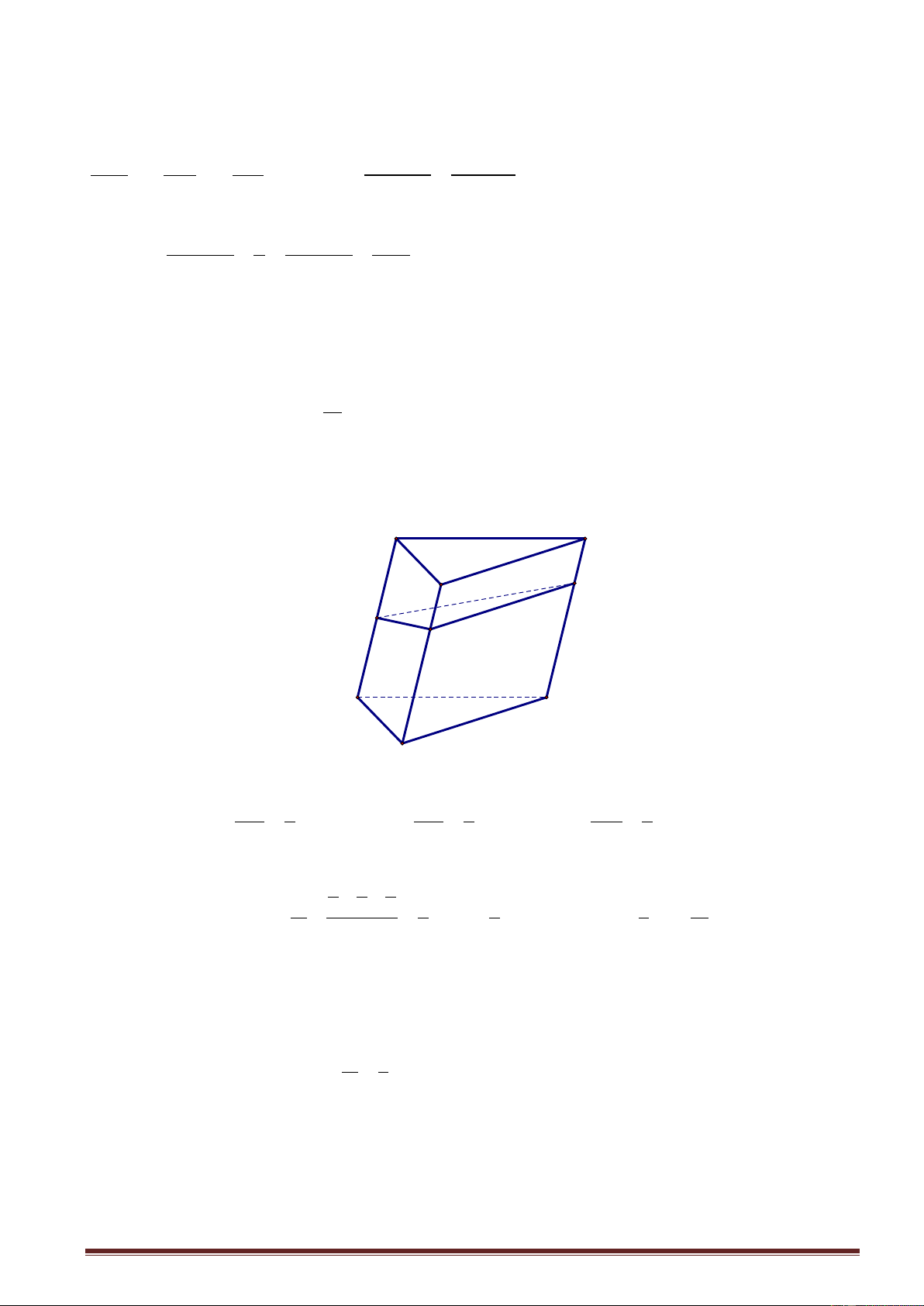
3. Tỉ số thể tích khối lăng trụ tam giác Cho lăng trụ AB . C A B  C
  có các điểm M , N, P lần lượt thuộc các cạnh AA , BB ,CC sao cho AM B N  C P     V    x y z x,  y,
 z . Khi đó A B C MNP  . AA BB CC V    3 A B C .ABC V x V y  z Đặc biệt: . A MNP M .  , BCPN  . V 3 V 3 ABC. 1 A 1 B 1 C ABC. 1 A 1 B 1 C
Ví dụ 7.Cho khối lăng trụ AB . C A B  C
 , có M , N, P lần lượt thuộc các cạnh AA , BB ,CC sao cho AM  MA ,
 BN  3NB ,CP  3PC . Đặt V là thể tích của khối đa diện ABCMNP , V là thể tích của 1 2 V
khối đa diện còn lại. Tính tỉ số 1 . V2 Lời giải A' C' B' P M N A C B MA 1 BN 3 CP 3
Ta có MA  MA 
 ; BN  3NB 
 ;CP  3PC   AA 2 BB 4 CC 4 1 3 3   V 2 2 1 V Đặt V  V . Suy ra 1 2 4 4 1 
  V  V  V  V V  V   2.
ABC. AB C   1 2 1 V 3 3 3 3 V2
Ví dụ 8.Cho khối lăng trụ AB . C A B  C
  có thể tích bằng V , các điểm M , N, P lần lượt thuộc các cạnh AA ,
 BB ,CC sao cho AM  2MA , BN  3NB ,CP  .
x PC . Đặt V là thể tích của khối đa diện 1 V 3 AB .
C MNP , tính giá trị của x để 1  . V 5 Lời giải Trang6 A' C' B' M P N A C B AM 2 BN 3 CP x
Ta có MA  2MA 
 ; BN  3NB 
 ; CP  xPC   AA 3 BB 4 CC x  1 2 3 x   V  3 17 x 9 x 23 23 Suy ra 1 3 4 x 1         x  . V 3 5 12 x 1 5 x 1 60 37
Ví dụ 9. Cho khối lăng trụ AB . C A B  C
  có thể tích bằng 3
60 cm , các điểm M , N , P lần lượt thuộc các cạnh AA ,
 BB ,CC sao cho AM  2MA , BN  3NB ,CP  4PC . Thể tích của khối đa diện B . C MNP . Lời giải A' C' B' P M N A C B AM 2 BN 3 CP 4
Ta có MA  2MA 
 ; BN  3NB 
 ;CP  4PC   AA 3 BB 4 CC 5 2 3 4   V 133 133 133 Nên ABCMNP 3 4 5    V  .60  V 3 180 ABCMNP 180 3
ABCA' B 'C ' 1 1 2 2 40 Mà V
 d M ; ABC .S
 . d A'; ABC .S  .V  . M . ABC    ABC    ABC
ABC. A' B 'C ' 3 3 3 9 3 Trang7 133 40 Vậy V    31 cm BCMNP  3. 3 3
Nhận xét. Các bài toán dạng này sẽ xuất hiện nhiều khối không phải là các khối có công thức tính thể
tích như chóp hay lăng trụ. Thay vì việc phải phân chia các khối này thành các khối có công thức tính,
nay ta có ngay một kết quả rất nhanh và chính xác.
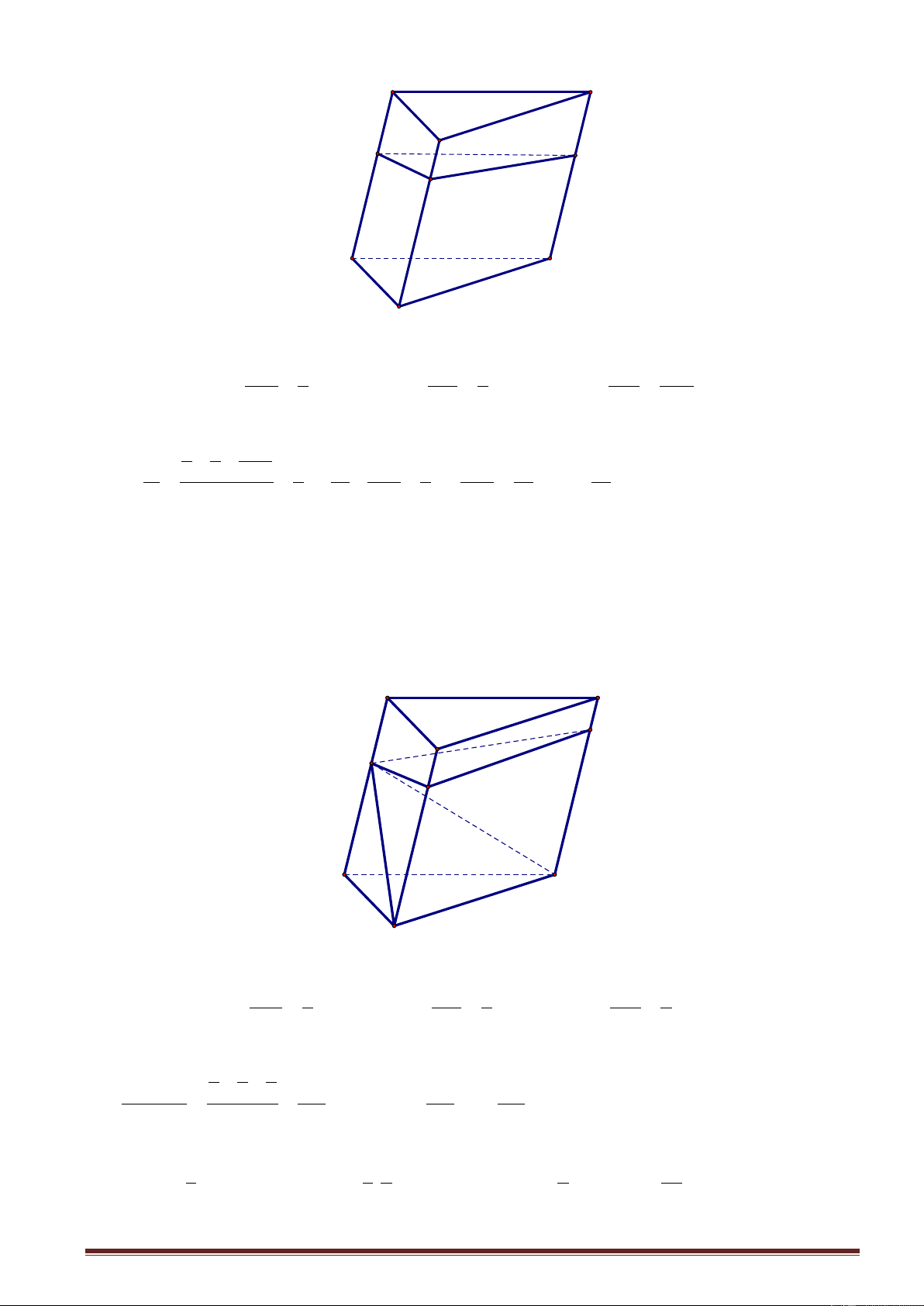
Ví dụ 10. Cho lăng trụ AB .
C A' B 'C 'có G, G ' lần lượt là trọng tâm của các tam giác ABC và A' B'C .
Mặt phẳng   cắt AA', BB ',CC ',GG ' lần lượt tại M , N, P, I . AM BN CP GI Chứng minh    3. . AA ' BB ' CC ' GG ' Chứng minh A' C' G' B' M P I N A C G B AM BN CP GI Đặt x  , y  , z  , t  ; V  V AA ' BB ' CC ' GG '
ABC. A' B 'C ' V Dễ thấy V V V  .
AGB .A 'G 'B '
CGB .C 'G 'B '
AGC .A 'G 'C ' 3 V
x  y  t V
z  y  t V
z  y  t Ta có AGBMIN  . Tương tự ta có CGBPIN  ; CGAPIN  V 3 V 3 V 3 A
V GB.A'G 'B' C
V GB.C 'G ' B' C
V GA.C 'G ' A'
Cộng vế với vế cả 3 đẳng thức trên ta được 3V
x  y  t
z  y  t
z  y  t
2 x  y  z ABCMNBP        t V 3 3 3 3 3V
x  y  z
x  y  z Mà ABCMNBP  3.
 x  y  z nên t 
. Ta được điều phải chứng minh. V 3 3 Trang8 V GI Từ kết quả trên ta có ABCMNBP  . V GG '
ABC.A' B 'C '
Nhận xét. Dựa vào kết quả trên ta thấy rẳng chỉ cần biết   cắt GG ' tại vị trí điểm I xác định là ta
đã biết   chia lăng trụ thành hai phần với tỉ số bao nhiêu rồi. Trang9
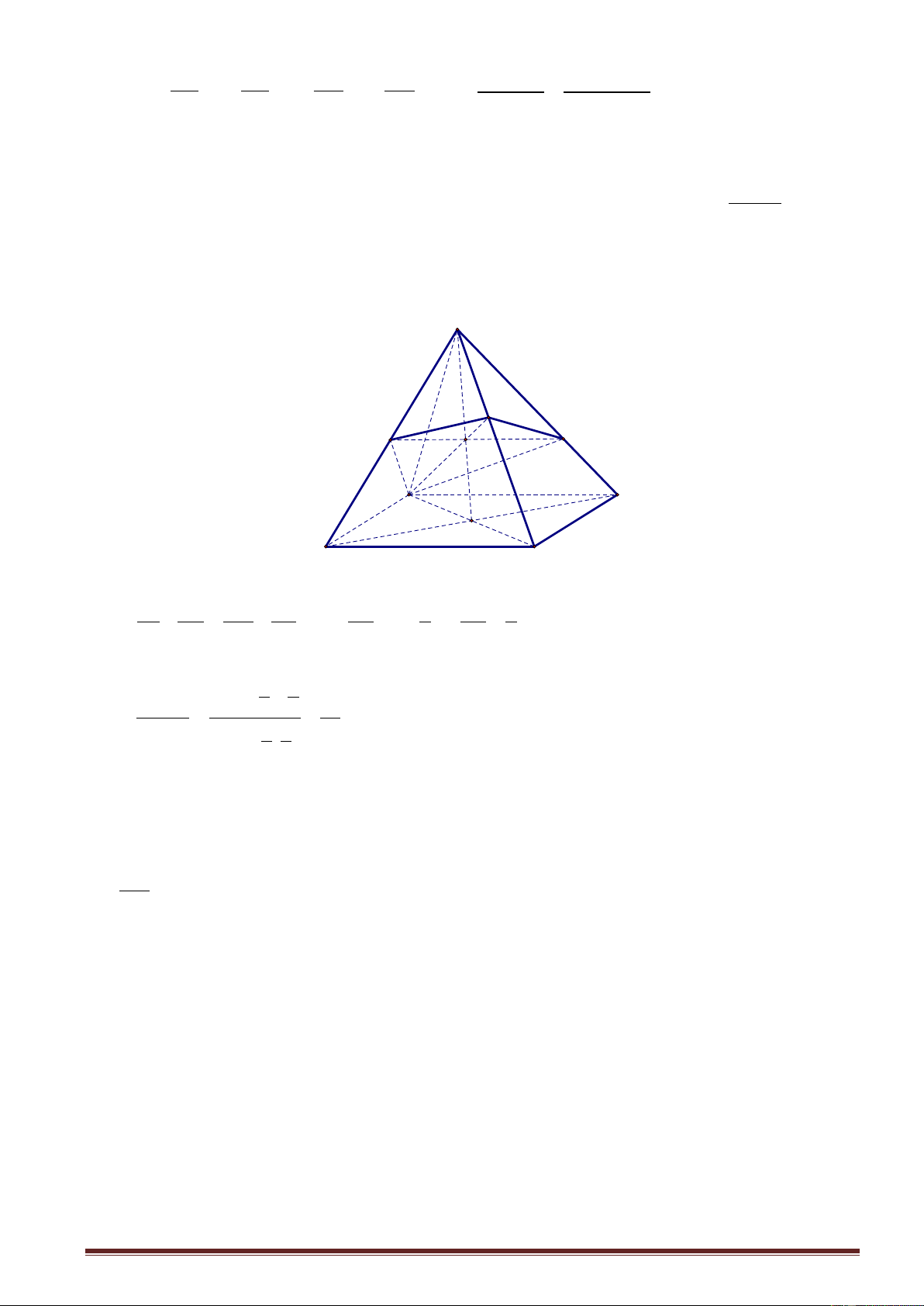
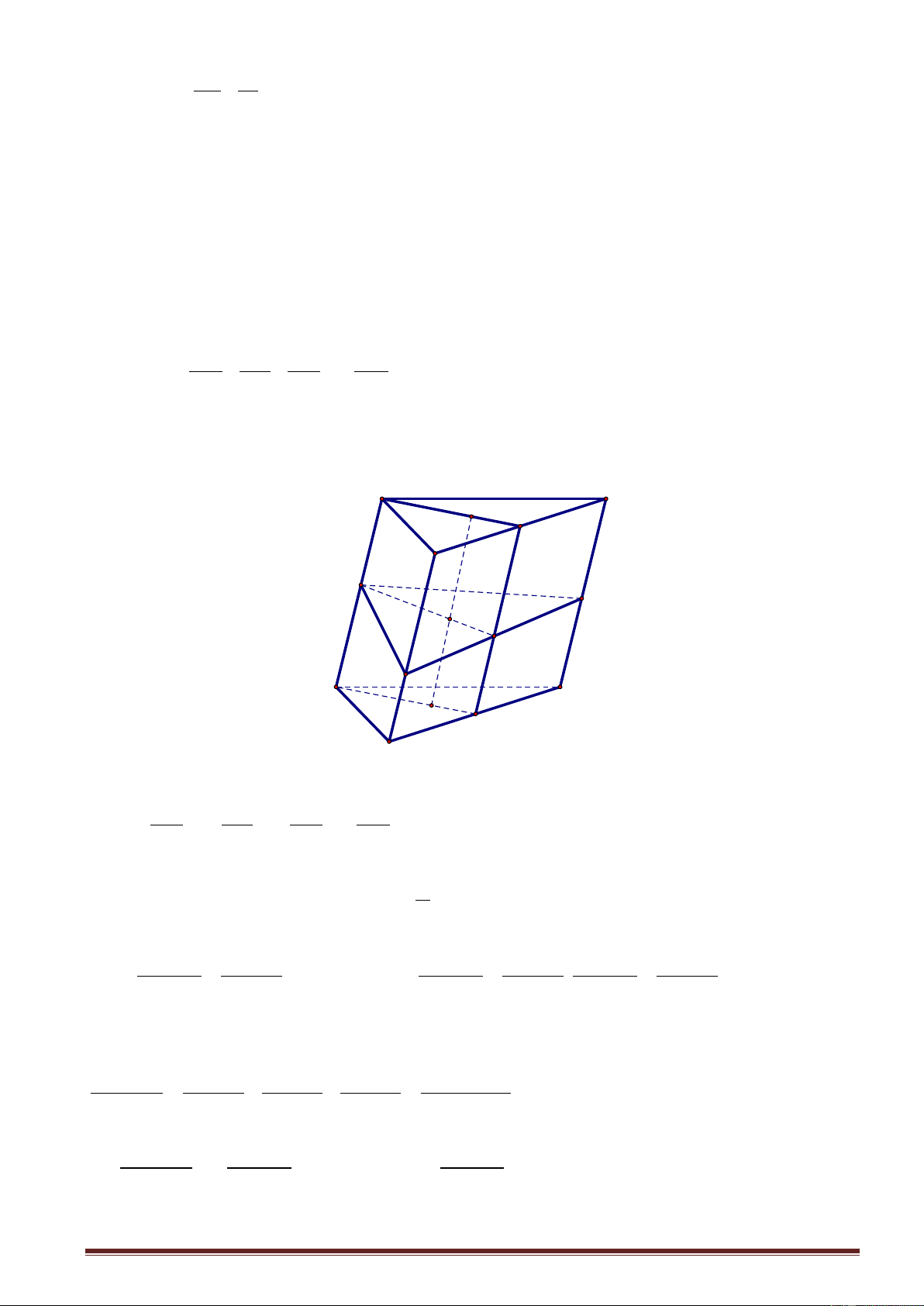
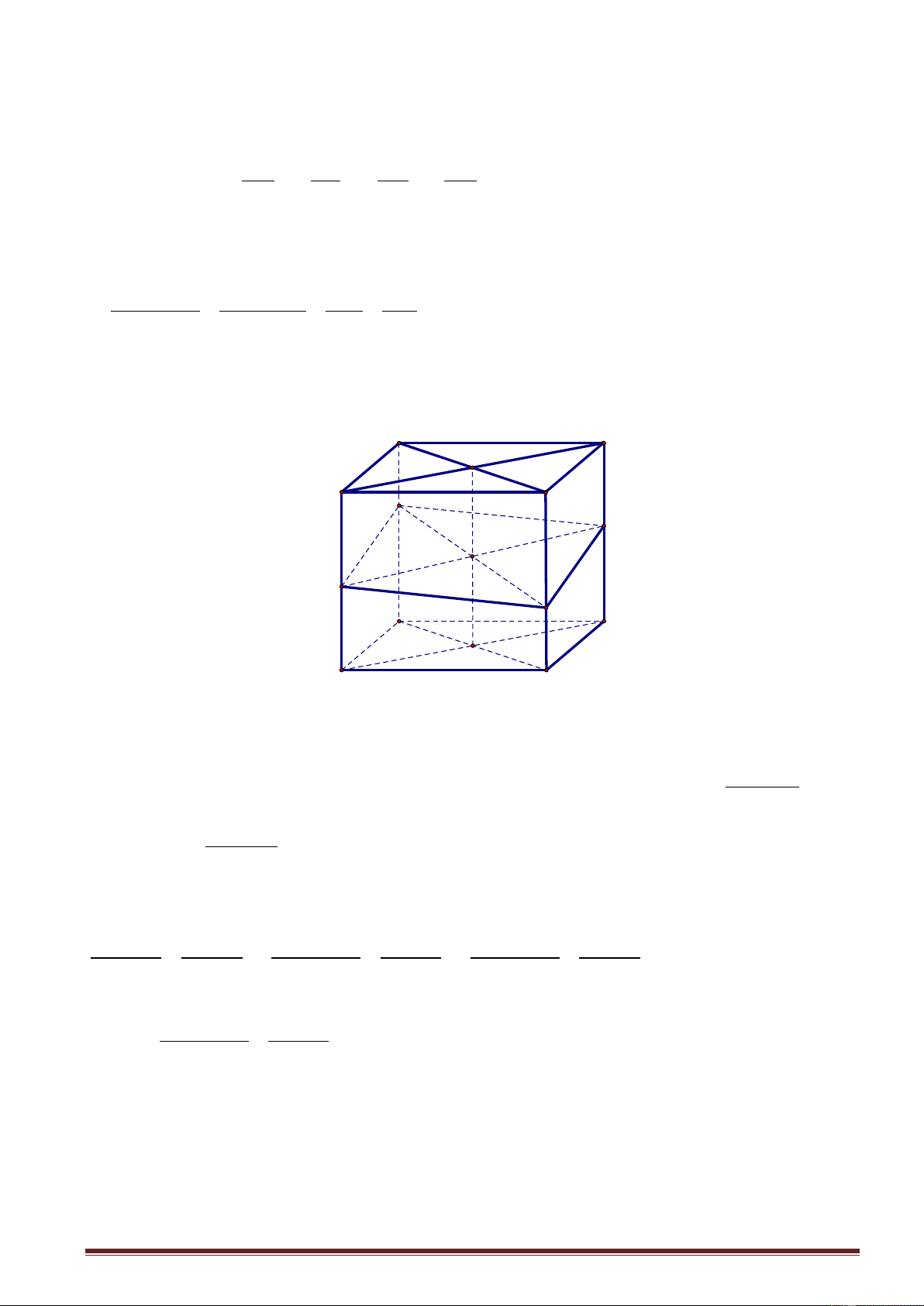
4. Tính chất 4: Tỉ số thể tích khối hộp Cho hình hộp ABC .
D A' B'C ' D' . Mặt phẳng   cắt các cạnh AA', BB ',CC ', DD ' lần lượt tại AM BN CP DQ
M , N , P, Q sao cho  x,  y,  z,
 t . Khi đó ta có: ' ' ' ' AA BB CC DD
a) x  z  y  t. V
x  y  z  t x  z y  t b) ABCDMNQP    . V 4 2 2
ABCD.A' B'C ' D' Chứng minh B C O A D N P I M B' Q C' O' A' D'
a. Dễ thấy tứ giác MNPQ là hình bình hành. Gọi I , O lần lượt là tâm của hình bình hành MNPQ và AM  CP
hình vuông ABCD . Ta có OI là đường trung bình của hình thang AMPC nên OI  . 2 BN  DQ Tương tự OI 
, do đó AM  CP  BN  DQ  xAA' zCC '  yBB ' tDD '  x  z  y  t 2
b. Áp dụng Tính chất 3 ta có V
x  y  t 2V
x  y  t V   ABDMNQ ABDMNPQ ABDMNQ x y t      V 3 V 3 V 6
ABD.A' B ' D'
ABCD.A' B'C ' D'
ABCD. A' B'C ' D' V
y  z  t tương tự BCDNPQ  V 6
ABCD.A' B 'C ' D ' Do đó, Trang10 V V V          ABCDMNPQ ABDMNQ BCDNPQ x y t y z t x y z t y t      V V V 6 6 6
ABCD. A' B 'C ' D '
ABCD. A' B 'C ' D '
ABCD. A' B 'C ' D '
x  y  z  t
x  y  z  t  2
x  y  z  t   6 4 V
x  y  z  t OI Chú ý : ABCDMNQP   . V 4 OO '
ABCD.A' B'C ' D'
Nhận xét. Một kết quả tương tự như Tính chất 3. Ở lăng trụ là tổng ba tỉ số chia ba, còn hình hộp là chia bốn.
Và cũng chỉ cần biết   cắt đoạn thẳng nối hai tâm đáy ở đâu là ta đã tìm được tỷ số hai khối tạo
thành do   cắt hình hộp. Tuy nhiên, Tính chất 4cũng khẳng định chỉ cần biết hai tỉ số ở hai cạnh
bên đối diện của hình hộp mà   cắt là ta cũng tìm được tỉ số thể tích các khối.
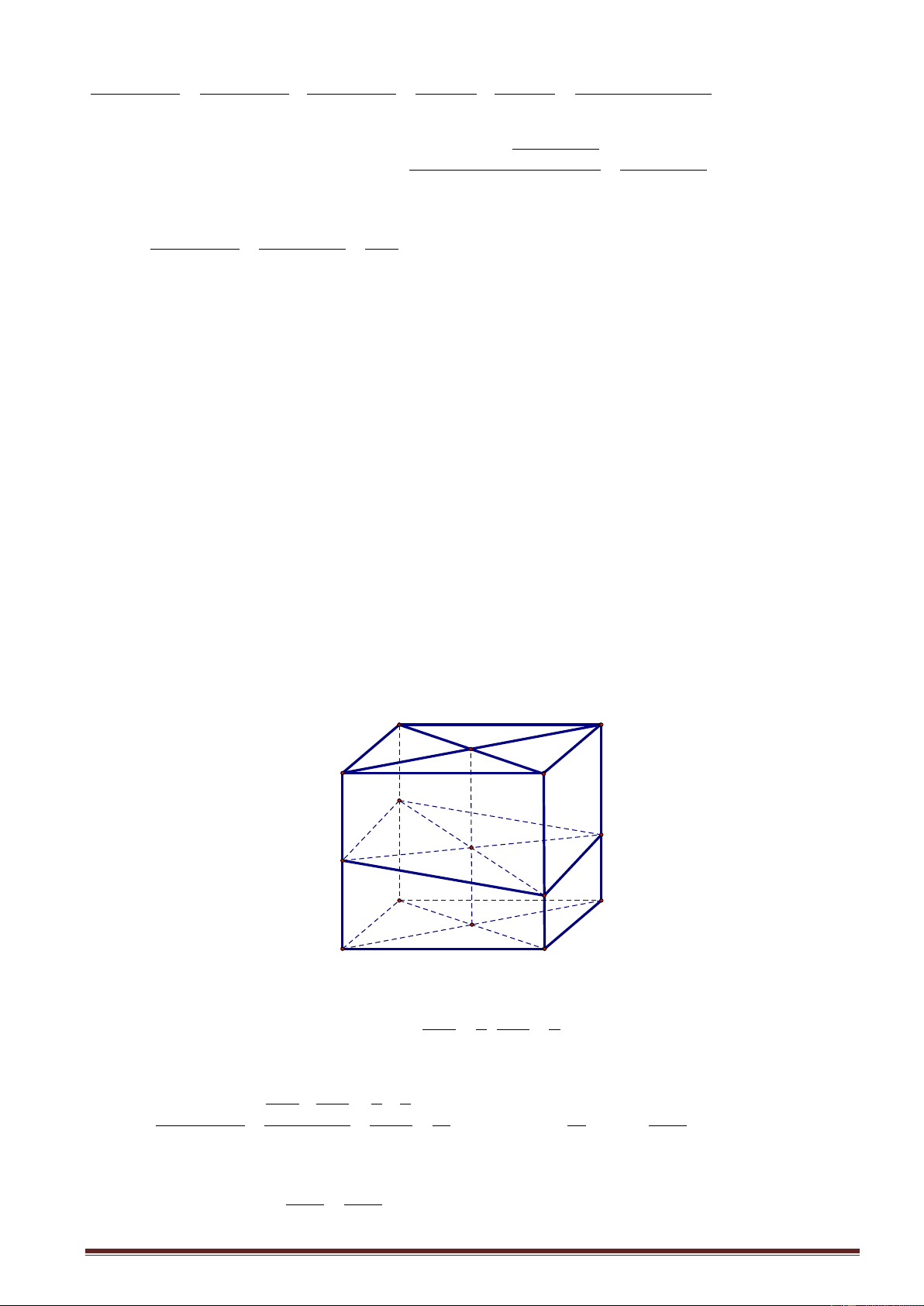
Ví dụ 11. Cho khối hộp chữ nhật ABC . D A B  C  D
  có thể tích bằng 2110 . Biết A M   MA ;
DN  3ND và CP  2C P
 . Mặt phẳng MNP chia khối hộp đã cho thành hai khối đa diện. Tính thể
tích khối đa diện nhỏ hơn. Lời giải B C O A D Q P M N B' C' O' A' D'  AM 1 CP 2 MNP cắt ’
BB tại Q . Từ giải thiết ta có  ;  . AA ' 2 CC ' 3 AM CP 1 2   V Do đó ABCDMNPQ 7 7 7385 AA' CC ' 2 3     V  .2110  V 2 2 12 ABCDMNPQ 12 6
ABCD. A' B 'C ' D ' 7385 5275 Vậy V  2110   .
A' B'C' D' MNPQ 6 6 Trang11
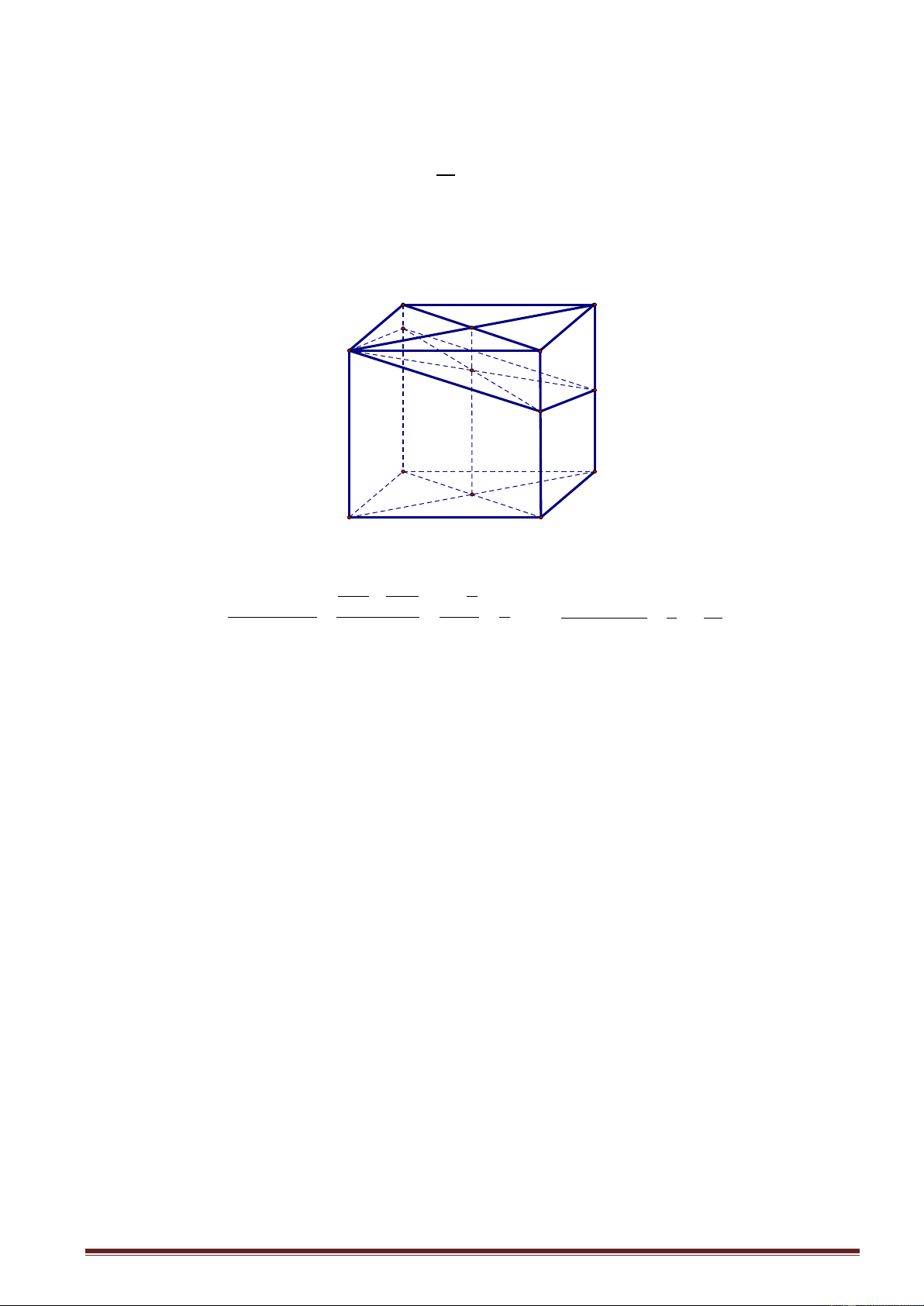
Ví dụ 12. Cho hình lập phương ABC . D A B  C  D
  có N là trung điểm CC . Mặt phẳng   đi qua
AN , cắt các cạnh BB ', DD lần lượt tại M , P ;   chia khối lập phương thành hai phần có thể tích tương ứ V
ng bằng V và V
V  V . Tính tỉ số 2 . 2  1 2  1 V1 Lời giải B C M O A D I N P B' C' O' A' D' AA CN 1  0  V 1 V 1 V Từ giải thiết ta có ABCDPNM AA ' CC ' 2    . Nên ABCDPNM 2    3. V 2 2 4 V 3 V
ABCD. A' B 'C ' D '
AMNPA' B 'C ' D ' 1 Trang12
B. CÂU HỎI TRẮC NGHIỆM Câu 1:
Cho khối chóp S.ABCD đáy ABCD là hình vuông cạnh a ; SA  a à
v SA   AB D C  . Gọi
B ', D ' lần lượt là trung điểm SB, SD . Mặt phẳng  AB ' D ' cắt SC tại C '. Đặt
VS.AB'C'D' k 
, giá trị của k bằng VS.ABCD 1 1 1 1 A. . B. . C. . D. . 12 3 4 6
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành; M , N lần lượt là trung điểm của
SA và SB . Gọi V , V lần lượt là thể tích của các khối chóp S.MNCD và S.ABC . D Tỷ số 1 2 V1 bằng V2 3 2 1 3 A. . B. . C. . D. . 8 3 8 4 Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của cạnh SC .
Mặt phẳng  P chứa AM và song song với BD lần lượt cắt các cạnh bên SB và SD tại V
N và Q . Tỷ số S.ANMO bằng VS.ABCD 1 1 2 1 A. . B. . C. . D. . 3 6 5 4 Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm I nằm trên cạnh SC sao
cho IS  2IC . Mặt phẳng  P chứa AI cắt các cạnh SB và SD lần lượt tại M và N . Gọi
V ' và V lần lượt là thể tích của khối chóp S.AMIN và S.ABCD . Giá trị nhỏ nhất của tỷ số V ' bằng V 4 5 8 5 A. . B. . C. . D. . 5 54 15 24 Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, điểm M thuộc cạnh SA , điểm SM 1 SN 2
N thuộc cạnh SD sao cho  ,
 . Mặt phẳng   thay đổi luôn chứa MN , cắt SA 2 SD 3
các cạnh SB và SC lần lượt tại Q và .
P Biết thể tích của khối chóp S.ABCD bằng V , khi
đó giá trị lớn nhất của thể tích khối chóp S.MNPQ bằng Trang13 V 2V 3V V A. . B. . C. . D. . 4 5 8 3 Câu 6:
Cho khối chóp S.ABC có G là trọng tâm tam giác SBC . Đường thẳng d đi qua G , cắt các
cạnh SB, SC lần lượt tại M và N. Gọi V ,V lần lượt là thể tích của các khối chóp S.AMN 1 V
và S.ABC . Tổng giá trị lớn nhất và giá trị nhỏ nhất của tỷ số 1 bằng V 17 21 37 10 A. . B. . C. . D. . 18 22 33 9 Câu 7:
Cho chóp S.ABC . Trên các cạnh S ,
A SB, SC lần lượt lấy các điểm A ,
 B ,C . Gọi G là SA SB SC
trọng tâm tam giác ABC và SG cắt  A B  C
 tại G. Khi đó   bằng SA ' SB ' SC ' 3SG SG ' 2SG 3SG ' A. . B. . C. . D. . SG ' SG SG ' SG Câu 8:
Cho khối lăng trụ AB . C A B  C
 . Gọi M , N lần lượt là trung điểm của hai cạnh AA và BB .
Mặt phẳng CMN  chia khối lăng trụ đã cho thành hai phần. Đặt V là thể tích của khối 1 V
chóp C '.MNB' A' và V là thể tích của khối đa diện AB .
C MNC '. Tỷ số 1 bằng 2 V2 2 1 3 A. . B. 2. C. . D. . 3 2 2 Câu 9:
Cho khối lăng trụ AB . C A B  C
  có thể tích bằng V . Các điểm M , N, P lần lượt thuộc các AM 1 BN CP 2 cạnh AA ,
 BB ,CC sao cho  , 
 . Thể tích của khối đa diện AA ' 2 BB ' CC ' 3 AB . C MNP bằng 2 9 20 11 A. V . B. V . C. V . D. V . 3 16 27 18
Câu 10: Cho khối lăng trụ đều AB . C A B  C
 . Gọi I là trung điểm của AA'. Mặt phẳng IB'C chia
khối lăng trụ thành hai phần: phần chứa đỉnh ,
A B có thể tích bằng V và phần còn lại có thể 1 V
tích bằng V . Tỉ số 1 bằng 2 V2 2 1 1 A. 1. B. . C. . D. . 3 3 2 Trang14
Câu 11: Cho hình hộp ABC . D A B  C  D
  . Trên các cạnh AA , BB ,CC lần lượt lấy ba điểm M , N, P A ' M 1 B ' M 2 C ' P 1 sao cho  ;  ;
 . Biết mặt phẳng MNP cắt cạnh DD ' tạiQ . Tỉ số AA' 3 BB ' 3 CC ' 2 D 'Q bằng DD ' 1 1 5 2 A. . B. . C. . D. . 6 3 6 3
Câu 12: Cho hình hộp chữ nhật ABC . D A B  C  D
  . Trên các cạnh AA , BB ,CC lần lượt lấy ba điểm
X ,Y , Z sao cho AX  2 AX , BY  B Y
 , CZ  3C Z
 . Mặt phẳng  XYZ  cắt cạnh DD' tại
điểmT . Tỉ số thể tích của khối XYZT.ABCD và khối XYZT.A B  C  D   bằng 7 7 17 17 A. . B. . C. . D. . 24 17 7 24
Câu 13: Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a . Mặt phẳng   cắt các cạnh 1 2 AA ,
 BB ,CC và DD lần lượt tại M , N, P,Q . Biết AM  a,CP  a . Thể tích của khối 3 5 đa diện . ABCD MNPQ bằng 11 3 a 3 2a 11 A. 3 a . B. . C. . D. 3 a 30 3 3 15
Câu 14: Cho khối lập phương ABC . D A B  C  D
  . Mặt phẳng   đi qua A cắt các cạnh BB ,
 CC , DD lần lượt tại M , N, P sao cho phần thể tích của khối đa diện chứa đỉnh B CN
bằng một nửa thể tích của khối đa diện còn lại. Tỉ số CC bằng 3 1 2 3 A. . B. . C. . D. . 4 2 3 2 BẢNG ĐÁP ÁN 1.D 2.A 3.A 4.C 5.D 6.A 7.A 8.C 9.D 10.A 11.A 12.B 13.A 14.C Trang15
BÀI TẬP TỔNG HỢP
Câu 1: Cho khối chóp S.ABCD đáy ABCD là hình vuông cạnh a . SA  a à
v SA   AB D C  . Gọi
B ', D ' lần lượt là trung điểm SB, SD . Mặt phẳng  AB ' D ' cắt SC tại C '. Đặt
VS.AB'C'D' k 
, giá trị của k bằng. VS.ABCD 1 1 1 1 A. . B. . C. . D. . 12 3 4 6
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M , N lần lượt là trung điểm của
SA và SB . Gọi V , V lần lượt là thể tích của các khối chóp S.MNCD và S.ABC . D Ttỷ số 1 2 V1 bằng. V2 3 2 1 3 A. . B. . C. . D. . 8 3 8 4 Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M là trung điểm của cạnh
SC . Mặt phẳng  P chứa AM và song song với BD lần lượt cắt các cạnh bên SB và SD V
tại N và Q . Tỷ số S.ANMO bằng. VS.ABCD 1 1 2 1 A. . B. . C. . D. . 3 6 5 4 Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm I nằm trên cạnh SC sao
cho IS  2IC . Mặt phẳng  P chứa cạnh AI cắt các cạnh SB và SD lần lượt tại M và N
. Gọi V ' và V lần lượt là thể tích của khối chóp S.AMIN và S.ABCD . Giá trị nhỏ nhất của V ' tỷ số bằng. V 4 5 8 5 A. . B. . C. . D. . 5 54 15 24 Câu 5:
Cho khối lăng trụ AB . C A B  C
  có thể tích bằng V . Các điểm M , N, P lần lượt thuộc các AM 1 BN CP 2 cạnh AA ,
 BB ,CC sao cho  , 
 . Thể tích của khối đa diện AA ' 2 BB ' CC ' 3 AB . C MNP bằng. 2 9 20 11 A. V . B. V . C. V . D. V . 3 16 27 18 Trang16