Chuyên đề tính đơn điệu và cực trị của hàm số từ cơ bản đến nâng cao

Tài liệu gồm 690 trang, được biên soạn bởi thầy giáo Huỳnh Văn Ánh, bao gồm lý thuyết, hệ thống bài tập trắc nghiệm và hệ thống bài tập tự luận chuyên đề tính đơn điệu và cực trị của hàm số từ cơ bản đến nâng cao. Mời bạn đọc đón xem!

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

690 trang 1 tháng trước

Tác giả:

Profile Lê Phương
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 1
Sưu tầm và biên soạn
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1. Khái niệm tính đợn điệu của hàm số.
Giả sử
K
là một khoảng, một đoạn hoặc một nữa khoảng và
()y fx
là hàm số xác định trên
K
.
+) Hàm số
()
y fx
được gọi là đồng biến trên
K
nếu
12 1 2 1 2
, , ( ) ( ).
x x K x x fx fx 
+) Hàm số
()y fx
được gọi là nghịch biến trên
K
nếu
12 1 2 1 2
, , ( ) ( ).x x K x x fx fx 
+) Hàm số đồng biến hoặc nghịch biến trên
K
được gọi chung là đơn điệu trên
.K
Chú ý:
+ Nếu hàm số đồng biến trên
K
thì từ trái sang phải đồ thị đi lên.
+ Nếu hàm số nghịch biến trên
K
thì từ trái sang phải đồ thị đi xuống.
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT VÀ VẼ
ĐỒ THỊ CỦA HÀM SỐ
I
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
Sưu tầm và biên soạn
2. Định lý: Cho hàm số
()y fx
có đạo hàm trên
K
, trong đó
K
là một khoảng, đoạn hoặc nữa
khoảng.
+) Nếu
( ) 0, fx x K

thì hàm số
()
y fx
đồng biến trên khoảng
K
.
+) Nếu
( ) 0, fx x K

thì hàm số
()y fx
nghịch biến trên khoảng
K
.
3. Định lý: (Tổng quát) Cho hàm số
()y fx
có đạo hàm trên
K
, trong đó
K
là một khoảng,
đoạn hoặc nữa khoảng.
+) Nếu
( ) 0,
fx x K

và
() 0fx
xảy ra tại một số hữu hạn điểm trên
K
thì hàm số
()y fx
đồng biến trên khoảng
K
.
+) Nếu
( ) 0, fx x K

và
() 0fx
xảy ra tại một số hữu hạn điểm trên
K
thì hàm số
()y fx
nghịch biến trên khoảng
K
.
4. Lưu ý:
+) Nếu hàm số
()y fx
liên tục trên đoạn
[;]ab
và
'( ) 0, ( ; )f x x ab 
thì ta nói hàm số đồng
biến trên đoạn
[ ; ].ab
+) Nếu hàm số
()y fx
liên tục trên đoạn
[;]ab
và
'( ) 0, (a; )fx x b 
thì ta nói hàm số
nghịch biến trên đoạn
[ ; ].
ab
+) Tương tự với các khái niệm hàm số đồng biến, nghịch biến trên các nửa khoảng.
5. Sử dụng bảng biến thiên để xét tính đơn điệu của hàm số.
Để xét tính đơn điệu của hàm số
()y fx=
ta thực hiện các bước sau:
Bước 1: Tìm tập xác định
D
.
Bước 2: Tính đạo hàm
()y fx
′′
=
. Tìm các điểm
( )
0;1; 2;...
i
xi=
mà tại đó
() 0fx
′
=
hoặc làm
cho
()fx
′
không xác định.
Bước 3: Sắp xếp các
( )
0;1; 2;...
i
xi=
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận
Chú ý: Đối với bài toán trắc nghiệm, ta có thể sử dụng Phương pháp sử dụng MTCT.
Cách 1: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính Casio. Quan sát bảng kết
quả nhận được về tính tăng, giảm giá trị của f(x) và dự đoán.
Cách 2: Tính đạo hàm, thiết lập bất phương trình đạo hàm. Sử dụng tính năng giải bất phương
trình INEQ của máy tính Casio (đối với bất phương trình bậc hai, bậc ba).
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 3
Sưu tầm và biên soạn
II. CỰC TRỊ CỦA HÀM SỐ
1. Khái niệm cực trị của hàm số: Cho hàm số
()y fx
=
xác định và liên tục trên khoảng
(;)ab
và điểm
0
(;)x ab∈
.
+) Nếu tồn tại số
0h >
sao cho
( ) ( )
0
fx fx
<
với mọi
00
(;)x x hx h∈− +
và
0
xx≠
thì ta nói
hàm số
()y fx
=
đạt cực đại tại
0
x
.
+) Nếu tồn tại số
0h >
sao cho
( ) ( )
0
fx fx>
với mọi
00
(;)x x hx h∈− +
và
0
xx≠
thì ta nói
hàm số
()
y fx=
đạt cực tiểu tại
0
x
.
* Chú ý
+) Nếu hàm số
()y fx
=
đạt cực đại tại
0
x
thì
0
x
được gọi là điểm cực đại của hàm số;
0
()fx
được gọi là giá trị cực đại của hàm số, kí hiệu là
()
CT
ff
CÑ
, còn điểm
00
( ; ( ))Mx fx
được gọi là
điểm cực đại của đồ thị hàm số.
+) Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại còn gọi là cực
đại và được gọi chung là cực trị của hàm số.
2. Cách tìm cực trị của hàm số
Định lí 2: Giả sử hàm số
()y fx=
liên tục trên
(;)ab
chứa điểm
0
x
và có đạo hàm trên
0
(; )ax
và
0
( ;)
xb
.
+) Nếu
(
)
'0
fx>
trên khoảng
0
(; )ax
và
'( ) 0fx<
trên
0
( ;)xb
thì
0
x
là một điểm cực đại của
hàm số
()y fx
=
.
+) Nếu
( )
0fx
′
<
trên khoảng
0
(; )ax
và
() 0fx
′
>
trên
0
( ;)
xb
thì
0
x
là một điểm cực tiểu của
hàm số
()y fx=
.
Minh họa bằng bảng biến thiến
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
Sưu tầm và biên soạn
NHẬN XÉT:
Để tìm cực trị của hàm số
()y fx=
ta thực hiện các bước sau:
Bước 1: Tìm tập xác định
D
.
Bước 2: Tính đạo hàm
()y fx
′′
=
. Tìm các điểm
( )
0;1; 2;...
i
xi=
mà tại đó
() 0fx
′
=
hoặc làm
cho
()fx
′
không xác định.
Bước 3: Sắp xếp các
( )
0;1; 2;...
i
xi=
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận.
DẠNG 1: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ CHO BỞI BIỂU THỨC
Câu 1: Tìm các khoảng đồng biến, nghịch biến của hàm số
32
31yx x=−+
.
Câu 2: Tìm các khoảng đồng biến, nghịch biến của hàm số
3
1
41
3
yx x= ++
.
Câu 3: Tìm các khoảng đồng biến, nghịch biến của hàm số
32
1
5 26 1
3
y xx x=− +−−
.
Câu 4: Tìm các khoảng đồng biến, nghịch biến của hàm số
32
1
3 91
3
yxx x
= + +−
.
Câu 5: Tìm các khoảng đơn điệu của hàm số
42
2yx x= −
.
Câu 6: Tìm các khoảng đơn điệu của hàm số
42
4yx x= +
.
Câu 7: Tìm các khoảng đơn điệu của hàm số
42
247y xx=−+ −
.
Câu 8: Tìm các khoảng đơn điệu của hàm số
31
1
x
y
x
+
=
−
.
Câu 9: Tìm các khoảng nghịch biến của hàm số
32
7
x
y
x
−
=
+
.
Câu 10: Tìm các khoảng nghịch biến của hàm số:
2
21
2
xx
y
x
−+ −
=
+
.
Câu 11: Tìm các khoảng đồng biến và nghịch biến của hàm số
2
44
1
xx
y
x
++
=
+
.
Câu 12: Tìm các khoảng đồng biến và nghịch biến của hàm số:
2
5
2
xx
y
x
− −+
=
+
.
Câu 13: Tìm các khoảng đơn điệu của hàm số
tan 2
tan 1
x
y
x
−
=
−
trên
4
;0
π
.
Câu 14: Tìm các khoảng đồng biến, nghịch biến của hàm số:
2
2 nÕu 1
2 2 7 nÕu 1 2
3 3 nÕu 2
xx
y
xx x
xx
− + <−
=
− + + −≤ ≤
−>
.
Câu 15: Tìm các khoảng đồng biến, nghịch biến của hàm số:
a)
2
23yx x=−−
. b)
2
4343
yx x x= − ++ +
.
II
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 5
Sưu tầm và biên soạn
Câu 16: Tìm các khoảng đơn điệu của hàm số
2
4yx x= −
.
DẠNG 2: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP CHO BỞI BBT HOẶC
ĐỒ THỊ CỦA HÀM SỐ
( )
y fx
=
HOẶC
( )
y fx
′
=
.
Câu 17: Cho hàm số
( )
y fx=
có đạo hàm trên
và có đồ thị hàm số
( )
y fx
′
=
như hình bên.
Xét tính đơn điệu của hàm số
(
) (
)
3y gx f x= = +
.
Câu 18: Cho hàm số
(
)
y fx=
xác định và liên tục trên
và có bảng biến thiên
Tìm các khoảng đồng biến của hàm số
( )
21yfx= +
.
Câu 19: Cho hàm số
( )
y fx
=
có bảng biến thiên
Tìm các khoảng nghịch biến của hàm số
( )
26
yf x= −+
.
Câu 20: Cho hàm số
(
)
y fx=
có bảng biến thiên
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 6
Sưu tầm và biên soạn
Hỏi hàm số
2
1
36
2
yf x x

= ++


nghịch biến trên các khoảng nào?
Câu 21: Cho hàm số
( )
y fx=
có bảng biến thiên
Tìm các khoảng đồng biến của hàm số
( )
2
2yf x x= −+
?
Câu 22: Cho hàm số
y fx
có đạo hàm liên tục trên
. Hàm số
(
)
y fx
′
=
có đồ thị như hình vẽ sau:
Tìm các khoảng đơn điệu của hàm số
1gx f x x 
.
Câu 23: Cho hàm số
y fx
có đạo hàm liên tục trên
. Đồ thị hàm số
( )
y fx
′
=
như hình vẽ bên.
Tìm các khoảng đồng biến của hàm số
( ) ( )
2020gx f x x= −+
.
O
x
y
1−
1−
1
2
1
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 7
Sưu tầm và biên soạn
Câu 24: Cho hàm số
( )
y fx=
. Hàm số
( )
y fx
′
=
có đồ thị như hình vẽ.
Hàm số
(
)
( )
2
y gx f x= = −
đồng biến trên khoảng nào?
Câu 25: Cho hàm số
( )
y fx=
. Hàm số
( )
y fx
′
=
có đồ thị như hình vẽ.
Hàm số
( ) ( )
24y gx f x= = −
nghịch biến trên khoảng nào?
Câu 26: Cho hàm số
( )
y fx=
có bảng biến thiên
Hỏi hàm số
( )
( )
y f fx=
đồng biến trên những khoảng nào?
Câu 27: Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên như sau
Tìm các khoảng đồng biến của hàm số
( ) ( )
3
2
5
42 6 1
32
x
y gx f x x x= = − −+ −+
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
Sưu tầm và biên soạn
Câu 28: Cho hàm số
( )
y fx=
liên tục trên
và có bảng xét dấu đạo hàm như sau
Biết
( )
13fx<<
,
x∀∈
. Hàm số
( ) ( )
( )
32
61y gx f f x x x= = +− −
có ít nhất bao nhiêu
khoảng đồng biến?
Câu 29: Cho hàm số
( )
=y fx
. Hàm số
( )
y fx
′
=
có đồ thị như hình vẽ.
Hàm số
(
)
(
)
2
12y gx f x x
= = +−
đồng biến trên khoảng nào?
Câu 30: Cho hàm số
( )
=y fx
. Hàm số
( )
y fx
′
=
có đồ thị như hình vẽ.
Hàm số
( )
( )
3
y gx f x= =
đồng biến trên khoảng nào?
Câu 31: Cho hàm số
( )
=y fx
. Hàm số
( )
y fx
′
=
có đồ thị như hình vẽ.
Hàm số
( )
(
)
2
22= = ++y gx f x x
đồng biến trên khoảng nào?
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 9
Sưu tầm và biên soạn
Câu 32: Cho hàm số
( )
y fx=
có đạo hàm liên tục trên
.
Đồ thị hàm số
( )
y fx
′
=
như hình bên dưới
Hàm số
(
)
( )
3
2
7
2 12 1
32
x
gx f x x x= −+ − + +
có ít nhất bao nhiêu khoảng nghịch biến?
DẠNG 3: TÌM ĐK CỦA THAM SỐ ĐỂ HÀM SỐ ĐỒNG BIẾN, NGHỊCH BIẾN TRÊN MỘT
MIỀN CHO TRƯỚC.
Câu 33: Tìm các giá trị của tham số
m
để hàm số đồng biến trên
.
1)
32
3
y x x mx m=+ ++
2)
( )
( )
32
21 2 2y mx m x m x= − + ++ −
Câu 34: Tìm các giá trị của tham số
m
để hàm số
32
( 1) 3( 1) 3(2 3)ymx mx m xm=− − − + −+
nghịch biến
trên
.
Câu 35: Tìm các giá trị của tham số
m
để hàm số
21
xm
y
x
−
=
−
đồng biến trên từng khoảng xác định.
Câu 36: Tìm
m
để hàm số
21x
y
xm
+
=
−
nghịch biến trên từng khoảng xác định?
Câu 37: Có bao nhiêu giá trị
m
nguyên để hàm số
( )
32 2
33 1yx x m x=+− −
đồng biến trên khoảng
( )
1; 2
?
Câu 38: Tìm
m
để hàm số
( )
32
31y x x m xm=−+ + − +
nghịch biến trên khoảng
( )
1;
− +∞
.
Câu 39: Tìm
m
để hàm số
( )
322
3 3 1 23
y x mx m x m=−+ − − − +
đồng biến trên khoảng
( )
1; 2
.
Câu 40: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32 2
362y x mx m x=−+ − −
nghịch biến
trên khoảng
( )
2; +∞
.
Câu 41: Có bao nhiêu giá trị nguyên dương bé hơn 2024 của tham số
m
sao cho hàm số
2
2 2 15xx m
y
xm
+ −−
=
−
nghịch biến trên khoảng
( )
1; 5
?
Câu 42: Có bao nhiêu giá trị nguyên dương không lớn hơn 2024 của tham số
m
sao cho hàm số
2
21
5
xx m
y
xm
+ −+
=
+
nghịch biến trên khoảng
( )
3;1−
?
Câu 43: Có bao nhiêu giá trị nguyên dương của tham số
m
sao cho hàm số
( )
2
21 1x mx m
y
xm
+ − ++
=
−
đồng biến trên khoảng
( )
1; +∞
?
Câu 44: Tìm tập hợp tất cả các giá trị của tham số
m
sao cho hàm số
2
1x
y
x xm
+
=
++
nghịch biến trên
khoảng
( )
1;1−
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 10
Sưu tầm và biên soạn
Câu 45: Xác định các giá trị của tham số m để hàm số
32
3y x mx m=−−
nghịch biến trên khoảng
(
)
0;1 ?
Câu 46: Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 22
39=−−y x mx m x
nghịch biến trên
khoảng
( )
0;1
.
Câu 47: Tìm các giá trị của tham số
m
để hàm số
( )
32
1
21 2
3
y x mx m x m= − + − −+
nghịch biến trên
khoảng
( )
2;0 .−
.
Câu 48: Tập hợp tất cả các giá trị của tham số
m
để hàm số
( )
32
61y x mx m x=− −− +
đồng biến trên
khoảng
( )
0; 4
là:
Câu 49: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
32
61y x mx m x=− −− +
đồng biến trên khoảng
(
)
0; 4
là:
Câu 50: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc
( )
2020;2020−
sao cho hàm số
32
22y x mx x
=++
đồng biến trên khoảng
( )
2;0−
. Tính số phần tử của tập hợp
S
.
Câu 51: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2
1
x xm
y
x
++
=
−
nghịch biến trên khoảng
(1; 3)
và đồng biến trên khoảng
(4;6)
.
Câu 52: Cho hàm số
( )
( )
3 22
1
1 21
3
y x m x m mx= −+ + + +
. Có tất cả bao nhiêu giá trị nguyên của
m
nằm trong đoạn
[ ]
100;100−
để hàm số đồng biến trên khoảng
( )
1;5
.
Câu 53: Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
(
)
15;15−
để hàm số
42
6 2526y x x mx=− −+
nghịch biến trên khoảng
( )
1;1−
.
Câu 54: Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
( 2021;2021)−
để hàm số
42
2 31y x mx m=− −+
đồng biến trên khoàng
(1; 2)
?
Câu 55: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32
33 1 1y x x m xm= − − + −−
nghịch biến
trên đoạn
[
]
1; 3
−
.
Câu 56: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
( )
3
22
1 21
3
x
y m x m mx=−+ + + +
nghịch biến trên đoạn
[ ]
2;3
?
Câu 57: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( )
32
33 1 1y x x m xm= − − + −−
nghịch biến
trên đoạn
[ ]
1; 3−
.
Câu 58: Cho hàm số
32
5y x x mx=−+ − +
với
m
là tham số thực. Có tất cả bao nhiêu giá trị nguyên của
m
trên đoạn
[ ]
50;50−
để hàm số đã cho đồng biến trên khoảng?
Câu 59: Có bao nhiêu giá trị của tham số
m
để hàm số
3 22
1
( 1) ( 2 ) 3
3
y x m x m mx 
nghịch
biến trên khoảng
1;1
.
Câu 60: Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 22
39=−−y x mx m x
nghịch biến trên
khoảng
( )
0; 2
.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 11
Sưu tầm và biên soạn
Câu 61: Tìm tất cả các giá thực của tham số
m
sao cho hàm số
( )
32
236 2y x x m xm=−− ++
nghịch
biến trên khoảng
(
)
1;1
−
.
Câu 62: Có bao nhiêu giá trị nguyên của tham số
[ ]
2022;2022m ∈−
để hàm số
3
2
1
2
y x mx
x
=+−
đồng
biến trên khoảng
( )
0; +∞
?
Câu 63: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
4xx
y
xm
−
=
+
đồng biến trên
(
)
1;
+∞
Câu 64: Cho hàm số
( )
2
2 2 31
1
x m xm
y
x
− ++ −+
=
−
. Tìm các giá trị của tham số m để hàm số nghịch biến
trên mỗi khoảng xác định.
Câu 65: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
xm
+
=
+
nghịch biến trên khoảng
(
)
10;
+∞
?
Câu 66: Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số
( ) ( )
32
3 2 1 12 5 2yx m x m x=− + + ++
đồng biến trên khoảng
( )
2; +∞
. Số phần tử của
S
bằng
Câu 67: Gọi
T
là tập hợp tất cả các giá trị nguyên dương của tham số
m
để hàm số
42
21y x mx=−+
đồng biến trên khoảng
( )
3; +∞
. Tổng giá trị các phần tử của
T
bằng
Câu 68: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[ ]
100;100
−
sao cho hàm số
( ) ( ) ( ) ( )
32
1 1 21 31=− +− + + +−fxmxmx mxm
đồng biến trên
?
Câu 69: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[
]
1; 25
sao cho ứng với mỗi
m
, hàm số
2
25
2
x xm
y
xm
−+ −+
=
−
đồng biến trên khoảng
( )
1; 3
.
Câu 70: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[
]
2;25
−
sao cho ứng với mỗi
m
, hàm
số
2
51
5
x xm
y
xm
+ −−
=
−
nghịch biến trên khoảng
( )
1; 4
.
Câu 71: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[ ]
25;3−
sao cho ứng với mỗi
m
, hàm
số
2
45
4
x xm
y
xm
−+ −−
=
−
đồng biến trên khoảng
( )
3; 1−−
.
Câu 72: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2sin 1
sin
x
y
xm
−
=
−
đồng biến trên khoảng
0;
2
π



.
Câu 73: Tìm
m
để hàm số
sin
sin 1
xm
y
x
+
=
−
nghịch biến trên khoảng
;
2
π
π



?
Câu 74: Có bao nhiêu giá trị nguyên
( )
10;10m∈−
sao cho hàm số
( )
42
24 1 1yx m x=− −+
đồng biến trên
khoảng
( )
1;
+∞
.
Câu 75: Tìm tập hợp các giá trị của tham số
m
để hàm số
2
11y x mx= +− −
đồng biến trên khoảng
(;)−∞ +∞
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 12
Sưu tầm và biên soạn
Câu 76: Tìm tất cả các giá trị thực của tham số
m
để hàm số
( ) ( )
32
2 32 1 6 1 1yx mxmmx=− + + ++
đồng biến trên khoảng
( )
2;+∞
.
Câu 77: Tìm tất cả các giá trị của
m
để hàm số
2cos 1
cos
x
y
xm
−
=
−
đồng biến trên khoảng
0;
2
π



.
Câu 78: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2cos 3
2cos
x
y
xm
+
=
−
nghịch biến trên khoảng
0; .
3
π



Câu 79: Tìm tất cả các giá trị thực của tham số
m
để hàm số
tan 2
tan 1
x
y
xm
−
=
−+
đồng biến trên khoảng
0;
4
π



.
Câu 80: Tìm các giá trị thực của tham số
m
để hàm số
tan
tan 1
xm
y
mx
+
=
+
nghịch biến trên khoảng
0; .
4
π



Câu 81: Tìm giá trị
m
để hàm số
cot 2
cot
x
y
xm
−
=
−
nghịch biến trên
;
42
ππ



?
Câu 82: Tìm
m
để hàm số
2cot 1
cot
x
y
xm
+
=
+
đồng biến trên khoảng
;
42
ππ



.
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 1
Sưu tầm và biên soạn
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1. Khái niệm tính đợn điệu của hàm số.
Giả sử
K
là một khoảng, một đoạn hoặc một nữa khoảng và
()y fx
là hàm số xác định trên
K
.
+) Hàm số
()
y fx
được gọi là đồng biến trên
K
nếu
12 1 2 1 2
, , ( ) ( ).x x K x x fx fx

+) Hàm số
()y fx
được gọi là nghịch biến trên
K
nếu
12 1 2 1 2
, , ( ) ( ).x x K x x fx fx 
+) Hàm số đồng biến hoặc nghịch biến trên
K
được gọi chung là đơn điệu trên
.K
Chú ý:
+ Nếu hàm số đồng biến trên
K
thì từ trái sang phải đồ thị đi lên.
+ Nếu hàm số nghịch biến trên
K
thì từ trái sang phải đồ thị đi xuống.
CHƯƠNG
I
ỨNG DỤNG ĐẠO HÀM
ĐỂ KHẢO SÁT VÀ VẼ
ĐỒ THỊ CỦA HÀM SỐ
I
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 2
Sưu tầm và biên soạn
2. Định lý: Cho hàm số
()y fx
có đạo hàm trên
K
, trong đó
K
là một khoảng, đoạn hoặc nữa
khoảng.
+) Nếu
( ) 0, fx x K

thì hàm số
()
y fx
đồng biến trên khoảng
K
.
+) Nếu
( ) 0, fx x K

thì hàm số
()y fx
nghịch biến trên khoảng
K
.
3. Định lý: (Tổng quát) Cho hàm số
()y fx
có đạo hàm trên
K
, trong đó
K
là một khoảng,
đoạn hoặc nữa khoảng.
+) Nếu
( ) 0,
fx x K

và
() 0fx
xảy ra tại một số hữu hạn điểm trên
K
thì hàm số
()y fx
đồng biến trên khoảng
K
.
+) Nếu
( ) 0, fx x K

và
() 0fx
xảy ra tại một số hữu hạn điểm trên
K
thì hàm số
()y fx
nghịch biến trên khoảng
K
.
4. Lưu ý:
+) Nếu hàm số
()y fx
liên tục trên đoạn
[;]ab
và
'( ) 0, ( ; )f x x ab 
thì ta nói hàm số đồng
biến trên đoạn
[ ; ].ab
+) Nếu hàm số
()y fx
liên tục trên đoạn
[;]ab
và
'( ) 0, (a; )fx x b 
thì ta nói hàm số
nghịch biến trên đoạn
[ ; ].
ab
+) Tương tự với các khái niệm hàm số đồng biến, nghịch biến trên các nửa khoảng.
5. Sử dụng bảng biến thiên để xét tính đơn điệu của hàm số.
Để xét tính đơn điệu của hàm số
()y fx=
ta thực hiện các bước sau:
Bước 1: Tìm tập xác định
D
.
Bước 2: Tính đạo hàm
()y fx
′′
=
. Tìm các điểm
( )
0;1; 2;...
i
xi=
mà tại đó
() 0fx
′
=
hoặc làm
cho
()fx
′
không xác định.
Bước 3: Sắp xếp các
( )
0;1; 2;...
i
xi=
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận
Chú ý: Đối với bài toán trắc nghiệm, ta có thể sử dụng Phương pháp sử dụng MTCT.
Cách 1: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính Casio. Quan sát bảng kết
quả nhận được về tính tăng, giảm giá trị của f(x) và dự đoán.
Cách 2: Tính đạo hàm, thiết lập bất phương trình đạo hàm. Sử dụng tính năng giải bất phương
trình INEQ của máy tính Casio (đối với bất phương trình bậc hai, bậc ba).
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 3
Sưu tầm và biên soạn
II. CỰC TRỊ CỦA HÀM SỐ
1. Khái niệm cực trị của hàm số: Cho hàm số
()y fx=
xác định và liên tục trên khoảng
(;)ab
và điểm
0
(;)x ab∈
.
+) Nếu tồn tại số
0h >
sao cho
( ) ( )
0
fx fx
<
với mọi
00
(;)x x hx h∈− +
và
0
xx≠
thì ta nói
hàm số
()y fx=
đạt cực đại tại
0
x
.
+) Nếu tồn tại số
0h >
sao cho
( ) ( )
0
fx fx>
với mọi
00
(;)x x hx h∈− +
và
0
xx≠
thì ta nói
hàm số
()
y fx
=
đạt cực tiểu tại
0
x
.
* Chú ý
+) Nếu hàm số
()y fx
=
đạt cực đại tại
0
x
thì
0
x
được gọi là điểm cực đại của hàm số;
0
()fx
được gọi là giá trị cực đại của hàm số, kí hiệu là
()
CT
ff
CÑ
, còn điểm
00
( ; ( ))Mx fx
được gọi là
điểm cực đại của đồ thị hàm số.
+) Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại còn gọi là cực
đại và được gọi chung là cực trị của hàm số.
2. Cách tìm cực trị của hàm số
Định lí 2: Giả sử hàm số
()y fx=
liên tục trên
(;)ab
chứa điểm
0
x
và có đạo hàm trên
0
(; )ax
và
0
( ;)xb
.
+) Nếu
(
)
'0
fx>
trên khoảng
0
(; )ax
và
'( ) 0fx<
trên
0
( ;)xb
thì
0
x
là một điểm cực đại của
hàm số
()y fx=
.
+) Nếu
( )
0fx
′
<
trên khoảng
0
(; )
ax
và
() 0fx
′
>
trên
0
( ;)xb
thì
0
x
là một điểm cực tiểu của
hàm số
()y fx=
.
Minh họa bằng bảng biến thiến
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 4
Sưu tầm và biên soạn
NHẬN XÉT:
Để tìm cực trị của hàm số
()y fx=
ta thực hiện các bước sau:
Bước 1: Tìm tập xác định
D
.
Bước 2: Tính đạo hàm
()y fx
′′
=
. Tìm các điểm
( )
0;1; 2;...
i
xi=
mà tại đó
() 0fx
′
=
hoặc làm
cho
()fx
′
không xác định.
Bước 3: Sắp xếp các
( )
0;1; 2;...
i
xi=
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận
DẠNG 1: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ CHO BỞI BIỂU THỨC
Câu 1: Tìm các khoảng đồng biến, nghịch biến của hàm số
32
31yx x=−+
.
Lời giải
Tập xác định:
D
=
.
Ta có:
2
36yx x
′
= −
;
2
0
03 60
2
x
y xx
x
=
′
=⇔ −=⇔
=
.
Bảng biến thiên
Vậy hàm số đồng biến trên các khoảng
( )
;0−∞
và
( )
2; +∞
, nghịch biến trên khoảng
( )
0; 2
.
Câu 2: Tìm các khoảng đồng biến, nghịch biến của hàm số
3
1
41
3
yx x= ++
.
Lời giải
Tập xác định:
D =
.
Ta có:
2
4 0,yx x
′
= + > ∀∈
.
Vậy hàm số đồng biến trên khoảng
( )
;−∞ +∞
.
Câu 3: Tìm các khoảng đồng biến, nghịch biến của hàm số
32
1
5 26 1
3
y xx x=−+−−
.
Lời giải
Tập xác định:
D =
.
Ta có:
( )
2
2
10 26 5 1 0,yx x x x
′
=− + − =− − −< ∀∈
.
II
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 5
Sưu tầm và biên soạn
Vậy hàm số nghịch biến trên khoảng
( )
;−∞ +∞
.
Câu 4: Tìm các khoảng đồng biến, nghịch biến của hàm số
32
1
3 91
3
yxx x= + +−
.
Lời giải
Tập xác định
D =
.
Ta có:
( )
2
2
6 9 3 0,yx x x x
′
= + + = + ≥ ∀∈
;
03yx
′
=⇔=−
.
Vậy hàm số đồng biến trên khoảng
(
)
;−∞ +∞
.
Câu 5: Tìm các khoảng đơn điệu của hàm số
42
2yx x= −
.
Lời giải
Tập xác định:
D =
.
Ta có
( )
32
4 44 1y x x xx
′
= −= −
;
0
0
1
x
y
x
=
′
= ⇔
= ±
.
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng
( )
1; 0−
và
( )
1; +∞
, nghịch biến trên các khoảng
( )
;1−∞ −
và
( )
0; 1
.
Câu 6: Tìm các khoảng đơn điệu của hàm số
42
4yx x= +
.
Lời giải
Tập xác định:
D =
.
Ta có
( )
32
4 84 2y x x xx
′
= += +
;
00yx
′
=⇔=
.
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng
( )
0; +∞
, nghịch biến trên khoảng
( )
;0−∞
.
Câu 7: Tìm các khoảng đơn điệu của hàm số
42
247y xx
=−+ −
.
Lời giải
Tập xác định:
D =
.
Ta có
( )
32
88 8 1y x x xx
′
=− +=− −
;
0
0
1
x
y
x
=
′
= ⇔
= ±
.
Bảng biến thiên:
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 6
Sưu tầm và biên soạn
Vậy hàm số đồng biến trên các khoảng
( )
;1−∞ −
và
( )
0;1
, nghịch biến trên các khoảng
( )
1; 0−
và
( )
1; +∞
.
Câu 8: Tìm các khoảng đơn điệu của hàm số
31
1
x
y
x
+
=
−
.
Lời giải
Tập xác định:
{ }
D \1=
.
Ta có
( )
22
3.1 1 .1
4
0,
(1 ) (1 )
y xD
xx
−−
′
= = > ∀∈
−−
.
Vậy hàm số đồng biến trên các khoảng
( )
;1−∞
và
( )
1; +∞
.
Câu 9: Tìm các khoảng nghịch biến của hàm số
32
7
x
y
x
−
=
+
.
Lời giải
Tập xác định:
{ }
D \7= −
.
Ta có
( )
( )
( )
22
2 .7 1.3
17
0,
77
y xD
xx
−−
−
′
= = < ∀∈
++
.
Vậy hàm số nghịch biến trên các khoảng
( )
;7−∞ −
và
( )
7;− +∞
.
Câu 10: Tìm các khoảng nghịch biến của hàm số:
2
21
2
xx
y
x
−+ −
=
+
.
Lời giải
Tập xác định:
{ }
D \2= −
. Ta có:
( )
2
2
45
2
xx
y
x
−− +
′
=
+
.
( )
2
2
45
'0 0
2
−− +
=⇔=
+
xx
y
x
2
5
4 50
1
= −
⇔− − + = ⇔
=
x
xx
x
.
Bảng biến thiên
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Page 7
Sưu tầm và biên soạn
Vậy hàm số nghịch biến trên các khoảng
(
)
;5−∞ −
và
( )
1; +∞
.
Câu 11: Tìm các khoảng đồng biến và nghịch biến của hàm số
2
44
1
xx
y
x
++
=
+
.
Lời giải
Tập xác định:
{
}
D \1
= −
. Ta có:
( )
2
2
2
2
'0
0
1
x
xx
yy
x
x
= −
+
′
= ⇒=⇔
=
+
.
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng
( )
−∞ −;2
và
( )
+∞0;
, nghịch biến trên các khoảng
( )
−−2; 1
và
( )
−1;0
.
Câu 12: Tìm các khoảng đồng biến và nghịch biến của hàm số:
2
5
2
xx
y
x
− −+
=
+
.
Lời giải
Tập xác định:
{ }
\2D = −
. Ta có:
( )
2
2
47
0,
2
xx
y xD
x
−− −
′
= < ∀∈
+
.
Vậy hàm số nghịch biến trên các khoảng
( )
−∞ −;2
và
( )
− +∞2;
.
Câu 13: Tìm các khoảng đơn điệu của hàm số
tan 2
tan 1
x
y
x
−
=
−
trên
4
;0
π
.
Lời giải
Trên khoảng
4
;0
π
thì
( )
0
cos;1;0tan
≠∈ xx
.
Ta có:
( )
2
2
1
cos
' 0, 0;
4
tan 1
x
yx
x
π

= > ∀∈


−
.
Vậy hàm số đồng biến trên khoảng
4
;
0
π
.
Câu 14: Tìm các khoảng đồng biến, nghịch biến của hàm số
2
2 nÕu 1
2 2 7 nÕu 1 2
3 3 nÕu 2
xx
y
xx x
xx
− + <−
=
− + + −≤ ≤
−>
.
Lời giải
Tập xác định:
D =
.
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Page 8
Sưu tầm và biên soạn
1 nÕu 1
4 2 nÕu 1 2
3 nÕu 2
x
y
xx
x
− <−
′
=
− + −< <
>
;
1
0
2
yx
′
=⇔=
.
Bảng xét dấu của
y
′
:
Từ bảng xét dấu của
y
′
ta có hàm số đồng biến trên các khoảng
1
1;
2

−


và
(
)
2; +∞
, nghịch biến trên các
khoảng
( )
;1−∞ −
và
1
;2
2



.
Câu 15: Tìm các khoảng đồng biến, nghịch biến của hàm số:
a)
2
23yx x=−−
. b)
2
4343yx x x= − ++ +
.
Lời giải
a) Tập xác định:
D
=
.
Cách 1:
( )
2
2
2
2 3 nÕu 1 hoÆc 3
23
2 3 nÕu 1 3
xx x x
yx x
xx x
− − ≤− ≥
= − −=
− − − −< <
.
( )
2 2 nÕu 1 hoÆc 3
2 2 nÕu 1 3
xx x
y
xx
− <− >
′
=
− − −< <
;
01yx
′
=⇔=
.
Bảng xét dấu
y
′
:
Vậy hàm số đồng biến trên các khoảng
( )
1;1−
và
( )
3; +∞
, nghịch biến trên các khoảng
( )
;1−∞ −
và
( )
1; 3
.
Cách 2: Ta có
( )
( )
( )
2
2
2
2 23 1
23
xx x
y
xx
−− −
′
=
−−
;
01yx
′
=⇔=
.
Bảng xét dấu của
y
′
:
| 1/690
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
ỨNG DỤNG ĐẠO HÀM NG ƯƠ
I ĐỂ KHẢO SÁT VÀ VẼ CH
ĐỒ THỊ CỦA HÀM SỐ
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ I LÝ THUYẾT.
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1. Khái niệm tính đợn điệu của hàm số.
Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và y f(x) là hàm số xác định trên K .
+) Hàm số y f(x) được gọi là đồng biến trên K nếu x , x K,
x x f (x )  f (x ). 1 2 1 2 1 2
+) Hàm số y f(x) được gọi là nghịch biến trên K nếu x , x K,
x x f (x )  f (x ). 1 2 1 2 1 2
+) Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K. Chú ý:
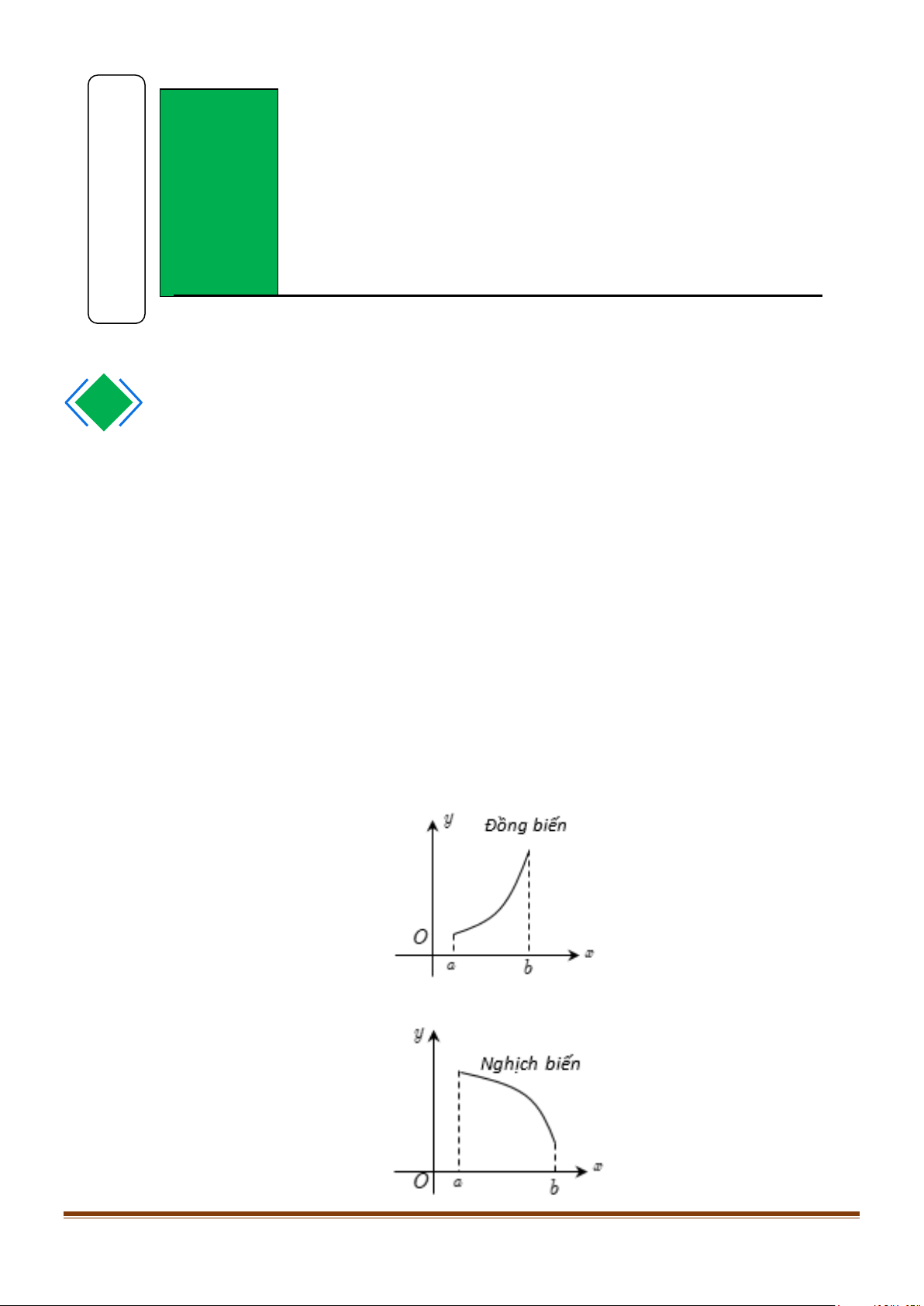
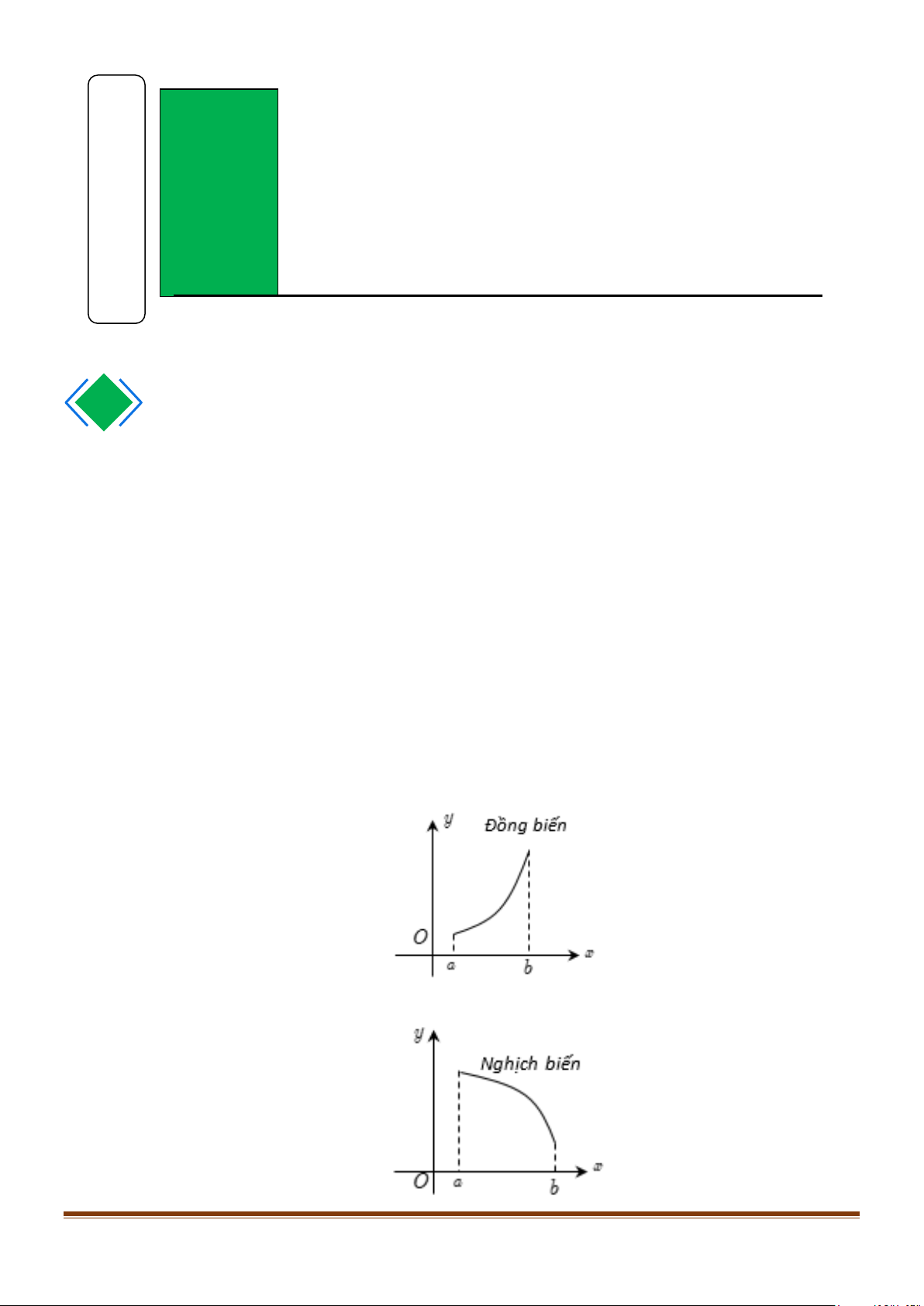
+ Nếu hàm số đồng biến trên K thì từ trái sang phải đồ thị đi lên.
+ Nếu hàm số nghịch biến trên K thì từ trái sang phải đồ thị đi xuống. Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
2. Định lý: Cho hàm số y f(x) có đạo hàm trên K   , trong đó K là một khoảng, đoạn hoặc nữa khoảng.
+) Nếu f (x)  0, x K thì hàm số y f(x) đồng biến trên khoảng K .
+) Nếu f (x)  0, x K thì hàm số y f(x) nghịch biến trên khoảng K .
3. Định lý: (Tổng quát) Cho hàm số y f(x) có đạo hàm trên K   , trong đó K là một khoảng,
đoạn hoặc nữa khoảng.
+) Nếu f (x)  0, x K và f (x)  0 xảy ra tại một số hữu hạn điểm trên K thì hàm số
y f (x) đồng biến trên khoảng K .
+) Nếu f (x)  0, x K và f (x)  0 xảy ra tại một số hữu hạn điểm trên K thì hàm số
y f (x) nghịch biến trên khoảng K .
4. Lưu ý: +) Nếu hàm số y f(x) liên tục trên đoạn [a;b] và f '(x)0, (
x a;b) thì ta nói hàm số đồng
biến trên đoạn [a;b].
+) Nếu hàm số y f(x) liên tục trên đoạn [a;b] và f '(x)  0, (
x  a;b) thì ta nói hàm số
nghịch biến trên đoạn [a;b].
+) Tương tự với các khái niệm hàm số đồng biến, nghịch biến trên các nửa khoảng.
5. Sử dụng bảng biến thiên để xét tính đơn điệu của hàm số.
Để xét tính đơn điệu của hàm số y = f (x) ta thực hiện các bước sau:
Bước 1: Tìm tập xác định D .
Bước 2: Tính đạo hàm y′ = f (′x) . Tìm các điểm x i =
mà tại đó f (′x) = 0 hoặc làm i ( 0;1;2;. .)
cho f (′x) không xác định.
Bước 3: Sắp xếp các x i =
theo thứ tự tăng dần và lập bảng biến thiên. i ( 0;1;2;. .)
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận
Chú ý: Đối với bài toán trắc nghiệm, ta có thể sử dụng Phương pháp sử dụng MTCT.
Cách 1: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính Casio. Quan sát bảng kết
quả nhận được về tính tăng, giảm giá trị của f(x) và dự đoán.
Cách 2: Tính đạo hàm, thiết lập bất phương trình đạo hàm. Sử dụng tính năng giải bất phương
trình INEQ của máy tính Casio (đối với bất phương trình bậc hai, bậc ba). Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
II. CỰC TRỊ CỦA HÀM SỐ
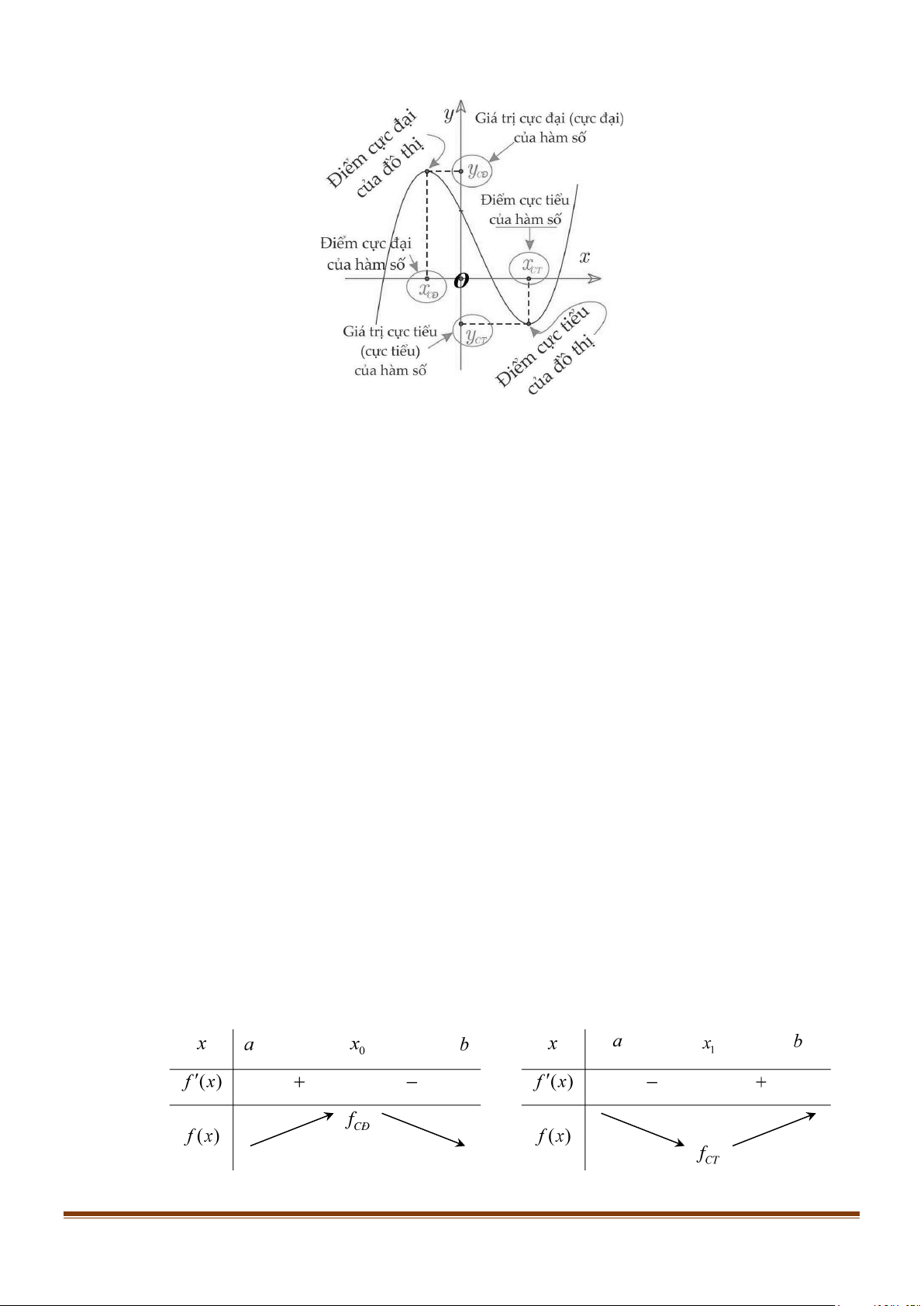
1. Khái niệm cực trị của hàm số: Cho hàm số y = f (x) xác định và liên tục trên khoảng ( ; a b) và điểm x ∈( ; a b) 0 .
+) Nếu tồn tại số h > 0 sao cho f (x) < f (x với mọi x∈(x − ;
h x + h) và x ≠ x thì ta nói 0 ) 0 0 0
hàm số y = f (x) đạt cực đại tại x0 .
+) Nếu tồn tại số h > 0 sao cho f (x) > f (x với mọi x∈(x − ;
h x + h) và x ≠ x thì ta nói 0 ) 0 0 0
hàm số y = f (x) đạt cực tiểu tại x0 . * Chú ý
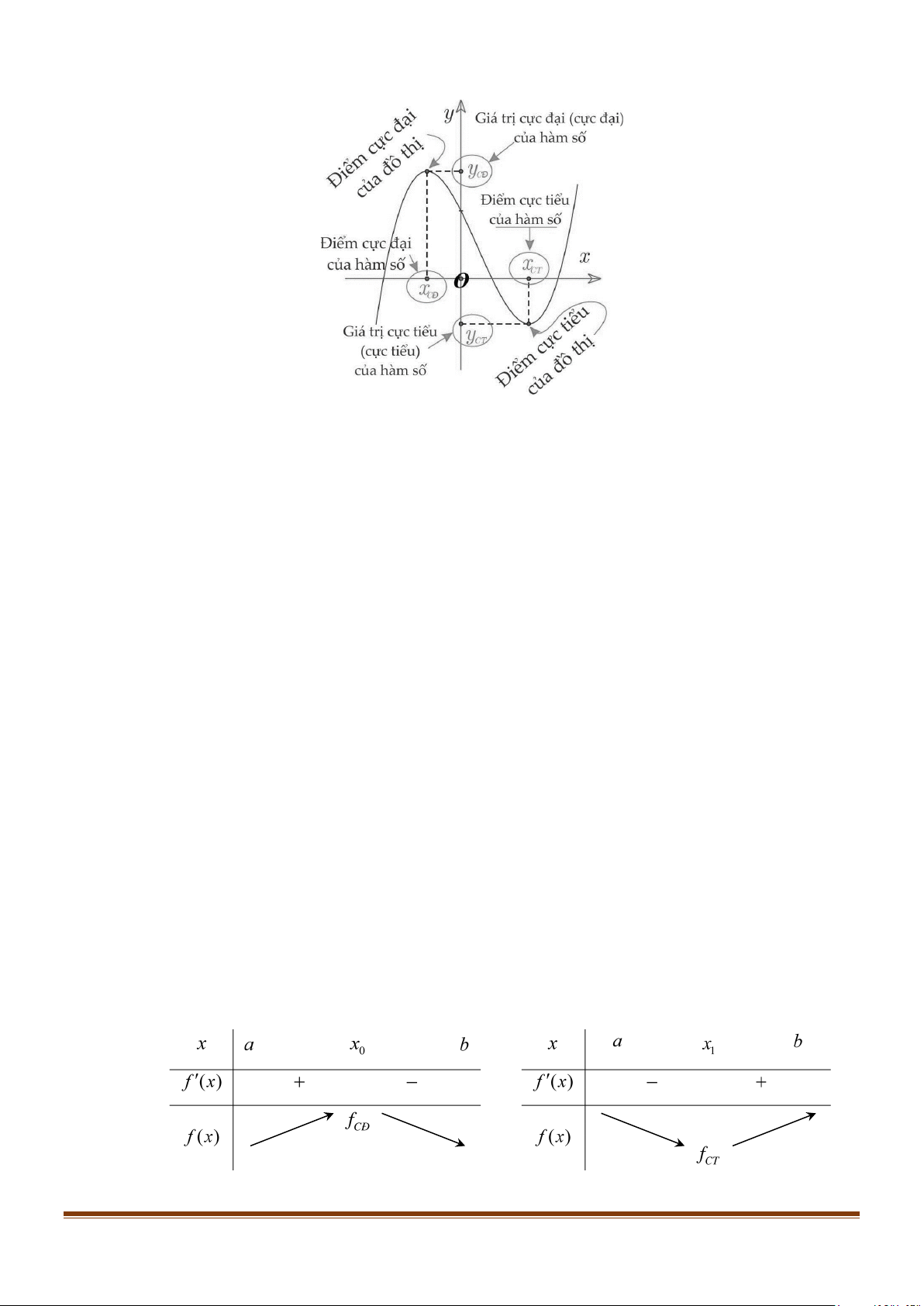
+) Nếu hàm số y = f (x) đạt cực đại tại x x f (x )
0 thì 0 được gọi là điểm cực đại của hàm số; 0
được gọi là giá trị cực đại của hàm số, kí hiệu là f
M (x ; f (x ))
CÑ ( fCT ) , còn điểm 0 0 được gọi là
điểm cực đại của đồ thị hàm số.
+) Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại còn gọi là cực
đại và được gọi chung là cực trị của hàm số.
2. Cách tìm cực trị của hàm số
Định lí 2: Giả sử hàm số y = f (x) liên tục trên ( ;
a b) chứa điểm x0 và có đạo hàm trên ( ; a x ) (x ;b) 0 và 0 .
+) Nếu f '(x) > 0 trên khoảng ( ; a x ) < (x ;b) x 0 và f '(x) 0 trên 0
thì 0 là một điểm cực đại của
hàm số y = f (x) .
+) Nếu f ′(x) < 0 trên khoảng ( ; a x ) ′ > (x ;b) x 0 và f (x) 0 trên 0
thì 0 là một điểm cực tiểu của
hàm số y = f (x) .
Minh họa bằng bảng biến thiến Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ NHẬN XÉT:
Để tìm cực trị của hàm số y = f (x) ta thực hiện các bước sau:
Bước 1: Tìm tập xác định D .
Bước 2: Tính đạo hàm y′ = f (′x) . Tìm các điểm x i =
mà tại đó f (′x) = 0 hoặc làm i ( 0;1;2;. .)
cho f (′x) không xác định.
Bước 3: Sắp xếp các x i =
theo thứ tự tăng dần và lập bảng biến thiên. i ( 0;1;2;. .)
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận.
II HỆ THỐNG BÀI TẬP TỰ LUẬN.
DẠNG 1: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ CHO BỞI BIỂU THỨC
Câu 1: Tìm các khoảng đồng biến, nghịch biến của hàm số 3 2
y = x − 3x +1.
Câu 2: Tìm các khoảng đồng biến, nghịch biến của hàm số 1 3
y = x + 4x +1. 3
Câu 3: Tìm các khoảng đồng biến, nghịch biến của hàm số 1 3 2
y = − x + 5x − 26x −1. 3
Câu 4: Tìm các khoảng đồng biến, nghịch biến của hàm số 1 3 2
y = x + 3x + 9x −1. 3
Câu 5: Tìm các khoảng đơn điệu của hàm số 4 2
y = x − 2x .
Câu 6: Tìm các khoảng đơn điệu của hàm số 4 2
y = x + 4x .
Câu 7: Tìm các khoảng đơn điệu của hàm số 4 2 y = 2
− x + 4x − 7 .
Câu 8: Tìm các khoảng đơn điệu của hàm số 3x +1 y = . 1− x
Câu 9: Tìm các khoảng nghịch biến của hàm số 3− 2x y = . x + 7 2
Câu 10: Tìm các khoảng nghịch biến của hàm số: −x + 2x −1 y = . x + 2 2
Câu 11: Tìm các khoảng đồng biến và nghịch biến của hàm số x + 4x + 4 y = . x +1 2
Câu 12: Tìm các khoảng đồng biến và nghịch biến của hàm số: −x − x + 5 y = . x + 2 −
Câu 13: Tìm các khoảng đơn điệu của hàm số tan x 2 y = trên  π   ; 0  . tan x −1  4   −x + 2 nÕu x < 1 −
Câu 14: Tìm các khoảng đồng biến, nghịch biến của hàm số:  2 y =  2
− x + 2x + 7 nÕu −1 ≤ x ≤ 2 .   3x − 3 nÕu x > 2
Câu 15: Tìm các khoảng đồng biến, nghịch biến của hàm số: a) 2
y = x − 2x − 3 . b) 2
y = x − 4x + 3 + 4x + 3 . Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 16: Tìm các khoảng đơn điệu của hàm số 2
y = x 4 − x .
DẠNG 2: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP CHO BỞI BBT HOẶC
ĐỒ THỊ CỦA HÀM SỐ y = f ( x) HOẶC y = f ′( x) .
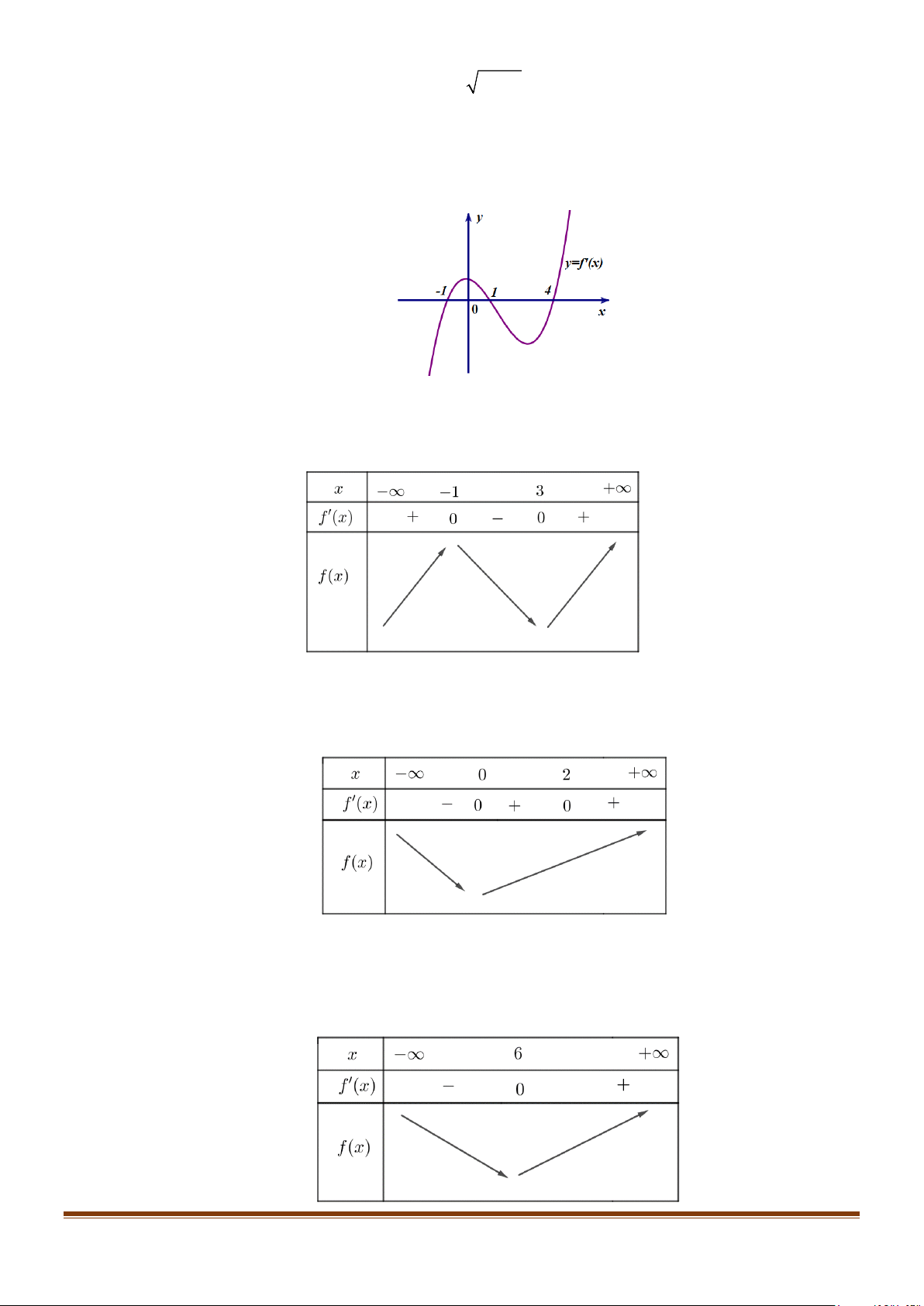
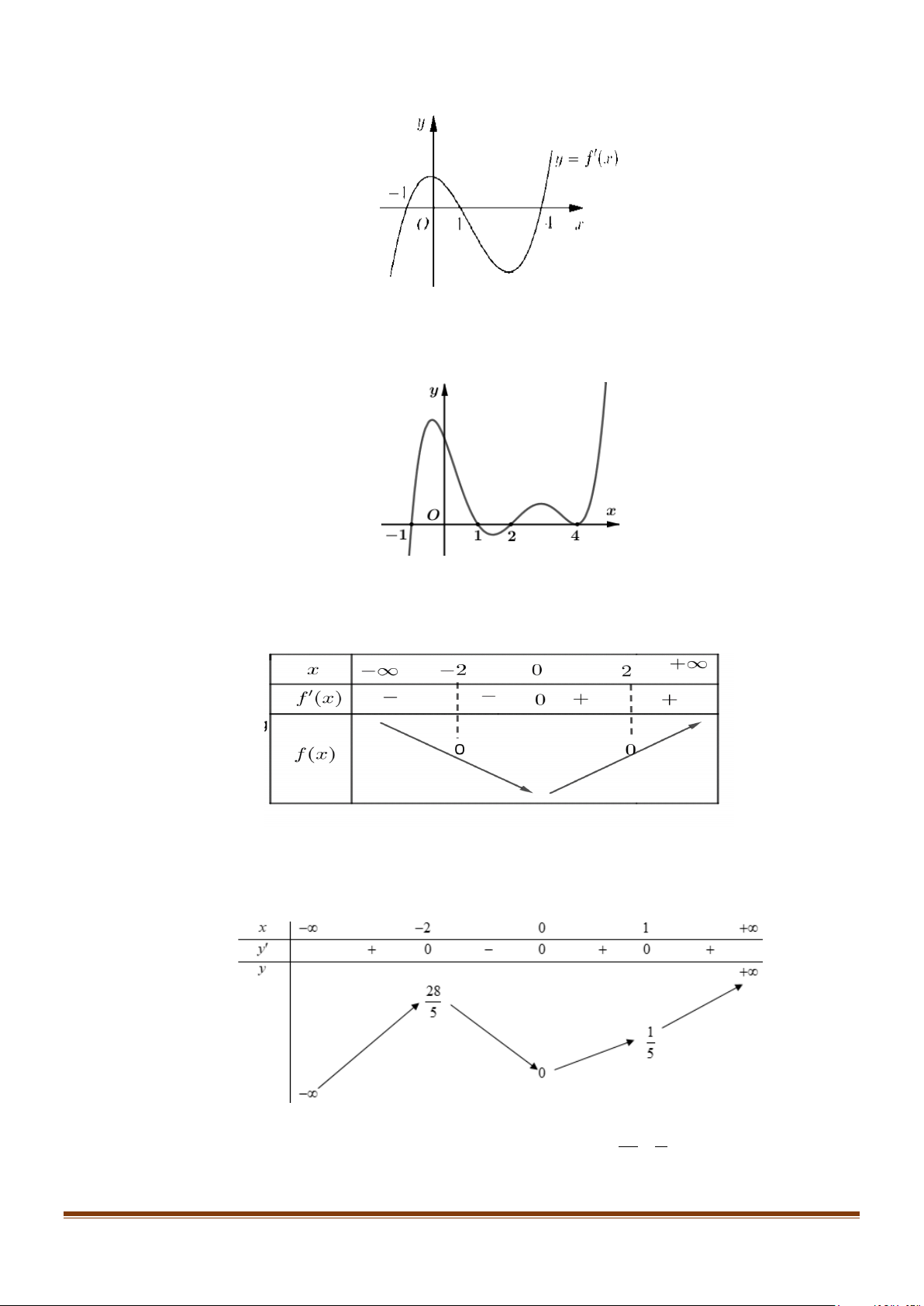
Câu 17: Cho hàm số y = f (x) có đạo hàm trên  và có đồ thị hàm số y = f ′(x) như hình bên.
Xét tính đơn điệu của hàm số y = g (x) = f (x) + 3.
Câu 18: Cho hàm số y = f (x) xác định và liên tục trên  và có bảng biến thiên
Tìm các khoảng đồng biến của hàm số y = f (2x + ) 1 .
Câu 19: Cho hàm số y = f (x) có bảng biến thiên
Tìm các khoảng nghịch biến của hàm số y = f ( 2 − x + 6).
Câu 20: Cho hàm số y = f (x) có bảng biến thiên Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ  1  Hỏi hàm số 2 y = f x + 3x + 
6 nghịch biến trên các khoảng nào? 2   
Câu 21: Cho hàm số y = f (x) có bảng biến thiên
Tìm các khoảng đồng biến của hàm số y = f ( 2
−x + 2x) ?
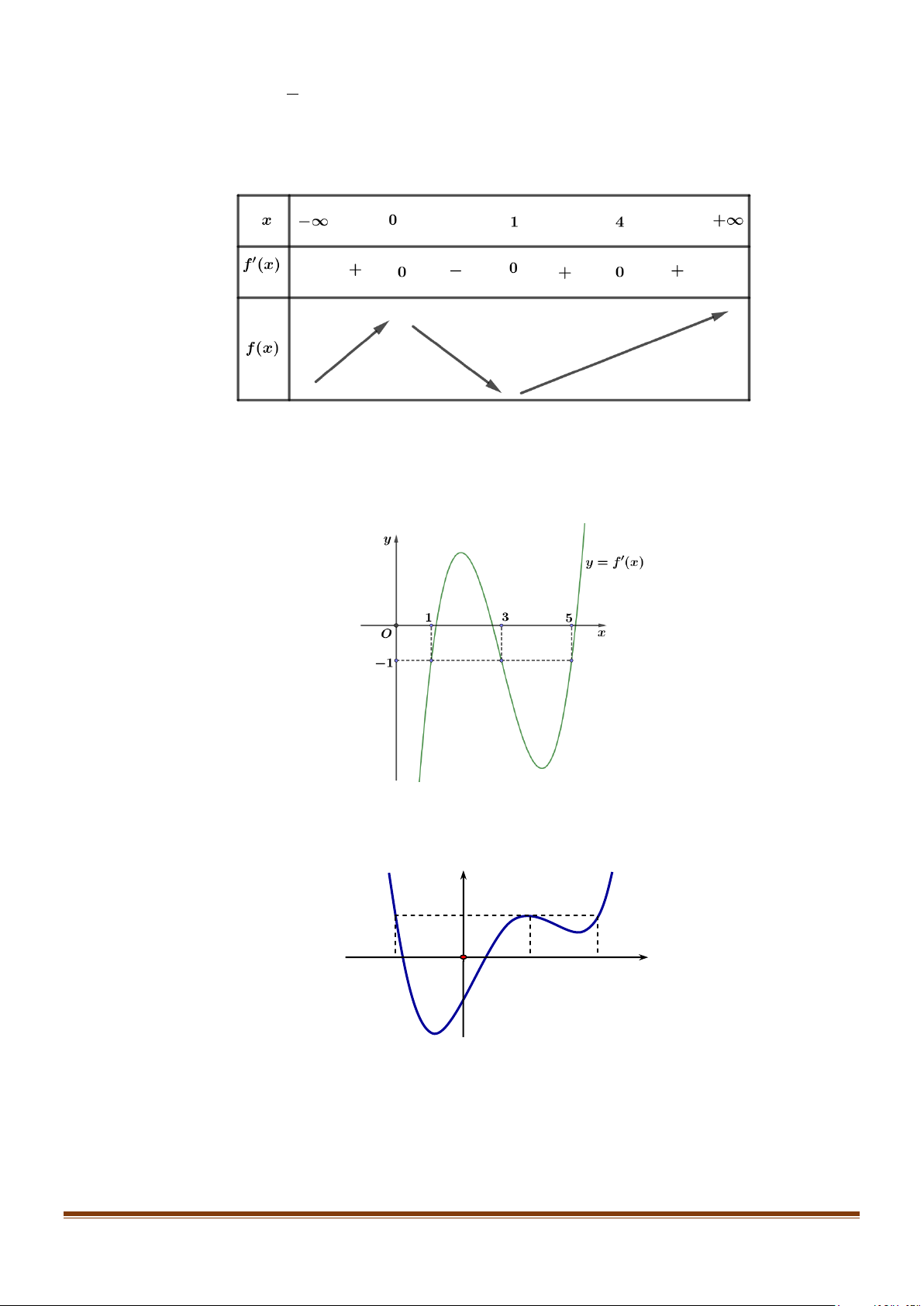
Câu 22: Cho hàm số y f x có đạo hàm liên tục trên  . Hàm số y = f ′(x) có đồ thị như hình vẽ sau:
Tìm các khoảng đơn điệu của hàm số gx f x x 1.
Câu 23: Cho hàm số y f x có đạo hàm liên tục trên  . Đồ thị hàm số y = f ′(x) như hình vẽ bên. y 1 1 − O 1 2 x 1 −
Tìm các khoảng đồng biến của hàm số g (x) = f (x) − x + 2020 . Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 24: Cho hàm số y = f (x) . Hàm số y = f ′(x) có đồ thị như hình vẽ.
Hàm số y = g (x) = f (2 − x) đồng biến trên khoảng nào?
Câu 25: Cho hàm số y = f (x) . Hàm số y = f ′(x) có đồ thị như hình vẽ.
Hàm số y = g (x) = f (2x − 4) nghịch biến trên khoảng nào?
Câu 26: Cho hàm số y = f (x) có bảng biến thiên
Hỏi hàm số y = f ( f (x)) đồng biến trên những khoảng nào?
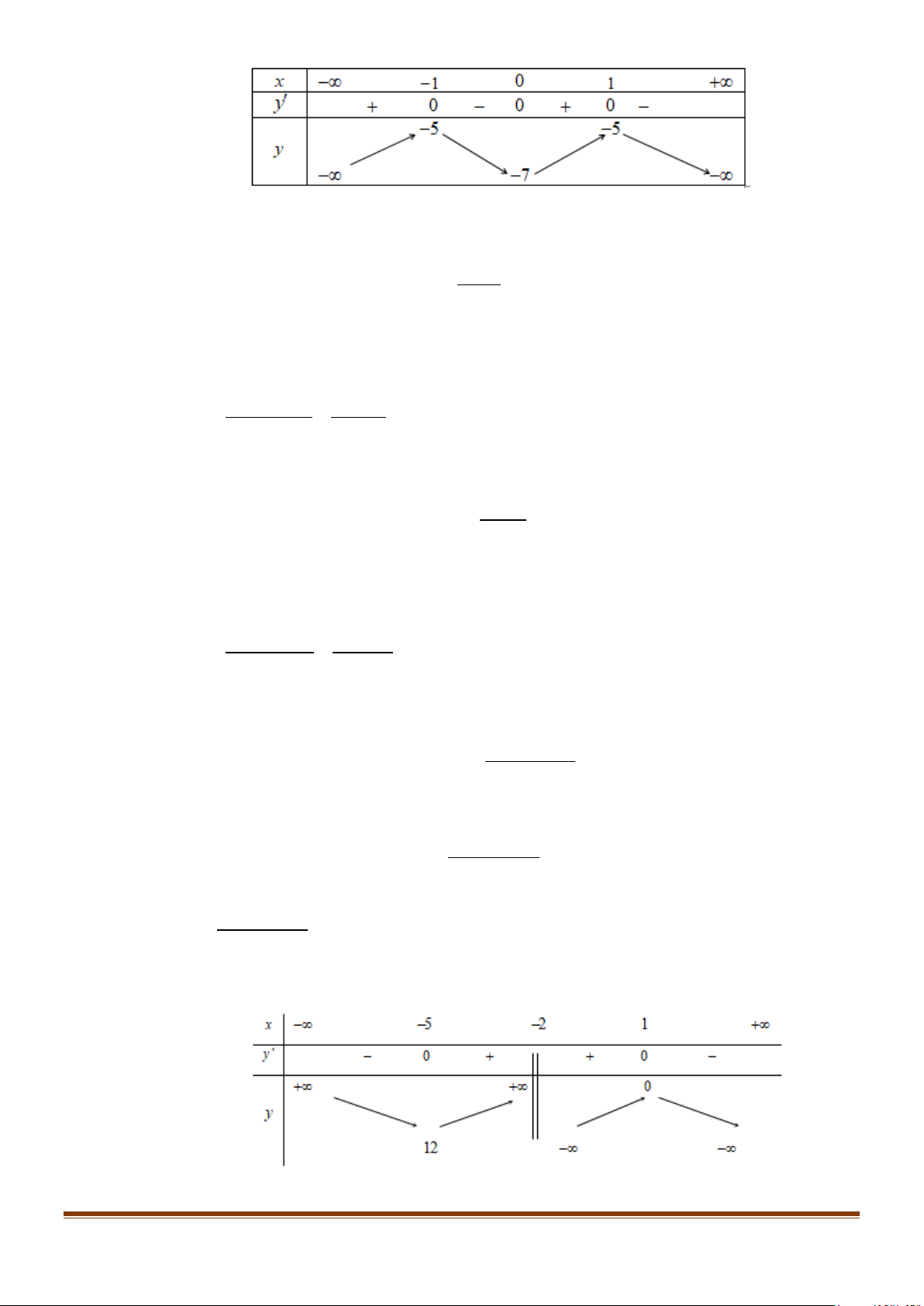
Câu 27: Cho hàm số y = f (x) liên tục trên  và có bảng biến thiên như sau 3 x 5
Tìm các khoảng đồng biến của hàm số y = g (x) = f (4 − 2x) 2 − + x − 6x +1 3 2 . Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
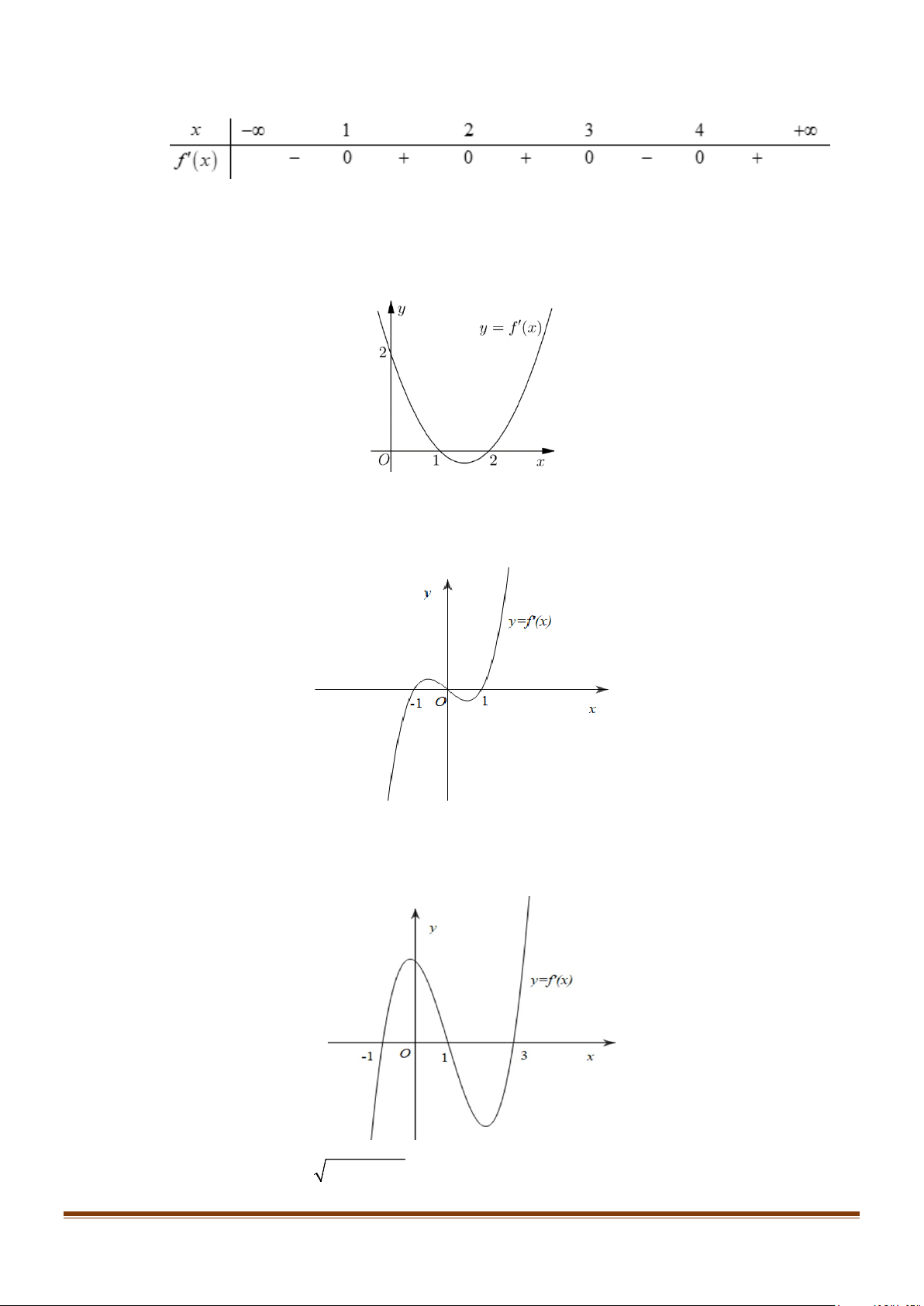
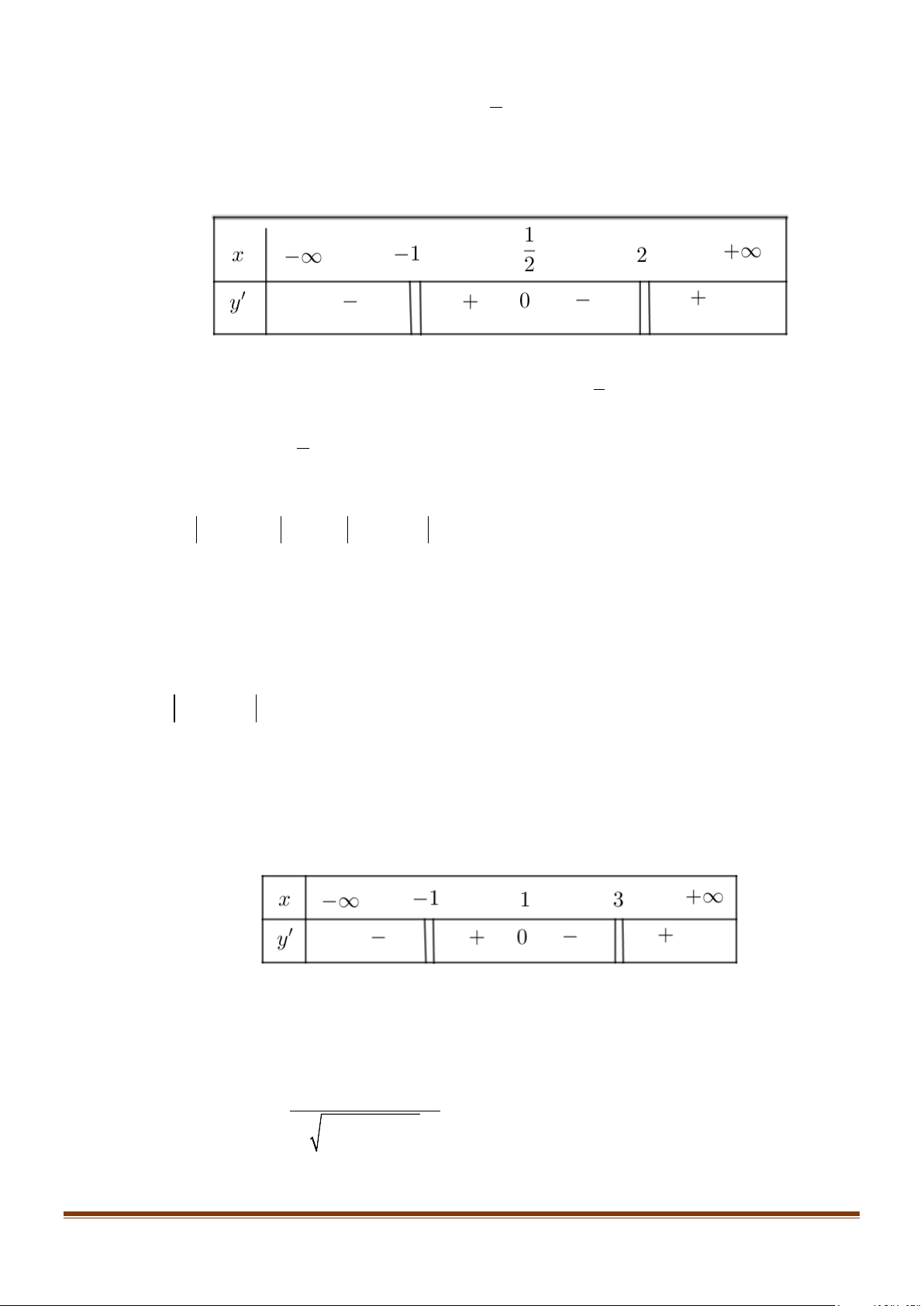
Câu 28: Cho hàm số y = f (x) liên tục trên  và có bảng xét dấu đạo hàm như sau
Biết 1< f ( x) < 3, x
∀ ∈  . Hàm số y = g (x) = f ( f (x)) 3 2
+ x − 6x −1 có ít nhất bao nhiêu
khoảng đồng biến?
Câu 29: Cho hàm số y = f (x) . Hàm số y = f ′(x) có đồ thị như hình vẽ.
Hàm số y = g (x) = f ( 2
1+ 2x − x ) đồng biến trên khoảng nào?
Câu 30: Cho hàm số y = f (x) . Hàm số y = f ′(x) có đồ thị như hình vẽ. Hàm số = ( ) = ( 3 y g x
f x ) đồng biến trên khoảng nào?
Câu 31: Cho hàm số y = f (x) . Hàm số y = f ′(x) có đồ thị như hình vẽ.
Hàm số y = g (x) = f ( 2x + 2x + 2) đồng biến trên khoảng nào? Page 8
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 32: Cho hàm số y = f (x) có đạo hàm liên tục trên .
 Đồ thị hàm số y = f ′(x) như hình bên dưới 3 x 7
Hàm số g ( x) = f ( x − 2) 2 + − x +12x +1 3 2
có ít nhất bao nhiêu khoảng nghịch biến?
DẠNG 3: TÌM ĐK CỦA THAM SỐ ĐỂ HÀM SỐ ĐỒNG BIẾN, NGHỊCH BIẾN TRÊN MỘT MIỀN CHO TRƯỚC.
Câu 33: Tìm các giá trị của tham số m để hàm số đồng biến trên  . 1) 3 2
y = x + 3x + mx + m 2) 3
y = mx − ( m + ) 2 2
1 x + (m + 2) x − 2
Câu 34: Tìm các giá trị của tham số m để hàm số 3 2
y = (m −1)x − 3(m −1)x + 3(2m − 3)x + m nghịch biến trên  .
Câu 35: Tìm các giá trị của tham số m để hàm số x − m y =
đồng biến trên từng khoảng xác định. 2x −1
Câu 36: Tìm m để hàm số 2x +1 y =
nghịch biến trên từng khoảng xác định? x − m
Câu 37: Có bao nhiêu giá trị m nguyên để hàm số 3 2
y = x + x − ( 2 3 3 m − )
1 x đồng biến trên khoảng (1;2) ?
Câu 38: Tìm m để hàm số 3 2
y = −x + 3x + (m − )
1 x + m nghịch biến trên khoảng ( 1; − +∞) .
Câu 39: Tìm m để hàm số 3 2
y = −x + mx − ( 2 3 3 m − )
1 x − 2m + 3 đồng biến trên khoảng (1;2) .
Câu 40: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = −x + mx − ( 2 3
6 m − 2) x nghịch biến
trên khoảng (2;+∞) .
Câu 41: Có bao nhiêu giá trị nguyên dương bé hơn 2024 của tham số m sao cho hàm số 2
2x + 2x −1− 5m y =
nghịch biến trên khoảng (1;5)? x − m
Câu 42: Có bao nhiêu giá trị nguyên dương không lớn hơn 2024 của tham số m sao cho hàm số 2
x + 2x −1+ m y =
nghịch biến trên khoảng ( 3 − ; ) 1 ? 5x + m 2
2x + (1− m) x +1+ m
Câu 43: Có bao nhiêu giá trị nguyên dương của tham số m sao cho hàm số y = x − m
đồng biến trên khoảng (1;+∞)?
Câu 44: Tìm tập hợp tất cả các giá trị của tham số m sao cho hàm số x +1 y = nghịch biến trên 2 x + x + m khoảng ( 1; − ) 1 . Page 9
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 45: Xác định các giá trị của tham số m để hàm số 3 2
y = x − 3mx − m nghịch biến trên khoảng(0; ) 1 ?
Câu 46: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2 2
y = x − 3mx − 9m x nghịch biến trên khoảng (0; ) 1 .
Câu 47: Tìm các giá trị của tham số m 1 để hàm số 3 2
y = x − mx + (2m − )
1 x − m + 2 nghịch biến trên 3 khoảng ( 2; − 0)..
Câu 48: Tập hợp tất cả các giá trị của tham số m để hàm số 3 2
y = x − mx − (m − 6) x +1 đồng biến trên khoảng (0;4) là:
Câu 49: Tìm tất cả các giá trị của tham số m để hàm số 3 2
y = x − mx − (m − 6) x +1 đồng biến trên khoảng (0;4) là:
Câu 50: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc ( 2020 − ;2020) sao cho hàm số 3 2
y = 2x + mx + 2x đồng biến trên khoảng ( 2;
− 0) . Tính số phần tử của tập hợp S . 2
Câu 51: Có bao nhiêu giá trị nguyên của tham số m để hàm số
x + 2x + m y =
nghịch biến trên khoảng x −1
(1;3) và đồng biến trên khoảng (4;6). Câu 52: Cho hàm số 1 3
y = x − (m + ) 2 1 x + ( 2
m + 2m) x +1. Có tất cả bao nhiêu giá trị nguyên của m 3 nằm trong đoạn [ 100 −
;100] để hàm số đồng biến trên khoảng (1;5) .
Câu 53: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( 15 − ;15) để hàm số 4 2
y = x − 6x − mx + 2526 nghịch biến trên khoảng ( 1; − ) 1 .
Câu 54: Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( 2021 − ;2021) để hàm số 4 2
y = x − 2mx − 3m +1 đồng biến trên khoàng (1;2) ?
Câu 55: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x −3x −3(m + )
1 x − m −1 nghịch biến trên đoạn [ 1; − ] 3 . 3
Câu 56: Có bao nhiêu giá trị nguyên của tham số m để hàm số x y = − (m + ) 2 x + ( 2 1
m + 2m) x +1 3
nghịch biến trên đoạn [2; ] 3 ?
Câu 57: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y = x −3x −3(m + )
1 x − m −1 nghịch biến trên đoạn [ 1; − ] 3 . Câu 58: Cho hàm số 3 2
y = −x + x − mx + 5 với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m trên đoạn [ 50
− ;50] để hàm số đã cho đồng biến trên khoảng?
Câu 59: Có bao nhiêu giá trị của tham số m để hàm số 1 3 2 2
y x (m 1)x (m  2m)x3 nghịch 3
biến trên khoảng 1;  1 .
Câu 60: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2 2
y = x − 3mx − 9m x nghịch biến trên khoảng (0;2) . Page 10
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Câu 61: Tìm tất cả các giá thực của tham số m sao cho hàm số 3 2
y = 2x − 3x − 6(m + 2) x + m nghịch biến trên khoảng ( 1; − ) 1 . 1
Câu 62: Có bao nhiêu giá trị nguyên của tham số m∈[ 2022 − ;2022] để hàm số 3
y = x + mx − đồng 2 2x
biến trên khoảng (0;+∞)? 2
Câu 63: Tìm tất cả các giá trị thực của tham số m để hàm số x − 4x y =
đồng biến trên (1;+∞) x + m 2 2
− x + (m + 2) x −3m +1
Câu 64: Cho hàm số y =
. Tìm các giá trị của tham số m để hàm số nghịch biến x −1
trên mỗi khoảng xác định.
Câu 65: Có bao nhiêu giá trị nguyên của tham số m để hàm số x + 6 y =
nghịch biến trên khoảng x + 5m (10;+∞)?
Câu 66: Gọi S là tập hợp các giá trị nguyên dương của m để hàm số 3
y = x − ( m + ) 2 3 2
1 x + (12m + 5) x + 2 đồng biến trên khoảng (2;+ ∞) . Số phần tử của S bằng
Câu 67: Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 4 2
y = x − 2mx +1
đồng biến trên khoảng (3;+∞) . Tổng giá trị các phần tử của T bằng
Câu 68: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 100 − ;100] sao cho hàm số
f (x) = (m − ) 3 x + (m − ) 2 1 1 x + (2m + )
1 x + 3m −1 đồng biến trên  ?
Câu 69: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [1;25] sao cho ứng với mỗi m, hàm số 2
−x + 2x − m + 5 y =
đồng biến trên khoảng (1;3) . 2x − m
Câu 70: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2;
− 25] sao cho ứng với mỗi m , hàm 2
x + 5x − m −1 số y =
nghịch biến trên khoảng (1;4) . 5x − m
Câu 71: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2 − 5; ]
3 sao cho ứng với mỗi m , hàm 2
−x + 4x − m − 5 số y =
đồng biến trên khoảng ( 3 − ;− ) 1 . 4x − m
Câu 72: Tìm tất cả các giá trị thực của tham số m để hàm số 2sin x −1  π y =
đồng biến trên khoảng 0; . sin x − m 2   
Câu 73: Tìm m để hàm số sin x + m  π y =
nghịch biến trên khoảng  ;π ? sin x −1 2   
Câu 74: Có bao nhiêu giá trị nguyên m∈( 10 − ;10) sao cho hàm số 4
y = x − ( m − ) 2 2 4
1 x +1 đồng biến trên khoảng (1;+∞).
Câu 75: Tìm tập hợp các giá trị của tham số m để hàm số 2
y = x +1 − mx −1 đồng biến trên khoảng ( ; −∞ +∞) . Page 11
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Câu 76: Tìm tất cả các giá trị thực của tham số m để hàm số 3
y = x − ( m + ) 2 2 3 2
1 x + 6m(m + ) 1 x +1
đồng biến trên khoảng (2;+ ∞).
Câu 77: Tìm tất cả các giá trị của m để hàm số 2cos x −1  π y =
đồng biến trên khoảng 0; . cos x − m 2   
Câu 78: Tìm tất cả các giá trị thực của tham số m để hàm số 2cos x + 3 y =
nghịch biến trên khoảng 2cos x − m 0;π   .  3  tan x − 2
Câu 79: Tìm tất cả các giá trị thực của tham số m để hàm số y =
đồng biến trên khoảng tan x − m +1  π 0;   . 4    tan x + m
Câu 80: Tìm các giá trị thực của tham số m để hàm số y =
nghịch biến trên khoảng  π 0;   . m tan x +1  4 
Câu 81: Tìm giá trị m để hàm số cot x − 2  π π y =
nghịch biến trên  ; ? cot x − m 4 2   
Câu 82: Tìm m để hàm số 2cot x +1  π π y =
đồng biến trên khoảng  ; . cot x + m 4 2    Page 12
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
ỨNG DỤNG ĐẠO HÀM NG ƯƠ
I ĐỂ KHẢO SÁT VÀ VẼ CH
ĐỒ THỊ CỦA HÀM SỐ
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ I LÝ THUYẾT.
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
1. Khái niệm tính đợn điệu của hàm số.
Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và y f(x) là hàm số xác định trên K .
+) Hàm số y f(x) được gọi là đồng biến trên K nếu x , x K,
x x f (x )  f (x ). 1 2 1 2 1 2
+) Hàm số y f(x) được gọi là nghịch biến trên K nếu x , x K,
x x f (x )  f (x ). 1 2 1 2 1 2
+) Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K. Chú ý:
+ Nếu hàm số đồng biến trên K thì từ trái sang phải đồ thị đi lên.
+ Nếu hàm số nghịch biến trên K thì từ trái sang phải đồ thị đi xuống. Page 1
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
2. Định lý: Cho hàm số y f(x) có đạo hàm trên K   , trong đó K là một khoảng, đoạn hoặc nữa khoảng.
+) Nếu f (x)  0, x K thì hàm số y f(x) đồng biến trên khoảng K .
+) Nếu f (x)  0, x K thì hàm số y f(x) nghịch biến trên khoảng K .
3. Định lý: (Tổng quát) Cho hàm số y f(x) có đạo hàm trên K   , trong đó K là một khoảng,
đoạn hoặc nữa khoảng.
+) Nếu f (x)  0, x K và f (x)  0 xảy ra tại một số hữu hạn điểm trên K thì hàm số
y f (x) đồng biến trên khoảng K .
+) Nếu f (x)  0, x K và f (x)  0 xảy ra tại một số hữu hạn điểm trên K thì hàm số
y f (x) nghịch biến trên khoảng K .
4. Lưu ý: +) Nếu hàm số y f(x) liên tục trên đoạn [a;b] và f '(x)0, (
x a;b) thì ta nói hàm số đồng
biến trên đoạn [a;b].
+) Nếu hàm số y f(x) liên tục trên đoạn [a;b] và f '(x)  0, (
x  a;b) thì ta nói hàm số
nghịch biến trên đoạn [a;b].
+) Tương tự với các khái niệm hàm số đồng biến, nghịch biến trên các nửa khoảng.
5. Sử dụng bảng biến thiên để xét tính đơn điệu của hàm số.
Để xét tính đơn điệu của hàm số y = f (x) ta thực hiện các bước sau:
Bước 1: Tìm tập xác định D .
Bước 2: Tính đạo hàm y′ = f (′x) . Tìm các điểm x i =
mà tại đó f (′x) = 0 hoặc làm i ( 0;1;2;. .)
cho f (′x) không xác định.
Bước 3: Sắp xếp các x i =
theo thứ tự tăng dần và lập bảng biến thiên. i ( 0;1;2;. .)
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận
Chú ý: Đối với bài toán trắc nghiệm, ta có thể sử dụng Phương pháp sử dụng MTCT.
Cách 1: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính Casio. Quan sát bảng kết
quả nhận được về tính tăng, giảm giá trị của f(x) và dự đoán.
Cách 2: Tính đạo hàm, thiết lập bất phương trình đạo hàm. Sử dụng tính năng giải bất phương
trình INEQ của máy tính Casio (đối với bất phương trình bậc hai, bậc ba). Page 2
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
II. CỰC TRỊ CỦA HÀM SỐ
1. Khái niệm cực trị của hàm số: Cho hàm số y = f (x) xác định và liên tục trên khoảng ( ; a b) và điểm x ∈( ; a b) 0 .
+) Nếu tồn tại số h > 0 sao cho f (x) < f (x với mọi x∈(x − ;
h x + h) và x ≠ x thì ta nói 0 ) 0 0 0
hàm số y = f (x) đạt cực đại tại x0 .
+) Nếu tồn tại số h > 0 sao cho f (x) > f (x với mọi x∈(x − ;
h x + h) và x ≠ x thì ta nói 0 ) 0 0 0
hàm số y = f (x) đạt cực tiểu tại x0 . * Chú ý
+) Nếu hàm số y = f (x) đạt cực đại tại x x f (x )
0 thì 0 được gọi là điểm cực đại của hàm số; 0
được gọi là giá trị cực đại của hàm số, kí hiệu là f
M (x ; f (x ))
CÑ ( fCT ) , còn điểm 0 0 được gọi là
điểm cực đại của đồ thị hàm số.
+) Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại còn gọi là cực
đại và được gọi chung là cực trị của hàm số.
2. Cách tìm cực trị của hàm số
Định lí 2: Giả sử hàm số y = f (x) liên tục trên ( ;
a b) chứa điểm x ( ; a x ) 0 và có đạo hàm trên 0 và (x ;b) 0 .
+) Nếu f '(x) > 0 trên khoảng ( ; a x ) < (x ;b) x 0 và f '(x) 0 trên 0
thì 0 là một điểm cực đại của
hàm số y = f (x) .
+) Nếu f ′(x) < 0 trên khoảng ( ; a x ) ′ > (x ;b) x 0 và f (x) 0 trên 0
thì 0 là một điểm cực tiểu của
hàm số y = f (x) .
Minh họa bằng bảng biến thiến Page 3
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ NHẬN XÉT:
Để tìm cực trị của hàm số y = f (x) ta thực hiện các bước sau:
Bước 1: Tìm tập xác định D .
Bước 2: Tính đạo hàm y′ = f (′x) . Tìm các điểm x i =
mà tại đó f (′x) = 0 hoặc làm i ( 0;1;2;. .)
cho f (′x) không xác định.
Bước 3: Sắp xếp các x i =
theo thứ tự tăng dần và lập bảng biến thiên. i ( 0;1;2;. .)
Bước 4: Căn cứ vào bảng biến thiên nêu kết luận
II HỆ THỐNG BÀI TẬP TỰ LUẬN.
DẠNG 1: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ CHO BỞI BIỂU THỨC
Câu 1: Tìm các khoảng đồng biến, nghịch biến của hàm số 3 2
y = x − 3x +1. Lời giải
Tập xác định: D =  . x = Ta có: 2
y′ = 3x − 6x ; 2 0
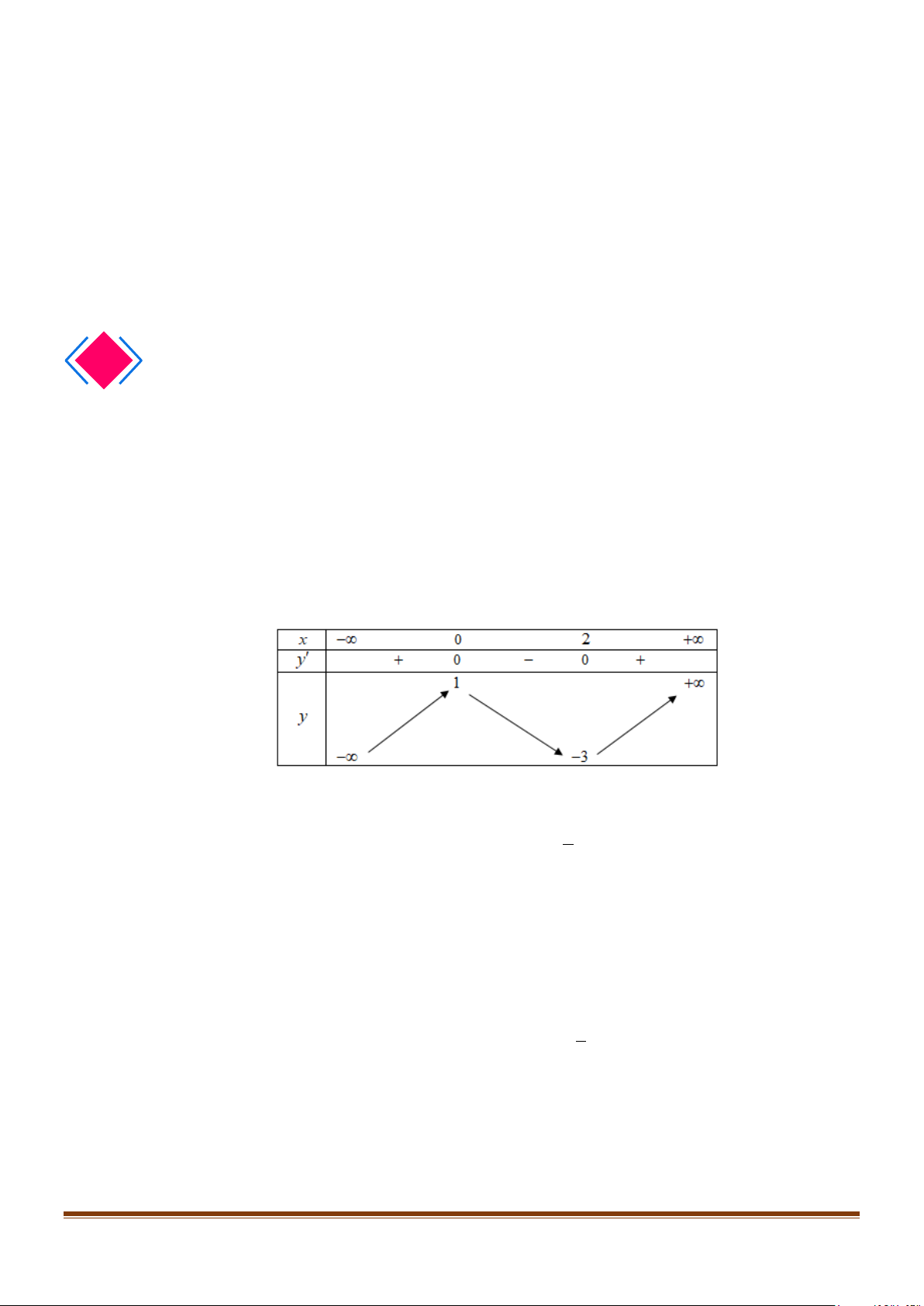
y′ = 0 ⇔ 3x − 6x = 0 ⇔  . x = 2 Bảng biến thiên
Vậy hàm số đồng biến trên các khoảng ( ;0
−∞ ) và (2;+∞) , nghịch biến trên khoảng (0;2) .
Câu 2: Tìm các khoảng đồng biến, nghịch biến của hàm số 1 3
y = x + 4x +1. 3 Lời giải
Tập xác định: D =  . Ta có: 2
y′ = x + 4 > 0, x ∀ ∈  .
Vậy hàm số đồng biến trên khoảng ( ; −∞ +∞) .
Câu 3: Tìm các khoảng đồng biến, nghịch biến của hàm số 1 3 2
y = − x + 5x − 26x −1. 3 Lời giải
Tập xác định: D =  . Ta có: 2
y′ = −x +10x − 26 = −(x −5)2 −1< 0, x ∀ ∈  . Page 4
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Vậy hàm số nghịch biến trên khoảng ( ; −∞ +∞) .
Câu 4: Tìm các khoảng đồng biến, nghịch biến của hàm số 1 3 2
y = x + 3x + 9x −1. 3 Lời giải
Tập xác định D =  . Ta có: 2
y′ = x + 6x + 9 = (x + 3)2 ≥ 0, x
∀ ∈  ; y′ = 0 ⇔ x = 3 − .
Vậy hàm số đồng biến trên khoảng ( ; −∞ +∞) .
Câu 5: Tìm các khoảng đơn điệu của hàm số 4 2
y = x − 2x . Lời giải
Tập xác định: D =  . x = 0 Ta có 3
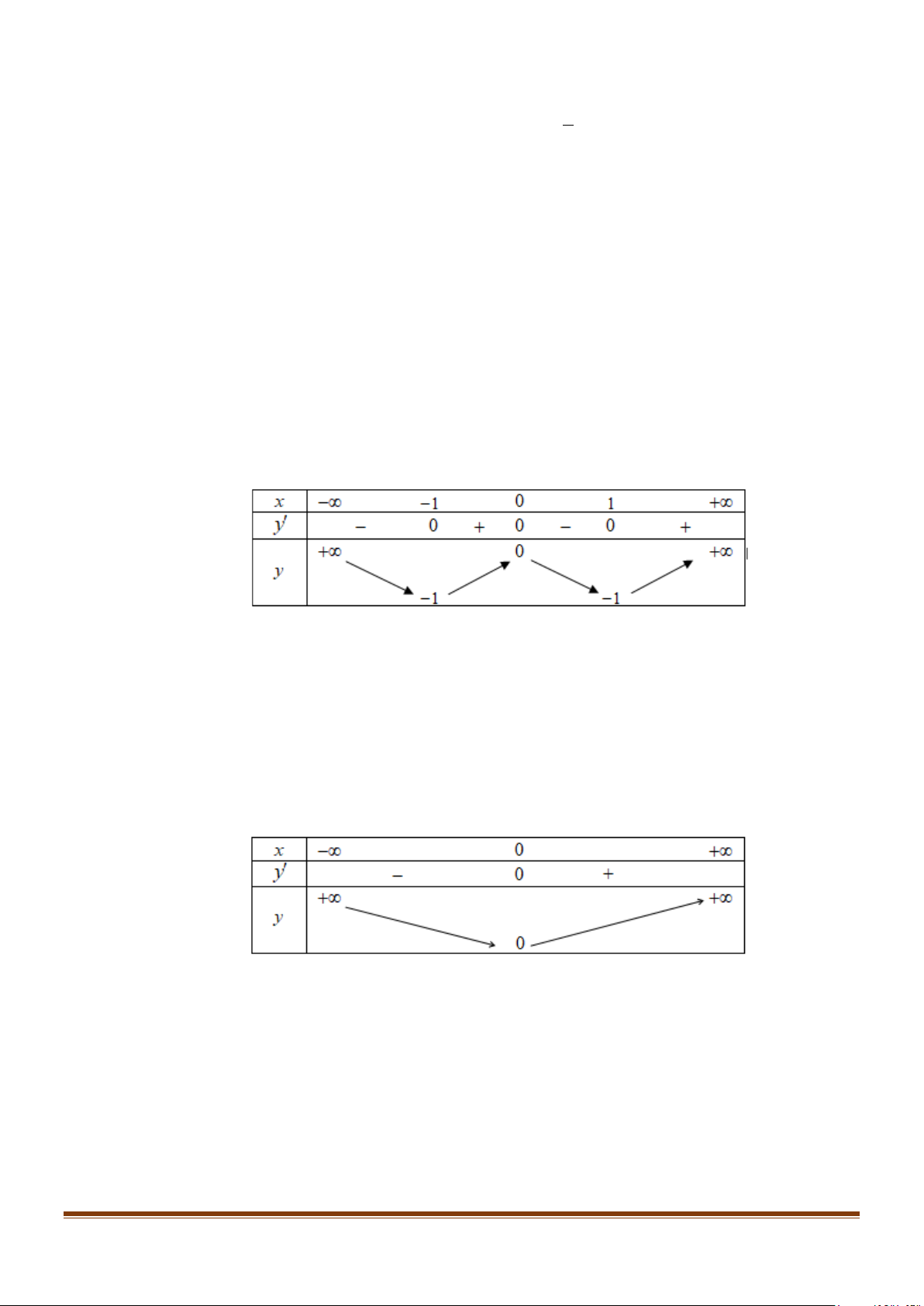
y′ = x − x = x( 2 4 4 4 x − ) 1 ; y′ = 0 ⇔  . x = 1 ± Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng ( 1;
− 0) và (1;+ ∞), nghịch biến trên các khoảng ( ; −∞ − ) 1 và (0; ) 1 .
Câu 6: Tìm các khoảng đơn điệu của hàm số 4 2
y = x + 4x . Lời giải
Tập xác định: D =  . Ta có 3
y′ = x + x = x( 2 4 8
4 x + 2) ; y′ = 0 ⇔ x = 0. Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng (0;+ ∞), nghịch biến trên khoảng ( ;0 −∞ ).
Câu 7: Tìm các khoảng đơn điệu của hàm số 4 2 y = 2
− x + 4x − 7 . Lời giải
Tập xác định: D =  . x = 0 Ta có 3
y′ = − x + x = − x( 2 8 8 8 x − ) 1 ; y′ = 0 ⇔  . x = 1 ± Bảng biến thiên: Page 5
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
Vậy hàm số đồng biến trên các khoảng ( ; −∞ − ) 1 và (0; )
1 , nghịch biến trên các khoảng ( 1; − 0) và (1; + ∞) .
Câu 8: Tìm các khoảng đơn điệu của hàm số 3x +1 y = . 1− x Lời giải
Tập xác định: D =  \{ } 1 . 3.1− (− ) 1 .1 Ta có 4 y′ = = > 0, x ∀ ∈ D . 2 2 (1− x) (1− x)
Vậy hàm số đồng biến trên các khoảng (−∞ ) ;1 và (1;+∞) .
Câu 9: Tìm các khoảng nghịch biến của hàm số 3− 2x y = . x + 7 Lời giải
Tập xác định: D =  \{− } 7 . ( 2 − ).7 −1.3 17 − Ta có y′ = = < 0, x ∀ ∈ D . (x + 7)2 (x + 7)2
Vậy hàm số nghịch biến trên các khoảng (− ;
∞ −7) và (−7;+∞). 2
Câu 10: Tìm các khoảng nghịch biến của hàm số: −x + 2x −1 y = . x + 2 Lời giải 2
Tập xác định: D =  \{− } 2 . Ta có: −x − 4x + 5 y′ = . (x + 2)2 2 −x − 4x + 5 x = 5 − y ' = 0 ⇔ = 0 2
⇔ −x − 4x + 5 = 0 ⇔ . (x + 2)2  x = 1 Bảng biến thiên Page 6
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Vậy hàm số nghịch biến trên các khoảng (− ; ∞ −5) và (1;+∞) . 2
Câu 11: Tìm các khoảng đồng biến và nghịch biến của hàm số x + 4x + 4 y = . x +1 Lời giải 2 x + 2xx = 2 −
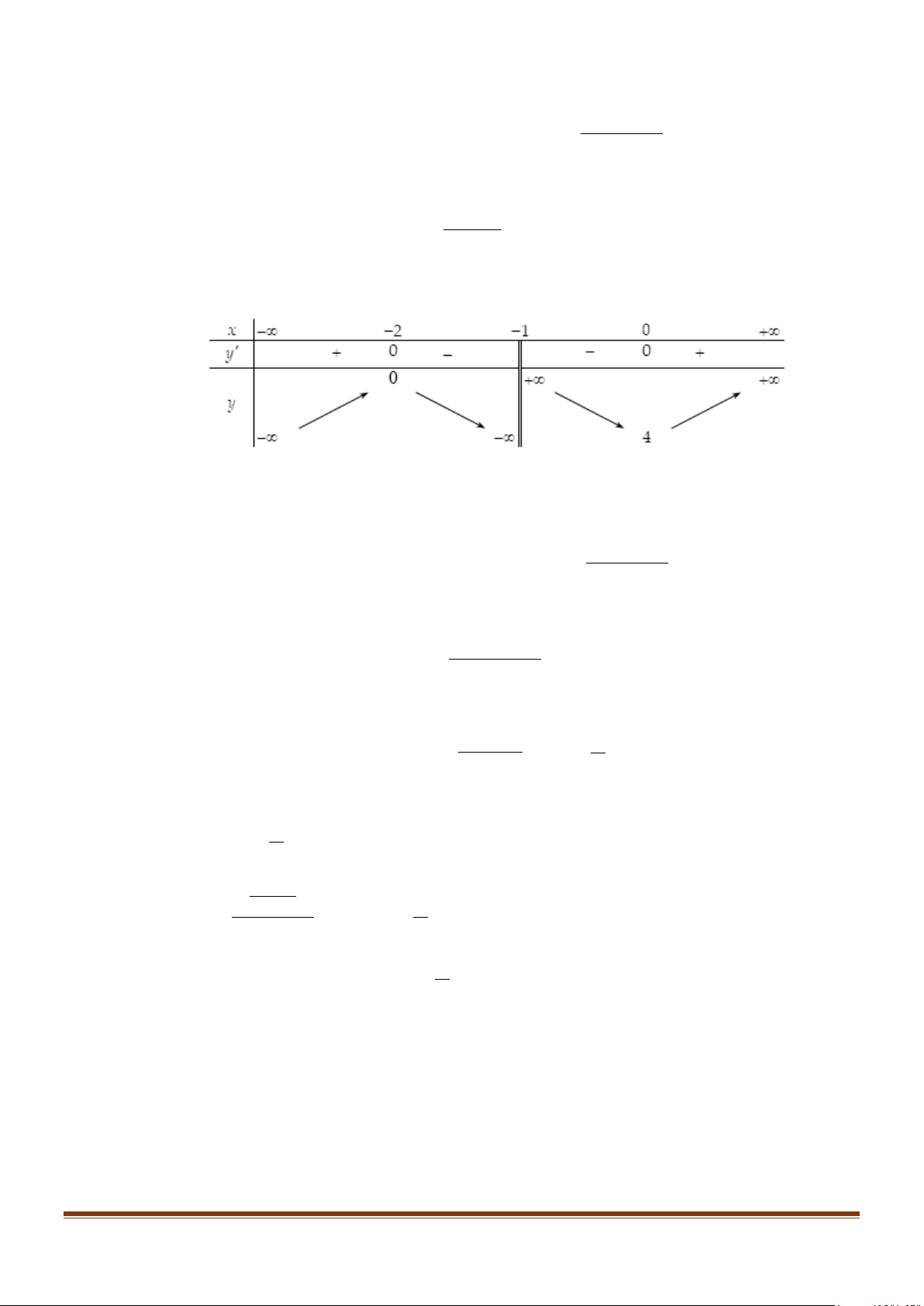
Tập xác định: D =  \{− } 1 . Ta có: y′ = ⇒ y ' = 0 ⇔ . (x + )2 1  x = 0 Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng (−∞;−2) và (0;+∞) , nghịch biến trên các khoảng (−2;−1) và (−1;0) . 2
Câu 12: Tìm các khoảng đồng biến và nghịch biến của hàm số: −x − x + 5 y = . x + 2 Lời giải 2
Tập xác định: D =  \ {− } 2 . Ta có:
−x − 4x − 7 y′ = < 0, x ∀ ∈ D . (x + 2)2
Vậy hàm số nghịch biến trên các khoảng (−∞;−2) và (−2;+∞). −
Câu 13: Tìm các khoảng đơn điệu của hàm số tan x 2 y = trên  π   ; 0  . tan x −1  4  Lời giải Trên khoảng  π   ;
0  thì tan x ∈ ( ) 1; 0 ; cos x ≠ 0 .  4  1 Ta có: 2 cos  π ' x y 0, x 0;  = > ∀ ∈ . (  tan x − )2 1  4 
Vậy hàm số đồng biến trên khoảng  π   ; 0  .  4 
Câu 14: Tìm các khoảng đồng biến, nghịch biến của hàm số  −x + 2 nÕu x < 1 −  2 y =  2
− x + 2x + 7 nÕu −1 ≤ x ≤ 2 .   3x − 3 nÕu x > 2 Lời giải
Tập xác định: D =  . Page 7
Sưu tầm và biên soạn
CHUYÊN ĐỀ I – GIẢI TÍCH 12 - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ  1 − nÕu x < 1 −  y′ =  4 − x + 2
nÕu −1 < x < 2 ; 1
y′ = 0 ⇔ x = .  2  3 nÕu x > 2
Bảng xét dấu của y′:  1 
Từ bảng xét dấu của y′ ta có hàm số đồng biến trên các khoảng 1; − 
và (2;+∞) , nghịch biến trên các 2     1  khoảng ( ; −∞ − ) 1 và  ;2 . 2   
Câu 15: Tìm các khoảng đồng biến, nghịch biến của hàm số: a) 2
y = x − 2x − 3 . b) 2
y = x − 4x + 3 + 4x + 3 . Lời giải
a) Tập xác định: D =  . Cách 1: 2
x − 2x − 3 nÕu x ≤ 1 − hoÆc x ≥ 3  2
y = x − 2x − 3 =  . −  ( 2 x − 2x − 3) nÕu −1 < x < 3
2x − 2 nÕu x < 1 − hoÆc x > 3 y′ = 
; y′ = 0 ⇔ x =1. −  (2x − 2) nÕu −1 < x < 3
Bảng xét dấu y′:
Vậy hàm số đồng biến trên các khoảng ( 1; − )
1 và (3;+∞) , nghịch biến trên các khoảng ( ; −∞ − ) 1 và (1;3) .
2( 2x − 2x −3)(x − )1
Cách 2: Ta có y′ = ; ′ = ⇔ = . ( y 0 x 1 x − 2x −3)2 2
Bảng xét dấu của y′: Page 8
Sưu tầm và biên soạn