Cơ sở trí tuệ nhân tạo - Cơ sở dữ liệu | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoARcPSD|46342985 lOMoARcPSD|46342985
CƠ SỞ TRÍ TUỆ NHÂN TẠO
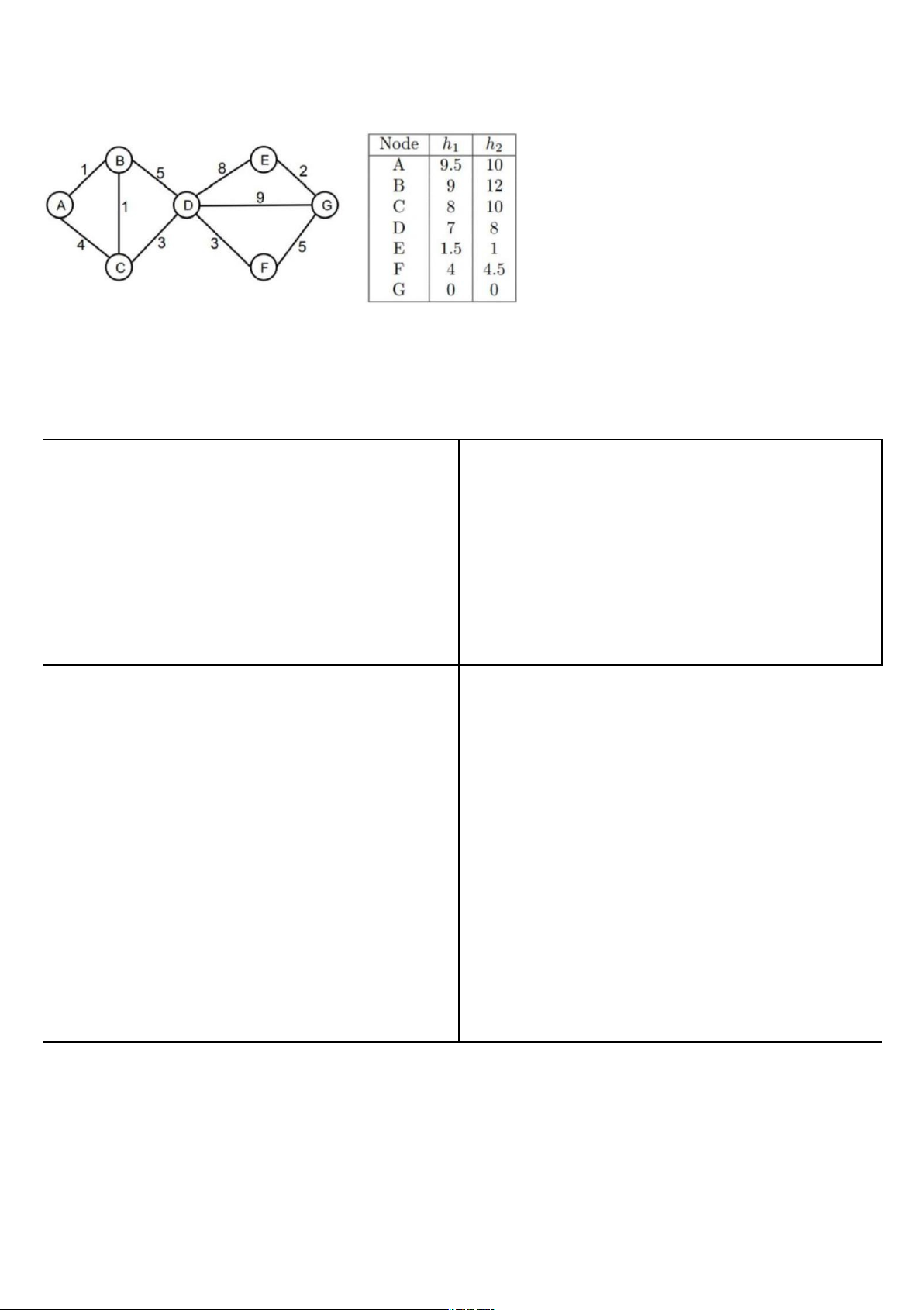
1. Tìm đường đi từ A đến G
Heuristic chấp nhận được
• Đặt h*(n) = chi phí tối thiểu thấp nhất từ n đến đích.
• Một heuristic h là chấp nhận được nếu h(n) <= h*(n) với mọi trạng thái n.
• Một heuristic chấp nhận được đảm bảo không bao giờ ước tính quá chi phí đến đích.
• Một heuristic chấp nhận được là tối ưu. a, BFS b, DFS Fringe = [A] Fringe = [A]
Fringe = [B C] //Lấy đầu Queue, B
Fringe = [C B] //Lấy đầu Stack, B
Fringe = [C D] //Lấy C
Fringe = [C D] //Lấy D Fringe = [D] //Lấy D
Fringe = [C G F E] //Lấy E
Fringe = [E F G] //Lấy E
Fringe = [C F G] //Tìm thấy đích, dừng giải thuật
Fringe = [F G] //Lấy F
➔ Đường đi từ A đến G: A, B, D, E, G
Fringe = [G] //Tìm thấy đích, dừng giải thuật
➔ Đường đi từ A đến G: A, B, C, D, E, G c, UCS Greedy: h1 Close_set: A, B, C, D, F, G Close_set: A, C, D, G PQ = [(A:0)] PQ = [A9.5]
PQ = [(B:1), (C:4)] //Lấy điểm nhỏ nhất: (B:1)
PQ = [(C:4), (C:2), (D:6)] //Lấy (C:2)
PQ = [B9, C8] //Lấy điểm nhỏ nhất: C
PQ = [(D:6), (D:5), (D:7)] //Lấy (D:5) PQ = [B9, D7] //Lấy D
PQ = [(E:13), (E:14), (E:15), (F:8), (F:9), (F:10), PQ = [E1.5, F4, G0] //Lấy G
(G:14), (G:15), (G:16)] // Lấy (F:8)
PQ = [(E:13), (E:14), (E:15), (G:14), (G:15),
Đường đi từ S đến G theo phương pháp
(G:16), (G:13), (G:14), (G:15)] // Lấy (G:13) Greedy là A, C, D, G
Đường đi từ S đến G theo phương pháp
UCS là A, B, C, D, F, G với chi phí đường đi là 13. A*: h1
Close_set: A, B, C, D, F, G PQ = [A0+9.5]
PQ = [B1+9, C4+8] //Lấy điểm nhỏ nhất, đầu hàng đợi: B
PQ = [C2+8, C4+8, D6+7] //Lấy C
PQ = [D5+7, D6+7] //Lấy D
PQ = [E13+1.5, F8+4, G14+0] //Lấy F
PQ = [E13+1.5, G13+0, G14+0] //Lấy G
➔ Đường đi ngắn nhất từ A đến G theo phương pháp A* là A, B, C, D, F, G. lOMoARcPSD|46342985
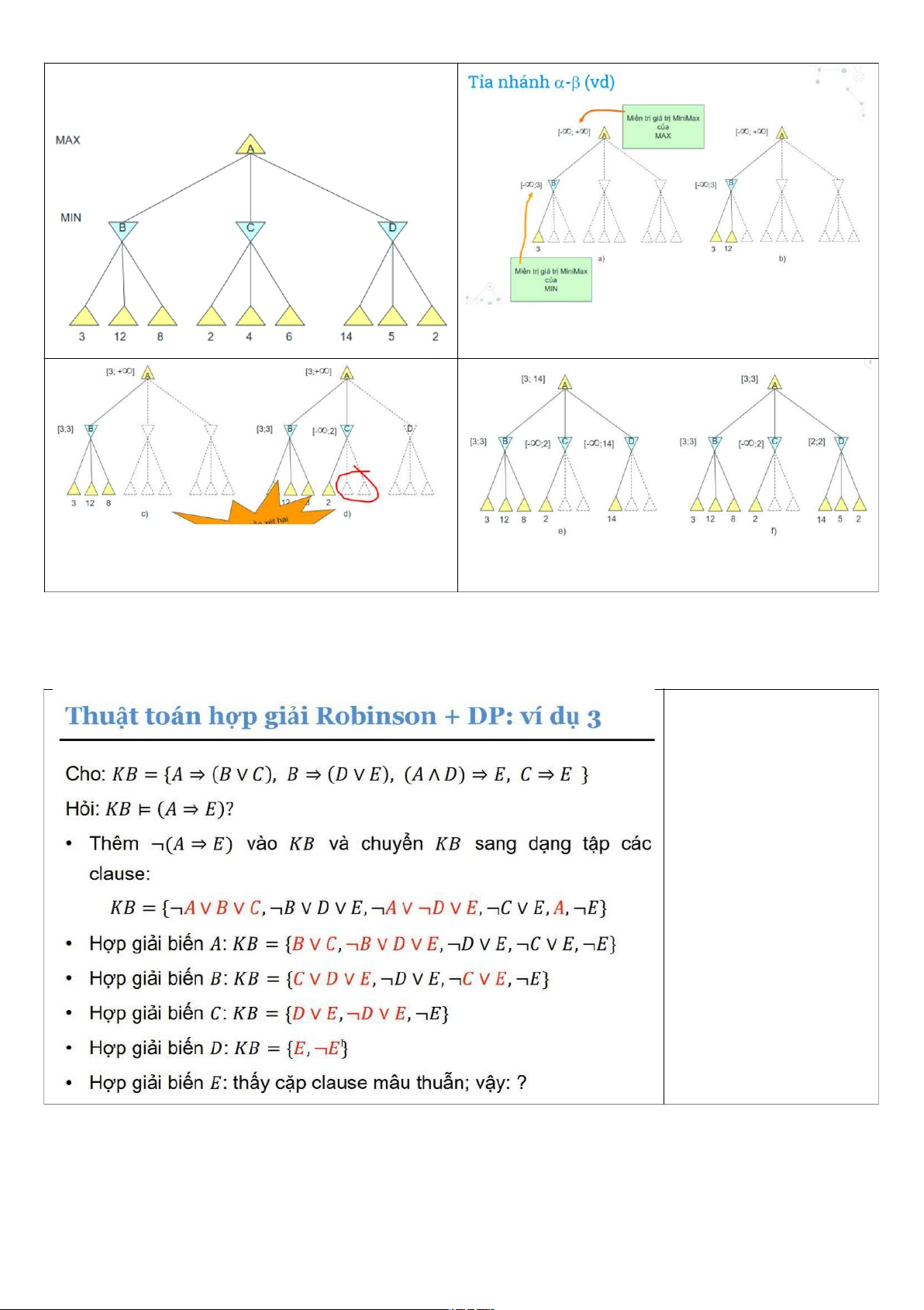
2. Tìm kiếm đối kháng B=3;C=2,D=2,A=3
α là giá trị max, β là giá trị Min
Để A chọn C thì C>=3, khi duyệt C <=2 Xét D, D>=3
không thỏa nên không cần duyệt tiếp
3. Logic mệnh đề (≡ trùng với, ¬ not, ˄ and, ˅ or)
Dạng viết tắt: α => β ≡ α ˅ β ; α <=> β ≡ (α => β) ˄ (β => α)
Hợp giải: KB = (α ˅ β, ¬ β ˅ γ) KL = (α ˅ γ) Sau khi hợp giải không thể ra câu mới được nữa, mà trong KB vẫn chưa xuất hiện mâu thuẫn, không thể đưa ra kết luận. Ví dụ 3: KB suy ra
được câu kết luận lOMoARcPSD|46342985 4. Logic bậc nhất Naïve Bayes
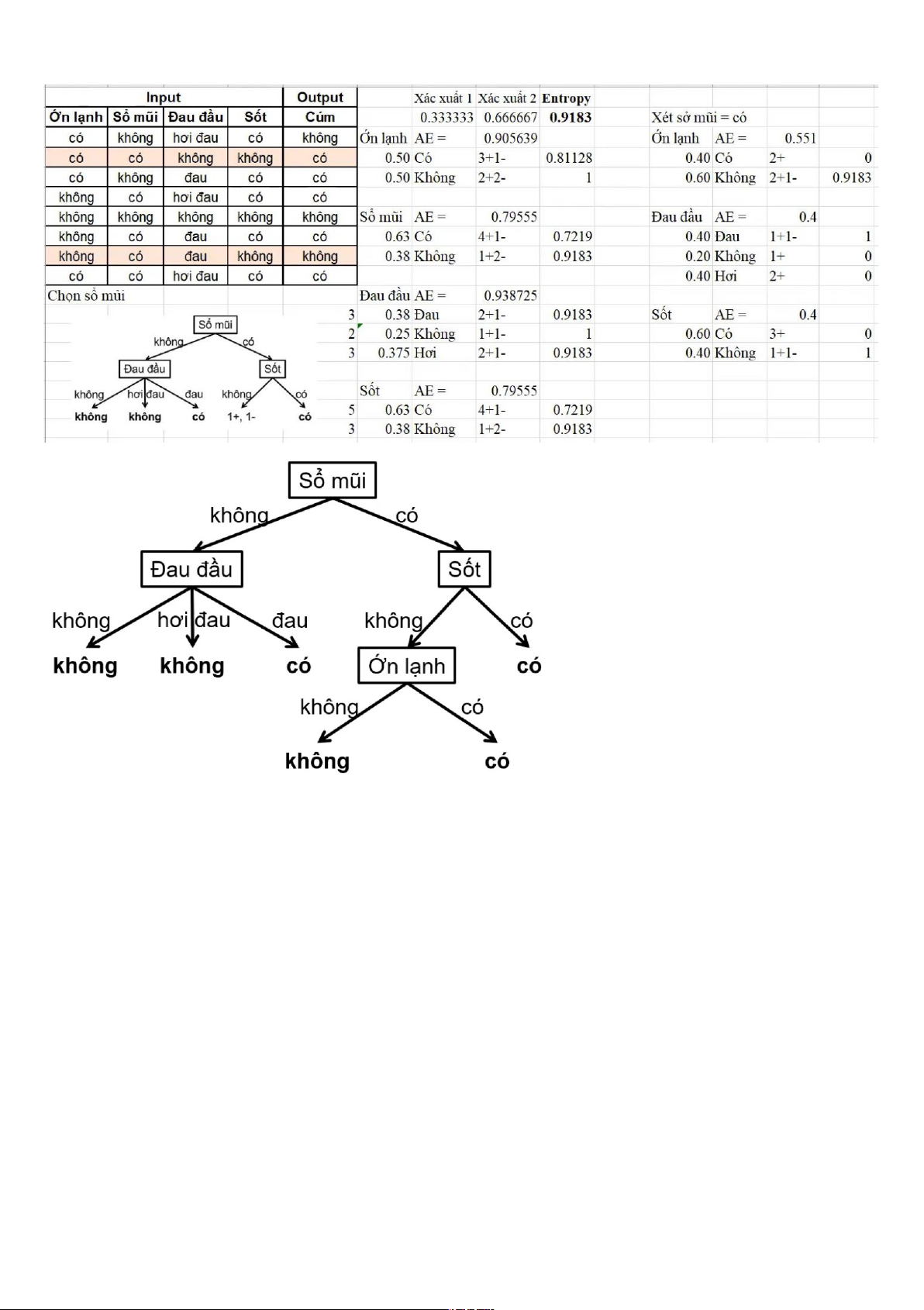
So sánh P(Y/X) = (P(X|Y) + P(Y))/P(X) lOMoARcPSD|46342985 ID3
Đi hết các node nhưng không ra được quyết định thì theo đa số