Đạo hàm theo hướng | Đại học Sư phạm Hà Nội 2

Đạo hàm theo hướng | Đại học Sư phạm Hà Nội 2. Tài liệu gồm 20 trang giúp bạn tham khảo, củng cố kiến thức và ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem!

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương trình đạo hàm riêng

Trường: Đại học Sư phạm Hà Nội 2

Thông tin:

20 trang 3 tháng trước

Tác giả:

Profile Phạm Thị Huyền
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
có đạo hàm riêng đến cấp n + 1 trong một lân cận của
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
f = f(x,y)
Véctơ đơn vị cùng phương
là góc tạo bởi và chiều dương
trục Ox và Oy tương ứng.
Phương trình tham số của tia
Đạo hàm của hàm f theo hướng véctơ tại điểm là giới hạn (nếu có)
0 0 0
( , )M x y
( , )M x y
u
0 1 2
,
u
l l l
u
0
cos ,cosl
u
,
0
:M M
0
0
cos
0
cos
x x t
t
y y t
u
0
M
'
0
( )
u
f M
1 2
( , )u u u
ox
oy
0
( )
f
M
u
0
0
0
( ) ( )
lim
M M
f M f M
MM
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Đây chính là đạo hàm của hàm f theo biến t
véctơ gradient của f tại M
0
Tích vô hướng của véctơ
gradient tại M
0
với véctơ đơn vị.
2 2
0 0 0
( ) ( )M M x x y y t
'
0 0
0
0
( , ) ( , )
( ) lim
u
t
f x y f x y
f M
t
'
0 0 0 0
0
0
( cos , cos ) ( , )
( ) lim
u
t
f x t y t f x y
f M
t
' '
0
( )
t
u
f M f
' ' ' '
x t y t
f x f y
' '
0 0 0 0
( , ) cos ( , ) cos
x y
f x y f x y
' '
0 0
'
00 0 0
( , ), cos ,c( , ) ,) s, o(
x
u
y
f x y f x yf x y
' '
0 0 0 0 0 0
( , ) ( , ), ( , )grad
x y
f x y f x y f x y
'
0 0 0 0
( ) ( , ),grad
u
f M f x y l
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Tương tự, ta có định nghĩa đạo hàm của f=f(x,y,z) tại M
0
theo hướng
Trong đó: véctơ đơn vị cùng phương với là:
là các góc tạo bởi và chiều dương trục 0x, 0y và 0z tương ứng.
Véctơ Gradient của f(x,y,z) tại M
0
là:
' ' ' '
0 0 0 0
( ) ( ) cos ( ) cos ( ) cos
x y z
u
f M f M f M f M
'
0 0 0 0 0
( ) ( , , ),grad
u
f M f x y z l
u
u
u
, ,
' ' '
0 0 0 0
( ) ( ), ( ), ( )grad
x y z
f M f M f M f M
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Tìm đạo hàm của tại điểm M
0
(1,1)
theo hướng của véctơ
Giải.
Véctơ đơn vị cùng phương với là:
2 4 5
( , ) 3f x y xy x y
(1, 2)u
0
1 2
,
5 5
l
u
' 2 3 5
12
x
f y x y
' 4 4
2 15
y
f xy x y
'
(1,1) 11
x
f
'
(1,1) 13
y
f
' ' '
(1,1) (1,1) (1,1)os os
x y
u
f f c f c
,os osc c
11 26
3 5
5 5
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Tìm đạo hàm của tại điểm M
0
(1,2)
theo hướng của véctơ tạo với chiều dương trục 0x một góc 30
0
.
Giải.
Véctơ đơn vị là:
3 2
( , ) 3 4f x y x xy y
' 2
3 3
x
f x y
'
3 8
y
f x y
'
(1,2) 3
x
f
'
(1,2) 13
y
f
0
' ' '
(1,2) (1,2) (1,2)os os
x y
l
f f c f c
0
l
,os osc c
3 3 13
2 2
0
3 1
cos ,cos ,
6 3 2 2
l
,
6 2 6 3
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Tìm đạo hàm của tại điểm
theo hướng pháp véctơ của đường tròn x
2
+ y
2
= 2x tại M
0
.
Giải.
Véctơ đơn vị là:
( , ) arctg
y
f x y
x
'
2 2
x
y
f
x y
'
2 2
y
x
f
x y
'
0
3
( )
2
x
f M
'
0
1
( )
2
y
f M
0
' ' '
0 0 0
( ) ( ) ( )os os
x y
l
f M f M c f M c
0
l
1 3
,
2 2
3
2
0
1 3
,
2 2
M
2 2
( , ) 2 0F x y x y x
' '
, 2 2,2
x y
n F F x y
( 1, 3)
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Tìm đạo hàm của tại điểm M
0
(3,3,1)
theo hướng của véctơ l=(2,1,2).
Giải.
Véctơ đơn vị là:
3 2 2
( , , ) 2 3f x y z x xy yz
' 2 2
3 2
x
f x y
' 2
4 3
y
f xy z
'
(3,3,1) 45
x
f
'
(3,3,1) 39
y
f
' ' ' '
0 0 0 0
( ) ( ) ( ) ( )os os os
x y z
l
f M f M c f M c f M c
0
l
2 1 2
, ,
3 3 3
(cos ,cos ,cos )
'
6
z
f yz
'
(3,3,1) 18
z
f
55
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Tìm đạo hàm của tại điểm M
0
(1,2,-1)
theo hướng của véctơ tạo với các trục tọa độ những góc nhọn bằng nhau.
Giải.
Véctơ đơn vị là:
2
( , , ) 3 4f x y z x yz
'
2
x
f x
'
3
y
f z
'
(1,2, 1) 2
x
f
'
(1,2, 1) 3
y
f
' ' ' '
0 0 0 0
( ) ( ) ( ) ( )os os os
x y z
l
f M f M c f M c f M c
0
l
(cos ,cos ,cos )
'
3
z
f y
'
(1,2, 1) 6
z
f
3
3
2 2 2
cos cos cos 1
2
3cos 1
1
cos
3
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Chú ý.
Nếu đạo hàm riêng theo x không tồn tại, thì đạo hàm theo hướng vẫn có thể
có.
Cho hàm f=f(x,y,z).
Đạo hàm của f tại M
0
theo hướng của véctơ (1,0,0) là:
Vậy đạo hàm theo hướng véctơ (1,0,0) tại M
0
là đạo hàm riêng theo x tại đó,
nếu đạo hàm riêng theo x tồn tại.
(vì theo định nghĩa, đạo hàm theo hướng là giới hạn một phía)
' ' ' '
0 0 0 0
( ) ( ) cos ( ) cos ( ) cos
x y z
i
f M f M f M f M
'
0
( )
x
f M
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Tìm đạo hàm của tại điểm M
0
(0,1, 1)
theo hướng của véctơ (1,0,0).
Giải.
Véctơ đơn vị là:
Không tồn tại đạo hàm riêng theo x tại M
0
.
Tìm đạo hàm của f theo hướng của véctơ (1,0,0) bằng định nghĩa
Lý do: trong định nghĩa đạo hàm theo hướng, M dần đến bên phải của
M
0
.
( , , ) | | 2f x y z x yz
0
l
1,0,0
'
0 0 0 0 0 0
0
( cos , cos , cos ) ( , , )
(0,1,1) lim
i
t
f x t y t z t f x y z
f
t
'
0
( ,1,1) (0,1,1)
(0,1,1) lim
i
t
f t f
f
t
0
| | 2 2
lim
t
t
t
0
| |
lim
t
t
t
0
lim 1
t
t
t
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Theo công thức tính đạo hàm đạo hàm theo hướng:
Đạo hàm của f tại M
0
đạt giá trị lớn nhất theo hướng của véctơ
Giá trị lớn nhất của đạo hàm theo hướng bằng:
Đạo hàm của f tại M
0
đạt giá trị nhỏ nhất theo hướng ngược với
Giá trị nhỏ nhất của đạo hàm theo hướng bằng:
'
0 0 0
( ) ( ),grad
u
f M f M l
0 0 0
( ) ( )grad gradf M l f M
0
( )gradf M
0 0
( , )gradf x y
0
( )gradf M
0 0
( , )gradf x y
0 0
( ) cosgradf M l
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Cho hàm và một điểm
1) Tìm hướng mà đạo hàm của f theo hướng đó tại M
0
đạt giá trị lớn
nhất.
Giải.
Tìm giá trị lớn nhất này.
2) Tìm hướng mà đạo hàm của f theo hướng đó tại M
0
đạt giá trị nhỏ
nhất.
Tìm giá trị nhỏ nhất này.
1) Hướng cần tìm là hướng của véctơ gradf (M
0
)
Giá trị lớn nhất bằng độ lớn véctơ gradf (M
0
):
2) Hướng cần tìm là ngược hướng của véctơ gradf (M
0
)
2 3
( , , ) 2f x y z xyz xy yz
0
1,1,2M
' ' '
0 0 0 0
( ) ( ), ( ), ( )grad
x y z
f M f M f M f M
0
'
( ) 0
| ( ) |
grad
grad
f M
f f M
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Cho hàm và một điểm
1) Tìm giá trị lớn nhất của đạo hàm theo hướng của f tại M
0
.
Giải.
1) Đạo hàm theo hướng của hàm f tại M
0
là một hàm phụ thuộc vào
hướng của véctơ l =(l
1
, l
2
,l
3
).
Giá trị lớn nhất của đạo hàm theo hướng bằng độ lớn véctơ gradf (M
0
)
2) Tìm giá trị nhỏ nhất của đạo hàm theo hướng của f tại M
0
.
Giá trị lớn nhất đạt được khi lấy đạo hàm theo hướng của véctơ gradf
(M
0
)
( , ) ln( )f x y xyz
0
1, 2, 3M
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Cho hàm và một điểm
Tìm hướng mà đạo hàm của f theo hướng đó tại M
0
có giá trị bằng 1
Giả sử hướng cần tìm là hướng của véctơ đơn vị:
Vậy có hai hướng:
hoặc
2
( , ) sin( )f x y x xy
0
1,0M
2 2
0
( , ), 1l a b a b
0
' ' '
0 0 0
( ) ( ) ( )
l x y
f M f M a f M b
'
2 cos( )
x
f x y xy
'
cos( )
y
f x xy
'
0
( ) 2
x
f M
'
0
( ) 1
y
f M
0
'
0
( ) 2 1
l
f M a b
0 4/5
;
1 3/5
a a
b b
0
(0,1)l
0
(4/5, 3/5)l
điểm đó là theo hướng của véctơ .
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Cho hàm
Tìm tất cả các điểm mà tốc độ thay đổi nhanh nhất của hàm f tại
những
Giả sử điểm cần tìm là M(a,b)
Tốc độ thay đổi nhanh nhất của f tại M là theo hướng của véctơ
gradf(M)
Theo đề: gradf(M) cùng hướng với véctơ i + j = (1,0) + (0,1) = (1,1)
Tập hợp các điểm là nửa đường thẳng.
2 2
( , ) 2 4 .f x y x y x y
i j
' '
( ) ( , ), ( , )grad
x y
f M f a b f a b
(2 2,2 4)a b
(2 2,2 4) (1,1), 0a b t t
1 / 2 1
, 0
2 / 2 2
a t a s
s
b t b s
1) Tìm tốc độ thay đổi của nhiệt độ tại điểm P(2,-1,2) theo hướng đến
điểm (3,-3,3).
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Ví dụ.
Nhiệt độ T tại một điểm (x,y,z) được cho bởi công thức
T tính bằng
0
C; x, y, z tính bằng mét.
2) Tìm hướng mà nhiệt độ thay đổi nhanh nhất tại điểm P(2,-1,2).
3) Tìm giá trị lớn nhất của tốc độ thay đổi tại điểm P(2,-1,2).
2 2 2
3 9
( , , ) 200
x y z
T x y z e
IV. Đạo hàm theo hướng, véctơ Gradient
--------------------------------------------------------------------------------------------------------------------
-------
Mặt phẳng tiếp diện
Mặt cong S có ptrình: F(x,y,z) =
0
P là một điểm thuộc S
Phương trình mặt phẳng
tiếp diện tại P với S:
Pháp véctơ của mặt phẳng tiếp diện chính là vectơ gradf(P)
0 0 0
( , , )gradf x y z
' ' '
0 0 0
( )( ) ( )( ) ( )( ) 0
x y z
F P x x F P y y F P z z
Ví dụ.
Viết phương trình mặt tiếp diện và phương trình của pháp tuyến với
mặt
tại điểm P(-2, 1, -3).
Phương trình mặt tiếp diện
Phương trình pháp tuyến qua P và có VTCP (-1, 2, -2/3):
2 2
2
3
4 9
x z
y
2 2
2
( , , ) 3 0
4 9
x z
F x y z y
' ' '
2
; 2 ;
2 9
x y z
x z
F F y F
2
1( 2) 2( 1) ( 3) 0
3
x y z
3 6 2 18 0x y z
2 1 3
1 2 2/3
x y z
| 1/20
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- -------
có đạo hàm riêng đến cấp n + 1 trong một lân cận của
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- -------
f = f(x,y)
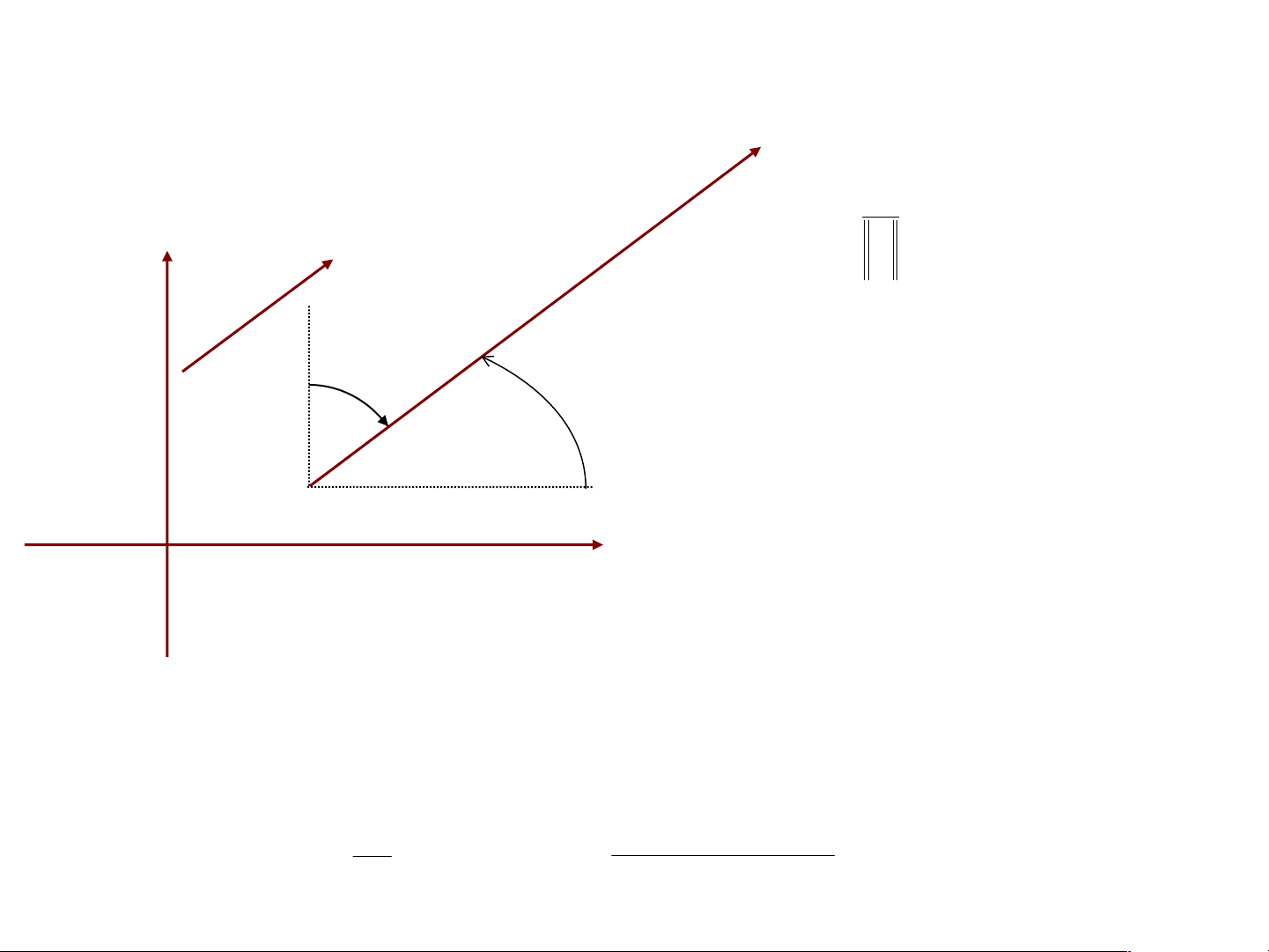
Véctơ đơn vị cùng phương u   u  0
l     1l, 2l u  ( oy 1 u ,u2)
M (x, y) u  0
l  cos,cos    
 ,  là góc tạo bởi u và chiều dương
trục Ox và Oy tương ứng. M0( 0 x , 0 y )  ox
x x t cos
Phương trình tham số của tia M 0  t  0
0M : y  0y tcos 
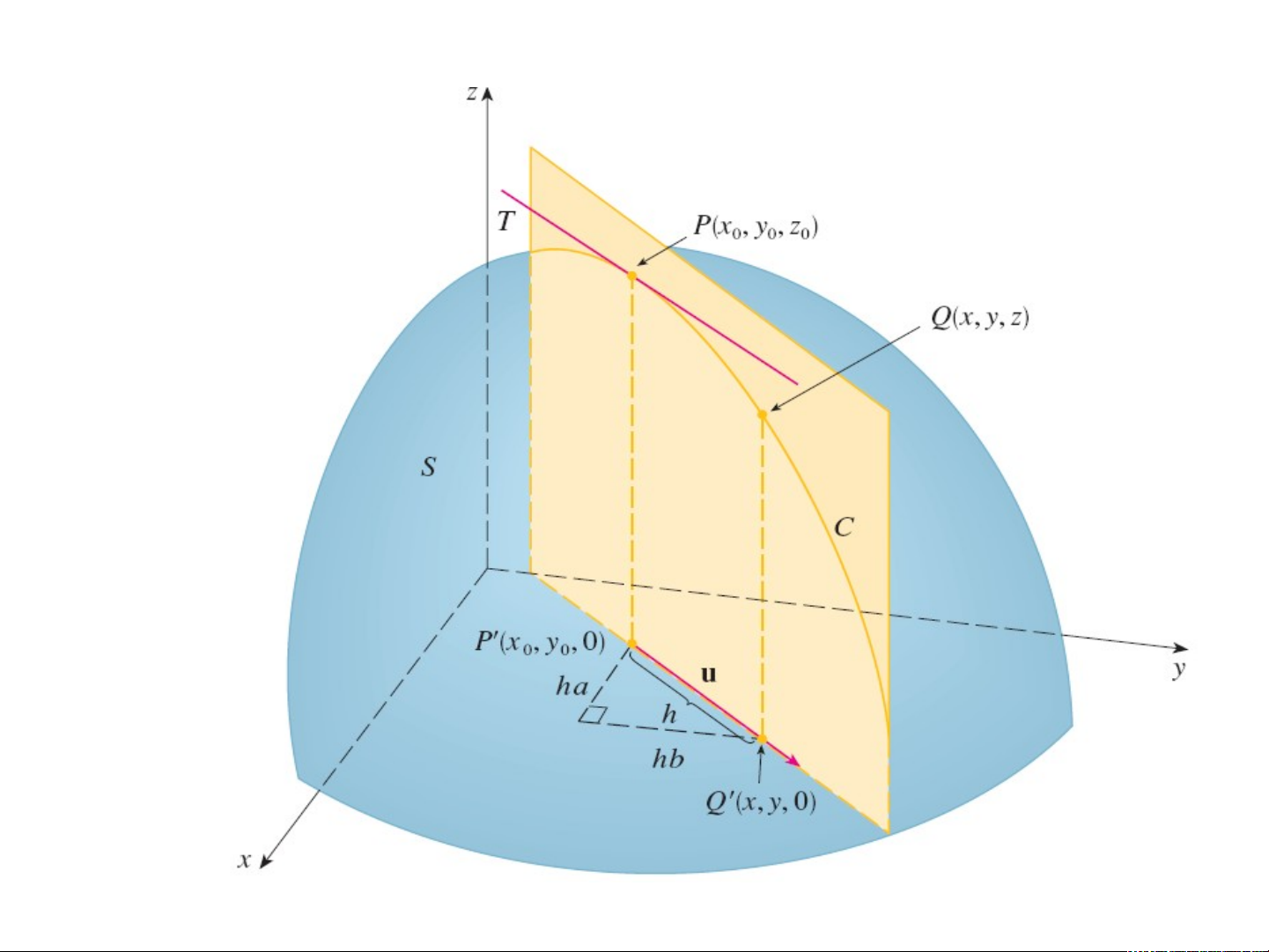
Đạo hàm của hàm f theo hướng véctơ u tại điểm
M 0 là giới hạn (nếu có) ' f(M f
f (M )  f (M0) 0 ) u  (M0)  lim u M M0 MM0
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- 2 2 M '
f (x, y)  f (  0 x , 0y) 0M  (x  0 x )  (y  0 y )  t f (M0)  lim u t 0  t ' f (  0
x t cos, 0y t cos)  f ( 0x, 0y) f (M0)  lim u t 0  t
Đây chính là đạo hàm của hàm f theo biến t ' '
f(M f ' ' ' '
f x f y ' '
fx(x , y )cos  fy(x , y )cos u 0) t x t y t 0 0 0 0 '
f(x y f x y f x y   u 0, 0 )  ' '
x ( 0, 0 ), y ( 0, 0 ),cos ,c s o  
gradf (x , y )   ' ' 0 0 fx( 0x, 0
y ), fy( 0x, 0
y ) véctơ gradient của f tại M0   '
Tích vô hướng của véctơ f(M f x y l u 0 )
grad ( 0, 0), 0 gradient tại M0 với véctơ đơn vị.
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- -------
Tương tự, ta có định nghĩa đạo hàm của f=f(x,y,z) tại M u 0 theo hướng ' ' ' '
f(M f M    f M    f M   u 0 ) x ( 0 ) cos y ( 0) cos z ( 0 ) cos   ' f(M f x y z l u 0 ) grad ( 0, 0, 0), 0  
Trong đó: véctơ đơn vị cùng phương với u là: l0   o c s, o c s, o c s  
 ,  ,  là các góc tạo bởi u và chiều dương trục 0x, 0y và 0z tương ứng. 
Véctơ Gradient của f(x,y,z) tại M là: gradf (M )   ' ' ' 0
fx(M0), fy(M0), fz(M0) 0
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Tìm đạo hàm của f x
y x y 2  x4 y5 ( , ) 3 tại điểm M0(1,1) 
theo hướng của véctơ u  (1, 2)  Giải.  
Véctơ đơn vị cùng phương với u là: 1 2  0 l    ,   o c s, o c s  5 5    ' 2 3 5 f '
x y 12x yfx(1,1)  1  1 ' 4 4 f '  fy(1,1)  13 
y  2xy 15x y ' ' ' f 11 26 (1,1)  fc   fc      3 5 u x (1,1) os y (1,1) os 5 5
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Tìm đạo hàm của f x y x 3
x y y2 ( , ) 3 4 tại điểm M0(1,2)
theo hướng của véctơ tạo với chiều dương trục 0x một góc 300. 
Giải. Véctơ đơn vị là: 0l   o c s, o c s            3 1   ,   
 0l  cos ,cos    , 6 2 6 3 6 3 2 2     ' 2 f '  fx(1,2)  3
x  3x  3y ' f '
y  3x  8yfy(1,2) 13 ' ' ' f 3 3 13  (1,2)  fc   fc     l x (1, 2) os y (1, 2) os 0 2 2
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.  1 3
Tìm đạo hàm của ( , )  a r ct g y f x y
tại điểm M   , x 0 2 2   
theo hướng pháp véctơ của đường tròn x2 + y2 = 2x tại M0.  Giải. 2 2
F(x, y)  x y  2x  0  n   ' ' x F , y
F  2x  2,2y  ( 1  , 3)   1  3 
Véctơ đơn vị là: 0l   , 2 2    ' y f ' 3 x   2 2
fx(M )   x y 0 2 ' x 1 f '  fy(M )  y  2 2 x y 0 2 ' ' ' 3
f (M f M c   f M c   l 0 ) x ( 0 ) os y ( 0 ) os 0 2
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Tìm đạo hàm của f x y z
x 3  xy 2  y z 2 ( , , ) 2 3 tại điểm M0(3,3,1)
theo hướng của véctơ l=(2,1,2).  Giải.  2 1 2 Véctơ đơn vị là:  0
l   , ,  (cos,cos,cos ) 3 3 3    ' 2 2 f '
x  3x  2 yfx(3,3,1)  45 ' 2 f '
y  4xy  3zfy(3,3,1)  39 ' f ' z  6 yzfz(3,3,1) 18 ' ' ' '
f(M f M c   f M c   f M c   55 l 0 ) x ( 0 ) os y ( 0) os z ( 0 ) os
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Tìm đạo hàm của f x y z x 2 ( , , )
 3 y z  4 tại điểm M0(1,2,-1)
theo hướng của véctơ tạo với các trục tọa độ những góc nhọn bằng nhau. 
Giải. Véctơ đơn vị là: 0l  (cos,cos ,cos ) 2 2 2
cos   cos   cos  1 2  3cos  1 1  cos  3 ' f ' x  2xfx(1,2,1)  2 ' f '  fy(1,2, 1  )  3 y  3z ' f ' z  3  yfz(1,2, 1  )  6 ' ' ' ' f 3
 (M f M c   f M c   f M c l 0 ) x ( 0 ) os y ( 0) os z ( 0 ) os   3
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- -------
Chú ý. Cho hàm f=f(x,y,z).
Đạo hàm của f tại M0 theo hướng của véctơ (1,0,0) là: ' ' ' '
f(M f M    f M    f M   '  fx(M ) i 0 ) x ( 0) cos y ( 0 ) cos z ( 0) cos 0
Vậy đạo hàm theo hướng véctơ (1,0,0) tại M là đạo hàm riêng theo x tại đó, 0
nếu đạo hàm riêng theo x tồn tại.
Nếu đạo hàm riêng theo x không tồn tại, thì đạo hàm theo hướng vẫn có thể có.
(vì theo định nghĩa, đạo hàm theo hướng là giới hạn một phía)
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Tìm đạo hàm của f ( x , y , z) |
x |  2 yz tại điểm M0(0,1, 1)
theo hướng của véctơ (1,0,0). 
Giải. Véctơ đơn vị là: 0l  1,0,0
Không tồn tại đạo hàm riêng theo x tại M0.
Tìm đạo hàm của f theo hướng của véctơ (1,0,0) bằng định nghĩa ' f (  0
x t cos, 0
y t cos , 0z t cos )  f ( 0x, 0y,z0) f (0,1,1)  lim i t 0  t '
f (t,1,1)  f (0,1,1) f | t | 2   2 | t | t  (0,1,1)  lim  lim  lim  lim 1 i t 0  t t 0  t t 0  t t 0  t
Lý do: trong định nghĩa đạo hàm theo hướng, M dần đến bên phải của M0.
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- -------
Theo công thức tính đạo hàm đạo hàm theo hướng:     ' f(M f M l
 gradf (M )  l cos u 0 ) grad ( 0), 0 0 0   
 gradf (M0)  0l  gradf (M0) 
Đạo hàm của f tại M gradf (M )
0 đạt giá trị lớn nhất theo hướng của véctơ 0 
Giá trị lớn nhất của đạo hàm theo hướng bằng: gradf ( 0 x , 0y) 
Đạo hàm của f tại M đạt giá trị nhỏ nhất theo hướng ngược vớigradf (M ) 0 0 
Giá trị nhỏ nhất của đạo hàm theo hướng bằng: gradf ( 0 x , 0 y )
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Cho hàm f x y z x
yzx y 2  y z3 ( , , ) 2
và một điểm M0  1,1,2
1) Tìm hướng mà đạo hàm của f theo hướng đó tại M0 đạt giá trị lớn nhất.
Tìm giá trị lớn nhất này.
2) Tìm hướng mà đạo hàm của f theo hướng đó tại M0 đạt giá trị nhỏ nhất.
Tìm giá trị nhỏ nhất này.
Giải. 1) Hướng cần tìm là hướng của véctơ gradf (M )0
gradf(M ) ' ' ' 0
fx(M0), fy(M0), fz(M0) 
Giá trị lớn nhất bằng độ lớn véctơ gradf (M ): 'fgradf M |  gradf (M ) | 0 ( 0) 0
2) Hướng cần tìm là ngược hướng của véctơ gradf (M )0
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Cho hàm f ( x , y )  l n ( x y z) và một điểm M0  1,2, 3  
1) Tìm giá trị lớn nhất của đạo hàm theo hướng của f tại M0.
2) Tìm giá trị nhỏ nhất của đạo hàm theo hướng của f tại M0.
Giải. 1) Đạo hàm theo hướng của hàm f tại M0 là một hàm phụ thuộc vào
hướng của véctơ l =(l1, l ,l 2 3).
Giá trị lớn nhất của đạo hàm theo hướng bằng độ lớn véctơ gradf (M0)
Giá trị lớn nhất đạt được khi lấy đạo hàm theo hướng của véctơ gradf (M )0
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Cho hàm f x yx 2 ( , )  s i
n( xy ) và một điểm M0  1,0
Tìm hướng mà đạo hàm của f theo hướng đó tại M0 có giá trị bằng 1
Giả sử hướng cần tìm là hướng của véctơ đơn vị: 2 2 0
l  (a,b),a b 1 ' ' '
fl (M )  fx(M )a fy(M )b 0 0 0 0 ' f ' ' '
x  2x y cos(xy)  fx (M )  2 f 0
y x cos(xy)  f y (M0 )  1 '
fl (M )  2a b 1 0 0 Vậy có hai hướng:
a  0  a  4/5  ; b 1 b     3/5 0
l  (0,1) hoặc 0l  (4/5, 3  /5)
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Cho hàm f x y
x 2  y 2 ( , )  2 x  4 . y
Tìm tất cả các điểm mà tốc độ thay đổi nhanh nhất của hàm f tại những  
điểm đó là theo hướng của véctơ i j .
Giả sử điểm cần tìm là M(a,b)
Tốc độ thay đổi nhanh nhất của f tại M là theo hướng của véctơ gradf(M)  gradf M   ' ' ( )
fx(a,b), fy(a,b)  (2a  2,2b 4)
Theo đề: gradf(M) cùng hướng với véctơ i + j = (1,0) + (0,1) = (1,1)
a 1 t / 2 a 1 s
(2a  2,2b  4)  t(1,1),t  0     , s  0
b  2  t / 2 b   2  s
Tập hợp các điểm là nửa đường thẳng.
IV. Đạo hàm theo hướng, véctơ Gradient
-------------------------------------------------------------------------------------------------------------------- ------- Ví dụ.
Nhiệt độ T tại một điểm (x,y,z) được cho bởi công thức 2 2 2 3 9 ( , , ) 200 x y z T x y z e    
T tính bằng 0C; x, y, z tính bằng mét.
1) Tìm tốc độ thay đổi của nhiệt độ tại điểm P(2,-1,2) theo hướng đến điểm (3,-3,3).
2) Tìm hướng mà nhiệt độ thay đổi nhanh nhất tại điểm P(2,-1,2).
3) Tìm giá trị lớn nhất của tốc độ thay đổi tại điểm P(2,-1,2).
IV. Đạo hàm theo hướng, véctơ Gradient
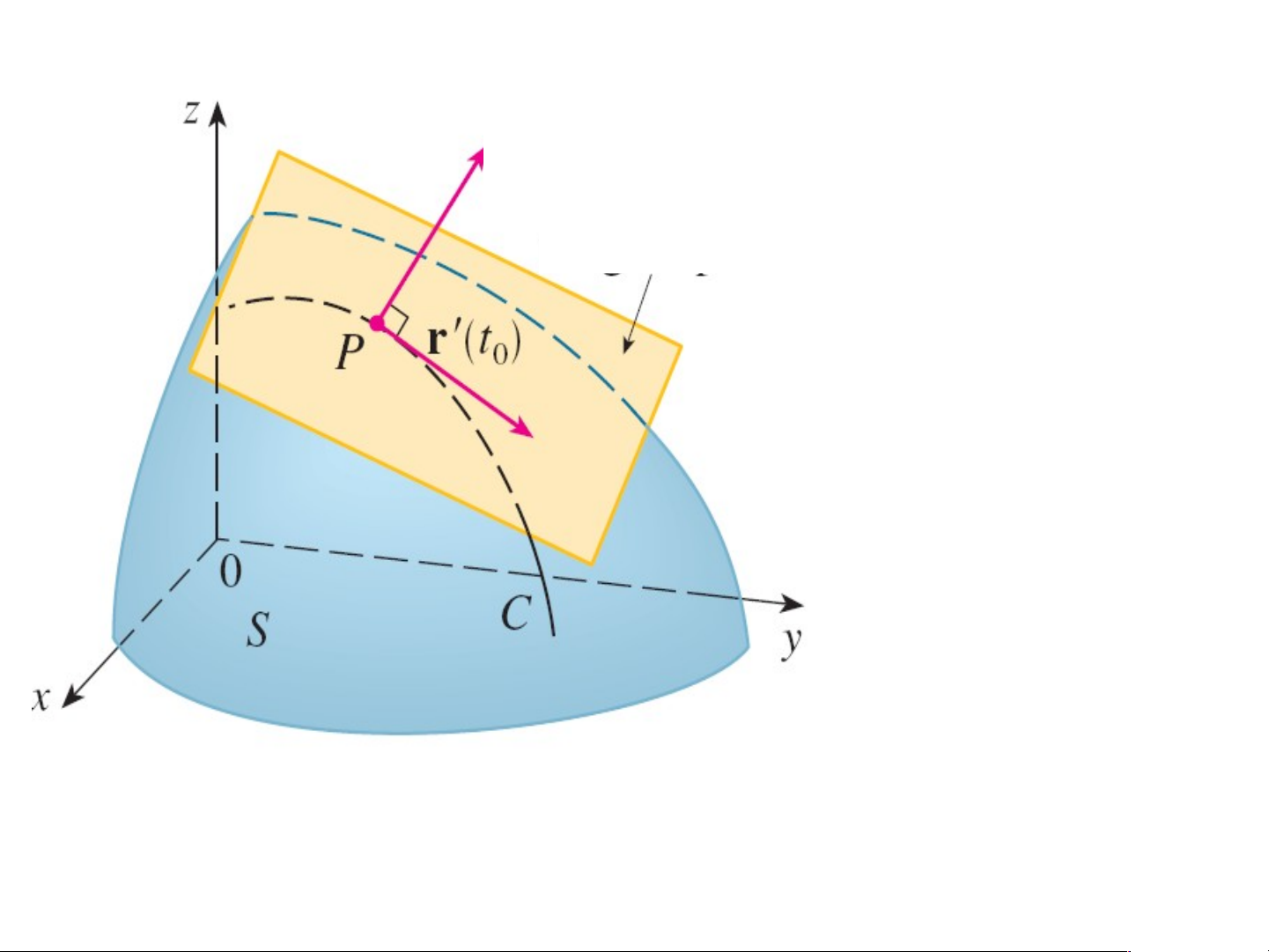
-------------------------------------------------------------------------------------------------------------------- -------  gradf ( 0x, 0 y , z0) Mặt phẳng tiếp diện
Mặt cong S có ptrình: F(x,y,z) = 0 P là một điểm thuộc S Phương trình mặt phẳng tiếp diện tại P với S: ' ' ' x
F (P)(x  0x)  y
F (P)(y  0 y )  z
F (P)(z z0)  0
Pháp véctơ của mặt phẳng tiếp diện chính là vectơ gradf(P) Ví dụ.
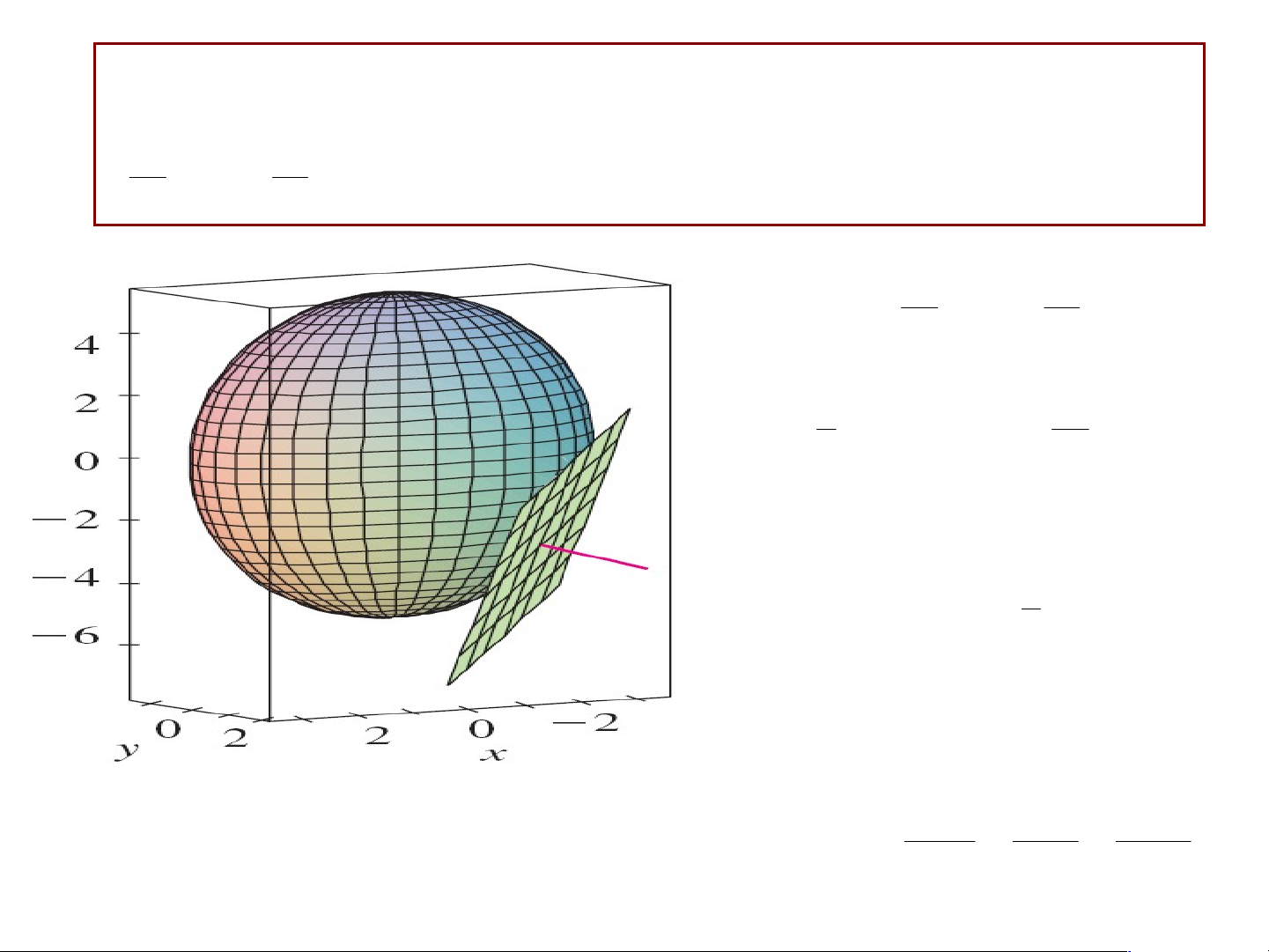
Viết phương trình mặt tiếp diện và phương trình của pháp tuyến với mặt2 2 x 2 zy
 3 tại điểm P(-2, 1, -3). 4 9 2 2 x 2 ( , , ) z F x y z   y   3  0 4 9 ' x ' ' 2z x F  ; y
F  2y;F  2 z 9
Phương trình mặt tiếp diện 2
1(x  2)  2(y 1)  (z  3)  0 3
3x  6y  2z 18  0
Phương trình pháp tuyến qua P và có VTCP (-1, 2, -2/3): x  2 y 1 z  3   1 2 2/3