Đáp án và lời giải chi tiết đề thi chính thức tốt nghiệp THPT 2021 môn Toán

Thứ Tư ngày 07 tháng 07 năm 2021, Bộ Giáo dục và Đào tạo tổ chức kỳ thi tốt nghiệp Trung học Phổ thông môn Toán năm học 2020 – 2021 đợt 1, nhằm làm căn cứ xét tuyển tốt nghiệp bậc Trung học Phổ thông và tuyển sinh vào các trường Đại học – Cao đẳng.

54 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2023

Môn: Toán

Thông tin:

99 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
KỲ THI TỐT NGHIỆP THPT QUỐC GIA
– ĐỢT 1 –
NĂM HỌC 2020 – 2021
Môn: Toán - Mã đề 101
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 90 phút (không kể thời gian phát đề)
LINK NHÓM
:
https://www.facebook.com/groups/1916660125164699
Câu 1. Tập nghiệm của bất phương trình
3 2
x
là
A.
3
;log 2
. B.
3
log 2;
. C.
2
;log 3
. D.
2
log 3;
.
Câu 2. Nếu
4
1
x 3f x d
và
4
1
x 2g x d
thì
4
1
xf x g x d
bằng
A.
1
. B.
5
. C.
5
. D.
1
.
Câu 3. Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
1; 4;0I
và bán kính bằng
3
. Phương trình
của
S
là
A.
2 2
2
1 4 9x y z
. B.
2 2
2
1 4 9x y z
.
C.
2 2
2
1 4 3x y z
. D.
2 2
2
1 4 3x y z
.
Câu 4. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua điểm
3; 1;4M
và có một vectơ chỉ
phương
2;4;5u
. Phương trình của
d
là:
A.
2 3
4
5 4
x t
y t
z t
. B.
3 2
1 4
4 5
x t
y t
z t
. C.
3 2
1 4
4 5
x t
y t
z t
. D.
3 2
1 4
4 5
x t
y t
z t
.
Câu 5. Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 6. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
4 2
2 4 1y x x . B.
3
3 1y x x . C.
4 2
2 4 1y x x . D.
3
3 1y x x .
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 7. Đồ thị hàm số
4 2
4 3y x x cắt trục tung tại điểm có tung độ bằng
A. 0. B. 3. C. 1. D.
3
.
Câu 8. Với
n
là số nguyên dương bất kì,
4n
, công thức nào dưới đây đúng?
A.
4
4 !
!
n
n
A
n
. B.
4
4!
4 !
n
A
n
. C.
4
!
4! 4 !
n
n
A
n
. D.
4
!
4 !
n
n
A
n
.
Câu 9. Phần thực của số phức
5 2z i
bằng
A.
5
. B.
2
. C.
5
. D.
2
.
Câu 10. Trên khoảng
0,
, đạo hàm của hàm số
5
2
y x
là:
A.
7
2
2
'
7
y x . B.
3
2
2
'
5
y x . C.
3
2
5
'
2
y x . D.
3
2
5
'
2
y x
.
Câu 11. Cho hàm số
2
4f x x
. Khẳng định nào dưới đây đúng?
A.
d 2f x x x C
. B.
2
d 4f x x x x C
.
C.
3
d 4
3
x
f x x x C
. D.
3
d 4f x x x x C
.
Câu 12. Trong không gian
Oxyz
, cho điểm
2;3;5A
. Tọa độ của véctơ
OA
là:
A.
2;3;5
. B.
2; 3;5
. C.
2; 3;5
. D.
2; 3; 5
.
Câu 13. Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
1
. B.
5
. C.
3
. D.
1
.
Câu 14. Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trong khoảng nào dưới đây?
A.
0;1
. B.
;0
. C.
0;
. D.
1;1
.
Câu 15. Nghiệm của phương trình
3
log 5 2x
là
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
A.
8
5
x
. B.
9
x
. C.
9
5
x
. D.
8
x
.
Câu 16. Nếu
3
0
d 4
f x x
thì
3
0
3 d
f x x
bằng
A.
36
. B.
12
. C.
3
. D.
4
.
Câu 17. Thể tích của khối lập phương cạnh
5
a
bằng
A.
3
5
a
. B.
3
a
. C.
3
125
a
. D.
3
25
a
.
Câu 18. Tập xác định của hàm số
9
x
y
là
A.
. B.
0;

. C.
\ 0
. D.
0;

.
Câu 19. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
16
S R
. B.
2
4
S R
. C.
2
S R
. D.
2
4
3
S R
.
Câu 20. Tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình:
A.
1
x
. B.
1
x
. C.
2
x
. D.
1
2
x
.
Câu 21. Cho
0
a
và
1
a
, khi đó
4
log
a
a
bằng
A.
4
. B.
1
4
. C.
1
4
. D.
4
.
Câu 22. Cho khối chop có diện tích đáy
2
5
B a
và chiều cao
h a
. Thể tích của khối chóp đã cho
bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5
a
. D.
3
5
3
a
.
Câu 23. Trong không gian
Oxyz
, cho mặt phẳng
:3 2 1 0
P x y z
. Véc tơ nào dưới đây là một
véc tơ pháp tuyến của
P
A.
1
( 3;1;2)
n
. B.
2
(3; 1;2)
n
. C.
3
(3:1;2)
n
. D.
4
(3;1; 2)
n
.
Câu 24. Cho khối hình trụ có bán kính đáy
6
r
và chiều cao
3
h
. Thể tích của khối trụ đã cho bằng
A.
108
. B.
36
. C.
18
. D.
54
.
Câu 25. Cho hai số phức
4 2 , w 3 4
z i i
. Số phức
w
z
bằng
A.
1 6
i
. B.
7 2
i
. C.
7 2
i
. D.
1 6
i
.
Câu 26. Cho cấp số nhân
n
u
có
1
3
u
,và
2
9
u
. Công bội của cấp số nhân bằng
A.
6
. B.
1
3
. C.
3
. D.
6
.
Câu 27. Cho hàm số
( ) 2
x
f x e
. Khẳng định nào dưới đây là đúng ?
A.
2
d
x
f x x e C
. B.
d 2
x
f x x e x C
.
C.
d
x
f x x e C
. D.
d 2
x
f x x e x C
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 28. Trong mặt phẳng tọa độ, điểm
3;4M
là điểm biểu diễn số phức nào dưới đây?
A.
2
3 4z i . B.
3
3 4z i . C.
4
3 4z i . D.
1
3 4z i .
Câu 29. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1a
có đồ thị như hình bên). Mệnh đề nào
dưới đây đúng?
A.
' 0, 1y x
. B.
' 0, 1y x
.
C.
' 0,y x
. D.
' 0,y x
.
Câu 30. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đó và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng
A.
7
44
. B.
2
7
. C.
1
22
. D.
5
12
.
Câu 31. Trên đoạn
0;3
, hàm số
3
3y x x đạt giá trị lớn nhất tại điểm
A.
0x
. B.
3x
. C.
1x
. D.
2x
.
Câu 32. Trong không gian
,Oxyz
cho điểm
1;3;2M
và mặt phẳng
: 2 4z 1 0.P x y
Đường
thẳng đi qua
M
và vuông góc với
P
có phương trình là
A.
1 3 2
1 2 1
x y z
. B.
1 3 2
1 2 1
x y z
.
C.
1 3 2
1 2 4
x y z
. D.
1 3 2
1 2 4
x y z
.
Câu 33. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
,B
2AB a
và SA vuông góc
với mặt phẳng đáy. Tính khoảng cách từ
C
đến mặt phẳng
( )SAB
bằng
A.
2a
. B.
2a
. C.
a
. D.
2 2a
.
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1;0;0A
,
4;1;2B
. Mặt phẳng đi qua A
và vuông góc với AB có phương trình là
A.
3 2 17 0x y z
. B.
3 2 3 0x y z
.
C.
5 2 5 0x y z
. D.
5 2 25 0x y z
.
Câu 35: Cho số phức
5 4iz i
. Số phức liên hợp của
z
là
A.
4 5z i
. B.
4 5z i
. C.
4 5z i
. D.
4 5z i
Câu 36: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng ( tham khảo hình bên). Góc giữa
đường thẳng
AA
và
BC
bằng
A.
0
30
. B.
0
90
. C.
0
45
. D.
0
60
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
Câu 37. Với mọi
,
a b
thỏa mãn
3
2 2
log log 6
a b
, khẳng định nào dưới đây đúng:
A.
3
64
a b
. B.
3
36
a b
. C.
3
64
a b
. D.
3
36
a b
.
Câu 38. Nếu
2
0
5
f x dx
thì
2
0
2 1
f x dx
bằng:
A.
8
. B.
9
. C.
10
. D.
12.
Câu 39. Cho hàm số
2
2 5, 1
3 4, 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2
F
. Giá trị của
1 2 2
F F bằng
A.
27
. B.
29
. C.
12
. D.
33
.
Câu 40. Có bao nhiêu số nguyên
x
thảo mãn
2
3
3 9 log 25 3 0
x x
x
?
A.
24
. B. Vô số. C.
26
. D.
25
.
Câu 41. Cho hàm số bậc ba
( )
y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt
của phương trình
( ( )) 1
f f x
là
A.
9
. B.
7
. C.
3
. D.
6
.
Câu 42: Cắt hình nón
( )
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
30
,
o
ta
được thiết diện là tam giác đều cạnh
4
a
. Diện tích xung quanh của
( )
N
bằng
A.
2
8 7 .
a
B.
2
4 13 .
a
C.
2
4 7 .
a
D.
2
4 13 .
a
Câu 43. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực). Có bao
nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
7
z
?
A.
2.
B.
3.
C.
1.
D.
4.
Câu 44. Xét các số phức
z
,
w
thỏa mãn
1
z
và
2
w
. Khi
6 8
z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
221
5
. B.
5
. C.
3
. D.
29
5
.
Câu 45: Trong không gian
Oxyz
, cho đường thẳng
1 2
:
1 1 1
x y z
d
và mặt phẳng
: 2 4 0
P x y z
. Hình chiếu vuông góc của
d
lên
P
là đường thẳng có phương trình:
A.
1 2
2 1 4
x y z
. B.
1 2
3 2 1
x y z
. C.
1 2
2 1 4
x y z
. D.
1 2
3 2 1
x y z
.
Câu 46. Cho hàm số
3 2
f x x ax bx c
với
, ,
a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
3
và
6
. Diện tích hình phẳng giới hạn
bởi các đường
6
f x
y
g x
và
1
y
bằng
A.
2ln 3
. B.
ln3
. C.
ln18
. D.
2ln 2
.
Câu 47. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;3
3
x
thỏa mãn
2
3 9
27 1 27
x xy x
xy
?
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
27
. B.
9
. C.
11
. D.
12
.
Câu 48. Cho khối hộp chữ nhật
. ' ' ' '
ABCD A B C D
có đáy là hình vuông,
2 ,
BD a
góc giữa hai mặt
phẳng
'
A BD
và
ABCD
bằng
0
30
. Thể tích khối hộp chữ nhật đã cho bằng
A.
3
6 3
a
. B.
3
2 3
9
a
. C.
3
2 3
a
. D.
3
2 3
3
a
.
Câu 49. Trong không gian
Ox
yz
, cho hai điểm
1; 3; 4
A
và
2;1;2
B . Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
2
MN
. Giá trị lớn nhất của
AM BN
bằng
A.
3 5
. B.
61
. C.
13
. D.
53
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
7 9 ,f x x x x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
5
g x f x x m
có ít nhất 3 điểm cực trị?
A.
6
. B.
7
. C.
5
. D.
4
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
BẢNG ĐÁP ÁN
1.A 2.C 3.B 4.D 5.D 6.A 7.D 8.D 9.A 10.C
11.C 12.A 13.C 14.A 15.C 16.B 17.C 18.A 19.B 20.A
21.B 22.D 23.B 24.A 25.B 26.C 27.B 28.B 29.B 30.A
31.C 32.D 33.B 34.B 35.A 36.C 37.A 38.A 39.A 40.C
41.B 42.D 43.B 44.D 45.C 46.D 47.C 48.D 49.D 50.A
LỜI GIẢI CHI TIẾT
Câu 1: Tập nghiệm của bất phương trình
3 2
x
là
A.
3
;log 2
 . B.
3
log 2;

. C.
2
;log 3
 . D.
2
log 3;

.
Lời giải
GVSB: Nguyễn Tấn Linh; GVPB: Dương Ju-i
Chọn A
Ta có
3
3 2 log 2
x
x
Vậy
3
S ;log 2
 .
Câu 2: Nếu
4
1
x 3
f x d
và
4
1
x 2
g x d
thì
4
1
x
f x g x d
bằng
A.
1
. B.
5
. C.
5
. D.
1
.
Lời giải
GVSB: Nguyễn Tấn Linh; GVPB: Dương Ju-i
Chọn C
Ta có
4 4 4
1 1 1
x x x 3 2 5
f x g x d f x d g x d
.
Câu 3: Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
1; 4;0
I và bán kính bằng
3
. Phương trình
của
S
là
A.
2 2
2
1 4 9
x y z
. B.
2 2
2
1 4 9
x y z
.
C.
2 2
2
1 4 3
x y z
. D.
2 2
2
1 4 3
x y z
.
Lời giải
GVSB: Nguyễn Tấn Linh; GVPB: Dương Ju-i
Chọn B
Mặt cầu
S
có tâm
1; 4;0
I có bán kính
3
có phương trình là
2 2
2
1 4 9
x y z
.
Câu 4: Trong không gian
Oxyz
, cho đường thẳng
d
đi qua điểm
3; 1;4
M
và có một vectơ chỉ
phương
2;4;5
u
. Phương trình của
d
là:
A.
2 3
4
5 4
x t
y t
z t
. B.
3 2
1 4
4 5
x t
y t
z t
. C.
3 2
1 4
4 5
x t
y t
z t
. D.
3 2
1 4
4 5
x t
y t
z t
.
Lời giải
GVSB: Trần Xuyến; GVPB: Dương Ju-i
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn D
Đường thẳng
d
đi qua điểm
3; 1;4M
và có một vectơ chỉ phương
2;4;5u
. Phương
trình của
d
là
3 2
1
4
4 5
x t
y t
z t
.
C
âu 5: Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
GVSB: Trần Xuyến; GVPB: Dương Ju-i
Chọn D
Dựa vào bảng xét dấu,
f x
đổi dấu khi qua các điểm
2; 1;1;4x
.
Vậy số điểm cực trị của hàm số đã cho là
4
.
Câu 6: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
4 2
2 4 1y x x . B.
3
3 1y x x . C.
4 2
2 4 1y x x . D.
3
3 1y x x .
Lời giải
GVSB: Trần Xuyến; GVPB: Dương Ju-i
Chọn A
Dựa vào dáng đồ thị, đây là hàm trùng phương nên loại câu B và D.
Đồ thị có bề lõm hướng xuống nên chọn câu A.
Câu 7. Đồ thị hàm số
4 2
4 3y x x cắt trục tung tại điểm có tung độ bằng
A. 0. B. 3. C. 1. D.
3
.
Lời giải
GVSB: Nam Đinh Ngọc; GVPB: Dương Ju-i
Chọn D
Đồ thị hàm số
4 2
4 3y x x sẽ cắt trục tung tại điểm có hoành độ
0x
Từ đó ta được
3y
.
Câu 8. Với
n
là số nguyên dương bất kì,
4n
, công thức nào dưới đây đúng?
A.
4
4 !
!
n
n
A
n
. B.
4
4!
4 !
n
A
n
. C.
4
!
4! 4 !
n
n
A
n
. D.
4
!
4 !
n
n
A
n
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
GVSB: Nam Đinh Ngọc; GVPB: Dương Ju-i
Chọn D
Ta có:
!
!
k
n
n
A
n k
4
!
4 !
n
n
A
n
Câu 9. Phần thực của số phức
5 2z i
bằng
A.
5
. B.
2
. C.
5
. D.
2
.
Lời giải
GVSB: Nam Đinh Ngọc; GVPB: Dương Ju-i
Chọn A
Số phức
z a bi
có phần thực là a do đó
5a
.
Câu 10. Trên khoảng
0,
, đạo hàm của hàm số
5
2
y x
là:
A.
7
2
2
'
7
y x . B.
3
2
2
'
5
y x . C.
3
2
5
'
2
y x . D.
3
2
5
'
2
y x
.
Lời giải
Chọn C
Ta có:
5
2
y x
3
2
5
'
2
y x
Câu 11. Cho hàm số
2
4f x x
. Khẳng định nào dưới đây đúng?
A.
d 2f x x x C
. B.
2
d 4f x x x x C
.
C.
3
d 4
3
x
f x x x C
. D.
3
d 4f x x x x C
.
Lời giải
Chọn C
Ta có:
2
4f x x
3
d 4
3
x
f x x x C
Câu 12. Trong không gian
Oxyz
, cho điểm
2;3;5A
. Tọa độ của véctơ
OA
là:
A.
2;3;5
. B.
2; 3;5
. C.
2; 3;5
. D.
2; 3; 5
.
Lời giải
Chọn A
Ta có:
OA
; ; 2;3;5
A A A
x y z
Câu 13. Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
A.
1
. B.
5
. C.
3
. D.
1
.
Lời giải
GVSB:Mai Thị Phương Lan GVPB:Châu Vũ
Chọn C
Ta có:
f x
đổi dấu từ
sang
khi đi qua nghiệm
1x
nên hàm số đã cho đạt cực
tiểu tại
1.x
Vậy hàm số đã cho có giá trị cực tiểu là
3.y
Câu 14. Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trong khoảng nào dưới đây?
A.
0;1
. B.
;0
. C.
0;
. D.
1;1
.
Lời giải
GVSB:Mai Thị Phương Lan; GVPB:Châu Vũ
Chọn A
Ta có: đồ thị hàm số đi xuống trên khoảng
0;1
nên hàm số nghịch biến trên khoảng
0;1
.
Câu 15. Nghiệm của phương trình
3
log 5 2x
là
A.
8
5
x
. B.
9x
. C.
9
5
x
. D.
8x
.
Lời giải
GVSB:Mai Thị Phương Lan; GVPB:Châu Vũ
Chọn C
TXĐ:
0;D 
.
Ta có:
2
3
9
log 5 2 5 3
5
x x x
.
Câu 16. Nếu
3
0
d 4f x x
thì
3
0
3 df x x
bằng
A.
36
. B.
12
. C.
3
. D.
4
.
Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Kim Liên
Chọn B
Ta có:
3
0
3 df x x
3
0
3 d 12f x x
.
Câu 17. Thể tích của khối lập phương cạnh
5a
bằng
A.
3
5a
. B.
3
a
. C.
3
125a
. D.
3
25a
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 11
Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB:Kim Liên
Chọn C
Thể tích của khối lập phương cạnh bằng
5
a
là:
3
3
5 125
V a a
Câu 18. Tập xác định của hàm số
9
x
y
là
A.
. B.
0;

. C.
\ 0
. D.
0;

.
Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB:Kim Liên
Chọn A
Vì hàm số
9
x
y
là hàm số mũ nên có tập xác định là tập
.
Câu 19. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
16
S R
. B.
2
4
S R
. C.
2
S R
. D.
2
4
3
S R
.
Lời giải
GVSB: Nguyen Nhan; GVPB: Kim Liên
Chọn B
Diện tích
S
của mặt cầu bán kính
R
là
2
4
S R
.
Câu 20. Tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình:
A.
1
x
. B.
1
x
. C.
2
x
. D.
1
2
x
.
Lời giải
GVSB: Nguyen Nhan; GVPB: Kim Liên
Chọn A
Ta có:
1 1
2 1
lim lim
1
x x
x
y
x

,
1 1
2 1
lim lim
1
x x
x
y
x

.
Do đó tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình
1
x
.
Câu 21. Cho
0
a
và
1
a
, khi đó
4
log
a
a
bằng
A.
4
. B.
1
4
. C.
1
4
. D.
4
.
Lời giải
GVSB: Nguyen Nhan; GVPB: Kim Liên
Chọn B
Ta có:
1
4
4
1
log log
4
a a
a a
.
Câu 22. Cho khối chóp có diện tích đáy
2
5
B a
và chiều cao
h a
. Thể tích của khối chóp đã cho
bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5
a
. D.
3
5
3
a
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
Lời giải
GVSB: Ngô Quang Minh; GVPB: Hoàng Dương
Chọn D
Thể tích của khối chóp đã cho bằng:
2 3
1 1 5
. 5 .
3 3 3
V B h a a a
.
Câu 23. Trong không gian
Oxyz
, cho mặt phẳng
:3 2 1 0
P x y z
. Véctơ nào dưới đây là một
véctơ pháp tuyến của
P
?
A.
1
( 3;1;2)
n
. B.
2
(3; 1;2)
n
. C.
3
(3;1;2)
n
. D.
4
(3;1; 2)
n
.
Lời giải
GVSB: Ngô Quang Minh; GVPB: Hoàng Dương
Chọn B
Véc tơ pháp tuyến của
P
là:
2
(3; 1;2)
n
.
Câu 24. Cho khối hình trụ có bán kính đáy
6
r
và chiều cao
3
h
. Thể tích của khối trụ đã cho bằng
A.
108
. B.
36
. C.
18
. D.
54
.
Lời giải
GVSB: Ngô Quang Minh; GVPB: Hoàng Dương
Chọn A
Thể tích của khối trụ đã cho là
2 2
.6 .3 108
V r h
.
Câu 25. Cho hai số phức
4 2 , w 3 4
z i i
. Số phức
w
z
bằng
A.
1 6
i
. B.
7 2
i
. C.
7 2
i
. D.
1 6
i
.
Lời giải
GVSB: Chau nguyen minh; GVPB:
Chọn B
Ta có:
w=4+2i+3- 4i=7 - 2i
z
.
Câu 26. Cho cấp số nhân
n
u
có
1
3
u
,và
2
9
u
. Công bội của cấp số nhân bằng
A.
6
. B.
1
3
. C.
3
. D.
6
.
Lời giải
GVSB: Chau nguyen minh; GVPB:
Chọn C
Ta có:
2
2 1
1
9
3.
3
u
u u q q
u
Câu 27. Cho hàm số
( ) 2
x
f x e
. Khẳng định nào dưới đây là đúng ?
A.
2
d
x
f x x e C
. B.
d 2
x
f x x e x C
.
C.
d
x
f x x e C
. D.
d 2
x
f x x e x C
.
Lời giải
GVSB: Chau nguyen minh; GVPB:
Chọn B
Ta có:
d 2 d 2
x x
f x x e x e x C
Câu 28. Trong mặt phẳng tọa độ, điểm
3;4
M
là điểm biểu diễn số phức nào dưới đây?
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 13
A.
2
3 4z i
. B.
3
3 4z i
. C.
4
3 4z i
. D.
1
3 4z i
.
Lời giải
GVSB: Vu Ngoc Anh; GVPB:
Chọn B
Ta có điểm
3;4M
là điểm biểu diễn cho số phức
3 4z a bi i
.
Câu 29. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1a
có đồ thị như hình bên). Mệnh đề nào
dưới đây đúng?
A.
' 0, 1y x
. B.
' 0, 1y x
. C.
' 0,y x
. D.
' 0,y x
.
Lời giải
GVSB:Vu Ngoc Anh; GVPB:
Chọn B
Ta có :
1
x a
y
x
2
1
' 0, 1
1
a
y x
x
(Dựa theo hướng của đồ thị)
Do
1a
nên dấu “
” không xảy ra.
Hàm đơn điệu không phụ thuộc vào
a
.
Câu 30. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đó và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng
A.
7
44
. B.
2
7
. C.
1
22
. D.
5
12
.
Lời giải
GVSB: Vu Ngoc Anh; GVPB:
Chọn A
Không gian mẫu
3
12
220n C
Gọi A là biến cố: “Lấy được 3 quả màu xanh”
3
7
35
35 7
220 44
A
A
n C
n
P A
n
Câu 31. Trên đoạn
0;3
, hàm số
3
3y x x
đạt giá trị lớn nhất tại điểm
A.
0x
. B.
3x
. C.
1x
. D.
2x
.
Lời giải
GVSB: Nguyễn Hồng Hiên; GVPB: Minh Văn Nguyễn
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn C
Tập xác định:
.
2
3 3y x
2
1 0;3
0 3 3 0
1 0;3
x
y x
x
Ta có
0 0; 1 2; 3 18.y y y
Vậy
0;3
max 1 2y y
.
Câu 32. Trong không gian
,Oxyz
cho điểm
1;3;2M
và mặt phẳng
: 2 4z 1 0.P x y
Đường
thẳng đi qua
M
và vuông góc với
P
có phương trình là
A.
1 3 2
1 2 1
x y z
. B.
1 3 2
1 2 1
x y z
.
C.
1 3 2
1 2 4
x y z
. D.
1 3 2
1 2 4
x y z
.
Lời giải
GVSB: Nguyễn Hồng Hiên; GVPB: Minh Văn Nguyễn
Chọn D
: 2 4z 1 0P x y
có vectơ pháp tuyến
1; 2;4n
.
Đường thẳng đi qua
M
và vuông góc với
P
nhận
1; 2;4n
làm vectơ chỉ phương nên có
phương trình
1 3 2
1 2 4
x y z
.
Câu 33. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
,B
2AB a
và SA vuông góc
với mặt phẳng đáy. Tính khoảng cách từ
C
đến mặt phẳng
( )SAB
bằng
A.
2a
. B.
2a
. C.
a
. D.
2 2a
.
Lời giải
GVSB: Thành đặng; GVPB: Lê Thị Phương
Chọn B
Vì
SA ABC
suy ra
CB SA
(1).
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 15
Tam giác
ABC
vuông tại
,B
nên
CB AB
(2).
Từ (1) và (2), ta suy ra
CB SAB
nên khoảng cách từ
C
đến mặt phẳng
( )SAB
bằng CB.
Mà tam giác
ABC
vuông cân tại
,B
suy ra
2AB BC a
Vậy
( ; ( ))
2 .
C SAB
d CB a
Câu 34. Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1;0;0A
,
4;1;2B
. Mặt phẳng đi qua A
và vuông góc với AB có phương trình là
A.
3 2 17 0x y z
. B.
3 2 3 0x y z
.
C.
5 2 5 0x y z
. D.
5 2 25 0x y z
.
Lời giải
GVSB: Thành đặng; GVPB: Lê Thị Phương
Chọn B
Ta có
3;1;2AB
Gọi
Q
là mặt phẳng đi qua
1;0;0A
và vuông góc với
AB
suy ra mặt phẳng
Q
nhận
vecto
3;1;2AB

làm véc tơ pháp tuyến. Vậy phương trình mặt phẳng
Q
cần tìm có dạng:
3( 1) 2 0 3 2 3 0x y z x y z
Câu 35: Cho số phức
5 4iz i
. Số phức liên hợp của
z
là
A.
4 5z i
. B.
4 5z i
. C.
4 5z i
. D.
4 5z i
Lời giải
Chọn A
Ta có
5 4
5 4 4 5
i
iz i z i
i
. Suy ra
4 5z i
.
Câu 36: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng ( tham khảo hình bên). Góc giữa
đường thẳng
AA
và
BC
bằng
A.
0
30
. B.
0
90
. C.
0
45
. D.
0
60
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn C
Vì
/ /AA BB
nên
, ',AA BC BB BC B BC
Ta có:
0
tan 1 45
B C
B BC B BC
BB
Câu 37. Với mọi
,a b
thỏa mãn
3
2 2
log log 6a b
, khẳng định nào dưới đây đúng:
A.
3
64a b
. B.
3
36a b
. C.
3
64a b
. D.
3
36a b
.
Lời giải
GVSB: Vũ Tuấn; GVPB:
Chọn A
Ta có
3 3 6 3
2 2
log log 6 2 64a b a b a b
.
Câu 38. Nếu
2
0
5f x dx
thì
2
0
2 1f x dx
bằng:
A.
8
. B.
9
. C.
10
. D.
12.
Lời giải
GVSB: Vũ Tuấn; GVPB: …
Chọn A
Ta có
2 2 2
0 0 0
2 1 2 2.5 2 8f x dx f x dx dx
.
Câu 39. Cho hàm số
2
2 5 khi 1
3 4 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
27
. B.
29
. C.
12
. D.
33
.
Lời giải
GVSB: Phạm Tính; GVPB:
Chọn A
Ta có
2
1
2
3
2
5 1
2 5 khi 1
3 4 khi 1
4 1
F x x x C x
x x
f x
x x
F x x x C x
.
Vì
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
nên
3
2
2 4 2C F x x x
.
Vì
F x
liên tục trên
nên
F x
liên tục tại
1x
nên:
1 1
1 1
lim lim 1 6 7 1
x x
F x F x F C C
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 17
Vậy ta có
2
3
5 2 1
1 2 2 3 2.15 27
4 1 1
F x x x x
F F
F x x x x
.
Câu 40. Có bao nhiêu số nguyên
x
thảo mãn
2
3
3 9 log 25 3 0
x x
x
?
A.
24
. B. Vô số. C.
26
. D.
25
.
Lời giải
GVSB: Phạm Tính; GVPB:
Chọn C
Điều kiện:
25 0 25x x
.
Ta giải các phương trình:
2
2
0
3 9 2
2
x x
x
x x
x
.
3
log 25 3 25 27 2x x x
.
Ta có bảng xét dấu sau:
Dựa vào bẳng xét dấu, để
2
3
3 9 log 25 3 0
x x
x
thì ta có
25 0 24 0
2 2
x
x x
x x

có 26 giá trị nguyên của
x
thỏa mãn.
Câu 41. Cho hàm số bậc ba
( )y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình
( ( )) 1f f x
là:
A.
9
. B.
7
. C.
3
. D.
6
.
Lời giải
GVSB: Quách Ngọc Giang, GVPB: Trần Đại Nghĩa
Chọn B
Ta có:
( ) 0
(
( )) 1 ( ) ( 1)
( ) (1< 2)
f x
f f x f x a a
f x b b
Ta dựa vào đồ thị:
P
hương trình
( ) 0f x
có 3 nghiệm.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Phương trình
( )f x a
có 1 nghiệm.
Phương trình
( )f x b có 3 nghiệm.
Vậy phương trình
( ( )) 1f f x
có 7 nghiệm phân biệt.
Câu 42. Cắt hình nón
( )N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc 30 ,
o
ta
được thiết diện là tam giác đều cạnh
4a
. Diện tích xung quanh của
( )N
bằng
A.
2
8 7 .a
B.
2
4 13 .a
C.
2
8 13 .a
D.
2
4 7 .a
Lời giải
Chọn D
Gọi hình nón
( )N
có đỉnh
S
, đường tròn đáy có tâm
O
, bán kính
r
. Thiết diện đã cho là tam
giác
SAB
cạnh
4a
và
I
là trung điểm của
AB
. Khi đó
,OI AB SI AB
nên góc giữa
( )SAB
và mặt phẳng đáy là
60
o
SIO .
2 3SI a nên .cos60 3.
o
OI SI a
Tam giác
OIA
vuông tại
I
có
2 2
7.r OA OI AI a
Vậy hình nón
( )N
có diện tích xung quanh bằng
2
4 7 .
xq
S rl a
Câu 43. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0z m z m
(
m
là tham số thực). Có bao
nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z thỏa mãn
0
7z
?
A.
2.
B.
3.
C.
1.
D.
4.
Lời giải
GVSB: Lê Mẫn; GVPB: Đồng Khoa Văn
Chọn B
Phương trình
2 2
2 1 0z m z m
.
Ta có
2 2
' ( 1) 2 1m m m
Trường hợp 1: Nếu
1
2 1 0
2
m m
thì phương trình có nghiệm thực nên
0
0
0
7
7
7
z
z
z
.
Với
0
7z thay vào phương trình ta được
2 2
7 14
7 2 1 .7 0
7 14
m
m m
m
(thoả
1
2
m
) .
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 19
Với
0
7
z
thay vào phương trình ta được
2 2 2
7 2 1 .7 0 14 63 0
m m m m
phương trình vô nghiệm .
Trường hợp 1: Nếu
1
2 1 0
2
m m
thì phương trình có hai nghiệm phức là
1 2 1
1 2 1
z m i m
z m i m
.
Khi đó
2
0
7
7 1 2 1 49
7
m
z m m
m
.
Kết hợp với
1
2
m
ta được
7
m
.
Vậy có 3 giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 44. Xét các số phức
z
,
w
thỏa mãn
1
z
và
2
w
. Khi
6 8
z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
221
5
. B.
5
. C.
3
. D.
29
5
.
Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Thị Thùy Nương
Chọn D
Đặt
z a bi
,
w c di
với
a
,
b
,
c
, d
.
Theo giả thiết
2 2
2 2
1
1
*
2
4
z
a b
w
c d
.
Ta có
6 8 6 8 6 8
z iw i a bi i c di i a d b c i
2 2 2 2
6 8 6 8
a d b c a d b c
.
Khi đó
2 2 2 2
2 2 2 2
6 8 6 8 10
a d b c a b d c
2 2 2 2
6 8 3 10 6 8 7
a d b c a d b c
.
Dấu “=” xảy ra khi
3
5
a
,
4
5
b
,
8
5
c
,
6
5
d
thỏa mãn (*).
Vậy
6 8
z iw i
đạt giá trị nhỏ nhất bằng
7
.
Khi đó
3 4
5 5
z i
,
8 6
5 5
w i
. Suy ra
2 29
1
5 5
z w i z w .
Câu 45: Trong không gian
Oxyz
, cho đường thẳng
1 2
:
1 1 1
x y z
d
và mặt phẳng
: 2 4 0
P x y z
. Hình chiếu vuông góc của
d
lên
P
là đường thẳng có phương trình:
A.
1 2
2 1 4
x y z
. B.
1 2
3 2 1
x y z
. C.
1 2
2 1 4
x y z
. D.
1 2
3 2 1
x y z
.
GVSB: Phạm Tuấn; GVPB: Trần Tú
Lời giải
Chọn C
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Ta có:
d P A
0;1;2
A .
Lấy
2;3;0
M d
.
Gọi
là đường thẳng qua
M
và vuông góc với
P
khi đó
2 3
:
1 2 1
x y z
.
Gọi
H P
2 ;3 2 ;
H t t t
.
Mặt khác
H P
2
2 2 3 2 4 0
3
t t t t
4 5 2
; ;
3 3 3
H
4 2 8
; ;
3 3 3
AH

.
Gọi
d
là hình chiếu của
d
lên
P
khi đó
d
đi qua
A
và có một VTCP
2;1; 4
u
1 2
:
2 1 4
x y z
d
.
Câu 46. Cho hàm số
3 2
f x x ax bx c
với
, ,
a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
3
và
6
. Diện tích hình phẳng giới hạn
bởi các đường
6
f x
y
g x
và
1
y
bằng
A.
2ln 3
. B.
ln3
. C.
ln18
. D.
2ln 2
.
Lời giải
GVSB: Nguyễn Hữu Chung Kiên; GVPB:Hoàng Ngọc Hùng
Chọn D
Ta có
3 2
3 2 6 2
g x f x f x f x x a x b a x a b c
.
Suy ra:
2
3 2 3 2 6
g x x a x b a
.
Xét phương trình
1
2
2
1 6 3 2 3 2 6 0 0
6
x x
f x
g x f x x a x a b g x
x x
g x
Ta có diện tích bằng
2 2 2
2
1
1 1 1
2 1
6
1 d d d ln 6
6 6 6
ln 6 ln 6 ln 4 2ln 2
x x x
x
x
x x x
f x f x g x g x
S x x x g x
g x g x g x
g x g x
.
Câu 47. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;3
3
x
thỏa mãn
2
3 9
27 1 27
x xy x
xy
?
A.
27
. B.
9
. C.
11
. D.
12
.
Lời giải
GVSB: …; GVPB: …
Chọn C
Xét
2
3 9
27 1
x x xy
f x xy
và áp dụng
1 1
x
a x a
.
Suy ra:
2 2
26 3 9 1 84 25 234 1 0, 10
f x x x xy xy x xy x y
.
Do đó
9
y
.
2
3 9 2
0 27 1 3 9 0
x x
y x x
: loại.
3 1 0
y xy VP
: loại.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 21
1, 2y y
: thỏa mãn.
Xét
0y
có
3
3 27 3 1 0, 0
y
f y y
.
Và
8
1
3 1 0, 1;2;3;...;9
3 3
y
y
f y
.
2; 1;1;2;3;4;5;6;7;8;9y
.
Câu 48. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình vuông,
2 ,BD a
góc giữa hai mặt
phẳng
'A BD
và
ABCD
bằng
0
30
. Thể tích khối hộp chữ nhật đã cho bằng
A.
3
6 3a . B.
3
2 3
9
a
. C.
3
2 3a . D.
3
2 3
3
a
.
Lời giải
GVSB: Phan Khắc Hy; GVPB:
Chọn D
Gọi
.O AC BD
Diện tích hình vuông
ABCD
là
2 2
2 2
2
2 .
2 2
ABCD
BD a
S AB a
Ta có:
0
' , ' ; 30 .A BD ABCD A O AO
Xét tam giác
'A OA
vuông tại
,A
ta có:
0
3
' tan 30 . .
3
A A AO a
Thể tích khối hộp chữ nhật đã cho là
2 3
3 2 3
' . .2 .
3 3
ABCD
V A A S a a a
Câu 49. Trong không gian
Oxyz
, cho hai điểm
1 3 4A ; ;
và
2 1 2B ; ;
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
2MN
. Giá trị lớn nhất của
AM BN
bằng
A.
3 5 . B.
61
. C.
13
. D.
53
.
Lời giải
Chọn D
O
C'
D'
B'
A
B
D
C
A'
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
Dễ thấy
A
,
B
nằm hai phía của mặt phẳng
Oxy
. Gọi
A'
đối xứng với
A
qua mặt phẳng
Oxy
suy ra
1 3 4A' ; ;
,
AM A M
.
Gọi
E
và
F
lần lượt là hình chiếu của
A'
và
B
lên mặt phẳng
Oxy
, ta có
1 3 0E ; ;
,
2 1 0F ; ;
. Do đó
3 4 0EF ; ;
5EF
.
Dựng
BK NM
suy ra
BN KM
.
Vậy
AM BN A M KM A K
.
Ta đi tìm giá trị lớn nhất của
A K
.
Do
MN
nằm trên mặt phẳng
Oxy
,
//BK MN
nên
//BK Oxy
. Suy ra
K
nằm trên mặt
phẳng chứa
B
, song song với
mp Oxy
. Mà
2BK MN
nên quỹ tích
K
là đường tròn
;2B
.
Kẻ
2BH AA A H
,
Có
2 2
2 2 2
4 2 4 5 2 53A K A H HK HB
. Dấu « = » khi
B
nằm giữa
,H K
.
Vậy GTLN của
AM BN
là
53
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
7 9 ,f x x x x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
5g x f x x m có ít nhất 3 điểm cực trị?
A.
6
. B.
7
. C.
5
. D.
4
.
Lời giải
Chọn A
Ta có:
2
7 9 ,f x x x x
.
7
0 3
3
x
f x x
x
.
3 3 3
5 5 . 5g x f x x m x x m f x x m
2 3
3
3
3 5 5
5
5
x x x
f x x m
x x
.
Nhận thấy:
0x
là 1 điểm cực trị của hàm số..
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 23
Cho
3 3
3 3 3
3 3
5 7 5 7
5 0 5 3 5 3
5 3 5 3
x x m x x m
f x x m x x m x x m
x x m x x m
.
Đặt
3 2
5 3 5 0,h x x x h x x x
.
Bảng biến thiên:
Từ bảng biến thiên suy ra: Yêu cầu bài toán tương đương với
7 0 7m m
1;2;3;4;5;6m
.
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Kú THI TN THPT N¡M 2021
M· §Ò: 102
TRAO ĐỔI & CHIA SẺ KIẾN THỨC THÔNG MINH DO HỌC TẬP MÀ CÓ THIÊN TÀI DO TÍCH LŨY MÀ NÊN
Câu 1. Trên khoảng
( )
0;+∞
, đạo hàm của hàm số
5
4
yx=
là
A.
9
4
4
9
x
. B.
1
4
4
5
x
. C.
1
4
5
4
x
. D.
1
4
5
4
x
−
.
Câu 2. Cho khối chóp có diện tích đáy
2
3Ba=
và chiều cao
ha=
. Thể tích của khối chóp đã cho
bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
1
3
a
. D.
3
a
.
Câu 3. Nếu
( )
4
1
6fx x=
∫
d
và
( )
4
1
5gx x= −
∫
d
thì
( ) ( )
4
1
fx gx−


∫
bằng
A.
1−
. B.
11−
. C.
1
. D.
11
.
Câu 4. Tập xác định của hàm số
7=
x
y
là
A.
{
}
\0
. B.
[
)
0;+∞
. C.
( )
0;+∞
. D.
.
Câu 5. Cho hàm số
(
)
=y fx
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho là
A.
3
. B.
1.−
C.
5−
. D.
1
.
Câu 6. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
4
π
=SR
. B.
2
16
π
=SR
C.
2
4
3
π
=SR
. D.
2
π
=SR
.
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua
( )
2;2;1M
và có một vectơ chỉ phương
( )
5;2; 3u = −
. Phương trình của
d
là:
A.
25
22
13
xt
yt
zt
= +
= +
=−−
. B.
25
22
13
xt
yt
zt
= +
= +
= +
. C.
25
22
13
xt
yt
zt
= +
= +
= −
. D.
52
22
3
xt
yt
zt
= +
= +
=−+
.
Câu 8. Cho hàm số
( )
y fx=
có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên
khoảng nào dưới đây?
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
A.
( )
1;1−
. B.
( )
;0−∞
. C.
( )
0;1
. D.
( )
0;+∞
.
Câu 9. Với
n
là số nguyên dương bất kì
5n ≥
, công thức nào dưới đây đúng?
A.
( )
5
!
5! 5 !
n
n
A
n
=
−
. B.
( )
5
5!
5!
n
A
n
=
−
. C.
( )
5
!
5!
n
n
A
n
=
−
. D.
( )
5
5!
!
n
n
A
n
−
=
.
Câu 10. Thể tích của khối lập phương cạnh
4a
bằng
A.
3
64a
. B.
3
32a
. C.
3
16a
. D.
3
8
a
.
Câu 11. Cho hàm số
( )
2
3fx x= +
. Khẳng định nào sau đây đúng?
A.
( )
2
d3fx x x xC=++
∫
. B.
( )
3
d3
3
x
fx x xC= ++
∫
.
C.
( )
3
d3
fx x x xC=++
∫
. D.
(
)
d2fx x xC
= +
∫
.
Câu 12. Trên mặt phẳng tọa độ, điểm
( )
3;2M −
là điểm biểu diễn của số phức nào dưới đây?
A.
3
32zi= −
. B.
4
32
zi= +
. C.
1
32
zi=−−
. D.
2
32zi=−+
.
Câu 13. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 5 3 0P x yz
− + +−=
. Véctơ nào dưới đây là một
véctơ pháp tuyến của
( )
P
?
A.
(
)
2
2;5;1n = −
B.
( )
1
2;5;1n =
C.
( )
4
2;5; 1n = −
D.
( )
3
2; 5;1n = −
.
Câu 14. Trong không gian
Oxyz
, cho điểm
( )
4; 1; 3A −
. Tọa độ vectơ
OA

là
A.
( )
4;1; 3−
B.
( )
4; 1; 3−
C.
( )
4;1; 3−−
D.
( )
4;1; 3
.
Câu 15. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
31yx x=−+
. B.
42
241y xx=−+ +
.
C.
3
31yxx=−+ +
. D.
42
241yx x=−+
.
Câu 16. Cho cấp số nhân
( )
n
u
với
1
3=u
và
2
12=u
. Công bội của cấp số nhân đã cho bằng
A.
9
. B.
9−
. C.
1
4
. D.
4
.
Câu 17. Cho
0a >
và
1a ≠
khi đó
3
log
a
a
bằng
A.
3−
. B.
1
3
. C.
1
3
−
. D.
3
.
Câu 18. Đồ thị của hàm số
42
23yx x=−− +
cắt trục tung tại điểm có tung độ bằng
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 19. Cho hai số phức
52
zi= +
và
w14i= −
. Số phức
wz +
bằng
A.
6 2.i+
B.
4 6.i+
C.
6 2.i−
D.
4 6.i−−
Câu 20. Cho hàm số
( )
1
x
fx e= +
. Khẳng định nào dưới đây đúng?
A.
( )
1
.
x
f x dx e C
−
= +
∫
B.
(
)
.
x
f x dx e x C= −+
∫
C.
( )
.
x
f x dx e x C= ++
∫
D.
( )
.
x
f x dx e C= +
∫
Câu 21. Cho hàm số
( )
y fx=
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
5.
B.
3.
C.
2.
D.
4.
Câu 22. Nếu
( )
3
0
d3fx x=
∫
thì
( )
3
0
2dfx x
∫
bằng
A.
3
. B.
18
. C.
2
. D.
6
.
Câu 23. Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
+
=
−
là đường thẳng có phương trình
A.
1x = −
. B.
2x
= −
. C.
2x =
. D.
1
x =
.
Câu 24. Trong không gian
Oxyz
, cho mặt cầu
( )
S
có tâm
( )
0; 2;1I −
và bán kính bằng
2
. Phương trình
của
( )
S
là
A.
( ) ( )
22
2
2 12xy z++ +− =
. B.
( ) ( )
22
2
2 12xy z+− ++ =
.
C.
( ) ( )
22
2
2 14xy z++ ++ =
. D.
( ) ( )
22
2
2 14xy z++ +− =
.
Câu 25. Phần thực của số phức
62zi= −
bằng
A.
2−
. B.
2
. C.
6
. D.
6−
.
Câu 26. Tập nghiệm của bất phương trình
25
x
<
là
A.
( )
2
5;log−∞
. B.
( )
2
log 5;+∞
. C.
( )
5
;log 2−∞
. D.
( )
5
log 2;+∞
.
Câu 27. Nghiệm của phương trình
( )
5
log 3 2x =
là
A.
25x =
. B.
32
3
x =
. C.
32x =
. D.
25
3
x =
.
Câu 28. Cho khối trụ có bán kính đáy bằng
4
và chiều cao
3h =
. Thể tích của khối trụ đã cho bằng
A.
16
π
. B.
48
π
. C.
36
π
. D.
12
π
.
Câu 29. Cho hình lăng trụ đứng
.ABC A B C
′′′
có tất cả các cạnh bằng nhau (tham khảo hình bên).
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Góc giữa hai đường thẳng
AA
′
và
BC
′
bằng
A.
0
90
. B.
0
45
. C.
0
30
. D.
0
60
.
Câu 30. Trên không gian
Oxyz
, cho hai điểm
( )
0;0;1A
và
(
)
2;1;3B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 11 0xy z
++ − =
. B.
2 2 20xy z++ −=
.
C.
2 4 40xy z++ −=
. D.
2 4 17 0xy z++ − =
.
Câu 31. Từ một hộp chứa
10
quả bóng gồm 4 quả màu đỏ và
6
quả màu xanh, lấy ngẫu nhiên đồng
thời
3
quả. Xác suất để lấy được
3
quả màu xanh bằng
A.
1
6
. B.
1
30
. C.
3
5
. D.
2
5
.
Câu 32. Cho số phức
z
thỏa mãn
65iz i= +
. Số phức liên hợp của
z
là
A.
56zi= −
. B.
56zi=−+
. C.
56zi
= +
. D.
56zi=−−
.
Câu 33. Biết hàm số
1
xa
y
x
+
=
+
(
a
là số thực cho trước,
1a ≠−
) có đồ thị như hình bên. Mệnh đề nào
dưới đây là đúng?
A.
0yx
′
< ∀∈
. B.
01yx
′
> ∀ ≠−
. C.
01yx
′
< ∀ ≠−
. D.
0yx
′
> ∀∈
.
Câu 34. Trong không gian
Oxyz
, cho điểm
( )
2;1; 1M −
và mặt phẳng
( )
: 3 2 1 0.Px y z− + +=
Đường
thẳng đi qua
M
và vuông góc với
( )
P
có phương trình là:
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
A.
211
1 31
x yz− −+
= =
−
. B.
211
1 32
x yz
− −+
= =
−
.
C.
2 11
1 31
x yz+ +−
= =
−
. D.
2 11
1 32
x yz+ +−
= =
−
.
Câu 35. Trên đoạn
[ ]
2;1−
, hàm số
32
31=−−yx x
đạt giá trị lớn nhất tại điểm
A.
2= −x
. B.
0=x
. C.
1= −x
. D.
1=x
.
Câu 36. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
C
,
3AC a=
và
SA
vuông góc với
mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
( )
SAC
bằng
A.
3
2
a
. B.
32
2
a
. C.
3a
. D.
32a
.
Câu 37. Nếu
(
)
2
0
dx 3
fx
=
∫
thì
( )
2
0
2 1 dxfx

−
∫
bằng
A.
6
. B.
4
. C.
8
. D.
5
.
Câu 38. Với mọi
,ab
thỏa mãn
3
22
log log 8ab+=
. Khẳng định nào dưới đây đúng?
A.
3
64
ab+=
. B.
3
256
ab
=
. C.
3
64ab=
. D.
3
256ab+=
.
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
( )
(
)
2
2
3 9 log 30 5 0
xx
x− + −≤


?
A.
30.
B. Vô số. C.
31.
D.
29.
Câu 40. Cho hàm số
( )
2
21 1
32 1
x khi x
fx
x khi x
−≥
=
−<
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
( )
02F
=
. Giá trị của
( ) ( )
122FF−+
bằng
A.
9
. B.
15
. C.
11
. D.
6
.
Câu 41. Cho hàm số bậc ba
(
)
y fx=
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt
của phương trình
( )
( )
1ffx =
là
A.
9
. B.
7
. C.
3
. D.
6
.
Câu 42. Xét các số phức
,zw
thỏa mãn
1z =
và
2w =
. Khi
68z iw i+ +−
đạt giá trị nhỏ nhất,
zw−
bằng
A.
5
. B.
221
5
. C.
3
. D.
29
5
.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Câu 43. Cho hàm số
( )
32
f x x ax bx c=+ ++
với
a
,
b
,
c
là các số thực. Biết hàm số
( ) ( ) ( ) ( )
gxfxfxfx
′ ′′
=++
có hai giá trị cực trị là
4−
và
2
. Diện tích hình phẳng giới hạn
bởi các đường
( )
( )
6
fx
y
gx
=
+
và
1y =
bằng
A.
2ln 2
. B.
ln 6
. C.
3ln 2
. D.
ln 2
.
Câu 44. Cho khối hộp chữ nhật
.ABCD A B C D
′′′′
có đáy là hình vuông,
4
BD a=
, góc giữa hai mặt
phẳng
( )
A BD
′
và
( )
ABCD
bằng
30
°
. Thể tích của khối hộp chữ nhật bằng
A.
3
16 3
9
a
. B.
3
48 3a
. C.
3
16 3
3
a
. D.
3
16 3a
.
Câu 45. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;4
3
x

∈


thỏa mãn
( )
2
3 12
27 1 .27
x xy x
xy
+
= +
?
A.
27
. B.
15
. C.
12
. D.
14
.
Câu 46. Trong không gian
Oxyz
, cho đường thẳng
11
:
112
+−
= =
x yz
d
và mặt phẳng
( )
:2 3 0P xyz+−+=
. Hình chiếu vuông góc của
d
trên
( )
P
là đường thẳng có phương trình
A.
11
4 5 13
x yz+−
= =
. B.
11
3 51
x yz+−
= =
−
. C.
11
3 51
x yz−+
= =
−
. D.
11
4 5 13
x yz−+
= =
.
Câu 47. Cắt hình nón
(
)
ℵ
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
60°
ta
được thiết diện là tam giác đều có cạnh
2a
. Diện tích xung quanh của
( )
ℵ
bằng
A.
2
7 a
π
. B.
2
13 a
π
. C.
2
27a
π
. D.
2
2 13 a
π
.
Câu 48. Trên tập hợp số phức, xét phương trình
( )
22
21 0z m zm− ++=
(
m
là tham số thực). Có bao
nhiêu giá trị của tham số
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
5
z =
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 49. Cho hàm số
( )
y fx=
có đạo hàm
( ) ( )
( )
2
8 9,fx x x x
¢
= - - "Î
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
( )
( )
3
6gx f x x m= ++
có ít nhất 3 điểm cực trị?
A.
5
. B.
8
. C.
6
. D.
7
.
Câu 50. Trong không gian, cho hai điểm
( )
1; 3; 2−A
và
( )
2;1; 3
−−B
. Xét hai điểm
M
và
N
thay đổi
thuộc mặt phẳng
( )
Oxy
sao cho
1=MN
. Giá trị lớn nhất của
−AM BN
bằng
A.
17
. B.
41
. C.
37
. D.
61
.
BẢNG ĐÁP ÁN
1.C
2.D
3.D
4.D
5.A
6.A
7.C
8.C
9.C
10.A
11.B
12.D
13.A
14.A
15.D
16.D
17.B
18.D
19.C
20.C
21.D
22.D
23.C
24.D
25.C
26.A
27.D
28.B
29.B
30.B
31.A
32.C
33.C
34.B
35.B
36.C
37.B
38.B
39.C
40.A
41.B
42.B
43.A
44.C
45.D
46.A
47.A
48.B
49.D
50.C
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
LỜI GIẢI CHI TIẾT MÃ ĐỀ 102
Câu 1. Trên khoảng
( )
0;+∞
, đạo hàm của hàm số
5
4
yx=
là
A.
9
4
4
9
x
. B.
1
4
4
5
x
. C.
1
4
5
4
x
. D.
1
4
5
4
x
−
.
Lời giải
GVSB: Thanh Hoa; GVPB: Nguyễn Ngọc Tuấn
Chọn C
51
44
5
4
xx
′

=


.
Câu 2. Cho khối chóp có diện tích đáy
2
3Ba
=
và chiều cao
ha
=
. Thể tích của khói chóp đã cho
bằng
A.
3
3
2
a
. B.
3
3a
. C.
3
1
3
a
. D.
3
a
.
Lời giải
GVSB: Thanh Hoa; GVPB: Nguyễn Ngọc Tuấn
Chọn D
Thể tích của khối chóp đã cho bằng
23
11
. .3 .
33
V Bh a a a= = =
.
Câu 3. Nếu
( )
4
1
6fx x=
∫
d
và
( )
4
1
5gx x= −
∫
d
thì
( ) ( )
4
1
fx gx−


∫
bằng
A.
1
−
. B.
11−
. C.
1
. D.
11
.
Lời giải
GVSB: Thanh Hoa; GVPB: Nguyễn Ngọc Tuấn
Chọn D
( ) ( ) ( ) ( ) ( )
4 44
1 11
6 5 11ddfx gx fx x gx x− = − = −− =


∫ ∫∫
.
Câu 4. Tập xác định của hàm số
7=
x
y
là
A.
{ }
\0
. B.
[
)
0;+∞
. C.
( )
0;+∞
. D.
.
Lời giải
GVSB: Thành Huy; GVPB: Nguyễn Ngọc Tuấn
Chọn D
Câu 5. Cho hàm số
( )
=y fx
có bảng biến thiên như sau
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Giá trị cực đại của hàm số đã cho là
A.
3
. B.
1.−
C.
5−
. D.
1
.
Lời giải
GVSB: Thành Huy; GVPB: Nguyễn Ngọc Tuấn
Chọn A
Dựa vào bảng biến thiên, giá trị cực đại của hàm số là
( )
13
= −=yf
.
Câu 6. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
4
π
=SR
. B.
2
16
π
=SR
C.
2
4
3
π
=
SR
. D.
2
π
=SR
.
Lời giải
GVSB: Thành Huy; GVPB: Nguyễn Ngọc Tuấn
Chọn A
Công thức diện tích mặt cầu:
2
4
π
=
SR
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua
( )
2;2;1M
và có một vectơ chỉ phương
( )
5;2; 3u = −
. Phương trình của
d
là:
A.
25
22
13
xt
yt
zt
= +
= +
=−−
. B.
25
22
13
xt
yt
zt
= +
= +
= +
. C.
25
22
13
xt
yt
zt
= +
= +
= −
. D.
52
22
3
xt
yt
zt
= +
= +
=−+
.
Lời giải
GVSB: Tuấn Minh; GVPB:Tấn Hậu
Chọn C
Phương trình của
d
đi qua
( )
2;2;1M
và có một vectơ chỉ phương
( )
5;2; 3u = −
là:
25
22
13
xt
yt
zt
= +
= +
= −
Câu 8. Cho hàm số
( )
y fx=
có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên
khoảng nào dưới đây?
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
A.
( )
1;1−
. B.
( )
;0−∞
. C.
( )
0;1
. D.
( )
0;+∞
.
GVSB: Tuấn Minh; GVPB:Tấn Hậu
Lời giải
Chọn C
Nhìn đồ thị ta thấy hàm số đã cho đồng biến trên
( )
0;1
.
Câu 9. Với
n
là số nguyên dương bất kì
5n ≥
, công thức nào dưới đây đúng?
A.
( )
5
!
5! 5 !
n
n
A
n
=
−
. B.
( )
5
5!
5!
n
A
n
=
−
. C.
( )
5
!
5!
n
n
A
n
=
−
. D.
( )
5
5!
!
n
n
A
n
−
=
.
GVSB: Tuấn Minh; GVPB:Tấn Hậu
Lời giải
Chọn C
Ta có:
( )
5
!
5!
n
n
A
n
=
−
.
Câu 10. Thể tích của khối lập phương cạnh
4a
bằng
A.
3
64a
. B.
3
32a
. C.
3
16a
. D.
3
8a
.
GVSB: Tuấn Minh; GVPB:Tấn Hậu
Lời giải
Chọn A
Thể tích của khối lập phương cạnh
4a
là
(
)
3
3
4 64Va a
= =
.
Câu 11. Cho hàm số
( )
2
3fx x= +
. Khẳng định nào sau đây đúng?
A.
( )
2
d3fx x x xC
=++
∫
. B.
( )
3
d3
3
x
fx x xC=++
∫
.
C.
( )
3
d3fx x x xC=++
∫
. D.
(
)
d2fx x xC= +
∫
.
GVSB: Tuấn Minh; GVPB:Tấn Hậu
Lời giải
Chọn B
( )
( )
3
2
d 3d 3
3
x
fx x x x xC= + = ++
∫∫
.
Câu 12. Trên mặt phẳng tọa độ, điểm
( )
3;2M −
là điểm biểu diễn của số phức nào dưới đây?
A.
3
32zi= −
. B.
4
32zi= +
. C.
1
32zi=−−
. D.
2
32zi=−+
.
GVSB: Tuấn Minh; GVPB:Tấn Hậu
Lời giải
Chọn D
Trên mặt phẳng tọa độ, điểm
( )
3;2M −
là điểm biểu diễn của số phức
2
32zi=−+
.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Câu 13. Trong không gian
Oxyz
, cho mặt phẳng
( )
:2 5 3 0P x yz− + +−=
. Véctơ nào dưới đây là một
véctơ pháp tuyến của
( )
P
?
A.
( )
2
2;5;1n = −
B.
( )
1
2;5;1n =
C.
( )
4
2;5; 1n = −
D.
( )
3
2; 5;1n = −
Lời giải
GVSB: Huỳnh Thanh Liêm; GVPB:Nguyễn Thị Hường
Chọn A
Ta có
( )
:2 5 3 0P x yz− + +−=⇒
VTPT là
(
)
2
2;5;1
n
= −
.
Câu 14. Trong không gian
Oxyz
, cho điểm
( )
4; 1; 3A −
. Tọa độ vectơ
OA

là
A.
( )
4;1; 3−
B.
( )
4; 1; 3−
C.
( )
4;1; 3−−
D.
( )
4;1; 3
Lời giải
GVSB: Huỳnh Thanh Liêm; GVPB:Nguyễn Thị Hường
Chọn B
Ta có
( )
4; 1; 3OA = −

.
Câu 15. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
31yx x=−+
. B.
42
241y xx=−+ +
.
C.
3
31yxx=−+ +
. D.
42
241yx x=−+
.
Lời giải
GVSB: Huynh Thanh Liem; GVPB: Nguyễn Thị Hường
Chọn D
Đây là đồ thị hàm số bậc
4
với hệ số
0a >
.
Câu 16. Cho cấp số nhân
( )
n
u
với
1
3=u
và
2
12=u
. Công bội của cấp số nhân đã cho bằng
A.
9
. B.
9−
. C.
1
4
. D.
4
.
Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB: Nguyễn Thị Hường
Chọn D
Ta có
21
12
.4
3
= ⇒= =u uq q
.
Câu 17. Cho
0a
>
và
1a ≠
khi đó
3
log
a
a
bằng
A.
3−
. B.
1
3
. C.
1
3
−
. D.
3
.
Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB: Nguyễn Thị Hường
Chọn B
3
11
log log
33
aa
aa= =
.
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Câu 18. Đồ thị của hàm số
42
23
yx x
=−− +
cắt trục tung tại điểm có tung độ bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB: Nguyễn Thị Hường
Chọn D
Giả sử
(
)
42
23
=−− +yx x C
Gọi
( ) ( )
00 0 0
; 03∩ = ⇒=⇒=C Oy M x y x y
.
Vậy đồ thị của hàm số
42
23yx x=−− +
cắt trục tung tại điểm có tung độ bằng
3
.
Câu 19. Cho hai số phức
52zi
= +
và
w14i= −
. Số phức
wz +
bằng
A.
6 2.i+
B.
4 6.i+
C.
6 2.i−
D.
4 6.i−−
Lời giải
GVSB: Văn Tuân; GVPB: Hà Thị Mai
Chọn C
Ta có :
( ) ( )
w 52 14 62z iii+ = + +− =−
.
Câu 20. Cho hàm số
( )
1
x
fx e= +
. Khẳng định nào dưới đây đúng?
A.
( )
1
.
x
f x dx e C
−
= +
∫
B.
( )
.
x
f x dx e x C= −+
∫
C.
(
)
.
x
f x dx e x C
= ++
∫
D.
( )
.
x
f x dx e C= +
∫
Lời giải
GVSB: Văn Tuân; GVPB: Hà Thị Mai
Chọn C
Ta có :
( )
( )
1.
xx
f x dx e dx e x C= + =++
∫∫
Câu 21. Cho hàm số
( )
y fx=
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
5.
B.
3.
C.
2.
D.
4.
Lời giải
GVSB: Văn Tuân; GVPB: Hà Thị Mai
Chọn D
Dựa vào bảng xét dấu suy ra đạo hàm của hàm
( )
y fx=
đổi dấu 4 lần nên hàm số đã cho có
4 điểm cực trị.
Câu 22. Nếu
( )
3
0
d3fx x=
∫
thì
( )
3
0
2dfx x
∫
bằng
A.
3
. B.
18
. C.
2
. D.
6
.
Lời giải
GVSB: Ngọc Thanh; GVPB:Hà Thị Mai
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Chọn D
( )
( )
33
00
2 d 2 d 2.3 6
fx x fx x
= = =
∫∫
.
Câu 23. Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
+
=
−
là đường thẳng có phương trình
A.
1x = −
. B.
2
x
= −
. C.
2x =
. D.
1x =
.
GVSB: Ngọc Thanh; GVPB:Hà Thị Mai
Lời giải
Chọn C
Ta có:
22
1
lim lim
2
xx
x
y
x
++
→→
+
= = +∞
−
(hoặc
22
1
lim lim
2
xx
x
y
x
−−
→→
+
= = −∞
−
).
Vậy
2x =
là tiệm cận đứng của đồ thị hàm số.
Câu 24. Trong không gian
Oxyz
, cho mặt cầu
( )
S
có tâm
( )
0; 2;1I −
và bán kính bằng
2
. Phương trình
của
( )
S
là
A.
( ) ( )
22
2
2 12xy z++ +− =
. B.
( ) ( )
22
2
2 12xy z+− ++ =
.
C.
( ) ( )
22
2
2 14xy z++ ++ =
. D.
( ) ( )
22
2
2 14xy z++ +− =
.
GVSB: Ngọc Thanh; GVPB:Hà Thị Mai
Lời giải
Chọn D
Mặt cầu
( )
S
có tâm
( )
0; 2;1I −
và bán kính bằng
2
có phương trình là
( ) ( )
22
2
2 14xy z++ +− =
.
Câu 25. Phần thực của số phức
62
zi
= −
bằng
A.
2−
. B.
2
. C.
6
. D.
6−
.
Lời giải
GVSB: Chí Tính; GVPB:Thanh Bui
Chọn C
Ta có:
62zi= −
có phần thực là 6.
Câu 26. Tập nghiệm của bất phương trình
25
x
<
là
A.
( )
2
5;log−∞
. B.
( )
2
log 5;+∞
. C.
( )
5
;log 2−∞
. D.
( )
5
log 2;+∞
.
Lời giải
GVSB: Chí Tính; GVPB:Thanh Bui
Chọn A
Ta có:
25
x
<
2
log 5x⇔<
Vậy tập nghiệm
( )
2
5;logS = −∞
.
Câu 27. Nghiệm của phương trình
( )
5
log 3 2x =
là
A.
25x =
. B.
32
3
x =
. C.
32x =
. D.
25
3
x =
.
Lời giải
GVSB: Chí Tính; GVPB:Thanh Bui
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Chọn D
Điều kiện:
0x
>
.
Với điều kiện phương trình đã cho tương đương
2
3 5 25x = =
25
3
x⇔=
.
Câu 28. Cho khối trụ có bán kính đáy bằng
4
và chiều cao
3h =
. Thể tích của khối trụ đã cho bằng
A.
16
π
. B.
48
π
. C.
36
π
. D.
12
π
.
GVSB: Thanh Sang; GVPB:Thanh Bui
Lời giải
Chọn B
Thể tích của khối trụ là
22
.4 .3 48V rh
ππ π
= = =
.
Câu 29. Cho hình lăng trụ đứng
.ABC A B C
′′′
có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng
AA
′
và
BC
′
bằng
A.
0
90
. B.
0
45
. C.
0
30
. D.
0
60
.
GVSB: Thanh Sang; GVPB:Thanh Bui
Lời giải
Chọn B
Ta có:
//CAA C
′′
nên:
( ) ( )
,,AA BC CC BC
′′ ′′
⇒=
Mặt khác tam giác
BCC
′
vuông tại
C
′
có
CC B C
′ ′′
=
nên là tam giác vuông cân.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Vậy góc giữa hai đường thẳng
AA
′
và
BC
′
bằng
0
45
.
Câu 30. Trên không gian
Oxyz
, cho hai điểm
( )
0;0;1A
và
( )
2;1;3B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 11 0
xy z
++ − =
. B.
2 2 20xy z++ −=
.
C.
2 4 40xy z++ −=
. D.
2 4 17 0xy z++ − =
.
Lời giải
GVSB: Vương Gia; GVPB:Dung Chang
Chọn B
Ta có:
( )
2;1;2AB =

.
Mặt phẳng đi qua
( )
0;0;1
A
và vuông góc với
AB
nên nhận
( )
2;1;2AB =

làm vectơ pháp
tuyến
Phương trình mặt phẳng là:
( ) ( ) ( )
2 0 1 0 2 1 0 2 2 20x y z xy z−+ −+ −=⇔ ++ −=
.
Câu 31. Từ một hộp chứa
10
quả bóng gồm 4 quả màu đỏ và
6
quả màu xanh, lấy ngẫu nhiên đồng
thời
3
quả. Xác suất để lấy được
3
quả màu xanh bằng
A.
1
6
. B.
1
30
. C.
3
5
. D.
2
5
.
Lời giải
GVSB: Nguyễn Thị Hải Yến; GVPB:Dung Chang
Chọn A
Lấy ngẫu nhiên đồng thời 3 quả cầu từ 10 quả bóng đã cho có
3
10
C
cách.
Lấy được
3
quả màu xanh từ
6
quả màu xanh đã cho có
3
6
C
cách.
Vậy xác suất để lấy được
3
quả màu xanh là
3
6
3
10
1
6
C
P
C
= =
.
Câu 32. Cho số phức
z
thỏa mãn
65iz i= +
. Số phức liên hợp của
z
là
A.
56
zi= −
. B.
56
zi=−+
. C.
56zi= +
. D.
56
zi=−−
.
GVSB: Luyen Duong; GVPB: Dung Chang
Lời giải
Chọn C
Ta có:
65 56 56
iz iz iz i=+ ⇒=− ⇒=+
.
Câu 33. Biết hàm số
1
xa
y
x
+
=
+
(
a
là số thực cho trước,
1a
≠−
) có đồ thị như hình bên. Mệnh đề nào
dưới đây là đúng?
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
A.
0yx
′
< ∀∈
. B.
01yx
′
> ∀ ≠−
. C.
01yx
′
< ∀ ≠−
. D.
0yx
′
> ∀∈
.
Lời giải
GVSB: Thanh Văn Nguyễn; GVPB: Dung Chang
Chọn C
Tập xác định
{ }
\1D = −
.
Từ đồ thị hàm số, ta thấy hàm số nghịch biến trên từng khoảng xác định.
Do đó
01yx
′
< ∀ ≠−
.
Câu 34. Trong không gian
Oxyz
, cho điểm
( )
2;1; 1M −
và mặt phẳng
(
)
: 3 2 1 0.Px y z
− + +=
Đường
thẳng đi qua
M
và vuông góc với
( )
P
có phương trình là:
A.
211
1 31
x yz
− −+
= =
−
. B.
211
1 32
x yz− −+
= =
−
.
C.
2 11
1 31
x yz+ +−
= =
−
. D.
2 11
1 32
x yz+ +−
= =
−
.
GVSB: Hà Hoàng; GVPB:Dung Chang
Lời giải
Chọn B
Đường thẳng đi qua
( )
2;1; 1M −
và vuông góc với
( )
P
nhận VTPT
(
)
1; 3; 2n
= −
của
( )
P
làm
VTCP nên có phương trình là:
211
1 32
x yz− −+
= =
−
.
Câu 35. Trên đoạn
[ ]
2;1−
, hàm số
32
31=−−yx x
đạt giá trị lớn nhất tại điểm
A.
2= −
x
. B.
0=x
. C.
1= −x
. D.
1=x
.
Lời giải
GVSB: Điểm Đàm; Ngô Minh Cường
Chọn B
Ta có
2
0
36 0
2
=
′′
= −⇒=⇔
=
x
y x xy
x
. Ta đang xét trên đoạn
[ ]
2;1−
nên loại
2=x
.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Ta có
( ) ( ) ( )
2 21; 0 1; 1 3
′ ′′
−=− =− =−f ff
. Do đó giá trị lớn nhất của hàm số trên đoạn
[ ]
2;1−
là
1−
, tại
0=x
.
Câu 36. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
C
,
3AC a=
và
SA
vuông góc với
mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
( )
SAC
bằng
A.
3
2
a
. B.
32
2
a
. C.
3a
. D.
32a
.
Lời giải
GVSB: Nguyễn Huệ; GVPB:Ngô Minh Cường
Chọn C
Ta có
ABC∆
vuông cân tại
C
nên
( )
1BC AC⊥
và
3AC BC a= =
.
Mặt khác
(
) ( )
2SA ABC SA BC⊥ ⇒⊥
.
Từ
( )
1
và
(
)
2
suy ra
( ) ( )
( )
,3BC SAC d B SAC BC a⊥⇒ ==
.
Vậy khoảng cách từ
B
đến mặt phẳng
( )
SAC
bằng
3a
.
Câu 37. Nếu
( )
2
0
dx 3fx =
∫
thì
( )
2
0
2 1 dx
fx

−

∫
bằng
A.
6
. B.
4
. C.
8
. D.
5
.
Lời giải
GVSB: Lê Trần Bảo An; GVPB:Ngô Minh Cường
Chọn B
( ) ( )
2 22
0 00
2 1 dx 2 dx dx 6 2 4

− = − =−=

∫ ∫∫
fx fx
Câu 38. Với mọi
,ab
thỏa mãn
3
22
log log 8ab+=
. Khẳng định nào dưới đây đúng?
A.
3
64ab+=
. B.
3
256ab=
. C.
3
64ab=
. D.
3
256ab+=
.
Lời giải
GVSB: Đoàn Yến; GVPB:Nguyễn Văn Ngọc
Chọn B
Ta có
( )
3 3 38
22 2
log log 8 log 8 2 256a b ab ab+ =⇒ =⇔==
.
Vậy
3
256ab=
.
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
( )
( )
2
2
3 9 log 30 5 0
xx
x− + −≤


?
A.
30.
B. Vô số. C.
31.
D.
29.
GVSB: Lê Thị Tiền; GVPB:Nguyễn Văn Ngọc
Lời giải
Chọn C
Xét hàm số:
( )
( )
( )
2
2
3 9 log 30 5
xx
fx x
= − +−


, với
30x >−
.
Cho:
( )
( )
2
2
2
5
2
2
390
33
0
0
log 30 5 0
30 2
xx
xx
x
fx
x
x
x
=
−=
=
=⇔ ⇔⇔
=
+ −=
+=
Ta có bảng xét dấu như sau:
Suy ra
( )
30 0
0
2
x
fx
x
− <≤
≤⇔
=
Mặt khác
x∈
nên
{ }
29; 28; 27;......; 2; 1;0;2x∈− − − − −
.
Vậy có
31
số nguyên
x
thỏa mãn.
Câu 40. Cho hàm số
( )
2
21 1
32 1
x khi x
fx
x khi x
−≥
=
−<
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
( )
02F =
. Giá trị của
(
) ( )
122FF−+
bằng
A.
9
. B.
15
. C.
11
. D.
6
.
Lời giải
GVSB: Lại Thị Quỳnh Nguyên; GVPB:Nguyễn Văn Ngọc
Chọn A
Tập xác định:
D =
.
Với
1x >
hay
1x <
thì hàm số
( )
fx
là hàm đa thức nên liên tục.
Mặt khác:
( )
( )
2
11
lim lim 3 2 1
xx
fx x
−−
→→
= −=
;
( ) ( )
11
lim lim 2 1 1
xx
fx x
++
→→
= −=
.
Ta có:
( ) ( ) ( )
11
lim lim 1 1
xx
fx fx f
−+
→→
= = =
nên hàm số
( )
fx
liên tục tại điểm
1x =
.
Suy ra hàm số
( )
fx
liên tục trên
.
Với
1x ≥
thì
( )
( )
2
1
d 2 1dfx x x x x x C= - = -+
òò
Với
1x <
thì
(
)
( )
23
2
d 3 2d 2fx x x x x x C= - =-+
òò
Mà
( )
02F =
nên
2
2C =
.
Khi đó
( )
2
1
3
1
2 2 1
x x C khi x
Fx
x x khi x
−+ ≥
=
−+ <
.
Đồng thời
( )
Fx
cũng liên tục trên
nên:
( ) ( ) ( )
1
11
lim lim 1 1 1
xx
Fx Fx F C
−+
→→
= = =⇔=
.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Do đó
( )
2
3
11
22 1
x x khi x
Fx
x x khi x
−+ ≥
=
−+ <
.
Vậy:
( ) ( )
1 2 2 3 2.3 9FF−+ =+ =
.
Câu 41. Cho hàm số bậc ba
(
)
y fx=
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt
của phương trình
(
)
( )
1
ffx =
là
A.
9
. B.
7
. C.
3
. D.
6
.
Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB:Thanh Nha Nguyen
Chọn B
Dựa vào đồ thị hàm số
( )
y fx=
suy ra
( )
( )
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
11
10 2
1 23
f x aa
ffx fx
fx b b
= <−
=⇔=
= <<
.
TH1
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
(
)
( )
1fx a a= <− ⇒
phương trình có một nghiệm.
TH2
( )
0fx= ⇒
phương trình có ba nghiệm phân biệt.
TH3
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
( ) ( )
12fx b b= << ⇒
phương trình có ba nghiệm phân biệt.
Các nghiệm của (1); (2); (3) là đôi một khác nhau.
Vậy
( )
( )
1ffx =
có
7
nghiệm nghiệm phân biệt.
Câu 42. Xét các số phức
,zw
thỏa mãn
1z
=
và
2w =
. Khi
68z iw i
+ +−
đạt giá trị nhỏ nhất,
zw−
bằng
A.
5
. B.
221
5
. C.
3
. D.
29
5
.
Lời giải
GVSB: Phạm Quốc Toàn; GVPB:Thanh Nha Nguyen
Chọn B
Ta có
68 68 10127z iw i i z iw+ + − ≥ − − − = −− =
.
Dấu “
=
” xảy ra khi
( )
( )
( )
( )
( )
(
)
( )
(
)
1 11
68
68 68 68
10 10 10
68, , 0
21 1
68 86 86
1, 2
10 5 5
zt i
zizizi
iw t i t t
iw i w i w i
zw

= −
=−− =−− =−−


′′
= − ∀ ≤⇔ ⇔ ⇔


=−− =+ =−
= =


.
Khi đó
221
5
zw−=
.
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Câu 43. Cho hàm số
( )
32
f x x ax bx c=+ ++
với
a
,
b
,
c
là các số thực. Biết hàm số
( ) ( ) ( ) ( )
gxfxfxfx
′ ′′
=++
có hai giá trị cực trị là
4−
và
2
. Diện tích hình phẳng giới hạn
bởi các đường
( )
( )
6
fx
y
gx
=
+
và
1y =
bằng
A.
2ln 2
. B.
ln 6
. C.
3ln 2
. D.
ln 2
.
Lời giải
GVSB: Trường Giang; GVPB: Yến Thoa
Chọn A
Ta có:
( )
32
f x x ax bx c=+ ++
( )
2
32f x x ax b
′
⇒ =++
;
( )
62fx x a
′′
= +
và
( )
6fx
′′
=
.
Phương trình hoành độ giao điểm của các đường
(
)
(
)
6
fx
y
gx
=
+
và
1y =
là:
( )
( )
( ) ( )
16
6
fx
fx gx
gx
=⇔=+
+
( ) ( )
( )
32 32 2
3 2 62 6x ax bx c x ax bx c x ax b x a⇔+ ++= + +++ + ++ + +
( )
( )
2
3 2 6 2 6 0*x a x ab⇔ + + + ++=
.
Gọi 2 nghiệm của phương trình
( )
*
là
1
x
và
2
x
.
Nhận xét:
( ) ( ) (
) ( )
gxfxfxfx
′ ′′
=++
( ) ( ) ( ) ( )
gxfxfxfx
′ ′ ′′ ′′′
⇒=++
( )
( )
( ) ( )
22
3 2 62 63 26 2 6gx x axb xa x a xab
′
⇔ = +++++=+++++
.
(
)
1
2
0
xx
gx
xx
=
′
⇒=⇔
=
.
Diện tích hình phẳng giới hạn bởi các đường
(
)
( )
6
fx
y
gx
=
+
và
1y =
là
( )
( )
( ) ( )
( )
22
11
6
1d d
66
xx
xx
fx fx gx
Sx x
gx gx

−−
= −=


++

∫∫
( )
( )
( )
2
2
1
1
d ln 6
6
x
x
x
x
gx
x gx
gx
′
= = +
+
∫
( )
(
)
21
ln 6 ln 6gx gx= +− +
ln8 ln 2 2ln 2=−=
.
Câu 44. Cho khối hộp chữ nhật
.ABCD A B C D
′′′′
có đáy là hình vuông,
4BD a=
, góc giữa hai mặt
phẳng
( )
A BD
′
và
( )
ABCD
bằng
30°
. Thể tích của khối hộp chữ nhật bằng
A.
3
16 3
9
a
. B.
3
48 3a
. C.
3
16 3
3
a
. D.
3
16 3
a
.
GVSB: Kieu Hung; GVPB: Yến Thoa
Lời giải
Chọn C
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Theo giả thiết
ABCD
là hình vuông nên có
22
2 22
AB BD AB a
= ⇒=
.
Do đó
22
8
ABCD
S AB a= =
.
Gọi
O
là tâm của đáy
ABCD
OA BD⇒⊥
và
1
2
2
OA BD a= =
.
Vì
.ABCD A B C D
′′′′
là hình hộp chữ nhật nên có
( ) ( )
A A ABCD A A BD BD A AO
′′ ′
⊥ ⇒ ⊥⇒⊥
. Do đó góc giữa
( )
A BD
′
và mặt phẳng
(
)
ABCD
là góc
A OA
′
30A OA
′
⇒=°
.
Tam giác
A OA
′
vuông tại
A
có
23
.tan
3
a
A A OA A OA
′′
= =
.
Vậy
23
.
2 3 16 3
8.
33
ABCD A B C D
a
Va a
′′′′
= =
.
Câu 45. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;4
3
x

∈


thỏa mãn
( )
2
3 12
27 1 .27
x xy x
xy
+
= +
?
A.
27
. B.
15
. C.
12
. D.
14
.
Lời giải
GVSB: Tran Nhung; GVPB: Hà Minh Yên
Chọn D
Xét
( ) ( )
2
3 12
27 1
x xy x
f x xy
+−
= −+
.
Áp dụng bất đẳng thức:
( )
11
x
a xa≥ −+
, ta có
( )
( )
( ) ( )
22
26 3 12 1 1 78 25 312 0, 13f x x xy x xy x y x y≥ + − +− + = + − > ∀≥
.
Do đó
12y ≤
.
2
3 12 2
0
0 27 1 3 12 0
4
xx
x
y xx
x
−
=
=⇒ =⇔−=⇔
=
(loại)
3 10y xy VP≤− ⇒ <− ⇒ <
(loại)
1, 2
yy=−=−
: thỏa mãn.
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Xét
0y >
có
( ) ( )
4
4 27 1 4 0, 0
y
f yy= − + ≥ ∀>
và
(
)
{
}
11
1
3 1 0, 1;2;...;12
33
y
y
f fx y
−

= = − −< ∀∈


.
Do đó phương trình
( )
0fx=
có nghiệm
1
;4
3
x

∈


,
{ }
1;2;...;12y∀∈
,
Vậy
{ }
2; 1;0;1;2;...;12y ∈− −
.
Câu 46. Trong không gian
Oxyz
, cho đường thẳng
11
:
112
+−
= =
x yz
d
và mặt phẳng
( )
:2 3 0P xyz+−+=
. Hình chiếu vuông góc của
d
trên
( )
P
là đường thẳng có phương trình
A.
11
4 5 13
x yz+−
= =
. B.
11
3 51
x yz+−
= =
−
. C.
11
3 51
x yz−+
= =
−
. D.
11
4 5 13
x yz−+
= =
.
Lời giải
GVSB: Đoàn Minh Tân; GVPB: Quy Tín
Chọn A
Đường thẳng
d
qua điểm
( )
1; 0;1A
−
và có véc-tơ chỉ phương
( )
1;1; 2
d
u =
.
Mặt phẳng
( )
P
có véc-tơ pháp tuyến
( )
( )
2;1; 1
P
n = −
.
Gọi
(
)
Q
là mặt phẳng chứa
d
và vuông góc với
( )
P
, khi đó
( )
Q
có một véc-tơ pháp tuyến là
( ) ( )
( )
, 3;5; 1
Q dP
n un

= =−−


.
Gọi
∆
là giao tuyến của hai mặt phẳng
( )
P
và
( )
Q
suy ra
∆
là hình chiếu của
d
trên
( )
P
.
Khi đó
∆
có một véc-tơ chỉ phương là
( ) ( )
( )
, 4;5;13
PQ
unn

= =


.
Ta có
( ) ( )
Ad Q A Q∈⊂ ⇒∈
và dễ thấy tọa độ
A
thỏa phương trình
( )
P
( )
AP⇒∈
.Do đó
A∈∆
.
Vậy phương trình đường thẳng
∆
là
11
4 5 13
x yz+−
= =
.
Câu 47. Cắt hình nón
(
)
ℵ
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
60°
ta
được thiết diện là tam giác đều có cạnh
2a
. Diện tích xung quanh của
( )
ℵ
bằng
A.
2
7 a
π
. B.
2
13 a
π
. C.
2
27a
π
. D.
2
2 13 a
π
.
Lời giải
GVSB: Đoàn Minh Tân; GVPB: Quy Tín
Chọn A
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Giả sử hình nón
(
)
ℵ
có
S
là đỉnh và
O
là tâm đường tròn đáy.
Giả sử mặt phẳng đề cho cắt nón theo thiết diện là tam giác đều
SAB
, khi đó ta có
2l SA a= =
.
Gọi
H
là trung điểm
AB
3
2. 3
2
SH a a⇒= =
.
Ta có góc giữa
(
)
SAB
và mặt phẳng chứa đáy là góc
60SHO = °
.
Xét
SHO∆
vuông tại
O
có
13
.cos60 3.
22
a
OH SH a= °= =
.
Xét
OAH∆
vuông tại
H
có bán kính đường tròn đáy là
2
2 22
37
42
aa
R OA AH OH a== + =+=
.
Vậy diện tích xung quanh của hình nón
( )
ℵ
là
2
xq
7
. .2 7
2
a
S Rl a a
ππ π
= = =
.
Câu 48. Trên tập hợp số phức, xét phương trình
( )
22
21 0z m zm− ++=
(
m
là tham số thực). Có bao
nhiêu giá trị của tham số
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
5z =
?
A.
2
. B.
3
. C.
1
. D.
4
.
GVSB: Minh Phạm; GVPB: Phạm Quốc Toàn
Lời giải
Chọn B
Cách 1. Ta có
( )
2
2
1 21m mm
′
∆= + − = +
.
Nếu
1
0
2
m
′
∆= ⇔ =−
thì phương trình có nghiệm
12
1
2
zz= =
(không thỏa mãn).
Nếu
1
0
2
m
′
∆ > ⇔ >−
thì phương trình có hai nghiệm phân biệt
1
121zm m= ++ +
và
2
121zm m= +− +
.
Trường hợp
1
.
( )
2
1
40
5 1215 214
2 14
m
zmm m m
mm
−≥
=⇔ ++ +=⇔ +=− ⇔
+= −
Trang 24 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
(
)
2
2
4
4
4
5 10
5 10
10 15 0
2 14
5 10
m
m
m
m
m
mm
mm
m
≤
≤
≤
⇔ ⇔ ⇔ ⇔=−
= +

− +=
+= −
= −
.
Trường hợp 2.
2
1 2 15
5 1 2 15
1215
mm
z mm
mm
+− + =
= ⇔ +− + = ⇔
+− + =−
( )
2
4
1215 21 4
21 4
m
m m mm
mm
≥
+− +=⇔ += −⇔
+= −
2
4
5 10
10 15 0
m
m
mm
≥
⇔ ⇔=+
− +=
( )
2
6
1215 21 6
21 6
m
m m mm
mm
≥−
+− +=−⇔ += +⇔
+= +
2
6
10 35 0
m
mm
≥−
⇔
+ +=
(vô nghiệm).
Nếu
1
0
2
m
′
∆ < ⇔ <−
thì phương trình ban đầu có hai nghiệm phức
12
,zz
và
12
5zz= =
.
Theo giả thiết, ta có
2
12 1 2
5( )
. . 25 25
5
m Loai
zz z z m
m
=
= =⇔=⇔
= −
.
Vậy có
3
giá trị của tham số
m
thỏa mãn yêu cầu bài toán.
Cách 2. Đặt
0
z x yi= +
( )
,xy∈
là nghiệm của phương trình ban đầu.
Theo giả thiết, ta có
( )
22
0
5 25 1z xy=⇔+=
.
Thay
0
z
vào phương trình ban đầu, ta có
( ) ( )( )
( )
( )
2
2 22 2
2 1 0 2 2 22 2 0x yi m x yi m x y mx x m xy my y i+ − + + + =⇔ −− −+ + − − =
( )
( ) ( )
22 2
22 2
2 2 02
22 0
2 2 20
10 3
x y mx x m
x y mx x m
xy my y
yx m
−− −+ =
−− −+ =
⇔ ⇔⇔

− −=
−−=
.
( )
0
3
1
y
xm
=
⇔
= +
.
Trường hợp 1. Với
( )
2
0 1 25 5y xx=⇒ ⇔ = ⇔=±
.
Nếu
( )
2
5 2 10 15 0 5 10x mm m=⇒ ⇔ − +=⇔=±
.
Nếu
( )
2
5 2 10 35 0x mm=−⇒ ⇔ + + =
(vô nghiệm).
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 25
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Trường hợp 2.
(
) (
)
( )
2
2
1 1 25 1 6 4
xm y m m= +⇒ ⇔ = − + −≤ ≤
.
(
)
(
)
(
) (
) (
)
(
)
22
22
5
2 1 25 1 2 1 2 1 0 25 0
5
m
m m mm m m m
mL
= −
⇔ + − + + − +− ++ =⇔ − =⇔
=
.
Vậy có
3
giá trị của tham số
m
thỏa mãn.
Câu 49. Cho hàm số
( )
y fx=
có đạo hàm
(
)
( )
(
)
2
8 9,
fx x x x
¢
= - - "Î
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
( )
( )
3
6gx f x x m= ++
có ít nhất 3 điểm cực trị?
A.
5
. B.
8
. C.
6
. D.
7
.
Lời giải
Chọn D
Cách 1 : GVSB: Đỗ Linh; GVPB:Hoa Tiên Phạm
( )
( )
( )
( ) ( )
3 33
6 6. 6gx fx xm gx x xmfx xm= ++⇒′= ++′′ ++
( ) ( )
( )
32
3
3
6 .3 6
.6
6
x xx
fx xm
xx
++
= ′ ++
+
.
Ta thấy
0x =
là một điểm tới hạn của hàm số
(
)
gx
.
Mặt khác
( )
33
33 3
33
6 8 68
6 0 6 3 63
6 3 63
xxm xx m
fxxm xxm xx m
xxm xx m

+ += + =−


′ ++=⇔ ++=⇔ +=−


+ + =− + =−−

.
Xét hàm số
(
)
3
6
hx x x
= +
, vì
( )
2
3 6 0,hx x x′ = + > ∀∈
nên
( )
hx
đồng biến trên
. Ta có
bảng biến thiên của hàm số
(
)
(
)
3
6kx hx x x
= = +
như sau:
Hàm số
( )
(
)
3
6gx f x x m
= ++
có ít nhất 3 điểm cực trị khi phương trình
( )
3
60fx xm′ ++=
có ít nhất hai nghiệm khác 0. Điều này xảy ra khi và chỉ khi
80m−>
hay
8m <
.
Kết hợp điều kiện
m
nguyên dương ta được
{ }
1;2;3...;7m∈
. Vậy có 7 giá trị của
m
thoả mãn.
Cách 2: GVSB: Đỗ Ngọc Nam; GVPB:Hoa Tiên Phạm
Nhận thấy hàm
( )
( )
( )
2
6gx f x x m= ++
là hàm số chẵn nên đồ thị đối xứng qua trục tung.
Để hàm
( )
( )
3
6gx f x x m= ++
có ít nhất 3 điểm cực trị thì hàm số
( )
( )
3
6hx fx x m= ++
có ít nhất 1 điểm cực trị có hoành độ dương, tức
Trang 26 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD
�
BIÊN SOẠN TOÁN GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
(
)
( )
( )
23
36 3 0hx x f x x m
¢¢
= + ++ =
có nghiệm dương bội lẻ hay
33
33
33
3 8 38
3 3 33
3 3 33
xxm xx m
xxm xx m
xxm xx m
éé
+ + = + - =-
êê
êê
+ + = Û + - =-
êê
êê
+ + =- + + =-
êê
ëë
có nghiệm dương bội lẻ.
Ta có bảng biến thiên (gộp)
Từ bảng biến thiên suy ra
0
08
8
m
m
m
ì
ï
>
ï
Û< <
í
ï
- >-
ï
î
.
Câu 50. Trong không gian, cho hai điểm
( )
1; 3; 2−A
và
( )
2;1; 3−−
B
. Xét hai điểm
M
và
N
thay đổi
thuộc mặt phẳng
( )
Oxy
sao cho
1
=MN
. Giá trị lớn nhất của
−AM BN
bằng
A.
17
. B.
41
. C.
37
. D.
61
.
GVSB: Nga Nguyen; GVPB: Tran Nhung
Lời giải
Chọn C
Nhận xét:
A
và
B
nằm khác phía so với mặt phẳng
( )
Oxy
.
Gọi
( )
P
là mặt phẳng qua
A
và song song với mặt phẳng
( ) ( )
:2⇒=Oxy P z
.
B
′
đối xứng với
( )
P
qua mặt phẳng
( ) ( )
2;1; 3Oxy B
′
⇒−
.
1
B
là hình chiếu của
B
′
trên mặt phẳng
(
) ( )
1
2;1; 2PB⇒−
.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 27
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 NHÓM WORD
�
BIÊN SOẠN TOÁN THPT
Gọi
( )
( )
′
=
′
= ⇒
′
MN
AA 1
AT A
AA Oxy

′
⇒ A
thuộc đường tròn
( )
C
có tâm
A
và bán kính
1=R
,
( )
C
nằm trên mặt phẳng
( )
P
.
Ta có:
AM BN AN BN AN BN AB
′ ′ ′ ′′
−= −= − ≤
11
5AB R B=>⇒
nằm ngoài đường tròn
( )
C
.
Do
( )
AP
′
∈
,
( )
BP
′
∉
mà
(
)
( )
P Oxy
suy ra
''AB
luôn cắt mặt phẳng
( )
Oxy
.
Ta lại có:
22
11
AB BB AB
′′ ′ ′
= +
mà
1
1BB
′
=
;
1
5AB =
11
6
max max
AB AB AB R
′′ ′
⇒ ⇔ = +=
37
max
AM BN
⇒− =
. Dấu
""=
xảy ra khi
'A
là giao điểm của
1
AB
với đường tròn
(
)
C
(
A
ở giữa
'A
và
1
B
và
N
là giao điểm của
''AB
với mặt phẳng
(
)
Oxy
.
Trang 28 TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
KỲ THI TN THPT- NĂM HỌC 2020 – 2021
Môn: Toán- Mã đề 103- Đợt 1
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 180 phút (Không kể thời gian phát đề)
LINK NHÓM
:
https://www.facebook.com/groups/1916660125164699
Câu 1. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
3
1
2
2
y x x
. B.
3
1
2
2
y x x
. C.
4 2
1
2
2
y x x
. D.
4 2
1
2
2
y x x
.
Câu 2. Cho cấp số nhân
n
u
với
1
3u
và
2
15u
. Công bội của cấp số nhân đã cho bằng
A.
12
. B.
1
5
. C.
5
. D.
12
.
Câu 3. Cho khối chóp có diện tích đáy
2
7B a
và chiều cao
h a
. Thể tích của khối chóp đã cho
bằng
A.
3
7
6
a
. B.
3
7
2
a
. C.
3
7
3
a
. D.
3
7a
.
Câu 4. Nếu
4
1
dx 5f x
và
4
1
dx 4g x
thì
4
1
dxf x g x
bằng
A.
1
. B.
9
. C.
1
. D.
9
.
Câu 5. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua điểm
3;1; 2M
và có một vectơ chỉ
phương
2;4; 1u
, phương trình của
d
là
A.
3 2
1 4
2
x t
y t
z t
. B.
3 2
1 4
2
x t
y t
z t
. C.
3 2
1 4
2
x t
y t
z t
. D.
2 3
4
1 2
x t
y t
z t
.
Câu 6. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
S R
. B.
2
4
3
S R
. C.
2
4S R
. D.
2
16S R
.
Câu 7. Trong không gian
Oxyz
, cho mặt phẳng
: 2 2z 3 0P x y
. Vectơ nào dưới đây là một
véctơ pháp tuyến của
P
?
A.
3
1;2;2n
. B.
1
1; 2;2n
. C.
4
1; 2; 3n
. D.
2
1;2; 2n
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 2 TÀI LIỆU ÔN THU THPT QUỐC GIA
Câu 8. Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
0;1; 2I
và bán kinh bằng
3
. Phương trình
của
S
là
A.
2 2
2
1 2 9x y z
. B.
2 2
2
1 2 9x y z
.
C.
2 2
2
1 2 3x y z
. D.
2 2
2
1 2 3x y z
.
Câu 9. Cho hàm số
2
1f x x
. Khẳng định nào dưới đây đúng?
A.
3
f x dx x x C
. B.
3
3
x
f x dx x C
.
C.
2
f x dx x x C
. D.
2f x dx x C
.
Câu 10. Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A. 2. B. 3. C. 4. D. 5.
Câu 11. Tập xác định của hàm số
6
x
y
là
A.
0; .
B.
\ 0 .
C.
0; .
D.
.
Câu 12. Nếu
3
0
d 2f x x
thì
3
0
3 df x x
bằng
A. 6. B. 2. C. 18. D. 3.
Câu 13. Trên mặt phẳng tọa độ, điểm
2;3M
là điểm biểu diễn của số phức nào dưới đây?
A.
3
2 3z i
. B.
4
2 3z i
. C.
1
2 3z i
. D.
2
2 3z i
.
Câu 14. Cho hàm số
3
x
f x e
. Khẳng định nào dưới đây đúng?
A.
d 3
x
f x x e x C
. B.
d
x
f x x e C
.
C.
3
d
x
f x x e C
. D.
d 3
x
f x x e x C
.
Câu 15. Cho hàm số
y f x
có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên
khoảng nào dưới đây?
A.
;2
. B.
0;2
. C.
2;2
. D.
2;
.
Câu 16. Đồ thị hàm số
3 2
2 1y x x
cắt trục tung tại điểm có tung độ bằng
A.
3
. B.
1
. C.
1
. D.
0
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
Câu 17. Trên khoảng
0;
, đạo hàm của hàm số
4
3
y x
là
A.
1
3
4
3
y x
. B.
1
3
4
3
y x
. C.
7
3
3
7
y x
. D.
1
3
3
4
y x
.
Câu 18. Cho
0a
và
1a
, khi đó
log
a
a
bằng
A.
2
. B.
2
. C.
1
2
. D.
1
2
.
Câu 19. Trong không gian
Oxyz
, cho điểm
(3;2; 4)A
, Tọa độ của vectơ
OA
là
A.
(3; 2; 4)
. B.
( 3; 2;4)
. C.
(3;2; 4)
. D.
(3;2;4)
.
Câu 20. Tập nghiệm của bất phương trình
2 3
x
là
A.
3
log 2; ,
B.
2
;log 3 ,
C.
3
;log 2
, D.
2
log 3;
.
Câu 21. Cho hai số phức
1 2z i
và
3 4w i
. Số phức
z w
bằng
A.
2 6i
B.
4 2i
C.
4 2i
D.
2 6i
.
Câu 22. Cho hàm số có bảng biến thiên như vẽ:
Giá trị cực đại của hàm số bằng
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 23. Thể tích khối lập phương có độ dài cạnh
3a
bằng
A.
3
27a
. B.
3
3a
. C.
3
9a
. D.
3
a
.
Câu 24. Tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình
A.
2x
. B.
1x
. C.
1
2
x
. D.
1x
.
Câu 25. Phần thực của số phức
3 2z i
bằng
A.
2
. B.
3
. C.
3
. D.
2
.
Câu 26. Nghiệm của phương trình
3
log 2 2x
là
A.
9
2
x
. B.
9x
. C.
4x
. D.
8x
.
Câu 27. Với
n
là số nguyên dương bất kì,
2n
, công thức nào dưới đây đúng?
A.
2
2 !
!
n
n
A
n
. B.
2
2!
2 !
n
A
n
. C.
2
!
2! 2 !
n
n
A
n
. D.
2
!
2 !
n
n
A
n
.
Câu 28. Cho khối trụ có bán kính
2r
và chiều cao
3h
.Thể tích khối trụ đã cho bằng
A.
12
. B.
18
. C.
6
. D.
4
.
Câu 29. Trong không gian
Oxyz
, cho điểm
1;2; 1M
và mặt phẳng
: 2 3 1 0P x y z
. Đường
thẳng đi qua
M
và vuông góc với
P
có phương trình là
A.
1 2 1
2 1 1
x y z
. B.
1 2 1
2 1 3
x y z
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 4 TÀI LIỆU ÔN THU THPT QUỐC GIA
C.
1 2 1
2 1 1
x y z
. D.
1 2 1
2 1 3
x y z
.
Câu 30. Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên dưới).
Góc giữa hai đường thẳng
A B
và
CC
bằng
A.
45
. B.
30
. C.
90
. D.
60
.
Câu 31. Cho số phức
z
thỏa mãn
3 2 .iz i
Số phức liên hợp của
z
là
A.
2 3z i
. B.
2 3z i
. C.
2 3z i
. D.
2 3z i
.
Câu 32. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
C
,
AC a
và
SA
vuông góc với mặt
phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
( )SAC
bằng
A.
1
2
a
. B.
2a
. C.
2
2
a
. D.
a
.
Câu 33. Từ một hộp chứa
10
quả bóng gồm
4
quả màu đỏ và
6
quả màu xanh, lấy ngẫu nhiên đồng
thời
3
quả. Xác suất để lấy
3
quả màu đỏ bằng
A.
1
5
. B.
1
6
. C.
2
5
. D.
1
30
.
Câu 34. Với mọi
,a b
thỏa mãn
2
2 2
log log 7a b
, khẳng định nào dưới đây đúng?
A.
2
49a b
. B.
2
128a b
. C.
2
128a b
. D.
2
49a b
.
Câu 35. Trong không gian
Oxyz
, cho hai điểm
0;0;1A
và
1;2;3B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 11 0x y z
. B.
2 2 2 0x y z
.
C.
2 4 4 0x y z
. D.
2 4 17 0x y z
.
Câu 36. Trên đoạn
0;3
, hàm số
3
3 4y x x
đạt giá trị nhỏ nhất tại điểm
A.
1x
. B.
0x
. C.
3x
. D.
2x
.
Câu 37. Nếu
2
0
d 6f x x
thì
2
0
2 1 df x x
bằng
A.
12
. B.
10
. C.
11
. D.
14
.
Câu 38. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1a
) có đồ thị như trong hình vẽ sau
A
B
C
C'
B'
A'
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
Mệnh đề nào dưới đây đúng?
A.
0, 1y x
. B.
0,y x
. C.
0,y x
. D.
0, 1y x
.
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
2 4 log 14 4 0
x x
x
?
A.
14
. B.
13
. C. Vô số. D.
15
.
Câu 40. Cho hàm số
2
2 3 1
3 2 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của hàm số
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
23
. B.
11
. C.
10
. D.
21
.
Câu 41. Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên dưới:
Số nghiệm thực phân biệt của phương trình
0f f x
là
A.
4
. B.
10
. C.
12
. D.
8
.
Câu 42. Xét số phức
,z w
thoả mãn
1z
và
2w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
3
. B.
29
5
. C.
5
. D.
221
5
.
Câu 43. Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
1 1 2
x y z
d
và mặt phẳng
: 2 6 0P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương trình
A.
1 2 1
3 1 1
x y z
. B.
1 2 1
3 1 1
x y z
.
C.
1 2 1
1 4 7
x y z
. D.
1 2 1
1 4 7
x y z
.
Câu 44. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;5
3
x
thỏa mãn
2
3 15
27 (1 )27
x xy x
xy
?
A. 17. B. 16. C. 18. D. 15.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 6 TÀI LIỆU ÔN THU THPT QUỐC GIA
Câu 45. Cho khối hộp chữ nhật .
ABCD A B C D
có đáy là hình vuông,
2
BD a
, góc giữa hai mặt
phẳng
vàA BD
ABCD
bằng
60
. Thể tích của khối hộp đã cho bằng
A.
3
2 3
9
a
. B.
3
6 3
a
. C.
3
2 3
3
a
. D.
3
2 3
a
.
Câu 46. Cho hàm số
3 2
f x x ax bx c
với
, ,
a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
3
. Diện tích hình phẳng giới hạn
bởi đường
6
f x
y
g x
và
1
y
bằng
A.
2ln3
. B.
ln 2
. C.
ln15
. D.
3ln2
.
Câu 47. Cắt hình nón
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30
, ta được thiết diện là tam giác đều cạnh
4
a
. Diện tích xung quanh của
bằng
A.
2
4 7
a
. B.
2
8 7
a
. C.
2
8 13
a
. D.
2
4 13
a
.
Câu 48. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(m là tham số thực ). Có
bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
8
z
.
A. 4. B. 3. C. 2. D. 1.
Câu 49. Trong không gian
Ox
yz
, cho hai điểm
1; 3;2
A
và
2;1; 4
B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
4
MN
. Giá trị lớn nhất của
AM BN
bằng
A.
5 2
. B.
3 13
. C.
61
. D.
85
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
' 10 25 ,f x x x x
.Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
8
g x f x x m
có ít nhất 3 điểm cực trị?
A.
9
. B.
25
. C.
5
. D.
10
.
------------------HẾT------------------
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
BẢNG ĐÁP ÁN
1B 2C 3C 4D 5C 6C 7B 8A 9B 10C 11D 12A 13C 14A 15B
16C 17B 18D 19C 20D 21C 22A 23A 24B 25C 26A 27D 28A 29B 30A
31A 32D 33D 34B 35B 36A 37B 38A 39D 40D 41B 42D 43D 44A 45D
46A 47D 48B 49B 50A
HƯỚNG DẪN GIẢI
Câu 1. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
3
1
2
2
y x x
. B.
3
1
2
2
y x x
. C.
4 2
1
2
2
y x x
. D.
4 2
1
2
2
y x x
.
Lời giải
GVSB: Trần Ngọc; GVPB:Hải Hạnh Trần
Chọn B
Đồ thị đã cho là đồ thị hàm số bậc ba có hệ số bậc ba
0a
. Chọn B.
Câu 2. Cho cấp số nhân
n
u
với
1
3u
và
2
15u
. Công bội của cấp số nhân đã cho bằng
A.
12
. B.
1
5
. C.
5
. D.
12
.
Lời giải
GVSB: Trần Ngọc; GVPB:Hải Hạnh Trần
Chọn C
Ta có:
2
1
15
5
3
u
q
u
.
Câu 3. Cho khối chóp có diện tích đáy
2
7B a
và chiều cao
h a
. Thể tích của khối chóp đã cho
bằng
A.
3
7
6
a
. B.
3
7
2
a
. C.
3
7
3
a
. D.
3
7a
.
Lời giải
GVSB: Trần Ngọc; GVPB:Hải Hạnh Trần
Chọn C
Thể tích khối chóp
2 3
1 1 7
7 .
3 3 3
V Bh a a a
.
Câu 4. Nếu
4
1
dx 5f x
và
4
1
dx 4g x
thì
4
1
dxf x g x
bằng
A.
1
. B.
9
. C.
1
. D.
9
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 8 TÀI LIỆU ÔN THU THPT QUỐC GIA
GVSB: Nguyễn Minh Hằng; GVPB: Hải Hạnh Trần
Chọn D
Ta có:
4 4 4
1 1 1
dx dx dx 5 4 9
f x g x f x g x
.
Câu 5. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua điểm
3;1; 2
M
và có một vectơ chỉ
phương
2;4; 1
u
, phương trình của
d
là
A.
3 2
1 4
2
x t
y t
z t
. B.
3 2
1 4
2
x t
y t
z t
. C.
3 2
1 4
2
x t
y t
z t
. D.
2 3
4
1 2
x t
y t
z t
.
Lời giải
GVSB: Nguyễn Minh Hằng; GVPB: Hải Hạnh Trần
Chọn C
Đường thẳng
d
đi qua điểm
3;1;2
M
và có một vectơ chỉ phương
2; 4; 1
u
, phương
trình của
d
là
3 2
1 4
2
x t
y t
z t
.
Câu 6. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
S R
. B.
2
4
3
S R
. C.
2
4
S R
. D.
2
16
S R
.
Lời giải
GVSB: Nguyễn Minh Hằng; GVPB: Hải Hạnh Trần
Chọn C
Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức
2
4
S R
.
Câu 7. Trong không gian
Oxyz
, cho mặt phẳng
: 2 2z 3 0
P x y
. Vectơ nào dưới đây là một
véctơ pháp tuyến của
P
?
A.
3
1;2;2
n
. B.
1
1; 2;2
n
. C.
4
1; 2; 3
n
. D.
2
1;2; 2
n
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Hải Hạnh Trần
Chọn B
Ta có mặt phẳng
: 2 2z 3 0
P x y
nên suy ra một vectơ pháp tuyến là
1
1; 2;2
n
.
Câu 8. Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
0;1; 2
I
và bán kinh bằng
3
. Phương trình
của
S
là
A.
2 2
2
1 2 9
x y z
. B.
2 2
2
1 2 9
x y z
.
C.
2 2
2
1 2 3
x y z
. D.
2 2
2
1 2 3
x y z
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Hải Hạnh Trần
Chọn A
Ta có mặt cầu tâm
0;1; 2
I
bán kính bằng
3
có phương trình là
2 2
2
1 2 9
x y z
.
Câu 9. Cho hàm số
2
1
f x x
. Khẳng định nào dưới đây đúng?
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
A.
3
f x dx x x C
. B.
3
3
x
f x dx x C
.
C.
2
f x dx x x C
. D.
2f x dx x C
.
Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Hải Hạnh Trần
Chọn B
Ta có
3
2
1
3
x
f x dx x dx x C
.
Câu 10. Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A. 2. B. 3. C. 4. D. 5.
GVSB: Bùi Minh Đức; GVPB: Phạm Tuyến
Lời giải
Chọn C
Từ bảng xét dấu ta thấy
f x
đổi dấu 4 lần
Suy ra hàm số
f x
có 4 điểm cực trị.
Câu 11. Tập xác định của hàm số
6
x
y
là
A.
0; .
B.
\ 0 .
C.
0; .
D.
.
GVSB: Bùi Minh Đức; GVPB: Phạm Tuyến
Lời giải
Chọn D
Tập xác định của hàm số
6
x
y
là
.D
Câu 12. Nếu
3
0
d 2f x x
thì
3
0
3 df x x
bằng
A. 6. B. 2. C. 18. D. 3.
GVSB: Bùi Minh Đức; GVPB: Phạm Tuyến
Lời giải
Chọn A
Ta có:
3 3
0 0
3 d 3. d 3.2 6f x x f x x
.
Câu 13. Trên mặt phẳng tọa độ, điểm
2;3M
là điểm biểu diễn của số phức nào dưới đây?
A.
3
2 3z i
. B.
4
2 3z i
. C.
1
2 3z i
. D.
2
2 3z i
.
Lời giải
GVSB: Nguyễn Linh Trang; GVPB: Phạm Tuyến
Chọn C
Điểm
2;3M
là điểm biểu diễn của số phức
1
2 3z i
.
Câu 14. Cho hàm số
3
x
f x e
. Khẳng định nào dưới đây đúng?
A.
d 3
x
f x x e x C
. B.
d
x
f x x e C
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 10 TÀI LIỆU ÔN THU THPT QUỐC GIA
C.
3
d
x
f x x e C
. D.
d 3
x
f x x e x C
.
Lời giải
GVSB: Nguyễn Linh Trang; GVPB: Phạm Tuyến
Chọn A
Nguyên hàm của hàm số
3
x
f x e
là:
d 3 d 3
x x
f x x e x e x C
.
Câu 15. Cho hàm số
y f x
có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên
khoảng nào dưới đây?
A.
;2
. B.
0;2
. C.
2;2
. D.
2;
.
Lời giải
GVSB: Nguyễn Linh Trang; GVPB: Phạm Tuyến
Chọn B
Dựa vào đồ thị hàm số ta có hàm số đồng biến trên khoảng
0;2
.
Câu 16. Đồ thị hàm số
3 2
2 1y x x
cắt trục tung tại điểm có tung độ bằng
A.
3
. B.
1
. C.
1
. D.
0
.
Lời giải
GVSB:Lê Thúy Hằng; GVPB: Phạm Tuyến
Chọn C
Từ hàm số:
3 2
2 1y x x
, cho
0 1x y
.
Vậy đồ thị hàm số
3 2
2 1y x x
cắt trục tung tại điểm có tung độ bằng
1
.
Câu 17. Trên khoảng
0;
, đạo hàm của hàm số
4
3
y x
là
A.
1
3
4
3
y x
. B.
1
3
4
3
y x
. C.
7
3
3
7
y x
. D.
1
3
3
4
y x
.
Lời giải
GVSB:Lê Thúy Hằng; GVPB: Phạm Tuyến
Chọn B
Ta có:
4 1
3 3
4
3
y x x
.
Câu 18. Cho
0a
và
1a
, khi đó
log
a
a
bằng
A.
2
. B.
2
. C.
1
2
. D.
1
2
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 11
GVSB:Lê Thúy Hằng; GVPB: Phạm Tuyến
Chọn D
Với
0a
và
1a
,ta có:
1
2
1 1
log log log
2 2
a a a
a a a
.
Câu 19. Trong không gian
Oxyz
, cho điểm
(3;2; 4)A
, Tọa độ của vectơ
OA
là
A.
(3; 2; 4)
. B.
( 3; 2;4)
. C.
(3;2; 4)
. D.
(3;2;4)
.
Lời giải
GVSB:Bạch Hưng Tình; GVPB: Nguyễn My
Chọn C
Ta có:
0; 0; 0O
,
(3;2; 4)A
3 0;2 0; 4 0 3;2; 4OA
.
Câu 20. Tập nghiệm của bất phương trình
2 3
x
là
A.
3
log 2; ,
B.
2
;log 3 ,
C.
3
;log 2
, D.
2
log 3;
.
Lời giải
GVSB:Bạch Hưng Tình; GVPB: Nguyễn My
Chọn D
Ta có:
2
2 3 log 3
x
x
.
Tập nghiệm của bất phương trình là
2
log 3; 
.
Câu 21. Cho hai số phức
1 2z i
và
3 4w i
. Số phức
z w
bằng
A.
2 6i
B.
4 2i
C.
4 2i
D.
2 6i
.
Lời giải
GVSB:Bạch Hưng Tình; GVPB: Nguyễn My
Chọn C
Ta có:
1 2 3 4 4 2z w i i i
.
Câu 22. Cho hàm số có bảng biến thiên như vẽ:
Giá trị cực đại của hàm số bằng
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
GVSB:Trần Thông GVPB:Nguyễn My
Chọn B
Câu 23. Thể tích khối lập phương có độ dài cạnh
3a
bằng
A.
3
27a
. B.
3
3a
. C.
3
9a
. D.
3
a
.
Lời giải
GVSB:Trần Thông GVPB:Nguyễn My
Chọn A
Thể tích khối lập phương là
3
3
3 27a a
.
Câu 24. Tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 12 TÀI LIỆU ÔN THU THPT QUỐC GIA
A.
2
x
. B.
1
x
. C.
1
2
x
. D.
1
x
.
Lời giải
GVSB:Trần Thông GVPB:Nguyễn My
Chọn B
Ta có
1
2 1
lim
1
x
x
x

và
1
2 1
lim
1
x
x
x

nên
1
x
là tiệm cận đứng của đồ thị hàm số.
Câu 25. Phần thực của số phức
3 2
z i
bằng
A.
2
. B.
3
. C.
3
. D.
2
.
Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Nguyễn My
Chọn C
Câu 26. Nghiệm của phương trình
3
log 2 2
x
là
A.
9
2
x
. B.
9
x
. C.
4
x
. D.
8
x
.
Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Nguyễn My
Chọn A
3
9
log 2 2 2 9
2
x x x
.
Câu 27. Với
n
là số nguyên dương bất kì,
2
n
, công thức nào dưới đây đúng?
A.
2
2 !
!
n
n
A
n
. B.
2
2!
2 !
n
A
n
. C.
2
!
2! 2 !
n
n
A
n
. D.
2
!
2 !
n
n
A
n
.
Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Nguyễn My
Chọn D
2
!
2 !
n
n
A
n
.
Câu 28. Cho khối trụ có bán kính
2
r
và chiều cao
3
h
.Thể tích khối trụ đã cho bằng
A.
12
. B.
18
. C.
6
. D.
4
.
Lời giải
GVSB: Nguyễn Trọng Thiện; GVPB: Hồ Quốc Thuận
Chọn A
Thể tích khối trụ:
2 2
.2 .3 12
V r h
.
Câu 29. Trong không gian
Oxyz
, cho điểm
1;2; 1
M
và mặt phẳng
: 2 3 1 0
P x y z
. Đường
thẳng đi qua
M
và vuông góc với
P
có phương trình là
A.
1 2 1
2 1 1
x y z
. B.
1 2 1
2 1 3
x y z
.
C.
1 2 1
2 1 1
x y z
. D.
1 2 1
2 1 3
x y z
.
Lời giải
GVSB: Nguyễn Trọng Thiện; GVPB: Hồ Quốc Thuận
Chọn B
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 13
Gọi
là đường thẳng cần tìm. Vì đường thẳng
vuông góc với mặt phẳng
P
nên
vectơ chỉ phương của
là:
2;1; 3
P
u n
.
Phương trình chính tắc của đường thẳng
đi qua điểm
1;2; 1M
và có vtcp
2;1; 3u
là:
1 2 1
2 1 3
x y z
.
Câu 30. Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên dưới).
Góc giữa hai đường thẳng
A B
và
CC
bằng
A.
45
. B.
30
. C.
90
. D.
60
.
Lời giải
GVSB: Nguyễn Trọng Thiện; GVPB: Hồ Quốc Thuận
Chọn A
Ta có:
'CC
//
'BB
. Nên
' ; 'A B CC
=
' ; 'A B BB
=
' 'A BB
(
' 'A BB
là góc nhọn). Mặt khác,
tam giác
' 'A BB
là tam giác vuông cân (
' 'A B BB
và
' 'A B BB
) suy ra
' ' 45A BB
.
Vậy
góc giữa hai đường thẳng
'A B
và
'CC
bằng
45
.
Câu 31. Cho số phức
z
thỏa mãn
3 2 .iz i
Số phức liên hợp của
z
là
A.
2 3z i
. B.
2 3z i
. C.
2 3z i
. D.
2 3z i
.
Lời giải
GVSB: Pham Thi Hong Van; GVPB: Hồ Quốc Thuận
Chọn A
A
B
C
C'
B'
A'
A
B
C
C'
B'
A'
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 14 TÀI LIỆU ÔN THU THPT QUỐC GIA
Ta có:
3 2
3 2 2 3
i
iz i z i
i
.
Do đó số phức liên hợp của z là:
2 3z i
Câu 32. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
C
,
AC a
và
SA
vuông góc với mặt
phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
( )SAC
bằng
A.
1
2
a
. B.
2a
. C.
2
2
a
. D.
a
.
Lời giải
GVSB: Pham Thi Hong Van; GVPB: Hồ Quốc Thuận
Chọn D
Ta có:
SA
vuông góc với mặt đáy suy ra
SA BC
Tam giác
ABC
vuông cân tại
C
suy ra
BC a
và
AC BC
Do đó ta có:
( )
SA BC
BC SAC
CA BC
.
Vậy khoảng cách từ
B
đến mặt phẳng
( )SAC
bằng
BC a
.
Câu 33. Từ một hộp chứa
10
quả bóng gồm
4
quả màu đỏ và
6
quả màu xanh, lấy ngẫu nhiên đồng
thời
3
quả. Xác suất để lấy
3
quả màu đỏ bằng
A.
1
5
. B.
1
6
. C.
2
5
. D.
1
30
.
Lời giải
GVSB: Phạm Quang Thiện; GVPB: Tran Phuc
Chọn D
Ta có:
3
10
n C
. Gọi biến cố A:“3 quả lấy ra màu đỏ”. Suy ra
3
4
n A C
.
Vậy Xác suất để lấy
3
quả màu đỏ bằng
1
30
n A
P A
n
.
Câu 34. Với mọi
,a b
thỏa mãn
2
2 2
log log 7a b
, khẳng định nào dưới đây đúng?
A.
2
49a b
. B.
2
128a b
. C.
2
128a b
. D.
2
49a b
.
Lời giải
GVSB: Phạm Quang Thiện; GVPB: Tran Phuc
Chọn B
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 15
Ta có:
2 2 2 7
2 2 2
log log 7 log 7 2 128a b a b a b
Câu 35. Trong không gian
Oxyz
, cho hai điểm
0;0;1A
và
1;2;3B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 11 0x y z
. B.
2 2 2 0x y z
.
C.
2 4 4 0x y z
. D.
2 4 17 0x y z
.
Lời giải
GVSB: Tuyet Trinh; GVPB: Phan Thị Thúy Hà
Chọn B
Ta có
1;2;2AB
.
Mặt phẳng đi qua
A
và vuông góc với
AB
nên nhận
1;2;2AB
làm vectơ pháp tuyến có
phương trình:
1 0 2 0 2 1 0x y z
2 2 2 0x y z
.
Câu 36. Trên đoạn
0;3
, hàm số
3
3 4y x x
đạt giá trị nhỏ nhất tại điểm
A.
1x
. B.
0x
. C.
3x
. D.
2x
.
Lời giải
GVSB: Tuyet Trinh; GVPB: Phan Thị Thúy Hà
Chọn A
Ta có
2
3 3y x
1 0;3
0
1 0;3
x
y
x
.
Lại có
0 4y
;
1 2y
;
3 22y
.
Vậy
0;3
min 1 2y y
.
Câu 37. Nếu
2
0
d 6f x x
thì
2
0
2 1 df x x
bằng
A.
12
. B.
10
. C.
11
. D.
14
.
Lời giải
GVSB: Phan Thị Thúy Hà; GVPB: Phan Thị Thúy Hà
Chọn B
Ta có:
2 2 2
0 0 0
2 1 d 2 d d 2.6 2 10f x x f x x x
.
Câu 38. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1a
) có đồ thị như trong hình vẽ sau
Mệnh đề nào dưới đây đúng?
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 16 TÀI LIỆU ÔN THU THPT QUỐC GIA
A.
0, 1y x
. B.
0,y x
. C.
0,y x
. D.
0, 1y x
.
Lời giải
GVSB: Phan Thị Thúy Hà; GVPB: Phan Thị Thúy Hà
Chọn A
Tập xác định của hàm số đã cho là
\ 1D
.
Ta có:
2
1
, 1
1
a
y x
x
.
Từ đồ thị của hàm số suy ra hàm số đã cho đồng biến trên mỗi khoảng xác định vì vậy
0, 1y x
.
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
2 4 log 14 4 0
x x
x
?
A.
14
. B.
13
. C. Vô số. D.
15
.
Lời giải
GVSB: Trương Hoài Bão; GVPB:ThanhQuach
Chọn D
Điều kiện:
14x
.
Bất phương trình tương đương:
2
2
2
2 2 log 14 4 0
x x
x
2 2
2 2
2 2
2 2
2 2
2 2
2 2 0 2 2
log 14 4 0 log 14 4
2 2 0 2 2
log 14 4 0 log 14 4
x x x x
x x x x
x x
x x
2
2
2
14 16
2
0
2
14 16
x x
x
x
x
x x
x
.
Kết hợp với điều kiện suy ra có 15 giá trị nguyên của
x
thỏa yêu cầu.
Câu 40. Cho hàm số
2
2 3 1
3 2 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của hàm số
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
23
. B.
11
. C.
10
. D.
21
.
Lời giải
GVSB: Trương Hoài Bão; GVPB:ThanhQuach
Chọn D
Khi
1x
thì
2
1
2 3 3F x f x dx x dx x x C
Khi
1x
thì
2 3
2
3 2 2F x f x dx x dx x x C
Theo giả thiết
2
0 2 2F C
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 17
Ta có
1 1
lim lim 1 5
x x
f x f x f
nên hàm số
f x
liên tục tại
1x
.
Suy ra hàm số
f x
liên tục trên
.
Do đó hàm số
F x
liên tục trên
1 2 1
1 1
lim lim 4 3 1
x x
F x F x C C C
Vậy
2 1
1 2 2 3 2 10 21F F C C
.
Câu 41. Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên dưới:
Số nghiệm thực phân biệt của phương trình
0f f x
là
A.
4
. B.
10
. C.
12
. D.
8
.
Lời giải
GVSB: Hoàng Văn Quảng; GVPB:
Chọn B
Ta có:
1
1 0
0
0 1
1
f x a a
f x b b
f f x
f x c c
f x d d
.
Phương trình
f x a
với
1a
vô nghiệm.
Phương trình
f x b
với
1 0b
có 4 nghiệm phân biệt.
Phương trình
f x c
với
0 1c
có 4 nghiệm phân biệt.
Phương trình
f x d
với
1d
có 2 nghiệm phân biệt.
Câu 42. Xét số phức
,z w
thoả mãn
1z
và
2w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
3
. B.
29
5
. C.
5
. D.
221
5
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 18 TÀI LIỆU ÔN THU THPT QUỐC GIA
GVSB: Trần Thị Vân; GVPB:Nguyễn Viết Thăng
Chọn D
6 8 6 8 10z iw i i z iw z iw
,
10 10 10 7z iw z iw z w
.
6 8z iw i
đạt giá trị nhỏ nhất khi
6 8
10
6 8 6 8
w 2.
10 5
i
z
i i
i
3 4
5
8 6
w
5 5
i
z
i
3 4 8 6 221
w
5 5 5 5
i
z i
.
Câu 43. Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
1 1 2
x y z
d
và mặt phẳng
: 2 6 0P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương trình
A.
1 2 1
3 1 1
x y z
. B.
1 2 1
3 1 1
x y z
.
C.
1 2 1
1 4 7
x y z
. D.
1 2 1
1 4 7
x y z
.
GVSB: Nguyễn Thị Kim Cúc; GVPB: Nguyễn Viết Thăng
Lời giải
Chọn D
Gọi
A
là giao điểm của
d
và
P
.
d
có phương trình tham số
1
2
1 2
x t
y t
z t
nên tọa độ giao điểm
A
của
d
và
P
thỏa mãn
1 1
2 2
1;2; 1
1 2 1
2 6 0 0
x t x
y t y
A
z t z
x y z t
.
Ta có
1;2; 1
P
n
và
1;1; 2
d
u
.
Gọi
Q
là mặt phẳng chứa
d
và
Q P
ta có
, 3;1; 1
Q P d
n n u
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 19
Hình chiếu vuông góc
của
d
lên
P
là giao tuyến của
P
và
Q
nên
, 1;4;7
P Q
u n n
và
đi qua
A
.
Phương trình
1 2 1
:
1 4 7
x y z
Câu 44. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;5
3
x
thỏa mãn
2
3 15
27 (1 )27
x xy x
xy
?
A. 17. B. 16. C. 18. D. 15.
Lời giải
GVSB: Trần Quốc Dũng; GVPB: …………
Chọn A
Xét
2
3 15
( ) 27 ( 1)
x x xy
f x xy
và áp dụng
( 1) 1
x
a x a
.
Suy ra
2 2
1
( ) 26 3 15 1 84 25 390 1 0, 16, ;5
3
f x x x xy xy x xy x y x
.
Do đó
16y
.
2
3 15 2
0 27 1 3 15 0
x x
y x x
: loại.
3 1 VP 0 :y xy
loại.
1, 2y y
: thỏa mãn (1)
Xét
0y
ta có
5
(4) 27 (5 1) 0, 0
y
f y y
và
14
1
3 1 0, {1;2;3; ;15}
3 3
y
y
f y
(2)
Từ (1) và (2)
2; 1;1; 2;3;4;5;6;7;8;9;10;11;15y
.
Câu 45. Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông,
2BD a
, góc giữa hai mặt
phẳng
vàA BD ABCD
bằng 60
. Thể tích của khối hộp đã cho bằng
A.
3
2 3
9
a
. B.
3
6 3a
. C.
3
2 3
3
a
. D.
3
2 3a
.
Lời giải
GVSB:Khanh Tam; GVPB: Hongnhung Nguyen
Chọn D
Gọi
O AC BD
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 20 TÀI LIỆU ÔN THU THPT QUỐC GIA
Ta có:
0
'
' 60 '
A BD ABCD BD
A O BD A OA
AC BD
.
Tam giác
AA O
có:
0
' tan 60 . 3AA OA a
và
2
2
ABCD
S a
.
Vậy
3
. ' ' ' '
'. 2 3
ABCD A B C D ABCD
V AA S a
.
Câu 46. Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
3
. Diện tích hình phẳng giới hạn
bởi đường
6
f x
y
g x
và
1y
bằng
A.
2ln3
. B.
ln 2
. C.
ln15
. D.
3ln2
.
Lời giải
GVSB: Phạm Tính; GVPB:Nguyễn Minh Thành
Chọn A
Ta có
3 2
3 2 6 2g x f x f x f x x a x b a x a b c
.
Suy ra:
2
3 2 3 2 6g x x a x b a
.
Xét phương trình
1
2
2
1 6 3 2 3 2 6 0 0
6
x x
f x
g x f x x a x a b g x
x x
g x
Ta có diện tích bằng
2 2 2
2
1
1 1 1
2 1
6
1 d d d ln 6
6 6 6
ln 6 ln 6 ln 9 2ln3
x x x
x
x
x x x
f x f x g x g x
S x x x g x
g x g x g x
g x g x
Câu 47. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30
, ta được thiết diện là tam giác đều cạnh
4a
. Diện tích xung quanh của
N
bằng
A.
2
4 7 a
. B.
2
8 7 a
. C.
2
8 13 a
. D.
2
4 13 a
.
Lời giải
GVSB:Nguyễn Thuỳ Dương GVPB:Thái Huy
Chọn D
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 21
Giả sử mặt phẳng
P
cắt đáy của hình nón theo dây
AB
. Suy ra tam giác
SAB
đều
4
AB a
.
Gọi
M
là trung điểm của
AB
30
SMO
.
Vì
SM
là đường cao của tam giác
SAB
nên
4 3
2 3
2
a
SM a
.
Tam giác
SMO
vuông tại
O
nên
1
sin .sin30 2 3. 3
2
SO
SMO SO SM a a
SM
.
Suy ra
2 2 2 2
12 3 3
OM SM SO a a a
;
2 2 2 2
9 4 13
OA OM MA a a a .
Vậy
2
. . . 13.4 4 13
xq
S Rl OA SA a a a
.
Câu 48. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(m là tham số thực ). Có
bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
8
z
.
A. 4. B. 3. C. 2. D. 1.
Lời giải
GVSB: …; GVPB: …
Chọn A
Vì
0
8
z
nên đặt
0
8 cos sin
z i
, với
.
Phương trình đã cho nhận
0
z
là nghiệm nên ta có:
2
64 cos 2 sin 16 1 cos sin 0
i m i m
.
Tách phần thực và phần ảo ta có:
2
64cos 2 16 1 cos 0 1
64sin 2 16 1 sin 0 2
m m
m
2 sin 4cos 1 0
m
sin 0
1
cos
4
m
* Nếu
sin 0
thì
cos 1
cos2 1
, thay vào (1) ta có:
2
64 16 1 0
m m
2
2
16 80 0 (vn)
16 48 0 (2 nghiem)
m m
m m
. Suy ra có 2 giá trị
m
.
* Nếu
1
cos
4
m
thì
2
2
1 1
cos 2 2 1 1 1
4 8
m
m
, thay vào (1) ta có:
2
2
1 1
64 1 1 16 1 . 0
8 4
m
m m m
Đặt
1
n m
, ta có:
2
2
1
64 1 16 . 1 0
8 4
n
n n n
2
2 2
8 64 4 1 0
n n n
2
5 2 63 0
n n
(Có 2 nghiệm). Suy ra có 2 giá trị
m
.
Dễ thấy các giá trị của
m
tìm được ở trên không trùng nhau. Vậy có 4 giá trị của
m
thỏa mãn
điều kiện bài toán.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Trang 22 TÀI LIỆU ÔN THU THPT QUỐC GIA
Câu 49. Trong không gian
Oxyz
, cho hai điểm
1; 3;2A
và
2;1; 4B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
4MN
. Giá trị lớn nhất của
AM BN
bằng
A.
5 2
. B.
3 13
. C.
61
. D.
85
.
Lời giải
GVSB: …; GVPB: …
Chọn B
Dễ thấy
A
,
B
nằm hai phía của mặt phẳng
Oxy
. Gọi
'A
đối xứng với
A
qua mặt phẳng
Oxy
suy ra
' 1; 3; 2A
.
Gọi
E
và
F
lần lượt là hình chiếu của
'A
và
B
lên mặt phẳng
Oxy
, ta có
1; 3;0E
,
2;1; 0F
. Do đó
3 ;4;0EF
5EF
.
1
A
là điểm thỏa mãn
1
AA MN k EF
  
( tức là
1
//AA EF
)
1
4 4 12 16
3;4;0 ; ;0
5 5 5 5
AA EF
*
Gọi
1
; ;A x y z
. Từ
*
12
1
5
16
3
5
2 0
x
y
z
17
5
31
5
2
x
y
z
1
17 31
; ;2
5 5
A
.
Ta có
1
27 36
; ; 6
5 5
A B

.
Do
1
AA MN
 
1
AM A N
.
2 2
2
1 1
27 36
6 3 13
5 5
T AM BN A N BN A B
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
' 10 25 ,f x x x x
.Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
8g x f x x m
có ít nhất 3 điểm cực trị?
A.
9
. B.
25
. C.
5
. D.
10
.
NHÓM TOÁN VDC&HSG THPT MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 23
Lời giải
GVSB: Nguyễn thị Thắm; GVPB:Trần Minh Quang
GVPB: Hoàng Hà
Chọn A
+ Ta có:
2
10 25 ,f x x x x
10
0 5
5
x
f x x
x
(*).
+
3 3 3
8 8 . 8g x f x x m x x m f x x m
2 3
3
3
3 8 8
8
8
x x x
f x x m
x x
.
Ta thấy:
2 3
3
3 8 8
0
8
x x x
x x
2 2
3
3 8 8
0
8
x x x
x x
có 1 nghiệm
0x
nên
0x
là 1
điểm cực trị của hàm số.
Cho
3 3
(*)
3 3 3
3 3
8 10 8 10
8 0 8 5 8 5
8 5 8 5
x x m x x m
f x x m x x m x x m
x x m x x m
(**).
Đặt
3 2
8 3 8 0,h x x x h x x x
.
Yêu cầu bài toán tương đương (**) có ít nhất 2 nghiệm phân biệt khác 0
10 0 10m m
1;2;3;4;5;6;7;8;9m
.
------------------HẾT------------------
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 1
Kú THI TN THPT N¡M 2021
M· §Ò: 104
TRAO ĐỔI & CHIA SẺ KIẾN THỨC THÔNG MINH DO HỌC TẬP MÀ CÓ THIÊN TÀI DO TÍCH LŨY MÀ NÊN
Câu 1. Cho hai số phức
3 2z i
và
1 4w i
. Số phức z w bằng
A.
4 2i
. B.
4 2i
. C.
2 6i
. D.
2 6i
.
Câu 2. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3 1y x x . B.
4 2
4 1y x x . C.
3
3 1y x x . D.
4 2
2 1y x x .
Câu 3. Nếu
4
1
d 4f x x
và
4
1
d = 3g x x
thì
4
1
df x g x x
bằng
A.
1
. B.
7
. C.
1
. D.
7
.
Câu 4. Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
là đường thẳng có phương trình
A.
2x
. B.
1x
. C.
2x
. D.
1x
.
Câu 5. Trong không gian
,Oxyz
cho mặt cầu
( )S
có tâm
( 1;3;0)I
và bán kính bằng
2
. Phương trình
của
( )S
là
A.
2 2 2
( 1) ( 3) 2x y z . B.
2 2 2
( 1) ( 3) 4x y z .
C.
2 2 2
( 1) ( 3) 4x y z . D.
2 2 2
( 1) ( 3) 2x y z .
Câu 6. Tập nghiệm của bất phương trình
2 5
x
là
A.
2
( ; log 5)
. B.
5
(log 2; ) . C.
5
( ;log 2) . D.
2
(log 5; )
Câu 7. Thể tích của khối lập phương cạnh 2a bằng
A. a
3
. B. 2a
3
. C. 8a
3
. D. 4a
3
.
Câu 8. Trên khoảng
0;
, đạo hàm của hàm số
5
3
y x
là
A.
8
3
3
8
y x
. B.
2
3
5
3
y x
. C.
2
3
5
3
y x
. D.
2
3
3
5
y x
.
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 2
Câu 9. Trong không gian
Oxyz
, cho điểm
2; 1;4A
. Tọa độ của véc tơ
OA
là
A. (-2; 1; 4). B. (2; -1; 4) . C. (2;1; 4). D.
(-2; 1; -4)
.
Câu 10: Nếu
3
0
d 3
f x x
thì
3
0
4 d
f x x
bằng
A.
3
. B.
12
. C.
36
. D.
4
.
Câu 11: Cho cấp số nhân
n
u
với
1
2u và
2
10u . Công bội của cấp số nhân đã cho bằng
A.
8
. B.
8
. C.
5
. D.
1
5
.
Câu 12: Với n là số nguyên dương bất kì,
3n
, công thức nào dưới đây đúng?
A.
3
3 !
!
n
n
A
n
. B.
3
3!
3 !
n
A
n
. C.
3
!
3 !
n
n
A
n
. D.
3
!
3! 3 !
n
n
A
n
.
Câu 13. Cho hàm số
2
2f x x
. Khẳng định nào dưới đây là đúng?
A.
d 2f x x x C
B.
3
d 2
3
x
f x x x C
C.
2
d 2f x x x x C
D.
3
d 2f x x x x C
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A.
0
B.
3
C.
1
D.
1
Câu 15. Trong không gian
Oxyz
, cho mặt phẳng
P
:
2 4 1 0x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng
P
A.
2
2; 4;1n
B.
1
2;4;1n
C.
3
2;4; 1n
D.
4
2;4;1n
Câu 16: Phần thực của số phức
4 2z i
bằng
A.
2
. B.
4
. C.
4
. D.
2
.
Câu 17: Nghiệm của phương trình
2
log 5 3x
là:
A.
8
5
x
. B.
9
5
x
. C.
8x
. D.
9x
.
Câu 18: Tập xác định của hàm số 8
x
y là
A.
\ 0
. B.
. C.
0;
. D.
0;
.
Câu 19. Cho
0a
và
a 1
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
1
5
. C.
5
. D.
5
Câu 20. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
d
đi qua điểm
1; 5 ; 2M
có
một véc tơ chỉ phương
3; 6 ;1u
. Phương trình của
d
là .
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 3
A.
3
6 5
1 2
x t
y t
z t
. B.
1 3
5 6
2
x t
y t
z t
. C.
1 3
5 6
2
x t
y t
z t
. D.
1 3
5 6
2
x t
y t
z t
.
Câu 21. Trên mặt phẳng toạ độ , điểm
4 ; 3M
là điểm biểu diễn số phức nào dưới đây hai số phức
nào dưới đây
A.
3
4 3z i
. B.
4
4 3z i
. C.
2
4 3z i
. D.
1
4 3z i
.
Câu 22. Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 23. Cho hàm số
e 4
x
f x
. Khẳng định nào dưới đây đúng?
A.
d e 4
x
f x x x C
. B.
d e
x
f x x C
.
C.
4
d e
x
f x x C
. D.
d e 4
x
f x x x C
.
Câu 24. Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;1
. B.
1;
. C.
;1
. D.
0;3
.
Câu 25. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
S R
. B.
2
16
S R
. C.
2
4
S R
. D.
2
4
3
S R
.
Câu 26. Đồ thị của hàm số
3 2
2 3 5 y x x cắt trục tung tại điểm có tung độ bằng
A.
5
. B.
0
. C.
1
. D.
2
.
Câu 27. Cho khối chóp có diện tích đáy
2
8B a
và chiều cao
h a
. Thể tích của khối chóp đã cho
bằng
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 4
A.
3
8a
. B.
3
4
3
a
. C.
3
4a
. D.
3
8
3
a
.
Câu 28. Cho khối trụ có bán kính đáy
5r
và chiều cao
3h
. Thể tích của khối trụ đã cho bằng
A.
15
. B.
75
. C.
25
. D.
45
.
Câu 29. Trong không gian
Oxyz
, cho điểm
2;1; 2M
và mặt phẳng
:3 2 1 0P x y z
. Đường
thẳng đi qua
M
và vuông góc với
P
có phương trình là:
A.
2 1 2
3 2 1
x y z
. B.
2 1 2
3 2 1
x y z
.
C.
2 1 2
3 2 1
x y z
. D.
2 1 2
3 2 1
x y z
.
Câu 30. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có tất cả các cạnh bằng nhau ( tham khảo hình bên).
Góc giữa hai đường thẳng
'AB
và
'CC
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 31. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
4AB a
và
SA
vuông góc với
mặt phẳng đáy. Khoảng cách từ
C
đến mặt phẳng
SAB
bằng
A.
4a
. B.
4 2a
. C.
2 2a
. D.
2a
.
Câu 32. Nếu
2
0
4
d
f x x
thì
2
0
2 1
d
f x x
bằng
A.
8
. B.
10
. C.
7
. D.
6
.
Câu 33. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1 a
) có đồ thị như trong hình bên. Mệnh đề
nào dưới đây đúng ?
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 5
A.
' 0, y x R
. B.
' 0, 1 y x
. C.
' 0, y x R
. D.
' 0, 1 y x
.
Câu 34. Cho số phức
z
thỏa mãn
4 3 iz i
. Số phức liên hợp
z
là
A.
3 4 z i
. B.
3 4 z i
. C.
3 4 z i
. D.
3 4 z i
.
Câu 35. Từ một hộp chứa
12
quả bóng gồm
5
quả màu đỏ và
7
quả màu xanh, lấy ngẫu nhiên đồng
thời
3
quả. Xác suất để lấy được
3
quả màu đỏ bằng
A.
1
22
. B.
7
44
. C.
5
12
. D.
2
7
.
Câu 36. Với mọi
,a b
thỏa mãn
3
2 2
log log 5a b
, khẳng định nào dưới đây là đúng?
A.
3
32a b
. B.
3
25a b
. C.
3
25a b
. D.
3
32a b
.
Câu 37. Trên đoạn
1;2
, hàm số
3 2
3 1y x x
đạt giá trị nhỏ nhất tại điểm
A.
2x
. B.
0x
. C.
1x
. D.
1x
.
Câu 38. Trong không gian
Oxyz
, cho hai điểm
1;0;0A
và
3;2;1B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 2 0x y z
. B.
4 2 17 0x y z
.
C.
4 2 4 0x y z
. D.
2 2 11 0x y z
.
Câu 39. Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình
0f f x
là
A.
12
. B.
10
. C.
8
. D.
4
.
Câu 40. Có bao nhiêu số nguyên
x
thỏa mãn
2
3
2 4 log 25 3 0
x x
x
?
A.
24
. B. Vô số. C.
25
. D.
26
.
Câu 41. Cho hàm số
2
2 2 1
.
3 1 1
x khi x
f x
x khi x
Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2.F
Giá trị của
1 2 2F F
bằng
y
x
O
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 6
A.
18
. B.
20
. C.
9
. D.
24
.
Câu 42. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30
, ta được thiết diện là tam giác đều cạnh
2
a
. Diện tích xung quanh của
N
bằng
A.
2
7
a
. B.
2
13
a
. C.
2
2 13
a
. D.
2
2 7
a
.
Câu 43. Trong không gian
Oxyz
, cho đường thẳng
1
:
1 1 2
x y z
d
và mặt phẳng
: 2 2 2 0
P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương
trình:
A.
1
2 4 3
x y z
. B.
1
14 1 8
x y z
. C.
1
2 4 3
x y z
. D.
1
14 1 8
x y z
.
Câu 44. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 1 .27
x xy x
xy
?
A.
19
. B.
20
. C.
18
. D.
21
.
Câu 45. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực). Có
bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
6
z
?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 46. Cho khối hộp chữ nhật .
ABCD A B C D
có đáy là hình vuông,
4
BD a
, góc giữa hai mặt
phẳng
A BD
và
ABCD
bằng
60
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
48 3
a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3
a
.
Câu 47. Cho hàm số
3 2
f x x ax bx c
với
, ,
a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
2
. Diện tích hình phẳng giới hạn
bởi đường
6
f x
y
g x
và
1
y
bằng
A.
ln3
. B.
3ln2
. C.
ln10
. D.
ln7
.
Câu 48. Xét các số phức
z
;
w
thỏa mãn
1
z
và
2
w
. Khi
6 8
z iw i
đạt giá trị nhỏ nhất,
z w
bằng:
A.
29
5
. B.
221
5
. C.
3
. D.
5
.
Câu 49. Trong không gian
Oxyz
, cho hai điểm
2;1 3
A
và
1; 3;2
B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
3
MN
. Giá trị lớn nhất của
AM BN
bằng:
A.
65
. B.
29
. C.
26
. D.
91
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
9 16 ,f x x x x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
7
g x f x x m
có ít nhất 3 điểm cực trị ?
A.
16
. B.
9
. C.
4
. D.
8
.
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 7
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
BẢNG ĐÁP ÁN
1.
B
2.
C
3.
D
4.
C
5.
C
6.
D
7.
C
8.
B
9.
B
10.
B
11.
C
12.
C
13
.
B
14.
C
15.
C
16.
C
17.
A
18.
B
19.
A
20.
D
21.
D
22.
B
23.
A
24.
A
25.
C
26.
A
27.
D
28.
B
29.
A
30.
D
31.
A
32.
D
33.
B
34.
A
35.
A
36.
A
37.
B
38.
A
39.
B
40.
D
41.
A
42.
B
43.
D
44.
B
45.
D
46.
D
47.
B
48.
B
49.
A
50.
D
LỜI GIẢI CHI TIẾT
Câu 1. Cho hai số phức
3 2z i
và
1 4w i
. Số phức z w bằng
A.
4 2i
. B.
4 2i
. C.
2 6i
. D.
2 6i
.
Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Đinh Ngọc
Chọn B
3 2 1 4 4 2z w i i i
.
Câu 2. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3 1y x x
. B.
4 2
4 1y x x
. C.
3
3 1y x x
. D.
4 2
2 1y x x
.
Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Đinh Ngọc
Chọn C
Dựa vào đồ thị ta thấy đây là hàm số bậc
3
có hệ số
0a
nên chọn C.
Câu 3. Nếu
4
1
d 4f x x
và
4
1
d = 3g x x
thì
4
1
df x g x x
bằng
A.
1
. B.
7
. C.
1
. D.
7
.
Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Đinh Ngọc
Chọn D
4 4 4
1 1 1
d d d 4 3 7f x g x x f x x g x x
.
Câu 4. Tiệm
cận đứng của đồ thị hàm số
1
2
x
y
x
là đường thẳng có phương trình
B.
2x
. B.
1x
. C.
2x
. D.
1x
.
Lời giải
GVSB: Trần Minh Tâm; GVPB: Đinh Ngọc
Chọn C
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 8
Ta có:
2 2
1 1
lim , lim
2 2
x x
x x
x x
 
.
Đồ thị hàm số có tiệm cận đứng là đường thẳng có phương trình
2
x
.
Câu 5. Trong
không gian
,
Oxyz
cho mặt cầu
( )
S
có tâm
( 1;3;0)
I
và bán kính bằng
2
. Phương trình
của
( )
S
là
A.
2 2 2
( 1) ( 3) 2
x y z
. B.
2 2 2
( 1) ( 3) 4
x y z
.
C.
2 2 2
( 1) ( 3) 4
x y z
. D.
2 2 2
( 1) ( 3) 2
x y z
.
Lời giải
GVSB: Trần Minh Tâm ; GVPB: Đinh Ngọc
Chọn C
Mặt cầu
( )
S
có tâm
( 1;3;0)
I
và bán kính
2
R
. Phương trình của mặt cầu
( )
S
là :
2 2 2
( 1) ( 3) 4
x y z
Câu 6. Tập nghiệm của bất phương trình
2 5
x
là
A.
2
( ; log 5)

. B.
5
(log 2; )
. C.
5
( ;log 2)

. D.
2
(log 5; )
Lời giải
GVSB: Trần Minh Tâm; GVPB: Đinh Ngọc
Chọn D
Ta có:
2
2 5 log 5.
x
x
Tập nghiệm của bất phương trình là :
2
(log 5; )
Câu 7. Thể tích của khối lập phương cạnh 2a bằng
B. a
3
. B. 2a
3
. C. 8a
3
. D. 4a
3
.
Lời giải
GVSB: Nguyễn Hòa; GVPB: Đinh Ngọc
Chọn C
Ta có
3
3
2 8
V a a
.
Câu 8. Trên khoảng
0;
, đạo hàm của hàm số
5
3
y x
là
B.
8
3
3
8
y x
. B.
2
3
5
3
y x
. C.
2
3
5
3
y x
. D.
2
3
3
5
y x
.
Lời giải
GVSB: Nguyễn Hòa; GVPB: Đinh Ngọc
Chọn B
Ta có:
5 2
1
3 3
5 5
3 3
y x x
.
Câu 9. Trong không gian
Oxyz
, cho điểm
2; 1;4
A
. Tọa độ của véc tơ
OA
là
A.
2;1;4
. B.
2; 1;4
. C.
2;1;4
. D.
2;1; 4
.
Lời giải
GVSB: Nguyễn Hòa; GVPB: Đinh Ngọc
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 9
Chọn B
Ta có:
2 0; 1 0;4 0OA
hay
2; 1;4OA
.
Câu 10: Nếu
3
0
d 3
f x x
thì
3
0
4 d
f x x
bằng
A.
3
. B.
12
. C.
36
. D.
4
.
Lời giải
GVSB: Đỗ Văn Trường; GVPB: Thanh Huyền
Chọn B
Ta có:
3 3 3
0 0 0
d 3 4 d 4 d 4.3 12f x x f x x f x x
.
Câu 11: Cho cấp số nhân
n
u
với
1
2u và
2
10u . Công bội của cấp số nhân đã cho bằng
A.
8
. B.
8
. C.
5
. D.
1
5
.
Lời giải
GVSB: Đỗ Văn Trường; GVPB: Thanh Huyền
Chọn C
Ta có:
2
2 1
1
10
. 5
2
u
u u q q
u
.
Câu 12: Với n là số nguyên dương bất kì,
3
n
, công thức nào dưới đây đúng?
A.
3
3 !
!
n
n
A
n
. B.
3
3!
3 !
n
A
n
. C.
3
!
3 !
n
n
A
n
. D.
3
!
3! 3 !
n
n
A
n
.
Lời giải
GVSB: Đỗ Văn Trường; GVPB: Thanh Huyền
Chọn C
Ta có:
3
!
3 !
n
n
A
n
.
Câu 13. Cho hàm số
2
2f x x
. Khẳng định nào dưới đây là đúng?
A.
d 2f x x x C
B.
3
d 2
3
x
f x x x C
C.
2
d 2f x x x x C
D.
3
d 2f x x x x C
Lời giải
GVSB: Nguyễn Thành Tiến; GVPB: Thanh Huyền
Chọn B
Ta có
3
2
d 2 d 2
2
x
f x x x x x C
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A.
0
B.
3
C.
1
D.
1
Lời giải
GVSB: Nguyễn Thành Tiến; GVPB: Thanh Huyền
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 10
Chọn C
Từ bảng biến thiên suy ra giá trị cực tiểu là
1
y
.
Câu 15. Trong không gian
Oxyz
, cho mặt phẳng
P
:
2 4 1 0
x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng
P
A.
2
2; 4;1
n
B.
1
2;4;1
n
C.
3
2;4; 1
n
D.
4
2;4;1
n
Lời giải
GVSB: Nguyễn Thành Tiến; GVPB: Thanh Huyền
Chọn C
Câu 16: Phần thực của số phức
4 2
z i
bằng
A.
2
. B.
4
. C.
4
. D.
2
.
Lời giải
GVSB: Nguyễn Bình; GVPB: Thanh Huyền
Chọn C
Phần thực của số phức
4 2
z i
là 4
Câu 17: Nghiệm của phương trình
2
log 5 3
x
là:
A.
8
5
x
. B.
9
5
x
. C.
8
x
. D.
9
x
.
Lời giải
GVSB: Nguyễn Bình; GVPB: Thanh Huyền
Chọn A
Điều kiện
0
x
2
log 5 3
x
3
5 2
x
5 8
x
8
5
x
(nhận).
Câu 18: Tập xác định của hàm số
8
x
y
là
A.
\ 0
. B.
. C.
0;

. D.
0;

.
Lời giải
GVSB: Nguyễn Bình; GVPB: Thanh Huyền
Chọn B
Tập xác định của hàm số
8
x
y
là
Câu 19. Cho
0
a
và
a 1
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
1
5
. C.
5
. D.
5
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Nguyễn Minh Luận
Chọn A
Ta có
1
5
5
1 1
log log log
5 5
a a a
a a a
.
Câu 20. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
d
đi qua điểm
1; 5 ; 2
M
có
một véc tơ chỉ phương
3; 6 ;1
u
. Phương trình của
d
là .
A.
3
6 5
1 2
x t
y t
z t
. B.
1 3
5 6
2
x t
y t
z t
. C.
1 3
5 6
2
x t
y t
z t
. D.
1 3
5 6
2
x t
y t
z t
.
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 11
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Nguyễn Minh Luận
Chọn D
Đường thẳng
d
có véc tơ chỉ phương là
3; 6 ;1u
và đi qua điểm
1; 5 ; 2M
nên có
phương trình tham số .
1 3
5 6
2
x t
y t
z t
.
Câu 21. Trên mặt phẳng toạ độ , điểm
4 ; 3
M
là điểm biểu diễn số phức nào dưới đây hai số phức
nào dưới đây
A.
3
4 3z i
. B.
4
4 3z i
. C.
2
4 3z i
. D.
1
4 3z i
.
Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Nguyễn Minh Luận
Chọn D
Điểm
4 ; 3M
là diểm biểu diễn số phức
1
4 3z i
.
Câu 22. Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
5
.
Lời giải
GVSB: Nguyễn Thảo; GVPB: Nguyễn Minh Luận
Chọn B
Từ bảng xét dấu ta thấy hàm số
y f x
đổi dấu khi qua
2x
;
1x
;
2x
;
4x
. Do
đó, hàm số đã cho có
4
điểm cực trị.
Câu 23. Cho hàm số
e 4
x
f x
. Khẳng định nào dưới đây đúng?
A.
d e 4
x
f x x x C
. B.
d e
x
f x x C
.
C.
4
d e
x
f x x C
. D.
d e 4
x
f x x x C
.
Lời giải
GVSB: Nguyễn Thảo; GVPB: Nguyễn Minh Luận
Chọn A
Ta có:
d e 4 d e 4
x x
f x x x x C
.
Câu 24. Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 12
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;1
. B.
1;
. C.
;1
. D.
0;3
.
Lời giải
GVSB: Nguyễn Thảo; GVPB: Nguyễn Minh Luận
Chọn A
Từ hình vẽ ta thấy hàm số đã cho nghịch biến trên khoảng
1;1
.
Câu 25. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
S R
. B.
2
16
S R
. C.
2
4
S R
. D.
2
4
3
S R
.
Lời giải
GVSB: Võ Sĩ Đạt; GVPB: Trương Minh Mỹ
Chọn C
Công thức diện tích
S
của mặt cầu bán kính
R
là:
2
4
S R
Câu 26. Đồ thị của hàm số
3 2
2 3 5 y x x
cắt trục tung tại điểm có tung độ bằng
A.
5
. B.
0
. C.
1
. D.
2
.
Lời giải
GVSB: Võ Sĩ Đạt; GVPB: Trương Minh Mỹ
Chọn A
Gọi
0 0
;M x y
là giao điểm của đồ thị hàm số
3 2
2 3 5y x x
và trục tung, ta có:
0 0
0 5x y
Câu 27. Cho khối chóp có diện tích đáy
2
8B a
và chiều cao
h a
. Thể tích của khối chóp đã cho
bằng
A.
3
8a
. B.
3
4
3
a
. C.
3
4a
. D.
3
8
3
a
.
Lời giải
GVSB: Võ Sĩ Đạt; GVPB: Trương Minh Mỹ
Chọn D
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 13
Thể tích của khối chóp có diện tích đáy
2
8B a
và chiều cao
h a
là:
32
1
. .
3 3
1
.
3
8
8 V aB h a a
Câu 28. Cho khối trụ có bán kính đáy
5r
và chiều cao
3h
. Thể tích của khối trụ đã cho bằng
A.
15
. B.
75
. C.
25
. D.
45
.
Lời giải
GVSB: Lê Thị Thu Trang; GVPB: Trương Minh Mỹ
Chọn B
Thể tích khối trụ:
2 2
.5 .3 75V r h
.
Câu 29. Trong không gian
Oxyz
, cho điểm
2;1; 2M
và mặt phẳng
:3 2 1 0P x y z
. Đường
thẳng đi qua
M
và vuông góc với
P
có phương trình là:
A.
2 1 2
3 2 1
x y z
. B.
2 1 2
3 2 1
x y z
.
C.
2 1 2
3 2 1
x y z
. D.
2 1 2
3 2 1
x y z
.
Lời giải
GVSB: Lê Thị Thu Trang; GVPB: Trương Minh Mỹ
Chọn A
Đường thẳng đi qua
M
và vuông góc với
P
có VTCP:
3;2; 1
P
u n
.
Phương trình đường thẳng cân tìm là :
2 1 2
3 2 1
x y z
.
Câu 30. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có tất cả các cạnh bằng nhau ( tham khảo hình bên).
Góc giữa hai đường thẳng
'AB
và
'CC
bằng
A.
30
. B.
90
. C.
60
. D.
45
.
Lời giải
GVSB: Lê Thị Thu Trang; GVPB: Trương Minh Mỹ
Chọn D
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 14
Ta có
'// 'BB CC
(do
'BB
và
'CC
là cạnh bên của hình lăng trụ).
Suy ra
', ' ', 'AB CC AB BB
.
Tứ giác
' 'ABB A
là hình vuông (do
. ' ' 'ABC A B C
là lăng trụ đứng có tất cả các cạnh bằng nhau)
nên
' 45AB B
.
Vậy
', ' ', ' ' 45AB CC AB BB AB B
.
Câu 31. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
4AB a
và
SA
vuông góc với
mặt phẳng đáy. Khoảng cách từ
C
đến mặt phẳng
SAB
bằng
A.
4a
. B.
4 2a
. C.
2 2a
. D.
2a
.
Lời giải
GVSB: Chương Huy; GVPB: Cô Long
Chọn A
Ta có:
:
gt
do
Trong mp
BC AB
BC SA SA ABC BC SAB
SAB AB SA A
tại
B
.
Suy ra
,d C SAB CB
.
Xét
ABC
vuông cân tại
B
có:
4BC AB a
.
Vậy
, 4d C SAB a
.
Câu 32. Nếu
2
0
4
d
f x x
thì
2
0
2 1
d
f x x
bằng
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 15
A.
8
. B.
10
. C.
7
. D.
6
.
Lời giải
GVSB: Chương Huy; GVPB: Cô Long
Chọn D
Ta có:
2 2 2
0 0 0
2 1 2 2.4 2 6
d d d
f x x f x x x
.
Câu 33. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1 a
) có đồ thị như trong hình bên. Mệnh đề
nào dưới đây đúng ?
A.
' 0, y x R
. B.
' 0, 1 y x
. C.
' 0, y x R
. D.
' 0, 1 y x
.
Lời giải
GVSB: Lương Công Hảo; GVPB: Trịnh Đềm
Chọn B
Ta có TXĐ:
\ 1D R
và
2
1
' 0, 1
( 1)
a
y x
x
và đồ thị là đường đi xuống trên từng
khoảng xác định nên hàm số đã cho nghịch biến trên mỗi khoảng xác định.
Câu 34. Cho số phức
z
thỏa mãn
4 3 iz i
. Số phức liên hợp
z
là
A.
3 4 z i
. B.
3 4 z i
. C.
3 4 z i
. D.
3 4 z i
.
Lời giải
GVSB: Lương Công Hảo; GVPB: Trịnh Đềm
Chọn A
Ta có:
2
2
4 3 (4 3 ).( ) 4 3
3 4
1
i i i i i
z i
i i
. Suy ra
3 4 . z i
Câu 35. Từ một hộp chứa
12
quả bóng gồm
5
quả màu đỏ và
7
quả màu xanh, lấy ngẫu nhiên đồng
thời
3
quả. Xác suất để lấy được
3
quả màu đỏ bằng
A.
1
22
. B.
7
44
. C.
5
12
. D.
2
7
.
Lời giải
GVSB: Phương Lan; GVPB: Nguyễn Chiên
Chọn A
Không gian mẫu
3
12
n C
.
Gọi A là biến cố “ cả
3
quả bóng lấy ra đều là màu đỏ”
3
5
n A C
.
y
x
O
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 16
Xác suất để lấy được
3
quả màu đỏ là:
3
5
3
12
1
22
n A
C
P A
n C
.
Câu 36. Với mọi
,a b
thỏa mãn
3
2 2
log log 5a b
, khẳng định nào dưới đây là đúng?
A.
3
32a b
. B.
3
25a b
. C.
3
25a b
. D.
3
32a b
.
Lời giải
GVSB: Phương Lan; GVPB:Nguyễn Chiên
Chọn A
Ta có:
3 3 3
2 2 2
log log 5 log 5 32a b a b a b
.
Câu 37. Trên đoạn
1;2
, hàm số
3 2
3 1y x x
đạt giá trị nhỏ nhất tại điểm
A.
2x
. B.
0x
. C.
1x
. D.
1x
.
Lời giải
GVSB: ThienMinh Nguyễn; GVPB:Nguyễn Chiên
Chọn B
Xét hàm số
3 2
3 1y f x x x
.
2
3 6y f x x x
.
+
2
0 1;2
0 3 6 0
2 1;2
x
f x x x
x
.
Ta có
1 3f
,
0 1f
và
2 21f
.
Nên
1;2
min
x
f x
1
khi
0x
.
Câu 38. Trong không gian
Oxyz
, cho hai điểm
1;0;0A
và
3;2;1B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 2 0x y z
. B.
4 2 17 0x y z
.
C.
4 2 4 0x y z
. D.
2 2 11 0x y z
.
Lời giải
GVSB: ThienMinh Nguyễn; GVPB:Nguyễn Chiên
Chọn A
Phương trình mặt phẳng
P
đi qua
1;0;0A
nhận vectơ
2;2;1AB
là VTPT có dạng:
2 1 2 0 1 0 0 2x 2 2 0x y z y z
.
Câu 39. Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình
0f f x
là
A.
12
. B.
10
. C.
8
. D.
4
.
Lời giải
GVSB: Duong Phan; GVPB: Nam Lê Hải
Chọn B
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 17
Nhìn vào đồ thị ta thấy
( ) 0f x
có 4 nghiệm phân biệt theo thứ tự
, , ,a b c d
.
Ta có:
, ; 1
, 1;0
0
, 0;1
, 1;
f x a a
f x b b
f f x
f x c c
f x d d

.
Dựa vào đồ thị ta thấy:
Phương trình
f x a
có
2
nghiệm thực phân biệt.
Phương trình
f x b
có
4
nghiệm thực phân biệt.
Phương trình
f x c
có
4
nghiệm thực phân biệt.
Phương trình
f x d
vô nghiệm trên
.
Vậy phương trình
0f f x
có
10
nghiệm thực phân biệt.
Câu 40. Có bao nhiêu số nguyên
x
thỏa mãn
2
3
2 4 log 25 3 0
x x
x
?
A.
24
. B. Vô số. C.
25
. D.
26
.
Lời giải
GVSB: Duong Phan; GVPB: Nam Lê Hải
Chọn D
Điều kiện:
25x
.
2
2
2
3
3
3
2 4 0
log 25 3 0
2 4 log 25 3 0
2 4 0
log 25 3 0
x x
x x
x x
x
x
x
.
Trường hợp 1:
2
2
3
0
2 4 0
2 0
2
25 27
log 25 3 0
2
x x
x
x x
x
x
x
x
.
Vì
25x
nên ta có:
25 0
2
x
x
mà
x
nên
24, 23,..., 1,0,2x
1
.
Trường hợp 2:
2
2
3
0 2
2 4 0
2 0
2
2
25 27
log 25 3 0
x x
x
x x
x
x
x
x
2
.
Từ
1
và
2
ta có
26
số nguyên
x
thỏa mãn
2
3
2 4 log 25 3 0
x x
x
.
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 18
GVPB đề xuất
ĐK:
25x
Xét
2
2
0
2 4 0 2 0
2
x x
x
x x
x
Xét
3
log 25 3 25 27 2x x x
Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta có: BPT
25 0
2
x
x
x
nguyên nên có 26 giá trị thỏa mãn bài toán.
Câu 41. Cho hàm số
2
2 2 1
.
3 1 1
x khi x
f x
x khi x
Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2.F
Giá trị của
1 2 2F F
bằng
A.
18
. B.
20
. C.
9
. D.
24
.
Lời giải
GVSB: Quốc Hưng; GVPB: Nam Lê Hải
Chọn A
Ta có:
1 1
2
0 0
3 1 2 1 0 1 2 0 4f x dx x dx F F F F
Trên khoảng
;1
, ta có:
2 3
3 1f x dx x dx x x C
Mà
3
0 2 2 2.F C F x x x
Trên nửa khoảng
1;
, ta có:
2
2 2 2f x dx x dx x x C
Mà
2
1 4 1 2 1.F C F x x x
Do đó:
1 2 2 0 2.9 18.F F
Câu 42. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30
, ta được thiết diện là tam giác đều cạnh
2a
. Diện tích xung quanh của
N
bằng
A.
2
7 a
. B.
2
13 a
. C.
2
2 13 a
. D.
2
2 7 a
.
Lời giải
GVSB: Đặng Minh Nhựt; GVPB: Cao Phi
Chọn B
+∞
+
+
-
+
-
-
+-+
0
0
0
0
0
VT
log
3
(x+25)-3
2
x
2
-4
x
2
0
-25
x
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 19
Xét hình nón
N
và mặt phẳng
SAB
đi qua đỉnh cắt
O
tại
A
,
B
.
Gọi
H
là trung điểm của đoạn thẳng
AB
.
Tam giác
SAB
đều nên
3 2 . 3
3
2 2
AB a
SH a
.
Ta có
, , 30
SAB OAB AB
SH AB SAB OAB SH OH SHO
OH AB
.
3
sin .sin 30
2
SO a
SHO SO SH
SH
.
2
2
2 2
3 13
2
2 2
a
OB SB SO a
.
Vậy
2
13
. . .2 . 13
2
xq
a
S SB OB a a
.
Câu 43. Trong không gian
Oxyz
, cho đường thẳng
1
:
1 1 2
x y z
d
và mặt phẳng
: 2 2 2 0P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương
trình:
A.
1
2 4 3
x y z
. B.
1
14 1 8
x y z
. C.
1
2 4 3
x y z
. D.
1
14 1 8
x y z
.
Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB:Cao Phi
Chọn D
Gọi
0;0;1A
,
1; 1;3B
là hai điểm thuộc đường thẳng
d
và
,A B
lần lượt là hình chiếu
vuông góc của
,A B
lên
P
.
Dễ thấy
A P
nên
A A
.
Gọi
là đường thẳng đi qua
B
và vuông góc với
P
Có
1;2; 2
P
u n

H
O
S
B
A
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 20
Đường thẳng
đi qua
1; 1;3
B
và có VTCP
1;2; 2
u
có dạng:
1
1 2 ,
3 2
x t
y t t
z t
Tọa độ điểm
B
là tọa độ giao điểm của
và
P
, tức là nghiệm của hệ
14
1
9
1 2
1 14 1 17
; ;
3 2
9 9 9 9
17
2 2 2 0
9
x
x t
y t
y B
z t
x y z
z
Gọi
d
là hình chiếu vuông góc của
d
lên
P
14 1 8
; ;
9 9 9
d
u A B
hay
14;1;8
d
u
PTCT của đường thẳng
d
đi qua
0;0;1
A
và có VTCP
14;1;8
d
u
có dạng:
1
14 1 8
x y z
.
Câu 44. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 1 .27
x xy x
xy
?
A.
19
. B.
20
. C.
18
. D.
21
.
Lời giải
GVSB: Bùi Thanh Sơn; GVPB:
Chọn B
Ta có:
2
3 18
27 1 .27
x xy x
xy
2
3 18
27 1
x xy x
xy
2
3 18
27 1 0
x xy x
xy
.
Mạt khác:
2
2
3 18
3 18 2
27 1 1 26 1 1 26 3 18 1
x xy x
x xy x
xy xy x xy x xy
2
78 25 468
x xy x
.
+ Với
19
y
2
3 18 2 2
1
27 1 78 25 468 84 7 0 ;6
3
x xy x
xy x xy x x x x
(loại).
+ Với
3
y
2
3 18
1
27 1 1 3 0 ;6
3
x xy x
xy x x
(loại).
+ Với
2
y
1
2
x
(thỏa mãn).
+ Với
1
y
1
x
(thỏa mãn).
+ Với
0
y
2
3 18
27 1
x x
2
3 18 0
x x
0
6
x
x
(loại).
+ Với
1
y
: Đặt
2
3 18
27 1
x xy x
f x xy
.
Do
17
1
3 1 0 1;2;....;18
3 3
y
y
f y
và
6
6 27 6 1 0 1;2;....;18
y
f y y
nên
phương trình
0
f x
luôn có nghiệm thuộc
1
;6
3
.
Tóm lại
2; 1;1;2;....;18
y
.
Vậy có
20
số nguyên
y
thỏa mãn yêu cầu bài toán.
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 21
Câu 45. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực). Có
bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
6
z
?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
GVSB: Bùi Thanh Sơn; GVPB: Vân Vũ
Chọn D
Ta có:
2
2
1 2 1
m m m
.
Nếu
0
1
2
m
: Phương trình có hai nghiệm phức
1 2 1.
z m m i
.
Ta có:
0
6
z
2
1 2 1 36
m m
2
36
m
6
6
m lo i
m th
¹
áa m·n
Nếu
0
1
2
m
: Phương trình có kép
1
2
z
.
Khi đó
1
2
z
nên
1
2
m
không thỏa mãn.
Nếu
0
1
2
m
: Phương trình có hai nghiệm thực phân biệt
1 2 1
z m m
.
Ta có:
0
6
z
0
0
6
6
z
z
+ Với
0
6
z
: Thay vào phương trình ta được:
2 2
6 2 1 .6 0
m m
2
12 24 0
m m
6 2 3
6 2 3
m th
m th
áa m·n
áa m·n
+ Với
0
6
z
: Thay vào phương trình ta được:
2
2
6 2 1 . 6 0
m m
2
12 48 0m m v
« nghiÖm
.
Vậy có
3
giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 46. Cho khối hộp chữ nhật .
ABCD A B C D
có đáy là hình vuông,
4
BD a
, góc giữa hai mặt
phẳng
A BD
và
ABCD
bằng
60
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
48 3
a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3
a
.
Lời giải
GVSB: Dương Quá; GVPB: Linh Pham
Chọn D
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 22
Gọi
O
là giao điểm của hai đường chéo
AC
và
BD
.
Ta có:
OA BD
BD A O
A A ABCD A A BD
Xét
A BD
và
ABCD
có:
A BD ABCD BD
AO BD
A O BD
góc giữa hai mặt phẳng
A BD
và
ABCD
là
A OA
.
60A OA
.
Ta có:
4BD a 2OA a
và
tan
AA
A OA
OA
.tan 60 2 3AA OA a
.
Vậy
.
.
ABCD A B C D ABCD
V AA S
1
. .
2
AA AC BD
2
3
1
2 3 . . 4 16 3
2
a a a
.
Câu 47. Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
2
. Diện tích hình phẳng giới hạn
bởi đường
6
f x
y
g x
và
1y
bằng
A.
ln3
. B.
3ln2
. C.
ln10
. D.
ln7
.
Lời giải
GVSB: Nguyễn Minh Thành; GVPB: Thanh Hảo
Chọn B
Ta có
6f x

.
Khi đó
6.g x f x f x f x f x f x
Giả sử
1 2 1 2
,x x x x
là hai điểm cực trị của hàm số
.g x
Vì
lim
x
g x


và
5
và
2
là hai giá trị cực trị của hàm số
g x
nên
1
2
2
.
5
g x
g x
Phương trình hoành độ giao điểm của
6
f x
y
g x
và
1y
là:
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 23
1
6
f x
g x
6
g x f x
6
f x f x f x f x
1
2
6 0 .
x x
f x f x
x x
Khi đó diện tích hình phẳng cần tìm là:
2 2
1 1
6
1 d d
6 6
x x
x x
f x f x f x
S x x
g x g x
2
2
1
1
d ln 6
6
x
x
x
x
g x
x g x
g x
2 1
ln 6 ln 6 ln8 3ln 2.
g x g x
Câu 48. Xét các số phức
z
;
w
thỏa mãn
1
z
và
2
w
. Khi
6 8
z iw i
đạt giá trị nhỏ nhất,
z w
bằng:
A.
29
5
. B.
221
5
. C.
3
. D.
5
.
Lời giải
GVSB: Bùi Thanh Sơn; GVPB:
Chọn B
Do
2
w
nên
. 2
iw iw i w
.
Ta có:
6 8 6 8 7
z iw i i z iw
.
Dấu bằng xảy ra
6 8 0
6 8 0
1
2
z k i k
iw m i m
z
iw
1
10
1
5
3 4
5 5
6 8
5 5
k
m
z i
iw i
1
10
1
5
3 4
5 5
8 6
5 5
k
m
z i
w i
Khi đó
3 4 8 6 221
5 5 5 5 5
z w i i .
Câu 49. Trong không gian
Oxyz
, cho hai điểm
2;1 3
A
và
1; 3;2
B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
3
MN
. Giá trị lớn nhất của
AM BN
bằng:
A.
65
. B.
29
. C.
26
. D.
91
.
Lời giải
GVSB: Nguyễn Cảnh Chiến; GVPB: Nguyễn Loan
Chọn A
ĐỀ CHÍNH THỨC ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Trang 24
Nhận xét:
A
và
B
nằm khác phía so với mặt phẳng
Oxy
.
Gọi
P
là mặt phẳng qua
A
và song song với mặt phẳng
: 3 Oxy P z
.
B
đối xứng với
B
qua mặt phẳng
1; 3; 2
Oxy B
.
1
B
là hình chiếu của
B
trên mặt phẳng
1
1; 3; 3 P B
.
Gọi
MN
AA 3
A T A
AA Oxy
A
thuộc đường tròn
C
có tâm
A
và bán kính
3R
,
C
nằm trên mặt phẳng
P
.
Ta có:
AM BN A N BN A N B N A B
1 1
5AB R B nằm ngoài đường tròn
C
.
Do
A P
,
B P
mà
P Oxy
suy ra
A B
luôn cắt mặt phẳng
Oxy
.
Ta lại có:
2 2
1 1
A B B B A B
mà
1
1B B
;
1
5AB
1 1
8
max max
A B A B AB R
65
max
AM BN . Dấu
" "
xảy ra khi
A
là giao điểm của
1
AB với đường tròn
C
,
A
ở giữa
A
và
1
B và
N
là giao điểm của
A B
với mặt phẳng
Oxy
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
9 16 ,f x x x x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
7g x f x x m
có ít nhất 3 điểm cực trị ?
A.
16
. B.
9
. C.
4
. D.
8
.
Lời giải
GVSB: Bùi Văn Huấn; GVPB: Lan Huong
Chọn D
Ta có:
9
0
4
x
f x
x
.
2 3
3
2
3
3 7 7
. 7
7
x x x
g x f x x m
x x
.
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
Trang 25
+)
g x
không xác định tại
0x
và
2 3
2
3
3 7 7
7
x x x
x x
đổi dấu khi qua
0x
nên
0x
là
một điểm cực trị của hàm số.
+)
3 3
3 3 3
3 3
7 4 7 4
7 0 7 4 7 4
7 9 7 9
x x m x x m
f x x m x x m x x m
x x m x x m
.
1
Ta có bảng biến thiên của hàm số
u x
với
3
7u x x x
Để hàm số
g x
có ít nhất 3 điểm cực trị thì hệ
1
phải có ít nhất 2 nghiệm đơn hoặc nghiệm
bội lẻ khác
0
. Mà ta lại thấy
9 4 4m m m
.
Nên suy ra
9 0 9m m
.
Vậy có 8 giá trị nguyên dương của
m
thỏa mãn yêu cầu bài toán là
1, 2,...,8m
.
| 1/99
| | Tải xuống

Có thể bạn quan tâm:

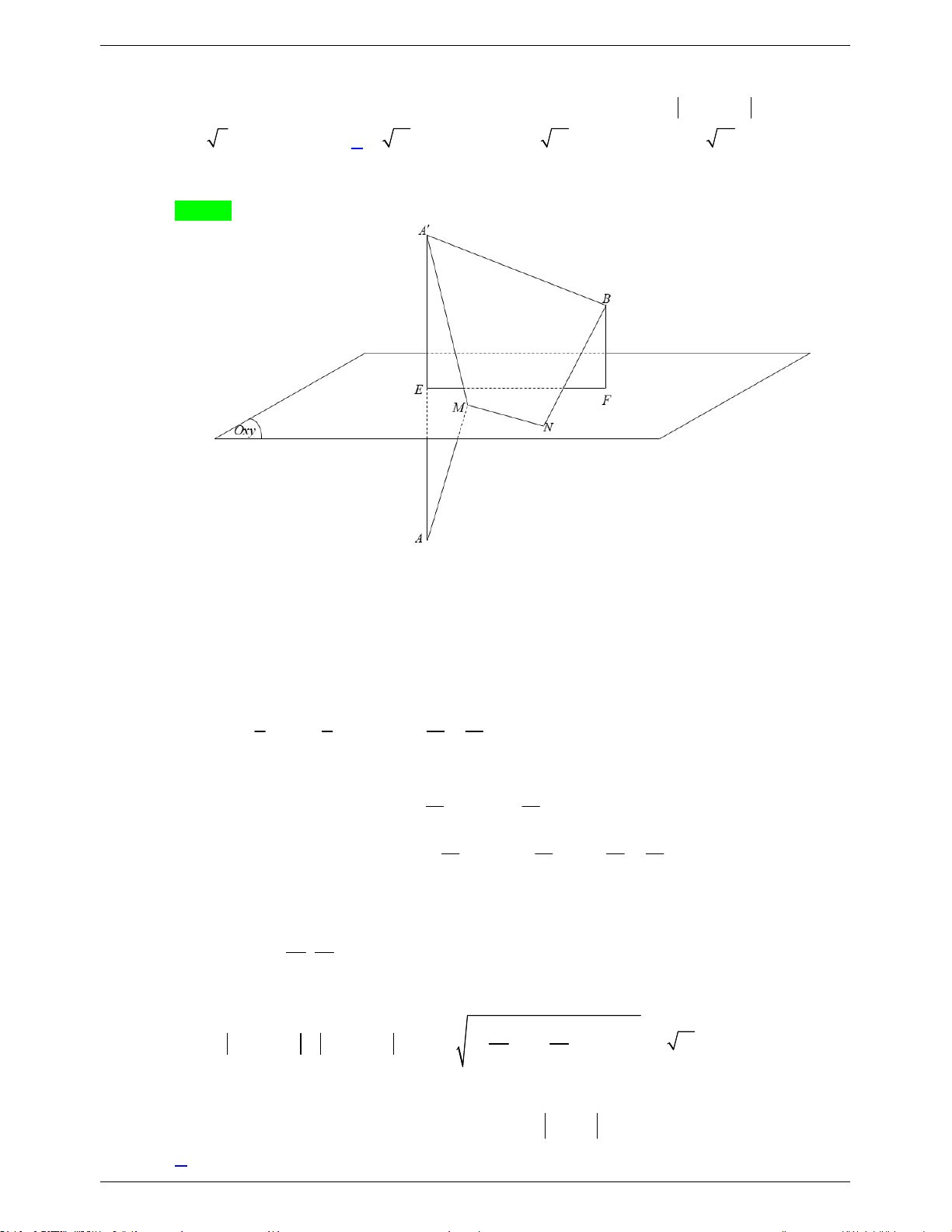
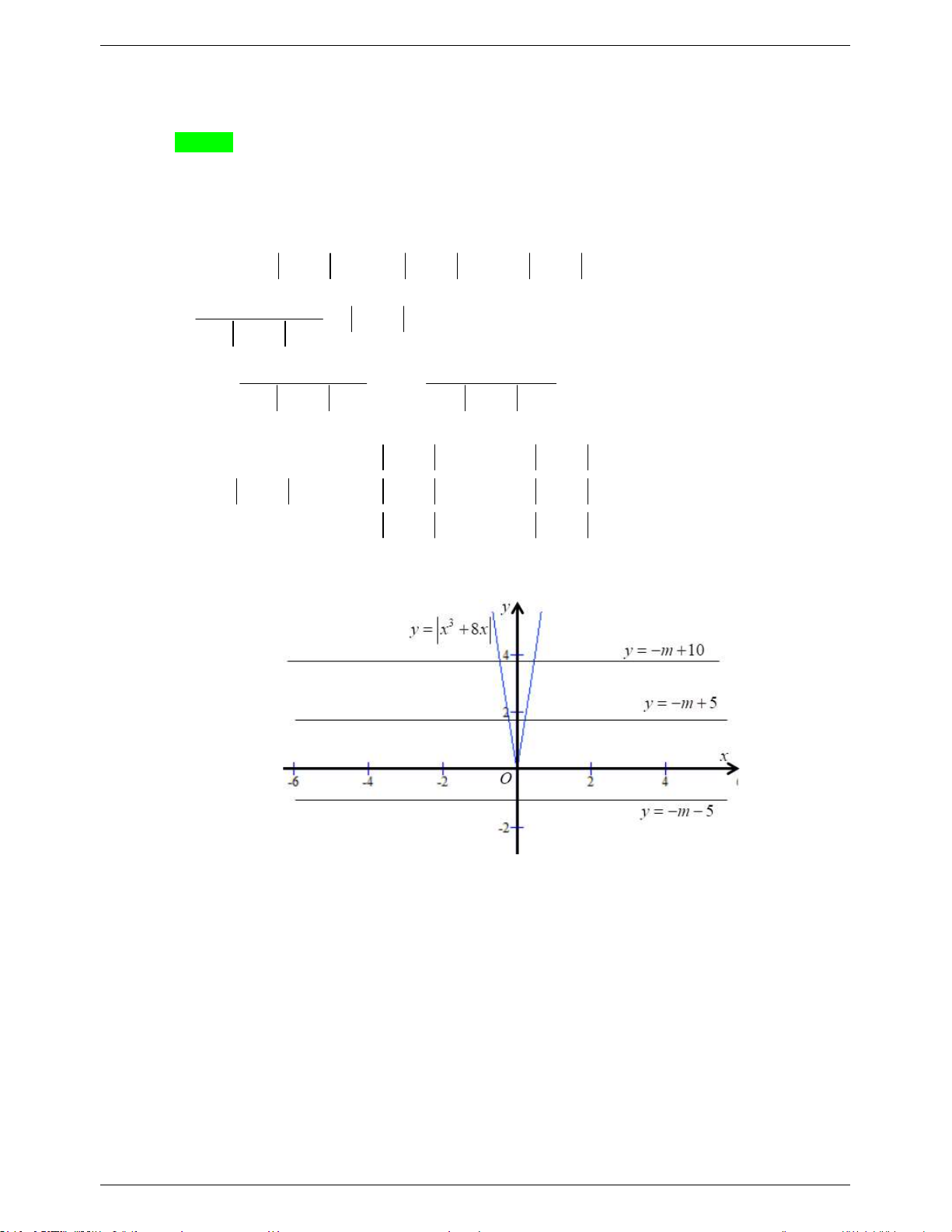
Preview text:

NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
KỲ THI TỐT NGHIỆP THPT QUỐC GIA – ĐỢT 1 – NĂM HỌC 2020 – 2021 Môn: Toán - Mã đề 101
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 90 phút (không kể thời gian phát đề)
LINK NHÓM: https://www.facebook.com/groups/1916660125164699
Câu 1. Tập nghiệm của bất phương trình 3x  2 là A.  ;  log 2 . B. log 2; . C.  ;  log 3 . D. log 3; . 2  2  3  3  4 4 4 Câu 2. Nếu f  xdx  3 và g
 xdx  2 thì  f
 x gxdx  bằng 1 1 1 A. 1. B. 5  . C. 5 . D. 1.
Câu 3. Trong không gian Oxyz , cho mặt cầu S  có tâm I 1; 4
 ;0 và bán kính bằng 3 . Phương trình của S  là
A.  x  2   y  2 2 1 4  z  9 .
B.  x  2   y  2 2 1 4  z  9 .
C.  x  2   y  2 2 1 4  z  3 .
D.  x  2   y  2 2 1 4  z  3 .
Câu 4. Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 3; 1
 ;4 và có một vectơ chỉ  phương u   2
 ;4;5 . Phương trình của d là: x  2  3t x  3 2t x  3  2t x  3  2t     A. y  4  t . B. y  1 4t . C. y 1 4t . D. y  1   4t . z  5 4t     z  4  5t  z  4  5t  z  4  5t 
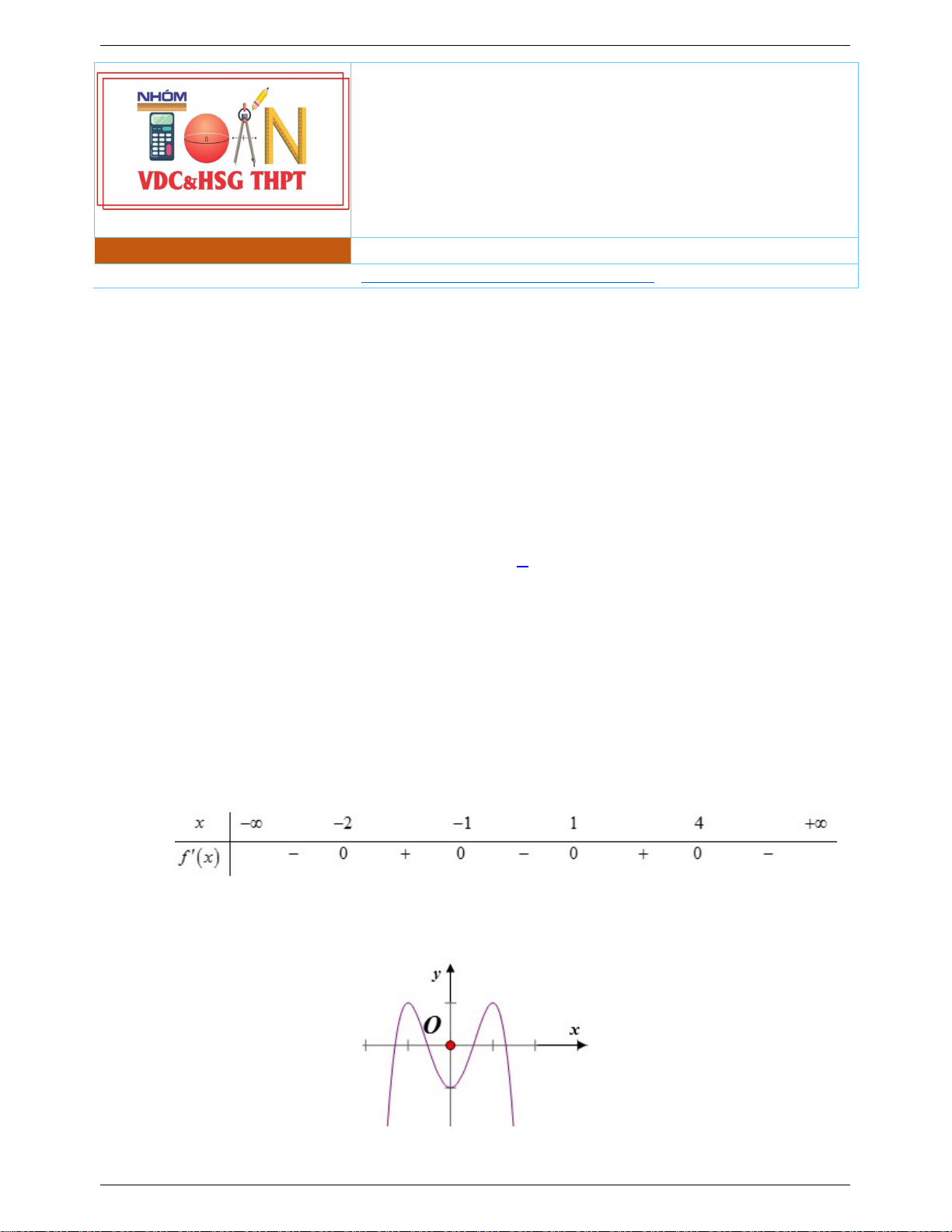
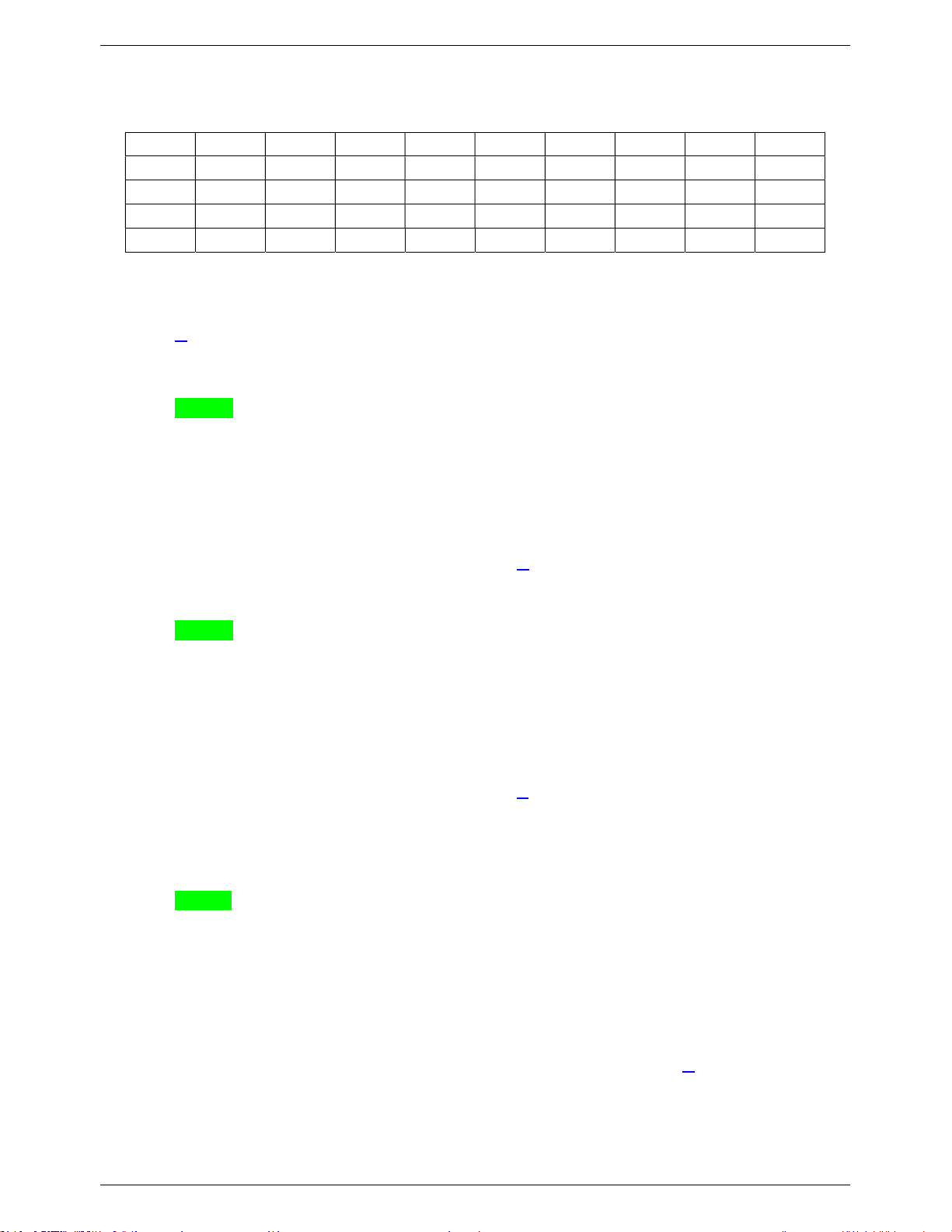
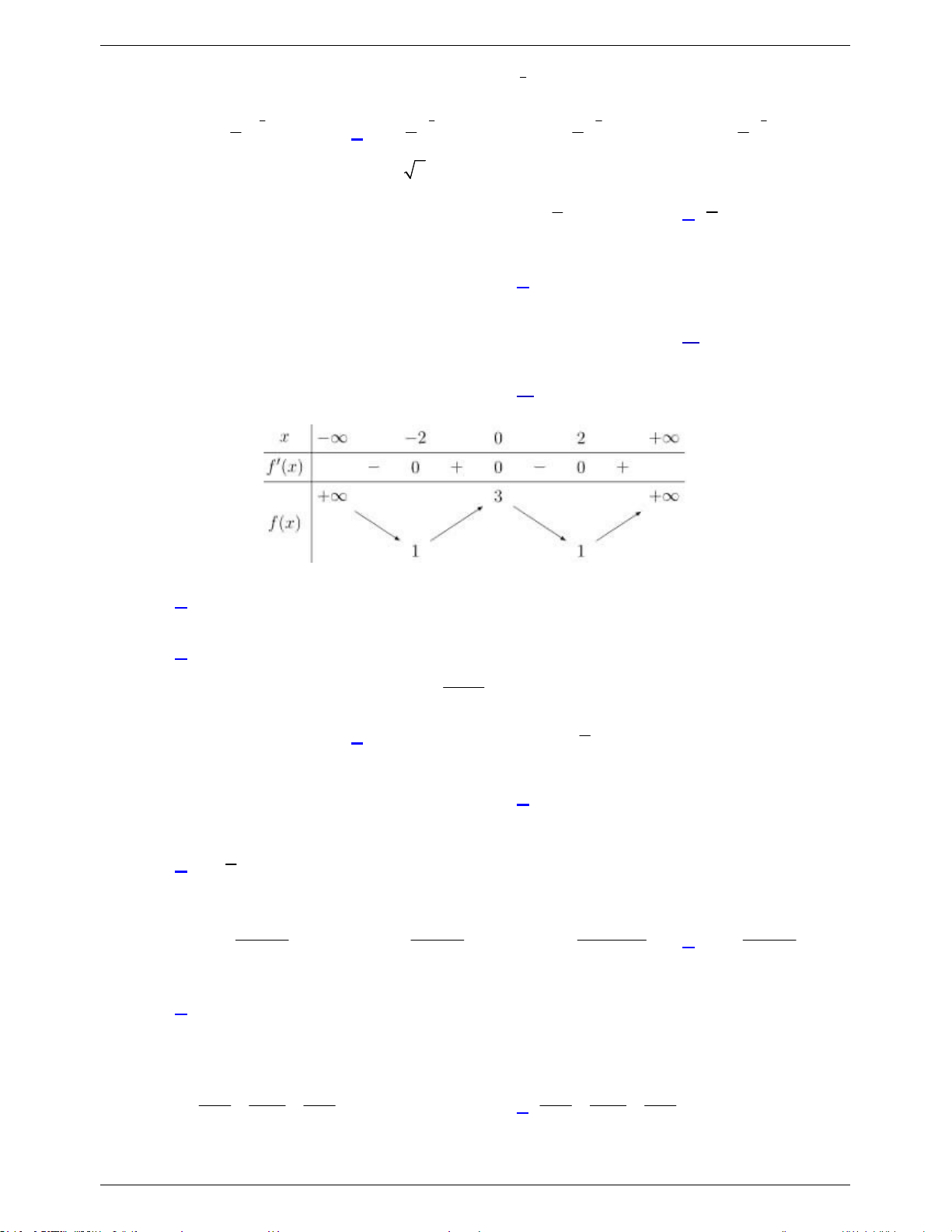
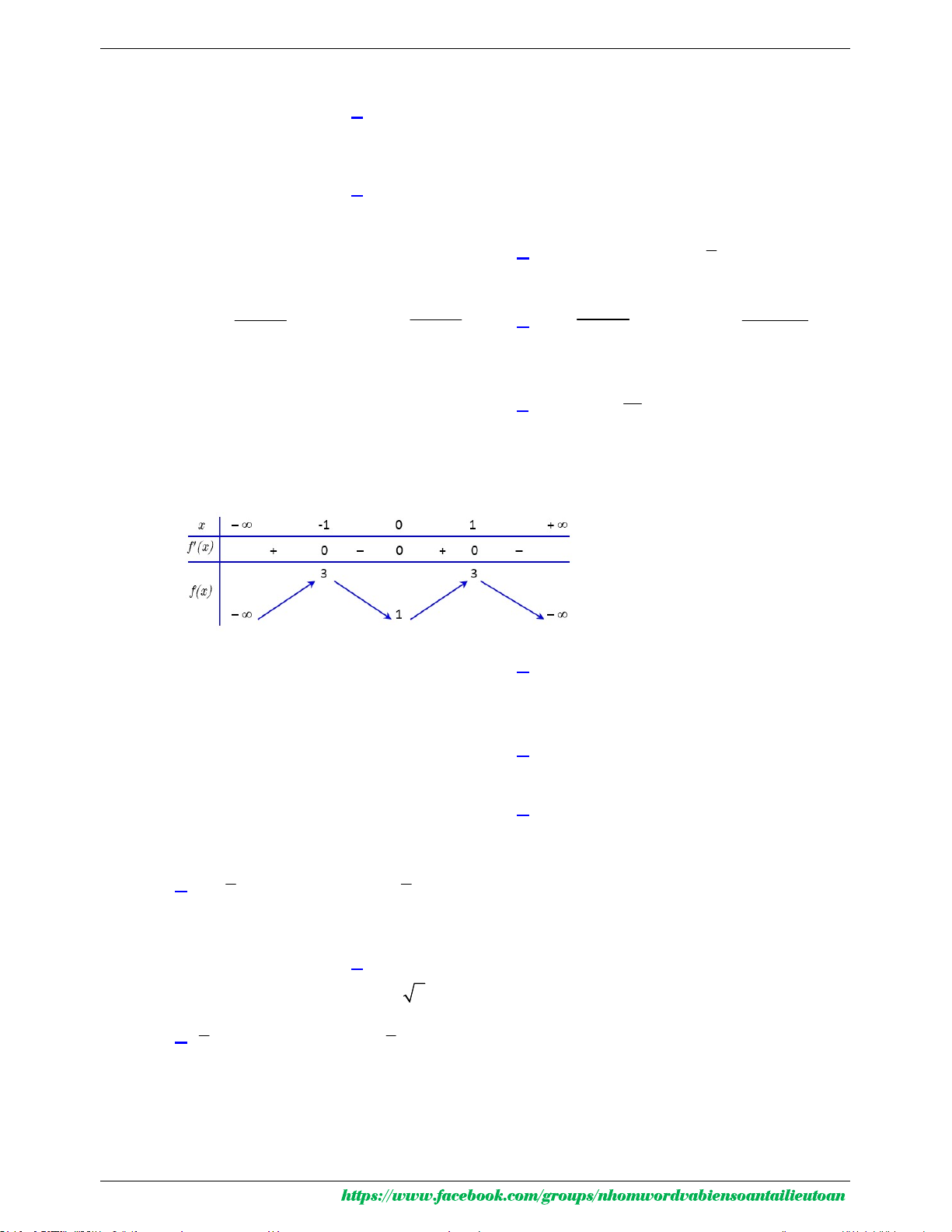
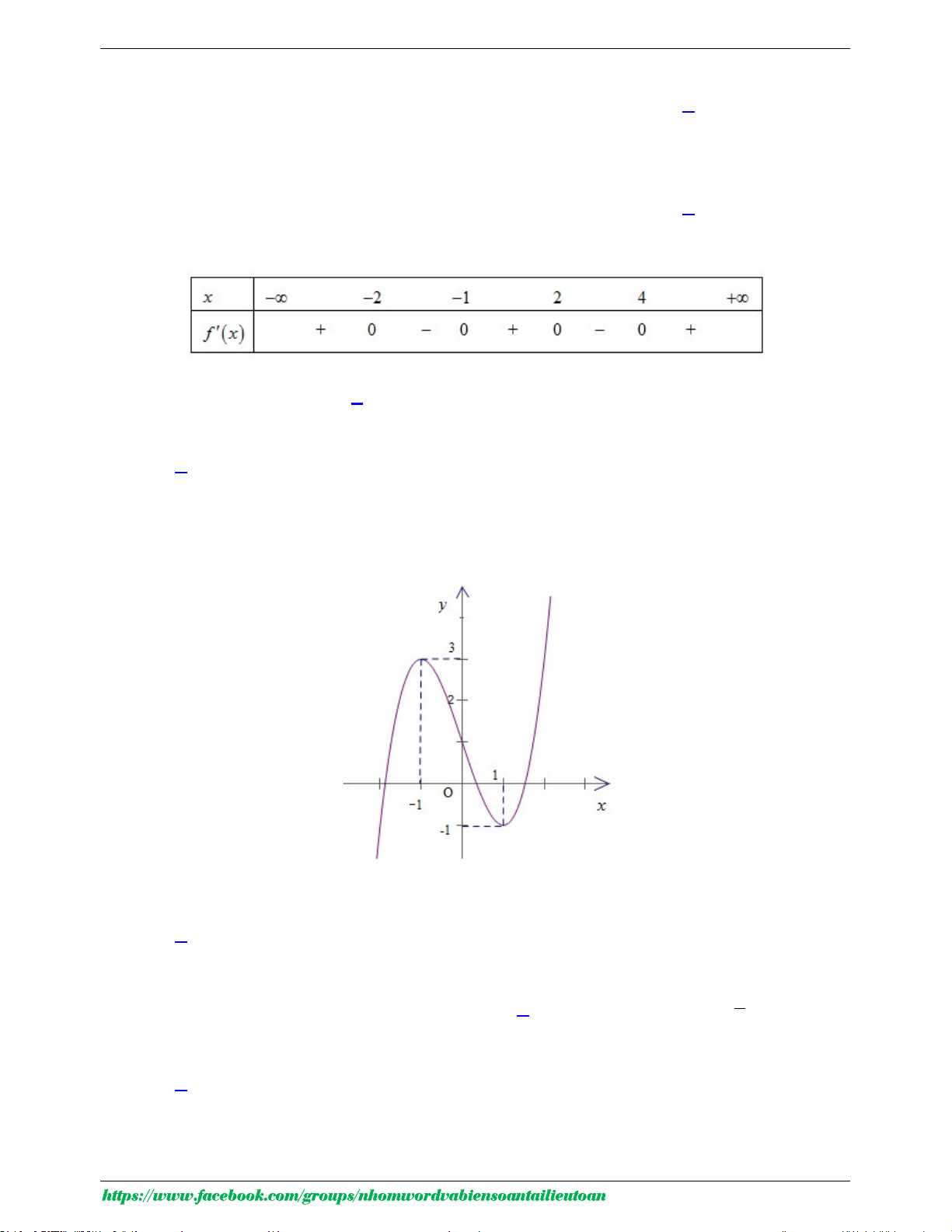
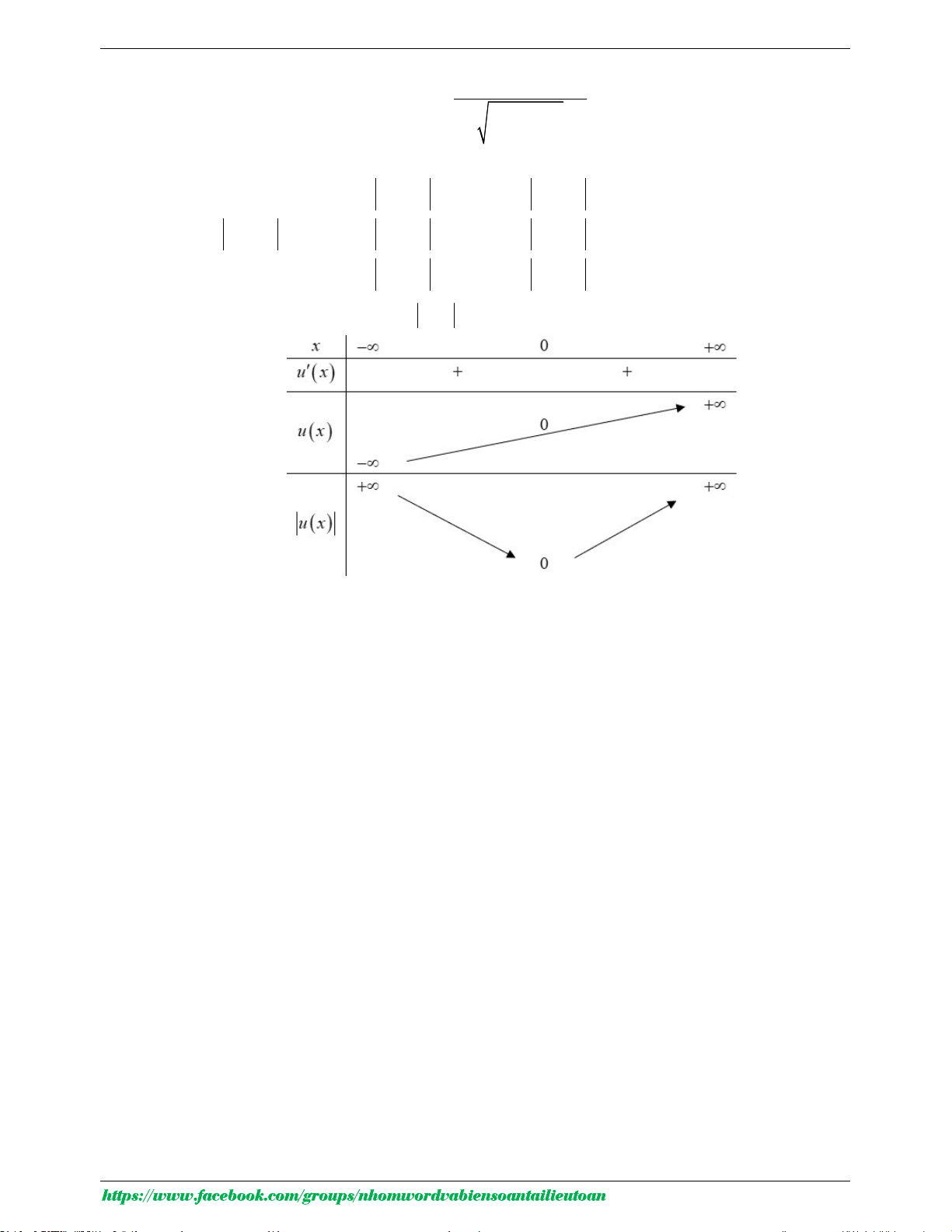
Câu 5. Cho hàm số y  f x có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là A. 5 . B. 3 . C. 2 . D. 4 .
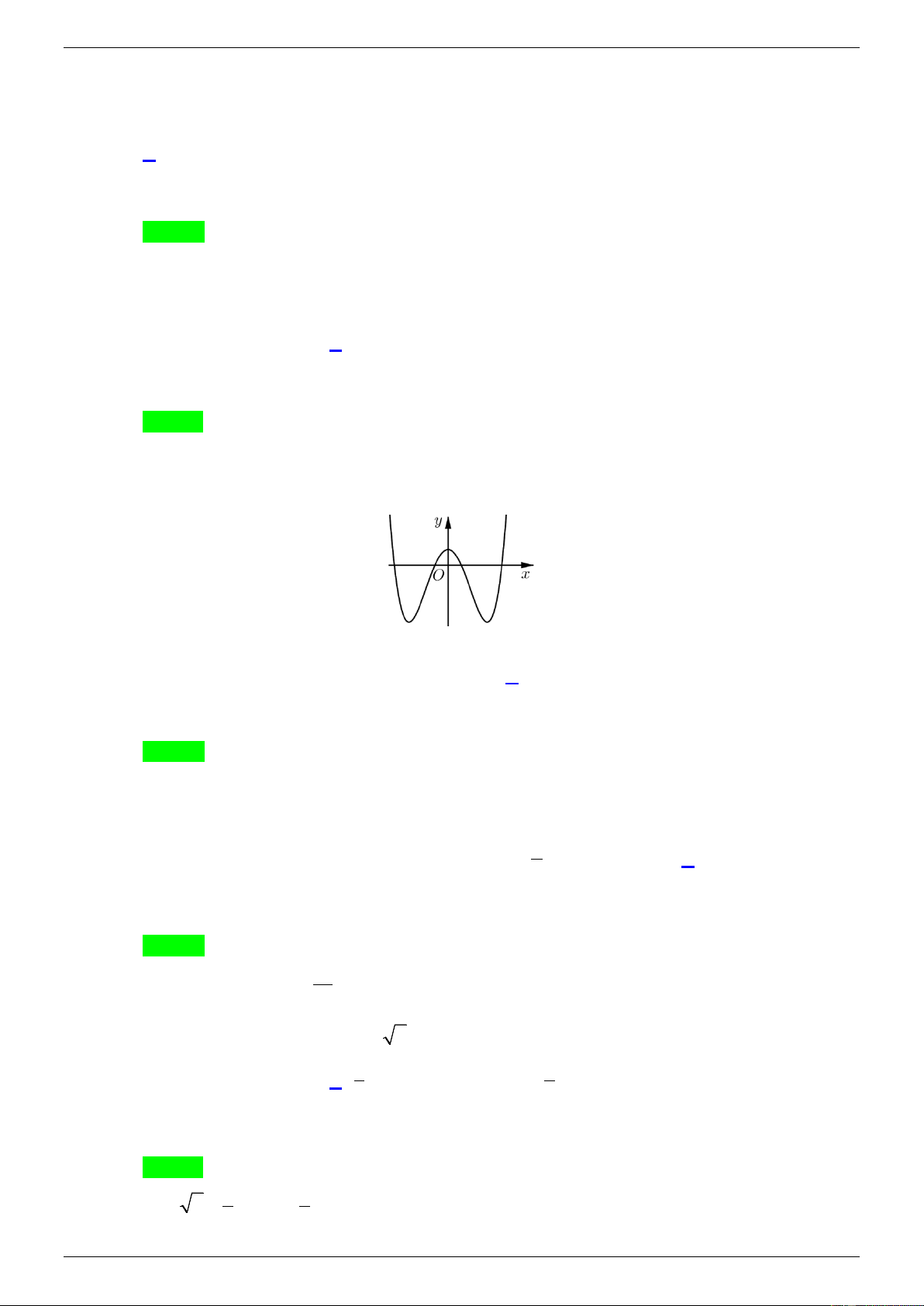
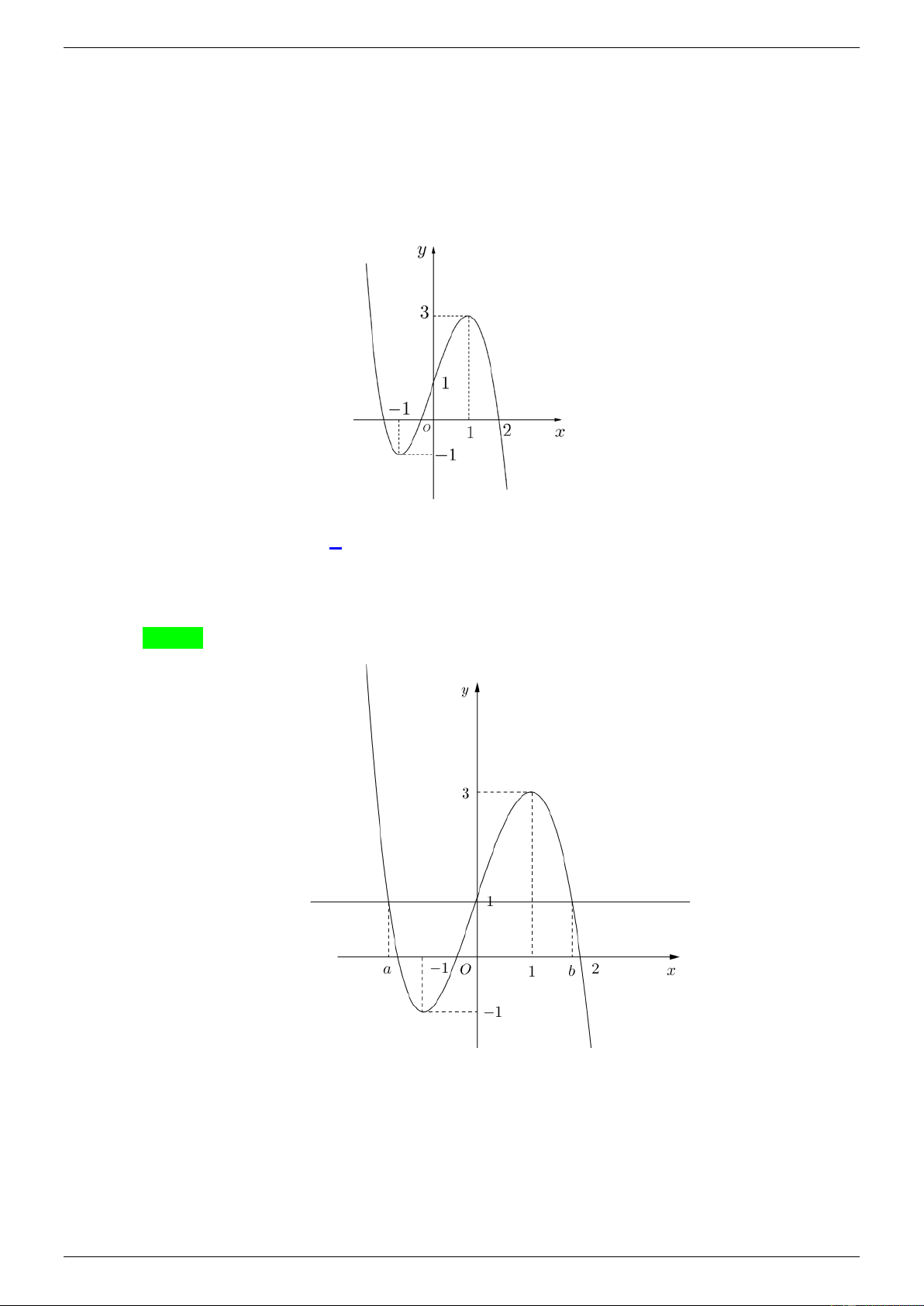
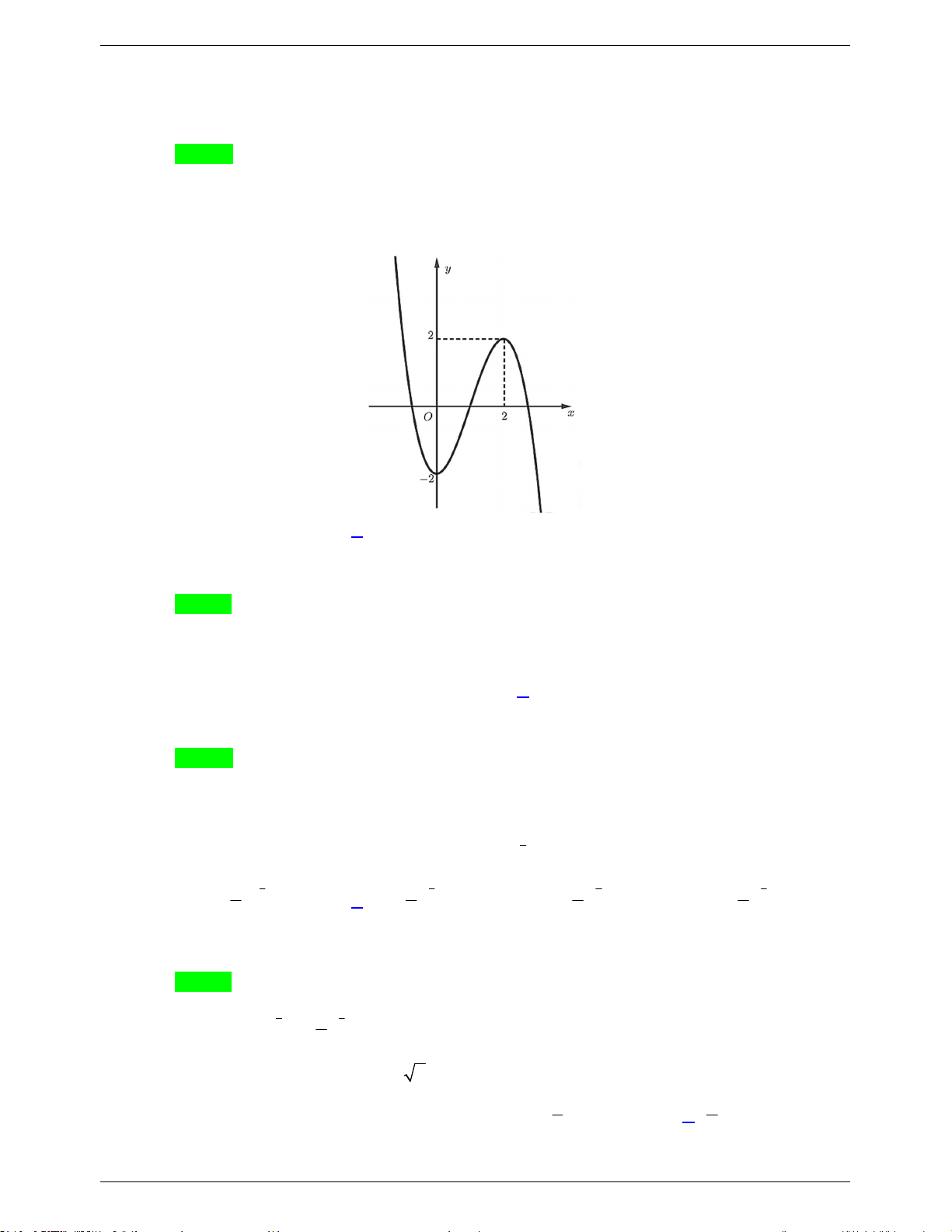
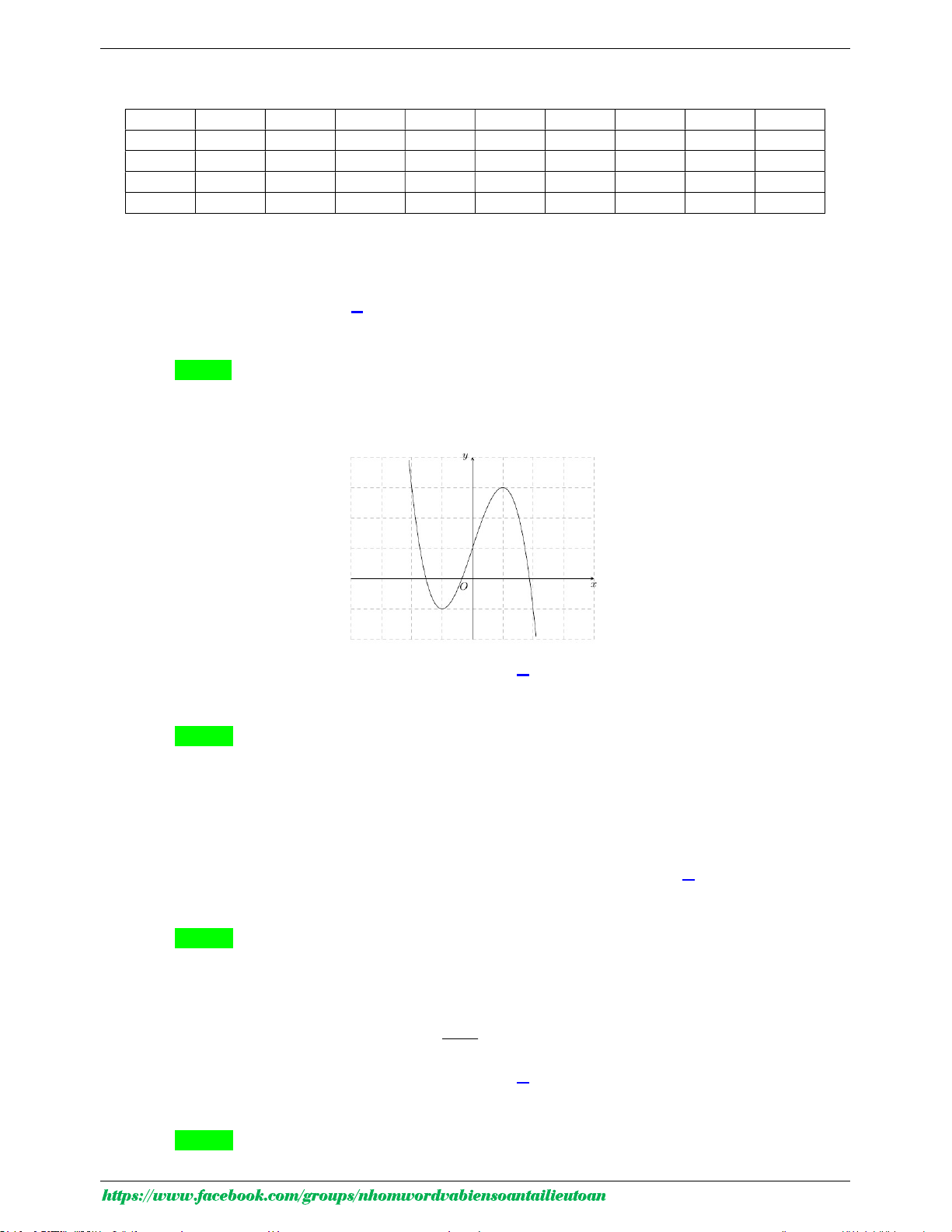
Câu 6. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? A. 4 2 y  2  x  4x 1. B. 3 y  x  3x 1. C. 4 2 y  2x  4x 1. D. 3 y  x  3x 1.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 Câu 7. Đồ thị hàm số 4 2
y  x  4x  3 cắt trục tung tại điểm có tung độ bằng A. 0. B. 3. C. 1. D. 3  .
Câu 8. Với n là số nguyên dương bất kì, n  4 , công thức nào dưới đây đúng? n  4 ! 4   n n A. A  . B. 4 4! A  . C. 4 ! A  . D. 4 ! A  . n n! n n  4! n 4!n  4! n n  4!
Câu 9. Phần thực của số phức z  5  2i bằng A. 5 . B. 2 . C. 5 . D. 2  . 5
Câu 10. Trên khoảng 0, , đạo hàm của hàm số 2 y  x là: 7 2 3 2 3 5 3 5  A. 2 y '  x . B. 2 y '  x . C. 2 y '  x . D. 2 y '  x . 7 5 2 2
Câu 11. Cho hàm số f  x 2
 x  4 . Khẳng định nào dưới đây đúng? A. f  xdx  2xC . B. f  x 2 dx  x  4x  C . 3 x C. f
 xdx   4xC . D. f  x 3 dx  x  4x  C . 3 
Câu 12. Trong không gian Oxyz , cho điểm A2;3;5 . Tọa độ của véctơ OA là: A. 2;3;5 . B. 2; 3  ;5 . C. 2;3;5 . D. 2;3;5 .
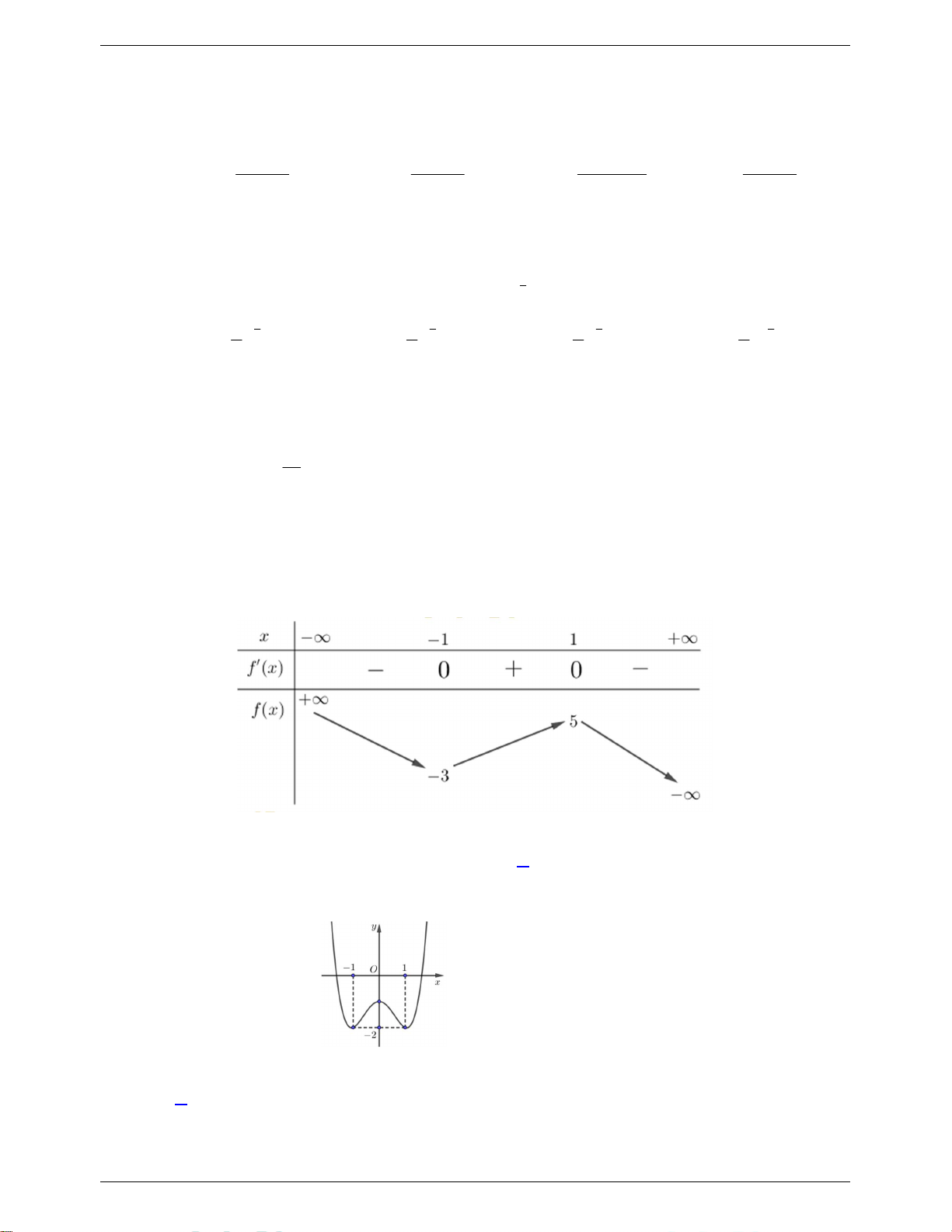
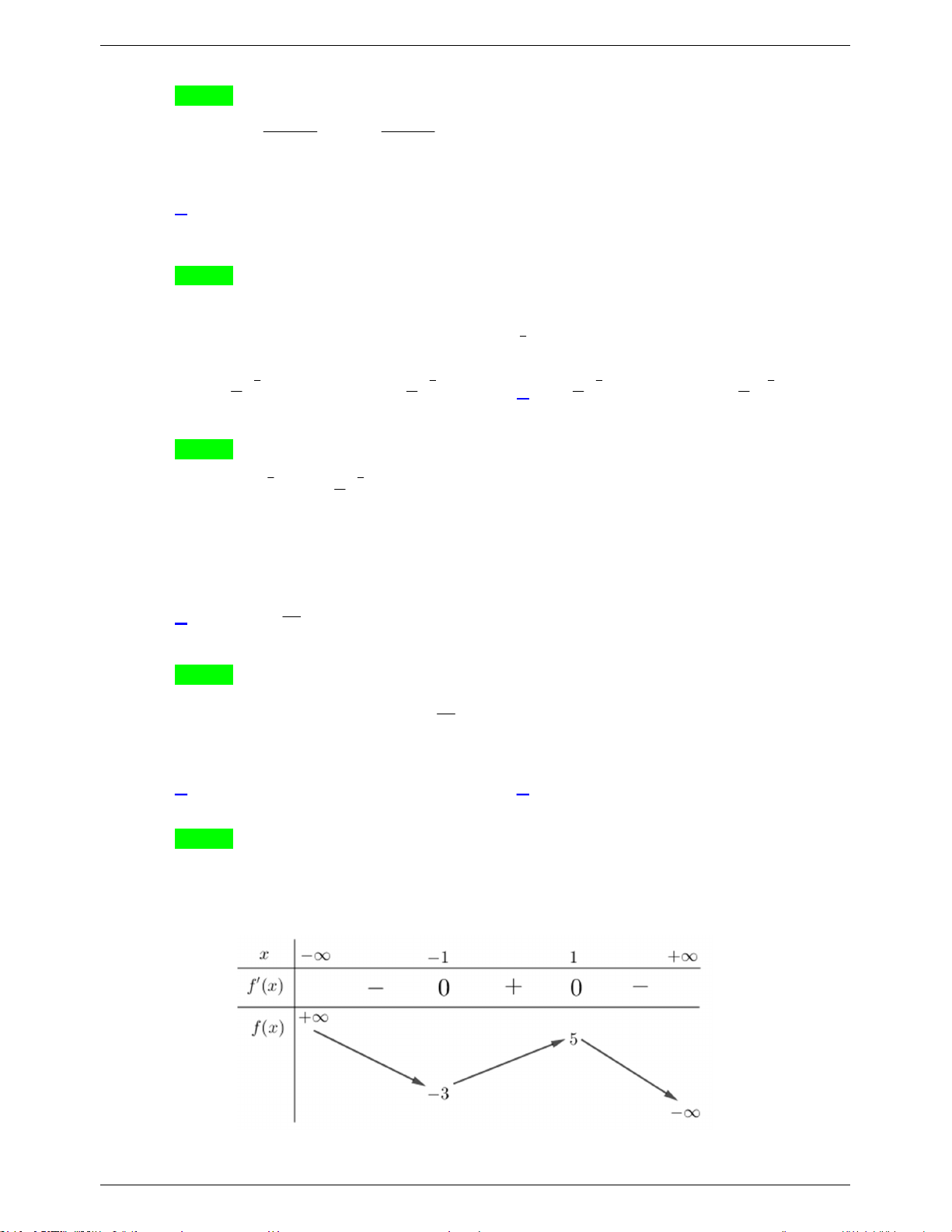
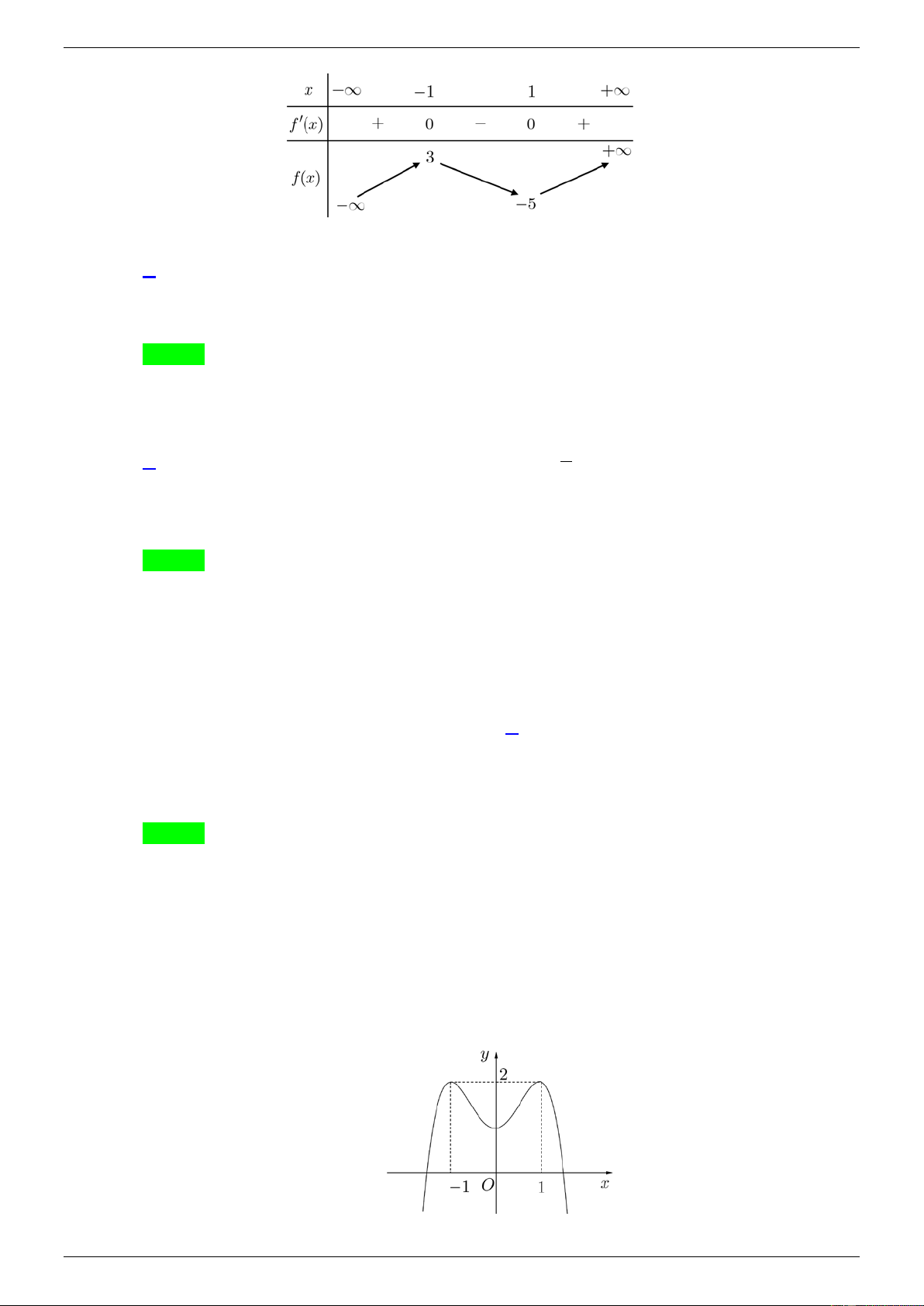
Câu 13. Cho hàm số y  f  x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 1  . B. 5 . C. 3  . D. 1.
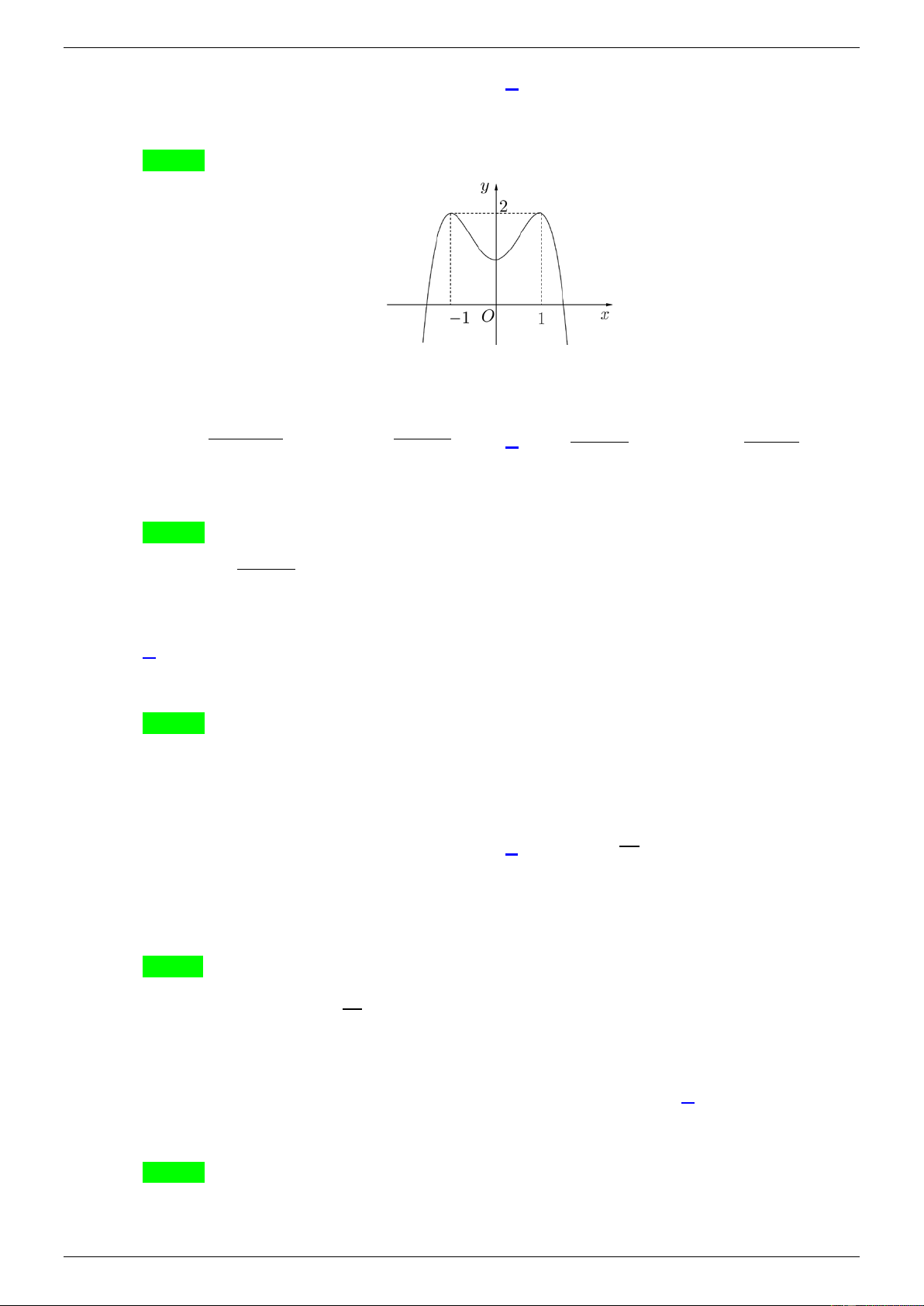
Câu 14. Cho hàm số y  f  x có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trong khoảng nào dưới đây? A. 0;  1 . B.  ;  0. C. 0; . D. 1;  1 .
Câu 15. Nghiệm của phương trình log 5x  2 là 3   Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 8 9 A. x  . B. x  9. C. x  . D. x  8 . 5 5 3 3 Câu 16. Nếu f
 xdx  4 thì 3f xdx  bằng 0 0 A. 36 . B. 12 . C. 3 . D. 4 .
Câu 17. Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a .
Câu 18. Tập xác định của hàm số 9x y  là A.  . B. 0; . C. \  0 . D. 0; .
Câu 19. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S  16 R . B. 2 S  4 R . C. 2 S   R . D. 2 S   R . 3 2x 1
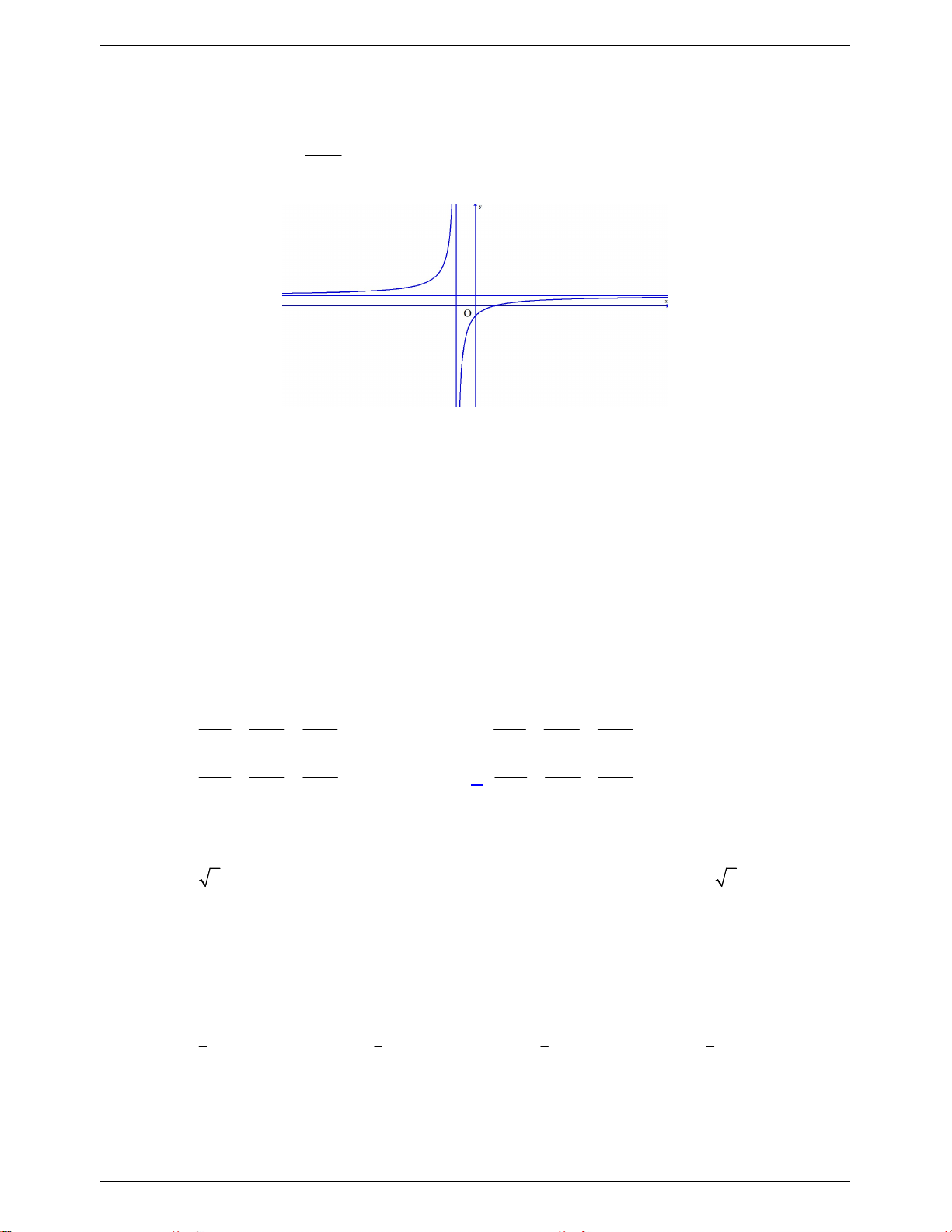
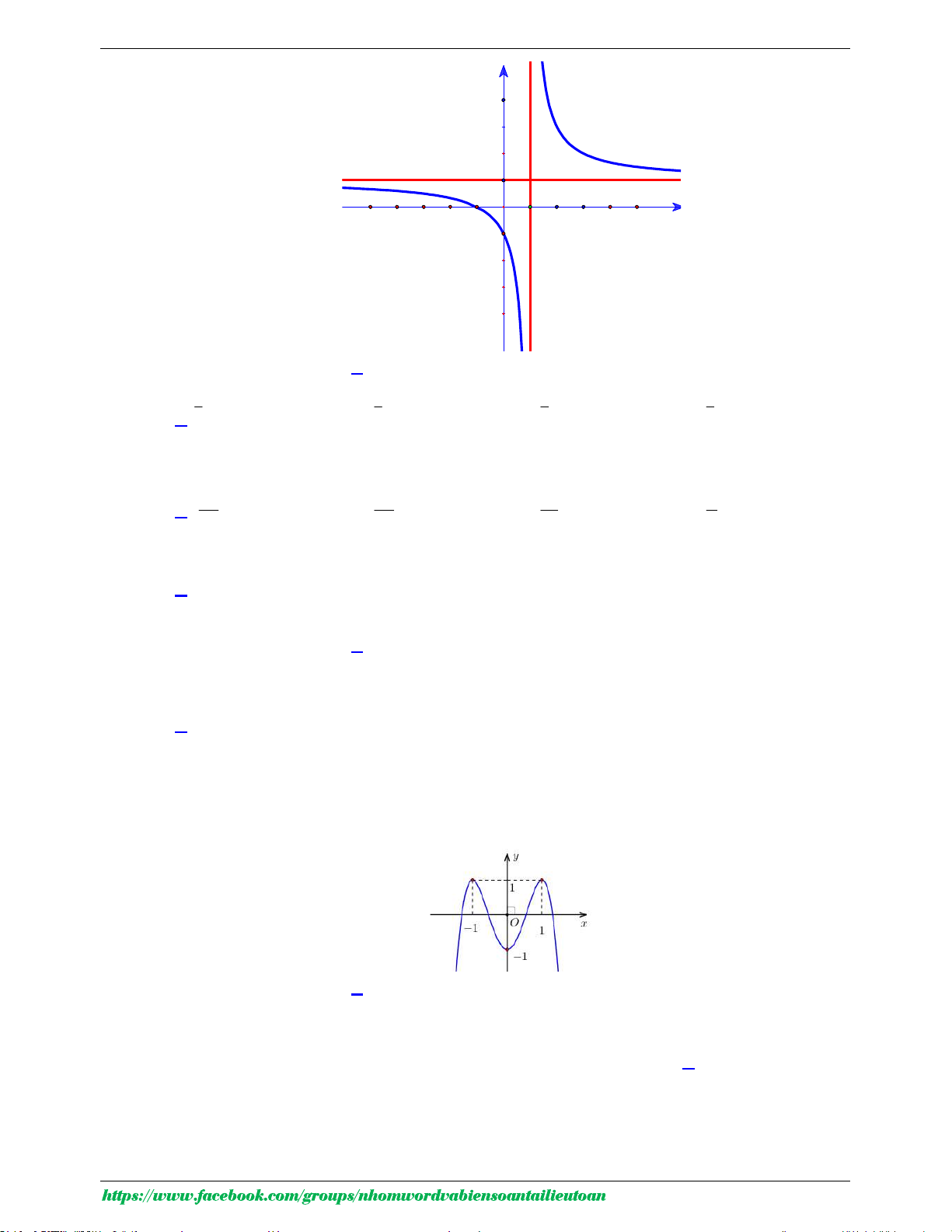
Câu 20. Tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình: x 1 1 A. x  1. B. x  1  . C. x  2 . D. x  . 2
Câu 21. Cho a  0 và a  1, khi đó 4 log a bằng a 1 1 A. 4 . B. . C.  . D. 4  . 4 4
Câu 22. Cho khối chop có diện tích đáy 2
B  5a và chiều cao h  a . Thể tích của khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
Câu 23. Trong không gian Oxyz , cho mặt phẳng P :3x  y  2z 1  0 . Véc tơ nào dưới đây là một
véc tơ pháp tuyến của P     A. n  (3;1; 2) . B. n  (3; 1  ; 2) . C. n  (3 :1; 2) . D. n  (3;1; 2) . 1 2 3 4
Câu 24. Cho khối hình trụ có bán kính đáy r  6 và chiều cao h  3. Thể tích của khối trụ đã cho bằng A. 108 . B. 36 . C. 18 . D. 54 .
Câu 25. Cho hai số phức z  4  2i , w  3  4i . Số phức z  w bằng A. 1 6i . B. 7  2i . C. 7  2i . D. 1 6i .
Câu 26. Cho cấp số nhân u
có u  3,và u  9 . Công bội của cấp số nhân bằng n  1 2 1 A. 6  . B. . C. 3 . D. 6 . 3 Câu 27. Cho hàm số ( ) x
f x  e  2 . Khẳng định nào dưới đây là đúng ? A.    2 d x f x x  e  C . B.   d x f x x  e  2x  C . C.   d x f x x  e  C . D.   d x f x x  e  2x  C .
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Câu 28. Trong mặt phẳng tọa độ, điểm M 3;4 là điểm biểu diễn số phức nào dưới đây? A. z  3  4i . B. z  3  4i . C. z  3   4i . D. z  3  4i . 2 3 4 1 x  a
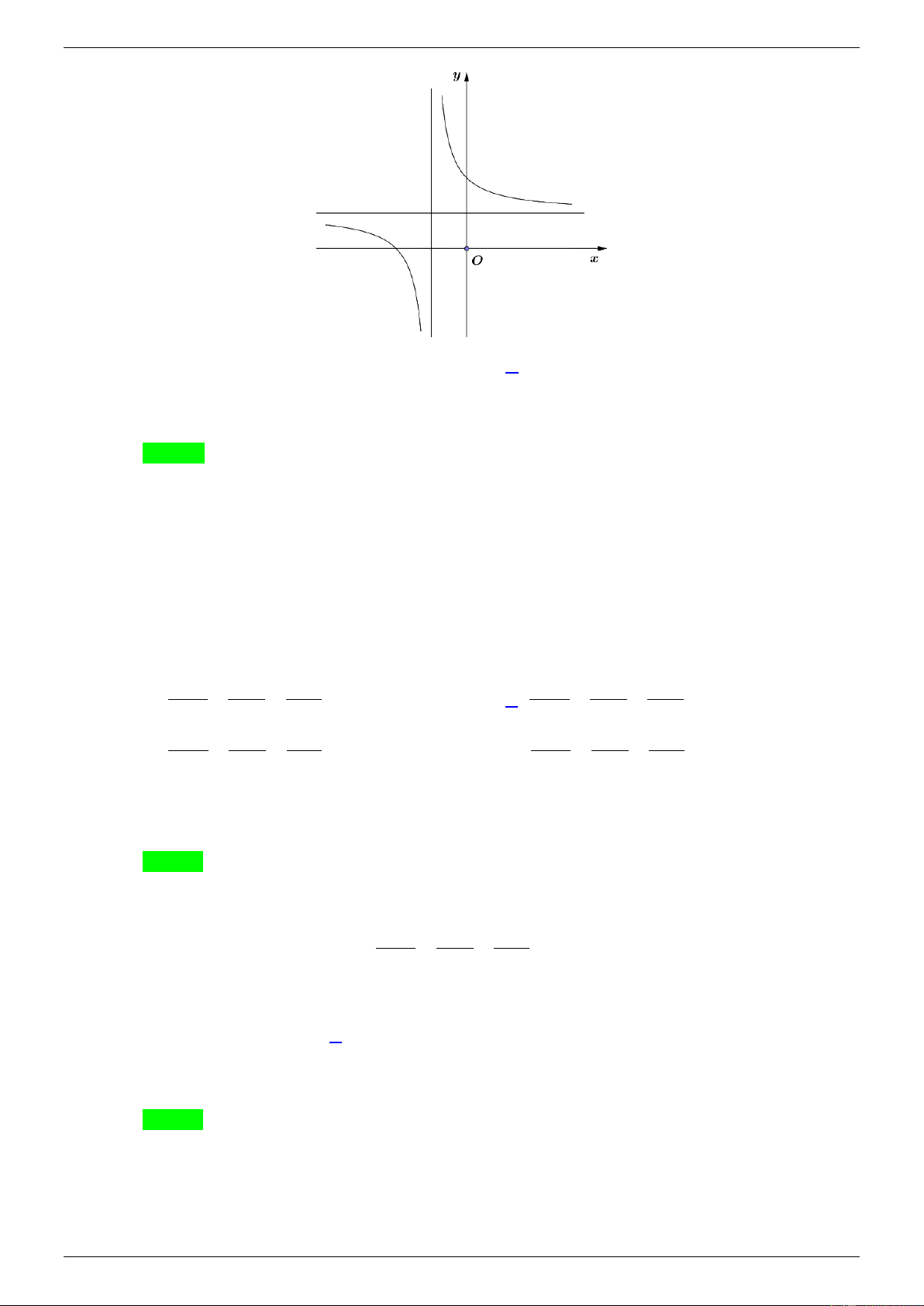
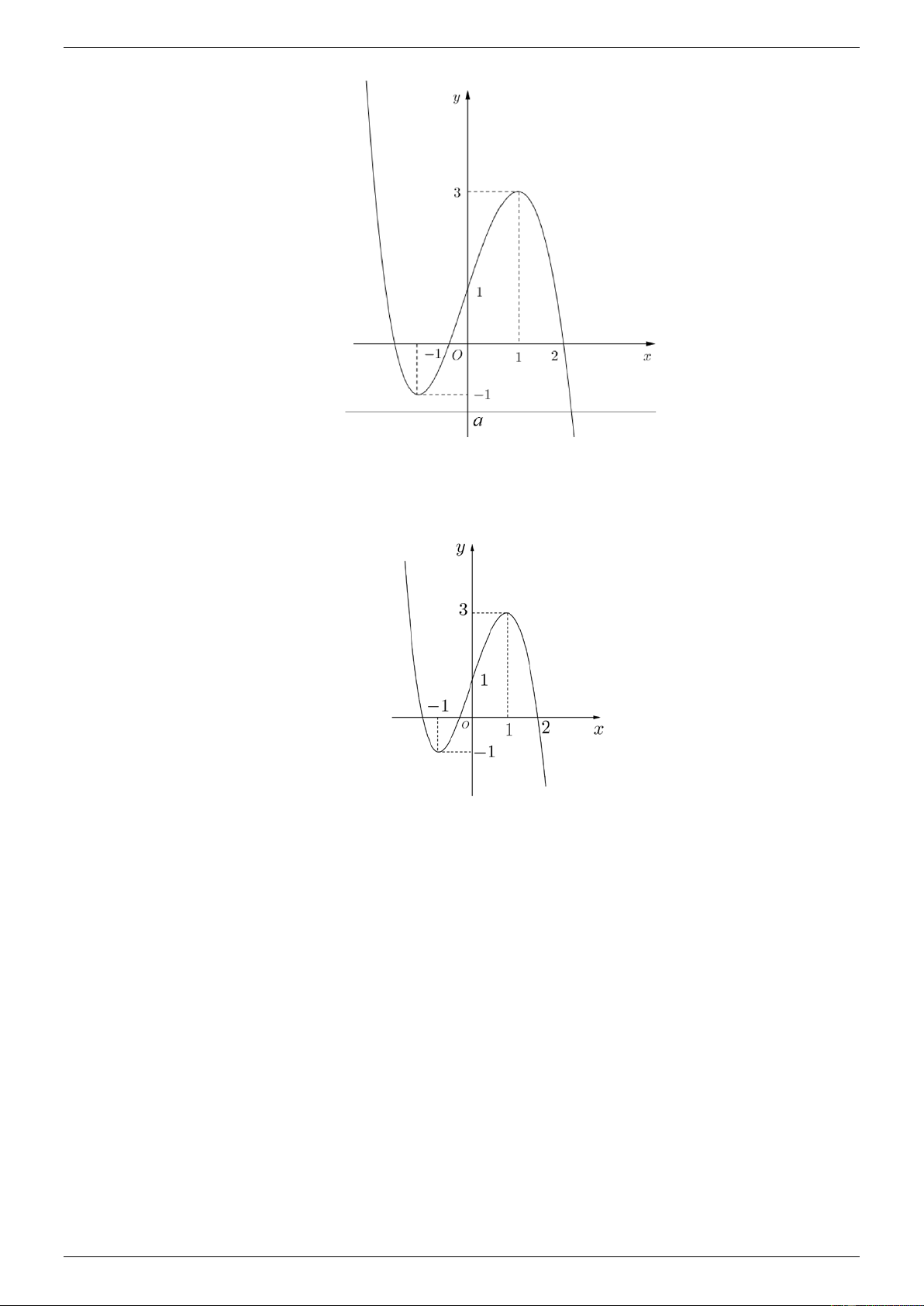
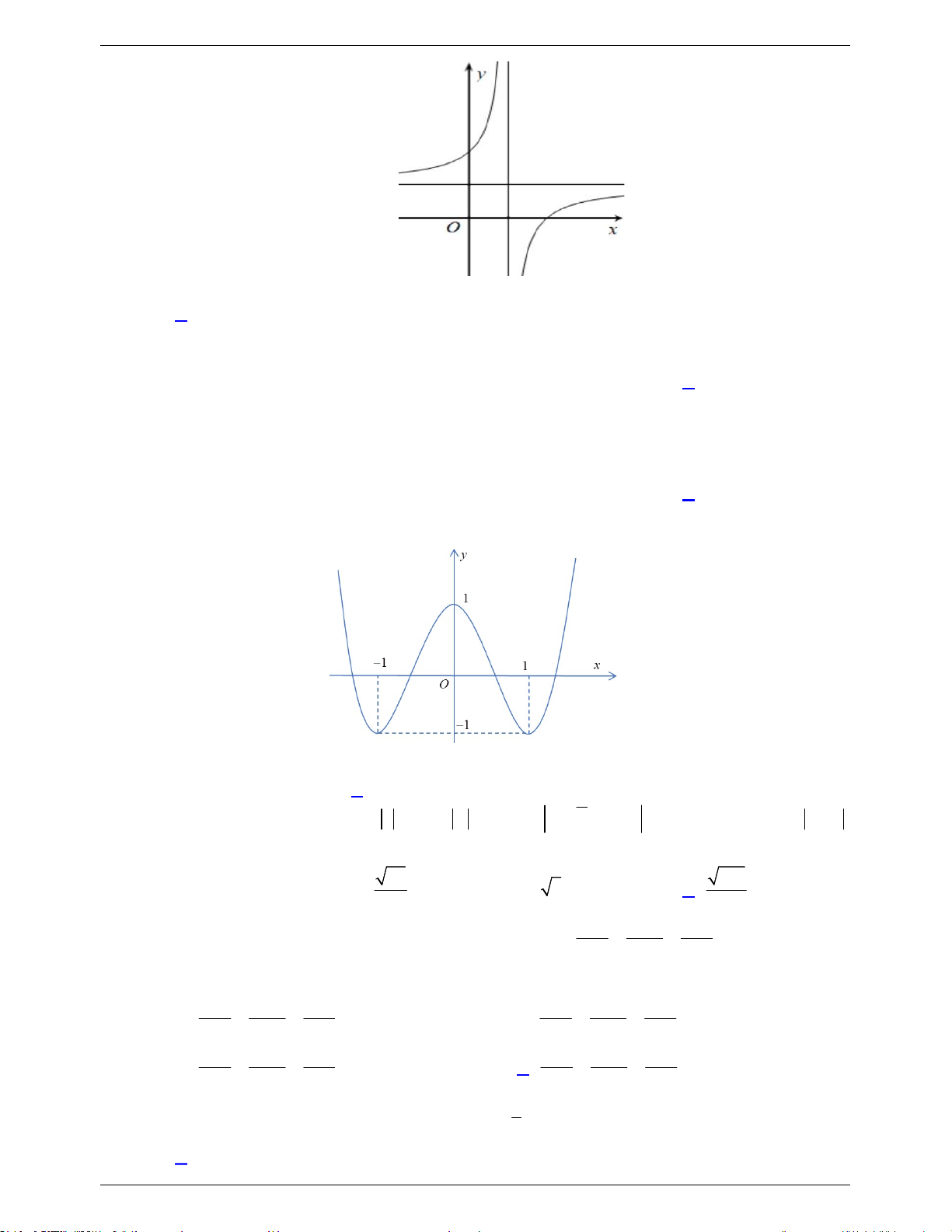
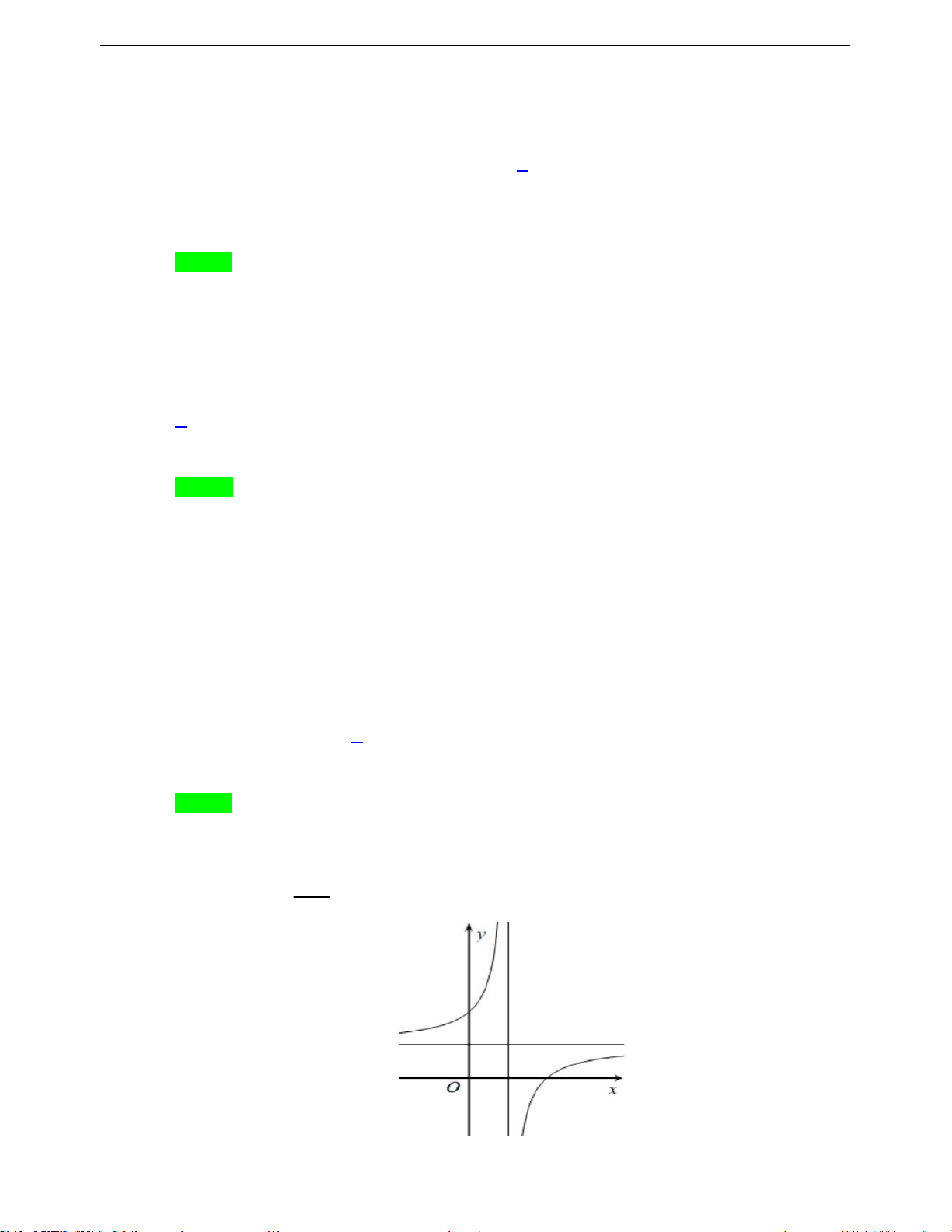
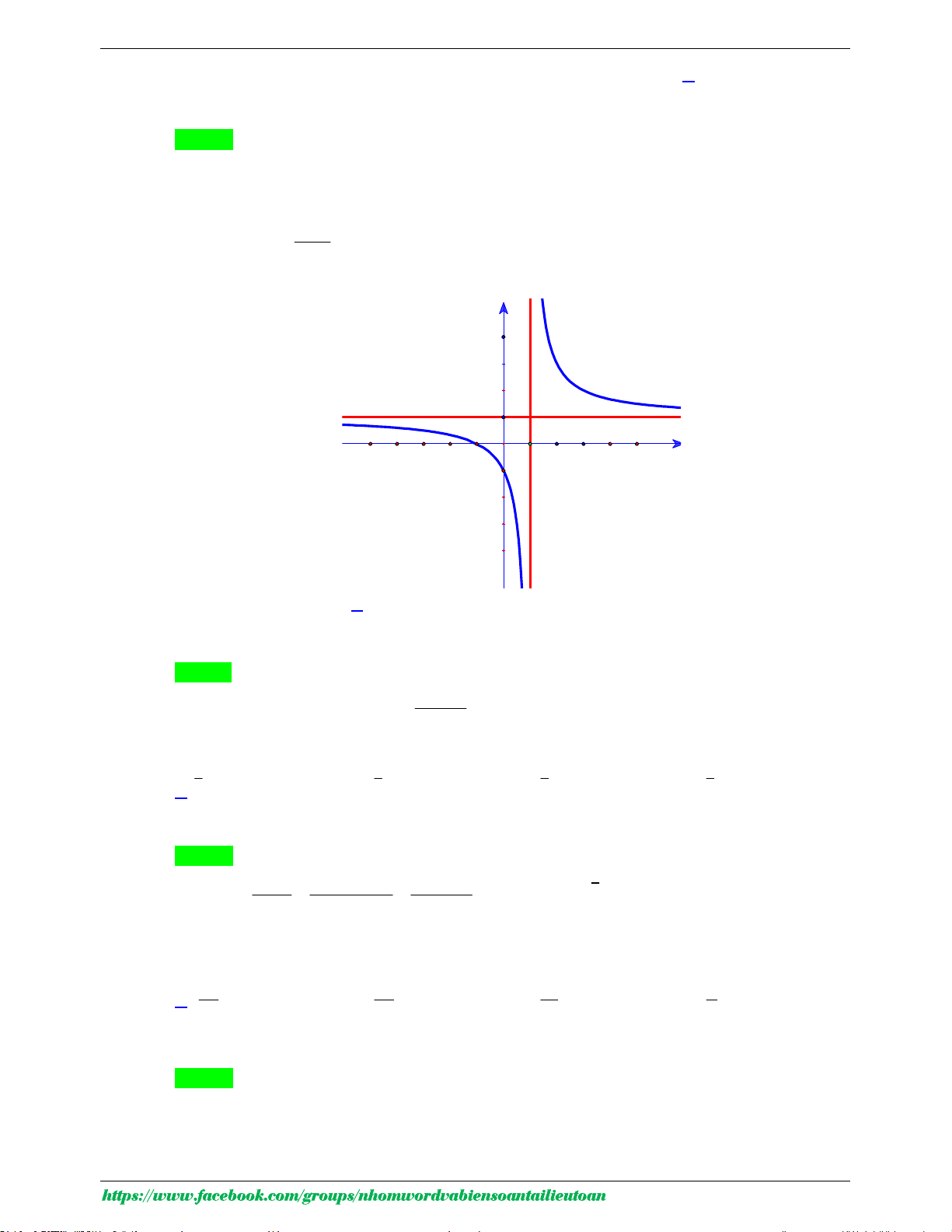
Câu 29. Biết hàm số y 
( a là số thực cho trước, a  1 có đồ thị như hình bên). Mệnh đề nào x 1 dưới đây đúng? A. y '  0, x   1  . B. y '  0, x   1. C. y '  0, x    . D. y '  0, x    .
Câu 30. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đó và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng 7 2 1 5 A. . B. . C. . D. . 44 7 22 12
Câu 31. Trên đoạn 0;  3 , hàm số 3
y  x  3x đạt giá trị lớn nhất tại điểm A. x  0 . B. x  3. C. x  1. D. x  2 .
Câu 32. Trong không gian Oxyz, cho điểm M 1;3;2 và mặt phẳng P : x  2y  4z 1  0. Đường
thẳng đi qua M và vuông góc với P có phương trình là x 1 y  3 z  2 x 1 y  3 z  2 A.   . B.   . 1 2 1 1 2  1 x 1 y  3 z  2 x 1 y  3 z  2 C.   . D.   . 1 2  4 1 2 4
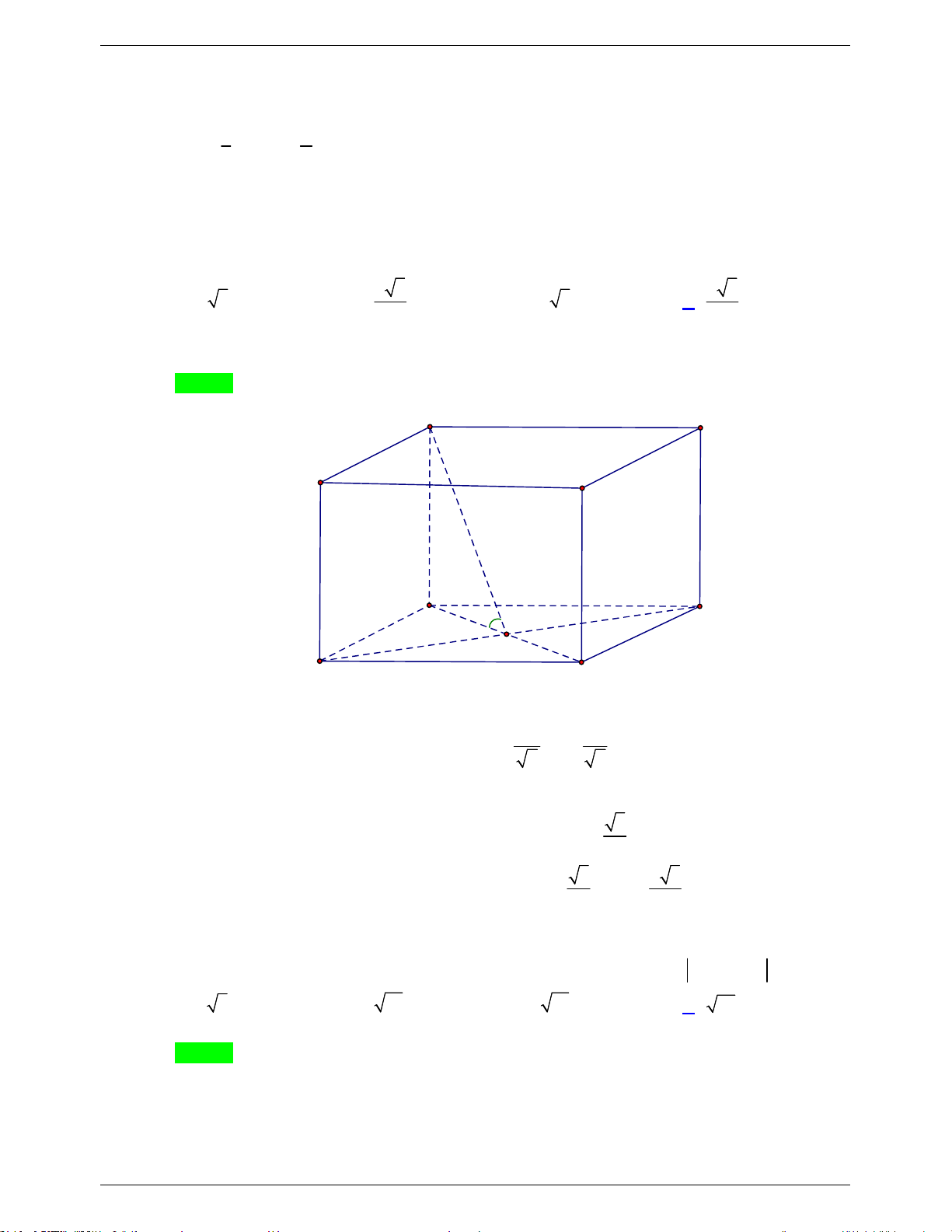
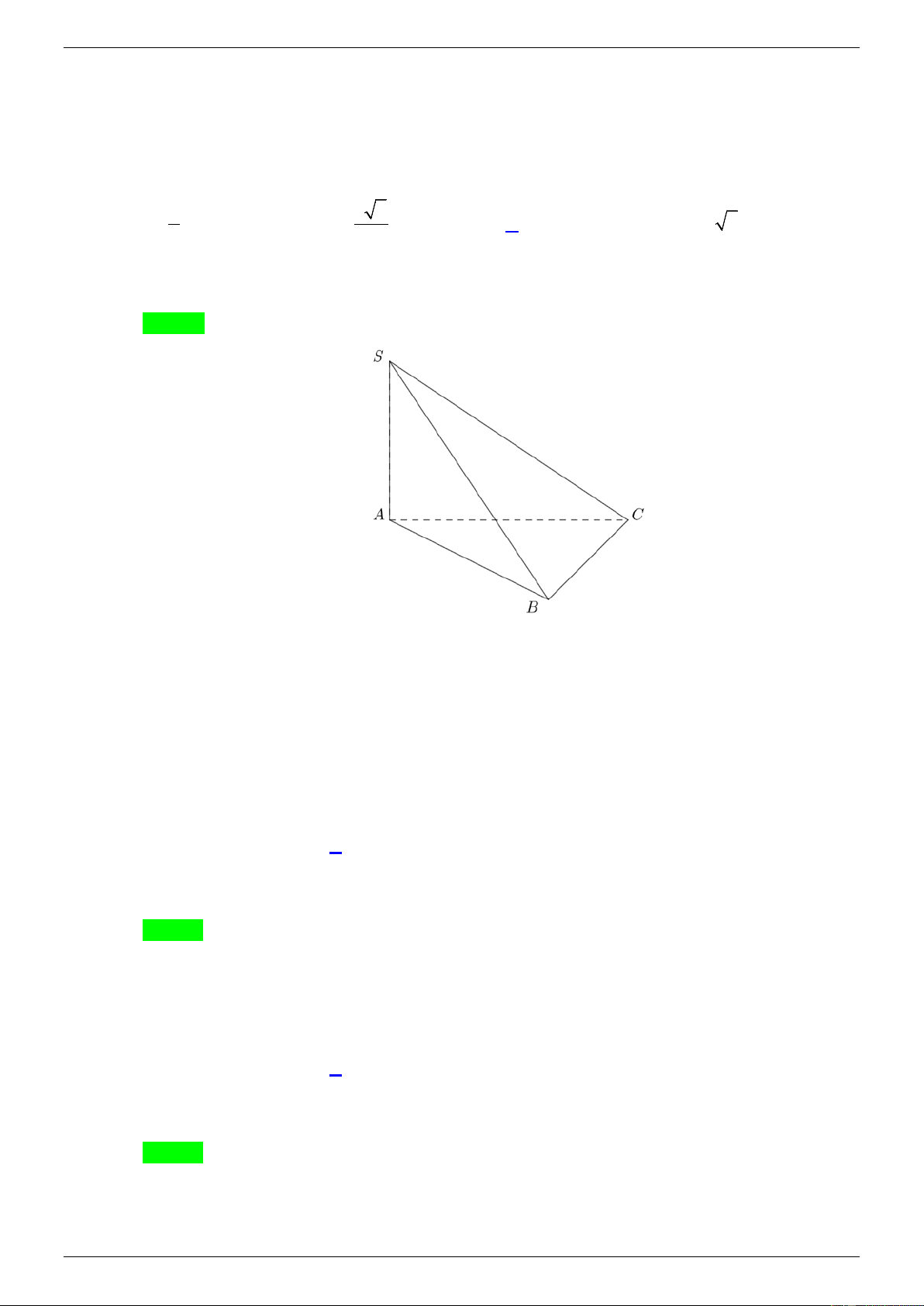
Câu 33. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB  2a và SA vuông góc
với mặt phẳng đáy. Tính khoảng cách từ C đến mặt phẳng (SAB) bằng A. 2a . B. 2a . C. a . D. 2 2a .
Câu 34. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;0;0 , B 4;1;2 . Mặt phẳng đi qua A
và vuông góc với AB có phương trình là
A. 3x  y  2z 17  0 .
B. 3x  y  2z  3  0 .
C. 5x  y  2z  5  0 .
D. 5x  y  2z  25  0 .
Câu 35: Cho số phức iz  5  4i . Số phức liên hợp của z là A. z  4  5i . B. z  4  5i . C. z  4   5i . D. z  4  5i
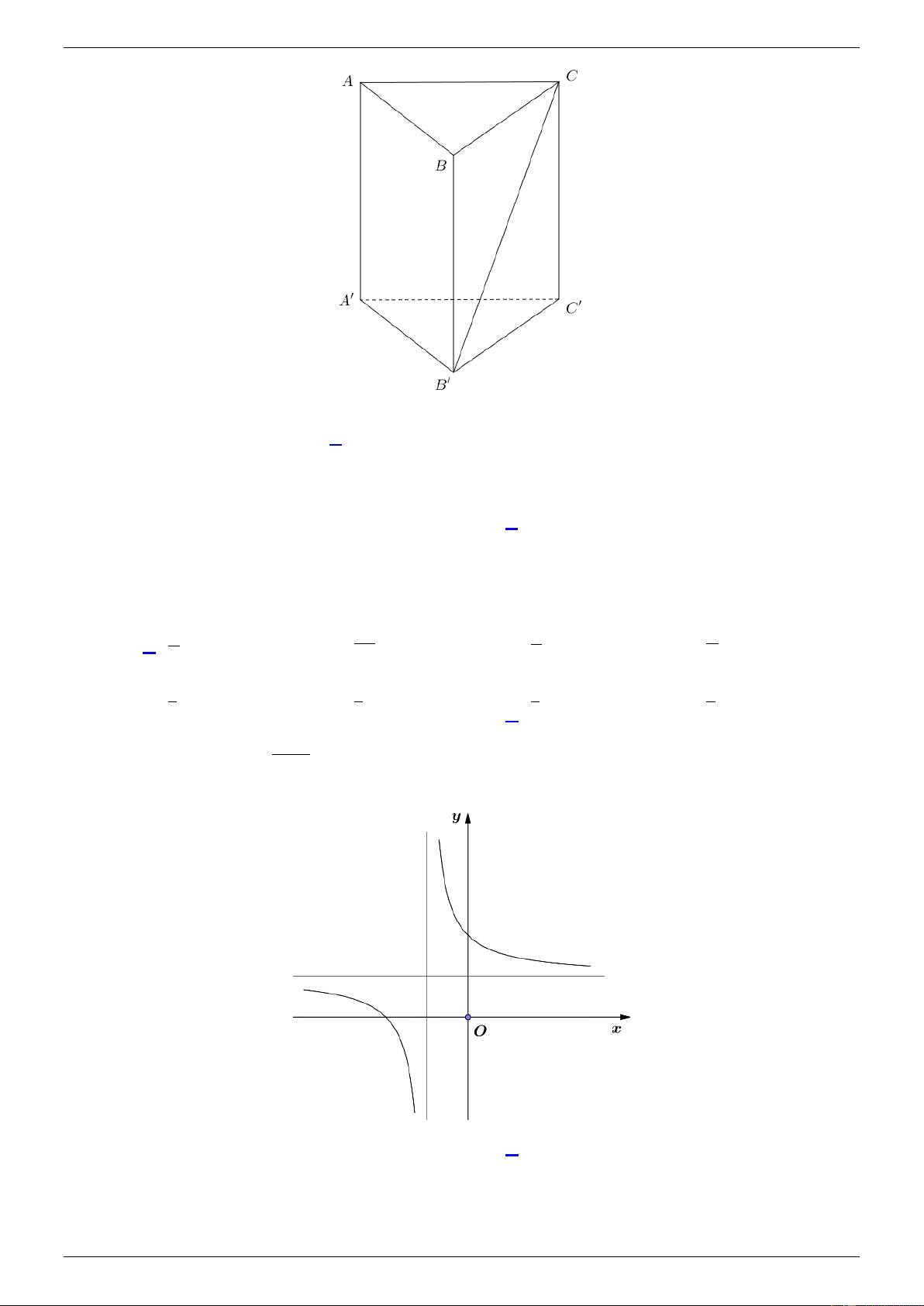
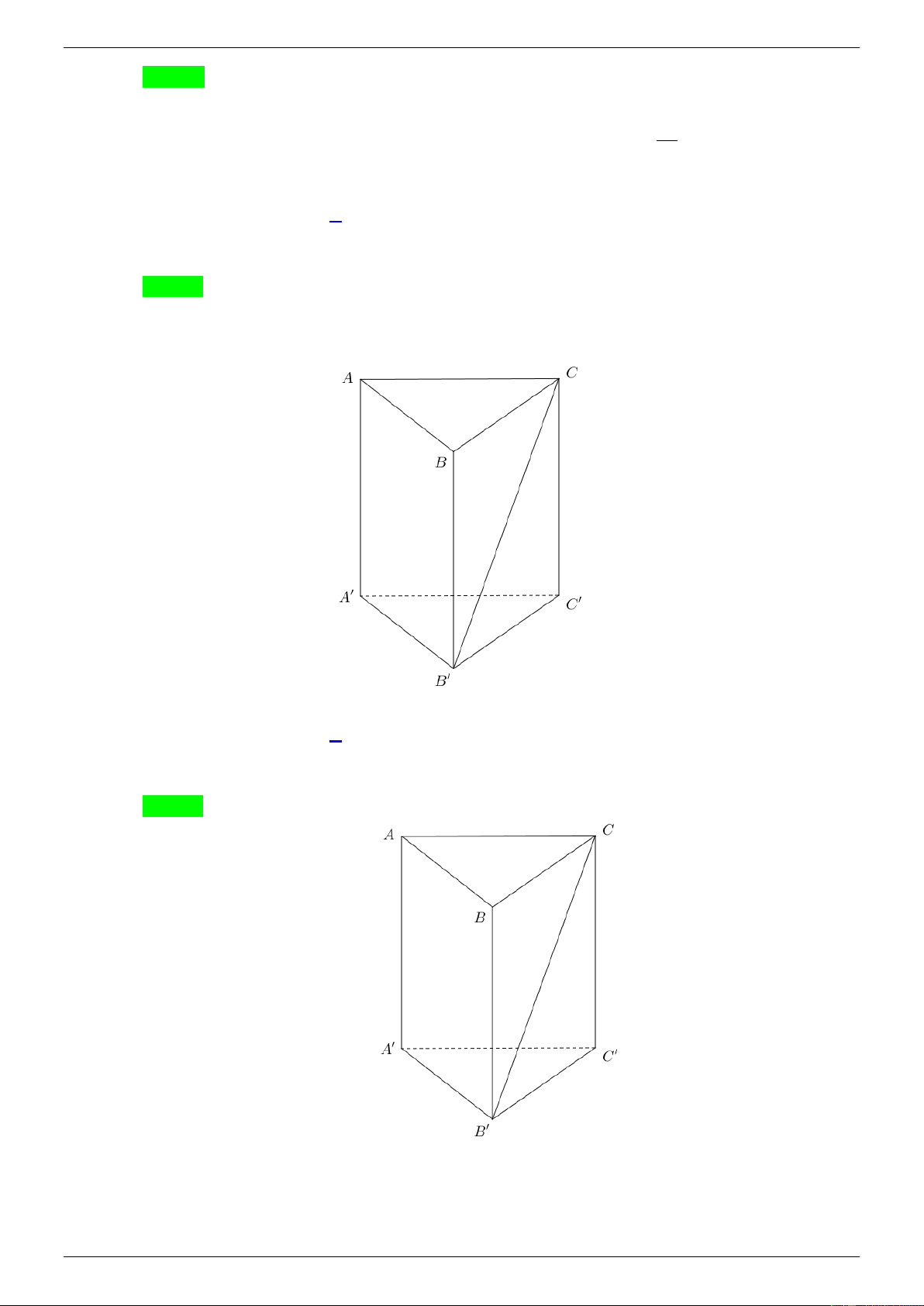
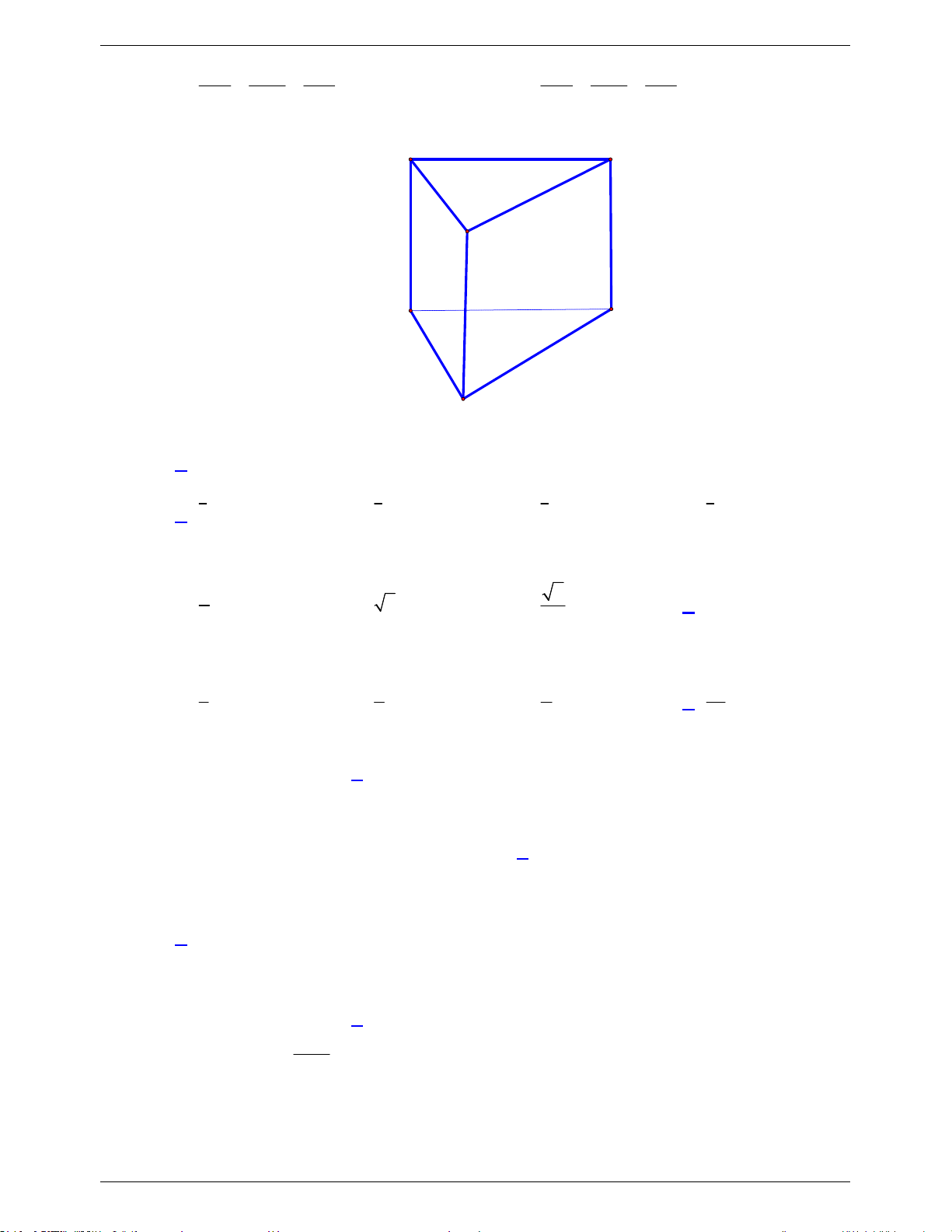
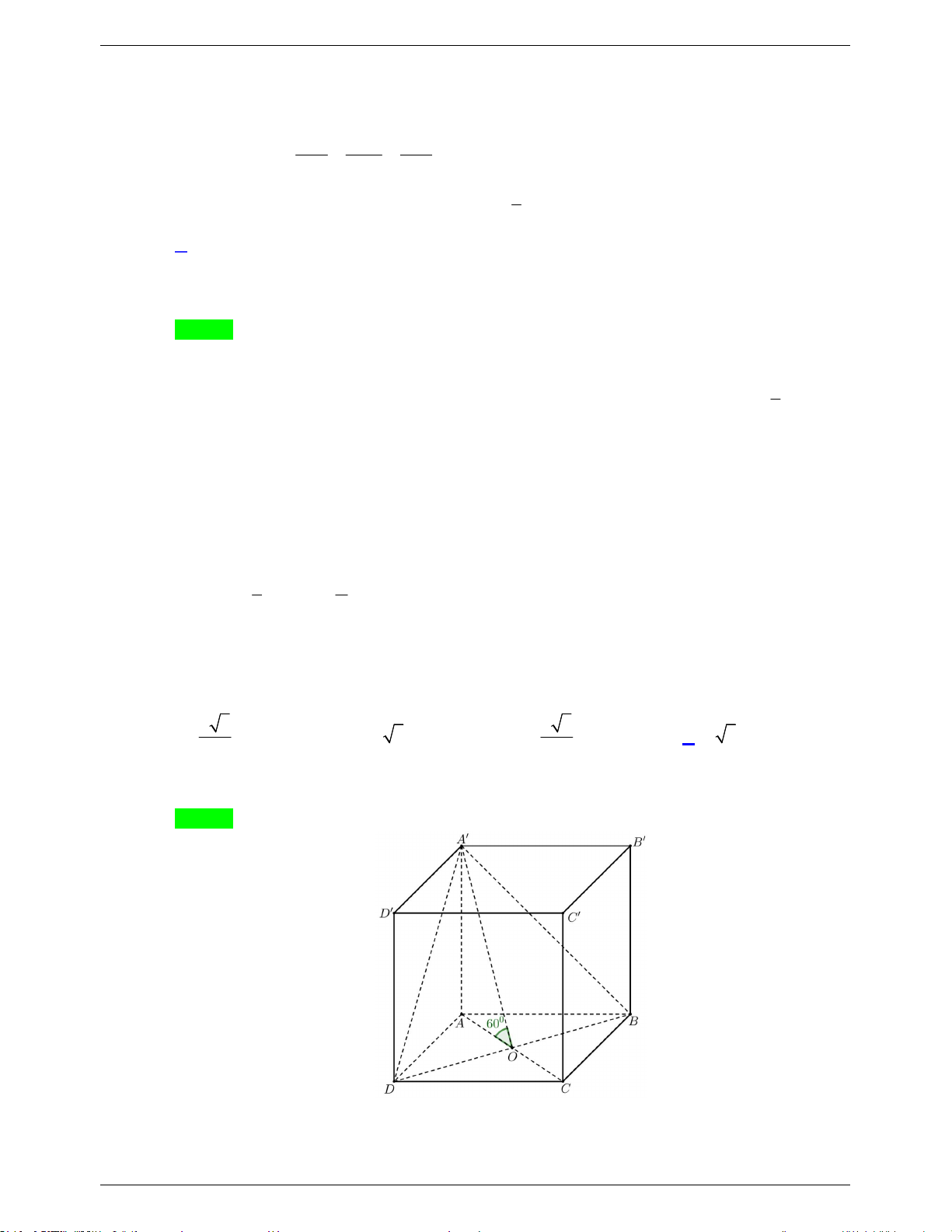
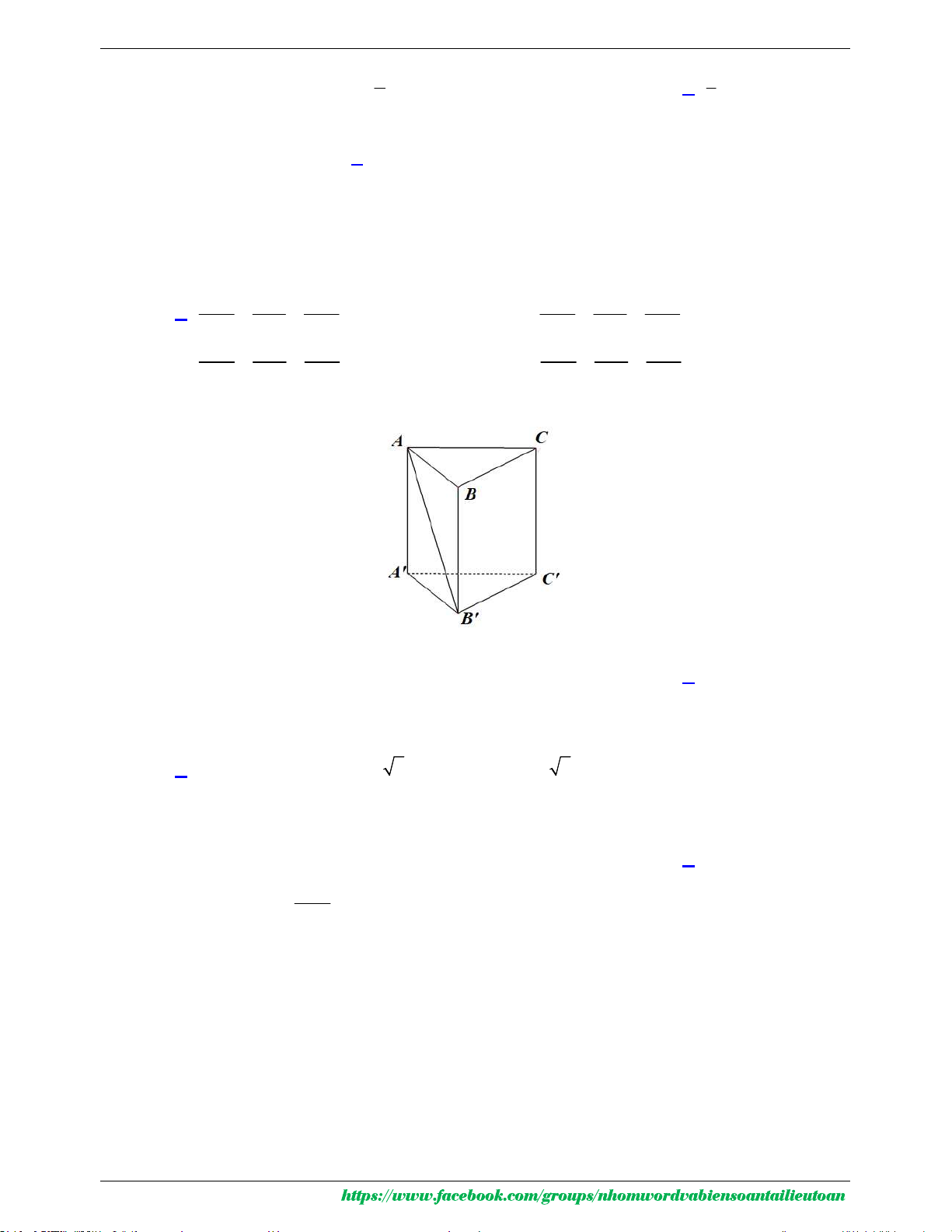
Câu 36: Cho hình lăng trụ đứng ABC.AB C
 có tất cả các cạnh bằng ( tham khảo hình bên). Góc giữa
đường thẳng AA và BC bằng A. 0 30 . B. 0 90 . C. 0 45 . D. 0 60 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Câu 37. Với mọi a,b thỏa mãn 3
log a  log b  6 , khẳng định nào dưới đây đúng: 2 2 A. 3 a b  64 . B. 3 a b  36 . C. 3 a  b  64 . D. 3 a  b  36 . 2 2 Câu 38. Nếu f
 xdx  5 thì 2 f   x1 dx  bằng: 0 0 A. 8 . B. 9. C. 10. D. 12. 2x  5, x  1
Câu 39. Cho hàm số f  x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3  x  4, x 1
F 0  2 . Giá trị của F   1  2F 2 bằng A. 27 . B. 29 . C. 12 . D. 33 .
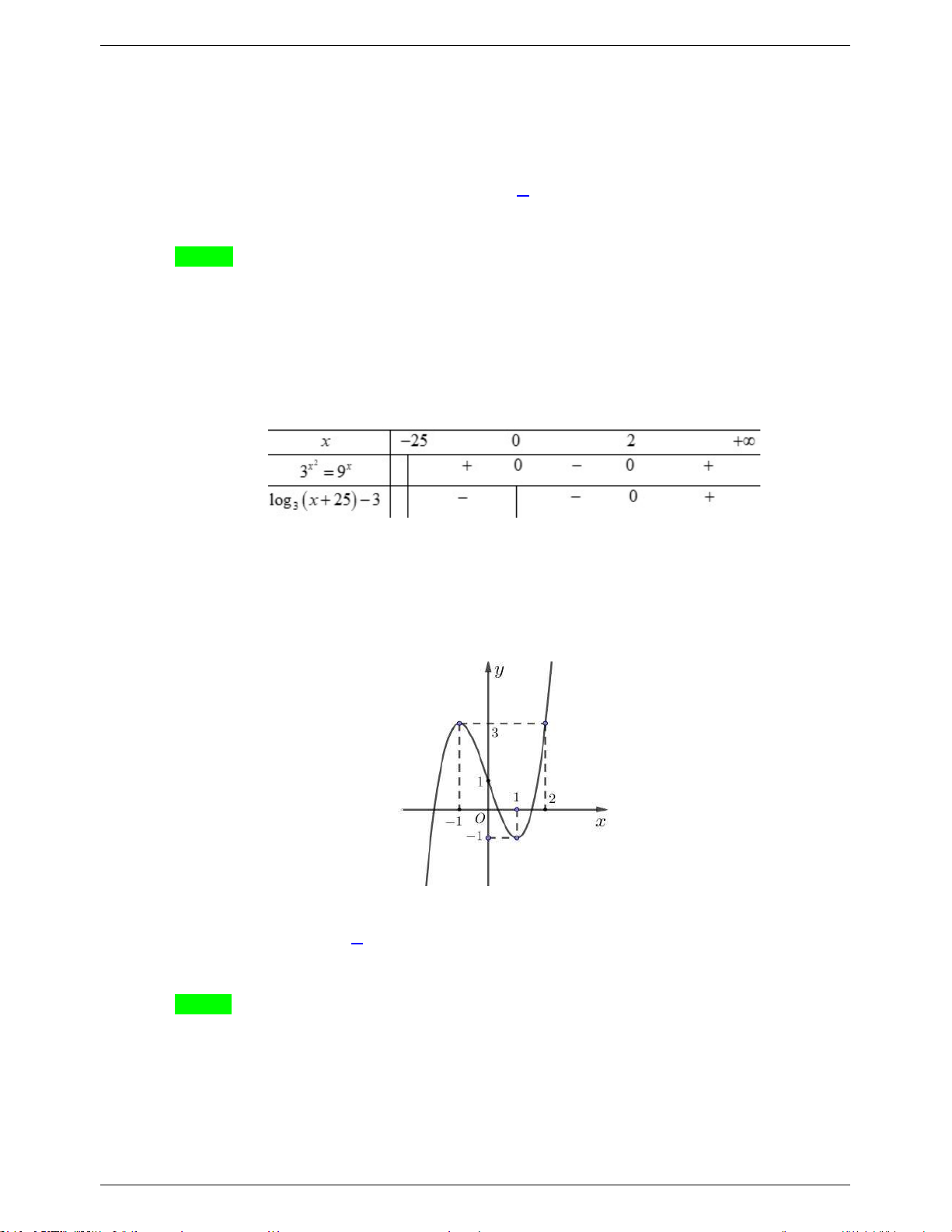
Câu 40. Có bao nhiêu số nguyên x thảo mãn  2
3x  9x log x  25 3  0  3    ? A. 24 . B. Vô số. C. 26 . D. 25 .
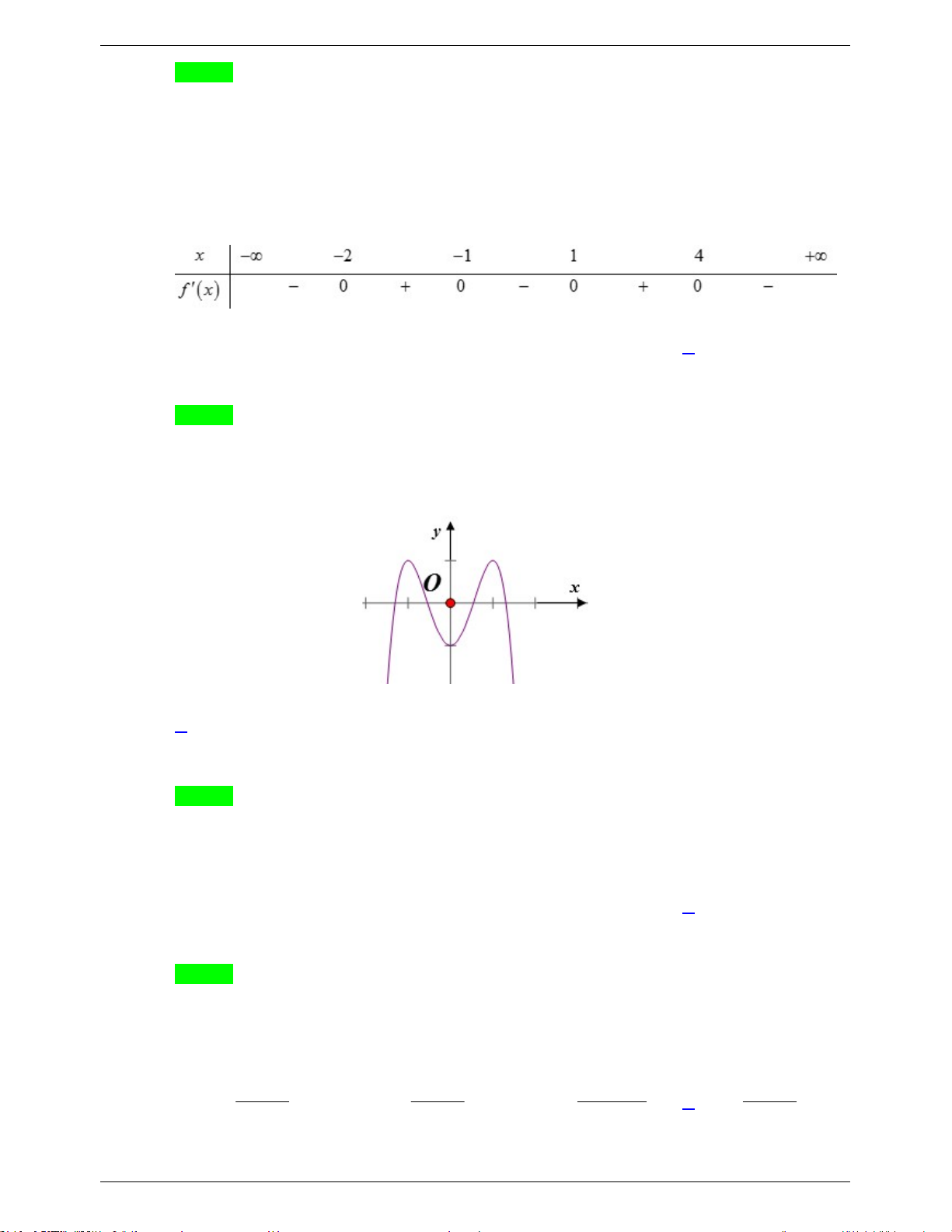
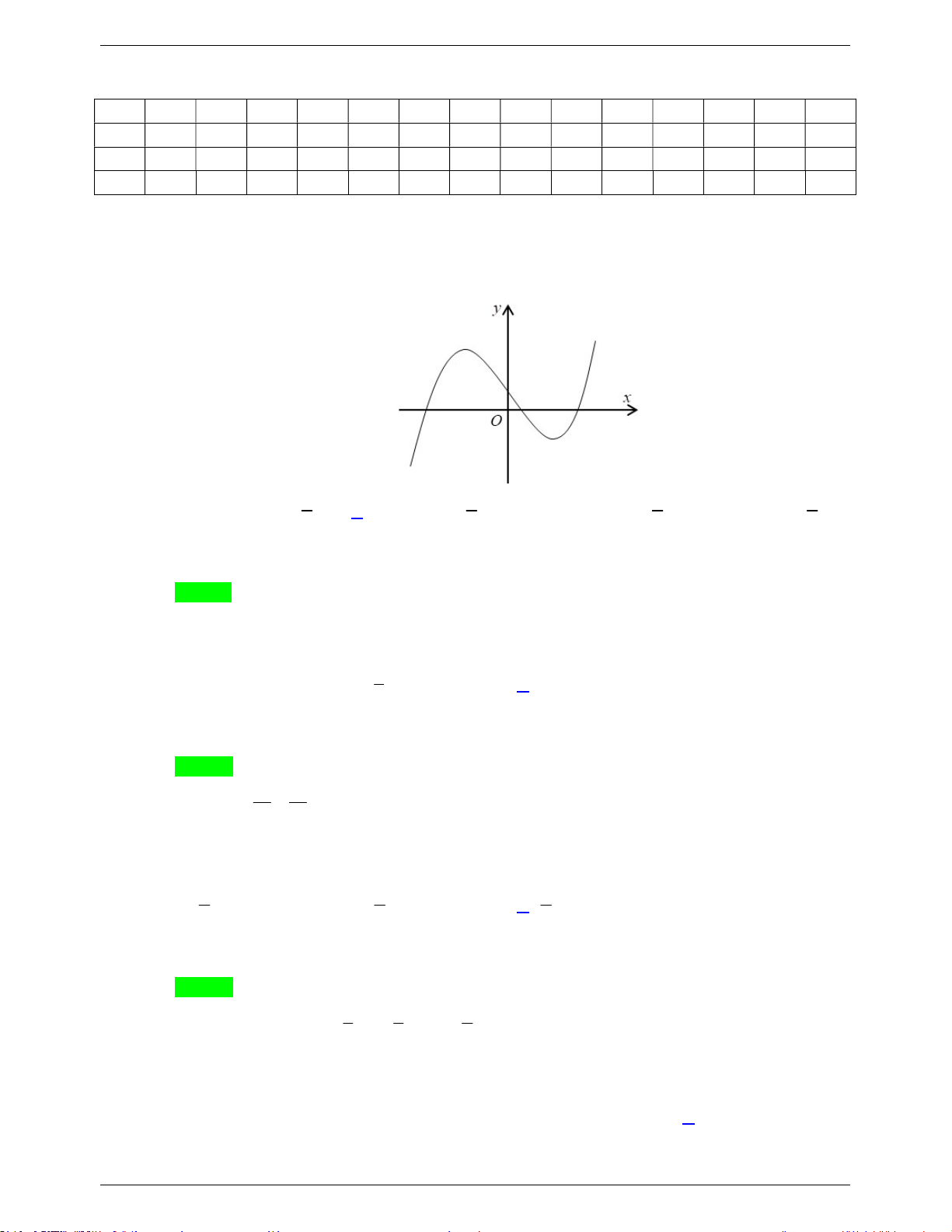
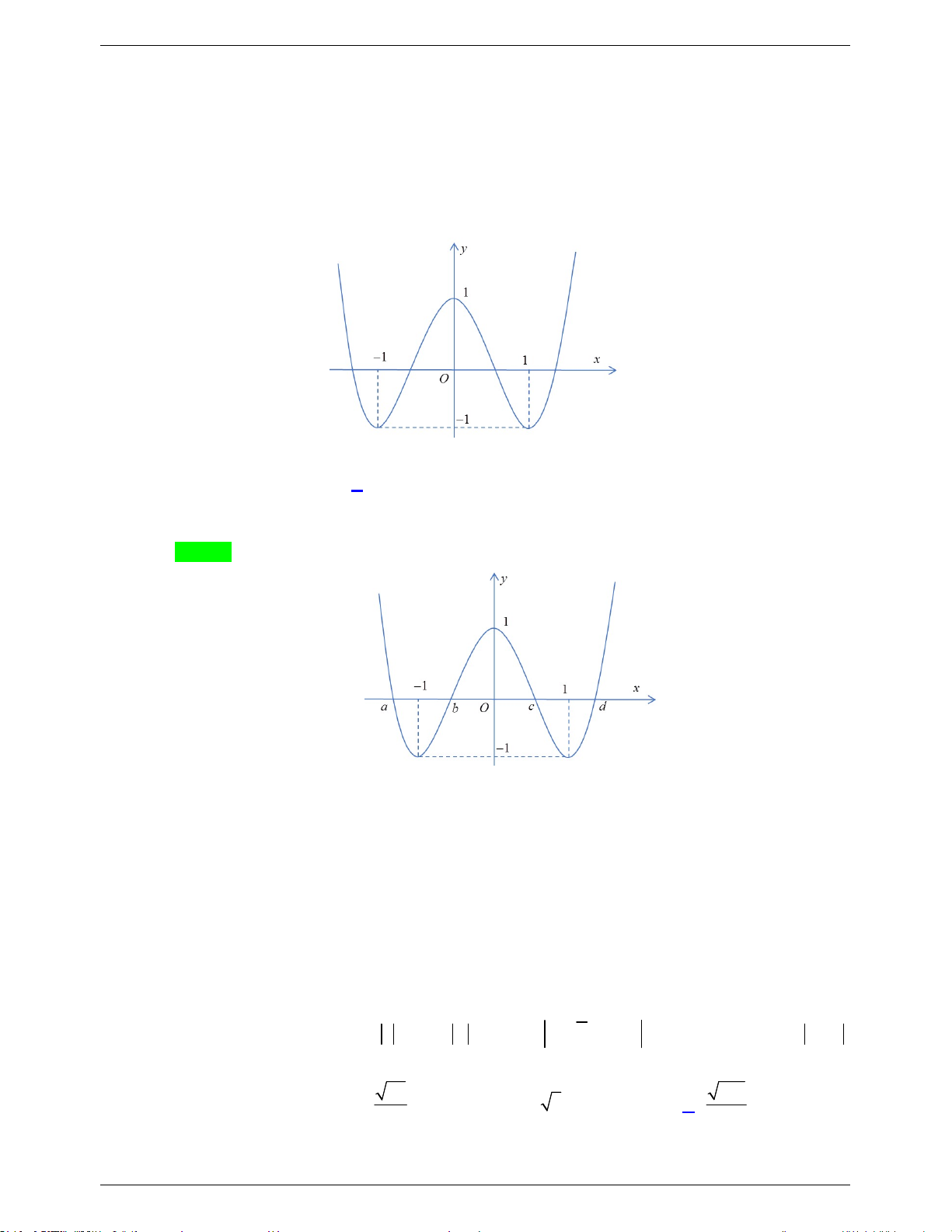
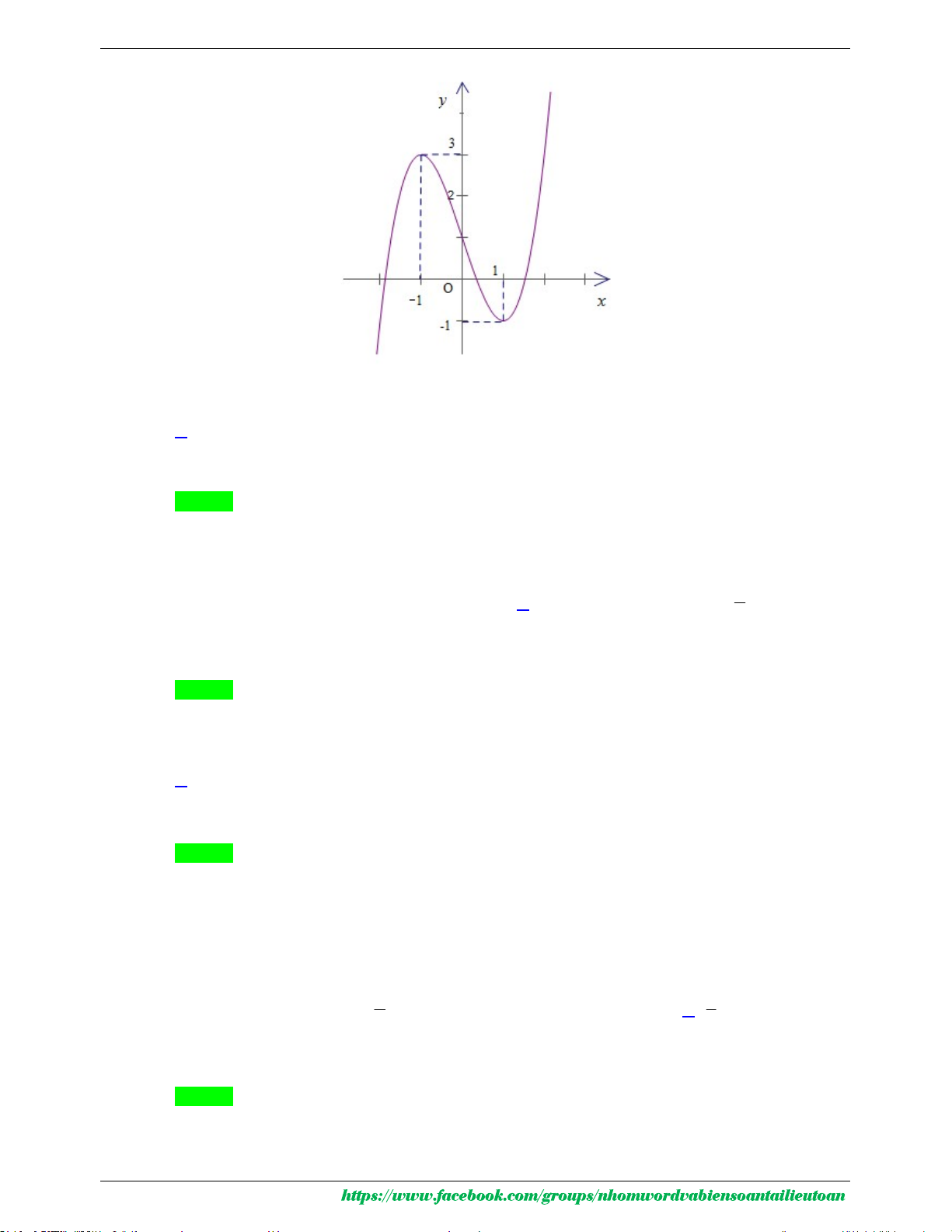
Câu 41. Cho hàm số bậc ba y  f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt
của phương trình f ( f (x))  1 là A. 9 . B. 7 . C. 3 . D. 6 .
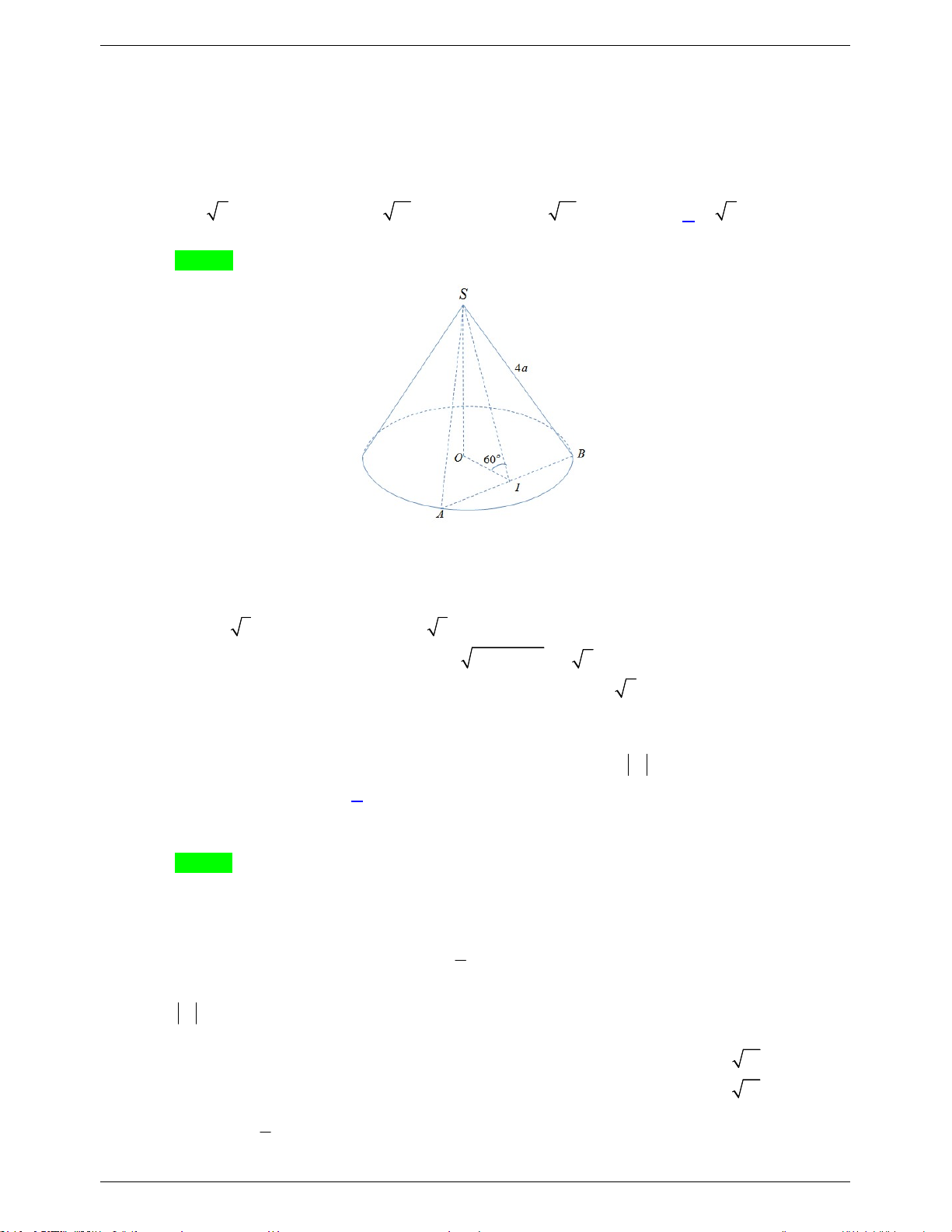
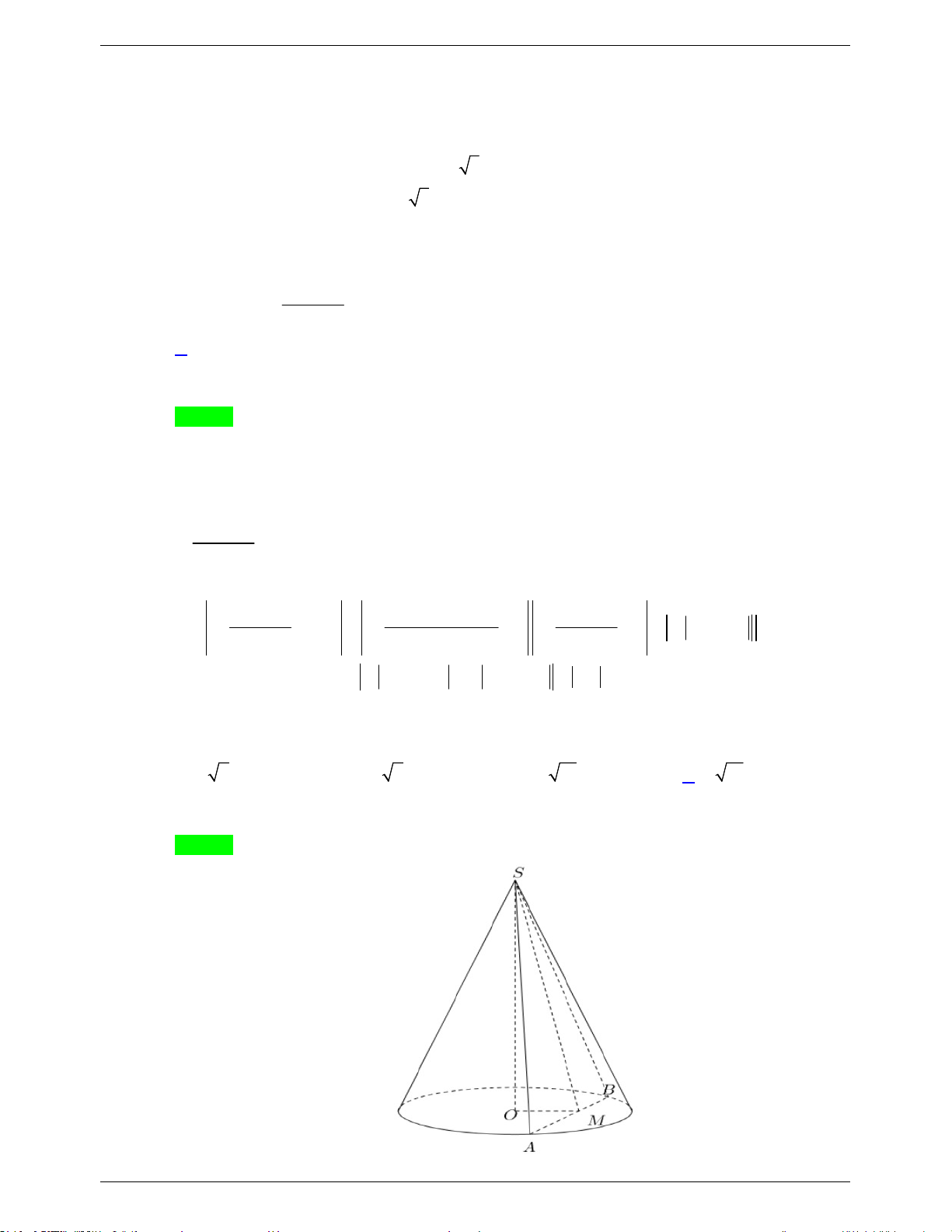
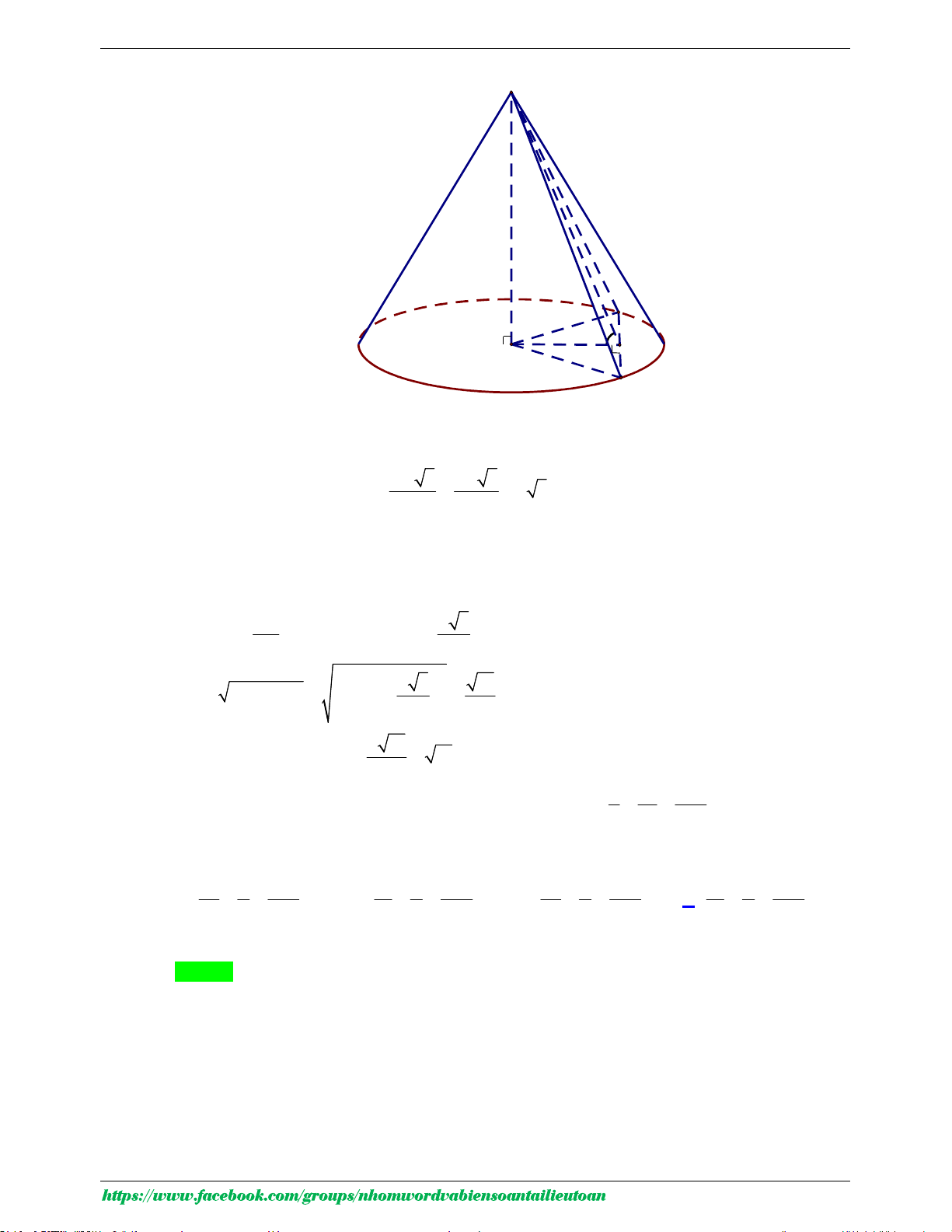
Câu 42: Cắt hình nón (N ) bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc 30o , ta
được thiết diện là tam giác đều cạnh 4a . Diện tích xung quanh của (N ) bằng A. 2 8 7 a . B. 2 4 13 a . C. 2 4 7 a . D. 2 4 13 a .
Câu 43. Trên tập hợp các số phức, xét phương trình 2 z  m   2 2
1 z  m  0 ( m là tham số thực). Có bao
nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  7 ? 0 0 A. 2. B. 3. C. 1. D. 4.
Câu 44. Xét các số phức z , w thỏa mãn z  1 và w  2 . Khi z  iw  6  8i đạt giá trị nhỏ nhất, z  w bằng 221 29 A. . B. 5 . C. 3 . D. . 5 5 x y 1 z  2
Câu 45: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 1 
P: x  2y  z  4  0 . Hình chiếu vuông góc của d lên P là đường thẳng có phương trình: x y 1 z  2 x y 1 z  2 x y 1 z  2 x y 1 z  2 A.   . B.   . C.   . D.   . 2 1 4 3 2 1 2 1 4 3 2  1 Câu 46. Cho hàm số   3 2
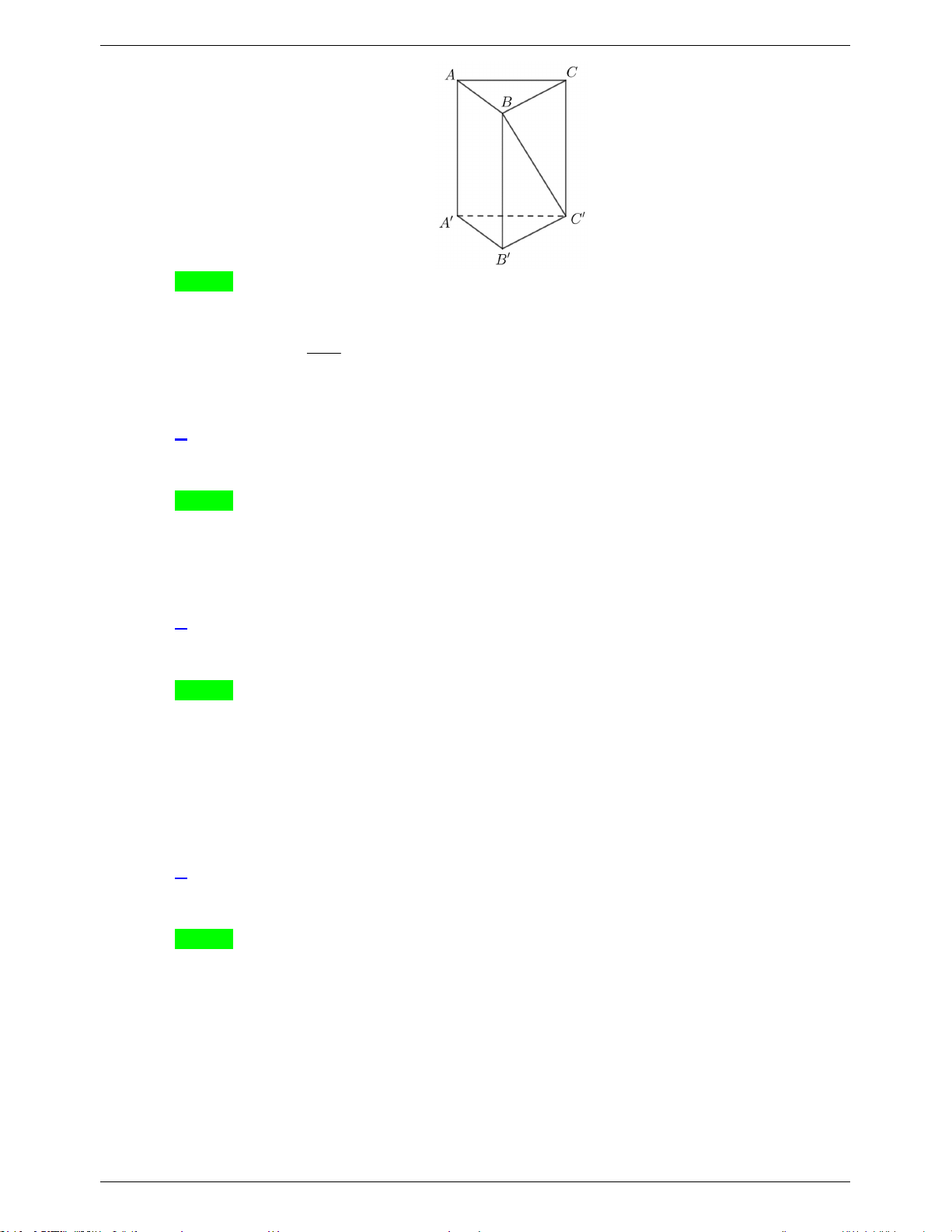
f x  x  ax  bx  c với a, ,
b c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 3
 và 6 . Diện tích hình phẳng giới hạn f  x bởi các đường y  và y  1 bằng g  x  6 A. 2ln 3 . B. ln 3 . C. ln18. D. 2ln 2 .  1 
Câu 47. Có bao nhiêu số nguyên y sao cho tồn tại x  ;3 2 
 thỏa mãn 3x xy     9 27 1 27 x xy ?  3 
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 A. 27 . B. 9 . C. 11. D. 12 .
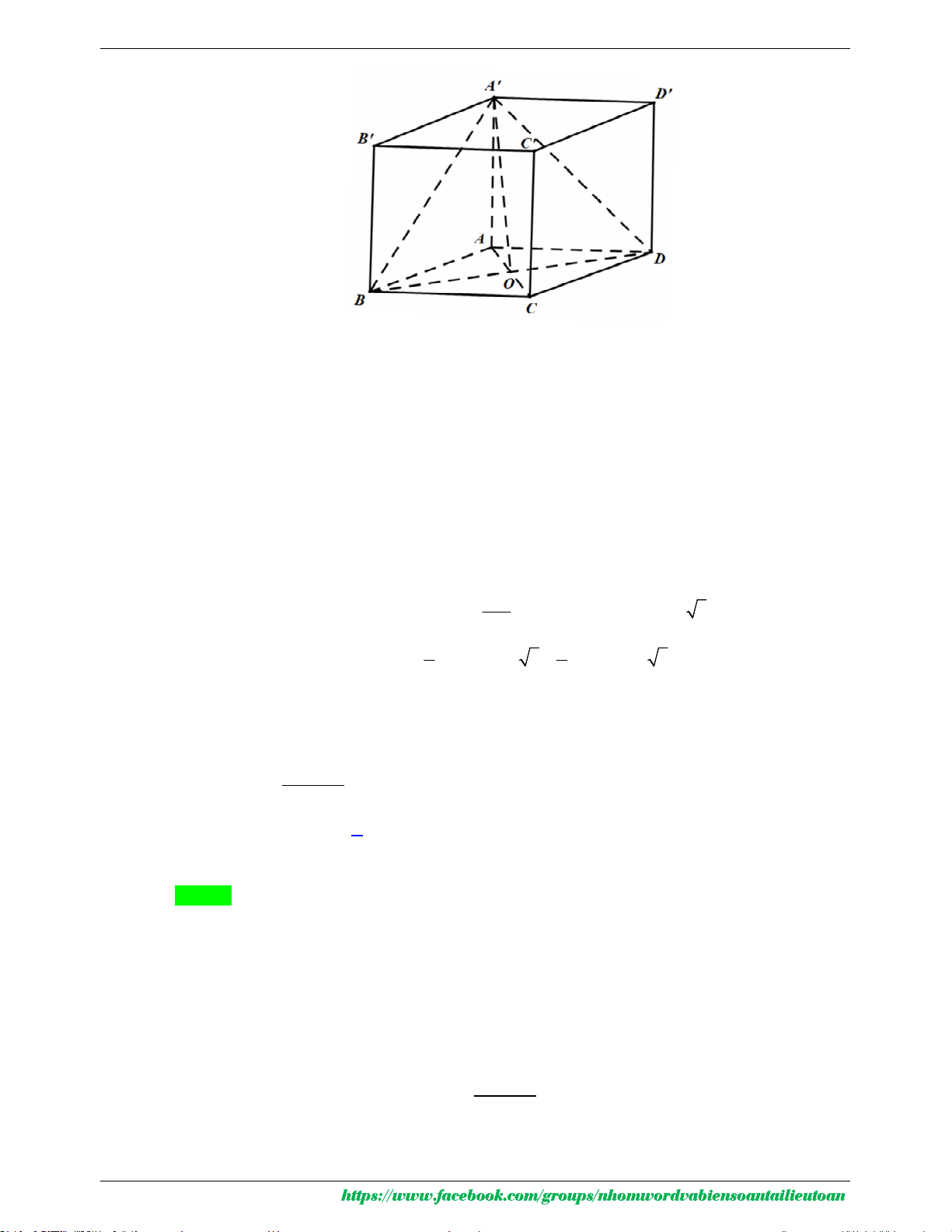
Câu 48. Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là hình vuông, BD  2a, góc giữa hai mặt
phẳng  A' BD và  ABCD bằng 0
30 . Thể tích khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3
Câu 49. Trong không gian Oxyz , cho hai điểm A1;3; 4
  và B2;1;2. Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  2 . Giá trị lớn nhất của AM  BN bằng A. 3 5 . B. 61 . C. 13 . D. 53 .
Câu 50. Cho hàm số y  f  x có đạo hàm f  x   x   2 7 x  9, x
   . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g  x  f  3
x  5x  m có ít nhất 3 điểm cực trị? A. 6 . B. 7 . C. 5 . D. 4 . Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN 1.A 2.C 3.B 4.D 5.D 6.A 7.D 8.D 9.A 10.C 11.C 12.A 13.C 14.A 15.C 16.B 17.C 18.A 19.B 20.A 21.B 22.D 23.B 24.A 25.B 26.C 27.B 28.B 29.B 30.A 31.C 32.D 33.B 34.B 35.A 36.C 37.A 38.A 39.A 40.C 41.B 42.D 43.B 44.D 45.C 46.D 47.C 48.D 49.D 50.A LỜI GIẢI CHI TIẾT
Câu 1: Tập nghiệm của bất phương trình 3x  2 là A.  ;  log 2 . B. log 2; . C.  ;  log 3 . D. log 3; . 2  2  3  3  Lời giải
GVSB: Nguyễn Tấn Linh; GVPB: Dương Ju-i Chọn A
Ta có 3x  2  x  log 2 3 Vậy S   ;  log 2 . 3  4 4 4 Câu 2: Nếu f  xdx  3 và g  x x d  2 thì  f
 x gxdx  bằng 1 1 1 A. 1. B. 5  . C. 5 . D. 1. Lời giải
GVSB: Nguyễn Tấn Linh; GVPB: Dương Ju-i Chọn C 4 4 4 Ta có  f
 x gxdx  f   xdx  g  x x d  3   2    5. 1 1 1
Câu 3: Trong không gian Oxyz , cho mặt cầu S  có tâm I 1;4;0 và bán kính bằng 3 . Phương trình của S  là
A.  x  2   y  2 2 1 4  z  9 .
B.  x  2   y  2 2 1 4  z  9 .
C.  x  2   y  2 2 1 4  z  3 .
D.  x  2   y  2 2 1 4  z  3 . Lời giải
GVSB: Nguyễn Tấn Linh; GVPB: Dương Ju-i Chọn B
Mặt cầu S  có tâm I 1; 4
 ;0 có bán kính 3 có phương trình là  x  2   y  2 2 1 4  z  9 .
Câu 4: Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 3;1;4 và có một vectơ chỉ  phương u   2
 ;4;5 . Phương trình của d là: x  2   3t x  3  2t x  3 2t x  3  2t     A. y  4  t . B. y  1   4t . C. y 1 4t . D. y  1   4t . z  5 4t     z  4  5t  z  4  5t  z  4  5t  Lời giải
GVSB: Trần Xuyến; GVPB: Dương Ju-i
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 Chọn D 
Đường thẳng d đi qua điểm M 3;1;4 và có một vectơ chỉ phương u   2  ;4;5 . Phương x  3  2t  trình của d là y  1   4t . z  4 5t 
Câu 5: Cho hàm số y  f x có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là A. 5 . B. 3 . C. 2 . D. 4 . Lời giải
GVSB: Trần Xuyến; GVPB: Dương Ju-i Chọn D
Dựa vào bảng xét dấu, f  x đổi dấu khi qua các điểm x 2; 1  ;1;  4 .
Vậy số điểm cực trị của hàm số đã cho là 4 .
Câu 6: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? A. 4 2 y  2  x  4x 1. B. 3 y  x  3x 1. C. 4 2 y  2x  4x 1. D. 3 y  x  3x 1. Lời giải
GVSB: Trần Xuyến; GVPB: Dương Ju-i Chọn A
Dựa vào dáng đồ thị, đây là hàm trùng phương nên loại câu B và D.
Đồ thị có bề lõm hướng xuống nên chọn câu A. Câu 7. Đồ thị hàm số 4 2
y  x  4x  3 cắt trục tung tại điểm có tung độ bằng A. 0. B. 3. C. 1. D. 3  . Lời giải
GVSB: Nam Đinh Ngọc; GVPB: Dương Ju-i Chọn D Đồ thị hàm số 4 2
y  x  4x  3 sẽ cắt trục tung tại điểm có hoành độ x  0 Từ đó ta được y  3  .
Câu 8. Với n là số nguyên dương bất kì, n  4 , công thức nào dưới đây đúng? n  4 ! 4   n n A. A  . B. 4 4! A  . C. 4 ! A  . D. 4 ! A  . n n! n n  4! n 4!n  4! n n  4! Lời giải Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
GVSB: Nam Đinh Ngọc; GVPB: Dương Ju-i Chọn D k n! n Ta có: A   4 ! A  n n  k! n n  4!
Câu 9. Phần thực của số phức z  5  2i bằng A. 5 . B. 2 . C. 5 . D. 2  . Lời giải
GVSB: Nam Đinh Ngọc; GVPB: Dương Ju-i Chọn A
Số phức z  a  bi có phần thực là a do đó a  5 . 5
Câu 10. Trên khoảng 0, , đạo hàm của hàm số 2 y  x là: 7 2 3 2 3 5 3 5  A. 2 y '  x . B. 2 y '  x . C. 2 y '  x . D. 2 y '  x . 7 5 2 2 Lời giải Chọn C 5 3 5 Ta có: 2 y  x  2 y '  x 2
Câu 11. Cho hàm số f  x 2
 x  4 . Khẳng định nào dưới đây đúng? A. f  xdx  2xC . B. f  x 2 dx  x  4x  C . 3 x C. f  xdx   4xC . D. f  x 3 dx  x  4x  C . 3 Lời giải Chọn C 3 x Ta có: f  x 2  x  4  f  xdx   4x C 3 
Câu 12. Trong không gian Oxyz , cho điểm A2;3;5 . Tọa độ của véctơ OA là: A. 2;3;5 . B. 2; 3  ;5 . C. 2;3;5 . D. 2;3;5 . Lời giải Chọn A 
Ta có: OA   x ; y ; z    2  ;3;5 A A A 
Câu 13. Cho hàm số y  f  x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 A. 1  . B. 5 . C. 3  . D. 1. Lời giải
GVSB:Mai Thị Phương Lan GVPB:Châu Vũ Chọn C
Ta có: f  x đổi dấu từ  sang  khi đi qua nghiệm x  1
 nên hàm số đã cho đạt cực tiểu tại x  1  .
Vậy hàm số đã cho có giá trị cực tiểu là y  3.
Câu 14. Cho hàm số y  f  x có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trong khoảng nào dưới đây? A. 0;  1 . B.  ;  0. C. 0; . D. 1;  1 . Lời giải
GVSB:Mai Thị Phương Lan; GVPB:Châu Vũ Chọn A
Ta có: đồ thị hàm số đi xuống trên khoảng 0; 
1 nên hàm số nghịch biến trên khoảng 0;  1 .
Câu 15. Nghiệm của phương trình log 5x  2 là 3   8 9 A. x  . B. x  9. C. x  . D. x  8 . 5 5 Lời giải
GVSB:Mai Thị Phương Lan; GVPB:Châu Vũ Chọn C TXĐ: D  0; . 9 Ta có: log 5x 2
 2  5x  3  x  . 3 5 3 3 Câu 16. Nếu f
 xdx  4 thì 3f xdx  bằng 0 0 A. 36 . B. 12 . C. 3 . D. 4 . Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB: Kim Liên Chọn B 3 3 Ta có: 3 f  xdx   3 f  xdx 12. 0 0
Câu 17. Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a . Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB:Kim Liên Chọn C
Thể tích của khối lập phương cạnh bằng 5a là: V   a3 3 5  125a
Câu 18. Tập xác định của hàm số 9x y  là A.  . B. 0; . C. \  0 . D. 0; . Lời giải
GVSB: Bùi Hoàng Nguyên; GVPB:Kim Liên Chọn A Vì hàm số 9x y 
là hàm số mũ nên có tập xác định là tập  .
Câu 19. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S  16 R . B. 2 S  4 R . C. 2 S   R . D. 2 S   R . 3 Lời giải
GVSB: Nguyen Nhan; GVPB: Kim Liên Chọn B
Diện tích S của mặt cầu bán kính R là 2 S  4 R . 2x 1
Câu 20. Tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình: x 1 1 A. x  1. B. x  1  . C. x  2 . D. x  . 2 Lời giải
GVSB: Nguyen Nhan; GVPB: Kim Liên Chọn A Ta có: 2x 1 2x 1 lim y  lim   , lim y  lim   . x 1 x 1   x 1 x 1 x 1   x 1 2x 1
Do đó tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình x  1. x 1
Câu 21. Cho a  0 và a  1, khi đó 4 log a bằng a 1 1 A. 4 . B. . C.  . D. 4 . 4 4 Lời giải
GVSB: Nguyen Nhan; GVPB: Kim Liên Chọn B 1 1 Ta có: 4 4 log a  log a  . a a 4
Câu 22. Cho khối chóp có diện tích đáy 2
B  5a và chiều cao h  a . Thể tích của khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 11
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 Lời giải
GVSB: Ngô Quang Minh; GVPB: Hoàng Dương Chọn D 1 1 5
Thể tích của khối chóp đã cho bằng: 2 3 V  . B h  5a .a  a . 3 3 3
Câu 23. Trong không gian Oxyz , cho mặt phẳng P :3x  y  2z 1  0 . Véctơ nào dưới đây là một
véctơ pháp tuyến của P ?     A. n  (3;1;2) . B. n  (3; 1; 2) . C. n  (3;1; 2) . D. n  (3;1;  2) . 1 2 3 4 Lời giải
GVSB: Ngô Quang Minh; GVPB: Hoàng Dương Chọn B 
Véc tơ pháp tuyến của P là: n  (3;1;2) . 2
Câu 24. Cho khối hình trụ có bán kính đáy r  6 và chiều cao h  3. Thể tích của khối trụ đã cho bằng A. 108 . B. 36 . C. 18 . D. 54 . Lời giải
GVSB: Ngô Quang Minh; GVPB: Hoàng Dương Chọn A
Thể tích của khối trụ đã cho là 2 2
V   r h   .6 .3  108 .
Câu 25. Cho hai số phức z  4  2i , w  3  4i . Số phức z  w bằng A. 1 6i . B. 7  2i . C. 7  2i . D. 1 6i . Lời giải GVSB: Chau nguyen minh; GVPB: Chọn B
Ta có: z  w=4+2i+3- 4i=7 - 2i .
Câu 26. Cho cấp số nhân u có u  3,và u  9 . Công bội của cấp số nhân bằng n  1 2 1 A. 6  . B. . C. 3 . D. 6 . 3 Lời giải GVSB: Chau nguyen minh; GVPB: Chọn C u 9 Ta có: 2 u  u q  q    3. 2 1 u 3 1 Câu 27. Cho hàm số ( ) x
f x  e  2 . Khẳng định nào dưới đây là đúng ? A.    2 d x f x x  e  C . B.   d x f x x  e  2x  C . C.   d x f x x  e  C . D.   d x f x x  e  2x  C . Lời giải GVSB: Chau nguyen minh; GVPB: Chọn B
Ta có:   d   x  2d x f x x e x  e  2x  C
Câu 28. Trong mặt phẳng tọa độ, điểm M  3
 ;4 là điểm biểu diễn số phức nào dưới đây? Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 A. z  3  4i . B. z  3  4i . C. z  3   4i . D. z  3  4i . 2 3 4 1 Lời giải GVSB: Vu Ngoc Anh; GVPB: Chọn B Ta có điểm M  3
 ;4 là điểm biểu diễn cho số phức z  a  bi  3   4i . x  a
Câu 29. Biết hàm số y 
( a là số thực cho trước, a  1 có đồ thị như hình bên). Mệnh đề nào x 1 dưới đây đúng? A. y '  0, x   1  . B. y '  0, x   1. C. y '  0, x    . D. y '  0, x    . Lời giải GVSB:Vu Ngoc Anh; GVPB: Chọn B x  a Ta có : y  x1 1 a  y '   0, x   1
 (Dựa theo hướng của đồ thị) x  2 1
Do a  1 nên dấu “  ” không xảy ra.
Hàm đơn điệu không phụ thuộc vào a .
Câu 30. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đó và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng 7 2 1 5 A. . B. . C. . D. . 44 7 22 12 Lời giải GVSB: Vu Ngoc Anh; GVPB: Chọn A Không gian mẫu 3 n  C  220  12
Gọi A là biến cố: “Lấy được 3 quả màu xanh” 3 n  C  35 A 7 P  A n 35 7 A    n 220 44 
Câu 31. Trên đoạn 0;  3 , hàm số 3
y  x  3x đạt giá trị lớn nhất tại điểm A. x  0 . B. x  3. C. x  1. D. x  2 . Lời giải
GVSB: Nguyễn Hồng Hiên; GVPB: Minh Văn Nguyễn
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 13
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 Chọn C Tập xác định:  . 2 y  3x  3 x  1 0;3 2
y  0  3x  3  0  x  1  0;3
Ta có y 0  0; y   1  2; y 3  18. Vậy max y  y   1  2 . 0; 3
Câu 32. Trong không gian Oxyz, cho điểm M 1;3;2 và mặt phẳng P : x  2y  4z 1  0. Đường
thẳng đi qua M và vuông góc với P có phương trình là x 1 y  3 z  2 x 1 y  3 z  2 A.   . B.   . 1 2 1 1 2  1 x 1 y  3 z  2 x 1 y  3 z  2 C.   . D.   . 1 2  4 1 2 4 Lời giải
GVSB: Nguyễn Hồng Hiên; GVPB: Minh Văn Nguyễn Chọn D  
P : x  2y  4z 1  0 có vectơ pháp tuyến n1;2;4 . 
Đường thẳng đi qua M và vuông góc với P nhận n1; 2
 ; 4 làm vectơ chỉ phương nên có x 1 y  3 z  2 phương trình   . 1 2  4
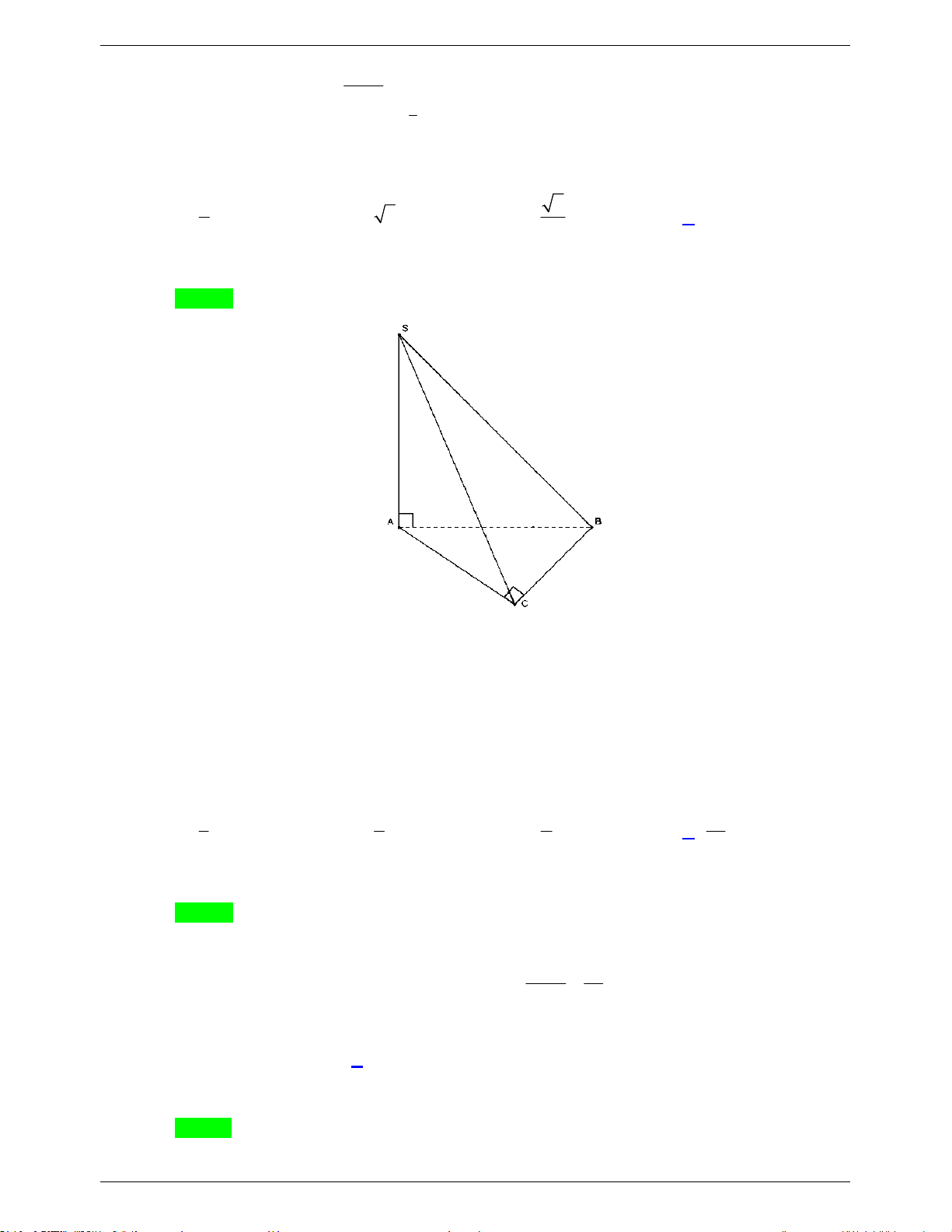
Câu 33. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB  2a và SA vuông góc
với mặt phẳng đáy. Tính khoảng cách từ C đến mặt phẳng (SAB) bằng A. 2a . B. 2a . C. a . D. 2 2a . Lời giải
GVSB: Thành đặng; GVPB: Lê Thị Phương Chọn B
Vì SA   ABC  suy ra CB  SA (1). Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Tam giác ABC vuông tại B, nên CB  AB (2).
Từ (1) và (2), ta suy ra CB  SAB nên khoảng cách từ C đến mặt phẳng (SAB) bằng CB.
Mà tam giác ABC vuông cân tại B, suy ra AB  BC  2a Vậy d CB  2 . a (C; (SAB))
Câu 34. Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1;0;0 , B 4;1;2 . Mặt phẳng đi qua A
và vuông góc với AB có phương trình là
A. 3x  y  2z 17  0 .
B. 3x  y  2z  3  0 .
C. 5x  y  2z  5  0 .
D. 5x  y  2z  25  0 . Lời giải
GVSB: Thành đặng; GVPB: Lê Thị Phương Chọn B  Ta có AB  3;1;2
Gọi Q là mặt phẳng đi qua A1;0;0 và vuông góc với AB suy ra mặt phẳng Q nhận 
vecto AB  3;1;2 làm véc tơ pháp tuyến. Vậy phương trình mặt phẳng Q cần tìm có dạng:
3(x 1)  y  2z  0  3x  y  2z  3  0
Câu 35: Cho số phức iz  5  4i . Số phức liên hợp của z là A. z  4  5i . B. z  4  5i . C. z  4   5i . D. z  4  5i Lời giải Chọn A 5  4i
Ta có iz  5  4i  z 
 4  5i . Suy ra z  4  5i . i
Câu 36: Cho hình lăng trụ đứng ABC.AB C
 có tất cả các cạnh bằng ( tham khảo hình bên). Góc giữa
đường thẳng AA và BC bằng A. 0 30 . B. 0 90 . C. 0 45 . D. 0 60 Lời giải
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 15
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 Chọn C
Vì AA / /BB nên  AA , BC  BB ', BC   B BC  B C   Ta có:  B BC      0 tan 1 B B  C  45 BB
Câu 37. Với mọi a,b thỏa mãn 3
log a  log b  6 , khẳng định nào dưới đây đúng: 2 2 A. 3 a b  64 . B. 3 a b  36 . C. 3 a  b  64 . D. 3 a  b  36 . Lời giải GVSB: Vũ Tuấn; GVPB: Chọn A Ta có 3 3 6 3
log a  log b  6  a b  2  a b  64 . 2 2 2 2 Câu 38. Nếu f
 xdx  5 thì 2 f  x 1 dx    bằng: 0 0 A. 8 . B. 9 . C. 10. D. 12. Lời giải GVSB: Vũ Tuấn; GVPB: … Chọn A 2 2 2 Ta có 2 f   x1 dx   2 f 
 xdx  dx  2.52  8  . 0 0 0 2x  5 khi x 1
Câu 39. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3  x  4 khi x  1
F 0  2 . Giá trị của F   1  2F 2 bằng A. 27 . B. 29 . C. 12 . D. 33 . Lời giải GVSB: Phạm Tính; GVPB: Chọn A 2x  5 khi x  1 F   x 2  x  5x  C x  1 Ta có f x 1     . 2 3  x  4 khi x  1 F   x 3  x  4x  C x  1 2
Vì F là nguyên hàm của f trên  thỏa mãn F 0  2 nên C  2  F  x 3  x  4x  2 . 2
Vì F  x liên tục trên  nên F  x liên tục tại x 1 nên:
lim F  x  lim F  x  F  
1  6  C  7  C  1.   1 1 x 1  x 1  Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 F   x 2  x  5x  2 x  1 Vậy ta có   F   1  2F 2     . F   x 3 2.15 27 3  x  4x 1 x  1
Câu 40. Có bao nhiêu số nguyên x thảo mãn  2
3x  9x log x  25 3  0  3    ? A. 24 . B. Vô số. C. 26 . D. 25 . Lời giải GVSB: Phạm Tính; GVPB: Chọn C
Điều kiện: x  25  0  x  25  .
Ta giải các phương trình: x  0  2 x x 2 3  9  x  2x   . x  2
 log x  25  3  x  25  27  x  2 . 3   Ta có bảng xét dấu sau:
Dựa vào bẳng xét dấu, để  2
3x  9x log x  25 3  0  3    thì ta có  25   x  0  24   x  0 x   
có 26 giá trị nguyên của x thỏa mãn. x 2   x  2
Câu 41. Cho hàm số bậc ba y  f (x) có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình f ( f (x))  1 là: A. 9 . B. 7 . C. 3 . D. 6 . Lời giải
GVSB: Quách Ngọc Giang, GVPB: Trần Đại Nghĩa Chọn B  f (x)  0 Ta có: f ( f (x)) 1    f (x)  a (a  1  )   f (x)  b (1 Ta dựa vào đồ thị:
Phương trình f (x)  0 có 3 nghiệm.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 17
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Phương trình f (x)  a có 1 nghiệm.
Phương trình f (x)  b có 3 nghiệm.
Vậy phương trình f ( f (x))  1 có 7 nghiệm phân biệt.
Câu 42. Cắt hình nón (N ) bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc 30o , ta
được thiết diện là tam giác đều cạnh 4a . Diện tích xung quanh của (N ) bằng A. 2 8 7 a . B. 2 4 13 a . C. 2 8 13 a . D. 2 4 7 a . Lời giải Chọn D
Gọi hình nón (N ) có đỉnh S , đường tròn đáy có tâm O , bán kính r . Thiết diện đã cho là tam
giác SAB cạnh 4a và I là trung điểm của AB . Khi đó
OI  AB, SI  AB nên góc giữa (SAB) và mặt phẳng đáy là  60o SIO  . SI  2a 3 nên  .cos 60o OI SI  a 3.
Tam giác OIA vuông tại I có 2 2
r  OA  OI  AI  a 7.
Vậy hình nón (N ) có diện tích xung quanh bằng 2 S   rl  4 7 a . xq
Câu 43. Trên tập hợp các số phức, xét phương trình 2 z  m   2 2
1 z  m  0 ( m là tham số thực). Có bao
nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  7 ? 0 0 A. 2. B. 3. C. 1. D. 4. Lời giải
GVSB: Lê Mẫn; GVPB: Đồng Khoa Văn Chọn B Phương trình 2 z  m   2 2 1 z  m  0 . Ta có 2 2
 '  (m 1)  m  2m 1 1
Trường hợp 1: Nếu 2m 1  0  m   thì phương trình có nghiệm thực nên 2 z  7 0 z  7  . 0 z  7   0 m  7  14
Với z  7 thay vào phương trình ta được 2 7  2m   2 1 .7  m  0   0 m  7  14 1 (thoả m   ) . 2 Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Với z  7 thay vào phương trình ta được 2  m   2 2 7 2
1 .7  m  0  m 14m  63  0 0
phương trình vô nghiệm . 1 Trường hợp 1: Nếu
2m 1  0  m   thì phương trình có hai nghiệm phức là 2
z  m 1 i 2m 1  .
z  m 1 i 2m 1 m  7
Khi đó z  7  m  2 1  2m 1  49  . 0  m  7  1
Kết hợp với m   ta được m  7  . 2
Vậy có 3 giá trị m thỏa mãn yêu cầu bài toán.
Câu 44. Xét các số phức z , w thỏa mãn z  1 và w  2 . Khi z  iw  6  8i đạt giá trị nhỏ nhất, z  w bằng 221 29 A. . B. 5 . C. 3 . D. . 5 5 Lời giải
GVSB: Trần Xuân Thiện; GVPB: Nguyễn Thị Thùy Nương Chọn D
Đặt z  a  bi , w  c  di với a , b , c , d   . 2 2  z 1  a  b 1 Theo giả thiết      * . 2 2  w  2  c  d  4 Ta có
z  iw  6  8i  a  bi  i c  di  6 8i  a  d  6  b  c  8i
 a  d  2  b  c  2  a  d  2   b   c  2 6 8 6 8 .
Khi đó a  d  2   b
  c  2  a  b  d  c   2   2 2 2 2 2 6 8 6 8  10 a d  2  b
  c  2    a  d  2  b  c  2 6 8 3 10 6 8  7 . 3 4 8 6
Dấu “=” xảy ra khi a  , b  , c  , d  thỏa mãn (*). 5 5 5 5
Vậy z  iw  6  8i đạt giá trị nhỏ nhất bằng 7 . 3 4 8 6 2 29
Khi đó z   i , w   i . Suy ra z  w  1 i  z  w  . 5 5 5 5 5 5 x y 1 z  2
Câu 45: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 1
P: x  2y  z  4  0 . Hình chiếu vuông góc của d lên P là đường thẳng có phương trình: x y 1 z  2 x y 1 z  2 x y 1 z  2 x y 1 z  2 A.   . B.   . C.   . D.   . 2 1 4 3 2 1 2 1 4 3 2  1
GVSB: Phạm Tuấn; GVPB: Trần Tú Lời giải Chọn C
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 19
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Ta có: d  P    A  A0;1;2 . Lấy M 2;3;0 d . x  2 y  3 z
Gọi  là đường thẳng qua M và vuông góc với P khi đó  :   . 1 2 1
Gọi H    P  H 2  t;3  2t;t .    4 2 8  
Mặt khác H P    t    t 2 2
2 3 2  t  4  0  t   4 5 2  H ; ;    AH ; ;   . 3  3 3 3   3 3 3  
Gọi d là hình chiếu của d lên P khi đó d đi qua A và có một VTCP u 2;1; 4   x y 1 z  2  d :   . 2 1 4 Câu 46. Cho hàm số   3 2
f x  x  ax  bx  c với a, ,
b c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 3
 và 6 . Diện tích hình phẳng giới hạn f  x bởi các đường y  và y  1 bằng g  x  6 A. 2ln 3 . B. ln 3 . C. ln18. D. 2ln 2 . Lời giải
GVSB: Nguyễn Hữu Chung Kiên; GVPB:Hoàng Ngọc Hùng Chọn D
Ta có g  x  f  x  f  x  f   x 3  x    a 2 3
x  b  2a  6 x  2a  b  c . Suy ra: g x 2
 3x  23 a x  b  2a  6 . Xét phương trình f  x x  x 2                 g  x 1 g  x f  x 6 3x 2a 3 x 2a b 6 0 g  x 1 0  6 x  x  2 Ta có diện tích bằng 2 x  f x 2 x   f x  g x 2  6 x   gx  x S      x     x    x  g x   g x   g x   g x     x    1 d 6  x    d 6  x    d ln   2 6 1 6 x  . 1 1 1
 ln g  x  6  ln g x  6  ln 4  2ln 2 2   1  1 
Câu 47. Có bao nhiêu số nguyên y sao cho tồn tại x  ;3 2 
 thỏa mãn 3x xy     9 27 1 27 x xy ?  3  A. 27 . B. 9 . C. 11. D. 12 . Lời giải GVSB: …; GVPB: … Chọn C Xét   2 3x 9  27 x xy f x  xy   1 và áp dụng x a  x a   1 1. Suy ra: f  x   2x  x xy 2 26 3 9
 xy 1  84x  25xy  234x 1  0, y   10. Do đó y  9 . 2 3x 9 x 2 y  0  27
 1 3x  9x  0 : loại. y  3  xy  1   VP  0 : loại. Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 y  1  , y  2  : thỏa mãn. Xét y  0 3 y
có f 3  27  3y   1  0, y   0 .  1   y Và y 8 f  3  1 0, y     1;2;3;...;  9 .  3  3  y 2; 1  ;1;2;3;4;5;6;7;8;  9 .
Câu 48. Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là hình vuông, BD  2a, góc giữa hai mặt
phẳng  A' BD và  ABCD bằng 0
30 . Thể tích khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3 Lời giải GVSB: Phan Khắc Hy; GVPB: Chọn D A' B' D' C' A B O D C Gọi O  AC  . BD 2 2  BD   2a 
Diện tích hình vuông ABCD là 2 2 S  AB    2a . ABCD      2   2 
Ta có:  A BD  ABCD   A O AO 0 ' , ' ;  30 .
Xét tam giác A'OA vuông tại , A ta có: 0 3 A' A  tan 30 .AO  . a 3 3 2 3
Thể tích khối hộp chữ nhật đã cho là 2 3 V  A' . A S  .2 a a  a . ABCD 3 3
Câu 49. Trong không gian Oxyz , cho hai điểm A1; 3; 4 và B 2  1
; ;2 . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  2. Giá trị lớn nhất của AM  BN bằng A. 3 5 . B. 61 . C. 13 . D. 53 . Lời giải Chọn D
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 21
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021
Dễ thấy A, B nằm hai phía của mặt phẳng Oxy . Gọi A' đối xứng với A qua mặt phẳng Oxy suy ra A'1; 3  ;4, AM  AM .
Gọi E và F lần lượt là hình chiếu của A' và B lên mặt phẳng Oxy , ta có  E 1; 3;0 , F  2  1 ; ;0 . Do đó EF   3  ;4;0  EF  5.  
Dựng BK  NM suy ra BN  KM . Vậy AM  BN  A M   KM  AK .
Ta đi tìm giá trị lớn nhất của AK .
Do MN nằm trên mặt phẳng Oxy , BK//MN nên BK // Oxy. Suy ra K nằm trên mặt
phẳng chứa B , song song với mpOxy . Mà BK  MN  2 nên quỹ tích K là đường tròn  ; B 2 . Kẻ BH  AA  A H   2 , Có A K 
 AH  HK   HB  2     2 2 2 2 4 2 4
5 2  53 . Dấu « = » khi B nằm giữa H , K .
Vậy GTLN của AM  BN là 53 .
Câu 50. Cho hàm số y  f x có đạo hàm f  x   x   2 7 x  9, x
   . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x  f  3
x  5x  m có ít nhất 3 điểm cực trị? A. 6 . B. 7 . C. 5 . D. 4 . Lời giải Chọn A
Ta có: f  x   x   2 7 x  9, x    . x  7 f  x 0     x  3  . x  3     g x   f   3 x  x  m  
 3x  x m f  3 5 5 . x  5x  m  2 3x  5 3 x  5x  f  3 x  5x  m . 3  x  5x
Nhận thấy: x  0 là 1 điểm cực trị của hàm số.. Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 101 – NĂM HỌC 2020 - 2021 3 3  x  5x  m  7  x  5x  7  m   Cho f  3 x  5x  m 3 3
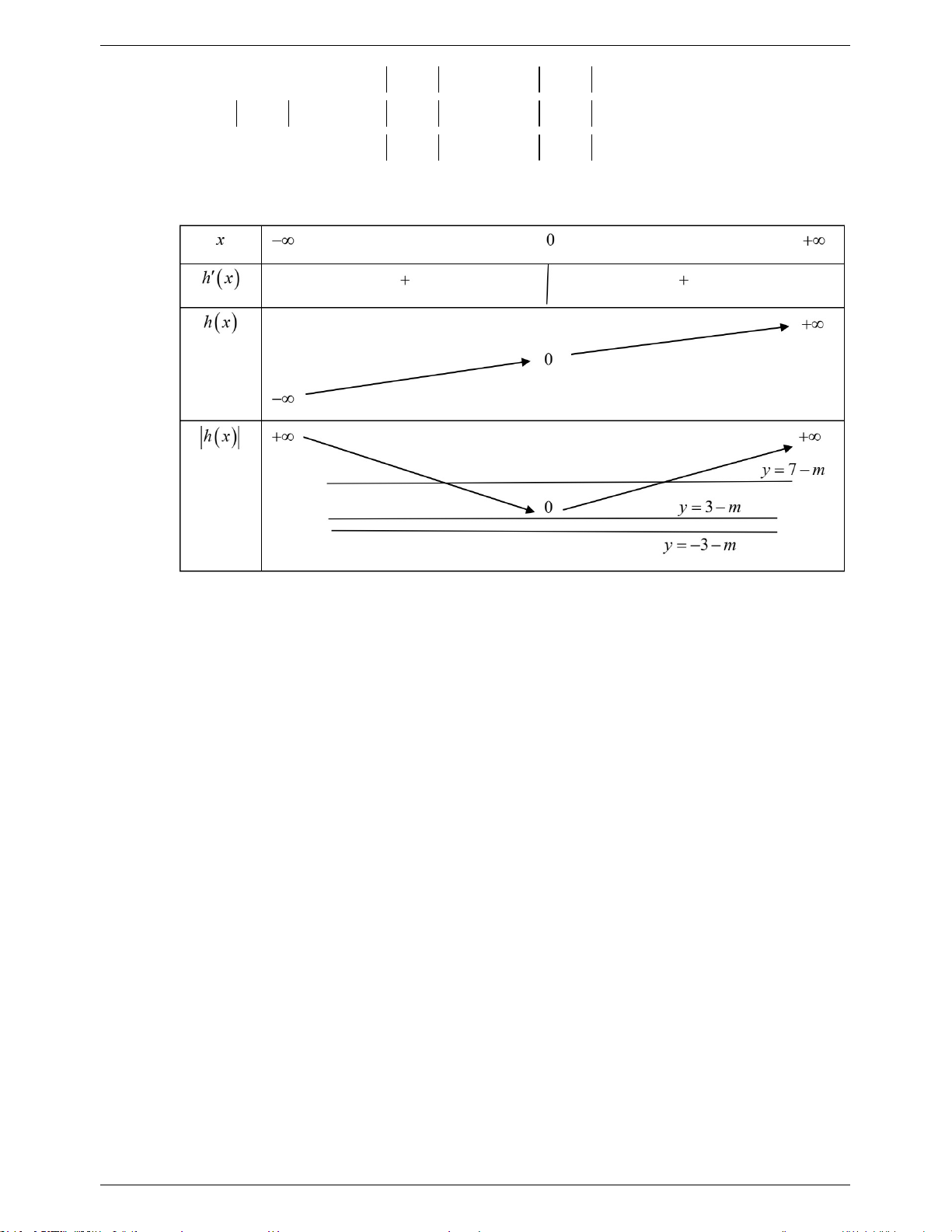
 0   x  5x  m  3   x  5x  3  m .   3 3  x  5x  m  3   x  5x  3   m   Đặt h  x 3  x  x  hx 2 5  3x  5  0, x    . Bảng biến thiên:
Từ bảng biến thiên suy ra: Yêu cầu bài toán tương đương với 7  m  0  m  7  m1;2;3;4;5;  6 .
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 23
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 Kú THI TN THPT N¡M 2021 M· §Ò: 102
TRAO ĐỔI & CHIA SẺ KIẾN THỨC
THÔNG MINH DO HỌC TẬP MÀ CÓ THIÊN TÀI DO TÍCH LŨY MÀ NÊN 5 Câu 1.
Trên khoảng (0; +∞) , đạo hàm của hàm số 4 y = x là 9 4 1 4 1 5 1 5 − A. 4 x . B. 4 x . C. 4 x . D. 4 x . 9 5 4 4 Câu 2.
Cho khối chóp có diện tích đáy 2
B = 3a và chiều cao h = a . Thể tích của khối chóp đã cho bằng 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 3 4 4 4 Câu 3. Nếu f
∫ (x)dx = 6 và g(x) x = 5 − ∫ d thì  f
∫ (x)− g(x)   bằng 1 1 1 A. 1 − . B. 11 − . C. 1. D. 11. Câu 4.
Tập xác định của hàm số = 7x y là A.  \ { } 0 . B. [0;+∞) . C. (0;+∞) . D.  . Câu 5.
Cho hàm số y = f ( x) có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho là A. 3 . B. 1. − C. 5 − . D. 1. Câu 6.
Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S = 4π R . B. 2 S = 16π R C. 2 S = π R . D. 2 S = π R . 3 Câu 7.
Trong không gian Oxyz , cho đường thẳng d đi qua M (2; 2; )
1 và có một vectơ chỉ phương
u =(5;2;−3). Phương trình của d là: x = 2 + 5tx = 2 + 5t   x = 2 + 5tx = 5 + 2t  
A. y = 2 + 2t .
B. y = 2 + 2t .
C. y = 2 + 2t .
D. y = 2 + 2t .   z = 1 − − 3tz = 1+ 3t    z = 1− 3tz = 3 − + tCâu 8.
Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT A. ( 1 − ; ) 1 . B. (−∞;0) . C. (0 ) ;1 . D. (0; + ∞) . Câu 9.
Với n là số nguyên dương bất kì n ≥ 5, công thức nào dưới đây đúng? n! 5! n! n − 5 ! 5 ( ) A. 5 A = 5 A = 5 = . D. = . n ( A A 5! n − . B. 5)! n (n − . C. 5)! n (n −5)! n n!
Câu 10. Thể tích của khối lập phương cạnh 4a bằng A. 3 64a . B. 3 32a . C. 3 16a . D. 3 8a .
Câu 11. Cho hàm số f ( x) 2
= x + 3. Khẳng định nào sau đây đúng? x A. f ∫ (x) 2
dx = x + 3x + C . B. f ∫ (x) 3 dx = + 3x + C . 3 C. f ∫ (x) 3
dx = x + 3x + C . D. f
∫ (x)dx = 2x +C .
Câu 12. Trên mặt phẳng tọa độ, điểm M ( 3;
− 2) là điểm biểu diễn của số phức nào dưới đây?
A. z = 3 − 2i .
B. z = 3 + 2i . C. z = 3 − − 2i . D. z = 3 − + 2i . 3 4 1 2
Câu 13. Trong không gian Oxyz , cho mặt phẳng ( P) : 2
− x + 5y + z − 3 = 0 . Véctơ nào dưới đây là một
véctơ pháp tuyến của (P) ?     A. n = − 2 ( 2;5; ) 1 B. 1 n = (2;5; ) 1 C. n = − 4 (2;5; )1 D. n = − 3 (2; 5; )1 . 
Câu 14. Trong không gian Oxyz , cho điểm A(4; 1
− ;3) . Tọa độ vectơ OA là A. ( 4 − ;1;3) B. (4; 1 − ;3) C. ( 4 − ;1; 3 − ) D. (4;1;3) .
Câu 15. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x +1. B. 4 2 y = 2 − x + 4x +1. C. 3
y = −x + 3x +1. D. 4 2
y = 2x − 4x +1 .
Câu 16. Cho cấp số nhân (u với u = 3 và u = 12 . Công bội của cấp số nhân đã cho bằng n ) 1 2 1 A. 9 . B. 9 − . C. . D. 4 . 4
Câu 17. Cho a > 0 và a ≠ 1 khi đó 3 log a bằng a 1 1 A. 3 − . B. . C. − . D. 3 . 3 3
Câu 18. Đồ thị của hàm số 4 2
y = −x − 2x + 3 cắt trục tung tại điểm có tung độ bằng Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 A. 1. B. 0 . C. 2 . D. 3 .
Câu 19. Cho hai số phức z = 5 + 2i và w = 1− 4i . Số phức z + w bằng A. 6 + 2 . i B. 4 + 6 . i C. 6 − 2 . i D. 4 − − 6 .i Câu 20. Cho hàm số ( ) x
f x = e +1 . Khẳng định nào dưới đây đúng? A. f ∫ (x) x 1 dx e − = + C. B. ∫ ( ) x
f x dx = e − x + C. C. ∫ ( ) x
f x dx = e + x + C. D. ∫ ( ) x
f x dx = e + C.
Câu 21. Cho hàm số y = f ( x) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 5. B. 3. C. 2. D. 4. 3 3 Câu 22. Nếu f
∫ (x)dx = 3 thì 2 f (x)dx ∫ bằng 0 0 A. 3 . B. 18 . C. 2 . D. 6 . x +1
Câu 23. Tiệm cận đứng của đồ thị hàm số y =
là đường thẳng có phương trình x − 2 A. x = 1 − . B. x = 2 − . C. x = 2 . D. x = 1 .
Câu 24. Trong không gian Oxyz , cho mặt cầu (S ) có tâm I (0; 2; − )
1 và bán kính bằng 2 . Phương trình của (S ) là 2 2 2 2 A. 2
x + ( y + 2) + ( z − ) 1 = 2 . B. 2
x + ( y − 2) + ( z + ) 1 = 2 . 2 2 2 2 C. 2
x + ( y + 2) + ( z + ) 1 = 4 . D. 2
x + ( y + 2) + ( z − ) 1 = 4 .
Câu 25. Phần thực của số phức z = 6 − 2i bằng A. 2 − . B. 2 . C. 6 . D. 6 − .
Câu 26. Tập nghiệm của bất phương trình 2x < 5 là A. ( ; −∞ log 5 . B. (log 5;+∞ . C. ( ; −∞ log 2 . D. (log 2;+∞ . 5 ) 5 ) 2 ) 2 )
Câu 27. Nghiệm của phương trình log 3x = 2 là 5 ( ) 32 25 A. x = 25 . B. x = . C. x = 32 . D. x = . 3 3
Câu 28. Cho khối trụ có bán kính đáy bằng 4 và chiều cao h = 3 . Thể tích của khối trụ đã cho bằng A. 16π . B. 48π . C. 36π . D. 12π .
Câu 29. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng nhau (tham khảo hình bên).
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT
Góc giữa hai đường thẳng AA′ và B C ′ bằng A. 0 90 . B. 0 45 . C. 0 30 . D. 0 60 .
Câu 30. Trên không gian Oxyz , cho hai điểm A(0;0; )
1 và B (2;1;3) . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 2x + y + 2z −11 = 0 .
B. 2x + y + 2z − 2 = 0 .
C. 2x + y + 4z − 4 = 0 .
D. 2x + y + 4z −17 = 0 .
Câu 31. Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy được 3 quả màu xanh bằng 1 1 3 2 A. . B. . C. . D. . 6 30 5 5
Câu 32. Cho số phức z thỏa mãn iz = 6 + 5i . Số phức liên hợp của z là
A. z = 5 − 6i .
B. z = − 5 + 6i .
C. z = 5 + 6i .
D. z = − 5 − 6i . x + a
Câu 33. Biết hàm số y =
( a là số thực cho trước, a ≠ 1
− ) có đồ thị như hình bên. Mệnh đề nào x +1 dưới đây là đúng? A. y′ < 0 x ∀ ∈  . B. y′ > 0 x ∀ ≠ 1 − . C. y′ < 0 x ∀ ≠ 1 − . D. y′ > 0 x ∀ ∈  .
Câu 34. Trong không gian Oxyz , cho điểm M (2;1; − )
1 và mặt phẳng ( P) : x − 3y + 2z + 1 = 0. Đường
thẳng đi qua M và vuông góc với ( P) có phương trình là: Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 x − 2 y − 1 z + 1 x − 2 y − 1 z + 1 A. = = . B. = = . 1 3 − 1 1 3 − 2 x + 2 y + 1 z − 1 x + 2 y + 1 z − 1 C. = = . D. = = . 1 3 − 1 1 3 − 2
Câu 35. Trên đoạn [ 2; − ] 1 , hàm số 3 2
y = x − 3x −1 đạt giá trị lớn nhất tại điểm A. x = 2 − . B. x = 0 . C. x = 1 − . D. x = 1 .
Câu 36. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C , AC = 3a và SA vuông góc với
mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SAC) bằng 3 3 2 A. a . B. a . C. 3a . D. 3 2a . 2 2 2 2 Câu 37. Nếu f
∫ (x)dx = 3 thì 2 f ∫ (x)−1dx  bằng 0 0 A. 6 . B. 4 . C. 8 . D. 5 .
Câu 38. Với mọi a,b thỏa mãn 3 log + = 2 a
log2 b 8 . Khẳng định nào dưới đây đúng? A. 3
a + b = 64 . B. 3 a b = 256 . C. 3 a b = 64 . D. 3
a + b = 256 . 2
Câu 39. Có bao nhiêu số nguyên x thỏa mãn (3x − 9x ) log x + 30 − 5 ≤ 0  2 ( )  ? A. 30. B. Vô số. C. 31. D. 29.
2x −1 khi x ≥1
Câu 40. Cho hàm số f ( x) = 
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3
x − 2 khi x <1
F (0) = 2 . Giá trị của F (− ) 1 + 2F (2) bằng A. 9 . B. 15 . C. 11. D. 6 .
Câu 41. Cho hàm số bậc ba y = f ( x) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt
của phương trình f ( f (x)) =1 là A. 9 . B. 7 . C. 3 . D. 6 .
Câu 42. Xét các số phức z, w thỏa mãn z = 1 và w = 2 . Khi z + iw + 6 − 8i đạt giá trị nhỏ nhất, z − w bằng 221 29 A. 5 . B. . C. 3 . D. . 5 5
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT Câu 43. Cho hàm số ( ) 3 2
f x = x + ax + bx + c với a , b , c là các số thực. Biết hàm số
g ( x) = f ( x) + f ′( x) + f ′′( x) có hai giá trị cực trị là 4
− và 2 . Diện tích hình phẳng giới hạn f ( x)
bởi các đường y = y = bằng g ( x) + và 1 6 A. 2 ln 2 . B. ln 6 . C. 3ln 2 . D. ln 2 .
Câu 44. Cho khối hộp chữ nhật ABC . D A′B C ′ D
′ ′ có đáy là hình vuông, BD = 4a , góc giữa hai mặt
phẳng ( A′BD) và ( ABCD) bằng 30° . Thể tích của khối hộp chữ nhật bằng 16 3 16 3 A. 3 a . B. 3 48 3a . C. 3 a . D. 3 16 3a . 9 3  1  2
Câu 45. Có bao nhiêu số nguyên +
y sao cho tồn tại x ∈ ; 4 
 thỏa mãn 3x xy = ( + ) 12 27 1 .27 x xy ?  3  A. 27 . B. 15 . C. 12 . D. 14 . x + y z −
Câu 46. Trong không gian Oxyz , cho đường thẳng 1 1 d : = = và mặt phẳng 1 1 2
(P):2x + y − z +3 = 0 . Hình chiếu vuông góc của d trên (P) là đường thẳng có phương trình x +1 y z −1 x +1 y z −1 x −1 y z +1 x −1 y z +1 A. = = . B. = = . C. = = . D. = = . 4 5 13 3 5 − 1 3 5 − 1 4 5 13
Câu 47. Cắt hình nón ( )
ℵ bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc 60° ta
được thiết diện là tam giác đều có cạnh 2a . Diện tích xung quanh của ( ) ℵ bằng A. 2 7π a . B. 2 13π a . C. 2 2 7π a . D. 2 2 13π a .
Câu 48. Trên tập hợp số phức, xét phương trình 2 z − (m + ) 2 2
1 z + m = 0 ( m là tham số thực). Có bao
nhiêu giá trị của tham số m để phương trình đó có nghiệm z thỏa mãn z = 5 ? 0 0 A. 2 . B. 3 . C. 1. D. 4 .
Câu 49. Cho hàm số y = f (x ) có đạo hàm f ¢(x ) = (x - )( 2 8 x - )
9 , "x Î  . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g (x) = f ( 3
x + 6x + m) có ít nhất 3 điểm cực trị? A. 5 . B. 8 . C. 6 . D. 7 .
Câu 50. Trong không gian, cho hai điểm A(1; 3 − ;2) và B( 2 − ;1; 3
− ) . Xét hai điểm M và N thay đổi
thuộc mặt phẳng (Oxy) sao cho MN = 1. Giá trị lớn nhất của AM − BN bằng A. 17 . B. 41 . C. 37 . D. 61 . BẢNG ĐÁP ÁN 1.C 2.D 3.D 4.D 5.A 6.A 7.C 8.C 9.C 10.A 11.B 12.D 13.A 14.A 15.D 16.D 17.B 18.D 19.C 20.C 21.D 22.D 23.C 24.D 25.C 26.A 27.D 28.B 29.B 30.B 31.A 32.C 33.C 34.B 35.B 36.C 37.B 38.B 39.C 40.A 41.B 42.B 43.A 44.C 45.D 46.A 47.A 48.B 49.D 50.C Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
LỜI GIẢI CHI TIẾT MÃ ĐỀ 102 5 Câu 1.
Trên khoảng (0; +∞) , đạo hàm của hàm số 4 y = x là 9 4 1 4 1 5 1 5 − A. 4 x . B. 4 x . C. 4 x . D. 4 x . 9 5 4 4 Lời giải
GVSB: Thanh Hoa; GVPB: Nguyễn Ngọc Tuấn Chọn C ′ 5 1   5 4 4  x  = x . 4   Câu 2.
Cho khối chóp có diện tích đáy 2
B = 3a và chiều cao h = a . Thể tích của khói chóp đã cho bằng 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 3 Lời giải
GVSB: Thanh Hoa; GVPB: Nguyễn Ngọc Tuấn Chọn D 1 1
Thể tích của khối chóp đã cho bằng 2 3 V = .
B h = .3a .a = a . 3 3 4 4 4 Câu 3. Nếu f
∫ (x)dx = 6 và g(x) x = 5 − ∫ d thì  f
∫ (x)− g(x)   bằng 1 1 1 A. 1 − . B. 11 − . C. 1. D. 11. Lời giải
GVSB: Thanh Hoa; GVPB: Nguyễn Ngọc Tuấn Chọn D 4 4 4  f
∫ (x)− g(x) = f
 ∫ (x)dx − g
∫ (x)dx = 6−( 5 − ) =11. 1 1 1 Câu 4.
Tập xác định của hàm số = 7x y là A.  \ { } 0 . B. [0;+∞) . C. (0;+∞) . D.  . Lời giải
GVSB: Thành Huy; GVPB: Nguyễn Ngọc Tuấn Chọn D Câu 5.
Cho hàm số y = f ( x) có bảng biến thiên như sau
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 7
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT
Giá trị cực đại của hàm số đã cho là A. 3 . B. 1. − C. 5 − . D. 1. Lời giải
GVSB: Thành Huy; GVPB: Nguyễn Ngọc Tuấn Chọn A
Dựa vào bảng biến thiên, giá trị cực đại của hàm số là y = f (− ) 1 = 3. Câu 6.
Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S = 4π R . B. 2 S = 16π R C. 2 S = π R . D. 2 S = π R . 3 Lời giải
GVSB: Thành Huy; GVPB: Nguyễn Ngọc Tuấn Chọn A
Công thức diện tích mặt cầu: 2 S = 4π R Câu 7.
Trong không gian Oxyz , cho đường thẳng d đi qua M (2; 2; )
1 và có một vectơ chỉ phương
u =(5;2;−3). Phương trình của d là: x = 2 + 5tx = 2 + 5t   x = 2 + 5tx = 5 + 2t  
A. y = 2 + 2t .
B. y = 2 + 2t .
C. y = 2 + 2t .
D. y = 2 + 2t .   z = 1 − − 3tz = 1+ 3t    z = 1− 3tz = 3 − + tLời giải
GVSB: Tuấn Minh; GVPB:Tấn Hậu Chọn C
Phương trình của d đi qua M (2;2; )
1 và có một vectơ chỉ phương u = (5; 2; − 3) là: x = 2 + 5t   y = 2 + 2t z =1−3tCâu 8.
Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 A. ( 1 − ; ) 1 . B. (−∞;0) . C. (0 ) ;1 . D. (0; + ∞) .
GVSB: Tuấn Minh; GVPB:Tấn Hậu Lời giải Chọn C
Nhìn đồ thị ta thấy hàm số đã cho đồng biến trên (0 ) ;1 . Câu 9.
Với n là số nguyên dương bất kì n ≥ 5, công thức nào dưới đây đúng? n! 5! n! n − 5 ! 5 ( ) A. 5 A = 5 A = 5 = . D. = . n ( A A 5! n − . B. 5)! n (n − . C. 5)! n (n −5)! n n!
GVSB: Tuấn Minh; GVPB:Tấn Hậu Lời giải Chọn C n! Ta có: 5 A = n (n − . 5)!
Câu 10. Thể tích của khối lập phương cạnh 4a bằng A. 3 64a . B. 3 32a . C. 3 16a . D. 3 8a .
GVSB: Tuấn Minh; GVPB:Tấn Hậu Lời giải Chọn A
Thể tích của khối lập phương cạnh 4a là V = ( a)3 3 4 = 64a .
Câu 11. Cho hàm số f ( x) 2
= x + 3. Khẳng định nào sau đây đúng? x A. f ∫ (x) 2
dx = x + 3x + C . B. f ∫ (x) 3 dx = + 3x + C . 3 C. f ∫ (x) 3
dx = x + 3x + C . D. f
∫ (x)dx = 2x +C .
GVSB: Tuấn Minh; GVPB:Tấn Hậu Lời giải Chọn B f
∫ (x) x = ∫(x + ) 3 x 2 d 3 dx = + 3x + C . 3
Câu 12. Trên mặt phẳng tọa độ, điểm M ( 3;
− 2) là điểm biểu diễn của số phức nào dưới đây?
A. z = 3 − 2i .
B. z = 3 + 2i . C. z = 3 − − 2i . D. z = 3 − + 2i . 3 4 1 2
GVSB: Tuấn Minh; GVPB:Tấn Hậu Lời giải Chọn D
Trên mặt phẳng tọa độ, điểm M ( 3;
− 2) là điểm biểu diễn của số phức z = 3 − + 2i . 2
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 9
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT
Câu 13. Trong không gian Oxyz , cho mặt phẳng ( P) : 2
− x + 5y + z − 3 = 0 . Véctơ nào dưới đây là một
véctơ pháp tuyến của (P) ?     A. n = − 2 ( 2;5; ) 1 B. 1 n = (2;5; ) 1 C. n = − 4 (2;5; )1 D. n = − 3 (2; 5; )1 Lời giải
GVSB: Huỳnh Thanh Liêm; GVPB:Nguyễn Thị Hường Chọn A  Ta có ( P) : 2
− x + 5y + z − 3 = 0 ⇒ VTPT là n = − 2 ( 2;5; ) 1 . 
Câu 14. Trong không gian Oxyz , cho điểm A(4; 1
− ;3) . Tọa độ vectơ OA là A. ( 4 − ;1;3) B. (4; 1 − ;3) C. ( 4 − ;1; 3 − ) D. (4;1;3) Lời giải
GVSB: Huỳnh Thanh Liêm; GVPB:Nguyễn Thị Hường Chọn B 
Ta có OA = (4; 1 − ;3) .
Câu 15. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y = x − 3x +1. B. 4 2 y = 2 − x + 4x +1. C. 3
y = −x + 3x +1. D. 4 2
y = 2x − 4x +1 . Lời giải
GVSB: Huynh Thanh Liem; GVPB: Nguyễn Thị Hường Chọn D
Đây là đồ thị hàm số bậc 4 với hệ số a > 0 .
Câu 16. Cho cấp số nhân (u với u = 3 và u = 12 . Công bội của cấp số nhân đã cho bằng n ) 1 2 1 A. 9 . B. 9 − . C. . D. 4 . 4 Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB: Nguyễn Thị Hường Chọn D 12
Ta có u = u .q ⇒ q = = 4 . 2 1 3
Câu 17. Cho a > 0 và a ≠ 1 khi đó 3 log a bằng a 1 1 A. 3 − . B. . C. − . D. 3 . 3 3 Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB: Nguyễn Thị Hường Chọn B 1 1 3 log a = log a = . a 3 a 3 Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
Câu 18. Đồ thị của hàm số 4 2
y = −x − 2x + 3 cắt trục tung tại điểm có tung độ bằng A. 1. B. 0 . C. 2 . D. 3 . Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB: Nguyễn Thị Hường Chọn D Giả sử 4 2
y = −x − 2x + 3 (C )
Gọi (C) ∩Oy = M (x ; y ⇒ x = 0 ⇒ y = 3. 0 0 ) 0 0
Vậy đồ thị của hàm số 4 2
y = −x − 2x + 3 cắt trục tung tại điểm có tung độ bằng 3 .
Câu 19. Cho hai số phức z = 5 + 2i và w = 1− 4i . Số phức z + w bằng A. 6 + 2 . i B. 4 + 6 . i C. 6 − 2 . i D. 4 − − 6 .i Lời giải
GVSB: Văn Tuân; GVPB: Hà Thị Mai Chọn C
Ta có : z + w = (5 + 2i) + (1− 4i) = 6 − 2i . Câu 20. Cho hàm số ( ) x
f x = e +1 . Khẳng định nào dưới đây đúng? A. f ∫ (x) x 1 dx e − = + C. B. ∫ ( ) x
f x dx = e − x + C. C. ∫ ( ) x
f x dx = e + x + C. D. ∫ ( ) x
f x dx = e + C. Lời giải
GVSB: Văn Tuân; GVPB: Hà Thị Mai Chọn C Ta có : ∫ ( ) = ∫( x + ) 1 x f x dx e dx e = + x + C.
Câu 21. Cho hàm số y = f ( x) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 5. B. 3. C. 2. D. 4. Lời giải
GVSB: Văn Tuân; GVPB: Hà Thị Mai Chọn D
Dựa vào bảng xét dấu suy ra đạo hàm của hàm y = f ( x) đổi dấu 4 lần nên hàm số đã cho có 4 điểm cực trị. 3 3 Câu 22. Nếu f
∫ (x)dx = 3 thì 2 f (x)dx ∫ bằng 0 0 A. 3 . B. 18 . C. 2 . D. 6 . Lời giải
GVSB: Ngọc Thanh; GVPB:Hà Thị Mai
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 11
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT Chọn D 3 3 2 f
∫ (x)dx = 2 f
∫ (x)dx = 2.3 = 6. 0 0 x +1
Câu 23. Tiệm cận đứng của đồ thị hàm số y =
là đường thẳng có phương trình x − 2 A. x = 1 − . B. x = 2 − . C. x = 2 . D. x = 1 .
GVSB: Ngọc Thanh; GVPB:Hà Thị Mai Lời giải Chọn C x +1 x +1 Ta có: lim y = lim
= +∞ (hoặc lim y = lim = −∞ ). + + − − x→2 x→2 x − 2 x→2 x→2 x − 2
Vậy x = 2 là tiệm cận đứng của đồ thị hàm số.
Câu 24. Trong không gian Oxyz , cho mặt cầu (S ) có tâm I (0; 2; − )
1 và bán kính bằng 2 . Phương trình của (S ) là 2 2 2 2 A. 2
x + ( y + 2) + ( z − ) 1 = 2 . B. 2
x + ( y − 2) + ( z + ) 1 = 2 . 2 2 2 2 C. 2
x + ( y + 2) + ( z + ) 1 = 4 . D. 2
x + ( y + 2) + ( z − ) 1 = 4 .
GVSB: Ngọc Thanh; GVPB:Hà Thị Mai Lời giải Chọn D
Mặt cầu (S ) có tâm I (0; 2; − )
1 và bán kính bằng 2 có phương trình là
x + ( y + )2 + ( z − )2 2 2 1 = 4 .
Câu 25. Phần thực của số phức z = 6 − 2i bằng A. 2 − . B. 2 . C. 6 . D. 6 − . Lời giải
GVSB: Chí Tính; GVPB:Thanh Bui Chọn C
Ta có: z = 6 − 2i có phần thực là 6.
Câu 26. Tập nghiệm của bất phương trình 2x < 5 là A. ( ; −∞ log 5 . B. (log 5;+∞ . C. ( ; −∞ log 2 . D. (log 2;+∞ . 5 ) 5 ) 2 ) 2 ) Lời giải
GVSB: Chí Tính; GVPB:Thanh Bui Chọn A
Ta có: 2x < 5 ⇔ x < log 5 2
Vậy tập nghiệm S = ( ; −∞ log 5 . 2 )
Câu 27. Nghiệm của phương trình log 3x = 2 là 5 ( ) 32 25 A. x = 25 . B. x = . C. x = 32 . D. x = . 3 3 Lời giải
GVSB: Chí Tính; GVPB:Thanh Bui Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 Chọn D
Điều kiện: x > 0 .
Với điều kiện phương trình đã cho tương đương 2 3x = 5 = 25 25 ⇔ x = . 3
Câu 28. Cho khối trụ có bán kính đáy bằng 4 và chiều cao h = 3 . Thể tích của khối trụ đã cho bằng A. 16π . B. 48π . C. 36π . D. 12π .
GVSB: Thanh Sang; GVPB:Thanh Bui Lời giải Chọn B
Thể tích của khối trụ là 2 2
V = π r h = π .4 .3 = 48π .
Câu 29. Cho hình lăng trụ đứng ABC.A′B C
′ ′ có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng AA′ và B C ′ bằng A. 0 90 . B. 0 45 . C. 0 30 . D. 0 60 .
GVSB: Thanh Sang; GVPB:Thanh Bui Lời giải Chọn B
Ta có: AA′//CC′ nên:
⇒ ( AA ,′ B C
′ ) = (CC ,′ B C ′ )
Mặt khác tam giác BCC′ vuông tại C′ có CC′ = B C
′ ′ nên là tam giác vuông cân.
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 13
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT
Vậy góc giữa hai đường thẳng AA′ và B C ′ bằng 0 45 .
Câu 30. Trên không gian Oxyz , cho hai điểm A(0;0; )
1 và B (2;1;3) . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 2x + y + 2z −11 = 0 .
B. 2x + y + 2z − 2 = 0 .
C. 2x + y + 4z − 4 = 0 .
D. 2x + y + 4z −17 = 0 . Lời giải
GVSB: Vương Gia; GVPB:Dung Chang Chọn B 
Ta có: AB = (2;1; 2) . 
Mặt phẳng đi qua A(0;0; )
1 và vuông góc với AB nên nhận AB = (2;1; 2) làm vectơ pháp tuyến
Phương trình mặt phẳng là: 2(x − 0) +1( y − 0) + 2(z − )
1 = 0 ⇔ 2x + y + 2z − 2 = 0 .
Câu 31. Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy được 3 quả màu xanh bằng 1 1 3 2 A. . B. . C. . D. . 6 30 5 5 Lời giải
GVSB: Nguyễn Thị Hải Yến; GVPB:Dung Chang Chọn A
Lấy ngẫu nhiên đồng thời 3 quả cầu từ 10 quả bóng đã cho có 3 10 C cách.
Lấy được 3 quả màu xanh từ 6 quả màu xanh đã cho có 36 C cách. 3 C 1
Vậy xác suất để lấy được 3 quả màu xanh là 6 P = = . 3 C 6 10
Câu 32. Cho số phức z thỏa mãn iz = 6 + 5i . Số phức liên hợp của z là
A. z = 5 − 6i .
B. z = − 5 + 6i .
C. z = 5 + 6i .
D. z = − 5 − 6i .
GVSB: Luyen Duong; GVPB: Dung Chang Lời giải Chọn C
 Ta có: iz = 6 + 5i ⇒ z = 5 − 6i ⇒ z = 5 + 6i . x + a
Câu 33. Biết hàm số y =
( a là số thực cho trước, a ≠ 1
− ) có đồ thị như hình bên. Mệnh đề nào x +1 dưới đây là đúng? Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 A. y′ < 0 x ∀ ∈  . B. y′ > 0 x ∀ ≠ 1 − . C. y′ < 0 x ∀ ≠ 1 − . D. y′ > 0 x ∀ ∈  . Lời giải
GVSB: Thanh Văn Nguyễn; GVPB: Dung Chang Chọn C
Tập xác định D =  \ {− } 1 .
Từ đồ thị hàm số, ta thấy hàm số nghịch biến trên từng khoảng xác định.
Do đó y′ < 0 x ∀ ≠ 1 − .
Câu 34. Trong không gian Oxyz , cho điểm M (2;1; − )
1 và mặt phẳng ( P) : x − 3y + 2z + 1 = 0. Đường
thẳng đi qua M và vuông góc với ( P) có phương trình là: x − 2 y − 1 z + 1 x − 2 y − 1 z + 1 A. = = . B. = = . 1 3 − 1 1 3 − 2 x + 2 y + 1 z − 1 x + 2 y + 1 z − 1 C. = = . D. = = . 1 3 − 1 1 3 − 2
GVSB: Hà Hoàng; GVPB:Dung Chang Lời giải Chọn B
Đường thẳng đi qua M (2;1;− )
1 và vuông góc với ( P) nhận VTPT n = (1; 3 − ;2) của (P) làm
VTCP nên có phương trình là: x − 2 y −1 z +1 = = . 1 3 − 2
Câu 35. Trên đoạn [ 2; − ] 1 , hàm số 3 2
y = x − 3x −1 đạt giá trị lớn nhất tại điểm A. x = 2 − . B. x = 0 . C. x = 1 − . D. x = 1 . Lời giải
GVSB: Điểm Đàm; Ngô Minh Cường Chọn B x = 0 Ta có 2
y′ = 3x − 6x ⇒ y′ = 0 ⇔ 
. Ta đang xét trên đoạn [ 2; − ] 1 nên loại x = 2 . x = 2
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 15
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT Ta có f ′( 2 − ) = 2 − 1; f ′(0) = 1 − ; f ′( ) 1 = 3
− . Do đó giá trị lớn nhất của hàm số trên đoạn [ 2; − ] 1 là 1 − , tại x = 0 .
Câu 36. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C , AC = 3a và SA vuông góc với
mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SAC) bằng 3 3 2 A. a . B. a . C. 3a . D. 3 2a . 2 2
Lời giải GVSB: Nguyễn Huệ; GVPB:Ngô Minh Cường Chọn C Ta có A
∆ BC vuông cân tại C nên BC ⊥ AC ( )
1 và AC = BC = 3a .
Mặt khác SA ⊥ ( ABC) ⇒ SA ⊥ BC (2) . Từ ( )
1 và (2) suy ra BC ⊥ (SAC ) ⇒ d ( B,(SAC )) = BC = 3a .
Vậy khoảng cách từ B đến mặt phẳng (SAC) bằng3a . 2 2 Câu 37. Nếu f
∫ (x)dx = 3 thì 2 f ∫ (x)−1dx  bằng 0 0 A. 6 . B. 4 . C. 8 . D. 5 . Lời giải
GVSB: Lê Trần Bảo An; GVPB:Ngô Minh Cường Chọn B 2 2 2 2
∫ f (x)−1dx = 2 
∫ f (x)dx − dx = 6−2 = 4 ∫ 0 0 0
Câu 38. Với mọi a,b thỏa mãn 3 log + = 2 a
log2 b 8 . Khẳng định nào dưới đây đúng? A. 3
a + b = 64 . B. 3 a b = 256 . C. 3 a b = 64 . D. 3
a + b = 256 . Lời giải
GVSB: Đoàn Yến; GVPB:Nguyễn Văn Ngọc Chọn B Ta có 3
log a + log b = 8 ⇒ log ( 3 a b) 3 8 = ⇔ = = 2 2 2 8 a b 2 256 . Vậy 3 a b = 256 . Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 2
Câu 39. Có bao nhiêu số nguyên x thỏa mãn (3x − 9x ) log x + 30 − 5 ≤ 0  2 ( )  ? A. 30. B. Vô số. C. 31. D. 29.
GVSB: Lê Thị Tiền; GVPB:Nguyễn Văn Ngọc Lời giải Chọn C 2
Xét hàm số: ( ) = (3x − 9x f x )log x+30 −5  x > − . 2 ( ) , với 30 2 2 x x x 2  3 −9 = 0 3 = 3 xx = 2
Cho: f ( x) = 0 ⇔  ⇔  ⇔  log  (x +30) 5 − 5 = 0 x + 30 = 2 x = 0 2
Ta có bảng xét dấu như sau: − < x ≤ Suy ra f ( x) 30 0 ≤ 0 ⇔   x = 2
Mặt khác x ∈  nên x ∈{ 29 − ; 28 − ; 27 − ;......; 2 − ; 1 − ;0; } 2 .
Vậy có 31 số nguyên x thỏa mãn.
2x −1 khi x ≥1
Câu 40. Cho hàm số f ( x) = 
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3
x − 2 khi x <1
F (0) = 2 . Giá trị của F (− ) 1 + 2F (2) bằng A. 9 . B. 15 . C. 11. D. 6 . Lời giải
GVSB: Lại Thị Quỳnh Nguyên; GVPB:Nguyễn Văn Ngọc Chọn A
Tập xác định: D =  .
Với x > 1 hay x < 1 thì hàm số f ( x) là hàm đa thức nên liên tục.
Mặt khác: lim f ( x) = lim −
= ; lim f (x) = lim (2x − ) 1 = 1. − − ( 2 3x 2) 1 + + x 1 → x 1 → x 1 → x 1 →
Ta có: lim f ( x) = lim f ( x) = f ( )
1 = 1 nên hàm số f ( x) liên tục tại điểm x = 1 . − + x 1 → x 1 →
Suy ra hàm số f ( x) liên tục trên  . Với x ≥ 1 thì f (x)dx = (2x- ) 2
1 dx = x - x + C ò ò 1 Với x < 1 thì f (x)dx = ò ò ( 2 3x - ) 3
2 dx = x - 2x + C 2
Mà F (0) = 2 nên C = 2 . 2 2  − + ≥ Khi đó F (x) x x C khi x 1 1 =  . 3
x − 2x + 2 khi x <1
Đồng thời F (x) cũng liên tục trên  nên: lim F (x) = lim F (x) = F ( ) 1 = 1 ⇔ C = 1. − + 1 x 1 → x 1 →
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 17
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT 2  − + ≥ Do đó F (x) x x 1 khi x 1 =  3  .
x − 2x + 2 khi x < 1 Vậy: F (− )
1 + 2F (2) = 3 + 2.3 = 9 .
Câu 41. Cho hàm số bậc ba y = f ( x) có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt
của phương trình f ( f (x)) =1 là A. 9 . B. 7 . C. 3 . D. 6 . Lời giải
GVSB: Tô Lê Diễm Hằng; GVPB:Thanh Nha Nguyen Chọn B
f (x) = a(a < − ) 1 ( )1 
Dựa vào đồ thị hàm số y = f (x) suy ra f ( f (x)) =1⇔  f (x) = 0 (2).  f
 ( x) = b(1 < b < 2) (3) TH1 Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
f ( x) = a (a < − )
1 ⇒ phương trình có một nghiệm. TH2
f ( x) = 0 ⇒ phương trình có ba nghiệm phân biệt. TH3
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 19
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT
f ( x) = b (1 < b < 2) ⇒ phương trình có ba nghiệm phân biệt.
Các nghiệm của (1); (2); (3) là đôi một khác nhau.
Vậy f ( f (x)) =1 có 7 nghiệm nghiệm phân biệt.
Câu 42. Xét các số phức z, w thỏa mãn z = 1 và w = 2 . Khi z + iw + 6 − 8i đạt giá trị nhỏ nhất, z − w bằng 221 29 A. 5 . B. . C. 3 . D. . 5 5 Lời giải
GVSB: Phạm Quốc Toàn; GVPB:Thanh Nha Nguyen Chọn B
Ta có z + iw + 6 − 8i ≥ 6 − 8i − z − iw = 10 −1− 2 = 7 . Dấu “ = ” xảy ra khi
z = t (6 −8i)  1   z = − (6−8i) 1 z = − (6−8i) 1 z = − (6−8i)         iw  = t′( − i) 10 10 10 6 8 , t ∀ ,t′ ≤ 0 ⇔  ⇔  ⇔  . 2  iw  = = ( i) 1 w ( i) 1 6 8 8 6  = − − = + w = (8−6 1, 2 i z w )   10  5  5 Khi đó 221 z − w = . 5 Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 Câu 43. Cho hàm số ( ) 3 2
f x = x + ax + bx + c với a , b , c là các số thực. Biết hàm số
g ( x) = f ( x) + f ′( x) + f ′′( x) có hai giá trị cực trị là 4
− và 2 . Diện tích hình phẳng giới hạn f ( x)
bởi các đường y = y = bằng g ( x) + và 1 6 A. 2 ln 2 . B. ln 6 . C. 3ln 2 . D. ln 2 . Lời giải
GVSB: Trường Giang; GVPB: Yến Thoa Chọn A Ta có: ( ) 3 2
f x = x + ax + bx + c ⇒ f ′( x) 2
= 3x + 2ax + b ; f ′′(x) = 6x + 2a và f ′′(x) = 6 . f ( x)
Phương trình hoành độ giao điểm của các đường y = y = là: g ( x) + và 1 6 f ( x) = ⇔ = + g ( x) 1
f ( x) g ( x) 6 + 6 3 2
⇔ x + ax + bx + c = ( 3 2
x + ax + bx + c) + ( 2
3x + 2ax + b) + (6x + 2a) + 6 2
⇔ 3x + (2a + 6) x + 2a + b + 6 = 0(*) .
Gọi 2 nghiệm của phương trình (*) là x và x . 1 2
Nhận xét: g (x) = f (x) + f ′(x) + f ′′(x)
⇒ g′(x) = f ′(x) + f ′′(x) + f ′′′(x)
⇔ g′(x) = ( 2
x + ax + b) + ( x + a) 2 3 2 6 2
+ 6 = 3x + (2a + 6) x + 2a + b + 6 .  = ⇒ g′( x) x x1 = 0 ⇔  . x = x  2 f ( x)
Diện tích hình phẳng giới hạn bởi các đường y = y = là g ( x) + và 1 6 2 x f ( x) 2 x
f ( x) − g ( x) − 6 2 x g′( x) 2 x S = ∫  −  x = x  ∫ = dx = ln g x + 6 ∫ g x  + g x + g x + x ( ) ( ) 6 x  ( ) 1 d  x ( ) d 6 6 x 1 1 1 1
= ln g (x + 6 − ln g x + 6 = ln8 − ln 2 = 2ln 2 . 2 ) ( 1)
Câu 44. Cho khối hộp chữ nhật ABC . D A′B C ′ D
′ ′ có đáy là hình vuông, BD = 4a , góc giữa hai mặt
phẳng ( A′BD) và ( ABCD) bằng 30° . Thể tích của khối hộp chữ nhật bằng 16 3 16 3 A. 3 a . B. 3 48 3a . C. 3 a . D. 3 16 3a . 9 3
GVSB: Kieu Hung; GVPB: Yến Thoa Lời giải Chọn C
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 21
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT
 Theo giả thiết ABCD là hình vuông nên có 2 2
2 AB = BD ⇒ AB = 2 2a . Do đó 2 2 S = AB = 8a . ABCD  1
Gọi O là tâm của đáy ABCD ⇒ OA ⊥ BD và OA = BD = 2a . 2 Vì ABC . D A′B C ′ D ′ ′ là hình hộp chữ nhật nên có
A′A ⊥ ( ABCD) ⇒ A′A ⊥ BD ⇒ BD ⊥ ( A′AO) . Do đó góc giữa ( A′BD) và mặt phẳng (ABCD) là góc  A′OA ⇒  A′OA = 30° .  a
Tam giác A′OA vuông tại A có ′ =  2 3 A A .
OA tan A′OA = . 3  2a 3 16 3 Vậy 2 3 V = = ′ ′ ′ ′ 8a . a . ABCD. A B C D 3 3  1  2
Câu 45. Có bao nhiêu số nguyên +
y sao cho tồn tại x ∈ ; 4 
 thỏa mãn 3x xy = ( + ) 12 27 1 .27 x xy ?  3  A. 27 . B. 15 . C. 12 . D. 14 . Lời giải
GVSB: Tran Nhung; GVPB: Hà Minh Yên Chọn D 2 Xét ( ) 3x + xy 12 = 27 − x f x − (1+ xy) .
Áp dụng bất đẳng thức: x
a ≥ x (a − ) 1 + 1 , ta có f ( x) ≥
( 2x + xy − x)+ −( + xy) 2 26 3 12 1 1
= 78x + (25y − 312) x > 0, y ∀ ≥ 13. Do đó y ≤ 12 .  = 2 x 0 3x 12 − x 2 y = 0 ⇒ 27
= 1 ⇔ 3x −12x = 0 ⇔  (loại) x = 4 y ≤ 3 − ⇒ xy < 1
− ⇒ VP < 0 (loại) y = 1 − , y = 2 − : thỏa mãn. Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 Xét y > 0 có ( ) 4 4 = 27 y f
− (1+ 4y) ≥ 0, y ∀ > 0 và  1  f = f (x) − y y 11 = 3 − −1 < 0, y ∀ ∈   {1;2;...; } 12 .  3  3 Do đó phương trình  1 
f ( x) = 0 có nghiệm x ∈ ; 4   , y ∀ ∈{1;2;...; } 12 ,  3  Vậy y ∈{ 2 − ;−1;0;1;2;...; } 12 . x + y z −
Câu 46. Trong không gian Oxyz , cho đường thẳng 1 1 d : = = và mặt phẳng 1 1 2
(P):2x + y − z +3 = 0 . Hình chiếu vuông góc của d trên (P) là đường thẳng có phương trình x +1 y z −1 x +1 y z −1 x −1 y z +1 x −1 y z +1 A. = = . B. = = . C. = = . D. = = . 4 5 13 3 5 − 1 3 5 − 1 4 5 13 Lời giải
GVSB: Đoàn Minh Tân; GVPB: Quy Tín Chọn A
Đường thẳng d qua điểm A( 1 − ;0; )
1 và có véc-tơ chỉ phương u = d (1;1;2). 
Mặt phẳng (P) có véc-tơ pháp tuyến n( = − P) (2;1; )1 .
Gọi (Q) là mặt phẳng chứa d và vuông góc với (P) , khi đó (Q) có một véc-tơ pháp tuyến là    n( =   = − − Q) ud , n(P) ( 3;5; ) 1   .
Gọi ∆ là giao tuyến của hai mặt phẳng (P) và (Q) suy ra ∆ là hình chiếu của d trên (P) .   
Khi đó ∆ có một véc-tơ chỉ phương là u = n(  = P) , n(Q) (4;5;13)   .
Ta có A ∈ d ⊂ (Q) ⇒ A∈(Q) và dễ thấy tọa độ A thỏa phương trình ( P) ⇒ A∈( P) .Do đó A ∈ ∆ .
Vậy phương trình đường thẳng + − ∆ x 1 y z 1 là = = . 4 5 13
Câu 47. Cắt hình nón ( )
ℵ bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc 60° ta
được thiết diện là tam giác đều có cạnh 2a . Diện tích xung quanh của ( ) ℵ bằng A. 2 7π a . B. 2 13π a . C. 2 2 7π a . D. 2 2 13π a . Lời giải
GVSB: Đoàn Minh Tân; GVPB: Quy Tín Chọn A
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 23
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT Giả sử hình nón ( )
ℵ có S là đỉnh và O là tâm đường tròn đáy.
Giả sử mặt phẳng đề cho cắt nón theo thiết diện là tam giác đều SAB , khi đó ta có l = SA = 2a . Gọi 3
H là trung điểm AB ⇒ SH = 2 . a = a 3 . 2
Ta có góc giữa (SAB) và mặt phẳng chứa đáy là góc  SHO = 60° . 1 a 3 Xét S
∆ HO vuông tại O có OH = SH.cos60° = a 3. = . 2 2 Xét OA ∆ H vuông tại H có bán kính đường tròn đáy là 2 3a a 7 2 2 2 R = OA = AH + OH = a + = . 4 2
Vậy diện tích xung quanh của hình nón ( ) ℵ a 7 là 2 S = π Rl = π. .2a = 7π a . xq 2
Câu 48. Trên tập hợp số phức, xét phương trình 2 z − (m + ) 2 2
1 z + m = 0 ( m là tham số thực). Có bao
nhiêu giá trị của tham số m để phương trình đó có nghiệm z thỏa mãn z = 5 ? 0 0 A. 2 . B. 3 . C. 1. D. 4 .
GVSB: Minh Phạm; GVPB: Phạm Quốc Toàn Lời giải Chọn B
Cách 1. Ta có ∆′ = (m + )2 2
1 − m = 2m +1. 1 1
Nếu ∆′ = 0 ⇔ m = − thì phương trình có nghiệm z = z = (không thỏa mãn). 2 1 2 2 1
Nếu ∆′ > 0 ⇔ m > − thì phương trình có hai nghiệm phân biệt z = m +1+ 2m +1 và 2 1
z = m +1− 2m +1 . 2 4 − m ≥ 0 Trườ 
ng hợp 1. z = 5 ⇔ m +1+ 2m +1 = 5 ⇔ 2m +1 = 4 − m ⇔  1 2m +1 =  (4− m)2 Trang 24
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 m ≤ 4 m ≤ 4  m ≤ 4  ⇔  ⇔  ⇔   m = + ⇔ m = − . 2m +1 =  (4− m) 5 10 5 10 2 2
m −10m +15 = 0  m =5− 10  + − + = Trườ m 1 2m 1 5
ng hợp 2. z = 5 ⇔ m +1− 2m +1 = 5 ⇔  2
m +1− 2m +1 = 5 − m ≥ 4 
m +1− 2m +1 = 5 ⇔
2m +1 = m − 4 ⇔  2m +1 =  (m − 4)2 m ≥ 4 ⇔  ⇔ m = 5 + 10 2
m −10m +15 = 0 m ≥ 6 − 
m +1− 2m +1 = 5
− ⇔ 2m +1 = m + 6 ⇔  2m +1 =  (m + 6)2 m ≥ 6 − ⇔  (vô nghiệm). 2
m +10m + 35 = 0 1
Nếu ∆′ < 0 ⇔ m < − thì phương trình ban đầu có hai nghiệm phức z , z và z = z = 5 . 2 1 2 1 2 m = 5 (Loai) Theo giả thiết, ta có 2
z .z = z . z = 25 ⇔ m = 25 ⇔ . 1 2 1 2  m = 5 −
Vậy có 3 giá trị của tham số m thỏa mãn yêu cầu bài toán.
Cách 2. Đặt z = x + yi ( x, y ∈ ) là nghiệm của phương trình ban đầu. 0 Theo giả thiết, ta có 2 2
z = 5 ⇔ x + y = 25 1 . 0 ( )
Thay z vào phương trình ban đầu, ta có 0
(x + yi)2 − (m + )(x + yi) 2 + m = ⇔ ( 2 2 2 2 1 0
x − y − 2mx − 2x + m ) + (2xy − 2my − 2y)i = 0 2 2 2 2 2 2
x − y − 2mx − 2x + m = 0
x − y − 2mx − 2x + m = 0 (2) ⇔  ⇔⇔  .
2xy − 2my − 2y = 0 y
 ( x − m − ) 1 = 0 (3) ( ) y = 0 3 ⇔  . x = m +1
Trường hợp 1. Với y = ⇒ ( ) 2 0
1 ⇔ x = 25 ⇔ x = 5 ± . Nếu x = ⇒ ( ) 2 5
2 ⇔ m −10m +15 = 0 ⇔ m = 5 ± 10 . Nếu x = − ⇒ ( ) 2 5
2 ⇔ m +10m + 35 = 0 (vô nghiệm).
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 25
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT Trườ 2
ng hợp 2. x = m + ⇒ ( ) 2 1
1 ⇔ y = 25 − (m + ) 1 ( 6 − ≤ m ≤ 4). ( m = − 2) ⇔ (m + ) 5 2 1 − 25 + (m + )2 1 − 2m (m + ) 1 − 2 (m + ) 2 2
1 + m = 0 ⇔ m − 25 = 0 ⇔  . m = 5  (L)
Vậy có 3 giá trị của tham số m thỏa mãn.
Câu 49. Cho hàm số y = f (x ) có đạo hàm f ¢(x ) = (x - )( 2 8 x - )
9 , "x Î  . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g (x) = f ( 3
x + 6x + m) có ít nhất 3 điểm cực trị? A. 5 . B. 8 . C. 6 . D. 7 . Lời giải Chọn D
Cách 1 : GVSB: Đỗ Linh; GVPB:Hoa Tiên Phạm
g ( x) = f ( 3
x + x + m) ⇒ g′( x) = ( 3
x + x + m)′ f ′( 3 6 6 .
x + 6x + m) ( 3x +6x).( 2 3x + 6) = . f ′( 3
x + 6x + m . 3 ) x + 6x
Ta thấy x = 0 là một điểm tới hạn của hàm số g ( x) . 3 3
x + 6x + m = 8
x + 6x = 8 − m   Mặt khác f ′( 3
x + 6x + m) 3 3
= 0 ⇔  x + 6x + m = 3 ⇔  x + 6x = 3 − m .   3 3
x + 6x + m = 3 −  x + 6x = 3 − − m  
Xét hàm số h ( x) 3
= x + 6x , vì h′(x) 2
= 3x + 6 > 0, x
∀ ∈  nên h(x) đồng biến trên  . Ta có
bảng biến thiên của hàm số k ( x) = h ( x) 3
= x + 6x như sau:
Hàm số g ( x) = f ( 3
x + 6x + m) có ít nhất 3 điểm cực trị khi phương trình f ′( 3
x + 6x + m) = 0
có ít nhất hai nghiệm khác 0. Điều này xảy ra khi và chỉ khi 8 − m > 0 hay m < 8 .
Kết hợp điều kiện m nguyên dương ta được m ∈{1; 2;3...; }
7 . Vậy có 7 giá trị của m thoả mãn.
Cách 2: GVSB: Đỗ Ngọc Nam; GVPB:Hoa Tiên Phạm
Nhận thấy hàm g (x ) = f ( 2 x + )
6 x + m) là hàm số chẵn nên đồ thị đối xứng qua trục tung.
Để hàm g (x) = f ( 3
x + 6x + m) có ít nhất 3 điểm cực trị thì hàm số
h (x) = f ( 3
x + 6x + m) có ít nhất 1 điểm cực trị có hoành độ dương, tức Trang 26
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM WORD � BIÊN SOẠN TOÁN
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102 h¢(x) = ( 2 x + )f ¢( 3 3 6
x + 3x + m) = 0 có nghiệm dương bội lẻ hay é 3 é 3
x + 3x + m = 8
x + 3x - 8 = m - ê ê ê 3 ê 3 x ê
+ 3x + m = 3 Û x ê + 3x - 3 = m
- có nghiệm dương bội lẻ. ê ê 3 3 x ê + 3x + m = -3 x ê + 3x + 3 = m - ë ë
Ta có bảng biến thiên (gộp) m ìï > 0 ï
Từ bảng biến thiên suy ra í Û 0 < m < 8 ï . m - > -8 ïî
Câu 50. Trong không gian, cho hai điểm A(1; 3 − ;2) và B( 2 − ;1; 3
− ) . Xét hai điểm M và N thay đổi
thuộc mặt phẳng (Oxy) sao cho MN = 1. Giá trị lớn nhất của AM − BN bằng A. 17 . B. 41 . C. 37 . D. 61 .
GVSB: Nga Nguyen; GVPB: Tran Nhung Lời giải Chọn C
Nhận xét: A và B nằm khác phía so với mặt phẳng (Oxy) .
Gọi ( P) là mặt phẳng qua A và song song với mặt phẳng (Oxy) ⇒ ( P) : z = 2 .
B′ đối xứng với ( P) qua mặt phẳng (Oxy) ⇒ B′( 2 − ;1;3) .
B là hình chiếu của B′ trên mặt phẳng ( P) ⇒ B 2 − ;1;2 . 1 ( ) 1
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 27
GIẢI CHI TIẾT ĐỀ CHÍNH THỨC 2021 – MÃ ĐỀ 102
NHÓM WORD � BIÊN SOẠN TOÁN THPT A ′ A =  1 Gọi ′
A = T ( A) ⇒  MN A ′
 A  (Oxy) ⇒ ′
A thuộc đường tròn (C ) có tâm A và bán kính R = 1 , (C ) nằm trên mặt phẳng ( P) .
Ta có: AM − BN = A′N − BN = A′N − B N
′ ≤ A′B′
AB = 5 > R ⇒ B nằm ngoài đường tròn (C ) . 1 1
Do A′ ∈ ( P) , B′∉( P) mà ( P)  (Oxy) suy ra A' B ' luôn cắt mặt phẳng (Oxy) . Ta lại có: 2 2 A′B′ =
B B′ + A′B mà B B
′ =1; AB = 5 ⇒ A′B′ ⇔ A′B = AB + R = 6 1 1 1 1 max 1 max 1 ⇒ AM − BN
= 37 . Dấu " = " xảy ra khi A' là giao điểm của AB với đường tròn (C) ( max 1
A ở giữa A' và B và N là giao điểm của A' B ' với mặt phẳng (Oxy) . 1 Trang 28
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
KỲ THI TN THPT- NĂM HỌC 2020 – 2021
Môn: Toán- Mã đề 103- Đợt 1
HỌC HỎI - CHIA SẺ KIẾN THỨC
Thời gian: 180 phút (Không kể thời gian phát đề)
LINK NHÓM: https://www.facebook.com/groups/1916660125164699
Câu 1. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? 1 1 1 1 A. 3 y  x  2x  . B. 3 y  x  2x  . C. 4 2 y  x  2x  . D. 4 2 y  x  2x  . 2 2 2 2
Câu 2. Cho cấp số nhân u với u  3 và u 15 . Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 1  2. B. . C. 5. D. 12 . 5
Câu 3. Cho khối chóp có diện tích đáy 2
B  7a và chiều cao h  a . Thể tích của khối chóp đã cho bằng 7 7 7 A. 3 a . B. 3 a . C. 3 a . D. 3 7a . 6 2 3 4 4 4 Câu 4. Nếu f
 xdx  5 và gxdx  4   thì  f
 x gxdx  bằng 1 1 1 A. 1  . B. 9 . C. 1. D. 9.
Câu 5. Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 3;1; 2 và có một vectơ chỉ  phương u 2;4; 
1 , phương trình của d là x 3  2t x   3  2t x   3  2t x  2  3t     A. y  1 4t . B. y 1 4t . C. y 1 4t . D. y  4  t . z 2 t     z  2  t  z  2  t  z  1 2t 
Câu 6. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S   R . B. 2 S   R . C. 2 S  4 R . D. 2 S  16 R . 3
Câu 7. Trong không gian Oxyz , cho mặt phẳng P : x  2 y  2z  3  0 . Vectơ nào dưới đây là một
véctơ pháp tuyến của P ?     A. n  1; 2;2 . B. n  1; 2;2 . C. n  1; 2  ; 3  . D. n 1;2; 2  . 2   4   1   3  
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 1
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Câu 8. Trong không gian Oxyz , cho mặt cầu S  có tâm I 0;1;2 và bán kinh bằng 3. Phương trình của S  là
A. x   y  2   z  2 2 1 2  9 .
B. x   y  2   z  2 2 1 2  9 .
C. x   y  2   z  2 2 1 2  3 .
D. x   y  2   z  2 2 1 2  3 .
Câu 9. Cho hàm số f  x 2
 x 1 . Khẳng định nào dưới đây đúng? 3 x A.    3 f x dx  x  x  C . B. f  xdx   xC . 3 C.    2 f x dx  x  x  C . D. f  xdx  2x C .
Câu 10. Cho hàm số y  f  x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 4. D. 5.
Câu 11. Tập xác định của hàm số 6x y  là A. 0;. B.  \  0 . C. 0; . D.  . 3 3 Câu 12. Nếu f
 xdx  2 thì 3f xdx  bằng 0 0 A. 6. B. 2. C. 18. D. 3.
Câu 13. Trên mặt phẳng tọa độ, điểm M 2;3 là điểm biểu diễn của số phức nào dưới đây? A. z  2  3i . B. z  2   3i . C. z  2   3i . D. z  2  3i . 3 4 1 2 Câu 14. Cho hàm số   x
f x  e  3 . Khẳng định nào dưới đây đúng? A.   d x f x x  e  3x  C . B.   d x f x x  e  C . C.    3 d x f x x  e  C . D.   d x f x x  e  3x  C .
Câu 15. Cho hàm số y  f  x có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ;2 . B. 0; 2 . C. 2; 2 . D. 2;  .
Câu 16. Đồ thị hàm số 3 2
y  x  2x 1 cắt trục tung tại điểm có tung độ bằng A. 3. B. 1. C. 1  . D. 0 . Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 4
Câu 17. Trên khoảng 0;  , đạo hàm của hàm số 3 y  x là 1 4  1 4 7 3 1 3 A. 3 y  x . B. 3 y  x . C. 3 y  x . D. 3 y  x . 3 3 7 4
Câu 18. Cho a  0 và a  1, khi đó log a bằng a 1 1 A. 2 . B. 2 . C.  . D. . 2 2 
Câu 19. Trong không gian Oxyz , cho điểm ( A 3; 2; 4
 ) , Tọa độ của vectơ OA là A. (3; 2  ; 4  ) . B. ( 3  ; 2  ;4) . C. (3;2; 4  ) . D. (3; 2;4) .
Câu 20. Tập nghiệm của bất phương trình 2x  3 là A. log 2; , B. ;log 3 , C.  ;  log 2 , D. log 3; . 2  3  2  3 
Câu 21. Cho hai số phức z 1 2i và w  3 4i . Số phức z  w bằng A. 2  6i B. 4  2i C. 4  2i D. 2   6i .
Câu 22. Cho hàm số có bảng biến thiên như vẽ:
Giá trị cực đại của hàm số bằng A. 3. B. 0 . C. 2 . D. 1.
Câu 23. Thể tích khối lập phương có độ dài cạnh 3a bằng A. 3 27a . B. 3 3a . C. 3 9a . D. 3 a . 2x 1
Câu 24. Tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình x 1 1 A. x  2 . B. x 1. C. x   . D. x  1  . 2
Câu 25. Phần thực của số phức z  3  2i bằng A. 2 . B. 3 . C. 3. D. 2  .
Câu 26. Nghiệm của phương trình log 2x  2 là 3   9 A. x  . B. x  9 . C. x  4 . D. x  8 . 2
Câu 27. Với n là số nguyên dương bất kì, n  2 , công thức nào dưới đây đúng? n  2 ! 2! n! n! 2   A. A  . B. 2 A  . C. 2 A  . D. 2 A  . n n! n n  2! n 2!n  2! n n  2!
Câu 28. Cho khối trụ có bán kính r  2 và chiều cao h  3.Thể tích khối trụ đã cho bằng A. 12 . B. 18 . C. 6 . D. 4 .
Câu 29. Trong không gian Oxyz , cho điểm M 1; 2;  
1 và mặt phẳng P : 2x  y  3z 1  0 . Đường
thẳng đi qua M và vuông góc với P có phương trình là x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 2 1 1 2 1 3 
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 2 1 1 2 1 3 
Câu 30. Cho hình lăng trụ đứng ABC.A B  C
  có tất cả các cạnh bằng nhau (tham khảo hình bên dưới). C A B A' C' B'
Góc giữa hai đường thẳng AB và CC bằng A. 45. B. 30 . C. 90 . D. 60 .
Câu 31. Cho số phức z thỏa mãn iz  3 2 .i Số phức liên hợp của z là A. z  2  3i . B. z  2  3i . C. z  2  3i . D. z  2  3i .
Câu 32. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C , AC  a và SA vuông góc với mặt
phẳng đáy. Khoảng cách từ B đến mặt phẳng (SAC) bằng 1 2 A. a . B. 2a . C. a . D. a . 2 2
Câu 33. Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy 3 quả màu đỏ bằng 1 1 2 1 A. . B. . C. . D. . 5 6 5 30 Câu 34. Với mọi , a b thỏa mãn 2
log a  log b  7 , khẳng định nào dưới đây đúng? 2 2 A. 2 a  b  49 . B. 2 a b 128 . C. 2 a  b 128. D. 2 a b  49 .
Câu 35. Trong không gian Oxyz , cho hai điểm A0;0; 
1 và B 1; 2;3 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. x  2y  2z 11  0 .
B. x  2y  2z  2  0 .
C. x  2y  4z  4  0 .
D. x  2y  4z 17  0 .
Câu 36. Trên đoạn 0;3, hàm số 3
y  x  3x  4 đạt giá trị nhỏ nhất tại điểm A. x 1. B. x  0 . C. x  3. D. x  2 . 2 2 Câu 37. Nếu f
 xdx  6 thì 2 f  x1dx  bằng 0 0 A. 12 . B. 10 . C. 11. D. 14 . x  a
Câu 38. Biết hàm số y 
( a là số thực cho trước, a  1
 ) có đồ thị như trong hình vẽ sau x 1 Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Mệnh đề nào dưới đây đúng? A. y  0, x   1. B. y  0, x    . C. y  0, x    . D. y  0, x   1.
Câu 39. Có bao nhiêu số nguyên x thỏa mãn  2
2x  4x log x 14  4  0  2    ? A. 14 . B. 13 . C. Vô số. D. 15 .  2x  3 khi x  1
Câu 40. Cho hàm số f  x  
. Giả sử F là nguyên hàm của hàm số f trên  2 3  x  2 khi x  1
thỏa mãn F 0  2 . Giá trị của F   1  2F 2 bằng A. 23. B. 11. C. 10 . D. 21.
Câu 41. Cho hàm số bậc bốn y  f  x có đồ thị là đường cong trong hình bên dưới:
Số nghiệm thực phân biệt của phương trình f  f  x  0 là A. 4 . B. 10 . C. 12 . D. 8 .
Câu 42. Xét số phức z, w thoả mãn z  1 và w  2 . Khi z  iw  6  8i đạt giá trị nhỏ nhất, z  w bằng 29 221 A. 3. B. . C. 5 . D. . 5 5 x 1 y  2 z 1
Câu 43. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2 
P: x  2y  z  6  0. Hình chiếu vuông góc của d trên P là đường thẳng có phương trình x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 3 1  1 3 1 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 4 7 1 4 7  1 
Câu 44. Có bao nhiêu số nguyên y sao cho tồn tại x  ;5   thỏa mãn 2 3x  xy 15 27  (1 )27 x xy ?  3  A. 17. B. 16. C. 18. D. 15.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Câu 45. Cho khối hộp chữ nhật ABC . D AB C  D
  có đáy là hình vuông, BD  2a , góc giữa hai mặt
phẳng  ABD và  ABCD bằng 60. Thể tích của khối hộp đã cho bằng 2 3 2 3 A. 3 a . B. 3 6 3a . C. 3 a . D. 3 2 3a . 9 3 Câu 46. Cho hàm số   3 2
f x  x  ax  bx  c với a, ,
b c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 5
 và 3. Diện tích hình phẳng giới hạn f  x bởi đường y  và y 1 bằng g  x  6 A. 2ln 3 . B. ln 2 . C. ln15. D. 3ln 2 .
Câu 47. Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 30
, ta được thiết diện là tam giác đều cạnh 4a . Diện tích xung quanh của  N  bằng A. 2 4 7 a . B. 2 8 7 a . C. 2 8 13 a . D. 2 4 13 a .
Câu 48. Trên tập hợp các số phức, xét phương trình 2 z  m   2 2
1 z  m  0 (m là tham số thực ). Có
bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  8 . 0 0 A. 4. B. 3. C. 2. D. 1.
Câu 49. Trong không gian Oxyz , cho hai điểm A1; 3;2 và B 2;1; 4 . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  4 . Giá trị lớn nhất của AM  BN bằng A. 5 2 . B. 3 13 . C. 61 . D. 85 .
Câu 50. Cho hàm số y  f  x có đạo hàm f  x   x   2 '
10 x  25,x  .Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g  x  f  3
x  8x  m có ít nhất 3 điểm cực trị? A. 9. B. 25 . C. 5. D. 10 .
------------------HẾT------------------ Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 BẢNG ĐÁP ÁN 1B 2C 3C 4D 5C 6C 7B 8A 9B 10C 11D 12A 13C 14A 15B
16C 17B 18D 19C 20D 21C 22A 23A 24B 25C 26A 27D 28A 29B 30A
31A 32D 33D 34B 35B 36A 37B 38A 39D 40D 41B 42D 43D 44A 45D 46A 47D 48B 49B 50A HƯỚNG DẪN GIẢI
Câu 1. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? 1 1 1 1 A. 3 y  x  2x  . B. 3 y  x  2x  . C. 4 2 y  x  2x  . D. 4 2 y  x  2x  . 2 2 2 2 Lời giải
GVSB: Trần Ngọc; GVPB:Hải Hạnh Trần Chọn B
Đồ thị đã cho là đồ thị hàm số bậc ba có hệ số bậc ba a  0 . Chọn B.
Câu 2. Cho cấp số nhân u với u  3 và u 15 . Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 1  2. B. . C. 5. D. 12 . 5 Lời giải
GVSB: Trần Ngọc; GVPB:Hải Hạnh Trần Chọn C u 15 Ta có: 2 q    5. u 3 1
Câu 3. Cho khối chóp có diện tích đáy 2
B  7a và chiều cao h  a . Thể tích của khối chóp đã cho bằng 7 7 7 A. 3 a . B. 3 a . C. 3 a . D. 3 7a . 6 2 3 Lời giải
GVSB: Trần Ngọc; GVPB:Hải Hạnh Trần Chọn C 1 1 7 Thể tích khối chóp 2 3 V  Bh  7a .a  a . 3 3 3 4 4 4 Câu 4. Nếu f
 xdx  5 và gxdx  4   thì  f
 x gxdx  bằng 1 1 1 A. 1  . B. 9 . C. 1. D. 9. Lời giải
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
GVSB: Nguyễn Minh Hằng; GVPB: Hải Hạnh Trần Chọn D 4 4 4 Ta có:  f
 x gxdx  f   xdx  g  xdx  5 4    9 . 1 1 1
Câu 5. Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 3;1; 2 và có một vectơ chỉ  phương u 2;4; 
1 , phương trình của d là x 3  2t x   3  2t x   3  2t x  2  3t     A. y  1 4t . B. y 1 4t . C. y 1 4t . D. y  4  t . z 2 t     z  2  t  z  2  t  z  1 2t  Lời giải
GVSB: Nguyễn Minh Hằng; GVPB: Hải Hạnh Trần Chọn C 
Đường thẳng d đi qua điểm M 3;1;2 và có một vectơ chỉ phương u 2;4;  1 , phương x   3  2t 
trình của d là y 1 4t z 2 t . 
Câu 6. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S   R . B. 2 S   R . C. 2 S  4 R . D. 2 S  16 R . 3 Lời giải
GVSB: Nguyễn Minh Hằng; GVPB: Hải Hạnh Trần Chọn C
Diện tích S của mặt cầu bán kính R được tính theo công thức 2 S  4 R .
Câu 7. Trong không gian Oxyz , cho mặt phẳng P : x  2 y  2z  3  0 . Vectơ nào dưới đây là một
véctơ pháp tuyến của  P ?     A. n  1;2; 2 . B. n  1; 2  ;2 . C. n  1; 2  ; 3  . D. n 1; 2; 2  . 2   4   1   3   Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Hải Hạnh Trần Chọn B 
Ta có mặt phẳng P : x  2 y  2z  3  0 nên suy ra một vectơ pháp tuyến là n  1; 2  ;2 . 1  
Câu 8. Trong không gian Oxyz , cho mặt cầu S  có tâm I 0;1;2 và bán kinh bằng 3. Phương trình của S  là
A. x   y  2   z  2 2 1 2  9 .
B. x   y  2   z  2 2 1 2  9 .
C. x   y  2   z  2 2 1 2  3 .
D. x   y  2   z  2 2 1 2  3 . Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Hải Hạnh Trần Chọn A
Ta có mặt cầu tâm I 0;1; 2 bán kính bằng 3 có phương trình là x   y  2   z  2 2 1 2  9 .
Câu 9. Cho hàm số f  x 2
 x 1. Khẳng định nào dưới đây đúng? Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 3 x A.    3 f x dx  x  x  C . B. f  xdx   xC . 3 C.    2 f x dx  x  x  C . D. f  xdx  2x C . Lời giải
GVSB: Nguyễn Đức Tài; GVPB: Hải Hạnh Trần Chọn B x Ta có f
 xdx  x   3 2 1 dx   x  C . 3
Câu 10. Cho hàm số y  f  x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 4. D. 5.
GVSB: Bùi Minh Đức; GVPB: Phạm Tuyến Lời giải Chọn C
Từ bảng xét dấu ta thấy f  x đổi dấu 4 lần
Suy ra hàm số f  x có 4 điểm cực trị.
Câu 11. Tập xác định của hàm số 6x y  là A. 0; . B.  \  0 . C. 0; . D.  .
GVSB: Bùi Minh Đức; GVPB: Phạm Tuyến Lời giải Chọn D
Tập xác định của hàm số 6x y  là D  .  3 3 Câu 12. Nếu f
 xdx  2 thì 3f xdx  bằng 0 0 A. 6. B. 2. C. 18. D. 3.
GVSB: Bùi Minh Đức; GVPB: Phạm Tuyến Lời giải Chọn A 3 3 Ta có: 3 f  xdx  3. f  xdx  3.2  6. 0 0
Câu 13. Trên mặt phẳng tọa độ, điểm M 2;3 là điểm biểu diễn của số phức nào dưới đây? A. z  2  3i . B. z  2   3i . C. z  2   3i . D. z  2  3i . 3 4 1 2 Lời giải
GVSB: Nguyễn Linh Trang; GVPB: Phạm Tuyến Chọn C
Điểm M 2;3 là điểm biểu diễn của số phức z  2  3i . 1 Câu 14. Cho hàm số   x
f x  e  3 . Khẳng định nào dưới đây đúng? A.   d x f x x  e  3x  C . B.   d x f x x  e  C .
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 C.    3 d x f x x  e  C . D.   d x f x x  e  3x  C . Lời giải
GVSB: Nguyễn Linh Trang; GVPB: Phạm Tuyến Chọn A
Nguyên hàm của hàm số   x
f x  e  3 là:   d   x  3d x f x x e x  e  3x  C .
Câu 15. Cho hàm số y  f  x có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ;2 . B. 0; 2 . C. 2; 2 . D. 2;  . Lời giải
GVSB: Nguyễn Linh Trang; GVPB: Phạm Tuyến Chọn B
Dựa vào đồ thị hàm số ta có hàm số đồng biến trên khoảng 0; 2 .
Câu 16. Đồ thị hàm số 3 2
y  x  2x 1 cắt trục tung tại điểm có tung độ bằng A. 3. B. 1. C. 1  . D. 0 . Lời giải
GVSB:Lê Thúy Hằng; GVPB: Phạm Tuyến Chọn C Từ hàm số: 3 2
y  x  2x 1, cho x  0  y  1  . Vậy đồ thị hàm số 3 2
y  x  2x 1 cắt trục tung tại điểm có tung độ bằng 1  . 4
Câu 17. Trên khoảng 0;  , đạo hàm của hàm số 3 y  x là 1 4  1 4 7 3 1 3 A. 3 y  x . B. 3 y  x . C. 3 y  x . D. 3 y  x . 3 3 7 4 Lời giải
GVSB:Lê Thúy Hằng; GVPB: Phạm Tuyến Chọn B 4  1   4 Ta có: 3 3 y   x   x . 3  
Câu 18. Cho a  0 và a  1, khi đó log a bằng a 1 1 A. 2 . B. 2 . C.  . D. . 2 2 Lời giải Trang 10
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
GVSB:Lê Thúy Hằng; GVPB: Phạm Tuyến Chọn D 1 1 1
Với a  0 và a  1,ta có: 2 log a  log a  log a  . a a 2 a 2 
Câu 19. Trong không gian Oxyz , cho điểm ( A 3; 2; 4
 ) , Tọa độ của vectơ OA là A. (3; 2  ; 4  ) . B. ( 3  ; 2  ;4) . C. (3;2; 4  ) . D. (3; 2;4) . Lời giải
GVSB:Bạch Hưng Tình; GVPB: Nguyễn My Chọn C  Ta có: O 0; 0; 0 , ( A 3;2; 4
 ) OA3 0;2  0; 4
  0  3;2; 4.
Câu 20. Tập nghiệm của bất phương trình 2x  3 là A. log 2; , B. ;log 3 , C.  ;  log 2 , D. log 3; . 2  3  2  3  Lời giải
GVSB:Bạch Hưng Tình; GVPB: Nguyễn My Chọn D
Ta có: 2x  3  x  log 3 . 2
Tập nghiệm của bất phương trình là log 3;  . 2 
Câu 21. Cho hai số phức z 1 2i và w  3 4i . Số phức z  w bằng A. 2  6i B. 4  2i C. 4  2i D. 2   6i . Lời giải
GVSB:Bạch Hưng Tình; GVPB: Nguyễn My Chọn C
Ta có: z  w  1 2i  3  4i  4  2i .
Câu 22. Cho hàm số có bảng biến thiên như vẽ:
Giá trị cực đại của hàm số bằng A. 3. B. 0 . C. 2 . D. 1. Lời giải
GVSB:Trần Thông GVPB:Nguyễn My Chọn B
Câu 23. Thể tích khối lập phương có độ dài cạnh 3a bằng A. 3 27a . B. 3 3a . C. 3 9a . D. 3 a . Lời giải
GVSB:Trần Thông GVPB:Nguyễn My Chọn A
Thể tích khối lập phương là  a3 3 3  27a . 2x 1
Câu 24. Tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình x 1
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 11
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 1 A. x  2 . B. x 1. C. x   . D. x  1  . 2 Lời giải
GVSB:Trần Thông GVPB:Nguyễn My Chọn B 2x 1 2x 1 Ta có lim   và lim
  nên x 1 là tiệm cận đứng của đồ thị hàm số. x 1  x 1 x 1  x 1
Câu 25. Phần thực của số phức z  3 2i bằng A. 2 . B. 3  . C. 3. D. 2  . Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Nguyễn My Chọn C
Câu 26. Nghiệm của phương trình log 2x  2 là 3   9 A. x  . B. x  9 . C. x  4 . D. x  8 . 2 Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Nguyễn My Chọn A 9
log 2x  2  2x  9  x  . 3   2
Câu 27. Với n là số nguyên dương bất kì, n  2 , công thức nào dưới đây đúng? n  2 ! 2   2! n! n! A. A  . B. 2 A  . C. 2 A  . D. 2 A  . n n! n n  2! n 2  ! n  2! n n  2! Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Nguyễn My Chọn D n! 2 A  . n n  2!
Câu 28. Cho khối trụ có bán kính r  2 và chiều cao h  3.Thể tích khối trụ đã cho bằng A. 12 . B. 18 . C. 6 . D. 4 . Lời giải
GVSB: Nguyễn Trọng Thiện; GVPB: Hồ Quốc Thuận Chọn A Thể tích khối trụ: 2 2
V   r h  .2 .3 12 .
Câu 29. Trong không gian Oxyz , cho điểm M 1;2; 
1 và mặt phẳng P : 2x  y  3z 1  0 . Đường
thẳng đi qua M và vuông góc với  P có phương trình là x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 2 1 1 2 1 3 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 2 1 1 2 1 3  Lời giải
GVSB: Nguyễn Trọng Thiện; GVPB: Hồ Quốc Thuận Chọn B Trang 12
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Gọi  là đường thẳng cần tìm. Vì đường thẳng  vuông góc với mặt phẳng P nên  
vectơ chỉ phương của  là:u  n    2;1; 3 . P  
Phương trình chính tắc của đường thẳng  đi qua điểm M 1;2;   1 và có vtcp u    2;1; 3 x 1 y  2 z 1 là:   . 2 1 3 
Câu 30. Cho hình lăng trụ đứng ABC.A B  C
  có tất cả các cạnh bằng nhau (tham khảo hình bên dưới). C A B A' C' B'
Góc giữa hai đường thẳng AB và CC bằng A. 45. B. 30 . C. 90 . D. 60 . Lời giải
GVSB: Nguyễn Trọng Thiện; GVPB: Hồ Quốc Thuận Chọn A C A B A' C' B' Ta có: CC '// BB ' . Nên  A'B;CC'=  A'B;BB'= A' BB ' ( 
A' BB ' là góc nhọn). Mặt khác,
tam giác A' BB ' là tam giác vuông cân ( A' B  BB ' và A' B  BB ') suy ra  A' BB '  45 . Vậy
góc giữa hai đường thẳng A' B và CC ' bằng 45.
Câu 31. Cho số phức z thỏa mãn iz  3 2 .i Số phức liên hợp của z là A. z  2  3i . B. z  2  3i . C. z  2  3i . D. z  2  3i . Lời giải
GVSB: Pham Thi Hong Van; GVPB: Hồ Quốc Thuận Chọn A
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 13
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 3  2i
Ta có: iz  3  2i  z   2  3i . i
Do đó số phức liên hợp của z là: z  2  3i
Câu 32. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C , AC  a và SA vuông góc với mặt
phẳng đáy. Khoảng cách từ B đến mặt phẳng (SAC) bằng 1 2 A. a . B. 2a . C. a . D. a . 2 2 Lời giải
GVSB: Pham Thi Hong Van; GVPB: Hồ Quốc Thuận Chọn D
Ta có: SA vuông góc với mặt đáy suy ra SA  BC
Tam giác ABC vuông cân tại C suy ra BC  a và AC  BC SA  BC Do đó ta có:   BC  (SAC) . C  A  BC
Vậy khoảng cách từ B đến mặt phẳng (SAC) bằng BC  a .
Câu 33. Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy 3 quả màu đỏ bằng 1 1 2 1 A. . B. . C. . D. . 5 6 5 30 Lời giải
GVSB: Phạm Quang Thiện; GVPB: Tran Phuc Chọn D Ta có: n  3
 C . Gọi biến cố A:“3 quả lấy ra màu đỏ”. Suy ra n  A 3  C . 10 4 n A 1
Vậy Xác suất để lấy 3 quả màu đỏ bằng P A     . n 30 Câu 34. Với mọi , a b thỏa mãn 2
log a  log b  7 , khẳng định nào dưới đây đúng? 2 2 A. 2 a  b  49 . B. 2 a b 128 . C. 2 a  b 128. D. 2 a b  49 . Lời giải
GVSB: Phạm Quang Thiện; GVPB: Tran Phuc Chọn B Trang 14
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 Ta có: 2
log a  log b  7  log  2 a b 2 7  7  a b  2  128 2 2 2
Câu 35. Trong không gian Oxyz , cho hai điểm A0;0; 
1 và B 1; 2;3 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. x  2y  2z 11  0 .
B. x  2y  2z  2  0 .
C. x  2y  4z  4  0 .
D. x  2y  4z 17  0 . Lời giải
GVSB: Tuyet Trinh; GVPB: Phan Thị Thúy Hà Chọn B  Ta có AB  1;2;2 . 
Mặt phẳng đi qua A và vuông góc với AB nên nhận AB  1;2;2 làm vectơ pháp tuyến có
phương trình: 1 x  0  2 y  0  2z 1  0  x  2y  2z  2  0 .
Câu 36. Trên đoạn 0;3, hàm số 3
y  x  3x  4 đạt giá trị nhỏ nhất tại điểm A. x 1. B. x  0 . C. x  3. D. x  2 . Lời giải
GVSB: Tuyet Trinh; GVPB: Phan Thị Thúy Hà Chọn A Ta có 2 y  3x  3 x 10;  3 y  0   . x  1    0; 3
Lại có y 0  4 ; y   1  2 ; y 3  22 . Vậy min y  y   1  2 . 0; 3 2 2 Câu 37. Nếu f
 xdx  6 thì 2 f  x1dx  bằng 0 0 A. 12 . B. 10 . C. 11. D. 14 . Lời giải
GVSB: Phan Thị Thúy Hà; GVPB: Phan Thị Thúy Hà Chọn B 2 2 2 Ta có: 2 f
 x1dx  2 f 
 xdx  dx  2.62 10  . 0 0 0 x  a
Câu 38. Biết hàm số y 
( a là số thực cho trước, a  1
 ) có đồ thị như trong hình vẽ sau x 1
Mệnh đề nào dưới đây đúng?
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 15
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 A. y  0, x   1. B. y  0, x    . C. y  0, x    . D. y  0, x   1. Lời giải
GVSB: Phan Thị Thúy Hà; GVPB: Phan Thị Thúy Hà Chọn A
Tập xác định của hàm số đã cho là D   \  1 . 1 a Ta có: y  , x   1. x  2 1
Từ đồ thị của hàm số suy ra hàm số đã cho đồng biến trên mỗi khoảng xác định vì vậy y  0, x   1.
Câu 39. Có bao nhiêu số nguyên x thỏa mãn  2
2x  4x log x 14  4  0  2    ? A. 14 . B. 13 . C. Vô số. D. 15 . Lời giải
GVSB: Trương Hoài Bão; GVPB:ThanhQuach Chọn D Điều kiện: x  1  4.
Bất phương trình tương đương:  2x 2
2  2 x log x 14  4  0  2    2 2 x 2x x 2 2  2  0 2  2 x 2   x  2x    log x 14  4  0   log x 14  4    2    2   x 14 16 x  2         . 2 2 x 2x x 2 2  2  0 2  2 x 2 x  2x x  0         log x 14  4  0  log x 14  4 x 14 16 2    2  
Kết hợp với điều kiện suy ra có 15 giá trị nguyên của x thỏa yêu cầu.  2x  3 khi x  1
Câu 40. Cho hàm số f  x  
. Giả sử F là nguyên hàm của hàm số f trên  2 3  x  2 khi x  1
thỏa mãn F 0  2 . Giá trị của F   1  2F 2 bằng A. 23. B. 11. C. 10 . D. 21. Lời giải
GVSB: Trương Hoài Bão; GVPB:ThanhQuach Chọn D
Khi x  1 thì F  x  f
 xdx  2x 3 2 dx  x  3x  C1
Khi x 1 thì F  x  f  xdx   2 3x  2 3 dx  x  2x  C2
Theo giả thiết F 0  2  C  2 2 Trang 16
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Ta có lim f  x  lim f  x  f  
1  5 nên hàm số f  x liên tục tại x 1. x 1 x 1  
Suy ra hàm số f  x liên tục trên  .
Do đó hàm số F  x liên tục trên   lim F  x  lim F  x  C  4  C  3  C 1   1 2 1 x 1  x 1  Vậy F  
1  2F 2  3  C  2 10  C  21. 2  1 
Câu 41. Cho hàm số bậc bốn y  f  x có đồ thị là đường cong trong hình bên dưới:
Số nghiệm thực phân biệt của phương trình f  f  x  0 là A. 4 . B. 10 . C. 12 . D. 8 . Lời giải
GVSB: Hoàng Văn Quảng; GVPB: Chọn B
 f  x  a a    1   f  x  b  1   b  0
Ta có: f  f  x  0   .
f  x  c 0  c   1   f x  d d   1
 Phương trình f x  a với a  1  vô nghiệm.
 Phương trình f x  b với 1
  b  0 có 4 nghiệm phân biệt.
 Phương trình f  x  c với 0  c 1 có 4 nghiệm phân biệt.
 Phương trình f x  d với d 1 có 2 nghiệm phân biệt.
Câu 42. Xét số phức z, w thoả mãn z  1 và w  2 . Khi z  iw  6  8i đạt giá trị nhỏ nhất, z  w bằng 29 221 A. 3. B. . C. 5 . D. . 5 5 Lời giải
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 17
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
GVSB: Trần Thị Vân; GVPB:Nguyễn Viết Thăng Chọn D
z  iw  6  8i  6  8i  z  iw  10  z  iw ,
10  z  iw  10   z  iw  10   z  w   7 .  6  8i z  
z  iw  6  8i đạt giá trị nhỏ nhất khi 10  6  8i 6  8i i  w  2.   10 5  3  4i z   5   3 4i  8 6  221   z  w     i    . 8 6  5  5 5  5 w    i  5 5 x 1 y  2 z 1
Câu 43. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2 
P: x  2y  z  6  0. Hình chiếu vuông góc của d trên P là đường thẳng có phương trình x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 3 1  1 3 1 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 4 7 1 4 7
GVSB: Nguyễn Thị Kim Cúc; GVPB: Nguyễn Viết Thăng Lời giải Chọn D
 Gọi A là giao điểm của d và P . x 1 t 
d có phương trình tham số y  2  t
nên tọa độ giao điểm A của d và  P thỏa mãn z  1   2t  x  1 t x  1   y 2 t     y  2     A1;2;  1 . z  1   2t z  1  
x  2y  z 6  0 t  0  
 Ta có n  1;2;  1 và u  1;1; 2  . d  P   
Gọi Q là mặt phẳng chứa d và Q  P ta có n  n ,u   3;1;  1 Q P d   Trang 18
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Hình chiếu vuông góc  của d lên P là giao tuyến của P và Q nên    u  n , n    và  đi qua A .   1;4;7 P Q    x 1 y  2 z 1 Phương trình  :   1  4 7  1 
Câu 44. Có bao nhiêu số nguyên y sao cho tồn tại x  ;5   thỏa mãn 2 3x  xy 15 27  (1 )27 x xy ?  3  A. 17. B. 16. C. 18. D. 15. Lời giải
GVSB: Trần Quốc Dũng; GVPB: ………… Chọn A Xét 2 3x 1  5 ( )  27 x xy f x  (xy 1) và áp dụng x a  x(a 1) 1.  1  Suy ra f (x)  26 2 3x 15x  xy 2
 xy 1  84x  25xy  390x 1  0, y  16, x   ;5   .  3  Do đó y  16 .  2 3x 1  5x 2 y  0  27
 1 3x 15x  0 : loại.  y  3   xy  1   VP  0 : loại.  y  1  , y  2  : thỏa mãn (1)  Xét y  0 ta có 5 (4)  27 y f  (5y 1)  0, y   0  1   y và y 14 f  3  1  0, y  {1;2;3;;15}   (2)  3  3
Từ (1) và (2)  y 2;1;1; 2;3; 4;5;6;7;8;9;10;11;1  5 .
Câu 45. Cho khối hộp chữ nhật ABC . D AB C  D
  có đáy là hình vuông, BD  2a , góc giữa hai mặt
phẳng  ABD và  ABCD bằng 60. Thể tích của khối hộp đã cho bằng 2 3 2 3 A. 3 a . B. 3 6 3a . C. 3 a . D. 3 2 3a . 9 3 Lời giải
GVSB:Khanh Tam; GVPB: Hongnhung Nguyen Chọn D Gọi O  AC  BD .
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 19
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
 A' BD  ABCD  BD  Ta có: 0 A'O  BD  60   A'OA . AC  BD  Tam giác AAO có: 0 AA'  tan 60 .OA  3a và 2 S  2a . ABCD Vậy 3 V  AA'.S  2 3a . ABCD.A' B 'C 'D ' ABCD Câu 46. Cho hàm số   3 2
f x  x  ax  bx  c với a,b,c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 5
 và 3. Diện tích hình phẳng giới hạn f  x bởi đường y  và y 1 bằng g  x  6 A. 2ln 3 . B. ln 2 . C. ln15 . D. 3ln 2 . Lời giải
GVSB: Phạm Tính; GVPB:Nguyễn Minh Thành Chọn A
Ta có g  x  f  x  f  x  f   x 3  x    a 2 3
x  b  2a  6 x  2a  b  c . Suy ra: g x 2
 3x  23  a x  b  2a  6 . Xét phương trình f  x x  x 2                 g  x 1 g  x f  x 6 3x 2a 3 x 2a b 6 0 g  x 1 0  6 x  x  2 Ta có diện tích bằng 2 x  f x x2   f x  g x x2  6   gx  x S      x     x    x  g x   g x   g x   g x     x    1 d 6  x    d 6  x    d ln   2 6 x1 6  1 1 1
 ln g x  6  ln g x  6  ln 9  2ln 3 2   1
Câu 47. Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 30
, ta được thiết diện là tam giác đều cạnh 4a . Diện tích xung quanh của  N  bằng A. 2 4 7 a . B. 2 8 7 a . C. 2 8 13 a . D. 2 4 13 a . Lời giải
GVSB:Nguyễn Thuỳ Dương GVPB:Thái Huy Chọn D Trang 20
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Giả sử mặt phẳng  P cắt đáy của hình nón theo dây AB . Suy ra tam giác SAB đều  AB  4a .
Gọi M là trung điểm của AB   SMO  30 . 4a 3
Vì SM là đường cao của tam giác SAB nên SM   2a 3 . 2 SO
Tam giác SMO vuông tại O nên  1 sin SMO 
 SO  SM.sin 30 2a 3.  a 3 . SM 2 Suy ra 2 2 2 2
OM  SM  SO  12a  3a 3a ; 2 2 2 2
OA OM  MA  9a  4a  a 13 . Vậy 2 S  Rl .O .
A SA .a 13.4a  4 13 a . xq
Câu 48. Trên tập hợp các số phức, xét phương trình 2 z  m   2 2
1 z  m  0 (m là tham số thực ). Có
bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  8 . 0 0 A. 4. B. 3. C. 2. D. 1. Lời giải GVSB: …; GVPB: … Chọn A
Vì z  8 nên đặt z  8 cos  i sin  , với    . 0   0
Phương trình đã cho nhận z là nghiệm nên ta có: 0    i    m     i   2 64 cos 2 sin 16 1 cos sin  m  0 .
Tách phần thực và phần ảo ta có:    m   2 64cos 2 16 1 cos  m  0   1  64sin 2 16  m  1sin  0 2 sin  0
2  sin 4cos    m   1   0   m 1 cos   4 cos  1  * Nếu sin  0 thì  , thay vào (1) ta có: cos 2 1 2 m 16m  80  0 (vn)  m   2 64 16 1  m  0   . Suy ra có 2 giá trị m . 2
m 16m  48  0 (2 nghiem) m 1 2  m 1 1 * Nếu cos   thì cos 2   2 1    m  2 1 1, thay vào (1) ta có: 4  4  8 1  m  64 m  2 1 1 16m   1 2 1 .  m  0 8    4 Đặt n  m 1, ta có: 1  n 64 n 1 16 . n  n  2 2 1  0  8    4  n   n  n  2 2 2 8 64 4 1  0 2
 5n  2n  63  0 (Có 2 nghiệm). Suy ra có 2 giá trị m .
Dễ thấy các giá trị của m tìm được ở trên không trùng nhau. Vậy có 4 giá trị của m thỏa mãn điều kiện bài toán.
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 21
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021
Câu 49. Trong không gian Oxyz , cho hai điểm A1; 3; 2 và B 2;1; 4 . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  4. Giá trị lớn nhất của AM  BN bằng A. 5 2 . B. 3 13 . C. 61 . D. 85 . Lời giải GVSB: …; GVPB: … Chọn B
Dễ thấy A , B nằm hai phía của mặt phẳng Oxy . Gọi A' đối xứng với A qua mặt phẳng
Oxy suy ra A'1;3;2 .
Gọi E và F lần lượt là hình chiếu của A' và B lên mặt phẳng Oxy , ta có 
E 1; 3;0 , F 2;1;0 . Do đó EF   3  ;4;0  EF  5 .   
A là điểm thỏa mãn AA  MN  k EF ( tức là AA //EF ) 1 1 1  4  4 12 16   AA   EF   3  ;4;0  ; ;0 * 1     5 5  5 5   12  17 x 1   x  5   5   16  31 17 31 
Gọi A x; y ; z . Từ *  y  3    y    A ; ; 2 . 1     5 1  5   5 5  z  2  0 z  2     27 36  Ta có A B   ; ;  6 . 1    5 5    Do AA  MN  AM  A N . 1 1 2 2  27   36 
 T  AM  BN  A N  BN  A B          6  2  3 13 . 1 1  5   5 
Câu 50. Cho hàm số y  f  x có đạo hàm f  x   x   2 '
10 x  25,x  .Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g  x  f  3
x  8x  m có ít nhất 3 điểm cực trị? A. 9. B. 25 . C. 5. D. 10 . Trang 22
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT
MÃ ĐỀ 103- ĐỢT 1 – NĂM HỌC 2020 - 2021 Lời giải
GVSB: Nguyễn thị Thắm; GVPB:Trần Minh Quang GVPB: Hoàng Hà Chọn A x  10
+ Ta có: f  x   x   2 10 x  25, x
    f x  0    x  5  (*). x  5    + g x   f   3 x  x  m    3x  x m f 3 8 8 . x  8x  m  2 3x  8 3 x  8x  f  3 x  8x  m . 3  x  8x  2 3x  8 3 x  8x  2 3x  8 x 2 x  8 Ta thấy:  0 
 0 có 1 nghiệm x  0 nên x  0 là 1 3 x  8x 3 x  8x
điểm cực trị của hàm số. 3 3  x  8x  m 10  x  8x 10  m   (*) Cho f  3 x  8x  m 3 3
 0   x  8x  m  5   x  8x  5  m (**).   3 3  x  8x  m  5   x  8x  5   m   Đặt h  x 3  x  x  hx 2 8
 3x  8  0,x   .
Yêu cầu bài toán tương đương (**) có ít nhất 2 nghiệm phân biệt khác 0
10  m  0  m 10  m 1;2;3;4;5;6;7;8;  9 .
------------------HẾT------------------
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 23
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104 Kú THI TN THPT N¡M 2021 M· §Ò: 104
TRAO ĐỔI & CHIA SẺ KIẾN THỨC
THÔNG MINH DO HỌC TẬP MÀ CÓ THIÊN TÀI DO TÍCH LŨY MÀ NÊN
Câu 1. Cho hai số phức z  3  2i và w  1 4i . Số phức z  w bằng A. 4  2i . B. 4  2i . C. 2   6i . D. 2  6i .
Câu 2. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 y  x  3x 1. B. 4 2 y  x  4x 1 . C. 3 y  x  3x 1. D. 4 2 y  x  2x 1. 4 4 4 Câu 3. Nếu f  xdx  4 và g  xdx= 3 thì  f
 x gxdx  bằng 1 1 1 A. 1. B. 7  . C. 1. D. 7 . x 1
Câu 4. Tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình x  2 A. x  2 . B. x  1 . C. x  2 . D. x  1 .
Câu 5. Trong không gian Oxyz, cho mặt cầu (S) có tâm I( 1
 ;3;0) và bán kính bằng 2 . Phương trình của (S) là A. 2 2 2
(x 1)  ( y  3)  z  2 . B. 2 2 2
(x 1)  ( y  3)  z  4 . C. 2 2 2
(x 1)  ( y  3)  z  4 . D. 2 2 2
(x 1)  ( y  3)  z  2 .
Câu 6. Tập nghiệm của bất phương trình 2x  5 là A. ( ;  log 5) . B. (log 2;  ) . C. ( ;  log 2) . D. (log 5; ) 2 5 5 2
Câu 7. Thể tích của khối lập phương cạnh 2a bằng A. a3. B. 2a3. C. 8a3. D. 4a3. 5
Câu 8. Trên khoảng 0; , đạo hàm của hàm số 3 y  x là 8 3 2 5 2 5  2 3 A. 3 y  x . B. 3 y  x . C. 3 y  x . D. 3 y  x . 8 3 3 5 Trang 1
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN 
Câu 9. Trong không gian Oxyz , cho điểm A2;1;4. Tọa độ của véc tơ OA là A. (-2; 1; 4). B. (2; -1; 4) . C. (2;1; 4). D. (-2; 1; -4). 3 3 Câu 10: Nếu f
 xdx  3 thì 4 f xdx  bằng 0 0 A. 3 . B. 12 . C. 36 . D. 4 .
Câu 11: Cho cấp số nhân u với u  2 và u  10 . Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 8 . B. 8 . C. 5. D. . 5
Câu 12: Với n là số nguyên dương bất kì, n  3 , công thức nào dưới đây đúng? n  3 ! 3! n 3   n! A. A  . B. 3 A  . C. 3 ! A  . D. 3 A  . n n! n n 3! n n 3! n  3! n  3!
Câu 13. Cho hàm số f  x 2
 x  2 . Khẳng định nào dưới đây là đúng? 3 x A. f  xdx  2xC B. f  xdx   2x C 3 C. f  x 2 dx  x  2x  C D. f  x 3 dx  x  2x  C
Câu 14. Cho hàm số y  f x có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng A. 0 B. 3 C. 1 D. 1
Câu 15. Trong không gian Oxyz , cho mặt phẳng P : 2x  4 y  z 1  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng P     A. n  2; 4;1 B. n  2; 4;1 C. n  2;4; 1  D. n  2  ;4;1 4   3   1   2  
Câu 16: Phần thực của số phức z  4  2i bằng A. 2 . B. 4  . C. 4 . D. 2 .
Câu 17: Nghiệm của phương trình log 5x  3 là: 2   8 9 A. x  . B. x  . C. x  8 . D. x  9 . 5 5
Câu 18: Tập xác định của hàm số 8x y  là A.  \  0 . B.  . C. 0; . D. 0;.
Câu 19. Cho a  0 và a  1, khi đó 5 log a bằng a 1 1 A. . B.  . C. 5 . D. 5  5 5
Câu 20. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d đi qua điểm M 1; 5 ;  2 có 
một véc tơ chỉ phương u 3 ;  6 ; 
1 . Phương trình của d là . Trang 2
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104 x  3  t x  1 3t x 1 3t x 1 3t     A.  y  6   5t . B.  y  5  6t . C.  y  5  6t . D. y  5  6t . z 1 2t     z  2  t  z  2  t  z  2  t 
Câu 21. Trên mặt phẳng toạ độ , điểm M  4
 ; 3 là điểm biểu diễn số phức nào dưới đây hai số phức nào dưới đây A. z  4  3i . B. z  4  3i . C. z  4  3i . D. z  4  3i . 3 4 2 1
Câu 22. Cho hàm số y  f  x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 5 .
Câu 23. Cho hàm số   ex f x 
 4 . Khẳng định nào dưới đây đúng? A.   d  ex f x x  4x  C . B.   d  ex f x x  C . C.    4 d  ex f x x  C . D.   d  ex f x x  4x  C .
Câu 24. Cho hàm số y  f x có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  1  ;  1 . B. 1; . C.  ;   1 . D. 0;3 .
Câu 25. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S   R . B. 2 S  16 R . C. 2 S  4 R . D. 2 S   R . 3
Câu 26. Đồ thị của hàm số 3 2 y  2
 x  3x  5 cắt trục tung tại điểm có tung độ bằng A. 5  . B. 0 . C. 1. D. 2 .
Câu 27. Cho khối chóp có diện tích đáy 2
B  8a và chiều cao h  a . Thể tích của khối chóp đã cho bằng Trang 3
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN 4 8 A. 3 8a . B. 3 a . C. 3 4a . D. 3 a . 3 3
Câu 28. Cho khối trụ có bán kính đáy r  5 và chiều cao h  3. Thể tích của khối trụ đã cho bằng A. 15 . B. 75 . C. 25 . D. 45 .
Câu 29. Trong không gian Oxyz , cho điểm M 2;1; 2
  và mặt phẳng P:3x  2y  z 1 0 . Đường
thẳng đi qua M và vuông góc với P có phương trình là:       A. x 2 y 1 z 2   . B. x 2 y 1 z 2   . 3 2 1 3 2 1       C. x 2 y 1 z 2   . D. x 2 y 1 z 2   . 3 2 1 3 2 1
Câu 30. Cho hình lăng trụ đứng ABC.A' B 'C ' có tất cả các cạnh bằng nhau ( tham khảo hình bên).
Góc giữa hai đường thẳng AB ' và CC ' bằng A. 30 . B. 90 . C. 60 . D. 45 .
Câu 31. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  4a và SA vuông góc với
mặt phẳng đáy. Khoảng cách từ C đến mặt phẳng SAB bằng A. 4a . B. 4 2a . C. 2 2a . D. 2a . 2 2 Câu 32. Nếu f
 xdx  4 thì 2 f  x1 dx  bằng 0 0 A. 8 . B. 10 . C. 7 . D. 6 . x  a
Câu 33. Biết hàm số y 
( a là số thực cho trước, a  1) có đồ thị như trong hình bên. Mệnh đề x 1 nào dưới đây đúng ? Trang 4
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104 y O x A. y '  0,x  R . B. y '  0,x  1. C. y '  0,x  R . D. y '  0,x  1.
Câu 34. Cho số phức z thỏa mãn iz  4  3i . Số phức liên hợp z là A. z  3  4i . B. z  3   4i . C. z  3  4i . D. z  3   4i .
Câu 35. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy được 3 quả màu đỏ bằng 1 7 5 2 A. . B. . C. . D. . 22 44 12 7
Câu 36. Với mọi a,b thỏa mãn 3
log a  log b  5 , khẳng định nào dưới đây là đúng? 2 2 A. 3 a b  32 . B. 3 a b  25 . C. 3 a  b  25 . D. 3 a  b  32 . Câu 37. Trên đoạn  1  ;2, hàm số 3 2
y  x  3x  1 đạt giá trị nhỏ nhất tại điểm A. x  2. B. x  0 . C. x  1  . D. x  1.
Câu 38. Trong không gian Oxyz , cho hai điểm A1;0;0 và B3;2; 
1 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 2x  2y  z  2  0.
B. 4x  2 y  z  17  0 .
C. 4x  2 y  z  4  0 .
D. 2x  2 y  z 11  0 .
Câu 39. Cho hàm số bậc bốn y  f  x có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình f  f  x  0 là A. 12 . B. 10 . C. 8 . D. 4 .
Câu 40. Có bao nhiêu số nguyên x thỏa mãn  2
2x  4x log x  25 3  0  3    ? A. 24 . B. Vô số. C. 25 . D. 26 . 2x  2 khi x 1
Câu 41. Cho hàm số f  x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3  x 1 khi x  1
F 0  2. Giá trị của F   1  2F 2 bằng Trang 5
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN A. 18 . B. 20 . C. 9 . D. 24 .
Câu 42. Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 30
, ta được thiết diện là tam giác đều cạnh 2a . Diện tích xung quanh của  N  bằng A. 2 7 a . B. 2 13 a . C. 2 2 13 a . D. 2 2 7 a . x y z 1
Câu 43. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1  2
P:x  2y  2z  2  0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình: x y z 1 x y z 1 x y z 1 x y z 1 A.   . B.   . C.   . D.   . 2  4 3 14 1 8 2  4 3 14 1 8  1 
Câu 44. Có bao nhiêu số nguyên y sao cho tồn tại x  ;6 2 
 thỏa mãn 3x xy     18 27 1 .27 x xy ?  3  A. 19 . B. 20 . C. 18. D. 21.
Câu 45. Trên tập hợp các số phức, xét phương trình 2 z  m   2 2
1 z  m  0 ( m là tham số thực). Có
bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  6 ? 0 0 A. 4 . B. 1. C. 2 . D. 3 .
Câu 46. Cho khối hộp chữ nhật ABC . D AB C  D
  có đáy là hình vuông, BD  4a , góc giữa hai mặt phẳng  A B
 D và  ABCD bằng 60. Thể tích của khối hộp chữ nhật đã cho bằng 16 3 16 3 A. 3 48 3a . B. 3 a . C. 3 a . D. 3 16 3a . 9 3 Câu 47. Cho hàm số   3 2
f x  x  ax  bx  c với a,b, c là các số thực. Biết hàm số
g  x  f  x  f  x  f   x có hai giá trị cực trị là 5
 và 2 . Diện tích hình phẳng giới hạn f  x bởi đường y  và y  1 bằng g  x  6 A. ln 3 . B. 3ln 2 . C. ln10. D. ln 7 .
Câu 48. Xét các số phức z ; w thỏa mãn z  1 và w  2 . Khi z  iw  6  8i đạt giá trị nhỏ nhất, z  w bằng: 29 221 A. . B. . C. 3 . D. 5 . 5 5
Câu 49. Trong không gian Oxyz , cho hai điểm A 2  ;13 và B1; 3
 ;2 . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  3. Giá trị lớn nhất của AM  BN bằng: A. 65 . B. 29 . C. 26 . D. 91.
Câu 50. Cho hàm số y  f  x có đạo hàm f x   x   2 9 x 16, x
   . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g  x  f  3
x  7x  m có ít nhất 3 điểm cực trị ? A. 16 . B. 9 . C. 4 . D. 8 . Trang 6
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT BẢNG ĐÁP ÁN 1.B 2.C 3.D 4.C 5.C 6.D 7.C 8.B 9.B 10.B 11.C 12.C 13.B 14.C 15.C 16.C 17.A 18.B 19.A 20.D 21.D 22.B 23.A 24.A 25.C 26.A 27.D 28.B 29.A 30.D 31.A 32.D 33.B 34.A 35.A 36.A 37.B 38.A 39.B 40.D 41.A 42.B 43.D 44.B 45.D 46.D 47.B 48.B 49.A 50.D LỜI GIẢI CHI TIẾT
Câu 1. Cho hai số phức z  3  2i và w  1 4i . Số phức z  w bằng A. 4  2i . B. 4  2i . C. 2   6i . D. 2  6i . Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Đinh Ngọc Chọn B
z  w  3  2i 1 4i  4  2i .
Câu 2. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 y  x  3x 1. B. 4 2 y  x  4x 1 . C. 3 y  x  3x 1. D. 4 2 y  x  2x 1. Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Đinh Ngọc Chọn C
Dựa vào đồ thị ta thấy đây là hàm số bậc 3 có hệ số a  0 nên chọn C. 4 4 4 Câu 3. Nếu f  xdx  4 và g  xdx= 3 thì  f
 x gxdx  bằng 1 1 1 A. 1. B. 7  . C. 1. D. 7 . Lời giải
GVSB: Đỗ Minh Vũ; GVPB: Đinh Ngọc Chọn D 4 4 4  f
 x gxdx  f   xdx  g
 xdx  4 3  7. 1 1 1 x 1
Câu 4. Tiệm cận đứng của đồ thị hàm số y 
là đường thẳng có phương trình x  2 B. x  2 . B. x  1 . C. x  2 . D. x  1 . Lời giải
GVSB: Trần Minh Tâm; GVPB: Đinh Ngọc Chọn C Trang 7
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN x 1 x 1 Ta có: lim   , lim   . x 2  x 2 x 2    x  2
Đồ thị hàm số có tiệm cận đứng là đường thẳng có phương trình x  2 . Câu 5.
Trong không gian Oxyz, cho mặt cầu (S) có tâm I( 1
 ;3;0) và bán kính bằng 2 . Phương trình của (S) là A. 2 2 2
(x 1)  ( y  3)  z  2 . B. 2 2 2
(x 1)  ( y  3)  z  4 . C. 2 2 2
(x 1)  ( y  3)  z  4 . D. 2 2 2
(x 1)  ( y  3)  z  2 . Lời giải
GVSB: Trần Minh Tâm ; GVPB: Đinh Ngọc Chọn C Mặt cầu (S) có tâm I ( 1
 ;3;0) và bán kính R  2 . Phương trình của mặt cầu (S) là : 2 2 2
(x 1)  ( y  3)  z  4 Câu 6.
Tập nghiệm của bất phương trình 2x  5 là A. ( ;  log 5) . B. (log 2;  ) . C. (;log 2) . D. (log 5; ) 2 5 5 2 Lời giải
GVSB: Trần Minh Tâm; GVPB: Đinh Ngọc Chọn D
Ta có: 2x  5  x  log 5. 2
Tập nghiệm của bất phương trình là : (log 5;  ) 2 Câu 7.
Thể tích của khối lập phương cạnh 2a bằng B. a3. B. 2a3. C. 8a3. D. 4a3. Lời giải
GVSB: Nguyễn Hòa; GVPB: Đinh Ngọc Chọn C Ta có V   a3 3 2  8a . 5 Câu 8.
Trên khoảng 0; , đạo hàm của hàm số 3 y  x là 8 3 2 5 2 5  2 3 B. 3 y  x . B. 3 y  x . C. 3 y  x . D. 3 y  x . 8 3 3 5 Lời giải
GVSB: Nguyễn Hòa; GVPB: Đinh Ngọc Chọn B 5 2 5 1  5 Ta có: 3 3 y  x  x . 3 3  Câu 9.
Trong không gian Oxyz , cho điểm A2;1;4. Tọa độ của véc tơ OA là A.  2  ;1;4. B. 2; 1  ;4 . C. 2;1;4 . D.  2  ;1; 4   . Lời giải
GVSB: Nguyễn Hòa; GVPB: Đinh Ngọc Trang 8
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104 Chọn B 
Ta có: OA  2  0;1 0;4  0 hay OA  2;1;4. 3 3 Câu 10: Nếu f
 xdx  3 thì 4 f xdx  bằng 0 0 A. 3 . B. 12 . C. 36 . D. 4 . Lời giải
GVSB: Đỗ Văn Trường; GVPB: Thanh Huyền Chọn B 3 3 3 Ta có: f  xdx  3 4 f  xdx  4 f  xdx  4.3 12. 0 0 0
Câu 11: Cho cấp số nhân u với u  2 và u  10 . Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 8 . B. 8 . C. 5. D. . 5 Lời giải
GVSB: Đỗ Văn Trường; GVPB: Thanh Huyền Chọn C u 10 Ta có: 2 u  u .q  q    5 . 2 1 u 2 1
Câu 12: Với n là số nguyên dương bất kì, n  3 , công thức nào dưới đây đúng? n  3 ! n! 3   n! A. A  . B. 3 3! A  . C. 3 A  . D. 3 A  . n n! n n 3! n n 3! n  3! n  3! Lời giải
GVSB: Đỗ Văn Trường; GVPB: Thanh Huyền Chọn C n! Ta có: 3 A  . n n3!
Câu 13. Cho hàm số f  x 2
 x  2 . Khẳng định nào dưới đây là đúng? 3 x A. f  xdx  2xC B. f  xdx   2x C 3 C. f  x 2 dx  x  2x  C D. f  x 3 dx  x  2x  C Lời giải
GVSB: Nguyễn Thành Tiến; GVPB: Thanh Huyền Chọn B x Ta có f
 x x  x   3 2 d 2 dx   2x  C 2
Câu 14. Cho hàm số y  f x có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng A. 0 B. 3 C. 1 D. 1 Lời giải
GVSB: Nguyễn Thành Tiến; GVPB: Thanh Huyền Trang 9
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN Chọn C
Từ bảng biến thiên suy ra giá trị cực tiểu là y  1.
Câu 15. Trong không gian Oxyz , cho mặt phẳng P : 2x  4y  z 1  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của mặt phẳng P     A. n  2; 4  ;1 B. n  2; 4;1 C. n  2;4; 1  D. n  2;4;1 4   3   1   2   Lời giải
GVSB: Nguyễn Thành Tiến; GVPB: Thanh Huyền Chọn C
Câu 16: Phần thực của số phức z  4  2i bằng A. 2 . B. 4  . C. 4 . D. 2  . Lời giải
GVSB: Nguyễn Bình; GVPB: Thanh Huyền Chọn C
Phần thực của số phức z  4  2i là 4
Câu 17: Nghiệm của phương trình log 5x  3 là: 2   8 9 A. x  . B. x  . C. x  8 . D. x  9 . 5 5 Lời giải
GVSB: Nguyễn Bình; GVPB: Thanh Huyền Chọn A Điều kiện x  0 8 log 5x  3 3
 5x  2  5x  8  x  (nhận). 2   5
Câu 18: Tập xác định của hàm số 8x y  là A.  \  0 . B.  . C. 0; . D. 0; . Lời giải
GVSB: Nguyễn Bình; GVPB: Thanh Huyền Chọn B
Tập xác định của hàm số 8x y  là 
Câu 19. Cho a  0 và a  1, khi đó 5 log a bằng a 1 1 A. . B.  . C. 5 . D. 5  5 5 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Nguyễn Minh Luận Chọn A 1 1 1 Ta có 5 5 log a  log a  log a  . a a 5 a 5
Câu 20. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d đi qua điểm M 1; 5 ;  2 có 
một véc tơ chỉ phương u 3 ;  6 ; 
1 . Phương trình của d là . x  3  t x  1 3t x  1 3t x  1 3t     A.  y  6   5t . B.  y  5  6t . C.  y  5  6t . D.  y  5  6t . z 1 2t     z  2  t  z  2   t  z  2   t  Trang 10
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Nguyễn Minh Luận Chọn D 
Đường thẳng d có véc tơ chỉ phương là u 3 ;  6 ; 
1 và đi qua điểm M 1; 5 ;  2 nên có x  1 3t 
phương trình tham số .  y  5  6t . z  2 t 
Câu 21. Trên mặt phẳng toạ độ , điểm M 4 ; 3 là điểm biểu diễn số phức nào dưới đây hai số phức nào dưới đây A. z  4  3i . B. z  4  3i . C. z  4  3i . D. z  4  3i . 3 4 2 1 Lời giải
GVSB: Hồng Hà Nguyễn; GVPB: Nguyễn Minh Luận Chọn D Điểm M  4
 ; 3 là diểm biểu diễn số phức z  4  3i . 1
Câu 22. Cho hàm số y  f x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 5 . Lời giải
GVSB: Nguyễn Thảo; GVPB: Nguyễn Minh Luận Chọn B
Từ bảng xét dấu ta thấy hàm số y  f  x đổi dấu khi qua x  2  ; x  1  ; x  2 ; x  4 . Do
đó, hàm số đã cho có 4 điểm cực trị.
Câu 23. Cho hàm số   ex f x 
 4 . Khẳng định nào dưới đây đúng? A.   d  ex f x x  4x  C . B.   d  ex f x x  C . C.    4 d  ex f x x  C . D.   d  ex f x x  4x  C . Lời giải
GVSB: Nguyễn Thảo; GVPB: Nguyễn Minh Luận Chọn A
Ta có:   d  ex  4d ex f x x x  4x  C .
Câu 24. Cho hàm số y  f  x có đồ thị là đường cong trong hình bên. Trang 11
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A.  1  ;  1 . B. 1; . C.  ;   1 . D. 0;3 . Lời giải
GVSB: Nguyễn Thảo; GVPB: Nguyễn Minh Luận Chọn A
Từ hình vẽ ta thấy hàm số đã cho nghịch biến trên khoảng  1  ;  1 .
Câu 25. Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S   R . B. 2 S  16 R . C. 2 S  4 R . D. 2 S   R . 3 Lời giải
GVSB: Võ Sĩ Đạt; GVPB: Trương Minh Mỹ Chọn C
Công thức diện tích S của mặt cầu bán kính R là: 2 S  4 R
Câu 26. Đồ thị của hàm số 3 2 y  2
 x  3x  5 cắt trục tung tại điểm có tung độ bằng A. 5  . B. 0 . C. 1. D. 2 . Lời giải
GVSB: Võ Sĩ Đạt; GVPB: Trương Minh Mỹ Chọn A
Gọi M x ; y là giao điểm của đồ thị hàm số 3 2
y  2x  3x  5 và trục tung, ta có: 0 0  x  0  y  5  0 0
Câu 27. Cho khối chóp có diện tích đáy 2
B  8a và chiều cao h  a . Thể tích của khối chóp đã cho bằng 4 8 A. 3 8a . B. 3 a . C. 3 4a . D. 3 a . 3 3 Lời giải
GVSB: Võ Sĩ Đạt; GVPB: Trương Minh Mỹ Chọn D Trang 12
NHÓM WORD & BIÊN SOẠN TÀI LIỆ U TOÁN
LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Thể tích của khối chóp có diện tích đáy 2
B  8a và chiều cao h  a là: 1 1 8 2 3 V  . B h  .8a .a  a 3 3 3
Câu 28. Cho khối trụ có bán kính đáy r  5 và chiều cao h  3. Thể tích của khối trụ đã cho bằng A. 15 . B. 75 . C. 25 . D. 45 . Lời giải
GVSB: Lê Thị Thu Trang; GVPB: Trương Minh Mỹ Chọn B Thể tích khối trụ: 2 2
V   r h   .5 .3  75 .
Câu 29. Trong không gian Oxyz , cho điểm M 2;1; 2
  và mặt phẳng P:3x  2y  z 1 0 . Đường
thẳng đi qua M và vuông góc với P có phương trình là:       A. x 2 y 1 z 2   . B. x 2 y 1 z 2   . 3 2 1 3 2 1       C. x 2 y 1 z 2   . D. x 2 y 1 z 2   . 3 2 1 3 2 1 Lời giải
GVSB: Lê Thị Thu Trang; GVPB: Trương Minh Mỹ Chọn A  
Đường thẳng đi qua M và vuông góc với P có VTCP: u  n  3;2;  1 . P   
Phương trình đường thẳng cân tìm là : x 2 y 1 z 2   . 3 2 1
Câu 30. Cho hình lăng trụ đứng ABC.A' B 'C ' có tất cả các cạnh bằng nhau ( tham khảo hình bên).
Góc giữa hai đường thẳng AB ' và CC ' bằng A. 30 . B. 90 . C. 60 . D. 45 . Lời giải
GVSB: Lê Thị Thu Trang; GVPB: Trương Minh Mỹ Chọn D Trang 13
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Ta có BB ' //CC ' (do BB ' và CC ' là cạnh bên của hình lăng trụ). Suy ra  AB',CC'  AB',BB'.
Tứ giác ABB ' A' là hình vuông (do ABC.A' B 'C ' là lăng trụ đứng có tất cả các cạnh bằng nhau) nên  AB ' B  45 . Vậy  AB',CC'  AB',BB'  AB ' B  45 .
Câu 31. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  4a và SA vuông góc với
mặt phẳng đáy. Khoảng cách từ C đến mặt phẳng SAB bằng A. 4a . B. 4 2a . C. 2 2a . D. 2a . Lời giải
GVSB: Chương Huy; GVPB: Cô Long Chọn A BC  AB gt 
Ta có: BC  SA do SA   ABC
 BC  SAB tại B .  Trong mp  SAB: AB  SA  A
Suy ra d C,SAB  CB . Xét A
 BC vuông cân tại B có: BC  AB  4a .
Vậy d C,SAB  4a . 2 2 Câu 32. Nếu f
 xdx  4 thì 2 f  x1 dx  bằng 0 0 Trang 14
NHÓM WORD & BIÊN SOẠN TÀI LIỆ U TOÁN
LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104 A. 8 . B. 10 . C. 7 . D. 6 . Lời giải
GVSB: Chương Huy; GVPB: Cô Long Chọn D 2 2 2 Ta có: 2 f
 x1 dx  2 f 
 xdx  dx 2.42  6  . 0 0 0 x  a
Câu 33. Biết hàm số y 
( a là số thực cho trước, a  1) có đồ thị như trong hình bên. Mệnh đề x 1 nào dưới đây đúng ? y O x A. y '  0,x  R . B. y '  0,x  1. C. y '  0,x  R . D. y '  0,x  1. Lời giải
GVSB: Lương Công Hảo; GVPB: Trịnh Đềm Chọn B 1 a Ta có TXĐ: D  R \  1 và y ' 
 0,x  1 và đồ thị là đường đi xuống trên từng 2 (x 1)
khoảng xác định nên hàm số đã cho nghịch biến trên mỗi khoảng xác định.
Câu 34. Cho số phức z thỏa mãn iz  4  3i . Số phức liên hợp z là A. z  3  4i . B. z  3   4i . C. z  3  4i . D. z  3   4i . Lời giải
GVSB: Lương Công Hảo; GVPB: Trịnh Đềm Chọn A 2 4  3i (4  3i).(i) 4i  3i Ta có: z   
 3  4i . Suy ra z  3 4 .i 2 i i 1
Câu 35. Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng
thời 3 quả. Xác suất để lấy được 3 quả màu đỏ bằng 1 7 5 2 A. . B. . C. . D. . 22 44 12 7 Lời giải
GVSB: Phương Lan; GVPB: Nguyễn Chiên Chọn A Không gian mẫu n  3  C . 12
Gọi A là biến cố “ cả 3 quả bóng lấy ra đều là màu đỏ”  n A 3  C . 5 Trang 15
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN 3 n A C 1
Xác suất để lấy được 3 quả màu đỏ là: P  A   5    . n  3 C 22 12
Câu 36. Với mọi a,b thỏa mãn 3
log a  log b  5 , khẳng định nào dưới đây là đúng? 2 2 A. 3 a b  32 . B. 3 a b  25 . C. 3 a  b  25 . D. 3 a  b  32 . Lời giải
GVSB: Phương Lan; GVPB:Nguyễn Chiên Chọn A Ta có: 3
log a  log b  5  log  3 a b 3  5  a b  32 . 2 2 2 Câu 37. Trên đoạn  1  ;2, hàm số 3 2
y  x  3x  1 đạt giá trị nhỏ nhất tại điểm A. x  2. B. x  0 . C. x  1  . D. x  1. Lời giải
GVSB: ThienMinh Nguyễn; GVPB:Nguyễn Chiên Chọn B
Xét hàm số y  f  x 3 2  x  3x 1.  y  f  x 2  3x  6x . x  0 1  ;2 + f x 2
 0  3x  6x  0   . x  2     1  ;2 Ta có f  
1  3 , f 0  1 và f 2  21.
Nên min f  x  1 khi x  0 . x   1  ;2
Câu 38. Trong không gian Oxyz , cho hai điểm A1;0;0 và B3;2; 
1 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 2x  2y  z  2  0.
B. 4x  2 y  z  17  0 .
C. 4x  2 y  z  4  0 .
D. 2x  2 y  z 11  0 . Lời giải
GVSB: ThienMinh Nguyễn; GVPB:Nguyễn Chiên Chọn A 
Phương trình mặt phẳng P đi qua A1;0;0 nhận vectơ AB  2;2;  1 là VTPT có dạng: 2x  
1  2 y  0 1z  0  0  2x  2y  z  2  0 .
Câu 39. Cho hàm số bậc bốn y  f  x có đồ thị là đường cong trong hình bên. Số nghiệm thực phân
biệt của phương trình f  f  x  0 là A. 12 . B. 10 . C. 8 . D. 4 . Lời giải
GVSB: Duong Phan; GVPB: Nam Lê Hải Chọn B Trang 16
NHÓM WORD & BIÊN SOẠN TÀI LIỆ U TOÁN
LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Nhìn vào đồ thị ta thấy f (x)  0 có 4 nghiệm phân biệt theo thứ tự a,b, c, d .
 f  x  a,a  ;    1 
 f  x  b,b  1  ;0
Ta có: f  f  x  0   .
f  x  c,c 0;  1 
 f x  d,d 1;   
Dựa vào đồ thị ta thấy:
Phương trình f x  a có 2 nghiệm thực phân biệt.
Phương trình f x  b có 4 nghiệm thực phân biệt.
Phương trình f  x  c có 4 nghiệm thực phân biệt.
Phương trình f  x  d vô nghiệm trên  .
Vậy phương trình f  f  x  0 có 10 nghiệm thực phân biệt.
Câu 40. Có bao nhiêu số nguyên x thỏa mãn  2
2x  4x log x  25 3  0  3    ? A. 24 . B. Vô số. C. 25 . D. 26 . Lời giải
GVSB: Duong Phan; GVPB: Nam Lê Hải Chọn D Điều kiện: x  2  5. 2 2x  4x  0   log x  25  3  0 2  2x  4x  3  
log x  25  3  0     . 3   2 2x  4x  0 
log x  25  3  0  3   x  0 2 x x 2 2  4  0 x  2x  0  Trường hợp 1:      x  2 . log x  25  3  0  x  25  27 3    x  2 25  x  0 Vì x  2  5 nên ta có:  mà x   nên x 2  4, 23,...,1,0,  2   1 . x  2 2 x x 2 2  4  0 x  2x  0 0  x  2 Trường hợp 2:       x  2 2 . log x  25  3  0  x  25  27 x  2 3   Từ  
1 và 2 ta có 26 số nguyên x thỏa mãn  2
2x  4x log x  25 3  0  3    . Trang 17
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN GVPB đề xuất ĐK: x  2  5 x  0 Xét 2x x 2
2  4  0  x  2x  0  x  2
Xét log x  25  3  x  25  27  x  2 3   Ta có bảng xét dấu: x -25 0 2 +∞ + 0 - 0 + 2x2-4x log3(x+25)-3 - - 0 + VT - + + 0 0  25   x  0
Dựa vào bảng xét dấu ta có: BPT  x  2
x nguyên nên có 26 giá trị thỏa mãn bài toán. 2x  2 khi x 1
Câu 41. Cho hàm số f  x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3  x 1 khi x  1
F 0  2. Giá trị của F   1  2F 2 bằng A. 18 . B. 20 . C. 9 . D. 24 . Lời giải
GVSB: Quốc Hưng; GVPB: Nam Lê Hải Chọn A 1 1 Ta có: f  xdx   2 3x   1 dx  2  F   1  F 0  F   1  2  F 0  4 0 0 Trên khoảng  ;   1 , ta có: f
 xdx   2x   3 3 1 dx  x  x  C
Mà F     C   F  x 3 0 2 2  x  x  2.
Trên nửa khoảng 1; , ta có: f
 xdx   x   2 2 2 dx  x  2x  C
Mà F     C   F x 2 1 4 1  x  2x 1. Do đó: F  
1  2F 2  0  2.9 18. Câu 42.
Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30 , ta được thiết diện là tam giác đều cạnh 2a . Diện tích xung quanh của  N  bằng A. 2 7 a . B. 2 13 a . C. 2 2 13 a . D. 2 2 7 a . Lời giải
GVSB: Đặng Minh Nhựt; GVPB: Cao Phi Chọn B Trang 18
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104 S A H O B
Xét hình nón  N  và mặt phẳng SAB đi qua đỉnh cắt O tại A , B .
Gọi H là trung điểm của đoạn thẳng AB . AB 3 2 . a 3
Tam giác SAB đều nên SH    a 3 . 2 2
SAB OAB  AB  Ta có SH  AB  SAB,OAB     SH,OH   SHO  30 . OH  AB   SO a 3 sin SHO   SO  SH.sin 30  . SH 2 2      a  OB SB SO 2a2 3 13 2 2      . 2  2   a 13 Vậy 2 S   .S . B OB   .2 . a  13 a . xq 2 x y z 1
Câu 43. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2
P:x  2y 2z  2  0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình: x y z 1 x y z 1 x y z 1 x y z 1 A.   . B.   . C.   . D.   . 2 4 3 14 1 8 2 4 3 14 1 8 Lời giải
GVSB: Hoàng Văn Tĩnh; GVPB:Cao Phi Chọn D Gọi A0;0;  1 , B 1; 1
 ;3 là hai điểm thuộc đường thẳng d và A , B lần lượt là hình chiếu vuông góc của , A B lên P .
Dễ thấy AP nên A  A .
Gọi  là đường thẳng đi qua B và vuông góc với P   Có u  n    1;2; 2 P  Trang 19
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN  x 1 t 
Đường thẳng  đi qua B 1; 1
 ;3 và có VTCP u  1;2;2 có dạng: y  1 2t , t  z  3 2t 
Tọa độ điểm B là tọa độ giao điểm của  và P , tức là nghiệm của hệ  14   1 x x  t   9   y  1   2t  1 14 1 17    y   B ; ;   z  3  2t 9    9 9 9 
x  2y  2z  2  0  17 z   9
Gọi d là hình chiếu vuông góc của d lên P
  14 1 8    u     u   14;1;8  A B ; ; hay d   d    9 9 9  
PTCT của đường thẳng d đi qua A0;0;  1 và có VTCP u   14;1;8 có dạng: d  x y z 1   . 14 1 8  1 
Câu 44. Có bao nhiêu số nguyên y sao cho tồn tại x  ;6 2 
 thỏa mãn 3x xy     18 27 1 .27 x xy ?  3  A. 19 . B. 20 . C. 18. D. 21. Lời giải GVSB: Bùi Thanh Sơn; GVPB: Chọn B Ta có: 2 3x  xy     18 27 1 .27 x xy  2 3x  xy 1  8 27 x  1 xy  2 3x xy 1  8 27 x 1 xy  0 . 2 Mạt khác: 2        3x xy 18 3 18  x x xy x xy   xy    2 27 1 1 26 1
1 26 3x  xy 18x 1 xy 2  78x  25xy  468x . x  xy x  1  + Với y  19  2 3 18 2 2 27
1 xy  78x  25xy  468x  84x  7x  0 x   ;6   (loại).  3  x  xy x  1  + Với y  3  2 3 18 27
 1 xy  1 3x  0 x   ;6   (loại).  3  + Với y  2   1 x  (thỏa mãn). 2
+ Với y  1  x  1 (thỏa mãn). x  0 + Với y  0  2 3x 18 27  x  1  2 3x 18x  0   (loại). x  6
+ Với y  1: Đặt   2 3x  xy 1  8  27 x f x 1 xy .  1   y Do y 17 f  3 1  0 y     1;2;....;1  8 và   6 6  27 y f  6y 1  0 y  1;2;....;1  8 nên  3  3  1 
phương trình f  x  0 luôn có nghiệm thuộc ;6   .  3  Tóm lại y  2  ;1;1;2;....;1  8 .
Vậy có 20 số nguyên y thỏa mãn yêu cầu bài toán. Trang 20
NHÓM WORD & BIÊN SOẠN TÀI LIỆ U TOÁN
LỜ I GIẢI CHI TIẾT - MÃ ĐỀ 104
Câu 45. Trên tập hợp các số phức, xét phương trình 2 z  m   2 2
1 z  m  0 ( m là tham số thực). Có
bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  6 ? 0 0 A. 4 . B. 1. C. 2 . D. 3 . Lời giải
GVSB: Bùi Thanh Sơn; GVPB: Vân Vũ Chọn D
Ta có:   m  2 2 1  m  2m 1.  Nếu   0  1
m   : Phương trình có hai nghiệm phức z  m 1 2m 1.i . 2 m  6 lo¹i
Ta có: z  6  m  2 1  2m 1  36  2 m  36  0  m  6   tháa m·n  1 Nếu   0  1
m   : Phương trình có kép z  . 2 2 1 1
Khi đó z  nên m   không thỏa mãn. 2 2  Nếu   0  1
m   : Phương trình có hai nghiệm thực phân biệt z  m 1 2m 1 . 2 z  6 Ta có: z  6  0 0 z  6  0
+ Với z  6 : Thay vào phương trình ta được: 0
m  6  2 3 tháa m·n 2  m   2 6 2 1 .6  m  0  2
m 12m  24  0  m  62 3  tháa m·n
+ Với z  6 : Thay vào phương trình ta được: 0
 2  m     2 6 2 1 . 6  m  0  2
m 12m  48  0 v« nghiÖm .
Vậy có 3 giá trị m thỏa mãn yêu cầu bài toán.
Câu 46. Cho khối hộp chữ nhật ABC . D AB C  D
  có đáy là hình vuông, BD  4a , góc giữa hai mặt phẳng  A B
 D và  ABCD bằng 60. Thể tích của khối hộp chữ nhật đã cho bằng 16 3 16 3 A. 3 48 3a . B. 3 a . C. 3 a . D. 3 16 3a . 9 3 Lời giải
GVSB: Dương Quá; GVPB: Linh Pham Chọn D Trang 21
ĐỀ CHÍNH THỨC ĐỢT 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Gọi O là giao điểm của hai đường chéo AC và BD . Ta có: OA  BD        BD  A O  A A ABCD  A A   BD
Xét  ABD và  ABCD có:
 ABD ABCD  BD AO  BD
  góc giữa hai mặt phẳng  ABD và  ABCD là  AOA. A O BD       A O  A  60 . AA
Ta có: BD  4a  OA  2a và tan  AOA   AA  O . A tan 60  2 3a . OA 1 1 Vậy V      2 3 . a .4a2 3      AA .S AA . AC.BD 16 3a . ABCD.A B C D ABCD 2 2 Câu 47. Cho hàm số   3 2
f x  x  ax  bx  c với a,b, c là các số thực. Biết hàm số
g x  f  x  f x  f   x có hai giá trị cực trị là 5
 và 2 . Diện tích hình phẳng giới hạn f  x bởi đường y  và y  1 bằng g  x  6 A. ln 3 . B. 3ln 2 . C. ln10. D. ln 7 . Lời giải
GVSB: Nguyễn Minh Thành; GVPB: Thanh Hảo Chọn B
Ta có f   x  6 .
Khi đó gx f x f  x f x f x f  x6.
Giả sử x , x x  x là hai điểm cực trị của hàm số gx. 1 2  1 2  gx  2 1 
Vì lim g x  và 5
 và 2 là hai giá trị cực trị của hàm số gx nên  .  x g  x  5 2   f  x
Phương trình hoành độ giao điểm của y  và y  1 là: g  x  6 Trang 22
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104
f x   gx6 f x  f x f x f x6  f x g x 1 6  
 f x f  x x x1 6  0   .  x  x2 
Khi đó diện tích hình phẳng cần tìm là: 2 x f x 2 x
f x f  x6 S   x  x   g x  g x  x   1 d x   d 6 6 1 1 2 x gx 2 x  x  g x  
 ln gx 6 ln g x 6  ln8  3ln 2. 2   1 g x  x   d ln   6 6 1 x 1
Câu 48. Xét các số phức z ; w thỏa mãn z  1 và w  2 . Khi z  iw  6  8i đạt giá trị nhỏ nhất, z  w bằng: 29 221 A. . B. . C. 3 . D. 5 . 5 5 Lời giải GVSB: Bùi Thanh Sơn; GVPB: Chọn B
Do w  2 nên iw  iw  i . w  2 .
Ta có: z  iw  6  8i  6  8i  z  iw  7 .  1  1 k    k   
z  k 6  8i k  0 10  10   1  1  i
 w  m6  8i m  0 m   m      Dấu bằng xảy ra  5 5      z  1  3 4  3 4 z    i z    i  iw  2  5 5  5 5   6 8  8 6 i  w    i w   i  5 5  5 5 3 4 8 6 221
Khi đó z  w    i   i  . 5 5 5 5 5
Câu 49. Trong không gian Oxyz , cho hai điểm A 2  ;13 và B1; 3
 ;2 . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  3. Giá trị lớn nhất của AM  BN bằng: A. 65 . B. 29 . C. 26 . D. 91. Lời giải
GVSB: Nguyễn Cảnh Chiến; GVPB: Nguyễn Loan Chọn A Trang 23
ĐỀ CHÍNH THỨ C ĐỢ T 1 NĂM 2021 – MÃ 104
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
Nhận xét: A và B nằm khác phía so với mặt phẳng Oxy .
Gọi P là mặt phẳng qua A và song song với mặt phẳngOxy  P : z  3 .
B đối xứng với B qua mặt phẳng Oxy  B1; 3;2 .
B là hình chiếu của B trên mặt phẳng P  B 1;3;3 . 1   1 A  A   3 Gọi 
A  T  A  MN A   A  Oxy  
A thuộc đường tròn C có tâm A và bán kính R  3 , C nằm trên mặt phẳng P .
Ta có: AM  BN  AN  BN  AN  B N   A B  
AB  5  R  B nằm ngoài đường tròn C . 1 1
Do A P , BP mà P  Oxy suy ra A B
  luôn cắt mặt phẳng Oxy . Ta lại có: 2 2 A B    B B  A B  mà B B  1; AB  5   A B   A B  AB  R  8 1 1 1 1 max 1 max 1  AM  BN
 65 . Dấu "  " xảy ra khi A là giao điểm của AB với đường tròn C, max 1
A ở giữa A và B và N là giao điểm của A B
  với mặt phẳng Oxy. 1
Câu 50. Cho hàm số y  f  x có đạo hàm f x  x   2
9 x 16,x  . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g  x  f  3
x  7x  m có ít nhất 3 điểm cực trị ? A. 16 . B. 9 . C. 4 . D. 8 . Lời giải
GVSB: Bùi Văn Huấn; GVPB: Lan Huong Chọn D x  Ta có: f x 9  0   . x  4   2 3x  7 3 x  7x g x  . f  3 x  7x  m . 2   3x7x Trang 24
NHÓM WORD & BIÊN SOẠN TÀI LIỆU TOÁN
LỜI GIẢI CHI TIẾT - MÃ ĐỀ 104  2 3x  7 3 x  7x
+) g x không xác định tại x  0 và
đổi dấu khi qua x  0 nên x  0 là x 7x2 3
một điểm cực trị của hàm số.  3  3 x  7x  m  4 x  7x  m  4     +) f  3 x  7x  m 3 3
 0  x  7x  m  4  x  7x  m  4   .   1   3 3  x  7x  m  9  x  7x  m  9  
Ta có bảng biến thiên của hàm số u  x với u x 3  x  7x
Để hàm số g  x có ít nhất 3 điểm cực trị thì hệ  
1 phải có ít nhất 2 nghiệm đơn hoặc nghiệm
bội lẻ khác 0 . Mà ta lại thấy m  9  m  4  m  4 .
Nên suy ra m  9  0  m  9 .
Vậy có 8 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán là m 1, 2,...,  8 . Trang 25
Document Outline

  • NHM-TO~1
  • NHM-WO~1
  • NHM-TO~2
  • NHM-WO~2