Đề chọn HSG Toán 10 năm 2024 – 2025 trường THPT Phùng Khắc Khoan – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HSG CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC KHOAN
KHỐI 10, 11-NĂM HỌC 2024-2025 - THẠCH THẤT
ĐỀ THI MÔN: TOÁN- LỚP 10
Thời gian làm bài 150 phút ĐỀ CHÍNH THỨC
(không kể thời gian giao đề) (Đề thi gồm 02 trang)
Số báo danh:..................... Họ và tên ............................................................................. Câu 1: ( 4 điểm)
1) Tìm tập xác định của hàm số 𝑦 = + √2𝑥 − 1 √ x 2 1
2) Tìm m để hàm số y 
có tập xác định là ℝ. 2 x  2x  m 1 Câu 2: ( 2điểm)
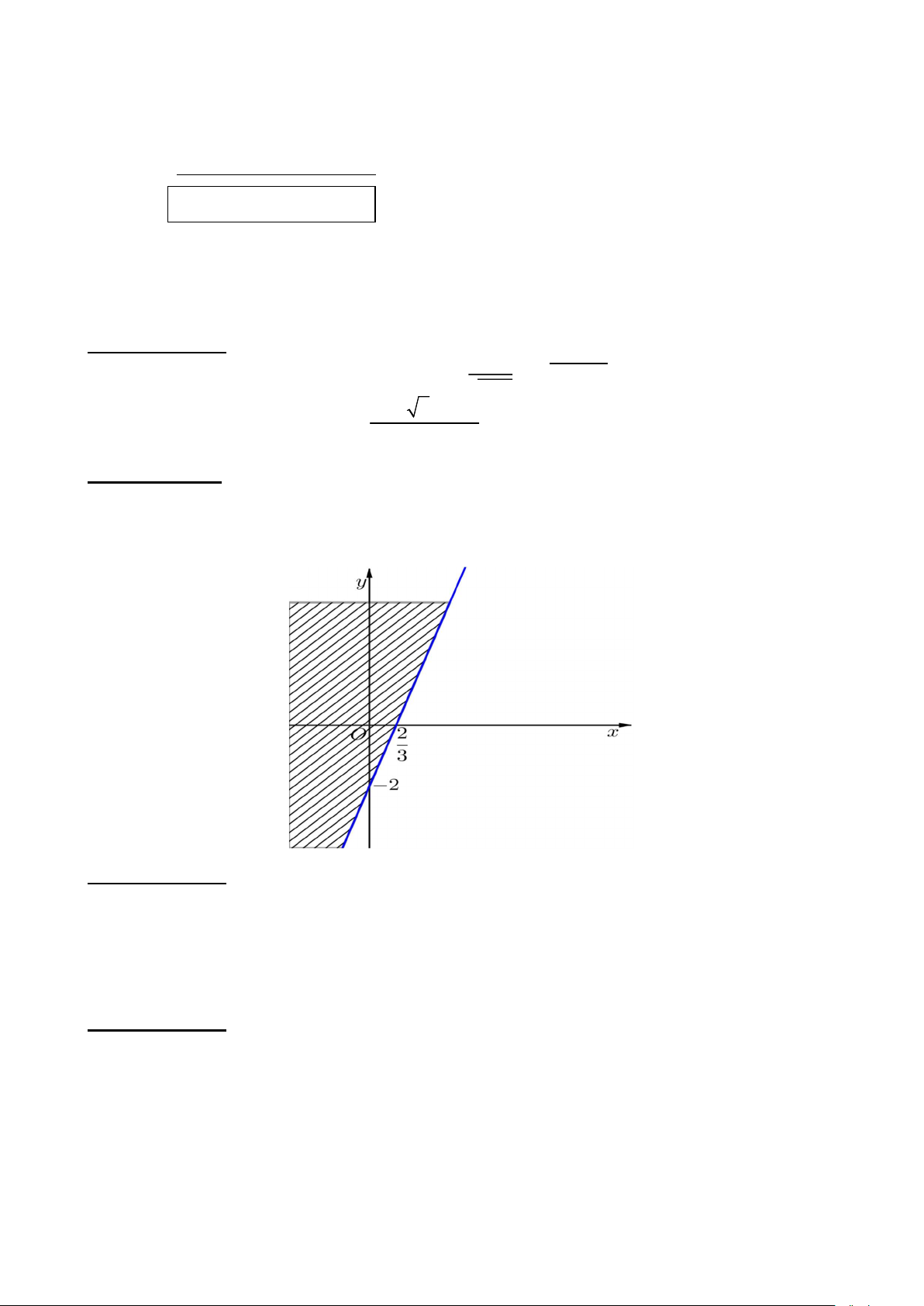
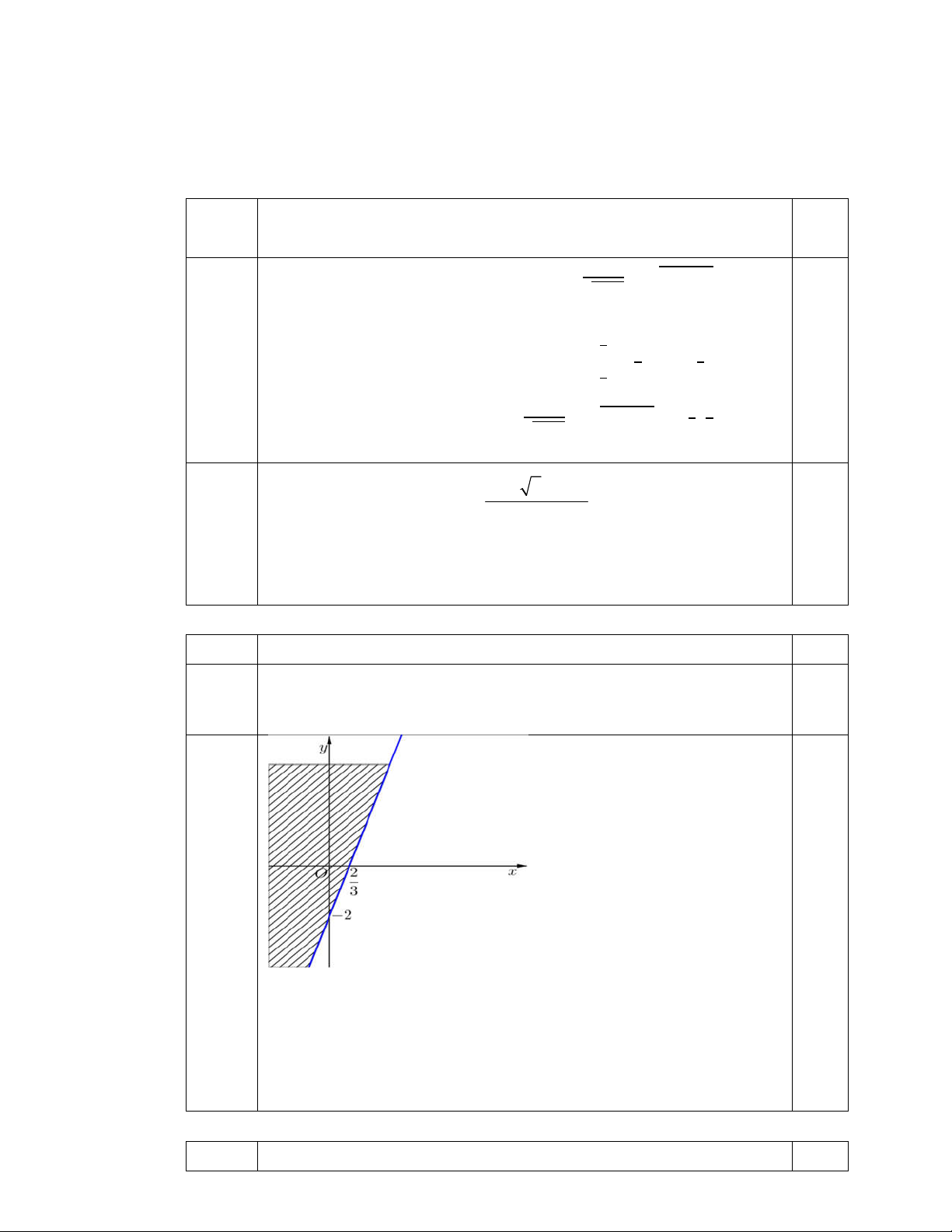
Khi biểu diễn hình học tập nghiệm của bất phương trình 𝑎𝑥 + 𝑏𝑦 + 2 ≤ 0. ta được miền
nghiệm trong hình vẽ sau đây. Hãy tìm giá trị a và b Câu 3: ( 3 điểm)
Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ℎ𝑎. Trên diện tích mỗi ℎ𝑎, nếu
trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu
đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ℎ𝑎 để thu được nhiều tiền
nhất, biết rằng tổng số công không quá 180 công. Câu 4: ( 2 điểm)
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình
tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính
của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả
như hình vẽ ( AB  4,3 cm; BC  3,7 cm; CA  7,5 cm). Tính đường kính của chiếc đĩa này.(kết
quả làm tròn đến phần trăm) Đề thi môn Toán 10 Trang 1/ 2 trang Câu 5: ( 4 điểm)
1) Cho tam giác ABC không cân, nội tiếp đường tròn tâm O và có trọng tâm G . Gọi
M , N, P lần lượt là trọng tâm các tam giác OBC, OC , A OAB và G' là trọng tâm
của tam giác MNP .Chứng minh ba điểm O,G,G ' thẳng hàng.
2) Cho tam giác 𝐴𝐵𝐶 có 𝐴(3; 4), 𝐵(2; 1), 𝐶(−1; −2). Tìm tọa độ điểm 𝑀 trên đường thẳng 𝐵𝐶 sao cho 𝑆 = 3𝑆 . ( S là diện tích) Câu 6: ( 5 điểm)
a) Cho hình vuông 𝐴𝐵𝐶𝐷 cạnh 𝑎. Tính giá trị biểu thức sau: (𝐴𝐵⃗ + 𝐴𝐷⃗)(𝐵𝐷⃗ + 𝐵𝐶⃗)
b) Cho tam giác ABC đều cạnh 𝑎. Lấy các điểm 𝑀, 𝑁, 𝑃 lần lượt nằm trên ba cạnh
𝐵𝐶, 𝐶𝐴, 𝐴𝐵 sao cho 𝐵𝑀 = 𝐵𝐶, 𝐴𝐶 = 2𝐴𝑁, 𝐴𝑃 = 𝑥, 0 < 𝑥 < 𝑎. Tính 𝑥 theo 𝑎
để 𝐴𝑀 vuông góc với 𝑁𝑃. c)
Cho tam giác ABC có AB = c, BC = a, CA = b. Trung tuyến CM vuông góc với phân giác trong CM AD và 3 
. Tính giá trị của cos A AD 2
------------- HẾT -------------
(Thí sinh không dùng tài liệu, cán bộ coi thi không giải thích gì thêm Đề thi môn Toán 10 Trang 2/ 2 trang ĐÁP ÁN THANG ĐIỂM
Để được điểm tối đa cần lập luận chính xác chặt chẽ, trình bày rõ ràng Câu 1 Nội dung Điểm 2
a) Tìm tập xác định của hàm số = + √2 − 1 √ 2 − 3 > 0 < xác định ⇔ ⇔ ⇔ ≤ < . 2 − 1 ≥ 0 1 ≥
Vậy tập xác định của hàm số =
+ √2 − 1 là [ ; . 1 √ 2 x 2 1
b) Tìm m để hàm số y 
có tập xác định là ℝ. 2
x  2x  m 1
Hàm số có tập xác định ℝ khi + 2 − + 1 ≠ 0, ∀ ⇔ 1 ′ = 1 + − 1 < 0 ⇔ < 0. 1 Câu 2 Nội dung Điểm
Biểu diễn hình học tập nghiệm của bất phương trình + + 2 ≤ 0. 2
ta được miền nghiệm tìm a và b
Biểu diễn hình học tập nghiệm của bất phương trình + + 2 ≤ 0. ta
được phần không chứa gốc tọa độ 0 1 phương trình +
+ 2 = 0 của (d) qua (0;-2) và (2/3;0) 1
thay vào tính được a = -3 và b=1 Câu 3 Nội dung Điểm 3
Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ℎ . Trên
diện tích mỗi ℎ , nếu trồng dứa thì cần 20 công và thu 3 triệu đồng,
nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng
mỗi loại cây trên với diện tích là bao nhiêu ℎ để thu được nhiều
tiền nhất, biết rằng tổng số công không quá 180.
Gọi , lần lượt là số ℎ trồng dứa và củ đậu. 3 Có 0 ≤ ≤ 8; 0 ≤ ≤ 8; +
≤ 8; 20 + 30 ≤ 180 ⇒ 2 + 3 ≤ 18.
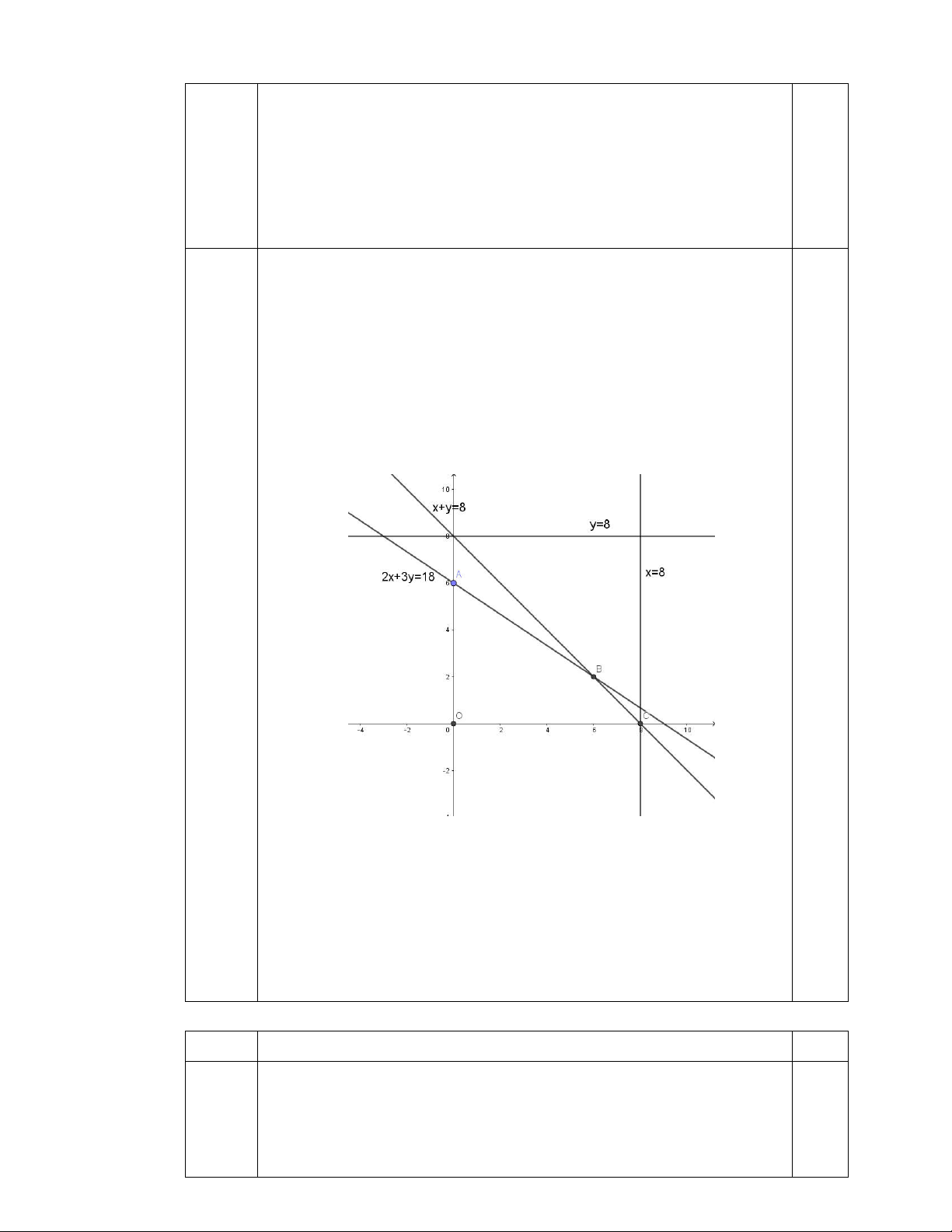
Số tiền thu được là ( , ) = 3 + 4 . 0 ≤ ≤ 8 0 ≤ ≤ 8 Ta có hệ 1 + ≤ 8 2 + 3 ≤ 18
Miền nghiệm của hệ là miền tứ giác
với (0; 6), (6; 2), (0; 8). 0,5
Khi đó ( , ) đạt cực đại tại một trong các đỉnh của .
Có (0,0) = 0; (0; 6) = 24; (6; 2) = 26; (8; 0) = 24. 0,5 0,5
Vậy cần trồng 6 ℎ dứa và 2 ℎ củ đậu. 0,5 Câu 4 Nội dung Điểm
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được 2
một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại
hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà
khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả 4
như hình vẽ ( AB  4, 3 cm; BC  3, 7 cm; CA  7,5 cm). Tính bán kính của chiếc đĩa này.
Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC .
Nửa chu vi của tam giác ABC là:
AB  BC  CA 4, 3  3, 7  7, 5 31 p    cm. 0,5 2 2 4
Diện tích tam giác ABC là: 0,5 S 
p  p  AB p  BC  p  CA  5, 2 cm2. . AB BC.CA . AB BC.CA Mà S   R   5, 73 cm. 4R 4S 2R = 11,46 cm 0,5 0,5 Câu 5 Nội dung Điểm 2
1) Cho tam giác ABC không cân, nội tiếp đường tròn tâm O và có
trọng tâm G . Gọi M , N , P lần lượt là trọng tâm các tam giác OBC, OC ,
A OAB và G ' là trọng tâm của tam giác MNP .Chứng
minh ba điểm O,G,G ' thẳng hàng.  1    1    1  
Ta có OM  OB  OC,ON  OC  OA,OP  OA  OB 0,5 3 3 3
   2    
Suy ra OM  ON  OP 
OA OB  OC  2OG 0,5 3
   
Lại có G ' là trọng tâm tam giác ABC nên OM  ON  OP  3OG '   0,5
Suy ra 3OG '  2OG  O, G, G ' thẳng hàng 0,5 5 2 2) Cho tam giác
có (3; 4), (2; 1), (−1; −2). Tìm điểm trên đường thẳng sao cho = 3 . ( S là diện tích) Ta có = 3 ⇔ = 3 ⇒ ⃗ = ±3 ⃗ 0,5 Gọi ( ; ) ⇒
⃗( − 2; − 1); ⃗(−3; −3) −3 = 3( − 2) = 1 0,5 Suy ra ⇔ −3 = 3( − 1) = 0 −3 = −3( − 2) = 3 0,5 hoặc ⇔ −3 = −3( − 1) = 2
Vậy có hai điểm thỏa mãn (1; 0), (3; 2). 0,5 Câu Nội dung Điểm 6 2 1-Cho hình vuông
cạnh . Tính giá trị các biểu thức sau: ( ⃗ + ⃗)( ⃗ + ⃗)
Theo quy tắc hình bình hành ta có ⃗ + ⃗ = ⃗ Do đó (
⃗ + ⃗)( ⃗ + ⃗) = ⃗. ⃗ + ⃗. ⃗ 0,5 = ⃗. ⃗ = ⃗ . ⃗ cos 0,5 ( ⃗. ⃗ = 0 vì ⃗ ⊥ ⃗) Mặt khác
= 45 và theo định lý Pitago ta có : 0,5 = √ + = √2 Suy ra (
⃗ + ⃗)( ⃗ + ⃗) = . √2 4 5 = 0,5 ABC 2 Cho tam giác
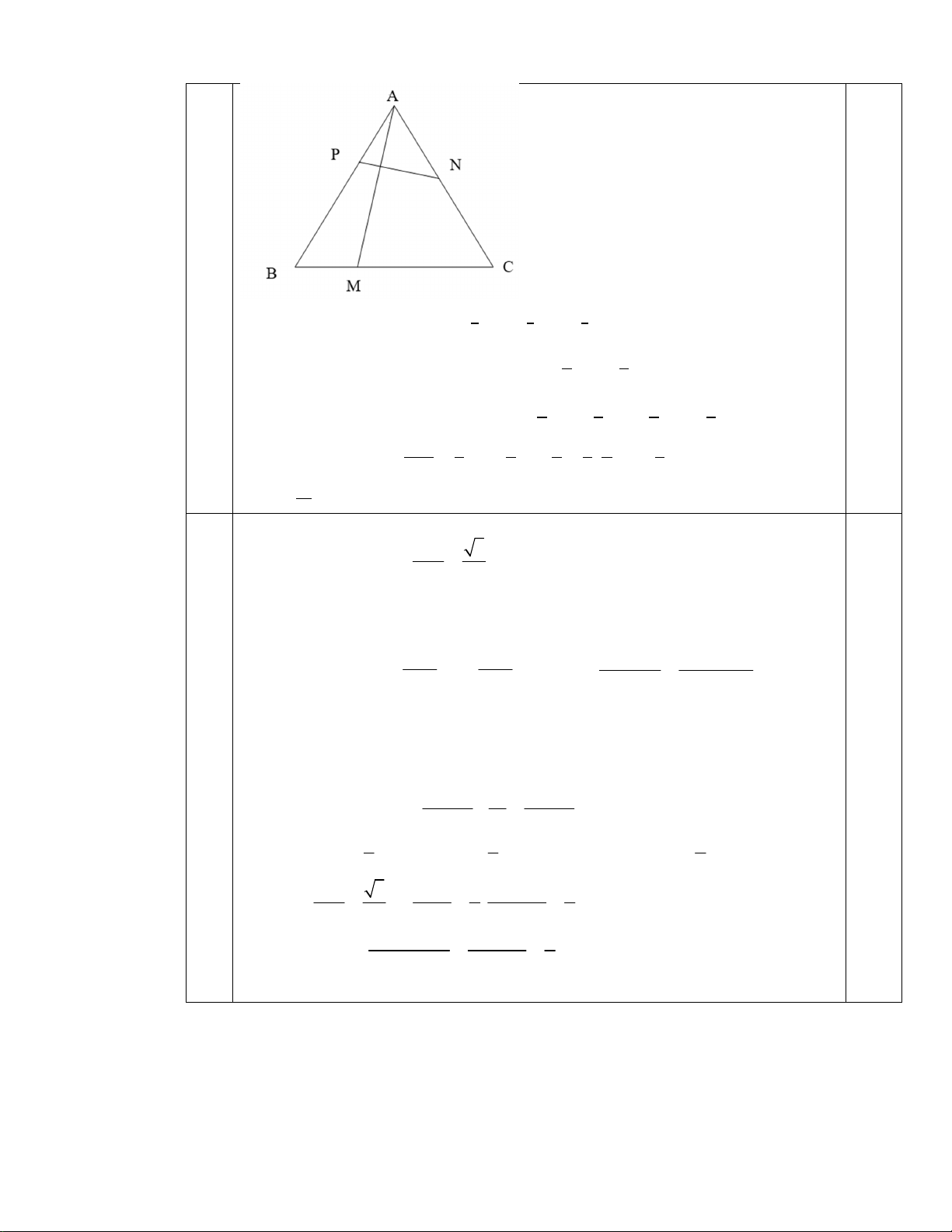
đều cạnh . Lấy các điểm ,
, lần lượt nằm trên ba cạnh , , sao cho = , = 2 , = , 0 < < . Tính theo để vuông góc với . 6 0,5 0,5 0,5 Ta có ⃗ = ⃗ + ⃗ = ⃗ + ⃗ = ⃗ + ⃗ 1 ⃗ = ⃗ − ⃗ = ⃗ − ⃗ 0,5 2 2 1 1 ⊥ ⇔ ⃗ ⊥ ⃗ = 0 ⇔ ⃗ + ⃗ ⃗ − ⃗ = 0 3 3 2 2 1 1 1 1 1 ⇔ − − . . + . . . . = 0 3 6 3 2 3 2 ⇔ = .
Cho tam giác ABC có AB  c , BC  a , CA  b . Trung tuyến CM vuông góc với 1 CM 3
phân giác trong AD và 
.Tính giá trị của cos A AD 2      b 
c   CA  CB AB  2 AC Ta có: AD  AB  AC , CM   b  c b  c 2 2 0,5  
Theo giả thiết: AD  CM  A . D CM  0    
 bAB  cAC AB  AC 2 2 2 2 2
 0  bc  bc cos A  2cb cos A  2cb  0
 c  2b1 cos A  0  c  2b (do cos A  1) 2 2 2 2 2 b  a c a  b Khi đó: 2 CM    2 4 2 1     AD 
 AB  2AC2 1 2 2   2 2
AB  4AC  4A . B AC    2 2 9b  a  0,5 9 9 9 2 2 2 CM 3 CM 9 a  b 3 2 2    .   a  3b 2 2 2 AD 2 AD 4 9b  a 4 2 2 2 2 2
b  c  a 5b  a 1 cos A    . 2 2bc 4b 2 7
Document Outline

• Toan 10-Dung.pdf (p.1-2)
• DE HSG LOP 10 nam 24-25.pdf (p.3-7)