PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ II CẨM GIÀNG
NĂM HỌC: 2022 - 2023 Môn: TOÁN 7 ĐỀ CHÍNH THỨC Thời gian: 90 phút
(Đề gồm có: 01 trang) Câu 1 (2,0 điểm)
a) Cho đa thức: P = 2x3+ 2x + 5x 2 + 7. Sắp xếp các hạng tử của đa thức P
theo lũy thừa giảm dần của biến rồi tìm bậc, hệ số cao nhất, hệ số tự do của đa thức P.
b) Tính giá trị của biểu thức A= 2
4x − 2x +1 tại x = 5.
Câu 2 (1,0 điểm) Chọn ngẫu nhiên một số trong bốn số 6; 7; 8 và 9. Xét ba biến
cố sau: A: “Chọn được số tự nhiên”.
B: “Chọn được số nguyên tố”.
C: “Chọn được số chia hết cho 5”.
a) Em hãy cho biết trong ba biến cố A, B, C biến cố nào là: biến cố chắc
chắn, biến cố không thể, biến cố ngẫu nhiên?
b) Tìm xác suất để chọn được số nguyên tố. Câu 3 (3,0 điểm)
a) Thực hiện phép tính: (3x + 2)(2x – 1)
b) Thực hiện phép tính: (x 2 – 5x – 8) + (4x 2 + 2x – 3)
c) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:
Q = 5x.2x – x(7x – 5) + (12x4 + 20x3 – 8x2):(– 4x2) Câu 4 (2,0 điểm)
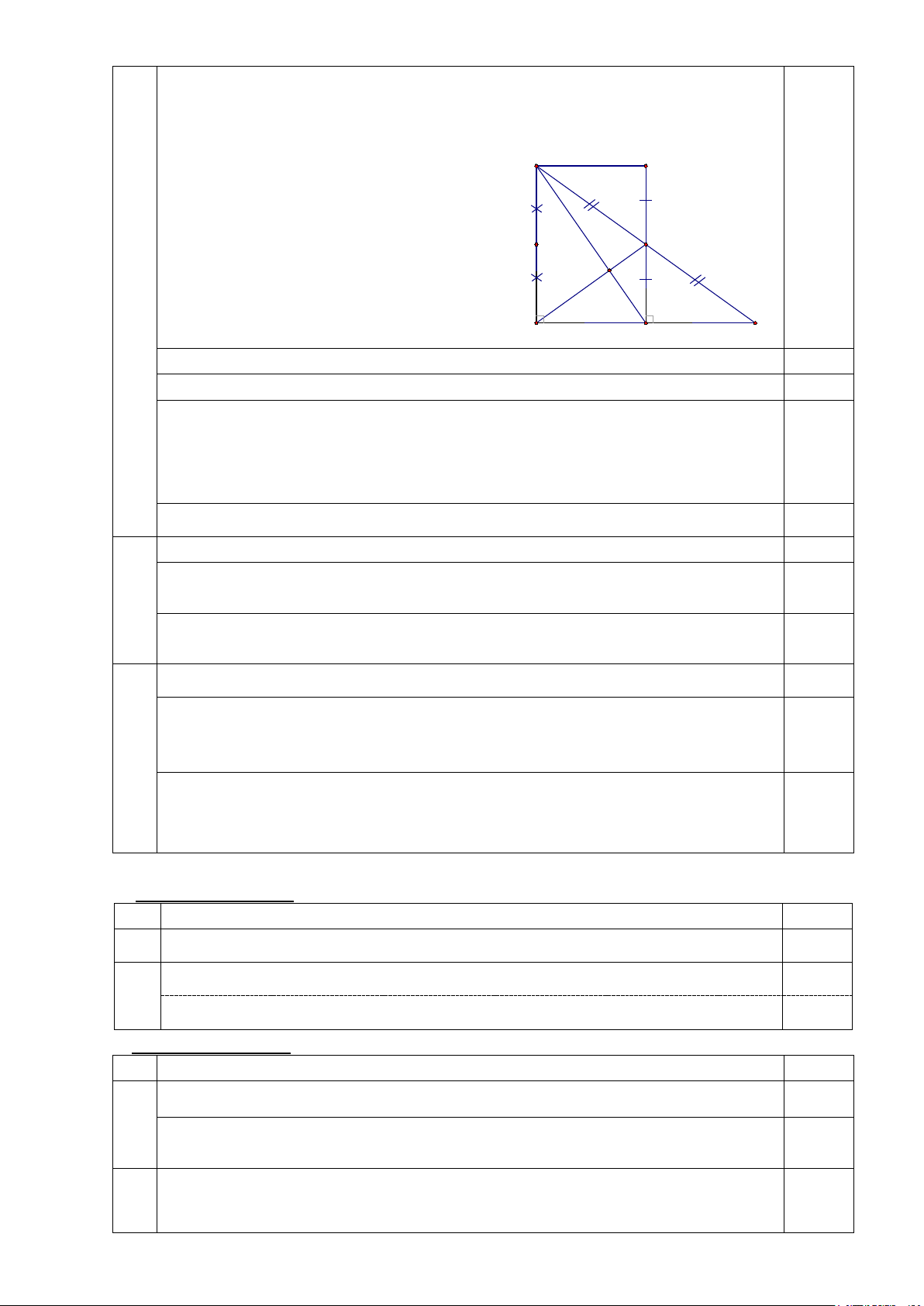
Cho ∆ABC vuông tại A, vẽ đường trung tuyến AM (M ∈ BC). Từ M kẻ
MH ⊥ AC (H ∈ AC), trên tia đối của tia MH lấy điểm K sao cho MK = MH.
a) Chứng minh: ∆MHC = ∆MKB.
b) Chứng minh: AB // MH và BK < MC.
c) Gọi G là giao điểm của BH và AM, I là trung điểm của AB. Chứng
minh: ba điểm I, G, C thẳng hàng. Câu 5 (1,0 điểm)
a) Tính diện tích xung quanh của một hình lăng trụ đứng có chiều cao 7 dm
và đáy là tam giác đều cạnh 4 dm.
b) Một hộp đựng đầy sữa tươi có dạng hình hộp chữ nhật có chiều dài 10 cm,
chiều rộng 7,5 cm và chiều cao 20 cm. Hỏi trong hộp chứa bao nhiêu lít sữa tươi? Câu 6 (1,0 điểm)
a) Tìm giá trị của a để đa thức F(x) = 2x3 – 7x2 + 12x + a chia hết cho đa thức G(x) = x + 2.
b) Cho đa thức A(x) thỏa mãn: (x − 4) A(x) = (x + 2) A(x − ) 1 . Chứng
minh rằng đa thức A(x) có ít nhất 2 nghiệm phân biệt. ----- Hết -----
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM CẨM GIÀNG
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
NĂM HỌC: 2022 - 2023 Môn: TOÁN 7 Thời gian: 90 phút
(HDC gồm có: 03 trang) Câu 1 (2,0 điểm). Ý Nội dung Điểm P = 2x3+ 5x 2 + 2x + 7 0,25 Bậc là 3 0,25 a Hệ số cao nhất là 2 0,25 Hệ số tự do là 7 0,25
Thay x= 5 vào biểu thức: 2
4x − 2x +1 ta được: A= 2 4.5 − 2.5 +1 0,5 b = 4.25-10+1 0,5 = 91
Vậy giá trị của biểu thức A tại x = 5 là 91 Câu 2 (1,0 điểm). Ý Nội dung Điểm
Biến cố A là biến cố chắc chắn 0,25 a
Biến cố C là biến cố không thể 0,25
Biến cố B là biến cố ngẫu nhiên 0,25 b
Xác suất để chọn được số nguyên tố là: 25% 0,25 Câu 3 (3,0 điểm). Ý Nội dung Điểm
(3x+2)(2x-1) = 6x2 – 3x + 4x - 2 0,5 a = 6x2 + x - 2 0,5
(x 2 – 5x – 8) + (4x 2 + 2x – 3) b
= x 2 - 5x – 8 + 4x 2 + 2x - 3 0,5 = 5x 2 - 3x - 11 0,5
Q =5x.2x – x(7x – 5) + (12x4 + 20x3 - 8x2):(-4x2)
Q = 10x2 – 7x2 + 5x – 3x2 – 5x + 2 0,5 c Q = 2
Vậy giá trị của biểu thức Q không phụ thuộc vào giá trị của 0,25 biến. 0,25 Câu 4 (2,0 điểm). Ý Nội dung Điểm
Vẽ hình đúng đến câu a K B 0,25 M I G A C H HS ghi đầy đủ GT và KL 0,25
a Chứng minh: ∆MHC = ∆MKB Xét ∆MHC và ∆MKB. MH = MK (gt)  0,25 =  HMC KMB (đối đỉnh) MC = MB (gt) ⇒ ∆MHC = ∆MKB (c.g.c) 0,25
Chứng minh: AB // MH và BK < MC Ta có : MH⊥ AC (gt) b AB⊥ AC (gt) nên MH // AB 0,25
Góc MHC vuông nên CH < MC Mà BK = CH nên BK < MC 0,25
Chứng minh: I, G, C thẳng hàng.
Chứng minh được: ∆ABH = ∆KHB(g.c.g) ⇒ AH = BK = CH 0,25
c ⇒ BH là đường trung tuyến của ∆ABC
Mà AM là đường trung tuyến của ∆ABC
⇒G là trọng tâm của ∆ABC 0,25
Mà CI là trung tuyến của ∆ABC ⇒ I, G, C thẳng hàng Câu 5 (1,0 điểm). Ý Nội dung Điểm
a Diện tích xung quanh của hình lăng trụ đứng đó là: 4.3.7 = 84 dm2 0,5
Thể tích của hộp đó là: 10.7,5.20 = 1500 cm3 0,25
b 1500 cm3 = 1,5 lít. Vậy trong hộp chứa 1,5 lít sữa tươi. 0,25 Câu 6 (1,0 điểm). Ý Nội dung Điểm
Chia F(x) cho G(x) được thương là 2x2 – 11x + 34 và dư là a – 68 0,25
a Để F(x) chia hết cho G(x) thì a – 68 = 0 ⇒ a = 68 Vậy a = 68 0,25
+ Với x = 4 ta có: (4 − 4) A(4) = (4 + 2) A(4 − ) 1 b ⇒0 = 6.A(3) ⇒ A( 3) = 0 0,25
⇒ x = 3là một nghiệm của A(x) . + Với x = 2 − ta có: ( 2 − − 4) A( 2 − ) = ( 2 − + 2) A( 2 − − ) 1 ⇒ 6. − A( 2 − ) = 0.A( 3 − ) ⇒ A( 2 − ) = 0 ⇒ x = 2
− là một nghiệm của A(x) . 0,25
Vậy đa thức A(x) có ít nhất 2 nghiệm phân biệt.
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa