Đề cương học kỳ 2 Toán 12 năm 2023 – 2024 trường THPT Xuân Đỉnh – Hà Nội

giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề cương ôn tập kiểm tra cuối học kỳ 2 môn Toán 12 năm học 2023 – 2024 trường THPT Xuân Đỉnh, thành phố Hà Nội.Mời bạn đọc đón xem!

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

16 trang 1 tháng trước

Tác giả:

Profile Lê Phương
TRƯỜNG THPT XUÂN ĐỈNH
1
NĂM HỌC 2023 – 2024
MÔN: TOÁN - KHỐI: 12
A. KIẾN THỨC ÔN TẬP
I. GIẢI TÍCH: TỪ ỨNG DỤNG ĐẠO HÀM ĐỂN HẾT ỨNG DỤNG TÍCH PHÂN VÀ SỐ PHỨC.
II. HÌNH HỌC: TỪ THỂ TÍCH KHỐI ĐA DIỆN ĐẾN HẾT PHƯƠNG TRÌNH MẶT CẦU, MẶT PHẲNG,
ĐƯỜNG THẲNG.
B. CÂU HỎI TRẮC NGHIỆM
I. GIẢI TÍCH
1. Ứng dụng đạo hàm khảo sát sự biến thên và vẽ đồ thị hàm số (Trong đề cương ôn tập giữa HK1).
2. Luỹ thừa, logarit – hàm số luỹ thừa, hàm số mũ, hàm số logarit – phương trình mũ, logarit (Trong đề cương ôn
tập HK1).
3. Ứng dụng hình học tích phân
Câu 1. Diện tích S của hình phẳng tô đậm trong hình dưới đây được tính theo công thức nào sau đây?
A.
2 4
0 2
( ) ( )S f x dx f x dx
B.
2 4
0 2
( ) ( )S f x dx f x dx
C.
2 4
0 2
( ) (x)dxS f x dx f
D.
4
0
( )S f x dx
Câu 2. Diện tích S của hình phẳng giới hạn giới hạn bởi đồ thị hàm số
3 2
3 2y x x
, hai trục tọa độ và
đường thẳng
2x
là
A.
3
2
S
B.
7
2
S
C. 4S D.
5
2
S
Câu 3. Thể tích khối tròn xoay được tạo thành khi quay quanh trục
Ox
hình phẳng giới hạn bởi các đường
y x
,
2y x
và
0y
là
A.
2
7
B.
C.
3
2
D.
5
6
Câu 4. Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số
2
, 2y x y x .
A.
3
20
S
. B.
20
3
S
. C.
4
3
S
. D.
3
4
S
.
Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
1 1
( )y f x C
,
2 2
( )y f x C
liên tục trên đoạn [a;b] và
hai đường thẳng x a , x b được xác định:
A.
1 2
x
b
a
S f x f x d
B.
1 2
x
b
a
S f x f x d
C.
1 2
1 2
1 2 2 1 1 2
x x x
c c
b
a c c
S f x f x d f x f x d f x f x d
D.
1
1
1 2 1 2
x x
c
b
a c
S f x f x d f x f x d
1
( )
C
2
( )
C
a
c
y
O
b
x
2
c
TRƯỜNG THPT XUÂN ĐỈNH
2
Câu 6. Diện tích hình phẳng giới hạn bởi các đồ thị
( )y f x
và
( )y g x
liên tục trên đoạn
[ ; ]a b
và hai
đường thẳng
;x a x b
là
A.
( ) ( ) .
b
a
f x g x dx
B.
( ) ( ) .
b
a
f x g x dx
C.
( ) ( ) .
b
a
f x g x dx
D.
( ) ( ) .
b
a
f x g x dx
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
1y x , trục hoành và 2 đường thẳng
1; 3x x
là
A.
3
2
1
1 .x dx
B.
3
2 2
1
( 1) .x dx
C.
3
2
1
( 1) .x dx
D.
3
2 2
1
( 1) .x dx
Câu 8. Cho đồ thị hàm số y = f(x)
Diện tích hình phẳng (gạch trong hình) là
A.
43
0 0
f x dx f x dx
B.
13
1 4
f x dx f x dx
C.
0
3 4
0
f x dx f x dx
D.
4
3
f x dx
Câu 9. Nếu gọi S là diện tích của hình phẳng được giới hạn bởi các đường
0; ; 0; .
2
x
x x y y cosx e
thì
khẳng định nào đây là đúng ?
A.
2
S e
B.
2
1S e
C.
2
1
1
2
S e
D.
S e
Câu 10. Diện tích miền hình phẳng giới hạn bởi các đường 2
x
y ,
3y x
,
1y
bằng
A.
1
3
ln 2
. B.
1 1
ln 2 2
. C.
1
1
ln 2
. D.
1
2
ln 2
.
Câu 11. Hình vuông OABC có cạnh bằng
4
được chia thành hai phần bởi đường cong
C
có phương trình
2
1
4
y x
. Gọi
1
S
,
2
S
là diện tích của phần không bị gạch và phần bị gạch (như hình vẽ sau). Tính tỉ số
1
2
S
S
A.
1
2
3
2
S
S
. B.
1
2
2
S
S
. C.
1
2
1
S
S
. D.
1
2
1
2
S
S
.
Câu 12. Diện tích hình phẳng giới hạn bởi hai đường:
2
4 3 ,y x x
1.x
bằng
A.
107
.
6
B.
109
.
6
C.
109
.
7
D.
109
.
8
Câu 13. Thể tích V của phần vật thể giới hạn bởi mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt
phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x
1 3
x
thì được thiết diện là một hình chữ nhật có
độ dài hai cạnh là 3x và
2
3 2x
.
A.
32 2 15V
. B.
124
3
V
. C.
124
3
V
. D.
32 2 15V
.
Câu 14. Cho hàm số
( )y f x
liên tục và không âm trên
[ ; ]a b
Hình phẳng giới hạn bởi đồ thị hàm số , trục
hoành và hai đường thẳng
;x a x b
quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích khối tròn
xoay là
TRƯỜNG THPT XUÂN ĐỈNH
3
A.
( ) .
b
a
f x dx
B.
( ) .
a
b
f x dx
C.
2
( ) .
b
a
f x dx
D.
2
( ) .
a
b
f x dx
Câu 15. Công thức thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung
quanh trục Ox là
A.
2
2
1
.ln d
e
x x e x
.
B.
1
.ln d
e
x x x
.
C.
1
.ln d
e
x x e x
.
D.
2
1
.ln d
e
x x x
.
Câu 16. Cho hàm số
f x
liên tục trên đoạn
;a b
.
Khi quay hình phẳng như hình vẽ trên quanh trục Ox ta được khối tròn xoay có thể tích là
A.
2
d
b
a
f x x
. B.
2
d
b
a
f x x
. C.
2
d
b
a
f x x
. D.
d
b
a
f x x
.
Câu 17.Công thức thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung
quanh trục
Ox
là
A.
2
4 3 2
2
4 8 16 16 dx x x x x
. B.
2
2
2
4 dx x
.
C.
2
4 3
2
4 16 16 dx x x x
. D.
2
2
2
4 4 dx x x
.
Câu 18.Công thức thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung
quanh trục Ox là
A.
1 2
2
0 1
2 d d
x x x x
. B.
1 2
2
0 1
d 2 d
x x x x
. C.
2
2
0
2 d
x x x
D.
2 4
2
0 2
d 2 d
x x x x
.
Câu 19. Miền phẳng trong hình vẽ giới hạn bởi hàm số
y f x
và parbol
2
2y x x . Biết
1
1
2
7
d
5
f x x
.
TRƯỜNG THPT XUÂN ĐỈNH
4
Khi đó diện tích hình phẳng được gạch chéo trong hình vẽ bằng
A.
1
S
. B.
71
40
S
. C.
41
40
S
. D.
2
S
.
Câu 20. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol
2
4
y x
và
2
2
y x
quay quanh trục
Ox
là kết quả nào sau đây?
A.
10 .
V
B.
12 .
V
C.
14 .
V
D.
16 .
V
Câu 21. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số
2
y = x
2
;
x y
quanh trục Ox
là
A.
2
10
B.
4
3
C.
10
D.
3
10
Câu 22. Ký hiệu (H) là hình phẳng giới hạn bởi các đường
sin cos , 0, 0,
2
y x x a y x x
với a là
tham số thực lớn hơn 2. Tìm a sao cho thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh
trục hoành bằng
2
3
2
.
A.
3
a
B.
4
a
C.
6
a
D.
9
a
Câu 23. Cho hình phẳng
H
giới hạn bởi
2
2 ,
y x x
0
y
. Tính thể tích của khối tròn xoay thu
được khi quay
H
xung quanh trục
Ox
ta được
1
a
V
b
với ,a b
và
a
b
là phân số tối
giản. Tính
, .
a b
A.
1, 15
a b
. B.
–7, 15
a b
. C.
241, 15
a b
. D.
16, 15
a b
2. Số phức – các phép toán – căn bậc hai – phương trình bậc hai
Câu 24. Cho các số phức
1 2
, ,
z z z
. Mệnh đề nào sau đây là mệnh đề sai
A.
1 2 1 2
z =z z = z
B.
z = 0 z = 0
C. Tập hợp điểm biểu diễn các số phức z thỏa mãn
z 1
là đường tròn tâm O, bán kính R = 1
D.
Hai s
ố
ph
ứ
c b
ằ
ng nhau khi và ch
ỉ
khi ph
ầ
n th
ự
c và ph
ầ
n
ả
o tương
ứ
ng b
ằ
ng nhau
Câu 25. Cho số phức
z
thỏa mãn
1
2 5
1
i
i z i
i
. Môđun của số phức
2
1 2
w z z
là
A. 10. B.
10
. C. 100. D.
100
.
Câu 26. Cho số phức thỏa mãn . Môđun của số phức là
A. 4 B. 9 C. 13 D.
13
Câu 27. Tính mô đun của số phức
2
1 i .z
w
, biết
z m
A.
4m
w
B.
2m
w
C.
2m
w D.
m
w
Câu 28. Cho hai số phức . Giá trị của biểu thức là
z
5( )
2
1
z i
i
z
2
1
z z
1 2
3 , 2
z i z i
1 1 2
z z z
TRƯỜNG THPT XUÂN ĐỈNH
5
A. B. C. D.
Câu 29. Cho số phức
3 4
z i
. Khi đó môđun của
z
1
là
A.
1
5
B.
1
5
C.
1
4
D.
1
3
Câu 30. Tìm phần thực, phần ảo của số phức z thỏa
3979
1 (1 )
2
z
i i i
?
A. Phần thực là
1990
2
và phần ảo là
2
. B. Phần thực là
1990
2
và phần ảo là
2
.
C. Phần thực là
1989
2
và phần ảo là
1
. D. Phần thực là
1989
2
và phần ảo là
1
.
Câu 31. Tìm phần ảo của số phức
z
thỏa mãn
2
2 1 3 1
i iz i
A.
8
B.
9
C. 9 D.
8
Câu 32. Cho số phức z = a + bi. Khi đó số
1
2
z z
i
là
A. Một số thực B. 0 C. Một số thuần ảo D. i
Câu 33. Cho
s
ố phức z thỏa mãn:
2
(3 2 ) (2 ) 4 .
i z i i
Hiệu phần thực và phần ảo của z là
A. 1 B. 0 C. 4 D. 6
Câu 34. Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức
'
z
z
có phần ảo là
A.
2 2
' '
aa bb
a b
B.
2 2
' '
' '
ba ab
a b
C.
2 2
' '
aa bb
a b
D.
2 2
2 '
' '
bb
a b
Câu 35. Thu gọn số phức z =
3 2 1
1 3 2
i i
i i
ta được
A.
21 61
26 26
i
B.
23 63
26 26
i
C.
15 55
26 26
i
D.
2 6
13 13
i
Câu 36. Biết điểm A(3;-2) là điểm biểu diễn của số phức z. Hỏi số phức liên hợp
z
của z là
A.
3 2
z i
B.
3 2
z i
C.
3 2
z i
D.
3 2
z i
Câu 37. Tìm số thực
,
x y
để số phức
2 5
1
9 4 10
z y xi
và
2 11
2
8 20
z y i
là liên hợp của nhau?
A.
2; 2
x y
. B.
2; 2
x y
. C.
2; 2
x y
. D.
2; 2
x y
.
Câu 38. Cho hai số thực
,
x y
thỏa mãn
2 1 1 2 2 2
x y i i yi x
. Giá trị của
2
3
x xy y
bằng
A.
1
. B.
1
. C.
2
. D.
3
.
Câu 39. Cho số phức
1
1 2
z i
và
2
1 2
z i
. Khẳng định nào sau đây là khẳng định đúng?
A.
1 2
0
z z
. B.
1
2
1
z
z
. C.
1 2
. 3 4
z z i
. D.
1 2
z z
.
Câu 40. Cho số phức
1 2
z i
. Khẳng định nào sau đây là khẳng định đúng?
A.
1
2
z
z
z
. B.
1
1 2
z i
C.
1
. 0
z z
. D.
1
1 2
5 5
z i
.
Câu 41. Tìm số phức
z
thỏa mãn
2
1 1 1
1 2
1 2
z i
i
A.
8 14
25 25
z i
B.
8 14
25 25
z i
C.
10 35
13 26
z i
D.
10 14
13 25
z i
Câu 42. Có bao nhiêu số phức z thỏa mãn z +
z
= 2024
A. 0 B. 1 C. 2 D. Vô số
Câu 43. Tìm số phức
z
thỏa mãn
1 1 2 3 2 0
i z i i
A.
4 3
z i
B.
3 5
2 2
z i
C.
5 3
2 2
z i
D.
4 3
z i
Câu 44. Tìm số phức
z
thỏa mãn
2 4 4
zi z i
A.
4 4
z i
B.
3 4
z i
C.
3 4
z i
D.
4 4
z i
0
10
10
100
TRƯỜNG THPT XUÂN ĐỈNH
6
Câu 45. Số phức
z
thỏa mãn:
2 3 1 9z i z i
là
A. 2 i . B. 2 i . C. 3 i . D. 2 i
Câu 46. Trong
R
, phương trình
2 4
z z i
có nghiệm là
A.
3 4 z i
B.
2 4 z i
C.
4 4 z i
D.
5 4 z i
Câu 47. Có bao nhiêu số phức z thỏa mãn
10z
đồng thời phần ảo gấp ba lần phần thực
A. 1 B. 2 C. 3 D. 4
Câu 48. Nghiệm của phương trình
4 7 5 2 6i z i iz
là
A.
18 13
7 7
i
B.
18 13
17 17
i
C.
18 13
7 17
i
D.
18 13
17 17
i
Câu 49. Phương trình
2
2 5 0z z
có nghiệm là
z a bi
(
,a b
). Khi đó
a
b
bằng
A.
1
2
B.
1
3
C.
1
4
D.
1
5
Câu 50. Kí hiệu
1 2 3
, ,z z z
và
4
z
là các nghiệm phức của phương trình
4 2
12 0z z . Tổng
1 2 3 4
T z z z z
bằng
A.
4.T
B.
2 3.T
C.
4 2 3.T
D.
2 2 3.T
Câu 51. Phương trình
2
2 0 ,i z az b a b
có hai nghiệm là
3 i
và
1 2i
. Khi đó
?a
A.
9 2i
B.
15 5i
C.
9 2i
D.
15 5i
Câu 52.
G
ọi
1
z
và
2
z lần lượt là nghiệm của phương trình:
2
2 5 0z z . Tính
1 2
z z
A.
2 5 B. 10 C. 3 D. 6
Câu 53. Giá trị của m thuộc khoảng nào sau đây để phương trình
2
z 2 m z 2 0
nhận số phức z = 1 – i
làm một nghiệm
A.
5;7m
B.
3;6m
C.
3; 1m
D.
1;4m
Câu 54. Gọi z
1
, z
2
, z
3
, z
4
là các nghiệm phức của phương trình
4 2
2 3 2 0z z
. Khi đó, giá trị
2 2 2 2
1 2 3 4
H z z z z
bằng:
A.
5H
. B.
3 2H
. C.
2H
. D.
5 2H
.
Câu 55. Gọi A và B lần lượt là hai điểm biểu diễn của hai số phức
5 3z i
và
' 3 5z i
. Kết luận nào sau đây
là đúng?
A. A và B đối xứng nhau qua trục hoành B. A và B đối xứng nhau qua trục tung
C. A và B đối xứng nhau qua gốc tọa độ D. A và B đối xứng nhau qua đt
y x
Câu 56. Cho số phức z thỏa mãn
| 1| 2z
. Biết rằng tập hợp điểm biểu diễn các số phức
1 3 2w i z
là một đường tròn. Tính bán kính
r
của đường tròn đó
A. 16r B. 4r C. 25r D. 9r
Câu 57. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn 2 2z i z z i là
A. Một đường thẳng B. Một đường tròn C. Một parabol D. Một elip.
Câu 58. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực của
z
bằng -2 là
A.
2x
. B.
2y
. C.
2y x
D.
2y x
Câu 59. Trong mặt phẳng phức , số phức
z
thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần
tô màu như hình vẽ
A.
1 2z
và phần ảo dương.
B.
1 2z
và phần ảo âm.
C.
1 2
z
và phàn ảo dương.
Oxy
TRƯỜNG THPT XUÂN ĐỈNH
7
D.
1 2
z
và phần ảo âm.
Câu 60. Cho các số phức
1 2 3 4
1 , 2 3 , 5 , 2
z i z i z i z i
lần lượt có các điểm biểu diễn trên mặt
phẳng phức là
, , ,
M N P Q
. Hỏi tứ giác
MNPQ
là hình gì?
A. Tứ giác
MNPQ
là hình thoi. B. Tứ giác
MNPQ
là hình vuông.
C. Tứ giác
MNPQ
là hình bình hành. D. Tứ giác
MNPQ
là hình chữ nhật.
Câu 61. Cho
A
,
B
,
C
lần lượt là các điểm biểu diễn của các số phức
6 3
i
;
1 2
i i
;
1
i
.Tìm số phức có điểm
biểu diễn
D
sao cho
ABCD
là hình bình hành.
A.
8 3
z i
. B.
8 4
z i
. C.
4 2
z i
. D.
8 5
z i
.
Câu 62. Trong mặt phẳng phức
Oxy
, các số phức
z
thỏa mãn
2 1
z i z i
. Tìm số phức
z
được biểu
diễn bởi điểm
M
sao cho
MA
ngắn nhất với
1, 3
A
.
A.
3
i
. B.
1 3
i
. C.
2 3
i
. D.
2 3
i
.
Câu 63. Xác định tập hợp các điểm
M
trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện:
| 1 | 1
z i
.
A. Đường tròn tâm I(-1;-1), bán kính R = 1.
B. Hình tròn tâm I(1;-1), bán kính R = 1.
C. Hình tròn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường tròn).
D. Đường tròn tâm I(1;-1), bán kính R = 1.
Câu 64. Điểm biểu diễn số thuần ảo nằm ở đâu trên mặt phẳng tọa độ?
A. Trục Ox B. Trục Oy C. Gốc tọa độ D. Phân giác của góc phần tư thứ I, III.
Câu 65. Điểm biểu diễn số phức
(2 3 )(4 )
3 2
i i
z
i
có tọa độ là
A. (1;-4) B. (-1;-4) C. (1;4) D. (-1;4)
Câu 66. Gọi D là tập hợp các số phức z thỏa mãn
1
z i
z i
. Khi đó D là
A. Trục hoành. B. Trục tung.
C. Đường phân giác y = x. D. Đường phân giác y = -x.
Câu 67. Gọi D là tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z sao cho
1
z i
là số thuần ảo.
Lựa chọn phương án đúng ?
A. D là trục tung. B. D là trục hoành.
C. D là đường phân giác thứ nhất y = x D. D là trục tung bỏ đi điểm I(0; 1).
Câu 68. Cho số phức
z
thỏa
1 2
z i z i
. Giá trị nhỏ nhất của
z
là
A.
1
2
B. 1
C.
2
D.
1
4
Câu 69. Xét các số phức z thỏa mãn
1 2
z z i
. GTNN của biểu thức
1 2 11 2
P i z i
bằng
A.
10
2
B.
5
2
C.
5
2
D.
2
5
II. HÌNH HỌC
Câu 70. Cho mặt cầu
2 2 2
: 2 4 2 0
S x y z x y z
. Tâm và bán kính mặt cầu
S
là
A.
1;2;1 , 6
I R
B.
1; 2; 1 , 6
I R
C.
1; 2; 1 , 6
I R
D.
1; 2;1 , 6
I R
Câu 71. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;-1) và đi qua điểm A(2;1;2). Mặt
phẳng nào sau tiếp xúc với (S) tại A ?
A. x + y - 3z - 8 = 0. B. x - y - 3z + 3 = 0. C. x + y + 3z - 9 = 0. D. x + y - 3z + 3 = 0.
Câu 72. Trong không gian Oxyz, mặt cầu có tâm thuộc
Ox
và tiếp xúc với hai mặt phẳng
: 2 5 0,
P x y z
: 2 3 0
Q x y z
có phương trình là
A.
2
2 2
1
4
5
x y z
. B.
2
2 2
1
4
6
x y z
. C.
2
2 2
1
4
7
x y z
. D.
2
2 2
1
4
8
x y z
.
TRƯỜNG THPT XUÂN ĐỈNH
8
Câu 73. Trong không gian Oxyz, mặt cầu
( )
S
đi qua
0;2;0
A
,
2;3;1
B
,
0;3;1
C
và có tâm nằm trên
Oxz
. Phương trình mặt cầu
( )
S
là
A.
2 2
2
6 4 9
x y z
B.
2
2 2
3 16
x y z
C.
2 2
2
7 5 26
x y z
D.
2 2
2
1 3 14
x y z
Câu 74. Trong không gian với hệ tọa độ Oxyz, cho hai điểm
2;0; 1 , 1; 1;3
P Q
và mặt phẳng
:3 2 5 0
R x y z
. Viết phương trình mặt phẳng
đi qua
,
P Q
và vuông góc với mp
R
A.
7 11 3 0
x y z
B.
7 11 1 0
x y z
C.
7 11 15 0
x y z
D.
2 0
x y z
Câu 75. Trong không gian tọa độ
,
Oxyz
cho đường thẳng
1 3
:
3 4 1
x y z
d
và điểm
1;2;3 .
A
Phương trình
mặt phẳng
đi qua
A
và chứa
d
là
A.
23 17 14 0.
x y z
B.
23 17 14 0.
x y z
C.
23 17 60 0.
x y z
D.
23 17 14 0.
x y z
Câu 76. Trong không gian tọa độ
,
Oxyz
cho 2 đường thẳng cắt nhau
1 2
: ,
1 2 3
x y z
d
1
' : 2
2 3
x t
d y t
z t
. Viết
phương trình mặt phẳng chứa d và d’.
A.
3 2 4 0.
y z
B.
3 2 4 0.
y z
C.
3 2 4 0.
y z
D.
3 2 4 0.
y z
Câu 77. Trong không gian
,
Oxyz
cho 2 đường thẳng song song
1
1 2
: , ': 2
1 1 2
1 2
x t
x y z
d d y t
z t
. Viết
phương trình mặt phẳng chứa d và d’.
A.
9 4 7 0.
x y z
B.
9 4 7 0.
x y z
C.
9 4 7 0.
x y z
D.
9 4 7 0.
x y z
Câu 78. Trong không gian với hệ tọa độ Oxyz cho
1;2;1
M . Viết phương trình mặt phẳng (P) qua M cắt trục
Ox, Oy, Oz lần lượt tại A, B, C sao cho
2 2 2
1 1 1
OA OB OC
đạt giá trị nhỏ nhất.
A.
: 2 3 8 0
P x y z
B.
: 4 0
P x y z
C.
: 2 6 0
P x y z
D.
: 1
1 2 1
x y z
P
Câu 79. Trong k/gian Oxyz cho đường thẳng
1 2
1
1 2
: 2 ; :
1 1 3
1 3
x t
x y z
d y t d
z t
. Khi đó
1
d
và
2
d
A. Cắt và vuông góc B. Song song D. Chéo nhau B. Cắt nhưng không vuông góc
Câu 80. Trong không gian Oxyz cho A(3;2;0), đường thẳng
x 1 y 3 z 2
d :
1 2 2
. Khoảng cách từ điểm A
đến đường thẳng d là
A. 2 B. 3 C. 4 D. 5
Câu 81. Trong không gian Oxyz gọi d là phương trình đường thẳng qua
1; 2;0
A
và có một véctơ chỉ
phương là
1;2; 3
u
. Khẳng định nào dưới đây là sai?
A.
1
: 2 2
3
x t
d y t
z t
B.
: 4 2
3 3
x t
d y t
z t
C.
1
: 2 2
3
x t
d y t
z t
D.
: 4 2
1 3
x t
d y t
z t
Câu 82. Trong không gian Oxyz cho hai đường thẳng
1
: 2
2
x t
d y t
z t
;
1 2
:
2 3 1
x y z
và gọi
là góc giữa
d
và
. Khi đó
cos
có giá trị bằng
TRƯỜNG THPT XUÂN ĐỈNH
9
A.
5 13
21
B.
5 14
21
C.
5 15
21
D.
5 17
21
Câu 83. Trong không gian Oxyz gọi d là phương trình đường thẳng qua
1; 2;0
A
và
2;0;1
B
. Khẳng định
nào sau đây là đúng?
A.
1
: 2 2
1
x t
d y t
z t
B.
2
: 2
1
x t
d y t
z t
C.
2 1
:
1 2 1
x y z
d
D.
3 2 1
:
1 2 1
x y z
d
Câu 84. Trong không gian Oxyz cho đường thẳng
1
: 2
2
x t
d y t
z t
mặt phẳng
: 2 3 1 0
P x y z
. Hình chiếu
của đường thẳng (d) trên mặt phẳng (P) có phương trình là
A.
3
1
2
5
9
2
x t
y t
z t
B.
3
1
5 9
x t
y t
z t
C.
3
1
2
5
9
2
x t
y t
z t
D.
3
1
5 9
x t
y t
z t
Câu 85. Phương trình đường thẳngtrong không gian Oxyz đi qua điểm
1; 2;1
A
và song song với đường
thẳng
1
:
2 1 1
x y z
d
có phương trình là
A.
1 2 1
2 1 1
x y z
B.
1 2 1
2 1 1
x y z
C.
3 1
2 1 1
x y z
D. Đáp án khác
Câu 86. Trong không gian tọa độ Oxyz, hình chiếu vuông góc của điểm
2; 1;3
P
trên
3
: 7 5
2 2
x t
d y t
z t
là điểm
có tọa độ nào sau đây?
A. (-3; 2; 4) B. (-3; -2 ;-4) C. (3;-2;4) D. (3;-2;-4 )
Câu 87. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
1
3 1
:
2 1 2
y
x z
d
và điểm M(1;2;-3).
Mặt cầu tâm M, tiếp xúc với đường thẳng d có bán kính R bằng bao nhiêu?
A.
2
R
B.
2 5
R
C.
2 2
R
D. R = 4.
Câu 88. Trong không gian tọa độ Oxyz, cho hai đường thẳng và . Góc
giữa hai đường thẳng trên là
A. B. C. D.
Câu 89. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
qua
1; 0; 1
A
và có véc tơ chỉ phương
2; 4; 6
u
. Phương trình tham số của đường thẳng
là
A.
1 2
: 4
1 6
x t
d y t
z t
B.
2
: 4
6
x t
d y
z t
C.
1
: 2
1 3
x t
d y t
z t
D.
1
: 2
1 3
x t
d y t
z t
Câu 90. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Vị trí
tương đối của và là
A. cắt
B.
C. và trùng nhau
D.
và chéo nhau
1 2
1 1 1
x y z
2 3 1
2 2 4
x y z
30
45
60
90
1
1 1
1
2 4
: 1 3
1 5
x t
d y t
z t
2
2 2
2
1 7
: 3 5
3
x t
d y t
z t
1
d
2
d
1
d
2
d
1 2
d d
1
d
2
d
2
d
1
d
TRƯỜNG THPT XUÂN ĐỈNH
10
Câu 91. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) song song với 2 đường thẳng
2
3 2
1
x t
y t
z t
và
2 1
2 3 4
x y z
. Mặt phẳng (P) có 1 véc tơ pháp tuyến là
A. (-5; 6;-7) B. (5; -6 ;7) C. (-5 ; -6 ; 7) D. (-5 ;6 ;7)
Câu 92. Mặt cầu
S
tâm
1;2; 3
I
và tiếp xúc với
: 2 2 1 0
P x y z
có phương trình là
A.
2 2 2
4
1 2 3 .
9
x y z
B.
2 2 2
4
1 2 3 .
9
x y z
C.
2 2 2
4
1 2 3 .
3
x y z
D.
2 2 2
16
1 2 3 .
3
x y z
Câu 93. Trong không gian với hệ trục tọa độ
Oxyz
, mặt phẳng
đi qua
0; 2;3
M
, song song với đường
thẳng
2 1
:
2 3
x y
d z
và vuông góc với mặt phẳng
: 0
x y z
có pt là
A.
2 3 5 9 0
x y z
. B.
2 3 5 9 0
x y z
. C.
2 3 5 9 0
x y z
. D.
2 3 5 9 0
x y z
.
Câu 94. Trong không gian
Oxyz
, đường thẳng
1 2 4
:
2 1 3
x y z
d
và
1
':
2 3
x t
d y t
z t
có vị trí tương đối là
A. trùng nhau. B. song song. C. chéo nhau. D. cắt nhau.
Câu 95. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
: 2 2 0
x y z m
và điểm
1;1;1
A
. Khi đó
m
nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng
bằng 1?
A.
2. B.
8. C.
2 hoặc
8
. D. 3.
Câu 96. Trong không gian với hệ tọa độ
,
Oxyz
phương trình nào sau đây là phương trình chính tắc của đường
thẳng
đi qua hai điểm
1; 2;5
A
và
3;1;1
B
?
A.
1 2 5
.
2 3 4
x y z
B.
3 1 1
.
1 2 5
x y z
C.
1 2 5
.
2 3 4
x y z
D.
1 2 5
.
3 1 1
x y z
Câu 97. Trong không gian với hệ tọa độ
,
Oxyz
phương trình đường thẳng
đi qua điểm
2;1; 5 ,
M
đồng
thời vuông góc với hai vectơ
1;0;1
a
và
4;1; 1
b
là
A.
2 1 5
.
1 5 1
x y z
B.
2 1 5
.
1 5 1
x y z
C.
2 1 5
.
1 5 1
x y z
D.
1 5 1
.
2 1 5
x y z
Câu 98. Trong không gian tọa độ
,
Oxyz
cho hai đường thẳng
1
2 1 1
:
1 3 2
x y z
d
và
2
1 3
: 2
1
x t
d y t
z t
. Phương
trình đường thẳng nằm trong
: 2 3 2 0
x y z
và cắt hai đường thẳng
1 2
,
d d
là
A.
3 2 1
.
5 1 1
x y z
B.
3 2 1
.
5 1 1
x y z
C.
3 2 1
.
5 1 1
x y z
D.
8 3
.
1 3 4
x y z
Câu 99. Trong không gian tọa độ
Oxyz
, cho hai đường thẳng
1
1
: 2
2
x t
d y t
z t
và
2
2
: 1 2
2
x t
d y t
z mt
. Để hai đường
thẳng hợp với nhau một góc bằng
0
60
thì giá trị của
m
bằng
A.
1
m
B.
1
m
C.
1
2
m
D.
1
2
m
Câu 100. Trong không gian tọa độ Oxyz, PT nào dưới đây là phương trình chính tắc của d:
1 2
3
2
x t
y t
z t
?
TRƯỜNG THPT XUÂN ĐỈNH
11
A.
1 2
2 3 1
x y z
. B.
1 2
2 3 2
x y z
. C.
1 2
1 3 2
x y z
. D.
1 2
2 3 1
x y z
.
Câu 101. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – 2y –z +1 = 0 và đường thẳng
1 2 1
:
2 1 2
x y z
. Tính khoảng cách d giữa đường thẳng
và (P) ?
A.
1
3
d
. B.
5
3
d
. C.
2
3
d
. D.
2
d
.
Câu 102. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
1
3 6 1
:
2 2 1
x y z
d
và
2
:
2
x t
d y t t
z
. Đường thẳng đi qua điểm
(0;1;1)
A
, vuông góc với
1
d
và cắt
2
d
có PT là
A.
1 1
1 3 4
x y z
B.
1 1
1 3 4
x y z
C.
1 1
1 3 4
x y z
D.
1 1
1 3 4
x y z
Câu 103. Trong không gian tọa độ
,
Oxyz
cho hai đường thẳng
1
1
: 0
5
x t
d y
z t
và
2
0
: 4 2 .
5 3
x
d y t
z t
Phương trình đường vuông góc chung của
1
d
và
2
d
là
A.
4 2
.
2 3 2
x y z
B.
4
3 .
2
x t
y t
z t
C.
4 2
.
2 3 2
x y z
D.
4 2
.
2 3 2
x y z
Câu 104. Trong không gian Oxyz, cho hai đường thẳng
1 2
,
d d
có phương trình lần lượt là
5
3
2 2
x t
y t
z t
và
1 3 '
1 '
5 '
x t
y t
z mt
. Tìm tham số thực m để hai đường thẳng
1
d
và
2
d
cắt nhau.
A.
1
m
B.
1
m
C.
2
m
D.
2
m
Câu 105. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
1 2
1 2 3
x y z
và mặt phẳng (P):
x y z
2 2 3 0
. Tọa độ điểm M thuộc đường thẳng (d) và cách mp (P) một đoạn bằng 2 là
A.
; ;M
1 3 5
B.
; ;M
2 3 1
C.
; ;M
2 5 8
D.
; ;M
1 5 7
C. ĐỀ MINH HOẠ
Câu 1: Trên mặt phẳng tọa độ
Oxy
, số phức
2
z i
được biểu diễn bởi điểm
A.
2; 0 .
M
B.
0; 2 .
N
C.
0; 2 .
P
D.
2; 0 .
Q
Câu 2: Hàm số
ln 2 1
y x
có đạo hàm là
A.
2
ln 2 1
y
x x
. B.
1
2 1
y
x
. C.
2
2 1
y
x
. D.
1
2 1 ln 2
y
x
.
Câu 3: Trên khoảng
0;
, đạo hàm của hàm số
5
3
y x
là
A.
8
3
5
3
y x
. B.
8
3
5
3
y x
. C.
2
3
5
3
y x
. D.
2
3
5
3
y x
.
Câu 4: Tập nghiệm của bất phương trình
2
1 1
7 49
x x
là
A.
;1
. B.
; 2 1;
 
. C.
1;

. D.
2;1
.
TRƯỜNG THPT XUÂN ĐỈNH
12
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
6 4
: 2
1 2
x t
d y t
z t
và điểm
1;1;1A .
Tìm tọa độ hình chiếu A
của A trên d.
A.
2;3;1 .A
B.
2;3;1 .A
C.
2; 3;1 .A
D.
2; 3; 1 .
A
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng
: 3 2 4 1 0x y z
. Vectơ nào dưới đây là một vectơ
pháp tuyến của
?
A.
2
3;2;4n
. B.
3
2; 4;1n
. C.
1
3; 4;1n
. D.
4
3;2; 4n
.
Câu 7: Cho hàm số
3 2
y ax bx cx d có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của
đồ thị hàm số đã cho và trục tung là điểm nào trong các điểm sau
Tìm giá trị của
d
.
A.
1;0
. B.
2;0
. C.
1;0
. D.
0;2
.
Câu 8: Nếu
3
1
2 1 5f x dx
thì
3
1
f x dx
bằng
A.
3.
B.
2.
C.
3
.
4
D.
3
.
2
Câu 9: Hình vẽ bên dưới là đồ thị của hàm số nào
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2 3
1
x
y
x
. D.
2 5
1
x
y
x
.
Câu 10: Trong không gian hệ tọa độ
Oxyz
, tìm tất cả các giá trị của
m
để phương trình
2 2 2
2 2 4 0x y z x y z m
là phương trình của một mặt cầu.
A.
6m
B.
6m
C.
6m
D.
6m
Câu 11: Trong không gian
Oxyz
cho đường thẳng
:
1 2 1
x y z
và mặt phẳng
: 2 0x y z
. Góc giữa
đường thẳng và mặt phẳng
bằng
A.
30
. B.
60
. C.
150
. D.
120
.
Câu 12: Cho hai số phức
1 3 , 2z i w i
. Tìm phần ảo của số phức
.u z w
.
A.
7
. B.
5i
. C. 5. D.
7i
.
TRƯỜNG THPT XUÂN ĐỈNH
13
Câu 13: Cho hình lăng trụ đứng
.ABCD A B C D
, có
ABCD
là hình vuông cạnh
2a
, cạnh
2 3
AC a
.Thể
tích khối lăng trụ
.ABC A B C
bằng
A.
3
4a
. B.
3
3a
. C.
3
2a
. D.
3
a
.
Câu 14: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 6a , góc giữa cạnh bên và mặt đáy bằng
0
60
.
Tính thể tích V của khối chóp S.ABC?
A.
3
9V a
B.
3
2V a
C.
3
3V a
D.
3
6V a
Câu 15: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
( ) : 1 2 3 16S x y z
và mặt phẳng
( ) : 2 2 6 0P x y z
. Khẳng định nào sau đây đúng?
A.
( )P
không cắt mặt cầu
( ).S
B.
( )P
tiếp xúc mặt cầu
( ).S
C.
( )P
đi qua tâm mặt cầu
( ).S
D.
( )P
cắt mặt cầu
( )S
.
Câu 16: Cho số phức
1 4z i
. Phần ảo của phức liên hợp
z
bằng
A.
1
. B.
4
. C.
1
. D.
4
.
Câu 17: Diện tích toàn phần của hình nón có bán kính đáy bằng 2 và độ dài đường sinh bằng
6
là
A. 8
. B. 16
. C. 12
. D. 24
.
Câu 18: Trong không gian với hệ tọa độ
,Oxyz
cho đường thẳng
d
có phương trình tham số
1 2
2 3
1 4
x t
y t t
z t
. Đường thẳng
d
không đi qua điểm nào dưới đây?
A.
2; 3;4Q
. B.
3; 1;5N
. C.
5; 4;9P
. D.
1;2;1M
.
Câu 19: Cho hàm số
y f x
có đồ thị như hình vẽ.
Giá trị cực tiểu của hàm số là
A.
2 x
. B.
2 y
. C.
0y
. D.
2y
.
Câu 20: Đồ thị hàm số
1 3
3
m x
y
x m
có tiệm cận ngang
2y
thì có tiệm cận đứng có phương trình:
A.
3y
. B.
6x
. C.
0x
. D.
6x
.
Câu 21: Tập nghiệm S của bất phương trình
2
log 2 3 0x
là
A.
; 1S 
. B.
1;S 
. C.
; 1S 
. D.
;0S 
.
Câu 22: Trong không gian với hệ tọa độ Oxyz, giá trị của m để hai mặt phẳng ( ) : 7 3 3 0x y mz và
( ): 3 4 5 0x y z vuông góc với nhau là
A.6. B.– 4. C.1. D.2.
Câu 23: Hàm số
2 sin 2F x x x
là một nguyên hàm của hàm số nào dưới đây?
A.
2 2cos 2f x x
. B.
2
1
cos2
2
f x x x
.
C.
2 2cos 2f x x . D.
2
1
cos2
2
f x x x
.
Câu 24: Nếu
2023
1
x 3f x d
và
2023
1
x 4g x d
thì
2023
1
2 1 xf x g x d
bằng
A. 2024 . B. 2023. C.
2025
. D. 2022 .
Câu 25: Tìm hàm số
( )y f x
biết rằng
( ) sin 2f x x
và
(0) 1f
TRƯỜNG THPT XUÂN ĐỈNH
14
A.
cos +2 +1x x
. B.
cos +2 +2x x
. C.
cos +2 +1x x
. D.
cos +2x x
.
Câu 26: Cho hàm số bậc ba
y f x
có đồ thị như hình sau
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
0;2
. B.
; 1
. C.
2;4
. D.
1;2
.
Câu 27: Cho hàm số
4 2
, ,y ax bx c a b c
có đồ thị là đường cong như hình vẽ. Điểm cực tiểu của đồ
thị hàm số đã cho là
A.
0
. B.
2
. C.
0;2
. D.
2;0
.
Câu 28: Cho các số thực dương
,a b
thỏa mãn
log 2log 1a b
. Mệnh đề nào sau đây đúng?
A.
2
1a b
. B.
2 10a b
. C.
2
10ab
. D.
2
10a b
.
Câu 29: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi
2
y x
và
2 3y x
quanh trục Ox là:
A.
1088
15
. B.
138
5
. C.
9
2
. D.
72
5
.
Câu 30: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại A , cạnh
AC a
, các cạnh bên
6
2
a
SA SB SC . Tính góc tạo bởi mặt bên
( )SAB
và mặt phẳng đáy
( )ABC
.
A.
6
. B.
4
. C.
arctan 2
. D.
arctan 2
.
Câu 31: Cho hàm số
y f x
xác định trên
\ 1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên
như sau:
Tìm tập hợp tất cả các giá trị thực của tham số
m
sao cho phương trình
f x m
có ba nghiệm
thực phân biệt.
A.
1;1
. B.
2 ; 1
. C.
2 ; 1
. D.
1;1
.
Câu 32: Cho hàm số
y f x
xác định trên tập và có
2
5 4f x x x
. Khẳng định nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng
1;4
.
B. Hàm số đã cho nghịch biến trên khoảng
3;
.
TRƯỜNG THPT XUÂN ĐỈNH
15
C. Hàm số đã cho đồng biến trên khoảng
;3
.
D. Hàm số đã cho đồng biến trên khoảng
1;4
.
Câu 33: Tìm tham số m để phương trình
2
4 1 3 2 2 0
x x
m m m có nghiệm.
A.
;
 
B.
;1 1;
 
C.
0;

D.
1;

Câu 34: Tích tất cả các nghiệm của phương trình
2
3 3
log 2log 7 0
x
là
A.
7
B.
9
C.
2
D.
1
Câu 35: Cho số phức
z
thỏa mãn
3 5 10
z i
và
2 1 3 9 14
w z i i
. Khẳng định nào đúng trong các
khẳng định sau?
A. Tập hợp điểm biểu diễn của số phức
w
là đường tròn tâm
33; 14
I
.
B. Tập hợp điểm biểu diễn số phức
w
là đường tròn có tâm
33;14
I
.
C. Tập hợp điểm biểu diễn số phức
w
là đường tròn có tâm
33;14
I
.
D. Tập hợp điểm biểu diễn số phức
w
là đường tròn có bán kính
10
R
.
Câu 36: Trong không gian
Oxyz
, cho tam giác
ABC
với
3; 1;2
A
,
1;3;5
B
,
3;1; 3
C
. Đường trung
tuyến
AM
của
ABC
có phương trình là
A.
1 2
2 3
1
x t
y t
z t
. B.
1 2
2 3
1
x t
y t
z t
. C.
1 2
2 3
1
x t
y t
z t
. D.
3 2
1 3
2
x t
y t
z t
.
Câu 37: Trong không gian
Oxyz
, cho điểm
2; 5;4
M . Tọa độ điểm
'
M
đối xứng với
M
qua mặt phẳng
Oyz
là
A.
2;5;4
. B.
2; 5; 4
. C.
2;5; 4
. D.
2; 5;4
.
Câu 38: Cho hình chóp
.
S ABC
có đáy là tam giác vuông tại
A
,
, 2
AB a AC a
và
SA ABC
,
SA a
. Khoảng cách từ
A
đến mặt phẳng
SBC
bằng
A.
3
2
a
. B.
2
a
. C.
2
5
a
. D.
10
5
a
.
Câu 39: Số nghiệm nguyên của bất phương trình
2
2
2
1
log 2 1
16 3
x x
x x
x
là
A.
2
. B.
3
. C.
10
. D.
11
.
Câu 40: Cho hàm số
f x
liên tục trên
. Gọi
,
F x G x
là hai nguyên hàm của
f x
trên
thỏa mãn
8 8 8
F G
và
0 0 2
F G
. Khi đó
8
1
1
5ln d
e
f x x
x
bằng
A.
1
. B.
1
. C.
5
. D.
5
.
Câu 41: Cho hàm số
2
2
2 4 3
f x x x x
với mọi
x
. Có bao nhiêu giá trị nguyên dương của
m
để hàm số
2
10 9
y f x x m
có
5
điểm cực trị?
A.
18
. B.
16
. C.
17
. D.
15
.
Câu 42: Gọi
1
z
,
2
z
là các số phức thoả mãn điều kiện
1 2
3 3
z z
và
1 2
3 1
z z
. Giá trị lớn nhất của biểu
thức
1 2
P z z
bằng
A.
5
. B.
4
9
. C.
2
. D.
1
.
Câu 43: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
. Khoảng cách từ tâm
O
của tam giác
ABC
đến mặt phẳng
A BC
bằng
6
a
. Thể tích khối lăng trụ bằng
TRƯỜNG THPT XUÂN ĐỈNH
16
A.
3
3 2
4
a
. B.
3
3 2
8
a
. C.
3
3 2
28
a
. D.
3
3 2
16
a
Câu 44: Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
0;1
và thỏa
3 2
2
2
2 5 5
1
x x x
f x f x
x x
;
1 0 2
f f
;
1
0
d 0
f x x
. Biết diện tích hình phẳng giới hạn bởi đồ thị
:
C y f x
, trục
tung và trục hoành có dạng
ln ln
S a b
với
,
a b
là các số nguyên dương. Tính
2 2
T a b
.
A.
13
T
. B.
25
T
. C.
34
T
. D.
41
T
.
Câu 45: Có bao nhiêu giá trị dương của số thực
a
sao cho phương trình
2 2
3 2 0
z z a a
có nghiệm
phức
0
z
thỏa
0
3
z
.
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 46: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(1;1;1)
A
,
(2;0;1)
B
và mặt phẳng
( ) : 2 2 0.
P x y z
Viết phương trình chính tắc của đường thẳng
d
đi qua
A
, song song với mặt
phẳng
( )
P
sao cho khoảng cách từ
B
đến
d
lớn nhất.
A.
1 1 1
:
3 1 2
x y z
d
. B.
2
:
2 2 2
x y z
d
.
C.
2 2
:
1 1 1
x y z
d
. D.
1 1 1
:
3 1 1
x y z
d
.
Câu 47: Biết rằng trong tất cả các cặp
;
x y
thỏa mãn
2 2
2 2
log 2 2 log 1
x y x y , chỉ có duy nhất
một cặp
;
x y
thỏa mãn
3 4 0
x y m
. Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20 B. 46 C. 28 D. 14
Câu 48: Hình nón tròn xoay có chiều cao
40
h cm
, bán kính đáy
50
r cm
. Một thiết qua đỉnh của hình nón
và khoảng cách từ tâm mặt đáy đến mặt phẳng chứa thiết diện là
24
d cm
. Tính diện tích S của thiết
diện.
A.
2
800
cm
. B.
2
1600
cm
. C.
2
200
cm
. D.
2
2200
cm
.
Câu 49: Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 2 4 6 13 0
S x y z x y z
. Lấy điểm
M
trong
không gian sao cho từ
M
kẻ được ba tiếp tuyến
MA
,
MB
,
MC
đến mặt cầu
S
thỏa mãn
60
AMB
,
90
BMC
,
120
CMA
(
A
,
B
,
C
là các tiếp điểm). Khi đó đoạn thẳng
OM
có độ
nhỏ nhất bằng
A.
14 3 3
. B.
14 6 3
. C.
14 6
. D.
6 14
.
Câu 50: Cho hàm số
3 2
3 2
y f x x x
. Hỏi có bao nhiêu giá trị nguyên của tham số
10;10
m để
hàm số
x f x m
g
nghịch biến trên
0;1
?
A.
7
. B.
8
. C.
9
. D.
10
.
--------------------------------------HẾT----------------------------------
| 1/16
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT XUÂN ĐỈNH NĂM HỌC 2023 – 2024 MÔN: TOÁN - KHỐI: 12 A. KIẾN THỨC ÔN TẬP
I. GIẢI TÍCH: TỪ ỨNG DỤNG ĐẠO HÀM ĐỂN HẾT ỨNG DỤNG TÍCH PHÂN VÀ SỐ PHỨC.
II. HÌNH HỌC: TỪ THỂ TÍCH KHỐI ĐA DIỆN ĐẾN HẾT PHƯƠNG TRÌNH MẶT CẦU, MẶT PHẲNG, ĐƯỜNG THẲNG. B. CÂU HỎI TRẮC NGHIỆM I. GIẢI TÍCH
1. Ứng dụng đạo hàm khảo sát sự biến thên và vẽ đồ thị hàm số (Trong đề cương ôn tập giữa HK1).
2. Luỹ thừa, logarit – hàm số luỹ thừa, hàm số mũ, hàm số logarit – phương trình mũ, logarit (Trong đề cương ôn tập HK1).
3. Ứng dụng hình học tích phân
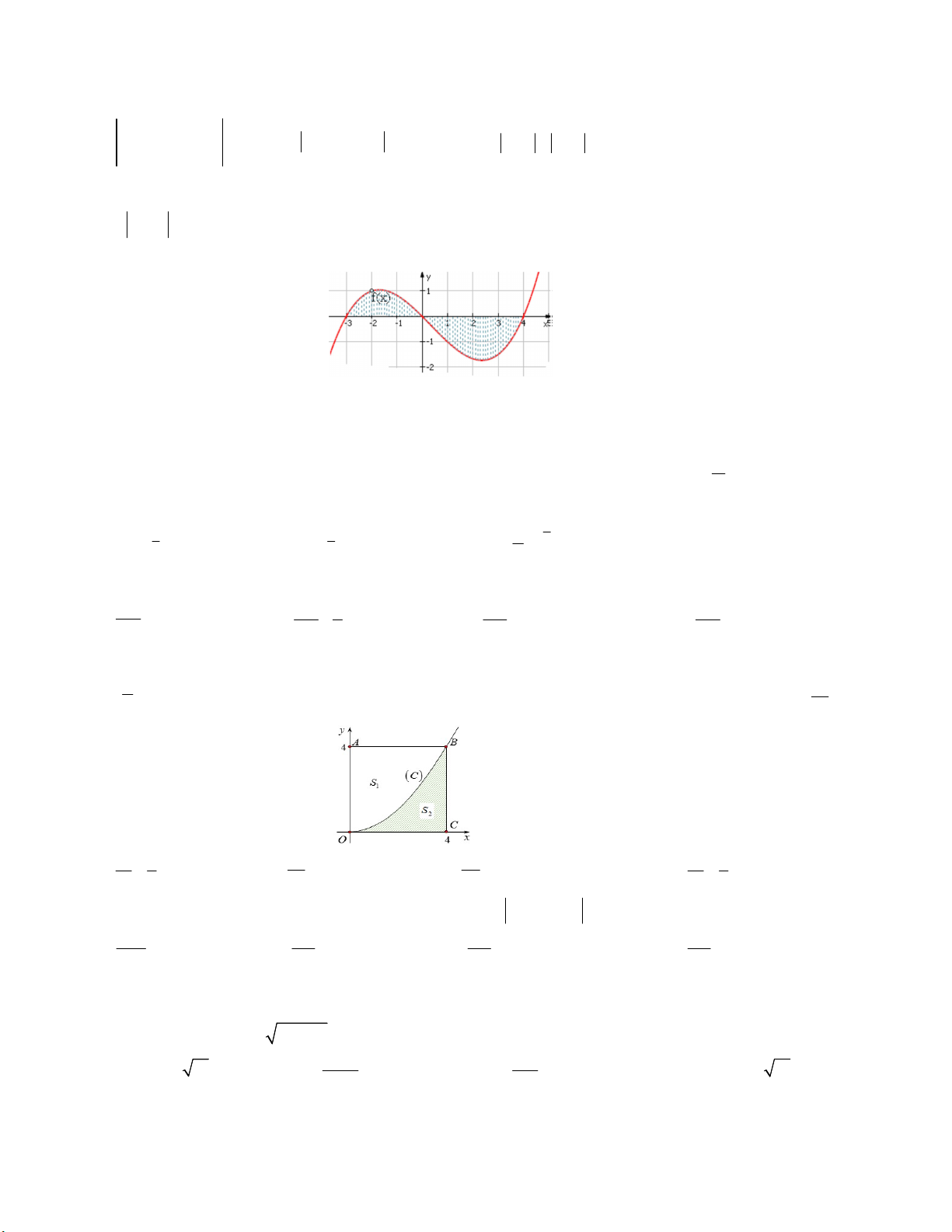
Câu 1. Diện tích S của hình phẳng tô đậm trong hình dưới đây được tính theo công thức nào sau đây? 2 4 2 4
A. S   f (x)dx  f (x)dx  
B. S   f (x)dx  f (x)dx   0 2 0 2 2 4 4 C. S  f (x)dx  f (x) dx   D. S  f (x)dx  0 2 0
Câu 2. Diện tích S của hình phẳng giới hạn giới hạn bởi đồ thị hàm số 3 2
y  x  3x  2, hai trục tọa độ và đường thẳng x  2 là 3 7 5 A. S  B. S  C. S  4 D. S  2 2 2
Câu 3. Thể tích khối tròn xoay được tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi các đường
y  x , y  2  x và y  0 là A. 2 B. C. 3 D. 5 7 2 6
Câu 4. Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số 2 y  x , y  2x . A. 3 S  . B. 20 S  . C. 4 S  . D. 3 S  . 20 3 3 4
Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f (x) C , y  f (x) C liên tục trên đoạn [a;b] và 1  1 2  2
hai đường thẳng x  a , x  b được xác định: b b y A. S   f x  f x  x d  B. S  f x  f x x d  (C ) 1   2   1   2   1 a a 1 c 2 c b (C ) C. 2
S   f x  f x  dx   f x  f x  x d   f x  f x  dx  1   2     2   1    1  2   a 1 c 2 c a c O c2 b x 1 c b 1
D. S   f x  f x  dx  f x  f x dx  1  2    1   2   a 1 c 1 TRƯỜNG THPT XUÂN ĐỈNH
Câu 6. Diện tích hình phẳng giới hạn bởi các đồ thị y  f (x) và y  g (x) liên tục trên đoạn [a;b] và hai
đường thẳng x  a; x  b là b b b b A. f (x)  g(x)dx .  B. f (x)  g(x) d . x 
C.  f (x)  g(x) d .x D.  f (x) g(x)d .x a a a a
Câu 7. Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y  x 1, trục hoành và 2 đường thẳng x  1; x  3 là 3 3 3 3 A. 2 x 1 d . x  B. 2 2  (x 1)d . x  C. 2  (x 1)d . x  D. 2 2 (x 1) d . x  1 1 1 1
Câu 8. Cho đồ thị hàm số y = f(x)
Diện tích hình phẳng (gạch trong hình) là 0 0 1 4 3  4 4 A. f
 xdx  f xdx B. f
 xdx  f xdx C. f
 xdx  f xdx D. f  xdx 3 4 3  1 0 0 3  
Câu 9. Nếu gọi S là diện tích của hình phẳng được giới hạn bởi các đường  0;  ;  0;  . x x x y y cosx e thì 2
khẳng định nào đây là đúng ?    1   A. S  e 1 2 S  e B. 2 S  e 1 C. 2  D. S  e 2  
Câu 10. Diện tích miền hình phẳng giới hạn bởi các đường 2x y 
, y  x  3 , y  1 bằng A. 1  3 . B. 1 1  . C. 1 1. D. 1  2 . ln 2 ln 2 2 ln 2 ln 2
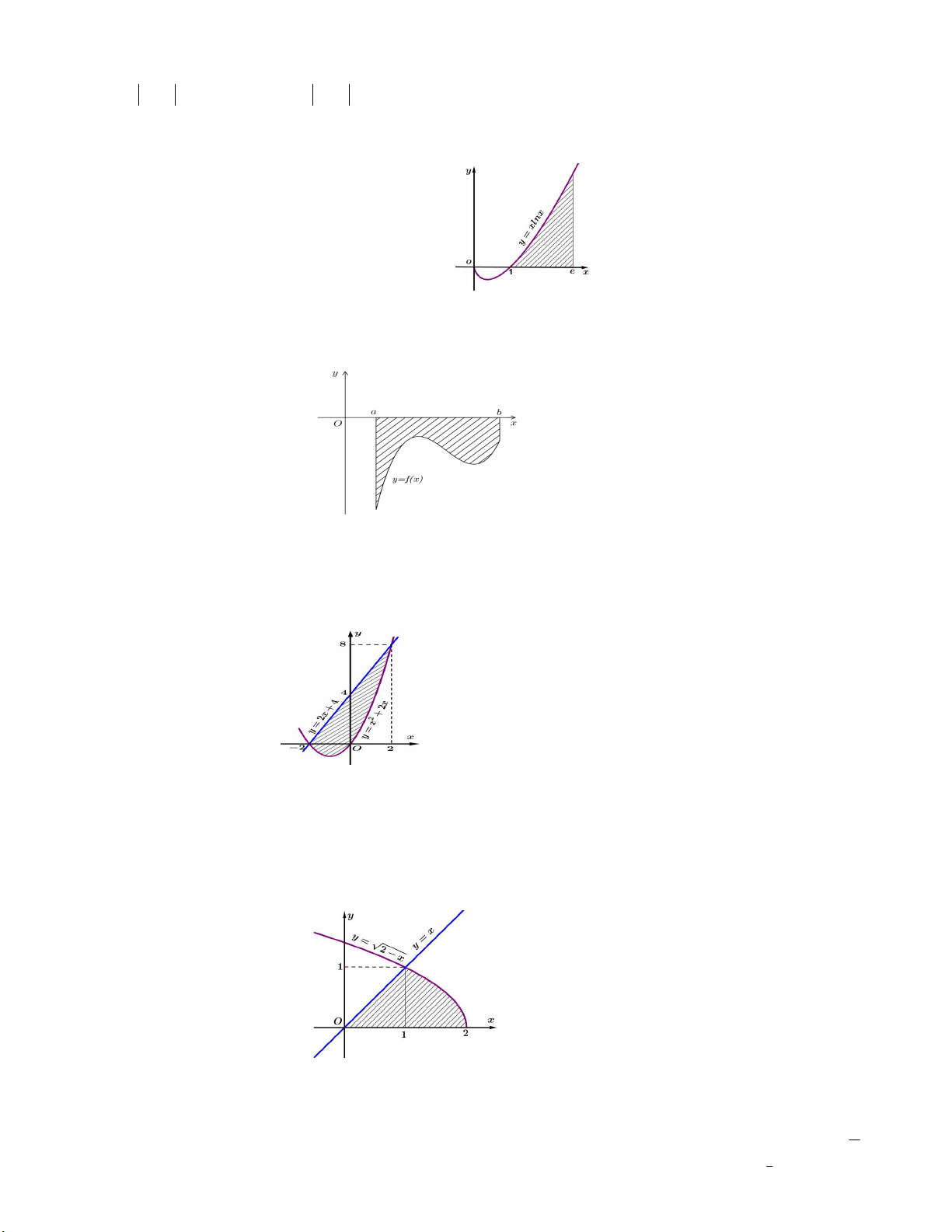
Câu 11. Hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong C có phương trình 1 2
y  x . Gọi S , S là diện tích của phần không bị gạch và phần bị gạch (như hình vẽ sau). Tính tỉ số S1 4 1 2 S2 A. S 3 S S S 1
1  . B. 1  2 . C. 1  1 . D. 1  . S 2 S S S 2 2 2 2 2
Câu 12. Diện tích hình phẳng giới hạn bởi hai đường: 2 y  x  4x  3 , x  1  . bằng
A. 107 . B. 109. C. 109. D. 109. 6 6 7 8
Câu 13. Thể tích V của phần vật thể giới hạn bởi mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt
phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x 1  x  3 thì được thiết diện là một hình chữ nhật có
độ dài hai cạnh là 3x và 2 3x  2 .  124 A. V  32  2 15 . B. 124 V  . C. V  .
D. V  32  2 15 . 3 3
Câu 14. Cho hàm số y  f (x) liên tục và không âm trên [a;b] Hình phẳng giới hạn bởi đồ thị hàm số , trục
hoành và hai đường thẳng x  a; x  b quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích khối tròn xoay là 2 TRƯỜNG THPT XUÂN ĐỈNH b a b a A.  f (x) d . x  B.  f (x) d . x  C. 2  f (x)d . x  D. 2  f (x)d . x  a b a b
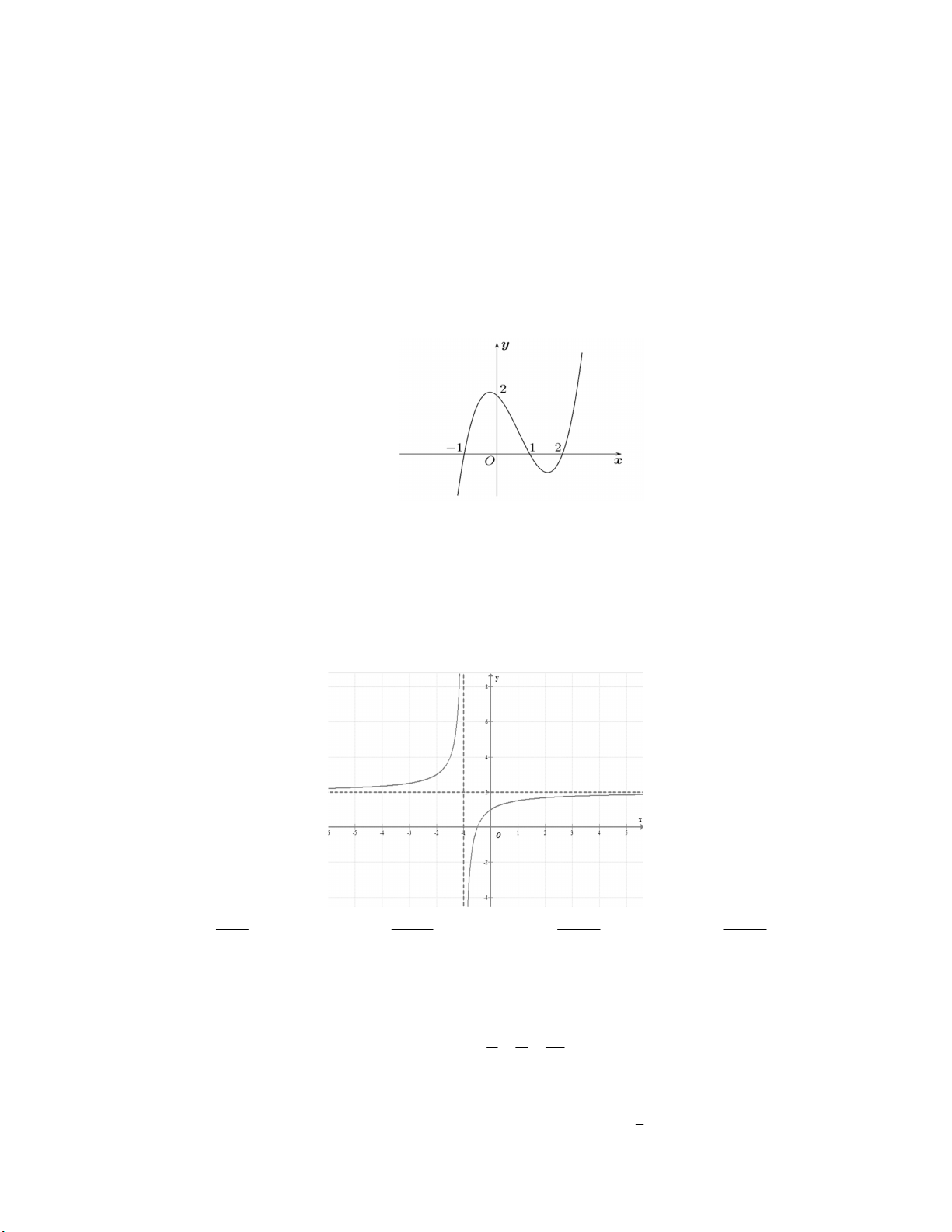
Câu 15. Công thức thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục Ox là e e e e A.     .xln x2 2  e  dx   . B.   .xln xdx  .
C.   .xln x edx. D.   .xln x2 dx  . 1 1 1 1
Câu 16. Cho hàm số f  x liên tục trên đoạn  ; a b .
Khi quay hình phẳng như hình vẽ trên quanh trục Ox ta được khối tròn xoay có thể tích là b b b b A.   f  x 2 dx  . B.  f  x 2 dx  . C.    f  x 2 dx  . D.  f  x dx . a a a a
Câu 17.Công thức thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục Ox là 2 2 A. 4 3 2
 x  4x 8x 16x 16 dx  2  
. B.   4 x dx . 2  2  2 2 C. 4 3
 x  4x 16x 16 dx  2   .
D.   x  4x  4dx . 2  2 
Câu 18.Công thức thể tích vật thể tròn xoay thu được khi quay hình phẳng (phần gạch sọc của hình vẽ) xung quanh trục Ox là 1 2 1 2 2 2 4 A.  2 x 2 dx   x dx  . B. 2  x dx  
 2 xdx . C.   2 2  x  x dx D. 2  x dx    2 xdx . 0 1 0 1 0 0 2 1 7
Câu 19. Miền phẳng trong hình vẽ giới hạn bởi hàm số y  f  x và parbol 2 y  x  2x . Biết f  xdx   . 5 1  2 3 TRƯỜNG THPT XUÂN ĐỈNH
Khi đó diện tích hình phẳng được gạch chéo trong hình vẽ bằng A. S  1. B. 71 S  . C. 41 S  . D. S  2 . 40 40
Câu 20. Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các parabol 2 y  4  x và 2 y  2  x
quay quanh trục Ox là kết quả nào sau đây? A. V  10 .  B. V  12 .  C. V  14 .  D. V  16 . 
Câu 21. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số 2 y = x 2 ; x  y quanh trục Ox là  2 4  3 A. B. C. D. 10 3 10 10 
Câu 22. Ký hiệu (H) là hình phẳng giới hạn bởi các đường y  sin x  cos x  a, y  0, x  0, x  với a là 2
tham số thực lớn hơn 2. Tìm a sao cho thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh 2 3 trục hoành bằng . 2 A. a  3 B. a  4 C. a  6 D. a  9
Câu 23. Cho hình phẳng H giới hạn bởi 2
y 2xx , y  0 . Tính thể tích của khối tròn xoay thu a a
được khi quay H xung quanh trục Ox ta được V     1 
 với a,b   và là phân số tối  b  b giản. Tính a, b.
A. a  1, b  15 . B. a  –7, b  15 . C. a  241, b  15. D. a  16, b  15
2. Số phức – các phép toán – căn bậc hai – phương trình bậc hai
Câu 24. Cho các số phức z, z , z . Mệnh đề nào sau đây là mệnh đề sai 1 2 A. z =z  z = z 1 2 1 2 B. z = 0  z = 0
C. Tập hợp điểm biểu diễn các số phức z thỏa mãn z  1 là đường tròn tâm O, bán kính R = 1
D. Hai số phức bằng nhau khi và chỉ khi phần thực và phần ảo tương ứng bằng nhau  i
Câu 25. Cho số phức z thỏa mãn   i 1 2 z 
 5  i . Môđun của số phức 2 w  1 2z  z là 1 i A. 10. B. 1  0. C. 100. D. 1  00. z  i Câu 26. Cho số phức z 5( ) thỏa mãn
 2  i . Môđun của số phức 2   1 z  z là z 1 A. 4 B. 9 C. 13 D. 13
Câu 27. Tính mô đun của số phức w    2 1 i .z , biết z  m
A. w  4m B. w  2m C. w  2m D. w  m
Câu 28. Cho hai số phức z  3  i, z  2  i . Giá trị của biểu thức z  z z là 1 2 1 1 2 4 TRƯỜNG THPT XUÂN ĐỈNH A. 0 B. 10 C. 1  0 D. 100
Câu 29. Cho số phức z  3  4i . Khi đó môđun của z1 là 1 1 1 1 A. B. C. D. 5 5 4 3  z 
Câu 30. Tìm phần thực, phần ảo của số phức z thỏa  i    i 3979 1  (1 i) ?  2  A. Phần thực là 1990 2
và phần ảo là 2 . B. Phần thực là 1990 2 và phần ảo là 2 . C. Phần thực là 1989 2
và phần ảo là 1. D. Phần thực là 1989 2 và phần ảo là 1.
Câu 31. Tìm phần ảo của số phức z thỏa mãn i   iz   i  2 2 1 3 1 A. 8 B. 9 C. 9 D. 8 1
Câu 32. Cho số phức z = a + bi. Khi đó số z z là 2i A. Một số thực B. 0
C. Một số thuần ảo D. i
Câu 33. Cho số phức z thỏa mãn: 2
(3  2i)z  (2  i)  4  .i Hiệu phần thực và phần ảo của z là A. 1 B. 0 C. 4 D. 6 z
Câu 34. Cho hai số phức z = a + bi và z’ = a’ + b’i. Số phức có phần ảo là z ' aa ' bb ' ba ' ab ' aa ' bb ' 2bb' A. B. C. D. 2 2 a  b 2 2 a '  b' 2 2 a  b 2 2 a '  b'  
Câu 35. Thu gọn số phức z = 3 2i 1 i  ta được 1 i 3  2i A. 21 61  i B. 23 63  i C. 15 55  i D. 2 6  i 26 26 26 26 26 26 13 13
Câu 36. Biết điểm A(3;-2) là điểm biểu diễn của số phức z. Hỏi số phức liên hợp z của z là A. z  3  2i B. z  3  2i C. z  3  2i D. z  3  2i
Câu 37. Tìm số thực x, y để số phức 2 5 z  9 y  4 10xi và 2 11
z  8y  20i là liên hợp của nhau? 1 2
A. x  2; y  2 . B. x  2; y  2 . C. x  2; y  2 . D. x  2; y  2 .
Câu 38. Cho hai số thực x, y thỏa mãn 2x 1 1 2yi  22  i  yi  x . Giá trị của 2 x  3xy  y bằng A. 1. B. 1. C. 2  . D. 3  .
Câu 39. Cho số phức z  1 2i và z  1
  2i . Khẳng định nào sau đây là khẳng định đúng? 1 2 z
A. z  z  0 . B. 1  1 . C. z .z  3  4i . D. z   z . 1 2 z 1 2 1 2 2
Câu 40. Cho số phức z  1
  2i . Khẳng định nào sau đây là khẳng định đúng?  z  1  2 A. 1 z  . B. 1 z  1 2i z z  . D. 1 z   i . 2 z C. 1 . 0 5 5 1 1 1
Câu 41. Tìm số phức z thỏa mãn   z 1 2i 1 2i2 8 14 A. 8 14 z   i B. z    i C. 10 35 z   i D. 10 14 z   i 25 25 25 25 13 26 13 25
Câu 42. Có bao nhiêu số phức z thỏa mãn z + z = 2024 A. 0 B. 1 C. 2 D. Vô số
Câu 43. Tìm số phức z thỏa mãn 1 i z 1 2i  3  2i  0 3 5 5 3 A. z  4  3i B. z   i C. z   i D. z  4  3i 2 2 2 2
Câu 44. Tìm số phức z thỏa mãn zi  2z  4  4i A. z  4  4i B. z  3  4i C. z  3  4i D. z  4  4i 5 TRƯỜNG THPT XUÂN ĐỈNH
Câu 45. Số phức z thỏa mãn: z  2  3i z  1 9i là A. 2  i . B. 2   i . C. 3  i . D. 2  i
Câu 46. Trong R , phương trình z  z  2  4i có nghiệm là
A. z  3  4i B. z  2  4i C. z  4  4i D. z  5  4i
Câu 47. Có bao nhiêu số phức z thỏa mãn z  10 đồng thời phần ảo gấp ba lần phần thực A. 1 B. 2 C. 3 D. 4
Câu 48. Nghiệm của phương trình 4  7i z 5  2i  6iz là A. 18 13   i B. 18 13  i C. 18 13  i D. 18 13  i 7 7 17 17 7 17 17 17 a Câu 49. Phương trình 2
z  2z  5  0 có nghiệm là z  a  bi ( , a b ). Khi đó bằng b 1 1 1 1 A. B. C. D. 2 3 4 5
Câu 50. Kí hiệu z , z , z và z là các nghiệm phức của phương trình 4 2 z  z 12  0 . Tổng 1 2 3 4
T  z  z  z  z bằng 1 2 3 4 A. T  4. B. T  2 3. C. T  4  2 3. D. T  2  2 3.
Câu 51. Phương trình   i 2 2
z  az  b  0a,b có hai nghiệm là 3 i và 1 2i . Khi đó a  ? A. 9
  2i B. 155i C. 9 2i D. 155i
Câu 52. Gọi z và z lần lượt là nghiệm của phương trình: 2
z  2z  5  0 . Tính   z  z 1 2 1 2 A. 2 5 B. 10 C. 3 D. 6
Câu 53. Giá trị của m thuộc khoảng nào sau đây để phương trình 2
z  2  mz  2  0 nhận số phức z = 1 – i làm một nghiệm
A. m  5;7 B. m 3;6 C. m3;  1 D. m  1;4
Câu 54. Gọi z1, z2, z3, z4 là các nghiệm phức của phương trình 4 2
2z  3z  2  0 . Khi đó, giá trị 2 2 2 2 H  z  z  z  z bằng: 1 2 3 4
A. H  5 . B. H  3 2 . C. H  2 . D. H  5 2 .
Câu 55. Gọi A và B lần lượt là hai điểm biểu diễn của hai số phức z  5  3i và z '  3  5i . Kết luận nào sau đây là đúng?
A. A và B đối xứng nhau qua trục hoành
B. A và B đối xứng nhau qua trục tung
C. A và B đối xứng nhau qua gốc tọa độ
D. A và B đối xứng nhau qua đt y  x
Câu 56. Cho số phức z thỏa mãn | z 1| 2 . Biết rằng tập hợp điểm biểu diễn các số phức w  1 i 3 z  2
là một đường tròn. Tính bán kính r của đường tròn đó A. r  16 B. r  4 C. r  25 D. r  9
Câu 57. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn 2 z  i  z  z  2i là
A. Một đường thẳng B. Một đường tròn C. Một parabol D. Một elip.
Câu 58. Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện phần thực của z bằng -2 là A. x  2
 . B. y  2 . C. y  2x D. y  x  2
Câu 59. Trong mặt phẳng phức Oxy , số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ
A. 1  z  2 và phần ảo dương.
B. 1  z  2 và phần ảo âm.
C. 1  z  2 và phàn ảo dương. 6 TRƯỜNG THPT XUÂN ĐỈNH
D. 1  z  2 và phần ảo âm.
Câu 60. Cho các số phức z  1 i,z  2  3i,z  5  i, z  2  i lần lượt có các điểm biểu diễn trên mặt 1 2 3 4 phẳng phức là M , N, ,
P Q . Hỏi tứ giác MNPQ là hình gì?
A. Tứ giác MNPQ là hình thoi.
B. Tứ giác MNPQ là hình vuông.
C. Tứ giác MNPQ là hình bình hành. D. Tứ giác MNPQ là hình chữ nhật. 1
Câu 61. Cho A , B , C lần lượt là các điểm biểu diễn của các số phức 6  3i ; 1 2ii ; .Tìm số phức có điểm i
biểu diễn D sao cho ABCD là hình bình hành.
A. z  8  3i . B. z  8  4i . C. z  4  2i . D. z  8  5i .
Câu 62. Trong mặt phẳng phức Oxy , các số phức z thỏa mãn z  2i 1  z  i . Tìm số phức z được biểu
diễn bởi điểm M sao cho MA ngắn nhất với A 1,3 .
A. 3  i . B. 1 3i . C. 2 3i . D. 2  3i .
Câu 63. Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: | z 1 i | 1 .
A. Đường tròn tâm I(-1;-1), bán kính R = 1.
B. Hình tròn tâm I(1;-1), bán kính R = 1.
C. Hình tròn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường tròn).
D. Đường tròn tâm I(1;-1), bán kính R = 1.
Câu 64. Điểm biểu diễn số thuần ảo nằm ở đâu trên mặt phẳng tọa độ?
A. Trục Ox B. Trục Oy C. Gốc tọa độ D. Phân giác của góc phần tư thứ I, III. (2  3i)(4  i)
Câu 65. Điểm biểu diễn số phức z  có tọa độ là 3 2i A. (1;-4) B. (-1;-4) C. (1;4) D. (-1;4)
Câu 66. Gọi D là tập hợp các số phức z thỏa mãn z  i 1. Khi đó D là z  i A. Trục hoành. B. Trục tung.
C. Đường phân giác y = x.
D. Đường phân giác y = -x.
Câu 67. Gọi D là tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z sao cho 1 là số thuần ảo. z  i
Lựa chọn phương án đúng ? A. D là trục tung. B. D là trục hoành.
C. D là đường phân giác thứ nhất y = x
D. D là trục tung bỏ đi điểm I(0; 1).
Câu 68. Cho số phức z thỏa z  i 1  z  2i . Giá trị nhỏ nhất của z là 1 1 A. B. 1 C. 2 D. 2 4
Câu 69. Xét các số phức z thỏa mãn z  z 1 2i . GTNN của biểu thức P  1 2i z 11 2i bằng 5 5 2 A. 10 B. C. D. 2 2 2 5 II. HÌNH HỌC
Câu 70. Cho mặt cầu S  2 2 2
: x  y  z  2x  4 y  2z  0 . Tâm và bán kính mặt cầu   S là A. I 1;2; 
1 , R  6 B. I 1;2;   1 , R  6 C. I 1;2;  
1 , R  6 D. I 1; 2;  1 , R  6
Câu 71. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;-1) và đi qua điểm A(2;1;2). Mặt
phẳng nào sau tiếp xúc với (S) tại A ?
A. x + y - 3z - 8 = 0. B. x - y - 3z + 3 = 0. C. x + y + 3z - 9 = 0. D. x + y - 3z + 3 = 0.
Câu 72. Trong không gian Oxyz, mặt cầu có tâm thuộc Ox và tiếp xúc với hai mặt phẳng
P: x  y  2z  5  0, Q: x  2y  z  3  0 có phương trình là 1 1 1 1 A.  x  42 2 2
 y  z  . B.  x  42 2 2
 y  z  . C. x  42 2 2  y  z  . D.  x  42 2 2  y  z  . 5 6 7 8 7 TRƯỜNG THPT XUÂN ĐỈNH
Câu 73. Trong không gian Oxyz, mặt cầu (S) đi qua A0;2;0 , B2;3;  1 , C 0;3;  1 và có tâm nằm trên
Oxz . Phương trình mặt cầu (S) là
A. x   y  2   z  2 2 6 4  9 B. x   y  2 2 2 3  z  16
C. x   y  2   z  2 2 7 5  26
D.  x  2  y   z  2 2 1 3  14
Câu 74. Trong không gian với hệ tọa độ Oxyz, cho hai điểm P 2;0; 
1 ,Q 1;1;3 và mặt phẳng
R:3x  2y  z 5  0 . Viết phương trình mặt phẳng   đi qua ,
P Q và vuông góc với mp R A. 7
 x 11y  z  3  0 B. 7x 11y  z 1 0 C. 7
 x 11y  z 15  0 D. 2x  y  z  0
Câu 75. Trong không gian tọa độ x y 1 z 3 Oxyz, cho đường thẳng   d :   và điểm A1;2;  3 . Phương trình 3 4 1
mặt phẳng  đi qua A và chứa d là
A. 23x 17y  z 14  0. B. 23x 1  7yz 1
 4 0. C. 23x 17y  z 60  0.
D. 23x 17y  z 14  0. x 1t x 1 y z  2 
Câu 76. Trong không gian tọa độ Oxyz, cho 2 đường thẳng cắt nhau d :   , d ' : y   2t . Viết 1 2 3 z  23t 
phương trình mặt phẳng chứa d và d’.
A. 3y  2z 4  0. B. 3y  2z  4  0. C. 3y 2z 4  0. D. 3y 2z  4  0. x 1t x 1 y 2 z    
Câu 77. Trong không gian Oxyz, cho 2 đường thẳng song song d :   , d ': y   2t  . Viết 1 1 2 z 12t 
phương trình mặt phẳng chứa d và d’.
A. 9x y 4z7  0. B. 9x  y  4z7  0. C. 9x y 4z 7  0. D. 9x y 4z 7  0.
Câu 78. Trong không gian với hệ tọa độ Oxyz cho M 1;2; 
1 . Viết phương trình mặt phẳng (P) qua M cắt trục 1 1 1
Ox, Oy, Oz lần lượt tại A, B, C sao cho  
đạt giá trị nhỏ nhất. 2 2 2 OA OB OC x y z
A.  P : x  2 y  3z  8  0 B.P : x  y  z  4  0 C. P : x  2y  z  6  0 D. P    : 1 1 2 1 x 1 t  x 1 y  2 z
Câu 79. Trong k/gian Oxyz cho đường thẳng d : y  2t ; d :   . Khi đó d và d 1 2 1 1 3 1 2 z 13t 
A. Cắt và vuông góc B. Song song D. Chéo nhau
B. Cắt nhưng không vuông góc x 1 y  3 z  2
Câu 80. Trong không gian Oxyz cho A(3;2;0), đường thẳng d :  
. Khoảng cách từ điểm A 1 2 2
đến đường thẳng d là A. 2 B. 3 C. 4 D. 5
Câu 81. Trong không gian Oxyz gọi d là phương trình đường thẳng qua A1; 2
 ;0 và có một véctơ chỉ  phương là u 1;2; 3
  . Khẳng định nào dưới đây là sai? x 1 t x  t x 1 t x  t     
A. d : y  2  2t B. d : y  4  2t C. d : y  2   2t D. d : y  4   2t z  3t     z  3  3t  z  3t  z  1 3t  x 1 t  x 1 y  2 z
Câu 82. Trong không gian Oxyz cho hai đường thẳng d : y  2t ;  : 
 và gọi  là góc giữa  2 3 1 z  2t 
d và  . Khi đó cos có giá trị bằng 8 TRƯỜNG THPT XUÂN ĐỈNH A. 5 13 B. 5 14 C. 5 15 D. 5 17 21 21 21 21
Câu 83. Trong không gian Oxyz gọi d là phương trình đường thẳng qua A1; 2  ;0 và B2;0;  1 . Khẳng định nào sau đây là đúng? x 1 t x  2  t   x  2 y z 1 x  3 y  2 z 1
A. d : y  2  2t B. d : y  2t C. d :   D. d :    1 2 1 1 2 1 z  1 t   z  1   t  x 1 t
Câu 84. Trong không gian Oxyz cho đường thẳng 
d : y  2t mặt phẳng  P : 2x  3y  z 1  0 . Hình chiếu z  2t 
của đường thẳng (d) trên mặt phẳng (P) có phương trình là   x  3t x  3t  x  3t  x  3t A.  1   1   y    t B. y  1 t C. y    t D. y 1 t 2   2 z  5  9t  z  59t  5   5  z   9t  z   9t  2  2
Câu 85. Phương trình đường thẳngtrong không gian Oxyz đi qua điểm A1; 2  ; 
1 và song song với đường  thẳng x y z 1 d :   có phương trình là 2 1 1        A. x 1 y 2 z 1     B. x 1 y 2 z 1   C. x 3 y 1 z   D. Đáp án khác 2 1 1  2 1 1 2 1 1  x  3t
Câu 86. Trong không gian tọa độ Oxyz, hình chiếu vuông góc của điểm 
P 2;1;3 trên d : y  7  5t là điểm z  2 2t 
có tọa độ nào sau đây?
A. (-3; 2; 4) B. (-3; -2 ;-4) C. (3;-2;4) D. (3;-2;-4 )
Câu 87. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng x  3 y  1 z  1 d :   và điểm M(1;2;-3). 2 1 2
Mặt cầu tâm M, tiếp xúc với đường thẳng d có bán kính R bằng bao nhiêu? A. R  2 B. R  2 5 C. R  2 2 D. R = 4.
Câu 88. Trong không gian tọa độ Oxyz, cho hai đường thẳng x 1 y z  2 x  y  z    và 2 3 1   . Góc 1 1 1 2 2 4
giữa hai đường thẳng trên là A. 30 B. 45 C. 60 D. 90
Câu 89. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng  qua A1;0; 1
  và có véc tơ chỉ phương
u2;4;6. Phương trình tham số của đường thẳng  là x  1  2t x  2  t x  1  t x  1  t A. d :   y  4t B. d :  y  4 C. d :  y  2t D. d : y  2t z  1 6t     z  6  t  z  1 3t  z  1 3t  x  2  4t x  1   7t 1 2
Câu 90. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng   d : y  1
  3t và d : y  3  5t . Vị trí 1 1 2 2 z  1   5t   z  3  t 1  2 tương đối của d d 1 và 2 là A. d d d  d d d d d 1 cắt 2 B. 1 2 C. 1 và 2 trùng nhau D. 2và 1 chéo nhau 9 TRƯỜNG THPT XUÂN ĐỈNH x  2  t
Câu 91. Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) song song với 2 đường thẳng y  3 2t và z 1t  x  2 y 1 z 
 . Mặt phẳng (P) có 1 véc tơ pháp tuyến là 2 3 4
A. (-5; 6;-7) B. (5; -6 ;7) C. (-5 ; -6 ; 7) D. (-5 ;6 ;7)
Câu 92. Mặt cầu S  tâm I  1  ;2; 3
  và tiếp xúc với P : x  2y  2z 1 0 có phương trình là
A.  x  2   y  2   z  2 4 1 2
3  . B.  x  2   y  2   z  2 4 1 2 3  . 9 9
C.  x  2   y  2   z  2 4 1 2
3  . D.  x  2   y  2  z  2 16 1 2 3  . 3 3
Câu 93. Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng   đi qua M 0;2;3 , song song với đường x  2 y 1 thẳng d : 
 z và vuông góc với mặt phẳng   : x  y  z  0 có pt là 2 3
A. 2x  3y  5z  9  0 . B. 2x  3y  5z  9  0 . C. 2x  3y  5z  9  0 . D. 2x  3y  5z  9  0 .  x  1 t   
Câu 94. Trong không gian Oxyz , đường thẳng x 1 y 2 z 4  d :   và d ':  y  t 
có vị trí tương đối là 2 1 3 z  23t 
A. trùng nhau. B. song song. C. chéo nhau. D. cắt nhau.
Câu 95. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng   : x  2 y  2z  m  0 và điểm A1;1;  1 . Khi đó
m nhận giá trị nào sau đây để khoảng cách từ điểm A đến mặt phẳng   bằng 1?
A.  2. B.  8. C.  2 hoặc 8 . D. 3.
Câu 96. Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình chính tắc của đường
thẳng  đi qua hai điểm A1; 2  ;5 và B3;1;  1 ? x 1 y  2 z  5 x  3 y 1 z 1 x 1 y  2 z  5 x 1 y  2 z  5 A.   . B.   . C.   . D.   . 2 3 4 1 2 5 2 3 4 3 1 1
Câu 97. Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng  đi qua điểm M 2;1;5, đồng  
thời vuông góc với hai vectơ a  1;0;  1 và b  4;1;   1 là x  2 y 1 z  5 x  2 y 1 z  5 x  2 y 1 z  5 x 1 y  5 z 1 A.   . B.   . C.   . D.   . 1 5 1 1 5 1 1 5 1 2 1 5 x 1 3t x  2 y 1 z 1
Câu 98. Trong không gian tọa độ Oxyz, cho hai đường thẳng d :   và      . Phương 1 d : y 2 t 1  3 2 2 z  1   t 
trình đường thẳng nằm trong  : x  2y 3z  2  0 và cắt hai đường thẳng d , d là 1 2 x  3 y  2 z 1    x  3 y  2 z 1   A.   x y z x y z . B. 3 2 1   . C.   . D. 8 3   . 5 1  1 5  1 1  5  1 1  1 3 4  x 1  t   x  2   t 
Câu 99. Trong không gian tọa độ d : 
Oxyz , cho hai đường thẳng y 2t d :  1     và y 1 2t . Để hai đường 2      z  2    t z  2   mt
thẳng hợp với nhau một góc bằng 0
60 thì giá trị của m bằng A. m  1
B. m  1 C. m  1 D. m  1 2 2 x  1 2t
Câu 100. Trong không gian tọa độ Oxyz, PT nào dưới đây là phương trình chính tắc của d: y  3t ? z  2   t  10 TRƯỜNG THPT XUÂN ĐỈNH x 1 y z  2 x 1 y z  2 x 1 y z  2 x 1 y z  2 A.   . B.   . C.   . D.   . 2 3 1 2 3 2 1 3 2  2 3 1
Câu 101. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x – 2y –z +1 = 0 và đường thẳng x 1 y  2 z 1  :  
. Tính khoảng cách d giữa đường thẳng  và (P) ? 2 1 2 1 5 2 A. d  . B. d  . C. d  . D. d  2 . 3 3 3 x  3 y  6 z 1
Câu 102. Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d :   và 1 2  2 1 x  t  d : y  t
 t   . Đường thẳng đi qua điểm (
A 0;1;1) , vuông góc với d và cắt d có PT là 2   1 2 z  2  x y 1 z 1 x y 1 z 1 x y 1 z 1 x 1 y z 1 A.   B.   C.   D.   1 3  4 1 3  4 1 3 4 1  3  4 x 1t  x  0  
Câu 103. Trong không gian tọa độ 
Oxyz, cho hai đường thẳng d : y  0     1  và d : y 4 2t .  2  z  5t  z  53t 
Phương trình đường vuông góc chung của d d 1 và là 2 x  4t x 4 y z 2  x  4 y z 2 A.   . B. y  3t . C.   . D. x  4 y z  2   . 2 3 2  2 3 2 2 3 2 z  2  t  x  5  t
Câu 104. Trong không gian Oxyz, cho hai đường thẳng d , d có phương trình lần lượt là  và 1 2  y  3  t z  2   2t  x  1   3t ' 
y 1 t ' . Tìm tham số thực m để hai đường thẳng d và d cắt nhau. 1 2  z  5  mt ' 
A. m  1 B. m  1 C. m  2 D. m  2
Câu 105. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x y 1 z  2   và mặt phẳng (P): 1 2 3
x  2y  2z  3  0 . Tọa độ điểm M thuộc đường thẳng (d) và cách mp (P) một đoạn bằng 2 là
A. M  ;1 ;35 B. M  ;2 ;3  1 C. M  ; 2  ;
5 8 D. M  ;1 ;57 C. ĐỀ MINH HOẠ
Câu 1: Trên mặt phẳng tọa độ Oxy , số phức z  2
 i được biểu diễn bởi điểm A. M 2; 0. B. N 0 ; 2. C. P 0; 2. D. Q 2; 0.
Câu 2: Hàm số y  ln 2x   1 có đạo hàm là 2 1 2 1 A. y  . B. y  . C. y  . D. y  . x ln 2x   1 2x 1 2x 1 2x  1ln 2 5 
Câu 3: Trên khoảng 0; , đạo hàm của hàm số 3 y  x là 8 5  8 5  2 5  2 5  A. 3 y   x . B. 3 y  x . C. 3 y   x . D. 3 y  x . 3 3 3 3 2  1 x x  1
Câu 4: Tập nghiệm của bất phương trình    là  7  49 A. ;1 . B.  ;  2
  1; . C. 1;. D. 2;  1 . 11 TRƯỜNG THPT XUÂN ĐỈNH x  6  4t 
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : y  2  t và điểm A1;1;  1 . z  1   2t 
Tìm tọa độ hình chiếu A của A trên d. A. A2;3;  1 . B. A2;3;  1 . C. A2; 3  ;  1 . D.  A 2;3;  1 .
Câu 6: Trong không gian Oxyz , cho mặt phẳng   : 3x  2 y  4z  1  0 . Vectơ nào dưới đây là một vectơ
pháp tuyến của   ?     A. n  3;2;4 . B. n  2; 4;1 .
C. n  3; 4;1 . D. n  3;2; 4 . 4   1   3   2   Câu 7: Cho hàm số 3 2
y  ax  bx  cx  d có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của
đồ thị hàm số đã cho và trục tung là điểm nào trong các điểm sau Tìm giá trị của d . A. 1;0 . B. 2;0 . C.  1  ;0 . D. 0;2 . 3 3 Câu 8: Nếu 2 f  x1 dx  5  thì f  xdx  bằng 1 1 3 3 A. 3. B. 2. C. . D. . 4 2
Câu 9: Hình vẽ bên dưới là đồ thị của hàm số nào x 1 2x 1 2x  3 2x  5 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Câu 10: Trong không gian hệ tọa độ Oxyz , tìm tất cả các giá trị của m để phương trình 2 2 2
x  y  z  2x  2y  4z  m  0 là phương trình của một mặt cầu. A. m  6 B. m  6 C. m  6 D. m  6 x y z
Câu 11: Trong không gian Oxyz cho đường thẳng  :  
và mặt phẳng   : x  y  2z  0 . Góc giữa 1 2 1 
đường thẳng  và mặt phẳng   bằng A. 30 . B. 60 . C. 150 . D. 120 .
Câu 12: Cho hai số phức z 1 3i, w  2  i . Tìm phần ảo của số phức u  z.w . A. 7 . B. 5i . C. 5. D. 7i . 12 TRƯỜNG THPT XUÂN ĐỈNH
Câu 13: Cho hình lăng trụ đứng ABCD.AB C  D
  , có ABCD là hình vuông cạnh 2a, cạnh AC2a 3.Thể
tích khối lăng trụ ABC.AB C   bằng A. 3 4 a . B. 3 3 a . C. 3 2 a . D. 3 a .
Câu 14: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 6 , góc giữa cạnh bên và mặt đáy bằng 0 60 .
Tính thể tích V của khối chóp S.ABC? A. 3 V  9a B. 3 V  2a C. 3 V  3a D. 3 V  6a
Câu 15: Trong không gian Oxyz , cho mặt cầu S  x  2   y  2   z  2 ( ) : 1 2 3  16 và mặt phẳng
(P) : 2x  2y  z  6  0 . Khẳng định nào sau đây đúng? A. ( )
P không cắt mặt cầu (S). B. ( )
P tiếp xúc mặt cầu (S). C. ( )
P đi qua tâm mặt cầu (S). D. ( ) P cắt mặt cầu (S) .
Câu 16: Cho số phức z 1 4i . Phần ảo của phức liên hợp z bằng A. 1. B. 4 . C. 1. D. 4 .
Câu 17: Diện tích toàn phần của hình nón có bán kính đáy bằng 2 và độ dài đường sinh bằng 6 là A. 8 . B. 16 . C. 12 . D. 24 .
Câu 18: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x 1 2t 
y  2  3t t  . Đường thẳng d không đi qua điểm nào dưới đây? z 1 4t  A. Q 2;3;4 . B. N 3; 1  ;5. C. P 5; 4  ;9 . D. M 1; 2;  1 .
Câu 19: Cho hàm số y  f  x có đồ thị như hình vẽ.
Giá trị cực tiểu của hàm số là A. x  2  . B. y  2 . C. y  0 . D. y  2 . m 1 x3
Câu 20: Đồ thị hàm số y 
có tiệm cận ngang y  2 thì có tiệm cận đứng có phương trình: x  m  3 A. y  3 . B. x  6 . C. x  0 . D. x  6  .
Câu 21: Tập nghiệm S của bất phương trình log 2x  3  0 là 2   A. S   ;    1 . B. S   1  ; . C. S   ;    1 . D. S   ;  0 .
Câu 22: Trong không gian với hệ tọa độ Oxyz, giá trị của m để hai mặt phẳng () : 7x  3y  mz  3  0 và ( )
 : x  3y  4z  5  0 vuông góc với nhau là A.6. B.– 4. C.1. D.2.
Câu 23: Hàm số F  x  2x  sin 2x là một nguyên hàm của hàm số nào dưới đây? 1
A. f  x  2  2cos 2x . B. f  x 2  x  cos2x . 2 1
C. f  x  2  2cos 2x . D. f  x 2  x  cos2x . 2 2023 2023 2023 Câu 24: Nếu f  x x d  3 và g
 xdx  4 thì 2 f x gx  1dx bằng 1 1 1 A. 2024 . B. 2023. C. 2025 . D. 2022 .
Câu 25: Tìm hàm số y  f (x) biết rằng f (x)  sin x  2 và f (0)  1 13 TRƯỜNG THPT XUÂN ĐỈNH A. cos x+2x+1. B. cos x+2x+2 . C.  cos x+2x+1. D. cos x+2x .
Câu 26: Cho hàm số bậc ba y  f  x có đồ thị như hình sau
Hàm số y  f  x nghịch biến trên khoảng nào dưới đây? A. 0;2 . B. ;  1 . C. 2;4 . D.  1  ;2 . Câu 27: Cho hàm số 4 2 y  ax  bx  ca, ,
b c  có đồ thị là đường cong như hình vẽ. Điểm cực tiểu của đồ thị hàm số đã cho là A. 0 . B. 2 . C. 0; 2 . D. 2;0 .
Câu 28: Cho các số thực dương a, b thỏa mãn log a  2logb  1. Mệnh đề nào sau đây đúng? A. 2 a  b 1. B. a  2b  10 . C. 2 ab 10 . D. 2 a  b 10.
Câu 29: Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi 2
y  x và y  2x  3 quanh trục Ox là: 1088 138 9 72 A. . B. . C. . D. . 15 5 2 5
Câu 30: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A , cạnh AC  a , các cạnh bên a 6 SA  SB  SC 
. Tính góc tạo bởi mặt bên (SAB) và mặt phẳng đáy (ABC) . 2   A. . B. . C. arctan 2 . D. arctan 2 . 6 4
Câu 31: Cho hàm số y  f  x xác định trên  \ 
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f  x  m có ba nghiệm thực phân biệt. A.  1  ;  1 . B.  2 ;  1 . C.  2 ; 1 1  ;1  . D.  .
Câu 32: Cho hàm số y  f  x xác định trên tập  và có f  x 2
 x 5x  4 . Khẳng định nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng 1;4 .
B. Hàm số đã cho nghịch biến trên khoảng 3; . 14 TRƯỜNG THPT XUÂN ĐỈNH
C. Hàm số đã cho đồng biến trên khoảng  ;  3 .
D. Hàm số đã cho đồng biến trên khoảng 1;4 .
Câu 33: Tìm tham số m để phương trình x    m x 2 4 1 3
2  2m  m  0 có nghiệm. A.  ;   B.  ;  
1  1; C. 0; D. 1;
Câu 34: Tích tất cả các nghiệm của phương trình 2
log x  2log  7  0 là 3 3 A. 7 B. 9 C. 2 D. 1
Câu 35: Cho số phức z thỏa mãn z  3  5i  10 và w  2z 1 3i  9 14i . Khẳng định nào đúng trong các khẳng định sau?
A. Tập hợp điểm biểu diễn của số phức w là đường tròn tâm I 33;14 .
B. Tập hợp điểm biểu diễn số phức w là đường tròn có tâm I 33;14.
C. Tập hợp điểm biểu diễn số phức w là đường tròn có tâm I 33;14 .
D. Tập hợp điểm biểu diễn số phức w là đường tròn có bán kính R 10.
Câu 36: Trong không gian Oxyz , cho tam giác ABC với A3;1;2 , B 1;3;5, C 3;1;3 . Đường trung
tuyến AM của ABC có phương trình là x  1 2t x  1 2t x  1 2t x  3  2t     A. y  2  3t . B. y  2  3t . C. y  2  3t . D. y  1   3t . z 1 t     z  1 t  z  1 t  z  2  t 
Câu 37: Trong không gian Oxyz , cho điểm M 2; 5
 ;4 . Tọa độ điểm M ' đối xứng với M qua mặt phẳng Oyz là A. 2;5;4 . B. 2; 5  ;4. C. 2;5; 4   . D.  2  ; 5  ;4.
Câu 38: Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  ,
a AC  a 2 và SA   ABC , SA  a
. Khoảng cách từ A đến mặt phẳng SBC bằng a 3 a 2 a 10 A. . B. a . C. . D. . 2 2 5 5 2 2  x  x 1
Câu 39: Số nghiệm nguyên của bất phương trình log    x  2  x  1 là 2    16x  3  A. 2 . B. 3 . C. 10 . D. 11.
Câu 40: Cho hàm số f  x liên tục trên  . Gọi F x,G  x là hai nguyên hàm của f  x trên  thỏa mãn 8 e 1
F 8  G 8  8 và F 0  G 0  2  . Khi đó f  5lnxdx bằng x 1 A. 1. B. 1. C. 5 . D. 5  .
Câu 41: Cho hàm số f  x   x  2  2 2
x  4x  3 với mọi x. Có bao nhiêu giá trị nguyên dương của m để hàm số y  f  2
x 10x  m  9 có 5 điểm cực trị? A. 18 . B. 16 . C. 17 . D. 15.
Câu 42: Gọi z , z là các số phức thoả mãn điều kiện z  3z  3 và 3z  z  1. Giá trị lớn nhất của biểu 1 2 1 2 1 2 thức P  z  z bằng 1 2 4 A. 5 . B. . C. 2 . D. 1 . 9
Câu 43: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm O a
của tam giác ABC đến mặt phẳng  A B
 C bằng . Thể tích khối lăng trụ bằng 6 15 TRƯỜNG THPT XUÂN ĐỈNH 3 3a 2 3 3a 2 3 3a 2 3 3a 2 A. . B. . C. . D. 4 8 28 16 3 2 Câu 44: Cho hàm số  
y  f  x có đạo hàm liên tục trên đoạn 0; 
1 và thỏa      2x 5x 5x f x f x  ; x  x 12 2 1 f   1  f 0  2 ; f
 xdx  0 . Biết diện tích hình phẳng giới hạn bởi đồ thị C: y  f x , trục 0
tung và trục hoành có dạng S  ln a  ln b với a, b là các số nguyên dương. Tính 2 2 T  a  b . A. T 13 . B. T  25 . C. T  34 . D. T  41.
Câu 45: Có bao nhiêu giá trị dương của số thực a sao cho phương trình 2 2
z  3z  a  2a  0 có nghiệm phức z thỏa z  3 . 0 0 A. 3 . B. 2 . C. 1. D. 4 .
Câu 46: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(1;1;1) , B(2; 0;1) và mặt phẳng
(P) :x  y  2z  2  0. Viết phương trình chính tắc của đường thẳng d đi qua A , song song với mặt
phẳng (P) sao cho khoảng cách từ B đến d lớn nhất. x 1 y 1 z 1 x y z  2 A. d :   . B. d :   . 3 1 2  2 2 2  x  2 y  2 z x 1 y 1 z 1 C. d :   . D. d :   . 1 1 1  3 1  1 
Câu 47: Biết rằng trong tất cả các cặp  ; x y thỏa mãn log  2 2
x  y  2  2  log x  y 1 , chỉ có duy nhất 2  2   một cặp  ;
x y thỏa mãn 3x  4y  m  0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được? A. 20 B. 46 C. 28 D. 14
Câu 48: Hình nón tròn xoay có chiều cao h  40cm, bán kính đáy r  50cm . Một thiết qua đỉnh của hình nón
và khoảng cách từ tâm mặt đáy đến mặt phẳng chứa thiết diện là d  24cm. Tính diện tích S của thiết diện. A. 2 800cm . B. 2 1600cm . C. 2 200cm . D. 2 2200cm .
Câu 49: Trong không gian Oxyz , cho mặt cầu S 2 2 2
: x  y  z  2x 4y 6z 13  0. Lấy điểm M trong
không gian sao cho từ M kẻ được ba tiếp tuyến MA, MB , MC đến mặt cầu S  thỏa mãn  AMB  60 ,  BMC  90 , 
CMA  120 ( A , B , C là các tiếp điểm). Khi đó đoạn thẳng OM có độ nhỏ nhất bằng A. 14  3 3 . B.  14  6 3 . C. 14  6 . D. 6  14 .
Câu 50: Cho hàm số y  f x 3 2
 x  3x  2 . Hỏi có bao nhiêu giá trị nguyên của tham số m  1  0;10 để
hàm số g  x  f  x  m  nghịch biến trên 0;  1 ? A. 7 . B. 8 . C. 9. D. 10.
--------------------------------------HẾT---------------------------------- 16