Đề cương môn Cấu trúc dữ liệu- Trường Đại học bách khoa - Đại học đà nẵng.

Bài tập
Trình bày thuật toán Linear Search và Binary Search. Sau đó vẽ hình từng bước
thực hiện của từng thuật toán trên để tìm kiếm lần lượt các số 54, 6, 20 trong dãy
số sau (không cần lập trình): 54, 26, 93, 17, 77, 31, 44, 55, 20. Chú ý đối với thuật
toán Binary Search thì cần phải sắp xếp mảng trước khi thực hiện tìm kiếm.
I. Linear Search :
- Cho trước mảng một chiều A có n phần tử. Tìm phần tử X có giá trị cho trước
trong mảng. Nếu phần tử đó tồn tại trong danh sách thì xuất vị trí của nó trong
danh sách. Nếu phần tử đó không tồn tại trong danh sách thì trả về giá trị -1.
- Ý tưởng : So sánh X lần lượt với phần tử thứ 1, thứ 2,…của mảng a cho đến khi
gặp được khóa cần tìm, hoặc tìm hết mảng mà không thấy.
- Các bước của thuật toán :
* Bước 1: Gán i = 0 // Giá trị khởi đầu
* Bước 2: So sánh a[i] với X. Có 2 khả năng xảy ra :
• Nếu a[i] = X thì trả về giá trị i là vị trí cần tìm
• Nếu a[i] != X thì tiếp tục bước 3
* Bước 3: i = i + 1 // Xét tiếp phần tử tiếp theo trong mảng
• Nếu i == n thì không tìm thấy à Trả về giá trị -1.
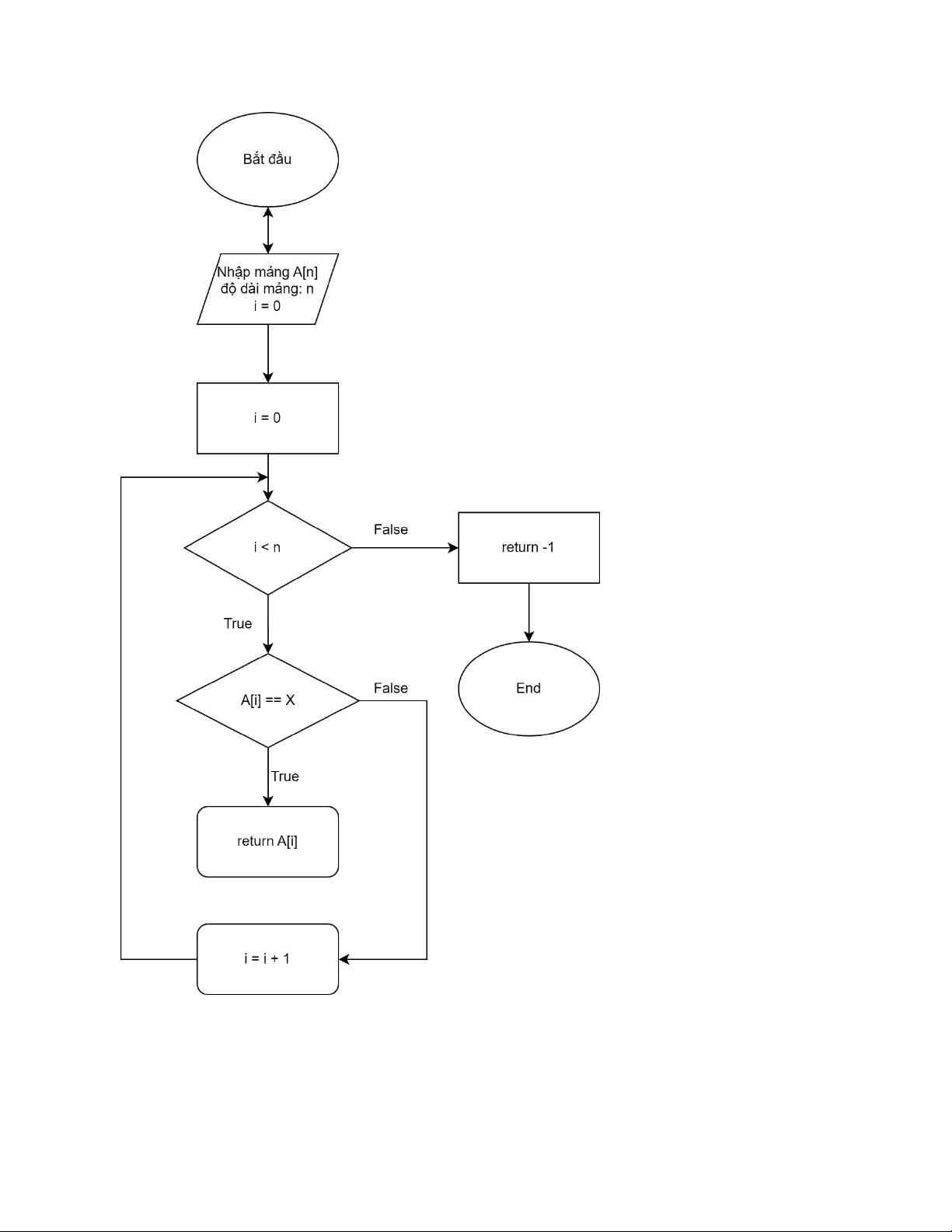
• Ngược lại: Tiếp tục bước 2. - Lưu đồ thuật toán : - Độ phức tạp :
+ Trong trường hợp tốt nhất, khi phần tử cần tìm nằm ở vị trí đầu tiên của mảng, độ
phức tạp sẽ là O(1), tức là tìm kiếm chỉ cần một bước.
+ Trong trường hợp của dãy số đã cho [54, 26, 93, 17, 77, 31, 44, 55, 20], nếu
chúng ta tìm lần lượt các số 54, 6 và 20, độ phức tạp sẽ là O(n), vì trong trường
hợp xấu nhất chúng ta phải kiểm tra qua tất cả các phần tử của mảng (9 phần tử) để
tìm được tất cả các số cần tìm.
II. Binary Search :
- Cho trước mảng một chiều A có n phần tử. Tìm phần tử X có giá trị cho trước
trong mảng. Nếu phần tử đó tồn tại trong danh sách thì xuất vị trí của nó trong
danh sách. Nếu phần tử đó không tồn tại trong danh sách thì trả về giá trị -1
- Ý tưởng : Binary search được áp dụng trên mảng đã có thứ tự.
+ Binary search dựa trên chiến lược “Chia để trị” (divide and conquer):
+ Bắt đầu tìm kiếm tại phần tử giữa của mảng.
+ Nếu giá trị tại phần tử giữa bằng giá trị cần tìm thì kết thúc.
+ Nếu giá trị tại phần tử giữa nhỏ hơn giá trị cần tìm thì loại bỏ nửa đầu tiên của
mảng trong lần xét kế tiếp.
+ Nếu giá trị tại phần tử giữa lớn hơn giá trị cần tìm thì loại bỏ nửa sau của mảng trong lần xét kế tiếp.
Lặp lại quá trình cho tới khi phần tử được tìm thấy, hoặc cho tới khi toàn bộ mảng được loại bỏ.
- Các bước của thuật toán :
* Bước 1: first = 0; last = N-1; * Bước 2:
+ middle=(first + last)/2; //chỉ số phần tử giữa dãy hiện hành
+ So sánh a[middle] với X. Có 3 khả năng:
a[middle] = X : tìm thấy. Dừng; // return middle
a[middle] > X : last = middle - 1;
a[middle] < X : first = middle + 1;
* Bước 3: Nếu first <= last ; // còn phần tử trong dãy hiện hành + Lặp lại bước 2
+ Ngược lại: Dừng;// return -1; - Độ phức tạp :
+ Độ phức tạp của thuật toán binary search để tìm lần lượt các số 54, 6, 20 là O(log
n), vì mảng này không được sắp xếp trước nên cần sắp xếp trước khi áp dụng binary search.
+ Độ phức tạp của thuật toán selection sort để sắp xếp dãy số này là O(n^2).
+ Do đó, tổng độ phức tạp của việc sử dụng binary search và selection sort để tìm
kiếm lần lượt các số 54, 6, 20 trong dãy số đã cho sẽ là O(n^2) + O(log n), với n là
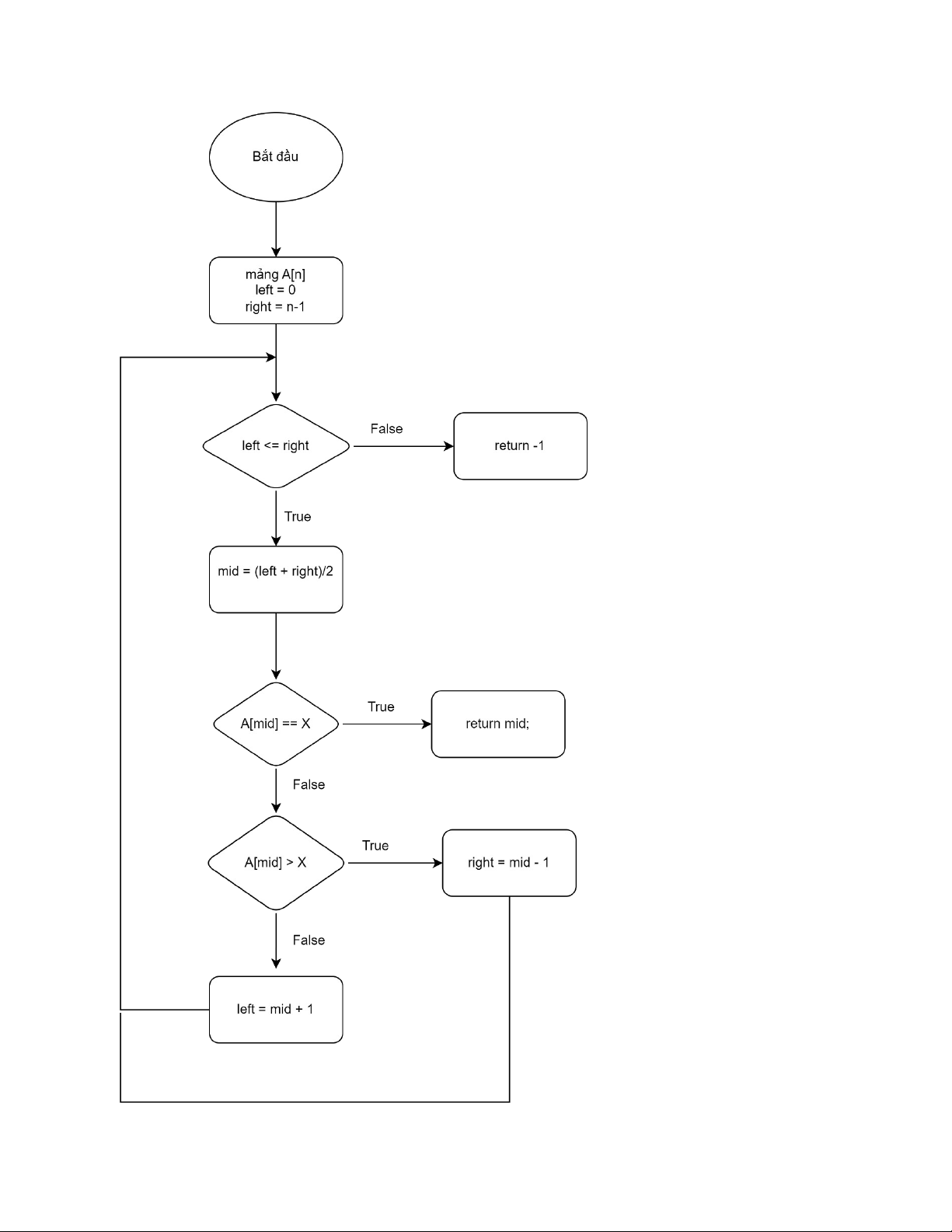
số lượng phần tử trong mảng. - Lưu đồ thuật toán :
III. Bài tập :
- Minh họa thuật toán Linear Search cho mảng : 54, 26, 93, 17, 77, 31, 44, 55, 20. * Tìm kiếm số 54 :
+ Gán i = 0. So sánh A[0] với số cần tìm
+ a[0] == 54: Tìm thấy giá trị tại vị trí i = 0
i = 0, tìm thấy giá trị 54 54 26 93 17 77 31 44 55 20 * Tìm kiếm số 6:
+ Gán i = 0. So sánh A[0] với số cần tìm. A[0] != 6: Di chuyển đến bước tiếp theo.
+ Cứ thế tăng i lên 1 và so sánh tiếp
+ Tiếp tục lặp lại quá trình cho tới khi hết dãy số mà không tìm thấy giá trị cần tìm. Trả về -1. i = 9, không tìm thấy 54 26 93 17 77 31 44 55 20 * Tìm kiếm số 20:
+ Gán i = 0. So sánh A[0] với số cần tìm. A[0] != 20 Di chuyển đến bước tiếp theo.
+ Cứ thế tăng i lên 1 và so sánh tiếp
+ Tiếp tục lặp lại quá trình cho tới khi hết dãy số
+ So sánh A[8] == 20 . Tìm thấy giá trị tại vị tr. Kết thúc tìm kiếm.
i = 8, tìm thấy giá trị 20 54 26 93 17 77 31 44 55 20
- Minh họa thuật toán Binary Search cho mảng : 54, 26, 93, 17, 77, 31, 44, 55, 20.
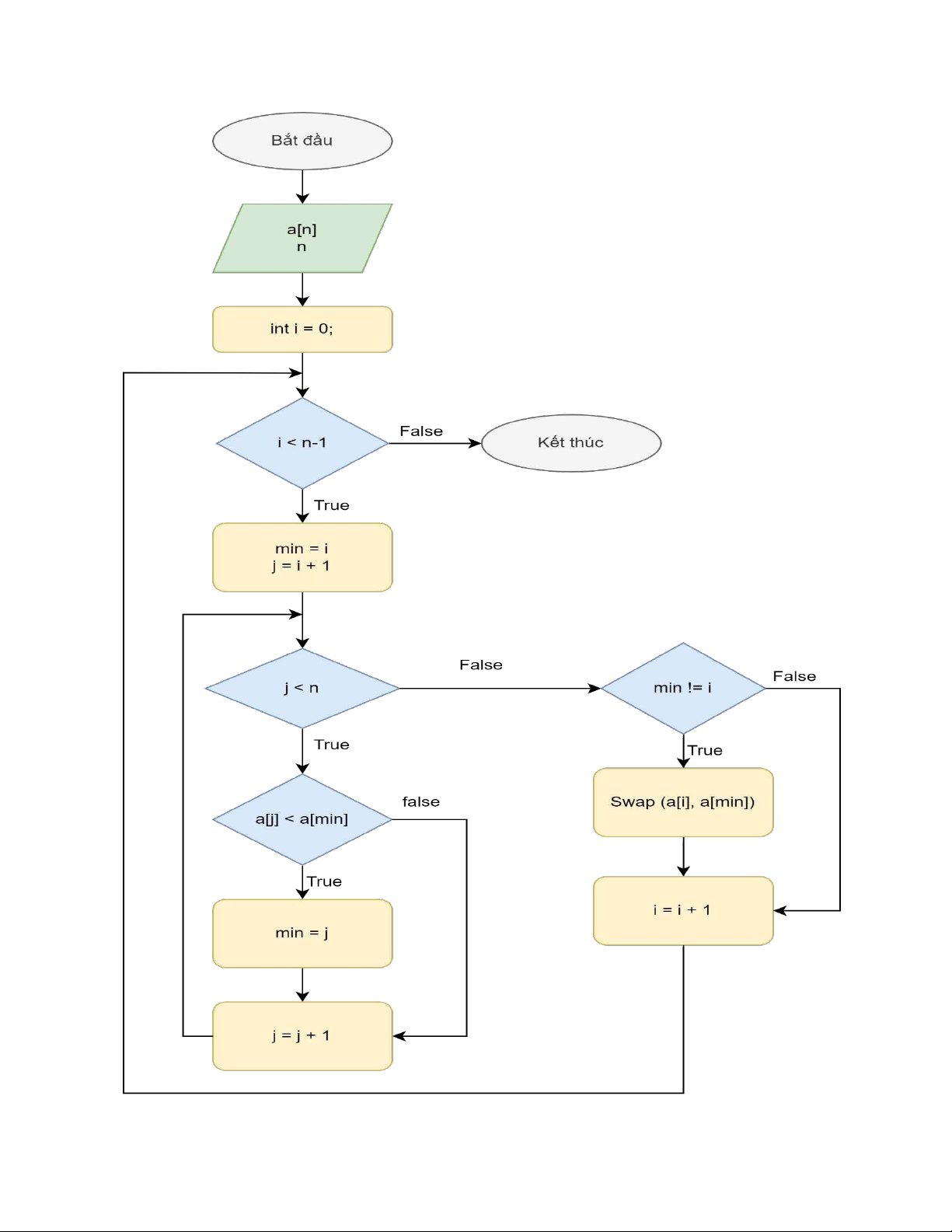
* Binary search được áp dụng trên mảng đã có thứ tự nên cần sắp xếp lại mảng
trước khi thực hiện tìm kiếm : 17, 20, 26, 31, 44, 54, 55, 77, 93. Ta sử dụng thuật
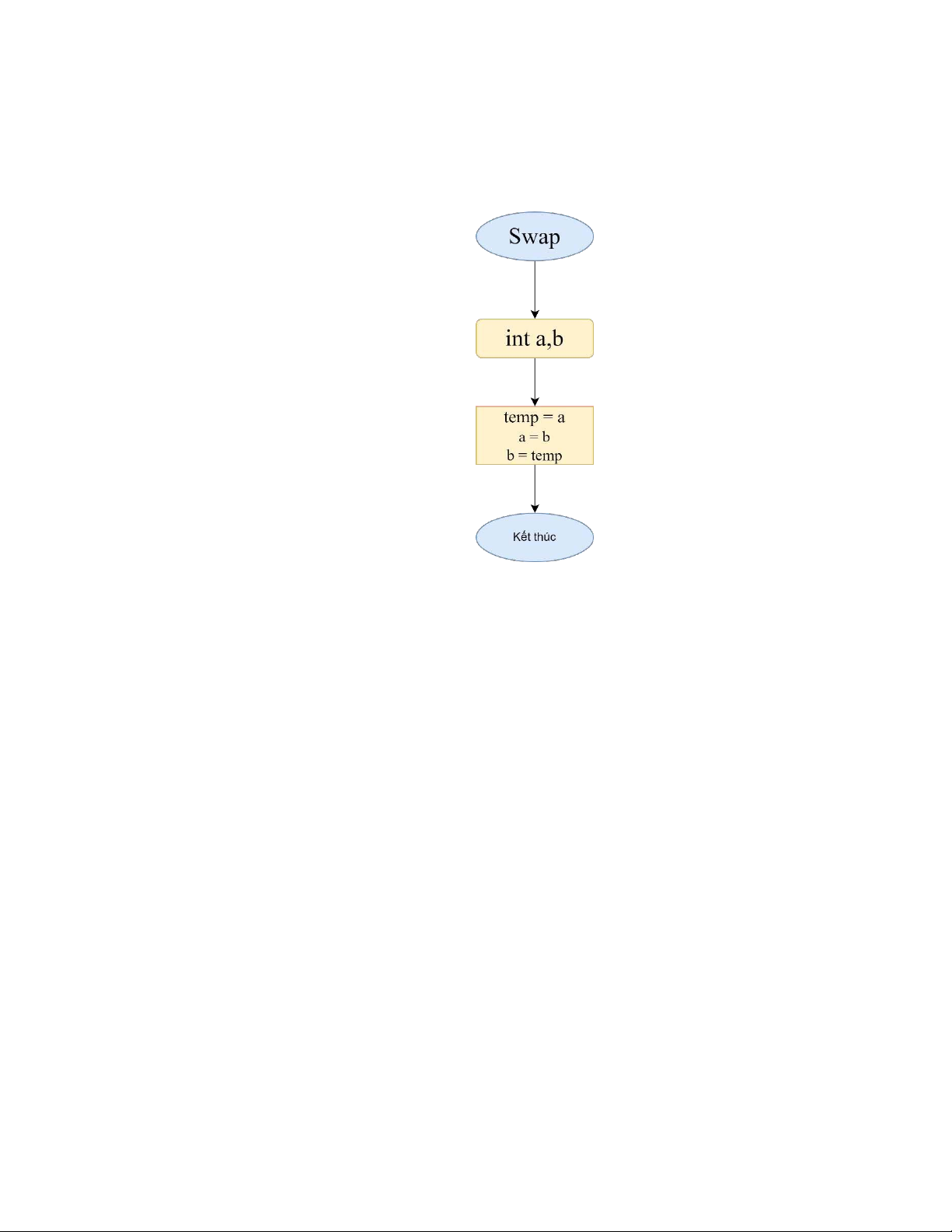
toán Selection Sort để sắp xếp. * Lưu đồ thuật toán : - Hàm swap : 17 20 26 31 44 54 55 77 93 f = 0 l = 8 * Tìm kiếm số 54 :
- Bước 1: first = 0, last = 8 (vì N = 9) - Bước 2: + middle = (0 + 8) / 2 = 4
+ So sánh a[4] = 44 với X= 54. (44 < 54). X 17 20 26 31 44 54 55 77 93 f = 0 m= 4 l = 8
+ Vì a[middle] - Bước 3: first (5) <= last (8) + Lặp lại bước 2 + middle = (5 + 8) / 2 = 6
+ So sánh a[6] = 55 với X = 54. (55 > 54). 17 20 26 31 44 54 55 77 93 f =5 m=6 l = 8
+ Vì a[middle] > X, nên last = middle - 1 = 6 - 1 = 5 17 20 26 31 44 54 55 77 93 f=l=5 * Khi first (5) = last (5) + middle = (5+ 5) / 2 = 5
+ So sánh a[5] = 54 với X= 54
* Kết quả: Số 54 được tìm thấy tại vị trí 5. a[mid] = X 17 20 26 31 44 54 55 77 93 * Tìm kiếm số 6:
- Bước 1: first = 0, last = 8 (vì N = 9) - Bước 2: + middle = (0 + 8) / 2 = 4
+ So sánh a[4] = 44 với X = 6. (44 > 6). 17 20 26 31 44 54 55 77 93 f = 0 m= 4 l = 8
+ Vì a[middle] >X, nên last = middle - 1 = 4 - 1 = 3
- Bước 3: first (0) <= last (3) + Lặp lại bước 2 + middle = (0 + 3) / 2 = 1 17 20 26 31 44 54 55 77 93 f = 0 m=1 l = 3
+ So sánh a[1] = 20 với X= 6. 20 > 6
+ Vì a[middle] > X, nên last = middle - 1 = 1 - 1 = 0 17 20 26 31 44 54 55 77 93 f = l=0 * Khi first (0) = last (0) + middle = (0 + 0) / 2 = 0
+ So sánh a[0] = 17 với X = 6. 17 > 6.
+ Vì a[middle] >X, nên last = middle - 1 = 0 - 1 = -1
- Bước 3: first (0) > last (-1) => Dừng
Kết quả: Số 6 không được tìm thấy trong dãy số. * Tìm kiếm số 20:
- Bước 1: first = 0, last = 8 (vì N = 9) - Bước 2: - middle = (0 + 8) / 2 = 4
- So sánh a[4] = 44 với X = 20. (44 > 20). X 17 20 26 31 44 54 55 77 93 f = 0 m= 4 l = 8
+ Vì a[middle] > X, nên last = middle - 1 = 4 - 1 = 3 * Khi first (0) < last (3) + m = (0+ 1) / 2 = 1 X 17 20 26 31 44 54 55 77 93 f = 0 m=1 l = 3
+ So sánh a[1] = 20 với X= 20
* Kết quả: Số 20 được tìm thấy tại vị trí 1 a[mid] = X 17 20 26 31 44 54 55 77 93