Đề cương ôn tập hè môn Toán lớp 6 năm 2025
Đề cương ôn tập hè môn Toán lớp 6 tổng hợp kiến thức và các dạng bài tập luyện tập trong chương trình học môn Toán lớp 6, giúp các em học sinh củng cố kiến thức đã học và ôn luyện để lên lớp 7 một cách hiệu quả. Mời các bạn tải về tham khảo trọn bộ tài liệu.
Chủ đề: Ôn hè Toán 6 3 tài liệu
Môn: Toán 6 2.4 K tài liệu
Sách: Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Tác giả:
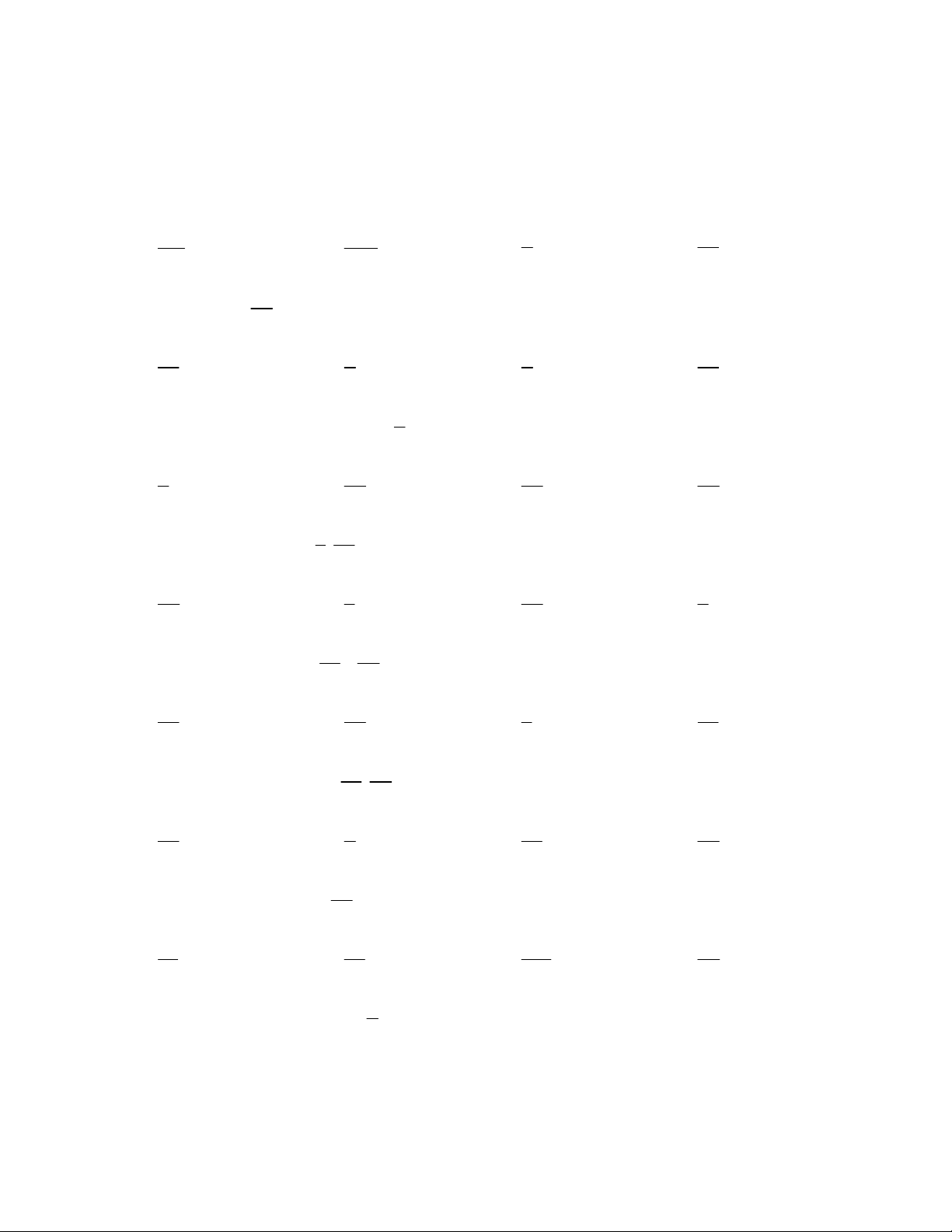
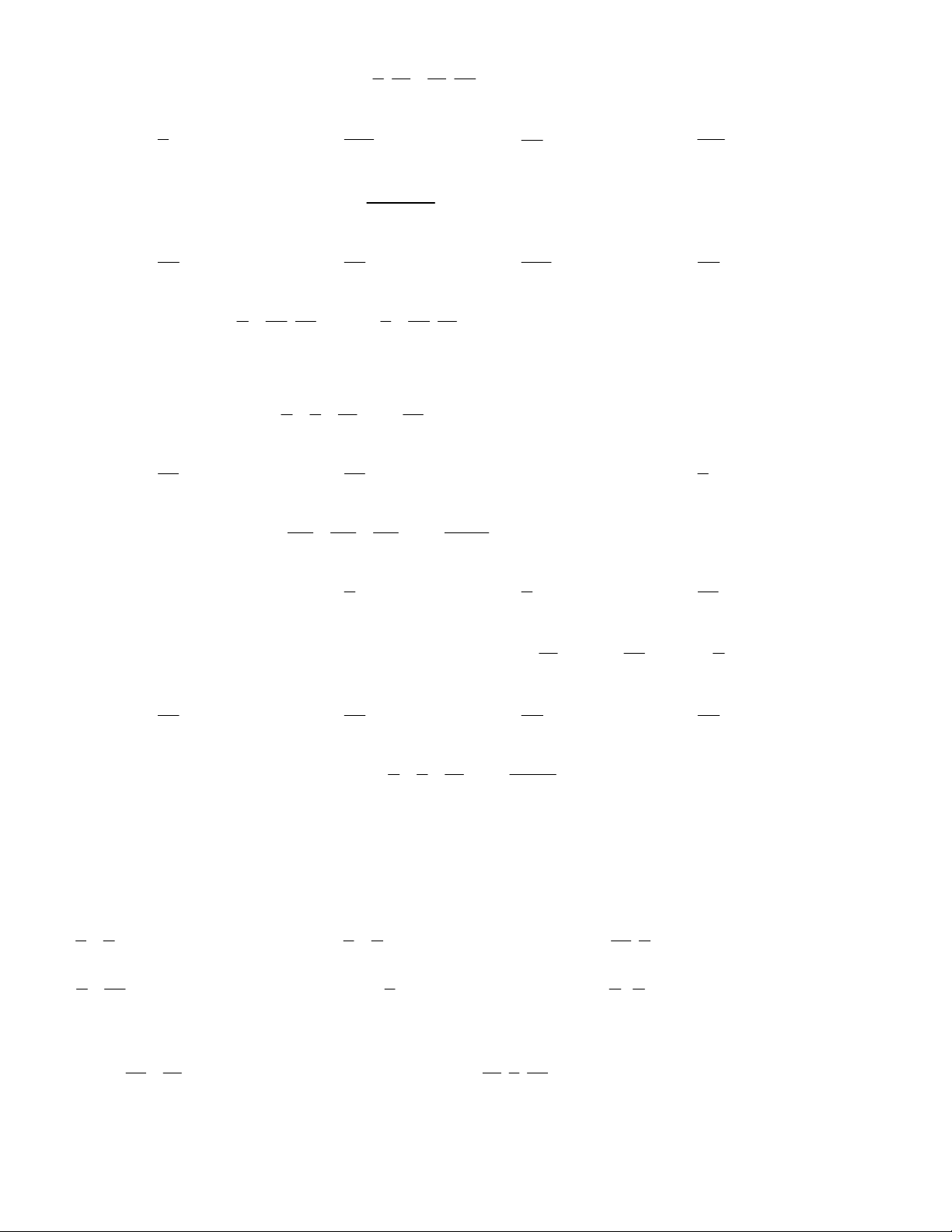
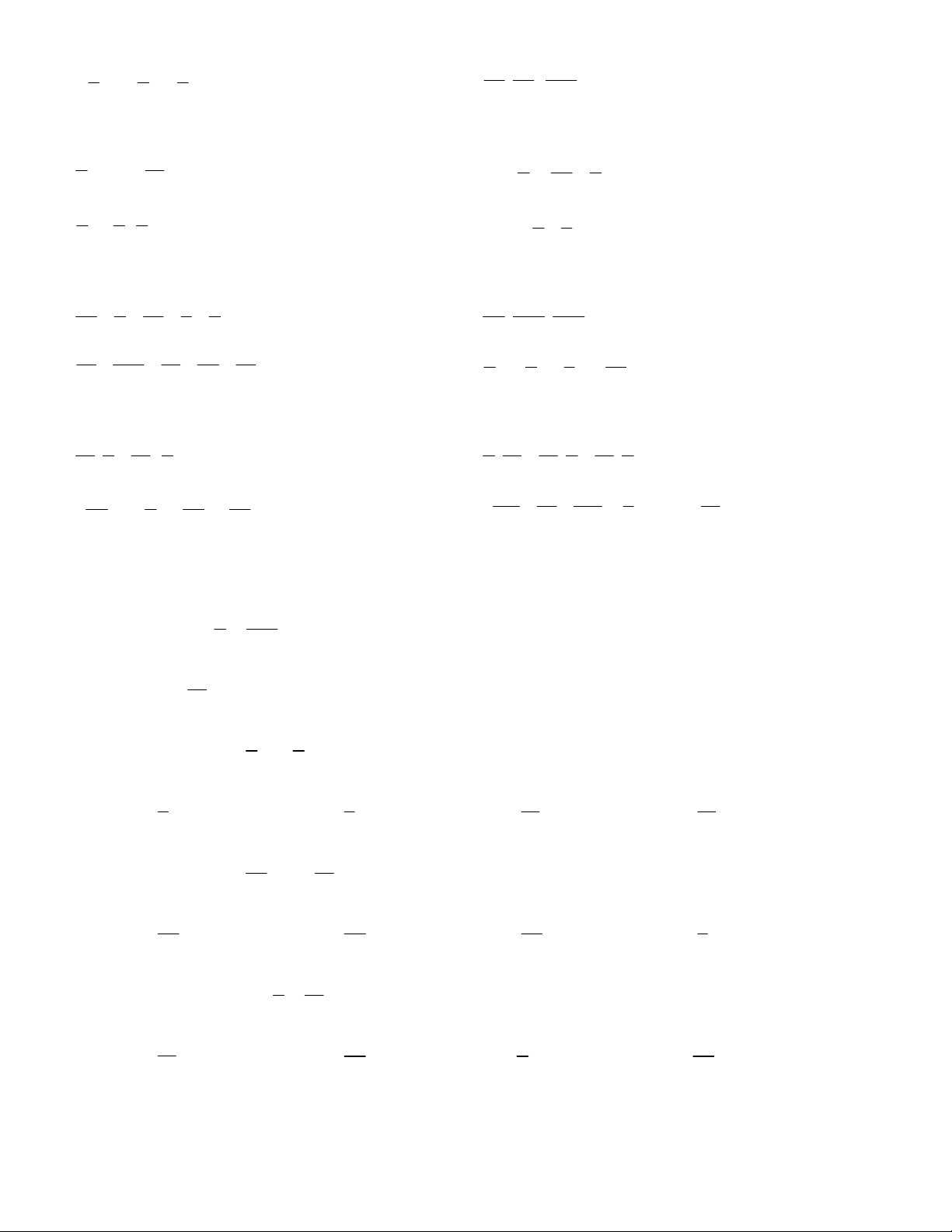
Preview text:
ĐỀ CƯƠNG ÔN TẬP HÈ – MÔN TOÁN LỚP 6
Chương I: Tập hợp các số tự nhiên 1. Tập hợp
- Sử dụng được thuật ngữ tập hợp, phần tử thuộc (không thuộc) một tập hợp; sử dụng được cách cho tập hợp.
- Nhận biết được tập hợp các số tự nhiên. 2. Cách ghi số tự nhiên
- Biểu diễn được số tự nhiên trong hệ thập phân.
- Biểu diễn được các số tự nhiên từ 1 đến 30 bằng cách sử dụng các chữ số La Mã.
3. Thứ tự trong tập hợp các số tự nhiên
- Nhận biết được (quan hệ) thứ tự trong tập hợp các số tự nhiên; so sánh được hai số tự nhiên cho trước.
4. Các phép toán trong tập hợp số tự nhiên (Phép cộng, trừ, nhân, chia, lũy thừa với sô mũ tự nhiên)
- Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số tự nhiên.
- Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng trong tính toán.
- Thực hiện được phép tính luỹ thừa với số mũ tự nhiên; thực hiện được các phép nhân và phép chia hai luỹ
thừa cùng cơ số với số mũ tự nhiên.
- Nhận biết được thứ tự thực hiện các phép tính.
- Vận dụng được các tính chất của phép tính (kể cả phép tính luỹ thừa với số mũ tự nhiên) để tính nhẩm, tính nhanh một cách hợp lí.
- Giải quyết được những vấn đề thực tiễn gắn với thực hiện các phép tính (ví dụ: tính tiền mua sắm, tính lượng
hàng mua được từ số tiền đã có, . .).
I. Bài tập trắc nghiệm
Câu 1: Tập hợp số tự nhiên được kí hiệu là: A. R B. N C. Z D. N*
Câu 2: Tập hợp các số tự nhiên khác 0 được kí hiệu là: A. R B. N C. N* D. Z
Câu 3: Số tự nhiên liền trước số 7428 là số: A. 7427 B. 7429 C. 7439 D. 7430
Câu 4: Số tự nhiên lớn nhất có hai chữ số là số: A. 97 B. 98 C. 99 D. 100
Câu 5: Có bao nhiêu số tự nhiên x thỏa mãn 748 < x < 760? 1 A. 10 số B. 11 số C. 12 số D. 13 số
II. Bài tập tự luận Bài 1:
Viết các tập hợp sau đây bằng cách liệt kê các phần tử :
A = {x ∈ N : 22 < x < 27} ; B = {x ∈ N*: x < 3} ;
C = {x ∈ N : 3 ≤ x < 8); D = {x ∈ N*:x ≤ 6}. Bài 2 Tìm X, biết x ∈ N và a) x < 1 ; b) x < 4 ;
c) x là số lẻ sao cho 6 < x ≤ 14. Bài 3:
a, Viết số tự nhiên liền sau mỗi số: 48; 957; 4782
b, Viết số tự nhiên liền trước mỗi số: 78, 167, 9479
c, Viết số tự nhiên liền trước và liền sau của số tự nhiên a (a khác 0)
Bài 4: Viết tập hợp A các số tự nhiên không vượt quá 7 bằng 2 cách. Biểu diễn các phần tử của tập hợp A trên tia số
Bài 5: Cho ba tập hợp: A là tập hợp các số tự nhiên không vượt quá 12, B là tập hợp các số tự nhiên lẻ nhỏ hơn 9
và C là tập hợp các số tự nhiên chẵn lớn hơn 3 và không vượt quá 14. Hãy viết các tập hợp trên theo hai cách
Bài 6: Viết tập hợp các số tự nhiên có hai chữ số, trong đó:
a, Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị là 4
b, Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị, tổng hai chữ số bằng 14 2
Chương II: Tính chia hết trong tập hợp các số tự nhiên
1. Quan hệ chia hết và tính chất 2. Dấu hiệu chia hết 3. Số nguyên tố
- Nhận biết được khái niệm số nguyên tố, hợp số.
- Thực hiện được việc phân tích một số tự nhiên lớn hơn 1 thành tích của các thừa số nguyên tố trong những trường hợp đơn giản.
4. Ước chung lớn nhất - Bội chung nhỏ nhất
- Xác định được ước chung, ước chung lớn nhất; xác định được bội chung, bội chung nhỏ nhất của hai hoặc ba
số tự nhiên; nhận biết được phân số tối giản; thực hiện được phép cộng, phép trừ phân số bằng cách sử dụng
ước chung lớn nhất, bội chung nhỏ nhất.
- Nhận biết được phép chia có dư, định lí về phép chia có dư.
- Vận dụng được kiến thức số học vào giải quyết những vấn đề thực tiễn (ví dụ: tính toán tiền hay lượng hàng
hoá khi mua sắm, xác định số đồ vật cần thiết để sắp xếp chúng theo những quy tắc cho trước, . .). Bài tập tham khảo:
Câu 1: Tìm tập hợp Ư (5)? A. Ư (5) = {0, 5} B. Ư (5) = {5, 10} C. Ư (5) = {0, 1} D. Ư (5) = {1, 5}
Câu 2: Trong các số: 16; 24; 35; 68. Số nào không là bội của 4? A. 24 B. 35 C. 16 D. 68
Câu 3: Không cần tính, hãy cho biết tổng (hiệu) chia hết cho cả 2 và 5 là: A. 138 + 210 B. 1.2.3.4.5 - 20 C. 325 – 45 3 D. 1.2.3.4.5 + 42
Câu 4: Phân tích một số ra thừa số nguyên tố là:
A. Phân tích số đó thành tích của các thừa số nguyên tố.
B. Phân tích số đó thành tích của hai thừa số nguyên tố.
C. Phân tích số đó thành tích của số nguyên tố với các hợp số.
D. Phân tích số đó thành tích của các số tự nhiên.
Câu 5: Cho A là tập hợp các số nguyên tố nhỏ hơn 30. Chọn đáp án đúng. A. 1 ∈ A B. 17 ∈ A C. 29 ∉ A D. 2 ∉ A
Câu 6: 8 là ước chung của A. 24 và 56 B. 14 và 48 C. 12 và 32 D. 18 và 24
Câu 7: ƯCLN của (18; 60) là A. 6 B. 12 C. 30 D. 18
Câu 8: Cho biết BC (4, 6) = {0; 12; 24; 36; 48; …}. Hãy cho biết BCNN (4, 6)? A. BCNN (4, 6) = 0 B. BCNN (4, 6) = 12 4 C. BCNN (4, 6) = 24 D. BCNN (4, 6) = 36
Câu 9: Nếu 20 ⋮ a và 20 ⋮ b thì 20 là ……của a và b. A. ước chung B. bội chung C. ước chung lớn nhất D. bội chung nhỏ nhất
Câu 10: Nếu 30 là số tự nhiên nhỏ nhất mà 30 ⋮ a và 3 ⋮ b thì 30 là ………của a và b. A. ước chung B. bội chung C. ước chung lớn nhất
D. bội chung nhỏ nhất
Câu 11: Viết tập hợp A = {x ∈ N | x là ước của 24} bằng cách liệt kê. A. A = {1; 2; 3; 4; 6; 12; 24}
B. A = {1; 2; 3; 6; 8; 12; 24}
C. A = {1; 2; 4; 6; 12; 16; 24} D. A = {1; 2; 3; 4; 6; 12}
Câu 12: Tìm các số tự nhiên x sao cho: x ∈ B (12) và x > 100
A. x ∈ {12k│k = 9; 10; 11; . .}
B. x ∈ {12k│k = 1; 2; 3; . .}
C. x ∈ {12k│k = 5; 10; 15 . .}
D. x = {105; 120; 135; 150; 165; 180; 195}
Câu 13: Một số tự nhiên a chia cho 45 có số dư là 15. Nhận định sau đây là đúng? A. a không chia hết cho 3
B. a không chia hết cho 9 5 C. a chia hết cho 2 D. Đáp án A và C
Câu 14: Ông Tuấn có hai đoạn ống thép, một đoạn dài 12 m và một đoạn dài 6m. Ông có thể cắt cả hai đoạn ống
thép này thành các đoạn dài bằng nhau, mỗi đoạn dài 5 m sao cho không có đoạn thép nào thừa được không?
Nếu không được thì ông có thể thay 5m bằng mấy mét thì được? A. Thay 5m thành 3m B. Thay 5m thành 2m C. Thay 5m thành 6m
D. Tất cả đáp án trên
Câu 15: Trong các số tự nhiên cho sau, số có ước nhiều nhất là: A. 1035 B. 496 C. 1517 D. 1464
Câu 16: Tích của hai số tự nhiên là 50. Tìm mỗi số đó. A. 50 và 1 B. 25 và 2 C. 10 và 5
D. Tất cả đáp án trên
Câu 17: Tìm tất cả các số tự nhiên khác 0, không vượt quá 60 sao cho ƯCLN của hai số đó là 17. A. 17; 34 và 51 B. 17; 34 và 41 C. 17 và 51 D. 17 và 34
Câu 18: Tìm số tự nhiên a, biết rằng khi chia số 111 cho a thì dư 115, còn khi chia 180 cho a thì dư 20. A. a = 30 6 B. a = 33 C. a = 32 D. a = 28
Câu 19: Tìm các số tự nhiên x sao cho x là bội của 6 và 20 ≤ x ≤ 36 A. x ∈ {30; 36} B. B. x ∈ {24; 30}
C. x ∈ {24; 30; 36} D. x = 24
Câu 20: Tìm hai số tự nhiên sao cho khi chia cho 3,7,15 đều dư 1 A. x ∈ X = {103,211}
B. x ∈ X = {106,211} C. x ∈ X = {106,201} D. x ∈ X = {103,201}
Câu 21: Phát biểu sai là
A. Những số có 9 chữ số giống nhau thì chia hết cho 9
B. Những số có 10 chữ số đôi giống nhau thì chia hết cho 9
C. n2 + n - 1 chia hết cho 2 với n là số tự nhiên D. Tất cả đáp án trên Chương III: Số nguyên
Số nguyên: Tập hợp các số nguyên âm, số 0 và các số nguyên dương gọi là tập hợp cá số nguyên. Tập hợp các
số nguyên được kí hiệu là . . .; 3 ; 2 ; 1 ;0;1;2;3;. .
Dạng 1: So sánh số nguyên
Dạng 2: Cộng, trừ, nhân, chia số nguyên. Dạng 3: Tìm
Dạng 4: Rút gọn số nguyên
Dạng 5: Tính chia hết trong tập số nguyên Dạng 6: Toán có lời văn 7
Dạng 7: Dãy số trong tập hợp số nguyên
BÀI TẬP CHƯƠNG III. SỐ NGUYÊN Bài 1. Tính a) (-26) + (- 32) b) (- 17) + 17 c) ( -327 ) + 1000 d) (-13) + 29 e) (-31) + (- 17) f) 317 + (- 421) Bài 2. Tính a) 100 – ( -19) b) 0 – ( -72) c) (-137) – ( -35) d) 156 – 31 e) (-5) – ( -7) f) 4 – ( -5) – 2 g) 17 – ( -19) -13 h) (-3) + 9 - 11 i) (-16) - 7 + 25
Bài 4. Thực hiện phép tính:
a) 367 + (- 30) + 1672 + (- 337) b) (-299) + (-300) + (-101)
c) 1 + (-4) + 7 + (-10) + 13 + (-16) d) (-103) - 95 + 83 + (-5) Bài 5: Tính nhanh
a) 234 + 117 + (-100) + ( -234)
b) -927 + 1421 + 930 + ( -1421) c) 2014 + [ 520 + ( -2014) ]
d) [ ( -851) + 5294] + [ ( -5294) + 851]
d) 921 + [ 97 + (- 921) + ( -47) ]
f) 2013 + 2014 + ( -2015) +( -2013)
Bài 1. Bỏ dấu ngoặc rồi tính các tổng sau:
a) (-28) + (-35) – 92 + (-82)
b) 15 – (-38) + (-55) – (+47).
c) (62 - 81) – (12 – 59 + 9);
d) 39 + (13 – 26) – (62 + 39).
Bài 2. Tính một cách hợp lí:
a) 32 – 34 + 36 – 38 + 40 – 42; b) 92 – (55 – 8) + (-45).
c) 386 – (287 + 386) – (13 + 0);
d) 332 – (681 + 232 – 431). Bài 3: Tính
a) 215 + ( -38) - ( -58) + 90 - 85
b) 31 – [ 26 – ( 209 + 35) ]
c) 215 + (-38) – ( -58) + 90 – 85 + (-90) – 130 d) 315 – ( 41 + 215) e) 917 – ( 417 – 65 )
Bài 4: Tìm x Z, biết: a) 16 – x = 21 – ( -8)
b) 4 – ( 27 – 3) = x – ( 13 – 4) c) 15 - ( 15 + x) = 21 d) 39 + ( x – 39) = 50
e) 25 – ( 25 – x) = 12 + ( 42 – 65) f) x – ( 77 – x) = x - 67 Bài 5: Tính: a) (-7) . 4 + 5. ( -3)
b) (-5) . ( 3 + 4) – 10 . (-2) c) 11. (-7) + (-6) . (-9) d) (-2)2. (-3) + (-1)7. (-6) e) (-23). 15 + 23. (-85) f) 65. (-9) + (-91). 65 Bài 6: Tính nhanh.
a) ( -4) . 125.(-25) . ( -126) . ( -8)
b) (-98) . ( 1- 296) – 296 . 98 c) 167 . ( -34) + 34 . 267 d) 87. (-125) -125 . ( -97)
e) 69 . ( -13) + 28 . ( -69) + ( -41) . ( -69) g) 17 . (-35) – 23 . 35 – 46 . ( -35)
Bài 7: Tính giá trị của các biểu thức sau với a = 8. a) ( -125) . ( -13) . ( -a)
b) (-1). ( -2) . ( -3) . ( -4) .a
Bài 8: Tìm x ∈ Z, biết: a) (2x - 5) + 17 = 6 b) 10- 2(4- 3x) = - 4 c) 24 : (3x- 2) = - 3 d)5 - 2x = - 17 + 12
e) ( x – 7) . ( x + 9) = 0
f) ( 2x – 1) . ( 3x + 6) = 0 8
Bài 9: Tính giá trị biểu thức sau : a/ (–26) + (–15) b/ (–37) + 4.(-6) c/ (-3) – (4 - 6) d/ -129 + [42. 5 – (-7)]: 3
e/ 5.32 + 60 : 2² – (11 – 6)² f/ (-115) + ( - 40) + 115 + 35 Bài 10: Tính nhanh. a/ 143.64 - 43.64 b/ 23.75 + 25.23 + 180 c/ 27.39 + 27.63 – 2.27 d/ 15.85 + 15.15 – 150.
e/ 46.37 + 93.46 + 54.61 + 69.54
Bài 11: Tìm x, biết: a/ (-2) + ( x + 6 ) = 9 - 23 b/ 219 – 7(x+1) = 100 c/ 7x – 10 = 27 : 25 d/ 2014. (x – 12) = 0 e/ 4.2x 3 125
Bài 12: Tính tổng của các số nguyên x, biết -2 Bài 13: Một đội văn nghệ có 60 nam và 72 nữ, được chia đều thành các nhóm sao cho số nam và số nữ của mỗi nhóm đều bằng nhau.
a) Có thể chia được nhiều nhất bao nhiêu nhóm?
b) Khi đó mỗi nhóm có bao nhiêu nam và bao nhiêu nữ?
Bài 14: Trong một buổi sinh hoạt lớp 6A, bạn lớp trưởng dự kiến chia các bạn thành từng nhóm sao cho sô bạn
nam trong mỗi nhóm đều bằng nhau và số bạn nữ cũng chia đều như thế. Hỏi lớp có thể chia được nhiều nhất là
bao nhiêu nhóm? Khi đó mỗi nhóm có bao nhiêu bạn nam, bao nhiêu bạn nữ? Biết rằng lớp 6A có 21 nữ và 14 nam.
Bài 15: Học sinh khối 6cuar một trường THCS khi xếp hàng 12, 15, 18 đều vừa đủ. Biết số học sinh trong
khoảng từ 200 đến 500. Tính số học sinh khối 6 của trường đó?
Bài 16: Học sinh khối 6 của một trường khi xếp hàng 4, 5, 6, 10 đều thừa ra 2 em, nhưng xếp hàng 7 thì vừa đủ.
Biết số học sinh của khối chưa đến 260 học sinh. Tính số học sinh khối 6 của trường đó. BÀI TẬP NÂNG CAO Bài 1: Tính tổng:
a/ S1 = 1 + (-2) + 3 + (-4) +. . + 2001 + ( -2002)
b/ S2 = 1 + (-3) + 5 + (-7) +. . + (-1999) + 2001
c/ S3 = 101 - 102 - (-103) - 104 - (-105) - 106 - (-107) - 108 - (-109) - 110
d/ S4 = 1 + (-2) + (-3) + 4 + 5 + (-6) + (-7) + 8 +. . + 1997 + (-1008) + (-1999) + 2000
Bài 2: Tính các tổng:
a/ S1 = 2 -4 + 6 - 8 +. . . + 1998 - 2000
b/ S2 = 2 - 4 -6 + 8 + 10- 12 - 14 + 16 +. . + 1994 - 1996 -1998 + 2000
Bài 3: So sánh P với Q biết:
P = a {(a - 3) - [( a + 3) - (- a - 2)]}.
Q = [ a + (a + 3)] - [( a + 2) - (a - 2)].
Chương IV, V: Một số hình phẳng trong thực tiễn
1. Hình tam giác đều. Hình vuông. Hình lục giác đều
- Nhận dạng được tam giác đều, hình vuông, lục giác đều.
- Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của: tam giác đều (ví dụ: ba cạnh bằng nhau, ba
góc bằng nhau); hình vuông (ví dụ: bốn cạnh bằng nhau, mỗi góc là góc vuông, hai đường chéo bằng nhau);
lục giác đều (ví dụ: sáu cạnh bằng nhau, sáu góc bằng nhau, ba đường chéo chính bằng nhau).
- Vẽ được tam giác đều, hình vuông bằng dụng cụ học tập. 9
- Tạo lập được lục giác đều thông qua việc lắp ghép các tam giác đều.
2. Hình chữ nhật, hình thoi, hình bình hành, hình thang cân
- Nhận dạng được tam giác đều, hình vuông, lục giác đều.
- Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của: tam giác đều (ví dụ: ba cạnh bằng nhau, ba
góc bằng nhau); hình vuông (ví dụ: bốn cạnh bằng nhau, mỗi góc là góc vuông, hai đường chéo bằng nhau);
lục giác đều (ví dụ: sáu cạnh bằng nhau, sáu góc bằng nhau, ba đường chéo chính bằng nhau).
- Vẽ được tam giác đều, hình vuông bằng dụng cụ học tập.
- Tạo lập được lục giác đều thông qua việc lắp ghép các tam giác đều.
3. Chu vi và diện tích của một số tứ giác đã học
- Công thức tính chu vi và diện tích của hình thang, hình chữ nhật, hình vuông
4. Hình có trục đối xứng,
5. Hình có tâm đối xứng
- Nhận biết được trục đối xứng của một hình phẳng.
- Nhận biết được những hình phẳng trong tự nhiên có trục đối xứng (khi quan sát trên hình ảnh 2 chiều).
- Nhận biết được tâm đối xứng của một hình phẳng.
- Nhận biết được những hình phẳng trong thế giới tự nhiên có tâm đối xứng (khi quan sát trên hình ảnh 2 chiều).
- Nhận biết được tính đối xứng trong Toán học, tự nhiên, nghệ thuật, kiến trúc, công nghệ chế tạo, . .
- Nhận biết được vẻ đẹp của thế giới tự nhiên biểu hiện qua tính đối xứng (ví dụ: nhận biết vẻ đẹp của một số loài
thực vật, động vật trong tự nhiên có tâm đối xứng hoặc có trục đối xứng).
BÀI TẬP CÓ HƯỚNG DẪN
Bài 1. Cho hình vuông ABCD có AB 9cm. Tính độ dài các đoạn thẳng DC và DA .
Hướng dẫn: Áp dụng kiến thức của hình vuông.
Bài 2. Cho lục giác đều ABCDEF với cạnh AB 8cm và đường chéo AD 16cm . Tính độ dài đoạn thẳng CD và CF.
Hướng dẫn: Áp dụng các kiến thức của hình lục giác đều.
Bài 3. Cho hình thoi ABCD với O là giao điểm của hai đường chéo. Biết AB 20cm , OA = 16 cm, OB 12cm . Tính
độ dài các cạnh và các đường chéo của hình thoi.
Hướng dẫn: Áp dụng các kiến thức của hình thoi.
Bài 4. Cho hình chữ nhật ABCD có AB 12cm,BC 9cm,BD 15cm . Tính cạnh AD,CD,AC .
Hướng dẫn: Áp dụng các kiến thức của hình chữ nhật.
Bài 5. Tính diện tích của hình vuông, biết chu vi của hình vuông đó bằng 16cm .
Hướng dẫn: Tìm cạnh của hình vuông rồi sau đó áp dụng công thức tính diện tích. 10 Đáp số: 2 16cm
Bài 6. Một hình vuông có chu vi bằng 20cm , một hình chữ nhật có chiều rộng bằng cạnh hình vuông và có chu vi 26cm .
Tính diện tích hình chữ nhật?
Hướng dẫn: Tìm cạnh của hình vuông, chiều rộng của hình chữ nhật, rồi sau đó áp dụng công thức tính diện tích. Đáp số: 2 40cm
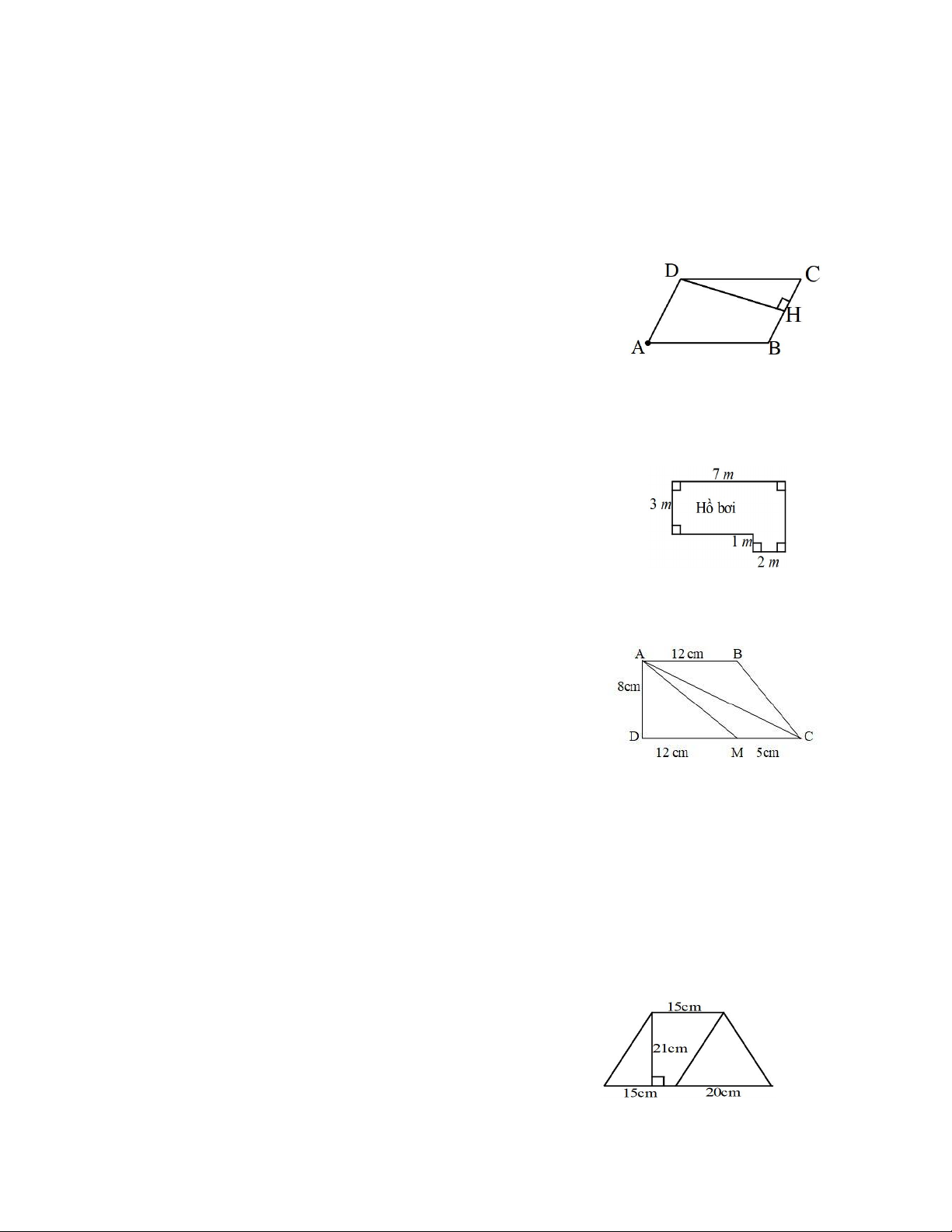
Bài 7. Tính chu vi và diện tích của hình bình hành ABCD (như hình
bên). Biết AD 6cm,AB 10cm,DH 9cm .
Hướng dẫn: Áp dụng công thức tính chu vi, diện tích hình bình hành. Đáp số: 2 P 32cm;S 54cm
Bài 8. Tính chu vi và diện tích của hồ bơi có kích thước như hình vẽ sau:
Hướng dẫn: Áp dụng công thức tính chu vi, diện tích chữ nhật. Có thể
chia nhỏ các hình để tính. Đáp số: 2 P 22cm;S 23cm
Bài 9. Hình thang ABCD có chiều cao AD và các kích thước như
hình vẽ bên. Hỏi diện tích hình Diện tích hình thang ABCD lớn hơn
diện tích hình tam giác AMC bao nhiêu xăng-ti-mét vuông?
Hướng dẫn: Áp dụng công thức tính diện tích hình thang, hình tam
giác. Lấy diện tích hình thang trừ diện tích tam giác. Đáp số: 2 2 S 116cm S ; 20cm hinh thang tamgiac 2 S S 96cm hinh thang tamgiac
Bài 10. Tính diện tích hình bên:
Hướng dẫn: Áp dụng công thức tính diện tích hình thang. 11 Đáp số: 2 S 252cm
Bài 11. Tính tổng độ dài hai đáy của hình thang. Biết diện tích là 2
2400cm và chiều cao là 48cm .
Hướng dẫn: Áp dụng công thức tính diện tích hình thang. Đáp số: 2 100cm
Bài 12. Tìm chiều cao hình thang. Biết diện tích là 2
6,4dm , đáy lớn là 1,8dm , đáy bé là 1,4dm .
Hướng dẫn: Áp dụng công thức tính diện tích hình thang. Đáp số: 4dm
Bài 13. Cho tam giác ABC , trên AC lấy điểm M sao cho AM CM . Hãy so sánh diện tích hai tam giác ABM và MBC.
Hướng dẫn: Áp dụng công thức tính diện tích hình tam giác. So sánh. Đáp số: S S ABM MBC
Bài 14. Cho hình thang ABCD (hình vẽ). Hãy so sánh diện tích tam giác ACD và
diện tích tam giác BCD; diện tích tam giác AOD và diện tích tam giác BOC.
Hướng dẫn: Áp dụng công thức tính diện tích hình tam giác. So sánh. Đáp số:S S S ; S ACD BCD AOD BOC
Chương VI, VII: Phân số. Số thập phân
1. Các quy tắc cộng, trừ, nhân, chia phân số a. Phép cộng phân số
+ B1: quy đồng mẫu các phân số (nếu cần)
+ B2: lấy tử cộng tử và giữ nguyên mẫu như công thức: a b a
b a,b,mZ;m 0 m m m
b. Phép trừ phân số
+ Số đối của phân số a a,b Z ;b 0 là a . Chú ý: a
a a . b b b b b
+ Quy tắc: muốn trừ hai phân số ta lấy SBT cộng với số đối của số trừ. a c a c . b d b d c. Phép nhân phân số
+ Quy tắc: muốn nhân hai phân số, ta lấy tử nhân tử, mẫu nhân mẫu. 12
a c a.c c a.c . a. . b d b.d d d m m
+ Lũy thừa của một phân số: a a m N b m b
d. Phép chia phân số
+ Số nghịch đảo của a là b . b a
+ Quy tắc: muốn chia hai phân số, ta lấy SBC nhân với số nghịch đảo của số chia.
a : c a d a.d : c a.d . a . b d b c b.c d c
2. Hỗn số, số thập phân, phần trăm a. Hỗn số
+ Hỗn số là tổng của một số nguyên và một phân số.
Kí hiệu: b b a a
Trong đó: a là phần nguyên còn b là phần phân số. c c c + VD: 2 2 5 1 1 là một hỗn số. 3 3 3 1 1 2 2 3 3 là một hỗn số. 3 3 3 Chú ý:
+ Mọi hỗn số đều có thể viết thành phân số.
+ Có những phân số không thể viết thành hỗ số. b. Số thập phân
+ Phân số thập phân là phân số được viết dưới dạng phân số có mẫu là lũy thừa của 10.
+ Các phân số thập phân đều có thể viết được dưới dạng số thập phân. + VD: 7 5 6 Phân số: ; ;
;. . . đều là các phân số thập phân. 3 100 10 10
Phân số 134 1,34 , khi đó 1,34 gọi là số thập phân. 100
Trong đó: phần số nguyên được viết bên trái dấu phẩy ( , ), Phần thập phân viết bên phải dấu ( , ).
+ Chú ý: Số chữ số ở phần thập phân đúng bằng sô chữ số 0 ở dưới mẫu của phân số thập phân. c. Phần trăm
+ Những phân số có mẫu là 100 có thể viết dưới dạng phần trăm với kí hiệu %.
+ VD: 6 6% , 23 23% ,…. 100 100
3. Thứ tự thực hiện phép tính
+ TH1: Khi biểu thức chỉ có cộng trừ hoặc nhân chia ta thực hiện từ trái qua phải. 13
+ TH2: Khi biểu thức không giống TH1 thì làm theo thứ tự sau:
Giá trị tuyệt đối/ lũy thừa Nhân/ chia Cộng/ trừ.
(lưu ý: biểu thức không có phép tính nào thì bỏ qua bước chứa phép tính đó)
+ Nếu biểu thức có ngoặc thì thực hiện trong ngoặc trước, ngoài ngoặc sau. A.
CÁC DẠNG TOÁN CƠ BẢN
Dạng 1: Thực hiện phép tính Phương pháp:
Ta làm đúng theo thứ tự thực hiện phép tính. Dạng 2: Tính hợp lý Phương pháp:
+ Sử dụng các tính chất cơ bản của phép cộng và phép nhân phân số để tính hợp lý. Tính chất Phép cộng Phép nhân Giao hoán
a c c a a c c a . . b d d b b d d b Kết hợp
a c p a c p
a c p a c p . . . .
b d q b d q
b d q b d q Cộng với số 0
a 0 0 a a b b b Nhân với số 1
a 11 a a . . b b b Số đối a a 0 b b Số nghịch đảo a b
. 1a,b 0 b a Phân phối của phép
a c p a c a p nhân đối với phép . . .
b d q b d b q cộng
+ Sử dụng một số kết quả đặc biệt: 1 1 1 a 1 1 ;
.n,a * N n.n 1
n n 1 n.n a n n a Dạng 3: So sánh Phương pháp:
+ Cách 1: Đưa về so sánh 2 phân số cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn. 14
+ Cách 2: Đưa về so sánh 2 phân số cùng tử dương, phân số nào có mẫu lớn hơn thì nhỏ hơn.
+ Cách 3: So sánh qua số trung gian a m b a b.
+ Cách 4: So sánh phần thừa, phần thiếu.
BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong các cách viết sau, cách viết nào cho ta phân số là A. 3 B. 3 1,2 C. 2 D. 2 . 2,5 2,4 0 3
Câu 2. Số đối của số 2 là 3 A. 3 B. 3 C. 2 D. 2 . 2 2 3 3
Câu 3. Phân số nghịch đảo của phân số 5 là 6 A. 6 B. 5 C. 5 D. 6 . 5 6 6 5
Câu 4. Kết quả đúng của tích 1 5 . là 3 3 A. 4 B. 5 C. 5 D. 5 . 3 3 9 9
Câu 5. Kết quả đúng của hiệu 1 2 là 5 5 A. 3 B. 1 C. 1 D. 1 . 5 5 5 10
Câu 6. Kết quả đúng của thương 1 2 : là 5 5 A. 2 B. 1 C. 1 D. 2 . 25 2 2 25
Câu 7. Tổng của hai số 0,75 và 5 là 2 A. 13 B. 26 C. 13 D. 7 . 4 8 4 4
Câu 8. Kết quả đúng của tích 1 6 .1 là 2 A. 9 B. 4 C. 4 D. 9 . 15
Câu 9. Viết hỗn số 2 3
dưới dạng một phân số ta được kết quả là: 3 A. 2 B. 7 C. 9 D. 11 . 1 3 3 3
Câu 10. Số thập phân 3,5 là cách viết khác của phân số nào? A. 7 B. 7 C. 5 D. 35 . 5 2 2 100
Câu 11. Giá trị đúng của biểu thức 4 9 1,5: là 5 4 A. 3 B. 22 C. 2 D. 2 . 4 15 15 15
Câu 12. Giá trị đúng của biểu thức 2 80%: là 3 A. 8 B. 8 C. 6 D. 6 . 15 15 5 5 3
Câu 13. Kết quả phép tính 3 1 1 . là 3 A. 1 B. 1 C. 1 D. 1 . 9 27 9 27 2 Câu 14. 2 21
Số nghịch đảo của tổng 1 là 10 35 A. 1 B. 35 C. 2 D. 35 . 2 44 66
Câu 15. Giá trị đúng của biểu thức 17.6 17 :5 là 3 20 A. 1 B. 1 C. 6 D. 6 . 5 5
Câu 16. Giá trị đúng của biểu thức 5 14 11 14 là 7 11 14 11 A. 1 B. 3 C. 3 D. 16 . 14 2 2 14 1 3 2 3
Câu 17. Số đối của : là 3 16 6 A. 5 B. 5 C. 24 D. 24 . 24 24 5 5 16
Câu 18. Giá trị đúng của biểu thức 5 7 6 5 . . là 9 13 13 9 A. 5 B. 5 C. 5 D. 5 . 9 117 9 117 2
Câu 19. Bình phương của phân số 4 3 2 . là 4 A. 5 B. 25 C. 25 D. 25 . 2 16 4 4 Câu 20. Cho 2 5 12 A . và 1 3 9 B :
. So sánh A và B , ta được 3 3 25 3 5 12
A. A B
B. A B
C. A B
D. A B .
Câu 21. Tính tổng 1 1 1 1 S . . 2 6 12 90 A. 9 B. 10 C. 1 D. 1 . 10 9 9
Câu 22. Giá trị của 5 5 5 5 A . . là
2.4 4.6 6.8 48.50 A. 3 B. 5 C. 6 D. 12 . 6 5 15
Câu 23. Tìm thương của B và nghịch đảo của B biết 13 11 2
B 1 .0,75 25% : là 15 20 5 A. 3 B. 16 C. 9 D. 9 . 5 25 25 25
Câu 24. So sánh giá trị biểu thức 3 8 15 9999 S . .
với các số 98 và 99. 4 9 16 10000
A. A 98 99
B. 98 99 A
C. 98 A 99
D. A 99 98 . BÀI TẬP TỰ LUẬN
Bài 1. Thực hiện phép tính a, 3 7 c, 1 1 e, 1 5 . 5 5 8 2 3 7 b, 1 5 d, 1 5 . f, 2 3 : 6 3 3 7 4
Bài 2. Thực hiện phép tính a, 1 5 0,75 c, 4 1 15 . . 3 18 15 3 20 17 3 5 3 b, 7 2 5 d, 1 15 25 . : 5 7 5 9 22 9
Bài 3. Thực hiện phép tính a, 2 10 20%. 1 3 1 2 3 7 c, 2 4 2 b, 3 4 3 1 : 1 7 5 1,5. .4 4 5 2 d, 3 3 Bài 4. Tính hợp lý a, 3 2 1 3 5 c, 5 12 8 . . .5,8 4 7 4 5 7 8 29 10 b, 6 12 10 1 18 3 2 1 19 . .2 .20. 21 44 14 4 33 d, 7 5 3 72 Bài 5. Tính hợp lý a, 9 3 9 7 . : c, 6 8 6 9 4 6 . . . 17 7 17 4 7 13 13 7 13 7 2 67 2 15 1 1 b, 9 2 3 22 .17 . d, 25% 25 3 5 3 111 33 117 3 12 TÌM x BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm x biết x 1 6 5 10 A. 12 x B. x 2 C. x 8 D. x 0. 15
Câu 2. Số x thỏa mãn 2 2 .x là 3 5 A. 5 B. 3 C. 4 D. 15 . 3 5 15 4
Câu 3. Số x thỏa mãn 5 7 x là 24 12 A. 3 B. 2 C. 19 D. 3 . 8 12 24 8
Câu 4. Số x thỏa mãn 1 7 x là 6 12 A. 5 B. 5 C. 3 D. 3 . 12 12 4 4 18
Câu 5. Số x thỏa mãn 4 x : 6 là 27 A. 9 B. 81 C. 2 D. 8 . 8 2 81 9
Câu 6. Số x thỏa mãn 3 3 : x là 5 11 A. 5 B. 11 C. 9 D. 55 . 11 5 55 9 Câu 7. Số x thỏa mãn 3 33 là x 77 A. 7 B. 7 C. 11 D. 11.
Câu 8. Trong các số dưới đây, số x thỏa mãn x 5 là 13 26 A. 5 B. 4 C. 3 D. 2 .
Câu 9. Giá trị của x thỏa mãn 1 1
x 5 là 4 3 A. 61 B. 59 C. 61 D. 59 . 12 12 12 12
Câu 10. Có bao nhiêu số tự nhiên x thỏa mãn 1 x 1 5 30 4 A. 1 B. 2 C. 3 D. 4. Câu 11.
Giá trị nào dưới đây của x thỏa mãn 3 4 4 .x ? 5 3 15 A. 1 B. 4 C. 8 D. 4 . 10 9 3
Câu 12. Tìm x , biết 4 2 7 4 .x : : 3 3 12 18 A. 2 7 B. 27 C. 1 D. 1 . 7 7 7 7
Câu 13. Với giá trị nào của x thỏa mãn 8 46 1 x 23 24 3 A. 1 B. 1 C. 1 D. 1 . 3 2 4 2 19 Câu 14.
Giá trị x thỏa mãn 3 5 12 x : . 4 6 3 A. 2 x B. 5 x C. 2 x D. 5 x . 5 2 5 2
Câu 15. Giá trị của x thỏa mãn 1 5 7 x là 7 21 3 A. 7 B. 17 C. 7 D. 17 . 17 7 17 7 BÀI TẬP TỰ LUẬN Bài 1. Tìm x biết: 3 1 a) x 2 b) 1 x 0 c) x d) 4 3 x e) 4 : x 13 . 5 3 2 4 2 7 2 7 Bài 2. Tìm x, biết a. 1 2 : x 7 b. 2 12 : x 1,4 c. x 4 11 4,5 2 .1 3 3 3 5 7 14 Bài 3. Tìm x a) 5 1 x 4 . b) 1 3 23 45 x . . 3 2 4 4 15 92 c) 3 1 3 1 x . d) 2 1 10 11 24 x . . 4 4 5 3 3 11 33 8 55 Bài 4. Tìm x biết a. 1 2 x 30% x 1,3
b. x x 1 0 c. 1 3 1 3 x 5 x x 3 5 2 5 5 BÀI TOÁN CÓ LỜI VĂN A. TÓM TẮT LÝ THUYẾT
1. Định nghĩa phân số: Phân số là số có dạng a, ,
a b Z,b 0 . b
2. Tính chất của phân số.
T/C1: Khi nhân cả tử và mẫu của một phân số với một số nguyên khác 0 ta được một phân số mới a . a m bằng phân số đã cho:
;a,b,m Z;b,m 0 b . b m 20