








































































Preview text:
lOMoARcPSD| 36067889 NGÂN HÀNG ĐỀ THI
Môn: LÝ THUYẾT THÔNG TIN S tín chỉ : 4
SỬ DỤNG CHO NGÀNH ĚIỆN TỬ - VIỄN THÔNG VÀ CÔNG NGHỆ THÔNG TIN
HỆ ĚẠI HỌC TỪ XA
CHƠNG I: NHỮNG VẪN ĚỀ CHUNG VÀ KHÁI NIỆM CƠ BẢN
1/ Chọn câu úng sau : a
Tin luôn ược biểu diễn dưới d ng số b Tấm nh, b
n nh c, bức thư . . . không ph i là các tin c Tin là một ánh x
liên tục ến người nhận d
Tin là d ng vật chất ể biểu diễn
hoặc thể hiện thông tin.
2/ Chọn phát biểu úng trong những câu sau : a
Thông tin là những tính chất xác ịnh của vật chất mà con người nhận ược từ thế giới vật chất bên ngoài b
Thông tin không thể xuất hiện dưới d ng hình nh c Thông tin tồn t i một cách
chủ quan, phụ thuộc vào hệ thụ c m. d
Thông tin không thể xuất hiện dưới d ng âm thanh
3/ Môn lý thuyết thông tin bao gồm việc nghiên cứu: a
Vai trò của thông tin trong kỹ thuật b Các quá
trình truyền tin và Lý thuyết mã hóa. c Lý thuyết
toán xác suất ứng dụng trong truyền tin. d Cách chống
nhiễu phi tuyến trong vô tuyến iện
4/ Chọn câu úng nhất về nguồn tin a Nguồn tin là nơi s n ra tin b
Nguồn tin là tập hợp các tin có xác suất và ký hiệu
như nhau c Nguồn tin liên tục sinh ra tập tin rời r c. d Nguồn
tin rời r c sinh ra tập tin liên tục.
5/ Chọn câu úng nhất về ường truyền tin a
Là môi trường Vật lý, trong
ó tín hiệu truyền i từ máy phát sang máy thu b Là môi trường Vật lý m b o an toàn thông tin c
Là môi trường Vật lý trong ó tín hiệu truyền i từ máy phát sang máy thu không làm mất thông tin của tín hiệu. d
Ěường truyền tin chính là kênh truyền tin.
6/ Ěể biến ổi một tín hiệu liên tục theo biên ộ và theo thời gian thành tín hiệu số, chúng ta cần thực
hiện quá trình nào sau ây: a Rời r c hóa theo trục thời gian và lượng tử hóa theo trục biên ộ b Gi i mã
dữ liệu c Mã hóa dữ liệu. d
Lượng tử hóa theo trục thời gian và rời r c hóa theo trục biên ộ
CHƠNG II: TÍN HIỆU VÀ NHIỄU lOMoARcPSD| 36067889
1/ Chọn câu úng về tín hiệu: a Tín hiệu là một ánh x
liên tục ến người nhận b
Tấm nh, b n nh c, bức thư . . .
không ph i là các tin c
Tin luôn ược biểu diễn dưới d ng số d
Tín hiệu là quá trình ngẫu nhiên .
2/ Chọn phát biểu úng nhất về ặc trưng thống kê : a
Ěặc trưng cho các quá trình ngẫu nhiên chính là các quy luật thống kê và các ặc trưng thống kê b
KǶ vọng, phương sai, hàm tự tương quan, hàm tương quan là các quy luật thống kê c
Các hàm phân bố và mật ộ phân bố là những ặc trưng thống kê d
Tín hiệu và nhiễu không ph i là quá trình ngẫu nhiên theo quan iểm thông kê
3/ Chọn câu úng nhất về hàm tự tương quan : a
Hàm tự tương quan là quy
luật thống kê thể hiện của quá trình ngẫu nhiên. R (t ,t ) b Hàm tự tương quan 2 x 1 luôn ược tính bằng biểu thức sau { } R [
x (t t1 2, )= M
X t( )−m tx ( )]2 R (t ,t ) c Hàm tự tương quan 2
x 1 ặc trưng cho sự phụ thuộc thống kê giữa hai giá trị ở hai thời iểm thuộc cùng một R (t ,t ) d Hàm tự tương quan
x 1 2 luôn bằng phương sai D t ( ) với mọi t x
4/ Việc biểu diễn một tín hiệu gi i hẹp thành tổng của hai tín hiệu iều biên biến thiên chậm sẽ làm cho
việc phân tích m ch vô tuyến iện dưới tác ộng của nó trở nên phức t p a Ěúng b Sai
5/ Người ta gọi tín hiệu gi i rộng nếu bề rộng phổ của nó tho mãn bất ẳng thức sau: Δω ≥1 ω0
. Các tín hiệu iều tần, iều xung, iều xung cốt, manip tần số, manip pha,… là các tín hiệu gi i rộng. a Sai b Ěúng
6/ Chọn câu úng về công thức xác ịnh mật ộ phổ công suất 1 ∞ ∞ •2 E = x π a 2 ω ω T
−∫∞ T (t)dt = 2 −∫∞ S ( ) dT
là công thức xác ịnh mật ộ phổ công suất của các quá trình ngẫu nhiên. lOMoARcPSD| 36067889 • 2 S ( ) ω T = G ( ) ω T b T
là công thức xác ịnh mật ộ phổ công suất của các quá trình ngẫu nhiên. • 2 S ( ) ω T G( )ω = M G ( ){ ω =} x M lim c T→∞ T
là công thức xác ịnh mật ộ phổ
công suất của các quá trình ngẫu nhiên. • 2 S ( ) ω T d
T T T là công thức xác ịnh mật ộ phổ công suất của các quá trình ngẫu nhiên.
7/ Chọn câu úng về công thức quan hệ giữa mật ộ phổ công suất và hàm tự tương quan • 2 S ( ) ω T G ( ) ω = ω = x lim G ( )T lim a T→∞ T→∞ T • 2 S ( ) ω T G( )ω = M G ( ){ ω =} x M lim b T→∞ T ∞ ∞ • 2 2 1 c
ET = ∫ xT (t)dt = 2π−∫∞ S ( ) dT ω ω −∞ ∞ G( )ω = ∫ R( )eτ −jωτdτ d −∞
8/ Trong trường hợp hệ thống tuyến tính thụ ộng có suy gi m thì ở những thời iểm t >> t 0 = 0 (thời iểm
ặt tác ộng vào), quá trình ngẫu nhiên ở ầu ra sẽ ược coi là dừng. Khi ó hàm tự tương quan và mật ộ phổ
công suất của quá trình ngẫu nhiên ở ầu ra sẽ liên hệ với nhau theo biểu thức sau : ∞ R ( )ra G ( )era d −∞ a Sai b Ěúng lOMoARcPSD| 36067889 9/ S* ( )
a t là hàm liên hợp phức của Sa t là tín hiệu gi i tích.
Ěường bao của tín hiệu gi i tích có thể biểu diễn bằng công thức sau: A t( ) = S ( ) ( ) a t .S*a t a Sai b Ěúng
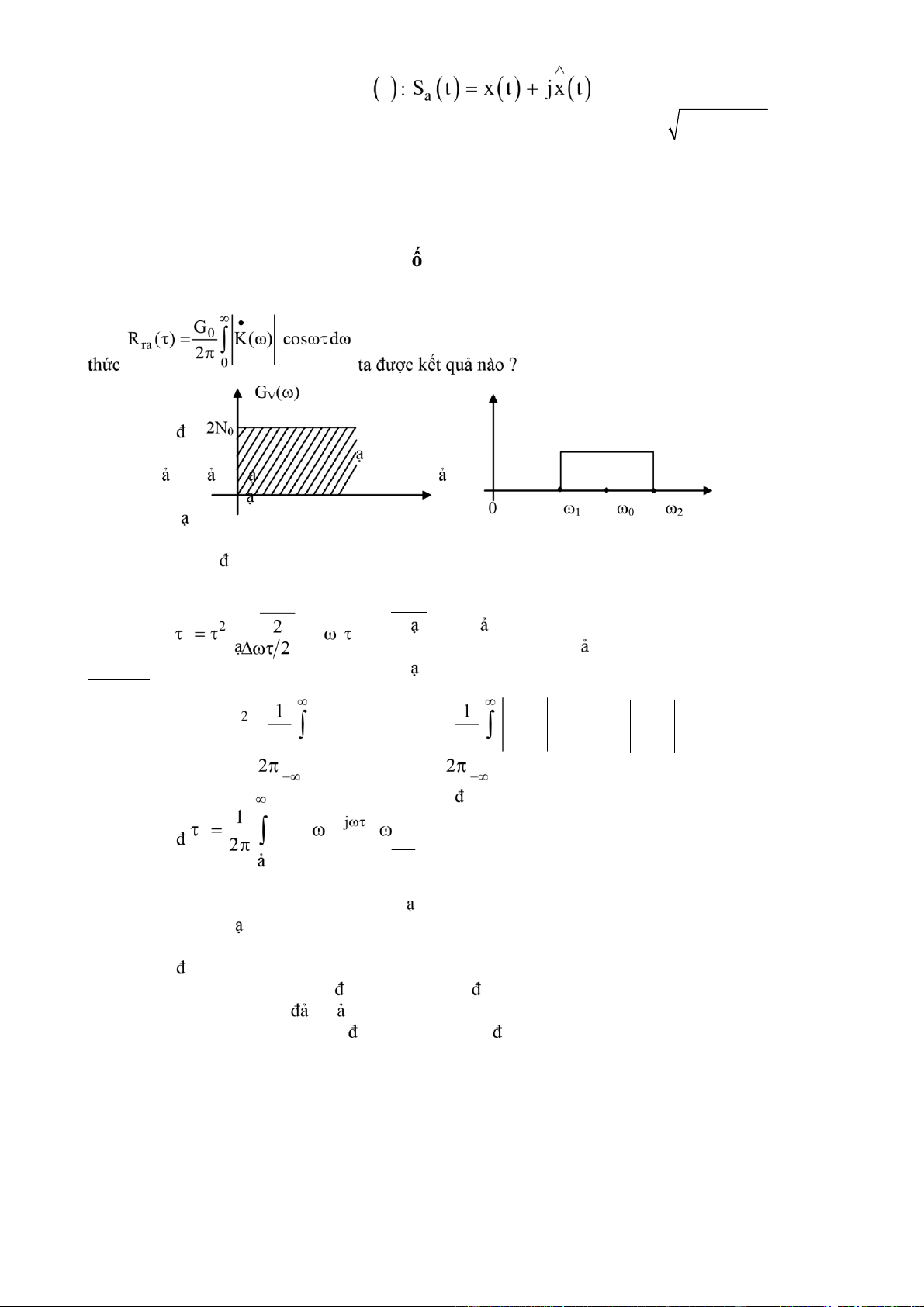
10/ Một m ch vô tuyến iện tuyến tính có tham số không ổi và ặc tính truyền t d ng chữ nhật (hình dưới)
chịu tác ộng của t p âm trắng dừng. Tìm hàm tự tương quan của t p âm ra theo công 2 | K(ω) | ω a. ω b. Δωτ c −∞ sin = R ( ) d Rra 0 ra ra cos 0 a • 2 K( ) G ( )dω ω ω v R (0) =τ = ra G ( )d ω ω= = ra Pra b R ( )ra G ( )era d
11/ Cho quá trình ngẫu nhiên dừng có biểu thức sau: X t( ) = Acos 2 f t( π +ϕ ) 0
Trong ó A = const, f0 = const, ϕ là
i lượng ngẫu nhiên có phân bố ều trong kho ng (−π π, ). π
Tính kǶ vọng M {X t( )} theo công thức M {X t( )}= ∫ X t w( ) ( )ϕdϕ ta ược giá trị nào dưới ây −π a M x t{ ( )}=0 b M x t{ ( )}=2 c M x t{ ( )}=1 lOMoARcPSD| 36067889 d M x t{ ( )}=−1
12/ Cho quá trình ngẫu nhiên dừng có biểu thức sau: X t( ) = Acos 2 f t( π 0 + ϕ) Trong ó A =
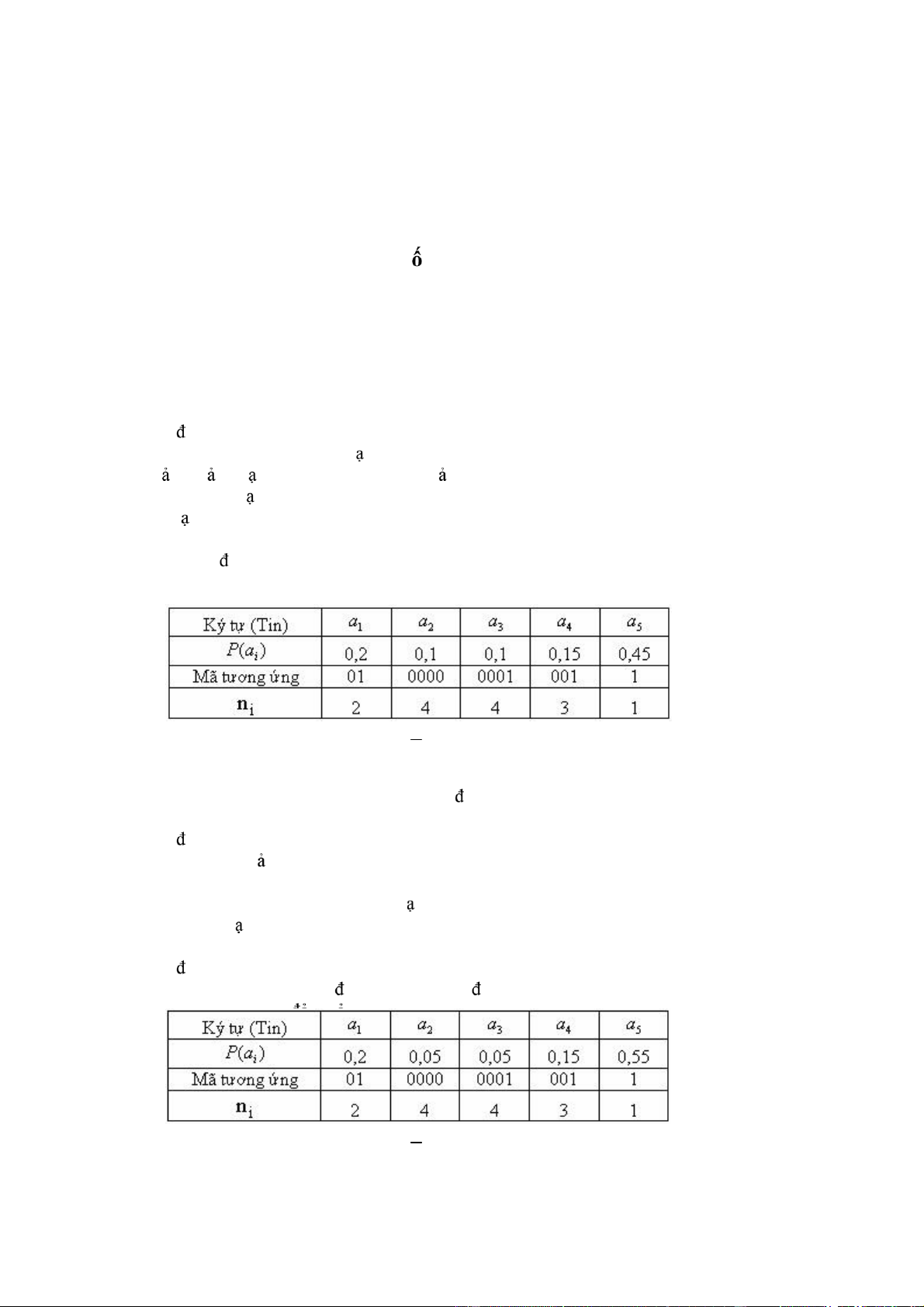
const, f0 = const, ϕ là i lượng ngẫu nhiên có phân bố ều trong kho ng (−π π, ). Tính hàm tự tương
quan R(t t , ) theo biểu thức 1 2
R t t( 1 2, ) = M X t X t{ ( ). ( +τ)} ta ược giá trị nào dưới ây: a R(t t1 2, ) = A2 cos2πf τ τ
0 b R t t( 1 2, ) = 0 c R(t t1 2, ) = A2 cos2πf0 d R(t t τ
1 2, ) =−A2 cos2πf0
13/ Tín hiệu iện báo ngẫu nhiên X(t) nhận các giá trị + a; - a với xác suất như nhau và bằng 1/2. Còn
xác suất ể trong kho ng τ có N bước nh y là:P N,( τ) = (λτ)N e−λτ τ > 0 N!
(theo phân bố Poisson). Từ các gi thiết trên tính ược hàm tự tương quan Rx ( )τ = a e2 2− λτ. Khi ó mật ộ
phổ công suất Gx ( )ω của X(t) ược tính theo công thức Gx( )
2 Rx( )cos d ta ược giá trị nào sau ây: a Gx ( )ω = b Gx ( )ω = c Gx ( )ω = 0 d Gx ( )ω =
14/ Một quá trình ngẫu nhiên dừng có hàm tự tương quan: Rx ( )τ =δ2e−ατcosωτ0 Khi ó
mật ộ phổ công suất của các quá trình ngẫu nhiên trên là ⎡⎣ + 2 2 + 2 (2 + 0)⎤⎥⎦ a G + x ( )ω ατ=
⎢α ω ω α ω ω2 ( − 0) ⎡ ⎤ b G ⎢⎣α ω ω α ω ω + + x ( )ω ατ= 2 2 (2 − 0) − 2 (2 + 0)⎥⎦ ⎡ ⎤ c G ⎢⎣α ω ω α ω ω + + x ( )ω ατ= 2 2 (1 − 0) − 2 (1 + 0)⎥⎦ lOMoARcPSD| 36067889 ⎡ 1 1 ⎤ d G ⎢⎣α ω ω α ω ω + + x ( )ω ατ= 2 2 ( − 0) + 2 ( + 0)⎥⎦
CHƠNG 3: CƠ SỞ LÝ THUYẾT THÔNG TIN TH NG KÊ
1/ Khái niệm lượng tin ược ịnh nghƿa dựa trên: a Nĕng
lượng của tín hiệu mang tin b
Ěộ bất ịnh của tin c
Ý nghƿa của tin d Nĕng lượng của tín hiệu mang tin và ý nghƿa của tin lOMoARcPSD| 36067889
2/ Chọn phát biểu úng nhất về Entropy của nguồn tin, H(X): a Là
i lượng ặc trưng cho ộ bất ịnh trung bình của nguồn tin b
Ěược tính theo công thức H c
Ě t cực tiểu khi nguồn là ẳng xác suất d Ě t cực
i khi nguồn là ẳng xác suất
3/ Chọn phát biểu sai về ộ bất ịnh a Ěộ bất ịnh của phép chọn tỷ lệ nghịch với xác
suất chọn một phần tử b Ěộ bất ịnh gắn liền với b n chất ngẫu nhiên của phép chọn
c Ěộ bất ịnh của một phần tử có giá trị 1 bit khi xác suất chọn phần tử ó là 1 d Ěộ
bất ịnh còn ược gọi là lượng thông tin riêng của biến cố tin
4/ Entropy của nguồn rời r c nhị phân H(A) =−plogp− −(1 p log 1)( − p)
Khi p=1/2 thì H(A) t max Chọn câu úng về H A( )max a
H A( )max =3/2 bít; b H A( )max =1/2 bít; c H A( )max =1
bít ; d H A( )max =0
5/ Trong một trận thi ấu bóng á Quốc tế, ội tuyển Việt Nam thắng ội tuyển Brazin, thông tin này có ộ bất ịnh là a bằng 0 ; b Vô cùng lớn c nhỏ hơn 0; d lớn hơn 0
6/ Học sinh A có thành tích 12 nĕm liền t danh hiệu học sinh giỏi, học sinh B lực học kém Thi tốt
nghiệp phổ thông trung học, học sinh A trượt, học sinh B ỗ thủ khoa Thông tin về học sinh B ỗ thủ
khoa, học sinh A trượt có ộ bất ịnh là: a bằng 0 ; b Vô cùng lớn c nhỏ hơn 0; d lớn hơn 0
7/ Chọn ngẫu nhiên một trong các số từ 0 ến 7 có xác suất như nhau Khi ó xác suất của số ược chọn ngẫu nhiên là: a 7 b 1/8 c 8 d -7
8/ Một thiết bị vô tuyến iện gồm 16 khối có ộ tin cậy như nhau và ược mắc nối tiếp Giả sử có một khối
nào ó bị hỏng, khi ó xác suất của một khối hỏng là: a 1/16 b 16 c -16 d -1/16
9/ Bộ tú lơ khơ 52 quân (không kể fĕng teo), A rút ra một quân bài bất kǶ Xác suất về quân bài mà A ã rút là: a Bằng 1/52 b Nhỏ hơn 5 c Lớn hơn 5 nhỏ hơn 6 d Bằng 1/52 lOMoARcPSD| 36067889
10/ Chọn câu sai trong các câu sau : a Ěộ bất ịnh sẽ
trở thành thông tin khi nó bị thủ tiêu b Ěộ bất ịnh chính là thông tin c
Lượng thông tin = ộ bất ịnh tiên nghiệm + ộ bất ịnh hậu nghiệm d
Lượng thông tin = ộ bất ịnh tiên nghiệm - ộ bất ịnh hậu nghiệm
11/ Chọn câu úng sau : a Lượng thông tin = thông tin tiên nghiệm -
thông tin hậu nghiệm b Thông tin hậu nghiệm chính là thông tin riêng
c Lượng thông tin = thông tin hậu nghiệm - thông tin tiên nghiệm d
Lượng thông tin = thông tin tiên nghiệm + thông tin hậu nghiệm
12/ Chọn câu sai trong các câu sau :
a Thông tin tiên nghiệm (ký hiệu I( x )) ược xác ịnh theo công thức sau:I( k
xk ) = log P( xk ); b Thông
tin tiên nghiệm còn gọi là lượng thông tin riêng; c Thông tin tiên nghiệm (ký hiệu I( x )) ược xác ịnh k
theo công thức sau:I( xk ) =- log P( xk ); d Thông tin tiên nghiệm còn gọi là lượng thông tin riêng ược
xác ịnh theo công thức sau : 1 I( xk ) = log ; P x( k ) 13/ (I x
)là lượng thông tin chéo về k , yl
xk do yl mang l i ược tính bằng công thức nào sau ây : 1 a log 1 −log
P x( k ) P x( k / yl ) b I(yj
)− I y( j / xk ) 1 c log −log P x( k / yl ) P x( k ) P y( / x ) d log l k P y( l ) 14/ (I x
)là thông tin hậu nghiệm về
k / yl ) =−log p x( k / yl
xk p x( k / yl ) =1 khi việc truyền tin không bị
nhiễu. Chọn câu sai trong những câu về (I x ) dưới ây: k / yl a I(x
)=0 khi kênh không có nhiễu k / yl b I(xk /
y ) là lượng tin bị mất i do nhiễu l
c I(xk / yl ) là lượng tin có iều kiện d I(x
)=1/2 khi kênh không có nhiễu k / yl 15/ (I x
)là thông tin hậu nghiệm về k / yl
xk p x( k / yl ) =1khi việc truyền tin không bị nhiễu Chọn câu sai
trong những câu về (I x ) dưới ây:
) là lượng tin bị tổn hao do nhiễu k / yl
a (I xk / yl
b (I xk / yl )= 0 khi
kênh không có nhiễu c (I x
)>1/2 khi kênh không có nhiễu
) là lượng thông tin về k / yl
d (I xk / yl xk khi ã biết yl lOMoARcPSD| 36067889 16/ (I x
) là lượng thông tin riêng của khi ã biết
) = 0 khi không có nhiễu Câu này k / yl xk
yl và (I xk / yl úng hay sai ? a Ěúng b Sai
17/ Chọn câu sai trong những câu sau: a Lượng tin còn l i của xk sau khi ã nhận ược yl ký hiệu là (I x
)là lượng tin riêng của
) là lượng tin ban ầu của
k / yl ) b (I xk , yl
xk và yl c Lượng tin (I xk xk d Lượng
tin (I x ) là lượng tin ban ầu của , Lượng tin còn l i của k xk
xk sau khi ã nhận ược yl ký hiệu là (I xk / yl )
18/ Cho tin x có xác suất là
)của tin này bằng các i lượng nào dưới i
P x( i ) = 0,5, lượng tin riêng (I xi ây : a 4 bít b 1 bít c 1/4 bít d 2 bít
19/ Cho tin x có xác suất là
)của tin này bằng các i lượng nào dưới i
P x( i ) =1/ 4, lượng tin riêng (I xi ây : a 2 bít b
4 bít c 3 bít d 1/2 bít e 1/4 bít
20/ Cho tin x có xác suất là
)của tin này bằng các i lượng nào dưới ây i
P x( i ) =1/8, lượng tin riêng (I xi : a 5 bít b 3 bít c 4 bít d 1/4 bít 21/ Cho tin x
)của tin này bằng các i lượng nào dưới
i có xác suất là P x( i ) =1/16, lượng tin riêng (I xi ây: a 1/4 bít b 2 bít c 3 bít d 4 bít 22/ Cho tin x
)của tin này bằng các dưới i lượng nào
i có xác suất là P x( i ) =1/ 27, lượng tin riêng (I xi ây: a 2log7 bít b
Log1/9 bít; c Log27 bít; d Log1/27 bít; lOMoARcPSD| 36067889
23/ Cho tin x có xác suất là )của tin này bằng các i lượng nào i
P x( i ) =1/9 , lượng tin riêng (I xi
dưới ây : a Log9 bít b Log1/3 bít c 2log3 bít d Log1/9 bít
24/ Cho tin x có xác suất là
)của tin này bằng các dưới i lượng nào i
P x( i ) =1/ 25, lượng tin riêng (I xi ây : a Log2/5 bít b 2log5 bít c Log1/25 bít d - Log25 bít
25/ Tìm câu sai trong những câu dưới ây a
Ěộ bất ngờ của tin x trong nguồn tin i
X N ược tính bằng entropy của lớp tin xi trong nguồn tin X N b
Ěộ bất ịnh của tin và lượng tin về ý nghƿa trái ngược nhau nhưng về giá trị l i bằng nhau c Ěộ
bất ịnh của tin và lượng tin có ý nghƿa như nhau nhưng giá trị khác nhau
d Lượng tin trung bình ược hiểu là lượng tin trung bình trong một tin bất kǶ của nguồn tin ã cho I
26/ Lượng thông tin riêng (ộ bất ịnh) của một biến ngẫu nhiên x ( ) k là xk I
Chọn biểu thức sai trong các biểu thức dưới ây a (x )=lnp( ) k xk ơn vị o I I là bit; b (x )=−lgp( ) ( )=−lnp( ) k
xk ơn vị o là hart; c xk xk ơn vị I o là nat; d (x )=− ( ) k
log p2 xk ơn vị o là bít I
27/ Lượng thông tin riêng (ộ bất ịnh) của một biến ngẫu nhiên x ( ) k là
xk ược tính bằng biểu thức nào dưới ây : I I a (x )= klnp( ) ( k xk ; b xk )=−lnp( I x ) (
k ơn vị o là bit; c xk )=− I log p ( ) (
2 xk ơn vị o là nat; d xk )=lgp(x ) k ơn vị o là hart; I I
28/ Lượng thông tin riêng (ộ bất ịnh) của một biến ngẫu nhiên x ( ) ( )= k là
xk ược tính như sau xk klnp(x )
k , trong ó k là hệ số tỷ lệ Tìm câu sai về cách chọn k trong các câu dưới ây : I a
Chọn k = 1 ta có (x )=lnp( ) k xk lOMoARcPSD| 36067889 I b
Chọn k =-1 ta có (x )=−lnp( ) k xk ; I I c Chọn k =− ta có (x )=−lgp( ) ( )=− ( ) k
xk ; d Chọn k =− ta có xk log p2 xk
29/ Entropy của nguồn tin rời r c A là trung bình thống kê của lượng thông tin riêng của các tin thuộc A Ký hiệu: H ( ( )= ⎤⎦ ) ⎞⎟⎠ 1 A); H A1
ΔM I a⎡⎣ ( )i với A =⎛⎜p a( )a11 p a(a22 ...... p a( )ass 0 ≤ p a( i )≤1; ⎝ s ∑p a( ) = ( ) i 1;H1
A ược tính bằng biểu thức nào dưới ây: i 1= s a H ( ) 1 A =∑p a( )i logp a( )i (bít) ; i 1= b H ( ) 1 A p a( )i logp a( )i (bít) ; c H A p a logp a (bít) ; ( ) s d H1 A
=−∑p a( )i logp a( )i (bít) ; i 1=
30/ Entropy của nguồn tin rời r c A là trung bình thống kê của lượng thông tin riêng của các tin thuộc A (A) ⎡ ; H A ( )= ⎦⎤ ) ( ) 1
ΔM I a ⎣ ( )i với A =⎛⎜⎝p a( )a11 p a(a22 ...... p a ass ⎞⎟⎠ Ký hiệu: H1 s 0 ≤ p a( )≤ ∑p a( ) = (A) i 1; i 1 H1
ược tính bằng biểu thức nào : ( ) i 1= s a H1 A =∑p a( )i logp a( )i (bít) ; lOMoARcPSD| 36067889 b H A p a logp a (bít) c H A p a log (bít) d H ( ) 1 A p a( )i logp a( )i (bít) ; i 1=
31/ Entropy của nguồn tin rời r c A là trung bình thống kê của lượng thông tin riêng của các tin thuộc A Ký hiệu: H ( ( ) ⎤⎦ ) 1 A); H1
A =Δ M I a⎡⎣ ( )i với A =⎛⎝⎜p a(a00 p a( )a11 ...... p a(as 1−s 1− )⎟⎠⎞ s 1− 0 ≤ p a( )≤ ∑p a( ) = (A) i 1; i 1 H1 ược tính như sau: ( ) i=0 s a H1 A =∑p a( )i logp a( )i (bít) i=0 b H ( ) 1
A =∑s 1− p a( )i logp a( )i (bít) c H A p a logp a (bít) ; ( ) s 1− d H1 A =−∑p a( )i logp a( )i (bít); i=0
32/ A và B là hai trường biến cố bất kǶ, Entropy của 2 trường biến cố ồng thời C=AB là H(AB)
Trong các tính chất của H(AB) dưới ây, tính chất nào sai: a H AB( )= H A( )+ H B A() ; b H AB( )= H B( )+ H A B(); ( ) s c H1 A =∑p a( )i logp a( )i (bít) ; i 1= lOMoARcPSD| 36067889 d H ( ) 1 A p a( )i logp a( )i (bít); i=0
33/ Entropy có iều kiện về 1 trường tin A khi ã rõ trường tin B là H(A/B)
Trong các tính chất của H(A/B) dưới ây, tính chất nào sai
a H A B( )≤ H B/A( ) ; b 0 ≤ H A B( ); c H A(
)≥ H A B( ) d H A B()≤ H A( ) ; H B/A H B/A
34/ Entropy có iều kiện về 1 trường tin B khi ã rõ trường tin A là
( ), Tính chất nào của ( ) dưới ây là úng
a 0 ≥ H B/A( ) ; b 0 ≤ H
B/A( ) ; c H A B()≤ H
B/A( ) ; d H B/A( )≤ H A( ) ;
35/ Entropy của trường biến cố ồng thời H(AB) ược tính bằng công thức nào sau ây a
H(A) + H(A/B); b H(A) + H(B) c
H(A) + H(B) - H(A/B) - H(B/A); d H(B) + H(A/B);
36/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B) có các tính chất nào sau ây I A,B a
( )=−H A( ) khi kênh có nhiễu; b 0 ≤ I A,B( )≤ H A( ); c H A( )≤ I A,B I A,B( )≤ 0; d
( )= H A( ) khi kênh có nhiễu;
37/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B) Trong các tính chất dưới ây, tính chất nào sai: a I A,B( )≤ H A( ); khi kênh có nhiễu; b I A,B()= H A( ) c 0 ≤ I A,B(); d
khi kênh không có nhiễu; I A,B()= H A( )
38/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B) có các tính chất nào sau ây a I A,B ( )=1 khi kênh bị ứt; I A,B I b 0 ≤ I A,B( ) v à
( )= 0 khi kênh bị ứt; c 0 ≥ I A,B( ) d
A,B( )= H A( ) khi kênh có nhiễu; lOMoARcPSD| 36067889
39/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B) ), trong các tính chất dưới ây của I(A,B), tính chất nào sai I A,B I A,B a
( )= H A( ) khi kênh không có nhiễu; b
( )= 0 khi kênh bị ứt; c H A( )≤ I A,B I A,B( ); d ( )≥1 khi kênh bị ứt;
40/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) , tìm biểu thức sai trong các biểu thức dưới ây
a I(A,B) = H(A) - H(A/B); ∑∑ ( ) ) s t p a( i b j log b I(A,B) = i 1= =j 1 p a bi j p a( )i c I(A,B) = H(A) - H(B/A); d I(A,B) = H(B) - H(B/A) ;
41/ Mệnh ề nào sau ây sai a H(A/B) ≤ H(A) ; b H(A,B) ≤ H(A) + H(B) c I(A,B) = H(A) + H(B) + H(AB); d
I(A,B) = H(A) + H(B) - H(AB);
42/ Chọn ngẫu nhiên một trong các số từ 0 ến 7 có xác suất như nhau Ěộ bất ịnh của số ược chọn ngẫu nhiên là a 1/8 bít; b -3 bít; c 3 bít; d 8 bít;
43/ Một thiết bị vô tuyến iện gồm 16 khối có ộ tin cậy như nhau và ược mắc nối tiếp Gi sử có một khối
nào ó bị hỏng, ộ bất ịnh của khối hỏng là: a 1/16 bít; b 16 bít; c 1/4 bít; d 4 bít;
44/ Bộ tú lơ khơ 52 quân (không kể fĕng teo), A rút ra một quân bài bất kǶ Ěộ bất ịnh về quân bài mà
A ã rút là: a Nhỏ hơn 5 bít; b Lớn hơn 5 nhỏ hơn 6 bít; c Bằng 6 bít d Lớn hơn 6 bít ;
45/ Một hộp có 8 ồng tiền kim lo i , trong ó có 02 ồng tiền 500 ồng; 02 ồng tiền 1000 ồng, 2 ồng tiền
2000 và 2 ồng tiền 5000 ồng Chọn ngẫu nhiên 1 trong 8 ồng tiền ó Khi ó xác suất của ồng tiền ược chọn ngẫu nhiên là: a 8 bít ; b -1/2 bít; c 1/8 bít; d 1/4 bít ; lOMoARcPSD| 36067889
46/ Một hộp có 8 ồng tiền kim lo i , trong ó có 02 ồng tiền 500; 02 ồng tiền 1000, 2 ồng tiền 2000 và 2
ồng tiền 5000 Chọn ngẫu nhiên 1 trong 8 ồng tiền ó Khi ó ộ bất ịnh của ồng tiền ược chọn ngẫu nhiên là: a 1/4 bít; b 8 bít ; c -1/2 bít; d 2 bít;
47/ Cho nguồn tin X = {x1, x2, x3} với các xác suất lần lượt là {1/2, 1/4, 1/4}, Entropy của nguồn tin H(X) ược tính là: a 1 1 1 log2 + log4 + log8 2 4 4 b 1 1 1 log2 + log4 + log4 2 4 2 c 1 1 1 log2 + log4 + log4 ; 2 4 4 d 1 1 1 log2 + log4 + log4 2 2 4
48/ Cho nguồn tin X = {x1, x2, x3, x4, x5, x6, x7, x8, x9} với các xác suất lần lượt là {1/4, 1/8, 1/8,
1/8, 1/16, 1/16, 1/8, 1/16, 1/16}. Trong các kết qu tính Entropy dưới ây, kết qu nào sai: a 1 1 1 log4 + 4 log8 + 4 log16 4 8 8 b 1 3 log4 + log2 + log2 2 2 c 1 1 1 log4 + 4 log8 + 4 log16 4 8 16 d 1 3 log4 + log2 + log2 4 2
49/ Entropy H ( ) 1
A của nguồn rời rạc ∑ ⎛ a ⎞ ( )≤ s = 1 a 2 ... as i 1; p a( )i 1 A =⎜p a( ) ) ⎟⎠ 1
p a( 2 ... p a( )s với 0 ≤ p a i 1= ⎝
Trong các tính chất của H(A) dưới ây tính chất nào là sai p a p a a Khi ( )= ( )= (A)= (A) = k 1, i 0 với ∀i ≠ k thì H1 H1 min 1 b Nguồn p
tin rời r c A có s dấu ồng xác suất cho entropy cực i H (A) = 1 max logs c Khi a( )= p a( )= (A)= (A) = k 1, i 0 với ∀i ≠ k thì H1 H1 min 0 d Entropy của nguồn rời r c A là một
i lượng giới nội 0 ≤ H (a)≤ 1 logs lOMoARcPSD| 36067889
50/ Cho nguồn rời r c A A =⎛⎝⎜p a( )a ) ⎞⎟⎠ )≤ ∑ = 11p a(a 22
......p a( )as s với 0 ≤ p a( i 1; i 1=s p a( )i 1
Gọi entropy của nguồn A là H ( ) ( )− 1
A , trong các biểu thức tính H1 Amax
logs dưới ây, biểu thức nào sai: ∑ 1 a H ( )− s + 1 Amax logs= p a( )i log logs i 1= p(a )i ∑ 1 ⎥ ⎤ b H ( )− s ⎢⎣⎡ − 1 Amax logs= p a( )i log p(a ) logs ⎦ ; c H1 Amax logs p ai log p(a )logsi ; i 1= p(a )i i 1= ∑ p a (A )− ( ) max logs= s i log 1 −logs ; d H1 i 1= p(a )i
51/ Cho nguồn rời r c A A =⎛⎜p a( )a ) ( ) ⎞⎟ 11 p a(a 22 ...... p a ass ⎠ với 0 ≤ p a( i )≤1; ∑ = i 1=s p a( )i 1 ⎝
Nếu nguồn A có s dấu ồng xác suất , khi ó biểu thức nào dưới ây là sai a ∑ ∑ = s 1 + s p a( )i 0 i 1= s i 1= p(a ) = 1 i ∑ ∑
b s ∀1≤ ≤i s ; c s 1 − = s p a( )i 0 ; i 1= s i 1= d H (A) − ≤ 1 logs ≤ ⇒0 H (A)1 logs lOMoARcPSD| 36067889
52/ Kh nĕng thông qua của kênh rời r c C’ là giá trị cực
i của lượng thông tin chéo trung bình
truyền qua kênh trong một ơn vị thời gian lấy theo mọi kh nĕng có thể có của nguồn tin A Δ C' = υK.C víi C =max I(A,B) C = ( )= ( ) ' maxI A,B' v maxI A,Bk (bps); A A A
υK biểu thị số dấu mà kênh ã truyền ược (ược truyền qua kênh) trong một ơn vị thời gian I’(A,B) là
lượng thông tin ã truyền qua kênh trong một ơn vị thời gian C ược gọi là kh nĕng thông qua của kênh
ối với mỗi dấu C’ có các tính chất nào dới ây : ≤υ
a C’ ≥ 0, C’ = 0 khi A và B ộc lập ; C’
K logs, C' = v logsk khi kênh không nhiễu b C’ =
0 khi và chỉ khi A và B có nhiễu c C' = v logsk khi kênh có nhiễu d C' = v logsk khi các kênh ộc lập
53/ I(A,B) là lượng thông tin trung bình ược truyền qua kênh rời r c có tính chất : I(A,B) ≤H(A) Và một số ịnh nghƿa : Δ C' = υK.C víi C =max I(A,B)
C' =maxI A,B' ( )= v maxI A,B ( ) k , A A A
υK biểu thị số dấu mà kênh ã truyền ược trong một ơn vị thời gian. Từ các tính chất và ịnh
nghƿa trên cho biết các biểu thức dưới ây, biểu thức nào sai ≥ υ a υK I(A,B) K H(A); b υK ≤ υ I(A,B) K H(A); c υK ≤ υ maxI(A,B) K maxH(A) υ d
max(υK I(A,B)) ≤ max( K H(A)); ⎛ a1 a 2 ⎞ =
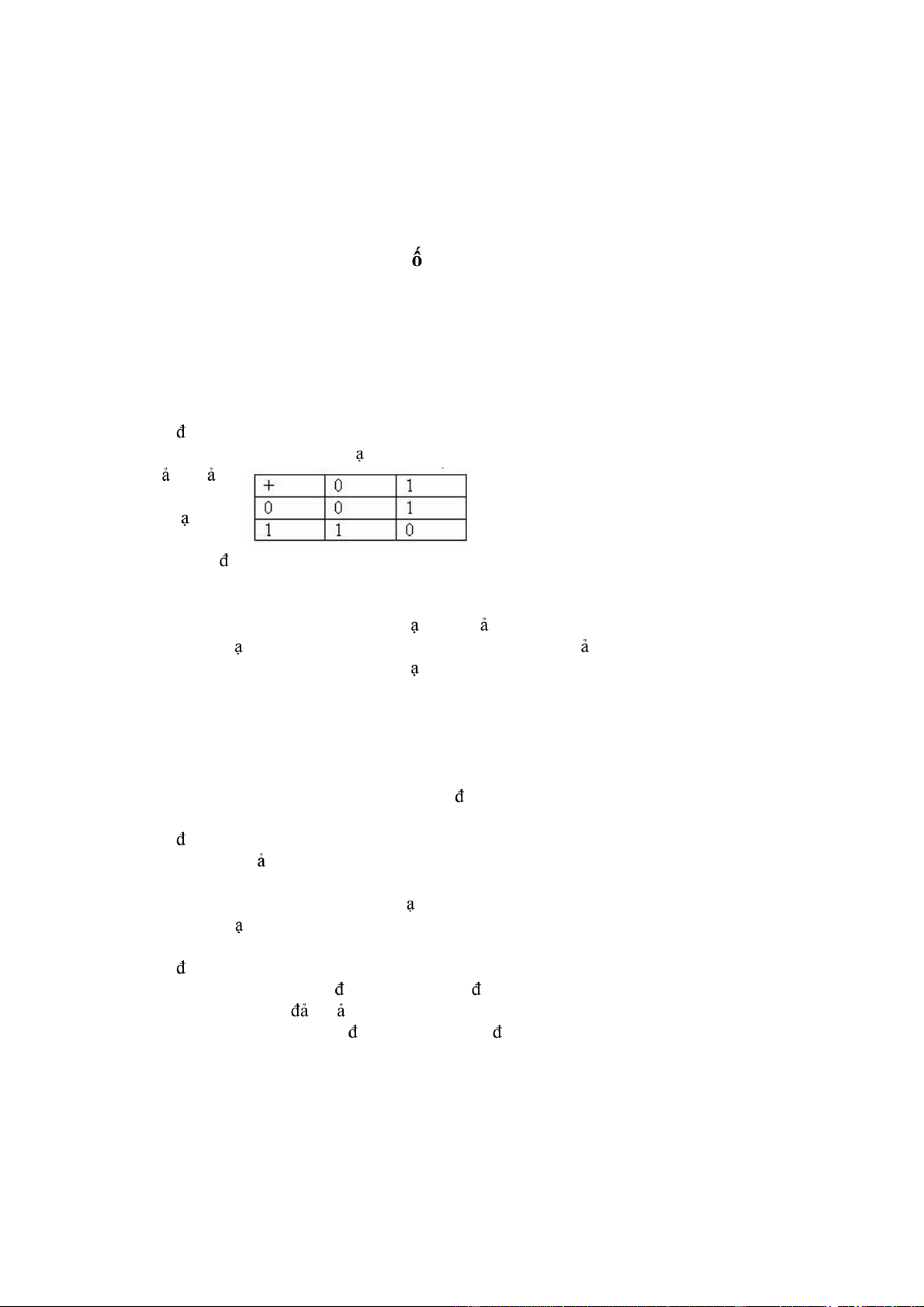
54/ Cho nguồn rời r c chỉ có hai dấu: A ⎜⎝p(a ) ⎟⎠ 1 p(a )2
Nguồn rời r c nhị phân là nguồn A trên tho mãn iều kiện sau ⎧a ⇔ ⇔ 1 "0"
víi x¸c suÊt p(a1) =p ⎨⎩a2 "1" víi x¸c suÊt p(a2) 1= −p
Khi ó nguồn rời r c nhị phân A có thể viết biểu thức nào lOMoARcPSD| 36067889 ⎛ p 1− p⎞ a A =⎜⎝a ⎟⎠ 1 a 2 ⎛ a1 p ⎞ b A =⎜⎝a 21− p⎟⎠ ⎛1 0 ⎞ c A =⎝⎜p 1− p⎟⎠ ⎛a ⎞ 1 a 2 d A =⎜⎝ p 1− p⎟⎠ ⎛a1 a2 ⎞ =⎜ ⎟ 55/ A p
1−p ⎠ là nguồn rời r c nhị phân Tho mãn iều kiện ⎝ ⎧a ⇔ 1 "0" víi x¸c suÊt p(a1) =p ⎩⎨a ⇔ 2 "1" víi x¸c suÊt p(a2) 1= −p Khi ó Entropy H (A) 1
ược tính bằng công thức nào sau ây a
−plogp − −(1 p)−log 1( − p) b
plogp− −(1 p log 1) ( −p) ; c p 1( −p log 1) ( −p)− plog ;
d −plogp− −(1 p log 1) ( − p) H A/b 56/
( )l là lượng thông tin tổn hao trung bình của mỗi tin ở ầu phát khi ầu thu ã thu ược bj H A/b( )=−∑ ) ) l
s p a /b( i l logp a( i bl ; H(B/a )i i 1=
là lượng thông tin riêng trung bình chứa trong mỗi tin ở ầu thu khi ầu phát ã phát i một tin
ai ược tính theo công thức t =− H(B/a ) ∑ i p(bj /a )logpi (bj /a )i j 1=
Trong trường hợp kênh bị ứt (bị nhiễu tuyệt ối) ta có biểu thức nào dưới ây là sai : a H A b( )= j H A( )+ H(B) lOMoARcPSD| 36067889 b H B a( )= i H B( ); c H B A()= H B( ) ) d H A b( = j H A( )=H A B() H A/b 57/
( )l là lượng thông tin tổn hao trung bình của mỗi tin ở ầu phát khi ầu thu ã thu ược bj s H(B/a ) H A/b( )=−∑ ) ) l p a /b( i l logp a( ibl ;
i là lượng thông tin riêng trung bình chứa i 1=
trong mỗi tin ở ầu thu khi ầu phát
ã phát i một tin ƶ ược tính theo công thức: t =− H(B/a ) ∑ i p(bj /a )logpi (bj /a )i j 1=
Trong trường hợp kênh không nhiễu biểu thức nào dưới ây là úng : a H A b H A b ( )= ( )= k H(A/A) = 0 ; b k H(B/A) = 0 c H A b H A b ( )= ( )= k H(B/B) = 0; d k H(A/B) = 0 ; H A/b 58/ (
)l là lượng thông tin tổn hao trung bình của mỗi tin ở ầu phát khi ầu thu ã thu ược s b )=−∑ ) ) H(B/a ) j . H A/b( l p a /b( i l logp a( ibl ;
i là lượng thông tin riêng trung bình chứa i 1=
trong mỗi tin ở ầu thu khi ầu phát ã phát i một tin ai ược tính theo công thức sau: t =− H(B/a ) ∑ i p(bj /a )logpi (bj /a )i j 1=
Trong trường hợp bị nhiễu tuyệt ối, A và B là ộc lập nhau suy ra :
p(a /bi j) = p(a )i ; p(b /aj i) = p(b )j ⇒ p(a bi j) =p(a )p(b )i j , khi ó ta có biểu thức nào sau ây là úng: ( ) s t a H A/b =−∑ j p a( )i logp a( )i và H B/a( i )=−∑p b( )j logp b( )j )=−∑ i 1= j 1= t b H B/a( i p b( )j logp a( )j lOMoARcPSD| 36067889 j 1= () c H A/b =−∑ )=−∑t j
s p a( )i logp b( )i vàH B/a(i p b( )j logp a( )j =−∑ i 1= j 1= s d H A/bj p ( ) a( )i logp b( )i i 1= H A B
59/ Entropy có iều kiện về 1 trường tin A khi ã rõ trường tin B là
(), ược xác ịnh theo công thức sau: s t ) )
H A B()=−∑∑p a b( ij logp a( i bj i 1 j 1= =
Trong trường hợp bị nhiễu tuyệt ối, A và B là ộc lập nhau, suy ra :
p(a /bi j) = p(a )i ; p(b /aj i) = p(b )j ⇒ p(a bi j) =p(a )p(b )i
j , khi ó biểu thức nào sau ây là úng: s t a H A B()=−∑∑p a b( ) ) i j logp a b( i j i 1 j 1= = t s b H A
B()=∑ ∑p b( )j p a( )i logp a( )i j 1= i 1= ) ) c
H A B( )=−∑∑st p a /b( ij logp a( i bj i 1 j 1= = t s d H A B()=−∑ ∑p b( )j p a( )i logp a( )i j 1= i 1= H B A
60/ Entropy có iều kiện về 1 trường tin B khi ã rõ trường tin A là
(), ược xác ịnh theo H s t công thức sau: B/A( )=−∑∑p b a( ) ) j i logp b( j ai i 1 j 1= = lOMoARcPSD| 36067889
Trong trường hợp bị nhiễu tuyệt ối, A và B là ộc lập nhau, suy ra : p(a /bi ⇒
j) = p(a )i ; p(b /aj i) = p(b )j p(a bi j) =p(a )p(b )i j
Khi ó biểu thức nào sau ây là úng ( ) ( ) a H B/A( )=−∑ ∑s p a( ) t i p b j logp b j ; i 1= j 1= ( ) b H B/A( )=−∑ ∑t p b s j p a( )i logp a( )i ; j 1= i 1= s t c H B/A( )=−∑∑p a b( ) ) i j logp a b( i j ; i 1 j 1= = s t d H B/A( )=−∑∑p a /b( ) ) i j logp a( i bj i 1 j 1= = H A B
61/ Entropy có iều kiện về 1 trường tin A khi ã rõ trường tin B là
(), ược xác ịnh theo H A s t công thức sau: B( )=−∑∑p a b( ) ) i j logp a( i bj i 1 j 1= =
Trong trường hợp bị nhiễu tuyệt ối, A và B là ộc lập nhau, suy ra :
p(a /bi j) = p(a )i ; p(b /aj i) = p(b )j ⇒ p(a bi j) =p(a )p(b )i
j , khi ó biểu thức nào sau ây là úng: t s a H A B()=−∑ ∑p b( ) = j p a( )i logp a( )i H(A) j 1= i 1= s t H A B()=−∑∑p a b( ) )= i j logp a b( i j H(A) b i 1 j 1= = ; ) ) c H A B( )=−∑∑s t p a /b( = i j logp a( i bj H(A) lOMoARcPSD| 36067889 i 1 j 1= = d H A B()=∑ ∑t p b( ) s = j p a( )i logp a( )i H(A) j 1= i 1= H B A
62/ Entropy có iều kiện về 1 trường tin B khi ã rõ trường tin A là
(), ược xác ịnh theo công thức sau: s t ) )
H B/A()=−∑∑p b a( ji logp b( j ai i 1 j 1= =
Trong trường hợp bị nhiễu tuyệt ối, A và B là ộc lập nhau, suy ra :
p(a /bi j) = p(a )i ; p(b /aj i) = p(b )j ⇒ p(a bi j) =p(a )p(b )i
j , khi ó biểu thức nào sau ây là úng: s t a H B/A( )=−∑∑p a /b( ) )= i j logp a( i bj H(B) i 1 j 1= = t s b H B/A( )=−∑ ∑p b( ) = j p a( )i logp a( )i H(B) j 1= i 1= ( ) ( ) c H B/A( )=−∑ ∑s p a( ) t = i p b j logp b j H(B) i 1= j 1= ) ) d H B/A( )=−∑∑s t p a b( = i j logp a b( i j H(B) i 1 j 1= = H A B
63/ Entropy có iều kiện về 1 trường tin A khi ã rõ trường tin B là
(), ược xác ịnh theo công thức sau: ) ) H A B( )=−∑∑ =
st p a b( ij logp a( i bj với p(a /b )ij p(a b )i j i 1 j 1= =p(b )j lOMoARcPSD| 36067889 H A B
Từ công thức này có thể khai triển
()thành công thức nào sau ây: s t ) ) a p a b( i j logp b( i a j s t ) ) b p a /b( i j logp a ,b( i j ∑ ( ) () ⎡ ∑ ⎤ t s c p(b ) ⎢− ⎥ j
p a /bi j logp aibj ; j 1= ⎣ i 1=⎦ s t ) ) d p a /b( i j logp a( i bj ;
64/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) : Δ I(A,B) = M ⎡⎣I(a ,b ) ) ) ij ⎤⎦ với I a ,b( = ij
log p a(p a( )i ibj Xác suất ể có thông tin I(a ,b )i j là p(a bi j)
Do ó có thể viết I(A,B))
bằng công thức nào sau ây: s t ) a p a b( i j log ; ( ) ) s t p a( i bj log b p a bi j p a( )i ; ( ) ) s t p a( i bj log c p a /bi j p a( )i ; lOMoARcPSD| 36067889 ( ∑∑ ( ) ( )) s t p a i bj
d p a bi j log i 1 j 1= = p a bi j
65/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) ược viết thành : ( ) ) s t p a( i bj I A,Bp a bi j log
p a( )i Khi ó có thể khai triển I(A,B) thành s t ) ) I(A,B)= p a b( ⎡⎣ − ⎤⎦ ij logp a( i bj logp a( )i a Sai b Ěúng s t pa b
66/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) ược ( i j) (IA,B = p ∑∑ (ab log i j ) ) viết thành : () pa
Khi ó có thể khai triển I(A,B) thành i 1 j 1= = i ) ) )logp a I(A,B)= p a b( ( ij logp a( i bj p a b( i j )i i 1 j 1= = i 1 j 1= = a Ěúng b Sai
67/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) ược viết thành : ( )=∑∑ )log p a( ) st p a b( ij
p a( )i ibj Khi ó có thể khai triển I(A,B) thành I A,B i 1 j 1= = s t )⎡ ) ⎤ I(A,B)= p a b( − p b( ) ij ⎣logp a( i bj i ⎦ a Sai b Ěúng lOMoARcPSD| 36067889
68/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) ược viết thành : ∑∑ I A,B( )= p a b b st ( )log p a( j ) i j p a( )i i
Trong các biểu thức khai triển I(A,B) dưới ây, biểu thức i 1 j 1= = nào sai s t a I(A,B) = − p a b( i )⎡ − )⎤ j
⎣logp a( )i logp a( i bj ⎦ ; ) s t b I(A,B) = p a b( i j ⎣⎡logp a( i b )+ logp b( ) j i ⎦⎤; c I(A,B) = ) p a b( i j logp a( i bj ) p a b( )logp a( ) i j i ; i 1 j 1= = i 1 j 1= = s t d I(A,B) = ⎤ p a b( ) )−logp a( ) i j ⎣⎡logp a( i bj i ⎦ ;
69/ Lượng thông tin chéo trung bình (ký hiệu là I(A,B)) ược viết thành : ) ) I A,B()=∑∑i 1 j 1= =s t p a b( i j log p a(p a( )i ibj H A B
Entropy có iều kiện về 1 trường tin A khi ã rõ trường tin B là
(), ược xác ịnh theo công thức sau: ) )
H A B( )=−∑∑st p a b( ij logp a( i bj i 1 j 1= =
Khi ó trong các kết qu tính I(A,B), kết qu nào sai a
I(A,B) = H(A) - H(A/B) ; b
I(A,B) = H(A)+ H(A/B) ; c I(A,B) = H(A) + H(B) - H(AB); d I(A,B) = H(B) - H(B/A); lOMoARcPSD| 36067889
70/ Xét 2 trường sự kiện A và B sau : A =⎧⎨p a( )ai i ⎫⎬⎭ i =1,s ;B =⎧⎪⎪⎩⎨ ( ) p b bj j ⎪⎫⎪⎭⎬ j=1,t ⎩
Khi ó, trường sự kiện ồng thời C = A.B Nếu A và B là ộc lập thì C có thể viết thành biểu thức nào dưới ây: a C =⎪⎨⎪⎩p a( )a /b i i /p b( )j ⎫⎪⎬ j ⎪⎭ ; ⎧ =⎧⎪⎨⎪⎩p a( )a ++ i i p bb( ) ⎫⎪⎬ j j ⎪⎭ b C ⎧ a ⎫⎪ i bj c
C =⎨⎩p(a ) p(b ) ⎬⎪⎭ j ; i d C ( ) =⎧⎪⎨⎪⎩p a( )a b ⎫⎪⎬ i i p bj j ⎪⎭ ; ( )
71/ Xét 2 trường sự kiện A và B sau : A =⎧⎨p a( )a ⎫ ⎪⎫⎬
i i ⎭⎬ i =1,s ;B =⎧⎪⎨⎪⎩p b bj j ⎪⎭ j=1,t ⎩
Trường sự kiện ồng thời C = A.B có entropy H(C) ược tính bằng công thức nào dưới ây: s t a H C( )=∑∑p a b( ) ) i j logp a b( i j i 1 j 1= = ) ) b H C( )=−∑∑s t p a b( i j logp a b( i j i 0 j 0= = ) ) c
H C( )=−∑∑s 1 t 1− − p a b( i j logp a b( i j ; lOMoARcPSD| 36067889 i 1 j 1= = ) ) d H C( )=−∑∑s t p a b( i j logp a b( i j ; i 1 j 1= = 72/ Chọn câu sai : a
Xác suất xuất hiện càng lớn, “lượng tin “ thu ược càng lớn b
Một tin x có xác suất xuất hiện là p(x), nếu p(x) càng nhỏ thì “lượng tin” khi nhận ược tin này cǜng sẽ càng lớn c
Nếu p(x) càng lớn thì 1/p(x) càng nhỏ d
Một tin x có xác suất xuất hiện là p(x), nếu p(x) càng lớn thì “lượng tin” khi nhận ược tin này cǜng sẽ càng nhỏ
73/ Chọn câu sai sau :
a Xác suất xuất p(x) càng lớn thì “lượng tin” khi nhận ược tin này cǜng sẽ càng lớn b Xác suất xuất
hiện của một tin tỉ lệ nghịch với ộ bất ngờ khi nhận ược một tin c Xác suất xuất p(x) càng lớn thì
“lượng tin” khi nhận ược tin này cǜng sẽ càng nhỏ d “Lượng tin” của một tin tỷ lệ thuận với số kh
nĕng của một tin và tỷ lệ nghịch với xác suất xuất hiện của tin ó x x y
74/ Lượng tin có iều kiện hậu nghiệm về K ( thông tin riêng về K sau khi có ) ược ịnh nghƿa là (I xk / y
) Chọn câu sai trong các câu sau :
l ) =−log p x( k / yl a
Xác suất P x( k / yl ) =1chỉ x y ra khi kênh truyền không có nhiễu b
Khi P x( k / yl ) →1 thì (I xk / yl ) →−1và ngược l i c
Xác suất P x( k / yl ) =1/ 2 → (I xk / yl ) =1bít , d
Khi P x( k / yl ) →1
thì (I xk / yl ) → 0 và ngược l i x y p(x
75/ Lượng thông tin về K khi ã rõ tin là I x( k k , yl ) = log / y )
l p x( ) Chọn câu sai sau : k x a p x(
K ược truyền nguyên vẹn
k / yl ) =1tức là là lượng tin của 1 b
Nếu p x( k / yl ) = 0suy ra I x( k , yl ) = log p(xk ) 1 c
Nếu p x( k / yl ) =1suy ra I x( k , yl ) = log p(xk ) y x d Nếu p x( K
k / yl ) =1, có nghƿa là khi
ã nhận ược tin thì chắc chắn ã phát x x y
76/ Lượng thông tin hậu nghiệm về K ( thông tin riêng về K sau khi cã ) ược viết là : lOMoARcPSD| 36067889 1 x 1 I x(
. Lượng thông tin riêng về K k / yl ) = log
là I x( k ) = log
p(xk / yl ) p(xk ) x y
Lượng thông tin chéo về K 1 1
do mang l i là : I x( − k , yl ) = log
log p(xk ) p x( k / yl ) Tìm câu sai sau : a
Lượng thông tin riêng bằng tổng lượng thông tin chéo và lượng thông tin hậu nghiệm b
Lượng thông tin riêng có thể âm c Tổng lượng thông tin chéo và lượng
thông tin hậu nghiệm bằng lượng thông tin riêng d Lượng thông tin riêng luôn dương
77/ Cho 2 nguồn tin A và B có các xác suất tương ứng là : ⎛⎝ a ⎞ =⎛⎜ ⎞⎟⎠ 1 a2 a3 a4 0b,15 0b,252 0,125b3 0,125b4 A =⎜1/2 1/4 1/8 1/8⎟⎠ ; B ⎝
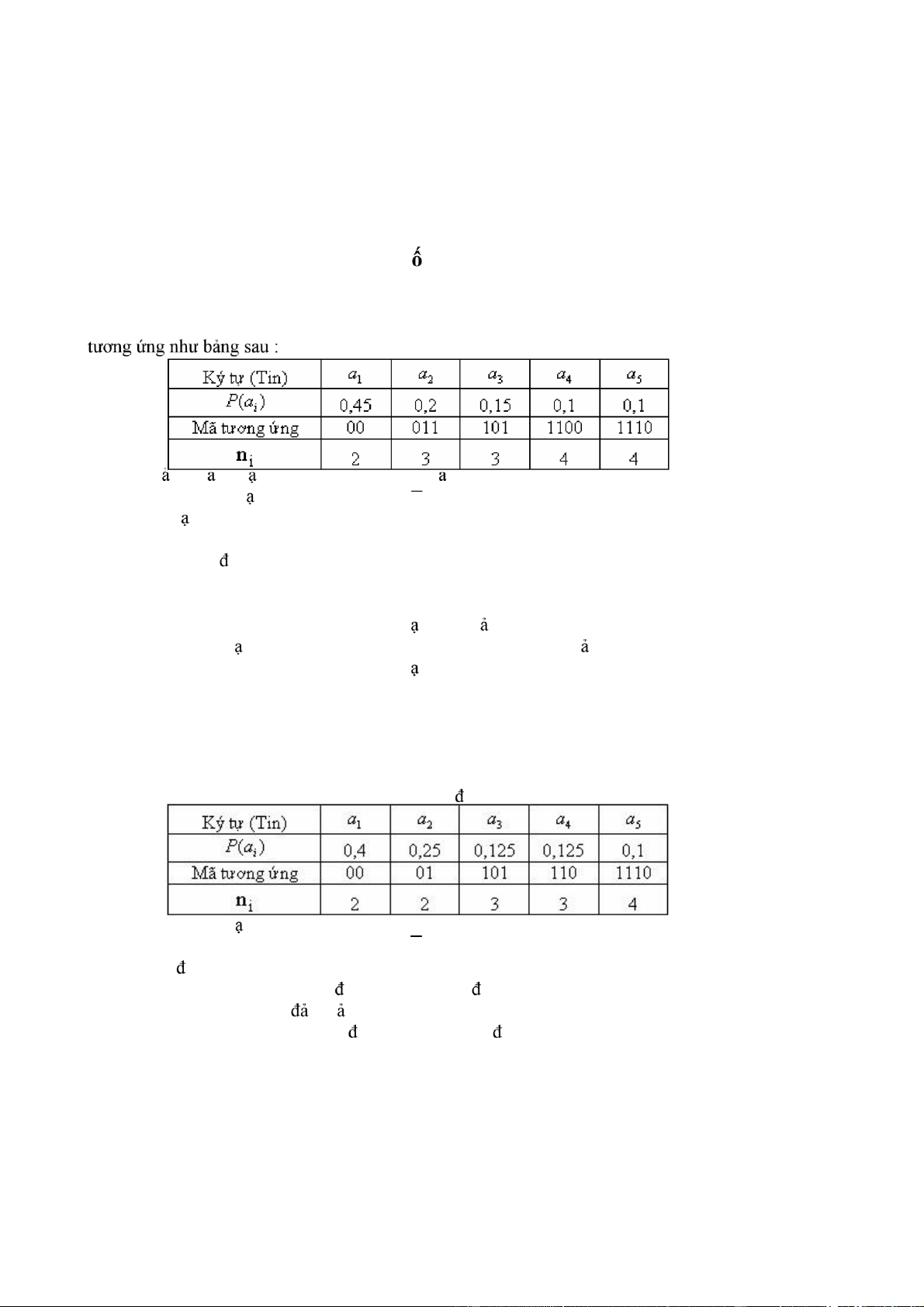
Entropy của nguồn A ( ký hiệu là H(A)), entropy của nguồn B ( ký hiệu là H(B)) có quan hệ theo các hệ thức nào dưới ây a H(A)=H(B); b H(A) > H(B); c H(B)>H(A); d H(A)=2H(B)
78/ Cho nguồn tin A có các xác suất tương ứng là : ⎛ a ⎞ 1 a2 a3 a4 A =⎜⎝1/2 1/4 1/8
1/8⎟⎠ ; Khi ó Entropy của nguồn A ( ký hiệu là H(A)) bằng các i
lượng nào dưới ây a H(A) = 1,85 bít; b H(A) = 1,75 bít ; c H(A) = 1,7 bít; d H(A) = 1,65 bít ;
79/ Cho nguồn tin A có các xác suất tương ứng là : ⎛ a ⎞ 1 a2 a3 a4 a5
A =⎜⎝0.45 0.2 0.15 0.1 0.1⎟⎠;
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a H(A) = 2,75 bít; b H(A) = 2,06 bít; c H(A) = 2,7 bít; d H(A) = 2,85 bít;
80/ Cho nguồn tin A có các xác suất tương ứng là : lOMoARcPSD| 36067889 ⎛ a ⎞ 1 a2 a3 a4 a5 A =⎜0.4 0.25 0.15 0.1 0.1⎟⎠; ⎝
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a
H(A) = 2,85 bít; b H(A) = 2,7 bít; c
H(A) = 2,75 bít; d H(A) = 2,1 bít;
81/ Cho nguồn tin A có các xác suất tương ứng là : ⎛ a a a a a ⎞ A =⎜0.4 ⎟⎠ 1 0.252 0.153 0.154 0.055 ; ⎝
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a
H(A) = 2,85 bít; b H(A) = 2,7 bít; c H(A) = 2,06 bít; d H(A) = 2,07 bít;
82/ Cho nguồn tin A có các xác suất tương ứng là : ⎛ a a a a a ⎞ A =⎜0.4 ⎟⎠ 1 0.252 0.23 0.14 0.055 ; ⎝
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a H(A) = 2,06 bít; b H(A) = 2,85 bít; c H(A) = 2,04 bít; d H(A) = 2,07 bít;
83/ Cho nguồn tin A có các xác suất tương ứng là : ⎛ a ⎞ 1 a 2 a3 a 4 a5
A =⎜⎝0.4 0.3 0.15 0.1 0.05⎟⎠ ;
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các a H(A) = 2,04 bít; b H(A) = 2,07 bít; c H(A) = 2,06 bít; d H(A) = 2,01 bít; i lượng nào dưới ây
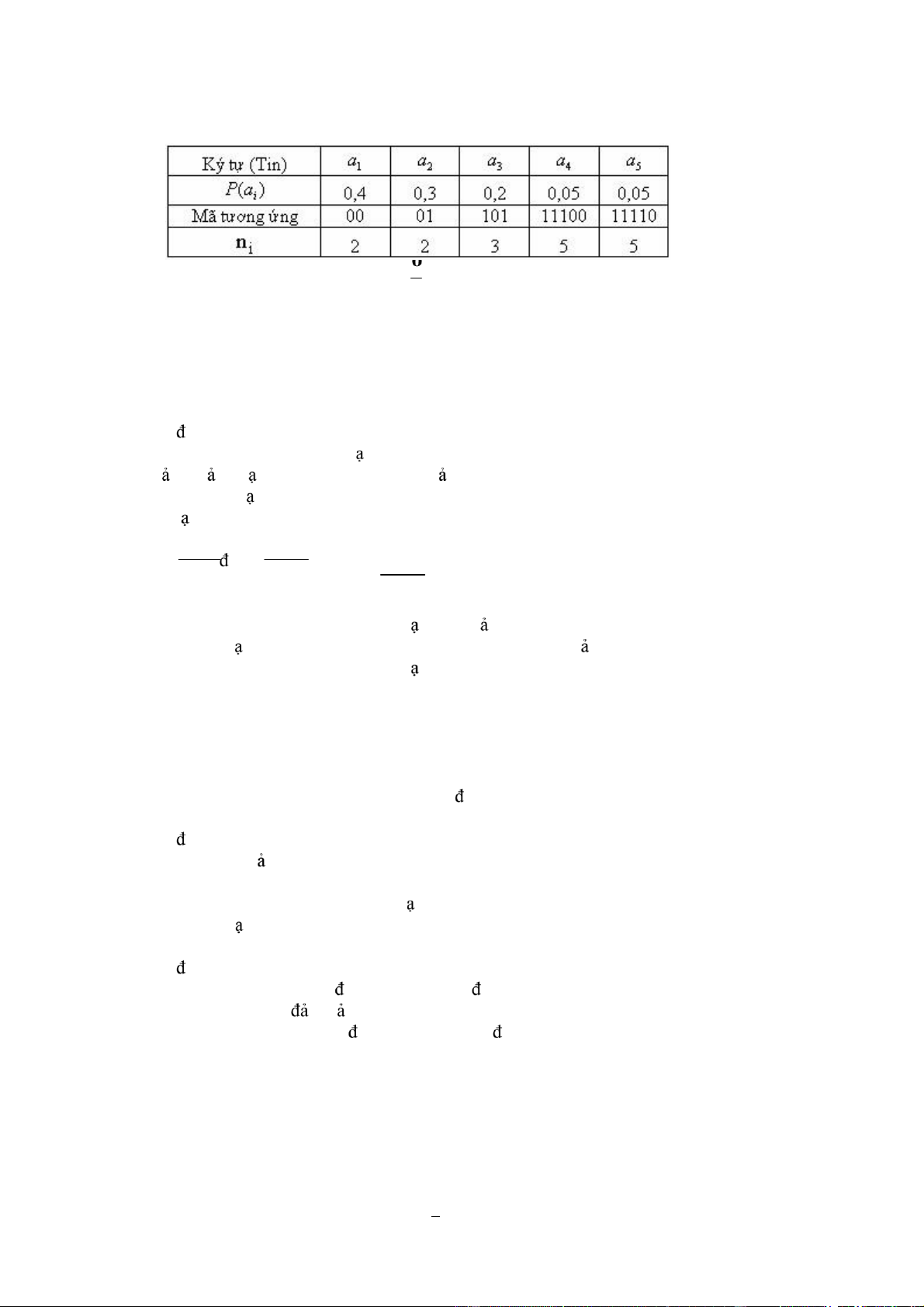
84/ Gi sử nguồn tin lOMoARcPSD| 36067889 A có các xác suất tương ứng là : ⎛ a ⎞ 1 a 2 a3 a 4 a5 A =⎜⎝0.4 0.3 0.2 0.05 0.05⎟⎠;
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a H(A) = 1,95 bít; b H(A) = 2,07 bít; c H(A) = 2,01 bít; d H(A) = 2,04 bít;
85/ Gi sử nguồn tin A có các xác suất tương ứng là : ⎛ a ⎞
1 a 2 a3 a 4 a5 A =⎜⎝0.35 0.35 0.2 0.05 0.05⎟⎠;
Khi ó Entropy của nguồn A (ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a
H(A) = 2,04 bít; b H(A) = 2,01 bít; c H(A) =
2,07 bít; d H(A) = 1,96 bít;
86/ Gi sử nguồn tin A có các xác suất tương ứng là : ⎛ a a a a a ⎞ A =⎜0.35 ⎟⎠ 1 0.32 0.253 0.054 0.055 ; ⎝
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a
H(A) = 2,01 bít; b H(A) = 1,9 bít; c H(A) =
1,98 bít; d H(A) = 2,04 bít;
87/ Gi sử nguồn tin A có các xác suất tương ứng là : ⎛ a a a a a ⎞ A =⎜0.35 ⎟⎠ 1 0.32 0.23 0.14 0.055 ; ⎝
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các i lượng nào dưới ây a H(A) = 2,06 bít; b H(A) = 1,98 bít; c H(A) = 2,01 bít; d H(A) = 1,9 bít;
88/ Gi sử nguồn tin A có các xác suất tương ứng là : lOMoARcPSD| 36067889 ⎛ a ⎞ 1 a 2 a3 a 4 a5
A =⎜⎝0.3 0.3 0.2 0.1 0.1⎟⎠ ;
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) gần bằng các a H(A) = 1,9 bít; b H(A) = 2,06 bít; c H(A) = 2,17 bít; d H(A) = 1,98 bít;
89/ Gi sử nguồn tin A và B có các xác suất tương ứng là : i lượng nào dưới ây ⎛ a ⎞ 1 a 2 a3 a 4 a5 a6 a7 a8 A =⎜⎝1/4 1/8 1/16 1/16 1/4 1/8 1/16 1/16⎟⎠; ⎛ b1 b2 b3 b4 b5 b6 b7 b8 ⎞ =⎜ ⎟ B ⎝0,25 0,125 0,0625 0,0625 0,25 0,125 0,0625 0,0625 ⎠
Entropy của nguồn A ( ký hiệu là H(A)), entropy của nguồn B ( ký hiệu là H(B)) có quan hệ theo các
hệ thức nào dưới ây a H(A) = 2H(B) b H(A)=H(B) ; c H(B)>H(A); d H(A) > H(B);
90/ Gi sử nguồn tin A có các xác suất tương ứng là : ⎛ a ⎞ 1 a 2 a3 a 4 a5 a6 a7 a8 A =⎜⎝1/4 1/8 1/16 1/16 1/4 1/8 1/16 1/16⎟⎠;
Khi ó Entropy của nguồn A ( ký hiệu là H(A)) bằng các i lượng nào dưới ây a H(A) = 2,7 bít; b
H(A) = 2,75 bít; c H(A) = 2,85 bít; d H(A) = 2,80 bít;
91/ Gi sử nguồn tin B có các xác suất tương ứng là : ⎛ b1 b2 b3 b4 b5 b6 b7 b8 ⎞ ⎟⎠ B =⎜⎝0,25 0,125 0,0625 0,0625 0,25 0,125 0,0625 0,0625 ;
Khi ó Entropy của nguồn B ( ký hiệu là H(B)) bằng các i lượng nào dưới ây a
H(B) = 2,80 bít; b H(B) = 2,7 bít; c H(B) = 2,75 bít; d H(B) = 2,85 bít;
92/ Cho một kênh nhị phân như hình bên: p(b 1/a1) = pd a1 b1 p(b1/a2) = ps lOMoARcPSD| 36067889 a2 b2 p(b2/a2) = pd Trong ó:
Phân bố xác suất của tin ở ầu ra p(b )ược tính theo công thức sau : 1 p( ) ( ) ( / ) i=1
Từ công thức này, có thể khai triển p(b ) thành công thức nào dưới ây: 1 a p b( )= ) )+ ) ) 1 p a( 1 .p b( 1a1 p a( 1 .p b( 1a 2 ; b p b( )= ) )+ ) ) )= 1 p a( 2 .p b( 1a1 p a( 2 .p b( 1a 2 ; c p b( 1 p a( ) )+ ) ) 1 .p b( 1a1 p a( 2 .p b( 1a 2 ; d p b( )= ) )− ) ) 1 p a( 2 .p b( 1 a1 p a( 2 .p b( 1 a 2 ;
93/ Cho một kênh nhị phân như hình bên: p(b 1/a1) = pd a1 b1 p(b1/a2) = ps a2 b2 p(b2/a2) = pd Trong ó:
Phân bố xác suất của tin ở ầu ra p(b )ược tính theo công thức sau : 2 p i=1
Từ công thức này, có thể khai triển p(b )thành công thức nào dưới ây: 1 a p b( )= ) )− ) ) 2 p a( 2 .p b( 1a1 p a( 2 .p b( 1a 2 b p b( )= ) )+ ) ) )= 2 p a( 1 .p b( 2a1 p a( 2 .p b( 2a 2 c p b( 2 p a( ) )+ ) ) )= 2 .p b( 2a1 p a( 2 .p b( 2a 2 d p b( 2 p a( 2 ).p b( )+ ) ) 1a1 p a( 2 .p b( 1a 2
94/ Cho kênh ối xứng nhị phân như hình bên: p(b 1/a1) = pd a1 b1 lOMoARcPSD| 36067889 p(b1/a2) = ps a2 b2 p(b2/a2) = pd Biết :
p(a1 )= p ; p(a2 )= −1 p p(b a )= 12 p b a( )= = − 21 ps 1 pd p(b /a ) = p(b /a ) = p 1 1 2 2 d H B A( )=−∑∑22 p a( ) ) ) i p b( j ai logp b( j ai i 1= =j 1
Khai triển H(B/A) theo p và p sẽ ược kết qu nào dưới ây d s a H B A()=⎡⎣p logp + −( d s 1 pd )log 1( − p )⎤⎦ + s
b H B A()=−⎡⎣p logps s −(1 p ) )⎤⎦ s log 1( − ps ; c H B A()=−⎡⎣p logp + −( ) )⎤⎦ d s 1 pd log 1( − ps d H B A()=⎡⎣p logp + −( ) )⎤⎦ s s 1 ps log 1( − ps ;
95/ Cho kênh ối xứng nhị phân như hình bên: p(b 1/a1) = pd a1 b1 p(b1/a2) = ps a2 b2 p(b2/a2) = pd Biết lOMoARcPSD| 36067889
p(a1 )= p ; p(a2 )= −1 p p(b a )= 12 p b a( )= = − 21 ps 1 pd p(b /a ) = p(b /a ) = p 1 1 2 2 d H B A()=−⎡⎣p logp + −( ) )⎤⎦ s s 1ps log 1( − ps = ⎡
Từ ó truyền tín hiệu cho kênh v = 1 ( )= 1 k 1 T và C' T maxI A,BA T max H BA ⎣ ( )−H B A( )⎦⎤ C' Khi ó
C'max ược tính theo biểu thức nào dưới ây C ' ( ) ( ) a C = − + − 'max 1 p logps s 1 ps log 1− ps C ' ( ) ( ) b C = + − − 'max 1 p logps s 1 ps log 1− ps C ' ( ) ( ) c C = + + − 'max 1 p logps s 1 ps log 1− ps C ' ( ) ( ) d C = + + − 'max 1 p logpd d 1 pd log 1− pd lOMoARcPSD| 36067889
CHƠNG 4: CƠ SỞ LÝ THUYẾT MÃ
1/ Chọn câu úng về mã hóa a
Mã hóa là phép biến ổi mọi d ng tín hiệu thành tín hiệu liên tục b
Mã hóa là ánh x che dấu thông tin c
Mã hóa là một ánh x 1- 1 từ tập các a α a →α tin rời r c n n
i lên tập các từ mã i i ; f : i i i d
Mã hóa là phép biến ổi d ng số nhị phân
thành d ng tín hiệu ban ầu
2/ Chọn câu úng về mã : a Mã là một tập các từ mã ược lập
nên một cách ngẫu nhiên b Mã là quá trình phục hồi tin tức c
Mã là ánh x che dấu thông tin d
Mã (hay bộ mã) là s n phẩm của phép mã hóa
3/ Chọn câu úng về mã : a Mã là quá trình phục hồi tin tức b
Mã là một tập các từ mã ược lập nên theo một luật ã ịnh c Mã (hay
bộ mã) là s n phẩm của phép biến ổi tín hiệu rời r c d Mã (hay
bộ mã) là s n phẩm của phép biến ổi tín hiệu liên tục n a
4/ Ěộ dài từ mã i là số các dấu mã cần thiết dùng ể mã hóa cho tin i Chọn câu úng về ộ dài từ mã a n n Ěộ dài từ mã =
i là một số phức b Nếu i
const với mọi i thì mọi từ mã ều có cùng ộ dài Bộ
mã tương ứng ược gọi là bộ mã ều n n c
Ěộ dài từ m· i càng lớn thì phép mã hóa càng tối ưu d Ěộ dài từ mã i
là một số nguyên có thể âm hoặc dương n a
5/ Ěộ dài từ mã i là số các dấu mã cần thiết dùng ể mã hóa cho tin i Chọn câu sai n
về ộ dài từ mã a Nếu = i
const với mọi i , khi ó bộ mã tương ứng ược gọi là bộ n n
mã ều b Ěộ dài từ mã =
i là một số nguyên luôn lớn hơn hoặc bằng 1 c Nếu i
const ∀ i có nghƿa là tất c các từ mã ều có cùng ộ dài n d
Ěộ dài từ mã i là một số nguyên có thể âm lOMoARcPSD| 36067889 n a
6/ Ěộ dài từ mã i là số các dấu mã cần thiết dùng ể mã hóa cho tin i n
Chọn câu úng về ộ dài từ mã a Nếu ≠ n i j thì bộ mã tương ứng n
ược gọi là bộ mã không ều b Ěộ dài từ mã i càng lớn thì phép mã hóa n
càng tối ưu c Nếu i = 1 thì bộ mã tương ứng ược gọi là bộ mã n không ều d Nếu = i
const ∀ i , có nghƿa là phép mã hóa là tối ưu
7/ Số các dấu mã khác nhau (về giá trị) ược sử dụng trong bộ mã ược gọi là cơ số mã Ta ký hiệu giá trị
này là m Chọn câu sai về các dấu mã m: a
Nếu m = 2 thì bộ mã tương ứng ược gọi là mã nhị phân b
Nếu m = 3 thì bộ mã tương ứng ược gọi là mã tam phân c Nếu m = 0 thì
bộ mã tương ứng ược gọi là mã ều d Nếu m = p thì bộ mã tương ứng ược gọi là mã p phân α = α
8/ Gi sử có từ mã 7 7
i 0 1 1 0 1 0 1 Chọn câu úng nhất về từ mã i a Từ α mã 7 i có ộ dài bằng 4 α b Từ mã 7
i trong bộ mã nhị phân có m=2 ( tức là có 2 dấu mã là 0 và 1) và có ộ dài là 7 c Từ α α mã 7 7
i có 7 dấu mã d Từ mã i có 3 dấu mã α = α
9/ Gi sử có từ mã 7 7
i 0 1 1 0 1 0 1 Chọn câu úng về từ mã i a Từ α m· 7 i có 7 dấu mã α b Từ mã 7
i trong bộ mã nhị phân có m=3, tức là có 3 dấu mã là 0 c α Từ mã 7 i có ộ dài bằng 7 α d Từ mã 7 i có ộ dài bằng 3
10/ Chọn câu úng về ộ dài từ mã a
Ěộ dài trung bình của từ mã n là kǶ vọng của
i lượng ngẫu nhiên ni ược xác ịnh như s sau : n =∑p a( )i ni i 1=
i lượng ngẫu nhiên ni ược xác ịnh như b
Ěộ dài trung bình của từ mã n là kǶ vọng của lOMoARcPSD| 36067889 s sau : n =−∑p a( )i ni i 1= n a c
Ěộ dài từ mã i là số các dấu mã cần thiết dùng ể gi i mã cho tin i n d
Ěộ dài từ mã i là Số các dấu mã khác nhau (về giá trị) ược sử dụng trong gi i mã
11/ Nội dung của ịnh lý mã hoá thứ nhất của Shannon (ối với mã nhị phân) ược phát biểu như sau: “Luôn
luôn có thể xây dựng ược một phép mã hoá các tin rời rạc có hiệu quả mà ộ dài trung bình của từ mã
có thể nhỏ tuǶ ý, nhưng không nhỏ hơn entropie xác ịnh bởi các ặc tính thống kê của nguồn” . Chọn
câu úng về ộ dài từ mã : a
Số từ mã nhỏ nhất b Số từ mã không ổi c Chiều dài trung bình
của các từ mã nhỏ hơn hoặc bằng entropy của nguồn d Chiều dài trung bình
các từ mã nhỏ nhất trong tất c các cách mã hóa
12/ Nội dung của ịnh lý mã hoá thứ nhất của Shannon (ối với mã nhị phân) ược phát biểu như sau:
“Luôn luôn có thể xây dựng ược một phép mã hoá các tin rời r c có hiệu qu mà ộ dài trung bình của từ
mã có thể nhỏ tuǶ ý, nhưng không nhỏ hơn entropie xác ịnh bởi các ặc tính thống kê của nguồn”. Chọn
câu sai về ộ dài từ mã : s =∑p a a
Chiều dài trung bình các từ mã tho mãn hệ thức n ( ) ≥ ( ) i ni H1 A i 1= b
Chiều dài trung bình các từ mã nhỏ nhất trong tất c các cách mã hóa c Chiều
dài trung bình của các từ mã lớn hơn hoặc bằng entropy của nguồn s =−∑p a d
Chiều dài trung bình các từ mã tho mãn hệ thức n ( ) = ( ) i ni H1 A i 0= α
13/ Kho ng cách giữa hai từ mã bất kǶ n
i và αnj là số các dấu mã khác nhau tính theo cùng một vị trí ( )
giữa hai từ mã này, ký hiệu d α α n 7
i , nj Gi sử α =i 0 1 1 0 1 0 1; α =7j 1 0 0 1 1 1 0 α (α )
Kho ng cách giữa 2 từ mã n 7 i và αnj là d i ,α7j bằng các i lượng nào dưới ây a 1; b 6 ; c 12; d 14; lOMoARcPSD| 36067889 α
14/ Kho ng cách giữa hai từ mã bất kǶ n
i và αnj là số các dấu mã khác nhau tính theo cùng một vị trí d(α α )
giữa hai từ mã này, ký hiệu n
i , nj . Tìm biểu thức sai về kho ng cách mã d trong các biểu thức sau: ( ) a n ≥ d α α n i , nj ; ( ) ( ) ( b d α α ≥ n α α ≤ α α n n n ) i , nj 0 c d i , nj d j , i ; ( ) ( d d α α = n α αn n ) i , nj d j , i α
15/ Kho ng cách giữa hai từ mã bất kǶ n
i và αnj là số các dấu mã khác nhau tính theo cùng một vị trí d(α α )
giữa hai từ mã này, ký hiệu n
i , nj Tìm biểu thức sai về kho ng cách mã d trong các biểu thức sau: ( ) ( ) a d α α + n α α ≥n i , nj d j , nk ( ) ( ) d α α n α α ≥ n i , nk ; b d i , nj ( ) ( 0; c d α α ≤ n α i , nj 0 d n ≥ d α n ) i , nj α
16/ Kho ng cách giữa hai từ mã bất kǶ n
i và αnj là số các dấu mã khác nhau tính theo cùng một vị trí (α α )
giữa hai từ mã này, ký hiệu d n
i , nj . Chọn câu úng sau : lOMoARcPSD| 36067889 ( ) a 0 ≤ α α ≤d in , nj 1; b ( ) ( ) ( d α α + n α α =n α i , nj d j , nk d α n n ) (α αn ) i , k c 1≥ d i , nj ; ( ) ( ) d d α α ≥ n α α = n n ≡αn i ,nj 0; d i ,nj 0 khi αi j ; W(α
17/ Trọng số của một từ mã n ) 7 i
là số các dấu mã khác không trong từ mã Ví dụ: α =i 0 1 1 0 ( ( 1 0 1 thì W α = 7 ) α n ) i
4. Chọn câu úng về các tính chất của trọng số W i : ( ) ( ) ( a d α α ≥ n α +α n n α ≤ n ) i , nj w i j b W i 0 c ( ) ( ) ( ) d α α ≤ n α +α n n α α = n i , nj W i j ; d d i , nj ( ) ( W α +α n n α ≤ n ) i j và 0 ≤ W i 1; W(α
18/ Trọng số của một từ mã n ) 7 i
là số các dấu mã khác không trong từ mã Gi sử α =i 0 1 1 0 1 (
0 1, thì trọng số W α 7 ) i bằng số nào dưới ây a 4 ; b 3; c 5 ; d 7 ; α V 19/ Coi mỗi từ mã n
i là một véctơ n chiều trong một không gian tuyến tính n chiều n , khi ó phép
cộng ược thực hiện giữa hai từ mã tương tự như phép cộng giữa hai véctơ tương ứng ược thực hiện
trên trường nhị phân GF(2) Phép cộng theo modulo 2 này ược mô t như sau: lOMoARcPSD| 36067889 Cho α = 7
i 0 1 1 0 1 0 1 ↔ (0, 1, 1, 0, 1, 0, 1)
α =7j 1 0 0 1 1 1 0 ↔ (1, 0, 0, 1, 1, 1, 0) Khi ó α =α +α7 7 7 k i
j bằng giá trị nào dưới ây a (0 1, 1, 1, 0, 1, 1); b
(1 1, 1, 1, 0, 1, 1); c (1 1, 1, 1, 1, 1, 1); d (1 1, 1, 1, 0, 1, 0); α V 20/ Coi mỗi từ mã n
i là một véctơ n chiều trong một không gian tuyến tính n chiều n , khi ó phép
cộng ược thực hiện giữa hai từ mã tương tự như phép cộng giữa hai véctơ tương ứng ược thực hiện
trên trường nhị phân GF(2) Phép cộng theo modulo 2 này ược mô t như sau:
Cho α =8i 1 1 1 0 1 0 1 0 ↔ (1, 1, 1, 0, 1, 0, 1, 0) α =8j 1 0
0 1 1 1 0 1 ↔ (1, 0, 0, 1, 1, 1, 0, 1) Khi ó α =α +α8 8 8 k i
j bằng giá trị nào dưới ây a (1 1, 1, 1, 0, 1, 1, 1 ); b (1 1, 1, 1, 0, 1, 0,1); c (0 1, 1, 1, 0, 1, 1, 1 ); d (1 1, 1, 1, 0, 1, 1, 1 );
21/ Chọn câu úng về mã tuyến tính a
Mã tuyến tính là mã mà từ mã của nó có các
dấu mã là phi tuyến b
Mã tuyến tính ộ dài n là mã mà từ mã của nó có các dấu mã
là các d ng tuyến tính c
Mã tuyến tính là mã mà từ mã của nó vừa có các dấu mã là
phi tuyến vừa ngẫu nhiên d Mã tuyến tính ộ dài n là mã mà từ mã của nó có các dấu mã là các d ng ngẫu nhiên
22/ Chọn câu úng về mã hệ thống tuyến tính : a
Mã hệ thống tuyến tính (n,k) là mã tuyến tính ộ dài n trong ó ta có thể chỉ ra ược vị trí của k-1 dấu thông tin trong từ mã b
Mã hệ thống tuyến tính (n,k) là mã tuyến tính ộ dài n trong ó ta có thể chỉ ra ược vị trí của k dấu thông tin trong từ mã c
Mã hệ thống tuyến tính (n,k) là mã tuyến tính ộ dài n trong ó ta có thể chỉ ra ược vị trí của n-k dấu thông tin trong từ mã d
Mã hệ thống tuyến tính (n,k) là mã tuyến tính ộ dài n trong ó ta có thể chỉ ra ược vị trí của r= n - k
dấu thông tin trong từ mã
23/ Chọn câu úng về mã tuyến tính ngẫu nhiên : lOMoARcPSD| 36067889 a
Mã tuyến tính ngẫu nhiên là mã tuyến tính có các dấu mã ược chọn ngẫu nhiên từ phép ánh x trong không gian phi tuyến b
Mã tuyến tính ngẫu nhiên là mã tuyến tính có các dấu mã ược chọn ngẫu nhiên từ các d ng tuyến tính có thể có c
Mã tuyến tính ngẫu nhiên là mã tuyến tính có phép ánh x phi tuyến ngẫu nhiên d
Mã tuyến tính ngẫu nhiên là mã ngẫu nhiên có các dấu mã ược chọn tuyến tính từ các d ng tuyến tính có thể có G
24/ Ěể mô t mã tuyến tính, có thể sử dụng ma trận sinh k,n Trong i số tuyến tính ta biết rằng với mỗi G H k,n sẽ tồn t i ma trận
r n× thỏa mãn: G.HT = 0 Chọn câu úng sau : a
H ược gọi là ma trận kiểm tra của mã tuyến tính (n,k) và H chứa r véc tơ
hàng trực giao với các véc tơ hàng của G G b
k,n là ma trận kiểm tra n hàng, r cột c H ược gọi là ma trận sinh của mã G tuyến tính (n,k) d
k,n không nhất thiết là ma trận sinh
25/ Gi sử sau khi thực hiện mã hóa, tin ai ược mã hóa thành 1001, khi ó ộ dài từ mã ni của tin này là : a 4; b 1; c 2; d 5;
26/ Sau khi thực hiện mã hóa nguồn rời r c A ( có entropy là H(A)=1,5 ) có thể tính ược ộ dài
trung bình n Với mỗi cách mã hóa khác nhau sẽ tính ược n khác nhau Trong các kết qu mã hóa, giá trị
n nào dưới ây ược gọi là tối ưu: n a =1,45; n n b =1,51; c =1,35; n d =1,81;
27/ Sau khi thực hiện mã hóa nguồn rời r c A ( có entropy là H(A)=1,4 ) có thể tính ược ộ dài
trung bình n Với mỗi cách mã hóa khác nhau sẽ tính ược n khác nhau Trong các kết qu mã hóa, giá trị n n
n nào dưới ây ược gọi là tối ưu nhất: a =1,51; b =1,45; c n =1,55; n d =1,75;
28/ Sau khi thực hiện mã hóa nguồn rời r c A (có entropy là H(A)=1,9) có thể tính ược ộ dài trung n
bình Với mỗi cách mã hóa khác nhau sẽ tính ược n khác nhau Trong các kết qu mã hóa, giá trị
n nào dưới ây ược gọi là tối ưu nhất: lOMoARcPSD| 36067889 n a =1,975; n b =1,91; n c =1,905; n d =1,95;
29/ Sau khi thực hiện mã hóa nguồn rời r c A ( có entropy là H(A)=1,905 ) có thể tính ược ộ dài n
trung bình Với mỗi cách mã hóa khác nhau sẽ tính ược n khác nhau Trong các kết qu mã hóa, giá trị
n nào dưới ây ược gọi là tối ưu nhất: n a =1,906; n b =1,907; n c =1,91; n d =1,95;
30/ Sau khi thực hiện mã hóa nguồn rời r c A (có entropy là H(A)=2,01 bít), có thể tính ược ộ dài n
trung bình Với mỗi cách mã hóa khác nhau sẽ tính ược n khác nhau Trong các kết qu mã hóa, giá trị
n nào dưới ây ược gọi là tối ưu: n a =2,07; n b =2,11; n c =2,09; n d =202;
31/ Cho mã Cyclic C(n, k) = C(7,4) có a thức sinh là g(x) thì a g(x) có bậc 4 ; b
g(x) là một ước của x7 4+ + 1 c g(x) có bậc 5 ; d
Từ g(x) có thể xác ịnh ược ma
trận sinh hệ thống G và ma trận kiểm tra H cho bộ mã
32/ Cho mã Cyclic C(n, k) = C(7,4), có a thức sinh g(x) là a g x( ) = + +1 x x4; b g x( ) = + +1 x
x2 + x4 c g x( ) = +1 x2 + x3; d
g x( ) = +1x2 + x3 + x4
33/ Cho mã Cyclic C(n, k) = C(7,4), có a thức sinh g(x) là
a g x( ) = + +1 x x2 + x3; b
g x( ) = + +1 x x3; c g x( )
= +1 x2 + x4 d g x( ) = +1 x3 + x4 lOMoARcPSD| 36067889
34/ Cho mã Cyclic C(n, k) = C(7,3) , tìm câu sai về g(x) a
g(x) không là ước của x7 + 1 ; b Từ g(x) có thể xác ịnh ược ma trận sinh hệ thống
G và ma trận kiểm tra H cho bộ mã c g(x) có bậc 4 ; d
g(x) là một ước của x7 + 1 ;
35/ Cho mã Cyclic C(n, k) = C(7,3), có a thức sinh g(x) là
a g x( ) = + +1 x x +
4 b g x( ) = + +1 x x2
x4 ; c g x( ) = +1 x + + + 2 x3
x5 d g x( ) = +1 x2 x3;
36/ Cho mã Cyclic C(n, k) = C(7,3), có a thức sinh g(x) là a
g x( ) = + +1 x
x5 b g x( ) = +1 x + + 2 x3
x5 c g x( ) = + +1 x x4; d g x( ) = + +1 x x + 2 x4 ;
37/ Phát biểu sau úng hay sai : Cho mã Cyclic C(n, k) = C(7,3) , g(x) là a thức bậc 4 a Sai b Ěúng
38/ Cho mã tuyến tính (7,4) Số ô nhớ cần thiết ể nhớ bộ mã là a 7; b 28; c 4; d 112;
39/ Cho mã Xyclic (7,4) Số các ô nhớ cần thiết ể nhớ bộ mã là a 7; b 112 c 28; d 8
40/ Cho mã tuyến tính (7,3) Số ô nhớ cần thiết ể nhớ bộ mã là a 7; b 21; c 3; d 56;
41/ Cho mã Xyclic (7,3) Số các ô nhớ cần thiết ể nhớ bộ mã là a 3 b 56 c 21; d 7;
42/ Cho mã tuyến tính (n,k) Số ô nhớ cần thiết ể nhớ bộ mã là a n.2k lOMoARcPSD| 36067889 b kn; c n+k; d n;
43/ Cho mã Xyclic (n,k) Số các ô nhớ cần thiết ể nhớ bộ mã là a kn; b n+k; c n.2k d n7;
44/ Chọn câu úng sau: x x x a
Các d ng tuyến tính của k biến ộc lập 1, 2, , k là các biểu thức có d ng: k f (x )=∑ ∈ 1, , xk
a xi i Trong ó: ai F, F là một trường i 1= x x x b
Các d ng tuyến tính của k biến ộc lập 1, 2, , k là các biểu thức có d ng: k f (x )=∑ ∈ 1, , xk
(a +xi i) Trong ã: ai F, F là một trường i 1= x x x c
Các d ng tuyến tính của k biến ộc lập 1, 2, , k là các biểu thức có d ng: k f (x )=∑ ∈ 1, , xk
a - xi i Trong ã: ai F, F là một trường i 1= x x x d
Các d ng tuyến tính của k biến ộc lập 1, 2, , k là các biểu thức có d ng: k f x ( )=∑ − ∈ 1, , xk ai
xi Trong ó: ai F, F là một trường i 1=
45/ Chọn câu sai về mã tuyến tính : a
2k các vétơ khác nhau là tất c các tổ hợp tuyến
tính có thể có của k véctơ hàng này G.H = 0 Trong ó:r = −n k H b
Trong i số tuyến tính ta biết rằng với mỗi G sẽ tồn t i ma trận r n× thỏa mãn: c H
Trong i số tuyến tính ta biết rằng với mỗi G sẽ tồn t i ma trận r n× thỏa mãn: d Ěể mô lOMoARcPSD| 36067889 G
t mã tuyến tính, có thể sử dụng ma trận sinh k,n , ma trận này chứa k véctơ hàng ộc lập V
tuyến tính t o nên không gian mã −(n,k) G.HT = 0 Trong ó :r = −n k G
46/ Ěể mô t mã tuyến tính, có thể sử dụng ma trận sinh k,n Trong i số tuyến tính ta biết rằng với mỗi G H k,n sẽ tồn t i ma trận
r n× thỏa mãn: G.HT = 0 Chọn câu sai sau : G a
k,n là ma trận k hàng, n cột b
HT ược gọi là ma trận k hàng, n cột ; c H
r n× là ma trận r hàng, n cột ; d
HT ược gọi là ma trận chuyển vị của H
47/ Khi xây dựng một mã tuyến tính (n,k,d )
0 người ta ph i tìm ược các mã có ộ thừa nhỏ nhưng l i có
kh nĕng khống chế sai lớn. Người ta thường xây dựng mã này dựa trên các bài toán tối ưu Tìm câu sai trong các câu dưới ây: d a
Với k và 0 xác ịnh, ta ph i tìm ược mã có ộ dài với từ mã là lớn nhấtTương ứng với bài toán này ta có giới h n n = k d b
Với n và k xác ịnh, ta ph i tìm ược mã có kho ng cách 0 là lớn nhất Tương ứng với bài ≥
toán này ta có giới h n Plotkin sau: n k 1i 0∑=− ⎡⎢⎢d20 ⎤⎥⎥ i d c
Với k và 0 xác ịnh, ta ph i tìm ược mã có ộ dài với từ mã là nhỏ nhấtTương ứng với bài n.2k 1− d ≤
toán này ta có giới h n Griesmer sau: − 0 2k 1 d
Với n và số sai khi sửa t xác ịnh, ta ph i tìm ược mã có số dấu thông tin k là lớn nhất (hay số dấu
thừaƶ là nhỏ nhất)Tương ứng với bài toán này ta có giới h n Hamming t sau:2n k− ≥∑Cin i 0=
48/ Chọn ịnh nghƿa sai về mã xyclic trong các ịnh nghƿa sau a Mã xyclic (n,
k) là Ideal I = g X( ) của vành a thức Z [x] 2 Xn +1 b
Mã xyclic (n, k) là một bộ mã mà a thức sinh có bậc r = n+k c
Mã xyclic là một bộ mã tuyến tính lOMoARcPSD| 36067889 a X a X
d Mã xyclic là một bộ mã , mà nếu
( ) là một từ mã thì dịch vòng của ( ) cǜng là một từ mã thuộc bộ mã này
49/ Chọn câu úng của ịnh lý về kh nĕng sửa sai a Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách +1⎤ Hamming d = ⎥⎦ 0
4 có kh nĕng sửa ược t sai tho mãn iều kiện: t ≤⎡⎢⎣d02 b
Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d > 0
1 có kh nĕng phát hiện t sai
tho mãn iều kiện t ≤ −d0 1 c
Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d ≥ 0
3 có kh nĕng sửa ược t sai tho ≤
mãn iều kiện: t ⎡⎢⎣d02−1⎤⎥⎦ và có kh nĕng phát hiện t sai tho mãn iều kiện t ≤ −d0 1 d
Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d ≥ 0
1 có kh nĕng sửa ược t sai tho −1⎤
mãn iều kiện: t ≤⎡⎢⎣d02 ⎥⎦ =
50/ Từ ịnh lý mã hoá thứ 1 của Shannon ối với mã nhị phân ta có : n ∑s p a( ) ≥ ( ) i ni H1 A i=1
Từ biểu thức trên tìm câu úng nhất trong các biểu thức sau : s a n =∑p a( )i logp a( )i ; i 1= s s ∑ =∑ b p a( )i ni p a( )i logp a( )i ; i 1= i 1= s s ∑ ≥−∑ c p a( )i ni p a( )i logp a( )i ; i 1= i 1= d p a( ) =− ) ) i ni p a( i logp a( i 51/ Theo ịnh lý mã hoá thứ 1 của Shannon ối với mã nhị phân ta có: s s n =∑p a( ) ≥ ( ) i ni H1 A =−∑p a( )i logp a( )i i 1= i 1= lOMoARcPSD| 36067889 p a
Từ biểu thức này suy ra ộ dài từ mã n ( ) i và xác suất i liên hệ với nhau: ni log (*)
Từ (*) tìm câu úng sau về nguyên tắc lập mã tiết kiệm: a Các từ mã có ộ dài lớn
sẽ ược dùng ể mã hóa cho các tin có xác suất lớn b Các từ mã có ộ dài n tỷ lệ thuận với xác suất P c
Các tin có xác suất xuất hiện lớn ược mã hóa bằng các từ mã có ộ dài nhỏ và ngược l i các tin có
xác suất xuất hiện nhỏ ược mã hóa bằng các từ mã có ộ dài lớn d
Các từ mã có ộ dài nhỏ sẽ ược dùng ể mã hóa cho các tin có xác suất nhỏ
52/ Cho nguồn tin X ={x x x x x }
1, 2, 3, 4, 5 với các xác suất lần lượt là {1/2, 1/4, 1/8, 1/16, 1/16}
Biết x1 ược mã hóa thành 0, x2 ược mã hóa thành 10, x3 ược mã hóa thành 110, x4 ược mã hóa thành
1110, x5 ược mã hóa thành 1111 Bộ mã tối ưu cho nguồn trên có chiều dài trung bình tính theo công thức : n p xi ni là : a 1,88 b 1,90 c 1,875 d 1,925
53/ Yêu cầu của phép mã hóa: những từ mã có ộ dài nhỏ hơn không trùng với phần ầu của từ mã có ộ
dài lớn hơn Các tin có xác suất xuất hiện lớn hơn ược mã hóa bằng các từ mã có ộ dài nhỏ và ngược l i.
Cho nguồn tin X ={x x x x x
}với các xác suất lần lượt là {1/2, 1/4, 1/8, 1/16, 1/16} 1, 2, 3, 4, 5
Biết x1ược mã hóa thành 0, x2 ược mã hóa thành 10 Chọn câu úng dưới ây ể mã hóa cho x3 a 101 b 011 c 110 d 100
54/ Yêu cầu của phép mã hóa: những từ mã có ộ dài nhỏ hơn không trùng với phần ầu của từ mã có ộ
dài lớn hơn Các tin có xác suất xuất hiện lớn hơn ược mã hóa bằng các từ mã có ộ dài nhỏ và ngược l
i.Cho nguồn tin X ={x x x x x
}với các xác suất lần lượt là {1/2, 1/4, 1/8, 1/16, 1/16} 1, 2, 3, 4, 5
Biết x1 ược mã hóa thành 0, x2 ược mã hóa thành 11, x3 ược mã hóa thành 100 Chọn
câu úng dưới ây ể mã hóa cho x4 a 000 b 110 c 001 d 1010
55/ Yêu cầu của phép mã hóa: những từ mã có ộ dài nhỏ hơn không trùng với phần ầu của từ mã có ộ
dài lớn hơn Các tin có xác suất xuất hiện lớn hơn ược mã hóa bằng các từ mã có ộ dài nhỏ và ngược l i
Cho nguồn tin X ={x x x x x
}với các xác suất lần lượt là {1/2, 1/4, 1/8, 1/16, 1/16} 1, 2, 3, 4, 5
Biết x1 ược mã hóa thành 0, x2 ược mã hóa thành 10, x3 ược mã hóa thành 110, x4 ược mã hóa thành
1110. Chọn câu úng dưới ây ể mã hóa cho x5 a
1010 b 1111 c 101 d 110
56/ Cho mã Cyclic C(7, 4) có a thức sinh là g x( ) =1+ +x x3 và a thức sinh G sau : lOMoARcPSD| 36067889 ⎛ 1 + +x x3 ⎞ ⎟ G = ⎜⎜⎜xx ++ ++ 2 xx32 xx54 ⎟⎟ ⎜⎜⎝x + + ⎟⎟⎠ 3 x4 x6
Ma trận nào sau ây là một ma trận sinh G ứng với mã Cyclic C(7,4) trên ⎡1101000⎤ a ⎢⎢0110100⎥⎥ ⎢0011010⎥ ⎢ ⎥ ⎣0001101⎦ ⎡1010100⎤ b ⎢0101100⎥⎥ ⎢ ⎢0010110⎥ ⎢ ⎥ ⎣0001011⎦ ⎡1000100⎤ c ⎢0100000⎥⎥ ⎢ ⎢0011001⎥ ⎢ ⎥ ⎣0001011⎦ ⎡1010100⎤ d ⎢⎢0101010⎥⎥ ⎢0010101⎥ ⎢ ⎥ ⎣0001101⎦
57/ Cho mã Cyclic C(7, 4) có a thức sinh là g x( ) =1+ x2 + x3 và a thức sinh G sau ⎛ 1 +x + ⎞ 2 x3 G=⎜⎜xx ++ 2 xx34 ++ ⎟ xx ⎟⎟ ⎜ 54 lOMoARcPSD| 36067889 ⎜⎜⎝x + + ⎟⎟⎠ 3 x5 x6
Ma trận nào sau ây là một ma trận sinh G ứng với mã Cyclic C(7,4) trên ⎡1010100⎤ a ⎢⎢0101010⎥⎥ ⎢0010101⎥ ⎢ ⎥ ⎣0001101⎦ ⎡1011000⎤ b ⎢0101100⎥⎥ ⎢ ⎢0010110⎥ ⎢ ⎥ ⎣0001011⎦ ⎡1010100⎤ c ⎢0101100⎥⎥ ⎢ ⎢0010110⎥ ⎢ ⎥ ⎣0001011⎦ ⎡1000100⎤ d ⎢0100000⎥⎥ ⎢ ⎢0011001⎥ ⎢ ⎥ ⎣0001011⎦
58/ Cho mã Cyclic C(7, 4) có a thức sinh là : g x( ) =1+ +x x3 và ma trận sinh G. Từ ma trận sinh G
tính ược ma trận kiểm tra H bên: ⎛ 1 +x x x2 + +3 4⎞ ⎜ = 3 4 + 5⎟⎟ H ⎜ x x x x+ + ⎜⎝ ⎟ x x x x + + + 2 4 5 6 ⎠
Chuyển ma trận kiểm tra H sang d ng không gian tuyến tính. Ma trận nào sau ây là một ma trận kiểm
tra H ( d ng không gian tuyến tính) lOMoARcPSD| 36067889 ⎡1011100⎤ ⎢ ⎥ a ⎢0101110 ⎥ ⎢⎣0010111⎥⎦ ⎡1010100⎤ ⎢ ⎥ b ⎢0101010 ⎥ ⎢⎣0010101⎥⎦ ⎡1000100⎤ c ⎢ ⎥ ⎢0100000 ⎥ ⎢⎣0011001⎥⎦ ⎡1010100⎤ ⎢ ⎥ d ⎢0101100 ⎥ ⎢⎣0010110⎥⎦
59/ Cho mã Cyclic C(7, 4) có a thức sinh là : g x( ) =1+ x2 + x3 và ma trận sinh G Từ ma trận sinh G
tính ược ma trận kiểm tra H bên : ⎛ 1 + +x x x2 + 4⎞ ⎟ H=⎜⎜ x x x x+ + + 2 3 5 ⎟ ⎜⎝x x ⎟ x x + + + 2 3 4 6 ⎠
Chuyển ma trận kiểm tra H sang d ng không gian tuyến tính. Ma trận nào sau ây là một ma trận kiểm
tra H ( d ng không gian tuyến tính) ⎡1110100⎤ ⎢ ⎥ a ⎢0111010 ⎥ ⎢⎣0011101⎥⎦ ⎡1010100⎤ ⎢ ⎥ b ⎢0101010 ⎥ ⎢⎣0010101⎥⎦ ⎡1010100⎤ c ⎢ ⎥ ⎢0101100 ⎥ ⎢⎣0010110⎥⎦ ⎡1000100⎤ ⎢ ⎥ d ⎢0100000 ⎥ ⎢⎣0011001⎥⎦ lOMoARcPSD| 36067889 a f a 60/ Tin rời r c ∈ (x) i A; RA: Từ mã i
tương ứng với i Thuật toán xây dựng từ mã xyclic gồm theo a
4 bước: M,N,P,Q ược sắp xếp ngẫu nhiên M: Mô t tin i trong tập tin cần mã hóa (gồm 2k tin) bằng một a thức a (X) (X)≤ i với deg ai k −1 N: Chia a ( ) ( ) i
X .xn k− cho a thức sinh g(X) ể tìm phần dư r Xi P: Nâng bậc a (
i X) bằng cách nhân nó với xn k−
Q : Xây dựng từ mã xyclic: f ( ( ( ) i x)= ai X .x) n k− + r Xi
Chọn các sắp xếp thứ tự úng thuật toán xây dựng từ mã xyclic: a
M-P-N-Q ; b P-Q-M-N; c M-N-P-Q; d Q-M-N-P;
61/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A. Ta có kết qu mã hoá sau : ⎧A1 A4 A5 A2 A3 ⎫ ⎨
⎬ Gi i mã cho dãy bít nhận ược có d ng 11100011010111100 sẽ ược
⎩00 10 110 1111 1110⎭ kết qu nào sau ây:
a A3-A1-A5-A4-A2-A2; b
A3-A1-A5-A4-A2-A1; c A3- A1-A5-A4-A2-A2; d A3-A2-A5-A4-A2-A1;
62/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A
⎧A1 A4 A5 A2 A3 ⎫
Ta có kết qu mã hoá sau :⎨
⎬ Gi i mã cho dãy bít nhận ược có d ng ⎩00 10 110 1111 1110⎭
11110011010111100 sẽ ược. kết qu nào sau ây: a A3-A1-A5-A4-A2-A2; b A3-A2-A5-A4-A2-A1; c A3-A1-A5-A4-A2-A1; d A2-A1-A5-A4-A2-A1;
63/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A
⎧A1 A4 A5 A2 A3 ⎫
Ta có kết qu mã hoá sau :⎨
⎬ Gi i mã cho dãy bít nhận ược có d ng ⎩00 10 110 1111 1110⎭
1111001101011110010 sẽ ược kết qu nào sau ây:
a A2-A1-A5-A4-A2-A1-A3;
b A3-A1-A5-A4-A2-A2; c A2- A1-A5-A4-A2-A1-A4 d A3-A1-A5-A4-A2-A1; lOMoARcPSD| 36067889
64/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A
⎧A1 A4 A5 A2 A3 ⎫
Ta có kết qu mã hoá sau :⎨
⎬ Gi i mã cho dãy bít nhận ược có d ng ⎩00 10 110 1111 1110⎭
11110011010111100110 sẽ ược kết qu nào sau ây: a A2-A1-A5-A4-A2-A1-A4 b
A2-A1-A5-A4-A2-A1-A5; c A3-A1-A5-A4-A2-A1; d A2-A1-A5-A4-A2-A1-A3;
65/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A
⎧A1 A4 A5 A2 A3 ⎫
Ta có kết qu mã hoá sau :⎨
⎬ Gi i mã cho dãy bít nhận ược có d ng ⎩00 10 110 1111 1110⎭
1111001101011110011000 sẽ ược kết qu nào sau ây: a A2-A1-A5-A4-A2-A1-A4 b
A2-A1-A5-A4-A2-A1-A5-A1 c A2-A1-A5-A4-A2-A1-A3; d A3-A1-A5-A4-A2-A1;
66/ Gi sử sau khi thực hiện mã hóa, các tin a ) ược mã hóa thành các
i với xác suất tương ứng P a( i mã
nhị phân có ộ dài mã ni tương ứng như b ng sau: 5 =
Tính ộ dài mã trung bình theo biểu thức n ∑ n p a ( ) i
i ta ược giá trị nào : i 1= a 4; b
3; c 2,1; d 1,2;
67/ Gi sử sau khi thực hiện mã hóa, các tin a
) ược mã hóa thành các mã
i với xác suất tương ứng P a( i
nhị phân có ộ dài mã ni tương ứng như b ng sau: 5 lOMoARcPSD| 36067889 =
Tính ộ dài mã trung bình theo biểu thức n ∑ n p a ( ) i i ta ược giá trí nào: i 1= a 1,8; b 4; c 2,4; d 3;
68/ Gi sử sau khi thực hiện mã hóa, các tin a
) ược mã hóa thành các mã
i với xác suất tương ứng P a( i
nhị phân có ộ dài mã ni 5 =
Tính ộ dài mã trung bình theo biểu thức n ∑ n p a ( ) i
i ta ược giá trí nào : i 1= a 1,8; b 2,1; c 4; d 2,75;
69/ Gi sử sau khi thực hiện mã hóa, các tin a
) ược mã hóa thành các mã
i với xác suất tương ứng P a( i
nhị phân có ộ dài mã ni tương ứng như b ng sau : 5 =
Tính ộ dài mã trung bình theo biểu thứ ∑ n p a c n ( ) i
i ta ược giá trí nào : i 1= a 2,1 dấu mã; b 1,8 dấu mã ; c 2,75 dấu mã; d 2,45 dấu mã; lOMoARcPSD| 36067889
70/ Gi sử sau khi thực hiện mã hóa, các tin a
) ược mã hóa thành các mã
i với xác suất tương ứng P a( i
nhị phân có ộ dài mã ni tương ứng như b ng sau : 5 =
Tính ộ dài mã trung bình theo biểu thức n ∑ n p a ( ) i
i ta ược giá trí nào : i 1= a 2,5; b 2,45; c 1,8; d 2,75;
71/ Một dãy tin X ={x x } ∈
1, 2,...,xn với xi
X i; =1→ n Lượng tin I(X) chứa trong dãy tin X sẽ là: 1 1 1 I X( ) = log +log +....+log
Gi sử cho nguồn X ={x x x x x1, 2, 3, 4, 5}với các xác P x( 1) P x( 2) P x( n )
suất lần lượt là {1/2, 1/4, 1/8, 1/16, 1/16}. Lượng tin I(X) chứa trong dãy x x x x x x x
tin X={x1 2 1 1 3 4 1 1 5 x } là: a 17 bít ; b 15 bít; c 18 bít; d 16 bít;
72/ Khi xây dựng một mã tuyến tính (n,k,d )
0 người ta ph i tìm ược các mã có ộ thừa nhỏ nhưng l i có
kh nĕng khống chế sai lớn Người ta thường xây dựng mã này dựa trên các bài toán tối ưu Tìm câu sai trong các câu dưới ây: d a
Với k và 0 xác ịnh, ta ph i tìm ược mã có ộ dài với từ mã là lớn nhất. Tương ứng với bài toán này ta có giới h n n = k d b
Với k và 0 xác ịnh, ta ph i tìm ược mã có ộ dài với từ mã là nhỏ nhất. Tương ứng với bài toán này
ta có giới h n Griesmer sau:
n ≥ k 1∑=− ⎡⎢⎢d20i ⎤⎥⎥ lOMoARcPSD| 36067889 i 0 c
Với n và số sai khi sửa t xác ịnh, ta ph i tìm ược mã có số dấu thông tin k là lớn nhất (hay số dấu
thừa ƶ là nhỏ nhất) Tương ứng n.2k 1− d0 ≤ 2k −1 d d
Với n và k xác ịnh, ta ph i tìm ược mã có kho ng cách 0 là lớn nhất Tương ứng với bài toán này ta có giới h n Plotkin sau: với bài toán này ta có giới h n Hamming sau: t 2n k− ≥∑Cin i = 0
73/ Chọn câu úng của ịnh lý về kh nĕng phát hiện sai sau a
Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d = 0
1 có kh nĕng phát hiện t sai tho mãn iều kiện t ≤ d + 0 1 b
Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d > 0
1 có kh nĕng phát hiện t sai tho
mãn iều kiện t ≤ d0 và có c
Mã ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d > 0
1 có kh nĕng phát hiện t sai tho ≤⎡⎢ mãn iều kiện t ≤ −d ⎣d0 0
1 kh nĕng sửa ược t sai tho mãn iều kiện:t 2−1⎤⎦⎥ d Mã
ều nhị phân có ộ thừa (D > 0) với kho ng cách Hamming d ≥ 0
3 có kh nĕng phát hiện ược t sai tho ≤⎡ −1⎤ mãn iều kiện: t ⎢⎣d02 ⎥⎦
74/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫ ⎧ a1 a2 a3 a4 a5 ⎫ A =⎨ ⎬ ⎨=
⎬ sẽ ược kết qu nào sau ây:
⎩p a( i )⎭ ⎩1/2 1/4 1/8 1/16 1/16⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 11 110 1110 1111⎭ lOMoARcPSD| 36067889 ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬ ⎩0 10 110 1110 1111⎭
75/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫ ⎧ a1 a2 a3 a4 a5 ⎫ A =⎨ ⎬ ⎨=
⎬sẽ ược kết qu nào sau ây:
⎩p a( i )⎭ ⎩1/16 1/16 1/8 1/4 1/ 2⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 10 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 111 1110 1111⎭ lOMoARcPSD| 36067889 ⎫ ⎧ a1 a2 a3 a4 a5 d ⎨ ⎬ ⎩1111 1110 110 10 0 ⎭
76/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫ sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/4 1/2 1/8 1/16 1/16⎭ ⎧a1 a2 a3 a4 ⎫ a5 a ⎨ ⎬ ⎩10 0 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 111 1110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬; ⎩0 10 110 1110 1111⎭
77/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/8 1/4 1/ 2 1/16 1/16⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 10 110 1110 1111⎭ ⎧ a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩110 10 0 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬; ⎩0 01 11 111 1111⎭ lOMoARcPSD| 36067889 a a ⎫
78/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/16 1/4 1/8 1/ 2 1/16⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 10 110 1110 1111⎭ ⎧ a1 a2 a3 a4 ⎫ a5 b ⎨ ⎬ ⎩1110 10 110 0 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬; ⎩0 11 110 1110 1111⎭
79/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau : A =⎨ ⎬ ⎨ ⎧⎩p a(a ⎬⎫⎭ i sẽ ược kết qu nào
i )⎫⎭=⎧⎩1a/2 1/4 1/16 1/8 1/1 a2 a3 a4 a165 sau ây: ⎧a1 a2 3 a4 5 a ⎨ ⎬; ⎩0 10 1110 110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ b ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬ ⎩0 10 111 1110 1111⎭
80/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫sẽ ược kết qu nào sau ây: lOMoARcPSD| 36067889 a a ⎫ A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/2 1/8 1/ 4 1/16 1/16⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 10 110 1110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ b ⎨ ⎬; ⎩0 11 01 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬ ⎩0 11 110 1110 1111⎭
81/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/ 2 1/16 1/8 1/4 1/16⎭
⎧a1 a2 a3 a4 a5 ⎫ a ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 1110 110 10 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬; ⎩0 10 110 1110 1111⎭
82/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/2 1/4 1/16 1/16 1/8⎭ lOMoARcPSD| 36067889 a a ⎫ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬ ⎩0 10 1111 1110 110⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬; ⎩0 10 110 1110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a1 a2 3 a4 5 d ⎨ ⎬; ⎩0 11 110 1110 1111⎭
83/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎬⎫sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/16 1/4 1/8 1/16 1/ 2⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 10 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬; ⎩0 11 110 1110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧ a1 a2 a3 a4 ⎫ a5 d ⎨ ⎬ ⎩1111 10 110 1110 0 ⎭
84/ Gi sử sau khi thực hiện mã hóa Shannon - Fano nguồn rời r c A : ⎧ a ⎫=⎧ ⎬⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩1/2 1/4 1/8 1/16 1/16⎭ ⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩0 10 110 1110 1111⎭ lOMoARcPSD| 36067889 a a ⎫
ược tính theo biểu thức H A logp a n p a ( )p a( ) ( ) i ni và i
i sẽ có kết qu nào sau ây : n a =H(A)=2,875; n n b =H(A)=1,875; c =1,875 và H(A)=1,95; n d =1,95 và H(A)=1,875
85/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.5 0.25 0.125 0.0625 0.0625⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a1 a2 a3 a4 a5 ⎫ d ⎨ ⎬; ⎩0 11 110 1110 1111⎭
86/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau : lOMoARcPSD| 36067889 a a ⎧ ai ⎫=⎧ 1 a2 3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.25 0.5 0.125 0.0625 0.0625⎭ ⎧a1 a2 a3 a4 a5 ⎫ a ⎨ ⎬; ⎩0 11 110 1110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ b ⎨ ⎬; ⎩10 0 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬ ⎩0 10 111 1110 1111⎭
87/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.125 0.25 0.5 0.0625 0.0625⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬ ⎩0 10 110 1110 1111⎭ ⎧ a1 a2 a3 a4 ⎫ a5 b ⎨ ⎬ ⎩110 10 0 1110 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬ ⎩0 10 111 1110 1111⎭
88/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.0625 0.25 0.125 0.5 0.0625⎭ lOMoARcPSD| 36067889 a ⎧ a1 a2 a3 a4 ⎫ a5 a ⎨ ⎬ ⎩1110 10 110 0 1111⎭
⎧a1 a2 a3 a4 a5 ⎫ b ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬ ⎩0 10 110 1110 1111⎭
89/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5⎬⎫ sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.0625 0.25 0.125 0.0625 0 ⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 110 1110 1111⎭ ⎧ a1 a2 a3 a4 5⎫ c ⎨ ⎬ ⎩1111 10 110 1110 0 ⎭
⎧a1 a2 a3 a4 a5 ⎫ d ⎨ ⎬; ⎩0 01 11 111 1111⎭
90/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.5 0.125 0.25 0.0625 0.0625⎭
⎧a1 a2 a3 a4 a5 ⎫ a ⎨ ⎬; ⎩0 01 11 111 1111⎭ lOMoARcPSD| 36067889 a ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a1 a2 a3 a4 a5 ⎫ c ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a1 a2 a3 a4 ⎫ a5 d ⎨ ⎬ ⎩0 110 10 1110 1111⎭
91/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.5 0.0625 0.125 0.25 0.0625⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬; ⎩0 11 110 1110 1111⎭ ⎧a1 a2 a3 a4 ⎫ a5 b ⎨ ⎬ ⎩1 00 010 0111 0101⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a1 a2 a3 a4 ⎫ a5 d ⎨ ⎬ ⎩0 1110 110 10 1111⎭
92/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.5 0.0625 0.125 0.0625 0.25⎭ ⎧a ⎫ 1 a2 a3 a4 a5 a ⎨ ⎬ ⎩0 10 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 111 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 lOMoARcPSD| 36067889 a c ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬; ⎩0 1111 110 1110 10⎭
93/ Thực hiện mã hóa Shannon - Fano nguồn rời r c A sau :
⎧ ai ⎫=⎧ a1 a2 a3 a4
a5 ⎫⎬sẽ ược kết qu nào sau ây: A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.5 0.25 0.0625 0.125 0.0625⎭
⎧a1 a2 a3 a4 a5 ⎫ a ⎨ ⎬; ⎩0 01 11 111 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 b ⎨ ⎬ ⎩0 10 110 1110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 c ⎨ ⎬ ⎩0 10 1110 110 1111⎭ ⎧a ⎫ 1 a2 a3 a4 a5 d ⎨ ⎬; ⎩0 11 110 1110 1111⎭
94/ Gi sử sau khi thực hiện mã hóa Shannon - Fano nguồn rời r c A : ⎧ a ⎫=⎧ ⎫⎬ i
a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨
⎩p a( i )⎭ ⎩0.5 0.25 0.125 0.0625 0.0625⎭ ⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩0 10 110 1111 1110⎭ H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : n n
a =H(A)=1,875; b n =H(A)=2,875; c =1,95 và H(A)=1,875; n d =1,875 và H(A)=1,95; lOMoARcPSD| 36067889 a
95/ Gi sử sau khi thực hiện mã hóa Shannon - Fano nguồn rời r c A : ⎧ a ⎫=⎧ ⎬⎫ i a1 a2 a3 a4 a5 a6 a7 a8 A =⎨ ⎬ ⎨ ⎩ ⎭
p a( i )⎭ ⎩0.25 0.125 0.0625 0.0625 0.25 0.125 0.0625 0.0625
⎧a1 a5 a2 a6 a3 a4 a7 a8 ⎫
Ta có kết qu mã hoá sau :⎨ ⎬
⎩00 01 100 101 1100 1101 1110 1111⎭
Ěộ dài từ mã trung bình n và
entropy H(A) ược tính theo biểu thức n p ai ni và H A
( ) p a( )i logp a( )i sẽ có kết qu nào sau ây : n a =1,875 và H(A)=1,95; n b =1,95 và H(A)=1,875 ; n c =H(A)=1,875; n d =H(A)=2,75;
96/ Gi sử sau khi thực hiện mã hóa Shannon - Fano nguồn rời r c A : ⎧ a ⎫=⎧ ⎬⎫ i a1 a2 a3 a4 a5 a6 a7 a8 A =⎨ ⎬ ⎨ ⎩ ⎭
p a( i )⎭ ⎩1/4 1/8 1/16 1/16 1/4 1/8 1/16 1/16 lOMoARcPSD| 36067889
Ta có kết qu mã hoá sau : ⎧a ⎫ 1 a5 a2 a6 a3 a4 a7 a8 ⎨ ⎬
⎩00 01 100 101 1100 1101 1110 1111⎭
Ěộ dài từ mã trung bình n và
entropy H(A) ược tính theo biểu thức n p ai ni và H A
( ) p a( )i logp a( )i sẽ có kết qu nào sau ây : n a =1,95 và H(A)=1,875 n n ; b =H(A)=2,75; c =H(A)=1,875; n d =1,875 và H(A)=1,95;
97/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬ ⎩ ⎭
p a( i )⎭ ⎩0.5 0.25 0.125 0.0625 0.0625 ⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩0 10 110 1111 11100⎭ H A
ược tính theo biểu thức: n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : n a =H(A)=2,875; n b =H(A)=1,875; n c =1,875 và H(A)=1,95; n d =1,9375 và H(A)=1,875;
98/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬
⎩p a( i )⎭ ⎩1/2 1/4 1/8 1/16 1/16⎭ ⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩0 10 110 1111 11100⎭ lOMoARcPSD| 36067889
Ta có kết qu mã hoá sau : H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : n a =1,875 và H(A)=1,95; n n b =H(A)=1,875; c =1,9375 và n H(A)=1,875; d =H(A)=2,875;
99/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬ ⎩ 16⎭
p a( i )⎭ ⎩1/2 1/4 1/8 1/16 1/ ⎧⎨a ⎫ 1 a4 a5 a2
a3 Ěộ dài từ mã trung bình n và entropy H(A) ⎬ ⎩00 10 110 1111 1110⎭ H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : n a =H(A)=1,75; b
n =2,375 và H(A)=1,875; c n =H(A)=2,875; d n = H(A)=1,85
100/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬ ⎩ 16⎭
p a( i )⎭ ⎩1/2 1/4 1/8 1/16 1/ ⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩0 10 1100 1111 1110⎭ H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau lOMoARcPSD| 36067889
Ta có kết qu mã hoá sau : ây : n n
a =H(A)=1,95; b =1,9375 và H(A)=1,75; n c =2 và H(A)=1,875; n d =1,87 và H(A)=1,87;
101/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬ ⎩ ⎭
p a( i )⎭ ⎩0.5 0.25 0.125 0.0625 0.0625 ⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩0 10 1100 1111 1110⎭ H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : a
n =1,87 và H(A)=2,1 b
n =H(A)=1,975 c n =1,9375 và H(A)=1,275;
d n =2 và H(A)=1,875;
102/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬ ⎩ ⎭
p a( i )⎭ ⎩0.5 0.25 0.125 0.0625 0.0625 ⎧⎨a ⎫ 1 a4 a5 a2
a3 Ěộ dài từ mã trung bình n và entropy H(A) ⎬ ⎩00 10 110 1111 1110⎭ H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : lOMoARcPSD| 36067889
Ta có kết qu mã hoá sau : a
n =2,5 và H(A)=1,85; b
n =1,9375 và H(A)=1,87; c
n =2,375 và H(A)=1,875 ; d n =2 và H(A)=1,9;
103/ Gi sử sau khi thực hiện mã hóa nguồn rời r c A : ⎧ a ⎫ ⎧ ⎫ i a1 a4 a5 a2 a3 A =⎨ ⎬ ⎨= ⎬ ⎩ ⎭
p a( i )⎭ ⎩0.5 0.25 0.125 0.0625 0.0625
⎧a1 a4 a5 a2 a3 ⎫ n và entropy H(A)
Ta có kết qu mã hoá sau :⎨ ⎬ Ěộ dài từ mã trung bình ⎩00 10 1100 1111 1110⎭ H A
ược tính theo biểu thức n p a ( ) p a( ) logp a( ) i ni và i i sẽ có kết qu nào sau ây : n a =2,5 và H(A)=1,875; n b =2,375 và n H(A)=1,975 c =2,55 và H(A)=1,775; n d =2 và H(A)=1,675;
104/ Cho mã Cyclic C(7,4) có
a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =x+x( )
3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống ta ược kết qu nào dưới ây : a 1100101 b 0101010; c 1000110; d 0110111;
105/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =1+x( )
2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống ta ược kết qu nào dưới ây: a 0101010; b 1000110; c 0011010; d 0110111; lOMoARcPSD| 36067889
Ta có kết qu mã hoá sau :
106/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =x+x( )
2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0101010; b 1110010; c 1000110; d 0110111; lOMoARcPSD| 36067889
107/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =1+x( )
3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0101010; b 1000110; c 1110010; d 0111001;
108/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =x +x(
) 2 3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây:
a 0111001; b 1000110; c 1110010; d 0100011;
109/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =1+x
+x( ) 2 3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0100011; b 0111001; c 1110010; d 1001011;
110/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3tương ứng a thức thông tin a x =1+x( )
Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1001011; b 0100011; c 1011100; d 1110010;
111/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =1+x+x(
) 2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1001011; b 0101110; c 1011100; d 1110010;
112/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =x+x( )
2 + x3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây :
a 1011100; b 0101110; lOMoARcPSD| 36067889 c 1001011; d 0010111;
113/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =( ) x3
Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0101110; b 1001011; c 1010001 d 1011100;
114/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =x( ) Sử
dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0010111; b 0110100; c 0101110; d 1011100;
115/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ +x x3 tương ứng a thức thông tin a x =x( ) 2
Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1110010; b 0101110; c 0110100; d 0010111;
116/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =x+x(
) 3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống ta ược kết qu nào dưới ây: a 0101110; b 0110111; c 1000101; d 0101010;
117/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =1+x(
) 2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống ta ược kết qu nào dưới ây: a 0011010; b 1000110; c 0101010; d 0111010;
118/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =x+x( )
2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1110010; lOMoARcPSD| 36067889 b 0110111; c 1000110; d 0010110;
119/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =1+x(
) 3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1101001; b 0101010; c 0111001; d 1000110;
120/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =x +x(
) 2 3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây: a 1010011; b
0111001; c 1000110; d 0100011;
121/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =1+x
+x( ) 2 3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0001011; b 0100011; c 0111001; d 1110010;
122/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3tương ứng a thức thông tin a x =1+x( )
Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1110010; b 1001011; c 0101100; d 0100011;
123/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =1+x+x(
) 2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1001011; b
1001110; c 1110010; d 1011100;
124/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =x+x(
) 2 + x3 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : lOMoARcPSD| 36067889 a 1001011; b 0100111; c 1011100; d 0101110;
125/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =( ) x3
Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1001011; b
0111011 c 1011100; d 0101110;
126/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =x( )
Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 1110100; b 1011100; c 0010111; d 0101110;
127/ Cho mã Cyclic C(7,4) có a thức sinh là g x( ) =1+ x2 + x3 tương ứng a thức thông tin a x =x( )
2 Sử dụng thuật toán 4 bước ể thiết lập từ mã hệ thống, sẽ ược kết qu nào dưới ây : a 0101110; b 0110100; c 1110110; d 0010111; lOMoARcPSD| 36067889
CHƠNG 5 : LÝ THUYẾT THU T I U
1/ Thu tín hiệu khi có nhiễu là một bài toán thống kê: a Ěúng b Sai
2/ Nhiệm vụ của máy thu là ph i chọn lời gi i, do ó máy thu còn ược gọi là sơ ồ gi i Yêu cầu của sơ ồ α β
gi i là ph i tìm lời gi i úng (phát i ta ph i tìm ược i ) Trong thực tế có rất nhiều sơ ồ gi i Trong tất c
các sơ ồ gi i có thể có thì t i một sơ ồ b o m xác suất nhận lớn ph i úng là lớn nhất (xác suất gi i sai là
bé nhất) Sơ ồ này ược gọi là sơ ồ gi i tối ưu. Khi ó người ta gọi “Máy thu xây dựng theo sơ ồ gi i tối ưu
ược gọi là máy thu tối ưu” Kết luận này úng hay sai ? a Sai b Ěúng 3/ λ ( ) )) l/i u > p((αli
Víi ⎨⎩ii =1,m≠ l là quy tắc gi i tối ưu viết dưới d ng hàm hợp lý. Chọn câu p α ⎧ λ
úng trong các câu sau: a Nếu mọi tín hiệu gửi i ều ồng xác suất thì (u)= l/i λ
0 Víi ∀ ≠i l b Nếu mọi tín hiệu gửi i ều ồng xác suất thì (u)> l/i 1 Víi ∀ ≠ λ
i l c Nếu mọi tín hiệu gửi i ều ồng xác suất thì (u)< l/i
1 Víi ∀ ≠i l d λ
Nếu mọi tín hiệu gửi i ều ồng xác suất thì (u)= l/i 1 Víi ∀ ≠i l lOMoARcPSD| 36067889
4/ Ěịnh nghƿa bộ lọc phối hợp tuyến tính thụ ộng :” Ěối với một tín hiệu xác ịnh, một mạch tuyến tính ⎛ ⎟ ⎞
thụ ộng ảm bảo tỷ số ρ =ra ⎜⎝ NS ⎠ ra cực ại ở một thời iểm quan sát nào ấy sẽ ược gọi là
mạch lọc phối hợp tuyến tính thụ ộng của tín hiệu ó Trong ó ρra là tỷ số giữa công suất trung bình của
nhiễu ở ầu ra bộ lọc ấy và công suất ỉnh của tín hiệu” Ěịnh nghƿa này úng hay sai ? a Sai b Ěúng
5/ Quá trình xử lý tín hiệu trong máy thu tối ưu ược gọi là xử lý tối ưu tín hiệu Xử lý ể nhận lời gi i có
xác suất sai bé nhất Chọn câu úng nhất về xử lý tối ưu các tín hiệu: a
Dựa vào các tiêu chuẩn tối ưu, bằng công cụ thống kê toán học người ta xác ịnh ược quy tắc gi i
tối ưu, do ó ngày nay lý thuyết truyền tin ã cho phép bằng toán học tổng hợp ược máy thu tối ưu. b
Việc tổng hợp các máy thu (xây dựng sơ ồ gi i) chỉ cĕn cứ vào các tiêu chuẩn chất lượng mang tính
chất chức nĕng mà không mang tính chất thống kê. c
nh hưởng của nhiễu lên chất lượng của máy thu tối ưu chỉ ược tính theo tỷ số tín/t p d Việc
tổng hợp máy thu tối ưu là dựa vào trực giác, kinh nghiệm, thí nghiệm α p 6/ Gi sử (α )
i là tín hiệu ã gửi i, có xác suất
i - ược gọi là xác suất tiên nghiệm ở máy thu ta nhận u t u t β α ược
( ), từ ( ) qua sơ ồ gi i ta sẽ có lời gi i l nào ó Như vậy l ã ược gửi i với một xác suất p(α /u) l
- ược gọi là xác suất hậu nghiệm. Do ó xác suất gi i sai sẽ là: p sai/u,( β = − ) l 1 p(αl /u) Xét hai sơ ồ gi i: u t β - Từ
( ) cho ta 1 - gọi là sơ ồ (1) u t β - Từ
( ) cho ta 2- gọi là sơ ồ (2) p sai/u, Nếu ( β < ) p sai/u,( β ) 1
2 ta rút ra kết luận sơ ồ (2) tối ưu hơn (1) Khẳng ịnh này úng hay sai ? a Sai b Ěúng )
7/ Tín hiệu tổng quát có d ng: C (t)= (t cos) (ω +φt(t)+ϕ i C0i 0
Chọn câu sai trong các câu sau: C
a Việc xử lý tối ưu tín hiệu không phụ thuộc ường bao (t) ( ) 0i
và tần số tức thời ωi t =ω+ dφ( )t lOMoARcPSD| 36067889 dt dφ t ω =ω+
b Khi xử lý tối ưu tín hiệu ta cần biết ường bao C (t) ( ) ( ) 0i và tần số tức thời i t dt c C ϕ C Nếu việc thu (t) (t) i
cần biết 0 (ể iều chỉnh hệ thống thu) thì ược gọi là thu kết hợp Nếu việc thu i ϕ
không cần biết 0 (ể iều chỉnh hệ thống thu) thì ược gọi là thu không kết hợp ϕ ϕ
d Thực tế khi τ thay ổi sẽ làm cho 0 thay ổi τ chỉ biến thiên ít nhưng cǜng ã làm cho 0 thay ổi rất
m nh Khi ó ta ph i chuyển sang thu không kết hợp.
8/ Cho ầu vào m ch tuyến tính thụ ộng một dao ộng có d ng: y t( )= C ( ) i t + n t( ) Trong ó C ( ) i
t là thể hiện của tín hiệu phát i (còn ược gọi là tín hiệu tới) n t( ) là nhiễu cộng, trắng, chuẩn Bài
toán tổng hợp m ch là tìm biểu thức gi i tích của hàm truyền phức K ( )ω i
của m ch tuyến tính thụ ộng
sao cho ở một thời iểm quan sát (dao ộng nhận ược) nào ó ể ρra t max, áp dụng ∞
công thức biến ổi ngược Fourier tính ược ρ ≤ N1 ( ( )ω ra
0 −∫∞ Siv 2πf )2 df Trong ó Siv là mật ộ phổ
(biên) phức của thể hiện tín hiệu ở ầu vào m ch tuyến tính
Theo ịnh lý Parseval, ta có: ρ = Ei ramax (*) N0 ∞ trong ó E = ∫ ( i
Siv 2πf )2 df là nĕng lượng của tín hiệu tới −∞
Chọn câu sai trong những nhận xét sau : ⎛⎜ S ⎞⎟ a
Từ (*) chứng tỏ tỷ số ρ = ⎝ ra
N ⎠ ra chỉ phụ thuộc vào nĕng lượng của tín hiệu và bài toán phát
hiện d ng của tín hiệu là không quan trọng b
Từ (*) chứng tỏ : Tỷ số giữa công suất ỉnh của tín hiệu và công suất trung bình của nhiễu ở ầu ra
bộ lọc ấy chỉ phụ thuộc vào nĕng lượng lOMoARcPSD| 36067889 ⎛⎜ S ⎞⎟ c
Từ (*) chứng tỏ tỷ số ρ = ⎝ ra
N ⎠ ra chỉ phụ thuộc vào nĕng lượng của tín hiệu mà hoàn toàn
không phụ thuộc vào d ng của nó ⎛⎜ S ⎞⎟ d
Từ (*) chứng tỏ tỷ số ρ = ⎝ ra
N ⎠ ra hoàn toàn phụ thuộc vào d ng của nó
của tín hiệu mà hoàn toàn không phụ thuộc vào d ng của nó.
9/ Cho kênh nhị phân, ối xứng, không nhớ có nhiễu cộng, trắng, chuẩn theo mô hình sau: p(α = ) 1 1 α1 p(β α1/ 1) β1 ( βα ) ( ) α ( ) α= α β ( βα ) p
Xác suất sai toàn phần ps( xác suất sai không iều kiện) là ps = p(α ) ) ) )
1 .p(β α + α2 / 1 p( 2 .p(β α1 / 2 Δ − ⎧⎪−η2⎫⎪ ⎛ ∫ π − ∞
Gi sử tính ược p(β α =2 / 1)exp⎨⎪⎩ 2 ⎬⎪⎭dη = φ −⎜⎜⎝ 2P TGΔ 0 ⎞⎟⎟⎠
khi ó ps sẽ bằng biểu thức nào dưới ây: a ps
= +φ1 ⎜⎜⎛⎝ 2P TGΔ 0 ⎞⎟⎟⎠ b ps = +φ12
⎛⎜⎜ 2P TGΔ 0 ⎞⎟⎟⎠ ⎝ c ps = + φ12
12 ⎛⎜⎜⎝ 2P TGΔ 0 ⎞⎟⎟⎠ lOMoARcPSD| 36067889 ⎛ P TΔ ⎞⎟⎟ d ps = − φ1 ⎜⎜ 2G0 ⎠ ⎝
10/ T i ầu vào bộ lọc tuyến tính tác ộng tín hiệu: x(t) = s(t) + n(t)
Trong ó n(t) là t p âm trắng, chuẩn, dừng Còn s(t) là xung thị tần ộc lập với n(t) và có d ng: s t(
) = ⎧⎪⎨A.eA t( − T) t ≤ T ⎪⎩0 t > T
Hàm truyền K (j )0 ω = kS (j )e* ω − ωj T ω = ω
Hàm truyền của bộ lọc (K (j ) kS (j )e − 0 *
jωT ) sao cho tỷ số tín trên t p ở ầu ra của bé lọc t cực i sẽ
là biểu thức nào dưới ây a K (j )0 ω =− AkA+ ωj b ω = K (j )0 AkA+ ωj c K (j )0 ω = AkA− ωj d K (j )0 ω = Ak+ ωjAj




