lOMoAR cPSD| 46560390
PHẦN I: Xác suất (3 điểm)
Câu 1. Tại một bệnh viện nhỏ có 2 khoa, tỷ lệ hai nhóm bệnh nhân khoa
ngoại, truyền nhiễm tương ứng là 0,35; 0,65. Xác suất gặp bệnh nhân nặng của
khoa ngoại bằng 0,5 và của khoa truyền nhiễm bằng 0,6. Xác suất gặp bệnh
nhân nặng của 2 khoa bằng bao nhiêu?
Khám tất cả bệnh nhân nặng, tìm tỷ lệ gặp bệnh nhân khoa truyền nhiễm? Giải:
Gọi A1 = “Bệnh nhân khoa ngoại”
A2 = “Bệnh nhân khoa truyền nhiễm” A = “Bệnh nhân nặng”
Theo đầu bài ta có: P(A1) = 0,35 ; P(A/A1) = 0,5 P(A2) = 0,65 ; P(A/A2) = 0,6
• Theo công thức xác suất đầy đủ ta có
Xác suất gặp bệnh nhân nặng của cả 2 khoa là:
P(A) = P(A1) . P(A/A1) + P(A2) . P(A/A2) = 0,35 . 0,5 + 0,65 . 0,6 = 0,565
• Theo công thức xác suất Bayes ta có
Khám bệnh nhân nặng thì tỷ lệ bệnh nhân đó thuộc khoa truyền nhiễm là
P(A2/A) = P(A 2)P.P(A(A) / A2) = 0,0,56565.0,6 = 0,69
Câu 2. Trong một quầy thuốc, tỷ lệ hai loại thuốc ngoại và nội, tương ứng
là 0,45; 0,55. Xác suất bán được loại thuốc nội bằng 0,3 và loại thuốc ngoại là
0,5. Xác suất bán được cả hai loại thuốc bằng bao nhiêu? lOMoAR cPSD| 46560390
Trong tất cả các loại thuốc đã bán được, tìm tỷ lệ bán được thuốc ngoại? Giải:
Gọi A1 = “ Thuốc ngoại” A2 = “ Thuốc nội”
A = “ Bán được thuốc”
Theo đầu bài ta có : P(A1) = 0,45 ; P(A/A1) = 0,5 P(A2) = 0,55 ; P(A/A2) = 0,3
• Theo công thức xác suất đầy đủ ta có
Xác suất bán được cả hai loại thuốc là:
P(A) = P(A1) . P(A/A1) + P(A2) . P(A/A2) = 0,45 . 0,5 + 0,55 . 0,3 = 0,39
• Theo công thức xác suất Bayes ta có
Trong các loại thuốc bán được thì tỷ lệ bán được thuốc ngoại là
P(A1/A) = P(A 1)P.P(A(A) / A1) = 0,450,39.0,5 = 0,58
Câu 3. Có 2 hộp đựng thuốc tiêm. Hộp 1 có 10 ống trong đó có 3 ống hết
hạn sử dụng. Hộp 2 có 13 ống trong đó có 4 ống hết hạn sử dụng. Từ hộp 1
chuyển ng u nhiên 2 ống thuốc sang hộp 2. Sau đó từ hộp 2 lấy ng u nhiên ra 1 ống. a)
Tìm xác suất để ống thuốc lấy ra từ hộp 2 là ống thuốc còn hạn sửdụng. b)
Biết ống thuốc lấy ra từ hộp 2 là ống thuốc còn hạn sử dụng. Tìm xác lOMoAR cPSD| 46560390
suất 2 ống thuốc chuyển từ hộp 1 sang hộp 2 đều còn hạn sử dụng. Giải:
Gọi A1 = “Hai ống thuốc lấy từ hộp 1 sang hộp 2 đều là 2 ống còn hạn sử dụng”
A2 = “Hai ống thuốc lấy từ hộp 1 sang hộp 2 thì 1 ống còn hạn sử dụng, 1 ống hết hạn sử dụng”
A3 = “Hai ống thuốc lấy từ hộp 1 sang hộp 2 đều là 2 ống hết hạn sử dụng”
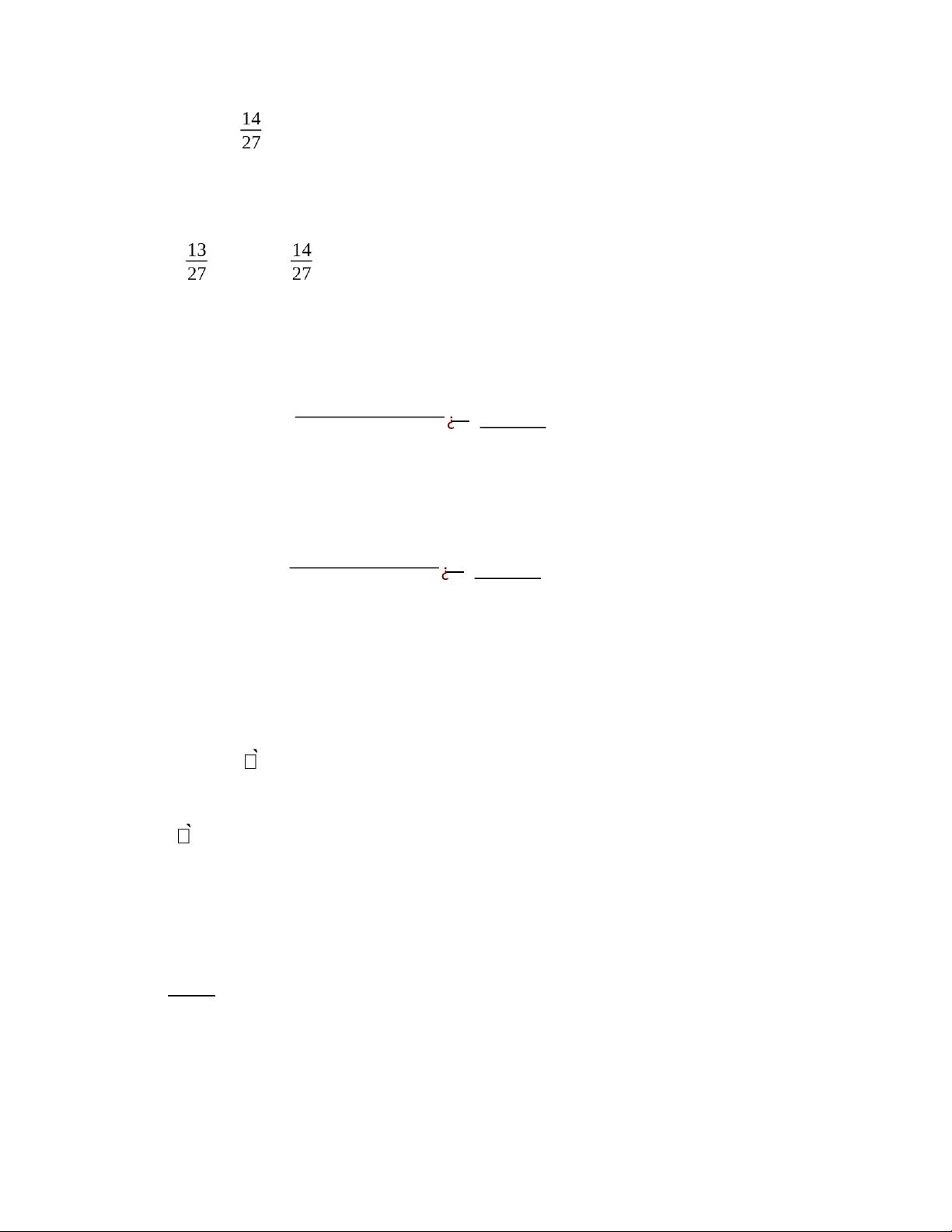
A = “Hai ống lấy từ hộp 2 còn hạn sử dụng” Theo đầu bài ta có C27 21 P(A1) = C = 2 45 P(A/A1) = 10 1 1 P(A2) = CC7.C 3 = 21 2 45 P(A/A2) = 10 C23 3 P(A3) = C210 = 45 P(A/A3) =
a) Theo công thức xác suất đầy đủ ta có
Xác suất để lấy 2 ống thuốc từ hộp 2 còn hạn sử dụng là
P(A) = P(A1) . P(A/A1) + P(A2) . P(A/A2) + P(A3) . P(A/A3) = . + . + . =0,69 lOMoAR cPSD| 46560390
b) Theo công thức Bayes ta có
Biết ống thuốc lấy ra từ hộp 2 là ống thuốc còn hạn sử dụng, xác suất 2
ống thuốc chuyển từ hộp 1 sang hộp 2 đều còn hạn sử dụng là: 11 P. P(A1/A) =
P(A) = 45 15 = 0,49 0,69
Câu 4. Một phòng hồi sức cấp cứu có 3 bệnh nhân nặng cần thở máy với xác
suất cần thở máy trong vòng 1 giờ của các bệnh nhân tương ứng là 0,6; 0,7;
0,75. Tính xác suất trong vòng 1 giờ:
1) Có 2 bệnh nhân cần thở máy.
2) Không có bệnh nhân nào cần thở máy.
3) Có 1 bệnh nhân cần thở máy. Giải
Gọi Ai = “ Bệnh nhân i cần thở máy trong vòng 1 giờ” ; i = { 1, 2, 3}
Ta có: P(A1) = 0,6 => P(A ) = 0,4 P(A 1 2)
= 0,7 => P(A2) = 0,3
P(A3) = 0,75 => P(A ) = 0,25 3
1. Gọi B = “Có 2 bệnh nhân cần thở máy”
P(B) = P(A1). P(A2). P(A ) + P(A ). P(A ). P(A 3 1). P(A2 3) + P(A1 2). P(A3)
= 0,6 . 0,7 . 0,25 + 0,6 . 0,3 . 0,75 + 0,4 . 0,7 . 0,75 = 0,45
2. Gọi C = “Không có bệnh nhân nào cần thở máy”P(C) = P(A ). P( ). P( ) 1 A2 A3 = 0,4 . 0,3 . 0,25 =0,03
3. Gọi D = “Có 1 bệnh nhân cần thở máy”
P(D) = P(A1). P(A ). P( ) + P( ). P(A ) + P( ). P( ). P(A 2 A3 A1 2). P(A3 A1 A2 3) lOMoAR cPSD| 46560390
= 0,6 . 0,3 . 0,25 + 0,4 . 0,7 . 0,25 + 0,4 . 0,3 . 0,75 = 0,205
Câu 5. Có 3 bác sỹ độc lập nhau khám bệnh. Xác suất chẩn đoán sai của các
bác sĩ tương ứng là 0,3; 0,2 và 0,1. Ba người đã khám cho một bệnh nhân. Tìm xác suất sao cho:
1) Không ai chẩn đoán sai.
2) Có 1 người chẩn đoán sai.
3) Có 2 người chẩn đoán sai. Giải:
Gọi Ai = “Bác sỹ i chẩn đoán sai” ; i = {1, 2, 3}
Ta có: P(A1) = 0,3 => P(A ) = 0,7 1
P(A2) = 0,2 => P(A2) = 0,8
P(A3) = 0,1 => P(A ) = 0,9 3
1. Gọi B = “Không ai chẩn đoán sai”
P(B) = P(A ). P( ). P( ) = 0,7 . 0,8 . 0,9 = 0,504 1 A2 A3
2. Gọi C = “Có 1 người chẩn đoán sai”
P(C) = P(A1). P(A ). P( ) + P( ). P(A ) + P( ). P( ). P(A 2 A3 A1 2). P(A3 A1 A2 3)
= 0,3 . 0,8 . 0,9 + 0,7 . 0,2 . 0,9 + 0,7 . 0,8 . 0,1 = 0,398
3. Gọi D = “Có 2 người chẩn đoán sai”
P(D) = P(A1). P(A2). P(A ) + P(A ). P(A ). P(A 3 1). P(A2 3) + P(A1 2). P(A3)
= 0,3 . 0,2 . 0,9 + 0,3 . 0,8 . 0,1 + 0,7 . 0,2 . 0,1 = 0,092
Câu 6. Có 2 loại thuốc có tác dụng tương đương trong điều trị bệnh A với
xác suất khỏi của thuốc 1 và thuốc 2 tương ứng là 0,75 và 0,85. Một người bị
bệnh A đã được điều trị khỏi bằng 1 trong 2 loại thuốc trên. Tìm xác suất người
đó được điều trị bằng thuốc 2. lOMoAR cPSD| 46560390 Giải:
Gọi A1 = “Bệnh nhân A điều trị bằng thuốc 1”
A2 = “ Bệnh nhân A điều trị bằng thuốc 2”
A = “Điều trị khỏi bệnh” Ta có: P(A1) = P(A2) = 0,5
P(A/A1) = 0,75 ; P(A/A2) = 0,8
Theo công thức xác suất đầy đủ
Ta có xác suất người đó được điều trị khỏi bệnh là
P(A) = P(A1). P(A/A1) + P(A2). P(A/A2) = 0,5 . 0,75 + 0,5 . 0,8 = 0,775 Theo công thức Bayes
Người bệnh A đã điều trị khỏi, xác suất để người đó điều trị bằng thuốc 2 là: P(A2/A) =
P ( A2). PP((AA)/A¿¿2)¿ = 00,775,5.0,8 = 0,52
Câu 7. Trong một xã X tỷ lệ nam: nữ là 13:14. Khả năng mắc bệnh bạch tạng ở
nam là 0,55 và ở nữ là 0,25.
a. Tính tỷ lệ mắc bệnh chung của cả xã?
b. Gặp ng u nhiên một bệnh án trong xã của một người không mắc
bệnh. Hãy cho biết khả năng người đó là nam hay nữ nhiều hơn? Giải:
Gọi A1 = “Người đó là nam trong xã X”
A2 = “Người đó là nữ trong xã X”
A = “Người mắc bệnh bạch tạng”
Ta có: P(A1) = ; P(A/A1) = 0,55 lOMoAR cPSD| 46560390 P(A2) = ; P(A/A2) = 0,25
1. Theo công thức xác suất đầy đủ, tỷ lệ mắc bệnh chung của cả xã là: P(A)
= P(A1). P(A/A1) + P(A2). P(A/A2) = . 0,55 + . 0,25 = 0,39 2. Theo công thức Bayes
Gặp người mắc bệnh, tỷ lệ người đó là nam là:
P(A1/A) = P ( A1). P(A/A¿¿1) = 1327 .0,55 = 0,68 P(A) 0,39
Gặp người mắc bệnh, tỷ lệ người đó là nữ là:
P(A2/A) = P ( A2). P(A/A¿¿2) = 1427 .0,25 = 0,33 P(A) 0,39
KL: Vậy khi gặp một người mắc bệnh thì khả năng người đó là nam sẽ nhiều hơn.
Câu 8: Thu m u bệnh phẩm từ 3 cơ sở sản xuất A; B; C theo tỉ lệ 45%; 35%;
20%. Tỉ lệ nhiễm khuẩn tương ứng của bệnh phẩm 3 cơ sở này là 8%; 6%; 3%.
Rút ng u nhiên ra một bệnh phẩm để kiểm tra.
a. Tìm xác suất để bệnh phẩm rút ra là dương tính.
b. Giả sử bệnh phẩm rút ra là âm tính. Tìm xác suất để bệnh phẩm
nàylà từ cơ sở A. Giải:
Gọi A = “Bệnh phẩm từ cơ sở sản xuất A”
B = “Bệnh phẩm từ cơ sở sản xuất B”
C = “Bệnh phẩm từ cơ sở sản xuất C” lOMoAR cPSD| 46560390
D = “Bệnh phẩm bị nhiễm khuẩn”
Theo đầu bài ta có: P(A) = 0,45 ; P(D/A) = 0,08 P(B) = 0,35 ; P(D/B) = 0,06 P(C) = 0,20 ; P(D/C) = 0,03
1. Theo công thức xác suất đẩy đủ
Xác suất bệnh phẩm bị nhiễm khuẩn (dương tính) là
P(D) = P(A).P(D/A) + P(B).P(D/B) + P(C).P(D/C)
= 0,45 . 0,08 + 0,35 . 0,06 + 0,20 . 0,03 = 0,063
2. Ta có P(D/A) = 0,08 => P(D/¿A) = 0,92 P(D) = 0,063 => P(D) = 0,937 Theo công thức Bayes
Một bệnh phẩm rút ra là âm tính, xác suất bệnh phẩm đó từ cơ sở A là:
P(A/D) = P ( AP). P(D(D) / A) = 0,450,937.0,92 = 0,44
Câu 9: Một bệnh viện nhận khám và điều trị cho bệnh nhân đến từ ba địa
phương A, B, C theo tỷ lệ 2: 5: 7. Theo điều tra, tỷ lệ người đóng bảo hiểm y tế
ở các địa phương trên theo thứ tự lần lượt là 86%; 90%; 92%.
1. Khám ng u nhiên một bệnh nhân. Tính xác suất để bệnh
nhân đó cóbảo hiểm y tế.
2. Giả sử bệnh nhân được khám có bảo hiểm y tế, theo Anh (Chị)
bệnhnhân đó có khả năng đến từ địa phương nào nhiều hơn cả? Giải:
Gọi A = “Bệnh nhân đến từ địa phương A”
B = “Bệnh nhân đến từ địa phương B” lOMoAR cPSD| 46560390
C = “Bệnh nhân đến từ địa phương C”
Bh = “Bệnh nhân có bảo hiểm”
Ta có: P(A) = ; P(Bh/A) = 0,86 P(B) = ; P(Bh/B) = 0,9 P(C) = ; P(Bh/C) = 0,92
1. Theo công thức xác suất đầy đủ
Xác suất để một bệnh nhân có bảo hiểm là:
P(Bh) = P(A). P(Bh/A) + P(B). P(Bh/B) + P(C). P(Bh/C) = . 0,86 + . 0,9 + . 0,92 = 0,9 2. Theo công thức Bayes
Khi gặp bệnh nhân có BHYT:
- Tỷ lệ bệnh nhân đó thuộc địa phương A là: 2
P(A/Bh) = P(A)P.P(Bh(Bh) /A) = 14 .o,86 = 0.14 0,9
- Tỷ lệ bệnh nhân đó thuộc địa phương B là: 5
P(B/Bh) = P(B)P.P(Bh(Bh) /B) = 14 .o,9 = 0.36 0,9
- Tỷ lệ bệnh nhân đó thuộc địa phương C là: 7
P(C).P(Bh/C) .o,92 P(C/Bh) = P(Bh) = 14 = 0,51 0,9 lOMoAR cPSD| 46560390
KL: Vậy khi gặp một bệnh nhân có BHYT thì khả năng bệnh nhân đó thuộc
địa phương C sẽ cao hơn cả.
Câu 10: Trong một trạm cấp cứu bỏng có 65% bệnh nhân bỏng do nóng, 35%
bệnh nhân bỏng do hóa chất. Loại bỏng do nóng có 25% bị biến chứng, loại
bỏng do hóa chất có 60% bị biến chứng. Từ tập hồ sơ bệnh nhân người ta rút
ng u nhiên ra một bệnh án.
a. Tìm xác suất để gặp bệnh án của bệnh nhân bị biến chứng.
b. Giả sử bệnh án lấy ra là của bệnh nhân bị biến chứng. Tìm xác suất
để bệnh án đó là của bệnh nhân bị biến chứng do hóa chất gây ra? Giải:
Gọi A1 = “Bệnh nhân bỏng do nóng”
A2 = “Bệnh nhân bỏng do hóa chất”
A = “Bệnh nhân bị biến chứng” Theo đầu bài ta có P(A1) = 0,65 ; P(A/A1) = 0,25 P(A2) = 0,35 ; P(A/A2) = 0,6
1. Theo công thức xác suất đầy đủ
Xác suất gặp bệnh án của bệnh nhân bị biến chứng là:
P(A) = P(A1) . P(A/A1) + P(A2) . P(A/A2)
= 0,65 . 0,25 + 0,35 . 0,6 = 0,3725 2. Theo công thức Bayes
Lấy ra bệnh án của bệnh nhân bị biến chứng, xác suất bệnh nhân đó bị
biến chứng do bỏng hóa chất gây ra là:
P(A2/A) = P(A 2)P.P(A(A) / A2) = 00,3725,35.0,6 = 0.56
PHẦN II: Thống kê (3 điểm) lOMoAR cPSD| 46560390
Câu 1: Khảo sát trọng lượng của óc người dưới 50 tuổi, thu được kết quả sau (tính theo gam):
Khoảng trọng 1175- 1225- 1275- 1325- 1375- 1425- 1475- lượng 1225 1275 1325 1375 1425 1475 1525
Số người dưới 50 7 16 25 35 29 22 10 tuổi 1.
Với độ tin cậy 95% xác định khoảng tin cậy của trọng lượng
trungbình của óc người dưới 50 tuổi. 2.
Có ý kiến cho rằng trọng lượng của óc người dưới 50 tuổi lớn
hơn1370gam. Với mức ý nghĩa α=0,05 hãy kết luận ý kiến đó.
Cho biết u0,975=1,96; u0,95=1,645. Giải : Ta có X = n ni Xi =
(7.1200 + 16.1250 + 25.1300 + 35.1350 + 29.1400 + 22.1450 +10.1500) = 1358,68 S = n ∑n – ( i X2i X)2 =
(7.12002 + 16.12502 + 25.13002 + 35.13502 + 29.14002
+ 22.14502 +10.15002) – (1358,68)2 = 6158,8 S = = 78,48 G = Chọn thống kê S
1. Với độ tin cậy bằng 95% => 1 – α = 0,95 => U α 1− 2 = U0,975 = 1,96
Khoảng tin cậy của trọng lượng trung bình của óc người dưới 50 tuổi là: S U + S . U ) 78,48 lOMoAR cPSD| 46560390 = (1358,68 - . 1,96 ; 1358,68 +
. 1,96) = (1345,82 ; 1371,54)
2. Theo đầu bài Có giả thuyết H0: µ = µ0 = 1370 (g) Đối thuyết H1: µ > µ0 . Ta có U qs = = = -1,72
Với mức ý nghĩa α=0,05 => U1 – α = U0,95 = 1,645
Với đối thuyết H1: µ > µ0 ta có miền bác bỏ Wα = { U1 – α ; + ∞ } => Wα = { 1,645 ; + ∞ }
Nhận thấy Uqs = -1,72 ∉ Wα
=> Chấp nhận giả thuyết Ho, bác bỏ đối thuyết H1
Vậy với mức ý nghĩa α = 0,05 không có cơ sở để cho rằng trọng lượng của óc
người dưới 50 tuổi lớn hơn 1370gam.
Câu 2: Người ta cân ng u nhiên 22 trẻ 2 tuổi ở một xã thu được số liệu sau: Trọng lượng (kg) 11,8 12,5 12,8 13,1 13,5 Số trẻ 3 4 8 5 2
Giả sử trọng lượng trung bình của trẻ tuân theo quy luật phân phối chuẩn.
Hãy ước lượng cân nặng trung bình của nhóm trẻ 2 tuổi ở xã này với độ tin cậy 95%. Biết . Giải: 1 Ta có X =
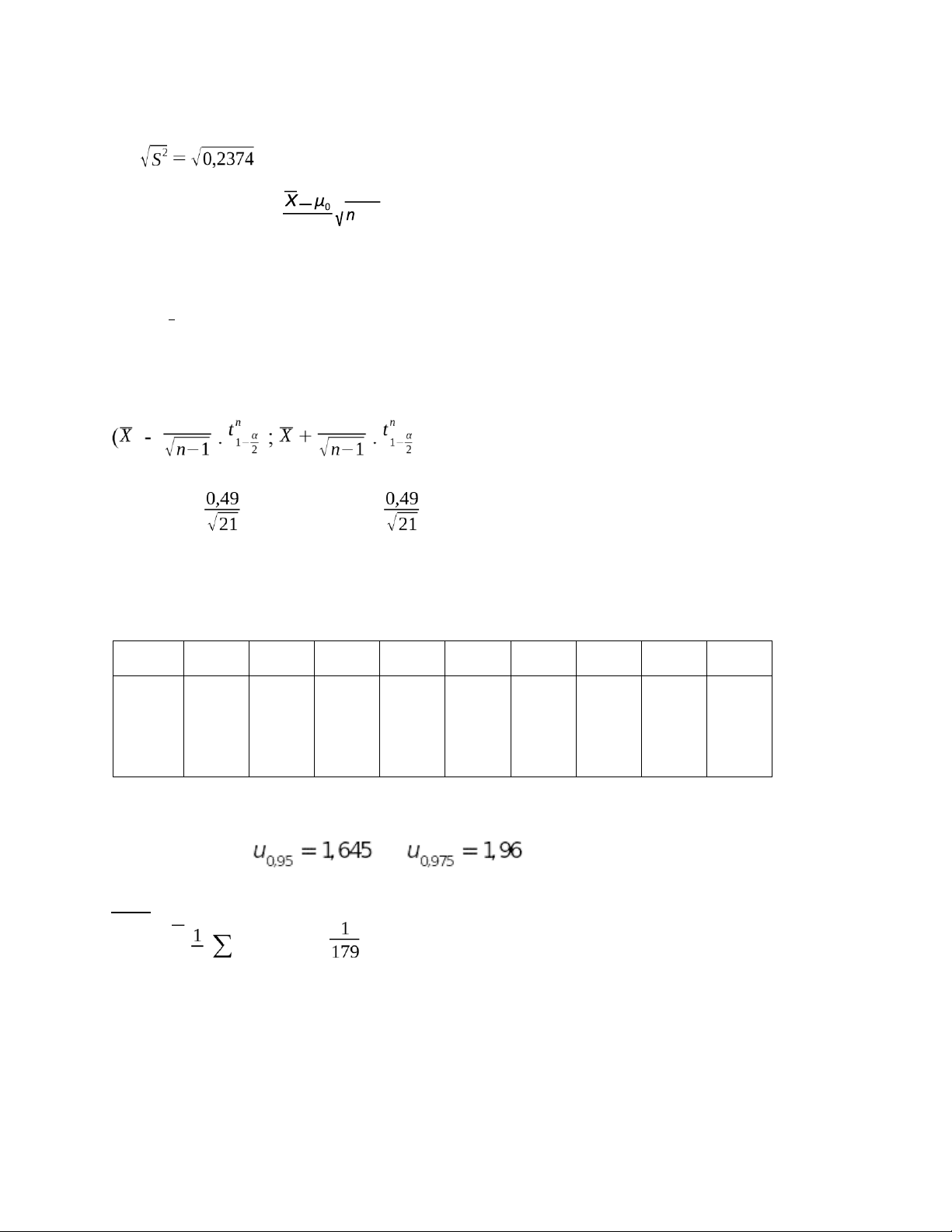
nni Xi = 22 ( 3.11,8 + 4.12,5 + 8.12,8 + 5.13,1 + 2.13,5) = 12,74 S
= n ∑ ni X2i – (X)2 = ( 3.11,82 + 4.12,52 + 8.12,82 + 5.13,12 + 2.13,52) – 12,742 lOMoAR cPSD| 46560390 = 0,2374 S = = 0,49 G = Chọn thống kê S −1
Với độ tin cậy 95% => 1 – α = 0,05 ; n = 22
=> tn1−−1α = t210,975 = 2,08 2
Vậy cân nặng trung bình của nhóm trẻ 2 tuổi ở xã này với độ tin cậy 95% trong khoảng là: S −1 S −1 ) = (12,74 - . 2,08 ; 12,74 + . 2,08) = (12,52 ; 12,96)
Câu 3: Sau khi cho uống xiro có chứa aslicylic acid. Người ta định phân chất
này (X) trong máu 1 giờ thu được kết quả như sau (đơn vị đó mg/l): X 118 57 166 136 130 90 131 132 110 Số 23 5 3 36 30 15 25 22 20 ngườ i
Với độ tin cậy 95% hãy ước lượng mức định phân trung bình của chất aslicylic acid. Cho biết và . Giải Ta có X = n ni Xi =
(23.118 + 5.57 + 3.166 + 36.136 + 30.130 + 15.90 + 25.131
+ 22.132 + 20.110) = 123,03 lOMoAR cPSD| 46560390 S =
+ 5.572 + 3.1662 + 36.1362 + 30.1302 + 15.902
+ 25.1312 + 22.1322 + 20.110)2 - 123,032 = 326,6 S = = 18,07 G = Chọn thống kê S −1
Với độ tin cậy 95% => 1 – α = 0,05 => U1−α2 = U0,975 = 1,96
Vậy mức định phân trung bình của chất aslicylic acid nằm trong khoảng là: S U + S . U ) = (123,03 - . 1,96 ; 123,03 + . 1,96) = ( 120,37 ; 125,68)
Câu 4: Để kiểm nghiệm loại thuốc A, người ta định phân chất Cl2 (X) trong nước
tiểu sau khi tiêm thuốc A (đơn vị: mEa/giờ). Thu được kết quả sau: X
6,32 6,98 8,39 6,01 0,59 7,5 9
7,71 3,05 6,68 Số 18 7 5 11 1 12 4 1 2 6 người
Có ý cho rằng sau khi tiêm thuốc A định mức Cl2 trong nước tiểu sau khi
tiêm cao hơn 6,5 mEa/giờ. Với mức ý nghĩa 5% cho biết ý kiến trên có
chấp nhận được không? Cho biết và . Giải: Ta có X = n ni Xi =
(18.6,32 + 7.6,98 + 5.8,39 + 11.6,01 + 1.0,59 + 12.7,5 +
4.9 + 2.3,05 + 6.6,68) = 5,83 lOMoAR cPSD| 46560390 S
= n ∑ ni X2i – (X)2 = (18.6,322 + 7.6,982 + 5.8,392 + 11.6,012 + 1.0,592 +
12.7,52 + 4.92 + 2.3,052 + 6.6,682) - 5,832 = 7,87 S = = 2,8 G = Chọn thống kê S −1
Theo đầu bài có Giả thuyết H0: µ = µ0 = 6,5 (mEa/giờ)
Đối thuyết H1: µ > µ0 . Ta có U qs = = −1 = -1,94
Với mức ý nghĩa α=0,05 => U1 – α = U0,95 = 1,645
Với đối thuyết H1: µ > µ0 ta có miền bác bỏ Wα = { U1 – α ; + ∞ } => Wα = { 1,645 ; + ∞ }
Nhận thấy Uqs = -1,94 ∉ Wα
=> Chấp nhận giả thuyết Ho, bác bỏ đối thuyết H1
Vậy với mức ý nghĩa 5% không có cơ sở cho rằng sau khi tiêm thuốc A định mức
Cl2 trong nước tiểu sau khi tiêm cao hơn 6,5 mEa/giờ.
PHẦN III: Tương quan hồi quy (4 điểm)
Câu 1: Cho bảng tương quan thực nghiệm sau X 6 7 8 9 Y 1 2 2 2 3 1 3 1 2 1 4 2
a. Tìm hệ số tương quan m u.
b. Viết phương trình hồi quy tuyến tính của Y đối với X. lOMoAR cPSD| 46560390 Giải: Ta có: X = n ni Xi =
( 1.6 + 2.6 + 2.7 + 2.7 + 3.8 + 1.8 + 2.9 + 1.9) = 7,5 S
ni X2i – (X)2 =
( 1.62 + 2.62 + 2.72 + 2.72 + 3.82 + 1.82 + 2.92 + 1.92) - 7,52 = 1,11 Sx Y = n niY i =
( 1.3 + 2.4 + 2.2 + 2.3 + 3.2 + 1.3 + 2.1 + 1.2) = 2,43 S
niY2i – (Y)2 =
( 1.32 + 2.42 + 2.22 + 2.32 + 3.22 + 1.32 + 2.12
+ 1.22) – 2,432 = 0,67 Sy = 0,82 XY = n ni XiY i =
( 1.6.3 + 2.6.4 + 2.7.2 + 2.7.3 + 3.8.2 + 1.8.3 + 2.9.1 + 1.9.2) = 17,43
1. Hệ số tương quan mẫu là:
r = XYS−x .SX.y Y = 17,431,05−7.0,5,82.2,43 = -0,92
Vậy X và Y có mối tương quan tuyến tính nghịch biến chặt chẽ.
2. Phương trình hồi quy tuyến tính của Y đối với X có dạng Y = aX + b S y 0,82
Với a = r. Sx = -0,92 . = -0,72 b =
Y – a. X = 2,43 – (-0,72).7,5 = 7,83
Vậy phương trình đường hồi quy của Y đối với X là lOMoAR cPSD| 46560390 Y = -0,72X + 7,83
Câu 2. Đo chiều cao và cân nặng của các học sinh thu được các số liệu sau: Chiều cao(m) 1,62 1,52 1,56 1,64 1,70 1,72 1,76
Cân nặng(kg) 48 52 60 74 58 60 34
a. Tính hệ số tương quan giữa chiều cao vào cân nặng của các học sinh trên.
b. Lập phương trình tương quan tuyến tính giữa chiều cao và cân nặng. Giải: Ta có: X =
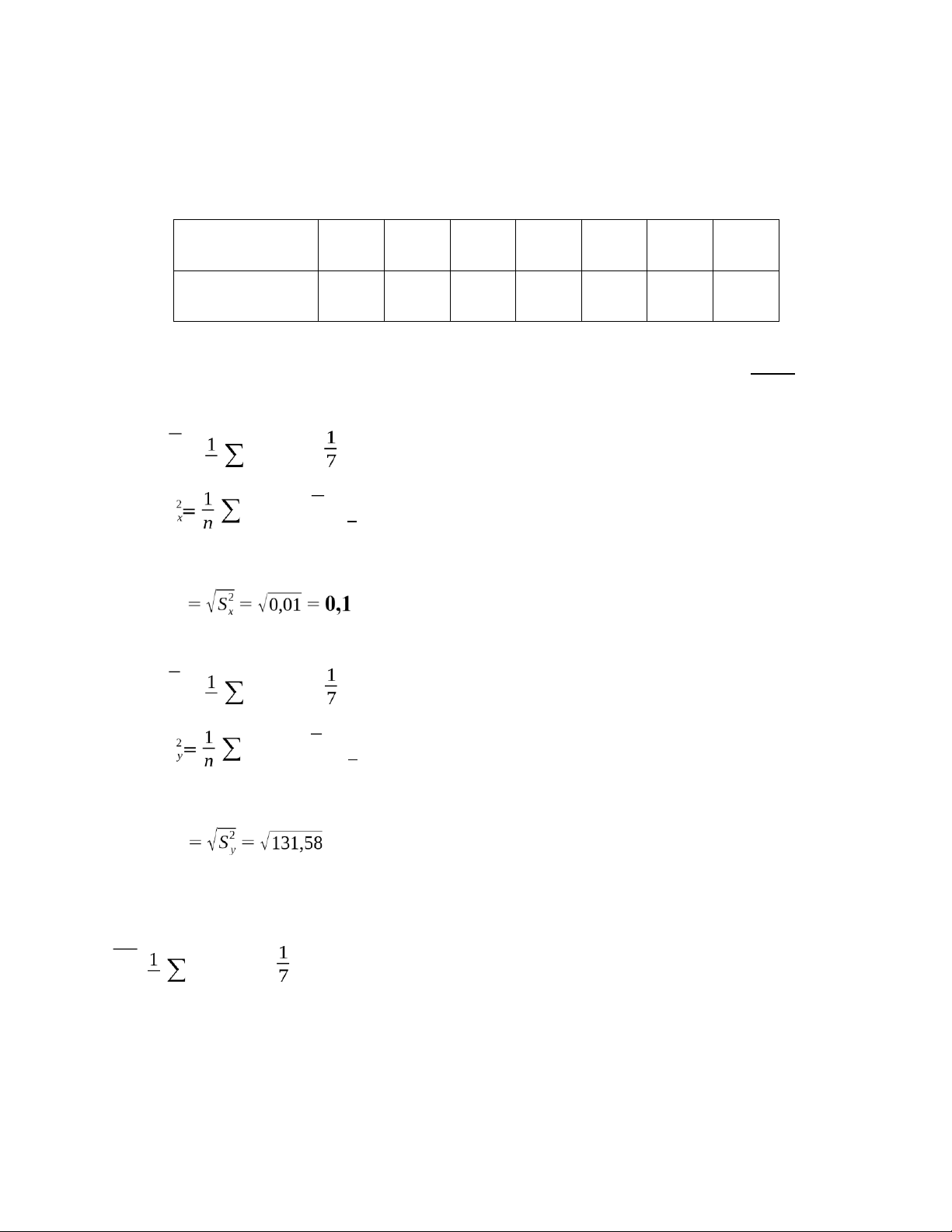
n ni Xi = ( 1,62 + 1,52 + 1,56 + 1,64 + 1,70 + 1,72 + 1,76) = 1,645 S n – ( i X2i
X)2 = 17 ( 1,622 + 1,522 + 1,562 + 1,642 + 1,702 + 1,722
+ 1,762) - 1,6452 = 0,01 Sx Y =
n niY i = ( 48 + 52 + 60 + 74 + 58 + 60 + 34) = 55,14 S n – ( iY 2i
Y)2 = 17 ( 482 + 522 + 602 + 742 + 582 + 602
+ 342) – 55,142 = 131,58 Sy = 11,47 XY =
n ni XiY i = ( 1,62.48 + 1,52.52 + 1,56.60 + 1,64.74 + 1,70.58 + 1,72.60 + 1,76.34) = 90,486
1. Hệ số tương quan mẫu là: lOMoAR cPSD| 46560390
r = XYS−x .SX.y Y = 90,4860−(,11,645.11,47.55,14) = - 0.2
Vậy X và Y có mối tương quan tuyến tính nghịch biến
2. Phương trình hồi quy tuyến tính của Y đối với X có dạng Y = aX + b S y 11,47
Với a = r. Sx = -0,2 . = -22,94 b = Y –
a. X = 55,14 – (-22,94).1,645 = 92,87
Vậy phương trình đường hồi quy của Y đối với X là Y = -22,94X + 92,87
Câu 3: Điều tra số đo chiều cao, cân nặng của một số em học sinh, người ta thu
được bảng số liệu sau Cân nặng 20 22 22 24 24 26 26 28 Chiều cao 115 115 120 120 125 125 130 130
Số học sinh 10 8 12 9 22 8 9 10
Tìm hệ số tương quan giữa chiều cao và cân nặng của nhóm học sinh này.
Viết phương trình hồi quy tuyến tính qua m u trên. Giải Ta có: X = n ni Xi =
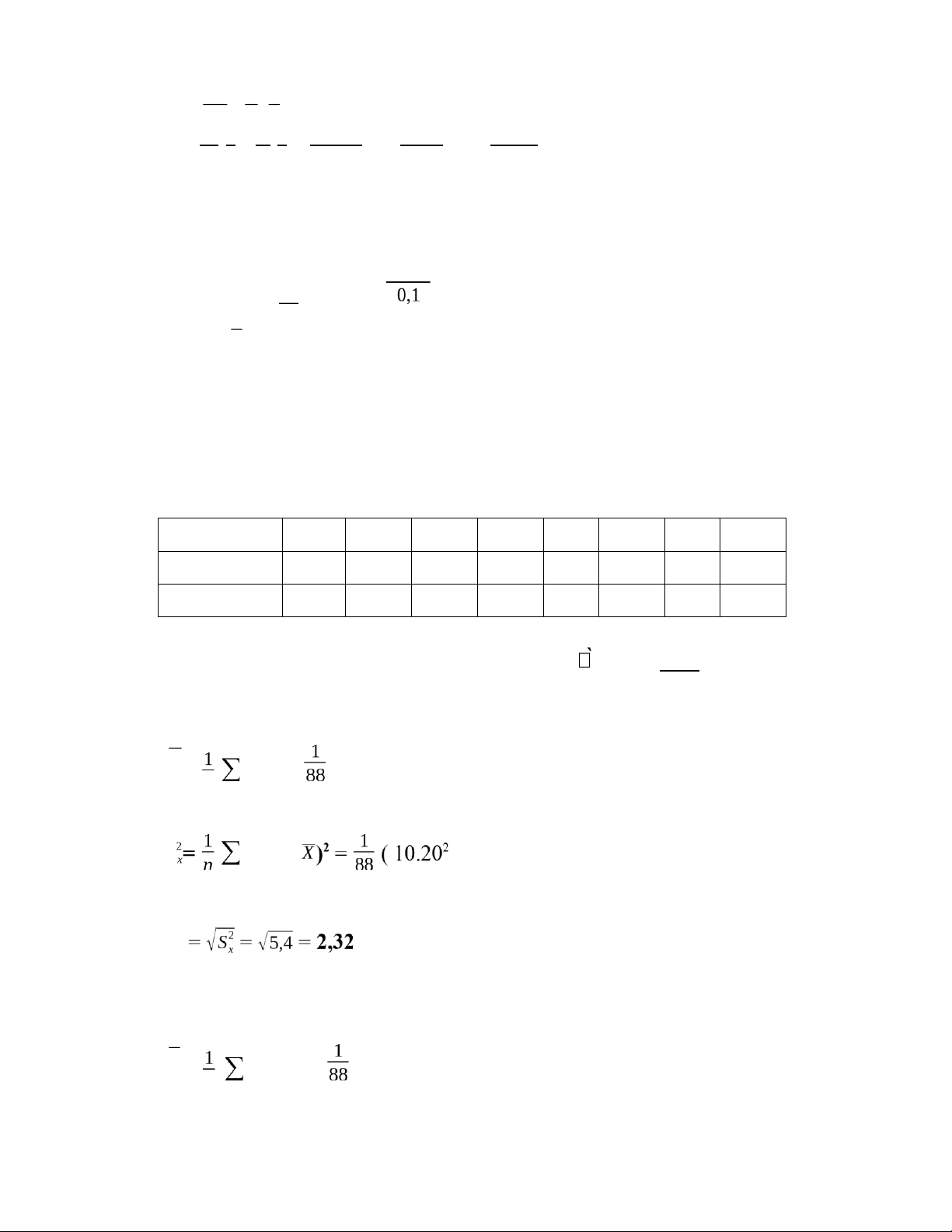
(10.20 + 8.22 + 12.22 + 9.24 + 22.24 + 8.26 + 9.26 + 10.28) = 23,93 S n – (
+ 8.222 + 12.222 + 9.242 + 22.242 + 8.262 i X2i
+ 9.262 + 10.282) - 23,932 = 5,4 Sx Y = n niY i =
( 10.115 + 8.115 + 12.120 + 9.120 + 22.125 + 8.125+ lOMoAR cPSD| 46560390 9.130 + 10.130) = 122,84 S
niY2i – (
+ 8.1252 + 9.1302 + 10.1302) - 122,84 = 27,38 Sy = 5,23 XY = n ni XiY i =
+ 22.24.125 + 8.26.125 + 9.26.130+ 10.28.130) = 2950,68
1. Hệ số tương quan mẫu là: XY−X.Y
2950,68−(23,93.122,84) r = Sx .S y = 2,32.5,23 = 0,92
Vậy X và Y có mối tương quan tuyến tính đồng biến chặt chẽ.
2. Phương trình hồi quy tuyến tính của Y đối với X có dạng Y = aX + b S y 5,23
Với a = r. Sx = 0,92 . = 2,07 b = Y –
a. X = 122,84 – 2,07.23,93 = 73,3
Vậy phương trình đường hồi quy của Y đối với X là Y = 2,07X + 73,3 lOMoAR cPSD| 46560390