Đề cương ôn tậpcác dạng câu hỏi môn Cơ sở khoa học vật liệu có gợi ý

lOMoARcPSD| 36991220
Ôn tập dạng câu hỏi Cơ sở khoa học vật liệu và gợi ý
Lý thuyết: Câu 1: Anh (chị) hiểu thế nào là chất rắn. Thế
nào là chất rắn tinh thể, chất rắn vô ịnh hình? Anh (chị) hãy dùng thuyết cấu trúc polymer giải thích sự
tồn tại khoảng biến mềm của các chất rắn có cấu trúc vô ịnh hình.
Chất rắn là một trạng thái tồn tại của vật chất, trong ó các phần tử cấu tạo (nguyên tử, phân
tử, ion) tập hợp ở trạng thái bền vững. Do ó, chất rắn có hình dạng và kích thước xác ịnh.
Theo khái niệm ộ nhớt, ta phân biệt chất rắn là những chất có ộ nhớt từ 1012 Pa.s trở lên.
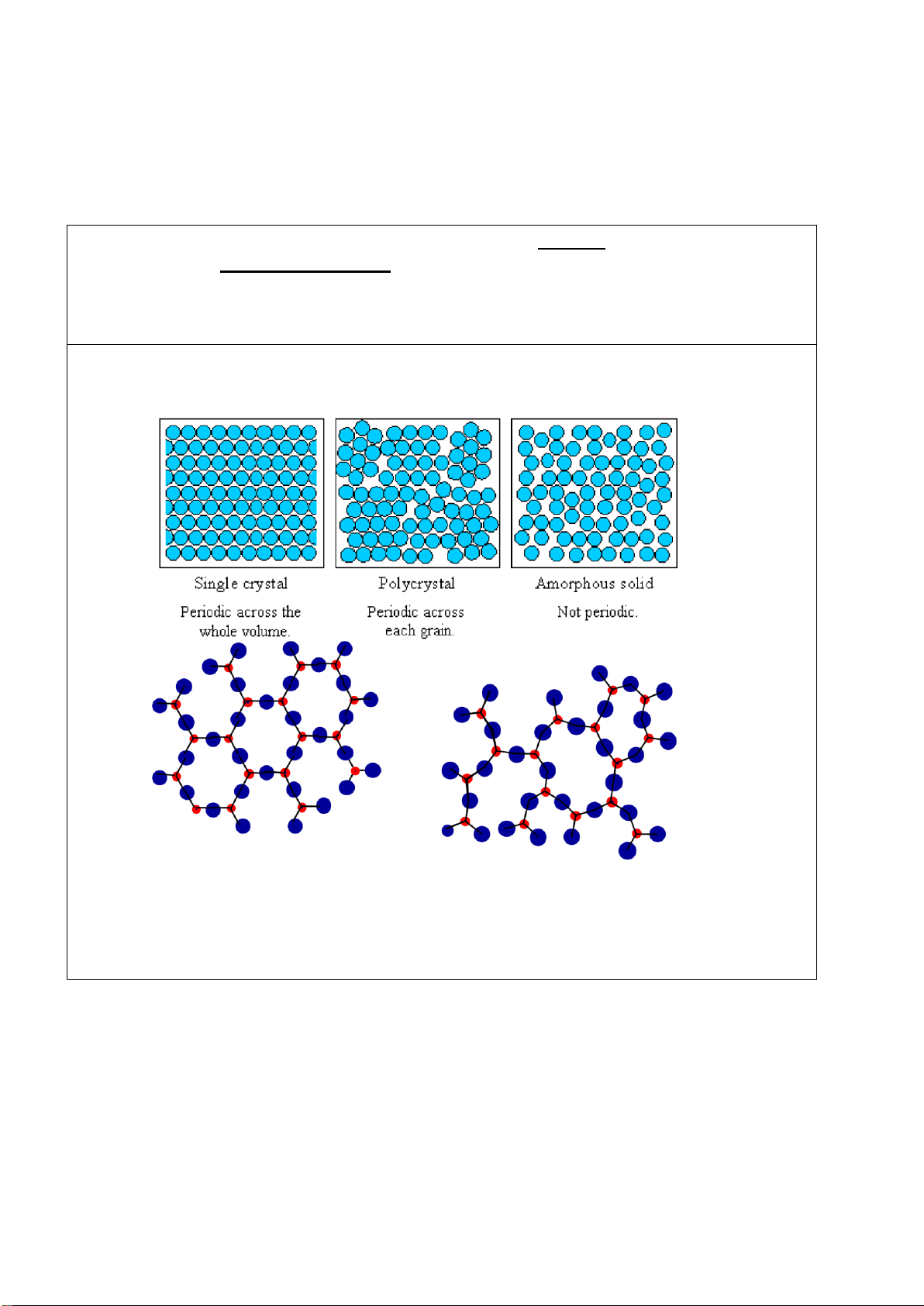
Chất rắn có các phần tử cấu tạo (nguyên tử, phân tử, ion) phân bố ối xứng, tuần hoàn ược
gọi là chất rắn có cấu trúc tinh thể.
Chất rắn có các phần tử cấu tạo phân bố không theo trật tự, ta gọi là chất rắn có cấu trúc vô ịnh hình.
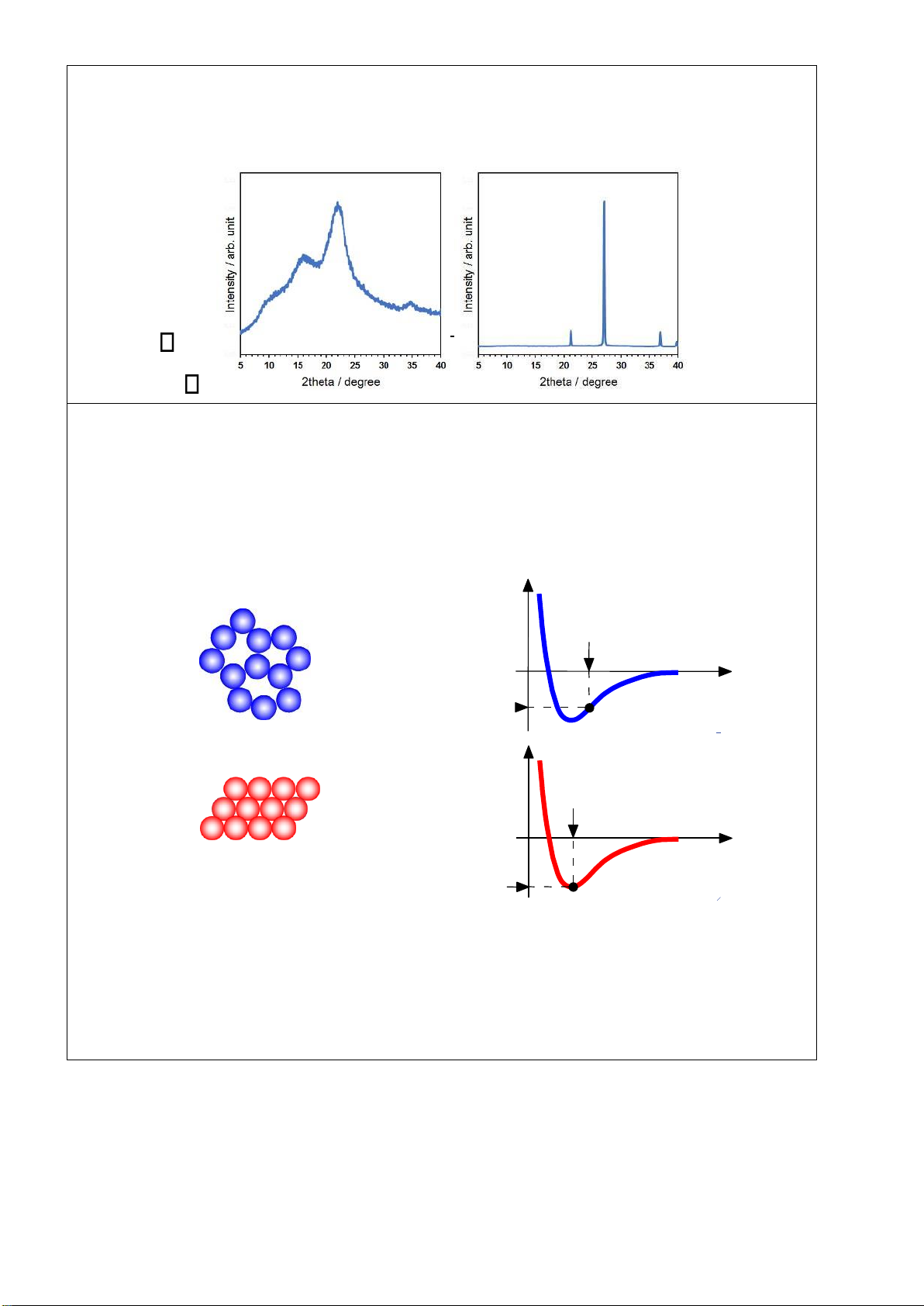
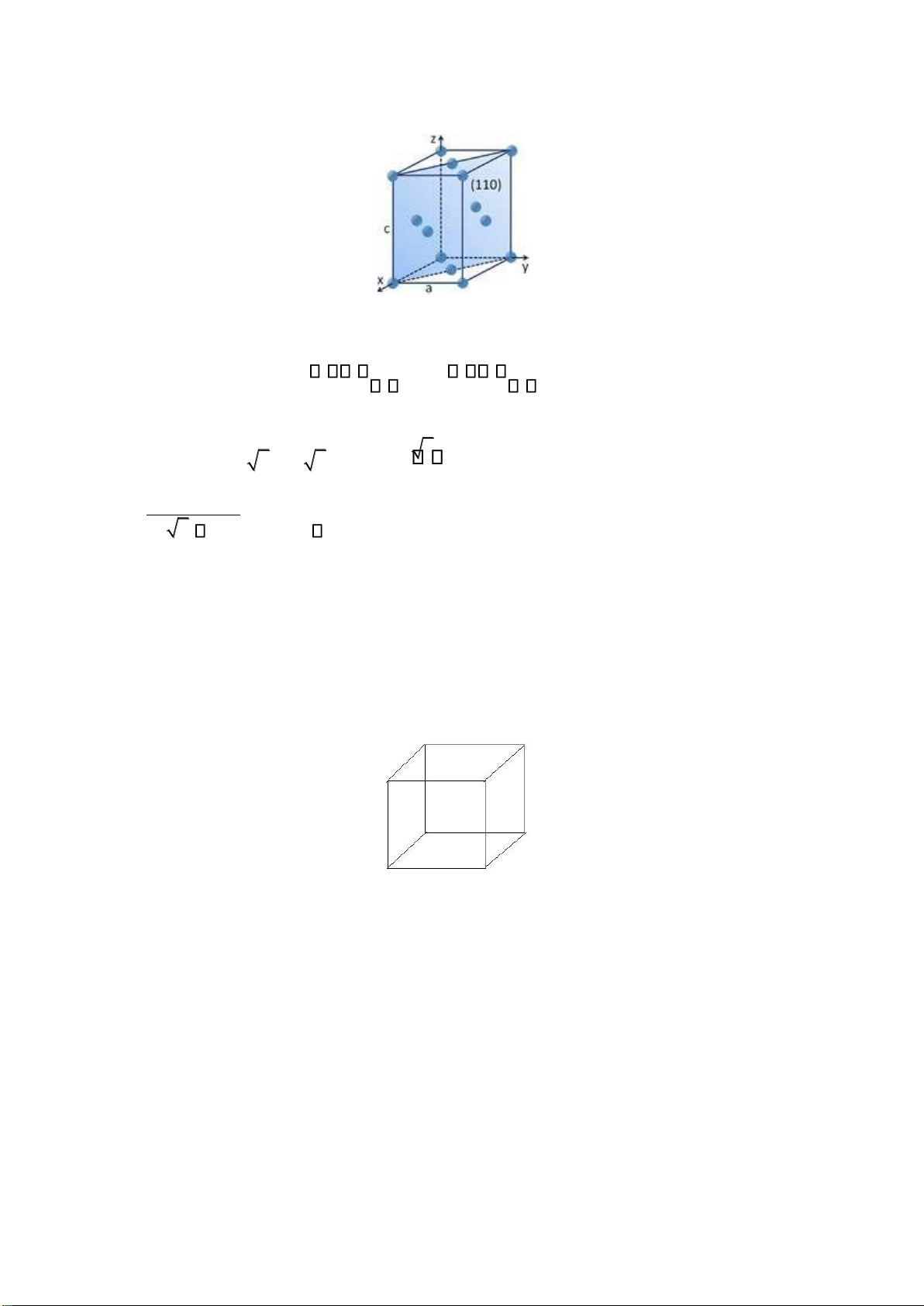
Công cụ phân biệt hiệu quả nhất chất rắn tinh thể và vô ịnh hình là nhiễu xạ tia X (XRD), dung phương trình Bragg Trang 1/4 lOMoARcPSD| 36991220 Phổ XRD của SiO2: Trái: vô ịnh hình SiO2; phải; tinh thể SiO2 d= n 2 sin
Khoảng biến ổi dần tính chất từ trạng thái rắn sang trạng thái lỏng gọi là khoảng biến mềm.
Khoảng biến mềm là dấu hiệu vật lý quan trọng nhất nhận biết trạng thái thủy tinh.
Nguyên nhân là do năng lượng mạng lưới thủy tinh không xác ịnh, các ô mạng bị phá hủy
dần, hoặc do mạng polymer vô cơ bị ứt dần. Mạch polymer không có năng lượng liên kết
ổn ịnh. Khi nóng chảy, các mạch liên kết bị phá hủy dần, vì vậy, không có Tnc cố ịnh, mà có khoảng biến mềm.
Nội năng của vật chất trạng thái thủy tinh sẽ lớn hơn nội năng vật chất ở trạng thái tinh thể
• Không sít chặt, E > Emin___ bond length
typical neighbor n n g • Sít chặt, Emin_____________ typical neighbor bond length typical neighbor r bond energy
Các liên kết trong chất rắn: 5 liên kết
1- Liên kết kim loại, ặc trưng cho vật liệu kim loại
2- Liên kết ion, cộng hóa tri: ặc trưng cho vật liệu ceramic
3- Liên kết phân tử Vanderwall, và liên kết H: ặc trưng cho vật liệu polymer
Liên kết kim loại, cộng hóa trị, ion có năng lượng liên kết lớn hơn liên kết phân tử
Vanderwall và liên kết Hydro Page 2 of 34 lOMoARcPSD| 36991220
Giải thích sự hình thành liên kết:
- LK cộng hóa trị: hình thành do việc ghép chung một hoặc nhiều cặp electron của các
nguyên tử, tạo lớp trạng thái bền vững của ám mây electron
- LK ion: do lực hút tính iện giữa các ion mang iện tích trái dấu
- LK kim loại: hình thành do các iện tử tự do trong nguyên tố kim loại - LK Vanderwall
: hình thành do sự phân cực của các phân tử thành các momen lưỡng cực,
- LK Hydro: hình thành do lực hút tĩnh iện giữa nguyên tử Hydro LK cộng hóa trị
với một nguyên tử hoặc nhóm có ộ âm iện cao hơn
Câu 2a: Kể tên các loại liên kết trong chất rắn. Vẽ sơ ồ ơn giản các mức năng lượng vùng cấm
Eg (band gap) theo quan iểm thuyết vùng năng lượng của chất rắn. Giải thích tính dẫn, cách iện
( iện môi) và bán dẫn của vật liệu theo Eg?
Câu 2b: Kể tên các loại liên kết trong chất rắn. Vẽ sơ ồ ơn giản các mức năng lượng vùng cấm
Eg (band gap) theo quan iểm thuyết vùng năng lượng của chất rắn. Giải thích tính dẫn, cách iện
( iện môi) và bán dẫn của vật liệu theo Eg? Gợi ý: Kể tên: Liên kết ion Liên kết cộng hóa trị Liên kết kim loại Liên kết Van der Waal Liên kết hydro Sơ ồ ơn giản: Page 3 of 34 lOMoARcPSD| 36991220
E Vùng dẫn (phản liên kết) : conduction band (CB) E g ( Vùng cấm )
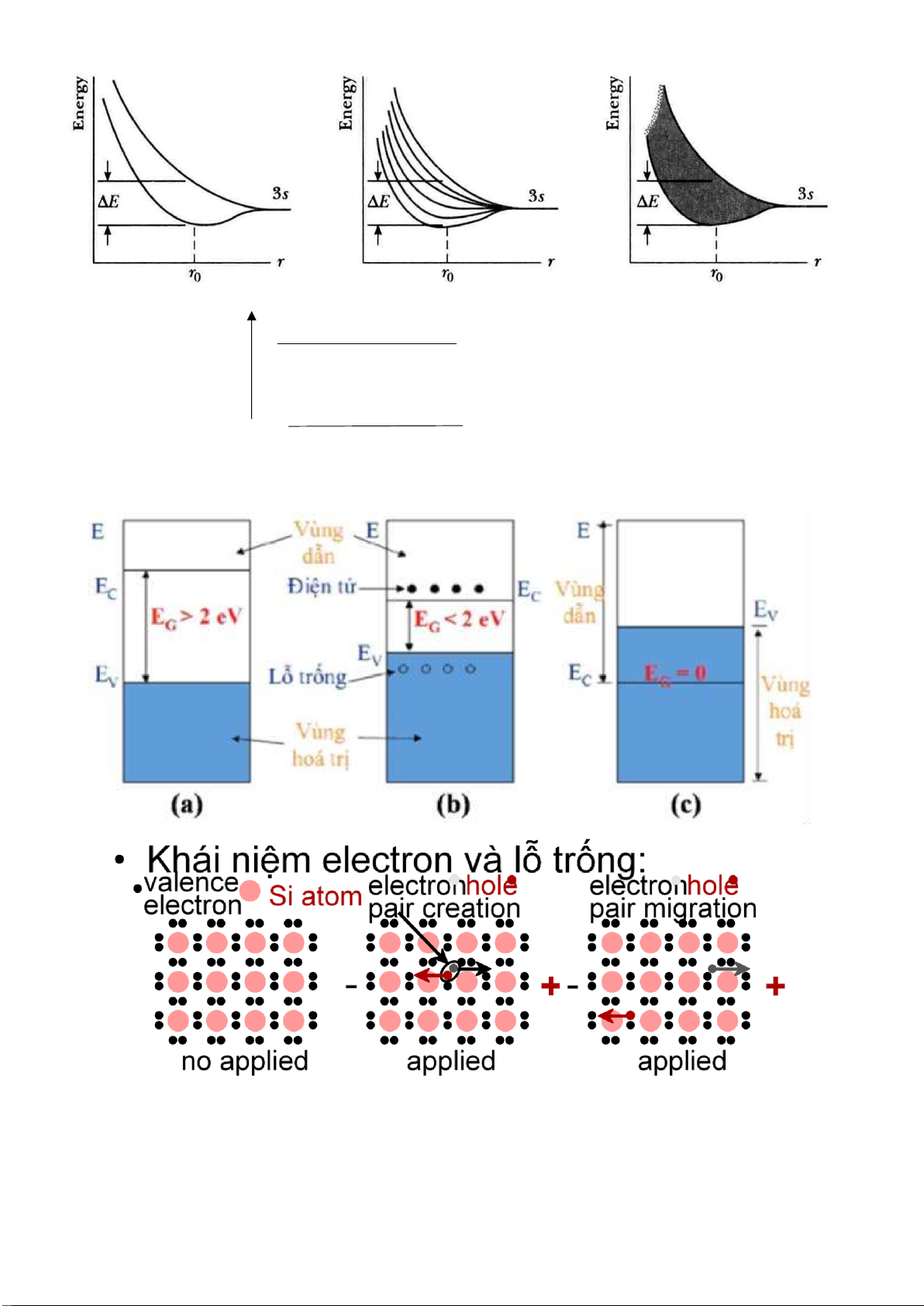
Vùng hóa trị (liên kết) : valence band (VB) • Cách iện: • Bán dẫn: -Band - Band gap rộng (> 2 eV) gap hẹp (< 2 eV) -
Một số electron bị kích thích qua -Nhiều electrons bị kích thích qua band gap band gap Page 4 of 34 lOMoARcPSD| 36991220 Energyempty Energyempty ? conductionconduction bandband GAPGAP s s et et a filled filled valence a st valence bandband st d d ell e i ll f if filled filled bandband
Khái niệm electron v valence electron Si atom no applied electric field
• n-type Tạp chất: (n >> p)
• p-type Tạp chất: (p >> n) Phosphorus atom Boron atom hole 4+ 4+ 4+ 4+ conduction 4+ 4+ 4+ 4+ electron 4+ 5+ 4+ 4+ 4+ 3+ 4+ 4+ valence ne e pe h 4+ 4+ 4+ 4+ electron 4+ 4+ 4+ 4+ 1 1 no applied Si atom no applied Adapted from Figs. 18.12(a) electric field
& 18.14(a), Callister & electric field Rethwisch 8e.
Chất dẫn: Vùng dẫn và liên kết chồng lấp (Eg = 0)
Điện môi (cách iện): Eg > 2eV Bán dẫn: Eg < 2eV. Page 5 of 34 lOMoARcPSD| 36991220
Câu 3a: Phân biệt chất rắn với chất lỏng thế nào? Dấu hiệu nhiệt – vật lý phân biệt chất rắn tinh
thể và rắn vô ịnh hình? Khoảng biến mềm là gì? Tại sao các chất rắn thủy tinh và polymer không
có nhiệt ộ nóng chảy cố ịnh?
Câu 3b: Anh (chị) hiểu thế nào là chất rắn. Thế nào là chất rắn tinh thể và chất rắn vô ịnh hình?
Dùng thuyết liên kết cấu trúc của polymer giải thích sự tồn tại khoảng biến mềm của các chất có cấu trúc vô ịnh hình. Gợi ý:
Chất rắn các phần tử cấu tạo (nguyên tử, phân tử, ion) liên kết bền vững. Do ó, chất rắn có hình
dạng và kích thước xác ịnh. Chất lỏng có các phần tử cấu tạo liên kết không bền, do ó bị biến ổi
hình dạng theo bình chứa.
Phân biệt: chất rắn là những chất có ộ nhớt từ 1012 Pa.s trở lên. Chất lỏng có ộ nhớt bé thua 1012 Pa.s.
Tinh thể: Có nhiệt ộ nóng chảy cố ịnh.
Vô ịnh hình: Không có nhiệt ộ nóng chảy cố ịnh.
Khoảng biến mềm: Khoảng nhiệt ộ chuyển trạng thái rắn – lỏng (và ngược lại) của các chất rắn vô ịnh hình.
Do năng lượng liên kết mạng lưới cấu trúc không ổn ịnh.
Dạng dung dịch rắn, các kiểu liên kết
Câu 1a: Kể tên các kiểu dung dịch rắn mà anh (chị) biết ? Hợp chất hóa học có phải là dung
dịch rắn không? Tại sao?
Câu 1b: Thế nào là dung dịch rắn? Phân biệt dung dịch rắn và hợp chất hóa học. Câu
1c: Thế nào là sai sót Frenkel, sai sót Schottky Gợi ý:
Phân biệt dung dịch rắn và hợp chất hóa học.
Dung dịch rắn: Thành phần biến ổi, không phải hàm trạng thái. Cấu trúc tương tự một trong hai
cấu tử thành phần. Dung dịch rắn chia ra dung dịch rắn lẫn, dung dịch rắn thế (thay thế), dung dịch rắn thiếu. Page 6 of 34 lOMoARcPSD| 36991220
Hợp chất hóa học: Thành phần cố ịnh (theo hệ số tỷ lượng), là hàm trạng thái. Cấu trúc khác biệt
các cấu tử thành phần. Hợp chất hóa học không phải dung dịch rắn
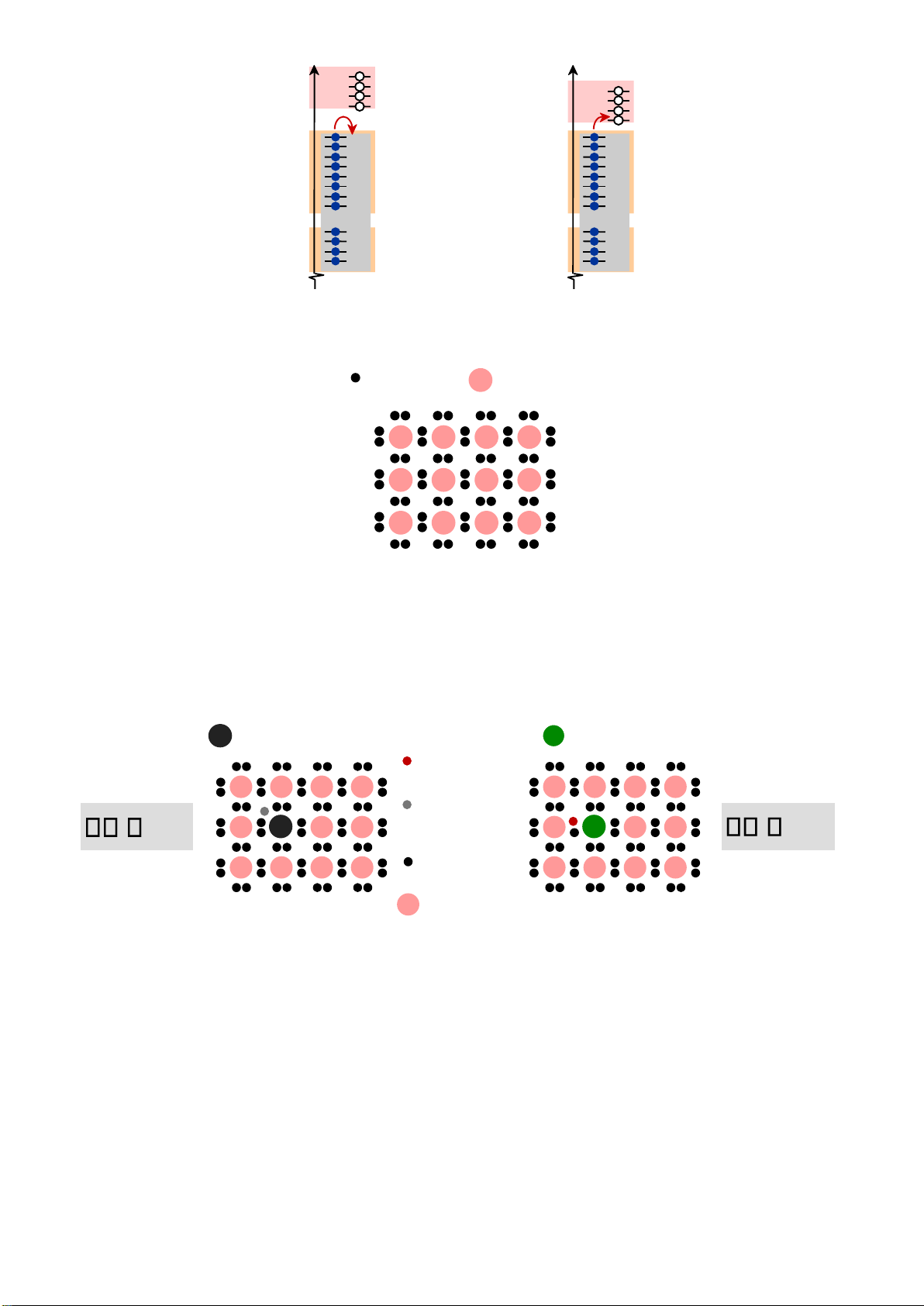
Sai sót Frenkel, tạo dung dịch rắn lẫn (intestial): iện tích hệ không ổi, tổng số phần tử hệ không ổi, tạo 1 lỗ trống
Sai sót Schotky: iện tích hệ không ổi , tổng số phần tử của hệ bị thay ổi (mất 1 cation và 1 anion, tạo 2 lỗ trống Schottky Defect Frenkel Defect
Câu 2: Theo quan iểm hóa học tinh thể, quan niệm thế nào về sự hình thành các hợp chất kép
kiểu AB, AB2, AB3 và A2B3 ? Tại sao không có kiểu cấu trúc riêng cho các hợp chất từ bốn phần tử trở lên? Gợi ý: Page 7 of 34 lOMoARcPSD| 36991220
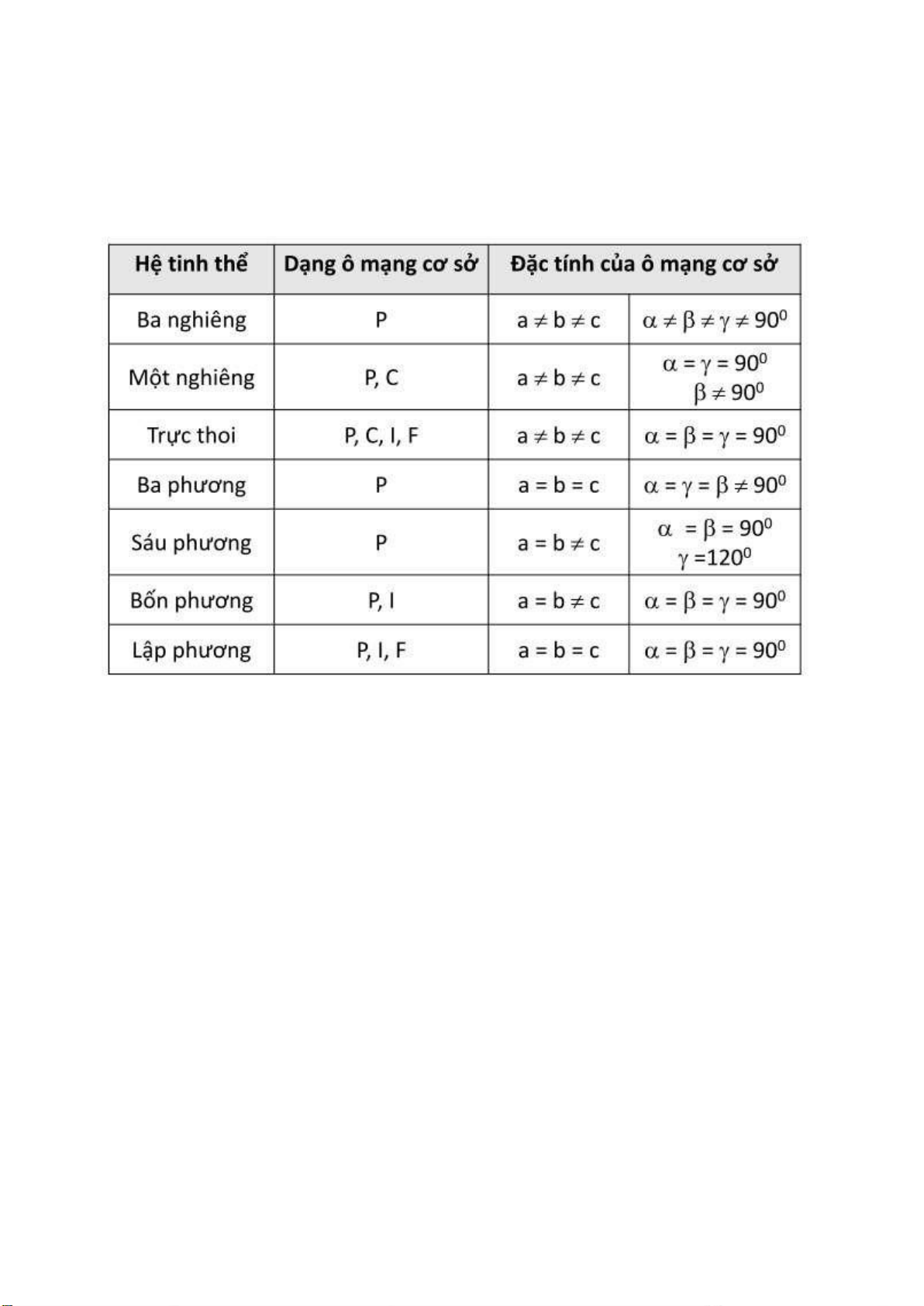
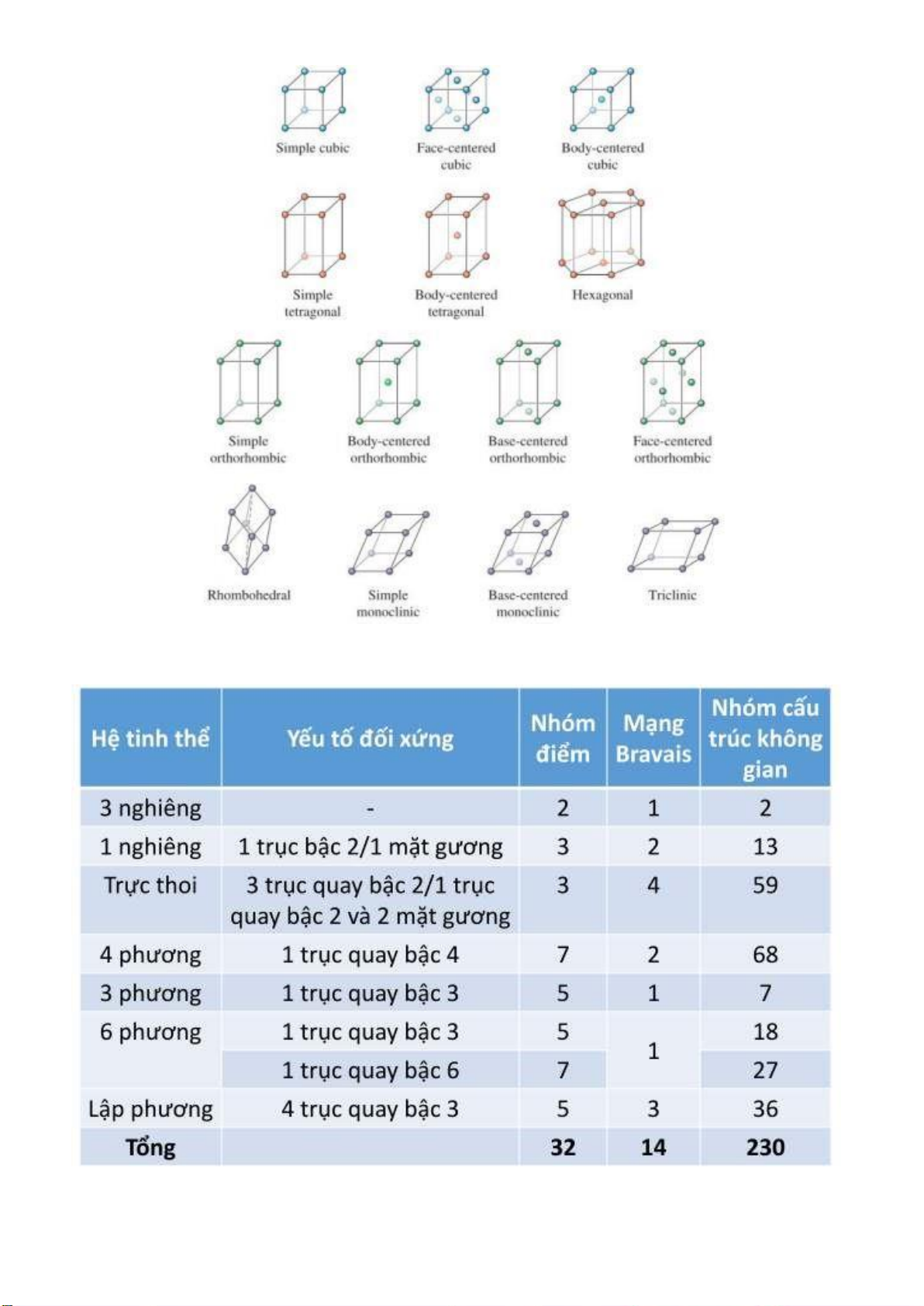
Các phần tử tạo thành 7 hệ tinh thể, 14 ô mạng Bravais, 32 yếu tố ối xứng, 230 nhóm cấu trúc
không gian ược phân loại thành 3 kiểu cấu trúc sắp xếp ặc trưng. Không có kiểu cấu trúc riêng
cho các hợp chất từ 4 phần tử trở lên. 7 hệ tinh thể 14 ô mạng Bravais Page 8 of 34 lOMoARcPSD| 36991220 Các yếu tố ối xứng Page 9 of 34 lOMoARcPSD| 36991220
Sự hình thành các hợp chất kép kiểu AB, AB2, AB3 và A2B3 : Các phần tử kích thước lớn tạo
cấu trúc sít chặt, các phần tử kích thước nhỏ xen vào lỗ trống LIÊN KẾT AB
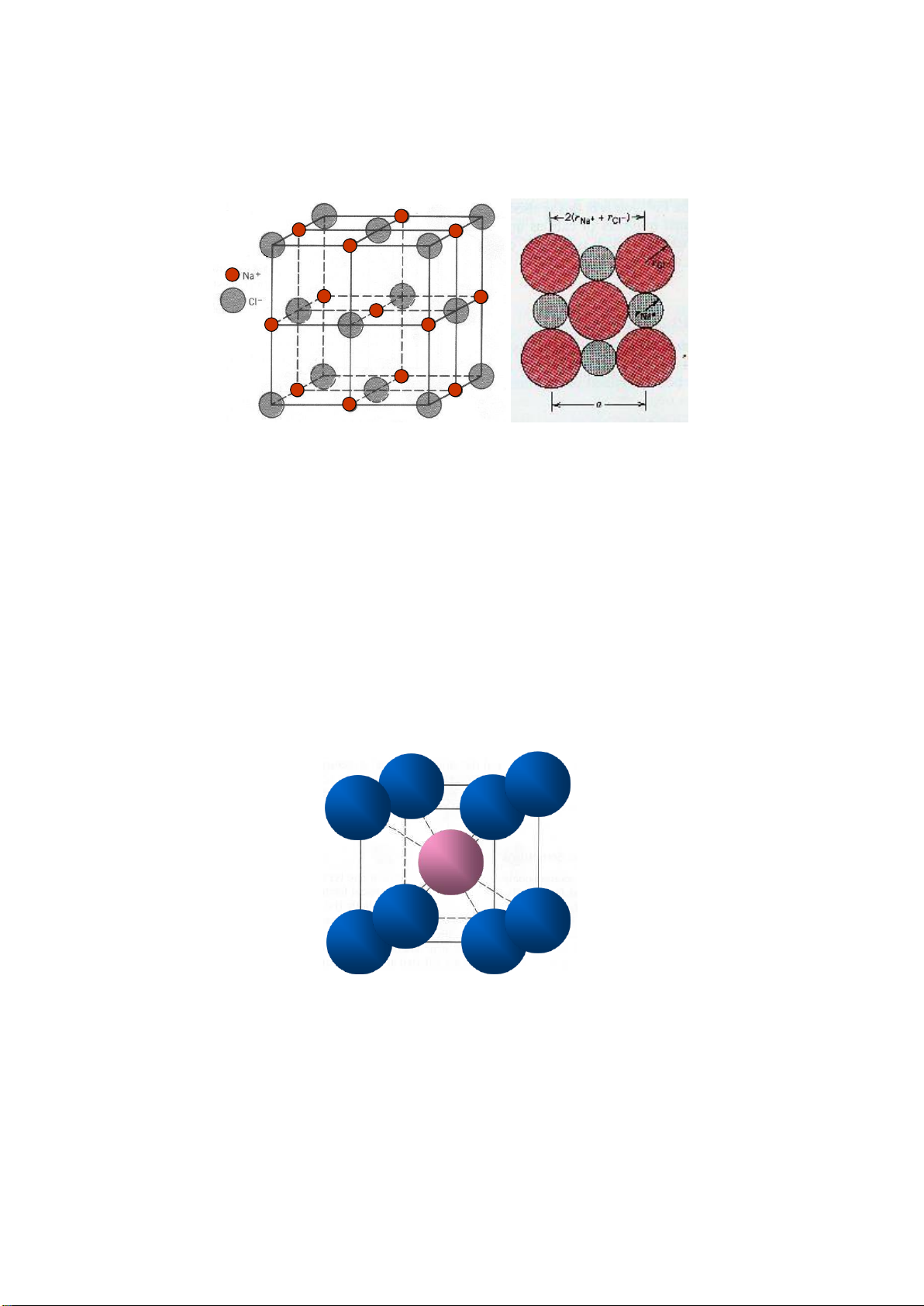
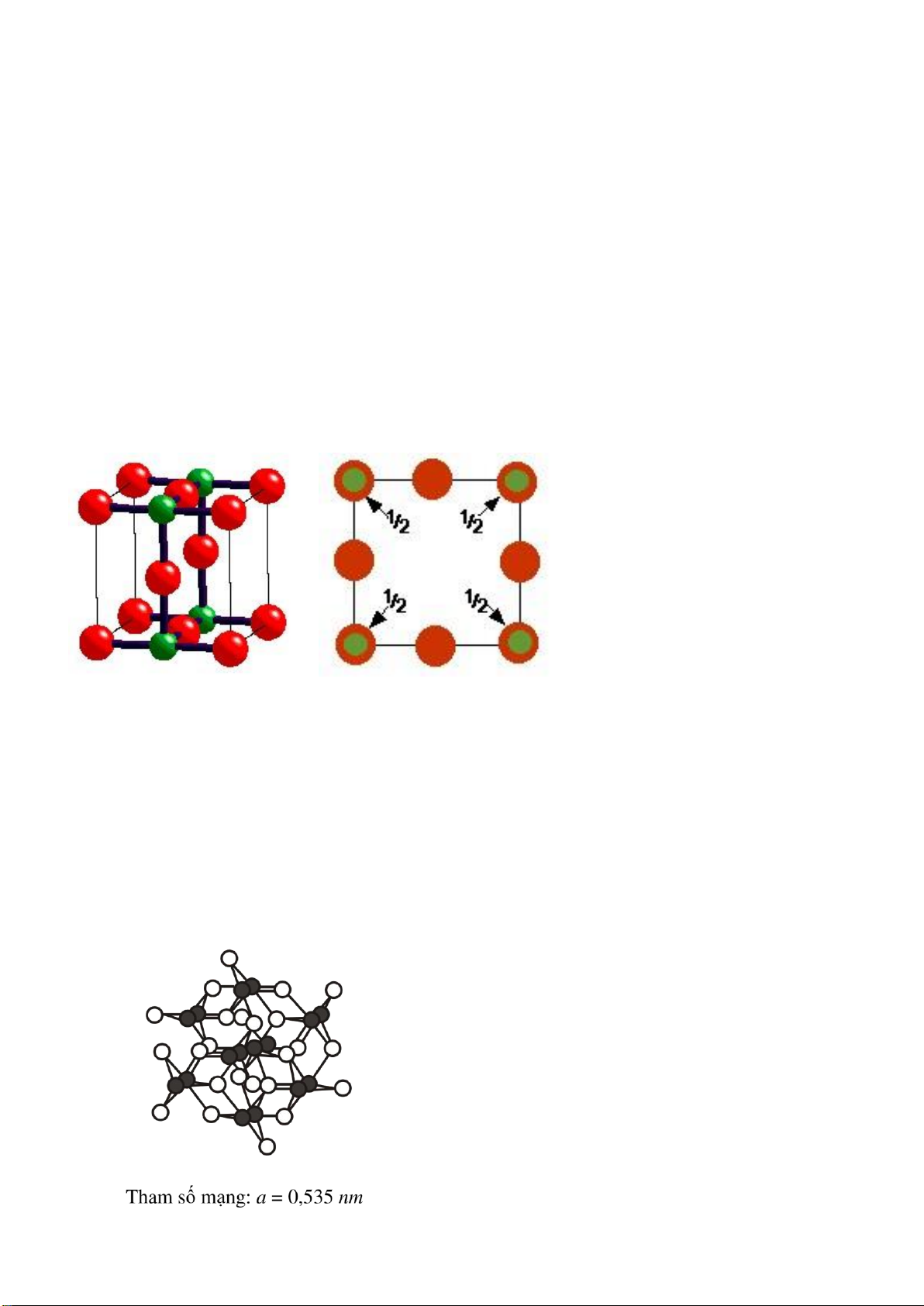
Liên kết AB: kiểu cấu trúc NaCl
• Tham số mạng a = 0.564nm
• Các ion trái dấu sắp xếp xen kẽ,
• Vị trí Na+ 1/2, 1/2, 1/2; Cl- 0,0,0.
• Số phối trí: Na+ 6; Cl- 6 (baùt dieän).
• Cl- sắp xếp vị trí lập phương (nút và tâm mặt)
• Kiểu cấu trúc NaCl: oxit (TiO, VO, NbO…), carbid, nitrid, sunfua, fosfua, selenit,
arsenit, telurid của các kim loại chuyển tiếp, một số halogenit kim loại kiềm halogenid kim loại kiềm thổ.
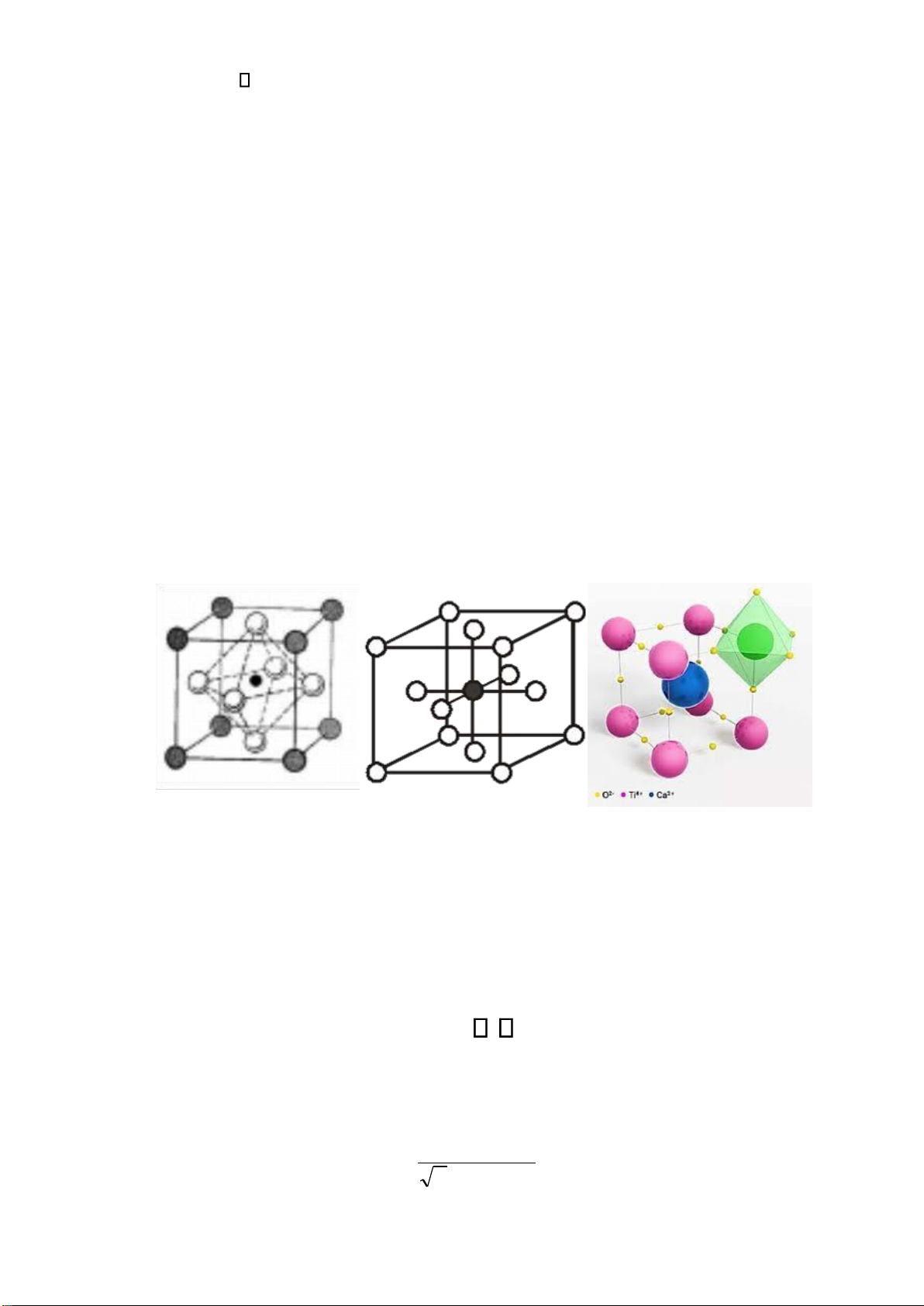
Liên kết AB: kiểu cấu trúc CsCl
• Tham số mạng: 0,412nm
• VVị trí các phần tử: Cs+: 0, 0, 0; Cl-: 1/2, 1/2, 1/2.
• Số phối trí Cs+ 8; Cl- 8.
• CsCl: cấu trúc liên kết ion iển hình, có ộ âm iện rất khác nhau
• Các chất có cấu trúc CsCl: CsBr, CsI, NH4Cl…
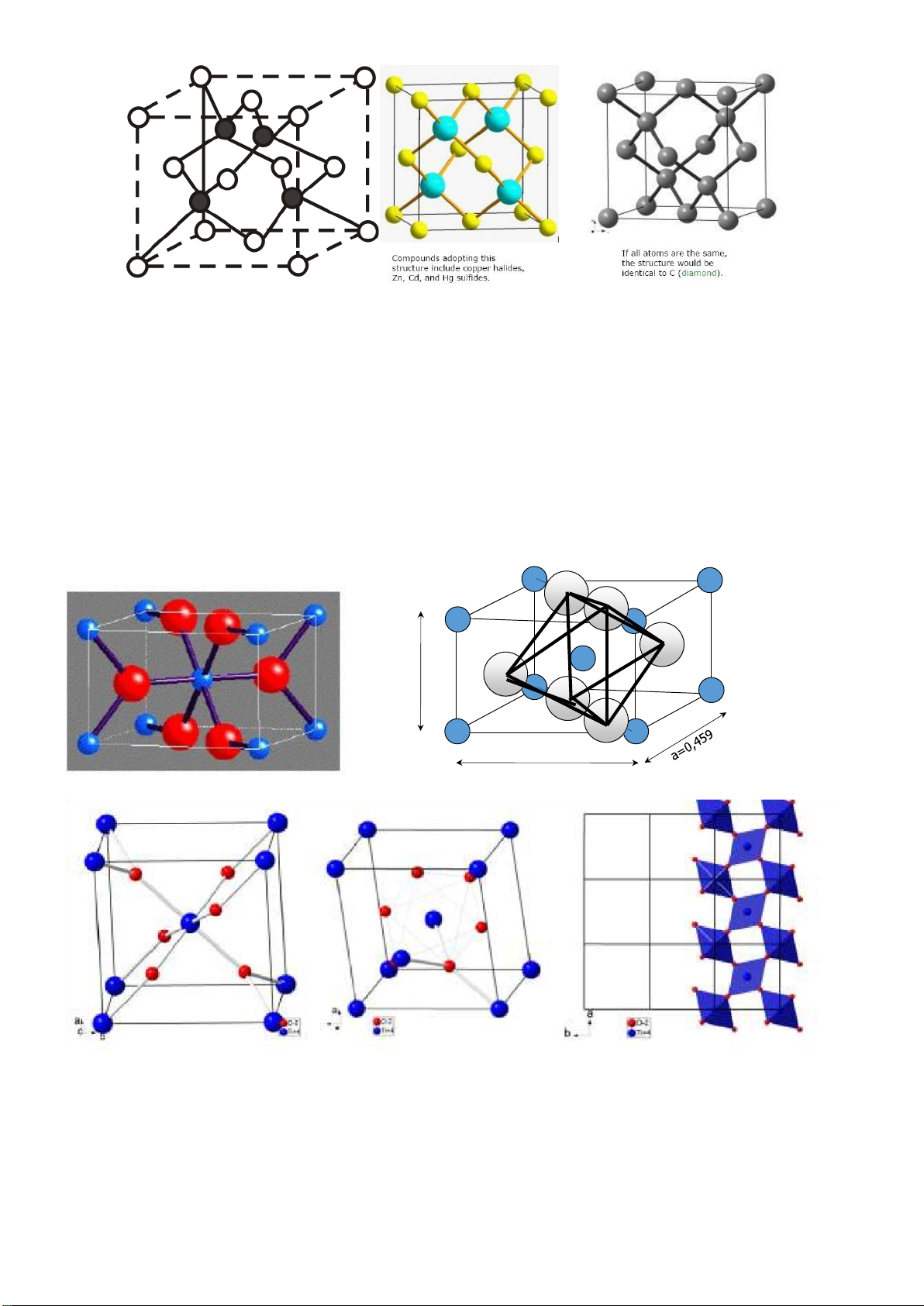
Liên kết AB: kiểu cấu trúc ZnS (Sfalerit), kiểu cấu trúc của kim cương Page 10 of 34 lOMoARcPSD| 36991220
• Tham số mạng: a = 0,541 nm
• Vị trí các phần tử:
• Zn2+:0, 0, 0; S2-: 1/4, 1/4, 1/4.
• Số phối trí Zn 4 (tứ diện), S 4 (tứ diện).
LIÊN KẾT AB2 hay MO2
Liên kết AB2: kiểu cấu TiO2, Rutil c=0,296 a=0,459 Đỏ: O2- Xanh: TI4+ • Tham số mạng: •
a = 0,459; c = 0,296 • Vị trí các phần tử: Page 11 of 34 lOMoARcPSD| 36991220 • Ti4+: 0,0,0; •
O2-: u,u,0 (u = 0,3053) •
Số phối trí Ti: 6 (bát diện); • O: 3 (tam giác). •
Rutil dạng thù hình nhiệt ộ cao của TiO2 là tứ diện, trong ó các bát diện
TiO6 liên kết ường tạo các dải hữu hạn. Các hợp chất có cấu trúc Rutil: CoF2, FeF2, CrO2, PbO2, SnO2, TeO2, WO2.
LIÊN KẾT AB3 hay MO3
Liên kết AB3: kiểu cấu ReO3, Rhenium trioxide
• Tham số mạng: a = 0,375 nm
• Vị trí các phần tử:
• Re6+ 1/2,1/2,1/2; O2-: 1/2, 0,1/2.
• Số phối trí Re là: 6 (bát diện), O là 2 ( ường thẳng).
• ReO3 là kiểu cấu trúc của nhiều oxit : Nb2O5; Nb12O29; Mo8O23; W20O58...
LIÊN KẾT A2B3 hay M2O3
Liên kết A2B3: kiểu cấu Cr2O3 Page 12 of 34 lOMoARcPSD| 36991220 = 55,10
Vị trí các phần tử: Cr3+: u,u,u; (u=0,3475); O2-: u, 1/2 -u, 1/4
• Số phối trí Cr: 6 (bát diện); O: 4 (tứ diện). Cấu trúc Cr2O3 hình thành từ bát diện CrO6
và tứ diện CrO4. Bát diện CrO6 nghiêng như hình chóp tam giác ngược, trong ó các
nguyên tử oxy trong kiểu cấu trúc Cr2O3 có dạng như hai hình chóp.
• Các oxit Al2O3, Ti2O3 ,V2O3 v Fe2O3 (hematít) có cấu trúc Cr2O3. LIÊN KẾT ABxOy
Oxy tạo cấu trúc sít chặt (nút mạng), các ion A và B thế vào các lỗ trống tứ diện hoặc bát
diện. Vì vậy, chỉ có thể có hai dạng cấu trúc:
-Perovskite ( ại diện: CaO.TiO2 ~ CaTiO3) hoặc Spinel ( ại diện: MgAl2O4 hoặc MgO.Al2O3)
Cấu trúc Perovskite ví dụ CaTiO3, có tính áp iện
• Tham số mạng: a = 0,384 nm
• Vị trí các phần tử: Ca2+ 0,0,0; Ti4+ 1/2, 1/2,1/2 ; O2- 1/2,1/2,0
• Số phối trí Ti: 6 (bát diện), O:6 (bát diện)
• Perovskit: cấu trúc lập phương iển hình của nhóm h/c ABX3. bán kính các ion thỏa mãn phương trình: 0,75 t 1 • Trong thực tế:
t = rA + rB =1 2(r + B rX) Page 13 of 34 lOMoARcPSD| 36991220
• Với perovskit, các yếu tố ối xứng mạng lập phương chuyển sang dạng thoi, một nghiêng…
• Các hợp chất sắt từ cấu trúc perovskit: BaTiO3, NaNbO3, KNbO3; GdFeO3 dạng trực
thoi, BaCeO3 một nghing và LaCoO3 thoi. Các h/c không tỷ lượng A1-X BX3 (ví dụ
NaxWO3) và ABX3-X (ví dụ CaFeO2,5) có cấu trúc perovskit.
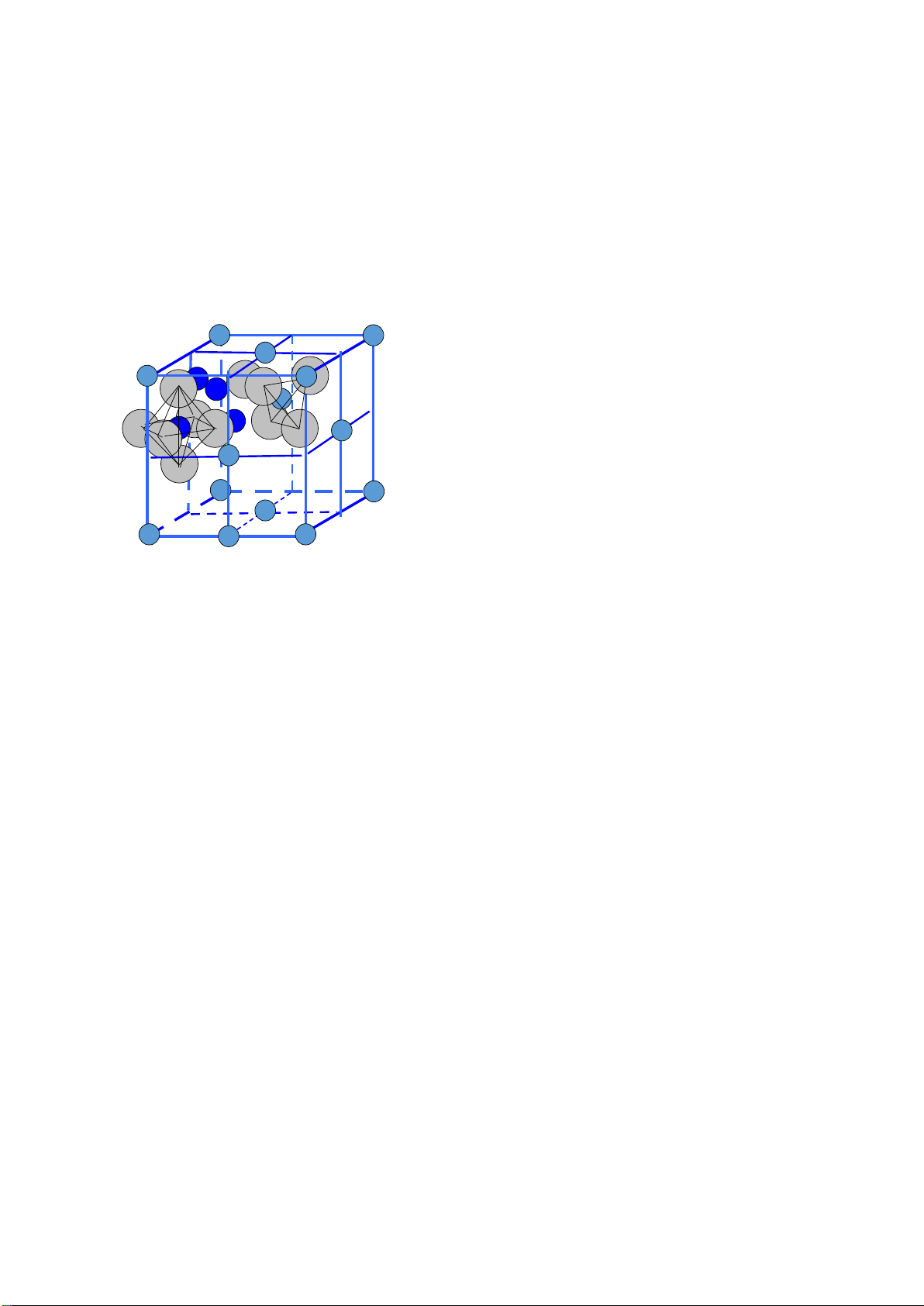
Cấu trúc Spinel ví dụ MgO.Al2O3 (AB2O4)
Tham s ố m ạ ng a = 0,809 nm .
Vị trí các phần tử: Mg2+ 0,0,0;
Al3+: 5/8,5/8,5/8; O2-: u,u,u (u = 0,387).
Số phối trí Mg2+: 4 (tứ diện); Al3+: 6 (bát diện).
• Mạng cơ sở: 8 cation Mg2+, 16 cation Al3+ & 32 anion O2-
• Độ dài liên kết: Al– O = a/4; Mg–O = 0,216 a. • Cấu trúc spinel :
• - O2- sắp xếp lập phương tạo lỗ trống bát diện và tứ diện.
• - Mg2+ chiếm 1/8 lỗ trống tứ diện, Al3+ chiếm 1/2 lỗ trống bát diện.
Các vị trí có thể chiếm chỗ: 1.Vị trí nút mạng;
2. Vị trí tâm (tâm mặt và tâm khối)
 vị trí nút mạng và tâm tạo cấu trúc xít chặt, có thể tích nhỏ nhất
3. Vị trí lỗ trống (các phần tử kích thước nhỏ hơn xen vào vị trí lỗ trống): gồm lỗ trống tứ diện
và lỗ trống bát diện. Các phần tử thứ tư sẽ tạo dung dịch rắn, không tạo cấu trúc kiểu mới Page 14 of 34 lOMoARcPSD| 36991220
Câu 5: Anh (chị) hãy cho biết thế nào là khuếch tán. Trình bày ịnh luật Fick I, II về khuếch tán do chênh
lệch nồng ộ trong chất rắn. Gợi ý:
Khuếch tán là quá trình chuyển chất nhằm cân bằng thế.
Khuếch tán trong chất rắn là quá trình chuyển vận nhằm cân bằng nồng ộ vật chất với ộng lực là
sự chênh lệch nồng ộ.
Ở nhiệt ộ lớn hơn nhiệt ộ 0 tuyệt ối, luôn tồn tại sai sót iểm. Do ó, luôn có khuếch tán trong tinh thể.
Định luật Fick I: trong iều kiện khuếch tán ổn ịnh, dòng khuếch tán các nguyên tử bằng hệ số
khuếch tán D nhân với gradient khuếch tán dc/dx. Phương trình ịnh luật Fick I
Cho dòng Ji khuếch tán nồng ộ ci theo phương x: J =− i Di ci x
Định luật Fick II cho dòng khuếch tán không ổn ịnh. Chứng minh:
Dòng Jx+dx tại khoảng cách x+dx, sau thời gian dt: J − x dx+ = +Jx Jx dx =−Di cxi x (Di cxi )dx
Dòng khuếch tán sau thời gian dt: ci = J = = x dx+ −Jx x Di cxi Di x2c2 t Kết luận: dC d C2 = D 2 dt dx
Câu 6: Cho phương trình “giả hóa học” ược mô tả bằng hệ thống ký hiệu Kröger – Vink như sau: ClClx →VCl/ + 1Cl2 2
Anh (chị) hãy giải thích các ký hiệu của phương trình”giả hóa học” trên. Theo
hệ thống ký hiệu Kröger – Vink, ta có bảng mô tả sau ây:
Nguyên tử Na ở vị trí cân bằng NaxNa Page 15 of 34 lOMoARcPSD| 36991220
Nguyên tử Cl ở vị trí cân bằng ClClx
Lỗ trống tại vị trí nguyên tử Cl, có iện tích hiệu dụng -1 VCl/
Khí Cl2 tách khỏi mạng tinh thể Cl2
Câu 7: Anh (chị) cho biết thế nào là số phối trí, a diện phối trí? Phân biệt ô mạng cơ sở và a diện phối trí.
Ô cơ sở là ơn vị nhỏ nhất của mạng tinh thể, mang tính ối xứng ặc trưng của mạng tinh thể.
Ô cơ sở có số cạnh bằng nhau và số góc bằng nhau nhiều nhất, các góc vuông giữa các
cạnh phải nhiều nhất và thể tích nhỏ nhất (cạnh bên ngắn nhất).
Mạng Bravais và ô cơ sở công cụ hiệu quả ể mô tả cấu trúc có trật tự, sắp xếp tuần hoàn.
Cách tiếp cận khác là xem xét một cấu trúc thông qua ếm số phần tử lân cận gần nhất của
mỗi phần tử trung tâm và dạng hình học của sự phân bố các phần tử xung quanh này.
Số nguyên tử hoặc ion lân cận gần nhất xung quanh nguyên tử hoặc ion ược xét ến ược gọi
là số phối trí của nguyên tử hoặc ion ó. Dạng hình học từ sự phân bố các nguyên tử hoặc
ion lân cận này gọi là a diện phối trí.
Câu 8: Nhiệt ộng học kết tinh có thể mô tả bằng phương trình dưới ây. Anh (chị) hãy giải thích ý nghĩa
của phương trình.
= + G4 .r .2 .r3 GV
Xác ịnh kích thước tới hạn r* ể G ạt giá trị cực trị
Câu b: Thiết lập phương trình tính năng lượng cho quá trình tạo mầm kết tinh từ pha lỏng ồng
chất ể ánh giá chiều hướng quá trình theo hàm thế nhiệt ộng ẳng áp G (coi các mầm có dạng hình cầu).
Câu 9: Viết phương trình tính năng lượng theo hàm thế nhiệt ộng ẳng áp G cho quá trình tạo
mầm kết tinh từ pha lỏng ồng chất (coi các mầm có dạng hình cầu). Gợi ý
Phương trình biến ổi năng lượng Gibbs. Giả thiết tinh thể dạng cầu, bán kính r.
r: là bán kính hạt γ: là năng lượng bề mặt
ΔGV: biến ổi năng lượng trên một ơn vị thể tích pha rắn
Năng lượng tạo pha mới (năng lượng bề mặt): 4 r2
Năng lượng phát triển pha mới với thể tích tăng (năng lượng phát triển khối): (4/3)πr3ΔGV
Hai quá trình trái ngược: γ lớn ể hạt bền, nhưng cần phá vỡ bề mặt cũ ΔGV tạo bề mặt mới. Năng
lượng tạo bề mặt mới và phát triển pha mới (năng lượng quá trình kết tinh) cân bằng khi hạt ạt
tới kích thước tới hạn (kích thước cân bằng) r* Page 16 of 34 lOMoARcPSD| 36991220 G=4 r2 +4/3 r3 GV
Để G ạt giá trị cực trị, d G/dr ( ạo hàm) bằng 0 tại r*
........................................................................................
Câu 10: Anh (chị) hãy cho biết thế nào là biến ổi thù hình? Nêu các loại biến ổi thù hình theo Bugger.
Thế nào là biến ổi martensite?
........................................................................................................................................................
Biến ổi thù hình là sự biến ổi cấu trúc tinh thể mà không thay ổi thành phần hóa học, chỉ xảy
ra với một số chất rắn. Phân loại theo Bugger:
− Biến ổi bậc một (biến ổi số phối trí)
− Biến ổi bậc hai (không biến ổi số phối trí)
− Biến ổi do sai sót cấu trúc
− Biến ổi do thay ổi kiểu liên kết hóa học.
Biến ổi martensite là nhóm biến ổi ặc biệt, ặc trưng kim loại và hợp kim. Biến ổi martensite
không thuận nghịch nhiệt ộng nhưng thuận nghịch cấu trúc. Martensite là biến ổi không
khuếch tán do một số nhóm các nguyên tử cùng mặt dịch chuyển ở khoảng cách nhỏ hơn
khoảng cách giữa các nguyên tử. Page 17 of 34 lOMoARcPSD| 36991220 PHẦN BÀI TẬP:
Phần chỉ số nút: [[abc]]
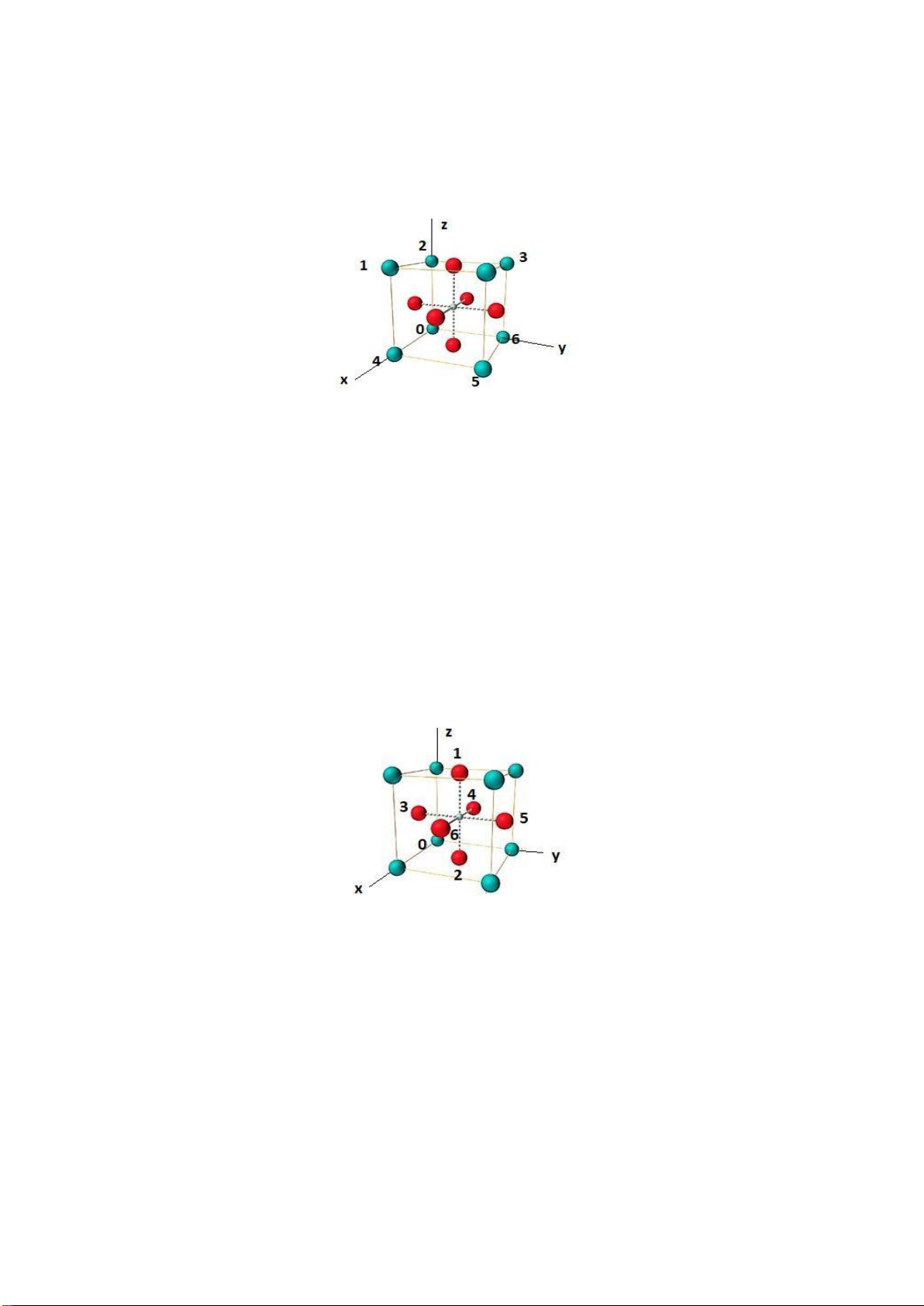
Câu 1. Xác ịnh các chỉ số nút của ion Ca2+ ( ánh dấu 1, 2, 3, 4, 5, 6 trên hình) trong cấu trúc
của BaTiO3 (cấu trúc perovskite). Gợi ý: Chỉ số nút Ca2+: 1: [[1 0 1]]; 2: [[0 0 1]]; 3: [[0 1 1]]; 4: [[1 0 0]]; 5: [[ 1 1 0 ]] 6: [[ 0 1 0 ]]
Câu 2. Xác ịnh các chỉ số nút của ion O2- ( ánh dấu 1, 2, 3, 4, 5, 6 trên hình) trong cấu trúc của
BaTiO3 (cấu trúc perovskite). Gợi ý: Chỉ số nút O2-: 1: [[1/2 ½ 1]]; 2: [[1/2 ½ 0]]; 3: [[1/2 0 1/2]]; 4: [[0 ½ 1/2 ]]; 5: [[ 1/2 1 1/2 ]] 6: [[ 1 1/2 1/2 ]] Page 18 of 34 lOMoARcPSD| 36991220
Phần chỉ số phương [abc]
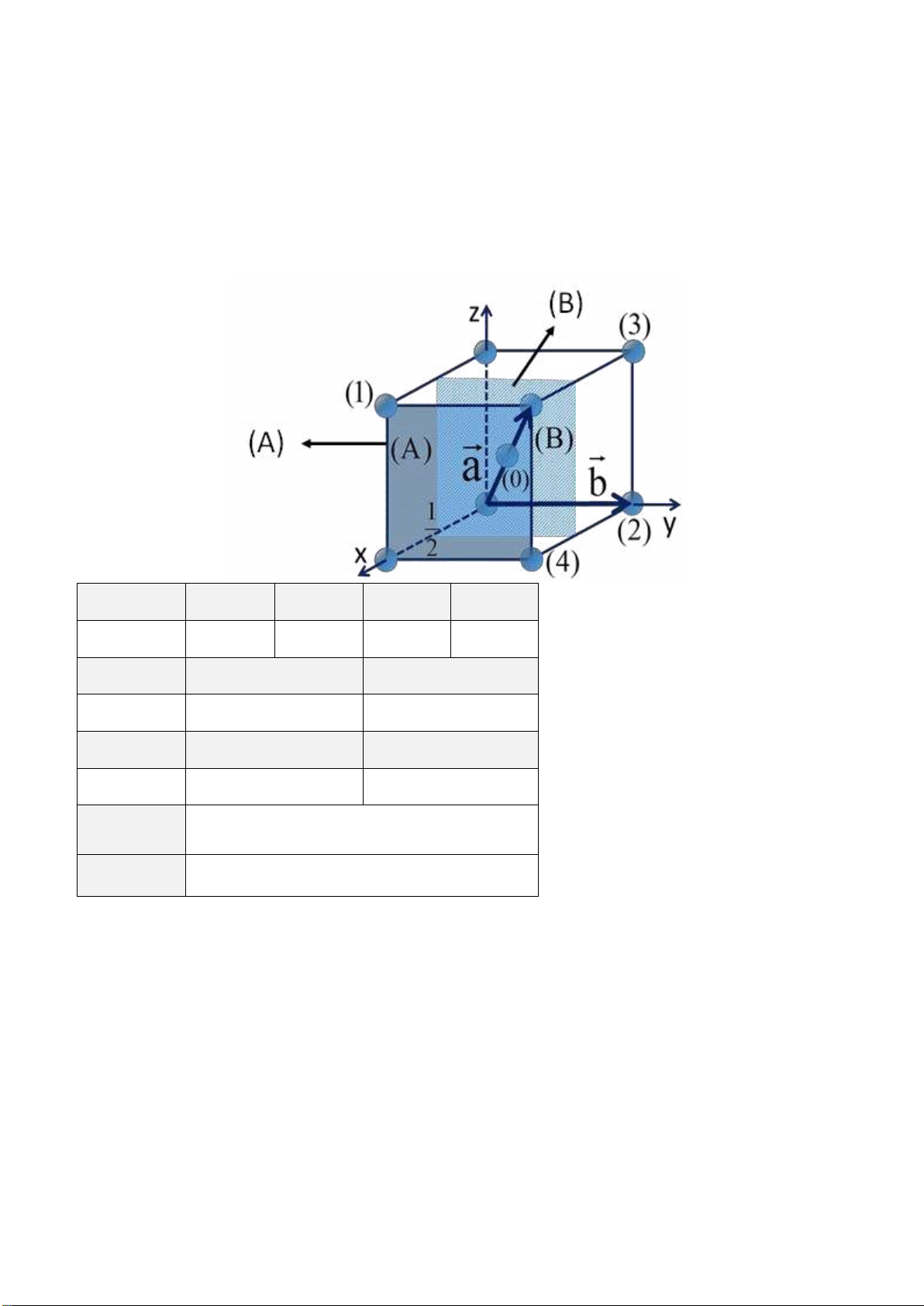
Câu 1: Cho hình vẽ ô mạng cơ sở như sau (tất cả các cạnh bằng nhau, tất cả các góc bằng 90o). Biết
nút (0) [[½½½]]. Anh (chị) hãy:
a). Xác ịnh chỉ số các nút mạng (1), (2), (3), (4).
b). Xác ịnh chỉ số các phương (a), (b) và các mặt mạng (A), (B).
c). Xác ịnh số phần tử thuộc về ô cơ sở.
d). Đây là mạng cơ sở gì? Nút (1) (2) (3) (4) Chỉ số Phương (a) (b) Chỉ số Mặt (A) (B) Chỉ số Số phần tử Kiểu mạng Gợi ý:
Nút (1): [[101]], nút (2): [[010]], nút (3): [[011]], nút (4): [[110]]
Phương a: [111], phương b: [010]
Mặt (A): (100), mặt (B): (200)
Số phần tử = 1/8x8 + 1 = 2 phần tử
Lập phương tâm khối (BCC) → →
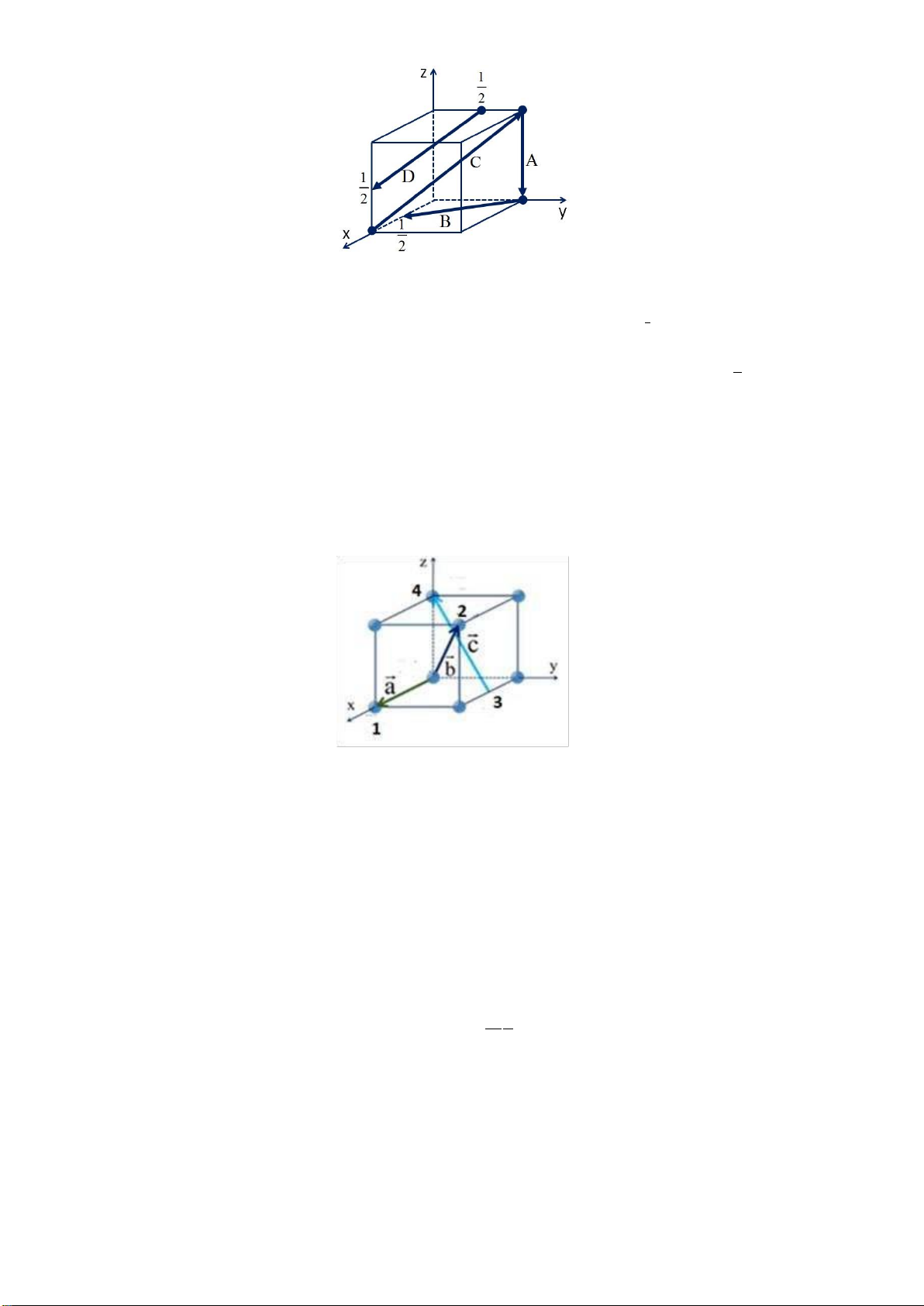
Câu 2. Xác ịnh chỉ số phương cho các phương A,B, C, D trong hình vẽ ô cơ sở sau. Page 19 of 34 lOMoARcPSD| 36991220 Gợi ý:
Chỉ số phương: Tọa ộ ỉnh trừ tọa ộ gốc
Phương A: Đỉnh [[0,1,0]] Gốc [[0,1,1]]  Đỉnh – gốc :[00-1] hay [001]
Phương B: Đỉnh [[1/2,0,0]] Gốc [[0,1,0]]  Đỉnh – gốc :[ 1/2,-1,0] ~[1-20] hay [120]
Phương C: Đỉnh [[0,1,1]] Gốc [[1,0,0]]  Đỉnh – gốc :[-111]
Phương D: Đỉnh [[1,0,1/2]] Gốc [[0,1/2,1]]  Đỉnh – gốc :[ 1,-1/2,-1/2] ~[2-1-1]
Câu 3: Xác ịnh chỉ số các nút ược ánh dấu 1, 2, 3, 4 trên hình dưới. Viết chỉ số phương các vec tơ i qua nút Gợi ý:
Chỉ số nút : Ký hiệu sai không cho iểm 1. [[100]], 2. [[111]] 3. [[1/2 10]] 4. [[001]] Chỉ số phương: Phương a : [100] Phương b : [111]
Phương c : [-1/2 -1 1] (quy ồng mẫu số)  [-1 -2 2] ~ [122] Page 20 of 34 lOMoARcPSD| 36991220
Phần chỉ số mặt Miller (hkl)
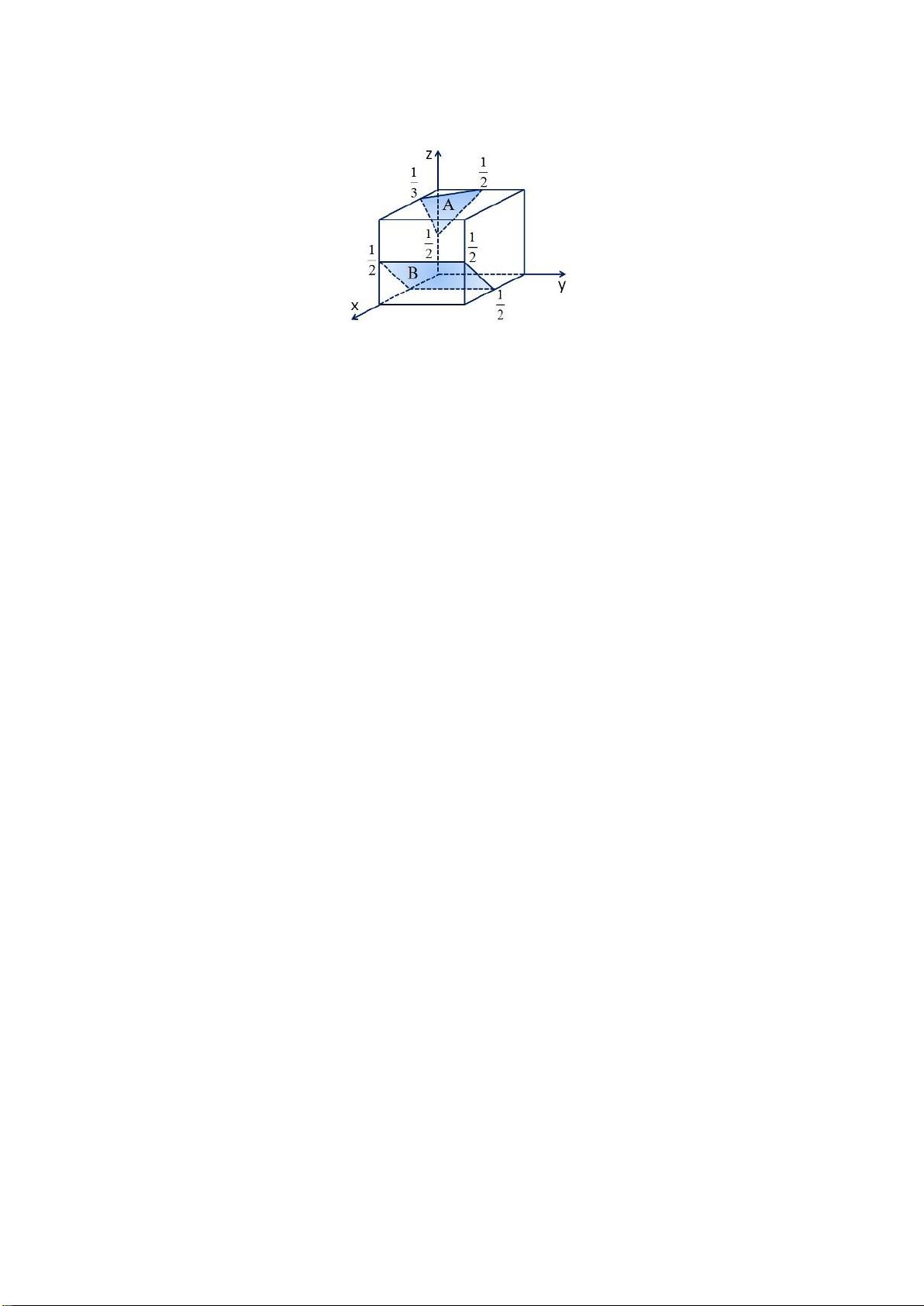
Câu 1. Xác ịnh chỉ số Miller cho các mặt mạng A, B trong hình vẽ ô cơ sở lập phương sau. Gợi ý:
Chỉ số Miller mặt mạng A:
Tọa ộ giao iểm: - 1/3, -1/2, 1/2.
Lấy nghịch ảo: - 3, - 2, 2.
Khử mẫu, có: (hkl) = (-3 -2 2)
Chỉ số Miller mặt mạng B:
Tọa ộ giao iểm: 1/2, ∞ , - 1/2 .
Lấy nghịch ảo: 2, 0, - 2.
Khử mẫu, có: (hkl) = (2 0 -2) Page 21 of 34 lOMoARcPSD| 36991220
Phần tính số phần tử theo ường, theo mặt, theo ô cơ sở:
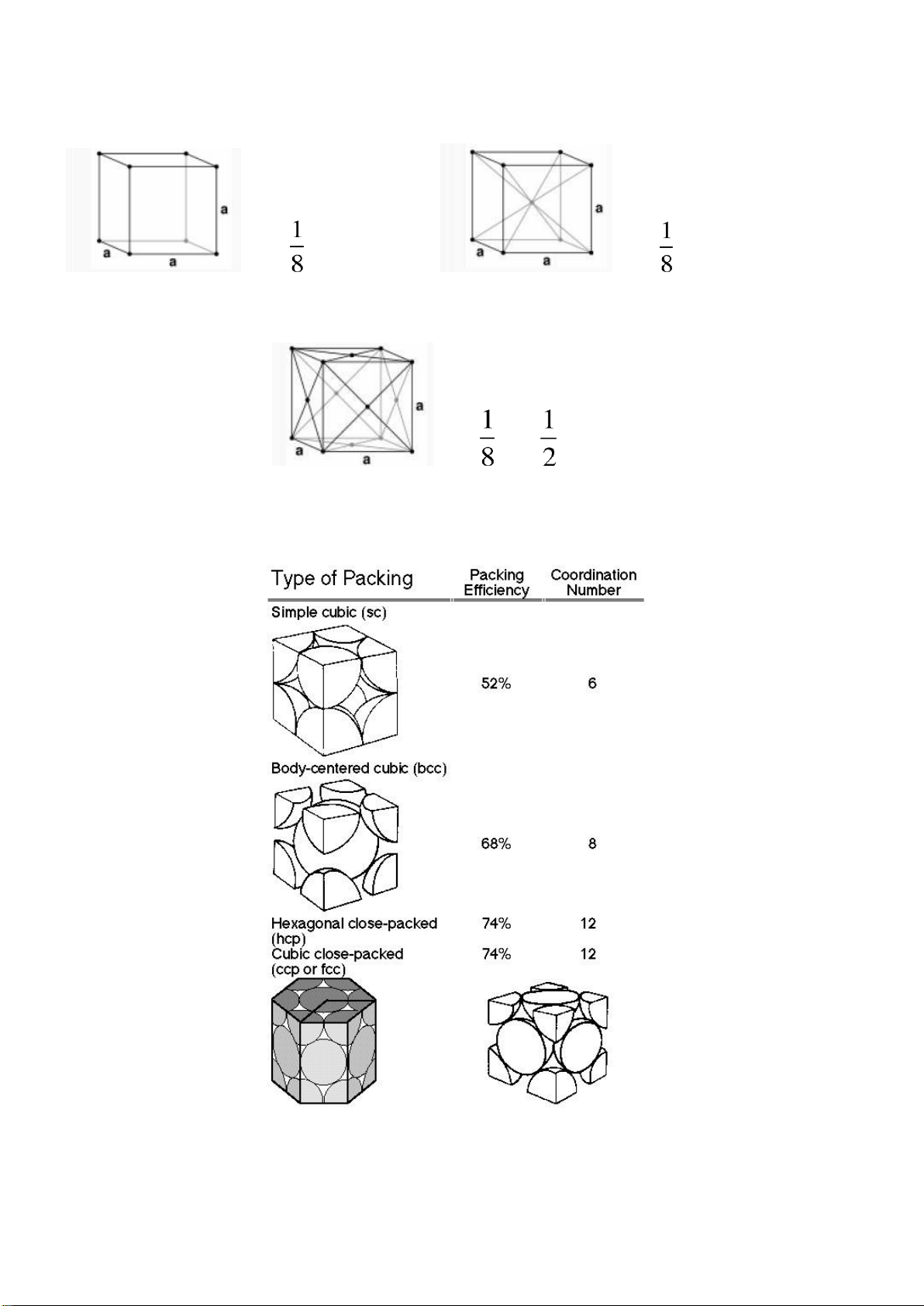
Kiến thức cần nhớ: n = .8 = 1 n = .8 + =1 2 Lập phương ơn giản Lập phương tâm khối n = .8 + .6 = 4 Lập phương tâm mặt
Mật ộ xít chặt theo thể tích (APF, APE) và số phối trí
Số phần tử theo mặt (thứ nguyên: số phần từ/diện tích mặt)
Câu 1: Anh (chị) hãy xác ịnh mật ộ sắp xếp nguyên tử (nguyên tử/m2) trên mặt (110) của một ô cơ sở
có cấu trúc lập phương tâm mặt có thông số a=b khác c. Biết thông số mạng a = 4Å, c = 6Å. Gợi ý: Page 22 of 34 lOMoARcPSD| 36991220
Vẽ ô cơ sở FCC và mặt (110)
Số phần tử mặt (110) i qua =2 12 +4 14 =2 o
Diện tích mặt (110) = 2ac= 2 4 6 24 2(A) =2 = Mật ộ 2 − = 20 5,89 10 18nguyên tử/m2 24 2 10
Số phần tử theo ô cơ sở (thứ nguyên: số phần tử/ ô cơ sở)
Câu 1: Cho ô lập phương sau. Hãy ánh dấu vị trí các phần tử cấu tạo nếu ô cơ sở là lập phương
tâm khối. Tính số phần tử thuộc về ô lập phương tâm khối. Gợi ý:
Đánh dấu: Các phần tử ở nút mạng (8).
Các phần tử ở giữa khối ( 1 )
Tính số phần tử thuộc về ô lập phương tâm khối (BCC): 8.(1/8) + 1 = 2
Dạng xác ịnh cách thông số của ô cơ sở, quan hệ với thông số với bán kính phần tử
Câu 1: Anh (chị) hãy xác ịnh bán kính nguyên tử Rhodium (Rh). Biết Rh có cấu trúc lập phương tâm mặt
(FCC) và thông số mạng a = 0,381nm.
Trong cấu trúc FCC, ta có: Page 23 of 34 lOMoARcPSD| 36991220 4 R =a2 2 2 R = a = 0,381 =0 ,135nm 4 4
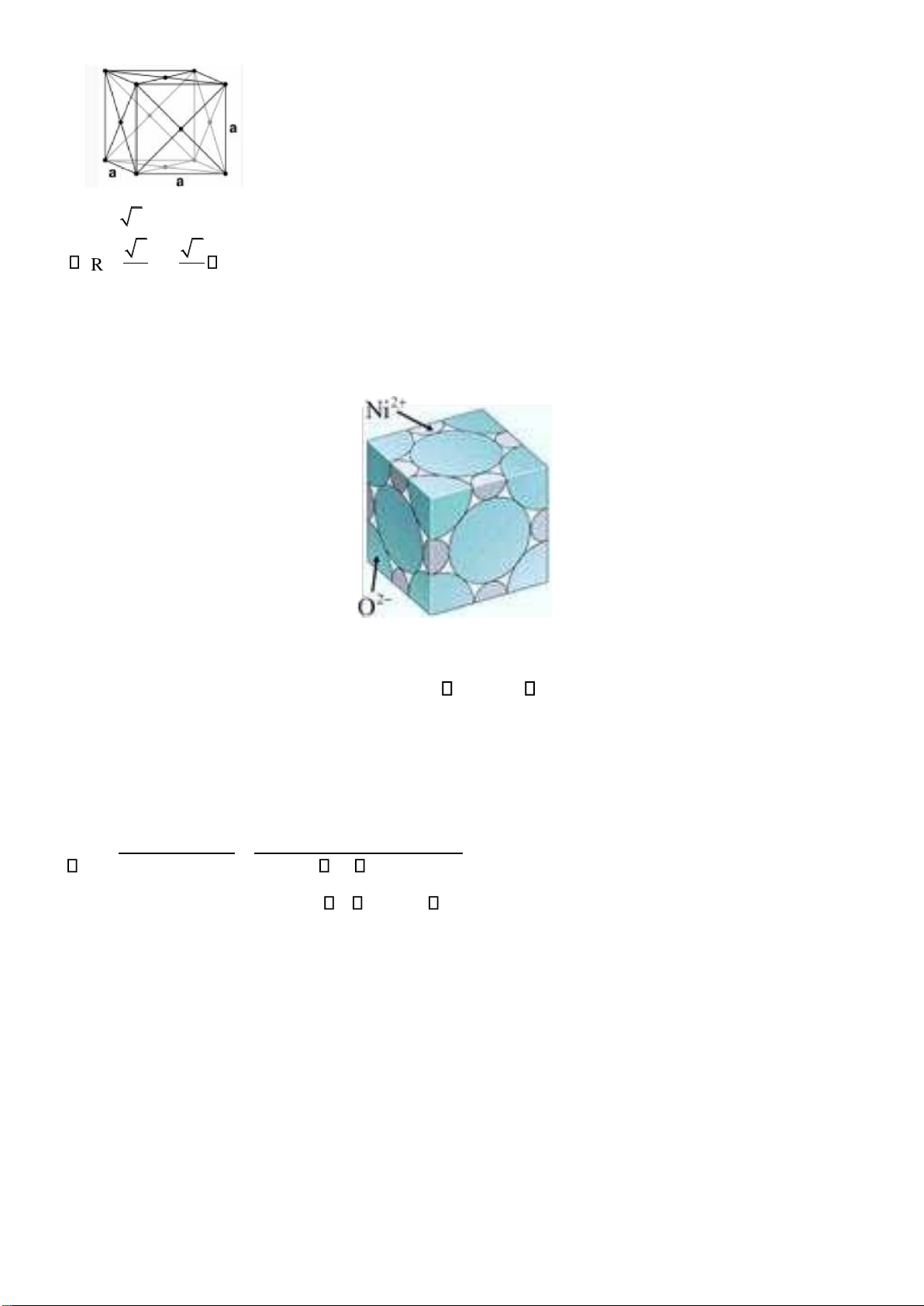
Câu 2: Anh (chị) hãy xác ịnh khối lượng riêng của NiO. Biết rằng, trong cấu trúc NiO, O2- sắp xếp ở
các nút lập phương, Ni2+ nằm trong tất cả các lỗ trống bát diện. Biết bán kính ion Ni2+ và O2- lần lượt
bằng 0,69Å và 1,32Å. Khối lượng mol của Ni và O lần lượt là 59g/mol và 16g/mol.
Số ion Ni2+ = số O2- trong 1 ô = 4 o
Thông số mạng của NiO: a = 2r + = 2+ 2R 2− 2 0 ,69+2 1 ,32= 4,02A Ni O
Trong 1 ô NiO, có 4 Ni2+ và 4 O2-.
Khối lượng riêng của NiO: = ) ) =
NiO4MNi23NiO+ +4AMO2− = (4 59 + 8 3 4 16( 23 7,67g/cm3 a N 4,02 10 − 6,02 10
Dạng ứng dụng phương trình nhiễu xạ tia X
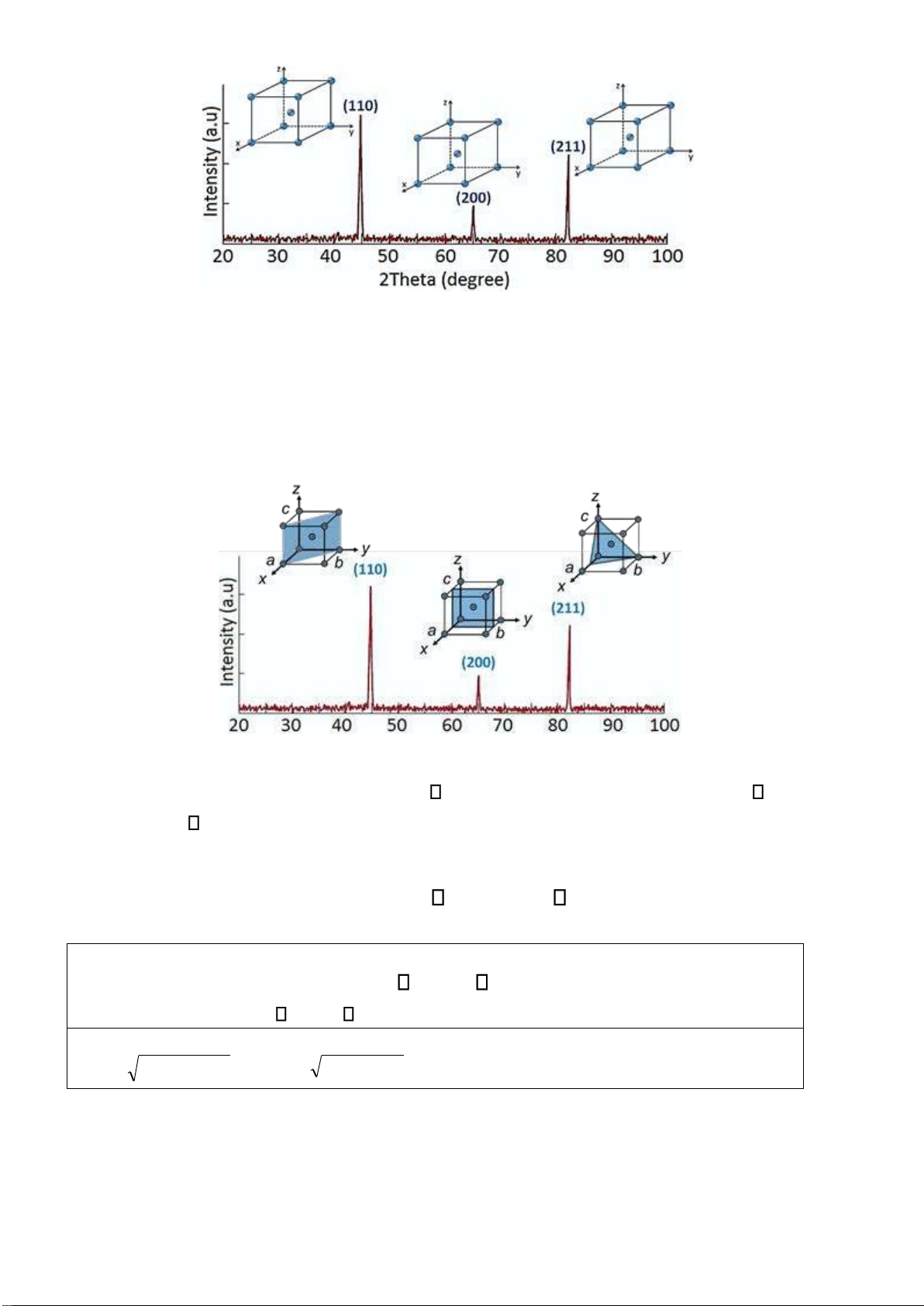
Câu 1: Cho phổ nhiễu xạ tia X (XRD) của sắt α (α-Fe) có cấu trúc tinh thể hệ lập phương như hình bên.
Anh (chị) hãy giải thích ý nghĩa của chỉ số (hkl) và vẽ các mặt mạng tương ứng với các chỉ số (vẽ trực tiếp vào hình). Page 24 of 34 lOMoARcPSD| 36991220 Gợi ý:
Chỉ số (hkl) tương ứng từng peak nhiễu xạ cho thông tin về chỉ số mặt mạng trong cấu trúc tinh thể.
Với cấu trúc lập phương, hệ trục tọa ộ cho trước, có thể vẽ lại các mặt mạng theo chỉ số (hkl) tương ứng.
Câu 2. Một vật liệu có cấu trúc tinh thể là lập phương tâm mặt (FCC). Sử dụng phương pháp
nhiễu xạ tia X (XRD) với bước sóng ơn sắc = 0,1028 nm ghi nhận góc nhiễu xạ cho mặt
mạng (311) là = 71,2o (n = 1). Chỉ ra cách xác ịnh các thông số d của họ mặt mạng này và
thông số mạng a của tinh thể này theo phương trình Wulf – Bragg (không cần tính ra con số).
(Phương trình nhiễu xạ Wulf-Bragg: n =2dsin , n =1). Gợi ý:
Các tia X giao thoa khi thỏa mãn phương trình Wuff-Bragg: n =2dsin
d(311) = n /2. sin = 1.0,1028/2. 0,95 (nm)= 0,04883 (nm)
Thông số mạng a: a =d h2 + + =k2 l2 0,04883 32 + + =12 12 0,04883.3,318= 0,162 (nm) Bài tập cơ tính
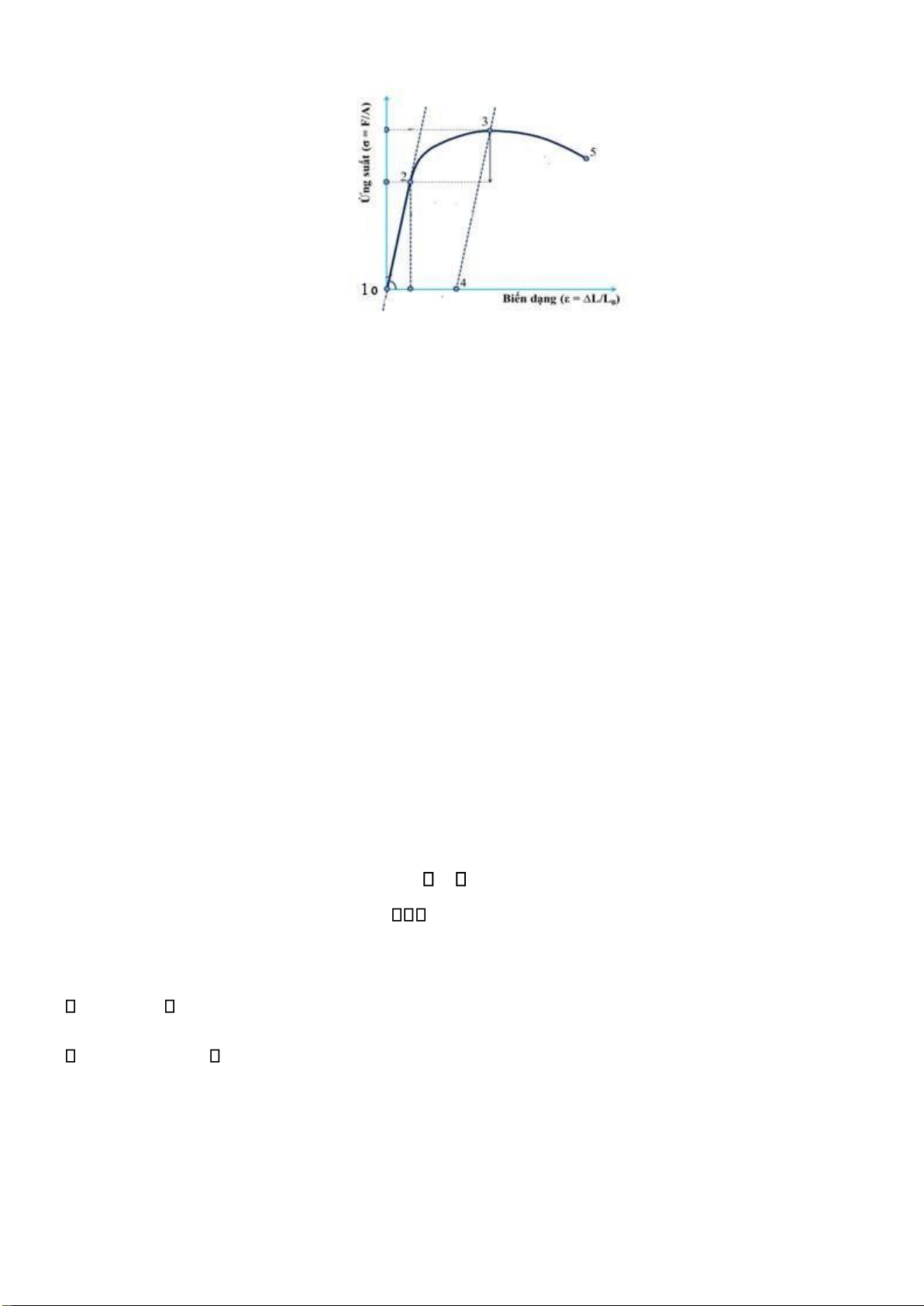
Câu 1: Thế nào là biến dạng àn hồi, biến dạng dẻo, phá hủy? Giải thích các iểm ký hiệu 1, 2, 3, 4, 5 trên
ường biến dạng kéo. Nếu sự khác nhau giữa biểu ồ ứng suất - biến dạng, biểu ồ lực kéo/nén – chuyển vị? Page 25 of 34 lOMoARcPSD| 36991220
Đường biến dạng kéo của vật liệu Gợi ý :
1.Biến dạng àn hồi (vùng tuyến tính, từ iểm 1 – 2),
2.Biến dạng dẻo (vùng phi tuyến, từ iểm 2 – 3),
3.Phá hủy (vùng phi tuyến 3- 5 tạo cổ và phá hủy tại 5).
Đường ứng suất – biến dạng sẽ theo oạn thẳng 3 – 4, song song với ường biến dạng àn hồi (1 – 2), trở
về iểm 4. Do hai ường song song, theo cả hai chiều biến dạng, mẫu thử vẫn có modul àn hồi là
E, nhưng ã bị biến dạng một oạn từ 1 – 4, ta ký hiệu oạn này là σy.
Sự tăng giới hạn àn hồi bởi biến dạng vĩnh viễn của vật liệu ược gọi là hóa bền (hay hóa cứng) do biến dạng. Câu 2 :
Tính modul àn hồi của một thanh kim loại có tiết diện 10mm x10mm. Biết rằng khi tác dụng lực kéo
3000N, thanh biến dạng dài từ 10cm thành 10,085cm (coi biến dạng là àn hồi, tuân theo ịnh luật Hooke) Gợi ý:
Biến dạng àn hồi ược coi là vùng tuyến tính 1-2, tuân theo ịnh luật Hooke: = E
E là mô-un àn hồi (hay mô-un Young) E =
Diện tích: 1cm x 1cm = 1cm2
: Ứng suất, = F/S = 3000 N/ 1 cm2 = 3000 (N/cm2) = 3.103 (N/cm2)
: Biến dạng (%). = 8,5.10-2 /10 = 8,5.10-3 = 0,85 %
Thế các giá trị, có: E = 3.103 /0,85 = 3,53.103 (N/cm2). Bài tập nhiệt:
Câu 1: Tính năng lượng cần thiết ể nâng nhiệt ộ mẫu 2 kg từ 20 lên 100oC của các vật liệu sau: Page 26 of 34 lOMoARcPSD| 36991220 (a) Nhôm; (b) Thép;
(c) Thuỷ tinh hệ soda – lime;
(d) High density polyethylene (HDPE)
Biết giá trị nhiệt dung riêng Cp
E(aluminum) = (900 J/kgK)*(2 kg)*(80K)=1.44 x 105 J
E(steel) = (486 J/kgK)*(2 kg)*(80K)=7.78 x 104 J
E(glass) = (840 J/kgK)*(2 kg)*(80K)=1.34 x 104 J
E(HDPE) = (1850 J/kgK)*(2 kg)*(80K)=2.96 x 105 J Giải:
NL ược tính từ PT 𝐸 = 𝐶𝑃 ∗ 𝑚 ∗ ∆𝑇 với ∆𝑇 = (100 + 273𝐾) − (20 + 273𝐾) = 80𝐾 và m = 2kg.
Tra bảng 19.1, ta có giá trị CP
(a) E(aluminum) = (900 J/kgK)*(2 kg)*(80K)=1.44 x 105 J (b)
E(steel) = (486 J/kgK)*(2 kg)*(80K)=7.78 x 104 J
(c) E(glass) = (840 J/kgK)*(2 kg)*(80K)=1.34 x 104 J
(d) E(HDPE) = (1850 J/kgK)*(2 kg)*(80K)=2.96 x 105 J
Câu 2: Tính nhiệt dung riêng (NDR) ẳng áp ở nhiệt ộ phòng cho các VL sau: (a) Nhôm (b) Bạc (c) Tungsten (W)
(d) Hợp kim 70Cu – 30Zn
Biết Cp(Al) = 900 J/kg.K Cp(Ag) 235 J/kg.K Cp(W)=138 J/kg.K
Cp(Hợp kim 70Cu – 30Zn)=375 J/kg.K Giải:
(a) Cho Al: CP = (900 J/kg.K)*(1 kg/1000 g)*(26.98 g/mol) = 24.3 J/mol.K
(b) Cho Ag: CP = (235 J/kg.K)*(1 kg/1000 g)*(107.87 g/mol) = 25.4 J/mol.K
(c) Cho W: CP = (138 J/kg.K)*(1 kg/1000 g)*(26.98 g/mol) = 25.4 J/mol.K
(d) Cho hợp kim 70Cu-30Zn, KLPTTB 𝐴𝑎𝑣𝑒 100 𝐶1∗𝐴1+𝐶2∗𝐴2 100 64.09𝑔/ 𝐴1 𝐴2 63.55 𝑔/𝑚𝑜𝑙 65.41 𝑔/𝑚𝑜𝑙 𝑚𝑜𝑙
Do vậy CP = (375 J/kg.K)*(1 kg/1000 g)*(64.09 g/mol) = 24.0 J/mol.K Page 27 of 34 lOMoARcPSD| 36991220
Câu 3: Làm lạnh 5 m Al từ 38oC xuống -1oC. Tính thay ổi chiều dài. Biết hệ số giãn nỡ nhiệt của
nhôm (Al) = [23.6 x 10-6 (oC)-1] Giải:
Ta có l = [23.6 x 10-6 (oC)-1] nên
l = lo* l* T = lo* l*(Tf – To) = (5 m)*[23.6 x 10-6 (oC)-1]*(-1oC – 38oC) = -4.6 x 10-3m = -4.6 mm Sợi nhôm bị co 4.6 mm
Câu 4: Sợi kim loại dài 0.1 m, thay ổi chiều dài △l là 0.2 m khi nung từ 20oC lên 100oC. Xác ịnh
hệ số giãn nở nhiệt (HSGNN) Giải:
HSGNN xác ịnh từ phương trình: 𝛼𝑙 = 𝑙
𝑜 ∆𝑙∗ ∆𝑇 = 𝑙𝑜 ∗ (𝑇∆𝑙− 𝑇 ) =
(0.1𝑚)0.2∗ (100 𝑥 10𝑜−3𝐶 −𝑚 20𝑜𝐶) = 25.0 𝑥 10−6( 𝑜𝐶)−1 𝑓 𝑜 Page 28 of 34 lOMoARcPSD| 36991220 Biểu ồ pha :
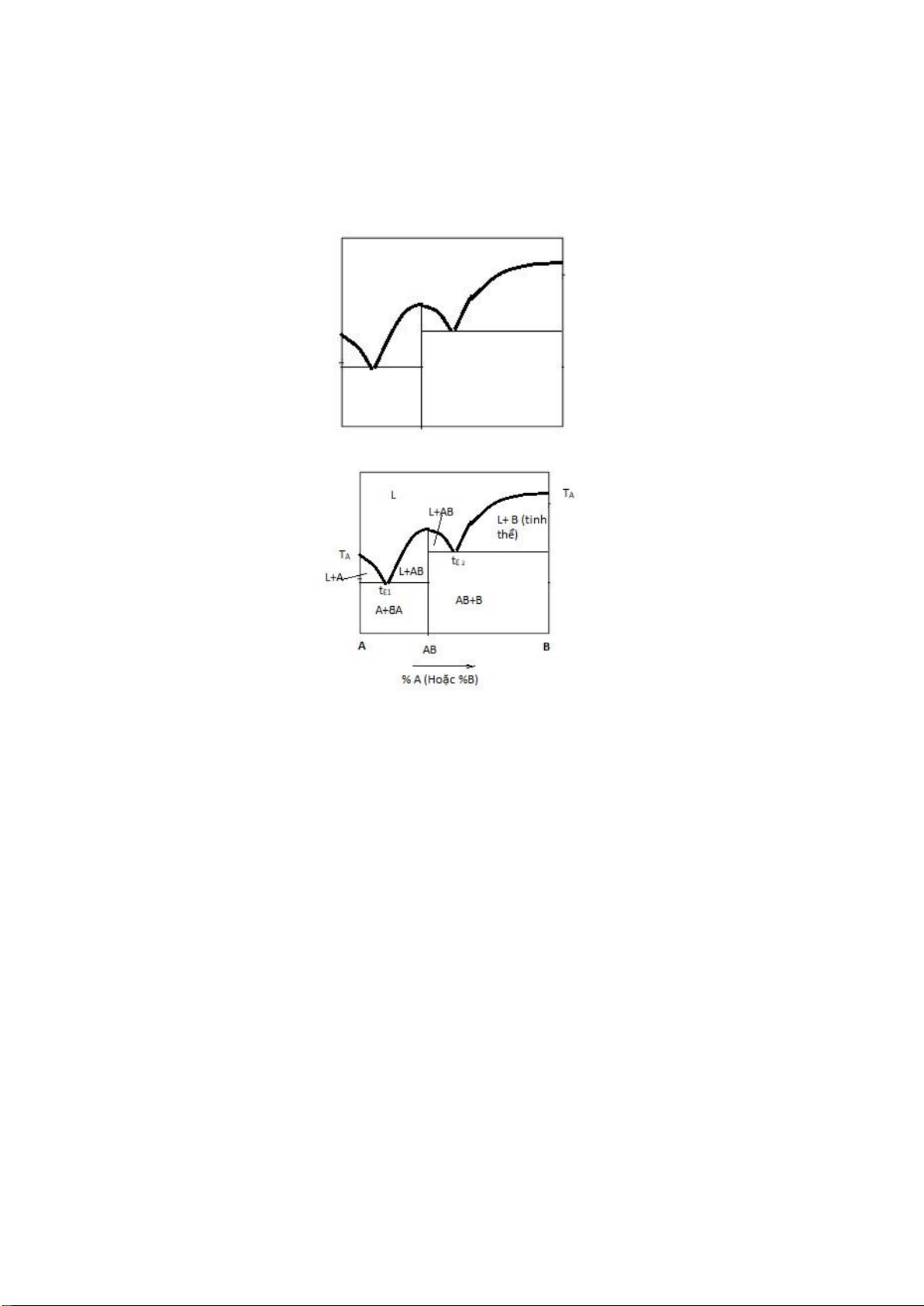
Câu 1: Cho biểu ồ pha hình dưới, anh (chị) hãy iền các ký hiệu cần thiết thể hiện hệ hai cấu tử (hai
nguyên) tạo hợp chất hóa học (Ký hiệu thành phần, nhiệt ộ nóng chảy, vùng pha lỏng, vùng kết tinh, vùng pha rắn tinh thể). Gợi ý
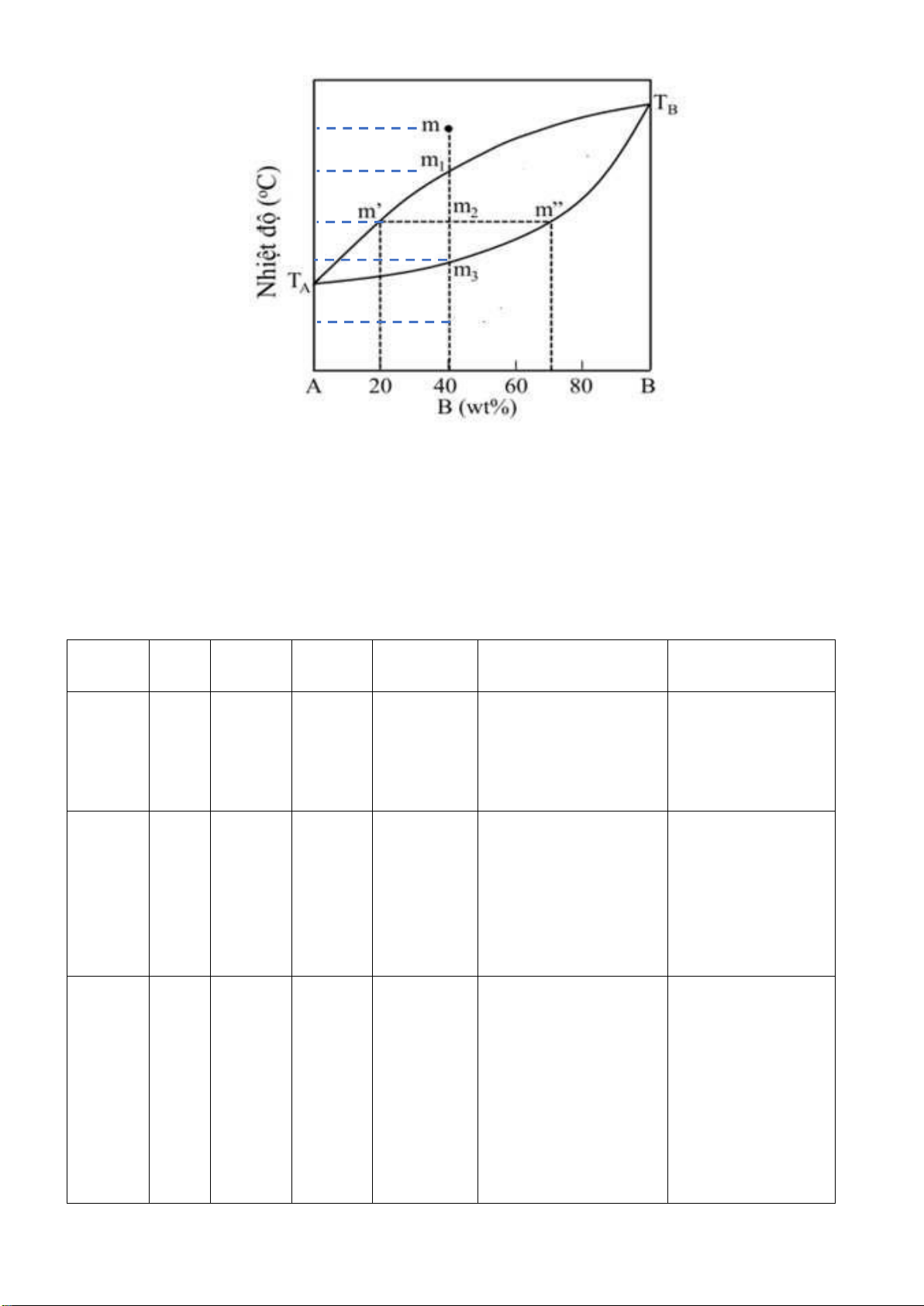
Câu 2 : Cho hệ ược biểu diễn bởi iểm m trên hình dưới, Biết hệ có khối lượng 100gram. Biết các iểm m,
m1, m2, m3 có nhiệt ộ tương ứng t, t1, t2, t3. Hãy :
1. Tính bật tự do tại iểm hê m, m1, m2, m3. Mô tả quá trình (lập bảng)
2. Tính lượng chất rắn, lỏng khi hệ ở trạng thái biểu diễn tại iểm m2.
3. Lượng mỗi cấu tử A và B trong pha lỏng, trong pha rắn tại m2? Gợi ý: Page 29 of 34 lOMoARcPSD| 36991220 (L ) t t ( L+R 1 AB ) t 2 t 3
( R AB ) t 4 m 4 1.
Bậc tự do F theo qui tắc pha Gibbs: F + P = K + 2.
P: số pha, K số cấu tử (nguyên), 2 nhiệt ộ và áp suất.
Áp dụng với K = 2, p = const (áp suất ít ảnh hưởng tới hệ ngưng tụ), khi ó F+P=K+1= 2+1=3, ta
có: F = 3 – P Điểm Nhiệt Bật tự Pha Pha rắn Diễn biến quá trình Nhận xét hệ ộ do F lỏng m t>t1 F=31=2 L -
Chỉ có 1 pha lỏng F=2, có thể thay ổi nóng chảy 2 thông số (nồng ộ, T) không làm thay ổi F m1 t1 F=32=1 L Rất ít
Pha lỏng nóng chảy Điểm hệ trên ường bắt ầu kết tinh cân bằng lỏng - rắn. F=1, có thể thay ổi 1 thông số (nồng ộ,) không làm thay ổi F m2 t2 F=32=1 L
Lượng pha Pha lỏng nóng chảy Điểm hệ trong rắn AB
kết tinh, tạo 2 pha: vùng cân bằng tăng dần
pha lỏng và dung lỏng - rắn. F=1, có
dịch rắn AB (lượng thể thay ổi 1 thông
pha rắn tăng dần khi số (nồng ộ,) không
hạ nhiệt ộ)l Lượng làm thay ổi F pha rắn, lỏng ược
tính từ quy tắc òn bẩy qua quan hệ Page 30 of 34 lOMoARcPSD| 36991220 m’m2 (Rắn) và m2m’’ (lỏng) m3 t3 F=32=1 - Rắn AB
Kết thúc kết tinh, Điểm hệ trên ường
toàn bộ lượng pha cân bằng lỏng -
lỏng kết tinh thành rắn. F=1, có thể rắn AB thay ổi 1 thông số (nồng ộ,) không làm thay ổi F m4 t4Rắn AB Rắn AB F=2, có thể thay ổi 2 thông số (nồng ộ, T) không làm thay ổi F
2. Lượng chất rắn R, lỏng L: R mm2 ' 20 2 = = = L mm2 '' 30 3
Nếu hệ có khối lượng 100 (g):
Lượng chất rắn sẽ là: 40 (g)
Lượng chất lỏng sẽ là: 60 (g)
3.Lượng A trong pha lỏng biểu diễn tại m’: 20% B, 80% A
Pha lỏng 60g. Vậy AL sẽ là 48, BL 12 (g)
Trong pha rắn (tỷ lệ thành phần tại m’’: 70%B, 30%A
Pha rắn 40g. Vậy AR 12g, BR 28g Câu 3:
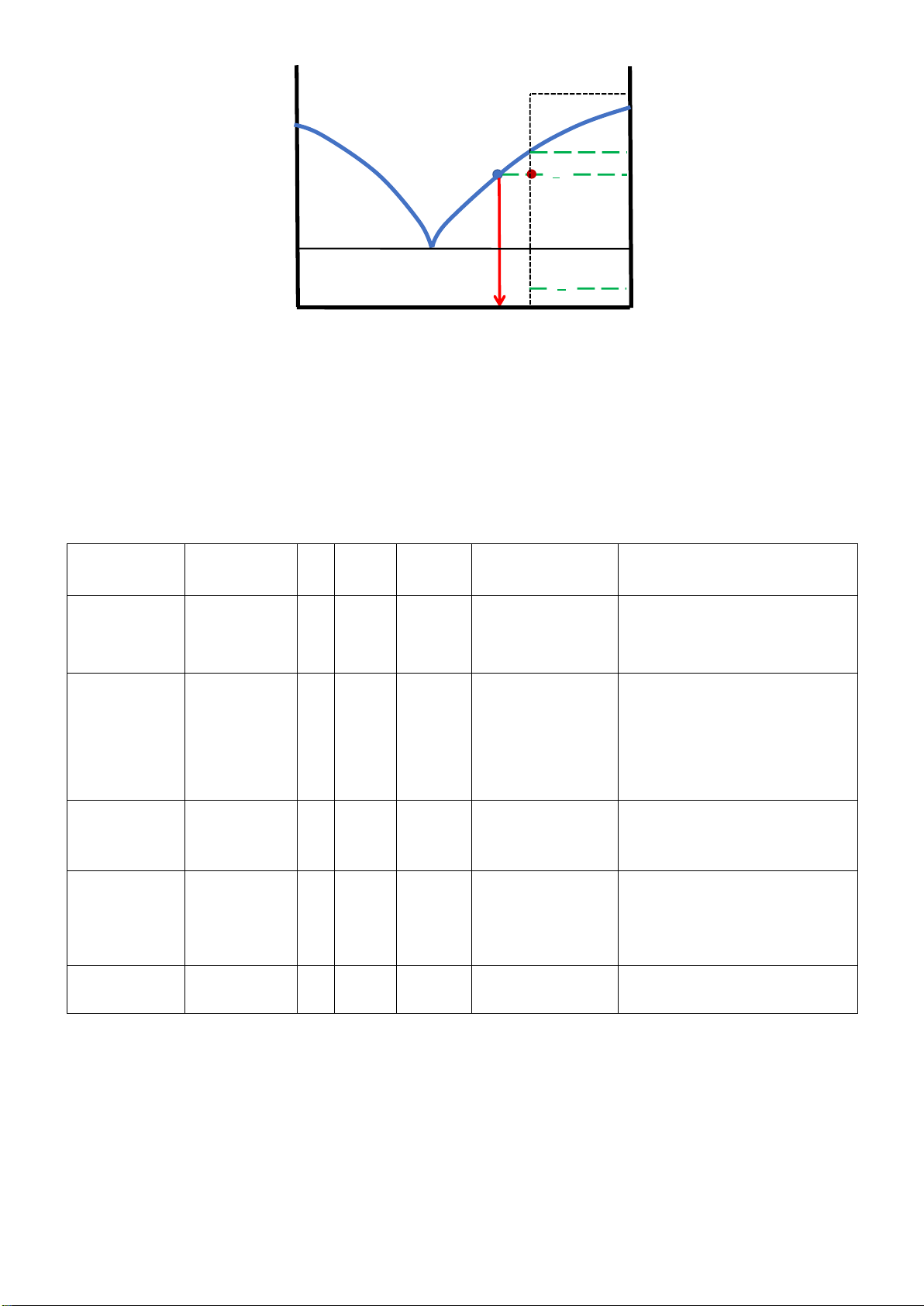
Câu 2 : Cho hệ ược biểu diễn bởi iểm m trên hình dưới, Biết hệ có khối lượng 100gram. Biết các iểm m,
m1, m2, m3 có nhiệt ộ tương ứng t, t1, t2, t3. Hãy :
1. Tính bật tự do tại iểm hê m, m1, m2, m3. Mô tả quá trình (lập bảng)
2. Tính lượng chất rắn, lỏng khi hệ ở trạng thái biểu diễn tại iểm m2.
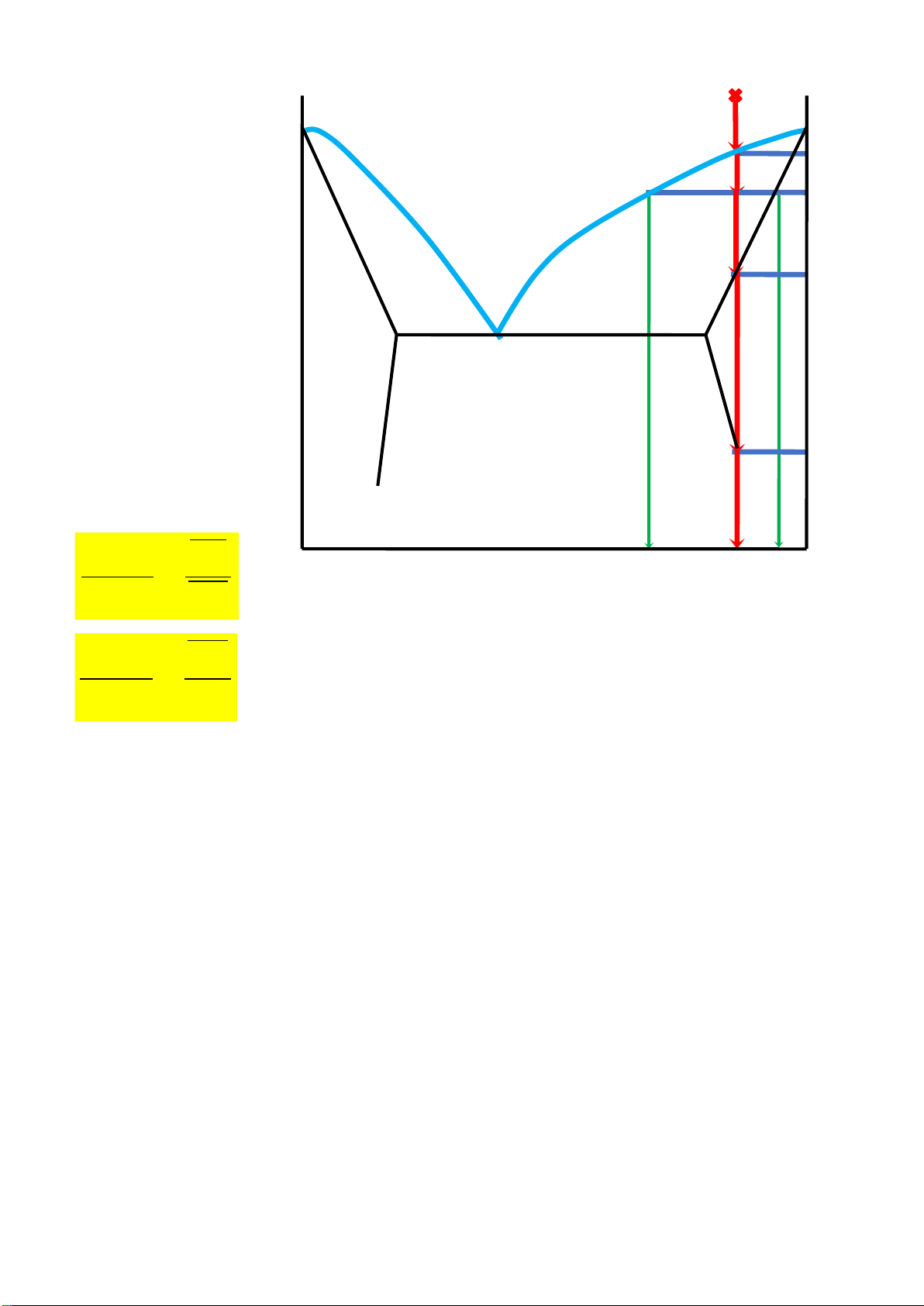
3. Lượng mỗi cấu tử A và B trong pha lỏng, trong pha rắn tại m2? Page 31 of 34 lOMoARcPSD| 36991220 L ( m t m ) T T B A m 1 a t m 1 2 t 2 L+R A L+R B m 3 t 3 e AB m 4 t 4 R A + R B A 100 100 B Gợi ý:
Bậc tự do F theo qui tắc pha Gibbs: F + P = K + 2.
P: số pha, K số cấu tử (nguyên), 2 nhiệt ộ và áp suất.
Áp dụng với K = 2, p = const (áp suất ít ảnh hưởng tới hệ ngưng tụ), khi ó F+P=K+1= 2+1=3, ta
có: F = 3 – P Điểm hệ Nhiệt ộ F Pha Pha rắn Diễn biến quá Nhận xét lỏng trình m tm > t1 2 L - Chỉ có 1 pha
F=2, có thể thay ổi 2 thông
lỏng nóng chảy số (nồng ộ, T) không làm thay ổi F m1 t1 1 L Rất ít Pha lỏng nóng
Điểm hệ trên ường cân RB
chảy bắt ầu kết bằng lỏng - rắn. F=1, có tinh RB thể thay ổi 1 thông số
(nồng ộ,) không làm thay ổi F m2 t1>t2>t3 1 L RB tăng Quy tắc òn bẩy: Lượng RB tăng dần m2a RB/L=m2a/m2t2 m3 t3 1 L RB tăng
RB tăng dần ến cực ại m3eAB dần ến cực ại m3eAB m4 t41 - RA +
Làm nguội hỗn hợp A, B. RA RB và RB cùng kết tính Page 32 of 34 lOMoARcPSD| 36991220 • m
S 1 : t A – a – a 1 • t A B L S t
2 : t B – b – b 1 . m 1
• E,a,b có F = 0. m 2 % L A CB = m 3 CA L + S 1 L + S 2 DB a b = E DA S 1 S 2
S 1 + S 2 m 4 3 A C M D B %BL %AS2 %BS2 Page 33 of 34