Đề giao lưu HSG Toán 6 năm 2023 – 2024 phòng GD&ĐT Thiệu Hóa – Thanh Hóa

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI GIAO LƯU HỌC SINH GIỎI THIỆU HOÁ NĂM HỌC 2023-2024 Môn: Toán 6 Đề chính thức
Thời gian: 120 phút (không kể thời gian giao đề)
Ngày thi: 16/4/2024 (Đề gồm 05 câu, 01 trang)
Câu 1. ( 4.0 điểm) Thực hiện phép tính: 1 1 1 1 1
a) A = -524 – {–224 – [–124 – (100 – 524) + 2024]} b) B  1      ...... 3 6 10 15 120 6 4 9 4 5.4 .9  3 .( 8  ) 1 1 1 c) C    ...... 13 8 4 3 4.2 .3  2.8 .( 2  d) D = 7) 1.2.3 2.3.4 98.99.100 Câu 2. (4.0 điểm) 1. Tìm x, biết:     x   2 2016 : 25 3 2   3 .7 
2. Tìm số tự nhiên a lớn nhất có ba chữ số sao cho khi chia a cho 5 dư 2, chia 7 dư 4 và chia 9 dư 6.
3. Tìm x, y nguyên biết: 3xy + 2x - 5y = 6 Câu 3. (4.0 điểm)
1. Cho p là số nguyên tố thỏa mãn p  2 và p  4 cũng là số nguyên tố.
Tìm số nguyên x sao cho p5 + 1782 = (2x – 5)2.
2. Cho n là số tự nhiên lớn hơn 1 thỏa mãn n + 1 và 2n +1 đồng thời là hai số chính phương.
Chứng minh rằng n chia hết cho 24. Câu 4. (6.0 điểm).
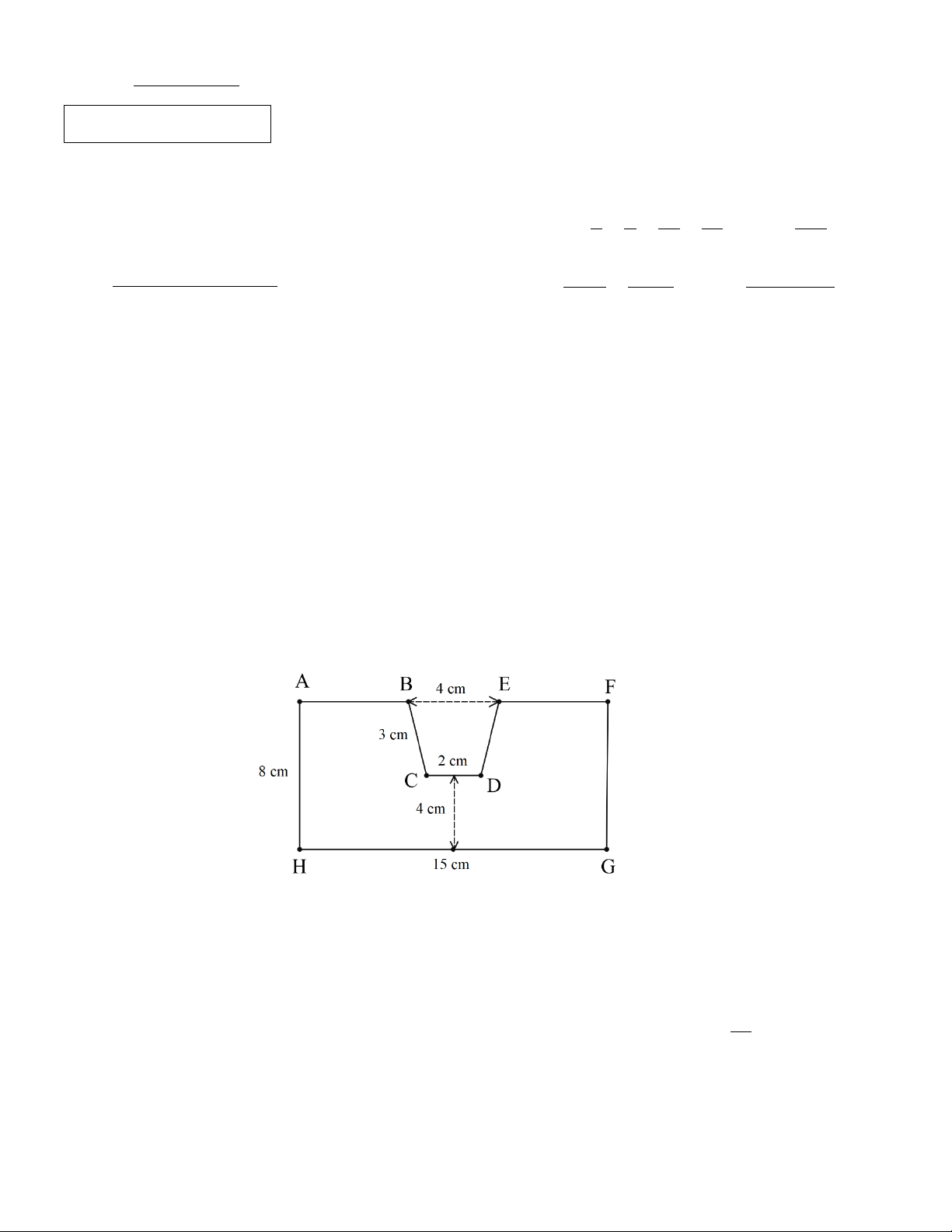
1. Một chi tiết máy có dạng và kích thước như hình biết AHGF là hình chữ nhật, BCDE là hình
thang cân. Hãy hãy tính chu vi và diện tích của chi tiết máy đó.
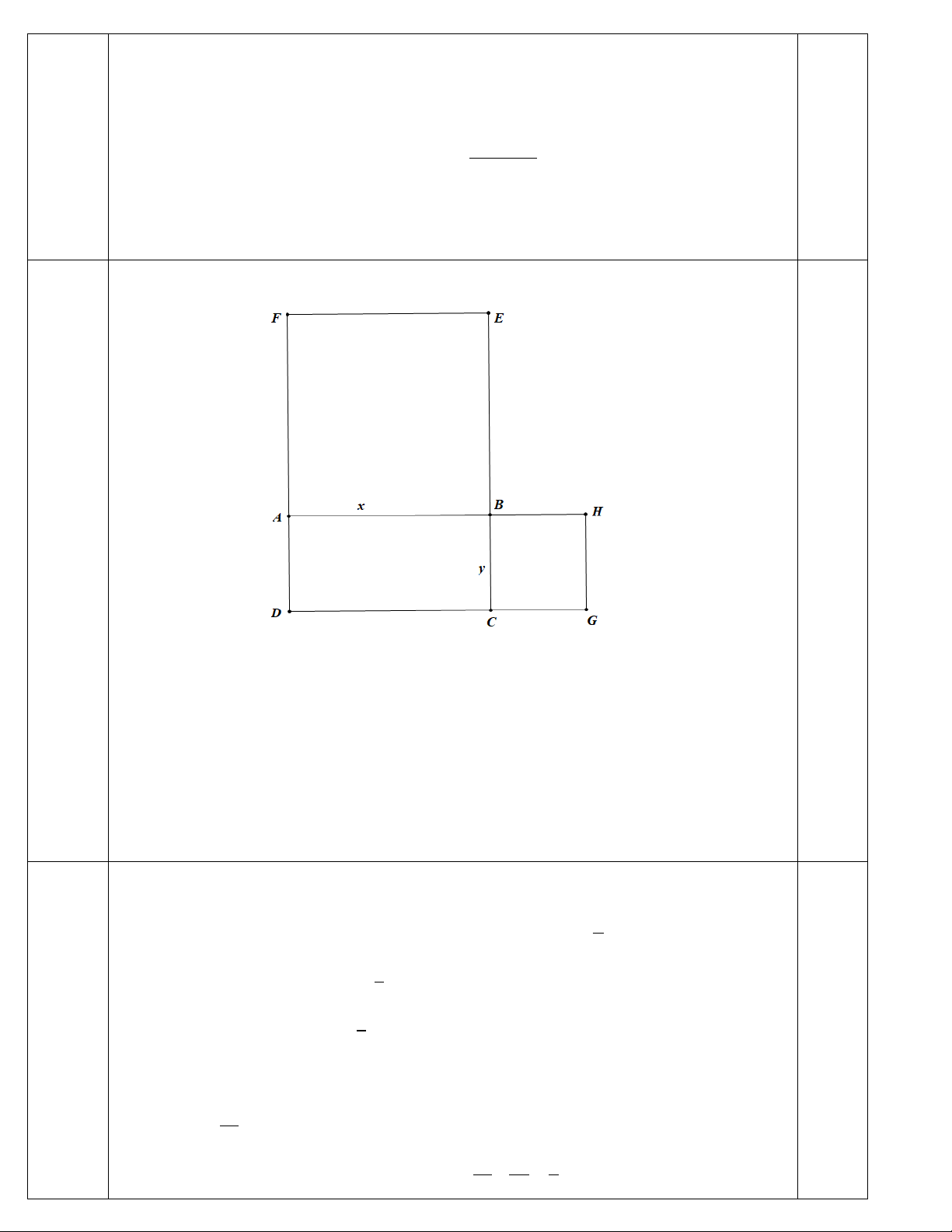
2. Cho hình chữ nhật ABCD , biết AB  ;
x BC  y , chu vi của nó là C . Vẽ ra phía ngoài hình chữ
nhật ABCD , các hình vuông ABEF, BCGH . Gọi C ,C theo thứ tự là chu vi các hình chữ nhật 1 2
CDFE, ADGH . Tính C, ,
x y và tỉ số diện tích của hình vuông ABEF với hình vuông BCGH . Biết
C  80cm;C  70cm . 1 2
3. Một khu đất hình chữ nhật có chu vi là 132m. Nếu giảm chiều rộng đi 5m và tăng chiều dài lên 5m
thì chiều dài gấp đôi chiều rộng. Người ta dùng 30% diện tích khu đất để trồng rau, 11 diện tích khu đất để 30
trồng cây ăn quả, diện tích còn lại để xây nhà. Hỏi diện tích xây nhà là bao nhiêu? Câu 5. (2.0 điểm)
Cho các số nguyên dương , a , b ,
c d thỏa mãn a < 3b + 1; b < 4c + 1; c < 5d + 1 và d < 2024.
Tìm giá trị lớn nhất có thể của a .
---------------- Hết ---------------
Họ tên thí sinh:............................................................SBD........................................ UBND HUYỆN THIỆU HÓA
HƯỚNG DẪN CHẤM ĐỀ GIAO LƯU HỌC SINH
PHÒNG GIÁO DỤC THIỆU HÓA
GIỎI LỚP 6 CẤP HUYỆN NĂM HỌC 2023 - 2024 MÔN: TOÁN Câu
Nội dung cần đạt Điểm A  524 
  224  124  100 (  524)  2024  524 
 224 124 100  524  2024 0,5 a)  ( 524   524)  (224 124  ) 100  2024  0,5 2024 1 1 1 1 1 1 1 15 15 1 b) A     .......   A 1   A  2 1.2 2.3 3.4 15.16 2 16 16 8 6 4 9 4 5.4 .9  3 .( 8  ) 6 4 9 4 5.4 .9  3 .8 0,5 c) C   13 8 4 3 4.2 .3  2.8 .( 2  7) 13 8 4 3 4.2 .3  2.8 .27 12 8 9 12 5.2 .3  3 .2 12 8 12 8 2 .3 .(5  3) 2 .3 .2 Câu 1.    1 15 8 13 9 2 .3  2 .3 13 8 2 13 8 2 .3 .(2  3) 2 .3 0,5 1 1 1 1 1 d) D =     ......   1.2.3 2.3.4 3.4.5 97.98.99 98.99.100 2 2 2 2D    ...... 1.2.3 2.3.4 98.99.100 1 1 1 1 1 1      ......  0,5 1.2 2.3 2.3 3.4 98.99 99.100 1 1 4949 4949 4949     D  : 2  1.2 99.100 9900 9900 19800 0,5 1.     x   2 2016 : 25 3 2   3 .7   2016 : 25  
3x  2  63 
 25 3x  2  2016:63 0,5
Câu 2.  25  3x  2  32  3x  2  25 32  3x  2  7   3x  9   x  3  Vậy x  3  0,5
2. Theo bài ra ta có: 99 < a < 1000 và a  2 5 a  2  5 5 a  3 5   
a  4 7  a  4  7 7  a  3 7  a  3 BC 5;7;9 0,5    a  6 9 a  6  9 9 a  3 9   
=> a  3 B315  0;315;630;945;1260... 
.  a 312;627;942;1257;..  . 0,5
Vì 99 < a < 1000 và a là số lớn nhất nhỏ hơn 1000 nên a = 942
Vậy số tự nhiên cần tìm là a = 942 0,25 3.
3xy + 2x - 5y = 6  x(3y  2)  5y  6
 3x(3y  2) 15y 18
 3x(3y  2) 15y 10 18 10
 3x(3y  2)  5(3y  2)  8 
(3x  5).(3y  2)  8  0,5
3y  2 U (8)   1  ; 2  ; 4  ;  8
Mà 3y+2 là số chia 3 dư 2 3y  2 1  ;2; 4  ;  8 Ta có bảng sau: 3y+2 -4 -1 2 8 3x-5 -2 -8 4 1 0,5 y -2 -1 0 2 x 1 -1 3 2 Vậy (x;y)   1; 2  ; 1  ;  1 ;3;0;2;2 0,25
1. Xét p  2 thì p  2  4 ; p  4  6 đều là hợp số (loại) 0,25
Xét p  3 thì p  2  5 ; p  4  7 đều là số nguyên tố (nhận) 0,25
Xét p  3 thì p có dạng 3k 1 hoặc 3k  2 , k là số nguyên dương
- Với p  3k 1thì p  2 chia hết cho 3, p  2  3 nên p  2 là hợp số.
- Với p  3k  2 thì p  4 chia hết cho 3, p  4  3 nên p  4 là hợp số. 0,5 Vậy p  3 Khi đó: 0,25
p5 + 1782 = (2x – 5)2 => (2x – 5)2 = 2025 2x  5  45 x  25     (thỏa mãn) 0,5 2x  5  45 x  20
Câu 3. Vậy x   25 ; 20 . 0,25
2. Do n + 1 và 2n + 1 đều là 2 số chính phương
nên đặt n+1 = k 2 và 2n +1= m 2 ( k và m thuộc N) 0,25
Ta có m lẻ nên m = 2a +1 suy ra m 2 = 4a( a+1) + 1 suy ra n = 2a( a +1)
do đó n chẵn suy ra k lẻ . 0,5
Đặt k = 2b + 1 suy ra b 2 = 4b( b+1) +1
suy ra n = 4b( b+1) nên n chia hết cho 8 (1) 0,5
Lại có k 2 + m 2 = 3n + 2 chia 3 dư 2
Mà k 2 và m 2 chia 3 dư 0 hoặc 1 do đó k 2 và m 2 đều chia 3 dư 1 suy ra m 2 – k 2 chia hết cho 3 0,5
hay ( 2n +1) – ( n + 1) = n chia hết cho 3. ( 2)
Mà ( 3; 8) = 1 Nên từ (1) và (2) ta suy ra n chia hết cho 24 0,25
Chu vi của chi tiết máy đó là: 8158 15 4 3 2
.  2  50cm . 0,25
Diện tích hình chữ nhật AFGH là 0,25 S  .   2 8 15 120 cm . AFGH  Câu
Độ dài đường cao của hình thang cân BCDE là 8  4  4cm . 0,25 4.1 4 2 4. 2.0
Diện tích hình thang cân BCDE là S  12 . BCDE  2 cm  điểm 2 0,5
Diện tích của chi tiết máy đó là S  S  S     2 120 12 108 cm . 0,5 AFGH BCDE 
Vậy chi tiết máy có chu vi bằng 50cm , diện tích bằng  2 108 cm  . 0,25 Ta có hình vẽ Câu 4.2 2.0 điểm
Chu vi hình chữ nhật ABCD là C  2x  y (cm) 0,25
Chu vi hình chữ nhật CDFE là C  4x  2y  2x  2 x  y (cm) 0,25 1  
Chu vi hình chữ nhật ADGH là C  2y  2 x  y (cm) 0,25 2   0,25
Suy ra C  C  4x  2y  2x  4y  6x  6y 1 2    
Mà C  80cm;C  70cm nên 6x  6y 150  x  y  25 (cm) 1 2 0,5
Vì C  2x  2 x  y  80  x  15cm , suy ra y  10cm, C  50cm 1   0,25
Vậy x 15cm, y 10cm, C  50cm . 0,25
Khi giảm chiều rộng 5m và tăng chiều dài 5m thì chu vi không đổi.
Ta có nửa chu vi lúc sau là: 132: 2 = 66 (m) 0,5
Lúc sau chiều dài gấp đôi chiều rộng hay chiều rộng bằng 1 chiều dài. 2
Suy ra chiều rộng lúc sau bằng 1 nửa chu vi. 0,25 Câu 3 4.3
Chiều rộng khu đất đó là: 66. 1 + 5 = 27 (m) 0,25 2.0 3 0,25
điểm Chiều dài khu đất đó là: 66 – 27 = 39 (m)
Diện tích khu đất đó là: 27.39 = 1053 (m2) 0,25 Đổi: 30% = 3 10
Diện tích đất làm nhà chiếm số phần là: 3 11 1 1   (diện tích khu đất) 0,25 10 30 3
Diện tích đất xây nhà là: 1053. 1 = 351 (m2) 3 0,25
Vì a là số nguyên dương mà a  b
3 1  a  b 3 0,25
Vì b là số nguyên dương mà b  c
4 1  b  c 4 0,25
Câu 5 Vì c là số nguyên dương mà c  d
5 1  c  d 5 0,25 2.0
Vì d là số nguyên dương mà d  2024  d  2023 điểm 0,25 Do đó a  2023 . 5 . 4 . 3  a 121380 0,5
Vậy giá trị lớn nhất có thể của a là 121380 khi b = 40460; c = 10115; d = 2023 0,5 Lưu ý:
- Điểm bài thi làm tròn đến 0,25.
- Nếu thí sinh làm cách khác mà đúng thì vẫn cho điểm tối đa.