Đề giao lưu HSG Toán 7 lần 7 năm 2023 – 2024 phòng GD&ĐT Nông Cống – Thanh Hóa

PHÒNG GD & ĐT HUYỆN NÔNG CỐNG
GIAO LƯU HỌC SINH GIỎI CỤM LẦN 7 Năm học 2023 - 2024 Môn: Toán 7
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề có 01 trang, gồm 05 câu)
Câu 1.(4.0 điểm).
1. Tính giá trị của các biểu thức sau (tính hợp lý nếu có thể) a) 2 2 1 − 0 1
A = 25 + (2 .3) .( ) + 2024 + − 4 4 b) 1.2.3 2.4.6 4.8.12 7.14.21 B + + + =
1.3.5 + 2.6.10 + 4.12.20 + 7.21.35 c)
2a 5b 6c 7d C = + + +
, biết 2a 5b 6c 7d = = =
và a,b,c,d ≠ 0
5b 6c 7d 2a
5b 6c 7d 2a
Câu 2. (4.0 điểm) a) Tìm x, biết 8
2x + 3 + 2x −1 = 5(x + )2 1 + 2
b) Bốn bao gạo có tổng cộng 375kg. Lần thứ nhất người ta lấy đi 1kg ở bao thứ nhất;
2kg ở bao thứ hai; 3kg ở bao thứ ba; 4kg ở bao thứ tư. Lần thứ hai người ta lấy đi tiếp 1 5
số kg gạo còn lại của bao thứ nhất; 1 số kg gạo còn lại của bao thứ hai; 1 số kg gạo còn 4 3
lại của bao thứ ba; 1 số kg gạo còn lại của bao thứ tư thì số kg gạo còn lại sau lần lấy 2
thứ hai của bốn bao bằng nhau. Tìm số kg gạo mỗi bao lúc đầu.
Câu 3.(4.0 điểm)
a) Tìm tất cả các cặp số nguyên (x ; y) thoả mãn: x + y − 2xy = 4
b) Tìm số nguyên tố ab (a > b > 0) , biết ab −ba là số chính phương.
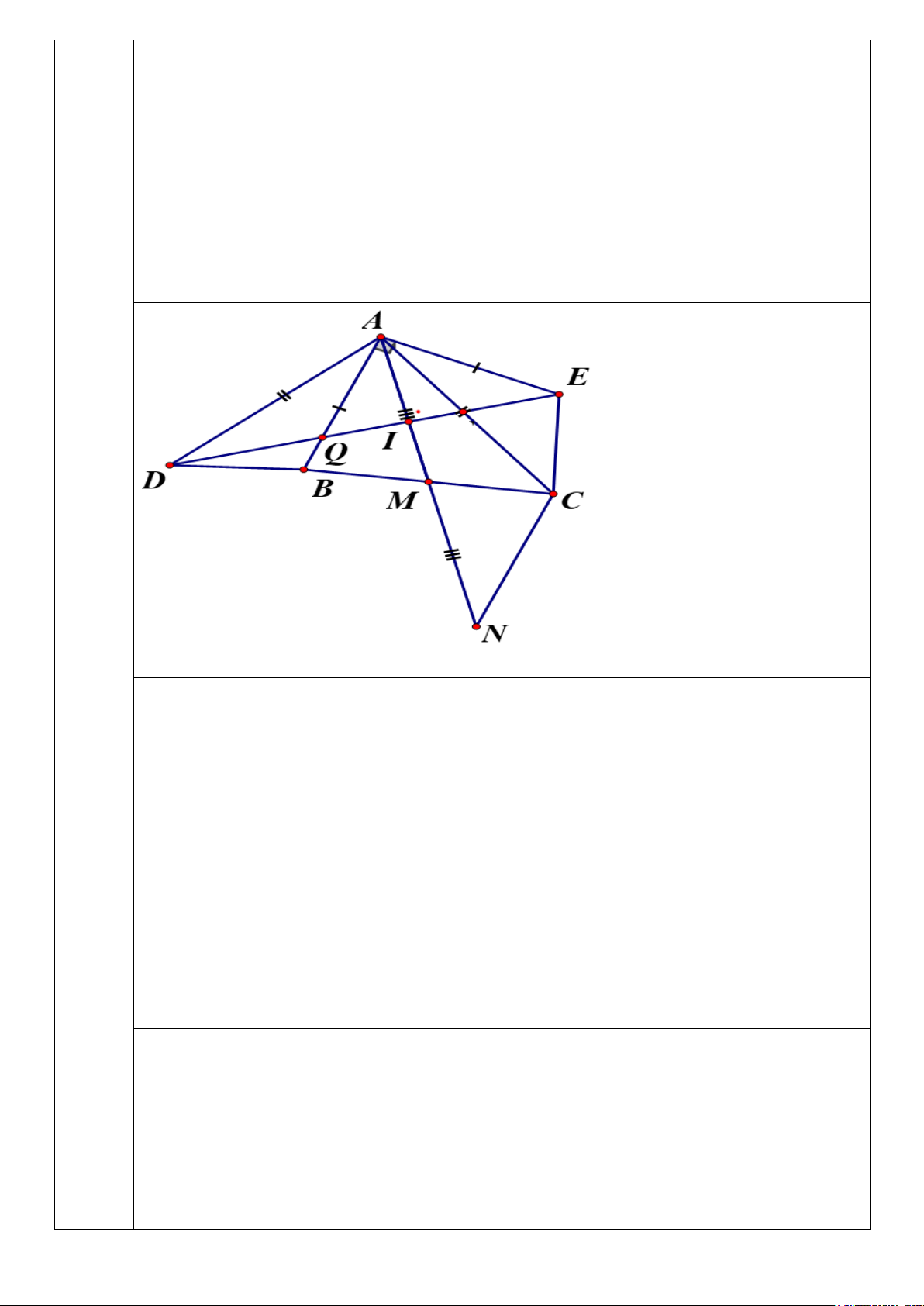
Câu 4.(6.0 điểm)Cho A
∆ BC có ba góc nhọn, AB < AC , trung tuyến AM. Trên nửa mặt
phẳng bờ AB chứa điểm C, vẽ đoạn thẳng AE vuông góc với AB và AE = A . B Trên nửa
mặt phẳng bờ AC chứa điểm B, vẽ đoạn thẳng AD vuông góc với AC và AD = AC. 1. Chứng minh: BD=CE
2. Trên tia đối của tia MA lấy N sao cho MN = . MA Chứng minh:  0 = − 
ACN 180 BAC.và A ∆ DE = C ∆ AN.
3. Gọi giao điểm của DE với AB, AC lần lượt là Q, P. Chứng minh: AP < AQ
Câu 5.(2 điểm) Cho P = 1 1 1 1 1+ + + + ... + và Q = 1 1 1 1 1+ + + + ... + 2 3 4 4034 3 5 7 4033 Chứng tỏ rằng: P 2017 < 1 Q 2018
……………………..Hết……………………
HƯỚNG DẪN CHẤM ĐỀ GIAO LƯU HỌC SINH GIỎI NĂM HỌC 2023 - 2024 MÔN: TOÁN - LỚP 7 Câu ĐÁP ÁN Điểm 1(4 a) 2 2 1 − 0 1 điểm)
A = 25 + (2 .3) .( ) + 2024 + − 4 4 0,5 4 2  1 −  1 = 5 + 2 .3 . +  1+  2  2  4 1 = 5 − 36 +1+ 4 119 − 0,5 = 4 b) 1.2.3 2.4.6 4.8.12 7.14.21 B + + + =
1.3.5 + 2.6.10 + 4.12.20 + 7.21.35
1.2.3(1+ 2.2.2 + 4.4.4 + 7.7.7) = 0,5
1.3.5.(1+ 2.2.2 + 4.4.4 + 7.7.7) 1.2.3 = 1.3.5 2 0,5 = 5 c)
2a 5b 6c 7d C = + + +
, biết 2a 5b 6c 7d = = =
và a,b,c,d ≠ 0
5b 6c 7d 2a
5b 6c 7d 2a 1,0
Đặt 2a 5b 6c 7d = = =
= k 2a 5b 6c 7d 4 ⇒ . . . = k ⇒ k = 1 ± ⇒ C = 4 ±
5b 6c 7d 2a
5b 6c 7d 2a 2.(4 a) Tìm x, biết 8
2x + 3 + 2x −1 = điểm) 5(x + )2 1 + 2
Ta có 2x +3 + 2x −1 = 2x +3 + 1− 2x ≥ 2x +3+1− 2x = 4 = 4 với mọi x Dấu ‘=’ xảy ra khi 3 − 1
(2x + 3)(1− 2x) ≥ 0 ⇒ ≤ x ≤ 0,5 2 2 Lại có 2 8 8 5(x +1) + 2 ≥ 2 ⇒ ≤ = 4 với mọi x 2 5(x +1) + 2 2 0,5
Dấu ‘=’ xảy ra khi x = -1  3 − 1 Do đó 8  ≤ x ≤ 2x 0,5 + 3 + 2x −1 = ⇒  2 2 ⇒ x = 1 − 5(x + )2 1 + 2   x = 1 − 0,5 Vậy x = -1
b) Bốn bao gạo có tổng cộng 375kg. Lần thứ nhất người ta lấy đi 1kg ở
bao thứ nhất; 2kg ở bao thứ hai; 3kg ở bao thứ ba; 4kg ở bao thứ tư. Lần
thứ hai người ta lấy đi tiếp 1 số kg gạo còn lại của bao thứ nhất; 1 số kg 5 4
gạo còn lại của bao thứ hai; 1 số kg gạo còn lại của bao thứ ba; 1 số kg 3 2
gạo còn lại của bao thứ tư thì số kg gạo còn lại sau lần lấy thứ hai của bốn
bao bằng nhau. Tìm số kg gạo mỗi bao lúc đầu.
Gọi số kg gạo 4 bao lúc đầu lần lượt là: x +1; y +2; z + 3; t + 4 (kg) Với x, y, z, t > 0 0,25
Sau khi lấy đi lần thứ nhất thì số kg gạo mỗi bao còn lại lần lượt là x, y, z,
t (kg) và tổng số kg gạo còn lại của 4 bao là 375 – (1+2+3+4) = 365 (kg) nên x + y + z + t = 365 0,25
Sau khi lấy đi lần thứ hai thì số kg gạo mỗi bao còn lại lần lượt là: 4 3 2 1 ;
x y; z; t 0,25 5 4 3 2
Ta có 4x 3y 2z t x y z t = = = ⇒ = = = 5 4 3 2 15 16 18 24 0,25
Áp dụng tính chất dãy tỉ số bằng nhau ta có x y z t
x + y + z + t 365 = = = = = = 5 0,25 15 16 18 24 15 +16 +18 + 24 73
Suy ra x = 5.15 = 75; y = 5.16 = 80; z = 5.18 = 90; t = 5.24 = 120 0,25
Vậy số kg gạo mỗi bao lúc đầu lần lượt là: 76; 82; 93; 124 (kg) 0,5 3
a) Tìm tất cả các cặp số nguyên (x ; y) thoả mãn: x + y − 2xy = 4 (4
x + y − xy =
x − xy + y − = 0,5 điểm) Ta có: 2 4 suy ra 2 4 0
⇔ 2x − 4xy + 2y − 8 = 0 ⇔ 2x − 4xy + 2y −1= 7
⇔ 2x(1− 2y) − (1− 2y) = 7 ⇔ (2x − ) 1 (1− 2y) = 7 0.5 Lập bảng 2x −1 1 7 -1 -7 1− 2y 7 1 -7 -1 0.5 x 1 4 0 -3 y -3 0 4 1
Thỏa mãn Thỏa mãn Thỏa mãn Thỏa mãn
Vậy (x; y) cần tìm là (1; -3) ; (4; 0) ; (0; 4) ; (-3; 1) 0.5
b) Tìm số nguyên tố ab (a > b > 0) , biết ab −ba là số chính phương. Ta có:
ab − ba =10a + b −10b − a
⇒ ab −ba = 9(a −b) 2
⇒ ab − ba = 3 (a − b) 0,25
ab − ba là số chính phương khi (a - b) là số chính phương
Do a, b là các chữ số và 0 < a,b ≤ 9,a > b > 0 nên 0 ≤ a −b ≤ 8 0,25
Suy ra (a - b) là SCP khi a - b = 1 hoặc a – b = 4
+ Nếu a – b = 1 ⇒ ab∈{21,32,43,54,65,76,87, } 98 0,5 Mà
ab là số nguyên tố nên ab = 43 thỏa mãn. 0,5
+ Nếu a – b = 4 ⇒ ab∈{51,62,73,84, }
95 mà ab là số nguyên tố ab = 73
Vậy ab = 43 và ab = 73 0,5 Bài 4 Cho A
∆ BC có ba góc nhọn, AB < AC , trung tuyến AM. Trên nửa mặt (6
phẳng bờ AB chứa điểm C, vẽ đoạn thẳng AE vuông góc với AB và
điểm) AE = A .
B Trên nửa mặt phẳng bờ AC chứa điểm B, vẽ đoạn thẳng AD
vuông góc với AC và AD = AC. 1. Chứng minh: BD=CE
2. Trên tia đối của tia MA lấy N sao cho MN = . MA Chứng minh:  0 = − 
ACN 180 BAC.và A ∆ DE = C ∆ AN.
3. Gọi giao điểm của DE với AB, AC lần lượt là Q, P. Chứng minh: AP < AQ P 1. Xét A ∆ BD và A ∆ EC có:
AD = AC(gt) và =  = 
AE AB(gt);BAD CAE(cùng phụ với  BAC) 2,0 ⇒ A ∆ BD = A ∆ EC( .
c g.c) ⇒ BD = CE(2 cạnh tương ứng) 2)Xét A ∆ BM và NCM ∆ có: 2,0 = =  = 
AM MN(gt);BM CM (gt); AMB NMC(đ đ) ⇒ ∆ = ∆ ⇒  =  ABM
NCM ( .cg.c)
ABM NCM (hai góc tương ứng)
Do đó:  =  +  =  +  0 = −  ACN ACB BCN ACB ABC 180 BAC(dfcm)
+Ta có:  =  +  −  0 = −  ⇒  =  DAE DAC BAE BAC 180 BAC DAE ACN Xét A ∆ DE và A ∆ CN có: CN = AE (cùng bằng AB), =  = 
AC AD(gt);DAE ACN(cmt) ⇒ A ∆ DE = C ∆ AN(cgc)
3)Theo tính chất góc ngoài, ta có:  =  +   =  +  AQP QAD QD ; A APQ PAE PEA 2,0
Mà AB < AC nên < ⇒  <  AE AD ADE AED
Theo chứng minh trên ta có:  =  QAD PAE
Từ đó suy ra  +  <  +  QAD QDA PAE PEA Hay  < 
AQP APQ ⇒ AP < AQ Bài 5 Cho P = 1 1 1 1 1+ + + + ... + và Q = 1 1 1 1 1+ + + + ... + (2 2 3 4 4034 3 5 7 4033
điểm) Chứng tỏ rằng: P 2017 < 1 Q 2018 Đặt K = P – Q = 1 1 1 1 + + + ... + 2 4 6 4034 Ta có : Q = 1 1 1 1 1+ + + + ... + > 1 1 1 1+ + + ... + = 1 + K (1) 0.5 3 5 7 4033 4 6 4034 2
Lại có: 2017 = 1 + 1 + 1 +...+ 1 1  + 1 + 1 + + 1 ... = K 2 2 2 2 2 2 4 6 4034 1 K ⇒  (2) 0.5 2 2017
Từ (1) và (2) suy ra Q > K + K 2018 = K 0.5 2017 2017 Do đó K 2017
K + Q 2017 + 2018 P 2017  ⇒  ⇔ 1 0.5 Q 2018 Q 2018 Q 2018