
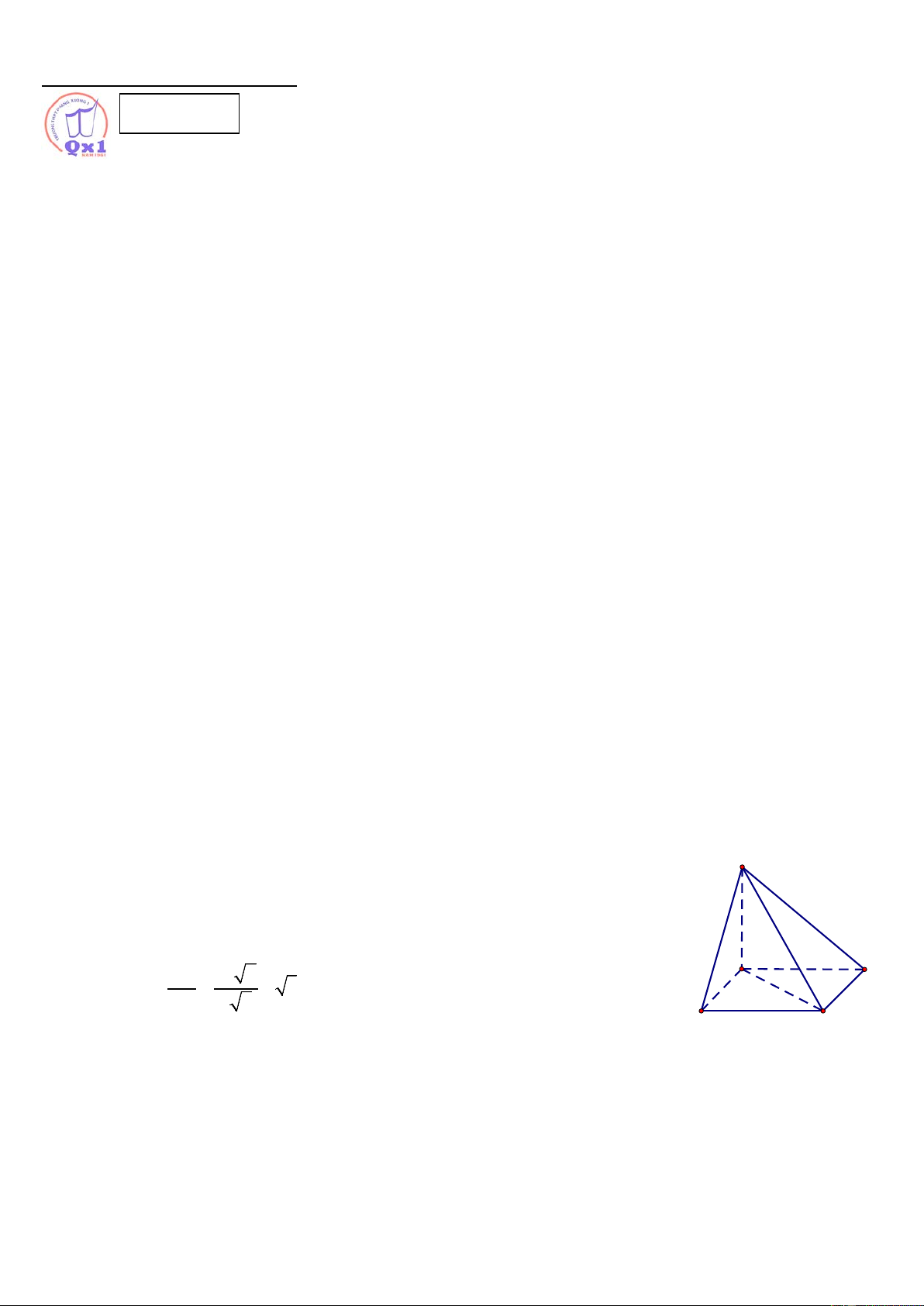


Preview text:
TRƯỜNG THPT QUẢNG XƯƠNG 1
GIAO LƯU KIẾN THỨC CÁC TRƯỜNG THPT
LẦN 2 - NĂM HỌC 2019 - 2020 MÃ ĐỀ 123 MÔN: TOÁN
(Đề gồm có 6 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD: . . . . . . . . Phòng: . . . . . . . . Câu 1.
Cho tập hợp A có 10 phần tử. Số tập hợp con có 3 phần tử được thành lập từ A là A. 3 A . B. 3 C . C. 10 3 . D. 3 10 . 10 10 Câu 2.
Cho cấp số nhân (u với u =
u = . Công bội của cấp số nhân đã cho bằng n ) 2 và 16 1 4 A. 4 . B. 2 . C. 2 − . D. 4 − . Câu 3.
Số nghiệm của phương trình 2 3 x = 1 là A. 0. B. 1. C. 2. D. 3. Câu 4.
Thể tích của khối lập phương có cạnh bằng a là A. 3 . a B. 2 a . C. 3 a . D. 2 3a . Câu 5.
Tập xác định của hàm số y = log (x −1) là 5 A. (0; +∞). B. [5; +∞). C. (1; +∞). D. [1; +∞). Câu 6.
Cho các hàm số f (x) và g (x) liên tục trên tập xác định. Mệnh đề nào sau đây sai? A. f
∫ (x)+ g(x)dx = f
∫ (x)dx+ g
∫ (x)dx. B. kf
∫ (x)dx = k f
∫ (x)dx (k là hằng số). C. f
∫ (x)g(x)dx = f ∫ (x)d .x g ∫ (x)dx . D. f ′
∫ (x)dx = f (x)+C , (C∈). Câu 7.
Cho khối chóp có diện tích đáy 2
B = 3a và chiều cao h = 3a . Thể tích khối chóp đã cho bằng 3 3 3a A. 3 3 3a . B. 3 3a . C. 3 9 3a . D. . 2 Câu 8.
Cho khối nón có chiều cao h = 3a và bán kính đáy r = a . Thể tích khối nón đã cho bằng 3 π 3a A. . B. 3 π 3a . C. 3 π a . D. 3 3π a . 3 Câu 9.
Cho mặt cầu có bán kính R = 3. Diện tích mặt cầu đã cho bằng A. 9π . B. 108π . C. 36π . D. 27π .
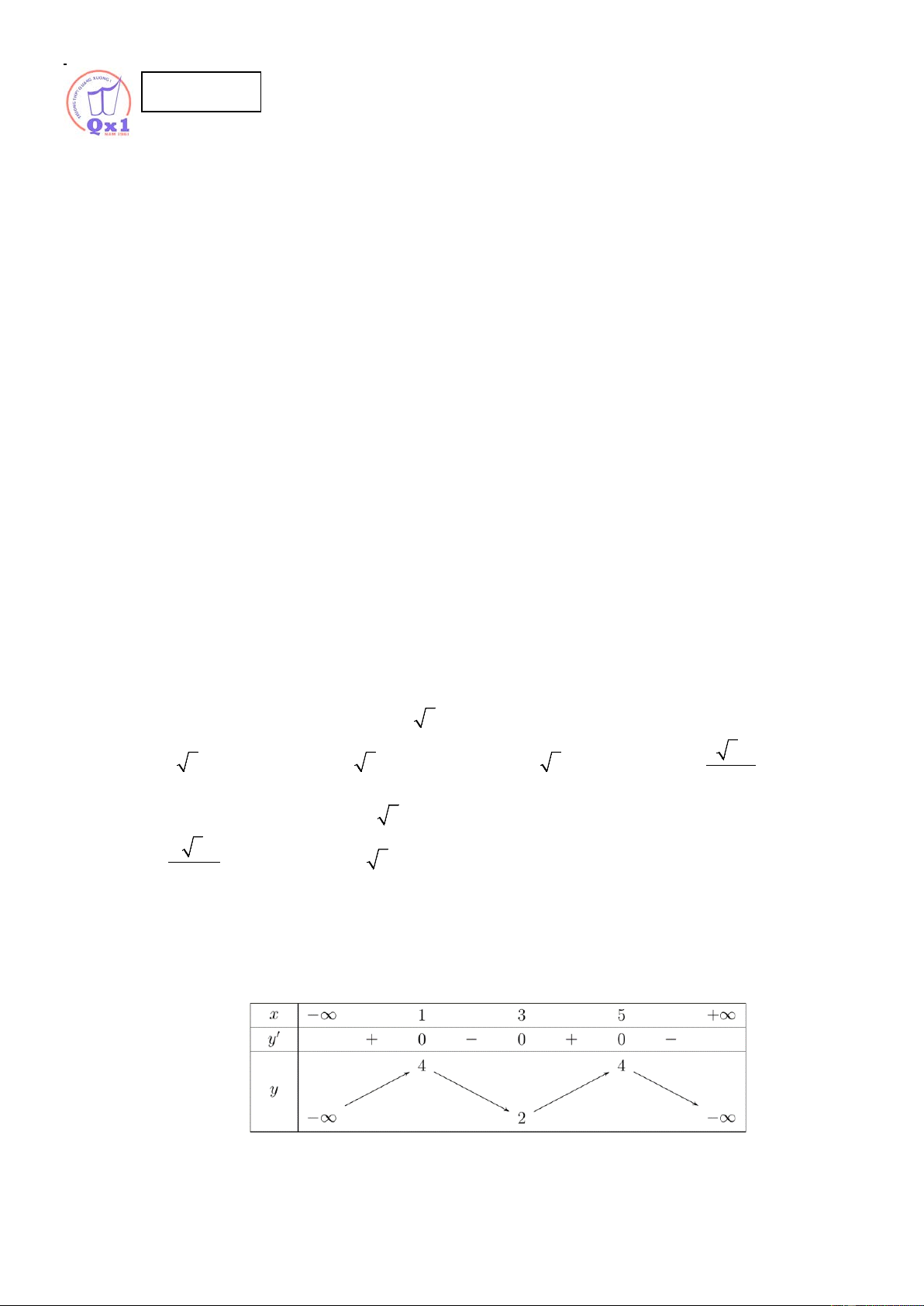
Câu 10. Cho hàm số y = f ( x) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ( ; −∞ 4) . B. (1;3) . C. (3; +∞) . D. (3;5) .
Trang 1/6 - Mã đề thi 123 Câu 11. Với ;
a blà các số thực dương (a 1), 3 log b bằng 2 a 3 2 3 A. 6 log b − b b b a . B. loga . C. loga . D. loga . 2 3 2
Câu 12. Diện tích xung quanh của mặt trụ có độ dài đường sinh bằng 2 bán kính đáy bằng 1 là 2π A. . B. π . C. 4π . D. 2π . 3
Câu 13. Cho hàm số f ( x) có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại A. x = 0 . B. x = 1 − . C. x = 1 . D. x = 4 .
Câu 14. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? x −1 A. y =
y = x − x +
y = x − x +
y = x − x + x + . B. 3 3 2 . C. 4 2 2 2 . D. 4 2 4 2 . 2 x −1
Câu 15. Tiệm cận đứng của đồ thị hàm số y = 2x + là đường thẳng 1 1 1 1 1 A. x = . B. x = − . C. y = . D. y = − . 2 2 2 2
Câu 16. Tập nghiệm của bất phương trình log x ≥ 3 là A. (10; +∞) . B. (0; +∞) . C. [1000; +∞) . D. ( ; −∞ 10).
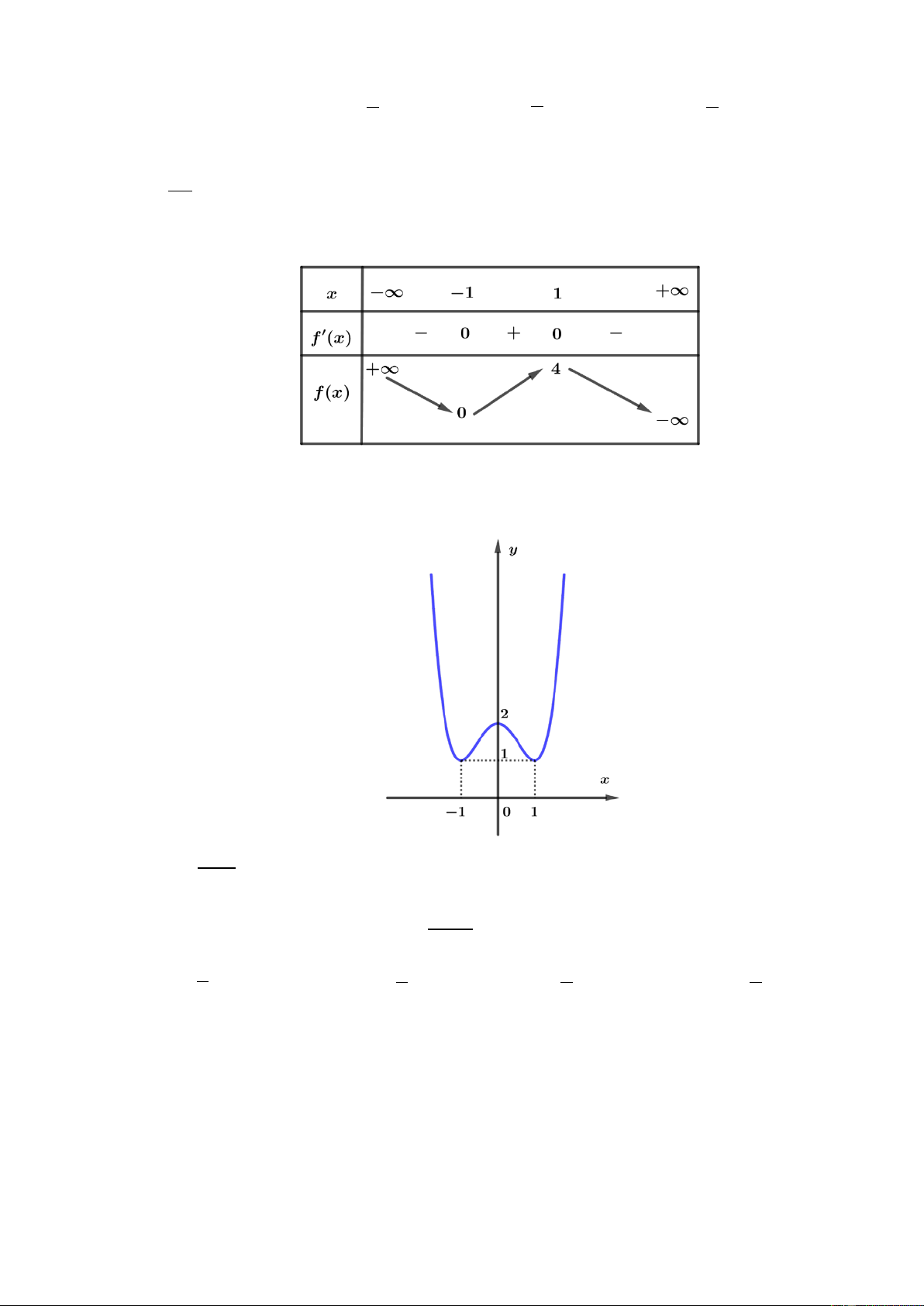
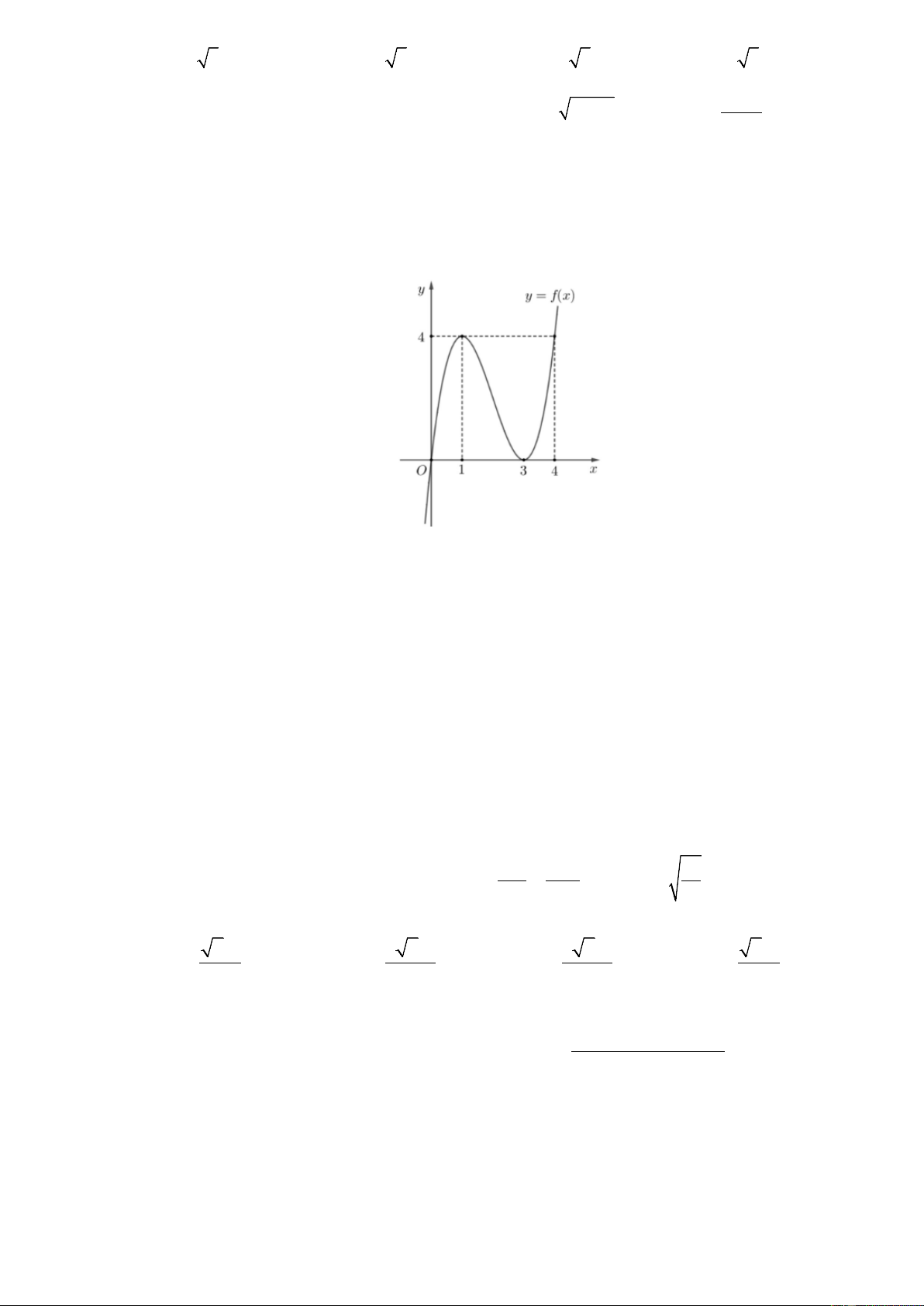
Câu 17. Cho hàm số bậc ba y = f ( x) có đồ thị trong hình dưới. Số nghiệm của phương trình
f (x) + 2 = 0 là
Trang 2/6 - Mã đề thi 123 A. 3. B. 1. C. 0. D. 2. 1 1 1
Câu 18. Nếu f (x)dx = 3 − ∫ và
g(x)dx = 4 − ∫ thì
[f (x) − 2g(x)]dx ∫ bằng bao nhiêu? 0 0 0 A. 5 . B. 1 − . C. 7 . D. 11. −
Câu 19. Số phức liên hợp của số phức 7 1 z = + i là 5 5 7 − 1 7 − 1 7 − 1 7 − 1 A. z = + i . B. z = − i . C. z = − i . D. z = + i . 5 5 5 5 3 5 3 3
Câu 20. Gọi z , z là 2 nghiệm của phương trình 2
z + 3z + 5 = 0 . Phần thực của số phức z + z bằng 1 2 1 2 3 − A. 3 − . B. 3 . C. . D. 0. 2
Câu 21. Trên mặt phẳng tọa độOxy , điểm biểu diễn của số phức z = 5 − 4i là điểm nào dưới đây? A. Q(5; 4 − ) . B. P( 5; − 4) . C. M ( 4; − 5) . D. N (4; 5 − ) .
Câu 22. Trong không gian Oxyz , hình chiếu vuông góc của điểm M (3; 2
− ;2) trên trục Oy có toạ độ là A. (3;0; 2) . B. (3;0;0) . C. (0; 2; − 0) . D. (0;0; 2) .
Câu 23. Trong không gian Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z − 2x + 4 y +10z −1 = 0. Tâm của (S ) có tọa độ là A. ( 2; − 4;10) . B. ( 1 − ;2;5) . C. (2; 4; − 1 − 0) . D. (1; 2 − ; 5 − ) .
Câu 24. Trong không gian Oxyz, cho mặt phẳng ( P) : x − 2 y − 2z + 3 = 0. Vectơ nào dưới đây là một
vectơ pháp tuyến của (P)? A. n = 1; 2 − ;2 . B. n = 1; 2 − ;3 . C. n = 1; 2 − ; 2 − . D. n = 1;0;3 . 4 ( ) 3 ( ) 2 ( ) 1 ( )
x 2 y 3 z 1
Câu 25. Trong không gian Oxyz , điểm nào dưới đây không thuộc đường thẳng d − + + : = = 1 2 − 2
A. M (2; − 3; − ) 1 .
B. N (1; −1; − 3) .
C. K (3; − 5; 2) .
D. P (0;1; − 5) .
Câu 26. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a 3 , SA vuông góc với mặt
phẳng đáy và SA =3 2a . Góc giữa đường thẳng SC và mặt phẳng ( ABCD) bằng A. 45° . B. 30° . C. 60° . D. 90° .
Câu 27. Cho hàm số y f x có bảng xét dấu đạo hàm như sau:
Trang 3/6 - Mã đề thi 123
Số điểm cực đại của hàm số đã cho là A. 3 . B. 2 . C. 1. D. 0 .
Câu 28. Giá trị nhỏ nhất của hàm số 4 2
f (x) = x − 2x + 2020 trên đoạn [ 2; − ] 1 bằng A. 2020 . B. 2019 . C. 2018 . D. 2028 .
Câu 29. Xét các số thực a a b ; b thỏa mãn log 4 .16
= log 4 . Trong các mệnh đề sau đây, mệnh đề nào 2 ( ) 8 là đúng?
A. a + 2b = 3 .
B. 6a + 3b = 1. C. 3ab = 1.
D. 3a + 6b = 1. 1
Câu 30. Số giao điểm của đồ thị hàm số 3 2
y = x + x + 2x +1 với trục hoành là 3 A. 0 . B. 1. C. 2 . D. 3 .
Câu 31. Tập nghiệm của bất phương trình x x 1 4 2 + − − 8 < 0 là A. (2; +∞) . B. (0; +∞) . C. (1; +∞) . D. ( ; −∞ 2) . Câu 32. Cho A
∆ BC vuông tại A có AB = 4a, AC = 3a . Quay A
∆ BC quanh AB , đường gấp khúc
ACB tạo nên hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón đó bằng A. 2 5π a . B. 2 15π a . C. 2 3π a . D. 2 20π a . e e 3ln x +1 3ln x +1
Câu 33. Xét I = dx, ∫
nếu đặt u = 3ln x +1 thì I = dx x ∫ bằng x 1 1 2 e e 2 2 3 2 3 A. 2 I = u du ∫ . B. 2 I = u du ∫ . C. 2 I = u du ∫ . D. 2 I = u du ∫ 3 3 2 2 1 1 1 1
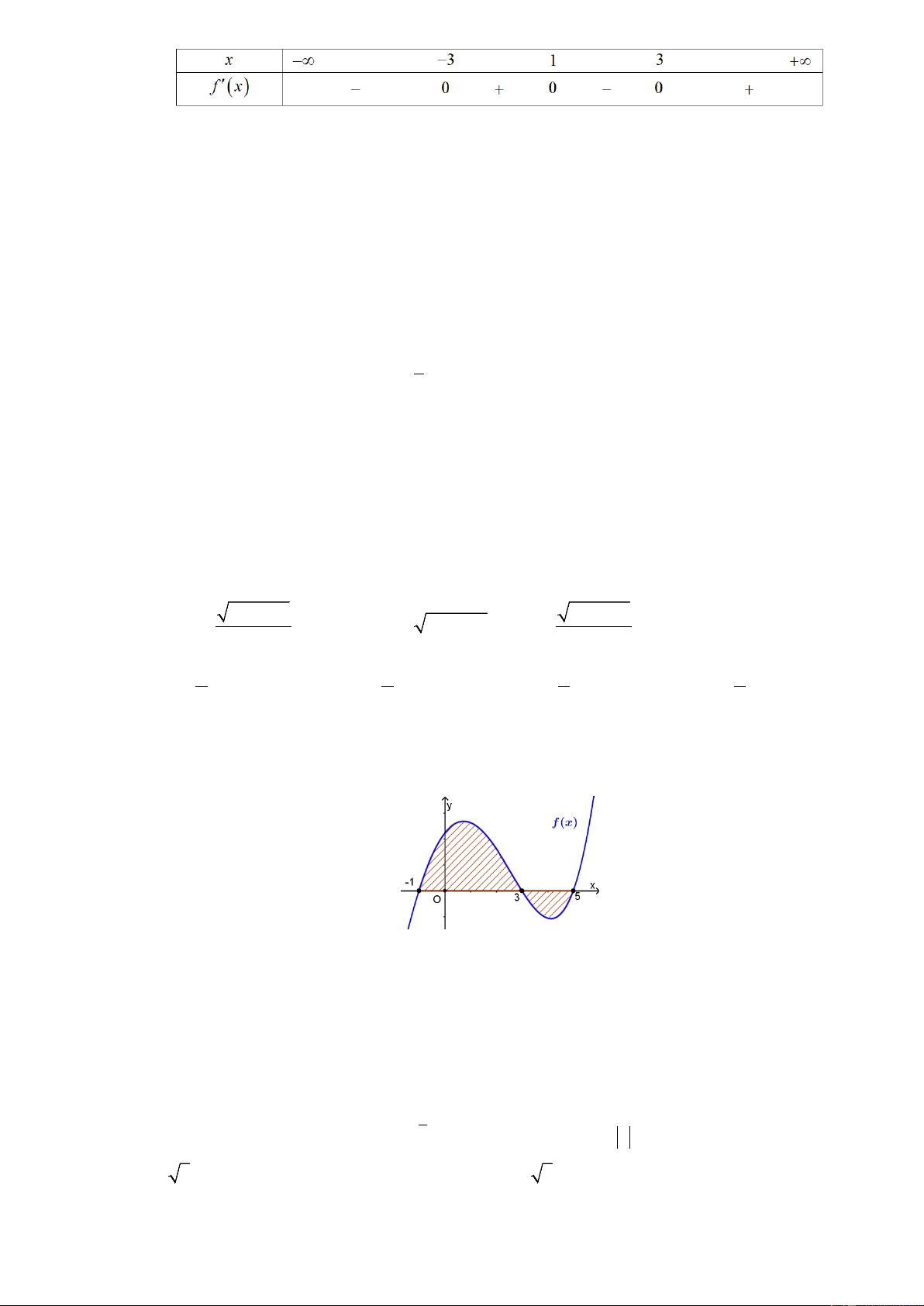
Câu 34. Cho phần hình phẳng (H ) được gạch chéo như hình vẽ. Diện tích của (H ) được tính theo
công thức nào dưới đây 5 3 5 A. S = f ∫ (x)dx. B. S = f
∫ (x)dx + f ∫ (x)dx. 1 − 1 − 3 3 5 3 5 C. S = f
∫ (x)dx − f ∫ (x)dx.
D. S = − f
∫ (x)dx + f ∫ (x)dx. 1 − 3 1 3
Câu 35. Cho hai số phức z = 2 − i và z = 2 − 4i . Phần ảo số phức z + z .z bằng 1 2 1 1 2 A. 2i . B. 2 . C. 11 − i . D. 11 − .
Câu 36. Cho số phức z thỏa mãn hệ thức z.(z − 2i) − 3 + 4i = 0. Giá trị z bằng: A. 5 . B. 2 . C. 3 . D. 1 .
Trang 4/6 - Mã đề thi 123
Câu 37. Trong không gian với hệ tọa độ Oxyz , cho hai mặt phẳng (P) : x − 2 y + 3z − 2 = 0 ,
(Q) : x − y + 3 = 0 .Mặt phẳng (α ) vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm
có hoành độ bằng 5. Phương trình của mp (α ) là:
A. 3x 3y z 15 0 . B. x y z 5 0 . C. 2x z 10 0 . D. 2x z 6 0 .
Câu 38. Trong hệ trục tọa độ Oxyz , cho các điểm M (1; 1 − ;1),N(2;0; 1 − ), P( 1
− ;2;1) . Xét điểm Q sao
cho tứ giác MNPQ là một hình bình hành. Tọa độ Q là A. ( 2; − 1;3) B. (2;1;3) C. ( 2; − 1; 3) − D. (4;1;3)
Câu 39. Một chiếc hộp đựng 8 viên bi màu xanh được đánh số từ 1 đến 8 , 9 viên bi màu đỏ được
đánh số từ 1 đến 9 và 10 viên bi màu vàng được đánh số từ 1 đến 10 . Một người chọn ngẫu
nhiên 3 viên bi trong hộp. Tính xác suất để 3 viên bi được chọn có số đôi một khác nhau. 772 209 512 2319 A. . B. . C. . D. . 975 225 2925 2915
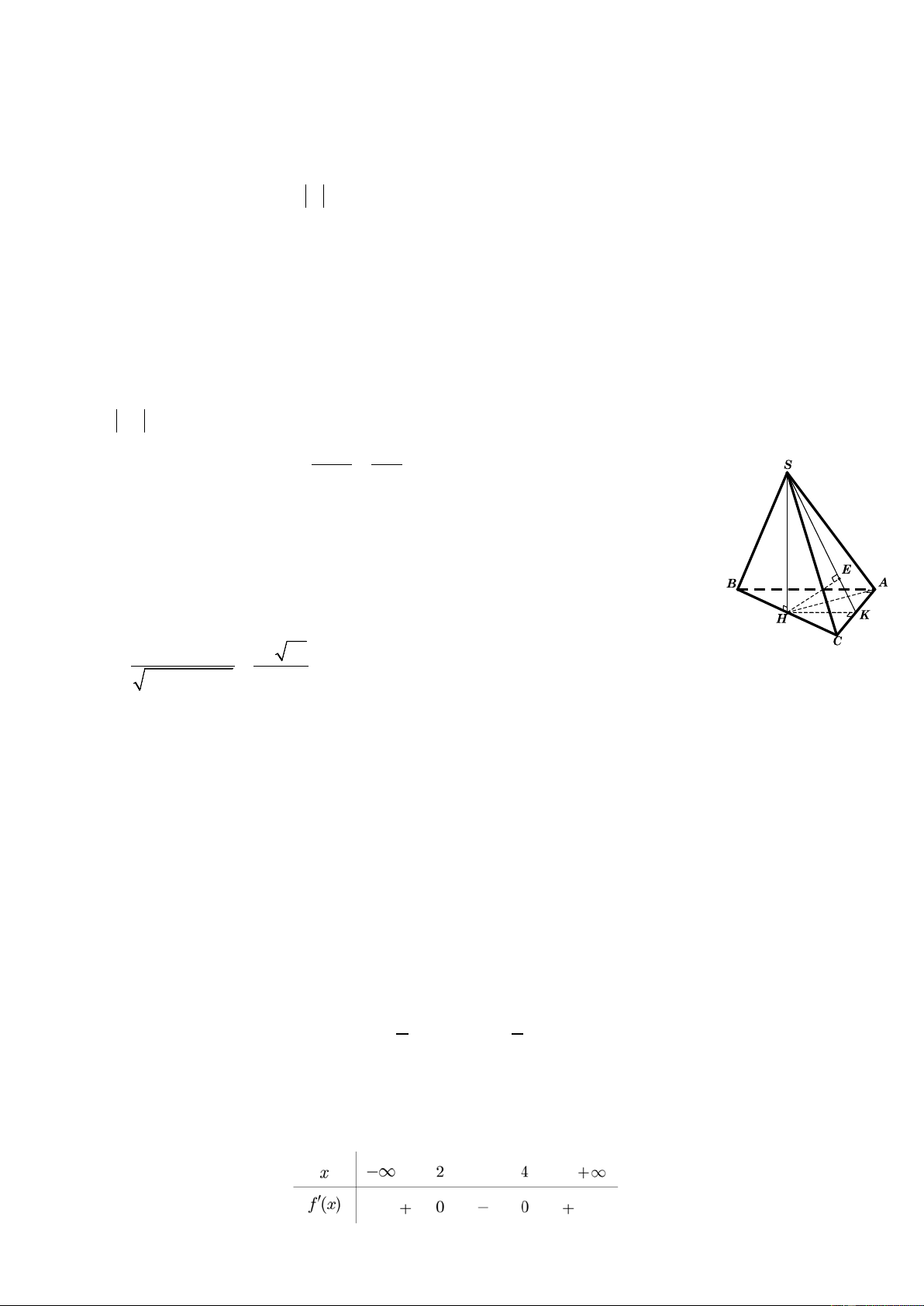
Câu 40. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , AB = a,
AC = a 3 . Tam giác
SBC đều và nằm trong mặt phẳng vuông với đáy. Tính khoảng cách từ B đến mặt phẳng (SAC). a 39 2a 39 a 3 A. . B. . a C. . D. . 13 13 2 Câu 41. Cho hàm số 3 2
f (x) = x − (2m +1)x + 3mx − m có đồ thị (C ) . Có bao nhiêu giá trị nguyên của m
tham số m thuộc ( 2020 −
; 2020] để đồ thị (C ) có hai điểm cực trị nằm khác phía so với trục m hoành. A. 4037 . B. 4038 . C. 4039 . D. 4040 .
Câu 42. Ông Hùng gửi 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn một năm, với công thức = ( n
C A 1+ r) , lãi suất r =12% một năm. Trong đó C là số tiền nhận được (cả gốc lẫn
lãi) sau thời gian n năm, A là số tiền gửi ban đầu. Tìm n nguyên dương nhỏ nhất để sau n
năm ông Hùng nhận được số tiền lãi hơn 40 triệu đồng. (Giả sử rằng lãi suất hằng năm không thay đổi). A. 5 . B. 2 . C. 4 . D. 3 . 4
Câu 43. Cho hàm số y f (x) có đồ thị như hình vẽ, biết f (
x) dx 12.
Tính m f (2). 1 A. 6 . B. 5 . C. 12 . D. 3 .
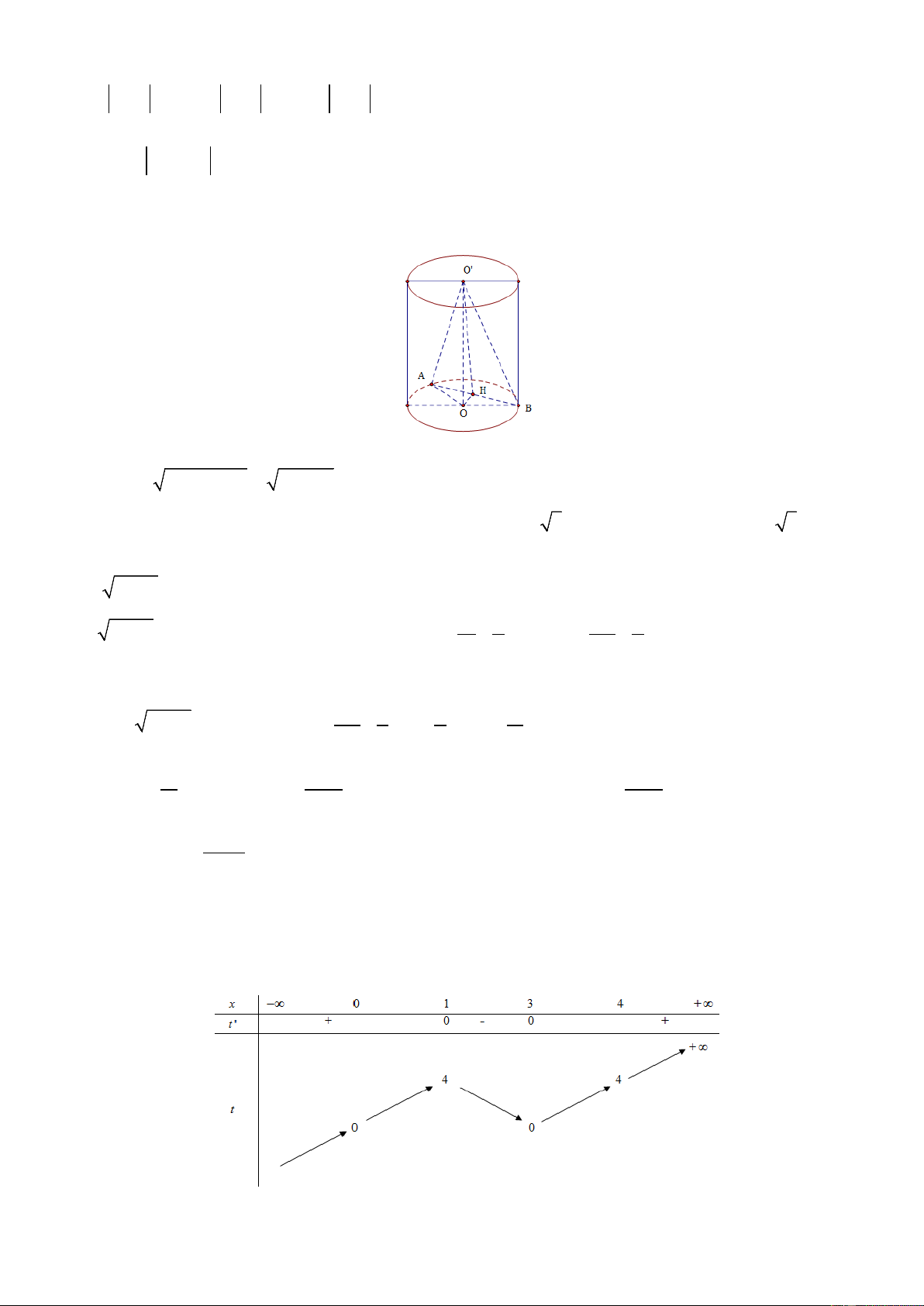
Câu 44. Cho hình trụ có 2 đáy là các đường tròn tâm O và O ' và có bán kính là R = 5 . Trên đường tròn (O) lấy 2 điểm ,
A B sao cho AB = 8 và mặt phẳng (O' AB) tạo với đáy một góc 0 60 . Thể
tích khối trụ đã cho bằng
Trang 5/6 - Mã đề thi 123 A. 15π 3 . B. 25π 3 . C. 125π 3 . D. 75π 3 . 2 5 f ( x)
Câu 45. Cho hàm số f (x) liên tục trên và thỏa mãn f
∫ ( 2x +5 − x)dx =1, dx = 3 ∫ . Tích 2 x 2 − 1 5 phân f (x)dx ∫ bằng 1 A. 15 − . B. 2 − . C. 13 − . D. 0 .
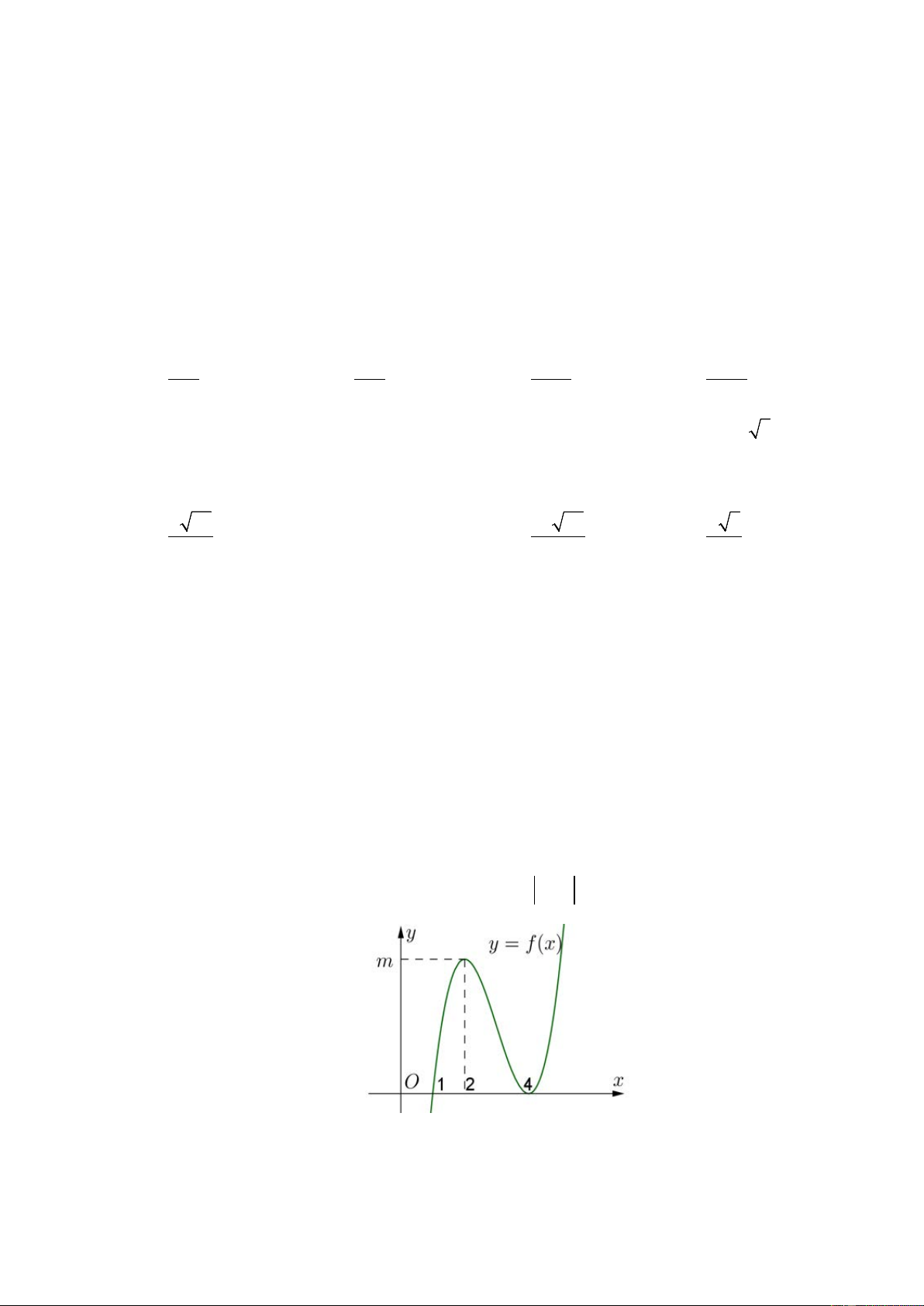
Câu 46. Cho hàm số y = f ( x) liên tục trên và có đồ thị như hình bên dưới
Với tham số thực m∈( 2
0; 4] thì phương trình f (x( x − 3) ) = m có ít nhất bao nhiêu nghiệm thực thuộc [0;4)? A. 4 . B. 3 . C. 7 . D. 5 .
Câu 47. Cho hàm số ( ) 2020x 2020 x f x − = −
. Tìm số nguyên m nhỏ nhất để f (m) + f (3m + 2020) > 0 A. 505 − . B. 504 − . C. 506 − . D. 503 − . 2 3
Câu 48. Cho các hàm số f ( x) 2
= x − 4x + m và g (x) = ( 2 x + )( 2 x + ) ( 2 1 2
x + 3) . Tổng tất cả các giá
trị nguyên của tham số m∈( 6;
− 6) để hàm số g ( f (x)) đồng biến trên (3;+∞) là A. 14 . B. 18 . C. 9 . D. 12 .
Câu 49. Cho khối chóp S.ABC có = = = 0 = 0 = 0
SA SB SC a, ASB 60 , BSC 90 ,CSA =120 . Gọi M, N lần
lượt là các điểm trên cạnh AB CN AM 11 và SC sao cho = MN = a
, tính thể tích V của SC AB và 12
khối chóp S.AMN. 3 2a 3 5 2a 3 5 2a 3 2a A. V = . B. V = . C. V = . D. V = . 72 432 72 432
Câu 50. Gọi S là tập hợp chứa tất cả các giá trị nguyên của tham số m để có đúng 2 bộ số thực ( ; x y) + + + +
thỏa mãn đồng thời hai hệ thức x y x y log (26x + 53) 2 2 2 4 5 2 .log + 8log m = 0 và 3 3 3 729
(x − )2 +( y + )2 12 2
=196 . Tổng giá trị các phần tử của tập S bằng A. 2 B. 82 C. 81 D. 32 −
--------------- HẾT ---------------
Trang 6/6 - Mã đề thi 123
TRƯỜNG THPT QUẢNG XƯƠNG 1
ĐÁP ÁN ĐỀ GIAO LƯU KIẾN THỨC CÁC TRƯỜNG THPT MÃ ĐỀ 123
LẦN 2 - NĂM HỌC 2019 - 2020
( Đáp án gồm có 6 trang) MÔN: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề) Câu 1. Chọn B Câu 2. Chọn B Câu 3. Chọn B Câu 4. Chọn C Câu 5. Chọn C Câu 6. Chọn C Câu 7. Chọn B Câu 8. Chọn A Câu 9. Chọn C Câu 10. Chọn D Câu 11. Chọn D
Câu 12. Chọn C Câu 13. Chọn B Câu 14. Chọn C Câu 15. Chọn B Câu 16. Chọn C Câu 17. Chọn A Câu 18. Chọn A Câu 19. Chọn B Câu 20. Chọn A Câu 21. Chọn A Câu 22. Chọn C Câu 23. Chọn D
Câu 24. Chọn C
Câu 25. Chọn C
Câu 26. Chọn C S
Do SA ⊥ ( ABCD) nên hình chiếu của SC lên mặt phẳng ( ABCD) là AC . Khi đó
góc giữa đường thẳng SC và mặt phẳng ( ABCD) là góc A SA 3a 2 B SCA . = = = ⇒ tan SCA 3 SCA = 60° . AC a 6 D
Vậy góc giữa đường thẳng C
SC và mặt phẳng ( ABCD) bằng 60° . Câu 27. Chọn C
Hàm số y f (x) có đạo hàm đổi dấu từ dương sang âm qua điểm x 1 nên hàm số có một điểm cực đại.
Câu 28. Chọn B
Trang 1/6 - Mã đề thi 123 x = 0∈[ 2; − ] 1 Hàm số 4 2
f (x) = x − 2x + 2020 liên tục trên đoạn [ 2; − ] 1 . 3 f (
′ x) = 4x − 4x . f (′x) = 0 ⇔ . x = 1 ± ∈ [ 2; − ] 1
f (0) = 2020; f ( 1
− ) = 2019; f (1) = 2019; f ( 2) − = 2028 ⇒ min f (x) = 2019 [ 2 − ] ;1
Câu 29. Chọn D log 4a.16b = log 4 log 4a log 16b ⇔ + = log 2 log 2 a log 2 b ⇔ + = log 2 2 ( 2 ) 2 ( 4 ) 2 2 ( ) 2 ( ) 2 2 ( ) 8 8 3 2 2
⇔ 2a + 4b = ⇔ 3a + 6b = 1. 3
Câu 30. Chọn B 1 Ta có 3 2 2 y =
x + x + 2x +1 ⇒ y′ = x + 2x + 2 > 0 , x ∀ ∈ . 3
Suy ra hàm số trên đồng biến trên và do đó đồ thị cắt trục hoành tại đúng 1 điểm. Câu 31. Chọn D Ta có: x x 1 4 2 + −
− 8 < 0 ⇔ 4x − 2.2x − 8 < 0 ⇔ 2
− < 2x < 4 ⇔ x < 2 . B
Câu 32. Chọn B 4a
Khi quay quanh cạnh AB , đường gấp khúc ACB tạo thành hình nón có r = AC = 3 ; a h = AB = 4 ;
a l = BC = 5a .Do vậy ta có 2 S = π rl = π.3 .5 a a = 15π a xq 3a
Câu 33. Chọn A A C • 3 dx 2 2
u = 3ln x +1 ⇒ u = 3ln x +1 ⇒ 2udu = dx ⇒ = udu . • x x 3 e 2 2 3ln x +1 2u I = dx = du ∫ ∫ . x 3 1 1
Câu 34. Chọn C 5 3 5 3 5 S =
f (x ) dx = f (x ) dx + f (x ) dx = f (x )dx − ∫ ∫ ∫ ∫
∫ f (x)dx. −1 −1 3 −1 3
Câu 35. Chọn D
Ta có z + z .z = 2 − i + 2 − i
2 − 4i = 2 −11i . 1 1 2 ( )( ) Câu 36. Chọn A
Gọi z = a + bi; a,b∈ .
Ta suy ra z (z − i) 2 .
2 − 3 + 4i = 0 ⇔ z − 2iz − 3 + 4i = 0 ⇔ ( 2 2
a + b ) − 2i (a + ib) − 3 + 4i = 0 ⇔ ( 2 2
a + b + 2b − 3) + i ( 2 − a + 4) = 0 2 − a + 4 = 0 a = 2 a = 2 ⇔ ⇔ ⇔
⇒ z = 2 − i ⇒ z = 5 2 2 2
a + b + 2b − 3 = 0 b + 2b +1 = 0 b = 1 −
Câu 37. Chọn A
(P) có vectơ pháp tuyến n = (1; 2
− ;3 , (Q) có vectơ pháp tuyến n = (1; 1 − ;0 . Q ) P )
n = n ; n = α α α
(3;3; )1 .( ) đi qua điểm M (5;0;0). Nên ( ) có phương trình: 3x +3y + z −15 = 0 . P Q
Câu 38. Chọn A Gọi Q( ; x y; z). = − = − − − − Ta có MN (1;1; 2), QP ( 1 ; x 2 y;1 z).
Trang 2/6 - Mã đề thi 123 1 = 1 − − x x = 2 − Tứ giác
MNPQ là một hình bình hành ⇔ MN = QP ⇔ 1
= 2 − y ⇔ y = 1 . Vậy, Q( 2; − 1;3) . 2 − = 1− z z = 3 Câu 39. Chọn A
Số phần tử của không gian mẫu là 3 Ω = C = 2925 27 . TH 1: một màu. Trường hợp này có 3 3 3
C +C +C = 260 8 9 10
phần tử (ứng với màu xanh, đỏ, vàng). TH 2: hai màu. Trường hợp này có 1 2 2 1 1 2 2 1 1 2 2 1
C .C +C .C +C .C +C .C +C .C +C .C = 1544 8 8 8 7 8 9 8 8 9 9 9 8
phần tử (ứng với các cặp màu xanh-
đỏ, xanh-vàng, đỏ-vàng).
TH 3: ba màu.Trường hợp này có 1 1 1
C .C .C = 512 8 8 8
phần tử (ứng với màu xanh, đỏ, vàng). Như vậy Ω = 2316 A .
Vậy xác suất của biến cố 2316 772 A là P = = . 2925 975 Câu 40. Chọn C
Gọi H là trung điểm của BC , suy ra SH ⊥ BC ⇒ SH ⊥ ( ABC) Gọi K là trung điểm
AC , HK ⊥ AC .
Kẻ HE ⊥ SK (E ∈ SK ). Khi đó d B,(SAC) = 2d H,(SAC) SH .HK 2a 39 = 2HE = 2. = . 2 2 + 13 SH HK Câu 41. Chọn B
Xét phương trình hoành độ giao điểm của đồ thị và trục hoành: x = 1 3 2 2
x − (2m +1)x + 3mx − m = 0 ⇔ (x −1)(x − 2mx + m) = 0 ⇔
Để thõa mãn thì phương trình 2
x − 2mx + m = 0 (1)
hoành độ giao điểm phải có 3 nghiệm phân biệt từ đó (1) có 2 nghiệm phân biệt khác 1. ⇒ m ∈ ( ;
−∞ 0) ∪ (1;+∞) Mà m là số nguyên và m∈( 2020 −
; 2020] nên có 4038 giá trị.
Câu 42. Chọn D Từ công thức = ( n C
A 1+ r ) với A = 100 , r = 0,12 và n nguyên dương.
Ta có: Số tiền thu được cả gốc lẫn lãi sau n
n năm là C = 100.(1+ 0,12) .
Số tiền lãi thu được sau n
n năm là L = 100.(1+ 0,12) −100 . n 7
L > 40 ⇔ 100 (1+ 0,12) −100 > n 7 40 ⇔ 1,12 > ⇔ n > log
≈ 2,97 .Số nguyên dương nhỏ nhất n = 3. 5 1,12 5
Câu 43. Chọn A
Từ đồ thị, ta có bảng xét dấu f (x) như sau:
Trang 3/6 - Mã đề thi 123 4 2 4 2 4 12 f ( x) dx f ( x) dx f ( x) dx 12 f (
x)dx f (x)dx 1 1 2 1 2 2 4
12 f (x) f (x) 12 f (2) f (1) f (4) f (2) f f f 1 2 12 2 (2) (1) (4)
12 2.m 0 0 m 6.
Câu 44. Chọn D
Gọi H là trung điểm của AB. Ta có: HA = HB = 4 Do vậy 2 2 2 2
OH = OA − HA =
R − 4 = 3 Mặt khác OO ' ⊥ AB ⇒ (O ' HO) ⊥ AB Do đó
O HO = ((O AB) (O)) 0 ' ' ; = 60 Khi đó 0
OO ' = OH tan 60 = 3 3 Vậy 2
V = S .h = π R h = 75π 3 d
Câu 45. Chọn C Đặt 2 t =
x + 5 − x suy ra t t + x =
x + 5 ⇒ (t + x)2 5 5 1 2 2 2
= x + 5 ⇒ t + 2tx = 5 ⇒ x = − ⇒ dx = − − dt 2 2t 2 2t 2 Đổi cận: x = 2
− ⇒ t = 5; x = 2 ⇒ t = 1. 2 1 5 5 1 1 5 Ta có: f
∫ ( 2x +5 − x)dx = f
∫ (t) − − dt = f t +1 dt = 1 ∫ . 2 ( ) 2 2t 2 2 t 2 − 5 1 5 5 5 f (t) 5 5 5 f t Suy ra f
∫ (t) +1 dt = 2 ⇔ 5 dt + f t dt = 2 ⇔ f t dt = 2 − 5 dt ∫ ∫ ∫ ∫ 2 ( ) ( ) ( ) 2 t 2 t t 1 1 1 1 1 5 5 ⇔ f ( x) f ( x) dx = 2 − 5 dx = 2 − 5.3 = 13 − ∫ ∫ . 2 x 1 1
Câu 46. Chọn A = Đặt 2 x 1
t = x ( x − )2
3 khi đó t′ = 0 ⇔ ( x − 3) + 2x ( x − 3) = 0 ⇔ . x = 3
Bảng biến thiên của t như sau
Trang 4/6 - Mã đề thi 123 < + Nếu t 0
phương trình t = x ( x − )2
3 không có nghiệm thuộc [0; 4) . t > 4
+ Nếu t = 0 phương trình t = x(x − )2
3 có đúng hai nghiệm thuộc [0; 4) .
+ Nếu t = 4 phương trình t = x(x − )2
3 có đúng một nghiệm thuộc [0; 4) .
+ Nếu 0 < t < 4 phương trình t = x(x − )2
3 có ba nghiệm phân biệt thuộc [0; 4) .
Vậy phương trình f (x(x − )2
3 ) = m có ít nhất 4 nghiệm thực phân biệt thuộc đoạn [0;4) khi m = 4 Câu 47. Chọn B
Hàm số ( ) 2020x 2020 x f x − = − xác định trên . Ta có:
(− ) = 2020−x − 2020x = −(2020x − 2020−x f x
) = − f (x)⇒ f (x) là hàm lẻ trên . −
Mà ′( ) = 2020x ln 2019 + 2020 x f x ln 2020 > 0, x
∀ ∈ nên hàm số f (x) đồng biến trên .
Do vậy: f (m) + f (3m + 2020) > 0 ⇔ f (3m + 2020) > − f (m) ⇔ f (3m + 2020) > f (−m)
⇔ 3m + 2020 > −m ⇔ m > 505 −
Do đó giá trị m nguyên nhỏ nhất thỏa mãn là 504 − .
Câu 48. Chọn D 2 3 f ( x) 2
= x − 4x + m ⇒ f ′(x) = 2x − 4. g (x) = ( 2 x + ) 1 ( 2 x + 2) ( 2 x + 3) 12 10 2
= a x + a x + ...+ a x + a 12 10 2 0 ⇒ g′(x) 11 9
=12a x +10a x +...+ 2a x . 12 10 2 ′ g
( f ( x)) = f ′( x).g′
( f (x)) = (2x −4) 11 12 a f (x) 9
+10a f x + ...+ 2a f x 12 10 ( ) 2 ( )
= (2x − 4). f (x) 10 . 12 a f (x) 8
+10a f x + ...+ 2a 12 10 ( ) 2
Vì a ; a ; ...; a ; a > 0 và 2x − 4 > 0 x ∀ ∈( 3; +∞) nên 12 10 2 0 (2x − 4) 10 12 a f (x) 8
+10a f x + ...+ 2a > 0 3 x ∀ ∈ ;+∞ 12 10 ( ) 2 ( ) . Hàm số ′
g ( f ( x)) đồng biến trên (3;+∞) ⇔ g
( f ( x)) ≥ 0 x ∀ ∈( 3; +∞) ⇔ f (x) ≥ x ∀ ∈( +∞) 2
⇔ x − x + m ≥ x
∀ ∈( +∞) ⇔ m ≥ h(x) 2 0 3; 4 0 3; = −x + 4x x ∀ ∈( 3; +∞)
⇒ m ≥ lim h(x) = 3 ⇒ m∈{3;4; } 5 . + x→3
Câu 49. Chọn B a
Ta có : AC = a 3, AB = a, BC = a 2 Gọi H là trung điểm của AC ta có SH là đường cao và SH = 2 S N C A H M 3 a 2
Ta có thể tích khối chóp S.ABC là B V = 0 12
Trang 5/6 - Mã đề thi 123 2 2
Đặ CN AM a a t =
= m(0 ≤ m ≤ 1), ta có SA = a, SB = b, SC = c, a = b = c = a, a.b =
, b.c = 0, c.a = − . SC AB 2 2 Theo đẳ
ng thức trên ta có SN = (1− m)c, SM = SA + AM = a + mAB = a + m(b − a)
⇒
MN = SN − SM = (1− m)c − a + m(b − a) = (m −1)a − mb + (1− m)c. Do đó = ( a MN
(m −1)a − mb + (1− m)c ) 2 2 11 2 2 2
= (3m − 5m + 3)a = . 12 3 3 5 SN SN AM 5 1 2a 5 2a ⇒ m = ⇒ V = V = .
V = m(1− m)V = . . = . S . AMC 0 0 6 SC SC AB 6 6 12 432 Câu 50. Chọn B Gọi M M ( ;
x y ) . Nhận thấy M nằm trên đường tròn (C) có tâm I (12; 2 − ) và bán kính R = 14 .
Ta biến đổi: x + y + x + y + = (x + )2 + ( y + )2 2 2 2 2 4 5 1 2
= AM ; trong đó điểm I A 13 A( 1 − ; 2 − ) .
Dễ dàng xác định được: 1≤ AM ≤ 27 như hình vẽ bên dưới.
Ta cũng để ý rằng từ: x + = x + −
+ (x − )2 + ( y + )2 = (x + )2 + ( y + )2 2 26 53 26 53 196 12 2 1 2 = AM . 2 2 2
x + y + 2x + 4 y + 5 AM Suy ra: 2 log (26x + 53) 2 .log + 8log m = 0 ⇔ log ( 2 AM .log + 8log m = 0 3 3 3 3 ) 3 3 729 729 ⇔ 2 log ( 2 AM ).( 2
log AM − 6 + 8 log m = 0 (*) 3 3 ) 3 Đặt 2 2 2
t = log AM ,ÐK : log 1 ≤ t ≤ log 27 ⇔ 0 ≤ t ≤ 6 . 3 3 3 = Để ý khi t 0
luôn cho ta duy nhất một bộ số ( ;
x y ) và với mỗi 0 < t < 6 cho ta hai bộ số ( ; x y ) t = 6
(Với hai điểm M đối xứng qua IA)
(*) trở thành 2t (t − 6) = 8
− log m ⇔ f (t) 3 2 = t − 6t = 8 − log m ** 3 3 ( )
Ta có bảng biến thiên của f (t) 3 2
= t − 6t trên 0;6 Với 8 − log m = 32
− ⇔ m = 81phương trình (**) có đúng một nghiệm t 4 có hai bộ ( ; x y ) 3 Với 8
− log m = 0 ⇔ m = 1 phương trình (**) có hai nghiệm t 0;t 6 có hai bộ ( ; x y ) 3
Vậy tổng các phần tử của tập S bằng 82.
--------------- HẾT ---------------
Trang 6/6 - Mã đề thi 123
Document Outline
- 123 -ĐỀ
- 123-DA




