PHÒNG GIÁO DỤC VÀ ĐÀO KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
TẠO THÀNH PHỐ VINH NĂM HỌC 2022- 2023
ĐỀ THI CHÍNH THỨC
Môn thi: Toán lớp 7
(Đề thi gồm có 01 trang)
Thời gian: 120 phút ( không kể thời gian giao đề)
Câu 1. (4,5 điểm)    
1. Tính giá trị biểu thức: a, 10. 1,44 24. 0,25 12 144 A =  +  :  + 3 7 7 9      5 4 9 b, 4 .9 2.6 N − = 10 8 8 2 .3 + 6 .20 2. Cho 4 8 1996 2000 A = 1+ 2 + 2 + ... + 2 + 2 và 2 4 2000 2002 B = 1+ 2 + 2 + ... + 2 + 2 . Tính tỷ số A B
Câu 2. (4,0 điểm)
a, Tìm x∈ Z biết 1 2x −1 + = 2 4
b, Tìm x, y, z biết: 2x = 3y = 5z và x + 3y − 2z = 66 3 c, Cho 2 2 b = ;
ac c = bd ( a, b, c, d khác 0). Chứng minh rằng:  12a + 3b − 5c  a = 
12b 3c 5d  + −  d
Câu 3. (3,5 điểm)
a, Cho x, y là các số nguyên dương thỏa mãn x + 2y 2023 =
. Tìm giá trị nhỏ nhất của x . x + y 2022
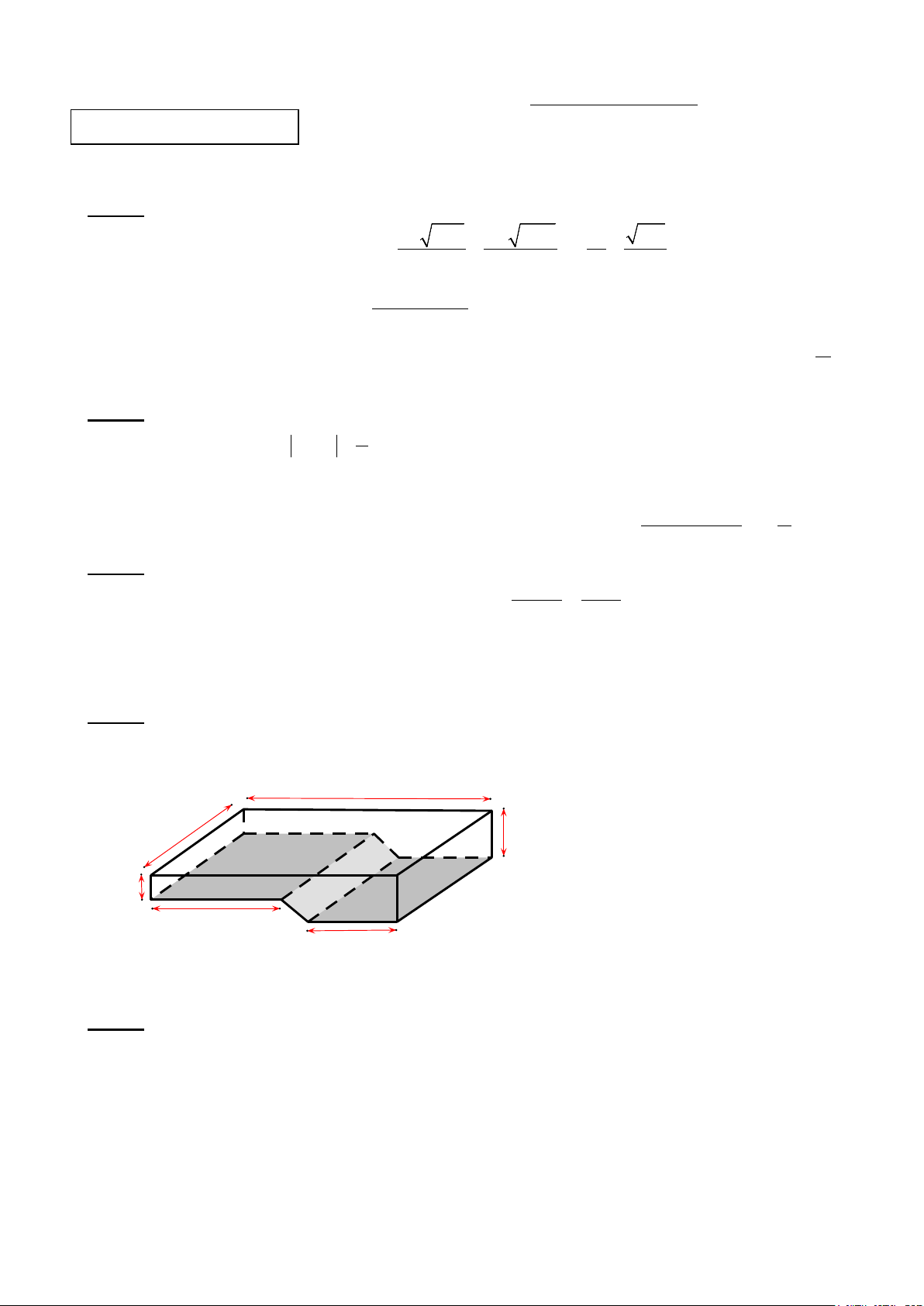
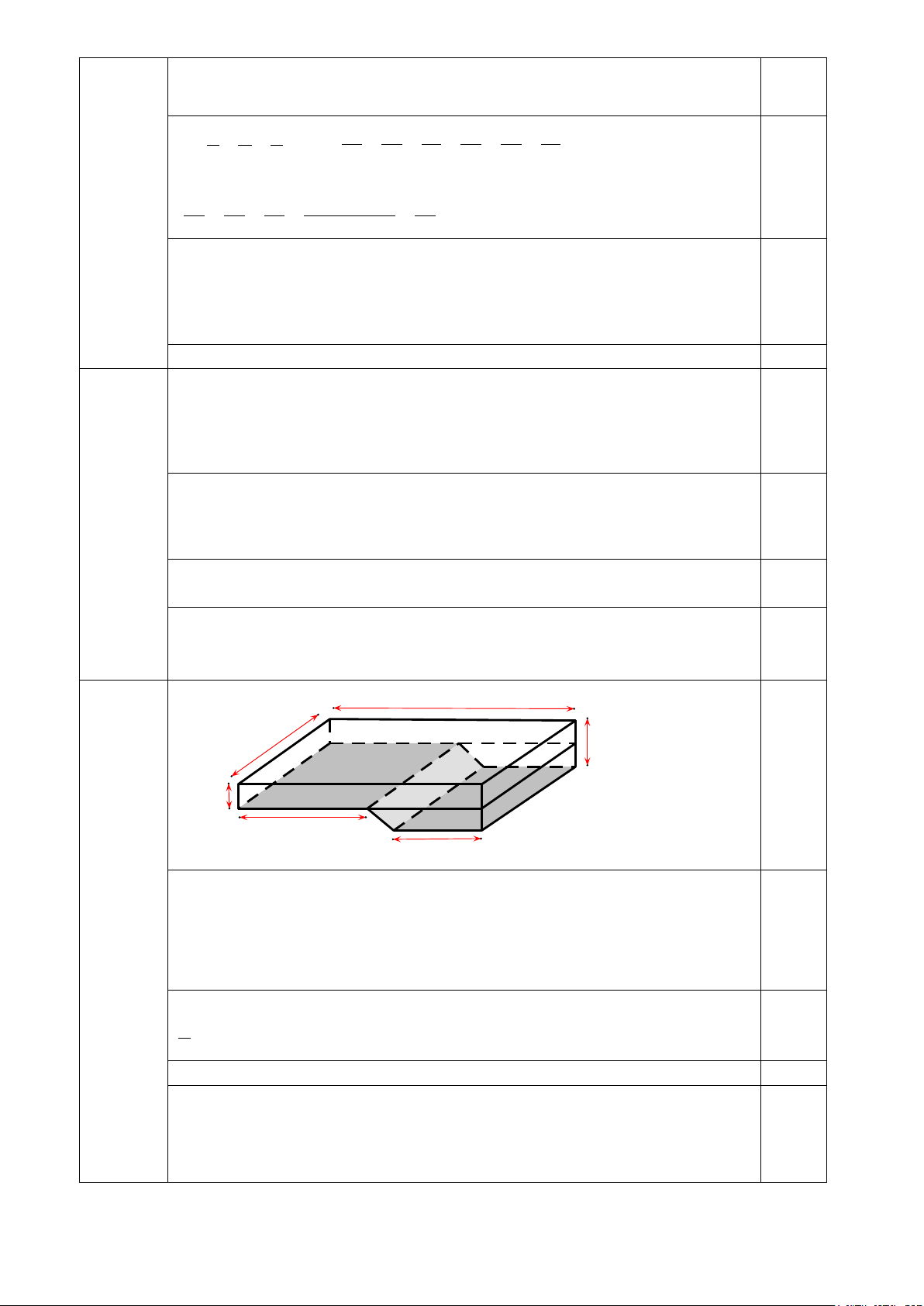
b, Một bể nước dạng hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao tỉ lệ với
1: 2: 4. Tổng diện tích sáu mặt của bể nước là 112m2. Tính thể tích bể nước.
c, Tìm các số nguyên dương a,b,c thỏa mãn: 3 2 + 3 + 5 = 5b a a và 3 5c a + =
Câu 4. (2,0 điểm)
Một bể bơi được xây dựng thành hai khu vực với độ sâu khác nhau cho trẻ em và người lớn và
các kích thước của lòng bể được cho như hình vẽ. 25 m 10 m 3 m 1,4 m 10 m 8 m
Hỏi sau bao lâu bể bơi được bơm đầy nước, biết cứ mỗi phút máy bơm được vào bể 500 lít nước.
Câu 5. (6,0 điểm)
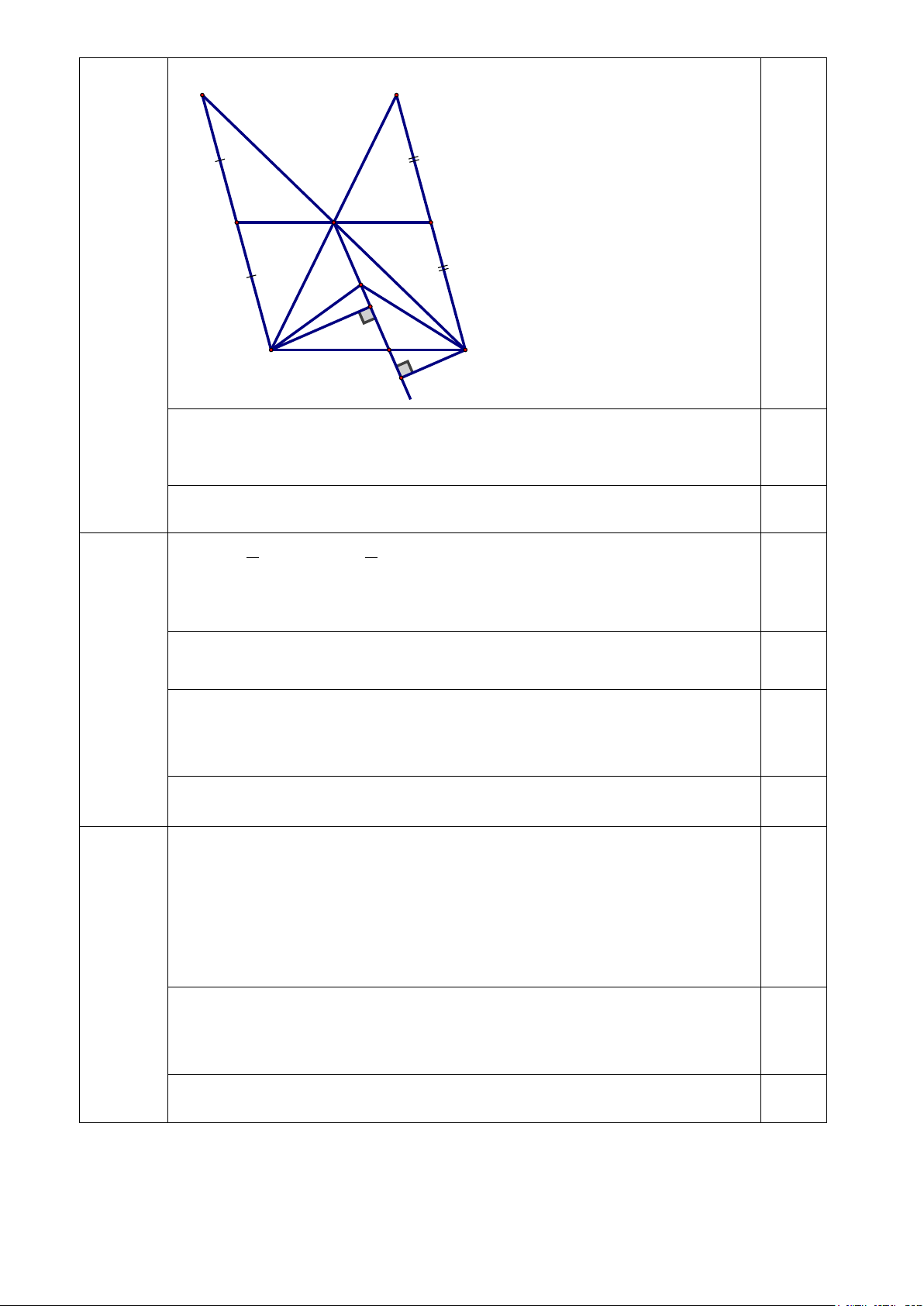
Cho tam giác ABC nhọn có AB < AC. Trên tia đối của tia AB lấy điểm D sao cho AB =
AD. Qua B kẻ đường thẳng song song với CD cắt đường thẳng AC tại E.
a, Chứng minh rằng BE = CD; ED =BC
b, Gọi P, Q lần lượt là trung điểm của BE, CD. Chứng minh rằng A là trung điểm của PQ
c, Gọi M là điểm bất kỳ nằm trong tam giác ABC. Xác định vị trí của M để biểu thức
MA.BC +MB.AC +MC.AB đạt giá trị nhỏ nhất.
……………….…. Hết …………………
PHÒNG GIÁO DỤC VÀ ĐÀO KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
TẠO THÀNH PHỐ VINH NĂM HỌC 2022- 2023
Hướng dẫn chấm môn Toán 7
(Hướng dẫn chấm gồm có 04 trang)
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa. Câu Đáp án Điểm 10. 1,44 24. 0,25  12 144  A =  +  :  + 3 7 7 9      0,5 10.1,2 24.0,5 12 12 A    :  = + +  3 7  7 9      12 12 12 12 Câu 1a  A   = + : +     (1,5 đ)  3 7   7 9  0,5 12.10 12.16 A = : 21 63 12.10 63 A = . 21 12.16 5 3 15 0,5 A = . = 1 8 8 5 4 9 4 .9 2.6 N − = 10 8 8 2 .3 + 6 .20 0,5 10 8 9 9 2 .3 2.2 .3 N − = 10 8 8 8 2 2 .3 + 2 .3 .2 .5 Câu 1b 10 8 10 9 2 .3 2 .3 (1,5 đ) N − = 10 8 10 8 2 .3 + 2 .3 .5 10 8 2 .3 .(1− 3) 0,5 N = 10 8 2 .3 (1+ 5) 2 1 N − − = = 0,5 6 3 4 8 1996 2000 A = 1+ 2 + 2 + ... + 2 + 2 4 4 8 12 2000 2004
2 .A = 2 + 2 + 2 + ... + 2 + 2 4 2004 2 .A − A = 2 −1 0,5 2004 2 1 A − = 15 Câu 1c 2 4 2000 2002 B = 1+ 2 + 2 + ... + 2 + 2 (1,5 đ) 2 2 4 6 2002 2004
2 .B = 2 + 2 + 2 + ... + 2 + 2 2 2004 2 .B − B = 2 −1 0,5 2004 2 1 B − = 3 A 2 −1 2 −1 3.( 2004 2004 2004 2 − ) 1 Do đó: 1 = : = = 0,5 B 15 3 15.( 2004 2 − ) 1 5 1
Câu 2a 2x −1 + = 2 4 (1,5 đ) 1 0,5 2x −1 = 2 − 4 7 2x −1 = 4 Trường hợp 1: 7 2x −1 = 4 0,5 Suy ra: 11 x = 8 Trường hợp 2: 7 2x 1 − − = 4 Suy ra: 3 x − = 0,5 8
Vì x nguyên nên không tồn tại x thỏa mãn bài ra x y z
Từ 2x = 3y = 5z suy ra = = . 0,5 15 10 6
Câu 2b Áp dụng tính chất dãy tỉ số bằng nhau, ta có: (1,5 đ) x y z
x + 3y − 2z 66 = = = = = 2 0,5 15 10 6 15 + 3.10 − 2.6 33
Khi đó: x = 2.15 = 30 ; y = 2.10 = 20; z = 2.6 =12 . 0,5 Từ 2
b = ac suy ra a b = ; b c Từ 2
c = bd suy ra b c = . 0,25 c d Do đó: a b c = = b c d
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Câu 2c a b c 12a + 3b −5c = = = 0,25 (1 đ)
b c d 12b + 3c − 5d 3 3
Suy ra  a   12a + 3b − 5c  =   b   
12b 3c 5d  + −  3
Hay a b c  12a + 3b − 5 . . c  = 0,5
b c d 12b 3c 5d  + −  3
Vậy a  12a + 3b − 5c  =
d 12b 3c 5d  + −  Từ x + 2y 2023 =
suy ra x + 2y x + y = x + y 2022 2023 2022
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: 0,5
x + 2y x + y (x + 2y) − (x + y) = = = y Câu 3a 2023 2022 2023 − 2022
(1 đ) Khi đó: x + y = 2022y Hay x = 2021y 0,25
Để x đạt GTNN khi 2021y đạt GTNN.
Mặt khác x, y là các số nguyên dương nên GTNN của y là 1. 0,25
Khi đó GTNN của x là 2021.
Gọi chiều dài, chiều rộng và chiều cao của bể nước lần lượt là x, y, z
(m). Điều kiện: x, y, z > 0 . Câu 3b 0,25
(1,5 đ) Khi đó: x y z = = 1 2 4
Tổng diện tích sáu mặt của bể nước là: 2.(x + y).z + 2xy (m2) 0,25
Theo đề ra, ta có: 2.(x + y).z + 2xy =112
Hay xz + yz + xy = 56 2 2 2 Từ x y z x y z xy yz xz = = suy ra = = = = = 1 2 4 1 4 16 2 8 4
Áp dụng tính chất dãy tỉ số bằng nhau, ta có: 0,5
xy yz xz xy + yz + xz 56 = = = = = 4 2 8 4 2 + 8 + 4 14 Khi đó: 2
x = 4.1 = 4 ⇒ x = 2 2
y = 4.4 =16 ⇒ y = 4 0,25 2
z = 4.16 = 64 ⇒ z = 8
(Vì x, y, z > 0 )
Vậy thể tích của bể nước là: 2.4.8 = 64 (m3) 0,25
Với a, b, c là các số nguyên dương, ta có: b 2 = ( + ) 2 5 .
3 + 5 = .5c + 5 > 5c a a a 0,25 5b 5c ⇒ > Do đó: 5b 5c  2
⇒ a .(a + 3) + 5a + 3
Câu 3c ⇒ 5a + 3 0,25
(1 đ) Hay a + 3∈Ư(5) ={ 1; ± ± } 5 .
Vì a là số nguyên dương nên a + 3 = 5. Do đó: a = 2 0,25 Khi đó: b 3 2
5 = 2 + 3.2 + 5 = 25 ⇒ b = 2
5c = 2 + 3 = 5 ⇒ c = 1. 0,25
Vậy a = 2, b = 2 , c =1 ( thử lại t/m) 25 m B C 10 m E 3 m C' B' M A N 1,4 m F D A' D' 10 m Q 8 m P
Để tính thể tích bể bơi, ta tính thể tích hình hộp chữ nhật
ABCD.A'B'C'D' và hình lăng trụ đứng EC'NM.FD'PQ có đáy là hình Câu 4 thang vuông. (2 đ) 0,5
Thể tích hình hộp chữ nhật ABCD.A'B'C'D' là: 10.25.1,4 = 350 (m3)
Thể tích hình lăng trụ đứng EC'NM.FD'PQ là:
1 .(25−10)+8.(3−1,4).10 =184 (m3) 0,5 2
Thể tích bể bơi là: 350 +184 = 534 (m3) 0,5 Đổi 534 m3 = 534 000 lít
Thời gian bể bơi được bơm đầy nước là: 534 000 : 500 =1 068 (phút) 0,5
Vậy sau 17 giờ 48 phút thì bể được bơm đầy nước. E D A P Q Câu 4a M (2 đ) H B I C K
Vì BE//CF nên  = 
ABD ADC (hai góc so le trong)
Chứng minh AEB =ACD (g.c.g) 1
Suy ra: BE = CD và AE = AC
Chứng minh AED =ACB (c.g.c)
Suy ra: DE = BC 1 Vì 1 PB = BE và 1 QD = CD 2 2 Mà BE = CD 0,5 Nên PB = QD
Chứng minh APB =AQD (c.g.c) Câu 4b 0,5 Suy ra:  = 
PAB QAD và AP = AQ
(2 đ) Mặt khác:  +  DAQ QAB =180° Do đó:  +  PAB QAB =180° . 0,5
Hay ba điểm A, P, Q thẳng hàng.
Vì AP = AQ và ba điểm A, P, Q thẳng hàng nên A là trung điểm của PQ. 0,5
Gọi I là giao điểm của AM và BC.
Kẻ BH ⊥ AM , CK ⊥ AM . Ta có: . MA BC = .
MA (BI + CI ) Mà 0,75
BI ≥ BH, CI ≥ CK . Do đó: . MA BC ≥ . MA BH + . MACK Câu 4c Hay . MA BC ≥ 2S +  S ABM 2 (2 đ) ACM Tương tự: . MB AC ≥ 2S +  S ABM 2 BCM
MC.AB ≥ 2S +  S ACM 2 BCM 0,75 Suy ra: . MA BC + .
MB AC + MC.AB ≥ 4S . ABC
Dấu bằng xảy ra khi AM ⊥ BC , BM ⊥ AC và CM ⊥ AB .
Khi đó M là trực tâm của tam giác ABC. 0,5